ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.04.26］ No.112
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
レイティング（評価）とランキングの数理
Amy Langville（ラングビル）
Professor, Mathematics Department, Operations Research Analyst,
College of Charleston

2012年にCarl Meyerとの共著 “No.1は誰か：レイティング（評価）とランキングの数理” が出版
［訳註：共立出版より同名の訳書あり］されると，企業，法律事務所，同僚，学生などから，
彼らのデータを解析支援する要棲を定期的に受けるようになった．
最近の興味深いプロジェクトのいくつかと，今年の数学月間のテーマ”予測の未来”
にふさわしいツールを説明しようと思う．
まず，タイムリーな応用［MAMは4月］は，3月の狂気（March Madness）です．
毎年恒例のNCAAカレッジ・バスケット・トーナメント．数百万人のファンが
この一月続くトーナメントの各試合の勝者を当てようとします．
［訳者より：ブラケット・チャレンジというのは，インターネットで行う
CBS sports serviceが提供する各試合の勝者を当てポイントを競うことらしいが，
よく知りません．米国事情に詳しい方，米国バスケットの3月の狂気と
ブラケット・チャレンジについて教えてください］．

まず，同僚Tim Chartier（Davidson College）と一緒に，数学モデルのみに基づき
ブラケットを提出する方法を学生に教えます．
そのときの2つのモデル（Colley and Masseyモデル）は，チームの評価に線形システムを用い，
もう一つのモデル（Eloモデル）は，反復更新を使います．
長年にわたって，学生のモデルはよい結果を出し，ある年などは提出された
すべてのブラケットの99のパーセントを得点しました．
毎年，モデルに洗練を加えるために，学生たちは質問をしデータを集めます．
例えば，コーチ，チーム団結，トーナメント経験のような因子をどのように導入したら良いのか？
怪我は因子にどのように入れることができるか？
我々は、今年のシンデレラ・チームを予測することができるだろうか？

もう一つのスポーツ応用：オリンピック・アスリートのデータ分析で，
私の学生と私は米国オリンピック委員会を支援しました．資源の効率利用の観点から，
委員会はどのアスリートがメダルをとるか予測したい．この問題を解くためには，
回帰とシミュレーションを用います．他の問題は，国の資金がどうであれ，
アスリートにより多くのメダルを獲得する動機を与えなければならない．
この第2の問題に関する適切なデータを得ることは困難だった．
それで，英国を含む他国の促進プログラムがうまくいったかどうかに調査を広げました．

次に，Amazonの「これを買った顧客はこれも買う」のような推薦システムを議論します．
また，どの映画を顧客に推薦するべきか，どの歌が特定のリスナーのプレイリストを満たすか，
どのスポーツ用品を顧客に推薦するべきかなどを予測したい小規模の新興企業からの要請に答えるために，
私は同僚Tim Chartierとチームを組みました．共通のテーマは，企業が集めたデータを，
顧客の行動に影響する役立つ予測のために，どのように使用するかということです．
この問題を解くために，典型的にはクラスタリング(クラス分け)と最隣接クラス分けのツールを用います．

昨年，Rootmetricsから，携帯電話を評価する現在の彼らのシステムの改良の依頼がありました．
学生Tyler Periniは，うまく接続し伝達できる物理過程をエレガントにモデルしたマルコフ連鎖を立て，
現在の評価システムのもつ多くのタイがある曖昧さをなくすことができました．
Charleston大の同僚，哲学教授と心理学教授，からは，
彼らの謙譲プロジェクトで集めたテキストデータの解析の要請がありました．
ゴールは，書かれたサンプルを解析して謙譲の個人レベルを決定することです．
学生 Tyler Perini は，テキストを混合するツールを開発しました．
それは，与えられた短いテキストサンプル（ツイートやfacebook今何してるより長くない）で，
著者が謙譲か謙譲でないか予測する．
謙譲な著者は，"and”，”we”，”all”，”each other”を含み，
謙譲でない著者は，"they", "people","them", 排除的"or"などの距離を取る言葉を使う．
次のステップで，人文科学教授が研究するのは，自己抑制である．
スピーチに基づき自己抑制の低さを予測する我々のツールが，
子供たちの行動訓練を提供することを願っています．

もう一つのテキスト・マイニング・プロジェクトでは，Charleston大の大学院生は，
今年の大統領選挙戦で候補のテキストを分析しています．
彼らは，若干の面白い傾向を見つけました．
たとえば，Donald Trumpの辞書（彼の使う語彙）は，Hillary Clintonのおよそ3分の1です．
フィールドが狭くなって，有権者がどのように1人の候補から他方の候補者へ支持を移すかを予測するために，
彼らは測度の同一性とマルコフ連鎖を使います．

最後に，同僚の妻は私に非常に難しい問題ー卒業の後の医学実習生と病院との安定結合問題ーを提案しました．

データが至る所にあることは，上述の問題の多様性から明白です．
衛星からスマートフォンまで，大小のソースから，データは絶えまなく集められています．
将来は，指数関数的に多くの予測解析法を持つことになり容易に予測ができるようになります．
現在は，数学，コンピューター・サイエンス，データ科学，統計学を専攻するには素晴らしい時代です．
これらの組み合わせはさらにうまく行きます．

ここまでは，MAMのエッセイ　http://www.mathaware.org/mam/2016/essay/　からの翻訳でした．

選挙の開票で，まだ開票率が35%なのに当確が出たりします．これはレイティングの予測で
トーナメントの勝ち数の推移から1番を予測するのと同じようなものです．
また，webサイトのページを渡り歩き，あるサイトで買い物をしたとすると，
それに導いたwebサイトの貢献率はどのようなものでしょうか．
googleのweb各ページのレイティングはどのように計算するのでしょうか．
サイト間の遷移行列を作り，この行列を作用させた結果新しい状態になると考えると
何度も遷移が繰り返された結果収束する状態が各ページのランキングになります．
つまり，遷移行列のn乗の固有ベクトルを求めることになります．
ここに線形代数が使われるし，現在の状態だけで次の状態が決まるというマルコフ連鎖にもとづき
遷移行列を決めることができます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.04.19］ No.111
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今月14日夜に，熊本県益城町で震度７の大きな地震が起きました．マグニチュードは6.5でした．
地震規模のスケールであるマグニチュードは，リヒターの発案当時は便宜的なものでしたが，
今日では，ずれの面積と変位，地面の剛性から計算できる地震の仕事エネルギーを対数で表示したものです．
14日の地震のマグニチュードは，巨大地震ほどではないが，震源が10kmと浅いため，
局地的に地表が激しい揺れとなり大きな被害がでました．
その上，この地域はフォッサマグナ（活断層が集まっているベルト地帯）の上にあり，
次々と余震が続きます．震源もフォッサマグナに沿って熊本県や大分県由布市に移ってきました．
心配ですね．被害お見舞い申し上げます．皆様のところは大丈夫でしょうか．

阿蘇の東側から佐伯，および，阿蘇の南側には，むかし行ったことがあります．
峡谷で囲まれた台地が島のようになった地形で，交通は大変だったそうですが，豊かな芸術文化が伝承されています．
通潤橋のある山都町では人形浄瑠璃が印象に残りました．怪我や避難やたいへんな日々と思います．
応援しております．はやく落ち着きますように．

■フォッサマグナは西日本では，佐田半島から大分，由布，九重，阿蘇を通り，天草，八代海に沿って走り，
川内原発の付近に至るようです．活断層の調査は露頭でできますが，川内原発の地下を通っていても見えません．
再稼働の根拠となった九電の調査は３つの断層延長上の1つのみの結果で，規制委は不十分のまま再稼働に踏み切りました．
フォッサマグナの走る佐田半島の付け根には伊方原発が，八代海側には稼働中の川内原発があります．
すべての原発は即時廃炉を進めるべきですが，特に地震の活動期にある九州で稼働させた川内原発は停止すべきです．
原発事故でどのような責任がとれるというのでしょうか．
川内原発は発電を続けています．それなのに送電先がなく被災地に電源車41台+81台を17日までに配るという．
役立たずの原発ですね．太陽光などの地域分散型の発電システムにすべきです．

■この機会に，手元にあった第４紀地図（1987年版で古いものです）を30年ぶりに開いてみました
（実は一時期，私は地学を教えていたことがあります）．参考までに地図を引用掲載しました．
伊方原発，益城町，フォッサマグナの大体の位置は，私がこの地図に書き込んだものです．
阿蘇の周りなどに見られる黒い線が活断層です．
活断層とは，第４紀後期（数十万年前）以降に何度か動いた断層で，地震の原因になる可能性があります．
第4紀は258万年前（寒冷化に向いだした）からで，人類出現の時代．
古い原人が発見されるたび，第3紀と第４紀の境は遡っていき，
258万年前は，2009年に国際地質科学連合が定義したものです．
地球が生まれた45億年前を1月1日の0時とし，現在を新年が始まる0時と例える地球カレンダーなら，
第4紀後期は大晦日の夕方以降です．ごく最近動き，まだ動きそうな断層が活断層ということになります．
活断層であるかどうかは露頭で，断層のできた時期の鑑定になります．

■この地域の乗るユーラシアプレートの下には，フィリピン海プレートがもぐり込んでいます．
地殻と上部マントルの地殻と一緒に動く部分を合わせてプレートと呼び，厚さはおよそ100kmです．
地球の半径は6,500kmですから，半径65mmのボールに例えるなら，プレートの厚さは1mmです．
プレートは，マントル対流に乗ってふわふわ動きぶっつかりもぐり込む皮みたいなもの，
その上に我々は暮らしています．

以下に，第4紀地図を掲載：
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/62/17401362/img_1_m?1460875928

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/62/17401362/img_2_m?1460875928

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.04.12］ No.110
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
数学と社会の架け橋＝数学月間
数学月間は7/22～8/22（22/7＝π，22/8=e）の期間です．
私たちは，この期間に数学への興味を惹き起こすイベントが
各地で盛んになるように応援しています．
数学月間の初日の7/22には毎年，懇話会を開催しています．
今年で数学月間懇話会は第12回になります．
計画中の懇話会情報：正式アナウンスに先立ちお知らせします．
無料です多くの方のご参加をお待ちしています．
日時：7月22日，14:00～17;00
場所：東大駒場キャンバス，数理科学研究科・002号教室
１．亀井哲治郎　数学の周辺
２．田渕健　統計と医学
３．松原望　統計と社会
（演題はいずれもまだ仮題です）
問い合わせ先：sgktani@gmail.com（日本数学協会，数学月間の会）
今年のテーマは，統計学です．
世の中は不確かなものやことばかりで確率で記述されます．確率の正しい理解が必要です．
従来，得られなかったようなデータも多量に収集できる時代になりました．
でも，データ収集が恣意的であったり，不合理な解析をしたりすると
どんな結論でも導くことができるので，だまされないように要注意です．

今年（4月に実施中）の米国MAM（Maths Awareness Month）のテーマは「予測の未来」．
・外れた世論調査ー予測の限界を知ろう
・あなたの健康のために
などの興味あるエッセイがあります．ちょっと紹介しましょう．

2015年5月の英国総選挙では，与党の保守党が過半数の326議席を獲得し，
労働党は232議席でした．スコットランド民族党は大躍進の56議席です．
選挙直前の世論調査では，保守党と労働党の差がこれほど広がる予測はありませんでした．
最後の世論調査と投票日の間に逆の一揺れがあったわけですが
なぜこれほど予測に誤差が出たのでしょうか？
調査委員会の報告書（2016年3月）によると，サンプリングが正しい代表値でなかった
ということですが，理想のランダム・サンプリングをすることはできるのでしょうか．
予測を頭から信じることは危ないことです．
今年は，日本も重要な選挙の年です．支持率調査などでも
現実が正しく反映されているのか怪しいところがあります．

2001年にフラミンガム心臓研究の研究者たちは，拡張期血圧，収縮期血圧，脈拍圧を，
冠動脈性心臓病リスク心の予測因子として使用できる結果を発表しました．
この研究により，冠動脈性心臓病の予測能力が向上しました．
異なる年齢層にたいする予測因子の強度を解析し，
それぞれの年齢層でどの予測因子が最も支配するか結論を得ました．
健康とウェルネスのための予測因子は，いろいろな理由で多くの分野で改善が進んでいます．
利用可能なデータは劇的に拡大し，モデリングや解析に用いる技術と手法は向上しています．
一つの分野での進歩は，別の分野の進歩につながり，また広がります．
研究者は以前よりも，より深くより洞察に満ちた結論に到達することができるようになりました．
フラミンガム心臓研究は1948年に始まったが，その後数回の拡大があり，
続く世代集団だけでなく，人口の多様性の増加を反映している集団を追加しました．
これにより，研究者達は，人口の幅，および，多様な健康問題の側面の両方を
表すデータの使用ができるようになった．
この研究のために，研究者達は，原初の集団に20才から79才の集団を統合した．
さらに，研究者達は，数年前には不可能だった場所でのデータ収集をしています．
フィットネスの追跡者は，活動レベルや睡眠パターンのような個人生活の情報を
容易に定量化できる恩恵を受けている．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.04.05］ No.109
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号（108号）に，色置換の性質の項で誤りがありました．お詫びして訂正します．
今号は，訂正した全文と，新たな話題の両方を載せますので，長くなります．

12枚のユニットで作るユニット折り紙の立体は下図のようなものです．

 この立体は，正8面体の面（正3角形）の上に，
頂角が直角の三角形ピラミッドが乗っている形です．
これから作る展開図では，ピラミッドは正8面体の面（正3角形）に
射影されているので，ぺちゃんこになっています．

正8面体の展開図の各面を，このように塗り分けるようにユニット折り紙を組み立てると，正8面体の各頂点のある4回回転軸（x,y,z軸の方向に3本ある）で4色置換が起こり，正８面体の面の真ん中を通る3回軸（4本ある）は，1色は保存し，残る3色を置換する3回軸だということがわかるでしょう．もちろん辺の真ん中を通る6本の2回軸の色置換も完璧です．

このような色の配置は実際にユニット折り紙で実現可能です．作ってみてください．
ユニット折り紙の規則では２つの直角3角形ピラミッドをつなぐユニットは1つのみですから，展開図の三角形の辺を越えて，対角上に同色の配置を作ります．展開図では，もう一つの対角上にも同色がある（辺を挟んで×になる配置）ように思うかもしれませんが，そちらは1つのユニットではありません．辺の両側で分かれる別々のユニット（同色だが）です．４色のバリエーションはいくらでもできますが，
配置に関しての解はただ一つのようです．
ただし，ユニットの作り方で右回りと左回りのものがあります．

この立体を眺めると4回軸の周りに，4つの色の帯の大円（緑，黄，青，ピンク）が見えます．
各色の帯の大円は，各3回軸を地球の地軸と見立てたとき赤道に相当します．
そして，その3回軸が保存する色が，帯状に現れるのです．

この立体には4色置換が行われる4回回転軸（3本）があり，外から（x,y,z軸の正方向）見て右回りに以下の順です：
x軸：黄→ピンク→青→緑，
y軸：黄→ピンク→緑→青，
z軸：黄→青→ピンク→緑

3色置換が行われる3回回転軸（4本）があります．
z軸（ｚ>0方向）の外から見て右回りに以下の順に置換が起こります：
黄→緑→青（保存：ピンク），黄→緑→ピンク（保存：青），
ピンク→青→緑（保存：黄），黄→ピンク→青（保存：緑）

ーーーーー
新たな話題
■正20面体（あるいは双対な正12面体）
60ユニット（正20面体の面の上にピラミッドが乗っている）の立体の塗り分けを考えます．
以下は展開図

6色を使って塗り分けます．
5回回転軸は6本ありますが，それぞれを地球の地軸とすると
それぞれの赤道に相当する大円に配置される1色が保存され，残りの5色が順番に置換されます．
3回回転軸は10本ありますが，それぞれ2組の3色置換になります．
ーーーーー
■平面
「大川組子」（さなさんブログから教えていただきました）という伝統工芸があります．
シンプルで精緻な組子で感動します．ななつ星の写真をご参照ください．

これらの組子はどちらも三角の格子でできています．ただし，どちらの組子も
格子の中身に，対称性は同じだが異なるモチーフが2種類（あるいは3種類）あり，
単純ではない面白い図案になっています．
さて今日は，この組子とユニット折り紙の関係についてです．

ユニット折り紙で作る多面体の場合と異なり，平面ですので正三角形が頂点で6つ集まっています．
そして正三角形の格子の上にピラミッドが乗っています．
図はユニット折り紙でこれを作り真上から見たものです．
6回軸の色置換を完全にするためにこの図では６色使いました
（地図の塗り分けで，4色問題というのがありましたね．長い間未解決の難問でしたが今は証明されています．この図の場合は，実は3色あれば塗り分けられます．一色の周りは4辺で，皆頂点で接続していますから）

そして，これは壁紙模様の平面群の一つで6回対称です．
色置換の対称性も完全にするには6色で塗り分ける必要があります．
色の区別ができる場合の単位胞タイルは大きな白い4辺形，
色の区別ができない場合の単位胞は小さな白い4辺形です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.03.29］ No.108
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
桜の季節がやって来ました．皆様のまわりはどうでしょうか．
私はこのところユニット折り紙に凝っています．今日はその話です．
ユニット折り紙とは，多数のユニットをつないで多面体を作る方法です．
1つのユニットは同じ大きさの直角3角形4個が連なった帯の様な形です．
まず，12枚のユニットで作られる多面体を取り上げましょう．
(Fig1)http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/36/17363336/img_0?1458990114

ユニット内の4つの直角3角形の両端のものはつなぎに使われますから，
立体の面となる直角3角形はユニットあたり２つ（合わせて正方形）です．
この立体の形は正8角面体の面の上に頂角が直角のピラミッドが乗っている形です．
1つのピラミッドは3枚のユニットで構成されています．
この立体をユニット色紙で塗り分ける方法を考察しました．
正8面体の各頂点のまわりに4回対称軸（それぞれ，x軸，y軸，z軸の方向）が3本あります．
色の巡回置換を4回対称軸に結び付けると4色要りますので，
全体を4色で対称操作と矛盾しないように塗り分けてみましょう．

■展開図
これから作るのは正8面体の展開図で，正三角形の面の上のピラミッドは
正8面体の面に射影してぺちゃんこになっています．
（fig.2）http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/65/17360665/img_0_m?1458989502
展開図の塗り分けをもとに，ユニット折り紙を組み立てます．
このような色の配置は実際にユニット折り紙で実現可能です．作ってみてください．
ユニット折り紙の規則では２つのピラミッドをつなぐユニットは
1つのみですから，展開図の三角形の辺を越えて，対角上に同色の配置を作ります．
展開図では，もう一つの対角上にも同色がある（辺を挟んで×になる配置）
ように思うかもしれませんが，そちらは1つのユニットではありません．
辺の両側で分かれている別々のユニット（同色だが）です．
４色のバリエーションはいくらでもありますが，配置に関しての解はただ一つのようです．
ただし，ユニットの作り方で右回りと左回りのものがあります．

■得られた立体の性質
正8面体の各頂点にある4回回転軸（3本あります）で4色置換が起こり，
正８面体の面の真ん中を通る3回軸（4本あります）は，1色は保存し，
残る3色を置換するということがわかるでしょう．
もちろん辺の真ん中を通る6本の2回軸の色置換も完璧です
この立体を眺めると立体の周りに，4つの色の帯の大円が見えます．
各色の帯の大円は，各3回軸を地球の地軸と見立てたとき赤道に相当します．
そして，その3回軸が保存する色が，帯状に現れるのです．

4色置換が行われる4回回転軸（3本）は，外から見て右回りに以下の順です：
x軸：黄→ピンク→青→緑，
y軸：黄→ピンク→緑→青，
z軸：黄→青→ピンク→緑

3色置換が行われる3回回転軸（4本）は，
黄→緑→青（保存：ピンク），黄→緑→ピンク（保存：青），
ピンク→青→緑（保存：黄），黄→青→ピンク（保存：緑）

■さらに色々な性質があることに気づきます．－－－－－－－

3回軸は軸の負方向から見ても正方向から見ても同じ順番の置換を起こしますが，
4回軸は軸の負方向から見ると正方向から見た場合と逆順の置換が起こします．
何故でしょうか？

正8面体の骨格をもつ今回の立体では，正３角形が頂点で4つ集まる展開図を作りましたが，
正20面体の展開図では正3角形が頂点で５つ集まります．そして，対称性を保った色の塗り替えは5色が要ります．
展開図で色の配置を考えてください？．
平面の3角格子では，正3角形が頂点に６つ集まります．
6回対称を保った色の塗り分けになるように，展開図で6色の配置を決定してください？．．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.03.22］ No.107
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
早いもので桜も咲き始めました．皆さまもお変わりなくお過ごしのことでしょう．

周期的空間（2次元に限定すれば壁紙模様）の数学－結晶空間群－の平易な解説法を色々工夫しています．
理論の本質が理解できるようにして，数学的な記述は最小限にしようとしています．
しかし，ある程度の数学的な記述をした方が反って理解し易いのです．
そこで，以下の様な記述に落ち着きました．皆様如何お感じでしょう．ご意見ご感想をお聞かせください．
さらに改良に活かしたいと思っています．
ーーーーー
有限図形の対称性を扱うのが点群．繰り返し模様（周期的な空間）の対称性を扱うのが結晶空間群です．
有限図形の対称性に比べて周期的な空間の対称性はなじみのない人が多いようです．
しかし，周期的な空間はとても重要です．例えば，もし体が縮む薬があり原子の大きさ位になって
結晶の中に入り込んだら，そこは無限に繰り返す世界（＝結晶空間）です．
ここで，点群から空間群への拡大方法にちょっと言及しておきましょう．
原理の骨格を簡明に示すために，扱う周期的空間は2次元（平面）に限定しました．
2次元での繰り返し模様（＝壁紙模様）は，エッシャー〈1944頃）の作品に見られます．

(1)格子
2次元空間では，互いに独立な2つの基本並進ベクトルa1,a2がとれ，
a1,a2の整数係数の1次結合をすべて集めたT={h･a1+k･a2丨h,kは整数｝を，
この平面の格子点の集合（あるいは単に“格子”）といいます.
集合Tは無限集合になりますが， 群の条件を満たしており，Tを並進群とも呼びます．
ブラべ格子とは，結晶点群の対称性を基準に，格子のタイプ分類をしたものです．

(2)点群一有限図形の対称性一
1点の周りの対称操作（点群の対称操作）を考察しましよう．
回転対称軸には,１， 2，3，4，5，6，･･･，∞回（回転対称）軸があり得ます [何もしないのは1回軸]．
n回軸Cnとは，360°/nだけの時計回りの回転操作で，n回続けるとCn^n=360°=0°(mod 360°)，
これは恒等操作1です．回転操作Cnからは，回転群Cn={Cn，Cn^2，…，Cn^n＝1}が生成されます．
その他の2次元点群で見られる対称操作には，鏡映m [対称心-1は，2次元空間では2回軸と同じ]があります．
鏡映操作mが生成する鏡映群はm={m,m^2=1}
（注）mod360°とは360°回転したら同じものとする［360°を法として同値］という意味です．
別の例では，時計の文字盤があります．我々は13時のことを1時とも言いますが，
これは，mod12［12を法として同値］を用いた結果です．

(3)結晶点群一格子と両立できる点群一
結晶では，点群の回転対称性と並進群（格子）の対称性とが両立しなければなりません．
2，3，4, 6回軸は，それぞれに両立できる格子 がありますが，5回軸の場合はどうでしょう．
1つの5回軸が支配する局所的な作用域として正5角形タイルを描きます．
平面に周期があり複数の5回軸が配列している状態を考えると，各5回軸は自分の局所的な作用域
（正5角形タイル）内でのみ有効なのではなく，全域でも有効です．
各5回軸の局所的な作用域は，互いに他の5 回軸により変換し合い，全体として不変な配置となるべきです．
これは2次元平面を正5角形タイルで隙間なく張り詰めることと同じで，そのようなタイル張りは実現不可能です．
したがって，5回軸と両立する格子はあり得ません．7回以上の回転対称軸に関しても同様で，
結局，格子と両立できる（＝結晶空間で許される）回転対称は，2， 3，4，6回軸に限られることになります
[ただし，2次元，3次元空間 での話]．

(4)空間群の作り方〈2次元の場合）
2次元空間では，10種の結晶点群G：1，m，2=-1，2mm， 3，3m，4，4mm，6，6mm，
および，5つのブラべ格子T：clino-P (斜交単純格子)，ortho-P（直交単純格子)，
ortho-C (直交C面心格子)，tetra-P(正方単純格子)，hexa-P(六方単純格子）が数え上げられます．

周期的な空間での対称操作が作る群が結晶空間群で，結晶空間群Φの要素は，
結晶点群Gの要素と並進群Tの要素との積（結合）です．Φ＝G×T

壁紙模様の平面群17種の構成を見てみましょう．
壁紙模様は，1つの“モチーフ”（＝単位胞の中身）を無限にある格子点の上に配置して構成されています．
格子点は無限にあり，どの格子点にいても常に世界の真ん中ですから，
「格子点距離の倍数だけ移動した点はすべて同価」との見方をします．
これを“格子を法として（mod T)同値”と言います．無限に繰り返す“モチーフ”の分布を，
単位胞内の１つの “モチーフ”に還元できます．
［準同型写像で，Φ/T=G のように表現します．ただし，並進群TはΦの正規部分群であることを用いています］
この見方をさらに進めると，“モチーフ”内部の対称性を記述する結晶点群G自体も，
格子を法として(mod T)閉じればよく，G(mod T)と拡張でき，
拡張された結晶点群G(mod T)と並進群Tとの積で作られる空間群もあります．
このような夕イプの空間群には, 映進面（鏡映 ＋ 鏡面に平行に格子距離/2の並進)，
n回螺旋軸(360°/nの回転 十 軸方向に格子距離/nの並進）などの操作があります．
ただし，螺旋軸が現れるのは3次元以上の空間です．
例として，平面群P2mm, P2mg, P2ggの作り方を図示します
(注）頭のPは格子を表し，続く2mmなどが結晶点群の対称要素です．後者の2つ平面群には，映進面gが現れます．
Fig
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/17/17352517/img_0_m?1458546408

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/17/17352517/img_1_m?1458546408

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.03.15］ No.106
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユークリッド幾何
アレクサンドリアにいたユークリッド(300BC)は，「原論」全13巻を著し，これがユークリッド幾何の誕生です．
彼が作った幾何学体系は，演繹を積み重ねて構築されるのですが，その演繹のスタートに，
彼は５つの公準（公理）を設定しました．公準とは無証明の命題で，常識的で直観的に違和感のないものでした．
公準の5番目が平行線に関してです．ユークリッド幾何は，測量や建築や物づくりに古代から活用され，
我々も日常的にその理論の活用をしています．
■非ユークリッド幾何
ユークリッドの第５公準（平行線の公準）を変えると，異なる幾何体系（非ユークリッド幾何）が構築できます．
これを考えたのが，ロバチェフスキー(1829,1840)，ボヤイ(1832,1835)です．
ガウスも同時代にすでにいくつかの結論を得ていたのですが発表はしませんでした．
双曲幾何の誕生です．ロバチェフスキーはロシアのカザン大学の数学者，ボヤイはハンガリーの数学者，
ガウスはドイツの数学者で当時すでに大御所でした．これらの研究はそれぞれ独立になされたものでした．
双曲幾何に続き，ドイツのリーマンは楕円幾何を生み出しました．
さらに，リーマン(1854)は，高次元の曲がった空間を扱うリーマン幾何を生み出します．
空間の曲率が楕円的であったり双曲的であったり位置ごとに変わるような空間の幾何学です．
これはアインシュタイン(1915)が一般相対性理論を構築する際に必要となる理論でした．
■非ユークリッド幾何とユークリッド幾何の整合
19世紀末から20世紀初頭に，ケーリー（イギリスの数学者，弁護士），クライン(ドイツの数学者)，
ポアンカレ(フランスの数学者)などが，射影幾何やユークリッド幾何空間の中に非ユークリッド空間のモデルを作ります．
機会をあらため，ポアンカレの円盤モデルはもう一度紹介するつもりです．
■射影幾何から非ユークリッド幾何へ
ダビンチなど画家たちは，遠近法や透視図法を古くから用いていました．
デザルグ（17c初頭，フランスの数学者建築家)は，透視図法を発展させた射影幾何の祖です．
ポンスレー(19c中葉)はフランス革命で開設されたエコール・ポリテクニークでモンジュの下で学び，
ナポレオンのロシア遠征に従軍．ロシアで捕虜になっている間に射影幾何学を研究しました．
射影変換というのは，物体から影を作る演算です．射影法には．平行光線や点光源からの発散光線を用いるなど色々あります．射影変換で失われる図形の性質もありますが，保存される性質もあります．
射影変換では，直線は直線に変換されるし，２つの直線の交点の性質も同様に保存されます．
しかし，長さや角度は保存されません．例えば，円を投影すると歪んでしまいます．
それぞれの変換で保存される性質に注目すると，色々な幾何学が生まれます．
群という概念も変換の集合に関する構造で，群に注目してた幾何学もあります．
クラインは，ユークリッド空間を運動群で規定されるものとして定義しました．
射影幾何やアフィン幾何もあるし，ポアンカレらによる位相幾何（図形のつながり方に注目）なども生まれています．
次のデザルグの定理を見るとわかるように，デザルグの定理を3次元で証明するのは容易ですが，
2次元で証明するのは非常に困難です．それは3次元から2次元への射影により，
長さの情報が失われてしまうからです（比率は保存されます）．
ーーーーー
■デザルグの定理
△ ABC と△A'B'C'があり，AA'，BB'，CC'が一点 O で交わるなら，
AB とA'B'の交点 P，BC と B'C'の交点 Q，CA と C'A'の交点 R は同一直線上にある．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/84/17335884/img_0_m?1457866730

（これを3次元の中で証明するのは非常に容易です）
この図が紙面に垂直な方向に高さをもつ3次元世界の中に置かれているものと想像しましょう．
△ABC　と△A'B'C'　は平行でなく，それぞれの三角形を含む平面は，線分QRを含む直線で交差しています．
当然，線分ABは△ABCを含む面内に，線分A'B'は△A'B'C'を含む面内にありますから，
ABとA'B'の交点Pは，両平面の交差する線分QRの延長上にあることになります．
ーーーーーーーーーー
（参考）ユークリッド幾何学と非ユークリッド幾何学
色々な幾何空間があります．大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．
非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．
我々の常識が通用するユークリッド幾何の世界では，
“直線l外の1点をA通り，その直線に平行な直線“は，唯一本だけ引けます．
平行線が1本も引けない世界や，無数に引ける世界とはどんな世界でしょうか？
これら3種類の幾何空間を，平面を例にとり比較します．

（１）ユークリッド幾何平面　　（２）楕円幾何平面　　（３）双極幾何平面
例⇒我々の常識の世界　　　　　球の表面　　　　　　ポアンカレの円盤モデル
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/28/17335928/img_0_m?1457866699

それぞれの空間で，“直線の定義を変えれば”，そのようなことが起こる世界があることを納得できるでしょう．
2点間を結ぶ直線とは，その世界で2点間の距離を最小とするものです．
（１）常識の通用するユークリッド幾何平面
2点間の距離が最少なのは我々の知っている直線です．
（２）球の表面は楕円幾何平面の例
球表面の世界では，大円（球中心を通る平面で切った球の表面）が直線です．
地球自体は3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面です．
地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，これは地表の大円上の線分のことです．
異なる２つの大円は必ず2点（直径の両端）で交わるので，直線外の1点を通る平行線はありません．
また，地球儀の緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面の例（ポアンカレ円盤モデル）
双曲幾何の世界のポアンカレ円盤モデルでは，円盤のフチに直交する円弧を，直線と定義します．
この世界では，ある直線に対する直線外の1点を通る平行線は無数に引けます．
円盤モデルの世界では，円盤のフチ（地平線）に近づくほど見かけの距離はどんどん縮んで見える
［あるいは旅をする自分がどんどん縮む］ので，永久に地平線に到達できません．
このような世界の最短距離（直線）は円盤のフチに直交する円弧となるのは納得できるでしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.03.08］ No.105
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
このブログやメルマガの表題になっている「数学月間」についての言及は少なかったように思います．
今日は，初心にもどって「数学月間」のことをお話します．
<数学と社会の架け橋>「数学月間」は，毎年7月22日～8月22日です．私たちはこの期間を中心に，
市民が数学に関心を向けるようなイベント開催を奨励しています．「数学月間」は，
市民が数学に関心を向けると同時に，数学者が社会に関心を向ける双方向の架け橋を目指しています．
何故7月22日～８月22日かと言えば，22/7≒π（円周率），22/8≒e（自然対数の底）
という数学の基本定数にちなんでいます．日本の「数学月間」は，今年で11年目．
毎年，初日に“数学月間懇話会”を開催し，今年の７月は第12回です．
正式アナウンスは4月末の予定ですが，以下の案で只今準備中です．
遠方の方もおられましょうが，ぜひ多くの方のご参加をお待ちしております．
今年のテーマは，現代社会で正しい理解が必要になる“確率や統計”がテーマです．
■第12回数学月間懇話会　7月22日（金）14:00-17:00（開場13:30）
場所●東京大学（駒場）数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
内容［演題は仮］●数学よもやま話（亀井哲治郎），医学と統計学（田渕健），社会と統計学（松原望）
問合せ先●数学月間の会（SGK），sgktani@gmail.com（SGK世話人）
17:30から構内（イタリアントマト）で懇親会（各自めいめい払い）
ーーーーーーー
■フランスの数学週間
2012年から始まったフランスの数学啓発活動－数学週間の今年（第5回）のテーマは“数学とスポーツ”です．
今年は，3月14日～20日が実施週間です．
http://www.education.gouv.fr/cid59384/la-semaine-des-mathematiques.html
パートナーと呼ばれる20数団体が参加して，毎年3月中旬に行われ，毎回一つのテーマが決められます．
“数学カンガルー”テスト・暗算大会と国内数学オリンピック大会とが同時開催されます．
数学カンガルーとは，1978年，オーストラリアの数学教授が考案した多項目選択式数学（算数）学力テストを，
フランスの二人の数学教授が更に発展させたもの（1991年）で，
現在は，“国境なきカンガルー協会”が，毎年3月の第3木曜日に実施し，
EUを中心に，世界50か国（600万人）以上が参加しています．
ーーーーーーーーー
■米国の数学月間
1986年4月のレーガン宣言で始まった米国の数学月間MAM（Maths Awareness Month）は，
長い歴史があります．米国MAMのスタートとなった歴史的なレーガン宣言は，
Webでは見当たらなくなりました．このブログの初期の項目に翻訳しておいたものがありますので，ご覧ください．
http://rdsig.yahoo.co.jp/blog/article/titlelink/RV=1/RU=aHR0cDovL2Jsb2dzLnlhaG9vLmNvLmpwL3Rhbmlkci8xNTc0NTU4My5odG1s
今年のテーマは“予測の未来”です．数学月間の先進国ですが，昨年あたりからあまりパッとしないように感じます．
ちなみに昨年のテーマは，“数学はキャリアを運ぶ”でした．
あまり数学の功利的な面を取り上げるのは私は好みません．
今年は数学に地道に根差したものになることを期待しています．
米国MAMの実施月は4月ですが，まだ準備が遅れているようです．
http://www.mathaware.org/mam/2016/essay/

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.03.01］ No.104
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
平面の非周期なタイル張りの一つが，
ロジャー・ペンローズが考案した（1966）ペンローズ・タイリングです．これは
2種類のタイルによる規則的ではあるが，周期的ではないタイル張りです．
2通りの方法でペンローズ・タイリングを作る．
（１）正10角形から出発して，分割・拡大を繰り返して作る
ペンローズ・タイリングに出てくる２つの2等辺3角形　A型とB型は，
正５角形の中にあります．この図形には黄金比１：φがたくさん出てきます．
A型やB型の2等辺3角形の等辺と底辺の比はφ：１（A型）や１：φ（B型）．
ただし，φ＝1.618･･･
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/95/17313295/img_0_m?1456754314
黄金比の3角形は，分割すると同じ型の3角形が含まれている性質があります．
A型およびB型の2等辺3角形は，それぞれ図示したように分割できます．
この性質を利用して，正10角形から出発して，分割とφ倍の拡大を繰り返すと
平面全体をA型とB型の２等辺3角形で埋め尽くすことができます．
こうしてペンローズのタイル張りを得ることができます．
タイルの分割が十分進んだときの，AのタイルとBのタイルの個数の比は，
φ(=1.618･･･)：１の黄金比になります．
図は3回の分割と拡大を繰り返して得た図形です．
この図形で見られる形は，凧(2A)と矢(2B)です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/95/17313295/img_1_m?1456754314

(2)正5角形のフラクタル配置を繰り返して作る
正5角形を一回り大きな正５角形の内に並べます．
これをさらに一回り大きな正5角形の内に並べます．
これを次々繰り返すと，全平面を埋め尽くすフラクタル図形ができます．
図上段は，この操作を3回繰り返したところです．
ギャップができますが，気にしないで配列を進めます．
実は，後でギャップの中も正五角形（白色）で埋めます．
すると最終的には，王冠型や星型のギャップが残されることがわかります．
この図をよく見ると，図中段のような2種類のタイル（黄色と青色の菱形）で
置換えると，図下段のようにペンローズ・タイリングであることがわかります．
図下段右の大きなペンローズ・タイリングはこのようにして得たものです．
このペンローズ・タイリングには，中心に5回回転対称が残っていますが，
中心の回転対称を消す配置も可能です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/07/17050507/img_3_m?1456754576

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.02.23］ No.103
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回は，話題の凍土遮水壁についての解説にしました．海への汚染を止めねばなりません．
■福一の事故から5年が経った．メルトダウンした原子炉の中がどのようになっているのか，
燃料棒のデブリが地下どこまで汚染しているのか，見た者はまだ誰もいない．
廃原子炉からデブリ取り出しの開始は，早くて2021年である．この間毎日，多量の地下水が原子炉建屋の下を流れ，
デブリを浸している高濃度の放射性汚染水と混ざり海に流れ込んでいる．豊富な地下水の流量は日に400トンと言われる．
読者も航空写真を見たことがおありかと思うが，汚染水貯蔵タンクが1,100基も立ち並び，
もはや敷地内にタンクを作る余地のない状態である．1～３号炉の冷却のために注入する水は400ton/日，
建屋地下を流れ去る地下水400ton/日のほかに，原子炉建屋を浸し冷却水と混合する地下水が400ton/日，
従って，建屋地下から汲み出す冷却水が800ton/日で，分離されてタンクに貯蔵される高濃度の汚染水は400ton/日という．
■従って，地下水を原子炉建屋のデ ブリに触れさせずに，バイパスさせ汚染のないまま海に放出したらどうか
という案は当初からあった．地下水脈は地上を流れる川のように迂回させるという工事 はできない．
緊急に短期間で実施できる対策に，トンネル工事などの水止めで実績のある凍土遮水壁を提案したのは
鹿島建設でこの案が採用された．
凍土遮水壁は原子炉建屋と建屋の周りのサブドレインを取り囲む周囲1,500mで，
深さ30mまで冷却パイプを打ち込み地盤，あるいは流水を凍らせるものである．
事業費約３５０億円は全額国費で賄われ，完成後も凍結を保つために，年間約２０億円の電気代がかかるので，
「国による東電の救済策」との批判もある．（北海道新聞，2/18社説）
■2014.4月に凍結し難い箇 所の試験凍結．5月に山側全体の凍結開始が，2015.3月に凍結開始，
さらにもっと計画がずれ込んだ．凍土遮水壁の工事は2014.6月に 開始し，
毎日約500人が働き，2年を費やしてやっと工事が完成したのだ．工事は犠牲者もでる難工事で現場の努力は評価したい．
凍土壁は，トンネル工事での短期間とか，局所現場に適応実績のあるもので，
このように周囲をぐるりと塀のように囲んだり，何年にもわたって凍結を維持した実績はない．
地下水脈の深度が深かったり，多量の地下流水が熱を運び去ったりして凍結できないのではないかと私も心配している．
原子力規制委員会は，凍結を実施 して地下水の侵入を止めると，サブドレインの水位より原子炉建屋中の水位が高くなり，
デブリに触れている高濃度の汚染水がサブドレインの方に出てくるリス クを懸念し，
やっと完成した凍土壁の稼働にストップをかけている．いまさら何を言っているのかと思う．
規制委員会，田中俊一委員長は効果が期待できないと，この件に関しては冷淡である
（2/17田中俊一委員長定例会見，iwj中継）．
3月初めに，水位の影響の少ない海側（建屋からの汚染水の排出側）だけ凍結 し，
様子を見ながら徐々に全周の凍結を行うという案を東電が提出し，これを規制委員会が認可して即実施に入る見込みである．
凍結が始まって順調だと8ヶ月 後に，流入地下水は日に90トンに低減されるという（2/15東電定例会見，iwj中経）
■凍土壁工法は，ローコストな救 急的な工法で，すぐ実施でき海洋の汚染を防止することに意味があったのだが，
計画より2年以上遅れ，今稼働しても凍結までまだ8ヶ月もかかる．この間汚染水は海に漏れま くっており，
対策時期を逸しいる．現場の苦労に同情しうまくいくことを望むが，抜本的な解決策ではないのが残念だ．
■規制委員会は，規制値内の汚染水なら海洋に放出してかまわない（抜本的な手立てを打っていない）との方針だ．
しかし，排水規制は放射能の濃度のみで総量は規制されないので，汚染水放出が続くと海洋汚染は深刻になる．
廃液の規制はCs134で60Bq/L，Cs137で90Bq/L，Sr90で30Bq/Lであり，これらの核種が混ざっていれば合計の放射能で規制され，
これら部分成分の濃度はさらに低く規制されるはずである．
ところが敷地内の海側の井戸水から規制値の何千倍もの汚染が観測されているのが現実で，
地下水も高濃度に汚染されている可能性が高い．
海水のモニタ値に変化が出るなら，海水の量を考えればそれはとんでもない汚染で死の海である．
現地漁協は風評被害というが， 食物連鎖による魚の汚染は進んでいる．
このことを考えると，一刻も早い汚染水の排出を止めるべきで，
規制委員会が効果が期待できないなどと無関心を決めることは許されることではない．
－－－－－－－
（注）ちょっとわかりにくいのだ が，原子炉建屋をぐるりと取り巻く凍土遮水壁は全部，陸側遮水壁とも呼ばれる，
それは，現存する海側遮水壁に対する名称で，海側遮水壁は，鋼管矢板594 本を使用し
海の前に作った全長約780mの壁（凍土ではない）で，2015年10月26日に作業終了している．
大雨の折などポンプの能力が追い付かずK排水路から高濃度の汚染水がオーバーフローすることがあるのはこの海側遮水壁である．
本文中で，陸側，海側と使われるのは凍土遮水壁の陸側の部分，海側の部分という意味である．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.02.16］ No.102
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
写真は，なかなか洒落たテーブル断面の模様です．最近入ったレストランで発見しました．
調べて見るとこの断面の孔は向こう側まで貫通しています．どうやって貫通孔を穿けたのでしょうか？
菱形，長方形，わざわざ貫通孔を穿けるのはとても困難な作業です．
そこで，さらによく観察すると，上・下面は貼り合わせて作ったようで，鏡映対称になっています．
片面をこのような溝つきに仕上げて，溝つき側を内側に貼り合わせれば，
このような上・下鏡映対称で貫通孔のある断面を作れます．
面白い断面模様ができるし，これらの溝が貼り合わせのマーカーになるのかもしれない．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/71/17285171/img_0_m?1455501541

このように考察したところで，とても面白かったのでこれをfacebookの記事にしました．
すると，友人から以下のコメントがありました．
「丸太の外周部分を使って背中合わせにしているのですね。
切れ込みはおそらく反り止めではないかと思います」
なるほど，溝は反り止めの効果があったのです．実に巧妙な木取です．
木目を頼りに木取の図を描いてみました．
1本の丸太材から柱を切り出した残りの外側廃材から4枚とれます．
幾何学的にも見事で，経験と知恵に感心します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/71/17285171/img_2_m?1455501541

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.02.09］ No.101
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
対称性が高いとか低いとか言いますが，これはいったいどのようなことでしょうか．
正方形の対称性4mmに限定して話を進めます．その他の平面図形についてはブログをご覧ください，

正方形の対称性（点群）は，4mmと表記されます．この記号中の４は，図形の中心にある4回回転対称軸です．
4回回転対称とは，図形を90°回転しても初めの状態と全く変わらないという図形の状態です．
このような操作を4回繰り返すと1回転しますから4回回転軸という名称が付きました．
４回回転対称の対称操作の数は，90°，180°，270°，360°＝0°の回転の４つがあります．
正方形の形に対する鏡映対称操作は，横辺の中点を結んだ鏡と，縦辺の中点を結んだ鏡の2枚（青色），
および対角線の方向に2分する2枚（赤色）の合計4枚があります．
前者の2枚の鏡は，4回軸の操作で互いに移り変われ，後者（対角線方向の2枚）の鏡同士も同様です．
しかしながら，前者の鏡と後者の鏡とは4回軸の操作で互いに移り変わることができませんから，
前者と後者は種類の異なる鏡です．そこで，正方形の対称性（点群）の記述では，
4mmというようにm［鏡（mirror）の意］を２つ並べて書きます（注）．
（注）正五角形は5mですが，5枚の鏡は5回軸で互いに変換されますので，１種類の鏡（赤の鏡）しかないからです．

点群4mmの対称操作（要素）の数（群の位数と呼ばれる）は，全部で8個になります．
対称性が高いとは，群の位数が大きいことですが，対称要素が次々に減じていく系列のなかで考えます．
これから説明しようとしているのは，それぞれの群の下に含まれる部分群の系統図についてです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568615/22/17246222/img_4_m?1454724698

正方形の系列で最も対称性の高い4mmには，４回軸と2種類（赤色と青色）の鏡がありました．
回転対称軸の対称性が下がって（４→2→１）行ったり，鏡映面がなくなったりして，
対称性の高い点群から対称性の低い点群（部分群）が得られます．
赤や青の矢印で結ばれたものは，群と部分群の関係にあります．
図表には，それぞれの点群の対称性を一目でわかる図形で表現しました．

対称要素の数（群の位数）をrとすると，各図形の1/rの領域（緑に塗った）を
対称操作で広げて全体を作ることができます．
つまり，対称性の高い図形ほどこの領域は小さくて済みます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.02.02］ No.100
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
おかげさまで100号発行になりました．今年は数学月間は11年目です．
７月の数学月間懇話会に向けての情報も，これから掲載していきますので
よろしくお願いします．日本の数学月間は7/22～8/22です．
さて，エッシャーのような繰り返し模様のモチーフをつくる平行6辺形タイルについては
085(2016/10/20)で言及したことがありましたが，再度ここにまとめてみます．

（１）平行4辺形とは下図の（A)のような形です．
これらは，向かい合った平行な辺どうしは同じ長さです．
向かい合った辺どうしを突き合わせて平面を敷き詰めることができます．
向かい合った辺に同じような変形を加えて図案のモチーフを作ります．
エッシャーの作品の2羽の鳥はこのようにして作られました．
　　　　（A)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/17260028/img_0_m?1454336049
（２）平行6辺形で平行な辺どうしが同じ長さの図形は下図の（B),（C)のような形です．
これらは，向かい合った平行な辺（同じ色に着色）どうしを突き合わせて平面を敷き詰めることができます．
向かい合った辺に同じような変形を加え，図案のモチーフを作るとエッシャーの様な繰り返す絵が作れます．
私は，ハロウイン魔女を作って見ました．
　　　（B)　　　　　　　　　（C)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/17260028/img_1_m?1454336049
（３）平行８辺形以上になると平面を敷き詰められないのは何故でしょうか？
平面は2次元のために独立な平行移動の方向は２つで，3つ目の方向は決まってしまいます．
可能な方向は全部で３つで，4つ目の方向は存在できません．
従って，敷き詰め可能なのは平行6面体までということになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/17260028/img_2_m?1454336049

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.01.26］ No.099
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆さまご機嫌いかがですか．東京でもちょっと雪が降ったりしました．
今は寒いですが，晴天の日が続いています．日本海側はだいぶ雪が降っているようですが
被害などありませんように．

今回取り上げる伝統工芸の「大川組子」は，FBの友達からの情報と
ブログの友達からの情報で知りました．ウエブやSNSで得られた情報がことの起こりです．
写真は，見事な伝統工芸の格子です．寸分も違わない見事な細工です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/64/17219564/img_3_m?1452480087
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/64/17219564/img_2_m?1452480087

この模様の対称性を鑑賞しましょう．
これらの組子は，正3角形２つでできている菱形の胞（セル）を単位としています．
そして，全体を一貫する格子があり，胞（セル）は格子の中に詰め込まれています．
第二の図の右側コラムに，そこに使われている胞（セル）の中身（5種類）を取り出しました．
これらはどの中身も周期的に繰り返すなら，どれもみんな6回対称（p6mm）になります．
違った中身へと移り変わる境界の状態は，対称性で記述するのは困難です．
その複雑さに，数学がまだ追着かない芸術の深さがあるようです．
胞の中身に変化があっても，格子が同じ一貫したものになっています．
これは，人工結晶などで見られる格子整合という状態を連想させます．

素晴らしい「大川組子」の写真をウエブで探してたくさん鑑賞しました．
「大川組子」の格子は，３角格子（正３角形２つの菱形），正方格子，
六角形格子の３タイプがありました．
多くの工芸作品は，みんなこのうちのどれかで，他の格子は使われないようです．
そこで思い当たったのですが，これは，正多角形のタイル張りが，
正３角形，正４角形，正６角形の３種であることと似ています．
そして，上で述べたように３角形の中に入る胞の中身の対称性は3mです．
正多角形の格子を用いることと，胞の中身も格子の対称性と同じにすることは
安定な釣り合いを考えれば当然のことで，
昔から職人は，寸分もたがわぬ組子を作るために
力のつり合いと対称性を直観的に理解していたことがわかります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.01.19］ No.098
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
鏡は左/右を逆転する（上/下は逆転しない）のが不思議だという人がいます．
そんなに不思議でしょうか？実物と鏡像とは，上は上に，下は下に，左は左に，右は右に映る
（対応する）のですから当たり前で，不思議でも何でもありません．
それでも，鏡像の世界はなんだか不思議な感じがするのは確かです．
この不思議さはどこに原因があるのでしょうか？実物と鏡像を考察してみましょう．
実物は我々の世界にあり，鏡像は鏡の中の世界にあります．
それなのに，鏡像を我々の世界の中にあるように思うことが，この混沌の原因なのです．

■ちょっと脱線ーーーーー
「太古の時代は，我々の世界と鏡の中の世界の行き来ができたそうだ．
（このようなことは4次元の世界なら実際に可能である．）
鏡の中の生き物とこちらの世界の生き物は仲良く一緒にいたのだそうです．
ある夜，突然，鏡の世界の住人達が我々の世界で好き勝手を始めるようになった．
そして人々は，鏡の中の住人の正体が「混沌」であることに気付いたという．
そこで，黄帝が魔力によって「混沌」を鏡の世界に閉じ込め，
姿や動きも我々の世界の模倣しかできないようにした．」*1)
混沌の中から湧き出るように次々と生まれてきたさまざまなものが宇宙を形作った．
そしてこれを神の技として語り伝えられた．

呪文の効果が切れて，鏡の世界の住人達が勝手に動き出すことが将来起こるかも知れない．
私は幻想怪奇小説が大好きです．そのようなテーマの小説*2,3)
のうちで私が好きなものは「パイプをすう男」です：
一人の男が寂しい一軒家に住んでいます．
毎夜，ランプを卓に置き食事をとる．正面の張出し窓の五枚の窓ガラスに，五つの人影が映る．
彼が食事をとれば人影も同じように食事をとって，
彼が食後の煙草に火をつければ，同じように火をつける．
ガラス窓が五稜形をしてるから当たり前だが，毎夜のことだった．
ところが，ある夜，恐ろしいことが起こった．彼は，煙草に火をつけて
いつものように正面の窓ガラスに映る自分の姿に眼をやった．
すると，その一番左の端の窓ガラスで，五番目の彼の姿が同じように火をつけた．
が，つけたのは，彼のように紙巻ではなくてパイプだった．．．．．」*2)

*1)Turbulent mirror, J Briggs & F. D. Peat, 訳：高安秀樹，高安美佐子
*2)パイプをすう男，M･アームストロング，幻想と怪奇 1（ハヤカワ）
*3)わな，Ｈ・Ｓ・ホワイトヘッド，怪奇幻想の文学(新人物往来社)
ーーーーーーー閑話休題

■鏡映像の左右反転
x軸に垂直な鏡面があるとします．鏡面内に原点(0,0,0)があり，上方向がy軸です．
この鏡面により，(x,y,z)の点は（-x,y,z）の点に映ります．
つまり，y,zは変わりません（上は上に，左は左に対応）が，xは-xに変わります（前向きが後向きに対応）．
この鏡面は，xの符号だけ反転します．だから，右手は鏡に映ると左手に変わります．

鏡像は鏡の世界にあるのですが，我々は，鏡の世界を我々の世界の延長のように認識しようとします．
つまり，鏡の世界の天井と地面を，我々の世界の天井と地面と共通のものと直観してしまいます．
そして，鏡像を我々の世界に連れ込んで，前後の向き（鏡像はｘ方向が反転している）を，揃えようとします．
上下方向（y軸）は，鏡の世界と我々の世界は共通，前後方向（ｘ軸）は鏡像では反転しているので，
我々の世界に鏡像を連れてくるなら，反転したｘ軸をそろえるため，y軸（左右方向）が反転してしまいます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.01.12］ No.097
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先週に引き続き，モアレの美しさを鑑賞ください．
（A)2枚の格子を全く傾けずに（交差角0°）重ねたもの
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/68/17214068/img_0_m?1452512081
（B)2枚の格子を交差角10°で重ねたもの
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/68/17214068/img_1_m?1452512081
(C)2枚の格子を交差角15°で重ねたもの
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/68/17214068/img_2_m?1452512081
(D)2枚の格子を交差角20°で重ねたもの
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/68/17214068/img_3_m?1452512081
(E)2枚の格子を交差角30°で重ねたもの
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/68/17214068/img_4_m?1452512081

2枚の全く同じ格子（3角格子）を重ねます．
３角格子（6mmの対称性）の非対称の領域は0°～30°です．
そこで交差角（回転角）を0°～30°の範囲を実験しました．
言及したい注目点は３つ：
（１）元の3角格子の格子点の集合（並進群A）と，重ね合わせで生じた共通格子点の集合（並進群B）の関係は，
BはAの部分群であることです．
例えば，交差角30°の時の2つの格子に共通な格子点（スーパーラティスという人もいる）は，
coincident-site-latticeで，Fig（E）に示します．
あたかも，結晶の表面構造や高分解能電顕による格子像観察の映像のようです．
（２）連続的に交差角度をかえると，生じた拡大された格子像がズーム・アップして面白いです．
交差角が小さいと拡大率は大きくなります．Fig(B～D)
（３）モアレ現象は，薄膜の干渉で生じる現象にも似ています．
例えば，複写機ドラムの感光体塗膜の厚さにより，界面と表面からの反射光の干渉があります．
望まない干渉縞を除去するそんな特許を昔書いたことがあります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.01.05］ No.096
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
新しい2016年がスタートしました．皆様のご健康とご成功を祈ります．
やる素振り，やった振りで国民を期待させ欺くのはもう化けの皮がはがれてきました．
日本にとって2016年は大事な年です．良い年になりますように．

■モアレMoire
2枚の同じグレーチング（格子模様）を重ねたとき，もとのグレーチングの拡大像のようなものが
新たに生じるのを見たことがありますか．これはモアレ現象の一種です．
The superposition of two regular nets produces a secondary enlarged net of the same shape.
2枚の全く同じグレーチング（格子模様）を重ねると，たいてい相互にわずか傾いていますから，モアレ（モワレ）縞を生じます．
これは，2枚のグレーチング模様の重なった場所はよく光を通し明るく見えるためです．
重なる場所の出現は周期的ですから，重ね合わせ像のコントラストに周期的な分布ができます
（ビート，うなりのようなものです）．そしてあたかも，グレーチングの拡大像を得たように見えます．
グレーチング相互の傾きがわずかなら生じる像の拡大率は大きく，傾きが大きくなると拡大率は小さくなります．
下の３つの写真は，最近ある店の中で撮影したもので，今回モアレのテーマを思い出したのもこのせいです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_2_m?1451706758
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_0_m?1451706758
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_1_m?1451706758

3枚の写真は，それぞれ全く同じ2枚のグレーチングが平行移動（傾きはなく）して重なっている状況です．
これらの写真を見ると，2次元的なビート・パターンが生じているのですが，
全く同じグレーチングが平行にずれても，新しいビート・パターンは生じないはずです．
ではなぜこのようなビート・パターンが生じたのでしょうか？
それは，2枚のグレーチングの間にスペース D があるために，観測者から視差（パララックス）があり，
前方のグレーチングよりも後方のグレーチングを小さく見込むためです．
これは，わずかに寸法の違うグレーチングを重ねたのと同じ現象なので，
このためにビート・パターンが生じているのです．
とても美しいので，よくわかるように以下の写真を追加します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_7_m?1451706758
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_8_m?1451706758
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_9_m?1451706758

■詳細考察
では，計算してみましょう：ノギスの副尺の原理を思い出すと良いかもしれません．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_6_m?1451706758
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/63/17194663/img_5_m?1451706758

本当のグレーチングの格子のサイズ　a
2枚のグレーチングの間隔　D
視点から表面のグレーチングまでの距離　L
後ろのグレーチングの縮小割合　δ/a≡q<1
として，生じるビートの周期　T　を求めて見ましょう．
a/(D+L)＝(a-δ)/L　より　δ/a＝D/(D+L)
T≡n･a=(n+1)(a-δ）より　δ/a＝a/(T+a)　⇒　T=a(1/q-1)　← D, L を消去した
　　あるいは，　T=a(L/D)　← q を消去した
さて，この例で生じた新しいビートの周期は，　T=5a　のように観測されます．
従って，L/D=5　が得られます．あるいは，1/q＝6，つまり　δ/a=1/6　です．

2枚の同一なグレーチングの間隔Dで重ねたとき生じるビートが，もとのグレーチングのn倍に見えたら，
観測点から表面のグレーチングまでの距離はL=n･D　です．これは，距離Lを測定する道具に応用できるでしょう．
ただし，n=1（T=a）はモアレとは言いません．a/2周期の均一なコントラスト分布です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.12.29］ No.095
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
いろいろあった2015年もあと数日で終わります．忙しい日々ですがどうぞ
お変わりなくお過ごしになりますよう．皆さまにとって良い2016年になりますように．
毎年7月22日に，数学月間懇話会を実施していますので，ご参加をお誘いします．
来年の計画が決まりましたらご案内いたします．

数学月間を日本数学協会が提唱して今年（2015年）で丸10年になりました．
今年の7月22日の数学月間懇話会（第11回）テーマは，十年目の数学月間（片瀬豊），
フランス数学週間（高窪正明），サッカーボールの対称性を解くトポロジカルシンメトリー（細矢治夫），
繰り返し模様の観賞法（谷克彦），テーラー展開の話（鈴木啓一）でした．
今年も例年のように大変暑い日で，教室付近の構内は自動販売機はないし熱中症も心配されましたが，
高校生5人を含む30人を超す参加があり熱心に質疑もなされました．参加者の過半数が懇親会にも参加されました．
今回のメルマガでは（１）の講演の概要を報告します．
（１）フランス数学週間（高窪正明）
2012年から始まったフランスの数学啓発活動－数学週間(La semaine des Mathématiques)－に付いて，
主にネットで得られた情報を中心に紹介がありました．
数学週間は，国民教育省の企画の下，“現在の生き生きとした魅力ある数学の提示”，
“数学が日常生活で果たしている重要性の提示”，などの五つの目的を掲げ，
パートナーと呼ばれる20数団体が参加して，毎年3月中旬に行われます．
加えて，毎回一つのテーマが決められています．2012年の第一回から2015年の第四回まで順にテーマを記すと，
”女子と数学”，”惑星である地球”，”様々な文化の交差点にある数学”，そして，”数学は，私たちを運ぶ”です．
この数学週間の特徴は，“数学カンガルー”テスト（後述）・暗算大会と国内数学オリンピック大会とが
同時開催されている点でしょう．前者二つは，遊び・身近なものを通じて，数学への関心を高める目的．
後者は，数学を専門として使う人材を養成する目的でしょう．
さて，数学カンガルーとは，1978年，オーストラリアの数学教授が考案した多項目選択式数学（算数）学力テストを，
フランスの二人の数学教授が更に発展させたもの（1991年）で，
現在は，“国境なきカンガルー協会”が，毎年3月の第3木曜日に実施し，
EUを中心に，世界50か国（600万人）以上が参加しています．
テスト問題は，学年・専攻別に12水準で用意され，代数，幾何学，および，
論理の三分野から出題される24問/50分から成り，参加国各国語に翻訳されます．
テスト結果は参加国それぞれで集計され，成績優秀者が表彰されます．
フランスでは，約4,000の学校・約3,000,000の小中高生が参加します．
これら三つの催しの他に，数学週間の期間中，その年のテーマに沿って多くの講演，
多彩な見学会（実習付），そして，教育映画上映会が，
フランス全土の30大学区（教育行政区）・パートナーによって執り行われます．
特に，第一回以来Cédric Villani 教授（2011年 Fields賞）が，活発な講演・啓発活動を行っている事も注目されます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.12.22］ No.094
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
本年もあと1週間です．本年お付き合いいただきありがとうございました．
今回は，前回のユニット折り紙の箱の考察の続きです．
■正6角形箱
２つの箱をユニット折り紙で作りました
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/29/17175629/img_0_m?1450707610

どちらの箱も正6角形です．色の見分けのできない（すべて灰色の見える）眼鏡をかけて見れば，
どちらもおなじで6回回転対称です．
左の箱は，6回回転軸の60°回転ごとに，色がオレンジ⇔青と入れ替わります．
このような色の交代と結び付いた6回軸を６’と書きます．
右の箱は，6回回転軸の60°回転ごと（左まわり）に，色は，青→ピンク→オレンジと置換します．
このような3色の置換と結び付いた6回回転軸を6^(3)と書きます［(3)は上付文字です］
左のような，2色交代と空間対称操作との結合はシュブニコフ，
右のような色置換と空間対称操作との結合はベーロフによって研究されました．
空間対称操作（空間群）はフェドロフにより研究されましたのでフェドロフ群と呼ばれるように，
これらの拡張された空間群は，シュブニコフ群，ベーロフ群と呼ばれます．
■シュブニコフ群
左の点群を６’＝｛6'，6'^2，6'^3，6'^4，6'^5，6'^6=1｝とします．
図形を見てわかるように，色の変化を起こさない点群３＝{3, 3^2，3^3=1}，
［ただし，６’^2=3，6'^4=3^2に注意］が，部分群［実は正規部分群］として含まれています．
したがって，対称操作の集合は2つの集合の和（剰余類展開）になります：
　6'=６’・３＋1・３
これは，点群6'を色を変えない正規部分群 3を法として６’/3＝｛１，6'（mod3）｝に単純化されるということです．
［注）群３を法としてとは，点群３で動くものはすべて同じものと思えということです．
時計は12を法としています．1時と13時は同じ位置に来ます］
■ベーロフ群
右の点群は６^(3)，色を変えない正規部分群は　2＝｛(6^(3))^3=2, 1｝ですから，
6^(3)/2=｛6^(3)(mod2)，(6^(3)(mod2))^2, 1｝
つまり，mod2というのは，2回軸で移るものは同じと思えということで，考察は図形の半分に帰着できます．
例えば図形の右側だけ見ると，青→ピンク→オレンジの置換が起きることがわかるでしょう．

■正8角形の箱
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/29/17175629/img_1_m?1450707610

左の箱は前回登場した正8角形のものです．点群は 8'
この中に含まれる色を変えない部分群は，4
8'/4={8'mod(4), 1} です．
ただし，正8角形のタイルで平面のタイル張りはできませんから，
有限図形の点群としての８はありますが，8回軸が周期的に並ぶと矛盾が起きます．
つまり，結晶点群として８は存在できません．
例えば，正8角形の分子（オクタテトラエン）が，周期的に配列して結晶を作ったとしても，
並進周期はせいぜい4回対称か2回対称でしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.12.15］ No.093
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ネットでこのような美しい正八角形の箱を見つけました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/99/17162399/img_0_m?1450074719

このなかに以下のような図形が見られます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/99/17162399/img_1_m?1450074719

一番外側の大きな正8角形の内に一回り小さな正8角形が
含まれています．そしてその正8角形の内に，さらに一回り小さい
正８角形が見えます．
この調子で，内部に作図を続けていくなら，どんどん小さな正8角形が
含まれて行きます．そのようなどんどん繰り込まれていく図形は
フラクタル図形です．
一回り小さくなる度に，その相似比はどのくらいでしょうか？
外側周は直角2等辺3角形でできていますからすぐわかると思います．
１：√2－1　が答えの相似比ですね．

外側を以下のように星形にすると
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/99/17162399/img_2_m?1450074719

レオナルドの星形8角形が得られます．
外側の星形と内部の星形の相似比は，やはり
１：√2－１　です．
老婆心ながら，この比率を√2＋1倍して
√2＋１：１
が相似比だと答えても正解です．

■私も折り紙でこの箱を作製してみました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/99/17162399/img_3_m?1450104156

以下のサイトに作り方が出ていますのでご参考まで．
同じ部品を作っておいて組み立てるこのような作り方を
ユニット折り紙というそうです．
正方形の千代紙が8枚必要です（フタ側の半身で）．
ただし，中心の白く見える部分は千代紙の裏側ですから
これが嫌な方は両面印刷の千代紙か，贅沢ですが
背中合わせで2枚重ねの千代紙を使うと良いでしょう．
折り紙では，45度や45度の半分の角度は簡単に作れます．
今回の箱作りでもそのような折り方（下写真）を使います．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/99/17162399/img_4_m?1450104156

■作り方は以下のサイトを参考にしました
https://www.youtube.com/attribution_link?a=CJItUT4Igow&u=/watch?v=RbSiETOOac4&feature=share
八角形の折り紙箱 1/2
http://origamisho.com/archives/1412
セツの折り紙処

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.12.09］ No.092
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
慌ただしい12月ですが，皆さまお風邪など召しませんように．私も危ない危ない．
今回は，4次元正多面体を理解するのに避けて通れないシュレーフリ記号についてです．
シュレーフリ（1814-1895）は，スイスの幾何学者．4次元の正多面体（ポリトープ：正多胞体）
が６つであることを示した人です．
ちょっと話を戻して，3次元の正多面体とは，　
（１）すべての面が同一の正多角形でできている．
（２）すべての頂点のまわりの状態は同一である．
を満たすもので，特に凸正多面体をプラトン正多面体と言いました．
プラトンの正多面体は5つであることはご存知でしょう．
注）5つの正多面体がプラトン多面体と呼ばれるのは，プラトンが著作に，ロクリス
（ギリシャの地名）のティマイオス（哲学者名）の宇宙観として“巨大な正12面体で囲まれている宇宙と，
四元素の正多面体”について述べているからです．この時代の四元素とは：
火→正4面体，　土→正６面体，　空気→正８面体，　水→正20面体．
正多面体が5種類であることは，プラトン以前のギリシャですでに知られていました．
ユークリッドの「原論」にも証明が載っています．

4次元の正多面体のことを正多胞体と呼ぶのが正しいのですが，
これは４次元の正多面体の面は，3次元の正多面体（プラトンの正多面体）なので，
面と言わずに胞Cellと呼ぶべきなのです．

さて，今回はこのようなものを記述するシュレーフリの記号についてです．
このような記号は面倒なようですが，この記号を理解すると多面体の性質のほとんどを理解したことになります．
シュレーフリの記号は本質をとらえた非常に優れた表記法であります．
■3次元の正多面体のシュレーフリ記号
｛面の形，頂点に集まる面の数｝
正4角形の面が頂点で3つ集まる図形を{4,3}と書きます．これは立方体ですね．
正3角形の面が頂点で4つ集まる図形｛3,4｝は？　これは正8面体です．
｛4,3｝と{3,4}の図形は互いに双対の関係にあります．つまり，
一方の図形の面→頂点，頂点→面に置き換えると他方の図形が得られます．
互いに双対な図形の対称性は全く同じです．
■ユークリッド平面のタイル張り
｛4,4｝なら，正方形による無限平面のタイル張り，{3,6}なら，正3角形によるタイル張りになります．

■半正多面体を記述するシュレーフリの記号
半正多面体というのは，複数の正多角形で作られる多面体で
どの頂点のまわりの状況も同じものです．半正多面体を記述する記号は，
頂点のまわりを1周するとき出会う正多角形を列挙します．
切頂正4面体（正4面体のとがった頂点を切断し，残りの面が正6角形になるようにする）の例では　
［3,6,6］となります．シュレーフリ記号が，正多面体に関するものか，
半正多面体に関するものかの混乱を避けるため，私は前者を｛｝，後者を［］と違うカッコを使い区別しています．

■4次元の正多胞体
正5胞体，正8胞体，正16胞体，正24胞体，正120胞体，正600胞体の6つです．
正5胞体は正4面体が5つでできています．
4次元正胞体のシュレ―フリの記号は｛胞の形，１辺が共有する胞数｝を指定します．
正5胞体は，正4面体が各辺の周りに3個集まっている図形ですので{ { 3,3},3｝={3,3,3}，
正16胞体は{3,3,4}，正600胞体は{3,3,5}というように，全く自然に3次元から延長できます．

■最後に３つの幾何平面（2次元）のタイル張りについてまとめます．
このような正ｎ多角形によるタイル張りを，平面の正則分割｛n,k｝といいます．
赤い色は楕円幾平面，緑色はユークリッド幾何平面，青色は双極幾何平面の出来事です
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/17152332/img_0_m?1449586423

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.12.01］ No.091
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ゼロとアラビア数字
最古の記数法は五進法だそうです．５をひとまとめにしたものを「１クワイン」といいました．
バビロニアには60進法，20進法を使ったところも，12進法を使った場所もありました．「１ダース」です．
12は約数が多いので10より便利なところがあります．けれども，大勢は10進法に落ち着きました．
われわれが指を折って数えるところから10進法が各所で使われるようになったと推測されています．
10進法での記数法には０と１～９までの数字が必要です．これからアラビア数字の起源に思いを馳せるわけですが，
0と1～9までの数に対応する何らかの記号があり，それ以前に十進法が確立していなければなりません．
参考書：「アラビア数学奇譚」マオバ・タハン（越智典子訳）白揚社
■イスラムの数学
フワーリズミー（780頃～850頃）は、アッバース朝のバクダッドで活躍しアラビアの数学を確立した代数学の創始者です．
彼の時代のバクダッドをのぞいてみましょう．
ゼロの役割には，位取りの役割と4則演算の対象となる数の役割があります．
まず位取りに関していえば，この時代，大勢は和算もイスラムも10進法でありましたから，
数を表示するには，････，十万，万，千，百，十，一，の位の場所に，0～9に相当する数字を書いたり，
マッチの軸木のような算木を置いたり，
そろばんでは玉で表示したりします．どんな記号を使っても似たようなもので，
ゼロの記号がないときはその位は空にしました．アラビア数字に関しては，エジプト，インドから
伝えられたゼロの概念がイスラムで発展しヨーロッパに伝わり完成されたという流れでしょう．
どのような数字でもかまいませんが，０があると空を位取りの場所に配置するよりも明瞭に数字を表示できます．
これが位を明瞭にするので，十，百，千，万，十万，百万，千万，億，...と際限なく単位が必要になることが避けられます．
これはイスラム数学の画期的な成果でしょう．
次に，4則演算の対象としてのゼロについてです．分数全体の集合（＝有理数）の中で4則演算を自由に行えます．
ただし，ゼロで割ることは禁じられていますのでご注意ください．
ギリシャでは幾何学が盛んでしたが，イスラムの数学ではアラビア数字の記数法を用いて，代数や方程式が進みました．
特に，三角関数が生まれて発展しました．われわれが高校で学んだ加法定理や倍角の公式やそのほか様々な三角関数の公式が証明され，本が出版され，三角関数の数表も発行されました
■平和の都，バクダッド
1100年前のバクダッドは人口100万人の世界最大の都市でした．
その賑わいはまさにアラビアンナイトの世界です．イスラムの教えのもとに
“平和の都”と呼ばれ，アッパース朝宮殿は建築工学，幾何学の粋を集めます．
イスラム帝国は，東ローマ帝国と中国（唐王朝）の間に位置し交易に便利です．
コーランは“神は商売を許したもうた”と商業を奨励し，売買の証人たる仲介人がいて契約と公正な取引が行われたそうです．
最古の小切手（エジプトの商人が振り出した）も発見されています．
チグリス川とユーフラテス川の間に円城都市（直径2.3km）が建設され，
これを中心とする見事な中央集権行政システムが出来上がりました．
バクダッドに集まる4本の街道は東西南北に延びヨーロッパはスエーデンまで交流があったということです．
（バイキングも正式に貿易しイスラム銀貨が流通しました）
■科学や医学，都市の発展
8世紀に成立したアッバース朝では，カリフや宮廷のワズィールたちが保護をうけ，第7代カリフ，
マアムーンが創設した研究施設バイト・アル＝ヒクマ（智恵の館）には多くの科学者が集まり，
ギリシャ科学のアラビア語への翻訳が進めらました．マアムーンに仕えた科学者・数学者のひとりが，
フワーリズミー（780頃～850頃）でした．
科学では，古代エジプトに起源を持つ錬金術の実験が繰り返され，元素記号が生まれ，
文学では，アラビアン＝ナイトが生まれ，唐で発明された製紙法もキルギスの戦いの際に伝わりました．
バクダッドには100軒を越す書店があったそうです．
百花繚乱．当時のバグダードのにぎわい言ったらすごい．見たかったですね．
イブン・シーナは最先端医学の医学典範を著し，世界初の総合病院がバクダッドに作られました．
病院は寄進され，その運営費も，周辺の市場の売り上げ寄付で行うワクフという相互扶助の制度が，公共施設を支えたそうです．
円城都市を中心に，モスク3万，多くの市場と市場には100店を超す店があったそうです．
500年間繁栄したイスラム帝国は，１万２千のモンゴル軍により滅亡しました．
チグリス川は血で染まり，本のインクで青く染まったそうです．
アラビア語に訳されたアリストテレスなどギリシャの古典や発展したイスラムの科学は，
その後ヨーロッパに伝わりラテン語に翻訳されルネッサンスが花開きます．
参考：
ドキュメンタリー 文明の道「第06集 バグダッド 大いなる知恵の都」
https://www.youtube.com/watch?v=ehEuTnLfOME&feature=share

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.11.24］ No.090
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
秋らしい日になりましたが，今年も慌ただしく過ぎて行きます．
皆様お変わりありませんか．
前号で双曲幾何平面（ポアンカレ円盤モデル）の正則分割（タイル張り）の話をしました．
そのような光景を万華鏡で作ってみることにします．
■コクセターの万華鏡
まず球表面（楕円幾何平面）の話から復習します．
球表面が球面正p多角形タイルで{p,q}のように張りつめられているとき，
1つのタイルの中を2p個の直角3角形に分割できます．
この直角3角形を鏡室とする万華鏡は“メビウスの万華鏡”です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/51/17096451/img_1_m?1447147230
直角3角形の内角は，それぞれ π/p，π/q，π/2で，この直角3角形を（p,q,2）と書きます．
ポアンカレ円盤の双曲幾何平面でも，双曲正p多角形で{p,q}のように張りつめられているとき，
１つのタイルを2p個の直角3角形に分割できます．
この直角3角形を鏡室とする万華鏡は“コクセターの万華鏡”です．
双曲面の｛6,4｝正則分割の場合の直角3角形(6,4,2)(赤い3角形）を図（左）に，
対応する“コクセターの万華鏡”の映像を図（右）に示します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/15/17104115/img_0_m?1447459606
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/15/17104115/img_1_m?1447459606
この3角形の2辺は平面鏡，残りの1辺は円盤のフ チに直交する円弧鏡よりなります．
しかしながら，この円弧鏡は，数学的には反転円として定義できるのですが，
現実の円柱鏡の反射には収差があるので，数学 の定義のようにはいきません．
従って，あまり鮮明な万華鏡映像にはなりません．

■(7,3,2)3角形によるコクセターの万華鏡
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/87/17106487/img_0_m?1447506664
(1){7,3}の正7角形タイル張り(赤)　(2)｛3,7｝の正3角形タイル張り（緑）　(3)菱形タイル張り（青）
3枚鏡（直線鏡2枚，円弧鏡1枚）の万華鏡により
ポアンカレ円盤内の双曲平面は市松模様に塗られますが，
正7角形のタイル張り，正3角形のタイル張り，菱形タイル張り
などを見ることができます．

話はこの先，エッシャーの作品「極限としての円」シリーズに続きます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.11.17］ No.089
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
非ユークリッド幾何の双曲幾何平面を訪ねて見ようと思います．
エッシャーの作品で「極限としての円」シリーズを見たことがおありでしょうか．
円盤の世界で周辺に行くほど，どんどん小さくなって行く構図です．
この作品は双曲幾何のポアンカレ円盤モデルを使い，
円盤内の正則分割（コクセターの万華鏡）が基礎になっています．
正多角形タイルによるタイル張り（正則分割という）は，
双曲幾何平面の場合は無限にあります．
例として，{6,4}と{5,4}を掲載しますので，まずはご鑑賞ください．
　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/02/17100202/img_0_m?1447229525
（注）
ポアンカレの双曲幾何のモデルは，円盤の中にすべての宇宙があります．
宇宙の果て（円盤のフチ）に近づけば近づくほど自分もどんどん小さくなるので
いつまでたっても宇宙の果てに到達できません（無限の時間がかかります）．

{6,4}は正6角形による双曲幾何平面の正則分割で，各頂点に4個の正6角形が集まっています．
円盤の中は双曲幾何の世界ですから，この世界の直線は円盤のフチに直交する円弧です．
正6角形の辺はすべて直線です．円盤の中に描かれた円弧は皆，縁と直交しており，
この世界ではすべて直線です．円盤の中の正6辺形はすべて同じ大きさです．
同様に，{5,4}の図は正5角形による双曲幾何平面の正則分割の例です．
　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/02/17100202/img_1_m?1447686193

例えば，赤い円弧で分けられた世界は左が大きく右が小さいようですが，
この円盤内の世界では同じ広さです．どちらの世界も無限に広い．
円弧は左右の世界を写し合う鏡です．鏡像は色が変るように市松模様に塗り分けました．

■エッシャーのトリック（引用先：コクセター論文）

M.C.エッシャーの「極限としての円」Circle limit IIIを鑑賞しましょう（図左）．
この円盤内は双曲幾何の世界（ポアンカレの円盤モデル）です．
この円盤内を旅する人は，円の縁（世界の果て）に近づくほど時間がかかる．
つまり，［世界の果てに到達するには無限の時間がかかる］ようになっています．
この世界で定義される直線（最短時間で移動できる経路）は，円盤世界の縁で直交する円弧です．
エッシャー作品（図（左））の円盤は，魚の流れを示す白い線で分割された双曲面の
[4,3,4,3,4,3]分割のように見えますが，実は図（中）に示すような，黒い線で分割した{8,3}正則分割です．
白い線は，双曲幾何の円盤世界の縁に80°で交差し，直線ではないのです．
図（中）の正8角形の黒い線がこの円盤世界の直線であることは，図（中）に書き込んだ赤い円弧
（いずれも円盤縁で直交する円弧）を見れば理解できるでしょう．
 

双曲平面の正８角形タイルは，双曲平面の直線（円盤の縁で直交する円弧）で囲まれています．
タイルの大きさは円盤の縁に行くほど小さく見えますが，円盤内は無限に広い双曲幾何平面なのですべて同じ大きさです．
１つのタイルの中には4匹の魚がおり中心に4回軸があります．
正8角形の頂点には3回軸があり，魚の白い流れは3回軸の場所に集まっています．
エッシャーは｛8,3｝分割に用いる直線をわざと隠し，白い流れが分割であるようなトリックを見せます．
もちろん，白い流れの円弧（直線ではない）に関して鏡映対称はありません．

■直角3角形(7,3,2) によるコクセターの万華鏡

正7角形のタイルは，直角3角形(7,3,2)［内角の組（π/7,π/3,π/2）の３角形のこと］の14個に分割できる．
直角3角形(7,3,2)を鏡室とする万華鏡を，コクセター万華鏡と呼びます．

(1)　{7,3}の正7角形タイル(赤)張り．　(2)   (1)の双対である{3,7}の正3角形タイル(緑)張り．(3)　菱形タイル(青)張り．

3枚鏡（直線鏡2枚，円弧鏡1枚）のコクセター万華鏡により，
ポアンカレ円盤内の双曲平面は市松模様に塗られます．
生じるタイル張りは，正7角形のタイル張り，正3角形のタイル張り，菱形タイル張り，に見えます．

■エッシャー作品の生まれるまで

コクセター　　　　　　　　　　　　　　　エッシャー
直角3角形（6,4,2)　　　　　　　　　　　　直線魚のモチーフ　　　　「極限としての円I」
双曲面の{6,4}分割を細分　　　　　　　　　　　　　　　　　　　　　　　Circle Limit I

コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました．
1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．

*By S.H.M.Coxeter
Crystal Symmetry and ItsGeneralizations (published in the Transactions of the RoyalSociety of Canada in 1957).

 続く⇒　極限としての円Ⅲ

■メビウスの万華鏡とコクセターの万華鏡

■楕円幾何平面の正則タイル張り
球表面が球面正p多角形タイルで{p,q}のように張りつめられているとき，1つのタイルの中を2p個の直角3角形に分割できます．この直角3角形を鏡室とする万華鏡は“メビウスの万華鏡”と名付けます．このときの直角3角形（鏡室）の内角は，それぞれ π/p，π/q，π/2で，この直角3角形を（p,q,2）と表記します．

■双曲幾何平面の正則タイル張り
ポアンカレ円盤の双曲幾何平面でも，双曲正p多角形で{p,q}のように張りつめられているとき，１つのタイルを2p個の直角3角形に分割できます．この直角3角形を鏡室とする万華鏡は“コクセターの万華鏡”と名付けます．
双曲面の｛6,4｝正則分割の場合の直角3角形(6,4,2)(赤い3角形）を図（左）に，対応する“コクセターの万華鏡”の映像を図（右）に示します．

■双曲面{6,4}分割の場合の“コクセターの万華鏡”を作る
双極面{6,4}分割の映像を，3角形の万華鏡で作るには，双曲面直角3角形(6,4,2)を用います．この3角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧鏡よりなります．この円弧鏡は，数学的には反転円として定義できるのですが，現実の円柱鏡の反射には収差があるので，数学の定義のように鮮明な万華鏡映像を作るのは困難です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.11.10］ No.088
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日は楕円幾何の世界である球表面のタイル張りを万華鏡で見て見ましょう．
シュレフリーの記号{p,q}は正p多角形が頂点でq個集まってできる正多面体を表します．
例えば，｛5,3｝は正5角形が各頂点で3つ集まっている正多面体（正12面体）を表します．
球面{p,q}多面体の面は球面正p-多角形です．
１つの球面正p-多角形タイルを2p個の球面3角形（p,q,2）に分割しましょう．
図は球面｛5,3｝多面体の例で，12個の面はすべて球面正5角形（黄色のタイル）から成ります．
１つの面は10個の球面三角形（5,3,2）（赤色タイル）に分割できます．
（注）3角形(p,q,2)とは，内角が（π/p，π/q，π/2）の直角3角形のことです．
球面幾何の世界では，直線は大円．球面正p-角形や球面3角形の辺はすべてこの世界の直線ですから，
大円です．球面三角形(5,3,2)の内角は，(π/5，π/3．π/2)で，内角の和は，(31/30)π>π とπを越しますが
楕円幾何の世界だからです(ユークリッド幾何の世界では3角形の内角の和はπ)．
ユークリッド平面では{5,3}は隙間ができタイル張りにならないが，
球表面ではタイル張りができ，これをユークリッド幾何の世界で見ると立体になります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/51/17096451/img_1_m?1447081624
球面3角形(p,q,2)の各辺を中心から見込む平面を鏡として，３枚鏡（△OHK，△OKA，△OAH）の万華鏡を作り，
球面3角形(p,q,2)の外側から覗きこむと，球面{ｐ,q}多面体が見えます．
以下に｛5,3｝多面体用の万華鏡の作り方を掲載します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568613/51/17096451/img_3_m?1447081624
（注）青色の3枚の3角形鏡（ただし，頂点Oの周りは半径2.5の円弧を切り取る）を組み立てる．図中の数字は長さ．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.11.03］ No.087
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
秋が深まりました．皆様お変わりありませんか．一寸，万華鏡の数学の話をしましょう．
万華鏡映像の美しさが我々の心をとらえるのは，空間の完全な対称性だけではありません．
時間の流れとともに映し出される「千変万化だが一度きり」の映像に，
生命を感じるからでもありましょう．
ワンドの中を降り行くすべてのガラス屑の運命は，運動方程式ですべて定まっているとはいえ，
ときおりカオスの起こる期待で目が離せません．
万華鏡は，対称性（秩序）とカオス（乱れ）の混在が魅力なのです．そして，
合わせ鏡が生みだす完全な秩序は，無限に繰り返される“結晶世界”に入り込んだようでもあります．
万華鏡　“カレイドスコープ”は，物理学者ブリュースター卿の特許（1817）［発明は1816年］
が起源です．特許には，2枚の合わせ鏡の交差角θ°が，360°を
偶数で割り切る角度にするということが書かれています．
今日はこの数学についてさらに考えて見ましょう．
■平面群と市松模様
本来の市松模様はチェス盤のように正方格子が交互に塗り分けられたものですが，
３角格子などの場合でも交互に塗り分けられていれば市松模様と呼ぶことにします．
Fig1 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_7_m?1446474652　
これらは皆，市松模様と呼ぶことになります．
万華鏡は鏡（位数２の対称操作）の組み合わせだけで作られます．
1回鏡で反射すると鏡像の向きは裏返っています．しかし，2回反射すると
鏡像の鏡像になり始めの向きと同じになります．
市松模様の黒-白は，物体のある鏡室タイル（グレイ色）と同じ向き＝"正置像”を黒；
“裏返像”を白に塗り分けています．

■正方形の鏡室の万華鏡がつくる市松模様
Fig2 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_8_m?1446474652
図(1）万華鏡の鏡室タイルをグレイの正方形とします．
鏡室のフチの赤線は鏡（4枚）です．
図(2)１回の反射で４個のタイルの裏返像(黄色)が生まれます．
図(3)２回の反射で，その外側に8個のタイルの正置像（緑色）が生まれます．
図(4)3回の反射で，その外側に12個のタイルの裏返像（黄色）が生まれます．
このようにして，鏡室タイルはその鏡像を全平面に広げて行き，
平面を市松模様で塗りつぶします．

■3角形の鏡室の万華鏡は市松模様をつくるか？
Fig3 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_9_m?1446474652
１．左図の鏡室3角形ABCは90°30°60°の3角形です．
各頂点で3角形が偶数個集まっています．３つの頂点のまわりはどれも市松模様ができており，
全平面が市松模様であることがわかります．
２．右図の鏡室3角形ABCは45°60°75°の3角形で，
AおよびBのまわりは3角形が偶数個集まりますが，Cのまわりでは偶数個あつまりません．
そのため，全平面では市松模様が出来ないことがわかります．
３．鏡映操作の集合が平面群を作っている場合は，全平面が市松模様になりますが，
逆に，市松模様が何処かで乱れているなら，その鏡の組み合わせは平面群が作れない場合です．
そのような万華鏡のもう一つの例を（Fig4)に示します．
Fig4　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_2_m?1446474652

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.10.26］ No.086
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ユークリッド幾何学と非ユークリッド幾何学

色々な幾何空間があります．
大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．
非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．
我々の常識が通用するユークリッド幾何の世界では，
“直線l外の1点をA通り，その直線に平行な直線“は，唯一本だけ引けます．

平行線が1本も引けない世界や，無数に引ける世界とはどんな世界でしょうか？

これら3種類の幾何空間を，平面を例にとり比較します．

（１）ユークリッド幾何平面　　（２）楕円幾何平面　（３）双極幾何平面
例⇒　我々の常識の世界　　　　　球の表面　　　　　　ポアンカレの円盤モデル

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/81/17061581/img_0?1445817357

それぞれの空間で，“直線の定義を変えれば”，
そのようなことが起こる世界があることを納得できるでしょう．
2点間を結ぶ直線とは，その世界で2点間の距離を最小とするものです．

（１）常識の通用するユークリッド幾何平面
2点間の距離が最少なのは我々の知っている直線です．
（２）球の表面は楕円幾何平面の例
球表面の世界では，大円（球中心を通る平面で切った球の表面）が直線です．
地球自体は3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面です．
地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，
これは地表の大円上の線分のことです．
異なる２つの大円は必ず2点（直径の両端）で交わるので，
直線外の1点を通る平行線はありません．また，地球儀の
緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面の例（ポアンカレ円盤モデル）
双曲幾何の世界のポアンカレ円盤モデルでは，
円盤のフチに直交する円弧を，直線と定義します．
この世界では，ある直線に対する直線外の1点を通る平行線は無数に引けます．
円盤モデルの世界では，円盤のフチに近づくほど見かけの距離はどんどん縮むので，
フチの近傍は実際は無限の距離があり，永久に地平線に到達できません．
確かにこのような円弧が最短距離です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.10.20］ No.085
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■平行４辺形や平行６辺形は，平面を敷き詰めることができます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/41/17047041/img_3_m?1445036597
平行6辺形とはこんな形です．
向かい合った辺（同じ色）を繋ぎ合わせて，平面を埋められます．
このような形のタイルを土台に向い合った辺を同じように変形し図案のモチーフにすると，
エッシャーのような繰り返す絵が作れます．
私はハロウィーン魔女を作ろうとしましたが未完成です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/41/17047041/img_4_m?1445042284
皆様完成させてください．
■任意の４辺形は，180°回転したものと組み合わせると平行６辺形になります．
下図の4種の組み合わせが可能ですが，どの平行６辺形のタイルを用いても
同じ敷き詰めになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/41/17047041/img_1_m?1445036597
■任意の3角形は，180°回転したものと組み合わせると
平行4辺形や平行6辺形になるので，平面を敷き詰めることができます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/41/17047041/img_2_m?1445036597
Q.　平行8辺形以上は平面を敷き詰められないのは何故でしょうか

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.10.13］ No.084
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■空間のデジタル化
最近の交通信号は，発光ダイオードのドットが円盤内に配置されています．
本来，円盤内は連続平面ですが，ドットの配置で表現される円盤は，
離散化（あるいはデジタル化）されています．
デジタル化された世界では，ドットを１つ２つと数えることができます．
ドットを十分小さくすれば，ドットはいくらでもこの世界に入ります．
このような世界を，“可算無限”の世界といいます．一方，連続平面は，
点を数えることすらできない“非可算無限”の世界です．
（例）整数や有理数（分数で書ける数）は可算無限個，
　　無理数（分数では書けない数）は非可算無限個です
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/44/17032344/img_0_m?1444646310
■無限に続く繰り返し
　周期的な空間－結晶世界
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/44/17032344/img_1_m?1444646310

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/44/17032344/img_2_m?1444646310
黒と白のタイルでできる市松模様が無限に広がっています．
もし，白いタイルのどれか一つの上にいたとしても，
市松模様の世界は無限に続いているのですから，
そこがいつも世界の真ん中に思えます．
つまり，どの白いタイルもすべて同価です．

この市松模様の世界の周期がわかりますか？　図には，
白いタイルから，隣の同価な白いタイルへの移動を示すベクトル（矢印）
が記入されています．
2次元の世界ですから2つの独立なベクトル a, bが基本周期になります．
白いタイルを基本周期a, bを繰り返して平行移動することを並進といいます．
（注）na+mbは，a方向にn個，b方向にm個の移動（並進）の意味です．
na+mb（整数n,m)の点（格子点）はすべて同価な点で，
これらの集合を格子といいます．
格子点の集合（格子，無限集合）は加法で閉じており
群という代数系になります（これを並進群といいます）．

上図の2つの市松模様は全く同じものですが，見渡す方向でずいぶん景色が違います．
このような性質を異方性と言います．
格子点に配置して，重ならず隙が出来ずに平面を張りつめるとき単位となる
ブロックタイル（単位胞）の形はどのようなものでしょうか？
これには色々なものを採用できますが，例えば，横並びの黒白ペアのタイル，
あるいは，a, bで囲まれた平行４辺形などがあります（上図の右側に図示）．
その面積はどちらも同じです．
無限に続く周期的な平面は，一つのブロックタイル（単位胞）で平面を張りつめる
こと（デジタル化）ができ，扱うのが簡単です．これに比べて，
周期的でない平面はアナログ平面で簡単化できません．つまり
一様な（平面のどの場所も同価であるような）デジタル化ができません．
デジタル化された信号のような円盤内も，一様でもなければ周期的でもありません．
周期的なデジタル化された空間は“結晶空間”と呼ばれ，
その性質は“格子”で抽象的に表現されます．

■繰り返し模様の観賞法
今年の数学月間懇話会(7/22)で，私は以下の話をしました：

周期的な空間(繰り返し模様)の対称性は有限図形の対称性にくらべて，
なじみのない人が多いようです．
これは，教科書で扱う対称性が有限図形だけであることによります．
しかし，周期的空間＝“結晶空間”は，最も基本的なデジタル化された空間で重要です．

デジタル画像や視細胞の配列した網膜など，自然界のほとんどが
デジタル化された平面です．特に，無限に広がる平面を，
一様で周期的にデジタル化した－“結晶空間”－は特に重要です．
結晶の内部構造は，単位となる平行6面体（単位胞）が，
空間を隙間なく埋め尽くしています．
このような例として，平面上の繰り返し模様の数学に親しみましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/68/17037468/img_0_m?1444646276
数学の言葉でいうと，繰り返し模様の対称性（空間群）と
有限図形（単位胞）の対称性（点群）との関係は，
「繰り返しの規則（並進群）を核（法）として，空間群は点群に準同型」
ということになります．あるいは，
「並進群を点群で拡大して空間群が得られる」ということもできます．
準同型という概念の心は，集合のもつ特徴を見つけるのに，
集合の要素の持つある特徴を同値と見做せれば（小異に目をつぶれば），
別の特徴が顕著に見えてくるという事．
日常生活の色々な場面でこの考え方が使えます．
「小異を捨てて大同に就く」といいますが，
「小異を同値と見做すなら，別の違いが見えてくる」
そして，「別の違いがない場合は，大同に就ける」という事でしょう．

平面のデジタル化の一つに，１種類の正多角形で平面を分割すること（正則分割）
がありますが，非ユークリッド平面の正則分割タイル張りに関しても言及しました．

■空間のデジタル化
最近の交通信号は，発光ダイオードのドットが円盤内に配置されています．
本来，円盤内は連続平面ですが，ドットの配置で表現される円盤は，
離散化（あるいはデジタル化）されています．
デジタル化された世界では，ドットを１つ２つと数えることができます．
ドットを十分小さくすれば，ドットはいくらでもこの世界に入ります．
このような世界を，“可算無限”の世界といいます．一方，連続平面は，
点を数えることすらできない“非可算無限”の世界です．
（例）整数や有理数（分数で書ける数）は可算無限個，
　　無理数（分数では書けない数）は非可算無限個です

■無限に続く繰り返し
　周期的な空間－結晶世界

黒と白のタイルでできる市松模様が無限に広がっています．
もし，白いタイルのどれか一つの上にいたとしても，
市松模様の世界は無限に続いているのですから，
そこがいつも世界の真ん中に思えます．
つまり，どの白いタイルもすべて同価です．

この市松模様の世界の周期がわかりますか？　図には，
白いタイルから，隣の同価な白いタイルへの移動を示すベクトル（矢印）
が記入されています．
2次元の世界ですから2つの独立なベクトル a, bが基本周期になります．
白いタイルを基本周期a, bを繰り返して平行移動することを並進といいます．
（注）na+mbは，a方向にn個，b方向にm個の移動（並進）の意味です．
na+mb（整数n,m)の点（格子点）はすべて同価な点で，
これらの集合を格子といいます．
格子点の集合（格子，無限集合）は加法で閉じており
群という代数系になります（これを並進群といいます）．

上図の2つの市松模様は全く同じものですが，見渡す方向でずいぶん景色が違います．
このような性質を異方性と言います．
格子点に配置して，重ならず隙が出来ずに平面を張りつめるとき単位となる
ブロックタイル（単位胞）の形はどのようなものでしょうか？
これには色々なものを採用できますが，例えば，横並びの黒白ペアのタイル，
あるいは，a, bで囲まれた平行４辺形などがあります（上図の右側に図示）．
その面積はどちらも同じです．
無限に続く周期的な平面は，一つのブロックタイル（単位胞）で平面を張りつめる
こと（デジタル化）ができ，扱うのが簡単です．これに比べて，
周期的でない平面はアナログ平面で簡単化できません．つまり
一様な（平面のどの場所も同価であるような）デジタル化ができません．
デジタル化された信号のような円盤内も，一様でもなければ周期的でもありません．
周期的なデジタル化された空間は“結晶空間”と呼ばれ，
その性質は“格子”で抽象的に表現されます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.10.06］ No.083
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
メルマガ09月29日号は休刊しました．ご了承ください．
実は，28日の朝6時50分に母は息を引き取りました．
救急車で入院した時は寒い冬で，病院の庭の梅の蕾も硬くこの梅が咲くころには退院しているだろうと
漠然と思ったものです．その梅が咲き，桜が咲き，つつじが咲き，暑い夏を越し，
帰るときには金木犀の香りが満ちていました．259日の病院生活を，ベットの上だけで過ごしました．
百歳の誕生日まで病気知らずで，寝込んだことは一度もありません．
いつも「大丈夫よ」「有難う」と言っていた母でした．
でも今回は，「いつ帰れるのか．さあ帰ろうか」と言ったことが一度ありました．
しかし，その後すぐ点滴づけになり帰る場所がなくなりました．
それでも負けずにこの長期間を頑張りぬきました．
最期の夜も最後の最後まで頑張りましたが朝に遂に力尽きました．スーパームーンの日でした．

葬儀は4,5日に，幡ヶ谷の代々幡斎場で，香典供物は辞退して母を知るご近所と身近な親戚で済ませました．
幡ヶ谷は，母と父が新所帯を持ち，つかの間の母の楽しい時期であった思い出の地です．
敗戦まじか，私はその家で生まれました．父がフィリピン・ボルネオの戦地にいるときです．
母は一人で，赤ん坊の私を押し入れで布団を積み上げ高射砲の破片から守ったのです．
幡ヶ谷の家は空襲で皆焼けてしまいました．父はジャングルでトカゲを食べたりマラリアになったり
破片で背中を負傷したり捕虜で働かされたりしましたが，終戦後3年たってから無事帰国できました．
母と私は父と再会し，暮らし始めた家は幡ヶ谷から1kmほど離れた所です．
ここには現在まで70年近く住んでおります．葬儀には母を知るご近所の方々が参列されましたし，
母方と父方の従兄弟たちも久しぶりに会しましたので，楽しい一時になりました．
ご報告とお詫びまで．次号から数学月間の話題にもどります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.09.22］ No.082
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
戦争法案が多くの世論を無視して強引に可決してしまいました．
本来，違憲である法案が国会に出されること自体あり得ないことですし，
国会の議論でもまともな答弁がなされていないことは誰の目にも明らかです．
政府の宣伝機関になったNHK始め大手メディアの罪はたいへんに重い．
さて，翁長沖縄県知事の国連人権理事会で演説に期待しよう．大手メディアの世論操作に負けてはならない．
イギリスで投獄を覚悟してインドの独立を主張したガンジーの姿が重なって見えます．
ーーーーーーーーーーーーーーーーーーーーーーーーーーー

戦時中の“科学朝日（1944年3月号）”に，「特集・戦争と数学」があります．
この特集号には，多くの著名な数学者が寄稿しており大変興味深い．
その中で，巻頭の弥永昌吉先生の論説が群を抜いており，言論も不自由であったろう戦時下に，
実に立派な意見を展開しておられます．
さらに，数学月間の考え方と同じ所も見受けられ我が意を得たりの感があります．
まず，弥永論説（対話形式）の概略を紹介します．

1年くらい前から始まった戦時下の米国の数学動員（米数学協会の記事の記憶）が紹介されます．
遅ればせながら日本でもこのような動きが始まっています．
米国の数学動員
委員長（モース）の下に６つの委員会がある
1.工業技術，2.航空力学，3.弾道学（ノイマン），4.確率統計，5.計算法，6.暗号解読
１は数学と工業の連携強化，2,3は微分方程式，高射砲の照準や電波兵器の数学，４は大量生産管理，5は計算機．
ーーーー以下抜粋－－－－－
■数学は魔術ではなく，合理的なものの中でも最も合理的なものですから，使い方も合理的でなくてはなりません．
この際，数学者の側で，数学を使えば何も彼も容易にできるというようなことを言いふらしたり，
まだ十分の研究を積まないのに現場の人たちのやり方が悪いと言ったりするようなことは一番いけないと思います．
ーーーーーーー
■大和魂が第一でも，それだけでは戦争に勝てないことがだんだんわかってきて，科学研究の動員が必要になった．
第一次大戦では「化学」，第二次大戦では「物理」→「数学」が必要だ．
米の他，ソ連，独，伊でも同様な数学動員の状況がある．
ソ連は，コルモゴロフ（確率の基礎）飛行機の乱流，ヴィノグラドフ（整数論）などがスターリン科学賞を受賞した．
ドイツからは，開所したばかりの米プリンストン研究所などに科学者が流出しており，
米国に最も豊富な人材が集まっている．
ーーーーーーー
■学問としてお留守にならず，その品位を下げぬような動員の仕方をすることが，戦争に勝つ道であると信じる．
日本では，それぞれの分野が功を急いだせいかも知れませんが，
学問が専門化しすぎて，それぞれ孤立化する危険がある．
この機会に横の結びつきが強化されるのは良いことだ．お互いに学問の理解を深め，
基礎理論の整備進展，新理論の展開という方向へ導かれれば日本の学問全体にとってもこんな有り難いことはない．
ーーーーー
■問題解決のためにも，数学では個々の小さな問題をそれぞれに突っつくよりも，
根本的なところまで遡って考えた方が，大きな成功を収めることがよくあるのです．
この戦争のために，目先のことばかりを考えてよいのでしょうか．
長期建設戦」ともなれば，文化が直接ものを言うことがますます多くなりましょう．
世界中のだれが見ても頭を下げるような高い立派な文化を我々が戦いつつ築きあげて行くことがぜひとも必要です．
この頃，この点について偏執な，浅慮短見の説をなす人があるのを慨いて，
渡辺慧さんはそれを「文化的敗北主義」と言っている．

戦争法案を多くの世論を無視して強引に可決してしまいました．
本来，違憲である法案が国会に出されること自体あり得ないことですし，
国会の議論でもまともな答弁がなされていないことは誰の目にも明らかです．
政府の宣伝機関になったNHK始め大手メディアの罪はたいへんに重い．
さて，翁長沖縄県知事の国連人権理事会で演説に期待しよう．
大手メディアの世論操作に負けてはならない．
イギリスで投獄を覚悟してインドの独立を主張したガンジーの姿が重なって見えます．
ーーーーーーーーーーーーーーーーーーーーーーーーーーー
■戦争と数学
戦時中の“科学朝日（1944年3月号）”に，「特集・戦争と数学」があります．
この特集号には，多くの著名な数学者が寄稿しており大変興味深い．その中で，巻頭の弥永昌吉先生の論説が群を抜いており，言論も不自由であったろう戦時下に，実に立派な意見を展開しておられます．さらに，数学月間の考え方と同じ所も見受けられ我が意を得たりの感があります．まず，弥永論説（対話形式）の概略を紹介します．

1年くらい前（1943年）から始まった戦時下の米国の数学動員（米数学協会の記事の記憶）が紹介されます．遅ればせながら日本でもこのような動きが始まっています．
米国の数学動員
委員長（モース）の下に６つの委員会がある
1.工業技術，2.航空力学，3.弾道学（ノイマン*），4.確率統計，5.計算法，6.暗号解読
１は数学と工業の連携強化，2,3は微分方程式，高射砲の照準や電波兵器の数学，４は大量生産管理，5は計算機．
ーーーー以下弥永論説からの抜粋－－－－－
■数学は魔術ではなく，合理的なものの中でも最も合理的なものですから，使い方も合理的でなくてはなりません．この際，数学者の側で，数学を使えば何も彼も容易にできるというようなことを言いふらしたり，まだ十分の研究を積まないのに現場の人たちのやり方が悪いと言ったりするようなことは一番いけないと思います．
ーーーーーーー
■大和魂が第一でも，それだけでは戦争に勝てないことがだんだんわかってきて，科学研究の動員が必要になった．第一次大戦では「化学」，第二次大戦では「物理」→「数学」が必要だ．米の他，ソ連，独，伊でも同様な数学動員の状況がある．
ソ連は，コルモゴロフ（確率の基礎）飛行機の乱流，ヴィノグラドフ（整数論）などがスターリン科学賞を受賞した．ドイツからは，開所したばかりの米プリンストン研究所などに科学者が流出しており，米国に最も豊富な人材が集まっている．
ーーーーーーー
■学問としてお留守にならず，その品位を下げぬような動員の仕方をすることが，戦争に勝つ道であると信じる．
日本では，それぞれの分野が功を急いだせいかも知れませんが，学問が専門化しすぎて，それぞれ孤立化する危険がある．この機会に横の結びつきが強化されるのは良いことだ．お互いに学問の理解を深め，基礎理論の整備進展，新理論の展開という方向へ導かれれば日本の学問全体にとってもこんな有り難いことはない．
ーーーーー
■問題解決のためにも，数学では個々の小さな問題をそれぞれに突っつくよりも，根本的なところまで遡って考えた方が，大きな成功を収めることがよくあるのです．
この戦争のために，目先のことばかりを考えてよいのでしょうか．
長期建設戦」ともなれば，文化が直接ものを言うことがますます多くなりましょう．世界中のだれが見ても頭を下げるような高い立派な文化を我々が戦いつつ築きあげて行くことがぜひとも必要です．この頃，この点について偏執な，浅慮短見の説をなす人があるのを慨いて，渡辺慧**さんはそれを「文化的敗北主義」と言っている．

*ノイマンはゲームの理論で有名になった若手でした．ドイツから米プリンストン研究所に多くの科学者が流出しました．そのうちの一人です．
**理論物理学者

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.09.15］ No.081
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号では，周期律表113番目の元素発見の話をしました．
今回は，原子番号96番のアメリシウムの話です．
原子番号92のU(ウラン)より大きい原子番号の元素(超ウラン元素)は天然には存在せず，
原子炉や原爆で人工的に生成された放射性の核種です．
これらの元素が我々の環境で検出されたなら，
原爆実験や原発事故や使用済核燃料の再処理などで排出されたものです．
これらの元素は大変不安定で，α線やβ線やγ線や中性子を放出して他の元素に姿を変えます．
超ウラン元素は，93番Np（ネプツニウム），94番Pu（プルトニウム），
95番Cm（キュリウム），96番Am（アメリシウム），の順で発見されました．
キュリウムやアメリシウムはマンハッタン計画（1944年）で発見されましたが，
発表されたのは1945年11月のことです．アメリシウムの中にも多くの核種がありますが，
質量数241のAm（アメリシウム）は，α線（5.4MeV），γ線（60keV）を放出して，
質量数237のNp（ネプツニウム）に変わります（半減期433年）．
　241Am　→　237Np　+α　+γ
さてアメリシウムはどのようにして生まれるのでしょうか．
稼働中の原子炉では，核燃料中の238Ｕは中性子を取り込み239Puに変わります．
生まれた239Puは，また中性子を取り込み241Puに変わり，これはβ線を出して241Amに変わります．
239Pu（2.41万年）+２n　→　241Pu（14.4年）→　241Am　+β
■
電気出力100万kWの軽水炉を２年間運転すると，使用済核燃料には１トン当たり，
アメリシウムが５g(放射能強度0.65×10^12Bq）含まれます．
奇妙に思えるでしょうが，原子炉から取り出した使用済核燃料の中で，
時間の経過とともにアメリシウム量が増えます．10年後に40g(放射能強度5.2×10^12Bq），
100年後には93g(放射能強度12×10^12Bq)という具合です．
使用済核燃料中には，核分裂生成物としてプルトニウムやアメリシウムを始め，
数百種類の放射性核種が生まれています．
使用済核燃料は，未使用の核燃料の1億倍もの放射能強度になり手に負えません．
だから原発を再稼働させてはいけないのです．
http://www.cnic.jp/knowledge/2611

原子力発電によって生み出される放射性物質は，「死の灰」あるいは「高レベル放射性廃棄物」と呼ばれます．
未使用燃料（1トン）　ーーーーー→　使用済燃料（1トン）
U-235(45kg)　　　　　　　　　　　　U-235(10kg)
U-238（955kg）　　　　　　　　　 　U-236（6kg)
　　　　　　　　　　　　　　　 核分裂生成物(46kg)
　　　　　　　　　　　　　　　 プルトニウム（10kg）
　　　　　　　　　　　　　　　 その他超ウラン核種（1kg）
　　　　　　　　　　　　　　　 U-234（0.2kg）
　　　　　　　　　　　　　　　U-238（926kg）
http://www5a.biglobe.ne.jp/~genkoku/kohza-002.htm

■アメリシウムの性質
Amは空気中で表面が酸化されAm2O3となり，また塩酸に容易に溶けます．
アメリシウムは，α線とγ線を放出するが，人体影響では，α線による内部被曝が怖い．
アメリシウムからのγ線のエネルギーは60keVでγ線としては低エネルギーの部類です．
ただし，人体影響では細胞に吸収されるエネルギーが細胞にダメージを与えるので，
低エネルギーの方が吸収されやすいということもあり，安全というわけではありません．

■核燃料中のアメリシウム-241
プルトニウムを核燃料として用いる立場からは，プルトニウム-241の核分裂に必要な遅い中性子を，
アメリシウム-241が無駄食いするので，核燃料中の阻害物です．
再処理によって分離したプルトニウムを核燃料として用いる場合には，
アメリシウム-241の量が増加しないうちに，核燃料として用いる必要があります．
http://www.cnic.jp/knowledge/2611

■川内原発
九州電力川内原発１号機が営業運転に移行し，川内２号機も炉心への燃料装荷が
11日から始まり13日朝に完了しました．10月中旬の再稼働を目指しています．
川内原発の1号機，2号機とも，軽水減速・加圧水型PWRで，出力89万ｋWで，
低濃縮（U-235が4～5%）二酸化ウラン（72トン/年）を使用します．
http://www.kyuden.co.jp/sendai_outline_index.html

ウラン燃料は，ペレットの型（直径8mm×10mm）で，ペレットを350個程度積み上げて棒状にした
燃料棒（長さ4m）を17×17あるいは15×15本まとめて燃料集合体（20cm角程度）を作る．
ただし，PWRの場合には制御棒クラスタや炉内計測用の案内管もあるので，集合体に燃料棒の入らない位置がある．
川内原発1号機，2号機ともにこのような燃料集合体が157体装荷された．
（注）沸騰水型BWRの原発の燃料は，燃料棒を9X9にまとめ燃料集合体として原子炉に装荷する．
制御棒の入る位置は燃料集合体の間になる．
http://www.nfi.co.jp/product/prod02.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.09.08］ No.080
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ウラン（原子番号92）より重い元素は，天然には無く人工的な手段でのみ得られる．
ウンウントリウムは原子番号113の元素だが，まだ認定されていない（元素の名称も仮のもの）．
理研・森田らは，線形加速器で亜鉛原子核をビスマス原子核に打ち込んで生じた不安定な元素が，
α崩壊する過程でウンウントリウムが存在することを発見した．2004年7月のことだ．
ウンウントリウムは，0.667msでα崩壊し次の元素へ姿を変える．次々とα崩壊が続き，
結局6回姿を変え135秒で101Md（メンデレビウム）に変わる．
http://www.riken.jp/pr/press/2012/20120927/
このようなウンウントリウムの詳細な崩壊経路をきちんと調べ上げた(2012年までかかっている）ので，
森田ら（理研）に，近々この元素の命名権が与えられるのではないかと思う．
しかしながら，2004年2月に，ロシアと米国のチームは、
カルシウムとアメリシウムの核融合で現れた元素115のα崩壊過程で0.48秒間113番元素を観測したと発表しており，
最初の発見者であると主張している．
https://www.youtube.com/watch?v=giuZaoxeKtY&feature=share

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.09.01］ No.079
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
電波干渉計の観測データから，ブラックホールの像を求める話題を
メルマガNo.070_統計数理研オープンハウス　で取り上げたことがある．
ここで用いられるスパースモデリングという手法はとても興味深いので，
NHKのサイエンスzero再放送（2015年8月23日）の
「情報科学の名探偵！魔法の数式 スパースモデリング」を楽しみに視聴した．
この題名は，ばかにおどろおどろしい．
「魔法の数式」とか実に持ってまわった言い方で嫌な予感がしたが，
案の定，題名も題名だが内容にも失望した．
番組中で，E(x)＝||y-Ax||^2＋λΣ|x_i|という式が何度も瞬間的に表示されるのだが，
この式をまともに説明する気は全く無い．実に視聴者をバカにしたプログラムで腹が立った．
この式自体は，測定した信号から画像をどのように推定するかの計算式で，
この式がどのようなことをするのか，素人にわかるように説明するのは
そんなに手間でもないし高度なことでもない．決して魔法の数式でもない．
それにもかかわらず魔法の呪文（ブラックボックス）のよう何度も表示される．
数学を魔法のように扱うのは，何の意味もない．
サイエンスカッフェなどで良くあることだが，結果ばかり紹介し手法の説明がない．
どのような考え方で得た結果なのか手法が納得できなければ，その結果を受け入れることはできない．
詳細な数式を説明されても困るが，素人相手だからこそ式の心を言葉で説明すべきであろう．
そのような努力を全くしない専門家は多いのだが，
特に，今回のサイエンスzeroの番組作りは踏み込みが全く足りない．大いに不満である．
ただし，今回の番組で良かった点にも触れておこう．
スパースモデリングがいろいろな分野で応用されていることが紹介され，
特にMRIの測定では，ほぼ同じ解像度の画像が1/3の測定時間で得られる例は興味深かった．

腹立ちついでに脱線し，物分かりの良すぎる国民に苦言を呈しておこう．
なぜ原発が必要なのか，戦争法案が必要なのか全く理解に苦しむ．
物分かりの良いふりは止めてわからないことはわからないと正直に言おう．
子供電話相談室を聞いていると，一寸違うんじゃないかな，本質の説明ではないなと思うことが多い．
「わかりません」「なぜですか」とさらに訊ねろとイライラしながら聞いているが，
子供は「なるほど」とか「判りました」とか答えている．どうして納得したふりをするのか
私はこういう予定調和は大嫌いだ．このような同調の習慣がいじめの温床であると思う．

■さて，サイエンスzeroでは説明されなかったが，私の理解している範囲で以下の数式を解説しておこう．
E(x)＝||y-Ax||^2＋λΣ|x_i|
yは観測データでxは得られた画像．評価関数E(x)が最小となるように画像が推定されるのだ．
右辺の第1項は最小二乗法であり，第2項は得られた画像のノルムである．
第1項の最小二乗法は元画像とフィルタを通した復元画像の誤差を最小にする画像処理でもよく使われる．
x線を観測しブラックホールの像を得る例では，AはFourier変換で，
像xのFourier変換が観測値yになるべきだから，両者の2乗誤差が最小になるところで落ち着く．
さて式全体の形をみれば，ラグランジュの未定乗数法を思い浮かべる方もいるだろう．
そうです．得られた像のノルムΣ|x_i|を最小にする条件下で，
最小二乗法を満たす解xを求めようとしている式にほかなりません．
スパースモデリングは新しい分野で，私は全く素人ですが，
像xは至る所ゼロの疎（スパース）行列だということから，そう呼ばれるのでしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.08.25］ No.078
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■8月22日にとっとりサイエンスワールドim鳥取が開催されました．今年で9年目です．
市民の参加者は700人ほどで，万華鏡のワークショップ参加者は110人弱，
先生方および高校生2名のボランテアを得て無事実施できました．
全体で高校生ボランティア50名，特に今回は中学生のボランティア10名が加わりました．
写真などは　
http://blogs.yahoo.co.jp/tanidr/16933900.html　をご覧ください．
このブログには，鳥取城址，久松山，仁風閣　の記事も掲載しました．

鳥取市歴史博物館，やまびこ館で，70年目の夏「昭和の戦争と鳥取」特別展がありました．
このテーマに関しての私の印象は，以下のブログにあります．どうぞお読みください．
http://blogs.yahoo.co.jp/tanidr/16935089.html

■さて，サイエンスワールドのワークショップの一つに
立体模型，小梁修（OSA工房）があります．
その中の問題の一つ「黄金三角形」の紹介をします．

正五角形の中を図のように分割して作った3種類の三角形
（これらはどれも2等辺三角形ですが何故でしょう）
の面積に関して，以下の関係があります．
（水色の三角形）＋（黄緑の三角形）＝（オレンジの三角形）
これを証明してください．図は以下にあります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/82/16936782/img_0_m?1440421136

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.08.18］ No.077
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆様，厳しい暑さの日が続きました．お元気でしょうか．私も関東で連日39℃を更新している日に
関東で一番熱い地域に黒服を着て行っていました．暑い暑い．

■地球温暖化のウソ
伊藤公紀(横国大教授)のIWJインタビューが以下のサイトにあります．
http://iwj.co.jp/wj/open/archives/256431
詳しくは，同氏らの「地球温暖化論のウソとワナ」KKベストセラーズ（2008）などをお読み下さい．
複雑系である気候決定の仕組みには，多くの要因が関与しており，現状の気候モデルではまだ説明できていない．
これらの要因には，人為的なものと自然的なものがあるが，人為的なもののうち温室効果ガスのCO2の増加
によるものだけが強調されている．
現実に起こっている現象は，グローバルな（地球全体としての）温暖化ではなく，
温暖化の地域と寒冷化の地域の両方が生じており，温室効果ガスCO2の増加で説明できるような単調なものではない．
種々の自然的な要因が気候の大勢を決めていることが近年の研究により明らかになってきた．
それは太陽風が影響を与えている北極海水温の振動や，海洋での熱移動などである．
海洋のコンベアベルトモデルも単純なものではなく，海洋での垂直熱移動は大きな関与をしているし，
大気の大循環のゆらぎもある．これらの影響が大きいことがわかってきたのだが，
現実を説明できるシミュレーションのできるモデリングにはほど遠いこともあり，
IPCCの報告書は，いまだに温室効果一辺倒に偏向したものになっている．

地球は閉じた系ではなく，エネルギーの出入りがある開放系なので，理論的に取り扱うのはとても難しい．
その上，都市化や大規模工事や砂漠化により気候が変わるのを実感し，
温室効果も現象としては真実（温室効果ガスはCO2だけではないH2Oもあるが）なので，
CO2排出削減ですべて解決するがごとく説得され，政策やビジネスに利用されている．
もちろん人為的な要因排除は我々の責任ですべきではある．
しかし，この問題は人間には手の下せない自然的な要因が大勢を決めているので，
CO2排出量削減をしても解決はしない．地球温暖化を原発推進の免罪符にするのは誤りである．
原発はCO2を出さないので温室効果を低減できるという論理は，
原発で生じる熱の大半が冷却水を介して海水に捨てられ海水を直接熱汚染していることを見れば
破綻していることがわかる．

■参考ー温室効果について
私は地学を教えていた（37年前のこと）ことがあるのだが，その頃は，温室効果と石炭消費量と温暖化の話をしていた．
地球の兄弟星の金星（400℃を越える）は，限度を超えたCO2の増加と気温上昇の正のフィードバックが暴走した結果
H2Oがなくなり，現在の金星大気の98%はCO2である．H2Oがなくなる前の金星の原始大気のCO2は多くて一割と推定されている．
現在の地球の大気のCO2濃度はずっと小さいが，ハワイのマウナロア山腹で，継続観測のデータがあり，
320ppm（1960年）から370ppm（2000年）と増加しているのは事実だ．
しかし，CO2増加による気温の上昇は，せいぜい２℃程度と計算される．
地球外から到来する可視光が地表を温め，地表が宇宙に放射される赤外線を温室効果ガスが吸収するので
地球が保温される．仕組みがシンプルで見積もり易いのだが，これだけで現実を説明しようとするのは無理がある．

■地球温暖化のデータ解析は信頼できるか？
・採用したデータ自体の信頼性
　　経年のデータの測定条件が一定でない．恣意的なデータ採用が行なわれた．
・統計学の正しい運用
　　主成分分析に誤りがあったらしい．
・シミュレーションの信頼度
　　シミュレーションはパラメータが３つもあれば，どのような結果にも合わせられるので，
　　モデリングの理論的根拠が大切である．
・相関関係よりの因果関係を問う

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.08.11］ No.076
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
とっとりサイエンスワールド2015が始まりました．
鳥取県と鳥取県数学教育会が主催です．8月2日が米子，コンベンションセンター，
8月９日が倉吉，未来中心，8月22日が鳥取，とりぎん文化会館で実施の予定です．
とっとりサイエンスワールドの開催時間は，各会場とも10:00～16:00です．
小さい子から大人まで，新しい人から顔なじみまで多くの市民の方々に定着した
楽しいイベントになっています．とっとりサイエンスワールドは今年で9年目です．
お近くの方，今年もお寄りください．
今年の万華鏡は次の3つを用意しています．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/29/16895829/img_0_m?1439204340

■米子
8月2日の米子，コンベンションセンターでは，全体で815人の入場者で盛況でした．
スタッフは，小・中・高の先生方および高校生ボランティアです．
万華鏡は，24人のクラスを5回実施し120人が自分の万華鏡を作りました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/29/16895829/img_1_m?1439204340
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/29/16895829/img_2_m?1439204340

■倉吉
8月9日のとっとりサイエンスワールドin倉吉は未来中心で実施され，
小，中，高の先生方90人＋高校生ボランティア40人のスタッフが働き，1024人の市民参加者がありました．
万華鏡のワークショップは110人分用意し，先生や高校生ボランティアの助けを得て
平均22人のクラスを5回順調にこなせました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/11/16907511/img_0_m?1439205601
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/11/16907511/img_1_m?1439205601

■鳥取
次の開催地は，8月22日，鳥取のとりぎん文化会館です．
こちらでは，万華鏡は160人分用意する予定です．

--------
万華鏡は合わせ鏡の仕組みから話を始めます．
平行な合わせ鏡により1つの物体が一直線上に無限に並んで見えます．
終わりというものがない．最後の映像があったとしてもこれが鏡に映れば
その先の映像が生まれてしまうからです．
次に，2枚の合わせ鏡が平行でなく角度θで傾いている場合を考えましょう．
生じる映像は一直線上でなく円周上に並びます．
そして，円周の向こう側ではきちんと重なって欲しい．
この条件から，360/θ＝偶数で割り切れる　という万華鏡の条件が生まれます．
今年の万華鏡は，鏡の交差角が作る3角形の1つの角度に　260/θ＝偶数　という条件が
わざと成り立たなくしたものです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.08.04］ No.075
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回は，数学らしくないと思うかもしれません．立体異性体の話です．
これは，右手と左手のように互いに鏡像となる分子の立体構造が関係しています．
この記事は，日刊ベリタに掲載(7/30）したものです．
暑さ厳しい夏です．健康に悪い油やマーガリンの取り過ぎに注意しましょう．

米食品医薬品局（ＦＤＡ）は１６日，食用油などに含まれ，肥満や心臓病との関連が指摘される
トランス脂肪酸を，２０１８年６月までに食品添加物から全廃すると発表しました．
日本でもトランス脂肪酸の低減をうたっている企業が出始めました．
トランス脂肪酸は，マーガリンやクッキーを焼くのに使うショートニングオイルなどに
含まれているそうです．トランス脂肪酸は悪玉コレステロールを増やすと言われています．
また，アトピーなどにも悪影響がありそうです．

脂肪酸のシス型とトランス型の分子構造について簡単にまとめておきます．
以下のサイトが参考になります：
http://www.maff.go.jp/j/syouan/seisaku/trans_fat/t_wakaru/
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%A9%E3%83%B3%E3%82%B9%E8%84%82%E8%82%AA%E9%85%B8

脂肪酸は，炭素原子が鎖状に並び，最後の炭素に=OとーOHが付いた分子です．
つまり，　　CーCーCー････ーCOOH　　　　＝は二重結合，－は一重結合　　
Hを省略せずに詳細に書くと
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16882908/img_0_m?1438241054

この例は，背骨となっている炭素原子の鎖は，すべて一重結合でできているので，
すべての結合手がふさがっており飽和脂肪酸と呼ばれます．
不飽和脂肪酸と言うのは，炭素原子の鎖の何ヶ所かに二重結合のあるものです．
二重結合でつながれた両側の炭素は回転できませんから（裏返しにできない）
シス型（左図）とトランス型（右図）の構造の区別ができます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16882908/img_1_m?1438241054

天然にある不飽和脂肪酸は，ほとんどシス型です（わずかな例外はあります）．
不飽和脂肪酸は酸化などで劣化しやすいし，大豆等の植物油の不飽和脂肪酸は常温で液体なので，
固体状にするため水素Hを付加してを飽和脂肪酸に変えることが工場で行われます．
このときトランス型の不飽和脂肪酸も生じ混ざるそうです．

(注)よく知られた不飽和脂肪酸の例
炭素の数18個で二重結合1個はオレイン酸，二重結合2個はリノール酸，
炭素の数22個で二重結合6個はドコサヘキサエン酸（DHA）．

■なぜシス型脂肪酸は安全な栄養で，トランス型脂肪酸は害があるのか
シス型，トランス型のような立体構造に差異があるものを“立体異性体”といいます．
炭素原子からは４本の結合手（二重結合ならそのうちの２つを使う）が出ていて，
それぞれの手に結合する原子が入れ替わると立体的に異なる構造になります．
右手と左手のように互いに鏡像である異性体も，この立体異性体の仲間です．例えば，
味の素はグルタミン酸ですが，立体異性体の右型と左型があり，
左型には旨みがあるが右型にはありません．これはおそらく，
人間のアミノ酸が左型であることに関係ありそうです．
不飽和脂肪酸の場合も，天然にあるものがほとんどシス型であることが
シス型が相性の良い理由と思われます．
サリドマイドでは，立体異性体の一方が副作用のない薬であるのに，他方には催奇性があった．
まるでジギルとハイドだが，このような大きな性質の違いがある理由はわからない．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.07.28］ No.074
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
暑い日が続きます．皆様いかがお過ごしでしょうか．
7月22日の数学月間懇話会（第11回）は無事に終了しました．参加の皆様ありがとうございました．
今回のゲスト講演者，細矢治夫先生は瑞宝中綬章を春に叙勲されました．
多角形百科（丸善）細矢・宮崎，および，七金三パズルの販売もありました．
今年も暑かったです．高校生5人を含む30人を超す参加があり熱心に質疑もなされました．
参加者の過半数が懇親会にも参加されました．
教室付近の構内は自動販売機がないし，飲み水に不便し私も熱中症気味．
でも今年は良い方です．一昨年の米沢興譲館の高校生がバスで団体参加したときのことが思い出されます．
バスから降りて炎天下グラウンドを歩かされて気の毒でした．
彼らはトイレも給水もそこそこ休む間もなく参加したのでした．
暑い最中に毎年こんな状況では，水くらい飲めるように改善したいものです．皆様ご要望などお寄せ下さい．
数学月間（7/22～8/22）はまだまだ続きます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/558900/79/16871179/img_0_m?1437962932
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/558900/79/16871179/img_1_m?1437962932
---------------------
■
私の講演内容 “繰り返し模様の観賞法” は，blog別項に掲載しています．
（そちらをご覧ください）http://blogs.yahoo.co.jp/tanidr/16859852.html
繰り返し模様の対称性は有限図形の対称性にくらべて，なじみのない人が多いようです．
教科書で取り上げているのは有限図形の話だけですからね．
しかし，周期的空間は，結晶などが実在する重要な世界です．
私は「空間を均一にデジタル化する」ということからスタートする教程を
構想しています．人間の視細胞を始め自然界のほとんどのものがデジタル空間です．
勉強会など機会があれば，繰り返し模様の数学の愛好者を増やしたいものです．

数学らしくいうと，繰り返し模様と有限図形との関係は
「並進群を核（法）として，空間群は点群に準同型」という事になります．
ここで，繰り返しの規則が「並進群」，繰り返し模様を表すのが「空間群」，
有限図形を表すのが「点群」です．「法として」というのは時計を想像してください．
12を法として無限に続く時間を表示しています．

準同型という概念の心は，集合のもつ特徴を見つける（整理する）のに，
集合の要素の持つある特徴を同じと見做せれば（その小異に目をつぶれば），
別の特徴が顕著に見えてくるという事．
日常生活の色々な場面でこの考え方が出てきます．
「小異を捨てて大同に就く」というは，この考え方に関係がありそうです．
つまり，「小異を同値と見做すなら，別の違いが見えてくる」
そして，「別の違いがない場合は，大同に就ける」という事でしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.07.21］ No.073
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
数学月間（＝数学と社会の架け橋）は今年で十年目になりました．
7月22日～8月22日を数学月間とすることは，2005年に日本数学協会が提唱しました．
この期間は，数学の土台となる2つの重要な定数
（円周率）π＝3.14･･･≒22/7と（自然対数の底）e＝2.71････≒22/8に因みます．
数学月間の会SGKは，月間初日の7月22日に「数学月間懇話会」を開催しています．

（注）今年の数学月間懇話会の案内は文末にあります．

我々は，この期間に各地で数学を楽しむイベントが盛んになるよう応援しています．
皆様の周りに数学イベントの情報などありましたらお知らせください．
SGK通信に掲載し連携イベントとして広報いたします．

漢字が読めないのは恥だが，数学なんて知らなくても構わないと思っていませんか．
数学は浮世離れしたものではありません．我々の社会は至る所で数学に支えられています．
数学月間は，“社会が数学を知るとともに，逆に数学が社会のニーズを知る”機会でもあります．
数学月間懇話会では，色々な分野で活躍する数学を鑑賞したり，
数学が生まれた現場に立ち戻りその生い立ちを観賞します．
完成された抽象数学は巨大山脈のようで，一般人には近寄りがたく感じるのものですが，
このように数学を見ることで共感できるのではないでしょうか．

我々の数学月間の手本となった米国の数学月間（スタート時は週間）の原点
“レーガン宣言（1986年）”を，以下に掲載します．今読んでも味わい深く格調高いものです．
ｰｰｰｰｰｰｰｰｰｰｰｰｰｰｰ
アメリカ合衆国大統領による宣言5461----
　｢国家的数学認識週間」1986年4月17日

宣言(National Mathematics Awareness Week)

　およそ5000年前、エジプトやメソポタミアで始まった数学的英知は、科学･通商･芸術発展の重要な要素である｡
ピタゴラスの定理からゲオルグ･カントールの集合論に至る迄、目覚ましい進歩を遂げ、
さらに、コンピュータ時代到来で、我々の発展するハイテク社会にとって、数学的知識と理論は、益々本質的になった。
　社会と経済の進歩にとって、数学が益々重要であるにも拘わらず、数学に関する学課が、
米国教育システムのすべての段階で低下する傾向にある｡
しかし、依然として、数学の応用が、医薬、コンビュータ･サイエンス、宇宙探究、ハイテク商業、
ビジネス、防衛や行政などの様々な分野で不可欠である｡
数学の研究と応用を奨励するために､すべてのアメリカ人が、日常生活において、
この科学の基礎分野の重要性を想起する事が肝要である｡
　上院の共同決議261で、国会が1986年4月14日から4月20日の週を、国家的な数学認識週間として制定し、
この行事に注目する宣言を出す事を大統領に要請した｡
　今日、アメリカ大統領、私、ロナルド･レーガンは、1986年4月14日から4月20日の週を
国家的数学認識週間とする事を、ここに宣言する｡私は、すべてのアメリカ人に対して、
合衆国における数学と数学的教育の重要性を実証する適切な行事や活動に参加する事を勧告する。
その証拠として、アメリカ合衆国の独立から210年の西暦1986年の４月17日、ここに署名する。
ロナルド･レーガン(Ronald Reagan)

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.07.14］ No.072
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ここでは，新国立競技場のキールアーチの不都合な力学についてのみ論評します．
その莫大な予算と環境破壊が不評な新国立競技場問題では，
発注前に設計図面の確定があったか，合意形成に必要な情報公開があったのか，
何処の誰が決定責任者なのか，全く見えないプロセスが最大の問題点ではあります．
工期がないと言ってはなし崩しに進めて行くやり口には，もう散々です．
以下の為末氏のブログの意見は全くの正論だと思います．
http://tamesue.jp/20150710/
-----------------

キール（竜骨）とは，船の船首から船底を通って船尾に至る鉄骨の背骨のことです．
新国立競技場の設計（ザハ案）には，巨大なキールアーチが2本使われています．
1本500億円かかると言われています．http://togetter.com/li/841805
この構造の問題点は，以下で評論されています．
http://ameblo.jp/mori-arch-econo/entry-11873045351.html

アーチの形は， http://blogs.yahoo.co.jp/tanidr/16586546.html で述べたことがあります．
アーチの曲線は，上下ひっくり返すと懸垂曲線と同じ形です．
中心から曲線に沿って測った距離をs，その点の曲線の接線の傾きをθとすると，
tanθ/s＝一定　の関係があることをそこで説明しました．
アーチの形は，曲線内部の全ての位置で圧縮応力でつりあっているのが特徴で，
大きな荷重を支えることができます．
しかし，あまりにも曲率の大きい平べったいアーチになるとポッキリ折れそうな気がしませんか．
圧縮応力よりもせん断応力の方が圧倒的に優勢になってしまいますからね．

アーチは最終的に，両側の接地点にすべての荷重がかかります．
370mのキールアーチ1本の重量は3万トンと言われていますので，
両端の各接地点はW=1.5万トンの重量に耐えねばなりません．
アーチの頂上の高さをどれくらいに抑えるかによりますが，
ザハ案のデザインのように低く抑えたい（大きな曲率にしたいなら）接地点の傾きθ0が小さくなりますから，
接地点での水平分力W･sinθ0は大きくなります（θ0＝30°なら，1.3万トン）．
アーチ橋の所で述べたように，アーチ橋の根元には大きな水平抗力が必要で，
両側が山に挟まれた峡谷などは，アーチ橋に適した立地条件です．しかし，
新国立競技場の場合は平地なので，アーチの根元の外側からガッチリ固定したい所ですが，
地下に地下鉄大江戸線があるのでできそうにありません．
そこでアーチ端の内側同志を鋼材で引っ張る（アーチを弓とすると弦のように引っ張る）ことにする．
この鋼材は両側から引っ張られますから，２.6万トン重ほどの大きな張力になります．
軟な鋼材では耐えられませんね．
ちなみに，コンクリートは圧縮には強いが引っ張りには弱い．
鉄筋コンクリートの鉄筋はコンクリートの引っ張り強度をカバーするために入れるのです．
アーチは圧縮力に強いコンクリートが使えますが，キールアーチでは使えません．
いろいろ補助手段を工夫するでしょうが，合理的な設計ではないので工夫のし甲斐がないでしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.07.07］ No.071
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
この所，雨の日が続いています．皆様如何お過ごしでしょうか．
7月22日は数学月間懇話会を開催しま．どうぞお出かけください．

昨年（2014年7月22日）の数学月間懇話会の話題の一つに，
中西達夫さんの「スパゲッティを巡る旅」がありました．
これはスパゲッティを適当に砕くと，破片の長さ分布がどのようなものになるかという興味ある実験でした．
興味おありの方は，「数学文化」第21号をご覧ください．このとき観察される「べき乗則」は，
社会の関心事の一つである「地震」にも関係があります．

この地震のテーマは，メルマガNo.031（'14/09/30発行）で，
複雑系（原発）の事故雪崩のテーマは，メルマガNo.006（'14/05/15発行）で，
取り上げたことがあります．

地震のマグニチュードMは，エネルギーの対数です．マグニチュードを決めるのにリヒターが発案した当初の定義は
便宜的なものでしたが，現在ではもっと理屈に合ったモーメント・マグニチュードが採用されています．
（注）震度というのはその地の揺れ（加速度[ガル]）の程度の段階です．
地震で解放されたエネルギーは，生じた断層面の面積×平均変位×地層の剛性の積です
（大雑把にいえば生じた断層の長さに比例します）．
生じた断層の長さが長い方が解放されたエネルギーは大きいし，
地層の剛性が大きいほど大きな歪エネルギーが蓄えられます．
これらを踏まえ，起こりうる地震の最大エネルギーを見積もるとM9.5程度と考えられています
（1960年のチリ地震ではM9.5が観測されている）．

地震のマグニチュードMと発生頻度（回/年）nの間にn=10^{a-bM}の関係があるのを，
グーテンベルクとリヒターが発見しました．a, bはその地域の地層の剛性などを表す定数で，
b≒1ですので，地震のマグニチューﾄﾞが1つ大きくなるごとに，地震の回数は1/10に減ります．
ゆえに，これを「べき乗則」とも言います．

地震では多く発生するマグニチュードというものがありません（正規分布ではない）．
大きな地震ほど少なくなりますが，M9あたりも起こり得る．そんな巨大な地震に見舞われたなら壊滅的です．
地震被害の低減対策は，被害のコスト（Mの関数）×発生確率（Mの関数）を小さく抑えることです．
従って，頻度は小さいけれど致命的な被害を惹起する巨大地震に対して，
被害が最小となるように備える必要があります．広域の汚染と何十年では済まない年月を要する
原発事故の被害コストは致命的です．原発の再稼働は止めましょう．

クリーン・ルームのチリのサイズ分布も「べき乗則」だと言われています．
もし正規分布のように頻度の高いサイズがあるなら，
そのサイズのチリの発生に特化した対策ができるのですが，「べき乗則」では特別な対策は困難です．
でもこの場合は，大きなサイズのチリが桁外れに大きな被害コストを与えると言う訳でもありません．

中西氏の実験したスパゲッティやクラッカーのほかに，分布関数を求める実験には色々あります．
凍ったジャガイモを投げて砕き，破片のサイズ分布を調べた人（南デンマーク大，1993年）などもいます．
ここでも「べき乗則」が確認されました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.30］ No.070
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
6月も末になりました．今年は梅雨らしい雨がありません．
皆様の方は如何でしょうか．いよいよ数学月間（7/22～8/22）
の月になりますね．
----------------
6月19日に統計数理研究所のオープンハウスがありました．
（統計数理研究所は立川にあります）
統計数理研究所には，
モデリング研究系，データ科学研究系，数理・推論研究系
の3つの系があり，各系にはそれぞれ３つのグループがあります．
オープンハウスでは，100件に近いポスター展示
（大学院生のポスター発表も27件含まれる）がありました．
午後は，「統計よろず相談室」や講演などがありこれも人気でした．
ポスターで興味深かったテーマを一つだけ紹介します．
--------------------------------------
電波干渉計の新たなイメージング法について，池田思朗准教授ほか

電波望遠鏡（アンテナ）を地球規模で複数個配置し，
各アンテナで受信する信号の相関処理をして，一つの仮想的な
巨大望遠鏡としたものを電波干渉計と呼ぶそうだ．
受光電波はcmオーダーのミリ波らしい．

(注)
*　ALMA望遠鏡（チリ共和国北部にあるアタカマ砂漠の標高約5000メートル
の高原に建設される）は，66台以上の電波望遠鏡を並べ，
これらの受信データを組み合わせて一つの巨大な仮想望遠鏡とする.

*　赤外線に近い電波を「サブミリ波」波長＝1~0.1mm，周波数＝300GHz~3THz
少し波長が長い電波を「ミリ波」波長＝10~1mm，周波数＝30GHz~300GHｚ

ブラック・ホールからは光が来ないと思っていたが，
ブラック・ホールの口で生じるプラズマから光（電波）が来るそうだ．
この光を受光して，光源の像を得ると円環状で，
ブラック・ホールの穴の形が見えるらしい．

これは宇宙オーダーの話だが，物質からのX線散乱を観測して
物質の原子的構造（nmオーダー）を見る話と非常に似ている．
そこで，私になじみのある結晶の例で理解を試みようと思う．
結晶（物体）ρ(r)からでる散乱X線F(R)は，Fourier変換の関係にあり
F(R)=W･ρ(r)，　ここで，WはFourier変換の演算行列．
もし，F(R)がわかれば，逆変換ρ(r)=W^-1･F(R)で，
ρ(r)が求められる．しかし，実際に観測できるのは，
複素数F(R)の大きさ|F(R)|のみで，位相はわからない．
だから，位相の推定法が，結晶学の主要な課題になっている．
位相推定には，逆空間をNyquist周波数以上でサンプリングする
オーバーサンプリングの測定も最近やられるようになった．

（注）
*　我々のいる観測空間は，物体ρ(r)のFourier変換スペクトルF(R)
の観測をするので，逆空間（R-空間）と呼ばれる．
これに対し，物体のある空間を実空間（r-空間）と呼ぶ．

宇宙からの電波の受光では，位相は計測できるようだ．
問題は，受光アンテナを乗せている地球が，
観測空間（逆空間）内の限られた軌道上を動く（自転や公転）だけなので，
限られた逆空間のデータしか観測できないところにあるらしい．

位相はわかるにしても，圧倒的に狭い逆空間内の観測データだけから，
逆Fourier変換で光源の形を求める課題である．
つまり，F(R)を観測できずに，圧倒的にゼロの多い2次元行列Fo(R)
しか得られず，この2次元行列を逆Fourier変換し，
光源のイメージ（2次元画像）を得なければならない．
おそらく，観測スペクトルFo(R)とモデルイメージのFourier変換像W･ρ(r)
との差||Fo(R)-W･ρ(r)||が最小となるように最小２乗法でρ(r)を求める
と同時に，観測できなかった範囲の逆空間の推定値も決まるのだろう．
もしかして，このプロセスで，光源の中心対称性などの光源の形に関する
何らかの束縛条件を仮定して推定を進めるのかもしれない？

（注意）この解説は私の推測を補っています．
発表内容の詳細を全部把握したわけでないので
不正確な部分があることをお断りしておきます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.23］ No.069
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆数学と諸科学・産業技術との連携
日本学術会議シンポジウム，“礎（いしずえ）の学問：数学
－数学研究と諸科学・産業技術との連携”-が，日本数学会，
日本学術会議数学委員会の主催で，2006.05.17に開催された．
このシンポジウムの狙いは，先端数学研究と異分野
（社会，医学，諸科学，産業など）との連携研究の拠点づくりにある．
その後数回の成果報告会がもたれ，直近では
“数学は世界を変えられるか？「忘れられた科学：数学」から10年
－数学イノベーションの現状と未来”が，2015.04.16に開催された．
異分野の課題の中に，数学が適用できるニーズや，
新しい数学が生れるシーズを発見できるかも知れないのだが，
数学者側から積極的に異分野の課題を理解し，課題の数学的命題化に
力を貸すことが必要だとの意見が出ている．
現実の課題から数学の命題を抽出する所が一番難しいのであり，
数学者はこの段階にも積極的に関与すべきである．

◆数学月間テーマから見る数理科学のトレンド
数学月間は，数学の価値を社会が知ると同時に，
社会からの要請を数学側が知る機会でもある．
国内外の数学月間テーマのトレンドを見ると，ビッグデータや統計学，
複雑系や非線形，モデリングやシミュレーションの話題が増加した．
これらはすべてコンピュータを駆使した数値計算によって
可能になった分野である．具体例を2つ紹介する：
（１）エネルギーの保存される系は，オイラー-ラグランジュ方程式を
立てることができるのだが，一般にはこれは解けない．
物理演習で学んだものは，線形近似で解けるようにしたものだった．
そして，解けない一般の場合にも解の挙動は似たものだろうと想像していた．
しかし，これがだいぶ違う．1900年ポアンカレは，
独立な因果列からなる可積分の方程式はわずかで，
大部分の方程式は非可積分（干渉し合う因果列）であると警鐘をならした．
明日の一つの出来事には，今日の全ての出来事が反映される
－遠方の地で過去に起きた蝶の羽ばたきが，
この地の明日の大風を引き起こす要因になり得る「バタフライ・エフェクト」
の世界である．初期パラメータのわずかな違いで分岐が起きカオスが生じる．
これらは方程式を積分して関数で書き表すことは不可能だが，
コンピュータを用いた数値計算で現象の追跡が可能である．
モデリングとシミュレーションにより現実現象を理解する
「現象数理科学」がさまざまな分野で盛んである．

（２）アモルファス（ガラス）物質の記述にトポロジーが登場した．
結晶は周期的な構造であるので，並進群を核とする準同型写像で
無限に広がる空間を単位胞の中に還元でき記述は簡単である．
アモルファス材料は均一ではあるが周期性はないので
多数の原子を全部記述せねばならず困難である．
アモルファス材料の記述は，古くは動径分布関数による統計的記述であった．
しかし，この記述では，特性の大きく異なるアモルファス構造でも，
同様な動径分布関数を与えてしまう．
そこで，アモルファス構造を特徴づけるいくつかのトポロジー量の定義が
導入された．ガラス構造のネットワーク中に，何員環がどれだけ存在するとか，
ベッチ数や連結数などの特性量，さらにパーシステントホモロジー群
の計算がなされている，これにより詳細なアモルファス構造の記述ができる．
これらのトポロジー量は，大きな原子数のアモルファス構造モデルで，
シミュレーションにより決定された全原子の座標値のビッグデータを
土台にして導出される．

◆市民のための数学月間
完成された抽象的な数学は，取りつき難くそびえる巨大な山脈だ．
身の回りの課題にどのような数学概念が使われているかを具体的に知ると，
数学学習へのモチベーションが高まる．
欧米は日本に比べこのような啓蒙活動がとても充実している．
多くの数学者が，他の領域の科学者と共同研究をしているのは
日本も同様であるが．英国では数学研究の大学生を学校に派遣し，
研究内容を説明させる（大使計画）．これは日本もぜひ見習ってほしい活動だ．
当協会の「数学月間」活動のような一般への啓蒙活動は，
成果が不明確なため国家的なプロジェクトから放置される傾向にある．
そして，危機意識のある数学愛好者によってボランテア・ベースの活動が
行われているのが現状である．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.16］ No.068
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆お知らせ
数学月間懇話会（第11回）
主催●日本数学協会，数学月間の会（SGK）
日時●７月２２日，13:50-17:20
－－－－
1.十年目の「数学月間」
　片瀬豊，高窪正明（SGK）
2.「サッカーボールの対称性を解くTopological Symmetry」
　細矢治夫（お茶の水女子大名誉教授）
3.繰り返し模様の観賞法
　谷克彦（SGK）
4.テーラー展開の話
　鈴木啓一（SGK）
ーーーー
会場●東京大学（駒場）数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●数学月間の会（SGK）
sgktani@gmail.com，谷克彦（SGK世話人）
直接会場においでください（開場13:30）

◆数学月間だより１
日本数学協会は，2005年に，7月22日--8月22日を数学月間と定めました．この期間は，数学の基礎定数 π(22/7=3.142..) とe(22/8=2.7..)に因みます．この期間に，数学への共感を高める活動が各地で盛んになるよう我々は応援しています．
数学が色々な分野で社会を支えていることを市民が知ることは，数学への共感の呼び起こしに直結します．逆に，社会が必要としている数学を数学者が知る--言い換えれば，異分野の課題の中に数学が適用できるニーズや新しい数学が生まれるシーズを見出す--ことも重要であります．

先ず隗より始めよで，SGKは毎年7月22日に数学月間懇話会を開催しています．
これまでのテーマを見て見ましょう．
（資料１）**********
◆数学月間懇話会10年の記録
第1回（2006.07.22）会場：シーボニア
数学月間のπとeの連分数展開，公開鍵暗号　山崎圭二郎
数学と社会　　　　　　　　　　　　　　 　真島秀行
ゲストスピーチ　　　　　　　　　　　　 鈴木裕道
第2回（2006.08.06）会場：議員会館
財政再建と数学：TQC手法　　　　　　　 （日科技連）
第3回（2007.07.22）会場：ルベソンヴェール
シミュレーション　　　　　　　　　　　 谷口健英
第4回（2008.07.22）
数学月間 　片瀬豊
ある数学者たちの物語 　 上野正
数学と基礎科学 　 谷克彦
秘宝－数学的オブジェの照明 　　　岡本和夫，河野俊丈
第5回（2009.07.22）
宇宙のかたち　　　　　　　　　　　 河野俊丈 　　　
造血幹細胞移植データベースと統計　　 田渕健
生体情報のゆらぎとフラクタル性　　　　 河野貴美子
MRIの数学的原理 真島秀行
第6回（2010.07.22）
手と目で観賞，数学曲面と多面体　　　　　手嶋吉法
教育数学の試み 　　　　　　　　　　　　岡本和夫
第7回（2011.07.22）
サイバー世界のモデリング　　　　　　　　北川源四郎
量子コンピューティングの考え方　　　　　荒井隆
米国MAM複雑系と日本の原発事故　　　　　谷克彦
第8回（2012.07.22）
物理化学の探検ー化学の中の数学の世界　　細矢治夫
じゃんけんの必勝法を論じて統計的思考に　石黒真木夫
第9回（2013.07.22）
考える楽しみわかる喜び　　　　　　　　　水谷一
最小二乗問題の新解法と逆問題への応用　　速水謙
数学祭り　　　　　　　　　　　　　　　　谷克彦
第10回（2014.07.22）
人口の集合関数としての「民力指数」　　　松原望
スパゲッティを巡る旅　　　　　　　　　　中西達夫
第11回（2015.07.22）
十年目の数学月間　　　　　　　　　　　　　　　　 　片瀬豊，高窪正明
サッカーボールの対称性を解くTopological Symmetry　細矢治夫
繰り返し模様の観賞法 　　　　　 　　　谷克彦
テーラー展開の話　　　　　　　　　　　　　　　　　　鈴木啓一
注）第4回以降の会場は，数理科学研究科棟・東大駒場キャンバス

次号に続く

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.09］ No.067
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
『数学 理性の音楽』，東京大学出版会(2015.4）刊行記念イベントが，
東京大学伊藤国際学術研究センター地下1階　ギャラリーにて開催された．
（6月8日，19:00-21:00）
同書の著者，東大名誉教授（岡本和夫・薩摩順吉・桂利行の三氏）による鼎談．

この書籍の副題は，自然と社会を貫く数学で，
まさに，数学月間のコンセプトが語られております．
ぜひ皆様が一読されることに期待し，ここでは書籍の内容には言及しません．
その代り，鼎談の内容を速報します（今夜，参加し帰宅したばかりでホットな情報です）．
----------
鼎談は，岡本氏の「数学の３つの側面」
ー道具としての数学．言葉としての数学，対象としての数学--の話から始まりました．
著者の3氏は，奇しくも歴代の東京大学大学院，数理科学研究科長です．
数学の大学院が理学部から抜けて，駒場に大学院数理科学研究科が創設されたのが
1992年のことで初代の科長が岡本氏，次いで薩摩氏，桂氏でした．
本郷キャンバスの理学部から大学院だけ抜けて，駒場キャンバスに
大学院数理科学研究科が設立できたのは，教養学部の数学の歴史があり，
基礎科学科もあったので，環境が整っていたことがあったようです．

20世紀の数学は，抽象化・純化に進んだわけですが，これは数学を学び難くしています．
どうも，学生・生徒たちは数学を人間が作ったという気がしないそうです．
完成された体系がそこにある．どうして生まれたかなど考える余裕もないようです．
完成された数学はそびえたつ山脈のようでとりつきがたい．
数学月間でも数学が生まれる所から親しむことを薦めています．

数学は役に立つのかというのは愚問です．
すぐ役に立っこともあるし，何十年もの後で役に立っものもあります．
岡本氏の研究したパンルヴェ方程式はソリトンの研究に使われるし，
暗号（公開鍵．楕円曲線），デジタル信号の誤り訂正，などの例が出ました．
1900年に，ヒルベルトは23の問題を出し，数学は抽象化の方向に進みだします．
同年，ポアンカレも人力で計算できるところまで行き着き，非可積分の方程式の
性質を示しました．その先はコンピュータの出現を待たねばなりませんでした．
現在はコンピュータによる数値計算が盛んで，非線形やカオス，分岐理論も研究されています．
モデリングやシミュレーションの現象数理科学も盛んです．

私は数学と数理科学の違いを質問してみました．
数理科学は数学のように厳密な証明の手順がないのではないか．
それとも数理科学というのはコンピュータを用た数学であるのか．
などという漠然とした感じがあったからです．
結論は，どちらも同じである（ニュアンスの個人差はあるが）という事でした．

コンピュータで計算は万能かというと，そうでもないようです．
例として出されたのは調和級数：
1/1+1/2+1/3＋・・・+1/n＋・・・＝lim_n→∞（log n）=∞
ですが，ｎをずいぶん先までたし行っても，対数ですから級数はなかなか∞にはなりません．

最後に岡本氏が面白い計算を提示しました．
方程式の問題より，数の問題の方が奥が深いということを象徴するためです：
2×3×5×7+11=13+17
2^2+3^2+5^2+････＋17^2=1+2+3+････+36=666

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.02］ No.066
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
日本数学協会・第14回総会および講演会のお知らせ
日時：　2015年　6月7日，
場所：　東京大学数理科学研究棟（駒場キャンバス）
11:30～12:30　総会
----------------------------------------
13:30～15:40　講演会
13:30～14:30
「十年目の数学月間，これまでとこれから」，片瀬豊・谷克彦（SGK）
14:40～15:40
「視覚と錯視の数学からアート，そして画像処理」，新井仁之（東京大学）
講演会にどうぞお気軽にご参加ください．
協会員は無料ですが，協会員外は参加費2千円かかります．

*******（私の話そうとしていること）*******
数学月間は，数学から社会を見ると同時に，社会からの要請を数学側が知る機会でもあります．
国内外の数学月間テーマのトレンドを見ると，ビッグデータや統計学，複雑系や非線形，
モデリングやシミュレーションの話題です．
これらはすべてコンピュータを駆使した数値計算によって可能になった分野です．
これまでの数学とは違う新しい数学分野が生まれているところと言えるかもしれません．
1900年ポアンカレは，独立な因果列からなる可積分の方程式はごくわずかで，
大部分の方程式は非可積分（干渉し合う因果列）であると警鐘をならしました．
明日の一つの出来事には，今日の全ての出来事の影響が反映される世界です．
遠方の地で過去に起きた蝶の羽ばたきが，この地の明日の大風を引き起こす要因の一つになり得る
「バタフライ・エフェクト」の世界です．
ちょっとした初期パラメータの違いでカオスが起きるかもしれません．
これらは方程式を積分して関数で書き表すことは不可能ですが，
コンピュータを用いた数値計算で現象の追跡ができます．
モデリングとシミュレーションにより現実の現象を理解する
「現象数理科学」がさまざまな分野で発展しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.26］ No.065
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
これは私の造語です．あまり耳慣れない言葉ですが，とても気に入っています．
結晶学では「空間格子」という言葉がでてきますが，「空間のデジタル化」はこれと同じ状況の表現です．
空間のデジタル化とは，「空間を，１つの多面体を並べ（面と面が接するよう）て隙間なく張りつめること」
を意味します．例えば，角砂糖のような立方体を並べて，空間を張り詰めたとすると，
このデジタル化された空間の対称性は，立方体の対称性と同じであることはわかりますね．
”立方体（A)”と同等な対称性の多面体で，空間のデジタル化ができる多面体に，
面心格子を生む”菱形12面体（B)”と，体心格子を生む”ケルビン立体（C)”があります．
これらは立方体の対称性に分類される3種類の空間充填です（Fig)．
（この図はpov-rayを用いて作成しました）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/85/16728485/img_0_m?1432564271

1種類の多面体を互いに面が隙間なく接するようにして空間に詰め込んだ状態を想像してください．
この状態が空間のデジタル化です．
空間のデジタル化の様式を分類したいなら，多面体の対称性に注目すべきでしょう．
一様で連続的な空間が，デジタル化によって，異方性があり周期的な空間に変わります．
無限に広がる空間が，単位となる１つの多面体に還元されます．
すでに，アモルファスと結晶の項目で述べましたが，デジタル化された空間はシンプルで扱いやすい．
このような空間を「結晶空間」と言います．
一寸脱線しますが，連続信号をサンプリングして得たデジタル信号の周波数帯域が抑えられるのと似ています．
結局，3次元では14種類の空間のデジタル化の様式があり，
これは結晶学でブラベー格子が14種類ということと同じことです．

(注)2種類の多面体を使って空間を充填することもいろいろ考察できます．
例えば正8面体と正4面体を使って空間を周期的に充填します．
2種類の多面体の混合による空間の充填では，必ず周期が生じるかといえばそうでもありません．
ペンローズのタイリングに相当する3次元非周期充填もあり得ます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.19］ No.064
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
このような不思議で奇麗な法則があります．
https://www.facebook.com/maxplancksociety/photos/a.10150979253928376.447707.324380493375/10153218754768376/?type=1

1³ + 5³ + 3³ = 153
16³ + 50³ + 33³ = 165033
166³ + 500³ + 333³ = 166500333
1666³ + 5000³ + 3333³ = 166650003333
and so on and om and on!

不思議な数式です．証明してみたくなるでしょう．
いや，なぜこのようなことが起こるのかが知りたいですね．
別の話ですが，似たような数式がまだあります．
ただし，こちらの場合は「数字の桁数が増えていっても，いつも成り立つ」
という性質ではありません．
https://twitter.com/Derektionary/status/484852762102857730

166³ + 500³ + 333³ = 166,500,333
296³ + 584³ + 415³ = 296,584,415
710³ + 656³ + 413³ = 710,656,413
828³ + 538³ + 472³ = 828,538472

閑話休題．初めの不思議な法則の証明法の問題に戻りましょう．
考え方は人さまざまで，証明法には色々あるでしょう．
論理が正しくて，命題が証明されるのならば，どのような証明方法でも正解です．
それでも，「美しい」証明とか「エレガント」な証明とか言われるものがあります．
そのような証明は，「命題の本質にズバリと触れている無駄のないシンプルな証明」
のことだと私は思っています．
補助線一本で解けてしまう図形問題の証明などはその例でしょう．
力ずくで計算して証明できても，命題の本質や現象の起こる仕組みが見えていないのでは，
本質にズバリと触れているとは言えません．
本質や仕組みがわかるということは，その仕組みを基礎とするもっと幅広い命題にも適用できる．
つまり「一般化できる」証明法でもあり価値が高いと思います．

小林昭七先生が「数学と美」というエッセイを，「いまを生きるための教室」角川文庫の中に掲載しています．
（私は小林先生がお亡くなりになる直前の夏の日本滞在中にお会いしこの本を頂きました）
この本から以下の部分を引用しておきます：
「他の科学と同様，数学でも新しい結果は重要である．しかし，数学では既に知られている結果の
別証明や新しい見地からの解釈もかなり評価されている．定理の本質を理解させるような証明，
「なるほどそういうことだったのか」と思わせるような美しい証明は，それが既知の定理の
証明であっても高く評価される」

「数学は美しい」と良く言われますが，美しいと言われても漠然として私にはピンときません．
これを言い換えるなら，「シンプルである」，「本質を見抜いてそれに言及している」，
「話を逸らさないで真摯に課題に集中している」という意味でしょう．

「問題の本質の議論から逃げて，話をそらし，周辺の議論にすり替える」という手法は，
政治や社会で良くみられることです．特に，今の安倍政権では目にあまるものがあります．
「丁寧に説明していく」とよく言いますが，これは聞く耳を持たないと言うことです．
我々の方が説明してあげたいくらい十分な知識があります．国民をバカ扱いしないでもらいたいものです．
論理や数学を軽視する社会に公正はありません．数学月間活動をもっと社会に広げる必要がある所以です．

もう一度，閑話休題で，この不思議な式に戻りましょう．
皆さん証明を考えてみてください．
n桁の数字を　$$ (x_n), (y_n), (z_n) $$と書くと，
　$$(x_n+1)=10(x_n)+6，(y_n+1)=10(y_n)，(z_n+1)=10(z_n)+3$$

$$(x_n)^3+(y_n)^3+(z_n)^3＝(10^2n)(x_n)+(10^n)(y_n)+(z_n)$$　が成立するとして，数学的帰納法で
力ずくで計算して証明することはできるでしょう．でも計算は大変ですし本質は別の所にありそうです．
この問題の本質が何処にあるのか私にもまだ理解できません．皆さん良い証明が出来たら教えてください．
ポイントは循環小数のように続く数字と数の表記法（10進法を使っている）にあるように思います．
多分，以下の表式が利用できます：
$$(x_n+1)＝(1+6/9)(10^n)-6/9，(y_n+1)＝5*(10^n)，(z_n+1)＝(3+3/9)(10^n)-3/9$$　

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.12］ No.063
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
2015年米国MAMのテーマ
「数学がキャリアを動かす」
（http://www.mathaware.org/mam/2015/highlighted/ より）

自分のキャリアに数学を利用している実在の人物
数学の才能や嗜好を報酬や多様なキャリアに変えた17人

数学が好きだが，数学専攻者にアカデミック以外のどのような仕事があるのかわからない？
幸いなことだが，「数学を専攻するのは今でしょう」というわけだ．
なぜなら，数学がイノベーションの原動力であるようにキャリアも運ぶからだ．
数学の才能と嗜好を，実業界や工業界や政府での多様なキャリアと報酬に替えた17人が紹介される．
彼らが影響を受けたものやそのキャリア・パス選択を見ることは，
アカデミックの外にキャリアを探す数学専攻者にとって，ユニークな見通しや有用なアドバイスになるだろう．

詳しく知るには
http://www.mathaware.org/mam/2015/highlighted/#sthash.gXM8A0oh.dpuf
に17人のプロフィールがあります．17人のうちIBM研究所の人が2人います．
そのほかは，data scientistという人が多いようで，
これらは統計学やコンピュータを用いた数学分野です．

■代表的なプロフィールの例
プロフィール：Jean Steiner
データ・サイエンティスト，Google社，ニューヨーク

私は、工学分野の広告組織Googleのデータ科学者です．
広告主が彼らのgoogle AdWordsアカウントを
どのように管理したらよいかを理解するためにデータを分析し，
彼らに良いツールの提供ができ，彼らのアカウント管理が容易になるようにしています．
私はデータから話を引出し，我々のソフトウエア技術者が良い製品を作るのを助けます．
データ・サイエンティストという役割をする人のほとんどは，
統計学，生物情報学，認知科学，物理学，数学，経済学などの背景を持っています．
私は，アカデミックの場の純粋数学からスタートした
（博士号を取った後，ポスドクフェローシップで研究と教育を行った）．
そして，私はやはり定量的であるが，応用的な何かをしたいと思った．
多くの可能なキャリア（例えば、疫学、定量的な金融、経営コンサルティング）
を探しての情報インタビューの結果，Googleで私の関心にぴったり合った仕事を見つけた．
データ解析と，わずかばかりの軽量シェル·スクリプト（コーディング），
ビジネスへの関心が組み合わさっている仕事だ．
当初，私は金融機関で，収益予測，分析，報告をしていたが，
最終的には，より深い分析とより少ない報告を望んでいたので，
データ・サイエンティスの役割に移動した．

■個人的な感想－－－－－
今年の米国MAMのねらいは，数学者の働き場所は大学教授や教員の他にも広範な分野があり
需要があるということにある．「だから数学を学ぶなら今でしょう」という調子だ．
この状況は日本でも全く正しいとは思う．

しかし，今年の米国MAMのキャンペーンのなかで，数学のキャリアは年収が高いとか言うのは眉唾物だと私は思う．
2014年度の高年収職業ベスト10とかワースト10とかは馬鹿げたデータだ．
だいたい高収入が欲しくて数学を専門にするなどおかしな話だ．
17人のプロファイルもそれほど面白くない．
広範な各分野で具体的にどのような数学を用いた仕事や研究をしているのかを知りたいと思ったのだが，
週刊誌の表題程度のレポートで，本年の米国MAMの内容には失望した．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.05］ No.062
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ゴールデン・ウイークの最中です．
皆様，よい休日をお過ごしでしょうか．
今週は2つの本を紹介しようと思います．

■「数学を楽しむ」西山豊，現代数学社
6174の不思議はこの本のp.130に出ています．

数学はなんでも証明されているかというとそうでもないらしい．
6174の不思議さを理解するのはちょっと大変．私はまだわかりません．
でも，6174に関する不思議な命題が成立しているのは事実です．
　
6174の各桁の数字の並びを変えて，最も大きい数字を作ると7641，
最も小さい数字を作ると1467です．
最大数字と最小数字の差は　7641-1467＝6174　になってしまいます．
6174という数字は不思議ですね．

いろいろな4ケタの数字で実験してみます．例えば，
2005なら
5200-0025＝5175
7551-1557=5994
9954-4599＝5355
5553-3555＝1998
.....
このような操作をカプレカー操作というそうです．
（カブレカーはなんでこんな操作を思いついたのでしょうか不思議です）
頑張って，この先をもう少し繰り返して行くと，結局6174に到着します．
全部同じ数字の場合を除き，どのような4ケタの数かtら出発しても
6174に到達するそうです．不思議ですね．なぜなのだろうか？

西山さんはプログラムを作り，パソコンですべての4ケタの数が，
有限回のカプレカー操作で6174に達することを確かめ，系統図をつくりました．

そのほかの桁数の数字ではどうかというと，
3ケタでは存在するけれど，5ケタでは存在しないそうです．

事実は確かめられましたが，なぜこのようなことが起こるのか？
その仕組みをしりたい．数学の不思議さを感じる例です．

■美しい幾何学，　丸善
高木隆司監訳
Eli Maor and Eugen Jost

ルネサンスの時代は，数学とアートの活動は協力して行われ，
心の中で補い合うものと考えられていた（イーリーによるまえがきより）．
オイゲンの数学的アートと数学者（数学史）イーリーの協同でできた本書は珍しい数学の本です．
説明には微積分などは出てきません．子供から大人まで数学アートを鑑賞しながら読み進むことができます．
テーマは系統的な幾何学とは異なります．初級の幾何学もあれば無限級数などもあります．
さらに意外なテーマが現れたり変化に富みます．
取り上げられたいくつかのテーマを見てみましょう．例えば，シュタイナーの円鎖．
これはアルベロスとかインドラの真珠などと呼ばれることもあります．
円の中に互いに接する円を詰め込んだ美しい図形です．円による反転操作もあります．
この図形は和算の算額にも登場しますが，それにも言及しているのは著者の専門が数学史だからでもあり，
本書の構成にもそれが現れています．本書の前半に，ピタゴラスから始まり，
素数，無限級数の収束，ユークリッドなどのテーマが現れます．
さらに続くのは，円周率，積み木による調和級数，自然対数の底，らせんや種々の曲線などです．
これらの説明も，数学アートの図が活きていて面白い本です．
本書の後半には，スノーフレーク曲線，シェルペンスキーの三角形などのフラクタル図形の特徴も，
美しく理解しやすい図による記述があります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.28］ No.061
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
面積がゼロで，周囲が無限大のフラクタル図形

フラクタル図形というのは，図形を拡大していくと，
どんどん細部が見えてくるが，それらがいつも同じ図形なのです．
http://upload.wikimedia.org/wikipedia/commons/6/6a/Sierpinski_zoom.gif

そのような図形のうち，ポーランドの数学者シェルピンスキーの図形の作り方を見てみましょう．

(1)シェルピンスキーのガスケット
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/58/16668258/img_2_m?1429928123

正3角形から出発します．正3角形を4分割して真ん中を通り覗きます．
残った3つの正三角形をそれぞれ4分割して，それぞれの真ん中を取り除きます．
この操作を際限なく（無限に）繰り返して得たフラクタル図形はシェルピンスキーのガスケットです．
面積は0に収束し，境界の長さは無限大に発散します．

(2)シェルピンスキーのカーペット
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/58/16668258/img_3_m?1429928123

正方形から出発し，9分割し真ん中の正方形を取り除きます．
残りの８つの正方形をそれぞれ9分割して，それぞれの真ん中を取り除きます．
この操作を際限なく（無限に）繰り返して得たフラクタル図形はシェルピンスキーのカーペットです．
やはり，面積は0に収束し，境界の長さは無限大に発散します．

これらの図形は，1次元でも，2次元でもありません．
「長さがx倍になった領域に，現在の図形をy個詰め込む」という操作を繰り返したわけですが
　　x^d=y　（dはフラクタル次元）　より，フラクタル次元は　d＝logy/logx　です．　
フラクタル次元は，(1)ガスケット3角形では1.585･･･，(2)カーペット4角形では1.89････になります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.21］ No.060
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■結晶とガラスについての話です．
まず，石英（水晶）と石英ガラスの2次元の模式図を見て下さい．
図はwikipediaから借りました．どちらも材料の化学式はSiO2で同じです．
Fig.1　結晶
http://upload.wikimedia.org/wikipedia/commons/f/fd/SiO2_-_Quarz_-_2D.png
Fig.2　ガラス
http://upload.wikimedia.org/wikipedia/commons/thumb/1/19/SiO2_-_Glas_-_2D.png/240px-SiO2_-_Glas_-_2D.png

結晶とガラスの違いは一目瞭然でしょう．
そう，結晶構造には繰り返し周期がありますが，ガラスにはありません．
Fig.3に示すように，結晶には単位となるタイルがあり，これで無限平面を隙間なく張りつめることができます．
石英の例では，正6角形のタイルを，赤点の場所に置けば，無限平面を隙間なく張り尽くせます．
赤点は格子点と呼ばれます．格子は，図中に示した2つの互いに独立なベクトルa1，a2の
一次結合ha1+ka2により生成されるベクトルを集めた無限集合（並進群）の図による表現でもあります．
Fig.3　結晶構造にある並進群
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/26/16652126/img_0_m?1429350335

■結晶空間は並進周期のある空間です．結晶構造は規則正しい秩序のある構造ですから，
並進操作以外にも回転対称操作とか鏡映対称操作などあり，
構造に存在するこれらの操作を続たとき生じる対称操作全体の無限集合は”群”をなしています．
生成される対称操作はこの集合に含まれるし，すべての操作に逆元があり，
何も動かさないという単位元もあります．
結晶空間（周期のある無限空間）の対称操作の集合のなす群を結晶空間群と言います．
今日，ここで扱ったような2次元の平面群（壁紙模様）は17種類あることが知られています．
並進（格子点間の移動）で重なるものは同値と定義すると，
無限に広がる結晶構造を，単位タイルの中に押し込めることができます．数学の言葉で言うと，
「並進群を核とする準同型写像で結晶空間群は結晶点群に帰着する」ということになります．
私はこの理論が大好きでした．しかし皮肉なもので，実際に扱った材料は結晶ではなく
群論の適用ができないガラスが中心になりました．

■ガラスの構造をどう解析し記述するかというのは，今日でも困難な課題です．
結晶で活躍する群論もFourier変換も役に立ちません．ガラス（一般化してアモルファスと言う）には，
単位タイルと言うものがありません．結晶構造では，
無限にある構成原子のパラメータは単位タイルに含まれる有限個に還元することができましたが，
ガラスでは無限個の構成原子のパラメータを減らせません（実際にコンピュータで扱うのは有限個）．
結晶空間は単位タイルによってデジタル化された空間，他方，アモルファス空間は連続空間（アナログ空間）です．
ガラス構造では，結晶のようにすべての構成原子のパラメータを記述するのは諦めねばなりません．
そこで古くから，1つの原子を中心に置いて．半径r+Δrの球殻上に何個の原子が存在するのか
というような確率的な記述（動径分布関数）が用いられてきました．
最近は，アモルファス構造を特徴づけるいくつかのトポロジー量を定義することもやられています．
Fig.2を見るとリングがたくさん見えるでしょう．ガラス構造の中に，何員環がどれだけ存在するかとか，
ベッチ数とか連結数などの特性量，さらにパーシステントホモロジーの計算がなされ，
これにより詳細なアモルファスの特徴量が得られるようになりました．
これらのトポロジー量は，大きな原子数のアモルファス構造のモデルから，
シミュレーションにより決定された原子の座標値のビッグデータを土台に導出されます．
******
（編集後記）
今回のメルマガでガラスの構造について書こうと思ったのは，
4月16日の文科省の講演会「数学は世界を変えられるか？」で数学イノベーションの紹介例3つの内に
ガラス構造への応用トポロジー（東北大）があったからです．
この講演会の主旨は，数学と社会・諸科学の連携です（ガラス構造の研究発表ではありません）．
数学連携に関する個人的感想は（メルマガ分量オーバーのため）．以下のサイトに書きました：
http://sgk2005.sakura.ne.jp/htdocs/index.php?key=joth4d0ko-36

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.14］ No.059
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
図
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556225/69/16381169/img_0_m?1428931802

計算することも大事ですが，このような感覚を体に身に着けることは有益です．
有限個の積み木を積んで長さの記録を競います．
無限個の積み木を積むなら，少しずつですが無限に伸びる対数曲線ができます．
（例１）発散する無限級数を体験する
　　１+1/2+1/3+1/4+.......+1/n+....=∞
積み木の長さの半分を１とする．
一番上の積み木の飛び出している長さは１
その下の積み木の飛び出している長さは1/2
その下の積み木の飛び出している長さは1/3
.....以下同様にいくらでも続きます．

（例２）収束する無限級数を体験する
　　1/2+1/4＋１/8＋1/16+........=1
総和でできる立方体の体積を１とする．
立方体の内部の1/2の体積(オレンジ）を取り除く
残りの体積から残りの体積の1/2（グリーン）つまり立方体の（1/2）^2を取り除く
その残りの体積の1/2（青）つまり立方体の(1/2)^3を取り除く
その残りの体積の1/2（赤）つまり立方体の(1/2)^4を取り除く
......以下同様にいくらでも続きます．

私達は子供の頃，積み木を積んで遊びました．そして自然に重心や釣合の感覚が身に着きました．
水遊びをして流体の性質を自然に身に着けました．
後に学校で物理学を学びますが，そのような理論を学ばずとも重力や力学の法則が身に着いていました．
身に着いていなければキャッチボールもできません．
吹きガラスの職人になるには，熔融ガラスの振る舞いを瞬時に判断できることが
身に着いていなければなりません．数学でもこのような体験は大事なことだと思います．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.07］ No.058
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
最近，我々のfacebook数学月間の会
https://www.facebook.com/sgk2014
に，Nishiyama氏から正方形の辺の長さの1/nを作る方法に関する
plusマガジンの以下の記事の紹介がありました．
https://plus.maths.org/content/folding-numbers?nl=0
皆様，正方形の折り紙を用いて試してみてください．
plusマガジンの記事は，下図の中に生じる黄色い２つの３角形が
互いに相似であること，直角3角形である（三平方の定理が成立）こと
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagak.jpg

を用いて，次の関係式を導びきます．
$$y/2＝k/(1+k)$$　
この関係式に，$$k$$の値（位置）として，得られた$$y/2$$の値（位置）を
代入するたびに，次の$$y/2$$の値（位置）が求まります．
$$k=1/2$$　→　$$y/2＝1/3$$
$$k=1/3$$　→　$$y/2＝1/4$$
$$k=1/4$$　→　$$y/2＝1/5$$
　　......
このようにして繰り返せば，一辺の長さの$$1/n$$まで順番に作れます．
正方形の上の辺に$$k$$の位置をとると，右側の辺に$$y/2$$に位置が決まります．
このように続けると，$$1/2，1/3，1/4，･･･$$の位置が正方形の周りを
ぐるぐる周りながら順次現れるのが大変面白いです．
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagaki.jpg

https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagakj.jpg

さて，紙の形が長方形の場合は如何でしょうか？
手紙を３つ折りにして封筒に入れるときにこのようなことが必要になります．
長方形の辺の1/3を作る方法では，Takakubo氏からの以下の２通りの情報が
寄せられました．以下の図をご覧ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_1_m?1428237203
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_2_m?1428237203
これらは一般の長方形（辺の比が１:√2に限らない）で使えます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.31］ No.057
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も桜が咲きました．関東地方は良いお花見日和です．
皆様のまわりは如何でしょうか．満開の桜はいいですね．
桜吹雪も私は好きです．年に一度の良い季節です．
一斉に花だけ咲く桜は確かに異常です．闇を背景の夜桜は怖いようですし，
森の中でただ一人，満開の桜の中に居れば，坂口安吾の小説にもあるように
気が変になりそうですね．
桜の花は，見事な5回対称をしています．今回は花見の季節という事で
平面図形の5回対称を観賞しましょう．今回は気楽にご覧ください．

（１）点群
桜の花びらの対称性は正5角形の対称性と同じで，
点群でいうと記号5mで表現します．これは，5回回転軸と鏡映面mとから
生成される点群だという意味です．図を見て下さい．
赤い5角形は，正五角形の中心に立てた5回回転軸を示します．
赤い線分は鏡映面を示します．鏡映面が１つあれば，5回回転軸のために
5枚の鏡映面が生じ，これらの鏡映面の交線が5回回転軸になっています．
ここで生じる5枚の鏡映面はすべて同じ性質です．それは5回回転軸で
互いに変換されるべきものだからです．
（群論の本では，すべての鏡映面は同じ共役類に類別されると表現されます）
群という言葉を出しましたが，あまり気にすることではありません．
5回回転軸と1枚の鏡映面mの操作を組み合わせ，次々新しい対称操作を
生んでいくことを，どんどんやっていくと，それまでに得たものと
同じ対称操作になってしまうことがわかります．
点群5mの例では，異なるものは10個の対称操作で全てです．
これら10個の対称操作で点群5mの対称操作の集合は閉じているといい．
点群5mの位数は10だと言います．
群となる条件は，集合が閉じているだけではありませんが，細かい定義は省略し，
ここでは，5回対称軸とそれを含む1枚の鏡映面だけで
10個の対称操作が生まれ，それで閉じていることを鑑賞ください．
点群と書いているのは群5mは1点を不動点にするものだからです．
出発点となった5回回転軸と1つの鏡映面を点群5mの生成元と言います．

老婆心ながら注意をうながしたいのは，奇数回転軸の点群で点群に生じた
鏡映面はすべて同一の共役類に入り，5mなどと記述すことです．
5mmではありません．
偶数回転軸の場合は，例えば，2mmのように記述し，鏡映面は
２つの共役類に分かれます．これらの違いは共役類の類別のためで
結晶学の本にときどき誤りが見受けられますのでご注意ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_0_m?1427715627

（２）部分群
点群5m（位数10）の部分群に点群5(位数5)や点群m（位数2）があります．
部分群は上位の群の対称要素を落とすことで得られます．
操作mを落とすことで点群５が，操作5を落とすことで点群mが得られます．

（３）5回回転対称性は，並進と両立しない
均一な2次元平面を，互いに独立なベクトル a, b を用いて
na+mb となる格子点（n,m）で，デジタル化したものが結晶空間です．
すべての格子点（n,m）は同値ですから，結晶空間は周期的です．
ベクトル a, b を並進ベクトルと言います．格子点を多角形のタイル
で表現すると，平面のデジタル化は平面のタイル張りの問題になります．
ここで，正五角形のタイルでは隙間なく平面をタイル張りできないことを
確認しましょう．結局，結晶空間（今考察中のものは2次元ですか，3次元でも）
では5回対称性は存在し得ないことがわかります．

（４）フラクタルのタイル張り
正五角形でフラクタルのタイル張りをしてみましょう．
この図には隙間だらけですが，隙間をさらに2種類のタイルを使って
埋めることを考えるとペンローズのタイル張りが得られます．

（５）黄金比
正五角形の中に次々と組み込まれる小さな正五角形には，黄金比1:x　
が随所に表れています．そのため，たいへんまとまりの良い感じの
図形になります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_1_m?1427715627

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_2_m?1427715627

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.24］ No.056
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
私が通潤橋（熊本県上益城郡山都町）を訪れたのは，2007年10月のことでした．
22日は，午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業，
午後は先生方と人形浄瑠璃注）観劇を経験しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_4_m?1426898367
－－－－－
注）人形浄瑠璃は，清和文楽館
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
で観賞しました．山都町の人形浄瑠璃の始まりは，江戸時代の嘉永年間（1850年ごろ）で，
山都町（旧・清和村）を訪れた淡路の人形芝居の一座から，
浄瑠璃好きな村人が人形を買い求め，技術を習ったのが始まりといいます．
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました．
良い話です.民衆の文化の高さに感激しました．三人で一体の人形を操ります．
首（かしら）と右手を操る「主遣い（おもづかい）」，左手を操る「左遣い」，
足を操る「足遣い」です．人形も触らしてもらいました．
－－－－－－－－－－－－－

■通潤橋
阿蘇山の南側のこの付近の地形は，島のように台地があり，台地から台地への移動が
大変で平家の落人が隠れ住むのに好都合だったようです．
台地（白糸台地）に農業用水を引くのが大変です．
水は台地のがけ下に汲みに行かなければなりません．
時の惣庄屋「布田保之助（ふたやすのすけ）」は，白糸台地に水を引くための
水路橋”通潤橋”を，肥後の石工たちの技術を用いて1854年に建設しました．
通潤橋は，石造りアーチ水路橋で，長さ75.6m，高さ20.2m。幅6.5m．
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています．
通潤橋の写真（放水事に撮影k.Tani）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_0_m?1426898367
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_1_m?1426898367

通水管の写真(撮影k.Tani)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_2_m?1426898367

長さ約127m．石をくりぬいた１尺（30cm）四方の函渠（圧力のかかる管水路）．
管と管の繋ぎ目には，振動吸収と漏水防止のための漆喰（しっくい）が塗られている．
さらに，通水管には5～6ケ所に地震対策のための板（緩衝材）を挟んでいる．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/tuusui.html
通潤橋は両側台地より低いので，サイフォンの原理で出口で水を押し上げています．
通潤橋の高さから流入側台地は7.5m高く，流出側台地は5.8m高い．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/kaisetu.html
通潤橋は，今でも周辺の田畑を潤しています．
放水は，通水管に詰まった堆積物を取り除くために行うものです．

「通潤橋史料館」　に行くと，どのようにアーチ石橋を施工したかわかります．
川の中に写真のような木枠を大工が組んで石工が石を置きました．
アーチ橋の高さを台地の高さまで上げられなかった理由は，
この木枠をこれ以上の高さにする木材がなかったためという事です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_3_m?1426898367

石橋の木枠を外す最終段階は，橋の中央に白装束を纏った布田翁が鎮座し，
石工頭も切腹用の短刀を懐にして臨んだといいます．

これから，アーチ曲線の数学の話をしようと思っています．
写真で見えるアーチ曲線を型どっている石の並びについてです．
アーチの頂点にある石を”かなめ石”と言います．
アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です．
それでも下の木枠を外すときは，とても心配で責任者は命がけだったでしょう．
ーーーーーーー

さて，石積の橋の形，アーチ曲線に関して考えましょう．
アーチの両側の根元はしっかり固定しなければなりませんが，
アーチの上の石の重さが重ければ重いほどアーチの石は互い押し合い引き締め合うので，
橋は大きな荷重に耐えられるのです．石積みは引張力に抗する力はないが，
石積の石に働く力はすべて圧縮力だけなので接着の必要はなく安定構造になります．
石は圧縮に強い材料ですからアーチ型の橋には最適です．ただし，アーチ根元の支点部には，
大きな水平力が発生するので，それとつり合う大きな水平反力が必要です．
山で挟まれた峡谷などはこの点では最適な立地条件でしょう．
通潤橋の根元をしっかり押さえつけている重そうな石積の写真を見てください．

■空き缶を積んで作ったアーチ
私が真剣に積んだのですが，できるのはどうしても缶5個のアーチまででした．
5個の缶で缶同志の接点は4点．すべての接点で同時につり合っていなければなりませんから，
とても難しいことです．もし，6個以上でアーチが出来た方は新記録です．ご一報ください．
缶の周りにラップを巻いていますが，摩擦力を増すためでアーチのつり合い条件を変えるものではありません．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/46/16586546/img_1_m?1426979031

ここから先は，釣合の5つの一次方程式を連立して解く線形代数の話になりますから
省略します．興味ある方は以下でご覧下さい．
http://blogs.yahoo.co.jp/tanidr/16586546.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.17］ No.055
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
とうとう桜の花も咲きだしました．やるふりだけの中身のない政治や仕組みに呆れます．
メルマガくらいは，実質のある楽しんでいただけるものをと心がけようと思います．
ご希望コメントなどをお寄せください．

■振幅の大きな2重振り子の動画がyoutubeなどに色々あります．
大変滑稽な動きをしますのでまずご覧ください．
http://blogs.yahoo.co.jp/tanidr/16560015.html
にはインターネットから拾った2つの例を掲載しています．
第１の動画は実験，第２の動画はシミュレーション結果です．
なぜこのような話をするのかと言えば，
２重振り子は，振幅の小さいうちは，皆が見たことのある自然な振動をしますが，
ある程度以上の振幅になると，とても不自然な滑稽な動きになるからです．
振幅が大きいときは，始めのスタート位置（初期値）によって結果が変わることにも気づくでしょう．

■このような系（エネルギーが保存される）の運動は，
ラグランジュ関数（運動エネルギーと位置エネルギーの差）に対する
オイラー=ラグランジュ方程式を解けば決定できます．
ラグランジュ関数　L(x(t),x'(t)，t)は，座標x(t),速度x'(t)，時間tの関数です．
オイラー=ラグランジュ方程式というのは変分原理とも呼ばれ，
ラグランジュ関数の時間積分（これを作用積分といいます）が
停留値となるようなx(t)の経路を見つける方法です．
ここでは，代表して変数はx(t)しか記述していませんが，
実際は自由度の数だけ変数があり，
これと同じ数だけオイラー=ラグランジュ方程式ができます．
エネルギーが保存される系では，ラグランジュ関数は作れるのですが，
オイラー=ラグランジュ方程式は，一般に解けません（解を関数で書けません）．
昔，私達が物理学で演習したのは，解のある特殊なケースばかりだったのです．
注）振幅の小さい範囲では，x(t)やx'(t)の2乗まで残す近似で，
線形な微分方程式の固有値問題に帰着します．
詳細はhttp://blogs.yahoo.co.jp/tanidr/16560687.html

■問題は振幅の大きいときの運動を知る方法です．
これは解析的な解が得られないので，
今日のようにコンピュータが使えるようになって数値計算ができるようになりました．
そのためのプログラムは，次のような手順です．
現在の位置と速度をx(n),x'(n)とします．
x(n)，x'(n)から加速度x''(n)を得るのは，オイラー=ラグランジュ方程式を使います．
一方，x'(n+Δ)＝x'(n)+x''(n)Δ，　x(n+Δ)＝x(n)+x'(n)Δ　ですから，
x(n), x'(n), x''(n)から，時間ステップΔ後の x(n+Δ)，x''(n+Δ)が更新できます．
このようにして，初期値から，逐一運動の様子を求めていきます．

■力学系を記述するラグランジュ方程式は存在するのだが，
解を関数で記述できない（解けない）方程式が大多数です．
系の運動を支配する法則（ニュートン力学）は明確なのに，
解が関数で記述できないのです．コンピュータによって
運動は逐一決定できますが，常識と違う予想もつかない挙動が起こる．
分岐やカオスです．このようなことを指摘したのはポアンカレでした．

・1766　オイラー「変分法の原理」
オイラー，　ラグランジュ
・1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ
・1900　ポアンカレ
可積分の方程式はごくわずか
大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．
－－－－－－
可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

力学系を記述するラグランジュ方程式は作れるのだが，これが解けるとは限らない．
物理の演習では，解けるものしか扱わなかったのです．
実際の世の中は，解を関数で記述できない（解けない）方程式が大多数．
系の運動を支配する法則（ニュートン力学の方程式）は明確なのに，
解が関数で記述できないのだ．でも，コンピュータによる数値計算により，
運動は逐一決定できる．しかも，予想もつかない挙動が起こる．
このようなことを指摘したのはポアンカレでした．

1766　オイラー「変分法の原理」
オイラー，　ラグランジュ

1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ

1900　ポアンカレ
可積分の方程式はごくわずかで，大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．

可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

分岐理論

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.10］ No.054
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回はホットなニュースです．
■錯視のシンポジウム
http://cmma.mims.meiji.ac.jp/…/jointrese…/demosillusion.html
International Symposium on Psychological vs Mathematical Approaches to Optical Illusion
が，明治大学中野キャンバスで，2015年3月4-6日に開催されました．
興味があるテーマでしたので多くのセッションを聞きたかったのですが，
私の時間の許す5日の14:00~17:20のセッションだけ参加しました．
https://www.facebook.com/sgk2014?fref=nf
注）
3月12-14日に明治大学駿河台キャンバスでサテライトミーティングがあるようです
http://www.mims.meiji.ac.jp/seminars/another/2011/20120313.html
ーーーーーーーーーーー
聴講したセッションの座長はYasushi Yamaguchi,
講演は次の3件；
Masanori Idesawa, A model for explaining tha anomalous motion illusion.
Akiyoshi Kitaoka, Color-dependent motion illusion in stationary images:
What causes illusory motion?
Stuart Anstis, Illusion of motion perception.
ーーーーーーーーーーー
会場は，明治大学中野キャンバス，5Fの新しい楕円型の階段ホール．
参加者は若者が多く４０人程度であった．この国際シンポジウムのオーガナイザーは，
Kokichi Sugihara(明治大学), Akiyoshi Kitaoka(立命館大学)です．
注）
明治大学は，2008年度，「現象数理学の形成と発展」グローバルCEOプログラムに採用された．
数学系では，東京大学，京都大学，九州大学，明治大学が採択されている．
大学院先端数理科学研究科，現象数理学専攻は2011年に開設，2013年に中野キャンバスがオープンした．
明治大学には錯視美術館（大学と少し離れた淡路町）があり，毎週土曜日だけ開館している．
博士前期課程では，学生1人に対し正副3人の指導教員が広がりを持った研究指導を行う．
後期課程では，学生の研究テーマに応じて，モデリング，シミュレーション，
数理解析の3分野から1人づつ計3人の指導教員がチームを組んで多角的な研究指導を行うという．
現象数理学は，微分方程式のモデルで定量的に記述し，コンピュータでシミュレーション．
分岐理論でなぜ違いが生じるのかを理解する．金融工学，進化ゲーム理論，錯視の仕組みなどが，
数理モデリングを通じて理解ができる．修了後の進路は，
ビッグデータを扱うIT系企業，金融機関，教員など．米国の例では，
投薬タイミングなどを分析して医師らにアドバイスする病院ポストなどまで広範である．

2006年の文科省科学技術政策研究所「忘れられた科学－数学」で
数学と他分野との共同研究実施に向けた体制整備が叫ばれた．
数学と諸科学の連携研究は，米国MAMでも盛んに報じられており，
活発化している数学の分野である．これが純粋な数学と呼べるかの疑問はさておき，
高性能のコンピュータと数値計算の発展により可能となった新しい分野である．
エネルギー散逸のない系を記述するオイラー=ラグランジュ方程式は存在するが，
その大部分は解けない（関数で書けない．非可積分という）．
学生時代に教科書で扱ったのはごく特殊なケースなのだ．
これらをコンピュータを用いて数値的に解くことになる．
安定軌道がなくカオス的で分岐が生じる現象が注目される．
同様にビッグデータを解析する統計学でもコンピュータが活躍する．
日本数学協会が，６月7日午後に予定している講演会（於大東文化大学）
「ヒトとモノづくり数学－10年目の数学月間」でも，
数学月間の経緯と並べて錯視を取り上げることになっている．
ーーーーーーーーーー
■静止画なのに動きを生じる錯視
見ているのは静止画なのに動きが出る（なぜ時間の要素が入る）のか？
と不思議に思うでしょう．見る側に原因があります．目の空間認識は，
TVのようなラスタースキャンではないが，サッケード運動，ドリフト，
中心視と周辺視の切り替わり，網膜の周期的なリセット，等々により，
これらは時間の関数だからです．私は形の認識の仕組みに興味があります．
図形の対称性を見て快いと感じるのは，単純なサッケードになるからだろうと考えていました．
そして今回，これは錯視と表裏一体の現象であると気付きました．図形の認識にかかわる
測度量で時間の関数であるものが，動きのある錯視を生む原因になるようです．
動きを生む錯視にも色々あります．北岡の回転する蛇に見るように，
黒/暗灰/白/明灰/黒/･･･の明暗のストライプで，白から黒の方向に動くように見える現象が，
色相のストライプでも起こり，周囲が明るいときと暗いときでは動く方法が逆になる．
このようなデザインは処々で活用されています．
http://www.ritsumei.ac.jp/~akitaoka/rotate.html
同じものを見ていても，全域的回転を認識するか局所的回転を認識するというように
注目現象が異なることがあります．どちらかを認識すると他方は見えないのです．
これは亜群の集合で核となる部分集合をどれに定義するかの問題と類似しています．
■青・黒ドレスの色が変わる
動きは生じない錯視の例として，青・黒の横縞のドレスが白・金の横縞に変わるのが，
このシンポジウムの紹介を兼ねて3月4日の夕方のTVニュースで取り上げられました．
youtube動画やtwitterなどで，この原因が，右脳，左脳による個人差だというような
説が流れていますがそれは嘘です．周囲の明るさに依存して変化するのです．
色相変化ではγ特性が効いています．
宮澤賢治が注文の多い料理店序文で「はたけや森の中で、ひどいぼろぼろのきものが、
いちばんすばらしいびろうどや 羅紗 や、宝石いりのきものに、
かわつているのをたびたび見ました」と言いましたが，これは錯視ではありません．
でも黄昏の光できものの模様が変わって見える錯視はあることでしょう．
フィルタリングや非線形γ特性などは，画像処理で日常使われているものですが，
これらも錯視を生む場合があります．
Stuart Anstis(University of California)は，動きを生む錯視の原理が理解できる例を
以下に掲載しています．http://anstislab.ucsd.edu/illusions/

■2重振り子（振幅の大きいとき）

微小な振幅であるならば，解析的な解があり，あまり複雑でない周期的な運動になることを前回に学習しました．
しかし，振幅が大きくなると，ラグランジュ関数 L の近似ができませんので，ラグランジュ方程式は解けません．
しかし，将来，誰かが巧妙な方法で解くのではないかと期待し，最悪そのような解析的な解は存在しないとしても，
振動範囲が小な場合と本質的に大差はないのではないかと想像するのが自然なことでした．
系のラグランジュ関数 L は全く正しいし，ラグランジュ方程式も正しいのですから，
解析的に解けないと言っても心配ないのではと思うでしょう．

しかし，実験ではとんでもない現象が見られました．
コンピュータを用いた計算が高度になり，力ずくで動きのシミュレーションがなされるようになりました．
正しい方程式は実在するのですから，関数による軌道記述は出来なくても，動きは逐一決定されるはずです．
しかし，初期条件（初期値）により，予想もつかない挙動が見られます（カオス）．

◆第１の動画は実験
スタートする初期値によって運動の様子は異なります：

◆第２の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1

■2重振り子（振幅の小さいとき）

図のような2重振り子の運動です．今回は物理演習のようになりましたが，
数式に囚われる必要はありません．重要なのは，振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので，2種類の周波数の振動が重畳
された運動になる．つまり，関数で記述できる安定な周期的な運動になる
という事です．そして，これに対比される次に話題になる振幅の大きい
2重振り子運動では，運動は関数で記述できず，予想もつかない
とんでもない運動をするということです．

◆それでは，振幅の小さいときの2重振り子の学習をしましょう．
ここでは，ラグランジュ関数やラグランジュ方程式を説明せずに用いています．
これらを学習したい方は，EMANの物理学などが参考になります．

m1の座標は

これは，Oから釣り下がる長さ l の糸と
mから釣り下がる長さ l₁ の糸の和であるからだ．

この2重振り子のラグランジュ関数Lは

Tは系全体の運動エネルギー，Uは系全体の位置エネルギー
解Φ，ψ を求めるには，次のラグランジュ方程式を解かねばならないのだが

解析的には解けない（関数で記述できる解がない）ので，
Φ，ψ の振動範囲を微小に制限して（Φ，ψの2次までを残す近似），

この近似した L=T-U を用いて，ラグランジュ方程式を解く．
これは解けるのだが物理の演習問題なので（参考）に示し，結論だけ述べる．
結論
Φ, ψ は，以下の2つの固有ベクトル（基準振動）の重畳（線形結合）で表せる．　

微小振動の範囲では，Φ，ψは，それぞれ２つの固有振動の重ね合わせであるということは，
それほど複雑な振動ではない．いずれにしろ周期的な振動である．
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
（参考）

続く⇒　振幅の大きい場合

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.03］ No.053
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
3月になりました．皆様，お元気にお過ごしでしょうか．
母が救急車で入院した1月には，硬い芽のようだった病院の梅も，
今はすっかり咲いてしまいました．白梅でした．
病院は遠方なのですが，見舞いにほぼ毎日通っています．
ここの梅の花の咲くのが見られるとは思っていませんでした．
でも，お陰様で無事に日々が過ぎています．

無限に繰り返す周期的な空間を結晶空間といいます．
このような空間を，正多面体（あるいは半正多面体）を組み合わせて，
すきまなく充填する様式を観賞しましょう．
これは立体パズルとしては難しいものですが，自然界ではめずらしくありません．
美しい鉱物結晶の構造として，結晶学の常識になっています．
空間分割の対称性，空間群の研究は，数学者ではなく
フェドロフなどの結晶学者や鉱山技師が偉大な業績を残しています．

■立方体（1種類）を積み重ねた周期空間から始めましょう．
Fig.1の4列目の最上行（右上隅）にあります．
http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16535749&no=1
（これらの図はPOV-Ray，v3.7を用いて作成しています）

1列目の図は，立方体と正8面体を重ねて表示したものです．
これらの2つの正多面体は互いに双対*の関係にあります．
（*立方体の面を頂点に，頂点を面に変えたものが正8面体）
立方体のサイズを固定して，正8面体のサイズを連続的に変化してみましょう．
第1列の上から下へ，正8面体のサイズを徐々に小さくしています．
そのとき，立方体と正8面体の共通部分として得られる半正多面体が第2列．
これら半正多面体の名前をシュレーフリ記号*で書くと，
第2列の上から順に［3,8,8］,［3,4,3,4］,［4,6,6］です．

*)記号の見方：例えば［3,8,8］は，頂点のまわりが，
正3角形，正8角形，正8角形で囲まれているという状態です

■第3列は，それぞれの多面体を2次元に配列させて作ったシート．
第3列の上段図には小さい正8面体，中段図には大きな正8面体を立てる穴が，
下段図では，正８面体ではなく同じ半正多面体［4,6,6］用の穴ができます．

■第4列に，空間を隙間なく埋め尽くす正多面体の組み合わせを示します．
第4列の最上段図は，立方体のみでできる配列．
立方体だけで隙間なく空間を充填した構造は単純格子といいます．
第２，第３の行に，正8面体の穴に正8面体を詰めて空間を充填する様式を示します．
これらも格子としては単純格子と同じです．
第４の行は，多面体［4,6,6］のみで空間を充填できることを示します．
このとき出来上がる構造は体心格子と呼ばれます．

■ペロブスカイト（CaTiO3）構造
Fig.1の下から2行目の配列構造を見てください．
正8面体と［3,4,3,4］多面体の組み合わせで，空間が充填されています．

Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/79/16539279/img_3_m?1425130572
正8面体の中心にTi原子，［3,4,3,4］多面体の中心にCa原子，
各多面体の頂点にはO原子を配置すると，ペロブスカイトの結晶構造が得られます．

余談ですが，この構造は，強誘電体や超伝導物質と係わりがありますし，
地球マントルの高密度物質の構造とも係わりがあります．

■ダイヤモンド構造
Fig.3
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_0_m?1425310851
こんどは，正8面体の稜を共通にして，平面シート状に並べます．
もちろん，正8面体だけでは空間の充填は出来ませんので，
正4面体の隙間がたくさんできます．正4面体の隙間はFig.3の緑のシートが
積み重なったようになり，頂点で８つの正4面体がつながり（シートが重なるため），
正4面体と正8面体の比率は2:1です．
空間の充填パズルはこれで正解なのですが，ついでにダイヤモンド構造を作ってみます．
Fig.4
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_1_m?1425310851
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_2_m?1425310851
正8面体（間隙）を取り囲む緑の正4面体の半分だけ使い，
各頂点で４つの正4面体がつながるようにします．
ダイヤモンドの結晶構造は， このような正4面体の配列が繰り返し，
青い正4面体の中心と頂点の位置に炭素原子を配置した構造*です．

*)正4面体の中心にある炭素原子から，4つの頂点方向に4本の結合が伸びています．
正四面体のどの頂点も4つの正4面体と規則正しくつながつているので，
正4面体の頂点の炭素原子からは，周りの４つの正4面体の中心にある炭素原子に向かって，
同様に4本の結合が伸びています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.24］ No.052
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
球表面を平面に投影するステレオ投影
地球儀を2次元平面の地図に

■性質1:　円は円として写像される
ステレオ投影というのは，球表面の点 Z(ξ，η，ζ)を，
北極 Nと結んで，南極 Sでの接平面 Π上の点 z=x+iyに投影することです．
N(0,0,1)，S(0,0,0)を直径とする球面の式は，ξ^2＋η^2+ζ^2=ζ　であり，
この球面はリーマン球と呼ばれます．
Z(ξ，η，ζ)は, (0,0,1）と（x,y,0）を結ぶ直線上にあるので，
ξ=x(1-ζ), η=y(1-ζ), これらを球の式に代入すると，ζ＝r^2/(1+r^2）となる.
ただし， r^2=x^2+y^2 である．　まとめると；
ξ＝x/(1+r^2) ，η＝y/(1+r^2)，ζ＝r^2/(1+r^2）
逆に解くと，x=ξ/(1-ζ)，y=η/(1-ζ)，r^2＝ζ(1+r^2）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_2_m?1424438241
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_3_m?1424438241

平面上の任意の円の方程式は　a(x^2+y^2)+bx+cy+d=0　である．
この円の方程式の x, yに，上記の表式を代入し，
ξ^2+μ^2＝ζ(1-ζ)を用い整理すると
(a-d)ζ+bξ+cη+d=0　が得られる．
この１次式は平面を表し，球表面との交線は円となる．従って，
「平面上の円は球面上の円から投影され」この逆も成立することがわかる．
以上で証明は終わりですが，直観的な説明を補足します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_4_m?1424438241

リーマン球上の円は平面Ωで球を切った切り口で，PQはこの円の直径です．
△NPQおよび△Nqpは，直径NSを含み，円の直径PQおよびpqを含む平面です．
図に示すように両三角形でα，βは互いに等しく，両三角形は互いに相似です．
PQを直径とする円に相似な円が，平面Π上にqpを直径として投影されるでしょう．

■性質2:　ステレオ投影は等角写像
複素関数 f が，複素平面領域 D のあらゆる点で微分可能*なら，Dで正則といいます．
*微分可能とは，どの方向からその点に近づいても同一の微分係数が確定することで，
微分係数が０や∞になる点は特異点といいます．
正則関数による写像は等角写像*です．
*写像された像が歪んでも，微小部分の角度は元の像の角度と変わらない．
ステレオ投影(複素平面からリーマン球面への写像 f )は，正則関数なので，
任意の点z0で交差する曲線の投影結果も，
それらの交差角度が保存されたまま投影されます（等角写像）．
（f(z1)-f(z0))/(f(z2)-f(z0))=(df/dz)(z1-z0)/(df/dz)(z2-z0)=(z1-z0)/(z2-z0)
ただし，z1,z2→z0 で成立．
lim arg(f(z1)-f(z2))=lim arg(z1-z2))
偏角について成立するこの式は，微小領域で写像による角度が保存されることを示す．
Fig.1に示した横倒しの地球儀のステレオ投影の様子を見ると
平面に投影した地球の下側半分の子午線は，大変歪んでいるが
互いに直交している状態は変わっていないことがわかる．

■諸科学への応用
等角写像は工学の色々な分野で利用されている．
色々な境界条件に合うようにする等角写像は，流体力学で活躍している．
何度でも微分可能であるという複素関数の性質も
我々の身の回りの現象を記述する方程式で頻繁に利用されている．

ご感想やコメントなど，以下のブログあるいはメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.17］ No.051
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号に引き続き双曲面分割の話です．

■エッシャーの「極限としての円」のシリーズが生まれるまで

コクセターとエッシャーは1951年の国際数学会で出会いました．
1958年にコクセターはこの分割を掲載した論文をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_0_m?1423875894

エッシャーの双曲面分割作品のシリーズ１は直線魚のモチーフでした，
天使と悪魔など，このシリーズの作品群があります．
そして，シリーズ3の洗練された作品に至り完成します．

■次に示すのは，エッシャーの作品「極限としての円3」です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_1_m?1423875894

白い線で分割されたタイル張りは，複数の正多角形による準正則タイル張り
[4,3,4,3,4,3]のように思うかもしれません．
しかし，白い線は直線ではないのです．白い線は，双曲世界のフチの円周と
直交しません（80°で交わる）．実は，右図に示される黒い線が直線です．
右図のように正8角形のタイルが頂点で３つづつ集まる正則分割{8,3}と
見るのが正しいのです．エッシャーの作品は，黒い線は顕に出さずに
白い線を見せて見事に数学的に正確で芸術的な作品に仕上げています．
このエッシャーのトリックについては，コクセターが論文で指摘しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.10］ No.050
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユークリッド幾何，楕円幾何，双曲幾何
色々な幾何空間があります．大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．これら3種を，平面を例にとり比較します．
（１）我々の常識の通用するのはユークリッド平面です．
ご存知のように，ユークリッド平面では，直線外の1点を通る平行線は唯一本だけ引けます．
（２）球の表面は楕円幾何平面の例です．地球の表面だけを想像しましょう．
地球自体は，3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面の例です．
楕円幾何平面の直線は大円（球の中心を含む平面による球の切り口）です．地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，これは地球の大円上の線分のことです．地球は3次元ユークリッド空間の物体ですから，地表の2点を地球内部を通る直線で結べば最短距離でありますが，地表だけの2次元平面では大圏コースが最短です．球表面の異なる２つの大円は必ず2点（直径の両端）で交わります．そのため楕円幾何平面では．平行線はありません．また，地球儀の緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面では，ある直線に対する直線外の1点を通る平行線は無数に引けます．双曲幾何平面は楕円幾何平面のように閉じていないので，イメージを持ちにくいのですが，ポアンカレがうまいモデルを提唱しました．このモデルはポアンカレの円盤モデルといいます．双曲幾何の世界を表すのに円盤を用い，この世界の直線は円盤のフチに直交する円弧とします．このように定義された世界では，ある直線に対する直線外の1点を通る平行線は無数に引けることがわかります．

■3種の幾何平面で，平面の正則分割を考える
さてこれからやることは，それぞれの幾何平面で，正多角形のタイルによるタイル張りを考えることです．このような問題は，平面の正則分割とも呼ばれます．
それぞれの幾何平面での多角形は，それぞれの幾何平面の定義による直線で囲まれているものです．それぞれの幾何平面で，3角形の内角の和Sは，S=π（ユークリッド平面），S>π（楕円平面），S<π（双曲平面）になります．
正p角形が頂点でq個集まってタイル張りがなされている状態{p, q}で，正p角形の内角の和を表す式を等号で置くと　(2π/q)p=(p-2)S　が成り立つので，
1/p+1/q=1/2　（ユークリッド幾何）
1/p+1/q>1/2　（楕円幾何）　
1/p+1/q<1/2　（双曲幾何）
となります．それぞれの幾何平面で，許される{p,q}の整数解を求めると，以下のことがわかります．
（１）ユークリッド平面での正多角形によるタイル張りは，正3角形，正4角形，正6角形で可能．｛3,6｝．｛4,4｝，{6,3}が解です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_0_m?1423315106
（２）楕円幾何の平面では，正6角形以上の正多角ではタイル張りができません（閉じた立体になりません）．
調べてみると，正5角形のタイルでは，頂点に3つのタイルが集まるもの{5,3}，正4角形のタイルでは，頂点に3つ集まるもの{4,3}，正3角形のタイルでは，頂点に5つ{3,5}，４つ{3,4}，３つ集まるもの{3,3}が作れます．結局，5種類の正多角形によるタイル張りがあり，これらはプラトンの正多角形に対応した球面立体です．ここでは｛5,3｝に対応するもののみ掲載します．黄色い球面正5角形が頂点で3つ集まっているものです．黄色いタイルに5mの対称性があるとき，赤で塗った三角形を中心から見込むような万華鏡を作るとこの映像が再現できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_1_m?1423315106
（３）双曲幾何の平面では，正則分割は無限にあります．
例として｛6,4｝と{5,4}のものをとりあげ掲載しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_3_m?1423315106
例えば，{6,4}の映像を3角形の万華鏡で作るには，
下図の中心に頂点のある三角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧の鏡を使います．しかしながら，この円弧は数学的に反転円として定義されているのですが，現実の光学法則では火線という収差があるので，あまり奇麗な万華鏡映像にはなりません
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_4_m?1423315106

■円盤の中の不思議な世界
私たちの宇宙は膨張していることが知られています．
遠方の宇宙のフチの後退速度はものすごく，光速に達すると，
こちらに光はやって来ません，そこが宇宙の果です．
宇宙銀河の回転速度は，宇宙のフチに行くほど大きく
高速で運動する世界の長さは，我々から見ると縮んで見えます
つまり，宇宙は双曲幾何の世界に似ています．
双曲幾何の円盤の内では，円盤のフチに近づくほど空間が縮みます．
この世界では，直線に沿って旅する自分自身もフチに行くほど縮むので
いつまで歩いても世界の果てに到達できません．
同様に，円盤の中心に近いほど距離が大きくはかどるので，
円盤の外から見ている我々には，直線が円盤の中心方向に膨らんで見えます．
一方，円盤内の世界にいる者にとってはこれが最短距離で直線なのです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.03］ No.049
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１種類の形（2等辺3角形）の赤色と黄色のタイル（赤タイルと黄タイルは互いに鏡像）
で作ったタイル張り模様を鑑賞しましょう．
1種類のタイルで，平面をタイル張りすると，必ず周期的なタイル張りになってしまう
と思い込むのは間違っています．確かに，
Fig.4　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_5_m?1422741853　や
Fig.5　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_6_m?1422741853
のような周期的なタイリングはすぐ思いつきます．
しかし，
Fig.2　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_1_m?1422741853　や
Fig.3　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_2_m?1422741853
のように非周期なもので，平面をタイル張りするものがあります．
Fig.2は中心に回転対称があるタイリング模様で，点群5mの対称性です．
Fig.3は，２つの目がある螺旋パターンのタイリングで，
水平線は映進面だと思うかもしれませんが，このパターンには周期がありませんから
映進操作はできません．螺旋の目の間（中心）に対称心があります．

さて，ここで万華鏡で作られるタイリング模様
Fig.1　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_0_m?1422741853
の登場です．
この万華鏡を生む3枚の鏡は１つの頂点では点群を生成しますが，他の２つの頂点では点群を生成しません．
従って平面を赤と黄色の市松模様で埋めることはありません．
全体の代数系は，群より緩いもの（特殊な亜群）になってしまいますから非常に複雑です．
対称操作は局所的で，独自の作用域と値域があり興味深いものです．
作用域，値域の制限のために，一つのタイル全体が無傷で写像されるパターン内の位置と，
部分が写像される位置があり，このような複雑なタイリング模様ができます．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊
ご感想コメントなどを，
http://blogs.yahoo.co.jp/tanidr/16430597.html　あるいは　以下のメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.01.27］ No.048
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１．万華鏡の美しさが我々の心をとらえる理由は，対称性とカオスの共存
完全な秩序は美しいが，死の世界のようだ．
一方，乱れは千変万化し同じ光景を見るのは一度きり．
そして現象は，いつ起こるかわからない．だから
我々は，はらはらしながら期待し目が離せない．
万華鏡は，秩序の中に乱れもある．生命も，秩序とカオスのただ中にある．
万華鏡の中を降りゆくガラス屑　定まると見し運命にカオスあり

２．対称性
それでは，まず対称性についての考察を始めようと思います．
対称性は自ずと決まるものとして，あるいは合理的なデザインとして生まれます．
環境や境界条件，自然科学の法則が，
その環境下の物質構造やふるまい/現象の対称性を自ずと決定する．
（例）人体，生物，乗り物，結晶，自己組織化，建築物．蜂の巣，花弁の形，柱状節理，etc．
■空間に関する対称性（１点の周りの対称性と周期）
タイル張り，壁紙模様，正多面体，結晶構造，エッシャーの版画．
■時間に関する対称性
時間反転．音楽（J.S.バッハ），詩の韻律，リズム，同期現象．
■現象の対称性
性質空間の対称性．因果律の対称性．

３．対称性はなぜ快いか？
インクの染みは汚らしいが，乾かないうちに紙を折り鏡映対称の染みになると美しく見える．
そしてなんだか想像力を駆きたてる（ロールシャッハ・テスト）．なぜ美しく感じるのだろうか．
私はその理由は次のようなものではないかと思っている：
物や事に対称性があると，我々の脳がその全貌を把握するための情報量が圧倒的に減る．
例えば，結晶とアモルファス（ガラス）で，それらの構造（構成する原子の位置）を
記述しようとすると，規則的な繰り返しのある結晶の方が圧倒的に単純だ．
人間の脳は，整理された少ない情報量だと負担が少なく，快いと感じるのではないだろうか．

４．鏡
万華鏡の話がテーマなのだが，ご存知のように万華鏡は合わせ鏡でできている．
万華鏡の対称性は，鏡映のみにより生成されたものに限ります．
我々は鏡をのぞきこむと何か変な気持がするものだが，以下のような話があります：
太古の時代は，我々の世界と鏡の中の世界の行き来ができたそうだ．＊

＊注）このようなことは4次元の世界なら実際に可能である．例えば，3次元空間で
右の手と左の手は，互いに鏡像になっている．右手が我々の世界にあり，
左手が鏡の世界にあると想像してみよう．左手が鏡の世界を抜け出して
我々の世界のなかで，右手と重なろうとしてもできない相談だ．
ただし，4次元空間なら左手の中身を裏返して，右手と同じにすることができる．
2次元の紙に描いた線画の右手と左手が，いくら紙表面の上で移動しても
ひったり重なることはできないが，紙を折り返す（3次元空間での操作）ならば
重ねることができることは実験で確かめられる．

話を戻すと，鏡の中の生き物とこちらの世界の生き物は仲良く一緒にいたのだそうだ．
ある夜，突然，鏡の世界の住人達が我々の世界で好き勝手を始めるようになった．
そして人々は，鏡の中の住人の正体が「混沌」であることに気付いたという．
そこで，黄帝が魔力によって「混沌」を鏡の世界に閉じ込め，
姿や動きも我々の世界の模倣しかできないようにした．*1)
呪文の効果が切れて，鏡の世界の住人達が勝手に動き出すことが将来起こるかも知れない．
そのようなテーマの小説に*2,3)がある．私は幻想怪奇小説が大好きです．

*1)Turbulent mirror, J Briggs & F. D. Peat, 訳：高安秀樹，高安美佐子
*2)パイプをすう男，M･アームストロング，幻想と怪奇 1（ハヤカワ）
*3)わな，Ｈ・Ｓ・ホワイトヘッド，怪奇幻想の文学(新人物往来社)

混沌の中から湧き出るように次々と生まれてきたさまざまなものが宇宙を形作った．
このようなプロセスを神の技と語られることもあります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.30］ No.044
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年もあと2日になりました．私は部屋の大整理掃除で3日間も満足にパソコンを開けません．
皆様には，よい年末でありますように．そして良い年をお迎えください．来年もよろしく．

クバンチックの問題は如何でした．私が一番好きなのは，第2問のビリヤードの問題です．
この問題に関する連想考察は，近いうちにぜひ書きたいと思っています．

さて，私は毎年「とっとりサイエンスワールド」で万華鏡のワークショップをやらせてもらっています．
正月まもなく（1月16日，PM3～）多摩センターでも開催しますので，お近くの方はご参加下さい．
詳細は，sgktani@gmail.com　にお問い合わせください．
これからメルマガでも，万華鏡の数学について何回か連載するつもりです．
ここで紹介する万華鏡のキットは，「その道の達人派遣事業」の時に開発し，
各地の学校を回り子供たちと作った万華鏡（当時は2種類）がもとで，
その後品種を増やしてできたものです．
-----
◆万華鏡の原理（１）
万華鏡は合わせ鏡の原理を使っていることはご存知ですね．fig1を見てください．
平行な合わせ鏡で挟まれた室（黄色）は1次元に無限に繰り返しています．
室内にある赤い物体もfig1に示したように繰り返します．
黄色い部屋の隣はその鏡像（左右が逆）．合わせ鏡で挟まれた黄色い部屋を（黒），
隣の鏡像の部屋を（白）と思うと，黒白の帯（1次元の市松模様）ができますね．
今度は，合わせ鏡のなす角度を平行でなくθ°とすると，
市松模様の帯は直線ではなく円を描くように延びて行きます．
円の反対側で市松模様がうまくつながるためには，
黒白のペアの数が整数でなければならない．
これは360°/2θ°＝n（整数）となります．これは，万華鏡の発明者
スコットランドの物理学者ブリュースターが1817年に提出した特許にあります．

FIg.1
以上の説明は2枚鏡の合わせ鏡でしたが，複数鏡の合わせ鏡でもできます．
3枚鏡の場合を考察しましょう．fig2には鏡が作る3角形の図です．
3角形の頂点で2枚の鏡が出会うわけですが，それぞれの頂点で，鏡のなす角度は
360°を偶数で割り切る角度である必要があります．3角形の３つの頂点で
この条件が満たされているなら3角形のタイルで平面が市松模様に張り尽くされます．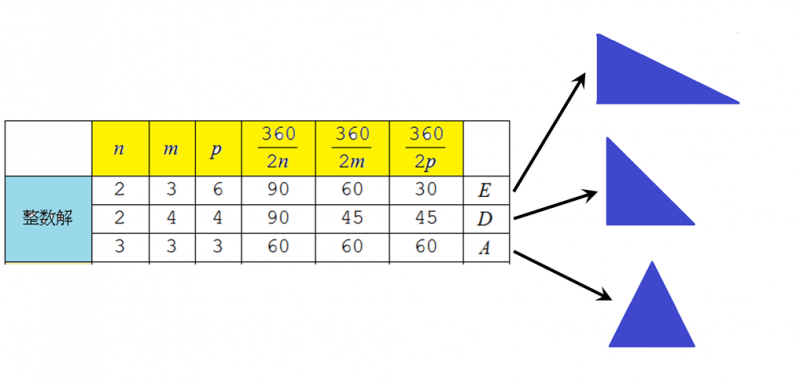

Fig.2
3つのどの頂点でも整数解を持つ場合は，平面をきれいに埋め尽くす市松模様ができます（3種類あります）．
1つの頂点でも整数解にならない場合には，市松模様は乱れますが，これも万華鏡としては美しいものです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.23］ No.043
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
«Квантик»クバンチク（量子っこ）というロシアの生徒向けの雑誌を知りました．
http://kvantik.org/
数学，言語学，物理学などの自然科学の疑問や問題を楽しく学ぶ新雑誌のようです．
onlineでは12ページまでしか出ていないので，その先は購入しなければなりません．
クバンチクで現在出題されている「4つの課題」を紹介します．
出来た人は解答を　kvantik@mccme.ru.　に送ると独創的な解答は公開されます．
面白い問題で私は出来ましたよ．問題もさることながら，
ロシア語の題意を解釈するのに時間がかかってしまいました．
翻訳を載せておきますのでご挑戦ください．

（第1問）監獄からの脱出
T字型の監獄で．2m幅の堀で囲まれている．1.9mの板が2枚ある．
ジャンプは出来ない．どのように脱出するか？
（第2問）ビリヤード
1:2のテーブルの真ん中の位置に球を置いて，テーブルの角のポケット
にビリヤードで（反射させて）玉を入れることは可能か？
（第3問）如何にしてビンをぶら下げるか
2本のマッチと50cmの糸がある．
これらを用いて水入りのビンを棚の縁（角ではない）にぶら下げなさい．
（第4問）物体の警護
物体点のまわりに，哨兵を何人か配置し，
物体にも哨兵にもこっそり近寄られることの無いようにすることはできるか？
ただし，各哨兵は，選んだ一つの方向だけまっすぐに100ｍだけ見ることができる．

解答は載せません．以下は，私からのヒントですーーー
１．Tという形がポイントです．
２．可能です．
３．マッチ2本をどう利用しますか
４．哨兵3人で済みますね．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.16］ No.042
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
パターンがどんどん内部に繰り込まれて行くデザインのいくつかを紹介します．
これらはフラクタルと呼ばれる性質と関係があります．
葛飾北斎（１８３０年代前半）の富嶽36景，神奈川沖の絵の
波しぶきを見たことがおありでしょう．あるいはこの季節の
すっかり葉を落とした木立の先が美しく枝分かれしていたり
雲や海岸線の輪郭が，拡大しても拡大しても同じような
形が現れてくるのにお気づきでしょう．
同じ形が繰り返し内部に繰り込まれているような仕組みを
フラクタルと言います．
フラクタルの詳しい説明は後回しにして
今回は応用されたデザインの例を鑑賞しましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_0_m?1418046938
グラスのこちら側の円が凹レンズになり，向こう側の円模様を
レンズ円内に縮小して映し出しているのが面白い．
（リュミナルク製）

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_2_m?1418046938
五芒星と黄金比　外部と内部の比(1+√5)/2＝1.618:1

http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16306916&no=1
レオナルドの星型8角形　外部と内部の比1+√2：1

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.09］ No.041
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆皆様，お元気でお過ごしでしょうか．選挙が迫り慌ただしい日々ですね．
大事な選挙です．私はもう期日前投票を済ませましたよ．
先週土曜日には，河合弘之弁護士の作ったドキュメンタリー「日本と原発」を
見てきました．皆様の近所でも有料試写会（自主上映）がきっとありますので，
ぜひご覧になることをお勧めします．
「原発は複雑系なので，事故が雪崩を起こす弱点（ここを攻撃されると過酷事故になる）
が思わぬところにある．その引き金となるのは，地震・津波だけではない」と，
メルマガ006に掲載したことがあります．ぜひお読みください．
バックナンバーはブログにもあります．私は，原発だけは止めたいと思っています．
高木仁三郎さんと「宮沢賢治をめぐる冒険」でお話したとき（1997年）のことが
昨日のように思い出されます．この本は，市民科学者として活躍した高木仁三郎さんが
羅須地人協会に打ち込んだ賢治と重なって見える良書です．
これら数学以外のことは，ブログの方に掲載することにしましょう．
ーーーーー

◆双曲幾何の円盤世界
Fig.1の灰色の円盤内の世界は，双曲幾何の世界です．
この世界の直線は，世界の果て（外周円）に直交する円弧
－例えば，Fig.1の赤い円－です．もちろん直径のような本当の直線も
灰色世界の円盤の外周円に直交しますのでこの世界の直線です．

赤い円で2分された灰色世界の左側と右側は
赤い円を反転円として，互いに反転鏡映像になっています．
Fig.1　
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_1_m?1418046545

2つの平面鏡と１つの円柱鏡で作られる万華鏡（Fig.2）を見てください．
赤く塗った3角形の各辺は，この円盤世界の直線です．
赤く塗った3角形の頂角は，30°－45°－90°．内角の和は165°で180°に
足りませんが，この円盤内の世界は双曲幾何の世界なので当然です．

赤く塗った3角形の辺を紙面に垂直な方向に伸ばした3角柱を考えると
平面2枚と円柱鏡からなる万華鏡ができます．
円柱鏡が生む映像は数学的な反転鏡映像としますと
Fig.2のような円盤内の分割（ポアンカレ万華鏡像）が得られます．
塗られた3角形と白い3角形は鏡映の度に入れ替わるので市松模様です．
Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_0_m?1418046545

実際に作ってみました．ポアンカレ万華鏡を再現するのは困難です．
円柱鏡での光の反射（物理的）は，数学的な反転操作とは異なり
厳密な数学的な反転鏡映は，光学的には実現できないのが残念です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.02］ No.040
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先に，「007_インドラの網と反転円」で言及したことがありますが，
円による反転鏡映について，その性質や利用例を鑑賞しましょう．

◆円による反転鏡映の性質
下図に赤い円による反転鏡映の代表的な例を２つ示します．
・反転円をよぎる直線aを反転すると，反転円の中心を通る円Aになる．
・円bを反転すると，円Bになる．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_0_m?1417183249

この性質を知っていると，色々なことに利用できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_3_m?1417183249
例えば，このような図形はアルベロス（靴屋のナイフ）
といいますが，この中の幾何学世界の面白さなどです．

下図のアポロニウスの窓の中にある黄色の円とピンクの円は，
緑色の円を反転円として，それぞれ反転円内の黄色とピンクの円が
鏡映像になります．これらの鏡映像は平行な直線（黒）に挟まれた
領域内に入ります．
平行直線の左はアポロニウスの窓の外周円の反転鏡映，
平行直線の右はアポロニウスの窓内にある左側の大きな円（灰）の
反転鏡映像です．なぜなら，外周円も左側の大きな円（灰）も
反転円の中心を通っているので，鏡映像はどちらも直線になるからです．
アポロニウスの窓内にある初めの黄色い円もピンクの円も，外周円と
内部の左側の大きな円（灰色）に接しているので，
それらの反転鏡映像でもそのような状態が保たれています．

このようなことがわかると，以下のパップスの定理が導かれます．
アルベロスの中で，右側の大きなピンクの円の上に生じる
黄色の円（ω1），続いて生じる灰色の円（ω2），の系列を考えると，
「円ωnの中心と直径ABとの距離は円ωnの直径のn倍である」
（パップスの定理）ことがわかります
以下の図は，ω2の場合の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_2_m?1417183249
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_1_m?1417183249

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.25］ No.039
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆平面のブラベー格子は５つのタイプがあることを036号で学びました．
ここに示す繰り返し模様のそれぞれは，どの格子に対応しますか？
日本の伝統文様には，美しい繰り返し模様がいろいろあり，それらは
着物や食器，籠バック，インテリアなどと色々な所で見られます．
これらの模様には，どのような対称性があるかを鑑賞しましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_3?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_4?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_5?1414573530

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.18］ No.038
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆正3角形の対称性
正3角形は，中心に回転軸を立て右回りに120°回転しても，
始めの状態と全く同じで，回転したかどうかわかりません．
この回転を続けて２回行い240°の回転になっても同様です．
120°の回転を3回続けて行うと1回転して始めの状態に戻ります．
つまり，正3角形には3回回転対称があります．
このような回転軸を3回軸といい，記号は3と書きます．
その他に，正3角形は鏡映対称があります．図に示した赤い線が鏡映面です．
ここにある3枚の鏡映面は3回軸の作用で互いに移り変われるわけで，
全部同じ性質です．従って，正3角形の対称性は，3回軸と1種類の鏡映面があり，記号では3mと書きます．
◆正4角形の対称性
正3角形の場合と同様に，こんどは中心に4回回転軸があります．記号は４です．
正4角形を見ると鏡映面が4枚あることがわかります．図で赤線で描いた2枚と
オレンジ線で描いた2枚です．4回軸によって，赤い鏡映面どうしは互いに移り変われるし，
オレンジ鏡映面どうしも移り変われますが，赤とオレンジの鏡映面は，互いに移り変わることができません．
従って，今度は2種類の鏡映面があることになります．正4角形の対称性は，記号で4mmと書くことに注意してください．
◆同様に，正5角形，正6角形の場合は，図のようになることを各自確かめてください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/42/16226942/img_0?1414074741

◆対称図形の重ね合わせ
正3角形の部品を複数重ね合わせると，一般に，全体の対称性は低下するが
配置の仕方により全体の対称性が上昇することもある．
このようなことをとり上げている本は見かけませんが，とても面白い現象です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/01/16227001/img_0?1414076174

◆対称性の重畳
正6角形は正3角形の対称性を含んでいますから，
正6角形と正3角形を鏡映面が共通になるよう重ね合わせる（下左）と正3角形の対称性が残ります．
正3角形と正6角形の回転軸をそろえて，鏡映面が共通でないように重畳すると，
結果は3回回転対称だけが残ります（上左）
他の図も同様ですので，各自確認ください．正6角形と正5角形の重畳の場合は，
6回回転対称と5回回転対称に含まれる下位の対称性（共通な部分群）はないので，
鏡映面の一致がなければ，対称性はなにも残りません（上右）．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/01/16227001/img_1?1414076174

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.11］ No.037
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆ことしは結晶学の生誕100年にあたります
結晶にX線ビ－ムを照てると，
結晶がブロック積みのような周期的な構造なら回折が起こります．
（結晶内部の繰り返し構造の周期と，X線の波長が好都合なことに同程度だったのです）
そう考えたのはラウエでしたのでこの実験をラウエの実験と言います（1912年）．
X線がレントゲンにより発見（1895年）されて間もない頃でした．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/23/16237223/img_0?1414563100

結果として得られたラウエの回折像には，その原因になった結晶内部の対称性が反映されているべきです．
これは「キューリーの原理」という因果律です．
回折像を撮影して，小さくて目に見えない（~nm）結晶の内部構造の解析をしたのがブラック親子（1913年）です．
レントゲン(1901)，ラウエ(1914)，ブラック(1915)，それぞれノーベル賞をもらっています．

◆結晶世界はデジタル
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/60/16237160/img_0?1414501713
大小いろいろな結晶がありますが，写真は全部，水晶の結晶です．
結晶個体は，いろいろな種類の結晶面で囲まれており，
その結晶面の大きさも結晶個体により様々です．
しかし，同じ組み合わせの結晶面どうしのなす角度は
どの結晶個体で測っても，同じになります．
例えば，黄色い面と青い面のなす角度は（各面に立てた垂線のなす角のこと）
どの結晶で測っても同じになります．⇒面角一定の法則（1772）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/60/16237160/img_1?1414501713
アウイ（1783）は，
「結晶は小さな単位胞がブロック細工のように積み重なって出来ている」
と考えました．→すなわち，結晶世界はデジタルな空間です！
それなら，現れる結晶面(上図の青い線)は格子点を載せている面なので，
面の傾きは有理数になります．→有理指数の法則（1783）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.04］ No.036
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆平面のデジタル化
写真フィルムは連続な平面ですが，デジカメの感光面は半導体のドットが並んでいます．
人間の網膜も視細胞が配列しているデジタル化された平面です．
最近の交通信号は円の中に発光ダイオードのドットが配列しています．
これらが平面のデジタル化の例です．結晶も原子や分子が詰まった単位ブロック（胞）があり，
これがきちんと積み重なりできている周期的な構造で，デジタル化された空間の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_0?1414413690

◆平面のデジタル化の様式
無限に広がる平面の何処も均一なようにデジタル化する（ドットを配列する）なら，
規則正しく周期的な構造になります．交通信号の円内は均一なデジタル化はできません．
平面のデジタル化は対称性の観点からどのように分類できるでしょうか？
結晶学でブラベ格子というものはデジタル化様式の分類にほかなりません．
そもそも結晶空間とはデジタル化された空間のことです．
（注）周期的なドットの配列は「格子」と呼ばれます．
格子の様式分類は，研究した人の名前をつけて「ブラベー格子」と呼ばれます．
2次元の「ブラベー格子」は5種類あることをこれから説明します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_3?1414413690

まずは，1次元の周期
2次元の周期は２つのベクトルの組み合わせでできる．
対称性から分類するとこれらの５つのタイップがある．

これらから格子を作ったものが以下の図です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_4?1414413690

上図に示した緑色のタイルは「W-S（ウイグナー・ザイツ）胞」といいます．
このタイルを赤い格子点に配置すると平面がタイル張りされることを確かめましょう．
さて，これらの周期的平面は，格子点（周期的な平行移動で生じる点）
をすべて同値と考えると，１つのタイルの中に引き戻せます．
以下の図には，それぞれのタイルの対称要素を記入しておきました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_8?1414413690
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_7?1414413690
上図左は，タイルの対称性が一目瞭然のW-S胞．右は，単位胞タイルです．
（注）単位胞の図を見るとわかるように，これらの５つはすべて単位胞に格子点が1つ含まれる1格子点胞です．
上段右の菱形胞を用いずに，面心型の2格子点胞を用いるのが慣例となっていることを申し添えます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.28］ No.035
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年の「数学月間懇話会」で松原望さんから「民力指数」についての
講演がありました．指数といえば「消費者物価指数」などが有名です．
数学で指数というのは桁（比率）の表現なので，例えば，基準年の物価
に対して何倍の変化があったかという「消費者物価指数」を，
指数というのは適当でありましょう．

しかし，「民力指数」の指数の意味はこれとは違うようです．
地域の「民力指数」とは，正の数値（スカラー）で，その地域の
生産・消費・文化，および，人口などの基本指標の関数として
（26種の経済統計量の関数として）定義されます．
これは朝日新聞が30年以上前に発案した定義だそうです．

地域の「民力指数」は，地域の経済活動力の表現になります．
都道府県に対する「民力指数」は全国を1,000に，市町村に対する
「民力指数」は全国を100,000になるように規格化します．

「民力指数」は数学的には測度であるので加法的であることが
松原さんの講演で指摘されました．
地域Aと地域Bの合併の「民力指数」の試算も合理性があり
色々な利用が期待できます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.21］ No.034
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆黄鉄鉱の結晶粒の外形には，多面体がいろいろ現れることを，
028号で述べました．整理すると下図のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_0?1413100917

さて，この図の中に正12面体や正20面体の外形が見られるようですが,
結晶（周期的な内部構造をもつ）では，5回対称軸は存在できず,
5回対称のある正12面体や正20面体は外形にも生じないはずです．
詳しく調べてみると，黄鉄鉱の正12面体のような5角12面体は，
(2,1,0)面で囲まれているようです．→◆ミラー指数
両者の多面体で二面角の比較をしてみましょう：
－－－－－－－－－－－－－－－－－－－－－
黄鉄鉱　　 　126.89°　(2回軸を挟む二面角）
正12面体　　116.57°
ーーーーーーーーーーーーーーーーーーーーー
黄鉄鉱の外形（5角12面体）は正12面体ではありません．

◆ミラー指数
ミラー指数とは面の傾きの表示です．
下図のブロックのサイズは，x,y,z各１単位
（x,y,zの各単位は等しくなくても良く，斜交軸でもかまいません）
例えば，(2,1,0)面の，x軸，y軸，z軸との切片は，1/2，1，∞です．
切片の逆数の比をとると，ミラー指数　2,1,0　が得られます．

結晶は単位ブロックが積み重さなった周期的な世界です．
周期的な世界（格子点が並んだデジタル世界）の格子点を載せた
面の傾きは有理数ですから，すべての結晶面のミラー指数は整数となります．
http://sgk2005.sakura.ne.jp/htdocs/?action=common_download_main&upload_id=88

周期的な世界に5回対称軸は存在できませんので
結晶（周期的な内部構造を持つ）は，正20面体の外形になることはできません．
（注）“準結晶”には5回対称がありますが，周期的な世界ではありません．
◆黄鉄鉱の6面体，5角12面体と準結晶（正12面体）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_1?1413100917
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_2?1413100917
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_3?1413100917

◆柘榴石garnetも立方晶系の結晶構造ですので
外形もさいころのような対称性を示します．
菱形12面体~24面体（これらは正多面体や半正多面体ではありません）
の晶系の変化があります．
http://www.museum.tokushima-ec.ed.jp/bb/chigaku/minerals/img/2-32.jpg

写真はwebで拾った岩手県和賀仙人鉱山産の柘榴石結晶です
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/36/16196636/img_0?1413101685

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.14］ No.033
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
大阪大学理学部数学教室は，
現代数学の様相と数学研究の実際，自然科学や社会科学に及ぼす数学の影響，
文化としての数学の在り方などについて，多角的な視点から易しく解説する公開講座を，
高校生を対象に夏休みのこの時期に開催しています（ オープンキャンパスも同日実施されます）．
まさに数学月間の模範になるイベントで，毎年，杉田洋教授より情報を頂きSGKのwebに掲載しています．
今年のテーマは，“多面体の不思議”でした．
2014年8月12日（火），10:00～12:00
会場：大阪大学豊中キャンパス　理学研究科 D棟 D307教室
講師：村井 聡（情報科学研究科情報基礎数学専攻　准教授）
毎年，興味深いテーマが選ばれ，私も参加したいと思いつつまだ参加できずにおります．
今回のイベントでは受講生が殺到し,準備した教室に定員の2倍近い人（約100人）が
集まり，来年は教室の選択を考える必要がありそうと伺っております．
（以下は私の勝手な解説ですみません）．
-----
多面体はとても古くから考えらてきた図形で、紀元前のギリシャ時代には既にその性質が調べられていました．
多面体で基本的な定理は，オイラーの定理V+F-E=2（３次元）が有名です．
これを使うとプラトンの正多面体（凸多面体）が５つというのがすぐ証明できます．
正多面体というのは，面が１種類の正多面体でできており，どの頂点のまわりの状態も同一なものです．
正多面体の記述は，定義の本質を捉えているシュレーフリの記号を用います．
正p角形が頂点にq個集まっている（同じことだが辺がq個集まっている）状態は，{p,q}と記述されます．
３次元の多面体は，面が３個以上集まらないと作れませんし，面が正３角形の場合には，
６個集まると平面になってしまいますので，正3角形の面をもつ凸多面体は，{3,q}，q=3,4,5しかありません．
q=3の場合は正4面体，q=4の場合は正８面体，q=5の場合は正20面体です．

全ての面が合同な正3角形であるが正多面体でないものまで数えると8種類になり
これらをまとめてデルタ多面体と呼びます．
1種類で空間を隙間なく充填できる正多面体は立方体だけですが，
2種類の組み合わせで空間を充填できる正多面体は，正4面体と正8面体です．
結晶学では良く知られていることですが，面心格子と体心格子というのも立方体と同じ対称性を持ち，
それぞれのウイグナー-ザイツ胞（デリクレ胞とも言う）は，それぞれ菱形12面体，切頂正8面体になります．
数学と諸科学［科学や造形］の関わり合いで現れる多面体の性質は，非常に興味を惹く話題です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.07］ No.032
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
「化学の日」10月23日は，化学4団体（日本化学会，化学工学会，日本化学工業協会，新化学技術推進協会）が
昨年制定しました．その日を含む月曜日から日曜日までの1週間が「化学週間」です．
もちろんこれはアボガドロ数6.02×10^23に因んでいます．
これも米国が先でNational Mole Foundationが10月23日をMole Dayと定め，
10月23日6時02分にイベントを行うなど色々な活動が盛んだそうです．

日本の「化学の日」初年度の今年は産官学一体となって，化学の普及活動が国民亭イベントとなるように
呼びかけています．我々の「数学月間」もこのような取り組みが必要で，「化学の日」の経緯は手本になります．

*****以下は，化学と工業,Vol67-9,2014,玉尾皓平氏（日本化学会前会長）の記事からの抜粋です*****
◆2年前の会長就任時に提案した2つの具体的提案を紹介します。
「全国一斉オープンキャンパス」：これが 「化学の日」と直結する提案です。
各大学. 研究機関や化学企業で独自に行っているオープンキャンパスやオープンファクトリーを，
「化学の日」「化学週間」にできるだけ 曰程を合わせて一斉に実施いただくことで，
国民的イベントとして認知度を高めようとの取組みです。
「『夢・化学-21』の全国統一ブランド化」： 「夢・化学-21」キャンペーンの強化策として，
そのロゴマークを意匠登録し，上で述ベたようなこれまでのすべての化学啓発活動にロゴマークを付して
ビジビリティの向上を目指すものです。

いずれもいわば全国区の活動ですが，期間限定型で集中的に盛り上げる企画と，
通年活動型で全国津々浦々いつでも「夢・化学-21」ロゴマーク付きのイベントが行わ れている，
という性格の異なる活動を2つ準備し，足並みをそろえて最大の効果を狙おうとする点が特徴です。
提案4団体だけではなく，経済産業省や文部科学省，さらにはマスコミ関係者の賛同も得ており，
産学官一体となった初めての本格的な取組みで，化学の啓発活動，
市民権獲得にとっての決め手となるものと期待しています。

◆「化学の日」「化学週間」のイベントは？
「化学の日」を長く定着させるためには. 活動現場に新たなロードを課さないことが 重要と考えます。
新たに企画するのではな くて，現在行われているイベントの開催日 をできるだけ「化学の日」「化学週間」
の日程に合わせていただくことで.最大の効 果を上げようとの考えです。
すでに，各支 部や産業界に対して，日程調整のご協力を お願いしています。
ただ，初年度の今年は，「化学の日@開成学園」「化学週間@東京大 学」「子ども実験ショー@近畿」
などのキックオフイベントを企画中です。
また，各種一般紙や月刊誌「ニュートン」「化学」「現代化学」「子供の科学」などへの
PR記事掲載の企画も進んでいます。

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.30］ No.031
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
地震に関心が高まっていますが，地震は地殻の破壊現象ですから
いつポッキリ折れるか予言できないように文字通りの予知はできません．

◆地震の規模（マグニチュード）M
まず，地震のマグニチュードMとは何でしょうか？
これは地震のエネルギーEの対数です．
大体，地震のエネルギーの大きさの桁と思ってよいでしょう．
リヒターが当初発案したマグニチュードの定義は，
震央から100kmに設置したと仮想した，特定な型の地震計で
観測される最大振幅の対数でした．しかし，現在では
もっと理屈に合ったモーメント・マグニチュード
（あるいは気象庁マグニチュード）が採用されています．

◆可能な最大地震
地震で解放されるエネルギーは，生じた断層面の面積と
その平均変位とその付近の地殻の剛性の積です
（大雑把にいえば生じた断層の長さに比例します）．
地殻に溜まった歪エネルギーが地震で解放されるわけですが，
断層の長さが長い方が解放されるエネルギーは大きいし，
地殻の剛性が大きいほど大きな歪エネルギーが蓄えられます．
これらから起こりうる地震の最大エネルギーを見積もると
M9.5程度と考えられています
（1960年のチリ地震ではM9.5が観測されている）．

◆べき乗則
地震の規模（マグニチュード）Mと発生頻度（回/年）ｎ
の間に　n=10^(a-bM)　の関係があります．
これはグテンベルクとリヒターが発見しました．
a,bはその地域の地殻の特性を表す定数でが，b≒1ですので
地震のマグにチューﾄﾞが1つ大きくなるごとに，地震の回数は1/10に減ります．
だからこれをべき乗則と言います．

地震の規模Mには最も発生しやすい典型というのがありません
（釣鐘型の正規分布ではありません）．
大きな地震は少なくなりますが，M=9あたりも起こり得るし，
そんな巨大な地震に見舞われると壊滅的なダメージです．
従って，頻度は小さいけれど致命邸なダメージとなる巨大地震が起きても
被害が最小となるように備える必要があります．原発は止めましょう．

クリーン・ルームのチリのサイズ分布もべき乗則だと言われています．
もし正規分布のように頻度の高いサイズがあるなら
そのサイズのチリの発生に注目した対策ができるのですが
べき乗則では特別な対策は困難です．

◆分布関数を求める実験
凍ったジャガイモを投げて砕き，破片のサイズ分布を調べた人が居ます
（南デンマーク大，1993年）．ここでもべき乗則が確認されました．
スパゲッティやクラッカーを砕くとどのようなサイズ分布になるか
実験した話が今年の数学月間懇話会で中西達夫さんからありました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.23］ No.030
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆今年のとっとりサイエンスワールド2014（矢部敏昭会長）が
9月21日（中部，倉吉）で無事終わりました．例年のように
8月31日（東部，鳥取），8月2日（西武，米子）の計3回開催され
各回,1000人に達する参加者が集まりました．
スタッフも先生方100人＋高校生ボランティア60人の規模です．
8年目ですが，小さい子供から，両親，お年寄りまで，楽しみに集まる
算数イベントに定着しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_0?1411477332

◆万華鏡は，各会場でそれぞれ異なる3角形の鏡の組み合わせを作りました．
西部110人，東部160人，中部110人用意しました．
鳥取でやったけれど倉吉にまた来たという小さい小学生もいたり，
彼女はすっかり内容を理解していてもうベテランです．大したものだ．
鏡の組み合わせが作る3角形が変われば，違うタイル張り模様が見られることを
知ることが眼目なので，色々な鏡の組み合わせの万華鏡や，
多面体が立体的に見える万華鏡などの展示物も用意して行きます．
これらの内で，2枚鏡の万華鏡の人気が高く
来年のリクエストとして聞いておきました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_2?1411477822
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_3?1411477822

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.16］ No.029
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
読者の皆様へ．
8月19日（025号）からまぐまぐの遅配が続いています．
特に，026号，027号はまだ配送されていない方があるようです．
届かない方がありましたら，ご一報ください．
これらの号では多面体に関する話を続けています．
メルマガ更新は毎火曜日の朝7:00に行っておりますので，
以下のサイトでもご覧になれます．
http://blogs.yahoo.co.jp/tanidr/folder/545271.html　あるいは
http://sgk2005.sakura.ne.jp/htdocs/?page_id=32
－－－－－－－－－－

◆4次元の正多面体は6種あるのですが，
3次元以上が見えない私たちには理解が困難です．
色々な図や説明が種々の本やwebで見られますが，どれもしっくりしません．
結局，4次元の正多胞体6種を最初に見つけたシュレーフリの説明が
最もわかり易いようです．（コクセター［幾何学入門］や
ヒルベルト，コーン・フォッセン［直観幾何学］に載っています）．
さて，このようなものを記述するシュレーフリの記号というのは
大変良くできています．この記号の仕組みを理解することが結局
4次元の理解に直結します．シュレーフリの記号を単純な図形で見てみましょう．

◆3次元の正多面体の例
面（2次元）が頂点（0次元）で3つ以上集まらないと立体（3次元）はできません．
シュレーフリの記号は以下のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_0?1410817831
（１）正4面体　　　　　　　　　{3,3}←シュレーフリ記号
正3角形の面（2次元）が頂点（0次元）で３つ集まっている．
（２）正6面体（立方体）　　　　{4,3}←シュレーフリ記号
正４角形の面（2次元）が頂点（0次元）で3つ集まっている．

正多面体が記述の対象ですから，どの頂点まわりの状態も同じです．

◆4次元の正多面体の例
胞（3次元の多面体）が辺（2次元）で３つ以上集まらないと
4次元の立体はできません．
シュレーフリの記号は以下のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_1?1410817831
（１）正5胞体　　　　　　　｛3,3,3｝
3次元正4面体｛3,3｝が辺（2次元）で３つ集まっている．
（２）正8胞体　　　　　　　｛4,3,3｝
3次元正6面体｛4,3｝が辺（2次元）で３つ集まっている．

正多胞体なので，どの辺まわりの状態も同じです．

（参考）　　｛4,3,4｝　というのはどのようなものでしょうか？
これは，3次元正6面体が辺のまわりに４つ集まっている状態ですから
角砂糖を頂点を合わせて無限に積み重ねたような状態．
これは3次元空間の中で無限に続く立方格子です（３次元で納まってしまいます）．

◆双対図形について
3次元の正多面体｛p,q｝の双対図形は｛q,p｝です．
｛p,q｝：正p角形の面が頂点でq個（辺がq本）集まっている．
この図形で面を頂点に変えた図形は，｛q,p｝となります．
同様に，｛p,q,r｝の双対図形は｛r,q,p｝になります．

◆4次元のイメージの万華鏡
雰囲気だけです（色々工夫していますが残念ながら困難なようです）．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_2?1410817831
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_3?1410817831

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.09］ No.028
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆プラトンの正多面体は5種類あります．
これら5種類の正多面体の対称性を考慮して
方位を合わせ重ね合わせた図が以下のものです．
この図のように２つの正多面体を重ね合わせると
それぞれの多面体の対称性で共通なもの（共通部分群）が残ります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/30/16103930/img_0?1410092475

◆黄鉄鉱FeS2の結晶は，色々な外形（晶相）のものが見られます．
黄鉄鉱は愚者の金とも言われ金色できれいです．
私は，川底に金色の砂がキラキラ光って貯まっているのを見つけて
採集したことがあります．1mm程度の結晶粒ですが
皆整った多面体の形をしていました．
結晶の外形は，正6面体，正8面体，正5角12面体が基本で，
ミラー指数で言うと，正6面体は結晶面(100)面，
正8面体は(111)面，正5角12面体は(210)面で囲まれています．
このほかに，これら正多面体の切頂多面体も見られ，
また，他の指数の面(211)，(321)が加わった複雑な多面体もあります．
多面体の形が連続的に変化することを示す良い自然の手本です．
黄鉄鉱の結晶は立方対称の内部構造（原子の配列）ですが，
結晶粒の外形は，どの指数の面が大きく成長するかによって変わります．

◆そこで，昔読んだ記憶のある砂川一郎の論文（1957）を
再度見てみました．奈良県や島根県にある絹雲母の鉱床や凝灰岩の
母岩中に晶出した黄鉄鉱の結晶粒の大きさと形の統計を述べています：
「小さい結晶粒では正6面体，大きい結晶粒では5角12面体の外形が多い」
晶相の変化を起こす機構は大変複雑で一概に言えませんが，
黄鉄鉱結晶の成長に伴って大きく成長する面が，
正6面体の面（100）→正8面体の面（111）→5角12面体の面（210）
と変化し晶相が変る．これは結晶面の性質と母岩（絹雲母化）との
化学的反応がかかわっているらしい．
◆今回，砂川一郎の論文中の図が，
Tシャツとして博物館グッズになっていることを知りました．
http://ameblo.jp/hakubutufes-sub/image-11876822744-12970852035.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.02］ No.027
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
「とっとりサイエンスワールド」in鳥取市（8月31日）に参加しました．
とっとりサイエンスワールドは今年で8年目になり，小さい子供から
お年寄りまで楽しめる市民イベントとしてすっかり定着しました．
学生ボランティア54人（短大・高45人，中9人）を含む先生方150人のスタッフで
運営され，大変さまざまなワークショップがあります．
私は万華鏡のワークショップで参加しました．
1時間のクラスを5回実施し，160人が自分の万華鏡を作りました．
イメージ 1,2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/03/16089803/img_0?1409575636
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/03/16089803/img_1?1409575636

◆今年，鳥取市で作ったものは，3枚鏡が作る3角形の角が，90°ー36°ー54°のものです．
交差する2枚の鏡が反射を繰り返し生じる結果が群をなすのは
2枚の鏡の交差角が360°を偶数で割り切る角度のときです．
通常の万華鏡はそのような鏡の交差角に設定されます：
例えば，60°(360/60＝６）．36°（360/36=10）などです．
これは，1817年のブリュースターの万華鏡の特許にも記載されています．
群をなすときには生じる映像は規則正しく美しく見えます．
しかし，今回作成した万華鏡は，3角形の１つの角の交差角だけが
54°（360/54＝6.666）と偶数で割り切れません．
このような角度に対応する所はどのような映像が見られるでしょうか？
数学では3周回ってもとに戻る（360°×3）ような空間を想像しても良く，
そのときは10回回転対称が完成するのですが，
実際の物理的な空間の光はそのようには回ってくれません．
他の2つの角の所では規則正しい映像になるのですが，
この角度の所だけ秩序が乱れることになります．
昨年のサイエンスワールドから，このようなシリーズの万華鏡を作っています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.26］ No.026
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
この所，正多面体による空間の充填などを見てきました．
今回は，最密充填構造の話です．以下の本が参考になります：
ケプラー予想，ジョージ・G・スピーロ（青木薫訳）新潮社

◆ケプラー予想とは：
「3次元空間で最も高密度に同じ大きさの球を充填した状態は，
１つの球のまわりを12個の球が取り囲む状態で，
その空間充填率は74.04％である」というものです．
これは，結晶学では最密充填構造として常識になっていることがらです．
立方最密充填(=立方面心格子)，６方最密充填，および，両者の混合のポリタイプは
無数にありすべて同じ充填率74.04％です．この起源は1883年，結晶学者ウィリアム・バーロウが
６方および立方の最密充填の２つの最密充填構造をネイチャーに掲載したことにあります．
バーロウは結晶空間群の数え上げ（フェドロフ，シェンフリーズもそれぞれ独立に数え上げた）でも有名です．

注：スピーロの著書p.23でバーロウの図に言及し，立方最密充填は6方最密充填とまったく同じ配置なのだ！」
と言っているのは，数学と結晶学との見解の相違．
111面（切断）が同一であるのは当たり前で，その積層様式に結晶学的違いがあるのだ．

◆ケプラー予想は多くの人が挑戦しましたが，どうやってもこれより稠密な充填構造はつくれません．
これより充填密度の高い構造はないという証明はとても難しいのです．このケプラー予想をヒルベルトは，
1900年8月，第2回国際数学者会議の講演で，未解決の23の問題（ケプラー予想は第18問題）として提起しました．
周期的に規則正しく並べる（結晶）という条件では，ケプラー予想は証明できるのですが，
不規則な並べ方まで含めてこれが最密であるということの証明はとても困難です．
正4面体でも正8面体でも正12面体でも正20面体でも，単一では空間の充填ができません．
前号で正4面体と正8面体を2:1で混ぜると周期的に空間が充填できることを示しましたが，
それは面心立方の最密充填構造にほかなりません．さらに高密度な様式はないのだろうか？
例えば，立方最密充填では1つの球の周りに6個の球が囲み，上の段，下の段に3個づつ球が接します．
上下の3角形が点対称であるような配置が立方最密充填，
上下の3角形が周りを囲む6角形を鏡として鏡映対称であるような配置が6方最密充填です．
このような１つの球のまわりに12個の球が配置する構造と言っても，次のようなものがあります．
中心球の赤道面の上側から5個の球，下側から5個の球が接し，上下の正5角形が点対称に配置し，
さらに，中心球の上下に球が1個づつ配置するのも12個配置です．これは正20面体配置と呼ばれます．
しかし，この配置は局所的には充填密度が高いが，正20面体だけでは空間の充填ができません．
どうも数学的にエレガントな証明は無理なようです．

◆ケプラー予想の証明は，トマス・ヘールズ（ミシガン大学）によってコンピュータを用いた
しらみつぶし法で完成したということです．ケプラー予想（1611年「六角形の雪について」
という友人向けの小冊子にあるという）から400年近く経過した1998年のことです．
ヘールズはドロネーの四面体分割を基礎に，シンプレックス法で計算されました．
評価関数を導入して，密度の低い配置は減点，密度の高い配置は加点を繰り返すものです．
300ページもあるヘールズの論文は，トート（Toth）ら審査員12人が4年かかってチェックしましたが
最後まで詰められず99%正しいと報告されました．
そこで，2003年にヘールズ自身が証明支援ツール（HOL Light，Isabelleなど）を使い
チェックを始めやっと証明できたと言います．コンピュータを用いる証明は「4色問題」の時にもありました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.19］ No.025
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
お盆休みも終わりました．皆様お元気でお過ごしのことと存じます．
お知らせがあります．今までバックナンバーをまぐまぐにすべて公開していましたが，
お盆休み中に，公開は最新号のみに変更しました．
バックナンバーをご覧になる場合には，
ブログ：http://blogs.yahoo.co.jp/tanidr/　あるいは，
公式HP: http://sgk2005.sakura.ne.jp/　で
メルマガ倉庫の項目をご覧ください．

◆今回は，空間を隙間なく充填できる正多面体についての話です．
正６面体（角砂糖の形）が隙間なく積み重ねられ空間を充填する
ことはご存知でしょう．
◆それでは，正４面体，正８面体はどうでしょうか？
どちらもそれだけでは隙間なく空間を充填することはできません．
しかし，正8面体と正4面体を1:2の比率で混ぜると
周期的に空間を隙間なく充填できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_1?1408372931

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_2?1408372931
このパズルは,osa工房，小梁さんが販売しています．
さて，幾何学的にこのようなうまい構造を思いつくのは
特殊なことなのですが，
自然界でこのような空間充填構造はたくさんあります．
結晶学では，ダイヤモンドがこのような構造であることは
古くから知られています．半導体で知られるシリコンも
ダイヤモンド型結晶構造です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_3?1408372931

他の例では，ペロブスカイトと言う鉱物があり，
常温超伝導などの多くの有用な材料がペロブスカイト型の結晶構造です．
正8面体が骨組みを作っています．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_4?1408372931

◆菱形12面体はこれだけで空間の充填ができる多面体です．
菱形12面体は，面心格子のウイグナー-ザイツ胞であるので
空間を充填できることは明らかです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_3?1407801148

切頂正8面体は，体心格子のウイグナー-ザイツ胞であり
もちろんこの多面体も空間を充填できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_0?1408372931

面心格子の格子点に原子を配置した結晶構造は，銅やアルミニウムなど
多くの金属の結晶構造で知られています．
また，体心格子構造は，鉄，タングステン，セシウムなど
多くの結晶構造で知られています．

◆今回の話の眼目は，純粋に数学的に空間充填構造を導くのは
とても大変なことですが，結晶学などでは昔から知られていたということです．
自然科学の分野から数学への多くの貢献がなされてきました．
結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.12］ No.024
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
お盆休みの時期ですが，皆様いかがお過ごしですか．
今回のメルマガは，No.023に続き多面体に関してです．

（１）多面体の分類を整理しておきます．
■正多面体
1種類の正多角形で囲まれた凸多面体です．
頂点のまわりに集まっている多角形の状態は，すべての頂点で同じです．
もちろん，辺のまわりの状態もすべての辺で同じです．
プラトンの正多面体とよばれる5種類があります．
■半正多面体
２種類以上の正多角形で囲まれた凸多面体です．
頂点のまわりに集まっている多角形の状態は，すべての頂点で同じです．
しかし，辺のまわりの状態は，すべての辺で同じとは限りません．
アルキメデスの半正多面体といい13種類あります．
（右回りと左回りを区別するなら15種類）
特に，辺のまわりの状態が．すべての辺で同じものは，準正多面体と言います．
■準正多面体（半正多面体に含まれる）
立方８面体と12･20面体の2種類があります．

（２）菱形12面体と菱形30面体について
これらの多面体は，準正多面体の双対として得られます．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_0?1407764464

■菱形12面体と菱形30面体を万華鏡で作ろう

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_1?1407764464

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_2?1407764464

■菱形12面体は空間を充填できる
実は，菱形12面体は，立方面心格子のウィグナー=ザイツ
（あるいはデリクレ）胞に他なりません．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_3?1407764464

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.05］ No.023
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆さま如何お過ごしでしょうか？書中お見舞い申し上げます！
現在，数学月間(7/22～8/22)の期間中です．暑い最中ですが
数学月間懇話会(7/22)，とっとりサイエンスワールドin米子
も無事終了しました．

■プラトンの正多面体

正多面体とは，次の（１），（２）を満たすもので，
特に凸多面体がプラトン正多面体と呼ばれる：
（１）すべての面が同一の正多角形でできている
（２）すべての頂点まわりの状態は同一である
従って，正p多角形が頂点まわりでq個集まっている正多面体は
{p,q}と表記できる．これを正多面体のシュレーフリの記号という．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_0?1407156023

■５つのプラトン正多面体を万華鏡で作る

上図の各多面体には鏡映対称面がたくさんあります
（煩雑になるので記入していません）．
各多面体で3つの鏡映面を選び，これを鏡とする万華鏡を作れば
それぞれの多面体の映像が見られるでしょう．
ここでは，幾つかの多面体に共通な鏡映対称面を利用して
まとめてプラトンの正多面体の映像を生成してみましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_1?1407156023

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_2?1407156023

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.29］ No.022
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
8月2日（土）は「とっとりサイエンスワールドin米子」です．
2014年度〔西部in 米子〕は，日本数学教育学会第96回全国算数・数学教育研究（鳥取）大会
とコラボで実施されるので，会場が例年の児童文化会館とは異なるようです．
米子コンベンションセンターにて（12：00～16：00）　

私も万華鏡で参加します．
米子では110人分用意しました．分数型の万華鏡を作製します．
以下に画像を掲載します：
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/37/15996337/img_0?1406563191

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/37/15996337/img_1?1406563191

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/18/15996418/img_0?1406562991

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/18/15996418/img_1?1406562991

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.22］ No.021
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
本日は数学月間（7/22-8/22）の初日です．
22/7＝3.14....＝π　，22/8＝2.7...＝e
数学に興味を集めるようなイベントが
各地で盛んになることを応援しています．
まず初日は数学月間懇話会です．
◆数学月間懇話会（第10回）
日時●７月２２日，14:00-17:10
1.人口の集合関数としての「民力指数」
　松原望（東京大学名誉教授，聖学院大学）
　14:10-15:10
2.スパゲッテイを巡る旅，
　中西達夫（株・モーション）
　15:20-16:20
3.数学月間の狙と効用，今年の米国MAM
　片瀬豊，谷克彦（日本数学協会）
　16:30-17:10
ーーーー
会場●東京大学（駒場）数理科学研究科棟，002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●日本数学協会，数学月間の会（SGK）
sgktani@gmail.com，谷克彦（SGK世話人）
直接会場においでください（開場13:30）．ご参加お待ちしています．
17:30より構内で各自払いの懇親会も予定しています．

◆幾何学的な消滅
さて，メルマガ020に掲載した　幾何学的な消滅　のその後の記事です．
メルマガ020の図面のように作製してみましたが，
断層を挟んだ行だけが明らかに（目立って）小さくなるのです．そこで，
初期状態のこの行だけ目立たない程度大き目に作ろうかと考えていたところ，
以下の動画を発見しました．
http://youtu.be/QbpfjM0NP7Q
さすがマジシャンもうひとひねりあったのです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_2?1405950272
パーツ２は表面が（A)で裏面が（B)です．
従ってこのパーツの断面形状は台形です

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.15］ No.020
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
幾何学的な消滅

◆7×9の板で1コマが幾何学的に消滅する
これは今年の米国MAMで取り上げられたマジックです．
http://www.mathaware.org/mam/2014/calendar/areapuzzles.html

まずは，アルゼンチンのマジシャン，ノルベルトジャンセンによるプレゼンを
ご覧ください．　http://youtu.be/3PszMaZ5Ipk
7x9のエリアにタイル片が配置されています，断層に沿って滑らせ
上部の左3コラム分と右4コラム分を入れ替えると，不思議なことにタイルが１つ減ります．
この操作を繰り返すたびにタイルが1つづつ減り３つまで減らせます．
タイルが1つ減っても，2つ減っても，3つ減っても，
元通りの7x9枠内にタイルはきちんと配置され変わらないように見えます．
これは不思議ですね．どうしてタイルが１つづつ余るのでしょうか？

ビデオを観察していると，タイルが消滅する原理がだんだんわかってきます．
原理理解を助ける図を以下に作成しました．
青色の面積がだんだん減じているのがわかります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_1?1405218032

このおもちゃを作製して見ようとする方は，この原理図を参考にしてください．
数学マジシャンの使っているタイルのパーツは目地が太いですね
私の原理図には，目地はありませんが，作製するときは目地の効果も考慮すべきでしょう．
結局，断層をはさんだある行だけ，1コマ縦の長さが1/7だけ縮むので，
7コラムあるから面積としては1コマ分取り出せることになります．

◆なぜタイルが１コマ減るのか
左のコラムと右の3列を入れ替えると，１コマ減る．
１コマの高さをbとすると，断層を挟んでb/4だけ縮みます．
ただし，右端のコラムの断層ではコマ間の目地が消えるのが残念！
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_3?1405215030

◆真ん中を取り除いたお札が再現できる
http://youtu.be/-h0AXeLIHqQ
お札の中心を取り除いて，裏向きにして並べると
完全な1枚が再現できたように見えます．
真ん中が消えるとは，あり得ないことが起ったように見えます．
数学マジシャンの使っているおさつの裏面には
再配列したときに完成するようなお札の裏面の絵が描いてあるので
お札が再現したように錯覚します．以下の原理図を参考に作製してください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_0?1405215030

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.12］ No.019b
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ロンドンシティホール
ロンドンシティホールは，ロンドン市長，ロンドン議会，大ロンドン当局を収容する．
ガラスの使用と内部の巨大ならせん階段が，
透明性と民主的プロセスへの近づき易さを象徴しているようである．
外部から見たとき，最も印象的なことは，建物の奇妙な形である．

http://plus.maths.org/issue42/features/foster/egg.jpg
テムズ川にかかるロンドンシティホール．

テムズ川の土手の上に置かれて，建物は，川原の小石を思わせる．
そのまるみが再び民主的な理想を思わせる．けれども，ガーキンと同じように，
形が決められたのは，単に形のためだけではなく，エネルギー効率を最大化するためでもある．
これを実現する１つの方法は，建物の表面積を最小にすることである．
それにより，望まない熱の損失と流入を防ぐことができる． 諸君の中の数学者は，
あらゆる形の中で，体積を基準にすると，球形が最も表面積が小さいことを知つている．
これが，ロンドンシティホールが球に近い形をしている理由だ．
建物の不均衡も同じくエネルギー効率に貢献する：南面のオーバーハングが，
ここの窓を上階の床で陰にして，夏季の冷房需要を低下させる．ガーキンでと同じく，
コンピュータモデリングが，建物の中で気流が如何動くか示し，
自然の換気が最大になるように建物内の形が選ばれた．実際，建物は冷房を必要としない．
同程度のオフィススペースのエネルギーに比べ，たつた1/4と伝えられる．
螺旋階段さえ，単に審美的理由で選ばれたのではない．それらの分析の一部として，
ロビーの音響効果，人々の声が適切に聞こえるような建物をSMGは設計した．
初めは音響効果は，広いホール内をエコーが跳ねるという状態でひどく，
何らかの対策が必要だった．Foster＋パートナーの過去のプロジェクトの１つが手がかりを提供した：
ベルリンの Reichstag は大きいホールを含むが，大きい螺旋の傾斜路があり反響が起きない．
SMG はロンドンのシティホールに同様な螺旋階段のモデルを作り，
Arup Acoustics会社がこの新モデルの音響効果を分析した．諸君は，
以下のアニメーションで，音が階段後ろに閉じ込められ，エコーが減じるのを見ることができる．
このアイデアは最終設計に採用された． (アニメーション © Arup Acoustics.)

ロンドンシティホール
http://plus.maths.org/issue42/features/foster/gherkin_outside_web.jpg
ガーキンの全貌．平面パネルが曲面を近似していることに注意．映像 © Foster + Partners

ガーキン，ロンドンシティホール，他の多くのFoster+パートナー作品がたいへんモダーンに見えるのは，
外側が曲面であるためだ． これらは，名うての困難さで，建設費が高くなる．
そこで幾何学者のチャレンジがある：単純な形から作る一番良い方法は何か？
” これは我々の主たるチャレンジの一つだ，”De Kestelierは語る，
”我々のプロジェクトの実に99％は，いかなる曲面も使っていない．
例えばガーキン，1種類の曲面パネルはトップにあるレンズのみ．
建物が曲面という印象は，多数の多角形の平面パネルで曲面を近似的に作ることで生じる．
パネルが多いほど錯視も真実味をおびる．
複雑な表面を記述するこのような平面パネル解を見いだすことで，
SMG は専門家になった．De Kestelier が説明するように，幾何学［その形]は，
しばしば経済により決定される：”我々は矩形に近いパネルを使う傾向がある．
なぜならそれはいっそう経済的であるからだ．資材をカットするとき安くなる．
三角形では，多くの材料ロスがあるが，矩形に近いとロスが少ない．
矩形に近いと構造が少ないので，視覚的にもさらによい．”これは，
表面が完全に矩形から成り立っているロンドンシティホールで例証される．
実際、ロンドンシテイホールは，理想的な幾何学形と建設容易さのバランスをとる必要性を
よく例証している：　扱い難い丸い形はスライスに切ることで扱われた．スライス一つ一つは，
僅かに傾いたコーンで，容易に数学的に記述でき，平面パネルでの近似も容易である．

合理的な設計
数学的な方程式で記述されるコーンのスライス，トーラス，球などの表面は，
しばしば，SMGデザインの基礎となる． これらを，バーチャルモデル創造に使うときに，
数学的に生成される表面はコンピュータ上で容易に表現できるので，たいへん利点がある．
多くの個別座標を蓄え記述する構造ではなく，方程式を蓄えるだけでよい．
表面の正確な形は方程式のパラメータを変じて制御できる（例として下図を見よ）．
平面解はやはり比較的容易に設計できる：ソフトウェアはオリジナルの表面の
ノードポイント集合に直線を引くようにする．

http://plus.maths.org/issue42/features/foster/surfaces_web.jpg
これらの表面は，関数z=e^-a(x^2-y^2) のグラフである．ここで，
３次元座標系は，ｘ，ｙと垂直ｚ軸である． a は表面の形を決める．
第一の表面はa=1 ，第二の表面はa=5 ，第三の表面はa=7 ．

数学的に定義された要素の集合からなる複雑な構造を考えるのは，
バーチャル世界では有用ではない：実際にどのようにそれを建設するべきかを，
建物モデルの建設の一歩一歩のガイドにつくる．合理化のこのプロセスは，
もう一つの SMG の仕事の重要な部分だ．前と同じように，数学的な完全性は，
実用性のために道を明渡さなければならない:"２～３週間前に，
誰かが楕円の一部である壁のプランのことで私のところに来た”De Kestelierは語る．”
もちろん楕円は数学的には描くのは易しい．それをさらに合理化することをなぜ望むのか？さて，
私は楕円のこの部分を３つの円弧に合理化することを決めた．
理由は，壁の建設で，コンクリート壁用の型が要るためだ．これは全体の形を建設するのに
多くの型パネルを使ってなされる．もし諸君が楕円にしたいなら，
すべての型パネルは異なっていなければならない：楕円の周囲を進むと，
楕円の曲率はたえず変化しつづけるのだから． もし楕円をやめて３つの弧にするなら，
諸君が必要とするのは，3セットのパネルだけで，各セットのパネルは同じである．
これはずっと簡単になる．" 数学者に理想的なものは常に建築家に理想的であるわけではない．”

http://plus.maths.org/issue42/features/foster/museum.jpg
英国博物館の屋根．設計Foster+パートナー

博才の人
SMG が，建物の外見と気流・音響のような物理現象の双方をモデル化するには，
コンピュータプログラミングを使う．幾何学［形］の理解は，デザインと建設プロセスに直結する．
建築家でなく数理科学の専門家なのか？SMGメンバーの8人中７人が，プロの建築家だが，
専門的知識は，複雑な幾何学，環境シミュレーションからパラメトリックなデザイン，
コンピュータプログラミングにまで及んでいる．
グループの８番目のメンバーはエンジニアで，主プログラマーである．
こみいった数学に基づき，物理的特徴をモデリングするとなれば，
チームはしばしば専門コンサルタントを使う．”チーム内で予備的な解析を行う．
もしさらに知りたければ，別の解析を行う．我々は，専門コンサルタントとデザイナー間の接点となる，
”Petersは説明する．純粋数学，幾何学は如何？ どれぐらい複雑なのか？
"オフィスに１Ａレベルの本がある． ” とDe Kestelierが語る．結局のところ，
それはすべて建設可能な構造を作ることに関わり，古典幾何学を越えるものはここでは用いない．
SMG の大部分の活動には数学が付随しているのだが，彼らのデザインとは，
仕事に対して制限を与えるものであるとPetersとDe Kestlierは主張する．
"悟るべき重要なことは，我々はアーキテクチャで働くプログラマーではなく，
プログラミングをするアーキテクトだということだ，”De Kestlierは語る．
Ptersは同意する：”我々の主な仕事はモデリングではない．
プロジェクトのパラメータは何かを理解し，噛み砕き定義できる規則にする．
我々は，何処に適応性があり何処に制限があるかを理解できるようにする．
”制限の最適化と建設可能な物体の創造．もちろん，建築家はいつもそうしてきたし，
PetersとDe Kesteierも建築の仕事は本質的には変わっていないと思っている．
現代のデジタルツールにより，今日の建築家は，
過去の世代には夢であったデザインオプションの領域も探索できるようになっただけだ．
形と模様，科学とコンピュータの言語として，これらのツールを譲渡処分にしたのは数学だ．
数学は，確かにその料金を取り戻している． （訳：谷克彦）
－－－－－－－－－－－－－－－－－
http://plus.maths.org/issue42/features/foster/xavier_brady.jpg
Xavier(左)とBrady（右）はFoster+Partnersのモデリング専門家メンバーである．
プラスは，ロンドンの数学と芸術ブリッジ会議（2006年）で，二人に出会った．
ブリッジ会議の詳細はウエブサイトにある．
著者：Marianne Freiberger（プラス編集者）

◆編集後記
019号はa,bで完結です．ところで，
ガーキンに良く似た超高層ビルが新宿にあります．2008年に完成した
東京モード学園が入っているコクーンタワーです．コクーンとは繭のことですが
どちらかというとセミに似ているビルです．設計は丹下都市建築設計です．
新宿で大変目立つビルです．写真は以下のブログにあります．