ブログ倉庫

私たちが学校で習った「水素イオン濃度指数 pH」の定義では，中性はpH=7で，pHは，（酸性）0～14（アルカリ性）までの数値でした．ときおり，強酸性でpHの－の数値や，強アルカリ性でpHが14を超える数値があるのはどう理解すればよいのでしょうか．わからないことばかりですので，以下で，pHの定義から復習を始めましょう．

以下のHORIBAのウエブサイトにたいへん分かり易い記述があります：

このウエブサイトの説明を要約すると次のようです：
セーレンセン(1909)のpHの定義 $${pH=－log_{10}[H^{+}]}$$ は，その後の研究で，水素イオン濃度$${[H^{+}]}$$ではなく，水素イオンの活量に関係することがわかりました．その結果，pHの定義は1920年に次のように改められました：

$$ {ｐH=-log_{10}a_{H^{+ } } }$$ ,   $${a_{H^{+ } }=f\times[H^{+}]}$$
これによると14を超えるpHも可能なようです．

■まず，私たちの学校教科書でのpHの定義では；
水溶液のpHは，水素イオン濃度$${ [H^{+}]}$$ の逆数の常用対数として定義されます:　$${pH=-log_{10}[H^{+}]}$$
この定義では，何故，逆数なのか考えてしまいます．単純に次のように言った方が良いと思います：pHは溶液中の水素イオン濃度の常用対数をとり，その符号を変えたものである．広範囲の濃度を対象にするので，水素イオン濃度の桁を指標にしたいので，常用対数をとり，符号を正にするためーをつけただけだ．

25℃の純粋の水には，$${1×10^{-7 } }$$mol/L［mol濃度という濃度の単位］の水素イオン$${[H^{+}]}$$（正確には，$${[H_{3}O^{+}]}$$の型）が含まれています．１Lに含まれる水分子のmol数を計算すると55.6molですから，含まれる$${[H^{+}]}$$イオンのmol数$${1×10^{-7 } }$$は，これに比べて非常に小さい．従って，ほとんどの水分子は電離していません．この数値は，「純粋な水」の電気伝導度を精密に測定することにより知ることができます．

多くの教科書には以下のような記述があります：---------------------
$${H_{2}O \rightleftharpoons H^{+}+OH^{- } }$$　の電離平衡定数Kは，水温で決まる定数で；$${\displaystyle \frac{[H^{+}][OH^{-}]}{[H_{2}O]}=K}$$ ．
引用終わり------------------

水のイオン積が一定であることは，電離反応速度の質量作用の法則から導かれ，この平衡定数と関連しているようです．しかし，電離度がわずかなために水のmol濃度に変化はないと説明があります．しかし，ここがとても気持ちが悪いのです．溶媒自身であり，同時に溶質でもある水分子のmol濃度とはいったい何なのだ！

ともかく，水分子が電離すれば，$$ H^{+} $$と$$ OH^{-} $$は等量ずつ生じるので，それらのイオン積（温度に依存する）は， $$ [H^{+}][OH^{-}]=1×10^{-14} $$であります．

希薄な水溶液の場合は，純粋な水の場合と同様，このイオン積は同じ一定値に保たれるようです．

従って，水素イオン濃度が減少すれば反比例して水酸基イオン濃度が増加する．それぞれのイオン濃度は１を越えることがないとすれば，pHの最大値は14になります．

pHは，酸・塩基の濃度が 1 mol/L よりも低い水溶液の酸性・アルカリ性の度合いを示すための指標として考案されたものです．濃度が 1 mol/L を超える濃厚な酸や濃厚アルカリ溶液では，pHが負になったり14を超えたりします．その上， $${[H^{+}]}$$ から求めると実態に合わない（塩基の場合も同様）ので，その代わりに水素イオン活量 $${a_{H^{+ } } } $$が導入されました．

希薄水溶液でなければ，イオン間の相互作用が強くなるので，溶液中の水素イオン濃度を，イオン活量$${a}$$で置き換えて定義しなおすことが必要になったのです．溶質成分$${i}$$のイオン活量の定義；
　$${a_{i}=e^{\Delta \mu _{i}/RT } }$$

ｐH緩衝液
緩衝液とは弱酸とその塩の混合液，あるいは，弱塩基とその塩の混合液で作られます．緩衝液は，酸や塩基を多少加えてもそのpHを変化させない性質（＝緩衝作用）を示します．
弱酸とその塩の混合液の場合，塩が電離して，水素イオンを発生するので，弱酸の電離を抑える．弱酸の濃度が多少増加しても電離は増えずpHの変動を抑えます．
このよう緩衝効果の例は，例えば，結晶成長に用いるゲル化シリカを，メタケイ酸ナトリウムと酢酸の中和反応で得て（ゲル化にともないpHは多少変化），ゲル中で結晶塩を成長させる反応イオン水溶液を加えるときにもみられます．

コンスタンチン・ノップ,「クバント」«КВАНТ»No8，2020　の記事より
ただし，原文の説明は分かりにくいので，訳者が説明をすこし変えました．

ジョン・ホートン・コンウェイは著名な数学者で，組み合わせゲーム理論だけではなく，面白​​い数学への多大な貢献をしています．

パズル－－－－－－－ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
■私はバスに乗っていて，2人の魔法使の会話を聞きました：

A：私には子供が何人かいて，それぞれの年齢は正の整数であり，それらの合計はこのバス番号に等しく，それらの積は私自身の年齢です．
Ｂ：面白い！　もし，あなたの年齢と子供の数を教えていただければ，私は彼らの年齢を計算することができますか？
A：いいえ，できません．
Ｂ：ああ！　ついにあなたの年齢がわかりました．
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

問: 　私たちの乗っていたバス番号はいくつですか？

■このパズルの背景
パズルの作者であるジョン・コンウェイが，バス内という場面を設定したのは，魔法使いAの年齢ａと彼の子供の数ｃの他に，もう1つの変数が必要だからで，それがバス番号ｂです．
（a,b,c）の三つ組数は，ａは魔法使いAの年齢，ｂはバス番号，ｃは魔法使いAの子供の数を表すとします．
ｂのバス番号は，私たちにはわかりませんが，魔法使いＢにはわかっています．

魔法使いAの「いいえ，できません」という意味は，魔法使いＢの知的能力に関することではなく，三つ組数（a,b,c ）が完全にわかっても，子供の年齢を明確に決めることができないということです．言い換えれば，同じ総和と積を与える［子供の年齢集合］で異なるものが存在することです．そのような年齢の集合をコンウェイ集合と呼びましょう．
訳者注）条件を満たす子供の年齢集合はｃ組数です．はじめの三つ組数と区別するために，私は［］で表示することにしました．

このパズルがめちゃくちゃ美しいのは，何から始めればよいかわからない．アプローチが非常に難しいからです．もし，魔法使いAの年齢ａが分かれば，その約数を調べて，その和のバリエーションをすべて見つけることができる．もし，バス番号ｂがわかれば，いろいろな方法でそれを総和に分解し，それらの積のバリエーションを求めることができる．もし，子供の数ｃだけ分かった場合でも，探索量はずっと少なくなる．
候補探索のプログラミングに数時間を費やし，ようやく正しい解に近づく方法を見出した人もいます．

この問題は，完全に定義されておらず，つまり，さまざまな解決策が存在するのです．

■例を示します：
21番のバス（b=21）内の会話で，魔法使いAは96歳（a=96），子供は3人（c=3）だとします．この状態を三つ組数（96, 21, 3）と書きます．
子供たちの年齢は，和が21，積が96で，この場合ｃ=３のため，たまたまですが，［3つ組数］になります．この条件を満たす子供の年齢は，［1，8，12］と［2，3，16］の2つがあり，確かに，魔法使いＢが（96,21,3）と完全な数字を知ったとしても，子供たちの具体的な年齢を割り出すことはできません．

魔法使いの会話から，条件を満たす子供の年齢が決まらないのは何故か？

同じbで異なるaを持つ数字のコンウェイ集合は他にないでしょうか？
この問いに答えるために，別の言い方をしましよう．bが小さく，aが異なるコンウェイ集合は他にないのでしょうか？なぜなら，もし見つけることができれば，それに1歳児を加えて，出来上がったコンウェイ集合の数の合計ｂを21になるようにすればよいからです．

［訳者注］子供の年齢集合に1歳を一人加えるとｂ（子どもの年齢の総和）は１つ増加しますが，積ａ（これは魔法使いＡの年齢）は変わりません．ただし，ｃは１つ増加します］．実際，このようなコンウェイ集合は簡単に見つかります．例えば，（40，14，３）の場合，［1, 5, 8］ や ［2, 2, 10］ がそうで，これに1歳児を加えると［1,1,5,8］や［1,2,2,10］で（40,15,4）に対応するコンウェイ集合が得られます（この両者で，魔法使いＡの年齢は40歳で変わりません）．
また，（36,13,3）の場合，コンウェイ集合 ［1, 6, 6］ と［2, 2, 9］があり，同様の操作で［1,1,6,6］と［1,2,2,10］のコンウェイ集合が得られ，これは（36,14,4）に対応します．この両者では魔法使いＡは36歳で変わりません．
この2つの例で，バス番号ｂ＝14が同じとき，魔法使いＡの年齢が40と36のように異なるものが作れます．

ここから，説明は冗長になり混乱しますから，ここで一息入れましょう．ここから先は，まず，自分でトライアンドエラーしてみた方が理解が深まります．各自試みてください．要するに，この問題は，［子供の年齢の集合］で，総和と積が一致する集合（コンウェイ集合）の中身に異なるものが複数存在し，子供の具体的な年齢が決まらない場合のｂ（子どもの年齢の総和でバス番号）を聞いているのです．「ああ！　ついにあなたの年齢がわかりました．」と言う発言があるので，そのとき，ａの数値は定まらなければいけません．

$$ \begin{split} 6 &= 2 + 2+2\ &(a=8) \\ \rhd 7 &= 2 + 2+ 3\ &(a=12) \\ \rhd 8 &= 2 + 2 + 2 + 2\ &(a=16) \\ \rhd 8 &= 2 + 2+ 4\ &(a=16) \\ \rhd 8 &= 2 + 3 + 3\ &(a=18) \\ \rhd 9 &= 2 + 2 + 2 + 3\ &(a=24) \\ 9 &= 2 + 2 + 5\ &(a=20) \\ \rhd 9 &= 2 + 3 + 4\ &(a=24) \\ 9 &= 3 + 3 + 3\ &(a=27) \\ \rhd 10 &= 2 + 2 + 2 + 2 + 2\ &(a=32) \\ \rhd 10 &= 2 + 2 + 2+ 4\ &(a=32) \\ \rhd 10 &= 2 + 2 + 3 + 3\ &(a=36) \\ \rhd 10 &= 2 + 2+ 6\ &(a=24) \\ \rhd 10 &= 2+3 + 5\ &(a=30) \\ \rhd 10 &= 2+4+4\ &(a=32) \\ \rhd 10 &= 3 + 3+ 4\ &(a=36) \\ \rhd 11 &= 2 + 2 + 2 + 2+ 3\ &(a=48) \\ 11 &= 2 + 2 + 2 + 5\ &(a=40) \\ \rhd 11 &= 2 + 2+ 3 + 4\ &(a=48) \\ \rhd 11 &= 2+3 + 3 + 3\ &(a=54) \\ 11 &= 2 + 2 + 7\ &(a=28) \\ \rhd 11 &= 2+3 + 6\ &(a=36) \\ 11 &= 2+4 + 5\ &(a=40) \\ 11 &= 3 + 3 + 5\ &(a=45) \\ \rhd 11 &= 3 + 4 + 4\ &(a=48) \\ 12 &= 2 + 2 + 2 + 2 + 2 + 2\ &(a=64) \\ 12 &= 2+2+2+2+4\ &(a=64) \\ 12 &= 2+2+2+3+3\ &(a=72) \\ \rhd 12 &=2+2+2+6\ &(a=48) \\ 12 &=2+2+3+5\ &(a=60) \\ 12 &= 2+2+4+4\ &(a=64) \\ 12 &=2+3+3+4\ &(a=72) \\ 12 &= 3+3+3+3\ &(a=81) \\ \rhd 12 &=2+2+8\ & (a=32) \\ 12 &=2+3+7\ &(a=42) \\ \rhd 12 &=2+4+6\ &(a=48) \\ 12 &= 2+5+5\ &(a=50) \\ \rhd 12 &= 3+3+6\ &(a=54) \\ 12 &=3+4+5\ &(a=60) \\ 12 &=4+4+4\ &(a=64)\end{split} $$

$$\begin{split}2 &= 2\ &(a=2) \\ 3 &= 3\ &(a=3) \\ \ldots \\ 11 &= 11\ &(a=11) \\ 4 &= 2+2\ & (a=4) \\ \rhd 5 &= 2+3\ &(a=6) \\ \rhd 6 &= 3+3\ &(a=9) \\ \rhd 6 &= 2+4\ &(a=8) \\ \rhd 7 &= 3+4\ &(a=12) \\ \rhd 7 &= 2+5\ &(a=10) \\ \rhd 8 &= 4+4\ &(a=16) \\ 8 &=3+5\ &(a=15) \\ \rhd 8 &= 2+6\ &(a=12) \\ 9 &= 4+5\ &(a=20) \\ \rhd 9 &=3+6\ &(a=18) \\ 9 &= 2+7\ &(a=14) \\ 10 &= 5+5\ &(a=25) \\ \rhd 10 &=4+6\ &(a=24) \\ 10 &=3+7\ &(a=21) \\ \rhd 10 &=2+8\ &(a=16) \\ \rhd 11 &=5+6\ &(a=30) \\ 11 &=4+7\ &(a=28) \\ \rhd 11 &=3+8\ &(a=24) \\ \rhd 11 &=2+9\ &(a=18)\end{split}
$$

$$\begin{split} \rhd 5 &= 2 + 3\ &(a=6) \\ \rhd 6 &= 6\ &(a=6) \\ \\ \rhd 6 &= 2 + 2 + 2 = 2 + 4\ &(a=8) \\ \rhd 8 &= 8\ &(a=8) \\ \\ \rhd 6 &= 3 + 3\ &(a=9) \\ \rhd 9 &= 9\ &(a=9) \\ \\ \rhd 7 &= 2 + 5\ &(a=10) \\ \rhd 10 &= 10\ &(a=10) \\ \\ \rhd 7 &= 2 + 2 + 3 = 3 + 4\ &(a=12) \\ \rhd 8 &= 2 + 6\ &(a=12) \\ \\ \rhd 8 &= 2 + 2 + 2 + 2 = 2 + 2+ 4 = 4 + 4\ &(a=16) \\ \rhd 10 &= 2+8\ &(a=16) \\ \\ \rhd 8 &= 2+3 + 3\ &(a=18) \\ \rhd 9 &= 3 + 6\ &(a=18) \\ \rhd 11 &= 2 + 9\ &(a=18) \\ \\ \rhd 9 &= 2 + 2 + 2+ 3 = 2+3+4\ &(a=24) \\ \rhd 10 &= 2+2 + 6\ &(a=24) \\ \\ \rhd 10 &= 2+3 + 5\ &(a=30) \\ \rhd 11 &= 5 + 6\ &(a=30) \\ \\ \rhd 10 &= 2 + 2 + 2 + 2 + 2 = 2 + 2 + 2+ 4 = 2+4 + 4\ &(a=32) \\ \rhd 12 &= 2+2 + 8\ &(a=32) \\ \\ \rhd 10 &= 2 + 2+ 3 + 3 = 3 + 3 + 4\ &(a=36) \\ \rhd 11 &= 2+3 + 6\ &(a=36) \\ \\ \rhd 11 &= 2 + 2 + 2 + 2 + 3 = 2 + 2+ 3 + 4 = 3 + 4 + 4\ &(a=48) \\ \rhd 12 &= 2 + 2 + 2 + 6 = 2+4 + 6\ &(a=48) \\ \\ \rhd 11 &= 2 + 3 + 3 + 3\ &(a=54) \\ \rhd 12 &= 3+3 + 6\ &(a=54)\end{split}
$$

$$ \begin{split} \rhd 11 &= 3+4 + 4\ &(a=48) \\ \rhd 12 &= 2+2 + 2 + 6\ &(a=48)\end{split} $$

（定義）語wordとは，順序つけられた記号の配列である．

（例）例えば，abcはアルファベット文字を用いた長さ３の語である．001101は，バイナリー語（各ビットには，0あるいは1が入る）で，長さ6ビットである．

（注）ビットbitとは，binaryとdigitを縮めて作った造語である．

（例題）$${a_{n } }$$ を連続して1が続くことのないようなb-ビット語の数とする．$${a_{n } }$$を求めなさい．

(実験)

n=0のとき：　空集合が１つ：　$${a_{0}=1}$$

n=1のとき：　0，1　：$${a_{1}=2}$$

n=2のとき：　00，01，10　：$${a_{2}=3}$$

n=3のとき：　000，010，100，001，101　：$${a_{3}=5}$$

n=4のとき：　0000，0100，1000，0010，1010，0001，0101，1001　：$${a_{4}=8}$$

$${a_{n } }$$はフィボナッチ数列，1,2,3,5,8,....…になることが予想される．

（証明）

１．任意のn-ビット語wを考える．語wが0で終わるとすると，末尾の1つ前(n-1)番ビットは，0でも１でも良いので，この場合の1～(n-1)番ビットでできる(n-1)-ビット語の数は，$${a_{n-1 } }$$個である．従って，0で終わり，連続する1を含まないn-ビット語は$${a_{n-1 } }$$個である．

２．語wが1で終わるとすると，(n-1)番ビットは0でなければならない．(n-2)番ビットは何の制約もなく，0でも1でもかまわない．従って，１で終わり，連続して１を含まないn-ビット語は$${a_{n-2 } }$$個ある．

1.,2.の２つのケースは互いに排他的であるので，加算原理により；$${a_{n}=a_{n-1}+a_{n-2 } }$$これは，フィボナッチ数列の定義に他ならない．

（練習問題）n個のコインを投げて，隣り合う２つのコインが連続して表を向くことがない確率を求めなさい．

写真は，今を盛りに咲いている花桃です．葉となる芽の位置を，枝の元から先に向かって調べると，５つごとに重なる位置になることがわかります．左回りの螺旋配置で，５つ目で重なるまでに２回転しますので，葉序比2/5といいます．２も５もフィボナッチ数です．　

一般に，植物や樹木の枝につく葉は螺旋配置をしています．１つの枝に沿って枝先に向かって，ある葉から出発しその葉に重なる上の葉までの葉の数を数えて見ましょう．その数は，だいたいフィボナッチ数になることが知られています．螺旋配置になるのは，木の枝が成長しながら，葉が重ならないよう葉が育つと考えると理解できます．同じ位置の上の葉と重なるまで（1周期）の葉の数がフィボナッチ数と言うことです．植物（精密な工業製品ではない）ですので，それほど厳密な話ではなく，だいたいの配置を言っているに過ぎません．重ならないようにするなら，周期が出来ない（∞周期）方が，良いのではないかとも思いますが，周期というのはだいたいのもので，結晶のように完全に周期的というわけではありませんから，目くじらを立てないでください．

シナノキとニレではこの数は２（左右交互）；ブナとハシバミでは３；アンズ，桜，カシでは５；梨とポプラでは８；アーモンドと柳では13と言われています．［Hoggatt，1979］

出発点の葉から終着点の葉までの時計回りあるいは反時計回りの回転数は，やはり通常はフィボナッチ数で，例えば，シナノキとニレでは1回転；ブナとハシバミではやはり1回転；アンズ，桜，カシでは2回転；梨とポプラでは3回転；アーモンドと柳では5回転だそうです．

樹木の枝の葉の配置は葉序と呼ばれます．葉が重なるまでの葉の数と，回転数の比は葉序比と呼ばれ，シナノキとニレの葉序比は1/2；ブナとハシバミでは1/3；アンズ，桜，カシでは2/5；梨とポプラでは3/8；アーモンドと柳では5/13です．［Fibonacci and Lucas numbers with applications, Thomas Koshy］

ここまでに観察される数値は，1,1,2,3,5,8,13までのフィボナッチ数です．さらに大きなフィボナッチ数が観測されるかどうかや，漸化式が葉の発芽の機構から必然的に導くことができるのかには言及しません．

■　電場$$\textrm{E}$$や電流密度$$\textrm{j}$$を極性ベクトルとすると，磁場$$\textrm{H}$$は軸性ベクトルになる．
それは，次のMaxwell方程式が成立しているためです．
$$ \nabla \times \textrm{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \textrm{E } }{ \partial t}+\displaystyle \frac{4\pi \textrm{j } }{c}$$の右辺は極性ベクトルですから，$$ \nabla \times \textrm{H}$$は極性ベクトルであることになり，$$ \nabla $$が極性ベクトルなので，$$\textrm{H}$$は軸性ベクトルでなければならない．
極性ベクトル$$ \times $$軸性ベクトル＝極性ベクトル 
極性ベクトル$$ \times $$極性ベクトル＝軸性ベクトル 
の関係があり，これを用いました．

$$ \nabla \times \textrm{H}$$，（あるいは，$$\textrm{rot H}$$）という演算の結果は，ベクトル$$\textrm{H}$$の回転面に垂直な軸性ベクトル（その方向は，回転を右ネジに見立てて進む方向）を与えます．この例の軸性ベクトルは$$ \nabla $$とHの2つのベクトルの外積で定義されたもので，その物理的実態は$$\textrm{H}$$の回転面の円軌道にそって流れる電流です．回転方向を，角速度などと同様に，外積を借りて定義しただけで，実態は円軌道という物理現象だけです．右手座標系でも，左手座標系でも，外積自体は右手系で定義するのが慣習です．右手座標系で定義された軸性ベクトルを左手座標系で記述すると，軸性ベクトルの向きは反転します．

詳細は：⇒極性ベクトル軸性ベクトルの項をご覧ください．

座標系を反転すると，右手系で見た座標値$$(x_{1}, x_{2}, x_{3})$$が左手系で見た座標値$$(x_{1}'=-x_{1}, x_{2}'=-x_{2}, x_{3}'=-x_{3})$$に変わります．

座標系の反転で，座標成分の符号が変るのが，極性ベクトル（変位，速度，力，運動量など）；
座標成分の符号が変わらないものが軸性ベクトル（角速度，角運動量，モーメントなど）と言われます．
軸性ベクトルとは，２つの極性ベクトル間の外積で定義されるものです．

軸性べクトルは，座標系の反転で座標成分の符号が変わらないというのは本当でしょうか？
納得できないので，これを確かめてみましょう．

■　右手系と左手系基底の定義 
２つの正規直交基底$$ \left[ e_{1}, e_{2}, e_{3} \right] $$，および，$$\left[ e_{1}', e_{2}', e_{3}' \right] $$があるとします．
正規直交基底は，　$$e_{i} \cdot e_{j}=\delta _{ij}$$，　$$e_{i} \times e_{j}=-e_{j} \times e_{i}$$，　$$e_{i} \times e_{i}=0$$が成立ちます．
右手系では，　$$e_{2} \times e_{3}=e_{1}$$，$$e_{3} \times e_{1}=e_{2}$$，$$e_{1} \times e_{2}=e_{3}$$ が成立します．
空間反転$$e_{1}'=-e_{1}，e_{2}'=-e_{2}，e_{3}'=-e_{3}$$して得られる基底$$\left[ e_{1}', e_{2}', e_{3}' \right] $$では， 
　$$(-e_{2}') \times (-e_{3}')=(-e_{1}')，(-e_{3}') \times (-e_{1}')=(-e_{2}')，(-e_{1}') \times (-e_{2}')=(-e_{3}')$$
すなわち，$$e_{3}' \times e_{2}'=e_{1}'，e_{1}' \times e_{3}'=e_{2}'，e_{2}' \times e_{1}'=e_{3}'$$が得られます．この座標系は左手系になります．

■　位置ベクトル，運動量ベクトル（ともに極性ベクトル）を，右手系と左手系で標示すると，
位置ベクトル：$$r=x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}=x_{1}'e_{1}'+x_{2}'e_{2}'+x_{3}'e_{3}'=-x_{1}e_{1}'-x_{2}e_{2}'-x_{3}e_{3}'$$
運動量ベクトル：$$p=p_{1}e_{1}+p_{2}e_{2}+p_{3}e_{3}=-p_{1}e_{1}'-p_{2}e_{2}'-p_{3}e_{3}'$$
このように，極性ベクトルの座標値は，座標系の反転で符号を変えることがわかる．

■　角運動量ベクトル（軸性ベクトル）を，右手系と左手系で標示する．
$$L=r \times p=\left( x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3} \right) \times \left( p_{1}e_{1}+p_{2}e_{2}+p_{3}e_{3} \right) =$$
$$=-x_{2}p_{1}e_{3}+x_{3}p_{1}e_{2}+x_{1}p_{2}e_{3}-x_{3}p_{2}e_{1}-x_{1}p_{3}e_{2}+x_{2}p_{3}e_{1}=$$
$$=\left( x_{2}p_{3}-x_{3}p_{2} \right) e_{1}+\left( x_{3}p_{1}-x_{1}p_{3} \right) e_{2}+\left( x_{1}p_{2}-x_{2}p_{1} \right) e_{3}=$$ 
$$=-\left( x_{2}p_{3}-x_{3}p_{2} \right) e_{1}'-\left( x_{3}p_{1}-x_{1}p_{3} \right) e_{2}'-\left( x_{1}p_{2}-x_{2}p_{2} \right) e_{3}'$$
最後の式で基底を反転している．左手系での座標値は，右手系の座標値の符号を反転したものになる．
$$e_{2} \times e_{3}=e_{1} \longrightarrow \left( -e_{2}' \right) \times \left( -e_{3}' \right) =\left( -e_{1}' \right)  \longrightarrow e_{3}' \times e_{2}'=e_{1}'$$

■（結論）
座標系の反転（右手系基底［$$e_{1}, e_{2}, e_{3}$$］$$ \longleftrightarrow $$左手系基底［$$e_{1}'=-e_{1}, e_{2}'=-e_{2}, e_{3}'=-e_{3}$$］
をしたときに； 
（１）　極性ベクトルは，
反転後の基底についての座標値は，反転前の基底に対する座標値の符号を変えたものになるが，基底自体も反転しているので実態は変わらない．
（２）　軸性ベクトルは， 
反転後の基底についての座標値は，反転前の基底に対する座標値の符号を変える．軸性ベクトルは外積で定義された向きを持つが，座標系が左手系であっても外積の定義は右手系でなされているので，左手系では向きを変える．

しかし，実態は回転現象でありこの状態が変わるわけではない．

$$e_{1}$$だけ反転（鏡映対称）：奇数パリティ⇒$$x_{1}$$だけ符号反転
$$e_{1}, e_{2}$$の２つを反転（$$e_{3}$$を軸とする2回対称）：偶数パリティ⇒符号の変化なし
$$e_{1}, e_{2}, e_{3}$$の３つを反転（対称心：奇数パリティ）⇒すべての座標値の符号を変える

ロシアがウクライナ東部のハリコフ占領の恐れと煽りたて，軍を進めるバイデン政権と，その米国の情報に追従する日本の大手新聞やテレビ報道を鵜呑みにしてはいけません．かつての湾岸戦争の勃発も米国の情報操作からでした．ロシアの中庭のようなウクライナをNATO軍事同盟に加盟させるのはおかしいし，米軍がウクライナ東部に軍を進めていること自体が，緊張を高める挑発です．ウクライナがNATOに加盟しなければ，ロシアは戦争を始めません．ロシア人同士が利益のない戦争を好むわけがありません．
https://iwj.co.jp/wj/open/archives/501693?fbclid=IwAR2G79BFL4C804PPmKIPhBl6pBh23tps_VRkQGG-V1JHYH8bDrZdvng4wHM

ウクライナ人民共和国は，第1次世界大戦では，ドイツ側でソ連と戦ったのですが，両国間で和平が成立し，その後，ソ連邦の一員となります．

第2次大戦では，ナチス・ドイツは，ソ連に対抗するのにウクライナ・ナショナリズムを利用します．一方，スターリンは大祖国戦争と呼び，ナチス・ドイツとの戦いにウクライナを利用します．都市ハリコフは，赤軍とナチス軍との激戦地になりました．ウクライナ･ナショナリズムは，東西の対立勢力にいつも利用されます．今日，米国がNATO軍事同盟にウクライナを加盟させようと，東部ウクライナで危機を煽り，ゼレンスキーは政権安定のためにナショナリズムを煽ります．ハリコフのあるウクライナ東部に住んでいるのは，ほとんどロシア人で親ロシア派です．ロシア軍との戦争は無意味です．

ここで，私は，ハリコフという都市にある，ソ連時代の物理学研究所の歴史を，シュブニコフの活動を軸に述べようと思います．

ハリコフはキエフとならぶウクライナの都市です．ソ連時代の1928年に，ヨッフェが物理学研究所を開設し，1931年にL.V.シュブニコフが極低温研究所を作りました．シュブニコフ＝ド･ハース効果に名前を冠したL.V.シュブニコフです．私は黒-白群（シュブニコフ群）に関心がありますが，これに名を冠しているのは，別人のA.V.シュブニコフです．

L.V.（レフ・ワシリエヴィチ）・シュブニコフは，1901年9月29日，レニングラードで生まれ，ペトログラード大学物理数学学部の数学科に入学．物理学を専門に学びました．その年の学生は彼一人だったので，一学年上の学生，S.E.フリッシュ，V.A.フォク，一学年下の学生，A.V.ティモレヴァ，O.N.トラペズニコヴァ（1925年に彼の妻となる）と一緒に講義を聴きました．

物理学科（1919年に分離）の学生や教師は，ヨットが好きでした．シュブニコフも熱心な一人で，1921年秋，フィンランド湾のヨットに見知らぬ人たちと一緒に行き，気がつくとフィンランドにおりました．そこからドイツに追放され，1922年にようやくペトログラードに戻ることができました．工科大学で勉強を続け1926年に卒業します．

研究室では，I.V.オブライモフといっしょに，ある形状の大きな金属単結晶を成長させる方法を完成させた．1926年，ドイツのライデンのド・ハース研究所で，この分野の専門家が必要になったときに，A.F.ヨッフェの推薦でシュブニコフが派遣されました．

当時のライデンは世界で唯一液体ヘリウムを持っている研究所で，さまざまな専門分野の物理学者がライデンに集まりました．P.エーレンフェストは，ライデン大学で理論物理学の講座を開いており，刺激的なエーレンフェストのセミナーでは，A・アインシュタイン，N・ボーア，W・パウリ，P・ディラックらとも知り合うことができました．

ライデン研究所では，ド・ハースと共同で，低温で不純物濃度の低いビスマス結晶の研究で，磁場中の磁気抵抗の振動（シュブニコフ＝ド・ハース効果）を発見しています．この効果が物性物理学に重要な意味を持つようになったのは，ずっと後の50〜60年代のことです．現在では，この効果は、固体の量子電子物性を調べるための主要な手段の一つとなっています．

ライデンのモットーは「測定から知識へ」で，シュブニコフにとって実験技術の良い学校でありました．常駐の研究所員やセミナーや研修のための訪問者との交流によって，彼は科学技術を習得ができました．

ヨッフェは1928年に，ウクライナのハリコフに物理学研究所を設立し，1930年にライデンから戻ったシュブニコフは，ここに低温研究所を作ることになります．1931年には早くも液体水素，1933年には液体ヘリウムを得て，1934年からは，当時世界で4番目の極低温センターの誕生の宣言をします．この成功は、シュブニコフの功績に間違いないが，ライデンの研究所長であるド・ハースと，当時ソ連では入手不可能な材料や器具をハリコフに移したキーソムの協力があって実現したものです．

シュブニコフの研究所では，低温技術は優れた監督者 I.P.コロレフが指揮し,
吹きガラスはE.V.ペトゥシコフが行いました．研究所の最初のスタッフにはYu.V.シュブニコフ，その後，ルデンコ，フェドロワ，ミルチン，ベレシュチャギン，ズルニツィン，アレクセーフスキー，キコイン，シャリュートと続き現在に至っています．ドイツからも，契約を結んだり，ナチスの迫害を逃れてきた物理学者たちが研究室で働いていました．

この研究所の主な活動の1つに，超伝導の研究があります．低温物理学の発展に貢献したL.V.シュブニコフの研究者の多くは，マイスナー効果はマイスナーとは無関係で，シュブニコフが彼とほぼ同時に発見したと考えています．また，クルト・メンデルスゾーンによると，合金の磁気特性の研究では，ハリコフ研究所はライデンやオックスフォードより進んでいたという．シュブニコフらの業績に敬意を表し，Hc1-Hc2磁場区間におけるタイプP超伝導体の状態は，シュブニコフ相と呼ばれています．

L.V.シュブニコフの研究室では，遷移金属塩化物の熱的，磁気的性質の研究に大きな成果を挙げ，これが反強磁性現象の実験的発見につながり，L.D.ランダウの興味を刺激したと考えられます．

L.V.シュブニコフとL.D.ランダウは，仕事だけでなく，親しい友人関係でもありました．どちらの名前もLevなので，太ったレオ，痩せたレオと呼ばれたのは面白い．二人ともハリコフ大学の物理学科で教鞭をとりました．

しかし，1937年8月6日，L.V.シュブニコフがL.D.ランダウと一緒にクリミアで過ごした休暇から戻った日に逮捕され，スターリンによる粛清の犠牲者となりました．いわれのない破壊活動の罪で起訴され，11月10日に銃殺刑になりました．記録は改竄され，死体もわからず，未亡人は彼が1945年死んだと知らされたといいます．

1956年にL.D.ランダウらにより名誉回復が行われました．ランダウが軍の検察官あてに出した書類は次のようです：
「彼の研究論文の多くは画期的な古典であります．彼がソ連のこの分野の創始者の一人であったことを考えると，低温物理学の分野での彼の破壊活動について話すのはまったくばかげています．彼の熱烈な愛国心は，彼がソ連での仕事のためにオランダでの仕事を自発的に辞めたという事実によって強調されています．L.V.シュブニコフの早すぎる死によって国内科学に引き起こされた損害は，いかなる過大評価も間に合わないほどです」

引用：http://www.ilt.kharkov.ua/bvi/info/shubnikov/shubnikov.html

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{1} & -\textrm{cos}\alpha _{3} \\[0mm]
-\textrm{cos}\alpha _{1} & 1 & -\textrm{cos}\alpha _{2} \\[0mm]
-\textrm{cos}\alpha _{3} & -\textrm{cos}\alpha_{2} & 1
\end{vmatrix} =1-\textrm{cos}^{2}\alpha _{1}-\textrm{cos}^{2}\alpha _{2}-\textrm{cos}^{2}\alpha _{3}+2\textrm{cos}\alpha _{1}\textrm{cos}\alpha _{2}\textrm{cos}\alpha _{3} \\　
=-4\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{2}+\alpha _{1}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{3}+\alpha _{1}+\alpha _{2 } }{2} \right)
$$

$$
=\begin{cases}
>0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}>\pi \\[0mm]
=0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}=\pi \\[0mm]
<0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}<\pi
\end{cases}
$$

立方格子の空間を見る万華鏡は，立方体の単位胞内の対称面を鏡に選び4枚鏡の万華鏡を作ります．
立方体にある対称面には立方体の正方形面に平行なものや，正方形の面と45°方位のものがあります．
上図の万華鏡では，（１）△ABC，△ABO，△ACO，△BCOを鏡映面にした万華鏡，（２）△ACO，△ACD，△AOD，△DCOを鏡映面にした(1)の半分体積の万華鏡，（３）△ABO'，△ABO，△AO'O，△BO'Oを鏡映面にした(1)の2倍体積の万華鏡を示しました．それら３つの万華鏡の作製と映像の記事は別項

これらは，3次元ユークリッド空間の「立体万華鏡」の例です．（上の写真は「美しい幾何学」p.47より引用）

ここでは，ユークリッド空間だけでなく，非ユークリッド空間（球面･楕円幾何，双曲幾何）の3角形面を用いた多面体についてまとめて数学の話をします．

正多面体の面のなす角（二面角）の話から始めます．凸正多面体Mとその頂点の１つを中心とする小球がよぎる線は，凸球面正多角形を形成します．
頂点から$${q}$$本の辺が出ているとすると，凸球面多角形の頂角（辺の二面角）の和は$${π(q-2)}$$よりも大きい．
正多面体Mのすべての二面角が$${π/2}$$を超えない（たとえば，コクセター多面体）場合，各頂点から出る辺は3本だけであることがわかります．この最後の性質を持つ多面体を単純多面体と呼びます．４面体や立方体は単純多面体ですが，８面体は単純多面体ではありません．

しかし，この単純な不等式だけでは，凸多面体の二面角の関係を網羅することはできません．最も単純なMが三角錐の場合について考えてみましょう．その面に番号をつけ，$${i}$$ 番目と$${ j}$$ 番目の面のなす角を $${α_{ij} = α_{ji } }$$ とします．ユークリッド三角錐の二面角が次の関係にあることは，線形代数によって簡単に証明できます．

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{12} & -\textrm{cos}\alpha _{13 } &
-\textrm{cos}\alpha _{14 } \\[0mm]
-\textrm{cos}\alpha _{12} & 1 & -\textrm{cos}\alpha _{23} &
-\textrm{cos}\alpha _{24} \\[0mm]
-\textrm{cos}\alpha _{13} & -\textrm{cos}\alpha _{23} & 1 &
-\textrm{cos}\alpha _{34} \\[0mm]
-\textrm{cos}\alpha _{14} & -\textrm{cos}\alpha _{24} &
-\textrm{cos}\alpha _{34} & 1
\end{vmatrix} =0
$$                                                

左辺の行列式は，ピラミッドの面に対する単位法線ベクトルのグラム行列式［ベクトルの内積が成分］で，０に等しいのは，これらのベクトルが線形従属であることによります．

注）二面角を$${α}$$とすると，対応する面の法線ベクトルの内積は，$$\textrm{cos}(π-α)＝-\textrm{cos}α$$となります．
試しに，ユークリッド三角形とすると，$${α_{12}＝α_{1}, α_{13}＝α_{2}, α_{23}＝α_{3 } }$$　になり，

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha_{1} & -\textrm{cos}\alpha_{2} \\[0mm]
-\textrm{cos}\alpha_{1} & 1 & -\textrm{cos}\alpha_{3} \\[0mm]
-\textrm{cos}\alpha_{2} & -\textrm{cos}\alpha_{3} & 1
\end{vmatrix} =0
$$

この簡単な場合からは，$${α_{1}＋α_{2}＋α_{3}＝π}$$　が得られます．

証明（Andreevより）

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{1} & -\textrm{cos}\alpha _{3} \\[0mm]
-\textrm{cos}\alpha _{1} & 1 & -\textrm{cos}\alpha _{2} \\[0mm]
-\textrm{cos}\alpha _{3} & -\textrm{cos}\alpha_{2} & 1
\end{vmatrix} =1-\textrm{cos}^{2}\alpha _{1}-\textrm{cos}^{2}\alpha _{2}-\textrm{cos}^{2}\alpha _{3}+2\textrm{cos}\alpha _{1}\textrm{cos}\alpha _{2}\textrm{cos}\alpha _{3} \\　
=-4\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{2}+\alpha _{1}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{3}+\alpha _{1}+\alpha _{2 } }{2} \right)
$$

$$
=\begin{cases}
>0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}>\pi \\[0mm]
=0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}=\pi \\[0mm]
<0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}<\pi
\end{cases}
$$

なぜならば，
$${0<\alpha _{1}, \alpha _{2}, \alpha _{3}<\pi /2}$$なので，$${-\pi <-\alpha _{i}+\alpha _{j}+\alpha _{k}<\pi}$$，$${\textrm{cos}\left( \displaystyle \frac{-\alpha _{i}+\alpha _{j}+\alpha _{k } }{2} \right) >0}$$であり，
従って，式の$${ \pm }$$は，$${\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) }$$の$${ \mp }$$で決まる（複合同順）．

始めに示した関係式は，先に導いた不等式と合わせて，二面角$${α_{ij } }$$を持つ三角錐がユークリッド空間に存在するための必要十分条件となります．これを利用すると，二面角が$${π/}$$整数であるユークリッド空間の三角錐をすべて求めることができ，その数は3つです．図7で，マークのない辺の二面角は$${π / 2}$$，マーク|あるいは||のついた辺の二面角は，それぞれ，$${π / 3}$$または$${π / 4}$$です．図7のピラミッドのうち，1つ目のピラミッドを対称面によって切断すると2つ目のピラミッドが得られ，2つ目のピラミッドを対称面で切断すると3つ目のピラミッドが得られます．

3次元ユークリッド空間には，この3つの万華鏡のほかに，ある意味で2次元に還元された万華鏡が4つだけあります．これは、直角プリズム（3角柱）の底面が2次元の万華鏡であるものです．

3次元ユークリッド万華鏡は，結晶学と密接な関係があります．このような万華鏡の中にいくつかの原子を配置し，万華鏡の壁で繰り返し反射させ得られる像をすべて調べると，結晶格子を得ることができます．つまり，図7に示した万華鏡のうち，1番目の万華鏡で，炭素原子Cを図に示した2つの頂点に置くとダイヤモンドの結晶格子が得られ，2番目の万華鏡で，ナトリウムNaと塩素Clの原子を図に示した頂点に置くと，食塩の結晶格子が得られます．

3次元球面上の万華鏡をすべて見つけることも難しくありません．このすべてが，球面三角錐です．この場合，ユークリッド平面から球面に移るとき，三角形の内角の和が$$π$$より大きくなるので，始めに示した式の等号が不等号$$>$$に置き換えられます．

引用：
E. B. Vinberg, published in the "Soros Educational Journal" (1997, No. 2)
«КВАНТ» No6, 2020

トレミーは2世紀のギリシャの天文学者プトレマイオスのことです．地球中心の天動説を確立したので有名です．トレミーの定理を導きました．

トレミーの定理（Ptolemy's Theorem）とは，円に内接する任意の４角形 ABCD で，AB･CD＋DA･BC＝AC･BD　が成立することです．高校の幾何ででてきた懐かしい定理です．

トレミーの定理を，以下のような特殊な円に内接する4角形＝長方形に適用すると，ピタゴラスの定理　a･a+b･b=c･c　が証明できます．この意味で，トレミーの定理はピタゴラスの定理の拡張定理と言えます．

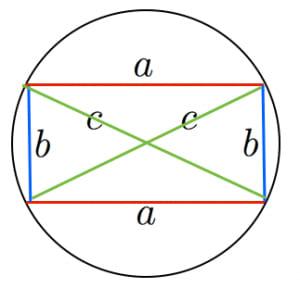
さて，トレミーの定理の証明には，三角関数を使うなど色々な方法がありますが，素朴に，下図の2つの図に示す3角形の相似を用いてやってみます．

両辺を足し合わせると　AB･CD+BC･DA＝AC･(BP+DP)が得られます．

<<KVANTIK>>, No.11, 2020; Фёдор Ниловフョードル・ニーロフより抜粋

https://kvantik.com/extra/parall/

セミパラレル図形

白い正方形は一斉にペチャンコにすると図形をコンパクトにできます．不思議ですね．

パラレルニクという多角形は，下図のどちらかの性質を持ちます．

任意の平行多角形はパラレルニクである．下図に示す例は5角形の平行多角形の例です．

次の図は，中央に任意の３角形（緑）があります．その外に白い正方形を３つ作ります．それら頂点は，6角形になり，その外に白い正方形を３つ作ると，また6角形が得られます．同じ色の多角形の面積はすべて等しく，4角形はすべて台形です．この定理は，2001年にアメリカの数学者D. DeTemple と M. Hudelsonが証明しました．

また，中央の３角形をどんな平行多角形に置き換えてもこの定理が成り立つことも発見しました．以下の図は，中央に平行４角形，平行５角形にした例です．

https://elementy.ru/nauchno-populyarnaya_biblioteka/435457/Kvantik_9_2020

«Квантик» No9, 2020に，アレクサンダー・ペレペチコによる次の問題があります：

１．サーシャは，1日2回，朝と夕方に，物忘れ治療薬を飲まなければならないのですが，忘れることもあります．続けて 2 回服用した後は，必ず忘れずに服用し，2 回服用しなかった後は，服用を忘れます．過去 1 日にちょうど 1 錠服用している場合は，次回服用する確率は1/2とします．

サーシャが，ある時点から完全に薬を飲むことを忘れてしまう確率はどれくらいありますか? ずっと飲み続けている確率は？

２．酔っぱらいは居酒屋と彼の家の間の道路に立ち，1 秒ごとに同じ確率でランダムな方向に道路に沿って 1m ステップします．家に着いたり居酒屋に着いたりすると，そこにとどまります．

家まで 3m，居酒屋まで 7mの距離にある場合，彼が帰宅できる確率はどれくらいですか．

https://elementy.ru/problems/

立方体の上の面の対角線にレールがあり，下の面の対角線（上の面の対角線とは直交）にもレールがあります．下のレールの端（頂点）と上のレールの中点（面の中心）とを結ぶ長さの「線分」があり，この線分（長さを変えない）の両端はレール上をすべることができます．線分が包絡線となり囲む図形（リノイド）の表面の形を推理してください．

立方体の1辺の長さを2aとすると，リノイド体積はいくらですか．

なかなか難しいですが，線分の動きを頭の中でシミュレーションした以下の図が参考になります．

立方体の1辺の長さを2aとすると，線分KFの長さはa√6です．
図のような，座標系で考えます：

$$K(x_{K} , 0, -a), F(0, y_{F} , a), M\left( x, y, z \right) $$とします．
$$\overrightarrow{KM}(x-x_{K} , y , Z+a), \overrightarrow{FM}(x, y-y_{F} , z-a)$$
なので，次の方程式が得られます．
$$\displaystyle \frac{x-x_{K } }{x}=\displaystyle \frac{z+a}{z-a}=\displaystyle \frac{y}{y-y_{F } }$$
これを解いて，　　$$x_{K}=\displaystyle \frac{2ax}{a-z} , y_{F}=\displaystyle \frac{2ay}{a+z}$$
一方，　$$\left\{ \begin{array}{@{\,} c @{\, } }
KF^{2}=x_{K}^{2}+y_{F}^{2}+4a^{2} \\[0mm]
KF=a\sqrt{6}
\end{array} \right. $$ 　⇒　 $$x_{F}^{2}+y_{F}^{2}=2a^{2}$$　であるので，$$x_{F} , y_{F}$$を代入して，
$$\left( \displaystyle \frac{2ax}{a-z} \right) ^{2}+\left( \displaystyle \frac{2ay}{a+z} \right) ^{2}=2a^{2}$$　 ⇒　$$ \displaystyle \frac{2x^{2 } }{\left( a-z \right) ^{2 } }+\displaystyle \frac{2y^{2 } }{\left( a+z \right) ^{2 } }=1$$
このリノイドの水平（すなわち軸Ozに垂直）断面の方程式を得るためには， 
zの値を区間$$\left( -a, a \right) $$でスライスする． 
この方程式は，半軸に$$x=\left( a-z \right) /\sqrt{2}, y=\left( a+z \right) /\sqrt{2}$$を持つ楕円の方程式になる．
楕円の面積$$S$$は，　$$S=\pi \cdot \displaystyle \frac{\left( a-z \right) }{\sqrt{2 } } \cdot \displaystyle \frac{\left( a+z \right) }{\sqrt{2 } }=\displaystyle \frac{\pi }{2}\left( a^{2}-z^{2} \right) $$
ゆえに，リノイドの体積$$V$$は，　$$V=\displaystyle \frac{\pi }{2}\displaystyle \int_{-a}^{a}\left( a^{2}-z^{2} \right) dz=\displaystyle \frac{2\pi a^{3 } }{3}$$ 

厚労省の公表値を用いて，日本の有病率を求めると0.6%，検査陽性率は5%程度です（5月14日時点）．このデータを用いて，ベイズ推定を用いPCR検査結果の考察をします．PCR検査の感度$$a$$と特異度$$b$$により，この結果は大きく変わります．PCR検査の感度$$a$$と特異度$$b$$は，従来の定説の0.7と0.99よりはるか高い，0.95と0.9992であることが，最近の研究で知られています．

今日のPCR検査で$$+$$判定の者には，罹患（真陽性）と非罹患（偽陽性）があります．同様に，今日のPCR検査で$$-$$判定の者にも，非罹患（真陰性）と罹患（偽陰性）があります．つまり，今日，罹患となった者には，真陽性と偽陰性があります．そして，今日の罹患者の病気期間は11日間とすると，今日の罹患者は，11日間先まで罹患者であり続け感染源となります．これを有病罹患と定義します．今日の有病罹患者は，11日前から今日までの罹患者の累積となります．11日を過ぎれば，PCR検査$$-$$となり，回復非罹患者（今日の非罹患者＋11日より以前の全検査数-累計死亡者）になるとします．ここで，PCR検査で$$-$$判定で，罹患であるのは，検査の確率の視点での話で，必ずしも，無症状の感染者と一致するものではありません．
日々発表される新規陽性（罹患）者数を累積すると，累積陽性者数になるので，差分としての新規陽性者数は，罹患率に似た傾向ですが，罹患率そのものではありません．ここで定義する有病罹患者は，日々の新規罹患者と病気期間（発症してから陰性になるまでの病気減衰関数$$A(t)$$）のコンボリューションとして得られます．
$$有病罹患者(T)=\displaystyle \int_{0}^{T}罹患者(t) \cdot A(T-t)dt$$

あるいは，$$現罹患者数=累積陽性者数-累積退院･回復者数-累積死亡者数$$で定義できます．

有病罹患者（現罹患者）

国内発生状況．厚労省（2021.5.15現在）

$$有病率(5.15現在）=有病罹患者数(5.15現在)/累積PCR検査数=5.8×10^{-3}$$
$$陽性率(5.15現在）=陽性者数(t)/PCR検査数(t)=5.2×10^{-2}$$

PCR検査の感度$$a$$と特異度$$b$$が与えられ，集団の有病率$$p(罹患)=x$$が与えられると，この集団で，PCR検査が+と判定されたとき罹患者である確率$$p(罹患|＋)$$，および，-と判定されたとき罹患者である確率$$p(罹患| - )$$を推定できます．
$$p(罹患| + )=p\left( + |罹患 \right) \cdot p\left( 罹患 \right) /p\left( + \right) =a \cdot x/\left( a \cdot x+(1-b)\left( 1-x \right) \right) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) \cdot x/\left( (1-a)x+b \cdot \left( 1-x \right) \right) $$，

従って，この集団の陽性率を$$p( + )=y$$とすると，有病率は，以下のように表現できます．
$$p(罹患)=p(罹患| + )･y+p(罹患|-)･(1-y) $$
$$x=a \cdot x \cdot y/\left( a \cdot x+\left( 1-b \right) \left( 1-x \right) \right) +\left( 1-a \right) \cdot x\left( 1-y \right) /\left( \left( 1-a \right) x+b \cdot \left( 1-x \right) \right) $$

$$有病罹患者(T)=\displaystyle \int_{}^{}罹患者(t) \ A(T-t)dt$$
病気減衰関数$$A(t)$$の半減期はおよそ10日ですので，近似的に，有病罹患者数(t)は本日の罹患者数(t)の10倍としたもので，この等式が成立/

特異度は，$$b$$>0.99（0.999）との説もあり$$b=1$$として，$$a$$を求めると，$$a=5.2×10^{-2}/5.8×10^{-3}=8.9$$

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 

■条件付き確率についての「ベイズの定理」とは次のように説明できます．$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$ 
ただし，記号の意味は例えば以下の様です．
$$p(X)$$：$$X$$が起こる確率
$$p(Y|X)$$：$$X$$が起こり，かつ$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きた後で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

■PCR検査の精度
「新型コロナ検査，どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）」によると，以下のようです：
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく判定される確率のことで，あまり大きくなく0.7程度です．真の罹患者でもPCR検査で陰性（－）（偽陰性）と判定される確率が0.3程度あります．
検査の特異度とは，非罹患者を正しく陰性（ー）と判定する確率のことでかなり高く0.99程度です．従って，非罹患者を陽性（＋）（偽陽性）と判定する確率は稀で0.01程度です．

有病率（現罹患者の比率）$$x$$が小さい集団では，非罹患者が大部分を占めるので，PCRで偽陽性の確率は0.01と非常に小さいとはいえ，PCRの偽陽性者数は多くなり，医療崩壊につながるという主張があります．しかしながら，陽性確定までにPCR検査は2度行われ，2度とも偽陽性となる確率は$$10^{-4}$$，1万人に1人です．さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．あるいは，PCR検査の感度のために偽陰性者をたくさん生むという主張もあります．確かに，検査数に比例する偽陰性者を出しますが，検査しない状況と変わりなく，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

（注）罹患者とは，真に感染しており現在感染源となるものと定義します．これには，PCR検査で陽性（真陽性）と判定されるものと，陰性（偽陰性）と判定されるものとを含みます．非罹患者とは，もともと感染していないか，回復した感染者で，感染源とならないものです．非罹患者はPCR検査で陰性になるのが原則ですが，例外（偽陽性）も0.01あります．有病率＝罹患者数／(罹患者数＋非罹患者数)　は，有病率の定義です．

■PCR検査の原理 
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です． 

■有病率の考察
日本疫学会の定義によると，有病率とは，ある時点で，疾病を有している人（罹患者）の全人口にたいする割合です：
（定義）有病率＝その時点の罹患者数／集団の人数
この有病率と混乱しそうな概念に，罹患率というものがあります：
（定義）罹患率＝ある期間の新規感染者数／集団内の感染感受性のある人数 

毎日発表される，COVID-19の新規感染者数は，罹患率の概念に近いが，罹患率に換算するのに必要な分母の「感染感受性のある人数」が不明です．ワクチン接種などで，感受性のある人数が減れば罹患率は上昇します．もし，その日の検査数（偏りのあるサンプルで，恣意的変動はある）を分母にするなら，その日の陽性率が得られます．
日々の新規感染者数や検査数は，恣意的な変動があるので，7日の移動平均をとり陽性率を定義します．検査の対象集団は症状のあるものや濃厚接触者なので，サンプル集団には陽性側に偏りがあります．

有病率，罹患率，陽性率は，時間で変化する関数で，感染拡大の指標になりますが，それぞれ意味合いが異なります．大雑把に言うと，陽性率は有病率の差分のような統計量です．

公開データから計算できる有病率$$p(罹患) $$を以下の2通りで定義することにしました．
（定義１）本日の有病者数＝累積陽性者数－累積回復者数－累積死亡者数
　　　　　本日の有病率＝本日の有病者数／累積検査数

厳密に言うと，累積陽性者数には非罹患者の陽性数（偽陽性）も混じりますが，累積回復者数を減じるので，これは相殺すると思われます．

有病率の分子からは回復者などが除外されるので，陽性率＝陽性者数／検査数よりも常に小さい値になります．

COVID-19の新規陽性者は，2週間隔離（症状の程度により，病院，宿泊施設，自宅などに）されますので，死亡者は無視して，本日の新規感染者は続く2週間は罹患者と見なされます［罹患期間を10日間とする見解もあります］．そして，2週間後にPCR検査が2度陰性になれば回復者に入ります．そこで，死亡者を無視すると次の定義も成り立ちます．便宜的に，新規感染者とは新規陽性者と同義語とします（厳密にいえば，偽陽性者が含まれるのですが，除去の根拠となるデータがありません）．

（定義２）本日の罹患者数＝日々の新規感染者数を2週間前まで遡り総和．
正確には，陽性持続曲線を用いて，新規感染者数と陽性持続曲線のコンボリューションとなります．
陽性持続の半減する期間はほぼ10日です．

英国国家統計局（ONS）は，オックスフォード大学，マンチェスター大学，英国公衆衛生サービスNHS，ウェルカムトラスト，IQVIA，グラスゴー・ライトハウス研究所，バイオセンター・ミルトンケインズと協力して，イングランドでパイロット調査を2020年4月に開始し，8月からは，サンプルのサイズを拡大し2021年3月まで大規模調査をしました．英国の４地域ベースのランダムな世帯サンプリングをし，得られた偏りのあるサンプルを英国全人口に外挿するには，多層回帰および事後層別化（MRP）を用いました．同じ世帯に対し長期間のCOVID-19検査を実施（最初の4週間は毎週，その後は毎月の検査）し，症状の有無にかかわらずCOVID-19の有病率と罹患率を，ほぼリアルタイムで観測し，病気期間（陽性持続確率）の関数を得ました．PCR検査の感度$$a$$と特異度$$b$$についても新しい知見が報告されました：$$a=0.95(0.85～0.98)$$，$$b=0.9992$$．スワブ採取が適切な監督下で行われれば，自己採取でも医療従事者が直接採取した場合と同様に正確な結果になることがわかりました．

COVID-19 Infection Survey: methods and further information，26 March 2021

 $$p_{a}(t)$$

 ■陽性率の考察
$$t$$時点の陽性率($$t$$）は，その時点でCOVID-19の検査で陽性となった人の割合です。現在のCOVID-19感染症は、鼻と喉から採取した綿棒で、症状の有無にかかわらず、SARS-CoV-2が陽性であることを意味します。これは、発生率とは異なります。発生率は、特定の期間における新しいポリメラーゼ連鎖反応（PCR）陽性の症例のみの測定値です。

ここで，陽性率$$p(+)$$に用いるべき数値を検討します．恐らく，毎日発表される検査陽性率（7日の移動平均された新規感染者数／7日の移動平均された検査数）を用いるのが適当でしょう．これは感染者数の微係数のようなもので，感染流行の傾向をある程度反映し注目すべき数値です．しかし，検査対象の制限（偏りがあるサンプリング）があり，かつ，サンプル数は少ない状況にあります．東京都の場合は，全人口1,400万人の集団に対して，症状のある集団1,000人程度を毎日サンプリングしています．日々の検査陽性率の4月14日時点の，厚労省の全国データを用いて，（検査）陽性率，$$p(+)=0.06$$を採用することにします．

引用）
1.厚労省データ，東京都データ，
2.COVID-19 Dashboard by the CSSE at Johns Hopkins University 

■問題：以下の２つを推定しましょう．ただし，ベイズの定理を使います． 
事前確率として，有病率を$$ p(罹患)＝x=0.003$$を用います．

（１）PCR検査で陽性と判定されたとき，罹患者（真陽性）である確率を求めなさい．この確率は，検査の「陽性的中率」と呼ばれます． 
$$p(罹患|+) =p( +|罹患) p(罹患) /p(+) =0.7x/(0.7x+0.01(1-x)) =$$
$$=7x/(6.9x+0.1)$$

（２）有病率を推定しなさい．
陰性と判定されたものの中に，見逃された罹患者（偽陰性）のいる確率は：
$$p(罹患|-) =p( -|罹患) p(罹患) /p( -) =0.3x/(0.3x+0.99(1-x)) =$$
$$=3x/(-6.9x+9.9)$$

集団の有病率$$x$$を変数に，$$p(患者|+)$$と$$P(患者|-)$$のグラフを示します．

従って，全人口に対して推定される有病率は，陽性率$$p(+)$$，陰性率$$p(-)=1-p(+)$$とすると，
有病率$$=p(罹患|+) p( + ) +p(罹患|-) (1-p(+) )$$　なので，

事前確率として有病率$$x=0.003$$を用いた場合は，真陽性の確率0.174，偽陰性の確率0.0009で，さらに，陽性率$$p(+)=0.06$$を用いると，真陽性の罹患者に，見逃された罹患者（偽陰性）を加えた有病率は$$0.174×0.06+0.0009×(1-0.06) =0.011$$と推定されます．

■PCR検査数は十分か

引用）
3.https://ourworldindata.org/coronavirus-testing

 ここに引用したのは，検査陽性数／1日（横軸）；検査数／1日（縦軸）の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは100万倍大きい（数値では30～20倍）のでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を全部拾う十分な検査が行われているようです．英国の例を見ると，始めは，陽性者がたくさん出て検査数が間に合わないほどでしたが，現在は十分な検査数が確保されていることがわかります．日本の例では，検査数と陽性者数の増減が微妙なバランスにあり，英国のグラフに見られる検査数を増やしても陽性者数が一定となる部分が見られません．検査数を増やせば，陽性者数も増加する可能性があります．

COVID-19では，無症状の罹患者が感染源となることが知られています．症状のあるグループだけをサンプリング対象にした限定されたPCR検査では，無症状の感染源は抜け落ちています．自由に活動する無症状の感染源がどの程度のウエイトかも未知ですので，PCR検査のサンプリング対象の拡大をはかるべきです．

■継続的検査のイギリス流戦略

引用文献）

4.https://plus.maths.org/content/testing-testing-schools
5.Assessing the impact of secondary school reopening strategies on within-school COVID-19 transmission and absences: a modelling study，Trystan Leng，etal.

英国では3月8日に学校を再開するにあたり，接触者継続的検査SCTという対策を決めました．英国JUNIPERコンソーシアムの研究者達が，数学モデルを用いて種々の検査戦略のシミュレーションをした結果です．

クリスマス前（閉鎖前）の生徒は，学年別「バブル」の一員として学校に通っていました．ある生徒が陽性と判定された場合，その「バブル」内の全員が10日間の自己隔離になります．この戦略は，学校内はもとより周囲コミュニティ内の感染伝播も防げる利点がありますが，多くの学校で生徒を欠席させるという欠点があります．

生徒が学校に行けない日数を減らすために，イムノクロマトグラフィー（LF検査）を使用した新しい戦略（SCT検査）が提案されました．COVID-19の症例が特定されると，その「バブル」内の他の生徒は，①「10日間の自己隔離」か，②「7日の間，毎日LF検査を受けて，その日の検査が陰性ならば学校に通う」のどちらかを選択します．この戦略の目標は，多くの生徒たちが学校に通えるようにすることにあります．生徒は，学期の初めにLF検査を2回受け，陰性である場合にのみ通学します．

■イムノクロマトグラフィー検査

イムノクロマトグラフィー（LF検査）は，抗体が配置されたセルローズ膜繊維の端に，採取した検体を滴下し，検体中にCOVID-19の抗原があるなら，それが抗体と反応しながらセルローズ繊維を移動し所定位置でキャプチャーされ呈色します．

LF検査はPCR検査よりも感度が低いかもしれませんが，30分以内に結果が出ます．ウイルス量が最も多く，感染性が最も高いと考えられる時点（感染してから約5日後）には，LF検査でCOVID-19陽性となる確率は十分高い［LF検査は，感度も特異度も95%以上との説もあります］のです．人々が感染を避け家にいるだけという状況から，活動できるように，常に検査を続けフィードバックを行うSCT検査への転換をしました．

■数学モデルで介入をシミュレーション

COVID-19に感染した中学生の12ー31％が，症状を発症すると考えられており，発症すると無症候よりも感染性が高いのですが，無症候の感染力はよくわかりません．このように未知の不確実性があるので，シミュレーションのモデル作りでは，パラメーターに不確実性を採り入れ，点推定ではなく範囲を推定しています．

ダイソンのグループ（レンら）は，それぞれ200人の生徒からなる5つの「バブル」で構成されるモデルを作成し，色々な検査戦略：何もしない；学年グループを隔離；SCT検査；毎週の集団検査；両方検査の組み合わせ；のそれぞれを，7週間にわたって毎日の時間ステップでシミュレーションしました．

もちろん，「SCT検査と毎週の集団検査の組み合わせ」が，欠席日数と感染数の両方を減らす最も効果的な戦略です．

検査をすれば，無症候性のCOVID症例が多数特定できます．しかし，組み合わせ検査の戦略では，7週間の半期の終わりに，生徒1人は平均して25回の検査を受けます．検査費用もかかり，若者の同意が必要です．毎日子供たちの鼻に綿棒を突き刺すのは素晴らしいことではありません．それらはトレードオフにあります．この調査は，パンデミックの際に政府や学校の指導者が下さなければならない難しい決定を浮き彫りにしています．ライブパンデミックの前例のない挑戦に対処するには，数学モデルが活躍します．

英国はロックダウンを間欠的に実施しました．長期にロックダウンを続ければ感染は減りますが生活ができなくなります．どのくらいの期間のロックダウンをどのくらいの期間を空けて実施するのが良いかのトレードオフも，感染拡大モデルでシミュレーションしています．英国の100万人当たりのPCR検査数は日本の20倍～30倍もあります．パンデミックを乗り越え現在の有病率は日本より小さい値に下がっています．

実効再生産数を減少させるには，次の3つを減少させることです：①感染者が感染力を持つ期間，②感染者が1日当たりに接触する人数，③感染者の接触で感染する確率．感染→潜伏期間→発症期間→検査→隔離の期間内でCOVID-19は感染します．COVID-19は，潜伏期間でも感染し，発症のない無症状も感染力があることが判明しています．「感染者が感染力を持つ期間」を短くするには，検査で早く感染者（有症状，無症状とも）を見つけ早く隔離することです．

検査陽性者数
日本国内（2021.03.23）

東京都（2021.03.17）

検体採集日と，判定確定日や発症日は医師判定までのタイムラグを含む．
検査数はPCRだけでなく抗原検査も含む．
＊ジョンズ・ホプキンス大学，東京都，厚労省のデータを用いました．

・検査陽性率＝陽性者数/検査数　はどのくらい？
上のデータより，国内では4.9%，東京都では6.5%と推定するのが適当であろう．

１．サンプリングの偏りが変化している
PCR検査を受診できるグループは限定されている．初期は，無症状者は検査対象外でした．その後，クラスター対策で局所的な検査対象になり，現在の対象者の限定は明確でないが，無症状者が増えているようだ．
状況に応じて対象カテゴリを広げるのは当然で，感染抑止のために無症状の有病者を把握することは必要である．感染疑いの濃いグループをサンプリングするので偏りがあるわけですが，この基準自体も変化している．
このように，統計のプラットホームが変化しているから，変化を時系列に並べて，単純に発生率の変化と解釈することはできません．

２．統計量の定義
日本疫学会の定義によると，集団の有病率とは，その時点で，疾病を有している人の集団人口にたいする割合．集団の疾病発生率（罹患率）とは，一定期間に発生した疾病者のその集団で疾病感受性のある人口にたいする割合です．
有病率(t)＝疾病を有する人数(t)/集団人数(t)
発生率(t)＝新規陽性者(t)/集団内の感受性のある人数(t)

毎日，発表される新規陽性者の数は，発生率に近い概念ですが，集団内の感受性のある人数が未知なので，発生率とは正確には同じではありません．
PCR検査陽性率＝新規陽性者/検査数で定義しますが，これも，サンプル集合の偏りと変化のために，単純比較はできません．そのため，累積数の比でこれを定義することにしました．

本来，有病率や罹患率などの統計量の時系列での変化を論じるには，ランダム・サンプリングの検査であるのが原則です．
ランダム・サンプリングで行われた調査としては，厚労省が抗体検査を行ったことがありますが，東京都で陽性率が0.1％程度だったと思います（2020．6）．現時点での陽性率（多分増加している）が知りたいです．
東京都の人口は約1,400万人，これまでの感染者累積11.7万人を用い，0.8４％が抗体保有者率が見積もれます．

現時点の感染者＝感染者累積ー回復者累計ー死亡者累計ですから，これを仮の有病者(t)と定義します．有病者(t)と新規陽性者(t)は同義語ではありませんが，比例すべきと予想します．しかし，推測される有病者数に対して，現在のPCR検査数で拾い上げられる陽性者は圧倒的に少ない．
PCR検査数の増加が必要な所以です．特に，無症状の有病者はPCR検査のサンプル集合から除外されているのも問題です．

いくつかの定義を明確にしたい
PCR検査陽性者は有病者と同じか？
有病者から無症状者が除外されるのは良くないだろう．どの時点で患者（罹患者）と呼ぶのか？

今後考慮すべき問題
無症状者も感染に寄与すること，PCR検査で陰性となる変異株の出現などあり，これらのパラメータをどう定義するか？実効再生産数には反映される．
感染拡大の結果やワクチン接種による持続的な抗体形成により，感受性のある人口を減少させます．

陽性率を，p(+)＝累積陽性者数/累積PCR検査数と定義すると，東京都の2021.3.17までのデータや厚労省の公表データを用いて，陽性率は，東京都で約6.5%（全国で4.9％，厚労省）になります．しかし，PCR検査の感度と特異度の情報（酒井健司，朝日デジタルなど）を入れてベイズ推定し，陽性的中率p(罹患|+)や偽陰性率p(罹患|-)を求めました．

ランダム･サンプリングのデータがないので，罹患率（有病率）も陽性率に等しいと仮定せざるを得ませんでした．
注）日本疫学会の定義によりますと，有病率と罹患率は異なります．

有病率＝ある時点における疾病を有する者の数/調査対象全数
罹患率＝ある時点における発生新規患者数/感染感受性のある人数

罹患率は，集団内の感染感受性のある人数に対して定義されるので，２つの定義で分母が異なります．さらに，有病率でいう「ある期間で疾病を有する者の数」は，罹患率でいう「新規感染者の数」とは異なるわけですが，タイムラグを考慮すれば，どちらも同様な傾向と近似ができそうです．

ここでは，有病率と罹患率を同義語として扱いました．毎日発表される，新規感染者数は，罹患率とは異なりますがよく似た指標であります．

東京都の2021.3.17までの陽性者累計116,293人，検査実施累計1,779,950人を用い，現在の陽性率はｘ＝6.5%程度（全国ではx=4.9%）程度と推定します．
ランダム･サンプリングではないし，データが不足しているので，罹患率（有病率）も陽性率に等しいと仮定します．

（注）ここで対象となるサンプル集合は，PCR検査を受診できる限定されたグループですので，ランダム･サンプリングではなく偏っており（発症条件が課さたグループ），その陽性率は一般集合より若干高値でしょう．また，サンプリング条件が感染状況とともに変化しているので，単純な時間変化の比較はできません．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
■条件付き確率についての「ベイズの定理」とは次のように説明できます．
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です．
p(X)　Xが起こる確率
p(Y|X)　Xが起こった後でYが起こる確率
p(X∩Y)　XかつYが起こる確率
ベイズの定理は，X（原因）が起きた後でY（結果）が起きる確率p(Y|X)と，XとYを入れ替えた確率p(X|Y)を結び付ける定理です．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
■PCR検査の精度
新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）などにより，次のように仮定します．
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく的中する確率のことで，あまり大きくなく0.7程度といわれます．真の罹患者でもPCR検査が陰性（－）（偽陰性）となる（罹患者を取りこぼす）確率が0.3程度あるそうです．
PCR検査の特異度とは，非罹患者を正しく陰性（ー）と判定する確率のことで0.99程度です．非罹患者を陽性（＋）（偽陽性）と判定するのは稀で0.01程度の確率ですが，非罹患者の割合が多い集団（罹患（有病）率が小さい集団）では，無視できない偽陽性数になります．

■これらの仮定の下で，以下の２つを推定しましょう．
ただし，ベイズの定理を使います．
罹患（有病）率をp(罹患)≡x，非罹患（非有病）率を1-xとします．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．

青線グラフ

つまり，PCRの結果が陽性のときでも，その的中率はp(罹患|+)＝83%（x=6.5%附近）程度です．
罹患していても，検査感度のため，検査の結果が陽性にならない偽陰性が30%あり，罹患者をとりこぼしている．
一方，検査の特異度が高いので，偽陽性率は0.1%と小さいにも関わらす，非罹患者の割合(1-x)が多い集団では，陽性判定中に占める偽陽性の数も無視できない．これらの原因のため的中率が低下します．
（２）罹患（有病率）を推定しなさい．
(陰性)判定されたものの中に見逃された罹患者のいる確率p(罹患|-)は，

赤線グラフ

陰性と判定されたものの中に見逃された患者である可能性は，p(罹患|-)＝2%(x=6,5%の付近）ほどある．
従って，全人口のなかで推定される罹患（有病）率は，
p(罹患)＝ｘ･p(罹患|+)＋(1-x)･p(罹患|-)

第1項：第2項＝真陽性：偽陽性＝5.40：1.87
x=6.5%のときには，陽性中に占める偽陽性の数は25%程度である．

物理の発展に先立ち，それが必要とする道具としての数学が，先回りして常に用意されていたという歴史観があります．
そのように言いたくなる事例は確かにたくさんあります．X線結晶学に先立ちすべての空間群が求められていたこともその例です．このような廻りあわせはドラマチックで面白いのですが，数学がすべてに先だってあるはずだと信じるのは妄想です．
ニュートンの微積分のように，現場が新しい数学の源泉であったことは多く，このような開拓場面に立ち会ったのは，
数学者ではなかった（物理学者，化学者，工学者，...様々，そして，新数学分野を開拓した後，彼らは数学者と呼ばれている）．つまり，新しい数学の源泉の多くは，自然の現象の中にありました．

（注）ニュートンは，自分の研究に必要な道具としての数学（微積分）も開発しました
（ニュートンは謙虚にも自分は巨人の肩に乗っただけだといいました）．
（注）ニュートンは，惑星の動きを理解するために新しい数学（微積分）を発明しなければなりませんでした．
このような19世紀は科学の発展局面で興味深い時期です．その後，偏微分方程式の理論が生まれ，
波の伝播，熱伝達を説明する最初の場の理論が構築されました．フーリエ，ラプラスのような数学者は、
この物理学を理解するために新しい数学を発明しました．
弦理論の現在は，このような興奮する局面にある．

自然（宇宙や現象）を数学は記述することができます．あたかも数学があって自然がそれに従って作られた
という反語的表現も実は同語反復です．数学が先にあってその通りに宇宙ができているわけではありませんが，
森羅万象の自然の中に数学も含まれるので，自然を記述する数学は存在するはずです．
人間も生命も自然の中に存在しますからやはり数学で記述されるはずです．
もし人間が宇宙に居なくてもそのような数学は存在すると私は思います．
ーーー
2004年5月のノーベル物理学賞を受賞したDavidGrossがモスクワを訪れ、弦理論と理論物理学の今後について講演し，
その時のインタビュー対談は，数学と物理学の協働テーマは啓蒙的で興味あるものです．

ーーーーー
20世紀の終わりに，新しいタイプの非常に緊密な協力（物理学者と数学者の間）が登場しました．
弦理論と場の量子論では，物理と数学が非常に密接に関連しています．

弦理論が非常にロシア的という理由は，物理学と一体となったロシアの数学者の伝統（オイラーに代表される）があるからです．
ゲルファンド，アーノルド，..など．

ハイゼンベルグが量子力学（行列力学とも呼ばれる）を発見したとき，彼は数学としての行列を知りませんでしたが，
今日では行列は大学の教養課程で教えられています．
弦理論の数学ツール経路積分も，時がたてば普及するでしょう．

1930年代に書かれた量子力学に関する最初の教科書を見ると，とてもひどいものです．教科書は時間とともに良くなります．
他の分野でもまったく同じことが起こっています．力学や電磁気学に関する最初の記事と教科書は非常に複雑でした．
アインシュタインが電磁気学を研究したとき，彼は苦労しました．今や学校で電磁気学を普通に習います．

私たちが自然や数学を発明していると言うのは間違っています．逆に，私たちは自然によって発明されました．
数学は，自然を理解し，その中で最適な生存を実現するためのツールとして，私たちが創造した言語から成長してきました．
だから数学は本質的に自然の一部であり，数学が自然を記述するのが得意です．

いつの日か，銀河の反対側にある別の文明とのつながりを確立するとしましょう．世界は1つしかないので，
宇宙人は私たちとほぼ同じ物理学を持つことに誰もが同意します．彼らは我々と同じ数学を持っているでしょうか？
一部の数学者はノーと言うでしょう．彼らは我々と全く異なる数学を発明する可能性はあります．
でもやはり，彼らの数学は私たちの数学と非常に似ていると思います．

■現代のコンピューターの数値計算能力は驚くべきもので，それらは理論物理学者の働く方法に強い影響を与えました．
多くの人はもはや微分方程式を解こうとはせず，単に数値的にシミュレートします．
例えば，スティーブン・ウルフラムはすべてを計算し尽くそうとします．

実際20〜30年前のデバイスの機能と比べると，今できることは驚くべきことのようですが，
コンピュータはまだそれほど賢くはありません．計算手法は幼児期に開発されたままです．
私たちが計算アルゴリズムについて話すときに使用または考えるすべてのコンピューターは古典的です．
量子コンピューターとコンピューティングのための量子力学システムを使用するプログラムを実装すれば，
従来のコンピューターよりも指数関数的に優れたパワーを得ることができることがすでに証明されています．

量子力学もパラドックスを背景に発生しました．一方では古典物理学であり，他方ではボーアの原子モデルであり，
このパラドックスは量子力学によって解決することができました．

弦理論の最も注目に値するアプリケーションの1つは宇宙論です．弦理論家は宇宙論者や天体物理学者と多くのことを話します．
宇宙論者たちは現在、ビッグバンとビッグバン自体の後の宇宙の発達の初期段階を理解しようとしています．
この分野では，私たちの関心のある領域が重なっています．
弦理論の他のアプリケーションもあります．特に，私たちが新しい数学を発見しているという事実．
この理論は科学の発展に不可欠なステップであり，量子力学と同じように多くの用途があります．
参考書：
リサ・ランドール，「ワープする宇宙―宇宙の隠された次元の謎を解き明かす」
バートン・ツバイバッハ，「弦理論の学生のための良い教科書」

あけましておめでとうございます．
今年はcovid19の感染拡大で先行き不透明な年になりました．
皆様それぞれに悔いのない良い年になりますように．私も気を引き締めて全力で努力していこうと思っています．
新年を迎えましたが，今，私は荷物ゴミの中におります．年末に多くの荷物を，私のところへ運び込んだからです．何故そんなことになったのかと言うと，来週には，私の育った家の取り壊しが始まるからです．私は，小，中，高校も地元の公立学校に通い，大学も歩いて通える距離でしたので，引っ越しをしたことがありません．
私の育った家は，戦後に建てた始めは2部屋だけの小さなものでした．戦後の焼け跡はそのようなバラックばかりがありました．その後の70数年に増築や補強が行われましたが，ずっと同じところに住んだので，父母の物や私の物が山ほどで，高価な物は何一つありませんがそれぞれに思い出があります．そのため，大変気が進まない断捨離でした．9月のまだ暑い最中から週に2日程度通い荷物の整理を進めましたが，とうとう年末が来てしまい，選別の間に合わない残りを全部私のもとに運び込む羽目になったのです．

母は編み物が好きでした．私が小さいときに見た光景は，いつも頼まれた編み物をしている母の姿でした．母は田舎の女学校を出て東京にでて来ました．あるとき，下宿でネクタイを編んでいて、金色の絹糸を色合わして買うために，お店にそれを持参したところ，お店の主人が「見本でウインドウに飾りたい」といって買い上げてくれたそうです。「そう，恥ずかしいわね」と口では言ったものの，かなりいい値だったのでうれしかったそうです。松坂屋の斜め前の大きな糸やでのことでした。市役所で洋裁も習う時間があったようです．東都服装学校にも少し行ったそうです．兵隊さんの猿股を作るにも，糸を何センチも無駄にしないような時代のことでした．
私は子供の頃，毛糸を両腕に通して母の毛糸玉を巻くのを手伝いました．長い時間腕を上げて振っていると疲れるものです．セーター1着作るのに，20玉が必要と母から聞いていました．
母の遺ししセーターに毛糸の玉巻きを手伝いし幼き日の想い出

今回，母の残した毛糸の編み物や和服など，大きな7つの段ボールを田舎に送りました．田舎では使ってくれるそうです．
未使用の毛糸は友人の知るグループで使うというので差し上げました．

庭に私の分身のような樹齢70の枇杷の木があります．今，白い花を盛りとつけています．可哀そうですが，実をつけることなく今年は切られてしまいます．木は動けませんから．合掌
我食いし枇杷の種より育ちたる樹齢は七十の白き花盛る

物置に釣り道具を見て悔やまれる父の釣行につき合わざりし日々
父の軍隊手帳をウエブに公開し見知らぬ方に難読箇所の教えを受く

 
■時宗総本山，遊行寺の御滅灯（おめっとう），一ッ火（ひとつび）は，11月27日の夕刻から行われます．

遊行寺のウエブサイトによると：－－－－－
「一ッ火」は遊行寺年中行事の中で最も荘厳な法要です。順に灯火が消えていき、やがて完全な暗闇に包まれた本堂に幽音の念仏が響きます。そして暗黒の世界にただ一つ灯される新たな灯明が、光り輝く念仏の世界を本堂内に映しだします。
この法要には、「一年間の悪業を懺悔し、来年の善行を志す」という意味合いもあります。
なお、本年、主役である「報土役ほうどやく」は、藤澤清孝ふじさわせいこう（鎌倉市材木座來迎寺住職かまくらしざいもくざらいこうじじゅうしょく）．「後灯役」は、望月輝山もちづききざん（総本山内近司そうほんざんないごんす）が務めます。
本年度は、新型コロナウイルス感染症対策のため、参拝人数を制限させていただきます。－－－－－

本堂内の火が次々に消され、最後にこの大光灯を報土役が消し、後灯を後灯役が消します。この漆黒の闇のなかで十八念仏が始まり、報土役・後灯役は、火打ち石で火を起こします。一度目は空中で火花を散らす「見せ火」で、二度目で「火口箱」に火花を打ち込みます。打ち込まれた火は、闇からしだいに灯明へと移され、再び弥陀と釈迦の光明に照らされた世界が戻ってくることを表現します。－－－－－

時宗のこの伝統行事は，京都，東山の西連寺でも行われていることをウエブで見ました．

現在、外灯も整備され夜遅くまで街の灯りも消えることもなく、「暗闇」の怖さや心細さというものを経験することも少ない。漆黒の闇につつまれた堂内で、徐々に明るくなっていく様を目の当たりして光の有り難さを経験することでしょう。

■2016年11月27日は，夕方からの雨でどんどん寒くなりました．私は，母の一周忌の折に，ご住職からお聞きしたばかりの「一ッ火」に参加してみようと思い，藤沢，遊行寺に出かけました．遊行寺は，落語（鈴振り）でも，箱根駅伝の中継でも，有名で知っていましたが，私が遊行寺に行ったのはこのときが初めてです．「一ッ火」は，5時に始まり9時近くまで行われました．外の雨は氷雨のようになり寒い夜でした．
「一つ火」の最後に，大僧正直々に全員（何百人でしょうか，例年より少ないそうです）が，お札をいただきました．その行列の長いこと．大僧正は97才．すごい大声でのお話，さすがです．（この方が，当時，運転免許返上で話題になった方ですね）．
「一っ火」というのは，本堂のロウソク（それぞれ或るものを象徴して配置され，20～30本位ある）の火を，複雑な手順（方法や役回りがいろいろ）に法り次々に消して行き真っ暗に...，そして静寂．十八念仏が始まり，火口箱に火花を打ち込み，灯明に移されます．再び弥陀と釈迦の光明に照らされた世界が戻ってきます．念仏は美しい合唱の音楽になって響ます．

■大きな百目蠟燭*)の炎は長く伸びて明るい．じっと見ていると，炎はピタッと動かない．それが突然瞬き始める．また，ピタッとまる．これが周期的に繰り返されます．この自励振動の機構**)に感嘆して見入ってしまいました．実に面白い．まるで活きているように間欠動作をします．
面白い現象です．ロウソクの炎の瞬きと，静止が何故繰り返されるのだろうか？どちらの状態も安定でないわけで，この移り変わりが起こる理由を考え込んでしまったのです．

注*）大きな和蠟燭です．100匁目あるかどうか知りません．明るく点燈し，嫌な臭いもしません．和ろうそくはハゼの実などから作るようです．ハゼの実や和ろうそくのことなどをどなたかお書きください．
　むかしの むかしの かざみの とりの
　ぼやけた とさかに はぜのは ひとつ
　はぜのは あかくて いりひいろ
　ちいさい あき ちいさい あき
　ちいさい あき みつけた

注**)　類似な現象として；
・近づけた2本のロウソクの瞬きの周期が揃う（協同する）という現象があります．以下に，協同現象のyoutube実験動画を引用します．
・蛍の明滅がそろってくる協同現象も知られています．
・私が昔係わったことのあるプラズマディスプレイ装置では，放電スポットが周期的に明滅する自励振動の現象がありました．

こんなクイズを何処かで聞いたことがありませんか？
１人10ドルのホテルに3人が止まり，30ドル支払いました．ホテルフロントが5ドル値引きしてくれ，女中を介して返金してきましたが，途中で女中が2ドル抜いたので，3人に渡ったのは1ドルづつです．結局，それぞれ9ドルづつ支払ことになり，全員でホテルに27ドル，女中が2ドル持っています．残りの1ドルはどこに消えたのでしょうか？
ややっこしくて変な気分ですが，お判りでしょう．27ドルと2ドルを足す意味は何でしょうか？

このような計算の笑い話は，落語のツボ算にも出てきます．買ったツボを返品するときに，支払った金額と返品するツボの値段を足してしまうのです．
数学の方程式を作るときに，左辺に足すか右辺に足すかよく意味を考えて式を作らないと，このようなとんでもないことになります．

落語の時そばでは，そば代金の16文を数える間に，8のときに時間（八つ）を混ぜ込むことで，１つスキップし金額を1文ごまかします．与太郎が真似をするときは，時間が（四つ）で，逆戻りし損をしてしまいます．これは，お金と時の呼び名という単位が異なり足すことのできないものを足すトリックです．我々ももう少し複雑な問題ではありますが．方程式を立てるときに単位の異なるものを足してしまうような式を立ててしまうことがよくあります．笑い話ではすみません．

話のついでにもう一つ，落語に出てくる不正な計算について述べましょう．落語花見酒では，酒だるを担いで売りに行く2人の間で，お金をやりとりしているうちに，お酒が全部なくなってしまう話です．これは売上金の公金横領に当たるわけですが，お金はお金でも，公金と自分の金というカテゴリーの違うものの区別ができなかったために起きた笑い話です．

最初の例に戻ると，ホテル取り分は25ドル，女中取り分は2ドル，客支払い分は3x9=27ドルで何の不思議もありません．

■以上をブログに掲載した時に，読者の方から「三方一両損」の話が出ました．
江戸っ子の職人が３両入りの財布を拾って，落とし主に届けると，落とし主はいらないと意地を張る．どちらも江戸っ子らしくていいですね．
大岡越前守が，1両出して4両にし，2両づつ分けさせる名裁きをします．
拾ったまま届けず手元に置けば3両ある．届けてもらって受け取っておけば3両ある．
奉行も関わらなければ1両出さずに済む．しかし，結局3人とも1両ずつ損をしたというのです．

■今回もう一つ，35頭のラクダと3人の兄弟（アラビア数学奇譚，３章より）を追加しましょう．

35頭のラクダを，父の遺言によれば，長男Aが1/2，次男Bが1/3，3男Cが1/9に分けろというものです．
かぞえびとペレズミがラクダをつれた友人と通りかかります．

ペレズミは言います「ここにある友人のラクダを上げますから36頭にしましょう」
36頭で計算すれば，すべて割り切れて，A,B,Cの3人のすべてが得をします．
なぜなら，
35/2<36/2=18
35/3<36/3=12
35/9<36/9=4

その結果，18+12+4＝34頭ですみますから，1頭は友人に返却して，余った1頭は相続の問題を解決したペレズミがもらいます．

2019.02月号より，文 Юрий Белецкий ＋図 Алексей Вайнер

■オデッサ州立フィルハーモニー協会（建築家-A.I.ベルナルダーツィ）
の窓は，円と弧のパターンで装飾されています．
この窓は，すばらしい幾何学問題を提供しています．

白板に描いたように，小さな３つの円の中心$$O_{1}，O_{2}，O_{3}$$は1つの直線上にのります．証明してください．

■この問題をみて思い浮かべるのは，以前掲載した以下の2つの記事です．
アポロニウスの窓，アルべロス（靴屋のナイフ）という形のなかに面白い幾何学世界があります．
反転の利用ーパップスの定理
https://note.com/sgk2005/n/n56056054e23c

インドラの網と反転円
https://note.com/sgk2005/n/nec1396b13bd4

アルべロス（下図のオレンジ色の形）の中で，パップスの定理が成立しています．しかし，円$$ω_{2}$$と円$$ω_{1}$$の中心を結ぶ線は，水平ではありません．

いま問題になっているオデッサの窓内の円では，$$O_{1}，O_{2}$$を結ぶ直線は水平になるのですが，その原因は，外側の大きな円（半径$$r$$）内で重なり合う2つの円（半径$$ar$$）に接するように，半径$$xr$$の円を決定することによります．しかる後に，この半径$$xr$$の円に接するように，半径$$yr$$の円を描くと，この円の中心は半径$$ar$$の中心線上に存在するようです．
問題のオデッサの建物図では，$$a=2/3$$（大きな円の直径を3等分する位置に柱がある）のようですが，実は，同じ半径の円が重なっていれば（任意の$$1/2<a<１$$）成り立つようです．

接する4つの円の半径の間にはデカルトの定理という式が成り立ちますが，それを計算するのは容易ではありません．幾何で解くことにしました．

円の接する条件を図示すると，辺の長さが，$$1-x，1-a，a+y，x+y$$の4角形になります．4角形の対角線は，$$a+x，1-y$$です．この条件は関係する円が接するための条件です．$$1-x$$の辺が垂直なのは対称性から明らか，半径$$yr$$の円の中心と，半径$$ar$$の円の中心を結ぶ$$a+y$$も垂直として，$$x$$と$$y$$を解くと，

この$$x，y$$を用いて，互いに対向する辺の長さを求めると，互いに等しいことが証明でき，矛盾は出ません．

従って，この4角形は長方形になり，辺$$x＋ｙ$$は水平であることがわかります．

この式を証明していきたいと思います。n桁の数字を$$(x_n),(y_n),(z_n)$$とすると、

$$ (x_n)=(10^n-4)/6 $$

$$(y_n)=(10^n)/2$$

$$(z_n)=(10^n-1)/3$$

と表せる。元記事より

$$ x_{n}^{3}+y_{n}^{3}+z_{n}^{3}=10^{2n}x_{n}+10^{n}y_{n}+z_{n} $$

を証明すれば良いことがわかる。

$$x_{n}^{3}+y_{n}^{3}+z_{n}^{3}＝((10^{n}-4)/6)^{3}+(10^{n}/2)^{3}+((10^{n}-1)/3)^{3}$$

$$ {10^{2n } }x_{n}+10^{n}y_{n}+z_{n}=10^{2n}(10^{n}-4)/6+10^{n}10^{n}/2+(10^{n}-1)/3 $$
$$=10^{3n}/6-10^{2n}/6+10^{n}/3-1/3$$

ゆえに

$$(x_n)^3+(y_n)^3+(z_n)^3＝{10^(2n)}(x_n)+(10^n)(y_n)+(z_n)$$

が成立する。

大まかなものだとこういう感じです。

菱形30面体とサッカーボール（あるいはフラーレン）の関係の続編です．
菱形は正多角形ではありませんから，菱形多面体は正多面体ではありませんが，正多面体や準正多面体と密接な関係がありますので，菱形多面体に集中して見直しましょう．菱形12面体と菱形30面体があります．それぞれの菱形多面体は，準正多面体6・8面体と12・20面体の双対多面体として得られます．
(注）双対多面体というのは，面と頂点を入れ替えて対応させて作る多面体です．例えば，準正多面体の6・8面体は，正6面体の面と正8面体の面よりなり，正6面体の面を対応させた頂点と，正8面体の面を対応させた頂点とで，菱形12面体の頂点は構成されています．

（美しい幾何学p.21より）

■菱形12面体は，空間を隙間なく充填できる立体です．菱形12面体の面を合わせて空間を充填すると，立方面心格子の配列ができます．

（美しい幾何学p.61より）

■菱形12面体の見える万華鏡を作る

（美しい幾何学p.44,45より）

 さて，菱形12面体の菱形面の対角線比は，1:√2であることを確かめてください．
菱形30面体の菱形面の対角線比は，黄金比2:1+√5であるを確かめてください．

■IQライトと呼ばれるランプシェードの話が，kvantik（2019.07）に載っていました．重さはたったの100グラムで，30枚の薄いフレキシブルプレートを組み立てて作ります．各プレートは菱形の形状で，4つのフックがついていて組み立てます．このデザインは，デンマークのデザイナーHolger Strömによって1973年に作られたそうです．
名称のIQはInterlocking Quadrilateralsーー連動した四角形の略．
菱形面が５つ集まる場所と３つ集まる場所があることに注意して，組み立てましょう．

 
カバー写真は私のバイオリンですが，低音域に共鳴点があり振幅が大きくなり音が開くような気がするのです．バイオリンの音質が何とかならないかと思って，昔，高い本だと思いながら気まぐれで買った「楽器の音響学」安藤由典という本が手元にあります（残念ながら役には立ちませんでした）．この本のp.132に，バイオリン胴板の振動モードの図（小橋,時田，日本音響学会誌，Vol.8,p.15,'52より引用したもの）があります．本自体古いし引用文献も大変古いので，もっと詳細な実験がその後どこかに発表されていると思います．特に調べていませんので，もしお気づきの方おられましたらお教えください．

バイオリンは駒から1cm付近の弦を弓で振動させ，駒から指板上の指で押さえた点までの長さの弦が振動し，その振動を胴で共鳴させます．共鳴箱の役割が重要です．定在波の振動の節となる場所は節点，2次元の面ですから，定在波の振動の節点は節線となって領域を取り囲んでいます．
振動モードの図で白い部分と斜線部分は振動方向が逆になっているので，斜線との境界線が節線です．周波数が上がるにつれて細かい領域に分かれて行くのは納得できるでしょう．楽器は特別な共振域ができないよう設計されあのような形になるのだ思いますが，ある音域が共振気味に耳元で鳴るのは良くありません．私はそれを見抜けずに迷った挙句良くない方を購入してしまいました．

■ここで，クラドニ図形の次の動画をご覧ください．

振動の腹では粉末は払いのけられ節線に集まります．この実験で見られる興味深い図形をクラドニ図形といいます．
振動から生じる節線についてのさまざまな疑問は，200年以上にわたって科学者を魅了してきました．1809年，クラドニがパリを訪問した後，フランス科学アカデミーはコンテストを発表しました．その目的は，「弾性表面の数学的理論を構築し，それが実験データとどの程度一致するかを示すこと」でした．この賞は1816年にソフィー・ジャーメインが受賞しました．その数学的モデルは，少し後のグスタフ・キルヒホフによって完成しました．

ここでこの話題を取り上げたのは，「トリニティオプション-サイエンス」第16号(310），2020年8月11日に，フョードル・ナザロフ，ミハイル・ソディン，アレクサンドル・ログノフによるこのテーマの紹介記事で，
アレクサンドル・ログノフが，2020年のヨーロッパ数学会のEME賞（数学への卓越した貢献が認められた35歳未満の10人の研究者に4年ごとに授与）を受賞したニュースを見たからです．

■周波数が上がると定在波の節線集合の形はだんだん細かくなりますが，どのように変わるのでしょうか．
バイオリンやギターなどの楽器は，圧縮に抵抗する弾性体の板を振動させますが，膜の振動であれば一定張力のみの弾性体ですみます．実際の楽器の振動計算をするのが目的ではなく，この節線集合サイズの振る舞いを知るのが目的ですので，アレクサンドル・ログノフは扱いが単純化できる膜モデルを用い，ラプラス微分方程式の各周波数に対する固有関数のゼロ節線集合のサイズに関するヤウ・シンツンとニコライ・ナディラシビリの予想を証明しました．

■この問題は，工学的には，2次元のFourier解析で膜の振動を正弦波の固有振動の重ね合わせに分解し，ラプラス方程式の固有関数を与えられた境界条件で解く有限要素法でコンピュータを用い数値解を得ることができます．
ラプラス演算子をΔ，振動数ωの固有関数 v_ω(x) は微分方程式
Δv_ω(x)+ 4(π^2)(ω^2)v_ω(x)= 0　の解です．節線集合は，条件 v_ω（x ）= 0を満たすｘの集合で，与えられた境界条件を満たすように解く問題です．

Fourierはナポレオン時代の数学者ですが，熱伝導の微分方程式の境界値問題を解くために開発したFourier解析を公開したのは1822年でした．従って，現代なら使う2次元のFourier変換もクラドニの時代にはありませんでした．

しかしながら，問題を精密に解くことと，現象の本質を理解することとは目的が違います．計算すればそうなるとか，一口ではいえないというのでは，本質が理解できたことになりません．

節線集合に関する有名な問題は，40年以上前に出された節線集合サイズに関するヤウ・シンツン予想です．節線の長さが，周波数ωの線形関数として増加する予想しました． それらは通常，膜を小さな正方形に分割し，それぞれのサイズを推定します．そのような推定のための便利なツールは，倍加指数（ハウスドルフ次元に似る）であり，立方体Qから倍の立方体2Qに変えたとき，固有関数の最大振幅の比の対数を倍加指数と定義しました．倍加指数が有界のままであれば，立方体Qに該当する節点集合のサイズも有界であるとの予想です．ニコライ・ナジラシビリは，ヤウ・シンツンによって提起された問は，調和関数の関連する質問に還元できることに気づきました．しかし，正方形が小さな断片に分割されたときに調和関数の倍加指数がどうなるかという問題は，2016年にアレクサンドル・ログノフとエフゲニア・マリンニコワの研究が発表されるまで進展していませんでした．

実効再生産数が東京では，まだ１を少し超えているようですが，他の県では1未満になってきたようです．以下のサイトに，都道府県別の実効再生産数の時系列の変化のグラフがあります．

Rt Covid-19 Japan都道府県別コロナウイルスの感染拡大・収束状況(実効再生産数Rt)をグラフ化したWebサイトrt-live-japan.com
実効再生産数Rというのは，1人の感染者が新たな感染者を作る人数のことです．Rが1未満なら感染流行は減少収束し，１より大きければ感染は拡大します．しかしながら，各都道府県の実効再生産数がすべて1未満になっても，感染拡大の起こる可能性を警告している論文を前回紹介しました．その論文では，全体をコミュニティと病院という２つのグループに分割したモデルで，コミュニティ内の感染に関する実効再生産数と病院内の感染に関する実効再生産数がともに1未満であっても，全体の実効再生産数が１を超す（感染拡大が起こる）可能性が指摘されました．その原因は，コミュニティから病院に感染させる場合も，病院からコミュニティに感染させる場合もあるからです．

都道府県別の実効再生産数が，それぞれ1未満になっても，各県間の人の移動接触により各県間の感染が起こるので，全体の実効再生産数が１より大きくなることは十分あり得ます．油断は危険です．

■数学の形式としては，次の行列を作ります：
対角要素には，各都道府県の実効再生産数を並べ．行列のその他の要素には，異なる県間の感染率を対応させます．県間の感染率は，相当する県間の人の接触確率のようなものです．このような行列を作るにはいろいろなデータが必要ですが，この行列ができたとすると，この行列の固有値を求める数学の問題になります．最大の固有値が１を超していれば，全体の実効再生産数は１を超し伝染の拡大が起こります．

私たちの社会は，都道府県がそれぞれ孤立して独立でいるわけではなく，互いに相互作用（人の接触がある）しているので，独立な個別地区の予測と，全体の予測は大変異なり，このような計算をしてみないとわかりません．

（注）実効再生産数の計算方法は，Anne RがCoriらによるものが，山中伸弥のホームページに紹介されています．

■直線上にｎ個の点が並んでいるとします．点が連続しないように選んで点の集合を作ります．そのような集合の選び方A_nは何通りありますか？　ただし，点を1つも含まない集合は空集合Φと言いますが，集合の選び方の１つに空集合もあります．

・n=1のとき：　Φ，{1}　　　　　→　$$A_1＝2$$
・n=2のとき：　Φ，{1}，{2}　　　→　$$A_2=3$$　
（注）{1,2}の集合は点が連続するので条件を満たしません．

・n=3のとき：　Φ，{1}，{2}，{3}，{1,3}　→　$$A_3＝5$$

・n=nのときは：　n点目を選ばない $$A_{n-1}$$個の方法と，n点目は選ぶがn-1点目は選ばない $$A_{n-2}$$個の方法があります．
従って，$$A_n＝A_{n-1}+A_{n-2}$$ ，これは，フィボナッチ数列$$F_n$$の定義ですが，初項が2なので，$$A_n=F_{n+2}$$になります．

■円周上にn個の点が並んでいる場合はどうでしょうか．今度はｎ番目の点と，1番目の点が連続してはダメです．この場合の集合の選び方をB_n個とします．

・n=1のとき：　Φ，{1}　　　　　→　$$B_1=2$$　
・n=2のとき：　Φ，{1}，{2}　　　→　$$B_2=3$$
・n=3のとき：　Φ，{1}，{2}，{3} 　→　$$B_3=４$$　
（注）｛1,3｝は繋がるので条件にあいません．
・n=nのとき：
n点を除いた場合は$$ A_{n-1}$$通り，n点がある場合には，自分n点と両隣り（n-1と１）の計３点は除くので$$A_{n-3}$$通りがあります．

この両者の合計が一般式です：$$B_n＝A_{n-1}＋A_{n-3}=F_{n+1}+F_{n-1}=L_n$$

このような数列 $$B_n$$ はルーカス数列$$L_n$$と呼ばれます．

今は閉鎖されてしまったyahooブログの仲間「さなのブログ」に大丸百貨店（心斎橋）の美しい幾何学模様の写真がありました．私は大阪にもずいぶん行ったのですが，心斎橋には縁がなく大丸百貨店もとうとう見ずじまいでした．さなさんから，ヴォーリズ設計の86年間皆に幸せを与え続けてきた美しい建物が取り壊されると教えられ惜しい限りです．そこで，私のyahooブログにこの記事を書きました（2015.12.31）．その後，新しい建物が完成し2019.9.20に大丸百貨店は再開しました．ウイリアム・メリル・ヴォーリス(*)の懐かしいデザインが極力残されて，懐かしい雰囲気が感じ取れよかったと思っています．

(*注)壁紙模様で有名なイギリス人William Morrisではありません．アメリカ人のWilliam Merrell Voriesです．ヴォーリズはプロテスタントの伝道者としてひとり来日し，戦争中も日本に帰化し日本で骨を埋めた人です．近江兄弟社の前進を設立しヴォーリズ建築事務所も設立しました．明治学院チャペルをはじめ数多くの美しい建物を手掛けています．「屋根をかける人」門井 慶喜著， KADOKAWAは，ヴォーリスのすがすがしさが伝わる良い本です（学校出たてのヴォーリスが日本への船に乗っている場面から始まります）

■取り壊し前の建物の美しい幾何学模様を鑑賞しましょう．以下で取り上げる模様は建築物でよく使われ，イスラム起源の模様の雰囲気があります．


この写真（貴重な取り壊し前）は，さなさんのブログの写真に遠近法の補正をかけて，模様を正面から見たように修正したものです．ただし，写真に見られる8回対称の花模様は窪んだドームの奥にあるため，視差の効果で中心から寄ってしまいました．実際はそれぞれドームの中心（4回回転軸のある位置）にあります．この写真の繰り返し模様にはp4mmの対称性があります．

次の図も，さなさんのブログの写真に遠近法の補正をかけて，正面から見たようにし切り出したものです．建築には半円しか使われていませんが，全円を想像してみると頂点のなまった星形10角形のようです．この星形は五芒星を2つ重ねたらできるもので，黄金比がたくさん現れます．このような模様は東京ジャーミーの説教壇や門扉にも見られます．

この写真の下側に見られる繰り返し模様も取り上げましょう．


この模様には6回回転対称軸が配列しています（3回や2回回転対称軸も生じています）．青い線は鏡映対称面です．繰り返し模様の対称性はp6mmです．

さなさんのブログのもう一つの写真から，切張りをして繰り返し模様を再現したものが以下の図です．ちょっとずれたところができましたが，パターン全体の様子は想像できるでしょう．


この模様も美しく大変複雑なものですが，4回対称性のある繰り返し模様であることがわかります．対称性はp4mmです．

■現在の大丸百貨店

これらの写真を見ると，建て替えられた建物にもヴォーリスのデザインが活かされているのがわかりますね．

国立数学博物館MoMath(National Museum of Maths)は，米国唯一の数学博物館で，ニューヨークのマディソン・スクエアに，2012年12月15日オープンしました．
ここには30以上の対話型展示がありますが，ホールの展示で目立つのは，正方形の車輪の3輪車が滑らかに走る光景です．

たいへん興味深いので，床面の曲線がどのような形であるかを計算してみました．
ここに掲載する結果は，2013年7月22日の数学月間懇話会（第9回）で谷が発表したものです．

ついでに，応用問題として計算した3角形の車輪の結果を（Fig.２）に掲載します．

■Fig.2　三角の車輪

注）2013年10月2日に開設された東京理科大学「数学体験館」にも同じ企画が採用されている．

昨年9月に表題の本（技術評論社）を出版しました．この本の構成は8つの章からなり，全章を通して万華鏡で繋がっています．1,2章は有限図形の対称性（点群）．3,4章は周期的な空間の対称性（平面群）．これらの映像は，万華鏡で作り出すことができます．5章は万華鏡．6章は円による反転という数学的な鏡を用いた万華鏡．7章はフラクタル操作という数学的な鏡を用いた万華鏡です．8章は東京ジャーミイで，イスラミック・デザインを鑑賞します．写真撮影にご協力いただいた東京ジャーミイの本屋さんにも本書を置いていただいています．

■この本に，第9章を続けて書くとすれば，イスラミック・デザインになります．イスラムデザインの特徴は，黄金比（すなわち5回対称や10回対称）がちりばめられていることです．しかし，5回対称性と2次元（あるいは3次元)世界の周期性とは両立できませんから，ちりばめられている5回（あるいは10回）対称性はロゼット内部だけに局所的に作用し，世界の全域を支配するものではありません．そのため，あたかも我々の住む3次元に高次元宇宙が投影しているようで不思議な魅力を感じます．イランのDarb-i Imam寺院（1453）の壁には,その500年後にヨーロッパで発見されるPenroseタイリング［自分の中に自分と同じパターンが繰り込まれる］と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています．イスラムの繰り返し模様は準結晶や基本領域が分割されて写像される万華鏡と似たところがあります．

まず写真をご覧ください．

同じ正３角形（正6角形）格子［あるいは，正３角形２つよりなる平行4辺形格子とみてもよい］のパンチングメタルを2枚重ね合わせました．
この図の状態は，2枚の格子どうしのなす角度が2θ＝30°になった場合です．初めの正3角形（正6角形）の格子より大きな新しい周期の格子が出現しているのがわかりますか．

■正方形格子（網目）を2枚重ねた場合を考察してみましょう．

両方の網目が重なった位置に，新しい網目の格子が見えて美しい．
2枚の正方形の格子（正方格子という）どうしの傾きを変えると，ときどきこのような新しい格子が現れます．
もとの格子の互いに直角な２つの並進ベクトルをa，ｂとすると（正方格子ならa=b），
もとの格子は，格子点 na+mb，（n,mは任意の整数）の集合です．
同じ正方格子を２枚傾けて重ねて，新しい周期の２つの並進ベクトル x, yが生じています．これらの図の状態は，

（左図）x=2a+b，y=a+2b ．（右図）x=3a+b，y=a+3b　（面心格子）

　　　　$$ \left( \begin{array}{@{\,} cc @{\, } } 2 & 1 \\[0mm] 1 & 2 \end{array} \right) $$，　　　　　$$ \left( \begin{array}{@{\,} cc @{\, } } ３ & 1 \\[0mm] 1 & 3 \end{array} \right) $$

この基底変換を行列で書き，行列式を求めると３（左図），8（右図）ですので，
新しくできた格子はもとの格子と比べて面積で3倍（左図），8倍（右図）粗くなっていることがわかります．

格子というのは，並進ベクトルの作る群＝並進群の”図的表現”です．
2枚の格子の干渉で生じた新しい格子の周期は，もとの格子の粗いサンプリングになっているわけで，
新しい格子は，もとの格子の部分群になります．

格子が重なって，拡大された（粗い）格子が見える現象は，干渉（ビート）と同じことです．
実際に，２つの原子網面が重なって，このようなビートが見えることは，
電子顕微鏡で格子像の観察をするときにもよく起こります．
結晶は周期的な構造をしているので，周期的な空間は「結晶空間」とも呼ばれます．
エッシャーの繰り返し模様や，壁紙模様などで，周期的空間の実例をたくさん目にしていると思います．

■2つの正方格子の平行なずれによる干渉（モワレ縞）

それぞれの正方格子の周期をλ_１，λ_２とすると，新しい周期Lは

$$ \displaystyle \frac{1}{L}=\displaystyle \frac{1}{\lambda _{1 } }-\displaystyle \frac{1}{\lambda _{2 } } $$　の関係があります．

私は，子供のころ家にあった織物検査器というもので遊んだことがあります．これは，標準となる格子模様がガラスに刻んであり，織物にこのガラスを重ねると繊維の周期とのビートで縞模様が観察できます．1mmの中に何本繊維があるかとか，織り方が均一でなくどの程度乱れているかが，モアレ縞からわかります．

次の写真は，工事現場のネットが折り返されて2重になっているために観察されるモアレ縞です．

私は3月24，26日のまぐまぐメルマガ(311,312号)で以下の内容の発表をしました．－－－－－
3月21日の厚労省の公表値を用いて，罹患率＝発症患者/PCR検査数と定義すると，罹患率は，約5%になります．しかし，PCR検査の，感度と特異性（酒井健司，朝日デジタル）の情報を入れてベイズ推定した罹患率は5.9%になります．この推定値の増加は，主としてPCR検査感度に原因があり，実際の罹患者を取りこぼすためです．（注）この数値は，PCR検査を受けた限定されたグループをサンプルとしているために，一般の集団に対しては少し割り引いた数値になるでしょう．－－－－－
今日PCR検査数も増加したので，4月24日時点の厚労省のデータを用いて，再計算をしてみました．ただし，PCR検査数が増加したといっても（検査を受ける条件はあまり緩和されていません）．したがって，陽性確率が高いサンプル集団について検査が行われている状況は同じです．
カバーの図を見てください．ここで推定する数値はあくまでもサンプル集団に関するもので，全体集団に対してはいくらか割り引いた数字になるでしょう．

ーーーーー
■PCR検査状況（厚労省4/23データ）

　【PCR検査陽性者数】　　　　【PCR検査陽性時の有症状・無症状の別】

新型コロナウイルスに対するPCR検査数は，4月23日の厚労省の発表で，135,983人になりました．1月前（3月21日）の数字の7.5倍です．PCR検査の陽性者数は11,919人，陽性者のうち発症患者（陽性者∩発症患者）は7,315人です．
発症患者/PCR検査数＝罹患率　と仮の罹患率を定義すると，罹患率は約5.4%です．
陽性率＝陽性者数/PCR検査数＝0.088（前回0.056）　，陰性率＝0.912（前回0.944）も定義します．

(要旨）＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
4月23日の厚労省の公表値を用いて，罹患率＝発症患者/PCR検査数と定義すると，罹患率は，約5.4%（前回5.0％）になります．しかし，PCR検査の，感度と特異性（酒井健司，朝日デジタル）の情報を入れてベイズ推定した罹患率は8.6%（前回5.9%）になります．この推定値の増加は，主としてPCR検査感度に原因があり，実際の罹患者を取りこぼすためです．
（注）この数値は，PCR検査を受けた限定されたグループをサンプル集合としているために，一般の集団に対しては少し割り引いた数値になるでしょう．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

■条件付き確率についての「ベイズの定理」とは次のように説明できます．
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
記号の意味は例えば以下の様です．
$$p(X)$$　　$$X$$が起こる確率
$$p(Y|X)$$　$$X$$が起こった後で$$Y$$が起こる確率
$$p(X \cap Y)$$ $$X$$かつ$$Y$$が起こる確率

ベイズの定理は，$$X$$（原因）が起きた後で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

■PCR検査の精度

新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）により，次のように仮定します．
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく判定される確率のことで，あまり大きくなく0.7．
真の罹患者でもPCR検査が陰性（－）（偽陰性）となる確率が0.3程度だそうです．
検査の特異性とは，非罹患者が陽性（＋）（疑陽性）と判定される確率で0.01程度だそうです．

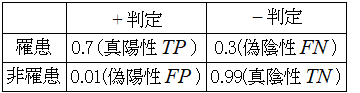
$$\begin{array}{|c|c|c|}
\hline
& ＋ & － \\[0mm]
\hline
罹患 & 0.7 & 0.３（偽陰性） \\[0mm]
\hline
非罹患 & 0.01（疑陽性） & 0.99 \\[0mm]
\hline
\end{array}$$

■これらの仮定の下で，以下の２つを推定しましょう．ただし，ベイズの定理を使います．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．
$$p(罹患|+)=\displaystyle \frac{p(+|罹患)p(罹患)}{p(+)}=\displaystyle \frac{0.7 \times 0.054}{0.054 \times 0.7+0.946 \times 0.01}=0.80$$
＋(陽性)でも，検査感度のせいで罹患者をとりこぼすことが多い．また，非罹患者の割合が多いので偽陽性の数も無視できず，全体として決定率を80%(前回79%)に下げている．

（２）罹患率を推定しなさい．
$$ p(罹患|-)=\displaystyle \frac{p(-|罹患)p(罹患)}{p(-)}=\displaystyle \frac{0.3 \times 0.054}{0.054 \times 0.3+0.946 \times 0.99}=0.017 $$
陰性と判定されたものの中に見逃された患者である可能性は1.7%(前回1.6%)ほどある．
従って，全人口のなかで推定される罹患率は$$0.088 \times 0.80+0.912 \times 0.017=0.086$$，すなわち，8.6%(前回5.9%)と推定できます．

 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝text

■条件付き確率についての「ベイズの定理」とは次のように説明できます．
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です．
p(X)　　Xが起こる確率
p(Y|X)　Xが起こった後でYが起こる確率
p(X∩Y) XかつYが起こる確率
ベイズの定理は，X（原因）が起きた後でY（結果）が起きる確率p(Y|X)と，XとYを入れ替えた確率p(X|Y)を結び付ける定理です．
■PCR検査の精度

新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）により，次のように仮定します．
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく判定される確率のことで，あまり大きくなく0.7．
真の罹患者でもPCR検査が陰性（－）（偽陰性）となる確率が0.3程度だそうです．
検査の特異性とは，非罹患者が陽性（＋）（疑陽性）と判定される確率で0.01程度だそうです．

■これらの仮定の下で，以下の２つを推定しましょう．ただし，ベイズの定理を使います．
（１）PCR検査で陽性（＋）と判定されたとき，真の罹患者である確率を求めなさい．
p(罹患|+)=p(+|罹患)p(罹患)/p(+)=0.7×0.054/(0.054×0.7+0.946×0.01)=0.80
＋（陽性）でも検査感度のせいで罹患者をとりこぼすことが多い，また，非罹患者の割合が大きいので偽陽性も無視できず，この2つの原因が，＋判定でも罹患者である確率80%（前回79%）を下げている．
（２）罹患率を推定しなさい．
p(罹患|−)=p(−|罹患)p(罹患)/p(−)=0.3×0.054/(0.054×0.3+0.946×0.99)=0.017
－（陰性）と判定されたものの中に見逃された患者である可能性は1.7%ほどある．

従って，サンプル集合全体で推定される罹患率は0.088×0.80+0.912×0.017=0.086
すなわち，8.6%（前回5.9%）と推定できます．

ナイチンゲールが50年間ベッドでの仕事を余儀なくされ，死因ともなったのは，クリミア戦争時に流行したマルタ熱（ブルセラ症）であることが明らかになった．D A B Young，Florence Nightingale's fever，(BMJ VOLUME 311 23-30 DECEMBER 1995)
ーーーーーーー
■ブルセラ症（brucellosis）
NIID国立感染症研究所https://www.niid.go.jp/niid/ja/kansennohanashi/513-brucella.html，および，wikiを参照した．－－－－
ブルセラ症はマルタ熱とも呼ばれる細菌に感染して起こる人獣共通感染症．クリミア戦争でマルタ熱が流行したことで世界的に注目されたが，紀元前400年頃のヒポクラテス著書にブルセラ症と思われる疾患がすでに記載されている．現在でも，世界中で毎年50万人を越える家畜ブルセラ菌感染患者が新規に発生（食料や社会・経済が家畜へ依存し，家畜ブルセラ病が発生している国や地域）発生している．マルタ熱の原因菌として，イギリス軍の軍医Sir David BruceによりB. melitensis が分離（1887）されて以降，種々のブルセラ属菌が発見されている．ヒトへの感染が報告されている主なものは，B. melitensis （自然宿主：ヤギ，ヒツジ），B. suis （ブタ），B. abortus （ウシ，水牛），B. canis （イヌ）の4菌種である．日本では，過去に牛のB. abortus感染が流行し問題になったが，家畜衛生対策の徹底により，1970年を最後に国内家畜から菌が分離された例はない．感染動物の加熱殺菌が不十分な乳・乳製品や肉の喫食による経口感染が最も一般的である．ヒト－ヒト感染は極めてまれである．
ブルセラ属菌は敵国の兵士や住民に罹患させて能力を低下させる生物兵器としても研究・培養された．アメリカは1942年、ソ連は1978年に兵器化を実現した．

■サビノワとリユドミラ物語．Екатерина Савинова и Людмила Сенчина
Приходите завтра「明日来なさい」(1963年，ソビエト映画)は，1540万観客の大ヒット映画（ロシア語）です．シベリアの寒村からИнститут имени Гнесиных モスクワの音楽学校に入ろうと出てきた才能ある少女の物語です．重い荷物を背負って一人で都会に出てきた元気で愉快な純粋な少女です．しかし，モスクワに来たときは既に遅く入学試験は終わっていました． 少女の役名はФросяフローシャ．これは実在のЕкатерина Савиноваサビノワの伝記映画で，サビノワ自身が主演し歌います．あの声はサビノワしか出せません．私がこの映画を知ったのも彼女の3.5オクターブ出るという魅力的な声の歌を耳にしたからです．音楽学校の玄関で有名なソコロフ教授に何度か訴えます．ついに引き出した教授の返事が Приходите завтра!「明日来なさい」でした．教授に学校のオーデトリウムで聞いてもらえた彼女の歌声がすばらしい．教授もフローシャの純粋さと素晴らしい声を見抜き，何とか入学させようと動きます．この映画はサビノワが自分で主演した愉快で楽しい映画で，私はとても好きです．しかし，残念ながら，その後のサビノワは，ブルセラ病（生牛乳を飲むと牛から感染する）が重くなり鉄道自殺（1970年，43歳）してしまいます．

興味深いのは，1963年にウクライナで高校生時代に，Людмила Сенчинаリュドミラ・センチナはきっとこの映画を見たのではないかと私は想像します．リュドミラは成功して，ロシア人民芸術家歌手になります．彼女は今年の1月25日に，ペテルブルクの病院で死去（６７歳）しました．
リュドミラは，高校を卒業して，歌手になるために，ウクライナからレニングラード（現ペテルブルグ）に出てきました．でも，そのとき音楽学校の試験は終わっていたのです．よく似た話があるものですね．サビノワと違うのはペテルブルグに親戚がいたことです．
リュドミラの代表曲は，Песня Золушкиシンデレラの歌
－－－－－－－

NHS Nightingale Hospital
NHS＝国民保険サービス，Nightingale Hospital＝臨時救急病院≒野戦病院
イギリスのNHSは4つの地域区分（イングランド，スコットランド，ウエールズ，北アイルランド）があります．イングランドのナイチンゲール病院は，London（4,000床）に4月3日オープンを皮切りに，7つ目のSunderland（460床）は日産自動車工場近くに準備が整いました．Covid-19患者の数に北東部の病院が対処できない場合に限り使われます．「人々が社会的距離を保ち，あるいはワクチンができ，この病院を使わないですむことを願っている」とNewcastle病院のNHS局長は語りました（Sunderland Echo紙）．
Stay at home, protect the NHS, and save lives
イギリスは，3月23日に3週間の全土封鎖に踏み切ったが，まだピークが去らないとしてさらに3週間の延長に入っています．4月19日現在．累積確認患者数は90,629，累積死者数は14,399に上りますが，一日の感染者の広がりは減少してきました．封鎖と並行して，PCR検査から抗体検査に転換し，抗体検査の大規模実施（現時点で1万3729人1日3万5000件の能力がある）と「NHSナイチンゲール病院」の設立を進めています．「ナイチンゲール病院」といはどのような病院でしょうか？

クリミア戦争(1853-1856)で野戦病院の衛生状態の改革を行ったナイチンゲールは，『看護覚え書』，『病院覚え書』など多くの著作を残し，そこにはワンルームの病院設計図も載っています．高い天井まで延びた3層の窓，3層目の窓を開放し換気，ベッドの間隔，等々，ナイチンゲールの病院概念が活かされた臨時救急病院≒野戦病院だからこう呼ぶのでしょう．
ーーーー

 Sunderland Echo↑

Getty Images↓

（注）以下のナイチンゲールの伝記的記事は，
草の実堂；https://kusanomido.com/study/history/western/21987/　を参考にした．
ナイチンゲールはクリミア戦争(1853-1856)で野戦病院の衛生状態を実践改革し死亡率を低下させました．帰国後のナイチンゲール・チームはバーリントンホテルに集結し，戦時の報告書をもとに病院の状況分析をして，数々の統計資料を作成，改革のためにつくられた各種委員会に提出しました．特に，死亡原因ごとに死者の数をひと目で分かるようにレーダーチャートの発明があります．
1860年にナイチンゲールが看護専門学校（ナイチンゲールスクール）を設立したのは広く知られていますが，ナイチンゲールが統計学者であることはあまり知られていません．疫学研究の元祖です．1859年にイギリス王立統計学会の初の女性メンバーに選ばれ，アメリカ統計学会の名誉メンバーにも選ばれました．ナイチンゲールは90歳で亡くなりますが，晩年50年間はほとんどベッドの上で，本の原稿や手紙を書く活動でした．その病因はブルセラ病に感染したこと（by D A B Young，Florence Nightingale's fever，1995)でした．ブルセラ病については，以前に述べたことがあるのでそちらを参照ください．

新型コロナウイルスの感染拡大が続いています．皆様お元気でしょうか．注意してお過ごしください．
緊急事態宣言下で，人と人の接触機会を最低7割，極力8割の削減を，政府は目標に掲げています（朝日新聞デジタル）．
接触機会をある閾値下に削減すると感染が減衰し収まるわけです．数学月間の会の石黒真木夫氏が，マクロの数理モデルでシミュレーションを行いました．その結果は，youtubeチャンネル「NPO数学月間の会」にアップロードし公開しました．そのリンクを探すには，数学月間のホーム・ページhttp://sgk2005.saloon.jpにアクセスします．現在そのトップ頁に掲載しています．そこで用いたシミュレーションのエクセルファイルは，同ホームページの記事中にリンクを張りましたので，各自がダウンロードしてシミュレーションを体験することができます．参考論文（西浦博・稲葉寿）へのリンクも，同ホームページの記事中に置きました．
＊youtubeチャンネル「NPO数学月間の会」の動画へのリンクは，数学月間の会のホーム・ページにアクセスし，youtubeチャンネルのタブを開くとそこに置かれています．

（１）石黒のシミュレーションの概要
ある人口集団を，未感染者，ウィルス感染源，免疫獲得者，死亡者に分類し，未感染者がウィルス感染源の一員と接触すると，ある感染確率で未感染者が感染してウィルス感染源となる．ウィルス感染源のウィルス拡散は１４日間つづき，１４日目に「死亡率」に従って死亡者と免疫獲得者に分かれ，免疫獲得者はもはやウィルスを拡散することも再感染することもなくなる．このようなルール(数理モデル）でシミュレーションを行った．このモデルに基づくと，時間の経過とともに未感染者は単調減少し，免疫獲得者は単調増加するので，感染の流行はかならず止まる．しかしそれは集団全員が感染した後である．

感染確率と死亡確率を適当に与えれば，シミュレーションは簡単である．いまの計算機をもってすれば人口集団の各個人の命運をたどるミクロシミュレーションもさして難しくない．ここで紹介するのは未感染者やウィルス感染源集団の大きさの変化を追跡するマクロシミュレーションである．確率的な現象の「期待値の動き」を追いかける決定論的なダイナミクスを採用する．もし，ミクロシミュレーションをして，算術平均の変化を見るとマクロシミュレーションの結果に「誤差」が乘ったような動きになるだろう．
石黒シミュレーションによる発見は，減少の後に揺り戻しが付随していることである．そのような波動を繰り返しながら徐々に減少し収束していきます．ワクチン等の発見がなくこの状態が続けば，ときおり感染者が増加する波動を繰り返しながら，生存者全員が免疫を獲得するまで続き．その間多数の死者がでるでしょう．

（２）ミクロシミュレーションについて
講演会「数学と生命科学--数理モデルを中心として」
主催：上智大学理工学部数学科/情報理工科（「数学月間」参加プログラム）
があったのは2008年8月4日（月）のことです．この中の講演に，「感染症対策における数理モデルの役割」（大日康史，国立感染症研究所）というのがありました．今回のCOVID-19の感染拡大にあたり，この国立感染症研究所の感染症対策のシミュレーションが，タイムリーに政策に活かされているとは思えません．原発事故の当時SPEEDIの結果が活用されなかったのに似ていると私は思います．

■感染症対策における数理モデルの役割，大日康史（国立感染症研究所）の概要
数理モデルによる感染拡大のシミュレーションは，新型インフルエンザやバイオテロなどの対策の有効性評価に必要である．
数理モデルには，SIRモデル，ibm（IndividualBasedモデル），Ribm（Realibm）などがある．
本研究で用いたRibmとは，実際に調査した個人の移動，所在の記録データ（首都圏では88万人）にもとづき，
6分ごとに人々の接触状態（感染の機会）が定義されるものである．新型インフルエンザには，種々のタイプがあり鳥類間の感染は起こるが，鳥から人への感染は血液の濃厚接触などの場合に限られる（豚と人の感染するインフルエンザのタイプは似る）．人に感染した場合に，人から人への感染が始まり拡大していく．シミュレーションには，例えば以下のシナリオを用いる：（第１日）初発例が外国で感染．（第３日）帰国．帰宅後（八王子）感染性を持つ．（第４日）出社（丸の内）．発症．（第５日）国際医療センターに受診．東京都健康安全研究センターで検査診断．（第６日）対策へ：シミュレーションの結果である首都圏への感染拡大の様子や全国への拡大の様子が示された．どのような対策（外出自粛，地域閉鎖，休校，住民全員が予防服用，....）をとると効果があるかが予測できるシミュレーションが示された．

■堆積岩は，岩石の砕屑物が水中で堆積して生まれたものです．この堆積物には，火山灰など火山由来のものも，石灰岩のような生物由来のものもありますが，岩石の風化などで生じた砕屑物は，その粒径により，礫（2mmより大きい)，2mm以下の細かい粒径のものは，砂($$2>･･･>1/2^4$$），シルト($$1/2^4>･･･>1/2^8$$)，粘土($$1/2^8>･･･$$)に分類されます．
静かな水中で，様々な粒径の砕屑土砂が沈降していくときの終端速度（一定になった速度）は，ストークスの法則で見積もることができ，大きい粒子の終端速度は大きく，小さい粒子の終端速度は小さいことがわかります．洪水で河口に運ばれてきた大小混合の砕屑物は，河口近くに大きい粒子を堆積させ，離れた海へ運ばれて堆積するのは小さい粒子ということになります．

■粘性液体中を静かに沈降していく粒子の速度が一定（終端速度）$$v$$のとき，次のように記述できます．
粒子は小さな球形で直径$$ d $$，密度を$$\rho _{s}$$とし，粘性液体の粘度$$\eta$$ ，密度を$$\rho_{f}$$ とします．
微粒子に働く力が釣り合うと（加速度０になり），粒子は一定速度（終端速度）で沈降します．つまり， 
重力$$＝$$浮力$$＋$$抵抗力，あるいは，重力$$-$$浮力$$=$$抵抗力  
従って，$$\displaystyle \frac{\pi ^{2}d^{3 } }{6}\left( \rho _{s}-\rho_{f} \right) g=3\pi \eta dv$$，ただし，$$g$$は重力加速度．
これを解いて，
$$v=\displaystyle \frac{\left( \rho _{s}-\rho_{f} \right) g}{18\eta }d^{2}$$
これがストークスの式です．

■ストークスの式を使って，水中の球形石英粒子の沈降速度を求めると，粒子径1 µm(粘土)の沈降速度は0.0001cm/s(およそ30m/年），粒子径10 µm(シルト)の沈降速度は0.01cm/s(およそ3000 m/年），少し大きな粒子径1 mm(砂)の粒子は1 m/sの沈降速度です．実験との比較では，100μm以下ではストークスの式はほぼ成り立ちますが，1mmになるとストークスの式から外れ沈降速度が大きくなります．これは，粒子径が大きくなると，沈降粒子の背後に渦流が発生しストークスの式が適用できないからです．

もし，水よりも粘性の大きい，あるいは密度も大きい分散媒を用いれば，もっと大きな粒子までストークスの式が適用できます．
私は，万華鏡の設計で，分散媒の中を沈降するガラスくずの速度を考察するのにストークスの式を用いました．

皆さまお元気でおお過ごしでしょうか．メルマガ311，312号で取り上げましたが罹患率5~6%でした．ただし，これはPCR検査を受けた人数に対してで，一般人に対しては少し割り引いた罹患率になるでしょう．3月30日現在の東京都の延べ患者数は443人とのことです．実際は都市封鎖をしてもおかしくない事態です．
この状況はしばらく続くので，数学月間の会の活動としてのイベントがいつ実施できるか見通せません（今年も7月22日に数学月間懇話会をやる予定です），
この対策として常時情報発信ができるyoutubeチャンネル（NPO数学月間の会）を立ち上げました．
このメルマガが皆様に届く朝には，このyutubeチャンネルも（3月31日0:00）公開されていると思います．ぜひお確かめの上，問題があるかどうかご報告くださいますようお願いいたします．
私個人のインターネット環境はwifiですので通信速度が遅く，
大きな動画のuploadに時間がかかり現在まだ５つくらいです．
今後，会員皆様の関連動画も載せられるように考えますので，ご協力のほどお願いいたします．

(要旨）ーーー
3月21日の厚労省の公表値を用いて，罹患率＝発症患者/PCR検査数と定義すると，罹患率は，約5%になります．
しかし，PCR検査の，感度と特異性（酒井健司，朝日デジタル）の情報を入れてベイズ推定した罹患率は5.9%になります．
この推定値の増加は，主としてPCR検査感度に原因があり，実際の罹患者を取りこぼしていたためです．
（注）この数値は，PCR検査を受けた限定されたグループをサンプルとしているために，一般の集団に対しては少し割り引いた数値になるでしょう．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

■条件付き確率についての「ベイズの定理」とは次のように説明できます．
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
記号の意味は例えば以下の様です．
$$p(X)$$　　$$X$$が起こる確率
$$p(Y|X)$$　$$X$$が起こった後で$$Y$$が起こる確率
$$p(X \cap Y)$$ $$X$$かつ$$Y$$が起こる確率

ベイズの定理は，$$X$$（原因）が起きた後で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

■新型コロナウイルスに対するPCR検査数は，厚生労働省の発表で，日本でも3月21日現在，18,134人になりました．
PCR検査による感染者数は1,007人，発症患者（＝罹患者と定義）はそのうちの884人です．

発症患者/PCR検査数＝罹患率　と仮の罹患率を定義すると，罹患率は約5%です．
陽性率＝感染者数/PCR検査数＝0.056　，陰性率＝0.944　も仮に定義します．

新型コロナ検査、どれくらい正確？　感度と特異度の意味査（酒井健司，朝日デジタル）をもとにして，次のように仮定します．PCR検査の感度というのは，罹患者がPCR検査で＋になる確率のことで，あまり大きくなく0.7, 罹患者でもPCR検査が－となる場合（偽陰性）の確率は0.3程度だそうです．
検査の特異性により，非罹患者が＋（疑陽性）と判定される確率は0.01だそうです．
＊注）3月24日のメルマガに使った仮定の数値は，実際とだいぶ違いましたので，修正した以下の表に差し替えました．
$$\begin{array}{|c|c|c|}
\hline
& ＋ & － \\[0mm]
\hline
罹患 & 0.7 & 0.３（偽陰性） \\[0mm]
\hline
非罹患 & 0.01（疑陽性） & 0.99 \\[0mm]
\hline
\end{array}$$
これらの仮定の下で，以下の２つを推定しましょう．ただし，ベイズの定理を使います．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．
$$p(罹患|+)=\displaystyle \frac{p(+|罹患)p(罹患)}{p(+)}=\displaystyle \frac{0.7 \times 0.05}{0.05 \times 0.7+0.95 \times 0.01}=0.79$$
＋（陽性）でも，検査感度のせいで罹患者をとりこぼすことが多い，非罹患者の割合が多いので偽陽性も無視できず，全体として決定率を下げている（79%）．

（２）罹患率を推定しなさい．
$$ p(罹患|-)=\displaystyle \frac{p(-|罹患)p(罹患)}{p(-)}=\displaystyle \frac{0.3 \times 0.05}{0.05 \times 0.3+0.95 \times 0.99}=0.016 $$
陰性と判定されたものの中に見逃された患者である可能性は1.6%ほどある．
従って，全人口のなかで推定される罹患率は$$0.056 \times 0.79+0.944 \times 0.016=0.059$$，すなわち，5.9%と推定できる．

＊注）ただし，PCR検査は限定されたグループに対してなされており，偏った集団をサンプルとしているので，全人口に対してなら少し割り引いた値が推定される．

一般の振幅

$$\left\{ \begin{array}{@{\,} c @{\, } }\displaystyle \frac{d}{dt}\displaystyle \frac{ \partial L}{ \partial \dot{\phi } }-\displaystyle \frac{ \partial L}{ \partial \phi }=0 \\[0mm]\displaystyle \frac{d}{dt}\displaystyle \frac{ \partial L}{ \partial \dot{\psi } }-\displaystyle \frac{ \partial L}{ \partial \psi }=0\end{array} \right. $$

ラグランジュ関数$$L$$は，

$$L=T-U$$

$$ T=\displaystyle \frac{m+m_{1 } }{2}l^{2}\dot{\phi }^{2}+\displaystyle \frac{m_{1 } }{2}l^{2}_{1}\dot{\psi }^{2}+m_{1}ll_{1}cos\left( \phi -\psi \right) \dot{\phi }\dot{\psi } $$

$$U=-\left( m+m_{1} \right) glcos\phi -m_{1}gl_{1}cos\psi $$

--------------------

$$\displaystyle \frac{ \partial L}{ \partial \dot{\phi } }=\left( m+m_{1} \right) l^{2}\dot{\phi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \dot{\psi }$$

$$\displaystyle \frac{ \partial L}{ \partial \dot{\psi } }=m_{1}l_{1}^{2}\dot{\psi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \dot{\phi }$$

$$\displaystyle \frac{ \partial L}{ \partial \phi }=-m_{1}ll_{1}\dot{\phi \psi }sin\left( \phi -\psi \right) -\left( m+m_{1} \right) glsin\phi $$

$$\displaystyle \frac{ \partial L}{ \partial \psi }=m_{1}ll_{1}\dot{\phi \psi }sin\left( \phi -\psi \right) -m_{1}gl_{1}sin\psi $$

--------------------

$$\left\{ \begin{array}{@{\,} c @{\, } }\left( m+m_{1} \right) l^{2}\ddot{\phi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \ddot{\psi }-m_{1}ll_{1}\dot{\psi }sin\left( \phi -\psi \right) \left[ \dot{\phi }-\dot{\psi } \right] =-m_{1}ll_{1}\dot{\phi \psi }sin\left( \phi -\psi \right) -\left( m+m_{1} \right) glsin\phi \\[0mm]m_{1}l_{1}^{2}\ddot{\psi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \ddot{\phi }-m_{1}ll_{1}\dot{\phi }sin\left( \phi -\psi \right) \left[ \dot{\phi }-\dot{\psi } \right] =m_{1}ll_{1}\dot{\phi \psi }sin\left( \phi -\psi \right) -m_{1}gl_{1}sin\psi\end{array} \right. $$

$$ \left\{ \begin{array}{@{\,} c @{\, } }\left( m+m_{1} \right) l^{2}\ddot{\phi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \ddot{\psi }+m_{1}ll_{1}\dot{\psi }^{2}sin\left( \phi -\psi \right) =-\left( m+m_{1} \right) glsin\phi \\[0mm]m_{1}l_{1}^{2}\ddot{\psi }+m_{1}ll_{1}cos\left( \phi -\psi \right) \ddot{\phi }-m_{1}ll_{1}\dot{\phi }^{2}sin\left( \phi -\psi \right) =-m_{1}gl_{1}sin\psi \end{array} \right. $$

$$ \left[ \begin{array}{@{\,} cc @{\, } }\left( m+m_{1} \right) l^{2} & m_{1}ll_{1}cos\left( \phi -\psi \right) \\[0mm] m_{1}ll_{1}cos\left( \phi -\psi \right) & m_{1}l_{1}^{2}\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } } \ddot{\phi } \\[0mm]\ddot{\psi }\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }-m_{1}ll_{1}\dot{\psi }^{2}sin\left( \phi -\psi \right) -\left( m+m_{1} \right) glsin\phi \\[0mm]m_{1}ll_{1}\dot{\phi }^{2}sin\left( \phi -\psi \right) -m_{1}gl_{1}sin\psi\end{array} \right] $$

$$\left[ \begin{array}{@{\,} cc @{\, } }\left( m+m_{1} \right) l^{2} & m_{1}ll_{1}cos\left( \phi -\psi \right) \\[0mm]m_{1}ll_{1}cos\left( \phi -\psi \right) & m_{1}l_{1}^{2}\end{array} \right] ^{-1}=\displaystyle \frac{1}{m_{1}\left( m+m_{1} \right) l^{2}l_{1}^{2}-m_{1}^{2}l^{2}l_{1}^{2}cos^{2}\left( \phi -\psi \right) }\left[ \begin{array}{@{\,} cc @{\, } }m_{1}l_{1}^{2} & -m_{1}ll_{1}cos\left( \phi -\psi \right) \\[0mm]-m_{1}ll_{1}cos\left( \phi -\psi \right) & \left( m+m_{1} \right) l^{2}\end{array} \right] $$

 $$ \left[ \begin{array}{@{\,} c @{\, } }\ddot{\phi } \\[0mm]\ddot{\psi }\end{array} \right] =\displaystyle \frac{1}{m_{1}\left( m+m_{1} \right) l^{2}l_{1}^{2}-m_{1}^{2}l^{2}l_{1}^{2}cos^{2}\left( \phi -\psi \right) }\left[ \begin{array}{@{\,} cc @{\, } } m_{1}l_{1}^{2} & -m_{1}ll_{1}cos\left( \phi -\psi \right) \\[0mm]-m_{1}ll_{1}cos\left( \phi -\psi \right) & \left( m+m_{1} \right) l^{2} \end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }-m_{1}ll_{1}\dot{\psi }^{2}sin\left( \phi -\psi \right) -\left( m+m_{1} \right) glsin\phi \\[0mm]m_{1}ll_{1}\dot{\phi }^{2}sin\left( \phi -\psi \right) -m_{1}gl_{1}sin\psi\end{array} \right] $$

$$=\displaystyle \frac{1}{m_{1}\left( m+m_{1} \right) l^{2}l_{1}^{2}-m_{1}^{2}l^{2}l_{1}^{2}cos^{2}\left( \phi -\psi \right) }\left[ \begin{array}{@{\,} c @{\, } }-m_{1}^{2}ll_{1}^{3}\dot{\psi }^{2}sin\left( \phi -\psi \right) -m_{1}\left( m+m_{1} \right) gll_{1}^{2}sin\phi -m_{1}^{2}l^{2}l_{1}^{2}\dot{\phi }^{2}cos\left( \phi -\psi \right) sin\left( \phi -\psi \right) +m_{1}^{2}gll_{1}^{2}cos\left( \phi -\psi \right) sin\psi \\[0mm]m_{1}^{2}l^{2}l_{1}^{2}\dot{\psi }^{2}cos\left( \phi -\psi \right) sin\left( \phi -\psi \right) +m_{1}\left( m+m_{1} \right) gl^{2}l_{1}cos\left( \phi -\psi \right) sin\phi + \sqcap - m_{1}\left( m+m_{1} \right) l^{3}l_{1}\dot{\phi }^{2}sin\left( \phi -\psi \right) -m_{1}\left( m+m_{1} \right) gl^{2}l_{1}sin\psi\end{array} \right] $$

$$\left[ \begin{array}{@{\,} c @{\, } }\dot{\phi }(n+1) \\[0mm]\dot{\psi }(n+1)\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }\dot{\phi }(n) \\[0mm]\dot{\psi }(n)\end{array} \right] +\left[ \begin{array}{@{\,} c @{\, } }\ddot{\phi }(n) \\[0mm]\ddot{\psi}(n)\end{array} \right] \mit\Delta t$$

 $$ \left[ \begin{array}{@{\,} c @{\, } } \phi (n+1) \\[0mm] \psi (n+1) \end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } } \phi (n) \\[0mm] \psi (n) \end{array} \right] +\left[ \begin{array}{@{\,} c @{\, } } \dot{\phi }(n) \\[0mm] \dot{\psi }(n) \end{array} \right] \mit\Delta t $$

$$\displaystyle \frac{E'}{E}=\displaystyle \frac{1}{1+\alpha (1-cos\theta )}$$
$$\alpha =\displaystyle \frac{E}{m_{0}c^{2 } }$$
クラインー仁科
$$\displaystyle \frac{d\sigma }{d\mit\Omega }=\displaystyle \frac{r_{0 } }{2}\left( \displaystyle \frac{E'}{E} \right) ^{2}\left( \displaystyle \frac{E'}{E}+\displaystyle \frac{E}{E'}-sin^{2}\theta \right) $$
$$E_{e}=E-E'=E\displaystyle \frac{\alpha (1-cos\theta )}{1+\alpha (1-cos\theta )}$$
$$\displaystyle \frac{d\sigma }{dE_{e } }=\displaystyle \frac{d\sigma }{d\mit\Omega }\displaystyle \frac{d\mit\Omega }{d\theta }\displaystyle \frac{d\theta }{dE_{e } }$$
$$ d\mit\Omega =2\pi sin\theta d\theta ,　　　　 \displaystyle \frac{d\mit\Omega }{d\theta }=2\pi sin\theta $$\

$$\displaystyle \frac{dE_{e } }{d\theta }=E\displaystyle \frac{\alpha sin\theta }{\left[ 1+\alpha \left( 1-cos\theta \right) \right] ^{2 } }$$

$$\displaystyle \frac{d\sigma }{dE_{e } }=\displaystyle \frac{d\sigma }{d\mit\Omega }2\pi sin\theta \displaystyle \frac{\left[ 1+\alpha \left( 1-cos\theta \right) \right] ^{2 } }{E\alpha sin\theta }=\displaystyle \frac{\pi r_{0 } }{E\alpha }\left( 1+cos^{2}\theta \right) \left\{ 1+\displaystyle \frac{\alpha ^{2}\left( 1-cos\theta \right) ^{2 } }{\left( 1+cos^{2}\theta \right) \left[ 1+\alpha \left( 1-cos\theta \right) \right] } \right\} $$

１種類の形（2等辺3角形）の赤色と黄色のタイル（赤タイルと黄タイルは互いに鏡像）で作ったタイル張り模様を鑑賞しましょう．1種類の形のタイルで，平面をタイル張りすると，必ず周期的なタイル張りになってしまうと思い込むのは間違っています．確かにFig.4,やFig.5のような周期的なタイリングはすぐ思いつきます．

しかし，Fig.2やFig.3のように非周期なもので，平面をタイル張りするものがあります．Fig.2は中心に回転対称があるタイリング模様で，点群5mの対称性です．Fig.3は，２つの目がある螺旋パターンのタイリングで，水平線は映進面だと思うかもしれませんが，このパターンには周期がありませんから映進操作はできません．
螺旋の目の中間に対称心があります．

さて，ここで万華鏡で作られるタイリング模様Fig.1の登場です．
この万華鏡を生む3枚の鏡は１つの頂点では点群を生成しますが，他の２つの頂点では点群を生成しません．従って平面を赤と黄色の市松模様で埋めることはありません．全体の代数系は，群より緩いもの（特殊な亜群）になってしまいますから非常に複雑です．
対称操作は局所的で，独自の作用域と値域があり興味深いものです．
作用域，値域の制限のために，一つのタイル全体が無傷で写像されるパターン内の位置と，部分が写像される位置があり，このような複雑なタイリング模様ができます．

シュロ縄で柵の竹竿を結びました．庭師は男結びと言う方法で結ぶそうですが，私は簡単にランニング・ノットという方法で結びました．実は，シュロ縄の扱いが大変だったので，一番作業の楽な結び方をして，後でこの結び方の名前を調べたら，ランニング・ノットという方法であることがわかりました．
ランニング・ノット（あるいは，スリップ・ノット）と言われる所以は，竹竿を通してから紐を引っ張って締めると結節ノットが移動して，自然に竹竿の周りの輪が締まるからです．結節になる輪から紐の両端が同じ方向に出ていますから，竹竿を通してから紐の一端を引っ張ると，輪が締り結節になると同時に，他端も同方向に引かれるので，両側から輪を締め，自分自身を締め緩みを防止しする一番シンプルな結び方になります．
ランニング・ノットの結び方で紐の両側を引っ張ると，輪の中に竹竿がなければ手品のように紐は結び目が出来ずに解けてしまいます．比較のために，もやい結びを見てみると，結びの両側を引っ張ると結節ノットは移動せず輪が出来てしまい，竹竿の周りを締める結び方にはなりませんし，竹竿がない状態で，もやい結びの紐の両側を引っ張ると解けずに固定した輪を残して結び目が出来てしまいます．

紐の始まりを竹竿の周りのランニング・ノットから始めて，柵を組んだ竹竿に巻きつけ固定し，紐の最後もランニング・ノットで収めようとするとなかなか難しい．巻いてきたひもが緩まないように締めながら出口の結節になる結び目を作る必要があるからです．
シュロ縄は水に湿らせた方がしなやかでよく締まります．シュロ縄を繰り返ししごいていると，縄に毛玉のような塊や細い箇所ができますから注意しましょう．

今回は，紐の両端をそれぞれ別の場所で固定したので，使いませんでしたが”かます結び”という方法もあります．これは紐の両端を結ぶ結び方です．

■連立線形微分方程式を解く

例えば，次の連立線形微分方程式は，行列を使って表現できます．

$$ \left\{ \begin{array}{@{\,} c @{\, } } \displaystyle \frac{d}{dt}x=y \\[0mm] \displaystyle \frac{d}{dt}y=-x \end{array} \right. $$

 $$ \displaystyle \frac{d}{dt}\left[ \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } } 0 & 1 \\[0mm] -1 & 0 \end{array} \right] \left[ \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right]　　 \Longleftrightarrow 　\displaystyle \frac{d}{dt}\vec{x }=M\vec{x } \\ $$

このような微分方程式の解は，初期値を $$\vec{x_{0} } =\vec{x }(t_{0})$$ として，

$$ \vec{x}(t)=\vec{x }_{0}+\displaystyle \int_{t_{0 } }^{t}M\vec{x}(\tau )d\tau　 $$  となります．

これの計算は，逐次近似で無限の関数列を作れば実行できます．

$$\vec{x_{1 } }(t)=\vec{x}_{0}+M\vec{x_{0 } }(t-t_{0})$$

$$\vec{x_{2 } }(t)=\vec{x}_{0}+\displaystyle \int_{t_{0 } }^{t}M\vec{x_{1 } }(\tau )d\tau =\vec{x}_{0}+M\vec{x_{0 } }(t-t_{0 } )+M^{2}\vec{x_{0 } }\displaystyle \frac{(t-t_{0})^{2 } }{2}$$

$$\vec{x_{n } }(t)=\displaystyle \sum_{0}^{n}M^{n}\vec{x_{0 } } \displaystyle \frac{(t-t_{0})^{n } }{n!}$$

ここで，$$n \longrightarrow \infty $$とすると収束して，次の指数関数の解が得られます．

$$\vec{x }(t)=e^{M\left( t-t_{0} \right) }\vec{x}_{0}$$ ただし，$$e^{Mt} $$の定義は　　$$e^{Mt}=\displaystyle \sum_{0}^{ \infty }\displaystyle \frac{1}{n!}(Mt)^{n}$$

この解は確かに，　$$\displaystyle \frac{d}{dt}e^{Mt}=Me^{Mt}$$を満たします.

■線形化

現実の連立微分方程式は非線形がほとんどです.

平衡点の近傍でテーラー展開し，局所的に方程式を線形化します．

例えば，一般的な反応拡散系の方程式で$$f(u,v)，g(u,v)$$は線形とは限りません．

$$ \left\{ \begin{array}{@{\,} c @{\, } } \displaystyle \frac{ \partial u}{ \partial t}=D_{u}\displaystyle \frac{ \partial ^{2}u}{ \partial x^{2 } }+f(u,v) \\[0mm] \displaystyle \frac{ \partial v}{ \partial t}=D_{v}\displaystyle \frac{ \partial ^{2}v}{ \partial x^{2 } }+g(u,v) \end{array} \right. $$

$$u(x,t), v(x,t)$$（それぞれ2種類の物質の濃度）を，平衡点のまわりでテーラー展開し，線形近似します．ただし，平衡点を$$(0,0)$$とする（このようにしても一般性を失わない）．

1次の偏微分係数が作る行列（ヤコビアン）$$J$$を定義し，次のように線形化する．

　　　$$ J \equiv \left[ \begin{array}{@{\,} cc @{\, } } \displaystyle \frac{ \partial f}{ \partial u} & \displaystyle \frac{ \partial f}{ \partial v} \\[0mm] \displaystyle \frac{ \partial g}{ \partial u} & \displaystyle \frac{ \partial g}{ \partial v} \end{array} \right] \equiv \left[ \begin{array}{@{\,} cc @{\, } } f_{u} & f_{v} \\[0mm] g_{u} & g_{v} \end{array} \right] $$，　　$$\left[ \begin{array}{@{\,} c @{\, } } f(u,v) \\[0mm] g(u,v) \end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } } f_{u} & f_{v} \\[0mm] g_{u} & g_{v} \end{array} \right] \left[ \begin{array}{@{\,} c @{\, } } u \\[0mm] v \end{array} \right] $$

$$f_{u} , f_{v} ,g_{u} ,g_{v}$$は，平衡点$$(0,0)$$での偏微分係数です．

線形化された反応拡散方程式を以下に示します．$$D_{u}, D_{v}$$はそれぞれの拡散係数（常に正）．

$$ \left\{ \begin{array}{@{\,} c @{\, } } \displaystyle \frac{ \partial u}{ \partial t}=D_{u}\displaystyle \frac{ \partial ^{2}u}{ \partial x^{2 } }+f_{u}u+f_{v}v \\[0mm] \displaystyle \frac{ \partial v}{ \partial t}=D_{v}\displaystyle \frac{ \partial ^{2}v}{ \partial x^{2 } }+g_{u}u+g_{v}v \end{array} \right. $$

$$u(x,t)=u^{*}e^{\sigma t}\textrm{sin}\alpha x$$， $$v(x,t)=v^{*}e^{\sigma t}\textrm{sin}\alpha x$$ と置くと

$$ \left\{ \begin{array}{@{\,} c @{\, } } \sigma u^{*}=-\alpha ^{2}D_{u}u^{*}+f_{u}u^{*}+f_{v}v^{*} \\[0mm] \sigma v^{*}=-\alpha ^{2}D_{v}v^{*}+g_{u}u^{*}+g_{v}v^{*} \end{array} \right. $$

行列形式で書くと，

$$ \left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right] =\displaystyle \frac{1}{\sigma }\left[ \begin{array}{@{\,} cc @{\, } } f_{u}-\alpha ^{2}D_{u} & f_{v} \\[0mm] g_{u} & g_{v}-\alpha ^{2}D_{v} \end{array} \right] \left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right] $$

$$A \equiv \left[ \begin{array}{@{\,} cc @{\, } } f_{u}-\alpha ^{2}D_{u} & f_{v} \\[0mm] g_{u} & g_{v}-\alpha ^{2}D_{v} \end{array} \right] $$

は平衡点$$(0,0)$$におけるヤコビアン．

■解の安定性

$$ \left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right] =\displaystyle \frac{1}{\sigma }A\left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right]      \Longrightarrow      P\left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right] =\displaystyle \frac{1}{\sigma }PAP^{-1}P\left[ \begin{array}{@{\,} c @{\, } } u^{*} \\[0mm] v^{*} \end{array} \right] $$

$$ PAP^{-1}=\left[ \begin{array}{@{\,} cc @{\, } } \lambda _{1} & 0 \\[0mm] 0 & \lambda _{2} \end{array} \right] $$

が対角化されると，固有値 $$\lambda _{1} , \lambda _{2}$$，固有ベクトルは $$P\left[ \begin{array}{@{\,} c @{\, } }u^{*} \\[0mm]v^{*}\end{array} \right] $$

平衡点 $$(0,0)$$ の解が安定であるためには，すべての固有値が負でなければならない．

$$\lambda _{1}<0,\lambda _{2}<0$$ が必要十分であり，$$\lambda _{1}+\lambda _{2}<0$$では少しゆるい条件になる.

$$A$$の固有値を求めるのは面倒なので，対角化により$$Tr$$は変わらない$$Tr[A]=Tr[PAP^{-1}]$$を利用し，ゆるく評価すると，$$Tr[A]=f_{u}+g_{v}-\alpha ^{2}(D_{u}+D_{v})<0$$

拡散項がない（$$D_{u}=D_{v}=0$$）時の安定性から　$$f_{u}+g_{v} < 0$$が成立するので，

例えば，　$$f_{u}>0, g_{v}<0$$，$$\left| \begin{array}{@{\,} c @{\, } }f_{u}\end{array} \right| <\left| \begin{array}{@{\,} c @{\, } }g_{v}\end{array} \right| $$が得られます．

$$u$$は加速剤，$$v$$は阻害剤として働き，互いの解が安定化することがわかります．

正3角形であるための必要十分条件は「３つの内角すべて（すくなくとも2つの内角）60°」です．

図形の対称性から，内角の１つが60°であることを証明すれば済みます．

これは，補助線1本引けば自明です．

■さて，ここに出てきた６辺形には面白い性質があるのを見つけました．

この６辺形の中にある正3角形の中に点Pを中心になるように，正3角形の外の6辺形の部分を折り込むことができます．

ナポレオンが発見したといわれるナポレオンの定理とは次のようなものです．

ナポレオンの定理
任意の⊿ABCの各辺上に正3角形を作図し，それら3つの正3角形の重心をD，E，Fとする．D,E,Fを結んでできる⊿DEFは正3角形である．

なかなか美しい形の定理ではありませんか，ナポオンの名を冠するのにふさわしい定理だと思います．ただし，ナポレオンが発見したかどうかは記録がなくわかりません．

ナポレオン (1769 －1821) は数学好きです．
陸軍幼年学校で，代数，三角法，幾何などを勉強し，数学で抜群の成績をおさめ，1784年にパリの陸軍士官学校に入学．数学が役に立つ砲兵科へと進みます．騎兵科，歩兵科でなく砲兵科に進んだのも戦術の時代の流れを見据えての決断でしょう．砲兵司令官，将軍，皇帝になりました．この時代にフランスには多くの数学者がいました．ラプラス，モンジュ，フーリエなどが近くにおり，エジプト遠征 (1798 年) にはモンジュやフーリエが同行しました．
ナポレオンは数学が大好き，このような幾何問題を考えるのが楽しみで，きっと定理を発見したのだと私は想像します．

 証明

与えられた任意の3角形を⊿ABCとします．その各辺上に作図した正3角形のそれぞれの重心がD,E,Fです．
点Oは⊿ABCの垂心（⊿ABCのそれぞれの辺の垂直2等分線が交差する点）で，点D，E，Fは，この垂直2等分線上にあります．

色々な角の角度は図中に記入してあります．我々が証明すべきことは，⊿DEFが正3角形であることで，例えば，∠DFE=60を証明すれば済みます．考えてみてください．

ヒントは，∠BFE=∠BXC　　と　　∠AFD＝∠AXC　を証明することです． 

 ➡　解答（証明）

反応拡散方程式

エンゼルフィッシュの縞模様やヒトデの星型はどうしてできるのでしょうか？
コンピュータの発明や暗号解読で有名な天才数学者アラン・チューリングが，”The chemical basis of morphogenesis”という論文を1952年に発表しました．今日，受精卵が細胞分裂を繰り返し分化し生物組織が出来ていく胚発生過程は遺伝子情報にプログラムされていることは公知です．1952年にチューリングが発表した理論は，「反応拡散系」が条件を満たせば，パターンや構造を自己成長形成するというものです．反応拡散系と言うのは，２つの物質（モルフォゲンと呼ぶ）が，反応し合いながら組織を介して拡散するもので，初期状態は均一であったものが，ランダムな外乱により，物質の濃淡の波が生じその波が生物の形や模様をつくりだすというものです．この数式でつくり出される模様は「チューリング・パターン」と呼ばれますが，コンピュータ・シミュレーションで描き出すと，条件により，動物の模様にそっくりな縞模様が出現したり，ヒトデの形を作ったりします．手の指が形づくられていくのは，その設計図が遺伝子により決定されているからと考えられていますが，もしかしたら，「指の形成はチューリングの理論のように波がつくっているのではないか」という論文が最近発表されたそうです．遺伝子はからだの構造の基本を決める設計図で，例えば，肺の形成の初期に気管支の分岐などを作るが，細かい肺胞の形成まではその設計図には書かれておらず，チューリング理論のように，現場の細胞同士のやり取り（反応と拡散）で作り上げられて行くのだろうと，近藤滋氏は言っています．

1952年に提唱されたチューリング理論は，現実の生物分野でそのような実験的証拠がなかったので，その後長い間，机上の空論と思われていました．1995年，近藤滋は，海洋エンゼルフィッシュのポマカンサスには，縞模様が皮膚に固定されていないことを発見しました．体の成長とともに，単純に比例して拡大する哺乳類の皮膚のパターンとは異なり，ポマカンサスの縞模様は，体の成長にともなうパターンの連続的な再配置が起こる．そして，縞間のスペースが維持されるという実験事実を観測しました．

実際，チューリング理論に基づくシミュレーションは，成長とともに形成されるパターンを正しく予測できたので，この理論の正しさを支持するものです．

■　チューリングの反応拡散系方程式
存在する２つの物質（モルフォゲン）が，反応したり拡散したりするのは，遺伝子情報で制御されるわけでもなく単純な化学反応で，以下の連立方程式で記述できます．u(t,r)，v(t,r)は振動し，いろいろな形が形成されます．

 ■数学的補足
チューリングの反応拡散方程式の解の安定性を調べる数学について
（解が不安定（暴走）では，縞模様ができません）
しかしながら，テキストのメルマガで数式を多用することができませんので，

ここでは，言葉で説明するにとどめます．
微分方程式の解は指数関数であること．
反応項f，gはそれぞれ物質の濃度u,vの関数で，平衡点の周りでテーラー展開（1次の項まで）して線形化します．
このような連立線形微分方程式の性質は，ヤコビアンと呼ばれる行列Aで決まるが，
この行列Aの固有値の実部がすべて負であれば，解は安定になります．
行列Aの固有値を求めるのは面倒なので，条件を緩くして，行列Aの対角要素の和（固有値の和に同じ）が
負であるとして，さらに，拡散係数も0の場合から始めると，結局，f_u＋g_v<0が得られます．
これは，促進剤と阻害剤が拮抗して働き，若干，阻害剤が強い条件を意味し，このようなときに縞模様が形成されます．

⇒　数学追補

■Turing AM. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 237(641):37-72, 1952.
形態形成の主要な現象が，モルフォゲンと呼ばれる（互いに反応し組織を介して拡散する化学物質）の系で説明できることを示しました．初期状態は全く均一の系ですが，ランダムな外乱によって引き起こされる均一平衡の不安定性により，パターンや構造が発展する可能性があります．このような反応拡散系は，生物学的には珍しいシステムですが，数学的には便利な孤立した細胞のリングの場合にある程度詳細に考慮されます。
調査は主に不安定性の開始に関係しています。これが取ることができる6つの本質的に異なる形式があることがわかります。最も興味深い形では、定常波がリングに現れます。これは、たとえば、ヒドラの触手パターンや渦巻きの葉の原因となる可能性があります。球体上の反応と拡散のシステムも考慮されます。
そのようなシステムは原腸形成を説明しているようです。 2次元の別の反応システムは、垂れ下がった模様を思い起こさせます。また、2次元の定常波が葉序の現象を説明できることも示唆されています。
この論文の目的は、受精卵の遺伝子が，生物の解剖学的構造を決定する可能性のあるメカニズムを議論することです．この理論は新しい仮説を立てません．特定のよく知られた物理法則だけで多くの事実を説明するのに十分です．この論文を完全に理解するには、数学の十分な知識が必要です．若干の生物学，基礎化学，読者がこれらすべての専門家になることは期待できないので，多くの基本的な事実を説明しました（それらは教科書で見ることができますが，省略すると論文が読み難くなるので）．

■Kondo S and Asai R. A reaction-diffusion wave on the skin of the marine angelfish Pomacanthus.Nature, 376(6543):765, 1995.
1952年にチューリングは,反応拡散系と呼ばれる分子的機構仮説を提案しました．これによると，均一な初期状態から周期的なパターンを作り出すことができます．形態形成でのパターン形成現象を説明するために，この反応拡散に基づいて多くの理論モデルが提案されましたが，生物学分野で，このような系の存在の決定的な実験的証拠はありません．海洋エンゼルフィッシュのポマカンサスには，皮膚に固定されていない縞模様があり，体の成長で単純に比例して拡大する哺乳類の皮膚のパターンとは異なり，ポマカンサスの縞模様はパターンの連続的な再配置により線間のスペースを維持します．パターンの変更はストライプの構造によって異なりますが，チューリング系に基づくシミュレーションプログラムは，将来のパターンを正しく予測できます．実際のパターンの再配置とシミュレートされたパターンの再配置の顕著な類似性は，反応拡散波がポマカンサスの縞模様の実行可能なメカニズムであることを強く示唆しています．

■Kondo S and Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation.Science, 329(5999):1616-1620, 2010.
チューリング,または反応拡散（RD）モデルは，発達中の動物胚における自己制御パターン形成を説明する最も有名な理論モデルの1つです．実世界での関連は長い間議論されてきましたが，多くの説得力のある例がモデルを取り巻く懐疑論の多くを説得しつつあります． RDモデルはさまざまな空間パターンを生成できます．数学的研究により，それぞれに必要な相互作用の種類が明らかになり，さまざまな形態現象の実験での仮説として，このモデルが適用できる可能性があります．
このレビューでは，RDモデルが効果的に組み込まれている実験研究の例を使用して，モデルに不慣れな実験生物学者のためにこの理論の本質を説明します．

1986年から始まった米国の数学月間MAMは，2017年から統計学を表に出して数学･統計学月間MSAMに衣替えした．これは，（2011年）解明進む複雑系，(2012年)統計学とデーターの氾濫，(2013年)持続可能性の数学，(2016年)予測の未来，と続くMAMテーマの流れから予想されたことです． 数学と統計学は，インターネット・セキュリティ，持続可能性，疫病，気候変動，データの氾濫，に見る現実世界の問題に対して重要な役割を果たしています．医学，製造，エネルギー，バイオテクノロジー，ビジネスなどの分野でも，日々新しい結果や応用が生まれています．数学と統計学は，システムや方法論がどんどん複雑化する技術世界で，革新の重要な推進力になっています． 些細な事故が雪崩となり大規模災害を惹起する危うさを持っているのが複雑系です．限界ぎりぎりで稼働している複雑系であるインフラの制御はAI（ディープラーニング）がなければどうにもなりません（ただし，事故の復旧では人間自身の手が必要で，AIで解決できるものではありません）．また，医療診断の画像識別エキスパートシステムでは，専門診断医を凌駕する状況であります．

日本政府の「AI戦略」は，AIを理解し各専門分野に応用できる人を，遅ればせながら2025年までに年25万人育てる体制を目標に掲げました．経済産業省が2019.3に出した報告書「数理資本主義の時代」（違和感のある表題だ）は，数学が国富の源泉であると謳い，GAFAを見ればそのような時代の流れであることは明白です．しかし，ことさらに数学をそのように強調し，強者になるための道具にすることには違和感があります．高い年収が得られるので数学を職業とするでは本末転倒と言わざるを得ません．
さらに経産省の当該報告書(p.19)には，<工学出身者に「数学は役に立たない」という時代遅れの先入観が残っている>との記述があます．時代遅れの先入観と言わようが，あえて言うと，私は「数学では物は作れない」と思っています．
アナログ制御の時代を担い応用数学を発展させた工学の扱う対象は物や反応であるのに，データサイエンス（コンピュータがなければ何もできない）の働きかける対象はいつも数値（データ）であり解析にとどまるからです．ただ，工学であれデーターサイエンスであれ，どちらも数学なので，「数学は役に立たない」とは誰も思ってはいないはずです．かつて，電気電子，計測などの工学部が応用数学の研究と教育を担っていた時代があったが，コンピュータの発展により，数学能力の低下はあると思います．数学理論を何も知らずとも優れたコンピュータ・ソフトを操り，良い結果を得るのをしばしば目撃したし，ディープラーニングのブラックボックス化の弊害もあると思います．今は，データーサイエンスの基礎を支える数学を押さえる時期であると思います．経産省の報告書の先に触れた部分は，<企業の工学出身者の時代遅れ先入観がAIを阻害している>と言いたいようだが，経産省の指摘を待つまでもなくこの分野の研究は多くの企業で先行していた．例えば，1987年に開設したリコーカリフォルニア研究センターでは，1990年にPeter E Hartを所長に迎えAIの研究を始めている．2000年に，Richard O Duda, Peter E Hart, David G Storkが”Pattern Classification”(2nd edition，尾上守夫監訳)を出版している．これはスタンフォード大の授業でも用いられ発売後半年で4,000部売れた．米国AI研究者の数学基礎の確かさと層の厚さが感じられる例である．

日本のある大学のポスターで，基幹工学（機械，電気・電子，工業化学），先端工学（ロボット，AI・データーサイエンス），建築工学の3分類の新し構えを見受けます．また，立教大学が2020年4月に開設する国内初となるAI（人工知能）に特化した大学院「人工知能科学研究科」（修士課程）は，機械学習やディープラーニングを中心としたAI領域についての学科で，機械学習の数理モデルを深く理解し，高度な情報科学や統計学の知識を持ち，論文から最新のAI技術を実装できる人材育成を目指すという．
ベイズ決定理論，最尤推定，パーセプトロン，多層ニューラルネットワークなどの基礎教育を行うのは必要ですが，数学以前の数理モデルを作る時点で，正しい解釈ができる能力，常識，読解力，AI倫理などはさらに重要であると考えます．統計学もAIも解釈次第でとんでもない結果を導く可能性があります．

前号では長さの問題をみましたが，今回は面積について少し考えましょう．
（掛谷の問題）
平面に置いた長さ１の針（線分）を平面上で１回転することができる平面図形のうちで
面積が最小なものは何かという問題です．この問題は1916年に掛谷宗一が提起したものです．

可能な図形候補の4つの図を，http://www.araiweb.matrix.jp/semi208/KakeyaProblem.html　から引用します．

多分，皆さんの思いつく答えは，この4つのタイプのうちの一つでしょう．

(1)　直径1の円　面積はπ/4=0.7854
(2)　ルーローの３角形　面積は(πー√3)/2=0.7048
　ルーローの3角形というのは，1辺１の正3角形の各頂点を中心に半径1の円弧を描いて囲まれた図形です．
　ルーローの3角形を断面に持つ棒は，円柱と同じように定幅曲線なのでコロとして使えます．
　その面積は，√3/4＋3x(π/6－√3/4)＝π/2－√3/2　と求まります．
(3)　高さが１の正3角形　面積は1/√3=0.5774

これらの図形の面積は，(1)>(2)>(3)の順で小さくなっています．
それで，(3)が最小面積の答えかと言うとそうでもありません．
(4)のように凸でない（内側に反った曲率の星型）図形でも針の回転が可能で，
そして，(4)の図形の面積はいくらでも小さく（面積0に）できることがわかります．
これは，1919年のベシュコビッチの定理からの一つの帰結でもあります．

さて，面積とは何かというのは難しものです．
われわれが常識で使っているのはジョルダンの面積です．
フラクタル図形の面積０ではジョルダンの面積の定義では面積が測れません．
無限回の操作がからむ図形にも使えるのがルベーグの面積です．

http://twitpic.com/8qlket　に，√2=2　というパラドックスが提起されています．
このパラドックスの原因は，非常に興味深いので，ここで考察することにします．

問題１

一辺の長さ１の正方形の対角線の長さは√2ですが，上図のように，X軸方向に1，y軸方向に１動く経路（n=０）を考えると長さは2になります．以降，このような折れ曲がり経路を繰り返して行きます（n=1,　2,　3,　4,････∞）．折れ曲がりを繰り返して行っても，いつも経路の長さは2で変わらないことがわかるでしょう．このような碁盤の目のような経路の長さは，マンハッタン距離と呼ばれることもあります（マンハッタンの市街の道は，碁盤の目の様だそうです）．マンハッタン経路は，ｎ→∞で対角線に限りなく近づきますので，√2=2　というパラドックスになります．

どこがいけないでしょうか？

問題２

同様な問題に以下の様なものがあります．https://note.com/keyneqq/n/n2ead38a59af5
半径1の円の円周は2πです．半径１の円に外接する正方形の一辺の長さは2ですから，半径１の円周のマンハッタン距離は８です．n=0から出発してx方向，y方向への折れ曲がり数を繰り返しマンハッタン経路は，限りなく円周に近づきますが，マンハッタン距離は8のままです．
従って，2π=8，すなわち，π＝４となります．　どこがいけないでしょうか？

 ■さて，これらの問題に見られるパラドックスは，どこに原因があるのでしょうか？
これらのすべての曲線はいずれも連続であることは確かです．碁盤の目に沿って辿るマンハッタン経路を∞回細かく繰り返した曲線は，至る所ギザギザで，微分不可能な曲線になっており，曲線の長さを微分係数を用いた積分で定義することができません．2点間（x1,y1)，(x2,y2)のマンハッタン距離の定義は|x1-x2|+|y1-y2|で，碁盤の目（メッシュ）を細かくすればするほど，マンハッタン経路はいくらでも目的とする曲線に近づけることはできるのですが，マンハッタン距離は不変です．
（メッシュで定義される碁盤の目のデジタル世界でも，差分により微分係数が定義できますが，そのときもユークリッド距離を用いて定義します）

マンハッタン経路で定義される曲線は，無限回折れ曲がりを繰り返すことで，目的とする曲線にいくらでも近づきますが，マンハッタン距離が変化するわけはありません．

繰り返しの手順を見て，折れ線のフラクタルとみなしフラクタル次元を求めると，この折れ線の次元はやはり１次元になりました．折れ線の幅がフラクタル次元を生むというような説明も見かけましたが，そうではなくフラクタルはこの問題では関係ありません．この問題で人を驚かせるパラドックスの原因は,単純に距離の定義の違いによるものです．
定義が違うものなので違って当然なのですが，2つの曲線は限りなく近づいて行きますので，定義の違いを忘れて同じ長さだと思ってしまうのが間違いの源です．

半径１の円に内接する正5角形の1辺の長さを求めましょう．
この正5角形の1辺の長さをxとします．
△BACと△ADCは相似(相似比が黄金比Φ)で，形は2等辺三角形(等辺xとすると，底辺Φ･x)です．
Φ･x＝x＋(x/Φ)　ですから，Φは黄金比の方程式　Φ²ーΦー１＝0を満たします．
この方程式の解（Φ>1のもの）は，Φ＝(1+√5)/2　です．

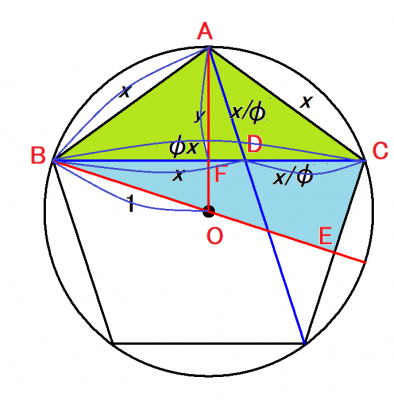
 ■次に，△BCEと△BOFとが相似であることを利用し，
1：(Φ･x）＝OF：CE=(1－y)：(x/2)　が成立するので，　y＝1ー1/(2Φ)　　

ただし，y＝√[(x/Φ)²－((Φ･x)/2－x/Φ)²]＝√[x²ー(Φ･x/2)²]＝x√[1－(Φ/2)²]　

x＝y/√[1－(Φ/2)²]＝[1－1/(2Φ)]/√[1－(Φ/2)²]＝(√[10－2√5])/2＝1.1756

■　作図
半径１の円に内接する正5角形の一辺の長さｘ＝(√[10－2√5])/2を作図する方法
（証明）ピタゴラスの定理を2回使います．

■　万華鏡への応用

■OECDのPISA（Programme for International Student Assessment）国際的な学習到達度調査で，日本の急激な読解力低下（2018年）が指摘されています．PISA調査は15歳（高校1年）を対象に，読解力，数学的リテラシー，科学的リテラシーの三分野について，３年ごとに実施する調査で，国立教育政策研究所が担当しています．
直近の2018年の試験では，読解力が前回の8位から15位に落ちました．

■日本の読解力の平均得点は504点で，OECD加盟国（移民など多数含む）の平均（487点）は上回ったものの，前回（2015年）から12点下がりました．内訳は408点未満の低得点の生徒の割合が全体の約17%を占め，前回調査から4ポイント増えている．生徒の6人に1人が十分な読解力を持っていないことになる．これほど低得点層が増えたにもかかわらず，平均点の低下は少なかった．これは，文章を解さない児童が増えたが，十分な読解力を備えた児童も同時に増える「二極化」が進んでいるということを意味します．得点分布が，平均中央に山を持つ標準的なグラフでなく，中央の左右に2つの山ができるグラフへと変化しました．
そのような変化は，少なくとも２つの因子が存在することを意味します，本来の読解力だけでなく，影響を与えるもう一つの因子なんでしょうか？それは家庭の経済力かもしれません．現在の日本社会では，貧富の2極化も進んでいますから．あるいは，文科省の言うようにデジタル機器への適応の問題である可能性も否定はしません．

■PISAは，紙に手書きで解答する方式から，パソコンで入力する方式に変更（2015年）したそうです．文科省は「日本の生徒は機器の操作に慣れていないことが影響した可能性がある」と分析しています．パソコンを介したテストの方式を私は良く知りませんが，まず，ディスプレイに問題文が表示され，次に進むと問が表示され，これに応えるという後戻りのできない方式ではないでしょうか．これに解答するのはかなり難しくなる．印刷物を介したテストでは，問を見てからまた問題文に戻り確認して答えるというやり方をすると思います．文科省の分析が，このようなテスト方式の変化のためであるというなら私もそうだろうと思います．しかし，「順位が落ちたのはパソコン入力に戸惑ったせいだ」との分析であるなら間違っていると思います．パソコン利用では，紙のときと違い，読解力だけでなく記憶力など総合的に影響し難しいテストに変わったかもしれません．

折り紙も数学ですが，この雪の結晶を折るアルゴリズムは複雑でわかりにくいです．
写真の１，２は完成した雪の結晶を，表面から見た写真（１）／裏面から見た写真（２）です．

（１）　　　　　　　　　　　　　　　　　　（２）　

■スタートに用いるのは，以下に示す6角形の折り紙（３）です．完成品を見ながら，
折り紙（表面側から見て）に，谷折りすべき線（赤色）／山折りすべき線（黄色）を描き込んでみました．

（３）

この線の通りに，谷折り／山折りをして，（４）に示す中間体が作れますから，
試行錯誤して，（４）図のような中間体を作るのを目標にしましょう．

（４）中間体

■中間体（４）の表面側に出た6か所の山尾根の部分を，平らに広げて帯状筋を作る．
この帯状筋の形成のときに，新たに山折りとなる箇所を，
折り紙（３）に青緑色の線で示しておきました．
中間体の山尾根をつぶして帯状筋にするところは，注意深くやりましょう．

■金沢に来ていますが北陸の海は８日は荒れ模様でした(この日はサンダーバードが運休しました)。海の色の変化が美しい。虹の撮影は小梁さん。

■ここは勧進帳の舞台です．腹芸とは相手の心を思いやり察することです．忖度は権力と利益が結びついていて汚いもので，人情や腹芸とは違うと私は思います．

中谷が雪の研究を進めたのには，シベリア出兵の時代で，雪や着氷などが軍事研究として必要だった背景がありますが，実際にやった中谷宇吉郎の雪の研究は基礎研究です．
この地に雪の科学館を設計した建築家は磯崎新です．

■氷の結晶模型はH-O-H分子が水素結合で連鎖しており，平面ではありませんが6角形が見えるでしょう．氷の結晶の内部構造の6回対称性が，樹脂状結晶成長にも反映され，成長した雪片の外形（「雪は天から送られた手紙である」というように上空の環境で様々な形の雪片が見られます）は，どれもすべて6回対称です．

中谷宇吉郎雪の科学館

ダイヤモンドダストの実験．

過冷却の霧（氷点以下なの水（液体）の状態を保っている）の中に，氷結の核となるダストを吹き込むと，一瞬にして水滴の霧が氷晶の霧となる．氷は光を当てるとキラキラして（屈折・分散・反射が強く起こる）ダイヤモンドのように輝く．

＊私は自販機でお茶を買い蓋を開けたとき一瞬でペットボトル内が凍るのを見ました．私の記憶では季節は夏だと思うのですが，自販機のペットボトルはギンギンに冷えていて過冷却だったのでしょう．

＊実験の動画を撮影しyoutubeに置きました．

鈴木大拙
■機械に何でも頼ると機心machine mindsになる.
A machine mind is a calculating mind. Such a mind is not clean and pure.「荘子」の外編

■You cannot understand yourself simply by thinking about yourself.
You can understand yourself better by understanding others．
〇△□

ドアや家具などに見られるイスラムの美しい模様は千年以上の歴史があります．
イスラムの星のデザインは，対称性の高い星型が配列しているのが特徴です．
繰り返し模様全体を支配する対称性は，17種類の平面群のどれかになるし，
並進（周期性）と両立しうる回転対称は，2,3,4,6回軸に限られます．
しかし，イスラムの模様に散らばる星形は対称性が高いのです．高い対称性はもちろん全域に作用はできず，その星形の内部にだけ作用する局所的なものです．

上図の模様を例にとると，8回対称の青い星型が，正方形格子の周期で配列していることがわかります．
青い星型にある8回対称性は，青い星型内部と緑の周囲領域，草色の星形5角形の領域までは有効ですが，
オレンジ色の８角形までは有効ではありません．
青い星の中心にある8回対称軸はオレンジ色8角形の付近では，4回対称軸に低下してしまいます．
これは，周期的な平面では8回対称軸は存在できない（正8角形のタイルでは平面を張れない）から当然のことです．
ある点のまわりの対称性という言葉は注意が必要で，その点周囲の「局所的」対称性を指す場合もありますが，平面「全域」で有効な対称性を指すのが普通です．この例では，青い星型の対称性は8回対称ですが，この星の中心にある回転対称軸は4回対称軸です．
このパターンの単位胞は，オレンジ色の8角形の中心を結んでできる正方形の格子で作られるタイル１つです．

■Girihタイル
正方形と正8角形を組み合わせた平面のタイル張りの例が下図(a)です．この例のテッセレーションを，（4,8,8）と記述します［１つの頂点のまわりに，正4角形，正8角形，正8角形が集まっている］．

(b)図は，正4角形および正8角形の内部に装飾線を描いたGirihタイルです．
平面をGirihタイルでタイル張りしておいて，タイルの縁の輪郭を消すと(c)図のパターンが得られます．

■ここで，始めに掲載したイスラムの模様も，上の例と全く同じであることを確認してください．
始めに掲載した模様の正4角形タイルや正8角形タイルの形は，草色の星型の中心を結んでいくと明らかでしょう．
正4角形や正8角形の内部の装飾線はどのようなものであるかもお確かめください．

Volume 90 Issue 50 | p. 64 | Newscripts
Issue Date: December 10, 2012

マイケル・フリッケ博士(オハイオ州のBoehringer Ingelheim's Ben Venue 研究所の化学者）は，2011年の化学ノーベル賞受賞者シェヒトマンの準結晶を知り，自宅の新しいパティオのデザインにこれを用いることを思いつきました．そしえ，フリッケは1年がかりで2012年11月にパティオを完成しました．
1200個の特製のコンクリート舗装石を準結晶パターンに配置したものです．
写真は，子供が準結晶タイル張りのパティオに立っているところです．彼のTシャツには「悪役のようにゆったり」と書かれています．

フリッケは，パティオに使う2種類の舗装石（太った菱形と痩せた菱形）の木製型を作製しました．木型を使用して彼は1日に15枚のコンクリート舗装石をキャストし，10か月生産した後，ペンローズの非周期タイルと呼ばれるパターンに配列し始めました．
この配列を作るのは「忍耐が必要」だったようです．準結晶が広く受け入れられるまでに，シェヒトマンが嘲笑や猜疑を乗り越えたように．

夜明け前の空の色が美しい．桔梗の色とオレンジ色の消えるところが良い．

新年おめでとうございます．2020年も宜しくお願いいたします．蕎麦好きな私ですが，年越し蕎麦を蕎麦屋で食べたのは初めて，除夜の鐘を撞きに行ったのも初めてです．行列があれば止める主義の私ですが，今回はどちらにも並んでしまいました．

4x4の16個のマスに0~15の数字が書かれたカードがあります．このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる．これをマスクカードを変えて4回行えば，相手が心の中で思っていた数が当てられるというのが，この数当てのゲームです．

どのような仕組みがあるのでしょうか．秋山久義さんが，2019年7月のパズル懇話会で発表されています．
今日は，秋山久義さんの発表「数当てカードの諸相」から引用して，その仕組みを解説します．

まず，16個の数の配列は，ランダムに配置したふりをしていますが隠れた規則があります．
例えば次の２つの方法があります．
（１）左右対称の位置にある2つの数字の和は常に15になる．
（２）回転対称（2回対称あるいは点対称）の位置にある２つの数字の和は常に15になる．

このために右半分（あるいは左半分）を知れば，全部の数の配置がわかります．
つまり，相手の意中の数が見えない場合は，その数との和が15となる数の方が見えているのです．

さて，0~15の数を2進数で表すと次の表のようになります．a,b,c,dはそれぞれ2^3，2^2，2^1，2^0の桁に相当します．

2進数表示で3桁目を表すマスクカードがa，2桁目を表すマスクカードがb，というように
4枚のマスクカードができます．
それぞれの数の上に乗る4種類のマスクカードで，2進数表示の１のところに孔を開ける（網掛け部分）
ことにします（逆に統一してもかまわないが）．
例えば，13の場合は，aとbとdのマスクカードに孔（網掛け部分）をあけ，ｃのマスクカードには
孔はあけません．

以上で，仕掛けの準備ができました．

これで，質問を開始して，数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます．
見えないといったマスクカードは
（１）の場合には裏返して重ね／（２）の場合は180°回転して重ねるのです．

結局，4枚のマスクカードを重ねたものは，
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2019.12.24］ No.298
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
12/20はアップリンク渋谷に映画，「エッシャー 視覚の魔術師」を見に行きました．
エッシャー（オランダ，2018）の版画作品からは，数学者としてのエッシャーは良く知られていますが，
どんな生活をした人物かはあまり気にしたことがありませんでした．
映画では，エッシャーの息子たちへの取材が面白かったです．作品にまつわるエピソード
［1955年作「表皮」から1956年作「婚姻のきづな」に発展］など，よくわかりました．
ムッソリーニ時代の全体主義に息子が染められるのを嫌いイタリアからスイスに移住しました．
人物像のわかる良い映画でした．

最後の方でエッシャーが国際結晶学会の講演に呼ばれていくところがありましたが，
私の専門は結晶学で，結晶学会では昔からエッシャーの周期的模様を教材にしており，
結晶学者には，エッシャー作品は馴染み深いものです．

アルハンブラのモザイクには平面群の17種のすべてがあるという説と1種類かけているという説があります．
どちらでしょうか？それともどちらも違うのか．実際にアルハンブラには行って調べて見たいものです．
ペンローズ・タイリングを発見したペンローズも，アルハンブラのタイルからヒントを得たと聞きます．
私も，イスラームのデザインに立戻って，タイル張りの見直しをしてみようと思っています．

映画のエンドロールにスナップ映像が流れますが，その映像の一つに，大道絵師の光景が写りました．
たまたま昨夏，ニューカッスルの通りで見かけたエッシャー作品ばかり道に描いていた大道絵師のようです．

http://cinejour2019ikoufilm.seesaa.net/article/escher-review.html シネマジャーナルへ掲載いただきました．

■エッシャー作品の生まれるまで
コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました．
1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/a655be2fc4e933a93af15e269d8b684e?frame_id=54

極限としての円の数学については，以下のブログを参照ください．
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/2e340c06148db50daae618a772629e15?frame_id=54

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

uplinkで上映中の「エッシャー視覚の魔術師」

極限としての円の数学については，過去のブログを参照⇒　「極限としての円」の作品

友達が本屋情報を教えてくれます．有難いことです．

12月のシジュウカラさんたちはとても活発です．ヒマワリの種もたくさん食べます．
2,3羽づつ飛来し，同時に4,5羽が来ることもあります．

クンデカリKundekariという技術は，接着剤も釘も使わず木のピースを組み立てていく技術です．イスラム模様の装飾のある説教壇（minbar），ドア，家具に用いられます．12世紀にアナトリア地区で生まれたこの技術は，その地のセルジューク帝国，オスマン帝国時代に洗練されました．杉，薔薇，梨，クルミ，黒檀，リンゴなどの木材が使われます．木材ピースを溝とホゾで組み立てるので．各ピース間は2~3mmのギャップがあり，それぞれのピースの膨張伸縮で歪みが生じることがありません．接着剤や釘で固定された作り方よりも，湿気などに対する耐久性があり，ひびが入らず700年持つといわれます．ジャーミイのドアは，5cm位の多くのパーツをクンデカリの技術で組み立てています．そしてさらに，このドアーを構成する木材ピースの総数は，数秘術的な意味があるそうです．
⇒数秘術的な意味については，アラビア文字のアブジャド数に続く．
（参考文献）クンデカリについては，Mugla Journal of Science and Technology, Vol2,No2,2016,110を引用

機械設計（日刊工業新聞社）1月号のSekkeiBookReviewに拙著「美しい幾何学」を取り上げてくださいました．本の狙いをよく理解いただいたようで工学分野で読まれるのは嬉しいです．
この雑誌は専門書なので初めて手にしますが，回転ステージやDCモーターなど，会社でＸ線反射率測定装置を作ったとき購入したものも色々載っていて懐かしいです．ロボットの分野はずいぶん進み洗練されましたね．

以下の記事が目につきます．これらは数学とも無縁ではありません．
・「歯車装置の設計計算」→表計算ソフトで歯車の歯切りに使うピニオンカッタのトコロイド曲線を描く．

・「Mathcad学ぶで力学解析」→Mathcadは数式通りの記述で計算ができるので，私も初期のMathcadを個人購入し（初期の頃はMathematicaに比べかなり安かった）愛用していたことがあります．いまはMathcad prime6.0になったようです．

・「鳥はなぜ飛べるのか」→非常に興味深い．翼まわりの渦輪など解析をしていますが，難しい流体力学なのでまだ読めていません．

12月4日の夕方から秋葉忠利さんの「数学書として憲法を読む」の出版記念パーティがありました．100人ほど集まり楽しいパーティでした．田中康夫さんや阿部知子さんも来られました．おりしも，PISAテストで15歳の読解力の低下が指摘されています．国民もマスコミも読解力のない社会になりました．論点を次々にずらしたり，揚げ足取りで本論から逸脱させたり，部分否定と全否定をすり替えたり，必要条件と十分条件を区別しなかったり，みな詭弁への道で，まともな議論になりません．論旨を素直にとらえて，正面から議論する当たり前のことが通じない社会になりました．特に，国会やマスコミの報道でこのようなまともな論理の劣化が気になります．

読解力は，読書をしたり話を聞いたりして自然に身に着くものです．私の子供の頃は，落語のラジオ放送を聞く毎日でしたが，まとまった話を最後まで聞くというのは，読解力を身に着けるための良い訓練であると思います．

論理的な普通の読解力で（いかめしく言うと数学的に）憲法を読むというアイデアは画期的な問題提起です．
秋葉さんの本の一読をお勧めします．この本は以下の様に憲法を舞台にしていますが，何の分野でも正しくあるがままに理解するということは重要なことです．

■改憲不可条項
憲法にある「義務」，「尊重」などの単語，特に，「永遠」，「永久」といった「絶対性」をもつ単語を，素直に受け入れ（「義務」という言葉は素直に法的義務と読むべきなのに，都合の悪いところになると道義的要請とよむ「憲法マジック」は詭弁の入り口），「全部否定」と「部分否定」，「必要条件」と「十分条件」との違いを峻別できないと，詭弁に引き込まれます．この他に，憲法に書かれていないこと（あるいは，他の文献）に依存せず，憲法全体は，無矛盾・自己完結するなど，９つのルール（9大律）を設定し，憲法の条文を公理に見立て，論理的な結論となるいくつかの「定理」を導きました．

「永久に」，「国民の総意」，「不断の」などの絶対的な表現と関連がある８つが「改憲不可条項」に当たります．改憲禁止の条項とは明示されてはいないが，論理的にそのような結論になる条文が8か条あるということです．この8か条も含めて，改正の対象にならない条文は30か条を超えることが示されました．改憲の手続き規定である96条は改憲のための必要条件に過ぎないわけです．時間的な極限を表す言葉，「永久に」が使われている9条を変えて，1946年以降の有限時間内のある時点で「戦争をすることが可能になる」ようにすることは，「永久に」という言葉に反します．したがって，9条を「改憲」することは憲法違反になります．

アラビア文字の各文字は数を割りあてられています．このシステムのことはアブジャドabjadと呼ばれ，十進法のインド数字が採用される以前は数値を表現するのに使われていました．また，単語や文章の数値はシンボリックな意味があります．
例えば，「アッラー」は66，このアナグラムの「ラーレ（チューリップ）」も66で，同じ数値ですので，チューリップ模様はジャーミイの装飾に使われます．

クンデカリを構成するピースの数も意味があります．例えば，ドアの文様を構成するセグメント数の165ピースは，「アッラーのほかに神はいない」を意味するそうです．

■私はアブジャドのことは聞きかじっただけで，正確な記述ではないかもしれません（アブジャドのことをご存知の方教えてください）．
私の理解した考え方だけおおざっぱに述べると，アラビア語でも，アルファベット（英語）で計算する数秘術のように，単語（スペル）の文字の数値を総計し，その単語の数値が決まります．ただし，数値を対応させるのはアブジャドに対してで，アラビア文字そのものに対してではないそうです．

（注）世界には，ギリシャ文字（ラテン文字，キリル文字，...），漢字，アラビア文字，などいろいろありますが，アラビア文字は子音を表記する文字に母音も含めるようで，文字も独立の場合と単語の中に使われる場合で異なるようです．漢字や速記文字なども記号全体で一定の意味もつのに似ています．単純なアルファベットではなくアブジャドという文字体系に数字を対応させます．

■クンデカリ技術で作られたドアを構成するピース数の意味

以下の写真のドアの文様の数値227は，次のようにして数えるそうです．この数値のシンボリックな意味は知りません．

面積１の正方形の数14個　→1x14=14
面積２の長方形の数11個　→2x11=22
面積３の長方形の数13個　→3x13=39
ーーーーーーーーーーーーーーーーーー　
　　　（全図形数）38個　　 　　75（全面積）
　　　　　　　　　x4
　　　　　　－－－－－
　（枠のピース数）152　＋（面積数）75　=227（全ピース数）

11月30日，10:00-17:00，東京ジャーミイの台風被災地復興支援チャリティ・バザーでにぎわいました．

新館内装も完成しました．

11月30日は東京ジャーミイのチャリティ・バザーの一環として万華鏡のワークショップを行いました．3クラス実施し，
66人の材料を使い切りました．新館の３Fの工事が終わったばかりの美しい部屋のHouse-warming partyになりました．

万華鏡の鏡室となる3角形は，頂角が15°の２等辺3角形です．従って，鏡室は（15°，82.5°，82.5°）ですから，分数解（12，24/11，24/11）の万華鏡になります．確かに，1/12＋11/24＋11/24＝1　ですから，条件を満たす分数解であることがわかります．

ーーーーーーーーーーーーーーーーーーーーーーーーーーーー

今週の土曜日（11月30日）は東京ジャーミイで万華鏡のワークショップをやります．これは東京ジャーミイのチャリティ・バザーの一環として実施されます．お近くの方は参加されることをお勧めします．詳細や参加申し込みは，以下の東京ジャーミイのウエブサイトをご覧ください．
https://tokyocamii.org/ja/event/1787/?fbclid=IwAR2JXV3GaFx5ruXfPabGC-reuY7VPFNKq1LPXtLpgdltl4hijMo0hT1Ot8I

■万華鏡の原理
平行な合わせ鏡の間に置いた物体は，物体像と鏡像のペアが無限に繰り返す市松模様を生じます．2枚の合わせ鏡が平行でなくθの角度で交差する場合は，一次元の市松模様は円周に沿って並びます．円周の向こう側で市松模様がきれいにつながる条件は，360/2θ＝n（整数）です．これは，万華鏡を発明した物理学者ブリュースターの特許（1817年）に書いてあります．

3枚鏡が3角形をなす場合は，3角形の各頂点でこの条件が成り立つので
1/n＋1/m+1/p＝１，（2=<n,m,p）が，平面がきれいな市松模様になる条件です．この条件を満たす3角形は図に示す3種類しかありません．

これだけではつまらないので，分数解も許すことにすれば，解は無限にあります．このような分数解の万華鏡は，平面の所々で市松模様が破綻しますが，やはり美しいものです．

→続く

■イスラーム模様の特徴　➡亜群

イスラーム模様の特徴は，局所的に対称性の高い星型ロゼットがちりばめられていることです．平面群で存在が許される回転対称は，2，3，4，6回に限られ，5回や，7回以上の回転対称は周期性と両立できません．その理由は正5角形のタイルや正7角形以上のタイルは平面を隙間なく埋めることができないからです．

イスラームの繰り返し模様中に，高い対称性（9回とか10回とか12回など）のロゼットをよく見かけますが，これらの対称性は各ロゼットの内部だけで，全域を支配することはあり得ません．そのため，対称性が高そうに見えても，平面群（17種類ある）のどれかに割り当てざるを得ないのです．

イスラームの特徴的な模様を，平面群で分類するのではなく，もっときめ細かい対称性の記述はできないものでしょうか？　群ではなく，亜群（1926）や混群という代数系などが提案されていますが，その発展が行き詰っているのは残念なことです．

■高次元の周期的な世界から2次元の世界への影　➡高次元格子からの射影

イスラーム模様を高次元の周期的空間からの2次元平面への影であると解釈する方法もあります．

周期性のないPenroseのタイル張り(1976)を，このような方法で作ることもできます．

左図は，周期的な2次元世界から1次元世界への射影で，2次元世界で存在した周期性が失われる事例です．5次元の周期的空間［3次元や2次元の周期的空間には存在できない5回対称軸が存在可能］を，2次元平面に射影すると，5回対称のロゼットを作れますが，５回対称性はロゼットの内部だけで2次元平面での周期性は壊れます．イスラーム模様にちりばめられた高い対称性の星型ロゼット（高次元空間からの影）を見ていると，高次元の宇宙の中に自分が存在する世界があることを実感し，不思議な気分になります．

■結晶は周期的な世界　➡平面群

結晶は単位胞を積み上げてできたブロック細工のようなもので，周期的な内部構造です．図は水晶の例です．水晶の6角柱の方向から見た投影図とM.C.Escherのこの版画作品は同じ対称性（平面群p31m）です．

系の秩序（対称性）は，対称操作［系全体を動かしたとき，系の初期位置と全く重なるような操作］の集合で記述します．対称操作には，並進，対称心，鏡映，回転などがあり，これらの対称操作（群の元という）の組み合わせが作る“群”という代数系［集合の元間の演算が，群の定義（注）を満たす集合］で分類できます．壁紙を記述する平面群は17種類あり，ジャーミイの繰り返し模様もこれらのどれかに分類できます．

注）群の定義：

1．集合Gの任意の２つの元a,bの積a・bは集合Gに属す．→集合は閉じている
2．(a･b)･c＝a･(b･c)　→結合の法則
3．任意の要素aに対して，a･e＝e･aとなるeが集合Gの中にある．→単位元eの存在
4．任意の要素aに対してx･a＝a･x＝eとなるxが集合Gの中にある．→逆元xの存在

■イスラームの模様の作り方　➡テッセレーション

イスラーム建築に使われている美しい模様は，コンパスと定規だけで厳密に作図できますが，1200年までに，5種類のGirihタイル[縁に模様のある等辺多角形タイル]を用いて，パズルのように平面を埋めて美しい複雑なデザインを作る手法が確立しました．

この方法は平面を多角形タイルで分割するテッセレーションの手法と同じです．イランのDarb-i Imam寺院（1453）の壁には,その500年後にヨーロッパで発見されるPenroseタイリング［自分の中に自分と同じパターンが繰り込まれる］と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています．

→（下）へ続く

ペンローズ・タイリングとは，次のような2種類のタイルから出来ているタイル張りです．
この図の例では周期ができてしまいましたが，周期ができないように作ることもできます．

ペンローズ・タイリングは，5次元の空間格子の2次元への射影として作れます．
5次元超立方体は頂点32個，辺の数80（各頂点が５次の同次グラフ）です．
超立方体は亀井図（多元構造グラフ）で表示するとわかり易い．
https://sgk2005.org/wysiwyg/image/download/1/526/medium
我々は５次元空間を見ることができないので，５次元空間の基底を，互いに直交する２つの部分空間の基底の直和（２次元＋３次元）に分けて考察することにします．
周期的な５次元空間［単位胞（5次元超立方体）］を，その5次元空間内をよぎる２次元平面（スクリーン）に射影するには，２次元平面にできる格子の影に，この2次元平面に対する３次元直交補空間（菱形20面体）を射影すればよい．

この３次元補空間内の基底ベクトル３本は互いに直交しているのだが，この３本のすべてがスクリーンとなる２次元平面にも直交している（想像しにくい状態だが５次元の世界だから可能）．
５次元超立方体を３次元に射影してできる立体は，菱形20面体（頂点数は22個，辺の数40）だが，
５次元空間の単位胞の体対角方向が２次元スクリーンに垂直になるように置いて，スクリーンへ射影を行う．つまり，菱形20面体の１つの5回対称軸を2次元スクリーンに垂直にして見下ろしたときの外形（ペトリー多角形と言う）を図に示します．ペトリー多角形とその内部の点は5次元の超立方体の頂点に対応します．

ペンローズ・タイリングに現れる特徴的なパターンが，ペトリー多角形内に作れることを図に示しました．

5次元の周期的な空間を，単位胞（5次元超立方体）の体対角線[1,1,1,1,1]方向に垂直な2次元平面に射影すると，この2次元平面は，3次元補空間の菱形20面体をいくつかの高さのレベルで切断したいくつかのサイズのペトリー多角形内のパターンが次々に現れ，ペンローズのタイル模様が作れます．

正10角形の外側を正5角形（辺の長さは正10角形の辺の長さと同じ）10個で取り囲んだ図が基本です．

この図形は，ジャーミイの説教壇横の装飾に使われています．

下図左のような３種（水色，黄緑色，ピンク）のタイルをGirihタイルと言います．この他に２種のタイル型もGirihタイルに加えて５種類のタイルを用いる場合もあります．Girihというのはタイルの中の模様の線のことです．水色の10角形のタイルの作図法を下図右に示します．この作図は赤い円を10等分することから始めます．

 さて，これらの3種類のタイルを用いて，色々な平面のタイル張りができます．

例えば，次の２つをご覧ください．

(1)

(2)

タイルの色は説明のために着色しただけで，タイルの輪郭線ではなく，各タイル内の線Girihが描く模様に注目してください．

これらのタイル張りの対称性は，(1)はP2mm，(2)はC2mm，もちろん，描かれるイスラーム模様の対称性も同様です．

このような３種（水色，黄緑色，ピンク）のタイルをGirihタイルと言います．この他に２種のタイルの型もGirihタイルに加えて５種類のタイルを用いる場合もあります．Girihというのはタイルの中の模様の線のことです．水色の10角形のタイルの作図法を次の図に示します．この作図は赤い円を10等分することから始めます．

さて，これらの3種類のタイルを用いて，色々な平面のタイル張りができます．

例えば，次の２つをご覧ください．

(1)

(2)

タイルの色は説明のために着色しただけで，各タイル内の線Girihが描く模様が求めるものです．

これらのタイル張りの対称性は，(1)はP2mm，(2)はC2mm，もちろん，描かれるイスラーム模様の対称性も同様です．

https://www.beautifulmosque.com/PostImages/Ulugh-Beg-Madrassa-in-Samarkand-Uzbekistan-21.jpg

ウルグ・ベク・マドラサ神学校

東京ジャーミイの玄関ホールの陳列棚に飾ってある美しい皿です．直径30cm程度です．

中心（花弁12枚）の大きな花には，花の内部だけで有効な12回対称軸があります．しかし，中心の花の周りに小さい花が6個配置されており，全域的に見ると，これは12回対称軸でなく6回対称軸になります．周囲の6個の花（花弁９枚）は，それぞれ自分の内部に有効な9回対称軸がありますが，全域的に見ると3回対称軸です．6回対称軸と6回対称軸の間，3回対称軸と3回対称軸の間には2回対称軸が生じます．その他，右図に実線で描いたように鏡映面があります．
ここで，全域的とは，この模様がお皿の外にも同様な繰り返し規則で無限に続いていると想定した模様のことです．つまり，無限に続くこの模様の対称性は右図のような対称要素の配列（平面群P6mm）になります．右図で水色に塗った部分が単位胞です．
この皿の模様は，この繰り返し模様から青い点線（右図中）で記した円の内部だけを切り取ったものです．

■それぞれの花の内部の局所的な高い対称性
中心の花の内部は，12回対称（その部分群としての6回対称は全域で通用），周りの6個の花の内部は，それぞれ9回対称(その部分群としての3回対称は全域で通用）です．
12回対称や9回対称は周期性と矛盾するので，繰り返し模様全域で，このように高い対称性は存在できません（周期性と両立できる回転対称性は，2,3,4,6回軸に限られます）．このような高い対称性が通用するのはそれぞれの花の内部だけです．
しかし，例えば，５次元空間では，５回対称性が周期と共存することが可能ですから，このような高い対称性が見える花の内部は，高次元空間の断面が2次元の皿の表面に投影されたものと想像することもできます．見えない次元の世界の投影を見るような不思議な魅力を感じるでしょう．

■説教壇横のイスラミックデザイン

写真は説教壇横にある装飾です．次の写真はステンドグラスです．

どちらもイスラミックデザインに特徴的な複雑な図形ですが美しい．
これらの図形の作図は，コンパスと直線定規だけでなされました．
中心に10回対称の星型ロゼットが見えるでしょう．
この「正5角形と180°回転した正5角形を重ね合わせた」星型ロゼット（点群10mm）を
内角が108°と72°の菱形を単位胞とする格子に配置して，繰り返し模様を作りました．
この菱形格子は正6角形（正3角形）のように見えますが，
上下の方向が左右の方向に比べてすこし長く，歪んでいます．
正5角形や正10角形（どちらも最低でも5回対称性がある）を
周期的に並べることは不可能ですから，5回対称性が全域で支配するような格子はできません．「正5角形とその180°回転したものを重ね合わせた」星型ロゼットの対称性（10mm）は，ロゼット内部だけを支配する（局所的）ものです．
この繰り返し模様の対称性（平面群）には，2回軸と水平および垂直に鏡映面があり，記号でいうとP2mmの対称性です．
このように高対称のロゼットをうまくつないで周期性のある模様ができるところがイスラムのデザインの特徴です．

10回(5回)対称は，周期的に並ぶことができません．10回(5回)対称タイルを周期的に配列したイスラームの繰り返しパターンを調べましょう．このようなパターンはイスラームに特徴的で，ジャーミイのいろいろな所で見かけます．

10回(5回)対称は周期性と矛盾しますから，それぞれの10回(5回)対称が支配するのはタイルの内部だけです．

このタイルの描き方を習得するのにだいぶ工夫をしました．
作図手順の足跡として，赤色の作図補助線を残しておきましたから，
皆さんも工夫してこの図を描いてみてください．

まず，中心にある円の円周を10等分することから始めます．
円周の10等分は中心角が36°の作図で，前回に正五角形（中心角72°）の作図をやりましたから，
それを応用して円周の10等分を作図してください．

この長方形のタイルが単位胞になり，これを並べることにより繰り返しパターンが作れます．

この繰り返しパターンの平面群はP2mmです．

10mmという対称性の高い部分があります．もし，そのような対称性が全域に作用するなら，
繰り返し（周期性）ができるわけがありません．10mmという点群の作用はそれぞれの赤い円内の領域に限られるので，周期性と両立できるのです．このようなイスラーム・パターンは色々な所に見受けられます．

次に，この繰り返しパターンを３つの部品によるタイル貼りと解釈してみましょう．
つまり，図に示したように正10角形タイルと，ピンクのタイルと黄緑色のタイルの3種類です．
今日は，この3種類のタイルで平面が隙間なくタイルhave貼りされていることを確認してください．

 ■応用例

Darb-e Imam寺院（イラン）のイスラミック・タイリングのパターン（1453年）は，その500年後に発見されるPenroseタイリング（1973年）と同じものであるのが興味深い．Penroseタイリングは，その10年後に発見される準結晶（1984年）の構造解明に用いられる．

■正5角形の性質

正5角形の中に相似な2等辺3角形（頂角36°）が次々に組み込まれていく様子を見てください．
赤い2等辺3角形→緑の2等辺3角形→青い2等辺3角形
辺の比率は，いつもΦ：1です．Φは正5角形の対角線（星形の辺）で，1は正5角形の1辺です．
このとき成立する方程式，Φ²－Φー１=0を解いて（Φ>1をとる），Φ＝(1+√5)/2＝1.6180･･が得られます．Φは黄金比の値です．

■正5角形の実用作図法で以下のものがあります．

この作図はつぎの式が成り立ちます．AH=HB=1/2，MH=√3/2　であるので，
PH=(√3ー1)/2，従ってPB=(√[(√3－1)²＋1])/2＝(√[5－2√3])/2
AB/PB＝2√(65－26√3)/13＝1.6138･･･
この作図法は，イスラームのタイル作図で便利ですが，厳密な正５角形ではありません．
しかし，誤差は0.26%なので実用上問題ない恐るべき精度です．

 ■厳密な正5角形の作図

AB=1，AH=1/2，PH=1　ですので，AP＝(√[1＋2²])/2＝√5/2
従って，QP＝(1＋√5)/2＝Φ
この作図で得られるのは厳密に正5角形であることが証明されました．

■折り紙で作る正5角形(1)の精度

この図は折り紙で正5角形を作る原理を示しました．y=3xの直線とx軸のなす角θを求めると
θ＝arctan3＝71.5651･･°　となりますが，正5角形では72°になるべきです．
この誤差は．0.6％ですのでかなり良い精度と言えましょう．

他の角度は，72.1087（0.2%），
72.6524（0.9%）程度です．（カッコ内は誤差）

■折り紙で作る正５角形(2)の精度

折り紙の一太刀切で大変作り易い星型です．この原理は以下の図を見てください．
正5角形（星型）の一辺の中心角は360°/5＝72°ですから，一太刀切りに対応する中心角は36°です．
以下の図を見ると，一太刀切りの中心角は，35.783°(36°からのハズレは-0.6%)to,36.870°（+2.4%）に収まっています．

「美しい幾何学」第8章はイスラミック・デザインです．

対称性10mmのタイルを周期的に配置するならば，10mm（あるいは5m）の対称性が全域で残ることはあり得ません．これらの対称性はタイルの内部だけ（局所的）に作用できます．
周期的なイスラームのデザインでタイル(10mm)はどのように配置されているのでしょうか．
大変興味深いことです．このようなタイルはどのように配置されているでしょうか．

（１）まず，一つの例を示します．並進周期をあらわす単位胞は内角が54°と126°の平行4辺形です．正3角形格子（菱形）のようにも見えますが，そうではありませんので注意しましょう．
オレンジの6角形ベース型は正10角形の内部にある花弁の6角形ベース型とまったく同じ型です．

10回対称軸の作用はそれぞれの正10角形内部でのみ有効で，オレンジの6角形ベースには作用できません．従って，それぞれの正10角形はそれぞれの独立した宇宙であるという解釈ができます．

（２）もう一つの配置例を示しましょう．MirzaAkbar

この例では並進を表す単位胞は長方形です．

（３）このほかにも，正10角形タイルを周期的につなぐ美しい配置の実例を発見することができるでしょう．探してみましょう．

次の写真はイスラムの美しい象嵌細工の一部分です．
今回は，この5回対称（あるいは10回対称）の模様を作図してみましょう．

中心部分の輪郭に，正5角形と，それを180°回転した正5角形とを重畳した
10回対称の形（右図）が見えるでしょう．
平面の正多角形タイルによるタイル張り（1種類の正多角形タイルで隙間なく張り詰めること）は，正3角形，正4角形，正6角形でのみ可能です．正5角形のタイルでは平面のタイル張りはできません．これは，平面全域に作用する5回対称軸が周期的に配列している状態があり得ないことと等価です．
イスラムのこの象嵌細工に見られる5回対称（10回対称）は，この模様が周期的に配置された平面全域で作用するものではありません．この図形を中心とする局所的な領域内で作用するものです．

このようなイスラムのデザインは色々な変形があり，各所の装飾に多用されています．大変美しいので，正5角形を基本とする以下の図を作図してみましょう．正10角形の周囲を10個の正5角形が取り囲んでいます．正5角形の１つの内角は108°，正10角形の１つの内角は144°ですから，このような作図（３つのタイルが出会う頂点では，108°x2+144°=360°が成立）は可能なはずです．

このような10回対称の部分を規則的に配列し，その隙間をうまくつなぎ合わせると，
高次元の世界を見るような不思議な模様ができます．どのようにつなぎ合わせるかは，次回考察することにします．5回対称（10回対称）は周期的な平面で不可能なわけですから，それぞれの5回対称軸は局所的な作用にとどまり，つなぎの領域には有効ではありません．そのために，我々は全体平面の中に小宇宙が分布しているような不思議な印象を持つのではないかと思います．

千葉県での広域停電は長期にわたり，大変な日々をお過ごしの方にお見舞い申します．送電網システムは，ケーブル・ネットワーク（ハードウエア），制御ソフトウエア，および行為者より構成されるが，完全に定義しきれない複雑系です．スマート・グリッドになったとはいえ複雑系には完全に制御しきれない要因が何処かにあるでしょう．台風により木立が揺れ，どこかで送電ケーブルが切れたとし，その場所が運悪く重要な結節点に属するなら，電力負荷が残りの送電線にかかり，あっという間に雪崩をうって広域なネットワークの事故に広がって行くことは良く知られています．複雑系はシステム全体として定義できるもので，システムの部分を切り出して定義できません．これは，どこかの事故がシステム全体に広がる可能性を意味します．引き金となる些細な事故はどこで起こるか予測できません．限界ぎりぎりで稼働している複雑系の社会インフラをもつ現代社会で複雑系の数学は重要です．

私は，大規模な送電網に頼らない社会に変えるべきだと思います．自然エネルギーによる発電は，地域で作りその地域で消費する（地域分散型の小規模な送電網）に適しています．そのような利点のあるソーラー発電なのに，森林を破壊しわざわざメガソーラーを作り，また大規模送電網で電気を運ぶのはナンセンスといわざるを得ません．もちろん原発自体が複雑系であり原発の稼働は論外です．

9月15日の日本数学協会の年会では，wowowドラマ，つるさんかめさん～ニッポン算額探訪～和算監修の小寺裕氏の講演がありました．この番組は各地の算額を訪れて問題を解くというドキュメンタリ風ドラマです．というのは，毎回，一人旅の旅行者に同行し，その人が問題を解くというドキュメンタリ仕立てですが，実はこの旅行者は俳優です．さすが俳優で，素人っぽいとぼけたいい味をだしておりなかなか面白いです．私はwowowを見ませんので知りませんでした．第1回の京都北野天満宮，第3回の仙台塩釜神社，第6回の東京金王八幡のそれぞれ30分番組が紹介されました．
脱線しますが奈良弘仁寺の近くで売っている算額最中とはこのような物らしい．

https://media-01.creema.net/user/1015506/exhibits/2498645/0_16f50200d1c23f016772a2a091f8d701_583x585.jpg?fbclid=IwAR1JHomrpu2ucRzQMMPm36vNlllUbq5ixYCEwsaw-1Q-R80C8HaPDgEePmM

■さて，ドラマで取り上げられた算額の問題を紹介しましょう．
第1問は辺2aの正方形内の帆の形に内接するピンクの円の半径を求める．
第2問は円r_a，r_b，r_c，直線が互いに接しているときのピンクの円の半径を求めることです．
私は問題中の数値を忘れたので，このように記号で書きましたが，算額の問題では，aやr_a，r_bは具体的に数字が与えられています．これらの問題は，直角3角形のピタゴラスの定理だけを使えば解けます．
両者とも互いに円が接するときの問題ですが，特に第2問はいわゆるアポロニウスのガスケットの特殊なケース（直線は半径∞の円）です．いろいろ挑戦してみてください．
第1問は　x²+6ax-3a²＝０を解くことになります．
第2問は1/√r_c＝1/√r_a＋1/√r_b　から求まります．
アポロニウスのガスケットの作図で描く互いに接する４つの円に関して，
もっと一般化されたデカルトの定理（1643年）があることに言及しておきます．
（第1問）

（第2問）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2019.09.10］ No.283
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日9/9の朝早く台風が通過しました．関東の皆様被害はありませんでしたか．
こちらでも草木がみななぎ倒されたり，街路樹の紅葉葉楓モミジバフウの枝や実が散乱していました．
今日9/9は，「美しい幾何学」の発売日です．やっと発売にこぎつけた記念すべき日です．
どうぞ書店で手に取って中身を一度ご覧ください．
以下の日刊ベリタに詳しい紹介記事があります．
http://www.nikkanberita.com/read.cgi?id=201909042302103&fbclid=IwAR2JFVjjl2EXJt7238PYL5IP4FwGc7-Fc4rj8xtZVn6SfsWAh2F2vrf6ZjU

この図鑑には美しい図形や不思議な図形がたくさん出てきます．
そのような図形の仕組みを「見ているだけで理解できるように」したかったのです．
数式を使えば正確な説明が楽にできますが，そのためには，
たくさんの数学準備の回り道があり，焦点がぼけてしまいます．
小学生から大学生までが，本書の図を眺めているうちに，
図形に隠された仕組みが自ずとわかることを狙いました．
普通の数学書のように抽象的な記述だけで終りません．
具体的な図を示し本質が理解できるようにしました．
内容には大学の専門課程レベルのものもあり，初めはわからないところもあるでしょうが，
何度も図を見ているうちに，不思議なことに理解できる時がきっと訪れます．

この本の各章は，万華鏡で繋がっています．
1,2章は有限図形の対称性，3,4章は周期的な空間の対称性，
これらの世界の映像は，万華鏡で作り出すことができます．
5章は万華鏡，6章は円による反転という数学的な鏡，7章はフラクタル操作という数学的な鏡，
8章ではイスラミック・デザインの特徴を鑑賞します．イスラムのデザインには，黄金比が多く，
かつ，局所的に高い対称性がちりばめられた周期平面なので，
あたかも我々の住む3次元に高次元宇宙が投影されているような不思議さが魅力です．