円に内接する正5角形の作図

投稿日時 : 2020/01/25  システム管理者 

半径１の円に内接する正5角形の1辺の長さを求めましょう．
この正5角形の1辺の長さをxとします．
△BACと△ADCは相似(相似比が黄金比Φ)で，形は2等辺三角形(等辺xとすると，底辺Φ･x)です．
Φ･x＝x＋(x/Φ)　ですから，Φは黄金比の方程式　Φ2ーΦー１＝0を満たします．
この方程式の解（Φ>1のもの）は，Φ＝(1+√5)/2　です．

　

 

 

 

 

 

 

 

 

 

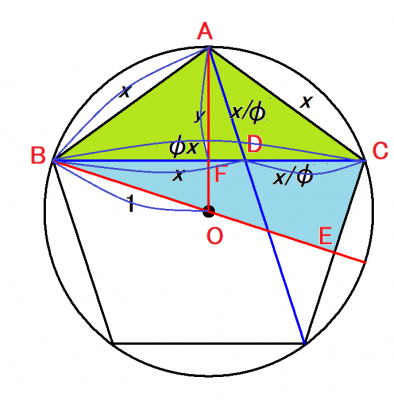
 ■次に，△BCEと△BOFとが相似であることを利用し，
1：(Φ･x）＝OF：CE=(1－y)：(x/2)　が成立するので，　y＝1ー1/(2Φ)　　

ただし，y＝√[(x/Φ)2－((Φ･x)/2－x/Φ)2]＝√[x2ー(Φ･x/2)2]＝x√[1－(Φ/2)2]　

x＝y/√[1－(Φ/2)2]＝[1－1/(2Φ)]/√[1－(Φ/2)2]＝(√[10－2√5])/2＝1.1756

■　作図
半径１の円に内接する正5角形の一辺の長さｘ＝(√[10－2√5])/2を作図する方法
（証明）ピタゴラスの定理を2回使います．

 

 

 

 

 

 

 

 

 

 

 

■　万華鏡への応用