2018年11月の記事一覧

菱形12面体が見える万華鏡を作りましょう．少し厚手（0.25mmとか0.31mm）のミラー紙（B5版）が手に入ると，簡単に作れます．
菱形12面体とは図１のような形で，空間を隙間なく埋め尽くすことのできる形でもあります．
菱形面ABA'B'を底面にして，立体の中心Oを結んだピラミッドADA'B-Oが，
中心のまわりに12個集まるとできる立体です．

①　ピラミッドABA'B-Oの側面OAB，OBA'，OA'B，OB'Aを鏡面にした万華鏡を作ります．非対称領域1/12
②　ピラミッドABA'B-Oの半分のABB'-OやABA'-Oでも万華鏡が作れます．非対称領域1/24
③　さらにそれらの半分のABH-Oも万華鏡が作れます．非対称領域1/48

菱形12面体の内部には立方体が含まれますので，
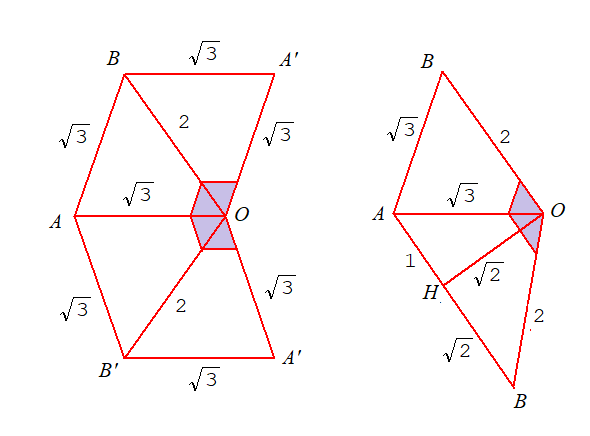
立方体の１辺を2とすると，菱形面ABA'B'の対角線の半分の長さは，
AH=1，BH=√2で，OH=√2，OA＝√3，OB=2となります．

                          図 1　                                                                            図2

 底面（＝菱形面ABA'B'）と頂点（立体の中心O）を結びピラミッドABA'B'-Oを作ります．ピラミッドの内面を鏡面とし，外部（ピラミッドの底側）から頂点Oを覗く万華鏡です．
ピラミッドABA'B'-O，あるいは，底面が直角3角形ABHのピラミッドABH-Oの2種類の万華鏡ができます．ピラミッドの各所の寸法は図２に示します．この寸法を用いて，作った展開図を図3a，bに示します．どちらの展開図でも，Oの周りのグレーに塗った部分は切り取り，窓（＝光の面）を開けます．それぞれの転開図で端辺どうし（左図ではOA'，右図ではOB）を，それぞれ貼り合わせると完成（写真は図4a，b）です．

展開図のグレーに塗った部分は切り取りる．

図3a,　図3b
実際に作る寸法はこの4倍位にすると良い．

完成した万華鏡の外側．鏡面はピラミッドの内側．

図4a　　　図4b

（a)および(b)に対応する万華鏡像

■２つの万華鏡はどちらも菱形12面体像が見えます．図4aのピラミッドには図4bが４つ入ります（図4bの非対称領域は図aの1/4）ので，図4bの万華鏡の方が「菱形面に2mmの対称性があり」，図4aの万華鏡より対称性は高いのです．

■菱形12面体の見える他の万華鏡の例は，⇒ここに掲載します．

トレチャコフ美術館展のポスターを飾る．19世紀末から20世紀初頭のロシア絵画の代表作，クラムスコイ作の「忘れえぬ女」は印象に残ります．表題のНеизвестнаяを直訳の「見知らぬ女」でなく「忘れえぬ女」とした翻訳は実に上手いですね．
この女性が誰だか謎です．すべてのものをありのままに見通すようなまなざしは，実に魅力的です．何も恐れず媚びず，勇敢にまっすぐにみる．あらゆる欺瞞を見抜いているようです．

トレチャコフ美術館展で気に入った絵画がありました．子供の世界のコーナーに展示されている「楽しいひととき」です．作者は，アントニーナ・レオナルドブナ・ルジェフスカヤ（女性）．Антонина Леонардовна Ржевская
ルジェフスキー家のレオナルドの娘アントニーナというわけで，ロシアの標記では，父称からも姓からも女性ということがわかります．この絵画は，男名のА Л Ржевский　と署名し1897年の展覧会に出品しました．

この絵画はパーベル・トレチャコフの目に留まり彼の所蔵となりました．
当時は絵画は男の仕事になっており偏見を心配したためです．

(注）父称や姓は，アントニーナ（女性名詞）を修飾する形容詞ですから女性の語尾変化をし，女性であることが明示されてしまいます．
彼女は没落した貧しい領主の家に生まれました．アレクサンドル2世による農奴解放令は1861年だが，農奴は土地を買わなければならなかったので不徹底改革でしたが，没落領主もあったでしょう．調べたら父は早く死に母と苦労したようです．
1880年にモスクワの絵画・彫刻・建築学校を卒業しました．
1899年に正式に移動派のメンバーになりました．
私立女子学校で教えたり，1920年には骨疾患の子供達のための教育芸術スタジオを組織しボランティア活動をしました．
「楽しいひととき」はこの絵です

エントロピーといえばボルツマンを思い浮かべます．天才ボルツマン（オーストリアの物理学者）の墓碑には，S=klogWと刻まれているそうです．Sはエントロピー，Wはとり得る微視的な”状態数”，kはボルツマン定数です．
対数をとると，log(A･B)=logA+logBのように，積が和になりますので，加算量であるエントロピーと，微視的な”状態数”という積で増加する量とを結び付けるには，対数の登場となるわけです．
熱力学のエントロピーのクラウジウス（1865年）による定義は，系の温度をTとし，可逆過程で熱量δQが系に流入すると，dS=δQ/Tだけ系のエントロピーが増加するというものです．
系の内部エネルギーやエントロピーは状態量です．状態量ならば，系の２つの状態間で，変化経路にかかわりなく，状態量の差が一意に確定します．従って，系のある状態から出発し一回りして戻る経路積分をすると積分値はゼロです．状態量として系の内部エネルギーを例にとると，∲dE=0．このような性質のdEを全微分といいます．
熱や仕事の流入がないとき内部エネルギーは保存（熱力学の第一法則）されます．
閉じた系の内部で何か変化が起きても，その系のエントロピーは増大することはあっても減少することはなく，可逆変化の時のみエントロピーは不変（熱力学の第２法則）です．
系の微視的状態の数はW＝N!/(n_1)!(n_2)!･･･(ｎ_m)!通りで，ここで，P_iを状態n_iをとる確率（n_i＝P_iN，Pi=1）とし，
スターリングの公式を用いlogWを近似すると logW=-(P_i)Nlog(P_i) が得られます．

情報エントロピーの定義もこれと同じ形になります．エントロピーを微視的な状態数の表現と解釈すれば，エントロピーが大きいと可能な状態数が多く，エントロピーが小さいとは予想がしやすいということです．

STEM教育（ステムきょういく）とは、"Science, Technology, Engineering and Mathematics" すなわち科学・技術・工学・数学の略語で，AIやArtも加えてSTEAM教育といわれる理数教科の統合教育であります．STEM教育は，米国で2003年ごろから始まりました．近年，日本でもSTEM教育の必要性が叫ばれるようになりました．これらの科目の中で統合的に数学を教える試みが重要ですが，まだ成功しているとはいえません．われわれが訴えている数学月間の視点は，STEM教育へも貢献できるものと思います．
数学はあらゆる文化・学術の基盤で，科学，工学，産業，芸術，医学，経済など，社会のあらゆる分野を数学が支えています．しかしながら，一般市民，特に，生徒・学生とその両親は，数学学習を敬遠する風潮にあり，これが数学力の低下をもたらしています．米国の「数学月間」MAM（Maths Awareness Month）は，議会上院が決議し、続くレーガン大統領の宣言（1986年4月17日）により国家的な行事として開始されて今日に至ります．米国MAMは，数学系の学協会が参加するJPBM（Joint Policy Boad for Maths）が，毎年，社会を反映した数学テーマを選定し，毎年4月に種々の数学イベントを展開し，国民からの事後評価も受けます．皆が知りたい時局の数学を，種々のレベルで学習できるウエブ・サイトが充実し，そこにエッセイや論文が集積され，そのテーマの数学を基礎から最先端まで，学生が独習できる優れたガイドになります．MAM期間には，一般から専門家まで，小学生から大学生まで，いろいろなレベルのイベントが全国で展開されます．レーガン宣言で国家的行事のMAMを決断した背景には，国民の数学力が低下し，米国の産業力も低下するとの焦りがあったといわれます．日本も同様な状況にあり，国家的行事の数学月間が望まれます．
社会のさまざまな分野と結び付けて数学を知るという数学月間はSTEM教育と精神は同じです．その活動も数学愛好者内にとどまっているのでは意味がなく，社会に横断的に呼びかけ活動し，「社会と数学の架け橋」になることが必要です．多くの方々が数学月間の会に参加されることを願っております．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2018.11.13］ No.241
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
いろいろな多面体の見える万華鏡（立体万華鏡と仮に呼ぶことにします）を作っています．
アルミ板やプラスチックの鏡は像がきれいに映りますが
ミラー紙を用いても，ここで取り上げているような立体万華鏡は良好に作れますので．
チャレンジしてみてください．

球面正多面体は，アラブの数学者，アブル・ワーファ（1000頃）に始まります．
球面正多面体｛p,q｝は，球面正p角形が，頂点でq個集まっているもので，
球面正p角形の１つの内角は2π/qです（図D）．そして，球面p-多角形の辺はすべて大円であることに注意しましょう．
ここで例に取り上げるのは，正12面体に相当する球面正12面体＝球面｛5,3｝多面体です．

メビウスは多面体万華鏡を発明します（1850）が，これは，球面p-多角形を．
2p個の球面直角３角形に分割することを使います（図A）．
分割された3角形の角度は，π/p，π/q，π/2，このような直角3角形を(p,q,2)のように記述します
万華鏡は，３角形（赤く塗った）の各辺となる大円を鏡にすると得られます．
Aは，メビウス万華鏡になり，正5角形の面を10個の直角3角形に分割しています．
Bは，正5角形の面を5個の2等辺3角形に分割しています．Bには，Aに存在した鏡映対称面が１つ消えています．
Cの赤く練った正3角形の周囲の辺の大円を鏡に置き換えて万華鏡を作れば，正20面体の映像が見えます．
それぞれの映像写真は続きに