
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
菱形12面体が見える万華鏡を作りましょう.少し厚手(0.25mmとか0.31mm)のミラー紙(B5版)が手に入ると,簡単に作れます.
菱形12面体とは図1のような形で,空間を隙間なく埋め尽くすことのできる形でもあります.
菱形面ABA'B'を底面にして,立体の中心Oを結んだピラミッドADA'B-Oが,
中心のまわりに12個集まるとできる立体です.
① ピラミッドABA'B-Oの側面OAB,OBA',OA'B,OB'Aを鏡面にした万華鏡を作ります.非対称領域1/12
② ピラミッドABA'B-Oの半分のABB'-OやABA'-Oでも万華鏡が作れます.非対称領域1/24
③ さらにそれらの半分のABH-Oも万華鏡が作れます.非対称領域1/48
菱形12面体の内部には立方体が含まれますので,
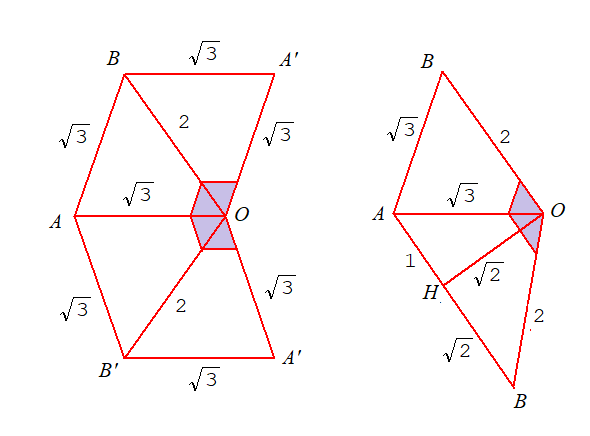
立方体の1辺を2とすると,菱形面ABA'B'の対角線の半分の長さは,
AH=1,BH=√2で,OH=√2,OA=√3,OB=2となります.
図 1 図2
底面(=菱形面ABA'B')と頂点(立体の中心O)を結びピラミッドABA'B'-Oを作ります.ピラミッドの内面を鏡面とし,外部(ピラミッドの底側)から頂点Oを覗く万華鏡です.
ピラミッドABA'B'-O,あるいは,底面が直角3角形ABHのピラミッドABH-Oの2種類の万華鏡ができます.ピラミッドの各所の寸法は図2に示します.この寸法を用いて,作った展開図を図3a,bに示します.どちらの展開図でも,Oの周りのグレーに塗った部分は切り取り,窓(=光の面)を開けます.それぞれの転開図で端辺どうし(左図ではOA',右図ではOB)を,それぞれ貼り合わせると完成(写真は図4a,b)です.
展開図のグレーに塗った部分は切り取りる.
図3a, 図3b
実際に作る寸法はこの4倍位にすると良い.
完成した万華鏡の外側.鏡面はピラミッドの内側.
図4a 図4b
(a)および(b)に対応する万華鏡像
■2つの万華鏡はどちらも菱形12面体像が見えます.図4aのピラミッドには図4bが4つ入ります(図4bの非対称領域は図aの1/4)ので,図4bの万華鏡の方が「菱形面に2mmの対称性があり」,図4aの万華鏡より対称性は高いのです.
■菱形12面体の見える他の万華鏡の例は,⇒ここに掲載します.
これらはすべて菱形12面体の見える万華鏡です.
非対称領域は,それぞれ,空間の1/8(写真1),空間の1/16(写真2,3),空間の1/32(写真4)です.1つの菱形面の中の分割数を観察すると,1(分割なし,写真1),2(写真2,3),4(写真4)であることからわかります.
写真1 写真2 写真3 写真4