2014年12月の記事一覧

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.30］ No.044
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年もあと2日になりました．私は部屋の大整理掃除で3日間も満足にパソコンを開けません．
皆様には，よい年末でありますように．そして良い年をお迎えください．来年もよろしく．

クバンチックの問題は如何でした．私が一番好きなのは，第2問のビリヤードの問題です．
この問題に関する連想考察は，近いうちにぜひ書きたいと思っています．

さて，私は毎年「とっとりサイエンスワールド」で万華鏡のワークショップをやらせてもらっています．
正月まもなく（1月16日，PM3～）多摩センターでも開催しますので，お近くの方はご参加下さい．
詳細は，sgktani@gmail.com　にお問い合わせください．
これからメルマガでも，万華鏡の数学について何回か連載するつもりです．
ここで紹介する万華鏡のキットは，「その道の達人派遣事業」の時に開発し，
各地の学校を回り子供たちと作った万華鏡（当時は2種類）がもとで，
その後品種を増やしてできたものです．
-----
◆万華鏡の原理（１）
万華鏡は合わせ鏡の原理を使っていることはご存知ですね．fig1を見てください．
平行な合わせ鏡で挟まれた室（黄色）は1次元に無限に繰り返しています．
室内にある赤い物体もfig1に示したように繰り返します．
黄色い部屋の隣はその鏡像（左右が逆）．合わせ鏡で挟まれた黄色い部屋を（黒），
隣の鏡像の部屋を（白）と思うと，黒白の帯（1次元の市松模様）ができますね．
今度は，合わせ鏡のなす角度を平行でなくθ°とすると，
市松模様の帯は直線ではなく円を描くように延びて行きます．
円の反対側で市松模様がうまくつながるためには，
黒白のペアの数が整数でなければならない．
これは360°/2θ°＝n（整数）となります．これは，万華鏡の発明者
スコットランドの物理学者ブリュースターが1817年に提出した特許にあります．

FIg.1
以上の説明は2枚鏡の合わせ鏡でしたが，複数鏡の合わせ鏡でもできます．
3枚鏡の場合を考察しましょう．fig2には鏡が作る3角形の図です．
3角形の頂点で2枚の鏡が出会うわけですが，それぞれの頂点で，鏡のなす角度は
360°を偶数で割り切る角度である必要があります．3角形の３つの頂点で
この条件が満たされているなら3角形のタイルで平面が市松模様に張り尽くされます．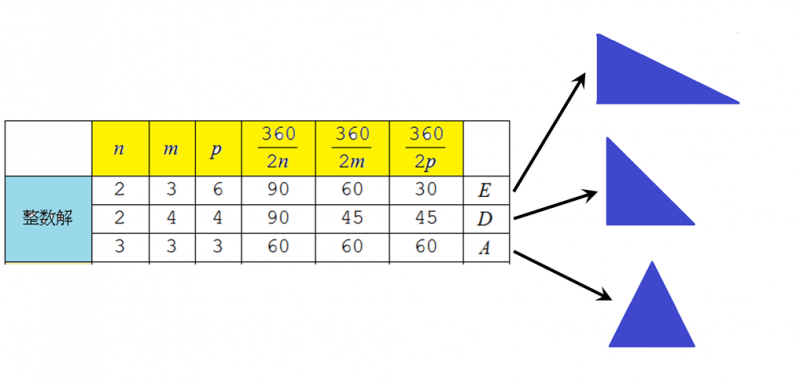

Fig.2
3つのどの頂点でも整数解を持つ場合は，平面をきれいに埋め尽くす市松模様ができます（3種類あります）．
1つの頂点でも整数解にならない場合には，市松模様は乱れますが，これも万華鏡としては美しいものです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.23］ No.043
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
«Квантик»クバンチク（量子っこ）というロシアの生徒向けの雑誌を知りました．
http://kvantik.org/
数学，言語学，物理学などの自然科学の疑問や問題を楽しく学ぶ新雑誌のようです．
onlineでは12ページまでしか出ていないので，その先は購入しなければなりません．
クバンチクで現在出題されている「4つの課題」を紹介します．
出来た人は解答を　kvantik@mccme.ru.　に送ると独創的な解答は公開されます．
面白い問題で私は出来ましたよ．問題もさることながら，
ロシア語の題意を解釈するのに時間がかかってしまいました．
翻訳を載せておきますのでご挑戦ください．

（第1問）監獄からの脱出
T字型の監獄で．2m幅の堀で囲まれている．1.9mの板が2枚ある．
ジャンプは出来ない．どのように脱出するか？
（第2問）ビリヤード
1:2のテーブルの真ん中の位置に球を置いて，テーブルの角のポケット
にビリヤードで（反射させて）玉を入れることは可能か？
（第3問）如何にしてビンをぶら下げるか
2本のマッチと50cmの糸がある．
これらを用いて水入りのビンを棚の縁（角ではない）にぶら下げなさい．
（第4問）物体の警護
物体点のまわりに，哨兵を何人か配置し，
物体にも哨兵にもこっそり近寄られることの無いようにすることはできるか？
ただし，各哨兵は，選んだ一つの方向だけまっすぐに100ｍだけ見ることができる．

解答は載せません．以下は，私からのヒントですーーー
１．Tという形がポイントです．
２．可能です．
３．マッチ2本をどう利用しますか
４．哨兵3人で済みますね．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.16］ No.042
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
パターンがどんどん内部に繰り込まれて行くデザインのいくつかを紹介します．
これらはフラクタルと呼ばれる性質と関係があります．
葛飾北斎（１８３０年代前半）の富嶽36景，神奈川沖の絵の
波しぶきを見たことがおありでしょう．あるいはこの季節の
すっかり葉を落とした木立の先が美しく枝分かれしていたり
雲や海岸線の輪郭が，拡大しても拡大しても同じような
形が現れてくるのにお気づきでしょう．
同じ形が繰り返し内部に繰り込まれているような仕組みを
フラクタルと言います．
フラクタルの詳しい説明は後回しにして
今回は応用されたデザインの例を鑑賞しましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_0_m?1418046938
グラスのこちら側の円が凹レンズになり，向こう側の円模様を
レンズ円内に縮小して映し出しているのが面白い．
（リュミナルク製）

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_2_m?1418046938
五芒星と黄金比　外部と内部の比(1+√5)/2＝1.618:1

http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16306916&no=1
レオナルドの星型8角形　外部と内部の比1+√2：1

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.09］ No.041
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆皆様，お元気でお過ごしでしょうか．選挙が迫り慌ただしい日々ですね．
大事な選挙です．私はもう期日前投票を済ませましたよ．
先週土曜日には，河合弘之弁護士の作ったドキュメンタリー「日本と原発」を
見てきました．皆様の近所でも有料試写会（自主上映）がきっとありますので，
ぜひご覧になることをお勧めします．
「原発は複雑系なので，事故が雪崩を起こす弱点（ここを攻撃されると過酷事故になる）
が思わぬところにある．その引き金となるのは，地震・津波だけではない」と，
メルマガ006に掲載したことがあります．ぜひお読みください．
バックナンバーはブログにもあります．私は，原発だけは止めたいと思っています．
高木仁三郎さんと「宮沢賢治をめぐる冒険」でお話したとき（1997年）のことが
昨日のように思い出されます．この本は，市民科学者として活躍した高木仁三郎さんが
羅須地人協会に打ち込んだ賢治と重なって見える良書です．
これら数学以外のことは，ブログの方に掲載することにしましょう．
ーーーーー

◆双曲幾何の円盤世界
Fig.1の灰色の円盤内の世界は，双曲幾何の世界です．
この世界の直線は，世界の果て（外周円）に直交する円弧
－例えば，Fig.1の赤い円－です．もちろん直径のような本当の直線も
灰色世界の円盤の外周円に直交しますのでこの世界の直線です．

赤い円で2分された灰色世界の左側と右側は
赤い円を反転円として，互いに反転鏡映像になっています．
Fig.1　
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_1_m?1418046545

2つの平面鏡と１つの円柱鏡で作られる万華鏡（Fig.2）を見てください．
赤く塗った3角形の各辺は，この円盤世界の直線です．
赤く塗った3角形の頂角は，30°－45°－90°．内角の和は165°で180°に
足りませんが，この円盤内の世界は双曲幾何の世界なので当然です．

赤く塗った3角形の辺を紙面に垂直な方向に伸ばした3角柱を考えると
平面2枚と円柱鏡からなる万華鏡ができます．
円柱鏡が生む映像は数学的な反転鏡映像としますと
Fig.2のような円盤内の分割（ポアンカレ万華鏡像）が得られます．
塗られた3角形と白い3角形は鏡映の度に入れ替わるので市松模様です．
Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_0_m?1418046545

実際に作ってみました．ポアンカレ万華鏡を再現するのは困難です．
円柱鏡での光の反射（物理的）は，数学的な反転操作とは異なり
厳密な数学的な反転鏡映は，光学的には実現できないのが残念です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.02］ No.040
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先に，「007_インドラの網と反転円」で言及したことがありますが，
円による反転鏡映について，その性質や利用例を鑑賞しましょう．

◆円による反転鏡映の性質
下図に赤い円による反転鏡映の代表的な例を２つ示します．
・反転円をよぎる直線aを反転すると，反転円の中心を通る円Aになる．
・円bを反転すると，円Bになる．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_0_m?1417183249

この性質を知っていると，色々なことに利用できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_3_m?1417183249
例えば，このような図形はアルベロス（靴屋のナイフ）
といいますが，この中の幾何学世界の面白さなどです．

下図のアポロニウスの窓の中にある黄色の円とピンクの円は，
緑色の円を反転円として，それぞれ反転円内の黄色とピンクの円が
鏡映像になります．これらの鏡映像は平行な直線（黒）に挟まれた
領域内に入ります．
平行直線の左はアポロニウスの窓の外周円の反転鏡映，
平行直線の右はアポロニウスの窓内にある左側の大きな円（灰）の
反転鏡映像です．なぜなら，外周円も左側の大きな円（灰）も
反転円の中心を通っているので，鏡映像はどちらも直線になるからです．
アポロニウスの窓内にある初めの黄色い円もピンクの円も，外周円と
内部の左側の大きな円（灰色）に接しているので，
それらの反転鏡映像でもそのような状態が保たれています．

このようなことがわかると，以下のパップスの定理が導かれます．
アルベロスの中で，右側の大きなピンクの円の上に生じる
黄色の円（ω1），続いて生じる灰色の円（ω2），の系列を考えると，
「円ωnの中心と直径ABとの距離は円ωnの直径のn倍である」
（パップスの定理）ことがわかります
以下の図は，ω2の場合の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_2_m?1417183249
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_1_m?1417183249