ブログ倉庫

私たちが学校で習った「水素イオン濃度指数 pH」の定義では，中性はpH=7で，pHは，（酸性）0～14（アルカリ性）までの数値でした．ときおり，強酸性でpHの－の数値や，強アルカリ性でpHが14を超える数値があるのはどう理解すればよいのでしょうか．わからないことばかりですので，以下で，pHの定義から復習を始めましょう．

以下のHORIBAのウエブサイトにたいへん分かり易い記述があります：

このウエブサイトの説明を要約すると次のようです：
セーレンセン(1909)のpHの定義 $${pH=－log_{10}[H^{+}]}$$ は，その後の研究で，水素イオン濃度$${[H^{+}]}$$ではなく，水素イオンの活量に関係することがわかりました．その結果，pHの定義は1920年に次のように改められました：

$$ {ｐH=-log_{10}a_{H^{+ } } }$$ ,   $${a_{H^{+ } }=f\times[H^{+}]}$$
これによると14を超えるpHも可能なようです．

■まず，私たちの学校教科書でのpHの定義では；
水溶液のpHは，水素イオン濃度$${ [H^{+}]}$$ の逆数の常用対数として定義されます:　$${pH=-log_{10}[H^{+}]}$$
この定義では，何故，逆数なのか考えてしまいます．単純に次のように言った方が良いと思います：pHは溶液中の水素イオン濃度の常用対数をとり，その符号を変えたものである．広範囲の濃度を対象にするので，水素イオン濃度の桁を指標にしたいので，常用対数をとり，符号を正にするためーをつけただけだ．

25℃の純粋の水には，$${1×10^{-7 } }$$mol/L［mol濃度という濃度の単位］の水素イオン$${[H^{+}]}$$（正確には，$${[H_{3}O^{+}]}$$の型）が含まれています．１Lに含まれる水分子のmol数を計算すると55.6molですから，含まれる$${[H^{+}]}$$イオンのmol数$${1×10^{-7 } }$$は，これに比べて非常に小さい．従って，ほとんどの水分子は電離していません．この数値は，「純粋な水」の電気伝導度を精密に測定することにより知ることができます．

多くの教科書には以下のような記述があります：---------------------
$${H_{2}O \rightleftharpoons H^{+}+OH^{- } }$$　の電離平衡定数Kは，水温で決まる定数で；$${\displaystyle \frac{[H^{+}][OH^{-}]}{[H_{2}O]}=K}$$ ．
引用終わり------------------

水のイオン積が一定であることは，電離反応速度の質量作用の法則から導かれ，この平衡定数と関連しているようです．しかし，電離度がわずかなために水のmol濃度に変化はないと説明があります．しかし，ここがとても気持ちが悪いのです．溶媒自身であり，同時に溶質でもある水分子のmol濃度とはいったい何なのだ！

ともかく，水分子が電離すれば，$$ H^{+} $$と$$ OH^{-} $$は等量ずつ生じるので，それらのイオン積（温度に依存する）は， $$ [H^{+}][OH^{-}]=1×10^{-14} $$であります．

希薄な水溶液の場合は，純粋な水の場合と同様，このイオン積は同じ一定値に保たれるようです．

従って，水素イオン濃度が減少すれば反比例して水酸基イオン濃度が増加する．それぞれのイオン濃度は１を越えることがないとすれば，pHの最大値は14になります．

pHは，酸・塩基の濃度が 1 mol/L よりも低い水溶液の酸性・アルカリ性の度合いを示すための指標として考案されたものです．濃度が 1 mol/L を超える濃厚な酸や濃厚アルカリ溶液では，pHが負になったり14を超えたりします．その上， $${[H^{+}]}$$ から求めると実態に合わない（塩基の場合も同様）ので，その代わりに水素イオン活量 $${a_{H^{+ } } } $$が導入されました．

希薄水溶液でなければ，イオン間の相互作用が強くなるので，溶液中の水素イオン濃度を，イオン活量$${a}$$で置き換えて定義しなおすことが必要になったのです．溶質成分$${i}$$のイオン活量の定義；
　$${a_{i}=e^{\Delta \mu _{i}/RT } }$$

ｐH緩衝液
緩衝液とは弱酸とその塩の混合液，あるいは，弱塩基とその塩の混合液で作られます．緩衝液は，酸や塩基を多少加えてもそのpHを変化させない性質（＝緩衝作用）を示します．
弱酸とその塩の混合液の場合，塩が電離して，水素イオンを発生するので，弱酸の電離を抑える．弱酸の濃度が多少増加しても電離は増えずpHの変動を抑えます．
このよう緩衝効果の例は，例えば，結晶成長に用いるゲル化シリカを，メタケイ酸ナトリウムと酢酸の中和反応で得て（ゲル化にともないpHは多少変化），ゲル中で結晶塩を成長させる反応イオン水溶液を加えるときにもみられます．

コンスタンチン・ノップ,「クバント」«КВАНТ»No8，2020　の記事より
ただし，原文の説明は分かりにくいので，訳者が説明をすこし変えました．

ジョン・ホートン・コンウェイは著名な数学者で，組み合わせゲーム理論だけではなく，面白​​い数学への多大な貢献をしています．

パズル－－－－－－－ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
■私はバスに乗っていて，2人の魔法使の会話を聞きました：

A：私には子供が何人かいて，それぞれの年齢は正の整数であり，それらの合計はこのバス番号に等しく，それらの積は私自身の年齢です．
Ｂ：面白い！　もし，あなたの年齢と子供の数を教えていただければ，私は彼らの年齢を計算することができますか？
A：いいえ，できません．
Ｂ：ああ！　ついにあなたの年齢がわかりました．
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

問: 　私たちの乗っていたバス番号はいくつですか？

■このパズルの背景
パズルの作者であるジョン・コンウェイが，バス内という場面を設定したのは，魔法使いAの年齢ａと彼の子供の数ｃの他に，もう1つの変数が必要だからで，それがバス番号ｂです．
（a,b,c）の三つ組数は，ａは魔法使いAの年齢，ｂはバス番号，ｃは魔法使いAの子供の数を表すとします．
ｂのバス番号は，私たちにはわかりませんが，魔法使いＢにはわかっています．

魔法使いAの「いいえ，できません」という意味は，魔法使いＢの知的能力に関することではなく，三つ組数（a,b,c ）が完全にわかっても，子供の年齢を明確に決めることができないということです．言い換えれば，同じ総和と積を与える［子供の年齢集合］で異なるものが存在することです．そのような年齢の集合をコンウェイ集合と呼びましょう．
訳者注）条件を満たす子供の年齢集合はｃ組数です．はじめの三つ組数と区別するために，私は［］で表示することにしました．

このパズルがめちゃくちゃ美しいのは，何から始めればよいかわからない．アプローチが非常に難しいからです．もし，魔法使いAの年齢ａが分かれば，その約数を調べて，その和のバリエーションをすべて見つけることができる．もし，バス番号ｂがわかれば，いろいろな方法でそれを総和に分解し，それらの積のバリエーションを求めることができる．もし，子供の数ｃだけ分かった場合でも，探索量はずっと少なくなる．
候補探索のプログラミングに数時間を費やし，ようやく正しい解に近づく方法を見出した人もいます．

この問題は，完全に定義されておらず，つまり，さまざまな解決策が存在するのです．

■例を示します：
21番のバス（b=21）内の会話で，魔法使いAは96歳（a=96），子供は3人（c=3）だとします．この状態を三つ組数（96, 21, 3）と書きます．
子供たちの年齢は，和が21，積が96で，この場合ｃ=３のため，たまたまですが，［3つ組数］になります．この条件を満たす子供の年齢は，［1，8，12］と［2，3，16］の2つがあり，確かに，魔法使いＢが（96,21,3）と完全な数字を知ったとしても，子供たちの具体的な年齢を割り出すことはできません．

魔法使いの会話から，条件を満たす子供の年齢が決まらないのは何故か？

同じbで異なるaを持つ数字のコンウェイ集合は他にないでしょうか？
この問いに答えるために，別の言い方をしましよう．bが小さく，aが異なるコンウェイ集合は他にないのでしょうか？なぜなら，もし見つけることができれば，それに1歳児を加えて，出来上がったコンウェイ集合の数の合計ｂを21になるようにすればよいからです．

［訳者注］子供の年齢集合に1歳を一人加えるとｂ（子どもの年齢の総和）は１つ増加しますが，積ａ（これは魔法使いＡの年齢）は変わりません．ただし，ｃは１つ増加します］．実際，このようなコンウェイ集合は簡単に見つかります．例えば，（40，14，３）の場合，［1, 5, 8］ や ［2, 2, 10］ がそうで，これに1歳児を加えると［1,1,5,8］や［1,2,2,10］で（40,15,4）に対応するコンウェイ集合が得られます（この両者で，魔法使いＡの年齢は40歳で変わりません）．
また，（36,13,3）の場合，コンウェイ集合 ［1, 6, 6］ と［2, 2, 9］があり，同様の操作で［1,1,6,6］と［1,2,2,10］のコンウェイ集合が得られ，これは（36,14,4）に対応します．この両者では魔法使いＡは36歳で変わりません．
この2つの例で，バス番号ｂ＝14が同じとき，魔法使いＡの年齢が40と36のように異なるものが作れます．

ここから，説明は冗長になり混乱しますから，ここで一息入れましょう．ここから先は，まず，自分でトライアンドエラーしてみた方が理解が深まります．各自試みてください．要するに，この問題は，［子供の年齢の集合］で，総和と積が一致する集合（コンウェイ集合）の中身に異なるものが複数存在し，子供の具体的な年齢が決まらない場合のｂ（子どもの年齢の総和でバス番号）を聞いているのです．「ああ！　ついにあなたの年齢がわかりました．」と言う発言があるので，そのとき，ａの数値は定まらなければいけません．

$$ \begin{split} 6 &= 2 + 2+2\ &(a=8) \\ \rhd 7 &= 2 + 2+ 3\ &(a=12) \\ \rhd 8 &= 2 + 2 + 2 + 2\ &(a=16) \\ \rhd 8 &= 2 + 2+ 4\ &(a=16) \\ \rhd 8 &= 2 + 3 + 3\ &(a=18) \\ \rhd 9 &= 2 + 2 + 2 + 3\ &(a=24) \\ 9 &= 2 + 2 + 5\ &(a=20) \\ \rhd 9 &= 2 + 3 + 4\ &(a=24) \\ 9 &= 3 + 3 + 3\ &(a=27) \\ \rhd 10 &= 2 + 2 + 2 + 2 + 2\ &(a=32) \\ \rhd 10 &= 2 + 2 + 2+ 4\ &(a=32) \\ \rhd 10 &= 2 + 2 + 3 + 3\ &(a=36) \\ \rhd 10 &= 2 + 2+ 6\ &(a=24) \\ \rhd 10 &= 2+3 + 5\ &(a=30) \\ \rhd 10 &= 2+4+4\ &(a=32) \\ \rhd 10 &= 3 + 3+ 4\ &(a=36) \\ \rhd 11 &= 2 + 2 + 2 + 2+ 3\ &(a=48) \\ 11 &= 2 + 2 + 2 + 5\ &(a=40) \\ \rhd 11 &= 2 + 2+ 3 + 4\ &(a=48) \\ \rhd 11 &= 2+3 + 3 + 3\ &(a=54) \\ 11 &= 2 + 2 + 7\ &(a=28) \\ \rhd 11 &= 2+3 + 6\ &(a=36) \\ 11 &= 2+4 + 5\ &(a=40) \\ 11 &= 3 + 3 + 5\ &(a=45) \\ \rhd 11 &= 3 + 4 + 4\ &(a=48) \\ 12 &= 2 + 2 + 2 + 2 + 2 + 2\ &(a=64) \\ 12 &= 2+2+2+2+4\ &(a=64) \\ 12 &= 2+2+2+3+3\ &(a=72) \\ \rhd 12 &=2+2+2+6\ &(a=48) \\ 12 &=2+2+3+5\ &(a=60) \\ 12 &= 2+2+4+4\ &(a=64) \\ 12 &=2+3+3+4\ &(a=72) \\ 12 &= 3+3+3+3\ &(a=81) \\ \rhd 12 &=2+2+8\ & (a=32) \\ 12 &=2+3+7\ &(a=42) \\ \rhd 12 &=2+4+6\ &(a=48) \\ 12 &= 2+5+5\ &(a=50) \\ \rhd 12 &= 3+3+6\ &(a=54) \\ 12 &=3+4+5\ &(a=60) \\ 12 &=4+4+4\ &(a=64)\end{split} $$

$$\begin{split}2 &= 2\ &(a=2) \\ 3 &= 3\ &(a=3) \\ \ldots \\ 11 &= 11\ &(a=11) \\ 4 &= 2+2\ & (a=4) \\ \rhd 5 &= 2+3\ &(a=6) \\ \rhd 6 &= 3+3\ &(a=9) \\ \rhd 6 &= 2+4\ &(a=8) \\ \rhd 7 &= 3+4\ &(a=12) \\ \rhd 7 &= 2+5\ &(a=10) \\ \rhd 8 &= 4+4\ &(a=16) \\ 8 &=3+5\ &(a=15) \\ \rhd 8 &= 2+6\ &(a=12) \\ 9 &= 4+5\ &(a=20) \\ \rhd 9 &=3+6\ &(a=18) \\ 9 &= 2+7\ &(a=14) \\ 10 &= 5+5\ &(a=25) \\ \rhd 10 &=4+6\ &(a=24) \\ 10 &=3+7\ &(a=21) \\ \rhd 10 &=2+8\ &(a=16) \\ \rhd 11 &=5+6\ &(a=30) \\ 11 &=4+7\ &(a=28) \\ \rhd 11 &=3+8\ &(a=24) \\ \rhd 11 &=2+9\ &(a=18)\end{split}
$$

$$\begin{split} \rhd 5 &= 2 + 3\ &(a=6) \\ \rhd 6 &= 6\ &(a=6) \\ \\ \rhd 6 &= 2 + 2 + 2 = 2 + 4\ &(a=8) \\ \rhd 8 &= 8\ &(a=8) \\ \\ \rhd 6 &= 3 + 3\ &(a=9) \\ \rhd 9 &= 9\ &(a=9) \\ \\ \rhd 7 &= 2 + 5\ &(a=10) \\ \rhd 10 &= 10\ &(a=10) \\ \\ \rhd 7 &= 2 + 2 + 3 = 3 + 4\ &(a=12) \\ \rhd 8 &= 2 + 6\ &(a=12) \\ \\ \rhd 8 &= 2 + 2 + 2 + 2 = 2 + 2+ 4 = 4 + 4\ &(a=16) \\ \rhd 10 &= 2+8\ &(a=16) \\ \\ \rhd 8 &= 2+3 + 3\ &(a=18) \\ \rhd 9 &= 3 + 6\ &(a=18) \\ \rhd 11 &= 2 + 9\ &(a=18) \\ \\ \rhd 9 &= 2 + 2 + 2+ 3 = 2+3+4\ &(a=24) \\ \rhd 10 &= 2+2 + 6\ &(a=24) \\ \\ \rhd 10 &= 2+3 + 5\ &(a=30) \\ \rhd 11 &= 5 + 6\ &(a=30) \\ \\ \rhd 10 &= 2 + 2 + 2 + 2 + 2 = 2 + 2 + 2+ 4 = 2+4 + 4\ &(a=32) \\ \rhd 12 &= 2+2 + 8\ &(a=32) \\ \\ \rhd 10 &= 2 + 2+ 3 + 3 = 3 + 3 + 4\ &(a=36) \\ \rhd 11 &= 2+3 + 6\ &(a=36) \\ \\ \rhd 11 &= 2 + 2 + 2 + 2 + 3 = 2 + 2+ 3 + 4 = 3 + 4 + 4\ &(a=48) \\ \rhd 12 &= 2 + 2 + 2 + 6 = 2+4 + 6\ &(a=48) \\ \\ \rhd 11 &= 2 + 3 + 3 + 3\ &(a=54) \\ \rhd 12 &= 3+3 + 6\ &(a=54)\end{split}
$$

$$ \begin{split} \rhd 11 &= 3+4 + 4\ &(a=48) \\ \rhd 12 &= 2+2 + 2 + 6\ &(a=48)\end{split} $$

（定義）語wordとは，順序つけられた記号の配列である．

（例）例えば，abcはアルファベット文字を用いた長さ３の語である．001101は，バイナリー語（各ビットには，0あるいは1が入る）で，長さ6ビットである．

（注）ビットbitとは，binaryとdigitを縮めて作った造語である．

（例題）$${a_{n } }$$ を連続して1が続くことのないようなb-ビット語の数とする．$${a_{n } }$$を求めなさい．

(実験)

n=0のとき：　空集合が１つ：　$${a_{0}=1}$$

n=1のとき：　0，1　：$${a_{1}=2}$$

n=2のとき：　00，01，10　：$${a_{2}=3}$$

n=3のとき：　000，010，100，001，101　：$${a_{3}=5}$$

n=4のとき：　0000，0100，1000，0010，1010，0001，0101，1001　：$${a_{4}=8}$$

$${a_{n } }$$はフィボナッチ数列，1,2,3,5,8,....…になることが予想される．

（証明）

１．任意のn-ビット語wを考える．語wが0で終わるとすると，末尾の1つ前(n-1)番ビットは，0でも１でも良いので，この場合の1～(n-1)番ビットでできる(n-1)-ビット語の数は，$${a_{n-1 } }$$個である．従って，0で終わり，連続する1を含まないn-ビット語は$${a_{n-1 } }$$個である．

２．語wが1で終わるとすると，(n-1)番ビットは0でなければならない．(n-2)番ビットは何の制約もなく，0でも1でもかまわない．従って，１で終わり，連続して１を含まないn-ビット語は$${a_{n-2 } }$$個ある．

1.,2.の２つのケースは互いに排他的であるので，加算原理により；$${a_{n}=a_{n-1}+a_{n-2 } }$$これは，フィボナッチ数列の定義に他ならない．

（練習問題）n個のコインを投げて，隣り合う２つのコインが連続して表を向くことがない確率を求めなさい．

写真は，今を盛りに咲いている花桃です．葉となる芽の位置を，枝の元から先に向かって調べると，５つごとに重なる位置になることがわかります．左回りの螺旋配置で，５つ目で重なるまでに２回転しますので，葉序比2/5といいます．２も５もフィボナッチ数です．　

一般に，植物や樹木の枝につく葉は螺旋配置をしています．１つの枝に沿って枝先に向かって，ある葉から出発しその葉に重なる上の葉までの葉の数を数えて見ましょう．その数は，だいたいフィボナッチ数になることが知られています．螺旋配置になるのは，木の枝が成長しながら，葉が重ならないよう葉が育つと考えると理解できます．同じ位置の上の葉と重なるまで（1周期）の葉の数がフィボナッチ数と言うことです．植物（精密な工業製品ではない）ですので，それほど厳密な話ではなく，だいたいの配置を言っているに過ぎません．重ならないようにするなら，周期が出来ない（∞周期）方が，良いのではないかとも思いますが，周期というのはだいたいのもので，結晶のように完全に周期的というわけではありませんから，目くじらを立てないでください．

シナノキとニレではこの数は２（左右交互）；ブナとハシバミでは３；アンズ，桜，カシでは５；梨とポプラでは８；アーモンドと柳では13と言われています．［Hoggatt，1979］

出発点の葉から終着点の葉までの時計回りあるいは反時計回りの回転数は，やはり通常はフィボナッチ数で，例えば，シナノキとニレでは1回転；ブナとハシバミではやはり1回転；アンズ，桜，カシでは2回転；梨とポプラでは3回転；アーモンドと柳では5回転だそうです．

樹木の枝の葉の配置は葉序と呼ばれます．葉が重なるまでの葉の数と，回転数の比は葉序比と呼ばれ，シナノキとニレの葉序比は1/2；ブナとハシバミでは1/3；アンズ，桜，カシでは2/5；梨とポプラでは3/8；アーモンドと柳では5/13です．［Fibonacci and Lucas numbers with applications, Thomas Koshy］

ここまでに観察される数値は，1,1,2,3,5,8,13までのフィボナッチ数です．さらに大きなフィボナッチ数が観測されるかどうかや，漸化式が葉の発芽の機構から必然的に導くことができるのかには言及しません．

■　電場$$\textrm{E}$$や電流密度$$\textrm{j}$$を極性ベクトルとすると，磁場$$\textrm{H}$$は軸性ベクトルになる．
それは，次のMaxwell方程式が成立しているためです．
$$ \nabla \times \textrm{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \textrm{E } }{ \partial t}+\displaystyle \frac{4\pi \textrm{j } }{c}$$の右辺は極性ベクトルですから，$$ \nabla \times \textrm{H}$$は極性ベクトルであることになり，$$ \nabla $$が極性ベクトルなので，$$\textrm{H}$$は軸性ベクトルでなければならない．
極性ベクトル$$ \times $$軸性ベクトル＝極性ベクトル 
極性ベクトル$$ \times $$極性ベクトル＝軸性ベクトル 
の関係があり，これを用いました．

$$ \nabla \times \textrm{H}$$，（あるいは，$$\textrm{rot H}$$）という演算の結果は，ベクトル$$\textrm{H}$$の回転面に垂直な軸性ベクトル（その方向は，回転を右ネジに見立てて進む方向）を与えます．この例の軸性ベクトルは$$ \nabla $$とHの2つのベクトルの外積で定義されたもので，その物理的実態は$$\textrm{H}$$の回転面の円軌道にそって流れる電流です．回転方向を，角速度などと同様に，外積を借りて定義しただけで，実態は円軌道という物理現象だけです．右手座標系でも，左手座標系でも，外積自体は右手系で定義するのが慣習です．右手座標系で定義された軸性ベクトルを左手座標系で記述すると，軸性ベクトルの向きは反転します．

詳細は：⇒極性ベクトル軸性ベクトルの項をご覧ください．

座標系を反転すると，右手系で見た座標値$$(x_{1}, x_{2}, x_{3})$$が左手系で見た座標値$$(x_{1}'=-x_{1}, x_{2}'=-x_{2}, x_{3}'=-x_{3})$$に変わります．

座標系の反転で，座標成分の符号が変るのが，極性ベクトル（変位，速度，力，運動量など）；
座標成分の符号が変わらないものが軸性ベクトル（角速度，角運動量，モーメントなど）と言われます．
軸性ベクトルとは，２つの極性ベクトル間の外積で定義されるものです．

軸性べクトルは，座標系の反転で座標成分の符号が変わらないというのは本当でしょうか？
納得できないので，これを確かめてみましょう．

■　右手系と左手系基底の定義 
２つの正規直交基底$$ \left[ e_{1}, e_{2}, e_{3} \right] $$，および，$$\left[ e_{1}', e_{2}', e_{3}' \right] $$があるとします．
正規直交基底は，　$$e_{i} \cdot e_{j}=\delta _{ij}$$，　$$e_{i} \times e_{j}=-e_{j} \times e_{i}$$，　$$e_{i} \times e_{i}=0$$が成立ちます．
右手系では，　$$e_{2} \times e_{3}=e_{1}$$，$$e_{3} \times e_{1}=e_{2}$$，$$e_{1} \times e_{2}=e_{3}$$ が成立します．
空間反転$$e_{1}'=-e_{1}，e_{2}'=-e_{2}，e_{3}'=-e_{3}$$して得られる基底$$\left[ e_{1}', e_{2}', e_{3}' \right] $$では， 
　$$(-e_{2}') \times (-e_{3}')=(-e_{1}')，(-e_{3}') \times (-e_{1}')=(-e_{2}')，(-e_{1}') \times (-e_{2}')=(-e_{3}')$$
すなわち，$$e_{3}' \times e_{2}'=e_{1}'，e_{1}' \times e_{3}'=e_{2}'，e_{2}' \times e_{1}'=e_{3}'$$が得られます．この座標系は左手系になります．

■　位置ベクトル，運動量ベクトル（ともに極性ベクトル）を，右手系と左手系で標示すると，
位置ベクトル：$$r=x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}=x_{1}'e_{1}'+x_{2}'e_{2}'+x_{3}'e_{3}'=-x_{1}e_{1}'-x_{2}e_{2}'-x_{3}e_{3}'$$
運動量ベクトル：$$p=p_{1}e_{1}+p_{2}e_{2}+p_{3}e_{3}=-p_{1}e_{1}'-p_{2}e_{2}'-p_{3}e_{3}'$$
このように，極性ベクトルの座標値は，座標系の反転で符号を変えることがわかる．

■　角運動量ベクトル（軸性ベクトル）を，右手系と左手系で標示する．
$$L=r \times p=\left( x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3} \right) \times \left( p_{1}e_{1}+p_{2}e_{2}+p_{3}e_{3} \right) =$$
$$=-x_{2}p_{1}e_{3}+x_{3}p_{1}e_{2}+x_{1}p_{2}e_{3}-x_{3}p_{2}e_{1}-x_{1}p_{3}e_{2}+x_{2}p_{3}e_{1}=$$
$$=\left( x_{2}p_{3}-x_{3}p_{2} \right) e_{1}+\left( x_{3}p_{1}-x_{1}p_{3} \right) e_{2}+\left( x_{1}p_{2}-x_{2}p_{1} \right) e_{3}=$$ 
$$=-\left( x_{2}p_{3}-x_{3}p_{2} \right) e_{1}'-\left( x_{3}p_{1}-x_{1}p_{3} \right) e_{2}'-\left( x_{1}p_{2}-x_{2}p_{2} \right) e_{3}'$$
最後の式で基底を反転している．左手系での座標値は，右手系の座標値の符号を反転したものになる．
$$e_{2} \times e_{3}=e_{1} \longrightarrow \left( -e_{2}' \right) \times \left( -e_{3}' \right) =\left( -e_{1}' \right)  \longrightarrow e_{3}' \times e_{2}'=e_{1}'$$

■（結論）
座標系の反転（右手系基底［$$e_{1}, e_{2}, e_{3}$$］$$ \longleftrightarrow $$左手系基底［$$e_{1}'=-e_{1}, e_{2}'=-e_{2}, e_{3}'=-e_{3}$$］
をしたときに； 
（１）　極性ベクトルは，
反転後の基底についての座標値は，反転前の基底に対する座標値の符号を変えたものになるが，基底自体も反転しているので実態は変わらない．
（２）　軸性ベクトルは， 
反転後の基底についての座標値は，反転前の基底に対する座標値の符号を変える．軸性ベクトルは外積で定義された向きを持つが，座標系が左手系であっても外積の定義は右手系でなされているので，左手系では向きを変える．

しかし，実態は回転現象でありこの状態が変わるわけではない．

$$e_{1}$$だけ反転（鏡映対称）：奇数パリティ⇒$$x_{1}$$だけ符号反転
$$e_{1}, e_{2}$$の２つを反転（$$e_{3}$$を軸とする2回対称）：偶数パリティ⇒符号の変化なし
$$e_{1}, e_{2}, e_{3}$$の３つを反転（対称心：奇数パリティ）⇒すべての座標値の符号を変える

ロシアがウクライナ東部のハリコフ占領の恐れと煽りたて，軍を進めるバイデン政権と，その米国の情報に追従する日本の大手新聞やテレビ報道を鵜呑みにしてはいけません．かつての湾岸戦争の勃発も米国の情報操作からでした．ロシアの中庭のようなウクライナをNATO軍事同盟に加盟させるのはおかしいし，米軍がウクライナ東部に軍を進めていること自体が，緊張を高める挑発です．ウクライナがNATOに加盟しなければ，ロシアは戦争を始めません．ロシア人同士が利益のない戦争を好むわけがありません．
https://iwj.co.jp/wj/open/archives/501693?fbclid=IwAR2G79BFL4C804PPmKIPhBl6pBh23tps_VRkQGG-V1JHYH8bDrZdvng4wHM

ウクライナ人民共和国は，第1次世界大戦では，ドイツ側でソ連と戦ったのですが，両国間で和平が成立し，その後，ソ連邦の一員となります．

第2次大戦では，ナチス・ドイツは，ソ連に対抗するのにウクライナ・ナショナリズムを利用します．一方，スターリンは大祖国戦争と呼び，ナチス・ドイツとの戦いにウクライナを利用します．都市ハリコフは，赤軍とナチス軍との激戦地になりました．ウクライナ･ナショナリズムは，東西の対立勢力にいつも利用されます．今日，米国がNATO軍事同盟にウクライナを加盟させようと，東部ウクライナで危機を煽り，ゼレンスキーは政権安定のためにナショナリズムを煽ります．ハリコフのあるウクライナ東部に住んでいるのは，ほとんどロシア人で親ロシア派です．ロシア軍との戦争は無意味です．

ここで，私は，ハリコフという都市にある，ソ連時代の物理学研究所の歴史を，シュブニコフの活動を軸に述べようと思います．

ハリコフはキエフとならぶウクライナの都市です．ソ連時代の1928年に，ヨッフェが物理学研究所を開設し，1931年にL.V.シュブニコフが極低温研究所を作りました．シュブニコフ＝ド･ハース効果に名前を冠したL.V.シュブニコフです．私は黒-白群（シュブニコフ群）に関心がありますが，これに名を冠しているのは，別人のA.V.シュブニコフです．

L.V.（レフ・ワシリエヴィチ）・シュブニコフは，1901年9月29日，レニングラードで生まれ，ペトログラード大学物理数学学部の数学科に入学．物理学を専門に学びました．その年の学生は彼一人だったので，一学年上の学生，S.E.フリッシュ，V.A.フォク，一学年下の学生，A.V.ティモレヴァ，O.N.トラペズニコヴァ（1925年に彼の妻となる）と一緒に講義を聴きました．

物理学科（1919年に分離）の学生や教師は，ヨットが好きでした．シュブニコフも熱心な一人で，1921年秋，フィンランド湾のヨットに見知らぬ人たちと一緒に行き，気がつくとフィンランドにおりました．そこからドイツに追放され，1922年にようやくペトログラードに戻ることができました．工科大学で勉強を続け1926年に卒業します．

研究室では，I.V.オブライモフといっしょに，ある形状の大きな金属単結晶を成長させる方法を完成させた．1926年，ドイツのライデンのド・ハース研究所で，この分野の専門家が必要になったときに，A.F.ヨッフェの推薦でシュブニコフが派遣されました．

当時のライデンは世界で唯一液体ヘリウムを持っている研究所で，さまざまな専門分野の物理学者がライデンに集まりました．P.エーレンフェストは，ライデン大学で理論物理学の講座を開いており，刺激的なエーレンフェストのセミナーでは，A・アインシュタイン，N・ボーア，W・パウリ，P・ディラックらとも知り合うことができました．

ライデン研究所では，ド・ハースと共同で，低温で不純物濃度の低いビスマス結晶の研究で，磁場中の磁気抵抗の振動（シュブニコフ＝ド・ハース効果）を発見しています．この効果が物性物理学に重要な意味を持つようになったのは，ずっと後の50〜60年代のことです．現在では，この効果は、固体の量子電子物性を調べるための主要な手段の一つとなっています．

ライデンのモットーは「測定から知識へ」で，シュブニコフにとって実験技術の良い学校でありました．常駐の研究所員やセミナーや研修のための訪問者との交流によって，彼は科学技術を習得ができました．

ヨッフェは1928年に，ウクライナのハリコフに物理学研究所を設立し，1930年にライデンから戻ったシュブニコフは，ここに低温研究所を作ることになります．1931年には早くも液体水素，1933年には液体ヘリウムを得て，1934年からは，当時世界で4番目の極低温センターの誕生の宣言をします．この成功は、シュブニコフの功績に間違いないが，ライデンの研究所長であるド・ハースと，当時ソ連では入手不可能な材料や器具をハリコフに移したキーソムの協力があって実現したものです．

シュブニコフの研究所では，低温技術は優れた監督者 I.P.コロレフが指揮し,
吹きガラスはE.V.ペトゥシコフが行いました．研究所の最初のスタッフにはYu.V.シュブニコフ，その後，ルデンコ，フェドロワ，ミルチン，ベレシュチャギン，ズルニツィン，アレクセーフスキー，キコイン，シャリュートと続き現在に至っています．ドイツからも，契約を結んだり，ナチスの迫害を逃れてきた物理学者たちが研究室で働いていました．

この研究所の主な活動の1つに，超伝導の研究があります．低温物理学の発展に貢献したL.V.シュブニコフの研究者の多くは，マイスナー効果はマイスナーとは無関係で，シュブニコフが彼とほぼ同時に発見したと考えています．また，クルト・メンデルスゾーンによると，合金の磁気特性の研究では，ハリコフ研究所はライデンやオックスフォードより進んでいたという．シュブニコフらの業績に敬意を表し，Hc1-Hc2磁場区間におけるタイプP超伝導体の状態は，シュブニコフ相と呼ばれています．

L.V.シュブニコフの研究室では，遷移金属塩化物の熱的，磁気的性質の研究に大きな成果を挙げ，これが反強磁性現象の実験的発見につながり，L.D.ランダウの興味を刺激したと考えられます．

L.V.シュブニコフとL.D.ランダウは，仕事だけでなく，親しい友人関係でもありました．どちらの名前もLevなので，太ったレオ，痩せたレオと呼ばれたのは面白い．二人ともハリコフ大学の物理学科で教鞭をとりました．

しかし，1937年8月6日，L.V.シュブニコフがL.D.ランダウと一緒にクリミアで過ごした休暇から戻った日に逮捕され，スターリンによる粛清の犠牲者となりました．いわれのない破壊活動の罪で起訴され，11月10日に銃殺刑になりました．記録は改竄され，死体もわからず，未亡人は彼が1945年死んだと知らされたといいます．

1956年にL.D.ランダウらにより名誉回復が行われました．ランダウが軍の検察官あてに出した書類は次のようです：
「彼の研究論文の多くは画期的な古典であります．彼がソ連のこの分野の創始者の一人であったことを考えると，低温物理学の分野での彼の破壊活動について話すのはまったくばかげています．彼の熱烈な愛国心は，彼がソ連での仕事のためにオランダでの仕事を自発的に辞めたという事実によって強調されています．L.V.シュブニコフの早すぎる死によって国内科学に引き起こされた損害は，いかなる過大評価も間に合わないほどです」

引用：http://www.ilt.kharkov.ua/bvi/info/shubnikov/shubnikov.html

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{1} & -\textrm{cos}\alpha _{3} \\[0mm]
-\textrm{cos}\alpha _{1} & 1 & -\textrm{cos}\alpha _{2} \\[0mm]
-\textrm{cos}\alpha _{3} & -\textrm{cos}\alpha_{2} & 1
\end{vmatrix} =1-\textrm{cos}^{2}\alpha _{1}-\textrm{cos}^{2}\alpha _{2}-\textrm{cos}^{2}\alpha _{3}+2\textrm{cos}\alpha _{1}\textrm{cos}\alpha _{2}\textrm{cos}\alpha _{3} \\　
=-4\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{2}+\alpha _{1}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{3}+\alpha _{1}+\alpha _{2 } }{2} \right)
$$

$$
=\begin{cases}
>0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}>\pi \\[0mm]
=0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}=\pi \\[0mm]
<0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}<\pi
\end{cases}
$$

立方格子の空間を見る万華鏡は，立方体の単位胞内の対称面を鏡に選び4枚鏡の万華鏡を作ります．
立方体にある対称面には立方体の正方形面に平行なものや，正方形の面と45°方位のものがあります．
上図の万華鏡では，（１）△ABC，△ABO，△ACO，△BCOを鏡映面にした万華鏡，（２）△ACO，△ACD，△AOD，△DCOを鏡映面にした(1)の半分体積の万華鏡，（３）△ABO'，△ABO，△AO'O，△BO'Oを鏡映面にした(1)の2倍体積の万華鏡を示しました．それら３つの万華鏡の作製と映像の記事は別項

これらは，3次元ユークリッド空間の「立体万華鏡」の例です．（上の写真は「美しい幾何学」p.47より引用）

ここでは，ユークリッド空間だけでなく，非ユークリッド空間（球面･楕円幾何，双曲幾何）の3角形面を用いた多面体についてまとめて数学の話をします．

正多面体の面のなす角（二面角）の話から始めます．凸正多面体Mとその頂点の１つを中心とする小球がよぎる線は，凸球面正多角形を形成します．
頂点から$${q}$$本の辺が出ているとすると，凸球面多角形の頂角（辺の二面角）の和は$${π(q-2)}$$よりも大きい．
正多面体Mのすべての二面角が$${π/2}$$を超えない（たとえば，コクセター多面体）場合，各頂点から出る辺は3本だけであることがわかります．この最後の性質を持つ多面体を単純多面体と呼びます．４面体や立方体は単純多面体ですが，８面体は単純多面体ではありません．

しかし，この単純な不等式だけでは，凸多面体の二面角の関係を網羅することはできません．最も単純なMが三角錐の場合について考えてみましょう．その面に番号をつけ，$${i}$$ 番目と$${ j}$$ 番目の面のなす角を $${α_{ij} = α_{ji } }$$ とします．ユークリッド三角錐の二面角が次の関係にあることは，線形代数によって簡単に証明できます．

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{12} & -\textrm{cos}\alpha _{13 } &
-\textrm{cos}\alpha _{14 } \\[0mm]
-\textrm{cos}\alpha _{12} & 1 & -\textrm{cos}\alpha _{23} &
-\textrm{cos}\alpha _{24} \\[0mm]
-\textrm{cos}\alpha _{13} & -\textrm{cos}\alpha _{23} & 1 &
-\textrm{cos}\alpha _{34} \\[0mm]
-\textrm{cos}\alpha _{14} & -\textrm{cos}\alpha _{24} &
-\textrm{cos}\alpha _{34} & 1
\end{vmatrix} =0
$$                                                

左辺の行列式は，ピラミッドの面に対する単位法線ベクトルのグラム行列式［ベクトルの内積が成分］で，０に等しいのは，これらのベクトルが線形従属であることによります．

注）二面角を$${α}$$とすると，対応する面の法線ベクトルの内積は，$$\textrm{cos}(π-α)＝-\textrm{cos}α$$となります．
試しに，ユークリッド三角形とすると，$${α_{12}＝α_{1}, α_{13}＝α_{2}, α_{23}＝α_{3 } }$$　になり，

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha_{1} & -\textrm{cos}\alpha_{2} \\[0mm]
-\textrm{cos}\alpha_{1} & 1 & -\textrm{cos}\alpha_{3} \\[0mm]
-\textrm{cos}\alpha_{2} & -\textrm{cos}\alpha_{3} & 1
\end{vmatrix} =0
$$

この簡単な場合からは，$${α_{1}＋α_{2}＋α_{3}＝π}$$　が得られます．

証明（Andreevより）

$$
\begin{vmatrix}
1 & -\textrm{cos}\alpha _{1} & -\textrm{cos}\alpha _{3} \\[0mm]
-\textrm{cos}\alpha _{1} & 1 & -\textrm{cos}\alpha _{2} \\[0mm]
-\textrm{cos}\alpha _{3} & -\textrm{cos}\alpha_{2} & 1
\end{vmatrix} =1-\textrm{cos}^{2}\alpha _{1}-\textrm{cos}^{2}\alpha _{2}-\textrm{cos}^{2}\alpha _{3}+2\textrm{cos}\alpha _{1}\textrm{cos}\alpha _{2}\textrm{cos}\alpha _{3} \\　
=-4\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{2}+\alpha _{1}+\alpha _{3 } }{2} \right) \textrm{cos}\left( \displaystyle \frac{-\alpha _{3}+\alpha _{1}+\alpha _{2 } }{2} \right)
$$

$$
=\begin{cases}
>0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}>\pi \\[0mm]
=0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}=\pi \\[0mm]
<0 & \Longleftrightarrow & \alpha _{1}+\alpha _{2}+\alpha _{3}<\pi
\end{cases}
$$

なぜならば，
$${0<\alpha _{1}, \alpha _{2}, \alpha _{3}<\pi /2}$$なので，$${-\pi <-\alpha _{i}+\alpha _{j}+\alpha _{k}<\pi}$$，$${\textrm{cos}\left( \displaystyle \frac{-\alpha _{i}+\alpha _{j}+\alpha _{k } }{2} \right) >0}$$であり，
従って，式の$${ \pm }$$は，$${\textrm{cos}\left( \displaystyle \frac{\alpha _{1}+\alpha _{2}+\alpha _{3 } }{2} \right) }$$の$${ \mp }$$で決まる（複合同順）．

始めに示した関係式は，先に導いた不等式と合わせて，二面角$${α_{ij } }$$を持つ三角錐がユークリッド空間に存在するための必要十分条件となります．これを利用すると，二面角が$${π/}$$整数であるユークリッド空間の三角錐をすべて求めることができ，その数は3つです．図7で，マークのない辺の二面角は$${π / 2}$$，マーク|あるいは||のついた辺の二面角は，それぞれ，$${π / 3}$$または$${π / 4}$$です．図7のピラミッドのうち，1つ目のピラミッドを対称面によって切断すると2つ目のピラミッドが得られ，2つ目のピラミッドを対称面で切断すると3つ目のピラミッドが得られます．

3次元ユークリッド空間には，この3つの万華鏡のほかに，ある意味で2次元に還元された万華鏡が4つだけあります．これは、直角プリズム（3角柱）の底面が2次元の万華鏡であるものです．

3次元ユークリッド万華鏡は，結晶学と密接な関係があります．このような万華鏡の中にいくつかの原子を配置し，万華鏡の壁で繰り返し反射させ得られる像をすべて調べると，結晶格子を得ることができます．つまり，図7に示した万華鏡のうち，1番目の万華鏡で，炭素原子Cを図に示した2つの頂点に置くとダイヤモンドの結晶格子が得られ，2番目の万華鏡で，ナトリウムNaと塩素Clの原子を図に示した頂点に置くと，食塩の結晶格子が得られます．

3次元球面上の万華鏡をすべて見つけることも難しくありません．このすべてが，球面三角錐です．この場合，ユークリッド平面から球面に移るとき，三角形の内角の和が$$π$$より大きくなるので，始めに示した式の等号が不等号$$>$$に置き換えられます．

引用：
E. B. Vinberg, published in the "Soros Educational Journal" (1997, No. 2)
«КВАНТ» No6, 2020

トレミーは2世紀のギリシャの天文学者プトレマイオスのことです．地球中心の天動説を確立したので有名です．トレミーの定理を導きました．

トレミーの定理（Ptolemy's Theorem）とは，円に内接する任意の４角形 ABCD で，AB･CD＋DA･BC＝AC･BD　が成立することです．高校の幾何ででてきた懐かしい定理です．

トレミーの定理を，以下のような特殊な円に内接する4角形＝長方形に適用すると，ピタゴラスの定理　a･a+b･b=c･c　が証明できます．この意味で，トレミーの定理はピタゴラスの定理の拡張定理と言えます．

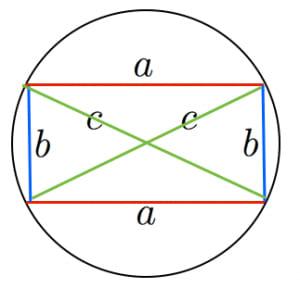
さて，トレミーの定理の証明には，三角関数を使うなど色々な方法がありますが，素朴に，下図の2つの図に示す3角形の相似を用いてやってみます．

両辺を足し合わせると　AB･CD+BC･DA＝AC･(BP+DP)が得られます．

<<KVANTIK>>, No.11, 2020; Фёдор Ниловフョードル・ニーロフより抜粋

https://kvantik.com/extra/parall/

セミパラレル図形

白い正方形は一斉にペチャンコにすると図形をコンパクトにできます．不思議ですね．

パラレルニクという多角形は，下図のどちらかの性質を持ちます．

任意の平行多角形はパラレルニクである．下図に示す例は5角形の平行多角形の例です．

次の図は，中央に任意の３角形（緑）があります．その外に白い正方形を３つ作ります．それら頂点は，6角形になり，その外に白い正方形を３つ作ると，また6角形が得られます．同じ色の多角形の面積はすべて等しく，4角形はすべて台形です．この定理は，2001年にアメリカの数学者D. DeTemple と M. Hudelsonが証明しました．

また，中央の３角形をどんな平行多角形に置き換えてもこの定理が成り立つことも発見しました．以下の図は，中央に平行４角形，平行５角形にした例です．

https://elementy.ru/nauchno-populyarnaya_biblioteka/435457/Kvantik_9_2020

«Квантик» No9, 2020に，アレクサンダー・ペレペチコによる次の問題があります：

１．サーシャは，1日2回，朝と夕方に，物忘れ治療薬を飲まなければならないのですが，忘れることもあります．続けて 2 回服用した後は，必ず忘れずに服用し，2 回服用しなかった後は，服用を忘れます．過去 1 日にちょうど 1 錠服用している場合は，次回服用する確率は1/2とします．

サーシャが，ある時点から完全に薬を飲むことを忘れてしまう確率はどれくらいありますか? ずっと飲み続けている確率は？

２．酔っぱらいは居酒屋と彼の家の間の道路に立ち，1 秒ごとに同じ確率でランダムな方向に道路に沿って 1m ステップします．家に着いたり居酒屋に着いたりすると，そこにとどまります．

家まで 3m，居酒屋まで 7mの距離にある場合，彼が帰宅できる確率はどれくらいですか．

https://elementy.ru/problems/

立方体の上の面の対角線にレールがあり，下の面の対角線（上の面の対角線とは直交）にもレールがあります．下のレールの端（頂点）と上のレールの中点（面の中心）とを結ぶ長さの「線分」があり，この線分（長さを変えない）の両端はレール上をすべることができます．線分が包絡線となり囲む図形（リノイド）の表面の形を推理してください．

立方体の1辺の長さを2aとすると，リノイド体積はいくらですか．

なかなか難しいですが，線分の動きを頭の中でシミュレーションした以下の図が参考になります．

立方体の1辺の長さを2aとすると，線分KFの長さはa√6です．
図のような，座標系で考えます：

$$K(x_{K} , 0, -a), F(0, y_{F} , a), M\left( x, y, z \right) $$とします．
$$\overrightarrow{KM}(x-x_{K} , y , Z+a), \overrightarrow{FM}(x, y-y_{F} , z-a)$$
なので，次の方程式が得られます．
$$\displaystyle \frac{x-x_{K } }{x}=\displaystyle \frac{z+a}{z-a}=\displaystyle \frac{y}{y-y_{F } }$$
これを解いて，　　$$x_{K}=\displaystyle \frac{2ax}{a-z} , y_{F}=\displaystyle \frac{2ay}{a+z}$$
一方，　$$\left\{ \begin{array}{@{\,} c @{\, } }
KF^{2}=x_{K}^{2}+y_{F}^{2}+4a^{2} \\[0mm]
KF=a\sqrt{6}
\end{array} \right. $$ 　⇒　 $$x_{F}^{2}+y_{F}^{2}=2a^{2}$$　であるので，$$x_{F} , y_{F}$$を代入して，
$$\left( \displaystyle \frac{2ax}{a-z} \right) ^{2}+\left( \displaystyle \frac{2ay}{a+z} \right) ^{2}=2a^{2}$$　 ⇒　$$ \displaystyle \frac{2x^{2 } }{\left( a-z \right) ^{2 } }+\displaystyle \frac{2y^{2 } }{\left( a+z \right) ^{2 } }=1$$
このリノイドの水平（すなわち軸Ozに垂直）断面の方程式を得るためには， 
zの値を区間$$\left( -a, a \right) $$でスライスする． 
この方程式は，半軸に$$x=\left( a-z \right) /\sqrt{2}, y=\left( a+z \right) /\sqrt{2}$$を持つ楕円の方程式になる．
楕円の面積$$S$$は，　$$S=\pi \cdot \displaystyle \frac{\left( a-z \right) }{\sqrt{2 } } \cdot \displaystyle \frac{\left( a+z \right) }{\sqrt{2 } }=\displaystyle \frac{\pi }{2}\left( a^{2}-z^{2} \right) $$
ゆえに，リノイドの体積$$V$$は，　$$V=\displaystyle \frac{\pi }{2}\displaystyle \int_{-a}^{a}\left( a^{2}-z^{2} \right) dz=\displaystyle \frac{2\pi a^{3 } }{3}$$ 

厚労省の公表値を用いて，日本の有病率を求めると0.6%，検査陽性率は5%程度です（5月14日時点）．このデータを用いて，ベイズ推定を用いPCR検査結果の考察をします．PCR検査の感度$$a$$と特異度$$b$$により，この結果は大きく変わります．PCR検査の感度$$a$$と特異度$$b$$は，従来の定説の0.7と0.99よりはるか高い，0.95と0.9992であることが，最近の研究で知られています．

今日のPCR検査で$$+$$判定の者には，罹患（真陽性）と非罹患（偽陽性）があります．同様に，今日のPCR検査で$$-$$判定の者にも，非罹患（真陰性）と罹患（偽陰性）があります．つまり，今日，罹患となった者には，真陽性と偽陰性があります．そして，今日の罹患者の病気期間は11日間とすると，今日の罹患者は，11日間先まで罹患者であり続け感染源となります．これを有病罹患と定義します．今日の有病罹患者は，11日前から今日までの罹患者の累積となります．11日を過ぎれば，PCR検査$$-$$となり，回復非罹患者（今日の非罹患者＋11日より以前の全検査数-累計死亡者）になるとします．ここで，PCR検査で$$-$$判定で，罹患であるのは，検査の確率の視点での話で，必ずしも，無症状の感染者と一致するものではありません．
日々発表される新規陽性（罹患）者数を累積すると，累積陽性者数になるので，差分としての新規陽性者数は，罹患率に似た傾向ですが，罹患率そのものではありません．ここで定義する有病罹患者は，日々の新規罹患者と病気期間（発症してから陰性になるまでの病気減衰関数$$A(t)$$）のコンボリューションとして得られます．
$$有病罹患者(T)=\displaystyle \int_{0}^{T}罹患者(t) \cdot A(T-t)dt$$

あるいは，$$現罹患者数=累積陽性者数-累積退院･回復者数-累積死亡者数$$で定義できます．

有病罹患者（現罹患者）

国内発生状況．厚労省（2021.5.15現在）

$$有病率(5.15現在）=有病罹患者数(5.15現在)/累積PCR検査数=5.8×10^{-3}$$
$$陽性率(5.15現在）=陽性者数(t)/PCR検査数(t)=5.2×10^{-2}$$

PCR検査の感度$$a$$と特異度$$b$$が与えられ，集団の有病率$$p(罹患)=x$$が与えられると，この集団で，PCR検査が+と判定されたとき罹患者である確率$$p(罹患|＋)$$，および，-と判定されたとき罹患者である確率$$p(罹患| - )$$を推定できます．
$$p(罹患| + )=p\left( + |罹患 \right) \cdot p\left( 罹患 \right) /p\left( + \right) =a \cdot x/\left( a \cdot x+(1-b)\left( 1-x \right) \right) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) \cdot x/\left( (1-a)x+b \cdot \left( 1-x \right) \right) $$，

従って，この集団の陽性率を$$p( + )=y$$とすると，有病率は，以下のように表現できます．
$$p(罹患)=p(罹患| + )･y+p(罹患|-)･(1-y) $$
$$x=a \cdot x \cdot y/\left( a \cdot x+\left( 1-b \right) \left( 1-x \right) \right) +\left( 1-a \right) \cdot x\left( 1-y \right) /\left( \left( 1-a \right) x+b \cdot \left( 1-x \right) \right) $$

$$有病罹患者(T)=\displaystyle \int_{}^{}罹患者(t) \ A(T-t)dt$$
病気減衰関数$$A(t)$$の半減期はおよそ10日ですので，近似的に，有病罹患者数(t)は本日の罹患者数(t)の10倍としたもので，この等式が成立/

特異度は，$$b$$>0.99（0.999）との説もあり$$b=1$$として，$$a$$を求めると，$$a=5.2×10^{-2}/5.8×10^{-3}=8.9$$

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 

■条件付き確率についての「ベイズの定理」とは次のように説明できます．$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$ 
ただし，記号の意味は例えば以下の様です．
$$p(X)$$：$$X$$が起こる確率
$$p(Y|X)$$：$$X$$が起こり，かつ$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きた後で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

■PCR検査の精度
「新型コロナ検査，どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）」によると，以下のようです：
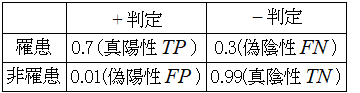
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく判定される確率のことで，あまり大きくなく0.7程度です．真の罹患者でもPCR検査で陰性（－）（偽陰性）と判定される確率が0.3程度あります．
検査の特異度とは，非罹患者を正しく陰性（ー）と判定する確率のことでかなり高く0.99程度です．従って，非罹患者を陽性（＋）（偽陽性）と判定する確率は稀で0.01程度です．

有病率（現罹患者の比率）$$x$$が小さい集団では，非罹患者が大部分を占めるので，PCRで偽陽性の確率は0.01と非常に小さいとはいえ，PCRの偽陽性者数は多くなり，医療崩壊につながるという主張があります．しかしながら，陽性確定までにPCR検査は2度行われ，2度とも偽陽性となる確率は$$10^{-4}$$，1万人に1人です．さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．あるいは，PCR検査の感度のために偽陰性者をたくさん生むという主張もあります．確かに，検査数に比例する偽陰性者を出しますが，検査しない状況と変わりなく，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

（注）罹患者とは，真に感染しており現在感染源となるものと定義します．これには，PCR検査で陽性（真陽性）と判定されるものと，陰性（偽陰性）と判定されるものとを含みます．非罹患者とは，もともと感染していないか，回復した感染者で，感染源とならないものです．非罹患者はPCR検査で陰性になるのが原則ですが，例外（偽陽性）も0.01あります．有病率＝罹患者数／(罹患者数＋非罹患者数)　は，有病率の定義です．

■PCR検査の原理 
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です． 

■有病率の考察
日本疫学会の定義によると，有病率とは，ある時点で，疾病を有している人（罹患者）の全人口にたいする割合です：
（定義）有病率＝その時点の罹患者数／集団の人数
この有病率と混乱しそうな概念に，罹患率というものがあります：
（定義）罹患率＝ある期間の新規感染者数／集団内の感染感受性のある人数 

毎日発表される，COVID-19の新規感染者数は，罹患率の概念に近いが，罹患率に換算するのに必要な分母の「感染感受性のある人数」が不明です．ワクチン接種などで，感受性のある人数が減れば罹患率は上昇します．もし，その日の検査数（偏りのあるサンプルで，恣意的変動はある）を分母にするなら，その日の陽性率が得られます．
日々の新規感染者数や検査数は，恣意的な変動があるので，7日の移動平均をとり陽性率を定義します．検査の対象集団は症状のあるものや濃厚接触者なので，サンプル集団には陽性側に偏りがあります．

有病率，罹患率，陽性率は，時間で変化する関数で，感染拡大の指標になりますが，それぞれ意味合いが異なります．大雑把に言うと，陽性率は有病率の差分のような統計量です．

公開データから計算できる有病率$$p(罹患) $$を以下の2通りで定義することにしました．
（定義１）本日の有病者数＝累積陽性者数－累積回復者数－累積死亡者数
　　　　　本日の有病率＝本日の有病者数／累積検査数

厳密に言うと，累積陽性者数には非罹患者の陽性数（偽陽性）も混じりますが，累積回復者数を減じるので，これは相殺すると思われます．

有病率の分子からは回復者などが除外されるので，陽性率＝陽性者数／検査数よりも常に小さい値になります．

COVID-19の新規陽性者は，2週間隔離（症状の程度により，病院，宿泊施設，自宅などに）されますので，死亡者は無視して，本日の新規感染者は続く2週間は罹患者と見なされます［罹患期間を10日間とする見解もあります］．そして，2週間後にPCR検査が2度陰性になれば回復者に入ります．そこで，死亡者を無視すると次の定義も成り立ちます．便宜的に，新規感染者とは新規陽性者と同義語とします（厳密にいえば，偽陽性者が含まれるのですが，除去の根拠となるデータがありません）．

（定義２）本日の罹患者数＝日々の新規感染者数を2週間前まで遡り総和．
正確には，陽性持続曲線を用いて，新規感染者数と陽性持続曲線のコンボリューションとなります．
陽性持続の半減する期間はほぼ10日です．

英国国家統計局（ONS）は，オックスフォード大学，マンチェスター大学，英国公衆衛生サービスNHS，ウェルカムトラスト，IQVIA，グラスゴー・ライトハウス研究所，バイオセンター・ミルトンケインズと協力して，イングランドでパイロット調査を2020年4月に開始し，8月からは，サンプルのサイズを拡大し2021年3月まで大規模調査をしました．英国の４地域ベースのランダムな世帯サンプリングをし，得られた偏りのあるサンプルを英国全人口に外挿するには，多層回帰および事後層別化（MRP）を用いました．同じ世帯に対し長期間のCOVID-19検査を実施（最初の4週間は毎週，その後は毎月の検査）し，症状の有無にかかわらずCOVID-19の有病率と罹患率を，ほぼリアルタイムで観測し，病気期間（陽性持続確率）の関数を得ました．PCR検査の感度$$a$$と特異度$$b$$についても新しい知見が報告されました：$$a=0.95(0.85～0.98)$$，$$b=0.9992$$．スワブ採取が適切な監督下で行われれば，自己採取でも医療従事者が直接採取した場合と同様に正確な結果になることがわかりました．

COVID-19 Infection Survey: methods and further information，26 March 2021

 $$p_{a}(t)$$

 ■陽性率の考察
$$t$$時点の陽性率($$t$$）は，その時点でCOVID-19の検査で陽性となった人の割合です。現在のCOVID-19感染症は、鼻と喉から採取した綿棒で、症状の有無にかかわらず、SARS-CoV-2が陽性であることを意味します。これは、発生率とは異なります。発生率は、特定の期間における新しいポリメラーゼ連鎖反応（PCR）陽性の症例のみの測定値です。

ここで，陽性率$$p(+)$$に用いるべき数値を検討します．恐らく，毎日発表される検査陽性率（7日の移動平均された新規感染者数／7日の移動平均された検査数）を用いるのが適当でしょう．これは感染者数の微係数のようなもので，感染流行の傾向をある程度反映し注目すべき数値です．しかし，検査対象の制限（偏りがあるサンプリング）があり，かつ，サンプル数は少ない状況にあります．東京都の場合は，全人口1,400万人の集団に対して，症状のある集団1,000人程度を毎日サンプリングしています．日々の検査陽性率の4月14日時点の，厚労省の全国データを用いて，（検査）陽性率，$$p(+)=0.06$$を採用することにします．

引用）
1.厚労省データ，東京都データ，
2.COVID-19 Dashboard by the CSSE at Johns Hopkins University 

■問題：以下の２つを推定しましょう．ただし，ベイズの定理を使います． 
事前確率として，有病率を$$ p(罹患)＝x=0.003$$を用います．

（１）PCR検査で陽性と判定されたとき，罹患者（真陽性）である確率を求めなさい．この確率は，検査の「陽性的中率」と呼ばれます． 
$$p(罹患|+) =p( +|罹患) p(罹患) /p(+) =0.7x/(0.7x+0.01(1-x)) =$$
$$=7x/(6.9x+0.1)$$

（２）有病率を推定しなさい．
陰性と判定されたものの中に，見逃された罹患者（偽陰性）のいる確率は：
$$p(罹患|-) =p( -|罹患) p(罹患) /p( -) =0.3x/(0.3x+0.99(1-x)) =$$
$$=3x/(-6.9x+9.9)$$

集団の有病率$$x$$を変数に，$$p(患者|+)$$と$$P(患者|-)$$のグラフを示します．

従って，全人口に対して推定される有病率は，陽性率$$p(+)$$，陰性率$$p(-)=1-p(+)$$とすると，
有病率$$=p(罹患|+) p( + ) +p(罹患|-) (1-p(+) )$$　なので，

事前確率として有病率$$x=0.003$$を用いた場合は，真陽性の確率0.174，偽陰性の確率0.0009で，さらに，陽性率$$p(+)=0.06$$を用いると，真陽性の罹患者に，見逃された罹患者（偽陰性）を加えた有病率は$$0.174×0.06+0.0009×(1-0.06) =0.011$$と推定されます．

■PCR検査数は十分か

引用）
3.https://ourworldindata.org/coronavirus-testing

 ここに引用したのは，検査陽性数／1日（横軸）；検査数／1日（縦軸）の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは100万倍大きい（数値では30～20倍）のでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を全部拾う十分な検査が行われているようです．英国の例を見ると，始めは，陽性者がたくさん出て検査数が間に合わないほどでしたが，現在は十分な検査数が確保されていることがわかります．日本の例では，検査数と陽性者数の増減が微妙なバランスにあり，英国のグラフに見られる検査数を増やしても陽性者数が一定となる部分が見られません．検査数を増やせば，陽性者数も増加する可能性があります．

COVID-19では，無症状の罹患者が感染源となることが知られています．症状のあるグループだけをサンプリング対象にした限定されたPCR検査では，無症状の感染源は抜け落ちています．自由に活動する無症状の感染源がどの程度のウエイトかも未知ですので，PCR検査のサンプリング対象の拡大をはかるべきです．

■継続的検査のイギリス流戦略

引用文献）

4.https://plus.maths.org/content/testing-testing-schools
5.Assessing the impact of secondary school reopening strategies on within-school COVID-19 transmission and absences: a modelling study，Trystan Leng，etal.

英国では3月8日に学校を再開するにあたり，接触者継続的検査SCTという対策を決めました．英国JUNIPERコンソーシアムの研究者達が，数学モデルを用いて種々の検査戦略のシミュレーションをした結果です．

クリスマス前（閉鎖前）の生徒は，学年別「バブル」の一員として学校に通っていました．ある生徒が陽性と判定された場合，その「バブル」内の全員が10日間の自己隔離になります．この戦略は，学校内はもとより周囲コミュニティ内の感染伝播も防げる利点がありますが，多くの学校で生徒を欠席させるという欠点があります．

生徒が学校に行けない日数を減らすために，イムノクロマトグラフィー（LF検査）を使用した新しい戦略（SCT検査）が提案されました．COVID-19の症例が特定されると，その「バブル」内の他の生徒は，①「10日間の自己隔離」か，②「7日の間，毎日LF検査を受けて，その日の検査が陰性ならば学校に通う」のどちらかを選択します．この戦略の目標は，多くの生徒たちが学校に通えるようにすることにあります．生徒は，学期の初めにLF検査を2回受け，陰性である場合にのみ通学します．

■イムノクロマトグラフィー検査

イムノクロマトグラフィー（LF検査）は，抗体が配置されたセルローズ膜繊維の端に，採取した検体を滴下し，検体中にCOVID-19の抗原があるなら，それが抗体と反応しながらセルローズ繊維を移動し所定位置でキャプチャーされ呈色します．

LF検査はPCR検査よりも感度が低いかもしれませんが，30分以内に結果が出ます．ウイルス量が最も多く，感染性が最も高いと考えられる時点（感染してから約5日後）には，LF検査でCOVID-19陽性となる確率は十分高い［LF検査は，感度も特異度も95%以上との説もあります］のです．人々が感染を避け家にいるだけという状況から，活動できるように，常に検査を続けフィードバックを行うSCT検査への転換をしました．

■数学モデルで介入をシミュレーション

COVID-19に感染した中学生の12ー31％が，症状を発症すると考えられており，発症すると無症候よりも感染性が高いのですが，無症候の感染力はよくわかりません．このように未知の不確実性があるので，シミュレーションのモデル作りでは，パラメーターに不確実性を採り入れ，点推定ではなく範囲を推定しています．

ダイソンのグループ（レンら）は，それぞれ200人の生徒からなる5つの「バブル」で構成されるモデルを作成し，色々な検査戦略：何もしない；学年グループを隔離；SCT検査；毎週の集団検査；両方検査の組み合わせ；のそれぞれを，7週間にわたって毎日の時間ステップでシミュレーションしました．

もちろん，「SCT検査と毎週の集団検査の組み合わせ」が，欠席日数と感染数の両方を減らす最も効果的な戦略です．

検査をすれば，無症候性のCOVID症例が多数特定できます．しかし，組み合わせ検査の戦略では，7週間の半期の終わりに，生徒1人は平均して25回の検査を受けます．検査費用もかかり，若者の同意が必要です．毎日子供たちの鼻に綿棒を突き刺すのは素晴らしいことではありません．それらはトレードオフにあります．この調査は，パンデミックの際に政府や学校の指導者が下さなければならない難しい決定を浮き彫りにしています．ライブパンデミックの前例のない挑戦に対処するには，数学モデルが活躍します．

英国はロックダウンを間欠的に実施しました．長期にロックダウンを続ければ感染は減りますが生活ができなくなります．どのくらいの期間のロックダウンをどのくらいの期間を空けて実施するのが良いかのトレードオフも，感染拡大モデルでシミュレーションしています．英国の100万人当たりのPCR検査数は日本の20倍～30倍もあります．パンデミックを乗り越え現在の有病率は日本より小さい値に下がっています．

実効再生産数を減少させるには，次の3つを減少させることです：①感染者が感染力を持つ期間，②感染者が1日当たりに接触する人数，③感染者の接触で感染する確率．感染→潜伏期間→発症期間→検査→隔離の期間内でCOVID-19は感染します．COVID-19は，潜伏期間でも感染し，発症のない無症状も感染力があることが判明しています．「感染者が感染力を持つ期間」を短くするには，検査で早く感染者（有症状，無症状とも）を見つけ早く隔離することです．

検査陽性者数
日本国内（2021.03.23）

東京都（2021.03.17）

検体採集日と，判定確定日や発症日は医師判定までのタイムラグを含む．
検査数はPCRだけでなく抗原検査も含む．
＊ジョンズ・ホプキンス大学，東京都，厚労省のデータを用いました．

・検査陽性率＝陽性者数/検査数　はどのくらい？
上のデータより，国内では4.9%，東京都では6.5%と推定するのが適当であろう．

１．サンプリングの偏りが変化している
PCR検査を受診できるグループは限定されている．初期は，無症状者は検査対象外でした．その後，クラスター対策で局所的な検査対象になり，現在の対象者の限定は明確でないが，無症状者が増えているようだ．
状況に応じて対象カテゴリを広げるのは当然で，感染抑止のために無症状の有病者を把握することは必要である．感染疑いの濃いグループをサンプリングするので偏りがあるわけですが，この基準自体も変化している．
このように，統計のプラットホームが変化しているから，変化を時系列に並べて，単純に発生率の変化と解釈することはできません．

２．統計量の定義
日本疫学会の定義によると，集団の有病率とは，その時点で，疾病を有している人の集団人口にたいする割合．集団の疾病発生率（罹患率）とは，一定期間に発生した疾病者のその集団で疾病感受性のある人口にたいする割合です．
有病率(t)＝疾病を有する人数(t)/集団人数(t)
発生率(t)＝新規陽性者(t)/集団内の感受性のある人数(t)

毎日，発表される新規陽性者の数は，発生率に近い概念ですが，集団内の感受性のある人数が未知なので，発生率とは正確には同じではありません．
PCR検査陽性率＝新規陽性者/検査数で定義しますが，これも，サンプル集合の偏りと変化のために，単純比較はできません．そのため，累積数の比でこれを定義することにしました．

本来，有病率や罹患率などの統計量の時系列での変化を論じるには，ランダム・サンプリングの検査であるのが原則です．
ランダム・サンプリングで行われた調査としては，厚労省が抗体検査を行ったことがありますが，東京都で陽性率が0.1％程度だったと思います（2020．6）．現時点での陽性率（多分増加している）が知りたいです．
東京都の人口は約1,400万人，これまでの感染者累積11.7万人を用い，0.8４％が抗体保有者率が見積もれます．

現時点の感染者＝感染者累積ー回復者累計ー死亡者累計ですから，これを仮の有病者(t)と定義します．有病者(t)と新規陽性者(t)は同義語ではありませんが，比例すべきと予想します．しかし，推測される有病者数に対して，現在のPCR検査数で拾い上げられる陽性者は圧倒的に少ない．
PCR検査数の増加が必要な所以です．特に，無症状の有病者はPCR検査のサンプル集合から除外されているのも問題です．

いくつかの定義を明確にしたい
PCR検査陽性者は有病者と同じか？
有病者から無症状者が除外されるのは良くないだろう．どの時点で患者（罹患者）と呼ぶのか？

今後考慮すべき問題
無症状者も感染に寄与すること，PCR検査で陰性となる変異株の出現などあり，これらのパラメータをどう定義するか？実効再生産数には反映される．
感染拡大の結果やワクチン接種による持続的な抗体形成により，感受性のある人口を減少させます．

陽性率を，p(+)＝累積陽性者数/累積PCR検査数と定義すると，東京都の2021.3.17までのデータや厚労省の公表データを用いて，陽性率は，東京都で約6.5%（全国で4.9％，厚労省）になります．しかし，PCR検査の感度と特異度の情報（酒井健司，朝日デジタルなど）を入れてベイズ推定し，陽性的中率p(罹患|+)や偽陰性率p(罹患|-)を求めました．

ランダム･サンプリングのデータがないので，罹患率（有病率）も陽性率に等しいと仮定せざるを得ませんでした．
注）日本疫学会の定義によりますと，有病率と罹患率は異なります．

有病率＝ある時点における疾病を有する者の数/調査対象全数
罹患率＝ある時点における発生新規患者数/感染感受性のある人数

罹患率は，集団内の感染感受性のある人数に対して定義されるので，２つの定義で分母が異なります．さらに，有病率でいう「ある期間で疾病を有する者の数」は，罹患率でいう「新規感染者の数」とは異なるわけですが，タイムラグを考慮すれば，どちらも同様な傾向と近似ができそうです．

ここでは，有病率と罹患率を同義語として扱いました．毎日発表される，新規感染者数は，罹患率とは異なりますがよく似た指標であります．

東京都の2021.3.17までの陽性者累計116,293人，検査実施累計1,779,950人を用い，現在の陽性率はｘ＝6.5%程度（全国ではx=4.9%）程度と推定します．
ランダム･サンプリングではないし，データが不足しているので，罹患率（有病率）も陽性率に等しいと仮定します．

（注）ここで対象となるサンプル集合は，PCR検査を受診できる限定されたグループですので，ランダム･サンプリングではなく偏っており（発症条件が課さたグループ），その陽性率は一般集合より若干高値でしょう．また，サンプリング条件が感染状況とともに変化しているので，単純な時間変化の比較はできません．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
■条件付き確率についての「ベイズの定理」とは次のように説明できます．
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です．
p(X)　Xが起こる確率
p(Y|X)　Xが起こった後でYが起こる確率
p(X∩Y)　XかつYが起こる確率
ベイズの定理は，X（原因）が起きた後でY（結果）が起きる確率p(Y|X)と，XとYを入れ替えた確率p(X|Y)を結び付ける定理です．
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
■PCR検査の精度
新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）などにより，次のように仮定します．
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく的中する確率のことで，あまり大きくなく0.7程度といわれます．真の罹患者でもPCR検査が陰性（－）（偽陰性）となる（罹患者を取りこぼす）確率が0.3程度あるそうです．
PCR検査の特異度とは，非罹患者を正しく陰性（ー）と判定する確率のことで0.99程度です．非罹患者を陽性（＋）（偽陽性）と判定するのは稀で0.01程度の確率ですが，非罹患者の割合が多い集団（罹患（有病）率が小さい集団）では，無視できない偽陽性数になります．

■これらの仮定の下で，以下の２つを推定しましょう．
ただし，ベイズの定理を使います．
罹患（有病）率をp(罹患)≡x，非罹患（非有病）率を1-xとします．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．

青線グラフ

つまり，PCRの結果が陽性のときでも，その的中率はp(罹患|+)＝83%（x=6.5%附近）程度です．
罹患していても，検査感度のため，検査の結果が陽性にならない偽陰性が30%あり，罹患者をとりこぼしている．
一方，検査の特異度が高いので，偽陽性率は0.1%と小さいにも関わらす，非罹患者の割合(1-x)が多い集団では，陽性判定中に占める偽陽性の数も無視できない．これらの原因のため的中率が低下します．
（２）罹患（有病率）を推定しなさい．
(陰性)判定されたものの中に見逃された罹患者のいる確率p(罹患|-)は，

赤線グラフ

陰性と判定されたものの中に見逃された患者である可能性は，p(罹患|-)＝2%(x=6,5%の付近）ほどある．
従って，全人口のなかで推定される罹患（有病）率は，
p(罹患)＝ｘ･p(罹患|+)＋(1-x)･p(罹患|-)

第1項：第2項＝真陽性：偽陽性＝5.40：1.87
x=6.5%のときには，陽性中に占める偽陽性の数は25%程度である．

物理の発展に先立ち，それが必要とする道具としての数学が，先回りして常に用意されていたという歴史観があります．
そのように言いたくなる事例は確かにたくさんあります．X線結晶学に先立ちすべての空間群が求められていたこともその例です．このような廻りあわせはドラマチックで面白いのですが，数学がすべてに先だってあるはずだと信じるのは妄想です．
ニュートンの微積分のように，現場が新しい数学の源泉であったことは多く，このような開拓場面に立ち会ったのは，
数学者ではなかった（物理学者，化学者，工学者，...様々，そして，新数学分野を開拓した後，彼らは数学者と呼ばれている）．つまり，新しい数学の源泉の多くは，自然の現象の中にありました．

（注）ニュートンは，自分の研究に必要な道具としての数学（微積分）も開発しました
（ニュートンは謙虚にも自分は巨人の肩に乗っただけだといいました）．
（注）ニュートンは，惑星の動きを理解するために新しい数学（微積分）を発明しなければなりませんでした．
このような19世紀は科学の発展局面で興味深い時期です．その後，偏微分方程式の理論が生まれ，
波の伝播，熱伝達を説明する最初の場の理論が構築されました．フーリエ，ラプラスのような数学者は、
この物理学を理解するために新しい数学を発明しました．
弦理論の現在は，このような興奮する局面にある．

自然（宇宙や現象）を数学は記述することができます．あたかも数学があって自然がそれに従って作られた
という反語的表現も実は同語反復です．数学が先にあってその通りに宇宙ができているわけではありませんが，
森羅万象の自然の中に数学も含まれるので，自然を記述する数学は存在するはずです．
人間も生命も自然の中に存在しますからやはり数学で記述されるはずです．
もし人間が宇宙に居なくてもそのような数学は存在すると私は思います．
ーーー
2004年5月のノーベル物理学賞を受賞したDavidGrossがモスクワを訪れ、弦理論と理論物理学の今後について講演し，
その時のインタビュー対談は，数学と物理学の協働テーマは啓蒙的で興味あるものです．

ーーーーー
20世紀の終わりに，新しいタイプの非常に緊密な協力（物理学者と数学者の間）が登場しました．
弦理論と場の量子論では，物理と数学が非常に密接に関連しています．

弦理論が非常にロシア的という理由は，物理学と一体となったロシアの数学者の伝統（オイラーに代表される）があるからです．
ゲルファンド，アーノルド，..など．

ハイゼンベルグが量子力学（行列力学とも呼ばれる）を発見したとき，彼は数学としての行列を知りませんでしたが，
今日では行列は大学の教養課程で教えられています．
弦理論の数学ツール経路積分も，時がたてば普及するでしょう．

1930年代に書かれた量子力学に関する最初の教科書を見ると，とてもひどいものです．教科書は時間とともに良くなります．
他の分野でもまったく同じことが起こっています．力学や電磁気学に関する最初の記事と教科書は非常に複雑でした．
アインシュタインが電磁気学を研究したとき，彼は苦労しました．今や学校で電磁気学を普通に習います．

私たちが自然や数学を発明していると言うのは間違っています．逆に，私たちは自然によって発明されました．
数学は，自然を理解し，その中で最適な生存を実現するためのツールとして，私たちが創造した言語から成長してきました．
だから数学は本質的に自然の一部であり，数学が自然を記述するのが得意です．

いつの日か，銀河の反対側にある別の文明とのつながりを確立するとしましょう．世界は1つしかないので，
宇宙人は私たちとほぼ同じ物理学を持つことに誰もが同意します．彼らは我々と同じ数学を持っているでしょうか？
一部の数学者はノーと言うでしょう．彼らは我々と全く異なる数学を発明する可能性はあります．
でもやはり，彼らの数学は私たちの数学と非常に似ていると思います．

■現代のコンピューターの数値計算能力は驚くべきもので，それらは理論物理学者の働く方法に強い影響を与えました．
多くの人はもはや微分方程式を解こうとはせず，単に数値的にシミュレートします．
例えば，スティーブン・ウルフラムはすべてを計算し尽くそうとします．

実際20〜30年前のデバイスの機能と比べると，今できることは驚くべきことのようですが，
コンピュータはまだそれほど賢くはありません．計算手法は幼児期に開発されたままです．
私たちが計算アルゴリズムについて話すときに使用または考えるすべてのコンピューターは古典的です．
量子コンピューターとコンピューティングのための量子力学システムを使用するプログラムを実装すれば，
従来のコンピューターよりも指数関数的に優れたパワーを得ることができることがすでに証明されています．

量子力学もパラドックスを背景に発生しました．一方では古典物理学であり，他方ではボーアの原子モデルであり，
このパラドックスは量子力学によって解決することができました．

弦理論の最も注目に値するアプリケーションの1つは宇宙論です．弦理論家は宇宙論者や天体物理学者と多くのことを話します．
宇宙論者たちは現在、ビッグバンとビッグバン自体の後の宇宙の発達の初期段階を理解しようとしています．
この分野では，私たちの関心のある領域が重なっています．
弦理論の他のアプリケーションもあります．特に，私たちが新しい数学を発見しているという事実．
この理論は科学の発展に不可欠なステップであり，量子力学と同じように多くの用途があります．
参考書：
リサ・ランドール，「ワープする宇宙―宇宙の隠された次元の謎を解き明かす」
バートン・ツバイバッハ，「弦理論の学生のための良い教科書」

あけましておめでとうございます．
今年はcovid19の感染拡大で先行き不透明な年になりました．
皆様それぞれに悔いのない良い年になりますように．私も気を引き締めて全力で努力していこうと思っています．
新年を迎えましたが，今，私は荷物ゴミの中におります．年末に多くの荷物を，私のところへ運び込んだからです．何故そんなことになったのかと言うと，来週には，私の育った家の取り壊しが始まるからです．私は，小，中，高校も地元の公立学校に通い，大学も歩いて通える距離でしたので，引っ越しをしたことがありません．
私の育った家は，戦後に建てた始めは2部屋だけの小さなものでした．戦後の焼け跡はそのようなバラックばかりがありました．その後の70数年に増築や補強が行われましたが，ずっと同じところに住んだので，父母の物や私の物が山ほどで，高価な物は何一つありませんがそれぞれに思い出があります．そのため，大変気が進まない断捨離でした．9月のまだ暑い最中から週に2日程度通い荷物の整理を進めましたが，とうとう年末が来てしまい，選別の間に合わない残りを全部私のもとに運び込む羽目になったのです．

母は編み物が好きでした．私が小さいときに見た光景は，いつも頼まれた編み物をしている母の姿でした．母は田舎の女学校を出て東京にでて来ました．あるとき，下宿でネクタイを編んでいて、金色の絹糸を色合わして買うために，お店にそれを持参したところ，お店の主人が「見本でウインドウに飾りたい」といって買い上げてくれたそうです。「そう，恥ずかしいわね」と口では言ったものの，かなりいい値だったのでうれしかったそうです。松坂屋の斜め前の大きな糸やでのことでした。市役所で洋裁も習う時間があったようです．東都服装学校にも少し行ったそうです．兵隊さんの猿股を作るにも，糸を何センチも無駄にしないような時代のことでした．
私は子供の頃，毛糸を両腕に通して母の毛糸玉を巻くのを手伝いました．長い時間腕を上げて振っていると疲れるものです．セーター1着作るのに，20玉が必要と母から聞いていました．
母の遺ししセーターに毛糸の玉巻きを手伝いし幼き日の想い出

今回，母の残した毛糸の編み物や和服など，大きな7つの段ボールを田舎に送りました．田舎では使ってくれるそうです．
未使用の毛糸は友人の知るグループで使うというので差し上げました．

庭に私の分身のような樹齢70の枇杷の木があります．今，白い花を盛りとつけています．可哀そうですが，実をつけることなく今年は切られてしまいます．木は動けませんから．合掌
我食いし枇杷の種より育ちたる樹齢は七十の白き花盛る

物置に釣り道具を見て悔やまれる父の釣行につき合わざりし日々
父の軍隊手帳をウエブに公開し見知らぬ方に難読箇所の教えを受く

 
■時宗総本山，遊行寺の御滅灯（おめっとう），一ッ火（ひとつび）は，11月27日の夕刻から行われます．

遊行寺のウエブサイトによると：－－－－－
「一ッ火」は遊行寺年中行事の中で最も荘厳な法要です。順に灯火が消えていき、やがて完全な暗闇に包まれた本堂に幽音の念仏が響きます。そして暗黒の世界にただ一つ灯される新たな灯明が、光り輝く念仏の世界を本堂内に映しだします。
この法要には、「一年間の悪業を懺悔し、来年の善行を志す」という意味合いもあります。
なお、本年、主役である「報土役ほうどやく」は、藤澤清孝ふじさわせいこう（鎌倉市材木座來迎寺住職かまくらしざいもくざらいこうじじゅうしょく）．「後灯役」は、望月輝山もちづききざん（総本山内近司そうほんざんないごんす）が務めます。
本年度は、新型コロナウイルス感染症対策のため、参拝人数を制限させていただきます。－－－－－

本堂内の火が次々に消され、最後にこの大光灯を報土役が消し、後灯を後灯役が消します。この漆黒の闇のなかで十八念仏が始まり、報土役・後灯役は、火打ち石で火を起こします。一度目は空中で火花を散らす「見せ火」で、二度目で「火口箱」に火花を打ち込みます。打ち込まれた火は、闇からしだいに灯明へと移され、再び弥陀と釈迦の光明に照らされた世界が戻ってくることを表現します。－－－－－

時宗のこの伝統行事は，京都，東山の西連寺でも行われていることをウエブで見ました．

現在、外灯も整備され夜遅くまで街の灯りも消えることもなく、「暗闇」の怖さや心細さというものを経験することも少ない。漆黒の闇につつまれた堂内で、徐々に明るくなっていく様を目の当たりして光の有り難さを経験することでしょう。

■2016年11月27日は，夕方からの雨でどんどん寒くなりました．私は，母の一周忌の折に，ご住職からお聞きしたばかりの「一ッ火」に参加してみようと思い，藤沢，遊行寺に出かけました．遊行寺は，落語（鈴振り）でも，箱根駅伝の中継でも，有名で知っていましたが，私が遊行寺に行ったのはこのときが初めてです．「一ッ火」は，5時に始まり9時近くまで行われました．外の雨は氷雨のようになり寒い夜でした．
「一つ火」の最後に，大僧正直々に全員（何百人でしょうか，例年より少ないそうです）が，お札をいただきました．その行列の長いこと．大僧正は97才．すごい大声でのお話，さすがです．（この方が，当時，運転免許返上で話題になった方ですね）．
「一っ火」というのは，本堂のロウソク（それぞれ或るものを象徴して配置され，20～30本位ある）の火を，複雑な手順（方法や役回りがいろいろ）に法り次々に消して行き真っ暗に...，そして静寂．十八念仏が始まり，火口箱に火花を打ち込み，灯明に移されます．再び弥陀と釈迦の光明に照らされた世界が戻ってきます．念仏は美しい合唱の音楽になって響ます．

■大きな百目蠟燭*)の炎は長く伸びて明るい．じっと見ていると，炎はピタッと動かない．それが突然瞬き始める．また，ピタッとまる．これが周期的に繰り返されます．この自励振動の機構**)に感嘆して見入ってしまいました．実に面白い．まるで活きているように間欠動作をします．
面白い現象です．ロウソクの炎の瞬きと，静止が何故繰り返されるのだろうか？どちらの状態も安定でないわけで，この移り変わりが起こる理由を考え込んでしまったのです．

注*）大きな和蠟燭です．100匁目あるかどうか知りません．明るく点燈し，嫌な臭いもしません．和ろうそくはハゼの実などから作るようです．ハゼの実や和ろうそくのことなどをどなたかお書きください．
　むかしの むかしの かざみの とりの
　ぼやけた とさかに はぜのは ひとつ
　はぜのは あかくて いりひいろ
　ちいさい あき ちいさい あき
　ちいさい あき みつけた

注**)　類似な現象として；
・近づけた2本のロウソクの瞬きの周期が揃う（協同する）という現象があります．以下に，協同現象のyoutube実験動画を引用します．
・蛍の明滅がそろってくる協同現象も知られています．
・私が昔係わったことのあるプラズマディスプレイ装置では，放電スポットが周期的に明滅する自励振動の現象がありました．