ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.16］ No.068
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆お知らせ
数学月間懇話会（第11回）
主催●日本数学協会，数学月間の会（SGK）
日時●７月２２日，13:50-17:20
－－－－
1.十年目の「数学月間」
　片瀬豊，高窪正明（SGK）
2.「サッカーボールの対称性を解くTopological Symmetry」
　細矢治夫（お茶の水女子大名誉教授）
3.繰り返し模様の観賞法
　谷克彦（SGK）
4.テーラー展開の話
　鈴木啓一（SGK）
ーーーー
会場●東京大学（駒場）数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●数学月間の会（SGK）
sgktani@gmail.com，谷克彦（SGK世話人）
直接会場においでください（開場13:30）

◆数学月間だより１
日本数学協会は，2005年に，7月22日--8月22日を数学月間と定めました．この期間は，数学の基礎定数 π(22/7=3.142..) とe(22/8=2.7..)に因みます．この期間に，数学への共感を高める活動が各地で盛んになるよう我々は応援しています．
数学が色々な分野で社会を支えていることを市民が知ることは，数学への共感の呼び起こしに直結します．逆に，社会が必要としている数学を数学者が知る--言い換えれば，異分野の課題の中に数学が適用できるニーズや新しい数学が生まれるシーズを見出す--ことも重要であります．

先ず隗より始めよで，SGKは毎年7月22日に数学月間懇話会を開催しています．
これまでのテーマを見て見ましょう．
（資料１）**********
◆数学月間懇話会10年の記録
第1回（2006.07.22）会場：シーボニア
数学月間のπとeの連分数展開，公開鍵暗号　山崎圭二郎
数学と社会　　　　　　　　　　　　　　 　真島秀行
ゲストスピーチ　　　　　　　　　　　　 鈴木裕道
第2回（2006.08.06）会場：議員会館
財政再建と数学：TQC手法　　　　　　　 （日科技連）
第3回（2007.07.22）会場：ルベソンヴェール
シミュレーション　　　　　　　　　　　 谷口健英
第4回（2008.07.22）
数学月間 　片瀬豊
ある数学者たちの物語 　 上野正
数学と基礎科学 　 谷克彦
秘宝－数学的オブジェの照明 　　　岡本和夫，河野俊丈
第5回（2009.07.22）
宇宙のかたち　　　　　　　　　　　 河野俊丈 　　　
造血幹細胞移植データベースと統計　　 田渕健
生体情報のゆらぎとフラクタル性　　　　 河野貴美子
MRIの数学的原理 真島秀行
第6回（2010.07.22）
手と目で観賞，数学曲面と多面体　　　　　手嶋吉法
教育数学の試み 　　　　　　　　　　　　岡本和夫
第7回（2011.07.22）
サイバー世界のモデリング　　　　　　　　北川源四郎
量子コンピューティングの考え方　　　　　荒井隆
米国MAM複雑系と日本の原発事故　　　　　谷克彦
第8回（2012.07.22）
物理化学の探検ー化学の中の数学の世界　　細矢治夫
じゃんけんの必勝法を論じて統計的思考に　石黒真木夫
第9回（2013.07.22）
考える楽しみわかる喜び　　　　　　　　　水谷一
最小二乗問題の新解法と逆問題への応用　　速水謙
数学祭り　　　　　　　　　　　　　　　　谷克彦
第10回（2014.07.22）
人口の集合関数としての「民力指数」　　　松原望
スパゲッティを巡る旅　　　　　　　　　　中西達夫
第11回（2015.07.22）
十年目の数学月間　　　　　　　　　　　　　　　　 　片瀬豊，高窪正明
サッカーボールの対称性を解くTopological Symmetry　細矢治夫
繰り返し模様の観賞法 　　　　　 　　　谷克彦
テーラー展開の話　　　　　　　　　　　　　　　　　　鈴木啓一
注）第4回以降の会場は，数理科学研究科棟・東大駒場キャンバス

次号に続く

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.09］ No.067
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
『数学 理性の音楽』，東京大学出版会(2015.4）刊行記念イベントが，
東京大学伊藤国際学術研究センター地下1階　ギャラリーにて開催された．
（6月8日，19:00-21:00）
同書の著者，東大名誉教授（岡本和夫・薩摩順吉・桂利行の三氏）による鼎談．

この書籍の副題は，自然と社会を貫く数学で，
まさに，数学月間のコンセプトが語られております．
ぜひ皆様が一読されることに期待し，ここでは書籍の内容には言及しません．
その代り，鼎談の内容を速報します（今夜，参加し帰宅したばかりでホットな情報です）．
----------
鼎談は，岡本氏の「数学の３つの側面」
ー道具としての数学．言葉としての数学，対象としての数学--の話から始まりました．
著者の3氏は，奇しくも歴代の東京大学大学院，数理科学研究科長です．
数学の大学院が理学部から抜けて，駒場に大学院数理科学研究科が創設されたのが
1992年のことで初代の科長が岡本氏，次いで薩摩氏，桂氏でした．
本郷キャンバスの理学部から大学院だけ抜けて，駒場キャンバスに
大学院数理科学研究科が設立できたのは，教養学部の数学の歴史があり，
基礎科学科もあったので，環境が整っていたことがあったようです．

20世紀の数学は，抽象化・純化に進んだわけですが，これは数学を学び難くしています．
どうも，学生・生徒たちは数学を人間が作ったという気がしないそうです．
完成された体系がそこにある．どうして生まれたかなど考える余裕もないようです．
完成された数学はそびえたつ山脈のようでとりつきがたい．
数学月間でも数学が生まれる所から親しむことを薦めています．

数学は役に立つのかというのは愚問です．
すぐ役に立っこともあるし，何十年もの後で役に立っものもあります．
岡本氏の研究したパンルヴェ方程式はソリトンの研究に使われるし，
暗号（公開鍵．楕円曲線），デジタル信号の誤り訂正，などの例が出ました．
1900年に，ヒルベルトは23の問題を出し，数学は抽象化の方向に進みだします．
同年，ポアンカレも人力で計算できるところまで行き着き，非可積分の方程式の
性質を示しました．その先はコンピュータの出現を待たねばなりませんでした．
現在はコンピュータによる数値計算が盛んで，非線形やカオス，分岐理論も研究されています．
モデリングやシミュレーションの現象数理科学も盛んです．

私は数学と数理科学の違いを質問してみました．
数理科学は数学のように厳密な証明の手順がないのではないか．
それとも数理科学というのはコンピュータを用た数学であるのか．
などという漠然とした感じがあったからです．
結論は，どちらも同じである（ニュアンスの個人差はあるが）という事でした．

コンピュータで計算は万能かというと，そうでもないようです．
例として出されたのは調和級数：
1/1+1/2+1/3＋・・・+1/n＋・・・＝lim_n→∞（log n）=∞
ですが，ｎをずいぶん先までたし行っても，対数ですから級数はなかなか∞にはなりません．

最後に岡本氏が面白い計算を提示しました．
方程式の問題より，数の問題の方が奥が深いということを象徴するためです：
2×3×5×7+11=13+17
2^2+3^2+5^2+････＋17^2=1+2+3+････+36=666

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.06.02］ No.066
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
日本数学協会・第14回総会および講演会のお知らせ
日時：　2015年　6月7日，
場所：　東京大学数理科学研究棟（駒場キャンバス）
11:30～12:30　総会
----------------------------------------
13:30～15:40　講演会
13:30～14:30
「十年目の数学月間，これまでとこれから」，片瀬豊・谷克彦（SGK）
14:40～15:40
「視覚と錯視の数学からアート，そして画像処理」，新井仁之（東京大学）
講演会にどうぞお気軽にご参加ください．
協会員は無料ですが，協会員外は参加費2千円かかります．

*******（私の話そうとしていること）*******
数学月間は，数学から社会を見ると同時に，社会からの要請を数学側が知る機会でもあります．
国内外の数学月間テーマのトレンドを見ると，ビッグデータや統計学，複雑系や非線形，
モデリングやシミュレーションの話題です．
これらはすべてコンピュータを駆使した数値計算によって可能になった分野です．
これまでの数学とは違う新しい数学分野が生まれているところと言えるかもしれません．
1900年ポアンカレは，独立な因果列からなる可積分の方程式はごくわずかで，
大部分の方程式は非可積分（干渉し合う因果列）であると警鐘をならしました．
明日の一つの出来事には，今日の全ての出来事の影響が反映される世界です．
遠方の地で過去に起きた蝶の羽ばたきが，この地の明日の大風を引き起こす要因の一つになり得る
「バタフライ・エフェクト」の世界です．
ちょっとした初期パラメータの違いでカオスが起きるかもしれません．
これらは方程式を積分して関数で書き表すことは不可能ですが，
コンピュータを用いた数値計算で現象の追跡ができます．
モデリングとシミュレーションにより現実の現象を理解する
「現象数理科学」がさまざまな分野で発展しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.26］ No.065
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
これは私の造語です．あまり耳慣れない言葉ですが，とても気に入っています．
結晶学では「空間格子」という言葉がでてきますが，「空間のデジタル化」はこれと同じ状況の表現です．
空間のデジタル化とは，「空間を，１つの多面体を並べ（面と面が接するよう）て隙間なく張りつめること」
を意味します．例えば，角砂糖のような立方体を並べて，空間を張り詰めたとすると，
このデジタル化された空間の対称性は，立方体の対称性と同じであることはわかりますね．
”立方体（A)”と同等な対称性の多面体で，空間のデジタル化ができる多面体に，
面心格子を生む”菱形12面体（B)”と，体心格子を生む”ケルビン立体（C)”があります．
これらは立方体の対称性に分類される3種類の空間充填です（Fig)．
（この図はpov-rayを用いて作成しました）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/85/16728485/img_0_m?1432564271

1種類の多面体を互いに面が隙間なく接するようにして空間に詰め込んだ状態を想像してください．
この状態が空間のデジタル化です．
空間のデジタル化の様式を分類したいなら，多面体の対称性に注目すべきでしょう．
一様で連続的な空間が，デジタル化によって，異方性があり周期的な空間に変わります．
無限に広がる空間が，単位となる１つの多面体に還元されます．
すでに，アモルファスと結晶の項目で述べましたが，デジタル化された空間はシンプルで扱いやすい．
このような空間を「結晶空間」と言います．
一寸脱線しますが，連続信号をサンプリングして得たデジタル信号の周波数帯域が抑えられるのと似ています．
結局，3次元では14種類の空間のデジタル化の様式があり，
これは結晶学でブラベー格子が14種類ということと同じことです．

(注)2種類の多面体を使って空間を充填することもいろいろ考察できます．
例えば正8面体と正4面体を使って空間を周期的に充填します．
2種類の多面体の混合による空間の充填では，必ず周期が生じるかといえばそうでもありません．
ペンローズのタイリングに相当する3次元非周期充填もあり得ます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.19］ No.064
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
このような不思議で奇麗な法則があります．
https://www.facebook.com/maxplancksociety/photos/a.10150979253928376.447707.324380493375/10153218754768376/?type=1

1³ + 5³ + 3³ = 153
16³ + 50³ + 33³ = 165033
166³ + 500³ + 333³ = 166500333
1666³ + 5000³ + 3333³ = 166650003333
and so on and om and on!

不思議な数式です．証明してみたくなるでしょう．
いや，なぜこのようなことが起こるのかが知りたいですね．
別の話ですが，似たような数式がまだあります．
ただし，こちらの場合は「数字の桁数が増えていっても，いつも成り立つ」
という性質ではありません．
https://twitter.com/Derektionary/status/484852762102857730

166³ + 500³ + 333³ = 166,500,333
296³ + 584³ + 415³ = 296,584,415
710³ + 656³ + 413³ = 710,656,413
828³ + 538³ + 472³ = 828,538472

閑話休題．初めの不思議な法則の証明法の問題に戻りましょう．
考え方は人さまざまで，証明法には色々あるでしょう．
論理が正しくて，命題が証明されるのならば，どのような証明方法でも正解です．
それでも，「美しい」証明とか「エレガント」な証明とか言われるものがあります．
そのような証明は，「命題の本質にズバリと触れている無駄のないシンプルな証明」
のことだと私は思っています．
補助線一本で解けてしまう図形問題の証明などはその例でしょう．
力ずくで計算して証明できても，命題の本質や現象の起こる仕組みが見えていないのでは，
本質にズバリと触れているとは言えません．
本質や仕組みがわかるということは，その仕組みを基礎とするもっと幅広い命題にも適用できる．
つまり「一般化できる」証明法でもあり価値が高いと思います．

小林昭七先生が「数学と美」というエッセイを，「いまを生きるための教室」角川文庫の中に掲載しています．
（私は小林先生がお亡くなりになる直前の夏の日本滞在中にお会いしこの本を頂きました）
この本から以下の部分を引用しておきます：
「他の科学と同様，数学でも新しい結果は重要である．しかし，数学では既に知られている結果の
別証明や新しい見地からの解釈もかなり評価されている．定理の本質を理解させるような証明，
「なるほどそういうことだったのか」と思わせるような美しい証明は，それが既知の定理の
証明であっても高く評価される」

「数学は美しい」と良く言われますが，美しいと言われても漠然として私にはピンときません．
これを言い換えるなら，「シンプルである」，「本質を見抜いてそれに言及している」，
「話を逸らさないで真摯に課題に集中している」という意味でしょう．

「問題の本質の議論から逃げて，話をそらし，周辺の議論にすり替える」という手法は，
政治や社会で良くみられることです．特に，今の安倍政権では目にあまるものがあります．
「丁寧に説明していく」とよく言いますが，これは聞く耳を持たないと言うことです．
我々の方が説明してあげたいくらい十分な知識があります．国民をバカ扱いしないでもらいたいものです．
論理や数学を軽視する社会に公正はありません．数学月間活動をもっと社会に広げる必要がある所以です．

もう一度，閑話休題で，この不思議な式に戻りましょう．
皆さん証明を考えてみてください．
n桁の数字を　$$ (x_n), (y_n), (z_n) $$と書くと，
　$$(x_n+1)=10(x_n)+6，(y_n+1)=10(y_n)，(z_n+1)=10(z_n)+3$$

$$(x_n)^3+(y_n)^3+(z_n)^3＝(10^2n)(x_n)+(10^n)(y_n)+(z_n)$$　が成立するとして，数学的帰納法で
力ずくで計算して証明することはできるでしょう．でも計算は大変ですし本質は別の所にありそうです．
この問題の本質が何処にあるのか私にもまだ理解できません．皆さん良い証明が出来たら教えてください．
ポイントは循環小数のように続く数字と数の表記法（10進法を使っている）にあるように思います．
多分，以下の表式が利用できます：
$$(x_n+1)＝(1+6/9)(10^n)-6/9，(y_n+1)＝5*(10^n)，(z_n+1)＝(3+3/9)(10^n)-3/9$$　

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.12］ No.063
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
2015年米国MAMのテーマ
「数学がキャリアを動かす」
（http://www.mathaware.org/mam/2015/highlighted/ より）

自分のキャリアに数学を利用している実在の人物
数学の才能や嗜好を報酬や多様なキャリアに変えた17人

数学が好きだが，数学専攻者にアカデミック以外のどのような仕事があるのかわからない？
幸いなことだが，「数学を専攻するのは今でしょう」というわけだ．
なぜなら，数学がイノベーションの原動力であるようにキャリアも運ぶからだ．
数学の才能と嗜好を，実業界や工業界や政府での多様なキャリアと報酬に替えた17人が紹介される．
彼らが影響を受けたものやそのキャリア・パス選択を見ることは，
アカデミックの外にキャリアを探す数学専攻者にとって，ユニークな見通しや有用なアドバイスになるだろう．

詳しく知るには
http://www.mathaware.org/mam/2015/highlighted/#sthash.gXM8A0oh.dpuf
に17人のプロフィールがあります．17人のうちIBM研究所の人が2人います．
そのほかは，data scientistという人が多いようで，
これらは統計学やコンピュータを用いた数学分野です．

■代表的なプロフィールの例
プロフィール：Jean Steiner
データ・サイエンティスト，Google社，ニューヨーク

私は、工学分野の広告組織Googleのデータ科学者です．
広告主が彼らのgoogle AdWordsアカウントを
どのように管理したらよいかを理解するためにデータを分析し，
彼らに良いツールの提供ができ，彼らのアカウント管理が容易になるようにしています．
私はデータから話を引出し，我々のソフトウエア技術者が良い製品を作るのを助けます．
データ・サイエンティストという役割をする人のほとんどは，
統計学，生物情報学，認知科学，物理学，数学，経済学などの背景を持っています．
私は，アカデミックの場の純粋数学からスタートした
（博士号を取った後，ポスドクフェローシップで研究と教育を行った）．
そして，私はやはり定量的であるが，応用的な何かをしたいと思った．
多くの可能なキャリア（例えば、疫学、定量的な金融、経営コンサルティング）
を探しての情報インタビューの結果，Googleで私の関心にぴったり合った仕事を見つけた．
データ解析と，わずかばかりの軽量シェル·スクリプト（コーディング），
ビジネスへの関心が組み合わさっている仕事だ．
当初，私は金融機関で，収益予測，分析，報告をしていたが，
最終的には，より深い分析とより少ない報告を望んでいたので，
データ・サイエンティスの役割に移動した．

■個人的な感想－－－－－
今年の米国MAMのねらいは，数学者の働き場所は大学教授や教員の他にも広範な分野があり
需要があるということにある．「だから数学を学ぶなら今でしょう」という調子だ．
この状況は日本でも全く正しいとは思う．

しかし，今年の米国MAMのキャンペーンのなかで，数学のキャリアは年収が高いとか言うのは眉唾物だと私は思う．
2014年度の高年収職業ベスト10とかワースト10とかは馬鹿げたデータだ．
だいたい高収入が欲しくて数学を専門にするなどおかしな話だ．
17人のプロファイルもそれほど面白くない．
広範な各分野で具体的にどのような数学を用いた仕事や研究をしているのかを知りたいと思ったのだが，
週刊誌の表題程度のレポートで，本年の米国MAMの内容には失望した．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.05.05］ No.062
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ゴールデン・ウイークの最中です．
皆様，よい休日をお過ごしでしょうか．
今週は2つの本を紹介しようと思います．

■「数学を楽しむ」西山豊，現代数学社
6174の不思議はこの本のp.130に出ています．

数学はなんでも証明されているかというとそうでもないらしい．
6174の不思議さを理解するのはちょっと大変．私はまだわかりません．
でも，6174に関する不思議な命題が成立しているのは事実です．
　
6174の各桁の数字の並びを変えて，最も大きい数字を作ると7641，
最も小さい数字を作ると1467です．
最大数字と最小数字の差は　7641-1467＝6174　になってしまいます．
6174という数字は不思議ですね．

いろいろな4ケタの数字で実験してみます．例えば，
2005なら
5200-0025＝5175
7551-1557=5994
9954-4599＝5355
5553-3555＝1998
.....
このような操作をカプレカー操作というそうです．
（カブレカーはなんでこんな操作を思いついたのでしょうか不思議です）
頑張って，この先をもう少し繰り返して行くと，結局6174に到着します．
全部同じ数字の場合を除き，どのような4ケタの数かtら出発しても
6174に到達するそうです．不思議ですね．なぜなのだろうか？

西山さんはプログラムを作り，パソコンですべての4ケタの数が，
有限回のカプレカー操作で6174に達することを確かめ，系統図をつくりました．

そのほかの桁数の数字ではどうかというと，
3ケタでは存在するけれど，5ケタでは存在しないそうです．

事実は確かめられましたが，なぜこのようなことが起こるのか？
その仕組みをしりたい．数学の不思議さを感じる例です．

■美しい幾何学，　丸善
高木隆司監訳
Eli Maor and Eugen Jost

ルネサンスの時代は，数学とアートの活動は協力して行われ，
心の中で補い合うものと考えられていた（イーリーによるまえがきより）．
オイゲンの数学的アートと数学者（数学史）イーリーの協同でできた本書は珍しい数学の本です．
説明には微積分などは出てきません．子供から大人まで数学アートを鑑賞しながら読み進むことができます．
テーマは系統的な幾何学とは異なります．初級の幾何学もあれば無限級数などもあります．
さらに意外なテーマが現れたり変化に富みます．
取り上げられたいくつかのテーマを見てみましょう．例えば，シュタイナーの円鎖．
これはアルベロスとかインドラの真珠などと呼ばれることもあります．
円の中に互いに接する円を詰め込んだ美しい図形です．円による反転操作もあります．
この図形は和算の算額にも登場しますが，それにも言及しているのは著者の専門が数学史だからでもあり，
本書の構成にもそれが現れています．本書の前半に，ピタゴラスから始まり，
素数，無限級数の収束，ユークリッドなどのテーマが現れます．
さらに続くのは，円周率，積み木による調和級数，自然対数の底，らせんや種々の曲線などです．
これらの説明も，数学アートの図が活きていて面白い本です．
本書の後半には，スノーフレーク曲線，シェルペンスキーの三角形などのフラクタル図形の特徴も，
美しく理解しやすい図による記述があります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.28］ No.061
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
面積がゼロで，周囲が無限大のフラクタル図形

フラクタル図形というのは，図形を拡大していくと，
どんどん細部が見えてくるが，それらがいつも同じ図形なのです．
http://upload.wikimedia.org/wikipedia/commons/6/6a/Sierpinski_zoom.gif

そのような図形のうち，ポーランドの数学者シェルピンスキーの図形の作り方を見てみましょう．

(1)シェルピンスキーのガスケット
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/58/16668258/img_2_m?1429928123

正3角形から出発します．正3角形を4分割して真ん中を通り覗きます．
残った3つの正三角形をそれぞれ4分割して，それぞれの真ん中を取り除きます．
この操作を際限なく（無限に）繰り返して得たフラクタル図形はシェルピンスキーのガスケットです．
面積は0に収束し，境界の長さは無限大に発散します．

(2)シェルピンスキーのカーペット
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/58/16668258/img_3_m?1429928123

正方形から出発し，9分割し真ん中の正方形を取り除きます．
残りの８つの正方形をそれぞれ9分割して，それぞれの真ん中を取り除きます．
この操作を際限なく（無限に）繰り返して得たフラクタル図形はシェルピンスキーのカーペットです．
やはり，面積は0に収束し，境界の長さは無限大に発散します．

これらの図形は，1次元でも，2次元でもありません．
「長さがx倍になった領域に，現在の図形をy個詰め込む」という操作を繰り返したわけですが
　　x^d=y　（dはフラクタル次元）　より，フラクタル次元は　d＝logy/logx　です．　
フラクタル次元は，(1)ガスケット3角形では1.585･･･，(2)カーペット4角形では1.89････になります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.21］ No.060
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■結晶とガラスについての話です．
まず，石英（水晶）と石英ガラスの2次元の模式図を見て下さい．
図はwikipediaから借りました．どちらも材料の化学式はSiO2で同じです．
Fig.1　結晶
http://upload.wikimedia.org/wikipedia/commons/f/fd/SiO2_-_Quarz_-_2D.png
Fig.2　ガラス
http://upload.wikimedia.org/wikipedia/commons/thumb/1/19/SiO2_-_Glas_-_2D.png/240px-SiO2_-_Glas_-_2D.png

結晶とガラスの違いは一目瞭然でしょう．
そう，結晶構造には繰り返し周期がありますが，ガラスにはありません．
Fig.3に示すように，結晶には単位となるタイルがあり，これで無限平面を隙間なく張りつめることができます．
石英の例では，正6角形のタイルを，赤点の場所に置けば，無限平面を隙間なく張り尽くせます．
赤点は格子点と呼ばれます．格子は，図中に示した2つの互いに独立なベクトルa1，a2の
一次結合ha1+ka2により生成されるベクトルを集めた無限集合（並進群）の図による表現でもあります．
Fig.3　結晶構造にある並進群
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/26/16652126/img_0_m?1429350335

■結晶空間は並進周期のある空間です．結晶構造は規則正しい秩序のある構造ですから，
並進操作以外にも回転対称操作とか鏡映対称操作などあり，
構造に存在するこれらの操作を続たとき生じる対称操作全体の無限集合は”群”をなしています．
生成される対称操作はこの集合に含まれるし，すべての操作に逆元があり，
何も動かさないという単位元もあります．
結晶空間（周期のある無限空間）の対称操作の集合のなす群を結晶空間群と言います．
今日，ここで扱ったような2次元の平面群（壁紙模様）は17種類あることが知られています．
並進（格子点間の移動）で重なるものは同値と定義すると，
無限に広がる結晶構造を，単位タイルの中に押し込めることができます．数学の言葉で言うと，
「並進群を核とする準同型写像で結晶空間群は結晶点群に帰着する」ということになります．
私はこの理論が大好きでした．しかし皮肉なもので，実際に扱った材料は結晶ではなく
群論の適用ができないガラスが中心になりました．

■ガラスの構造をどう解析し記述するかというのは，今日でも困難な課題です．
結晶で活躍する群論もFourier変換も役に立ちません．ガラス（一般化してアモルファスと言う）には，
単位タイルと言うものがありません．結晶構造では，
無限にある構成原子のパラメータは単位タイルに含まれる有限個に還元することができましたが，
ガラスでは無限個の構成原子のパラメータを減らせません（実際にコンピュータで扱うのは有限個）．
結晶空間は単位タイルによってデジタル化された空間，他方，アモルファス空間は連続空間（アナログ空間）です．
ガラス構造では，結晶のようにすべての構成原子のパラメータを記述するのは諦めねばなりません．
そこで古くから，1つの原子を中心に置いて．半径r+Δrの球殻上に何個の原子が存在するのか
というような確率的な記述（動径分布関数）が用いられてきました．
最近は，アモルファス構造を特徴づけるいくつかのトポロジー量を定義することもやられています．
Fig.2を見るとリングがたくさん見えるでしょう．ガラス構造の中に，何員環がどれだけ存在するかとか，
ベッチ数とか連結数などの特性量，さらにパーシステントホモロジーの計算がなされ，
これにより詳細なアモルファスの特徴量が得られるようになりました．
これらのトポロジー量は，大きな原子数のアモルファス構造のモデルから，
シミュレーションにより決定された原子の座標値のビッグデータを土台に導出されます．
******
（編集後記）
今回のメルマガでガラスの構造について書こうと思ったのは，
4月16日の文科省の講演会「数学は世界を変えられるか？」で数学イノベーションの紹介例3つの内に
ガラス構造への応用トポロジー（東北大）があったからです．
この講演会の主旨は，数学と社会・諸科学の連携です（ガラス構造の研究発表ではありません）．
数学連携に関する個人的感想は（メルマガ分量オーバーのため）．以下のサイトに書きました：
http://sgk2005.sakura.ne.jp/htdocs/index.php?key=joth4d0ko-36

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.14］ No.059
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
図
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556225/69/16381169/img_0_m?1428931802

計算することも大事ですが，このような感覚を体に身に着けることは有益です．
有限個の積み木を積んで長さの記録を競います．
無限個の積み木を積むなら，少しずつですが無限に伸びる対数曲線ができます．
（例１）発散する無限級数を体験する
　　１+1/2+1/3+1/4+.......+1/n+....=∞
積み木の長さの半分を１とする．
一番上の積み木の飛び出している長さは１
その下の積み木の飛び出している長さは1/2
その下の積み木の飛び出している長さは1/3
.....以下同様にいくらでも続きます．

（例２）収束する無限級数を体験する
　　1/2+1/4＋１/8＋1/16+........=1
総和でできる立方体の体積を１とする．
立方体の内部の1/2の体積(オレンジ）を取り除く
残りの体積から残りの体積の1/2（グリーン）つまり立方体の（1/2）^2を取り除く
その残りの体積の1/2（青）つまり立方体の(1/2)^3を取り除く
その残りの体積の1/2（赤）つまり立方体の(1/2)^4を取り除く
......以下同様にいくらでも続きます．

私達は子供の頃，積み木を積んで遊びました．そして自然に重心や釣合の感覚が身に着きました．
水遊びをして流体の性質を自然に身に着けました．
後に学校で物理学を学びますが，そのような理論を学ばずとも重力や力学の法則が身に着いていました．
身に着いていなければキャッチボールもできません．
吹きガラスの職人になるには，熔融ガラスの振る舞いを瞬時に判断できることが
身に着いていなければなりません．数学でもこのような体験は大事なことだと思います．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.07］ No.058
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
最近，我々のfacebook数学月間の会
https://www.facebook.com/sgk2014
に，Nishiyama氏から正方形の辺の長さの1/nを作る方法に関する
plusマガジンの以下の記事の紹介がありました．
https://plus.maths.org/content/folding-numbers?nl=0
皆様，正方形の折り紙を用いて試してみてください．
plusマガジンの記事は，下図の中に生じる黄色い２つの３角形が
互いに相似であること，直角3角形である（三平方の定理が成立）こと
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagak.jpg

を用いて，次の関係式を導びきます．
$$y/2＝k/(1+k)$$　
この関係式に，$$k$$の値（位置）として，得られた$$y/2$$の値（位置）を
代入するたびに，次の$$y/2$$の値（位置）が求まります．
$$k=1/2$$　→　$$y/2＝1/3$$
$$k=1/3$$　→　$$y/2＝1/4$$
$$k=1/4$$　→　$$y/2＝1/5$$
　　......
このようにして繰り返せば，一辺の長さの$$1/n$$まで順番に作れます．
正方形の上の辺に$$k$$の位置をとると，右側の辺に$$y/2$$に位置が決まります．
このように続けると，$$1/2，1/3，1/4，･･･$$の位置が正方形の周りを
ぐるぐる周りながら順次現れるのが大変面白いです．
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagaki.jpg

https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagakj.jpg

さて，紙の形が長方形の場合は如何でしょうか？
手紙を３つ折りにして封筒に入れるときにこのようなことが必要になります．
長方形の辺の1/3を作る方法では，Takakubo氏からの以下の２通りの情報が
寄せられました．以下の図をご覧ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_1_m?1428237203
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_2_m?1428237203
これらは一般の長方形（辺の比が１:√2に限らない）で使えます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.31］ No.057
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も桜が咲きました．関東地方は良いお花見日和です．
皆様のまわりは如何でしょうか．満開の桜はいいですね．
桜吹雪も私は好きです．年に一度の良い季節です．
一斉に花だけ咲く桜は確かに異常です．闇を背景の夜桜は怖いようですし，
森の中でただ一人，満開の桜の中に居れば，坂口安吾の小説にもあるように
気が変になりそうですね．
桜の花は，見事な5回対称をしています．今回は花見の季節という事で
平面図形の5回対称を観賞しましょう．今回は気楽にご覧ください．

（１）点群
桜の花びらの対称性は正5角形の対称性と同じで，
点群でいうと記号5mで表現します．これは，5回回転軸と鏡映面mとから
生成される点群だという意味です．図を見て下さい．
赤い5角形は，正五角形の中心に立てた5回回転軸を示します．
赤い線分は鏡映面を示します．鏡映面が１つあれば，5回回転軸のために
5枚の鏡映面が生じ，これらの鏡映面の交線が5回回転軸になっています．
ここで生じる5枚の鏡映面はすべて同じ性質です．それは5回回転軸で
互いに変換されるべきものだからです．
（群論の本では，すべての鏡映面は同じ共役類に類別されると表現されます）
群という言葉を出しましたが，あまり気にすることではありません．
5回回転軸と1枚の鏡映面mの操作を組み合わせ，次々新しい対称操作を
生んでいくことを，どんどんやっていくと，それまでに得たものと
同じ対称操作になってしまうことがわかります．
点群5mの例では，異なるものは10個の対称操作で全てです．
これら10個の対称操作で点群5mの対称操作の集合は閉じているといい．
点群5mの位数は10だと言います．
群となる条件は，集合が閉じているだけではありませんが，細かい定義は省略し，
ここでは，5回対称軸とそれを含む1枚の鏡映面だけで
10個の対称操作が生まれ，それで閉じていることを鑑賞ください．
点群と書いているのは群5mは1点を不動点にするものだからです．
出発点となった5回回転軸と1つの鏡映面を点群5mの生成元と言います．

老婆心ながら注意をうながしたいのは，奇数回転軸の点群で点群に生じた
鏡映面はすべて同一の共役類に入り，5mなどと記述すことです．
5mmではありません．
偶数回転軸の場合は，例えば，2mmのように記述し，鏡映面は
２つの共役類に分かれます．これらの違いは共役類の類別のためで
結晶学の本にときどき誤りが見受けられますのでご注意ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_0_m?1427715627

（２）部分群
点群5m（位数10）の部分群に点群5(位数5)や点群m（位数2）があります．
部分群は上位の群の対称要素を落とすことで得られます．
操作mを落とすことで点群５が，操作5を落とすことで点群mが得られます．

（３）5回回転対称性は，並進と両立しない
均一な2次元平面を，互いに独立なベクトル a, b を用いて
na+mb となる格子点（n,m）で，デジタル化したものが結晶空間です．
すべての格子点（n,m）は同値ですから，結晶空間は周期的です．
ベクトル a, b を並進ベクトルと言います．格子点を多角形のタイル
で表現すると，平面のデジタル化は平面のタイル張りの問題になります．
ここで，正五角形のタイルでは隙間なく平面をタイル張りできないことを
確認しましょう．結局，結晶空間（今考察中のものは2次元ですか，3次元でも）
では5回対称性は存在し得ないことがわかります．

（４）フラクタルのタイル張り
正五角形でフラクタルのタイル張りをしてみましょう．
この図には隙間だらけですが，隙間をさらに2種類のタイルを使って
埋めることを考えるとペンローズのタイル張りが得られます．

（５）黄金比
正五角形の中に次々と組み込まれる小さな正五角形には，黄金比1:x　
が随所に表れています．そのため，たいへんまとまりの良い感じの
図形になります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_1_m?1427715627

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_2_m?1427715627

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.24］ No.056
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
私が通潤橋（熊本県上益城郡山都町）を訪れたのは，2007年10月のことでした．
22日は，午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業，
午後は先生方と人形浄瑠璃注）観劇を経験しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_4_m?1426898367
－－－－－
注）人形浄瑠璃は，清和文楽館
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
で観賞しました．山都町の人形浄瑠璃の始まりは，江戸時代の嘉永年間（1850年ごろ）で，
山都町（旧・清和村）を訪れた淡路の人形芝居の一座から，
浄瑠璃好きな村人が人形を買い求め，技術を習ったのが始まりといいます．
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました．
良い話です.民衆の文化の高さに感激しました．三人で一体の人形を操ります．
首（かしら）と右手を操る「主遣い（おもづかい）」，左手を操る「左遣い」，
足を操る「足遣い」です．人形も触らしてもらいました．
－－－－－－－－－－－－－

■通潤橋
阿蘇山の南側のこの付近の地形は，島のように台地があり，台地から台地への移動が
大変で平家の落人が隠れ住むのに好都合だったようです．
台地（白糸台地）に農業用水を引くのが大変です．
水は台地のがけ下に汲みに行かなければなりません．
時の惣庄屋「布田保之助（ふたやすのすけ）」は，白糸台地に水を引くための
水路橋”通潤橋”を，肥後の石工たちの技術を用いて1854年に建設しました．
通潤橋は，石造りアーチ水路橋で，長さ75.6m，高さ20.2m。幅6.5m．
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています．
通潤橋の写真（放水事に撮影k.Tani）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_0_m?1426898367
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_1_m?1426898367

通水管の写真(撮影k.Tani)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_2_m?1426898367

長さ約127m．石をくりぬいた１尺（30cm）四方の函渠（圧力のかかる管水路）．
管と管の繋ぎ目には，振動吸収と漏水防止のための漆喰（しっくい）が塗られている．
さらに，通水管には5～6ケ所に地震対策のための板（緩衝材）を挟んでいる．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/tuusui.html
通潤橋は両側台地より低いので，サイフォンの原理で出口で水を押し上げています．
通潤橋の高さから流入側台地は7.5m高く，流出側台地は5.8m高い．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/kaisetu.html
通潤橋は，今でも周辺の田畑を潤しています．
放水は，通水管に詰まった堆積物を取り除くために行うものです．

「通潤橋史料館」　に行くと，どのようにアーチ石橋を施工したかわかります．
川の中に写真のような木枠を大工が組んで石工が石を置きました．
アーチ橋の高さを台地の高さまで上げられなかった理由は，
この木枠をこれ以上の高さにする木材がなかったためという事です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_3_m?1426898367

石橋の木枠を外す最終段階は，橋の中央に白装束を纏った布田翁が鎮座し，
石工頭も切腹用の短刀を懐にして臨んだといいます．

これから，アーチ曲線の数学の話をしようと思っています．
写真で見えるアーチ曲線を型どっている石の並びについてです．
アーチの頂点にある石を”かなめ石”と言います．
アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です．
それでも下の木枠を外すときは，とても心配で責任者は命がけだったでしょう．
ーーーーーーー

さて，石積の橋の形，アーチ曲線に関して考えましょう．
アーチの両側の根元はしっかり固定しなければなりませんが，
アーチの上の石の重さが重ければ重いほどアーチの石は互い押し合い引き締め合うので，
橋は大きな荷重に耐えられるのです．石積みは引張力に抗する力はないが，
石積の石に働く力はすべて圧縮力だけなので接着の必要はなく安定構造になります．
石は圧縮に強い材料ですからアーチ型の橋には最適です．ただし，アーチ根元の支点部には，
大きな水平力が発生するので，それとつり合う大きな水平反力が必要です．
山で挟まれた峡谷などはこの点では最適な立地条件でしょう．
通潤橋の根元をしっかり押さえつけている重そうな石積の写真を見てください．

■空き缶を積んで作ったアーチ
私が真剣に積んだのですが，できるのはどうしても缶5個のアーチまででした．
5個の缶で缶同志の接点は4点．すべての接点で同時につり合っていなければなりませんから，
とても難しいことです．もし，6個以上でアーチが出来た方は新記録です．ご一報ください．
缶の周りにラップを巻いていますが，摩擦力を増すためでアーチのつり合い条件を変えるものではありません．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/46/16586546/img_1_m?1426979031

ここから先は，釣合の5つの一次方程式を連立して解く線形代数の話になりますから
省略します．興味ある方は以下でご覧下さい．
http://blogs.yahoo.co.jp/tanidr/16586546.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.17］ No.055
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
とうとう桜の花も咲きだしました．やるふりだけの中身のない政治や仕組みに呆れます．
メルマガくらいは，実質のある楽しんでいただけるものをと心がけようと思います．
ご希望コメントなどをお寄せください．

■振幅の大きな2重振り子の動画がyoutubeなどに色々あります．
大変滑稽な動きをしますのでまずご覧ください．
http://blogs.yahoo.co.jp/tanidr/16560015.html
にはインターネットから拾った2つの例を掲載しています．
第１の動画は実験，第２の動画はシミュレーション結果です．
なぜこのような話をするのかと言えば，
２重振り子は，振幅の小さいうちは，皆が見たことのある自然な振動をしますが，
ある程度以上の振幅になると，とても不自然な滑稽な動きになるからです．
振幅が大きいときは，始めのスタート位置（初期値）によって結果が変わることにも気づくでしょう．

■このような系（エネルギーが保存される）の運動は，
ラグランジュ関数（運動エネルギーと位置エネルギーの差）に対する
オイラー=ラグランジュ方程式を解けば決定できます．
ラグランジュ関数　L(x(t),x'(t)，t)は，座標x(t),速度x'(t)，時間tの関数です．
オイラー=ラグランジュ方程式というのは変分原理とも呼ばれ，
ラグランジュ関数の時間積分（これを作用積分といいます）が
停留値となるようなx(t)の経路を見つける方法です．
ここでは，代表して変数はx(t)しか記述していませんが，
実際は自由度の数だけ変数があり，
これと同じ数だけオイラー=ラグランジュ方程式ができます．
エネルギーが保存される系では，ラグランジュ関数は作れるのですが，
オイラー=ラグランジュ方程式は，一般に解けません（解を関数で書けません）．
昔，私達が物理学で演習したのは，解のある特殊なケースばかりだったのです．
注）振幅の小さい範囲では，x(t)やx'(t)の2乗まで残す近似で，
線形な微分方程式の固有値問題に帰着します．
詳細はhttp://blogs.yahoo.co.jp/tanidr/16560687.html

■問題は振幅の大きいときの運動を知る方法です．
これは解析的な解が得られないので，
今日のようにコンピュータが使えるようになって数値計算ができるようになりました．
そのためのプログラムは，次のような手順です．
現在の位置と速度をx(n),x'(n)とします．
x(n)，x'(n)から加速度x''(n)を得るのは，オイラー=ラグランジュ方程式を使います．
一方，x'(n+Δ)＝x'(n)+x''(n)Δ，　x(n+Δ)＝x(n)+x'(n)Δ　ですから，
x(n), x'(n), x''(n)から，時間ステップΔ後の x(n+Δ)，x''(n+Δ)が更新できます．
このようにして，初期値から，逐一運動の様子を求めていきます．

■力学系を記述するラグランジュ方程式は存在するのだが，
解を関数で記述できない（解けない）方程式が大多数です．
系の運動を支配する法則（ニュートン力学）は明確なのに，
解が関数で記述できないのです．コンピュータによって
運動は逐一決定できますが，常識と違う予想もつかない挙動が起こる．
分岐やカオスです．このようなことを指摘したのはポアンカレでした．

・1766　オイラー「変分法の原理」
オイラー，　ラグランジュ
・1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ
・1900　ポアンカレ
可積分の方程式はごくわずか
大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．
－－－－－－
可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

力学系を記述するラグランジュ方程式は作れるのだが，これが解けるとは限らない．
物理の演習では，解けるものしか扱わなかったのです．
実際の世の中は，解を関数で記述できない（解けない）方程式が大多数．
系の運動を支配する法則（ニュートン力学の方程式）は明確なのに，
解が関数で記述できないのだ．でも，コンピュータによる数値計算により，
運動は逐一決定できる．しかも，予想もつかない挙動が起こる．
このようなことを指摘したのはポアンカレでした．

1766　オイラー「変分法の原理」
オイラー，　ラグランジュ

1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ

1900　ポアンカレ
可積分の方程式はごくわずかで，大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．

可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

分岐理論

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.10］ No.054
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回はホットなニュースです．
■錯視のシンポジウム
http://cmma.mims.meiji.ac.jp/…/jointrese…/demosillusion.html
International Symposium on Psychological vs Mathematical Approaches to Optical Illusion
が，明治大学中野キャンバスで，2015年3月4-6日に開催されました．
興味があるテーマでしたので多くのセッションを聞きたかったのですが，
私の時間の許す5日の14:00~17:20のセッションだけ参加しました．
https://www.facebook.com/sgk2014?fref=nf
注）
3月12-14日に明治大学駿河台キャンバスでサテライトミーティングがあるようです
http://www.mims.meiji.ac.jp/seminars/another/2011/20120313.html
ーーーーーーーーーーー
聴講したセッションの座長はYasushi Yamaguchi,
講演は次の3件；
Masanori Idesawa, A model for explaining tha anomalous motion illusion.
Akiyoshi Kitaoka, Color-dependent motion illusion in stationary images:
What causes illusory motion?
Stuart Anstis, Illusion of motion perception.
ーーーーーーーーーーー
会場は，明治大学中野キャンバス，5Fの新しい楕円型の階段ホール．
参加者は若者が多く４０人程度であった．この国際シンポジウムのオーガナイザーは，
Kokichi Sugihara(明治大学), Akiyoshi Kitaoka(立命館大学)です．
注）
明治大学は，2008年度，「現象数理学の形成と発展」グローバルCEOプログラムに採用された．
数学系では，東京大学，京都大学，九州大学，明治大学が採択されている．
大学院先端数理科学研究科，現象数理学専攻は2011年に開設，2013年に中野キャンバスがオープンした．
明治大学には錯視美術館（大学と少し離れた淡路町）があり，毎週土曜日だけ開館している．
博士前期課程では，学生1人に対し正副3人の指導教員が広がりを持った研究指導を行う．
後期課程では，学生の研究テーマに応じて，モデリング，シミュレーション，
数理解析の3分野から1人づつ計3人の指導教員がチームを組んで多角的な研究指導を行うという．
現象数理学は，微分方程式のモデルで定量的に記述し，コンピュータでシミュレーション．
分岐理論でなぜ違いが生じるのかを理解する．金融工学，進化ゲーム理論，錯視の仕組みなどが，
数理モデリングを通じて理解ができる．修了後の進路は，
ビッグデータを扱うIT系企業，金融機関，教員など．米国の例では，
投薬タイミングなどを分析して医師らにアドバイスする病院ポストなどまで広範である．

2006年の文科省科学技術政策研究所「忘れられた科学－数学」で
数学と他分野との共同研究実施に向けた体制整備が叫ばれた．
数学と諸科学の連携研究は，米国MAMでも盛んに報じられており，
活発化している数学の分野である．これが純粋な数学と呼べるかの疑問はさておき，
高性能のコンピュータと数値計算の発展により可能となった新しい分野である．
エネルギー散逸のない系を記述するオイラー=ラグランジュ方程式は存在するが，
その大部分は解けない（関数で書けない．非可積分という）．
学生時代に教科書で扱ったのはごく特殊なケースなのだ．
これらをコンピュータを用いて数値的に解くことになる．
安定軌道がなくカオス的で分岐が生じる現象が注目される．
同様にビッグデータを解析する統計学でもコンピュータが活躍する．
日本数学協会が，６月7日午後に予定している講演会（於大東文化大学）
「ヒトとモノづくり数学－10年目の数学月間」でも，
数学月間の経緯と並べて錯視を取り上げることになっている．
ーーーーーーーーーー
■静止画なのに動きを生じる錯視
見ているのは静止画なのに動きが出る（なぜ時間の要素が入る）のか？
と不思議に思うでしょう．見る側に原因があります．目の空間認識は，
TVのようなラスタースキャンではないが，サッケード運動，ドリフト，
中心視と周辺視の切り替わり，網膜の周期的なリセット，等々により，
これらは時間の関数だからです．私は形の認識の仕組みに興味があります．
図形の対称性を見て快いと感じるのは，単純なサッケードになるからだろうと考えていました．
そして今回，これは錯視と表裏一体の現象であると気付きました．図形の認識にかかわる
測度量で時間の関数であるものが，動きのある錯視を生む原因になるようです．
動きを生む錯視にも色々あります．北岡の回転する蛇に見るように，
黒/暗灰/白/明灰/黒/･･･の明暗のストライプで，白から黒の方向に動くように見える現象が，
色相のストライプでも起こり，周囲が明るいときと暗いときでは動く方法が逆になる．
このようなデザインは処々で活用されています．
http://www.ritsumei.ac.jp/~akitaoka/rotate.html
同じものを見ていても，全域的回転を認識するか局所的回転を認識するというように
注目現象が異なることがあります．どちらかを認識すると他方は見えないのです．
これは亜群の集合で核となる部分集合をどれに定義するかの問題と類似しています．
■青・黒ドレスの色が変わる
動きは生じない錯視の例として，青・黒の横縞のドレスが白・金の横縞に変わるのが，
このシンポジウムの紹介を兼ねて3月4日の夕方のTVニュースで取り上げられました．
youtube動画やtwitterなどで，この原因が，右脳，左脳による個人差だというような
説が流れていますがそれは嘘です．周囲の明るさに依存して変化するのです．
色相変化ではγ特性が効いています．
宮澤賢治が注文の多い料理店序文で「はたけや森の中で、ひどいぼろぼろのきものが、
いちばんすばらしいびろうどや 羅紗 や、宝石いりのきものに、
かわつているのをたびたび見ました」と言いましたが，これは錯視ではありません．
でも黄昏の光できものの模様が変わって見える錯視はあることでしょう．
フィルタリングや非線形γ特性などは，画像処理で日常使われているものですが，
これらも錯視を生む場合があります．
Stuart Anstis(University of California)は，動きを生む錯視の原理が理解できる例を
以下に掲載しています．http://anstislab.ucsd.edu/illusions/

■2重振り子（振幅の大きいとき）

微小な振幅であるならば，解析的な解があり，あまり複雑でない周期的な運動になることを前回に学習しました．
しかし，振幅が大きくなると，ラグランジュ関数 L の近似ができませんので，ラグランジュ方程式は解けません．
しかし，将来，誰かが巧妙な方法で解くのではないかと期待し，最悪そのような解析的な解は存在しないとしても，
振動範囲が小な場合と本質的に大差はないのではないかと想像するのが自然なことでした．
系のラグランジュ関数 L は全く正しいし，ラグランジュ方程式も正しいのですから，
解析的に解けないと言っても心配ないのではと思うでしょう．

しかし，実験ではとんでもない現象が見られました．
コンピュータを用いた計算が高度になり，力ずくで動きのシミュレーションがなされるようになりました．
正しい方程式は実在するのですから，関数による軌道記述は出来なくても，動きは逐一決定されるはずです．
しかし，初期条件（初期値）により，予想もつかない挙動が見られます（カオス）．

◆第１の動画は実験
スタートする初期値によって運動の様子は異なります：

◆第２の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1

■2重振り子（振幅の小さいとき）

図のような2重振り子の運動です．今回は物理演習のようになりましたが，
数式に囚われる必要はありません．重要なのは，振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので，2種類の周波数の振動が重畳
された運動になる．つまり，関数で記述できる安定な周期的な運動になる
という事です．そして，これに対比される次に話題になる振幅の大きい
2重振り子運動では，運動は関数で記述できず，予想もつかない
とんでもない運動をするということです．

◆それでは，振幅の小さいときの2重振り子の学習をしましょう．
ここでは，ラグランジュ関数やラグランジュ方程式を説明せずに用いています．
これらを学習したい方は，EMANの物理学などが参考になります．

m1の座標は

これは，Oから釣り下がる長さ l の糸と
mから釣り下がる長さ l₁ の糸の和であるからだ．

この2重振り子のラグランジュ関数Lは

Tは系全体の運動エネルギー，Uは系全体の位置エネルギー
解Φ，ψ を求めるには，次のラグランジュ方程式を解かねばならないのだが

解析的には解けない（関数で記述できる解がない）ので，
Φ，ψ の振動範囲を微小に制限して（Φ，ψの2次までを残す近似），

この近似した L=T-U を用いて，ラグランジュ方程式を解く．
これは解けるのだが物理の演習問題なので（参考）に示し，結論だけ述べる．
結論
Φ, ψ は，以下の2つの固有ベクトル（基準振動）の重畳（線形結合）で表せる．　

微小振動の範囲では，Φ，ψは，それぞれ２つの固有振動の重ね合わせであるということは，
それほど複雑な振動ではない．いずれにしろ周期的な振動である．
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
（参考）

続く⇒　振幅の大きい場合

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.03］ No.053
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
3月になりました．皆様，お元気にお過ごしでしょうか．
母が救急車で入院した1月には，硬い芽のようだった病院の梅も，
今はすっかり咲いてしまいました．白梅でした．
病院は遠方なのですが，見舞いにほぼ毎日通っています．
ここの梅の花の咲くのが見られるとは思っていませんでした．
でも，お陰様で無事に日々が過ぎています．

無限に繰り返す周期的な空間を結晶空間といいます．
このような空間を，正多面体（あるいは半正多面体）を組み合わせて，
すきまなく充填する様式を観賞しましょう．
これは立体パズルとしては難しいものですが，自然界ではめずらしくありません．
美しい鉱物結晶の構造として，結晶学の常識になっています．
空間分割の対称性，空間群の研究は，数学者ではなく
フェドロフなどの結晶学者や鉱山技師が偉大な業績を残しています．

■立方体（1種類）を積み重ねた周期空間から始めましょう．
Fig.1の4列目の最上行（右上隅）にあります．
http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16535749&no=1
（これらの図はPOV-Ray，v3.7を用いて作成しています）

1列目の図は，立方体と正8面体を重ねて表示したものです．
これらの2つの正多面体は互いに双対*の関係にあります．
（*立方体の面を頂点に，頂点を面に変えたものが正8面体）
立方体のサイズを固定して，正8面体のサイズを連続的に変化してみましょう．
第1列の上から下へ，正8面体のサイズを徐々に小さくしています．
そのとき，立方体と正8面体の共通部分として得られる半正多面体が第2列．
これら半正多面体の名前をシュレーフリ記号*で書くと，
第2列の上から順に［3,8,8］,［3,4,3,4］,［4,6,6］です．

*)記号の見方：例えば［3,8,8］は，頂点のまわりが，
正3角形，正8角形，正8角形で囲まれているという状態です

■第3列は，それぞれの多面体を2次元に配列させて作ったシート．
第3列の上段図には小さい正8面体，中段図には大きな正8面体を立てる穴が，
下段図では，正８面体ではなく同じ半正多面体［4,6,6］用の穴ができます．

■第4列に，空間を隙間なく埋め尽くす正多面体の組み合わせを示します．
第4列の最上段図は，立方体のみでできる配列．
立方体だけで隙間なく空間を充填した構造は単純格子といいます．
第２，第３の行に，正8面体の穴に正8面体を詰めて空間を充填する様式を示します．
これらも格子としては単純格子と同じです．
第４の行は，多面体［4,6,6］のみで空間を充填できることを示します．
このとき出来上がる構造は体心格子と呼ばれます．

■ペロブスカイト（CaTiO3）構造
Fig.1の下から2行目の配列構造を見てください．
正8面体と［3,4,3,4］多面体の組み合わせで，空間が充填されています．

Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/79/16539279/img_3_m?1425130572
正8面体の中心にTi原子，［3,4,3,4］多面体の中心にCa原子，
各多面体の頂点にはO原子を配置すると，ペロブスカイトの結晶構造が得られます．

余談ですが，この構造は，強誘電体や超伝導物質と係わりがありますし，
地球マントルの高密度物質の構造とも係わりがあります．

■ダイヤモンド構造
Fig.3
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_0_m?1425310851
こんどは，正8面体の稜を共通にして，平面シート状に並べます．
もちろん，正8面体だけでは空間の充填は出来ませんので，
正4面体の隙間がたくさんできます．正4面体の隙間はFig.3の緑のシートが
積み重なったようになり，頂点で８つの正4面体がつながり（シートが重なるため），
正4面体と正8面体の比率は2:1です．
空間の充填パズルはこれで正解なのですが，ついでにダイヤモンド構造を作ってみます．
Fig.4
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_1_m?1425310851
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_2_m?1425310851
正8面体（間隙）を取り囲む緑の正4面体の半分だけ使い，
各頂点で４つの正4面体がつながるようにします．
ダイヤモンドの結晶構造は， このような正4面体の配列が繰り返し，
青い正4面体の中心と頂点の位置に炭素原子を配置した構造*です．

*)正4面体の中心にある炭素原子から，4つの頂点方向に4本の結合が伸びています．
正四面体のどの頂点も4つの正4面体と規則正しくつながつているので，
正4面体の頂点の炭素原子からは，周りの４つの正4面体の中心にある炭素原子に向かって，
同様に4本の結合が伸びています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.24］ No.052
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
球表面を平面に投影するステレオ投影
地球儀を2次元平面の地図に

■性質1:　円は円として写像される
ステレオ投影というのは，球表面の点 Z(ξ，η，ζ)を，
北極 Nと結んで，南極 Sでの接平面 Π上の点 z=x+iyに投影することです．
N(0,0,1)，S(0,0,0)を直径とする球面の式は，ξ^2＋η^2+ζ^2=ζ　であり，
この球面はリーマン球と呼ばれます．
Z(ξ，η，ζ)は, (0,0,1）と（x,y,0）を結ぶ直線上にあるので，
ξ=x(1-ζ), η=y(1-ζ), これらを球の式に代入すると，ζ＝r^2/(1+r^2）となる.
ただし， r^2=x^2+y^2 である．　まとめると；
ξ＝x/(1+r^2) ，η＝y/(1+r^2)，ζ＝r^2/(1+r^2）
逆に解くと，x=ξ/(1-ζ)，y=η/(1-ζ)，r^2＝ζ(1+r^2）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_2_m?1424438241
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_3_m?1424438241

平面上の任意の円の方程式は　a(x^2+y^2)+bx+cy+d=0　である．
この円の方程式の x, yに，上記の表式を代入し，
ξ^2+μ^2＝ζ(1-ζ)を用い整理すると
(a-d)ζ+bξ+cη+d=0　が得られる．
この１次式は平面を表し，球表面との交線は円となる．従って，
「平面上の円は球面上の円から投影され」この逆も成立することがわかる．
以上で証明は終わりですが，直観的な説明を補足します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_4_m?1424438241

リーマン球上の円は平面Ωで球を切った切り口で，PQはこの円の直径です．
△NPQおよび△Nqpは，直径NSを含み，円の直径PQおよびpqを含む平面です．
図に示すように両三角形でα，βは互いに等しく，両三角形は互いに相似です．
PQを直径とする円に相似な円が，平面Π上にqpを直径として投影されるでしょう．

■性質2:　ステレオ投影は等角写像
複素関数 f が，複素平面領域 D のあらゆる点で微分可能*なら，Dで正則といいます．
*微分可能とは，どの方向からその点に近づいても同一の微分係数が確定することで，
微分係数が０や∞になる点は特異点といいます．
正則関数による写像は等角写像*です．
*写像された像が歪んでも，微小部分の角度は元の像の角度と変わらない．
ステレオ投影(複素平面からリーマン球面への写像 f )は，正則関数なので，
任意の点z0で交差する曲線の投影結果も，
それらの交差角度が保存されたまま投影されます（等角写像）．
（f(z1)-f(z0))/(f(z2)-f(z0))=(df/dz)(z1-z0)/(df/dz)(z2-z0)=(z1-z0)/(z2-z0)
ただし，z1,z2→z0 で成立．
lim arg(f(z1)-f(z2))=lim arg(z1-z2))
偏角について成立するこの式は，微小領域で写像による角度が保存されることを示す．
Fig.1に示した横倒しの地球儀のステレオ投影の様子を見ると
平面に投影した地球の下側半分の子午線は，大変歪んでいるが
互いに直交している状態は変わっていないことがわかる．

■諸科学への応用
等角写像は工学の色々な分野で利用されている．
色々な境界条件に合うようにする等角写像は，流体力学で活躍している．
何度でも微分可能であるという複素関数の性質も
我々の身の回りの現象を記述する方程式で頻繁に利用されている．

ご感想やコメントなど，以下のブログあるいはメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.17］ No.051
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号に引き続き双曲面分割の話です．

■エッシャーの「極限としての円」のシリーズが生まれるまで

コクセターとエッシャーは1951年の国際数学会で出会いました．
1958年にコクセターはこの分割を掲載した論文をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_0_m?1423875894

エッシャーの双曲面分割作品のシリーズ１は直線魚のモチーフでした，
天使と悪魔など，このシリーズの作品群があります．
そして，シリーズ3の洗練された作品に至り完成します．

■次に示すのは，エッシャーの作品「極限としての円3」です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_1_m?1423875894

白い線で分割されたタイル張りは，複数の正多角形による準正則タイル張り
[4,3,4,3,4,3]のように思うかもしれません．
しかし，白い線は直線ではないのです．白い線は，双曲世界のフチの円周と
直交しません（80°で交わる）．実は，右図に示される黒い線が直線です．
右図のように正8角形のタイルが頂点で３つづつ集まる正則分割{8,3}と
見るのが正しいのです．エッシャーの作品は，黒い線は顕に出さずに
白い線を見せて見事に数学的に正確で芸術的な作品に仕上げています．
このエッシャーのトリックについては，コクセターが論文で指摘しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.10］ No.050
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユークリッド幾何，楕円幾何，双曲幾何
色々な幾何空間があります．大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．これら3種を，平面を例にとり比較します．
（１）我々の常識の通用するのはユークリッド平面です．
ご存知のように，ユークリッド平面では，直線外の1点を通る平行線は唯一本だけ引けます．
（２）球の表面は楕円幾何平面の例です．地球の表面だけを想像しましょう．
地球自体は，3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面の例です．
楕円幾何平面の直線は大円（球の中心を含む平面による球の切り口）です．地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，これは地球の大円上の線分のことです．地球は3次元ユークリッド空間の物体ですから，地表の2点を地球内部を通る直線で結べば最短距離でありますが，地表だけの2次元平面では大圏コースが最短です．球表面の異なる２つの大円は必ず2点（直径の両端）で交わります．そのため楕円幾何平面では．平行線はありません．また，地球儀の緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面では，ある直線に対する直線外の1点を通る平行線は無数に引けます．双曲幾何平面は楕円幾何平面のように閉じていないので，イメージを持ちにくいのですが，ポアンカレがうまいモデルを提唱しました．このモデルはポアンカレの円盤モデルといいます．双曲幾何の世界を表すのに円盤を用い，この世界の直線は円盤のフチに直交する円弧とします．このように定義された世界では，ある直線に対する直線外の1点を通る平行線は無数に引けることがわかります．

■3種の幾何平面で，平面の正則分割を考える
さてこれからやることは，それぞれの幾何平面で，正多角形のタイルによるタイル張りを考えることです．このような問題は，平面の正則分割とも呼ばれます．
それぞれの幾何平面での多角形は，それぞれの幾何平面の定義による直線で囲まれているものです．それぞれの幾何平面で，3角形の内角の和Sは，S=π（ユークリッド平面），S>π（楕円平面），S<π（双曲平面）になります．
正p角形が頂点でq個集まってタイル張りがなされている状態{p, q}で，正p角形の内角の和を表す式を等号で置くと　(2π/q)p=(p-2)S　が成り立つので，
1/p+1/q=1/2　（ユークリッド幾何）
1/p+1/q>1/2　（楕円幾何）　
1/p+1/q<1/2　（双曲幾何）
となります．それぞれの幾何平面で，許される{p,q}の整数解を求めると，以下のことがわかります．
（１）ユークリッド平面での正多角形によるタイル張りは，正3角形，正4角形，正6角形で可能．｛3,6｝．｛4,4｝，{6,3}が解です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_0_m?1423315106
（２）楕円幾何の平面では，正6角形以上の正多角ではタイル張りができません（閉じた立体になりません）．
調べてみると，正5角形のタイルでは，頂点に3つのタイルが集まるもの{5,3}，正4角形のタイルでは，頂点に3つ集まるもの{4,3}，正3角形のタイルでは，頂点に5つ{3,5}，４つ{3,4}，３つ集まるもの{3,3}が作れます．結局，5種類の正多角形によるタイル張りがあり，これらはプラトンの正多角形に対応した球面立体です．ここでは｛5,3｝に対応するもののみ掲載します．黄色い球面正5角形が頂点で3つ集まっているものです．黄色いタイルに5mの対称性があるとき，赤で塗った三角形を中心から見込むような万華鏡を作るとこの映像が再現できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_1_m?1423315106
（３）双曲幾何の平面では，正則分割は無限にあります．
例として｛6,4｝と{5,4}のものをとりあげ掲載しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_3_m?1423315106
例えば，{6,4}の映像を3角形の万華鏡で作るには，
下図の中心に頂点のある三角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧の鏡を使います．しかしながら，この円弧は数学的に反転円として定義されているのですが，現実の光学法則では火線という収差があるので，あまり奇麗な万華鏡映像にはなりません
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_4_m?1423315106

■円盤の中の不思議な世界
私たちの宇宙は膨張していることが知られています．
遠方の宇宙のフチの後退速度はものすごく，光速に達すると，
こちらに光はやって来ません，そこが宇宙の果です．
宇宙銀河の回転速度は，宇宙のフチに行くほど大きく
高速で運動する世界の長さは，我々から見ると縮んで見えます
つまり，宇宙は双曲幾何の世界に似ています．
双曲幾何の円盤の内では，円盤のフチに近づくほど空間が縮みます．
この世界では，直線に沿って旅する自分自身もフチに行くほど縮むので
いつまで歩いても世界の果てに到達できません．
同様に，円盤の中心に近いほど距離が大きくはかどるので，
円盤の外から見ている我々には，直線が円盤の中心方向に膨らんで見えます．
一方，円盤内の世界にいる者にとってはこれが最短距離で直線なのです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.03］ No.049
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１種類の形（2等辺3角形）の赤色と黄色のタイル（赤タイルと黄タイルは互いに鏡像）
で作ったタイル張り模様を鑑賞しましょう．
1種類のタイルで，平面をタイル張りすると，必ず周期的なタイル張りになってしまう
と思い込むのは間違っています．確かに，
Fig.4　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_5_m?1422741853　や
Fig.5　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_6_m?1422741853
のような周期的なタイリングはすぐ思いつきます．
しかし，
Fig.2　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_1_m?1422741853　や
Fig.3　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_2_m?1422741853
のように非周期なもので，平面をタイル張りするものがあります．
Fig.2は中心に回転対称があるタイリング模様で，点群5mの対称性です．
Fig.3は，２つの目がある螺旋パターンのタイリングで，
水平線は映進面だと思うかもしれませんが，このパターンには周期がありませんから
映進操作はできません．螺旋の目の間（中心）に対称心があります．

さて，ここで万華鏡で作られるタイリング模様
Fig.1　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_0_m?1422741853
の登場です．
この万華鏡を生む3枚の鏡は１つの頂点では点群を生成しますが，他の２つの頂点では点群を生成しません．
従って平面を赤と黄色の市松模様で埋めることはありません．
全体の代数系は，群より緩いもの（特殊な亜群）になってしまいますから非常に複雑です．
対称操作は局所的で，独自の作用域と値域があり興味深いものです．
作用域，値域の制限のために，一つのタイル全体が無傷で写像されるパターン内の位置と，
部分が写像される位置があり，このような複雑なタイリング模様ができます．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊
ご感想コメントなどを，
http://blogs.yahoo.co.jp/tanidr/16430597.html　あるいは　以下のメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.01.27］ No.048
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１．万華鏡の美しさが我々の心をとらえる理由は，対称性とカオスの共存
完全な秩序は美しいが，死の世界のようだ．
一方，乱れは千変万化し同じ光景を見るのは一度きり．
そして現象は，いつ起こるかわからない．だから
我々は，はらはらしながら期待し目が離せない．
万華鏡は，秩序の中に乱れもある．生命も，秩序とカオスのただ中にある．
万華鏡の中を降りゆくガラス屑　定まると見し運命にカオスあり

２．対称性
それでは，まず対称性についての考察を始めようと思います．
対称性は自ずと決まるものとして，あるいは合理的なデザインとして生まれます．
環境や境界条件，自然科学の法則が，
その環境下の物質構造やふるまい/現象の対称性を自ずと決定する．
（例）人体，生物，乗り物，結晶，自己組織化，建築物．蜂の巣，花弁の形，柱状節理，etc．
■空間に関する対称性（１点の周りの対称性と周期）
タイル張り，壁紙模様，正多面体，結晶構造，エッシャーの版画．
■時間に関する対称性
時間反転．音楽（J.S.バッハ），詩の韻律，リズム，同期現象．
■現象の対称性
性質空間の対称性．因果律の対称性．

３．対称性はなぜ快いか？
インクの染みは汚らしいが，乾かないうちに紙を折り鏡映対称の染みになると美しく見える．
そしてなんだか想像力を駆きたてる（ロールシャッハ・テスト）．なぜ美しく感じるのだろうか．
私はその理由は次のようなものではないかと思っている：
物や事に対称性があると，我々の脳がその全貌を把握するための情報量が圧倒的に減る．
例えば，結晶とアモルファス（ガラス）で，それらの構造（構成する原子の位置）を
記述しようとすると，規則的な繰り返しのある結晶の方が圧倒的に単純だ．
人間の脳は，整理された少ない情報量だと負担が少なく，快いと感じるのではないだろうか．

４．鏡
万華鏡の話がテーマなのだが，ご存知のように万華鏡は合わせ鏡でできている．
万華鏡の対称性は，鏡映のみにより生成されたものに限ります．
我々は鏡をのぞきこむと何か変な気持がするものだが，以下のような話があります：
太古の時代は，我々の世界と鏡の中の世界の行き来ができたそうだ．＊

＊注）このようなことは4次元の世界なら実際に可能である．例えば，3次元空間で
右の手と左の手は，互いに鏡像になっている．右手が我々の世界にあり，
左手が鏡の世界にあると想像してみよう．左手が鏡の世界を抜け出して
我々の世界のなかで，右手と重なろうとしてもできない相談だ．
ただし，4次元空間なら左手の中身を裏返して，右手と同じにすることができる．
2次元の紙に描いた線画の右手と左手が，いくら紙表面の上で移動しても
ひったり重なることはできないが，紙を折り返す（3次元空間での操作）ならば
重ねることができることは実験で確かめられる．

話を戻すと，鏡の中の生き物とこちらの世界の生き物は仲良く一緒にいたのだそうだ．
ある夜，突然，鏡の世界の住人達が我々の世界で好き勝手を始めるようになった．
そして人々は，鏡の中の住人の正体が「混沌」であることに気付いたという．
そこで，黄帝が魔力によって「混沌」を鏡の世界に閉じ込め，
姿や動きも我々の世界の模倣しかできないようにした．*1)
呪文の効果が切れて，鏡の世界の住人達が勝手に動き出すことが将来起こるかも知れない．
そのようなテーマの小説に*2,3)がある．私は幻想怪奇小説が大好きです．

*1)Turbulent mirror, J Briggs & F. D. Peat, 訳：高安秀樹，高安美佐子
*2)パイプをすう男，M･アームストロング，幻想と怪奇 1（ハヤカワ）
*3)わな，Ｈ・Ｓ・ホワイトヘッド，怪奇幻想の文学(新人物往来社)

混沌の中から湧き出るように次々と生まれてきたさまざまなものが宇宙を形作った．
このようなプロセスを神の技と語られることもあります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.30］ No.044
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年もあと2日になりました．私は部屋の大整理掃除で3日間も満足にパソコンを開けません．
皆様には，よい年末でありますように．そして良い年をお迎えください．来年もよろしく．

クバンチックの問題は如何でした．私が一番好きなのは，第2問のビリヤードの問題です．
この問題に関する連想考察は，近いうちにぜひ書きたいと思っています．

さて，私は毎年「とっとりサイエンスワールド」で万華鏡のワークショップをやらせてもらっています．
正月まもなく（1月16日，PM3～）多摩センターでも開催しますので，お近くの方はご参加下さい．
詳細は，sgktani@gmail.com　にお問い合わせください．
これからメルマガでも，万華鏡の数学について何回か連載するつもりです．
ここで紹介する万華鏡のキットは，「その道の達人派遣事業」の時に開発し，
各地の学校を回り子供たちと作った万華鏡（当時は2種類）がもとで，
その後品種を増やしてできたものです．
-----
◆万華鏡の原理（１）
万華鏡は合わせ鏡の原理を使っていることはご存知ですね．fig1を見てください．
平行な合わせ鏡で挟まれた室（黄色）は1次元に無限に繰り返しています．
室内にある赤い物体もfig1に示したように繰り返します．
黄色い部屋の隣はその鏡像（左右が逆）．合わせ鏡で挟まれた黄色い部屋を（黒），
隣の鏡像の部屋を（白）と思うと，黒白の帯（1次元の市松模様）ができますね．
今度は，合わせ鏡のなす角度を平行でなくθ°とすると，
市松模様の帯は直線ではなく円を描くように延びて行きます．
円の反対側で市松模様がうまくつながるためには，
黒白のペアの数が整数でなければならない．
これは360°/2θ°＝n（整数）となります．これは，万華鏡の発明者
スコットランドの物理学者ブリュースターが1817年に提出した特許にあります．

FIg.1
以上の説明は2枚鏡の合わせ鏡でしたが，複数鏡の合わせ鏡でもできます．
3枚鏡の場合を考察しましょう．fig2には鏡が作る3角形の図です．
3角形の頂点で2枚の鏡が出会うわけですが，それぞれの頂点で，鏡のなす角度は
360°を偶数で割り切る角度である必要があります．3角形の３つの頂点で
この条件が満たされているなら3角形のタイルで平面が市松模様に張り尽くされます．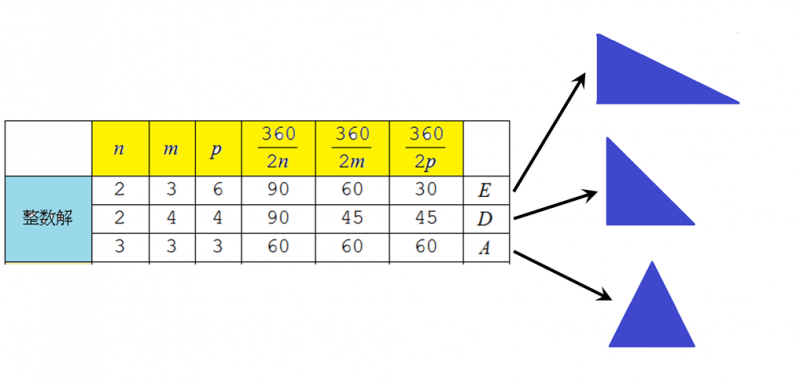

Fig.2
3つのどの頂点でも整数解を持つ場合は，平面をきれいに埋め尽くす市松模様ができます（3種類あります）．
1つの頂点でも整数解にならない場合には，市松模様は乱れますが，これも万華鏡としては美しいものです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.23］ No.043
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
«Квантик»クバンチク（量子っこ）というロシアの生徒向けの雑誌を知りました．
http://kvantik.org/
数学，言語学，物理学などの自然科学の疑問や問題を楽しく学ぶ新雑誌のようです．
onlineでは12ページまでしか出ていないので，その先は購入しなければなりません．
クバンチクで現在出題されている「4つの課題」を紹介します．
出来た人は解答を　kvantik@mccme.ru.　に送ると独創的な解答は公開されます．
面白い問題で私は出来ましたよ．問題もさることながら，
ロシア語の題意を解釈するのに時間がかかってしまいました．
翻訳を載せておきますのでご挑戦ください．

（第1問）監獄からの脱出
T字型の監獄で．2m幅の堀で囲まれている．1.9mの板が2枚ある．
ジャンプは出来ない．どのように脱出するか？
（第2問）ビリヤード
1:2のテーブルの真ん中の位置に球を置いて，テーブルの角のポケット
にビリヤードで（反射させて）玉を入れることは可能か？
（第3問）如何にしてビンをぶら下げるか
2本のマッチと50cmの糸がある．
これらを用いて水入りのビンを棚の縁（角ではない）にぶら下げなさい．
（第4問）物体の警護
物体点のまわりに，哨兵を何人か配置し，
物体にも哨兵にもこっそり近寄られることの無いようにすることはできるか？
ただし，各哨兵は，選んだ一つの方向だけまっすぐに100ｍだけ見ることができる．

解答は載せません．以下は，私からのヒントですーーー
１．Tという形がポイントです．
２．可能です．
３．マッチ2本をどう利用しますか
４．哨兵3人で済みますね．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.16］ No.042
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
パターンがどんどん内部に繰り込まれて行くデザインのいくつかを紹介します．
これらはフラクタルと呼ばれる性質と関係があります．
葛飾北斎（１８３０年代前半）の富嶽36景，神奈川沖の絵の
波しぶきを見たことがおありでしょう．あるいはこの季節の
すっかり葉を落とした木立の先が美しく枝分かれしていたり
雲や海岸線の輪郭が，拡大しても拡大しても同じような
形が現れてくるのにお気づきでしょう．
同じ形が繰り返し内部に繰り込まれているような仕組みを
フラクタルと言います．
フラクタルの詳しい説明は後回しにして
今回は応用されたデザインの例を鑑賞しましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_0_m?1418046938
グラスのこちら側の円が凹レンズになり，向こう側の円模様を
レンズ円内に縮小して映し出しているのが面白い．
（リュミナルク製）

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_2_m?1418046938
五芒星と黄金比　外部と内部の比(1+√5)/2＝1.618:1

http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16306916&no=1
レオナルドの星型8角形　外部と内部の比1+√2：1

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.09］ No.041
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆皆様，お元気でお過ごしでしょうか．選挙が迫り慌ただしい日々ですね．
大事な選挙です．私はもう期日前投票を済ませましたよ．
先週土曜日には，河合弘之弁護士の作ったドキュメンタリー「日本と原発」を
見てきました．皆様の近所でも有料試写会（自主上映）がきっとありますので，
ぜひご覧になることをお勧めします．
「原発は複雑系なので，事故が雪崩を起こす弱点（ここを攻撃されると過酷事故になる）
が思わぬところにある．その引き金となるのは，地震・津波だけではない」と，
メルマガ006に掲載したことがあります．ぜひお読みください．
バックナンバーはブログにもあります．私は，原発だけは止めたいと思っています．
高木仁三郎さんと「宮沢賢治をめぐる冒険」でお話したとき（1997年）のことが
昨日のように思い出されます．この本は，市民科学者として活躍した高木仁三郎さんが
羅須地人協会に打ち込んだ賢治と重なって見える良書です．
これら数学以外のことは，ブログの方に掲載することにしましょう．
ーーーーー

◆双曲幾何の円盤世界
Fig.1の灰色の円盤内の世界は，双曲幾何の世界です．
この世界の直線は，世界の果て（外周円）に直交する円弧
－例えば，Fig.1の赤い円－です．もちろん直径のような本当の直線も
灰色世界の円盤の外周円に直交しますのでこの世界の直線です．

赤い円で2分された灰色世界の左側と右側は
赤い円を反転円として，互いに反転鏡映像になっています．
Fig.1　
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_1_m?1418046545

2つの平面鏡と１つの円柱鏡で作られる万華鏡（Fig.2）を見てください．
赤く塗った3角形の各辺は，この円盤世界の直線です．
赤く塗った3角形の頂角は，30°－45°－90°．内角の和は165°で180°に
足りませんが，この円盤内の世界は双曲幾何の世界なので当然です．

赤く塗った3角形の辺を紙面に垂直な方向に伸ばした3角柱を考えると
平面2枚と円柱鏡からなる万華鏡ができます．
円柱鏡が生む映像は数学的な反転鏡映像としますと
Fig.2のような円盤内の分割（ポアンカレ万華鏡像）が得られます．
塗られた3角形と白い3角形は鏡映の度に入れ替わるので市松模様です．
Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_0_m?1418046545

実際に作ってみました．ポアンカレ万華鏡を再現するのは困難です．
円柱鏡での光の反射（物理的）は，数学的な反転操作とは異なり
厳密な数学的な反転鏡映は，光学的には実現できないのが残念です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.02］ No.040
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先に，「007_インドラの網と反転円」で言及したことがありますが，
円による反転鏡映について，その性質や利用例を鑑賞しましょう．

◆円による反転鏡映の性質
下図に赤い円による反転鏡映の代表的な例を２つ示します．
・反転円をよぎる直線aを反転すると，反転円の中心を通る円Aになる．
・円bを反転すると，円Bになる．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_0_m?1417183249

この性質を知っていると，色々なことに利用できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_3_m?1417183249
例えば，このような図形はアルベロス（靴屋のナイフ）
といいますが，この中の幾何学世界の面白さなどです．

下図のアポロニウスの窓の中にある黄色の円とピンクの円は，
緑色の円を反転円として，それぞれ反転円内の黄色とピンクの円が
鏡映像になります．これらの鏡映像は平行な直線（黒）に挟まれた
領域内に入ります．
平行直線の左はアポロニウスの窓の外周円の反転鏡映，
平行直線の右はアポロニウスの窓内にある左側の大きな円（灰）の
反転鏡映像です．なぜなら，外周円も左側の大きな円（灰）も
反転円の中心を通っているので，鏡映像はどちらも直線になるからです．
アポロニウスの窓内にある初めの黄色い円もピンクの円も，外周円と
内部の左側の大きな円（灰色）に接しているので，
それらの反転鏡映像でもそのような状態が保たれています．

このようなことがわかると，以下のパップスの定理が導かれます．
アルベロスの中で，右側の大きなピンクの円の上に生じる
黄色の円（ω1），続いて生じる灰色の円（ω2），の系列を考えると，
「円ωnの中心と直径ABとの距離は円ωnの直径のn倍である」
（パップスの定理）ことがわかります
以下の図は，ω2の場合の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_2_m?1417183249
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_1_m?1417183249

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.25］ No.039
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆平面のブラベー格子は５つのタイプがあることを036号で学びました．
ここに示す繰り返し模様のそれぞれは，どの格子に対応しますか？
日本の伝統文様には，美しい繰り返し模様がいろいろあり，それらは
着物や食器，籠バック，インテリアなどと色々な所で見られます．
これらの模様には，どのような対称性があるかを鑑賞しましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_3?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_4?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_5?1414573530

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.18］ No.038
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆正3角形の対称性
正3角形は，中心に回転軸を立て右回りに120°回転しても，
始めの状態と全く同じで，回転したかどうかわかりません．
この回転を続けて２回行い240°の回転になっても同様です．
120°の回転を3回続けて行うと1回転して始めの状態に戻ります．
つまり，正3角形には3回回転対称があります．
このような回転軸を3回軸といい，記号は3と書きます．
その他に，正3角形は鏡映対称があります．図に示した赤い線が鏡映面です．
ここにある3枚の鏡映面は3回軸の作用で互いに移り変われるわけで，
全部同じ性質です．従って，正3角形の対称性は，3回軸と1種類の鏡映面があり，記号では3mと書きます．
◆正4角形の対称性
正3角形の場合と同様に，こんどは中心に4回回転軸があります．記号は４です．
正4角形を見ると鏡映面が4枚あることがわかります．図で赤線で描いた2枚と
オレンジ線で描いた2枚です．4回軸によって，赤い鏡映面どうしは互いに移り変われるし，
オレンジ鏡映面どうしも移り変われますが，赤とオレンジの鏡映面は，互いに移り変わることができません．
従って，今度は2種類の鏡映面があることになります．正4角形の対称性は，記号で4mmと書くことに注意してください．
◆同様に，正5角形，正6角形の場合は，図のようになることを各自確かめてください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/42/16226942/img_0?1414074741

◆対称図形の重ね合わせ
正3角形の部品を複数重ね合わせると，一般に，全体の対称性は低下するが
配置の仕方により全体の対称性が上昇することもある．
このようなことをとり上げている本は見かけませんが，とても面白い現象です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/01/16227001/img_0?1414076174

◆対称性の重畳
正6角形は正3角形の対称性を含んでいますから，
正6角形と正3角形を鏡映面が共通になるよう重ね合わせる（下左）と正3角形の対称性が残ります．
正3角形と正6角形の回転軸をそろえて，鏡映面が共通でないように重畳すると，
結果は3回回転対称だけが残ります（上左）
他の図も同様ですので，各自確認ください．正6角形と正5角形の重畳の場合は，
6回回転対称と5回回転対称に含まれる下位の対称性（共通な部分群）はないので，
鏡映面の一致がなければ，対称性はなにも残りません（上右）．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/01/16227001/img_1?1414076174

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.11］ No.037
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆ことしは結晶学の生誕100年にあたります
結晶にX線ビ－ムを照てると，
結晶がブロック積みのような周期的な構造なら回折が起こります．
（結晶内部の繰り返し構造の周期と，X線の波長が好都合なことに同程度だったのです）
そう考えたのはラウエでしたのでこの実験をラウエの実験と言います（1912年）．
X線がレントゲンにより発見（1895年）されて間もない頃でした．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/23/16237223/img_0?1414563100

結果として得られたラウエの回折像には，その原因になった結晶内部の対称性が反映されているべきです．
これは「キューリーの原理」という因果律です．
回折像を撮影して，小さくて目に見えない（~nm）結晶の内部構造の解析をしたのがブラック親子（1913年）です．
レントゲン(1901)，ラウエ(1914)，ブラック(1915)，それぞれノーベル賞をもらっています．

◆結晶世界はデジタル
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/60/16237160/img_0?1414501713
大小いろいろな結晶がありますが，写真は全部，水晶の結晶です．
結晶個体は，いろいろな種類の結晶面で囲まれており，
その結晶面の大きさも結晶個体により様々です．
しかし，同じ組み合わせの結晶面どうしのなす角度は
どの結晶個体で測っても，同じになります．
例えば，黄色い面と青い面のなす角度は（各面に立てた垂線のなす角のこと）
どの結晶で測っても同じになります．⇒面角一定の法則（1772）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/60/16237160/img_1?1414501713
アウイ（1783）は，
「結晶は小さな単位胞がブロック細工のように積み重なって出来ている」
と考えました．→すなわち，結晶世界はデジタルな空間です！
それなら，現れる結晶面(上図の青い線)は格子点を載せている面なので，
面の傾きは有理数になります．→有理指数の法則（1783）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.04］ No.036
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆平面のデジタル化
写真フィルムは連続な平面ですが，デジカメの感光面は半導体のドットが並んでいます．
人間の網膜も視細胞が配列しているデジタル化された平面です．
最近の交通信号は円の中に発光ダイオードのドットが配列しています．
これらが平面のデジタル化の例です．結晶も原子や分子が詰まった単位ブロック（胞）があり，
これがきちんと積み重なりできている周期的な構造で，デジタル化された空間の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_0?1414413690

◆平面のデジタル化の様式
無限に広がる平面の何処も均一なようにデジタル化する（ドットを配列する）なら，
規則正しく周期的な構造になります．交通信号の円内は均一なデジタル化はできません．
平面のデジタル化は対称性の観点からどのように分類できるでしょうか？
結晶学でブラベ格子というものはデジタル化様式の分類にほかなりません．
そもそも結晶空間とはデジタル化された空間のことです．
（注）周期的なドットの配列は「格子」と呼ばれます．
格子の様式分類は，研究した人の名前をつけて「ブラベー格子」と呼ばれます．
2次元の「ブラベー格子」は5種類あることをこれから説明します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_3?1414413690

まずは，1次元の周期
2次元の周期は２つのベクトルの組み合わせでできる．
対称性から分類するとこれらの５つのタイップがある．

これらから格子を作ったものが以下の図です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_4?1414413690

上図に示した緑色のタイルは「W-S（ウイグナー・ザイツ）胞」といいます．
このタイルを赤い格子点に配置すると平面がタイル張りされることを確かめましょう．
さて，これらの周期的平面は，格子点（周期的な平行移動で生じる点）
をすべて同値と考えると，１つのタイルの中に引き戻せます．
以下の図には，それぞれのタイルの対称要素を記入しておきました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_8?1414413690
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/31/16234231/img_7?1414413690
上図左は，タイルの対称性が一目瞭然のW-S胞．右は，単位胞タイルです．
（注）単位胞の図を見るとわかるように，これらの５つはすべて単位胞に格子点が1つ含まれる1格子点胞です．
上段右の菱形胞を用いずに，面心型の2格子点胞を用いるのが慣例となっていることを申し添えます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.28］ No.035
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年の「数学月間懇話会」で松原望さんから「民力指数」についての
講演がありました．指数といえば「消費者物価指数」などが有名です．
数学で指数というのは桁（比率）の表現なので，例えば，基準年の物価
に対して何倍の変化があったかという「消費者物価指数」を，
指数というのは適当でありましょう．

しかし，「民力指数」の指数の意味はこれとは違うようです．
地域の「民力指数」とは，正の数値（スカラー）で，その地域の
生産・消費・文化，および，人口などの基本指標の関数として
（26種の経済統計量の関数として）定義されます．
これは朝日新聞が30年以上前に発案した定義だそうです．

地域の「民力指数」は，地域の経済活動力の表現になります．
都道府県に対する「民力指数」は全国を1,000に，市町村に対する
「民力指数」は全国を100,000になるように規格化します．

「民力指数」は数学的には測度であるので加法的であることが
松原さんの講演で指摘されました．
地域Aと地域Bの合併の「民力指数」の試算も合理性があり
色々な利用が期待できます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.21］ No.034
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆黄鉄鉱の結晶粒の外形には，多面体がいろいろ現れることを，
028号で述べました．整理すると下図のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_0?1413100917

さて，この図の中に正12面体や正20面体の外形が見られるようですが,
結晶（周期的な内部構造をもつ）では，5回対称軸は存在できず,
5回対称のある正12面体や正20面体は外形にも生じないはずです．
詳しく調べてみると，黄鉄鉱の正12面体のような5角12面体は，
(2,1,0)面で囲まれているようです．→◆ミラー指数
両者の多面体で二面角の比較をしてみましょう：
－－－－－－－－－－－－－－－－－－－－－
黄鉄鉱　　 　126.89°　(2回軸を挟む二面角）
正12面体　　116.57°
ーーーーーーーーーーーーーーーーーーーーー
黄鉄鉱の外形（5角12面体）は正12面体ではありません．

◆ミラー指数
ミラー指数とは面の傾きの表示です．
下図のブロックのサイズは，x,y,z各１単位
（x,y,zの各単位は等しくなくても良く，斜交軸でもかまいません）
例えば，(2,1,0)面の，x軸，y軸，z軸との切片は，1/2，1，∞です．
切片の逆数の比をとると，ミラー指数　2,1,0　が得られます．

結晶は単位ブロックが積み重さなった周期的な世界です．
周期的な世界（格子点が並んだデジタル世界）の格子点を載せた
面の傾きは有理数ですから，すべての結晶面のミラー指数は整数となります．
http://sgk2005.sakura.ne.jp/htdocs/?action=common_download_main&upload_id=88

周期的な世界に5回対称軸は存在できませんので
結晶（周期的な内部構造を持つ）は，正20面体の外形になることはできません．
（注）“準結晶”には5回対称がありますが，周期的な世界ではありません．
◆黄鉄鉱の6面体，5角12面体と準結晶（正12面体）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_1?1413100917
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_2?1413100917
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/55/16194255/img_3?1413100917

◆柘榴石garnetも立方晶系の結晶構造ですので
外形もさいころのような対称性を示します．
菱形12面体~24面体（これらは正多面体や半正多面体ではありません）
の晶系の変化があります．
http://www.museum.tokushima-ec.ed.jp/bb/chigaku/minerals/img/2-32.jpg

写真はwebで拾った岩手県和賀仙人鉱山産の柘榴石結晶です
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/36/16196636/img_0?1413101685

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.14］ No.033
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
大阪大学理学部数学教室は，
現代数学の様相と数学研究の実際，自然科学や社会科学に及ぼす数学の影響，
文化としての数学の在り方などについて，多角的な視点から易しく解説する公開講座を，
高校生を対象に夏休みのこの時期に開催しています（ オープンキャンパスも同日実施されます）．
まさに数学月間の模範になるイベントで，毎年，杉田洋教授より情報を頂きSGKのwebに掲載しています．
今年のテーマは，“多面体の不思議”でした．
2014年8月12日（火），10:00～12:00
会場：大阪大学豊中キャンパス　理学研究科 D棟 D307教室
講師：村井 聡（情報科学研究科情報基礎数学専攻　准教授）
毎年，興味深いテーマが選ばれ，私も参加したいと思いつつまだ参加できずにおります．
今回のイベントでは受講生が殺到し,準備した教室に定員の2倍近い人（約100人）が
集まり，来年は教室の選択を考える必要がありそうと伺っております．
（以下は私の勝手な解説ですみません）．
-----
多面体はとても古くから考えらてきた図形で、紀元前のギリシャ時代には既にその性質が調べられていました．
多面体で基本的な定理は，オイラーの定理V+F-E=2（３次元）が有名です．
これを使うとプラトンの正多面体（凸多面体）が５つというのがすぐ証明できます．
正多面体というのは，面が１種類の正多面体でできており，どの頂点のまわりの状態も同一なものです．
正多面体の記述は，定義の本質を捉えているシュレーフリの記号を用います．
正p角形が頂点にq個集まっている（同じことだが辺がq個集まっている）状態は，{p,q}と記述されます．
３次元の多面体は，面が３個以上集まらないと作れませんし，面が正３角形の場合には，
６個集まると平面になってしまいますので，正3角形の面をもつ凸多面体は，{3,q}，q=3,4,5しかありません．
q=3の場合は正4面体，q=4の場合は正８面体，q=5の場合は正20面体です．

全ての面が合同な正3角形であるが正多面体でないものまで数えると8種類になり
これらをまとめてデルタ多面体と呼びます．
1種類で空間を隙間なく充填できる正多面体は立方体だけですが，
2種類の組み合わせで空間を充填できる正多面体は，正4面体と正8面体です．
結晶学では良く知られていることですが，面心格子と体心格子というのも立方体と同じ対称性を持ち，
それぞれのウイグナー-ザイツ胞（デリクレ胞とも言う）は，それぞれ菱形12面体，切頂正8面体になります．
数学と諸科学［科学や造形］の関わり合いで現れる多面体の性質は，非常に興味を惹く話題です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.10.07］ No.032
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
「化学の日」10月23日は，化学4団体（日本化学会，化学工学会，日本化学工業協会，新化学技術推進協会）が
昨年制定しました．その日を含む月曜日から日曜日までの1週間が「化学週間」です．
もちろんこれはアボガドロ数6.02×10^23に因んでいます．
これも米国が先でNational Mole Foundationが10月23日をMole Dayと定め，
10月23日6時02分にイベントを行うなど色々な活動が盛んだそうです．

日本の「化学の日」初年度の今年は産官学一体となって，化学の普及活動が国民亭イベントとなるように
呼びかけています．我々の「数学月間」もこのような取り組みが必要で，「化学の日」の経緯は手本になります．

*****以下は，化学と工業,Vol67-9,2014,玉尾皓平氏（日本化学会前会長）の記事からの抜粋です*****
◆2年前の会長就任時に提案した2つの具体的提案を紹介します。
「全国一斉オープンキャンパス」：これが 「化学の日」と直結する提案です。
各大学. 研究機関や化学企業で独自に行っているオープンキャンパスやオープンファクトリーを，
「化学の日」「化学週間」にできるだけ 曰程を合わせて一斉に実施いただくことで，
国民的イベントとして認知度を高めようとの取組みです。
「『夢・化学-21』の全国統一ブランド化」： 「夢・化学-21」キャンペーンの強化策として，
そのロゴマークを意匠登録し，上で述ベたようなこれまでのすべての化学啓発活動にロゴマークを付して
ビジビリティの向上を目指すものです。

いずれもいわば全国区の活動ですが，期間限定型で集中的に盛り上げる企画と，
通年活動型で全国津々浦々いつでも「夢・化学-21」ロゴマーク付きのイベントが行わ れている，
という性格の異なる活動を2つ準備し，足並みをそろえて最大の効果を狙おうとする点が特徴です。
提案4団体だけではなく，経済産業省や文部科学省，さらにはマスコミ関係者の賛同も得ており，
産学官一体となった初めての本格的な取組みで，化学の啓発活動，
市民権獲得にとっての決め手となるものと期待しています。

◆「化学の日」「化学週間」のイベントは？
「化学の日」を長く定着させるためには. 活動現場に新たなロードを課さないことが 重要と考えます。
新たに企画するのではな くて，現在行われているイベントの開催日 をできるだけ「化学の日」「化学週間」
の日程に合わせていただくことで.最大の効 果を上げようとの考えです。
すでに，各支 部や産業界に対して，日程調整のご協力を お願いしています。
ただ，初年度の今年は，「化学の日@開成学園」「化学週間@東京大 学」「子ども実験ショー@近畿」
などのキックオフイベントを企画中です。
また，各種一般紙や月刊誌「ニュートン」「化学」「現代化学」「子供の科学」などへの
PR記事掲載の企画も進んでいます。

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.30］ No.031
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
地震に関心が高まっていますが，地震は地殻の破壊現象ですから
いつポッキリ折れるか予言できないように文字通りの予知はできません．

◆地震の規模（マグニチュード）M
まず，地震のマグニチュードMとは何でしょうか？
これは地震のエネルギーEの対数です．
大体，地震のエネルギーの大きさの桁と思ってよいでしょう．
リヒターが当初発案したマグニチュードの定義は，
震央から100kmに設置したと仮想した，特定な型の地震計で
観測される最大振幅の対数でした．しかし，現在では
もっと理屈に合ったモーメント・マグニチュード
（あるいは気象庁マグニチュード）が採用されています．

◆可能な最大地震
地震で解放されるエネルギーは，生じた断層面の面積と
その平均変位とその付近の地殻の剛性の積です
（大雑把にいえば生じた断層の長さに比例します）．
地殻に溜まった歪エネルギーが地震で解放されるわけですが，
断層の長さが長い方が解放されるエネルギーは大きいし，
地殻の剛性が大きいほど大きな歪エネルギーが蓄えられます．
これらから起こりうる地震の最大エネルギーを見積もると
M9.5程度と考えられています
（1960年のチリ地震ではM9.5が観測されている）．

◆べき乗則
地震の規模（マグニチュード）Mと発生頻度（回/年）ｎ
の間に　n=10^(a-bM)　の関係があります．
これはグテンベルクとリヒターが発見しました．
a,bはその地域の地殻の特性を表す定数でが，b≒1ですので
地震のマグにチューﾄﾞが1つ大きくなるごとに，地震の回数は1/10に減ります．
だからこれをべき乗則と言います．

地震の規模Mには最も発生しやすい典型というのがありません
（釣鐘型の正規分布ではありません）．
大きな地震は少なくなりますが，M=9あたりも起こり得るし，
そんな巨大な地震に見舞われると壊滅的なダメージです．
従って，頻度は小さいけれど致命邸なダメージとなる巨大地震が起きても
被害が最小となるように備える必要があります．原発は止めましょう．

クリーン・ルームのチリのサイズ分布もべき乗則だと言われています．
もし正規分布のように頻度の高いサイズがあるなら
そのサイズのチリの発生に注目した対策ができるのですが
べき乗則では特別な対策は困難です．

◆分布関数を求める実験
凍ったジャガイモを投げて砕き，破片のサイズ分布を調べた人が居ます
（南デンマーク大，1993年）．ここでもべき乗則が確認されました．
スパゲッティやクラッカーを砕くとどのようなサイズ分布になるか
実験した話が今年の数学月間懇話会で中西達夫さんからありました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.23］ No.030
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆今年のとっとりサイエンスワールド2014（矢部敏昭会長）が
9月21日（中部，倉吉）で無事終わりました．例年のように
8月31日（東部，鳥取），8月2日（西武，米子）の計3回開催され
各回,1000人に達する参加者が集まりました．
スタッフも先生方100人＋高校生ボランティア60人の規模です．
8年目ですが，小さい子供から，両親，お年寄りまで，楽しみに集まる
算数イベントに定着しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_0?1411477332

◆万華鏡は，各会場でそれぞれ異なる3角形の鏡の組み合わせを作りました．
西部110人，東部160人，中部110人用意しました．
鳥取でやったけれど倉吉にまた来たという小さい小学生もいたり，
彼女はすっかり内容を理解していてもうベテランです．大したものだ．
鏡の組み合わせが作る3角形が変われば，違うタイル張り模様が見られることを
知ることが眼目なので，色々な鏡の組み合わせの万華鏡や，
多面体が立体的に見える万華鏡などの展示物も用意して行きます．
これらの内で，2枚鏡の万華鏡の人気が高く
来年のリクエストとして聞いておきました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_2?1411477822
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/81/16147181/img_3?1411477822

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.16］ No.029
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
読者の皆様へ．
8月19日（025号）からまぐまぐの遅配が続いています．
特に，026号，027号はまだ配送されていない方があるようです．
届かない方がありましたら，ご一報ください．
これらの号では多面体に関する話を続けています．
メルマガ更新は毎火曜日の朝7:00に行っておりますので，
以下のサイトでもご覧になれます．
http://blogs.yahoo.co.jp/tanidr/folder/545271.html　あるいは
http://sgk2005.sakura.ne.jp/htdocs/?page_id=32
－－－－－－－－－－

◆4次元の正多面体は6種あるのですが，
3次元以上が見えない私たちには理解が困難です．
色々な図や説明が種々の本やwebで見られますが，どれもしっくりしません．
結局，4次元の正多胞体6種を最初に見つけたシュレーフリの説明が
最もわかり易いようです．（コクセター［幾何学入門］や
ヒルベルト，コーン・フォッセン［直観幾何学］に載っています）．
さて，このようなものを記述するシュレーフリの記号というのは
大変良くできています．この記号の仕組みを理解することが結局
4次元の理解に直結します．シュレーフリの記号を単純な図形で見てみましょう．

◆3次元の正多面体の例
面（2次元）が頂点（0次元）で3つ以上集まらないと立体（3次元）はできません．
シュレーフリの記号は以下のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_0?1410817831
（１）正4面体　　　　　　　　　{3,3}←シュレーフリ記号
正3角形の面（2次元）が頂点（0次元）で３つ集まっている．
（２）正6面体（立方体）　　　　{4,3}←シュレーフリ記号
正４角形の面（2次元）が頂点（0次元）で3つ集まっている．

正多面体が記述の対象ですから，どの頂点まわりの状態も同じです．

◆4次元の正多面体の例
胞（3次元の多面体）が辺（2次元）で３つ以上集まらないと
4次元の立体はできません．
シュレーフリの記号は以下のようです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_1?1410817831
（１）正5胞体　　　　　　　｛3,3,3｝
3次元正4面体｛3,3｝が辺（2次元）で３つ集まっている．
（２）正8胞体　　　　　　　｛4,3,3｝
3次元正6面体｛4,3｝が辺（2次元）で３つ集まっている．

正多胞体なので，どの辺まわりの状態も同じです．

（参考）　　｛4,3,4｝　というのはどのようなものでしょうか？
これは，3次元正6面体が辺のまわりに４つ集まっている状態ですから
角砂糖を頂点を合わせて無限に積み重ねたような状態．
これは3次元空間の中で無限に続く立方格子です（３次元で納まってしまいます）．

◆双対図形について
3次元の正多面体｛p,q｝の双対図形は｛q,p｝です．
｛p,q｝：正p角形の面が頂点でq個（辺がq本）集まっている．
この図形で面を頂点に変えた図形は，｛q,p｝となります．
同様に，｛p,q,r｝の双対図形は｛r,q,p｝になります．

◆4次元のイメージの万華鏡
雰囲気だけです（色々工夫していますが残念ながら困難なようです）．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_2?1410817831
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/41/16122741/img_3?1410817831

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.09］ No.028
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆プラトンの正多面体は5種類あります．
これら5種類の正多面体の対称性を考慮して
方位を合わせ重ね合わせた図が以下のものです．
この図のように２つの正多面体を重ね合わせると
それぞれの多面体の対称性で共通なもの（共通部分群）が残ります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/30/16103930/img_0?1410092475

◆黄鉄鉱FeS2の結晶は，色々な外形（晶相）のものが見られます．
黄鉄鉱は愚者の金とも言われ金色できれいです．
私は，川底に金色の砂がキラキラ光って貯まっているのを見つけて
採集したことがあります．1mm程度の結晶粒ですが
皆整った多面体の形をしていました．
結晶の外形は，正6面体，正8面体，正5角12面体が基本で，
ミラー指数で言うと，正6面体は結晶面(100)面，
正8面体は(111)面，正5角12面体は(210)面で囲まれています．
このほかに，これら正多面体の切頂多面体も見られ，
また，他の指数の面(211)，(321)が加わった複雑な多面体もあります．
多面体の形が連続的に変化することを示す良い自然の手本です．
黄鉄鉱の結晶は立方対称の内部構造（原子の配列）ですが，
結晶粒の外形は，どの指数の面が大きく成長するかによって変わります．

◆そこで，昔読んだ記憶のある砂川一郎の論文（1957）を
再度見てみました．奈良県や島根県にある絹雲母の鉱床や凝灰岩の
母岩中に晶出した黄鉄鉱の結晶粒の大きさと形の統計を述べています：
「小さい結晶粒では正6面体，大きい結晶粒では5角12面体の外形が多い」
晶相の変化を起こす機構は大変複雑で一概に言えませんが，
黄鉄鉱結晶の成長に伴って大きく成長する面が，
正6面体の面（100）→正8面体の面（111）→5角12面体の面（210）
と変化し晶相が変る．これは結晶面の性質と母岩（絹雲母化）との
化学的反応がかかわっているらしい．
◆今回，砂川一郎の論文中の図が，
Tシャツとして博物館グッズになっていることを知りました．
http://ameblo.jp/hakubutufes-sub/image-11876822744-12970852035.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.09.02］ No.027
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
「とっとりサイエンスワールド」in鳥取市（8月31日）に参加しました．
とっとりサイエンスワールドは今年で8年目になり，小さい子供から
お年寄りまで楽しめる市民イベントとしてすっかり定着しました．
学生ボランティア54人（短大・高45人，中9人）を含む先生方150人のスタッフで
運営され，大変さまざまなワークショップがあります．
私は万華鏡のワークショップで参加しました．
1時間のクラスを5回実施し，160人が自分の万華鏡を作りました．
イメージ 1,2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/03/16089803/img_0?1409575636
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/03/16089803/img_1?1409575636

◆今年，鳥取市で作ったものは，3枚鏡が作る3角形の角が，90°ー36°ー54°のものです．
交差する2枚の鏡が反射を繰り返し生じる結果が群をなすのは
2枚の鏡の交差角が360°を偶数で割り切る角度のときです．
通常の万華鏡はそのような鏡の交差角に設定されます：
例えば，60°(360/60＝６）．36°（360/36=10）などです．
これは，1817年のブリュースターの万華鏡の特許にも記載されています．
群をなすときには生じる映像は規則正しく美しく見えます．
しかし，今回作成した万華鏡は，3角形の１つの角の交差角だけが
54°（360/54＝6.666）と偶数で割り切れません．
このような角度に対応する所はどのような映像が見られるでしょうか？
数学では3周回ってもとに戻る（360°×3）ような空間を想像しても良く，
そのときは10回回転対称が完成するのですが，
実際の物理的な空間の光はそのようには回ってくれません．
他の2つの角の所では規則正しい映像になるのですが，
この角度の所だけ秩序が乱れることになります．
昨年のサイエンスワールドから，このようなシリーズの万華鏡を作っています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.26］ No.026
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
この所，正多面体による空間の充填などを見てきました．
今回は，最密充填構造の話です．以下の本が参考になります：
ケプラー予想，ジョージ・G・スピーロ（青木薫訳）新潮社

◆ケプラー予想とは：
「3次元空間で最も高密度に同じ大きさの球を充填した状態は，
１つの球のまわりを12個の球が取り囲む状態で，
その空間充填率は74.04％である」というものです．
これは，結晶学では最密充填構造として常識になっていることがらです．
立方最密充填(=立方面心格子)，６方最密充填，および，両者の混合のポリタイプは
無数にありすべて同じ充填率74.04％です．この起源は1883年，結晶学者ウィリアム・バーロウが
６方および立方の最密充填の２つの最密充填構造をネイチャーに掲載したことにあります．
バーロウは結晶空間群の数え上げ（フェドロフ，シェンフリーズもそれぞれ独立に数え上げた）でも有名です．

注：スピーロの著書p.23でバーロウの図に言及し，立方最密充填は6方最密充填とまったく同じ配置なのだ！」
と言っているのは，数学と結晶学との見解の相違．
111面（切断）が同一であるのは当たり前で，その積層様式に結晶学的違いがあるのだ．

◆ケプラー予想は多くの人が挑戦しましたが，どうやってもこれより稠密な充填構造はつくれません．
これより充填密度の高い構造はないという証明はとても難しいのです．このケプラー予想をヒルベルトは，
1900年8月，第2回国際数学者会議の講演で，未解決の23の問題（ケプラー予想は第18問題）として提起しました．
周期的に規則正しく並べる（結晶）という条件では，ケプラー予想は証明できるのですが，
不規則な並べ方まで含めてこれが最密であるということの証明はとても困難です．
正4面体でも正8面体でも正12面体でも正20面体でも，単一では空間の充填ができません．
前号で正4面体と正8面体を2:1で混ぜると周期的に空間が充填できることを示しましたが，
それは面心立方の最密充填構造にほかなりません．さらに高密度な様式はないのだろうか？
例えば，立方最密充填では1つの球の周りに6個の球が囲み，上の段，下の段に3個づつ球が接します．
上下の3角形が点対称であるような配置が立方最密充填，
上下の3角形が周りを囲む6角形を鏡として鏡映対称であるような配置が6方最密充填です．
このような１つの球のまわりに12個の球が配置する構造と言っても，次のようなものがあります．
中心球の赤道面の上側から5個の球，下側から5個の球が接し，上下の正5角形が点対称に配置し，
さらに，中心球の上下に球が1個づつ配置するのも12個配置です．これは正20面体配置と呼ばれます．
しかし，この配置は局所的には充填密度が高いが，正20面体だけでは空間の充填ができません．
どうも数学的にエレガントな証明は無理なようです．

◆ケプラー予想の証明は，トマス・ヘールズ（ミシガン大学）によってコンピュータを用いた
しらみつぶし法で完成したということです．ケプラー予想（1611年「六角形の雪について」
という友人向けの小冊子にあるという）から400年近く経過した1998年のことです．
ヘールズはドロネーの四面体分割を基礎に，シンプレックス法で計算されました．
評価関数を導入して，密度の低い配置は減点，密度の高い配置は加点を繰り返すものです．
300ページもあるヘールズの論文は，トート（Toth）ら審査員12人が4年かかってチェックしましたが
最後まで詰められず99%正しいと報告されました．
そこで，2003年にヘールズ自身が証明支援ツール（HOL Light，Isabelleなど）を使い
チェックを始めやっと証明できたと言います．コンピュータを用いる証明は「4色問題」の時にもありました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.19］ No.025
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
お盆休みも終わりました．皆様お元気でお過ごしのことと存じます．
お知らせがあります．今までバックナンバーをまぐまぐにすべて公開していましたが，
お盆休み中に，公開は最新号のみに変更しました．
バックナンバーをご覧になる場合には，
ブログ：http://blogs.yahoo.co.jp/tanidr/　あるいは，
公式HP: http://sgk2005.sakura.ne.jp/　で
メルマガ倉庫の項目をご覧ください．

◆今回は，空間を隙間なく充填できる正多面体についての話です．
正６面体（角砂糖の形）が隙間なく積み重ねられ空間を充填する
ことはご存知でしょう．
◆それでは，正４面体，正８面体はどうでしょうか？
どちらもそれだけでは隙間なく空間を充填することはできません．
しかし，正8面体と正4面体を1:2の比率で混ぜると
周期的に空間を隙間なく充填できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_1?1408372931

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_2?1408372931
このパズルは,osa工房，小梁さんが販売しています．
さて，幾何学的にこのようなうまい構造を思いつくのは
特殊なことなのですが，
自然界でこのような空間充填構造はたくさんあります．
結晶学では，ダイヤモンドがこのような構造であることは
古くから知られています．半導体で知られるシリコンも
ダイヤモンド型結晶構造です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_3?1408372931

他の例では，ペロブスカイトと言う鉱物があり，
常温超伝導などの多くの有用な材料がペロブスカイト型の結晶構造です．
正8面体が骨組みを作っています．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_4?1408372931

◆菱形12面体はこれだけで空間の充填ができる多面体です．
菱形12面体は，面心格子のウイグナー-ザイツ胞であるので
空間を充填できることは明らかです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_3?1407801148

切頂正8面体は，体心格子のウイグナー-ザイツ胞であり
もちろんこの多面体も空間を充填できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16052778/img_0?1408372931

面心格子の格子点に原子を配置した結晶構造は，銅やアルミニウムなど
多くの金属の結晶構造で知られています．
また，体心格子構造は，鉄，タングステン，セシウムなど
多くの結晶構造で知られています．

◆今回の話の眼目は，純粋に数学的に空間充填構造を導くのは
とても大変なことですが，結晶学などでは昔から知られていたということです．
自然科学の分野から数学への多くの貢献がなされてきました．
結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.12］ No.024
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
お盆休みの時期ですが，皆様いかがお過ごしですか．
今回のメルマガは，No.023に続き多面体に関してです．

（１）多面体の分類を整理しておきます．
■正多面体
1種類の正多角形で囲まれた凸多面体です．
頂点のまわりに集まっている多角形の状態は，すべての頂点で同じです．
もちろん，辺のまわりの状態もすべての辺で同じです．
プラトンの正多面体とよばれる5種類があります．
■半正多面体
２種類以上の正多角形で囲まれた凸多面体です．
頂点のまわりに集まっている多角形の状態は，すべての頂点で同じです．
しかし，辺のまわりの状態は，すべての辺で同じとは限りません．
アルキメデスの半正多面体といい13種類あります．
（右回りと左回りを区別するなら15種類）
特に，辺のまわりの状態が．すべての辺で同じものは，準正多面体と言います．
■準正多面体（半正多面体に含まれる）
立方８面体と12･20面体の2種類があります．

（２）菱形12面体と菱形30面体について
これらの多面体は，準正多面体の双対として得られます．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_0?1407764464

■菱形12面体と菱形30面体を万華鏡で作ろう

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_1?1407764464

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_2?1407764464

■菱形12面体は空間を充填できる
実は，菱形12面体は，立方面心格子のウィグナー=ザイツ
（あるいはデリクレ）胞に他なりません．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/62/16035662/img_3?1407764464

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.08.05］ No.023
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆さま如何お過ごしでしょうか？書中お見舞い申し上げます！
現在，数学月間(7/22～8/22)の期間中です．暑い最中ですが
数学月間懇話会(7/22)，とっとりサイエンスワールドin米子
も無事終了しました．

■プラトンの正多面体

正多面体とは，次の（１），（２）を満たすもので，
特に凸多面体がプラトン正多面体と呼ばれる：
（１）すべての面が同一の正多角形でできている
（２）すべての頂点まわりの状態は同一である
従って，正p多角形が頂点まわりでq個集まっている正多面体は
{p,q}と表記できる．これを正多面体のシュレーフリの記号という．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_0?1407156023

■５つのプラトン正多面体を万華鏡で作る

上図の各多面体には鏡映対称面がたくさんあります
（煩雑になるので記入していません）．
各多面体で3つの鏡映面を選び，これを鏡とする万華鏡を作れば
それぞれの多面体の映像が見られるでしょう．
ここでは，幾つかの多面体に共通な鏡映対称面を利用して
まとめてプラトンの正多面体の映像を生成してみましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_1?1407156023

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/27/16014627/img_2?1407156023

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.29］ No.022
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
8月2日（土）は「とっとりサイエンスワールドin米子」です．
2014年度〔西部in 米子〕は，日本数学教育学会第96回全国算数・数学教育研究（鳥取）大会
とコラボで実施されるので，会場が例年の児童文化会館とは異なるようです．
米子コンベンションセンターにて（12：00～16：00）　

私も万華鏡で参加します．
米子では110人分用意しました．分数型の万華鏡を作製します．
以下に画像を掲載します：
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/37/15996337/img_0?1406563191

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/37/15996337/img_1?1406563191

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/18/15996418/img_0?1406562991

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/18/15996418/img_1?1406562991

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.22］ No.021
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
本日は数学月間（7/22-8/22）の初日です．
22/7＝3.14....＝π　，22/8＝2.7...＝e
数学に興味を集めるようなイベントが
各地で盛んになることを応援しています．
まず初日は数学月間懇話会です．
◆数学月間懇話会（第10回）
日時●７月２２日，14:00-17:10
1.人口の集合関数としての「民力指数」
　松原望（東京大学名誉教授，聖学院大学）
　14:10-15:10
2.スパゲッテイを巡る旅，
　中西達夫（株・モーション）
　15:20-16:20
3.数学月間の狙と効用，今年の米国MAM
　片瀬豊，谷克彦（日本数学協会）
　16:30-17:10
ーーーー
会場●東京大学（駒場）数理科学研究科棟，002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●日本数学協会，数学月間の会（SGK）
sgktani@gmail.com，谷克彦（SGK世話人）
直接会場においでください（開場13:30）．ご参加お待ちしています．
17:30より構内で各自払いの懇親会も予定しています．

◆幾何学的な消滅
さて，メルマガ020に掲載した　幾何学的な消滅　のその後の記事です．
メルマガ020の図面のように作製してみましたが，
断層を挟んだ行だけが明らかに（目立って）小さくなるのです．そこで，
初期状態のこの行だけ目立たない程度大き目に作ろうかと考えていたところ，
以下の動画を発見しました．
http://youtu.be/QbpfjM0NP7Q
さすがマジシャンもうひとひねりあったのです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_2?1405950272
パーツ２は表面が（A)で裏面が（B)です．
従ってこのパーツの断面形状は台形です

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.15］ No.020
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
幾何学的な消滅

◆7×9の板で1コマが幾何学的に消滅する
これは今年の米国MAMで取り上げられたマジックです．
http://www.mathaware.org/mam/2014/calendar/areapuzzles.html

まずは，アルゼンチンのマジシャン，ノルベルトジャンセンによるプレゼンを
ご覧ください．　http://youtu.be/3PszMaZ5Ipk
7x9のエリアにタイル片が配置されています，断層に沿って滑らせ
上部の左3コラム分と右4コラム分を入れ替えると，不思議なことにタイルが１つ減ります．
この操作を繰り返すたびにタイルが1つづつ減り３つまで減らせます．
タイルが1つ減っても，2つ減っても，3つ減っても，
元通りの7x9枠内にタイルはきちんと配置され変わらないように見えます．
これは不思議ですね．どうしてタイルが１つづつ余るのでしょうか？

ビデオを観察していると，タイルが消滅する原理がだんだんわかってきます．
原理理解を助ける図を以下に作成しました．
青色の面積がだんだん減じているのがわかります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_1?1405218032

このおもちゃを作製して見ようとする方は，この原理図を参考にしてください．
数学マジシャンの使っているタイルのパーツは目地が太いですね
私の原理図には，目地はありませんが，作製するときは目地の効果も考慮すべきでしょう．
結局，断層をはさんだある行だけ，1コマ縦の長さが1/7だけ縮むので，
7コラムあるから面積としては1コマ分取り出せることになります．

◆なぜタイルが１コマ減るのか
左のコラムと右の3列を入れ替えると，１コマ減る．
１コマの高さをbとすると，断層を挟んでb/4だけ縮みます．
ただし，右端のコラムの断層ではコマ間の目地が消えるのが残念！
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_3?1405215030

◆真ん中を取り除いたお札が再現できる
http://youtu.be/-h0AXeLIHqQ
お札の中心を取り除いて，裏向きにして並べると
完全な1枚が再現できたように見えます．
真ん中が消えるとは，あり得ないことが起ったように見えます．
数学マジシャンの使っているおさつの裏面には
再配列したときに完成するようなお札の裏面の絵が描いてあるので
お札が再現したように錯覚します．以下の原理図を参考に作製してください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_0?1405215030

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.07.12］ No.019b
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ロンドンシティホール
ロンドンシティホールは，ロンドン市長，ロンドン議会，大ロンドン当局を収容する．
ガラスの使用と内部の巨大ならせん階段が，
透明性と民主的プロセスへの近づき易さを象徴しているようである．
外部から見たとき，最も印象的なことは，建物の奇妙な形である．

http://plus.maths.org/issue42/features/foster/egg.jpg
テムズ川にかかるロンドンシティホール．

テムズ川の土手の上に置かれて，建物は，川原の小石を思わせる．
そのまるみが再び民主的な理想を思わせる．けれども，ガーキンと同じように，
形が決められたのは，単に形のためだけではなく，エネルギー効率を最大化するためでもある．
これを実現する１つの方法は，建物の表面積を最小にすることである．
それにより，望まない熱の損失と流入を防ぐことができる． 諸君の中の数学者は，
あらゆる形の中で，体積を基準にすると，球形が最も表面積が小さいことを知つている．
これが，ロンドンシティホールが球に近い形をしている理由だ．
建物の不均衡も同じくエネルギー効率に貢献する：南面のオーバーハングが，
ここの窓を上階の床で陰にして，夏季の冷房需要を低下させる．ガーキンでと同じく，
コンピュータモデリングが，建物の中で気流が如何動くか示し，
自然の換気が最大になるように建物内の形が選ばれた．実際，建物は冷房を必要としない．
同程度のオフィススペースのエネルギーに比べ，たつた1/4と伝えられる．
螺旋階段さえ，単に審美的理由で選ばれたのではない．それらの分析の一部として，
ロビーの音響効果，人々の声が適切に聞こえるような建物をSMGは設計した．
初めは音響効果は，広いホール内をエコーが跳ねるという状態でひどく，
何らかの対策が必要だった．Foster＋パートナーの過去のプロジェクトの１つが手がかりを提供した：
ベルリンの Reichstag は大きいホールを含むが，大きい螺旋の傾斜路があり反響が起きない．
SMG はロンドンのシティホールに同様な螺旋階段のモデルを作り，
Arup Acoustics会社がこの新モデルの音響効果を分析した．諸君は，
以下のアニメーションで，音が階段後ろに閉じ込められ，エコーが減じるのを見ることができる．
このアイデアは最終設計に採用された． (アニメーション © Arup Acoustics.)

ロンドンシティホール
http://plus.maths.org/issue42/features/foster/gherkin_outside_web.jpg
ガーキンの全貌．平面パネルが曲面を近似していることに注意．映像 © Foster + Partners

ガーキン，ロンドンシティホール，他の多くのFoster+パートナー作品がたいへんモダーンに見えるのは，
外側が曲面であるためだ． これらは，名うての困難さで，建設費が高くなる．
そこで幾何学者のチャレンジがある：単純な形から作る一番良い方法は何か？
” これは我々の主たるチャレンジの一つだ，”De Kestelierは語る，
”我々のプロジェクトの実に99％は，いかなる曲面も使っていない．
例えばガーキン，1種類の曲面パネルはトップにあるレンズのみ．
建物が曲面という印象は，多数の多角形の平面パネルで曲面を近似的に作ることで生じる．
パネルが多いほど錯視も真実味をおびる．
複雑な表面を記述するこのような平面パネル解を見いだすことで，
SMG は専門家になった．De Kestelier が説明するように，幾何学［その形]は，
しばしば経済により決定される：”我々は矩形に近いパネルを使う傾向がある．
なぜならそれはいっそう経済的であるからだ．資材をカットするとき安くなる．
三角形では，多くの材料ロスがあるが，矩形に近いとロスが少ない．
矩形に近いと構造が少ないので，視覚的にもさらによい．”これは，
表面が完全に矩形から成り立っているロンドンシティホールで例証される．
実際、ロンドンシテイホールは，理想的な幾何学形と建設容易さのバランスをとる必要性を
よく例証している：　扱い難い丸い形はスライスに切ることで扱われた．スライス一つ一つは，
僅かに傾いたコーンで，容易に数学的に記述でき，平面パネルでの近似も容易である．

合理的な設計
数学的な方程式で記述されるコーンのスライス，トーラス，球などの表面は，
しばしば，SMGデザインの基礎となる． これらを，バーチャルモデル創造に使うときに，
数学的に生成される表面はコンピュータ上で容易に表現できるので，たいへん利点がある．
多くの個別座標を蓄え記述する構造ではなく，方程式を蓄えるだけでよい．
表面の正確な形は方程式のパラメータを変じて制御できる（例として下図を見よ）．
平面解はやはり比較的容易に設計できる：ソフトウェアはオリジナルの表面の
ノードポイント集合に直線を引くようにする．

http://plus.maths.org/issue42/features/foster/surfaces_web.jpg
これらの表面は，関数z=e^-a(x^2-y^2) のグラフである．ここで，
３次元座標系は，ｘ，ｙと垂直ｚ軸である． a は表面の形を決める．
第一の表面はa=1 ，第二の表面はa=5 ，第三の表面はa=7 ．

数学的に定義された要素の集合からなる複雑な構造を考えるのは，
バーチャル世界では有用ではない：実際にどのようにそれを建設するべきかを，
建物モデルの建設の一歩一歩のガイドにつくる．合理化のこのプロセスは，
もう一つの SMG の仕事の重要な部分だ．前と同じように，数学的な完全性は，
実用性のために道を明渡さなければならない:"２～３週間前に，
誰かが楕円の一部である壁のプランのことで私のところに来た”De Kestelierは語る．”
もちろん楕円は数学的には描くのは易しい．それをさらに合理化することをなぜ望むのか？さて，
私は楕円のこの部分を３つの円弧に合理化することを決めた．
理由は，壁の建設で，コンクリート壁用の型が要るためだ．これは全体の形を建設するのに
多くの型パネルを使ってなされる．もし諸君が楕円にしたいなら，
すべての型パネルは異なっていなければならない：楕円の周囲を進むと，
楕円の曲率はたえず変化しつづけるのだから． もし楕円をやめて３つの弧にするなら，
諸君が必要とするのは，3セットのパネルだけで，各セットのパネルは同じである．
これはずっと簡単になる．" 数学者に理想的なものは常に建築家に理想的であるわけではない．”

http://plus.maths.org/issue42/features/foster/museum.jpg
英国博物館の屋根．設計Foster+パートナー

博才の人
SMG が，建物の外見と気流・音響のような物理現象の双方をモデル化するには，
コンピュータプログラミングを使う．幾何学［形］の理解は，デザインと建設プロセスに直結する．
建築家でなく数理科学の専門家なのか？SMGメンバーの8人中７人が，プロの建築家だが，
専門的知識は，複雑な幾何学，環境シミュレーションからパラメトリックなデザイン，
コンピュータプログラミングにまで及んでいる．
グループの８番目のメンバーはエンジニアで，主プログラマーである．
こみいった数学に基づき，物理的特徴をモデリングするとなれば，
チームはしばしば専門コンサルタントを使う．”チーム内で予備的な解析を行う．
もしさらに知りたければ，別の解析を行う．我々は，専門コンサルタントとデザイナー間の接点となる，
”Petersは説明する．純粋数学，幾何学は如何？ どれぐらい複雑なのか？
"オフィスに１Ａレベルの本がある． ” とDe Kestelierが語る．結局のところ，
それはすべて建設可能な構造を作ることに関わり，古典幾何学を越えるものはここでは用いない．
SMG の大部分の活動には数学が付随しているのだが，彼らのデザインとは，
仕事に対して制限を与えるものであるとPetersとDe Kestlierは主張する．
"悟るべき重要なことは，我々はアーキテクチャで働くプログラマーではなく，
プログラミングをするアーキテクトだということだ，”De Kestlierは語る．
Ptersは同意する：”我々の主な仕事はモデリングではない．
プロジェクトのパラメータは何かを理解し，噛み砕き定義できる規則にする．
我々は，何処に適応性があり何処に制限があるかを理解できるようにする．
”制限の最適化と建設可能な物体の創造．もちろん，建築家はいつもそうしてきたし，
PetersとDe Kesteierも建築の仕事は本質的には変わっていないと思っている．
現代のデジタルツールにより，今日の建築家は，
過去の世代には夢であったデザインオプションの領域も探索できるようになっただけだ．
形と模様，科学とコンピュータの言語として，これらのツールを譲渡処分にしたのは数学だ．
数学は，確かにその料金を取り戻している． （訳：谷克彦）
－－－－－－－－－－－－－－－－－
http://plus.maths.org/issue42/features/foster/xavier_brady.jpg
Xavier(左)とBrady（右）はFoster+Partnersのモデリング専門家メンバーである．
プラスは，ロンドンの数学と芸術ブリッジ会議（2006年）で，二人に出会った．
ブリッジ会議の詳細はウエブサイトにある．
著者：Marianne Freiberger（プラス編集者）

◆編集後記
019号はa,bで完結です．ところで，
ガーキンに良く似た超高層ビルが新宿にあります．2008年に完成した
東京モード学園が入っているコクーンタワーです．コクーンとは繭のことですが
どちらかというとセミに似ているビルです．設計は丹下都市建築設計です．
新宿で大変目立つビルです．写真は以下のブログにあります．