ブログ倉庫

1986年から始まった米国の数学月間MAMは，2017年から統計学を表に出して数学･統計学月間MSAMに衣替えした．これは，（2011年）解明進む複雑系，(2012年)統計学とデーターの氾濫，(2013年)持続可能性の数学，(2016年)予測の未来，と続くMAMテーマの流れから予想されたことです． 数学と統計学は，インターネット・セキュリティ，持続可能性，疫病，気候変動，データの氾濫，に見る現実世界の問題に対して重要な役割を果たしています．医学，製造，エネルギー，バイオテクノロジー，ビジネスなどの分野でも，日々新しい結果や応用が生まれています．数学と統計学は，システムや方法論がどんどん複雑化する技術世界で，革新の重要な推進力になっています． 些細な事故が雪崩となり大規模災害を惹起する危うさを持っているのが複雑系です．限界ぎりぎりで稼働している複雑系であるインフラの制御はAI（ディープラーニング）がなければどうにもなりません（ただし，事故の復旧では人間自身の手が必要で，AIで解決できるものではありません）．また，医療診断の画像識別エキスパートシステムでは，専門診断医を凌駕する状況であります．

日本政府の「AI戦略」は，AIを理解し各専門分野に応用できる人を，遅ればせながら2025年までに年25万人育てる体制を目標に掲げました．経済産業省が2019.3に出した報告書「数理資本主義の時代」（違和感のある表題だ）は，数学が国富の源泉であると謳い，GAFAを見ればそのような時代の流れであることは明白です．しかし，ことさらに数学をそのように強調し，強者になるための道具にすることには違和感があります．高い年収が得られるので数学を職業とするでは本末転倒と言わざるを得ません．
さらに経産省の当該報告書(p.19)には，<工学出身者に「数学は役に立たない」という時代遅れの先入観が残っている>との記述があます．時代遅れの先入観と言わようが，あえて言うと，私は「数学では物は作れない」と思っています．
アナログ制御の時代を担い応用数学を発展させた工学の扱う対象は物や反応であるのに，データサイエンス（コンピュータがなければ何もできない）の働きかける対象はいつも数値（データ）であり解析にとどまるからです．ただ，工学であれデーターサイエンスであれ，どちらも数学なので，「数学は役に立たない」とは誰も思ってはいないはずです．かつて，電気電子，計測などの工学部が応用数学の研究と教育を担っていた時代があったが，コンピュータの発展により，数学能力の低下はあると思います．数学理論を何も知らずとも優れたコンピュータ・ソフトを操り，良い結果を得るのをしばしば目撃したし，ディープラーニングのブラックボックス化の弊害もあると思います．今は，データーサイエンスの基礎を支える数学を押さえる時期であると思います．経産省の報告書の先に触れた部分は，<企業の工学出身者の時代遅れ先入観がAIを阻害している>と言いたいようだが，経産省の指摘を待つまでもなくこの分野の研究は多くの企業で先行していた．例えば，1987年に開設したリコーカリフォルニア研究センターでは，1990年にPeter E Hartを所長に迎えAIの研究を始めている．2000年に，Richard O Duda, Peter E Hart, David G Storkが”Pattern Classification”(2nd edition，尾上守夫監訳)を出版している．これはスタンフォード大の授業でも用いられ発売後半年で4,000部売れた．米国AI研究者の数学基礎の確かさと層の厚さが感じられる例である．

日本のある大学のポスターで，基幹工学（機械，電気・電子，工業化学），先端工学（ロボット，AI・データーサイエンス），建築工学の3分類の新し構えを見受けます．また，立教大学が2020年4月に開設する国内初となるAI（人工知能）に特化した大学院「人工知能科学研究科」（修士課程）は，機械学習やディープラーニングを中心としたAI領域についての学科で，機械学習の数理モデルを深く理解し，高度な情報科学や統計学の知識を持ち，論文から最新のAI技術を実装できる人材育成を目指すという．
ベイズ決定理論，最尤推定，パーセプトロン，多層ニューラルネットワークなどの基礎教育を行うのは必要ですが，数学以前の数理モデルを作る時点で，正しい解釈ができる能力，常識，読解力，AI倫理などはさらに重要であると考えます．統計学もAIも解釈次第でとんでもない結果を導く可能性があります．

前号では長さの問題をみましたが，今回は面積について少し考えましょう．
（掛谷の問題）
平面に置いた長さ１の針（線分）を平面上で１回転することができる平面図形のうちで
面積が最小なものは何かという問題です．この問題は1916年に掛谷宗一が提起したものです．

可能な図形候補の4つの図を，http://www.araiweb.matrix.jp/semi208/KakeyaProblem.html　から引用します．

多分，皆さんの思いつく答えは，この4つのタイプのうちの一つでしょう．

(1)　直径1の円　面積はπ/4=0.7854
(2)　ルーローの３角形　面積は(πー√3)/2=0.7048
　ルーローの3角形というのは，1辺１の正3角形の各頂点を中心に半径1の円弧を描いて囲まれた図形です．
　ルーローの3角形を断面に持つ棒は，円柱と同じように定幅曲線なのでコロとして使えます．
　その面積は，√3/4＋3x(π/6－√3/4)＝π/2－√3/2　と求まります．
(3)　高さが１の正3角形　面積は1/√3=0.5774

これらの図形の面積は，(1)>(2)>(3)の順で小さくなっています．
それで，(3)が最小面積の答えかと言うとそうでもありません．
(4)のように凸でない（内側に反った曲率の星型）図形でも針の回転が可能で，
そして，(4)の図形の面積はいくらでも小さく（面積0に）できることがわかります．
これは，1919年のベシュコビッチの定理からの一つの帰結でもあります．

さて，面積とは何かというのは難しものです．
われわれが常識で使っているのはジョルダンの面積です．
フラクタル図形の面積０ではジョルダンの面積の定義では面積が測れません．
無限回の操作がからむ図形にも使えるのがルベーグの面積です．

http://twitpic.com/8qlket　に，√2=2　というパラドックスが提起されています．
このパラドックスの原因は，非常に興味深いので，ここで考察することにします．

問題１

一辺の長さ１の正方形の対角線の長さは√2ですが，上図のように，X軸方向に1，y軸方向に１動く経路（n=０）を考えると長さは2になります．以降，このような折れ曲がり経路を繰り返して行きます（n=1,　2,　3,　4,････∞）．折れ曲がりを繰り返して行っても，いつも経路の長さは2で変わらないことがわかるでしょう．このような碁盤の目のような経路の長さは，マンハッタン距離と呼ばれることもあります（マンハッタンの市街の道は，碁盤の目の様だそうです）．マンハッタン経路は，ｎ→∞で対角線に限りなく近づきますので，√2=2　というパラドックスになります．

どこがいけないでしょうか？

問題２

同様な問題に以下の様なものがあります．https://note.com/keyneqq/n/n2ead38a59af5
半径1の円の円周は2πです．半径１の円に外接する正方形の一辺の長さは2ですから，半径１の円周のマンハッタン距離は８です．n=0から出発してx方向，y方向への折れ曲がり数を繰り返しマンハッタン経路は，限りなく円周に近づきますが，マンハッタン距離は8のままです．
従って，2π=8，すなわち，π＝４となります．　どこがいけないでしょうか？

 ■さて，これらの問題に見られるパラドックスは，どこに原因があるのでしょうか？
これらのすべての曲線はいずれも連続であることは確かです．碁盤の目に沿って辿るマンハッタン経路を∞回細かく繰り返した曲線は，至る所ギザギザで，微分不可能な曲線になっており，曲線の長さを微分係数を用いた積分で定義することができません．2点間（x1,y1)，(x2,y2)のマンハッタン距離の定義は|x1-x2|+|y1-y2|で，碁盤の目（メッシュ）を細かくすればするほど，マンハッタン経路はいくらでも目的とする曲線に近づけることはできるのですが，マンハッタン距離は不変です．
（メッシュで定義される碁盤の目のデジタル世界でも，差分により微分係数が定義できますが，そのときもユークリッド距離を用いて定義します）

マンハッタン経路で定義される曲線は，無限回折れ曲がりを繰り返すことで，目的とする曲線にいくらでも近づきますが，マンハッタン距離が変化するわけはありません．

繰り返しの手順を見て，折れ線のフラクタルとみなしフラクタル次元を求めると，この折れ線の次元はやはり１次元になりました．折れ線の幅がフラクタル次元を生むというような説明も見かけましたが，そうではなくフラクタルはこの問題では関係ありません．この問題で人を驚かせるパラドックスの原因は,単純に距離の定義の違いによるものです．
定義が違うものなので違って当然なのですが，2つの曲線は限りなく近づいて行きますので，定義の違いを忘れて同じ長さだと思ってしまうのが間違いの源です．

半径１の円に内接する正5角形の1辺の長さを求めましょう．
この正5角形の1辺の長さをxとします．
△BACと△ADCは相似(相似比が黄金比Φ)で，形は2等辺三角形(等辺xとすると，底辺Φ･x)です．
Φ･x＝x＋(x/Φ)　ですから，Φは黄金比の方程式　Φ²ーΦー１＝0を満たします．
この方程式の解（Φ>1のもの）は，Φ＝(1+√5)/2　です．

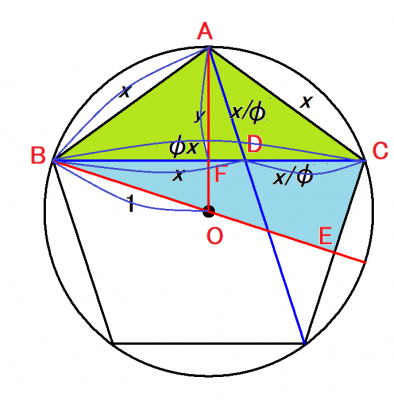
 ■次に，△BCEと△BOFとが相似であることを利用し，
1：(Φ･x）＝OF：CE=(1－y)：(x/2)　が成立するので，　y＝1ー1/(2Φ)　　

ただし，y＝√[(x/Φ)²－((Φ･x)/2－x/Φ)²]＝√[x²ー(Φ･x/2)²]＝x√[1－(Φ/2)²]　

x＝y/√[1－(Φ/2)²]＝[1－1/(2Φ)]/√[1－(Φ/2)²]＝(√[10－2√5])/2＝1.1756

■　作図
半径１の円に内接する正5角形の一辺の長さｘ＝(√[10－2√5])/2を作図する方法
（証明）ピタゴラスの定理を2回使います．

■　万華鏡への応用

■OECDのPISA（Programme for International Student Assessment）国際的な学習到達度調査で，日本の急激な読解力低下（2018年）が指摘されています．PISA調査は15歳（高校1年）を対象に，読解力，数学的リテラシー，科学的リテラシーの三分野について，３年ごとに実施する調査で，国立教育政策研究所が担当しています．
直近の2018年の試験では，読解力が前回の8位から15位に落ちました．

■日本の読解力の平均得点は504点で，OECD加盟国（移民など多数含む）の平均（487点）は上回ったものの，前回（2015年）から12点下がりました．内訳は408点未満の低得点の生徒の割合が全体の約17%を占め，前回調査から4ポイント増えている．生徒の6人に1人が十分な読解力を持っていないことになる．これほど低得点層が増えたにもかかわらず，平均点の低下は少なかった．これは，文章を解さない児童が増えたが，十分な読解力を備えた児童も同時に増える「二極化」が進んでいるということを意味します．得点分布が，平均中央に山を持つ標準的なグラフでなく，中央の左右に2つの山ができるグラフへと変化しました．
そのような変化は，少なくとも２つの因子が存在することを意味します，本来の読解力だけでなく，影響を与えるもう一つの因子なんでしょうか？それは家庭の経済力かもしれません．現在の日本社会では，貧富の2極化も進んでいますから．あるいは，文科省の言うようにデジタル機器への適応の問題である可能性も否定はしません．

■PISAは，紙に手書きで解答する方式から，パソコンで入力する方式に変更（2015年）したそうです．文科省は「日本の生徒は機器の操作に慣れていないことが影響した可能性がある」と分析しています．パソコンを介したテストの方式を私は良く知りませんが，まず，ディスプレイに問題文が表示され，次に進むと問が表示され，これに応えるという後戻りのできない方式ではないでしょうか．これに解答するのはかなり難しくなる．印刷物を介したテストでは，問を見てからまた問題文に戻り確認して答えるというやり方をすると思います．文科省の分析が，このようなテスト方式の変化のためであるというなら私もそうだろうと思います．しかし，「順位が落ちたのはパソコン入力に戸惑ったせいだ」との分析であるなら間違っていると思います．パソコン利用では，紙のときと違い，読解力だけでなく記憶力など総合的に影響し難しいテストに変わったかもしれません．

折り紙も数学ですが，この雪の結晶を折るアルゴリズムは複雑でわかりにくいです．
写真の１，２は完成した雪の結晶を，表面から見た写真（１）／裏面から見た写真（２）です．

（１）　　　　　　　　　　　　　　　　　　（２）　

■スタートに用いるのは，以下に示す6角形の折り紙（３）です．完成品を見ながら，
折り紙（表面側から見て）に，谷折りすべき線（赤色）／山折りすべき線（黄色）を描き込んでみました．

（３）

この線の通りに，谷折り／山折りをして，（４）に示す中間体が作れますから，
試行錯誤して，（４）図のような中間体を作るのを目標にしましょう．

（４）中間体

■中間体（４）の表面側に出た6か所の山尾根の部分を，平らに広げて帯状筋を作る．
この帯状筋の形成のときに，新たに山折りとなる箇所を，
折り紙（３）に青緑色の線で示しておきました．
中間体の山尾根をつぶして帯状筋にするところは，注意深くやりましょう．

■金沢に来ていますが北陸の海は８日は荒れ模様でした(この日はサンダーバードが運休しました)。海の色の変化が美しい。虹の撮影は小梁さん。

■ここは勧進帳の舞台です．腹芸とは相手の心を思いやり察することです．忖度は権力と利益が結びついていて汚いもので，人情や腹芸とは違うと私は思います．

中谷が雪の研究を進めたのには，シベリア出兵の時代で，雪や着氷などが軍事研究として必要だった背景がありますが，実際にやった中谷宇吉郎の雪の研究は基礎研究です．
この地に雪の科学館を設計した建築家は磯崎新です．

■氷の結晶模型はH-O-H分子が水素結合で連鎖しており，平面ではありませんが6角形が見えるでしょう．氷の結晶の内部構造の6回対称性が，樹脂状結晶成長にも反映され，成長した雪片の外形（「雪は天から送られた手紙である」というように上空の環境で様々な形の雪片が見られます）は，どれもすべて6回対称です．

中谷宇吉郎雪の科学館

ダイヤモンドダストの実験．

過冷却の霧（氷点以下なの水（液体）の状態を保っている）の中に，氷結の核となるダストを吹き込むと，一瞬にして水滴の霧が氷晶の霧となる．氷は光を当てるとキラキラして（屈折・分散・反射が強く起こる）ダイヤモンドのように輝く．

＊私は自販機でお茶を買い蓋を開けたとき一瞬でペットボトル内が凍るのを見ました．私の記憶では季節は夏だと思うのですが，自販機のペットボトルはギンギンに冷えていて過冷却だったのでしょう．

＊実験の動画を撮影しyoutubeに置きました．

鈴木大拙
■機械に何でも頼ると機心machine mindsになる.
A machine mind is a calculating mind. Such a mind is not clean and pure.「荘子」の外編

■You cannot understand yourself simply by thinking about yourself.
You can understand yourself better by understanding others．
〇△□

ドアや家具などに見られるイスラムの美しい模様は千年以上の歴史があります．
イスラムの星のデザインは，対称性の高い星型が配列しているのが特徴です．
繰り返し模様全体を支配する対称性は，17種類の平面群のどれかになるし，
並進（周期性）と両立しうる回転対称は，2,3,4,6回軸に限られます．
しかし，イスラムの模様に散らばる星形は対称性が高いのです．高い対称性はもちろん全域に作用はできず，その星形の内部にだけ作用する局所的なものです．

上図の模様を例にとると，8回対称の青い星型が，正方形格子の周期で配列していることがわかります．
青い星型にある8回対称性は，青い星型内部と緑の周囲領域，草色の星形5角形の領域までは有効ですが，
オレンジ色の８角形までは有効ではありません．
青い星の中心にある8回対称軸はオレンジ色8角形の付近では，4回対称軸に低下してしまいます．
これは，周期的な平面では8回対称軸は存在できない（正8角形のタイルでは平面を張れない）から当然のことです．
ある点のまわりの対称性という言葉は注意が必要で，その点周囲の「局所的」対称性を指す場合もありますが，平面「全域」で有効な対称性を指すのが普通です．この例では，青い星型の対称性は8回対称ですが，この星の中心にある回転対称軸は4回対称軸です．
このパターンの単位胞は，オレンジ色の8角形の中心を結んでできる正方形の格子で作られるタイル１つです．

■Girihタイル
正方形と正8角形を組み合わせた平面のタイル張りの例が下図(a)です．この例のテッセレーションを，（4,8,8）と記述します［１つの頂点のまわりに，正4角形，正8角形，正8角形が集まっている］．

(b)図は，正4角形および正8角形の内部に装飾線を描いたGirihタイルです．
平面をGirihタイルでタイル張りしておいて，タイルの縁の輪郭を消すと(c)図のパターンが得られます．

■ここで，始めに掲載したイスラムの模様も，上の例と全く同じであることを確認してください．
始めに掲載した模様の正4角形タイルや正8角形タイルの形は，草色の星型の中心を結んでいくと明らかでしょう．
正4角形や正8角形の内部の装飾線はどのようなものであるかもお確かめください．

Volume 90 Issue 50 | p. 64 | Newscripts
Issue Date: December 10, 2012

マイケル・フリッケ博士(オハイオ州のBoehringer Ingelheim's Ben Venue 研究所の化学者）は，2011年の化学ノーベル賞受賞者シェヒトマンの準結晶を知り，自宅の新しいパティオのデザインにこれを用いることを思いつきました．そしえ，フリッケは1年がかりで2012年11月にパティオを完成しました．
1200個の特製のコンクリート舗装石を準結晶パターンに配置したものです．
写真は，子供が準結晶タイル張りのパティオに立っているところです．彼のTシャツには「悪役のようにゆったり」と書かれています．

フリッケは，パティオに使う2種類の舗装石（太った菱形と痩せた菱形）の木製型を作製しました．木型を使用して彼は1日に15枚のコンクリート舗装石をキャストし，10か月生産した後，ペンローズの非周期タイルと呼ばれるパターンに配列し始めました．
この配列を作るのは「忍耐が必要」だったようです．準結晶が広く受け入れられるまでに，シェヒトマンが嘲笑や猜疑を乗り越えたように．

夜明け前の空の色が美しい．桔梗の色とオレンジ色の消えるところが良い．

新年おめでとうございます．2020年も宜しくお願いいたします．蕎麦好きな私ですが，年越し蕎麦を蕎麦屋で食べたのは初めて，除夜の鐘を撞きに行ったのも初めてです．行列があれば止める主義の私ですが，今回はどちらにも並んでしまいました．

4x4の16個のマスに0~15の数字が書かれたカードがあります．このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる．これをマスクカードを変えて4回行えば，相手が心の中で思っていた数が当てられるというのが，この数当てのゲームです．

どのような仕組みがあるのでしょうか．秋山久義さんが，2019年7月のパズル懇話会で発表されています．
今日は，秋山久義さんの発表「数当てカードの諸相」から引用して，その仕組みを解説します．

まず，16個の数の配列は，ランダムに配置したふりをしていますが隠れた規則があります．
例えば次の２つの方法があります．
（１）左右対称の位置にある2つの数字の和は常に15になる．
（２）回転対称（2回対称あるいは点対称）の位置にある２つの数字の和は常に15になる．

このために右半分（あるいは左半分）を知れば，全部の数の配置がわかります．
つまり，相手の意中の数が見えない場合は，その数との和が15となる数の方が見えているのです．

さて，0~15の数を2進数で表すと次の表のようになります．a,b,c,dはそれぞれ2^3，2^2，2^1，2^0の桁に相当します．

2進数表示で3桁目を表すマスクカードがa，2桁目を表すマスクカードがb，というように
4枚のマスクカードができます．
それぞれの数の上に乗る4種類のマスクカードで，2進数表示の１のところに孔を開ける（網掛け部分）
ことにします（逆に統一してもかまわないが）．
例えば，13の場合は，aとbとdのマスクカードに孔（網掛け部分）をあけ，ｃのマスクカードには
孔はあけません．

以上で，仕掛けの準備ができました．

これで，質問を開始して，数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます．
見えないといったマスクカードは
（１）の場合には裏返して重ね／（２）の場合は180°回転して重ねるのです．

結局，4枚のマスクカードを重ねたものは，
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2019.12.24］ No.298
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
12/20はアップリンク渋谷に映画，「エッシャー 視覚の魔術師」を見に行きました．
エッシャー（オランダ，2018）の版画作品からは，数学者としてのエッシャーは良く知られていますが，
どんな生活をした人物かはあまり気にしたことがありませんでした．
映画では，エッシャーの息子たちへの取材が面白かったです．作品にまつわるエピソード
［1955年作「表皮」から1956年作「婚姻のきづな」に発展］など，よくわかりました．
ムッソリーニ時代の全体主義に息子が染められるのを嫌いイタリアからスイスに移住しました．
人物像のわかる良い映画でした．

最後の方でエッシャーが国際結晶学会の講演に呼ばれていくところがありましたが，
私の専門は結晶学で，結晶学会では昔からエッシャーの周期的模様を教材にしており，
結晶学者には，エッシャー作品は馴染み深いものです．

アルハンブラのモザイクには平面群の17種のすべてがあるという説と1種類かけているという説があります．
どちらでしょうか？それともどちらも違うのか．実際にアルハンブラには行って調べて見たいものです．
ペンローズ・タイリングを発見したペンローズも，アルハンブラのタイルからヒントを得たと聞きます．
私も，イスラームのデザインに立戻って，タイル張りの見直しをしてみようと思っています．

映画のエンドロールにスナップ映像が流れますが，その映像の一つに，大道絵師の光景が写りました．
たまたま昨夏，ニューカッスルの通りで見かけたエッシャー作品ばかり道に描いていた大道絵師のようです．

http://cinejour2019ikoufilm.seesaa.net/article/escher-review.html シネマジャーナルへ掲載いただきました．

■エッシャー作品の生まれるまで
コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました．
1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/a655be2fc4e933a93af15e269d8b684e?frame_id=54

極限としての円の数学については，以下のブログを参照ください．
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/2e340c06148db50daae618a772629e15?frame_id=54

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

uplinkで上映中の「エッシャー視覚の魔術師」

極限としての円の数学については，過去のブログを参照⇒　「極限としての円」の作品

友達が本屋情報を教えてくれます．有難いことです．

12月のシジュウカラさんたちはとても活発です．ヒマワリの種もたくさん食べます．
2,3羽づつ飛来し，同時に4,5羽が来ることもあります．

クンデカリKundekariという技術は，接着剤も釘も使わず木のピースを組み立てていく技術です．イスラム模様の装飾のある説教壇（minbar），ドア，家具に用いられます．12世紀にアナトリア地区で生まれたこの技術は，その地のセルジューク帝国，オスマン帝国時代に洗練されました．杉，薔薇，梨，クルミ，黒檀，リンゴなどの木材が使われます．木材ピースを溝とホゾで組み立てるので．各ピース間は2~3mmのギャップがあり，それぞれのピースの膨張伸縮で歪みが生じることがありません．接着剤や釘で固定された作り方よりも，湿気などに対する耐久性があり，ひびが入らず700年持つといわれます．ジャーミイのドアは，5cm位の多くのパーツをクンデカリの技術で組み立てています．そしてさらに，このドアーを構成する木材ピースの総数は，数秘術的な意味があるそうです．
⇒数秘術的な意味については，アラビア文字のアブジャド数に続く．
（参考文献）クンデカリについては，Mugla Journal of Science and Technology, Vol2,No2,2016,110を引用

機械設計（日刊工業新聞社）1月号のSekkeiBookReviewに拙著「美しい幾何学」を取り上げてくださいました．本の狙いをよく理解いただいたようで工学分野で読まれるのは嬉しいです．
この雑誌は専門書なので初めて手にしますが，回転ステージやDCモーターなど，会社でＸ線反射率測定装置を作ったとき購入したものも色々載っていて懐かしいです．ロボットの分野はずいぶん進み洗練されましたね．

以下の記事が目につきます．これらは数学とも無縁ではありません．
・「歯車装置の設計計算」→表計算ソフトで歯車の歯切りに使うピニオンカッタのトコロイド曲線を描く．

・「Mathcad学ぶで力学解析」→Mathcadは数式通りの記述で計算ができるので，私も初期のMathcadを個人購入し（初期の頃はMathematicaに比べかなり安かった）愛用していたことがあります．いまはMathcad prime6.0になったようです．

・「鳥はなぜ飛べるのか」→非常に興味深い．翼まわりの渦輪など解析をしていますが，難しい流体力学なのでまだ読めていません．

12月4日の夕方から秋葉忠利さんの「数学書として憲法を読む」の出版記念パーティがありました．100人ほど集まり楽しいパーティでした．田中康夫さんや阿部知子さんも来られました．おりしも，PISAテストで15歳の読解力の低下が指摘されています．国民もマスコミも読解力のない社会になりました．論点を次々にずらしたり，揚げ足取りで本論から逸脱させたり，部分否定と全否定をすり替えたり，必要条件と十分条件を区別しなかったり，みな詭弁への道で，まともな議論になりません．論旨を素直にとらえて，正面から議論する当たり前のことが通じない社会になりました．特に，国会やマスコミの報道でこのようなまともな論理の劣化が気になります．

読解力は，読書をしたり話を聞いたりして自然に身に着くものです．私の子供の頃は，落語のラジオ放送を聞く毎日でしたが，まとまった話を最後まで聞くというのは，読解力を身に着けるための良い訓練であると思います．

論理的な普通の読解力で（いかめしく言うと数学的に）憲法を読むというアイデアは画期的な問題提起です．
秋葉さんの本の一読をお勧めします．この本は以下の様に憲法を舞台にしていますが，何の分野でも正しくあるがままに理解するということは重要なことです．

■改憲不可条項
憲法にある「義務」，「尊重」などの単語，特に，「永遠」，「永久」といった「絶対性」をもつ単語を，素直に受け入れ（「義務」という言葉は素直に法的義務と読むべきなのに，都合の悪いところになると道義的要請とよむ「憲法マジック」は詭弁の入り口），「全部否定」と「部分否定」，「必要条件」と「十分条件」との違いを峻別できないと，詭弁に引き込まれます．この他に，憲法に書かれていないこと（あるいは，他の文献）に依存せず，憲法全体は，無矛盾・自己完結するなど，９つのルール（9大律）を設定し，憲法の条文を公理に見立て，論理的な結論となるいくつかの「定理」を導きました．

「永久に」，「国民の総意」，「不断の」などの絶対的な表現と関連がある８つが「改憲不可条項」に当たります．改憲禁止の条項とは明示されてはいないが，論理的にそのような結論になる条文が8か条あるということです．この8か条も含めて，改正の対象にならない条文は30か条を超えることが示されました．改憲の手続き規定である96条は改憲のための必要条件に過ぎないわけです．時間的な極限を表す言葉，「永久に」が使われている9条を変えて，1946年以降の有限時間内のある時点で「戦争をすることが可能になる」ようにすることは，「永久に」という言葉に反します．したがって，9条を「改憲」することは憲法違反になります．

アラビア文字の各文字は数を割りあてられています．このシステムのことはアブジャドabjadと呼ばれ，十進法のインド数字が採用される以前は数値を表現するのに使われていました．また，単語や文章の数値はシンボリックな意味があります．
例えば，「アッラー」は66，このアナグラムの「ラーレ（チューリップ）」も66で，同じ数値ですので，チューリップ模様はジャーミイの装飾に使われます．

クンデカリを構成するピースの数も意味があります．例えば，ドアの文様を構成するセグメント数の165ピースは，「アッラーのほかに神はいない」を意味するそうです．

■私はアブジャドのことは聞きかじっただけで，正確な記述ではないかもしれません（アブジャドのことをご存知の方教えてください）．
私の理解した考え方だけおおざっぱに述べると，アラビア語でも，アルファベット（英語）で計算する数秘術のように，単語（スペル）の文字の数値を総計し，その単語の数値が決まります．ただし，数値を対応させるのはアブジャドに対してで，アラビア文字そのものに対してではないそうです．

（注）世界には，ギリシャ文字（ラテン文字，キリル文字，...），漢字，アラビア文字，などいろいろありますが，アラビア文字は子音を表記する文字に母音も含めるようで，文字も独立の場合と単語の中に使われる場合で異なるようです．漢字や速記文字なども記号全体で一定の意味もつのに似ています．単純なアルファベットではなくアブジャドという文字体系に数字を対応させます．

■クンデカリ技術で作られたドアを構成するピース数の意味

以下の写真のドアの文様の数値227は，次のようにして数えるそうです．この数値のシンボリックな意味は知りません．

面積１の正方形の数14個　→1x14=14
面積２の長方形の数11個　→2x11=22
面積３の長方形の数13個　→3x13=39
ーーーーーーーーーーーーーーーーーー　
　　　（全図形数）38個　　 　　75（全面積）
　　　　　　　　　x4
　　　　　　－－－－－
　（枠のピース数）152　＋（面積数）75　=227（全ピース数）

11月30日，10:00-17:00，東京ジャーミイの台風被災地復興支援チャリティ・バザーでにぎわいました．

新館内装も完成しました．

11月30日は東京ジャーミイのチャリティ・バザーの一環として万華鏡のワークショップを行いました．3クラス実施し，
66人の材料を使い切りました．新館の３Fの工事が終わったばかりの美しい部屋のHouse-warming partyになりました．

万華鏡の鏡室となる3角形は，頂角が15°の２等辺3角形です．従って，鏡室は（15°，82.5°，82.5°）ですから，分数解（12，24/11，24/11）の万華鏡になります．確かに，1/12＋11/24＋11/24＝1　ですから，条件を満たす分数解であることがわかります．

ーーーーーーーーーーーーーーーーーーーーーーーーーーーー

今週の土曜日（11月30日）は東京ジャーミイで万華鏡のワークショップをやります．これは東京ジャーミイのチャリティ・バザーの一環として実施されます．お近くの方は参加されることをお勧めします．詳細や参加申し込みは，以下の東京ジャーミイのウエブサイトをご覧ください．
https://tokyocamii.org/ja/event/1787/?fbclid=IwAR2JXV3GaFx5ruXfPabGC-reuY7VPFNKq1LPXtLpgdltl4hijMo0hT1Ot8I

■万華鏡の原理
平行な合わせ鏡の間に置いた物体は，物体像と鏡像のペアが無限に繰り返す市松模様を生じます．2枚の合わせ鏡が平行でなくθの角度で交差する場合は，一次元の市松模様は円周に沿って並びます．円周の向こう側で市松模様がきれいにつながる条件は，360/2θ＝n（整数）です．これは，万華鏡を発明した物理学者ブリュースターの特許（1817年）に書いてあります．

3枚鏡が3角形をなす場合は，3角形の各頂点でこの条件が成り立つので
1/n＋1/m+1/p＝１，（2=<n,m,p）が，平面がきれいな市松模様になる条件です．この条件を満たす3角形は図に示す3種類しかありません．

これだけではつまらないので，分数解も許すことにすれば，解は無限にあります．このような分数解の万華鏡は，平面の所々で市松模様が破綻しますが，やはり美しいものです．

→続く

■イスラーム模様の特徴　➡亜群

イスラーム模様の特徴は，局所的に対称性の高い星型ロゼットがちりばめられていることです．平面群で存在が許される回転対称は，2，3，4，6回に限られ，5回や，7回以上の回転対称は周期性と両立できません．その理由は正5角形のタイルや正7角形以上のタイルは平面を隙間なく埋めることができないからです．

イスラームの繰り返し模様中に，高い対称性（9回とか10回とか12回など）のロゼットをよく見かけますが，これらの対称性は各ロゼットの内部だけで，全域を支配することはあり得ません．そのため，対称性が高そうに見えても，平面群（17種類ある）のどれかに割り当てざるを得ないのです．

イスラームの特徴的な模様を，平面群で分類するのではなく，もっときめ細かい対称性の記述はできないものでしょうか？　群ではなく，亜群（1926）や混群という代数系などが提案されていますが，その発展が行き詰っているのは残念なことです．

■高次元の周期的な世界から2次元の世界への影　➡高次元格子からの射影

イスラーム模様を高次元の周期的空間からの2次元平面への影であると解釈する方法もあります．

周期性のないPenroseのタイル張り(1976)を，このような方法で作ることもできます．

左図は，周期的な2次元世界から1次元世界への射影で，2次元世界で存在した周期性が失われる事例です．5次元の周期的空間［3次元や2次元の周期的空間には存在できない5回対称軸が存在可能］を，2次元平面に射影すると，5回対称のロゼットを作れますが，５回対称性はロゼットの内部だけで2次元平面での周期性は壊れます．イスラーム模様にちりばめられた高い対称性の星型ロゼット（高次元空間からの影）を見ていると，高次元の宇宙の中に自分が存在する世界があることを実感し，不思議な気分になります．

■結晶は周期的な世界　➡平面群

結晶は単位胞を積み上げてできたブロック細工のようなもので，周期的な内部構造です．図は水晶の例です．水晶の6角柱の方向から見た投影図とM.C.Escherのこの版画作品は同じ対称性（平面群p31m）です．

系の秩序（対称性）は，対称操作［系全体を動かしたとき，系の初期位置と全く重なるような操作］の集合で記述します．対称操作には，並進，対称心，鏡映，回転などがあり，これらの対称操作（群の元という）の組み合わせが作る“群”という代数系［集合の元間の演算が，群の定義（注）を満たす集合］で分類できます．壁紙を記述する平面群は17種類あり，ジャーミイの繰り返し模様もこれらのどれかに分類できます．

注）群の定義：

1．集合Gの任意の２つの元a,bの積a・bは集合Gに属す．→集合は閉じている
2．(a･b)･c＝a･(b･c)　→結合の法則
3．任意の要素aに対して，a･e＝e･aとなるeが集合Gの中にある．→単位元eの存在
4．任意の要素aに対してx･a＝a･x＝eとなるxが集合Gの中にある．→逆元xの存在

■イスラームの模様の作り方　➡テッセレーション

イスラーム建築に使われている美しい模様は，コンパスと定規だけで厳密に作図できますが，1200年までに，5種類のGirihタイル[縁に模様のある等辺多角形タイル]を用いて，パズルのように平面を埋めて美しい複雑なデザインを作る手法が確立しました．

この方法は平面を多角形タイルで分割するテッセレーションの手法と同じです．イランのDarb-i Imam寺院（1453）の壁には,その500年後にヨーロッパで発見されるPenroseタイリング［自分の中に自分と同じパターンが繰り込まれる］と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています．

→（下）へ続く

ペンローズ・タイリングとは，次のような2種類のタイルから出来ているタイル張りです．
この図の例では周期ができてしまいましたが，周期ができないように作ることもできます．

ペンローズ・タイリングは，5次元の空間格子の2次元への射影として作れます．
5次元超立方体は頂点32個，辺の数80（各頂点が５次の同次グラフ）です．
超立方体は亀井図（多元構造グラフ）で表示するとわかり易い．
https://sgk2005.org/wysiwyg/image/download/1/526/medium
我々は５次元空間を見ることができないので，５次元空間の基底を，互いに直交する２つの部分空間の基底の直和（２次元＋３次元）に分けて考察することにします．
周期的な５次元空間［単位胞（5次元超立方体）］を，その5次元空間内をよぎる２次元平面（スクリーン）に射影するには，２次元平面にできる格子の影に，この2次元平面に対する３次元直交補空間（菱形20面体）を射影すればよい．

この３次元補空間内の基底ベクトル３本は互いに直交しているのだが，この３本のすべてがスクリーンとなる２次元平面にも直交している（想像しにくい状態だが５次元の世界だから可能）．
５次元超立方体を３次元に射影してできる立体は，菱形20面体（頂点数は22個，辺の数40）だが，
５次元空間の単位胞の体対角方向が２次元スクリーンに垂直になるように置いて，スクリーンへ射影を行う．つまり，菱形20面体の１つの5回対称軸を2次元スクリーンに垂直にして見下ろしたときの外形（ペトリー多角形と言う）を図に示します．ペトリー多角形とその内部の点は5次元の超立方体の頂点に対応します．

ペンローズ・タイリングに現れる特徴的なパターンが，ペトリー多角形内に作れることを図に示しました．

5次元の周期的な空間を，単位胞（5次元超立方体）の体対角線[1,1,1,1,1]方向に垂直な2次元平面に射影すると，この2次元平面は，3次元補空間の菱形20面体をいくつかの高さのレベルで切断したいくつかのサイズのペトリー多角形内のパターンが次々に現れ，ペンローズのタイル模様が作れます．

正10角形の外側を正5角形（辺の長さは正10角形の辺の長さと同じ）10個で取り囲んだ図が基本です．

この図形は，ジャーミイの説教壇横の装飾に使われています．

下図左のような３種（水色，黄緑色，ピンク）のタイルをGirihタイルと言います．この他に２種のタイル型もGirihタイルに加えて５種類のタイルを用いる場合もあります．Girihというのはタイルの中の模様の線のことです．水色の10角形のタイルの作図法を下図右に示します．この作図は赤い円を10等分することから始めます．

 さて，これらの3種類のタイルを用いて，色々な平面のタイル張りができます．

例えば，次の２つをご覧ください．

(1)

(2)

タイルの色は説明のために着色しただけで，タイルの輪郭線ではなく，各タイル内の線Girihが描く模様に注目してください．

これらのタイル張りの対称性は，(1)はP2mm，(2)はC2mm，もちろん，描かれるイスラーム模様の対称性も同様です．

このような３種（水色，黄緑色，ピンク）のタイルをGirihタイルと言います．この他に２種のタイルの型もGirihタイルに加えて５種類のタイルを用いる場合もあります．Girihというのはタイルの中の模様の線のことです．水色の10角形のタイルの作図法を次の図に示します．この作図は赤い円を10等分することから始めます．

さて，これらの3種類のタイルを用いて，色々な平面のタイル張りができます．

例えば，次の２つをご覧ください．

(1)

(2)

タイルの色は説明のために着色しただけで，各タイル内の線Girihが描く模様が求めるものです．

これらのタイル張りの対称性は，(1)はP2mm，(2)はC2mm，もちろん，描かれるイスラーム模様の対称性も同様です．

https://www.beautifulmosque.com/PostImages/Ulugh-Beg-Madrassa-in-Samarkand-Uzbekistan-21.jpg

ウルグ・ベク・マドラサ神学校

東京ジャーミイの玄関ホールの陳列棚に飾ってある美しい皿です．直径30cm程度です．

中心（花弁12枚）の大きな花には，花の内部だけで有効な12回対称軸があります．しかし，中心の花の周りに小さい花が6個配置されており，全域的に見ると，これは12回対称軸でなく6回対称軸になります．周囲の6個の花（花弁９枚）は，それぞれ自分の内部に有効な9回対称軸がありますが，全域的に見ると3回対称軸です．6回対称軸と6回対称軸の間，3回対称軸と3回対称軸の間には2回対称軸が生じます．その他，右図に実線で描いたように鏡映面があります．
ここで，全域的とは，この模様がお皿の外にも同様な繰り返し規則で無限に続いていると想定した模様のことです．つまり，無限に続くこの模様の対称性は右図のような対称要素の配列（平面群P6mm）になります．右図で水色に塗った部分が単位胞です．
この皿の模様は，この繰り返し模様から青い点線（右図中）で記した円の内部だけを切り取ったものです．

■それぞれの花の内部の局所的な高い対称性
中心の花の内部は，12回対称（その部分群としての6回対称は全域で通用），周りの6個の花の内部は，それぞれ9回対称(その部分群としての3回対称は全域で通用）です．
12回対称や9回対称は周期性と矛盾するので，繰り返し模様全域で，このように高い対称性は存在できません（周期性と両立できる回転対称性は，2,3,4,6回軸に限られます）．このような高い対称性が通用するのはそれぞれの花の内部だけです．
しかし，例えば，５次元空間では，５回対称性が周期と共存することが可能ですから，このような高い対称性が見える花の内部は，高次元空間の断面が2次元の皿の表面に投影されたものと想像することもできます．見えない次元の世界の投影を見るような不思議な魅力を感じるでしょう．

■説教壇横のイスラミックデザイン

写真は説教壇横にある装飾です．次の写真はステンドグラスです．

どちらもイスラミックデザインに特徴的な複雑な図形ですが美しい．
これらの図形の作図は，コンパスと直線定規だけでなされました．
中心に10回対称の星型ロゼットが見えるでしょう．
この「正5角形と180°回転した正5角形を重ね合わせた」星型ロゼット（点群10mm）を
内角が108°と72°の菱形を単位胞とする格子に配置して，繰り返し模様を作りました．
この菱形格子は正6角形（正3角形）のように見えますが，
上下の方向が左右の方向に比べてすこし長く，歪んでいます．
正5角形や正10角形（どちらも最低でも5回対称性がある）を
周期的に並べることは不可能ですから，5回対称性が全域で支配するような格子はできません．「正5角形とその180°回転したものを重ね合わせた」星型ロゼットの対称性（10mm）は，ロゼット内部だけを支配する（局所的）ものです．
この繰り返し模様の対称性（平面群）には，2回軸と水平および垂直に鏡映面があり，記号でいうとP2mmの対称性です．
このように高対称のロゼットをうまくつないで周期性のある模様ができるところがイスラムのデザインの特徴です．

10回(5回)対称は，周期的に並ぶことができません．10回(5回)対称タイルを周期的に配列したイスラームの繰り返しパターンを調べましょう．このようなパターンはイスラームに特徴的で，ジャーミイのいろいろな所で見かけます．

10回(5回)対称は周期性と矛盾しますから，それぞれの10回(5回)対称が支配するのはタイルの内部だけです．

このタイルの描き方を習得するのにだいぶ工夫をしました．
作図手順の足跡として，赤色の作図補助線を残しておきましたから，
皆さんも工夫してこの図を描いてみてください．

まず，中心にある円の円周を10等分することから始めます．
円周の10等分は中心角が36°の作図で，前回に正五角形（中心角72°）の作図をやりましたから，
それを応用して円周の10等分を作図してください．

この長方形のタイルが単位胞になり，これを並べることにより繰り返しパターンが作れます．

この繰り返しパターンの平面群はP2mmです．

10mmという対称性の高い部分があります．もし，そのような対称性が全域に作用するなら，
繰り返し（周期性）ができるわけがありません．10mmという点群の作用はそれぞれの赤い円内の領域に限られるので，周期性と両立できるのです．このようなイスラーム・パターンは色々な所に見受けられます．

次に，この繰り返しパターンを３つの部品によるタイル貼りと解釈してみましょう．
つまり，図に示したように正10角形タイルと，ピンクのタイルと黄緑色のタイルの3種類です．
今日は，この3種類のタイルで平面が隙間なくタイルhave貼りされていることを確認してください．

 ■応用例

Darb-e Imam寺院（イラン）のイスラミック・タイリングのパターン（1453年）は，その500年後に発見されるPenroseタイリング（1973年）と同じものであるのが興味深い．Penroseタイリングは，その10年後に発見される準結晶（1984年）の構造解明に用いられる．

■正5角形の性質

正5角形の中に相似な2等辺3角形（頂角36°）が次々に組み込まれていく様子を見てください．
赤い2等辺3角形→緑の2等辺3角形→青い2等辺3角形
辺の比率は，いつもΦ：1です．Φは正5角形の対角線（星形の辺）で，1は正5角形の1辺です．
このとき成立する方程式，Φ²－Φー１=0を解いて（Φ>1をとる），Φ＝(1+√5)/2＝1.6180･･が得られます．Φは黄金比の値です．

■正5角形の実用作図法で以下のものがあります．

この作図はつぎの式が成り立ちます．AH=HB=1/2，MH=√3/2　であるので，
PH=(√3ー1)/2，従ってPB=(√[(√3－1)²＋1])/2＝(√[5－2√3])/2
AB/PB＝2√(65－26√3)/13＝1.6138･･･
この作図法は，イスラームのタイル作図で便利ですが，厳密な正５角形ではありません．
しかし，誤差は0.26%なので実用上問題ない恐るべき精度です．

 ■厳密な正5角形の作図

AB=1，AH=1/2，PH=1　ですので，AP＝(√[1＋2²])/2＝√5/2
従って，QP＝(1＋√5)/2＝Φ
この作図で得られるのは厳密に正5角形であることが証明されました．

■折り紙で作る正5角形(1)の精度

この図は折り紙で正5角形を作る原理を示しました．y=3xの直線とx軸のなす角θを求めると
θ＝arctan3＝71.5651･･°　となりますが，正5角形では72°になるべきです．
この誤差は．0.6％ですのでかなり良い精度と言えましょう．

他の角度は，72.1087（0.2%），
72.6524（0.9%）程度です．（カッコ内は誤差）

■折り紙で作る正５角形(2)の精度

折り紙の一太刀切で大変作り易い星型です．この原理は以下の図を見てください．
正5角形（星型）の一辺の中心角は360°/5＝72°ですから，一太刀切りに対応する中心角は36°です．
以下の図を見ると，一太刀切りの中心角は，35.783°(36°からのハズレは-0.6%)to,36.870°（+2.4%）に収まっています．

「美しい幾何学」第8章はイスラミック・デザインです．

対称性10mmのタイルを周期的に配置するならば，10mm（あるいは5m）の対称性が全域で残ることはあり得ません．これらの対称性はタイルの内部だけ（局所的）に作用できます．
周期的なイスラームのデザインでタイル(10mm)はどのように配置されているのでしょうか．
大変興味深いことです．このようなタイルはどのように配置されているでしょうか．

（１）まず，一つの例を示します．並進周期をあらわす単位胞は内角が54°と126°の平行4辺形です．正3角形格子（菱形）のようにも見えますが，そうではありませんので注意しましょう．
オレンジの6角形ベース型は正10角形の内部にある花弁の6角形ベース型とまったく同じ型です．

10回対称軸の作用はそれぞれの正10角形内部でのみ有効で，オレンジの6角形ベースには作用できません．従って，それぞれの正10角形はそれぞれの独立した宇宙であるという解釈ができます．

（２）もう一つの配置例を示しましょう．MirzaAkbar

この例では並進を表す単位胞は長方形です．

（３）このほかにも，正10角形タイルを周期的につなぐ美しい配置の実例を発見することができるでしょう．探してみましょう．

次の写真はイスラムの美しい象嵌細工の一部分です．
今回は，この5回対称（あるいは10回対称）の模様を作図してみましょう．

中心部分の輪郭に，正5角形と，それを180°回転した正5角形とを重畳した
10回対称の形（右図）が見えるでしょう．
平面の正多角形タイルによるタイル張り（1種類の正多角形タイルで隙間なく張り詰めること）は，正3角形，正4角形，正6角形でのみ可能です．正5角形のタイルでは平面のタイル張りはできません．これは，平面全域に作用する5回対称軸が周期的に配列している状態があり得ないことと等価です．
イスラムのこの象嵌細工に見られる5回対称（10回対称）は，この模様が周期的に配置された平面全域で作用するものではありません．この図形を中心とする局所的な領域内で作用するものです．

このようなイスラムのデザインは色々な変形があり，各所の装飾に多用されています．大変美しいので，正5角形を基本とする以下の図を作図してみましょう．正10角形の周囲を10個の正5角形が取り囲んでいます．正5角形の１つの内角は108°，正10角形の１つの内角は144°ですから，このような作図（３つのタイルが出会う頂点では，108°x2+144°=360°が成立）は可能なはずです．

このような10回対称の部分を規則的に配列し，その隙間をうまくつなぎ合わせると，
高次元の世界を見るような不思議な模様ができます．どのようにつなぎ合わせるかは，次回考察することにします．5回対称（10回対称）は周期的な平面で不可能なわけですから，それぞれの5回対称軸は局所的な作用にとどまり，つなぎの領域には有効ではありません．そのために，我々は全体平面の中に小宇宙が分布しているような不思議な印象を持つのではないかと思います．

千葉県での広域停電は長期にわたり，大変な日々をお過ごしの方にお見舞い申します．送電網システムは，ケーブル・ネットワーク（ハードウエア），制御ソフトウエア，および行為者より構成されるが，完全に定義しきれない複雑系です．スマート・グリッドになったとはいえ複雑系には完全に制御しきれない要因が何処かにあるでしょう．台風により木立が揺れ，どこかで送電ケーブルが切れたとし，その場所が運悪く重要な結節点に属するなら，電力負荷が残りの送電線にかかり，あっという間に雪崩をうって広域なネットワークの事故に広がって行くことは良く知られています．複雑系はシステム全体として定義できるもので，システムの部分を切り出して定義できません．これは，どこかの事故がシステム全体に広がる可能性を意味します．引き金となる些細な事故はどこで起こるか予測できません．限界ぎりぎりで稼働している複雑系の社会インフラをもつ現代社会で複雑系の数学は重要です．

私は，大規模な送電網に頼らない社会に変えるべきだと思います．自然エネルギーによる発電は，地域で作りその地域で消費する（地域分散型の小規模な送電網）に適しています．そのような利点のあるソーラー発電なのに，森林を破壊しわざわざメガソーラーを作り，また大規模送電網で電気を運ぶのはナンセンスといわざるを得ません．もちろん原発自体が複雑系であり原発の稼働は論外です．

9月15日の日本数学協会の年会では，wowowドラマ，つるさんかめさん～ニッポン算額探訪～和算監修の小寺裕氏の講演がありました．この番組は各地の算額を訪れて問題を解くというドキュメンタリ風ドラマです．というのは，毎回，一人旅の旅行者に同行し，その人が問題を解くというドキュメンタリ仕立てですが，実はこの旅行者は俳優です．さすが俳優で，素人っぽいとぼけたいい味をだしておりなかなか面白いです．私はwowowを見ませんので知りませんでした．第1回の京都北野天満宮，第3回の仙台塩釜神社，第6回の東京金王八幡のそれぞれ30分番組が紹介されました．
脱線しますが奈良弘仁寺の近くで売っている算額最中とはこのような物らしい．

https://media-01.creema.net/user/1015506/exhibits/2498645/0_16f50200d1c23f016772a2a091f8d701_583x585.jpg?fbclid=IwAR1JHomrpu2ucRzQMMPm36vNlllUbq5ixYCEwsaw-1Q-R80C8HaPDgEePmM

■さて，ドラマで取り上げられた算額の問題を紹介しましょう．
第1問は辺2aの正方形内の帆の形に内接するピンクの円の半径を求める．
第2問は円r_a，r_b，r_c，直線が互いに接しているときのピンクの円の半径を求めることです．
私は問題中の数値を忘れたので，このように記号で書きましたが，算額の問題では，aやr_a，r_bは具体的に数字が与えられています．これらの問題は，直角3角形のピタゴラスの定理だけを使えば解けます．
両者とも互いに円が接するときの問題ですが，特に第2問はいわゆるアポロニウスのガスケットの特殊なケース（直線は半径∞の円）です．いろいろ挑戦してみてください．
第1問は　x²+6ax-3a²＝０を解くことになります．
第2問は1/√r_c＝1/√r_a＋1/√r_b　から求まります．
アポロニウスのガスケットの作図で描く互いに接する４つの円に関して，
もっと一般化されたデカルトの定理（1643年）があることに言及しておきます．
（第1問）

（第2問）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2019.09.10］ No.283
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日9/9の朝早く台風が通過しました．関東の皆様被害はありませんでしたか．
こちらでも草木がみななぎ倒されたり，街路樹の紅葉葉楓モミジバフウの枝や実が散乱していました．
今日9/9は，「美しい幾何学」の発売日です．やっと発売にこぎつけた記念すべき日です．
どうぞ書店で手に取って中身を一度ご覧ください．
以下の日刊ベリタに詳しい紹介記事があります．
http://www.nikkanberita.com/read.cgi?id=201909042302103&fbclid=IwAR2JFVjjl2EXJt7238PYL5IP4FwGc7-Fc4rj8xtZVn6SfsWAh2F2vrf6ZjU

この図鑑には美しい図形や不思議な図形がたくさん出てきます．
そのような図形の仕組みを「見ているだけで理解できるように」したかったのです．
数式を使えば正確な説明が楽にできますが，そのためには，
たくさんの数学準備の回り道があり，焦点がぼけてしまいます．
小学生から大学生までが，本書の図を眺めているうちに，
図形に隠された仕組みが自ずとわかることを狙いました．
普通の数学書のように抽象的な記述だけで終りません．
具体的な図を示し本質が理解できるようにしました．
内容には大学の専門課程レベルのものもあり，初めはわからないところもあるでしょうが，
何度も図を見ているうちに，不思議なことに理解できる時がきっと訪れます．

この本の各章は，万華鏡で繋がっています．
1,2章は有限図形の対称性，3,4章は周期的な空間の対称性，
これらの世界の映像は，万華鏡で作り出すことができます．
5章は万華鏡，6章は円による反転という数学的な鏡，7章はフラクタル操作という数学的な鏡，
8章ではイスラミック・デザインの特徴を鑑賞します．イスラムのデザインには，黄金比が多く，
かつ，局所的に高い対称性がちりばめられた周期平面なので，
あたかも我々の住む3次元に高次元宇宙が投影されているような不思議さが魅力です．