
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
ナイチンゲールが50年間ベッドでの仕事を余儀なくされ,死因ともなったのは,クリミア戦争時に流行したマルタ熱(ブルセラ症)であることが明らかになった.D A B Young,Florence Nightingale's fever,(BMJ VOLUME 311 23-30 DECEMBER 1995)
ーーーーーーー
■ブルセラ症(brucellosis)
NIID国立感染症研究所https://www.niid.go.jp/niid/ja/kansennohanashi/513-brucella.html,および,wikiを参照した.----
ブルセラ症はマルタ熱とも呼ばれる細菌に感染して起こる人獣共通感染症.クリミア戦争でマルタ熱が流行したことで世界的に注目されたが,紀元前400年頃のヒポクラテス著書にブルセラ症と思われる疾患がすでに記載されている.現在でも,世界中で毎年50万人を越える家畜ブルセラ菌感染患者が新規に発生(食料や社会・経済が家畜へ依存し,家畜ブルセラ病が発生している国や地域)発生している.マルタ熱の原因菌として,イギリス軍の軍医Sir David BruceによりB. melitensis が分離(1887)されて以降,種々のブルセラ属菌が発見されている.ヒトへの感染が報告されている主なものは,B. melitensis (自然宿主:ヤギ,ヒツジ),B. suis (ブタ),B. abortus (ウシ,水牛),B. canis (イヌ)の4菌種である.日本では,過去に牛のB. abortus感染が流行し問題になったが,家畜衛生対策の徹底により,1970年を最後に国内家畜から菌が分離された例はない.感染動物の加熱殺菌が不十分な乳・乳製品や肉の喫食による経口感染が最も一般的である.ヒト-ヒト感染は極めてまれである.
ブルセラ属菌は敵国の兵士や住民に罹患させて能力を低下させる生物兵器としても研究・培養された.アメリカは1942年、ソ連は1978年に兵器化を実現した.
■サビノワとリユドミラ物語.Екатерина Савинова и Людмила Сенчина
Приходите завтра「明日来なさい」(1963年,ソビエト映画)は,1540万観客の大ヒット映画(ロシア語)です.シベリアの寒村からИнститут имени Гнесиных モスクワの音楽学校に入ろうと出てきた才能ある少女の物語です.重い荷物を背負って一人で都会に出てきた元気で愉快な純粋な少女です.しかし,モスクワに来たときは既に遅く入学試験は終わっていました. 少女の役名はФросяフローシャ.これは実在のЕкатерина Савиноваサビノワの伝記映画で,サビノワ自身が主演し歌います.あの声はサビノワしか出せません.私がこの映画を知ったのも彼女の3.5オクターブ出るという魅力的な声の歌を耳にしたからです.音楽学校の玄関で有名なソコロフ教授に何度か訴えます.ついに引き出した教授の返事が Приходите завтра!「明日来なさい」でした.教授に学校のオーデトリウムで聞いてもらえた彼女の歌声がすばらしい.教授もフローシャの純粋さと素晴らしい声を見抜き,何とか入学させようと動きます.この映画はサビノワが自分で主演した愉快で楽しい映画で,私はとても好きです.しかし,残念ながら,その後のサビノワは,ブルセラ病(生牛乳を飲むと牛から感染する)が重くなり鉄道自殺(1970年,43歳)してしまいます.
興味深いのは,1963年にウクライナで高校生時代に,Людмила Сенчинаリュドミラ・センチナはきっとこの映画を見たのではないかと私は想像します.リュドミラは成功して,ロシア人民芸術家歌手になります.彼女は今年の1月25日に,ペテルブルクの病院で死去(67歳)しました.
リュドミラは,高校を卒業して,歌手になるために,ウクライナからレニングラード(現ペテルブルグ)に出てきました.でも,そのとき音楽学校の試験は終わっていたのです.よく似た話があるものですね.サビノワと違うのはペテルブルグに親戚がいたことです.
リュドミラの代表曲は,Песня Золушкиシンデレラの歌
-------

■この本に,第9章を続けて書くとすれば,イスラミック・デザインになります.イスラムデザインの特徴は,黄金比(すなわち5回対称や10回対称)がちりばめられていることです.しかし,5回対称性と2次元(あるいは3次元)世界の周期性とは両立できませんから,ちりばめられている5回(あるいは10回)対称性はロゼット内部だけに局所的に作用し,世界の全域を支配するものではありません.そのため,あたかも我々の住む3次元に高次元宇宙が投影しているようで不思議な魅力を感じます.イランのDarb-i Imam寺院(1453)の壁には,その500年後にヨーロッパで発見されるPenroseタイリング[自分の中に自分と同じパターンが繰り込まれる]と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています.イスラムの繰り返し模様は準結晶や基本領域が分割されて写像される万華鏡と似たところがあります.
シュロ縄で柵の竹竿を結びました.庭師は男結びと言う方法で結ぶそうですが,私は簡単にランニング・ノットという方法で結びました.実は,シュロ縄の扱いが大変だったので,一番作業の楽な結び方をして,後でこの結び方の名前を調べたら,ランニング・ノットという方法であることがわかりました.
ランニング・ノット(あるいは,スリップ・ノット)と言われる所以は,竹竿を通してから紐を引っ張って締めると結節ノットが移動して,自然に竹竿の周りの輪が締まるからです.結節になる輪から紐の両端が同じ方向に出ていますから,竹竿を通してから紐の一端を引っ張ると,輪が締り結節になると同時に,他端も同方向に引かれるので,両側から輪を締め,自分自身を締め緩みを防止しする一番シンプルな結び方になります.
ランニング・ノットの結び方で紐の両側を引っ張ると,輪の中に竹竿がなければ手品のように紐は結び目が出来ずに解けてしまいます.比較のために,もやい結びを見てみると,結びの両側を引っ張ると結節ノットは移動せず輪が出来てしまい,竹竿の周りを締める結び方にはなりませんし,竹竿がない状態で,もやい結びの紐の両側を引っ張ると解けずに固定した輪を残して結び目が出来てしまいます.
紐の始まりを竹竿の周りのランニング・ノットから始めて,柵を組んだ竹竿に巻きつけ固定し,紐の最後もランニング・ノットで収めようとするとなかなか難しい.巻いてきたひもが緩まないように締めながら出口の結節になる結び目を作る必要があるからです.
シュロ縄は水に湿らせた方がしなやかでよく締まります.シュロ縄を繰り返ししごいていると,縄に毛玉のような塊や細い箇所ができますから注意しましょう.
今回は,紐の両端をそれぞれ別の場所で固定したので,使いませんでしたが”かます結び”という方法もあります.これは紐の両端を結ぶ結び方です.
アラビア文字の各文字は数を割りあてられています.このシステムのことはアブジャドabjadと呼ばれ,十進法のインド数字が採用される以前は数値を表現するのに使われていました.また,単語や文章の数値はシンボリックな意味があります.
例えば,「アッラー」は66,このアナグラムの「ラーレ(チューリップ)」も66で,同じ数値ですので,チューリップ模様はジャーミイの装飾に使われます.
クンデカリを構成するピースの数も意味があります.例えば,ドアの文様を構成するセグメント数の165ピースは,「アッラーのほかに神はいない」,
66ピースは,「アッラー」を意味するそうです.
■私はアブジャドのことは聞きかじっただけで,正確な記述ではないかもしれません(アブジャドのことをご存知の方教えてください).
私の理解した考え方だけおおざっぱに述べると,アラビア語でも,アルファベット(英語)で計算する数秘術のように,単語(スペル)の文字の数値を総計し,その単語の数値が決まります.ただし,数値を対応させるのはアブジャドに対してで,アラビア文字そのものに対してではないそうです.
(注)世界には,ギリシャ文字(ラテン文字,キリル文字,...),漢字,アラビア文字,などいろいろありますが,アラビア文字は子音を表記する文字に母音も含めるようで,文字も独立の場合と単語の中に使われる場合で異なるようです.漢字や速記文字なども記号全体で一定の意味もつのに似ています.単純なアルファベットではなくアブジャドという文字体系に数字を対応させます.
■クンデカリ技術で作られたドアを構成するピース数の意味
以下の写真のドアの文様の数値227は,次のようにして数えるそうです.この数値のシンボリックな意味は知りません.
面積1の正方形の数14個 →1x14=14
面積2の長方形の数11個 →2x11=22
面積3の長方形の数13個 →3x13=39
ーーーーーーーーーーーーーーーーーー
(全図形数)38個 75(全面積)
x4
-----
(枠のピース数)152 +(面積数)75 =227(全ピース数)
クンデカリKundekariという技術は,接着剤も釘も使わず木のピースを組み立てていく技術です.イスラム模様の装飾のある説教壇(minbar),ドア,家具に用いられます.12世紀にアナトリア地区で生まれたこの技術は,その地のセルジューク帝国,オスマン帝国時代に洗練されました.杉,薔薇,梨,クルミ,黒檀,リンゴなどの木材が使われます.木材ピースを溝とホゾで組み立てるので.各ピース間は2~3mmのギャップがあり,それぞれのピースの膨張伸縮で歪みが生じることがありません.接着剤や釘で固定された作り方よりも,湿気などに対する耐久性があり,ひびが入らず700年持つといわれます.ジャーミイのドアは,5cm位の多くのパーツをクンデカリの技術で組み立てています.そしてさらに,このドアーを構成する木材ピースの総数は,数秘術的な意味があるそうです.
⇒数秘術的な意味については,アラビア文字のアブジャド数に続く.
(参考文献)クンデカリについては,Mugla Journal of Science and Technology, Vol2,No2,2016,110を引用
■ダイヤモンドの価値は,4C[Carat重量,Color色,Cralityキズ,Cutカット]で評価されます.ここでは,数学的に興味のあるカットのプロポーションについて述べました.ラウンド・ブリリアン・カットのダイヤモンドが最も輝くようにしたプロポーションを理想カットといいます.理想カットは1919年にベルギーのMarcel Tolkowsky(数学者でダイヤモンドのカッター)が計算しました.今なら,コンピュータもあるし,光線追跡のソフトウエアもある時代で,理想カットの形(プロポーション)を見つけることは容易でしょうが.1919年にどのように計算したのか,興味深いことです.多分,閉じ込められた光線が全反射を繰り返す光路に注目したのでしょう.
ダイヤモンドのブリリアン・カットの各部の名称を図に記載してあります.正面の平らな面をテーブル面,上半分をクラウン,下半分をパビリオンと呼びます.真ん中のガードル面に対してクラウン斜面のなす角度をβ,パビリオン斜面のなす角度をαとしました.
テーブル面の左隅Aに入った光線(赤色)が,ダイヤモンド内部を進み,後方の左パビリオン斜面で全反射され,次に,右パビリオン斜面で全反射され,テーブル面右隅Bに戻り,前方に出て行く光線もありますが,テーブル面右隅Bで一部は反射され内部に戻る光線(青色)になります.この光線は全反射を繰り返し内部に閉じ込められることになります(青色).
この図で追跡した光線は,テーブル面の左隅Aから出て,テーブル面の右隅Bに達する左右対称の光路です.ダイヤモンドの屈折率n≒2.417を用いて,この光路のテーブル面での入射角φ,屈折角γに対する屈折の式,sinφ=n・sinγ から,左右対称になる入射角φ(テーブル面の垂線と入射光線のなす角)を求めると,21°になります.というのは,左右のパビリオン間でテーブル面と平行になる光路ですから,左のパビリオン斜面での反射の法則(反射角αはパビリオン角αに等しい)から,γ=90°ー2α=8.5°となることが決まるからです.ここで,パビリオン角α=40.75°を用いました.
■屈折率の高い媒質中に光が閉じ込められるのは,全反射を起こし易いからで,ダイヤモンドの全反射の臨界角θ(入射角でいうと)は,sinθ=1/nだから,θ=24.4°(反射面から測った反射角で言うと,65.6°)です.
テーブル面の出口で反射されて内部に戻った一部の光線は,パビリオン面とクラウン面で全反射を繰り返し内部に閉じ込められます.パビリオン角α=40.75°,クラウン角β=34.50°というのは実によくできた設計です.
全反射によりブリリアン・カット内に閉じ込められた光線の経路は,一周すると,これに平行な経路に戻ることを証明するために,次の作図をしてみました.BC(赤色)の直線はダイヤモンド内部で全反射を繰り返す光線(青色)を外に引き伸ばしたものです.その代わりに,ダイヤモンドも反射面を共通にしてつないで並べました.結局,全反射を4回繰り返すと光線が平行になるということは,このように配置したダイヤモンドが4つで回転角が0に戻る(初めの向きと同じ)ことからわかります.
■カットの形を評価するには,そのカットの形を磨き直して理想カットにするとしたら,重量がどれだけ減るか(カット減点%)で表します.カット減点5%までは理想カットと見做されます.さて最後になりましたが,トルコフスキーの理想カットのプロポーションを表紙の図に示しました.トルコフスキーはガードル厚には言及せず,ナイフ・エッヂだったそうですが,現実にはナイフ・エッヂは作れず,ガードル厚は必要です.
■(注)ラウンド・ブリリアン・カットとは,58のファセット面を磨き上げた形(キューレットも1面と数えます)です.ダイヤモンドは立方晶系の結晶ですから,複屈折はありません.また,光の分散もそれほど強くなく上品です.虹色にぎらぎらするようならキュービック・ジルコニアなどの疑いがあります.
クラウン面の高さや,パビリオンの深さが最適でないと,テーブル面の中が暗くなります.
折り紙では近似的な正5角形(星型)が出てきましたが,これから扱うのは数学的に厳密な正5角形についてです.
半径1の円に内接する正5角形の1辺の長さを求めましょう.
この正5角形の1辺の長さをxとします.
△BACと△ADCは相似(相似比が黄金比Φ)で,形は2等辺三角形(等辺xとすると,底辺Φ・x)です.Φ・x=x+(x/Φ) ですから,Φは黄金比の方程式
Φ^2ーΦー1=0を満たします.この方程式の解(Φ>1のもの)は,Φ=(1+√5)/2 です.
■次に,△BCEと△BOFとが相似であることを利用し,
1:(Φ・x)=OF:CE=(1-y):(x/2) が成立するので, y=1ー1/(2Φ)
ただし,y=√[(x/Φ)^2-((Φ・x)/2-x/Φ)^2]=√[x^2ー(Φ・x/2)^2]=x√[1-(Φ/2)^2]
x=y/√[1-(Φ/2)^2]=[1-1/(2Φ)]/√[1-(Φ/2)^2]=(√[10-2√5])/2=1.1756
■ 作図
半径1の円に内接する正5角形の一辺の長さx=(√[10-2√5])/2を作図する方法
(証明)ピタゴラスの定理を2回使います.
私は,yahooブログ 「数学と社会の架け橋<数学月間>(2012.5~2019.3)」に,発行している同名のメルマガまぐまぐのバックナンバーを保存していました.メルマガはテキストなので,必要な図はどこかに保存したもののリンクを張らねばなりません.そこで,必要な図や写真はyohooブログに保存していました.しかし,昨年yahooブログが閉鎖しましたので,ブログ機能はlivedoorブログと数学月間の会のホームページに引っ越しました.
テキストは移動できたのですが,移動できなかった画像や写真があります.yahooブログに張ったリンク先が消えてしまったので後の祭りです.
今回Noteを始めて,それらの記事中から面白いものを優先し,図を作り直し再現しようとしています(新規の記事も並行して随時書きます).お付き合いのほどよろしくお願いします.記事の候補全体は,数学月間の会ホームページにありますので訪問ください.その中で再現すべき記事のリクエストがありましたらお寄せください.まだNoteの使い方になれないので皆さまのお気づきのことをお教えください.記事に数式が必要なこともありますが,Texが使えないようなので,まとまった数式は画像にして埋め込むことにしています.
今回再現するのは,以下のメルマガの記事です.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2018.10.23] No.238
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日は,たいへん古典的だが,重要な証明問題を扱いましょう.
ギリシャの幾何学者達が研究した不可能作図とは
以下のものがあります.
(1)与えられた正立方体の2倍の体積の正立方体を作れ
(2)与えられた円と同じ面積の正方形を作れ
(3)任意に与えられた角を3等分せよ
これらは,定規とコンパスだけを有限回使って作図できるか?
ということです.
■なぜ作図できないか
(1)は,2の3乗根の作図が必要です.
(2)の円と同じ面積の正方形を作る方針を以下の図に示します.
どうしてこの作図ができないのかわかりますか?
与えられた円の半径をrとします.まず,円と同じ面積の長方形を作りましょう.もし,縦r,横aの長方形が作れたら,r・a=x^2 となるxの作図は可能です.問題は,円の面積と同じ縦 r,横 a=πrの長方形を作るところで,
円周の半分の長さπrの線分を作図する方法が,定規とコンパスではないからです.無理数πが作図できません.
■直線定規とコンパスだけを有限回繰り返し用いて作図できる長さは
2つの有理数の,加法,減法,乗法,除法,開平だけです.
作図方法は,以下をご覧ください.
条規とコンパスで作図
開平を繰り返せは,2のべき乗根(4乗根,8乗根,...)は作図できますが,例えば,立方根は作図できません(この証明は難かしいのでスキップ).
(3)任意の角度の3等分が作図できないわけ.
角度3等分の方程式は x^3-3x-a=0 で,
例えば,与えられた角度が60°ならa=1の方程式です.
60°の3等分の方程式は,x^3-3x-1=0 となりますが,この3次方程式は,p+q√r (ただし,p,q,rは有理数)の型の解を持たないので
この角度の作図は,定規とコンパスでは不可能です.
もちろん,60°の3等分の20°は存在しますが,
定規とコンパスだけを使う方法では作図できないということです.
詳しくは,以下をご覧ください.
■任意の角度の3等分
任意の角度∠XOYの3等分がなされたとします.
フィボナッチ数列F(n)は,1,1,2,3,5,8.13,21,34,.....のような数列です.
F(n)=F(n-1)+F(n-2) と再帰的に定義されます.
この数列は,いろいろな所に現れます.得られた数列が,フィボナッチ数列であることを証明するには数学的帰納法を用います.
今回は,その典型的な例として,抵抗ラダー回路を取り上げましょう.
■抵抗ラダー回路
ラダーとは梯子のことで,梯子型に抵抗を並べた回路を,抵抗ラダー回路といいます.例えば,表紙の図は3段のラダー回路です.
A-Bの端子(入力側)から見たインピーダンスをZ_i,
C-Dの端子(出力側)から見たインピーダンスをZ_oとします.
この3段のラダー回路は,A-B側(入力側)にR1の抵抗があるが,C-D側(出力側)にはないので,左右対称ではありません.入力側から見たインピーダンスと出力側から見たインピーダンスの比から,減衰率Z_i/Z_o≡Aが定義されますが,A>1なのでこの回路はアッテネータ(減衰器)として使えます.
抵抗値をすべて同じR1=R2=1とすると,
ラダーの段数mを増やしていくと,減衰率A(m)=F(2m+1)/F(2m-1)は,2/1,5/2,13/5,34/13,...とフィボナッチ数列が出てきます.
(参考)n=1から3までの計算は以下にありますのでご覧ください.
証明は数学的帰納法を使う練習になりますので,各自試みてください.
■ラダー回路の応用例
ラダー回路は,アナログ信号が入力されたときに,そのアナログ信号の大きさを,瞬時に8水準に分類する(8ビットのデジタル化)回路(これを8ビットのAD変換といいます)に使われたりもします.次の図をご覧ください.
コンパレータが7個並列に並んでいますね(カスケード結合).
入力信号の大きさを8水準に分類するのは,7個のコンパレータの働きで,
その境界値となる7段階の基準電位をそれぞれに供給します.
この7つの基準電位を発生するのが,一番左の直列に並んだ抵抗ラダー回路です.nビットのAD変換には(2^n)-1個のコンパレータと基準電位がいります.
■正5角形の性質
正5角形の中に相似な2等辺3角形(頂角36°)が次々に組み込まれていく様子を見てください.赤い2等辺3角形→緑の2等辺3角形→青い2等辺3角形の順です.2等辺3角形の辺の比率は,いつもΦ:1で,Φは正5角形の対角線(星形の辺),1は正5角形の1辺です.このとき成立する方程式,Φ2-Φー1=0を解いて(Φ>1をとる),Φ=(1+√5)/2=1.6180・・が得られます.Φは黄金比の値です.
■正5角形の実用作図法
この作図はつぎの式が成り立ちます.AH=HB=1/2,MH=√3/2 であるので,PH=(√3ー1)/2,従ってPB=(√[(√3-1)2+1])/2=(√[5-2√3])/2
AB/PB=2√(65-26√3)/13=1.6138・・・
この作図法は,イスラームのタイル作図で便利ですが,厳密な正5角形ではありません.しかし,誤差は0.26%なので実用上問題ない恐るべき精度です.
■厳密な正5角形の作図
AB=1,AH=1/2,PH=1 ですので,AP=(√[1+22])/2=√5/2
従って,QP=(1+√5)/2=Φ
この作図で得られるのは厳密に正5角形であることが証明されました.
■折り紙で作る正5角形(1)の精度
この図は折り紙で正5角形を作る原理を示しました.y=3xの直線とx軸のなす角θを求めると,θ=arctan3=71.5651・・° となりますが,正5角形では72°になるべきです.この誤差は.0.6%ですのでかなり良い精度と言えましょう.他の角度は,72.1087(0.2%),72.6524(0.9%)程度です.(カッコ内は誤差)
■折り紙で作る正5角形(2)の精度
折り紙の一太刀切で大変作り易い星型です.この原理は以下の図を見てください.正5角形(星型)の一辺の中心角は360°/5=72°ですから,一太刀切りに対応する中心角は36°です.
以下の図を見ると,一太刀切りの中心角は,35.783°(36°からのハズレは-0.6%)to,36.870°(+2.4%)に収まっています.
ある折り紙の本に正5角形の作り方がありました.
複雑な手順なので整理して原理だけ説明しましょう.
正5角形の中心角72度を作るミソは,以下のようです.
これで,Θは72°になることを証明できますか?
答,72°になりません.
約71.56...°です.
この折り紙手順で作れる角度は,72°に非常に近いので
実際の折り紙工作では非常に良い方法といえるでしょう.
でも,幾何の命題としては正しくないのです.
話は別になりますが,
正5角形を,コンパスと直線定規で作図できます;
例えば http://www.natubunko.net/zukei/png/penta03.png
ここから図を引用しましょう.
さてそれでは,この作図を折り紙の手順で追いかけてみましょう.
折り紙の手法で,「円を描く」というのは,可能でしょうか?
コンパスの使い方には2通りあます;
1)所定の長さを所定の方向にとる.
2)2つの円の交点を求める
(与えられた2点から,それぞれ与えられた距離だけ離れた点を求める).
このうち,1)は折り紙手順で可能ですが,2)は折り紙手順で不可能ではありませんが工夫がいります.折り紙の手順で,正5角形の作図を追いかけてみると,(4)の段階で,2つの円の交点を求めることが必要になり,ここが困難です.でも不可能ではないようなので,皆様,挑戦されて,もし,うまい方法を発見したら教えてください.
まったく別の方法でも,折り紙で正5角形を作ることができます.例えば,表紙の写真は定幅紙(帯)を用いて正5角形を折ったものです.この場合はどのような手順の作図になるのかを考察してみてください.このような折り紙は手順が全部完成してからつじつまが合うように最初から調整しますから,漸近的に正5角形を得る作図のようなもので,無限の手順がかかるので幾何学の作図としては認められません.
■NHS Nightingale Hospitalについて
NHS=国民保険サービス,Nightingale Hospital=臨時救急病院≒野戦病院
イギリスのNHSは4つの地域区分(イングランド,スコットランド,ウエールズ,北アイルランド)があります.イングランドのナイチンゲール病院は,London(4,000床)にオープン(4月3日)を皮切りに,7つ目のSunderland(460床)は日産自動車工場近くに整いました.Covid-19患者の数に北東部の病院が対処できない場合に限り使われます.「人々が社会的距離を保ち,あるいはワクチンができ,この病院を使わないですむことを願っている」とNewcastle病院のNHS局長は語りました(Sunderland Echo紙).
Stay at home, protect the NHS, and save livesがスローガンで,
イギリスは,3月23日に3週間の全土封鎖に踏み切ったが,まだピークが去らないとしてさらに3週間の延長しています.4月19日現在.累積確認患者数は90,629,累積死者数は14,399に上りますが,一日の感染者の広がりは減少始めたようです.封鎖と並行して,PCR検査から抗体検査に転換し,抗体検査の大規模実施(現時点で1万3729人1日3万5000件の能力がある)と「NHSナイチンゲール病院」の設立を進めました.
クリミア戦争(1853-1856)で野戦病院の衛生状態の改革を行ったナイチンゲールは,『看護覚え書』,『病院覚え書』など多くの著作を残し,そこにはワンルームの病院設計図もあり,高い天井まで延びた3層の窓,3層目の窓を開放し換気,ベッドの間隔,等々要点が記されています.
NHSが設立した病院は,ナイチンゲールの病院概念が活かされた臨時救急病院≒野戦病院だからこう呼ぶのでしょう.
■ナイチンゲールについて(以下のウエブサイト記事を参照しました)
草の実堂;https://kusanomido.com/study/history/western/21987/
ナイチンゲールはクリミア戦争(1853-1856)で野戦病院の衛生状態を実践改革し死亡率を低下させました.帰国後のナイチンゲール・チームはバーリントンホテルに集結し,戦時の報告書をもとに病院の状況分析をして,数々の統計資料を作成,改革のためにつくられた各種委員会に提出しました.特に,死亡原因ごとに死者の数をひと目で分かるようにレーダーチャートの発明があります.
1860年にナイチンゲールが看護専門学校(ナイチンゲールスクール)を設立したのは広く知られていますが,ナイチンゲールが統計学者であることはあまり知られていません.疫学研究の元祖です.1859年にイギリス王立統計学会の初の女性メンバーに選ばれ,アメリカ統計学会の名誉メンバーにも選ばれました.ナイチンゲールは90歳で亡くなりますが,晩年50年間はほとんどベッドの上で,本の原稿や手紙を書く活動でした.その病因はブルセラ病に感染したこと(by D A B Young,Florence Nightingale's fever,1995)でした.
ブルセラ病については,次号に続きます.
新型コロナウイルスCovid-19の感染拡大が止まりません.皆様お元気でお過ごしでしょうか.現在,日本では「人と人との接触機会を8割減にしよう」との呼びかけがなされています.規制を遵守し感染機会を減らすことはこの時期非常に重要です.
8割減は,感染拡大の転換点であるとされています.その根拠となる手法の総説には,例えば,「感染症流行の予測:感染症数理モデルにおける定量的課題」(西浦・稲葉;統計数理,第54巻第2号,461-480,2006)があります.しかし,接触機会8割減が転換点であるという具体的なシミュレーションはまだ見ておりません.
いろいろな感染症はそれぞれの特異な伝染状況があり,それに合わせた数理モデルを作る必要があるので一般論ではかたづきません.Covid-19の感染拡大に対しての数理モデルと,感染率,ウイルスの活性期間,患者の死亡率,感染者が感染源になりうる期間,等々の係数を仮定する必要があります.Covid-19は,まだ解明されない特異な感染の振る舞い(無症状の保菌者が感染源になる,感染回復後も再度感染する,等々)があり,完全な数理モデルができず確定的予測は困難です.
今回,石黒真木夫が,簡単な仮定に基づくCovid-19の特徴を考慮した数理モデルを作り,教育的なシミュレーション結果を得ました.その詳細は.「NPO数学月間の会」のホームページhttp://sgk2005.saloon.jpにありますのでご覧ください.
■ここでは,数式を用いずに,石黒の数理モデルとシミュレーションの内容要点を紹介します.
(1)ある人口集団を未感染者,ウィルス感染源,免疫獲得者,死亡者に分類し,未感染者がウィルス感染源の一員と接触したときにある感染確率で未感染者が感染してウィルス感染源となるものとする[実際は,Covid-19では,人-物ー人の感染ルートもあるといわれる].
(2)ウィルス感染源のウィルス拡散は14日間つづき,14日目に「死亡率」に従って死亡者と免疫獲得者に分かれ,免疫獲得者はもはやウィルスを拡散することも再感染することもなくなる[実際は,再感染するケースも稀にある].
(3)このモデルでは時間の経過とともに未感染者は単調減少,免疫獲得者は単調増加するので,感染の流行はかならず止まる.しかしそれは集団全員が感染した後である.
(4)感染確率と死亡確率を適当に与えればシミュレーションは簡単である.いまの計算機をもってすれば人口集団の各個人の命運をたどるミクロ・シミュレーションもさして難しくないが,以下で紹介するのは未感染者やウィルス感染源集団の大きさの変化を追跡するマクロ・シミュレーションである.確率的な現象の「期待値の動き」を追いかける決定論的なダイナミクスを採用する.ミクロ・シミュレーションをして,算術平均の変化を見るとマクロシミュレーションの結果に「誤差」が乘ったような動きになるだろうと考えられる.
(5)感染が感染源と未感染者の接触でおきるので,接触規制で感染源率を下げて「医療崩壊」は防ぐことは可能だが,これは未感染率を「高止まり」させ,規制をはずすと残った未感染者が感染する事態が発生することを示している.接触規制で再流行時期を遅らせて得た時間的余裕を有効に使って致死率を下げることが重要.それができないと、結局は死者の数は減らせないということになる.
■石黒の数理モデルを用いたシミュレーション・プログラム(Excelファイル)は,NPO数学月間の会のウエブサイトhttp://sgk2005.saloon.jpに公開しています.各自このファイルをダウンロードし,パラメータも色々変えてシミュレーション実験をすると面白いだろう.各種規制の効果は接触機会数に乗じるパラメータを変えて見ることができます.
感染者数のピークが過ぎても,揺れ戻しの感染者数の小さなピークが観測され,このような波動を繰り返しながら収束に向かうことがわかるでしょう.
私は3月24,26日のメルマガまぐまぐ(311,312号)で以下の内容の発表をしました.-----
3月21日の厚労省の公表値を用いて,罹患率=発症患者/PCR検査数と定義すると,罹患率は,約5%になります.しかし,PCR検査の,感度と特異性(酒井健司,朝日デジタル)の情報を入れてベイズ推定した罹患率は5.9%になりました.この推定値の増加は,主としてPCR検査感度に原因があり,実際の罹患者を取りこぼすためです.(注)この数値は,PCR検査を受けた限定されたグループをサンプルとしているために,一般の集団に対しては少し割り引いた数値になるでしょう.-----
今日,PCR検査数も増加したので4月23日厚労省のデータを用いて,再計算をしてみました.どのように変わったでしょうか?
ただし,PCR検査数が増加したといっても(多少はPCR検査を受ける条件の緩和があるかもしれませんが),陽性の確率が高いサンプル集団について検査が行われている状況は変わりません.
カバーの図を見てください.ここで推定する数値はあくまでもサンプル集団に関するもので,一般集団に対してはいくらか割り引いた数字になるでしょう.
ーーーーーーーーーーーーーーーーーーーーー
■条件付き確率についての「ベイズの定理」とは次のようなものです.
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です.
p(X) Xが起こる確率
p(Y|X) Xが起こった後でYが起こる確率
p(X∩Y) XかつYが起こる確率
ベイズの定理は,X(原因)が起きた後でY(結果)が起きる確率p(Y|X)と,XとYを入れ替えた確率p(X|Y)を結び付ける定理です.
ーーーーーーーーーーーーーーーーーーーー
■新型コロナウイルスに対するPCR検査数は,厚労省の発表https://www.mhlw.go.jp/stf/newpage_11012.html で,4月23日現在,
135,983人になりました(1月前の3月21日の数字の7.5倍です).
PCR検査数 135,983
PCR検査陽性者数 11,919
陽性者のうち発症患者(陽性者∩発症患者)7,315人
発症患者/PCR検査数=罹患率 と仮の罹患率を定義すると,罹患率は約5.4%です.
陽性率=陽性者数/PCR検査数=0.088 ,陰性率=0.912 と定義できます.
■PCR検査の精度
新型コロナ検査、どれくらい正確? 感度と特異度の意味(酒井健司,朝日デジタル)に基づき,次のように仮定します.PCR検査の感度というのは,罹患者がPCR検査で陽性+と正しく判定される確率のことで,あまり大きくなく0.7, 罹患者でもPCR検査が陰性-となる(偽陰性)の確率は0.3程度.
検査の特異性により,非罹患者が+(疑陽性)と判定される確率は0.01だそうです.
■これらの仮定の下で,以下の2つを推定しましょう.ただし,ベイズの定理を使います.
(1)PCR検査で陽性と判定されたとき,罹患者である確率を求めなさい.
p(罹患|+)=p(+|罹患)p(罹患)/p(+)=0.7×0.054/(0.054×0.7+0.946×0.01)=0.80
+(陽性)でも検査感度のせいで罹患者をとりこぼすことが多い.また,非罹患者の割合が大きいので偽陽性の数も無視できない.この2つの原因が,+判定でも罹患者である確率を80%(前回79%)に下げている.
(2)罹患率を推定しなさい.
p(罹患|−)=p(−|罹患)p(罹患)/p(−)=0.3×0.054/(0.054×0.3+0.946×0.99)=0.017
-(陰性)と判定されたものの中に見逃された患者である可能性は1.7%(前回1.6%)ほどある.
従って,サンプル集団で推定される罹患率は0.088×0.80+0.912×0.017=0.086
すなわち,8.6%(前回5.9%)と推定できます.
ナポレオンが発見したといわれるナポレオンの定理とは次のようなものです.
ーーーーーーーーーーーーーーーーーーーーーーーーー
ナポレオンの定理
任意の⊿ABCの各辺上に正3角形を作図し,それら3つの正3角形の重心をD,E,Fとする.D,E,Fを結んでできる⊿DEFは正3角形である.
ーーーーーーーーーーーーーーーーーーーーーーーーー
なかなか美しい形の定理ではありませんか,ナポオンの名を冠するのにふさわしい定理だと思います.ただし,ナポレオンが発見したかどうかは記録がなくわかりません.
ナポレオン (1769 -1821) は数学好きです.
陸軍幼年学校で,代数,三角法,幾何などを勉強し,数学で抜群の成績をおさめ,1784年にパリの陸軍士官学校に入学.数学が役に立つ砲兵科へと進みます.騎兵科,歩兵科でなく砲兵科に進んだのも戦術の時代の流れを見据えての決断でしょう.砲兵司令官,将軍,皇帝になりました.この時代にフランスには多くの数学者がいました.ラプラス,モンジュ,フーリエなどが近くにおり,エジプト遠征 (1798 年) にはモンジュやフーリエが同行しました.
ナポレオンは数学が大好き,このような幾何問題を考えるのが楽しみで,きっと定理を発見したのだと私は想像します.
証明
与えられた任意の3角形を⊿ABCとします.
その各辺上に作図した正3角形のそれぞれの重心がD,E,Fです.
点Oは⊿ABCの垂心(⊿ABCのそれぞれの辺の垂直2等分線が交差する点)で,点D,E,Fは,この垂直2等分線上にあります.
色々な角の角度は図中に記入してあります.我々が証明すべきことは,⊿DEFが正3角形であることで,例えば,∠DFE=60を証明すれば済みます.考えてみてください.
ヒントは,∠BFE=∠BXC と ∠AFD=∠AXC を証明することです.
正3角形であるための必要十分条件は「3つの内角すべて(すくなくとも2つの内角)60°」です.
図形の対称性から,内角の1つが60°であることを証明すれば済みます.
これは,補助線1本引けば自明です.三角関数を使って計算で証明する方法もありますが,補助線1本で自明になるのが幾何の醍醐味です.
■さて,ここに出てきた6辺形には面白い性質があるのを見つけました.
この6辺形の中にある正3角形の中に点Pを中心になるように,正3角形の外の6辺形の部分を折り込むことができます.
特定方位に切り出した水晶Quartzの両側の面に電圧をかけると結晶は変形します.逆に両側から力をかけると両端に電圧(分極)を生じます.この性質を圧電効果といいます.圧電効果は,結晶構造に対称心がある場合には生じません.なぜなら,結晶中のいかなる方向に電圧(分極)ベクトルが生じたとしても,対称心に矛盾するからです.
所定の方位で所定の厚さに切り出した水晶片の両面に交流を印加すれば,水晶片は振動します.水晶片の共振の起こる周波数で安定な発振器を作ることができます.水晶振動子(通常32.768kHz=2^15Hzの水晶音叉)を用い,精度の高いクォーツ時計が作られており,実際の標準時計もこれです.
現在の時間標準は,セシウム(133Cs)の原子時計と定められました.原子時計とは,水晶時計を含む総合システムで,水晶発振器の周波数の校正標準に原子の状態遷移の周波数を用います.
セシウム原子は,最外殻の電子が1つ(水素原子型)なので,解析的にエネルギー準位の計算ができます.磁場を印加して縮退している準位を分離させた状態で,基底状態から励起状態への遷移を起こさせると,マイクロ波領域の9.192631770GHzのエネルギーで遷移します.そこで,水晶発振器により,この近傍のマイクロ波を発生させ,セシウム原子による吸収が最大になったときの水晶発振器の周波数を,9.192631770GHzであると校正しています.
ちなみに,GPS衛星は,ルビジュウムの原子時計を積載しています.最近はMEMS(Micro Electric Mechanical Systems)技術により,ルビジュウムの腕時計の開発も進んでいるそうです.
長さの標準は,地球の経線の1/4を10,000mと定めたのが始まりでした.しかし,1983年に,真空中の光速でこれを定義することになりました.1mの定義は「光が真空中を1/299,792,458秒間に進む長さ」です.長さの標準も時間に基礎を置くことになったのです.
数学と基礎科学,谷克彦(数学文化15号P82より抜粋)
2017年の数学月間懇話会(第13回)の講演の一つとして,ブラックホールの形を見る(池田思朗)をとりあげました.ブラックホールはなんでも引っ張り込み光も脱出できません.しかし,ブラックホールの穴に荷電粒子が引き込まれるときに電波やX線が放出されるので,ブラックホールの形は,この放出される電波を観測(地球上の6地点の電波望遠鏡を結んで電波干渉計を作り,電波の強度とその位相を観測)して,それらのデータをFourier変換すると形が見えるはずです.しかし,Fourier変換に用いる観測データは,地球が宇宙空間で旅した範囲の観測点で得られるのは圧倒的に限られたデータしかありません.
ブラックホールの穴画像を$$x$$,観測されたデータを$$y$$とすると,$$y=Ax$$
(行列$$A$$や,形式的な逆行列$$A^{-1}$$は線形演算子で,Fourier変換やその逆変換のことです).
行列Aが正則ならば逆行列を両辺に左から乗じて,$$x=A^{-1}y$$と簡単に解くことができるのですが,$$y$$の次元$$N$$は非常に小さく,$$x$$の次元$$M$$は非常に大きい(行列$$A$$は$$N$$x$$M$$行列でランク落ち)ために解けません.多数($$M$$個)の未知数のある$$x$$を解くのに,式の数($$N$$個)が少ないので,不定解になります.もし,解$$x$$にたくさんの0要素(スパース)があるとしランクを下げれば,一意解を持ちます.なぜこのようなスパースな解が合理的なのかは難しいのですが,我々のまわりの画像は統計的にスパースなようです.この方法は,LASSO(Least Absolute Shrinkage and Selection Operator)といいます.数学的には,$$x$$がスパースであるという条件を,$$Σ|x_{i}|$$が最小という条件にして,最小2乗法$$||y-Ax||^{2}$$ を解き,少ない観測値$$y$$から$$x$$を求めます.このための数学には,ラグランジュの未定乗数法が適用できます.
■圧縮センシング
このような手法は,医学画像(MRIなど)解析で用いられており,高速で高解像度の画像が測定できる圧縮センシングとして役立っています.得られる画像の解像度を上げるには,観測空間でも細かくたくさんのデータを収集し,それらを用いてFourier変換を行うのが正攻法です.これは情報理論でシャノンのサンプリング定理(注)と呼ばれるものであります.
しかし,実際には画像内で急峻な変化がある場所は少なく大体がだらだら変わっています.そのような性質のある実際画像では,観測空間内を細かい分解能で測定するのは時間がかかり過ぎてもったいない.観測空間の少数の点だけのデータで十分なのです(この考え方はjpgなどの画像圧縮と同じ).得られる画像は至る所0(スパース)という仮定は,大胆であるが良い結果をもたらします.
観測空間のサンプリングをナイキスト・レート(注)より細かく行う場合はオーバーサンプリング,ナイキスト・レートより粗い場合はアンダーサンプリングと呼ばれますが,画像がスパースという条件があれば,アンダーサンプリングのデーター集合を用いて解像度の高い原画像が再現できるのです. 解のスパース性を利用するこの手法は,医学画像(MRIなど)の撮影で利用でき,高解像度の画像を短時間で得られるようになりました.
ーーーーーーーーーーーーーーーーーーーーーー
(注)シャノンのサンプリング定理(1949年)
アナログ信号をあるサンプリング・レートでデジタル化すると,元のアナログ信号に含まれる周波数成分のうち,サンプリング周波数(ナイキスト間隔とも呼ばれます)の1/2の周波数成分までが再現できます.ナイキストは,サンプリング定理を1928年に予想していました(シャノンの証明が広く知られています).
デジタル音源のサンプリング周波数は44.1kHzが使われていますが,この周波数でサンプリングすれば,人間の耳が聞き分ける高音限界といわれる20kHzの音まで十分に再現できるからです.
ーーーーーーーーーーーーーーーーーーーーーー
病院でMRI(核磁気共鳴イメージング)を撮ったことがある方もおられることでしょう.私も3年前にMRIの診断を受けたことがあります.お陰様で現在は絶好調です.このMRIの記事はそのころ書いたものです(記事の中で1.5Tの静磁場と記述しましたが,3年たち3.0Tの装置の普及も多少進んだようです).
MRIの測定中に聞こえる”カタカタ”や”ビー”というほとんど冗談かと思うようなふざけた音は何でしょうか? あれは,1.5T(テスラ)という強い磁場中で装置が動くために,あたかもスピーカーと同じように装置が振動して出す音です.それにしてもなんとかならないものか?振動しないようにガッチリ作るのは,今でも何トンという重量ですから無理なのでしょうが.
さて,画像の分解能を良くすれば,測定時間は増えるわけです.しかし,
分解能を上げて,かつ,測定時間も短縮できる「圧縮センシング」という数学的な方法があり,これに言及するのが後編の主題です.その前に,前編では,まず,MRIの装置の仕組みについてお話しましょう.
■プロトン(水素の原子核)はスピンを持ち,磁石の性質(核磁気)があります.強い静磁場下に置かれたプロトン核磁気は,磁場に沿ってだいたい向きが揃い,歳差運動している状態です.歳差運動の周波数(ラーモア周波数という)は,磁場が強いほど高く,MRI装置の静磁場は1.5T程度と超強力なので,ラーモア周波数は64MHz(ラジオ電波の周波数領域)程度です.
静磁場下のプロトンに,このラーモア周波数の電波が照射されると吸収共鳴が起こり,核磁気の歳差運動の振幅(周波数は変わらない)が増大しほとんど横倒しの状態で回転(古典論的なイメージ)しています.
一方,歳差運動をしているプロトン核磁気からは同じ周波数の電波が放射されるので,これを検出することができます.
■生体組織は,水をはじめ水素原子と結合した分子からなる組織です.
つまり,プロトン(水素の原子核)核磁気は組織の至る所に分布していて,
その水素の属する組織の環境(診断される情報)がそのプロトン核磁気の性質(緩和現象)に反映されています.
すなわち,核磁気の歳差運動の縦緩和,横緩和という現象は,そのプロトン(水素)が含まれる(結合している)組織内の状態で違いが出ます.
緩和というのは,電波の照射を止めると,励起されていた核磁気の歳差運動が定常状態に戻ることで,静磁場方向の核磁気成分の復元緩和を「縦緩和」,静磁場に垂直面内の成分の減衰緩和を「横緩和」といいます.
組織の各点で,これらの緩和定数を測定し,マップに表示できれば,
診断に役立つ組織の特徴を反映したイメージングになります.
■さて,組織画像の位置情報はどのようにして得られるのでしょうか.
これがなければ画像として見ることができません.断層測定をするには,検出器に到来する電波が,1つのスライス平面から来るものだけ集める必要があります.このためには,静磁場の他に傾斜磁場を印加します.
傾斜磁場はさきほどの静磁場とは別で,ペアのコイルによって発生する
(数十mT/m程度の強さ)もので,たとえば,z軸方向の静磁場があり,加えて,z方向に沿って変化する傾斜磁場,x方向に沿って変化する傾斜磁場,y方向に沿って変化する傾斜磁場の3種類があります.
傾斜磁場があると,空間内で磁場の大きさが一定になるのは平面になります.例えば,静磁場方向と同じz方向の傾斜磁場を印加すると,磁場一定の平面はz軸に垂直な平面です.
プロトン核磁気のラーモア周波数は,磁場の強度に比例するので,
共鳴吸収する電波の周波数をスキャンすれば,z軸に垂直な各断層平面に並ぶ核磁気からの電波を順次採取することができます.
次に,各断層面内の(x,y)位置情報はどのように得たらよいでしょうか?
断層内のプロトンの歳差運動を励起した後に,x傾斜磁場,引き続きy傾斜磁場の印加を行うとします.
x傾斜磁場印加でx軸に沿って歳差運動の周波数が変化し,その場所から放射される電波のx座標情報(周波数エンコーディング)が得られます.
xおよびy傾斜磁場の印加でy軸に沿って歳差運動の位相が変化し,
y座標情報(位相エンコーディング)が得られます.
傾斜磁場を印加して,空間の位置情報を得,画像化を可能にしたのは,
Lautergur(1972)の発明で,2003年のノーベル賞を受賞しました.
■緩和時間の測定は,歳差運動の励起後,照射電波を切って行うので,
立ち上がり時間も考慮した電波照射の複雑なパルスシークエンスになり,
256x256画素の測定でもかなりの時間を要します.高分解能画像を得るには,正攻法で行うならさらに細分化した画素数の測定が必要になり膨大な測定時間になるでしょう.
これを解決し,MRIの高分解能かつ高速化を実現したのは,
後編で言及する予定の「圧縮センシング」という数学方法です.
同じ正3角形(正6角形)格子[あるいは,正3角形2つよりなる平行4辺形格子とみてもよい]のパンチングメタルを2枚重ね合わせました.
この図の状態は,2枚の格子どうしのなす角度が2θ=30°になった場合です.初めの正3角形(正6角形)の格子より大きな新しい周期の格子が出現しているのがわかりますか.
■正方形格子(網目)を2枚重ねた場合を考察してみましょう.
(Coincidence-site-lattice)
両方の網目が重なった位置に,新しい網目の格子が見えて美しい.
2枚の正方形の格子(正方格子という)どうしの傾きを変えると,ときどきこのような新しい格子が現れます.もとの格子の互いに直角な2つの並進ベクトルをa,bとすると(正方格子ならa=b),
もとの格子は,格子点 na+mb,(n,mは任意の整数)の集合です.
同じ正方格子を2枚傾けて重ねて,新しい周期の2つの並進ベクトル x, yが生じています.これらの図の状態は,
(上図)x=2a+b,y=a+2b .(下図)x=3a+b,y=a+3b(面心格子,2格子点胞)
この基底変換を行列で書き,行列式を求めると3(左図),8(右図)ですので,新しくできた格子はもとの格子と比べて面積で3倍(左図),8倍(右図)粗くなっていることがわかります.
格子というのは,並進ベクトルの作る群=並進群の”図的表現”です.2枚の格子の干渉で生じた新しい格子の周期は,もとの格子の粗いサンプリングになっているわけで,新しい格子は,もとの格子の部分群になります.
格子が重なって,拡大された(粗い)格子が見える現象は,干渉(ビート)と同じことです.
実際に,2つの原子網面が重なって,このようなビートが見えることは,電子顕微鏡で格子像の観察をするときにもよく起こります.
結晶は周期的な構造をしているので,周期的な空間は「結晶空間」とも呼ばれます.エッシャーの繰り返し模様や,壁紙模様などで,周期的空間の実例をたくさん目にしていると思います.
■2つの正方格子の平行なずれによる干渉(モワレ縞)
それぞれの正方格子の周期をλ1,λ2とすると,新しい周期Lは
1/L=1/λ1−1/λ2 の関係があります.
私は,子供のころ家にあった織物検査器というもので遊んだことがあります.これは,標準となる格子模様がガラスに刻んであり,織物にこのガラスを重ねると繊維の周期とのビートで縞模様が観察できます.1mmの中に何本繊維があるかとか,織り方が均一でなくどの程度乱れているかが,モアレ縞からわかります.
次の写真は,工事現場のネットが折り返されて2重になっているために観察されるモアレ縞です.
4月25日,10:30から,Zoomを用いてリモートでの同志社中学校のDo★MATH博物館の見学がありました.10分間ほどの休憩をはさんで1時間ほど園田先生が出演され,見学会と,一太刀切りでハートや星形を作ったり,誕生日を当てる数あてカードを楽しみました.今年は,「数学月間」のイベント(毎年7月22日に実施し今年は第16回)もリモートで実施することになりそうです.
誕生日(1~31の数)を当てるには,4x4の数字が書かれた5種類のカードを見て,自分の誕生日が書かれているカードを選び出します.そして,それらのカードの左上の数を足し合わせると誕生日が当たるのです.
なかなか不思議ですね.この原理を今日は解説します.
■これからの説明は,誕生日を当てるゲームの変種で,15までの数を当てるゲームについて語りましょう.ゲームの実施方法も,数字が書かれてあるカードを選ぶのではなく,数字が書かれたカードの上にマスクをかぶせて当てようとしている数が見えているかどうか訊ねる方法になります.この両方のゲームとも同じ原理(2進数表記)を利用しています.
4x4の16個のマスに0~15の数字が書かれたカードがあります.このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる.これをマスクカードを変えて4回行えば,相手が心の中で思っていた数が当てられるというのが,この数当てのゲームです.
どのような仕組みがあるのでしょうか.秋山久義さんが,2019年7月のパズル懇話会で発表されています.今日は,秋山久義さんの発表「数当てカードの諸相」から引用して,その仕組みを解説します.
まず,16個の数の配列は,ランダムに配置したふりをしていますが隠れた規則があります.
例えば次の2つの方法があります.
(1)左右対称の位置にある2つの数字の和は常に15になる.
(2)回転対称(2回対称あるいは点対称)の位置にある2つの数字の和は常に15になる.
このために右半分(あるいは左半分)を知れば,全部の数の配置がわかります.つまり,相手の意中の数がマスクに隠されて見えない場合は,その数との和が15となる数の方が見えているのです.
さて,0~15の数を2進数で表すと次の表のようになります.下図をご覧ください.a,b,c,dはそれぞれ2^3,2^2,2^1,2^0の桁に相当します.
2進数表示で3桁目を表すマスクカードがa,2桁目を表すマスクカードがb,というように4枚のマスクカードができます.
それぞれの数の上に乗る4種類のマスクカードで,2進数表示の1のところに孔を開ける(逆に統一してもかまわないが)ことにします.
例えば,13に場合は,aとbとdのマスクカードに孔(網掛け部分)をあけ,cのマスクカードには孔はあけません.
以上で,仕掛けの準備ができました.
これで,質問を開始して,数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます.
見えないといったマスクカードは
(1)の場合には裏返して重ね/(2)の場合は180°回転して重ねるのです.
結局,4枚のマスクカードを重ねたものは,
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです.
60÷5(7-5)=?
この答えは24ですか6ですか
60÷5x2=?と聞かれれば,24と迷わず答えられる人が,なぜ6と答えたくなるのでしょうか.これは5と()の間にxが書かれていないことが心理的に影響すると思います.
5(7-5)は文字式のような錯覚に陥り,ひとまとめにして数値を出したくなります.÷とxの演算が並んだ式は,前から順番に演算するのが決まりです.割り算を使わず掛け算だけで書き直すこともできます.例えば,
60÷5x2=60x(1/5)x2 のようにです.
60÷5(7-5)=を,分数で書いてみましょう.しかし,5だけが分母に来るのか,5(7-5)が分母に来るのか不明確です.(60/5)(7-5)のことなのか,60/(5(7-5))のことなのか,かっこを1組追加すれば明確になります.
逆ポーランド式に,二項に対する演算の繰り返しとして計算手順のグラフを書くと,解釈の異なるそれぞれの計算手順は表紙カバーの図のようになります.
■さて,文字式の場合は係数と文字の間のx記号は省略されるのが普通です.9a^2÷3a=の答えは,3a か,3a^3 のどちらが正しいのでしょうか?
雰囲気的には3aですが,式の機械的な記述は曖昧です.
このような曖昧さを避けるために,()を用いて明確にすべきです.
9a^2÷(3a)=3a あるいは,(9a^2÷3)a=3a^3 のようにはっきりさせましょう.
■ここまでの記事を,私がメルマガに掲載したことがあります.すると,以下のコメントを読者からいただきました.この問題はなかなか面白いですね.ここに掲載させていただきます.
理学系では『省略演算の優先』を意識している傾向がいくつか見られます。たとえば化学業界では省略演算は優先することが国際的なルールとして明記されていて、先の計算は6と答えなければならないように定められているそうです。
また、物理学のフィジカルレビュー誌の投稿規定にも同様な省略演算の優先が書かれているということですので、こちらも6と答えることが義務付けられていることになります。
算数の世界では、帯分数の計算部分に同様な様子が見られます。{以下テキストの都合上帯分数には()をつけ、整数部分と分数部分の間に『と』を挟みますが、実際には無いものと思ってください}
(2と1/3)×3 は,2+1/3×3 なら,+より×優先なので =2+1=3 と計算するはずですが、実際には省略演算である+を先に行い、7/3×3=7 と計算します。
ところで、マセマティカで計算すると、メルマガの計算は24が出力されるようです。ソフトのいくつかは24を出力すると聞いています。
以下は想像です。
理学系では古くから省略演算を優先する感覚があったため、そのようなルールが少なくとも上記の物理化学ではルールとして明記された。数学はともかく算数でもそのように教えている部分がある。
一方で後発の計算機業界ですが、こちらはそもそも昔は省略演算は文法違反でエラー扱いでした。それがハードが強力になり対応可能となった時に、理学系の慣習など頭になく、ただ省略演算を補うだけだったために、結果24と計算するソフトが多いのではないかと。実際、カシオの関数電卓では、古い機種では24を答えに出し、新しい機種で6を出力するケースを確認しています。おそらく化学業界あたりから苦情が来てユーザーニーズに合わせたのではないでしょうか?
数学では化学業界と違って国際組織が演算順序をルールとして明記するなんて多分やってないと思います。×が+に優先するなことすら学会による明文化はなく慣習によるものだと思われます。明文化されない以上慣習として定着するまではどちらが正しいとは言い切らないのが無難に思います。ただ、化学業界のルールでも但し書きとして、『ただし、誤解を招かないよう括弧を十分に補うことを推奨する』とあるそうですから、メルマガの式は
(60÷5)(7-5) なり、60÷(5(7-5)) なりにするのが大人の対応ということになりそうです。
エンゼルフィッシュの縞模様やヒトデの星型はどうしてできるのでしょうか?
コンピュータの発明や暗号解読で有名な天才数学者アラン・チューリングが,”The chemical basis of morphogenesis”という論文を1952年に発表しました.今日,受精卵が細胞分裂を繰り返し分化し生物組織が出来ていく胚発生過程は遺伝子情報にプログラムされていることは公知です.1952年にチューリングが発表した理論は,「反応拡散系」が条件を満たせば,パターンや構造を自己成長形成するというものです.反応拡散系と言うのは,2つの物質(モルフォゲンと呼ぶ)が,反応し合いながら組織を介して拡散するもので,初期状態は均一であったものが,ランダムな外乱により,物質の濃淡の波が生じその波が生物の形や模様をつくりだすというものです.この数式でつくり出される模様は「チューリング・パターン」と呼ばれますが,コンピュータ・シミュレーションで描き出すと,条件により,動物の模様にそっくりな縞模様が出現したり,ヒトデの形を作ったりします.手の指が形づくられていくのは,その設計図が遺伝子により決定されているからと考えられていますが,もしかしたら,「指の形成はチューリングの理論のように波がつくっているのではないか」という論文が最近発表されたそうです.遺伝子はからだの構造の基本を決める設計図で,例えば,肺の形成の初期に気管支の分岐などを作るが,細かい肺胞の形成まではその設計図には書かれておらず,チューリング理論のように,現場の細胞同士のやり取り(反応と拡散)で作り上げられて行くのだろうと,近藤滋氏は言っています.
1952年に提唱されたチューリング理論は,現実の生物分野でそのような実験的証拠がなかったので,その後長い間,机上の空論と思われていました.1995年,近藤滋は,海洋エンゼルフィッシュのポマカンサスには,縞模様が皮膚に固定されていないことを発見しました.体の成長とともに,単純に比例して拡大する哺乳類の皮膚のパターンとは異なり,ポマカンサスの縞模様は,体の成長にともなうパターンの連続的な再配置が起こる.そして,縞間のスペースが維持されるという実験事実を観測しました.
実際,チューリング理論に基づくシミュレーションは,成長とともに形成されるパターンを正しく予測できたので,この理論の正しさを支持するものです.
■ チューリングの反応拡散系方程式
存在する2つの物質(モルフォゲン)が,反応したり拡散したりするのは,遺伝子情報で制御されるわけでもなく単純な化学反応で,以下の連立方程式で記述できます.u(t,r),v(t,r)は振動し,いろいろな形が形成されます.
■チューリングの反応拡散方程式の解の安定性を調べる数学について
(解が不安定(暴走)では,縞模様ができません)
数式を多用することができませんので,ここでは,言葉で説明するにとどめます.⇒ Texによる数式追補http://sgk2005.saloon.jp
反応項 f,g はそれぞれ物質の濃度 u, v の関数で,平衡点の周りでテーラー展開(1次の項まで)して線形化します.このような連立線形微分方程式の性質は,ヤコビアンと呼ばれる行列Aで決まるが,この行列Aの固有値の実部がすべて負であれば,解は安定になります.
行列Aの固有値を求めるのは面倒なので,条件を緩くして,行列Aの対角要素の和(固有値の和に同じ)が負であるとし,さらに,拡散係数も0の場合から始めると,結局,f_u+g_v<0が得られます.
これは,f_uとg_vが異符号で負の絶対値が大(促進剤と阻害剤が拮抗して働き,若干,阻害剤が強い)の条件を意味し,このようなときに縞模様が形成されます.
表紙写真のグラス(リュミナルク製)のデザインは,こちら側の模様の円が凹レンズとして働き,向こう側の模様の円を円内に縮小して映し出すので,あたかもアポロニウスの窓のようです.
■映像が果てしなく繰り返す「インドラの網」
網の上に置かれた真珠は互いに反射し合って,他の真珠を映しだすだけでなく,映っている他の真珠の映像の中に自身の姿をも映しています.世界全体が真珠一つ一つの上に映り,またその姿が別の真珠に映り,これが永遠に続くのです.「インドラの真珠」D.マンフォード, C.シリーズ, D.ライト, 小森洋平 (翻訳),日本評論社は,美しく興味深い数学の本です.
この美しい図形の2次元版は,「アポロニウスの窓」ApolloniusGasketとも呼ばれます.
互いに 接し合う3つの円に接する第4の円を描くのですが,これを次々と繰り返して,どんどん小さくなる円で埋め尽くされる円盤内の世界はフラクタルです.
4つの円の曲率(半径の逆数)をa,b,c,dとすると,
2(a^2+b^2+c^2+d^2)=(a+b+c+d)^2 という,デカルトの発見(1643)した定理が成り立っています.
(参考)⇒三角形の七不思議 (ブルーバックス), 細矢 治夫
■反転によるフラクタル構造
2つの円β,γが互いに接し,かつそれらがアポロニウスの窓の外周円Ωとも接しているとき,これらの接点を通り外周円と直交する円(赤色)を考えましょう.すると,この円で分断された2つのアポロニウスの窓の世界(若草色と黄色)は,この円(赤色)を反転円として,互いに鏡像(反転鏡映)となっています. もし反転円がどんどん小さくなれば,
その小さな領域に大きな世界がどんどん繰り込まれていくので,不思議なフラクタル世界 の美しさが見られます.表紙の図はこのような様子を表しています.色々な反転円を考えれば,無限にある大小さまざまな大きさの円は,
みんな同じ大きさであるとも言えます.それゆえに,円盤内の世界は無限に広いと言い張るのも良いでしょう.
上図は Cinderellaというフリーソフトを用いて描きました.
■円による反転
中心Oの半径rの円による反転は,反転円外の点r1を反転円内の点r2への写像
で,反転像どうしは,r1・r2=r^2を満たします.
もし,反転円の円周上に点があれば,反転像は元の点と同じ位置です(r1=r2=r).
反転操作では,円は円に写像されます.もし,反転円に直交するような円周の円をこの反転円で反転すれば,同一の円の上に写像されます.したがって,円周に直交するような反転円で分断された円の2つの部分は,反転円によるそれぞれの鏡像になります.
反転円が直線なら,反転鏡映は普通の鏡映像になります.
直線鏡の組み合わせで作られる映像は,良く知られた万華鏡ですので,反転円を用いたインドラの網の鏡映像も拡張された万華鏡の映像とみなせます.
■仏教では,「宇宙の一切のものが,一切のものの原因になっていて,
無限の過去からの無数の原因が,どの一人にも,それぞれ反映されている」と考えます.これはまさに単純な因果列ではなく複雑系の考え方ですね.
宮澤賢治に「インドラの網」という小品があります.インドラの網目に縫い付けられた珠玉は,互いに映じ合うと同時に,自分自身も輝いています.
この項目は,反転円の幾何学のほかに,フラクタル,複雑系,双曲幾何の円盤モデル,エッシャーの不思議な世界,万華鏡,などに関連があります.
これらは順次取り上げる予定ですが,拙著「美しい幾何学」技術評論社(2019.9刊)をご覧いただけると幸いです.
■円による反転鏡映の性質
①反転円の円周上の点は,反転しても元の点と同じ位置.
②反転では,円は円に変換される(直線も半径∞の円の仲間)
下図に反転円(赤い円)による,反転鏡映の例を示します.
●図1・反転円Oと交差する円Cは,交差の2点を共有する円cに変換される.
●図2・反転円Oと直交する円Cは,自分の上に変換される.
円周に直交するような反転円で分断された円の2つの部分は,反転円によるそれ
ぞれの鏡像になる.
●図3・反転円Oの中心を通る円Aは,直線aに変換される.
特に,円Bが反転円Oと交差する場合は,交差する2点をよぎる直線bに変換される.
③反転円が直線なら,普通の鏡映像になります.
直線鏡の組み合わせで作られる映像は,良く知られた万華鏡です.
反転円を用いたアポロニウスの窓も拡張された万華鏡の映像と言えるでしょう.
■反転の利用
反転の性質を使うと,パップスの定理の様な難しいものを簡単に証明できます.
このような図形はアルベロス(靴屋のナイフ)といいます.
この中に面白い幾何学があります.
円弧αと円弧βに挟まれたア
ルベロスの領域に,互いに接す
るように円のチェーンω0, ω1,
ω2, … があるとき, 円ωnの
中心と直径ABとの距離は円ωn
の直径のn倍である.
(パップスの定理)
[以下の証明ができます]
円ω2の中心は,線分ABから円ω2の直径の2倍だけ離れていること.
① 点Aから円ω2へ接線を引く.両接点を通りAを中心とする円γは,円ω2
と直交します.(なぜなら,円の接線は接点での半径と直交するから)
② γを反転円にして,色々なものを反転してみましょう.
円ω2 は自分自身に.円α,β は,それぞれ 直線α’,β’に,
円ω1,ω0 は,それぞれ円ω1’,ω0’に,なります.
③ 円ω2,ω1’, ω0’の直径はすべて同じだから,パップスの定理が証明
された. (なぜなら,平行な直線α‘とβ’に挟まれているから)
■楕円幾何平面の正則タイル張り
球表面が球面正p多角形タイルで{p,q}のように張りつめられているとき,1つのタイルの中を2p個の直角3角形に分割できます.この直角3角形を鏡室とする万華鏡を“メビウスの万華鏡”と名付けます.このときの直角3角形(鏡室)の内角は,それぞれ π/p,π/q,π/2で,この直角3角形を(p,q,2)と略記します.
■双曲幾何平面の正則タイル張り
ポアンカレ円盤の双曲幾何平面が,双曲正p多角形で{p,q}のように張りつめられているとき,1つのタイルを2p個の直角3角形に分割できます.この直角3角形を鏡室とする万華鏡を“コクセターの万華鏡”と名付けます.
双曲面の{6,4}正則分割を例に,直角3角形(6,4,2)(赤い3角形)を図(左)に,対応する“コクセターの万華鏡”の映像を図(右)に示します.
■双曲面{6,4}分割の場合の“コクセターの万華鏡”を作る
双極面{6,4}分割の映像を,3角形の万華鏡で作るには,双曲面直角3角形(6,4,2)を用います.この3角形の2辺は平面鏡,残りの1辺は円盤のフチに直交する円弧鏡よりなります.この円弧鏡は,数学的には反転円として定義できるのですが,現実の円柱鏡の反射には収差があるので,数学の定義のように鮮明な万華鏡映像を作るのは困難です.
■エッシャー作品の生まれるまで
(1) (2) (3)
(1)コクセター:直角3角形(6,4,2)による双曲面の{6,3}分割の細分
(2)エッシャー:直線魚のモチーフ
(3)エッシャー:「極限としての円Ⅰ」CircleLimitⅠ
コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました.1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り,これがエッシャーの「極限としての円」の作品群(Ⅰ~Ⅲ)を生むことになります.
*By S.H.M.Coxeter
Crystal Symmetry and ItsGeneralizations (published in the Transactions of the RoyalSociety of Canada in 1957).
■エッシャーのトリック(引用先:コクセター論文)
M.C.エッシャーの「極限としての円」Circle limit IIIを鑑賞しましょう(図左).
この円盤内は双曲幾何の世界(ポアンカレの円盤モデル)です.
この円盤内を旅する人は,円の縁(世界の果て)に近づくほど時間がかかる.つまり,[世界の果てに到達するには無限の時間がかかる]ようになっています.
この世界で定義される直線(最短時間で移動できる経路)は,円盤世界の縁で直交する円弧です.
エッシャー作品(図(左))の円盤は,魚の流れを示す白い線で分割された双曲面の[4,3,4,3,4,3]分割のようにも見えますが,実は,図(中)に示すような,黒い線で分割した{8,3}正則分割です.
白い線は,双曲幾何の円盤世界の縁に80°で交差し,直線ではないのです.
図(中)の正8角形の黒い線がこの円盤世界の直線であることは,図(中)に書き込んだ赤い円弧(いずれも円盤縁で直交する円弧)を見れば理解できるでしょう.
双曲平面の正8角形タイルは,双曲平面の直線(円盤の縁で直交する円弧)で囲まれています.
タイルの大きさは円盤の縁に行くほど小さく見えますが,円盤内は無限に広い双曲幾何平面なのですべて同じ大きさです.
1つのタイルの中には4匹の魚がおり中心に4回軸があります.
正8角形の頂点には3回軸があり,魚の白い流れは3回軸の場所に集まっています.
エッシャーは{8,3}分割に用いる直線をわざと隠し,白い流れが分割であるようなトリックを見せます.もちろん,白い流れの円弧(直線ではない)に関して鏡映対称はありません.
参照:「美しい幾何学」p.142,143
■パイレックス・ガラスとは
シリカガラスSiO2の軟化点は1700°Cと高温です.ガラスには明確な融点はありません.初めから乱れた構造ですから液体状態の固体ともいわれます.固体での変形が起こるのは軟化点~1900°Cあたりまでで,それ以上の温度では液体になります.シリカの正4面体ネットワーク中の所々にCaイオンやNaイオンが入ったものが,ソーダーライムガラス(青板ガラスとも呼ばれる)で,ガラスの融点も軟化点も下がり成型が容易になります.しかし,Naの熱振動振幅は大きく,ガラスの熱膨張率は大きくなります.ホウケイ酸ガラスは,ホウ素Bを添加したガラスで,ナトリウムNaの量を減らせるので,熱膨張率を小さくできます.これがpyrexパイレックスガラス(Corningの商標)で軟化点は820℃位で,Nonexという非膨張ガラスの処方も開発されました.パイレックスガラスは,キッチンのベーキング皿にも,温度計にも,ビーカーなどの理化学機器にも,1949年に完成したパロマーのヘール望遠鏡の巨大鏡(回転放物面)にも使われています.この巨大鏡はパイレックスガラスの直径5mのガラスのキャストディスクで20トンもあります.この巨大なガラスのキャストディスクの製造では,アニーリング・オーブンに入れて10か月もかけて徐冷したそうです.これを現場に運び凹面(回転放物面)に研磨しました.
■パイレックス・ガラス製造中止
2008年3月14日に パイレックス・ロール板の生産中止をコーニング社は決めました.パイレックスと言えば耐熱ガラスの代名詞で,理化学機器にも使われていますが,望遠鏡用の 大きなガラスも作らなくなりました.どうなることか心配です.
今日,コーニング社の製品は,スマートフォン用のGorillaGlassというカバーガラスやエレクトロニクス用の薄い強化ガラスにシフトしたようです.
以下の写真はコーニングガラス博物館の様子で面白そうです.
https://media-cdn.tripadvisor.com/media/photo-m/1280/19/bd/64/98/corning-museum-of-glass.jpg
力学系を記述するラグランジュ方程式は作れるのだが,これが解けるとは限らない.
物理の演習では,解けるものしか扱わなかったのです.
実際の世の中は,解を関数で記述できない(解けない)方程式が大多数です.
系の運動を支配する法則(ニュートン力学の方程式)は明確なのに,解が関数で記述できないのだ.
でも解は存在するのです.コンピュータによる数値計算により,運動は逐一決定できる.
しかも,予想もつかない挙動ーカオスーが起こる.このようなことを最初に指摘したのはポアンカレでした.
ーーーーーーーーーーーーーーーーーーー
●1766 オイラー「変分法の原理」
(オイラー, ラグランジュ)
●1800 ラグランジュ「解析力学」
エネルギー散逸がない系は,オイラー=ラグランジュ方程式が作れる.
(オイラー, ハミルトン, ヤコービ)
●1900 ポアンカレ
可積分の方程式はごくわずかで,大部分の方程式は非可積分(関数で記述できない)
ニュートンの法則に従う系の運動は,可積分と決めつけてはいけない.
可積分 → 予測可能(安定な軌道) 互いに独立な因果列
非可積分→ カオス的 干渉し合う因果列
ーーーーーーーーーーーーーーーーーーー
■2重振り子の例
上図のような2重振り子の運動です.今回は物理演習のようですが,
数式に囚われる必要はありません.重要なのは,振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので,2種類の周波数の振動が重畳
された運動になる.つまり,関数で記述できる安定な周期的な運動になる
という事です.そして,これに対比される次に話題になる振幅の大きい
2重振り子運動では,運動は関数で記述できず,予想もつかない
とんでもない運動をするということです.
(注)ここでは,ラグランジュ関数やラグランジュ方程式を説明せずに用いています.
これらを学習したい方は,EMANの物理学https://eman-physics.net/analytic/lagrange.html
などが参考になります.
2重振り子のラグランジュ関数は正確に作れます.
次に,ラグランジュ方程式を解かねばならないのだが,これが解析的には解けない(関数で記述できる解がない).
◆振幅の小さいとき
Φ,ψ の振動範囲を微小に制限して(Φ,ψの2次までを残す近似)解く.
これは解けます(物理の演習問題).
計算の詳細は以下に載せました.http://sgk2005.saloon.jp/blogs/blog_entries/view/46/ddf8d815a70840c192d0532618218407?frame_id=54
結論
ラグランジュ方程式(連立方程式)を微小振動の範囲とし線形近似したので,解のΦ,ψは,それぞれ2つの固有振動(基準振動)の重ね合わせになり,それほど複雑な振動ではない.いずれにしろ周期的な(予測できる)振動になります.
◆一般論(振幅の大きいとき)
振幅が大きくなると,ラグランジュ関数の線形近似がなり立たないので,ラグランジュ方程式は解析的には解けません.でも解は実在するはずです.
将来,誰かが巧妙な方法で解くのではないかと期待しつつ,得られたその解は,解析的ではないにしろ振動範囲が小な場合と本質的に大差はないのではないかと想像するのは自然なことです.
系のラグランジュ関数 は完全に正しいし,ラグランジュ方程式も正しいのですから,解析的に解けないと言っても心配ないのではと思うでしょう.
これが誤りであることを証明したのがポアンカレでした.
現代は,コンピュータを用いた計算が高度になり,力ずくで動きのシミュレーションがなされるようになりました.正しい方程式は実在するのですから,関数による軌道の記述は出来なくても,動きは逐一決定されるはずです.
しかし,初期条件(初期値)により,予想もつかない挙動が見られます(カオス).ともかく,そのような運動の実験とシミュレーションの例を,youtube動画で見てください.とんでもない現象が見られます.
◆第1の動画は実験
スタートする初期値によって運動の様子は異なります:
◆第2の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1
ドアや家具や壁に見られるイスラムの美しい模様を作製する技術は千年以上の歴史があります.イスラムのデザインの特徴は,対称性の高い星型がちりばめられていることです.
繰り返し模様全体を支配する対称性は,17種類の平面群のどれかであるはずだし,並進(周期性)と両立しうる回転対称は,2,3,4,6回軸に限られるはずです.しかし,イスラムの模様の中に散らばる星形は対称性が高いのです.高い対称性はもちろん模様全域に作用はできません.その星形の内部にだを作用域とする局所的なものです.
上図の模様を例にとると,8回対称の青い星型が,正方形格子の周期で配列していることがわかります.青い星型にある8回対称性は,青い星型内部と緑の周囲領域,草色の星形5角形の領域までは有効ですが,オレンジ色の8角形までは有効ではありません.
青い星の中心にある8回対称軸はオレンジ色8角形の付近では,4回対称軸に低下してしまいます.これは,周期的な平面では8回対称軸は存在できない(正8角形のタイルでは平面を張れない)から当然のことです.
ある点のまわりの対称性という言葉は注意が必要で,その点周囲の「局所的」対称性を指す場合もありますが,平面「全域」で有効な対称性を指すのが普通です.この例では,青い星型の対称性は8回対称ですが,この星の中心にある回転対称軸は4回対称軸です.
このパターンの単位胞は,オレンジ色の8角形の中心を結んでできる正方格子の1つの内部です.
■Girihタイル(装飾線が描かれたタイル)
イスラムの繰り返し模様の壁はGirihタイルという手法で作れます.
正方形と正8角形を組み合わせた平面のタイル張りの例を,下図(a)に示します.このテッセレーションは,シュレーフリの記法で(4,8,8)と記述されます[1つの頂点のまわりに,正4角形,正8角形,正8角形が集まっている状態].
(b)図は,正4角形および正8角形の内部に装飾線を描いたGirihタイルです.
平面をGirihタイルでタイル張りしておいて,タイルの縁の輪郭を消すと(c)図のパターンが得られます.
デザインを作れる以下のウエブサイトがありますのでお試しください.
https://girihdesigner.com/
■ここで,始めに掲載したイスラムの模様も,上の例と全く同じであることを確認してください.
始めに掲載した模様の正4角形タイルや正8角形タイルの形は,草色の星型の中心を結んでいくと明らかでしょう.正4角形や正8角形の内部の装飾線はどのようなものであるかもお確かめください.
私たちは,ものごとを考え解決困難なときに,次元を1つ上げて(失われている視点を一つ加えて)見ると,思わぬ解決策にはっと気づくことがあります.たとえば,今,新型コロナウイルス禍にあり,医学・疫学的視点と,経済活動視点の2つの視点に集中して,この危機を乗り越えようと必死の活動がなされています.しかし,政治的視点がなおざりにされています.不安定な遺伝子のウイルスはやがて消滅し我々は生き残るでしょうが,見えない次元に無関心でいると,そのときの社会体制は,監視や権力集中の社会に変貌しているかもしれません.歴史学者のハラリ氏は,そのように警告しています.パンデミックが変える世界ユヴァル・ノア・ハラリとの60分:
https://www.dailymotion.com/video/x7tjaoq
視点を上げる(次元を上げる)効果は,デザルグの定理を考えるとよくわかります.
ーーーーーーー
デザルグの定理とは
「⊿ABCと⊿A'B'C'があり,AA',BB',CC'を通る直線が1点Oで交わるなら.
直線ABとA'B'の交点P,直線BCとB'C'の交点Q,直線CAとC'A'の交点Rは,同一直線上にある」
ーーーーーーー
高校とき幾何の教科書にこの問題が載っていました.
このデザルグの定理の証明は,実はとても難しいのです.3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります.
ところが,下図のように,この図形を平面(2次元)と見ずに,立体(3次元)にあると見ると,ごく当たり前のことを言っていることに気づきます.
2つの平面Ω(薄緑)とΩ’(薄青)が交差しており,△ABCは平面Ω上に,△A'B'C'は平面Ω'上にあるとイメージするのです.
光源Oから出る光が,△ABCの影を△A'B'C'に作っています(辺ABの影が辺A'B').従って,O,A,B,A',B' は,同一平面上にあり,この平面をΣ(薄燈)と名付けます.A,Bを通る直線も,A',B'を通る直線もこの平面Σ上にあり,P点で交差します.
一方,A,B,Pは平面Ω上に,A',B',Pは平面Ω’上にあります.
結局,P点は平面Ωと平面Ω’の交線上にあることになります.
同様にして,QもRも,平面Ωと平面Ω’の交線上にあり,デザルグの定理が証明できました.
高校の教科書では,このような証明は厳密でないとみなされるせいか,チェバやメネラウスの定理を使ってあくまでも平面図形として扱われます.
■デザルグの定理は,2次元で証明するのは難しいが,3次元では証明が要らないほど自明なのは何故でしょうか.
3次元でこの図のような模型があったとして,これを2次元に射影する(高さ方向をぺちゃんこ)と,直線が交差する状況は変わらないのですが,長さや角度の情報が失われてしまいます.△ABCと△A'B'C'は,それぞれ別の2次元平面にあったものですが,ぺちゃんこにされて1つの平面(紙面)に入ってしまいました.
私たちは,高い次元(2次元の世界から3次元の世界)を想像するのは困難です.デザルグの定理でこれを思い知らされます.
■デザルグは,17世紀初頭のフランスの数学者,建築家.透視図法を発展させた射影幾何学の祖です.ダビンチなどの画家たちは,遠近法や透視図法を古くから用いていましたが,その数学を固め射影幾何学の本を出したのはデザルグが最初です.
その後,射影幾何学が本格的に研究されるのは,200年後の19世紀中葉,ポンスレー(フランスの数学者.ナポレオンのロシア遠征に従軍し,ロシアで捕虜のときに射影幾何学を研究した)を待たねばなりませんでした.
射影幾何学自体,作図など重要な応用がありますが,やはり,19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました.
千川論文[千川純一,ひょうご科学財団]は,実用化も期待でき興味深いが難解なので,ここで解説を試みます.厳密な記述は原著論文を参照ください:
・Chikawa et al.,"Hair growth at a solid-liqid interface as a protein crystal without cell division", Progress in Crystal Growth and Characterization of Materials, Volume 65, Issue 3, August 2019, 100452
・Chikawa et al.,"Cancer development in the hair spectra by X-ray
fluorescence using synchrotron radiation",International Journal of Cancer, in press
■千川論文の意義
毛根にある毛球から毛髪は成長してきます.毛球の中は液体で,毛髪の成長は,あたかも,固液界面で成長する無期結晶のようです.固液界面には毛母細胞[毛球と毛幹(毛髪のこと)の境界]があり,その液体側の毛球に,S, K, Ca, Srなどの元素が偏析し,血液から毛母細胞に流入する元素量と,成長した毛幹の元素量が等しい状態が維持されています.
毛髪の成長は,純化学的過程(化学ポテンシャルの勾配が成長を駆動する)で行われることが示されました.[細胞分裂で成長するときのように遺伝子の関与もなく,チューリング反応拡散系と同じように純化学的な過程です]
この平衡関係から毛髪の元素濃度は血液の元素濃度から計算できるので,毛髪の分析をすると毛母細胞のイオンチャンネルの開閉の記録(癌の発生と成長に密接に関係している)が分かるというのがこの研究のミソです.
臨床データとリンクし収集した多数の毛髪の分析が実施されました.
毛髪1本の毛根から先端へとX線蛍光分析をし,種々の元素の分布するパターンのデータを収集しました.これらを解析し,大気汚染(黄砂)による心筋梗塞,脳梗塞の死亡率の増加の原因も毛髪分析で示されましたが,特に重要な結果は,癌発生の機構とCaの分布パターンが関係のあることを見出したことです.
■毛髪のCaの分布と癌発生のメカニズム
Caが不足すると,副甲状腺ホルモン(PTH) が分泌され,PTHが各細胞の「受容体」に結合すると,細胞のチャンネルが開いてCaを取り込むので,毛髪カルシウムは正常値を超えます.他方,血清Caが正常値以下に低下すると,小胞体に備蓄のCaを使うために別のチャンネルが開きます.これら2種類のチャンネルの開閉の記録が毛髪Ca 濃度に残されています.
情報伝達の主役であるカルシウム(Ca)の毛髪濃度は,毛母細胞のCaチャンネルが閉じた状態の正常値と,その5倍も高いPTH制御Caチャンネルは開いたときの値があります.また,正常値以下で小胞体の備蓄Ca量制御のチャンネルが開いた状態も起こりますが,これらは識別できます.
癌患者の毛髪を先端から毛根へと分析すると,癌の種類によらず,癌は必
ずPTH 制御チャンネル開のCa高値で発生し,癌成長とともに1~2年かけて正常値に降下し,さらに,小胞体の備蓄Ca量制御のチャンネルが開くCa正常値未満の状態(癌の「成熟」と呼ぶ)が続くことがわかりました.即ち,癌の発生から成熟までが,毛髪に特有のパターンとして記録されるわけです.
■(注)放射光実験の方法
毛髪の元素分析は,2003年から千川純一らが実施しており,臨床とリンクし採取した多数の毛髪分析のデータを集積しました.放射光を用いる蛍光X線分析は,毛髪一本で長さ1mm以下でも精密に測定できます.放射光施設利用にボトルネックはあるものの,毛髪だけ提供すれば済むので,人体に安全な診断方法であります.
血液は採取した瞬間の結果しか知ることができないが,毛髪には過去の記録が残されていて[1カ月に約1cm成長]変化のパターンを知ることができるところが,この方法の優れたところである.
さて,毛髪1 本(直径は100μm 程度)中のX 線照射点から出てくる蛍光X 線を観測すれば,その点に含まれる元素を検出することができますが,毛髪の元素濃度を得るには,蛍光X線強度を照射された部位の体積(質量)で規格化する必要があります.これにはそのとき観測されるバックグランド強度を用います.バックグランドは毛髪母体のタンパクによる散乱X 線(小角散乱領域ではない.コンプトン散乱が主体)で,一定の方位にセットした検出で,散乱X線も蛍光X線も測定できます.これらの比をとれば毛髪の太さや形状によらない値になり,濃度指標が得られます.
このマガジンの数学月間とは題名に違和感を感じている方もおられるでしょう.「数学月間」とは7/22-8/22のひと月を指します.この期間は22/7=3.14・・・(π)と22/8=2.7・・・(e)に因みます.
日本の数学月間は,(故)片瀬豊さんの提案により2005年に日本数学協会が7/22-8/22を数学月間と定めたことに始まります.2005年の発足以来,ボランティア・ベースながら,毎年,「数学月間」の初日7/22に,「数学月間懇話会」を開催し,啓蒙的な講演を一般市民に対し実施してきました.2020年の7月22日にも第16回の開催予定です.今年は,集会の実施は困難が予想されるので,初のZOOMによるリモート開催の計画です.
「NPO法人数学月間の会」のホームページhttp://sgk2005.saloon.jpに情報を随時掲載します.
(注)2005年から始まった「数学月間の会(代表:片瀬豊)」は,昨年から,「NPO法人(理事長:岡本和夫)」になりました.このような数学月間活動は米国MAMに学んで始めたものですが,米国MAMのように国家的行事として行うべき性質のものです.現在は個人寄付金とボランティア・ベースで実施していますが,活動を社会に波及させたいものです.「NPO法人数学月間の会」は,数学同好会ではありません.数学の内部にとどまらず社会の諸分野に横断的に呼びかけ活動し,「社会と数学の架け橋」を目指します.情報を共有しましょう.仲間に入りませんか.
問い合わせ先や詳細はhttp://sgk2005.saloon.jp にあります.
ーーーーーーーーーーーーーーーーーーーーーーーーーー
■米国MAM(Maths Aeareness Month)はレーガン宣言から始まった
全文を掲載します.どなたの草稿か知りませんが,格調高く今日でも心を打ちます.米国MAMのスタート時は月間行事ではなく,週間行事MAWでした.
原文は以下にあります.
https://www.gpo.gov/fdsys/pkg/STATUTE-100/pdf/STATUTE-100-Pg4430.pdf
----------------------------------------------------------------------
アメリカ合衆国大統領による宣言5461
「国家的数学週間」1986年4月17日
宣言(National Mathematics Awareness Week)
およそ5000年前,エジプトやメソポタミアで始まった数学的英知は,科学・通商・芸術発展の重要な要素である.ピタゴラスの定理からゲオルグ・カントールの集合論に至る迄,目覚ましい進歩を遂げ,さらに,コンピュータ時代の到来で,我々の発展するハイテク社会にとって,数学的知識と理論は
益々本質的になった.社会と経済の進歩にとって,数学が益々重要であるにも拘わらず,数学に関する学課が米国教育システムのすべての段階で低下する傾向にある.しかし依然として,数学の応用が医薬,コンビュータ・サイエンス,宇宙探究,ハイテク商業,ビジネス,防衛や行政などの様々な分野で不可欠である.数学の研究と応用を奨励するために,すべてのアメリカ人が日常生活において,この科学の基礎分野の重要性を想起する事が肝要である.上院の共同決議261で,国会が1986年4月14日から4月20日の週を,
国家的な数学週間に制定し,この行事に注目する宣言を出す事を
大統領に要請した.今日,アメリカ大統領,私ロナルド・レーガンは,
1986年4月14日から4月20日の週を国家的数学週間とする事を,ここに宣言する.私はすべてのアメリカ人に対し,合衆国における数学と数学的教育の重要性を実証する適切な行事や活動に参加する事を勧告する.
その証拠として,アメリカ合衆国の独立から210年の西暦1986年の4月17日,ここに署名する.ロナルド・レーガン(Ronald Reagan)
----------------------------------------------------------------------
長くなりますので,活動の様子は省略し,年度別テーマのリストを掲載します.(注)2017年からMSAMに変わりました.追加されたSはStatistics統計学です.
■MAMの年度別テーマの推移
http://www.mathstatmonth.org/mathstatmonth/msamhome
1986数学----基礎的訓練
1987美と数学の挑戦
1988米国数学の100年
1989発見のパターン
1990通信数学
1991数学----それが基本
1992数学と環境
1993数学と製造業
1994数学と医学
1995数学と対称性
1996数学と意思決定
1997数学とインターネット
1998数学と画像処理
--MAWからMAMへ------
1999数学と生物学
2000数学は全次元に
2001数学と海洋
2002数学と遺伝子
2003数学と芸術
2004ネットワークの数学
2005数学と宇宙
2006数学とインターネット保全
2007数学と脳
2008数学と投票
2009数学と気候2013持続可能性の数学
2010数学とスポーツ
2011解明進む複雑系
2012統計学とデータの洪水
2013持続性の数学
2014マス,マジック,ミステリー(Martin Gardner記念)
2015数学はキャリアを駆動する
2016予測の未来
2017年より,MSAMがテーマになる
注)略語表
MAM:Mathematics Awareness Week
MAM: Mathematics Awareness Month(4月)
AMS:American Mathematical Society米国数学会
MAA: Mathematical Association of America米国数学協会
SIAM: Society for Industrial and Applied Mathematics工業応用数学会
ASA: American Statistical Association米国統計学協会
JPMB: Joint Policy Board for Mathematics米国連結政策協議会
*)2006年から、ASAが加盟することになった.
■編集後記
数学月間は数学者のものではなく,一般人が対象です.数学は,ものごとの本質を追求し,装飾を剥ぎとり,その本質をあぶりだします.
出来上がった抽象化された概念体系(定理)を,数学者は美しいと感じます.数学とは,そのような理論体系であるべきことは確かです.
しかし,このようにして出来上がった抽象的な数学を見せられても,
一般人は興味が湧かない.そこで,数学月間は<数学と社会の架け橋>として,数学が実際の課題に使われていることを示して行こうと考えています.
かつて,物理学の現場で数学が生まれている時代がありました(ニュートンの微積分もその例です).数学は自分の生まれた源泉を離れて抽象化に専念していることに,著書の前文で警鐘をならしたのはクーラントとヒルベルトでした.源泉に立ち返って数学を見るときっと共感を感じることでしょう.
大学の数学では,完成され抽象化された数学を,数学科の先生が教えます.
これは,数学科の学生に対する教程としてはオーソドックスなものですが,
数学科でない学生には不親切であります.工学,薬学,経済学など,
それぞれの専門に適した数学の基礎教程が必要でありましょう.
安倍内閣が今週にも通過させようとしている検察庁法改正案は,権力分立の精神に反し憲法違反です.以下のメルマガを発行した2015.9.22のことを思い出しました.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2015.09.22] No.082
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
戦争法案が多くの世論を無視して強引に可決してしまいました.
本来,違憲である法案が国会に出されること自体あり得ないことですし,
国会の議論でもまともな答弁がなされていないことは誰の目にも明らかです.
政府の宣伝機関になったNHK始め大手メディアの罪はたいへんに重い.
さて,翁長沖縄県知事の国連人権理事会で演説に期待しよう.大手メディアの世論操作に負けてはならない.
イギリスで投獄を覚悟してインドの独立を主張したガンジーの姿が重なって見えます.
ーーーーーーーーーーーーーーーーー
■戦時中の“科学朝日(1944年3月号)”「特集・戦争と数学」
https://twitter.com/oburo72 自由古書園「海つばめ」さんの写真借用
戦争一色の特輯:南方の科学 飛行機 精密機械と兵器 戦車と偽装
防空の科学 潜水艦 戦争と数学 航空母艦 基地建設と進攻兵器...
-------
この特集号には,多くの著名な数学者が寄稿しており大変興味深い.
その中で,巻頭の弥永昌吉先生の論説が群を抜いており,言論も不自由であったろう戦時下に,実に立派な意見を展開しておられます.
さらに,数学月間の考え方と同じ所も見受けられ我が意を得たりの感があります.まず,弥永論説(対話形式)の概略を紹介します.
1年くらい前から始まった戦時下の米国の数学動員(米数学協会の記事の記憶)が紹介されます.遅ればせながら日本でもこのような動きが始まっています.
ーーーーー
米国の数学動員
委員長(モース)の下に6つの委員会がある
1.工業技術,2.航空力学,3.弾道学(ノイマン),4.確率統計,5.計算法,6.暗号解読
1は数学と工業の連携強化,2,3は微分方程式,高射砲の照準や電波兵器の数学,4は大量生産管理,5は計算機.
ーーーー以下抜粋-----
■数学は魔術ではなく,合理的なものの中でも最も合理的なものですから,使い方も合理的でなくてはなりません.
この際,数学者の側で,数学を使えば何も彼も容易にできるというようなことを言いふらしたり,まだ十分の研究を積まないのに現場の人たちのやり方が悪いと言ったりするようなことは一番いけないと思います.
ーーーーーーー
■大和魂が第一でも,それだけでは戦争に勝てないことがだんだんわかってきて,科学研究の動員が必要になった.
第一次大戦では「化学」,第二次大戦では「物理」→「数学」が必要だ.
米の他,ソ連,独,伊でも同様な数学動員の状況がある.
ソ連は,コルモゴロフ(確率の基礎)飛行機の乱流,ヴィノグラドフ(整数論)などがスターリン科学賞を受賞した.
ドイツからは,開所したばかりの米プリンストン研究所などに科学者が流出しており,米国に最も豊富な人材が集まっている.
ーーーーーーー
■学問としてお留守にならず,その品位を下げぬような動員の仕方をすることが,戦争に勝つ道であると信じる.
日本では,それぞれの分野が功を急いだせいかも知れませんが,
学問が専門化しすぎて,それぞれ孤立化する危険がある.
この機会に横の結びつきが強化されるのは良いことだ.お互いに学問の理解を深め,基礎理論の整備進展,新理論の展開という方向へ導かれれば日本の学問全体にとってもこんな有り難いことはない.
ーーーーー
■問題解決のためにも,数学では個々の小さな問題をそれぞれに突っつくよりも,根本的なところまで遡って考えた方が,大きな成功を収めることがよくあるのです.
この戦争のために,目先のことばかりを考えてよいのでしょうか.
長期建設戦」ともなれば,文化が直接ものを言うことがますます多くなりましょう.世界中のだれが見ても頭を下げるような高い立派な文化を我々が戦いつつ築きあげて行くことがぜひとも必要です.
この頃,この点について偏執な,浅慮短見の説をなす人があるのを慨いて,
渡辺慧さんはそれを「文化的敗北主義」と言っている.
2014年の米国の数学月間MAMのテーマは,Mathematics, Magic, and Mystery でした.
このMAMのテーマは,Martin Gardner (1914-2010)の生誕100年を記念したものです.
ガードナーのことは,『サイエンティフィック・アメリカン』誌に,コラム「数学ゲーム」を25年に渡って連載したのでご存じの方も多いでことしょう.MAM(2014)のサイトに掲載されている組み紐のパズルに挑戦してください.
http://www.mathaware.org/mam/2014/calendar/braids.html
■魔法の三つ編み組み紐 (James Tanton)
James Tantonのウエブサイトは http://www.jamestanton.com/?p=1072
■次のパズルはどうでしょうか.
これは可能ですので,チャレンジされてください・
こんにゃくでこんな形にした料理がありましたか?
回答は以下にあります.
■それでは,次の四つ編みは実現可能でしょうか?
■可能なことを証明するのは簡単です.作って見せればよい!しかし,不可能であることを証明するのは難しい.何度も試行して失敗すれば,不可能と思えるかもしれません.しかし,もう一度試してみたらうまくいくかも知れない.
4つ編の組み紐の完成例が左図です.4本の紐の上端と下端がそれぞれ閉じている状態で始めて,このような完成例にすることが可能でしょうか.この四つ編み組み紐の完成例には,交差点が全部で12あります.上から出発して,左から来る紐の上に右から来る紐が乗る交差点を̟⊕,左から来る紐の下に右から来る紐が潜る交差点を̠⊖として,図示したのが左図です.12の交差の後,四本の紐は,上端での順番と下端での順番とが同じになります.全体で,⊕が8個,⊖が4個ですので,全体のIndexは+4と定義します.
いろいろな四つ編みを試してみてもIndexを0にできないようです.
まだ詰めが必要ですが,これが四つ編みで組み紐を完成できない理由のようです.
同じことをやってみると,三つ編み組み紐の場合は,交差点数6で,3本の紐の上端での順番と下端での順番が同じになり,Indexは0になることがわかります.
(参考)http://www.jamestanton.com/wp-content/uploads/2012/03/Cool-Math-Newsletter_June-2013.pdf
■「30年以内に震度6弱以上の地震が起こる確率は,横浜市が78%で最も高く,九州では大分市が54%」などと言われていました.あくまでも確率ですから,いつ地震が起きるかはわかりません.熊本の方が先に大地震が起きてしまいましたね.このような確率はどのようにして出たものでしょうか?(このSGK通信を書いた2016.7時点の数字)
震度(揺れ方)6弱といっても,震源が浅い場合もありますから,
震度が大きいものが必ずしも巨大地震(マグニチュードMが大きい)とは限りません.
■地上の被害は震度(揺れの程度)に比例します.
地下の岩盤には色々な原因で歪が蓄積していき,岩盤の耐えられる歪の限界を超えると,岩盤がポッキリ折れて地震が発生するというイメージです.岩盤が強靭なほど溜め込める歪エネルギーの限界は大きく,限界まで溜め込んだ岩盤が地震で放出するエネルギーは大きい(地震のエネルギーの対数がマグニチュードM).
地震は破壊現象なので,限度まで歪を蓄えた岩盤がいつどこで破壊するかを予知することは不可能だが,破壊が始まってからの前駆現象を少しでも早く観測することは可能です.
■日本の地震の発生メカニズムを調べると,大雑把に言って2つのタイプがあります.
1.海溝型(海洋プレート沈み込み境界)
Mは大きい巨大地震で,頻度分布は数十年~100年.
2.内陸型(陸側プレート内)
震源は地下5~20kmと浅い.Mは小さいが震源が浅いので,直上の被害は大きい.頻度分布は数百年ー数十万年.
日本で起きた最近の大地震は,内陸型です.
1923年の関東地震,2011年の東日本大震災,心配されている東海地震や南海トラフ地震は海溝型です.
■地層に残る地震の記録や,古文書の記録を調べると,日本の各地で,数多くの地震が繰り返し起こっていることがわかります.この地震発生の繰り返し周期はどうなのか,地震発生の予測のために,経過年に対する地震頻度の分布を調べてみます.過去の地震記録はどのような分布と合うでしょうか.地震は破壊現象なので発生確率はランダム(ポアソン分布)が予想されます.沈み込むプレートに引き込まれた陸地が時折り弾性反発するモデルは,Brown酔歩時間の分布(BPT)が予想されます.
全国を250kmのメッシュに切り,その地に影響を与える活断層起因の地震やプレート境界起因の地震で,地表の震度が6弱以上となる地震について発生確率を算出します.
メッシュに切った各地の30年以内の震度6弱以上の地震発生確率を着色した地図が以下のサイトにあります:
http://www.j-shis.bosai.go.jp/map/
■ここで用いられる地震の発生確率の定義では,分布密度関数を積分した全面積を確率1とします.
現時点は分布密度関数内のどこかですが,現時点から分布密度関数の0となる将来時点までの積分値に対する,現時点から30年先の時点までの積分値の比の値が30年以内にその地震が発生する確率となります.
現時点がどこか(過去の最新活動時期が不明)わからない場合には,地震の発生が「ポアソン過程」に従うとします.
地震は繰り返し発生しますが,正確な周期があるわけではありません.
今日地震が起こらなければ,明日地震が起こる確率は、今日より高くなる
今日より明日,明日より明後日と大地震がやってくる確率はどんどん高まって行きます.
(注)地震のマグニチュードMとその発生確率は,べき乗測が成り立つことが知られています.
被害の大きい巨大地震(Mの大きいもの)も,発生数は少ないですが必ず起こり,その時の被害は甚大です.
ここで話題にして来たのは,時間(年)の経過に対するある大きさ(震度8弱)をもたらす地震の発生確率に関するもので,べき乗測とは別の話です.
■さて,地図を見てください.日本の活断層の話に移りましょう.
赤い線は活断層です.関東地方では,高崎-熊谷-深谷の西側を流れる荒川に沿いに走り,荒川は江戸区で東京湾に注ぐ.断層地帯の荒川上流は長瀞など風光明美な処です.富士山側の活断層は,諏訪-甲府-富士山の西側を富士川沿いに走り,駿河湾に至ります.活断層は繰り返し地震を起こしており注意が必要です.
DNAの2重らせん構造が解明されて,ノーベル賞を受賞したのは1962年のことです.
受賞者の一人ワトソン博士は,後に本(二重らせん,講談社文庫(1986))を出版し話題になりました.
もう旧聞に属しますが,今回はこの二重らせんがテーマです.
カバーのDNAの図はlivedoorblog美惑星フィロソフィアからお借りしました.
このブログの主は存じ上げませんが,SARS,MERSが同定されてまもないころ(2015年6月)に,コロナ・ウイルスは,一本鎖のRNAリボ核酸でアビガンか効きであることに言及されています.
DNAの2重らせんの話がしたくなりました.
■Rosalind Franklin,ロザリンドは,ロンドン大学のキングス・カレッジに職を得て,X線結晶学者としてDNA結晶の構造解析を行っていた.DNAには水分含量の差によって2タイプ(A型とB型)があることを明らかにし,それらを別々に結晶化し,X線回折写真撮影に成功した(1952年).X線構造解析では単結晶をつくることがとても大事で,難しい仕事です.物質によっては方法をいろいろ変えてもどうしても結晶が育たない(微細な沈殿になってしまう)ので,私もずいぶん苦労し断念したことがあります.
撮影したX線回折写真を見れば,X線結晶学者なら,らせん構造があることはすぐわかります.
らせんのピッチや周期はすぐ計算できます.
しかし,彼女のまとめた非公開研究データのレポートは,予算権限を持つクリックの指導教官のマックス・ペルーツが入手し,クリックの手に渡ってしまいます.一方,ウイルキンス(彼女が赴任する前からDNAの研究をしていた)は,
ケンブリッジ大学キャベンディッシュ研究所のワトソンとクリックに彼女の撮影した写真を内緒で見せてしまいます.
ワトソンは,複製の能力のあるDNAのモデルを考えていたので,彼女の写真を見て2重らせん構造モデルを確信します.
■ワトソン,クリックの論文は,Nature(1953.4.25)に掲載されます.同じ号に,ロザリンド・フランクリンらの論文,
ウイルキンスらの論文を,同号に同時掲載の体裁(合わせて3篇)をとっています.
ワトソン,クリック,ウイルキンスがノーベル賞を受賞したとき(1962),
フランクリンはその4年前に37歳で亡くなっています.
■X線構造解析の定石は,回折像の逆Fourier計算し,DNAの詳しい構造を見つけることです.ロザリンドの時代にはコンピュータはなく,Fourier合成の計算は,数表Beevers-Lipson短冊を用いて行う手計算(多分機械式のタイガー計算機でしょう)でありました.また,試料たんぱく質の結晶化も不十分で,回折像のスポットもぼんやりしている写真しか撮影できませんでした.
良い結晶を作製して,X線自動回折系で6,000個もの反射スポットを得て,コンピュータで計算し精密な構造を得るのは1981年になってからです.
◆Matt Parker:エジンバラ・フェスティバルでは切符完売のコメディ・ショーを持ち,ロンドン数学会の人気講師という権威ある肩書きも持つのは,マット・パーカーただ一人だろう.
彼は,数学とコメディという彼の2つの情熱の混合に没頭している.
オーストラリアの数学教師であったが,今はロンドンに住み,コメディと数学コミュニケータをしている.
彼は,数学への情熱を,著書,ラジオ,TVショー,新聞,学校訪問,ライヴ・コメディ・ショー,そして時折の街頭パフォーマンスで広めている.
彼には,ロンドンのクイーン・メリー大学の数学フェローという公的契約もある.
⇒ http://www.standupmaths.com/
--------
◆マット・パーカーが鮮やかに演じる「27枚のカード・トリック」の背景には3進法がある.しかし,見ているとそんな背景は思いもつかず,楽しくも不思議である.
ビデオの後半で,マットがトリックの仕組みに3進法が使われていることを解説するので納得できる.この27枚のカードトリックはマーチン・ガードナーが1956年に発表したものだ.マットはこの発展として47枚カードのトリックを演じるが,7進法を使うものであってマットの発明である.
Martin Gardner; Mathematics, Magic and Mystery(ドーバー,1956)
27枚カードのトリックは次のように演技される:
観客に任意のカード1枚(例えば,スペードA)を選ばせ,27以下の数字(例えば18)を選ばせる.演技者は,選んだカードが何んであるか知らない.選ばれたカードを含む27枚のカードは十分に混ぜられ,裏向きの束に積み上げられている.演技の最後には,27枚のカード束の上から18番目の位置に,選ばれたカードを移動しておく必要がある.つまり,スペードAの上に17枚のカードがあるようにしたい.
この演技のプロセスに,3進法が利用されている.
3進法で17を表すと17=2x3^0+2x3^1+1x3^2で,221と表記される (ここでは,1の位から先に表記していて,慣れている表記と逆順なのに注意せよ).
演技者は,27枚のカードを,3つの山に,1枚づつ配り分けていく.選ばれたカードがどの山に入っているか聞いてから,出来上がった3つの山を,さりげなく重ね合わせる.
再度,同じ操作を繰り返し,結局全部で,操作が3セット繰り返されて,得られた3つの山を1つの束に重ね合わせると,不思議なことに求めるカードは,上から18番目に置かれている.
このトリックのミソは,3つの山を重ねる順番にある.重ねる機会は3回あるのだが,各回,どの山を上(Top=0),中(Middle=1),下(Bottom=2) の何処に置いたら良いか?
さりげなく手際が良いので見分け難いが,マットの仕組み説明で良くわかる.18番目に置くには,17の3進法表記221を使い,求めたいカードの入っている山の位置を,1回目は底(Bottom),2回目は底(Bottom),3回目は中(Middle)になるように積み上げるのだ.もし,10番目の位置に置きたければ,9=0x3^0+0x3^1+2x3^2 で,3進法表記では 001なので,1回目,2回目,3回目の積み上げでは,Top,Top,Middleの位置に置くようにすれば,求めるカードは10番目の位置になる.
今年の「とっとりサイエンスワールド」は,新型コロナウイルスのため急遽中止になりました.残念です.

とっとりサイエンスワールド---美しい数学・楽しい算数---は,鳥取大学,地域学部,矢部敏昭教授(現副学長)が中心になって2007年にスタートし,今年で第14回でした.発足時は,東部(鳥取市)だけの開催でしたが,すぐに西部(米子市)と東部の2か所で開催するようになり,4年目からは,西部,東部,中部(倉吉市)の3会場で開催に広がりました.鳥取県,鳥取県数学教育会が主催,鳥取県教育委員会,各地区教育委員会が後援し,小・中学校の先生方が活動の中心になっています.多数の高校生,短大生のバランティア参加もあり頼もしい.いまやすっかり地域から愛されるイベントになり,子供,両親から老人までが楽しみに集まる数学フェスティバルとなっています.
この13年の間に,豪雪被害の年も,台風被害の年も,倉吉地震の年もありましたが,乗り越えて毎年開催することができました.2020年は中止せざるを得ない状況は残念なことです.
とっとりサイエンスワールドは,毎年夏休みの日曜日に開催(無料のイベント)されます.昨年の例では,鳥取(7/28),米子(8/4),倉吉(8/25)に開催され,各会場に1,000人程度の参加者があります.私も万華鏡のワークショップで参加しています.万華鏡作りの参加者は3会場で400人ほどの子供や大人です.
■数学まつり
多くの人々が数学に関心をもつようになるイベントを数学月間では応援しています.講演会,講習会,数学カフェ,ワークショップ,様々な活動形態がありますが,子供たちが楽しめて数学感覚が身に着く”数学まつり(フェスティバル)”というのがあり,英国のMMPでも米国のMAMでも大変人気があります.
国立数学博物館MoMath(National Museum of Maths)は,米国唯一の数学博物館で,ニューヨークのマディソン・スクエアに,2012年12月15日オープンしました.ここには30以上の対話型の展示があります.
東京でもMoMathのような常設の数学展示のあるものは,科学技術館,リスーピア,東京理科大「数学体験館」(2013年オープン)などがあります.一度見学されると良いでしょう.
Do Math 同志社中学校数学博物館www.facebook.com
■同志社中学校数学博物館 Do★Math
同志社中学校数学博物館 Do★Mathは,2016年6月にオープンしました.Do★Mathは,生徒以外にも,一般市民にも公開されています.
一つの学校の教育の場で実現した,米国のMoMath(数学フェスティバル)や,米国の地域の数学サークル活動を思わせる意欲的な活動です.今年の数学月間懇話会(ZOOMによるリモート開催の計画.詳細が決まり次第http://sgk2005.saloon.jpに掲載します)のテーマの一つとして,Do★Mathを園田毅先生(同志社中)にご案内いただく予定です.
国立数学博物館MoMath(National Museum of Maths)は,米国唯一の数学博物館で,
ニューヨークのマディソン・スクエアに,2012年12月15日オープンしました.
ここには30以上の対話型の展示があります.
ホールの展示で目立つのは,正方形の車輪の3輪車が滑らかに走る光景(動画の2分半経過ごろ)です.
たいへん興味深いので,床面の曲線がどのような形であるかを計算してみました.
ここに掲載する結果(Fig.1)は,2013年7月22日の数学月間懇話会(第9回)で
谷が発表したものです.
■Fig.1 四角い車輪
床の形状
ついでに,応用問題として計算した3角形の車輪の結果を(Fig.2)に掲載します.
■Fig.2 三角の車輪
床の形状
注)2013年10月2日に開設された東京理科大学「数学体験館」にも,同じような4角い車輪の車の展示があります.
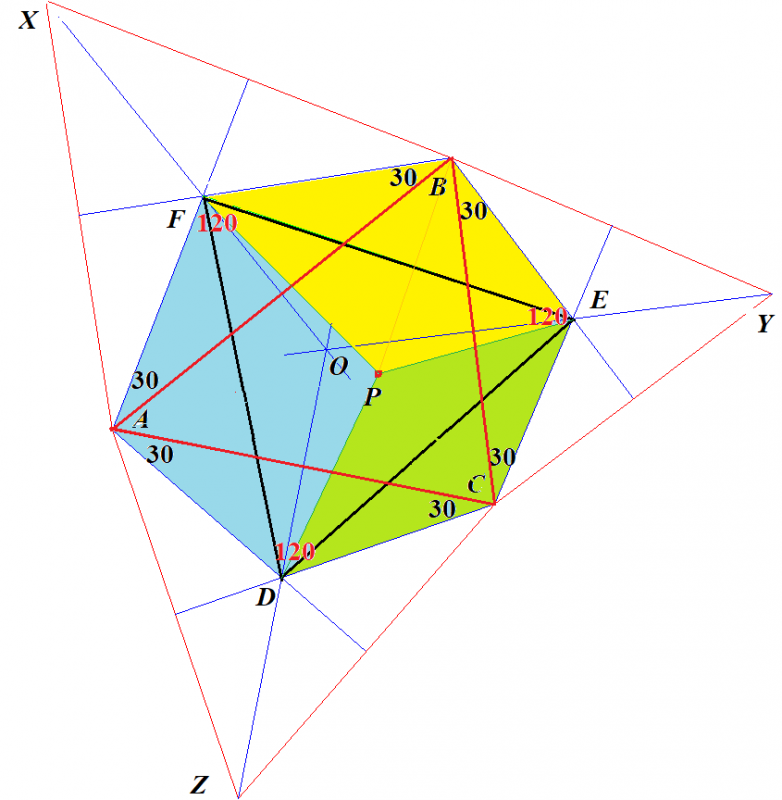
これはオーボールという赤ちゃんのおもちゃです.球の表面は互いに接する大きい円20個と小さい円12個でできています.円を正多角形にすれば,いわゆるサッカーボールの形です.つまり,小さい円は正5角形,大きい円は正6角形に対応します.
(問)大きい円と小さい円の半径の比は?
球面多面体の正多角形の辺は球の大円でできていますが,多面体の正多角形の辺は直線でできています.この多面体の1つの頂点の周りには,正5角形,正6角形,正6角形が集まっています.このような多面体は[5,6,6](シュレーフリの表記法)と記述します.正3角形の面だけが頂点で5つ集まっているのは正20面体で{3,5}と記述します.正20面体の頂点を切って(切り口は図の白い面),残りの面が正6角形になるようにすると,多面体[5,6,6]が得られます.
これは,上図のC60[フラーレン(60個の炭素原子からなる)分子.青球は炭素原子C]と同じ形です.
■さて,問の答えですが,オーボールの大きい円と小さい円は,フラーレンの正6角形と正5角形に対応することがわかります.
下図を見てください.
辺の長さの等しい正5角形と正6角形の外接円(内接円)半径比が答えです.計算すると 1:1/2sin36°≒1.176:1
■次の図に示す「組み合わさった立体」は,正20面体(水色)と正12面体(黄色)が組み合わさっています.それぞれの多面体のサイズは,辺の中央でちょうど重なるようにしました.入り組んで組み合わされている多面体は,正20面体{3,5}と正12面体{5,3}です.これらの正多面体は互いに双対です.
(注){3,5}←→{5,3}のように,面の形と頂点に集まる数を入れ替えると,”互いに双対”な多面体が得られます.
サッカーボールもオーボールも,正20面体由来の正6角形(正3角形)の面と正12面体由来の正5角形の面からできています.サッカーボールの面に対応する頂点をもつ双対な多面体を作ると菱形30面体が得られます.
(注)正5角形の面に対応する頂点間と正6角形の面に対応する頂点間が,それぞれ菱形面の対角線になります.
下図の「組み合わさった多面体」で,黄色い頂点と水色の頂点を結ぶと菱形30面体が得られます.
菱形面の1つを赤い線で図に記入しました.この菱形面の対角線比は黄金比です.
多面体の見える万華鏡
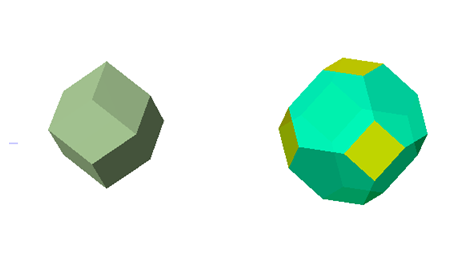
reciprocalという言葉があります.経済などでは,互恵的とか対等とかいう意味で使われます.
結晶学では,結晶格子crystal latticeに対して,逆格子のことをreciprocal latticeといいます.
両者の関係は,多面体でいうと,面を頂点に,頂点を面に変換した多面体
(これを双対dualな多面体という)の関係と同じです.
例えば,シリコンの結晶格子は面心格子で,ディリクレ胞を描くと菱形12面体(左図)です.シリコンの逆格子は体心格子で,ディリクレ胞を描くと[6,6,4]半正多面体[いわゆるケルビン立体](右図)です.
結晶格子中のデリクレ胞と逆格子中のデリクレ胞は,このように互いに双対です.格子latticeに対して逆格子reciprocal latticeとはうまく名付けたものです.
もちろん,対称性はどちらも同じ,正6面体(角砂糖)と同じ対称性です.菱形12面体と[6,6,4]半正多面体(ケルビン立体)の形が見える万華鏡を作りました.この万華鏡は,左から覗くと菱形12面体が,右から覗くとケルビン立体が観察され,両者の対称性は同じであることを理解するのに役立ちます.
ーーーー
(注)用語(ディリクレ胞,格子,逆格子,面心格子,体心格子,半正多面体)は,説明なしに用いたので,別の機会に補足説明をいたします.
参考 「美しい幾何学」 今,試し読みができるようです.
p.44~ 45 万華鏡で作る多面体
p.60~ 62 ディリクレ胞,格子
今年(2020年)のとっとりサイエンスワールドは,新型コロナウイルスのために残念ながら中止になりました.
2017年のとっとりサイエンスワールドin倉吉は,8月27日に開催されました.1,250人の来訪者があり,例年のように盛況でした.万華鏡ワークショップは30人クラスを4回実施し120人が作りました.2016年は,鳥取サイエンスワールドの終わった直後,翌々日に倉吉地震がありびっくりしました.多くの方が避難生活をし,サイエンスワールドの会場だった梨っこ館もガラス天井が落ちたそうです.隣のプールは2017年7月20日になってやっと利用開始にこぎつけました.白壁土蔵群,赤瓦館でも地震の被害がありました.
2017年に,その赤瓦二号館を訪れたとき見つけた御殿まりの写真です.
これらはみんな一人のご婦人が作ったものだそうです.お会いしたいものでしたが,残念ながら不在でした.
どれも美しく良いできですね.
正4面体群:正6面体群(正8面体群):正12面体群(正20面体群)のどれがあるでしょうか?
Q1:さて私は,正6面体群(正8面体群)と正12面体群(正20面体群)のうちのどちらを選んだでしょう?
私が選んだのは,前者の方でした.
参考に,これと同じ対称性の図形を掲載しましょう.
これらはともに,半正多面体[4,6.6]ですが,立方体のx,y,zの方向に,4回軸があり,体対角線の方向に3回軸があります.2回軸のある方向も確認してください.(注)シュレーフリの記号[4,6,6]は,頂点の周りに正4角形,正6角形,正6角形が集まっていることを示しています.
結局,これらは皆,球面正6面体{4,3}や正8面体{3,4}と同じ対称性(点群)になります.(注){4,3}もシュレーフリの記号と呼ばれますが,正4角形が頂点に3つ集まっていることを示しています.
Q2: 球面正12面体{5,3}や菱形30面体の御殿まりを見つけましょう.このなかにありますか?
これらの対称性(点群)は,正12面体やその双対の正20面体と同じです.
一番下の立体の形は,菱形30面体です.菱形30面体は,12・20面体(半正多面体[3,5,3,5])と双対な多面体なので,対称性としては,上の3つの立体はすべて同じです.
別項目・サッカーボール(フラーレン)に関連記事があります.
Q3: この他に,半正多面体[6,3,6,3]があります.探してみましょう.
ーーーーーーーーーー
美しい幾何学,p21,p46,p48 が関連します.ご参照ください
1.立方体(角砂糖)を積み重ねて,空間を隙間なく周期的に埋めることができます.下図の出発点にある黄色い立方体(シュレーフリの記号で{4,3})を並べた図がそれです.このときの空間充填では「立方単純格子」ができます.
2.立方体の頂点を切り落とした(切頂といいます)立体を考えましょう.頂点の切り口は正3角形で,立方体の正方形の面が正8角形になる位置で切頂します.すると,下図の2番目のように,切頂正6面体(シュレーフリの記号で[3,8,8])と正8面体{3,4}が組み合わさって空間を充填することがわかります.
3.下図の3番目は,立方体の切頂の切り口がさらに大きくなった場合です.立方体の正方形の面は45°回転した小さな正方形になります.このときは,正8面体{3,4}と半正多面体[3,4,3,4](あるいは6・8面体と呼ぶ)とで空間を充填することがわかります.
4.切頂でできる正3角形をさらに大きく,切り口が正6角形になる位置で切頂します.このとき,組み合わされる2つの立体は同じ形になります.つまり,切頂正8面体(あるいは半正多面体[4,6,6],ケルビン立体とも呼ぶ)だけで,空間を充填できます.このときの空間充填では「立方体心格子」ができます.
■図の3番目,半正多面体[3,4,3,4]と正8面体{3,4}の組み合わせの図で,正8面体だけを抜き出すと,以下のように頂点でつながっています.
このような構造は,ペロブスカイト CaTiO3 という物質の結晶構造に見られます.正8面体の頂点に酸素原子Oがあり,正8面体をつないで骨組みを作っています. 正8面体(青色)の中心にはチタンTi原子,骨組み中の空いた穴(黄色)の中心にはカルシウムCa原子があります.
ペロブスカイト構造は,強誘電体や酸化物高温超伝導材料などの結晶構造に見られます.また地殻を作るケイ酸塩鉱物MgSiO3(カンラン石など)はマントル下部の超高圧下でこの構造になることが知られています.
美しい幾何学,p.63,64をご覧ください.
■エッシャーの繰り返し模様のようなモチーフをつくる
平行4辺形や平行6辺形タイルは,平面を敷き詰めることができます.
(1)平行4辺形とは下図の(A)のような形です.
これらは,向かい合った平行な辺どうしは同じ長さです.
向かい合った辺どうしを突き合わせて平面を敷き詰めることができます.
向かい合った辺に同じような変形を加えて図案のモチーフを作ります.
エッシャーの作品の2羽の鳥はこのようにして作られています.
(2)平行6辺形で平行な辺どうしが同じ長さの図形は下図の(B),(C)のような形です.
これらは,向かい合った平行な辺(同じ色に着色)どうしを突き合わせて平面を敷き詰めることができます.
向かい合った辺に同じような変形を加えて図案のモチーフを作るとエッシャーの様な繰り返す絵が作れます.私は,ハロウイン魔女を作って見ました.
(3)平行8辺形以上になると平面を敷き詰められないのは何故でしょう?平面は2次元ですから独立な並進ベクトルは2つa,b です.a,b を2辺とする平行4辺形が平面を充填する並進の単位(単位胞)となります.3つの平行辺のある6辺形もタイル張りが可能ですが,2次元平面内の3つ目の並進ベクトルをcとすると,a,b,c の間に c=b−a の関係があり自由はききません.4つ目は作れません.
■一つのタイルを配置するときに回転を許すと,凸6角形タイルで平面の充填ができるものは,以下に図示する3つのタイプがあります.
(注)任意の4辺形は,180°回転したものと組み合わせると平行6辺形になります.任意の3角形も,180°回転したものと組み合わせると
平行4辺形や平行6辺形になるので,平面を敷き詰めることができます.
■凸5角形によるタイル張り4種を発見した主婦マジョリー・ライスの話は,別の機会にします.凸5角形の場合は全部で15種類をコンピュターで数え上げ2017年に至り決着しました.
「美しい幾何学」p.68~71
■5つの正多面体(プラトン立体)のうちで,最も面の数が多い(球に近い)ものは正20面体です.正3角形の面が20個でできています.最も対称性が高いものという言い方も間違いではありませんが,互いに双対な正12面体と正20面体は同じ点群です.互いに双対な正6面体と正8面体は同じ点群です.
(注)正多面体とは,正多角形(正p角形)の面でできていて,どの頂点の周りも同数の面(q個の面)が会している立体です.この立体を,シュレーフリの記号で{p,q}と記述します.pとqを入れ替えた正多面体どうしを互いに双対と言います.
正多面体(プラトン立体)は,正4面体{3,3},正8面体{3,4},正6面体{4,3},正12面体{5,3},正20面体{3,5}の5つしかないことは証明できますから,面数20より多い正多面体が存在するはずはありません.
しかし,例えばゴルフ球のディンプルはいくらでもたくさん作れるように思えなす.正多面体の面を分割し続けると,いくらでも球に近い正多面体が作れるように思うかもしれません.しかし,そのようなことが可能なはずがありません.ここで作るいくらでも球に近い多面体は,面が正多角形からわずかに歪むので,正多面体ではないのです.
正20面体の1つの正3角形の面を4つの三角形に細分化します.このとき,中心の三角形は正3角形ですが,その周りの3つの3角形は正3角形から歪むのを確認ください.以下,細分化の操作を繰り返すたびに,面の数は4倍ずつ増加します.そして,細分化された面で正3角形のものは,初めの正20面体の面の中心にあるものだけです.だから,正20面体を細分化して,球に近い多面体を作っても,その対称性は正20面体と同一(細分化しても対称性は上昇しません).素性は隠せないのです.細分化された多面体の面は正3角形ではないので,細分化でできる多面体は正多面体ではありません.(この細分化で用いたjavaプログラムは郡山彬氏が作成しました)
美しい幾何学p.23より
私が「メビウス万華鏡」と呼ぶ万華鏡は,球面多面体の見える万華鏡です.
上図の万華鏡と下図の万華鏡では,3枚の鏡の組み合わせ角度はもちろん異なります.
上図の万華鏡は,球面正3角形を面とする「球面正20面体」が見えます.
球面正3角形が5つで作る球面正5角形を一つの面と解釈すれば,「球面正12面体」が見えるという人もいるかもしれません.
下図の万華鏡は,球面直角3角形が10個で作る球面正5角形の面で囲まれた「球面正12面体が見えます」.
(注)直角3角形を鏡室に使った下図の万華鏡をコクセター万華鏡と呼びたくなりますが,これは球面正多面体なので,私はメビウス万華鏡と呼びます.
双曲幾何の円盤内にできる万華鏡のみコクセター万華鏡と呼ぼうと思います.
作り方は,「美しい幾何学」p.134~135にあります.
平面張り詰めができる凸5角形タイルの形は,フランスの数学者マイケル・ラオがコンピュータを使い,全部で15種類を数え上げ(2017)決着したようです.このような数え上げの問題が難しいのは,演繹的な数学が使えないからです.
米国サンディエゴの主婦マジョリー・ライスが,タイル張りの問題を知ったのは,1975年のScientific American 誌のマーチン・ガードナーのコラムでした.平面のタイル張り,別の言い方をすれば,一つのタイルで平面を分割する(テッセレーション)問題です.
平面のタイル張りは,任意の3角形,任意の4角形タイルで可能,凸7角形以上では不可能です.凸6角形の場合は,全部で3タイプのタイル形で可能なことをラインハルトが証明しました(1918).残されたのは凸5角形の場合で,1975年のガードナーのコラムには,ラインハルトの5タイプと1967年にカーシュナーが発見した3タイプの計8タイプが掲載されていました.ところが新しいタイプがまだあったのです.
マージョリ(フロリダ州生まれ)が,高等学校で数学を学んだのは1年だけでした.
1945年,結婚しワシントンD.C. に移り,幼い息子と一緒に,その地で商業デザイナーとして働き,後にサンディエゴに移住します.数学が楽しみで,黄金比とピラミッドに魅了されていたといいます.子どもたちが学校に通っている間に自分も読めるようにと,息子達にScientific American の定期購読を許しました.
この問題では,5角形タイルのタイプ分けがとても難しい.連続変形によりどちらのタイプにも属するタイルがあるし,同じタイプでも出来上がったパターンが全く違うように見えたりもします.彼女は発見に驚き喜んで,自分の仕事をガードナーに送りました.ガードナーはそれをペンシルバニア州のモラヴィアン・カレッジのタイリング問題の専門家であるドリス・シャトシュナイダーに送ってくれました.シャトシュナイダーは,彼女の発見が正しいことを確認したのです.彼女は,張り詰め可能な4つの新しい凸五角形タイプと,それらによるほぼ60種類のテッセレーションを発見しました(1977).1975年以降にマジョリーの4種を含む計7種が発見されていま
す.最後に発見(2015) された15番目は,やはり周期的なものですが,単位胞が12個の5角形で構成される大きなもので,発見にスーパーコンピュータが使われました.
マジョリーは2017年7月2日94歳で亡くなりました.認知症のため,5角形タイリングの問題がついに完結したのを知ることはありませんでした.ワシントンにある数学協会のロビーの床タイルに,彼女の発見した5角形テッセレーションの1つ(エッシャー風の絵)が見られるといいます.
マジョリー・ライスについては,Natalie Wolchover の記事
(Quantamagazine, 2017)
https://www.quantamagazine.org/marjorie-rices-secret-pentagons-20170711/
をご覧ください.
注) 凸5角形タイルの非周期タイル張りに関しては,3回以上の任意の回転対称のものが作れることが知られています.
表紙は結晶空間のイメージです.同じ造作の部屋が無限に並んでいるホテルです.電子を1個だけ入れたら,電子はどの部屋に居るべきでしょうか?どの部屋にも同じように出現せねばなりません.電子の存在確率は結晶空間の周期をもった関数であることが知られています.
一種類の多面体を積み重ねて空間を充填します.許されるのは平行移動のみとします.
これを考えるのは「格子」を考えるのと同じことです.3次元の場合は,独立な移動方向は3つあります:それらのベクトルをa, b, c としましょう.
na+mb+lc,(n,m,lは整数)を格子点といいます.無限に続く格子点全体を格子と呼びます.ベクトルa, b, cの組みを対称性で分類したものがブラベー格子と呼ばれ,2次元では5種類,3次元では14種類,4次元では74種類ります.
無限に繰り返す「周期的空間」(「結晶空間」とも呼ぶ)の幾何学的表現が「格子」です.周期的空間は,点の集合と考えるとデジタル化された空間といえます.(注)整数全体は可算無限個の世界です.
■格子からディリクレ胞をつくる
ディリクレ胞は格子点1個の占有領域です.単位胞とは少し意味合いが異なります.物理ではウイグナー&ザイツ胞と呼ぶことが多いです.ボロノイ分割と似ているところもありますが,ボロノイ分割と異なり格子の分割に限定しています.
立方体(角砂糖)を積み上げたような格子の場合に,ディリクレ胞の作り方を説明します.手順を見ると,ディリクレ胞とは格子点1つが占有する多面体の形なのがわかります.格子点にディリクレ胞を配置すれば,空間が隙間なく充填されるのは明らかです.
そして,ディリクレ胞の対称性(点群)に格子の対称性が現れています.
◆立方面心格子→菱形12面体
面心格子のディリクレ(ウイグナー&ザイツ)胞を作図すると「菱形12面体」が得られます.
◆立方体心格子→半正多面体[4,6,6](ケルビン立体「切頂正8面体」の一つ)
体心格子のディリクレ(ウイグナー&ザイツ)胞を作図すると,この立体が得られます.
図は省略しますが立方体(角砂糖)を積み上げた形と,ここに示した菱形12面体やケルビン立体は周期的空間を隙間なく埋め尽くすことができ,これら3つの対称性は同じです.
■格子というのは,無限に続く周期的構造の<幾何学的表現>でした.格子点に置くのは繰り返される単位モチーフです.格子点に本当に点を置くのは最も単純な構造,面心格子の格子点に原子を配置した構造は,銅やアルミニウムなどの金属結晶で,体心格子の格子点に原子を配置した構造は,鉄,タングステン,セシウムなどの金属結晶で知られています.
◆純粋に数学的に空間充填構造を導くのはとても大変なことですが,結晶学者は昔から知っていました.
自然科学の分野に数学への源泉がいろいろありました.結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です.
美しい幾何学 今,試し読みができます
◆立方面心格子→菱形12面体
面心格子のディリクレ(ウイグナー&ザイツ)胞を作図すると「菱形12面体」が得られます.
◆立方体心格子→半正多面体[4,6,6](ケルビン立体とも呼ばれる「切頂正8面体」の一つ)
体心格子のディリクレ(ウイグナー&ザイツ)胞を作図すると,この立体が得られます.

■格子というのは,無限に続く周期的構造の<幾何学的表現>です.格子点に置くのは繰り返される単位モチーフです.格子点に本当に点を置くのは一番単純な構造です.面心格子の格子点に本当に原子を配置した構造は,銅やアルミニウムなどの金属結晶で知られています.体心格子の格子点に本当に原子を配置した構造は,鉄,タングステン,セシウムなどの金属結晶で知られています.
■格子からディリクレ胞を作る手順を見ると,ディリクレ胞とは格子点1つが占有する多面体の形なのがわかります.
従って,格子点にディリクレ胞を配置すれば,空間が隙間なく充填されるのは明らかです.
そして,ディリクレ胞の対称性(点群)に格子の対称性が現れています.
図は省略しましたが立方体(角砂糖)を積み上げた形,菱形12面体や,ケルビン立体,は周期的空間を隙間なく埋め尽くすことができます.これら3つの対称性は同じです.
◆純粋に数学的に空間充填構造を導くのはとても大変なことですが,結晶学者は昔から知っていました.
自然科学の分野に数学への源泉がいろいろありました.結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です.
■ドリルが動かなくなったので分解しました.こんな減速機構になっています.グリスの詰め替えをしましょう.
先端のカバー内に遊星歯車による減速機構があります.
表面に見えている3個の歯車(歯数20,遊星歯車と呼ぶ)の中心に,モーターからの回転軸(歯数6,太陽歯車と呼ぶ)が入ります.この3個の歯車は,周囲の円(歯数48,リング歯車と呼ぶ)とも接しています.
中心軸(モーターのシャフト)が右回転すると,3個の歯車は左回転し,この3個の歯車を乗せている台は,周囲の歯に沿って右回転します.
■原理図を以下のサイトからお借りします.この原理図の歯数は,私のドリルの場合とは違いますのでご注意ください.https://www.monotaro.com/s/pages/readingseries/kikaikiso_0112/
■私のドリルの減速機構に戻りましょう.
中心の回転軸が右回りに1回転すると,台は6/48=1/8だけ右回転します.
このドリルでは,このような機構が2段になっていました.
つまり,3つの遊星歯車を載せている回転台の中心軸(出力軸)に,また6枚歯の歯車が付いていて,これが2段目の入力となっています.
こうして,下段の同様な遊星歯車に回転を伝えるので,結局,(1/8)^2=1/64だけ減速することになります.
遊星歯車は入力の回転軸と出力の回転軸は同一線上にあるので,このように段数を重ねることができます.
■遊星歯車を,toyotaプリウスでは,うまく使っています.
ガソリンエンジンにつながっているのは遊星歯車の台,発電機につながっているのは太陽歯車,モーター(車輪)につながっているのは,外周のリング歯車です.3つの歯車のうちの1つをロックすると残りの2つ間で回転の伝達が起こるので,切り替えて,いろいろな使い分けができます.
遊星歯車機構とTHSのしくみ - まっつん総研連絡用ブログ《免責事項》 自分なりに調べたことを書いていますが、間違っている点があれば資料と...matsun-ri.cocolog-nifty.com
以下の図は上記サイトからお借りしました.
■歯面に垂直なカの伝達のできる互いにかみ合う歯面の曲線については,別の機会に取り上げます.
インボリュート曲線の歯
このサイトにあるgif動画です
左の図をクリックすると見られます
■インボリュート曲線
右図をご覧ください.黒い円(半径1)が糸巻きで,この糸巻きに巻いてある糸をほどいているときに糸(赤い線)の先端が描く曲線(青い色)をインボリュートといいます.
ほどく糸の巻き始めは,黒い糸巻き表面の点(1,0)でこれがインボリュート曲線の出発点です.
糸が引っ張られる方向(赤い線)は,いつもインボリュート曲線(青い線)に垂直であることに注目してください.
インボリュート曲線は歯車の歯の形に利用されます.
上図のように,黄色い歯車どうしがかみ合っている状態を考えて見て下さい.
歯車の形がインボリュートならば,2つの歯車の接点を通る糸の方向はそれぞれの歯車の面に垂直です.
これらの歯は回転中いつも互いに垂直に押し合って力を伝えるので理想的な歯車になります.
下図で,2つの糸巻きに巻かれた糸(青色)を見てください.糸巻きが回転して一方の糸巻きに糸が巻かれ,他方の糸巻きの糸がほどかれて行きます.このとき両者の歯車の間に張られた糸の方向は動きません.
■懸垂曲線とアーチ
懸垂曲線は,密度一定のひもが両端で固定されて垂れ下がった時の形です.
石積の橋が描くアーチもこれと同じです(懸垂曲線の上下を逆にしたもの).円柱状のジュースの缶を5つ積んで,アーチを作りつり合いを保っ実験をしてみました.テーブル上のアーチの根元にある左右のブロックは,一番下の円柱を両側から押しています.
円柱の間は点接触ですのでバランスをとって積むのは非常に難しいが落ち着いてやればできます.この形は石積の橋と同じ懸垂曲線です.
私が通潤橋(熊本県上益城郡山都町)を訪れたのは,2007年10月のことでした.22日は,午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業,午後は先生方と人形浄瑠璃を観劇しました.
■通潤橋の写真(放水時に撮影k.Tani)
阿蘇山の南側のこの付近の地形は,島のように台地があり,台地から台地への移動が大変で平家の落人が隠れ住むのに好都合だったようです.台地(白糸台地)に農業用水を引くのが大変です.
水は台地のがけ下に汲みに行かなければなりません.
時の惣庄屋「布田保之助(ふたやすのすけ)」は,白糸台地に水を引くための水路橋”通潤橋”を,肥後の石工たちの技術を用いて1854年に建設しました.通潤橋は,石造りアーチ水路橋で,長さ75.6m,高さ20.2m,幅6.5m.
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています.
◆通水管
長さ約127m.石をくりぬいた1尺(30cm)四方の函渠(圧力のかかる管水路).管と管の繋ぎ目には,振動吸収と漏水防止のための漆喰(しっくい)が塗られている.さらに,通水管には5~6ケ所に地震対策のための板(緩衝材)を挟んでいる.
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/tuusui.html
通潤橋は両側台地より低いので,サイフォンの原理で出口で水を押し上げています.通潤橋の高さから流入側台地は7.5m高く,流出側台地は5.8m高い.
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/kaisetu.html
通潤橋は,今でも周辺の田畑を潤しています.
放水は,通水管に詰まった堆積物を取り除くために行うものです.
「通潤橋史料館」 に行くと,どのようにアーチ石橋を施工したかわかります.川の中に写真のような木枠を大工が組んで石工が石を置きました.
アーチ橋の高さを台地の高さまで上げられなかった理由は,
この木枠をこれ以上の高さにする木材がなかったためという事です.
石橋の木枠を外す最終段階は,橋の中央に白装束を纏った布田翁が鎮座し,
石工頭も切腹用の短刀を懐にして臨んだといいます.
写真に見えるアーチ曲線を型どっている石の並びについて話しましょう.
アーチの頂点にある石を”かなめ石”と言います.アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です.それでも下の木枠を外すときは,とても心配で責任者は命がけだったでしょう.布田翁も石工頭も命がけで臨んだのがよくわかります.
近年の熊本地震でも残ったのは,その堅牢さ(石の配管の修理をしたと聞きます)の証明です.
■人形浄瑠璃
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
人形浄瑠璃は,清和文楽館で観賞しました.山都町の人形浄瑠璃の始まりは,江戸時代の嘉永年間(1850年ごろ)で,山都町(旧・清和村)を訪れた淡路の人形芝居の一座から,浄瑠璃好きな村人が人形を買い求め,技術を習ったのが始まりといいます.
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました.良い話です.江戸時代の庶民の文化の高さに感激しました.三人で一体の人形を操ります.首(かしら)と右手を操る「主遣い(おもづかい)」,左手を操る「左遣い」,足を操る「足遣い」です.人形も触らしてもらいました.
長くなったので,本題のアーチの数学については,次号に回します.
さて,石積の橋の形,アーチ曲線に関して考えましょう.
アーチの両側の根元はしっかり固定しなければなりませんが,
アーチの上の石の重さが重ければ重いほどアーチの石は互い押し合い引き締め合うので,橋は大きな荷重に耐えられるのです.石積みは引張力に抗する力はないが,石積の石に働く力はすべて圧縮力だけなので接着の必要はなく安定構造になります.
石は圧縮に強い材料ですからアーチ型の橋には最適です.ただし,アーチ根元の支点部には,大きな水平力が発生するので,それとつり合う大きな水平反力が必要です.山で挟まれた峡谷などはこの点では最適な立地条件でしょう.通潤橋の根元をしっかり押さえつけている重そうな石積の写真を見てください.
■空き缶を積んで作ったアーチで実験
私が真剣に積んだのですが,できるのはどうしても缶5個のアーチまででした.5個の缶で缶同志の接点は4点.すべての接点で同時につり合っていなければなりませんから,作るのがとても難しい.もし,6個以上でアーチが出来た方は新記録です.ご一報ください.
缶の周りにラップを巻いていますが,摩擦力を増すためでアーチのつり合い条件を変えるものではありません.
ここから先は,釣合の5つの一次方程式を連立して解く線形代数の話になります.興味ある方はお読みください.
http://sgk2005.saloon.jp
空き缶を積んで作ったアーチです.左右対称ですから,左半分だけ解析しましょう.缶の中心を①,②,③と名づけます.すると,缶同士の接点は,線分①-②の中点と,線分②-③の中点にあります.線分①-②,線分②-③には,それぞれ圧縮応力 $$ f_{1}, f_{2} $$があります.すべての缶は点で接触しており,モーメントは考える必要がありません(トラス構造).線分①-②,および線分②-③の水平となす角度をそれぞれ$$ α,β $$としてつり合いの式を立てます.各缶には下向きに力gがかかっています.つり合いの式は,①点,②点,③点でx, y成分ごとに書きます.

$$ f_{1}, f_{2}, r_{x}, r_{y}, g $$が,ゼロででない解であるための必要十分条件は,行列式がゼロとなることでした.この行列式を計算すると,
$$ tanβ=3tanα $$ の関係が得られます.
この釣り合いの結果は,①から測った曲線に沿った距離sと,その点の接線の傾き$$ tanθ $$が比例する $$ tanβ/3=tanα/1=tanθ/s $$の関係(懸垂曲線で導ける)と一致します(下図参照).
ガーキンの全貌.平面パネルが曲面を近似していることに注意.映像 © Foster + Partners
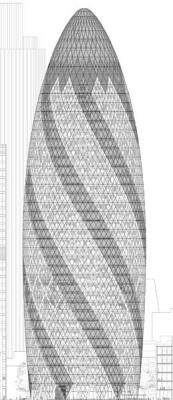
ガーキンやロンドンシティホールや,他の多くのFoster+パートナーズの作品がたいへんモダーンに見えるのは,外側が曲面であるためです. しかし,曲面を作るのはとても困難で,建設費が高くなります.そこに幾何学者のチャレンジがあります:単純な形から作る一番良い方法は何か?
「これが我々の主たるチャレンジの一つだ」とDe Kestelier(SMGメンバーの一人)は語ります.
「我々のプロジェクトの実に99%は,いかなる曲面も使っていない.
例えばガーキン,1種類の曲面パネルはトップにあるレンズのみだ.
建物が曲面という印象は,多数の多角形の平面パネルで曲面を近似的に作ることで生じる.パネルが多いほど錯視も真実味をおびる」
複雑な表面を記述するこのような平面パネル解を見いだすのが,SMGの仕事です.De Kestelier が説明するように,幾何学[その形]は,しばしば経済により決定される:「我々は矩形に近いパネルを使う傾向がある.なぜならそれはいっそう経済的であるからだ.資材をカットするとき安くなる」
三角形では,多くの材料ロスがあるが,矩形に近いとロスが少ない.
また,矩形に近いと構造が少ないので,視覚的にもさらによい.これは,
表面が完全に矩形から成り立っているロンドンシティホールで実証されました.
実際,ロンドンシテイホールは,理想的な幾何学形と建設容易さのバランスがよく取れている例です: 扱い難い丸い形はスライスに切ることにし,スライスの一つ一つは,僅かに傾いたコーンで容易に数学的に記述できて平面パネルでの近似も容易です.
■合理的な設計
数学的な方程式で記述されるコーンのスライス,トーラス,球などの表面は,しばしば,SMGデザインの基礎となります. これらを,バーチャル・モデルの創造に使うときに,数学的に生成される表面はコンピュータ上で容易に表現できるのでたいへん利点があります.
たくさんの個別座標を蓄え記述する構造ではなく,方程式を蓄えるだけでよい.表面の正確な形は方程式のパラメータを変じて制御できます(例として下図を見よ).[記述に必要なメモリが圧倒的に少なくなる]
平面解はやはり比較的容易に設計できる:ソフトウェアはオリジナルの表面のノードポイント集合に直線を引くようにする.
http://plus.maths.org/issue42/features/foster/surfaces_web.jpg
これらの表面は,関数z=e^-a(x^2-y^2) のグラフである.ここで,
3次元座標系は,x,y,z(上向き)軸であり, a は表面の形を決める.
第一の表面はa=1 ,第二の表面はa=5 ,第三の表面はa=7 .
数学的に定義された要素の集合からなる複雑な構造を考えるのは,
バーチャル世界では有用ではない:建物モデルから実際の建設手順のガイド作りを支援する合理化のこのプロセスは,もう一つの SMG の仕事の重要な部分だ.
同様に,数学的な完全性は,実用性のために道を譲る必要がある:「2~3週間前のことだが,楕円の一部である壁のプランのことで私のところに来た建築家がいる」とDe Kestelierは語った・・・
もちろん楕円は数学的には描くのは易しいのだが,それをさらに合理化することを望むのはなぜか?
私は楕円の弧を3つの円弧に合理化することを決めた.理由は,壁の建設でコンクリート壁用の型が要るためだ.これは全体の形を建設するのに多くの型パネルを使ってなされる.もし諸君が正確に楕円にしたいなら,すべての型パネルは異なっていなければならない:楕円の周囲を進むと,楕円の曲率はたえず変化しつづけるのだから. もし楕円をやめて3つの弧にするなら,諸君が必要とするのは,3セットのパネルだけで,各セットのパネルは同じである.
これならずっと簡単になる.「 数学者に理想的なものは,建築家に理想的であるとは限らない」
http://plus.maths.org/issue42/features/foster/museum.jpg
英国博物館の屋根.設計Foster+パートナー
■博才の人
SMG が,建物の外見と気流・音響のような物理現象の双方をモデル化するには,コンピュータプログラミングを使う.幾何学[形]の理解は,デザインと建設プロセスに直結する.
「建築家でなく数理科学の専門家なのか? SMGメンバーの8人中7人が,プロの建築家だが,専門的知識は,複雑な幾何学,環境シミュレーションからパラメトリックなデザイン,コンピュータ・プログラミングにまで及んでいる.グループの8番目のメンバーはエンジニアで,主プログラマーである.
こみいった数学に基づき,物理的特徴をモデリングするとなれば,
チームはしばしば専門コンサルタントを使う.チーム内で予備的な解析を行ない,もしさらに知りたければ別の解析を行う.「我々は,専門コンサルタントとデザイナー間の接点となる」とPetersは説明する.
純粋数学,幾何学は如何? どれぐらい複雑なのか?
「オフィスに1Aレベルの本がある」と,De Kestelierは語る.結局のところ,それはすべて建設可能な構造を作ることに関わり,古典幾何学を越えるものはここでは用いない.
SMG の大部分の活動には数学が付随しているのだが,彼らのデザインとは,
仕事に対して制限を与えるものであるとPetersとDe Kestlierは主張する.
「悟るべき重要なことは,我々はアーキテクチャで働くプログラマーではなく,プログラミングをするアーキテクトだということだ」とDe Kestlierは語った.
Petersも同意する:「我々の主な仕事はモデリングではない.
プロジェクトのパラメータは何かを理解し,噛み砕き定義できる規則にする.我々は,何処に適応性があり何処に制限があるかを理解できるようにする」 制限の最適化と建設可能な物体の創造.もちろん,建築家はいつもそうしてきたし,PetersとDe Kesteierも建築の仕事は本質的には変わっていないと思っている.
現代のデジタルツールにより,今日の建築家は,過去の世代には夢であったデザインオプションの領域も探索できるようになっただけだ.
形と模様,科学とコンピュータの言語として,これらのツールを自由に使えるようにしたのは数学だ.数学は確かにその料金を取り戻している.(訳:KT)
-----------------
◆編集後記
ガーキンとロンドンシティホールを設計したFoster+Partnersについての記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者(KT)が翻訳し若干編集しました.
原著エッセイを,3つに分割して(その3)に当たるものです.
Perfect buildings: the maths of modern architecture
By Marianne Freiberger
http://plus.maths.org/issue42/features/foster/xavier_brady.jpg

Xavier(左)とBrady(右)はFoster+Partnersのモデリング専門家メンバーである.プラス編集者は,ロンドンの数学と芸術ブリッジ会議(2006年)で,二人に出会った.ブリッジ会議の詳細はウエブサイトにある.
Marianne Freiberger(プラス編集者)
◆ところで,ガーキンに良く似た超高層ビルが新宿にあります.2008年に完成した東京モード学園が入っているコクーンタワーです.コクーンとは繭のことですがどちらかというとセミに似ているビルです.設計は丹下都市建築設計です.新宿で大変目立つビルです.
◆専門家モデリンググループ(SMG)について
Foster+パートナーズの専門家モデリンググループ(SMG)は,De KestelierとPetersがメンバーになっており,1997年に設立された.SMGの仕事は,建築家を助けて,プロジェクトのバーチャルモデルを創造することだ.
「通常,チームは概念を持って我々のもとにやって来る」と,De Kestelierは語る.「それはスケッチのようなものであったり,より発展させたものであったりする.そこで我々は,CADツールを用いるかツールを開発し,モデル作りで彼らを助ける」
http://plus.maths.org/issue42/features/foster/populated_surfaces.jpg
パネルを収めた数学的表面.映像提供 ΕBradyPeters
コンピュータの助けを借り,その物理から外観まで,建物のほぼすべての様相を設計することができる.コンピュータ モデルで,建物の周囲を風が流れる様や,建物内部の音波の反響をシミュレートできる.グラフィックプログラムで,異なった数学的な表面を探究し,それらに異なった柄のパネルをはめてみることもできる.
そして,これらのモデルから手に入る情報のすべては,近年の建築 CAD ツールで最も重要な発明であるパラメトリックモデリングに連動できる.
http://plus.maths.org/issue42/features/foster/gherkin_model.jpg
30St Mary Axeの建築モデル.
映像 © Foster + Partners.
パラメトリックモデリングは,1960年代からあった.しかし,建築家がその力をフルに利用できるようになったのはつい最近である.
モデルは,諸君が建物に加えた変化により影響を受ける他の特徴を再計算せずに,建物のある特定の特徴をいじることを可能にする.
これはたいへん強力なデザインツールである.ガーキンを例にとろう.もし,建物をもっとスリムにしようと思うなら,他の何らかの特徴が犠牲になるだろう.外側ライニングカーブやダイヤモンド型の角度など再計算が必要となる.これはまったくたいへんな仕事量で,もしなされたとしても,手書きであれ再プログラミングであれ,新しいスケッチを描きなおさねばならない.
パラメトリックモデルはこれらのすべてを諸君のためにやってくれる.
変えないようにしようと決めた特性は固定されたままで,幾何学的特徴を色々変えることができる.モデルはスプレッドシートのような働きで,建物の特徴を変えることは, スプレッドシートの項目を変えるようなものだ.変化に応じ,ソフトウエアは先に決めた関係を保ちつつ,モデルを再度生成する.
丁度スプレッドシートがそのすべての項目を再計算するように,SMG によって提供されたデジタルのツールが装備され,デザインチームは短期間のうちにデザインオプションの莫大な範囲を探検することができる.チームは建物の幾何学的な特徴を変えて,変化がどのように・・・例えば気流,あるいは音響特性・・・に影響を与えるかを見ることができる.
建てるのが難しいようなどのような複雑な形でも,探究することができ,単純な形へと分解することもできる.必要な材料はどれほどで,
コストはいくらかもすばやく見積ることができる.
複雑な形がほとんど建設不可能であったためと,最良な環境へ適合させる科学を充分使いこなせなかったため,数十年前には実現不可能であった建物を建設できるようになった.
◆ガーキン [ガーキンとは”キュウリ”のこと]
http://plus.maths.org/issue42/features/foster/gherkin_wind_web.jpg
ガーキンの周囲の気流のモデル.映像 © Foster + Partners.
ガーキンは SMG が関与したプロジェクトの1つで,形がどのようにして制約を満たすように選ばれたかがわかる主要な例である.このビルは30St mary Axe の公式名称で,高さ180m(ナイアガラの滝の3倍の高さ).他の高層建築に比べて,3つの際立った特徴がある:
形は方形でなくむしろ丸い.膨らむ中央と先細るトップ.螺旋のデザインに基づいている.これらすべてが,純粋に審美的特徴となることに容易に気づく.だがそれだけでなく,これらは特定の制約を満足させている.
ガーキンサイズの建物の主要な課題は,周囲を吹き抜ける気流だ.
ベースから旋風がまきおこり,近隣地域を不快な地にする. この問題を扱うために,SMG は,建築家に乱気流の数学に基づき建物の空気力学特性を
シミュレートするコンピュータモデルを使うように助言した.
モデルは円筒状が方形のものより空気の流れへの応答が良く,旋風を減らすことを示した.中央が太く16階で最大直径に達するものが,スリムなものより風の低減の助けになるということもわかった.
強風でくちゃくちゃにならないとしても,高層ビルの隣に立つのは恐ろしい.高層ビルは諸君を小さく見せ,低い建物の輝きを奪い,日光を奪い取る.これらの効果を最小に抑えるのは,ガーキンの特有な形である.
膨らんだ中央と先細のトップは,下からトップが見えないようにする.
かくして,諸君を小さいとは感じさせないし,太陽と他の景観も底から覗き込める可能性がある.
ガーキンの床面プラン. 映像 © Foster + Partners.
最初に決めたことは,ガーキンが可能な限り持続可能な建物であるべきということだ.そしてこれは,自然な換気(エアコンの節約のため)と自然の日光照射(光熱費の節約)を最大にする形の選択を意味する.6つの三角形のくさび形を,建物の内部に貫入するように各フロアの円形プランから切り取る.これらは光の井戸の役をする.
それらが作る光線は,自然の喚気を促進する.しかしながら,くさび形はお互いの直上には位置していない.空気力学のモデリングは,1つの床のプランが下の床のに対して数度回転していると,換気が最大になることを示した.それで,くさび形が作るシャフトは建物を昇る螺旋を作り,建物の外形により起こる空気の流れと,最適に相互作用する.くさび形のファサドの窓が自動的に開いて,新鮮な空気を建物に引き込む.慎重に選んだ幾何学の結果として,この建物は,同程度の他の建物に比べて,エネルギーが50%削減されたという.
http://plus.maths.org/issue42/features/foster/gherkin_inside.jpg
ガーキンの内部.三角形のくさび形は,床面プランから切り取られる.
それらは,光の井戸の役をするし,喚気も促進する.映像 © Foster + Partners.
◆この記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者が翻訳し若干編集しました.
原著エッセイを,3つに分割して(その2)に当たるものです.
http://plus.maths.org/issue42/features/foster/LCH_web.jpg

テームス川にかかるロンドンシティホール.内部の巨大な螺旋階段ケースに注目.映像©Foster + Partners
■Foster+パートナーズについて
Foster+パートナーズは,Norman Foster とシニアーパートナーグループ
が指導する国際的に著名な建築スタジオである.
ロンドンのガーキンGherkin(キュウリ)として知られる建物や,この
ロンドンシティホールや,大英博物館の大広場の屋根のようなランドマークは彼らの設計です.地上最大建設の一つワシントンDCのスミソニアン研究所の中庭,ロンドンのウエンブリースタジアム,北京国際空港第3ターミナル(龍のイメージ)なども手掛けています.
大英博物館の大広場の屋根 ガーキンの全貌
■Foster+パートナーズのプロジェクトがもつ共通点は:巨大
巨大は,環境に最大限の影響を与えます.巨悪のデザインとならずにすむかどうかは,微妙なバランスの技であります.
建造物は構造的に健全で,美的に快いものであるだけでなく,
設計規制,工費の制約,目的に良く合うこと,エネルギー効率の極大化
など,多角的に満たさなければなりません.デザインの過程は,複雑な最適化問題になります.この問題を解く方法が,モダーン建築術と古代エジプトの建築術とでは異なるのです:
先進的なデジタルツールが,制約の膨大な配列を分析統合し,最適解を見出します.数学は建設される構造の形,要求される物理的特徴を記述できます.数学はコンピュータの言語で,モデリングのすべての段階の基礎になっています.
■ロンドンシティホール
ロンドンシティホールは,ロンドン市長,ロンドン議会,大ロンドン当局を収容します.ガラスの使用と内部の巨大ならせん階段が,透明性と民主的プロセスへの親近感を象徴しているかのようです.
外見の強いインパクトは,この建物の奇妙な形です.
テムズ川の土手の上に置かれて,建物は川原の小石を思わせます.
その丸みも民主的な理想を思わせます.けれども,ガーキンと同じように,
形が決められたのは,みかけの形のためだけではなく,エネルギー効率を最大化するためでもありました.
これを実現する1つの方法は,建物の表面積を最小にすること(望まない熱の損失と流入を防ぐことができる)です.諸君は,体積が同じあらゆる形の中で,球形が最も表面積が小さいことを知つているでしょう.
これが,ロンドンシティホールが球に近い形をしている理由です.
建物を非対称にしたのもエネルギー効率に貢献しています:南面のオーバーハングが,ここの窓を上階の床で陰にして,夏季の冷房需要を低下させる.
ガーキンの場合と同様に,コンピュータ・モデリングで建物の中の気流が如何動くか把握でき,自然の換気が最大になるように建物内の形が選ばれました.実際,この建物は冷房を必要としないといいます.
同程度のオフィススペースのエネルギーに比べ,たつたの1/4と伝えられます.
螺旋階段さえ,単に審美的理由で選ばれたのではありません.それらの分析の一部として,ロビーの音響効果,人々の声が適切に聞こえるような建物をSMG(専門家モデリンググループ)は設計しました.
初期の音響効果は,広いホール内をエコーが跳ねるという状態でひどく,
何らかの対策が必要だったが,Foster+パートナーの過去のプロジェクトの1つが手がかりを提供したのです:
ベルリンの Reichstag は大きいホールがありますが,大きい螺旋の傾斜路があり反響が起きません.SMG はロンドンのシティホールに同様な螺旋階段のモデルを作り,Arup Acoustics会社がこの新モデルの音響効果を分析しました.諸君は,以下のアニメーションで,音が階段後ろに閉じ込められ,エコーが減じるのを見ることができます.このアイデアは最終設計に採用されました. (アニメーション © Arup Acoustics)
https://plus.maths.org/content/sites/plus.maths.org/files/Flashfix/arup.mov

arup.mov1.62 MB
◆この記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者が翻訳し若干編集しました.原著エッセイを,3つに分割して(その1)に当たるものです.
proccessingという使いやすいオープンソースのプログラムがあります.私も使っています.現在はver.3.5.4が出ています.これで何ができるか粒子モデルの紹介です.
この記事は,英国MMPのplusマガジン42号(2004)の翻訳(訳:KT)です.
http://plus.maths.org/issue42/features/dartnell/index.html
Matrix: Simulating the world Part I - Particle models by Lewis Dartnell
鳥の群れが黄昏空に飛び交う様,魚群が敵をかわす様を見たことがあるなら,その完璧に振り付けられた動きに驚愕したことだろう.この行動は,
複雑に思えるかもしれないが,コンピュータでそのモデル化を行うのは,
それほど難しくはない.Lewis Dartnellが諸君自身のシュミレーションの
実地ガイドをする⇒経験不要.
粒子モデルにより,鳥の群れの運動,銀河系誕生,原子分子の物質構成,
などをシミュレート!
■マトリックス[訳注:1999年アメリカ映画]
世界をシミュレート 第1部---粒子モデル
モデルの構築は,科学や工学の多くの研究分野の核心である.
モデルの本質は複雑な系の表現であり,複雑な系のふるまいを理解するのに
異なった種々の方法で系の単純化がなされてきた.例えば,航空技師は,風胴テストのために戦闘機のミニチュア模型を作るかもしれないが,現代は,数学モデルをコンピュータ上でたいへん高速に走らせるモデリングが,ますます盛んになっている.超音速気流のコンピュータモデルは,信じられないくらい複雑だが,プログラムのデザインとシミュレーションは非常に基礎的な原理に基づいている.
モデルのふるまいに関するこの論文の前半で,たいへん興味深い自然系研究のコンピュータモデルが,いとも簡単にプログラムできることを述べる.
先端研究にこのようなモデルを用いている科学者の何と少ないことか.
◆はじめよう
http://plus.maths.org/issue42/features/dartnell/fish.jpg

Fig.1 どちらに行くのか?魚の行動をシミュレートする方法を見出せ.
これは,数学的なモデリングとコンピュータ・シミュレーションへの体験入門である.だが,プログラミングそのものの学習には深入りしない.これまでにプログラムを見たことがないとしても,心配は要らない.
シミュレーションのすべては,このウエブサイトでJavaビデオとして見ることができる.もし諸君がコンピュータプログラミングをすこしやったことがあるなら,この論文で用いた全コードをダウンロードして,改良したり調節したり試してみたいだろう.これらのシミュレーションを書いたり,アニメーション作りに用いたソフトウェアはプロセッシングと呼ばれ,無料でダウンロードでき,PCやMac バージョンで利用可能だ.
プロセッシングはコンピュータ科学者とアーティストの協力でリリースされ,自分で容易に改良や開始ができる.http://processing.org/download/index.html
プロセッシングが使われた世界中の種々のプロジェクトすべてのリストを
ホームページで一見されたし.http://processing.org/
よいモデルを組み立てる本質は,複雑な問題をいかにうまく単純化し,
系の重要な特徴を抽出し,モデルのふるまい解析を混乱させるものは取り除くように考えることだ.
例えば、ライフル銃から発射された銃弾弾道の単純なモデルは,明らかに重力の影響を考慮する必要があるが,空気抵抗のわずかな影響は無視してよい.この場合の空気抵抗は,2次オーダーの効果と呼んでよい.
別の系のモデリング,航空機の翼による揚力では,空気の影響を無視することはできないが他の因子は無視できる.
コツは,そのふるまいが理解しやすいように,モデルをできうる限り単純に保つことと,意味のない結果が生じないように重要と思われる因子をあまりカットしないようにし,入力因子の一つを変えて全系の応答の影響を見ることとのバランスにある.
この最初の論文のすべての例は,各点が空間内を色々な規則に従い動き回る粒子モデルとして知られるものである.
◆箱の中のガス分子
最初のモデルは,箱につめられたガス分子の大変基礎的な物理シミュレーションだ.見やすく単純にするため正方形内に閉じ込められた2次元粒子とする.この場合の物理は簡単である.各粒子は,箱の壁に当たるまで,
出発したときと同方向・同スピードで直線運動し続ける.壁に衝突すると,粒子は跳ね返り方向を変えるがスピードは変えない.映画と同じで,この論文のアニメーションは流体の運動を印象づけるフレームのシリーズからなる.
プログラムの仕事は各粒子の位置,方向,スピードを各時間ステップごとに前のステップの情報に基づき計算することである.この論文のすべての例では,各時間ステップごとのデータを配列または行列に蓄える.
行列の各行は異なる粒子に関する必要な情報を蓄える.このガスの例では,各粒子の状態は4つの数で記述される.
これらのうちの2つは平面内の位置(x,y)である.残りの2つは,粒子の運動の2成分を記述する.これらはdeltaX, deltaYと呼ばれる(”X位置の変化”,”Y位置の変化”の意).粒子の速度も定義する.
この場合の行列は4つの列と,全粒子に対する十分な行数を持つ.
シミュレーションの各時間ステップごとに,各粒子の位置(x,y)は,その速度に依存した更新を受ける.このプロセスのモデルを記述するプログラムの構造は,かなり直接的である.
どのように機能するか一般的な要点がつかめるかコードを見てみよう.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules.pde
最初にするのは,モデルの最も重要なパラメータ(含まれる分子の数,各粒子の位置と速度の情報を格納する行列など)
の定義である.次に,プロセッシングは,世界の大きさ-この例では正方形,アニメーションのフレームレート-を決め,シミュレーションのセットアップをする必要がある.
それからシミュレーションの初期化をする.これはデータを蓄える行列で,各粒子の初期位置,速度の必要な情報を順次蓄える.今回は,粒子のランダム散布を選んだ.
次に,トルコ石色の背景と各粒子の(x,y)位置に置かれた赤い円で系の現状を記述するコードがある.
最後に,シミュレーションの中核,アップデート関数が来る.
各時間ステップごとに,この関数は,行列中の各粒子に順番にあたり,時間ステップ内に,その速度が箱の境界を越えその粒子を飛び出させないかどうか計算する.
もし飛び出すなら,箱の壁で跳ね返り,粒子速度は変化するが,そうでなければ,その速度ベクトルで決められる距離だけ前進し続ける.
かくして,各粒子は新しい位置と新しい速度ベクトルをもち,行列は新しい値にアップデートされる.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules_web.jpg
Fig
箱に閉じ込められたガス分子のモデル.Java始動には映像をクリック.
全プログラムは,粒子が系をアップデートした後,再び描画し,
粒子はもう一度アップデートされ,これが繰り返されるように,
ループにセットされる.高速な現在のコンピュータでは,
これがたいへん高速に行われるので,ガス分子のスムーズなアニメーションになる.
この絵はプログラムのJAVAバージョンを開くようになっているので,
プロセッシングソフトウエアをインストールしなくても,動作を見ることができる.
この過剰に単純化したモデルは,2つの問題点があることに気づくだろう.第一に,我々のプログラムではdeltaX,deltaYに整数値だけ使っていること.このため粒子が動ける異なる方向の多くがなくなってしまう.
粒子のいくつかは,両サイドでバウンドし往ったり来たりするので,完全に水平や垂直に動くのが見られる.
第二に,このコードは,分子間の相互作用を考慮していない.分子は決して互いに衝突せず,箱の中を跳ね回るだけで,
完全予測可能である.周期的に,はじめがそうであったように,全分子が外向きに散らばる前に,真ん中で密なクラスターが形成される.これは明らかに部屋の中の空気分子では起こらないことだ.
空気分子は絶えず互いにぶっつかりあい予測不可能な運動を生み出している.
もし諸君が,少しコンピュータプログラム知っているなら,この単純な例をスタートとして,もっと洗練され現実的なものを作りたいと思うだろう.これをどのように行うかの若干の助言は,プログラムファイルの末尾にある.
運動のモデリングのもう一つの例に移ろう.今度は,粒子の相互作用の規則がもう少し複雑である.
◆鳥の群れ
モデル化する系は鳥の群れである.分子の例のように完全に独立に動くのではなく,各粒子は他の粒子の動きに反応して動く.
同様な標準構造をガスのプログラムにも用いるだろう.
最初はパラメータと世界の大きさを決め,全粒子の位置と速度を初期化する.次に,系の現在の状態を表示する関数のループをまわし,
次のタイムステップでの系の変化の計算を行う規則を実施する.
最初の例は,閉空間に閉じ込められた粒子の運動のシミュレーションをねらった.
今度は,開かれた戸外で飛ぶ鳥がどのように群れを作るか調べるのが関心事だ.エッジがあるような世界は困る.なぜなら,そのような人工的な特徴の周りでは,シミュレーションが適切にふるまわないであろうから.
モデリングの共通のコツは,世界空間を,粒子が左から去れば右から現れる,上下も同様[周期的境界条件]に世界空間を定義することだ.
上下は互いにつながりチューブのよう.左右端を丸く曲げてつなぐ.
ドーナツの表面の世界のようだ(数学ではトーラスという).
http://plus.maths.org/issue42/features/dartnell/flocking_index.html
Fig
鳥の群れモデル.単純な規則の集合が,他の鳥との相互作用を定義し各粒子の運動に作用する.燈色の円は視野範囲を示す.イメージをクリックすると
シミュレーションのJavaバージョンが走る.
再スタートは[Ctrll]+[F5](Windows)または,[z]+[R](Mac).
このモデルでの第二の発展は,直線運動を続ける粒子のかわりに,
鳥たちは互いに相互作用をし近隣者に依存し飛ぶ方向を変化させることだ.
各時間ステップごとに,プログラムは,次々に各鳥を選び,選んだレンジ内で他のすべての鳥の飛行方向の平均を計算し,選んだ鳥はこの方向に舵をとる.
ランダムに選んだある鳥の視野レンジの場を燈色の円で表示させる.
プログラムで値を蓄える変数はeyeSight.
プログラムがどのように機能するか一般的な要点を拾い上げるため,
コンピュータ・コードを一寸見てみよう.
http://plus.maths.org/issue42/features/dartnell/Flocking.pde
次に左のイメージのシミュレーションを走らせて見よう.
始めはランダムであった鳥たちの運動が,直ちに秩序のある振る舞いに変わる.
鳥の巨大な群れが,大体同じ方向に飛び行くように自己組織化される.
孤立した鳥が一団の中に引き込まれる.そして時折2つの大きいグループがお互いに近づいて迷うとき,個々の鳥は他の群れに参加するために引き剥がされる.2つの雲がスムーズに混ざり合うようだ.
ちょっと迷って,そして次に新しいグループの先頭が決まる.
この設計された行動を本当の鳥一団の動的関係と比較してみよう.
これを書く時点で,あるホップベースの飲物の英国テレビで放映されている素晴らしい広告がある.
夕映え空のツバメの群れに魅せられる.タグ ライン「属します」で終わる.
この広告はYouTube から見ることができる.たとえすでに消されていたとしても,他の鳥の群れビデオを見いだすのは全く容易であろう.
http://www.youtube.com/watch?v=RHHfynLYW1I
Fig 巨大スケール鳥群れを示すYouTube広告
この運動は優雅な振り付けに見える.
個々の鳥が次に何処に飛ぶか正確に知っているように見える.
鳥の巨大な流れが,滑らかに調和し一斉に方向を変える.
群れの中にリーダーはいない.基本計画もない.
すべての決定はグループ力学だけで決まる.
何千という群れをなす鳥の魅了される複雑さのすべては,
最近接の隣を越えた残りのグループが何をするかを知ることなしに,
個人が行動するというたいへん単純な規則から発する.
これはボトムアップ制御として知られる.
単純な規則で相互作用している個体から,
たいへん複雑なグループ行動が出現する例だ.
たくさんの動物,ミツバチ,スズメバチ,アリ,シロアリ,...が,
この種の「群れ知性」を使う.
しかし,群れの振る舞いの基礎となっているこれらの単純な規則は異常な環境では,まったく馬鹿な行動を惹き起こすことがある.
自分自身ではまだ試す機会がなかったが,友達の友達から,
諸君が羊の一団と一種にやれる面白いトリックの信頼できる情報を得ている.
羊達の前で突然走ったとする.羊達は脅威を察知し動き去ろうとする.
まだ可能な限り,諸君の隣人に近い状態を保って,同じ方向に動作することが最も安全であるという規則は働いている.
もしあなたが羊より少し速く走り続けるなら,あなたは追いつき,
そして一団の中央を通過して先頭で今走っている.グループの動的力学が,
侵略者から逃げ出すという初期の個体の決断から引き継がれていて,
あなたは,群れ全体をあなたの後ろに従えていることになる.
◆コウモリとタカ
プロセッシングソフトとこのモデルのプログラッミングコードをダウンロードしたら,グループ全体のふるまいにどのように影響するかモデルのある特徴をいじることができる.
例えば,鳥同士は何処まで見えているのか,eyeSight変数はたいへん重要なパラメータだ.我々のプログラムでは,この変数は20にセットされている
(とりの視野を表している燈色の円の半径が20単位).
このパラメータは諸君の望む如何なる値にもセットできる.
2つの異なるシナリオを見てみよう:
”コウモリのように目が見えない”eyeSightは1とする.
もう一つは地図をよぎって見渡せる”タカの目”eyeSightは100とする.
下の2つのリンクの図をクリックすればjavaが動き,どちらのシミュレーションも見ることができる.
http://plus.maths.org/issue42/features/dartnell/eyeSight1_web.jpg
http://plus.maths.org/issue42/features/dartnell/eyeSight100_web.jpg
Figコウモリのように目が見えないeyeSight=1 タカの目eyeSight=100
第一のシナリオでは鳥たちは相互作用をまったくしない.だから実際は世界空間内でランダムに走るガス分子と同じだ.
第二のシナリオでは,鳥たちはグループの反対側にいる個々の鳥の飛行方向に反応するくらい,たいへん遠くまでコミュニケーションする.グループのふるまいはたいへん速く一体化した固まった運動になる.
どちらの場合にも,少なすぎるか多すぎる相互作用のために,すべての複雑な群れのふるまいは失われる.
系のアウトプットはこのパラメータにたいへん敏感である.気体的ふるまいと固体的なふるまいの間にある種の相転移がある.興味あるダイナミックスの見地ではどちらも死んだも同然だが,自然ではeyeSightの値がこれら両極端の中間値のときにのみ緊急行動が起こることが見られる.
◆揺動させる
もう一つの重要なモデリングパラメータはランダムジグリングである
(プログラム中にrandomJiggleと記す).
「各鳥の周囲の鳥の平均飛行方位の査定が,いつも正確になされている訳ではない」という事実を考慮に入れる.プログラムが時時刻,各鳥の方位を更新するとき,ランダムジグリング変数により与えられる範囲内のランダム角に調整される.
10°より小さいrandomJigle値なら,群れは最終的に一方向への一体運動になる.randomJiggleを180°にセットすると系は塵微粒子のブラウン運動の
シミュレーションと同じになる.
ガス分子の例のように,このモデルをさらに自然に近づけるいくつかの方法がある.このヒントのいくつかはプログラムファイルの末尾にある.
◆単純さと速度
モデル記述で重要な因子は,用いるアルゴリズムの効率である.
”アルゴリズム”の起源は,アラブの数学者al-Khowarazmiの名前であるが,
”仕事を完成させるための一連の指示”を意味するようになった.
鳥の群れの例で用いたアルゴリズムは,おそらくそれほど自然ではない.
本当の鳥は,他のすべての鳥の位置を記録し,
自身と他のすべての鳥間の斜辺距離を計算し,
正確に5m内のものを選択し,
それらの進路の算術平均の方位に向けて舵を切るなどということはしない.
これらのステップは,追従が容易で,望ましい結果が得られるので,モデルとして選ばれたのだ.これは,なかなか冗長な方法だ.
一つの鳥から他のすべての鳥までの距離を計算しなければならない.
これを順番にそれぞれの鳥について,各時間ステップごとに行う.
高速なデスクトップコンピュータでも,鳥の数が500より大きいとシミュレーションはゆっくりゆっくり進む.
そこで,モデルのデザインでは,仕事をどのように達成するかを考える必要がある.可能な限り速いアルゴリズムを使うか,系でできる限り現実の方法に近づけるか,効率は悪いが仕事が達成できる方法にするか.
プログラミングで,しばしば,特定の仕事部分のアルゴリズムを関数にするのは良いアイディアだ.こうすればプログラム内で特定の計算が必要になったときいつでも呼び出せる.
(鳥の群れのコードを見れば,MeanHeading()関数でこれがなされる
のを見るだろう.)
見守る間にシミュレーションがずっと速く走るようにしたければ,
プログラムを2つの段階に分割するとよい.
最初は,コンピュータを貪り尽くすようなすべての計算を通して行い,
各時間ごとに系の状態を別々な行列として記録する.
この計算の後は,例えば1000回の時間間隔の行列リストの束のような3次元行列に行き着く.
シミュレーションを一回通しで行えば,すべての情報が保存される.
第二のステージは時間ステップごとに順番に表示する
(今度は計算処理のために待つ必要はない).
あたかもアニメーションを見るのに,行列の本の頁をパラパラするようなものだ.我々は,鳥の群れの単純なシミュレーションに絞ってきた.
コンピュータプログラムの構造,特定の仕事をするアルゴリズムや関数の記述などのコンピュータモデリングの重要な様相が浮彫りになるからだ.
このように単純なモデルでも,複雑で大変自然に近い群れのふるまいが作れる.これはまさに,動物研究者が作ろうとし,理解しようとした鳥の群れのふるまいや,魚の群れのコンピュータモデルだ.
例えば,Iain Couzin博士が動物のふるまいを理解するために巨大グループのコンピュータモデルを使つている.彼のモデルは,この論文で見てきたものとまったく同じ原理に基づいており,同様の複雑性がみごとに出現する.
モデルはさらに複雑になっており,(我々の2次元平面を超え)
3次元で動き,冗長だが現実に近い各個体のふるまいを制御する規則の集合を持つ.
-------------------------------------------------------------------------
◆Iain Couzin
イアンは,プリンストン大学とオックスフォード大学の両方に拠点を置く
動物行動の専門家だ.バッタから魚,鳥に至るまでの群れのダイナミックスのコンピュータモデルを作った.
彼の研究は,如何に動物の群れが集団としての決定をなすか驚異的な特徴を見いだすことと,アフリカの政府機関の行うバッタの致命的な群移動コントロールを手伝うことだ.最近まで,イアンは群れがどのように肉食動物の
アプローチに反応するかに集中していた.
諸君はイアンの研究の詳細を
http://www.princeton.edu/̃icouzin/で読むことができる.
下の映像は彼のモデルの一つから作ったビデオの静止画だ.
BBCのドキュメンタリシリーズ”肉食動物”で使われた.
http://plus.maths.org/issue42/features/dartnell/SimImage.jpg
------------------------------------------------------------------------
◆重力モデル
この種類の粒子運動モデリングの拡張は,画面をよぎって伸びる効果を含めることである.このわかりやすい例は,重力である.
重力は消えそうなほどわずかかもしれないが,太陽の重力の影響は非常に長距離まで達する.processingを使い単純な重力モデルを作るには,太陽としてスクリーンの中心に小円を描き,他のすべての点から太陽までの方位と距離を計算する関数を記述する.これで,諸君のモデル化した世界にある
粒子が影響を被り速度を変じる重力を計算できる.
ランダムな位置に置かれランダムな速度を持った惑星でシミュレーションを初期化し,これらの太陽の周りの円弧運動をアニメートしよう.
次の時間ステップのこれらの位置は,現在の重力と速度で決定される.諸君はプログラムを,各惑星が後ろに軌道の軌跡を残すように変更することもできる.
(draw()関数BYの背景コマンドを取り除く.ラインの始めに//でコメントにする).
http://plus.maths.org/issue42/features/dartnell/collision.jpg
Fig. 何十億という星がアンテナ銀河の衝突の間に形成された.
下に示した銀河衝突モデリングで色々見いだそう.
このイメージはハッブル宇宙望遠鏡で撮影された(NASA提供).
太陽系の表示のために,各惑星の円軌道を生む速度を注意して解く必要がある.太陽系の圧倒的な支配力,太陽の重力だけを含めば,第一近似で正確なモデルができる.だが,巨大ガスの木星は他の惑星に注目すべき影響を与える.このような二次的な効果を含めるなら,さらに正確なモデルができる.
水星の軌道を完全に観察に合わせるには,もっと複雑なレベルが必要で,
アインシュタインの相対性理論-これはNewtonの重力の法則よりも,
ある特定の状況では正確-を含める必要がある.
繰り返すが,モデリングのコツは,無視できない詳細の最小量を巧妙に考慮することだ.月面に人を着陸させたアポロプログラムは,単純な Newtonの重力モデルで地球と月の影響以外のすべてを無視した.
すべての粒子が互いに相互作用するもっと大きな重力系ダイナミックス
のモデリングは,非常に高速なコンピュータを使い膨大な計算が必要で,
極端な”計算浪費”である.
しかし,そのような数値シミュレーションも多くの研究者にとって
極めて重要だ.例えば,下の枠中に,2人の主導的な研究者の仕事に焦点を合わせ,過去と未来の数十億年のイベントを見ることができる.
世界を打ち砕く衝突を通して月が作られ,我々自身の銀河と我々に最も近い隣人銀河が,巨大な重力で引き合い,数十億年の先に互いを分裂させられるであろう.
----------------------------------------------------------------
◆Robin Canup
ロビンはテキサスのサウスウエスト研究所の宇宙科学者だ.
彼女は月がいかにして形成されたかに興味を持ち,
太陽系生成の初期に,若い地球がより小さい原始の惑星に衝突した時の
イベントから月が生まれたという理論をテストした.
彼女のコンピュータモデルは衝突の熱で地球全体が融け
大量の岩が宇宙に放出され,その多くは衛星の軌道でに合体し月になった.
http://www.boulder.swri.edu/̃robin/でもっと多くを見ることができる.
http://plus.maths.org/issue42/features/dartnell/Moon_impact1.jpg
-----
◆John Dubinski
ジョンはトロント大学で全銀河のダイナミックスを研究している宇宙物理学者.我々の銀河,天の川,アンドロメダと呼ばれるらせん銀河の隣人は
重力的に互いに引き合っていて,500,000km/時間でお互いに向かって落ちて行く.
ジョンはスーパーコンピュータを使用し,これらの2つの巨大な銀河が合体し始め,2つの星が互いに引き裂かれるときに星の大きな帯を引き裂き始める約30億年後の時間をモデル化した.驚くべきことに,このすべての混乱にもかかわらず個々の星の間のギャップは非常に大きいため,実際には一つも衝突はないであろう.
我々の太陽の運命は不確実である.太陽は銀河間の宇宙の暗虚に排出されるか,混合銀河の密集しているコアに飛び込むかである.諸君は,
http://www.cita.utoronto.ca/̃dubinski/tflops/で,
地球の夜空の景色も含めて,さらに色々な映画を見ることができる.
http://plus.maths.org/issue42/features/dartnell/galaxy1.jpg
-----
◆著者:Lewis Dartnell
著者のルイスはオックスフォード,クイーンズ・カレッジで生物科学を専攻している.現在[訳注:2004年当時],生命科学と実験生物学の数学と物理センター,学際科学のロンドン大学センターの生物学的複雑系モデリングの
4年間のMRes-PhD課程にいる.彼は宇宙生物学の分野で研究している.
火星の放射線レベルのコンピュータ・モデルを用い,火星の表面付近で
生命が生きられるかの予測をし,最近ニュースで報じられた.
彼はデイリーテレグラフ/ BASFの若手科学ライター賞などを4回受賞した.
彼のポピュラーサイエンス本,宇宙での生活:初心者向けガイドは,
2007年3月に出版された.彼のウェブサイトで多くの作品を読むことができる.(訳:KT)
中西達夫さんの「スパゲッティを巡る旅」は,スパゲッティを適当に砕くと,破片の長さの分布がどのようなものになるかという興味ある実験でした.
興味おありの方は,「数学文化」第21号(2013年)をご覧ください.数学月間懇話会(第10回,2014)でも講演していただきました.このとき観察される「べき乗則」は,社会の関心事の一つである「地震」でも見られます.
地震のテーマはメルマガNo.031('14/09/30)に,複雑系原発の事故雪崩のテーマは「数学文化」第16号(2011年)やメルマガNo.006('14/05/15)に掲載しました.今回は地震のマグニチュードと頻度のべき乗則の話です.
地震のマグニチュードMはエネルギーの対数です.マグニチュードを決めるのにリヒターが発案した当初の定義は便宜的なものでしたが,現在ではもっと理屈に合ったモーメント・マグニチュードが採用されています.
(注)震度というのはその地の揺れ(加速度[ガル])の程度をもとにした段階区分です.
地震で解放されるエネルギーは,生じた断層面の面積×平均変位×地層の剛性の積です(大雑把にいえば生じた断層の長さに比例します).
生じた断層の長さが長い方が解放されたエネルギーは大きいし,
地層の剛性が大きいほど大きな歪エネルギーが蓄えることができます.
これらを踏まえ,起こりうる地震の最大エネルギーを見積もるとM9.5程度と考えられています(1960年のチリ地震ではM9.5が観測されている).
地震のマグニチュードMと発生頻度(回/年)nの間にn=10^{a-bM}の関係があるのを,グーテンベルクとリヒターが発見しました.a, bはその地域の地層の剛性などを表す定数(b≒1)ですので,地震のマグニチュードが1つ大きくなるごとに,地震の頻度(回数)は1/10に減ります.ゆえに,これを「べき乗則」とも言います.
地震では,多発しやすいマグニチュードというものがありません(中心値があるようなガウス分布やポアソン分布ではない).べき乗則では,大きな地震ほど少なくはなりますが,M9あたりも起こり得ます.めったにないことですが,そんな巨大な地震に見舞われたなら壊滅的で,大きな地震の被害コストは莫大です.
地震被害コストの総額=Σ被害コスト(Mの関数)×発生確率(Mの関数)
を小さく抑えるのが,最善のリスク対策です.
工場の品質管理を考えましょう.不良品の多くでる日と少なく出る日がありますが,不良品の個数とそのような数の不良品を出す頻度の分布は,ガウス分布,ポアソン分布,ワイブル分布などの中心値を持つ分布ですから,中心値を出した普通の日の対策を検討すればよいわけです.
しかしながら,分布がべき乗則の場合は全く異なります.
頻度は小さいけれど致命的な被害を惹起する巨大地震に対して,
被害が最小となるように備える必要があります.
広域を汚染し人間の尺度に合わない百年もの年月要する原発事故の被害コストは致命的です.原発の再稼働は止めましょう.
クリーン・ルームの塵のサイズ分布も「べき乗則」だと言われています.
もし正規分布に従い,頻度の高い塵サイズがあるなら,そのサイズの塵の発生に特化した対策ができるのですが,「べき乗則」では特別な対策は困難です.幸いなことにこのケースでは,大きなサイズの塵が桁外れに大きな被害コストを与えると言う訳でもありませんし命に係わることもありません.
べき乗則は,大規模停電,原発事故,ハリケーン被害などの複雑系でみられます.べき乗則は,小さな事故が雪崩をうって全体に広がる性質と関係があります.関連テーマのバタフライ効果は稿を改めます.
■砕いた破片の分布関数を求める実験は,中西氏の実験したスパゲッティやクラッカーのほかに,凍ったジャガイモを投げて砕く(南デンマーク大,1993年)などいろいろあります.砂山が雪崩を起こす限界傾斜の実験も面白いものです.これらでも「べき乗則」が確認されました.
Maths goes to the movies By Joan Lasenby
Submitted by plusadmin on March 1, 2007
http://www.plus.maths.org/issue42/features/lasenby/index.html
今回も,MMP,plusマガジン42号の筆者KTによる翻訳です(2回に分けて掲載).
数式が読みにくい場合は,数学月間の会http://sgk2005.saloon.jp,社会を支える数学科学でご覧ください(ホームページではTexを用いている).これは,2007年の数学月間懇話会で配布したものです.この後の13年でコンピュータビジョンの分野は非常に進化しましたが,原理の紹介には非常によく書かれたこのエッセイが役に立ちます.
------------------------------------------------------------------
ポップコーンは手に入れたか?よい席は選んだか?座り心地は良いか?それではタイトルロール....
■数学が誇らしげにプレゼント....
映画の中の信じられないほど真に迫ったコンピュータで作られた映像に皆な驚く.ジュラシック・パークの恐竜,ロード・オブ・ザ・リングズの不思議 ---- 特に,ガーラムの出演者 --- は,数学なしではできなかったということを知らない人が何と多いことか.どのようにして,これらの驚くべき映像が作られるのだろう?
コンピュータ・グラフィックス,コンピュータ・ビションは大きな課題だ.この記事では,完成作品に使われる数学のいくつかを簡単に概観する.最初に映画の世界を創造し,次にそれを生活へ持ち込もう.
■場面を作る
pblk0001.png
最初の対象物は,三角形のような単純多角形よりなる針金骨格として作られる.
コンピュータ生成映画を作る第一ステップは,物語中のキャラクターや,
それらが棲む世界を創造することだ.これら対象物のそれぞれは,
接続された多角形(通常は三角形)で構成された表面として作られる.
各三角形の頂点は, コンピュータメモリにストアされる.
どの三角形のどちらの面が,物体やキャラクターの外側であるかを知ることは重要だ.この情報は, ストアされている頂点の順番として,右ネジの規則に従い記号化される.これで,どちらが外か一意に決まる.
[頂点の順番に従い,三角形の周りを右手の指を人差し指,中指,..と回したとき]
諸君の親指が向いているのが三角形の外側だ.例でやってみよう.
三角形(A,B,C)の外側方向(外側法線)は,三角形(A,C,B)の外側方向と反対であることがわかるだろう.
pblk0002.png
右ネジ規則で定義された(A,B,C)の外側法線は(A,C,B)とは反対方向
pblk0003.png
諸君の視点からファセット面までの光線を追跡しよう.光線は反射して光源を通過するか?
いまや対象物の表面は三角形の針金網だ.網のコンポーネントのそれぞれを彩色する準備ができた.
我々がモデル化している光景のライティングを,実際と同じにすることが重要である.これは光線追跡と呼ばれるプロセスを用いなされる.視点から物体へと遡り光線追跡し,反射させる.もし,目から出た光線がファセット面(針金網三角形の中の一つ)で反射され,光源を通過するなら,そのファセット面は光源に照らされ明るい色,もし,反射された光線が,光源を通過しないなら,そのファセット面は暗い色の影付をする.
光線を特定のファセット面まで追跡するには,表面を数学的に記述し,光線とファセット面の平面とが係わる幾何学方程式を解くことが必要になる.これはベクトルを用いなされる.光景の3次元座標系に,視点となる原点(0,0,0)を加える.
ベクトル v =( a, b, c ) は,原点から発し座標 a, b, c で終わる矢である.
例えば, v にスカラー2を乗ずるのは,規則 2v =2( a,b,c )=(2a, 2b, 2c ) に従い行う.
2v は v と同じ方向で2倍長い矢だ.
表現 λ v を見よう. λ は変数(言い換えれば,任意の実数).これはもはや,ある長さの矢ではない.長さが変数になったのだから.矢の方向だけを表している.別の言葉でいえば,この表現はベクトル v を含む直線を表す.
それは我々の視点からベクトル v の方向に発する光線を記述する.
三角形のファセット面で定義される平面は,3つの情報で表現される:
3頂点のうちの1つの位置頂点 $$a_{1}$$と, $$a_{1}$$から $$a_{2}$$へのベクトルと, $$a_{1}$$から $$a_{3}$$へのベクトルである.
下の囲みの中に,目とファセットで決定される面から発する一本の光線の方程式を与える.
光線がファセットをよぎるか否か,何処でよぎるかを知り,反射された光線の方程式を計算するには,
これらの2式を解かねばならぬ.
------------------------------------------
-------------------------------------------
(光線追跡の数学の詳細は,Turner Whittedの革新的な論文 ”影付け表示のための改良された照明モデル”,
Communication of the ACM,Vol.23,Isuue6に見ることができる.)
光線追跡は現実味ある光景を作り出すことができるが,たいへん遅い.
これはコンピュータが作る映画の製作には用いることができるが,コンピュータゲームのようにリアルタイムで照明を変化させることが必要な場合問題である.
影や火線束(コースティク)[収差による回り込みでできる光像],多重反射のような複雑な現象は,モデル化が困難で,動的あるいはもっと巧妙な数学的な手法,事前計算放射輝度伝搬(PRT)やラジオシティ(R)が使われる.
pblk0004.png
コンピュータゲームDOOM3,Neverwinter nights はダイナミックライティングが必要だ.
■必要なのは若干の想像力
光景,照明が出来てしまえば,監督が”アクション!”と叫び,キャラクターが動き出すのを待っばかりだ.いまや,数学がイメージに命を吹き込むのを確かめよう.
最も基本的な物体の動きの一つは,与えられた軸の回りの与えられた角度の回転である.
座標幾何学は,回転後の物体各点各点の位置を計算するツールを提供する.だがこれらのツールは効率的で高速であることが重要だ.これらのツールを見るにあたり,数学授業に一寸立ち寄って見る....
[この後,複素平面のこと,複素数に虚数iを乗じると反時計回りの90度回転になること,などの説明があるが略]
........
1806年にアマチュア数学者Jean Ribert Argandは複素数とiに幾何学的な解釈を与えた.複素数を乗ずることは,幾何学的には回転を表す.
■3Dへ
pblk0006.png
Broone橋にある記念プレート,Hamiltonが4元数を発明したときこの橋の下を散歩していた.
数学者William Rowan Hamilton卿はDublinのTrinityCollegeの最も著名な子であろう.
彼は最後の20年,複素数が2次元の回転を表すのと同様な,
3次元の回転の表現を捜し求め,人生の最後にHamiltonは,4元数という答えを見出した.
⇒次号に続く
←wikiより
■3Dへ
Broone橋にある記念プレート,
Hamiltonが4元数を発明したときこの橋の下を散歩していた.
数学者William Rowan Hamilton卿はDublinのTrinityCollegeが産んだ最も著名な子であろう.
彼は最後の20年,複素数が2次元の回転を表すのと同様な
3次元の回転の表現を捜し求め,人生の最後にHamiltonは,4元数という答えを見出した.
$$q=a_{0}+a_{1}i+a_{2}j+a_{3}k$$
ここで,$$i^{2}=j^{2}=k^{2}=ijk=-1$$, $$a_{0}, a_{1}, a_{2}, a_{3}$$は実数.
複素数でしたように,4元数を幾何学的に記述し,回転の表現に用いよう.
今度は2次元でなく3次元の回転だ.
$$i, j, k$$は,3次元内の単位平面:$$i$$は$$yz$$平面,$$j$$は$$xz$$平面,$$k$$は$$xy$$平面で,外側向き法線はそれぞれ$$ x,-y,z$$方向である.
$$i, j, k$$は,3次元空間の単位平面という幾何学的解釈ができる.
点$$ a=(a_{1},a_{2},a_{3}) $$を,角βだけ原点を通る$$b=(b_{1},b_{2},b_{3})$$軸の回りに回転してみよう.
2つの4元数$$q_{1}, q_{2}$$を$$b, \beta $$から作る.
$$q_{1}=\textrm{cos}(\beta /2)+\textrm{sin}(\beta /2)(b_{1}i+b_{2}j+b_{3}k)$$
$$q_{2}=\textrm{cos}(\beta /2)-\textrm{sin}(\beta /2)(b_{1}i+b_{2}j+b_{3}k)$$
$$a$$($$x,y,z$$方向の単位ベクトルの線形結合)に,これら2つの4元数を乗じて
$$a'=q_{1}aq_{2}$$
この積で得られる点$$a'$$は$$a$$を与えられた軸の回りに角度$$\beta $$だけ回転したものだ.
複素数は平面内の回転記述,4元数は3次元空間内の回転記述に用いられる.
ダブリンの橋の下を通りかかったとき,Hamiltonのひらめきは,
3次元で物体を回転させる最も効率の良い方法であることがわかった.
だが彼の新しい乗法で,だれも幸福にならなかった.
物理学者Kelvin卿は4元数のことを:”....美しく巧妙だが,とにかく,これに触れるものには,純粋邪悪である...と評した.
とりわけ厄介なのは,2つの4元数を掛け合わせるとき,答えがかける順番で変わることだ.この特性を非可換という.
Hamiltonの積則をみれば,$$ij=k, ji=-k$$が示せる.
もし,$$i, j, k$$を単位平面のように扱えば,Kelvinや彼の同時代の人々を困らせた特性は直接導ける.
■映像を生活へ
Hamiltonの発明はいまや多数の物体を動かしたり,運動の創出へのグラフィック応用に使われる.コンピュータグラフィックで最も重要なツールの2つは,変形と補間である.
補間とキーフレーミング技術は,物体の初めと終わりの形と位置の特定と,その間の様子をコンピュータに計算させることだ.以下に示す映像のように:
一連のフレームにわたって徐々に変形するティーポットの形
諸君は,未発達のへびのアニメーション(Richard Wareham製作)を見ることができる.
ここではへび全体が,いくつかの特定な点の運動から,
補間を用いてコンピュータで作られた.
[訳注:ファイルのダウンロード先は略]
変形は単純なものから複雑なものを作り出す方法だ.
下の映像のように,変形球を覆っている布は,
普通の球面で起こる同じ光景を数学的な変形をして得られる.
変形も補間も速くて安定な数学的技術を必要とし,
4元数関連の手法がこれを提供する.
http://plus.maths.org/issue42/features/lasenby/sphere.png
http://plus.maths.org/issue42/features/lasenby/deformed_sphere.png
■ガーラムを信じさせる
http://plus.maths.org/issue42/features/lasenby/motioncapture1.jpg
http://plus.maths.org/issue42/features/lasenby/dots.jpg
http://plus.maths.org/issue42/features/lasenby/skeleton.jpg
データは体の色々な部分に付属しているリフレクターの運動からキャプチャーされる.....
....骨格は,データに数学的にフィットさせる.
上で記述したテクニークは古典的なアニメーションでも基本的なツールである.
漫画キャラクターでは,我々はその結果が信じられるのはとても幸せだ.
しかし,人間のアニメーションでは,たちまち偽者とわかってしまう.
現実味ある動きを作り出すにはモーションキャプチャーが必要になる.
ロードオブザリングズのフィルムバーションから,ガーラムのような
多数のキャラクターを作るにはモーションキャプチャーによる.
これらは,身体,頭,肩,ひじ,ひざなどの回転点に,本当の人のリフレクターを付加して作られる.それぞれは,多重のカメラによってフィルム化されリフレクターの位置の変化をコンピュータに記録する.
骨格は3次元データでフィットされる.
最後に,上に記述された技術はすべて,骨格上に具体化し,生活し,呼吸し,動くキャラクターを作り出す.
もしまだ諸君がタイトルロールを完全に見るために留まっているなら,首尾よい映画作製で使われた種々の製作タレントに気づくだろう.作者,ディレクタ,俳優,衣装デザィナー,プロップビルダー,....
これらのクレジットリストが続々流れる.
しかし一つの名前がしばしばタイトルロールから忘れられている-数学だ.
今日の映画の多くは,光線追跡の幾何学,4元数による空間内の回転なくしてはできない.
次回は,あなたの映画シートで,CGスペクタクルを楽しむために,数学に対してポップコーンを掲げよう.ショーの隠れたスターへ.
(訳:KT)
-----------------------
著者
http://plus.maths.org/issue42/features/lasenby/jl_small.jpg
Joan Lasenbyはケンブリッジ,トリニティカレッジで数学を専攻し,
電波天文学グループ物理学科のPhDをとった.
マルコーニの企業で短期間働いた後に,大学に戻り,現在,
ケンブリッジ大学工学部の信号処理グループの講師や
トリニティカレッジの研究のディレクター,研究員である.
彼女の興味は,コンピュータビジョン,コンピュータグラフィックス,
画像処理,モーションキャプチャと幾何代数の分野にある.
2019.10.26に開催した数学月間企画講演会では,約数の構造をわかり易く表示するグラフ(亀井図)を取り上げました.例えば,210の約数の系統的な構造を示すグラフは以下のようです.
210は4つの互いに素な素数の積210=2・3・5・7から出来ているので,4次元超立方体と同じこのような構造になります.210の約数は,自分自身の210と1を含めて全部で16個ありますが,系統的に並べると上の図のように整理できます.
頂点1のレベルには1個,頂点2のレベルには4つの素数,頂点6のレベルには2つの素数の積で4C2=6個,頂点30のレベルには3つの素数の積で4C3=4個,頂点210のレベルは4つの素数の積で1個です.4次元の超立方体には対称心があり,互いに点対称な頂点の積は210になることも理解できます.
このようなグラフは,数学のいろいろな分野で出会います.半順序を表現するハッセ図というのは,このグラフを逆順に描いたものと同じです.
210の約数の構造といえば,210をトップに置き逆順(ハッセ図と同じ)に並べる表示もありでしょう.
約数の構造に関しては,数学Aの研究課題として高校生にもなじみやすいものであるし,このグラフは高次元立方体の理解にも役立ち興味深いでしょう.
(注)数学ではハッセ図と呼ばれるものですが,美しくバランスのとれた4次元立方体は,亀井のアルゴリズムで描けるので亀井図とも呼ばれます.
4次元の超立方体の1つの次元(例えば,素数2の方向)を消すと,3次元の立方体の2つに分離します(下図).同様なことを,それぞれの3次元立方体で考え,例えば,素数7の方向の次元を消すと,3次元の立方体は2次元の面(例えば1-3-15-5)に分離します.このような性質は高次元の超立方体の成り立ちの理解に役立つでしょう.
(演習)2310=2・3・5・7・11ですから,2310の約数の構造を示すグラフを描いてください.これは5次元の超立方体になるはずです.
解答
(演習) $$420=2^2・3・5・7$$ の約数の構造を示すグラフを描いてください.
直角3角形△ABCの面積(赤色)は,直角を挟む2辺上の三日月の面積(水色,黄緑色)の和です.証明してください.
∠ABCは直角,3つの円はそれぞれ,各辺を直径とする円です.
ピタゴラスの定理 $$ AB^{2}+BC^{2}=CA^{2} $$ を持ち出してかまいませんが,
この問題は,ピタゴラスの定理と同じことを言っています.
問題41.
プレイヤーの前に,3つの箱が並んでいます.そのうちの1つに賞品があります.図のように,張り紙が箱につけられています.張り紙のうち1つだけが正しいことが知られています.賞品を受け取るには,どの箱を選びますか?
箱の張り紙は,左から次のようです:
賞品はありません 賞品はここ 賞品は隣の箱
Здесь приза нет. Приз лежит здесь. Приз в соседней шкатулке.
ーーーーーーー
この問題は,”クバンチク”,(5月号,2020)の「私たちのコンペ・オリンピック」第Ⅸラウンド(問41~45)のうちの第41問です.残念ながら,この問題の解答締め切りは6月5日で終わってしまいました.
クバンチクквантикはロシアの青少年向けの数学雑誌です.www.kvantik.com
クバンチクとはクバント(Quantum)の指小形ですので「量子ッ子」というような意味でしょう.子供向けの非常に優れた雑誌で,数学月間の会でも手本にすべき活動だと思います.
журнал для любознательных школьников — «Квантик»
好奇心旺盛な小学生のための雑誌ーー「クバンチク(量子っ子)」
ロシアのクバンチク誌にお化け煙突のパズルが載っています.
煙突の本数が見る方向によって変わるので,自転車に乗った主婦がびっくりする場面の記憶があります.子供のころですから何の映画か覚えていませんが,「煙突の見える場所」(昭和28年)でしたら名画ですね.私が見たのは違う映画かもしれません.お化け煙突がロシアにまで有名だったとは....
それで,クバンチクのこの記事が目にとまりました.
クバンチク,2018年10月号,p.16 (訳:KT)
以下はその翻訳です:
東京の千住火力発電所は1926年から1963年まで稼働した.
その "お化け”煙突は当時の多くの写真や映画に残されており,地域のシンボルの一つとなった.発電所には4本の煙突があった.高さ83.5メートル,幅5-6メートル; 建設された当時は,東京で最も高い建造物だった.
なぜこれらはお化けと呼ばれるようになったのか?
次の2つの説明が推測される.
第一は,これらの煙突からの煙の出没が幽霊のようだった.というのは,この発電所は余裕があり(full稼働ではなかった),煙はまれに予期せぬときに出現した.
別の推測では,煙突の興味深い特性によりこの名前が付けられた:遠くから発電所を見るので,煙突は,4つ,3つ,2つ,またはただ1つに見えたりした.たとえば,図1では4つの煙突が見えている.
どのように煙突が配置されていたでしょうか?
図1の写真のように4本に見えるのは,方向4.
図3のように1本に見えるのは,方向1(ただし,前後の2本をまっすぐ重ねずに,煙突の幅が外れない程度斜めの方がもっと良さそうだと私は思います).
図4では2本(方向2),図5では3本(方向3)です.
コンペは5年生から8年生を対象としていますが,若い学生は解答を送ることができます.今は,7月5日締め切りの第 Xラウンドの問46~50の5つのタスクがあります.面白いがかなり難しい問題です.またご紹介したいと思います.姓名,都市,学校,クラス,返信先を明記して,メールか手紙で解答を,モスクワのジャーナル「クバンチク」に送るシステムです.
ーーーーー
過去の例から
■第Ⅶラウンドの問32(ミハイル・エヴドキモフ)
正方形ABCDのBC側に,正三角形BMCがあります.線分ACとMDは点Oで交差します。OA = OMであることを証明しなさい.
お前がどのように解いたか不思議だ.
妹が僕のノートに描いただけ.
■第Ⅴラウンドの問24(グレゴリー・メルゾン)
計算しなさい.
ごめんなさい,グーグルはこの問題は解けません.ごきげんよう!
■第Ⅳラウンドの問18
点Kは二等辺三角形BACの底辺BCを長さxとyの線分に分割します.∠AKC=60°の場合,長さAKを求めなさい.
解けなかったのが何か? 2点だったので隅に立たせるなんて非教育的.
YouTubeにある動画について.たいへん興味を引く動画なので,ぜひご覧ください.この動画の発信元3Blue1Brownは,Grant Sandersonが作ったYouTubeのチャンネルで,なかなかよくできた可視化された数学入門です.
動画は,物体mは静止しており,物体Mは初速度v0で摩擦のない台上を滑る所から始まります.
Mやmはそれぞれの物体の質量(M>m)で,左側は壁です.
衝突はすべて弾性衝突とすると,エネルギー保存(1)と運動量保存(2)が成り立ちます.
(1)は楕円の式ですが
の変数変換をすれば,新しい変数$$v_{3}$$を採用した$$v_{1},v_{3}$$平面では半径$$v_{0}$$の円になります.
(2)は,2つの物体m,Mが衝突したとき2つの物体から成る系全体の運動量が保存される(運動量変化が0)ことを示しています.こちらの式も,$$ v_{2} $$から$$v_{3}$$へ変数変換すると,$$v_{1},v_{3}$$平面で傾き-√M/mの直線になります.物体mとMの衝突後に分配される速度変化$$⊿v_{1}$$と$$⊿v_{2}$$の比は,それぞれの質量に反比例するわけですが,質量mの速度$$v_{2}$$を変換した$$v_{3}$$に対しては,$$v_{1},v_{3}$$の速度変化の比はそれぞれの質量の平方根に反比例します(2').つまり,$$ v_{3}=-\sqrt{M/m} ・v_{1}+C $$で,傾き$$-\sqrt{M/m}$$の直線です.
物体mが壁と衝突するときは,壁は動きませんから,$$v_{3}$$の符号のみ変えます.横軸を速度$$v_{1}$$,縦軸を速度$$v_{3}$$としてグラフを描くと,式(1')は,半径が$$v_{0}$$の円で,エネルギーが保存される系の状態はいつもこの円上にあるべきです.式(2')は運動量保存を示すグラフで,$$(-v_{0},0)$$の点から出発し傾き$$ー\sqrt{M/m}$$の直線です.
この直線が円と交差する点が,物体mと物体Mの最初の衝突後の速度$$v_{1},v_{3}$$の状態です.
その後,物体mはそのまま滑り壁に衝突し,$$v_{3}$$だけが符号を変えます.これは,最初の衝突点の$$v_{3}$$の符号を変えた円上の点になります.
このように続けると,円内に納まるのこぎり歯状のグラフができます.
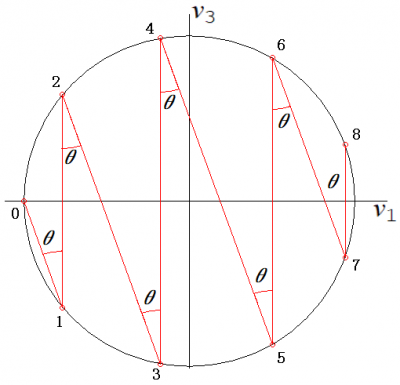
YouTubeのアニメーションのように,Mの質量を増加させると,直線(1')の傾きが急になり,のこぎり歯が細かくなるので衝突回数は増加します.
きちんと計算すると,$$tanθ=\sqrt{m/M}$$として$$\theta =\textrm{tan}^{\textrm{-1 } }\sqrt{m/M}$$,衝突回数Nは,N=2[π/2θ]となり(中心角2θだから),Mが大きくなればなるほど,Nは大きくなります.([]は数値の整数部分)
$$m/M=10^{-2p}$$とおくと,$$M$$が大きくなる($$p→∞$$)とき,$$N→π×10^{p}の整数部分になります.
上の数表のミソは,$$M/m=10^{2p}$$のときしか調べていないので,$$π$$の$$10^{p}$$ 倍の整数部分が並ぶことになる.
まぐまぐに投稿したメルマガ(html版)のリメイクです.
数式はうまく表示できているでしょうか?
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2014.05.09] No.002
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
■無限の脅威(2014年米国MAMよりhttp://www.mathaware.org/mam/2014/calendar/infinity.html)
今回は,奇妙な数学の話です.
■発散する級数
$$ S=1+2+3+4+....+n+....=-1/12 $$
正の整数すべての総和が無限大でなく-1/12であるという.正気の沙汰なのか?
このとんでもない結果は,1748年に偉大なオイラーにより導かれた.
発散する数列は悪魔の発明であり,無限級数を用いると,どんな結論でも導くことができる.
発散する級数の研究は,アーベル(1802-1829)に端を発する.
数学者がこの悪魔の細部を解決するのに続く百年を要したのだ.
すなわち,リーマンの解析接続の理論(1859)を待ち理論的解決した.
現代では,物理学(超弦理論,量子計算)や数学(ζゼータ関数)で利用している.
リーマンは素数の分布を調べるためにζ関数に解析接続をした関数の0点を研究し,
リーマン予想を提示した(1856).これはまだ解かれていない.
■オイラーの発見が現実に
オイラー+リーマンの ζ関数は無限級数の形で定義される.
$$ ζ(s)=1+2^{-s}+3^{-s}+4^{-s}+5^{-s}+.... $$
この関数は,実部が1より大きいRe(s)>1複素平面で収束するが,
実部が1あるいは1より小さいRe(s)=<1複素平面では発散する.
そこで,全複素平面(ただし1は極)に,ζ 関数の定義域を拡張
するのに解析接続という手段が役立つ.
$$ S=ζ(-1)=1+2+3+4+5+.... $$
$$S_{1}=1-1+1-1+1-1+....=1 $$(奇数項までの和), $$=0 $$(偶数項までの和)
この和は,偶数項で止めれば0,奇数項まで止めれば1になる.
しかし,解析接続という理論を使うと1/2になることを以下に示す.
$$f(x)=1+x+x^2+x^3+x^4+x^5+....=1/(1-x) $$
この多項式は公比$$x$$の等比級数だから,$$|x|<1$$なら収束し$$1/(1-x)$$になる.
もとの多項式は$$|x|<1$$の外では発散するので定義できないが,
級数を解析接続した関数$$1/(1-x)$$に繋ぎ,形式的だが
$$x=-1$$を入れると 1/2 が得られる.
$$S_1=f(-1)=1-1+1-1+1-1+....=1/2$$
級数$$S_1, S_2$$ などを等式と見立て加減演算をし,$$S$$を求めてみよう.
$$∞+∞$$などの無限大を数値のように演算しているのが気持ち悪いが
解析接続で収束した級数を用いているので実は正しい結果になる.
$$S_2=1-2+3-4+5-6+.... $$とすると,
$$2S_2=1-2+3-4+5-6+....+[1-2+3-4+5-6+....]=1-1+1-1+1-1+.... =1/2$$
ゆえに,$$S_2=1/4$$が得られる.
$$S-S_2=1+2+3+4+5+6+....-[1-2+3-4+5-6+....]=4(1+2+3+....)=4S$$
であるから,$$S=-S_2/3=-1/12$$ が得られる.
■参考
http://www.mathaware.org/mam/2014/calendar/infinity.html
超弦理論入門,大栗博司,ブルーバックス
リーマン予想を解こう,黒川信重,技術評論社
メルマガNo.075(2015.08.04発行)のリメイク版です.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2015.08.04] No.075
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回は,数学らしくないと思うかもしれませんが,3次元立体と関係があります.
右手と左手のように互いに鏡像となる立体構造の分子のことを立体異性体といいます.
この記事は,日刊ベリタに掲載(2015/7/30)したものです.
暑さ厳しい夏です.健康に悪い油やマーガリンの取り過ぎに注意しましょう.
米食品医薬品局(FDA)は16日,食用油などに含まれ,肥満や心臓病との関連が指摘される
トランス脂肪酸を,2018年6月までに食品添加物から全廃すると発表しました.
日本でもトランス脂肪酸の低減をうたっている企業が出始めました.
トランス脂肪酸は,マーガリンやクッキーを焼くのに使うショートニングオイルなどに
含まれているそうです.トランス脂肪酸は悪玉コレステロールを増やすと言われています.
また,アトピーなどにも悪影響がありそうです.
脂肪酸のシス型とトランス型の分子構造について簡単にまとめておきます.
以下のサイトが参考になります:
http://www.maff.go.jp/j/syouan/seisaku/trans_fat/t_wakaru/
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%A9%E3%83%B3%E3%82%B9%E8%84%82%E8%82%AA%E9%85%B8
脂肪酸は,炭素原子が鎖状に並び,最後の炭素に=OとーOHが付いた分子です.
つまり, CーCーCー・・・・ーCOOH =は二重結合,-は一重結合
Hを省略せずに詳細に書くと
この例は,背骨となっている炭素原子の鎖は,すべて一重結合でできているので,すべての結合手がふさがっており飽和脂肪酸と呼ばれます.
不飽和脂肪酸と言うのは,炭素原子の鎖の何ヶ所かに二重結合のあるものです.二重結合でつながれた両側の炭素は回転できませんから(裏返しにできない),シス型(左図)とトランス型(右図)の構造の区別ができます.
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16882908/img_1_m?1438241054
天然にある不飽和脂肪酸は,ほとんどシス型です(わずかな例外はあります).不飽和脂肪酸は酸化などで劣化しやすいし,大豆等の植物油の不飽和脂肪酸は常温で液体なので,固体状にするため水素Hを付加してを飽和脂肪酸に変えることが工場で行われます.
このときトランス型の不飽和脂肪酸も生じ混ざるそうです.
(注)よく知られた不飽和脂肪酸の例
炭素の数18個で二重結合1個はオレイン酸,二重結合2個はリノール酸,
炭素の数22個で二重結合6個はドコサヘキサエン酸(DHA).
■なぜシス型脂肪酸は安全な栄養で,トランス型脂肪酸は害があるのか
シス型,トランス型のような立体構造に差異があるものを“立体異性体”といいます.
炭素原子からは4本の結合手(二重結合ならそのうちの2つを使う)が出ていて,
それぞれの手に結合する原子が入れ替わると立体的に異なる構造になります.
右手と左手のように互いに鏡像である異性体も,この立体異性体の仲間です.例えば,
味の素はグルタミン酸ですが,立体異性体の右型と左型があり,
左型には旨みがあるが右型にはありません.これはおそらく,
人間のアミノ酸が左型であることに関係ありそうです.
不飽和脂肪酸の場合も,天然にあるものがほとんどシス型であることが
シス型が相性の良い理由と思われます.
サリドマイドでは,立体異性体の一方が副作用のない薬であるのに,他方には催奇性があった.
まるでジギルとハイドだが,このような大きな性質の違いがある理由はわからない.

無限に食べられるチョコレートをご覧ください.不思議ですね.
How to eat chocolate indefinitely [fixed]109159 views and 3505 votes on Imgurimgur.com
◆7×9の板で1コマが幾何学的に消滅する
これは2014年の米国MAMで取り上げられたマジックです.
http://www.mathaware.org/mam/2014/calendar/areapuzzles.html
まずは,アルゼンチンのマジシャン,ノルベルトジャンセンによるプレゼンをご覧ください. http://youtu.be/3PszMaZ5Ipk
7x9のエリアにタイル片が配置されています,断層に沿って滑らせ
上部の左3コラム分と右4コラム分を入れ替えると,不思議なことにタイルが1つ減ります.
この操作を繰り返すたびにタイルが1つづつ減り3つまで減らせます.
タイルが1つ減っても,2つ減っても,3つ減っても,
元通りの7x9枠内にタイルはきちんと配置され変わらないように見えます.
これは不思議ですね.どうしてタイルが1つづつ余るのでしょうか?
ビデオを観察していると,タイルが消滅する原理がだんだんわかってきます.原理の理解を助ける図を以下に作成しました.
青色の面積がだんだん減じているのがわかります.
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_1?1405218032
このおもちゃを作製して見ようとする方は,この原理図を参考にしてください.
数学マジシャンの使っているタイルのパーツは目地が太いですね.
私の原理図には,目地はありませんが,作製するときは目地の効果も考慮すべきでしょう.
結局,断層をはさんだある行だけ,1コマ縦の長さが1/7だけ縮むので,
7コラムあるから面積としては1コマ分取り出せることになります.
◆なぜタイルが1コマ減るのか
左のコラムと右の3列を入れ替えると,1コマ減る.
1コマの高さをbとすると,断層を挟んでb/4だけ縮みます.
ただし,右端のコラムの断層ではコマ間の目地が消えるのが残念!
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_3?1405215030
◆真ん中を取り除いたお札が再現できる
http://youtu.be/-h0AXeLIHqQ
お札の中心を取り除いて,裏向きにして並べると
完全な1枚が再現できたように見えます.
真ん中が消えるとは,あり得ないことが起ったように見えます.
数学マジシャンの使っているお札の裏面には
再配列したときに完成するようなお札の裏面の絵が描いてあるので
お札が再現したように錯覚します.以下の原理図を参考に作製してください.
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_0?1405215030
今回も以下のメルマガのリメイク版です
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2014.06.10] No.013
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆数を記憶する
http://plus.maths.org/issue31/features/eastaway/index-gifd.html
Rob Eastaway
今回は,2004年の英国MMP,plusマガジン31の記事の翻訳(byKT)です.
肩のこらない読み物なので長文ですが全文掲載し,さらに新たに,編集後記を追加しました.
2004年3月, Kent のDaniel Tammet が,π(パイ)を小数22,511位まで暗唱してみせ,
ヨーロッパ新記録が達成された.この仕事を完了するのに5時間を費やした.
それでも,日本の後藤裕之が1995年に達成した小数点以下42,195桁のやっと半分である.
[訳注:その後の2006年10月3~4日に,16時間28分をかけて,
原口 證(当時60歳)が100,000桁を暗誦している.ギネス社申請中とのことだ.
http://www.worldrecord314.com/pi01.html
原口の方法は,数字を1,000桁ずつ区切り,語呂合わせで物語として暗記するもの.
今回の物語のテーマは「世界旅行」.北海道に住んでいる武士が全国各地を歩いて
いるうちにいろいろな人物や物件に出会い,10万桁にもなれば,
朝鮮半島を通り過ぎてシルクロードまでたどりつくストーリーになっているという.
柴田昭彦http://www5f.biglobe.ne.jp/̃tsuushin/sub1.htmlによる]
人間はいかにしてこのような信じられない(むしろ無意味な)記憶の業績を
やり遂げるのだろうか? それらから学べるものが何かあるだろうか?
数字を覚えていなければならぬもっと実際的な必要性---
例えば,南京錠のコード,キャッシュカードの暗証番号---などもある.
◆記憶と数
記憶は諸君が考えるために重要だ.諸君はほとんどすべての活動に記憶を使用する.
記憶は事実と名前を学ぶために必要だが,新規に身体技能を獲得するためや,
冗談を言うためにでさえ必要となる.素質はそれぞれの人によって大変異なる.
同じ人の記憶能力も仕事によって大変違う.例えば,数を良く記憶する人が,
ジョークも覚えているとは限らない(私は苦い経験がある).
数を覚えているという特別な素質はどこから来るのだろう?
数学者は他の人より数を覚えているようだが,
この領域で卓越した能力を持っことが数学者になるための必須条件ではない.
例えば,Daniel Tammetは,数字の順番を記憶するすばらしい能力を,
数字を色と映像として”見る”ことに置き換えている.
彼にとってπは数字の抽象的なセットではなく,物語か映じられるフィルムのように現れる.
Tammetは,稀有だが詳しい記載のある症候群---共感---と呼ばれるもので,
感覚のある一つが刺激されると,他の感覚も反応を引き起こすのだ.
共感はさまざまな様子で現れる.ある人達は,数字にさらされるとき,多重の感覚の反応を得る.
有名なロシアの”記憶男”Shereshevskyは,数字2は常に暗い矩形として見えるさまを記述している.
私は別の人間で,数字4はトマトの味とリンクしている人に出会ったことがある.
彼らにとってこれらの関連に理屈はない.共感は,記憶をしようと思ったときに自然な利点がある.
なぜなら,脳は,感覚と結びついたものを長期間記憶しようとするからだ.
出来事や物体は,音や映像や素材や特に匂いに結びついているときに,さらに記憶し易くなる.
ほとんどの人と同じく諸君も匂いに関する奇妙な経験があるだろう.
例えば古い家具の匂いをかぐことが,遠い過去に起こった何かを思い出させる.
匂いは記憶と特別に強い結合がある.多分,匂いを扱う脳の部分が,
長期記憶を形作ると考えられている海馬と近いためだろう.もし諸君が,
何かを記憶しようとするとき,わざと特定の匂いに囲まれるようにすれば,
後に思い出す必要があるとき,その匂いは記憶を引き出すのに役立つ可能性が高い.
記憶と感覚の間のこのリンクは,勉強の助ける記憶術の基礎である.
数を記憶しておくためによく提案される方法は,各数字を韻を踏んでいる言葉と結び付ける方法である.
oneワン=バンbun
twoトゥー=シューshoe
threeスリー=ツリーtree
fourフォー=ドォーdoor
......
このアイデアは,抽象的な数字を付随するイメージと音とともに,実質のあるものに変える.
もし,数字24を覚えていようと思ったら”シュードア”と覚え,正面ドアを蹴っ飛ばす絵を描く
(このイメージはなぜか容易に記憶される).
ドアをける記憶は数字24より長く維持されるだろう.私が1週間,数を覚えていようとするとき,
私はすぐにイメージを考える.思い出すにはただそれを数に変換するだけだ.
明らかにこれは小さい数を記憶しておく助けになるテクニックであろう.
しかし,もし何桁かの数を記憶する必要があるなら,信じられないほど厄介である.
1492は,bun-door-wine-shoe.この順番を記憶するのに必要となるイメージ---
オドビンスの[ワイン]店にパンを投げ込む適切な事件---を思い浮かべようと奮闘する.
もっとよい方法がきっとある....
◆数の記憶の数学的アプローチ
数を良く覚えている人のほとんどは,何らかの感覚的経験によるわけではない.
数が彼らにとって意味をもっているということはありそうな理由である.
数学者はここに強力な有利さがある.なぜなら,本職で数にさらされているので,
数の特徴に親しんでいるからだ.数学者に4832を見せる.彼らは,
その数字はどのような種類(4桁,偶数)か直ちに認識できる.
時には,数学者は数で遊ばずにはいられない.
この場合,4832を4×8=32と言っている自分を見出すかもしれない.
この種の遊びは,数字の意味付けを助け覚えやすくする.
数で遊ぶというこの衝動の有名な例がある.記憶で有名だった
Alexander Aitkenアレクサンダー・エイトケンは,エジンバラ大学の数学教授で,
かつて以下のようなコメントをした:
私が散歩している時に,モーターカーが通り過ぎ,登録ナンバーが731なら,
それは17×43と観察せざるをえない.....折襟に数字のついたバスの車掌を見ると,
その数字を2乗してしまう.....これは故意ではなく,どうしてもそうしてしまうのだ.
....時々は,数字が811のように特徴をまったくもたないものもある.
時には41のように諸君ご存知の多くの定理に登場するものもある.
さて,どっちが興味深い数字だろうか?
数学的な特性により数を記憶する最も有名な例の一つに,
病院に友人のRamanujanをたずねた時の数学者G H Hardyの話がある.
Hardyはタクシーできて,Ramanujanに挨拶した後お詫びを言った.
”私のタクシーナンバーは, 1729 だった.あまりぱ っとしな い数 ですみません.”
”それは逆です.1729はたいへん興味深い.”とRamanujanは言った.
”それは2種類の答えがある2つの立方体の和の最小の数字だ.”
(1729=12^3+1^3,または,10^3+9^3 )
しばしば,数字の背景にあるパターンと意味が努力なしに心に残るだろう.
それほどでなくても,数字を意識的に記憶する方法の基礎になりうる.
諸君はそれらを暗証番号や電話番号の記憶に使うかもしれない.
これらはもっと長い数にも適用できる.例えば,この数を覚えてみよう.
10秒間の猶予がある:15222936435057
書いて覚えようとするなら,多分苦しむだろう.数の短期間の記憶保持は通常7桁までである.
これより長いものは,最初の数桁より先は覚えられそうもない.
(上の例では,たいがいの人が15222は簡単に覚えるが,それ以降はごちゃごちゃになってしまう)
今,数学の頭になってみよう.諸君は,数字のパターンのなかに,
それをもっと簡単に覚えるものを見つけることができるか?
おそらくここの仕事を単純化する複数の方法があるだろう.もし見つけたなら,
仕事をなんでもないものにしてしまう一つの特別なパターンがある.
実は,数字が二桁づつに分解されて,15 22 29 36 43 50 57,7つの対は
だんだん大きくなる順に並んでいる.諸君がすることは始まる数字と規則を覚えればよい.
[訳注:7ずつ増えていく数列]
◆πの記憶
すべての数がそんな都合のいいパターンとは限らない,だがどの数のなかにも,
数学的な意味のある数のサブグループがあるものだ.
実際上はランダムな順序と思える数πに適用して見る.ここにπの始めの100桁を記す:
ほとんどの人は,一桁の数字の列として覚えることはできないだろう.
だが,もし諸君が面白い数の固まりを選び出すなら,仕事はもっと容易になる.
3.141592653589793238462643383...
例えば,最初の10桁は連番14-15を含む,足すと100になる数65-35,
後の方には偶数のクラスター846-264がある.これらはともに,二番目以降の数を
逆転すると(864は846,246は264になる)単純な数列になる.
これらのパターンにリンクさせ,数学的ストーリーを組み立てることができる.
これはプロフェッショナル記憶者が使う種類のアプローチだ.彼らは,
それを他のテクニック-数字を,文字に置き換え言葉にするなど-と結びつけている.
良く使われる数字と文字の対応規則は:
1 becomes the letter T (a single downstroke),
2 is n (two downstrokes),
3 is M (three downstrokes),
4 is R (r is the fourth letter of four!),
5 is L (L is the Roman fifty, which is close...),
6 is J (J is a bit like a backwards 6),
7 is K (K is like two sevens stuck together),
8 is F (a cursive f resembles an eight),
9 is P (P is a backwards 9),
0 is Z (Z is for zero).
πは次のように始まる M-T-R-T-L-P-N-J-L...,思いつきで母音を時々入れる
(これは数字にカウントしない).例えば,My TuRTle oPeN JaiL....,
諸君の亀が牢やぶりするイメージを描く.ほら,πの最初の9桁を記憶出来た.
これを42,187桁続ける.世界記録は諸君のものだ.幸いなことに諸君が記憶演者になるか,
あるいは物理学,数学,天文学の非常に特別な分野を追求する予定がない限り,
πを3~4桁以上記憶している必要性はなく,
この重要な数のその程度の桁を思い出すときには,忘れにくい文章がある.
”May I have a large container of coffee?" [コーヒー大カップをいただけますか]
この文中の各単語の文字数を数える.πの数字が小数7桁まで現れていることがわかるだろう.
[訳注:日本語では,“産医師異国に向かう....”などとやるのです]
最後に,覚えていたい数字が何であろうとも,πでも,歴史の日付でも,
ナンキン錠のコードでも,最も忘れ難い記憶術は,諸君が諸君自身のために発明するものである.
諸君のアプローチがどんなに風変わりでも問題ではない.
それが諸君のために働くならそれで良いのだ.(訳:KT)
■編集後記(KT)
折り紙も数学が必要ですが,この雪の結晶を折るアルゴリズムは複雑でわかりにくいです.写真の1,2は完成した雪の結晶を,表面から見た写真(1)/裏面から見た写真(2)です.
(1) (2)
■スタートに用いるのは,以下に示す6角形の折り紙(3)です.完成品を見ながら,折り紙(表面側から見て)に,谷折りすべき線(赤色)/山折りすべき線(黄色)を描き込んでみました.
(3)
この線の通りに,谷折り/山折りをして,(4)に示す中間体が作れますから,試行錯誤して,(4)図のような中間体を作るのを目標にしましょう.
(4)中間体
■中間体(4)の表面側に出た6か所の山尾根の部分を,平らに広げて帯状筋を作る.この帯状筋の形成のときに,新たに山折りとなる箇所を,
折り紙(3)に青緑色の線で示しておきました.
中間体の山尾根をつぶして帯状筋にするところは,注意深くやりましょう.
3Blue1Brownのyoutube動画をご覧ください.
コーヒーカップの表面に,3つの家と3つのソース(ガス,電気,水)があり,
パイプラインが交差しないように,3つのソースと3つの家を繋ぎます.
いくら頑張っても交差箇所が1つできてしまいます.
頂点の数V,辺の数E,面の数Fとすると,V-E+F=2 がオイラーの多面体定理ですが,
図のように面(領域)の数は4つ(黒い地の部分も1つと数えます)で,
6-8+4=2とオイラーの定理が成立しています.
3つの家はそれぞれ3つのソースに結ばれるわけですから,辺(パイプライン)の数は9本ありますが,頂点6と面の数4ですから,最後のパイプラインはどうしても繋げません.
さてここで,コーヒーカップで実験をしている理由がわかります.
コーヒーカップの取っ手の部分をうまく使うのです.取っ手の中を通り抜けるパイプラインと取っ手の上を這わせるパイプラインで立体交差になります.
コーヒーカップは,穴が1つある浮袋のような位相表面です.先のオイラーの多面体定理は穴のない位相表面に対する表現なので,穴の開いている位相表面では定理が少し変わります.
注)トーラスでは,面の数が2つ減り,頂点の数が3つ減り,辺の数が3つ減るので,V-E+F=0 が成り立ちます)
このような教育グッズがたくさんあり提供されるようすが,国民数学祭NMFのサイトで見ることができます.
このエッセイは,2020年3月30日にマリアンヌによってプラスマガジンに提出されたものの翻訳(by KT)です.
How can maths fight a pandemic? By Marianne Freiberger ,https://plus.maths.org/content/
■ケンブリッジ大学の疫学者であるジュリア・ゴグは,「人生は長期間同じように過ごすことが許されない」と語った.ゴグ自身の人生は2月の初めに突然変化した.彼女は数理科学センターの通常の職務を辞し,緊急事態のための科学諮問グループ(SAGE)に結果を供給するモデリンググループであるSPI-Mに専念することになった.
SPI-Mは,インフルエンザパンデミックへ備えて活動をしてきたが,現在はCOVID-19のパンデミックに焦点を当て活動が引き継がれている.ゴグは,王立協会が率いる全国コンソーシアムの運営委員会にも所属し,パンデミックに対処している.
SPI-Mの仕事は,次に何が起こり,さまざまな介入でそれがどのように変化するかを予測するのに役立つ数理モデルを開発し使用することだ.COVID-19パンデミックがどのように進展し,我々の生活している社会の介入はどのような影響を与えるのか.これらのモデルは何か,それらは正しいか?
モデル
COVID-19パンデミックの報道については、こちらをご覧ください:https://plus.maths.org/content/tags/covid-19
諸君は意識しないで,数理モデリングを使っている可能性は十分にあります.COVID-19の感染数が3日ごとに2倍になると聞いて,きっと予測計算をしたことでしょう.今日$$ x $$件があり,この傾向が続くと,
3日間で$$ 2x $$件,6日間で$$ 4x $$件,9日間で$$ 8x $$件,一般的に,3 $$ n $$日で$$ 2 ^ nx $$.
このように急増加して今回の災害に至りました.
この外挿は単純ですがモデルの基本的な要素,時間の経過とともに起こる変化の一般的な性質を表す数式と,変化の正確な形状を特定するパラメーターがわかります.
この例では,時間の経過とともに指数関数的に増加し,この増加の急峻さは2倍に増加する時間パラメーター(3日間)で決まっています.
ーーーーーーーーーーーーーーーー
SIRモデル
$$ S $$を感染しやすい人の数,$$ I $$を感染した人の数,$$ R $$を回復した人の数とする.
SIRモデルの方程式は次のとおりです。
$$ \displaystyle \frac {dS} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle-\beta SI $$
$$ \displaystyle \frac {dI} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle \beta SI-\nu I $$
$$ \displaystyle \frac {dR} {dt} $$ $$ \displaystyle = $$ $$\displaystyle \nu I $$
ここで、$$ \beta $$は感染速度で,$$ \nu $$は回復速度, $$ d / dt $$という表現は,時間の経過に伴う変化率を表すため,$$ dS / dt $$は時間の経過に伴う感受性の数の変化率の意味.
数値$$ R_0 = \beta / \nu N, $$($$ N $$は母集団のサイズ)は、疾患の基本的な複製数と呼ばれる.
SIRモデルの詳細については,この記事https://plus.maths.org/content/mathematics-diseasesをご覧ください.
ーーーーーーーーーーーーーーーーーーーーーー
長期の予測や介入の影響を詳細にシミュレートするには,さらに洗練されたモデルが必要です.短期予測,長期予測,学校閉鎖など特定の介入効果のシミュレーション,さまざまな目的のためにさまざまなモデルが設計されています.モデルが異なっても,それらのモデルは1910年代以降のアプローチであるSIRモデルに基づいて構築される傾向があります.
SIRモデルの背景となる考え方の理解には,すべての人を,病気にかかりやすい(S),感染している(I),回復し免疫がある(R)のどれかの集団に属するとします.人が,SクラスからIクラスに,IクラスからRクラスに,進む方法を数式によって記述します. これらの方程式は,病気の感染率と回復率にも依存します. Iクラスの人口が少ないモデルから開始し,時間の経過とともにモデルを進化させて,病気がどのように広がり,人々が回復して免疫力を得て治まるかが見られます.
単純なSIRモデルは,寄宿学校の生徒などの単純な母集団に対して適切な予測を提供します. より複雑な母集団に関しては,さまざまな地理的場所やサブ母集団を表す個々のSIRモデル(個々の町や学校など)を繋ぎ合わせます.
接触がカギ
背景で非常に重要なのは人の接触パターンです:誰が誰にどのくらい会ったか.これに関する情報は,社会混合研究から得られます.例えば,BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります.人々は彼らの動きを追跡するアプリをダウンロードし,彼らに出会った人々(すべて適切に匿名化されている)を追跡するように求められます.このような接触データは,モデルに組み込まれている数値の配列( 行列 )(下図を参照)によって数学的に表されます.
異なる年齢グループ間の平均的な接触を表示する接触マトリックス.濃い色はより多くの接触を示します(ここでは,マトリックスを理解しやすくするために,数値ではなく色が使用されています).図は論文
Contagion! The BBC Four Pandemic – The model behind the documentaryから許可を得て使用.
学校閉鎖などの特定の社会的介入が,病気蔓延にどのように影響するかを確認するには,介入に関連する部分を削除または縮小して,接触データを適宜調整してみます.
ただし,「学校要因を完全オフに切り替えるのは現実的とはいえません.子供たちがまだ学校に通っているので減じるだけです」とGog氏は言います.「そして明確なガイダンスがない場合,学校外の子供たちは他の方法などや,祖父母と混ざってしまう可能性があります.これは,考慮に入れるべき追加の接触が発生していることを意味します.それらの範囲での推測になります」. 教師のストライキ中に何が起こったかに関する情報などの既存のデータは,接触データを補正し介入による流行への影響を予測するのに役立ちます.簡単に言うと,これが疫学モデリングの仕組みです.
だが,モデルは正しいか?
英国,ヨーロッパ,さらには世界全体を表すように設計された壮大なモデルは1つだけではありません.代わりに,さまざまなことを実行するように設計された多くの異なるモデルがあり,SIRモデルのコンパートメントアプローチは支配的なパラダイムですが,モデルの性質は依然として異なる可能性があります.完全に確定的なものもあれば,ある程度のランダム性を含むものもあれば,特定の要因の役割を示すために1回だけ実行されるように設計されているものや,不確実性に直面して予測の範囲を取得するために何度も実行されるものもあります.
大きな問題は,モデルが現実的であるかどうかです. 1つには,COVID-19が新しい病気で,既存モデルは季節性インフルエンザのために開発されたものなのです.「私たちのモデルは,みなインフルエンザから始まったもので,コロナパンデミックモデルは誰も作っていませんでした」とGog氏.COVID-19とインフルエンザのためとでは構築した典型的モデルで何が違うのかを調べなければなりません.
パンデミックのダイナミクスはインフルエンザとコロナウイルスで似ていますが,違いもあります.1つは,COVID-19にはかなりの潜伏期があるということです.人は何の症状も示さずに感染する可能性があります.「インフルエンザの場合は数時間かかるかもしれませんが,このコロナウイルスの場合は数日かかる可能性があります」モデルは,SEIRモデルを用いることを意味します.E「露出」が追加されます.このクラスの人々は感染していますが,まだ症状はありません.Eクラスは,人に感染させる人と感染させない人にさらに分けることができます.すべてのモデルは近似であり,「インフルエンザの場合,目的によってはSIRを回避できることがよくあります.ただし,このウイルスの場合,潜伏期間を無視すると,近似が非常に悪くなる.特に,短期予測のときは,これを考慮する必要があります」とGog氏は語った.
これは,単純SIRモデルによる典型的な結果で,感染しやすい(可能性がある)人の数は青,感染した人の数は緑,回復した人の数は赤で表示されます.
COVID-19について私たちが知らないことが他にもたくさんあります.「1日目や2日目の感染力など詳細はわかりません」.「不完全なデータからそれを推測することは非常に困難ですが,現在,中国や他の国からのデータがいくつかあり,クルーズ船からのデータも非常に興味深い.限られた情報から推測するために最善を尽くしています」 十分な情報がない場合,モデラーは不確実性を取り除くために何が最も重要な未知数か決定します—これがモデリングで非常重要なことです.
1つのパラメーターの重要性は,実行しようとしていることに厳密に依存する場合があります.「明日何件の発病があるかを予測するためには,多くのことを知る必要はありません.現時点では指数関数的です」.「しかし,第2波が発生するかどうかを予測するには,非常に異なるいくつかのことを知る必要があります」
長期予測の重要な数値は,疾患の基本的な再生産数です(多くの場合,$$ R_0 $$と表示される).人口の全員が疾患感受性がある(かかる可能性がある)と仮定すると,感染者が平均して感染させる人の数(それは 伝送速度に関連する,上記の枠記事を参照).COVID-19の場合,これは2から2.5の間にあると推定されます.モデラーは,可能な値の範囲ごとにモデルを実行し,対応する予測の範囲を考えます.
感染したが病気ではない
現在,多くの疫学者に必要なもう1つの重要な数は,集団内での感染の真の症例数で,これには,病気にかかったが症状を示さなかった人々の症例数が含まれます.「無症候性の数は,私が現時点で睡れなくなる数です.これを知ることは,私たちの出口戦略にとって非常に重要です」とGog氏は言います.
現在の指数関数的成長を減らすことができるものが基本的に2つあります.「1つ目は,学校の閉鎖や身体的な距離などの介入により接触率が変化することです」とGog氏は述べます.「指数関数的プロセスを変える2番目のことは,感受性の枯渇です」 病気になったことでしばらくの間免疫があり,無症候性を含む真の症例数を知ることで,感受性の高い人々のクラスがどれほど速く小さくなるかがわかります.議論されている集団の免疫のメカニズムは,感受性の数が減少するにつれて,病気の指数関数的成長が平らになり,その後指数関数的減衰になることを意味します.
幸いなことに,無症候性に関するデータを知ることに関しては望みがあります. 人が病気にかかっているかどうかを知ることのできる抗体検査をしていますが,これらの最初の波は当然NHSスタッフにのみ公開されます.
しかし、不完全な情報があったとしても,モデリングの予測は,特に不確実性の範囲を考慮して提示する場合,暗闇の中で突き刺すだけではありません.優れたモデルは,私たちが持っているすべての関連情報で構成されています.優れたモデラーは,モデルの制限とモデル内の不確実性を注意深く追跡します.多くの場合,可能なパラメーター値の範囲を含み,予測の範囲につながります.これは,さまざまな介入戦略の下で発生する可能性のある将来のシナリオの範囲です.予測は完璧ではありませんが,私たちが持っている情報を使用して実行できる最善の予測です.
では何が起こるのでしょうか?
誰も何が起こるか正確に言うことはできません.地平線に見える大きな望みはワクチンの到着です.これは,群れの免疫を構築するためのもう1つの手段であり,最も脆弱な人を優先的に保護するオプションを備えています.問題は,最小限のダメージでどのように自分自身をそのポイントに到達させるかです.
誰もが同意することの1つは,これには長期的な犠牲が伴うということです.「1週間だけシャットダウンして,この状況がなくなることを期待することはできません」とGog氏は言います.「それはまだここにあり(社会的距離の措置が早すぎる場合),集団の免疫はありません.現時点では,ヘルスケアシステムが容量を超えないようにするためにシャットダウンせざるを得ません.しかし,これは恒久的な戦略ではないことは十分に認識しています」
先週 ,Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では,季節変動も考慮して,再発の問題について詳細に検討しました.呼吸器疾患の発生は,秋と冬に悪化する傾向があります.季節性インフルエンザの発生と同時に,ヘルスケアシステムにさらに大きな負担をかけます.キスラーと彼のチームは,そのような季節変動を反映する要因を含むSEIRモデルを使用しました.社会的距離測定の効果は,COVID-19の基本的な生殖数が最大60%減少することでモデルに反映され,中国で観察されたものと同等です.
この最新の研究の結論は,必ずしも明るいものではありません.社会的距離の1期間では、救急医療能力が圧倒されるのを防ぐのに十分ではありません(調査では,英国ではなく米国の救急医療能力を調べましたが,英国でも同様の結果が当てはまります).「[この調査によると]シリアルロックダウンの期間を検討しています」とGog氏は言います.「批判的なケアが始まろうとしているときにロックダウンするという考えです.しかし,英国で起こっていることは,NHSが規定を拡大しているため,ロックダウンがより短く,それほど深刻ではなく,あまり頻繁ではないことです」
これらの社会的距離の断続的な期間がどれだけ長く,頻繁に異なる仮定(米国の数値に基づく)になる可能性が高いかを,論文から抜粋した以下の図に示します.
これらのグラフは,断続的な社会的距離(青色の領域)の下でのウイルスの有病率(黒い曲線)と重大なケース(赤い曲線)を示しています.最初と3番目のグラフには,季節的な強制がありません.2番目と4番目の季節の強制.クリティカルケア能力は、水平の黒い実線で示されます.最初の2つのグラフは現在の米国の救急医療能力のあるシナリオであり,3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです.基本再生数の最大値は冬期は2であり,季節的なシナリオでは夏期は1.4です.この図は,キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からのものです.許可を得て使用.
悲観的状況ですが,希望の光がいくつかあります.1つは,COVID-19の重症例に対する投薬とより良い治療プロトコルが,ある時点で到来する可能性です.これは,人々が短期間で病気にならないことを意味し,NHSへの圧力を軽減します.社会的距離を縮める措置の深刻さの多くは,NHSが崩壊しないようにする必要があるため,深刻な病気の人々を効果的にケアすることができ,短期間の過酷な措置が少なくなる可能性もあります.
もう1つの希望の光は,軽度で無症候性の感染者の未知な総数です.これがモデルで想定されているよりもはるかに高いければ,より多くの人々が病気になり免疫力があれば,上記の図が示唆するほど見通しは悪くありません.私たちはこれが事実であることを期待し,それがわかるまでは,ルールを守って家にいるだけです.
この記事について
Julia Gogはケンブリッジ大学の数理生物学の教授です.彼女は,その結果を緊急事態用科学諮問グループ (SAGE)にフィードするモデリンググループSPI-Mのメンバーです.彼女は王立協会が率いる全国コンソーシアムの運営委員会のメンバーでもあり,COVID-19パンデミックに対処しています.
プラスマガジンの編集者,マリアンヌフライバーガーは,2020年3月24日にGogにインタビューしました.
■今回の記事は,2020年3月30日にマリアンヌによってプラスマガジンに提出されたエッセイの解説です.
How can maths fight a pandemic? By Marianne Freiberger ,https://plus.maths.org/content/
プラスマガジンの編集者,マリアンヌフライバーガーは,2020年3月24日にGogにインタビューしました.
エッセイの全文翻訳(by KT)は数学月間ホームページに掲載しておきます
これは大変長いエッセイで読み難いので,ここにレジメを作成しました.
このエッセイの書かれた3月30日ころは,Covid-19の感染について未知なことばかり(感染させるが症状の出ない保菌者など)だったでしょう.しかし,2.5か月経過した現時点では,これらは皆さんの常識になりましたね.最後に出てくる医療崩壊をさせないための断続的なロックダウン方法のシミュレーションは参考になるかもしれません.
■ケンブリッジ大学の疫学者ジュリア・ゴグGogは,2月の初めに,数理科学センターの通常の職務を辞し,緊急事態のための科学諮問グループ(SAGE)に結果を報告するモデリンググループ,SPI-Mに専念することになった.
SPI-Mは,インフルエンザパンデミックへ備えてこれまで活動をしてきたのだが,現在はCOVID-19のパンデミックに焦点を絞った活動をしている.ゴグは,王立協会が率いる全国コンソーシアムの運営委員会にも所属し,このパンデミックに対処している.
SPI-Mの仕事は,次に何が起こるか,さまざまな介入でそれがどのように変化するかを,予測できる数理モデルを開発し働かせることだ.COVID-19パンデミックがどのように進展するか?社会的介入はどのような影響を与えるか?これらのモデルはどのようなものか?それらは正しいのか?
COVID-19パンデミックの報道については、こちらをご覧ください:https://plus.maths.org/content/tags/covid-19
ーーーーーーーーーーーーーーーー
■SIRモデルとは(訳者補足)
S 感受性保持者数,(感染可能な数)
I 感染者数,(患者数)
R 免疫保持者数,(回復患者数)
全人口Nは一定と仮定して,N=S+I+R が成り立ちます.
SIRモデルの方程式は次のとおりです.
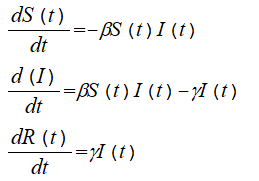
(1)(感染可能な数)の増加速度は,(患者数)と(感染可能な数)の積に比例する.比例定数βは感染率.
(2)(患者数)の増加速度は,(感染可能な数)の増加速度から,(回復患者数)の増加速度を減じたもの.
(3)(回復患者数)の増加速度は,(患者数)に比例する.比例定数γは回復率.
SIRモデルの詳細については,以下の記事https://plus.maths.org/content/mathematics-diseasesをご覧ください.
S, I, Rの間の状態遷移をブロック図で描くと上図のようです.
このモデル(単純SIR)で得られる結果は,下のグラフのようです.
S:青い線,I:緑の線,R:赤い線
赤い線は,「始めは免疫のあるものが誰もいなかったが,全員免疫ができて終わる」という当たり前の特別面白くない結果ではあります.
ーーーーーーーーーーーーーーーーーー
単純なSIRモデルは,寄宿学校の生徒などの単純な母集団に対して適切な予測を提供しますが,複雑な母集団に関しては,さまざまな母集団ごとのSIRモデルを繋ぎ合わせます.
実際には,これに色々な介入が加わるのですが,この影響を詳細にシミュレートするには,SIRモデルよりもさらに洗練されたモデルが必要です.
接触がカギ
このようなモデルの世界の背景で,非常に重要なのは人の接触パターンです(いわゆる動態調査):誰が誰にどのくらい会ったか.例えば,BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります.人々は,彼らの動きを追跡するアプリをダウンロードし,出会った人々(すべて適切に匿名化されている)を追跡するように求められます.モデルに組み込むこのような接触データは数値の配列( 行列 )です(下図を参照).
異なる年齢グループ間の平均的な接触を表示する接触行列.濃い色はより多くの接触を示します(ここでは,理解しやすくするために,数値ではなく色が使用されています).Contagion! The BBC Four Pandemic – The model behind the documentary.
学校閉鎖などの特定の社会的介入が,感染拡大にどのように影響するかを確認するには,介入に関連する部分を削除または縮小して,接触データを適宜調整してみます.
学校要因を完全にオフにするのは現実的とはいえません.減じるだけです.学校外で子供たちは,他のルートがあり(祖父母と混ざってしまう可能性など)ます.これは,考慮に入れるべき追加の接触が発生していることを意味します. 教師のストライキ中に起ったことなどの既存データは,接触データを補正し介入による流行への影響予測に役立ちます.
モデルが現実的であるかどうかは重大な問題です.COVID-19は新しい病気.既存モデルは季節性インフルエンザのために開発したもので,コロナパンデミックモデルは誰も作っていませんでした.COVID-19とインフルエンザとではモデルのどこが違うのかを調べなければなりません.
パンデミックのダイナミクスは,インフルエンザとコロナウイルスで似ていますが,違いもあります.
COVID-19はかなりの潜伏期があり,何の症状も示さずに感染している可能性があります.発症までに,インフルエンザの場合は数時間,コロナウイルスの場合は数日かかる可能性があります.
モデルに関して言えば,これは,SIRではなく,SEIRのモデルになることを意味します.Eは「露出」.
クラスEの人々は感染していますが,まだ症状は出ていません.クラスEの人は,他人に感染させる人と感染させない人に分けられます.すべてのモデルは近似であり,インフルエンザの場合は,目的によってSIRを回避できることがよくあります.ただし,コロナウイルスの場合,潜伏期間を無視すると,近似が非常に悪い.特に,短期予測のときは,これを考慮する必要があります.
COVID-19については,私たちが知らないことが他にもたくさんあります.1日目や2日目の感染力など,詳細はわかりません.不完全なデータからそれを推測するのは非常に難しい.中国や他の国のデータがいくつか(クルーズ船からのデータは非常に興味深い)あり,限られた情報から推測するのに最善を尽くしています.十分な情報がない場合,モデラーは不確実性を取り除くために,最も重要な未知数は何か決定します.これがモデリングで非常に重要なことです.
明日,何人の患者が出るか予測するなら,多くのことを知る必要はなく,現時点では指数関数的増加です. しかし,第2波が発生するかどうかを予測するには,非常に異なるいくつかのことを知る必要があります.
長期予測で重要なパラメータは,疾患の再生産数(1人の患者が平均何人に感染させるか.多くの場合,R_0と表示される)です.これは 感染速度に関連する.COVID-19の場合,R_0は2~2.5の間にあると推定されます.モデラーは,可能な値の範囲ごとにモデルを実行し,対応する予測の範囲を考えます.
感染したが病気ではない
多くの疫学者が知りたいもう1つの重要なパラメータは,集団内での感染の症例数で,これには,病気にかかったが症状を示さない人々の症例数も含まれます.無症候感染者数は,睡れなくなるほどの多数で,これを知ることは,私たちの出口戦略にとって非常に重要です.とGog氏は語りました.
現在の指数関数的成長を止める要素が2つあります.
1つは,学校の閉鎖や身体的な距離をとるなどの介入うぃして接触率を減らすことです.
2つ目は,罹患感受性のある人をなくすことです.病気になったらしばらくの間免疫があるので,無症候性を含む真の症例数を知ることから,罹患感受性の高い人々のクラスがどれほど速く減少するかがわかります.
議論されている集団免疫のメカニズムは,罹患感受性のある人数が減少するにつれて,病気の指数関数的成長が平担になり,指数関数的減衰になるという仕組みのことです.
幸い,無症候性に関するデータは知ることができます. 病気に罹ったか罹っているか抗体検査が実施されています.これらの第一波は当然NHSスタッフにのみ公開されます.
では何が起こる?
何が起こるか誰も正確に言うことはできません.地平線に見える大きな望みはワクチンの到着です.これは,集団に免疫を備えるもう1つの手段です.最も脆弱な人を優先的に,最小限のダメージでどのようにその目標に到達させるかです.誰もが同意するのは,これには長期的な犠牲が伴うということです.「1週間だけシャットダウンして,この状況がなくなることを期待することはできません」「社会的距離の措置が早すぎる場合,感染かまだ残っていて,集団免疫はありません.現時点では,ヘルスケアシステムが容量を超えないようにするために,シャットダウンせざるを得ませんが,これは恒久的な戦略ではないことは十分に認識しています」とGog氏は語る.
先週 ,Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では,季節変動も考慮して,再発の問題について詳細に検討しました.呼吸器疾患の発生は,秋と冬に悪化する傾向があります.季節性インフルエンザの発生と同時に,ヘルスケアシステムにさらに大きな負担をかけます.キスラーと彼のチームは,そのような季節変動を反映する要因を含むSEIRモデルを使用しました.社会的距離測定の効果は,COVID-19の基本的な再生産数が最大60%減少することでモデルに反映され,中国で観察されたものと同等です.
この最新の研究の結論は,必ずしも明るいものではありません.
「シリアルロックダウンの期間を検討しています」とGog氏は言います.(医療崩壊が始まろうとしているときにロックダウンするという考え)英国のナイチンゲール病棟NHSのことは,noteの記事の1号に書きましたので,そちらをご覧ください.
社会的距離(ロックダウン)の断続的な期間の長さと頻度の仮定(米国の数値に基づく)のシミュレーション.
これらのグラフは,断続的な社会的距離(青色の領域)の下でのウイルスの有病率(黒い曲線)と重症なケース(赤い曲線)を示しています.最初と3番目のグラフには,季節的な強制がありません.2番目と4番目の季節の強制.ケア能力臨界は,水平の黒い実線で示されます.最初の2つのグラフは現在の米国の救急医療能力でのシナリオ,3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです.再生産数の最大値は冬期は2であり,夏期は1.4です.この図は,キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からです.
悲観的状況の中に,希望の光がいくつかあります.1つは,COVID-19の重症例に対して,投薬と良い治療プロトコルが,ある時点で追いつく可能性があることです.これで,NHSへの負荷の軽減でき,重症患者のケアができるます.
もう1つの希望の光は,軽度で無症候の感染者が,想定されているよりもはるかに多い(多くの人々がすでに病気になり免疫力がある場合)かもしれません.私たちはこれが事実かどうかわかるまでは,ルールを守って家にいるだけしかできません.
これがどうして私の手元にあるのか思い出せません.
その他にも球状のものや,いくつか組木のパズル(箱根細工と呼んでいました)で子供の頃遊んだのを覚えています.それは遠い昔のことで,いつの間にか失くなってしまいました.複雑な組木もあったように思い残念です.なぜかこの組木だけが,今私の手元にあります.多分,この組木を手に入れたのが一番新しいためでしょう.この組木はとてもシンプルですが,職人のすばらしいアイデアだと思います.
全体の対称性は立方晶系の最も対称性の高い点群です.
4回対称軸が3本,3回対称軸が4本,2回対称軸が6本あります.
(鏡映面はたくさんありますが表示略).
全体はこのような同じパーツが6個で出来ています.
3回対称軸に沿って引き抜くことができ,二つに割れます.
写真は3回軸に沿って引き抜き開いて(内部をこちらに向けて)並べたところです.

対称性を考えないと,引き抜く方向がわからず難しいパズルです.
3つのパーツでできた風車のような形を一体として引き抜くのがミソです.(この方法がわかっていても,特に,分解と逆の組立てのときは,手作業的にはなかなか難しい.手が3本欲しいということになります)
3つのパーツは一体として扱わなければ,互いに組み合っているので,バラせません.3回対称軸は4本あるので,引く抜く方向は4通りありどれでも可能です.
(図)4回対称軸の方向から見る↓ (図)3回対称軸の方向から見る↓

(図)3回軸(上下方向)に沿って引き抜く↓(今度,動画にしたい)
■この組木は,x平面,y平面,z平面がかみ合っているという見方もできます.それぞれの平面は2つのパーツからなります.
直交するx平面,y平面を作り,z平面の部品の1つだけ(下側)は置けるが,残り1つ(上側)をどう入れるかと,普通の人は苦闘します.
この手順では入りません.3つのパーツで組んだ風車型を一体として扱うのがミソでした.
(図)最後の1つはどうしても入りません.↓
フィボナッチ数はいろいろな所に現れます.この記事はThomas Koshyの著書からの引用で,2018.09.25発行のメルマガSGK通信No.234のリメイクです.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2018.09.25] No.234
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
フィボナッチ数列は次のように定義されます.
F(n)=F(n-1)+F(n-2).F(1)=1,F(2)=1として数列を作ると
1,1,2,3,5,8,13,21,.......の数列が得られます.
ピアノの鍵盤は,フィボナッチ数と音楽のつながりの可視化の良い例です.
鍵盤上で1オクターブとは,2音の間の音程で高音の周波数が低音の2倍になっていることです.鍵盤でいうと,1オクターブは,5つの黒鍵と8つの白鍵,合わせて13の鍵で構成されます(図).この5つの黒鍵は2つのグループをなしています;一方は2鍵よりなるグループ,他方は3鍵よりなるグループ.
1オクターブに入る13の音は,西洋音楽で最も一般的な音階であるクロマチック音階(半音階)を作ります.クロマチック音階に先行して,2つの他の音階;5音からなるペンタトニック音階と8音からなるダイアトニック音階がありました. お馴染みの"Mary had a Little Lamb” と “Amazing Grace” は,ペンタトニック音階を使い演奏でき,また, “Row, Row, Row Your Boat” のメロディーはダイアトニック音階を使い演奏できます.
長6度と短6度(6つ離れた音,および,5+1/2離れた音)は,耳を最も喜ばす2つの音程(和音)です.長6度は,例えば,音CとAから成る:それぞれの音は,1秒当たり264と440の振動数で(図),264/440 = 3/5はフィボナッチ比であるに注目しましよう.
短6度は,例えば,1秒当たりの振動数330と528の音であるEとCから構成され,それらの比もフィボナッチ比です: 330/528 = 5/8.
[訳注)自音の音程は1度という.1オクターブの音程は8度である.]
正12面体や球面正12面体は,正5角形(あるいは,球面正5角形)の面12枚が囲んでできる立体です.
3枚鏡の組み合わせで万華鏡を作り,正12面体や球面正12面体が見える万華鏡を作りましょう.
正12面体の点群(対称性)を生成する3枚の鏡に,次のものを選びます.
(Aタイプ)1つの正5角形の面を10個の直角3角形(若草色)に分割し,
その領域を立体の中心から見込む「3角錘」が万華鏡になります.
(Bタイプ)1つの正5角形の面を5つの2等辺3角形(水色)に分割し,
その領域を立体の中心から見込む「3角錘」が作る万華鏡になります.
(Aタイプ) (Bタイプ)
作製したそれぞれの万華鏡で見られる映像を対応させて掲載します.
どちらも正12面体の映像が見えますが,両者の正5角形の面を観察して比較しましょう.
Aの映像では直角3角形10個で正5角形の1つの面を作っていますが,Bの映像では2等辺三角形5個で正5角形の1つの面を作っているのがわかります.
■正12面体および球面正12面体の見える万華鏡(Aタイプ)の作り方
ミラー紙(厚さ0.25mm以上が良い)に次の展開図を描きます.青色の部分を使います(赤線に沿って光の窓を作ります).赤線の円に沿って切ると「球面正12面体像が見える光の窓」,赤線の直線に沿って切ると「正12面体像が見える光の窓」ができます.どちらかを選びます.辺OHが共通につながるように3角錐(鏡面は三角錐の内側)を組み立てます.完成した万華鏡は△KAHから覗きます.
「美しい幾何学」球面正多面体とメビウス万華鏡p.133~p135に,この万華鏡の説明があります.
いろいろな多面体の見える万華鏡(立体万華鏡と呼びましょう)を作ります.アルミ板やプラスチックの鏡は像がきれいに映りますが,ミラー紙(厚手0.25mmくらい)を用いても,ここで取り上げているような立体万華鏡は良好に作れますので,チャレンジしてみてください.
球面正多面体は,アラブの数学者,アブル・ワーファ(1000頃)に始まります.球面正多面体{p,q}は,球面正p角形が,頂点でq個集まっているもので,球面正p角形の1つの内角は2π/qです(図D).
そして,球面p-多角形の辺はすべて大円であることに注意しましょう.
ここで具体的に取り上げるのは,正12面体に相当する球面正12面体=球面{5,3}多面体です.
メビウスは多面体万華鏡を発明します(1850)が,これは,球面p-多角形を,2p個の球面直角3角形に分割することを使います(図A).
分割された3角形の角度は,π/p,π/q,π/2,このような直角3角形を(p,q,2)と記述します.
万華鏡は,3角形(赤く塗った)の各辺となる大円を鏡にすると得られます.
(A)メビウス万華鏡になり,正5角形の面を10個の直角3角形に分割しています.
(B)正5角形の面を5個の2等辺3角形に分割しています.Bには,Aに存在した鏡映対称面が1つ消えています.
(C)赤く塗った正3角形の周囲の辺の大円を鏡に置き換えて万華鏡を作れば,正20面体の映像が見えます.
では,AとBを作ってみましょう:展開図は,前号の[正12面体の見える万華鏡を作ろう]に掲載してあります.
A(左写真) B(右写真)
p.132~p.133 美しい幾何学より
私はこの問題が気に入っています.中学生向きですが,読解力と身に着いた科学的な常識があれば解けます.算数・数学というのは,数式の記述や論理の学習が目標ですが,そんな堅苦しい学習よりも必要なことは,生活や遊びで自然に身に着いた,読解力と常識が大事だと思います.
次の「アルプスを渡る」の問題では,以下の5つ(とりわけ出だしの2つ)がポイントです:
①題意を正しく理解する読解力→山頂を越えろとは言っていません.
②糸巻に糸を巻くなど生活の遊びの場で,自然に身に着いた力学感覚(力のバランスや手応え)★←特に大事
③円錐の展開図がひらめく(最短距離を引くのは展開だから)
④状況を読んで,2√2≒3と大胆に近似(融通の利かない数学バカでは行き詰る)
⑤半径2√2の円に内接する正3角形の一辺の長さは(ここだけが数学)
★物理学や円錐曲線などを知っている必要はありません.子供の頃に,積み木や水遊びや泥んこ遊びなどで,自然に体感したことのある手応えのことを,私はここで常識と言っています.
別に,物理や数学で数式を習わなくても,手応えが身についていれば,簡単に箸で豆をつかめるし,卵を握りつぶしたりはしません.職人は,器用にガラス細工をします.これは流体の粘性など面倒な計算をしても無駄なことで,その時の手応えで瞬時に反応できないと知識は役に立ちません.色々な分野で同様な身に着いた常識が大切でしょう.私は教室で知識を学ぶよりも,身についている手応えが一番大事だと思っています.
最近の子供は,ゲームやバーチャルな世界で間違った手応えを身に着けていますし,実際の泥んこの手応えや積み木のバランスや卵の殻の複雑な手ごたえを身に着けていないようです.大人になって機械設計をしても,構造の強度の感覚を持ち合わせていない.常識が身に着いていれば,直感(見た目でわかる)でわかる不安定なものを作ってしまう(計算結果がとんでもない数値になってもおかしいと思わない).
さて,この問題では,円錐の斜面に糸を巻くときの手ごたえをイメージしましょう.とがった頂点を通るように糸を巻いたり,山麓の円周に糸を巻いたりを,安定にできますか?斜面のどこかを経由するとき一番きつく糸を巻きつけられるはずですね.
■問:「アルプスを渡る」
一定の傾斜角45度の円錐形の山のふもとに人々が集まりました.山の高さは2000メートルです.グループは、山のふもとの正反対の地点に行きたいと考えています(図の点Aから点Bに移動します).AからBへの最短ルートは...
この仕事で地獄行? もう降りようよ.
解答選択肢(私は,Bを選びました.皆様はどうですか)
A. 4.5 km
B. 5 km
C. 5.5 km
D. 6 km
E. 6.5 km
なかなか面白い手頃な問題を引用します.
(問2)
3人の農民が宿に入り,休憩と食事をしました.彼らはホステスにジャガイモをゆでるように命じた後,眠りました.ホステスは客を起こさなかったが,ゆでたジャガイモをテーブルに置いて去りました.
まもなく,彼らのうちの一人Aが目を覚まし,自分の分け前を食べ,そして再び眠りに落ちました.
それから二人目の農民Bが目を覚まし,ジャガイモを数え,1/3だけ食べてまた眠りに落ちました.
それから,三人目の農民が目を覚まし,自分が最初に目を覚ましたと仮定して,ジャガイモを数えて1/3だけ食べました.
それから彼の仲間たち全員が目を覚まし,まだ8つのジャガイモが残っているのを見ました.3人はこれからそれぞれ何個のジャガイモを食べれば,最終的に公平に同じ個数のジャガイモ食べたことになりますすか?
(問3)
数学者は庭のプロットでヤギを飼っています.彼は,20 mの長さのロープの一端を結び付け,他端はヤギの首に結びました.ロープの中間は,フェンスに沿ってスライドできるリングにするワイヤーに沿ってスライドできるリングを通してあります(図を参照).結局,ヤギは移動できる範囲にある草を全部食べました.ヤギの到達範囲の境界となる弧を描きなさい.
図の説明
дерево(木) ,кольцо(リング)
クバンチクの問題は,小中学生が対象ですが無理のない興味ある問題です.
第一に必要なのは,問題の意味を理解する読解力です.
■クバンチクの問題1(私の解答例)
クバンチクの問題は解答が定まるとは限りません.解答は5択の選択肢があります.クバンチク問題1として前回紹介したのは解答できる問題の例でした.私の解答例をここに掲載します.
●問2
全体をXとして,Aが食べた後の残りはX(2/3),続いてBが食べた後の残りはX(2/3)^2,さらにCが食べた後の残りはX(2/3)^3=8個でした.
従って,Cは4個食べ,Bは6個食べ,Aは9個食べています.
Aの9個は全体の1/3に相当します.B, Cも9個づつ食べられますので,Bは後3個,Cは後5個食べられます.こうして8個の残りはBとCが食べてなくなります.
●問3
===============================================================
■クバンチクの問題2
今回はクバンチクの問題2として,新たな例題を3つ紹介します.これらはみな2016年の年間ツアー(毎月4~5題を出題)で出されたものです.
挑戦してください.私の解答は,C,D,D です.
●問:島で
島の成人男性の40%と成人女性の60%は未婚です.島の成人人口のうち,結婚していない割合はいくらですか(一夫多妻制および同性婚は島では禁止されています)?
解答選択肢
A. 48%
B. 50%
C. 52%
D. 68.5%
E.結婚について考えるのは早すぎる
●問:都市計画
図は,ある都市の道路地図を示しています.合計2つの環状道路(共通の中心を持つ2つの円)と,この中心で等しい角度で合流する6つの道路があります.バーシャ(名前)は,AからBへの行き方を考えています.外部環状道路または内部環状道路を通る2つのルートのうちどちらが短いですか?
解答選択肢
A.同じ
B.内側の円
C.外側の円
D. 2つの円の半径の比率に依存
E.地下鉄はまだ速いです!
●問:平均速度
2つの山村AとBの間の道路は,上り坂または下り坂のどちらかになります.古いバスは,上り坂では平均時速30 km / h,下り坂では平均速度60 km / hです.AからBまで行き来する通しの平均速度はいくらですか?
解答選択肢
A.時速40 km
B. 45 km / h
C. 50 km / h
D.明確な答えを得るための十分なデータがない
E.古いバスは間違いなく道で壊れます
■2008年8月4日に上智大が主催した数学月間参加プログラムで,
「感染症対策における数理モデルの役割」大日康史(国立感染症研究所)
という講演がありました.
数理モデルによる感染拡大のシミュレーションは,新型インフルエンザやバイオテロなどの対策の有効性評価に必要です.数理モデルには,SIRモデル,ibm(IndividualBasedモデル),Ribm(Realibm)などがあります.本研究で用いたRibmとは,実際に調査した個人の移動,所在の記録データ(首都圏では88万人)にもとづき,6分ごとに人々の接触状態(感染の機会)が定義されるものです.新型インフルエンザには,種々のタイプがあり鳥類間の感染は起こるが,鳥から人への感染は血液の濃厚接触などの場合に限られる(豚と人の感染するインフルエンザのタイプは似る).人に感染した場合に,人から人への感染が始まり拡大していく.[注)Covid-19は,また別のタイプで異なる数理モデルの開発が必要です]
このシミュレーションに用いたのは,例えば,以下のシナリオでした:
(第1日)初発例が外国で感染.(第3日)帰国.帰宅後(八王子)感染性を持つ.(第4日)出社(丸の内).発症.(第5日)国際医療センターに受診.東京都健康安全研究センターで検査診断.(第6日)対策へ:
このシミュレーションの結果として,
首都圏への感染拡大の様子や全国への拡大の様子が示されました.どのような対策(外出自粛,地域閉鎖,休校,住民全員が予防服用,....)をとると効果があるかを予測できるシミュレーションでした.
この現実的なシミュレーションのシナリオには,首都圏での人の動き(動態調査)のデータが使われています.
このような,人々の接触を考慮した感染拡大のシミュレーションはミクロなシミュレーションといいます.これに対して,統計集団としての陽性率,罹患率などのマクロな量の変化を追うのはマクロなシミュレーションといいます.
■つぎは,英国のハスルミアで行われたスマホアプリを用いた動態調査の実験です.インフルエンザ感染拡大のミクロなシミュレーションに必要な動態調査は,スマホアプリを開発して2018年になされました.それは以下のようなものです.
英国の全国的な市民科学実験は,BBC Pandemicというアプリを使いました.このアプリは,App StoreまたはGoogle Playからスマートフォンにダウンロードできます.
アプリを使用して,ボランティアは次の2つの研究に参加できました:
(1)サリー州の町ハスルミア(ロンドンの近く)に焦点を当てたもので,それはかなりの数の人々を登録するキャンペーンでした.ボランティアのスマートフォンの位置の連続3日以上の追跡を許可を得て実施します.
(2)英国全体の規模の大きい調査は,許可を得てボランティアが選んだ24時間にわたりボランティアの毎時の位置(1km^2のメッシュ精度)を記録します.
各研究期間の終わりに,ボランティアはその期間中に遭遇した人を入力するように求められます.
記録された移動データと自己申告した接触データとで構成された国のデータセットのみを取り出します.このデータを使用して,インフルエンザの蔓延に関する数学的モデルを開発し,それによってインフルエンザのパンデミックがどのようにイギリス全体に蔓延するかをシミュレートするのが仕事でした.
このバーチャルの大流行は,イギリス南部のサリー州にある町ハスルミアで始まり,番組シナリオに従い,BBCドキュメンタリーのプレゼンターはバーチャル実況をしました.ハスルミアで収集した詳細なデータは,バーチャルな国内感染爆発の火種となるハスルミア内の感染爆発のシミュレートに使用されました.結果の感染拡大地図(Kissler,Klepac, Tang, Gog,2018)を見るとロンドンで始まった感染は,何の規制もしなければ1週間でニューカッスルまで広がるようです.
■しかし,Covid-19では全く違う(まだわからない)
パンデミックの感染拡大は,インフルエンザとコロナウイルスで似ているようで,非常に異なるところが多いのです.上で述べたミクロなシミュレーションは2018年以前のCovid-19出現前のインフルエンザに対するものであることを再度強調しておきます.ご注意ください.
Covid-19はかなりの潜伏期があり,何の症状も示さずに感染している可能性があります.発症までに,インフルエンザの場合は数時間,コロナウイルスの場合は数日かかる可能性があります.そして,無症状の感染源があるので非常にやっかいです.潜伏期の考慮は本質的に重要で,単純なSIRモデルではなくSEIRモデルになることを,Gogらが指摘しています.そして,Gogらはインフルエンザで開発した感染モデルと全く違う感染モデルを作らなければならずまだ研究中です.
キューリー夫人は皆さまご存じでしょう.マリ・キューリーの夫の
ピエール・キューリーは,私の最も好きな科学者の一人です.
キューリーの原理も学生の頃からずっと心を奪われている事柄です.
水晶などの結晶に圧力をかけると電位が発生する圧電効果(ピエゾ効果)の発見で有名です.水晶振動子はこの性質を使ったデバイスです.
半導体や誘電体など色々な材料で,色々なデバイスが作られます.
例えば,半導体結晶を舞台にして,光子や電子が演じるパフォーマンス
を制御利用して,種々の半導体デバイスが作られます.舞台となる結晶世界は周期的なデジタル世界です.(周期的な空間は「結晶空間」とも呼ばれます)
周期的空間の数学(対称性)はとても重要で魅力的です.
この分野では,フェドロフ,シュブニコフ,ベーロフ,ザモルザエフなどの学者を輩出したロシアに伝統があり,1970年代にはロシアの本を一生懸命勉強したものです.
結晶の幾何学(古典結晶学の歴史)を,速足でレビューしましたが,
ここで,「キューリーの原理」について紹介しようと思います.
色々な「系(もの)」や「そこで起こる現象(こと)」の理解に,「対称性」の考え方が使われます.
ピエール・キューリーは,“結晶という舞台”で起こる”物理現象の対称性”を研究しました(1894).水晶結晶の圧電効果(対称心のある構造では起こりません)はその例です.
「舞台の対称性は,その舞台で起こる現象の対称性に反映されるべきだ」という因果律は,キューリーの原理と呼ばれます.
色々な分野で,原因(舞台)と結果(現象)のそれぞれの対称性の間でこの因果律がなりたちます.例えば,原因(結晶)の対称性G_cryst,結果(その結晶で起こる現象)の対称性G_pとすると,G_cryst⊆G_pです.
この逆が成り立たないのは,結果には注目している原因の他にも別の原因が反映されてもかまわないからです.
例えば,結晶にX線ビームをあてたとき,結晶を通過したX線の作る回折パターンの対称性には,その原因となった結晶の対称性が反映されています.
あるいは,運動量保存則が成り立つのは,空間が無限に広く一様であり,
平行移動しても環境が変わらないからです.
エネルギー保存則が成り立つのは,時間に関して変化がない時です.
因果律のいろいろな例を思いつくでしょう.舞台環境とそこで生きる生物の形.結晶構造とそこで起こる物理現象.万華鏡の鏡室と生じる繰り返し模様.こられもみんな対称性の因果律が支配しています.
「もの」や「こと」の対称性とは,変換をほどこしても,「もの」や「こと」が全体として変わらない性質のことで,
例えば,回転や鏡映で系全体が不変なら,その系には回転対称,鏡映対称があるといいます.
音楽や詩歌の形式や韻律.
絵画,壁紙模様,タイル張り模様,建物,などのデザイン.
.....,芸術を始め色々な分野で,対称性の考え方が役立ちます.
■群の考え方は色々な数学分野に現れます.そして,群論が適用される対象も様々な分野にあります.
群論を作ったのは天才ガロアで,群論は代数方程式の解法にかかわって生まれました.2次方程式,3次方程式,4次方程式は,その解法が発見されていましたが,5次方程式の解法はどうしても見つけられないでいた時代のことです.
f(x)=x^5+ax^4+bx^3+cx^2+dx+eという5次式は,連続なグラフで,
xが負の方向に絶対値が大きくなれば,f(x)<0,xが正の方向に絶対値が大きければ,f(x)>0になるので,グラフy=f(x)はどこかでx軸を過るはずです.5次方程式f(x)=0には必ず1つの解xが存在し,そのxは係数で表されるはずだと誰もが思っていました.しかし,係数の加減乗除と冪根で表せる解は存在しなかったのです.1820年,アーベルは「5次以上の方程式には解の公式は存在しない」という証明を自費出版しました.アーベルは注目を浴びることなく1829年結核で死亡します.
根の対称性に注目し,群の理論を作り,これを証明したのはガロワですが,ガロワはこの証明を残して,決闘の銃弾により20歳で死亡します.1832年のことでした.
群論が生まれるまでに,ラグランジュ(1770),コーシー,アーベル,ガロア(1832)が関わっています.
■群論が生まれたのは,方程式の解法に関する分野でしたが,
群の概念は,正多面体の対称性(シンメトリー)と相性がよく,この応用の現場で群論を理解するのが良いと思います.結晶は原子や分子で構成される周期的な世界です.無限に繰り返す周期的な空間(結晶空間とも呼ぶ)には,構造の単位となるものが存在し(単位胞と呼ぶ),単位胞が周期的に積み重なって周期的な空間を作ります.単位胞を1つの点で表示すると,周期的な空間は点が配列した格子になるでしょう.つまり,周期的な空間は,(連続な空間ではなく)デジタル化された空間であるといえます.
結晶空間という舞台は,対称操作の集合が作る群という数学系が活躍するのに絶好な分野です.というわけで,結晶空間で群論が活躍するのを具体的に見て行きましょう.
■古典的結晶学について
水晶のいろいろな面の大きさは個体ごとに違うが,「対応する面どうしのなす角度を測ると,どの水晶でも同じ値だ」ということを発見したのはステノ(1669).この現象を,多くの鉱物で調べて「面角一定の法則」としたのは,ロメデリル(1772)です.
この法則は,「結晶の内部構造に原因がある」と洞察したのがアウイ(1783)で,彼は「結晶には単位胞が存在し.この単位胞が繰り返し並ぶブロック細工のようなものだ」と推論しました.
19世紀に入ると,結晶に座標軸(結晶軸)を導入し,結晶面に指数をつける方法が種々定義されました.それらの方法のうち,ミラー (1801~1880〉によるミラー指数が,今日,最も広く用いられています.
「その結晶の単位胞の形に合った座標軸を決めると,すべての結晶面のミラー指数は,簡単な整数で表せる」=結晶面の有理指数の法則といいます.
これは,アウイの述べた「結晶=ブロック細工説」を裏付けるすることにほかなりません.
この時期には, 結晶面の方位(=結晶内部に置いた原点から,各結晶面へ垂線を立てて,結晶内部の原点を中心とした単位球表面に投影する)を,2次元平面へ写像する種々の等角投影法(ステレオ投影など)も生まれています.
3次元の結晶点群は32種(ヘッセル,1830〉,3次元の空間格子(結晶格子)のタイプ=ブラべ格子(1848)は14種が数え上げられ,続いて,3次元の空間群の夕イプが230種であることが,フェドロフ,シェンフ リーズ,バーロー(1885~1894〉により(3名は互いに独立に研究した)数え上げられました.これらは,すべてX線の発見(1895)以前の純粋な数学的業績であるのが興味深いことです.ラウエの回折実験(1912)は,結晶が周期的な内部構造であることの決定的な証拠です.
ーーーーー
今後の計画
空間群をΦとすると,並進群(格子)Tは,空間群Φに正規部分群として含まれるので,並進を法とした群Φ/Tは,点群Gに同型である.ということを徐々に説明します.
■ゼロとアラビア数字
最古の記数法は五進法だそうです.5をひとまとめにしたものを「1クワイン」といいました.バビロニアには60進法,20進法を使ったところも,12進法を使った場所もありました.「1ダース」です.
12は約数が多いので10より便利なところがあります.けれども,大勢は10進法に落ち着きました.われわれが指を折って数えるところから10進法が各所で使われるようになったと推測されています.
10進法での記数法には0と1~9までの数字が必要です.これからアラビア数字の起源に思いを馳せるわけですが,0と1~9までの数に対応する何らかの記号があり,それ以前に十進法が確立していなければなりません.
参考書:「アラビア数学奇譚」マオバ・タハン(越智典子訳)白揚社
■イスラムの数学
フワーリズミー(780頃~850頃)は、アッバース朝のバクダッドで活躍しアラビアの数学を確立した代数学の創始者です.
彼の時代のバクダッドをのぞいてみましょう.
ゼロの役割には,位取りの役割と4則演算の対象となる数の役割があります.まず位取りに関していえば,この時代,大勢は和算もイスラムも10進法でありましたから,数を表示するには,・・・・,十万,万,千,百,十,一,の位の場所に,0~9に相当する数字を書いたり,
マッチの軸木のような算木を置いたり,そろばんでは玉で表示したりします.どんな記号を使っても似たようなもので,ゼロの記号がないときはその位は空にしました.アラビア数字に関しては,エジプト,インドから
伝えられたゼロの概念がイスラムで発展しヨーロッパに伝わり完成されたという流れでしょう.
どのような数字でもかまいませんが,0があると空を位取りの場所に配置するよりも明瞭に数字を表示できます.
これが位を明瞭にするので,十,百,千,万,十万,百万,千万,億,...と際限なく単位が必要になることが避けられます.これはイスラム数学の画期的な成果でしょう.
次に,4則演算の対象としてのゼロについてです.分数全体の集合(=有理数)の中で4則演算を自由に行えます.
ただし,ゼロで割ることは禁じられていますのでご注意ください.
ギリシャでは幾何学が盛んでしたが,イスラムの数学ではアラビア数字の記数法を用いて,代数や方程式が進みました.
特に,三角関数が生まれて発展しました.われわれが高校で学んだ加法定理や倍角の公式やそのほか様々な三角関数の公式が証明され,本が出版され,三角関数の数表も発行されました
■平和の都,バクダッド
1100年前のバクダッドは人口100万人の世界最大の都市でした.
その賑わいはまさにアラビアンナイトの世界です.イスラムの教えのもとに
“平和の都”と呼ばれ,アッパース朝宮殿は建築工学,幾何学の粋を集めます.イスラム帝国は,東ローマ帝国と中国(唐王朝)の間に位置し交易に便利です.コーランは“神は商売を許したもうた”と商業を奨励し,売買の証人たる仲介人がいて契約と公正な取引が行われたそうです.
最古の小切手(エジプトの商人が振り出した)も発見されています.
チグリス川とユーフラテス川の間に円城都市(直径2.3km)が建設され,
これを中心とする見事な中央集権行政システムが出来上がりました.
バクダッドに集まる4本の街道は東西南北に延びヨーロッパはスエーデンまで交流があったということです.
(バイキングも正式に貿易しイスラム銀貨が流通しました)
■科学や医学,都市の発展
8世紀に成立したアッバース朝では,カリフや宮廷のワズィールたちが保護をうけ,第7代カリフ,マアムーンが創設した研究施設バイト・アル=ヒクマ(智恵の館)には多くの科学者が集まり,ギリシャ科学のアラビア語への翻訳が進めらました.マアムーンに仕えた科学者・数学者のひとりが,
フワーリズミー(780頃~850頃)でした.
科学では,古代エジプトに起源を持つ錬金術の実験が繰り返され,元素記号が生まれ,文学では,アラビアン=ナイトが生まれ,唐で発明された製紙法もキルギスの戦いの際に伝わりました.
バクダッドには100軒を越す書店があったそうです.
百花繚乱.当時のバグダードのにぎわい言ったらすごい.見たかったですね.イブン・シーナは最先端医学の医学典範を著し,世界初の総合病院がバクダッドに作られました.
病院は寄進され,その運営費も,周辺の市場の売り上げ寄付で行うワクフという相互扶助の制度が,公共施設を支えたそうです.
円城都市を中心に,モスク3万,多くの市場と市場には100店を超す店があったそうです.500年間繁栄したイスラム帝国は,1万2千のモンゴル軍により滅亡しました.チグリス川は血で染まり,本のインクで青く染まったそうです.
アラビア語に訳されたアリストテレスなどギリシャの古典や発展したイスラムの科学は,その後ヨーロッパに伝わりラテン語に翻訳されルネッサンスが花開きます.
参考:
ドキュメンタリー 文明の道「第06集 バグダッド 大いなる知恵の都」
https://www.youtube.com/watch?v=ehEuTnLfOME&feature=share
壁紙模様の対称性は,平面群で17種類に分類できますが,平面群p3m1とp31mの対称性はとてもよく似ています.
以下の2つはともにエッシャーの作品です.比較鑑賞しましょう.
p3m1 p31m
どちらも3回回転対称のある繰り返し模様ですが,鏡映面の入り方に違いがあります.
白い線は鏡映面です.
P31mの方には,鏡映面が集まっていない3回対称軸がありますが
P3m1の方の3回対称軸の場所には,鏡映面が集まっています.
両者の絵から受ける微妙な印象の差は,図のモチーフもあるでしょうが,このような対称性の違いの影響もありそうです.
■正三角形の鏡室の万華鏡を作ると,p3m1の壁紙模様が観察できます.
しかしながら,p31mの壁紙模様は自然には得られません.
その理由は,p31mでは鏡室の内部の図柄が3回対称である必要があるからです.
鏡室の図柄は,ガラス屑が自然に分布して作る図柄なので,
それが3回対称であるなどという偶然はあり得ません.
p3m1の例 万華鏡映像 p31mの例 石英の結晶構造
(注)平面群の記号p31m,p3m1の記法について:
p:単純格子,3:紙面に垂直な3回回転軸,
単位胞の辺(並進方向)に垂直な鏡mの有無,その他の方向の鏡mの有無,
(鏡のないときは1と記す)
美しい幾何学,p.100,p.110~112
https://i1.wp.com/vectorfield.net/wp/wp-content/uploads/2017/11/PB180047.jpg?resize=880%2C1024
東京都庭園美術館,姫宮の部屋
■ 星型正多角形(ダ・ビンチの星型)
下の青や緑の図形は,星型正多角形の例で星型5角形(五芒星)と星型8角
形(ダ・ビンチの星型)です.頂点同士を結んだ赤い輪郭線は,それぞれ正5
角形と正8角形になり,凸多角形(凹所のない多角形)です.星型自体は,星状凸集合(領域内の点で,領域内の任意の点と結ぶ線分が領域内にあるよう点が存在する図形)ではあるが,凸多角形ではありません.
青い星型5角形について詳しくみていきましょう.頂点Aから辺をA→C→E→B→D→A
と1周りたどると,辺の向き(→)が2回転することがわかります.あるいは,「5角形の頂点
を1つ飛ばしでたどって,2周して始めの頂点に戻る」という言い方もできます.このような
星形を { 5/2 } と表記します.
星型8角形(ダ・ビンチの星型)でも同様で,右の図形は { 8/3 } です.
星型5角形を 5/2 と書くのは,2×360˚/5=360˚/(5/2) だからです.この星型5角形が頂
点で5つずつ集まる { 5/2, 5 } は,星型小12面体になります.
■星型正多面体(ケプラーの星形正多面体より)
(1)正12面体をコア(芯)にしてできる星型「星型小12面体」
右の写真の星型は,東京都庭園美術館,旧朝香宮邸,姫宮の部屋の照明器具にも使われています.
コアになるのは正12面体で,その12個の正5角形の面の上に,それぞれ正5角錘を取り付けた形
をしています.正5角錐の頂点は,それぞれ,芯となる正12面体の面に対応していますから,頂
点を結んでできる図形(赤の多面体)は,正12面体に双対な正20面体です.
正5角錐の頂点(例えばA)の周りに,星型正5角形 { 5/2 } が5個集まっている立体です.
芯に正5角形の穴のある五芒星の板を,各頂点で5枚ずつ組み合わせると,この立体になりま
す.したがって,この星型正多面体はシュレーフリの記号で { 5/2, 5 } となります.
さて,この星型小12面体 { 5/2, 5 } は,プラトンの正多面体(正12面体)を芯にして,その
正5角形の面に正5角錐を貼りつけた形でした.同様に,プラトンの正多面体(正20面体)を
芯にして,その正3角形の面に正3角錘(正4面体)を貼り付けてできる形は, 星型大12面体
{ 5/2, 3 } と呼ばれます.これら2つの星型は,ケプラーの星型多面体とも呼ばれます.序に,
この2つの星型に双対な,{ 5, 5/2 },{ 3, 5/2 } は ポアンソの星型と呼ばれます.
星型小12面体は,五芒星の面F が12枚,稜の数E が30,頂点の数V が12ですので,
F−E+V= −6( 私たちの知っているオイラーの多面体定理では2)となります.これは星型
小12面体の空間が,球の位相と異なり,穴が4つ空いた浮輪と同じ位相であるためです.
(穴が1つ開くごとにF-E+Vは2づつ減ります)
■万華鏡映像の美しさが我々の心をとらえるのは,「空間の完璧な対称性」のせいだけではありません.時間の流れとともに映し出される「千変万化だが一度きり」の映像に,生命を感じるからでもありましょう.
ワンドの中を降り行くすべてのガラス屑の運命は,運動方程式ですべて定まっているとはいえ,ときおりカオスの起こる期待に目が離せません.万華鏡は,対称性(秩序)とカオス(乱れ)の混在が魅力なのです.そして,合わせ鏡が生みだす完璧な秩序は,無限に繰り返される“結晶世界”に迷い込んだようでもあります.
万華鏡 “カレイドスコープ”は,物理学者ブリュースター卿の特許(1817)[発明は1816年]が起源です.特許には,2枚の合わせ鏡の交差角θ°が,360°を偶数で割り切る角度にする:
$$360/θ=2n$$,だたし,$$n=2,3,4,・・・$$ということが書かれています.
■平面群と市松模様
本来の市松模様はチェス盤のように正方格子が交互に塗り分けられたものですが,
3角格子などの場合でも交互に塗り分けられていれば市松模様と呼ぶことにします.
Fig1
これらは皆,市松模様と呼ぶことになります.頂点で偶数個のタイルが会合している場合に市松模様が作れます.この状況は,ブリュースターの特許の「合わせ鏡の交差角θ°が,360°を偶数で割り切る角度」と同じことです.
万華鏡は鏡(位数2の対称操作)の組み合わせだけで作られます.
物体が1回鏡で反射すると鏡像(向きが裏返る),2回反射すると鏡像の鏡像になり始めの向きと同じになります.
市松模様の黒-白は,物体のある鏡室タイル(グレイ色)と同じ向き="正置像”を黒;鏡像=“裏返像”を白に塗り分けています.
■正方形の鏡室の万華鏡がつくる市松模様
Fig2 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_8_m?1446474652
図(1)万華鏡の鏡室タイルをグレイの正方形とします.
鏡室のフチの赤線は鏡(4枚)です.
図(2)1回の反射で4個のタイルの裏返像(黄色)が生まれます.
図(3)2回の反射で,その外側に8個のタイルの正置像(緑色)が生まれます.
図(4)3回の反射で,その外側に12個のタイルの裏返像(黄色)が生まれます.
このようにして,鏡室タイルはその鏡像を全平面に広げて行き,
平面を市松模様で塗りつぶします.
■3角形の鏡室の万華鏡は市松模様をつくるか?
Fig3 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_9_m?1446474652
1.左図の鏡室3角形ABCは90°30°60°の3角形です.
各頂点で3角形が偶数個集まっています.3つの頂点のまわりはどれも市松模様ができており,
全平面が市松模様であることがわかります.
2.右図の鏡室3角形ABCは45°60°75°の3角形で,
AおよびBのまわりは3角形が偶数個集まりますが,Cのまわりでは偶数個あつまりません.
そのため,全平面では市松模様が出来ないことがわかります.
3.鏡映操作の集合が平面群を作っている場合は,全平面が市松模様になりますが,
逆に,市松模様が何処かで乱れているなら,その鏡の組み合わせは平面群が作れない場合です.
そのような万華鏡のもう一つの例を(Fig4)に示します.
Fig4 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/27/17073327/img_2_m?1446474652
--研究したのはガロワと同級生だったこともあるブラベーBravais(1848)--
■ 周期(デジタル化で生じる),格子,並進群
2次元世界では,互いに独立な2つの基本並進ベクトルが採れます.これを$$a, b$$(両者の長さが同じときは$$a_1,a_2$$と書く)としましょう.
$$a,b$$の整数係数の1次結合をすべて集めた $$ T={h・a+k・b| h,kは整数} $$を,
この平面の格子点の集合(あるいは単に“格子”)といいます.
集合$$T$$は無限集合になりますが, 群の条件を満たしており,$$T$$を並進群とも呼びます.格子を発生させる源となった$$a,b$$の組みの対称性で,格子のタイプが分類できます.これを研究したのはブラベーBravaisで,3次元のブラベ格子は14種であることを数え上げました(1848年).
ブラべ格子とは,結晶点群の対称性を基準に,格子のタイプ分類をしたもの2次元のブラベー格子は5種類,3次元では14種類,4次元では64種類あります.今回のシリーズでは,よく理解できることを優先し,すべて2次元世界に限定して話を進めています.
■ 図の見方
格子点●が並んでいます.この格子は,ベクトルa,bの一次結合で生じます.
格子点の1つを原点にし,自分に隣接する格子点と結び,それを垂直2等分する線で囲まれた領域をディリクレ胞(あるいは,ウイグナー=ザイツ胞)などと呼びます.ディリクレ胞タイルの形は,このタイルで平面を隙間なく埋め尽くせる形です.格子の対称性は,ディリクレ胞タイルの形に反映されています.ディリクレ胞は格子点をただ1つ含みます.単位胞というのは,並進の基本ベクトルa, bで囲まれた平行4辺形のことで,格子点を1つ含む単位胞は(one point cell)と呼ばれ,この場合は単純格子pになります.複数の格子点を含む単位胞は(multi point cell)で,複合格子(体心格子I,面心格子F,C面心格子C,A面心格子Aなどが3次元以上で出現)になります.2次元世界では,面心(or体心)格子(私はここで”菱形格子”と名付けました)だけが複合格子です.複合格子というものは,図形の特徴を見やすくするためだけのものなので,複合格子(multi point cell)をいっさい用いず,単位胞の格子(one point cell)だけで統一することもできます.
■5つの2次元ブラベー格子
美しい幾何学,p50~51, p54~55
この記事は,SGK通信No298(2019.12.24)をリメイクしたものです.
その時の感想の抜粋をシネマジャーナルに掲載いただきました.
http://cinejour2019ikoufilm.seesaa.net/article/escher-review.html
私が,映画「エッシャー 視覚の魔術師」を見たのは,アップリンク渋谷で(2019.12.20),
まだ新型コロナウイルスを知らなかったころです.
最近は,新型コロナウイルスの流行で,私たちは映画館から足がすっかり遠のいてしまいました.
『エッシャー 視覚の魔術師』6/28-7/4(土)深谷シネマにて上映決定!!という情報をお聞きしました.
遠出をしないで済む地元の方々は,ご覧になる良い機会かもしれません.
━━━━━━━━━━━━━━━━━━━━
■エッシャーは数学者といえる
エッシャー(オランダ,2018)の版画作品を見たことのある方は多いでしょう.
エッシャーの作品はどれも数学的でありますが,いくつかの幾何学分野に分類できます.
・錯視や空間認識,
・パズルやテッセレーション,
・非ユークリッド幾何学,
・周期的壁紙模様(2次元結晶学)
などの分野に分類できます.
数学を駆使したエッシャーの作品は良く知っていましたが,
エッシャーがどんな生活をした人物かはあまり気にしたことがありませんでした.
映画では,エッシャーの息子たちへの取材が面白い.
作品にまつわるエピソードの証言があります:
1955年作「表皮」から1956年作「婚姻のきづな」に作品が発展した状況がよくわかります.
ムッソリーニ時代の全体主義に息子が染められるのを嫌い,イタリアからスイスに移住します.
エッシャーの人物像がよくわかる,とても良い映画でした.
■映画の最後の方で,エッシャーが国際結晶学会の講演に呼ばれて行くところがありました.
私の専門は結晶学で,結晶学会では昔からエッシャーの周期的版画を,2次元結晶の教材にしており,
2次元のブラベー格子や,平面群(壁紙模様)に親しむことができます.
結晶学者には,エッシャー作品は馴染み深いものです.
アルハンブラのモザイクには平面群の17種のすべてがあるという説と1種類欠けているという都市伝説があります.
どちらでしょうか?それとも....? 実際にアルハンブラには行って調べて見たいものです.
ペンローズ・タイリングを発見したペンローズも,アルハンブラのタイルからヒントを得たと聞きます.
エッシャーの周期的版画の原点はアルハンブラのモザイク・タイルにあります.
私も,局所的に高い対称性の星型ロゼットをちりばめた,あたかも高次元宇宙からさす影を思わせる
イスラームのデザインに興味をもっています.
映画のエンドロールにスナップ映像が流れますが,その映像の一つに,大道絵師の光景が写りました.
2018年夏,たまたま行ったニューカッスルの通りで見かけた,エッシャー作品ばかり道に描いていた大道絵師のようです.
■エッシャー作品の生まれるまで
コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました.
1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り,
これがエッシャーの「極限としての円」の作品群を生むことになります.
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/a655be2fc4e933a93af15e269d8b684e?frame_id=54
極限としての円の数学については,以下のブログを参照ください.
http://sgk2005.saloon.jp/blogs/blog_entries/view/46/2e340c06148db50daae618a772629e15?frame_id=54
(参考)美しい幾何学,p142~143
STXM(走査型透過X線顕微鏡)は,有機材料の化学状態のマッピングができる重要な評価技術です.実験を計画されている方々のお役に立つように,私たちの過去の実験(2000年10月)を紹介しましょう.
■私たちは,1粒のトナーの中に練り込まれている有機物分子の分布状態を知る必要がありました.高精細のトナー1粒のサイズは5~10μmです.その1粒のトナー中には,種々の有機材料(レジン,ワックス,色素,電荷制御剤,など)の分子を練り込んでいます.それらの分子がどのように分布しているか観察したいものです.特徴的な元素を含む分子の分布をみることはさして困難な課題ではありません.蛍光X線を用いれば元素分布のマップを簡単に得ることができます.電子顕微鏡でもエネルギーロスEELSで見ることができます.しかし,トナーの場合は,分布しているのがすべて有機物(炭素原子Cが主体の分子)ですから,蛍光X線分析は役に立ちません.
分子内の炭素Cの結合状態の違いで有機材料を見分ける必要があります.分子のC原子の結合状態(1重結合か,2重結合が,π電子系か,どんな官能基が付いているか)で,炭素の1s電子の吸収端近傍のスペクトルの形がわずかにことなることが手掛かりです.炭素1s電子の吸収端は285eV程度ですので,この付近の吸収スペクトルは,軟X線領域(真空中で測定)になり,この実験のできる装置は,2000年当時は,Hitchcock(McMaster大)教授が,米国バークレイの放射光施設ALSに作ったBL5.3.2とBL7.0でした.エネルギー分解能0.1eV,ビームの空間分解能35nmという素晴らしい性能です(aXis2000という解析ソフトも完成していました).これを用いて2000年から数年間共同実験をしました.
(写真)左からDr. Araki,Dr. Kilcoyne,Dr. Hitchcock
吸収端のちょっと上の50eV~1000eV程度までの範囲に現れるスペクトをEXAFSといい,吸収原子周囲の配位構造の解析に使えることはご存じかもしれません.一方,吸収端近傍のせいぜい50eVまでは,XANESとかNEXAFSと呼ばれます.原子は吸収端のエネルギーを吸収して,光電子波を発しますが,吸収端近傍では電子波の持つエネルギーが小さく波長が長いため多重反射が起こり,周囲の配位原子に反射され吸収原子の位置に作る電場は非常に複雑なので,EXAFSのように配位構造の解析には使えません.しかし,吸収原子周囲の化学状態に特徴的な吸収スペクトルになり,分子を知る手がかり(指紋のような)になります.
■ここで初期の結果(2000年10月)を紹介しましょう.
2次元にスライスした試料の1点1点ごとに,Cの吸収端付近でX線の波長をスキャンすると,その点に存在する物質分子(一般的に,数種の分子が重畳されている)に特徴的な吸収端に対応して透過X線のコントラストが変化しますから,画面を見ていると物質の分布状態がわかります.上の写真では,エネルギーをスキャンしていくと,赤や青でマークした部分のコントラストが逆転したりして,違う物質が分布していることがわかります.
■用いる数学について
このデータ処理のための数学は特異値分解といいaXis2000で実行します.
X線のエネルギーEのときの,サンプルの点(x,y)のコントラストは,
Σμ_i(E)・t_i(E) ,iは分子の種類,μ_iとt_iは分子iの吸収率と存在量です.
各点(x,y)でΣμ_i・t_iのデータを測定しますが,1画面の測定ができると,エネルギーをΔEスキャンしまた画面の各点を測定するので,Eのステップ数分の各点(x,y)の吸収データが得られます.結局,各点(x,y)でスペクトルが得られたことになります.各点でi種類の分子をどのような比率で混ぜると観測したスペクトルと同じにできるかという問題を解くことになり特異値分解を用います.
研究のまとめは,トナー1粒内の立体的な分布の再現です.各スライス断面で測定し解析した分布を積み重ねて3D像を再現しました.
J.Phys.Ⅳ France 104(2003)509, A.P.Hitchcock, et al.
■ この装置のゾーンプレートの光学系の仕組みはとても面白いのですが,今回はここまでにします.
X線は光(電磁波)の仲間です.次の図をご覧ください.波長で言うと左の長い方にはラジオ波,マイクロ波,などの電波があります.われわれの目に見える可視光線はvisibleと記載したほんのわずかな領域です.波長がさらに短くなっていくと,ultrvaiolet,softXrays,hardXraysの領域になります.
さて,X線を集光する凸レンズは作れません.その理由は,X線に対する物質の屈折率(n=1-δ-iβ)が,真空中(n=1)とほとんど同じ[わずかに1より小さい(δ~10^-6,従って,n≒1)]だからです.
物質による電磁波の散乱現象は,電場中に置かれた物質中の電子(それぞれの原子核に束縛されて存在)が,電場と同じ周波数で振動子し,振動する双極子(原子核と電子)から同じ周波数の電磁波が放射されることです.
原子核に束縛されながら振動している電子の周波数(原子の種類jにより固有の値)ω_jが,入射した電波の周波数ωに比べて,可視光線の場合はω<<ω_j,X線領域ではω_j<<ωの違いがあり,これが,物質の光に対する屈折率が1より大きく,X線に対する屈折率が1より小さく(ほとんど1)なる原因です.
■X線に対する物質の屈折率はほとんど1でしたから,物資に入射したX線は屈折せず直進します.しかし,物質の屈折率が,1より小さいので,物質表面で全反射させることはできます.これを利用して,X線を集光する反射光学系がいろいろ作られています.
■もう一つのX線を集光する素子はゾーンプレート
2種類のX線顕微鏡の光学系を上に掲載しました.トロイダル・ミラーやシュワルツシルト光学系が使われる例と,ゾーンプレートが使われる例です.
Hichcock教授のSTXMでもゾーンプレートが用いられています.
以下で,ゾーンプレートの仕組みを解説します.ゾーンプレートは光に対しても,X線にたいしても効果がありますが,光源は単色光(波長λ)である必要があります.
ゾーンプレートは,下図のような同心の輪帯環よりなります.図の黒い輪帯環はX線をストップする金属膜がある輪帯環で,白い輪帯環はX線が通過できる輪帯環です.ゾーンプレート前面に入射するX線は,単色(波長λ)である必要があります.最初の白い輪帯環を通過したX線と,次の白い輪帯環を通過したX線の行路差は,焦点位置でちょうど波長分λだけ異なるようします.他の白い輪帯環でも同様で,すべての白い輪帯環を通り抜けたX線は,焦点までの行路で波長λの整数倍だけずれるようにするので,焦点位置で位相が全部そろい強め合います.こうして,単色(波長λ)のX線が焦点に集光できることになります.
■10回(5回)対称のタイルを周期的に並べる
10回(5回)対称は,周期的に並ぶことができません.周期的に並べることが可能な回転対称軸は,2回,3回,4回,6回対称に限られます.
10回(5回)対称タイルを周期的に配列したイスラームの繰り返しパターンを調べましょう.もちろん,5回対称軸が周期的に並んでいるはずはありませんので,自然に並べるのにうまい工夫があるはずです.このようなパターンはイスラームに特徴的で,ジャーミイのいろいろな所で見かけます.
10回(5回)対称は周期性と矛盾しますから,それぞれの10回(5回)対称が支配するのはタイルの内部だけです.
このタイルの描き方を習得するのにだいぶ工夫をしました.
作図手順の足跡として,赤色の作図補助線を残しておきましたから,
皆さんも工夫してこの図を描いてみてください.
まず,中心にある円の円周を10等分することから始めます.
円周の10等分は中心角が36°の作図で,前回に正五角形(中心角72°)の作図をやりましたから,それを応用して円周の10等分を作図してください.
この長方形のタイルが単位胞になり,これを並べることにより繰り返しパターンが作れます.
この繰り返しパターンの平面群はP2mmです.
10mmという対称性の高い部分(正10角形)があります.もし,そのような対称性が全域に作用するなら,繰り返し(周期性)ができるわけがありません.10mmという点群の作用はそれぞれの赤い円内の領域に限られるので,周期性と両立できるのです.このようなイスラーム・パターンは色々な所に見受けられます.
次に,この繰り返しパターンを3つの部品によるタイル貼りと解釈してみましょう.つまり,図に示したように正10角形タイルと,ピンクのタイルと黄緑色のタイルの3種類です.
今日は,この3種類のタイルで平面が隙間なくタイル貼りされていることを確認してください.
■応用例
周期的な2次元平面では,互いに独立な並進ベクトルを2方向とれます.
これら2本の並進ベクトルが挟む平行4辺形を単位胞といいます.
並進ベクトルの組み(単位胞の形)を対称性で分類したものがブラベー格子です.
2次元のブラベー格子には,図に示す5種類があります.
そして,それぞれに対応する格子の図も掲載しておきました.
■さて,以下に伝統文様を10種挙げました.
図中に赤色ベクトルで,並進の周期を描き込んであります.
図中に描き込んだ並進ベクトルの位置はいろいろ可能で,図示したものは一例です.赤色ベクトルの選び方もいろいろ可能ですが,
単位胞の形(赤色ベクトルで囲まれた平行4辺形)が
(A)正方形,(B)長方形,(C)120°の菱形,(D)任意角度の菱形,
の4種類のどれかにあてはめるようにとれます.
2次元のブラベー格子の5種類のうち,(E)一般形の平行4辺形に属する伝統文様は,ここの例には挙げていません.
Q.それぞれの伝統文様は,A,B,C,Dのどのタイプに属するでしょうか.
詳しくは,美しい幾何学,p86~88
X線に対する物質の屈折率が$$n<1$$になること
古典的原子モデル(原子核を中心に電子が公転している)を考え,
Lorentz振動子モデル(原子核+と電子ーが互いに束縛されて振動している)を適用する.
X線電場により,原子核に束縛された電子が振動する運動方程式:
電子の電荷:$$-q$$, X線電場: $$E=E_{0}exp\left( i\omega t \right) $$
$$\ddot{r}=-\mit\Gamma \dot{r}-\omega _{0}^{2}r+\left( \displaystyle \frac{-q}{m} \right) E_{0}exp\left( i\omega t \right) $$
$$r=\displaystyle \frac{(q/m)}{\omega ^{2}-\omega ^{2}_{0}-i\mit\Gamma \omega }E_{0}exp\left( i\omega t \right) $$
分極$$P$$,分極率$$\chi ,j$$は電子の番号(単位体積に$$N$$個あるとする)
$$P \equiv \chi E=(-q)\displaystyle \sum_{unit vol}^{N}r_{j}=-\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{unit vol}^{N}f_{j}E_{0}exp\left( i\omega t \right) $$
ただし,
$$f_{j}=\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega _{0j}^{2}-i\mit\Gamma _{j}\omega }=\displaystyle \frac{\omega ^{2}\left( \omega ^{2}-\omega _{0j}^{2} \right) }{\left( \omega ^{2}-\omega _{0j}^{2} \right) ^{2}+\mit\Gamma _{j}^{2}\omega ^{2 } }+\displaystyle \frac{\mit\Gamma _{j}\omega ^{3 } }{\left( \omega ^{2}-\omega _{0j}^{2} \right) ^{2}+\mit\Gamma _{j}^{2}\omega ^{2 } }i$$
原子散乱因子(atomic scattering factor)の定義:
$$a$$原子の原子散乱因子$$f$$とは,$$a$$原子に属する$$n$$個の電子に対して$$f_{j}$$を総和したものである.
$$f=\displaystyle \sum_{an atom}^{n}f_{j}=f_{0}+\mit\Delta f ' +i\mit\Delta f '' $$
$$f_{0}$$は,原子中の電子数$$n$$(原子番号);$$\mit\Delta f ' $$,$$\mit\Delta f '' $$は,異常分散項という.
マクロな光学定数の定義: 屈折率$$n$$,誘電率$$\varepsilon $$,分極率$$\chi $$
$$n=(1-\delta )-i\beta $$, $$\delta , \beta \sim 10^{-6}$$, $$\delta ( \sim 10^{-6}) \propto N$$
$$\varepsilon =\varepsilon _{1}+i\varepsilon _{2}$$
$$D=\varepsilon E=E+4\pi P=\left[ 1+4\pi \chi \right] E$$
$$\varepsilon =n^{2} \approx (1-2\delta )-2i\beta $$
$$\chi =-\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{unit vol}^{N}f_{j}$$
原子内の電子はそれぞれの$$\mit\Gamma _{j}(\omega ), \omega _{0j}(\omega )$$を持ち,$$\omega _{0j}<<\omega $$の電磁場追従ではそれぞれの位相遅れを生じる[特に,原子核に強く束縛されるK殻電子は顕著].これが$$\omega \approx \omega _{0j}$$近傍で,”異常分散”を起こす.$$j$$個の電子は吸収端の振動数$$\omega _{0j}$$から高振動数側に分布する多数の振動子の集まりと見なせる.
(1)$$\omega <<\omega _{0}$$ 光と物質
$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{in unit vol}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega ^{2}_{0j}-i\mit\Gamma _{j}\omega } \cong 1+4\pi \displaystyle \sum_{in unit vol}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega _{0j}^{2 } } \right) $$
$$n \approx 1+2\pi \displaystyle \sum_{in unit vol}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega _{0j}^{2 } } \right) >1$$
(2)$$\omega _{0}<<\omega $$ X線と物質
$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{in unit vol}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega ^{2}_{0j}-i\mit\Gamma _{j}\omega } \cong 1-4\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) $$
$$n \approx 1-2\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) <1$$ $$N$$: (電子数 $$ \textrm{in unit volume)=} $$電子密度
単位体積中の電子数 $$N$$
Fig. X線電場により,原子核に束縛された電子が振動する.
振動ゆらぎ分だけ分極し双極子が生じる.
異なる媒質間の界面をよぎつて進行する電磁波は,運動量保存則が成り立たない.運動量保存則は,一様な媒質中で成り立つからである.この場合,運動量の界面接線成分は保存されるが,界面法線成分は変化する.このため,界面で屈折が起こる.屈折の法則とは,運動量の界面接線成分の保存の表現である:
$$p_{0t}=p_{1t}$$ → $$p_{0}cos\theta _{0}=p_{1}cos\theta _{1}$$
X線で用いる入射角(grazing angle)$$\theta _{0}$$,屈折角$$\theta _{1}$$の定義は,それぞれ,界面と光線のなす角である[光学で,一般に用いられているのは,”界面の法線”と光線のなす角なので,特に注意を要する].
$$n_{1} \equiv \displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{cos\theta _{0 } }{cos\theta _{1 } }$$
物質1の屈折率は,真空に対するものとして定義され: \\
$$n_{1}=\displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{\lambda _{0 } }{\lambda _{1 } }=\displaystyle \frac{c}{v_{1 } }$$
$$v_{1}=\displaystyle \frac{c}{n_{1 } }$$であることがわかる.$$v_{1}$$は,物質1中の電磁波の位相速度.
$$E=E_{0}exp\left[ i\left( \omega t-2\pi kz \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{2\pi k}{\omega }z \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{n}{c}z \right) \right] $$
$$n$$を複素数にすると:$$n=(1-\delta )-i\beta $$
$$E=E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{1-\delta }{c}z \right) \right] exp\left( -\displaystyle \frac{\omega \beta }{c}z \right) $$
$$\displaystyle \frac{\left| E \right| ^{2 } }{\left| E_{0} \right| ^{2 } } \equiv exp\left( -\mu z \right) =exp\left( -\displaystyle \frac{2\omega \beta }{c}z \right) $$
1)虚数部$$-\beta $$は,線吸収係数$$\mu $$に比例:
$$\mu =\displaystyle \frac{2\omega \beta }{c}=\displaystyle \frac{4\pi \beta }{\lambda }$$ $$ln\displaystyle \frac{\left| E_{0} \right| ^{2 } }{\left| E \right| ^{2 } }=\mu z$$ をoptical density という.
2)実数部$$1-\delta $$は,位相速度$$v$$と関係がある.$$\delta $$が正で大きくなれば,位相速度は増加:
$$v \equiv \displaystyle \frac{\omega }{2\pi k}=\displaystyle \frac{c}{1-\delta }$$
漫画が面白いので,問題を訳してみました.問題3は難しいです.
■空間的な想像力を練習してみませんか?
数学,プログラミング,物理学など,科学技術のさまざまな分野で役立ちます.
ステレオメトリ(空間幾何学)の知識がなくても解決できるいくつかの問題を次に示します.
1.平面で立方体をカットして,切り口が3角形や4角形にするのは簡単です(図参照).
切り口が正6角形になるようなカットの仕方を描きなさい.
2.立方体「キューブ」は3×3×3個の単位立方体からできています.
次のものを描きなさい;
a)中央の立方体と中央の立方体と共通の面を持つ立方体で構成される「ハリネズミ」.
[(訳注)「ハリネズミ」とは,中央の立方体に面でくっついている立方体を含む立体の形と解釈します.エッジだけではない]
b)角の立方体を取り除いたときの「ハリネズミ」.
c)「キューブ」から「ハリネズミ」を削除するとどうなりますか.
3.問2のばらばらの「ハリネズミ」で空間全体を埋めることは可能ですか?
4.四面体のそれぞれの面ごとに,面に平行な2つの平面を描きます.これらの平面は四面体をいくつの部分に分割しますか?
ロビンソンは,円形の無人島に流れ着きました.ロビンソンが海岸の小屋を出て,西に3 km,南に4 km移動した後,彼は海岸に出ました(その日は小屋に戻りました.).翌日は,ロビンソンは小屋を出て南西に10 km行くと海岸に出ました.1日後,ロビンソンは海岸沿いに島を一周することにしました.彼が歩く一周の距離はどのくらいありますか?
A.約16 km
B.約31 km
C.約63 km
D.約113 km
E.正解は異なります。
■解答です.図を描いて考えましょう.
最初の日は,AからBに行きます.(その日はまたAに戻ります)次の日は,AからCに行きます.A,B,Cは海岸にある点ですから,この3点を通る円の中心を求めれば円の半径rがわかり,島の全周囲は2πrとなります.
解答は,Dです.
この問題で紛らわしいのは,最初の日はAの小屋にもどると書いていないところです.(小屋にもどる)というのは私が補足しました.次の日の出発点をBとすると,非常に大きな円になります.半径51kmで全円周320kmになります.無人島の探検なのだから,小屋はAしかないのでしょうが,紛らわしいのではっきり出発点に戻ることを書いてほしかったです.
この問題は作図で解くのが良いと思いますが,座標を用いて計算で解くこともできます.西,南の方向を+にした座標で書くと,A(0,0),B(3,4),C(10/√2,10/√2)で,円の中心(a,b),半径rの円の方程式(x-a)^2+(y-b)^2=r^2
に,A,B,Cの座標を入れた3つの式を連立させて解き,半径rを知ればよいのです.