--研究したのはガロワと同級生だったこともあるブラベーBravais(1848)--
■ 周期(デジタル化で生じる),格子,並進群
2次元世界では,互いに独立な2つの基本並進ベクトルが採れます.これを$$a, b$$(両者の長さが同じときは$$a_1,a_2$$と書く)としましょう.
$$a,b$$の整数係数の1次結合をすべて集めた $$ T={h・a+k・b| h,kは整数} $$を,
この平面の格子点の集合(あるいは単に“格子”)といいます.
集合$$T$$は無限集合になりますが, 群の条件を満たしており,$$T$$を並進群とも呼びます.格子を発生させる源となった$$a,b$$の組みの対称性で,格子のタイプが分類できます.これを研究したのはブラベーBravaisで,3次元のブラベ格子は14種であることを数え上げました(1848年).
ブラべ格子とは,結晶点群の対称性を基準に,格子のタイプ分類をしたもの2次元のブラベー格子は5種類,3次元では14種類,4次元では64種類あります.今回のシリーズでは,よく理解できることを優先し,すべて2次元世界に限定して話を進めています.
■ 図の見方
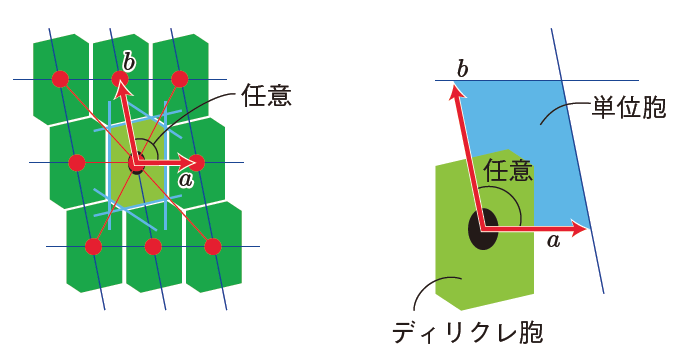
格子点●が並んでいます.この格子は,ベクトルa,bの一次結合で生じます.
格子点の1つを原点にし,自分に隣接する格子点と結び,それを垂直2等分する線で囲まれた領域をディリクレ胞(あるいは,ウイグナー=ザイツ胞)などと呼びます.ディリクレ胞タイルの形は,このタイルで平面を隙間なく埋め尽くせる形です.格子の対称性は,ディリクレ胞タイルの形に反映されています.ディリクレ胞は格子点をただ1つ含みます.単位胞というのは,並進の基本ベクトルa, bで囲まれた平行4辺形のことで,格子点を1つ含む単位胞は(one point cell)と呼ばれ,この場合は単純格子pになります.複数の格子点を含む単位胞は(multi point cell)で,複合格子(体心格子I,面心格子F,C面心格子C,A面心格子Aなどが3次元以上で出現)になります.2次元世界では,面心(or体心)格子(私はここで”菱形格子”と名付けました)だけが複合格子です.複合格子というものは,図形の特徴を見やすくするためだけのものなので,複合格子(multi point cell)をいっさい用いず,単位胞の格子(one point cell)だけで統一することもできます.
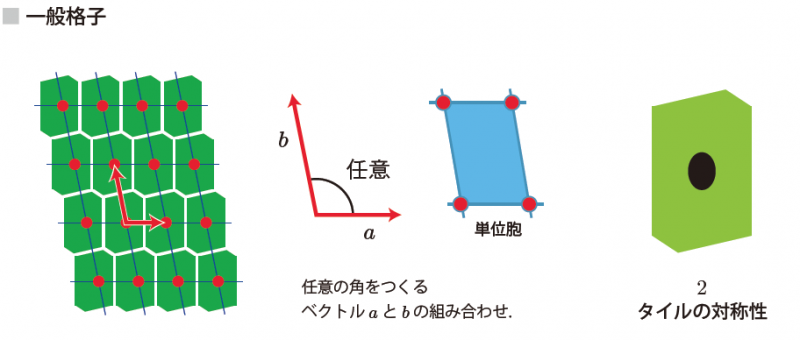
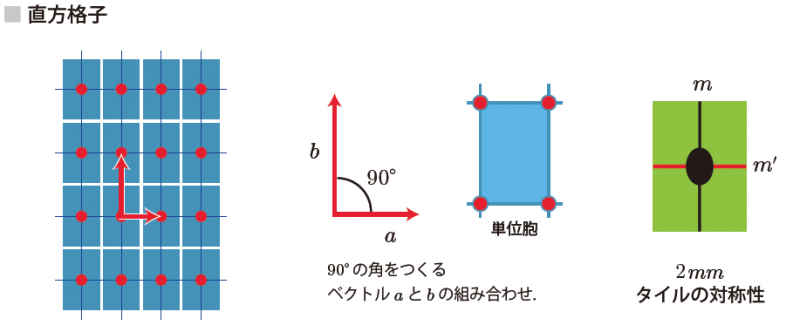
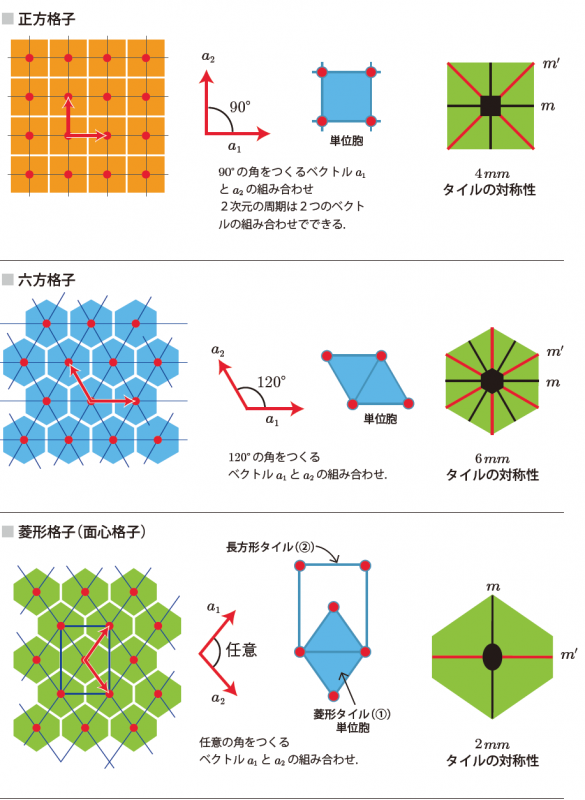
■5つの2次元ブラベー格子
美しい幾何学,p50~51, p54~55