ジョゼフ゠ルイ・ラグランジュ(1736年 - 1813年);数学者,物理学者,天文学者は,オイラーの弟子で,フランス革命の前後の時代を生きた.
彼は,微分積分学を物理学へ適用し,最小作用の原理,解析力学を創出した.
ラグランジュによる『解析力学』は,ラプラスの『天体力学』と共に18世紀末の古典的名著とされる.
最小作用の原理の起源といえば,1696年のスイスの数学者ヨハン・ベルヌーイの「最速降下曲線」問題に言及せねばなりませんが,そのトピックは以下でご覧ください:
https://note.com/sgk2005/n/n7b4803b9a981
■ 変分原理
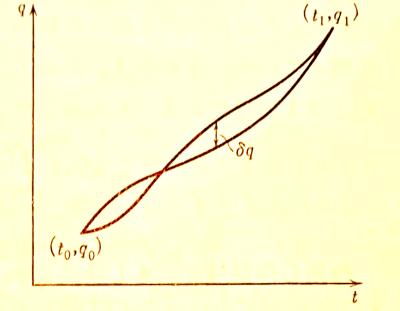
始点$${(t_0, q_0)}$$と終点$${(t_1, q_1)}$$に対し,この2点を結ぶ2つの道筋が図示されている.2つの道筋は始点と終点では一致している.同一時間における道筋の差$${\delta q}$$を変分という.
ラグランジュ関数$${L(q, \dot{q}, t)}$$ として,$${S=\int_{t_0}^{t_1}L(q,\dot{q},t)dt}$$ をラグランジュ関数$${L}$$の作用という.$${L}$$の変分は
$${\delta L=\frac{\partial L}{\partial q}\delta q+\frac{\partial L}{\partial \dot{q } }\delta \dot{q}=\frac{d}{dt}(\frac{\partial L}{\partial\dot{q } }\delta q)+\delta q(\frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial\dot{q } })}$$
$${\delta S=\int_{t_0}^{t_1}\delta q(\frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial\dot{q } })dt}$$
現実に起こる運動はラグランジュの方程式を満たすので,変分は0で作用は停留値をとる.
$${\displaystyle \frac{d}{dt}\displaystyle \frac{ \partial L}{ \partial \dot{q}_{\alpha } }-\displaystyle \frac{ \partial L}{ \partial q_{\alpha } }=0}$$
Lagrangeラグランジュの方程式
$${L(\dot{q}_{\alpha } , q_{\alpha }, t)=T-U}$$
Lagrange関数(系の運動エネルギーと位置エネルギーの差)$${\dot{q}, q}$$は一般座標での速度と位置
ラグランジュの方程式から,ニュートンの方程式を導くことができるが,複雑な系でもラグランジュ関数を書き下すことは容易なので,広範に応用できる.
Lagrange関数から色々な力学量を導くこともできる.
例えば,系の全エネルギーは$${E=\dot{q}_{\alpha}\frac{\partial L}{\partial \dot{q}_{\alpha } }-L=T+U}$$
中心力場で角運動量を求めたり,軌道を決定したりできる.
ニュートンの運動方程式がケプラーの法則と一致することも示せる.
量子力学への移行では,エネルギー(ハミルトン演算子)$${E=\frac{p^2}{2m}+U}$$で,運動量演算子の置き換え$${p→ \frac{h}{2\pi i}▽}$$ をして,ハミルトン演算子$${H}$$を作ったことを記憶しているだろう.
$${H=-\frac{(h/2\pi)^2}{2m}+U}$$
■最小作用(停留値)の原理
ある力学系でLagrange 関数$${L(q, \dot{q}, t)}$$が与えられたとする.
$${S=\int_{t_0}^{t_1} L(q, \dot{q}, t)dt}$$をその系の作用という.
モーペルテュイは,「始状態から終状態への運動経路には,作用と呼ばれる 量が定義でき,作用が最小となる経路が実現される.これが物理学のみならず,万物の運命を決める外界の原理である」という着想ーーー”最小作用の原理”(1744)を得た.モーペルテュイは,1744年に光学現象(光の直進・反射・屈折)に即してこの原理を述べた.
たしかに,現実の運動では,しばしば作用が極小になるものが見られるが,正確には,「作用が停留値をとる経路が実現する」というのが正しいことが後にわかる.適当な作用を見つければ万物の運命が分るというのは神秘的だが魅力的な着想ではある.
オイラーは,モーペルテュイの作用量の定義を積分に拡張し,最小作用の原理をさまざまな力学課題に適用できるようにし,最大または最小の性質をも つ経路曲線を見出す方法を発表した(1744). これを読んだ若き日のラグランジュは変分法を発明し,オイラーに手紙(1755)を送った.オイラーは,ラグランジュの方法を採用し,『変分法の原理』 (1766)を出版する.
変分法により導かれる運動方程式が,オイラー=ラグランジュ方程式といわれる所以だ.
その後,ラグランジュは,『解析力学』(1788)を出版する.その序文に「 本書には図はーつも出てこな い.・・・・所定の手続きに従い進める代数計算だけだ.・・・・」と高らかに宜言する.こうして,複雑な力学問題も解ける一般化された手法が確立された.
力学系を記述するラグランジュ関数を求め,ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと,オイラー=ラグランジュ方程式が得られる.
系のラグランジュ関数は,$${L(q, \dot{q}, t)=T-U}$$,ここで,
$${T, U}$$はそれぞれ,運動エネルギー,位置エネルギーである.
普通,位置エネルギーは座標$${q}$$だけの関数だが,複雑な系では,位置エネルギーも速度$${\dot{q } }$$に依存することもある.
ラグランジュ関数は,電磁場に置かれた荷電粒子にも定義され,光(電磁力学)も力学も統一して扱える原理ができた.
変分原理から,ニュートンの運動方程式は導出できる.その上,変分原理は,ニュートン力学より一般化された外界の原理である.20世紀に入り,量子力学が誕生した時もこの原理が手掛かりになった.光や物体の運動が,作用積分を停留化する経路を選択するというのは不思議といえば不思議,当然といえば当然だ.