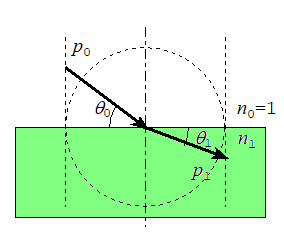
異なる媒質間の界面をよぎつて進行する電磁波は,運動量保存則が成り立たない.運動量保存則は,一様な媒質中で成り立つからである.この場合,運動量の界面接線成分は保存されるが,界面法線成分は変化する.このため,界面で屈折が起こる.屈折の法則とは,運動量の界面接線成分の保存の表現である:
$$p_{0t}=p_{1t}$$ → $$p_{0}cos\theta _{0}=p_{1}cos\theta _{1}$$
X線で用いる入射角(grazing angle)$$\theta _{0}$$,屈折角$$\theta _{1}$$の定義は,それぞれ,界面と光線のなす角である[光学で,一般に用いられているのは,”界面の法線”と光線のなす角なので,特に注意を要する].
$$n_{1} \equiv \displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{cos\theta _{0 } }{cos\theta _{1 } }$$
物質1の屈折率は,真空に対するものとして定義され: \\
$$n_{1}=\displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{\lambda _{0 } }{\lambda _{1 } }=\displaystyle \frac{c}{v_{1 } }$$
$$v_{1}=\displaystyle \frac{c}{n_{1 } }$$であることがわかる.$$v_{1}$$は,物質1中の電磁波の位相速度.
$$E=E_{0}exp\left[ i\left( \omega t-2\pi kz \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{2\pi k}{\omega }z \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{n}{c}z \right) \right] $$
$$n$$を複素数にすると:$$n=(1-\delta )-i\beta $$
$$E=E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{1-\delta }{c}z \right) \right] exp\left( -\displaystyle \frac{\omega \beta }{c}z \right) $$
$$\displaystyle \frac{\left| E \right| ^{2 } }{\left| E_{0} \right| ^{2 } } \equiv exp\left( -\mu z \right) =exp\left( -\displaystyle \frac{2\omega \beta }{c}z \right) $$
1)虚数部$$-\beta $$は,線吸収係数$$\mu $$に比例:
$$\mu =\displaystyle \frac{2\omega \beta }{c}=\displaystyle \frac{4\pi \beta }{\lambda }$$ $$ln\displaystyle \frac{\left| E_{0} \right| ^{2 } }{\left| E \right| ^{2 } }=\mu z$$ をoptical density という.
2)実数部$$1-\delta $$は,位相速度$$v$$と関係がある.$$\delta $$が正で大きくなれば,位相速度は増加:
$$v \equiv \displaystyle \frac{\omega }{2\pi k}=\displaystyle \frac{c}{1-\delta }$$