これはオーボールという赤ちゃんのおもちゃです.球の表面は互いに接する大きい円20個と小さい円12個でできています.円を正多角形にすれば,いわゆるサッカーボールの形です.つまり,小さい円は正5角形,大きい円は正6角形に対応します.
(問)大きい円と小さい円の半径の比は?
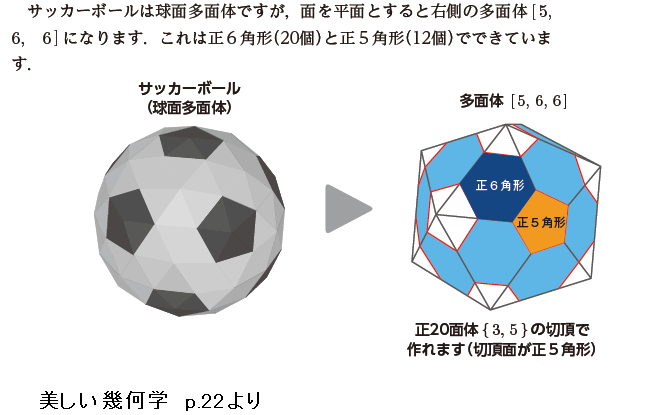
球面多面体の正多角形の辺は球の大円でできていますが,多面体の正多角形の辺は直線でできています.この多面体の1つの頂点の周りには,正5角形,正6角形,正6角形が集まっています.このような多面体は[5,6,6](シュレーフリの表記法)と記述します.正3角形の面だけが頂点で5つ集まっているのは正20面体で{3,5}と記述します.正20面体の頂点を切って(切り口は図の白い面),残りの面が正6角形になるようにすると,多面体[5,6,6]が得られます.
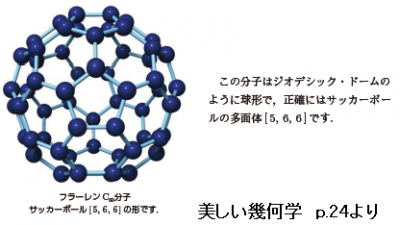
これは,上図のC60[フラーレン(60個の炭素原子からなる)分子.青球は炭素原子C]と同じ形です.
■さて,問の答えですが,オーボールの大きい円と小さい円は,フラーレンの正6角形と正5角形に対応することがわかります.
下図を見てください.
辺の長さの等しい正5角形と正6角形の外接円(内接円)半径比が答えです.計算すると 1:1/2sin36°≒1.176:1
■次の図に示す「組み合わさった立体」は,正20面体(水色)と正12面体(黄色)が組み合わさっています.それぞれの多面体のサイズは,辺の中央でちょうど重なるようにしました.入り組んで組み合わされている多面体は,正20面体{3,5}と正12面体{5,3}です.これらの正多面体は互いに双対です.
(注){3,5}←→{5,3}のように,面の形と頂点に集まる数を入れ替えると,”互いに双対”な多面体が得られます.
サッカーボールもオーボールも,正20面体由来の正6角形(正3角形)の面と正12面体由来の正5角形の面からできています.サッカーボールの面に対応する頂点をもつ双対な多面体を作ると菱形30面体が得られます.
(注)正5角形の面に対応する頂点間と正6角形の面に対応する頂点間が,それぞれ菱形面の対角線になります.
下図の「組み合わさった多面体」で,黄色い頂点と水色の頂点を結ぶと菱形30面体が得られます.
菱形面の1つを赤い線で図に記入しました.この菱形面の対角線比は黄金比です.