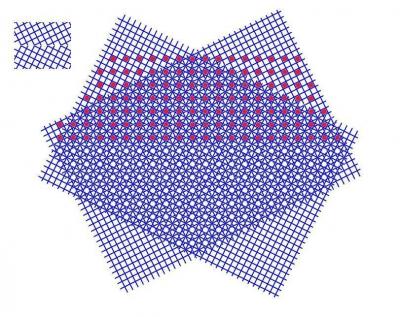
同じ正3角形(正6角形)格子[あるいは,正3角形2つよりなる平行4辺形格子とみてもよい]のパンチングメタルを2枚重ね合わせました.
この図の状態は,2枚の格子どうしのなす角度が2θ=30°になった場合です.初めの正3角形(正6角形)の格子より大きな新しい周期の格子が出現しているのがわかりますか.
■正方形格子(網目)を2枚重ねた場合を考察してみましょう.
(Coincidence-site-lattice)
両方の網目が重なった位置に,新しい網目の格子が見えて美しい.
2枚の正方形の格子(正方格子という)どうしの傾きを変えると,ときどきこのような新しい格子が現れます.もとの格子の互いに直角な2つの並進ベクトルをa,bとすると(正方格子ならa=b),
もとの格子は,格子点 na+mb,(n,mは任意の整数)の集合です.
同じ正方格子を2枚傾けて重ねて,新しい周期の2つの並進ベクトル x, yが生じています.これらの図の状態は,
(上図)x=2a+b,y=a+2b .(下図)x=3a+b,y=a+3b(面心格子,2格子点胞)
この基底変換を行列で書き,行列式を求めると3(左図),8(右図)ですので,新しくできた格子はもとの格子と比べて面積で3倍(左図),8倍(右図)粗くなっていることがわかります.
格子というのは,並進ベクトルの作る群=並進群の”図的表現”です.2枚の格子の干渉で生じた新しい格子の周期は,もとの格子の粗いサンプリングになっているわけで,新しい格子は,もとの格子の部分群になります.
格子が重なって,拡大された(粗い)格子が見える現象は,干渉(ビート)と同じことです.
実際に,2つの原子網面が重なって,このようなビートが見えることは,電子顕微鏡で格子像の観察をするときにもよく起こります.
結晶は周期的な構造をしているので,周期的な空間は「結晶空間」とも呼ばれます.エッシャーの繰り返し模様や,壁紙模様などで,周期的空間の実例をたくさん目にしていると思います.
■2つの正方格子の平行なずれによる干渉(モワレ縞)
それぞれの正方格子の周期をλ1,λ2とすると,新しい周期Lは
1/L=1/λ1−1/λ2 の関係があります.
私は,子供のころ家にあった織物検査器というもので遊んだことがあります.これは,標準となる格子模様がガラスに刻んであり,織物にこのガラスを重ねると繊維の周期とのビートで縞模様が観察できます.1mmの中に何本繊維があるかとか,織り方が均一でなくどの程度乱れているかが,モアレ縞からわかります.
次の写真は,工事現場のネットが折り返されて2重になっているために観察されるモアレ縞です.