今年(2020年)のとっとりサイエンスワールドは,新型コロナウイルスのために残念ながら中止になりました.
2017年のとっとりサイエンスワールドin倉吉は,8月27日に開催されました.1,250人の来訪者があり,例年のように盛況でした.万華鏡ワークショップは30人クラスを4回実施し120人が作りました.2016年は,鳥取サイエンスワールドの終わった直後,翌々日に倉吉地震がありびっくりしました.多くの方が避難生活をし,サイエンスワールドの会場だった梨っこ館もガラス天井が落ちたそうです.隣のプールは2017年7月20日になってやっと利用開始にこぎつけました.白壁土蔵群,赤瓦館でも地震の被害がありました.
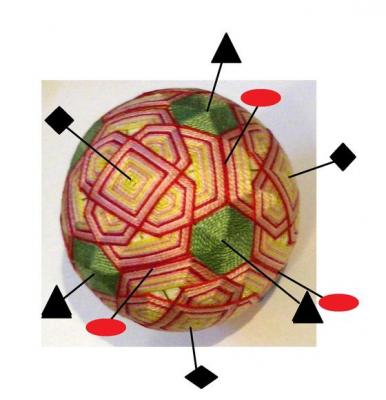
2017年に,その赤瓦二号館を訪れたとき見つけた御殿まりの写真です.
これらはみんな一人のご婦人が作ったものだそうです.お会いしたいものでしたが,残念ながら不在でした.
どれも美しく良いできですね.
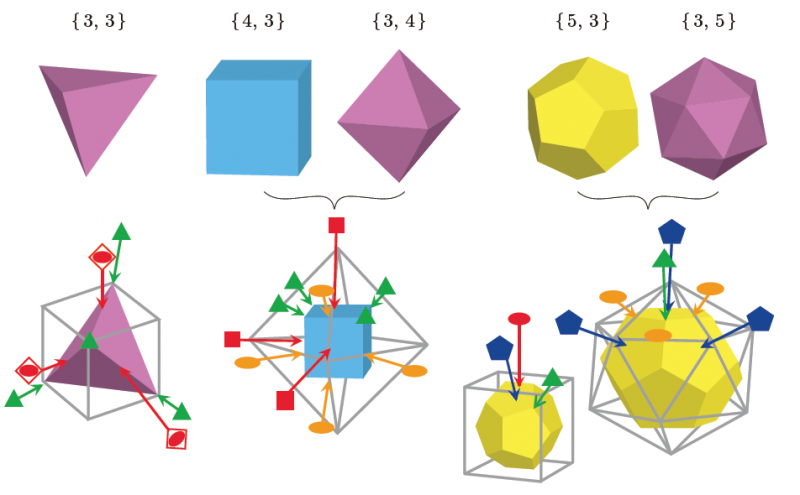
正4面体群:正6面体群(正8面体群):正12面体群(正20面体群)のどれがあるでしょうか?
Q1:さて私は,正6面体群(正8面体群)と正12面体群(正20面体群)のうちのどちらを選んだでしょう?
私が選んだのは,前者の方でした.
参考に,これと同じ対称性の図形を掲載しましょう.
これらはともに,半正多面体[4,6.6]ですが,立方体のx,y,zの方向に,4回軸があり,体対角線の方向に3回軸があります.2回軸のある方向も確認してください.(注)シュレーフリの記号[4,6,6]は,頂点の周りに正4角形,正6角形,正6角形が集まっていることを示しています.
結局,これらは皆,球面正6面体{4,3}や正8面体{3,4}と同じ対称性(点群)になります.(注){4,3}もシュレーフリの記号と呼ばれますが,正4角形が頂点に3つ集まっていることを示しています.
Q2: 球面正12面体{5,3}や菱形30面体の御殿まりを見つけましょう.このなかにありますか?
これらの対称性(点群)は,正12面体やその双対の正20面体と同じです.
一番下の立体の形は,菱形30面体です.菱形30面体は,12・20面体(半正多面体[3,5,3,5])と双対な多面体なので,対称性としては,上の3つの立体はすべて同じです.
別項目・サッカーボール(フラーレン)に関連記事があります.
Q3: この他に,半正多面体[6,3,6,3]があります.探してみましょう.
ーーーーーーーーーー
美しい幾何学,p21,p46,p48 が関連します.ご参照ください