システム管理者
「群」や「体」などの数学概念は，ガロアが５次以上の方程式には代数的な解法が存在しないものがあることを証明する過程で生み出されました．
２次，３次，４次の有理数を係数とする（有理数体上の）多項式方程式には解の公式［係数の四則演算とベキ根で表現される］が必ず存在するが，５次以上の方程式には代数的に解けないものがあることをガロアが証明しました．
ガロア（1811～1832年）は短い悲劇的な生涯でしたが，「群」，「体」などの新しい数学概念を生み出しました［このことが認識されるのは死後40年も経過してからでした］．
「群」や「体」の概念を用いると，以下のような古典的な問題の証明を，新しい観点から理解することができます．
（１）ギリシャ時代の３大不可能作図
ギリシャの幾何学者たちが研究した３つの作図不可能問題：
①デロス島のアポロンの祭壇(立方体)を倍積に
一辺１の立方体に対してちょうど2倍の体積の立方体を作る．
1 → $${\sqrt[3]{2 } }$$ の長さの作図
②円を同じ面積の正方形に
円の半径1 → 正方形の一辺$${\sqrt{\pi } }$$ の長さの作図
③任意の角度を3等分する
任意に与えられた$${a}$$に対して，3次方程式$${x^3-3x-a=0}$$
の$${x}$$を作図する．
ギリシャでは幾何学が基本で，数は線分の長さで表現します．
数直線は実数（有理数と無理数）で構成されています．
もちろん①～③の解は存在しますが，コンパスと直線定規だけを繰り返し用いて作図せよという問題です．
コンパスと直線定規で作図出来るのは，長さの加減乗除（四則演算），開平$${\sqrt{ } }$$のみで，これらの操作の繰り返しで作図できるものだけが可能です．
作図法は下図参照．
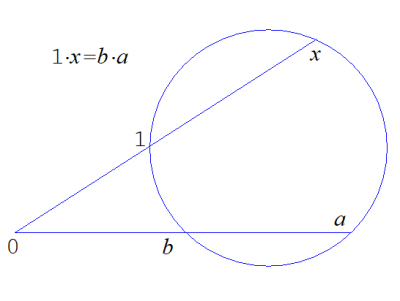
乗除は方べきの定理
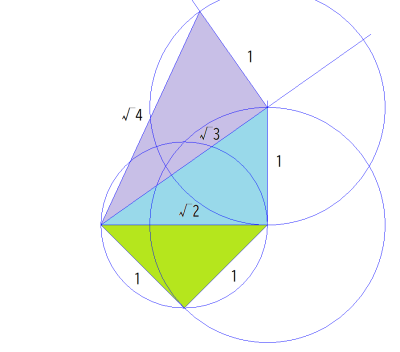
任意の整数の開平の作図
有理数体$${Q}$$の数字に加減乗除の操作を繰り返して得られる結果は同じ$${Q}$$の中にあります．作図条件に開平$${\sqrt{ } }$$の操作も許されますから，この結果は有理数の集合$${Q}$$からはみ出します．そこで，有理数体$${Q}$$を開平（平方根）$${\sqrt{ } }$$を加えて拡大した拡大体$${Q(\sqrt{})}$$を作れば，作図可能な数（長さ）はこの拡大体の中にあるはずです．つまり，立方根などはこの拡大体のなかにないので，立方根の作図は不可能とわかります．
①は立方根の作図だから不可能．
②は$${\pi}$$自体が超越数なので代数式の解ではなく作図できない．
③は$${a}$$の値により ［与えられた角度により］解$${x}$$が四則演算と開平で表現できることもあり，その場合は作図できる．例えば，90°の角に相当する$${a=0}$$の場合は，$${x=0, \sqrt{3}, -\sqrt{3 } }$$であるので作図できる．一般の3次方程式の解は立方根を含み作図できない．
この続きは次号へ
体の拡大 （２）ガロアの時代
明日7月22日は 数学月間懇話会（第21回）です。この問題にも少し触れます。案内は，https://sgk2005.org/ をご覧ください。