力学系を記述するラグランジュ方程式は作れるのだが,これが解けるとは限らない.
物理の演習では,解けるものしか扱わなかったのです.
実際の世の中は,解を関数で記述できない(解けない)方程式が大多数です.
系の運動を支配する法則(ニュートン力学の方程式)は明確なのに,解が関数で記述できないのだ.
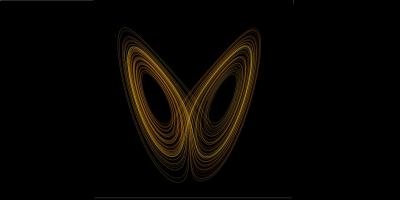
でも解は存在するのです.コンピュータによる数値計算により,運動は逐一決定できる.
しかも,予想もつかない挙動ーカオスーが起こる.このようなことを最初に指摘したのはポアンカレでした.
ーーーーーーーーーーーーーーーーーーー
●1766 オイラー「変分法の原理」
(オイラー, ラグランジュ)
●1800 ラグランジュ「解析力学」
エネルギー散逸がない系は,オイラー=ラグランジュ方程式が作れる.
(オイラー, ハミルトン, ヤコービ)
●1900 ポアンカレ
可積分の方程式はごくわずかで,大部分の方程式は非可積分(関数で記述できない)
ニュートンの法則に従う系の運動は,可積分と決めつけてはいけない.
可積分 → 予測可能(安定な軌道) 互いに独立な因果列
非可積分→ カオス的 干渉し合う因果列
ーーーーーーーーーーーーーーーーーーー
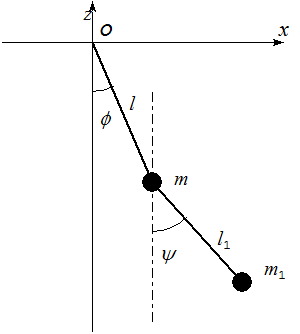
■2重振り子の例
上図のような2重振り子の運動です.今回は物理演習のようですが,
数式に囚われる必要はありません.重要なのは,振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので,2種類の周波数の振動が重畳
された運動になる.つまり,関数で記述できる安定な周期的な運動になる
という事です.そして,これに対比される次に話題になる振幅の大きい
2重振り子運動では,運動は関数で記述できず,予想もつかない
とんでもない運動をするということです.
(注)ここでは,ラグランジュ関数やラグランジュ方程式を説明せずに用いています.
これらを学習したい方は,EMANの物理学https://eman-physics.net/analytic/lagrange.html
などが参考になります.
2重振り子のラグランジュ関数は正確に作れます.
次に,ラグランジュ方程式を解かねばならないのだが,これが解析的には解けない(関数で記述できる解がない).
◆振幅の小さいとき
Φ,ψ の振動範囲を微小に制限して(Φ,ψの2次までを残す近似)解く.
これは解けます(物理の演習問題).
計算の詳細は以下に載せました.http://sgk2005.saloon.jp/blogs/blog_entries/view/46/ddf8d815a70840c192d0532618218407?frame_id=54
結論
ラグランジュ方程式(連立方程式)を微小振動の範囲とし線形近似したので,解のΦ,ψは,それぞれ2つの固有振動(基準振動)の重ね合わせになり,それほど複雑な振動ではない.いずれにしろ周期的な(予測できる)振動になります.
◆一般論(振幅の大きいとき)
振幅が大きくなると,ラグランジュ関数の線形近似がなり立たないので,ラグランジュ方程式は解析的には解けません.でも解は実在するはずです.
将来,誰かが巧妙な方法で解くのではないかと期待しつつ,得られたその解は,解析的ではないにしろ振動範囲が小な場合と本質的に大差はないのではないかと想像するのは自然なことです.
系のラグランジュ関数 は完全に正しいし,ラグランジュ方程式も正しいのですから,解析的に解けないと言っても心配ないのではと思うでしょう.
これが誤りであることを証明したのがポアンカレでした.
現代は,コンピュータを用いた計算が高度になり,力ずくで動きのシミュレーションがなされるようになりました.正しい方程式は実在するのですから,関数による軌道の記述は出来なくても,動きは逐一決定されるはずです.
しかし,初期条件(初期値)により,予想もつかない挙動が見られます(カオス).ともかく,そのような運動の実験とシミュレーションの例を,youtube動画で見てください.とんでもない現象が見られます.
◆第1の動画は実験
スタートする初期値によって運動の様子は異なります:
◆第2の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1