ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.03.07］ No.157
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
桜もずいぶん早く咲いているのを見かけますね．皆様のところでは如何でしょうか．
今回もダ・ビンチの星型を取り上げますが，「星型小12面体」とも呼ばれる形を見てみましょう．
イメージ 1
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_0_m?1488810835
シュレフリの記号で書くと｛5/2，5｝です．
（注）シュレフリの記号｛p,q｝というのは，
正p角形の面が，頂点でq個集まっているような正多面体を表す記号でした．
この形は，東京都庭園美術館，朝香宮邸，姫宮の部屋の照明器具にも使われている美しい形です．
芯になるのは正5角12面体で，その12個の正５角形の面の上に，それぞれ正5角錘を取り付けた形をしています．
正5角錐の頂点は，それぞれ，正12面体の面に対応していますから，
頂点を結んでできる図形（赤の多面体）は，正12面体に双対な正20面体です．
2次元の断面を見ると，以下の左図の様な星型正多角形（ダビデの星）が見えます．
イメージ 2
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_1_m?1488810835
上図の図形は,星型5角形（ダビデの星）と星型8角形（ダ・ビンチの星型）です．
それぞれの図にある赤い輪郭線（それぞれ正5角形と正8角形）は，
凸多角形（凹所のない多角形）で，赤い輪郭線の多角形内部に，黒い線分で描いた図形が星型です．
左のダビデの星を見て下さい．
星型正5角形の辺をA→B→C→･･･→Aと1周りたどると，
辺の向き（→）が2回転することがわかります．（あるいは，
「5角形の頂点を１つ飛ばしで辿って，2周して始めの頂点に戻る」
ということもできます）
このような星形を｛5/2｝と表記します．
（もし，1点の周りが2x360°という世界があれば，この星型は凸多角形になります）
星型８角形でも同様で，この図形は｛8/3｝です．

■さて，星型正多面体を見て下さい，正5角錐の頂点の周りに，星型正多角形{5/2}が，
5個集まっていることがわかるでしょう．
従って，この星型正多面体をシュレフリの記号で書くと{5/2,5}となります．

このダ・ビンチの星型は，「星型小12面体」とも呼ばれます．
イメージ 1

シュレーフリの記号で書くと｛5/2，5｝です．
（注）シュレフリの記号｛p,q｝というのは，正p角形の面が，頂点でq個集まっているような正多面体を表す記号でした．
この形は，東京都庭園美術館，朝香宮邸，姫宮の部屋の照明器具にも使われている美しい形です．芯になるのは正12面体で，その12個の正５角形の面の上に，それぞれ正5角錘を取り付けた形をしています．正5角錐の頂点は，それぞれ，芯となる正12面体の面に対応していますから，頂点を結んでできる図形（赤の多面体）は，正12面体に双対な正20面体です．
この星型多面体の面は，以下の左図の様な星型正多角形（五芒星）です．
イメージ 2

　Fig.　星型5角形（五芒星）と星型8角形（ダ・ビンチの星型）

それぞれの図の赤い輪郭線（それぞれ正5角形と正8角形）は，
凸多角形（凹所のない多角形）で，赤い凸多角形内部に星型が作図されています．

■五芒星（図左）
星型正5角形の辺をA→C→E→B→D→Aと1周りたどると，
辺の向き（→）が2回転することがわかります．あるいは，
「5角形の頂点を１つ飛ばしで辿って，2周りすると始めの頂点に戻る」
ということもできます．
このような星形を｛5/2｝と表記します．
（もし，1点の周りが2x360°という世界があれば，この星型は凸多角形になります）
凸多角形では，1周すると辺の向きは360°回転し，正n角形では，頂点で360°/nずつ回ります．従って，正n角形の頂角（内角）は180°-360°/nです．五芒星の頂角は36°で，正n角形の頂角が36になるのはn=5/2ですから，五芒星を｛5/2｝と表記するのは妥当でしょう．

星型８角形でも同様で，この図形は｛8/3｝です．

■さて，星型正多面体に戻りましょう．正5角錐の頂点の周りに，星型正多角形{5/2}が，5個集まっていることがわかるでしょう(例えば，頂点Aの周りに右図のような五芒星の板を5枚集める)．芯に正5角形の穴の開いた五芒星の板を，各頂点で5枚ずつ組み合わせると，この立体を作ることができます．
従って，この星型正多面体をシュレーフリの記号で書くと{5/2,5}となります．
イメージ 3

デザルグの定理とは
「⊿ABCと⊿A'B'C'があり，AA'，BB'，CC'を通る直線が1点Oで交わるなら．
直線ABとA'B'の交点P，直線BCとB'C'の交点Q，直線CAとC'A'の交点Rは，同一直線上にある」

 このデザルグの定理の証明は，実はとても難しいのです．3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります．
ところが，下図のように，この図形を平面（2次元）と見ずに，立体（3次元）にあると見ると，ごく当たり前のことを言っていることに気づきます．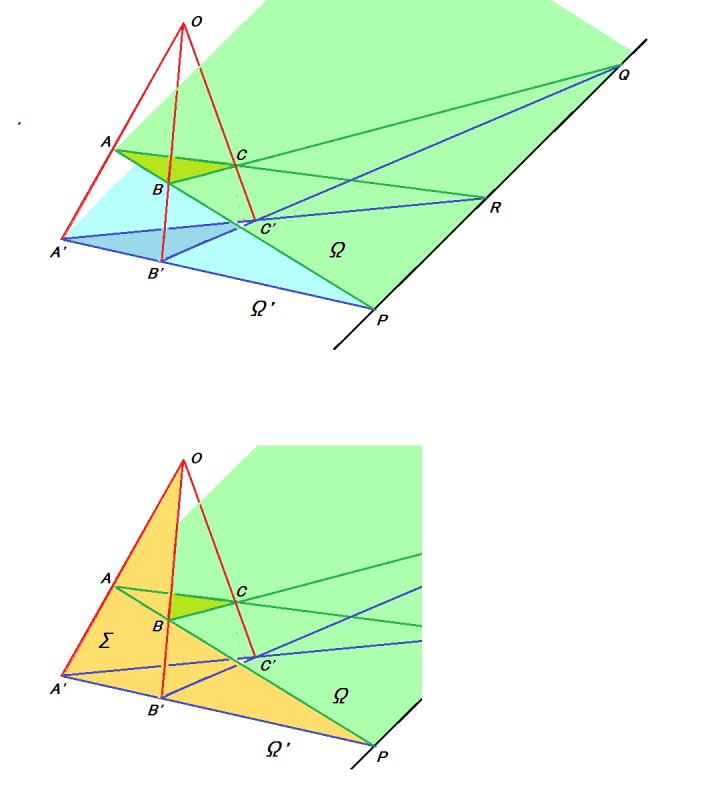
２つの平面Ω（薄緑）とΩ’（薄青）が交差しており，△ABCは平面Ω上に，△A'B'C'は平面Ω'上にあります．
光源Oから出る光が，△ABCの影を△A'B'C'に作っています（辺ABの影が辺A'B'）．
従って，O，A，B，A'，B' は，同一平面上にあり，この平面をΣ（薄燈）と名付けます．A，Bを通る直線も，A'，B'を通る直線もこの平面Σ上にあり，P点で交差します．
一方，A，B，Pは平面Ω上に，A'，B'，Pは平面Ω’上にあります．
結局，P点は平面Ωと平面Ω’の交線上にあることになります．
同様にして，QもRも，平面Ωと平面Ω’の交線上にあり，デザルグの定理が証明できました．

■デザルグの定理は，2次元で証明するのは難しいが，3次元では証明が要らないほど自明なのは何故でしょうか．
3次元でこの図のような模型があったとして，これを2次元に射影する（高さ方向をぺちゃんこ）と，直線が交差する状況は変わらないのですが，長さや角度の情報が失われてしまいます．△ABCと△A'B'C'は，それぞれ別の2次元平面にあったものですが，ぺちゃんこにされて1つの平面（紙面）に入ってしまいました．
私たちは，高い次元（2次元の世界から3次元の世界）を想像するのは困難です．デザルグの定理でこれを思い知らされます．
■デザルグは，17世紀初頭のフランスの数学者，建築家．透視図法を発展させた射影幾何学の祖です．ダビンチなどの画家たちは，遠近法や透視図法を古くから用いていましたが，その数学を固め射影幾何学の本を出したのはデザルグが最初です．
その後，射影幾何学が本格的に研究されるのは，200年後の19世紀中葉，ポンスレー（フランスの数学者．ナポレオンのロシア遠征に従軍し，ロシアで捕虜のときに射影幾何学を研究した）を待たねばなりませんでした．
射影幾何学自体，作図など重要な応用がありますが，やはり，19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました．

デザルグの定理とは
「⊿ABCと⊿A'B'C'があり，AA'，BB'，CC'を通る直線が1点Oで交わるなら．
直線ABとA'B'の交点P，直線BCとB'C'の交点Q，直線CAとC'A'の交点Rは，同一直線上にある」

このデザルグの定理の証明は，実はとても難しいのです．3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります．
ところが，下図のように，この図形を平面（2次元）と見ずに，立体（3次元）にあると見ると，ごく当たり前のことを言っていることに気づきます．
イメージ 2

２つの平面Ω（薄緑）とΩ’（薄青）が交差しており，△ABCは平面Ω上に，△A'B'C'は平面Ω'上にあります．
光源Oから出る光が，△ABCの影を△A'B'C'に作っています（辺ABの影が辺A'B'）．
従って，O，A，B，A'，B' は，同一平面上にあり，この平面をΣ（薄燈）と名付けます．A，Bを通る直線も，A'，B'を通る直線もこの平面Σ上にあり，P点で交差します．
一方，A，B，Pは平面Ω上に，A'，B'，Pは平面Ω’上にあります．
結局，P点は平面Ωと平面Ω’の交線上にあることになります．
同様にして，QもRも，平面Ωと平面Ω’の交線上にあり，デザルグの定理が証明できました．

■デザルグの定理は，2次元で証明するのは難しいが，3次元では証明が要らないほど自明なのは何故でしょうか．
3次元でこの図のような模型があったとして，これを2次元に射影する（高さ方向をぺちゃんこ）と，直線が交差する状況は変わらないのですが，長さや角度の情報が失われてしまいます．△ABCと△A'B'C'は，それぞれ別の2次元平面にあったものですが，ぺちゃんこにされて1つの平面（紙面）に入ってしまいました．
私たちは，高い次元（2次元の世界から3次元の世界）を想像するのは困難です．デザルグの定理でこれを思い知らされます．
■デザルグは，17世紀初頭のフランスの数学者，建築家．透視図法を発展させた射影幾何学の祖です．ダビンチなどの画家たちは，遠近法や透視図法を古くから用いていましたが，その数学を固め射影幾何学の本を出したのはデザルグが最初です．
その後，射影幾何学が本格的に研究されるのは，200年後の19世紀中葉，ポンスレー（フランスの数学者．ナポレオンのロシア遠征に従軍し，ロシアで捕虜のときに射影幾何学を研究した）を待たねばなりませんでした．
射影幾何学自体，作図など重要な応用がありますが，やはり，19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.02.21］ No.155
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユニット折り紙で作ったダビンチの星型の続きです．これは，
芯に置いた正8面体の各面に正3角錘が乗っている形です．Fig.4
星型の頂点を結ぶと芯にある正8面体に双対な正6面体ができます．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/19/17902919/img_0_m?1486823996

このユニット折紙では，正３角錐の面は正3角形ではなく直角3角形です．
そして，各面はツートンカラーになっています．
対称性を調べると，芯の正8面体の頂点方向に（x,y,ｚ軸）4回回転対称軸，
各正3角形の面に垂直に3回回転対称軸，2つの4回回転軸の中間（同じことだが，2つの3回回転軸の中間）に
2回回転対称軸があります．色の変化を調べると，
4回回転軸により4色の置換，3回回転軸により3色の置換と1色の保存，
2回回転軸により2色の置換と2色の保存が起こります．

この図形には4回軸があるので，色置換の操作も含めて完全な対称性にするには，
塗り分けには4色用いる必要があります．
3回軸の方向から見ると3色見え，見えないもう一色は，
3回軸で保存され，3回軸に垂直な面の大円上にあります．
3回軸の方向は4本あり，3回軸それぞれは，軸に垂直な大円上の色を保存するので，
結局，塗り分けには全部で4色使うという言い方もあります．

■写真(Fig.5)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_0_m?1487566646
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_1_m?1487566646

この星型は，立方体の6つの面に，正3角形の面で出来ている正4角錐が乗っています．
芯になる立方体の1辺の長さを１とすると，星型の頂点の高さは√2/2，
もし，星型頂点の高さを立方体の辺の長さの1/2に短縮すると，
星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_4_m?1487566646
(Fig.6)左が星型正24面体，右が菱形12面体

展開図は色々なものができますが，作りやすいものにするのがよい設計です．
星型24面体と菱形12面体の展開図を比較して見て下さい．（Fig.7）
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_6_m?1487566646
美しい形ですので作って見ると良いでしょう．

■正20面体を芯にして，正3角形の各面の上に正3角錘（正4面体）を乗せた星型が，星型正60面体です．
正3角形の面が10個集まっている点と3個集まっている点（頂点）が交互にある星型です．
1枚の連続した紙に展開図を描くことはできません．

写真の星型は，立方体の6つの面に，正3角形の面で出来ている正4角錐が乗っています．芯になる立方体の1辺の長さを１とすると，星型の頂点の高さは√2/2，もし，星型頂点の高さを立方体の辺の長さの1/2に短縮すると，星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります．

■星型の展開図です．

展開図はいろいろなものが考えられますが，作りやすいように設計するとよいと思います．

■星型正24面体と菱形12面体

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.02.14］ No.154
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
星型を作って見ました．展開図を考えて組み立てました．展開図には色々な変形があり，
紙の使用量が小さくなるようにくふうするのも面白いです．糊代に立体内部から糊付けするのはちょっと面倒でした．
■この金平糖のような形（Fig.1）はダ・ビンチの星型の一つです．芯の部分に正12面体があり，
その正5角形の12個の面の上に，正5角錘が乗っています．だから星の頂点は12個で，
12個の頂点を結んでできるのは正12面体に双対な正20面体です．一つの頂点の真上から見ると，
五芒星と五芒星の中に正5角形が見えます．五芒星の腕の長さと中にある正５角形の辺の比は黄金比です．
この星型多面体の面（2等辺3角形）は，黄金比の三角形です．
もし，面の形を正3角形にすれば，星形正60面体が得られます．どちらもダ・ビンチの橋形と言います．
特にこの写真の黄金比が出て来る方は美しいですね．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/58/17899558/img_1_m?1486673391

■プラトンの正多面体は正多角形の面で出来ている凸の正多面体で5種類あります．
プラトンの正多面体を芯にして，正多角形の各面の上に正多角錘（面は正3角形）を乗せると，
ダ・ビンチの星型ができまので，ダ・ビンチの星型も5種類できます．その作り方から自明ですが，
それぞれのダ・ビンチの星型と対応するプラトンの多面体は互いに双対です．

■例えば，正4面体の4つの面のそれぞれに正4面体を貼り付けた形（Fig.2）を見ましょう．
この星型の頂点は４つで，頂点を結ぶと，また正4面体になります．
これは，正4面体の双対図形が正4っ面体であることからわかります．
正4面体が５つ(芯にあるのは見えません)で出来ています．
これを4次元の世界で組み立てると4次元の正5胞体（５つの3次元の正4面体を面に持つ4次元の立体のこと．
4次元多面体の面は3次元の多面体）ができます．その意味で，この星型は，4次元正5胞体の3次元の展開図といえます．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/65/17901765/img_1_m?1486690977

■もう一つ例をあげれば，正8面体を芯にして，
正8面体の8つの正3角形の面にそれぞれ正4面体が乗っている形の星型（Fig.3）です．
互いに点対称にある２つの大きな正4面体が噛み合った形です．星型の頂点を結んでできる図形は，
正8面体に双対な正6面体です．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/01/17905101/img_0_m?1486868408

■次に示すユニット折り紙も，ダビンチの星型です．正8面体の各面に正3角錘が乗っています．
この折紙では，正３角錐の面は正3角形ではなく直角3角形です．そして，各面はツートンカラーになっています．
この図形には4回回転対称軸や3回回転対称軸，2回回転対称軸などがあります．
これから先はこの図形の対称性と色置換の話ですが，長くなるので次号にします．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/19/17902919/img_0_m?1486823996

星型を作って見ました．展開図を考えて作り，それを組み立てました．展開図には色々な変形があり，紙の使用量を小さくするような工夫も面白いです．糊代に立体内部から糊付けするのはちょっと面倒でした．
■この金平糖のような形（Fig.1）はダ・ビンチの星型の一つです．芯の部分に正12面体があり，その正5角形の12個の面の上に，正5角錘が乗っています．だから星の頂点は12個で，12個の頂点を結んでできるのは正12面体に双対な正20面体です．一つの頂点の真上から見ると，五芒星と五芒星の中に正5角形が見えます．五芒星の腕の長さと中にある正５角形の辺の比は黄金比です．この星型多面体の面（2等辺3角形）は，黄金比の三角形です．
もし，面の形を正3角形にすれば，星型正60面体が得られます．どちらもダ・ビンチの星型と言います．特にこの写真の黄金比が出て来る方は美しいですね．
■プラトンの正多面体は正多角形の面で出来ている凸の正多面体で5種類あります．プラトンの正多面体を芯にして，正多角形の各面の上に正多角錘（面は正3角形）を乗せると，ダ・ビンチの星型ができまので，ダ・ビンチの星型も5種類できます．その作り方から自明ですが，それぞれのダ・ビンチの星型と対応するプラトンの多面体は互いに双対です．

■例えば，正4面体の4つの面のそれぞれに正4面体を貼り付けた形（Fig.2）を見ましょう．この星型の頂点は４つで，頂点を結ぶと，また正4面体になります．これは，正4面体の双対図形が正4っ面体であることからわかります．
正4面体が５つ(芯にあるのは見えません)で出来ています．これを4次元の世界で組み立てると4次元の正5胞体（５つの3次元の正4面体を面に持つ4次元の立体のこと．4次元多面体の面は3次元の多面体）ができます．その意味で，この星型は，4次元正5胞体の3次元の展開図といえます．

■もう一つ例をあげれば，正8面体を芯にして，正8面体の8つの正3角形の面にそれぞれ正4面体が乗っている形の星型（Fig.3）です．互いに点対称にある２つの大きな正4面体が噛み合った形です．星型の頂点を結んでできる図形は，正8面体に双対な正6面体です．

ーーーー
■次に示すユニット折り紙も，ダビンチの星型です．芯にある正8面体の各面に正3角錘が乗っています．この折紙では，正３角錐の面は正3角形ではなく直角3角形です．そして，各面はツートンカラーになっています．
対称性を調べると，芯の正8面体の頂点方向（x,y,ｚ軸上にある）4回回転対称軸，体対角線の方向に3回回転対称軸，2つの4回回転軸の中間（同じことだが，2つの3回回転軸の中間）に2回回転対称軸があります．
4回回転軸により4色の置換，3回回転軸により3色の置換と1色の保存，2回回転軸により2色の置換と2色の保存が起こります．星型の頂点を結ぶと芯にある正8面体に双対な正6面体ができます．
(Fig.4)

この図形には4回軸があるので，色置換の操作も含めて完全な対称性にするには，塗り分けには4色用いる必要があります．3回軸の方向から見ると3色見えます．見えないもう一色は，3回軸で保存され，3回軸に垂直な面の大円上にあります．
立方体では，3回軸の方向が体対角線方向に4本あり，3回軸それぞれに，軸に垂直な大円が色を保存するので，結局，全部で4色使うという言い方もあります．

■写真(Fig.5)の星型は，立方体の6つの面に，正3角形の面で出来ている正4角錐が乗っています．芯になる立方体の1辺の長さを１とすると，星型の頂点の高さは√2/2，もし，星型頂点の高さを立方体の辺の長さの1/2に短縮すると，星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります．(Fig.6)
イメージ 1イメージ 2

Fig.5

■星型正24面体の展開図
イメージ 3イメージ 4

 　
展開図はいろいろなものが考えられますが，作りやすいものを設計するとよいと思います．

■星型正24面体と菱形12面体
イメージ 5

Fig.6

　　　星型正24面体　　　　　菱形12面体

以下に星型正24面体と菱形12面体の展開図の比較を示します．

イメージ 6

■正20面体を芯にして，正3角形の各面の上に正3角錘（正4面体）を乗せた星型が，
星型正60面体です．正3角形の面が10個集まっている点と3個集まっている点（頂点）が交互にある星型です．1枚の連続した紙に展開図を描くことはできません．

日刊ベリタ（2月3日）に掲載

■2月2日，17時からの東電会見で，福一2号機の格納容器内の映像についての報告がありました．この会見は定例で月・木に行われ，各社の記者にまじって，おしどりマコさんも必ず出席されています．私は，IWJのインタネット中継でこれを見ています．皆様もご覧になることをお勧めします．ただし，東電の説明はとても下手で，一般向けに説明しません．そこで，東電の発表事実を踏まえた上で，私の解説を加えてこの記事を書きました．
■2月2日に発表されたのは，1月30日に実施した挿入カメラによる画像を解析した結果です．この実験は24日，5:30-8:00，26日，5:45-9:10，にも実施されています．カメラは格納容器のX6ペネという導入窓に直径11cmの穴を穿孔（この穿孔も大変でした．詳細は私のブログにあります），物干し竿の先につけた固定焦点のカメラをレールに沿って移動させ挿入しました．2月に，「原子炉圧力容器」を下から支える，コンクリートの部屋（ペデスタル）の中に，自走式のサソリ型ロボットを投入して観察しようというのです．これはそのための偵察実験です．
■原子炉格納容器内で，「圧力容器（原子炉容器）」を支えているコンクリート製の構造物が「ペデスタル」．ペデスタル内に入り天井を見上げると，「圧力容器」の底から出ている多数の制御棒挿入機構や配管が配列しています（正常なら）．
原子炉建屋で言うと，「原子炉圧力容器」は2,3階を占め，ペデスタルは地下から1階を占めます．「原子炉圧力容器」を包む格納容器は地階から４階を占めています．
「原子炉圧力容器」の直径は７mほど，高さは22mあり，格納容器はこれを内部に含む大きなフラスコの様な形をしています．
ペデスタルの入り口は，高さ1mほどで，屈まないと入れません．広さは直径7mほどの円形の空間で，天井には「原子炉圧力容器」の制御棒駆動機構に繋がるスタブチューブフランジが並んでいます．この配管に水圧をかけると，上にある制御棒が上昇し，燃料体に挿入される仕組みになっています．3.11の時も，制御棒の挿入まではうまく行ったということです．
■1号機，3号機は，事故当時，ウエットベントが出来ましたが，それぞれの建屋は水素爆発しました．1号機は白煙，3号機は黒煙をあげて爆発したことを記憶されていることでしょう．どちらも核燃料はメルトダウンして，ほぼすべてが溶け落ちた可能性が高いと東電も認めています（2014.8.6）．続いて，2号機も2011.3.14日深夜に格納容器圧力が異常上昇するもベントに失敗，圧力抑制室が破損し，直接放射性物質をばらまきました．15日，6時10分に圧力抑制室の圧力が外気と同じ1気圧になったのです．
圧力抑制室というのは，建屋の地下にある直径33.5mのドーナツの様な形の水の入ったプールです．格納容器とはベント管というパイプ（直径2m，8本ある）で繋がっています．
■2号機では，メルトダウンした核燃料の70％~100％が圧力容器の底にたまっているらしいことは，ミュー粒子（宇宙線）を用いた透視で判明しています（2015.３）．同様の透視法で1号機のメルトダウンした核燃料は圧力容器にはとんどなく，圧力容器から抜け落ちたことがわかります（IRID資料，2016.10.4）．
(注）装荷核燃料の量は，１機あたり約１トンです．
特に，3号機はプルサーマルで，我々の反対を押し切り，プルトニウムを含むMOX燃料が装荷されて運転を始めたところでした．

■1月30日までの2号機での偵察実験でわかったことは以下のようなものです．

サソリ型ロボットを走行させる床（グレーチング）の一部（1m^2）に脱落しかかった場所や脱落や障害物があり，可能であるかも含めて走行ルートの検討が必要である．X6ペネから格納容器内にカメラを挿入したとき，X6の内側で50Sv/h，原子炉直下のペデスタルに達する手前の2.3mの位置で530Sv/h，ペデスタルの入り口付近では20Sv/hの線量率が観測された．東電は明言を避けていますが，格納容器内のペデスタルの外が線量率が高いというのは予想外で，デブリがペデスタルの外に落ちているのではないか．おそらくデブリは水の外に出ていて遮蔽されていないし，事故の経緯を思い出すと，デブリの一部は，格納容器も破り地下の圧力抑制室に達した可能性も考えなければいけないと私は推測します．
核燃料デブリは，高い放射能を持ちます．原子炉に核燃料が入っているから，止めていても稼働しても同じことで，使わないのは損だというような暴論を言う経済評論家が居ります．とんでもない．新しい核燃料は人がそばにいても大丈夫ですが，使用済み核燃料には，核分裂で生じた放射性の高い核種がたくさん含まれます．さらに，核分裂が起きている核燃料からは中性子がたくさん出て，周りの物質を放射化（例えば，構造物のステンレスに当たると，普通の鉄やコバルトを放射性のある同位体に変える）し，これらを含むデブリは高い放射性を持ち人が扱えません．
■今回の放射線量率の算定は，画像のノイズから（誤差が30％と大きい）ということで，東電は確定的な判断は避けています．ちょっと説明不足なので，解説を加えると，画像のノイズは，カメラの中にあるCCD（半導体）に入るγ線のためで，画像に写っている場所から来ているのではない．カメラの通った場所の線量率であります．
今後，ロボット走行のルートが確保でき投入したとしも，サソリ型ロボットの眼となるCCDの累積寿命は1,000Svなので，高い線量率の場所があると短時間で壊れてしまう恐れがあります．また，デブリが地下の圧力抑制室に達しているなら，除去は無駄

ではないかと思います．作業者の被ばく量（現在3mSv/日で管理）はさらに増加するでしょう．

「雪は天から送られた手紙（中谷宇吉郎）」という言葉がありますが，雪の結晶が生まれ・成長した気圏の状況により，様々な形の雪片が観察できます．これらの写真の中で，絶対にありえない雪の結晶が２つあります．どれとどれでしょうか？

 （以下は，追補）
雪片の形の対称性は6mmです．これは雪（氷）の結晶の内部構造（分子配列）が外に反映されたものです．以下に氷の結晶構造の2次元模式図を示します．水分子はH2O(酸素原子O●の両側に水素原子H●が結合し，その結合角度は約120°）で，両端の水素原子は，隣の分子の酸素原子と弱い相互作用（水素結合）をしています．そのためこのような6mmの対称性の結晶になります．

（注）雪片（雪の結晶）の形は，デンドライトという形です．
これは，比較的速く結晶が成長するときにできます．
金平糖も似たような現象で出来るデンドライトといえますが，
1粒の金平糖全体で砂糖結晶の方位が揃った単結晶というわけでは
ないので，それが雪の結晶とは違うところです．

東京ジャーミイの礼拝ホール

　祭壇の方向（西）に向かって礼拝

東京ジャーミイは，東京，代々木上原にあります．トルコ文化センターも併設されています．
この地には，昔，ロシアカザン州から避難したトルコ人によりモスクが建てられていました．
私の子供の頃，近隣の者は「マジスト寺院」と呼んでいた風情のあるモスクでした．
老朽化のため1986年に取り壊され，東京トルコ人協会の人々が中心になり，
東京ジャーミイの建設が1998年から始まり2000年に完成しました．
トルコから送られた資材を用い，オスマントルコ様式で設計され，2階の礼拝場のドームが印象的です．仕上げにはトルコ人建築家や職人が100人もかかったそうです．
毎日礼拝が行われコーランの声が流れます．特に金曜日には300人以上のイスラムの人々が礼拝に訪れます．皆，西に向かって絨毯にすわり礼拝します．ステンドガラスに西日が入ると，青い光線が，青緑色のカーペットに重なり，とても美しい光で溢れます．
イスラム教は偶像崇拝をしません．幾何学的な完璧な規則で描かれた模様が
宇宙を作った神の原理を思わせるのでしょう．
スペイン，グラナダのアルハンブラ宮殿の，さまざまな幾何学的な繰り返し模様を
表現したタイルは美しいので有名ですが，ここ東京ジャーミイも東アジアでもっとも美しいモスクと言われます．ここで見られるいくつかの幾何学模様を取り上げ鑑賞しましょう．

説教壇

 
東京ジャーミイ（代々木上原，東京）にある装飾です．写真左Fig.1は説教壇の横にある装飾です．写真右Fig.2はステンドグラスです．
どちらも複雑な図形ですが美しい．
これらの図形の構成を調べて見ましょう．

　　Fig.1　　　　　　　　　　　　　　　　　Fig.2　
■Fig.1の図形の構成を，以下のFIg.3で説明します．
Fig.3の一番左は辺の長さが黄金比の2等辺三角形です．
つまり底辺を１とすると，等しい２辺は1.618...，頂角は36°，両底角は72°です．
真ん中の図は，正5角形の中にできる星形で，
星の頂角は黄金比の三角形にでてくる頂角36°と同じです．
一番右の図は，この星型とこの星型を180°回転したものを重ね合わせたものです．
東京ジャーミイの美しい図形Fig.1には，星形を２つ重ね合わせたものが中心にあることに，お気づきでしょうか．

Fig.3

Q:星形をこのように重ね合わせた図形の対称性は？
A:まず，星形の対称性は．点群5mです（５は5回回転対称軸，mは鏡映面）．
2回回転対称軸２が生じるように重ね合わせたので，
重ね合わせた星形の対称性は，結局，2⊗5m＝10mmの点群になります．
あるいは，星形の点群5mを「法」にすると，10回回転操作（36°の回転）は
｛１，10(mod5m)｝のような，位数2の対称操作として理解できます．
注）数学の言葉を使うと，次のように表現されます．
点群10mmは，点群5m（これは点群10mm内の正規部分群）を核として，
群｛1,10(mod5m)｝に準同型．
この考え方は，奇妙なもので，36°回転を2回続けると元の星形に重なるから
これを振り出しに戻ったと見なすと，我々の3次元ユークリッド空間では
360°回転しないと元に戻らないのに，この奇妙な空間では，
2x36°＝72°回転すると元に戻ることになります．
■Fig.2のステンドグラス窓の模様は，繰り返し模様の一部です．
この繰り返し模様をFig.5に再現してみました．

　　　　　　　Fig.4　　　　　　　　　　　　　Fig.5

「正5角形と180°回転した正5角形を重ね合わせた」星型パーツ（点群10mm）を内角が108°と72°の菱形を単位胞とする格子に配置して（Fig.4）繰り返し模様を作ります(Fig.5）です．
この菱形格子は正6角形（正3角形）のように見えますが，
上下の方向が左右の方向に比べてすこし長く，歪んでいます．
正5角形や正10角形（どちらも最低でも5回対称性がある）を周期的に並べることは不可能ですから，5回対称性が全域で支配するような格子はできません．「正5角形とその180°回転したものを重ね合わせた」星型パーツの対称性（10mm）は，そのパーツの内部だけを支配する（局所的）ものです．
この繰り返し模様の対称性（平面群）には，2回軸と水平および垂直に鏡映面があり，記号でいうとP2mmの対称性です．

■電力を遠方の原子力発電所の様な大規模施設で発電し，消費地に送電するのは無駄ではないでしょうか．それぞれの地域で発電し消費する（地産地消）「分散型」がこれからの合理的なシステムです．遠距離送電も原子力発電も止めましょう．家庭の屋根で太陽光発電しても，100V交流に変換して東電に売っていたのでは，原子力発電の電力の一部とされ，現在の課金システムの枠内です．将来目指すべきシステムの姿は，大規模な送電網から独立した電気エネルギーの自給自足です．
皆さんの家電で必要となる電気の質を考えて見ましょう．ラジオ，TV，パソコン，携帯,発光ダイオード，...これらはどれも，直流（５V,９V,12V,15V,19V,24Vなど）で動くものです．交流100Ｖのコンセントから使うために，わざわざそれぞれACアダプターが付属し，アダプターだらけで嫌になります．掃除機や工具の様なモーターを使うものでも電池で働きますし，冷蔵庫やエアコンも車載では，12V（あるいは24V）のバッテリーで動かしているではありませんか．交流100Vはいらないということになりませんか．低電圧直流用の家電は，需要が出れば生産できます．その他，各種ヒータや湯沸かしなどは，電気で加熱する必要もありません．目的に合った電気以外のエネルギーもさまざまあります．何でも電気でやろうとするのは止めましょう．
■さて，皆さんの家庭に送電される電気は，ほとんどが，100Vの交流です．電気が送られてくる2本の電線の一方は接地されていてほとんど0V，電線の他方の電位は，±100V（正確には±141V）の間で周期的に変動（sin波の形）しています．その周波数は50Hz（東日本），あるいは60Hz(西日本）です．さわると感電し危険な方は，±100Vで周期的に変動している方です．家庭のコンセントを観察すると，コンセントのプラグの挿入口の切れ込みの長さに違いがあるでしょう．切れ込みの長い方が接地側．こちらを触っても感電しません（電気工事がJIS規格通りに正しく実施されていればの話です）．直流は，電圧の周期的変化のない電気で，電池からの電気はその例です．
■エジソンがアメリカ合衆国で電気事業を始めた頃（1880年代），発電所でできた電気を送電するのに直流が良いか交流が良いかの議論がありました．エジソンが直流送電（DC），それに対して，ウエスティングハウスとニコラ・テスラが交流送電（AC）を主張しました．直流送電/交流送電のどちらにも長所・短所があります．例えば，交流は，トランスで変圧できる利点がありますが，表皮効果で電線表面ばかりに電流が集まり電線内部が無駄になる欠点もあります．結局，エジソンの直流送電方式で，アメリカ合衆国の電力事業が始まりましたが，1888年の大寒波のときにニューヨークでは，雪の重みで直流電力送電網が崩壊するなどの事件がありました．ナイヤガラ発電プロジェクトでは，GE社＋エジソンに対し，ウエスチングハウス社＋テスラが契約を勝ち取り．バッファロー工業地帯への交流送電が1896年に開始されました．現在まで，直流送電/交流送電のどちらも，世界各地でそれぞれに実用化されています．電車では架線に直流を送電しているのはご存知でしょう．
■しかしながら，発電および送電の主流は，現在では交流です．
電力は電圧Vと電流Iの積V･Iですから，同じ電力を送るにも，電圧を高くすれば電流を小さくできます．送電線での発熱による損失は，電線の抵抗をRとすると，R･I^2ですから，電流の2乗に比例し，電流が小さいと損失が減ります．従って，高圧送電方式が採用されています．高圧送電のときは交流送電の方が有利なのは，トランスにより容易に変圧できるからです．
■ここで，立ち止まって現状を見てみましょう．現代は半導体技術の発展により，直流のままでの変圧（DC-DCコンバータ）は容易です．変圧原理は，ACを介することには変わりないのですが，半導体内部で昇圧も降圧も容易にできます．需要のある電力も低電圧の直流になりました．真空管から半導体に，ブラウン管からLCDに，白熱電球からLEDに変ったのです．消費する電力も桁違いに低下し，高電圧でもなくなりました．そのため，太陽光パネルで発電した低電圧の直流電力を，送電せずにそのまま消費することが出来そうです．ただし，このためには鉛畜電池などの2次電池の用意が新たに必要となります．
■私は今，12Vの「ディープサイクル鉛蓄電池」(32Ah)と太陽光パネル（50W級の小型のもの）を用いて検証実験中です．この実験程度の電池（1万円以内）の蓄電量ですと，300W×1時間程度の電気量の貯えしかできません．LED照明などは，たいして電力を消費しませんが，冷蔵庫は1時間40W，冷房は1時間90W程度の電力を消費します．太陽光で発電できない夜間は，電池に蓄えられた電力を使いますから，何を何時間動かすか節約を考えましょう．そうでないと，際限なく電池の容量を増設することになります．DC-DCコンバータによる直流出力（５V,19V,24Vとバッテリ－直結の12V），および，DC-ACコンバータによるAC100Vが利用可能です．使用機器に合わせた１度の変圧は避けられませんが，コンバータの効率は90%以上なのでロスは最小限です．昇圧と交流化後にAC100Vの東電の送電線に上げ，AC100Vの送電線から機器に必要な低圧直流に再度変換する2度手間と比べるとロスがありません．

日刊ベリタ(2017.01.09)に掲載

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.01.03］ No.148
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆様，新年おめでとうございます．こちらは晴天に恵まれたとてもよいお正月でした．
良い年であることを祈ります．今年は，ゴミ屋敷状態だった私の部屋から，
書類ファイルや文献コピーファイルなどを，不要なものを捨て，必要なものを選んで搬出しました．
何も正月にやりたくなかったのですが，皆が留守のときでないとできないので，
31日，1日，2日と突貫工事的に働きました．まるでブラック企業の社員のようです．
毎日こんな仕事をやらされたら体がもちません．
重い段ボールを持ち上げて運び，ちょっとまた腰痛が心配です．予定通り2日の夕方に一応けりをつけました．
今年はまだ街にも，神社にも行っていません．異例な年の始まりでしたが，良い年にしたいものです．
ですから，私にとっては明日が元旦というこにします．
正月ですので，「アラビア数学奇譚（白揚社）」から，軽い問題です．お考えください．

■（第3話より）
「あっしらは兄弟なんですがね．ここにいる35頭のらくだを遺産として3人で相続したんでさ．
で，おやじの遺言によれば，半分があっしのもん，3分の1が弟のハメド，9分の1が末のハリムのもんなんです．
とはいうものの，どう分けりゃいいのか，さっぱりわからねえんで」
35頭の1/2も，1/3も，1/9も割り切れません．
この問題に出会った数え人（ベレミズ）は，友人と一緒に，
1頭のらくだでバクダットに向って砂漠の旅の途中でした．
うまく解決したベレミズは自分のらくだ１頭を手に入れることになります．．．．．
さて，どうしたのでしょうか？
（コメント）3人合わせても残ります．1-(8.5/9)=0.5/9=2/36

■（第28話より）
2,025ですが，ちゃんと計算すれば平方根が45であることがわかります．
つまり，45x45は2,025ということです．ところで，45は2,025をまんなかで分けた2組の数字，20と25の合計でもあります．
同じことが3,025でも起こります．この平方根は55です．
55は3,025を2つに分けた30と25の和でもあるのです．同じことは9,801についても言えます．
平方根は99，つまり，98+1なのです．
これら3つの例から，不注意な数学者は次のような規則があると考えてしまうかもしれません．
4桁の数字の平方根は，4桁の数字をまんなかから左右に分けた2組の数をたしたものである，と．
明らかに誤りであるこの法則は，3つの実例から導き出されました．
数学では，単なる観察だけでは真実に到達できません．
ことに，こうした誤った推論を避けるように注意を払う必要があります．
（コメント）99まであっても，100回目で違えば正しくありません．証明するとは，そのようなことが起きないことです．

2,025ですが，ちゃんと計算すれば平方根が45であることがわかります．つまり，45x45は2,025ということです．ところで，45は2,025をまんなかで分けた2組の数字，20と25の合計でもあります．同じことが3,025でも起こります．この平方根は55です．55は3,025を2つに分けた30と25の和でもあるのです．同じことは9,801についても言えます．平方根は99，つまり，98+1なのです．これら3つの例から，不注意な数学者は次のような規則があると考えてしまうかもしれません．
4桁の数字の平方根は，4桁の数字をまんなかから左右に分けた2組の数をたしたものである，と．
明らかに誤りであるこの法則は，3つの実例から導き出されました．数学では，単なる観察だけでは真実に到達できません．ことに，こうした誤った推論を避けるように注意を払う必要があります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.12.27］ No.147
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も残りわずかになりました．私の方は何もかにも来年に持ち越しで，毎日バタバタと過ごしておます．
まっだく，まだ年賀状に取り組む雰囲気になりません．
皆様の年末の日々は如何でしょうか．皆様にとって来年は良い年でありますように．
先週の20日は久しぶりの放射光実験で，名古屋を日帰りし大変疲れました．今日26日はこのデータの検討会がありました．
そして，明27日は，ユーロスペースで上映されているアニメ「算法少女」を見に行く予定です．
このアニメの上映期間は，24日~28日ですので，明日，明後日の内に見なければなりません．
http://sampo-shojo.oops.jp/index.html　
遠藤寛子さんの「算法少女」，ちくま学芸文庫は，大変すがすがしい物語です．皆様もご覧になることをお勧めします．

■さて，今年も色々なことがありました．以下は，日刊ベリタ（2016.12.23）に掲載したものです
安倍晋三首相とプーチン大統領の会談は2日間にわたって行われ，12月16日夕方に共同記者会見が行われました．
内容のない会見でしたが40分にわたり，安倍首相がプーチン大統領をファーストネームで「ウラジーミル」と何度も呼びかけ，
「君（きみ）」という呼びかけも使いました．
http://www.j-cast.com/2016/12/16286354.html　によると，
「プーチン大統領、ウラジーミル。ようこそ日本へ。日本国民を代表して君を歓迎したいと思います。
私が2013年にモスクワを訪れた時に、出来るだけ頻繁に会談を重ねようと、君と約束をしました」と切り出し，
結局，安倍首相は発言の中で，「ウラジーミル」を5回，「君（きみ）」を3回使ったといいます．
質疑応答でも，5回「ウラジーミル」と口にしたということです．
■日本語の感覚では，とても失礼な感じがします．
そして，これはロシア語としても中途半端で気持ちの悪い感じがします．
「ウラジーミル」といったら，父称まで続けるのが普通です．「ウラジーミル・ウラジーミロビッチ」です．
プーチンの場合は，お父さんの名前も「ウラジーミル」です．
あるいはもっと親しければ，愛称の「ヴォロージャ」と呼ぶべきでしょう．
安倍さんは，ドストエフスキーなどのロシアの小説を読んだことがないのだろうか？
■日本国民向けに，「やっている振り」や「親密さのアピール」を企んだことでしょうが，
見え見えで違和感があります．プーチンが「晋三」と返事をしたわけでなく．全く噛み合いませんでした．
だいたい，個人的信頼関係で国策を決められても困ります．
トップの個人プレーで何かするのは，全くの議会軽視．国会無視の姿勢の表れであります．
よく考えると「ウラジーミル」て怖い名前ですね「世界を支配する」という意味です
（「ウラジオストーク」は「東方を支配する」です）．安倍さんはそんな言葉を連呼したことになります．
参考までに，これが噂のプーチンカレンダー，私の部屋につるしてあります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556223/62/17813962/img_0_m?1481887010

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.12.20］ No.146
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
本日（12月20日）は，放射光を用いた毛髪の蛍光X線分析に参加しています．
私にとっては，十年ぶりの放射光実験です．
励起X線ビーム（20keV）で毛髪を照射すると，毛髪に含まれているほとんどの原子の（原子核に捉えられている
1番内側の電子）K殻電子を，原子から飛び出させることができます．
こうしてできたK殻電子の空孔に，外側の電子（高いエネルギーのL殻やM殻）が落ちてきて埋め，安定な原子になりますが，
このとき放出されるX線が蛍光X線で，そのエネルギーは元素によって決まっています．
これが蛍光X線で元素分析ができる原理です．
この蛍光X線の測定で，観測されるバックグラウンドに影響する現象を，
ここで，数式に頼らず平易に解説してみようと思います．
■X線は電磁波
X線は周波数の高い（エネルギーの大きい）光（電磁波）です．eVというエネルギーの単位で表すと，
可視光線は，1.6eV（赤）～3.2eV（紫）の程度ですが，今日，私が実験で使うＸ線は20keVです．
■弾性散乱
物質をこのX線ビームで照らすと，どんなことが起こるでしょうか？物質は原子が集まってできており，
１つの原子は，原子核とその周りのいくつかの電子からなります．電磁波の電場は+-が入れ替わる振動電場です．
水平に飛んで来る放射光ビームの電場は，水平面内で振動しています（水平偏波）．
その周波数は，20keVのエネルギーですと4.8x10^18ヘルツです．
この振動電場のなかに置かれた原子の電子も，電場の周波数と同じ周波数で振動します．
原子の内部が分極し双極子となり，これが+-振動する．振動する双極子は，電波の源になり，同じ周波数の電磁波を出します．
これをX線の散乱といいます．電線を張って，高周波の電流を流すと，電線に垂直な方向に電波が飛んで行きます．
これをダイポール（双極子）アンテナと言いますが，原子の1つ1つが小さなダイポールアンテナになるわけです．
物質に入って来るビームと散乱されていくビームのなす角度χを散乱角と言いますが，
散乱角0°や180°の方向（アンテナの腹に垂直）に強い散乱があり，
散乱角90°の方向（アンテナの先端方向）にはほとんど散乱されません．
電磁波の強度は振幅の2乗に比例しますから，入射波の電場ベクトルと散乱波の電場ベクトルの内積の2乗（cosχ)^2が，
散乱波強度の大雑把な方位依存性を決め，これを偏光因子と言います．
１つの原子には原子番号だけの複数の電子がありますから，原子によってその散乱能力が異なります．
電子のたくさんある原子の方が強く散乱を起こします．
ある原子により散乱角χの方向に散乱されるX線の散乱強度は散乱振幅の2乗で，
ボルン近似で求めた散乱振幅は，その原子の電子分布密度のFourier変換になっています．
実験では，散乱Ｘ線がほとんど消える水平面内で散乱角χ=90°の位置に検出器を置きます．
ここまでの説明は散乱によりX線のエネルギーが変化しない（いわゆる弾性散乱）についてでした．
■コンプトン散乱
X線のエネルギーが変化する非弾性散乱で重要なのは，コンプトン散乱と呼ばれるものです．
これは，入射するX線のエネルギーの一部が電子の運動に渡され，散乱されるX線のエネルギーが減少する散乱です．
散乱の前後で，エネルギー保存則と，運動量の保存則が成り立ちます．計算すると，
散乱角が0°ではX線のエネルギー損失はありませんが，散乱角が大きいほどエネルギー損失は大きく，
散乱角χ=90°では，入射光20keVの場合，0.754keVの損失になることがわかります．
コンプトン散乱を考慮してバックグラウンドの理論値を見積もることができます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.12.13］ No.145
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
Mathematicaという数学，情報処理ソフトウエアがあります．価格は高いが定評のある大変優れたソフトウエアです．
ウルフラムWolfram reseach Inc.がコンファレンスを東京で開催（12月12日）しましたので参加して来ました．
Mathematicaは，今年の8月にversion11がリリースされました．
mathematicaは，version8まではいわゆる数式処理のソフトウエアでしたが，
version9あたりからAI（人工知能）のようなソフトウエアに変貌しています．
このソフトの創始者で最高経営責任者のstephen Wolframは，世界中のあらゆるデータを計算し尽くすと豪語しています．
wolfram alphaというウエブサイトhttps://www.wolframalpha.com/をご覧になったことがありますか？
ここのinput boxにどんなことを書き込んでも，AIがそれを理解し適切な答えを返してくるのです．
もし，数式や方程式を書けば，それを解いたりグラフで可視化表示したりします．これくらいは驚きませんね．
しかし，入力するものが数式でなくて，imageや音声ファイルや，地図や，キ－ワードや，その他なんでも，
コンピュータが解釈し答えを返してきます．ただし，無料のウエブサービスですから，
計算時間に制限があり時間切れを知らせてくることはあります．AI技術の進歩には驚くばかりです．
測定した色々な生データを入れると，何も知らなくても論文ができて出て来るという時代が到来
しているというと一寸大げさですが，そのような感があります．
■数学の教育にMathematicaを用いる動きもあります．研究や大学の授業では用いていますが，
高校の数1から数3までの教程があるそうです．計算はコンピュータにやらせるわけですから，
パラメータを色々変えて傾向をみたり，不動点を発見したりなどの面白い教育的な使い方があるでしょう．
しかし，私たちが高校時代に味わった，因数分解がうまく行ったときの喜びや，
補助線一本を発見して幾何が解けたときの喜びはもうないでしょうね．
基礎理論を知らなくてもうまく行ってしまうのにも不安を感じます．
コンピュータがないと簡単な積分もできないということにならないように．
そして，数式処理の大変高度な能力が手に入りますからこれをうまく利用しましょう．
美しいグラフィックは理解を助けるし，出力を３Dプリンターにつなぎ，3次元の物体として出すこともできる時代です．
■AIは，多層のニューラルネットワークの学習機能を持っていてトレイニング（教師付き）させると，
データの識別（それが特定できる確率が示される）や診断結果のクラス分けができます．
データから傾向の予測をしたりもします．
■東京慈恵会医科大学の関根宏氏は，ビッグバンモデルに基づき増殖する腫瘍に対する放射線治療の話をしました．
がんというのは自律的な増殖と転移をするものだそうです．がんに放射線を照射するとがん細胞が減っていきます．
臨床例はがん細胞にガンマ線照射を60Gy/30回/6週などです．何回に分けてどのくらいの期間に照射すると効果的か，
照射の仕方と再発の有無をGLQモデル（照射パラメータ２つがあり，照射で指数関数的にがん細胞が減るモデル）により，
シミュレーションしている．ただし，最近の研究ではがん幹細胞があり，
ここを攻撃しないとがん細胞は死なないという説があるそうだ．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.12.06］ No.144
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
数学月間は，数学同好者のためでもないし数学の講習会でもありません．
<数学と社会の架け橋>を目指しています．毎年，数学月間の初日7/22（これは，22/7≒3.14･･･にちなみます）
に懇話会を実施しています．ご参加ください．
今年の「数学月間懇話会」の講演から紹介しましょう．
がん登録の可能性．田渕　健（都立駒込病院，東京都がん登録室）

駒込ピペットは，感染症の避病院であったこの病院の発明（140年前）だそうだ．
今年(2016年)新たにがんと診断される患者は，101万人を超える予測で，98万人（2015年），88万人（2014年）と増加し，
この3年間のがん死亡も，年間37万人程度ですが．増加傾向です．
2014年から，多いがんのランキングや死亡率などが話題になり，がん検診も叫ばれています．
一方，過剰検診の問題もあり，がん検診を増やすことがどれほど有効なのかはわからない．
がん罹患率の統計が整備されると，過去年のがん罹患数のデータを用いて，
今年のがん罹患数を予測したり，次のような質問に答えることができるようになります．
・助かるのか，助からないのか，どのくらいの人が助かるのか?
・同じような病気の人がどのくらいいるのだろうか?
・この病気を治してくれる病院があるのだろうか?
・どんな治療法があるのだろうか?　治療成績に違いがあるのだろうか?
がん登録推進法が，遅ればせながら今年スタートしました（人口統計は，明治に確立している）．
がん統計は，データ収集→処理登録→統計解析の流れで行い，
特に，生データからがん登録を行うところが，混沌としていてとても難しい．
これは数学者の仕事なのだが，数学者の参入がないのが問題です．
（注）統計解析は，良いツールソフトがあり実施に問題はない．
具体的には，がん登録の届け出がされていない/複数病院からダブって届けられる/一人で多重がんをもつ，
などの混沌とした状態が生データで，まず，同一性の判定が必要になります．
死亡状況から，届け出がなかったがんを判定発見することも必要です．
病院は電子カルテに変わり，医者が患者の顔を見なくなった弊害に加え．
そのカルテ情報が構造化されておらず，残念ながら統計には役に立たないそうだ．
病気を分類し，がんの定義を満たすリストを作る．そして，いろいろな届け出病名から，がんを特定する．
例えば，肺炎には肺がんが含まれているかもしれない．
心不全というのは死因ではなく，死因の特定には，第1次原因，第2次原因，...，第5次まで見ることが必要とのことだ．
いずれにしろ，生のデータは斯様に混沌としている．同値関係を定義したり，
同値分類したりしてデータの構造化が必要であり，これは数学者の仕事なのです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.29］ No.143
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
寒くなりました．皆様お元気でお過ごしでしょうか．
11月27日は，夕方からの雨でどんどん寒くなりましたが，
藤沢，遊行寺の「一ッ火」に参加していました．5時に始まり9時近くまで行われました．
遊行寺に行ったのは初めてです．落語でも，箱根駅伝の中継でも，遊行寺は有名ですね．
会の最後に，大僧正直々に全員（何百人でしょうか，例年より少ないそうです）がお札をいただきました．
その行列の長いこと．大僧正は97才．すごい大声でのお話さすがです．（この方が免許返上で話題になった方ですね）．
「一っ火」というのは，本堂のロウソク（それぞれ或るものを象徴して配置され，20～30本位ある）の火を，
複雑な手順（方法や役回りがいろいろ）に法り次々に消して行き真っ暗に...，静寂．十八念仏が始まり，
火口箱に火花鵜を打ち込み，灯明に移されます．再び弥陀と釈迦の光明に照らされた世界が戻ってきます．
念仏は美しい合唱の音楽です．
大きな百目ろうそくの炎は長く伸びて明るい．じっと見ていると，炎はピタッと動かない．
それが突然瞬き始める．また，ピタッとまる．これが周期的に繰り返されます．
この自励振動の機構に感嘆して見入ってしまいました．実に面白い．
近づけた2本のロウソクの瞬きの周期が揃う（協同する）というのは知っていますが，
そもそも，ロウソクの炎の瞬きと，静止が何故繰り返されるのだろうか？どちらの状態も安定でないわけで，
この移り変わりが起こる理由を考え込んでしまったのです．この話題は後日取り上げたいと思います．

今日は，福１の事故原子炉の話をします．
■福1のメルトダウンした2号機のペデスタル（原子炉（圧力）容器を支えるコンクリートの部屋（地階と1階））
の観察を来年1月に実施する計画です．ペデスタルは格納容器（建屋の地階から4階までを含んでいる）の中にありますので，
格納容器のX-6ペネ（貫通窓のこと，ケーブルや配管を通しているが，X-6はコンクリートのメクラ蓋）に穿孔（115Φ）し，
自走式のサソリ型ロボットをいれる．実は，この穿孔の準備のため，X-6ペネの前にある遮蔽ブロックを取り外す工事で，
X-6ペネ周辺にダメージを与え放射能が漏れだし，昨年10月から最近まで，その作業エリアの放射能除去対策に苦闘していた．
いよいよ遮蔽盾に隠れて穿孔作業が始まるが，作業場は高線量のため１日の被曝限度3mSvをすぐ超えるので10分といられない．
3人ぐらいの班で，次々と入れ替わりのリレー作業となる．
計画は観察だけ．その後．どうやってデブリをとりだすか，どこに保管するかなど問題だらけで可能かどうかも危惧される．
（だいたい，燃料プールには，4号機の燃料を入れたままだし）
■現在判明している状態
メルトダウンした福1原発1号機～3号機のデブリの観察
1号機，3号機は，ウエットベントが出来ましたが，建屋は水素爆発しました．
どちらも核燃料はメルトダウンして，ほぼすべてが溶け落ちた可能性が高いと東電も認めています（2014.8.6）．
2号機は，ベントに失敗．圧力抑制室が破損し，直接放射性物質をばらまきました．建屋の水素爆発も起きました．
2号機では，メルトダウンした核燃料の70％~100％が圧力容器の底にたまっていることは，
ミュー粒子（宇宙線）を用いた透視で判明しています（2015.３）．
同様の透視法で1号機のメルトダウンした核燃料は圧力容器にはとんどなく，
圧力容器から抜け落ちたことがわかります（IRID資料，2016.10.4）．
(注1）装荷核燃料の量は，１機あたり約１トンです．
特に，3号機はプルサーマルで，プルトニウムを含むMOX燃料が装荷されていました．

（注2）ミュー粒子（宇宙線）による透過像
宇宙線，ミュー粒子は大気で発生し，一様に振り注ぎます．透過力が強いが，高密度の物質を通過すると減衰するので，
火山の山体のマグマや原子炉の核燃料位置を見ることができます．
ミュー粒子の飛んで来た方向の検出には，
原子核乾板を複数重ねて感光させる方法や，同じ原理ですが，シンチレータバー（1cm角）と呼ばれる棒を並べた面検出器を，
間隔をとって平行に置き，ミュー粒子の軌跡がどのように貫いたか知ります．
シンチレータバーの中心には波長変換ファイバー1mmΦが通っていて，ミュー粒子をとらえた位置のシンチレータの発光を，
可視光の波長に変えてファイバー端面に伝え，ファイバー端面の半導体検出素子に入れます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.22］ No.142
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ドリルが動かなくなったので，分解しました．こんな減速機構になっています．
グリスの詰め替えをしましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/70/17750970/img_1_m?1478607599
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/70/17750970/img_2_m?1478607599
表面に見えている3個の歯車（歯数20）の中心にモーターからの回転軸（6枚歯）が入ります．
この3個の歯車は，周囲の円（歯数48）とも接しています．
中心軸（モーターのシャフト）が右回転すると，3個の歯車は左回転し，
この3個の歯車を乗せている台は，周囲の歯に沿って右回転します．
このような機構を遊星歯車と言います．
中心の回転軸が右回りに1回転すると，台は6/48=1/8だけ右回転します．
このドリルでは，このような機構が2段になっている［回転台の中心軸（6枚歯）が，
下段の同様な遊星歯車に回転を伝える］ので，
(1/8)^2＝1/64だけ減速することになります．
遊星歯車では入力の回転軸と出力の回転軸は同一線上にあります．

**************************
前号の補足
■今年の米国大統領選の予測はずれ
米大統領選は，1票でも得票が多かった陣営がその州の選挙人を総取りするシステム
（実質的に州が一人区）なので，ゲリマンダー状態を起こし，効率的に票獲得をすれば，
少ない総獲得票数でも，選挙人数で逆転が可能です．そのため事前予測では，
各州の得票数にある少しの不確定さが非線形に増幅され，それらが積み重なる傾向があります．
今回，大方の予想は，クリントンがトランプに選挙人で70人近い差で圧勝と報じました．
しかし，結果は逆でした．ただし，総獲得票数は拮抗（反ってクリントンの方が若干多い）しています．
支持率世論調査の全米平均値では，ほぼ正しく予測したものの，州によっては大きく外れ，
これが獲得選挙人の数の大逆転を起こした原因です．
正しくランダム・サンプリングが出来なかったのは，生産拠点の国外流出で労働者，
黒人層に移動混乱があるミシガン州（すたれたベルト地帯）などで，
その層のサンプルが少なく母集団の構成比が反映されなかったことがあると思われます．
また，ほとんどのメディアが，クリントン支持を意図的に流し，世論誘導をしたので，
これが隠れトランプ支持を生み，正しいサンプリングにならなかったのも原因の一つです．
世論調査には数学的に批判されるべき問題がかなり存在するようです．

（注）ゲリマンダー（wikipediaより引用）
1812年，アメリカ合衆国マサチューセッツ州の当時の知事エルブリッジ・ゲリーが，
自分の所属する政党に有利なように選挙区を区割りした結果，幾つかの選挙区の形が奇妙なものとなった．
そのうちのひとつがサラマンダーの形をしていたことから，ゲリーとサラマンダーを合わせた造語・ゲリマンダーが生まれた．
https://upload.wikimedia.org/wikipedia/commons/thumb/6/63/The_Gerry-Mander.png/330px-The_Gerry-Mander.png

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.15］ No.141
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ドナルト・トランプ大統領が誕生しました．
大方の世論調査でも，期日前投票や投票当日の出口調査でも，ヒラリー・クリントンが優勢でした．
トランプをとんでもない候補だとする，新聞やTVによる刷り込みが激しかったこともあり，
多くの人々がこの逆転結果に驚きました．選挙戦中のメディアの報道は明らかにクリントン支持に偏っていました．
しかし，クリントンは現政権の中枢におり，既成勢力の政治はもうたくさんだとトランプに共感する人々は多かったのです．
今回も外れてしまった世論調査はどれほど信用できるのでしょうか．
選挙直前の世論調査を振り返ってみましょう．
10/29-11/01の期間に行われたワシントンポストとABCテレビによる世論調査は,50州の1,767人を対象とし，
トランプ45%，クリントン47%でした．
同時期のロイターによる世論調査は，1,700人の回答を得て，トランプ39%，クリントン45%だった．
直前11/7のロイター/イプソスの調査は，全米50州とワシントンDCの15,000人に対して行われ，
獲得選挙人を，トランプ235人，クリントン303人と予想しました．
政治専門サイト「リアル・クリア・ポリティクス」によると，７日午後時点の支持率は，
トランプ44.3%，クリントン47.2%で，猛追してきたトランプだが，
差は前日の1.8ポイントから2.9ポイントに広がっています．
そして，選挙人獲得見込は，トランプ164人，クリントン203人でした．
調査会社「ファイブサーティエイト」の最終の選挙人獲得予測も，
70人近い差でクリントン圧勝としていました．
大統領選挙の結果は，獲得選挙人数で，トランプはクリントンに60人以上の差をつけましたので，
これらの予測は大きく外れました．しかし，獲得票数は拮抗しています（トランプの方が若干少ない）ので，
予測できたと言えないこともありません．
選挙人に換算するところで，わずかな誤差が積算されるために予測が困難なのです．
（注）アメリカの大統領選挙は,州ごとの集計で獲得票が1票でも上回った候補が，
その州の選挙人を総取りする方式なので，得票数と獲得選挙人の数は比例せず，
場合によっては逆転することもあります．

■世論調査はなぜ外れたのか
世論調査は，有権者全員（母集団）を対象にすべきですが，現実にはこれは不可能なので，
母集団から掬い取ったサンプル集合に対して調査を行います．
サンプル集合が母集団の性質を代表していると見做せるのは，ランダム・サンプリングがなされた場合です．
しかし，これが難しい．サンプル集合に偏りが生じてしまうのが普通です．
これを少しでも避けるために，サンプリングの方法に色々な工夫があります．
母集団を，性質（人口規模，地方性，産業構成，人種，....）が似ている地域（1つの層とする）ごとに層別し
その中でサンプリングします．
各層のサンプルについての調査結果に母集団内での構成比に応じた荷重をかけ結果を得ます．
このとき色々な誤差が入ります．例えば，ある層の人たちの回答が，少ない/多いとか，
あるいは，ある層のサンプリングが過剰になるなどのことが起こります．
これらに対して適切な補正ができればよいのですが実際はなかなか難しい．
もし，サンプル集合が完全なランダム・サンプリングであるならば，話は単純です．
信頼区間95%として，非常に大きい母集団でも，1,600のサンプル数があれば，
最も誤差の大きくなる拮抗状態でも，±2.5%の誤差が保証されます．
今回の世論調査による両者の支持率の差では，この誤差中に入り，まさに拮抗状態です．
実際の得票数もほとんど拮抗しています．
ワシントンポストとABCテレビのサンプリングはうまく行ったといってよいのではないでしょうか．
直前のロイター/イプソスの調査はサンプル数15,000なので，ランダム・サンプリングが正しければ
誤差は±0.8%程度になるはずです．各州ごとにサンプル数と支持率を検証しないとわかりませんが，
全体が大きく外れているのでサンプル集合の偏りが疑われます．
2015年の英国の総選挙の例では，保守党と労働党の票獲得は，予測された「統計的デッドヒート」状態にはならずに，
保守党が労働党に対し7ポイントの優位で下院の多数を勝ち取りました．
世論調査組織が使ったサンプル補集の方法が，労働党有権者を過剰に系統的に集め偏ったサンプル集合だったからです．
適用された統計的補正も働かず予想が外れたのです．
特に，米国大統領選挙の予測では，得票数予測の正確さが要求されます．
一人の差で，獲得選挙人の数が大幅に変わってしまう選挙制度なのですから．
以下で，サンプル集合を偏らせる原因のいくつかを並べてみましょう．
■固定電話の激減
世論調査はRDD（ランダムに選んだ固定電話に行う）方式です．固定電話が対象ですが，
米国でも携帯電話による固定電話の置き換えが進んでいます．
固定電話がつながった場合でも応答に出る確率は以下のように激減しているそうです．
　72%(1980)→81%(2000)→5.5&(2012)→0.9%(2016)
そして，固定電話に応答の確率は，高齢白人女性が若いヒスパニック男性より21倍も高いことや，
生産拠点の国外流出で労働者，黒人層に移動混乱があるミシガン州での固定電話の調査が困難なことなどです．
（Garret M. Graff；WIRED，2016,7による）
■隠れトランプ
いわゆる「隠れトランプ支持者」の存在が調査結果を歪ませ，影響を与えたと言われています．
人種差別者と誤解されたくないので「私はトランプ支持者です」と答えることを躊躇する有権者や，
逆に，ヒラリー支持と言いながら投票に行かない人の存在が考えられます．
多くのメディアが反トランプの立場で報道した反作用として，この影響がでているのでしょう．
日本で，NHKが報じないと信用しないというほど，多くの庶民がTV報道による歪曲を受けています．
世論誘導に利用する調査の数字では困ったものです．
■投票機における不正
実際の投票数の方がゆがめられて予測と合わなくなる場合の話です．
大統領選の本選では，このようなことはなかったと信じますが，
クリントンが勝ち，サンダースが負けた米民主党の５月の予備選挙で不思議なことが起こったようです．
米国の選挙には投票機（90年代に作られそのOSはwindowsCE）が用いられるので，
ROMを差し替えておくと改造プログラムが立ち上がり不正が可能といいます．
５月の予備選挙の後，米スタンフォード大学の大学院生らが，
この選挙でサンダースを不利にクリントンを有利にする不正が行われたとの研究結果を発表しています．
それによると，印字機能がついている投票機が使われている州だけを集計すると，
クリントンの得票率が49%，サンダースの得票率が51%でサンダースの勝ちだったが，
印字機能がついていない投票機の州だけを集計すると，クリントン65%，サンダース35%でクリントンの勝ちだったという．
このことから民主党本部は，印字機能がついていない投票機のＲＯＭを細工を施したものに差し替えて，
サンダースに投票した党員の何割かの投票結果をクリントンにすりかえることを実現したのだと推測されています．
（田中宇，2016年10月26日より）
トランプはこのことを受けて，不正が行われたなら自分は負けを受け入れないといったのだが，
クリントン支持の米マスコミに，「トランプは，大統領選の負けを受け入れないひどい候補者だ」
と歪曲キャンペーンに利用されました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.08］ No.140
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前回の予告したペンローズ・タイル張りの後編です．
(2)正5角形のフラクタル配置からペンローズ・タイリングを作る
図をご覧ください
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/07/17050507/img_4_m?1478536819
正5角形の周囲に正5角形を配置し，一回り大きな正５角形
［平面を隙間なく埋められないのでギャップはあります］を作ります．
これを単位とし，さらに一回り大きな正5角形の内に並べます．
このような操作を次々繰り返すと，全平面に広がる正5角形のフラクタル配置ができます．
ギャップがたくさんできますが，気にしないで配置を進めます．
実は，これらのギャップの中も正五角形（白色）で埋めれば，
最終的には，王冠型や星型のギャップのみが残されることになります．
この図には，この操作を3回繰り返したところまで載せました．

この図をよく見ると，2種類のタイル（黄色と青色の菱形）で置き換えて，
隙間なく平面を張り詰めることがわかります．
黄色いタイル（太った菱形），青いタイル（痩せた菱形）の中の
正5角形のフラクタル配置の名残を参考にしてください．
説明図は
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/07/17050507/img_6_m?1478536819

このように置き換えると，よく知られたペンローズ・タイリングと同じであることがわかります．
図
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/07/17050507/img_5_m?1478536819

ここで作ったペンローズ・タイリングには，中心に5回回転対称が残っていますが，
中心の回転対称を消す配置も可能です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.01］ No.139
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ペンローズ・タイル張りのことは，以前に触れたことがあるのですが
面白いがわかりにくいとのコメントもいただいているので，
図も少し変えて，もう一度2回に分けて掲載しようと思います．

ロジャー・ペンローズが考案した（1966）ペンローズ・タイリングは，
2種類のタイルによる規則的ではあるが，周期的ではないタイル張りの一つです．

（１）正10角形から出発して，ペンローズのタイル張りを作る
このタイル張りで用いられているのは2種類のタイル（A型とB型）です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/95/17313295/img_6_m?1477918345

二等辺3角形　A型とB型は，正５角形の中にある形で，
それぞれ，等辺と底辺の長さの比が黄金比になっています．
等辺:底辺=Φ：１（A型），あるいは，等辺：底辺=１：Φ（B型），
ただしΦ＝1.618･･･

黄金比の3角形は，分割すると，自分自身と同じ型の3角形が含まれている性質があります．
この性質を利用して，A型の3角形(10枚)が作る正10角形から出発して，分割とΦ倍の拡大を繰り返し，
平面全体をA型とB型の２等辺3角形で埋め尽くすことができます．
分割してもΦ倍拡大をするのでタイルの大きさは変わらず，外周の正10角形の形も変わりませんが，
タイルの数はどんどん増えていき，無限の広さを覆いつくします．
タイルの分割が充分進んだときの，AのタイルとBのタイルの個数の比は，
Φ(=1.618･･･)：１の黄金比になります．
４番目の図は，3回目の分割と拡大を繰り返した結果です．
この図形で見られる形は，2A(凧型，青色)と2B(矢型，緑色)の2種類のタイルです．
このようにして，ペンローズ・タイリングの一つを得ることができます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/95/17313295/img_7_m?1477918345

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.10.25］ No.138
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
21日の倉吉の地震，お見舞いいたします．しっかりした古い建物が多いし周りに余裕があるので，
浅い直下型の地震にも関わらず死者がなかったのは幸いです．東京は密集しているのでこうは行きません．
崩壊した家や白壁土蔵の町の陳列散乱の様子が報道されていますが，余震はおさまりつつあるようです．
600人の方々が学校などに避難されて居られます．ご無事でありますように．
どこも大地震の発生確率は高まっています．逃げようがありません．
そういいながら原発を再稼働するなんてばかです．

■毛髪1本でがん検診
毛髪は約1cm/月の割合で伸びます．15cmの長さの毛髪ならその中に15か月間の健康状態の記録が残されているはずです．
毛髪中に含まれるいくつかの元素（カルシウム，ストロンチウム，カリウム，ナトリウム，など）の分布状態
（濃度の変化の記録）を調べて，ガン検診（特に乳がん）ができるという新手法を，千川純一先生（ひょうご科学技術創造協会）が，2003年からSPring8で研究を始め，結果を2015年に論文を発表しています．
毛髪1本を抜いて送れば，がんの検診ができるとなると，画期的ですね．この検査の人体への危険は全くありません．
この実用化のために，病院の先生方と協力して多くの臨床例を集め，実証研究を進める段階に来ています．
■測定方法
毛髪1本（直径は100μm程度）に放射光X線を照射し，毛髪のX線照射点から出てくる蛍光X線を観測することで，
その点に含まれる元素を検出することができます．そのとき観測されるバックグランドは，
毛髪母体のタンパクによる散乱X線ですから，蛍光X線のピークの強度P，バックグランド強度Sとして，
そのピークを与えた元素の濃度[X]を，[X]＝P/Sと定義すると，この値は毛髪の太さや形状によらない値になり，
濃度指標に使えます．
■放射光X線
SPring-8というのを聞いたことがありますか．姫路にある大きな放射光施設で，周囲1.5kmほどのリング内を電子を走らせます．
正確に言うと電子の軌道は多角形で，偏向磁石のある角で曲げられ，その時強いX線を放射します．
実験室のX線源の輝度を1等星の明るさとすれば，太陽の輝度に相当します．
指向性がよく広がりませんので，スポットに絞って照射できるので，小さい場所の分析に威力を発揮できます．
■イオンチャンネル
細胞外液（血清）から細胞への各種イオンの取り込みは細胞膜のイオンチャンネル開閉で制御されます．
血清から毛根の細胞への各種イオンの取り込みも同様に制御され，毛根細胞に取り込まれた各元素は．
成長して行く毛髪中に記録されて行きます．
細胞にカルシウムが不足すると，副甲状腺ホルモンPTHが分泌されて，
細胞のカルシウムチャンネルが開きカルシウムを細胞に取り込みます．
イオンチャンネル開はデジタル・パルス的（PTHが細胞の受容体に付着するたびにチャンネルが開く）
に行われるそうです．がん細胞からは副甲状腺ホルモン関連タンパクPTHrPが分泌され，
細胞のPTH受容体にPTHの1,500倍も長く滞在するので，カルシウムチャンネルの開閉が阻害されるということです．
■がん判定の仕組み
正常な人は，カルシウムイオンチャンネル開の時は，毛髪中のカルシウム濃度は50（単位は，上記の濃度定義に基づく），
カルシウムイオンチャンネル閉の時は，10です．がんが発生すると分泌されるPTHrPにより，
イオンチャンネル機能が阻害されるために，カルシウム濃度が50と10の中間値を数ケ月かけてゆっくり下降します．
このような変化パターンを検出することにより，初期の乳ガンの発見が他のマーカーより鋭敏にできます．
現在，病院の先生と協力して，検体の数を増加し実証を進める計画が進んでいます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.11.18］ No.137
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■10月12日，午後3時半ごろ起きた東京都内の停電で，58万戸が停電．都心中心部も停電した．
埼玉県，新座付近の地下送電ケーブルの火災が原因という．
社会インフラは限界ぎりぎりで稼動している状態です．東京の送電ネットワークもその例にもれません．
ネットワークに流入する交流電力を繋ぐには，電圧をそろえるだけではなく，交流の周波数も位相もそろえなければなりません．
つまり，流れ込む交流の山と山が重なるようにタイミングを合わせて合流させる（山と谷が重なったら一瞬で電流が流れて危ない）．ネットワークの結合点には，このような調整装置があり，ネットワークを作っています．
このようなネットワークの一部分を切り取って解析しても正しくありません．
予想もしないネットワークの部分から影響が来る可能性があり，ネットワークは全体を解析機する必要があります．
このような性質の系を「複雑系」といいます．
バタフライ・エフェクトというのは，海を隔てた地での蝶の羽ばたきが，明日のこの地の大風に影響を与えるかもしれない．
という極端な比喩ですが，複雑系とはこのようなことが起こり得る世界です．
複雑系のネットワークでは，どこかで起きた些細な事故が引き金となり，
次々と被害が雪崩を打ってネットワーク全体に広がる性質があります．

■些細な事故が，広域の大停電になった例は色々あります：
2003年８月14日，午恨１時42分，米国中西部の独立システム送電網オペレータの１人が異変に気づき，
ルイビルのガスと電気のオペレータに向かって，｢おい，どうした？」と問いかけたが，
その２時間半後には，北東合衆国から南東カナダにかけて，５千万人の人々の送電網の電力が失われた．
その3年後の2006年11月４日，夜の9:30に，ドイツの送電網オベレータが，クルーズ・ボード，ノルウェーの真珠号
の安全通行を許すために，Ems川をよぎる１対の配電線の接続を切り，
それから半時間以内に，１千５百万人のヨーロッパ人が暗やみに座ることになった.
日本でも，2006年８月に大規模停電が起きている.
2006年８月14日，午前７時38分(日本時間)．旧江戸川を航行中のクレーン船がアームを高圧線に接触させ，
これを切断した．アーム長33mのクレーン船が，現場に到着後すぐに浚渫作業にかかれるように，
曳航中にアームを上げたため，旧江戸川上の高さ16mの位置にある高圧線を破損したためである．
米国の大規模停電は，乾燥した樹木が送電線にふれスパークしたという些細なことが引き金になったのかもしれない．
ドイツや日本の原因は人為的な誤操作である．いずれにしても些細なことがトリガーとなり，
あっという間に事故の連鎖が雪崩を打って広域の大規模停電につながった．

■送電網は複雑系ですから，その部分部分を切り離して見たのでは，正しい理解にはならない．
送電網全体を対象にしなければだめなのでとても面倒だ．
送電網は，何百万という物理的なハードウェア／ソフトウェアと行為者(人間)によって構成されている．
大きな事故の引き金は，ほんの些細なイベントで予測もつかないことから起こる．
今回の火災は，ケーブル周囲被覆の油紙の劣化により，絶縁性能が低下し過大な電流が流れたためと伝えられる．
あるコンポーネントで事故（例えば，送電ケーブルの火災）が起こり，送電線回路のブレーカが落ちる．
そして，そのコンポーネントにかかっていた負荷は，ネットワークの残りを介して直ちに再分配され，
再分配された負荷は別のコンポーネントを過負荷にし，事故に導くかも知れない．
この過程は，雪崩のように繰り返され，広域な大規模停電となる可能性を持っている.
今回は，新座から離れた場所のケーブルにも負荷がかかった形跡があるらしいが，
それ以上の大きな事故雪崩にならずに済んだのは幸運であった．

［日刊ベリタ(10月13日)に掲載した]
http://www.nikkanberita.com/read.cgi?id=201610132037164

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.10.11］ No.136
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
表面だけのスカスカの立体は，面がシェルピンスキーのカーペットでできている
メンガーのスポンジが知られています．この図形は穴を開けるたびに，表面積は増加し，
体積は減少するので，質量はゼロで，表面積が∞の不思議な図形です．
メンガーのスポンジの次元は，　2.7268....になります．

■ここでは，正4面体から出発し似たような図形を作って見ましょう．
正8面体の４つの面に正4面体を組み合わせると，2倍の辺長の正4面体ができます．
この手順を繰り返すと，だんだん大きな正4面体ができます．
図1 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/80/17708080/img_0_m?1476098595
図2 http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/80/17708080/img_1_m?1476098595
この手順を逆にしてみましょう．
正4面体体積を１とすると，正4面体の中にできる正8面体の体積は1/2です．
（Q何故でしょう？）
この正8面体をくり抜くと，正4面体が4つ残り，合計の体積は1/2．
元の正4面体の表面積と，残された４つの正4面体の表面積合計は不変です．
（Q何故でしょう？）
次に，4つの正4面体からそれぞれの正8面体をくり抜くと，
残りの体積がさらに1/2になりますが，表面積はやはり不変です．

■この操作をn回繰り返すと，体積は(1/2)^nになるが，表面積は不変です．
この調子で，無限に操作を繰り返すと，表面積はスタートの正4面体と同じだが，
質量はゼロであるようなスカスカの物体が得られます．
この図形の作り方は，メンガーのスポンジと呼ばれる図形に似ていますが，
質量はゼロになるが表面積は∞にはなりません．
この図形の次元は，2倍の長さのところに４つの1世代前の図形が入るから，
log4/log2=2　で2次元です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.10.04］ No.135
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆様，早いもので10月になりました．昨夜はノーベル賞のニュースが入りました．
大隅さんは，東大，基礎科学科の2期生ということ（私は3期生）で，
消滅した基礎科学科ですが，開拓時の良さに思いが巡ります．

さて，世論調査で無作為で1,000人のデータを得たとして
そのうち有効なサンプル集合に入れられるのはどのくらいでしょうか？
統計処理では都合の悪い点を除外することがよくやられる．
実験測定などでは，明らかな間違いで除外する正当な理由がある場合もあるが，
“外れ値”と称して除外する処理手順の乱発は曲者である．

都合の悪いデータを除外することで，意図的な結論を得ることもできる．
“外れ値”とは正規分布から外れた点で，正規分布から外れた点だから除外してよいとする．
標本（サンプル集合）の平均から，標準偏差の2～3倍離れた点を“外れ値”として除外する．
この点を取り除いたサンプル集合で，さらに“外れ値”があればまたこれを除外する．
こうして続けて行くと都合の悪いものが除外され，
“外れ値”はなくなり正規分布はますます確かになっていく，
大変都合よくもあり恐ろしくもある処理手順である．

サンプル集合の分布は，平均を中心にして釣り鐘型の正規分布とは限りません．
我々は，どうして正規分布の１点でなければいけないのか？
正規分布から外れた点は“外れ値”として除外されねばならないのか？
私はどうしても納得できない．
“外れ値”を除外することを乱発され，正規分布に入っていないと生きていけない．
恐ろしい社会になってしまったものだ．
なにがなんでも正規分布にして済ますのはいやですねぇ．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.09.27］ No.134
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
早いもので9月も終わりです．皆様いかがお過ごしでしょうか．
台風や雨続きでしたが，秋らしい落ち着いた日々が待ち遠しいですね．
今回の発行は134号です．133号を飛ばしたのは，間違って131号を2回続けたためです．

■平田森三（物理学者，寺田寅彦の弟子）が「キリンのまだら」というエッセイを書きました．
古い本ですが再刊されていますのでご覧になることをお勧めします．
キリンのまだら模様と田んぼのひび割れの形が似ているというのです．
平田は1933年の「科学」に「キリンの斑模様について」の論文を掲載します．
田んぼのひび割れは地面が乾燥して縮むために生じます．
体の成長に皮膚の伸長が追いつかないと皮膚にひび割れができるというのです．
胎児のキリンの成長過程で皮膚にひび割れは生じませんから，
専門外の分野に口を出した平田は動物学者から攻撃されました．
田んぼのひび割れと同じ仕組みで，いろいろな分野のまだら模様ができるということが言いたいのですが，
キリンをアナロジーにしたのがいかにもまずい．メロンの縞模様をアナロジーにすれば，
この理論もまったく正しかったのです．
このような膨張収縮の力で縞模様ができるという現象はたくさんあります．
お餅を焼いたときの表面のひび，パン皮のひび，パン皮状溶岩，皆同じ機構によります．
基板につけた蒸着膜が，時間が経っと膜中の残留応力のために膜が膨張し，
面白い皺模様ができるのを私も経験したことがあります．

■1952年に，アラン・チューリング（英）が”反応拡散波”という考えを出し，
化学反応が波状に進む問題を解決しました．年輪のようなメノウの縞模様も，
周期的な模様ができる化学反応（ジャボチンスキー反応）も，すべてこの理論で説明できます．
キリンのまだらも，その他の動物の皮膚の色々な模様も，
チューリングの方程式のパラメータを変えればすべて再現できます．
だいぶ前のことになりますが，このメルマガでも自励振動の発生について触れたことがありました．
これらの現象は，新しく生まれた複雑系という分野と係わりがあります．

■形が似ているということは，それを抽象化した数式が同じということです．
全然違う分野の現象といえども，そこに働く力をふさわしい概念のものに入れ変え対応させれば，
両者を統一的に理解できるのではないでしょうか．
私が，ギブスの相律とオイラーの定理での”系内部の自由度”
のアナロジーの謎を捨てきれない理由は，そこにあります．
色々な異なる分野の現象を統一して記述できるのは数学の威力でしょう．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.09.20］ No.132
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
突然ですが，化学にGibbsの相律というものがあります．
物質の系（閉じた）を考えます．この系はc個の成分からなりたっています．
例えば，水とアルコールの混合した系なら，成分数は２です．
各成分の状態の数（相の数）をpとします．水とアルコールの混合系の場合は，
それぞれの成分ごとに，気体，液体，の2つの相（場合によっては固体を入れて3つ）があります．

成分数cの系で独立（に変化できる）変数の数はc-1個で，
それぞれにp個の相があるから，（c-1)pの変数があるが，
これ全部が独立なものではありません．
p個の相の間には，p-1個の平衡条件があります．
したがってc(p-1)個の束縛条件が課せられます．
結局，系の自由度fは
f=(c-1)p-c(p-1)+2
第3項に加えた2は，系全体の温度と圧力の２つの独立変数です．
これを計算整理すると
f=c-p+2　，あるいは　f+p-c=2　　となります．

何処かで見たことがありませんか．そう，オイラーの多面体定理V+F-E=2
を思わせます．今日，唐突に化学の相律の話をしたのは
この類似性を不思議と感じた十数年前のことが蘇ったからです．
ーーーーーーーーーーーーー
相律　　　f-2=c-p
オイラー　F-2=E-V　（FとVを入れ替えたものは互いに双対なので同じ）
ーーーーーーーーーーーーー
このように並べて，両者の類似性を見ていると，
幾何学的な本質に関係があるような気がしてならないのです．
これは，偶然の一致だと言ってしまえばそれまでです．
それが正しいようでもあります．私も昔，そう結論を下しました．
しかし，まだ考えつかないことがあるような気がしてなりません．
皆さん何か良いアイデアは無いでしょうか？

■考えがまとまりませんので，3成分系の具体例をたたき台に示します．
石英SiO2，橄欖石２MgOSiO2，灰長石CaOAl2O32SiO2の系を例にします．
各成分に，固体，液体の2相があります．今，圧力一定の切り口を考えるとf-1=c-pです．
3成分＋液の4相が共存するなら，自由度　f=0
3相が共存するなら　f=1（線上を動く）
2相が共存するなら　f=2（面上を動く）

融液を冷やしていくと，1,360～1,280℃で，橄欖石の晶出と液組成の変化
（橄欖石＋液の共存）すなわちここではf=2．
1,280～1,260℃で，灰長石の晶出と液組成の変化
（橄欖石＋灰長石＋液の共存），すなわちここではf=1．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.09.13］ No.131
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆さん，いよいよ９月になりました．お変わりありませんか．
私は，11日（日）に倉吉で開催される”とっとりサイエンスワールド”に参加するために，
もうすぐ家を出発します（今，9月11日の17時過ぎで，夜行バスは21時に出ます）．
このメルマガの発行される13日の朝は，まだ倉吉にいます．そのため今週号も予約発行です．
お近くの方は，倉吉の未来中心にお出かけ下さい．色々なワークショップがあります．

＊＊＊＊＊＊＊＊＊＊＊＊＊
これがどうして私の手元にあるのか出所は忘れてしまいました．
その他の組木もいくつかあったのですが，遠い昔に失くしてしまいました．
この組木を手に入れたのが一番新しく，今手元にこれだけがあります．
この組木はシンプルですが，職人のすばらしいアイデアだと思います．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/72/17658372/img_0_m?1473494896

全体の対称性は立方晶系の完面像（最も対称性の高い点群）を思わせます．
4回対称軸が3本，3回対称軸が４本，2回対称軸が6本あります．
鏡映面はたくさんあります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/72/17658372/img_1_m?1473494896

全体はこのようなパーツが6個で出来ています．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/72/17658372/img_2_m?1473494896

3回対称軸に沿って引き剥くことができ，二つに割れます．
写真は3回軸に沿って引き抜き開いて（内部をこちらに向けて）並べたところです．
3回軸に沿ってスライドできるのは，この分海図を見ると理解できるでしょう．
対称性を考えないと，引き抜く方向がわからず難しいパズルです．
3回対称軸は４本あるので，引く抜く方向には4通りあります．

■この組木は，x平面，y平面，z平面がかみ合っているという見方もできるでしょう．
それぞれの平面はパーツ2つからなります．
直交するx平面，y平面を作り，z平面の部品一つだけ置けるが，残り一つをどう入れるか苦闘します．
そうして，3回軸に沿ってスライドさせてできた空間に残り1つのパーツを入れることに気がつきます．
けれども，この方法で実行しようとすると，手作業的にはなかなか難しい．
手が3本欲しいということになります．
対称性を考慮すると，1つの方向にスライドして２つに割るという綺麗な解を思いつきます．
そして，この2つの部分を内側から見ると互いに鏡像にになっていることもわかります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.09.06］ No.131
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
始めにお詫びです．先週発行した”黄金三角形パズル”の図のリンクが切れていたようです．
以下のサイトに掲載しておりますので，こちらをご覧ください．
http://blogs.yahoo.co.jp/tanidr/16936782.html

さて今回は，高次元の世界から低次元の世界への影についてです．
高い次元の空間の周期性は，低い次元の空間に必ずしも遺伝しません．
ここではそのような例を見てみましょう．

■2次元の周期的な世界から1次元の非周期の世界へ
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/37/17648237/img_2_m?1472990935

1辺の長さが１の正方形のタイル（赤色）を隙間なく張り詰めた周期的な2次元世界があります．
タイルの中心に格子点があるとして，格子点を”1次元世界（水平な青色の線）”に射影しましょう．
この1次元世界（青色の水平線）が過るタイルだけが影を作る対象になります．
■2次元の世界は，1次元の世界1,2,3,4,6,8.....(それぞれ色を変えた)を束ねてできています．
射影のスクリーンとなる1次元世界（水平な青色直線）は，これらの1次元世界1,2,3,4,5,6,...と
角度αで交わっています．
tanα=n/mと有理数なら，１つの格子点が青色の直線に載れば，
その格子点がある部分空間の中でm個のタイルを動き，他の部分空間に向ってn個のタイルを動いた場所にある格子点は，
また青色の直線に載っているはずで，青色の１次元世界にも周期が出来ています．
もしtanαが無理数なら，１つの格子点が水平な青色直線に載ったら，
他の格子点でこの直線に載るものはないはずです．この時は，青色の１次元世界は非周期になります．
■射影されてできた1次元の非周期格子を，図の下に取り出しました．
この非周期格子の格子点は，各1次元空間1,2,3,4,5,6,....内に起源をもつ間隔と，
次の1次元世界に飛び移るときに生じる間隔との２種類の間隔が混ざってできています．

■この非周期格子は，周期的2次元空間から1次元空間への射影で作りました．
周期的2次元空間の1次元の断面そのものではありません．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.08.30］ No.130
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
暑かった8月も終わろうとしています．学校の夏休みも終わりですね．
今日は図形のパズルです．難しい計算は必要ありません．
図形を見て考えるのみです．ユークリッド幾何の世界ですから
我々が身に着けた直観や常識で間に合い，特別な知識は要りません．
「錯角（平行線とこれに交わる直線があるときにできる角度）は等しい」
ことを使いますが，これも日常生活で身についている直観でしょう．
このように，図形の問題は特別な知識は必要ありません．
諦めずに図形を眺めていましょう．そのうちわかります．

小梁修（OSA工房）の黄金三角形パズルの一つを紹介します．
(1)正五角形の中を図のように分割して作った3種類の三角形があります．
Q1.これらはどれも2等辺三角形ですが，何故でしょうか．
ヒント：両底角が等しいと2等辺三角形になります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/558900/82/16936782/img_3_m?1472477472

これらの3種類の三角形の面積に関して，以下の関係があります．
（水色の三角形）＋（黄緑色の三角形）＝（オレンジ色の三角形）
Q2.これを証明してください．
(補助線一本でわかります)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/558900/82/16936782/img_0_m?1472477472

(2)水色と黄緑色とオレンジ色の三角形パーツを使って
色々な大きさの正五角形を作りました．
(1)の正五角形（基本正五角形と呼ぶ）の面積を１とすると
Q3.作った色々な大きさの正五角形の面積はいくらでしょうか．
（5a^2：c^2：a^2：b^2　の面積比になります）
ここには基本正五角形（辺長a）の他に，
5x基本正五角形(辺長√5a)，大正五角形（辺長c），小正五角形（辺長b）
が出てきます．
c^2＝a^2+b^2　の関係があることを証明してください．
（この関係は，これらの三角形の面積が S_c＝S_a+S_b であること
　［Q2でも証明している］から得られます）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/558900/82/16936782/img_2_m?1472477472

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.08.23］ No.129
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
8月21日は，とっとりサイエンスワールドin鳥取です．
とっとりサイエンスワールドは，鳥取県と鳥取数学教育会が主催し今年で十年目．
すっかり市民に定着したイベントになりました．
このメルマガが皆様に配信される日は，数学月間最終日の翌日23日です．
数学月間は7/22～8/22：これは22/7=3.14･･･，22/8=2.７･･･にちなみます．
今年のとっとりサイエンスワールドは，この期間内に，西部と東部の2か所で
実施されました（さらに，9/11は中部で実施の計画があります）．
私はとっとりサイエンスワールドに参加するために鳥取に行き不在ですので，
今週のメルマガは予約発行です．
サイエンスワールドの様子は，後日のメルマガにご期待ください．

■さて，今回はランプシェードのデザインに利用される多面体の鑑賞です．
これは，球に近い多面体（いわゆるジオデシック構造）です．

www.creema.jpにある広告の写真を見て下さい．
これは,日球（https://www.creema.jp/c/hitamaya/item/onsale）さんの作品．
球面正20面体の面の細分で得られるジオデシック構造です．基礎となる球面正20面体の頂点は，
球面正3角形の頂点が５つ集まっている点の12個です．
20の面をそれぞれ細分化しジオデシック構造を作るには，各球面正3角形を4つに細分します．
全体で80個の球面三角形の面からなります．
https://d12ciics2fd1e.cloudfront.net/user/108977/exhibits/516682/1_c1e528919e76aed18f78765ae22229c698360adb_583x585.jpg

参考となる正20面体の形のランプシェードは，以下のところで見ることができます．
おりあるて（https://www.creema.jp/c/holiarte）さんの作品です．
https://d12ciics2fd1e.cloudfront.net/user/73358/exhibits/555659/1_f1e2caf473c660f6ddf04858aef8e7bdaf110412_583x585.jpg

■ジオデシック・ドームは建築家フラーが好んで作った建造物で，
炭素原子だけ60個で作るサッカー・ボールの様な構造の分子C60（フラーレン）
の語源になったものです．
バックミンスター・フラーのジオデシック・ドーム
https://upload.wikimedia.org/wikipedia/commons/thumb/8/8c/Biosph%C3%A8re_Montr%C3%A9al.jpg/800px-Biosph%C3%A8re_Montr%C3%A9al.jpg
（wikipedia.orgより）
正20面体からスタートして，各面を細分化していくのですが，日球さんのランプシェードの形は，
正20面体の最初の細分化で得られ，正20面体の各面となる3角形の各辺の2等分点を球面に投影して作ります．
この細分化を何度も繰り返すとだんだん球に近い多面体（ジオデシック構造）になります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.08.16］ No.128
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
お元気でしょうか？皆様のところではお盆は如何お過ごしでしょうか．
このところ先週の猛暑は少しおさまり助かりますね．
私は，日曜日からお盆で田舎に来ております．
母の新盆は7月に済ませましたが，８月は田舎のお盆で，従兄の新盆や，義父母の墓参に来ています．
そして，17日は父の祥月命日ですので，田舎からとって返してこちらの墓参に行きます．
そうこうするうちに，とっとりサイエンスワールドin鳥取（8月21日）が迫ってきました（私は前夜の夜行バスで出かけます）．
17日には墓参に行く前に，材料を発送しないと....もうタイムリミットです．今週は全く余裕がありません．

■鳥取サイエンスワールドin鳥取（8/21，とりぎん会館）
お近くの方はぜひご参加ください．子供も大人も楽しめる数学祭りです．すっかり市民に定着したイベントになりました．鳥取県，鳥取数学教育会のスタートから11年の活動に敬意を表します．

私の万華鏡ワークショップは，30人のクラスを5回実施する計画でいます．
なかなか予定通り行きませんので，10人分ほど予備も準備します．
さて，今回作る万華鏡の映像写真をとりあえず掲載しておきます．
映像を見ると12回の回転対称性があり，点群の対称性は12mmです．
この対称性は2枚の交差する鏡で生成されるのですが，鏡の交差角は何度でしょう？（答え15度）．
万華鏡の映像写真↓
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/07/17616707/img_0_m?1471269173

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.08.09］ No.127
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
子供たちが楽しそうな夏休みの最中です．7月31日の鳥取サイエンスワールドin米子では
約800人の入場者があり，120人分用意した万華鏡は，3時で材料がなくなりました．
次回開催は，8月21日の鳥取です．お近くの方お寄りください．

■正多面体とは，1種類の正多角形の面で囲まれた立体で，どの頂点の周りも同じ状態になっている立体です．
正多面体は「プラトンの多面体」とも呼ばれ，3次元では5種類（正4面体，正6面体，正8面体，正12面体，正20面体）
しかないことが知られています．正多面体の記述には，シュレーフリの表記法が用いられます．
例えば，｛3,5｝という表記は，正3角形の面が，どの頂点でも５つ集まっている状態です．
これは正20面体で，もっとも球に近い正多面体です．
■もっと球に近い多面体（正多面体ではない）を作るにはどうしたらよいでしょう．
例えば，ゴルフボールのディンプルを思い浮かべてください．
均一にデインプルを配置するにはどうしたら良いか？1つのディンプルの正面から見て．
その点の周りが均一ということは，ディンプルを面に見立てて，その面が正多角形であること．
すべてのディンプルが同じということは，同じ正多角形で囲まれているということ．
つまり，正多面体になっていることと同じです．したがって，厳密に均一な対称性でディンプルを配置するということは，
プラトンの多面体に相当する5種類しかあり得ません．
■しかし，近似的には，例えば，正20面体から出発して，面を分割していくと，
多面体の面の数がどんどん増加し，形も球に近づけることができます．
ジオデシック・ドーム（フラーの設計した建築物．C60分子（フラーレン）の語源になった）は，
このような形です．ドームの壁は，すべて3角形でできたトラス構造です．
■さて，図を参照しながらその作り方を説明しましょう．
出発点となる正20面体（灰色の球内部に内接する青色の正20面体）（A)から出発します．
外接球の中心Oから，正20面体の正３角形面の辺の中点に向かって線を伸ばし，
外接球面をよぎる点を三角形面の分割点とします（B).
この操作により，1つの正３角形の面は４つの三角形の面に分割されます．
この分割で生じた小さな3角形は，正3角形ではありません．
こうしてできた4倍の面をもつ80面体の多面体を図(c)に示します．
さて，(C)をもう一度分割すると，320面体の多面体(E)が得られます．
このようにして，ますます球に近い多面体を作ることができます．
各3角形の面にディンプルを配置すれば，いくらでも多くのディンプルを，近似的に均一に配置できますが，
この作り方からわかるように，スタートとなった正20面体の対称性は変わりません．素性は隠せないのです．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/60/17605260/img_0_m?1470654264　←Fig

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.08.02］ No.126
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も鳥取サイエンスワールド（10年目）の夏がやって来ました．
とっとりサイエンスワールドのFacebook　←（ここをクリック）
主催は，鳥取県，県数学教育会です．鳥取大学，地域教育学部が中心になり
小中学校の先生方や多くの高校生ボランティアが活躍します．　
7月31日（米子），8月21日（鳥取），9月11日（倉吉）です．
楽しいイベントがたくさんありますから．皆さんお寄りください．
私も万華鏡で参加します．万華鏡は1時間くらいで完成します．楽しいですよ．
今年作る万華鏡は，新型です．
予習になるように，万華鏡の仕組みを簡単にまとめておきます．
この記事は31日の米子に出かけるために事前に書き予約配信です．実際の配信は事後になります．

■万華鏡の原理
互いに平行に向かい合った「合わせ鏡」は，1列に無限に並ぶ像を作ります．
合わせ鏡に挟まれた部屋（緑色）を「鏡室」と呼んでおきます．
鏡室が鏡でひっくり返った鏡像は白いままの部屋にしました．
もう一回，鏡でひっくり返ると鏡室と同じ向きの映像になります．
詳しく言うと，緑（あるいは黄色）と白色の部屋が並んで市松模様ができます．
繰り返しの単位は，このペア（鏡室の2倍）です．
合わせ鏡が互いに平行でなく，交差角がθのときの図も合わせて掲載しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/77/17588477/img_0_m?1469773013

交差角がθのときは，1列に並ぶ像は円周上に並びます．円周上に並んだ像が，反対側でうまくつながる条件を考えると，
全円周角360°が，繰り返しの単位2θで割り切れることであることがわかるでしょう．つまり
360°／2θ＝n（整数）　このとき生じる万華鏡の映像には，n回回転対称性があります．
もちろん，この回転対称性の生じる原因になったのは，2枚の鏡です．

■今年，皆さんが作る万華鏡は，2枚の鏡の交差角が15°のものです．
これなら，360°／30°＝12 となり割り切れます．12回回転対称性が生じるはずですね．
以下のような映像が観察できるでしょう．この対称性をもたらした原因は2枚の鏡（赤と青）です．
この図形の対称性を点群の記号で書くと 12mm となります．
http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=17588477&no=1

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.07.26］ No.125
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆様のところは梅雨が明けましたでしょうか．お変わりありませんか．
私は，この日曜日（都知事選投票日）に米子で，サイエンスワールドに参加するために
万華鏡の材料の準備であたふたしています．
7月22日の数学月間懇話会は，無事実施できました．ご参加の皆さま有難うございます．

１．数学者って，どんな顔をしている？
　　亀井哲治郎・河野裕昭（亀書房・写真家）
２．世論調査は正しいか
　　松原望（東京大学名誉教授，聖学院大学）
３．がん登録の可能性
　　田渕　健（都立駒込病院・東京都がん登録室）
■今年の数学月間懇話会は，数式の出てこない一風変わった講演会になりました．
数学月間は数学同好者のためでもないし数学の講習会でもありません．
数学と社会の架け橋を目指しているのですから，今回の数学月間のテーマは，
数学月間の原点の姿であると言えるでしょう．今年の数学月間懇話会参加賞は35人を数えました．
以下，講演の要点をまとめました．それぞれの講演は1時間弱ありますから，
講演の要旨を数行にまとめるのは私の偏見によります（分責．谷）．
（１）
お二人が掛け合いで写真の説明をされ，撮影時の様子やエピソードをお聞きしました．
まず，色々な講義風景がありました．200人入る教室に4人の学生の贅沢な風景や，
無意識のオーケストラの指揮者よろしいポーズなどがりました．写真に切り取ってみると案外面白いものです．
一方では，数学者の教室外の生活感のあふれる写真－耕運機を運転している姿など－もありました．
（２）
議席事前予想（いわゆる世論調査）と開票実況中継（いわゆる「当確」打ち）の話がありました．
世論調査では，ランダムサンプリングによるサンプル集合が必要ですが，これが難しい．
性質（人口規模，地方性，産業構成）などが似ている範囲を1つの層として，全国を180層別し，
これをもとに3600人をサンプリングする方法が実施された（1963年の例）．ビッグデータによる解析も最近行われ，
当たったことも記憶に新しい．データ保護，調査の倫理，政治への従属，操作誘導が心配な問題点である．
開票は田舎から開いて都市部が遅い.開票の結果が出るの待てば良いのだが，各社一刻も早く当確を打ちたがる．
自分の投票が開票されていないのに，当確が決まるとは私は許せない気がする．
過去には，当確が取り消しになった事例もあるそうだ．少なくとも開票50％，あるいは，60%当たりで，
当確を打てば大体間違いはない．実際に当確判定に携わった1983年総選挙の新潟3区の田中角栄に得票率推移が例に出た．
（３）
駒込ピペットは，感染症の避病院であったこの病院（140年前）の発明である．
ガンの今年の患者が102万人を超えたという．2014年から，多いガンのランキングや死亡率ばどが語られ，
ガン検診も叫ばれているが．ガン検診をすることがどれほど有効かはわからない．ガン罹患率の統計はまだない．
統計解析は，良いソフトツールがあり実施に問題はないが，ガン登録を行うところがドロドロしていてとても難しい．
これは数学者の仕事なのだが，数学者が参入していないのが問題である．
ガン登録の届け出がされていない．複数病院からダブっている．一人で多重ガン．などがあり，同一性の判定が必要だ．
死亡状況から届け出がなかったのを判定する．例えば，病院は電子カルテになって，医者は患者の顔を見なくなった上に．
情報が構造化されていないので，あまり役に立たない．
発生場所と下水処理の相関を見つけた疫学調査がロンドンのコレラを鎮圧したそうである．
ガン登録推進法今年スタートした（人口統計は，明治に確立しているのだが）．
ガンの定義．病気を分類しガンの定義を満たすリストを作る．
届にもいろいろな言葉が使われる．色々な病名がある．肺炎には肺ガンが含まれているかもしれない．
心不全というのは死因ではない．第1次原因，第2次原因，第5次まで記入するそうだ．
いずれにしろ，生のデータは意味がダブったり混沌としている．同値関係を定義したり，
同値分類したりしてデータの構造化が必要であり数学者の仕事である．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.07.19］ No.124
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■「30年以内に震度６弱以上の地震が起こる確率は，横浜市が78％で最も高く，九州では大分市が54％」などと言われていました．
あくまでも確率ですから，いつ地震が起きるかはわかりません．熊本の方が先に大地震が起きてしまいましたね．
このような確率はどのようにして出たものでしょうか？
震度（揺れ方）6弱といっても，震源が浅い場合もありますから，
震度が大きいものが必ずしも巨大地震（マグニチュードMが大きい）とは限りません．

■地上の被害は震度（揺れの程度）に比例します．
地下の岩盤には色々な原因で歪が蓄積していき，岩盤の耐えられる歪の限界を超えると，
岩盤がポッキリ折れて地震が発生するというイメージです．
岩盤が強靭なほど溜め込める歪エネルギーの限界は大きく，限界まで溜め込んだ岩盤が地震で放出するエネルギーは大きい
（地震のエネルギーの対数がマグニチュードM）．
地震は破壊現象なので，限度まで歪を蓄えた岩盤がいつどこで破壊するかを予知することは不可能だが，
破壊が始まってからの前駆現象を少しでも早く観測することは可能です．

■日本の地震の発生メカニズムを調べると，大雑把に言って2つのタイプがあります．
１．海溝型（海洋プレート沈み込み境界）
Mは大きい巨大地震で，頻度分布は数十年～100年．
２．内陸型（陸側プレート内）
震源は地下5～20kmと浅い．Mは小さいが震源が浅いので，直上の被害は大きい．頻度分布は数百年ー数十万年．
日本で起きた最近の大地震は，内陸型です．
海溝型の地震は，1923年の関東地震以降起きていません．心配されている東海地震や南海トラフ地震は海溝型です．

■地層に残る地震の記録や，古文書の記録を調べると，日本の各地で，数多くの地震が繰り返し起こっていることがわかります．
この地震発生の繰り返し周期はどうなのか，地震発生の予測のために，経過年に対する地震頻度の分布を作ります．
過去の地震記録はどのような分布と合うでしょうか．地震は破壊現象なので発生確率はランダム（その時はポアソン分布）
が予想されます．沈み込むプレートに引き込まれた陸地が時折り弾性反発するモデルは，Brown酔歩時間の分布(BPT)が予想されます．

全国を250kmのメッシュに切り，その地に影響を与える活断層起因の地震やプレート境界起因の地震で，
地表の震度が６弱以上となる地震について発生確率を算出します．
メッシュに切った各地の30年以内の震度6弱以上の地震発生確率を着色した地図が以下のサイトにあります：
http://www.j-shis.bosai.go.jp/map/

■ここで用いられる地震の発生確率の定義では，分布密度関数を積分した全面積が確率１とします．
現時点は分布密度関数内のどこかですが，現時点から分布密度関数の０となる将来時点までの積分値に対する，
現時点から30年先の時点までの積分値の比の値が30年以内にその地震が発生する確率となります．
現時点がどこか（過去の最新活動時期が不明）わからない場合には，地震の発生が「ポアソン過程」に従うとします．

地震は繰り返し発生しますが，正確な周期があるわけではありません．
今日地震が起こらなければ，明日地震が起こる確率は、今日より高くなる
今日より明日，明日より明後日と大地震がやってくる確率はどんどん高まって行きます．

（注）地震のマグニチュードMとその発生確率は，べき乗測が成り立つことが知られています．
被害の大きい巨大地震（Mの大きいもの）も，発生数は少ないですが必ず起こり，その時の被害は甚大です．
上で，議論して来たのは，時間（年）の経過に対するある大きさ（震度８弱）をもたらす地震の発生確率に関するもので，
べき乗測と混乱しないでください．

■さて，地図にある日本の活断層の話に移りましょう．
赤い線は活断層です．関東地方では，高崎-熊谷-深谷の西側を流れる荒川に沿いに走り，荒川は江戸区で東京湾に注ぐ．
断層地帯の荒川上流は長瀞など風光明美な処です．富士山側の活断層は，諏訪-甲府-富士山の西側を富士川沿いに走り，
駿河湾に至ります．活断層は繰り返し地震を起こしており注意が必要です．

ーーーーーーーーーー
7月22日から数学月間が始まります．暑い日が予想されますが皆さまお変わりなくお過ごしでしょうか
お近くの数学イベントにご参加ください．
◆数学月間懇話会（第12回）
日時：7月22日，14:00～17;00（開場13:30)
場所：東大駒場キャンバス，数理科学研究科・002号教室
１．数学者って，どんな顔をしてる？
　　亀井哲治郎・河野裕昭（亀書房・写真家）
２．世論調査は正しいか
　　松原望（東京大学名誉教授，聖学院大学）
３．がん登録の可能性
　　田渕　健（都立駒込病院・東京都がん登録室）
参加費無料．直接会場にお出で下さい．
例年，暑い最中です，教室には冷房がありますが，
近くに水飲み場や販売機はありません．水筒を持参されることをお勧めします．
17:30より構内カフェテリア（イタリアントマト）にて懇親会（めいめい払い）
問い合わせ先：sgktani@gmail.com（日本数学協会，数学月間の会）
◆三鷹ネットワーク大学　国際基督教大学寄付講座
題目：数学の夕べ　「関係性の数学 - カテゴリー(圏)論入門」
日時：７月２２日（金）19:00?20:30 　
https://www.kouza.mitaka-univ.org/kouza/B1651000
場所：三鷹ネットワーク大学 　　　（東京都三鷹市下連雀３－２４－３　三鷹駅前協同ビル３階）
◆ICUオープンキャンパスでのモデル授業
題目：シンメトリー ? 多項式で楽しむ
講師：清水勇二
日時：８月１３日（土）　１２：０５?１２：５０ および １５：０５?１５：５０
　 (同じ講義を2回します。)
場所：国際基督教大学 理学館２F　２２０ 教室
(東京都三鷹市大沢 3-10-2)
◆とっとりサイエンスワールド
7/31（米子），8/21（鳥取），9/11（倉吉）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.07.12］ No.123
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
昨日参院選が終わりました．改憲勢力が2/3になりました．
RDDによる世論調査やビッグデータによる選挙予測通りの状況になってしまいました．
RDDによる今回の世論調査では，母集団の性質を代表する正しいサンプル集合であったことになります．
特に，ビッグデータによる予測では，今回さらに実証データが増えましたから，
モデルの精度はますます向上することが期待できます．

デッドヒート状態にある選挙区では，結果予測のアナウンス効果で，正あるいは負のフィードバックが
最後の一揺れを起こす場合があるのですが，今回は予測をひっくり返すほどのものではなかったようです．
そもそも投票率が低い54.4%（世論調査ではこれより高い予測）．
「改憲勢力が2/3になるのが良くない」が世論調査では47%でしたが，
結果は，改憲勢力が追加公認も入れ77人で64％でした．世論調査では「まだ決めていない」が35%もあったので，
これが棄権につながったように思います．比例区の支持政党なしの党に1.2%の得票がありなんたることだ．

選挙予測は当てなければならないが，別の見方をすると，結果が予測できるような安定な選挙ではだめだ．
この安定さは，NHKを始めとする大手TV・メディアが選挙の様子を報じないために作られたものだ．
私はインタネットの中継で，各政党候補の街宣演説を聞いているが，特に自民党候補の質は低い．
名前だけを連呼する内容のないものが多い．安倍総理の演説も低俗なものであった．
TVの報道だけではこの差はわからない．各党の街宣演説に出会うこともなかった人には，
今回の選挙は行く気にもなれない盛り上がらないと感じただろう．争点を隠し投票日を迎え，
無風状態で予測通りの安定な結果となったわけだが，これを予測が正しいと喜ぶわけにはいかない．
メディアは予測よりも現場と政策内容に切り込んでもらいたいし，市民はアナウンス効果に鋭敏に反応するようでありたい．
社会は複雑系なのだから，バタフライ効果はいつ起こっても良いはずだ．
このような選挙結果の鈍感安定さは，選挙制度（小選挙区）にあることは間違いない．

■次回取り上げるテーマ：地震の発生確率．
今日地震が起こらなかった．明日は今日より地震発生確率は高いのだが？

－－－－－－記－－－－
数学月間懇話会（第12回）
主催●日本数学協会，数学月間の会（SGK）
日時●７月２２日，14:00-17:10
－－－－
１．数学者って，どんな顔をしてる？
　　亀井哲治郎・河野裕昭（亀書房・写真家）
２．世論調査は正しいか
　　松原望（東京大学名誉教授，聖学院大学）
３．がん登録の可能性
　　田渕　健（都立駒込病院・東京都がん登録室）
ーーーー
会場●東京大学（駒場）数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●数学月間の会（SGK）
sgktani@gmail.com，谷克彦（SGK世話人）
直接会場においでください（開場13:30）
17:30より構内カフェテリアにて懇親会（各自払い）
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.07.05］ No.122
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■現代は，衛星からスマートフォンまで大小のソースから，さまざまなデータが絶えまなく集められています．
検索サイトのgoogleやyahooにはビッグデータが蓄積しています．
ビッグデータの様々な利用法やそのための解析法も急速に発展しつつあります．
世論調査は従来から，RDD（無作為抽出）の電話によるアンケート形式で実施されているのだが，
先日，yahooのビッグデータを用いた参院選挙当選予測が発表された．
http://docs.yahoo.co.jp/info/bigdata/election/2016/01/
それによると改憲勢力が2/3に達しそうな情勢という．

■webサイトを渡り歩き，あるサイトで買い物をしたとする．そこに導いた各webサイトの貢献率は如何様なものだろうか？
googleの各webサイトのレイティングはどのように計算しているのだろうか？
サイト間の遷移確率を成分とする遷移行列＊)を作り，この行列を各サイトの状態に作用させた結果，
各サイトの状態は新しい状態になる．何度も遷移が繰り返されると，状態が収束するとして，
各webサイトの状態（貢献度，ランキング）を求めることができる．
*)各webサイトを頂点とし，頂点間の遷移を矢印で表すと，有向グラフができる．
サイト間の遷移確率をこれに書き込むと遷移行列になる．

■さて，選挙の当選予想に戻るが，Amazonの「これを買った顧客はこれも買う」のような推薦システムや，
企業が集めたデータから，顧客の行動を予測をしている．これにはクラスタリングと最隣接クラス分けのツールが用いられる．
投票行動の予測もこれに類似したものであろう．
ビッグデータをどのように解析したのかわからないので，何とも言えないが，
過去に実績のある推測法らしいので当たるかもしれない．
http://searchblog.yahoo.co.jp/2012/12/yahoobigdata_senkyo.html
例えば，ある本の購入数，あるワードの検索数など，関係のなさそうな事柄と各政党の得票との相関を重ね合わせ予測がなされる
（投影法という）．定義した注目度という量を各候補の当落の評価関数に用いている．
なぜ各事柄と得票に相関があるのか，各相関を重ね合わせる時のウエイト付の意味など説明できないことだらけだが，
予測結果が実際と合うように決める．因果関係の筋が通っていないものは，私には信用できないが，
絡み合った因果関係の“複雑系の世界”とはそういうものなのでしょう．
地球のどこかで起きた蝶の羽ばたきが，後日離れた地でハリケーンの進路を変える原因になる
かもしれないという“バタフライ・エフェクト”の世界ですから．

そして，思いもよらぬ事柄の些細な変化で結果の逆転も起こり得ます．
予測は不安定ですので信じるのはほどほどにしないと誘導され易い運命論者になってしまいます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.06.28］ No.121
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
選挙戦たけなわです．皆様の周りは如何でしょうか．
TVニュースはもともと政治報道は少ないのですが，選挙期間中はさらに少なく，国民を眠らせておけとばかりです．
街宣の様子や市民の反応など中継して欲しいものです．政治討論でも，
選挙後に安倍連合政権が緊急事態条項の成立を狙っていることは触れないように話題をそらしています．
私たちは，支持率や選挙結果の予測や政局は，結果ですので知ったって意味がありません．
その根拠となる政策の賛否を議論したいのです．
しかし，支持率を見せて世論を誘導するというマスコミもあるようです．
内閣支持率が高いことを知って，戦っても無駄だとやめるのですか？
支持率が低いことを見て，見捨てて大勢につくのですか？
あるいはこれらの逆で，弱い方につくのですか？
支持率結果は，市民の投票行動に複雑なフィードバックを起こします．
雪崩をうって体制につく（正のフィードバック）のと，バランスをとろうとする（負のフィードバック）の混合でしょう．
24日朝刊トップは参院選情勢調査の結果で，いずれも自民党が勝利し、公明やお維新を加えると、
改憲に必要な３分の２に届く勢いであるとのニュースです．
それほど与党が優勢でしょうか？私の感じでは，まさにデッドヒートを演じていると思います．
野党統一候補が頑張っている所をもっと報道するのが公平だと思います．
さて，各社同じような世論調査を出したわけですが，出所は日経リサーチ社のもの．
読売は，日経と同じデータを使って，同じような記事を載せました．
これは，意図的で悪質です．以下の記事をご覧ください．
http://hunter-investigate.jp/news/2016/06/-24-300.html

さて，世論調査の結果と本番の選挙結果が逆転した例が，しばしば見られるようです．
直前の世論調査の結果のフィードバック効果により，揺さぶられることもありましょう．
しかし，それはさておき，世論調査はサンプリングで集めたした小さな集合（サンプル集合）で行いますから，
ランダムサンプリングを心がけても，一方の陣営の意見が多く集まって偏ったサンプル集合ができる危険性は避けられません．
このサンプル集合が，安倍内閣の支持率が高いという，世論誘導に都合のよいものを意図的に選ぶということも起こりえます．
そのような意図的なサンプル集合でないとしても，賛否が半々（50%付近）で，拮抗している場合には，
統計学的に誤差が大きくなります．別のサンプル集合をとれば別の支持率がでます．
サンプル集合の撮り方による支持率のばらつきが標本（サンプル）誤差です．
賛否が拮抗している（50%付近のデッドヒート状態）ときは，信頼度95％（100回中95回はこの幅に収まる）で考えると，
7.1%（サンプル数200），4.1%（標サンプル600）の誤差があります．

さて，皆さんはEUに残留か離脱かの英国の選挙結果をどう思いますか．
私は英国が自分だけ離脱したことは，大変残念なことだと思います．
この国民投票前の世論調査では，どちらが過半数をとるか，さまざまな予測がありました．
ほぼ半々の予測だったわけです．
このようなデッドヒート状態の時には，予測の誤差は最も大きく，
今回のように３～4%くらいの逆転が起こっても不思議ではありません．
サンプル集合のサイズ（サンプル数）を大きくすると，この誤差は小さくなりますが
よほど大きくしなくてはならず，本番の投票のようになってしまいます．
英国の国民投票の結果は，離脱51.9%，残留48.1%（投票率72.2%）でした．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.06.21］ No.120
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
世論調査に関する記事は，日刊ベリタ（6/18）に掲載していただきました
http://www.nikkanberita.com/read.cgi?id=201606181029266
今週号は，これをもとに書き足したものです．
以前にも，英国世論調査(5/24号)，ビデオリサーチ(5/31号）は，すでに取り上げています．
こういったものがどれほど正しいのか，疑問に思いませんか？
自分は聞かれたことがないのにどうして意見が反映されるのか？
わずかなサンプル集合で行った統計的推論が母集団の性質になるのか？素朴な疑問ですが，
これらは根拠のない不安ではありません．
明後日は参院選の公示で，それから選挙戦に突入します．
世論調査は週末に行われ，調査の方法はだいたいRDDという
「コンピューターでランダムに発生させた番号に調査員が電話をかける」方式です．
母集団は全国の全有権者で，調査に選ばれた回答数「サンプル集合」は，2,000から700程度です．
サンプル集合はこの程度のサイズだから，私は選ばれたことは一度もありません．
各地域からできるだけ均一なランダムサンプリングになるように，色々工夫をしているようですが，
誰もランダムサンプリングがなされたことを保証できません．
実際に偏ったサンプリングが行われて（意図的ではなかったが）予測が外れた例が昨年の英国総選挙でも起きました．
意図的に偏ったサンプル集合や小さなサンプル集合を採用することも可能で，世論操作は可能です．
出された数値は独り歩きします．
メディアのコメンテータは，世論調査で出た政党支持のわずかな変化を過剰に解釈する傾向があり，
証拠が推論をサポートしていない（統計的に有意でない）のに，公衆に党の運命が変わってきたと印象づけたりする．
何ポイント支持率上昇とかいうが，そのような変化を起こす因果関係を説明できる事実はあるのか私は問いたい．
アンケートの作り方（問の文章，およびそれらの配列順，回答用選択肢）は，回答結果に影響を与えます．
複数ある設問は，互いに独立に見えるが，実際はある種のパラメータで関連し合っている．
設問の配列順で，そして，回答を誘導していくことも可能です．
問題を良く理解している人しか答えにくいようにすることも可能です．
「○○のために，▲▲するのはどう思いますか」というような問いかけは巧みです．
条件付きで答えが決まるなら，条件がない問いには答えようがありませんから．
このような論理と因果関係は明瞭にして欲しいものです．
とにかく色々な原因で，サンプル集合には偏りが生じます．そのようなサンプル集合で解析した結果は，
サンプリング理論の予想外の誤差が起こります．
ーーーーーーーーーーーーー
最後に，先週末（6/17～19）時点の各社の世論調査から内閣支持率だけ掲載します：
日本テレビ：世帯数1487，回答数725，回答率48.76%，
内閣支持43.3%，内閣不支持39.5%
NHK：世帯数3035，　回答率66%，
内閣支持47%，　内閣不支持34%
朝日新聞：世帯数2371，有効回答1163，回答率49%，
内閣支持45%，内閣不支持36%
読売新聞：
内閣支持49%，内閣不支持38%

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.06.14］ No.119
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
空間充填パズル

空間は正8面体だけでは隙間なく充填することは出来ません．
（１）正８面体と立方8面体を組み合わせて空間を充填することができます．
ペロブスカイト構造に見られる正8面体と立方8面体による空間の充填構造
（２）正8面体と正4面体を組み合わせて空間を充填することができます．
ダイヤモンド構造に見られる正4面体と正8面体による空間の充填構造

（１）の場合は，正8面体と立方8面体の個数比は1:1です．
どのようにして数えますか？
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/14/17051514/img_2?1445217129
（解答）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/10/17507610/img_0_m?1465832802
赤い立方体の中に立方8面体が１つ納まっています．立方体の８つの頂点に
隙間がありますが，この隙間は正8面体の1/8の形です．したがって8つ集めると正8面体１つになります．
よって，個数比は，正8面体：立方8面体＝1:1　です．

（２）の場合は，正8面体と正4面体の個数比は，1:2です．
どのようにして数えますか？
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/62/17051462/img_1_m?1453416995

（解答）
正8面体が辺を共有するように配列しています．赤枠の正方柱の中に正８面体が2つ入ります．
なぜなら，１つは丸々入り，赤枠内の8つの頂点周りにある間隙には正8面体の1/8の形が入るからです．
さらに，正8面体間には間隙があり，その形は正4面体（橙色）です．
ただし，赤枠の中に入るのは正4面体の1/2の形で，上側に（1/2）x4個，
下側も同様ですので合計4個が赤枠内に入ります．結局，個数比は；　正8面体：正4面体=1:2　です．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/28/16779028/img_7_m?1453418256
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/10/17507610/img_2_m?1465832802

■小梁（OSA工房）によるCube充填パズル
周期的な空間でできるこの詰め込み構造を，立方体の単位胞の中につくります．
そのためには正8面体を分割した部品にする必要があります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/568616/28/16779028/img_5_m?1453418256

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.06.07］ No.118
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
早いものでもう6月です．私は，どれも進まないまま大変焦っています．
皆様は，順調な日々をお過ごしでしょうか？
これから，万華鏡と繰り返し模様の話を始めようと思います．

平面群P3m1とP31mの対称性はとてもよく似ています．
以下の２つはともにエッシャーの作品です．比較鑑賞しましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/566714/93/17489893/img_0_m?1465078055

どちらも3回回転対称のある繰り返し模様ですが
鏡映面の入り方が違います．
P31mの方には，鏡映面が集まっていない3回対称軸がありますが
P3m1の方の3回対称軸の場所には，すべて鏡映面が集まっています．
両者の絵から受ける微妙な感覚の差は，
このような所にあるのではないでしょうか？

■正三角形の鏡室の万華鏡を作ると，P3m1の壁紙模様が観察できます．
しかしながら，P31mの壁紙模様は自然には得られません．
その理由は，P31mでは鏡室の内部の図柄が3回対称である必要があるからです．
鏡室の図柄は，ガラス屑が自然に分布して作る図柄なので，
それが3回対称であるなどという偶然はあり得ません．

（注）平面群の記号P31m，P3m1の記法について：
P:単純格子，3：紙面に垂直な3回回転軸，
単位胞の辺（並進方向）に垂直な鏡mの有無，その他の方向の鏡mの有無
鏡のないときは１と記す．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.05.31］ No.117
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
いよいよここにきて選挙の動きが激しくなってきました．
はたしてダブル選挙があるのかないのか？
今回は，前回の「世論調査は正しいか」に続いて，「視聴率調査は正しいか」です．
これは，日刊ベリタに掲載（05/30)したものです：
http://www.nikkanberita.com/read.cgi?id=201605300831101

アメリカの視聴率調査会社ニールセンが，機械による視聴率調査をスタートさせたのは1961年．
日本でも1962年9月にビデオリサーチが設立され，12月より機械による視聴率調査が始まりました．
（ビデオリサーチは電通系列）
関東，関西，名古屋の3つの地区では，それぞれ600世帯にピープルメーターPMと呼ばれる装置がテレビに取り付けられ，
分ごとのデータが蓄積・送信されています．このシステムはPMシステムと呼ばれます．
この他に，オンラインメーターシステムというものがあり，全国に24地区（各地区の200世帯）で実施されています．
http://www.videor.co.jp/rating/wh/03.htm
例えば，関東地区には15,000,000世帯ありますが，そのうちから選ばれた600世帯だけが調査の対象になります．

全対象（母集団）の調査をするのが正確なのですが，実際には，“選ばれた”（サンプル集合）について調査をします．
全対象の調査（全数検査）は，国勢調査などの限られた調査だけです．統計量の解析は，サンプル集合について実施し，
それを母集団のものと推測します．
それが意味を持つ根拠には，サンプル集合は母集団の性質を代表しているということが前提にあります．
つまり，サンプル集合の作り方が，ランダムサンプリングによるということが前提にあります．
しかし，それがランダムサンプリングであるかどうか誰も保証できない．無作為に細心の準備をして実施しても，
サンプリングにバイアスがあり，サンプル集合に偏りがあることはしばしばあります．
2015年の英国総選挙で起こった外れた世論調査の原因研究報告については，前回のメルマガで述べました．

ビデオリサーチのサンプル数は，如何にも少ない感じがするでしょう．
サンプル数600は母集団の1/25,000（抽出率）です．ところがこれで大丈夫だというのです．
標本誤差（600世帯のサンプル集合で解析した統計量の母集団の統計量からのずれ）は，
視聴率10%（90%）では±2.4，20%（80%）では，±3.3，30%(70%）では±3.7，40%(60%)では，±4.0%，
50%では±4.1％です．
大きな母集団に対して，意外に少ないサンプル数でよい解析ができることになり，これが現在実施されている根拠です．
しかしながら，サンプル集合が母集団を代表している（ランダムサンプリングである）という保証はありません．
これらの議論はランダムサンプリングでなければ崩れてしまいます．
そして，サンプル数が少なければランダムサンプリングから外れる危険性は増加すると言わざるを得ません．
私たちの感じる心配は，いわれのないことではないのです．
視聴率調査結果を皆さんはどこまで信じますか？
出された数字が独り歩きし，人々を誘導するのは，前回の世論調査と同じです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.05.24］ No.116
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年は選挙の年ですが，世論調査を鵜呑みにしてはいけません．
世論調査のためのサンプル集合は信用できますか？
母集団からサンプル集合を作るのに，
意見を聞く集団が偏っていることは良くあります．
視聴率調査のビデオリサーチのように，サンプル数の少ないものもあります．
母集団を代表しない偏ったサンプル集合では正しい情報が得られません．
ランダムサンプリングであるのが前提ですが
ランダムサンプリングであるかどうか事前に判定できません．
昨年６月の英国総選挙の世論調査では実際にそのようなことが起こり
保守党と労働党の票獲得は，予測された「統計的デッドヒート」が実現せず，
保守党が労働党に対し7ポイントの優位で下院の多数を勝ち取った．
選挙直後に，外れた世論調査の原因研究が
英国世論調査会議BPCと市場調査協会MRSによって立ち上げられ，
2016年3月に報告書（120ページの長文）が出た．
この報告書は大部のため，本稿への引用は，Tarranのエッセイによる（注）．

報告書によると，サンプルが母集団を代表するものでなかったことが，
世論調査ミスの主原因であるというのだ．
世論調査組織が使ったサンプル補集の方法が，
労働党有権者を過剰に，保守党有権者を過少に系統的に集め，
適用された統計的調整手順も，これらのエラーの低減に効果がなかったという．
報告書が勧告する改善提案は，将来起こりうる世論調査ミスのリスクを低減するが，
リスクそのものを取り除くものではないことに注意しよう．

世論調査では，今後も非ランダムサンプリングを使用せざるを得ない．
ランダムサンプリング（確率的サンプリング）は，実行するのに，費用と時間がかかる．
しかし，非ランダムサンプリング（非確率的サンプリング）に比べて明らかに優れている．
非確率的サンプリングではサンプルに偏り（バイアス）が生じ易いのだ．
回答者がランダムに選択されるなら，母集団のすべてのメンバーに，調査参加者となる一定のチャンスがある．
これ自体は，得られたサンプルが，母集団の完全な代表であると保証するものではないが，
選択のランダム性は，代表されるグループの外部/内部を調整するためのサンプリング理論の適用を可能にする．
また，サンプルへ自己選択される可能性を下げ，回答者の採用過程で，バイアスがかかるリスクを軽減できる．
研究報告書を読んで失望する読者もいるだろうが，失望が畢竟実用主義への道を与え，
世論調査の難しさと不確実性を理解することになる．母集団でなくサンプルで解析するのだから限界がある．
世論調査は将来起こるかもしれない行動について，
有権者のようなよくわからない母集団を調べるので苦しい闘いに直面している．
世論調査の実施方法の高い透明性と，その推定の不確実性レベルを明確に伝える責任がある．
それぞれの政党の支持率の信頼区間と前回公開世論調査に対するそれぞれのシェア変化
の統計学的有意差検定を合わせて報告することを報告書は勧告している．

メディアのコメンテータは，世論調査で出た政党支持のわずかな変化を過剰に解釈する傾向があり，
証拠が推論をサポートしていない（統計的に有意でない）のに，公衆に党の運命が変わってきたと印象づける．
このようなことは避けるべきだ．

（注）https://www.statslife.org.uk/politics/2752

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.05.17］ No.115
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
皆さんお変わりありませんか．良い季節になりました．
今日は町の歩道で見かけたタイルの景色についての軽い話です．

■問
Fig.1Aをご覧ください．綺麗な市松模様が見えます．
確かに斜めから見ると（Fig.1B）コントラストがあります．
しかし真上から見ると（Fig.1C）コントラストがつきません．何故か？

Fig.1
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/77/17449077/img_3_m?1463289592

■正解発表
タイルの条線がコントラストに差を生じると思ったでしょう．その通りです．
条線に直角な横方向から浅い視射角で見下ろす場合Aと，
条線方向から浅い視射角で見下す場合Bを比較すると，前者Aの方が暗く見えます．
だから，条線が市松模様になっているタイル張りを，浅い視射角で見下すとコントラストの市松模様が見えます．
見る方向を90°変えると，いままで条線方向を見せていたタイルは，条線が横方向になりますので，
タイル張りの市松模様コントラストは逆転します．

では，条線の横方向から浅い視射角で見下すAは，条線方向から見るBより，
タイルが暗く見えるのは何故でしょうか？

Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/06/17451706/img_2_m?1463289812

Fig.2をご覧ください．視射角θが浅い（A)の場合は，条線の底（図中の緑）が見えません．
しかし，（A)の場合でも視射角θが大きくなれ条線の底（図中の緑）が見えます．
実地にタイルを観察してみると，条線は１ｍｍ程度凹んだ底で，
その上，条線の底はタイルの凸部より白くなっている（散乱光の光量が多い）のです．
従って，視射角が浅くなると条線（図中の緑）から散乱光が視点まで来なくなりタイルは暗く見えます．
一方，条線の方向から見た（B)の場合は，視射角にかかわらず，いつも条線の底（図中の緑）が見えますので，
タイルは大体明るく見えます．
この解答へのヒントとして，浅い視射角で撮影した写真（Fig.1B）と，
タイルの真上から撮影した写真（Fig.1C）を掲載しました．

■以上で，この話は完結で，私のfacebookに掲載したところ．読者の方から反響やコメントがありました．
写真(Fig.1A)で，横方向の条線タイルの中がさらに明・暗のコントラストに2分されている所があるのは何故かという疑問です．

写真（Fig.1A）の写真撮影では，できるだけ見やすく，均一な効果が出る場所を選ぶのに苦労しました．
説明通りに均一な市松模様のできる場所はありますが，1枚のタイルの中が明・暗に2分される場所もあるのです．
言及しないつもりでしたが，その説明が必要になり考えました．
タイル真上から見た写真(Fig.1C）を詳しく見なおしても，タイルの条線の幅も深さも均一です．
このような1種類のタイルで市松模様を作るという条件で，この現象の説明を考えるなら，
タイルが平面ではなく，タイルの表面が円柱表面のように（条線方向を円柱の軸方向）わずかに反っている場合
しか考えつきません．しかし，facebookの読者は，タイルの反りでの説明は満足しないようです．
そこで，タイル張りの別の場所（Fig.3A）で，真上から撮影した写真（Fig.3B）がありましたので，それも調べて見ました．
写真（Fig.3B）を見ると，タイル内の半分領域の条線がつぶれているタイルもあることがわかります．
これでこの疑問は解決しました．
つまり，完璧な条線のタイルだけで市松模様を作るという仮定から導けるパターンではなかったのです．
Fig.3
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/06/17451706/img_3_m?1463289812

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.05.10］ No.114
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
連休も終わってしまいましたが，皆さまお元気でお過ごしでしょうか．
大変な日々をお過ごしの方もおられるでしょう・お見舞い申し上げます．

今回は，対称性とキューリーの原理について紹介します．
ピエール・キューリーは，私の最も好きな科学者で，
キューリーの原理も学生の頃から今までずっと心を奪われている事柄です．
半導体や誘電体など色々な材料で，色々なデバイスが作られています．
例えば，半導体結晶を舞台にして，光子や電子が演じるパフォーマンス
を利用するのが，半導体デバイスです．舞台となる結晶世界は周期的なデジタル世界です．
（周期的な空間は「結晶空間」とも呼ばれます）
周期的な空間の数学（対称性）はとても重要で魅力的，いつも私の心をとらえていました．
この分野では，フェドロフ，シュブニコフ，ベーロフ，ザモルザエフなどの学者を輩出した
ロシアが大変魅力的で，1970年代にはロシアの本を一生懸命勉強したものです．

結晶の幾何学（数理結晶学発展史），結晶空間（周期的空間）の対称性
の話は，ぜひ取り上げたいと思っていますが，
今回は，キューリーの原理の易しい紹介にもどります．

色々な「系（もの）」や「そこで起こる現象（こと）」の理解に，「対称性」の考え方が使われます．
ピエール・キューリーは，“結晶という舞台”で起こる”物理現象の対称性”を研究しました（1894）．
水晶結晶の圧電効果はその例です．
「舞台の対称性は，その舞台で起こる現象の対称性に反映されるべきだ」という因果律は，
キューリーの原理と呼ばれます．
色々な分野で，原因（舞台）と結果（現象）のそれぞれの対称性間でこの因果律がなりたちます．
例えば，結晶にX線ビームをあてたとき，結晶を通過したX線の作る回折パターンの対称性には，
その原因となった結晶の対称性が反映されています．
あるいは，運動量保存則が成り立つのは，空間が無限に広く一様であり，
平行移動しても変わらないからです．
エネルギー保存則が成り立つのは，時間に関して変わらない時です．

環境舞台とそこで生きる生物の形．結晶構造とそこで起こる物理現象．
万華鏡の鏡室と生じる繰り返し模様．
こられもみんな対称性の因果律が支配しています．
「もの」や「こと」の対称性とは，変換をほどこしても，
「もの」や「こと」が全体として変わらない性質です．
例えば，回転や鏡映で系全体が不変なら，その系には回転対称，鏡映対称があるといいます．

音楽や詩歌の形式や韻律．
絵画，壁紙模様，タイル張り模様，建物，などのデザイン．
.....，芸術を始め色々な分野で，対称性の考え方が役立ちます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2016.05.03］ No.113
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
連休の中日となりました．良い休日でありますように．しかし，
地震で落ち着かない日々を過ごされている方もおありでしょう．
お見舞い申し上げます．

今年の数学月間懇話会（第12回）のお知らせです．
日時：7月22日，14:00～17;00
場所：東大駒場キャンバス，数理科学研究科・002号教室
１．数学者って，どんな顔をしてる？
　　亀井哲治郎・河野裕昭（亀書房・写真家）
２．世論調査は正しいか
　　松原望（東京大学名誉教授，聖学院大学）
３．ガン登録とガン統計
　　田渕健（東京都立駒込病院）
参加費無料．
17:30より構内カフェテリアにて懇親会（各自払い）
問い合わせ先：sgktani@gmail.com（日本数学協会，数学月間の会）
みなさんのご参加をお待ちします．

始めの話題は，JIR（ジャーナリスト・イン・レジデンス）という活動の紹介です．
編集者の亀井さんは，写真家の河野さんと組んで，
数学者へのインタビューと写真撮影を続けて，すでに１５０人を超える人たちを取材しました．
今年のテーマは統計学です．次に，２つの話題を取り上げます．
世の中は不確かなものやことばかりで確率で記述されます．
確率の正しい理解が必要です．
従来，得られなかったようなデータも多量に収集できる時代になりました．
でも，データ収集が恣意的であったり，不合理な解析をしたりすると
どんな結論でも導くことができるので，だまされないように要注意です．

（その他お知らせ）
5月22日に，日本数学協会のシンポジウムがあります．
こちらの方は，協会員は無料ですが一般の方は若干の参加費がかかります．
場所：大東文化大学
13:30－14:30　岡本龍明（NTT)，暗号
14:50－15:50　加藤文元（東工大),ライプニッツ

■雑談：エンブレム
このデザインの生まれるまでを，勝手に推理してみました．
おそらく次の順番で，右端のデザイン（パラリンピック）に到着したのでしょう．
地球（ステレオ投影）のイメージ（左端）から，2番目の市松模様を作り，
赤い円領域をくり抜くと，パラリンピックのエンブレムになります．
ここまでは自然ですが，これからくり抜く穴を中心に持っていくのは，
平行移動のパズルで難しい．でもいくつかのユニットを平行移動だけで入れ替えると
オリンピックのエンブレムができます．
そこで，次の疑問が浮かびました（未解決です）．
オリンピックのエンブレムが3回回転対称に落ち着くのは何故でしょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/572283/97/17424497/img_0_m?1461891630