note.com投稿記事

Интервью с Семёном Гиндикиным
«Троицкий вариант» №10(229), 23 мая 2017 года

撮影は，Natalia Demina

Natalia Demina が，Semyon G. Gindikin（ロシア系アメリカ人の数学者、教師、数学の普及者）に，モスクワ生涯数学教育センターで，インタビューをしました．
反ユダヤ運動が才能ある若者にどのように影響したか，I. M. ゲルファントのセミナーについて語る．

О том, как отразилась на талантливых ребятах антисемитская кампания, о семинаре И. М. Гельфанда Наталия Демина поговорила с Семёном Григорьевичем Гиндикиным, российско-американским математиком, педагогом, популяризатором математики. Беседа с этим веселым, остроумным человеком состоялась в Московском центре непрерывного математического образования.

--------- 以下用紙抜粋---------- 

◆ピーター・セルゲイビッチ・ノビコフは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学の力学数学学部（мехмат）で反ユダヤ主義について話し始めるのが嫌いでした。数学者になり、「暗い20代」を強い人々が生き残ることができたという例です. それは本当ではない。これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に本物の数学者になることができたように私には思えます. 私は本当にラッキーでした。まず第一に、すぐに私の仲間と素晴らしい数学者の両方が私の近くにいることがわかったからです。

◆ イスラエル・モイセービッチ・ゲルファントについて一言いただけますか? 彼のセミナーに参加したことがありますか？

- もちろん。彼の90歳の誕生日に、これらのセミナーに関する記事を書きました。ゲルファントはこれについて議論するのをためらっていましたが、ランダウの物理学セミナーが彼のセミナーに強い影響を与えたように私には思えます。ある時点で、ゲルファントは物理学を学びたいと思っていたので、セミナーでは多くの物理学のプレゼンテーションがありました。レフ・ダビドビッチ・ランダウはイスラエル・モイセビッチ・ゲルファントをやや見下そうとしたと思います。

ランダウを初めて見たときのことを正確に知っています。これは1955年のことです。関数解析に関する会議があり、国内で最高の数学者がすべて集まりました - モスクワでの大きなイベントです。その時まで、実質的に会議はありませんでした。最初は戦前に行われました。モスクワ全体がこの会議の開会式に参加しました。そして、イスラエル・モイセエビッチはそこで君臨しましたが、彼のセミナーではいつもより少し控えめに振る舞いました。最初の報告は、ランダウによって行われました。そして、彼らはそれぞれのパートを完璧にリードした 2 人の偉大なアーティストであることがわかりました。その時までに、Israel Moiseevich は Bob Minlos と一緒に、経路積分と呼ばれるものを考え出していました (Bob は私の友人であり、素晴らしい人物であり、数学者でもあります)。

Landau の報告の後、Gelfand は、これらの積分はおそらく場の理論を作成する正しい方法であると彼に非常に穏やかに説明しようとしました。そしてランダウはこっそりと彼に答えました：「イズレール・モイセエビッチ、鶏は秋に数えます（捕らぬ狸の皮算よ）」。このフレーズは、ピョートル・セルゲイヴィッチ・ノヴィコフが好んで言ったことを覚えています。

ところで、私は、レニングラードで開催された数学会議 (1960 年頃) で、ゲルファントとランダウの間の別の会話を目撃しました。I. M. と一緒にネフスキーに沿って、Baltiyskaya Hotel の近くを歩き、Landau に会いました。真剣な現代数学を再び適用する可能性についての話題が会話の中で生じたことを覚えています。I. M. はいくつかの例 (ローレンツ群の表現だと思います) を引用しましたが、L. D. は断固として彼に同意しませんでした。彼は、何年にもわたって「数理物理学の方程式」に関するセクションがあったが、物理学への本格的な数学の重要な応用を知らないと述べた.

今日、現代の理論物理学でどのような精巧な数学が使用されているかを見ると、ゲルファントが正しかった可能性が高いように思えます。どうやら、ランダウは将来の物理学における数学の役割を過小評価していたようです (私の物理学者の友人から聞いたところによると、おそらく彼の学生の何人かはこれに多額のお金を払ったようです)。

ゲルファントのセミナーに戻ったら、私の見解を繰り返します。イスラエル・モイセービッチが民主主義を認めなかったことに多くの人が腹を立てた。彼にとってセミナーは、ある意味で彼の人生の本業でした。

第一印象は、セミナーのすべてが即興であるということでした。セミナーは大幅に遅れて始まりました。Gelfand 氏は、セミナーを待つことがコミュニケーションの最適な時間であると説明しました。これは、人々が（無意識のうちに！）互いに話し合う、科学的コミュニケーションにとって貴重な時間でした。

そのような完全に意識的な混乱は、彼の性格の特徴でした。彼はすべてを時間通りに行う必要があるとは考えていませんでした。彼は、自分にとって都合の良いことをする権利を獲得し、一般に受け入れられている規則を考慮しないと信じていました。少し大げさですが、あなたは素晴らしい人なので、導かれるように振る舞う必要があります。そして、これは最良の結果をもたらします。礼儀正しさは、イスラエル・モイセヴィッチの強みではありませんでした。しかしいつもではない。彼は誰とどのように話すかを知っていました。それでも、彼はスターリン時代を生き抜いた男でした。しかし、しばしばある時点で彼は崩壊し、すべての宝石外交は裏社会に陥りました.

セミナーに関しては、彼にとってそれは人生の主な仕事でした。それは彼自身が数学のほとんどを理解した場所であり、彼は他の人にこの数学を理解する機会を与えたと信じていました. そして、彼は完全にリラックスしていました。彼の態度は、すべての人に適しているとは限らなかったかもしれませんが、このセミナーから利益を得たいと思った場合、他の人が支払わなければならない種類の賛辞でした.

セミナーの数日前、彼はセミナーの内容について考え始めました。ゼミにいた有名な数学者で、普及にも携わったポール・ハルモス（ポール・リチャード・ハルモス）の思い出がある。セミナー、ゲルファントとの交流、彼がクレムリンをどのように案内したかについての章全体があります。そこでハルモスはセミナーに来て、綿密なレポートを作成しました。彼は偉大な達人であり、彼の本は高い教育レベルで書かれていました。そして、ここで外向きに-ある種の完全な障害：Gelfandは、スピーカーに発言権を与える代わりに、彼に質問をし、他の人と話します。

しかし、ゲルファントの世界モデルでは、そのような無秩序はありませんでした。最初のセミナーは彼にとってトランスのようなものでした。彼は数学を際限なく聞く準備ができていました。このため、彼は交霊会のように、導かれたように振る舞いました。そして、誰もがそれを気に入ったわけではありません。さらに、数学者は他の人のためにゲルファントに腹を立てることがありました。

しかし、イスラエル・モイセビッチは、名誉ある教授に「あなたは何も理解していない！」と言うことができれば、常に信じていました。-これは、彼が彼を平等に扱っていることを意味します。そして、彼が丁寧に彼に話しかけると、彼は彼を人として、そして確かに数学者として保持していないことがわかります。それがスタイルでした。

Gelfandは、人々が自分のキッチンに入るのを許可した場合、数学をどのように聞いたか、それについてどう考えたかを隠さなかった場合、そのように振る舞う権利があると信じていました。これは、このセミナーの心理学を再構成したものです。すでに説明しました。外国の数学者にとって、ゲルファントのセミナーに出席することは、ボリショイ劇場に出席することと同じくらい義務的でした。それはその娯楽の一部でした。

私が西側でアーノルドとマスロフと一緒に行った最初のことの 1 つは、モスクワとレニングラードでの一連のセミナーの開会式でした。彼女のアイデアは、モスクワのセミナーのスタイルを伝えようとする試みでした。西洋では、セミナーは短い純粋にビジネス的なものです。若い科学者たちは大学院での研究を完了し、博士号を擁護し、独自の軌跡に沿って世界のさまざまな場所に行きました。そしてモスクワでは、彼らは永遠に残りました。彼らはどこにも連れて行かれず、実際、彼らの専門分野で働くことができず、「箱」に座って、夕方にはアーノルドまたはゲルファンドのセミナーに来て、彼らの職業生活の最良の部分が始まりました。

そして、その学校は永遠のように見えました-それは決して終わらない学校でした. しかし、それは皆の個人的な選択であり、彼らは予期せずそこで厄介になる可能性がありました... I.M.にとってセミナーは本当に彼の人生でした. 私が見つけられなかった困難な時期がありました。しかし、大学とステクロフカを追放されたとき、彼が戦った唯一のことは、セミナーを開いたままにすることでした。

彼はセミナーで見知らぬ人が現れて最前列に座る様子を語った. 彼らはショルダーストラップを着用していませんでしたが、すべてが見えました。クルチャトフ研究所で働いていたミハイル・アレクサンドロヴィッチ・レオントヴィッチから、「私服を着た男が歩いていて、肩に何か青いものを持っている」という非常に適切なフレーズを聞いた。

生物セミナーもありました。これも面白かったです。私たちが若い頃、私たちはすべてを理解していると思っていました-どうすればそれを少し改善できるか、そして人々がそれほど引っ張られないようにすることができます.

Izrail Moiseevich はこれらのセミナーをほとんど欠席しませんでした。非常に気分が悪いとき、彼はしばしば彼らを導きました。かつて、実験として、彼が私と A. A. キリロフにこのセミナーを行うように指示したことを覚えています。セミナーは短く、素晴らしく、すぐに終了し、すべてのレポートはスムーズに進み、誰にも邪魔されませんでした。しかし、それはゲルファントのセミナーではありませんでした!

すでにアメリカにいますか？

— いいえ、モスクワです。アメリカでのセミナーについても、ご希望があればお伝えできます。私はラトガース大学でイスラエル・モイセービッチと一緒に仕事をしました。そして、このセミナーは行きませんでした...

――社会に民主主義がなければ、科学は正常に発展しないという命題があります。一方、スターリン主義ロシアにおける数学の隆盛は、このテーゼと矛盾するように思われる現象です。これらの「メールボックス」、「鉄のカーテン」がなければ、ゲルファントのセミナーはそれほど成功しなかったでしょうか?

- いいえ。Gelfand のセミナーの成功は、主に彼の人柄によるものだと思います。彼はこの数学的生活様式を発明しました。私は、モスクワの数学が独特で、他に類を見ない現象であったことを強調します。私たちの会話の時までに、私が行ったことのない場所と私が見たことのないもの。しかし、私はこれを他の場所で見たことがありません。この現象の起源と性質は、別の議論のトピックです。

数学は単なる科学ではありません。私にとっては、最高の状態で、ハイアート、音楽、詩に近いです。アルキメデスの時代から適用された側面は、しばしば重要で注目に値するものでした。権力者との関係は異なり、長い歴史があります。数学がアテネで栄えたのにスパルタでは栄えなかった理由、プラトンが未来の王たちのアカデミーで数学を教えた理由、ギリシャの衰退とともに幾何学が消えた理由、ギリシャから多くを奪ったローマは数学なしでした...

ソビエト連邦では、数学は生物学や言語学と同じようには破壊されませんでした。一番上には、政府の問題、主に軍事的な問題を解決するために、少なくともしばらくの間、数学が必要であるという幻想があったからです。多くの人にとって、当時の数学はそのようなはけ口でした。まず、この世界ではなく、「眼鏡をかけた」若者が常にそこに引っ張られていました。一方で、マルクス・レーニン主義に言及せずに記事を書くことができる、比較的非政治的な場所はほとんどここだけでした。他のどの科学でこれを行うことができますか?

そして、一般的に民主主義は複雑なものです。彼女の原始的な理解は、彼女の不在よりもはるかに優れているわけではありません. 彼らが理解しているように、彼らの権利のために戦う暴徒。民主主義の大部分を大金で買う能力...

- 民主主義に関するテーゼの確認は、科学の分野で最も先進的な国が民主主義の例と見なされている国であるという事実である可能性があります: 米国、英国、フランス、ドイツ。

-主なことは、これらの国の若者は数学があまり得意ではないということです. それが問題です！私が推測するように、あなたはさまざまな数学者に会いました。そして、ユーリー・イワノビッチ・マニンのように、人道的に才能のある人々を何人見ましたか? 非常に人道的に才能のある人々は、しばしば数学に進みました。他の地域に行くのはほとんど自殺行為でした。

ソ連で何が起こったのですか？数学は、通常の状況下では、通常の社会では絶対に数学に入ることはなかったであろう一定数の人々を食い物にしてしまった。この国に数学に専念する準備ができている若者がどれだけいるのか、私は今でも驚いています. 米国では同様のことは何も起きていません。民主主義があるように見えますが。

- アメリカでは、数学サークルが盛んに行われていないのですか? 最近、アメリカでは子供向けの数学的教育が発展しているという記事がありました。アメリカ全土で非常に多くのサークルが作成されており、子供たちが数学に興味を持っているということです...

「見えない。誰が言っているのかわからない。

――丸ごと記事でした。もしよろしければリンクを送ります... [2]

- しましょう。あなたが知っている、彼らはしません。しかし、去った人々のほとんどは、私たちがソ連で行ったことを開始する必要があると考えていました。サークル、数学の学校...アメリカでは、これらすべてが利用可能ですが、これは比較的小さいです。ソ連では、まだ行くことができる「誘惑」はありませんでした。素晴らしい音楽があり、素晴らしいアーティストが登場しました。選択肢はあまりありませんでした。

アメリカでは、数学を勉強した人は銀行やビジネスに行きます。そして、私は悲しみでそれをする人を知っています. しかし、社会におけるそのような価値観。彼らは家族や将来を犠牲にしたくないので、そのような選択をしなければなりません。私の見解では、数学をするのにより助長している国があります。いいえ、この社会の好みの尺度では、純粋な科学はかなり低い位置にあります.

— 科学や数学の大衆化に関わった経緯を教えてください。Kvant にすばらしい記事があります [1] . このコラボレーションはどのように始まったのですか？

- 私はオリンピック関係者です。さまざまな種類のオリンピックに常に参加してきました。これには常に関心がありました。数学の普及は、さまざまな数学サークルへの参加を通じて自然に生じました。

科学の大衆化の中で、私は自分自身のために別のニッチを思いついた. 「物理学者と数学者の話」という本が生まれた最初の記事は、数学の歴史に関する記事でした。当時、数学の歴史は公式イデオロギーが数学に圧力をかけようとするトロイの木馬でした。

そして、私はこのトリックを思いつきました。私は、数学についてのように、数学の歴史について書こうと決心しました。みんながガウスの最初の2つの発見について理解できるように、正直に書くことにしました。ガウスは、彼が数学者になることをまだ決めていなかった時代に、ほぼ男の子として、通常の 17 角形の構築に関する作業を行いました。数学。

そして、私はそれを正直に受け止めて、この証明をどこからでもどこへでも書いてみようと思いました。それがクヴァントでの私の最初の出版物でした。そして、それは良い考えだったと思います。それから私は互恵の法則について書きました。

数学者は最も興味深い思想家ではありませんでした。難しい問題やパズルを解けるメガネ男子がいたからです。でもすごい人もいました。そして、私が最初に書いた人物はブレイズ・パスカルでした。

そして始まりました。私は普及者の役割を選びました。私は数学史家ではなく、数学史を語る数学者です。

セミョン・ギンディキン (1984) (「TrV」No. 10 (229), 05/23/2017)
セミョン・ギンディキン (1984)
- 現在、そのようなアクセスしやすいスタイルで、科学に関する本物の科学者の話が不足しています。

- アクセスしやすいだけではありません。つまり、科学の人間的側面です。私たちはすでにこの方向に進んでいたので、ある少年またはその両親が私に何か言ってくれたことを思い出しました。私の記事について、「彼は偉大な科学者を人として語る」と言われました。そして、それはまさに私の自己注文であり、私が望んでいたものでした. 数学の普及の分野での私の仕事はしばらく続きましたが、その後終了しました。

- なぜ？最後の記事は、1985 年から 1986 年に Kvant で公開されましたか?

「それから私は別のことを書きました。私はロシアを離れました。他の言語で書きたくないことに気づきました。数学について英語で書くことはできますが、ノンフィクションの物語や本はできません。たまに講義で話します。私はまだこれらすべてに興味があります。

- 雑誌はたくさんありますが、ロシアには同じKvantが存在します。仕事を続けたいですか？

— 今日の Kvant が何であるかはわかりませんが、当時は単なる人気のある科学雑誌ではありませんでした...

- 過ぎ去った時代...

— アメリカで開催された Gelfand のセミナーについては十分に話しませんでした。アメリカでのセミナーは失敗しました。イスラエル・モイセビッチは楽観主義者でしたが、うまくいかないと確信していました。私はこの失敗にとても腹を立てていたので、行くことさえしませんでした。第一に、モスクワでのゲルファンドのセミナーは無期限に続く可能性があり、その後、夜にモスクワを散歩しました。先日、レニンスキー大通りを車で走っていたとき、昔の考えがよみがえってきました。毎週月曜日は苦痛でした。

そしてアメリカでは反射神経があります。カップルが終わったら、全員が立ち上がって去りました。廊下で出会った方法を覚えています。まったく理解できなかったゲルファンドを完全に失いました。

アメリカの同僚に最初に言ったのは、私は I. M. Gelfand の教師ではなく、彼についての苦情は受け付けないということでした。しかし、イスラエル・モイセビッチはあらゆる種類のトリックを投げ出しました。そこでの生活のすべての民主的な性質のために、セミナーで話す人に「何も理解していない」と言うのは習慣的ではありません。そしてゲルファントは、「はい、彼は素晴らしい人物であり数学者です。私は数学者として彼にこれを話しました。」

非線形方程式を扱った有名で非常に優秀な数学者、Martin David Kruskal がいました。これは、I. M. と同じ強さと気質の男です。 Gelfand が Kruskal の宿題を出したことがあります。彼はレポートを作成し、優秀な学生のように最初の机に座って、マスターの先生が彼に電話するのを待ちます。そして彼は別のことを話します... クラスカルはゲルファントに思い出させます：「イスラエル、あなたが私に仕事を与えたことを覚えていますか？」I.M. は彼にすべてを覚えていると厳しく言います。そして時間が経ちます。ペアがなくなると、全員が去ります。マーティンは再び彼に思い出させます。I. M. は、彼がこれに興味を失ったと彼に話します。しかし、クルスカルのような男でさえ、そのような態度を理解するユーモアのセンスに欠けていました...

それにもかかわらず、セミナーは引き続き運営されており、さまざまな人がそこに来ました。そして、私ははっきりと理解していました。別の言語でいくつかのことを行うのは非常に難しいということです。一番下の息子が結婚したとき、突然、息子の結婚式で外国語を話すのはただの悲劇だと痛感しました。「シンメトリー」という本（この本は非常に数学的な本です）の冒頭で、ヘルマン・ヴェイユは私に非常に近い言葉を言いました。

- ロシアでの科学の普及は盛んです。人気のある科学の講義や科学の祭典に参加する人がますます増えています。同時に、優れた科学はもはや成り立たなくなり、科学に対する一般の関心が高まっているようです。もしかしたら、科学は人々にとってある種のはけ口になるのでしょうか？

- プロレベルではなく、アマチュアレベルで普及が行われています...

「科学者もこれをやっています。たとえば、ゲルファントの孫は講義をよく読んでいます。

- 私は彼の博士論文の監督者でしたが、彼の論文が何について書かれているかはよく知りませんでした. ミーシャはおしゃべりがうまい。教育的能力は彼の祖父から彼に受け継がれました、それは素晴らしいです!

ロシア社会はますます西洋社会に似てきており、同じ価値観を持っていますが、これは非常に危険なことです。科学者が後援を必要とするとき、それは非常に危険です。応用もいいのですが、文化にとって基礎科学はとても重要だと思います。絵画は常に抽象的だったわけではなく、音楽は必ずしもメロディーなしではありませんでした。

数学も比較的遅く抽象化されました。80歳までに、数学のような私たちの生活の驚くべき現象の何かを理解したいと思っています. 今日、このすべてについて書くとしたら、社会の生活についてすべてを説明する強力な教えがあったソビエト時代の生活がどれほど良かったかについて話すでしょう。

また、ある時点ですべての数学者が、あることを研究し始め、別のことを研究しなくなる理由についても考えます。たとえば、17 世紀になると、誰もが突如として微分積分や積分計算、つまり解析幾何学を取り上げるようになったのです。そして、これらの分野で働いている膨大な数の数学者がいました。世紀ごとの分布さえありました-各世紀に何人の偉大な数学者がいました. 18世紀にはほとんどいませんでしたが、6人の名前を付けることができます.

なぜピエール・ド・フェルマーだけが数論に従事し、次の世紀になって初めてこれに関心が現れたのですか? 不明。物理学者はこれを理解しています。彼らは、素粒子の理論や場の理論を、それが可能だと思われる瞬間に構築したいと考えています。あるいは、日本人が首都を放棄して新しい首都を建設したように、なぜ数学者は特定の分野の知識を放棄するのでしょうか?

— 数学的オブジェクトは、ある種の理想的な世界に存在すると思いますか?

「存在は危険で曖昧な言葉です。しかし、少なくともある時点で、何かがあなたの選択を後押しし、目的が達成され、定理が証明されると信じ込ませるような感覚を避けることはできません。数学は、最低限、論理的な結論を伴う形式的な真珠のゲームです。上のどこかからたくさん来ているような気がします。偉大な人でさえありませんが、平均的な数学者です。

詩人たちは、詩がどこから来ているのかを理解しようとし続けました...なぜ、特定のアイデアが数学者の生涯を悩ませているのでしょうか? I. M. Gelfand がこのことについて教えてくれました。もちろん、彼に会うことは私の人生の主な成功です。偉大な人がとても近くにいると、彼はあなたを悩ませ、時には些細なことをあなたに話しますが、一時的なものはすべて排除されます. そして、この人が別の世界と直接通信したことがわかります。これについては他に説明がない場合があるためです。彼はどのようにしてこれまたはあれを知ったのですか？

あなたは彼と一緒に本を書きました。彼は扱いが難しいと聞きました。

「彼と一緒に仕事をするのは難しくありませんでした。でもまた… 50年前に聞いていたら、彼と一緒に仕事をするのは無理だと言っていたでしょう！あなたが彼の家に来ると、彼は電話で誰かと話し、それから別のことをします。私はあなたに、彼は仕事を組織するという点であまり自分自身をコントロールしていなかったと言いました. それはあなたが望む誰のためでもあります。彼は、おそらく、私に向かって叫んだことはなく、誓うこともありませんでした。私自身、性格が悪いのでしょう。

最近、モスクワの数学者の 1 人が、I. M. Gelfand がかつて彼に (彼を仕事に呼んだとき)、Semyon Gindikin と一緒に仕事をすることの否定的な側面について話すことができると言ったことを思い出しました。でも今日、あなたがそのことを私に話してくれたとき、私は少し驚きました。その瞬間、この殻がすべてなくなったとき、彼は数学について話し始めました...そしてそれは奇跡でした! 特にしばらくすると、これの価値が理解できます。

今、私は以前に彼にしようとしたことを何とかすることができました. この本以外にも、かなりの数の作品を書いています。その時、いくつかのことがうまくいかなかった理由がわかりました。

あなたは現在教えていますか、それとも引退しましたか？

-正式にはまだ引退していません。しかし、私は健康上の問題を抱え始めました。両手がうまく動かない。新しい技術がたくさんあるので、ボードに書くのをやめる時が来たと思います。どうやら、もうすぐ教え終わるらしい。

- 何を教えていますか？

- 私の教育​​活動は狭い枠組みの中で行われています。これはモスクワ大学でも、プリンストン大学でもハーバード大学でもありません。それでも、ここの学生の入学はあまり良くありません。しかし、私は最善を尽くそうとしています。私はよく旅行をし、さまざまなイベントで数学について話すのが好きです。日本やオーストラリアに共著者がいると、全く違う人生が開けます。

- あなたが持っている？

- もちろん。そういう意味で、私は世界の一部になりました...

— ロシアの数学は、この解散によって何かを失ったり、得たりしたと思いますか?

— 他のどの国でも、モスクワにあったような数学的生活の集中はないと思います。しかし、常識の観点からは、すべての数学が巨大な国の 1 つの中心に集中することは悪夢のように見えます。そして、モスクワに原爆を投下してすべての科学を失う可能性があるという理由だけでなく、一般的に。しかし、結果は素晴らしかったです。

今日でも、モスクワ生涯数学教育センターの建物の周りを歩いていると、よく知っている数学者や数学学校や数学大学の卒業生にいつも会います。昨日、ここで働いている女性が私に近づき、50 年前に私が第二高校で彼女を教えていたことを思い出させてくれました。モスクワのような数学者の集中は、どこにも見当たりません。パリでは夏に集まることもあります。しかし、1990 年代初頭以前にモスクワにあったようなものは、どこにもありませんでした。しかし、それは消えました。

はい、ロシアの数学は存在し続けています。数学を教え、学び続けている人がいるからです。私たちが会話をしているMTsNMO、ドゥブナのサマースクールがあります - これらすべてが存在します。そして、世界にはそのようなプロジェクトはあまりありません。数学の教え方を知っている数学者がここに残っていますが (私の仲間はほとんどいなくなりました)、これを行うのは非常に困難です。

ニュージーランドやオーストラリアにも行ったことがありますが、シベリアやコラ半島の景色も悪くなく、若い頃に欠けていたという感覚はありません。はい、私は多くの外国の数学者を見たことがありませんでしたが、ここにいた人たちは本当に楽しかったです。私はこの偉大な時代の同時代人であったことを嬉しく思います.

ピーター・セルゲイビッチは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学のメフマートで反ユダヤ主義について話し始めるのが本当に好きではありません。私が例として挙げられているのは、彼が数学者になり、強い人々が「黒い20代」で生き残ることができたということです.それは本当ではない。私は、これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に真面目な数学者になることができたように私には思えます.本当にラッキーでした。まず第一に、すぐに私の同僚や素晴らしい数学者が私の近くにいることがわかったからです。

— Я увидела в «Википедии», что Вы не поступили в МГУ. Вы стали жертвой антисемитской кампании?

— Так я подозреваю. Я никогда не пытался собрать точные доказательства, но...

— Золотая медаль — и не быть принятым на мехмат?!

— Золотая медаль, а еще вторая премия на Московской математической олимпиаде, и не приняли.

— Вас на экзамене заваливали?

— Да, конечно, заваливали!

— Давали сложные задачи?

— Просто нерешаемые. Либо ты знал решение задачи, либо решить ее не мог. Это был не экзамен, это было собеседование. Но мой год был уже сравнительно вегетарианский. Если за пару лет до меня при таких начальных параметрах на мехмат не поступал никто, то в тот год поступили уже несколько человек. А у меня была золотая медаль — и разочарование. Я немало слышал об антисемитизме при приеме, о том, что происходит, но думал, что у меня есть запас прочности и меня это не коснется.

— А как Вы решили, куда поступать, если не в МГУ?

— У меня не было особых советчиков, у меня была довольно простая семья. Я настолько был настроен на мехмат и уверен в положительном исходе... В итоге я поступил в Ленинский пединститут. И более того, для медалиста было уже поздно поступать на физико-математический факультет. Это был случайный выбор от полной безысходности (в 16 лет!).

Я начал учиться на дефектологическом факультете, там было что-то связанное с математикой. Семестр я там проучился. Потом с большим трудом меня перевели на физмат. К тому времени к моей судьбе уже подключились несколько математиков. В учебе в педагогическом институте было много положительных сторон. Во-первых, там работали несколько очень хороших математиков. Из них наиболее ярким был Пётр Сергеевич Новиков. Знаете ли Вы его сына Сергея Петровича?

— Конечно!

— Пётр Сергеевич был удивительным человеком. Мне так повезло с ним встретиться. Он занимался математической логикой и был совершенно фантастическим математиком. Но яркость его таланта не передается полностью ни через статьи, ни через лекции. При множестве хороших математиков он был сингулярной точкой. Умнейший, интереснейший человек во всех отношениях. Помню, на стенах его квартиры я увидел картины «неслыханных» художников (Фальк, Крымов...).

Он был удивительно открыт, охотно поддерживал разговоры на любые темы. Хотя я выбрал заниматься вещами далекими от того, чем занимался П. С. (да и не очень интересными ему!), я много лет пытался сделать что-нибудь достаточно ему близкое, несколько лет вел с ним общий семинар, и опубликовал в связи с этим несколько статей, и даже написал книгу по логике «Алгебра логики в задачах».

Довольно скоро я познакомился с Израилем Моисеевичем Гельфандом. И больше всего моя студенческая жизнь проходила около Гельфанда, которого я считаю одним из двух главных своих математических учителей. Другим был Илья Иосифович Пятецкий-Шапиро. Это был тоже счастливый случай.

Я очень не люблю, когда начинаются разговоры про антисемитизм на мехмате МГУ; меня приводят в пример, мол, он-то стал математиком и сильные люди могли выжить в «черное двадцатилетие». Это неправда. Я знаю многих людей, которым эти события полностью сломали жизнь. И мне кажется, что те, кому не дали поступить, могли стать абсолютно серьезными математиками. Мне действительно повезло. В первую очередь потому, что довольно быстро около меня оказались и мои сверстники, и замечательные математики.

— Вы учились в Педагогическом институте им. Ленина. Вы встречали там Юрия Визбора, Юлия Кима и других?

— Конечно, я многих из них знал, хотя и не очень близко. Многие мои однокурсники стали поэтами, замечательными артистами. Это был один из бонусов той жизни. Культурная жизнь бурлила и интересовала меня, но я участвовал в ней ограниченно, тратя основное время на математику. Рядом был туризм, который увлек меня на всю жизнь.

Там были хорошие очень математики, и там были замечательные ребята, которые поступили туда по разным причинам. Там учился, например, Петя Фоменко, известный режиссер... Вдруг вспомнил, как оказался в конце 1960-х в Алибеке на горных лыжах с Петей Фоменко. Он только что ушел с Таганки. Вижу его на втором этаже двуспальных нар, читающего «Бесов» и уверявшего меня (пессимиста), что он поставит это! А еще его фантастические экспромты... Кстати, и Визбора я встретил — на лыжах, на Кольском полуострове. Он был уже звездой! Мы успели поговорить один вечер, а на следующее утро он страшно сломался, пытаясь съехать с крутого ледяного склона.

— Можете несколько слов сказать об Израиле Моисеевиче Гельфанде? Посещали ли Вы его семинары?

— Конечно. Я написал статью про эти семинары к его 90-летию. Израиль Моисеевич неохотно это обсуждал, но мне кажется, что на его семинары оказал сильное влияние физический семинар Ландау. Гельфанд в какой-то момент хотел заниматься физикой, и поэтому на семинаре было много физических докладов. Я думаю, что Лев Давидович пытался несколько свысока смотреть на Израиля Моисеевича.

Я точно знаю, когда увидел Ландау в первый раз. Это было в 1955 году. Была конференция по функциональному анализу, на которую съехались все лучшие математики страны, — большое событие в Москве. До того времени практически не было конференций. Первая проходила еще до войны. Вся Москва пришла на открытие этой конференции. И Израиль Моисеевич там царствовал, но вел себя чуть сдержаннее, чем обычно на своем семинаре. Первый доклад делал Ландау. И это надо было видеть, это были два великих артиста, которые прекрасно вели свои партии. К тому моменту Израиль Моисеевич придумал вместе с Бобом Минлосом то, что они назвали континуальными интегралами (Боб — мой друг, замечательный человек и математик).

После доклада Ландау Гельфанд пытался ему очень мягко объяснять, что, наверное, эти интегралы — правильный путь для создания теории поля. А Ландау хитро ему отвечал: «Израиль Моисеевич, цыплят по осени считают». Помню, что эта фраза понравилась Петру Сергеевичу Новикову, который сказал: «Да И. М. любит считать цыплят весной!»

Кстати, я был свидетелем еще одного диалога Гельфанда и Ландау во время математического съезда в Ленинграде (около 1960 года). Мы гуляли с И. М. по Невскому, около гостиницы «Балтийская», и встретили Ландау. Помню, что в разговоре опять возникла тема возможности применения серьезной современной математики. И. М. приводил какие-то примеры (кажется, представления группы Лоренца), а Л. Д. был категорически с ним не согласен. Он говорил, что много лет существует раздел «Уравнения математической физики», но он не знает ни об одном существенном применении серьезной математики к физике.

Сегодня мне кажется, что Гельфанд скорее был прав, если посмотреть, какая изысканная математика применяется в современной теоретической физике. По-видимому, Ландау недооценил роль математики в будущей физике (я слышал от моих друзей-физиков, что, возможно, некоторые его ученики дорого заплатили за это).

Если вернуться к семинару Гельфанда, то повторю свою точку зрения. Многих раздражало, что Израиль Моисеевич не допускал никакой демократии. Для него семинар был в некотором смысле главным делом жизни.

Первым впечатлением было, что всё на семинаре происходило экспромтом. Семинар начинался с огромным опозданием. Это Гельфанд объяснял тем, что ожидание семинара было лучшим временем для общения. Этот был ценный для научной коммуникации час, когда люди (поневоле!) разговаривали друг с другом.

Такая абсолютно осознанная неорганизованность была чертой его характера. Он не считал нужным делать всё вовремя. Он полагал, что заслужил право делать то, что ему удобно, и не считаться с общепринятыми правилами. Несколько утрируя: раз ты великий человек, то нужно вести себя так, как тебе ведется. И это даст лучшие результаты. Вежливость не была сильной стороной Израиля Моисеевича. Но не всегда. Он понимал, как и с кем говорить. Все-таки это был человек, который пережил сталинские годы. Впрочем, часто в какой-то момент он срывался и вся ювелирная дипломатия проваливалась в преисподнюю.

Что касается семинаров, для него это было главным делом жизни. Это было место, где он сам понимал большую часть математики, и он считал, что дает другим возможность разобраться в этой математике. И там он был абсолютно раскован. Его манеры, которые, может быть, не всех устраивали, были такой данью, которую должны были заплатить остальные, если хотели получить бенефиты от этого семинара.

За несколько дней до семинара он начинал обдумывать, что на нем будет. Есть воспоминания Пола Халмоша (Paul Richard Halmos), известного математика, занимавшегося также популяризацией, который бывал на семинаре. Там есть целая глава о семинаре, о взаимодействии с Гельфандом, как он его по Кремлю водил. И вот Халмош пришел на семинар, подготовил тщательно доклад; он был большим мастером, его книги были написаны на высоком педагогическом уровне. А тут внешне — какой-то полный беспорядок: Гельфанд задает ему вопросы, разговаривает с другими, вместо того чтобы дать слово докладчику.

Но в модели мира Гельфанда этого беспорядка не было. Сначала семинар был для него как транс, он был готов слушать математику бесконечно; для этого он, как на спиритическом сеансе, вел себя так, как ему велось. И совершенно не всем это нравилось. Причем иногда математики обижались на Гельфанда за других людей.

Но Израиль Моисеевич всегда считал, что, если он позволяет себе сказать какому-то заслуженному профессору: «Ты же ничего не понимаешь!» — то это означает, что к нему он относится хорошо, как к равному. А если он с ним вежливо будет разговаривать, то получается, что он его за человека не держит, и уж точно не за математика. Таким был этот стиль.

Гельфанд считал, что если он допускает людей в свою кухню — не скрывает, как он слушает математику, что он о ней думает, — то имеет право вести себя так. Это моя реконструкция психологии этого семинара, я ее уже описывал. Для любого зарубежного математика посещение семинара Гельфанда было не менее обязательным делом, чем посещение Большого театра. Это было частью такого entertainment’а.

Одной из первых вещей, которую я сделал на Западе вместе с Арнольдом и Масловым, было открытие серии трудов семинаров в Москве и Ленинграде. Ее идеей была попытка передать стиль московских семинаров. На Западе семинары — это короткая чисто деловая вещь. Молодые ученые закончили аспирантуру, защитили PhD и отправились в разные места мира по своим траекториям. А в Москве они оставались навечно. Их не брали никуда, фактически они не могли работать по специальности, они сидели в «ящике», а вечерами приходили на семинар Арнольда или Гельфанда, и начиналась лучшая часть их профессиональной жизни.

И та школа казалась вечной — это была школа, которая никогда не кончалась. Но это был личный выбор каждого, там могли неожиданно нахамить... Для И. М. семинар был действительно его жизнью. Были трудные времена, которых я не застал. Но единственное, за что он боролся, когда его выгнали из университета и из Стекловки, — это сохранить возможность работы семинара.

Он рассказывал, как на семинаре появлялись и садились в первом ряду незнакомые люди. Они погон не носили, но по ним всё было видно. Я слышал от Михаила Александровича Леонтовича, который работал в Курчатовском институте, очень меткую фразу: «Идет человек в штатском, а у него что-то синее на плечах».

Еще был биологический семинар. Это тоже было интересно. Мы по молодости думали, что всё понимаем — как можно было бы это чуть-чуть улучшить и чтобы людей так не дергало.

Израиль Моисеевич эти семинары почти не пропускал; часто он их вел, когда очень плохо себя чувствовал. Помню, один раз в качестве эксперимента он нам с А. А. Кирилловым поручил провести этот семинар. Семинар прошел коротко, с блеском, быстро закончился, все доклады шли гладко, никто никого не прерывал. Но это не был семинар Гельфанда!

— Уже в США?

— Нет, в Москве. Про семинары в США, если Вы хотите, я тоже могу рассказать. Я же с Израилем Моисеевичем работал в Ратгерском университете (Rutgers University). И там этот семинар не пошел...

— Есть такой тезис, что наука не может нормально развиваться без демократии в обществе. Между тем расцвет математики в сталинской России — феномен, который, казалось бы, противоречит этому тезису. Если бы не было этих «почтовых ящиков», «железного занавеса», то семинар Гельфанда не был бы таким успешным?

— Нет. Думаю, что успех семинара Гельфанда был прежде всего обусловлен его личностью. Он придумал такой способ математической жизни. Подчеркну, что московская математика была уникальным, неповторимым феноменом. К моменту нашего разговора где я только не был и чего только не видел. А вот этого я нигде больше не встречал. В чем истоки и природа этого феномена — тема для отдельного разговора.

Математика — это не только наука; для меня она в своих лучших проявлениях ближе к высокому искусству, музыке, поэзии. Ее прикладные аспекты со времен Архимеда часто бывали существенны и замечательны. Взаимоотношения с власть имущими бывали разными и имеют давнюю историю. Почему математика цвела в Афинах, но не в Спарте, почему Платон учил математике в Академии будущих королей, почему геометрия исчезла с закатом Греции, а Рим, взяв многое из Греции, без математики обошелся...

В Советском Союзе математика не была разгромлена так, как биология или лингвистика. Потому что наверху была такая иллюзия (может, и не совсем иллюзия!), что математика хоть на какое-то время нужна для решения государственных задач, в первую очередь военных. Для многих математика в те времена была такой отдушиной. Во-первых, туда всегда тянулись молодые люди «в очках», не от мира сего. А с другой стороны, э

«Кот Шрёдингера» №1–2(39–40), 2018，Математика как очки より
数学者Igor KricheverにGrigory Tarasevichがインタビュー

Igor Krichever:
宇宙の法則は内部のどこかで保護されているように思えてならない．

■証拠に基づく世界
数学者は日常生活の中でどのように決定を下すのですか？誰と結婚するか，休暇にどこに行くか，夕食に何を買うか，ジャーナリストとの会合に同意するかなど．このような問題の解決には，スーパーコンピューターが1日動作しても足りない複雑な多基準モデルの構築が必要です．そのような場合，数学者はどのように行動するのでしょうか？

皆さんと同じです．私は，人生においては数学者も普通の人でなければならないと信じています．そして数学はこれを妨げるべきではありません．

知り合いの数学者の多くは，どんな決定も痛々しいほど受け入れます．そして，それを痛々しいほど後悔します．私にとってすべて簡単なことです．子供の頃，両親が読んでくれたマルシャークの詩（*注）を覚えています．猟師の網に引っかかった鳥についての物語です．鳥は猟師に言います：私は小さく，一口で食べてしまう肉しかありません．放してください．私はあなたに貴重な３つのアドバイスができます．持っていないものを後悔する必要はありません．

私はこのルールに従い，何が欠けているのかではなく，何が先にあるのかを考えようとしています．しかし，これは私が数学者であるということと関係はありません．

（*訳者注）サムイル・マルシャークは，「森は生きている（12か月）」で，私たち日本の子供にも知られている児童文学者，詩人です．ここに引用されている鳥と猟師の会話は，詩「愚かさの物語」の一節にあることを探し当てました．たいへん哲学的な詩なので，私の語学力では十分に理解ができないのですが，概略は以下のようです：３つのアドバイスがあるというので，猟師は鳥を自由にしてあげます．３つのアドバイスとは：
持っていないものを後悔する必要はありません．
過去を取り戻すために無駄なことをして血を流さないよう．
ナンセンスを信じるな世界に奇跡はありません．
ということでした．鳥は猟師をだましたようです．

Самуил Маршак　サムイル・マルシャーク
Сказка о глупости　「愚かさの物語」

http://www.world-art.ru/lyric/lyric.php?id=4351

確かに，引用されている一節があります．
Я ростом с ноготок, Всего комочек пуха Да мяса на глоток. 
Пусти меня на волю, Доволен будешь сам.
Хороших три урока Тебе за это дам.

Запомни мой совет;
Жалеть о том не надо,
Чего уж больше нет.

この詩全体は，上記ウエブサイトをご覧くださいーーーーーーーーーーー

■数学は、考え方を変えますか？

「数学はあなたに考えることを教えます．どんなステートメントも批判的に知覚し，それが何で構成されているか，それがどのように受け取られたか，そしてそれから何が続くのかを分析することを教えます．「証明する」の意味を，人々が常に理解しているとは限りません．
レーニンの古典的な言葉「マルクスの教えは真実であるので全能だ」は，数学者の観点からすると，悪循環です．そのような発言は信頼できません．
数学は私たちにすべてのことを当然と思わないように教えています．丸ごと信じることはできません．

私はアメリカのコロンビア大学でたくさん働きました．
初等数学のコースでは：数式を与え，生徒に何かを計算させます．その後，上級コースが始まります．これは証明がベースのコース，つまり，証明とは何かを説明するコースです．すでに証明されているか，証明されているものから直接派生した要素の連鎖に，ステートメントを分解することは素晴らしい芸術です（*注）．これは長くて難しい旅であるに違いありません．特に，学生時代ではなく，大人としてこの芸術を理解し始めた場合はなおさらです．
（*訳者注）あるステートメント（声明，命題）を，証明済みとその証明から派生するものの連鎖に分解することは，論理的な推論に必要な構造化です．

■ロシアの学校では，「人文科学」という言葉がよく使われます．これは賢いようだが，正確な科学との関係が築かれていないのです．数学を必要としないのでしょうか？

数字を操る機能としての数学は，おそらく必要ありません．統計は社会学や心理学で使われていますが．私の意見では，思考を発達させる科学としての数学は誰もが必要としています．

個人的な例を挙げましょう．私の孫は第57学校の数学の授業を卒業し，現在は高等経済学部の言語学部で勉強しています．数学は彼にとって非常に有用であり，モデルを構築し，何かを計算します．数字を操る算術はまったく役に立たなかったと信じています．彼は論理的に推論し，パターンを特定し，構造化することを学びました．それが最も重要なことであり，算術能力ではありません．退屈な算術は数学ではありません．

繰り返しますが，これは証拠に基づく考え方です．数学は良い眼鏡のようなものです．絵がぼやけないように世界をよりはっきりと見たい場合は，数学を学びましょう．

■信仰と公式

ここでは，厳密な証拠に基づくことがいかに重要であるかを繰り返します．数学的思考は道徳的な選択をするのを邪魔しませんか？会議で手を挙げて，道徳的に間違った決定に反対する必要があるとしましょう．人はこれをしません：論理的な根拠が十分ではないと言って...

この場合，数学的証明を持ち出す必要はないと思います．これは市民の勇気の問題です．あなたの人間の感性で，これが正しいとか間違っているとか感じます．

道徳的な選択は数学的な正当化を必要としませんか？

おそらくそうではありません．宇宙の法則は私たちの内部のどこかで保護されているように見えることがあります．数学は，独自の規則と公理に基づいて，純粋に内部法に従って発展しているように思われます．実験や観察は使用しません．論理のみを使用します．これらはゲームのルールです．しかし，結局のところ，数学は現実の世界を不思議な方法で表現していることがわかりました．つまり，自然の法則は私たちの思考の中に非常に深く隠されています．どのように？誰によって？なんで？私にとって，これは私が答えを見つけることができない謎です．ここであなたは神について考え始めさえします．誰かがそれを私たちの中に置いたのです．おそらく，道徳の法則は同じカテゴリーのものです：それらは私たちの内側のどこかにあります．あなたは何かを信じ，あなたの良心に従って，あなたの考えに従って行動します．少なくともそれが私がそれを理解する方法です．

信仰と証拠の必要性は互いに矛盾していますか？

はい，それらは矛盾しています．しかし，私の仕事では，私はしばしば原則に導かれます：それは美しいので，それは正しくなければなりません．これらは形式化できない概念です．何かがあるという信念，私たちの世界を定義する調和．ただそれを神の奇跡についての素朴な考えと混同しないでください．むしろ，それは世界の正しさへの信念です．私はそれを持ってます．

あなたは世界が正しく配置されていると信じますか？それともあなたはそれを知っていますか？

「信じる」または「知っている」と言うのは完全に正しいわけではありません．私は自然の法則が合理的であると信じています．同時に，私たちの社会の世界は私には深く間違っているように見えます．それは間違った方向に進んでいます．すべてが悪化します．しかし，おそらくこれはただの時代への不平でしょう．

私たちの世界の何が問題になっていますか？例を

人々の考えがシフトし引き裂かれているのは間違っているように思えます．これは特に子供に顕著です．彼らが一人でいることはますます難しくなっています．人々はただ座って考える時間がますます少なくなっています．それは正しくありません．しかし，それは避けられないことだと私は理解しています．

進歩はありませんか？

進歩はそれが進むところに行くのは，自然なプロセスです．それが正しいかどうかはわからない．私はそれが好きではありません．誰もが本は死ぬだろうと言います．本は何か他のものに置き換えられるでしょう．私はそのようなことは好きではありません．しかし，これについて議論することは，風に逆らって唾を吐くようなものです．

避けられない事故
当初は，世界の構造における偶然と必然性の比率をインタビューのメイントピックにしたかったのです．たとえば，シュレディンガーの猫の運命は，粒子の完全にランダムな振る舞いによって決定されることが知られています．そして，ローレンツ蝶はブラジルで羽ばたき，それによってテキサスでハリケーンを引き起こします．それが非常に複雑であっても，非常に異なる現象の間に因果関係があるという事実についての話です．あなたの意見では，チャンスと必然性はどのように相関していますか？

新しい数学的解決策を提案するとき，あなたは創造するようです．しかし，その一方で，あなたはただ何であるかを発見します．会議で，私の偉大な同僚は，詩人がその行を書かなければ，それは二度と現れないだろうと言いました．しかし，あなたが定理を証明しなければ，遅かれ早かれ他の誰かがそれを証明するでしょう．結局のところ，それなしでは，あなたは先に進むことができません．ある意味で，これは必然性であり，数学の発展における予定説です．ここにはランダムなものは何もありません．

しかし，ランダム性は時間の文脈に存在します．発見が今日行われなかった場合，それは後，たぶん5年後，あるいは50年後，あるいは150年後かもしれません．科学の発展は事前に決定されていますが，科学が進む道はほとんど偶然です．

物理プロセスの数学的モデルを構築する場合，ランダムな要素はどの程度重要ですか．

それはすべて，モデル，実際のプロセスの必要な単純化の程度に依存します．コインを投げるとしましょう．実際，表または裏がでるのは常に事前に決定されています．それは，体の初期位置，指によって加えられる力，風，および他の多くの要因に依存します．しかし，表裏のどちらかが偶然にでると想定します．これは実際のプロセスの近似です．十分に正確な場合もあれば，そうでない場合もあります．

あなたの伝記では，偶然と必然性はどのように相関していますか？

私の人生はかなり退屈で，まっすぐです．私がモスクワ州立大学のコルモゴロフ寄宿学校を卒業した後，すべてが比較的明確でした．したがって，おそらく，私は人生における事件の重要性を誇張する傾向はありません．私には，すべてが論理的であり，一方が他方に続いているように思われます．ランダム性は，一般的な背景の小さな波紋です．

あなたがこの寄宿学校に行き着かなかったら？

わかりません...私はタガンログで最高の学校の1つであるチェーホフ学校で勉強しました．数学の先生が，コルモゴロフ寄宿学校に入学した元生徒と一緒に私を連れてきました．もしこれが起こらなかったら，私はモスクワにたどり着くことはなかっただろうし，私の人生は違ったものになっていただろう．しかし，これを証明するのは非常に困難です．私はやはり数学者になると思います．道のりが長くなるでしょうけれど．

物理学など，他の分野の科学者になることもできます．

はい，私は現在の専門分野の数学物理学者です．しかし実際，私はもちろん数学者です．そして，物理学が常に私にとって問題の発生源であったというだけです．

昔々，上司，そして同僚で友人のセルゲイ・ペトロヴィッチ・ノヴィコフと私はボソン弦の量子化の問題に取り組みました．そして彼らはよく言いました：結果として物理理論が何を得るのかは不明であり，任意の代数曲線のために私たちが思いついたローラン-フーリエ基底は数学に永遠に残ります．

同時に，私は問題は外の世界から来るべきだと信じている数学者のその部分に属しています．原則として，それらは最も興味深いものです．過去20〜30年間で，数学の最も注目すべき成果が物理学から生まれたアイデアに関連していることは不思議ではありません．

今日の日本でも，大学教育はグローバル化，ユニバーサル化に対応する必要があり，高校教程で学ぶべきミニマム数学の内容やその達成度テストも適切なものでなければならない．これらの議論は教育数学の研究集会の記事をご覧ください．カリキュラム改革はいつの時代でもなかなか難しい．
改革では今日の数学（統計学やデータ解析など）に目配りする必要があるでしょう．６0年前に遡り，その時代に議論された新数学教科書改革；ソ連，フランス，欧米の先行事例を知ることは大事ではないでしょうか．以下の記事(アレキサンドル･ブヘトフ)からコルモゴロフの改革は何だったか学びましょう．

Падение преобразователя: четыре вопроса о реформе Колмогорова
Александр Буфетов, профессор РАН
«Троицкий вариант» №2(346), 25 января 2022 года

Падение преобразователя: четыре вопроса о реформе Колмогорова • БиблиотекаПятьдесят лет назад в советских средних школах появился учебнelementy.ru
■学校教育の数学コースの改革の一環として，アンドレイ・ニコラエヴィッチ・コルモゴロフが編集した幾何学の教科書がソビエトの中等学校に登場したのは60年前だった．

10年制学校の6年生から8年生向けの幾何学の教科書

学校の数学授業を20世紀の数学に近づけたいという願望は，戦前から叫ばれており，1950年代に活発に議論されました． この論説の著者が10歳の少年の頃，学校の数学の授業が17世紀の数学者の業績(*)で終わっているのを，どこかで偶然読み，非常に驚いたことを覚えているという． その後に行われたことを知る時間はいつあるのでしょうか？（*訳者注）ニュートン，ライプニッツ，デカルト，ベルヌーイ，フェルマーなどの時代.
この論説の著者の生まれる20年前も，アレキサンダー大王の継承戦争の時代の数学者の業績(*)で学校の幾何学コースが終わっていることを知っていたら，もっと驚いたことでしょう．（*訳者注）アレキサンダー大王の死は紀元前323年です．アルキメデス，ピタゴラス，ユークリッドなどの時代．

ユーリ・アレクサンドロヴィッチ・ネレチンは次のように書いています．「私たちの3次元空間は，私たちの考え方と同様に，その時以来，あまり変わっていません」しかし，私たちの3次元空間の考え方が，ユークリッドやアルキメデスの考え方と同じではありません．その時代には，ベクトル計算，平面運動の分類，第5公準の独立性の証拠がありませんでした（ユークリッドの第5公準の解釈はロバチェフスキーの驚くべき業績です）．3つのトピックのうち，キセリョフの注目すべき教科書（改革前の好評な教科書）で触れられているのはそのうちの1つだけ(ロバチェフスキーの幾何学は，キセリョフの教科書の余白に現れています）です．それ以来，学校のコースでの議論はこれ以上詳細にはなりませんでした．その一方，学校の幾何学コースにベクトルと幾何学変換が欠けているのは古くさいとの認識は，戦前からありました．

改革の主な熱狂者の1人は，RSFSRの教育副大臣であり，解析関数の理論に関する古典的な大学の教科書の著者であり，多くの言語に翻訳され，今日まで積極的に使用されている著名な数学者Алексей Иванович Маркушевичアレクセイ･イヴァノビッチ･マルクシェビッチでした．

1960年代初頭，コルモゴロフは改革の作業に参加しました．彼のリーダーシップの下で，新しいカリキュラムが作成され，その後，彼自身が共著者の小さなチームと協力して，非常に短い時間で，代数と解析入門と，幾何学に関する新しい教科書を書きました．

しかし，特に幾何学の教科書は厳しい批判を受け，批判は改革全体に広がりました． 1978年，ソ連科学アカデミーの数学科は，数学の教科書と学校のカリキュラムの現状は不十分であると認識し，コルモゴロフの改革は公式に却下されました．

一方、コルモゴロフによって編集された代数と解析入門教科書は，学校に残り，ソビエト連邦時代を無事に生き延びました．昨年，卒業前と卒業のクラスのための教科書の第26版が出版されました．幾何学の教科書の方は，取り返しのつかないほどの後退をしました．
コルモゴロフの改革は，西側の改革，つまり米国の新数学，そして特にフランスの急進的な数学の近代よりも比類のないほど穏やかでした．たとえば，フランスのリセウムの大学院クラスの1972年の幾何学教科書の目次を開いてみましょう：ベクトル空間，線形写像，多重線形形式，行列式があります．

フランスの最新数学の研究は，膨大な（そしてあまり簡単に見ることができない）文献に結び付けられている．詳細なモノグラフ「新数学の政治史」が最近米国で出版されました．3)
Yu.A.Neretinの注目すべき最近の論文は，コルモゴロフの改革に捧げられています．4)

3） The New Math: A Political History by Christopher J. Phillips. University of Chicago Press, 2015.
4） Ю.А. Неретин, Реформа Колмогорова математического образования, 1970–1980-е годы. arxiv.org/abs/1911.06108

------------------------------------------------

コルモゴルフ　wikiより抜粋ーーーーー
(1903年4月25日 - 1987年10月20日）は、ロシアの数学者。確率論および位相幾何学の大きな発展に寄与した。彼以前の確率論はラプラスの『確率の解析的理論』に基づく古典的確率論が中心であったが、彼が『測度論に基づく確率論』『確率論の基礎概念』（1933年）』で公理主義的確率論を立脚させ、現代確率論の始まりとなった。
1931年に彼はモスクワ大学で教授になり、1935年に、コルモゴロフはモスクワ大学で第1代議長になった。1939年に、彼はソ連科学アカデミーの正会員に選出された。ーーーーーーーーーー

結局，コルモゴロフの教科書改革は失敗でした．改革が不徹底の原因背景について種々論じられています．ここで取り上げたАлександр Буфетовブヘトフの論説の後半部分でも，４つの問題点が語られています．
例えば，数学に割り当てられた時間の15〜20％の大幅な削減．8年制から10年制への移行にともない，なぜ時間を短縮されたのか​​わかりません．週に６時間の数学を決めたのは誰でしょうか？幾何学試験の廃止を決定したのは誰でしょうか？
制約がいろいろあったようです．コルモゴロフが非常に急いでプロジェクトを進めたのは何故でしょうか？健康問題もあったようです．費用も少なかったようです．しかし，当時の時代背景や状況の理解が十分にできていない筆者にはわからない点が多く，現時点でのこれ以上の深入りは止めておきます．もう少し調べる必要があります．
詳細な調査を掲載している別の論説も以下にあります：

Реформа Колмогорова (Kolmogorov reform)mat.univie.ac.at

Замыслы Колмогорова о школьном курсе геометрии • ВидеотекаПоселок Московский, 29.06.2009. Конференция лауреатов Всероссelementy.ru

Вспоминая Колмогорова • ВидеотекаПоселок Московский, 04.07.2006. II конференция лауреатов Всерelementy.ru

 https://elementy.ru/nauchno-populyarnaya_biblioteka/431665/Aleksandr_Shen_Uchenikom_Kolmogorova_ya_ne_byl?from=rxblock

 Александр Шень: «Учеником Колмогорова я не был» • БиблиотекаАлександр Ханиевич Шень — кандидат физико-математических наукelementy.ru
■50年代後半から60年代前半にかけて，さまざまな人々が，微分積分，幾何学変換，ベクトル代数，組み合わせ論，確率論（および統計），複素数，集合論的アプローチ，数理論理学を，詰め込む可能性について議論しました．学校のカリキュラムは，現在のプログラムから何かを省略する必要があり困難な問題です．リストのほぼすべての要素を押し込むことが比較的合理的な方法でできました（統計，積分，および論理を除く）．しかし，いくつかの夢を犠牲にしなければならない難しい決断でした...
幾何学変換で不変となる量に注目していろいろな幾何学（ユークリッド，非ユークリッド，アフィン，射影，トポロジー等々）が定義できます．幾何学的変換の概念に基づいて幾何学のコースを作成するというアイデアは，1905年にエミール･ボレルによってフランスで成功裏に実装され，ソビエト連邦では戦前でも詳細に繰り返し議論されました．ベクトルは，キセリョフにも，ニキチンの初等教科書（コルモゴロフの前身）にも，1969年のポゴレロフの教科書にも含まれていないが，コルモゴロフの改革の枠組みの中で学校の幾何学コースに入りました．

■ポゴレロフの教科書が完成し，使用されました．これは，早くも1969年に行われた可能性があります．

Atanasyan-Butuzov-Kadomtsev-Poznyak-Yudinaの教科書，A.D.Aleksandrov-Werner-Ryzhikによる教科書が書かれ発売されました．教科書の全連合大会が開催されました．

作家が誰にでも好かれることはないのと同じように，1冊の教科書が誰にでも愛されることはありません．すべての教科書には欠点があることがわかります．Wernerによると，教師は教科書を選択できました．1980年代初頭，サンクト・ペテルブルグ市のさまざまな地区で3つの異なる教科書が使用されました．

 https://note.com/sgk2005/n/naa3e06512eb1

ガウス積分

$$I^{2}=\displaystyle \frac{1}{4}\displaystyle \int_{- \infty }^{ \infty }\displaystyle \int_{- \infty }^{ \infty }e^{-(x^{2}+y^{2})}dxdy=\displaystyle \frac{1}{4}\displaystyle \int_{0}^{2\pi }\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdrd\theta =\displaystyle \frac{2\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdr$$
$$r^{2}=X$$とおく，　$$2rdr=dX$$
$$I^{2}=\displaystyle \frac{\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-X}dX=\displaystyle \frac{\pi }{4}$$, $$I=\displaystyle \frac{1}{2}\sqrt{\pi }$$
--------------------------------------------
$$\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\sqrt{\displaystyle \frac{\pi }{\alpha } }$$
$$\displaystyle \frac{d}{d\alpha }\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\displaystyle \int_{- \infty }^{ \infty }dx\displaystyle \frac{d}{d\alpha }e^{-\alpha x^{2 } }=\displaystyle \int_{- \infty }^{ \infty }dx(-x^{2})e^{-\alpha x^{2 } }$$
$$\displaystyle \frac{d}{d\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }=\sqrt{\pi }\displaystyle \frac{d}{d\alpha }\alpha ^{-1/2}=\sqrt{\pi }\left( -1/2 \right) \alpha ^{-3/2}$$
$$\displaystyle \int_{- \infty }^{ \infty }x^{2}e^{-\alpha x^{2 } }dx=\displaystyle \frac{1}{2\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }$$

フレネル積分　　$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{ix^{2 } }dx$$を求めなさい． 
ただし，$$S(x)=\displaystyle \int_{0}^{x}\textrm{sin}t^{2}dt$$, $$C(x)=\displaystyle \int_{0}^{x}\textrm{cos}t^{2}dt$$もFresnel積分と呼ばれる．
ただし，$$S( \infty )=C( \infty )=\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }$$を既知とすると，
$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx+i\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }\left( 1+i \right) $$が得られます．
（参考）Gauss積分　$$\displaystyle \int_{0}^{ \infty }\textrm{exp}[-t^{2}]dt=\sqrt{\pi }/2$$

－－－－－－－－－－－－－－－－－－－－－－－－－－－
これを複素積分法で計算してみます： 
$$I=\displaystyle \int_{0}^{ \infty }\textrm{exp}[ix^{2}]dx=\displaystyle \int_{0}^{ \infty }\textrm{exp}[-(e^{-i\pi /2})x^{2}]dx$$
$$z=xe^{-i\pi /4}$$とおくと，$$dz=dxe^{-i\pi /4}$$だから，　$$I=e^{i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{Re^{-i\pi /4 } }\textrm{exp}[-z^{2}]dz$$

被積分関数$$\textrm{exp}[-z^{2}]$$は，周回積分の領域$$C$$で正則だから，コーシー・リーマンの定理により周回積分は０になる：
$$0=\displaystyle \int_{(C)}^{}\textrm{exp}[-z^{2}]dz=\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz$$
$$z=te^{i\theta }$, $dz=dte^{-i\pi /4}$, $dz=d\theta iRe^{i\theta }$$
$$C_{1}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz = e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}e^{-i\pi /2}]dt=e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{it^{2 } }dt$$
$$C_{2}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}\textrm{exp}[-R^{2}e^{i2\theta }]e^{i\theta }d\theta =$$
$$=\displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}e^{-R^{2}\textrm{2cos}2\theta }e^{-iR^{2}\textrm{sin}2\theta }e^{i\theta }d\theta \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}\textrm{cos}2\theta }|d\theta \leqq $$
$$ \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}(4\theta /\pi +1)}|d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\displaystyle \int_{-\pi /4}^{0}e^{-(4R^{2}/\pi )\theta }d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left[ \displaystyle \frac{e^{-(4R^{2}/\pi )\theta } }{-4R^{2}/\pi } \right] _{-\pi /4}^{0}$$
$$=\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left( 1-e^{R^{2 } } \right) /\left( -4R^{2}/\pi \right) =\displaystyle \lim_{R \to \infty }i\pi (1-e^{-R^{2 } })/4R=0$$

$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }-\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}]dt=-\sqrt{\pi }/2$$
従って，$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}=-\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}$$ より，
$$\displaystyle \frac{\left( 1-i \right) }{\sqrt{2 } }\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\sqrt{\pi }/2$$
$$\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }(1+i)$$

オーギュスタン・ジャン・フレネルFresnel（1788-1827）は，ナポレオン時代のフランスの数学者です．

■フレネルレンズ

フレネルレンズの概念（断面図はwikiより）

フレネルは，フレネルレンズ(1819)やゾーンプレートに名前が残っています．注）ブリタニカ（https://www.britannica.com/technology/Fresnel-lens）によると，レンズの表面を同心円状のリングに分割するというアイデアはFresnelよりも古く，Georges-Louis Leclerc de Buffon（1748）で，フレネルは，1821年に灯台レンズの製造に採用したとあります．ビュフォンもフランスの数学者で確率論の実験「ビュフォンの針」で有名です． 

灯台の凸レンズは巨大で重いのが問題でしたが，フレネルはフレネルレンズを採用してこの問題を解決しました．今日ではプラスチックを用いることで，この原理を使った平板レンズが，ルーペなどの小さいものから，太陽光集光用の大型の製品まで作られています．

https://www.ntkj.co.jp/products/#lens1

 製品情報 | NTKJ Co., Ltd. - 日本特殊光学樹脂日本特殊光学樹脂株式会社(NTKJ)より

■ゾーンプレート

フレネルゾーンプレートは，単色の光を集光することができます．X線や光や電波は，皆，電磁波の仲間ですが，ゾーンプレートは，屈折させて集光するレンズが作れないX線に対しても集光することができます．

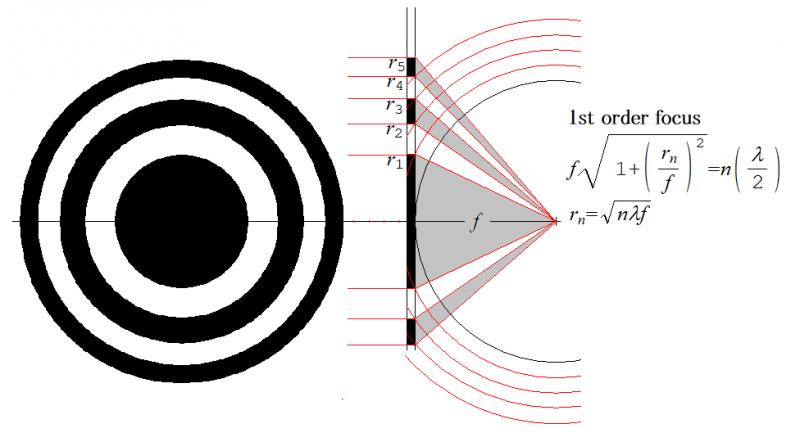
 STXMで使われるX線の集光（バークレイALS，BL5）

■アンテナとフレネルゾーン

フレネルゾーンは，無線通信でも使われる言葉です．無線通信で「見通しが良い」ということは，送信アンテナと受信アンテナの間に障害物がなく，お互いにアンテナが見通せるという意味ではなく，フレネルゾーンが確保されている状態を指します．フレネルゾーンは，送信アンテナと受信アンテナの位置を軸とする楕円体の形で，第1フレネルゾーン，その外側に，第2フレネルゾーン…と広がっていき，隣り合うゾーンの位相は互いに反対です．

私の家の立地では，携帯４Gの電波強度が非常に弱いので，屋外にドナーアンテナを設置してもらっています．私の場合では，800MHz（18バンド）ですが，例えば基地アンテナからdの距離があるとすると，第1フレネルゾーン半径r_1は，r_1＝√(λ･d)/2=9.7mとなります．ただし，λは800MHz電波の波長37.5cm，d=1,000mを用いた．第1フレネルゾーンの楕円体の60%程度が確保できれば良い通信状況と言えますが，この途中で障害物が邪魔をするのです．一般的な話をすれば，地上から高い位置に受信アンテナを設置できれば，第１フレネルゾーンの60%確保がしやすいということになります．

フレネルゾーン計算ツール | 株式会社サーキットデザインwww.circuitdesign.jp

レンズアンテナと反射型アンテナ

電波望遠鏡，衛星放送アンテナは，良く知られるように反射型のパラボラアンテナが使われます．これは，特定の方向からやってくる平行電波を集光する反射型アンテナです．しかし，ゾーンプレートの原理を使って集光するアンテナもあります．

一寸，脱線しますが，ルネベルグレンズは，球形の誘電体レンズ（同心殻で誘電率を変化させている）で，マイクロ波電波を屈折させて集光するレンズアンテナです．球体が乗っているレーターの写真を見たことがおありでしょう．私は昔，衛星放送受信用のルネQアンテナを使用していました．残念ながら今は販売されていないようです．

■フレネル反射率

フレネルは若くして（39歳）で亡くなりましたが，フレネル反射率は死の4年前の発表（1932）です．

物質の表面や界面で反射や透過する光の電場の振幅は，電場の界面平行成分と電束密度の界面垂直成分は連続になります．
物質0と物質1との界面を問題にするとき，この界面で反射される電場の振幅の比ρをフレネルの振幅反射率といいます．エネルギー反射率はρ^2です．
屈折率の低い物質から高い物質に向かう界面で反射するときには，ρが負になりますが，これは振幅の位相が180°変わることを意味します．エネルギー反射率はρの2乗なので負にはなりません．

■フレネルは，光学の分野で色々な研究をしました．そこで現れる数学「フレネル積分」の話をするのが，実は本題ですが，長くなったので，稿を改めて別の機会にします．

Maxwell方程式　[c.g.s.単位系使用] 
$$rot\overrightarrow{E}=-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{B } }{ \partial t}$$    (1a)    電場$$\overrightarrow{E}$$
$$rot\overrightarrow{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$ （変位電流）    （1b）    磁場$$\overrightarrow{H}$$
$$div\overrightarrow{B}=0$$    （1c）    磁束密度$$\overrightarrow{B}$$
$$div\overrightarrow{D}=4\pi \rho$$ (空間電荷)    (1d)    電束密度$$\overrightarrow{D}$$

弱い場では，線形応答が成り立つ： 
$$\overrightarrow{B}=\mu\overrightarrow{H}$$ (透磁率$$\mu=1$$の物質を対象とする)    (2a)    magnetic susceptibility$$\mu$$
$$\overrightarrow{D}=\varepsilon \overrightarrow{E}$$    (2b)    dielectric constant$$\varepsilon $$
$$\overrightarrow{j}=\sigma \overrightarrow{E}$$    (2c)    current density$$\overrightarrow{j}$$，conductivity$$\sigma $$
---------------------------------------------------- 
参考） [MKSA単位系の場合]
$$ \bigtriangledown \times E=-\displaystyle \frac{ \partial B}{ \partial t}$$
$$ \bigtriangledown \times H=\displaystyle \frac{ \partial D}{ \partial t}+j$$
$$ \bigtriangledown \cdot B=0$$
$$ \bigtriangledown \cdot D=\rho $$
ベクトルポテンシャル，スカラーポテンシャルの定義
$$E=- \bigtriangledown \cdot \phi -\displaystyle \frac{ \partial A}{ \partial t}$$
$$B= \bigtriangledown \times A$$
---------------------------------------------------- 
公式　$$[ \bigtriangledown \times \left[ \bigtriangledown \times E \right] ]= \bigtriangledown \left( \bigtriangledown \cdot E \right) - \bigtriangledown ^{2}E$$を使うと，
(1a,b)　→ $$ \bigtriangleup \overrightarrow{E}=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{E } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}$$， $$ \bigtriangleup \overrightarrow{H}=\displaystyle \frac{\varepsilon}{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{H } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{H } }{ \partial t}$$ （３）
（３）の解  → $$\overrightarrow{E}=\overrightarrow{E}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$，$$\overrightarrow{H}=\overrightarrow{H}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$ 　　　（４）
解（４）は，条件（５）の下で成立する．もし，変位電流がなければ，（５）の右辺第２項はない． 
$$\left( \displaystyle \frac{2\pi kc}{\omega } \right) ^{2}=\varepsilon -i4\pi \left( \displaystyle \frac{\sigma }{\varepsilon } \right) $$ (5)
(4)を(1a,b)に代入（$$\sigma =0$$の物質を対象とする．）： 
$$\overrightarrow{k} \times \overrightarrow{E}_{0}=\displaystyle \frac{\omega }{2\pi c}\overrightarrow{H}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
kE_{x} \\[0mm]
0
\end{array} \right] =\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
H_{y} \\[0mm]
0
\end{array} \right] $$ (6a)
$$\overrightarrow{k} \times \overrightarrow{H}_{0}=-\displaystyle \frac{\omega }{2\pi c}\overrightarrow{E}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
-kH_{y} \\[0mm]
0 \\[0mm]
0
\end{array} \right] =-\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
E_{x} \\[0mm]
0 \\[0mm]
0
\end{array} \right] $$ (6b)
$$\displaystyle \frac{c}{n}=\displaystyle \frac{\omega }{2\pi k}$$ (7)
$$\displaystyle \frac{H_{y } }{E_{x } }=\displaystyle \frac{\omega \varepsilon }{2\pi ck}=\displaystyle \frac{2\pi ck}{\omega }\left( =\displaystyle \frac{\varepsilon }{n}=n \right) $$ (8)
$$n^{2}=\varepsilon $$, $$\displaystyle \frac{H_{y } }{E_{x } }=\sqrt{\varepsilon }$$ (9)

境界条件

物質１と物質２の境界では，電束密度の界面垂直成分，電場の界面平行成分が連続することがMaxwell方程式から導ける．
$$D_{1z}=D_{2z}$$ $$ \Leftarrow $$ $$div\overrightarrow{D}=0$$ (10a)
$$\displaystyle \int_{}^{}(D_{2z}-D_{1z})dxdy=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}D_{z}df_{z}=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}div\overrightarrow{D}dV=0$$
$$E_{1x}=E_{2x}$$ $$ \Leftarrow $$ $$div\overrightarrow{B}=0$$ (10b)

$$\displaystyle \int_{}^{}(E_{1x}-E_{2x})dx=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}(rotE)_{y}df_{y}=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \int_{}^{}\displaystyle \frac{ \partial B_{y } }{ \partial t}df_{y}=$$

$$=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial }{ \partial t}\displaystyle \int_{}^{}div\overrightarrow{B}dV=0$$

垂直入射
$$E_{1x}+E_{1x}^{R}=E_{2x}$$
$$H_{1y}+H_{1y}^{R}=H_{2y}$$ $$ \Rightarrow $$ $$n_{1}\left( E_{1x}-E_{1x}^{R} \right) =n_{2}E_{2x}$$
$$\displaystyle \frac{H_{1y } }{E_{1x } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$-\displaystyle \frac{H_{1x}^{R } }{E_{1x}^{R } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$\displaystyle \frac{H_{2y } }{E_{2x } }=\sqrt{\varepsilon _{2 } }=n_{2}$$
振幅反射率 $$\displaystyle \frac{E_{1x}^{R } }{E_{1x } }=\displaystyle \frac{n_{1}-n_{2 } }{n_{1}+n_{2 } }$$， $$n_{1}<n_{2}$$で位相反転
振幅透過率 $$\displaystyle \frac{E_{2x } }{E_{1x } }=\displaystyle \frac{2n_{1 } }{n_{1}+n_{2 } }$$
--------------------------------------------------------
$$n_{1}, n_{2}$$が実数なら，$$\displaystyle \frac{\left| E_{1x}^{R} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }+\displaystyle \frac{\left| E_{2x} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }=1$$
-------------------------------------------------------- 
$$\displaystyle \frac{ \partial \rho }{ \partial t}+div\overrightarrow{j}=0$$
$$\displaystyle \frac{ \partial }{ \partial t}div\overrightarrow{D}=4\pi \displaystyle \frac{ \partial \rho }{ \partial t}=-4\pi div\overrightarrow{j}$$
$$div\left( \displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+4\pi \overrightarrow{j} \right) =0$$
$$rot\overrightarrow{H}=\displaystyle \frac{\varepsilon }{c}\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$
第１項：第２項の寄与率＝$$\varepsilon \omega :4\pi \sigma $$
$$\omega \gg \displaystyle \frac{4\pi \sigma }{\varepsilon }$$ $$\to $$ 誘電体

４．特異値分解の数学

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n

簡単のために，m=5，n=3として，具体的に演習してみましょう．

今回は，昔，私がリコーで関わった懐かしい実験の話をして，特異値分解の数学の話への導入にしたいと思います．まず，実験の話をしますが，私がSTXMに係わったのは，2000年～2004年で，もう20年も前のことです．その後の進歩は著しいに違いありません．当時，実用になるSTXM装置は，Hitchcoch博士が，サンフランシスコ，バークレーのALS（Advanced Light Source）に建設した，BL5.3.2（bending magnet光源利用）　とBL7.0.1（undulator光源利用）の2台だけでした．後年，岡崎の分子研のUVSORに，やはり，Hitchcock博士がSTXMを建設しました．

（注）放射光とは初耳の読者もおられるので，放射光施設とは何かを簡単にお話しておきます．ドーナツのような真空リングの中を，光速に近い速度に加速された電子が回転しています．回転するといっても電子の軌道が円形というわけはなく，リングの要所要所に偏向磁石bending magnetが配置されていて，偏向磁石の所で電子は曲げられるので，電子の軌道は多角形です．電子が方向を変えるときには，電磁波（白色光の光やX線）を放出します．これが放射光で，いろいろな測定に放射光を利用します．リングの電子蓄積エネルギーとはリング内を回転する電子のエネルギーのことです．ALSでは1.9GeV，兵庫県のSPring8では8GeVです．蓄積エネルギーの大きさは，放出される放射光のエネルギーの最大値を決めるので，SPring8は硬X線の光源，ALSは軟X線の光源となります．
放射光の光源は，偏向磁石bending magnet光源とundulator光源とがあります．undulatorというのは周期的に配列した磁石のことで，蓄積リングの電子軌道の直線部に挿入します．周期的磁場で電子は蛇行運動をしますが，その軌道のFourier変換に相当する波長のX線（準単色光）が放射されます．

さて，STXMに使うALSの放射光リング（蓄積電子のエネルギーが1.9GeV）は，軟X線の光源です．軟Ｘ線の領域は10^2eV～10^4eVの範囲で，炭素など軽元素の1s（K殻電子）の励起（光電効果による電子の放出）は，このX線の領域にあります．硬X線と違い，軟X線は空気で減衰しますからその測定は，He置換した真空チェンバー内で行います．炭素の1sの吸収スペクトルNEXAFS(吸収端近傍の吸収微細構造)は，分光して単色化したX線ビームを薄膜試料に透過させ，その吸収を測定して得ます．スキャンするエネルギー範囲は，280eV～310eVで，スキャンステップは0.1eVですので，スペクトルは300点ほどのデータ数になります．

目次
これから始まるこのテーマの話には4つの側面があります．
第１は，ニュースとしての一般向け報道．
第２は，STXMの装置の仕組み．
第３は，材料科学の側面．炭素1s吸収端近傍の吸収スペクトルNEXAFS．
第４は，データ解析の数学．特異値分解．

技術者向け教育の場合にお話しするのは，第１，２の部分です．第４の部分は，Hitchcock博士らの開発したaXis2000というソフトウエアを用いるので，数学を意識することはないのですが，今回は，特に，第４の数学の話に注目することにします．番号順に順を追って話ます．

１．一般向け報道

せっかくの記事ですが，技術の解説が正しくありません．ここで言及しているデータベースは無関係で，この記事はピントがずれているのが残念です．

２．STXM（ScanningTransmissionX-rayMicroscopy）装置

放射光X線をFresnel Zone Plateで，試料薄膜上にフォーカス（22nmΦ）させ，その微小ビームを試料薄膜に透過させ，微小ポイントの吸収スペクトルを測定します．スペクトルを得るには入射するX線のエネルギーを280eV～310eVの範囲で，0.1eVの分解能で変化させます．これは，色を変えて見る実験に例えるとわかりやすいでしょう．同じ材料薄膜でも，赤い色を透過させてみた場合と青い色を透過させてみた場合とでは異なるでしょう．試料薄膜（ミクロトームで加工した厚さ100nmの切片）上をラスタースキャンすることで，そのエネルギーで見た薄膜の吸収画像が得られます．
薄膜に入射するＸ線エネルギーを280eV～310eVの範囲で変えて測定した300枚ほどの吸収画像をスタックすれば，薄膜試料の各点(x, y)の吸収スペクトルμ(x, y)が，point to pointで得られたことになります．試料上の空間分解能は約30nm，スペクトルのエネルギー分解能は0.1eVという高性能な測定です．私たちは装置を使う純粋ユーザーでしたが，私は，このような装置を開発したHichcock博士グループの技術と装置の仕組みに興味を持ちました．ここでは，STXM装置の重要な要素であるゾーンプレートとその制御についてとり上げましょう．

ゾーンプレートの焦点距離は波長で変わります．入射するX線ビームのエネルギーがスキャンされれば，そのつど瞬時にフォーカスしなければなりません．これは，レーザー干渉計とゾーンプレートの載るピエゾステージで行われます．試料点の（x, y)スキャンは試料台のピエゾステージで行われます．
BL5.3.2はbending mgnetからの放射光（undulator光源よりは光強度は弱い）ですが，照射された点の有機物はダメージを受けますので，できるだけ高速で測定します．そして，試料の変質がなかったかどうか測定前後でチェックする測定ルーチンもあります．X線のエネルギーを変えて測定した吸収画像をスタックしたとき，サンプル位置のずれがあれば自動修正できます．

以下で，STXM装置で最も主要な素子であるFresnel zone plateについて，詳述しましょう．zone plateは，外径45000nm，最外輪帯幅35nm程度のものです．下図のゾーンプレートは，波長λのX線の単色光を集光します．黒い部分はX線を通しません．例えば，中心の黒丸はダイレクト光をストップし，輪帯環の白い部分を通過してくる行路長　f+λ/2，f+3λ/2，f+5λ/2，････のものが，焦点距離fに集光できます．

 このようなフレネルゾーンプレートの後ろにOSAという絞りを置いて，行路差λずつの光線（１次のフォーカス）のみが試料位置に集光するように調整します．

 入射X線のエネルギーを変えたときのゾーンプレートの焦点距離の調整は，レーザー干渉計を用い精密制御されています．

３．炭素の1s電子の吸収端直上の微細構造スペクトルNEXAFS

電子写真で使われるトナーは，カーボンブラックとか顔料色素で出来ていると思っている人がほとんどでしょう．実際には，このような黒やカラーの色素だけでなく，樹脂，ワックス，電荷制御剤など，複数の有機物分子が，1粒のトナー中に分散されており，それらの分散状態は，トナーの性能に影響を与えます．設計通りの分散状態が実現しているか評価することが必要です．高精細トナー1粒のサイズは数μmという微細さで，その中の物質の分布状態を30nmΦの分解能で調べる必要があります．しかも，混合されている物質は，皆，有機物ポリマーで元素分析をすれば，どれも主成分は炭素です．つまり，炭素が骨格のよく似た有機分子が混合している状態の分布マップが知りたいのです．これを化学状態マッピングといいます．

下図には，色々な物質の炭素1s電子のNEXAFS吸収スペクトルを載せました．X線のエネルギーを変えて観察した透過像も載せています．例えば，①カーボンブラックの分布する場所は292.5eVのX線エネルギーで見ると吸収が大きいため白っぽく見え，②ワックスの分布する場所は，287.8eVで見ると吸収のためX線の透過が悪く白っぽく見えます．同様に，③樹脂の分布する場所は，284.3eVのX線の透過像では白っぽく見えます．
エネルギースキャンにともなう画像変化のパラパラ動画を作って見るとわかりやすく面白いものです．

 化学状態（元素分析ではない）という意味は，トナー中に分散している物質は，すべて有機分子（どの分子もほとんど炭素元素で出来ている）なので，元素分布のマッピングでは差がありません．炭素原子が骨格の有機分子の吸収スペクトルは，炭素の1sの吸収端285eV付近にあり，その炭素原子がどのような化学結合状態にあるのか（1重結合か，2重結合か，π電子系か，どのような官能基と結合しているか）により，吸収端から高エネルギー側に観測される吸収スペクトルの微細構造（NEXAFSという）に違いがでます．
トナー中の有機ポリマー分子の分布マップを得るには，化学状態マッピングがどうしても必要になります．
元素に特有な特性X線を検出すれば良い元素分布マッピング［TEM（分析電顕）でも，放射光でも，微小領域の蛍光X線分析は普及している］と，化学状態マッピング［微小領域のpoint to pointで炭素1sのNEXAFSの測定が必要］は，全く異なる技術であり，我々の目的には，STXMでの実験が必要でありました．

リコーが，Adam P. Hitchcock（McMaster University）博士が開発したALS（バークレー，AdvancedLightSource）のBL5.3.2に設置されたSTXMで共同研究を行ったのは，2000~2004年のことです．

実験で得られるデーターセットは，試料表面の座標を（x, y）とすると，試料表面のラスタースキャンと，透過させるX線のエネルギーωのエネルギースキャンを行って，point to pointで収集した吸収スペクトルμ(ω；x, y)です．
再度たとえ話をすると，膜を透過する光のコントラスト像は，光の色を変化させると透過光の像のコントラストが変わって見えるというわけだ．

このような，データセットの収集と解析は，Hitchcock博士の開発したソフトウエアaXis2000を用います．この解析のために用いる数学は，特異値分解です．この先は，４．特異値分解の数学に続きます．

４．特異値分解

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n
簡単のために，m=5，n=3として，続編で演習してみましょう．続く...

参考-----
特異値分解を使いますが，特異値分解の概念図は以下のようなものです．

以下の拙著の第3章p64～p84から抜粋転載しました．

https://www.amazon.co.jp/dp/4774143936?tag=note0e2a-22&linkCode=ogi&th=1&psc=1

■特異値分解

複素行列$$A(m \times n),m \ge n$$は，適当なユニタリー行列$$U(m \times m)$$と$$V(n \times n)$$を用いれば，
$$UAV^{ \dagger }=\mit\Sigma $$，あるいは，$$A=U^{ \dagger }\mit\Sigma V$$に分解できる．これを，Aの特異値分解という．
(ただし，$$V^{ \dagger }$$は$$V$$の共役転置行列．$$A$$が実数行列の場合は転置のみ$$V^{'}$$）．

$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$

ここで，$$\sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$を$$A$$の特異値と呼ぶ．
$$r$$は$$\textrm{rank}(A)$$に等しい．

$$AA^{ \dagger }=U^{ \dagger }\mit\Sigma VV^{ \dagger }\mit\Sigma ^{'}U=U^{ \dagger }\mit\Sigma ^{2}U$$,      $$ \because \Sigma \Sigma ^{'}=\Sigma ^{2}(m×m) $$
$$AA^{ \dagger }$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$m-r$$）
$$A^{ \dagger }A=V^{ \dagger }\Sigma ^{'}UU^{ \dagger }\Sigma V=V^{ \dagger }\Sigma ^{2}V$$,      $$ \because \Sigma ^{'}\Sigma =\Sigma ^{2}(n×n)$$
$$A^{ \dagger }A$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$n-r$$）

線形写像 $$ y=Ax  (x∈C^{n}，y∈C^{m})$$があり，それぞれの空間でユニタリ変換； 
$$ x'=Vx$$, $$y'=Uy$$をすると，$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている．

■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して，
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める．
特異値分解ができたら；$$UAV'=\Sigma$$，$$A=U'\Sigma V$$が成立している．
（$$A$$は実行列なので，$$U，V$$は直交行列となり$$U'＝U^{-1}$$などの性質がある．）
最小2乗法は，$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる．
$$\textrm{rank}(A)=r≦n<m$$とする．$$\Sigma (m×n), V(n×n), U(m×m)，x(n×1)$$の型であった．

$$r=n$$の場合を考える．

$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$,　$$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから，
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方， 
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って，$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると，第1項は0になり，第２項は残差の２乗を与える，

$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る．

１．結晶空間群．結晶点群

結晶は周期的な内部構造を持ちます．周期的な離散空間を＜結晶空間＞と言い，
その対称性は<結晶空間群>で記述します．結晶空間群の種類は，3次元では230種類です．
3次元の周期構造の幾何学的な表現を＜格子＞と言ったり，その数学的な表現を＜並進群＞と言ったりします．
結晶空間の中で，格子分だけ移動しても，周囲の状況は移動する前の状況と全く同じなので，無限に繰り返す結晶の中で自分がどこにいるか区別できません．そこで，格子分だけ移動した点はすべて同値とみなして，
無限に広い結晶空間を１つの単位胞の中に畳み込んでしまうことができます．
あたかも，無限に続く時間を，時計の文字盤（12時間）に畳み込んでしまうのと同じです．
＜単位胞＞（有限図形）の対称性は＜点群＞で記述でき，3次元の＜結晶点群＞は32種類です．

（注）＜結晶点群＞の対称操作は周期性と両立しなければならないので，ただの点群とは異なり，
回転対称は２，３，４，６回軸に限定されます．

格子を法として（あるいは，並進群を核として）準同型写像をすると，結晶空間群の230種類を，結晶点群の32種類に還元できます．

 $$\mit\Phi /T \cong G$$ ,     $$T \vartriangleleft \mit\Phi $$    ($$\mit\Phi $$結晶空間群，$$T $$並進群，$$G$$結晶点群）

２．双対空間．コンボリューションのFourier変換．Curieの原理（因果律）

結晶格子をFourire変換すると逆格子が得られます．結晶格子（$$r-$$空間）と逆格子（$$R-$$空間）は，Fourier変換で移り変わる互いに双対な空間です．結晶の電子密度関数$$ρ(r)$$とそのFourier変換F(R)は，1:1に対応し，両者の対称性は同じです．

電子密度分布$$ρ(r)$$により散乱されるX線の散乱振幅は$$F(R)$$で，$$ρ(r)$$のFourier変換にほかなりません．観測される散乱強度は$$|F(R)|^{2}$$で散乱振幅$$F(R)$$の位相情報は失われます．

 $$Tr[\rho (r)]=F(R)$$,     $$Tr[\rho (r)*\rho (r)]=|F(R)|^{2}$$

結晶の対称心の有無にかかわらず，観測されるX線散乱強度には，対称心が生じます：$$|F(-R)|=|F(R)|$$，これをFriedel則と言います．

Friedel則は，もっと大きい次のCurieの原理の一部です．

原因である「結晶構造の対称性」は，結果である「その結晶で生じる現象の対称性」に反映される．

（例1）結晶構造に，4回対称性が存在すれば，Ｘ線回折像の対称性に，少なくとも4回対称性は反映される．しかし，Ｘ線回折像に4回対称性が存在しても，結晶に必ずしも4回対称性が存在するわけではない．
これを回折対称の上昇という．

（例2）Ｘ線回折像に10回対称（5回対称⊗Friedel則）があったとしても，その原因たる結晶構造に5回対称性があるとは限らない．結晶構造の5回対称性は周期性（結晶の定義）と矛盾するのであり得ない．しかし，周期性を外せばあり得る．準結晶のモデルは，非周期のペンローズ・タイリングで実現できる．

３．点集合とベクトル集合．ホモメトリック

結晶構造（点集合）の対称性と，回折強度像（点集合のベクトル集合が作るスター）の対称性の関係を考察しましょう．両者の対称性では，回折強度像の対称性が高いわけで，与えられたベクトル集合から点集合を推理するのは，面倒な逆問題になる場合がある．

一般に，回折強度像の対称性から結晶構造の対称性は，一意に定まらず，同一の回折強度像を与える結晶構造が複数存在する可能性があります．これらをホモメトリック構造という．
下の2つの図は，1次元のホモメトリック構造の例［Patterson(1944)］．
（注）この図の見方は，1次元の単位胞が全円周（長さ1）です．図中に描き込まれた長さは円弧に沿って測ります（弦の長さではない）．円周（長さ１）のどこか1点で切って，線分（長さ１）に延ばします．この線分を1次元のタイルのように並べていくと1次元の周期的な図形になります．この図形には黒い点が並んでいますが，2つの図形で黒点の配列は異なります．それにもかかわらず，出現する黒点間の間隔の種類は2つの図形で同じになります．

PCR検査の統計と論理　　　　　　　　　　　　　　　谷　克彦

（要旨）
◆PCR検査の感度と特異度は，遥かに1に近い確率でした．偽陰性や偽陽性を理由に検査数をコントロールする理由は成り立ちません．検査を拡大し有病者を発見し早期隔離しましょう（感染から5日目頃が最もウイルスを放出し，有病者の半減期は10日位です）．◆日本の陽性率は7%と計算できますが，最近の変動の勾配（末尾に掲載）から見ると10%を越えたように見えます．このグラフがそのように見えるのは，検査数を抑制しているために陽性者数のオーバーフローが起きている証拠かもしれません．
---------------------------------

COVID-19パンデミックは，実効再生産数を1より低下させると鎮まります．この対策は，次の３つの数値を下げることです；①感染者が感染力を持つ期間，②感染者が接触する人数，③感染者との接触で感染する確率．そして，それぞれに対する施策は以下のようです；
①感染者を早期に発見し隔離する．このためにPCR検査の拡充が必要．
②効果的なロックダウンの期間，地域，方法を，シミュレーションで予測し戦略的に介入する．
③ワクチン接種で，感染感受性のある人の割合を減らす． 

COVID-19に感染すると，次のような経過になります． 

感染（陽性）→潜伏無症状期→発症期（無症状もありうる）→回復（陰性）or死亡
陽性の期間［潜伏無症状期＋発症期（無症状もありうる）］は，「罹患者」が感染源となる有病状態なので「有病罹患」と呼ぶことにします．感染源となる「有病罹患」（症状の有無にかかわらず）を早く発見し隔離する必要があります．
有病罹患者の発見はPCR検査でなされます．検査の目的は蔓延率の推定だけではなく，感染源となる有病罹患者をできるだけ早期に探し出し隔離するという緊急な役割があります．検査対象を限定し，検査の陽性的中率を上げることが検査の目的になってはいけません．
実世界の現象は，多数の原因と結果が複雑に絡んだ因果関係をなし，数学（統計）で論理的に推論するのは，その一部を切り取った世界です．その範囲で得た数学（統計）的推論の結果を，系全体の中で解釈できる論理的な思考が必要です．
正しい数学（統計）推論で得られた結果でも，複雑な全体系で非論理的に利用されるとしたら，社会を誤った方向へ導く主張に，数学が加担してしまうことになります．PCR検査の規模拡大は有病率の低い集団ではすべきではないというのは正しい主張ではありますが，その主張の根底にあるPCR検査の性能から見直し，これを論理的に考察してみましょう．

■有病率とは
日本感染症学会の定義によると，有病率とは，「その疾患をもっている人数の全人口に対する割合」ですが，日々発表される厚労省の新規陽性者数と検査数のデータから，日本の有病率を計算できるように，有病率$$x_{0}$$の解釈を次のようにします．
（定義）$$有病率=有病罹患数/累積PCR検査数$$
　　　　 　　　$$有病罹患数＝累積検査陽性者数－累積回復退院者数－累積死亡者数$$
これにより，日時（$$T=$$5月15日）の日本の有病率を求めると$$x_{0}=0.58$$％になります．
ここでは，陽性者=罹患者と見なしています．
この検査集団の陽性率($$T$$)と罹患率($$T$$)は，7日平均（8～１５日）を用いて，
$$陽性率(T)=陽性者(T)/検査数(T)=6288/92167=0.068$$，
罹患率(*)$$(T) =陽性者(T)/累積検査数(T)=6288/13015244=0.0005$$

日時$$T$$の有病罹患数$$(T)$$を別の定義で表現してみましょう．有病罹患状態は，14日位で回復（陰性になる）します（運悪く死亡の場合もありますが，少数のため無視します）．今日$$T$$の有病罹患者（感染源となる罹患）の中には，$$t$$日前に罹患した者も残っています．そこで，次の定義が成り立ちます：
有病罹患数$$(T)=\displaystyle \int_{0}^{T}$$罹患数$$(t)p_{a}(T-t)dt$$，
ここで，$$p_{a}(t)$$は，陽性保持確率（病気の減衰関数のような性質）で，（付録３）の大規模調査の結果に報告されています．病気の感染初日を推定するのは大変難しいのです．PCR検査で見つかった日が感染日という訳ではないでしょう．感染から5日目あたりが，感染者が最も多くウイルスを放出するので，その頃が最も発見され易いのではないかと思います．
病気減衰関数の半減期は約10日ですので，コンボリューション積分は次のように近似できます：
有病罹患数$$(T)=10×罹患数(T)$$．この集団の累積検査数で規格化すると．
$$有病率(T)=10×罹患率(T)$$が得られます．
注*）感染症学会の定義では，罹患率の分母は，「集団の感受性のある人数」ですが，ここでは「集団の人数」としています．

■PCR検査の感度と特異度
PCR検査の感度$a$とは，罹患者をPCR検査で陽性（$$+$$）と正しく判定する確率のことで，真の罹患者でもPCR検査が陰性（$$-$$）（偽陰性）と判定される確率は$$1-a$$程度あります．検査の特異度$$b$$とは，非罹患者を正しく陰性（$$-$$）と判定する確率のことで，非罹患者を陽性（$$+$$）（疑陽性）と判定する確率は$$1-b$$程度です．

確率$$a , b$$は１に近いほど，優秀な検査になります．従来の議論に用いられてきたこれらの数値は，$$a=0.70, b=0.99$$ですが，昨年の英国ONSによる大規模調査（付録３．)で判明した数値は，$$a=0.95(0.85 ~ 0.98)$$，$$b=0.9992$$です．
低い有病率の集団でPCR検査対象を拡大すると，莫大な偽陽性が出て医療崩壊につながるので，有症状者や濃厚接触者に限定して検査を行っているとの主張がありますが，英国ONS調査の感度と特異度を採用すると，この主張の根拠が覆えることを検証します． 

■ベイズ推定による有病罹患の内訳

この集団の罹患率を$$p(罹患)=x$$，とします．この集団で，PCR検査が$$+$$判定のとき，罹患者である確率$$p(罹患|＋)$$，および，$$-$$判定のとき，罹患者である確率$$p(罹患| - )$$，などを推定しましょう．
$$p(罹患| + )=p( + |罹患)･p( 罹患) /p( +) =a･x/( a･x+(1-b)( 1-x)) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) x/\left( (1-a)x+b\left( 1-x \right) \right) $$， 
$$p(非罹患|+)=p\left( + |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( + \right) =(1-b)(1-x)/\left( (1-b)(1-x)+a \cdot x \right) $$,
$$p(非罹患| - )=p\left( - |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( - \right) =b\left( 1-x \right) /\left( b(1-x)+(1-a)x \right) $$，
下に$$x$$を変数とするグラフを示します．ベイズの定理は線形システムなので，重ね合わせができ，罹患状態を束ねた状態で定義される有病率$$x_{0}$$を入力にしても良いでしょう． 
■集団の有病率 $$x=0.006$$に対して，感度$$a$$，特異度$$b$$を変えて比較
（１）$$a=0.95, b=0.9992$$（英国ONS）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.9:0.1$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.9:0.0003$$
（２）$$a=0.7, b=0.99$$（従来）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.3:0.7$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.3:0.002$$
PCR検査が$$+$$判定であるときに，真陽性の確率$$p(罹患|+)$$と，偽陽性の確率$$p(非罹患|+)$$を比較すると，従来用いられている感度，特異度では，偽陽性確率が真陽性確率の$$2.3$$倍もありますが，英国ONSの数値では，逆に1/10になり，医療崩壊を懸念する根拠にはなりません．
いずれにしろ，陽性確定までにPCR検査は2度行われ，さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．

次に，真陽性の確率$$p(罹患|+)$$と偽陰性の確率$$p(罹患|-)$$を比較すると，
（１）では，$$1:3 \times 10^{-3}$$，（２）では，$$1:7 \times 10^{-3}$$で偽陰性は小さい確率です．これを人数で比較するには，陽性率$$y=0.07$$，陰性率$$1-y=0.93$$を，それぞれ，$$p(罹患|+)$$と$$p(罹患|-)$$に乗じます．
（１）では，$$真陽性人数:偽陰性人数=1:4 \times 10^{-2}$$，
（２）では，$$真陽性人数:偽陰性人数=1:9$$
この集団の陽性率は$$7$$％と低いので，陰性集団が大多数で，偽陰性の確率が小さくても偽陰性者数は多いとの主張もあります．確かに，従来の数値（２）を用いると，真陽性者の9倍もの偽陰性者がいます．しかし，数値（１）を用いると，偽陰性者の数は1/100で，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

■PCR検査数は十分か
ここに引用した２つの図は，1日の$10^{6}$人あたりの（横軸）検査陽性数：（縦軸）検査数の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは日本のものより縦軸で25倍，横軸で16倍大きいのでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間経過とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を拾い出す十分な検査が行われているようです．英国の例を見ると，始めは，陽性者が多く検査数が間に合わないほどでしたが，現在みられる検査数を増しても陽性者が一定となる状態は，十分な検査数が確保されている証拠です．日本の例で，検査数と陽性者数の増減の比例が見られる傾向は，検査数を増やせば，陽性者数も増加する可能性があります．
これらの図は，2020.1.25～2021.5.25の期間のもので，赤細線は，日本の図では，陽性率5{\%}と10{\%}の勾配，英国の図では，0.5{\%}と２０{\%}の勾配を示しています．
これらのグラフは，https://ourworldindata.org/coronavirus-testingから引用しました．

■付録－－－－－
付録１．ベイズの定理
条件付き確率についての「ベイズの定理」とは次のように説明できます．
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
ただし，記号の意味は例えば以下の様です．
$$p(X)$$:$$X$$が起こる確率 
$$p(Y|X)$$：$$X$$が起きる条件下で，$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きる条件下で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

付録２．PCR検査の原理
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を40回程度繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です．

付録３．英国ONSのcovid-19感染の大規模調査
英国国家統計局（ONS)によるcovid-19の大規模感染調査は，パイロット調査としてイングランド（2020.4末）で開始されました．7月以降，規模を拡大し，住所リストから世帯のランダム・サンプリングを行い，8月には，2週間ごとにテストされるサンプルを，イングランドで15万人，ウエールズ，スコットランド，北アイルランドで各1.5万人の規模に拡げました．調査は，小児の症候性および無症候性感染の有病率と発生率を知るため，2歳以上の子供を含みます（参照：covid-19学校感染調査）．16歳以上の成人の20{\%}は血液サンプルの提供を求められました．2020.7.31～9.10の6週間で，208,730の検体調査を行いました．偽陽性は症状のない人で発生すると予想されましたが，調査研究のデータからは，症状の有無によらず同じでした．血液サンプルは，オックスフォード大学で，抗体検査，IgG免疫グロブリンのテストをしました．
PCR検査に関する知見は；その感度が，85{\%}～９８{\%}(95{\%}である可能性が最も高い)にあり，特異度は，99.92{\%}でした．
綿棒スワブの検体採取は，適切な監督下で行えば，自己採取でも医療従事者が直接採取した場合と同様の正確な結果になることも報告されています.

引用データ

1)厚生労働省 
2) Coronavirus (COVID-19) Infection Survey, UK Statistical bulletins
3) Keeping up with COVID-19, Rachel Thomas;
https://plus.maths.org/content/keeping-covid-19
4) https://ourworldindata.org/coronavirus-testing

2021年3月に，2021年のアーベル賞の受賞者が発表されました．ラズロ・ロヴースLászló Lovász（ハンガリー科学アカデミー・レニェイ数学研究所）とアヴィ・ウィグダーソンAvi Wigderson（プリンストン高等研究所）です．
プレスリリースによると，「理論計算機科学および離散数学への基本的な貢献，および，これらの分野を現代数学の中心的な分野として確立するのに果たした主導的な役割」が評価されました．
アーベル賞は，2002年にノルウェー科学アカデミーによって設立された数学で最も権威のある賞の1つです．ノルウェーの天才数学者ニールス・ヘンリック・アーベル（1802–1829）にちなんで名付けられ，この分野の発展に多大な貢献をした科学者に毎年授与されます．

2021年の受賞者について，ステクロフ数学研究所，シカゴ大学（米国）の数学科アレクサンドル・ラズボロフ教授による解説記事を要約紹介します．
「トリニティオプション-科学」第6号（325），2021年3月23日号
https://elementy.ru/nauchno-populyarnaya_biblioteka/435811/Troitskiy_variant_Nauka_6_325_23_marta_2021_goda

離散数学は，有限の離散的オブジェクトの特性を研究します．その重要な部分は，伝統的には組み合わせ論と呼ばれ，「純粋」数学で生じる構造に動機付けられています．たとえば，組み合わせの観点から，トポロジーの基本である複体の概念は，複体の面に対応する有限集合の閉じたファミリーにすぎません．組み合わせの抽象化は顕著な結果をもたらし，「有用な」（つまり，基本的な数学に適用される）組み合わせ論は，数学界で常に重視されてきたのは当然です．

離散数学は，「ハンガリーの数学」と長い間関連しており，その最も活発な支持者および宣伝者は，ポール・エルデシュでした．ラズロ・ロバースは1948年にブダペスト（ハンガリー）で生まれ，この数学的文化の中で育ちました．特に，彼はかなり早い年齢でエルデシュに会いました．そしてこれは彼のその後のキャリアと展望に非常に大きな影響を与えました．ラズロ・ロバースは，ポール・エルデシュの直接の後継者と見なすことができます．

　　　　　　　　　ラズロ・ロバース

理論情報学の形成
理論計算機科学，または，コンピュータサイエンスは，一般に「計算の複雑さの理論」の基礎が築かれた1970年代頃に独立した分野として出現しました．この分野では，大まかに言えば，アルゴリズムの存在の問題，または多くの場合，それらの効率に与えられた制約を伴うアルゴリズムの非存在が研究されます．

その名称にもかかわらず，理論計算機科学は厳密に数理科学であり，そのすべての成果は，数学の他の分野と同様に，厳密な定義，定理，および補題の形で定式化されています．それにもかかわらず，開発の内部論理とともに，理論情報学もまた，実際のアプリケーションによって大部分が導かれ，時には非常に具体的であります．他の「半応用」分野と同様，それに対する「純粋」数学者の態度は，穏やかではあるが長い間警戒していたことは明らかです．

アヴィ・ウィグダーソンは，1956年にハイファ（イスラエル）で生まれました．彼の学生時代は，理論計算機科学，特に独立した分野としての計算の複雑さの理論の形成に費やされました．プリンストンでの大学院での研究中，アヴィは，複雑性理論の創設者の1人である彼の学術顧問Richard JayLiptonの影響を大きく受けました．ロバースの場合と同様に，理論計算機科学が彼の人生の仕事になりました．

　　　　　　　　　アヴィ・ウィグダーソン

両受賞者の主な成果の1つは，数十年にわたる両方の分野の成熟と形成の過程で，彼らの科学的研究と国際的な教育および普及活動が大きな貢献をしたことです．
理論計算機科学は，コンピュータが操作する対象のほとんどが離散的であるという自然な理由から，離散数学の成果，アイデア，概念を積極的に利用しています．その多くは「純粋な」数学では需要がありませんでした．一方，理論計算機科学のニーズは，離散数学の全く新しい分野の創造につながっており，これは科学の歴史の中で最も成功した共生関係の一つであると思います．この分野から他分野への「アイデアの移転」における最大の功労者は，今年のアーベル賞受賞者なのです．
「純粋」数学者や数学者との関係も，より良い方向に変化しました．たとえば，ラズロ・ロバース（ちなみに，ロシア科学アカデミーの外国人会員）は4年間（2007〜 2010年）国際数学連合の会長を務め，プリンストン高等研究所（IAS）でのアヴィ・ウィグダーソンの役職は数学学校に属しています．この道を歩み始めた当初は，どちらも考えられないことでした．これは，抽象数学の多くの分野に密接に関連する問題，アイデア，定式化が両分野に蓄積され，多くの場合，抽象数学自身の発展に影響を与えることによって，多かれ少なかれ自然な形で起こったことです．この点において，ラズロとアヴィは誰もが認めるリーダー的存在です．

離散性から連続性へ
離散数学の特徴として，連続的ではなく有限的な対象への関心が高まっていることを前述しました．ラズロ・ロバースは，正反対の仮定に基づいた非常に重要なプロジェクトの創設者の一人であり，おそらく主人公です．その結果，非常に大きなグラフやその他の組み合わせ対象物は，10進法の分数が無理数の近似値とみなされるのとほぼ同じ意味（ロバースのアナロジー）で，幾何学的または代数的な性質を持つ自然な連続構造の近似値とみなすことができることがわかりました．その結果，美しく一貫した理論が生まれ，当然のことながら組合せ論だけでなく，代数学，解析学，測度論，統計力学，エルゴード理論など，数学や物理学のさまざまな分野と驚くほど関連していることがわかりました．

ラズロ・ロバースは，優れたモノグラフのLarge Networks and Graph Limitsを書き，すぐにこの分野の古典的なテキストになりました．興味のあるすべての読者にお勧めします．

疑似乱数理論
アヴィ・ウィグダーソンに最も関連するトピックに名称を付けると，疑似ランダム性の理論でしょう．最初の動機から始めると，最も重要なアルゴリズムの多くが本質的に確率的なことです．つまり，作業で乱数検出器を使用します．ただし，絶対的なランダム性はまれであり，実際には，いわゆる疑似乱数発生器がほとんどの場合使用されます．これは，アルゴリズムがそのような置換に「気付かない」ことを期待して，決定論的手順によって生成されたランダムビットとして渡されます．

擬似乱数理論とは，大まかに言えば，この希望に理論的根拠を与えようとするもので，さまざまなアーキテクチャやパラメータを持つ発生器を構築し，それらが必要な特性を持つことを数学的に証明することができ，同時に，これらの対象や概念は，計算複雑さの理論において，まったく独立した別の用途があることや，対応する構造が，たとえば代数幾何学のような，数学のきわめて古典的な分野に関連していることも，すぐに判明しました．アヴィ・ウィグダーソンは，この分野で誰もが認めるリーダーです．特に，最も重要な構成要素（Nisan-Wigderson発生器）と，複雑さの理論における顕著な影響（Impagliazzo-Wigderson定理）の両方があります．

Kneser仮説
ラズロ・ロバースは，クネーザー予想の証明があります．クネーザーグラフは，代数的組み合わせ論で発生する非常に自然な有限グラフで，タスクは，その色数を計算することです．つまり，エッジで接続された頂点が常に異なる色になるように頂点に色を付けることができる最小の色数を計算します．

おそらく，最適な着色を作成するのは簡単です．問題は，それを改善できないことを証明することです．この問題は，25年近くの間，組合せ学的な努力を必要としていましたが，1978年にロバースが発表したエレガントな論文で，厳密に離散的な絵全体を多次元の球体に浸し，実数位相幾何学の基礎的な結果の1つであるBorsuk-Ulamの定理を適用することで解決されました．この証明から，今日では位相幾何学的組合せ論と呼ばれる学問全体が発展し，その方法によって，他のアクセスできない問題の数々が解決されました．

解の系

証明の複雑さの理論では，数学の定理や，あるグラフが与えられた数の色に着色できないという主張，あるコードにエラーが含まれていないという主張など，さまざまな自然な主張の効果的な証明が可能かどうかを研究します．最も重要な証明系は，いわゆる解の系であり，それに基づくアルゴリズムが最も広く実用化されているからです．

解の系を研究する方法はかなり昔から知られていましたが，2001年にEli Ben-SassonとA. Wigdersonが研究するまでは，せいぜい私的なものでした．本研究では，このような証明を分析するための驚くほど簡単な一般的手法を，幅と呼ばれるもう一つの複雑さの尺度の関与に基づいて提案しました．この論文は，証拠の複雑性に関する理論のパラダイムとなり，多くの新しいアイデアやコンセプトを生み出しました．

イベルメクチンは，北里大学特別栄誉教授の大村智博士が１９７４年，静岡県・川奈のゴルフ場近くで発見した微生物が生み出す「アベルメクチン」をもとにした化合物（誘導体）で，アメリカの製薬会社のメルク社との共同研究で，もともとは家畜やペットの寄生虫，回虫などの治療薬として１９８１年に開発されました．イベルメクチンは，家畜の寄生虫や皮膚病，イヌのフィラリア症などの特効薬となり，動物抗生物質として２０年以上にわたって売上高世界トップを維持する記録的なヒット薬剤です．

人間のオンコセルカ症 （アフリカ・中南米・中東などの河川流域で蔓延していた河川盲目症）に効果があっただけではありません．その作用の範囲は驚くほど広いことが判明しました．線虫，ほとんどの昆虫，ダニに効果があります．そして，多くの寄生虫（またはそれらが運ぶ病気）は動物から人間に伝染するので，寄生虫のペットを取り除くことも重要な仕事です．そして，人々はオンコセルカ症や他のフィラリア症に苦しんでいるだけでなく ，1億人以上が桿虫症に感染しており，私たちが忘れていた疥癬とアタマジラミは世界のどこでも消えていません．イベルメクチンはこれらすべての病気に適応されます．イベルメクチンはノーベル賞を受賞した英雄的な薬です．

ーーー

■以下のサイトより引用します

イベルメクチンはコロナ治療に有効か無効か　世界的論争の決着に日本は率先して取り組め : NEWS特集 : 記事・論考 : 調査研究ＰＯＩＮＴ ■北里大学の大村智博士が発見した抗寄生虫病の特効薬イベルメクチンが、コロナウイルス感染症（ＣＯＶＩＤ−１９）にwww.yomiuri.co.jp
　河川に生息するブユ（ブヨ、ブト）がヒトを刺した際に，ミクロフィラリア（回旋糸状虫）という線虫をうつし，それが体内で繁殖して失明する人が多数出ていた．この治療に役立てようと，１９７５年に大村博士がメルク社のウィリアム・キャンベル博士と共同研究を進め，オンコセルカ症や脚のリンパ腺に線虫がはびこって太いむくみが出るリンパ系フィラリア症（象皮症）の特効薬としてイベルメクチン（薬剤名はメクチザン）を開発した．世界保健機関（ＷＨＯ）の研究者は「これまで出てきたどの熱帯病薬剤と比較しても，けた外れに優れた効果を持つ」とイベルメクチンを高く評価し，メルク社と北里大学に協力を求め，１９８７年から熱帯地方の住民に無償で配布することにした．何よりも年に１回，錠剤を水で飲むだけという簡単な服用法がＷＨＯの評価を高めたポイントだった．この特効薬が出てきたため，盲目になる人が続出していたオンコセルカ症は急速に減少し，コロンビア，メキシコなどでは，オンコセルカ症を撲滅したと宣言している．その後，ダニによる疥癬かいせん症や糞線虫症など重篤な風土病の予防・治療薬になることもわかり，イベルメクチンは世界中に広がった．臨床現場では，副作用がほとんど報告されないことも評価を一層高めた．大村・キャンベル両博士は，この業績を評価され，２０１５年にノーベル生理学・医学賞を受賞した．

■ＣＯＶＩＤ－１９の大流行で浮上したイベルメクチン
　イベルメクチンは今，新型コロナ（ＣＯＶＩＤ－１９）のパンデミック（世界的大流行）で再び世界中の注目を集めている．試験管レベルの研究で，新型コロナウイルスがヒトの細胞内で増殖する際に，ウイルスのたんぱく質の核内移行を妨害し，増殖を抑制することがわかったからだ．

　ＷＨＯは２０２０年３月１１日，ＣＯＶＩＤ－１９のパンデミックを宣言し，世界中に厳戒態勢を求めた．しかし，感染が拡大しても有効な治療薬がないことから，中南米・中東諸国を中心に，イベルメクチンをＣＯＶＩＤ－１９治療に投与する事例が広がった．

　最初に臨床試験の結果が発表されたのは，アメリカ・南フロリダの４病院での臨床試験だった．２０年６月に発表された試験結果によると，イベルメクチン投与患者１７３人の死亡率は１５.０％で，非投与群１０７例の２５.２％と比べて有意（ｐ＝０.０３）に優れているというものだった．

ーーー

■北里大学病院の治験

新型コロナウイルスに対するイベルメクチンの現状・世界的の状況と北里大学の取り組み

■以下は，セルゲイ・グラゴレフによる記事から抜粋

Герой и злодей • ЗадачиБезопасное для животных и людей лекарство от паразитов —elementy.ru

日本の科学者大村智が伊東・川奈で土壌を採取

土壌から 分離した放線菌Streptomyces avermitilisの二次代謝産物である 8つの成分を発見しました．45年間，森林は伐採されていません．
長い間，この種のバクテリアは他の場所では見つけることができなかったようです．これは生物多様性の保全を支持する大きな根拠です．ジャイアントパンダや ミンククジラだけでなく，土壌や植生がある場所ならどこでも重要です．

アベルミクチンは，マクロライド系抗生物質に関連する 16員の大環状ラクトンで，それらの品種の多くは，この放線菌と密接に関連する種の放線菌から得られ，次にそれらから多くの半合成誘導体が得られ，そのうちの約5つが駆虫薬として使用されました．

詳細は，Andy Crump（2017）のレビューを参照ください．
Ivermectin: enigmatic multifaceted ‘wonder’ drug continues to surprise and exceed expectations

https://www.nature.com/articles/ja201711.pdf

数学の未解決問題は無数にあります．
未解決の数学の問題のリスト（書ききれないので以下をご覧ください）

Открытые математические проблемы — Википедияru.wikipedia.org
このリストに挙がっているものだけでも，あまりにたくさんあるので驚くでしょう．
挑戦してみたくなるものもあるかもしれません．

実際に，数学上の未解決問題は，無数に存在します．そのうちから，ここには，リーマン予想のようにその証明結果が数学全域と関わりを持つような命題，P≠NP予想のようにその結論が現代科学，技術のあり方に甚大な影響を及ぼす可能性があるような命題，問いかけのシンプルさ故に数多くの数学者や数学愛好家達が証明を試みてきたような有名な命題を７つ列挙します：

以下の7つの問題はミレニアム懸賞問題と呼ばれ，クレイ数学研究所によってそれぞれ100万ドルの懸賞金が懸けられています．
P≠NP予想
ホッジ予想
ポアンカレ予想（解決済み）
リーマン予想
ヤン-ミルズ方程式と質量ギャップ問題
ナビエ–ストークス方程式の解の存在と滑らかさ
バーチ・スウィンナートン＝ダイアー予想（BSD予想とも）

真空ギャップを通り抜けるフォノンのトンネリング。左側に入射する音波は、表面に交流電場を生成し、右側の2番目の物体の原子の同期振動を生成します。Phys.Rev.Lett.105,125501より
https://elementy.ru/novosti_nauki/431440/Mozhet_li_zvuk_peredavatsya_cherez_vakuum?from=rxblock　
2010 年10月27日• イゴール･イワノフ

■固体媒体で見られる新しい現象、つまりフォノンが真空（空隙）を介して、右の固体から左の固体に「ジャンプ」することが説明されています。音波は薄い真空の隙間を乗り越え伝わり、熱は通常の熱放射が伝えるより何十億倍も効果的に真空を介して伝達できます。
[訳者注）真空中を熱が伝わる様式は放射（輻射）のみと思い込んでいました．魔法瓶は壁の中に真空層があるために，真空中は熱伝導がなく放射だけなので熱流の遮断ができます．熱放射は真空中を伝搬できますが，それ程高温でない物体からの熱放射は小さいものです．物質の熱は原子の振動ですので，原子の振動を伝えることができれば非常に高効率な伝達でしょう．この発見の面白さはここにあります．ここで引用されているphys.rev.letters（フィンランドのグループ）によると，近接場熱伝達は音響フォノンが真空中をトンネルする現象で，フォノンによって誘起されるエバネッセント波が固体間を結合するので離れた誘電体間で起こり，いわゆる電流加熱でもないようです．近接場放射熱伝達の測定法はよくわかりませんが，以下の論文（入手していません）が引用されています．A. Narayanaswamy, S. Shen, and G. Chen, Phys. Rev. B,78, 115303 (2008)］．

音波とは、物質の原子が平衡位置を基準にして同期的に振動することです。音が伝播するためには、これらの振動を支える物質媒体が必要です。真空中では、音はそこには存在できないので、伝搬することはできません。しかし、最近になって発見されたこの現象は、音の振動は、サブミクロンの厚さの真空隙間を突き抜けて、固体から固体へとジャンプすることです。この効果は「真空フォノン・トンネリング」と呼ばれ、Physical Review Letters誌の最新号に掲載された2つの論文で説明されました。結晶格子の振動は音だけでなく熱も運ぶため、真空中での熱伝導が異常に大きいことに注目が集まっています。

新しい効果は、結晶の音波と電界の間の相互作用によって起こります。１番目の結晶格子の振動は、結晶の端面に到達し、その表面近くに交互の電界を生成します。これらの場は真空ギャップを越えたもう一方の端面で「感じられ」、2番目の結晶の格子振動を起こします（図1を参照）。全体として、フォノン（結晶格子振動の「量子」）が1つの結晶から別の結晶にジャンプし、その中でさらに伝播するように見えますが、もちろん、２つの結晶間の真空空間にはフォノンは存在できません。

発見者は、効果を説明するために「トンネリング」という言葉を使用しました。この現象は、量子粒子がエネルギー的に禁止された領域を飛び越えるときのトンネリングをイメージしています。ただし、この新しい現象は古典物理学で完全に記述でき、量子力学の関与をまったくないことを強調しておく必要があります。これは、変圧器、誘導ホットプレート、ガジェットの非接触充電装置などで使用される電磁誘導の現象に少し関連しています。固体で起こるなんらかのプロセスで電磁界を生成し、電磁界は、非放射的に（電力の損失なく）真空ギャップを介して別の固体に伝達され、そこで応答を引き起こします。両者の違いは、電磁気学のインダクタンスでは電流（つまり電子の動き）が「働く」のに対し、真空フォノン･トンネルでは原子そのものが動くということです。

このような結晶振動と電界が効果的に結びつく具体的なメカニズムはいろいろあるでしょう。フィンランドの研究者による理論論文では、この目的のために圧電素子（水晶などの電場で変形し，かつ変形すると電荷を生じる物質）を使うことを提案しています。加えて：効果的に真空ギャップを突き抜けフォノンが伝わるには、 "対向 "フォノン、交流電場と "エスケープ "フォノンの間の共振同調が必要です。計算によると、物質の現実的なパラメータの下では、このような共鳴が実際に存在し、特定の入射角でフォノンが100%の確率でトンネリングさせられることが示されます。

図2. 走査型トンネル顕微鏡の針の先端にある最後の原子と基板との間の熱交換が異常に強い。原子は基板上に電荷を誘導し、原子の熱ジッタを追従して基板上にフォノンを発生させ、その過程で原子からエネルギーを奪う。 Phys.Rev.Lett.105，166101より

別の論文では、物理学者たちは、一見まったく技術的な問題を研究して、議論されているこの効果に行きつきました：走査型トンネル顕微鏡の針の最先端の熱は、冷たい基板（図2参照）に（触れることがない）運ばれるのか？繊細な実験方法を用いて、彼らは針の先端の文字通り最後の原子の温度を測定することができ、驚くべき事実を発見しました：この原子は、針ではなく、基板の温度でした！これは、基板と先端の最後の原子の非接触熱交換が（真空を通して！）先端の残りの部分の針よりもはるかに強力であったことを意味します。

このようなことから、通常の熱放射だけ考えても、かなり不十分であることが判明します。研究者らは、針から基板への熱伝達は、熱放射が作り出すことができるものよりも数十億（！）倍も効率的であると推定しました。このことは、詳細な測定結果と相まって、真空中のフォノンのトンネル現象がここでも起こっていることを示しています。

論文の著者は、この効果のメカニズムを次のように説明します。金属表面近傍に置かれた電荷は、金属に電荷を誘起します（静電気の問題では、仮想電荷イメージ）。初期電荷が、例えば熱振動によって揺れている場合、誘起された電荷もまた同じ周波数と振幅で揺れます（電子は原子よりもはるかに軽いという事実のため、原子のそれぞれの動きには "適応 "する時間がかかります）。その結果、基板の表面にある種の電子塊が現れ、「熱い」原子のように揺れる。この塊は、基板上の原子の振動を励起しエネルギーが費やされる。それは、電子塊から、したがって、電気力によって電子塊としっかり接続されているの元の原子の熱を奪う！　これが、針の残りの部分が暖かい場合でも、先端の最後の原子は、クールダウンされるメカニズムです。

どうやら、応用はいろいろありそうです。新しい効果は、特定の状況で以前に考えられていたよりもはるかに効率的なので、熱伝達の観点から興味深いものになります。この観察は、マイクロメカニカルデバイスの設計や、多結晶圧電体サンプルの熱伝導率の研究において非常に重要なものとなるでしょう。また、圧電部品と金属部品を組み合わせたマイクロデバイスでは、電子が活躍します。これは、真空を介して電子とフォノンの間で、ある物質から別の物質へのエネルギー移動を迅速に行う現象のすべては、まだ探求されていません。

■Источники:
1) Mika Prunnila, Johanna Meltaus. Acoustic Phonon Tunneling and Heat Transport due to Evanescent Electric Fields // Phys. Rev. Lett. 105, 125501 (14 September 2010); текст статьи находится в свободном доступе в архиве е-принтов под номером arXiv:1003.1408.
2) Igor Altfeder, Andrey A. Voevodin, Ajit K. Roy. Vacuum Phonon Tunneling // Phys. Rev. Lett. 105, 166101 (11 October 2010).

См. также:
Структура электромагнитных полей в веществе оказалась сложнее, чем считалось ранее // «Элементы», 29.11.2005.

Игорь Иванов

4. 時空の構造
これらの考え方は、時空の構造に深く根ざしています。2+1次元時空の境界の粒子論から始まり、3+1次元時空の重力論に至りました。時空の次元の一つがどこからともなく現れたのです。この次元は、2+1次元の粒子の相互作用から出現しました。

そして、これは時空が最も基本的な概念ではないということを意味しています。それは、より基本的な概念によって生成され、その法則は、研究対象から観察者の一定の距離の後にのみ有効になります。例え話をしてみましょう。湖面を観察したとします。波が見えたり、水面に浮いている虫が走っていたり。湖の表面は透明度が高く、非常に描写しやすいように見えます。確かに、波の伝搬や表面張力などを記述する方程式を書くこともできます。さて、水面の構造をもっと詳しく調べたいと思ったとします。顕微鏡で見ると、以前のように水面がはっきりと観察されていないことがわかります。そして、電子顕微鏡で見てみると、水の蒸発分子が絶えず表面から出てきて、その場所は空気中の水の分子が凝縮したものに取られていることがわかります。よくよく考えてみると、水の表面が十分に明確に定義されていないことがわかり、個々の分子のレベルで起こる現象をなんとか含めなければならないことがわかりました。同様に、時空は近距離では明確に定義された概念ではなくなります。 明確に定義された概念は、境界に存在する粒子であり、時空は集合的な特性としてのみ出現します。

もし我々が負の曲率を持つ時空の中だけに住んでいるとしたら、我々の宇宙で起こっているすべてのことを理解するためには、その中の粒子の振る舞いを記述する境界層の適切な理論を作くることで十分でしょう。

しかし、興味深いのは、すべての利用可能なデータから判断すると、巨視的なスケールでは、私たちの宇宙の時空は、残念ながら、正の曲率を持っています。現時点では、正の曲率を持つ時空の重力場を同様に記述できる可能性があるかどうかはわかっていません。このような記述が存在し、それを見つけることができれば、ビッグバンの特異点問題は解決するでしょう。

 https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/25571

Juan Maldacena,　
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

3. これらの謎を解く
3.1. ひも理論
量子力学と重力は、あまりうまくいっていない2つの理論です。物理学者たちは、この二つの理論を整合性のある理論にまとめようとしてきました。私たちが遭遇するほとんどの物理現象は、重力の影響を無視してもいいし、量子力学の影響を無視してもいいようなものなので、日常生活の実用上、量子重力の理論を開発することはあまり重要ではありません。一方で、ビッグバンの最初の瞬間に宇宙の起源を理解しようとするならば、一貫した理論が必要です。そもそも量子力学と重力の両方が重要なのです。これが、量子重力の理論を見つけるための大きな動機の一つです。

ひも理論は量子重力の理論です。量子力学と重力をまとめて管理している。それが正しい理論なのかどうかはわかりませんが、我々が持っている理論の中では最も有力な候補です。それは，「ひも理論」と呼ばれますが、そのわけはここでの議論で重要ではありません。重要なのは、それが量子重力の理論であるということです。

3.2. ひも理論におけるブラックホール
ひも理論では、ブラックホールを考えることができる。いくつかの特殊な状況下で、これらのブラックホールの微視的な記述を見つけることが可能です。技術的な理由から、一定の負の曲率を持つ時空の中に存在するブラックホールを理解する方が簡単です。このような時空は、平面空間の最も単純な一般化で、平らな空間は曲率がゼロ、正の曲率を持つ空間の例は球体の表面です。図１では，一定の負の曲率を持つ２次元空間の「地図」を見ることができます．また，ゼロ，正，負の曲率を持つ時空を考えることもできます．負の曲率を持つ時空は、実質的に無限大に境界を持っています。粒子は有限時間内に無限大に行き、有限時間内に戻ることができますが、これは時間の流れが異なる位置で異なるため、遠くに行くほど時間の流れが速くなります。

図１：このエッシャーの描画は、双曲空間の幾何学を捉えようとしたもので、双曲空間を円盤に投影したものです。元の双曲空間では、それぞれの図は同じ大きさなのですが、投影の歪みの影響で、円盤の境界に行くに従って小さく見えます。実際には，円盤の境界は内部のどの点からも無限の距離にあるのです．世界地図を平面上に表現する場合も同様の歪みがあります．標準的な投影［訳者注）メルカトール図法のこと］では，地図上では極点付近の領域が不釣り合いに大きく見える．ここの双曲空間の投影では，逆の効果があり、双曲空間の大きさは無限大なのに、境界付近の領域がどんどん縮小されて投影されるので、全体が円盤内に収まって見えます。

1997年に、私はこの空間における重力物理学の全体が、境界上の普通粒子の理論で記述できると推測しました。これは、ガブサーS. Gubser，クレバノフ I. Klebanov，ポリャコフA. Polyakov，ウィッテンE. Witten らによってさらに発展しました。詳細はやや複雑ですが：境界理論は、私たちが理解していなかった重力理論を、私たちが理解している普通の素粒子理論と同等のものにします。さらに重要なのは この境界理論が 量子力学の原理に従うことです。

内部のブラックホールは、境界にある粒子と比べて熱状態にあります。ブラックホールのエントロピーは、これらの粒子のエントロピーに過ぎません。時空幾何学の「素粒子」とは、境界に存在する粒子のことです。

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

2. ブラックホールと量子力学
次に驚いたのは、量子効果が研究されたときです。量子力学では、真空は単に粒子が存在しないだけではありません。真空は非常に興味深い状態で、常に粒子のペアが生成されたり破壊されたりしています。平らな空間では、エネルギーが保存されているので、粒子の純生産はありません。生成された粒子はすべて、非常に早く消滅しなければなりません。1974年にスティーブン・ホーキング博士は、地平線が存在すると、もはやそうではないことを示しました。地平線の近くに正のエネルギーを持つ粒子と負のエネルギーを持つ粒子ができてしまうのです。負のエネルギーを持つ粒子はブラックホールに落ち、正のエネルギーを持つ粒子は飛び去る。平面空間では、負のエネルギーの粒子を持つことができないので、このようなことはありえません。しかし、地平線の反対側では、遠くの観測者から見て負のエネルギーを持つ粒子が、地平線の内側の観測者から見て正のエネルギーを持つことができます。正味の効果は、ブラックホールが粒子を放出することです。放出された粒子は、ブラックホールの質量に反比例する温度を持つ熱分布を持っています。太陽質量のブラックホールでは、この温度はこの効果を測定するには小さすぎます。もしブラックホールが空の空間にあったら、ブラックホールはゆっくりと質量を失い、小さくなるでしょう。質量の小さいブラックホールの方が高温になる可能性があります。1018キログラム（山脈の質量）の質量を持つブラックホールは、1000度の温度を持ち、白く見える。1ミリワットの電球1個分の光を出すことになる。その質量がどんどん小さくなるにつれて、その温度は上昇し、おそらく完全に蒸発するまで、どんどん速く蒸発していきます。実際、数キログラムの質量をブラックホールに崩壊させた場合（実際にはとても難しいことですが）、1ミリ秒もしないうちに完全に蒸発し、核爆弾よりも多くのエネルギーを放出します。

ブラックホールのこの熱的性質は、2つの謎を生み出します：1) 何がエントロピーを生み出すのか？2) 情報パラドックス？
これらについて詳しく説明しましょう。

2.1. ブラックホールのエントロピー
通常の物理学では、熱的性質は常に構成要素の運動から生じます。例えば、空気の温度は、空気分子の平均速度に関係しています。これと密接に関連した概念として、"エントロピー "と呼ばれるものがあります。エントロピーは、すべての構成要素の運動に関連する無秩序の量です。エントロピーは熱力学の法則で温度と関係しているので、システムのミクロな詳細を知らなくても計算できる。ホーキングとベッケンシュタインは、ブラックホールのエントロピーは、地平線の面積をプランク長の2乗で割ったものと同じであることを示しました。巨視的なブラックホールにとって、これは巨大なエントロピーです。このエントロピーにブラックホールの寄与が含まれていても、熱力学の法則は有効であることがわかりました。ブラックホールの「構成要素」が何であるかが全く分かっていないため、非常に不可解な結果となっています。ブラックホールは時空の穴なので、その構成要素を見つけることは、時空幾何学の最も基本的な構成要素を見つけることと密接に関係しています。

ブラックホールのエントロピーは体積ではなく面積に比例するというのは非常に興味深いことです。1990年代初頭、トホーフトHooftとサスキンドSusskindは、量子力学と重力を含む理論では、系を記述するために必要な構成要素の数は、系を取り囲む表面の面積よりも大きくてはならないことを提唱しました。このことは、時空が普通の固体とはかなり異なることを意味しています。ほとんどの実用的な目的のためには、このエントロピーの束縛はそれほど厳密ではありませんが、時空のある領域は、その領域の境界に住む構成要素によって記述できることを示唆しているので、理論的には興味深い意味合いを持っています。

2.2. 情報のパラドックス
これまでブラックホールはいろいろな方法で作れることを述べてきましたが、結局はいつも同じブラックホールになってしまうようです。物理学では、通常、異なる初期状態から始めると、最終的には異なる状態になります。時々、その違いは非常に微妙なものですが、違いがあります。例を挙げてみましょう。2枚のお皿を用意して、片方にAの文字を書き、もう片方にBの文字を書きます。最初の概算では、最終的な結果は同じで、たくさんの破片が割れていることになる。しかし，破片を詳しく調べれば，どの文字が書かれているかが分かります．

そのうちの一つをブラックホールに放り込んだとしましょう。どうやら、ブラックホールはホーキング博士の放射線を放出して完全に蒸発してしまうらしい。ホーキング博士の計算では、この放射は完全に熱的で、ブラックホールの初期状態とは無関係のようだ。つまり、元々プレートの上にあった文字の情報を完全に復元することはできなさそうです。

これは非常に難解な学術的な問題のように思えます。私たちはいつも物事を忘れているので、そんなことは気にしていません！（笑）。なぜこの問題が非常に重要な問題なのかというと、量子力学では、このプロセスを支配する法則は、原理的に情報を復元できるようなものでなければならないと教えてくれているからです。だから、情報の問題を解決することが、量子重力の一貫した理論に必要なのです。そのような理論は、情報の謎を解決しなければなりません。

ホーキング博士を含む多くの著名な物理学者は、これは不可能だと考えていました。彼らは、ブラックホールが本当に情報を破壊していると考え、量子力学を捨てなければならないと考えていました。彼らは、量子力学と重力は根本的に相容れないものであり、正しい理論は情報が失われないことを暗示する量子力学の原理に従わないと考えていた。

この疑問を考えることで、弦理論や素粒子物理学の分野で興味深い進歩を遂げてきました。

ーーー続く

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/3_Solving_These_Puzzles

Black Holes and the Structure of Space-Time • БиблиотекаBlack holes are very puzzling objects that are predicted by gelementy.ru
Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

1. ブラックホール
ブラックホールは、アインシュタインの一般相対性理論によって予測された最も魅力的な天体の一つです。ブラックホールには興味深い歴史があり、時空の性質の理解を深めるために多くの理論的な驚きの源となってきました。

まず、ニュートンの重力理論を考えてみましょう。ここ地球の表面では、重力の力を感じることができます。石を上に投げると、重力の力で石が下に戻ってきます。では、物を上に投げても下に落ちてこないようにすることはできるのでしょうか？はい、できます。秒速11km以上の速度で投げると、地球の重力場から離れてしまいます。この「脱出速度」は、地球の質量と半径に依存します。もし地球がもっと質量があり、同じ半径であれば、脱出速度はもっと高くなります。では、もし、光の速度よりも脱出速度が速いほど密度が高く、質量のある物体があったとしたらどうなるだろうか？そうすると、光が逃げられなくなり、それは黒く見えます。例えば、大きさが

より小さい星は黒く見えるでしょう。ここでG_{N}はニュートン定数、cは光速です。計算式に慣れていない方のために、いくつか例を挙げてみましょう。地球の質量の物体がブラックホールになるためには、その大きさが1cm以下でなければならない。太陽の質量を持つ物体は、1km以下の領域に集中していなければなりません。このことは1800年代にP.ラプラスによって指摘されましたが、誰も注目していませんでした。

1905年に特殊相対性理論が登場して、光の速度は他の普通の速度とは違うことがわかりました。それは宇宙の速度の限界であり、光より速く進ませることができるものはないのです。アインシュタインの相対性理論は、空間と時間が密接に結びついていることも教えてくれます。時間の流れは、お互いに相対的に移動している観測者によって異なります。あなたが通りのそばに立って車が通るのを見ているとしましょう。車に乗っている人の時間の流れは、あなたの時間の流れとは異なります。2 つの別々の街灯が同時に赤になるのを見たとしましょう。運転手にとっては、同時に赤になることはないでしょう。これはもちろん、光が両人の目に届くまでの時間を考慮に入れた上でのことです。両者とも光の速度で進んでいる光を見ていますが、時間の流れ方は異なります。時間は相対的なものであり、光の速度は絶対的なものである。私たちは通常、光の速度よりもはるかに小さい速度で移動し、私たちは非常に正確に時間を追跡していないので、これは私たちにとって非常に小さな効果であるため、これは逆に直感的に思えます。これは、粒子加速器では常に見られる効果です。粒子は光速に近い速度で移動しているときには、はるかに長く生きています。

空間と時間は、一つの概念である時空にまとめられています。時間は、お互いに相対的に移動している二人の観測者によって異なる知覚をします。どちらの観測者も同じ時空を見ています。この二つの観測者の観測を関連付けるための正確な公式があります。

重力の話に戻りましょう。重力には、ガリレオによって発見された非常に特殊な特徴があり、真空中では、羽と石が一緒に落ちる。これは他の力では起こりません。電場の中の粒子は、その質量や電荷が変われば、異なる動きをする。ニュートンの重力理論では、すべての粒子が同じように落ちるのは、重力の力が質量に比例するからです。これを "等価原理 "と呼ぶこともあります。

アインシュタインは、ニュートンの理論では重力が瞬間的に伝播するので、ニュートンの理論は特殊相対性理論と両立しないことに気づきました。1915年、アインシュタインはこの問題を、等価性の原理も自然に取り入れた方法で解決しました。彼はこの理論を一般相対性理論と名付けた。彼は、重力は時空の湾曲に起因することを提案しました。湾曲した時空の中の粒子は最短の線に従う。湾曲した空間上で最初は平行な線は、後になってお互いに向かって移動するかもしれない。例えば、地球の赤道にある2本の子午線は、最初は赤道で平行だったが、北極で交差する。時空の形は、その上を移動する物質に依存しています。一般相対性理論は、時間の流れが重力場に依存していることを暗示しています。したがって、同じ建物の最上階と最下階に住んでいる二人の人は、時間の流れが違って見えることになります。下の階に住んでいる人の方が時間の流れが遅くなります。これは、この地球上の建物にとっては非常に小さな効果であり、1/1015の効果です。私たちが学んだことは、巨大な物体が空間と時間をゆがめるということです。特に、これは巨大な物体の近くの時間は、遠くの時間よりもゆっくりと流れることを意味します。

物理学者は常に最初に最も単純な状況を研究しようとします。そこで、一般相対性理論が発明されて間もない1916年、カール・シュワルツシルトという若いドイツ人が、アインシュタインの方程式の最も単純な球対称解を発見しました。これらの方程式は、点状の質量によって生成される幾何学であると考えられていた特定の幾何学を記述しています。その幾何学が何であるかを語るのではなく、その特徴の一つである静止した時計がチックする速度に焦点を当ててみよう。太陽の表面にある時計は、遠くにある時計よりも100万分の1の速度で動いています。中性子星の表面にある時計は、遠くにある時計の70%の速度で動いています。この場合、大きな効果があることがわかります。シュワルツシルトが発見した解は、「中心」にある時計が完全に止まってしまうことを示しています。当初、ほとんどの物理学者は、これは物理的ではない結果であり、過度に単純化された解析の産物だと考えていました。

さらに研究を進めると、シュワルツシルトの解の「中心」は、実際には完全に滑らかな表面であることがわかりました。時空を旅している観察者は、この領域を何の違和感も奇妙さも感じずに通過することができます。ブラックホールの外にいる人は、落下してくる観測者からの信号が、すべての実用的な目的のために、最終的には消滅するまで減速することを見ています。静止した時計がゼロに減速する表面は "地平線 "と呼ばれ、この地平線は戻りがない点を示し、この表面を横切った観測者は、再び出てくることができず、内部の「特異点」に押しつぶされてしまいます。特異点とは、非常に高い時空の曲率の領域で、彼は引き裂かれてしまいます。アインシュタインの理論におけるブラックホールの大きさは、今でもニュートンの理論でラプラスが計算した式で与えられていることが判明しましたが、物理的な解釈は大きく異なっています。

ブラックホールは、太陽の数倍の質量を持つ星が核燃料を使い果たし、その重力の下で爆発することで、天体物理学的な過程で形成されることがあります。宇宙にはブラックホールが存在することを示す多くの観測的証拠があります。これらの天体物理学的ブラックホールには、大きく分けて2つのタイプがあります。太陽の数倍の質量を持つものと、恒星が崩壊してできたものです。ブラックホールは黒いので、なかなか見ることができません。運よくブラックホールの中にガスが落ちてくることがあります。ガスが落下すると、このガスは熱を帯びて独特の放射線を発しそれを検出します。このガスは、ブラックホールを周回している別の星から来ることもあります。つまり、お互いに公転している2つの星があって、一方の星が崩壊してブラックホールになったとすると、もう一方の星からガスが出てきます。そして、もう一方の星からのガスがブラックホールに落ち始めます。また、銀河の中心には、もっと質量の大きなブラックホールがあります。これらは10億個の太陽の質量を持っています。これらのブラックホールに物質が落下すると、熱を帯びて放射線を発し、それが最終的には地球上の私たちによって検出されます。私たちのような大きな銀河はすべて、中心にブラックホールがあると考えられています。

この講演の焦点は、天体物理学的なブラックホールの説明ではなく、ブラックホールが時空の構造に与える影響を探ることにあります。

アインシュタインの理論によれば、ブラックホールは時空の穴であり、一度落ちたら二度と戻れない。ブラックホールに投げ込まれたものは永遠に失われる。ブラックホールは非常に興味深い普遍的な性質を持っています。星がブラックホールに崩壊したとき、その最終的な形は質量と角運動量の2つのパラメータだけに依存します。つまり、ブラックホールは普遍的なものであり、ブラックホールを形成した物質の特異な詳細な性質に依存しないのです。最初の星の化学組成に関係なく、常に同じブラックホールを得ることができます。つまり、ブラックホールは重力の理論だけに依存しており、他の力の詳細な性質には依存しないのです。

ブラックホールのもう一つの特異な特徴は次のようなことです：ブラックホールが関与しているプロセスがあるとします。例えば、2つのブラックホールの衝突を考えてみましょう。ブラックホールが衝突して、より大きなブラックホールを形成する。ちなみに、この過程では重力波を出すことができ、それを測定しようとしている検出器があります。この過程を計算するのはかなり難しく、複雑な方程式を解かなければなりません。それでも、いくつかの簡単な結果があります。最終的なブラックホールの面積は、最初のブラックホールの面積の合計よりも常に大きい。面積は常に大きくなる。これは「面積定理」と呼ばれ、1970年にホーキング博士によって証明された。

https://elementy.ru/nauchno-populyarnaya_biblioteka/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

漠然とした質問の性質
AS：私の友人は、基礎物理学の現在の状態を、コペルニクス理論が出現する前の時代と比較できるかどうか尋ねています。惑星の動きを予測することを可能にしたプトレマイオスシステム[訳者注)天動説]がすでにありましたが、その背後にある現象の物理学の理解はありませんでした。今は、方程式の背後にある物理的な意味が現れるのを待っていると言えますか？

DG：もちろん、私たちは何かを待っています。おそらくホーキングは私たちが何を待っているのかを正確に教えてくれるでしょう。しかし、ご存知のように、歴史が正確に繰り返されることは決してありません。私たちは未来が何であるかわからないので、私たちの時間を過去にあったものと比較することは非常に困難です。

AS：あなたが今構築している新しい基本理論には多くの希望があります。それは万物の一種の究極の理論になるはずです。しかし、新しいコンセプトが最終的なものになると考える理由は何ですか？今、重力の性質とは何かを尋ねているのなら、なぜ疑問が生じないのでしょうか、弦の性質は何ですか？等...

DG：自然！あなたがそれらを形成するとき、質問は非常に曖昧です。「自然とは何か」という質問は曖昧すぎて、ほとんど哲学的です。たとえば、私たちの多くは、微細構造定数［訳者注）微細構造定数とは、水素原子のスペクトル線の分裂を説明するときにアーノルド・ゾンマーフェルトにより導入された］が1/137である理由を理解したいと思っていますか？これは適切な質問です。しかし、そのような明確な質問への回答を受け取ったとしても、漠然とした質問のいくつかはより正確な定式化を見つけ、より正確な回答を必要とするため、私たちはまだ満足できません。答えを求めているすべての質問に答えることができたとしても、新しい質問が生まれます。これが科学の歴史です。そして、これは無期限に続きます。しかし、おそらくいつか私たちは、非常に満足のいく答えを見つけて、やめるでしょう。私はこの問題にとらわれません。おそらく、決定的な理論、「万物の理論」があります。しかし、そうでないかもしれない。だれも知りません。

自分自身を計算する世界
SP：数学は自然を表現するための言語であり、普遍的でなければならないとおっしゃいました。物理学で使用される分析法の言語を数値法に置き換えるという最近発表された提案についてどう思いますか？結局のところ、方程式を書く能力を奪われているので、これの背後にはまったく異なる哲学があります。

AS：はい、一部のプログラマーは、私たちの世界が計算可能かどうかに常に関心を持っていますか？

DG：コンピューター...現代のコンピューターの数値計算能力は驚くべきものだと思います。そしてもちろん、それらは理論物理学者が今日働く方法に強い影響を与えました。多くの人はもはや微分方程式を解こうとはせず、単に数値的にシミュレートします。そのため、一部のコンピューター科学者は、この傾向を限界まで押し上げています。

SP：スティーブン・ウルフラム、例えば？

DG：その通りです。Wolframは実際には計算の専門家であり、物理学者ではありません。彼は私の友人であり、私たちが会ったとき、私は彼に非常に強い議論をしました。彼は落胆したと思います。

SP：あなたの間で公開討論をするのは素晴らしいことです...

DG：私たちもそう思いますし、実際に議論するつもりですが、それはまだうまくいきません。

AS：私のコンピューターの友達はよく尋ねます：量子論はある意味で世界の基本的な離散性と同等であると言えますか？連続体の古典的なアイデアは現実の世界に関連していますか？

DG：いいえ、量子力学は離散理論ではありません。多くの人が無限大を非常に複雑な概念だと考えています。19世紀以来、世界のすべてのものが離散的で、有限で、計算可能であるべきであることを示す試みがなされてきました。ただし、無限大は非常に強力な概念です。そして、私は本当にそれをあきらめたくありません。

実際、計算手法は現在、幼児期に開発されています。20〜30年前のデバイスの機能と比べると、今できることは驚くべきことのように思えますが、将来の機能と比べると何もありません。コンピュータはまだそれほど賢くはありません。

そして、ウォルフラムについて話す文脈で特に興味深いもう1つのことは、完全に古典的なままである思考の性質です。私たちが計算アルゴリズムについて話すときに使用または考えるすべてのコンピューターは古典的です。しかし、過去10年間で、量子力学を使用することにより、計算、さらには実際のコンピューターの構築にも信じられないほどの可能性があることに気づきました。この方向にはすでに目覚ましい進歩があります。私の研究所は現在、量子コンピューターとコンピューティングのための量子力学システムの使用に関するプログラムを実装しています。また、場合によっては、従来のコンピューターよりも指数関数的に優れたパワーを得ることができることがすでに証明されています。

したがって、ある意味で、世界が独自の状態を計算していることは完全に真実です。これだけが量子力学の制御下で起こります。これは量子コンピューターであり、古典的なコンピューターではありません。そして、あなたのコンピュータの友達のほとんどは、量子力学について何も知りません。したがって、彼らはこれらすべてを50年前の観点から議論しており、強力なコンピューターは複雑な問題を解決できると言っています。そろばんの前に座って、現代のプログラミングの利点について話すようなものです。非常に原始的です。

弦理論には真の競合はありません
SP：弦理論と競合する理論について何が言えますか？

DG：実際、弦理論には本当の競合はいない。これが、非常に多くの人々が弦理論に取り組んでいる理由です。強い競争相手がいたら、他のことに取り組んでいる人もいるでしょう。重力のループ理論には何かがありますが、量子重力の理解など、限られた問題の枠組みの中でさえ、あまり成功していないように思えます。そらは古典的な重力を再現することさえできません。

SP：単一の理論の開発にそれほど多くの労力を費やすのはリスクが高すぎませんか？

DG：弦理論は、実際には特定の理論というよりもパラダイムだと思います。さらに、弦理論と場の量子論の間には非常に密接な関係があります。実際、この2つを区別することはさらに困難です。場の量子論は、強い相互作用、弱い相互作用、つまりすべての自然の力を説明するために使用されるツールです。したがって、弦理論には、このような幅広い問題に対処するための強力な競争相手はありません。そして、ある意味で、弦理論は代替手段ではないので破壊することはできませんが、逆に、ご存知のように、一般に受け入れられている物理学の理論的基礎として機能する場の量子論と密接に関連しています。

来たるべき物理学の革命について話すとき、私は弦理論を完全理論とは考えていません。私たちはまだそれが何であるかを理解しようとしています。そして、私たちはすでにそれに成功しているとは思いません。しかし、私が言ったように、私は革命が進行中であると信じています。そうは言っても、弦理論は根本的に新しいものではなく、実際には古い物理学と密接に関連しています。そして実際、私たちはすでに、核力をよりよく理解するために、すべての基本理論であると主張する、いわゆる弦理論の主要なセクションの1つを使用しています。したがって、弦理論は私たちの観察に関連しているため、反駁することはできません。

SP：では、理論的基礎だけでなく、弦理論の研究には直接的な観察の動機がありますか？

DG：それは理論的なつながりの問題です。弦理論はあなたがしなければならない多くのことに非常に役立ちます。あなたはそれを宇宙論の分野の研究に適用することを試みることができます、あなたはそうすることができます-核物理学をよりよく理解することを試みること。数学やゲージ理論へのリンクを調べることができます。若い研究者ができることはたくさんあります。

基本的な物理学における人々の仕事の方向性を決定するものについて話す場合、これらはまだほとんどない重要な実験結果（それらが現れることを願っています、少し待ってみましょう）、またはエキサイティングな領域のいずれかです。弦理論には強力な競合概念はありませんが、人々が取り組むことができる良い問題を提供します。本当にそうです。

量子対相対性理論
AC：「時間の簡単な歴史」、スティーブン・ホーキング（スティーブン・ホーキング）、ロジャー・ペンローズ（ロジャー・ペンローズの ）による「皇帝の新しい心」、「エレガントな宇宙」グリーン・ブライアン（ブライアン・グリーン）などのノンフィクションの本から-その弦理論は一般相対性理論と量子論の間の矛盾を解決する試みであると結論付けることができます。この印象は正しいですか？

DG：非常に異なる本...実際、これは弦理論が有用であることが証明された問題の1つにすぎませんが、それを解決することは当初の目標ではありませんでした。弦理論は核相互作用の理論として始まりましたが、それは（カントの力学と相対性理論の間の矛盾を取り除いたこと- AS）は弦理論の最も重要な成功の1つです。そして、矛盾を含まない量子力学的相対論的不変式論であるという事実により、それが成功を収めたことは間違いありません。弦理論のブラックホールは、量子力学の原理に違反するクレイジーなオブジェクトではありませんが、通常のオブジェクトは弦理論にとって大きな成功を収めています。ホーキングのような男でさえそれを認めなければなりませんでした。ホーキングは何年もの間私に説得されましたが、彼は同意しませんでした。彼は一般相対性理論の量子力学が深刻な問題に直面していることを固く確信しており、私たちは量子力学を変えなければならないでしょう...

AS：そしてペンローズは一般相対性理論を変えたいと思っています...

DG：ペンローズは数学者で物理学者ではありません。真面目に受け止めてはいけません。ホーキング博士は自分が間違っていたと認めた 弦理論のおかげで、量子力学を変える必要がないことがわかってきました。これは弦理論にとって大きな成功です。そして、その理由の1つ、理論的動機の1つ（実験的証拠ではなく理論的動機！）は、まだ正確な予測を行うことができないにもかかわらず、人々を弦理論の軌道にとどめるものであり、概念を解決できるという事実です。パラドックス。これは物理学の発展にとって非常に重要です。量子力学もパラドックスを背景に発生しました。一方では古典物理学であり、他方ではボーアの原子モデルには互換性がありませんでした。これは理論的な問題であり、量子力学によって解決することができました。

そして、私たちはこれから何を得るでしょうか？
AS：あなたが話している基本的な物理学の新しい革命は、原子力や半導体の発見のようなものに、私たちの世界を変える何かに、いくつかの重要な社会的変化をもたらすでしょうか？

DG：誰が知っているのか...わかりません。実際、基本的な科学的知識の開発よりも、テクノロジーやアプリケーションを予測することははるかに難しいと思います。テクノロジーを予測し、科学を知っていても科学がどのように使用されるかを予測することは非常に難しいビジネスであり、関係する要因が多すぎます。

AS：しかし、そのような変化の可能性を期待していますか？

DG：実際、私たちがすでに理解し、実験でテストし、確認を受けたものについて質問するのもよいでしょう。たとえば、素粒子の標準模型や核相互作用の理解についてです。それらのアプリケーションはどうですか？たとえば、量子色力学の応用について何度も聞かれました。記者は常にこの質問に悩まされています：「これの用途は何ですか？」そして、私は何も考えることができません。

しかし、歴史は、あなたが何も考えられないときでさえ...同じ量子力学を取りなさい-量子力学の用途は何ですか？ハイゼンベルグに量子力学の使用法を尋ねた場合、彼がトランジスタやレーザーについて教えてくれるとは思えません。しかし、それらは現れました。アプリケーションを予測することは非常に困難です。20世紀に私たちが達成した基本的な相互作用の信じられないほどのレベルの理解でさえ、まだ何かにとって有用か有害かわかりません。新しい武器、新しい薬、または新しい道具は作られませんでした。しかし、誰が知っているでしょうか？技術を予測することは非常に困難です。誰もトランジスタを予測しませんでした。IBMが1950年代にコンピューターについて考えたとき、彼らはコンピューターを、ラップトップの処理能力を備えたこのホテルのサイズの建物と考えていました。

応用科学としてのビッグバン
SP：あなたの講義には、理論物理学全般、特に弦理論が「好奇心からだけでなく、私たちの世界の起源を理解しているかどうかを知りたいから」発展しているという声明があります。個人的には、研究の主な動機は好奇心ですが、世界の起源の問題は実用的だと思いますか？

DG：もちろん、主な動機は好奇心です。これが基礎科学を前進させるものです。しかし、好奇心を通じて得られた質問への回答が、ある意味で有用である場合、科学者は誰でも大きな道徳的満足を得ることができます。それで、私は物理学の基本法則の新しい知識を他の科学分野に適用することについて話しました。

最も注目に値するアプリケーションの1つは宇宙論です。そのため、弦理論家は宇宙論者や天体物理学者と多くのことを話します。宇宙論者たちは現在、ビッグバンとビッグバン自体の後の宇宙の発達の初期段階を理解しようとしています。そして、この分野では、私たちの関心のある領域が重なっています。したがって、弦理論で私たちが尋ねる質問を理解せずに、包括的な宇宙論や宇宙の歴史を構築することはできません。

しかし、弦理論の他のアプリケーションもあります。これは弦の物理学者をとても幸せにします。特に、私たちが新しい数学を発見しているという事実。または、核の相互作用について異なる考え方をする能力。これにより、計算を改善できます。これはすべて非常に満足のいくものです。この理論は科学の発展に不可欠なステップであり、量子力学と同じように多くの用途があります。

何を読むか
AS：そして最後の質問です。弦理論の一般的な説明を探している人にどのようなアドバイスをすることができますか？あなたの講義では、「二重性」、「量子測定」、「ゲージ理論」など、かなり複雑な用語を使用しています。多くの人にとって、これは完全に理解できないように聞こえます。一般の人に何をすすめますか？

DG：あまりありません。ブライアングリーンの本があります...

SP：エレガントな宇宙のことですか？

DG：はい、そして2冊目の本はすでに書かれています- 「宇宙の構造：空間、時間、そして現実の質感」。リサ・ランドールによって書かれた、余分な次元についての良い新しい本があります- 「ワープする宇宙―宇宙の隠された次元の謎を解き明かす」。私自身、このような公開講座をもとに小さな本を書くつもりです。しかし、あなたが知っている、良い人気のある科学の本を書くことは非常に難しいです。そして、Barton Zwiebachによって書かれた、弦理論の学生のための良い教科書があります。これは、場の量子論をまだ研究していない物理学の学生向けに設計されたこの種の最初の教科書です。そして、これはとても良い本です。

［訳者注↓］

https://elementy.ru/nauchno-populyarnaya_biblioteka/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

思考プロセスはどのように進んでいますか？
AS：弦理論（ひも理論）では、弦のアイデア自体が現実の良いモデルですか、それとも単なるイラストですか？
DG：弦理論の観点から現実を説明することは、粒子の観点から場の量子論を説明することに似ています。量子色力学（核力の理論）では、クォーク、グルーオン、およびそれらの間の距離に関して便利な説明があります。しかし、これはおおよその説明にすぎません。場の量子論の観点から、量子色力学のより良い説明があります。弦理論では、実際には最初の記述だけがあり、2番目のより正確な記述はありません。特定の側面なら弦理論の多くの説明がありますが、多かれ少なかれ完全な説明は、ある時空で動く弦に関するものだけです。弦理論では、場の量子論の経路積分に相当するものはまだありません。これ以上の基本的な定式化がなく、これは弦理論におけるテーマの1つです。

SP：しかし、ひもとしてのこの説明は、実際の物理的な直感に役立ちますか？

DG：はい、もちろんです。

AS：個人的に仕事をしていく上でより頼りにするのは、物理的直観と数学的直観のどちらでしょうか？

DG：それらを区別するのはかなり難しいです。数学は言語であり、非常に発達した言語です。私たちが考えるとき、私たちは視覚的なイメージで操作します。しかし、私たちは思考を言語で整理し、数学は非常に高度な言語形式です。したがって、理論物理学者は数学的に考える傾向があります。しかし、もちろん、思考のプロセスがどのように進行するかを正確に説明することはできません。私はそれをしようとさえも思いませんし、多くは無意識のうちに起こります。

数学の現実は宇宙人が証明する
SP: 数学は言語だとおっしゃいましたね。自然を言語で記述する際に、私たちはこの記述を発明したのでしょうか、それとも自然現象の根底にあるのは数学的法則なのでしょうか？例えば、ガリレオにとっては、そのような疑問はありませんでした - 彼は、自然の本は数学の言語で書かれており、誰が書いたかは非常に明白だと述べました。

DG：私たちが自然や数学を発明していると言うのは間違っています。それどころか、私たちは自然によって発明されました。同時に、私たちは自発的に現れなかったと思います。いいえ、私たちは私たちが神によって創造されたとは信じていません。私たちは自然の一部として進化してきました。ですから、自然環境の中で生き残るために進化してきた私たちの心が、自然を十分に理解するために必要な能力を発達させてきたのは当然のことです。違った結果になったとしたら不思議です。したがって、ほとんどの数学者はある程度物理学者であると思います。物理学者は現実の世界を説明し、自然界に存在するものを発見します。そして数学者は一般的に同じことをします。学者アーノルドがこれについてどう思っているかを尋ねる人もいるかもしれませんが、ほとんどの数学者は自分たちが物を発明するのではなく、発見すると信じていると思います。

プリンストン大学の同僚で有名な物理学者ユージン・ウィグナーは、「自然科学における数学の不可解な効率性」を好んで話していました。私は彼に同意していないし、理解できないことは何も見ていない。数学は、自然を理解し、その中で最適な生存を実現するためのツールとして、私たちが創造した（あるいは自然進化によって進化した）言語から成長してきました。だから私は、数学は本質的に自然の一部であり、それを発見していると考えています。数学が自然を記述するのが得意だという主張は、ほとんど同語反復に近い。

ちなみに、これは実験的に検証することができます。私はこれについて数学者と話し合いました-私に同意する人もいれば、同意しない人もいます。このように確認できます。いつの日か、銀河の反対側にある別の文明とのつながりを確立するとしましょう。世界は1つしかないので、私たちとほぼ同じ物理学を持つことに誰もが同意します。（そして、彼らが私たちよりも弦理論をよりよく理解することを願っています。）しかし、私たち自身に問いかけましょう：彼らは同じ数学を持っているでしょうか？一部の数学者はノーと言います、彼らは完全に異なる数学を発明することができます。しかし、私はそうは思いません。彼らの数学は私たちの数学と非常に似ていると思います。実はその歴史も彼らの数学の発達は私たちとほぼ同型であるでしょう。もちろん、わずかな外部の違いも可能です。しかし、何世紀にもわたる規模を見ると、彼らの数学は同様の道に沿って発展するでしょう。いつかこの仮説を検証できることを願っています。

人類原理の認識論的悲観論
SP：これはかなり楽観的な見方です。人類の将来がどうなるかはまだ分からないからです。

DG：そうですね、それでも勝ちます。私たちの手法が課題に適さないという指摘はありません。それらは完璧に機能していて、私たちはすでに驚くべき結果を得ています。では、なぜ悲観的になるのか？ロシアでは悲観論者になるのが流行なのは知っています。また、科学者の間だけではありません。ビジネスパーソンの間でも見たことがあります。

SP: 講演の中で、人類学的な原理に非常に批判的なご意見がありましたが、どのようにお考えでしょうか？しかし、あなたが今言ったことは、同じではないにしても、少なくとも人類学的原理の精神で推論することと非常に似ています。

DG：いや、そうでもないですね。もちろん、人類学的原理には一定の論理があります。私たちはここに座っているので、私たちは生きているので、私たちの世界は私たちの存在に必要な一定の性質を持っていることを意味します。しかし、私の直感がこれを教えてくれます。歴史がこれを教えてくれます。私たちの存在のために特別に作られたように見えるものは、最終的には自然な説明を得ることができるでしょう。

たとえば、氷は水よりも軽く、その表面に浮かんでいるという事実を考えてみましょう。それは私たちにとって非常に重要です。氷が浮かなければ、夏には海が溶けず、生命が発達しません。これは人間原理によるものと言えます。水は確かに非常に珍しい液体ですが、今日、私たちは化学のおかげでその特性を理解しています。実際には、原子物理学、化学、生化学、生物学、そして最後に、生命とそれに基づく私たちの心さえも、ご存知のように、量子力学、電磁気学によって記述されています。これは信じられないほど強力な理論の例であり、原則として-もちろん実際にはありませんが、原則として-電気的相互作用の力を除いて、任意の仮定と自由パラメーターは含まれていません。非常に簡単な理論と1つの数字で、水、有機物、生命のすべての性質を計算することができます... まさに反人類主義の勝利です。

100年前は、科学で生命を説明することはできないと多くの人が考えていました。今は基本的なレベルで生命を理解していると考えれば、十分な理論を持っています。もちろん、原子から始まって、脳を構築して理解することはできません。そしてもちろん、すべての仕組みを理解するために必要な方法を開発するには、長い時間が必要になります。しかし、その理解は最終的には恣意的な要素を持たない理論の上に成り立つ。私の考えでは、人々はしばしば、非常に難しい質問に答えることができないために、自分たちの力への不信感から、議論を求めて人類学的原理に目を向けることがあります。しかし、歴史を見れば、解けないと思われる質問でも、最終的には答えが出てくることがわかります。

もちろん、それらはいくつかの点で正しが-いくつかの質問には答えることができません。宇宙の発展には多くの事故があり、科学がそれらを説明しようとして失敗することがあります。たとえば、ケプラーは、太陽系の惑星軌道の半径を計算できると信じていました。彼は正多面体の美しいシステムを構築し、そこから半径のセットを取得しました。そして、それらは太陽系の軌道のサイズに似ていましたが、軌道半径を予測することは、1年後-2007年5月13日の午前11時のモスクワの天気を予測するようなもので、これは計算できるものではなく、計算しても面白くありません。

もちろん、基本量として物理法則に含まれている私たちの世界のパラメータは、同じランダムな性質を持っていることが判明するかもしれません。これは、人類原理に従う人々が言うことです。この可能性は捨てることができません。人々は無力感からこれらの考えにたどり着くのではないかと思います。そうすれば、歴史は彼らが間違っていたことを示すでしょう。しかし、それらが間違っていることを証明する唯一の方法は、過去に起こったように、予測力を備えた実用的な理論を提供することです。したがって、たとえば、物理学が生命を説明できる科学を証明する唯一の方法は、DNAの構造の発見、量子力学、原子物理学、生化学などの理解でした。

SP：それで、あなたは辛抱強くなるようにアドバイスしますか？

DG：一生懸命働くことをお勧めします。

空間の次元は実験的な課題です

AS：主に実験材料を扱う多くの物理学者や天文学者は、これらの多次元理論は物理的現実からかけ離れていると信じており、現実世界の科学というよりは数理ゲームです。

DG：たぶんそうです。科学は興味深いものです。なぜなら、予測力のある発見をするまで、誰も答えを知らないからです。だからそれは実験の問題です-時空は多次元です。多くのモデル、特に弦理論では、これが当てはまると想定しています。これらはおそらく非常に小さい寸法であり、見るのが難しいと考えられています。ただし、これらが十分に大きく、観察にアクセスできる可能性があることを除外していません。これは純粋に科学的な質問です。

今日、天文学者や天体物理学者は、アインシュタインによって開発された非常識な数学的理論をほとんど認識しています。そしてそれを認識すれば、時空は動的な物体であり、次元の数の問題は科学的な問題であることが理解できます。これらの寸法の一部は非常に小さく、検出が難しい場合がありますが、正直な方法はそれらの存在を確認することだけです。

正しい科学的アプローチは次のとおりです。物事をより深く理解することがあなたに新しい質問を提起し、新しい可能性を開く場合（たとえば、一般相対性理論のように）、これらの新しい質問と可能性を探求する必要があります。弦理論の場合、追加の次元が必要な理由はおおいにあり得ます。しかし、これは未解決の科学的問題です。現在、それらの存在の確固たる証拠はありません。しかし、これは常に当てはまります。新しいアイデアに対処するのは簡単ではありません。

大型ハドロン衝突型加速器が優れている理由
JV：あなたの講義で、CERN大型ハドロン衝突型加速器（大型ハドロン衝突型加速器、LHC）の建設現場-弦理論の検証のための最も有望な装置であると述べました。ただし、そのエネルギーは、アメリカのテバトロンなどの既存の加速器のエネルギーよりも1桁高いだけです。大統一のエネルギーが少なくとも10桁高いのに、なぜ1桁のステップだけが根本的に新しいデータを取得するのに役立つと思いますか？

DG：この加速器は、標準モデルの予測を完全にカバーするために必要なエネルギーのスケールへの脱出を初めて可能にするので、非常に重要です。

もう一つの重要な理由は、新しい物理学、新しい基礎物理学に関連した効果がこのエネルギースケールで現れ始めることを示す、非常に説得力のある実験結果が多数存在することです。このようなエネルギーでは、弦理論の重要な要素である量子（超対称）時空の新しい次元が発見されると期待されている理由を説明します。新しい対称性、新しい量子時空次元が、LHCで達成可能なテラ電子ボルトのエネルギーで最初に発見される可能性を支持する3つの独立した議論があります。

これらの議論の1つは、相互作用の組み合わせに由来します。力の統一の簡単なスキームは、超対称性の存在を必要とします。これは、LHCで利用可能なエネルギーのオーダーのエネルギーで顕著になりますが、これを確実に予測することはできません。

2番目の議論は、重力が強いスケールとそれが非常に弱い核スケールとの間の巨大な格差を理解しようとすることと関係があります。繰り返しになりますが、超対称性は、このスケールの大きな違いを自然で美しい説明にしています。

最後に、宇宙物理学から学んだことは、宇宙に存在する物質のほとんどは、目には見えないが重力を感じる暗黒物質という未知のタイプに属しているということです。暗黒物質が構成するかもしれない粒子をたくさん発明することができますが、標準モデルの超対称版では、暗黒物質の候補となる粒子が自動的に存在することが保証されています。これらの粒子がLHCで観測可能な質量を持っていれば、宇宙の物質の9割が何からできているのかがすぐにわかります。

これらは3つの非常に強力な議論です。超対称性の兆候がどこでどのように観察されるかについての証拠や正確な予測はありませんが、定性的なレベルでは、超対称性の発見を支持する非常に説得力のある議論があります。だから私は50：50で誰とでもこれに賭ける準備ができています。そして超対称性が発見されなければ私はたくさんのお金を払わなければなりません！

---続く---

https://elementy.ru/nauchno-populyarnaya_biblioteka/izbrannoe/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

2004年5月のノーベル物理学賞を受賞したDavidGrossがモスクワを訪れました。彼は、弦理論と理論物理学の今後の革命について公開講演を行うために、王朝財団と国際基礎物理学センターの招待を受けて来ました。講義の前に、DavidGrossはElementsWebサイトからの質問に答えました。

デイビッド・グロスへの質問は次のとおりです。
セルゲイ・ポポフ、天体物理学者、モスクワ州立大学の研究者、アレクサンダー・セルゲイエフ、ジャーナリスト、ラジオ・リバティの科学オブザーバー、ウェブサイトElements

左から：セルゲイ・ポポフSP、アレクサンダー・セルゲイエフAS、デイビッド・グロスDG（写真：オルガ・レビナ）

数学と物理学はそれほど異なる科学ではありません
セルゲイ・ポポフ：グロス教授、私たちの会話は、主に現代の理論の複雑さとそれらで使用されている概念の問題に触れたいと思います。したがって、最初の質問は、素粒子物理学の分野で働く若い科学者、理論物理学者からです。現代の理論物理学者が数学の最新の研究を知り、過去10〜20年にわたって出版されたオリジナルの数学記事を読むことの重要性を教えてください。それとも、ほぼ同じ時間スケールで発行されたモノグラフに精通するだけで十分ですか？

David Gross：それはあなたが扱っている問題に部分的に依存します。弦理論のいくつかの分野では、物理学者は自分たちで新しい数学を発明することを余儀なくされています。そして、彼らは数学者と非常に緊密に協力しています。彼らが直面している課題のいくつか（および行われている発見）は、数学者が以前は知らなかった新しい数学的構造の出現につながります。そのため、弦理論のいくつかの分野では、物理学と数学が協力して、本だけでなく元の記事でも読むことが不可能な新しい数学を発見しています。

素粒子物理学は多くの現代数学を必要としますが、何か新しいものを発明する必要はありません。しかし、現代の物理学（場の量子論と弦理論）は、50年または100年前よりも数学の最先端にはるかに近づいています。

アレクサンダーセルゲイエフ：これは、物理学者が数学的解析を発明したニュートンの時代と比較できますか？

DG：そうですね、時代は変わりつつあります。現在、多くの人々が数学と物理学の両方に従事しています。そして、ニュートン自身が惑星の動きを理解するために新しい数学（数学的解析）を発明しなければなりませんでした。しかし、多くの点で、これはかなり珍しい時期です。これは19世紀にはすでに当てはまりました。その後、偏微分方程式の理論が生まれました。波の伝播、熱伝達を説明する最初の場の理論の構築に必要でした。フーリエ、ラプラスのような数学者は、物理学を理解するために新しい数学を発明しました...

しかし、20世紀の終わりに、初めて、新しいタイプの非常に緊密な協力（物理学者と数学者の間）が登場しました。私は数学と基本的な理論物理学をそれほど異なる科学とは考えていないとだけ言っておきましょう。結局のところ、物理学者のような数学者も、本質的に自然の中で起こる現実の何かを発見します。

弦理論はロシア的です

SP：その場合、弦理論は今日の数学者にとって最も刺激的な主題であると言えますか？それとも、他にも同様に有望な分野はありますか？

DG：弦理論と場の量子論は非常に密接に関連しています。当初、数学は場の量子論から強力な後押しを受け、その作用は弦理論でも続いています。もちろん、物理学と数学がうまく相互作用している他の分野もありますが、弦理論で起こることほどよく似ているものはありません。

ご存知のように、私はカリフォルニアで理論物理学研究所を運営しています。毎年何百人もの物理学者が集まって、共通のトピックに取り組んでいます。そして昨年の秋、弦理論の数学的構造に関するプログラムがあり、参加者の半数は世界をリードする数学者でした。弦理論家と数学者は非常に緊密に協力しています。これは本当に素晴らしいです。そして、これは非常にロシア的です-物理学に近づき続けるロシアの数学者の伝統のように。ゲルファンドを覚えています...
SP：そしてアーノルド..。
DG：はい、これらは良い例です。アーノルドの仕事は主に力学系などの古典物理学に関連していました。

[訳者注]ロシアの数学の特徴はオイラーの流れをくむというか，物理に密接しているようです．対話で言及された本を以下に引用します：

関数とグラフ (ゲルファント先生の学校に行かずにわかる数学 1)www.amazon.co.jp1,400円(2021年02月02日 07:27時点 詳しくはこちら)
Amazon.co.jpで購入する
古典力学の数学的方法www.amazon.co.jp9,900円(2021年02月02日 07:27時点 詳しくはこちら)
Amazon.co.jpで購入する
量子力学は学校で教えられます
SP：弦理論の数学は非常に複雑です...

DG：複雑なのはその目新しさのためだけです。ニュートンにとって数学的解析は非常に困難でした。そして、ご存知のように、ハイゼンベルグが量子力学（行列力学とも呼ばれる）を発見したとき、彼は行列について聞いたことがありませんでした。しかし、ハイゼンベルグはなんとか関係式を書きました。「それはマトリックスのように見えます！」と言われて、彼は：「マトリックスとは何ですか？」と応じました。したがって、ハイゼンベルグにとって、行列（マトリックス）は非常に困難なものでしたが、今日では大学で教えられています。

SP：弦理論の数学ツールは、時間の経過とともにアクセスしやすくなると思いますか？結局のところ、何と言っても、たとえば経路積分は通常の積分よりもはるかに複雑です。

DG：すべて時間の問題です。

SP：人々はこれらの難しいことに慣れているだけですか、それとももっと理解しやすいアプローチを発明していますか？

DG：アイデアが最初に浮かんだとき、開拓者自身でさえそれをよく理解していません。新しい概念を十分に理解して生徒に教えることができるのは、多くの場合、長年の研究の後でのみです。時にはそれは数世代かかる。たとえば、多くの物理学者はまだ量子力学に苦労しています。私たちはまだそれを正しく教えるのに十分に理解していません。そしてこれは80年が経過したという事実にもかかわらず。そして、1930年代に書かれた量子力学に関する最初の教科書を見ると、それらはひどいものです。教科書は時間とともに良くなります。彼らは改善を続け、高校生に量子力学を教え始めると、彼らはより自然に感じ、それをよりよく理解するようになります。

ほら、他の分野でもまったく同じことが起こっています。力学や電気と磁気に関する最初の記事と教科書は非常に複雑でした。アインシュタインが電気と磁気を研究したとき、彼は苦労しました。結局のところ、それは大学の4年生でしか教えられず、それでも非常に難しい記事と見なされていました。そして今や私たちは学校で電気と磁気を普通に習います。

---続く

[訳者注）この節の放射線医学に関する内容は不十分です．iwjの以下のyoutube動画をお勧めします．]

https://iwj.co.jp/wj/open/archives/233698

「内部被曝の影響は、これから出てくる」 放射線治療の第一人者が語る、被曝問題の隠された真実～岩上安身によるインタビュー 第517回 ゲスト 西尾正道氏 第一弾 | IWJ Independent Web Journal　北海道がんセンター名誉院長で、臨床医として約40年もの間、放射線治療に携わってきた西尾正道氏は、3.11後、全国各地で内iwj.co.jp

なぜ放射性セシウムが必要ですか、それを不注意に扱うとどうなりますか？ 

セシウム137は、強力なガンマ線源として工学や医学で使用されています。医師は、腫瘍の領域に放射性薬物のエンドウ豆を置くことによって前立腺癌の治療をします-ガンマ線はそれを焼き切ります。また、工学の分野では、構造欠陥の探索から種々のタンク内の充填レベルの決定まで、さまざまな測定にガンマ線が必要とされています。放射性セシウムを含む機器の普及は、無知や不注意と相まって、悲惨な結果をもたらす可能性があります。捨てられた機器の無責任な所有者が放射性元素の入ったシリンダーから取り出すのを忘れて、ゴミ捨て場行になったことが時々ありました。そこから他のスクラップと一緒に冶金工場に運ばれ、精錬されることもあります。その結果金属が放射性物質になり、危険なバッチが見落とされると、最悪の場合、悲劇を招くことになります。

最悪の事態は1985年にブラジルの都市ゴイアニアで起こりました。そこで、地元の診療所は新しい建物に移転し、一部の機器が古い建物に残りました。診療所は建物の所有者に借金を負っており、裁判が進行中で機器が差し押さえられていましたが、セキュリティが十分でなく、社会的責任の低い二人が機器を盗み、部品のためにそれを解体し売りました。部品の中には放射性セシウムを含むアンプルがありました。泥棒はアンプルを売ることができず、お祭りに持ち帰り、彼らが発見した-夜に青く光る素晴らしい結晶について自慢しました。

近所の人は奇跡の粉を歯につけて味見をしたり、肌にこすりつけたり、ポケットの中でつまんだだけの人もいました。そして、しばらくして、人々は病気になり始めました。医者は症状にはほとんど注意を払わず、いつもの「何かを食べたからか、アレルギーがあるからか」と言っていましたが、病状が悪化し、被害者の中の誰かが、粉末を医師に見せると、すぐにすべてが理解されました。全体で200人以上の人が苦しみ、4人が放射能病で亡くなった。

ブラジル人が自分たちの過失と文盲のために苦しんだとすれば、クラマトルスクの家の住人は無実の被害者で、恐ろしい事故の犠牲者であります。複数のマンションの入居者が長期にわたって体調不良を訴え、数人が血液がんで死亡した。結局、1989年には検査が行われました。建物の壁に埋め込まれたセシウムのシリンダーを発見した。調査の結果、このボンベは70年代に消えていて、どうやらコンクリートを作るための砂利の中にあったらしい（セメント工場にはセシウムの器具がある）。このコンクリートは不運な壁に注がれたのです。

1997年の事件は死傷者には至りませんでした。ジョージアの兵士たちは古いソビエト軍の兵舎を解体しました、そして彼らの一人は磨かれた金属の美しくて暖かいシリンダーを見つけました。幸いなことに、彼はそれを開けませんでしたが、彼のポケットに入れました。兵士が放射線熱傷を受けた後、発見の性質が明らかになりました。

セシウムは薬ですか？
［訳者注）ここの話題のセシウム治療薬はほとんど与太話です．著者も懐疑的記述をしています．誤解を招くといけないので念のためお断りします．］
ルビジウム（「化学と生命」第9号、2020年参照）と同様に、医学者は精神疾患の治療にセシウムを使用しようとしてきたが、成功していないようだ。文献には矛盾する証拠がある。例えば、躁鬱病患者の血液中のセシウム含有量は、健康な人に比べて低く、治療後に症状が改善した患者に比べて低いという研究者もいます。しかし、他の人は、違いを見つけることができません。いずれにしても、これらの研究は20世紀後半に上演されたもので、今では話題性がありません。腫瘍学者の間では、セシウムはかなりスキャンダラスな名声を得ています。

事実、代替医療の支持者たちは、人が塩化セシウムを服用する、いわゆる高アルカリ性癌治療法を推進しています。この方法の達人によれば、セシウムは腫瘍細胞に濃縮され、そこで細胞を破壊するアルカリ性環境を作り出します。この方法の批評家は、この方法には化学的または生物学的根拠がないことを指摘しています。さらに、塩化セシウムを提案された用量、1日6グラム、さらには静脈内投与で食物と一緒に定期的に摂取すると、心臓の働きに深刻な問題が生じ、頻脈とその停止さえ引き起こします。さて、米国食品医薬品局は、承認された方法の数に癌のセシウム療法を含めなかっただけでなく、時々手紙を送ります、この方法の危険性についての警告。しかし、支持者は主張します：科学的根拠はそこに非常にあり、結果は認められた薬の結果より悪くはなく、時にはさらに良くなります。しかし、この紛らわしい話の本質を理解するためには、詳細を掘り下げる必要があります。

https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

福島事故後、放射性セシウムはどうなりましたか？
原子炉で発生する放射性同位元素の中で、セシウム137が最も有害なのは、第一に、セシウム137の量が多いこと、第二に、半減期が30年以上で、放射能汚染が長く続くことによります。たとえば、2011年の福島事故では、約20kgの放射性セシウムが放出されました。これは莫大な量です。このような放射性セシウムの放射能は9〜36 PBq［訳者注）ペタという単位は10^15です］、つまり1秒あたり数千万の崩壊［γ線光子が出ます］です。

福島の事故は、放射性セシウムの最新データを研究者に提供しました。原子炉の爆発で放出されたセシウムは、可溶性の化合物ではなく、鉄とケイ素の酸化物を主成分とする粒子の形で放出されました。どうやらこれらの粒子はかなり安定しているようです。いずれにしても、事故から1年後に、福島の学校の校庭から採取した土壌サンプルからも容易に発見されました。事故現場から数百キロ離れたタケノコの表面やシイタケの笠から放射性セシウムを含む単一粒子が検出されたが、その多くはタケノコの葉屑や切り株に付着した茎の先端から検出された。そして、タケノコやキノコの果肉の内部では、放射性セシウムは観測されなかった。このことは、放射性セシウムの移動性と植物組織への移行能力がやや誇張されていることを示唆している。

福島の原子力発電所の爆発後に散乱した粒子のオージェ分光分析（「化学と生命」第11号、2020年）
電子顕微鏡とオージェ分光法を用いて、サンプル中の元素の分布マップを得ることができます。福島の原子力発電所の爆発後に拡散した粒子をこの方法で分析すると、それらは主に酸化鉄に、シリコン、塩素、亜鉛、放射性セシウムを含むものでした。Scientific Reports、2013年8月30日

セシウムで汚染された土壌はどうか？
汚染された物や土壌を埋葬地に送ることで、小さな地域を埋め立てることができますが、原子力発電所での原子爆発や大事故は、放射性元素が畑や森林に散らばり、必然的に食物になってしまうため、主に農業の大惨事になります。セシウムの場合、この汚染がバックグラウンドレベルになるのに何十年もかかります。広大な農地を開墾したり、使用をやめたりすることは事実上不可能です。なぜなら、これらの土地で労働者として生活している膨大な数の人々を再定住させる必要があるからです。したがって、わずかに汚染された土地での生産が停止されることはなく、結果として生じる汚染された製品をきれいな製品と混合して、許容可能なレベルの放射能となります。

しかし、他の方法もあります。セシウムは植物に存在する必然性はないので、植物組織におけるセシウムの存在は単なる運の問題です。さまざまな種とさまざまな種類の飼料草で実施された実験は、それらに入り込むセシウムの蓄積は10倍以上も異なる可能性があります！　季節的にも同様の変動が見られます。葉や茎の成長が活発な夏の初めには、葉や茎の成長が終わる頃に比べてセシウムの量が著しく少なくなります。このおかげで、通常の農法を変えることなく、品種の選択と正しい農業技術のおかげで、汚染された土地でも比較的きれいな生産を受けることが可能になりました。遺伝学者が努力すれば、農家は土壌からセシウムをほとんど吸収しない品種を自由に使えるようになるだろう。原発の事故で汚染された土地ばかりになれば、そのような種に頼ることになってしまうが．．．。

しかし、研究者は汚染された土地をきれいにするためいろいろな方法を試しています。たとえば、福島の事故後、次のようなジレンマが発生しました。この県の住民は野生のキノコやベリーを採取するのが大好きです。さらに、それは彼らにとって重要な収入源です。しかし、セシウムを蓄積するハーブを育てることで畑をある程度きれいにすることができるが、この方法は森林では機能しませんが、キノコがその仕事に対処できる可能性があります。

横浜国立大学の研究者は、この仮説を確認しました。彼らは、セシウムが腐敗した落葉落枝に蓄積し、その含有量が菌類のバイオマスに比例することに気づきました。新鮮な葉にはセシウムが含まれておらず、キノコは処理中にすでに危険な金属を土壌からごみに汲み上げるという考えが生まれました。次に、彼らは菌類の成長に最も適した条件を作成することを決定し、汚染された森林の実験エリアの土壌を厚い木材チップの層で覆いました。確かに、わずか6か月で、キノコは土壌から放射性セシウムの半分を吸い込み、腐った木に濃縮しました。

ただし、一部の木は土壌自体からセシウムを吸引するのが得意であるため、これはすべての木で機能するとは限りません。これは、蜂蜜の研究におけるドイツの実験によって証明されています。したがって、すでに1988年以降、土壌放射性セシウムの菜種蜂蜜への変換係数は2％を超えませんでした。そして、針葉樹の新芽を食べているアブラムシからミツバチが集める甘露蜂蜜の場合、係数ははるかに高かった。その後のトウヒの針葉と若い芽の分析により、それらに高含有量の放射性セシウムが含まれていることが明らかになりました。土壌から蜂蜜への放射性セシウムの最も高い変換係数は、ヘザー蜂蜜で観察されました。土壌の含有量と比較して、40倍も多いことが観察されました。

セシウムで汚染された土地での山火事は危険ですか？
広島と長崎へのアメリカの原爆投下から75年後、マヤック事故から63年後の現在、チェルノブイリと福島の地域には、放射性セシウムで汚染された土壌に2つの大きな森しかありません。最初のケースでは、それらの面積は3000平方キロメートルであり、2番目のケースでは400平方キロメートルです。2011年11月の福島の森林地域では1平方メートルあたり1MBq以上でした（自然のバックグラウンドは数十万分の1です）。森林から落ちた放射性元素は森林から消えず、そこで崩壊し続けていると考えるのが論理的で、放射性セシウムはこの例です。

おそらく、それは森のゴミに蓄積し、そこから針葉に入り、枯れていくと、実際にその場所から移動することなく、ゴミに戻ります。そして、火事が発生すると、この場で放射性粒子が灰に変わり、火事の場所から遠くに散乱する可能性があります。しかし、それらはどこまで行くかを簡単に体験できます。両方の汚染された森林の松やもみの針を集め、木の下にゴミを捨て、セシウム塩の溶液（もちろん非放射性）に浸し、それらを燃やし、燃焼生成物を吹き飛ばすのに15〜20メートルの高さのパイプを通します：これは、山火事で炎が舞い上がる状況の再現です...

この実験は、2018年にミズーラ（モンタナ州）の米国森林局消防研究所のブースで実施され、非常に重要な結果を受け取りました。特に、ごくわずかなセシウム（3％以下）だけが煙とともに残り、残りは火の場所に散らばった灰の中に残っていることが判明しました。そして、セシウムの煙の粒子は遠くまで飛ぶことはありません。圧倒的多数で、それらは大きく、直径は10ミクロンです。したがって、消防士が最も危険にさらされています。

この結論は、2020年4月から5月にチェルノブイリゾーンで発生したひどい山火事の際の実践によって確認されたようです。メディアの報道によると、ゾーン外の過剰な放射線レベルは認められませんでした。また、京都大学の研究者による実験では、汚染地域のごみは高温で燃焼する必要があることが示されました。そうすると、放射性セシウムがボトムアッシュに集まり、低い燃焼温度で煙の粒子が濃縮されます。

［訳者注）ここでのテーマは，量の多い放射性セシウム汚染に関するものです．放射能は消せないのですが，農作物に取り込まない方法はありそうです．放射性セシウムからのガンマ線は外部被ばくに関与しますが，ベータ線やアルファー線を放出する核種は細胞に取り込まれると深刻な内部被ばくに関与します．例えば，トリチウム水は大きな問題です．］

ーー続く

セシウムはどのようにして原子力施設に行き、そこで何をするのでしょうか？

セシウムは2つの理由でそこにある可能性があります。第一に、放射性セシウムは、ウランが原子炉で核分裂するときに生成されます。そのようなセシウムはまだましな方です。結局のところ、それは強い放射能と長い寿命を持っているので、原発事故後の長期的な悪影響につながるのは放射性セシウムです。そして第二に、原発を設計するエンジニアは、セシウムを核または熱核施設に意識的に配置します。その理由は、電子管の陰極にセシウム層を塗布すると、電子の仕事関数が急激に低下するためです。つまり、追加の努力をしなくても、このようなランプの電流が増加します。原子力施設はそれとどのように係るのかだろうか？

惑星間宇宙工学の開発者は、原子力発電所がなければ、太陽系の惑星へ宇宙船の飛行は不可能であると確信しています。ただし、このような施設では、熱を地球に適用できる電気に変換するという原則は使用できません。この寸法では、蒸気エンジンを宇宙に配置することはできません。そのため、1970年代には、ソビエトのライプンスキー物理・電力工学研究所とクラスナヤ・ズヴェズダ研究・生産協会の技術者が、別の原理に基づいてトパーズ核施設を設計しました。

熱は熱放射によって直接電気に変換されました。対応するデバイスは電子ランプであり、電子は加熱された陰極から飛び出して冷たい陽極に飛んで、回路に電流を供給します。陰極は原子炉の熱で加熱されます。そのため、陰極にセシウムの層があれば、電子電流は何倍にもなります。

しかし、どのようにしてセシウムを熱陰極に保つのですか？このために彼らはそのようなトリックを思いついた。電極間のギャップは非常に小さく、数百ミクロンです。したがって、セシウムは陰極に堆積しませんでしたが、その原子からのガスはこのギャップを通してポンプで送られました。いくつかの原子は最終的に陰極表面に到達し、陰極表面からの電子の脱出を促進しました。「トパーズ」のテストは1987年と1988年にそれぞれ衛星「コスモス-1818」と「コスモス-1867」で成功しましたが、チェルノブイリ事故後、この種の作業は削減されました。彼らはアメリカ人と協力して再開しましたが、90年代後半にこのプログラムも終了しました。

セシウムは、核物理学SB ASソ連の研究所からノボシビルスクの物理学者によって発明された施設で同様の役割を果たしたが、発電のためではなく、全く別のタスクのためのものである。彼らは、加速器で使用するために、負に帯電した水素イオンのビームを生成する必要がありました。正イオンを作る方法は多かれ少なかれ明らかであるが、それは原子をイオン化することが必要である - 光で電子を引き裂くために、例えば。しかし、どうやってマイナスイオンを作るのか？このようなイオンは、電子管の陰極に水素分子を衝突させることで得られる。それを残して電子を拾うことによって、分子はその安定性を失い、すぐに水素原子とマイナスイオンに崩壊します。陰極にセシウムをコーティングすることで、電子が逃げやすくなり、水素イオンが何十倍も生成されやすくなることがわかりました。

現在、熱核科学者はそのようなイオン源を使用したいと考えています。彼らの仕事は、燃料、つまり重水素原子を加熱して、プラズマに入るときに冷却しないようにすることです。そして、加熱するということは、原子に高速の動きを与えることを意味します。ただし、中性原子の加速はイオンよりもはるかに困難です。そのため、イオンを作り、分散させ、中和するという発想が生まれました。中和は他の原子との衝突で行われますが、電荷が正の場合、イオンの速度が速いほど衝突の確率は低くなります。電荷が負ならばそうではありません。そのため、ITERAの建設に伴い、強力なマイナス水素イオン源を作ることが急務となり、セシウムを使わずにはいられなくなりました。このようなソースでは大電流が予想されるため、セシウムを含む陰極だけでなく、その層を常時再生するシステム全体が必要となる。開発されています。

セシウムは宇宙エンジンで使用されていますか？
いいえ、アメリカ人は加速されたセシウムイオンのジェット気流を宇宙船に提供しようとしましたが、成功しませんでした。現在、宇宙イオンエンジンの作動流体はキセノンであり、これはセシウムと同じくらい重い。

https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

油田ではなぜ、何立方メートルものセシウム塩溶液を井戸に流し込むのか？［訳者注］自然に存在するセシウム同位体は安定な133で，放射性セシウムではありません．まず安定なセシウムの利用の話の続きです．

そのような塩は、現代の掘削流体のユニークな成分であることが判明し、専門家が年間生産量と見積もっているセシウム50トンの半分以上を必要としています。掘削泥水は、掘削プロセスの間に井戸に直接汲み上げられます。これは複数の機能を持っています。その中でも特に重要なのは、掘削によって破壊された岩石を持ち上げることと、地層中の流体によって破壊されないように井戸内に反圧を生じさせることです。そのためには濃い泥が必要で、密度を高めるために、粘土のような充填材を追加します。
しかし、別の方法として、重くて均質な流体を使用するという方法もあります。セシウムは自然界に存在するすべてのアルカリ金属の中で最も重いので、セシウム塩を水に溶かしたものが使われます。実際、ギ酸セシウムはこのような塩として機能します：その溶液の密度は、水の密度の2倍を超えており、2.2 g/cm^3に達することがあります。また、ギ酸塩は分解しやすく、ある程度の量のセシウムで汚染することを除けば、環境に全く害を及ぼさないというメリットがあり、危険なことではありません。

ギ酸セシウムを掘削流体にする歴史は1999年までさかのぼります。その時にトータル社が抱えた問題からです。1997年には、北海の英国領エルジン・フランクリン油田の掘削を開始しました。石油は地表から約6キロ下にあり、貯留層の圧力と温度は前例のないほど高く、1000気圧以上、摂氏205度にも達しています。1999年までに7つの井戸が掘削され、2つの井戸には貯留層からの油の流れを増やすために壁に穴が開けられていました。

すべての井戸に、欠陥のあるエレベータ・ストリング（油を地表に送り出すパイプ）が設置されていることがわかりました。どうすればいいのか？井戸を殺して新しい井戸を掘るのか？そこで、エンジニアは別の方法を考え出しました：井戸を一時的にシャットダウンし、パイプを取り出し、ハンガーを変更し、すべてを元のラインに戻す。同じ泥で井戸を浸水させて殺してしまっうのですが、この場合は泥を使うことができませんでした。油田の油層は砂岩で構成されており、粘土の粒子が気孔に堆積し、それを詰まらせる可能性があります。これは、塩水が修理に必要であることを意味します：その密度を確保できる固体粒子ではなく塩溶液です。しかし、当時は臭化亜鉛という塩しか使えませんでした。この溶液は深刻な腐食を引き起こすだけでなく、海の生物を死滅させるほどの量の亜鉛が海に流れ込む可能性があります。何らかの無害な液体を探す必要がありました。

そして、会社にとって幸運なことに、遠くないスコットランドのアバディーンで、キャボット・スペシャルティ・フルイーズ社が所有する4,000m^3という十分な量のギ酸セシウム溶液のバッチがあったことです。この液体を借りて、一つづつ井戸を埋めて修理して、液体を汲み上げて別の井戸に送りました。このような丁寧な処理のため、貴重な液体はわずか10％しか失われていませんでした。全体としては、1つの井戸につき100万ドルの費用がかかりました。これは、不良品のバネを工場から出荷した品質管理部の社員とこのようなバネを導入した管理職の給料よりもはるかに高いものでしょう。

それ以来、油田労働者は掘削泥水の成分としてギ酸セシウムを頻繁に使用します。高密度で安全なギ酸セシウムは、掘削時間を2～4週間（掘削の複雑さにもよりますが）短縮し、機器の消耗を抑え、腐食速度を低下させ、油回収量を増加させます。最も重要なことは、作業員や環境に無害であることのおかげで、そのような掘削油は油田での環境に優しい作業のための新しい基準になりました。

ーーー続く

Цезий: факты и фактики • БиблиотекаЦезий — это первый элемент, открытый благодаря спектроскопии:elementy.ru
https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

A.Motylyaev 「ChemistryandLife」 No。11、2020

1860年、シュヴァルツシルトのミネラルウォーターサンプルの発光スペクトルを研究していたロバート・ブンセンとグスタフ・キルヒホフは、その中に明るい青色の線を発見しました。その元素を "空色 "という意味のラテン語のcaesiusからセシウムと呼びました。医師はすぐに新しい元素を使おうとしましたが、あまり成功しませんでした。20世紀には、セシウムは光を励起しやすいことがわかったため、荷電粒子の崩壊生成物を分析するための検出器をはじめ、さまざまな光学機器に使われました。［訳者注）ヨウ化セシウム（NaやTlドープ）は，ガンマ線で発光するシンチレータとして安価に販売されています．］

唯一の天然の同位体であるセシウム133が存在し、大きな原子質量、電子殻がシンプルなので、セシウムガスは、現在世界の時間を設定する超精密時計の動作体となりました。［訳者注）自然に存在するのは安定な安定な同位体だけですが，2011年の原発事故で放射性の同位体137などが環境に放出されました．セシウム時計については，現代の標準時計をご覧ください］https://note.com/sgk2005/n/n5a0079b99920

また、触媒としての役割も証明されています。しかし、時間が経ち、生産量が増え、新しい応用（時にはかなり議論の的になることもある）が見だされています。

グリーンエネルギーの創造者たちは、なぜセシウムに注目しているか。
材料科学者はセシウムペロブスカイト太陽電池に大きな期待を寄せています。少し前の2009年には、いわゆるペロブスカイト太陽電池への関心の波が押し寄せ始め（化学と生活#7、2019参照）。今ではそれは津波のようです。結局、太陽光を電気に変換する効率は14％とかなり許容範囲内になり、シリコンを導入したペロブスカイト電池では28％という記録的な効率になっています。ソーラーパネルの技術者は、これらのセルが安価に作られる方法に非常に魅力を感じており、専門家はペロブスカイトの大量生産が開始された後、ソーラーパネルの価格が急落すると予測している。そして、もう始まっています! 　中国企業のMicroquantaは2020年8月、小州市に70ヘクタールの工場を開設し、年内に20万平方メートルの純ペロブスカイトセルを生産すると発表しています。ドイツでは2021年に、イギリスのオックスフォード・フォトボティクス社の技術を用いたタンデム型シリコンペロブスカイトセルの生産を開始します。
ーーーーー
［訳者注）以下のmicroquantaのサイトをご覧ください］https://www.pv-magazine.com/2019/10/24/microquanta-achieves-14-24-efficiency-with-large-area-perovskite-solar-module/

Microquanta achieves 14.24% efficiency with large-area perovskite solar moduleThe four-year-old Hangzhou-based business says it already haswww.pv-magazine.com
ーーーーー

しかし、これらの成功はすべて、ハロゲン化鉛にメチルアンモニウムなどの有機カチオンが結合した有機無機ペロブスカイトで達成されました。実践では、これらの化合物は太陽光や大気中の水分の影響を受けてあまり安定ではないことがわかっています。その上、技術者たちは、そのような化合物の効率を向上させるための手段をすでに使い果たしており、理論的な限界に非常に近づいています。そして2015年には、有機カチオンを金属に置き換えるためのアイデアが生まれました：セシウムは、その外殻電子が簡単に分離する性質［訳者注）水素様原子］から、そのような選択がなされました。こうして無機セシウム系ペロブスカイトが登場しました。

セシウムには、量子ドット（光を放出したり吸収したりできるナノ粒子）と、太陽電池の2つの用途があります。5 年間で、セシウム・セルによる光から電気への変換の効率は 5 からほぼ 20 ％ （実験室のサンプルで）、実験者のデータではなく、認証機関のデータでは - ちょうど 15 ％ 未満まで増加しました。まだ理論上の限界からは程遠く、実際には道半ば、改善の余地は十分にあります。しかし、これらの素子の安定性は、まだ多くの問題があります。国際電気標準会議の加速規制下でテストされた最高のセルは、規制下では少なくとも1000時間は持たなければならないのに対し、240時間で10％の効率低下を示した。材料科学者は安定性を高めるための多くのツールを持っています。現在の主要課題は、安価なセシウムペロブスカイトセルで、高価なシリコンセルよりも日光の変換効率をよくすることです。これが実現しないと、すべての努力が報われません。

ーーー続くーー
安定な同位体セシウムの利用の話から始めました：
今回は，太陽電池への利用の話でした．
次回は，「油田掘削での利用」

Академик Георгий Сергеевич Голицын　ゴリツィン
«Природа» No6, 2007
https://elementy.ru/nauchno-populyarnaya_biblioteka/430479/Portret_neizvestnogo_K_300_letiyu_Leonarda_Eylera

レオナルド・オイラーは18世紀の偉大な科学者です。その前世紀の偉大な科学者はアイザック・ニュートン、そして、次の世紀はオイラー（1707–1783）であったことは確かです。オイラーは、現代の数学の主要な分野を提唱開発しました：変分法、複素変数の関数理論、解析的整数論、特種関数の理論。彼は、天体力学理論、流体力学、弾性の理論などに関する数多くの研究を残しました。A.S.プーシキンによる「テーブルトーク」では ,オイラーについてのセクションがあります。

1730年から1740年に統治したアンナ・イオアナブナの甥であり、将来の皇帝ジョン6世となるイワン・アントノビッチの誕生時に、宮廷はオイラーに王位継承者のための星占いを命じました。オイラーは占星術を信じていなかったので、最初は拒否したが、宮廷の要請を受けました。ホロスコープを作成するためのルールを知っていたオイラーは、イワン・アントノビッチのためにそれを作成しました。ホロスコープは酷いものであることが判明したため、オイラーはあえてそれを使用せず、別の非常に成功したものを提案しました。一年後、エリザベタ・ペトロヴナは赤ん坊の王を退位させシュリッセルブルク要塞に幽閉し、（ミロビッチ中尉がイワンアントノビッチを釈放しようとしたとき）1764年にエカテリーナ2世の密令で殺されました。オイラーは優秀な計算機でした。1783年の彼の死後、誰かが「オイラーは死んで計算をやめた」と言いました．

■1972年3月、レニングラード水文気象研究所の大気物理学部長であるデイビッド・L・ライヒツマン教授から、惑星大気の力学に関する講義を2週間で4回行うように招かれました。
私（ゴリツィン）は週に半日2回忙しく、残りの時間は美術館で過ごし、街を歩き回りました。ネフスキープロスペクト近くのルビンスタイン通りに部屋を提供してくれた友人のネイルBと滞在しました。

ある日、モスクワ駅近くのネフスキーにある古着屋に行きました。1階にはあらゆる種類の衣類があり、2階には絵画やその他のオブジェがありました。そこには、巨大な金箔の額縁に入った大きな暗い肖像画があった。漆喰が所々落ちていましたが、まともな状態でした。近づいてみると、その肖像画にはレオンハルト・オイラーが描かれていることがすぐにわかりました。オイラーの肖像画は、無名の画家の無名の人物の肖像画として売り出されていた。キャンバスは所々破れていたり、絵の具がボロボロになっていたりしていました。この肖像画は買わないと一生後悔すると実感しましたが、それは、93ルーブルで 50カペイカだった。

私はそのようなお金を持っていませんでした（当時、理学博士の給料は月に400ルーブルでした）。ネイルに足りないものを借りて、翌朝の開店に行きました。支払った後、なぜそんなに安い価格なのかと尋ねました。店員は私がラッキーだったと言った。肖像画は3か月以上店にあり、最近15％割引にしたと。したがって、肖像画の元の価格は110ルーブルだったのです。

フレーム付きの肖像画の重さは15キログラムで、裏には指の太さのロープが付いていました。ネイルは彼の肩に肖像画を掛け、私たちは彼の家に行きました。翌日、私はモスクワに向けて出発しました。ネイルが私に同行しました。車掌が、120×140cm巨の大な絵を車内に乗せないと言い、私はそれをコンパートメントの頭上の荷物棚に置くと言いましたが、確かに、棚ははるかに狭いのです。チェックインする時間がありません。電車が出発する約10分前です。ネイルは送ってくれると約束し、電車に沿って歩いて行ったが、数分後戻って、肖像画が別の車の前デッキに乗せたと言いました。私はボロゴエで、肖像画が乗客の出入りを妨げないことを確認し、モスクワでは私が最初に電車を降りることにしました。車掌には5ルーブルを支払いました。

モスクワのレニングラード駅で、重くて公共交通機関が不便だったので、一人では家にも仕事場にも肖像画を運ぶことができないのに気づき、保管室に渡しました。駅にある十数台のロッカーのうちで、そのような大サイズのものを受け入れられるのは最も遠くにある1台だけでした。数日後、私は研究所「カジク」に、絵を持ち込みました。

肖像画は明らかに修復が必要な状態でした。いとこのイラリオン・ウラジミロヴィチ・ゴリーツィン（ロシア人民芸術家、芸術院議長会会員、2003年の国家賞受賞者）に電話してみました。 イラリオンは、ペトリーヌ時代からの家族の肖像画をすべて保管しており、その中のいくつかは、この事件の少し前にトレチャコフ・ギャラリーで修復したものです。プロの修復業者の電話番号を教えてくれました。汚れを落とし、新しいキャンバスの裏に貼り、落ちていたところを塗り直して、すべて70ルーブルでできました。似顔絵は新品同様に良くなりました!　 右下隅には署名がありました：I. Konig, 1881.

肖像画は私のオフィスの壁に取り付けられました。USSR科学アカデミーの大気物理学研究所の所長である学者のアレクサンダー・ミハイロヴィッチ・オブホフがそれを見に来て、それを賞賛した後、突然「ゴガ、私に肖像画を売ってください」と言いました。数秒経過の後、私は次の返事を返しましたが、それには数十年後の今でも驚いています。「アレクサンダーミハイロヴィッチ、あなたはすでにあなたのオフィスに必須で良い肖像画をぶら下げていますが、これはそれより芸術的に優れ、政治的に間違っています。」オブホフはうなって立ち去り、このトピックに戻ることはありませんでした。

1973年、科学アカデミー250周年記念式典の準備が始まりました。その年の雑誌『自然』9号には、V.I.ヴェルナドスキーの論文「科学アカデミーの最初の年」が掲載されており、父パヴェルの息子キリル・パブロヴィッチ・フロレンスキーの資料に基づいて作成されています。他の肖像画の中で、私はレオンハルト・オイラーの自分の肖像画を見ました。キャプションには、E. ハンドマン（1756年、バーゼル大学）の肖像画が掲載されています。

スイスのこの街でオイラーは生まれ、1720年から1724年にかけて上記の大学でヨハン・ベルヌーイの数学の講義を受けた。若きオイラーは毎週土曜日に彼と数学の話をし、子供のニコラスとダニエルと仲良くなった。この二人は1724年にサンクトペテルブルク・アカデミーへの招待状を受け取り、翌年には同アカデミーに入学しています。オイラーは本当に一緒に行きたかった。しかし、彼が招待を受けたのは翌年の1726年12月でした。ニコライ･ベルヌーイが、かの地の気候に慣れることができなかったため、アカデミーに空席が発生したからです。オイラーは1727年5月に20歳でロシアに来て、1741年までここに住み、数学と力学の約80の論文を作成しました。

1740年、アンナ・イオアンノブナ皇后が亡くなりました。幼児ジョン6世の下の摂政は彼の母親アンナ･レオポルドブナでした。彼女の治世の数年間、ロシア国家の情勢は完全に混乱、アカデミーは1年間給与を支払わなかった。1741年オイラーは、ベルリン科学アカデミーを組織た若いプロイセン王フリードリッヒ2世（後にグレートの愛称で呼ばれる）の招待を受け入れた。オイラーが数学教室長に就任。彼はベルリンに25年間滞在しました。1759年には、このアカデミーの初代学長であるモーペルチュイ（力学における最小作用の原理の発案者として知られていますが、オイラーの貢献が大きい）、モーペルチュイの死後、オイラーはアカデミーのマネージャーに任命されましたが、フルードリッヒは給料を上げませんでした。厳格なフリードリッヒは、常に服装が正式でないオイラーを非常に嫌っており、これは数年間続きました。

王位に就くと、エカテリーナ2世はすぐにサンクトペテルブルクアカデミーに注目をしました。ベルリンでの25年間を通じて、オイラーはサンクトペテルブルクでの出来事を追跡し、アカデミーのメンバー、特に彼が常に支援していたロマノソフとの広範な通信を維持していました。エカテリーナは、首相であるN.I.パニンに、どうしてもオイラーをロシアに戻すように指示し、彼はベルリンでの給料よりもはるかに高い給料を約束され、1766年7月にオイラーと彼の家族はぺテルブルグに戻りました。ここで過ごした最後の17年間で、彼は約400点の論文を作りました。

（続く）－－－－－

ハンドマンと私の肖像画では、オイラーは明らかに生命のない右目をしています。これには独自の物語があり一度は聞いたことがありますが、今は正確なリンクを与えることができません。1740年代か1750年代には、パリのアカデミーが帆船のマストの配置を競うコンテストを発表しています。オイラーは長年造船業に携わっており、大会に参加したかったのですが、コンテストの論文提出期限が迫っていた。ついに彼は計算のために座り、丸3日間机から離れませんでした。その間、彼は他の人が少なくとも1か月を費やしたであろう計算を完了し、賞を受賞しました。しかし、彼は目を失った。第二の目で、レナード・オイラーはすでにサンクトペテルブルクで盲目になりました。それから彼は彼の長男に彼の仕事を口述した。オイラーの子孫はまだサンクトペテルブルクに住んでいます。

1981年1月、私はソ連科学アカデミーの対応メンバー3名の代表団を率いて、「気象・気候予測モデルのための大気プロセスパラメータ化に関する国際シンポジウム」に参加しました。ワシントンDCのすぐ北にあるメリーランド大学コンベンションセンターで開催されました。そこから私は同僚の海洋学者オーウェン・フィリップス氏（ボルチモアのジョンズ・ホプキンス大学教授）に電話をかけました。1時間足らずでワシントンからボルチモアまで 送ってくれました。地球惑星科学専攻では、回転流体の対流に関する講義を行いました。講演会の後、私はもう一人の同僚である有名な乱流研究者のスタンリー・コルシン（Stanley Corrsin）という研究所の友人を訪ねました。彼と一緒に、私は偉大な流体力学の写真の肖像画を見ました：ジョシュア・レイノルズ、乱流の科学の創始者、ルートヴィヒ・プラントル、セオドア・フォン・カルマン、ジェフリー・テイラー、そして、レオナルド・オイラーの肖像画の小さなカラー写真を見せてくれました。コルリジンは、"科学と芸術の歴史の中で、こんなに素晴らしい題材を個人的に所有することができるのか？"と質問し、どうすればいいと思っているのか聞いてみました。答えは、"科学史博物館か、せめて科学アカデミーに渡した方がいい "というものでした。私には、その後、前述の流体力学者の肖像画の写真が郵送されてきました。

コルジンの事務所を出ると、世界的に有名な力学者であるトゥルースデル教授に会いました。その本の多くは、1960年代と1970年代にロシア語に翻訳されました。この教授の主な趣味はレナナルド・オイラーの人生と仕事の研究であることを私は知っていました。コルジンは私たちをお互いに紹介しました。幸いなことに、私はオイラーの肖像画の写真の別のコピーを持っていました。私はこれをトゥルースデルに渡し、飛行機に遅れたことを謝罪し、必要に応じてフィリップスとコルジンが私の住所を持っていると言いました。

当時、まだメールもファックスもありませんでした。約1か月後、トゥルースデルから手紙を受け取りました。彼は、私が偉大な科学者のこのような素晴らしい肖像画を持っていたことがどれほど幸運であったかについて、ほぼ文字通りコルジンの言葉を繰り返しました。彼は次のように書いています。「あなたがこの肖像画を継承したと仮定させてください。」彼は続けて、この肖像画の最初の所有者が誰であったかについて2つの提案をしました。最初の可能な所有者である彼は、啓蒙された慈善家であるアレクサンダー・ミハイロヴィッチ・ゴリツィン副首相（1722-1806）を指名しました。もう1人は、当時の有名な科学者であり、すべてのヨーロッパのアカデミーのメンバーであり、エルミタージュの絵画や芸術作品を購入するエカテリーナ大王の主な代理人であり、フランスとオランダのロシア大使であるドミトリー・アレクシーヴィッチ・ゴリツィン（1734-1803）である可能性があります。彼については別の話があります。

（訳者注）著者名も含めて，ゴリツィンが3人も出てきて私も混乱しましたが，皆別人（ゲエオルギィ，アレクサンダー，ドミトリー）です．

トゥルースデルは、オイラーの肖像画が3か月以上誰も興味を持たなかったため、古着屋で割引価格で購入されたと聞いてがっかりしました。1989年12月にアカデミックA.M.オブホフが亡くなり、すでにUSSRの科学アカデミーの正会員であったので、1990年1月1日から私は大気物理学研究所の所長に任命されました。最初の2年間、私は古い小さなオフィスを研究所と気候理論部門の責任者として維持しました。オイラーの肖像画がそこにありました。1991年の終わりに、USSRの崩壊、ソビエト連邦の共産党の主導的役割の廃止、そして部屋を空ける必要性とともに、私は小さな古い事務所を空け、壁からウラジミール・イリイチ（レーニン）のかなりまともな肖像画を取り除き、そこにレナルド・オイラーの肖像画を置きました。

2000年末までは肖像画の関連することは何も起こりませんでした。その全容は不明のままでした。2000年12月、モスクワ石油ガスアカデミーの数学教師である末娘のマーシャは、パイプ内の非定常ガス運動に関する博士論文の防衛戦に臨んでいました。彼女の結果によると、パイプの2つの場所で希薄化波の振幅と通過時間を測定すると、ガスパイプライン（例えばウクライナ）からの不正なガス抽出の場所と量を特定することができました。防衛に成功した後、出席者全員が部署に招待され、少しお祝いをしました。論文評議会のメンバーであるグレブ・ミハイロフ教授は、何気なくレオナルド・オイラーのことを口にしていた。マーシャはすぐに、父親が科学者の大きな肖像画を持っていると答えた。教授は珍しく興奮して、この肖像画を見ることができるかどうか尋ねました。マーシャは彼に私の電話番号を教えてくれました。翌日、彼は私に電話し、私たちは彼が私の研究所に来ることに同意しました。「この肖像画を見てもいいですか？」マーシャは私の電話番号を教えてくれた。次の日、彼は私に電話をかけてきて、私の研究所に来ることになりました。

到着すると、グレブ・コンスタンティノヴィッチは、オイラーが彼の人生の主なテーマであると言いました。ソビエト（後にロシア）委員会の事務局長、そして流体力学はサービスです。本職はオイラー。これまでサンクトペテルブルク、ベルリン、スイスの彼のアーカイブは完全に解かれていませんでした。レオンハルト・オイラーの遺産に関する国際委員会のメンバーとして、毎年1ヶ月間をスイスやドイツで過ごしており、その活動は後を絶たない。「この素晴らしい肖像画に出会えて何と嬉しいことでしょう。2、3日でロシアでの歴史が調べられると思います」と、ミハイロフ教授は別れを告げました。

その日のうちに電話が鳴った。興奮したグレブ・コンスタンチノビッチが次のように言っていた。1875年、ロシアアカデミーは創立150周年を迎えていました。その中でも特に目立つメンバーの肖像画があることが決まった。オイラーの肖像画は、ドイツの画家ヨハン・ケーニッヒに依頼され、彼は1756年のバーゼルの肖像画の非常に正確なコピーを作成しました。 その後、このコピーやコピーから、質が著しく低く、色調が異なる多くの新しいコピーが作成されました。このような二次コピーは、モスクワ大学、ロシア科学アカデミー学長の応接室にあります。

1881年にケーニッヒによって実行されたこの命令は、最初にサンクトペテルブルクのワシリエフスキー島にある科学アカデミーの建物に吊るされました。1889年は、プルコボ天文台の開館50周年の年でした。オイラーは天体力学の分野でも多くのことをしていたので、彼の肖像画はこの天文台に贈られました。1918年、天文台は革命家船乗りによって2度略奪されました。54年後、私はネフスキーのコミッションショップで「不明」の暗い肖像画を見たのです。

［訳者注］量子力学の数学的基礎(ノイマン）がベルリンで出版されたのは1932年，みすずから日本語訳の出版がされたのは1957年です．ソボレフ達がスミルノフ主催のセミナーで勉強したのはこの本でした．ディラックのデルタ関数を厳密に扱うにはルベーク積分やヒルベルト空間の理論を基礎に置くことが必要でした．ソボレフの名はソボレフ空間に残っています．
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

Семен Кутателадзе，«Наука из первых рук» №1(86), 2020　より

https://elementy.ru/nauchno-populyarnaya_biblioteka/435305/Sobolev_iz_shkoly_Eylera

数学は思考の形を研究します。最も一般的な意味で、微分はプロセスのトレンドを決定し、積分はトレンドの将来を予測します。

現代の人類は、積分と微分なしでは思考ができません。ニュートンとライプニッツによって、微分積分が発見され、この概念を使用して、オイラーは変数の新しい数学を育て、多くの独創的な発見をし、驚くべき公式と定理の数えきれない集大成を行いました。

200年間、解析学はニュートン、ライプニッツ、オイラーの微積分にとどまりましたが、20世紀に入ると、古典微積分は分布の理論へと進化していきます。近代解析学の主要な対象は、ルベーグの意味での積分と、S.L.ソボレフの意味での微分であります。古典的な微分と積分の操作対象とならない一般的な依存関係のために、これらは定義されています。ルベーグとソボレフは、積分と微分への新しいアプローチを提案し、数学の影響力と応用の範囲を大幅に拡大することで歴史を作りました。

歴史上の人物や発見は、歴史的な並立と分析に値する。数学の賜物は、先生から生徒に受け継がれます。この交互に続く連鎖こそが、数学スクールの物質的な担い手で、ソボレフは、レオンハルト・オイラーにまで遡るスクールに属しています。

オイラーからソボレフへ
人間は物理的な物体であり、４次元時空の世界線で部分的に表現できます。オイラーの世界線の大部分はロシアに属します。スイス出身のオイラーは、ロシアに第二の故郷を見つけ、サンクトペテルブルクに住みました。数学の "ダ・ヴィンチ "たる彼は、ずっと前にロシアの精神の不可欠な部分になっていました。

スイスの数学もロシアの数学もありませんが、ロシアには数学があり、国家的な数学の伝統があり、国家的な数学スクールがあります。我々の同胞は、オイラーをロシアの数学スクールの創始者と考えることを誇りに思っています。

オイラーの努力により、ペテルブルクは18世紀に世界の数学の中心地となりました。 ダニエル・ベルヌーイはオイラーに次のような手紙を書いて、時代をリードする科学雑誌となった有名な「サンクトペテルブルクアカデミーのコメント」の話をしています。この出版物は何度か名前を変え、時を経てIzvestiya RAN (Mathematical Series)となりました。サンクトペテルブルク科学アカデミー紀要にはオイラーの論文473本が掲載されており、オイラーの死後1830年まで何年もの間、順番に掲載されていました。

サンクトペテルブルクの家。ここにL.オイラーは住んでいた。撮影：M.パンフィロフ 。オイラーのサイン。ロシア科学アカデミーアーカイブのサンクトペテルブルク支部

19世紀の初めに、数学的思考の中心はフランスに移り、ラプラス、ポアソン、フーリエ、コーシーが活動しました。生み出される数学の新しいアイデアは、ハリコフ帝国大学から合法的に取得した卒業証明書を剥奪され、パリに留学したM.V. オストログラドスキーによって受け入れられました。オストログラドスキーがフランスで獲得した名声と、科学アカデミーに提出された多くの彼の回想録は、ロシアでの彼の功績を認識させ、彼はすぐにロシアの数学のリーダーとして認められるようになりました。

[訳者注）ベクトル解析のガウスの定理のことを，ロシアではガウスーオストログラドスキーの定理と呼ぶのをロシアの物理本で見たことがあるでしょう]

［訳者注）オストログラドスキーがハリコフ帝国大学の博士号を拒否した状況はwiki参照］

オストログラドスキーは、ロシア科学にとってのオイラーの重要性を十分に認識していた。オイラーの遺産を出版するという問題を精力的に提起したのは彼でした。「オイラーは、近代解析学を創始し、それだけでも彼のすべての前任者を合わせたよりも豊富で、それを人間の心の最も強力な道具にした 」とオストログラドスキーは書いています。全28巻の出版は10年以内に完了する予定でしたが、当時も現在も科学アカデミーはそのための資金を確保できず......。

ロシアの有名な数学者や力学者の多くは、M.V.オストログラドスキーの影響を受けています。その中には、オストログラドスキースクールのサンクトペテルブルク支部のチェビシェフ、リアプノフ、ステクロフがいた。チェビシェフの教え子には、コルキン、マルコフらがおり、ソボレフの大学院の顧問となったギュンターはその下で学んでいた。ソボレフは、V.A.ステクロフやA.M.リャプノフの弟子であるV.I.スミルノフを、彼の第二の師と考えていた。ソボレフの科学的系図の華麗なる連鎖はこのようなものでした。

"1951年、セルゲイ・リヴォヴィッチはモスクワ国立大学で数学物理学の方程式の講義した。メモを取る時間がないほど、鮮かで素早い講義だった。生徒たちはスローダウンと彼にメモを送ったが、10分ももたずに、また夢中になり始めた。セルゲイ・リヴォヴィッチは授業中に気を散らすことはありません。とても律儀で、自分の講座を自分のテキストを使って明瞭な講義をしました。［訳者注）リヴォヴィッチは，ソボレフの父称。名前だけでなく，名前と父称で尊敬をこめて呼ぶのがロシアでは普通］
私たちは彼の試験を受けることを恐れませんでした。彼は学生が主題を知っていることを確認し、すぐに成績を上げました。
当時、私たちはソボレフが有名な数学者であることをすでに知っていましたが、もう一つの仕事である原子力研究所で彼がどのような責任を担っているのかは知らなかった。”ーー物理学と数学の博士号、RRCクルチャトフ研究所の教授、最高科学責任者、IVM RAS V. I. レベデフーー

1930年代のロシアにおける数学
大発見とは、自然には発生しないが必然のマイルストーンである。必要性はチャンスが密集した雑木林を通り抜けていく。ソボレフの発見は、世界と国家の数学の大躍進の年に属していました。

20世紀は当然のことながら自由の世紀と見なされます。自由とは、個人間の対立を解決する方法を反映した歴史的概念であり、多様性に制限はなく、集団的共存の形態を制限します。歴史的な環境は、すべての勝利とすべての悲劇の不可欠な要素です。

レニングラード大学の学生時代。S.L.ソボレフと同志のS.A.クリスティアノビッチ、教師のV.I.スミルノフ。

民主主義の社会制度の発展は、人々の精神生活のあらゆる側面の解放と同時に起こりました。数学は、自由な思考の科学としての本質を明らかにしました。

微分方程式を解くという概念を改訂するというアイデアは、20世紀初頭の数学的な雰囲気の中で身につけられました。1957年の彼の業績を理解するにあたり、ソボレフ自身は次のように述べています。”偏微分方程式を満たす関数を見つけるさまざまな問題を研究する過程で、必要な次数の連続導関数を持たない関数のクラスを使用することが有用であることがわかりました。どこにでもありますが、ある意味では方程式の実際の解を制限しています。このような一般化された解は、さまざまな関数空間で自然に求められ、時には完全であり、時には新しい「理想的な要素」を導入することによって特別に補完されます”。

科学は、個々の解から関数空間、その中の演算子、そして解の要素の研究へと移行していきました。
これらの一般化された解が、いつ古典的な意味での解になるのかという問題は、この考察下では独立したものとなりました。

私たちが見ることができるように、ソボレフは、カントールの集合理論に基づいて、彼の理論とヒルベルトの考えとが不可分に結びついていることを示しました。

ソボレフがこの問題に注目したのは、集合関数論に基づいて数理物理学の方程式へのアプローチを見直す必要があるというルベーグの考えを推し進めたギュンターと関係があることは間違いない。

ソボレフは、スミルノフ主催のセミナーで関数解析の考え方を紹介されました。そのゼミで、量子力学の数学的方法についてのJ・フォン・ノイマンの古典書を研究したのがきっかけでした。ノイマンのアイデアはまた、スミルノフのセミナーの別の参加者の興味を喚起しました。ソボレフの大学の友人であるL.V.カントロヴィッチは、K.フリードリヒの関数の概念を拡張する問題に専念し、中等度周期分布の一般化された微分の記述を含む2つのノートを1935年にソ連のDANに発表しました。

親しい友人であり、同じセミナーの参加者でもあるソボレフとカントロヴィッチが、関連する話題でお互いの研究を知らなかったことは、絶対に信じられないように思えます。しかし、後にこのエピソードに触れたことは二人とも一度もありません。当時、ソボレフとカントロヴィッチの間には一時的な疎遠感があったことは明らかであり、彼らは最後まで温かく心のこもった友情を保っていた。その本質は、レニングラードとモスクワの数学界で当時繰り広げられていた非常に鋭い政治的な出来事を理解することによって理解することができます。

この国の数学界の状況は、当時の一般的なモラルとあまり変わらなかった。北の都の旧教授に対抗して「レニングラード数学戦線」が展開された。主な攻撃対象は、ペトログラード数学会を率いたギュンターであり、理想主義と実践からの離脱を全面的に非難され、「公共生活における反動的」「科学における保守的」という烙印を押されていた。ギュンターへの痛ましい告発を含む1931年3月10日の「レニングラード物理数学協会の再編成に関するイニシアチブグループの宣言」に署名した人々の中には、カントロヴィッチがいる。ギュンターは、部門の指導者を去り、悔い改めの手紙を書くことを余儀なくされたが、「唯物論の数学者」とも呼ばれた。ステクロフも理想主義者の中にランクされました。ソボレフとスミルノフの名誉のために、彼らは彼らの指導者の公の迫害に加わっていませんでした。教師と生徒の科学的見解の明らかな近さは解毒剤として役立ちました。

モスクワでも老教授たちは嫌がらせを受けていた。ムスコビテスもカントロヴィッチを論争に巻き込もうとしたが、彼はルージンへの攻撃を控え、ソボレフは残念ながら「ルージン事件」に関する学術委員会の活動に積極的に参加した。

 ロシアの数学の悲劇は普遍的なものだった。その勝利はまた、普遍的なものであった。

ソボレフと原子爆弾
人間の力は、理想的な無形の価値を創造し伝達する能力にあります。数学は、無謬の知的技術の最古の技術を保持しています。根拠のある計算の科学と芸術、数学は文化の中心に位置しています。思想の自由は、個人の自由の必須条件です。世界観の基礎である数学は、自由の基礎となり保証人となります。オイラーとそのスクールの最高の代表者の仕事は、これの無数の例を提供しています。ソボレフの運命も例外ではなかった。

20世紀に入って、人類は第一次世界大戦と第二次世界大戦の扇動者を止めることができずに、安全な存在の境界線に来た。抑止力は自由の保障人であるが、アメリカとロシアの原爆製造は、科学の驚異的な力、つまり人類生存の最後の予備軍であることを示している。数学者は、このプロセスに同僚が参加していることを誇りに思う。ノイマンとウラムはマンハッタン計画で働き、ソボレフとカントロヴィッチは国内のエノモルモズ計画に関わっていた。 

今日では、核兵器開発の歴史に関わる文書のほとんどが機密解除され公開されており、あの英雄的な時代の熱気を感じることができます。

我が国における原子力事業の開始は、1942年9月28日付のGKO令No 2352号「ウランに関する事業の組織化について」に関連づけられています。 数ヶ月後、GKOは、原子力エネルギーの研究のためにソ連科学アカデミーの第2研究所を組織することを決定した。クルチャトフは、研究所の管理と原子問題に関するすべての作業を任されました。すぐにクルチャトフはソボレフを副官に任命し、キコインのグループに加わり、同位体分離のためのカスケード型拡散装置を用いたウラン濃縮を担当した。

特別フォルダーには、1945年8月のクルチャトフとキコインの報告書が入っています。 この文書の前文には次のように書かれています。

"海外で知られている4つの原子爆弾（ウラン235とプルトニウム239）の製造方法のうち、「ウラン235とプルトニウム239の製造方法」と「プルトニウム239とプルトニウム239の製造方法」の2つを紹介します。ウラングラファイトボイラ法、ウラン重水ボイラ法、拡散法、磁気法、第二研究室の第一人者（学識経験者のクルチャトフ、ソボレフ、科学アカデミーのキコイン、ボズネセンスキーに相当するメンバー）は、これらの最初の3つの方法について、第二研究室は現在、施設を設計し、建設するのに十分なデータを持っていると考えています。”

早くも1946年には最初のガス濃縮器が製造され、大量生産が可能になりました。ガス状六フッ化ウラン濃縮実験開始 その仕事は、膨大な数の多様な科学的、技術的、組織的な問題を解決しなければならず、ソボレフの本業となった。ソボレフは、プルトニウム239とウラン235の両グループで働き、計算機の組織化と指導、工業用同位体分離の規則の開発、損失削減の責任者、その他多くの組織的・技術的な問題の解決を行った。原子力プロジェクトでの彼の役割は大きくなっていた。

1949年8月29日、セミパラチンスク近郊でRDS-1の実験が行われ、そのちょうど2ヶ月後には、800人以上の参加者が原爆計画に参加していたことが明らかになりました。ソボレフはレーニン勲章を受章した。

1949年半ばには、第2研究室は「LIPAN-科学アカデミー計測研究所」に改称されました。LIPANでは、ソボレフは、彼の人生の主要な本、"数理物理学における関数解析のいくつかの応用 "を書いた。

原子計画はソボレフの科学的、個人的な可能性を豊かにした。計算数学は、彼の人生の最後まで彼の仕事の中心を占めていました。1952年から1960年までは、モスクワ国立大学の計算数学科を率いました。すでにシベリアで、ソボレフは、その普遍性の驚くべき美しさ、立方式の理論を構築しました。ソボレフは、古典的な近似法と分布理論の概念を統合しました。

LIPANでの仕事は、ソボレフの数学の理解に新たな明るい色を加えました。彼によれば、多くの問題において重要なのは、解決策があるかどうかという抽象的な問題ではなく、合理的な近似変形を規定の期限までに具体的に提示することであることに気付いたのは、この頃だったそうです。

新しい微分-新しい微積分
ずっと前の1755年に、オイラーは関数の普遍的な定義を与えましたが、それはほぼ200年間、最も一般的で完璧なものと考えられていました。彼の有名な微分積分のコースで、以下のように書いています：

"ある量が，他の量に依存し，他の量が変化するときに、変化を受けるなら、前者は後者の関数と呼ばれる。この呼称は非常に広範で、ある量を他の方法で決定するすべての方法をカバーしています。したがって，もし x が変数量を表すならば，何らかの方法で x に依存するすべての量，すなわち x によって決定されるすべての量は，その関数と呼ばれる．

 ソボレフの研究は、微分方程式の解の概念の再考に関連している。

ソボレフはコーシー問題を汎関数空間で解くことを提案した．すなわち，関数としての解を理解するのを止めた．ソボレフは、プロセスの挙動のすべての積分特性が使える場合でさえ、微分方程式を解いたものとして考えることを始めた。この場合、時間の関数としての解は未知であるだけでなく、存在しないこともあります。予測の重要な原理の質的に新しい理解が科学に入りました。

ソボレフの一般化された導関数はオイラー関数の概念には該当しない。ソボレフが提案した微分は、数学的数量の相互依存性の新しい理解に基づいています。一般化された関数は、あらかじめ選択されたサンプル関数のクラスのすべての代表に対するその効果の積分特性によって暗黙的に定義される。

ソボレフは、関数分析を数学物理学に応用した先駆者の一人であり、1935年に理論を発表した。 10年後に独立して同じ考えに到達したローラン・シュワルツの研究により、新しい微積分が一般に利用可能になり、代数学、幾何学、位相幾何学の多くの進歩的な考えを利用した、優雅で強力で極めて透明性の高い分布の理論として発表された。

17世紀の微分積分は、古典力学の一般的な見解と切り離せないものである。一般化された関数の理論は量子力学と結びついています。

特に強調したいのは、量子力学は古典力学の単純な一般化ではなく、新しい法則に基づいた科学的な世界観を表しているということです。古典的な決定論と連続性は、量子化と不確定性に取って代わられました。二十世紀の人類は、自然過程の理解度の全く異なるレベルに達しました。

現代の数学理論も同様である。現代の論理は、アリストテレスの論理を一般化したものではありません。バナッハ空間の幾何学は、ユークリッド平面幾何学の一般化ではありません。現代の微積分となった分布理論は、微分方程式による物理過程の数学的記述の技術全体を激変させた。

ニュートンとライプニッツの発見は、何世紀にもわたって続いてきた微分・積分の前史を総括し、新たな研究への道を開いた。ルベークとソボレフの業績は、創意に富んだ先人たちの反省を継続し、現代の数学者の道を照らすものであった。

ソボレフは未来を聞き、自分のスペースを持って人々に贈り物をしました。彼の発見は、数学における多くの革命的な変化のきっかけとなりました。

ソボレフは最後の一連の数学研究では、オイラー多項式の根の微妙な特性に専念していました...

"セルゲイ・リヴォヴィッチを見た多くの人は、彼がハンサムだったと言うだろう。背が高く、エネルギッシュな動き、素早い足取り。彼の演説は常に非常に明快で、優れた論争家とみられていましたが、めったに論争しなかったのは、彼が正しいことが多かったからかもしれません。セルゲイ・リヴォヴィッチは常に慈悲深く、他人の意見を尊重しました。

ソボレフは優秀なプロモーターであり、様々な聴衆の前で講演していました。たまたま小学生に関数解析とは何かを説明したとき、彼は最も難しいことにまで言及しせんでしたが、非常に明確でわかりやすく数学のこの分野の立場と重要性について生徒たちに伝えることができました。”ーーАкадемик, д. ф.-м. н., советник РАН Ю. Г. Решетняк, ИМ СО РАН

Редакция и автор благодарят Е. С. Соболеву, пресс-секретаря Президиума СО РАН О. В. Подойницыну, сотрудников библиотеки ИМ СО РАН, директора издательства Т. Н. Рожковскую за помощь в подготовке публикации.

В статье использованы материалы из архивов семьи С. Л. Соболева, Института математики им. С. Л. Соболева СО РАН, Президиума СО РАН.

Литература
1. Атомный проект СССР. Документы и материалы. Т. II: Атомная бомба 1945–1954 / Ред. Рябев Л. Д. М.; Саров: Наука, 2000.
2. Кутателадзе С. С. Сергей Соболев и Лоран Шварц // Вест. РАН. 2005. Т. 75, вып. 4. С. 354–359.
3. Нейман, Иоганн фон. Математические методы квантовой механики. М.: Наука, 1964.
4. Николай Петрович Дубинин и XX век / Сост. Дубинина Л. Г., Овчинникова И. Н. М.: Наука, 2006.
5. Сергей Львович Соболев. Страницы жизни в воспоминаниях современников / Ред. Рамазанов М. Д. Уфа: ИМВЦ УНЦ РАН, 2003.
6. Смирнов В. И., Соболев С. Л. Биографический очерк [Николай Максимович Гюнтер (1871–1941)] // Гюнтер Н. М. Теория потенциала и ее применение к основным задачам математической физики. М.: ГИТТЛ, 1953. С. 393–405.
7. Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука, 1974.
9. Соболев С. Л. Избранные труды. Т. 2. Новосибирск: Ин-т математики СО РАН, 2006.
10. Философские проблемы современного естествознания / Ред. Федовеев Н. П. и др. М.: Изд-во АН СССР, 1959.
11. Эйлер Л. Дифференциальное исчисление. Л.: Гостехиздат, 1949.
12. Lutzen J. The Prehistory of the Theory of Distributions. New York etc.: Springer, 1982.
13. Schwartz L. A Mathematician Grappling with His Century. Basel etc.: Birkhauser, 2001.

［訳者注］19世紀には，数学がその源泉として物理学と一体でした．ニュートンは自分の力学の研究のために新しい数学（微分や積分）が必要で，自分で開発しました．ニュートンは物理学者兼数学者です．ストークスの数学も現実の物理現場に対応する中から誕生し実験現場に適用されました．今日，高度に分化し抽象化した数学を数学の中で扱うことだけに興味をもつ数学者を，私は嫌いです．数学者が現場に足を入れることを願います．このエッセイを私が好んで読んだ理由はここにあります．
**********************

科学者の研究に対する評価
J.ニュートンによって始められた光のスペクトルの研究は、W.H.ウォラストン、J.フラウンホーファー、J.F.W.ハーシェル、C.ホイートストン、J.H.ストークスの研究によって発展しました。黒体放射のH.R.キルヒホフの研究も有名です。化学者R.W.ブンゼンと彼の実験的研究は、スペクトル線の反転効果の発見、フラウンホーファー線の説明、物理学、化学、天文学のための重要なスペクトル分析法の創出につながりました。

同時代のW.トムソンは、J.G.ストークスの物理学のこの分野への貢献について書いています。彼は、ストークスの太陽化学と恒星化学の原理が、ここ8、9年の間、公開講座で概説されていたことを思い出しました。ブンゼンとキルヒホフ（ストークスとは独立して理論を発見した）の研究は応用されて、太陽には鉄、マグネシウム、その他の既知の金属が存在することが示されました。すでに何年も前に会話の中でストークスは、太陽スペクトルの暗い線によって、太陽大気の化学的性質について結論を出すことができるという考えを表明していました[8, p.114]。

同時にストークスは、地球の基準表面［訳注）ジオイド面を近似した回転楕円体］、質量、軸を中心とした自転の角速度によって地球の外部重力場を決定するという問題も解決しました。この問題の解答可能性を証明し、ポテンシャル理論の最初の境界問題として、圧縮されたスフェロイドの収縮の二乗のオーダーの相対誤差を持つ近似解を与えた。楕円体のストークス問題のかなり正確な解は、1945年にイタリアのP.ピツェッティとロシアのM.M.モロデンスキーによって与えられた。

ケンブリッジでは、自然科学や技術科学における数学的手法の使用が奨励され、ストークスもまた、それらを広く活用していました。これは、ヴァイルが指摘したように、ベクトル解析とテンソル解析のすべての積分定理が、座標 x_i で囲まれた空間にある r 次元（方向性のある）多様体上の次数 r の微分形に対するストークスの一般定理の特別な場合であるという事実に現れていた [9, p. 192]。

実際、ストークスは数学の発展に重要な貢献をしました。ベクトル解析の主要な公式の一つであるストークスの定理は、ベクトル場の回転を、閉曲線を境界とする有向曲面上で面積分したものが、元のベクトル場を有向曲面の境界の閉曲線上で線積分したものに等しいという彼の名を冠した定理で、1849年にW.トムソンによって得られました。J.G.ストークスは、半収束無限級数の指摘をし、無限級数の完全収束（絶対収束？）や限定収束（条件収束？）を研究しました。
[訳注）収束する無限級数には、絶対収束級数と条件収束級数（半収束級数）があります]

1848年、J.G.ストークスはドイツの数学者F.L.vonザイデルとともに、級数と級数の一様収束の概念を科学的に導入しました。彼は純粋な数学だけでなく、物理学の様々な分野（力学や光学）、天文学や工学への応用にも興味を持っていました。漸近解析におけるストークス現象、流体力学におけるストークスパラメータとベクトル、微分幾何学における彼の定理、光学におけるストークス線、結合、せん断、Navier-Stokes方程式、ストークスドリフト、ストークス電流と波動関数、流体力学におけるストークス境界層などが科学の歴史に登場しています。

彼の研究結果の修正は、ストークスの科学におけるメリットを損なうものではありませんでした。P.N. レベデフ と彼の教え子である N.P. ネクレパエビム は、音響ストークス波とキルヒホッフ波の公式の係数の正確性に疑問を持ち [10, p.349]、W.G.ブラッグは、ストークスのインパルス理論（加速された電子がエーテル中でインパルスを発す）では、X線と電子の交換性を説明できないと指摘し、R.E.ミリカンは、液滴の運動法則がストークスの法則と一致するのは、連続的な媒体の場合だけであることを強調しました。その他にもストークスの研究結果に対する多くの議論が起きました。

ストークは晩年も研究を続けていましたが、レントゲンの発見を乗り越えることができませんでした。1898年には「X線の性質について」という論文の中で、陰極ビーム粒子の制動の結果として反陰極（陽極）上での短時間の電磁的インパルスを理論的に扱おうとしました。ドイツの物理学者J.E.ウィーチェルトと同様に、J.G.ストークスは、X線が非常に短い波長の発光であることは、X線の発生モードから明らかであるという結論に達しました。

科学のオーガナイザー、教育者としてのストークス
生前、ストークスはM.ファラデーからE.ファラデーに至るまで、イギリスの著名な科学者たちに囲まれていました。まだまだスターダムの瞬間を待っていたラザフォードら。

ストークスは最後の日が来るまで、科学的な出来事に関心を持ち、批判的に（いつも評価が正しかったわけではないが）評価していました。例えば、W.トムソンのように、J.K.マクスウェルの 論文に対しては寡黙でしたが、W.レントゲンによるX線による発見はすぐに認め急いで手紙で知らせました。

ストークスとその仲間たちは、精密科学と応用科学の発展、物理現象の解明方法の解明、自然哲学と科学的知識の区別、経験的活動と科学的活動の区別に多大な貢献をしました。彼や彼のような人たちのおかげで、大学教育の質が将来の研究者のニーズに沿ったものになリ、ストークは何十年も講義をしました。マクスウェルも彼の意見に耳を傾け、やがてストークの親友となりました。

ストレットの回想によると、ストークの講義や実験は彼に感銘を与え、教えることについて多くの有益なことを教えられたという。ストークスのコースの学生が、自分たちが理解していない光学現象の解明を彼に訴えたとき、彼は大抵の場合、親身になって対応してくれました。

19世紀後半と20世紀初頭の英語教育の伝統では、まず、生徒に説明する際には、自分自身がその質問を理解しているかどうかを確認することが大切だと指摘しています。第二に、クリアーの形を探すときに... プレゼンの... 新しいアイデアが浮かんできます。第三に、学生の質問は思考を刺激し、私たちがいつも標準的な方法でアプローチしている現象を新しい視点から見させてくれるので、創造的な思考にも役立ちます[11, p.261]。かつてストークがやっていたことです。

彼のコレクションから、ストークスは、学生が物理学や数学の問題に関連する1つまたは別の問題を解くことを勧めます。そのうちの一人は、等高線上の積分が、等高線を通過する流れの大きさに関係していることを証明することを提案した。今日では、このためにはストークスの定理を証明する必要があると言われていますが、ストークス自身はその証明を発表したことはありませんでした。1854年、トライポサス（ケンブリッジ大学の優等学士号取得のための公開試験）に合格したとき、ストークスの大学院生だったマクスウェルは、気体中の速度による分子の分布の問題を解きました。

1887年から1892年まで、ストークスはケンブリッジ大学の国会議員の一人であった。そのような責任ある立場にもかかわらず、合理的な心と冷静な性格のためか、下院での発言はほとんどせず、注意深く聞き役に徹していました。

強い宗教的信条を持つ家庭で育ったストークは、保守的な価値観と人生の信念を堅持していました。1886年にはヴィクトリア・インスティテュートの会長に就任しました。ダーウィンの進化論からキリスト教の原則を守るために設立されました（ストークスもダーウィンの進化論を批判していた）。また、イギリスと外国の聖書協会の副会長を務め、その宣教活動を支援していました。

1851年、ストークスはロンドン王立協会の会員となり、その後その幹事となり、1885年～1890年にはロンドン王立協会の会員-社長となりました。1849年から1903年までケンブリッジ大学のルーカス教授。1852年に光の研究で王立協会からラムフォード・メダル、1893年にはコプリー・メダルを受賞。ストレットのおかげで、1889年には男爵に昇格し、フランス学士院からアラゴ勲章を授与され、ロシア帝国軍医学校のメンバーとなりました。

ストークスのスタイルを評価し、彼についての本を書いたJ.ラーモアは、次のように述べています：ストークスの極端に慎重な研究発表の特徴は 質量で捉えた物質の性質と規則性に言及した定義の一般的なトーンで、正確さ、厳格な定式化は、分子という概念を使用することも必要としないようです [12, p.329]。

ストークスの仕事は、当時の科学文化の有機的な一部となりました。19世紀や20世紀の科学者たちがストークスの仕事を数多く紹介していますが、彼らの研究でストークスの研究結果に磨きがかけられ、発展したことは、彼の努力が無駄ではなかったことを証明しており、現代の科学のさらなる進歩を刺激する肥沃な材料となっています。

科学の古典の遺産
ストークスの発見-まず、ストークスの法則、ストークスの定理、ストークス・シフト、ストークスの方程式とそのパラメータ-は、科学技術の世界に入り込み、外国とロシアの科学者の開発活動を活性化させた。1909年にN. ボーアがレイリー理論を指定してストークス法にも言及していることを思い出していただければ十分です。

J.G.ストークスの存命中、彼の科学研究はM.ファラデー、J.C.マックスウェル、D.P.ジュール、H.R.ヘルツ（彼らはそれぞれ1867年、1879年、1889年、1894年に他界）、W.トムソン、W.ラムジー、J.W.ストラット、そして他の同僚たちによって続けられました。彼らとの会話や議論の中で、彼は新しいアイデアを得て、豊かになり、インスピレーションを得て、創作活動の中でさらなる発見をするきっかけを得ました。

彼の発見は、ストークがいなくなった後も科学者たちの想像力をかきたて、新たな成果へと導きましたが、今度は量子論と相対性理論の観点からです。H.A.ローレンツ、M.K.E.L.プランク、A.アインシュタイン、N.ボーア、A.A.マイケルソン、R.E.ミリカン、A.H.コンプトン、A.F.ヨッフェ、Y.I.フレンケル、S.I.バビロフなどの20世紀の科学者たちが、J.G.ストークスの思想の発展に貢献してきました。

ストークスは研究に関する本を書かなかったが、王立協会、英国科学振興協会（1869年に会長に就任）、ヴィクトリア研究所などの科学団体の論文発表数では、最も多作であった。彼の研究の成果は論文に反映され、各国の同僚との文通の対象となった。

ストークスの著作は、『数学・物理学論文』（1880-1905）の5巻に集められて出版されたが、そのうちの最初の3巻は彼自身が編集したものである。最後の2巻は1905年に彼の死後に出版されたもので、ストレットが書いた死亡記事が掲載されています。

1907年には、ストークスの簡単な伝記と、J.ラーモアが作成した彼の科学的な書簡が2巻で出版されました。また、若い才能を奨励するためにストークス財団（英語や外国人科学者による講演講座）も設立されました。

ジョージ・ガブリエル・ストークスは1903年2月1日、ケンブリッジで83歳で死去した。ミルロード墓地に埋葬されている。残念なことに、彼の墓は妻と二人の子供の墓とは違って保存されていません。ストークスの名誉を冠して命名されたのは：CGS単位系の粘度単位、月と火星のクレーター、鉱物ストークサイトです。

Литература
1. Клейн Ф. Лекции о развитии математики в XIX столетии. Т. 1. М., 1989.
2. Столетов А. Г. Собрание сочинений. Т. 1. М.; Л., 1939.
3. Погребысский И. Б. От Лагранжа к Эйнштейну. М., 1996.
4. Стрэтт Дж. В. (лорд Рэлей). Волновая теория света. М., 2015.
5. Эйнштейн А. Собрание научных трудов. Т. III. М., 1966.
6. Творцы физической оптики: Сборник статей. М., 1973.
7. Эйнштейн А. Собрание научных трудов. Т. I. М., 1965.
8. Кирхгоф Г. Избранные труды. М., 1988.
9. Вейль Г. Математическое мышление. М., 1989.
10. Лебедев П. Н. Собрание сочинений. М., 1963.
11. Капица П. Л. Эксперимент. Теория. Практика. М., 1981.
12. Тимошенко С. П. История науки о сопротивлении материалов. М., 1957.

1 Ротор векторного поля показывает, насколько и в каком направлении закручено поле в каждой точке.

2 Луи Мари Анри Навье (1785–1836) — французский математик и механик, один из основоположников теории упругости, с 1824 г. член Парижской академии наук.

3 Кинематическая вязкость — отношение динамической вязкости плотности среды к жидкости, дает понятие о ее вязкости под действием силы тяжести (измеряется вискозиметром по времени вытекания из калиброванной емкости).

4 Аберрация света — изменение видимого положения светила в небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли.

5 Михаил Сергеевич Молоденский (1909–1991) — советский геофизик, гравиметрист и геодезист. Разработал теорию использования измерений гравитационного поля Земли для целей геодезии. Предложил метод астрономо-гравиметрического нивелирования, новый метод определения.

6 Николай Павлович Неклепаев (1886–1942), ученик П. Н. Лебедева, исследовал вместе с ним поглощение акустических волн, преподавал в Московском университете, затем был ассистентом при кафедре физики Саратовского университета.

7 Институт Виктории (или Философское общество Великобритании) был основан в 1865 г. как ответ на публикацию книги Ч. Дарвина «О происхождении видов...». Институт Виктории пользовался значительным успехом в конце XIX в., когда Дж. Г. Стокс был его президентом (с 1886 г. до своей смерти). Максимальное число членов — 1246 человек — было в 1897 г., но быстро упало до менее чем трети от этого количества в первые два десятилетия XX в. Дж. К. Максвелл неоднократно приглашался для вступления в институт, но, хотя он и был набожным евангелистом-христианином, он отказался от приглашений из-за узости тематики и консерватизма института.

ストークスの光の波動理論の研究
ちょうどこの頃の科学の世界では、物理学の機械化や弾性理論の基礎とともに、光の波動説が生まれ、O.J.フレネルの「準固体エーテルは動く物体に部分的に付随する」という仮説が出て、エーテルの数学的な理論も登場してきました。このような展開の中で、ストークスは重要な役割を担い、特に光学の発展に大きく貢献しました。ストークスは生涯にわたって光の波動理論の支持者であり続け、適切な数学的装置を使用し、実験はニュートンとほぼ同じ条件で行われました。［訳注）ニュートンは光の粒子説でした］

上図は，ストークスシフトの概念図．これは、吸収スペクトルと放出蛍光スペクトルのずれを示しています．横軸は波長です．蛍光スペクトルは吸収スペクトルより波長が長い．

ストークス（彼の多くの同時代人と同様に）は光の収差、ニュートンリング、光の干渉と偏光、および媒質を通過する波動、スペクトルなど光学現象を研究しました。ストークスの波動理論への貢献は非常に大きい。彼の学生であるストレットは論文「波動光学理論」で、J.G.ストークスを（O. J.フレネルに次ぐ）引用数2位としました。 [ 4、p.206]

1852年、ストークスは電磁波の偏光ベクトルを表す量を提案しました。彼によって導入されたパラメータは、列ベクトルであり、光強度の次元を持つています。詳細なパラメータは、総強度、偏光度、および楕円偏光度を使って、インコヒーレント光や部分偏光を記述できます。

ストークスは、蛍石（フルオライト）の観察中に発見した発光も扱っています。同じ1852年に、ストークスは、フルオライトによって放出された光線は吸収された光線よりも屈折が少ないという結論に達しました（後にE.K.J. vonロンメルとS.I.バビロフによって一般化された）。蛍光の波長は励起光の波長より長い。ストークスにちなんで名付けられたこの規則は、蛍光（フォトルミネッセンス）の量子性を示すものだったのです。

1879年、ロンメルは、スペクトルの一部で放射周波数が励起光の周波数よりも高いことを発見しました。ストークスの法則と矛盾するスペクトルのそのような部分は、反ストークス線と呼ばれていました。ストークスは、ニュートンが提案したクロスプリズムの方法に続き、クロスフィルターの方法による発光の観測を導入し、発光を利用した近紫外領域の検出・研究方法を提案しました。

1905年、アインシュタインは彼の記事「光の出現と変換に関する発見的観点について」で次のように述べています [ 5、p.103]。光が量子で構成されている場合、ストークス規則からの逸脱は2つの理由で可能です。1つは、単位体積あたりの量子の数が多い場合（励起された光の量子は多くの励起された量子からエネルギーを受け取ることができます）。第二に、発光中に放出された量子のエネルギーが励起量子のエネルギーよりも大きい場合。

ストークスの時代には、発光に関する研究は偶然の性格を持つものでした。バビロフはその基礎研究に人生の30年を捧げました。ストークスの法則の限界を決定し、熱力学の第二法則の始まりとストークスの法則を関連付け、発光の絶対収量を定式化し、その種類を分類し、放射体の性質に関連づけたのは彼でした。そして1950年には「光の微細構造」にまとめている。その少し後にバビロフは、主にストークスのルールを含むいくつかの一般的な法則を発見したにもかかわらず、発光は物理学の人里離れた島のままであると書いた。アインシュタインがストークスの法則の意味を説明できたのは、1905年の量子論に基づいてのことです。1913年にはボーアの原子構造の量子論によって、発光の全分野、そのすべてのセクションの主要な特徴が明らかになりました[6, p.335, 338]。

エーテル理論のどれが正しいと考えられていますか？
ストークスは長寿だったので、エーテルのいくつかの理論の変遷を見ました-エーテルとは、その振動が可視光を含む電磁波として現れるような一種の万能媒体です。O. J.フレネル、O.L.コーシー、W.トムソン、H.A.ローレンツ、J.A.ポアンカレ、M.C.E. L. プランク、等がエーテルの解釈を提案しました。ストークスも関心がありました。

異なる科学者の考えにおけるエーテルは、均質性、圧縮性などの程度、および軌道上を移動するときに地球によって運び去られる程度が異なっていました。エーテルの特性についての理解に応じて、科学者はマクスウェルの方程式をさまざまな方法で解釈しました。ご存知のように、ストークスとトムソンはそれを抑制して扱いました。エーテルの否定は、アインシュタインによる相対性の理論の後です。

特に、フレネルはエーテルが非圧縮性であるという仮説を提唱しましたが、それは物質中を透過するのが困難である横方向のせん断を可能にします。ストークスは、樹脂のように、エーテルは急速な変形の間は剛体のように振る舞い、惑星が動くときはプラスチックのように振る舞うという事実によってこの困難を説明しました。1839年、コーシーは収縮するエーテルの理論を作りこのモデルを改善、これは後にトムソンによって洗練されました。

1845年に収差の理論（ある基準座標系から別の基準座標系に移るときの光の伝播方向の変化）を作りました。ストークスは、地球が移動するときに周囲のエーテルも運び去ると仮定して、その結果、地球表面のエーテルの速度は惑星の速度に等しくなります。科学者は、いっしょに運ばれるエーテルの動きが、惑星を取り巻く空間とそれが静止している領域の両方で渦なしの特徴を持っていることを認めました。ストークスによれば、エーテルは硬くも柔らかくもあり、通常は液体媒体のような振る舞いをします。

銀河のエーテル風の流れによる地球表面の流れの架空図（左）（1- エーテル圧力が上昇したゾーン; 2- エーテル圧力が低いゾーン; 3- 海からの水分捕捉のゾーン; 4- エーテルのトロイダル渦が冬に大気を捕捉する）、および、科学者が自然界にエーテルを探せなかったことの風刺画。

ストークスは、収差効果について次のような説明を提案しました。地球の表面から一定の距離になると、エーテルの巻き込み部分とエーテル全体の速度差が現れるはずで、この差により、光学素子に当たる光波の前面が回転してしまう。これが収差を惹き起こします。ストークスは、エーテルの運動が渦なしの速度ポテンシャルの形であることを証明する計算で説明を補足しました。その後、プランクはストークスの理論を肯定的に捉え、それを救おうとしたが、役に立たちませんでした。

ストークスは、エーテルの巻込み程度が、その密度の違いだけに依存するのではないことも指摘しました。エーテルは物質の中に入ると圧縮され、離れると希薄化して物質の粒子に引き寄せられることが予想されます。弾力性のあるエーテル論は、非常に長い間、科学界に根付いていました。実際、ストークスをはじめとする当時の著名な物理学者たちは皆、その性質や本質を一般的に解明することに取り組んでいました。

1846年、ストークスは次のように書いています：我々は、よほどの理由がないと、エーテルが地球の固体質量の中を完全に妨げられずに移動するのを信じることができません。しかし、それを正しいと考える理論をチェックする決定的実験は非常に有用であろう[7, p.235]。1881年、A.A.マイケルソンは、J.G.ストークスが仮定したように、エーテル風が地球によって運び去られることを実験で確立したように見えた。しかし、エーテル否定の結論はまじかに迫っていました。

ストーク自身も、エーテルの概念に固執した彼の同僚も、その本格的な理論を作ることができません。I.フィゾーの発言によると、1851年に提示されたエーテル仮説の中には多かれ少なかれ可能性はあるが、どれも証明されたとは考えられません[6, c.214]。10年後のストークスは、仮説の長所と短所について議論を続けたが、彼自身はこれが成功するとは期待していませんでした。

ストークの死後、1905年には、アインシュタインは、相対性理論と光速不変を提唱しました。その結論によると、これらの前提条件は単純で矛盾のない移動体の電磁気学を構築できる。光を運ぶエーテル」の導入は、余計なものに見えます[7, с. 8]。この瞬間から、ストークスの理論だけでなくエーテルに関する数多くの理論がその価値を失うことになりました。

■今回の節では，ストークスの研究のうち，光の波動論とエーテル仮定を扱います．前者は成功しましたが，後者は無意味でした．

偏光状態を表示するストークス・パラメータ，反ストークス線については，
訳者が別稿で解説する予定です．

科学者であるストークスは、数学から美的快楽と実用的満足感を得た。半収束級数の指摘、完全収束または限定的収束の無限級数の研究、整数列と級数の一様収束の概念の導入、ベクトル解析に取り組んだ。彼が提案した最も重要な公式の一つは、彼の名が冠されたストークスの公式です。

［訳注］
ベクトル場の回転を閉曲面上で面積分したものは、ベクトル場を閉曲面の縁で周回線積分したものに一致するというものです。

ベクトル場A(x,y,z)とは、平面あるいは空間の各点でベクトルが定義されているものです。例えば、天気予報で風の向きと強さが矢印で描き込まれたマップをよく目にすることがあるでしょう。
ベクトルの回転は，上の式でrotAと書かれているものですが，ベクトル解析は別の稿にまわします。話をもとに戻します。

1849年には友人のトムソンがストークスからこの公式を入手しています。ストークス自身は、1849年から1882年まで毎年行っていた数学の試験にこれを含めることが有用であると考えていました。 1910年には、ドイツの理論物理学者A.I.W. Sommerfeldがストークスの結論を4次元空間に一般化しました。J.C.マクスウェルは、彼の論文 "On Faraday Force Lines" (1885-1886)で、ストークスの結論をベクトル解析の重要な定理として、C.F.ガウス、J.グリーン、M.W.オストログラドスキ、W.トムソン、そしてもちろん、J.G.ストークスの名を冠した。

当初、科学者たちは、液体や気体の力学と固体の力学には共通点がないと考えていました。しかし、1845年、ストークスは固体と粘性液体の共通の性質を発見しました。固体物質の可塑性が高まると弾性が低下し、固体は液体状態になっていくという結論です。ストークスの考えは価値あるものであることが証明され、その後の一連の科学的研究を刺激しました。

フランスの科学者L.M.A. ナビエ, O.L. コーシー, S.D. ポアソンなどが粘性流体の研究に成功しました。ストークスは1849年に彼の論文「移動する流体の内部摩擦の理論と弾性固体の平衡と運動について」で、粘性流体と気体の微分方程式を導出することによって、ナヴエの理論を補完しました（分子の概念とは無関係です）。これらは今日ではナビエ・ストークス方程式として知られています。この科学者に敬意を表して、CGS単位系で動粘度の単位は、後にストークス（ロシア語表記：St、国際St）と呼ばれるようになりました。国際単位系では、粘度のSI単位はm^2/sです。

ストークスは層状境界層の理論も構築しました。彼は乱流における層流の遷移の事実を確立した - 最初は液体の流れる水道管や物体に対して（研究は抵抗の値に境界層の剥離の影響を研究するために実施された）。時を経て、船、航空機、タービン、蒸気機関の高速化に起因する乱流の理論が大きく発展しました。

科学史家 I.B. Pogrebyskii が定義したような、物理的側面への注目、実験結果の考察、運動の明確な運動学的描写、オリジナルの動的原理の網羅的な定式化、これらすべてが、理論の成功した応用と組み合わされて、ストークスの研究は粘性流体の理論に関する更なる研究の主要な出発点となりました [3, p.127]。

分子間の距離や分子間の相互作用による液体速度の不規則な成分を無視して、ストークスは液体粒子の近傍での液体の平均的な規則速度のみで計算しました。彼が粘性流体の運動方程式を導出することを可能にしたのは、流体粒子のひずみ速度の6つの成分に対する応力の6つの成分の線形依存性に基づくと仮定したからです。

流体を連続的な媒体として考えたストークスは、「内部摩擦」の概念を採り入れ、その計算に基づいて、円柱内の粘性流体の回転に関して、ニュートンの解析を修正した。ストークスが示したように、ニュートンの間違いは、液体中の隔離された各層の外部表面と内部表面に作用する摩擦力のモーメントの代わりに、力そのものを考慮したことである。ニュートンは、流体粒子の1回転の時間が円筒状の層の半径に線形に依存することを発見し、ストークスの結果から、時間は半径の2乗に比例することがわかりました。その結果、円筒管内の定常流における粘性非圧縮性流体の流量についても、ハーゲン-ポワズイユ式を理論的に説明できるようになった。やがてストークス自身も、速度の時間変化の法則を記述した微分方程式を得ました。

1851年、科学者は、束縛されていない粘性流体の中で、そのゆっくりとした均一な運動の間に小さな固体球に作用する抗力Fの公式を導出しました。ストークスの公式はＦ＝６πＲηｕ形です。ここでＲとｕは球の半径と速度、ηは流体の動的粘性係数で、この法則は非常に小さな半径でも真であることが判明し、A.アインシュタインは後に糖分子の半径を測定するためにこれを使用しました。

ストークスの法則は、新しい研究で広く使われました。私は、A.アインシュタインによるブラウン運動の計算、J.J.トムソンによるイオンの電荷の決定、R.ミリカンによる電子電荷の決定を思い出します。ミリカンの実験と自身の実験を分析した結果、ミリカンがストークスの公式で誤って空気粘度の値を使ったので、素電荷を正確に決定することができなかったことがわかりました。このチェックの結果は、ストークスの法則の正しさの確認になりました。

論文 "移動する流体の内部摩擦の理論について" (1845) で、ストークスは物体が等時性振動を起こすのは、小さな変形範囲では、物体に生じる応力が変形量に比例するという事実によることを示し [4, p. 116]、橋梁のたわみについても研究しました。ウェールズの鉄道橋の崩壊を知り、変形したときの鋳鉄の脆さが原因であると解明しました。ストークスの橋梁の動的たわみに関する研究は、工学的な応用研究に近いものです。
弾性の理論を扱い、弾性体と塑性体を考察し、自然界では弾性と塑性は切り離せないものであり、実際には両者の間には急激な変化はないと考えました。

ストークスはまた、液体の中での音の吸収についても研究した。しかし、彼は粘性を散逸（散逸）メカニズムと考えながらも、熱伝導率を考慮に入れていなかったため、彼の分析は不完全なものでした。しかし、J. R. von マイヤー、J. P. ジュール、H. L. F. von ヘルムホルツがエネルギー保存法則を発見（当初は不信感を持って科学界に受け入れられていた）をするまでは、これを解決できませんでした。

ストークスは科学活動の初期の頃から、主要な力学者、流体力学者としての地位を確立していました。F. E. ノイマン、J.A.ポアンカレ、P.M.M. デュエム、T.レヴィ＝チヴィタ、M.V.オストログラドスキー、P.L.チェビシェフのように、彼は力学の理論的基礎の開発に貢献しました。同時に、弾性理論は、彼によって開発されました。 1860年代までに。若いジョージ・ストークスは、ケンブリッジの科学界で、理論力学、数理物理学、水力学の熟練した研究者として、光学の専門家として、同時に新世代の科学者たちの辛抱強く親しみやすい教育者としても知られるようになりました。

ジョージ・ガブリエル・ストークスの生誕200周年の節目に
«ПРИРОДА» №1, 2020，ロバート・シュチェルバコフより，
教育学博士（エストニア，タリン）

https://elementy.ru/nauchno-populyarnaya_biblioteka/435633/Dzhordzh_Gabriel_Stoks_klassik_matematicheskoy_fiziki_KhIKh_veka

J.G.ストークス（1819-1903）は、アイルランド出身の英国の数学者、機械工学者、物理学者：理論力学、流体力学、弾性理論、振動理論、光学、数理物理学、数理解析。彼はロンドン王立協会の会員であり、その秘書兼会長を務め正確な科学を推進した。

19世紀のイギリスでは、数学的分野とともに物理学的分野も発展しました。伝統的な自然哲学（当時は自然科学と呼ばれていた）から、独自のアプローチと方法を持つ独立した科学、物理学が誕生し、最初の物理研究所が誕生しました。

彼の同胞の多くと同様に、J.G.ストークスは、19世紀の自然科学の中心地であったケンブリッジの伝統を大切に守り発展させました。理論的な力学と光学の問題を解くために、まず第一に数学的方法を用いることです。研究に実験を適用することはごくまれでした。

科学者としてのストークスの形成

プロテスタント福音司祭ガブリエル・ストークスの6人の子供の末息子であるジョージは、1819年8月13日にアイルランドの村で生まれました。

家族は宗教的であり、彼の兄の3人は後に司祭になりました。そして彼自身、科学に専念し、生涯を通じて世界に対する彼の宗教的な世界観を保持しました。

1835年には 16歳のジョージはイギリスに渡り、ブリストルカレッジに入学しました。2年間の見習い生活は、彼の数学的能力の開発に重要な瞬間であり、ケンブリッジでの彼の研究のために自分を準備するのに役立ちました。1841年、ストークは大学で教育を受け、ケンブリッジでは教職にも就き、1849年には数学のルーカス・チェア（世界で最も権威のある学術的地位であるルーカス数学教授を、記録的な54年間務めた）を受けました。当時はJ.ニュートンが会長を務めていました。

ストークスは66年間の科学的活動において、機械工学と光学の古典的な研究から、地球の重力場、仮想エーテル、スペクトル分析の応用まで、彼の世紀の物理学のほぼすべての分野をカバーしました。ただし、電磁気学だけは彼の興味の外になりました。これらの科学分野では、ストークスは、数学的方法のエキスパートだったので非常な成功を収めました。

F.クラインが強調したように、イギリスの数理物理学は、ストークスとウィリアム・トムソン［訳注）やはりアイルランド出身で同時代の物理学者］がケンブリッジの若い才能に現れて以来、途切れることなく華麗な上昇を続けました。ストークスは1837年から死までの66年間、最初は研究者として、次に教育者および管理者として、ケンブリッジに住みました。優しい個性で、彼の広範で継続的な非常に有益な活動を行いました [1, p. 259]。

ストークスは、ケンブリッジのペンブローク大学の部屋で数学を応用して実験を開始しました。1871年から1872年にかけて、イギリスの科学者たちがオックスフォード研究所や（J.C.Maxwellの努力により）ケンブリッジ大学のキャベンディッシュ研究所などの物理学研究所を設立したのは、正確な体積測定の必要性が高まってきたからに他なりません。52歳のストークスにとっては残念ながら、少し遅かった。

開所当時、J.K.マクスウェルの研究室を訪れたA.G.ストレトフによると、当時、物理学の研究は長い間、数学のコースに含まれており、物理学のための特別な学科の存在は、その用語自体と同様に新しいものでした。1871 年までケンブリッジでは数学の一部としての光学と化学の一部としての熱の章だけが教えられていました。電気と磁気の広範な科学は全く教えられていませんでした [2, p. 342]。

おそらく、このことが、数学、理論力学、光学、仮想エーテルなどの科学活動の方向性と、そのような英国の科学者（ストークスを含む）の選択ができたのでしょう。ストークスは時折、今日の基準では最も単純な実験的調査を用いて、彼が既に行った理論的な結論を徹底的にチェックしました。

ストークスの研究における力学と流体力学
J.G.ストークスは、J.グリーン、W.トムソン（ケルビン卿）、W.J.M.ランキン、O.レイノルズ、J.W.ストラット（レイリー卿）らとともに、数学的手法の開発に成功した。- 数学的方法の開発に成功し、古典的な数学物理学の発展に貢献し、当時の物理学や工学の問題に数学を適用した。その世代の科学者のおかげで、熱伝導、拡散、弾性と運動の安定性の理論、振動と波動の過程、光学、電位理論と電気力学の多くの問題を解決するために数理物理学の方法が開発されました。これらの方法は、現代の物理学、工学、産業界に関連しています。

J.G.ストークスの親しい同僚、教え子、友人たち。
左から、J.C.マックスウェル、J.W.ストラット（レイリー公）、W.トムソン（ケルビン公）。

コンスタンチン・ボグダノフ
「クォンタム」2014年第4号、第5号、第6号、第7号、第8号

エンペドクレスは、2500年前にシチリア島に住んでいた古代ギリシャの哲学者、医師、司祭でした。

エンペドクレスは、万物は土、空気、火、水の4つの要素で構成されていると考えました。愛と憎しみ、あるいは好きと嫌いという二つの対立する力は、これらの要素に影響を与え、それらを統合しあるいは分離し無限の様々な形を作る。

私たちの時代は、物質は原子と分子で構成されていることを誰もが知っており、エンペドクレスの推論は、笑われてしまいますが、エンペドクレスが語った無限の多様な自然は、分子および原子の化学反応に置き換えることができます。

そして、愛と憎しみ、共感と反感はどのような関係があるのでしょうか？
例えば、一枚の紙がコップ一杯の水を愛したり、マッチが石けんを憎んだりすることは、どのようにしてできるのでしょうか？

有名なレオナルド・ダ・ヴィンチが言ったように、真実を判定する唯一の基準は実験であるから、これらの質問に答えるために、簡単な実験を設定しましょう。

実験1.一枚の紙は水の入ったグラスを好むのか？

厚手の紙から一辺15cmの正方形を切り取ります。壁のカレンダーのカバーはこの目的に最適です。水道水の入ったグラスを取り、それを四角い紙で覆い、そっと裏返し、紙をグラスにしっかりと押し付けます。

グラスを裏返し、水の動きが止まったら、紙の保持をやめて手を横に離します。私たちがすべてを正確に行えば、一枚の紙は水の入ったグラスからはがれず、いわばそれに引き付けられます（下の写真を参照）。エンペドクレスは正しい。一枚の紙が水の入ったグラスに恋をしました？なぜこのようなことが起こるのでしょうか？

実験2.なぜマッチは石鹸を嫌うのか？

大きな容器（料理やゼリーの下ごしらえ用のトレー、直径30cm以上の深鍋や鍋、バケツや湯船でもOK）を持っていく。石鹸液の残りを洗い流し、冷たい水道水で満たしておきましょう。次にマッチを持って、その頭を任意のシャンプーに一瞬だけ浸してから、このマッチを水面にそっと置いて離します。マッチの頭が水に触れた「石けんスポット」からすぐに離れるのがわかります（下の写真）。それはまるでマッチがエンペドクレスの言葉を借りれば、石鹸液を嫌って純粋な水に寄り添うかのようだ。なぜ？

実験１と実験２を説明するためには、まず、エンペドクレスの要素の一つである空気が何であるかを知る必要があります。人間は空気なしでは生きられないことを誰もが知っています。私たちの体は空気中に含まれる酸素を必要としています。空気の存在を検出するのは非常に簡単です。これを行うには、あなたが紙のシートを持ち、団扇のようにそれを振ると、移動する空気を顔に感じるでしょう。

 地球の表面の上にある空気の層の厚さ-約100キロ。この地球の空気層は大気と呼ばれています。空気は水の約1,000倍の軽さですが、大気はかなり大きな力で私たちの体の表面のあらゆる部分を押しています - １平方センチメートルあたりの力は、１kgの重さに等しいのです。この圧力を大気圧といいます。

山上の大気の厚さは海上よりも薄いので、山上の高いところの空気は圧縮されておらず、気圧が低いということになります。例えば、エルブルス山の頂上では、気圧がソチの半分になっています。

気圧は登山時だけでなく、気温や湿度の変化でも変化します。モスクワの気圧がトゥラ［訳注）モスクワの南100kmにある］よりも低くなると、トゥラからの圧縮された空気がモスクワに向かって移動し始め、南風が吹きます。そのため、気圧を測定することで、天気予報に役立ちます。

フランスの有名な科学者ブレイズ・パスカルは、登山中に気圧の存在を証明し、その低下を実証した最初の科学者です。さらに、パスカルは最初の機械式計算機を設計しました。圧力測定の単位（1パスカル＝1N/m^2）とプログラミング言語の一つにパスカルの名前がついています。

実験3.水から空気を作る方法は？
これは大人の目の前で行うのが一番です。ビニール袋に少量（30ml）の水を入れ、空気を絞り、上部でしっかりと縛ります。そして、袋を電子レンジに入れてスイッチを入れます。数秒後に袋が膨らみ始め、約1分後には電子レンジのほぼ全容量を占めるほど膨らみます。

袋がかなり熱くなることがあるので注意が必要です。2つの質問に答えてください。
1.密閉された袋の中の空気はどこから来たのか？
2. 密閉された袋の中に水を入れていない場合、電子レンジはスイッチを入れたらどうなるでしょうか？

この実験と実験１の説明("一枚の紙はコップの水が好きなのか？") の動画があります。

実験３「水から空気を作るには」では、エンペドクレスの一つの要素（水）から別の一つの要素（空気）が生まれました。実験では、水と空気は熱したり冷やしたりするとお互いに変化し、なんとなく似たような感じになることがわかりました。電子レンジで加熱すると密閉された水の入った袋が膨らんでしまう理由がわからなかった方は、こちらで解説しています。

実験４．グラスはなぜ歌うのか？

この実験は、大人の目の前でやった方がいいと思います。実験には2つの同じグラスが必要です。片方は半分を水で満たし、もう片方は空けておきます。空のグラスの足（スタンド）を左手でテーブルの表面に押し付けます。次に右手の人差し指を水で湿らせ、空になったグラスの上端に沿ってゆっくりとまわしながら、端の指の圧力を少しずつ高めていきます。圧力が十分であれば、この指の円運動で音が出ます。次に、半分が水で満たされたグラスで同じことをします。水の入ったグラスが低い音を出すのが聞こえてきます。

2つの質問に答えてください。
1. なぜグラスが歌い始めるのか？
2. 歌うグラスに水を入れると音程が下がるのはなぜ？

この実験の動画は、Quanticsのウェブサイトに掲載されています。https://old.kvantik.com/files/materials_2014_06.html

イギリスの科学者ロバート・フック(1635-1703)は1660年に、力とそれが引き起こす固体の変形を結びつける法則を発見しました。この法則は、現在ではフックの法則と呼ばれていますが、身体の弾性変形は力の大きさに正比例するというものです。ラテン語では、フックはこの法則を次のように記しています。"Ut tensio, sic uis" 文字通りの意味は "力と同じくらい伸びも同じくらい" 当時、科学者たちは、他人に流用されることを恐れて、発見を暗号化することがありました。フックは彼の法律のラテン語の言葉からアナグラムを作った - アルファベット順に文字を並べ替えた。"ceiiinosssttuu". 彼は1676年にこのアナグラムを発表し、1678年に解読しました。

フックが残した多くの発見や発明の中でも、彼の最も重要な技術的発明である、当時としては前例のない精度を持つ懐中時計について言及しなければなりません。1日1分の誤差を達成しました。このような高い精度を確保するために、フックはアンカー機構（図1）とスパイラルスプリング（図2）を時計のデザインに取り入れました。フックの発明以前は、時計は15分以上の誤差で進んだり、遅れたりするので、毎日巻かなければなりませんでした。19世紀末までにフックのゼンマイ時計は改良され、その精度はさらに10倍に向上し、船乗りは正午の時刻を確定し、海上での経度を0.5度の精度で知ることができるようになりました。

実験４「グラスはなぜ歌うのか」では、ガラスの縁に沿って濡れた指を動かすとガラスが鳴りました。ガラスは川の砂でできており、他の岩石（花崗岩、大理石、石灰岩など）とともに地球の地殻の一部であることが知られています。このように、ほとんどすべての固体は、エンペドクレスの「土」の要素と考えることができ、そのすべてが音源となりうる。では、なぜ固体の接触が音の発生につながるのか、その疑問に答えてみましょう。

実験4 "グラスはなぜ歌うのか？"

グラスがなぜ歌うのかを理解するためには、まず音とは何かを理解する必要があります。これは別の記事で取り上げますが、今のところは「音は空気の振動である」と言っておけば十分です。

固体の振動を伝達して、空気が振動することがよくあります。例えば、人が話すと声帯が喉の中で振動して声が出る。人がギターを弾くとき、弦を揺らしたり、捻ったり、指で叩いたりして音を出します。少し違うのは、バイオリンを弾いた時の音です。ミュージシャンが弓で弦をこすると、摩擦で弦が引っ張られている状態になりますが、弾性力はそれを引き戻す傾向があり、この力が摩擦力を超えるとすぐに、弦は戻り繰り返され、音が聞えます。

歌うグラスは、バイオリンとほとんど同じです：グラスの縁に沿って指を走らせると、皮膚の小さな凹凸がグラスにまとわりついて、グラスが振動します。バイオリンの弦との違いは、これらの振動がミクロなもので、目で見ることができないことです（指で感じることはできますが）。しかし、グラスの中に水がある場合は、グラスの水面に波が現れるのを見ることができます。これは、ガラスが本当に振動していることを意味します。

実験を成功させるためには、ガラスと指が油っぽくないことが重要です（摩擦力がここで働くので）。

水の入ったグラスの方が水の入っていないグラスよりも低い音がするのはなぜでしょうか？
正確な説明は簡単ではありませんが、おおよその現象は次のように説明できます。
空気の振動をゆっくりとさせるような音が、私たちには低く見える。
ここで、バネ振り子で、バネに重りをつけたものを想像してみましょう。Kvantikのサイトに投稿された動画では、プラスチック製のバネとミカンで作れるバネ振り子の振動を確認することができます。経験上、ミカンのあるバネは、ない場合に比べて、はるかに振動数が小さいことがわかります。実際、荷重が大きくなるほど、バネが元の位置に戻るまでに時間がかかります。グラスに水を入れると質量が増えるので、ミカンをくっつけたときのバネのように振動数が小さくなります。

http://kvantik.com/files/materials_2014_07.html

ーーー

2つのフォークを取り、それらを組み合わせ、それらの間の隙間に木製のつまようじを刺します。次に、この構造をガラスのゴブレット（または背の高いグラス）に置き、つまみでガラスの端にのみ触れるようにします（右の写真を参照）。同時に、構造物が落ちないように、端にしっかりとぶら下がるようにしてください。これが実際に実行できるという事実は、Kvantik Webサイトのビデオに示されています。

次に、2つの質問に答えましょう。
1. 　2つのフォークと1つのつま先の構造が非常に安定しているのはなぜですか？
2.　この構造の重心はどこにありますか？

古代ギリシャの有名な科学者アルキメデス（紀元前287～212年頃）は、彼の2世紀前に世界の根源を4つの要素としたエンペドクレスがいたアクラガス（現在のアグリジェント）の町から100キロ離れたシラクーサ（シチリア島）に住んでいました。アルキメデスは幾何学が好きだったので、いくつかの物理法則を発見し、そのうちの1つには彼の名前が付けられています。

アルキメデスの法則は次のように述べています：液体（または気体）の中に沈められた身体は、身体によって変位された液体（または気体）の重量に等しい力を受けます。紀元前1世紀に生き、ユリウス・シーザーの時代にローマの水道橋を設計したローマの建築家ヴィトルヴィウスの書物から、世界は初めてアルキメデスの法則を知った。ヴィトルヴィウスによると、アルキメデスは入浴中に自分の法則を発見し、その直後に裸で家から飛び出し、ギリシャ語で「見つけた！」という意味の「ユリイカ！」と叫び始めたという。

アルキメデスが発見した同じように有名な法則に「てこの法則」があります。古代ギリシアの作家プルターク（45-127）は、アルキメデスが「てこの法則」を利用しようとした珍しい方法を伝えます。アルキメデスは、友人でもあり身内でもあるギエロン王に、与えられた力でどんな重さでも動かすことができると書いたことがあります。要するに「支点をくれたら世界をひっくり返す」ということです。

アルキメデスは、物体の重心の概念を最初に導入し、三角形や平行四辺形の形をした平たい物体の重心の位置を求めた。忘れてしまった方のために、物体の重心とは、その物体の重力の力（地球に引き寄せられる力）が集まる点です。覚えておきましょう。

壁に打たれた釘に物体を吊るすと、数回の振動の後、物体は静止し、その重心は懸垂点の下、つまり懸垂点から垂直に下っていく線上にある。この重心の性質を利用して、図に示した図形の重心の位置を求めてみましょう（Kvantikのサイトの動画も参照してください）。まず、A点から物体を吊り下げ、落ち着いたらA点を通って赤い線を縦に引きます（右図のように）。次に、同じようにB点から物体を吊り下げて青い線を引きます（右図のように）。この図の重心であるC点で線が交差していることがわかります。多くの場合、物体の重心がこの物体の外にあることもあります。Kvantikのサイトに掲載されている動画を見ると、2つのフォークを繋いだ時の重心が2つのフォークの間にあることがわかります。

実験5　 なぜフォークは落ちないのか？

2本のフォークをつまようじで固定した構造が、ガラスの端に置いたときに非常に安定していることを示しています。安定している理由は、構造物の重心が支点の下にあるからです（左の図で重心が青、支点が赤で表示されています）。この説明が本当なのかどうかは、もう一回実験してみると（Kvantikのサイトの動画を見てください）わかると思います。

実験６　ボールはどうしてグラスの中に入るのか？

卓球のボールとグラスを持って、テーブルの上にあるように置きます。手などでボールを触らずにグラスに入れることは可能でしょうか？ボールをテーブルの端に押し付けて、グラスでキャッチするなどは禁止です。実際にこれが可能であることは、Kvantikのウェブサイトに掲載されている動画でも紹介されています。

では、2つの質問に答えてください。
1. 　グラスの中にボールを引きあげ保持する力は何か？
2. 　この実験は、グラスの壁が上に伸びている形状でも可能でしょうか？

実験6 　ボールはどうやってグラスの中に入ったか？
グラスを逆さにしてボールにかぶせ、グラスを回転させる。ボールがグラスの中で回転するようにグラスの壁をボールに押し付け続けます。グラスの口（首）の近くでは壁が先細りになっていて、その傾斜のために横だけでなく上にもボールを押し上げます。ボールの立場で見た場合、それは、遠心分離機や回転木馬のように、ガラスの壁に強く押し付けられ、グラスの軸から最も遠い領域（グラスの壁）に押し出されます。（動画を見るとよくわかります）https://old.kvantik.com/files/materials_2014_08.html

口（首）が拡大しているグラスの場合、この方法は適していません：ボールはグラスから排除されます。

アーティスト アルチョム・コシュチュケヴィッチ

参照
コンスタンチン・ボグダノフ氏による大衆科学講演会「私たちの中の物理学」，2007年12月13日，モスクワ，ФИАН

http://video.elementy.ru/fian/Bogdanov-fpff.mp4

https://elementy.ru/nauchno-populyarnaya_biblioteka/izbrannoe/432676/Chetyre_stikhii_Empedokla

https://elementy.ru/kartinka_dnya/53/Dvoynoe_lucheprelomlenie?from=rxblock
2016年5月11日 • Pavel Plechov　
この記事は簡単なので入門にはよいのですが，あまり正確ではありません．結晶光学については，物の記事で解説します．

岩塩haliteと方解石calciteの結晶
写真は、岩塩とアイスランドスパー（方解石）の結晶の大きな断片を示しています。外見上、それらは類似していますが、光学特性が大きく異なります。

岩塩結晶は立方晶系に属します。光は方向に関係なく同じ速度で結晶を通過します。このような結晶は、光学的に等方性と呼ばれます。

一方、方解石結晶は顕著な光学的異方性を持っています。結晶に入った光線は2つの互いに垂直に電場が振動する光線に分かれ、異なる速度で結晶内を移動します。一方の光線の速度は、もう一方の光線の速度より11.5％高速です［訳注：光軸に垂直に伝播する異常光のこと］。このため、複屈折、または複屈折の光学現象が発生します。各光線には独自の屈折率があり、結晶内で異なる方法で屈折します。結晶のある点に入った光線は、結晶内で異なる経路をたどり異なる場所に出て、そのうちの1つは遅れて現れます。写真は、方解石の後ろにある「кальцит」の刻印が二重に見えるのに対し、岩塩の後ろにある「Галит」の刻印では何も起こらないことを示しています。

-----
［訳注］もう少し正確に言うと，方解石の結晶構造は，３方晶系（光学的には１軸性です）．光軸方向に進む２つの偏光は同じように進む（分かれません）．それ以外の方向に進む光線は複屈折を示します．複屈折の大きさは，光軸に垂直な方向に進む光で最も大きくなります．
結晶内を伝搬する２つの偏光は，通常光と異常光と呼ばれます．通常光の伝播速度は結晶内のどの方向に伝播しても同じです．
ここで，使われている光の速度とは伝播する光の位相速度のことで，物質の屈折率をnとすれば，物質内で光の速度は1/nになります．
-----

一枚の紙にカルサイト結晶
箱の中の紙の上に横たわる方解石結晶による複屈折。
en.wikipedia.orgからの写真

偏光面を回転させて方解石の複屈折を見る
結晶の方位に対する偏光面の方向によって方解石の複屈折の大きさが変わります：en.wikipedia.orgからの描画

複屈折の効果は、1669年にデンマークの科学者エラスムスバルトリン（1625-1698）によって最初に説明されました。彼はそれをアイスランドからの船員によって運ばれたアイスランドスパーの結晶で見つけました。E.バルトリンの出版は、「神は1つの無生物を創造したので、それだけでは2つになることはできない」という同時代の人々からの大きな批判を引き起こしました。方解石の複屈折の現象そのものが、アイザック・ニュートン、クリスチャン・ホイヘンス、ジョージ・ストークスなどの科学者を悩ませました。19世紀初頭、トーマス・ヤング（1801）とオーガスティン・ジャン・フレネル（1820）による光の理論に関する研究により、アイスランドのスパーの効果が理解できるようになり、開発の可能性が開かれました。結晶光学の誕生です。

ウィリアムニコールは、1829年に最初の偏光器を設計し（したがって、偏光器はしばしばニコルプリズムまたは略してニコラと呼ばれます）、1851年から1854年にヘンリークリフトンソルビー卿は最初の偏光顕微鏡の設計を提案し、多くの分野で科学的革命を引き起こしました。偏光顕微鏡を使用すると、さまざまな鉱物や合成材料の複屈折など、物質の多くの光学定数を定量的に測定できます。［訳注：岩石を構成する鉱物の同定に使われたのが歴史的な用途です］

写真©アレクサンダーSigachev commons.wikimedia.org
サンプルはAEFersman MineralogicalMuseum

「回折の物理理論におけるエッジ波の方法」
Konstantin Bobrov, "Popular Mechanics" No. 9，2020　に，
「ロシアが起源の重要な発見と発明」という記事が載っていました．
ここには，医学・生物学，物理学，材料デバイスなどの現在発展し実用化されている科学技術で，ロシア発祥の研究が12例紹介されています．
その中で私の興味を惹いたものの第一位は，ステルス・テクノロジー（1962）の起源です．そこで，少し調べてみました．
ステルス戦闘機の技術は軍事研究ですが，1962年のUfimtevの論文は「回折の物理理論におけるエッジ波の方法」ウフィムツェフ（1962年出版）という，基礎的な電磁波回折散乱方程式で，X線散乱の論文と同程度にたいへん地味な装いです．
この論文の著者の，Peter Yakovlevich Ufimtsev（1931年生まれ），電波工学者，物理学者，数学者です．彼はさまざまな形状の航空機に対するレーダビームの散乱面積を計算できる方程式を作りました．散乱面積（レーダー反射断面積RCS）とはレーダ反射が作る飛行機の像がどのくらいの大きさかというもので，現在最新鋭のステルス機F-35などでは，野球ボールや雀位の大きさと言います．1960年代初頭に、彼が開発したエッジ波法は、推測がまだ多かったことと，散乱面積を小さくする構造は、空気力学の原理と両立せず，戦闘機の運動性能を低下させるので実用性はないと考えられていました．

したがって、Ufimtsevの論文はソ連では重要とは見なされず，世界に公開されました．この論文に注目したのは，デニスDenis Overholzerです．
1970年代初頭にロッキード社のオフィスで働いていた若いデニスは，ロシア語ができたので，ソビエト連邦で出版された技術出版物を調べることが仕事でした．デニスは高度な工学教育を受けていたため，Peter Ufimtsevの科学的研究に興味を持ち，深く掘り下げ英語に翻訳しました．
「回折の物理理論におけるエッジ波の方法」ウフィムツェフ（1962年出版）

デニスはこの論文の重要性を上級管理職に訴えましたが取り上げられず，その後，デニスはエンジニアリングスタッフに直接渡しました．その分野の真の専門家であるエンジニアリングスタッフは，Ufimtsevの仕事の重要性を理解しました．

Ufimtsevによって発見されたアルゴリズムは，ステルス技術を使用して製造された最初の航空機であるF-117ナイトホークの設計に使用され，これは1981年に離陸しました．

Ufimtsevの論文は，防空レーダーから飛行機を事実上見えなくする方法を説明しています．翻訳者のデニス・オーバーホルツァーは，技術的に有能な人物で米国の偉大な愛国者でありました．彼は，Ufimtsevの仕事がアメリカ空軍に前例のない機会をもたらすことにすぐ気づきました．ソビエト連邦は，この論文を秘密にしなかったので，アメリカは完全に合法的に技術を手に入れたのです．

ソビエト連邦がステルス技術の利点を認識したのは，米国がすでにナイトホーク航空機を完全に使用していた1980年代の終わりになってからでしたが，それはすでに手遅れでした．さらに，ミハイル・ゴルバチョフの時代の冷戦雪解けになり，ステルス機は不要になりました．

1990年はソビエト連邦の存在の最後の年でした．Peter Yakovlevich Ufimtsevにとっても1990年は転機で，当時ソビエト連邦科学アカデミーの無線電子工学研究所で働いていた彼は，カリフォルニア大学の客員教授として，アメリカ合衆国に招待を受けました．

彼がアメリカに到着したとき，デニス・オーバーホルツァーは彼に会いに来ました．しかし，Ufimtsevは，ロッキードの競合-ノースロップグラマンとの契約になり，アメリカのB-2爆撃機の戦闘能力の改善に取り組み始めました。

Peter Yakovlevich Ufimtsevの生涯と運命，そしてステルス技術の歴史全体は，科学者に対する国家の不注意がもたらす深刻な結果の典型的な例です．1990年代，ソビエト後のロシアでは「頭脳流出」が深刻な問題となりました．何万人もの有望な科学者，エンジニア，技術者が，お金だけでなく，より注意深く敬意を払う態度を求めてロシアを去りました．

残念ながら，この問題は今のところ解決されていません．国内科学への資金提供には多くの要望が残されています．そのため，若い科学者たちは西側に，そして今では東側にも向けて出発しています．米国，そして中国にも，彼らの知識は需要があります．

以下のサイトを参照しました
https://en.topwar.ru/162805-russkij-stels-kto-razrabotal-tehnologiju-samoleta-nevidimki.html>

補足
レーダーの仕組み：
電波が機体に当たり、機体表面に誘導電流が発生する．
誘導電流から電波が発生する（これは反射波となる）
見えなくするには：
電波が来た方向へ電波を反射しなければ良い（あらぬ方向へ受け流す）．
金属は電波を反射し易いので，電波を反射し難い・吸収する物質に換える．
厚さ1/4波長の表面と裏面から反射させて，反射波同士を打ち消し合わせることも可能である．
ステルス機の形は多面体を思わせるが，どちらから見ても来た方向に電波を戻さず横に受け流すにはこのような形が良いのだろう．

光学的ステルス
可視光で見えなくなる隠れ蓑のような衝立が2019.12にカナダの企業から発表されたのを覚えている方もおられるだろう．可視光に対するステルスも研究されている．

Алексей Левинのエッセイ（ИСТОРИЯ НАУКИ，14.10.2016）
http://www.csmonitor.com/Books/Book-Reviews/2015/1209/The-Invention-of-Science-tells-the-story-of-the-shaping-of-the-modern-world

ウートン著 科学の発明：科学革命の新しい歴史

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．
この著書についてのアレクセイ・レビンのエッセイ（ИСТОРИЯ НАУКИ • 14.10.2016）から抜粋編集。

■ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年

ニコラウス・コペルニクスの モノグラフ「天球の回転について」が、ニュールンベルクの出版社 Johann Petraeusから出版されたのが1543年です。ウートンは2つの理由から、コペルニクスの1543年を科学革命の開始とする従来の見解に異を唱えています。
第一の理由は、太陽を不動中心とする（地動説のこと）コペルニクスモデルは、ケプラーとガリレオの後の17世紀の初めになってから、革命の要因になれるからです。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、その物理的な基盤が不確かだと思いました。たとえば、砲弾がどの方向にも同じ距離を飛ぶという当時の事実は、地球回転の仮説を反駁するに十分でした。1580年代と90年代には、天文学界のコペルニクス信者は3人以下でした。しかも、そのうちの1人、ドイツのクリストフ・ロスマンは、最終的に敵の陣営に移りました。第二の理由は、コペルニクスのモデルが、アリストテレスと古代の天文学者から受け継いだ、地上世界とは全く異なる月以遠（天上界）の世界の絶対不変の概念をそのまま保持したからです。ご存知のように、この概念は17世紀に完全に拒否されました。
コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象で、すべての天体は大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は、毎晩、天で同じ経路をたどり、明るさも変化しません。彗星は唯一の例外で、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者になるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月にこの星が完全に消滅するまで、輝きが徐々に薄れていくのを追跡しました。彼は1573年に、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusavimemoriapriusvisaStella」を出版し、彼の観察を説明しました。そのため、ブラーエはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見たのです。この現象は、11月6日に韓国、2日後に中国で記録されました。これより古い1054年の超新星観察は明月記や中国，アラビアで記録されましたが、ヨーロッパでの記録はありません。

その数年後、彼は、彗星は月以遠の世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定をすることを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積しました。これは、品質と幅の点で、ヨーロッパだけでなく、中国やイスラム教徒の最高の天文台でこれまでに行われたすべての観測をはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することを、ケプラーが厳密に証明できたのはこれらの材料を用いてであり、それによってコペルニクスモデルの弱点が修正されました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。
この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていました）。ウートンが提案する科学革命の最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。
科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較します。 16世紀の終わりの、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく解釈された夢は未来を予測すると信じていました。彼らは、地球は動かず、宇宙の中心にあるという公理を受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたと思われますが）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの著作、または、おそらくそれらのポピュラー書に限定されていました。 彼らは、個人的な図書室に、2～3ダースの本を持っていました。

1730年頃までの150年間を早送りで見ます。当時、同じ社会的および教育的地位を持つ英国人は、フランス、イタリア、ドイツ、さらにはオランダの同時代の人よりもはるかに優れた科学的知識を持っていました。おそらく、彼らはすでに望遠鏡と顕微鏡を通して見る機会があり、太陽系の機能がどのようなものかを知っていました。彼らは良い時計や、おそらく水銀気圧計を持っていて、それを使って天気を追跡していました。彼らは魔女、狼狼、魔法使い、または彗星関連の前兆を信じていませんでした。彼らは、虹が神の啓示ではなく、雨滴が日光を屈折させる結果であることをよく理解していました。彼らは蒸気エンジンについて聞いたり読んだりしていて、おそらく仕事でそれらを観察していました。彼らは目に見えない生物がたくさんいること、心臓は機械式ポンプのように血液を送り出すことを知っていました。彼らは未来を予測する可能性を否定し、おそらく聖書の奇跡を詩的な比喩と見なしました。彼らはニュートンを世界で最も偉大な科学者であり、進歩と科学への熱狂的な信念であると考えました。彼らの図書室は数百、さらには数千冊にのぼり、現代人類があらゆる点で古代世界をはるかに超えたことを疑いませんでした。

ウートンは科学の発明（この本のタイトル）を可能にした知的道具立ての出現と進化をたどります。さまざまなヨーロッパ言語による発見と出現の重要なアイデアから始めます。このプロセスの開始は、彼の意見では、クリストファーコロンブスや他のスペインの航海士の旅が、中国ではなく巨大な新大陸への大西洋横断ルートを開拓したことを、ヨーロッパが知った16世紀初頭です。「アメリカ発見が幸せな偶然だったとしたら、それはさらに驚くべき偶然、つまり発見の発見につながりました」（p.61）。この結論は奇妙に思えるかもしれません。結局のところ、最大の地理的発見は以前にあり、アフリカ沿岸のポルトガル人の航海ではないでしょうか。しかし、彼らの旅は、新しいルートに沿っているとはいえ、すでに知られ予想されている目標への旅と認識されていました。そして、これは決して地理分野に留まりません。コロンブス以前の時代のルネッサンス精神の著名人は、失われた古代の文化的価値を取り戻そうとしましたが、新しい知識の誕生には至りませんでした。さらに、「カトリックの宗教、ラテン文学、アリストテレスの哲学は、新しい知識がまったく存在しないということを共通認識にしていました」（p.74）。知ることができるすべてはすでに知られており、時間の経過とともに蓄積された破損したテキストと誤解釈の修復が研究対象となりました。繰り返す循環過程としての歴史認識が支配していたのが１6世紀です。華麗なイタリアの歴史家でマキャヴェリの友人であるフランチェスコ・ギチャルディーニは、「過去に起こったことはすべて、将来も繰り返されるだろう」と書いています。当然のことながら、そのような態度は、17世紀の初めにフランシス・ベーコンを始めとする、磁気学の研究者ウィリアム・ヒルベルト、ヨハネス・ケプラー、ガリレオ・ガリレイの発見が影響を与えるまで、知識の絶え間ない進歩の可能性を考慮する余地を締め出していました。

発見のアイデアを「育てる」ことは多くの結果をもたらしました。それは、16世紀の前半に、3次方程式、4次方程式の解法の探求に関連し始まり、その後、数学以外の研究にも広がり、誰が先に発見したかの議論が活発になりました。「このような論争は、知識が公になり、進歩的で、発見指向になったことを明確に示しています」（p.96）。17世紀には、個々の著者を発見に帰属させ、それに応じて、その著者の名前を認定された発見に冠するという伝統が生まれました。たとえば、ボイルの法則として知られている理想気体の法則は1708年にこの名前を受け取り 、ニュートンの重力の法則は1713年にこの名前を受け取りました。

----------------------------------------------------------------------------------------------------------------------------------------------

前号から始まったデビッド・ウートン（ヨーク大学の歴史教授）の表題の著書の紹介の続きです．
アレクセイのエッセイ（ИСТОРИЯ НАУКИ， 14.10.2016）より抜粋編集しています．
今回は17世紀あたりまでの科学の流れを概観します．

http://www.csmonitor.com/Books/Book-Reviews/2015/1209/The-Invention-of-Science-tells-the-story-of-the-shaping-of-the-modern-world

まず，前号のレジメから
■ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年

ニコラウス・コペルニクスの モノグラフ「天球の回転について」が出版されたのは1543年です。
ウートンがこの年を科学革命の開始とする従来の見解には，賛成しません。前号ではその２つの根拠を述べました。

このパラダイムは、1572年11月11日に最初の衝撃を受けました。その夜、ティコ・ブラーエは、
カシオペア星座の明るい星に気づきました。彼は、1574年3月にこの星が完全に消滅するまで、毎日観測を続けました。
ブラーエは、彗星の軌道は天球の運動とは異なるので、彗星は地球の大気圏内の現象とした当時の説を否定し、
彗星も月以遠の宇宙世界に属していることを証明しました。
ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点と宣言します。
ウートンが提案する科学革命の最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）
の出版された1704年です。

ウートンは科学の発明（この本のタイトル）について，
その発明者の名を冠して呼ぶようになったヨーロッパの歴史にも言及します。
それは、17世紀のことです。たとえば、ボイルの法則として知られている理想気体の法則は1708年に、
ニュートンの重力の法則は1713年にこの名前を受け取りました。

■15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。
コペルニクスは、すでにプトレマイオス世界を改訂しました（具体的には1514年）。
地球を固体の球と見なし、その表面には海と海が点在するものです。地軸の周りを１日に1回転します。
この視点は当時非常に新しく、まだ共有できいませんでした。
たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。
居住地は丸い島のようにこの表面から突き出ており、その形は半球で、決して球ではありませんでした。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。
アメリゴ・ベスプッチが赤道を越え南緯50度のブラジルの海岸に航海した後で初めて現実になりました。
この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版され、
ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。
それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマンが
地球の表面を完全な球とした新しい地図を描きました（1507年に公開されたWaldseemullerの地図では、
コロンブスによって発見された大陸を、アメリカと名付けられました）。
ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかったでしょう」。

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。
これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、
前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。
TubingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉は、フクシア属の植物に名前が付けられています）。

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。
どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。
当時のグラフィック印刷技術の向上があって出版が可能になりました。
フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、
各植物が彼の本のページに描かれていると考えたのは偶然ではありません。
これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。
実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、
中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、
早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、
共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。
15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、
幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。
視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、
特にアルブレヒト・デュラーによって使用され、開発されました。
彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。
しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。
彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、
初期の科学界の集団心理学の基礎となりました。
彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。
1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。
そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、
ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。
彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。
その中にはDoge Leonardo Donato自身が含まれていました。
上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、
彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。
数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。
この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、
天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、
ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。
最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、
1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、
木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。
彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。
コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているかの説明の説得力がありませんでした。
これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本
「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。
同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、
新しく発見されたジュピターの衛星をメディチの星と名付けました。

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。
英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、
ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。
しかし、ハリオットは彼の結果をまったく公表しませんでしたし、
マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、
科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、
ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。
1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。
その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。
実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。
6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、そこまででした。
（惑星の輪についての最初の明確な声明は、1655年にChristian Huygensによって行われました）
1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、
実際には太陽系の8番目の惑星であるネプチューンを星座Virgoの恒星（固定星）と思いました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙では
存在できないことを完全に理解していました。それらは、太陽中心理論（地動説）によって自然に説明されました。
プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、
これらのオプションの間で明確な選択はできませんでした。
前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、
後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。
対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、
月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。
ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、
ローマのコッレジオロマーノイエズス会アカデミーの教授，そしてグレゴリア暦の創設者の1人に知らせました。
これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、
「有能な天文学者はプトレマイオスのシステムを守ることができなかった」。
ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

*************************************

ウートンは、すべての追加補充された発見のアイデアをヨーロッパの文化分野に含めることが、科学発明の基礎となった体系的な認知革新の重要な要因になったと結論付けています。歴史的に、彼らの最初の製造業者は、新しい土地を説明した地図製作者でした。このプロセスでは、数学者がすぐに参加し、次に解剖学者、植物学者、天文学者、物理学者、化学者が加わりました。彼らは皆、印刷機を利用して、テキストや図を正確かつ大量に再現することを可能にしました。「その結果、革新的で批判的で競争力のある新しいタイプの知的文化が出現しましたが、同時に正確さと信頼性に重点が置かれました」（p.107）。この文化は科学的活動の基礎を形成しました。

15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。コペルニクスは、すでにプトレマイオス世界の改訂を開始（具体的には1514年まで）していました。地球を固体の球と見なし、その表面には海と海が点在するものです。この球は、両方の極を結ぶ軸の周りの空間空間で回転し、１日に1回転します。この視点は当時非常に新しく、誰もがまだ共有できいませんでした。たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。居住地は丸い島のようにこの表面から突き出ており、その形は半球に近づいていますが、決して球になることはできません。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。彼女は、アメリゴ・ベスプッチが赤道の南50度を離れてブラジルの海岸に航海した後で初めて、彼らと実際に衝突しました。この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版された後、ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマン地球の表面が完全な球の表面のように見える新しい地図を描きました（1507年に公開されたWaldseemullerの地図では、コロンブスによって発見された大西洋横断の土地は最初に大陸として表され、アメリカと名付けられました）。コペルニクスはこの概念に精通しており、彼の反省の中でそれを信頼していました。したがって、この場合の新しい地理は、新しい天文学の誕生の前提条件になりました。ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかっただろう」。（p.143）

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。 これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。 ）、TubingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉で、フクシア属の植物に名前が付けられています）。

画像1

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。当時のグラフィック印刷技術の向上により出版が可能になりました。フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、各植物が彼の本のページに描かれていると考えたのは偶然ではありません。これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

画像2

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。 15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、特にアルブレヒト・デュラーによって使用され、開発されました。彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、初期の科学界の集団心理学の基礎となりました。彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。その中にはDoge Leonardo Donato自身が含まれていました。上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているの説明の説得力がありませんでした。これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。 同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、新しく発見されたジュピターの衛星をメディチの星と名付けました。

画像3

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。しかし、ハリオットは彼の結果をまったく公表しませんでしたし、マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。 1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。 6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、それで終わりです（惑星の鳴動についての最初の明確な声明は、1655年にChristian Huygensによって行われました）。 1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、実際には太陽系の8番目の惑星であるネプチューンである星座Virgoで「固定星」を観察しました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙に存在できないことを完全に理解していましたが、それらは、太陽中心理論（地動説）によって自然に説明されました。プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、これらのオプションの間で明確な選択はできませんでした。前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、ローマのコッレジオロマーノイエズス会アカデミーの教授、そしてグレゴリアンカレンダーの創設者の1人に知らせました。これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、「有能な天文学者はプトレマイオスのシステムを守ることができなかった」（p.226）。ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

画像4

金星の段階の発見と分析は、ウートンが科学の相対論的歴史学の支持者、特にトーマス・クーンとの論争において重要な位置を占めることを可能にします。それらのすべては、科学的知識がその生産に関与する特定のコミュニティの信仰の対象であると考えています。このことから、科学的信念のさまざまな「シンボル」のキャリア（Kuhnによると、代替パラダイムの支持者）はコンセンサスに達する可能性がほとんどないことがほぼ自動的にわかります。したがって、パラダイムの変化は、クーンが科学革命と呼んでいる科学コミュニティ内の対立に関連しています。ウートンが書いているように、「クーンの科学革命の構造の後、科学の歴史家は科学内紛争の研究に焦点を合わせてきました。この傾向は、そのような論争は事実上すべての主要な科学的発見によって必然的に生じ、科学理論を競合する概念に置き換えることは決して避けられないという仮定から生じた」（p.246）。しかし、金星の相（変化段階）の発見はまさに望遠鏡の発明の必然的な結果となり、そのおかげで、天文学界は遅滞なく、ほぼ完全にそして多くの議論なしに、プトレマイオスの理論を放棄しました。ウートンが強調するように、そのような状況は典型的です。これは、科学の歴史学における相対論的イデオロギーとは対照的に、経験が科学の進歩的な進化における決定的な要因になる可能性があることを意味します（そして、原則として役立ちます！）。これはウートンの主要な結論の1つであり、本全体で何度も繰り返され、他の多くの例で確認できることは簡単にわかります。

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。 これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。 ）、TübingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉が、フクシア属の植物に名前が付けられています）。

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。当時のグラフィック印刷技術の向上により出版が可能になりました。フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、各植物が彼の本のページに描かれていると考えたのは偶然ではありません。これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。 15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、特にアルブレヒト・デュラーによって使用され、開発されました。彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、初期の科学界の集団心理学の基礎となりました。彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。その中にはDoge Leonardo Donato自身が含まれていました。上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているの説明の説得力がありませんでした。これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。 同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、新しく発見されたジュピターの衛星をメディチの星と名付けました。

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。しかし、ハリオットは彼の結果をまったく公表しませんでしたし、マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。 1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。 6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、そこまでです（惑星の輪についての最初の明確な声明は、1655年にChristian Huygensによって行われました）。 1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、実際には太陽系の8番目の惑星であるネプチューンを見つけましたが、星座Virgoの恒星（動かぬ星）と思いました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙に存在できないことを完全に理解していましたが、それらは、太陽中心理論（地動説）によって自然に説明されました。プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、これらのオプションの間で明確な選択はできませんでした。前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、ローマのコッレジオロマーノイエズス会アカデミーの教授、そしてグレゴリアンカレンダーの創設者の1人に知らせました。これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、「有能な天文学者はプトレマイオスのシステムを守ることができなかった」（p.226）。ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

金星の段階の発見と分析は、ウートンが科学の相対論的歴史学の支持者、特にトーマス・クーンとの論争において重要な位置を占めることを可能にします。それらのすべては、科学的知識がその生産に関与する特定のコミュニティの信仰の対象であると考えています。このことから、科学的信念のさまざまな「シンボル」のキャリア（Kuhnによると、代替パラダイムの支持者）はコンセンサスに達する可能性がほとんどないことがほぼ自動的にわかります。したがって、パラダイムの変化は、クーンが科学革命と呼んでいる科学コミュニティ内の対立に関連しています。ウートンが書いているように、「クーンの科学革命の構造の後、科学の歴史家は科学内紛争の研究に焦点を合わせてきました。この傾向は、そのような論争は事実上すべての主要な科学的発見によって必然的に生じ、科学理論を競合する概念に置き換えることは決して避けられないという仮定から生じた」（p.246）。しかし、金星の相（変化段階）の発見はまさに望遠鏡の発明の必然的な結果となり、そのおかげで、天文学界は遅滞なく、ほぼ完全にそして多くの議論なしに、プトレマイオスの理論を放棄しました。ウートンが強調するように、そのような状況は典型的です。これは、科学の歴史学における相対論的イデオロギーとは対照的に、経験が科学の進歩的な進化における決定的な要因になる可能性があることを意味します（そして、原則として役立ちます！）。これはウートンの主要な結論の1つであり、本全体で何度も繰り返され、他の多くの例で確認できることは簡単にわかります。

ウートンの著作を紹介したアレクセイのエッセイを読んでいます（続きです）．1730年頃までの150年間を早送りで見ます。当時、同じ社会的および教育的地位を持つ英国人は、フランス、イタリア、ドイツ、さらにはオランダの同時代の人よりもはるかに優れた科学的知識を持っていました。おそらく、彼らはすでに望遠鏡と顕微鏡を通して見る機会があり、太陽系の機能がどのようなものかを知っていました。彼らは良い時計や、おそらく水銀気圧計を持っていて、それを使って天気を追跡していました。彼らは魔女、狼狼、魔法使い、または彗星関連の前兆を信じていませんでした。彼らは、虹が神の啓示ではなく、雨滴が日光を屈折させる結果であることをよく理解していました。彼らは蒸気エンジンについて聞いたり読んだりしていて、おそらく仕事でそれらを観察していました。彼らは目に見えない生物がたくさんいること、心臓は機械式ポンプのように血液を送り出すことを知っていました。彼らは未来を予測する可能性を否定し、おそらく聖書の奇跡を詩的な比喩と見なしました。彼らはニュートンを世界で最も偉大な科学者であり、進歩と科学への熱狂的な信念であると考えました。彼らの図書館は数百、さらには数千冊にのぼり、現代人類があらゆる点で古代世界をはるかに超えたことを疑ったりしませんでした。

ウートンは科学の発明（この本のタイトル）を可能にした知的道具立ての出現と進化をたどります。さまざまなヨーロッパ言語による発見と出現の重要なアイデアから始めます。このプロセスの開始は、彼の意見では、クリストファーコロンブスや他のスペインの航海士の旅が、中国ではなく巨大な新大陸への大西洋横断ルートを開拓したことを、ヨーロッパが知った16世紀初頭です。「アメリカの発見が幸せな偶然だったとしたら、それはさらに驚くべき偶然、つまり発見の発見につながりました」（p.61）。この結論は奇妙に思えるかもしれません。結局のところ、最大の地理的発見は以前にあり、アフリカ沿岸のポルトガル人の航海ではないでしょうか。しかし、彼らの旅は、新しいルートに沿っているとはいえ、すでに知られ予想されている目標への旅と認識されていました。そして、これは決して地理分野に留まりません。コロンブス以前の時代のルネッサンス精神の著名人は、失われた古代の文化的価値を取り戻そうとしましたが、新しい知識の誕生には至りませんでした。さらに、「カトリックの宗教、ラテン文学、アリストテレスの哲学は、新しい知識がまったく存在しないということを共通認識にしていました」（p.74）。知ることができるすべてはすでに知られており、時間の経過とともに蓄積された破損したテキストと誤解釈の修復が研究対象となりました。繰り返す循環過程としての歴史認識が支配していたのが１6世紀です。華麗なイタリアの歴史家でマキャヴェリの友人であるフランチェスコ・ギチャルディーニは、「過去に起こったことはすべて、将来も繰り返されるだろう」と書いています。当然のことながら、そのような態度は、17世紀の初めにフランシス・ベーコンを始めとする、磁気学の研究者ウィリアム・ヒルベルト、ヨハネス・ケプラー、ガリレオ・ガリレイの発見が影響を与えるまで、知識の絶え間ない進歩の可能性を考慮する余地を締め出していました。

発見のアイデアを「育てる」ことは多くの結果をもたらしました。それは、16世紀の前半に、3次方程式、4次方程式の解法の探求に関連し始まり、その後、数学以外の研究にも広がり、誰が先に発見したかの議論が活発になりました。「このような論争は、知識が公になり、進歩的で、発見指向になったことを明確に示しています」（p.96）。17世紀には、個々の著者を発見に帰属させ、それに応じて、その著者の名前を認定された発見に冠するという伝統が生まれました。たとえば、ボイルの法則として知られている理想気体の法則は1708年にこの名前を受け取り 、ニュートンの重力の法則は1713年にこの名前を受け取りました。

ウートンは、すべての追加補充された発見のアイデアをヨーロッパの文化分野に含めることが、科学発明の基礎となった体系的な認知革新の重要な要因になったと結論付けています。歴史的に、彼らの最初の製造業者は、新しい土地を説明した地図製作者でした。このプロセスでは、数学者がすぐに参加し、次に解剖学者、植物学者、天文学者、物理学者、化学者が加わりました。彼らは皆、印刷機を利用して、テキストや図を正確かつ大量に再現することを可能にしました。「その結果、革新的で批判的で競争力のある新しいタイプの知的文化が出現しましたが、同時に正確さと信頼性に重​​点が置かれました」（p.107）。この文化は科学的活動の基礎を形成しました。

15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。コペルニクスは、すでにプトレマイオス系の改訂開始（具体的には1514年まで）した。地球を固体の球と見なし、その表面には海と海が点在するものです。この球は、両方の極を結ぶ軸の周りの空間空間で回転し、１日に1回転します。この視点は当時非常に新しく、誰もがまだ共有できいませんでした。たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。居住地は丸い島のようにこの表面から突き出ており、その形は半球に近づいていますが、決して球になることはできません。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。彼女は、アメリゴ・ベスプッチが赤道の南50度を離れてブラジルの海岸に航海した後で初めて、彼らと実際に衝突しました。この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版された後、ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマン地球の表面が完全な球の表面のように見える新しい地図を描きました（1507年に公開されたWaldseemüllerの地図では、コロンブスによって発見された大西洋横断の土地は最初に大陸として表され、アメリカと名付けられました）。コペルニクスはこの概念に精通しており、彼の反省の中でそれを信頼していました。したがって、この場合の新しい地理は、新しい天文学の誕生の前提条件になりました。ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかっただろう」。（p.143）

wikiより拝借

Алексей Левинのエッセイより抜粋　ИСТОРИЯ НАУКИ • 14.10.2016

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．

'The Invention of Science' tells the story of the shaping of the modern worldThe central subject of this vibrant work is not really the inwww.csmonitor.com

ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年。

ニコラウス・コペルニクスの モノグラフ天球の回転について（ニュールンベルクの出版社 Johann Petraeusから1543年に出版）。

ウートンは2つの理由から、コペルニクスの1543年を革命の開始とする従来の見解に同意しません。第一に、太陽中心（地動説のこと）［正確には太陽不動］コペルニクスモデルは、ケプラーとガリレオの研究の後の、17世紀の初めになってから天文学革命の要因になりました。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、それが物理的な基盤を持っていることは否定しました（たとえば、砲弾がどの方向にも同じ距離を飛ぶという事実からも、地球回転の仮説は反駁できたと信じられました）。1580年代と90年代には、コペルニクスは天文学界に3人以下の信者しか持っていません、さらにそのうちの1人、ドイツのクリストフ・ロスマンは最終的に彼の敵の陣営に移りました。第二に、コペルニクスのモデルは、アリストテレスと古代の天文学者から受け継いだ地上世界とは根本的反する、月を越える（天上界）世界の絶対不変の概念をそのまま保持しています。ご存知のように、この概念は17世紀に完全に拒否されました。

コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象でした。すべての天体は、大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は毎晩、天の同じ経路をたどり、明るさと数の両方で変化しません。彗星は唯一の例外でしたが、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者であるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月に完全に消滅するまで、その輝きが徐々に薄れていくのを追跡しました。その前から、彼は1573年に出版され、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusævimemoriapriusvisaStella」で彼の観察を説明しました。そのため、ブラヘはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見ました。（11月6日に韓国で、2日後に中国で、日本でも記述があります）。

左：TychoBraheの著書「DenovaetnulliusævimemoriapriusvisaStella」からの星座Cassiopeiaの描画。 超新星は文字Iでマークされています。
右：スペクトルのさまざまな部分のフレームを合計して得られた超新星の残骸のスナップショット。 チャンドラ望遠鏡のウェブサイトで、この残骸が2000年から2015年の間にどのように変化したかを見ることができます。
http://mvshelter.blogspot.ruからの画像

数年後、彼は、彗星は月を越える世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定を実行することを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積してきました。これは、品質と幅の点で、ヨーロッパだけでなく、中国とイスラム教徒の東の最高の天文台でこれまでに行われたすべてをはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することをケプラーが厳密に証明することを最終的に可能にしたのはこれらの材料であり、それによってコペルニクスモデルの主な弱点を修正しました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていましたが、真に無限の宇宙には中心はありません）。ウートンが提案する最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。

科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較することを提案しています。 16世紀の終わりに、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく理解された夢は未来を予測すると信じていました。彼らは、地球が動かず、宇宙の中心にあるという公理として受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたでしょう）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの研究、またはおそらくそれらのポピュラー書に限定されていました。 彼らはまた、個人的な図書館-2、3ダースの本を持っていました。

https://elementy.ru/nauchno-populyarnaya_biblioteka/431670/Vsego_lish_stepeni_dvoyki

И. Акулич，«Квант» №2, 2012　に２の累乗の大きな数を求める問題があります．

（問題） 

$$S = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{63}$$

$$S$$の値を計算しなさい．

$$2 S = 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{64}$$

$$2S-S＝S=2^{64}-1$$

計算機を使えば，$$2^{64}-1=18446 744 073 709551615$$ と計算できるでしょう．
計算機が無くても，許容できる精度でおおよその答えを見つけることができます。原則として、日常生活では（そしてほとんどの自然科学では）2～3%の誤差が許容されます．
$$2^{64}$$をどのように概算したらよいかという問題です．

 $$2^4 = 16$$，$$2^{10} = 1024≒1000=10^3$$　だから，

$$2^{64}＝2^4・(2^{10})^6≒16・(10^3)^6$$

しかし，この誤差はかなり大きい．結局，1024を1000に置き換えること続けて6回．
このため，1.024倍の誤差の6乗$$1.024^6$$の誤差になります．

1よりも何倍も小さい数xについては、次の近似式を使うと精度が高い．

$$(1 + x)^n ≒ 1 +n･x$$　これを使うと，

$$(1+0.024)^6≒1+6×0.024＝1.144$$

従って，$$2^{64}≒16･10^{18}･1.144=18304･10^{18}$$　と補正します．その結果，

$$S≒2^{64}≒18,304,000,000,000,000,000,000$$となり（18304の後ろに0が18個），
これは正解と1%未満の誤差になります．

■注

１．数字を2のべき乗の和で表すのは，数字を2進数で表すときに必要になります．

たとえば，$$2^{10}+2^9+2^8+2^7＋2^6＋2^4＋2^3+2^2＝2042$$，　2進数で表記すると$$11111011100$$

２．この問題の最初の式は，次の一般式の$$m=64$$の場合になります．

$$2^m = (2^{m–1} + 2^{m–2} + ... + 2^0) + 1$$

３．次の性質も役に立ちます：

$$10^{10}＝(2･5)^{10}＝2^{10}・5^{10}$$

$$2^{10}>10^3$$，　$$5^{10}<10^7$$

Григорий Мерзон, «Квантик» №5, 2020　より

この記事の図には，不要なものもありましたので，必要なものだけ掲載します．文章は冗長ですので私が全部書き換えました．解が1つしかないような記述も私は気に入りません．要するに，この問題は，以下の図（ラクダと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れという主旨です．パズルの問題として予備知識なしで考えるとなかなか難しいかもしれません．

この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

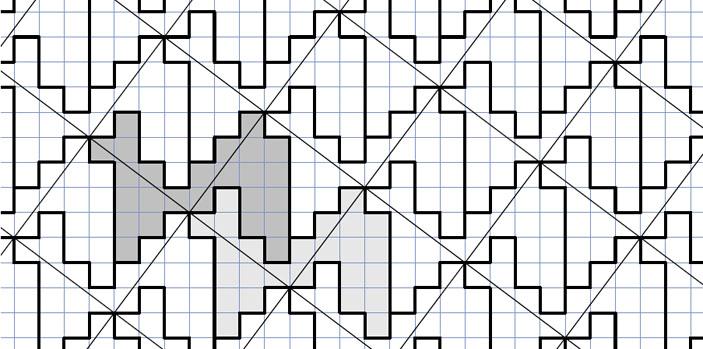
このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞と呼びます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の答ですが，私は答えはこれだけではないことを指摘しておきたいです．

ラクダが3分割できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Григорий Мерзон, «Квантик» №5, 2020

この記事の図はすべて掲載しますが，文章は冗長ですので私が全部書き換えました．要するに，この問題は，以下の図（らくだと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れということです． 

 この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞とよぶます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の回答ですが，私は答えはこれだけではないことを指摘しておきたいとおもいます．

ラクダが3等分できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

そして彼が帰宅したとき、クヴァンチクは上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
のエッセイのまとめです．今回は短いが，彼の最も言いたかったことはここにあるのでしょう．最後に私（訳者）の感想を述べます．

そして今、第四の定理について、少しだけ、多分最も恐ろしいことを話します - "教えても、誰も興味を示さない”。この問題のいくつかの断片はすでに話しました。人々は有限群の研究に興味を持たなくなりました。やる人が減ってきて、テキストという形で保存されてきた知識の塊が不要になり、誰も読めなくなってきている。これは数学の多くの分野を脅かす不幸でもあります。

数学の分野によっては運がいい分野があります。例えば、グラフ理論と組み合わせの理論は同じです。本気でやり始めるにも、ほんの少し学べばよい。少し勉強して、数学オリンピックの問題が解ける。一歩踏み出して、未解決の問題があり、～やったーとなります。しかし、数学の多くの分野は、本当に美しく、それをやりたいと感じるためにも、あなたは多くのことを学ぶ必要があります。そして、その道中では、他にも多くの美しいことを学ぶことができます。しかし、道中で出会うこれらの美しさに気を取られてはいけません、そして、最後には、まさに迷路の中で、美しさを見て、そして、多くのことを学んで、この分野の数学ができるようになっていくのです。そして、この難しさは、そういった部分の問題です。数学の分野が発展するためには、それに従事しなければなりません。全ての困難を乗り越えて、そこに登って、その後もやり続けるというのは、多くの人には面白いはずです。そして今、数学はその難易度の高みに達しており、多くの分野で人知の限界が大きな問題となっています。

人類がこれらすべての問題にどのように対処するのか-私にはわかりませんが、それは興味深いものになるでしょう。

実はそれだけです。

訳注）感想：私は、このエッセイで例にあげられている有限群の問題に興味があります。しかし、この分野は数学者たちは興味を失っているようです。それは、数学の確立された分野で，これ以上研究するのは人間の理解できる限界だからです。これを乗り越えるのは、他のすべての分野の知識もマスターしている数学者ができる仕事でしょう。それを乗り越えられる人がいるのか，その人知はもう人間業ではないのか。そして、たとえ誰かが乗り越えても他の誰にも理解できず，その結果に誰も関心をもたないという状況が恐ろしい．

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
3番目の定理-何かがわかっている場合、それは隣人には説明できません。

これらはまさに現代の数学で最も燃えている問題であり、おそらく最も誇張された問題です。人は何かを証明しましたが、その証明を他の人に伝えることはできません。または、彼が本当にそれを証明したことを他の人に納得させます。この範疇で最初の例であり、一般に最も有名なのは、4色問題です。しかし、これはまだここで発生する最も困難な状況ではありません。ここで、4色問題について少しお話しした後、さらに異常な状況を示します。

図： 5.
4色問題とは何ですか？これはグラフ理論の質問です。グラフは、エッジで接続されたいくつかの頂点です。これらの頂点を平面上に描画し、エッジが互いに交差しないようにそれらをエッジに接続できる場合、フラットと呼ばれるグラフが得られます。グラフカラーリングとは何ですか？トップスはさまざまな色で塗装しています。エッジに沿って隣接する頂点が常に異なる色になるようにこれを行った場合、色は正しいと呼ばれます。できるだけ少ない色でグラフを正しく描きたいです。たとえば、図5には、ペアで接続された3つの頂点があります。つまり、どこにも移動できません。これらの頂点は、必ず3つの異なる色になります。しかし、一般的に、このグラフを描くには4色で十分です（3色では不十分です。確認できます）。

百年の間、問題がありました：平面上に描くことができるどんなグラフも4色で着色できるというのは本当ですか？誰かが信じて4色で十分であることを証明しようとしましたが、誰かが信じずに4色では不十分な例を考え出そうとしました。また、そのような厄介な問題もありました。問題は非常に簡単に定式化されます。したがって、多くの人々は、軽薄な数学者でさえ、それに襲いかかり、それを証明しようとし始めました。そして、彼らは膨大な量の疑惑の証拠または疑惑の否定を提示しました。彼らはそれらを数学者に送り、新聞で叫んだ。私は4色の問題を証明しました！」 -そして誤った証拠のある出版された本さえ。要するに、ノイズが多かったのです。

結局、K。AppelとV.Hakenがそれを証明しました。ここで、証明のスキームについて説明します。同時に、この証拠が他の人には説明できない理由もわかります。人々は、フラットグラフがどのように機能するかを真剣に研究することから始めました。彼らは数十の構成のリストを提示し、すべてのフラットグラフでこれらの構成の1つを見つける必要があることを証明しました。これは証明の前半です。そして、証明の後半-これらの構成のそれぞれについて、それがグラフにある場合は、4色で色付けできることを確認できます。

より正確には、証明は反対からさらに進んでいます。グラフを4色で着色できないとします。前半から、リストからいくつかの構成があることがわかります。その後、これらの構成のそれぞれについて、そのような推論が実行されます。グラフにこの構成が含まれているとします。捨てましょう。誘導により、残ったものは4色に塗られます。そして、残りを4色でどのように着色しても、まさにこの構成をペイントできることを確認します。

カスタマイズ可能な構成の最も単純な例は、他の3つだけに接続されている頂点です。グラフにそのような頂点がある場合は、最後に色を付けたままにしておくことができることは明らかです。他のすべてに色を付けましょう。次に、この頂点がアタッチされている色を確認し、4番目を選択します。他の構成の場合、推論は似ていますが、より複雑です。

さて、これはどのように行われたのですか？このように多数の構成のそれぞれが常に手でペイントされていることを確認することは不可能です-時間がかかりすぎます。そして、このチェックはコンピューターに割り当てられました。そして、彼は多くの事件を調べて、これがそうであることを本当に確認しました。その結果、4色の問題が証明されました。

当初はこんな感じでした。厚い本に記録された推論の人間的な部分には、すべてが着色されていることの最終チェックがコンピューターに委ねられ、コンピュータープログラムのテキストさえも与えられたというフレーズが付随していました。このプログラムはすべてを計算し、すべてをチェックしました-実際、すべてが正常です。つまり、4色の定理が証明されています。

すぐに騒動が起こりました-そのような証拠は信じられませんでした。結局のところ、証拠のほとんどは人間ではなくコンピューターで生成されたものです。 「コンピュータが間違っていたらどうしますか？」 -そんな偏狭な人たちが言った。

そして、この証明の問題は実際に始まりましたが、それらはコンピューターの部分ではなく、人間の部分にあることが判明しました。証拠に欠陥が見つかりました。もちろん、複雑な検索を含むこのような長さのテキストにはエラーが含まれている可能性があることは明らかです。これらのエラーは見つかりましたが、幸いなことに修正されました。

ヨハネスケプラー

コンピュータ部分は残り、それ以来、同じ種類の検索を行うだけで、プログラムを書き直しさえして、複数のコンピュータでチェックされました。結局のところ、正確に何を列挙すべきかが言われれば、誰もが独自のプログラムを作成して、結果が期待どおりになることを確認できます。たとえば、証明にこのような大規模なコンピュータ列挙を使用することは問題ではないように思われます。どうして？しかし、同じ理由で、4色の問題の例ですでに明らかになっています。つまり、人間の証拠よりもコンピューターの証拠の方がはるかに信頼されており、少なくはありません。彼らはコンピューターが機械だと叫びました、そして突然それはどこかで故障し、道に迷いました、そこで何かが間違っていました...しかしこれはただありえません。コンピュータが誤ってどこかで誤動作し、エラーが発生した場合（0が誤って1に置き換えられた場合）、これによって誤った結果が生じることはありません。これは結果につながりません、それはプログラムが最終的に壊れることだけです。コンピューターが実行する典型的な操作は何ですか？彼らは、そのようなレジスターからそのような番号を取得し、そこに制御を移しました。当然、この数に1ビットの変更が発生した場合、制御は誰にも移されませんでした。そこにいくつかのコマンドが書き込まれ、すぐにすべてが破壊されます。

もちろん、コンピューター用のプログラムを書く際にエラーが発生する可能性がありますが、これはすでに人為的なエラーです。人はプログラムを読んで、それが正しいかどうかを確認することができます。人は他人の証明を読んで、それが正しいかどうかを確認することもできます。しかし、人間はコンピューターよりも間違っている可能性がはるかに高いです。他の人の十分な長さの証拠を読んでいて、それに間違いがある場合、あなたがそれに気付かない可能性があります。どうして？まず第一に、証明の作者自身がこの間違いを犯したので、それはそれが心理的に正当化されることを意味します。つまり、彼は偶然にそれをしたのです-これは原則として、典型的な人がそのような間違いを犯すことができる場所です。これは、この一節を読んで、それに気づかないことで同じ間違いを犯す可能性があることを意味します。したがって、人間による証明の人間による検証は、コンピュータプログラムの結果を他のマシンで再度実行して検証するよりも、信頼性の低い検証方法です。 2つ目はほぼすべてが正常であることを保証し、1つ目はどれほど幸運かです。

そして、この問題（人々が書いた数学のテキストの誤りを見つけること）では、それはますます困難になり、時には不可能にさえなります-これは現代の数学の深刻な問題です。あなたはそれと戦わなければなりません。まだ誰も知らない。しかし、問題は大きく、現在発生しています。これにはいくつかの例があります。これはおそらくあまり知られていませんが、最も近代的なものの1つです。これはケプラーの古い仮説です。彼女は三次元空間にボールを置くことについて話します。

図： 6
まず、2次元空間、つまり平面で何が起こるかを見てみましょう。同じサークルを作りましょう。それらが交差しないように平面上にそれらを描くための最良の方法は何ですか？答えがあります-あなたは六角形の格子のノードに円の中心を置く必要があります。このステートメントは完全に些細なことではありませんが、簡単です。

3Dでは、どのようにボールをしっかりと詰めますか？まず、図6に示すように、平面上にボールを配置します。次に、図7に示すように、同じ層の別の層を上に置き、止まるまで押します。次に、同じ層の別の層を上に置きます。直感的には、これは3次元空間にボールを置くための最もタイトな方法です。ケプラーは、このパッケージは3次元空間で最も密度の高いパッケージでなければならないと主張しました（そして最初に作成したようです）。

それは17世紀に起こりました、それ以来、この仮説はそれだけの価値がありました。 21世紀の初めに、その証拠が現れました。そして、あなたの誰もがそれを手に入れて読むことができます。インターネット上のパブリックドメインにあります。この記事は200ページです。それはある人によって書かれ、コンピュータ計算だけでなく、純粋に数学的な推論も含まれています。

図： 7
まず、著者は数学的な推論を使用して、問題を有限数のケースをチェックするように減らしようとします。その後、時々コンピューターを使用して、彼はこの有限の、しかし非常に多くのケースをチェックし、すべてが収束します、そして-万歳！ -ケプラーの仮説が証明されました。そして、これがこの記事の問題です-誰もそれを読むことができません。それは重いので、場所によっては検索が本当に完了したかどうかが完全に明確ではないので、それを読むのは単に退屈だからです。 200ページの退屈な計算。人はそれを読むことができません。

一般的に言って、誰もがこの記事にはこの定理の証拠が含まれていると信じています。しかし一方で、これまで正直にチェックした人は誰もいません。特に、この記事はピアレビューされたジャーナルに掲載されていません。つまり、自尊心のある数学者は、「はい、すべてが正しく、ケプラーの推測が証明された。」

そして、これは唯一の状況ではなく、これは数学の他の分野でも起こります。最近では、セット理論、モデル理論、さまざまな分野で未解決の問題のリストに出くわしました。そして、ある仮説に対するコメントがあります。それは、このような記事で反駁されていると言われていますが、誰もそれを信じていません。

これが状況です。その人はその声明を証明しましたが、それを他の人に伝えることも、他の人に伝えることもできません。

最も恐ろしい例は、もちろん、有限の単純なグループの分類です。必要に応じて、それらが何であるか、グループが何であるか、有限グループが何であるかを正確に定式化することはしません。有限グループはすべて、ある意味で、単純なグループと呼ばれる単純なブロックから組み立てられます。これは、小さなブロックに分解することはできません。これらの有限の単純なグループは無限にあります。それらの完全なリストは次のようになります。これらは17のエンドレスシリーズであり、最後に26の個別のグループが追加されます。これらは個別の方法で構築され、どのシリーズにも含まれていません。このリストには、すべての有限の単純なグループが含まれていると言われています。この仕事は数学にとってひどく必要です。したがって、70年代に、その解決策に対するいくつかの特別なアイデアと希望が現れたとき、さまざまな国、さまざまな機関の数百人の数学者が問題を攻撃し、それぞれが独自の作品を取り上げました。いわば、このプロジェクトのアーキテクトがいて、これらすべてをまとめて1つの証明にまとめる方法を大まかに想像していました。人々が急いで競争していたことは明らかです。その結果、彼らが行った作品は合計で約10,000の雑誌ページになり、それが出版されたものです。また、プレプリントまたはタイプライトされたコピーのいずれかの形式で存在した記事もあります。私自身、そのような記事をやがて読みました。この完全な証拠の注目すべき部分が含まれていますが、公開されることはありませんでした。そして、これらの10,000ページは、さまざまな人によって書かれたさまざまなジャーナルに散在しており、さまざまな程度の理解力があります。これに関係がなく、この理論の設計者ではない一般の数学者にとって、10,000ページすべてを読むことは不可能であるだけでなく、非常に困難です。証拠の構造そのものを理解します。そしてそれ以来、これらの建築家の何人かは単に死にました。

証明は誰も読めないテキストの形でしか存在しないが、分類が完了したことが発表され、次のトラブルにつながった。新しい数学者は、有限グループの理論に行く気がありませんでした。これを行う人はますます少なくなっています。そして、50年後には、この証拠で何かを理解できる人が地球上にまったくいないということが起こるかもしれません。伝説があります：私たちの偉大な祖先は、すべての有限の単純なグループがこのリストにリストされており、他にはないことを証明する方法を知っていましたが、今ではこの知識は失われています。かなり現実的な状況。しかし、幸いなことに、この状況が現実的だと思っているのは私だけではないので、彼らはそれに苦労しており、彼らは特別なプロジェクト「有限の単純なグループの分類の証明に関連する哲学的および数学的問題」を組織したとさえ聞いた。この証拠を読みやすい形にしようとしている人々がいます、そして多分いつかそれは本当にうまくいくでしょう。これらすべての困難をどうするかを考えようとしている人々がいます。人類はこの仕事を覚えているので、最終的にはそれに対処します。しかし、それにもかかわらず、他の同様に複雑な定理が現れる可能性があり、それは証明できますが、誰も読むことができず、誰も誰にも言うことができないという証拠です。

Дмитрий Германович Фон-Дер-Флаасс, «Квант» №5, 2010
Gorgiasの2番目の定理は次のようです-
何かが存在する場合、それは人にはわかりません。
ここで、このカテゴリに分類される文の例をいくつか示します。

集合理論に問題がありました。「選択の公理は本当ですか？」のような質問をする権利はあるのでしょうか？矛盾することなく数学をやりたいだけなら、原則として、選択公理を受け入れることも、それが真実ではないことを受け入れることもできます。どちらの場合でも、私たちは数学を開発することができ、ある場合にはいくつかの結果を、別の場合には他の結果を得ることができますが、矛盾は決してありません。

しかし、今は状況が異なります。明らかに、結果があり、その答えは明らかに存在し、明らかにそれは明確に決定されていますが、人類はおそらくそれを知ることは決してないでしょう。最も単純な例は、いわゆる（3 N + 1）問題です。これについては、これから説明します。自然数を選択しましょう。偶数の場合は、半分に分割します。そして、それが奇数の場合は、3を掛けて1を足します。結果の数値についても同じことを行います。たとえば、3から始めると、次のようになります。

7から始めると、プロセスに少し時間がかかります。いくつかの小さな数から始めて、このチェーンはかなり長いことが判明するかもしれませんが、常に1で終わります。どの自然数から始めても、そのようなチェーンを構築すると、常に1になるという仮説があります。これは（3 N + 1）-問題です-この仮説は本当ですか？

すべての現代の数学者はそれが正しいと信じているように私には思えます。そして、無謀にもそれを証明しようとさえします。しかし、誰も成功しませんでした。そして何十年も経過しています。したがって、これは魅力的な課題の1つです。もちろん、真面目な数学者はそれを軽蔑します-まるで楽しいパズルのようです。何がそこにあるのか、そこに何があるのか​​を知る必要が誰にあるか​は不明です。しかし、軽薄な数学者は、仮説が真実であるかどうかにまだ興味を持っています。それが証明されないうちは、ここで何でも起こり得る。まず、この質問には明確なyesまたはnoの答えがあることは明らかです。自然数から始めて、1に到達するというのは本当か、本当でないかのどちらかです。ここでの答えは、公理の選択や人間の意志に依存しないことは直感的に明らかです。人類はこの質問に対する答えを決して知らないという仮定があります。

ベルンハルト・リーマン
もちろん、誰かがこの仮説を証明すれば、私たちは答えを知るでしょう。証明するとはどういう意味ですか？これは、自然数が1に収束する理由を彼が説明することを意味し、理由を私たちに明らかにするです。

誰かが73桁の数字がまさにそのような特性を持っていることを証明するかもしれません。それからこのチェーンを実行することによって、私たちは間違いなく任意の大きな数字を得るでしょう。または、このチェーンが別の場所でループすることを証明します。繰り返しますが、これが仮説が間違っている理由になります。

しかし、たとえば、私にはひどい悪夢があります。この命題が真実であるが、理由がない場合はどうなるでしょうか。確かに、この命題には、ある人が別の人に理解して説明できる理由はまったくありません。そうすれば、私たちは答えを知ることは決してありません。残っているのは、すべての自然数を繰り返し、それぞれの仮説をテストすることだけだからです。そして、これは当然、私たちの力を超えています。エネルギー保存の法則は、有限の時間内に無限の数の操作を実行することを許可していません。または光の速度の有限性。一般に、物理的な法則では、有限の時間内に無限の数の操作を実行して結果を見つけることは許可されていません。

多くの未解決の問題は、この領域に正確に関連しています。つまり、原則として、彼らは本当にそれらを解決したいと考えています。それらのいくつかは決定する可能性が高いです。リーマン仮説という名前を聞いたことがあると思います。たぶんあなた方の何人かはこの仮説が何を言っているかを漠然と理解しているでしょう。個人的には漠然と理解しています。しかし、リーマンの仮説では、少なくともそれが真実であることは多かれ少なかれ明らかです。すべての数学者はそれを信じています、そして私は彼らが近い将来それを証明することを願っています。そして、まだ誰も証明も反証もできないという命題がいくつかあり、仮説においてさえ、2つの答えのどちらが正しいかは定かではありません。人類は、原則として、これらの質問に対する回答を決して受け取ることはない可能性があります。

Дмитрий Германович Фон-Дер-Флаасс (1962–2010)カバー写真より
数学者が、例えば複素関数を研究するとき、複素数が実数の対であること、実数が有理数の無限集合であること、有理数が整数の対であることなどをいちいち思い出すわけではありません。出来上がったいろいろな数学対象を使っています。しかし、非常に長い話になりますが、原理的にはすべてのものは基礎から組上がっています。

では、数学者は何をするのか？彼らは、これらの数学対象のいろいろな特性を証明します。何かを証明するためには、すでに何かを知っている必要があります。何よりも、一人の数学者が得た結果が他のすべての人に受け入れられるためには、どのような初期特性から議論を始めるかの完全な合意がなければなりません。

これらの初期特性のいくつかを書き出す（それらは公理と呼ばれる）ことから始め、多くの複雑な数学対象の他のいろいろな特性を証明します。しかし、自然数では困難があります。正しいと直感的に感じる公理から導くことができないが、それにもかかわらず真実と思える自然数に関する命題があることが判明しました。

すぐに疑問が湧いてきますが、この性質が自然数にも当てはまることをどのようにして知ることができるのでしょうか？困難な問題です。自然数の公理しか扱えないのであれば、多くのことを語ることは不可能です。例えば、自然数の任意の無限部分集合について語ることはできません。それにもかかわらず、人々はそれが何であるかを想像し、これらの部分集合がどの特性によって決定されるか直感的に理解します。したがって、公理から推論できない自然数のいくつかの特性について、人々はそれらが真実であることを知ることができました。自然数のある性質を明示的に示したのは、おそらく数学者のクルト・ゲーデルが最初で、それは直感的には真実である（つまり、数学者はそれが真実であることに異議を唱えない）が、当時受け入れられていた自然数の公理からは推論できないということになる。

部分的、実際には非常に大きな範囲（数学のほとんどの分野）で、この問題は、慎重にすべてを集合に持ちこんで、直感的に正しいと思える集合理論の公理のいくつかを書き出すことによって対処されました。

言ってみれば、連想の公理。もし、いくつかの集合の集合があれば、次のように言うことができます：この集合からこれらの集合のすべての要素を含む集合を形成しましょう。このような集合が存在することには、合理的な反論はありません。また、もう少しトリッキーな公理もあります。ここでは、集合理論の中で、原理的に疑問視される可能性のある3つのトリッキーな公理を考えてみます。

例えば、こんな公理があります。要素をたくさん有すると集合で、それぞれの要素上のある関数の値を曖昧なく決めることができるとします。この公理は、この集合の各要素にこの関数を適用すると、集まったものが再び集合を形成するというものです（図2）。最も単純な例：xをx^2に変換する関数なら、自然数の集合があれば、それをそれぞれの正方形に入れるイメージで、また自然数の集合に対応させます。 直感的に理解できる公理ではありませんか？もし、これらの関数が非常に複雑な方法で定義されると、集合が非常に大きくなる恐れがあります。また、私たちの関数が明確に定義されていないことは証明できるが、集合の各要素についてこの関数の具体的な意味を計算することは非常に難しい、あるいは無限に難しいという状況もあり得ます。何かしらの答えがあることは確かで、それは曖昧なものではありません。このような複雑な状況でも、この公理は適用可能と考えられており、集合論の問題の源泉の一つは、このような非常に一般的な形です。

図3
一方では自明、他方では問題をもたらす第二の公理は、この集合のすべての部分集合を抜き出せるという公理です。ある集合があれば、その集合のすべての部分集合からなる集合が存在するという。有限集合の場合は当然のことながら N個の要素の有限集合があれば、それは2^N個の部分集合しか持ち得ないことになります。基本的には、全部書き出すことも可能です。最も単純な無限集合でも問題はありません。1,2,3,4,5,6,7などの自然数の集合を取ってみましょう。自然数の集合のすべての部分集合の族が存在することは、なぜ明らかなのでしょうか？要素がわかっているからです。自然数の部分集合を想像するにはどうしたらいいのでしょうか？取り出す要素には１を、取らない要素には０を対応させる。この配列が無限に続く２進数であることを想像してみましょう（図３）。［訳注）いくつか抜き取った状態は0.1010････など頭に０．をつけて無限に続く2進数で表現できる］これで、実数は自然数の部分集合とほぼ同じであることがわかります。 すべての実数が順に並ぶことを直感的に知っているので、それらは実線として明確に表すことができます。与えられた集合のすべての部分集合の集合に関する公理も成り立つのです。

さらに考えてると、ちょっと怖くなってきますが、数学者は、この公理は常に実行されると信じています：我々がある集合を持っている場合、それはまた、そのすべての部分集合が存在することを意味します。そうでなければ、何かを構築するのは非常に困難になります。

そしてもう一つ、最初は信じていなかった公理があります。その名を聞いたことがあるかもしれません。「選択の公理」です。様々な方法で定式化することができ、非常に複雑なものもあれば、非常にシンプルなものもあります。今から、選択公理の定式化の方法をお話ししますが、その中で、それが正しいことが本当に明白になります。いくつかの集合を用意しておきましょう。それらは実際には重なっているかもしれませんが、それは重要ではありません。 簡単に言えば、それらはまだ重なっていないかもしれません。そうすれば、これらのセットを全部まとめたものを作ることができます。これはどういうことかというと、その要素はこれらのものになる、つまり、それぞれの要素から1つの要素を取り出して、それらすべてで1つの集合を形成する（図4）。集合から一つの要素を選択するそれぞれの方法は、これらの集合から作られるものの要素を与えます。

もちろん、これらの集合の中に空集合があり、そこから選択するものがない場合、作られるすべてのものも空になります。そして、選択の公理は、そのような完全に明白な事実を主張します。これらの集合がすべて空でない場合、作られるものは空ではありません。これは明らかに、選択の公理が実際に正しいという事実を支持する最も強力な議論の1つです。他の定式化では、選択の公理はこれほど明白に聞こえません。

すべての数学を集合理論の言語に翻訳しようとして、数学者が命題をどのように証明するかを観察すると、多くの場所で、数学者はそれに気付かずにこの公理を使用していることがわかりました。これに気がつくと、別の命題に分ける必要があることが明らかになりました。私たちはそれを使用していたので、どこかからそれを取り出さなければなりませんでした。それを証明するか、これが基本的な明白な事実であり、それを公理として使用することを許可されていることを宣言する必要があります。これは本当に基本的な事実であり、他のすべての事実だけを使用して証明することは不可能であり、反論することも不可能であることが判明しました。したがって、それを受け入れる場合は、公理として受け入れます。そして、もちろん、受け入れる必要があります。

ここで大きな問題が起こりました。この事実が明確な形で定式化され、「使用できます」と宣言されるとすぐに、数学者はすぐにそれを使用し、直感的には全く非自明な命題を多数証明しました。直感的に間違っているように見える命題すら証明しました。

選択の公理を使用して証明された、そのような命題の最も衝撃的な例は以下です。ボールがあります。それをいくつかのピースに分割し、これらのピースから2つのまったく同じボールが作れます。ここで「いくつかの部分に分割する」とは、たとえば7とすると、各点ごとに、これらの7つの部分のどれに該当するかの話で、これはナイフでボールを切るようなものではありません。はるかに難しい場合があります。たとえば、これは想像するのは非常に難しいですが、ボールを2つにカットする方法なら、座標が有理数であるすべての点を1つのピースに取り、もう1つのピース（無理数の座標を持つすべての点）も作ります。各点について、どのピースに分類されたかがわかります。つまり、これはボールを2つのピースに合法的に分割したものです。しかし、これを視覚化することは非常に困難です。これらの各ピースは、遠くから見ると、まるでボールのように見えます。これらのピースの1つは実際には非常に小さく、もう1つは非常に大きくなりますが。そこで、選択した公理の助けを借りて、この方法でボールを7つのピースにカットできることを証明しました。次に、これらのピースを少し動かして（つまり、空間内で動かしたり、歪ませたり、曲げたりすることなく）、もう一度組み立てて、2つのボールを得ることができます。当初のものと同じです。この命題は証明されていますが、やや風変わりに聞こえます。しかし、それにもかかわらず、数学者は、選択の公理のそのような結果を完全に放棄するよりも我慢する方がよいことに気づきました。他に方法はありません。選択した公理を放棄すると、それをどこでも使用できなくなり、多くの重要で美しく直感的な数学的な結果が証明できないことが判明します。結果は安全に証明できるようになりますが、同時にそのような異常な結果もあります。しかし、人々は多くのことに慣れており、これらの異常にも慣れています。一般的に、現在選択されている公理には問題がないようです。

集合理論の一連の公理があり、数学があります。そして多かれ少なかれ、人間が数学でできることはすべて、集合理論の言語で表現できるようです。しかし、ここでは、ゲーデルが算術の時代に発見したのと同じ問題が発生します。私たちの集合の世界（すべての数学の世界）を説明するかなり豊富な公理のセットがある場合、それらが真実であるかどうかを知ることは決してできないという命題があります。これらの公理から証明することはできず、反論することもできません。集合理論は強力に発展しており、今ではこの問題に最も近いものです。いくつかの問が非常に自然に聞こえる状況に直面することがよくあります。それらに対する答えを得たいのですが、答えも未知で、公理から導き出すこともできないことが証明されています。

何をすべきか？集合理論では、彼らはどういうわけかこれに対処しようとします。つまり、彼らは新しい公理を考え出そうとします。人類にとって直感的に明らかなことはすべて、20世紀の初めに開発された集合理論の公理にすでに還元されているように思われますが、まだ何か他のものが欲しいことがわかりました。数学者は直感をさらに訓練して、いくつかの新しい命題が何らかの理由ですべての数学者に突然直感的に明白に見えるようにし、それらを使用できるようにするでしょう。

もちろん、これがどのように行われるのかはわかりません。非常に複雑な命題があります。まず、集合理論を深く掘り下げて、それらが主張する内容を理解し、次に理解する必要があります。 これらの命題は、実際に直感的に明白であると見なすことができ、公理と見なすことができます。 これは、数学の最も神秘的な分野の集合理論が現在行っていることです。

Dmitry Germanovich Fon-Der-Flaass "Kvant" No. 5、2010

https://elementy.ru/nauchno-populyarnaya_biblioteka/431269/Teoremy_sofista_Gorgiya_i_sovremennaya_matematika

Dmitry Germanovich Fon-Der-Flaass（1962–2010）が早すぎる死を遂げました。クバントの読者はこの名前に何度も会ったことがあります。クバント誌はしばしば彼の問題を発表しました。ドミトリー・ゲルマノビッチは大きな科学で成功を収めましたが、それは彼の活動の一部にすぎません。彼は、学童のための数学オリンピック、全連合および全ロシアのオリンピック、そして近年では国際審査員を務めました。彼はさまざまな数学キャンプや学校で講義を行い、国際数学オリンピックロシアチームのトレーナーの一人でした。この文は，2009年に全ロシア子供センター「Орленокオルリョノク（わし）」で、D.Fon-der-Flaassが行った講演に基づいています。

■古代のソフィスト、ゴルジウスは、三つの定理を立てたことで有名です。第一の定理は、世界には何も存在しないということです。第二の定理は、もし何かが存在するならば、それは人間にはわからないということです。第三の定理は、もし何かが認識可能であるならば、それは隣人には言い表せない。
言い換えれば、何もありませんし、何かがあれば、それについて何も知りませんし、何かを知っていても、誰にも言えません。
これらの三つの定理に四番目を追加します。何かを言うことができたとしても、誰も興味を持ちません。
これらの四つの定理は、実は、現代数学の主要な問題です。

ゴルジウスの第一定理
世界には何も存在しない。数学の言語に翻訳すると、数学は理解できないことをしています。ある意味、これは真実です。結局のところ、数学的なものは世界に存在しません。私たちは皆、自然数が何であるかを知っています。それらは1，2，3，4，などです。そして、私たち全員が「など」という言葉の意味を理解しているという事実は大いなる謎です。 「など」は「無限に多い」数を意味するからです。この世界には、無限に多くのものが存在する余地はない。しかし、私たち全員が自然数について考えるとき、私たちは皆同じことを考えていると信じています。私は7の次は8と思うが、あなたも7の次は8と思う。私が19を素数と思うが、あなたも19を素数と思う。この対象物は世に存在しないようですが、私たちはそれを知っており、私たち全員が同じことを知っています。もちろん、これは数学的な謎ではなく、哲学的な謎なので、議論は哲学者にさせます。幸いなことに、私たちは数学的対象の概念を持っているだけで十分で、それらについて考えるすべての人にとって同じです。だから数学が可能なのです。しかし、哲学的な大きな問題は残っています。

数学者が、これを厳密に考えようとすると、問題が発生します。それがこれからお話しすることです。それらが人類の記憶に出現したのはごく最近（過去100年間）のことです。

自然数に加えて、数学にはもっとたくさんのことがあります。ユークリッド平面があり、そこにあらゆる種類の三角形、角度を描き、それらについての定理を証明します。実数がある、複素数がある、関数がある、もっと恐ろしいものもある...。19-20世紀の変わり目（もちろん、それは少し前に始まった）で大きな転機がありました。人々は、多様な数学的対象の全体は、単一の概念 （集合の概念）に還元できることに気付きました。確かに、単純に「集合」とは何か、「など」とは何かということを直感的に理解していれば、基本的にはすべての数学を構築することができます。

問題は、集合で何ができるかということです。集合が存在する場合、それはどういう意味でしょうか？つまり、私たちの世界、数学的対象の世界のどの要素についても、それがこの集合に含まれているか否かを尋ねられたら、はっきりした答えを得られることを意味しています。答えは明確で、私たちの意志とは完全に独立しています。これは、集合を使ってできる最初の基本的なことで、要素が集合に属するかどうかを調べることです。

もちろん、集合自体は何らかの方法で構築する必要があります。そして、最終的には、すべての豊富な数学的対象がそれらから構築されます。それらはどのように構築されるでしょう？たとえば、空集合Øを作成できます。この集合に属しているかどうかに関係なく、どの要素について質問しても、答えは常に「no，属していません」となり、空集合はすでに一意に決定されています。空集合に関するすべての質問は即座に答えられます。

そして、空集合だけしか含まない集合{Ø}を作成できます。繰り返しますが、この集合があるとはどういう意味ですか？これは、どの要素についても、それがこの集合に属しているかどうかを判定できることを意味します。そして、この要素が空集合である場合、答えは「yes」、この要素が他の要素である場合、答えは「no」になります。したがって、この集合もできました。

ここからすべてが始まります。より直感的な操作をいくつか使います。 2つの集合がある場合は、それらを結合できます。これは、一方または他方の集合の要素を含む集合があると言えます。繰り返しますが、要素が結果集合に属するか否かという質問に対する明確な答えができます。だから私たちは結合を築くことができます。等々。

ある時点で、無限に多くの要素が存在する集合があることを宣言する必要があります。自然数があることを知っているので、無限の数が存在すると信じます。自然数の集合も利用できることを宣言します。無限の集合が現れると、整数を定義できます。整数は、ゼロまたはマイナス記号の有無にかかわらず自然数のいずれかです。これはすべて、集合理論の言語で行うことができます。

有理数を定義できます。有理数とは、分子と（ゼロ以外の）分母の2つの数値のペアです。それらの間に加法と乗法を定義する必要があるだけです。そして、そのようなペアが同じ有理数と見なされるときの条件は何でしょうか。

実数とは何か？これが興味深いステップです。たとえば、それは無限小数であると言うのも良い定義でしょう。無限小数とはどういう意味ですか？つまり、各自然数は実数に含まれます。

ところで、数学者は実数をこのように定義するわけではありません。我々がすでに押さえた有理数の集合を見れば、厳密には実数の集合よりも小さいものであることを宣言しておきましょう。これは非常に厄介な定義です。実は、以前の定義と非常に似ています。例えば実数3,1415926だとすると (無限の数の連鎖が続いている)例えば、それよりも小さい有理数は何でしょうか？小数点以下の端数を切ります。3.14という数字が出てきますが、考えた実数よりも小さいです。小数点以下第4位の端数を切ると3,1415個になり、これも考えている実数よりも小さい有理数が1つ増えます。自分の数よりも小さい有理数をすべて知っていれば、その数だけで決まることは明らかです。そのような絵を視覚的にイメージすることができます。直線はすべて実数で、その中でどこかに私たちの未知数があり、その左に私たちの未知数よりも小さい多くの有理数があります。他の側のすべての有理数は、それよりも大きくなるだろう。これら2つの有理数の間に1つのチップがあることは直感的に明らかで、このチップを実数と呼ぶことにします。集合の概念から始まって、数学全体が少しずつできていきます。

 
plus magazine（November 5, 2020）を要約した

11月18日の東京都のCOVID19新規陽性者数は493人となり，指数関数的な増加予測グラフに乗りました．予断を許さない状況になりました．
ここで紹介する（plusmagazine，Nov.５，2020）記事は，マスク着用の効果とエアロゾルを介しての伝染を予防するための換気について語っています．たぶん，皆様の常識になっている事実の確認で新規性はないので，この記事は圧縮して紹介します．

■　COVID-19を引き起こすウイルスは、主に大きな液滴と小さなエアロゾルを介して伝染する。これらは、呼吸、会話、咳、または笑いの際に排出され、「ウイルスを含む小さな呼吸エアロゾルは、呼吸によって生成された二酸化炭素と一緒に、換気の流れによって部屋の周りに運ばれる」とリンデンらは論文で言う［Paul Linden, Rajesh Bhagat, Stuart Dalziel, and Megan Davies　Wykesによる］。「換気が不十分だと二酸化炭素濃度が高くなり、ウイルスにさらされるリスクが高まる可能性がある」

オフィス、病院、レストランなどの多くの近代的な屋内スペースの換気システムはさまざまです：　風と熱によって駆動される自然換気、または機械システムによります。混合換気は、空間内の空気を十分に混合して維持することを目的とし、置換換気は、部屋の上部から暖かい空気を抽出し、床近くの通気口から冷たい空気を供給することで、より涼しい下部ゾーンとより暖かい上部ゾーンを生成します。

COVID-19の感染に関しては、空気を混ぜることは望ましくない。「混合換気は、すべてを空中に浮遊させてかき混ぜることを目的としています」とリンデン氏は説明します。「置換換気ならば、私たちが吐き出す暖かく潜在的に危険な空気は天井に上がり、そこで抽出することができます」。

置換換気を使用しても問題が発生する可能性があります。部屋にさまざまな熱源がある場合、呼気は暖かい天井層の下に閉じ込められ、他の人によって再び吸い込まれる可能性があります。

人々の呼気の正確な挙動と病気の伝染におけるその役割を予測することは非常に難しいので、リンデンと彼の同僚は、流体力学研究所（ケンブリッジ大学の数学科学センター）で実験を行いました。

■　呼吸、会話、笑い
人がじっと座って息を止めているときでさえ、彼らの体の熱は天井に上がる暖かい空気のプルームを生成します。人が呼吸を始めたり、口を開いて話したり、歌ったり、咳をしたり、笑ったりすると、吐き出された息が2番目のプルームを生成します。伝達に関しては、この2番目のプルームが本体のプルームに同伴されて天井に運ばれるのが最善です。

もちろん、空気は見えませんが、リンデンと彼のチームは、暖かい空気を追跡できる画像技術を使用しました。「誰かが暖かい空気を吐き出すと、温度と密度の変化を見ることができます。それは光を屈折させ、あなたはそれを測定することができます」とバガットは説明します。

チームが作成した画像を以下に示します。左側の画像では、人は静かに座って鼻から呼吸し、中央の画像では通常の音量で話し、右側の画像では笑っています。各画像では、体のプルームが穏やかに上昇していることもわかります。3つのケースのそれぞれで、吐き出されたプルームが体のプルームに吸収されていないことがわかります。

上段の写真はマスクなし．下段の写真はマスクありです．

■　実験と数学

このような実験は非常に重要ですが、実験はリンデンと彼のチームの研究の一部に過ぎません。同様に重要なのは、ガスやその中の汚染物質の挙動を記述する数学モデルで、ウェルズ・ライリーの方程式があります。これは、空気感染性の病気にかかっている人と部屋を共有することで感染する人の予想される数I　を推定しています。

ここで、Sは、部屋の中で病気にあらたに感染可能な人の数であり、Γは部屋の中の既に感染している者がウイルスを排出する率を記述し、qは一人当たりの平均呼吸率、tは人々が部屋を共有している時間幅を記述する。Qは部屋の換気率、つまり新鮮な空気が部屋に入る率です。

この式をよく見てみると、Qが大きいほど（部屋の換気が良いほど）感染する人の数Iが少ないことがわかります。ウェルズ-ライリー方程式は、換気 Q は空間全体で均一であることを前提としており、リンデンと彼のチームが示したように、これは通常、人や家電製品によって生じる空気の流れも問題になり現実にはそうではありません。しかし、ウェルズ-ライリー方程式（他の多くの関連する数式とともに）は、現実の生活をより正確に記述する、より複雑なモデルの一部を形成するでしょう。

■　結論

置換換気システムは、適切に設定されている場合は、より良い選択である。
マスクは有益である。

この研究はまた、もう一つの興味深い可能性を示唆している。ウイルスを含んだエアロゾルは、私たちが息を吐くCO₂と同じように振る舞うので、部屋のCO₂レベルは警告システムに使える。CO₂レベルは非常に簡単に測定することができ、それが高い場合は、空気感染のリスクも高くなるので、リンデンらは、信号機のような警報システムを考えている。

疫学において、次世代行列（じせだいぎょうれつ、英: next-generation matrix）は、感染症の流行に関する区画モデルの基本再生産数を得るのに用いられる。個体群動態においては、構造化個体群モデルの基本再生産数を計算するのに用いられる[1]。マルチタイプの分岐過程でも、同様の計算に用いられる[2]。

次世代行列を用いて基本再生産数を計算する方法はDiekmann et al. (1990)[3] と van den Driessche and Watmough (2002)[4]によって与えられた。次世代行列を用いて基本再生産数を計算するために、集団全体を n 個の区画に分割し、はじめの m 個を感染集団の区画とする。時刻 t における区画の個体数を$$  {\displaystyle x=(x_{1},\dotsc ,x_{n})^{T } }   $$とおき、流行モデル

$$ {\displaystyle {\frac {dx_{i } }{dt } }={\mathcal {F } }_{i}(x)-{\mathcal {V } }_{i}(x)\qquad ({\mathcal {V } }_{i}(x)={\mathcal {V } }_{i}^{-}(x)-{\mathcal {V } }_{i}^{+}(x))} $$
を考える。ここで $${\displaystyle {\mathcal {F } }_{i}(x)}$$  は i 番目の区画における新規感染の発生率を表しており、$${\displaystyle {\mathcal {V } }_{i}^{+}(x)}$$  は他のコンパートメントから i 番目の区画への遷移率を、$${\displaystyle {\mathcal {V } }_{i}^{-}(x)}$$  は i 番目の区画から他の区画への遷移率を表している。このとき

$${\displaystyle {\mathcal {F } }(x)=({\mathcal {F } }_{1}(x),\dotsc ,{\mathcal {F } }_{n}(x))^{T},\qquad {\mathcal {V } }(x)=({\mathcal {V } }_{1}(x),\dotsc ,{\mathcal {V } }_{n}(x))^{T } }$$ 
とおけば、上のモデルは

$$ {\displaystyle {\frac {dx}{dt } }={\mathcal {F } }(x)-{\mathcal {V } }(x)} $$ 
と書くこともできる。いま $$x0$$ を感染症のない定常状態とする。このとき $${\displaystyle {\mathcal {F } }(x)}$$  と $${\displaystyle {\mathcal {V } }(x)}$$  のヤコビ行列は $$x0$$ において

  $$ {\displaystyle D{\mathcal {F } }(x_{0})={\begin{bmatrix}F&0\\0&0\end{bmatrix } },\quad D{\mathcal {V } }(x_{0})={\begin{bmatrix}V&0\\J_{3}&J_{4}\end{bmatrix } } }{\displaystyle D{\mathcal {F } }(x_{0})={\begin{bmatrix}F&0\\0&0\end{bmatrix } },\quad D{\mathcal {V } }(x_{0})={\begin{bmatrix}V&0\\J_{3}&J_{4}\end{bmatrix } } } $$

となる。ここで F と V は

$$ {\displaystyle F={\begin{bmatrix}{\frac {\partial {\mathcal {F } }_{i } }{\partial x_{j } } }(x_{0})\end{bmatrix } }_{1\leq i,\,j\leq m},\quad V={\begin{bmatrix}{\frac {\partial {\mathcal {V } }_{i } }{\partial x_{j } } }(x_{0})\end{bmatrix } }_{1\leq i,\,j\leq m } } $$

で定義される m 次正方行列である。このとき K = FV −1 は次世代行列と呼ばれる。その最大固有値、すなわちスペクトル半径 R0 = ρ(K) がこのモデルの基本再生産数である。

■氷山の水面下

2020年のSARS-CoV-2コロナウイルスのパンデミックは、前例のないものです。このウイルスが、季節性インフルエンザや他の急性呼吸器ウイルス感染症を引き起こすウイルスと相互作用をし、惹き起こす多くの問題が明るみに出たのは意外ではありません。

例えば、インフルエンザの予防接種を受けて、流行期に健康を維持していれば、感染を回避できていると考えられます。それでも、インフルエンザウイルスはまだ上気道の少数の細胞に感染している可能性があり、明らかな病気の兆候を引き起こすことなく、そこで「軽く」増殖しています。もしそうであれば、SARS-CoV-2のケースですでに証明されているように、ワクチンを接種した人でも無症候性の感染キャリアになる可能性があります。

COVID-19の患者は、最初の症状が現れる2日前に感染を広げ始める。無症状の場合でも、感染した人は呼吸やくしゃみ、咳だけでなく、糞便と一緒に最大2週間ほど環境中にウイルスを放出します。そのため、患者はウイルスの検査で陰性になって初めて隔離所から解放されるのです。

現在、人類は呼吸器感染症の90％を診断することができます。しかし、少なくともロシアでは、実際にはこれを実施していません。急性呼吸器ウイルス感染症ARVIとインフルエンザの診断は、症状によってのみ行われます。そして、ARVIの症状のほとんどはほとんど同じであるため、これではわかりません。インフルエンザはほとんどの場合、鼻水が出ずに消えますが、これはCOVID-19を含む他のいくつかの感染症でも一般的です。ARVIの特定の原因（病因）についての答えは、正確な実験室診断によってのみ与えられます。これは可能ですが、現在有料です。ARVIのPCR診断は、強制医療保険の資金調達には含まれていません。

「かぜ」やインフルエンザの特定の症例は目で判断されるため、わが国で実際に特定の病原体に一度に感染したと思われるARVI患者数を知ることはできません。これらの感染のそれぞれからの真の損傷を評価することと、最も危険で疫学的に重要なものを決定することの両方を妨げます。したがって、インフルエンザウイルスを除いて、これらの病原体に対する新しいワクチンや抗ウイルス薬を開発したり、それらの進化の長期的な傾向を追跡したりすることができません。ARVI病原体のグループに新しいウイルスがどのように侵入しているかにすぐに気付かないのは当然でした。

フランス． 2020（ "Science First Hand" No. 3（88）、2020）
2020年の写真：Jacques Paquier

 ただし、一部の国では、関連する研究がいわゆるパイロット都市で実施され、PCRを使用して、いくつかの総合病院からのSARSの兆候があるすべての患者のサンプルが分析されます。それは非常に費用がかかり、1つのサンプルのそのような分析は、現在7〜8千ルーブルの費用です。しかし、病原体の全範囲を見ると、どの感染症に対してワクチンを開発する価値があるのかが明らかになります。

ちなみに、これらの病気の原因のうち、細菌感染症はわずか20％、残りはウイルス性です。今日のワクチンはインフルエンザに対してのみ開発および生産されており、ARVIの病因におけるその割合は10〜15％です。さらに、一部の国では同じコロナウイルス感染がより一般的です（15-30％）。そして、これらの「習慣的な」コロナウイルスは無害とはほど遠い。COVID-19のように、重度を含む3種類の病気があり、感染自体の結果と機械的換気による二次性肺炎の両方で死亡する患者もいます。

もちろん、ARVIのすべての患者に対して一般的な診断を行ってそのようなウイルス感染を検出することは意味がありません。特定の抗ウイルス治療がないため、今のところ症状があるものだけです。通常の治療コースは、診断自体よりも約7倍安くなります。ウイルス感染の場合、上記の理由で選択的研究を行う必要がありますが、どのワクチンを開発し、どの診断をCHIに導入する必要があるかを理解するためです。

モスクワでのそのような研究は、適切に組織された場合、1年以内に数千人の患者をテストするために約1500万ルーブルを必要とします。モスクワの「3DKマンション」の価格ほどで，最も高価なベントレークロスオーバーほどではありません。しかし、保健省はそのような提案に対する答えを1つだけ持っています-お金がありません。

新しいコロナウイルス感染によって引き起こされたパンデミックが私たちに教えてくれた主な教訓は、実際、私たちはウイルスの流行と感染一般についてほとんど知らないということです。それは、そのような将来の出来事に備える方法と、それらに対処する効果的行動方法を私たちは学ばねばなりません。そして、それはCOVID-19自体についてだけに留まらず、危険な季節的な感染ではありますが、別のものになる可能性があります。自然界に動物や鳥がいる限り、新しい未知の病気のパンデミックのリスクは残ります-「野生の」病原体の自然の貯蔵所。

そして、私たちが本当に人口を保護したいのであれば、私たちが今しなければならない最初のことは、私たちがまだ病気であるもの、私たちの中で最も危険なSARSを引き起こす病原体、ロシア人を見つけることです。モスクワ、サンクトペテルブルク、ノボシビルスク、クラスノダール、イェカテリンブルク、カザン、ウファ、ウラジボストークなど、SARSが特に多い主要都市でモニタリング研究を実施するためには、まず、健康問題の解決に今よりも有能かつ効果的に多くのお金を費やす必要があります。他の百万以上の都市と同様に。

SARS-CoV-2に関しては、明らかに、抗流行作用だけでそれを根絶することはほとんど不可能でしょう。おそらく、少なくとも効果的なワクチンが広く実践に導入されるまで、それは人間の集団で循環し続けるでしょう。しかし、私たちはまた、この病気を簡単にまたは無症状で経験し、おそらく免疫を持っている人々の層が徐々に増えています。ワクチン接種は彼らの数を増やすべきであり、そうすれば流行は減少するでしょう。

その間、マスマスキングと社会的距離は感染の拡大を減らすことができ、それは人口の最も脆弱なセグメントを保護します。厳しい対策（企業、学校、大学、カフェ、レストラン、ショップの仕事をやめること）に戻ることは経済の崩壊につながり、ひいてはヘルスケアの状況を悪化させることになることを心に留めておくべきです。

Литература
1. Bendavid E., Mulaney B., Sood N. et al. COVID-19 Antibody Seroprevalence in Santa Clara County, California // MedRxiv. 2020. DOI: 10.1101/2020.04.14. 20062463.
2. Logunov D. Y., Dolzhikova I. V., Zubkova O. V. et al. Safety and immunogenicity of an rAd26 and rAd5 vector-based heterologous prime-boost COVID-19 vaccine in two formulations: two open, non-randomised phase ½ studies from Russia // Lancet. 2020. V. 396. N. 10255. P. 887–897.
3. Moghadas S. M., Fitzpatrick M. C., Sah P. et al. The implications of silent transmission for the control of COVID-19 outbreaks // PNAS. 2020. V. 117(30). P. 17513–17515.
4. Peccia J., Zulli A., Brackney D. E. et al. SARS-CoV-2 RNA concentrations in primary municipal sewage sludge as a leading indicator of COVID-19 outbreak dynamics // MedRxiv. 2020. DOI: 10.1101/2020.05.19.20105999.
5. Zhanga R., Li Y., Zhang A. L. et al. Identifying airborne transmission as the dominant route for the spread of COVID-19 // PNAS. 2020. V. 117(26). P. 14857–14863.

著者について
Sergey Viktorovich Netesov- ロシア科学アカデミーの対応するメンバー、生物科学の博士、ノボシビルスク州立大学自然科学部のバイオナノテクノロジー、微生物学およびウイルス学の研究所の責任者。国際的に引用されたジャーナルと10以上のモノグラフで150以上の出版物の著者。生物医学の分野でロシア政府賞を2回受賞。

«НАУКА ИЗ ПЕРВЫХ РУК» №3, 2020
Sergey Viktorovich Netesov
- Corresponding Member of the Russian Academy of Sciences, Doctor of Biological Sciences, Head of the Laboratory of Bionanotechnology, Microbiology and Virology, Faculty of Natural Sciences, Novosibirsk State University.

公式の統計から判断すると、パンデミックの最初の6か月におけるSARS-CoV-2コロナウイルスの犠牲者の数は、2009年から2011年の1年半の悪名高い豚インフルエンザの流行を越えました。さまざまな推定によれば、7〜14億件の症例のうち、15万人から50万人が死亡しました。COVID-19については、9月の公式症例数は3,300万人を超え、死亡者数は100万人を超えました。[訳者注）11月26日現在，症例数6,030万人，死亡者数142万人]

SARS-CoV-2は、人類にとっては困難な問題であることが判明しました。一方、COVID-19の大流行では、当初から前例のない急速な証拠の積み上げとこの問題に関する科学出版物数の増加を惹き起こしている（2020年6月の初めまでに、その数は20万を超えました）、WHOは150以上の候補ワクチンを登録しました。一方で、この病気の原因物質に対して本当に効果的な薬はまだ1つも現れておらず、SARS-CoV-2と身体との相互作用のメカニズム、および広範な病理学的症状の出現はまだ研究中です。

過去数か月にわたって、専門家は新しいコロナウイルス感染について多くの有用な情報を学んだだけでなく、私たちが慣れ親しんでいる急性呼吸器ウイルス感染症（ARVI）についても 、たとえば、以前はあまり注目されていなかった無症候性のよく知られた現象など、違った見方になりました。現在、このような現象はコロナウイルスだけでなく固有のものであることが明らかになりました。

私たちがパンデミックとの戦いから学び、どのように進むかを考える時が来ました。いずれにせよ、人類の最優先事項は、この病気が日常生活と経済に与える影響を最小限に抑えるために可能な限りのことをすることです。

■先駆病原体SARS-COV-2
今世紀の初めまで、コロナウイルスは通常の季節的なSARSの原因になっていましたが、2000年代になり状況は変わり始めました。非定型肺炎の原因物質であるSARS-CoV-1は、2002年11月に中国の広東省で最初に「特定」されました。それはコウモリのコロナウイルスに由来し、その中間の宿主は明らかにヒマラヤのコガネムシ（ウィーバーラ）だったようです。これらの動物は、コーヒー［世界で最も高価なコーヒーの品種の一つであるliuvak kopiになる］の果実を食べ、肉が美味しく、毛皮も美しい。その内臓や体の部分は、中国の民間療法で使用されています。そのため、かつては中国など東南アジア諸国で集中的に飼育されていました。コウモリから、そして次に人間にもたらされたウイルスの偶発的な適応は、2003年に世界37カ国で8000件以上の感染と800人近くの死をもたらしました。

SARS-CoV-2が属するOrthocoronavirinaeサブファミリーは、広範なCoronaviridaeファミリーのメンバーです（Science First Hand No. 3（88）、2020）。

SARS-CoV-2が属するOrthocoronavirinaeサブファミリーは、広範なCoronaviridaeファミリーのメンバーです。それはいくつかの亜属を含む4つの属で構成されています。これらのうち、SARS-CoV-2、SARS-CoV-1に加えて、重度の急性呼吸症候群（SARS）を引き起こす2002- 2003年のSARSウイルス、および中東を引き起こす肺肺炎の原因物質であるMERS-CoVは、人間にとって特に危険です。呼吸器症候群。他のヒトコロナウイルスは、肺および中等度のARVIの原因物質です

MERS-CoVは、2012年にサウジアラビアで最初に特定されました。これは、エジプトのロゼットコウモリコロナウイルスに由来し、中間宿主である片こぶのラクダを通過した後、ヒトに感染し始めました。この病原体は8年間（2012年9月から2020年1月まで）、実験で確認された感染症例を2.5千件以上引き起こし、そのうち約800件（35％以上！）が致命的でした。ラクダと接触した人のほとんどが病気になりましたが、人から人への感染の事例も知られています。韓国でのこの病気の発生は広く知られ、1人の患者から150人以上が連続して感染しました。

■コウモリから人間へ
コロナウイルスは1960年代半ばに発見されました。その名前（ラテンのコロナから'太陽コロナ'）は、英国のウイルス学者で顕微鏡学者のジューンアルメイダによって電子顕微鏡で最初に見られたウイルスの形状に由来します。「クラウン」は、表面タンパク質、スパイクによって形成され、膜貫通受容体 （アンギオテンシン変換酵素2（ACE2、またはACE2）の分子）に結合することにより、ウイルスが細胞に浸透することを保証します。

同じ1960年代以来、長い間人間に感染してきた一般的なコロナウイルスが徐々にわかってきました。それらのうちの2つはアルファコロナウイルスNL63と229Eです。さらに2つ-ベータコロナウイルスHKU1およびOC43。後者には、SARS-CoV- 1SARSウイルスと現在のSARS-CoV-2が含まれます。

過去10年間、中国とアメリカの科学者たちは、コロナウイルスを含む数十種類のカブトコウモリウイルスのゲノムを詳細に研究してきたので、かなり早く新しい病原体を特定することができました。2020年1月10日までに、中国疾病管理予防センター（北京）の専門家は、患者から得られたSARS-CoV-2の9つの分離株のゲノムを解読した。新型ウイルスは、SARS-CoV-1（約79％の類似度）とMERS-CoV（約50％の類似度）の両方とは遺伝的に異なることが判明した。その違いは非常に深刻です。

SARS-CoV-2を分離する（ "Science First Hand" No. 3（88）、2020）
米国で最初の症例からSARS-CoV-2（球状ウイルス粒子、青）を分離します。粒子の内側に黒い点が表示され ます-ウイルスゲノムの断面。透過電子顕微鏡法。写真：疾病管理センター

ただし、SARS-CoV-2はスナッフボックスの悪魔［訳注）キノコ］ではありません。その特徴づけられた分離株はすべて、2018年に中国東部で発見された2つの既知のコウモリコロナウイルスに遺伝的に近く（88％以上の類似性）、このウイルスのヒト細胞との結合部位は、SARSウイルスのものと類似していました。少し後に、RatG13株がコウモリで同定されました。これは、新しい病原体にさらに近く、96％以上の類似性があります。

SARS-CoV-2の最初の8つの完全なゲノムは、互いに99.98％以上同一であり、ヒト集団における最近の出現を示しています。同時に、コウモリがこのウイルスにとって「孵卵器インキュベーター」であったかどうかはまだ決定されていません。このウイルスの起源については多くの仮説が提唱されていますが、最も現実的なのは、ウイルスが人間にとって病原性になり、中間宿主、おそらくパンゴリン（アルマジロの遠い「相対的」）の生物を「通過」するというものです。

SARS-CoV-2の人工的な起源をめぐる論争については、この理論に賛成して、「ソファーに座った」ウイルス学者は、2015年のNature誌の記事に記載されているハイブリッドを指摘しています。これはコロナウイルスの自然な進化を模倣する実験に言及しています。この研究の主な目的は、SARS-CoV-1ウイルスのスパイクタンパク質をコードするわずかに修飾された遺伝子が挿入されたコウモリコロナウイルスの1つです。主な変更は、科学者がそのゲノムにヒトACE2受容体への結合に関与する領域を挿入したという事実にありました。

北京の動物園のコウモリ（Science First Hand No. 3（88）、2020）
コウモリは、人間にとって潜在的に危険な多くのウイルスのキャリアですが、コウモリ自体は病気にならず、ウイルス感染で死亡することもありません。写真 は北京（PRC）の動物園のコウモリです。写真：愚かなウサギ、トリックスは子供向けです

この組換えウイルスは、ノースカロライナ大学（米国）で構築され、ウーハンウイルス学研究所（PRC）でテストされました。そのようなキメラの特徴は細胞培養でテストされ、それが人間にとって潜在的に危険であることが判明しました。ちなみに、Gain-of-Functionという英語名のこのような実験は、過去10年間で2回禁止され、世界の科学界によって2回許可されています。

ただし、このハイブリッドウイルスは、パンデミックなSARS-CoV-2とは大きく異なります。遺伝的類似性は87％以下です。別の「陰謀」シナリオによると、別のコウモリウイルスであるRatG13が誤ってウーハンの中心から放出される可能性があり、SARS-CoV-2の類似性ははるかに高くなっています。

陰謀研究は魅力的で非常に伝染性の高い活動ですが、新しい感染性物質の起源と拡散に関する有能な科学的調査とは異なり、病原体との戦いには役立ちません。

たとえば、人間と接触して生活しているさまざまな動物のSARS-CoV-2に対する感度をテストすると、犬、豚、鶏、アヒルの生物では再現性が非常に低いが、フェレットや猫ではよく再現され、呼吸管によって、そして感染した動物から人間へ。これはデンマークや他のいくつかの国のミンク農場で起こり、ミンクは人間からのウイルスにしか感染できませんでした。したがって、コロナウイルス感染の可能性のある貯蔵所として、野生動物と家畜をさらに研究する必要があります。

人への道
ウイルスは、人間と家畜のすべての感染症の70％以上を引き起こします。工業用抗ウイルスワクチンがなければ、人間の寿命ははるかに短くなり、人類が動物性食品を提供することは非常に困難になります。

数十年前、いわゆる新規または新たな感染症はすべて、野生動物から飼いならされた動物、そして人間への「飛躍」による動物病原体の適応進化の結果であることが示されました。人間と動物のウイルスゲノムの分子遺伝学的研究によって証明されるように、これは、はしか、おたふく風邪、風疹、C型肝炎、HIVの古くから知られているウイルスに関しても当てはまります。したがって、戦略的な目的のために、人間の病気を防ぐために、最も危険な病気に対して動物にワクチンを接種するだけでなく、野生動物の病原体の全範囲を特定するためのモニタリング研究を実施し、その後、人間の新たな感染を防ぐための対策を開発する必要があります。

家畜の産業繁殖において、野生の親類の病原体から動物を保護することも同様に重要です。同時に、閉鎖状態でのみ家畜を飼育する必要があり、生きた動物を販売するための「野生の」市場は禁止されるべきです。現代の養鶏場では、空気がフィルターを通って鳥に入り、労働者は完全に着替え、飼料は消毒されます。中国の同じ手のひらのシベットも、コウモリがそこに行けないように、閉鎖された保育園でのみ飼育されています。

 
真空の屈折率は１です．例えば，ダイヤモンドの屈折率は2.42で，物質の屈折率は，波長589.3 nm（振動数$$5×10^{14}$$Hz）の光（ナトリウムD線589.0nmと589.6nmの平均値）で測定するのが慣例です．屈折率nの物質に入ると光の位相速度は真空中の光速の1/nで伝播します．屈折率が１より小さいならば真空中の光速より速くなると心配する必要はありません．ここでいう光速は位相速度のことです．物質（ダイヤモンドでも）の屈折率は，X線領域では，1よりわずかに小さく$$n=1-δ，δ～10^{-6}$$になります．何故でしょうか？

■X線，可視光，電波などは，電磁波（振動電場）の仲間です．可視光に比べてX線の周波数は$$10^4$$倍も大きく，30keVのX線の周波数は$$10^{19}$$Hzです．
ダイヤモンドに限らず，物質は原子が集まって構成されており，物質が振動電場に置かれると，物質中に種々の振動する双極子が生じ，これらが物質の置かれた振動電場と同じ周波数で振動し，同じ周波数の電磁波を放射します．これが物質による電磁波の散乱現象です．
物質中に生じる分子分極やイオン分極による双極子の固有振動は赤外や可視光の領域にあります．これらの種々の分極は赤外や可視光領域の誘電率（振動電場に対する応答）に寄与しますが，振動電場の周波数が高くなると，これらの振動は追従できずに次々に落ちていきます．特に，X線の周波数域になると，原子内に束縛されている電子の振動による「電子分極」だけが追従できます．

さて，電子分極だけに注目しましょう．原子内のいろいろな軌道に束縛された電子の固有振動数は10^15Hz程度（この振動数の付近では共鳴が起こります）です．

$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{j=1}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega _{0j}^{2}-i\mit\Gamma _{j}\omega } \cong \left\{ \begin{array}{@{\,} cc @{\, } }
1+4\pi \displaystyle \sum_{j=1}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega ^{2}_{0j } } \right) & for \omega <<\omega _{0} \\[0mm]
1-4\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) & for \omega _{0}<<\omega
\end{array} \right. $$

以下の式を見ると，（１）電子の固有振動数よりはるかに小さい周波数の可視光の領域では，屈折率は１よりわずかに大きく，（２）束縛電子の固有振動数より遥かに大きい周波数のX線領域では屈折率は１よりわずかに小さいことがわかります．

結局，電子分極だけが振動に追従できるX線領域での物質の屈折率nは，１よりごくわずか小さいことになります．

■応用
X線に対する物質の屈折率は１より小さいので，空気中（≒真空中）から，物質表面へ臨界角以内ですれすれに入射するX線ビームは，表面で全反射します．X線を曲げるレンズの光学系は作れませんが，全反射を使うと，適当な形状のミラーを組み合わせてX線ビームを集光させる光学系を作ったり，光ファイバーのようなX線導波路を作ったりすることが可能になります．

全反射するX線は，スキンデプスと呼ばれる物質の極表面しか侵入しませんから，極表面の分析に利用できます．
物質の深さ方向に種々の屈折率層の積層モデルを作り，フレネル反射率をシミュレーションできます．これは，種々の入射角で反射率の測定を行い，物質表面の深さ方向の情報を得る反射率測定実験で利用されています．

$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{j=1}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega _{0j}^{2}-i\mit\Gamma _{j}\omega } \cong $$
$$ \cong \left\{ \begin{array}{@{\,} cc @{\, } }
1+4\pi \displaystyle \sum_{j=1}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega ^{2}_{0j } } \right) & for \omega <<\omega _{0} \\[0mm]
1-4\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) & for \omega _{0}<<\omega
\end{array} \right. $$

Сергей Нетесов，«Наука из первых рук» № 3(88), 2020　より

■治療薬はどうか？
残念ながら、2020年1月以降、治療用抗体を含む新薬の模索が続いていますが、COVID-19に対してウイルス特異的効果が証明された有効な薬剤はまだありません。

米国食品医薬品局（FDA）で事前承認を受けている製品は、RNAポリメラーゼのウイルス酵素阻害剤であるレムデシビルのみです。エボラの治療のために開発されたこともありましたが、その効果はあまり期待できませんでした。

SARS-CoV-2による肺炎患者の第1陣が、早くも2020年2月に中国で正式に服用を開始したが、その時点では効果が証明されていません。しかし、後にアメリカで行われた2つの臨床試験では、重症期間が15日から11日に短縮され、致死率が20～25％低下するという結果が出ています。しかし、他の2つの臨床試験では、これらの結果は確認されていません。レムデシビルは現在、米国ではCOVID-19治療薬として承認されていますが、ロシアでは登録されていません。

他の薬の有効性も研究されています。インターロイキン-6（IL-6）阻害剤は、免疫反応や急性炎症反応を調整する低分子で、患者の免疫系が「制御不能」のときに、いわゆるサイトカインの嵐を防ぐのに役立ちます。そのような薬には、モノクローナル抗体に基づくトシリズマブが挙げられる。イタリアの医師によると、それは肺炎を予防することで病気の経過を改善し、病気の初期段階で有効です。

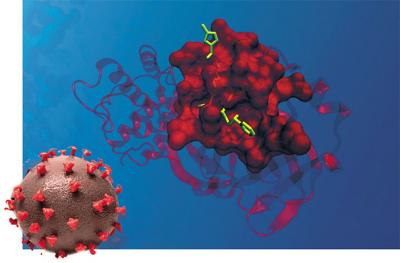
SARS-CoV-2ウイルスプロテアーゼの主酵素と潜在的阻害剤の組み合わせの分子モデル．X線構造解析による．
写真：ツヴィティリオ・クロメナーレ
左：SARS-CoV-2ウイルス粒子．芸術的な構成．写真：NIAID

英国の医師によると 、抗炎症作用と免疫抑制作用を持つ合成グルココルチコステロイドであり、古くから知られているはるかに安価な薬剤であるデキサメタゾンは、サイトカインの嵐を抑制し、重篤な疾患の死亡率を低下させることができます。英国では、この薬は非常にうまく機能しましたが、COVID-19の軽度の症例では、その使用は禁じられています。

抗マラリア薬ヒドロキシクロロキンと抗生物質アジスロマイシンの組み合わせも、ウイルスによる肺炎の治療にテストされました。前者は肺の炎症反応を抑え、後者は付着細菌感染を予防すると考えられていました。しかし、この組み合わせの第一成分の効果のなさを指摘する多くの出版物があり，テストに終止符が打たれました。さらに、ヒドロキシクロロキンとアジスロマイシンは、それ自体で心血管合併症による死亡のリスクを高める可能性があり、このような問題を抱える人々は特にコロナウイルスに対して脆弱です。

免疫不全状態の重症インフルエンザの治療薬として、2015年に日本でアビガンという名前で登録されたファビピラビルをベースにした薬剤に大きな期待が寄せられました（催奇形性効果のため、妊婦には使用できません）。この物質は、レムデシビルのようなRNAポリメラーゼの阻害剤であり、ヒトウイルスではなくRNA含有ウイルス酵素のみに作用する。2020年2月に中国でCOVID-19患者を対象とした臨床試験が開始され、3月に薬効が発表されましたが、その後の説明はありませんでした。

ファビピラビル/アビガンのライセンスは2019年に失効しており、2020年夏にはロシアのメーカー3社からコロナウイルス感染症治療薬として位置づけられている「コロナビル」「アビファビル」「アレプリビル」の3つのファビピラビル系薬剤が国内向けに発売されています。9月には、これらの処方薬がロシアの最低生活レベルに匹敵する価格で小売販売されました。

その有効性については、最近日本でコロナウイルス患者を対象としたファビピラビルの臨床試験の第3フェーズが完了し、平均的な重症度で、摂取により病気の期間が14.7日から11.9日に短縮されることが示されました。これらのデータは、ロシアのパイロット研究の結果と一致しています。中程度および軽度の疾患では、ファビピラビルは「臨床的回復期間を約3.5日短縮し」、鼻腔からのウイルス排除を加速し1～3日短縮することができます。全治療には、体重に応じて40錠1.5～2パックが必要です。

赤外線非接触温度計を使用して人々の健康状態をチェックします。インド。写真：グウィディオンM.ウィリアムズ

■ワクチン接種を受けるや否や？
2020年8月末現在、世界で約160の候補ワクチンが開発されており、そのうち約50は臨床試験のさまざまな段階にあり、そのうち9つはフェーズ３にあります。この段階では、通常、多施設で慎重に管理された研究で、安全性を判断し、実際の流行における薬剤の予防効果を評価するために、大規模な患者グループ（少なくとも1〜3千人）の参加を得て実施されます。

同時に、ロシアと中国の2つのワクチンは、フェーズ３の臨床試験が終了するまで、国レベルでの限定的な使用が許可されました。これは前例のないケースです。

まず、これは、コロナウイルススパイクタンパク質の遺伝子が挿入されたゲノムに第5血清型のアデノウイルスをベースにした中国企業CanSinoBiologicsのワクチンです。フェーズ３の臨床試験は、サウジアラビアの保健省と協議して、サウジアラビアの何万人ものボランティアを対象に8月に開始されました。しかし、早くも2020年6月25日、中国国防省は、一部の軍隊の医師にワクチン接種のために、このワクチンを1年間使用することを正式に承認しました。これが任意接種なのか強制接種なのかは不明です。今日、このワクチンが、アデノウイルスワクチンの中で最も「先進的」なワクチンです。

2つ目の「冬ツバメ」は、M.V.ロマノソフ記念・モスクワ疫学・微生物学研究センターとモスクワ疫学・微生物学研究センターが共同開発した2成分ワクチン「スプートニクV」です。このワクチンは、モスクワの疫学・微生物学研究センター（Gamaleya Research Center for Epidemiology and Microbiology）とロシア国防省の48中央研究所が共同で開発しました。また、コロナウイルス蛋白質遺伝子Ｓを組み込んだアデノウイルス（第５、２６回ヒト血清型）をベースにするこのような方法論に基づいて、この研究センターでは、これまでに我が国のエキゾチックエボラおよび中東呼吸器症候群に対するワクチン候補が開発され、フェーズ1およびフェーズ2の臨床試験に合格しています。

このような組換えワクチンはすべて、比較的無害なウイルスをベースにしており、これらのウイルスは、人体内での繁殖能力を弱める（減衰させる）か、あるいは奪うかのいずれかです。実際、このようなウイルスは、ＤＮＡやＲＮＡワクチンの場合のように、病原体の遺伝物質を細胞に送達し、特異的な免疫応答を誘発するためのベクターとなります。このようなウイルスが細胞に入ると、そのDNAが放出されて細胞核に入り、そこでメッセンジャーRNAが合成され、コロナウイルスの表面Sタンパク質を含むウイルスタンパク質が組み立てられます。これらのタンパク質が細胞膜に組み込まれると、細胞は免疫原性になります。つまり、体内で特定の免疫を形成することができます。

スプートニク Vワクチンの特定のアデノウイルスベースに関しては、これらのウイルスが人体での増殖能力をどのように失ったかについての情報はありません。

「スプートニクV」の正式登録は、2020年8月11日に発表されました。これは、臨床試験のフェーズIIIの開始とフェーズ１〜２の結果の公開のほぼ1か月前です。その後、この登録は条件付きで、2021年1月1日まで有効であることが発表され、最終的な登録は、最大4万人が参加することになっているテストの完了後に行われます。

マスクの少女（「サイエンス・ファースト・ハンド」第3号（88）、2020年）写真：ニックアンダーソン

2020年の夏に、コロナウイルススパイクタンパク質をコードするメッセンジャーRNAに基づくさらに2つのワクチンがフェーズ３の臨床試験用にリリースされました。1つは米国の革新的なバイオテクノロジー企業であるModerna社が、もう1つはドイツのBionTech社、米国のPfizer社、中国のFOSUN Pharma社が共同で開発しているワクチン、そして中国で国有製薬企業の参加を得て開発された不活化ウイルスSARS-CoV-2をベースにした3種類のワクチンです。

これとは別に、Sタンパク質遺伝子が挿入された組換えワクチンも注目に値します。これもアデノウイルスに基づいて作成されていますが、ヒトではなくチンパンジーに基づいています。オックスフォード大学（英国）で、英スウェーデンの製薬大手AstraZenecaと共同で開発されました。ステージ３の臨床試験は、8月初旬にブラジル、米国、南アフリカで開始されました。これらのテストのいくつかはロシアで実施される予定との情報があります。

なぜ開発者の中には、組み換えワクチンの基礎としてサルアデノウイルスや希少なヒトアデノウイルスの血清型を選ぶ人がいるのでしょうか？実は、最近の研究によると、かなりの割合の人がすでに共通の血清型5に対する抗体を持っている可能性があるということです。例えば、このような抗体は、がん研究プロジェクトの一環として中国で調査された人の67％、中国の青海省の子供の75％以上、米軍の新兵の4分の1にも見られた。また、このアデノウイルスをベースにしたワクチンが、以前に接触したことのある人にどの程度効果があるかは不明です。

ワクチン製造の世界的リーダーの育成に関連し最低限の宣伝と「PR」をしているのは：米国に本社を置く国際的なバイオ製薬企業メルク・シャープ＆ドーム、英国グラクソ・スミスクラインに本社を置く国際的な企業、免疫生物学的製剤の多国籍メーカーであるフランスのサノフィ・パスツール

ロシアでは、さらにいくつかの候補ワクチンが様々な拠点で開発されており、その中には、Rospotrebnadzorの国立ウイルス学・バイオテクノロジー研究センター「Vector」（Koltsovo、ノボシビルスク州）、A.A. Smorodintsevインフルエンザ研究所（サンクトペテルブルグ）、M.P. Chumakov免疫生物学的製剤の研究開発のための連邦研究センター（モスクワ）などが含まれています。また、ロシアでワクチンを生産するために、外国の開発者との交渉が進んでいます。ということで、2021年には選択肢が出てきます。

■ワクチンの2ショット
「スプートニクV」の使用説明書には、臨床試験のフェーズ１の結果から、発生頻度の点で有害事象（AE）は、頻繁かつ非常に頻繁に発生していると見なせます。ワクチン接種後、次のAEが記録されました：一般的な障害と反応注射部位：高体温、痛み、浮腫、ワクチン接種部位のかゆみ、無力症、倦怠感、発熱、ワクチン接種部位の皮膚温度の上昇、食欲減退。神経系障害：頭痛、下痢。呼吸器系、胸部および縦隔器官からの障害：中咽頭の痛み、鼻のうっ血、喉の痛み、鼻漏。現在の臨床試験でワクチンの投与量を減らすことにより、これらの現象を減らすことができる可能性があります。

実際のワクチンの保護効果は、20年9月に始まったフェーズ３の臨床試験で検討されるためまだ評価されていません。この場合は破られましたが臨床試験のフェーズ３は通常のアルゴリズムで行います。フェーズ２の試験では、通常、薬剤の投与量が変化するが、既に公表されているスプートニクVの臨床試験結果では、そのようなデータは得られていません。

ワクチン「Gam-COVID-Vac」（「ScienceFirstHand」No.3（88）、2020）

フェーズ３に関しては、独自の規則があります。各テスト参加者には「幸福」の特別な日記が与えられ、セラピストが割り当てられます。すべてのテスト参加者は少なくとも4つのグループに分けられ、そのうちの1つはワクチンの代わりにプラセボを投与され、もう1つは同様のワクチン製剤、3つ目はワクチン自体、4つ目は可変用量などです。スプートニクVの場合、前例のないことに直面し、臨床試験のフェーズ３の開始を待たずに、2020年9月8日、ロシア保健省は、ワクチンの最初のバッチを民間循環に放出する許可を発表し、地域を含むリスクグループからの集団の大量ワクチン接種が計画されています。

ちなみに、「スプートニクV」の指示には、子供だけでなく、主なリスクグループである60歳以上の人（75歳以上の人の死亡率は20～30％）にもワクチンを使用してはいけないと書かれています。

ここまでnote公開･･･････････････

■氷山の水面下
2020年のSARS-CoV-2コロナウイルスのパンデミックは、人間のスクリーニングでは前例のないものです。このウイルスが、さまざまな人々の生物と病原体、主に季節性インフルエンザや他の急性呼吸器ウイルス感染症を引き起こすものと相互作用で，多くの問題が明らかなったのは驚きではありません。

たとえば、インフルエンザの発作を起こし、流行中に健康を維持することで、感染を回避できたと考えています。ただし、この場合、インフルエンザウイルスは、明らかな病気の兆候を引き起こすことなく、上気道の少数の細胞に感染し、そこで「わずかに」増殖する可能性があります。そしてこれが事実であるならば、SARS-CoV-2の場合にすでに証明されているように、ワクチン接種された人々でさえ感染の無症候性の保因者である可能性があります。

COVID-19患者は、最初の症状が現れる2日前に感染を広げ始めます。病気が無症候性である場合でも、感染した人々は、呼吸、くねくね、または咳だけでなく、糞便によっても、最大2週間ウイルスを環境に放出する可能性があります。そのため、ウイルスの存在について陰性の検査を行った後にのみ、患者は検疫から解放されます。

問題の反対側：現在、人類は原則として呼吸器感染症の90％を診断することができます。しかし、少なくともロシアでは、実際にはこれを行っていません。急性呼吸器ウイルス感染症とインフルエンザの診断は、症状によってのみ行われます。そして、ARVIの症状のほとんどはほとんど同じであるため、これは冒涜です。ただし、インフルエンザはほとんどの場合、鼻水が出ずに消えますが、これはCOVID-19を含む他のいくつかの感染症では一般的です。ARVIの特定の原因（病因）についての答えは、正確な実験室診断によってのみ与えられます。現在は可能ですが、有料です。ARVIのPCR診断は、強制医療保険の資金調達には含まれていません。

「寒さ」やインフルエンザの特定の症例は目で判断されるため、わが国で実際に特定の病原体に一度に感染したARVI患者の数を概算することすらできません。そしてこれは、これらの感染のそれぞれからの真の損傷を評価することと、最も危険で疫学的に重要なものを決定することの両方を防ぎます。したがって、インフルエンザウイルスを除いて、これらの病原体に対する新しいワクチンや抗ウイルス薬を開発したり、それらの進化の長期的な傾向を追跡したりすることはありません。したがって、ARVI病原体のグループに新しいウイルスがどのように補充されているかにすぐに気付かないのは当然のことです。

フランス。 2020（ "Science First Hand" No. 3（88）、2020）
フランス。2020年の写真：Jacques Paquier

ただし、一部の国では、関連する研究がいわゆるパイロット都市で実施され、PCRを使用して、いくつかのポリクリニックからのSARSの兆候があるすべての患者のサンプルが分析されます。はい、それは非常に費用がかかります。1つのサンプルのそのような分析は、現在7〜8千ルーブルの費用がかかります。しかし、病原体の全範囲を見ると、どの感染症に対してワクチンを開発する価値があるかが明らかになります。

ちなみに、これらの病気の原因のうち、細菌感染症はわずか20％、残りはウイルス性です。今日のワクチンはインフルエンザに対してのみ開発および生産されており、ARVIの病因におけるその割合は10〜15％です。さらに、一部の国では同じコロナウイルス感染がより一般的です（15-30％）。そして、これらの「習慣的な」コロナウイルスは無害とはほど遠いです。COVID-19のように、重度を含む3種類の病気があり、感染自体の結果と機械的換気による二次性肺炎の両方で死亡する患者もいます。

もちろん、ARVIのすべての患者に対して一般的な診断を行ってそのようなウイルス感染を検出することは意味がありません。特定の抗ウイルス治療がないため、これまでのところ症状があるだけです。通常の治療コースは、診断自体よりも約7倍安くなります。ウイルス感染の場合、上記の理由で選択的研究を行う必要があります。どのワクチンを開発し、どの診断をCHIに導入する必要があるかを理解するためです。

モスクワでのそのような研究は、適切に組織された場合、1年以内に数千人の患者をテストするために約1500万ルーブルを必要とします-モスクワの「3ルーブルノート」の価格または最も高価なベントレークロスオーバーではありません。しかし、保健省はそのような提案に対する答えを1つだけ持っています-お金がありません。

新しいコロナウイルス感染によって引き起こされたパンデミックが私たちに教えてくれた主な教訓は、実際、私たちはウイルスの流行と感染一般についてほとんど知らないという理解です。それは、そのような将来の出来事に備える方法と、それらに対処する上で効果的に行動する方法を私たちに教えなければなりません。そして、それはCOVID-19自体についてでさえありません。それは、危険な季節的な感染ではありますが、別のものになる可能性があります。自然界に動物や鳥がいる限り、新しい未知の病気のパンデミックのリスクは残ります-「野生の」病原体の自然の貯蔵所。

そして、私たちが本当に人口を保護したいのであれば、私たちが今しなければならない最初のことは、私たちがまだ病気であるもの、私たちの中で最も危険なSARSを引き起こす病原体、ロシア人を見つけることです。モスクワ、サンクトペテルブルク、ノボシビルスク、クラスノダール、イェカテリンブルク、カザン、ウファ、ウラジボストークなど、SARSが特に多い主要都市でモニタリング研究を実施するためには、まず、健康問題の解決に今よりも有能かつ効果的に多くのお金を費やす必要があります。他の百万以上の都市と同様に。

SARS-CoV-2に関しては、明らかに、抗流行作用だけでそれを根絶することはほとんど不可能でしょう。おそらく、少なくとも効果的なワクチンが広く実践に導入されるまで、それは人間の集団で循環し続けるでしょう。しかし、私たちはまた、この病気を簡単にまたは無症状で経験し、おそらく免疫を持っている人々の層が徐々に増えています。ワクチン接種は彼らの数を増やすべきであり、そうすれば流行は減少するでしょう。

その間、マスマスキングと社会的距離は感染の拡大を減らすことができ、それは人口の最も脆弱なセグメントを保護します。厳しい対策（企業、学校、大学、カフェ、レストラン、ショップの仕事をやめること）に戻ることは経済の崩壊につながり、ひいてはヘルスケアの状況を悪化させることになることを心に留めておくべきです。

文献･････　　略

 
セルゲイ・ネテソフ, "SCIENCEFIRSTHAND" №3（88）,2020
ノボシビルスク州立大学自然科学部，バイオナノテクノロジー，微生物学およびウイルス学研究所長

前半の章（以下の３つ）は略
■先駆病原体SARS-COV-2，■コウモリから人間へ，■人への道，

■エピデミックを止める方法
病原体の最も重要な特徴は、感染の基本再生産数（R0）で、まだ感染していない集団で，1人の患者から感染する平均人数のことです。通常のインフルエンザウイルスのR0は0 1.4まで、そして新しいコロナウイルスで、おそらく3から5までです。この指標は徐々に変わりますが、感染拡大は国によって定義がわずかに異なるためです。

ドイツ連邦共和国は、第１波の流行克服では最も成功した国の1つです。2020年5月には、ドイツの研究によると，患者の隔離も、マスクなしの社会的距離も、学校の閉鎖も、R0減衰に効果がありませんで。最大の効果は、大規模なイベントの禁止、過酷な導入、罰金、マスク体制、および集中的なコミュニケーションが行われている組織の閉鎖から得られました。これらの措置の結果、実効再生産数は1を下回り、流行は収まり始めました。

ドイツでの抗流行対策の早期導入と広範なテストは、ウイルスの実効再生産数を迅速に低下させ、多くの死亡を防ぐのに役立ちました。
（National Geographic、2020年5月1日）

同様の状況がオーストリア、ノルウェー、イタリアおよび他のヨーロッパ諸国で観察されました。そこでも、学校の閉鎖は効果がないことが判明し（学童は教育機関の外で積極的にコミュニケーションをとっています）、流行を止めるための有効な介入は、マスク着用、集団行動停止、社会的距離を置く、患者の隔離でした。同時に、そのような措置がすぐに導入されず、完全ではなかったスウェーデンでは、主に高齢者の死亡率はヨーロッパで最も高いものの1つでした。そして、イラン、イラク、サウジアラビアでは、検疫措置が弱まった後、病的状態の第二の波が始まりました。

バルセロナ（スペイン）の診療所にいるCOVID-19の患者。
写真：フランシスコアビアホスピタルクリニックデバルセロナ

抗流行対策の有効性の最も顕著な例は、サンフランシスコとニューヨークという2つの最大のアメリカの都市の行政の行動で見られました。サンフランシスコ政府（カリフォルニア州知事および市長）は3月16日、州が自己隔離、マスクの着用、事業活動のほぼ完全な停止などの厳しい検疫措置を課していると発表しました。ニューヨークでは、同じことがわずか6日後に行われました。その結果、米国で最大の都市で2か月以内に約2万人が死亡しましたが、2番目に人口密度が高く13番目に人口の多いサンフランシスコでは35人しか死亡していません。これは、抗ウイルス予防策の採用が少し遅れただけでも、その結果がどれほど広範囲に及ぶ可能性があるかを明確に示しています。

ニューヨーク市では、コロナウイルスと診断された死亡患者の77％が糖尿病、肺疾患、高血圧や喘息などの心血管疾患も患っており、死亡者の1.5％のみが比較的健康でした。参考までに、米国では約66％の人が太りすぎまたは非常に肥満であり、コロナウイルス感染による死亡のリスクが高くなっています。また、ニューヨーク市の成人人口の約半数が高血圧です。

■Covidかどうか？
コロナウイルスはRNA含有ウイルスに属し、リボ核酸自体に加えて、脂質とウイルス特異的タンパク質も含み、さまざまな方法で診断できます。第一に、患者の鼻咽頭からのサンプル中のウイルス自体の成分の存在による：RNA（逆転写PCR、RT-PCR）およびウイルス抗原-表面Sタンパク質（免疫学的測定法）。

SARS-CoV-2ウイルス粒子では、スパイクSタンパク質がはっきりと見え、そこからウイルスの名前が付けられました。透過電子顕微鏡法。画像：NIAID

別の方法は、体の免疫の構成要素、例えば、特定の抗体ができているかを評価することです。これを行うには、症状の発症と同時に現れる、患者の血液サンプル中のIgMクラスの「一次」抗体の含有量が測定されます。過去に疾患に罹ったかは、「二次」IgG抗体の存在によって識別できます。これらのテストは、酵素免疫測定法を使用して実行されます。

2020年8月20日の時点で、157の異なる検査システムがロシアで登録されました。126はコロナウイルスに対する抗体を検出し、31はウイルスRNAです。しかし、なぜ、そのような多数のシステムで、診断の信頼性を論じるのでしょうか？

第一に、ウイルスRNAの試験システムを使用する場合、鼻咽頭から材料を正しく採取することが非常に重要です。さらに、ウイルスRNAの分離と保存のために、特別なサンプラーを必要とする特別な液体にすばやく入れる必要があります。第二に、今日、テストが実行される多くの研究所がありますが、テスト手順のすべての段階で正しく実行されるわけではありません。

患者の鼻咽頭からCOVID-19テスト用の生物学的材料を採取します。写真：フランシスコアビアホスピタルクリニックデバルセロナ

第三に、上気道からRNAを検出する可能性は、鼻咽頭からのウイルスの「逃避」のために、病気の後期に減少します。最後に、RT-PCRテストでは、患者が回復した後でも、長期間にわたって陽性の結果が得られることがよくあります。その理由は次のとおりと考えられます。体は生きているウイルスではなく、ウイルスRNAの断片を循環し続けます。

ウイルス抗原の信頼性の高いテストシステムが開発され、最近医療現場に導入されましたが、状況によってはウイルスRNAの結果が陰性または不明確な場合に正確な診断を行うことができるため、患者の正確な診断に有用であることがすでに示されています。

実験室培養におけるSARS-CoV-2ウイルス粒子（青い物体）。この株は、米国の患者から分離されています。走査型電子顕微鏡写真：NIAID

IgG抗体の検査システムに関しては、ARVIを引き起こす一般的なコロナウイルスに感染していて、検査システム自体が十分に特異的でなかった場合、検査システムの中には偽陽性を示すものもあります。その結果、私たちの人口のほとんどがSARS-CoV-2に対する抗体を持っているように見えるかもしれませんが、最も特異性の高い検査のデータから判断すると、この割合はまだ10〜12％を超えていません。

一方、IgG抗体を持っていなくても、ウイルスに対する免疫防御が欠如しているわけではありません。個々の保護を評価するための追加の検査は、免疫細胞が活性化され、サイトカイン誘導が検出される特異的Ｔ細胞免疫の有無の判定であります。しかし、このような診断や抗体解析の複雑さやコストは比類のないものであるため、限られた規模の科学研究でのみ使用されます。 

ほとんどの場合（症例の40〜90％）、COVID-19は無症候性または軽度であるが、中程度の重症度の疾患では、体温が上昇し、ODSの1つ以上の臨床徴候を示しています：乾いた咳、急速または困難な呼吸、味覚と嗅覚の喪失、血中酸素飽和度の低下。重いフォームが特徴です：38℃以上の体温、脱力感、食欲不振、下痢、筋肉痛、肺炎の記録された徴候。感染してから重篤な症状が現れるまでには、実際には約2週間かかります。（ニューイングランド医学ジャーナル2020年5月16日号）

問題は、今日のロシアでは、外国で行われているように、実際の患者からの対照サンプルとCOVID-19に感染していない人々からの陰性血清の広範なパネルを使用して実施された、すでに適用されている診断法の特異性と感度の比較分析のためのデータをパブリックドメインで持っていないことです。そして、そのようなデータは、特定の診断ツールの購入を決定する際に、ロシア保健省と地域の保健当局の両方で役立ちます。質が大切で安ければ良いというのもではないからです。

感染性物質による人間の感染の実験は、世界のほぼすべての国で犯罪です。したがって、ヒトに対するウイルスの感染量、すなわち、疾患を引き起こすために体内に侵入しなければならないウイルス粒子の数はまだ決定されていません。病人が単位時間あたりにどれだけの量のウイルスを環境に放出するか、テーブルやボタンなどの家庭用品の表面に接触しているときに指に付着するウイルスの粒子の数は不明です。しかし一方で、ウイルスが環境内でどれだけ迅速に、どのような条件下で不活性化されるかがわかりました。このための実験は、倫理基準に違反しませんので。

たとえば、デンマークの科学者は、感染者が多く、これらの人々が病気の最初の症状を感じる前でさえ、下水でコロナウイルスを特定しました。同時に、人をテストするときと実質的に同じテストが下水域のウイルスを検出するために使用されます。しかし、それらはサンプル中のウイルスRNAの存在を明らかにするだけであり、「生きている」ウイルス粒子ではないことを常に覚えておく必要があります。したがって、研究者は、細胞培養物中の生きたウイルスの実際の検出とPCR試験の結果を時々検証する必要があります。

以下続く･････

■治療薬は？，■ワクチン接種を受けるか？否か？，■氷山の隠れた部分

コーシー (1789-1857)、リーマン (1826-1866)

これも19世紀の数学で重要な発見の一つです．「数学が社会（科学技術も含まれる）とどのように係わるかを知る」のが私たちの目的で，数学の勉強会とは別物です．そのような視点で見ても，複素関数論は19世紀に確立した重要な数学分野で，広い応用をもちます．そこで，この数学概念の意義を理解できることを目指します．

私たちの使う関数論は19世紀の数学で確立しました．先に，Fourierフーリエ級数（変換）,Laplaceラプラス変換を取り上げましたが，もう少しだけ複素関数に言及する必要があります．今回は，コーシー-リーマンの方程式を取り上げます．

複素平面（$$x$$軸が実数，$$y$$軸が虚数）に定義域$$D$$をもつ複素関数$$f(z)$$を考えましょう．この関数は領域$$D$$で正則（微分可能）であるとします．微分可能な関数ですから，この領域$$D$$で連続であることはいうまでもありません．

ある点$$z∈D$$での微分は，$$ｘ$$軸に沿って（$$x$$で偏微分）行う微分係数と，$$y$$軸に沿って（$$y$$で偏微分）行う微分係数がありますが，複素関数$$f(z)$$が正則であるとすると，どちらの微分係数も一致し，点$$z$$での微分係数は確定しなければなりません．
関数$$f(z)$$が$$D$$で正則とは，定義域$$D$$のすべての点$$z∈D$$で微分係数が確定する（微分可能）ことです．

関数$$f(z)$$に領域$$D$$での正則性を要請します．定義域内のすべての$$z=x+iy$$に対して，

$$\displaystyle \frac{df(z)}{dz}=\displaystyle \frac{ \partial u}{ \partial x}+i\displaystyle \frac{ \partial v}{ \partial x}=\displaystyle \frac{ \partial u}{ \partial (iy)}+i\displaystyle \frac{ \partial v}{ \partial (iy)}$$が成立します．$$x$$で偏微分しても，$$iy$$で偏微分しても等しい．
実部と虚部をそれぞれ等しいとおいて，
$$\displaystyle \frac{ \partial u}{ \partial x}=\displaystyle \frac{ \partial v}{ \partial y},　 \displaystyle \frac{ \partial v}{ \partial x}=-\displaystyle \frac{ \partial u}{ \partial y}$$が得られます．これをコーシー-リーマンの方程式（条件）と言います．

逆に，コーシー-リーマンの方程式が成立するなら，複素関数f(z)は正則であることが証明できます．
従って，複素関数が正則であるための必要十分条件は，コーシー-リーマンの方程式が成立することです．

■閉曲線$$C$$とその内部で，$$f(x)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$　←コーシーの積分定理

（コーシーの積分定理の証明）
$$\displaystyle \int_{C}^{}f(z)dz=\displaystyle \int_{C}^{}\left[ u(x,y)+iv(x,y) \right] \left( dx+idy \right) =\displaystyle \int_{C}^{}\left( udx-vdy \right) +i\displaystyle \int_{C}^{}\left( udy+vdx \right) =$$

$$ =\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial v}{ \partial x}+\displaystyle \frac{ \partial u}{ \partial y} \right) dxdy+i\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial u}{ \partial x}-\displaystyle \frac{ \partial v}{ \partial y} \right) dxdy=0 $$

（参考）
$$\displaystyle \int_{C}^{}\displaystyle \frac{f(z)}{z-z_{0 } }dz=f(z_{0})\displaystyle \int_{\mit\Gamma }^{}\displaystyle \frac{dz}{z-z_{0 } }=2\pi if(z_{0})$$

■正則な複素関数$$f(x,y)＝u(x,y)+iv(x,y)$$はその実数部$$u(x,y)$$あるいは虚数部$$v(x,y)$$のどちらか一方を知れば他方は決まってしまう．

例えば，虚数部$$v(x,y)$$を知り，コーシー-リーマンの方程式を使うと，実数部$$u(x,y)$$を求めることができる．

例えば，以下のyoutube動画には，このような問題の演習があります．

■応用について

実数部を知って虚数部を求める例として，私のやった実験の話をします．

複素屈折率を　$$ \tilde{n}(\omega )=n(\omega )+iK(\omega ) $$と書きます．$$ω$$は光の周波数で実数．複素屈折率$$ \tilde{n}(\omega ) $$は，複素数値をとり，実数部$$n(ω)$$と虚数部$$K(ω)$$があります．
実数部の$$n(ω)$$は反射率に，虚数部の$$K(ω)$$は吸収率に関係があります．

反射率を測定し$$n(ω)$$を知り，$$K(ω)$$を計算し吸収率を求めます．このとき，実数部$$n(ω)$$と虚数部$$K(ω)$$を結ぶのは，クラマース-クローニッヒ変換です．$$ω$$は複素数ではないので，コーシー-リーマンの方程式にははなりませんが，$$ \displaystyle \frac{\tilde{n}(\omega )}{z-\omega } $$は実軸より上側で正則（$$ω$$は極）なので，コーシーの積分定理を使うと，クラマース-クローニッヒ変換を導くことができます．

$$0=\displaystyle \int_{}^{}\displaystyle \frac{n(z)}{z-\omega }dz+i\displaystyle \int_{}^{}\displaystyle \frac{K(z)}{z-\omega }dz=P\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{z-\omega }dz-i\pi n(\omega )+iP\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(z)}{z-\omega }dz+\pi K(\omega )$$
$$\left\{ \begin{array}{@{\,} c @{\, } }
-\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{Z-\omega }=K(\omega ) \\[0mm]
\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(\omega )}{z-\omega }=n(\omega )
\end{array} \right. $$

■コーシーの積分定理

閉曲線$$C$$および，その内部で$$f(z)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$

■ローラン展開と留数

関数$$G(s)$$に，極（分母が0となる特異点）がある場合，例えば，１つの極$$s_1$$の周りで，次のようにローラン展開ができます．$$s_1$$が$$n$$次の極とすると，
$$G(s)=\displaystyle \frac{a_{-n } }{\left( s-s_{1} \right) ^{n } }+\displaystyle \frac{a_{-\left( n-1 \right) } }{\left( s-s_{1} \right) ^{n-1 } }+ \cdots +\displaystyle \frac{a_{-2 } }{\left( s-s_{1} \right) ^{2 } }+\displaystyle \frac{a_{-1 } }{\left( s-s_{1} \right) }+a_{0}+a_{1}\left( s-s_{1} \right) + \cdots $$
この展開中の係数$$a_{-1}$$を留数と言います．

実は，$$G(s)$$を複素関数と見たとき，極$$s=s_1$$で，$$G(s)$$は正則ではありません．$$s=s_1$$を内部に含むような閉曲線$$C$$に沿って左回りに1周$$G(s)$$を積分すると
$$\displaystyle \int_{C}^{}G(s)ds=2\pi ia_{-1}$$  となります．これを留数の定理といいます．

さてこれらの証明は，難しくはありません．興味おありでしたら，親切な解説をしているyoutube動画がありますので，そちらをご覧ください．

関数をローラン展開すると，いろいろな次数の項がでて来ますが，閉曲線に沿って1周積分すると，なぜ-1次の項の係数（留数）だけが残るのか不思議ですね．youtube動画で証明を確認ください．たいへん都合の良い便利な性質です．

■いろいろな場面で，いろいろな積分をするのに，留数定理を使います．「道具としての数学」の代表でしょう．複素関数論は活躍しています．

話は変わりますが，ちょっと似た手法で，ラプラス逆変換をするときに，部分分数に展開します．以下の例題をご覧下さい．

複素関数$$G(s), s=x+iy$$を，ラプラス逆変換するときに，$$G(s)$$を部分分数に展開することが必要になります．

■Fourier変換
フーリエ解析のときに触れた事柄をまとめておきます：

$$F(\nu )=\displaystyle \int_{- \infty }^{+ \infty }f(t)e^{-2\pi i\nu t}dt$$
$$f(t)=\displaystyle \int_{- \infty }^{+ \infty }F(\nu )e^{2\pi i\nu t}d\nu $$

関数$$f(t)$$のフーリエ変換を$$F(ν)$$といい，$$F(ν)$$から$$f(t)$$に戻る変換をフーリエ逆変換といいます．

変数$$t，ν$$は実数です．積$$ν･t$$は無次元なので，変数$$t$$の空間と，変数$$ν$$の空間は，互いに双対な空間になります．フーリエ変換は，互いに双対な空間同士を結びつける線形写像です．フーリエ変換を用いると，同じ現象を，異なる世界（空間）で見ることができ，現象の理解に威力を発揮します．

適用例
事例１．$$t$$を時間とすると，$$ν$$は周波数ですから，フーリエ変換は，時間空間から，周波数空間への線形写像になります．
事例２．もし，$$t$$を実空間とすると，$$ν$$は逆空間になります．

■ラプラス変換

ラプラス変換はフーリエ変換とよく似ています．歴史的にはフーリエ変換より先だったのですが，フーリエ変換の紹介を先にしてしまいました． 

$$ {\displaystyle F(s)=\int _{0}^{\infty }f(t)\mathrm {e} ^{-st}\mathrm {d} t} $$

$$ {\displaystyle f(t)=\lim _{p\to \infty }{\frac {1}{2\pi i } }\int _{c-ip}^{c+ip}F(s)\mathrm {e} ^{st}\,\mathrm {d} s} $$

（第一の式）$$F(s)$$を$$f(t)$$のラプラス変換といいます．関数$$f(t)$$は実数 $$t ≥ 0$$ について定義されており，積分範囲は$$0≦t<+∞$$になっています．ここで， $$s$$ は複素数（2 つの実数 $$σ, ω$$ を用いて $$s = σ + iω$$ と書ける）．もし,$$s$$を純虚数$$s=iω$$とすれば，フーリエ変換になります．
（第二の式）$$c > 0$$ として，関数 $$F(s)$$ から元の関数 $$f (t)$$ を計算することを逆ラプラス変換といいます．複素平面$$s$$での積分をするので難しそうですが，複素関数論の定理が役に立ちます．複素平面内の積分経路を閉曲線となるように広げ，内部にある特異点の留数の総和を求めれば計算できます．

ラプラス変換は，$$0≦t<+∞の$$実数の空間から複素平面$$s$$への線形写像です．
なぜ，このような面倒な変換が必要なのでしょうか．それは，微分方程式を解くのに有用です．ラプラスは，1812年の著書で，微分方程式の解法に使っています．

ラプラス変換，逆変換を，次のように簡略表記することがあります．
$$ {\displaystyle F(s)={\mathcal {L } }[f(t)]} $$
$$ {\displaystyle f(t)={\mathcal {L } }^{-1}[F(s)]} $$

■ラプラス（1749-1827），フーリエ（1768-1830），ヘビサイド（1850-1925）
フーリエはラプラスより20歳若いのですが，どちらもナポレオンに仕えて，大臣や知事を任命され政治の場でも活躍したところが似ています．
ラプラス変換は，後の演算子法（ヘビサイド）や複素関数論とのつながりがありますので，ここでまとめて紹介しましょう．

ヘビサイド（英国人）は，ラプラスよりも100年後の時代の電気技師ですが，微分方程式の解法に演算子法という素晴らしく便利な方法を開発（1880-1887）しました．これは，微分方程式を代数のように簡単に解く手法です．しかし，その解法の導出過程は数学的厳密さを欠いていたため，当時の数学者から非難されました．ヘビサイドは，「数学は実験的科学であり，定義が先にくるわけではない」，「私は消化のプロセスを知らないからといって食事をしないわけではない」と言ったそうです（wikiより引用）．

その後，ヘビサイドの演算子法は，ラプラス変換により理論づけがなされました．今日，私たちが，微分方程式を解くのに，ラプラス変換をして，周波数空間に移り，そこで簡単な代数計算をして，それをラプラス逆変換して，私たちの世界の時間の関数の解を得るという手順を使います．

ヘビサイドはユニークな天才です．1884年に，当時は20の式から構成されていたマクスウェル方程式を，今日知られる4つのベクトル形式の式に直したというのもとても興味深い逸話です．

Q．正4面体を，平面を切り口に，合同な２つの図形に分割すること．

この問題を考えるのに，まず，正四面体の対称性から説明を始めましょう．図を見てください．正4面体の回転対称軸を調べると，3回回転対称軸が，各頂点にあります．2回回転対称軸は直角に対向している稜の中点を通ります．正4面体の場合は対称心もあるので，2回回転対称軸は，4回回反軸の性質もありますが，今，この問題で必要なのは2回回転対称軸の性質で十分です．鏡映対称面もありますが，この問題では関係ないので略します．

正4面体を，平面で切って，2つの合同な部分に2分割するのですが，対称性を考慮すると，2回回転軸を含む平面で2分割すると，合同な２つの部分に分割できることが理解できるでしょう．例えば，以下の2つの解答例を思いつきます．ついでに，Q．それぞれの例の場合に，その切り口の形はどのような図形でしょうか？という問題も追加します．

解答例１（指で挟んでいるのが，2回軸の正4面体への入口と出口）

解答例２（指で挟んでいるのが，2回軸の正4面体への入口と出口）

■さて私が言いたいのは，「解答例はそれだけでしょうか？」ということです．

実はそのような解は無数にあります．一つの直線を含む平面は無数にありますから，どれも解になります．下図（正4面体の1つの2回回転軸の真上から眺めた図）をご覧ください．黒い線が表現する平面は解答例１，赤い線が表現する平面は解答例２の場合です．2回回転軸を含む平面は無数に作れるので，例えば緑の線も解答例になります．

私がこの問題を作ったのは，対称性の概念は，物事を見通し良く整理して理解するのに役立つことを示したかったからです．

■大発明たる所以
色々な分野でフーリエ解析（フーリエ変換）が使われます．現在の科学におけるフーリエ変換の貢献は偉大です．フーリエ変換なしでは何も考えられません．例えば，時間とともに変化する信号$$f(t)$$は，いろいろな周波数$$ω$$のサイン波の信号の振幅が時々刻々変化するものを重畳$$\displaystyle \sum_{}^{}a_{n\omega }(t)\textrm{sin(}n\omega t)$$して表現できます．線形システムというのは，時間の関数の入力$$f(t)$$があれば$$A･f(t)$$が出力され，入力に，$$f(t)$$と$$g(t)$$があれば，$$A･(f(t)+g(t))$$が出力され，いわゆる重ね合わせが成立します．入力信号も出力信号も，重畳成分のいろいろな周波数のサイン波に分解できるというのがフーリエ変換です．分解された個々周波数のサイン波ごとに，ある周波数帯域を除去するフィルタを通すなどして，それらの出力を再び重畳する信号処理が可能です．

赤外吸収IRスペクトルの測定を例にとりましょう．これは，サンプルを透過する光はどのような波長で吸収されるかの測定です．光の波長を順次スキャンし分光しながら測定する方法は普通ですが，FTIRという方法では，分光せず白色光をマイケルソンの干渉計でインターフェログラムにし，これに対するサンプルの吸収を測定して得たデータをフーリエ変換をすれば，波長スキャンのときと同様に吸収スペクトル測定ができます．

結晶学では，結晶空間と逆空間という互いに双対な空間を扱いますが，この両空間は互いにフーリエ変換で変換し合う空間です．イメージが把握できるように，双対という概念に簡単に説明しましょう．例えば，正6面体と正8面体は互いに双対な立体です．この両立体は，面を頂点に，頂点を面に取り換えると互いに移り変われる立体です．置き換える面と頂点の関係とは，結晶格子の基本ベクトルと逆格子の基本ベクトルの関係と言い換えることができます．

■さて，フーリエ級数（展開）とフーリエ変換は，同じ性質のものなのですが，細かいことをいうと違いもあります．

フーリエ級数展開は：
周期的などのような波形も、単純な波形（サイン波）の重ね合わせとして表すことができます。
フーリエ変換では：
周期的でない波形を扱えます．ここで用いる単純な波形（サイン波）の周波数は，フーリエ級数のときのように離散的な倍音のみではなく，周波数のステップが細かくなり，級数は積分になります．

■ジョセフ・フーリエは，熱が固体中をどのように移動するか（熱伝導現象 ）を数学的に研究しました．この研究のために，新しい数学的方法を開発しました．これがフーリエ解析の始まりです．

彼が熱伝導に興味を持ったきっかけが，いつのことだか定かではありません．北アフリカにいたときに生じたと推定しているのは，以下のエッセイです．

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
1798 年, フーリエはナポレオン のエジプト遠征に科学顧問として, モンジ ュやマリ ュ スとともに同行し， エジプトでは考古学上の調査や， カイロ学士院の創設に力を注ぎ，カイロ学士院の書記官にも選出されました． ナポレオンは 1799 年にパリに帰還しますが，フーリエはその後 2 年間エジプトに残りました.　1801 年, フーリエはフランスに帰還し, 再び諸工芸学校の解析学の教授になりますが，翌年 2 月にナポレオンはフーリエをイゼール 県の知事に任命しました．以下のエッセイによると，熱伝導研究の開始は 1802 年頃らしいとされています．

タイトル未設定www.kurims.kyoto-u.ac.jp
1807，1811年 に論文で，連続物体の温度分布の問題を解いており，フーリエ展開公式を導いています．

彼の研究結果は1822年に、熱の解析理論（Theorie analytique de la chaleur)に掲載され、そこでは、複雑な物理問題をより単純なものに分解して解析する方法が示されました。

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
フーリエは，複雑な波形を単純な波形の重ね合わせとして表せることを示しました．一般に，古典的な系を説明する方程式は，これらの単純な波のそれぞれについては簡単に解けます．フーリエは，これらの単純な波形を重ね合わせて，複雑な問題全体の解を得る方法を示しました．数学的に言えば，フーリエ級数は，周期的な任意の関数を単純なsin波の種々な高調波（倍音）の重ね合わせとして表す方法で，フーリエ解析は調和解析とも呼ばれます．（下図参照）

周期的でない任意の波形の場合は，整数倍音の高調波の重ね合わせではなく，連続的に変化する高調波の積分で表現するフーリエ変換の概念に拡張できます．

フーリエ解析の登場フーリエ解析の登場energychord.com

■20世紀半ばにコンピューターが登場するまで，自然の複雑さに立ち向かう武器は，フーリエ解析でした．フーリエ解析の出現以来，科学者はニュートン力学の法則や他の基本的な方程式を直接適用して解ける単純な問題だけではなく，複雑な問題にもそれを使用して解くことができました．19世紀のニュートン科学の偉大な成果の多くは，実際には，フーリエによって最初に提案された方法を使用しなければ不可能でした．その後，これらの方法は，天文学から機械工学まで，さまざまな分野の問題を解決するために使用されました．現在は，画像処理などでコンピュータを用いた高速離散フーリエ解析が行われています．

■ジャン・バプティスト・ジョセフ・フーリエ（1768-1830）
フランスの数学者．オセールに生まれ，9歳で孤児となる．若くして数学の才能を発揮した．フーリエは教会学校や軍人学校で教育を受けた後，フランス革命にあう．彼は数学教師として働いたが，生涯を通じて政治の世界で活躍した．1794年にはテロの被害者を保護して逮捕されたが，ロベスピエールの死後，獄中から釈放され，パリの有名なエコール・ポリテクニークの創設に参加し，その地位はナポレオン政権下での昇進の橋頭堡となった．ナポレオンに同行してエジプトに行き，下エジプト総督に任命された．1801年にフランスに帰国すると，州知事に任命された．1822年にはフランス科学アカデミーの常任書記官に就任し，フランスの科学界で影響力のある地位に就いた．熱伝導の論文は1807，1811年．フーリエ解析の本の出版は1822年．

今年の数学月間（7月29日）は，稲葉寿氏（東大）の表題の講演をZOOMでお送りしました．covid19の感染拡大第３波に見舞われている今日，お読みいただくと役に立つと思います．gotoトラベルは，それぞれR<1を保っている複数の状態（都市）の相互作用により，R>1に変わる可能性を誘発する危険な政策です．

■これまでに人類はいろいろなパンデミックを経験してきました．1918年のインフルエンザ（スペイン風邪）は4000万人以上の死者，2015年のＨＩＶ感染者は3670万人，マラリアは年間3億～5億人の患者を生む．最近のSARS，エボラなどの新興感染症や，再興感染症などにより感染症撲滅という1980年代までの楽観論は消滅しました．人口増加，都市集中，環境破壊などによって，感染症流行リスクはますます増大しています. 現在COVID-19は予断をゆるさない状況です．

■感染症の数理モデルは，SIRモデルを基本とします．これは，ケルマックとマッケンドリックが提唱(1927)したものです．全人口をS（感染感受性のある集団），I（感染者集団）,　R（免疫のできた回復者）の３つのグループに分け，それらのグループ間の相互作用（遷移）を数式で記述し数理モデルができます．
数理モデルは，感染拡大の様子を予測でき，種々の介入（ワクチン接種，隔離，接触制限，ロックダウンなど）を行うことで，感染性人口を絶滅させる（感染源にならないようにする）対策の策定に必要です．

COVID-19では，もう少し進化させた，SEIR数理モデルが必要です．これは，E（潜伏期間にある感染者集団）が加わったモデルです．特にCOVID-19は，Eグループのものが感染源になることや，免疫のできた回復者の免疫が消えることなどがわかり始めており，一筋縄では行かないモデリングになります．

■基本再生産数R0（R-naught)
感染感受性のある集団に居る一人の感染者が，その全感染期間に再生産する（感染させる）2次感染者の数を基本再生産数R0と定義します．全員感受性のある集団で，1次感染者数，2次感染者数，3次感染者数，･･･と等比級数で増加するときの公比がR0です．
R0は患者数と感染感受性のある人（未感染者）との接触回数に比例するので，環境状況でこの数値は変化します．感染が広がると未感染者が減り，実際の集団には免疫のある人も混ざった状態になるので，全員感受性がある集団で定義したR0よりも小さいR（実効再生産数）が期待できますが，適切でない介入があれば，逆にRの増加もあり得ます．
結局，R>1であればその集団の感染者人口の成長率は正になり，流行は拡大していくが，R<1であればその集団の感染者人口の成長率は負であって流行は自然に消滅する．何らかの介入をして，すみやかに，R<1とすることが対策になります．

■多状態のSEIRモデル
集団に2つの状態（例えば，学童と社会；病院と社会；東京と地方；大学と社会；等々）がある場合は，それぞれにSEIRモデルを作り，さらに２つの状態間の相互作用を考える複雑なモデル（コンパートメント・モデルという）になります．２つの状態にはそれぞれの実効再生産数Rがあります．
現実に近い多状態SEIRモデルを作り，その次世代行列の最大固有値として，Rを計算します．そして，どのような介入（例えば，ワクチン接種，ロックダウン，外出制限，休校）をすれば，Rが下げられるかを検討します．
集団の２つの状態のRが1未満であるため，感染が制御されているように見え，通常の生活に戻り始めるかもしれません．
イギリスでも約200万人の大学生が全国から復帰し，フレッシャーズフルー［注）フレッシャーズフルーとは，大学で最初の数週間に新入生が発症した一連の病気に付けられたイギリス英語］のようなCOVID-19感染拡大が懸念されるそうです．若者が無症候で感染を広げる最悪モデルでは，学年末までに96％感染と予測されました．学生集団は軽症ですが，体力の弱いスタッフや周囲のコミュニティと相互作用をするコンパートメントモデルでシミュレーションし，いろいろな介入施策の検討がなされています．
［注）Isaac Newton Instituteによって実施された「感染症のパンデミックのダイナミクスを理解する上での数学的および統計的課題」（IDP）　https://www.newton.ac.uk/event/idp］

日本でも，東京と他都市のRが，それぞれ１をわずかに下回っている状況ですが安心はできません．東京と他都市の相互作用により全体が増加し１を超えるRになる可能性はあります．

■免疫は持続するか
もし，回復したものの再感染を許容するモデルにするならば，新規感染率に対する，回復者再感染率の比をσとし，σR0＜１なら収束に向かいます．
従来の感染症の常識では，免疫を得ると再感染はしないということを前提にしていますが，COVID-19に関しては，再感染をしないような免疫が獲得できないかもしれません．免疫抗体が数か月で減衰するという報告が中国やスペインからなされている状況です．もし，免疫が獲得できないのであればワクチン自体が成立しないことにもなります．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
次回の数学月間企画講演（第3回）のお知らせ
「3Dジグソーパズルのデザインと数学」
手嶋吉法（千葉工業大学）
12月26日（土），15:00～17:00，参加無料です．
ZOOMにてリモートで実施します．多くの皆様の参加をお待ちします．
ホームページhttp://sgk2005.saloon.jp/　で申し込みができ，
参加登録されると，実施日の1週間前までにZOOMのURLをお知らせします．
主催：NPO法人数学月間の会

ロシアの義務教育は6歳から17歳までの11年間の一貫教育です．この年代の生徒が読む科学啓蒙雑誌も各種あり，いろいろ工夫されており面白く自分で深く学ぶこともできます．

 ●「科学の世界で」

月刊誌、ロシア版サイエンティフィックアメリカン。2003年から発行されています（それ以前は1983年から1993年に発行されました）。

●知識は力

1926年1月にティーンエイジャー向けの月刊ポピュラーサイエンス&アドベンチャーマガジンとして創刊し、困難な発展の道を歩んできました。戦後、「冒険」の要素を失くし、「働く若者に人気の科学雑誌」になりました。60年代の初めにかけて、人道的知識の割合が増加しました。
「科学と社会の架け橋」として、あらゆる年齢や専門分野の人々との交流を重視しています。

●量子っ子　クバンチク

2012年から発行されている、あらゆる年齢の好奇心旺盛な学童のための月刊イラストマガジン。数学、物理学、言語学、生物学、化学の面白い話や問題があります。

●量子　クバント

学童と学生のためのソビエトとロシアの人気のある科学、物理学と数学のジャーナル。1970年から発行されています。アカデミアンP.L. Kapitsaは、「KVANT」の創刊という提案をしました。アカデミアのIKKikoinがジャーナルの最初の編集長になり、アカデミックのA.N.Kolmogorovが最初の副編集長になりました。

高校生とその教師、および中学生を対象としています。
「Quant」セクションのタスクは、通常、6年生から学者まで、誰にとっても興味深いものです。

●トリニティオプションサイエンス

「TrV-Science」はロシアの人気科学新聞です。2008年4月1日から2週間ごとに発行されています。

●コマーサントサイエンス

出版社「Kommersant」の情報速報。Kommersant新聞と一緒に配布されます。2011年から（断続的に）公開されています。

●シュレーディンガーの猫

2014年10月から発行されている月刊「科学祭」。

●科学と生活

ロシアとソビエトのイラスト科学の月刊誌。1890年に創刊され、1934年に更新されました。

●サイエンスファーストハンド

科学の学際的なジャーナル。2004年以来、世界最大の科学センターの1つであるNovosibirskAcademgorodokで発行されています。ロシア語の印刷版は年に6回発行されます。Science First Hand （英語の電子版）は年に3回発行されます。

●ポピュラー機械

2002年から公開されています。1902年以来発行されているアメリカの人気科学雑誌PopularMechanicsのロシア版。

●可能性：化学。生物学。薬

学生と教師のための月刊教育雑誌。2005年から生産。

●可能性：数学。物理。コンピュータサイエンス

学生と教師のための月刊教育雑誌。シリーズ「数学。物理。情報」は2005年から発行されています。

●自然

ロシア科学アカデミーの月刊自然科学ジャーナル。1912年1月から公開されています。

●化学と生命

月刊科学誌。1965年に「Chemistry＆Life」という名前で創刊されました。1997年以来、「化学と生命-XXIセンチュリー」というタイトルで出版されています。

●科学技術の最新情報（販売終了）
雑誌「現代の大都市のハイテクライフスタイルについて、革新と科学的発見について」、アメリカの雑誌ポピュラーサイエンスのロシア版。2002年から2009年に終了。
●エコロジーとライフ
エコロジーアンドライフマガジン（販売終了）
月刊の科学教育誌。1996〜2012年に公開されました。

Грегори Чейтин　科学の世界«В мире науки» №6, 2006

数学と物理学
数学と物理学は完全に異なるものと一般に思われています。物理学者は、実験と観察の結果に基づいて世界を説明します。ニュートンの法則であれ、量子物理学の標準モデルであれ、宇宙を支配する法則は、経験的に確立され、論理的に証明するのではなく、実験的にのみ検証できる公理と見なされなければなりません。数学者は、ある意味で世界から独立しています。彼らの結論や定理、たとえば整数や実数の性質は、私たちの周りの現実にまったく依存していません。数学的な真実はどの世界でも真実でなければなりません。それでも、類似点があります。物理学、そして一般的に自然科学では、科学者は観察結果を昇華させることによって法則を生みだします。それから、結果の法則から観察結果をどのように推定できるか示します。数学でも同様のことが起こります。数学者は計算実験の結果を公理に圧縮し、それらから定理を推定します。

ヒルベルトが正しければ、数学は閉じたシステムであり、新しいアイデアの場所はありません。数学のすべてを説明する静的な閉じた理論があり、それは独裁者のようになります。数学を発展させるには、創造のための新しいアイデアと範囲が必要です。いくつかの基本原理から考えられるすべての結果を推測するために最善を尽くすだけでは十分ではありません。個人的には、オープンシステムの方が好きで、厳格で権威のある考え方は好きではありません。

1956年にハンガリーから脱出し、その後イギリスで科学の哲学に従事したイムレ・ラカトスも、数学は物理学のようなものだと信じていました。彼は、実験が数学にとって異質ではないことを示すために、準経験性の概念を導入しました。たとえば、1742年に、Christian Goldbachゴールドバッハは、2を超える偶数は2つの素数の合計として表すことができるという経験的な結論に達しました。ゴールドバッハの推測は、10^{14}までの数で正常にテストされていますが、厳密には証明されていません。数学は準経験的であるように私には思えます。言い換えれば、それは物理学（本当に経験的です）とは異なりますが、おそらくほとんどの人が考えるほどではありません。

新しい公理
新しい公理を追加するという考えは、数学者にとって異質ではありません。たとえば、ユークリッドの5番目の仮定を考えてみましょう。直線の外側に選んだ任意の点を通る指定された直線に平行線な直線は、1つだけ描くことができます。何世紀にもわたって、幾何学は、ユークリッドの他の仮定に基づいてそれを証明しようと頭を悩ませてきましたが、失敗しました。最後に、数学者は、5番目の公理を置き換えて、曲線空間の非ユークリッド幾何学、特に球面形と鞍形を得ることができることに気づきました。他の例としては、論理学における除外平均の法則や集合論における選択の公理などがありますが、これはほとんどの数学者が進んで証拠として使っています。しかし、それを認めず、いわゆる直観主義的な論理や構成主義的な数学を探求する科学者がいます。数学はまだ絶対的な真理の一枚岩のシステムになっていないことが判明しました!

もう一つの非常に興味深い公理は、「PはNPと等しくない」という文で、PとNPは課題クラスの名称です。NPクラスには、提案された解を非常に迅速にチェックできる課題が含まれています。例えば、「数字8633の因数を求める」という問題では、提案された解「97と89」を簡単な掛け算ですぐに確認することができます。（「速い」には厳密な定義がありますが、ここでは詳細は重要ではありません）クラスPは、事前の想定がなくてもすぐに解ける課題です。誰も答えを知らない問題は、どんなNPクラスの問題でもすぐに解けるかどうかということです。(数8633の因数を素早く求める方法はないのでしょうか？)つまり、クラスPとNPは同じなのでしょうか？これは、クレイ数学研究所のミレニアム賞問題リストにある項目の一つで、それぞれ100万ドルの賞が与えられています。

ほとんどのコンピュータ科学者は、PがNPと同等ではないと確信しているが、厳密な証拠はまだ見つかっていない。このような仮定の真偽は多くの経験的証拠に支えられているが、それを前提にして公理として受け入れられるのだろうか。それこそコンピュータの専門家がやっていることです。確かに、広く使われているいくつかの暗号システムの信頼性については疑問が残ります。
ハッキングできないと考えられていますが、誰もそれを証明することはできません。

実験数学
物理学と数学の交差点で、実験的な数学が生まれました。多数の例のコンピュータ処理による新しい数学の法則の発見です。このアプローチは、短い証明ほどの説得力がありませんが、長くて複雑な証明よりも説得力があり、場合によっては非常に受け入れられます。この概念は、過去に、ヒューリスティックスと数学の準経験的性質の強力な支持者であるジョージ・ポリヤとラカトスの両方によって支持されてきました。これは、2002年に発行されたStephen Wolfram（Stephen by Wolfram）の著書「NewKind of Science»（A the New Kind of Science）」に適用され、正当化されています。

大規模なコンピューティングは非常に説得力がありますが、それは証明の必要性を排除しますか？はいでもありいいえでもある。計算と証拠は、さまざまな種類の証拠を提供します。特に重要なケースでは、証明に誤りが含まれている可能性があり、コンピュータの計算は、残念ながら、想定されている結論を反証するような反例を見つける直前に停止されることがあるので、両方とも必要だと考えます。

議論された問題は非常に興味深いものですが、解決にはほど遠い。ゲーデルの証明に関する記事が発表されてから50年が経過しましたが、2006年の今でも、その不完全性がどれほど深刻なのか、それが原因で数学的方法を修正すべきかどうかはまだわかりません。おそらく50年以内に答えが見つかるでしょう。

追加の文献：

・Leibnizの章については、Men ofMathematicsを参照してください。ETベル。再発行します。タッチストーン、1986年。
・数学の準経験的見解のより完全な議論については、数学の哲学の新しい方向性を参照してください。ThomasTymoczkoによって編集されました。プリンストン大学出版局、1998年。
・ゲーデルの証明。改訂版。E.ネーゲル、JRニューマン、DRホフスタッター。ニューヨーク大学出版局、2002年。
・実験による数学：21世紀のもっともらしい推論。J.BorweinとD.Bailey。AK Peters、2004年。
・ゲーデルの哲学と彼の作品とライプニッツの作品との関係については、不完全性：カートゲーデルの証明と逆説を参照してください。レベッカゴールドスタイン。WWノートン2005。
・メタ数学！：オメガの探求。グレゴリィ・チェイチン。パンテオンブックス、2005年。
・数学者の経歴は、スコットランドのセントアンドリュース大学の数学統計学部のウェブサイトで入手できます。
・グレゴリィ・チェイチンのホームページ。

数値Ω
Ωの発見に向けた第一歩は、ライプニッツのエッセイが出版されてからちょうど250年後に出版された有名な記事でした。1936年、ロンドン数学協会プロシーディングスに、アラン・チューリングが単純なユニバーサルコンピューティングマシンの数学モデルを発表しました。さらに、彼はコンピュータ・プログラムが停止するか否かの判断が可能かどうか疑問を持ちました。これが有名な停止問題の定式化です。

数値Ωは、数学未知な部分を表しています。有限長のコンピュータプログラムは、この数の有限数のビットしか決定できません。後続のものはすべて、あいまいな暗闇の中に残ります（画像：www.sciam.ru）

 オメガの中は暗闇！

もちろん、プログラムを実行すると、最終的には停止していることに気付く場合があります。基本的な問題は、プログラムが停止しない場合に、いつあきらめて停止するかを決定することです。多くの特殊なケースでは解決できますが、チューリングは一般的な解決策がないことを示しました。アルゴリズムも数学理論も、どのプログラムが停止し、どのプログラムが停止しないかを決定することはできません。（このチューリングの状態の近代的な証明は、サイエンティフィック・アメリカンのウェブサイト上で見つけられます。）ちなみに、私は現代的な意味で「プログラム」という言葉を使用していて、それはコンピュータプログラム自体の全体と、それが処理するデータを意味しています。 

数値Ωに向けた次のステップは、考えられるすべてのプログラムのセットを検討することです。ランダムに選択されたプログラムが停止することはありますか？停止確率は Ωです。まず、プログラムをランダムに選択する方法を決めましょう。プログラムはビットの列であるため、後続の各ビットの値を選択するには、単にコイン投げをします。プログラムには何ビットを含める必要がありますか？コンピューターが次のビットを要求しなくなるまで、コイン投げをします。数値 Ωは、このようなランダムなビット列が導入されたときに、マシンが停止する確率です。（数値Ωはプログラミング言語の選択に依存しますが、この数の驚くべき特性はプログラム言語によりません。言語を選択すると、Ω はπや5のような特定の数値をとり ます。）

数値Ωは確率を表すため、 ゼロより大きく、1より小さい必要があります。一部のプログラムは停止し、一部は停止しません。バイナリコードで記述されたΩの数は 0.1110100...のようになり、小数点以下のビットの列は還元不可能であり、それら自体も還元不可能な数学的事実であることがわかります（各事実は特定のビットが0か1かです）。

Ωの決定方法

数値Ωがどのように決定されるか理解するために、簡単な例を考えてみましょう。特定のコンピュータのすべてのプログラムのうち、停止するのは3つだけで、それぞれ110、11100、11110、これらは、それぞれ3、5、5ビットの長さであるとします。我々はランダムに連続する各ビットの値を決定するためにコインを投げ、それらの各々の確率は1/2です。各プログラムの確率は

$$1/2^{3}, 1/2^{5} , 1/2^{5}$$, です。次に、そのようなコンピューターのプログラムを停止する確率は、次の式によって決定されます。

$$Ω = 1/2^{3} + 1/2^{5} + 1/2^{5} = 0.001 + 0.00001 + 0.00001 = 0.00110$$

［訳注）1/2^{3}は10進数表現，0.001は2進数表現です．他も同様］

ここで、2進数は、3つの停止プログラムの1つをランダムに選択する確率を表します。プログラム110が停止するため、1100や1101など、110で始まる3ビットより長いプログラムは考慮しません。したがって、それぞれの合計に0.0001を追加しません。

このように開始にプログラム110が含まれる、長いプログラム（1100など）すべては，停止すると見なします。言い換えると、プログラムデータは停止した後、それ以上のビットを要求しないので自己制限的です。
 
数Ωは無限の合計として定義でき 、長さがNビットの各プログラムはΩに$$1/2^{N}$$だけ寄与します。言い換えると、停止する各Nビットプログラムは、Ωのバイナリ表現のN番目のビットに1を追加します。停止したプログラムに対応するすべてのビットを合計することにより、Ωの正確な値を取得できます 。このように数値Ωは√2やπのように正確に計算できるように見えますが、そうではありません。数値Ωは厳密に定義されており、非常に具体的な意味がありますが、実際には解決策がない停止の問題を解決するので、計算することはできません。具体的には、Ωの最初のN ビットを 知ることで、最大N ビットの長さのプログラムが停止するかどうかを判断できます。つまり 、ΩのNビット を見つけるには、少なくともN ビットの長さのプログラムが必要です。Ωで特定のビット数を定義できないことを示唆しているわけではないことに注意してください。たとえば、コンピュータプログラム　0、10、および110が停止することを知っていると、Ωの最初の3ビットまでと言えます。0.111の形式です。重要なのは、Ωの最初のNビットは、Nビットよりも大幅に短いプログラムを使用して計算できないということです。

最も重要なことは、  Ωが無限の数の還元不可能なビットを与えることです。有限の長さのプログラムは、何十億ビットも含まれていても、残りのビットを決定するのに役立ちません。残りのビットは無限にあります。言い換えれば、公理の有限集合に対して、この集合を使用して証明できない真実の数は無限です。

数値Ωが非圧縮であるのはなぜか？

数値が非圧縮であること、つまり、最初のNビットがNビットより短いプログラムで決定できないことを証明してみましょう。チューリングの停止問題に照らして、Ωの特性を分析しましょう。Nビット長までのプログラムは、それより短いプログラムでは問題を解決できないという命題を使用します。

Ωの非圧縮性を実証するために、最初のNビットを知ることで、Nビットまでの長さのプログラムのチューリング問題を解くことができることを示します。N ビット以下の長さのプログラムでは、Ωの最初の N ビットを計算できないことがわかります。(もしそのようなプログラムが存在するならば、その助けを借りて、最初のNビットΩを計算して、Nビットの長さのプログラムのチューリング問題を解くのに使うことができます。)

それでは、ΩのNビット知ることで、停止問題を解くことができ、Nビット長までのプログラムのうち、どのプログラムが停止するかを決定することができるかを見てみましょう。一歩一歩やっていきましょう。Ｋステップでは、各プログラムをＫ秒間実行し、停止したプログラムの数によって、停止する確率$$Ω_{K}$$を決定します。Ωが全てのプログラムを用いて算出されるのに対し、最終的に停止するプログラムのサブセットのみを用いて取得されるため、Ωよりも小さいが、Ｋが増加するにつれて、$$Ω_{K}$$の値はΩに近づき、$$Ω_{K}$$の最初のビットの多くがΩの対応するビットと等しくなります。 $$Ω_{K}$$とΩの最初のNビットが一致する場合、これは、Nビット長までのすべてのプログラムが考慮され、遅かれ早かれ停止することを意味します。

(他にもNビット長のプログラムがあったとしたら、後段Kで停止してしまい、$$Ω_{K}$$がΩよりも大きくなってしまうので、あり得ない)。

つまり、Ωの最初のNビットを知ることで、Nビットまでの長さのすべてのプログラムの停止問題を解くことができます。今、Ωの最初のNビットの長さがNビットよりも有意に短いプログラムで検出できるとしましょう。そして、$$Ω_{K}$$を計算するプログラムと組み合わせて、Ｎビット以下のプログラム長を求めることで、Ｎビットまでのすべてのプログラムの停止問題を解決することができるが、上記のように、そのようなプログラムは存在し得ない。したがって、Ωの最初のＮビットを計算するためには、ほぼＮビットの長さのプログラムが必要となる。これは、数Ωが非圧縮性であること、すなわち、適用できないことを認めれば十分である。(大きなNビットの場合、NビットからほぼNビットへの長さ短縮は重要ではありません)。

Ωという数が受け入れられないことから、包括的な数学的理論が存在し得ないことは、次のとおりである。無限のビット数Ωは、ビット列よりも単純な、いかなる原理からも導き出すことのできない数学的事実の無限集合（選択された各ビットが１であろうと0であろうと）である。このように、数学の複雑さは無限であるのに対し、「世界の万物」のいかなる個々の理論も有限の複雑さを特徴とし、その結果、数学的真理の世界の豊かさをすべてカバーすることはできない。これまで言われてきたことから証明に意味がないということではありませんし、私は決して論理的な推論に反対しているわけではありません。実際、説明不能な原理（公理）は、常に数学の一部である。Ωという数字を見ただけで、今まで考えられていたよりもはるかに多いことがわかります。

数学者は何でも証明しようとする必要はないのかもしれません。彼らは真実ではない事実については、新しい公理を追加するべきです。問題は、彼らが説明不能であることを理解し、証明できないことを認めることです。しかし、厳密な証明ではなく、常にもっともらしい推論を用い、新しい法則を導き出して新鮮な実験データを理解しようとする物理学者とは異なり、数学者は決してあきらめることはありません。数学は物理学に似ているのだろうか？

概要：還元不可能な複雑さ
＊ゲーデルは、数学にある不可避の不完全性を示しました。厳密に証明できない真の命題があります。特異数Ωはさらに大きな不完全性を明らかにし、有限の公理集合から推論できない定理が無数に存在することを証明しました。

＊Ωという数値は厳密に定義されており、非常に具体的な意味がありますが、有限のコンピュータプログラムを使用して計算することはできません。

＊数値Ωの特性の分析は、数学者が新しい公理を仮定する必要があることを示しています。これは、物理学者が実験の結果を一般化し、論理の助けを借りて証明できない基本的な法則を導き出すときに行うことです。

アイク・アコピアン АЙК АКОПЯН • МАТЕМАТИКА • 21 КОММЕНТАРИЙ

https://elementy.ru/problems/2390/Samye_spravedlivye_vybory 

さまざまな形式の選挙がいたるところで実施されています。選挙結果が有権者の意思をあまり反映しない場合もあれば、大多数の意志を反映する場合もあります。選挙を数学の観点から検討し、このプロセスに2つの自然で明白な特性を要求すると、予期せぬ結論が得られることを示します。しかし、最初に、選挙とは何を意味するのか、そして選挙の正義とは何かを形式化しておきましょう。

複数の候補者が選挙に参加し、各有権者がこれらの候補者の特定の評価、つまり、候補者を有権者の個人的な好みの降順で並べたリストを持っていると仮定します。ワシントン、フランクリン、ジェファーソンの3人の候補者がいる例を考えてみましょう（ただし、以下のすべての推論は、もっと多くの候補者でも有効です）。その場合、ある有権者の評価は次のようです。「フランクリン>ワシントン≥ジェファーソン」。すべての候補者を優先度の高い順に1行に並べることができるこのような評価は、推移的と呼ばれます。

私たちが慣れ親しんでいる選挙では、各有権者が候補者の1人だけに投票を行う、たとえば、ある有権者がジェファーソンに投票したい場合、これは彼の評価が「ジェファーソン>フランクリン=ワシントン」のようになることを意味します。

選挙制度は、「大多数の意見」を反映した評価を出力するべく、すべての投票を評価する方法であると理解します。もう少し数学的な言葉で言えば、選挙はすべての有権者の好みを入力として受け、これらのデータに基づいて集合の好みの評価を出力する機能です。

このようなシステムの特殊なケースは、ロシア（日本でも）で使われている各候補者の総投票数です。別の特殊はケースは、例えば、候補者のランダムな最終選択で、これは投票者の意見がまったく考慮に入れられません。

選挙制度が公正と呼ばれるために必要な特性は何でしょうか？
まず、すべての有権者が2番目の候補よりも1番目の候補を好む場合、最終結果はこれを反映する必要がある、つまり、最終選挙手順は、1番目の候補が2番目の候補よりも高くなるのが論理的です。このプロパティは、全会一致と呼ばれます。第二に、これも非常に論理的ですが、最終評価における2人の候補者の相対位置は、有権者の好みの評価による相互位置にのみ依存し、他の候補者の位置に依存するべきではありません。これは、選挙結果で、一方の候補者が他方の候補者を追い抜いたことが判明した場合、3番目の候補者が投票に追加（または除外）された場合もまったく同じ結果になることを意味します。2番目のプロパティは、無関係な選択肢からの独立（またはバイナリ独立）と呼ばれます。

これらの2つの特性を満たす選挙は、公正であると見なされます。

課題
これらの定義を満たす唯一の公正な選挙制度は独裁である。つまり選挙の結果が一人の人の好みによって完全に決定され（そして、他の人の好みはまったく考慮されない）システムであることを証明しなさい。

ヒント1
結果は3人以上でも当てはまりますが、3人の候補者による選挙で行うのが最も簡単です。

ヒント2
最初はすべての有権者が個人的な評価でリンカーンを最初に置き、フランクリンを最後に置いたとしましょう。そのような評価で最終的な選挙結果はどのようになりますか？有権者がリンカーンとフランクリンの場所を次々と変え始めたら、選挙結果はどのように変わるでしょうか？

解答
有権者が6人しかいないとします。まず、候補者が2人だけの場合にどうなるかを考えてみましょう。ワシントン（W）をジェファーソン（J）と競争させ、フランクリン（F）をしばらく忘れます。

すべての有権者がジェファーソンよりもワシントンを好む場合（つまり、評価がW≥Jの場合）、全会一致規則に従った公正な選挙の最終手順は、W≥Jになることに注意してください。この平凡な状況を図1に示します。.逆に、すべての有権者がワシントンよりもジェファーソンを好む場合（すべてJ≥W）、明らかに、ジェファーソンもワシントンを打ち負かす必要があります。

図1.

それでは、ダイナミクスで何が起こるかを見てみましょう。誰もがワシントンに賛成している状況から始めて、有権者が順番に個人の評価を変更し始めたらどうなるかを見てみましょう。最終結果はどのように変わりますか？
最初はワシントンが勝つことは明らかであり、最終的には、すべての有権者が好みを変えると、ジェファーソンが勝たなければなりません。最終手順で結果が逆転する、ある有権者i（私たちの場合は、1≤ i≤6）があります。私たちの場合では、i=4（図2）。

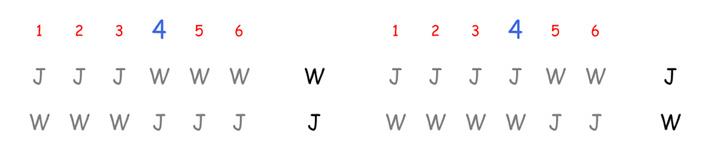
図2.

フランクリンを思い出して、図2の左側のケース（主要な候補者のランキングでW≥Jの場合）を考えてみましょう。フランクリンは、i<4の場合投票の真ん中に位置を占め、i≥4の場合に最下位になるとしましょう（図3）。選挙結果はどうなりますか？フランクリンが入る前に、ワシントンがジェファーソンを倒したことを思い出してください。私たちの選挙は公正なので、この結果は、バイナリの独立性のために変わるべきではありません。また、すべての有権者についてJ≥Fであることがわかります。全会一致プロパティから、最終結果もJ≥Fである必要があります。したがって、最終手順はW≥J≥Fとなります。

図3.

もし4番目の有権者がWとJを入れ替える決定した場合、この有権者はペア（W,J）のキーであり、個々の評価の相対位置（J,F）と(W,F)は変わらないので、最終結果はJ≥W≥Fに変わります（図4）。主要な有権者の個人的な評価は、最終的な評価と一致することに注意してください。

図4.

このキー有権者がどれほど強力であるかを理解するために、他の有権者の票を変えることによって選挙の結果に影響を与えようとしましょう。たとえば、フランクリンとジェファーソンの個人的な評価の場所を交換します(図5)．結果は変わりましたか?

図5.

個々の評価におけるWとFの相対的な位置は変更されていないため、W≥Fは最終手順に残ります（無関係な選択肢からの独立性のため）。また、JとWの相対位置は変更されていません。つまり、最終手順ではJ≥Wになります。結果はまったく変更されず、ジェファーソンが常に勝ちます。そしてこれは、4番目の有権者が、彼の個人的な評価でジェファーソンを1位にした唯一の人であるということです。キー有権者の個人的な評価がJ≥Fである限り、この問題に関する他の有権者の意見は最終的な投票結果に考慮されないことがわかります。

では、何を証明したのでしょうか。候補者のペア（この場合はワシントンとジェファーソン）について、他の人の意見に関係なく、投票結果で3番目の候補者の位置を明確に決定するキー有権者がいることを示しました。

しかし、候補者の任意のペアのキー有権者の存在から、独裁者の存在自体は導かれません。理論的には、このキー有権者は候補者のペアごとに異なる可能性があるためです。それにもかかわらず、キーは常に同じ有権者であることが判明しました（正確には、彼が実際に評価におけるFの位置を指示しているためです）。これは、上記と同様の推論を実行することで簡単に示すことができます。このキー有権者による評価が最終的な選挙結果を完全に決定することが判明しました。

あとがき
上で議論された問題は長い間古典的な結果でした。これは、1951年の論文で、アメリカの数学者で経済学者のケネス・アローによって最初に定式化され、証明されました。今では、民主主義の不可能性またはアローのパラドックスについてのアローの定理と呼ばれています。
一般的なケースの完全な証明は、J.Geanakoplos，2005にあります。
Arrowの不可能性定理の3つの簡単な証明https://link.springer.com/article/10.1007/s00199-004-0556-7

この定理は実際には次のように述べています。人々の好みが独立していて一過性であり（評価を表す）、選挙が全会一致と、無関係な選択肢からの独立の原則を尊重する場合、他の評価に関係なく、個人の評価が結果を完全に決定する独裁者が常に自動的に存在します。これらの条件を少し緩和しても、たとえば、独裁者ではないにしても、選挙の最終結果における任意の2人の候補者の相対的な位置を常に決定する「拒否」する権利を持つ人が常に存在することを示すことができます。

定理が成立するために必要な有権者の選好要件は、通常のアプローチと呼ばれます。このアプローチでは、個人の好みは量的ではなく質的に考慮されます。つまり、いくつかの選択肢は他の選択肢よりも優れている、悪い、または同等である可能性がありますが、ある選択肢が別の選択肢よりどれだけ優れているかを判断する手段はありません。

これらの条件はすべて、非常に論理的ですが、実際には常に満たされているわけではありません。たとえば、基本的に選挙の特定の客観性の要件であるバイナリ独立（無関係な選択肢からの独立）の原則（候補は互いにのみ比較され、他のコンテキストでは比較されません）は、非常に簡単に破られます。100人の有権者がいて、その個人的な評価が次のように分布している状況を想像してみてください。25人の有権者の評価はW> J> F、40人の有権者の評価はJ> F> W、残りの35人の有権者の評価はF> W> Jです。いずれにせよ、選択はバイナリ独立の原則に違反します（W、J、またはFが勝つ場合を個別に検討してこれを示すようにしてください）。

この例は、一般に、候補者が3人以上いる場合、大多数の「意見」が互いに矛盾する可能性があることも示しています。公的選択の理論におけるこの現象は、コンドルセパラドックスまたは公的選択の循環的性質と呼ばれます。これは、社会全体の観点から（つまり、「選挙」の結果を合計した後）、次の逆説的な状況が発生するためです。W> J> F> W> ...、にもかかわらず各有権者の個々の好みは一時的なものであること。

このパラドックスは、2段階の投票システムで重要です。最も明白な例は、米国大統領選挙です。そこでは、各党（共和党と民主党）の候補者が最初にいわゆるプライマリーを通過します。そこでは、各党から1人の候補者が選ばれ、主要な大統領選挙で党を代表します。

今年の民主党の初等協会では、主な戦いはバーニーサンダースとジョーバイデンの間でした。ジョー・バイデンが予備選挙で勝利し、選挙で民主党の候補者になります。彼は現職の共和党大統領ドナルド・トランプと競争するでしょう..。コンドルセのパラドックスはアメリカ社会の好みで起こっているのかもしれません：トランプ>バイデン>サンダース>トランプ> ...そして、バイデンは世間の心にあまりないので、すべての選挙の結果は選挙の第一段階（プライマリー）の結果に依存することがわかりますトランプよりも優先され（サンダースよりも優先されますが）、サンダースはトランプよりも優先されます（バイデンよりは優先されませんが）。そして、この状況では、大統領選挙に参加したバイデンは（プライマリーではサンダースよりも好ましいため）、トランプに負けます。したがって、ある意味で、民主党が選挙に勝つチャンスがあるにもかかわらず、あまり好まれない民主党の候補者を指名することは「より有益」です。しかし、そのような場合の世論を評価する問題は、社会学の分野に属します。

ーーーーーーー
（参考）11月4日現在

https://elementy.ru/nauchno-populyarnaya_biblioteka/430319/Predely_dokazuemosti

グレゴリー・チェイチン
「科学の世界で」2006年第6号より

ゴットフリート・ライプニッツが、「形而上学の議論」(1686年)で、最初に表現した複雑さとランダム性の考え方と、現代の情報理論におけるそれらの確認から、数学が「すべての中で最も一般的な理論」を作ることは不可能です。

1956年、Scientific American誌は、Ernest NagelとJames R.Newmanによる記事「Gödel's Proof」を発表しました。2年後、その著者は同じ名前の本をリリースしました（まだ再版されています）。当時はまだ子供でしたが、ニューヨーク公立図書館で本を開いたときのスリルを今でも覚えています。

Kurt Gödelゲーデルが、数学を使って、数学自身の可能性の限界を示していることに私は驚いた。彼は、数学の完全な理論の存在についてDavid Hilbertヒルベルトが約1世紀前に行った命題に反論しました。数学的論理の規則を一貫して使用することにより、数学のすべての命題を導き出すことができる究極の公理系はあるか。ゲーデルは、この方法では証明できない真の数学的命題が存在することを示しました。彼の結論は、「この命題は誤りである」と「この命題は証明できない」という2つの自己関連のパラドックスに基づいています。（ゲーデルの不完全性定理の詳細については、 Scientific Americanを参照してください。）

有限のコンピュータプログラムを使用して、計算できない特定の厳密に定義された数Ωの存在は、真の命題を厳密に証明できる包括的な数学システムを作る希望を打ち砕きました。（画像：www.sciam.ru）

私は生涯を通じてゲーデルの証明を扱い、半世紀後、自分の本を出版しました。ある程度、これはNagelとNewmanネーゲルとニューマンの本の私のバージョンですが、ゲーデルの証明はその主要なテーマではありません。私の仕事は、情報を測定し、いくつかの数学的な事実は複雑すぎるために理論に詰め込むことができないことを証明することに基づいています。私のアプローチによると、ゲーデルは氷山の一角を発見しただけです。有限の公理体系からは証明できない正しい数学的定理が無数にあります。

複雑さと科学の法則

ライプツィヒに記念碑が建てられたゴットフリート・ライプニッツは、300年前にアルゴリズム情報の多くの特性を予見していました（www.uni-leipzig.deからの写真）

1686年、ライプニッツの哲学的エッセイDiscoursdemétaphysique形而上学の議論が出版されました。提起された問題は：特定の法則によって記述できる事実を、どの法則にも従わない事実からどのように区別するか？
彼のエッセイの4章で、ライプニッツは非常に単純で深遠な考えを表現しました。理論は、それが説明するデータよりも単純でなければなりません。そうでなければ、何も説明しません。科学法則の概念は、それが無制限のレベルの数学的複雑さを許容する場合、意味がなくなります。なぜなら、事実がどれほどランダムで乱雑であっても、法則を定式化することが常に可能だからです。逆に、一部のデータを説明する単一の法則が複雑すぎることが判明した場合、問題のデータは実際にはどの法則にも従いません。

アルゴリズム情報の現代の数学理論は、複雑さと単純さの概念の正確な定量的定義を与えることを可能にしました。従来の情報理論は、情報をエンコードするために必要なビット数によって情報量を定義します。たとえば、単純な「はい/いいえ」の回答をエンコードするには、1ビットが必要です。対照的に、アルゴリズム情報量は、データを生成するために必要なコンピュータプログラムの長さによって決定されます。プログラムを格納するために必要な最小ビット数は、アルゴリズムデータ情報量と呼ばれます。たとえば、自然数1，2，3，...　の無限のシリーズには、アルゴリズム情報がほとんど含まれていません。シリーズのすべての数は、短いコンピュータプログラムを使用して取得できます。計算を完了するのにかかる時間や、使用するメモリ量は関係ありません。プログラムの長さ（ビット単位）のみが重要です。（もちろん、アルゴリズム情報量の正確な値は、選択したプログラミング言語によって異なりますが、この記事で説明する問題については、これは関係ありません。）

別の例として、3.14159...に等しい数πを考えてみましょう。そのアルゴリズム情報量は少ない：すべての符号を順次計算するには、かなり短いアルゴリズムですむ。しかし、100万文字のみを含むランダムな数値、たとえば1.341285 ... 64は、はるかに大量のアルゴリズム情報によって特徴付けられます。そのような数字には定義構造がないため、それを書き込むために必要なプログラムの長さは、数字自体の長さに近くなります。

科学理論は、観察結果を予測するコンピュータプログラムのようなものです。有用な理論は、実験データの昇華です。いくつかの法則と方程式を使用して、さまざまな現象の全世界を記述することができます（画像：www.sciam.ru）

（...で置き換えたすべての数字をプログラムに含める必要があります。）このような数字の列を計算できる短いプログラムはありません。プログラムは圧縮できず冗長性もありません。最善の方法は、そのまま書き出すので、このような列は、還元不可能またはアルゴリズム的にランダムと呼ばれます。

上記は科学法則や事実との関連は如何でしょうか？
アイデアは、プログラマーの目を通して科学を見ることです。科学理論は、観察の結果すなわち実験データを予測するコンピュータプログラムのようなものです。この見方は、2つの基本原則に基づいています。最初の（Occam's razor「オッカムのかみそり」）によると、いくつかのデータを説明する2つの理論のうち、より単純なものが優先されるべきです。言い換えれば、最良の理論は、観測結果を計算するための最短のプログラムです。ライプニッツによって示された2番目の原則は、現代の用語では次のように言います。ビット単位のサイズが説明するデータ量に等しい理論は、完全にランダムなデータを記述できるため、役に立ちません。有用な理論は情報の削減を提供します：データを理解することは、それらを短いアルゴリズムの説明に圧縮することです。理論が単純であるほど、現象の本質をよりよく理解できます。

十分な理由
コンピュータプログラム登場の2世紀半前に生きていたライプニッツは、現代のアルゴリズム情報の概念に非常に近づいていました。ライプニッツは、すべてがバイナリコードの形式で表現できることを知っており、最初のコンピューティングデバイスの1つを作成しました。複雑さと単純さの概念を考慮して、彼はコンピューティングの巨大な可能性を認識していました。ライプニッツが知っていたすべての要素を組み合わせていたとしたら、彼はおそらく自分の哲学の基礎の一つである十分な理由の原理（起こったものにはすべて理由がある）を疑っていただろう。ポジションが真であれば、何らか真の理由があります。しかし、日常の喧騒の中で、信じられないことが起こります。理由が常にわかるとは限りません（おそらく、推論の連鎖が長すぎて混乱しているため）、神のみぞ知る。それですべてです！

数学者は、常にすべてを証明しようと努力しているため、ライプニッツの十分な理由の原理を無条件に受け入れることは間違いありません。たとえ定理の真実が明白であり、何百万もの例がそれを確認したとしても、数学者は依然として一般化された証明を必要とします。そして、アルゴリズム情報の概念は、知識の出所と限界についての哲学的推論に驚くべき貢献をすることができます。それは、いくつかの数学的事実が理由もなく真実であることを示しており、十分な理由の原理に異議を唱えています。以下に示すように、還元不可能な数学的事実は無数にあり、その真実はいかなる理論によっても説明ができません。それらは計算上還元できないだけでなく、論理的にも還元できません。これらの事実を「証明」する唯一の方法は、理由なしでそれらを公理として認識することです。

「公理」の概念は、論理的な還元不可能性と密接に関連しています。公理は、私たちが自明であると考え、かつ単純な原理から証明できない数学的提案です。すべての数学理論は、公理から導かれる定理で、これは、ユークリッドが2000年前に行ったことです。幾何学に関する彼の著書は数学的な表現の手本になりました。

古代ギリシャでは、他の方法ではなく、この方法で投票するように仲間の市民を説得するために、あなたの理由を述べる必要がありました。これがおそらく、ギリシャ人が数学的な提案は証明されるべきであり、経験的に推論されるべきではないという考えに至った理由です。（ギリシャ人とは異なり、メソポタミアとエジプトの初期の文明は実験に依存していたようです。）論理的推論の方法は非常に実り多いことが判明しました。現代の数学、数学的物理学、そしてコンピュータ構築技術を含むすべての精密科学は、現代の数学と論理機械の助けを借りて作られました。
私は2千年かけて構築した数学とすべての科学のアプローチが失敗だったと主張しているのでしょうか? ある意味そうです。私の反論例は、論理と推論の限界を示し、証明できない数学的規則の無限の流れの源を、私が「オメガ」Ωと呼ぶ数に担わせることです。

こうして、3千年ぶりに、数学者は彼らの分野の最も深い基礎を研究することに近づきました。そして、奇妙な構図が浮かび上がりました。数字ファンは、計算を行うルールを明確に記述することを学び、パラドックスによって生じる疑念を排除するために、使われた根拠の「正当性」を証明すれば済みました。そして1920年代の前半までに優れた研究学派を形成した偉大なヒルベルトは、一連の論文で数学の基礎の研究計画（後に「ゲッティンゲンプログラム」の名前が付けられた）を講演しました。最も単純化された形式で、それは次のように表すことができます。数学は、特定の公理体系から導き出された一連の結果として表すことができ、次のことを証明できます。

１．数学は完全です。すなわち、いかなる数学的な記述も、その分野自体の規則に基づいて証明または反証することができます。
２．数学は一貫しています。受け入れられている推論の規則に違反せずに、いかなる命題も証明すると同時に反駁することは不可能です。
３．数学は決定可能です。つまり、ルールを使用して、それが証明可能であるか反駁可能であるかどうか、任意の数学命題について調べることができます。

実際、ヒルベルトのプログラムは、すべての数学的な質問に答えるための、または少なくともそのような存在を証明するためのいくつかの一般的な手順を開発しようとしました。科学者自身は、彼が作成した3つの質問すべてに対して肯定的な答えを確信していました。彼の意見では、数学は確かに完全で、一貫性があり、解決可能でした。残ったことはそれを証明するだけでした。

さらに、ヒルベルトは、公理的方法が数学だけでなく、科学一般の基礎にもなり得ると信じていました。1930年に、彼の記事「自然と論理の認識」で、彼は次のように書いています。

科学のさらなる発展のために、ヒルベルトと彼の学派は成功したでしょうか？彼が信じていたように、すべての数学（および科学全体）が公理のシステムに還元された場合、一般的な論理規則に従ったプログラムに従って、元の命題から次の命題を実証する（つまり、定理を証明する）ことがコンピューターでできます。

ヒルベルトの理論が実現されれば、24時間稼働するスーパーコンピューターは、ますます多くの新しい定理を継続的に証明し、World WideWeb上の無数のサイトに投稿します。数学に続いて、「公理の時代」は物理学、化学、生物学に広がり、そして最後に、人間の意識の科学に変わります。私たちの周りの世界、そして私たち自身は、そのような場合には多少異なって見えるでしょう。

しかし、「普遍的な公理化」は行われませんでした。世界の数学者が数十年にわたって取り組んできた、非常に野心的で壮大なプログラム全体が、単一の定理によって反駁されました。それは、当時わずか25歳のKurt Gödelゲーデルによってでした。

1930年、ケーニヒスベルクのウィーンサークルが主催した会議で、彼は”論理計算の完全性”に関する発表をし、翌年の初めに、”Principia Mathematica と関連システムの根本的な困難”に関する論文を発表しました。彼の仕事の中心は、数学のさらなる発展において基本的な役割を果たす定理の定式化と証明でしたが、不完全さについてのゲーデルの有名な定理は、「どのような一貫した公理システムであっても、受け入れられた公理系内で、証明または反証することができない命題が存在する」と述べています。このように、ゲーデルはヒルベルトの最初の命題に否定的な反応を示しました。 興味深いことに、ヴェルナー・ハイゼンベルグは同じ会議で「因果関係の知識と量子力学」について講演しました。このレポートで、”不確定性原理”の最初のアプローチが提示されました。

■ゲーデルの定理

それから四半世紀が経過しましたが、ゲーデルが何を証明したかについての議論は続いています。特に熱狂的な議論が疑似科学界で起こっています。「ゲーデルの不完全性定理は本当にユニークです。神々の存在から理由の欠如まで、"世界のすべて"を証明したいときはいつでも言及されます」と、優れた現代数学者V.A.Uspenskyは書いています。

多くの推測はさておき、科学者はゲーデルの評価で二分されました。ラッセルに続いて、現代の数学論理の基礎となるこの有名な定理は、この分野以外の研究にほとんど影響を与えないと信じる人もいます。

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

新しい定理を絶えず証明し続けるコンピューターの幻想に関しては、そのような活動の意味に多くの専門家から、大きな疑問が投げかけられています。確かに、数学にとって、証明された定理の定式化だけでなく、その理解も重要です。これにより、さまざまなオブジェクト間の接続を識別し、どの方向に進むことができるかを理解できるからです。そのような理解がなければ、形式化された推論ルールに基づいて生成された定理は、一種の「数学的なスパム」にすぎません。これは、モスクワ州立大学の数学論理および機械と数学のアルゴリズム理論部門のメンバーであるアレクサンドル・ シェニの意見です。

ゲーデル自身も同様の方法で推論しました。数学の基礎の完全性を破壊したとして彼を非難した人々に、彼は、「実際には何も変わっておらず基礎は揺るぎないままで、彼の定理は論理の鉄の法則に支配される科学分野で、直感と個人的なイニシアチブの役割の再評価につながっただけ」と答えました。これには何かメリットがあるというわけではありません。

ゲーデルとアインシュタイン（写真：「科学の世界で」）

ゲーデルの定理
それから四半世紀が経過しましたが、ゲーデルが何を証明したかについての議論は続いています。特に熱狂的な議論が疑似科学界で起こっています。「ゲーデルの不完全性定理は本当にユニークです。神々の存在から理由の欠如まで、"世界のすべて"を証明したいときはいつでも言及されます」と、優れた現代数学者V.A.Uspenskyは書いています。

多くの推測はさておき、科学者はゲーデルの評価で二分されました。ラッセルに続いて、現代の数学論理の基礎となるこの有名な定理は、この分野以外の研究にほとんど影響を与えないと信じる人もいます。

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

新しい定理を絶えず証明し続けるコンピューターの幻想に関しては、そのような活動の意味に多くの専門家から、大きな疑問が投げかけられています。確かに、数学にとって、証明された定理の定式化だけでなく、その理解も重要です。これにより、さまざまなオブジェクト間の接続を識別し、どの方向に進むことができるかを理解できるからです。そのような理解がなければ、形式化された推論ルールに基づいて生成された定理は、一種の「数学的なスパム」にすぎません。これは、モスクワ州立大学の数学論理および機械と数学のアルゴリズム理論部門のメンバーであるアレクサンドル・ シェニの意見です。

ゲーデル自身も同様の方法で推論しました。数学の基礎の完全性を破壊したとして彼を非難した人々に、彼は、「実際には何も変わっておらず基礎は揺るぎないままで、彼の定理は論理の鉄の法則に支配される科学分野で、直感と個人的なイニシアチブの役割の再評価につながっただけ」と答えました。これには何かメリットがあるというわけではありません。

ゲーデルとアインシュタイン（写真：「科学の世界で」）

ーーー

しかし、一部の科学者は異なる意見を持っています。確かに、論理的に推論する能力が人間の心の特徴（少なくともその主なツール）であると考える場合、ゲーデルの定理は私たちの脳の限界を直接示しています。無限の思考力を信じて育った人が、その力の限界についての論文を受け入れることは非常に難しいことでありましょう。

むしろ、私たちは自分の精神的能力の思考限界について話すことができます。多くの専門家は、論理的思考の根底にある計算の「アリストテレス」プロセスは、人間の意識の一部にすぎないと考えています。彼の他の分野、「非計算的」分野は、直感、創造的な洞察、理解などに責任があります。そして、心の前半がゲーデルの制限に該当するとしても、後半はそのような枠組みから解放されます。

この観点の立つ最も一貫した支持者である数学と理論物理学の著名な専門家、ロジャー・ペンローズは、さらに進めて、創造的意識行為の実現にかかわる非計算的性質のいくつかの量子効果の存在を示唆しました。彼の同僚の多くは、人間の脳に仮想の量子メカニズムを与えるという考えに批判的ですが、ペンローズと彼の共同研究者は、その存在を確認する実験スキームをすでに開発しています。

ペンローズの仮説の多くの結果の1つに、量子コンピューターの出現がコンピューティング分野の途方もないブレークスルーであるとしても、現代のコンピューティングデバイスに基づいて人工知能を作るのは基本的に不可能であるという結論があります。事実、どのコンピューターでも、人間の意識の形式的で論理的な「計算」活動を詳細にシミュレートすること以外はできず、知性の「非計算的」能力にはアクセスできません。

これは、75年前に発表された若いゲーデルの数学的定理によって引き起こされた自然科学と哲学的論争のほんの一部にすぎません。他の偉大な同時代の人々と一緒に、彼は人に自分の周りの世界と自分自身を異なって見させました。

ゲーデルの定理、相対性理論および量子論の創造を含む、20世紀の最初の3分の1の最大の発見は、過去2世紀の科学的研究に基づいて創造された自然の機械的決定論の構図の限界を示しました。宇宙の発展の道と道徳的義務の両方が根本的に異なる法則に従うことが判明しました。そこには、取り返しのつかない複雑さ、不確実性、偶然、そして不可逆性があります。

しかし、科学革命の偉大な結果は、すでに述べたものに限定されません。20世紀の初めまでに、ラプラス-ニュートンの決定論思想は、社会科学の発展に大きな影響を与えました。すべての要素が厳格な法則に従い、厳格な機械的構造の形で自然を表現した古典的な自然科学の先覚者に続き、現在の状態を知れば未来を明確に予測することができ、司祭、社会科学者は不変の法則に従い、所定の方向に発展する人間社会を描きました。そのような世界像を保存するための最後の試みの1つは、明らかに、「唯一の真の科学的教義」の概念に取り組んだマルクシズム-レニニズムであり、その一部は「歴史の物質主義的理解」でした。 「大きな工場」のような社会主義社会を構築するというレーニンの考えを思い出すだけで十分です。

宇宙の自然科学の全体像に定着していた複雑さ、ランダム性、不確実性についての考えが、徐々に、社会科学や人間科学に浸透し始めました。社会では、個人の自由という現象を通じて、不確定が実現します。歴史的プロセスを複雑にし、普遍的な発展の不変の法則に従わないのは、自由で予測不可能な選択をする主題としての自然界の人間の存在です。

しかし、わが国の複雑な世界の新しい構図の取得は非常に困難でした。これに気付くのは間違いありません。70年間支配していたイデオロギーは、普遍的な権威秩序の哲学としてのラプラス型の決定論に引き寄せられました。厳格な階層法に支配されている社会工場の支配的なソビエトの官僚機構が決して離さなかった夢の中心に、この事前決定の原則がありました。

したがって、複雑さ、多元性、多様性に関しては、それが相対性の理論、量子力学、遺伝学、サイバネティクス、社会学的研究、心理分析などであるかどうかにかかわらず、イデオロギー検閲のメカニズムがすぐに働きました。これは、自然と社会の両方からの自由へのすべての言及を排除することを目的としていました。

悲しいかな、不活性な遺産は、今でも多くの同胞や同時代の人々の心を暗い影として支配しています。これは、共産主義の教義の終焉によって空けられた場所を埋めるために、当局によって開始された新しい「国民的イデオロギー」探求の苦悶によって証明されています。

このようにして、クルト・ゲーデルと彼の偉大な同時代人たちは、頭上の星空と私たちの内なる道徳法則、そして私たちが住む社会を、新しい方法で私たちに見せました。

Александр Музыкантский，«В мире науки» №3, 2007

アレクサンダー・ムジカンツキー,  「科学の世界で」2007年第3号より

訳者より口上：私はラッセルのパラドックスがよく理解できません．その簡易な解説は，次のような表現で語られることが多いのでここから始めましょう．

アレクサンダー・ムジカンツキー,  「科学の世界で」2007年第3号より

訳者(SGK)より口上：私はラッセルのパラドックスがよく理解できません．その簡易な解説は，次のような表現で語られることが多いのでここから始めましょう．

町の人々は，自分で自分の髭を剃る（Ａ）か，剃らない（Ｂ）かのグループに完全に2分割できます．どちらの集合にも属さないという人はあり得ませんし，両方に属するということも不可能です．そして，床屋も町の人のうちに入りますから，（Ａ）or（Ｂ）のどちらかの集合に属します．床屋が自分に課したルールで，他人の髭を剃ることができるのは（Ｂ）に属する人に対してです．床屋自身はどちらの集合に属していてもかまいません．もし，（Ａ）に属していれば，自分の髭は自分で剃りますが，（Ａ）の人のひげは剃らないという床屋のルールに反します．もし，（Ｂ）に属していれば床屋の手で髭を剃りますが，自分＝床屋なので，自分で剃ることになり（Ｂ）に存在することが矛盾になります．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
訳者のウォーミングアップはここまでにし，
Александр Музыкантский，В мире науки，№3, 2007
によるゲーデルの紹介に入りましょう：

■20世紀の最も優れた発見といえば、アインシュタインの相対性理論、量子力学、ハイゼンベルグの不確定性原理などです。しかし、多くの著名な科学者（数学者や哲学者）は、前世紀の科学的思想の最大の成果の中にゲーデルの定理を含めています。物理学分野の画期的な進歩が、人間の心の自然の新しい法則への理解をもたらすなら、ゲーデルの仕事は人間の心自体の動作原理をさらによく理解する可能性で、私たちの時代の世界観と文化に大きな影響を与えました。

ゲーデルとは誰か？
Kurt Gödelゲーデルは1906年4月28日、オーストリア-ハンガリーのモラヴィアの都市ブルノ（当時はブルンと呼ばれていました）で生まれました。18歳で、彼は最初に物理学を学んだウィーン大学に入学しましたが、2年後に数学に転向しました。このような科学的関心の変化は、主にバートランド・ラッセルの著書「数学の哲学の紹介」の影響下で起こったことが知られています。科学者としてのゲーデルの形成に大きな影響を与えたもう1つは、ウィーンサークルの活動への彼の参加でした。これは、1920年代後半から1930年代半ばまで定期的にウィーンに集まった、数学者、論理学者、哲学者などの優秀な科学者の集団です。ルドルフ・カルナップ、オットー・ニューラス、ハーバート・フェイグル、モリッツ・シックなどの科学者は、さまざまな時期にウィーンサークルの活動に参加しました。哲学的な積極性の形成は、彼らの活動に関連しています。サークルのトピックスは、自然と社会の知識のうち、科学的知識のすべてをカバーしていました。さまざまなヨーロッパの科学センターで開催された国際会議では、20世紀の基本的な科学的知識の形成で、ウィーンサークルが果たした卓越した役割がありました。ゲーデルは、木曜日のサークルのほぼすべての会議と、彼が主催する国際会議に参加しました。オーストリアでのサークルの活動は1936年に中断され、そのリーダーであるモリッツ・シュリックがウィーン大学の階段でナチスの学生に殺されました。サークルのメンバーのほとんどは米国に移住し、ゲーデルも移住しました。時が経ち、彼はアメリカ市民になり、プリンストンの高等研究所で働き、同じ都市で1978年に亡くなりました。これが彼の人生の輪郭です。職場の友人や同僚は、彼を閉じた人、痛々しいほど傷つきやすく、周囲の世界から切り離され、完全に彼の考えに没頭している人であったことを思い出します。

Kurt Gödel（1906-1978）．写真：「科学の世界で」

世界の論理的理解が、ゲーデルの人生の中心を占めていたという事実は、彼の伝記の奇妙な詳細によって証明されています。1948年、アメリカ市民権の取得の問題が決定されたとき、ゲーデルは、決められた手順に従って、アメリカ憲法の基本に関する口頭試験のようなものに合格しなければなりませんでした。彼はすべての科学的良識をもってこの問題に取り組み、文書を徹底的に研究し、憲法に違反することなく合法的に独裁権を確立することができるという結論に達しました。そのような発見は、彼がテストを受ける役人と話し合うとき、テストに失敗させるだけです。彼はもちろん、合衆国基本法の彼の理解を政治思想の最大の成果であると考えました。彼が市民権を取得したときにゲーデルの2人の保証人の1人として行動したアルバート・アインシュタインは友人です。少なくとも誓いが立てられるまで、彼の議論の展開を延期するように彼を説得しました。その後、歴史は興味深いエピローグとなります。四半世紀後、別のアメリカ人、ケネス・アローは、ゲーデルがアメリカの憲法を研究して到達した命題を一般的に証明したことでノーベル賞を受賞しました。

ゲーデルは何を証明したか？
ゲーデルの名前を不滅にした定理の提示に進む前に、1920年代の終わりまでに数学が直面した問題、正確には、19世紀と20世紀の変わり目に際立っていたその断面を簡単に話す必要があります。それは「数学の基礎」と呼ばれました。
最初に、幾何学の学校コースに立ち寄る価値があります。それは今日まで、2000年以上前に書かれたユークリッドの「原論」を大部分繰り返しています。伝統的な教科書では、最初に、平面上の点と線の特性に関するいくつかの命題が与えられ、そこから「アリストテレス」論理の規則［訳注）三段論法］に従った論理的構築によって、さまざまな重要で有用な幾何学的事実（定理）が推論されます。たとえば、公理の1つは、たった1本の直線が2点を通過すると主張しますが、平行線は無数にあるとする別の公理（ロバチェフスキーが非ユークリッド幾何学で拒否した有名な第5の仮定）もあります。公理の真実は、明白なものと見なされ証明は必要ありません。ギリシャの幾何学の特徴は公理から定理を導くことです。
19世紀の終わりに、ユークリッド原論のすべてのギャップ（数学者の厳密さと推論の正確さの観点で）が埋められました。
ドイツの数学者David Hilbertの本「Foundations of Geometry」は、最新の研究の結果となりました。
ユークリッドの方法の成功は、科学者に彼の原理を数学の他の分野に拡張することを促します。幾何学の後に算術の番が来ました。1889年、イタリアの数学者ジュゼッペ・ピアノは、最初に算術の公理を定式化しました。これは、ばかばかしいほど明白に見えました（ゼロがあり、各数字の後に別の数字が続くなど）が、実際には完全に網羅的です。彼らは幾何学において偉大なギリシャ人の仮定と同じ役割を果たしました。このような記述に基づいて、論理的推論を使用して、基本的な算術定理を得ることができました。
同じ時期に、ドイツの数学者ゴットリーブ・フレーゲはさらに野心的な問題を提起しました。彼は、研究中のオブジェクトの主な特性を公理的に承認するだけでなく、推論の方法を形式化、体系化することを提案しました。これにより、特定の規則に従って、記号のチェーンの形で数学的な推論を書くことができました。フレーゲは彼の結果を「算術の基本法則」で発表しました。その最初の巻は1893年に出版され、2番目の巻はさらに10年間の努力を必要とし、1902年に完全に完成しました。
おそらく、数の科学の発展で最も劇的な物語の1つは、フレーゲの名前と科学的研究に関連しています。第2巻がすでに印刷されていたとき、フリーゲは若い英国の数学者バートランド・ラッセルから手紙を受け取りました。ラッセルは、同僚の素晴らしい結果を祝福しながら、それでも著者の注意を引いた1つの状況を指摘しました。陰湿な「状況」は「ラッセルのパラドックス」であり、後に広く知られるようになりました。
自分自身を要素として含まない集合の集合は、自分自体は要素として含まれるか。フレーゲはすぐに謎を解くことができませんでした。彼は、印刷されていない彼の本の第2巻に、苦味に満ちた言葉を追加するしかありませんでした。「科学者にとって、発見することほど望ましくないことはありません。やっと完成した仕事の基盤が崩壊したこと。バートランド・ラッセルから受け取った手紙は、私をまさにそのような立場に置きました...」苦しんでいる数学者は、大学を卒業し、理論を正すために多くのエネルギーを費やしましたが、それはすべて無駄でした。彼は20年以上研究しましたが、算術に関するこれ以外の論文を書きませんでした。

しかし、ラッセルは、すべての数学をカバーし、フレーゲのアイデアと仕事に正確に依存して、当時知られているすべてのパラドックスのない正式なシステムのバージョンを1902年に導き出すことができました。Principia Mathematica（Alfred North Whiteheadと共著）という本で発表された彼の結果は、実際には論理の公理化になり、David Hilbertは、これが「科学を公理化するためのあらゆる努力の頂点と見なせる」と信じていました。
数学者が彼らの分野の基礎に強い関心を持っているもう一つの理由がありました。事実、19世紀と20世紀の変わり目に、集合理論に矛盾が発見され、そのために傲慢な「集合理論のパラドックス」が生み出されました。これらの中で最も有名な—ラッセルの有名なパラドックス—は、残念ながら、それだけではありませんでした。さらに、ほとんどの科学者にとって、新しい奇妙な発見が当てはまらないことは明らかでした。集合理論は数の科学の建物全体が建てられている基礎の役割をしているので、ヒルベルトが言ったように、この発見は数学の世界に「壊滅的な影響」を及ぼしました。「これらのパラドックスに直面して、私たちは今の状況が長い間耐えられないことを認めなければなりません。考えてみてください：数学（信頼と真実のモデル－概念と推論）は、研究し、教え、適用することが無意味であることになります。では、数学的な思考自体が破綻した場合、どこで信頼性と真実を探すことができるでしょうか？ヒルベルトは1925年6月の数学者会議の彼の報告で嘆きました。

 ーーー

こうして、3千年ぶりに、数学者は彼らの分野の最も深い基礎を研究することに近づきました。そして、奇妙な構図が浮かび上がりました。数字ファンは、計算を行うルールを明確に記述することを学び、パラドックスによって生じる疑念を排除するために、使われた根拠の「正当性」を証明すれば済みました。そして1920年代の前半までに優れた研究学派を形成した偉大なヒルベルトは、一連の論文で数学の基礎の研究計画（後に「ゲッティンゲンプログラム」の名前が付けられた）を講演しました。最も単純化された形式で、それは次のように表すことができます。数学は、特定の公理体系から導き出された一連の結果として表すことができ、次のことを証明できます。

１．数学は完全です。すなわち、いかなる数学的な記述も、その分野自体の規則に基づいて証明または反証することができます。
２．数学は一貫しています。受け入れられている推論の規則に違反せずに、いかなる命題も証明すると同時に反駁することは不可能です。
３．数学は決定可能です。つまり、ルールを使用して、それが証明可能であるか反駁可能であるかどうか、任意の数学命題について調べることができます。

実際、ヒルベルトのプログラムは、すべての数学的な質問に答えるための、または少なくともそのような存在を証明するためのいくつかの一般的な手順を開発しようとしました。科学者自身は、彼が作成した3つの質問すべてに対して肯定的な答えを確信していました。彼の意見では、数学は確かに完全で、一貫性があり、解決可能でした。残ったことはそれを証明するだけでした。

さらに、ヒルベルトは、公理的方法が数学だけでなく、科学一般の基礎にもなり得ると信じていました。1930年に、彼の記事「自然と論理の認識」で、彼は次のように書いています。

科学のさらなる発展のために、ヒルベルトと彼の学派は成功したでしょうか？彼が信じていたように、すべての数学（および科学全体）が公理のシステムに還元された場合、一般的な論理規則に従ったプログラムに従って、元の命題から次の命題を実証する（つまり、定理を証明する）ことがコンピューターでできます。

ヒルベルトの理論が実現されれば、24時間稼働するスーパーコンピューターは、ますます多くの新しい定理を継続的に証明し、World WideWeb上の無数のサイトに投稿します。数学に続いて、「公理の時代」は物理学、化学、生物学に広がり、そして最後に、人間の意識の科学に変わります。私たちの周りの世界、そして私たち自身は、そのような場合には多少異なって見えるでしょう。

しかし、「普遍的な公理化」は行われませんでした。世界の数学者が数十年にわたって取り組んできた、非常に野心的で壮大なプログラム全体が、単一の定理によって反駁されました。それは、当時わずか25歳のKurt Gödelゲーデルによってでした。

1930年、ケーニヒスベルクのウィーンサークルが主催した会議で、彼は”論理計算の完全性”に関する発表をし、翌年の初めに、”Principia Mathematica と関連システムの根本的な困難”に関する論文を発表しました。彼の仕事の中心は、数学のさらなる発展において基本的な役割を果たす定理の定式化と証明でしたが、不完全さについてのゲーデルの有名な定理は、「どのような一貫した公理システムであっても、受け入れられた公理系内で、証明または反証することができない命題が存在する」と述べています。このように、ゲーデルはヒルベルトの最初の命題に否定的な反応を示しました。 興味深いことに、ヴェルナー・ハイゼンベルグは同じ会議で「因果関係の知識と量子力学」について講演しました。このレポートで、”不確定性原理”の最初のアプローチが提示されました。

■ゲーデルの定理

それから四半世紀が経過しましたが、ゲーデルが何を証明したかについての議論は続いています。特に熱狂的な議論が疑似科学界で起こっています。「ゲーデルの不完全性定理は本当にユニークです。神々の存在から理由の欠如まで、"世界のすべて"を証明したいときはいつでも言及されます」と、優れた現代数学者V.A.Uspenskyは書いています。

多くの推測はさておき、科学者はゲーデルの評価で二分されました。ラッセルに続いて、現代の数学論理の基礎となるこの有名な定理は、この分野以外の研究にほとんど影響を与えないと信じる人もいます。

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

新しい定理を絶えず証明し続けるコンピューターの幻想に関しては、そのような活動の意味に多くの専門家から、大きな疑問が投げかけられています。確かに、数学にとって、証明された定理の定式化だけでなく、その理解も重要です。これにより、さまざまなオブジェクト間の接続を識別し、どの方向に進むことができるかを理解できるからです。そのような理解がなければ、形式化された推論ルールに基づいて生成された定理は、一種の「数学的なスパム」にすぎません。これは、モスクワ州立大学の数学論理および機械と数学のアルゴリズム理論部門のメンバーであるアレクサンドル・ シェニの意見です。

ゲーデル自身も同様の方法で推論しました。数学の基礎の完全性を破壊したとして彼を非難した人々に、彼は、「実際には何も変わっておらず基礎は揺るぎないままで、彼の定理は論理の鉄の法則に支配される科学分野で、直感と個人的なイニシアチブの役割の再評価につながっただけ」と答えました。これには何かメリットがあるというわけではありません。

ゲーデルとアインシュタイン（「科学の世界で」より）

フリーマンダイソンの講演の続きです．（１）の主張がメインです．まだ（１）をお読みでないない方は，以下の（１）からご覧ください．　　https://note.com/sgk2005/n/n329b63ad54a4　

2番目の異端は濡れたサハラの謎です。私はいつもこの謎に魅了されてきました。今日は乾燥していて無人であるサハラの多くの場所で、人や動物の群れを描いた岩絵が見られます。これらの絵はかなりの数あり、驚くほど芸術的です。フランスやスペインの有名な洞窟の絵に匹敵します。サハラ砂漠の絵は、それらの洞窟の絵ほど古くはありません。それらは多くの異なるスタイルがあるので、数千年の期間にわたって創作されたように見えます。それらの最新のものはエジプトの影響を示しており、おそらく古代エジプトの墓を飾る図面と同時に作られました。50年前の1958年に出版されたアンリ・ロットの本「タッシリ・フレスコを求めて」には、そのような50の絵の驚くべき複製があります。それらのうち最高のものは約6,000年前にさかのぼります。彼らは、サハラが当時湿気を持っていたことを強く示唆しています。草や木の枝を食べているはずの牛やキリンの群れを支えるのに十分な降雨量がありました。象とカバもいました。当時のサハラは、今日のセレンゲティ*)の姿を見るはずだった。（＊訳注：タンザニある国立公園）

フリーマンダイソン． 2009年3月23日、モスクワ、FIAN。

約6,000年前、針葉樹が優勢なロシア北部には落葉樹林があり、当時の北部の気候は今よりもはるかに穏やかであったことを示唆しています。今日有名な氷河が横たわるスイスの山の谷には、当時も木が生えていました。今日溶けているこれらの氷河は、6000年前は現在よりもはるかに小さかった。6,000年前は間氷期でも最も暖かく湿った時期であり、最後の氷河期が終わった12,000年前から始まった時期です。この点に関して、私は2つの質問を提起したいと思います。まず、大気中の二酸化炭素濃度をさらに上げていくと、サハラが湿気を帯びていた6,000年前と同じような気候になるのでしょうか。そして第二に、サハラが乾燥している現在の気候と、サハラが湿気を帯びていた6000年前の気候のどちらかを選択する機会があった場合、現在の気候を選択する必要がありますか？私は、最初の質問には肯定的に答え、2番目の質問には否定的に答えます。私の意見では、サハラが湿気を帯びていた6,000年前の暖かい気候が好ましく、大気中の二酸化炭素の増加は、当時の気候を再び作るのに役立つかもしれません。私はこの異端の考えが真実であると主張しているのではありません。私にはわかりません。ただ考えても害はないと言っているだけです。サハラが湿気を帯びていた6,000年前のことは好ましいことであり、大気中の二酸化炭素の増加は、当時の気候を再び作るのに役立つかもしれません。

フリーマン講演のこの部分の主旨を理解するのは私にはとても難しい．この第４の異端の紹介はスキップしていましたが，それも公正を欠くので掲載します．ただし，私の理解できるものに要約しました．私というフィルターを通して書き直したものですので，フリーマンの意図と異なるかもしれませんが，私の主張でもないことをお断りしておきます．
フリーマンの4番目の異端の考えは，生物学に関するもの－オープンソース生物学です．オープンソースソフトウェアとのアナロジーでこう呼ぶのでしょう．ゲノム操作をすべての生命を共同体とし水平伝播をどんどんやるとも聞こえ，私は主旨の理解ができません．

■ダーウインの幕間

種間競争によるダーウインの進化の時代は幕間だった．それ以前の時代も，それ以降の時代も遺伝子の水平伝播の時代である．約1万年前に単一種のホモサピエンスが生物界を支配し始め，文化の進化（ゲノムではなくアイデアの水平伝播）が原動力になる進化に変わった．そのスピードは1,000倍も速く，グローバリゼーションが進んだ．

カール・ウーズは，微生物のゲノム間の類似点と相違点を追跡することにより，微生物の祖先を調査し，すべての生き物が3つの原始的な枝から降りている生命の木の大規模な構造を発見しました．
ダーウインの進化の前に，水平遺伝子伝達と呼ぶプロセス（無関係な種間での遺伝子の共有）があったというのです．そして今もそうだというのです．遺伝子の水平伝播が普遍的であり，別個の種が存在しなかったダーウィン以前の生命の黄金時代を仮定しています．その頃，生命はさまざまな種類の細胞の共同体であり，ウイルスによって遺伝情報を共有し，進化は共同体の問題であり，最も効率的な細胞の遺伝子が共有されたため，共同体全体が代謝効率と生殖効率を向上させました．

新しい化学デバイスは、並行して動作するさまざまな種類のセルによって同時に進化し、その後、遺伝子の水平伝播によって単一のセルに再構築されるため、進化は急速である可能性があります。

しかし，ある日，原始的なバクテリアに似た細胞がたまたま隣人よりも1つ先に進んでいることに気づき，共同体から離れ共有することを拒否しました．その優れた効率により，共同体の残りの部分が共同生活を続けている間は，それは繁栄し，別々に進化し続けました．数百万年後，別の細胞がコミュニティから分離し，2番目の種になりました．．．．．

そして，おそらくウイルスを除いてコミュニティに何も残らなくなるまで続き，すべての生命は種に分けられました．現在はこうしてダーウィンの幕間に至っています．

数学パズルで有名な問題　$$ X^3 + Y^3 + Z^3 = k $$，（$$ k $$はゼロ以上の整数）を解く話です。まず、$$ k $$=1から100までの個々の場合の整数解$$X, Y, Z$$を求めよというのが1954年に提示された問題です。似ている問題　$$x^2+y^2=z^2$$　を満たすピタゴラス数を求めよというのもあります。この種の方程式はディオファントス方程式とよばれ、紀元前300年のギリシャ以来研究されています。

さて、$$X^3+Y^3+Z^3＝k$$　，　（$$ k$$=０，･･･，100)　に戻りましょう。
求める整数解$$X, Y, Z$$は正数だけとは限りませんので、問題は難問になります。

長年の研究で、$$k=4, 5, 13, 14, 22, 23, 31, 32$$の場合には解がないことがわかっています．これらを除くほとんどの$$ k $$に対して解が求まりました($$ k $$によっては解が無数に存在する場合もあります)が、$$k$$=33と42の場合の解がどうしても見つかっていません（解がないという証明もできません）でした。2019年になり、ブリストル大学のAndrew Booker教授は、スーパーコンピューターを３週間連続使用して、$$ k $$＝33の場合の解を見つけました。以下のものです。

$$ (8,866,128,975,287,528)^3+(-8,778,405,442,862,239)^3+(-2,736,111,468,807,040)^3＝33 $$

私（筆者）はこれが正解かどうか確認しようとしましたが、数字が大きすぎて計算もできません。$$k$$=42の場合は、もう一桁大きな数を扱わなければならないのでスーパーコンピュータといえども困難なのが理解できるでしょう。
そこで、Booker教授は、大きな数の解をチェックできる効率的なアルゴリズムを作り、MITの計算数理学者Andrew Sutherland教授の協力を得て、地球規模のコンピューティングプラットフォーム「Charity Engine」を利用した。Charity Engineには、世界規模で50万台を超える家庭用PCが接続され、各PCの空き時間を使って計算を実行するものです。Charity Engineによる100万時間を越える計算の結果、やはり2019年に次の解が得られました。

$$X = -80538738812075974$$
$$Y = 80435758145817515$$
$$Z = 12602123297335631$$

現在は，$$k$$が100～1,000までの場合の整数解を求めることに挑戦中である。
$$k$$が100～1000の間で解けていないのは10個位あるという。

 
フリーマンダイソンの講演の続きです．彼の最後の異端意見は核兵器についてです。折しも10月24日に，核兵器禁止条約発効に必要な50ケ国の参加を得た。90日後の2021.1.22に発効することになった。米露や日本は参加していないのは残念である。（訳者注）

Еретические мысли о науке и обществе • ВидеотекаМосква, ФИАН, 23.03.2009 • Наука и общество, Климат, Эволюцияelementy.ru
核兵器
そして最後の異端は核兵器についてです。私の意見では、これが最も重要なことです。異端者としての意見では、私たちと環境への最大の危険は核兵器であり、私たちの最も重要な仕事はそれらをできるだけ早く取り除くことです。私はこの異端の意見を最後に残しましたが、私自身はそれが最初であると考えています。私は少なくとも25年間それを主張して、さらに今日でもそれを主張します。世界は過去25年間で劇的に変化しました。何かが良くなり、何かが悪くなりました。想像もできなかった最高の変化は、ソビエト連邦が平和的に崩壊したことでした。私も想像もできなかった最悪の変化は、米国が予防戦争［訳注）テロとの戦いのこと］を開始したことでした。これらの変化の結果として、核兵器に対する人々の見方は変化しましたが、核兵器に関連する根本的な危険とそれらに対する手段は、少なくともほとんど変化していません。

今日、人々は、イラン、北朝鮮、パキスタン、いわゆる「不正国家」の手にある核兵器、アルカイダのようなテロリストグループの手にある核兵器について懸念します。この問題は核増殖問題と呼ばれます。本当に50年間そのような問題がありました。しかし、それを自分たちで解決することができません。私たちの主要問題は、自身の核兵器の問題です。私たちには、地球の人口のかなりの部分を一掃するのに十分な約1万の核兵器があります。ロシア連邦もアメリカとほぼ同じ量を持っています。これらの大量の武器の備蓄は、イランやパキスタンが手に入れることができる少量よりも、世界全体にはるかに大きな脅威をもたらします。ロシアは自分たちの核兵器を追跡できない懸念がありますが、私が米国の核兵器保管場所で、41個の水素爆弾が床に横たわり、つながれていないのを見た瞬間を忘れられません。私はそれらを注意深く数え、41個あることを確認しました。そのうちの1つか2つが欠けていても気付く人はいないだろうと思います。したがって、私たちの側もその武器を最善の方法で監視してはいません。

フリーマンダイソン．2009年3月23日，モスクワ，FIAN

あなたが核兵器について話すにあたり、2つの視点ー宗教と道徳があります。核兵器は大量殺戮の兵器であるため比類のない悪であり、神の前での犯罪であり、私たちの道徳的および宗教的義務はそれらを取り除くことです。他方、軍事的ニーズについて実践的に考えることもできます。核兵器は実用的な観点からは効果がない。皆さんご存じなので宗教的な議論はここでは語りません。核兵器は原則として悪であると同意しましょう。したがって、私は軍事的議論に焦点を当て、核兵器は実際には戦争勝利に役立たないと、皆様に説得しましょう。イランや北朝鮮が独自の核兵器を取得するのを防ぐために、核兵器で意味のあることはできません。私たちの理性は、いかなる軍事目的にも自分の爆弾の使用を許しません。いくつかの貧しい国との戦争に勝つために核兵器を使用することは問題です。核兵器は多くの人々を殺し、生き残った人々を私たちを深く憎むようにさせますが、それは戦争に勝利したことになりません。

このことから、私たちの外交政策の最も重要な目標の1つは、核兵器の完全廃絶であるべきと結論します。敵や友人が、秘密の武器をどこにも隠していないことを確認するのは難しい。ご存知のように、核兵器を隠すのは簡単です。私たちが核兵器を取り除くことを話すとき、私たちは、生物学的兵器が今日禁止されているように、これらの兵器は法律によって禁止されるべきです。これは、残りのすべての武器は、大規模で明確な搬送システムがなければ、違法で秘密にせざるを得ないことを意味します。それは、私たち自身がもはや核兵器を持っていないことを確信できます。私たちの核兵器がなければ世界はより安全になると私は信じています。奇襲攻撃の最も魅力的な標的は、例えば、原子力航空機運搬船であり、私たちは主にそのような標的を持っています。このような標的を取り除くことで、公海やペルシャ湾での戦争の可能性を大幅に減らすことができます。

武器は、一方的に、または多国間合意に達することによって、2つの方法で処分することができます。これらの方法は両方とも過去50年間にわたって試行され、時には成功しました。歴史から4つの例を簡単に紹介します。最初の懸念は、1963年に私が米国の武器管理および武装解除局で働いていたときです。当時、武器レースの過程でますます大きな水素爆弾が作られていました。その後、ソビエト連邦は、プロトタイプの100メガトン爆弾として宣言した65メガトン爆弾で首位に立ちました。レースの次のステップは、飛行機やロケットで運ぶには重すぎる1ギガトンの爆弾になるのではないかと思えました。ギガトン爆弾は、大きな潜水艦コンテナまたは無人自動潜水艦に配置され、海辺の都市を破壊するために使用され、巨大な津波を引き起こす可能性があります。しかし、最も血に飢えた空軍の将軍と海軍の提督でさえ、そのような爆弾を望んでいませんでした。ケネディ大統領と[大臣評議会]フルシチョフ議長は、この狂気を終わらせ、大気中での核実験を禁止することに合意した。その後のすべての核実験は地下で行われなければなりませんでした。そして実際の地下試験は約10メガトンに制限されています。その後、武器レースは別の方向の競争になり－より小さくてより強力でない爆弾に向かいました。しかし、ケネディとフルシチョフは、武器競争をさらに遅らせるであろう完全な核実験禁止を交渉する機会を逃しました。

私の2番目の例は、1969年のニクソン大統領による生物兵器の破壊に関するものです。それはニクソンが大騒ぎせずに静かに行った一方的な決定でした。国際交渉も上院の承認手続きも必要ありませんでした。この決定の反対者は、彼らの異議を公に表明したり、この決定の採択を法的に遅らせたりする機会を得ませんでした。ニクソンは、生物兵器に関連するすべての政府プログラムを停止し、すべての在庫を破壊する必要があると単に発表しました。これは、ハーバードの生物学者マシュー・メセルソンが、ニクソンの国家安全保障顧問であったヘンリー・キッシンジャーの隣に​​、いわゆるダチャであるケープコッド半島に夏の家を持っていたという事実によるものでした。メセルソンはキッシンジャーを説得した 生物兵器を取り除く時が来たと、キッシンジャーはニクソンを説得した。この件に関する議会会議で、メセルソンは生物兵器プログラムを担当する陸軍将軍に「これらの兵器をどの程度正確に使用する予定ですか」と尋ねました。そして彼らは答えることが何もありませんでした。将軍たちは、私たちが生物兵器で攻撃されたとしても、それに応じて私たち自身の生物兵器を使用する現実的な計画がなかったことを認めざるを得ませんでした。純粋に軍事的な理由で、私たち自身の武器は役に立たなかった。ニクソンがこの決定を下した3年後の1972年に、彼は生物兵器を非合法化する国際条約を交渉し、ソビエト連邦はその条約に署名しました。この大会の条件が満たされているかどうかを確認することは不可能でした、そして実際、その後のソビエト連邦では、秘密の生物兵器プログラムが続けられました。それでも、このコンベンションでは、それがない場合よりもはるかに良い結果が得られました。ソビエトのプログラムは秘密のままであり、生物兵器の公開展開はありませんでした。テロリストによる生物兵器の使用の脅威は残っていますが、テロリストが盗むことができる生物兵器の独自の在庫がまだある場合、この脅威ははるかに深刻になります。

私が与える3番目の例では、武器を取り除く試みは失敗しました。1986年、レーガン大統領と[最高ソビエトの幹部会の議長、当時CPSU中央委員会の事務局長]ゴルバチョフはレイキャビクで会合し、武器管理協定を交渉しました。レーガンは核兵器の完全廃絶を熱心に支持しており、ゴルバチョフも同様の見解を持っていました。彼らは顧問から逃げ出し、1対1で話し始めました。彼らは、あらゆる種類の核兵器をすべて排除するという合意に非常に近づいています。しかし、2つの理由で彼らはこの合意に達することができませんでした。第一に、彼らは両方とも現状の劇的な変化を致命的に恐れていた公式の顧問を持っていました。第二に、レーガンは彼のミサイル防衛プログラム「スターウォーズ」を非常に大切にしていました。ゴルバチョフはスターウォーズシステムが先制攻撃システムに変換されるのではないかと恐れていたが、彼はそれをあきらめたがらなかった。ゴルバチョフの恐れは誇張されていましたが、根拠のないものではありませんでした。スターウォーズに無関心だったため、レーガンは歴史の流れを変えるチャンスを逃しました。

4番目の例では、彼らはなんとか武器を取り除くことができ、完全に成功しました。これは、ジョージW.ブッシュがアメリカの大統領だった1991年に起こりました。2年前、ゴルバチョフはドイツがベルリンの壁を破壊することを許可しました。そこでは冷戦は本質的に終わりました。ブッシュ大統領は、合衆国陸軍と海軍がすべての戦術的な核システムを取り除く時が来たと決定しました。その結果、警戒しているすべての武器の約半分が1日で一方的に削除されました。それは歴史上最大の核武装解除でした。これが起こる数年前に、私はロングビーチハーバーのミサイルクルーザープリンストンを訪れました。この巡洋艦は、私が住んでいる都市にちなんで名付けられました。それは2つの大きな箱に98個のトマホーククルーズミサイルを運びました、1つは核弾頭を備えた49で、もう1つは非核弾頭を備えた49です。キャプテンはどれを忘れないように努めなければなりませんでした。いつでも何らかの事故が発生し、海上で核戦争が始まる可能性があります。世界中の多くのオープンな場所で警戒している軍事戦術核兵器も同様に危険でした。今、これはもうありません。現在、軍隊と水上艦隊の両方が核兵器を処分したことを喜んでいます。彼らは今や核兵器の世話をする手間をかけずに、はるかにうまく仕事をすることができます。誰もこの武器を返還したくない。ブッシュ大統領は、タバコ産業に対する訴訟が解決すると同時に、作戦が発表されることを確認した。それで、アメリカのメディアはこのタバコビジネスに焦点を合わせました、そして核の武装解除は見過ごされて滑った。しばらくすると、ゴルバチョフはソビエトの戦術的な核兵器を取り除いたと答えた。

これらの4つの例は、一方的に取られた行動は、多国間交渉よりも効果的に根本的な武装解除をもたらす傾向があることを私に確信させます。もちろん、あなたは両方の方法で行動しようとする必要があります、両方が必要です。核兵器を排除するための最新のステップは、2006年に、レイキャビクでレーガンと一緒にいて、それらの武器管理交渉でレーガンのコミッショナーであったマックス・カンペルマンによって行われました。カンペルマンは、ヘンリー・キッシンジャー、ウィリアム・ペリー、サム・ナン、レーガン国務長官のジョージ・シュルツを含む他の著名な政治家とともに、米国の外交政策の目標として世界中で核兵器の廃絶を求める宣言を発表した。彼らはロシアとの交渉に戻ることを申し出た、レイキャビクで戦った後、他の国々を巻き込んで核兵器の破壊に関する多国間合意に達した。彼らはそのような合意をどのように実施するかを強調しすぎており、それが守られていることを確認していると思います。誰にも何も強制せずに、一方的な手順から始める方がよいでしょう。イスラエルとイランにいくつかの隠された保護区が残っていたとしても、主要な核兵器が公然と警戒されなければ、世界ははるかに安全になるでしょう。イスラエルとイランが参加することを望まない場合、そのような合意を実施する合理的な方法はありません。各国は、6か月以内に協定に参加または脱退しない権利を有するべきです。撤退の可能性は、すべての武器管理協定の別個の条項として詳しく説明されています。

アメリカやロシアの国民に核兵器を取り除くよう説得するために克服しなければならない主な困難は、核兵器がある程度の安全を提供するという深い確信です。この信念は、いくつかの神話、特に広島と長崎のアメリカの核兵器が第二次世界大戦の終結をもたらしたという神話によって支持されています。歴史家の長谷川らによる最近の研究は、この神話は真実ではないと私に確信させました。最も重要な証拠は、1945年8月に署名されたヒロヒト天皇の軍隊に宛てた公式の書簡に含まれており、そこで彼らは降伏を命じられました。この記述は核爆弾については言及しておらず、1945年に発生した状況と状況との類似性を強調しています。日中戦争の終わりに1895年に開発されました。ヒロヒトは日本の歴史をよく知っていたからです。1895年、日本は中国を破り、満州を占領した。ロシアを中心とするヨーロッパの勢力がこの戦争に介入し、満州に侵攻した。ロシア人はポートアーサーを占領しました。日本を近代大国に変えた明治天皇は、屈辱的な平和を受け入れました。明治はヨーロッパ人と恥ずべき和平を結び、ロシア人の日本への侵入を阻止した。ヒロヒトの書き言葉は、降伏を決意したとき、この類推を覚えていたことを示しています。彼は主に技術ではなく歴史に関心を持っていました。決定的な要因は広島と長崎の爆撃ではなく、ロシア人が戦争と満州への侵略を宣言した。

暴かれる必要があるいくつかの神話があります。ヒットラーが私たちより先に核兵器を受け取っていたら、それで世界を征服できたはずだという神話があります。ヒットラーが核兵器を持っていれば、ロンドンとここモスクワの多くの人々をーおそらく私もー殺すためにそれを使用する可能性は高かったですが、私たちの軍隊は1年前に戦争を終わらせ、1944年にベルリンに到着しました。水素爆弾の発明が核兵器の本質そのものを変えたという別の神話があります。実際、現在の核兵器の在庫を見ると、水素爆弾が発明されていなかった場合とほとんど変わりません。武器の破壊に関する国際協定は、厳密に施行されなければ意味がないという神話もあります。しかし実際には、多くの国際協定の実施を監視している人は誰もおらず、違反さえしているが、それでもなお、それらは引き続き有用です。良い例は、1817年のラッシュバゴット協定であり、これは米国とカナダの国境で平和を維持しました。したがって、これらすべての神話は真実ではありません。それらが暴かれるとき、核兵器のない世界への決定的なステップが可能になるでしょう。しかし、それが起こるためには、平和な市民と実用的な大統領と軍隊がこれに協力しなければなりません。

■以下で紹介するフリーマンの第３の異端に関しては，私は異なる見方をします．私の視点もここで簡単に述べておきます．

フリーマンの言うように，コンピュータが研究所に設置さる大型機械から，各家庭で子供も使う家畜化になったと同様な足跡をたどり，バイオテクノロジーは，モンサントなどのグローバル企業の独占ではなく，ユーザーフレンドリーな道具として生活に浸透し家畜化しするというバラ色の未来に，私はあえて異は唱えません．
しかし，そのような世界になる前に，人類が破滅に向かう多くの岐路があり，これらを正しく乗り越えてバラ色の未来に向かえるか私は懸念します．日本の食糧自給率は低下の一途です．TPP協定に合意し，主要農作物種子法（種子法）の「廃止法」が2017年4月に成立，2018年3月末に廃止されました．地域に適した優良種子は地元の地で長期間の品種改良で得た人類の宝です．しかし．グローバル企業に種子を握られ，肥料も農薬もセットで生産性優先の産業農法の道を進むことになります．これとバイオテクノロジーが手を結んでいるのが現状です．自然農法を守ろうとする良心的な農家も存続が難しく，グローバル企業による遺伝子組換え（GM）種子，F1種子などが支配する産業としての農業は誰のためにもならないはずです．

■バイオテクノロジーの家畜化
フリーマンダイソンの講演の続き
https://elementy.ru/video/20/Ereticheskie_mysli_o_nauke_i_obshchestve?
3番目の異端はバイオテクノロジーの家畜化です。

50年前、プリンストンで、数学者のジョン・フォン・ノイマンは、エンコードされた命令、つまりコンピューター・プログラムを実行する最初のコンピューターを私の目の前で開発構築しました。コンピューターはフォンノイマンによって発明されたのではありませんが、コンピュータープログラムを発明したのは彼でした。ENIACと呼ばれるこのコンピューターは、5年前にペンシルベニア大学ですでに稼働していました。しかし、パンチカードに書かれたソフトウェアと電子ハードウェアの組み合わせにより、1台のマシンで天気を予測し、生物集団の進化をシミュレートし、熱核爆弾を作成する可能性をテストすることができました。フォンノイマンは、彼の発明が世界を変えることを理解していました。彼は、そのような機械の次世代が科学、ビジネス、政府の仕事の基礎になることを理解していました。しかし、コンピューターは常に巨大で高価になるのが彼には見えました。彼は、コンピューターが研究所や大企業を運営する大規模なセンターに設置されると想像しました。彼は、コンピューターが非常に小型で安価になり、主婦がコンピューターを使用して所得税申告書を計算し、学童がコンピューターで宿題をすることになるとは予測できませんでした。彼は、コンピューターが最終的に3歳児向けのおもちゃになるまで飼いならされ家畜化するとは予見できませんでした。彼は、21世紀にコンピューターゲームが日常生活の基盤の1つになることを予見することすらできませんでした。コンピュータゲームのおかげで、私たちの孫は今、不治のコンピュータ中毒を持つ人々として成長しています。
良かれ悪しかれ、健康か不健康かにかかわらず、人とコンピュータは今では夫と妻よりも強く結ばれ、死がそれらを分かつ時まで強く結ばれています。

フリーマンダイソン． 2009年3月23日，モスクワ，FIAN

この話は、フォンノイマンコンピュータとコンピュータゲームのバイオテクノロジーへの進化と何の関係があるでしょうか？　次のとおりです。
特別なセンターに設置された巨大機械としてのコンピュータのフォン・ノイマンの見方は、モンサントのような大規模な製薬会社や農業会社専用の職業としての遺伝子工学の一般的な認識と共通しています。
モンサントはコンピューターを使って水素爆弾を開発したため、フォンノイマンの活動を警戒するのと同じように、モンサントは有毒な農薬遺伝子を食用作物に導入しているため、一般の人々はモンサントを警戒しています。
遺伝子工学が大企業が所有する特別なセンターの特権であり続ける限り、それは不人気で議論の余地のある活動形態であり続けるだろう。

しかし、私は、コンピュータ業界の足跡をたどるバイオテクノロジー産業の偉大な未来を予見します。巨大機械が家庭に入ったように。この方向への最初のステップは、ペットショップで遺伝子組み換え熱帯魚が、新しく非常に明るい色になったのを見ました。バイオテクノロジーの国内化に向けた次のステップは、それがユーザーフレンドリーになるときです。私は最近、世界中の生産者が彼らの労働の成果を披露する世界最大のショーであるフィラデルフィアフラワーショーである幸運な日を過ごしました。サンディエゴ爬虫類ショーにも参加しました。爬虫類を繁殖させる人。フィラデルフィアには最高級のバラと蘭があり、サンディエゴには最高級のトカゲとヘビがいます。孫を爬虫類展に連れて行く祖父母にとって、主な問題はヘビやトカゲを買わずにそこから抜け出すことです。これらすべてのバラと蘭、そしてこれらすべてのトカゲとヘビは、情熱的で経験豊富な花と爬虫類の栽培者の努力の成果です。プロとアマチュアの両方の何千人もの人々が、このビジネスや他のビジネスに人生を捧げています。しかし、これらの人々が遺伝子工学的手法を利用できるようになるとどうなるか想像してみてください。庭師のためのDIYキットがあり、遺伝子工学によって新しい種類の蘭やバラを開発します。鳩の飼育者、オウムの飼育者、トカゲやヘビのためのキットもあり、新しい品種を育てることができます。

遺伝子工学は、それが子供や主婦の手に渡ると、新しい生物の多様性に巨大な急増をもたらし、大企業によって植え込まれた単一文化に終止符を打つでしょう。新しい品種が普及し、単文化農業と工業化の欠陥のために消えたものに取って代わります。ゲノムの作成は、絵画や彫刻のように創造的な、個人的な事柄、新しい芸術形態になります。傑作となる新しい作品はほとんどありませんが、それらはすべてクリエイターに喜びをもたらし、私たちの動植物の多様性を高めます。

バイオテクノロジーの家畜化の最終段階は、幼稚園の年齢までの子供のためのコンピュータゲームと同様にバイオテクノロジーゲームの作成ですが、コンピュータ画面上の画像の代わりに子供たちが本物の種子や卵で遊ぶという点で異なります。これらのゲームをプレイすると、子供たちは生物の成長が何であるかを深く感じるでしょう。勝者は、種子が最も傷ついたサボテンを成長させるか、卵のハッチからかわいい恐竜を育てる子供かもしれません。このようなゲームでは、多くの困難と可能な危険に関連付けられます。私たちは、子供たちが遊ぶときに自分自身や他の人を危険にさらさないように、厳格なルールを開発する必要があります。

フリーマンダイソン． 2009年3月23日，モスクワ，FIAN

将来、家畜化バイオテクノロジーの普及を待っているなら、この点で5つの質問に答える必要があります。まず、この流入を止めることができますか?
第二に、それは停止する必要がありますか?第三に、それを止めることができない、または望ましくない場合、社会はそれをどのように制限すべきでしょうか?第四に、このような制限をどのように正確に交渉するのでしょうか?
第五に、彼らは国家レベルまたは国際レベルで実施されていますか?
コンピュータ技術とバイオテクノロジーのたとえは、これらすべての質問に対する答えを深く考えるのに役立つかもしれません。家畜化バイオテクノロジーを不正に使用するほとんどの人は、おそらくインターネット上にコンピュータウイルスを広める若いハッカーのように、ささいなものになるでしょう。一方、コンピュータウイルスとインフルエンザウイルスや免疫不全ウイルスなどの実ウイルスとの間には有意な差がある。子供たちにバラやヘビと遊ぶことを許可したとしても、ウイルスとのゲームをどのように防ぐかという問題に直面します。

これが私がバイオテクノロジーについて言いたかったことです。

カバーの図は，「美しい幾何学」p.76-84，p84準結晶より引用

 
ロジャー・ペンローズは，ブラックホールの研究で2020年のノーベル物理学賞を受賞しました．

ここでは，ペンローズのタイリングと準結晶を話題にしましょう．
参考：Alexey Panov、Pyotr Panov "Kvantik" No. 9，2019，アーティストAnnaGorlach
No.7と No.8の記事は，すでに別項で取り上げましたので，そちらをご覧ください．

■　ロジャーペンローズの非周期モザイク

ロジャーペンローズ．
写真：Biswarup Ganguly，Wikimedia Commons; CC-BA-3.0

準結晶の発見に先んじて，数学者の準備はできていた．
1960年代に，数学者は新しいオブジェクト－非周期モザイク－を発見し，研究を始めました．
モザイクとは，平面を完全に埋め尽くすような多角形のタイルで作られたパターンのことです．
非周期モザイクは，どのような平行移動でも自分自身に重ね合わせできないものです．

非周期モザイクの中で最も有名なのはペンローズモザイクです．このようなモザイクの断片を図22に示します．
これは，いくつかのタイプのポリゴンを使い特定のルールに従って組み立て，平面全体を埋め尽くします．
これは，宇宙の調和に掲載されたケプラーによる絵（図23）とよく比較され ます．
ペンローズ自身は，「彼は私がやったことに近いことをしようとしましたが，うまくいかなかった」と述べています．
＊）ケプラーのトリアコンタヘドロンは，現代の結晶学のシンボルの1つです．

図：22（左）ペンローズモザイクの断片．

図：23. 宇宙の調和から.

別のタイプの非周期なペンローズタイリングについてもう少し詳述します．
それらは2種類の菱形で構成されています（鋭角36°の 痩せたものと鋭角72°の太いものです）．
そのうちの1つを図24に示します．もちろん，前号の記事の図18ほど対称的ではありません．
並進で自分自身と重ね合わせができず，回転対称軸もありません
［訳注：局所的な回転対称はありますが，全域的な回転対称はありません］．
ただし，繰り返し五角形の星が表示され，72°= 360°/ 5回転するとそれぞれが重なります
［訳注：局所的な5回回転対称］，さらに，これらの星は2つのクラスに分けられ（図25），
一方のクラスの星は別のクラスの星と36°= 360°/ 10の回転だけ異なります．

図：24.　鋭角36°および72°の菱形のモザイク

有限数の平行四辺形からなる各領域は，モザイク内で無限に繰り返し，36°回転したものも無限に繰り返します．

図：25.　異なる色の星は36°回転だけ異なります

ここで，ペンローズモザイクの物理的特性について少し説明します．
■　アラン・マッケイ：モザイクの回折

アランマッケイ．
写真：Julyan-cartwright、Wikimedia Commons; CC-BY-SA-3.0

Alan McKayは，標準的物理実験手法を非標準的数学オブジェクトであるペンローズモザイクに適用することを提案しました．モザイクの各頂点を小さな円［ドット］に置き換えたドットパターンを縮小し，ドット間の距離が光の波長程度にしました．このミニチュアにレーザー光を入射し，シェヒトマンの実験のように，回折パターンは10回対称となることを得ました*)．マッケイの論文は，シェヒトマンが最初の実験を行った同じ1982年に発表されました．
シェヒトマンがマッケイのこの仕事について知っていれば，彼はそれを参照し，彼の業績の早期承認が得られたところですが，シェヒトマンは当時マッケイの発見に気付いていなかったと言います．
［＊）訳注：このような標準的物理実験は，オプティカルトランスフォームといいます．
縮小されたドットパターンがらの回折像が得られます．
ドットパターンと回折像の関係は，互いに2次元のFourier変換の関係にありますが，
厳密に言うと得られる回折像は位相の情報が打ち消された振幅の絶対値2乗になります．
そのため，回折像の対称性には必ず対称心が生じます．
回折像の対称性は5回対称ではなく10回対称になります．］

■　トリアコンタヘドロン（菱形30面体）とヘキサコンタヘドロン（星型60面体）

ロジャーペンローズとロバートアンマン．　
写真：Ludwig Danzer; MarjorieSenechalの記事「アンマンの奇跡」より

ペンローズの非周期タイリングの3次元アナロジーがあります．
そのようなモザイクの1つが，RobertAmmannによって発見されました．
これらは，前号の記事の図16の下部に示されているものとまったく同じ，
細長い平らな2種類の菱形の平行線から組み立てられています．
五角形の星が2次元のペンローズモザイクでよく見られるのと同じように（図24および25），
菱形30面体（トリアコンタヘドロン）は，アンマンの非周期空間モザイクや，60面の菱形の六面体でよく見られます．
星型60面体（ヘキサコンタヘドロン）は，菱形の多面体のリストにはありませんが，これは12個の凹所がある非凸多面体であるためです(図26)．

図：26.　黄金比菱形［訳注：対角線比が］から組み立てられた星型60面体（ヘキサコンタヘドロン）

その後，物理学者は菱形30面体（トリアコンタヘドロン）と星型60面体（ヘキサコンタヘドロン）の形で実際の準結晶構造を作ることができました．

最後に，ヘキサコンタヘドロンとペンローズのモザイクに関するいくつかの演習を行います．
• 60個の黄金比菱形を使用してヘキサコンタヘドロンを作りましょう．また，トリアコンタヘドロンと菱形のフェドロフイコサヘドロンの両方が，このヘキサコンタヘドロンの12個のキャビティすべてにきちんと収まっていることを確認してください．
• トリアコンタヘドロンとヘキサコンタヘドロンがアンマンのモザイクによく見られるという事実について話しました．実際，ヘキサコンタヘドロンは20個の細長い平行6面体で構成でき，トリアコンタヘドロンは10個の細長い平行6面体と10個の扁平平行6面体で構成できることを確認してください．
• ペンローズタイリングの十分に大きな部分では，痩せた菱形の数に対する太い菱形の数の比が黄金比φ= 1.618に近いことが証明されています．
図24を使用して，このステートメントを確認しましょう．
• ペンローズモザイクは，他のすべての多面体と同様に，菱形で構成されているためゾーン［訳注：晶帯］もあります．今回のゾーンは，無限に続く菱形のチェーンです．各菱形は、共通の側に隣接する2つがあり，これらの側は平行です．

Haydar Nurligareev "Kvantik"＃ 10，2019より．Alexey Weiner画

正3角形，正4角形，正6角形は，それぞれ無限に広い平面をタイル張りできます（図１）．

１つのタイルを中心に置き，その周囲を同じタイルで［重ならず隙間も空けず］取り巻きます（レイヤー１）．
次のその周りを取り巻きます（レイヤー２）．何周取り巻けるかがHeesh数です．1周も取り負けなければHeesh数は０．
正3角形，正4角形，正5角形は，それぞれ平面のタイル張りができる（図１）ので，Heesh数は∞です．

（図１）

正5角形のタイルは平面タイル張りができません（図２）．正5角形のHeesh数は０です．

(図２） 

ランダムに選択されたタイルにもHeesh数があり，通常は0または∞のいずれかです．
Heesh数が1，2，3，...の多角形はありますか？
1968年にハインリッヒヒーシュHeeshがこの問題を定式化する前は，Heesh数が0か∞以外の既知のタイルは1つしかありませんでした（図3）．このタイルは多角形でさえなく，1922年にWalterLitzmanの著書「AmusingandStrangeNumbersandShapes」に最初に登場しました．Heesh数は１です．

(図３）

Heesh自身が，Heesh数が1に等しい別のタイルを見つけました．これは，正方形，通常の三角形，および同じ三角形の半分で構成される5角形です（図4）．

(図４）

Anne Fontaineは，1991年にHeesh数が2のタイルの最初の例を示し，そのようなタイルを無数に作成しました．それらはすべて同じ正方形で構成されています．つまり，それらはポリオミノ図形です（図5）．

(図５）

同年，ロバート・アンマンは通常の６角形に2つの突起を追加し，同じ溝を3つ切り取り，Heesh数が3の図を作りました（図6）．アンマンのアイデアはシンプルでエレガントです．突起と同じ溝があるタイルを探す必要がありますが，その数は異なります．

(図６）

2001年にCasey Mannによって発見されたタイルの例を使用して，このアイデアがどのように機能するかを示しましょう．これは，4つの突起と5つの溝を持つ4セルの長方形の形をしています（図7）．そのようなタイルのHeesh数が大きすぎない理由を以下で述べましょう．タイルのコピーで完全に覆われた正方形Sを考えてみましょう．各溝は同じ突起でしか閉じることができないため，正方形Sの内側にある溝と突起の数は 同じです．一方，正方形内の突起の数は、その面積（セル内）にほぼ等しくなります-タイルの各セルには突起が1つだけあり，溝の数はその面積の5/4にほぼ等しいためです-タイルでは，4つの突起ごとに5つの溝があるためです．しかし，大きな正方形では，これらの数を等しくすることはできません．

(図７）

サイズ2n × 2nの正方形 Sをタイルで完全に覆います。これには少なくとも$$2n･2n/4=n^{2}$$のタイルが必要です．それらには合計$$5n^{2}$$の 溝があり，すべて埋める必要があります．一方，これらのスロットは$$2(n+4)×2(n+4)$$の正方形S 'の内側にあります（図8）．したがって，$$2(n+5)2(n+5)$$個以下のセルからの突起で埋められます．したがって，突起の最大値は$$2(n+5)2(n+5)= 4n^{2} + 40 n +100$$です．n > 100の場合，不等式$$n^{2}>40n+100$$は確実に満たされ，$$5n^{2}>4n^{2}+ 40n+100$$，つまり，突起よりも多くの溝があります．矛盾-すべてのスロットを埋めることはできません．したがって、このタイルのHeesh数は有限です．実際には3に等しい（図9）が，これまでのところ，コンピューター検索によってのみ証明することができます．

 (図８）

フィギュアを研究するのに最も簡単なのは，ポリオミノ，ポリアマンド， ポリヘックスです．それらはまた，互いに隣接する同じ「セル」で構成されており，ポリアマンドではセルは通常の三角形で，ポリヘックスでは通常の六角形です．ポリオミノ，ポリアマンド，またはポリヘックスからタイリングするときは，「市松模様」の紙にレイアウトします（図1）．このような紙なら，コンピュータ検索を整理するのは簡単です．これが，Casey Mannケーシー・マンがHeesh数3のポリアモンドを見つけた方法です（図10）．

（図９）

また，ケーシー・マンはHeesh数が有限であるがゼロに等しくない，突起と溝を備えたいくつかの新しい一連のポリオミノとポリヘックスを何とか入手しました．これが，ケーシー・マンのポリヘックスで，5つの六角形（突起と溝付き）で構成されています-このHeesh数は5で（図11），今日人類に知られている最大の有限のHeesh数を持つタイルです．

(図10）

（図11）

 
 
レムデシベルが新型コロナ治療に有効であるのか/ないのかの議論があります．このような疑問に終止符を打つには，十分な統計的解析が行えるデータが必要です．偏見のある仮設に立って解析を始めてはなりません．統計的解析のスタート台は，帰無仮説（ヌル仮説）が鉄則です．これは，証拠がないので因果関係はないと見なすことです［推定無罪のようなもの］．ただし，統計的結論がでた後でも，一つの症例が発見されただけでひっくり返る可能性があるのが，統計的結論というものです．これは結論に影響を与える非常に多くの要因があるからです．さらに，統計的結論を待っては手遅れになるという一面もあります．
統計的研究を行う際には，ヌル仮説に立ちます．そして，科学的実験あるいは臨床データに基づき，仮説の証明または反証を目指します．
ほとんどの場合，単一の「クリーンな」現象ではないため，結果の信頼性を保証するために測定を何度も繰り返す必要があります．したがって，得られたデータの統計的解析が必要になります．結果は多くの要因に依存するので，メインの要因とマイナーな要因を分離する必要があります．

たとえば，科学者が喫煙と肺がんの関連性を見つけたい場合，肺がんを患っている（または発症しなかった）喫煙者を1人見つけるだけでは不十分です．この科学者が喫煙と肺癌の間に関係があると主張できるようになるには，かなりの量のデータを収集して分析する必要があります．この種の研究では，ヌル仮説が重要な役割を果たします．ヌル仮説は，結果（あらゆる研究の最終目標）が存在しないという仮定です．喫煙と肺がんの関係を探る限り，そのような因果関係は存在しないというのがヌル仮説です．問題は，収集されたデータがこの主張を無効にするのにどのような意味で十分であるかということです．
実際は，喫煙と肺癌発生ではヌル仮説はずっと前に卒業しました．しかし，それを実証するための十分なデータがなかった頃は，これが単なる偶然の問題ではないということを証明できませんでした．大量のデータを得たので，ランダムな結果の可能性を最小限に抑えられ，ヌル仮説を卒業することができました．

ヌル仮説を卒業するためには，大量のデータを蓄積する必要がありました．科学者は「大きなサンプル」と言うでしょう．しかし，大きくなくても「質の良いサンプル」というものもあります．たとえば，ティコ・ブラーエの長年の正確な観測は，ケプラーの惑星運動の法則の発見につながりました．これは，ヌル仮説を拒否し，ケプラーの結果が正しいことを確認するのに十分でした．

病気とその疑わしい原因との間に相関関係があると主張する論文を読むときには，ヌル仮説を除外する前に，研究者が実際に十分な症例を調べたかどうかに注意してください．新型コロナの治療薬やワクチンに関しても同様です．

結晶空間は周期的な世界です．周期的な空間を，対称性で分類すると，3次元では230種類の空間群になります．2次元では壁紙群とも呼ばれ17種類です．

注）群というのは，
集合の元elementの間に演算が定義されて，任意の2元間で演算を繰り返して生じる元も集合に属する集合で，
（有限集合の場合も無限集合の場合もあります）

群の演算定義を満たす代数系のことです．

例えば，2次元の周期は，2つの独立なベクトル$$a,b$$を与えて，$$na+mb$$（格子点の集合）で表現できます．ただし，$$n,m$$は整数．格子点の集合の対称性は並進群で記述されます．格子点は，無限可算個ですから，並進群は無限群です．

結晶点群は32個ですが，この中の単純群は1,2,3,4(mod2),-1,mで，1は例外,3以外は位数2です．

　工事中！

数学は何処へ行くより2, 
Brian Davies, Notices of the American Mathematical Society, декабрь 2005, vol. 52, №11.

コンピュータプログラムを書いたことのある人は誰でも、最も単純で最も短いものでさえ、数学者とは異なり、間違いを許さないことをよく知っています。構文のわずかなエラーはコンパイラーによって認識され、そのようなプログラムの実行は即座に停止されます。コンパイラは2つの異なる変数に同じ名前を使用することをスキップしますが、プログラムの出力はほとんど意味がないため、このようなエラーに気付くことは困難です。多くの場合、数学的なエラーは、同様のタイプの単純な問題に対してプログラムを実行することによって検出されます。その解決策は事前にわかっています。この場合、問題の入力パラメーターを変更することで、モデルが予測どおりに動作することを確認できます。

標準ソフトウェアパッケージに含まれているユーティリティで発生する可能性のあるエラーと不正確さは、それらの重要性と発現の希少性のために、識別することははるかに困難です。それにもかかわらず、わずか数百行の長さのプログラムは、数学者の生活を信じられないほど楽にすることができ、プログラムをデバッグすることで最終的に正しく動作できることを示しています。長くて複雑なプログラムを使用すると、本当の問題が発生します。最近、すべての部門のコンピューターに誤ったソフトウェア更新がインストールされたため、英国政府の管理がほぼ1週間麻痺しました。

ソフトウェアの正確さの正式な検証は、応用数学論理の分野の専門家とビジネス担当者の両方の関心事です。特に、Windows XP［訳注）この論文は2005年］の信頼性の向上は、プログラムの機能の根底にある数学的アルゴリズムの正式な整合性チェックの数学的方法に基づく強力なソフトウェアの正確性分析ツールのおかげで達成されました。ただし、いくつかの点で、サイバネティクスと数学の問題は根本的に異なる面にあります。 Javaなどの一部のプログラミング言語の技術文書は、数百ページの長さになる可能性があります。これは、最も洗練された定理が必要とするよりもはるかに長いものです。ソフトウェアの「特異な」動作がバグなのか、プログラムの機能なのかを判断するのが難しい場合もあります。ハング（多くの場合、バッファオーバーフローが原因）は、間違いなくプログラマの欠陥です。たとえば、LATEXが、ユーザーの要求に応じず、何かをすることを拒否した場合、開発者がそのような機能を必要であるとは全く考えていなかったためで，明確なことを言うのはより困難です。一般に、大規模なソフトウェアパッケージの開発に不適切な技術仕様は、プログラマーによる技術仕様の不適切なパフォーマンスよりも、予測できない経済的影響を伴う壊滅的な障害を起こす原因です。

ソフトウェアの正しさの公式的証明により、一部のサイバーネティシストは厳密な数学に同じ方法を適用しようと試みましたが、現時点でこの分野の活動は明らかにうまく行っていません。以下の発言から、私が分析している分野では、正当性の公式的証明の実施に大きな困難が予見されていることがはっきりとわかります。他の分野では（たとえば、数学論理や代数で）価値のあるアプリケーションを見つけるかもしれませんが、これらの分野で働く専門家にこれを判断させてください。たとえこれらの詳細が重要でなくても、起こっていることの雰囲気を読者に伝えるために、ここで詳細を少しだけお話しましょう。数学的分析におけるほとんどすべての定理の証明は、外部の事実に基づいています。これらは読者が知っていることを意図しているため、通常は説明されません。例えば、ディリクレ境界条件を持つ有界ユークリッド領域でのラプラシアンのスペクトル分析に専念していると述べることから始めるなら、このトピックだけでもおそらく数百のモノグラフと数千の出版物があり、著者はそれらのほとんどに精通しているとして、この場合、著者は、読者が気付かない可能性のある、新しくてあまり知られていない論文のみを参照します。これは、そのような記事を読む人が、このジャンルの古典に精通している可能性が高いことを意味します。

この道筋に沿って多くの罠があり、時折それらに陥ります。数学的な分析では、同じ定理の複数のバージョンが存在することが多く、異なる初期の仮定に基づいて同様の結論が出されることを忘れがちです。モノグラフには、多くの場合、セクションまたは章の冒頭に、最初の仮定の単一の表示がされ、定理を使用して、その後、著者はどこにも仮定に言及しません。

多くの場合、証明のステップを正当化するとき、著者は元のソースを引用せずに、いくつかの古典的な結果を参照します。最近、私の学生の一人がマーサーの定理の誤適用を見つけました。マーサー自身の定式化は、1次元間隔でカーネルを使用して動作しますが、私はより一般的な定式化を使用し、説明はなしでした。学生が私のバージョンを立証するように私に依頼したとき、私が使用した解釈をカバーするのに十分な一般的な定理の主張を文献で見つけることができませんでした。半ダースの本をめくった後、私はこの証明を自分で書くことにしました。私のように、線形間隔の元の証明に精通している人なら誰でも、有限数の次元を持つケースにそれを拡張可能なことは明らかに見えます。しかし、一般的な形で定理を厳密に証明するのに4ページかかりました。私は、この場合に必要な結果の証明可能性が明らかであったため、重大な教育上の間違いを犯しませんでした。残ったのは、マーサーの証明のすべての論理ステップを1次元のケースから多次元のケースに丹念に転送することだけでした。結局、生徒は私の証明に満足しました。

専門家は、議論中の文脈に合うように古典的な定理を修正することが可能である場合、ほとんど本能的に「理解」します。どうやら、専門家を区別するのはこの能力です。時折、集まって、あらゆる領域の多かれ少なかれ完全な説明を含むモノグラフを書く力を持った数学者がいます。同僚は後で参照するものがあるので、これは大きな問題です。しかし、そのようなモノグラフは、作者が自発的または無意識に均質な文脈でそれを構築するため、実際の状況を歪めるだけである場合があり、そのようなモノグラフで与えられる多くの定理は、より弱い条件下でも当てはまります。

Т-квадратelementy.ru
このフラクタルは、T定規の形をしています（英語ではT定規をT-squareと呼ぶそうです）。レース模様のようです。

始めに与えられた辺の長さ１の正方形（暗い部分）の中心に,①辺1/2の正方形を白く塗ります。次に，②正方形の4つの頂点を中心に，①の正方形の辺の1/2の辺の正方形を白く塗ります。このように繰り返し，次の世代で追加する正方形は，前の世代の正方形の頂点を中心に，辺の長さは前の世代の1/2にします。
無限回繰り返したときにできるフラクタルのフラクタル次元は，
log_{2}4 = 2　です。

無限に繰り返すと，始めに与えられた正方形のどの点をとっても、その近傍には白く塗りつぶされた点があり，始めに与えられた正方形のほとんどすべてが白くなり，残りの領域は0に等しく，フラクタルは始めに与えられた正方形（面積１）全体を占めます。しかし、塗りつぶされた部分の境界の長さは無限です。

(訳者による要約)

単純群とは，自明な正規部分群以外の正規部分群を含まない群です．乱暴な言い方をすれば，自然数では素数のようなものです．有限群を単純群の積で表すのは，自然数を素因数分解するイメージです．

（定理）有限単純群は次のいずれかと同型である．
１．素数位数の巡回群
２．5次以上の交代群
３．Lie型の単純群
４．26個の散在型単純群

 １～３は系列ですが，どちらにも属する群も存在し，この分類は重複を許すものです．４は系列に属さず存在する群なので散在型と呼ばれます．モンスター群は散在型単純群に分類されます．この記事の趣旨はこのような数え上げの問題では分類完了と言い切れないということで，有限単純群の分類に踏み込んで理解する必要はありません．

 この分類定理は，10年を越える500以上もある論文を繋ぎ合わせて得られる結論ですが，論理の繋ぎにギャップがある可能性はあり．分類に抜けがないとは言えません．理論全体を理解している人は10人いるかどうかで，今後とも証明が完全であることを証明できるかどうか疑わしいと言うことです．

結晶点群は32個ですが，この中の単純群は1,2,3,4(mod2),-1,mで，1は例外,3以外は位数2です．

ーーー 

■数学は何処へ行くより３， Brian Davies（ロンドンキングスカレッジ）

https://elementy.ru/nauchno-populyarnaya_biblioteka/164681/164685

これから説明する3番目の危機も、不必要な複雑さに関連していますが、ある意味ではもっと深刻です。この場合、私たちはコンピュータは使いませんが、「純粋数学」におけるコンピュータの証明が容認できない理由です。私が提供する例は、現代数学の中心的な分野の1つである群論に関連します。

1970年代に、100人を超える群論専門家が一種のコンソーシアムを結成し、単純な有限群の完全な分類を目標にしました。この問題は非常に骨の折れるものとして提起され、その解決策は、純粋数学で「フロー法」と「分業」を使用した唯一の例です。ダニエル・ゴレンシュタインの指導の下で、問題は「パッケージ」に分解され、世界中の数学者のさまざまなグループに割り当てられました。10年間の集中的な作業の後、3つの可算無限の系列族と、26個の散在型で構成されるすべての有限単純群の完全な分類をまとめることに成功しました［訳注）約500編の論文］。 「モンスター」と呼ばれる最高位数の散在型の存在は、コンピューターの助けを借りてのみ証明することができました。 幸いなことに、この問題をめぐる危機は、群分類の詳細に立ち入ることなく議論することができます。有限単純群が何であるかを知る必要さえありません。

1980年代には、群分類自体と同じくらい興味深いことが起こりました。外向きのポジティブな変化です。コンピューターを使わずに「モンスター」の存在を証明する方法の発見です。さまざまな数学者グループの努力を組み合わせて、模索された証明の大規模な研究を実施することが決定されましたが、期待される結果の代わりに、以前に受け入れられた証明の多くのギャップが特定されました。ほとんどの穴にはパッチが適用されていましたが、1990年に単純な有限グループの完全な分類が得られたという記述は時期尚早であると見なされるほど、深刻であることが判明しました。時が経つにつれて、このギャップはアシュバッハーとスミスの証明で埋められ、再びその証明は非常に正しいように見えました[3]。この最終的な証明の20巻のうち、これまでに公開されたのは不完全な5巻だけであり、これは定理が「証明」されてから四半世紀後のことです。詳細については、[3]、[27]を参照してください。プロジェクトに最も関心のある参加者の1人であるミハエル・アッシュバッハーは、いつの日か新しい有限単純群が発見される可能性を排除していません。
その特性がすでに知られているどれかに関連しているなら、大したことではありませんが，
アッシュバッハーは、根本的に新しい有限単純群である可能性を排除していません。その場合は、分類に関するすべての作業を最初から始めなければなりません [4]。Jean-Pierre Serre は用いられる証明の正しさと完全さに懐疑的であることを記しておきます [24]．

アッシュバッハーは、証明は「外見は十分に強い」と考えています。それは、特定された欠点が、証明のメインラインに影響を与えることなく、適度な量の追加作業でこれまでに修正できたからです。残念ながら、これは証明が正しいことを意味するものではありません。証明の強さは、そのリンクの最も弱いものによって決定されます。これまで、ドロップされたリンクが比較的簡単に新しいリンクに置き換えられたという事実は、これが将来何度も成功することを保証するものではありません。

個々のスレッドの切断があるネットワークの形の証明をイメージしましょう。ネットワーク全体の整合性を脅かさないで、どこかにハエが這うのに十分な大きさの穴があることは排除できません。ハエ（この場合は有限単純群）の大部分は捕らえられますが、すべてではありません。

数学的知識を相互に関連する事実のウェブと比較するという考えは、線形論理の役割を減らし、数学的証明の問題を確率論的平面に移します。これは必然的に不必要な複雑な構造につながります。この考えは新しいものではありませんが、数学者自身が向かうのは比較的最近です。同様の類似点は、特にアシュバッはー [4]によって与えられており、「古典的な数学」とは対照的に、データを整理するさまざまな方法が豊富な、情報集約型の科学としての現代の数学と生物学の類似点を示しています。

有限単純群の最終分類案の完成（徹底的な最終報告書を発行するという意味で）に関しては、自然な老齢化で主要な参加者を失ったために危機に瀕しています。さらに10年後、それらのほとんどは生命や数学から消え、分類を完了するのに十分なほど問題を深く理解している科学者は少ないでしょう。しかし、プロジェクトが徹底的な最終報告で終わったとしても、少なくともマルチボリューム証明の主要な行を理解していると主張する権利を持っている数学者は、おそらく世界に10人もいないでしょう。

したがって、次のような状況になります。数文で定式化された問題の解決には、数万ページのテキストが必要です。証明は完全に書き留められておらず、一貫して書き留められているわけではなく、おそらく書き留められることはなく、最後に、1人の個人が完全に理解することはできません。しかし、得られた結果は重要であり、群理論の枠組みの中でさまざまな問題を解決するために広く使用されていますが、その正確性は依然として大きな問題です。

もちろん、群分類の問題を解決する簡単なアプローチができる可能性もあります。しかし、同じように、これが起こらない可能性もあります。アシュバッハーは、（まだ記録されていない）利用可能な証明の推定全長が過去四半世紀で減少していないという事実を考えると、比較的単純な証明の可能性について懐疑的です。チューリングの研究から、証明が定式化よりも何倍も長い定理があることがわかります。実際、これら2つの長さの比率は任意に大きくすることができます。コーエンは、「中程度に複雑さの数理論の基本問題でさえ、圧倒的多数が合理的な理解を超えている」と確信しています[13]。したがって、将来的には、この種の新しい発見のみが期待できます。

https://elementy.ru/posters/fractals/Levy

このオブジェクトは1906年にイタリアのエルネスト･セサロによって研究されましたが、その自己相似性とフラクタル特性は、1930年代にフランス人のポール･ピエール･レヴィによって研究されました。このフラクタルの境界のフラクタル次元は、 1.9340にほぼ等しい...。しかし、これはかなり複雑な数学的結果であり、正確な意味はわかっていません。

華やかなフォントで書かれた文字「C」に似ていることから、レビィCカーブとも呼ばれます。よく見ると、レヴィの曲線がピタゴラスの木の冠の形に似ていることがわかります。

バリエーション
歪んだ曲線は、各ステップで等角線の右三角形の代わりに他の右三角形を使用することによって得られます。

Levyレヴィ Cカーブの別バージョンは、セグメントではなく文字Pで開始する場合に作成できます。以下は、このカーブを作成する最初の3、8、および11番目のステップです。

レヴィ島は、正方形を基準にすると得られます。

https://elementy.ru/posters/fractals/Pythagoras

上記ウエブサイトの図を利用していますが，説明文はわかりやすくするために書き換えています．

この図形は正方形ばかりでできています．３つ組の正方形が囲む3角形が直角3角形なので，ピタゴラスの定理が成立するので，ピタゴラスの木と呼ばれます．

この構成規則のため木全体が制限されるので，最大の正方形を1とすると，木は6×4の長方形に収まります。したがって，その面積は24を超えません．各ステップで，正方形の辺は1/√2倍に縮小され（面積は1/2）ますが，生じる縮小された正方形の数は2倍ですので，いつも同じ面積が追加されて行きます．このため，木の領域は無限大になるはずです．しかし実際には，正方形がかなり速くから重なり始め，領域がそれほど速く成長できません．それは有限ですが，正確なことはわかっておらず，これは未解決の問題です．

３角形の底辺の角度を変えると，木の形が少し異なります．そして，60°の角度で，3つの正方形すべてが等しくなり，木は平面上で周期的なパターンに変わります．

正方形を長方形に置き換えることもできます．そうすれば，木は本物の木のように見えます．そして，いくつかの芸術的な処理により，かなりリアルな画像が得られます．

https://elementy.ru/posters/fractals/Sierpinski

このフラクタルは、1915年にポーランドの数学者シェルピンスキーVaclavSierpinskiによって記述されました。これを作るには、正3角形の内部に、中線3本を引き、生じた4つの小さな３角形の中央の1つを捨てます。次に、残りの3つの三角形のそれぞれについて同じ手順を繰り返します。この図は、最初の3つの手順を示しています。

Sierpinski三角形を作る手順

中央の３角形を捨てることは、Sierpinskiの３角形を作る唯一の方法ではありません。「反対」のやり方も可能です。最初は「空の」三角形を取り、その中の中線で形成される３角形を作り、3つの角の三角形のそれぞれで同じことを行います。最初は、図は大きく異なりますが、反復回数が増えるにつれて、それらはますます互いに類似し、無限回繰り返す極限では両者は一致します。

Sierpinski3角形を作る「反対」の手順

Sierpinski3角形を得る次の方法は、次の反復の一部に縮小された自分を置き換えることで幾何学的フラクタルを構築する通常の手順にさらに似ています。各ステップで、ポリラインを構成するセグメントが3つ折れのポリライン（最初の反復で形ができた）に置き換えます。この3つ折れを右と左に交互に置き換えて行きます。8回目の反復でフラクタルに非常に近いものが出来上がっています。

Sierpinski３角形を得る別の方法

しかし、それだけではありません。Sierpinski３角形は、平面上の点のランダム歩行の種類の1つの結果として得られます。この方法は「カオスゲーム」と呼ばれています。他のいくつかのフラクタルはそれを使って構築することができます。

カオスゲーム

「ゲーム」の本質は次のとおりです。正３角形をA1 A2 A3とします。任意の始点 B0が与えられます。３角形の3つの頂点の1つがランダムに選択され、もしA1が選ばれたとすると、B0とA1の中点B1 がマークされます。同様に、次にA2が選ばれたとすると、B2がマークされます。その後、A3が選ばれたとすると、B3がマークされます。つまり、前の手順で何を選択したかに関係なく、三角形の頂点がランダムに選択されるたびにマークされる点がジャンプして生じます。驚くべきことに、シェルピンスキーの三角形がすぐに表示されるようになります。以下に、100、500、2500ポイントがマークされたときに何が起こるかを示します。

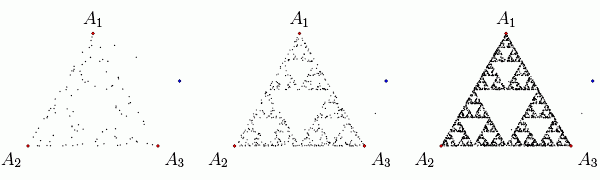
カオスゲーム：100、500、2500ポイント

いくつかの性質

フラクタル次元$$log_{2}3=1.584962･･･$$。 Sierpinski３角形は、自分自身を1/2に縮小した3つのコピーで構成されます。それらの相対位置は、グリッドセルが半分になると、フラクタルと交差する正方形セルの数が3倍になるようなものです。つまり、$$ N( δ/2)= 3N(δ)$$です。最初のセルサイズが1で、フラクタルがそれらの$$N_{0}$$と交差する場合（$$N(1)=N_{0}$$）， $$N(1/2)=3N_{0}，N(1/4)=3^2N_{0},･･･， N(1/2^k) =3^k$$ $$N_{0}$$。　　　したがって、$$N(δ)$$は$$ (1/δ)^{log_{2}3} $$に比例しており、フラクタル次元の定義により、次元は$$log_{2}3$$に等しいことがわかります。
Sierpinski３角形の面積はゼロです。これは、単一の、非常に小さな円でさえ、フラクタルに収まらないことを意味します。つまり、最初の方法で構築を開始した場合、内部全体が３角形から「取り出され」ました：各反復のたびに、残っている領域は3/4倍されます。つまり、ますます小さくなり、0に収束します。これは厳密な証明ではありませんが、他の構築方法も、この特性が真実であるという確信を高めるだけです。
コンビナトリクスとの予期せぬつながり。$$2^n$$ 本の線があるパスカルの三角形で、すべての偶数を白で、奇数を黒で着色すると、目に見える数字はSierpinski３角形を形成します。
オプション
Sierpinskiによるカーペット（正方形、ナプキン）。正方形のバージョンは、1916年にVaclavSierpinskiによって記述されました。彼は、自己交差することなく平面上に描くことができる曲線は、このスカスカの正方形のサブセットと同形であることを証明することができました。３角形のときと同様に、正方形はさまざまなデザインから取得できます。右側は古典的な方法です。正方形を9つの部分に分割し、中央の部分を捨てます。次に、残りの8つの正方形についても同じことが繰り返されます。

Sierpinskiカーペット、最初の5回の繰り返し

３角形と同じに、正方形の面積はゼロです。シェルピンスキーカーペットのフラクタル次元は、3角形と同様に算出し　log_{3}8

シエルピンスキーのピラミッド。Sierpinski３角形の3次元類似物の1つ。起こっていることの3次元性を考慮して、同様に構築されます。1/2に圧縮された最初のピラミッドの5つのコピーが最初の反復を構成し、その5つのコピーが2番目の反復を構成します。フラクタル次元はlog_{2} 5です。図の体積はゼロです（各ステップで、体積の半分が破棄されます）が、表面積は反復ごとに保持され、フラク​​タルの場合は最初のピラミッドの場合と同じです。

メンガーのスポンジ。Sierpinskiカーペットの3次元空間への一般化。スポンジを作成するには、手順を無限に繰り返す必要があります。繰り返しを構成する各立方体は、27個の1/3に縮小された立方体に分割され、中央の立方体とその6つの隣接する立方体が破棄されます。つまり、各立方体は20個の新しい立方体を生成します。これは3分の1です。したがって、フラクタル次元はlog_{3} 20です。このフラクタルは普遍的な曲線です。3次元空間の曲線は、スポンジの一部のサブセットに対して同形です。スポンジの体積はゼロですが（各ステップで20/27倍されるため）、表面積は無限大です。

表紙の3D図形は，コッホピラミッドと呼ばれます．
https://elementy.ru/posters/fractals/Koch

コッホの雪片

この図は，最初に研究されたフラクタルの1つです．これは，1904年のスウェーデンの数学者Helge vonKochの論文に初めてでたKoch曲線の3つです．この曲線は，連続ではあるが至る所接線を引くことができない線の例として提案されました．このような特性を持つ線は以前から（Karl Weierstrassは1872年）知られてはいましたが，Koch曲線はその構造の単純さで注目に値します．

コッホ曲線の作り方　以下の操作を無限に続けます．

コッホ曲線の基本的な特性
0.拡大しても拡大しても同じパターンがでて来ます。

1.連続ですが、至る所で微分できません（接線が引けません）。

2.無限の長さを持っています。元の線分の長さを1とすると、各ステップごとに；　1，4/3，(4/3)^2，．．．．のように長さが増えていきます。nステップごの線の全長は(4/3)^nですから、n→∞で全長は無限大になります。

3.コッホの雪片が囲むのは有限な領域ですが、その周囲が無限であるというのは不思議です。興味のある方は、面積を計算してみてください。

始めにあるのは面積S_0の正3角形１つ．step１で出来るのは，2つの正3角形を重ねたダビデの星形（ピンク色の星形）．この面積S_1は，中心の正6角形［面積は(2/3)S_0］と外側の小さな３角形［面積は(1/9)S_0］が6個です．S_1=S_0［2/3＋6(1/9)］．step3では，青色の小さな正3角形［面積S_0x(1/9)^2］が2×6個分付け加わります．S_2=S_1+2･6･S_0(1/9)^2．このように継続していくと，面積は単調に増加一方ですが，付け加わる面積は指数関数的に減少し，n→∞で面積はある値に収束するはずです．

4.フラクタル次元はlog4 / log3 =1.26･･･
自分の中に1/3に縮小した自分が4個入って次の世代ができる

美しい幾何学p159,160

https://elementy.ru/posters/fractals/H-fractal

Hフラクタル
文字Hの形の図形からすべてが始まります。Hの垂直な線分と水平な線分の長さは等しくなっています。
次ステップで、図の4つの端のそれぞれに、半分に縮小されたコピーが描画されます。
次ステップで，両端にあるのは，4分の１に縮小された16個のHです。
このように無限に繰り返して、フラクタルは視覚的にほぼ正方形を埋めます。

Hフラクタルはどの場所でも密。つまり、正方形の任意場所のいくらでも小さい近傍に、フラクタルがあります。よく見ると、各文字Hが、同じステップで完成した独自の小さな正方形に含まれていることがわかります。

Hフラクタルは正方形を埋める（空間充填曲線）ので、そのフラクタル次元は2で、すべてのセグメントの全長は無限大です。

Hフラクタルを構築する原理は、電子マイクロ回路の製造に使用されます。複雑な回路内の多数の要素が同時に同じ信号を受信する必要がある場合、Hフラクタルの適切な反復セグメント端に配置し、接続します。

オプション
Mandelbrotマンデルブロの木は、線セグメントではなく長方形でできた厚いHを描画することで作られます。

www.flickr.com/photos/29915793@N08からの画像
平面の一部を埋める線のいくつかの例（空間充填曲線）は、1890年にイタリアの数学者ジュゼッペペアノの論文に初めて登場しました。Peanoペアノは、曲線と正方形が等しい性質（点集合と見なす場合）である、つまり「同じ」密度の点を持っているということの視覚的な説明を見つけようとしました。この定理は、Georg Cantorカントールによって、彼が創始した集合理論の枠組みの中で証明されていましたが、この直感に反する新理論の結果は、大きな懐疑論を引き起こしました。ペアノの例（セグメントから正方形への連続写像）は、カントールの正しさの良い確認となりました。

ペアノ曲線、最初の3回の繰り返し
不思議なことに、ペアノの論文には1つのイラストも含まれていませんでした。ペアノ曲線という表現は、特定の例ではなく、平面または空間の一部を埋める曲線を指す場合があります。

下の曲線（ヒルベルト曲線）は、1891年にデビッドヒルベルトによって発表されました。見ることのできるのは，私たちの念頭にある数学的オブジェの有限回近似です。本当の曲線は、無限回の操作後にのみ実現します。

ペアノ曲線の変種-ヒルベルト曲線、最初の6回の反復

ゴスパーカーブ、またはゴスパー雪片（ビル ゴスパー）：

ゴスパーの曲線（雪片）

そして、そのような線の三次元版もあります。たとえば、3次元のヒルベルト曲線、またはヒルベルトキューブ：

カリフォルニア大学バークレー校のコンピューターサイエンスの教授であるCarloH.Séquinによって作成された、3Dヒルベルト曲線のエレガントなメタリックバージョン（3回目の反復）。 www.cs.berkeley.eduからの画像

このようなモデルは、64個のプラスチック製コーナー配管を用い自分で作れます。

ヒルベルトのプラスチックキューブ（2回目の繰り返し）。momath.orgからの画像

モーペルテュイは，
「始状態から終状態への運動経路には，作用と呼ばれる積分量が定義でき，作用が最小となる経路が実現される．これが物理学のみならず，万物の運命を決める外界の原理である」
という着想－”最小作用の原理”(1744年)を得ました．たしかに，現実の運動では，しばしば作用が極小になりますが，正確には，「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります．
オイラーは，モーペルテュイの作用量の定義を積分に拡張し，最小作用の原理をさまざまな力学課題に適用できるようにし，”最大，または最小の性質をもつ曲線を見出す方法”（1744）を発表しました．これを読んだ若きラグランジュは変分法を発明し，オイラーに手紙（1755）を送ります．オイラーは，ラグランジュの方法を採用し，”変分法の原理”（1766）を出版します．変分法で導かれる運動方程式が，オイラー＝ラグランジュ方程式といわれる所以です．その後，ラグランジュは，”解析力学”（1788)を出版します．その序文に「本書には図は一つも出てこない．...所定の手続きに従い進める代数計算だけだ．...」と高らかに宣言します．こうして，複雑な力学問題も解ける一般化された手法が確立されます．
変分法は，19世紀のハミルトン，ヤコービにより完成に至ります．ハミルトンは，系の状態を表示する空間に，座標と速度を座標軸とした相空間を導入し，「作用量は最小化や最大化するのではなく，停留化する」ことを示しました．
１つの物体は，座標x,y,zと速度x˙,y˙,z˙を変数に持ち，その状態は6次元の空間の１点で表現できます．同様に，N個の物体よりなる系は，6N次元の空間の１点で表現できます．この空間を相空間といいます．系のエネルギーを
H(xi,yi,zi,xi˙,yi˙,zi˙)，i=1,2,･･･,Nとすると，エネルギーが保存される運動の軌跡は，相空間内の超平面H(xi,yi,zi,xi˙,yi˙,zi˙)=hに含まれます．超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです．解けるかどうかは別として，周期解（軌道）が存在することは，証明（1986年）されています．（文献10）
■　最小作用の原理の理解には，ホイヘンスの光の波動説の説明が参考になります．ホイヘンスは，空間は見えない媒質で満たされており，光は波紋（球面波）が拡がるように伝わると考えました．波面上の各点はまた新たな波源となり，そこを中心として新たな波紋が広がって行きます．生じた無数の波紋は重なりあったり打ち消しあったりの結果，新しい波面ができます．これは多数の波面の包絡面で，この面に垂直な方向に光は進むと考えます．この様なプロセスで決定された方向は，作用を停留値にするものです．

量子力学の世界の運動には，軌道の概念がなく，電子などはランダムに動き回ります．しかし，我々の日常（マクロ世界）では，電子の運動でも軌道はあります．ここで，マクロ世界でも物体はランダムな経路をとれるとしてみましょう．あらゆる経路に実現可能性があるが，各経路の実現率は，それぞれの確率に従う．これらの確率は，波紋が伝播するときのように互いに干渉し合い，その結果として現実の経路が決まってくると言うわけです．最も確からしい経路は，近くからの干渉の最も少ない経路であって，これがちょうど作用積分を停留化するもののようです．「ファインマンの原理」（文献10）
■　運動方程式が解ける問題を”可積分な問題”といいますが，実際は，”非可積分の問題”がほとんどです．ニュートン力学は，可積分で安定な周期軌道が解になる特殊な範疇を扱っています．一方，非可積分の問題からは，カオスが生じます．１つの軌道は，1本の因果列の存在を意味しています．単純な世界は，今日の現象（原因）１が明日の結果１につながり，今日の現象（原因）２が明日の結果２につながる世界ですが，一般には，今日の現象のすべてが，明日のある結果１の原因になりうる複雑な世界です．バタフライ・エフェクトという映画＊）があったようですが，今日，上空で蝶が羽ばたいたことが，遠い未来に竜巻きを起こす原因の一つになるかも知れません．「風が吹けば，桶屋が儲かる」世界です．この世界は，独立な因果列はないので，周期的な軌道にはなりません．コンピュータを用いて，すべてのステップを計算していけば，結果を予測できるのですが，遠い先の結果は予測もつかないものになります．「最小作用（停留値）の原理」は，ニュートン力学も含むが，このようなカオスも含む原理であります．
＊注）過去に戻れる能力を持ったエヴァンは，過去に戻りやり直すことにする．しかし，過去に戻り選択肢を変えて始めた人生は，どれも，自分を含め自分が愛する誰かが，幸せではないものだった．
 
■　最小作用の原理の起源といえば，1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません．「決まった二点の間を，始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です．ライプニッツの提案により，ベルヌーイはこの問題を海外の数学者にも公開することにしました．ベルヌーイは，ライプニッツの友人で，ニュートンとライプニッツの微積分の先取権論争にも加わり，ライプニッツを応援しています．きっと，ニュートンを困らせてやろうと思ったのでしょう．ところがこの問題を受け取ったニュートンは，「当時，造幣局の仕事で忙しく疲れて帰宅したが，問題が解けるまでは寝なかった．とは言っても朝４時までには解けてしまった」と日記に書いています．そして，解答を匿名で返したということです（文献１，5）．

最速降下曲線の答えは，円板の縁（１点）に目印をつけ，直線上を転がしたときに，目印が描く”サイクロイド曲線”です．ホイヘンスが振り子時計に用いたあの曲線です．

■　解析力学の手順
力学系を記述するラグランジュ関数 を求め，ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと，オイラー＝ラグランジュ方程式が得られます．簡単な系のラグランジュ関数は，（運動エネルギー）－（位置エネルギー）の型になりますが，複雑な系では，位置エネルギーが速度に依存することもあります．
ラグランジュ関数は，電磁場に置かれた荷電粒子にも定義され，光（電磁力学）も力学も統一して扱える原理であります．変分原理から，ニュートンの運動方程式は導出されます．その上，変分原理はニュートン力学よりさらに一般化された外界の原理です．（文献１１）
20世紀に入り，量子力学が誕生するときにもこの原理が手がかりになりました．光や物体の運動が，作用積分を停留化するような，手の混んだ経路を選択するというのは，何と不思議なことでしょう．

（文献）
１．物理と数学の不思議な関係，マルコム・E・ラインズ（青木薫訳），ハヤカワ文庫,　2004
５．古典物理学を創った人々，エミリオ・セグレ（久保亮五，矢崎裕二訳），みすず書房，1992
１０．数学は最善世界の夢を見るか？，エクランド（南條郁子訳），みすず書房, 2009
１１．理論物理学，カンパニエーツ（山内恭彦，高見穎郎訳），岩波書店, 1964

（「数学文化」谷，NO.15(2010)，p.79-87　より抜粋）

ストローと輪ゴムで凸多面体を作ります．
輪ゴムの働きは，結節点でストローの長さを変えないように固定しますが，ストロー間の角度は固定しません．つまり，このような構造を建築ではトラス構造と言います．

皆様の常識通り，２次元の多角形では，３角形は安定で，４角形は安定ではありません.

多面体の面がすべて３角形で出来ていれば，変形しない多面体になりますが，１つでも3角形でない面（４角形や，5角形や，....）があると変形が起こる多面体になります．
例えば，以下の多面体は，すべて３角形の面で出来ているので安定です．

これらが安定なことは，皆様の経験通りで感覚的にわかるでしょう．オルルクは１つだけ4角形の面を含む以下の模型を提案しましたが，実験するとこれも変形してしまいました．

これらの事実は，力学的には常識で自明と思いますが，数学的には証明が必要で，自明なものほど証明は難しいものですが，コーシー＆アレクサンドロフの定理が関係あります．

今回の記事は，KVANTIK，No3（2018）のDmitry Panov, Alexandra Pushkar, Dmitry Chebasov の記事を参考に作成しました．

 
フリーマンダイソンFreeman Dyson（1923年12月15日ー2020年2月28日）
フリーマン・ジョン・ダイソンは、イギリス・バークシャー生まれのアメリカ合衆国の理論物理学者、宇宙物理学者、サイエンスライター。ケンブリッジ大学トリニティ・カレッジ卒業、コーネル大学大学院中退。プリンストン高等研究所名誉教授。 若くしてダイソン方程式を発表、量子電磁気学の完成に大きな寄与をなした。（wikiより引用）

1949年に彼は、トモナガと独立してシュウィンガー、ファインマンによって提案された、当時の量子電磁気学である量子場理論のさまざまな定式化が実際に同じ理論の説明であることを示しました。これにより量子電磁気学が定式化されました。　　繰り込み理論＝renormalization theory
（ヴァレリー・アナトリエビッチ・ルバコフの開会の辞2009.3.23より抜粋）
＊訳注）朝永、シュウィンガー、ファインマンはノーベル賞（1965年）をもらいましたが、ダイソンは受賞を逃しましたね。

■訳者（私）の意見
  二酸化炭素は温室効果ガス（地表から放射される赤外線を閉じ込める）でありますが，水蒸気の温室効果は二酸化炭素に倍するほど強力です．大気中にある水蒸気や二酸化炭素は地球大気に広がり地球を包み地球全体としての温暖化を起こすでしょう．それでも，水蒸気や二酸化炭素の濃度には場所により濃淡があります．飽和水蒸気量は気温依存しますので，寒いほど水蒸気量は少なく温室効果は減少するので，寒いところはますます寒くなります．水蒸気の豊富にあるところの温室効果は水蒸気が主体となります．
大気中の二酸化炭素量だけが地球全体の温暖化に結び付けるのは，その他のもっと重要な温暖化原因を故意に見落とすことになります．二酸化炭素を減らしたが温暖化は解決しないということが起こる危険があります．二酸化炭素を削減するために原発が必要という我田引水な理由で原発稼働がなされてきたのは間違いです．

それでは，ダイソン博士の講演を拝聴しましょう．
https://elementy.ru/video/20/Ereticheskie_mysli_o_nauke_i_obshchestve

２．土地管理と気候
これから5つの問題について私は異論を述べます。
最初の異論：地球温暖化をめぐる現在の誇張されたヒステリックな宣伝です。ここで私は、気候モデル専門家の聖なる兄弟と、気候モデルにより予測された数値を信じる惑わされた市民の群衆に反対します。もちろん、私はこの分野の専門家でないので話す資格がないと言われます。しかし、私は気候モデルを研究し、それらの能力を知っています。このモデルは、流体力学の方程式を解き、大気と海洋の流体運動を非常によく記述します。しかし、この方程式は，雲、ほこり、化学、畑、農地、森林の生物を説明することはできません。この方程式は，私たちが住んでいる現実の世界を説明できません。現実の世界は泥だらけで乱雑で、私たちがまだ理解していないことがたくさんあります。科学者がエアコンの効いた建物に座ってコンピューターでモデルを実行する方が、防寒着を着て沼や雲の中で実際に何が起こっているのかを測定するよりもはるかに簡単です。その故に、気候モデルの専門家は自分たちのモデルを信じてしまうのです。

地球上のいくつかの場所で、気候が実際に温暖化していることは間違いありません。私は，この温暖化が問題を引き起こしていないと言っているのではありません。明らかに問題は起こっています。私たちはそれをもっとよく理解すべきです。 この問題がひどく誇張されていると言いたいのです。これを語り，貧困、感染症、公教育、公衆衛生、陸と海の生物の保護など、緊急でもっと重要な他の問題から目をそらさせ，お金を奪っています。 とりわけ、戦争と平和と核兵器の問題についてもお話します。

地球温暖化の問題は、その重要性が誇張されていますが、興味深い問題なので、少しお話します。大気や生物圏における炭素の流れを詳細に理解するには、多くのパラメーターの数値を測定する必要があります。たくさんの数字と混同したくないので、1つの数字だけを覚えておいてください。覚えておいていただきたいのは、年間1/3mmです。次に、この数字の意味を説明します。砂漠、極地の氷、都市、道路、駐車場などではい地球の土地面積の半分を想像してください。農地、森林、沼地など、さまざまな種類の植物を支える土壌で覆われています。毎年、地表のこの半分は、その二酸化炭素の一部を吸収してバイオマスに変換します。それを大気中に放出します。バイオマスの増減を測定していないため、この割合がどれだけ大きいかはわかりません。バイオマスは生き物であり、すでに死んだ生き物の残骸でもあります。私が覚えておくように頼んだ数字（年間1/3mm）は、化石燃料を燃やすときに放出されるすべての二酸化炭素の吸収によって、地表の半分で起こるバイオマスの厚さの平均増加です。

これらの計算の意味するところは、土壌による大気中の炭素の吸収が非常に良好な速度で進行する可能性があるということです。大気中の二酸化炭素濃度の上昇を止めるには、土壌バイオマスを年間わずか1/3mmだけ増加させる必要があります。肥沃な上層土はバイオマスの約10％を占めるため、1年に1/3mmのバイオマスの増加は、1年に約3ミリメートルの表土の増加に対応します。耕作回避など農業慣行の変化は、同様に急速なバイオマスの増加につながります。土を耕さずに作物を育てれば、より多くのバイオマスが根に行き、それが地面に残り、より少ない大気に戻る炭素は少なくなります。遺伝子工学を通じて、根のバイオマスがより高い品種を入手すれば、明らかに、達成することができるでしょう。土の厚さの成長がさらに速くなるように。これらの簡単な計算から、二酸化炭素の大気への放出の問題は気象学の問題ではなく、土地管理の問題であるという結論が導かれます。大気と海洋のコンピュータモデルでは、土地をどのように管理するかを予測することはできません。

地球全体の規模でバイオマスの平均増加を計算することはできないかもしれませんが、この問題を局所的な側面で検討しましょう。この将来の可能性を想像してみてください。中国は、石炭の燃焼に大きく依存する産業大国として発展を続けていますが、米国は、土壌バイオマスの増加によって排出される二酸化炭素を吸収することを決定しています。植物や木の生きている部分に蓄積できるバイオマスの量は限られていますが、土壌に沈着できるバイオマスの量を制限するものは何もありません。大規模な土壌増強は、遺伝子操作された作物の経済的パフォーマンスに応じて、有益な場合とそうでない場合があります。しかし、少なくとも、石炭を燃やすことによって中国が豊かになる可能性については、非常に議論の余地があります。一方、米国は、大気が中国の鉱山から米国の土壌に炭素を自由に輸送できるようにし、大気中の二酸化炭素を一定に保つことによって土壌を貯蔵することにより、環境を祝福しています。化石燃料と気候変動についての予測を聞くとき、このような機会は検討する価値があります。コンピュータ技術が過去50年間に君臨したように、バイオテクノロジーが次の50年間に地球上で最高に君臨する場合、気候ゲームのルールは根本的に変化します。大気中の二酸化炭素含有量は一定に保たれます。

フリーマンダイソン，2009年3月23日，モスクワFIAN

気候変動についての公開討論に耳を傾けると、私たちの知識の巨大なギャップ、私たちの観察の不完全さ、そして私たちの理論の表面性に驚かされます。私たちの地球生態学における多くの基本的なプロセスの理解はまだ乏しい。それらをよりよく理解した場合にのみ、地球の現在の状態を正確に診断することができます。病気の人の世話をするのと同じ方法で地球の世話をしようとすると、最初に病気を診断し、次にそれを治療する必要があります。このためには、生物圏で起こっているプロセスを観察し、それらのパラメーターを測定する必要があります。

大気中の二酸化炭素濃度の増加は、気候と非気候の2つの重要な結果をもたらすことは全員が同意します。1つは、大気中のエネルギーの放射伝達の物理的変化であり、2つ目は、陸上および世界の海の植生の生物学的変化です。これらの結果のどれがより重要であるか、またこれらの結果が個別にまたは一緒にか、有益であるか有害であるかについての意見は異なります。物理的影響は、降水量、雲の被覆、風の強さ、温度の変化に現れます。これらは通常、一緒に積み上げられ、誤解を招く用語「地球温暖化」と呼ばれます。湿った空気では、二酸化炭素によって引き起こされる放射輸送の変化は、水蒸気のはるかに強い温室効果によって本質的に相殺されます。

二酸化炭素の影響は、空気が乾燥している場所で重要であり、空気は通常、冷たい場所でのみ乾燥します。 二酸化炭素の温暖化効果は、空気が冷たく乾燥している場所で最も強く、主に熱帯ではなく北極で、主に夏ではなく冬に、そして主に昼間ではなく夜間に発生します。 温暖化は、暑い場所を暑くするのではなく、寒い場所を暖かくします。 この局所的な温暖化を世界平均で表すことが、人々に誤解を生じさせています。

大気中の二酸化炭素の濃度が生物学的に非常に重要である本当の理由は、この濃度が非常に低いことです。晴れた日の午後に太陽の下で育つトウモロコシやその他の穀物の畑は、地上1メートルの二酸化炭素を約5分ですべて吸収します。対流と風によって空気が継続的に混合されない場合、トウモロコシは成長を停止します。大気中の二酸化炭素の約1/10は、毎年夏にバイオマスの成長に費やされ、毎年秋に大気に戻ります。これが、化石燃料の燃焼の影響を植物の成長と衰退の影響から切り離すことができない理由です。
数千年の時間スケールでしか利用できない炭酸塩岩と深海を除いて、短い時間スケールで生物学的にアクセスできる炭素に5つのプールがあります。これらの5つのプールは、大気、陸上植物、陸上植物が成長する土壌、海洋植物が成長する海の表層、および化石燃料の実証済みの埋蔵量です。大気はこれらのプールの中で最も小さく、化石燃料は最も大きいが、5つすべてが同等のサイズです。それらはすべて互いに強く相互作用し、それらのいずれかを理解するには、それらすべてを理解する必要があります。インテリジェントな土地管理によって、大気中の二酸化炭素の増加を止めるのに必要な量である年間40億トンの炭素が土壌プールの成長を増加させられるかどうかはわかりません。確かに言えることは、これは理論的な可能性であり、真剣に検討する必要があるということです。

地球温暖化の科学的および経済的側面について私が知っている議論のほとんどは、最も重要な問題を回避しています。これは科学的な問題というよりは宗教的な問題です。そのような世界の世俗的な宗教-それは環境主義と呼ぶことができます-それによると、地球上の人々の役割は経済管理者の役割であり、私たちの贅沢の無駄で地球を台無しにすることは罪であり、正しい方法は可能な限り経済的に生きることです。環境倫理の基本は、世界中の幼稚園、学校、大学の子供たちに教えられています。環境主義は社会主義に取って代わり、主要な世俗的な宗教になりました。この宗教には強力な倫理的基盤があります。科学者や経済学者は、仏教の僧侶やキリスト教の説教者たちに、私たちの自然の生息地の破壊は悪であることに同意することができます。鳥や蝶を注意深く保護することは祝福です。グローバル環境主義コミュニティは非常に強い道徳的立場を持っており、より良い未来への希望の道に沿って人間社会をリードしています。自然への希望と尊敬の宗教としての環境主義は、真剣にそして長い間やって来ました。これは、地球温暖化の危険性を信じているかどうかに関係なく、私たち全員が共有できる宗教です。

しかし、残念ながら、環境保護運動は、地球温暖化が何よりも地球の生態系を脅かしているという信念の信条の1つとして採用されています。これが、地球温暖化についての論争が非常に熱く激しくなっている理由です。地球温暖化の危険な影響に懐疑的な人は誰でも環境の敵であると国民は信じています。今、私のような懐疑論者は、そうでなければ大衆を説得するという困難な課題に直面しています。これらの懐疑論者の多くは熱心な環境保護主義者です。彼らは、地球温暖化への一般的な執着が、今日私たちの惑星をすでに脅かしているはるかに深刻な危険から国民の注意をそらすのを恐れて見ています。例えば、環境に対する真に深刻な脅威は、世界の人口の制御されていない成長から来ています。しかし同時に、人間の人口の幸福の増加と出生率の低下の間には強い正の相関関係があります。

20世紀の後半、メキシコが豊かになると、メキシコの平均的な家族の人数は7人の子供から2.5人に減少しました。アイルランドやイタリアなどの繁栄しているヨーロッパ諸国の家族規模はさらに急速に減少しています。世界の人口を安定させ、地球を保護する最も簡単な方法は、すべての人を豊かにすることです。先進国は一般的に人口が安定しているか減少しており、環境に配慮する余裕があります。ベルトルト・ブレヒトが三文オペラでずっと前に述べたように、「最初のコムト・ダス・フレッセン、ダン・コムトは道徳的に死ぬ」、「最初に餌を与え、次に道徳が来る」。環境にとって最悪のことは、産業技術の助けを借りずに、成長し、飢え、貧しい人々が土地に住もうとしていることです。中国とインドの政府が地球温暖化との戦いよりも貧困との戦いを優先するとき、彼らは道徳的にも科学的にも正しいといえます。

By Marianne Freiberger; plus magazineより　

今，学校の再開が注目されていますが，もう1つのパンデミックの課題にも直面しています．今月と来月，全国の大学が秋学期を開始します．

約200万人の大学生が全国から選択した教育機関に動きだします．フレッシャーズフルー*)［*注）フレッシャーズフルーとは，大学で最初の数週間に新入生が発症した一連の病気に付けられたイギリス英語．］の感染は大学のキャンパス全体に簡単に広がる可能性があります． COVID-19では，若者が無症候である可能性が高いということから，発生しても迅速に発見されない可能性があります．若者のCOVID-19は深刻な病気になる可能性は低くいのですが，学生より脆弱な可能性のあるスタッフや周囲のコミュニティと混ざり合うため，大学での流行は無視できないリスクとなります．

大学を可能な限り安全に保つのに，何ができるでしょうか？ 7月に2つのオンラインブレーンストーミングセッションがありました．Isaac Newton Instituteによって実施された「パンデミックの感染症のダイナミクス：感染症のパンデミックのダイナミクスを理解する上での数学的および統計的課題」（IDP）　https://www.newton.ac.uk/event/idp　の一部で，数学者と教育省および高等教育機関の代表者が集まり，数学がいくつかの問題の敏速な解決にどのように役立つかを確認しました．

数学者が提供しなければならないのは，数学モデルを使用してさまざまな状況下で病気の広がりをシミュレートし，緩和策が感染拡大にどのように影響を与えるか確認することです．

「この問題の見方で，数学は学際的なタペストリーの一部になりたい」と講演者でサウザンプトン大学のレベッカ・ホイルは言いました．「すべての答えがあると感じているわけではありませんが，そのパッチワークの一部を提供します」

■ベースライン
病気が典型的な学生集団にどのように広がるか，IDPの会議で，Ellen Brooks Pollockはブリストル大学のチームの仕事について報告しました． チームは、2010年に実施された社会的接触調査のデータとブリストルの学生の家庭の状況に関する匿名の情報を使用して，学生の接触パターン（誰が、どのくらいの頻度で会うか）を把握しました． チームは，学期の初めに到着したときに学生が通常どこから来るのかを見て，COVID-19に感染して到着する学生の数も推定しました． 彼らは，この情報を確率的コンパートメントモデル*)https://plus.maths.org/content/how-can-maths-fight-pandemic　に組み込みました．
このモデルによると，ブリストルの学生の約20％が最初の学期中に感染する可能性があり，大学生活が通常どおり継続する場合，約74％が学年末までに感染することを示唆しています．新入生は感染率が最も高く，発生の初期段階を促進します．ブリストル大学では，他の多くの大学と同様に，新しく到着した学生が好む宿泊施設であるホールは，さまざまな混合場所になるため，1年目の期待と社交への熱意を考慮すると驚くべきことではありません．

モデリングは，発症の症例と比較して，気づかれずに忍び込む無症候性の症例が，どれほどの感染性であるかに依存することも示しました．上記の結果は，無症候性が対症療法の約半分の感染性であるという仮定（入手可能なデータに照らして妥当な推定値）に基づいています．しかし，ブルックス・ポロックと彼女の同僚は，この相対的な感染率の他の値も試し，流行の最終的なサイズがその数に非常に敏感であることを発見しました．たとえば，無症候性の人が症状を示している人と同じくらい感染性があると仮定すると，学生の約96％が学年末までに感染します．

すべてのモデルと同様に，ブリストルのチームによって開発されたモデルは，仮定に基づいており限界があります．これについては，https://www.medrxiv.org/content/10.1101/2020.09.10.20189696v1.full.pdf　この論文に書きます．大学の流行は，本当にリスクがあることを確認しています．これらの発生をよりよくシミュレートするために，無症候性の症例の感染性に関するより多くの研究が必要であることを示唆しています．

■テスト、テスト、テスト
今では誰もが知っているように，エピデミックを回避または少なくとも軽減するには，感染の連鎖を早期に断ち切ることです．したがって，大規模な大学が独自の学内テストおよびトレースシステムを導入することは理にかなっているでしょう？ IDPセッションは，まさにそれを調査しているウォーリック大学のチームからも聞いた． チームは，接触パターンを反映するネットワークと組み合わせたコンパートメントモデルを使用して，ワーウィックキャンパスでの病気の蔓延をシミュレートしました．

IDPセッションで報告された最初の結果は，最も効果的にするために，テスト＆トレースがスムーズに機能する必要があることを示唆しています．症状を発症する十分な数の人が実際に行ってテストを受け，症状がでるまでとテスト＆トレースシステムの遅延を短くする． これらの問題の両方で，学内のテスト＆トレースシステムが明らかに役立ちます．

潜在的に危険な無症候性の症例を見つける唯一の方法は，学生の体全体の定期的なテストを実行することです．問題は，そのようなプログラムが効果的であるために，学生はどのくらいの頻度でテストされる必要があるかということです．これはブリストルの研究が検討したもう1つの問題であり，モデルによるとその答えは少なくとも2週間ごとです．

すべての英国の大学にスケールアップすると，これは多くのテストを意味し，問題はそれらすべてのテストがどこから来るのかということです．一部の大学は独自のラボを使用してテスト能力を構築していますが，ほとんどの大学はこれを行うことができません．そのため，大学のテストでは，現在医療従事者や症状のある人々のために確保されている国の能力を利用する必要があります．

テストに関する現在の問題を考えると，より経済的なアプローチを検討することも理にかなっています． 「検討するかもしれないのはバッチテストです」とHoyle氏は説明します． 「アイデアは，サンプルを組み合わせて一度に複数の人をテストすることです．そのテストが陰性に戻った場合，個別のテストを行う必要はありません．陽性のバッチにあった人を個別にテストするだけで済みます．多くの人を定期的にテストできるかもしれません」

IDPセッションの参加者は，個々の機関がどのような種類のテスト体制が彼らに適しているかを見つけるために使用できる適応モデリングツールを作成することを目的として，テスト＆トレースモデルに取り組んでいます．モデリングはまた，大学での流行が周囲のコミュニティにとってどれほど危険であるかについてのより多くの考えを私たちに与えるでしょう．危険性が高い場合は，国の政策でこれを考慮に入れる必要があります．国の試験能力の一部は，実際に大学のために確保する必要があるかもしれません．

その間，教育機関は，テストで陽性となった学生をどうするかについても考える必要があります．モデルでは，これらの人々は感染性がなくなるまで検疫に入ると常に想定されていますが，現実はそれほど単純ではありません． 20歳の子供に，家から遠く離れた小さな学生部屋で2週間自己隔離するように言うと，規則の違反やさらに悪いことに，深刻なメンタルヘルスの問題につながる可能性があります．誰もが家に帰ることを期待している学期の終わりにテストが行われる場合，これはさらに悪いことになります．モデラーだけでなく，学生の福祉や支援を担当する人たちにもやるべきことがあります．

もちろん，大学が実施できる手段はテストだけではありません．対面教育と学生間の接触を減らすことは，他の2つの明白なオプションです．これらについて詳しくは，
https://plus.maths.org/content/going-back-uni-during-pandemic-part-ii

ブライアンデイビス，ロンドンキングスカレッジ
Notices of American Mathematical Society 52,No11(2005)12月
Элементы，数学は何処へ行くより抜粋翻訳（１）：　
https://elementy.ru/nauchno-populyarnaya_biblioteka/164681/Dokazatelstva_s_ispolzovaniem_kompyutera

コンピューター支援で証明された主要な数学的定理の最初の例は，1976年にAppelとHakenによって証明された4色定理でした．これは2つの理由で，多くの数学者を大いに心配させました．第一に，機械が実行した計算のすべてを，手動で再チェックすることなしに証明の正しさを検証することは不可能であると主張されました．当時，「正しい」定理の証明は，ほとんどすべての数学者にとって，まだ完璧に見えました．証明の偶発的なエラーの可能性は認識されましたが，それらを修正するのは時間の問題であると考えられました．もう一つは，一部の数学者は，その定理が正しいかどうかではなく，なぜそれが正しいと見なされるのかについて考え始めたからです． 本質を理解していない証明は彼らに興味がありません．

4色定理は重要な応用がなく，長い間，面白い逸脱と見なされていました．おそらく，誇張された関心が高まったのは，この定理の単純な定式化のせいでしょう．しかし，時が経ち，コンピューターはますます利用可能になり，コンピューターの証明が広く受け入れられるようになりました．
最も新しい事例，ケプラー問題をここで取り上げます．

ケプラー問題は，最大平均密度となるように，同じ直径の球体を3次元空間に最も密に充填する方法を見つけることです．期待される解決策は昔から知られおます．1998年，トムヘイルズは，幾何学的分析と複雑なコンピュータ計算を組み合わせて，ケプラー問題に対する厳密な数学的解決策を見つけたと発表しました．ジャーナル"Annals of Mathematics"は，この論文を審査のために受け入れ，この分野の20人の主要な専門家からなる委員会を立ち上げ,専門家の委員会は，全体的な戦略を決めるためにプリンストン大学で会議を開始しました．数年が経過し，レフェリーは徐々に委員会を去りました．そして2004年の初めには，記事のレビューを続けられなくなりやめることが最終的に決定されました．ジャーナルの編集委員会は，論文の「理論的部分」を公開し，「コンピュータに基づく部分」をより適切なジャーナルに送るすることを決定しました．ジャーナルの編集委員会のメンバーであるロバート・マクファーソンは，このような論文に対するジャーナルの編集方針は破綻したことを認めた．

王立協会の会合では，コンピュータプログラムの操作の正しさを正式に証明し，それによってコンピュータを使用して証拠を調べる手順を明確にする可能性について活発な議論が行われました．マクファーソンによれば，コンピュータプログラムの正しさを証明するための実際の技術を提供できる人は学術評議会にいなかったので，問題を明確にすることはできませんでした．プログラムは，正式な数学的正しさの専門家による評価の必要性を念頭に置いて作成されたものではないので，これが大きな妨げとなりました．

証明の理論的部分に含まれるアイデアを完全に実装する完全に新しいプログラムを「ゼロから」作成することは可能です．しかし，この可能性は，専門家のレフェリーグループにとって耐え難いものとして却下されました．これは，他の科学分野のプロジェクト（土星へのカッシーニ宇宙探査機など）を完了させるために必要な労力の価値を認めている数学者はほとんどいないからです．

レフェリーの過程で，実行される計算は非常に具体的で特定の問題に特化しているため，引き出された結論を他の同様の問題に適用することはほとんどできないことが明らかになりました．

特に，ケプラーの問題は，互いにさまざまな相互作用を起こすランダムな形状とサイズの異なる物体の大規模なシステムの最小静止エネルギーを決定する問題と密接に関連しています．このような最小化の問題の例は非常に多く，個別の数値手法を開発してコンピューターで計算するので，１つづつが別物でこの分野の理解は不可能です．数学的モデリングを除いて，これらすべての問題を解決する他の方法がない場合，これらの問題のほとんどはそれほど興味深いものではありません．ただし，ケプラーの問題自体は，エラー修正コードの理論などの重要な他のいくつかの問題と関係があります．

コンピューター支援の良い面としては，コンピューターが純粋な数学者を面倒な日常的な計算から大幅に解放したことです．これは，いくつかのカテゴリに分類できます．数式処理は，絶望的に長い計算を変換することができ，さまざまな分野で広く使用されています．カオスの力学系の研究は，数値実験なしには進展しなかったでしょう．カオス現象の存在が19世紀の終わりにアンリポアンカレによって発見されたのは事実ですが，主題を理解と進歩は，コンピューターの開発を待たなければなりませんでした．自己結合行列と非自己結合行列のスペクトルの振る舞いの大きな違いは，数値実験の結果として明らかになり，現在、それ自体が厳密な数学の分野として研究されている疑似スペクトルの新しい分野を生み出しました．特に高次非線形微分方程式の分野では，コンピューター法のみが解の存在を証明することを可能にしました．

写真の石垣は美しいですね．石積みの改修は番号をふって再現するのでパズルのようです．素晴らしい石工の技です．
ボロノイ分割のような網目で各所の釣り合いの条件を書いて計算できたとしても物づくりの役にたちません．石工の技術は直感と身に着けたバランス感覚そのものです．ガラス職人は熔けたガラスの粘性の手応えに反射的に反応し細工をします．機械の設計でも常識や力学感覚が身に着いていない技術者の計算まかせはとんでもなく危うい．
私たちは，幼児の頃に，積み木をしたり水遊びや泥団子などで遊び，物の柔らかさや脆さ，それを扱うバランス感覚，力学感覚を自然に身に着けました．物理や数学を学ぶよりもこの常識を身に着けることはとても大事なことだと思います．壊れやすいものを不器用に扱う若者が増えています．もっとも，理論と器用さは関係ないようで，教授でも子供より不器用な人はたくさんいます．

■通潤橋のアーチと通潤橋のアーチの数学に関し，私はnoteに以下の2つの記事を書きましたがあまり目につかなかったようです．
https://note.com/sgk2005/n/n5eccdef5315a
https://note.com/sgk2005/n/n4356f184665d
リンク切れになっているウエブサイトやブログもあるので，再度，概要を紹介をしましょう．

表紙の写真は，石積みの美しい橋，通潤橋（熊本県，山都町）です．アーチの形は懸垂曲線，放水の軌跡は放物線です．逆さにした懸垂曲線のグラフをアーチに重ねてみました．

鎖の両端を持ち水平に広げたときに，鎖が作る曲線が懸垂曲線です．鎖の各部分は重力で下向きに引かれ，鎖の一つ一つの繋ぎ目はどこも引張あって釣り合っています．この形の上下をひっくり返すとアーチができ，アーチの各部に働く力はすべて圧縮力になります．アーチには圧縮力しか働きません．石たちは自分の重量で互いに押し合い，圧縮され引き締め合います．接着されていない石積みは引張力ではバラバラになりますが，自分の重量で圧縮され良く締まります．石が割れると困りますが，石は圧縮力には強いのです．すべての荷重がかかるアーチの根元には，大きな水平反力が必要ですが，山に挟まれた峡谷などは建設するのに最適な立地条件です．

■私が通潤橋（熊本県上益城郡山都町）を訪れたのは，2007年10月のことでした．22日は，午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業，午後は先生方と人形浄瑠璃を観劇しました．
最近の通潤橋の様子は，以下のウエブサイトにでています．2016年の熊本地震で被災し，修理工事中だった2019年5月にも豪雨で石垣の一部が崩落しましたが，2020年3月までに工事を終え，翌4月から4年ぶりに放水を再開しているそうです．
通潤橋の近況ですが，山都町のウエブサイトよりhttps://d38mttjwbmxw55.cloudfront.net/files/6c2868f8-675e-4dac-b6f3-079b3d5bf224_l.jpg?1585873042

阿蘇山の南側のこの付近の地形は，島のように台地があり，台地から台地への移動が大変で，平家の落人が隠れ住むのに好都合だったようです．
台地（白糸台地）に農業用水を引くのが大変です．
水は台地のがけ下に汲みに行かなければなりません．
時の惣庄屋「布田保之助（ふたやすのすけ）」は，白糸台地に水を引くための水路橋”通潤橋”を，肥後の石工たちの技術を用いて1854年に建設しました．通潤橋は，石造りアーチ水路橋で，長さ75.6m，高さ20.2m，幅6.5m．
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています．

◆通水管
長さ約127m．石をくりぬいた１尺（30cm）四方の函渠（圧力のかかる管水路）．管と管の繋ぎ目には，振動吸収と漏水防止のための漆喰（しっくい）が塗られている．さらに，通水管には5～6ケ所に地震対策のための板（緩衝材）を挟んでいる．
通潤橋は両側台地より低いので，サイフォンの原理で出口で水を押し上げています．通潤橋の高さから流入側台地は7.5m高く，流出側台地は5.8m高い．
通潤橋は，今でも周辺の田畑を潤しています．
放水は，通水管に詰まった堆積物を取り除くために行うものです．
「通潤橋史料館」　に行くと，どのようにアーチ石橋を施工したかわかります．川の中に写真のような木枠を大工が組んで石工が石を置きました．
アーチ橋の高さを台地の高さまで上げられなかった理由は，
この木枠をこれ以上の高さにする木材がなかったためという事です．
石橋の木枠を外す最終段階は，橋の中央に白装束を纏った布田翁が鎮座し，
石工頭も切腹用の短刀を懐にして臨んだといいます．

写真に見えるアーチ曲線を型どっている石の並びについて話しましょう．
アーチの頂点にある石を”かなめ石”と言います．アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です．それでも下の木枠を外すときは，とても心配で責任者は命がけだったでしょう．布田翁も石工頭も命がけで臨んだのがよくわかります．
近年の熊本地震でも残ったのは，その堅牢さ（石の配管の修理をしたと聞きます）の証明です．
2007年当時の「通潤橋資料館」のウエブサイト資料がなくなりましたので，http://www.kumamotokokufu-h.ed.jp/kumamoto/isibasi/ab_sakus.html
のウエブサイトより以下の説明図を引用しました．

■人形浄瑠璃
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
人形浄瑠璃は，清和文楽館で観賞しました．山都町の人形浄瑠璃の始まりは，江戸時代の嘉永年間（1850年ごろ）で，山都町（旧・清和村）を訪れた淡路の人形芝居の一座から，浄瑠璃好きな村人が人形を買い求め，技術を習ったのが始まりといいます．
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました．良い話です．江戸時代の庶民の文化の高さに感激しました．三人で一体の人形を操ります．首（かしら）と右手を操る「主遣い（おもづかい）」，左手を操る「左遣い」，足を操る「足遣い」です．人形も触らしてもらいました．

■空き缶を積んで作ったアーチで実験

私は真剣に積んだのですが，どうしても缶5個のアーチまでしかできませんでした．5個の缶で缶同志の接点は4点．すべての接点で同時につり合っていなければなりませんから，作るのがとても難しい．もし，6個以上でアーチが出来た方は新記録です．ご一報ください．
缶の周りにラップを巻いていますが，摩擦力を増すためでアーチのつり合い条件を変えるものではありません．

5個の空き缶を積んで作ったアーチです．左右対称ですから，左半分だけ解析しましょう．缶の中心を①，②，③と名づけます．すると，缶同士の接点は，線分①－②の中点と，線分②－③の中点にあります．線分①-②，線分②-③には，それぞれ圧縮応力f_{1}, f_{2}があります．すべての缶は点で接触しており，モーメントは考える必要がありません（トラス構造）．線分①-②，および線分②-③の水平となす角度をそれぞれα，βとしてつり合いの式を立てます．各缶には下向きに力gがかかっています．つり合いの式は，①点，②点，③点でx, y成分ごとに書きます．

$$ f_{1}, f_{2}, r_{x}, r_{y}, g $$が，ゼロででない解であるための必要十分条件は，行列式がゼロとなることでした．この行列式を計算すると，
$$ tanβ=3tanα $$　の関係が得られます．
この釣り合いの結果は，①から測った曲線に沿った距離$$ s $$と，その点の接線の傾きtanθが比例する　$$ tanβ/3＝tanα/1=tanθ/s $$の関係（懸垂曲線で導ける）と一致します(下図参照)．

懸垂曲線のグラフ（赤）と放水軌跡のグラフ（緑）を表紙の写真の上に重ねました．ご鑑賞ください．アーチの形とアーチの屋根の左右の石の詰め物を見て，この橋の安定なバランスに感動するなら，あなたは常識の力学感覚が身に着いていると思われます．
 

■球面上のオイラーの定理
球表面の３角形メッシュに関して，オイラーの定理は T-E+V=2　です．
（ここで，3角形（面）の数 T，エッジの数 E，頂点の数 V）

球表面を３角形メッシュに分割したとき，すべての３角形のすべての角度の総和は，2πVになります（すべての頂点のまわりに2πがあるから）．

球面3角形の面積（球面過剰）
球面３角形が半径１の球上にあり，例えば，頂点がｘ軸，ｙ軸，z軸にあれば，各頂点の角度θ1，θ2，θ3は，それぞれ，π/2なので，内角の総和は，θ1＋ θ2+ θ3＝３π/2です．

もちろん，ユークリッド幾何学では，いつでも，θ1＋ θ2+ θ3＝πです．
一般に，内角がθ1，θ2，θ3の球面3角形の面積は，θ1＋ θ2+ θ3-πで定義されます（この量は球面過剰とよばれます）．

この例では，球面3角形の面積は球全表面の1/8で，球面3角形の球面過剰は３π/2－π＝π/2ですので，全球表面は確かに４πになります．

■球面上のオイラーの定理のルジャンドルの証明
球面上の3角メッシュ全体で，次の面積の関係が成り立ちます．
（3角メッシュの角度総和）＝（球面3角メッシュの面積総和）+πT
すなわち，2πV=4π＋πT　　→　V=2+T/2

他方，3角メッシュ全体でエッジの数を2重に数えると，→　3T=2E

ゆえに，T-E+V=T-3T/2+(2+T/2)=2　となりオイラーの定理が証明された．

３角メッシュではなく，多角形の面からなる多面体についてもオイラーの定理は成立します．多面体の面の数F，エッジの数E，頂点の数Vとして，球表面でのオイラーの定理は　
F-E+V=2

■多面体の不足角
多面体の頂点の不足角は，2πー（その頂点に集まる面の内角の和）
例えば，立方体の場合は，１つの頂点で，2πー3π/2=π/2ですから，立方体全体では４πとなります．これは，球と同じトポロジーの面上の任意の多面体で成り立ちます．
多面体全体の全不足角は，いつも4πであることの証明．

多角形F1，F2，･･･，Fkのk個の面で構成される多面体を考えましょう．これにオイラーの定理を適用し，エッジ数と頂点数を計算しましょう．
面FjはNj個のエッジとNjの頂点がある（Nj多角形）とします．
２E=N1+N2+･･･+Nk
V=E-F+2=(N1+N2+･･･+Nk)/2-k+2　→　２V=(n1+N2+･･･+Nk)-2k+4

多面体全体の全不足角Θは
Θ＝2πV－[(N1-2)π+(N2-2)π+････+(Nk-2)π]=
　=π(2V-(N1+N2+････+Nk)+2k)=4π
定理　　任意の多面体全体の全不足角は4πである．

（参考）
Nrich Article by Alan Beardon，Published December 2000,February 2011.

Kvantikの数学コンクールの問35（2012-07）に，次の問題を見つけました．

■問
1から始まる次の数列の規則がわかりますか？数列の規則を理解し，続く数字を書きなさい．
この素晴らしい数列は，有名な数学者ジョン・コンウェイによって発明されました．

1,
11,
21,
1211,
111221,
312211,
13112221,
1113213211,
31131211131221, …

（ヒント）各項は，数値というよりも記数法と見なした方が良いでしょう．
それは，この数列を作ったのがコンウェイだからでもあります．

■ジョン・ホートン・コンウェイ (John Horton Conway) はライフゲーム を1970年に考案したイギリスの数学者です．プリンストン大学．新型コロナウイルスで，2020年4月11日に死去（82歳）しました．
https://www.princeton.edu/news/2020/04/14/mathematician-john-horton-conway-magical-genius-known-inventing-game-life-dies-age

■生命の誕生，進化，淘汰などのプロセスを簡易なモデルで再現したシミュレーションゲームで有名です．コンウェイは，「セル・オートマトン」を実証するためのコンピュータを使った実験プログラムとして，生態系をシミュレートした「ライフゲーム」を開発しました．
「近辺が4つ以上のセルで埋まると，混みすぎて死亡」「近辺のセルが1つ以下になっても孤独で死亡」といった，簡易なモデルで生命現象や結晶成長などの過程を再現した研究です．

ライフゲームシミュレータ
https://algoful.com/Archive/Algorithm/LifeGame

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　谷　克彦 
科学の発展局面で，それが必要としている数学が用意されていたというのは，ドラマティクです．そのような脚色をした本も多いようです（分献１）．しかし，必要な数学が手品のように出現したわけはなく，その数学の源泉にはやはり語るべき背景があります．
科学の発展と平行し，それに必要な数学が開拓されるのは興味深いものです．数学と基礎科学は，密接に牽引しあいながら発展してきました．R.クーラントは，”物理数学の方法”の序文（1924）で，次のように述べています．「．．．多くの数学者は物理学その他の分野との関連を見失い，一方，物理学者は数学者の関心と問題意識，その方法と語法が理解できなくなっている．これでは，科学の発展の流れは次第に細かく枝分かれし水量を失い，ついには干上がってしまうであろう．．．」（文献２）
数学月間の趣旨は，数学が種々の分野に影響を与え，「数学が社会を支えている」ことを，専門家でない一般の人に説明することです．数学嫌いの一般の人々が，数学は知的遊戯で自分の生活には関係ないと思っているとすれば，その誤解を解かねばなりません．
数学が基礎科学を支えているのですが，それにもまして，その数学は基礎科学を源泉にして生まれたことを，ここで述べたいと思います．
中谷宇吉郎は随筆”科学と文化”（昭和12年）のなかで，科学の普及に役立つ文章作法に４つのタイプを挙げ，そのうちでも，テーマを不思議と感じた所から，今までに知られた事実を列挙することを特に推奨しています（分献３）．この手法に則りこの小論を進めようと思います．

１． 外界を知る手段としての数学 

我々は感覚（センサー）により，森羅万象を知ることができます．しかし，森羅万象を動かしている外界は，感覚では知り得ず数学の力により初めて知ることができます．始めに，外界についてのクラインの言葉を引用します．「感覚では知り得ない外界がある．数学の目標は，感覚では知り得ない外界を知ることである．そこから予想もしなかった知識，時には感覚と矛盾するような知識が引き出される．それは物質界の知識の精髄であり，感覚をはるかに凌駕している．」（文献４）
例えば，天体の運行を調べて，それを支配している外界の原理を知るには，数学が必要でした．これは，ニュートンにより完成されます．すなわち，運動方程式と万有引力の式から，２体問題ならすべての運動が説明できます．巨大な宇宙の星雲の運動から，分子の集合である気体の圧力などの巨視的性質まで，宇宙のあらゆる力学現象（粒子間の相互作用は無視）を説明し，ニュートン力学と電磁気学（ﾏｯｸｽｳｪﾙ方程式）の２つのパラダイムにより，森羅万象の外界が解明できたと思われ19世紀が終わりました．

2．ニュートンの解明した外界 

ニュートンの時代に遡ってみましょう．ニュートンがプリンキピアを刊行したのは，1687年，44歳のときです．若き日のニュートンは，1676年2月5日のフックへの書簡に，「私が，ほかの人たちよりわずかでも遠くを見たとすれば，それは巨人たちの肩の上に乗っているからです」と書いています（注１）．巨人たちとは，ガリレオを始めとする先人の研究や数学の蓄積のことで，これらが彼の研究の基礎になったと言っているのです． 
しかし，ニュートンの力学に必要だった微積分が用意されていたわけではありません．自分自身で開拓せねばなりませんでした．ニュートンより少し早いと言われますが，独自にライプニッツも同等な業績を上げます．日本でも関孝和がおります．遅かれ早かれ，まさに微積分の扉が開かれる時代の流れではありました． 
ニュートンのプリンキピアは，「観測できる事物の因果関係を示す」という立場を堅持しています．引力がなぜ発生するかは言及せず，従って仮説は何もありません．これが，今日の科学的方法論の手本であります． 
ポアンカレは，「科学と仮説」で，「数学的理論は事物の本性を我々に解き示すことを目的とするものではない．．．そのただ一つの目的は実験が我々に知らせる物理法則に定まった場所を与えることである」（第12章，光学と電磁気）といっています（文献７）． 
数学と自然科学の違いは，数学は観測事物にこだわらず，どのような仮定から数学的理論を構築してもかまわぬ所にあります．例えば，「引力が距離の逆３乗に比例する」として理論を構築することも価値があります．非ユークリッド幾何学は数学として構築されましたが，今日の宇宙論では実在性をおびております． 
－－－－－－－－－－－－－－－－－－－ 
（注１） 
この時代の科学者達は，たいへんまめに文通しています．その上，論文公開のシステムは不完全であったので，揉め事が起こりがちでした．特に，ニュートンは自分が得た結果の大部分を秘密にしており，誰かに督促されるか，他の人が同じことを見出したときになってから，公表に踏み切ったといいます．そして自分の先取権が認められなかったり，批判されたりすると逆上したそうです．（文献５）
フックは，ニュートンより７つ年長で，王立協会の実験主任，後ちに書記でした．協会の書記は，外国の科学会とつながりを保つ要職です．他の協会の書記に手紙を書き，関心のある人々に情報を伝えてもらうのです．
ニュートンは，1672年に，”光と色”の論文を王立協会の雑誌に発表します（文献６）．この内容をフックが批判したことから，フックを嫌うようになります．
プリンキピア発表後，力の逆２乗法則は，ニュートンに文通で伝えたものであるとフックが主張し，因縁の論争が再度起こります．フックはバネの伸びと力が比例するというフックの法則で有名ですが，やはり大変多才な人です．1679年のフックからニュートンへの書簡には，惑星の運動を，接線方向と中心方向の運動の合成とする見方が示されています．しかしながら，これらの規則から生じる軌道の証明には，微積分が必要で，ニュートンの業績の偉大さは．そこにありましょう．フックは背中の曲がった背の低い人だったそうで，ニュートンの書簡にある巨人の肩に乗るとは，私は肩に乗れたが，フックには乗れないだろうとの皮肉が含まれているということです．ニュートンは，フックの死後の1703年に，12代目の王立協会会長に就任するや，フックの肖像や実験装置などの業績をすべて消し去ったと言われています．
なお，「巨人の肩に乗った小人は遠くを見ることが出来る」という名言自体は，12世紀のシャルトル（仏）のベルナールの言葉として，ニュートン時代の知識人には知られていたそうです（文献１）．
－－－－－－－－－－－－－－－－－－－－－ 

３．時間と空間の計測

さらに，ニュートンより前のガリレオ（イタリア，1564-1642年）の時代に遡りましょう．空間と時間の計測は最も基本的なものです．空間の測量は，紀元前に幾何学とともに発達しました．しかし，時間の計測は，地球の日周運動を利用した日時計，あるいは，水時計や砂時計でした．その後，ロウソク時計，線香時計などが生活に現れ，やがて，歯車やゼンマイを用いた機械時計が作られるようになります．しかし，正確な時計は，18世紀の振り子時計まで待たねばなりません．
ガリレオの”振子の等時性”の発見は，エポックメーキングです．正確な時計を持たなかったガリレオ以前の時代には，正確な観測に基づいた運動の研究は不可能だったわけです．振り子を時計に取り入れたのは，ホイヘンス（オランダ，1656年)で，1675年には，ホイヘンスは ヒゲゼンマイのついたテンプ時計も製作し，フランスで特許取得しました（フック（英）も考案した（1664年）と主張します）．これが，「世界初の実用的な機械式時計」の始まりです．
ガリレオの発見した”振り子の等時性”は，振り子の周期が，振り子の長さ$$l$$の平方根にのみ比例し，振幅や重りの重さによらないというものです．周期は$$T=2\pi \sqrt{l/g}$$と表せ，現在では$$g$$は重力の加速度で地球の場所により，僅かに異なることがわかっています．正確には，”振り子の等時性”は，振幅が小さいときに成り立つ線形近似です．振幅が大きくなると振り子の周期は長くなります．
$$T=2\pi \sqrt{\displaystyle \frac{l}{g } }\left( 1+\displaystyle \frac{1}{4}sin^{2}\left( \displaystyle \frac{\theta _{0 } }{2} \right) + \cdots \right) $$，ここで$$\theta _{0}$$は振幅の半分の角度．
普通の振り子の軌道は，円弧ですが，サイクロイド曲線に沿って動く振り子は，振幅が大きくても小さくても周期は不変です．ホイヘンスは，これを利用したサイクロイド振り子時計も作りました（図１）．ホイヘンスは，振り子時計の本と光の本を書き，微積分の先駆的研究もし，ニュートンと重なる時代を生きました．

その後の大航海時代には，海上で正確に経度を知る方法が必要になりました．船の経度は，船の時刻と経度のわかっている地点の時刻の差から求めます．地球は24時間で一回転するから，1時間で経線15度の差です．
1714 年，イギリス議会は「経度を精度良く決定できる方法」に2 万ポンドの懸賞を出しました．時計技師ジョン・ハリソン（イギリス）は，30年近くも試作を繰り返し，苦心の4号機H4はポーツマスからジャマイカへの81日間の航海を済ました（1762年1月19日）に，時計から求めた経度と現地の天文観測から求めた経度との誤差が5秒という議会の要求（2分）をはるかに上回る成績を収めました．
彼は，今日の懐中時計にも使われているグラスホッパー脱進機構を発明しています．（文献8）
－－－－－－－－－－－－－－－－－－－－－－－－－－ 
（コラム）　現代の標準時計－－クォーツ時計，原子時計（文献9）
切り出した水晶（クォーツ）の両側の面に電圧をかけると結晶は変形します．逆に両側から力をかけると両端に電圧（分極）を生じます．この性質を圧電効果といいます．圧電効果は，結晶構造に対称心がある場合には生じません．なぜなら，結晶中のいかなる方向に電圧（分極）ベクトルが生じても，対称心に矛盾するからです．
所定の方位で所定の厚さに切り出した水晶片の両面に交流を印加すれば，水晶片は振動します．水晶片の共振の起こる周波数で安定な発振器を作ることが出来ます．水晶振動子（通常，32.768kHz=$$2^{15}$$Hzの水晶音さ）を用い，精度の高いクオ－ツ時計が作られており，実際の標準時計もこれです．
現在の時間標準は，セシウム（$$^{133}Cs$$）の原子時計と定められました．原子時計とは，水晶時計を含む複合システムで，水晶発振器の周波数の校正標準に原子の状態遷移の周波数を用います．
セシウム原子は，最外殻の電子が１つ（水素原子型）なので，解析的にエネルギー準位の計算が出来ます．磁場を印加して縮重している準位を分離させた状態で，基底状態から励起状態への遷移を起こさせると，マイクロ波領域の9.192631770GHzのエネルギーで遷移します．そこで，水晶発振器により，この近傍のマイクロ波を発生させ，セシウム原子による吸収が最大になったときの水晶発振器の周波数を，9.192631770GHzであると校正しています．
ちなみに，GPS衛星は，ルビジュウムの原子時計を積載しています．最近はMEMS（Micro Electro Mechanical Systems）技術により，ルビジュウムの腕時計の開発も進んでいるそうです． 
長さの標準は，地球の経線の1/4を$$10,000m$$と定めたのが始まりでした．しかし，1983年に，真空中の光速でこれを定義することになりました．１$$m$$の定義は「光が真空中を1／299,792,458秒間に進む長さ」です．長さの標準にも時間を基礎に置くこととなったのです． 
－－－－－－－－－－－－－－－－－－ 

４． 最小作用（モーペルテュイ）の原理，あるいはオイラーの原理（注２）

モーペルテュイは，「始状態から終状態への運動経路には，作用と呼ばれる積分量が定義でき，作用が最小となる経路が実現される．これが物理学のみならず，万物の運命を決める外界の原理である」という着想－”最小作用の原理”(1744年)を得ました．たしかに，現実の運動では，しばしば作用が極小になりますが，正確には，「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります．
オイラーは，モーペルテュイの作用量の定義を積分に拡張し，最小作用の原理をさまざまな力学課題に適用できるようにし，”最大，または最小の性質をもつ曲線を見出す方法”（1744）を発表しました．これを読んだ若きラグランジュは変分法を発明し，オイラーに手紙（1755）を送ります．オイラーは，ラグランジュの方法を採用し，”変分法の原理”（1766）を出版します．変分法で導かれる運動方程式が，オイラー＝ラグランジュ方程式といわれる所以です．その後，ラグランジュは，”解析力学”（1788)を出版します．その序文に「本書には図は一つも出てこない．...所定の手続きに従い進める代数計算だけだ．...」と高らかに宣言します．こうして，複雑な力学問題も解ける一般化された手法が確立されます（注３）．
変分法は，19世紀のハミルトン，ヤコービにより完成に至ります．ハミルトンは，系の状態を表示する空間に，座標と速度を座標軸とした相空間を導入し，「作用量は最小化や最大化するのではなく，停留化する」ことを示しました．
１つの物体は，座標$$x, y, z$$と速度$$\dot{x}, \dot{y}, \dot{z}$$を変数に持ち，その状態は6次元の空間の１点で表現できます．同様に，$$N$$個の物体よりなる系は，$$6N$$次元の空間の１点で表現できます．この空間を相空間といいます．系のエネルギーを$$H(x_{i}, y_{i}, z_{i}, \dot{x}_{i}, \dot{y}_{i}, \dot{z}_{i}, )$$とすると，エネルギーが保存される運動の軌跡は，相空間内の超平面$$H(x_{i}, y_{i}, z_{i}, \dot{x}_{i}, \dot{y}_{i}, \dot{z}_{i})=h$$に含まれます．超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです．解けるかどうかは別として，周期解（軌道）が存在することは，証明（1986年）されています．（文献10）
最小作用の原理の理解には，ホイヘンスの光の波動説の説明が参考になります．ホイヘンスは，空間は見えない媒質で満たされており，光は波紋（球面波）が拡がるように伝わると考えました．波面上の各点はまた新たな波源となり，そこを中心として新たな波紋が広がって行きます．生じた無数の波紋は重なりあったり打ち消しあったりの結果，新しい波面ができます．これは多数の波面の包絡面で，この面に垂直な方向に光は進むと考えます．この様なプロセスで決定された方向は，作用を停留値にするものです．

量子力学の世界の運動には，軌道の概念がなく，電子などはランダムに動き回ります．しかし，我々の日常（マクロ世界）では，電子の運動でも軌道はあります．ここで，マクロ世界でも物体はランダムな経路をとれるとしてみましょう．あらゆる経路に実現可能性があるが，各経路の実現率は，それぞれの確率に従う．これらの確率は，波紋が伝播するときのように互いに干渉し合い，その結果として現実の経路が決まってくると言うわけです．最も確からしい経路は，近くからの干渉の最も少ない経路であって，これがちょうど作用積分を停留化するもののようです．「ファインマンの原理」（文献10）
運動方程式が解ける問題を”可積分な問題”といいますが，実際は，”非可積分の問題”がほとんどです．ニュートン力学は，可積分で安定な周期軌道が解になる特殊な範疇を扱っています．一方，非可積分の問題からは，カオスが生じます．１つの軌道は，1本の因果列の存在を意味しています．単純な世界は，今日の現象（原因）１が明日の結果１につながり，今日の現象（原因）２が明日の結果２につながる世界ですが，一般には，今日の現象のすべてが，明日のある結果１の原因になりうる複雑な世界です．バタフライ・エフェクトという映画（注４）があったようですが，今日，上空で蝶が羽ばたいたことが，遠い未来に竜巻きを起こす原因の一つになるかも知れません．「風が吹けば，桶屋が儲かる」世界です．この世界は，独立な因果列はないので，周期的な軌道にはなりません．コンピュータを用いて，すべてのステップを計算していけば，結果を予測できるのですが，遠い先の結果は予測もつかないものになります．「最小作用（停留値）の原理」は，ニュートン力学も含むが，このようなカオスも含む原理であります．
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
（注２）
最小作用の原理の起源といえば，1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません．「決まった二点の間を，始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です．ライプニッツの提案により，ベルヌーイはこの問題を海外の数学者にも公開することにしました．ベルヌーイは，ライプニッツの友人で，ニュートンとライプニッツの微積分の先取権論争にも加わり，ライプニッツを応援しています．きっと，ニュートンを困らせてやろうと思ったのでしょう．ところがこの問題を受け取ったニュートンは，「当時，造幣局の仕事で忙しく疲れて帰宅したが，問題が解けるまでは寝なかった．とは言っても朝４時までには解けてしまった」と日記に書いています．そして，解答を匿名で返したということです（文献１，5）．
 
最速降下曲線の答えは，円板の縁（１点）に目印をつけ，直線上を転がしたときに，目印が描く”サイクロイド曲線”です．ホイヘンスが振り子時計に用いたあの曲線です． 

（注３）解析力学の手順 
力学系を記述するラグランジュ関数 を求め，ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと，オイラー＝ラグランジュ方程式が得られます．簡単な系のラグランジュ関数は，（運動エネルギー）－（位置エネルギー）の型になりますが，複雑な系では，位置エネルギーが速度に依存することもあります． 
ラグランジュ関数は，電磁場に置かれた荷電粒子にも定義され，光（電磁力学）も力学も統一して扱える原理であります．変分原理から，ニュートンの運動方程式は導出されます．その上，変分原理はニュートン力学よりさらに一般化された外界の原理です．（文献１１）
20世紀に入り，量子力学が誕生するときにもこの原理が手がかりになりました．
光や物体の運動が，作用積分を停留化するような，手の混んだ経路を選択するというのは，何と不思議なことでしょう．

（注４）

過去に戻れる能力を持ったエヴァンは，過去に戻りやり直すことにする．しかし，過去に戻り選択肢を変えて始めた人生は，どれも，自分を含め自分が愛する誰かが，幸せではないものだった．
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 

５． 結晶の世界

結晶は，原子や分子が規則正しく並んでできています．水晶の結晶構造を図3(a)に示します．簡単のため$$c$$軸に沿って投影した平面図にしました．大きい丸は，シリコン原子，小さい丸は酸素原子です．図3(a)を見ると，基本タイルで，平面が隙間なく張り詰められているのがわかります．実際の結晶は，基本ブロック（平行６面体）を隙間なく積み重ねた3次元に周期を持つ構造です．結晶の基本ブロック（単位胞といいます）は，一辺のサイズが$$nm$$の程度なので，その実在を観測したのは，X線の発見（レントゲン，1895年）以降になります．発見まもないX線は，波長の短い（$$nm$$オーダー）光らしいので，空間に周期を持つ結晶が回折格子になるだろうとラウエは考えました．これが有名なラウエの実験（1912年）です．結晶が持つ対称性は，その回折像の対称性に反映されるはずです（”因果律”図3）．逆に，X線回折像から結晶構造を推定できるわけで，その手法は，ブラック親子により開発（1915年）されます．この時点で，結晶構造解析に必要な，空間群タイプ230種類の数え上げは，「さあ，お使い」とばかりに準備されていました．何とドラマティックでありましょう．

しかしながら，ここで空間群を突然出現させるのは演出にすぎません．それが生まれるまでの背景を辿って見ましょう．結晶は単位胞が積み重なった「デジタル世界だ」という推論は，18世紀後半に遡ります．（文献12）
デンマークの鉱物学者ステノ（1669年）が，水晶で発見して以来，種々の鉱物結晶の外形の研究が積み重ねられ，「同一物質の結晶では，対応する面と面のなす角度は一定不変である」という法則（1772年）を，フランスのリスルが確立します． 
アウイ（1783年）は”有理指数の法則”を見出します．方解石は劈開が顕著で，どこまでも同じ形の平行６面体に割れます．これなどは，単位胞の存在や，結晶格子の存在を思わせます（図４）．結晶が単位胞の積み重ねでできるデジタルの世界ならば，観測されるどの結晶面も，格子点を載せた平面だから，結晶面の座標軸上の切片の比は，必ず整数比になるはずです．これが有理指数の法則の心です．結晶面の記載に用いるミラー指数は（1839年）に考案されました．これらの観測事実から，結晶は単位胞が並んだデジタル世界でなければならないと推論されました．
基本タイルを点で表すと，結晶構造は点の配列になり，このような点の配列を格子といいます．つまり結晶はデジタル（離散量）の世界です．格子の対称性タイプの数え上げ14種（ブラベー，1848年）がなされます．また，結晶外形の対称性から，結晶点群の数え上げ32種（ヘッセル，1830年）がなされました．
結晶点群と格子（並進群）の組み合わせで，結晶空間群が生成されます．1890～1894年に，フェドロフ，シェンリース，バーローがそれぞれ独立に，３次元の空間群230種類を数え上げました．（文献１３）（注５）
－－－－－－－－－－－－－－－－－－－－－ 
（注５）
結晶空間群には，並進群が正規部分群として含まれています．
基本タイルを点にしてしまうような写像なら，空間群に含まれる格子があぶりだされます．格子の周期で並進した物は同値とみなすならば，空間に広がった結晶構造や平面にひろがった繰り返し模様は，1つの単位胞の中に集約され，空間群は結晶点群に準同型となります．（文献１３，１４）
－－－－－－－－－－－－－－－－－－－－－ 

６．おわりに 
「科学者がその肩に乗ろうと懸命に探し求めた巨人は，とうの昔に死んだ数学者だった．しかし，数学者の側からみれば，自分が科学者の肩の上に乗っていた，などということはまずありそうにない」（文献１）という見方もあります．しかし，私は，新しい数学の誕生は，その背景に，科学の発展があったことに注目し，大きな過去の世界からこの小論への写像を試みました．論点を浮き彫りにするには，準同型写像です．同値と見做そうとする項目は束ねて，写像の核にすると，大きな世界にあった特徴の一つが浮き上がります．写像の核は，数学自体にしたので，数学と他の基礎科学の関係が見えたでしょうか．この先，”線形写像の世界”を訪れる予定でしたが，紙数が尽きました．これに関しては，拙著（文献14）をお読みいただけると幸甚です．
――――――――――― 
参考文献 

１．物理と数学の不思議な関係，マルコム・E・ラインズ（青木薫訳），ハヤカワ文庫,　2004 
２．数理物理学の方法，クーラン，ヒルベルト（斎藤利弥監訳），東京図書，1985 
３. 中谷宇吉郎随筆集，樋口敬二編，岩波文庫，1988 
４．何のための数学か，クライン（雨宮一郎訳），紀伊国屋書店, 1987 
５．古典物理学を創った人々，エミリオ・セグレ（久保亮五，矢崎裕二訳），みすず書房，1992 
６．http://trailblazing.royalsociety.org/ 
英国王立協会は，2010年１１月30日で創立350周年になります．これを記念し，17世紀から協会が発行しているPhilosophical Transactions誌に掲載された論文の科学史的に重要ないくつかが，このwebsiteで公開されています． 
７． 科学と仮説，　ポアンカレ（河野伊三郎訳），岩波文庫, 1966 
８. http://www.nmm.ac.uk/harrison 
９.尾上守夫，私信 \\
１０．数学は最善世界の夢を見るか？，エクランド（南條郁子訳），みすず書房, 2009 
１１．理論物理学，カンパニエーツ（山内恭彦，高見穎郎訳），岩波書店, 1964 
１２．結晶の話，伊藤正時，斎藤喜彦，倍風館，1984 
１３．結晶の幾何学，谷克彦，数学教育p.41-46，明治図書，2003.11 
１４．物理と工学で使う行列と固有値，谷克彦，技術評論社, 2010 
----------------------------------- 

「数学文化」，NO.15(2010)，p.79-87　より

数学と基礎科学，谷，「数学文化」p.79-87，No15 (2010)より抜粋

以前の号に，現代の標準時計 を掲載しています．現代の標準時計は，水晶発振子と原子時計です．長さの標準は今日では「メートル原器」ではなく，真空中の光速で定義します．長さを光速で定義するには正確な時計が必要ですが，原子時計はそのような長さの定義に使用されています．GPSが位置を割り出すときにも正確な時計が活躍しています．

■今回の記事は，ガリレオの時代から始めます．
時間と空間の計測は最も基本的なものです．空間の測量は，紀元前に幾何学とともに発展しました．しかし，時間の計測は，地球の日周運動を利用した日時計，あるいは，水時計や砂時計から始まりました．その後，ロウソク時計，線香時計などが生活に現れ，やがて，歯車やゼンマイを用いた機械時計が作られるようになります．しかし，正確な時計は，18世紀の振り子時計まで待たねばなりませんでした．ガリレオ（イタリア，1564-1642）の”振り子の等時性”の発見は，エポックメーキングです．
正確な時計を持たなかったガリレオ以前の時代には，正確な観測に基づいた運動の研究は不可能だったわけです．
振り子を時計に取り入れたのは，ホイヘンス（オランダ，1656年）で，1675年には，ホイヘンスはヒゲゼンマイのついたテンプ時計も制作し，フランスで特許を取得しました［フック（英）も考案した（1664年）と主張します］．これが，「世界初の実用的な機械式時計」の始まりです．
ガリレオの発見した”振り子の等時性”は，振り子の周期が，振り子の長さ$$l$$の平方根にのみ比例し，振幅や錘の重さにはよらないというものです．
周期は　 $$T=2\pi \sqrt{l/g }$$ 

と表せ，現在では$$g$$は重力の加速度で地球の場所により，わずかに異なることがわかっています．正確には，”振り子の等時性”は，振幅が小さいときに成り立つ線形近似です．振幅が大きくなると振り子の周期は長くなります．

 $$T=2\pi \sqrt{\displaystyle \frac{l}{g } }\left( 1+\displaystyle \frac{1}{4}sin^{2}\left( \displaystyle \frac{\theta _{0 } }{2} \right) + \cdots \right) $$，ここで$$\theta _{0}$$は振幅の半分の角度．

普通の振り子の軌道は円弧ですが，サイクロイド曲線に沿って動く振り子は，振幅が大きくても小さくても周期は不変です．ホイヘンスは，これを利用したサイクロイド振り子時計も作りました（図1）．

ホイヘンスは，振り子時計の本と光の本を書き，微積分の先駆的研究もし，ニュートンと重なる時代を生きました．

その後の大航海時代には，海上で正確に経度を知ることが必要になりました．船の現在地（経度＊）は，船の時刻と経度のわかっている地点の時刻の差から求めます．地球は24時間で一回転するから，1時間で経線15度の差です．＊注）緯度は太陽の高度や北極星の高度からわかります．
1714年，イギリス議会は「経度を精度よく決定できる方法」に2万ポンドの懸賞を出しました．時計技師ジョン・ハリソン（英）は，30年近くも試作を繰り返し，苦心の4号機H4はポーツマスからジャマイカへの81日間の航海をすませた1762年1月19日に，時計から求めた経度と現地の天文観測から求めた経度との誤差が5秒という議会の要求（2分）をはるかに上回る成績を収めました．彼は，今日の懐中時計にも使われているグラスホッパー脱進機構を発明しています．

参考文献
http://www.nmm.ac.uk/harrison

■ディリクレ胞

結晶内部は周期的空間で，その繰り返しの単位を単位胞と言います．もし，単位胞を点で表現するなら，点が周期的に並んだ格子ができます．［慣用的な述語としての”単位胞”の用法は，格子点を複数含む単位胞（面心格子，体心格子など）もありますが，格子点をただ一つ含むもの”単純格子”だけを単位胞と呼ぶことにします］．

１つの格子点を原点に置き，原点と隣接する格子点とを結ぶ線分の垂直2等分面を作ります．これらの垂直2等分面で囲まれた立体はディリクレ胞と呼ばれます．ディリクレ胞には，格子点がただ一つ含まれます．ディリクレ胞の形は平行多面体で，面と面をぴったり合わせて隙間なく空間の充填ができることは，ディリクレ胞の作図の仕方から明らかでしょう．ディリクレ胞の形は，その結晶格子の対称性を表現しています．結晶格子の対称性の分類（14種のブラベー格子）や7種の晶系はディリクレ胞の対称性に基づく分類です．

■結晶の物性量（スカラー，ベクトル）

結晶のスカラー特性（温度・密度など）は，測定の方位によらず１つの数にで定義されます．しかし，結晶は異方性のある物質なので，単位胞が$$10^{20}$$以上も並ぶ巨視的には均一一様であると見なせるが，充分小さいとも言える程度の体積要素を点として定義できます．

例えば，誘電体結晶（焦電性pyroelectricや強誘電性ferroelectric）は，その構造に起因する自発分極（外部電場が存在しなくても分極している）を持つ．対称性$$1$$（対称性がない）の結晶中の分極ベクトル$$P$$は，３つの独立なパラメータ：$$P_{1}, P_{2}, P_{3}$$で記述される．対称性$$m$$の結晶では，生じるベクトル$$P$$は，２つの成分$$P_{1}, P_{2}$$で記述できる．鏡映対称があると，成分$$P_{3}=0$$となる訳は，平面$$m$$内にない斜めのベクトルには鏡映同価なベクトルが必ずあるので，互いに打ち消し合うからである．回転対称軸のある対称類$$2,3,4,6,mm2,3m,4mm$$の結晶では，生じるベクトル$$P$$は，１つのパラメータ$$P_{3}$$で記述される．対称心$$\bar{1}$$ がある結晶類では，ピロ焦電性はない；すなわち$$P=0$$である．

■分極ベクトル

極性ベクトルの変換則$$r'=[D|0]r=Dr$$ を思いだそう．この法則で，$$r$$ を分極ベクトル$$P$$ に置き換え：$$P_{i}'=D_{ij}P_{j}$$ と行列形式で書く．例えば群$$2$$で，$$X_{3 }$$軸回りの2回軸（180°回転）を，以前に得た行列$$D$$のあらわな形式を用い，対称操作の行列積を行うと，以下の結果を得る．
$$\left( \begin{array}{@{\,} c @{\, } }
P_{1}' \\[0mm]
P_{2}' \\[0mm]
P_{3}'
\end{array} \right) =\left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & 1
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
P_{1} \\[0mm]
P_{2} \\[0mm]
P_{3}
\end{array} \right) =\left( \begin{array}{@{\,} c @{\, } }
-P_{1} \\[0mm]
-P_{2} \\[0mm]
P_{3}
\end{array} \right) $$　　　(1)

軸対称のため，系の180°回転後，

$$\left( \begin{array}{@{\,} c @{\, } }
P_{1}' \\[0mm]
P_{2}' \\[0mm]
P_{3}'
\end{array} \right) =\left( \begin{array}{@{\,} c @{\, } }
P_{1} \\[0mm]
P_{2} \\[0mm]
P_{3}
\end{array} \right) $$, 　すなわち，　　$$\left\{ \begin{array}{@{\,} c @{\, } }
P_{1}'=-P_{1}=P_{1}=0 \\[0mm]
P_{2}'=-P_{2}=P_{2}=0 \\[0mm]
P_{3}'=P_{3}=\textrm{const}
\end{array} \right. $$

さらにもう１つ，２階の極性テンソルで記述される特性例：誘電体に誘起される分極現象（図220）を考察する．結晶中の変位ベクトルDは一般には印加される電場E方向と一致しない（等方媒質では一致する）．これらの極性ベクトルの成分D_{i}とE_{j} との関係は，
D_{i}=?_{ij}E_{j}　　または， { { {D_{1}=?_{11}E_{1}+?_{12}E_{2}+?_{13}E_{3 } },{D_{2}=?_{21}E_{1}+?_{22}E_{2}+?_{23}E_{3 } },{D_{3}=?_{31}E_{1}+?_{32}E_{2}+?_{33}E_{3 } } }
係数?_{ij}は，誘電率テンソルの形で，べクトルD　と　E　を結び付ける．一般に，要素の対称性?_{ij}=?_{ji} があり，９つではなく６つの独立なパラメータをもつ．これから先は，テンソル?_{ij} の行列を，簡単化して，非ゼロの独立なパラメータのみの行か列の形式に書くことにする：
{ { ?_{11},?_{12},?_{13 } },{?_{12},?_{22},?_{23 } },{?_{13},?_{23},?_{33 } } }＝(?_{１１},?_{12},?_{13},?_{22},?_{23},?_{33})　　　
?_{ij}を係数とする２次の表面
?_{11}x_{1}^{2}+?_{22}x_{2}^{2}+?_{33}x_{3}^{2}+2?_{12}x_{1}x_{2}+2?_{13}x_{1}x_{3}+2?_{23}x_{2}x_{3}=1
は，対称テンソルに一意に関係づけられている；この表面は誘電率楕円体ellipsoid，あるいは一般に，観察される効果の特性を明確にする物理特性の屈折率楕円体indicatrixである．結晶の対称群G_{k} は，この表面の形（３軸あるいは１軸性の楕円体，球）と結晶物理軸 X_{1}, X_{2}, X_{3}に対する楕円体の主軸X_{1}', X_{2}', X_{3}' の方位を決定する。群G_{k} は，実験的に決定しなければならない?_{ij} の独立な数をも決定する。これを理解するために，テンソル成分?_{ij} の変換式を
?_{i'j'}=?(D)D_{i'i}D_{j'j}?_{ij}　　　　　　 　i', j', i, j=1,2,3　　　　　　　　　　　　　（２）
と書く，ここで，D_{i',i}=cos(X_{i}', X_{i}) ，?(D) は極性テンソルでは+1，右辺の総和は繰り返されるi,j に対し，１から３で行われる。項の和を取り，６つの未知数を求めるのに９方程式の冗長系（ 3つの方程式?_{i'j'}=?_{j'i'}は，この場合は成立しない；非対称テンソルの一般の場合には，成立しない）を得る．
　　　読者諸君にこの手順を実行するのを残しておく。上記の等式系の行列を導くのに他の手法を使う－３次元空間の座標変換の直交行列の（自分自身との）直積（p.241）．行列Dの自分自身との直積は，
D^{2}={ { D_{11},D_{12},D_{13 } },{D_{21},D_{22},D_{23 } },{D_{31},D_{32},D_{33 } } }?{ { D_{11},D_{12},D_{13 } },{D_{21},D_{22},D_{23 } },{D_{31},D_{32},D_{33 } } }={ { D_{11}(D_{ij}),D_{12}(D_{ij}),D_{13}(D_{ij})},{D_{21}(D_{ij}),D_{22}(D_{ij}),D_{23}(D_{ij})},{D_{31}(D_{ij}),D_{32}(D_{ij}),D_{33}(D_{ij}) } }
ここで，(D_{ij})は３×３行列で，例えば
D_{23}(D_{ij})={ { D_{23}(D_{11}),D_{23}(D_{12}),D_{23}(D_{13})},{D_{23}(D_{21}),D_{23}(D_{22}),D_{23}(D_{23})},{D_{23}(D_{31}),D_{23}(D_{32}),D_{23}(D_{33}) } } ，等々．
例えば，2∥X_{3} 軸まわりの180°回転の行列D（D_{11}=D_{22}=-1, D_{33}=1，残りの行列要素はゼロ）を知れば，テンソル?_{ij} の空間でのこの回転を記述するD^{2}を見出せる。すなわち，対称群G_{k}=2 に対して，変換式?_{i'j'}=?(D)D^{2}?_{ij} は以下の形となる：

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

変換則と物理量の対称性（一様連続体の近似） \\
反対称と色対称の極限群 \\
\ \\
　　　結晶のスカラー特性は，測定の方位によらないので，１つの数により定義される。このように，均一一様な結晶での温度・密度は，巨視的なサンプルに比べて，十分小さい体積要素で，単位胞よりは遥かに大きいような全ての"点" で同一である． \\
　　　誘電体結晶（焦電性\textrm{pyroelectric}，強誘電性\textrm{ferroelectric}と呼ばれる）は，その構造起因の自発分極（外部電場が存在しなくても分極している）を持つ．対称性\texttt{1}の結晶中の分極ベクトル\textrm{\textsl{P } }は，３つの独立なパラメータ：$P_{1}, P_{2}, P_{3}$で記述される（図219a）．対称性\textrm{\textsl{m } }の結晶では，生じるベクトル\textrm{\textsl{P } }は，２つの成分$P_{1}, P_{2}$で完全に決定される（図219b）．成分$P_{3}=0$となる訳は，平面\textrm{\textsl{m } }内にない斜めのベクトルには，鏡映同価なベクトルが必ずあるからである．軸対称類$2,3,4,6,mm2,3m,4mm$の結晶では，生じるベクトル\textrm{\textsl{P } }は，１つのパラメータ$P_{3}$で記述される（図219c）．$\overline{1}$ のような残りの類の結晶では，ピロ焦電性はない；すなわち$P=0$である． \\
　　　極性ベクトルの変換則$$r'=\left[ D|0 \right] r=Dr$$ を思いだそう（P.204参照）．この法則で，$$r$$ を$$P$$ で置き換え：$$P_{i}'=D_{ij}P_{j}$$ と行列形式で書く．例えば，軸性群$$2$$における軸$$2 /\!\!/ X_{3}$$の周りの180°回転を，行列$$\textrm{\textsl{D } }$$のあらわな形式を用い，対称操作の行列積を行うと，以下の結果を得る． \\
$$\left( \begin{array}{@{\,} c @{\, } }
P_{1}' \\[0mm]
P_{2}' \\[0mm]
P_{3}'
\end{array} \right) =\left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & 1
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
P_{1} \\[0mm]
P_{2} \\[0mm]
P_{3}
\end{array} \right) =\left( \begin{array}{@{\,} c @{\, } }
-P_{1} \\[0mm]
-P_{2} \\[0mm]
P_{3}
\end{array} \right) $$ \\
軸対称のため，系の180°回転後， \\
$\left( \begin{array}{@{\,} c @{\, } }
P_{1}' \\[0mm]
P_{2}' \\[0mm]
P_{3}'
\end{array} \right) =\left( \begin{array}{@{\,} c @{\, } }
P_{1} \\[0mm]
P_{2} \\[0mm]
P_{3}
\end{array} \right) $　，すなわち，$ \left\{ \begin{array}{@{\,} c @{\, } }
P_{1}'=-P_{1}=P_{1}=0 \\[0mm]
P_{2}'=-P_{2}=P_{2}=0 \\[0mm]
P_{3}'=P_{3}=const
\end{array} \right. $ \\
\ \\
さらにもう１つ，２階の極性テンソルで記述される特性例：誘電体に誘起される分極現象（図220）を考察する．結晶中の変位ベクトル\textrm{\textsl{D } }は一般には印加される電場\textrm{\textsl{E } }方向と一致しない（等方媒質では一致する）．これらの極性ベクトルの成分$D_{i}とE_{j} $との関係は， \\
$D_{i}=\varepsilon _{ij}E_{j}$　　または，$ \left\{ \begin{array}{@{\,} c @{\, } }
D_{1}=\varepsilon _{11}E_{1}+\varepsilon _{12}E_{2}+\varepsilon _{13}E_{3} \\[0mm]
D_{2}=\varepsilon _{21}E_{1}+\varepsilon _{22}E_{2}+\varepsilon _{23}E_{3} \\[0mm]
D_{3}=\varepsilon _{31}E_{1}+\varepsilon _{32}E_{2}+\varepsilon _{33}E_{3}
\end{array} \right. $ （１） \\
係数$\varepsilon _{ij}$は，誘電率テンソルの形で，べクトル\textrm{\textsl{D } }　と　\textrm{\textsl{E } }　を結び付ける．一般に，要素の対称性$\varepsilon _{ij}=\varepsilon _{ji}$ があり，９つではなく６つの独立なパラメータをもつ．これから先は，テンソル$\varepsilon _{ij}$ の行列を，簡単化して，非ゼロの独立なパラメータのみの行か列の形式に書くことにする： \\
$$\left( \begin{array}{@{\,} ccc @{\, } }
\varepsilon _{\texttt{\textsl{11 } } } & \varepsilon _{12} & \varepsilon _{13} \\[0mm]
\varepsilon _{12} & \varepsilon _{22} & \varepsilon _{23} \\[0mm]
\varepsilon _{13} & \varepsilon _{23} & \varepsilon _{33}
\end{array} \right) ＝\left( \varepsilon _{１１},\varepsilon _{12},\varepsilon _{13},\varepsilon _{22},\varepsilon _{23},\varepsilon _{33} \right) 　　　 $$
$\varepsilon _{ij}$を係数とする２次の表面 \\
$\varepsilon _{11}x_{1}^{2}+\varepsilon _{22}x_{2}^{2}+\varepsilon _{33}x_{3}^{2}+2\varepsilon _{12}x_{1}x_{2}+2\varepsilon _{13}x_{1}x_{3}+2\varepsilon _{23}x_{2}x_{3}=1$ \\
は，対称テンソルに一意に関係づけられている；この表面は誘電率楕円体\textrm{ellipsoid}，あるいは一般に，観察される効果の特性を明確にする物理特性の屈折率楕円体\textrm{indicatrix}である．結晶の対称群$G_{k}$ は，この表面の形（３軸あるいは１軸性の楕円体，あるいは，球）と結晶物理軸 $X_{1}, X_{2}, X_{3}$に対する楕円体の主軸$X_{1}', X_{2}', X_{3}'$ の方位を決定する．群$G_{k}$ は，実験的に決定しなければならない$\varepsilon _{ij}$ の独立な数をも決定する．これを理解するために，テンソル成分$\varepsilon _{ij}$ の変換式を \\
$\varepsilon _{i'j'}=\chi (D)D_{i'i}D_{j'j}\varepsilon _{ij}$　　　　　　 　$i', j', i, j=1,2,3$　　　　　　　　　　　　　（２） \\
と書く，ここで，$D_{i',i}=\textrm{cos}(X_{i}', X_{i})$ ，$\chi (D)$ は極性テンソルでは+1，右辺の総和は繰り返される$i,j$ に対し，１から３で行われる。項の和を取り，６つの未知数を求めるのに９方程式の冗長系（ 3つの方程式$\varepsilon _{i'j'}=\varepsilon _{j'i'}$は，この場合は成立しない；非対称テンソルの一般の場合には，成立しない）を得る． \\
　　　読者諸君にこの手順を実行するのを残しておく。上記の等式系の行列を導くのに他の手法を使う－３次元空間の座標変換の直交行列の（自分自身との）直積（p.241）．行列Dの自分自身との直積は， \\
$$D^{2}=\left( \begin{array}{@{\,} ccc @{\, } }
D_{11} & D_{12} & D_{13} \\[0mm]
D_{21} & D_{22} & D_{23} \\[0mm]
D_{31} & D_{32} & D_{33}
\end{array} \right) \times \left( \begin{array}{@{\,} ccc @{\, } }
D_{11} & D_{12} & D_{13} \\[0mm]
D_{21} & D_{22} & D_{23} \\[0mm]
D_{31} & D_{32} & D_{33}
\end{array} \right) =\left( \begin{array}{@{\,} ccc @{\, } }
D_{11}(D_{ij}) & D_{12}(D_{ij}) & D_{13}(D_{ij}) \\[0mm]
D_{21}(D_{ij}) & D_{22}(D_{ij}) & D_{23}(D_{ij}) \\[0mm]
D_{31}(D_{ij}) & D_{32}(D_{ij}) & D_{33}(D_{ij})
\end{array} \right) $$ \\
ここで，$(D_{ij})$は$3 \times 3$行列で，例えば \\
$D_{23}(D_{ij})=\left( \begin{array}{@{\,} ccc @{\, } }
D_{23}(D_{11}) & D_{23}(D_{12}) & D_{23}(D_{13}) \\[0mm]
D_{23}(D_{21}) & D_{23}(D_{22}) & D_{23}(D_{23}) \\[0mm]
D_{23}(D_{31}) & D_{23}(D_{32}) & D_{23}(D_{33})
\end{array} \right) $ ，等々． \\
例えば，$2 /\!\!/ X_{3}$軸まわりの180°回転の行列$D$（$D_{11}=D_{22}=-1, D_{33}=1$，残りの行列要素はゼロ）を知れば，テンソル$\varepsilon _{ij}$ の空間でのこの回転を記述する$D^{2}$を見出せる．すなわち，対称群$G_{k}=2$ に対して，変換式$\varepsilon _{i'j'}=\chi (D)D^{2}\varepsilon _{ij}$ は以下の形となる： \\
$\left[ \begin{array}{@{\,} c @{\, } }
\varepsilon _{1'1'} \\[0mm]
\varepsilon _{1'2'} \\[0mm]
\varepsilon _{1'3'} \\[0mm]
\varepsilon _{2'1'} \\[0mm]
\varepsilon _{2'2'} \\[0mm]
\varepsilon _{2'3'} \\[0mm]
\varepsilon _{3'1'} \\[0mm]
\varepsilon _{3'2'} \\[0mm]
\varepsilon _{3'3'}
\end{array} \right] =\left[ \begin{array}{@{\,} ccccccccc @{\, } }
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\[0mm]
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\[0mm]
0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\[0mm]
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\[0mm]
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\[0mm]
0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\[0mm]
0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 \\[0mm]
0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 \\[0mm]
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
\varepsilon _{11} \\[0mm]
\varepsilon _{12} \\[0mm]
\varepsilon _{13} \\[0mm]
\varepsilon _{21} \\[0mm]
\varepsilon _{22} \\[0mm]
\varepsilon _{23} \\[0mm]
\varepsilon _{31} \\[0mm]
\varepsilon _{32} \\[0mm]
\varepsilon _{33}
\end{array} \right] $ \\
\ \\
系の対称性を考慮して， \\
$\varepsilon _{1'1'}=\varepsilon _{11}$ \\
$\varepsilon _{1'2'}=\varepsilon _{12}$ \\
$\varepsilon _{1'3'}=-\varepsilon _{13}=\varepsilon _{13}=0$ \\
$\varepsilon _{2'1'}=\varepsilon _{21}$ \\
$\varepsilon _{2'2'}=\varepsilon _{22}$ \\
$$\varepsilon _{2'3'}=-\varepsilon _{23}=\varepsilon _{23}=0$$
$$\varepsilon _{3'1'}=-\varepsilon _{31}=\varepsilon _{31}=0$$
$\varepsilon _{3'2'}=-\varepsilon _{32}=\varepsilon _{32}=0$ \\
$$\varepsilon _{3'3'}=\varepsilon _{33}$$
\ \\
行列$D^{2}$の４，７，８行，４，７，８列を抜き取り，$9 \times 9$行列から，対称テンソルの変換則を完全に記述する$6 \times 6$行列に移行する．この行列を２つの行列の対称化積（あるいは対称化平方）と呼び$D^{(2)}$と標す． \\
　　　群$G=\left\{ g_{1},g_{2}, \ldots ,g_{j} \right\} $ の同形な行列群$\left\{ D_{1}(g_{1}),D_{2}(g_{2}), \ldots ,D_{j}(g_{j}) \right\} $ は，行列表現$G$　を作る．この表現は，$3 \times 3$行列$D_{j}$が点の配置の変換のみでなく３次元空間のベクトル成分を変換するので，ベクトル表現と呼ばれる． \\
　　　群G　の群$\left\{ D_{1}^{2}(g_{1}),D_{2}^{2}(g_{2}), \ldots ,D_{j}^{2}(g_{j}) \right\} $ による表現は，ベクトル表現の平方あるいはテンソル表現と呼ばれる。この術語を用いれば，誘電率テンソル$\varepsilon _{ij}$はベクトル表現 $\left\{ D_{1}(g_{1}),D_{2}(g_{2}), \ldots ,D_{j}(g_{j}) \right\} $の対称化された平方により変換される．テンソル量の定義自体は，成分の変換を支配する法則を特化すること，すなわち対応するテンソル表現の特化に基づいている． \\
　　　各32の結晶群に対する表現$\left\{ D_{1}^{2}(g_{1}),D_{2}^{2}(g_{2}), \ldots ,D_{j}^{2}(g_{j}) \right\} $ から，これらの群のどれに対しても，群$G_{k}=2$ に対して行ったのと全く同様に，テンソル$\varepsilon _{ij}$ の形を決定できる．テンソル$\varepsilon _{ij}$ の行列は，成分$\varepsilon _{ij}$ が対応する座標 $x_{i}x_{j}$の積と同様に変換されることに注目すれば，もっと速く決定できる．この方法を用い，方位$m \bot X_{3} $の群$G_{k}=m $に対し，テンソル$\varepsilon _{ij}$の行列の形を見出すことにする．この平面での鏡映により，座標$x_{1}, x_{2}$ は保存され，座標$x_{3}$は符号を変える：　$$x_{1} \to x_{1}, x_{2} \to x_{2}, x_{3} \to -x_{3} $$ \\
従って，座標の積は以下のように変化する： \\
$$x_{1}x_{1} \to x_{1}x_{1}, x_{1}x_{2} \to x_{1}x_{2}, x_{1}x_{3} \to -x_{1}x_{3}, x_{2}x_{1} \to x_{2}x_{1}, x_{2}x_{2} \to x_{2}x_{2} $$
$$x_{2}x_{3} \to -x_{2}x_{3}, x_{3}x_{1} \to -x_{3}x_{1}, x_{3}x_{2} \to -x_{3}x_{2}, x_{3}x_{3} \to x_{3}x_{3} $$
この変換は対称変換であるので，変換の前後で，成分$\varepsilon _{ij} \leftrightarrow x_{i}x_{j}$ は等しい．従って，群\textrm{\textsl{m } }の行列$\varepsilon _{ij}$ が，群２に対するものと同じ形となる：$（\varepsilon _{11}, \varepsilon _{12}, \varepsilon _{22}, \varepsilon _{33}）$ \\
　　　以下のリストに，結晶学的な群に対する誘電率テンソルの一般形を与える： \\
$$三斜晶系G_{k}=1, \overline{1} ：（\varepsilon _{11}, \varepsilon _{12}, \varepsilon _{13}, \varepsilon _{22}, \varepsilon _{23}, \varepsilon _{33}）$$
$$単斜晶系　2, m, 2/m　 ：（\varepsilon _{11}, \varepsilon _{12}, \varepsilon _{22}, \varepsilon _{33}）$$
$$斜方晶系　2, 222, mmm ：（\varepsilon _{11}, \varepsilon _{22}, \varepsilon _{33}）$$
$$三方－，正方－，六方－：（\varepsilon _{11}, \varepsilon _{22}=\varepsilon _{11}, \varepsilon _{33}）$$
$$等軸晶系　23, m\overline{3}, 432, \overline{4}3m, m\overline{3}m :（\varepsilon _{11}, \varepsilon _{22}=\varepsilon _{11}, \varepsilon _{33}=\varepsilon _{11}）$$
全く同様に，軸性ベクトルに対するテンソル不変量（対応する群の変換により変わらない行列）を見出すことが出来る．テンソル成分の変換則で，第１種の変換（回転，並進）に対しては，$\chi (D)=+1$ ，第２種の変換（鏡映，反転）に対しては$\chi (D)=-1$ とする所が異なる． \\
　　　テンソル本来の斜方晶対称－テンソル行列の一般形を保存する斜方晶[直交]変換の最も対称性の高い群により決定される－は，もとの結晶の対称性よりも高くなる可能性があることに注意しよう．例えば，立方晶系に対し，誘電率楕円体は対称性$ \infty \infty m$ の球に縮退する．３方晶系，正方晶系，６方結晶に対しては，１軸性誘電率楕円体は対称性$ \infty /mmm$である．残りの結晶に対しては，誘電率楕円体は，対称性 \textrm{\textsl{mmm } }の３軸性である．これは，楕円体（図220）をprincipal axes主軸$X_{1}', X_{2}', X_{3}'$に参照することにより理解出来る：群\textrm{\textsl{mmm } } のすべての変換は，テンソル行列$（\varepsilon '_{11}, \varepsilon '_{22}, \varepsilon '_{33}）$を保存する．さらに低い対称性の結晶系では，結晶物理主軸$X_{1}, X_{2}, X_{3}$ に対する楕円体の方位を標示するために，パラメータが（これらの３つ以上に）増える． \\
\ \\
\ \\
　　　均一なテンソル場の対称群の中で，極限キューリーCurie群（図74）に加えて，反対称と色対称群のlimiting orthogonal極限斜方晶［直交］群に出会う． \\
　　　7つの中性と7つの2-色のlimiting antisymmetry極限反対称群が，拡大の理論により得られる： \\
$$ \infty 1', \infty 221', \infty mm1', \infty /m1', \infty /mmm1', \infty \infty 1', \infty \infty m1',$$
$$ \infty /m', \infty 2'2', \infty m'm', \infty /m'mm, \infty /mm'm', \infty /m'm'm', \infty \infty m' $$
これらの群の具体化としての物質図形は，キュリーCurie群に対するそれらと同じ形を持つ．中性群では，図形の全ての点は中性，2-色群では，2色である（2色は，各点ごとに，混合されたり塗り分けられたりする）．反対称の磁気的解釈では，電気，磁気，Poyntingポインティングベクトルは，それぞれ，磁気対称の極限群$ \infty mm1', \infty /mm'm', \infty /m'mm$を持つ（図221）．反対称の極限群の導出では，読者はShubunikov（1958，1959），Sirotin（1962），Koptsik（1966）による扱いを参照するとよい． \\
　　　この系列に，無限にcolored limiting groups色極限群が存在し： \\
$$ \infty 1^{(p)}, \infty 221^{(p)}, \infty mm1^{(p)}, \infty /m1^{(p)}, \infty /mmm1^{(p)},$$
$$ \infty \infty 1^{(\texttt{\textsl{p } })}, \infty \infty \texttt{\textsl{m } }1^{(\texttt{\textsl{p } })};$$
$$ \infty ^{( \infty )}, \infty ^{( \infty )}\texttt{\textsl{m } }^{(2)}\texttt{\textsl{m } }^{(2)}, \infty ^{( \infty )}/\texttt{\textsl{m } }, \infty ^{( \infty )}/\texttt{\textsl{mm } }^{(2)}\texttt{\textsl{m } }^{(2)},$$
$$ \infty ^{( \infty )}2^{(2)}2^{(2)}, \infty ^{( \infty )}/\texttt{\textsl{m } }^{(2)}, \infty ^{( \infty )}/\texttt{\textsl{m } }^{(2)}\texttt{\textsl{m } }^{(2)}\texttt{\textsl{m } }^{(2)} $$
$$ \infty ^{( \infty )} \infty ^{( \infty )}, \infty ^{( \infty )} \infty ^{( \infty )}\texttt{\textsl{m } }^{(2)} $$
色群の具体化となる典型的な図形は，Curieキューリー図形の周りに色調が連続的に変化（虹のように）する色紙を接着すると得られる． \\
例えば，単色光線がコーンの頂点からその底面へ通過すると，色は，コーンの回転にともない，自然のスペクトル順に変化する．コーンが回転するなら， \\
群の系列$ \infty ^{( \infty )}(1), \infty ^{( \infty )}(2), \ldots , \infty ^{( \infty )}(n)$，静止しているコーンには，系列$ \infty ^{( \infty )}m^{(2)}m^{(2)}(1), \infty ^{( \infty )}m^{(2)}m^{(2)}(2), \ldots , \infty ^{( \infty )}(n)$ を得る \\
［ここで，\texttt{(1)}\textrm{\textsl{, } }\texttt{(2)}\textrm{\textsl{, } }\texttt{(}\textrm{\textsl{n } }\texttt{)}は，古典的軸性部分群である；色コーンの群が，部分群\textrm{\textsl{n } }を含むなら，１回転でカラーサイクルは\textrm{\textsl{n } }回繰り返すことを意味する]. \\
底をシリンダーとし，その周りに色サイクルを一回貼りつけ，群$ \infty ^{( \infty )}/mm^{(2)}(1)$ （静止したシリンダー），$ \infty ^{( \infty )}/m(1)$ （回転シリンダー）を得る． \\
色が連続的に，シリンダーを１周（円周に沿い）するのみでなく，すべての生成元に沿い変化するなら，対称性$ \infty ^{( \infty )}/m^{(2)}m^{(2)}m^{(2)}(1)$（静止時），$ \infty ^{( \infty )}/m^{(2)}(1)$（回転シリンダー），$ \infty ^{( \infty )}2^{(2)}2^{(2)}(1)$（ねじれシリンダー）の２回の色シリンダーを得る． \\
これらの全てで，部分群$1$を$n$で置き換えると，オリジナルのものから群の無限系列が導びける．色シリンダーの群は，古典的部分群$mmm,n22$, あるいは，何らかの性質を保存する部分群の系列に形式化できる． \\
色極限群の最後の２つは，全点が$ \infty $-色で，かつ，中性でない球で具体化される：各点の色は，セクターに沿って分布するか，あるいは，混合されずに層をなして互いに重畳され，同様に群$ \infty ^{( \infty )}$ と$ \infty ^{( \infty )}m^{(2)}m^{(2)}$ ではコーンのチップに分布する．群$ \infty ^{( \infty )} \infty ^{( \infty )}$ では，球の直径は群 $ \infty ^{( \infty )}2^{(2)}2^{(2)}$でのように捩れている．一方，群$ \infty ^{( \infty )} \infty ^{( \infty )}m^{(2)}$では，捩れがない．極限群の別の解釈では，初期に見たすべての図形でのように，１つの固定色は，一般点のすべてに帰属せしめられる。捩れたシリンダーの対称性は，もっと完全には２回色反対称群により記述される． \\
$\displaystyle \frac{ \infty ^{( \infty ) } }{m'^{ \ast } }\displaystyle \frac{2^{(2) } }{m'^{ \ast } }\displaystyle \frac{2^{(2) } }{m'^{ \ast } }$ \\
ここで＊星印はシリンダー低部の周囲の順序で，色を変え，′ダッシュは捩れの方向を変える． \\
　　　さらに，中性群では，色同一部分群$1^{( \infty )}$は冪によって異なることに注意する．具体化に加え，言及したように，古典的なCurieキューリ群，反対称の極限群，Waerden-Burckhardt群，Wittke-Garrido群，およびこれらの許容される積（p.248，256参照）により記述される色図形がある．すべての有限色群（結晶学的および非結晶学的の位数の）は，これらの極限群の部分群であり，非常に早く本書で与えてある。完全な構造対象の物理で，極限色群は通常の極限斜方晶群よりも役割が低いわけではない． \\

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2020.08.25］ No.335
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
実効再生産数が東京では，まだ１を少し超えているようですが，他の県では1未満になってきたようです．
以下のサイトに，都道府県別の実効再生産数の時系列の変化のグラフがあります．

Rt Covid-19 Japan都道府県別コロナウイルスの感染拡大・収束状況(実効再生産数Rt)をグラフ化したWebサイト
rt-live-japan.com

実効再生産数Rというのは，1人の感染者が新たな感染者を作る人数のことです．
Rが1未満なら感染流行は減少収束し，１より大きければ感染は拡大します．
しかしながら，各都道府県の実効再生産数がすべて1未満になっても，
感染拡大の起こる可能性を警告している論文を前号で紹介しました．その論文では，
全体をコミュニティと病院という２つのグループに分割したモデルで，
コミュニティ内の感染に関する実効再生産数と病院内の感染に関する実効再生産数がともに1未満であっても，
全体の実効再生産数が１を超す（感染拡大が起こる）可能性が指摘されました．
その原因は，コミュニティから病院に感染させる場合も，病院からコミュニティに感染させる場合もあるからです．

都道府県別の実効再生産数が，それぞれ1未満になっても，各県間の人の移動接触により各県間の感染が起こるので，
全体の実効再生産数が１より大きくなることは十分あり得ます．油断は危険です．

■数学の形式としては，次の行列を作ります：
対角要素には，各都道府県の実効再生産数を並べ．行列のその他の要素には，異なる県間の感染率を対応させます．
県間の感染率は，相当する県間の人の接触確率のようなものです．
このような行列を作るにはいろいろなデータが必要ですが，この行列ができたとすると，
この行列の固有値を求める数学の問題になります．最大の固有値が１を超していれば，
全体の実効再生産数は１を超し伝染の拡大が起こります．

私たちの社会は，都道府県がそれぞれ孤立して独立でいるわけではなく，
互いに相互作用（人の接触がある）しているので，
独立な個別地区の予測と，全体の予測は大変異なり，このような計算をしてみないとわかりません．

（注）実効再生産数の計算方法は，Anne RがCoriらによるものが，山中伸弥のホームページに紹介されています．

<東京おもちゃまつり>は，東京おもちゃ美術館にて，毎年10月半ばに開催されています．今年は，新型コロナウイルスの感染拡大のために開催は困難でしょうね．

この記事の写真は，2017年10月14,15日に開催されたときのものです．
両日とも冷たい雨の降るあいにくの天気でしたが盛況でした．私は10月15日に出かけ，バクウ研究所の富川義朗先生と佐藤芳弘先生にお会いしました．

振動で廻すトントン・コマなど，いろいろな「ばくうコマ」の展示がありしたが，その原理はなかなか奥が深い．富川先生たちは，振動を回転運動に変える超音波モータの発明者です．

■私は，ミラクル・ツインという「ばくうコマ」に興味をもちました．左右の回転子の回転は互いに逆回転で，右の回転子は5回対称の模様が見え，左の回転子は3回対称の模様が見えます．

富川先生によるミラクル・ツインの解説はここにありますが，まだ，基本的仕組みの解明はされていないようです．私自身，考えるほど疑問が沸き上がりますので整理しました：

①なぜ，左右の回転子は逆回転するのか？
②なぜ，台座の回転モーメントを軸心は逆回転するのか？
③なぜ，4回対称の図形が，5回対称や3回対称に見えるのか？

納得のいかない現象ばかりですので，高速度撮影をして観察することにしました：

この観察をもとに，みんなで考えてみましょう．私が解明した仕組みについて解説しましょう．

 高速度撮影・解析１

右側の回転子の軸は回転子と接着していますが，左側の回転子の軸受け穴と軸心は接着されていません．さらに，回転子の軸受け穴径は，軸心径の1.5倍程度あり歳差運動を起こします．

回転の向きを観察すると，中央の偏芯回転子の回転方向に対して，左の回転子は逆回転，右の回転子は同方向に回転します．そして，右の回転子には5回対称の模様が見え，左の回転子には3回対称の模様が見えます．

高速度撮影・解析２

撮影の前に，左側の回転子の軸受けに細工をして，軸受けと軸心が固定されるようにしました．すると予想通り，左側の回転子の運動は右側と全く同じになりました．

■解析１の観察に基づく仕組みの考察

中央の偏心した回転子が生み出すのは単純な振動ではなく，台座全体の回転モーメントです．台座全体（台座の左右にある軸受け穴も）が公転と言われる軌道を描き平行移動します(決して，軸受け穴が回転するわけではありません．平行移動です）．

左右の軸受け穴の中には，軸心が通っていますが，少しの”ガタ”があります［軸受け穴径は軸心径の1.2倍程度］．軸心は公転の向きと逆向きに自転をします（これはコペルニックスの定理）．軸心は歳差運動もしているはずで,

軸心の自転と歳差運動の位相との相互作用が，軸心に結合した回転子の上下波打ち運動を生み，5回対称模様が静止して見えるのではないかと推理します．

左側の回転子については，軸心と回転子は一体ではなく，回転子の軸受け穴径は軸心の1.5倍ほどあり，かなりの”ガタ”があります．軸心の歳差運動の位相は，軸心の回転と逆方向で，回転子への回転の伝達は，ちょうど皿回しと同じで，歳差運動により伝えられます．左側の回転子の軸受け穴の”ガタ”は大きいため，大きな上下波打ち運動になり，3回対称が現れるものと思います．