モーペルテュイは,
「始状態から終状態への運動経路には,作用と呼ばれる積分量が定義でき,作用が最小となる経路が実現される.これが物理学のみならず,万物の運命を決める外界の原理である」
という着想-”最小作用の原理”(1744年)を得ました.たしかに,現実の運動では,しばしば作用が極小になりますが,正確には,「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります.
オイラーは,モーペルテュイの作用量の定義を積分に拡張し,最小作用の原理をさまざまな力学課題に適用できるようにし,”最大,または最小の性質をもつ曲線を見出す方法”(1744)を発表しました.これを読んだ若きラグランジュは変分法を発明し,オイラーに手紙(1755)を送ります.オイラーは,ラグランジュの方法を採用し,”変分法の原理”(1766)を出版します.変分法で導かれる運動方程式が,オイラー=ラグランジュ方程式といわれる所以です.その後,ラグランジュは,”解析力学”(1788)を出版します.その序文に「本書には図は一つも出てこない....所定の手続きに従い進める代数計算だけだ....」と高らかに宣言します.こうして,複雑な力学問題も解ける一般化された手法が確立されます.
変分法は,19世紀のハミルトン,ヤコービにより完成に至ります.ハミルトンは,系の状態を表示する空間に,座標と速度を座標軸とした相空間を導入し,「作用量は最小化や最大化するのではなく,停留化する」ことを示しました.
1つの物体は,座標x,y,zと速度x˙,y˙,z˙を変数に持ち,その状態は6次元の空間の1点で表現できます.同様に,N個の物体よりなる系は,6N次元の空間の1点で表現できます.この空間を相空間といいます.系のエネルギーを
H(xi,yi,zi,xi˙,yi˙,zi˙),i=1,2,・・・,Nとすると,エネルギーが保存される運動の軌跡は,相空間内の超平面H(xi,yi,zi,xi˙,yi˙,zi˙)=hに含まれます.超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです.解けるかどうかは別として,周期解(軌道)が存在することは,証明(1986年)されています.(文献10)
■ 最小作用の原理の理解には,ホイヘンスの光の波動説の説明が参考になります.ホイヘンスは,空間は見えない媒質で満たされており,光は波紋(球面波)が拡がるように伝わると考えました.波面上の各点はまた新たな波源となり,そこを中心として新たな波紋が広がって行きます.生じた無数の波紋は重なりあったり打ち消しあったりの結果,新しい波面ができます.これは多数の波面の包絡面で,この面に垂直な方向に光は進むと考えます.この様なプロセスで決定された方向は,作用を停留値にするものです.
量子力学の世界の運動には,軌道の概念がなく,電子などはランダムに動き回ります.しかし,我々の日常(マクロ世界)では,電子の運動でも軌道はあります.ここで,マクロ世界でも物体はランダムな経路をとれるとしてみましょう.あらゆる経路に実現可能性があるが,各経路の実現率は,それぞれの確率に従う.これらの確率は,波紋が伝播するときのように互いに干渉し合い,その結果として現実の経路が決まってくると言うわけです.最も確からしい経路は,近くからの干渉の最も少ない経路であって,これがちょうど作用積分を停留化するもののようです.「ファインマンの原理」(文献10)
■ 運動方程式が解ける問題を”可積分な問題”といいますが,実際は,”非可積分の問題”がほとんどです.ニュートン力学は,可積分で安定な周期軌道が解になる特殊な範疇を扱っています.一方,非可積分の問題からは,カオスが生じます.1つの軌道は,1本の因果列の存在を意味しています.単純な世界は,今日の現象(原因)1が明日の結果1につながり,今日の現象(原因)2が明日の結果2につながる世界ですが,一般には,今日の現象のすべてが,明日のある結果1の原因になりうる複雑な世界です.バタフライ・エフェクトという映画*)があったようですが,今日,上空で蝶が羽ばたいたことが,遠い未来に竜巻きを起こす原因の一つになるかも知れません.「風が吹けば,桶屋が儲かる」世界です.この世界は,独立な因果列はないので,周期的な軌道にはなりません.コンピュータを用いて,すべてのステップを計算していけば,結果を予測できるのですが,遠い先の結果は予測もつかないものになります.「最小作用(停留値)の原理」は,ニュートン力学も含むが,このようなカオスも含む原理であります.
*注)過去に戻れる能力を持ったエヴァンは,過去に戻りやり直すことにする.しかし,過去に戻り選択肢を変えて始めた人生は,どれも,自分を含め自分が愛する誰かが,幸せではないものだった.
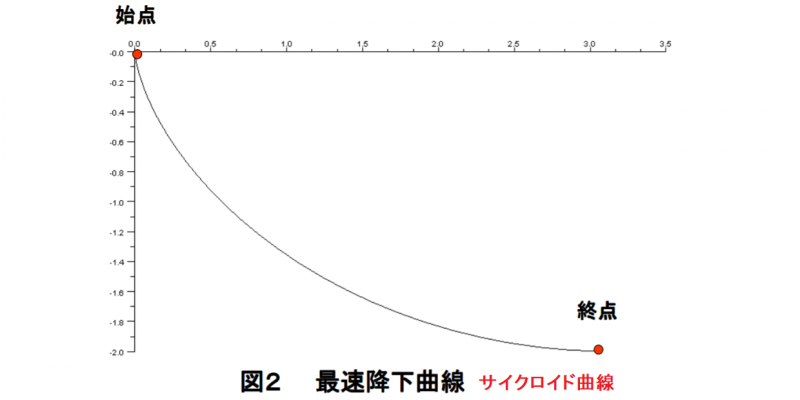
■ 最小作用の原理の起源といえば,1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません.「決まった二点の間を,始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です.ライプニッツの提案により,ベルヌーイはこの問題を海外の数学者にも公開することにしました.ベルヌーイは,ライプニッツの友人で,ニュートンとライプニッツの微積分の先取権論争にも加わり,ライプニッツを応援しています.きっと,ニュートンを困らせてやろうと思ったのでしょう.ところがこの問題を受け取ったニュートンは,「当時,造幣局の仕事で忙しく疲れて帰宅したが,問題が解けるまでは寝なかった.とは言っても朝4時までには解けてしまった」と日記に書いています.そして,解答を匿名で返したということです(文献1,5).
最速降下曲線の答えは,円板の縁(1点)に目印をつけ,直線上を転がしたときに,目印が描く”サイクロイド曲線”です.ホイヘンスが振り子時計に用いたあの曲線です.
■ 解析力学の手順
力学系を記述するラグランジュ関数 を求め,ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと,オイラー=ラグランジュ方程式が得られます.簡単な系のラグランジュ関数は,(運動エネルギー)-(位置エネルギー)の型になりますが,複雑な系では,位置エネルギーが速度に依存することもあります.
ラグランジュ関数は,電磁場に置かれた荷電粒子にも定義され,光(電磁力学)も力学も統一して扱える原理であります.変分原理から,ニュートンの運動方程式は導出されます.その上,変分原理はニュートン力学よりさらに一般化された外界の原理です.(文献11)
20世紀に入り,量子力学が誕生するときにもこの原理が手がかりになりました.光や物体の運動が,作用積分を停留化するような,手の混んだ経路を選択するというのは,何と不思議なことでしょう.
(文献)
1.物理と数学の不思議な関係,マルコム・E・ラインズ(青木薫訳),ハヤカワ文庫, 2004
5.古典物理学を創った人々,エミリオ・セグレ(久保亮五,矢崎裕二訳),みすず書房,1992
10.数学は最善世界の夢を見るか?,エクランド(南條郁子訳),みすず書房, 2009
11.理論物理学,カンパニエーツ(山内恭彦,高見穎郎訳),岩波書店, 1964
(「数学文化」谷,NO.15(2010),p.79-87 より抜粋)