アイク・アコピアン АЙК АКОПЯН • МАТЕМАТИКА • 21 КОММЕНТАРИЙ
https://elementy.ru/problems/2390/Samye_spravedlivye_vybory
さまざまな形式の選挙がいたるところで実施されています。選挙結果が有権者の意思をあまり反映しない場合もあれば、大多数の意志を反映する場合もあります。選挙を数学の観点から検討し、このプロセスに2つの自然で明白な特性を要求すると、予期せぬ結論が得られることを示します。しかし、最初に、選挙とは何を意味するのか、そして選挙の正義とは何かを形式化しておきましょう。
複数の候補者が選挙に参加し、各有権者がこれらの候補者の特定の評価、つまり、候補者を有権者の個人的な好みの降順で並べたリストを持っていると仮定します。ワシントン、フランクリン、ジェファーソンの3人の候補者がいる例を考えてみましょう(ただし、以下のすべての推論は、もっと多くの候補者でも有効です)。その場合、ある有権者の評価は次のようです。「フランクリン>ワシントン≥ジェファーソン」。すべての候補者を優先度の高い順に1行に並べることができるこのような評価は、推移的と呼ばれます。
私たちが慣れ親しんでいる選挙では、各有権者が候補者の1人だけに投票を行う、たとえば、ある有権者がジェファーソンに投票したい場合、これは彼の評価が「ジェファーソン>フランクリン=ワシントン」のようになることを意味します。
選挙制度は、「大多数の意見」を反映した評価を出力するべく、すべての投票を評価する方法であると理解します。もう少し数学的な言葉で言えば、選挙はすべての有権者の好みを入力として受け、これらのデータに基づいて集合の好みの評価を出力する機能です。
このようなシステムの特殊なケースは、ロシア(日本でも)で使われている各候補者の総投票数です。別の特殊はケースは、例えば、候補者のランダムな最終選択で、これは投票者の意見がまったく考慮に入れられません。
選挙制度が公正と呼ばれるために必要な特性は何でしょうか?
まず、すべての有権者が2番目の候補よりも1番目の候補を好む場合、最終結果はこれを反映する必要がある、つまり、最終選挙手順は、1番目の候補が2番目の候補よりも高くなるのが論理的です。このプロパティは、全会一致と呼ばれます。第二に、これも非常に論理的ですが、最終評価における2人の候補者の相対位置は、有権者の好みの評価による相互位置にのみ依存し、他の候補者の位置に依存するべきではありません。これは、選挙結果で、一方の候補者が他方の候補者を追い抜いたことが判明した場合、3番目の候補者が投票に追加(または除外)された場合もまったく同じ結果になることを意味します。2番目のプロパティは、無関係な選択肢からの独立(またはバイナリ独立)と呼ばれます。
これらの2つの特性を満たす選挙は、公正であると見なされます。
課題
これらの定義を満たす唯一の公正な選挙制度は独裁である。つまり選挙の結果が一人の人の好みによって完全に決定され(そして、他の人の好みはまったく考慮されない)システムであることを証明しなさい。
ヒント1
結果は3人以上でも当てはまりますが、3人の候補者による選挙で行うのが最も簡単です。
ヒント2
最初はすべての有権者が個人的な評価でリンカーンを最初に置き、フランクリンを最後に置いたとしましょう。そのような評価で最終的な選挙結果はどのようになりますか?有権者がリンカーンとフランクリンの場所を次々と変え始めたら、選挙結果はどのように変わるでしょうか?
解答
有権者が6人しかいないとします。まず、候補者が2人だけの場合にどうなるかを考えてみましょう。ワシントン(W)をジェファーソン(J)と競争させ、フランクリン(F)をしばらく忘れます。
すべての有権者がジェファーソンよりもワシントンを好む場合(つまり、評価がW≥Jの場合)、全会一致規則に従った公正な選挙の最終手順は、W≥Jになることに注意してください。この平凡な状況を図1に示します。.逆に、すべての有権者がワシントンよりもジェファーソンを好む場合(すべてJ≥W)、明らかに、ジェファーソンもワシントンを打ち負かす必要があります。
図1.
それでは、ダイナミクスで何が起こるかを見てみましょう。誰もがワシントンに賛成している状況から始めて、有権者が順番に個人の評価を変更し始めたらどうなるかを見てみましょう。最終結果はどのように変わりますか?
最初はワシントンが勝つことは明らかであり、最終的には、すべての有権者が好みを変えると、ジェファーソンが勝たなければなりません。最終手順で結果が逆転する、ある有権者i(私たちの場合は、1≤ i≤6)があります。私たちの場合では、i=4(図2)。
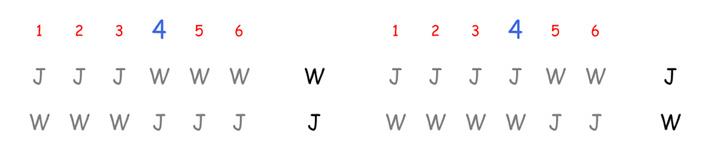
図2.
フランクリンを思い出して、図2の左側のケース(主要な候補者のランキングでW≥Jの場合)を考えてみましょう。フランクリンは、i<4の場合投票の真ん中に位置を占め、i≥4の場合に最下位になるとしましょう(図3)。選挙結果はどうなりますか?フランクリンが入る前に、ワシントンがジェファーソンを倒したことを思い出してください。私たちの選挙は公正なので、この結果は、バイナリの独立性のために変わるべきではありません。また、すべての有権者についてJ≥Fであることがわかります。全会一致プロパティから、最終結果もJ≥Fである必要があります。したがって、最終手順はW≥J≥Fとなります。
図3.
もし4番目の有権者がWとJを入れ替える決定した場合、この有権者はペア(W,J)のキーであり、個々の評価の相対位置(J,F)と(W,F)は変わらないので、最終結果はJ≥W≥Fに変わります(図4)。主要な有権者の個人的な評価は、最終的な評価と一致することに注意してください。
図4.
このキー有権者がどれほど強力であるかを理解するために、他の有権者の票を変えることによって選挙の結果に影響を与えようとしましょう。たとえば、フランクリンとジェファーソンの個人的な評価の場所を交換します(図5).結果は変わりましたか?
図5.
個々の評価におけるWとFの相対的な位置は変更されていないため、W≥Fは最終手順に残ります(無関係な選択肢からの独立性のため)。また、JとWの相対位置は変更されていません。つまり、最終手順ではJ≥Wになります。結果はまったく変更されず、ジェファーソンが常に勝ちます。そしてこれは、4番目の有権者が、彼の個人的な評価でジェファーソンを1位にした唯一の人であるということです。キー有権者の個人的な評価がJ≥Fである限り、この問題に関する他の有権者の意見は最終的な投票結果に考慮されないことがわかります。
では、何を証明したのでしょうか。候補者のペア(この場合はワシントンとジェファーソン)について、他の人の意見に関係なく、投票結果で3番目の候補者の位置を明確に決定するキー有権者がいることを示しました。
しかし、候補者の任意のペアのキー有権者の存在から、独裁者の存在自体は導かれません。理論的には、このキー有権者は候補者のペアごとに異なる可能性があるためです。それにもかかわらず、キーは常に同じ有権者であることが判明しました(正確には、彼が実際に評価におけるFの位置を指示しているためです)。これは、上記と同様の推論を実行することで簡単に示すことができます。このキー有権者による評価が最終的な選挙結果を完全に決定することが判明しました。
あとがき
上で議論された問題は長い間古典的な結果でした。これは、1951年の論文で、アメリカの数学者で経済学者のケネス・アローによって最初に定式化され、証明されました。今では、民主主義の不可能性またはアローのパラドックスについてのアローの定理と呼ばれています。
一般的なケースの完全な証明は、J.Geanakoplos,2005にあります。
Arrowの不可能性定理の3つの簡単な証明https://link.springer.com/article/10.1007/s00199-004-0556-7
この定理は実際には次のように述べています。人々の好みが独立していて一過性であり(評価を表す)、選挙が全会一致と、無関係な選択肢からの独立の原則を尊重する場合、他の評価に関係なく、個人の評価が結果を完全に決定する独裁者が常に自動的に存在します。これらの条件を少し緩和しても、たとえば、独裁者ではないにしても、選挙の最終結果における任意の2人の候補者の相対的な位置を常に決定する「拒否」する権利を持つ人が常に存在することを示すことができます。
定理が成立するために必要な有権者の選好要件は、通常のアプローチと呼ばれます。このアプローチでは、個人の好みは量的ではなく質的に考慮されます。つまり、いくつかの選択肢は他の選択肢よりも優れている、悪い、または同等である可能性がありますが、ある選択肢が別の選択肢よりどれだけ優れているかを判断する手段はありません。
これらの条件はすべて、非常に論理的ですが、実際には常に満たされているわけではありません。たとえば、基本的に選挙の特定の客観性の要件であるバイナリ独立(無関係な選択肢からの独立)の原則(候補は互いにのみ比較され、他のコンテキストでは比較されません)は、非常に簡単に破られます。100人の有権者がいて、その個人的な評価が次のように分布している状況を想像してみてください。25人の有権者の評価はW> J> F、40人の有権者の評価はJ> F> W、残りの35人の有権者の評価はF> W> Jです。いずれにせよ、選択はバイナリ独立の原則に違反します(W、J、またはFが勝つ場合を個別に検討してこれを示すようにしてください)。
この例は、一般に、候補者が3人以上いる場合、大多数の「意見」が互いに矛盾する可能性があることも示しています。公的選択の理論におけるこの現象は、コンドルセパラドックスまたは公的選択の循環的性質と呼ばれます。これは、社会全体の観点から(つまり、「選挙」の結果を合計した後)、次の逆説的な状況が発生するためです。W> J> F> W> ...、にもかかわらず各有権者の個々の好みは一時的なものであること。
このパラドックスは、2段階の投票システムで重要です。最も明白な例は、米国大統領選挙です。そこでは、各党(共和党と民主党)の候補者が最初にいわゆるプライマリーを通過します。そこでは、各党から1人の候補者が選ばれ、主要な大統領選挙で党を代表します。
今年の民主党の初等協会では、主な戦いはバーニーサンダースとジョーバイデンの間でした。ジョー・バイデンが予備選挙で勝利し、選挙で民主党の候補者になります。彼は現職の共和党大統領ドナルド・トランプと競争するでしょう..。コンドルセのパラドックスはアメリカ社会の好みで起こっているのかもしれません:トランプ>バイデン>サンダース>トランプ> ...そして、バイデンは世間の心にあまりないので、すべての選挙の結果は選挙の第一段階(プライマリー)の結果に依存することがわかりますトランプよりも優先され(サンダースよりも優先されますが)、サンダースはトランプよりも優先されます(バイデンよりは優先されませんが)。そして、この状況では、大統領選挙に参加したバイデンは(プライマリーではサンダースよりも好ましいため)、トランプに負けます。したがって、ある意味で、民主党が選挙に勝つチャンスがあるにもかかわらず、あまり好まれない民主党の候補者を指名することは「より有益」です。しかし、そのような場合の世論を評価する問題は、社会学の分野に属します。
ーーーーーーー
(参考)11月4日現在