フレネル積分 $$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{ix^{2 } }dx$$を求めなさい.
$$S(x)=\displaystyle \int_{0}^{x}\textrm{sin}t^{2}dt$$, $$C(x)=\displaystyle \int_{0}^{x}\textrm{cos}t^{2}dt$$もFresnel積分と呼ばれる.
ただし,$$S( \infty )=C( \infty )=\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }$$を既知とすると,
$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx+i\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }\left( 1+i \right) $$が得られます.
(参考)Gauss積分 $$\displaystyle \int_{0}^{ \infty }\textrm{exp}[-t^{2}]dt=\sqrt{\pi }/2$$
---------------------------
これを複素積分法で計算してみます:
$$I=\displaystyle \int_{0}^{ \infty }\textrm{exp}[ix^{2}]dx=\displaystyle \int_{0}^{ \infty }\textrm{exp}[-(e^{-i\pi /2})x^{2}]dx$$
$$z=xe^{-i\pi /4}$$とおくと,$$dz=dxe^{-i\pi /4}$$だから, $$I=e^{i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{Re^{-i\pi /4 } }\textrm{exp}[-z^{2}]dz$$
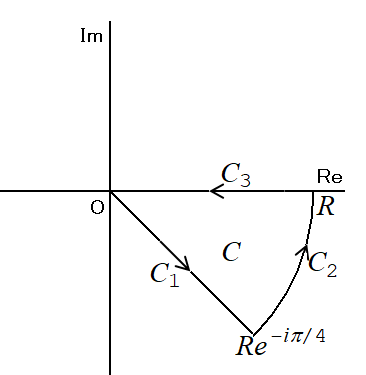
被積分関数$$\textrm{exp}[-z^{2}]$$は,周回積分の領域$$C$$で正則だから,コーシー・リーマンの定理により周回積分は0になる:
$$0=\displaystyle \int_{(C)}^{}\textrm{exp}[-z^{2}]dz=\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz$$
$$z=te^{i\theta }$$, $$dz=dte^{-i\pi /4}$$, $$dz=d \theta iRe^{i\theta }$$
$$C_{1}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz = e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}e^{-i\pi /2}]dt=e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{it^{2 } }dt$$
$$C_{2}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}\textrm{exp}[-R^{2}e^{i2\theta }]e^{i\theta }d\theta =$$
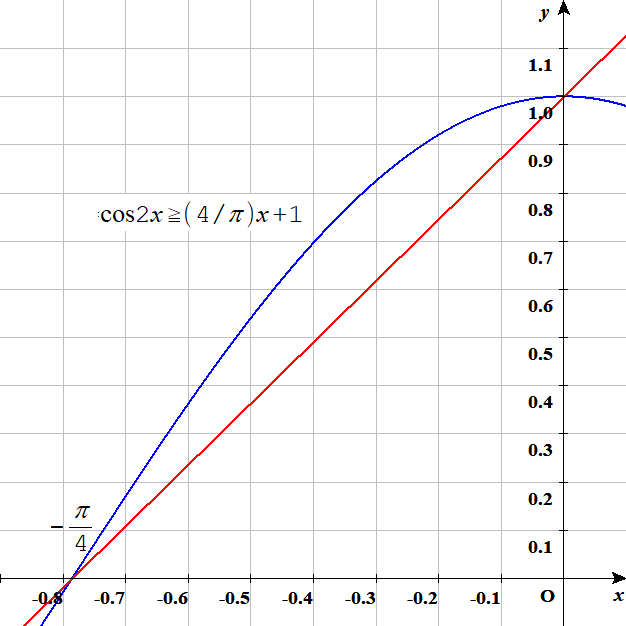
$$=\displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}e^{-R^{2}\textrm{2cos}2\theta }e^{-iR^{2}\textrm{sin}2\theta }e^{i\theta }d\theta \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}\textrm{cos}2\theta }|d\theta \leqq $$
$$ \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}(4\theta /\pi +1)}|d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\displaystyle \int_{-\pi /4}^{0}e^{-(4R^{2}/\pi )\theta }d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left[ \displaystyle \frac{e^{-(4R^{2}/\pi )\theta } }{-4R^{2}/\pi } \right] _{-\pi /4}^{0}$$
$$=\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left( 1-e^{R^{2 } } \right) /\left( -4R^{2}/\pi \right) =\displaystyle \lim_{R \to \infty }i\pi (1-e^{-R^{2 } })/4R=0$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }-\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}]dt=-\sqrt{\pi }/2$$
従って,$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}=-\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}$$ より,
$$\displaystyle \frac{\left( 1-i \right) }{\sqrt{2 } }\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\sqrt{\pi }/2$$
$$\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }(1+i)$$