note.com投稿記事

Интервью с Семёном Гиндикиным
«Троицкий вариант» №10(229), 23 мая 2017 года

撮影は，Natalia Demina

Natalia Demina が，Semyon G. Gindikin（ロシア系アメリカ人の数学者、教師、数学の普及者）に，モスクワ生涯数学教育センターで，インタビューをしました．
反ユダヤ運動が才能ある若者にどのように影響したか，I. M. ゲルファントのセミナーについて語る．

О том, как отразилась на талантливых ребятах антисемитская кампания, о семинаре И. М. Гельфанда Наталия Демина поговорила с Семёном Григорьевичем Гиндикиным, российско-американским математиком, педагогом, популяризатором математики. Беседа с этим веселым, остроумным человеком состоялась в Московском центре непрерывного математического образования.

--------- 以下用紙抜粋---------- 

◆ピーター・セルゲイビッチ・ノビコフは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学の力学数学学部（мехмат）で反ユダヤ主義について話し始めるのが嫌いでした。数学者になり、「暗い20代」を強い人々が生き残ることができたという例です. それは本当ではない。これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に本物の数学者になることができたように私には思えます. 私は本当にラッキーでした。まず第一に、すぐに私の仲間と素晴らしい数学者の両方が私の近くにいることがわかったからです。

◆ イスラエル・モイセービッチ・ゲルファントについて一言いただけますか? 彼のセミナーに参加したことがありますか？

- もちろん。彼の90歳の誕生日に、これらのセミナーに関する記事を書きました。ゲルファントはこれについて議論するのをためらっていましたが、ランダウの物理学セミナーが彼のセミナーに強い影響を与えたように私には思えます。ある時点で、ゲルファントは物理学を学びたいと思っていたので、セミナーでは多くの物理学のプレゼンテーションがありました。レフ・ダビドビッチ・ランダウはイスラエル・モイセビッチ・ゲルファントをやや見下そうとしたと思います。

ランダウを初めて見たときのことを正確に知っています。これは1955年のことです。関数解析に関する会議があり、国内で最高の数学者がすべて集まりました - モスクワでの大きなイベントです。その時まで、実質的に会議はありませんでした。最初は戦前に行われました。モスクワ全体がこの会議の開会式に参加しました。そして、イスラエル・モイセエビッチはそこで君臨しましたが、彼のセミナーではいつもより少し控えめに振る舞いました。最初の報告は、ランダウによって行われました。そして、彼らはそれぞれのパートを完璧にリードした 2 人の偉大なアーティストであることがわかりました。その時までに、Israel Moiseevich は Bob Minlos と一緒に、経路積分と呼ばれるものを考え出していました (Bob は私の友人であり、素晴らしい人物であり、数学者でもあります)。

Landau の報告の後、Gelfand は、これらの積分はおそらく場の理論を作成する正しい方法であると彼に非常に穏やかに説明しようとしました。そしてランダウはこっそりと彼に答えました：「イズレール・モイセエビッチ、鶏は秋に数えます（捕らぬ狸の皮算よ）」。このフレーズは、ピョートル・セルゲイヴィッチ・ノヴィコフが好んで言ったことを覚えています。

ところで、私は、レニングラードで開催された数学会議 (1960 年頃) で、ゲルファントとランダウの間の別の会話を目撃しました。I. M. と一緒にネフスキーに沿って、Baltiyskaya Hotel の近くを歩き、Landau に会いました。真剣な現代数学を再び適用する可能性についての話題が会話の中で生じたことを覚えています。I. M. はいくつかの例 (ローレンツ群の表現だと思います) を引用しましたが、L. D. は断固として彼に同意しませんでした。彼は、何年にもわたって「数理物理学の方程式」に関するセクションがあったが、物理学への本格的な数学の重要な応用を知らないと述べた.

今日、現代の理論物理学でどのような精巧な数学が使用されているかを見ると、ゲルファントが正しかった可能性が高いように思えます。どうやら、ランダウは将来の物理学における数学の役割を過小評価していたようです (私の物理学者の友人から聞いたところによると、おそらく彼の学生の何人かはこれに多額のお金を払ったようです)。

ゲルファントのセミナーに戻ったら、私の見解を繰り返します。イスラエル・モイセービッチが民主主義を認めなかったことに多くの人が腹を立てた。彼にとってセミナーは、ある意味で彼の人生の本業でした。

第一印象は、セミナーのすべてが即興であるということでした。セミナーは大幅に遅れて始まりました。Gelfand 氏は、セミナーを待つことがコミュニケーションの最適な時間であると説明しました。これは、人々が（無意識のうちに！）互いに話し合う、科学的コミュニケーションにとって貴重な時間でした。

そのような完全に意識的な混乱は、彼の性格の特徴でした。彼はすべてを時間通りに行う必要があるとは考えていませんでした。彼は、自分にとって都合の良いことをする権利を獲得し、一般に受け入れられている規則を考慮しないと信じていました。少し大げさですが、あなたは素晴らしい人なので、導かれるように振る舞う必要があります。そして、これは最良の結果をもたらします。礼儀正しさは、イスラエル・モイセヴィッチの強みではありませんでした。しかしいつもではない。彼は誰とどのように話すかを知っていました。それでも、彼はスターリン時代を生き抜いた男でした。しかし、しばしばある時点で彼は崩壊し、すべての宝石外交は裏社会に陥りました.

セミナーに関しては、彼にとってそれは人生の主な仕事でした。それは彼自身が数学のほとんどを理解した場所であり、彼は他の人にこの数学を理解する機会を与えたと信じていました. そして、彼は完全にリラックスしていました。彼の態度は、すべての人に適しているとは限らなかったかもしれませんが、このセミナーから利益を得たいと思った場合、他の人が支払わなければならない種類の賛辞でした.

セミナーの数日前、彼はセミナーの内容について考え始めました。ゼミにいた有名な数学者で、普及にも携わったポール・ハルモス（ポール・リチャード・ハルモス）の思い出がある。セミナー、ゲルファントとの交流、彼がクレムリンをどのように案内したかについての章全体があります。そこでハルモスはセミナーに来て、綿密なレポートを作成しました。彼は偉大な達人であり、彼の本は高い教育レベルで書かれていました。そして、ここで外向きに-ある種の完全な障害：Gelfandは、スピーカーに発言権を与える代わりに、彼に質問をし、他の人と話します。

しかし、ゲルファントの世界モデルでは、そのような無秩序はありませんでした。最初のセミナーは彼にとってトランスのようなものでした。彼は数学を際限なく聞く準備ができていました。このため、彼は交霊会のように、導かれたように振る舞いました。そして、誰もがそれを気に入ったわけではありません。さらに、数学者は他の人のためにゲルファントに腹を立てることがありました。

しかし、イスラエル・モイセビッチは、名誉ある教授に「あなたは何も理解していない！」と言うことができれば、常に信じていました。-これは、彼が彼を平等に扱っていることを意味します。そして、彼が丁寧に彼に話しかけると、彼は彼を人として、そして確かに数学者として保持していないことがわかります。それがスタイルでした。

Gelfandは、人々が自分のキッチンに入るのを許可した場合、数学をどのように聞いたか、それについてどう考えたかを隠さなかった場合、そのように振る舞う権利があると信じていました。これは、このセミナーの心理学を再構成したものです。すでに説明しました。外国の数学者にとって、ゲルファントのセミナーに出席することは、ボリショイ劇場に出席することと同じくらい義務的でした。それはその娯楽の一部でした。

私が西側でアーノルドとマスロフと一緒に行った最初のことの 1 つは、モスクワとレニングラードでの一連のセミナーの開会式でした。彼女のアイデアは、モスクワのセミナーのスタイルを伝えようとする試みでした。西洋では、セミナーは短い純粋にビジネス的なものです。若い科学者たちは大学院での研究を完了し、博士号を擁護し、独自の軌跡に沿って世界のさまざまな場所に行きました。そしてモスクワでは、彼らは永遠に残りました。彼らはどこにも連れて行かれず、実際、彼らの専門分野で働くことができず、「箱」に座って、夕方にはアーノルドまたはゲルファンドのセミナーに来て、彼らの職業生活の最良の部分が始まりました。

そして、その学校は永遠のように見えました-それは決して終わらない学校でした. しかし、それは皆の個人的な選択であり、彼らは予期せずそこで厄介になる可能性がありました... I.M.にとってセミナーは本当に彼の人生でした. 私が見つけられなかった困難な時期がありました。しかし、大学とステクロフカを追放されたとき、彼が戦った唯一のことは、セミナーを開いたままにすることでした。

彼はセミナーで見知らぬ人が現れて最前列に座る様子を語った. 彼らはショルダーストラップを着用していませんでしたが、すべてが見えました。クルチャトフ研究所で働いていたミハイル・アレクサンドロヴィッチ・レオントヴィッチから、「私服を着た男が歩いていて、肩に何か青いものを持っている」という非常に適切なフレーズを聞いた。

生物セミナーもありました。これも面白かったです。私たちが若い頃、私たちはすべてを理解していると思っていました-どうすればそれを少し改善できるか、そして人々がそれほど引っ張られないようにすることができます.

Izrail Moiseevich はこれらのセミナーをほとんど欠席しませんでした。非常に気分が悪いとき、彼はしばしば彼らを導きました。かつて、実験として、彼が私と A. A. キリロフにこのセミナーを行うように指示したことを覚えています。セミナーは短く、素晴らしく、すぐに終了し、すべてのレポートはスムーズに進み、誰にも邪魔されませんでした。しかし、それはゲルファントのセミナーではありませんでした!

すでにアメリカにいますか？

— いいえ、モスクワです。アメリカでのセミナーについても、ご希望があればお伝えできます。私はラトガース大学でイスラエル・モイセービッチと一緒に仕事をしました。そして、このセミナーは行きませんでした...

――社会に民主主義がなければ、科学は正常に発展しないという命題があります。一方、スターリン主義ロシアにおける数学の隆盛は、このテーゼと矛盾するように思われる現象です。これらの「メールボックス」、「鉄のカーテン」がなければ、ゲルファントのセミナーはそれほど成功しなかったでしょうか?

- いいえ。Gelfand のセミナーの成功は、主に彼の人柄によるものだと思います。彼はこの数学的生活様式を発明しました。私は、モスクワの数学が独特で、他に類を見ない現象であったことを強調します。私たちの会話の時までに、私が行ったことのない場所と私が見たことのないもの。しかし、私はこれを他の場所で見たことがありません。この現象の起源と性質は、別の議論のトピックです。

数学は単なる科学ではありません。私にとっては、最高の状態で、ハイアート、音楽、詩に近いです。アルキメデスの時代から適用された側面は、しばしば重要で注目に値するものでした。権力者との関係は異なり、長い歴史があります。数学がアテネで栄えたのにスパルタでは栄えなかった理由、プラトンが未来の王たちのアカデミーで数学を教えた理由、ギリシャの衰退とともに幾何学が消えた理由、ギリシャから多くを奪ったローマは数学なしでした...

ソビエト連邦では、数学は生物学や言語学と同じようには破壊されませんでした。一番上には、政府の問題、主に軍事的な問題を解決するために、少なくともしばらくの間、数学が必要であるという幻想があったからです。多くの人にとって、当時の数学はそのようなはけ口でした。まず、この世界ではなく、「眼鏡をかけた」若者が常にそこに引っ張られていました。一方で、マルクス・レーニン主義に言及せずに記事を書くことができる、比較的非政治的な場所はほとんどここだけでした。他のどの科学でこれを行うことができますか?

そして、一般的に民主主義は複雑なものです。彼女の原始的な理解は、彼女の不在よりもはるかに優れているわけではありません. 彼らが理解しているように、彼らの権利のために戦う暴徒。民主主義の大部分を大金で買う能力...

- 民主主義に関するテーゼの確認は、科学の分野で最も先進的な国が民主主義の例と見なされている国であるという事実である可能性があります: 米国、英国、フランス、ドイツ。

-主なことは、これらの国の若者は数学があまり得意ではないということです. それが問題です！私が推測するように、あなたはさまざまな数学者に会いました。そして、ユーリー・イワノビッチ・マニンのように、人道的に才能のある人々を何人見ましたか? 非常に人道的に才能のある人々は、しばしば数学に進みました。他の地域に行くのはほとんど自殺行為でした。

ソ連で何が起こったのですか？数学は、通常の状況下では、通常の社会では絶対に数学に入ることはなかったであろう一定数の人々を食い物にしてしまった。この国に数学に専念する準備ができている若者がどれだけいるのか、私は今でも驚いています. 米国では同様のことは何も起きていません。民主主義があるように見えますが。

- アメリカでは、数学サークルが盛んに行われていないのですか? 最近、アメリカでは子供向けの数学的教育が発展しているという記事がありました。アメリカ全土で非常に多くのサークルが作成されており、子供たちが数学に興味を持っているということです...

「見えない。誰が言っているのかわからない。

――丸ごと記事でした。もしよろしければリンクを送ります... [2]

- しましょう。あなたが知っている、彼らはしません。しかし、去った人々のほとんどは、私たちがソ連で行ったことを開始する必要があると考えていました。サークル、数学の学校...アメリカでは、これらすべてが利用可能ですが、これは比較的小さいです。ソ連では、まだ行くことができる「誘惑」はありませんでした。素晴らしい音楽があり、素晴らしいアーティストが登場しました。選択肢はあまりありませんでした。

アメリカでは、数学を勉強した人は銀行やビジネスに行きます。そして、私は悲しみでそれをする人を知っています. しかし、社会におけるそのような価値観。彼らは家族や将来を犠牲にしたくないので、そのような選択をしなければなりません。私の見解では、数学をするのにより助長している国があります。いいえ、この社会の好みの尺度では、純粋な科学はかなり低い位置にあります.

— 科学や数学の大衆化に関わった経緯を教えてください。Kvant にすばらしい記事があります [1] . このコラボレーションはどのように始まったのですか？

- 私はオリンピック関係者です。さまざまな種類のオリンピックに常に参加してきました。これには常に関心がありました。数学の普及は、さまざまな数学サークルへの参加を通じて自然に生じました。

科学の大衆化の中で、私は自分自身のために別のニッチを思いついた. 「物理学者と数学者の話」という本が生まれた最初の記事は、数学の歴史に関する記事でした。当時、数学の歴史は公式イデオロギーが数学に圧力をかけようとするトロイの木馬でした。

そして、私はこのトリックを思いつきました。私は、数学についてのように、数学の歴史について書こうと決心しました。みんながガウスの最初の2つの発見について理解できるように、正直に書くことにしました。ガウスは、彼が数学者になることをまだ決めていなかった時代に、ほぼ男の子として、通常の 17 角形の構築に関する作業を行いました。数学。

そして、私はそれを正直に受け止めて、この証明をどこからでもどこへでも書いてみようと思いました。それがクヴァントでの私の最初の出版物でした。そして、それは良い考えだったと思います。それから私は互恵の法則について書きました。

数学者は最も興味深い思想家ではありませんでした。難しい問題やパズルを解けるメガネ男子がいたからです。でもすごい人もいました。そして、私が最初に書いた人物はブレイズ・パスカルでした。

そして始まりました。私は普及者の役割を選びました。私は数学史家ではなく、数学史を語る数学者です。

セミョン・ギンディキン (1984) (「TrV」No. 10 (229), 05/23/2017)
セミョン・ギンディキン (1984)
- 現在、そのようなアクセスしやすいスタイルで、科学に関する本物の科学者の話が不足しています。

- アクセスしやすいだけではありません。つまり、科学の人間的側面です。私たちはすでにこの方向に進んでいたので、ある少年またはその両親が私に何か言ってくれたことを思い出しました。私の記事について、「彼は偉大な科学者を人として語る」と言われました。そして、それはまさに私の自己注文であり、私が望んでいたものでした. 数学の普及の分野での私の仕事はしばらく続きましたが、その後終了しました。

- なぜ？最後の記事は、1985 年から 1986 年に Kvant で公開されましたか?

「それから私は別のことを書きました。私はロシアを離れました。他の言語で書きたくないことに気づきました。数学について英語で書くことはできますが、ノンフィクションの物語や本はできません。たまに講義で話します。私はまだこれらすべてに興味があります。

- 雑誌はたくさんありますが、ロシアには同じKvantが存在します。仕事を続けたいですか？

— 今日の Kvant が何であるかはわかりませんが、当時は単なる人気のある科学雑誌ではありませんでした...

- 過ぎ去った時代...

— アメリカで開催された Gelfand のセミナーについては十分に話しませんでした。アメリカでのセミナーは失敗しました。イスラエル・モイセビッチは楽観主義者でしたが、うまくいかないと確信していました。私はこの失敗にとても腹を立てていたので、行くことさえしませんでした。第一に、モスクワでのゲルファンドのセミナーは無期限に続く可能性があり、その後、夜にモスクワを散歩しました。先日、レニンスキー大通りを車で走っていたとき、昔の考えがよみがえってきました。毎週月曜日は苦痛でした。

そしてアメリカでは反射神経があります。カップルが終わったら、全員が立ち上がって去りました。廊下で出会った方法を覚えています。まったく理解できなかったゲルファンドを完全に失いました。

アメリカの同僚に最初に言ったのは、私は I. M. Gelfand の教師ではなく、彼についての苦情は受け付けないということでした。しかし、イスラエル・モイセビッチはあらゆる種類のトリックを投げ出しました。そこでの生活のすべての民主的な性質のために、セミナーで話す人に「何も理解していない」と言うのは習慣的ではありません。そしてゲルファントは、「はい、彼は素晴らしい人物であり数学者です。私は数学者として彼にこれを話しました。」

非線形方程式を扱った有名で非常に優秀な数学者、Martin David Kruskal がいました。これは、I. M. と同じ強さと気質の男です。 Gelfand が Kruskal の宿題を出したことがあります。彼はレポートを作成し、優秀な学生のように最初の机に座って、マスターの先生が彼に電話するのを待ちます。そして彼は別のことを話します... クラスカルはゲルファントに思い出させます：「イスラエル、あなたが私に仕事を与えたことを覚えていますか？」I.M. は彼にすべてを覚えていると厳しく言います。そして時間が経ちます。ペアがなくなると、全員が去ります。マーティンは再び彼に思い出させます。I. M. は、彼がこれに興味を失ったと彼に話します。しかし、クルスカルのような男でさえ、そのような態度を理解するユーモアのセンスに欠けていました...

それにもかかわらず、セミナーは引き続き運営されており、さまざまな人がそこに来ました。そして、私ははっきりと理解していました。別の言語でいくつかのことを行うのは非常に難しいということです。一番下の息子が結婚したとき、突然、息子の結婚式で外国語を話すのはただの悲劇だと痛感しました。「シンメトリー」という本（この本は非常に数学的な本です）の冒頭で、ヘルマン・ヴェイユは私に非常に近い言葉を言いました。

- ロシアでの科学の普及は盛んです。人気のある科学の講義や科学の祭典に参加する人がますます増えています。同時に、優れた科学はもはや成り立たなくなり、科学に対する一般の関心が高まっているようです。もしかしたら、科学は人々にとってある種のはけ口になるのでしょうか？

- プロレベルではなく、アマチュアレベルで普及が行われています...

「科学者もこれをやっています。たとえば、ゲルファントの孫は講義をよく読んでいます。

- 私は彼の博士論文の監督者でしたが、彼の論文が何について書かれているかはよく知りませんでした. ミーシャはおしゃべりがうまい。教育的能力は彼の祖父から彼に受け継がれました、それは素晴らしいです!

ロシア社会はますます西洋社会に似てきており、同じ価値観を持っていますが、これは非常に危険なことです。科学者が後援を必要とするとき、それは非常に危険です。応用もいいのですが、文化にとって基礎科学はとても重要だと思います。絵画は常に抽象的だったわけではなく、音楽は必ずしもメロディーなしではありませんでした。

数学も比較的遅く抽象化されました。80歳までに、数学のような私たちの生活の驚くべき現象の何かを理解したいと思っています. 今日、このすべてについて書くとしたら、社会の生活についてすべてを説明する強力な教えがあったソビエト時代の生活がどれほど良かったかについて話すでしょう。

また、ある時点ですべての数学者が、あることを研究し始め、別のことを研究しなくなる理由についても考えます。たとえば、17 世紀になると、誰もが突如として微分積分や積分計算、つまり解析幾何学を取り上げるようになったのです。そして、これらの分野で働いている膨大な数の数学者がいました。世紀ごとの分布さえありました-各世紀に何人の偉大な数学者がいました. 18世紀にはほとんどいませんでしたが、6人の名前を付けることができます.

なぜピエール・ド・フェルマーだけが数論に従事し、次の世紀になって初めてこれに関心が現れたのですか? 不明。物理学者はこれを理解しています。彼らは、素粒子の理論や場の理論を、それが可能だと思われる瞬間に構築したいと考えています。あるいは、日本人が首都を放棄して新しい首都を建設したように、なぜ数学者は特定の分野の知識を放棄するのでしょうか?

— 数学的オブジェクトは、ある種の理想的な世界に存在すると思いますか?

「存在は危険で曖昧な言葉です。しかし、少なくともある時点で、何かがあなたの選択を後押しし、目的が達成され、定理が証明されると信じ込ませるような感覚を避けることはできません。数学は、最低限、論理的な結論を伴う形式的な真珠のゲームです。上のどこかからたくさん来ているような気がします。偉大な人でさえありませんが、平均的な数学者です。

詩人たちは、詩がどこから来ているのかを理解しようとし続けました...なぜ、特定のアイデアが数学者の生涯を悩ませているのでしょうか? I. M. Gelfand がこのことについて教えてくれました。もちろん、彼に会うことは私の人生の主な成功です。偉大な人がとても近くにいると、彼はあなたを悩ませ、時には些細なことをあなたに話しますが、一時的なものはすべて排除されます. そして、この人が別の世界と直接通信したことがわかります。これについては他に説明がない場合があるためです。彼はどのようにしてこれまたはあれを知ったのですか？

あなたは彼と一緒に本を書きました。彼は扱いが難しいと聞きました。

「彼と一緒に仕事をするのは難しくありませんでした。でもまた… 50年前に聞いていたら、彼と一緒に仕事をするのは無理だと言っていたでしょう！あなたが彼の家に来ると、彼は電話で誰かと話し、それから別のことをします。私はあなたに、彼は仕事を組織するという点であまり自分自身をコントロールしていなかったと言いました. それはあなたが望む誰のためでもあります。彼は、おそらく、私に向かって叫んだことはなく、誓うこともありませんでした。私自身、性格が悪いのでしょう。

最近、モスクワの数学者の 1 人が、I. M. Gelfand がかつて彼に (彼を仕事に呼んだとき)、Semyon Gindikin と一緒に仕事をすることの否定的な側面について話すことができると言ったことを思い出しました。でも今日、あなたがそのことを私に話してくれたとき、私は少し驚きました。その瞬間、この殻がすべてなくなったとき、彼は数学について話し始めました...そしてそれは奇跡でした! 特にしばらくすると、これの価値が理解できます。

今、私は以前に彼にしようとしたことを何とかすることができました. この本以外にも、かなりの数の作品を書いています。その時、いくつかのことがうまくいかなかった理由がわかりました。

あなたは現在教えていますか、それとも引退しましたか？

-正式にはまだ引退していません。しかし、私は健康上の問題を抱え始めました。両手がうまく動かない。新しい技術がたくさんあるので、ボードに書くのをやめる時が来たと思います。どうやら、もうすぐ教え終わるらしい。

- 何を教えていますか？

- 私の教育​​活動は狭い枠組みの中で行われています。これはモスクワ大学でも、プリンストン大学でもハーバード大学でもありません。それでも、ここの学生の入学はあまり良くありません。しかし、私は最善を尽くそうとしています。私はよく旅行をし、さまざまなイベントで数学について話すのが好きです。日本やオーストラリアに共著者がいると、全く違う人生が開けます。

- あなたが持っている？

- もちろん。そういう意味で、私は世界の一部になりました...

— ロシアの数学は、この解散によって何かを失ったり、得たりしたと思いますか?

— 他のどの国でも、モスクワにあったような数学的生活の集中はないと思います。しかし、常識の観点からは、すべての数学が巨大な国の 1 つの中心に集中することは悪夢のように見えます。そして、モスクワに原爆を投下してすべての科学を失う可能性があるという理由だけでなく、一般的に。しかし、結果は素晴らしかったです。

今日でも、モスクワ生涯数学教育センターの建物の周りを歩いていると、よく知っている数学者や数学学校や数学大学の卒業生にいつも会います。昨日、ここで働いている女性が私に近づき、50 年前に私が第二高校で彼女を教えていたことを思い出させてくれました。モスクワのような数学者の集中は、どこにも見当たりません。パリでは夏に集まることもあります。しかし、1990 年代初頭以前にモスクワにあったようなものは、どこにもありませんでした。しかし、それは消えました。

はい、ロシアの数学は存在し続けています。数学を教え、学び続けている人がいるからです。私たちが会話をしているMTsNMO、ドゥブナのサマースクールがあります - これらすべてが存在します。そして、世界にはそのようなプロジェクトはあまりありません。数学の教え方を知っている数学者がここに残っていますが (私の仲間はほとんどいなくなりました)、これを行うのは非常に困難です。

ニュージーランドやオーストラリアにも行ったことがありますが、シベリアやコラ半島の景色も悪くなく、若い頃に欠けていたという感覚はありません。はい、私は多くの外国の数学者を見たことがありませんでしたが、ここにいた人たちは本当に楽しかったです。私はこの偉大な時代の同時代人であったことを嬉しく思います.

ピーター・セルゲイビッチは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学のメフマートで反ユダヤ主義について話し始めるのが本当に好きではありません。私が例として挙げられているのは、彼が数学者になり、強い人々が「黒い20代」で生き残ることができたということです.それは本当ではない。私は、これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に真面目な数学者になることができたように私には思えます.本当にラッキーでした。まず第一に、すぐに私の同僚や素晴らしい数学者が私の近くにいることがわかったからです。

— Я увидела в «Википедии», что Вы не поступили в МГУ. Вы стали жертвой антисемитской кампании?

— Так я подозреваю. Я никогда не пытался собрать точные доказательства, но...

— Золотая медаль — и не быть принятым на мехмат?!

— Золотая медаль, а еще вторая премия на Московской математической олимпиаде, и не приняли.

— Вас на экзамене заваливали?

— Да, конечно, заваливали!

— Давали сложные задачи?

— Просто нерешаемые. Либо ты знал решение задачи, либо решить ее не мог. Это был не экзамен, это было собеседование. Но мой год был уже сравнительно вегетарианский. Если за пару лет до меня при таких начальных параметрах на мехмат не поступал никто, то в тот год поступили уже несколько человек. А у меня была золотая медаль — и разочарование. Я немало слышал об антисемитизме при приеме, о том, что происходит, но думал, что у меня есть запас прочности и меня это не коснется.

— А как Вы решили, куда поступать, если не в МГУ?

— У меня не было особых советчиков, у меня была довольно простая семья. Я настолько был настроен на мехмат и уверен в положительном исходе... В итоге я поступил в Ленинский пединститут. И более того, для медалиста было уже поздно поступать на физико-математический факультет. Это был случайный выбор от полной безысходности (в 16 лет!).

Я начал учиться на дефектологическом факультете, там было что-то связанное с математикой. Семестр я там проучился. Потом с большим трудом меня перевели на физмат. К тому времени к моей судьбе уже подключились несколько математиков. В учебе в педагогическом институте было много положительных сторон. Во-первых, там работали несколько очень хороших математиков. Из них наиболее ярким был Пётр Сергеевич Новиков. Знаете ли Вы его сына Сергея Петровича?

— Конечно!

— Пётр Сергеевич был удивительным человеком. Мне так повезло с ним встретиться. Он занимался математической логикой и был совершенно фантастическим математиком. Но яркость его таланта не передается полностью ни через статьи, ни через лекции. При множестве хороших математиков он был сингулярной точкой. Умнейший, интереснейший человек во всех отношениях. Помню, на стенах его квартиры я увидел картины «неслыханных» художников (Фальк, Крымов...).

Он был удивительно открыт, охотно поддерживал разговоры на любые темы. Хотя я выбрал заниматься вещами далекими от того, чем занимался П. С. (да и не очень интересными ему!), я много лет пытался сделать что-нибудь достаточно ему близкое, несколько лет вел с ним общий семинар, и опубликовал в связи с этим несколько статей, и даже написал книгу по логике «Алгебра логики в задачах».

Довольно скоро я познакомился с Израилем Моисеевичем Гельфандом. И больше всего моя студенческая жизнь проходила около Гельфанда, которого я считаю одним из двух главных своих математических учителей. Другим был Илья Иосифович Пятецкий-Шапиро. Это был тоже счастливый случай.

Я очень не люблю, когда начинаются разговоры про антисемитизм на мехмате МГУ; меня приводят в пример, мол, он-то стал математиком и сильные люди могли выжить в «черное двадцатилетие». Это неправда. Я знаю многих людей, которым эти события полностью сломали жизнь. И мне кажется, что те, кому не дали поступить, могли стать абсолютно серьезными математиками. Мне действительно повезло. В первую очередь потому, что довольно быстро около меня оказались и мои сверстники, и замечательные математики.

— Вы учились в Педагогическом институте им. Ленина. Вы встречали там Юрия Визбора, Юлия Кима и других?

— Конечно, я многих из них знал, хотя и не очень близко. Многие мои однокурсники стали поэтами, замечательными артистами. Это был один из бонусов той жизни. Культурная жизнь бурлила и интересовала меня, но я участвовал в ней ограниченно, тратя основное время на математику. Рядом был туризм, который увлек меня на всю жизнь.

Там были хорошие очень математики, и там были замечательные ребята, которые поступили туда по разным причинам. Там учился, например, Петя Фоменко, известный режиссер... Вдруг вспомнил, как оказался в конце 1960-х в Алибеке на горных лыжах с Петей Фоменко. Он только что ушел с Таганки. Вижу его на втором этаже двуспальных нар, читающего «Бесов» и уверявшего меня (пессимиста), что он поставит это! А еще его фантастические экспромты... Кстати, и Визбора я встретил — на лыжах, на Кольском полуострове. Он был уже звездой! Мы успели поговорить один вечер, а на следующее утро он страшно сломался, пытаясь съехать с крутого ледяного склона.

— Можете несколько слов сказать об Израиле Моисеевиче Гельфанде? Посещали ли Вы его семинары?

— Конечно. Я написал статью про эти семинары к его 90-летию. Израиль Моисеевич неохотно это обсуждал, но мне кажется, что на его семинары оказал сильное влияние физический семинар Ландау. Гельфанд в какой-то момент хотел заниматься физикой, и поэтому на семинаре было много физических докладов. Я думаю, что Лев Давидович пытался несколько свысока смотреть на Израиля Моисеевича.

Я точно знаю, когда увидел Ландау в первый раз. Это было в 1955 году. Была конференция по функциональному анализу, на которую съехались все лучшие математики страны, — большое событие в Москве. До того времени практически не было конференций. Первая проходила еще до войны. Вся Москва пришла на открытие этой конференции. И Израиль Моисеевич там царствовал, но вел себя чуть сдержаннее, чем обычно на своем семинаре. Первый доклад делал Ландау. И это надо было видеть, это были два великих артиста, которые прекрасно вели свои партии. К тому моменту Израиль Моисеевич придумал вместе с Бобом Минлосом то, что они назвали континуальными интегралами (Боб — мой друг, замечательный человек и математик).

После доклада Ландау Гельфанд пытался ему очень мягко объяснять, что, наверное, эти интегралы — правильный путь для создания теории поля. А Ландау хитро ему отвечал: «Израиль Моисеевич, цыплят по осени считают». Помню, что эта фраза понравилась Петру Сергеевичу Новикову, который сказал: «Да И. М. любит считать цыплят весной!»

Кстати, я был свидетелем еще одного диалога Гельфанда и Ландау во время математического съезда в Ленинграде (около 1960 года). Мы гуляли с И. М. по Невскому, около гостиницы «Балтийская», и встретили Ландау. Помню, что в разговоре опять возникла тема возможности применения серьезной современной математики. И. М. приводил какие-то примеры (кажется, представления группы Лоренца), а Л. Д. был категорически с ним не согласен. Он говорил, что много лет существует раздел «Уравнения математической физики», но он не знает ни об одном существенном применении серьезной математики к физике.

Сегодня мне кажется, что Гельфанд скорее был прав, если посмотреть, какая изысканная математика применяется в современной теоретической физике. По-видимому, Ландау недооценил роль математики в будущей физике (я слышал от моих друзей-физиков, что, возможно, некоторые его ученики дорого заплатили за это).

Если вернуться к семинару Гельфанда, то повторю свою точку зрения. Многих раздражало, что Израиль Моисеевич не допускал никакой демократии. Для него семинар был в некотором смысле главным делом жизни.

Первым впечатлением было, что всё на семинаре происходило экспромтом. Семинар начинался с огромным опозданием. Это Гельфанд объяснял тем, что ожидание семинара было лучшим временем для общения. Этот был ценный для научной коммуникации час, когда люди (поневоле!) разговаривали друг с другом.

Такая абсолютно осознанная неорганизованность была чертой его характера. Он не считал нужным делать всё вовремя. Он полагал, что заслужил право делать то, что ему удобно, и не считаться с общепринятыми правилами. Несколько утрируя: раз ты великий человек, то нужно вести себя так, как тебе ведется. И это даст лучшие результаты. Вежливость не была сильной стороной Израиля Моисеевича. Но не всегда. Он понимал, как и с кем говорить. Все-таки это был человек, который пережил сталинские годы. Впрочем, часто в какой-то момент он срывался и вся ювелирная дипломатия проваливалась в преисподнюю.

Что касается семинаров, для него это было главным делом жизни. Это было место, где он сам понимал большую часть математики, и он считал, что дает другим возможность разобраться в этой математике. И там он был абсолютно раскован. Его манеры, которые, может быть, не всех устраивали, были такой данью, которую должны были заплатить остальные, если хотели получить бенефиты от этого семинара.

За несколько дней до семинара он начинал обдумывать, что на нем будет. Есть воспоминания Пола Халмоша (Paul Richard Halmos), известного математика, занимавшегося также популяризацией, который бывал на семинаре. Там есть целая глава о семинаре, о взаимодействии с Гельфандом, как он его по Кремлю водил. И вот Халмош пришел на семинар, подготовил тщательно доклад; он был большим мастером, его книги были написаны на высоком педагогическом уровне. А тут внешне — какой-то полный беспорядок: Гельфанд задает ему вопросы, разговаривает с другими, вместо того чтобы дать слово докладчику.

Но в модели мира Гельфанда этого беспорядка не было. Сначала семинар был для него как транс, он был готов слушать математику бесконечно; для этого он, как на спиритическом сеансе, вел себя так, как ему велось. И совершенно не всем это нравилось. Причем иногда математики обижались на Гельфанда за других людей.

Но Израиль Моисеевич всегда считал, что, если он позволяет себе сказать какому-то заслуженному профессору: «Ты же ничего не понимаешь!» — то это означает, что к нему он относится хорошо, как к равному. А если он с ним вежливо будет разговаривать, то получается, что он его за человека не держит, и уж точно не за математика. Таким был этот стиль.

Гельфанд считал, что если он допускает людей в свою кухню — не скрывает, как он слушает математику, что он о ней думает, — то имеет право вести себя так. Это моя реконструкция психологии этого семинара, я ее уже описывал. Для любого зарубежного математика посещение семинара Гельфанда было не менее обязательным делом, чем посещение Большого театра. Это было частью такого entertainment’а.

Одной из первых вещей, которую я сделал на Западе вместе с Арнольдом и Масловым, было открытие серии трудов семинаров в Москве и Ленинграде. Ее идеей была попытка передать стиль московских семинаров. На Западе семинары — это короткая чисто деловая вещь. Молодые ученые закончили аспирантуру, защитили PhD и отправились в разные места мира по своим траекториям. А в Москве они оставались навечно. Их не брали никуда, фактически они не могли работать по специальности, они сидели в «ящике», а вечерами приходили на семинар Арнольда или Гельфанда, и начиналась лучшая часть их профессиональной жизни.

И та школа казалась вечной — это была школа, которая никогда не кончалась. Но это был личный выбор каждого, там могли неожиданно нахамить... Для И. М. семинар был действительно его жизнью. Были трудные времена, которых я не застал. Но единственное, за что он боролся, когда его выгнали из университета и из Стекловки, — это сохранить возможность работы семинара.

Он рассказывал, как на семинаре появлялись и садились в первом ряду незнакомые люди. Они погон не носили, но по ним всё было видно. Я слышал от Михаила Александровича Леонтовича, который работал в Курчатовском институте, очень меткую фразу: «Идет человек в штатском, а у него что-то синее на плечах».

Еще был биологический семинар. Это тоже было интересно. Мы по молодости думали, что всё понимаем — как можно было бы это чуть-чуть улучшить и чтобы людей так не дергало.

Израиль Моисеевич эти семинары почти не пропускал; часто он их вел, когда очень плохо себя чувствовал. Помню, один раз в качестве эксперимента он нам с А. А. Кирилловым поручил провести этот семинар. Семинар прошел коротко, с блеском, быстро закончился, все доклады шли гладко, никто никого не прерывал. Но это не был семинар Гельфанда!

— Уже в США?

— Нет, в Москве. Про семинары в США, если Вы хотите, я тоже могу рассказать. Я же с Израилем Моисеевичем работал в Ратгерском университете (Rutgers University). И там этот семинар не пошел...

— Есть такой тезис, что наука не может нормально развиваться без демократии в обществе. Между тем расцвет математики в сталинской России — феномен, который, казалось бы, противоречит этому тезису. Если бы не было этих «почтовых ящиков», «железного занавеса», то семинар Гельфанда не был бы таким успешным?

— Нет. Думаю, что успех семинара Гельфанда был прежде всего обусловлен его личностью. Он придумал такой способ математической жизни. Подчеркну, что московская математика была уникальным, неповторимым феноменом. К моменту нашего разговора где я только не был и чего только не видел. А вот этого я нигде больше не встречал. В чем истоки и природа этого феномена — тема для отдельного разговора.

Математика — это не только наука; для меня она в своих лучших проявлениях ближе к высокому искусству, музыке, поэзии. Ее прикладные аспекты со времен Архимеда часто бывали существенны и замечательны. Взаимоотношения с власть имущими бывали разными и имеют давнюю историю. Почему математика цвела в Афинах, но не в Спарте, почему Платон учил математике в Академии будущих королей, почему геометрия исчезла с закатом Греции, а Рим, взяв многое из Греции, без математики обошелся...

В Советском Союзе математика не была разгромлена так, как биология или лингвистика. Потому что наверху была такая иллюзия (может, и не совсем иллюзия!), что математика хоть на какое-то время нужна для решения государственных задач, в первую очередь военных. Для многих математика в те времена была такой отдушиной. Во-первых, туда всегда тянулись молодые люди «в очках», не от мира сего. А с другой стороны, э

«Кот Шрёдингера» №1–2(39–40), 2018，Математика как очки より
数学者Igor KricheverにGrigory Tarasevichがインタビュー

Igor Krichever:
宇宙の法則は内部のどこかで保護されているように思えてならない．

■証拠に基づく世界
数学者は日常生活の中でどのように決定を下すのですか？誰と結婚するか，休暇にどこに行くか，夕食に何を買うか，ジャーナリストとの会合に同意するかなど．このような問題の解決には，スーパーコンピューターが1日動作しても足りない複雑な多基準モデルの構築が必要です．そのような場合，数学者はどのように行動するのでしょうか？

皆さんと同じです．私は，人生においては数学者も普通の人でなければならないと信じています．そして数学はこれを妨げるべきではありません．

知り合いの数学者の多くは，どんな決定も痛々しいほど受け入れます．そして，それを痛々しいほど後悔します．私にとってすべて簡単なことです．子供の頃，両親が読んでくれたマルシャークの詩（*注）を覚えています．猟師の網に引っかかった鳥についての物語です．鳥は猟師に言います：私は小さく，一口で食べてしまう肉しかありません．放してください．私はあなたに貴重な３つのアドバイスができます．持っていないものを後悔する必要はありません．

私はこのルールに従い，何が欠けているのかではなく，何が先にあるのかを考えようとしています．しかし，これは私が数学者であるということと関係はありません．

（*訳者注）サムイル・マルシャークは，「森は生きている（12か月）」で，私たち日本の子供にも知られている児童文学者，詩人です．ここに引用されている鳥と猟師の会話は，詩「愚かさの物語」の一節にあることを探し当てました．たいへん哲学的な詩なので，私の語学力では十分に理解ができないのですが，概略は以下のようです：３つのアドバイスがあるというので，猟師は鳥を自由にしてあげます．３つのアドバイスとは：
持っていないものを後悔する必要はありません．
過去を取り戻すために無駄なことをして血を流さないよう．
ナンセンスを信じるな世界に奇跡はありません．
ということでした．鳥は猟師をだましたようです．

Самуил Маршак　サムイル・マルシャーク
Сказка о глупости　「愚かさの物語」

http://www.world-art.ru/lyric/lyric.php?id=4351

確かに，引用されている一節があります．
Я ростом с ноготок, Всего комочек пуха Да мяса на глоток. 
Пусти меня на волю, Доволен будешь сам.
Хороших три урока Тебе за это дам.

Запомни мой совет;
Жалеть о том не надо,
Чего уж больше нет.

この詩全体は，上記ウエブサイトをご覧くださいーーーーーーーーーーー

■数学は、考え方を変えますか？

「数学はあなたに考えることを教えます．どんなステートメントも批判的に知覚し，それが何で構成されているか，それがどのように受け取られたか，そしてそれから何が続くのかを分析することを教えます．「証明する」の意味を，人々が常に理解しているとは限りません．
レーニンの古典的な言葉「マルクスの教えは真実であるので全能だ」は，数学者の観点からすると，悪循環です．そのような発言は信頼できません．
数学は私たちにすべてのことを当然と思わないように教えています．丸ごと信じることはできません．

私はアメリカのコロンビア大学でたくさん働きました．
初等数学のコースでは：数式を与え，生徒に何かを計算させます．その後，上級コースが始まります．これは証明がベースのコース，つまり，証明とは何かを説明するコースです．すでに証明されているか，証明されているものから直接派生した要素の連鎖に，ステートメントを分解することは素晴らしい芸術です（*注）．これは長くて難しい旅であるに違いありません．特に，学生時代ではなく，大人としてこの芸術を理解し始めた場合はなおさらです．
（*訳者注）あるステートメント（声明，命題）を，証明済みとその証明から派生するものの連鎖に分解することは，論理的な推論に必要な構造化です．

■ロシアの学校では，「人文科学」という言葉がよく使われます．これは賢いようだが，正確な科学との関係が築かれていないのです．数学を必要としないのでしょうか？

数字を操る機能としての数学は，おそらく必要ありません．統計は社会学や心理学で使われていますが．私の意見では，思考を発達させる科学としての数学は誰もが必要としています．

個人的な例を挙げましょう．私の孫は第57学校の数学の授業を卒業し，現在は高等経済学部の言語学部で勉強しています．数学は彼にとって非常に有用であり，モデルを構築し，何かを計算します．数字を操る算術はまったく役に立たなかったと信じています．彼は論理的に推論し，パターンを特定し，構造化することを学びました．それが最も重要なことであり，算術能力ではありません．退屈な算術は数学ではありません．

繰り返しますが，これは証拠に基づく考え方です．数学は良い眼鏡のようなものです．絵がぼやけないように世界をよりはっきりと見たい場合は，数学を学びましょう．

■信仰と公式

ここでは，厳密な証拠に基づくことがいかに重要であるかを繰り返します．数学的思考は道徳的な選択をするのを邪魔しませんか？会議で手を挙げて，道徳的に間違った決定に反対する必要があるとしましょう．人はこれをしません：論理的な根拠が十分ではないと言って...

この場合，数学的証明を持ち出す必要はないと思います．これは市民の勇気の問題です．あなたの人間の感性で，これが正しいとか間違っているとか感じます．

道徳的な選択は数学的な正当化を必要としませんか？

おそらくそうではありません．宇宙の法則は私たちの内部のどこかで保護されているように見えることがあります．数学は，独自の規則と公理に基づいて，純粋に内部法に従って発展しているように思われます．実験や観察は使用しません．論理のみを使用します．これらはゲームのルールです．しかし，結局のところ，数学は現実の世界を不思議な方法で表現していることがわかりました．つまり，自然の法則は私たちの思考の中に非常に深く隠されています．どのように？誰によって？なんで？私にとって，これは私が答えを見つけることができない謎です．ここであなたは神について考え始めさえします．誰かがそれを私たちの中に置いたのです．おそらく，道徳の法則は同じカテゴリーのものです：それらは私たちの内側のどこかにあります．あなたは何かを信じ，あなたの良心に従って，あなたの考えに従って行動します．少なくともそれが私がそれを理解する方法です．

信仰と証拠の必要性は互いに矛盾していますか？

はい，それらは矛盾しています．しかし，私の仕事では，私はしばしば原則に導かれます：それは美しいので，それは正しくなければなりません．これらは形式化できない概念です．何かがあるという信念，私たちの世界を定義する調和．ただそれを神の奇跡についての素朴な考えと混同しないでください．むしろ，それは世界の正しさへの信念です．私はそれを持ってます．

あなたは世界が正しく配置されていると信じますか？それともあなたはそれを知っていますか？

「信じる」または「知っている」と言うのは完全に正しいわけではありません．私は自然の法則が合理的であると信じています．同時に，私たちの社会の世界は私には深く間違っているように見えます．それは間違った方向に進んでいます．すべてが悪化します．しかし，おそらくこれはただの時代への不平でしょう．

私たちの世界の何が問題になっていますか？例を

人々の考えがシフトし引き裂かれているのは間違っているように思えます．これは特に子供に顕著です．彼らが一人でいることはますます難しくなっています．人々はただ座って考える時間がますます少なくなっています．それは正しくありません．しかし，それは避けられないことだと私は理解しています．

進歩はありませんか？

進歩はそれが進むところに行くのは，自然なプロセスです．それが正しいかどうかはわからない．私はそれが好きではありません．誰もが本は死ぬだろうと言います．本は何か他のものに置き換えられるでしょう．私はそのようなことは好きではありません．しかし，これについて議論することは，風に逆らって唾を吐くようなものです．

避けられない事故
当初は，世界の構造における偶然と必然性の比率をインタビューのメイントピックにしたかったのです．たとえば，シュレディンガーの猫の運命は，粒子の完全にランダムな振る舞いによって決定されることが知られています．そして，ローレンツ蝶はブラジルで羽ばたき，それによってテキサスでハリケーンを引き起こします．それが非常に複雑であっても，非常に異なる現象の間に因果関係があるという事実についての話です．あなたの意見では，チャンスと必然性はどのように相関していますか？

新しい数学的解決策を提案するとき，あなたは創造するようです．しかし，その一方で，あなたはただ何であるかを発見します．会議で，私の偉大な同僚は，詩人がその行を書かなければ，それは二度と現れないだろうと言いました．しかし，あなたが定理を証明しなければ，遅かれ早かれ他の誰かがそれを証明するでしょう．結局のところ，それなしでは，あなたは先に進むことができません．ある意味で，これは必然性であり，数学の発展における予定説です．ここにはランダムなものは何もありません．

しかし，ランダム性は時間の文脈に存在します．発見が今日行われなかった場合，それは後，たぶん5年後，あるいは50年後，あるいは150年後かもしれません．科学の発展は事前に決定されていますが，科学が進む道はほとんど偶然です．

物理プロセスの数学的モデルを構築する場合，ランダムな要素はどの程度重要ですか．

それはすべて，モデル，実際のプロセスの必要な単純化の程度に依存します．コインを投げるとしましょう．実際，表または裏がでるのは常に事前に決定されています．それは，体の初期位置，指によって加えられる力，風，および他の多くの要因に依存します．しかし，表裏のどちらかが偶然にでると想定します．これは実際のプロセスの近似です．十分に正確な場合もあれば，そうでない場合もあります．

あなたの伝記では，偶然と必然性はどのように相関していますか？

私の人生はかなり退屈で，まっすぐです．私がモスクワ州立大学のコルモゴロフ寄宿学校を卒業した後，すべてが比較的明確でした．したがって，おそらく，私は人生における事件の重要性を誇張する傾向はありません．私には，すべてが論理的であり，一方が他方に続いているように思われます．ランダム性は，一般的な背景の小さな波紋です．

あなたがこの寄宿学校に行き着かなかったら？

わかりません...私はタガンログで最高の学校の1つであるチェーホフ学校で勉強しました．数学の先生が，コルモゴロフ寄宿学校に入学した元生徒と一緒に私を連れてきました．もしこれが起こらなかったら，私はモスクワにたどり着くことはなかっただろうし，私の人生は違ったものになっていただろう．しかし，これを証明するのは非常に困難です．私はやはり数学者になると思います．道のりが長くなるでしょうけれど．

物理学など，他の分野の科学者になることもできます．

はい，私は現在の専門分野の数学物理学者です．しかし実際，私はもちろん数学者です．そして，物理学が常に私にとって問題の発生源であったというだけです．

昔々，上司，そして同僚で友人のセルゲイ・ペトロヴィッチ・ノヴィコフと私はボソン弦の量子化の問題に取り組みました．そして彼らはよく言いました：結果として物理理論が何を得るのかは不明であり，任意の代数曲線のために私たちが思いついたローラン-フーリエ基底は数学に永遠に残ります．

同時に，私は問題は外の世界から来るべきだと信じている数学者のその部分に属しています．原則として，それらは最も興味深いものです．過去20〜30年間で，数学の最も注目すべき成果が物理学から生まれたアイデアに関連していることは不思議ではありません．

今日の日本でも，大学教育はグローバル化，ユニバーサル化に対応する必要があり，高校教程で学ぶべきミニマム数学の内容やその達成度テストも適切なものでなければならない．これらの議論は教育数学の研究集会の記事をご覧ください．カリキュラム改革はいつの時代でもなかなか難しい．
改革では今日の数学（統計学やデータ解析など）に目配りする必要があるでしょう．６0年前に遡り，その時代に議論された新数学教科書改革；ソ連，フランス，欧米の先行事例を知ることは大事ではないでしょうか．以下の記事(アレキサンドル･ブヘトフ)からコルモゴロフの改革は何だったか学びましょう．

Падение преобразователя: четыре вопроса о реформе Колмогорова
Александр Буфетов, профессор РАН
«Троицкий вариант» №2(346), 25 января 2022 года

Падение преобразователя: четыре вопроса о реформе Колмогорова • БиблиотекаПятьдесят лет назад в советских средних школах появился учебнelementy.ru
■学校教育の数学コースの改革の一環として，アンドレイ・ニコラエヴィッチ・コルモゴロフが編集した幾何学の教科書がソビエトの中等学校に登場したのは60年前だった．

10年制学校の6年生から8年生向けの幾何学の教科書

学校の数学授業を20世紀の数学に近づけたいという願望は，戦前から叫ばれており，1950年代に活発に議論されました． この論説の著者が10歳の少年の頃，学校の数学の授業が17世紀の数学者の業績(*)で終わっているのを，どこかで偶然読み，非常に驚いたことを覚えているという． その後に行われたことを知る時間はいつあるのでしょうか？（*訳者注）ニュートン，ライプニッツ，デカルト，ベルヌーイ，フェルマーなどの時代.
この論説の著者の生まれる20年前も，アレキサンダー大王の継承戦争の時代の数学者の業績(*)で学校の幾何学コースが終わっていることを知っていたら，もっと驚いたことでしょう．（*訳者注）アレキサンダー大王の死は紀元前323年です．アルキメデス，ピタゴラス，ユークリッドなどの時代．

ユーリ・アレクサンドロヴィッチ・ネレチンは次のように書いています．「私たちの3次元空間は，私たちの考え方と同様に，その時以来，あまり変わっていません」しかし，私たちの3次元空間の考え方が，ユークリッドやアルキメデスの考え方と同じではありません．その時代には，ベクトル計算，平面運動の分類，第5公準の独立性の証拠がありませんでした（ユークリッドの第5公準の解釈はロバチェフスキーの驚くべき業績です）．3つのトピックのうち，キセリョフの注目すべき教科書（改革前の好評な教科書）で触れられているのはそのうちの1つだけ(ロバチェフスキーの幾何学は，キセリョフの教科書の余白に現れています）です．それ以来，学校のコースでの議論はこれ以上詳細にはなりませんでした．その一方，学校の幾何学コースにベクトルと幾何学変換が欠けているのは古くさいとの認識は，戦前からありました．

改革の主な熱狂者の1人は，RSFSRの教育副大臣であり，解析関数の理論に関する古典的な大学の教科書の著者であり，多くの言語に翻訳され，今日まで積極的に使用されている著名な数学者Алексей Иванович Маркушевичアレクセイ･イヴァノビッチ･マルクシェビッチでした．

1960年代初頭，コルモゴロフは改革の作業に参加しました．彼のリーダーシップの下で，新しいカリキュラムが作成され，その後，彼自身が共著者の小さなチームと協力して，非常に短い時間で，代数と解析入門と，幾何学に関する新しい教科書を書きました．

しかし，特に幾何学の教科書は厳しい批判を受け，批判は改革全体に広がりました． 1978年，ソ連科学アカデミーの数学科は，数学の教科書と学校のカリキュラムの現状は不十分であると認識し，コルモゴロフの改革は公式に却下されました．

一方、コルモゴロフによって編集された代数と解析入門教科書は，学校に残り，ソビエト連邦時代を無事に生き延びました．昨年，卒業前と卒業のクラスのための教科書の第26版が出版されました．幾何学の教科書の方は，取り返しのつかないほどの後退をしました．
コルモゴロフの改革は，西側の改革，つまり米国の新数学，そして特にフランスの急進的な数学の近代よりも比類のないほど穏やかでした．たとえば，フランスのリセウムの大学院クラスの1972年の幾何学教科書の目次を開いてみましょう：ベクトル空間，線形写像，多重線形形式，行列式があります．

フランスの最新数学の研究は，膨大な（そしてあまり簡単に見ることができない）文献に結び付けられている．詳細なモノグラフ「新数学の政治史」が最近米国で出版されました．3)
Yu.A.Neretinの注目すべき最近の論文は，コルモゴロフの改革に捧げられています．4)

3） The New Math: A Political History by Christopher J. Phillips. University of Chicago Press, 2015.
4） Ю.А. Неретин, Реформа Колмогорова математического образования, 1970–1980-е годы. arxiv.org/abs/1911.06108

------------------------------------------------

コルモゴルフ　wikiより抜粋ーーーーー
(1903年4月25日 - 1987年10月20日）は、ロシアの数学者。確率論および位相幾何学の大きな発展に寄与した。彼以前の確率論はラプラスの『確率の解析的理論』に基づく古典的確率論が中心であったが、彼が『測度論に基づく確率論』『確率論の基礎概念』（1933年）』で公理主義的確率論を立脚させ、現代確率論の始まりとなった。
1931年に彼はモスクワ大学で教授になり、1935年に、コルモゴロフはモスクワ大学で第1代議長になった。1939年に、彼はソ連科学アカデミーの正会員に選出された。ーーーーーーーーーー

結局，コルモゴロフの教科書改革は失敗でした．改革が不徹底の原因背景について種々論じられています．ここで取り上げたАлександр Буфетовブヘトフの論説の後半部分でも，４つの問題点が語られています．
例えば，数学に割り当てられた時間の15〜20％の大幅な削減．8年制から10年制への移行にともない，なぜ時間を短縮されたのか​​わかりません．週に６時間の数学を決めたのは誰でしょうか？幾何学試験の廃止を決定したのは誰でしょうか？
制約がいろいろあったようです．コルモゴロフが非常に急いでプロジェクトを進めたのは何故でしょうか？健康問題もあったようです．費用も少なかったようです．しかし，当時の時代背景や状況の理解が十分にできていない筆者にはわからない点が多く，現時点でのこれ以上の深入りは止めておきます．もう少し調べる必要があります．
詳細な調査を掲載している別の論説も以下にあります：

Реформа Колмогорова (Kolmogorov reform)mat.univie.ac.at

Замыслы Колмогорова о школьном курсе геометрии • ВидеотекаПоселок Московский, 29.06.2009. Конференция лауреатов Всероссelementy.ru

Вспоминая Колмогорова • ВидеотекаПоселок Московский, 04.07.2006. II конференция лауреатов Всерelementy.ru

 https://elementy.ru/nauchno-populyarnaya_biblioteka/431665/Aleksandr_Shen_Uchenikom_Kolmogorova_ya_ne_byl?from=rxblock

 Александр Шень: «Учеником Колмогорова я не был» • БиблиотекаАлександр Ханиевич Шень — кандидат физико-математических наукelementy.ru
■50年代後半から60年代前半にかけて，さまざまな人々が，微分積分，幾何学変換，ベクトル代数，組み合わせ論，確率論（および統計），複素数，集合論的アプローチ，数理論理学を，詰め込む可能性について議論しました．学校のカリキュラムは，現在のプログラムから何かを省略する必要があり困難な問題です．リストのほぼすべての要素を押し込むことが比較的合理的な方法でできました（統計，積分，および論理を除く）．しかし，いくつかの夢を犠牲にしなければならない難しい決断でした...
幾何学変換で不変となる量に注目していろいろな幾何学（ユークリッド，非ユークリッド，アフィン，射影，トポロジー等々）が定義できます．幾何学的変換の概念に基づいて幾何学のコースを作成するというアイデアは，1905年にエミール･ボレルによってフランスで成功裏に実装され，ソビエト連邦では戦前でも詳細に繰り返し議論されました．ベクトルは，キセリョフにも，ニキチンの初等教科書（コルモゴロフの前身）にも，1969年のポゴレロフの教科書にも含まれていないが，コルモゴロフの改革の枠組みの中で学校の幾何学コースに入りました．

■ポゴレロフの教科書が完成し，使用されました．これは，早くも1969年に行われた可能性があります．

Atanasyan-Butuzov-Kadomtsev-Poznyak-Yudinaの教科書，A.D.Aleksandrov-Werner-Ryzhikによる教科書が書かれ発売されました．教科書の全連合大会が開催されました．

作家が誰にでも好かれることはないのと同じように，1冊の教科書が誰にでも愛されることはありません．すべての教科書には欠点があることがわかります．Wernerによると，教師は教科書を選択できました．1980年代初頭，サンクト・ペテルブルグ市のさまざまな地区で3つの異なる教科書が使用されました．

 https://note.com/sgk2005/n/naa3e06512eb1

ガウス積分

$$I^{2}=\displaystyle \frac{1}{4}\displaystyle \int_{- \infty }^{ \infty }\displaystyle \int_{- \infty }^{ \infty }e^{-(x^{2}+y^{2})}dxdy=\displaystyle \frac{1}{4}\displaystyle \int_{0}^{2\pi }\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdrd\theta =\displaystyle \frac{2\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdr$$
$$r^{2}=X$$とおく，　$$2rdr=dX$$
$$I^{2}=\displaystyle \frac{\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-X}dX=\displaystyle \frac{\pi }{4}$$, $$I=\displaystyle \frac{1}{2}\sqrt{\pi }$$
--------------------------------------------
$$\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\sqrt{\displaystyle \frac{\pi }{\alpha } }$$
$$\displaystyle \frac{d}{d\alpha }\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\displaystyle \int_{- \infty }^{ \infty }dx\displaystyle \frac{d}{d\alpha }e^{-\alpha x^{2 } }=\displaystyle \int_{- \infty }^{ \infty }dx(-x^{2})e^{-\alpha x^{2 } }$$
$$\displaystyle \frac{d}{d\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }=\sqrt{\pi }\displaystyle \frac{d}{d\alpha }\alpha ^{-1/2}=\sqrt{\pi }\left( -1/2 \right) \alpha ^{-3/2}$$
$$\displaystyle \int_{- \infty }^{ \infty }x^{2}e^{-\alpha x^{2 } }dx=\displaystyle \frac{1}{2\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }$$

フレネル積分　　$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{ix^{2 } }dx$$を求めなさい． 
ただし，$$S(x)=\displaystyle \int_{0}^{x}\textrm{sin}t^{2}dt$$, $$C(x)=\displaystyle \int_{0}^{x}\textrm{cos}t^{2}dt$$もFresnel積分と呼ばれる．
ただし，$$S( \infty )=C( \infty )=\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }$$を既知とすると，
$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx+i\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }\left( 1+i \right) $$が得られます．
（参考）Gauss積分　$$\displaystyle \int_{0}^{ \infty }\textrm{exp}[-t^{2}]dt=\sqrt{\pi }/2$$

－－－－－－－－－－－－－－－－－－－－－－－－－－－
これを複素積分法で計算してみます： 
$$I=\displaystyle \int_{0}^{ \infty }\textrm{exp}[ix^{2}]dx=\displaystyle \int_{0}^{ \infty }\textrm{exp}[-(e^{-i\pi /2})x^{2}]dx$$
$$z=xe^{-i\pi /4}$$とおくと，$$dz=dxe^{-i\pi /4}$$だから，　$$I=e^{i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{Re^{-i\pi /4 } }\textrm{exp}[-z^{2}]dz$$

被積分関数$$\textrm{exp}[-z^{2}]$$は，周回積分の領域$$C$$で正則だから，コーシー・リーマンの定理により周回積分は０になる：
$$0=\displaystyle \int_{(C)}^{}\textrm{exp}[-z^{2}]dz=\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz$$
$$z=te^{i\theta }$, $dz=dte^{-i\pi /4}$, $dz=d\theta iRe^{i\theta }$$
$$C_{1}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz = e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}e^{-i\pi /2}]dt=e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{it^{2 } }dt$$
$$C_{2}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}\textrm{exp}[-R^{2}e^{i2\theta }]e^{i\theta }d\theta =$$
$$=\displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}e^{-R^{2}\textrm{2cos}2\theta }e^{-iR^{2}\textrm{sin}2\theta }e^{i\theta }d\theta \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}\textrm{cos}2\theta }|d\theta \leqq $$
$$ \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}(4\theta /\pi +1)}|d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\displaystyle \int_{-\pi /4}^{0}e^{-(4R^{2}/\pi )\theta }d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left[ \displaystyle \frac{e^{-(4R^{2}/\pi )\theta } }{-4R^{2}/\pi } \right] _{-\pi /4}^{0}$$
$$=\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left( 1-e^{R^{2 } } \right) /\left( -4R^{2}/\pi \right) =\displaystyle \lim_{R \to \infty }i\pi (1-e^{-R^{2 } })/4R=0$$

$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }-\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}]dt=-\sqrt{\pi }/2$$
従って，$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}=-\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}$$ より，
$$\displaystyle \frac{\left( 1-i \right) }{\sqrt{2 } }\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\sqrt{\pi }/2$$
$$\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }(1+i)$$

オーギュスタン・ジャン・フレネルFresnel（1788-1827）は，ナポレオン時代のフランスの数学者です．

■フレネルレンズ

フレネルレンズの概念（断面図はwikiより）

フレネルは，フレネルレンズ(1819)やゾーンプレートに名前が残っています．注）ブリタニカ（https://www.britannica.com/technology/Fresnel-lens）によると，レンズの表面を同心円状のリングに分割するというアイデアはFresnelよりも古く，Georges-Louis Leclerc de Buffon（1748）で，フレネルは，1821年に灯台レンズの製造に採用したとあります．ビュフォンもフランスの数学者で確率論の実験「ビュフォンの針」で有名です． 

灯台の凸レンズは巨大で重いのが問題でしたが，フレネルはフレネルレンズを採用してこの問題を解決しました．今日ではプラスチックを用いることで，この原理を使った平板レンズが，ルーペなどの小さいものから，太陽光集光用の大型の製品まで作られています．

https://www.ntkj.co.jp/products/#lens1

 製品情報 | NTKJ Co., Ltd. - 日本特殊光学樹脂日本特殊光学樹脂株式会社(NTKJ)より

■ゾーンプレート

フレネルゾーンプレートは，単色の光を集光することができます．X線や光や電波は，皆，電磁波の仲間ですが，ゾーンプレートは，屈折させて集光するレンズが作れないX線に対しても集光することができます．

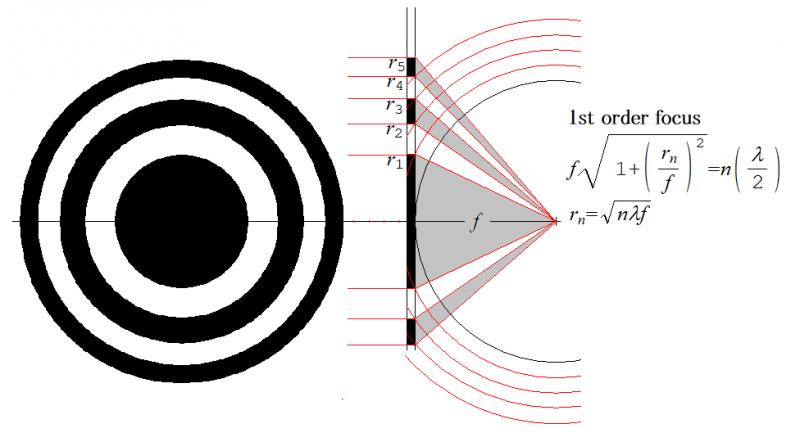
 STXMで使われるX線の集光（バークレイALS，BL5）

■アンテナとフレネルゾーン

フレネルゾーンは，無線通信でも使われる言葉です．無線通信で「見通しが良い」ということは，送信アンテナと受信アンテナの間に障害物がなく，お互いにアンテナが見通せるという意味ではなく，フレネルゾーンが確保されている状態を指します．フレネルゾーンは，送信アンテナと受信アンテナの位置を軸とする楕円体の形で，第1フレネルゾーン，その外側に，第2フレネルゾーン…と広がっていき，隣り合うゾーンの位相は互いに反対です．

私の家の立地では，携帯４Gの電波強度が非常に弱いので，屋外にドナーアンテナを設置してもらっています．私の場合では，800MHz（18バンド）ですが，例えば基地アンテナからdの距離があるとすると，第1フレネルゾーン半径r_1は，r_1＝√(λ･d)/2=9.7mとなります．ただし，λは800MHz電波の波長37.5cm，d=1,000mを用いた．第1フレネルゾーンの楕円体の60%程度が確保できれば良い通信状況と言えますが，この途中で障害物が邪魔をするのです．一般的な話をすれば，地上から高い位置に受信アンテナを設置できれば，第１フレネルゾーンの60%確保がしやすいということになります．

フレネルゾーン計算ツール | 株式会社サーキットデザインwww.circuitdesign.jp

レンズアンテナと反射型アンテナ

電波望遠鏡，衛星放送アンテナは，良く知られるように反射型のパラボラアンテナが使われます．これは，特定の方向からやってくる平行電波を集光する反射型アンテナです．しかし，ゾーンプレートの原理を使って集光するアンテナもあります．

一寸，脱線しますが，ルネベルグレンズは，球形の誘電体レンズ（同心殻で誘電率を変化させている）で，マイクロ波電波を屈折させて集光するレンズアンテナです．球体が乗っているレーターの写真を見たことがおありでしょう．私は昔，衛星放送受信用のルネQアンテナを使用していました．残念ながら今は販売されていないようです．

■フレネル反射率

フレネルは若くして（39歳）で亡くなりましたが，フレネル反射率は死の4年前の発表（1932）です．

物質の表面や界面で反射や透過する光の電場の振幅は，電場の界面平行成分と電束密度の界面垂直成分は連続になります．
物質0と物質1との界面を問題にするとき，この界面で反射される電場の振幅の比ρをフレネルの振幅反射率といいます．エネルギー反射率はρ^2です．
屈折率の低い物質から高い物質に向かう界面で反射するときには，ρが負になりますが，これは振幅の位相が180°変わることを意味します．エネルギー反射率はρの2乗なので負にはなりません．

■フレネルは，光学の分野で色々な研究をしました．そこで現れる数学「フレネル積分」の話をするのが，実は本題ですが，長くなったので，稿を改めて別の機会にします．

Maxwell方程式　[c.g.s.単位系使用] 
$$rot\overrightarrow{E}=-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{B } }{ \partial t}$$    (1a)    電場$$\overrightarrow{E}$$
$$rot\overrightarrow{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$ （変位電流）    （1b）    磁場$$\overrightarrow{H}$$
$$div\overrightarrow{B}=0$$    （1c）    磁束密度$$\overrightarrow{B}$$
$$div\overrightarrow{D}=4\pi \rho$$ (空間電荷)    (1d)    電束密度$$\overrightarrow{D}$$

弱い場では，線形応答が成り立つ： 
$$\overrightarrow{B}=\mu\overrightarrow{H}$$ (透磁率$$\mu=1$$の物質を対象とする)    (2a)    magnetic susceptibility$$\mu$$
$$\overrightarrow{D}=\varepsilon \overrightarrow{E}$$    (2b)    dielectric constant$$\varepsilon $$
$$\overrightarrow{j}=\sigma \overrightarrow{E}$$    (2c)    current density$$\overrightarrow{j}$$，conductivity$$\sigma $$
---------------------------------------------------- 
参考） [MKSA単位系の場合]
$$ \bigtriangledown \times E=-\displaystyle \frac{ \partial B}{ \partial t}$$
$$ \bigtriangledown \times H=\displaystyle \frac{ \partial D}{ \partial t}+j$$
$$ \bigtriangledown \cdot B=0$$
$$ \bigtriangledown \cdot D=\rho $$
ベクトルポテンシャル，スカラーポテンシャルの定義
$$E=- \bigtriangledown \cdot \phi -\displaystyle \frac{ \partial A}{ \partial t}$$
$$B= \bigtriangledown \times A$$
---------------------------------------------------- 
公式　$$[ \bigtriangledown \times \left[ \bigtriangledown \times E \right] ]= \bigtriangledown \left( \bigtriangledown \cdot E \right) - \bigtriangledown ^{2}E$$を使うと，
(1a,b)　→ $$ \bigtriangleup \overrightarrow{E}=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{E } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}$$， $$ \bigtriangleup \overrightarrow{H}=\displaystyle \frac{\varepsilon}{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{H } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{H } }{ \partial t}$$ （３）
（３）の解  → $$\overrightarrow{E}=\overrightarrow{E}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$，$$\overrightarrow{H}=\overrightarrow{H}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$ 　　　（４）
解（４）は，条件（５）の下で成立する．もし，変位電流がなければ，（５）の右辺第２項はない． 
$$\left( \displaystyle \frac{2\pi kc}{\omega } \right) ^{2}=\varepsilon -i4\pi \left( \displaystyle \frac{\sigma }{\varepsilon } \right) $$ (5)
(4)を(1a,b)に代入（$$\sigma =0$$の物質を対象とする．）： 
$$\overrightarrow{k} \times \overrightarrow{E}_{0}=\displaystyle \frac{\omega }{2\pi c}\overrightarrow{H}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
kE_{x} \\[0mm]
0
\end{array} \right] =\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
H_{y} \\[0mm]
0
\end{array} \right] $$ (6a)
$$\overrightarrow{k} \times \overrightarrow{H}_{0}=-\displaystyle \frac{\omega }{2\pi c}\overrightarrow{E}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
-kH_{y} \\[0mm]
0 \\[0mm]
0
\end{array} \right] =-\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
E_{x} \\[0mm]
0 \\[0mm]
0
\end{array} \right] $$ (6b)
$$\displaystyle \frac{c}{n}=\displaystyle \frac{\omega }{2\pi k}$$ (7)
$$\displaystyle \frac{H_{y } }{E_{x } }=\displaystyle \frac{\omega \varepsilon }{2\pi ck}=\displaystyle \frac{2\pi ck}{\omega }\left( =\displaystyle \frac{\varepsilon }{n}=n \right) $$ (8)
$$n^{2}=\varepsilon $$, $$\displaystyle \frac{H_{y } }{E_{x } }=\sqrt{\varepsilon }$$ (9)

境界条件

物質１と物質２の境界では，電束密度の界面垂直成分，電場の界面平行成分が連続することがMaxwell方程式から導ける．
$$D_{1z}=D_{2z}$$ $$ \Leftarrow $$ $$div\overrightarrow{D}=0$$ (10a)
$$\displaystyle \int_{}^{}(D_{2z}-D_{1z})dxdy=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}D_{z}df_{z}=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}div\overrightarrow{D}dV=0$$
$$E_{1x}=E_{2x}$$ $$ \Leftarrow $$ $$div\overrightarrow{B}=0$$ (10b)

$$\displaystyle \int_{}^{}(E_{1x}-E_{2x})dx=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}(rotE)_{y}df_{y}=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \int_{}^{}\displaystyle \frac{ \partial B_{y } }{ \partial t}df_{y}=$$

$$=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial }{ \partial t}\displaystyle \int_{}^{}div\overrightarrow{B}dV=0$$

垂直入射
$$E_{1x}+E_{1x}^{R}=E_{2x}$$
$$H_{1y}+H_{1y}^{R}=H_{2y}$$ $$ \Rightarrow $$ $$n_{1}\left( E_{1x}-E_{1x}^{R} \right) =n_{2}E_{2x}$$
$$\displaystyle \frac{H_{1y } }{E_{1x } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$-\displaystyle \frac{H_{1x}^{R } }{E_{1x}^{R } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$\displaystyle \frac{H_{2y } }{E_{2x } }=\sqrt{\varepsilon _{2 } }=n_{2}$$
振幅反射率 $$\displaystyle \frac{E_{1x}^{R } }{E_{1x } }=\displaystyle \frac{n_{1}-n_{2 } }{n_{1}+n_{2 } }$$， $$n_{1}<n_{2}$$で位相反転
振幅透過率 $$\displaystyle \frac{E_{2x } }{E_{1x } }=\displaystyle \frac{2n_{1 } }{n_{1}+n_{2 } }$$
--------------------------------------------------------
$$n_{1}, n_{2}$$が実数なら，$$\displaystyle \frac{\left| E_{1x}^{R} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }+\displaystyle \frac{\left| E_{2x} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }=1$$
-------------------------------------------------------- 
$$\displaystyle \frac{ \partial \rho }{ \partial t}+div\overrightarrow{j}=0$$
$$\displaystyle \frac{ \partial }{ \partial t}div\overrightarrow{D}=4\pi \displaystyle \frac{ \partial \rho }{ \partial t}=-4\pi div\overrightarrow{j}$$
$$div\left( \displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+4\pi \overrightarrow{j} \right) =0$$
$$rot\overrightarrow{H}=\displaystyle \frac{\varepsilon }{c}\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$
第１項：第２項の寄与率＝$$\varepsilon \omega :4\pi \sigma $$
$$\omega \gg \displaystyle \frac{4\pi \sigma }{\varepsilon }$$ $$\to $$ 誘電体

４．特異値分解の数学

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n

簡単のために，m=5，n=3として，具体的に演習してみましょう．

今回は，昔，私がリコーで関わった懐かしい実験の話をして，特異値分解の数学の話への導入にしたいと思います．まず，実験の話をしますが，私がSTXMに係わったのは，2000年～2004年で，もう20年も前のことです．その後の進歩は著しいに違いありません．当時，実用になるSTXM装置は，Hitchcoch博士が，サンフランシスコ，バークレーのALS（Advanced Light Source）に建設した，BL5.3.2（bending magnet光源利用）　とBL7.0.1（undulator光源利用）の2台だけでした．後年，岡崎の分子研のUVSORに，やはり，Hitchcock博士がSTXMを建設しました．

（注）放射光とは初耳の読者もおられるので，放射光施設とは何かを簡単にお話しておきます．ドーナツのような真空リングの中を，光速に近い速度に加速された電子が回転しています．回転するといっても電子の軌道が円形というわけはなく，リングの要所要所に偏向磁石bending magnetが配置されていて，偏向磁石の所で電子は曲げられるので，電子の軌道は多角形です．電子が方向を変えるときには，電磁波（白色光の光やX線）を放出します．これが放射光で，いろいろな測定に放射光を利用します．リングの電子蓄積エネルギーとはリング内を回転する電子のエネルギーのことです．ALSでは1.9GeV，兵庫県のSPring8では8GeVです．蓄積エネルギーの大きさは，放出される放射光のエネルギーの最大値を決めるので，SPring8は硬X線の光源，ALSは軟X線の光源となります．
放射光の光源は，偏向磁石bending magnet光源とundulator光源とがあります．undulatorというのは周期的に配列した磁石のことで，蓄積リングの電子軌道の直線部に挿入します．周期的磁場で電子は蛇行運動をしますが，その軌道のFourier変換に相当する波長のX線（準単色光）が放射されます．

さて，STXMに使うALSの放射光リング（蓄積電子のエネルギーが1.9GeV）は，軟X線の光源です．軟Ｘ線の領域は10^2eV～10^4eVの範囲で，炭素など軽元素の1s（K殻電子）の励起（光電効果による電子の放出）は，このX線の領域にあります．硬X線と違い，軟X線は空気で減衰しますからその測定は，He置換した真空チェンバー内で行います．炭素の1sの吸収スペクトルNEXAFS(吸収端近傍の吸収微細構造)は，分光して単色化したX線ビームを薄膜試料に透過させ，その吸収を測定して得ます．スキャンするエネルギー範囲は，280eV～310eVで，スキャンステップは0.1eVですので，スペクトルは300点ほどのデータ数になります．

目次
これから始まるこのテーマの話には4つの側面があります．
第１は，ニュースとしての一般向け報道．
第２は，STXMの装置の仕組み．
第３は，材料科学の側面．炭素1s吸収端近傍の吸収スペクトルNEXAFS．
第４は，データ解析の数学．特異値分解．

技術者向け教育の場合にお話しするのは，第１，２の部分です．第４の部分は，Hitchcock博士らの開発したaXis2000というソフトウエアを用いるので，数学を意識することはないのですが，今回は，特に，第４の数学の話に注目することにします．番号順に順を追って話ます．

１．一般向け報道

せっかくの記事ですが，技術の解説が正しくありません．ここで言及しているデータベースは無関係で，この記事はピントがずれているのが残念です．

２．STXM（ScanningTransmissionX-rayMicroscopy）装置

放射光X線をFresnel Zone Plateで，試料薄膜上にフォーカス（22nmΦ）させ，その微小ビームを試料薄膜に透過させ，微小ポイントの吸収スペクトルを測定します．スペクトルを得るには入射するX線のエネルギーを280eV～310eVの範囲で，0.1eVの分解能で変化させます．これは，色を変えて見る実験に例えるとわかりやすいでしょう．同じ材料薄膜でも，赤い色を透過させてみた場合と青い色を透過させてみた場合とでは異なるでしょう．試料薄膜（ミクロトームで加工した厚さ100nmの切片）上をラスタースキャンすることで，そのエネルギーで見た薄膜の吸収画像が得られます．
薄膜に入射するＸ線エネルギーを280eV～310eVの範囲で変えて測定した300枚ほどの吸収画像をスタックすれば，薄膜試料の各点(x, y)の吸収スペクトルμ(x, y)が，point to pointで得られたことになります．試料上の空間分解能は約30nm，スペクトルのエネルギー分解能は0.1eVという高性能な測定です．私たちは装置を使う純粋ユーザーでしたが，私は，このような装置を開発したHichcock博士グループの技術と装置の仕組みに興味を持ちました．ここでは，STXM装置の重要な要素であるゾーンプレートとその制御についてとり上げましょう．

ゾーンプレートの焦点距離は波長で変わります．入射するX線ビームのエネルギーがスキャンされれば，そのつど瞬時にフォーカスしなければなりません．これは，レーザー干渉計とゾーンプレートの載るピエゾステージで行われます．試料点の（x, y)スキャンは試料台のピエゾステージで行われます．
BL5.3.2はbending mgnetからの放射光（undulator光源よりは光強度は弱い）ですが，照射された点の有機物はダメージを受けますので，できるだけ高速で測定します．そして，試料の変質がなかったかどうか測定前後でチェックする測定ルーチンもあります．X線のエネルギーを変えて測定した吸収画像をスタックしたとき，サンプル位置のずれがあれば自動修正できます．

以下で，STXM装置で最も主要な素子であるFresnel zone plateについて，詳述しましょう．zone plateは，外径45000nm，最外輪帯幅35nm程度のものです．下図のゾーンプレートは，波長λのX線の単色光を集光します．黒い部分はX線を通しません．例えば，中心の黒丸はダイレクト光をストップし，輪帯環の白い部分を通過してくる行路長　f+λ/2，f+3λ/2，f+5λ/2，････のものが，焦点距離fに集光できます．

 このようなフレネルゾーンプレートの後ろにOSAという絞りを置いて，行路差λずつの光線（１次のフォーカス）のみが試料位置に集光するように調整します．

 入射X線のエネルギーを変えたときのゾーンプレートの焦点距離の調整は，レーザー干渉計を用い精密制御されています．

３．炭素の1s電子の吸収端直上の微細構造スペクトルNEXAFS

電子写真で使われるトナーは，カーボンブラックとか顔料色素で出来ていると思っている人がほとんどでしょう．実際には，このような黒やカラーの色素だけでなく，樹脂，ワックス，電荷制御剤など，複数の有機物分子が，1粒のトナー中に分散されており，それらの分散状態は，トナーの性能に影響を与えます．設計通りの分散状態が実現しているか評価することが必要です．高精細トナー1粒のサイズは数μmという微細さで，その中の物質の分布状態を30nmΦの分解能で調べる必要があります．しかも，混合されている物質は，皆，有機物ポリマーで元素分析をすれば，どれも主成分は炭素です．つまり，炭素が骨格のよく似た有機分子が混合している状態の分布マップが知りたいのです．これを化学状態マッピングといいます．

下図には，色々な物質の炭素1s電子のNEXAFS吸収スペクトルを載せました．X線のエネルギーを変えて観察した透過像も載せています．例えば，①カーボンブラックの分布する場所は292.5eVのX線エネルギーで見ると吸収が大きいため白っぽく見え，②ワックスの分布する場所は，287.8eVで見ると吸収のためX線の透過が悪く白っぽく見えます．同様に，③樹脂の分布する場所は，284.3eVのX線の透過像では白っぽく見えます．
エネルギースキャンにともなう画像変化のパラパラ動画を作って見るとわかりやすく面白いものです．

 化学状態（元素分析ではない）という意味は，トナー中に分散している物質は，すべて有機分子（どの分子もほとんど炭素元素で出来ている）なので，元素分布のマッピングでは差がありません．炭素原子が骨格の有機分子の吸収スペクトルは，炭素の1sの吸収端285eV付近にあり，その炭素原子がどのような化学結合状態にあるのか（1重結合か，2重結合か，π電子系か，どのような官能基と結合しているか）により，吸収端から高エネルギー側に観測される吸収スペクトルの微細構造（NEXAFSという）に違いがでます．
トナー中の有機ポリマー分子の分布マップを得るには，化学状態マッピングがどうしても必要になります．
元素に特有な特性X線を検出すれば良い元素分布マッピング［TEM（分析電顕）でも，放射光でも，微小領域の蛍光X線分析は普及している］と，化学状態マッピング［微小領域のpoint to pointで炭素1sのNEXAFSの測定が必要］は，全く異なる技術であり，我々の目的には，STXMでの実験が必要でありました．

リコーが，Adam P. Hitchcock（McMaster University）博士が開発したALS（バークレー，AdvancedLightSource）のBL5.3.2に設置されたSTXMで共同研究を行ったのは，2000~2004年のことです．

実験で得られるデーターセットは，試料表面の座標を（x, y）とすると，試料表面のラスタースキャンと，透過させるX線のエネルギーωのエネルギースキャンを行って，point to pointで収集した吸収スペクトルμ(ω；x, y)です．
再度たとえ話をすると，膜を透過する光のコントラスト像は，光の色を変化させると透過光の像のコントラストが変わって見えるというわけだ．

このような，データセットの収集と解析は，Hitchcock博士の開発したソフトウエアaXis2000を用います．この解析のために用いる数学は，特異値分解です．この先は，４．特異値分解の数学に続きます．

４．特異値分解

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n
簡単のために，m=5，n=3として，続編で演習してみましょう．続く...

参考-----
特異値分解を使いますが，特異値分解の概念図は以下のようなものです．

以下の拙著の第3章p64～p84から抜粋転載しました．

https://www.amazon.co.jp/dp/4774143936?tag=note0e2a-22&linkCode=ogi&th=1&psc=1

■特異値分解

複素行列$$A(m \times n),m \ge n$$は，適当なユニタリー行列$$U(m \times m)$$と$$V(n \times n)$$を用いれば，
$$UAV^{ \dagger }=\mit\Sigma $$，あるいは，$$A=U^{ \dagger }\mit\Sigma V$$に分解できる．これを，Aの特異値分解という．
(ただし，$$V^{ \dagger }$$は$$V$$の共役転置行列．$$A$$が実数行列の場合は転置のみ$$V^{'}$$）．

$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$

ここで，$$\sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$を$$A$$の特異値と呼ぶ．
$$r$$は$$\textrm{rank}(A)$$に等しい．

$$AA^{ \dagger }=U^{ \dagger }\mit\Sigma VV^{ \dagger }\mit\Sigma ^{'}U=U^{ \dagger }\mit\Sigma ^{2}U$$,      $$ \because \Sigma \Sigma ^{'}=\Sigma ^{2}(m×m) $$
$$AA^{ \dagger }$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$m-r$$）
$$A^{ \dagger }A=V^{ \dagger }\Sigma ^{'}UU^{ \dagger }\Sigma V=V^{ \dagger }\Sigma ^{2}V$$,      $$ \because \Sigma ^{'}\Sigma =\Sigma ^{2}(n×n)$$
$$A^{ \dagger }A$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$n-r$$）

線形写像 $$ y=Ax  (x∈C^{n}，y∈C^{m})$$があり，それぞれの空間でユニタリ変換； 
$$ x'=Vx$$, $$y'=Uy$$をすると，$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている．

■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して，
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める．
特異値分解ができたら；$$UAV'=\Sigma$$，$$A=U'\Sigma V$$が成立している．
（$$A$$は実行列なので，$$U，V$$は直交行列となり$$U'＝U^{-1}$$などの性質がある．）
最小2乗法は，$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる．
$$\textrm{rank}(A)=r≦n<m$$とする．$$\Sigma (m×n), V(n×n), U(m×m)，x(n×1)$$の型であった．

$$r=n$$の場合を考える．

$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$,　$$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから，
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方， 
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って，$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると，第1項は0になり，第２項は残差の２乗を与える，

$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る．

１．結晶空間群．結晶点群

結晶は周期的な内部構造を持ちます．周期的な離散空間を＜結晶空間＞と言い，
その対称性は<結晶空間群>で記述します．結晶空間群の種類は，3次元では230種類です．
3次元の周期構造の幾何学的な表現を＜格子＞と言ったり，その数学的な表現を＜並進群＞と言ったりします．
結晶空間の中で，格子分だけ移動しても，周囲の状況は移動する前の状況と全く同じなので，無限に繰り返す結晶の中で自分がどこにいるか区別できません．そこで，格子分だけ移動した点はすべて同値とみなして，
無限に広い結晶空間を１つの単位胞の中に畳み込んでしまうことができます．
あたかも，無限に続く時間を，時計の文字盤（12時間）に畳み込んでしまうのと同じです．
＜単位胞＞（有限図形）の対称性は＜点群＞で記述でき，3次元の＜結晶点群＞は32種類です．

（注）＜結晶点群＞の対称操作は周期性と両立しなければならないので，ただの点群とは異なり，
回転対称は２，３，４，６回軸に限定されます．

格子を法として（あるいは，並進群を核として）準同型写像をすると，結晶空間群の230種類を，結晶点群の32種類に還元できます．

 $$\mit\Phi /T \cong G$$ ,     $$T \vartriangleleft \mit\Phi $$    ($$\mit\Phi $$結晶空間群，$$T $$並進群，$$G$$結晶点群）

２．双対空間．コンボリューションのFourier変換．Curieの原理（因果律）

結晶格子をFourire変換すると逆格子が得られます．結晶格子（$$r-$$空間）と逆格子（$$R-$$空間）は，Fourier変換で移り変わる互いに双対な空間です．結晶の電子密度関数$$ρ(r)$$とそのFourier変換F(R)は，1:1に対応し，両者の対称性は同じです．

電子密度分布$$ρ(r)$$により散乱されるX線の散乱振幅は$$F(R)$$で，$$ρ(r)$$のFourier変換にほかなりません．観測される散乱強度は$$|F(R)|^{2}$$で散乱振幅$$F(R)$$の位相情報は失われます．

 $$Tr[\rho (r)]=F(R)$$,     $$Tr[\rho (r)*\rho (r)]=|F(R)|^{2}$$

結晶の対称心の有無にかかわらず，観測されるX線散乱強度には，対称心が生じます：$$|F(-R)|=|F(R)|$$，これをFriedel則と言います．

Friedel則は，もっと大きい次のCurieの原理の一部です．

原因である「結晶構造の対称性」は，結果である「その結晶で生じる現象の対称性」に反映される．

（例1）結晶構造に，4回対称性が存在すれば，Ｘ線回折像の対称性に，少なくとも4回対称性は反映される．しかし，Ｘ線回折像に4回対称性が存在しても，結晶に必ずしも4回対称性が存在するわけではない．
これを回折対称の上昇という．

（例2）Ｘ線回折像に10回対称（5回対称⊗Friedel則）があったとしても，その原因たる結晶構造に5回対称性があるとは限らない．結晶構造の5回対称性は周期性（結晶の定義）と矛盾するのであり得ない．しかし，周期性を外せばあり得る．準結晶のモデルは，非周期のペンローズ・タイリングで実現できる．

３．点集合とベクトル集合．ホモメトリック

結晶構造（点集合）の対称性と，回折強度像（点集合のベクトル集合が作るスター）の対称性の関係を考察しましょう．両者の対称性では，回折強度像の対称性が高いわけで，与えられたベクトル集合から点集合を推理するのは，面倒な逆問題になる場合がある．

一般に，回折強度像の対称性から結晶構造の対称性は，一意に定まらず，同一の回折強度像を与える結晶構造が複数存在する可能性があります．これらをホモメトリック構造という．
下の2つの図は，1次元のホモメトリック構造の例［Patterson(1944)］．
（注）この図の見方は，1次元の単位胞が全円周（長さ1）です．図中に描き込まれた長さは円弧に沿って測ります（弦の長さではない）．円周（長さ１）のどこか1点で切って，線分（長さ１）に延ばします．この線分を1次元のタイルのように並べていくと1次元の周期的な図形になります．この図形には黒い点が並んでいますが，2つの図形で黒点の配列は異なります．それにもかかわらず，出現する黒点間の間隔の種類は2つの図形で同じになります．

PCR検査の統計と論理　　　　　　　　　　　　　　　谷　克彦

（要旨）
◆PCR検査の感度と特異度は，遥かに1に近い確率でした．偽陰性や偽陽性を理由に検査数をコントロールする理由は成り立ちません．検査を拡大し有病者を発見し早期隔離しましょう（感染から5日目頃が最もウイルスを放出し，有病者の半減期は10日位です）．◆日本の陽性率は7%と計算できますが，最近の変動の勾配（末尾に掲載）から見ると10%を越えたように見えます．このグラフがそのように見えるのは，検査数を抑制しているために陽性者数のオーバーフローが起きている証拠かもしれません．
---------------------------------

COVID-19パンデミックは，実効再生産数を1より低下させると鎮まります．この対策は，次の３つの数値を下げることです；①感染者が感染力を持つ期間，②感染者が接触する人数，③感染者との接触で感染する確率．そして，それぞれに対する施策は以下のようです；
①感染者を早期に発見し隔離する．このためにPCR検査の拡充が必要．
②効果的なロックダウンの期間，地域，方法を，シミュレーションで予測し戦略的に介入する．
③ワクチン接種で，感染感受性のある人の割合を減らす． 

COVID-19に感染すると，次のような経過になります． 

感染（陽性）→潜伏無症状期→発症期（無症状もありうる）→回復（陰性）or死亡
陽性の期間［潜伏無症状期＋発症期（無症状もありうる）］は，「罹患者」が感染源となる有病状態なので「有病罹患」と呼ぶことにします．感染源となる「有病罹患」（症状の有無にかかわらず）を早く発見し隔離する必要があります．
有病罹患者の発見はPCR検査でなされます．検査の目的は蔓延率の推定だけではなく，感染源となる有病罹患者をできるだけ早期に探し出し隔離するという緊急な役割があります．検査対象を限定し，検査の陽性的中率を上げることが検査の目的になってはいけません．
実世界の現象は，多数の原因と結果が複雑に絡んだ因果関係をなし，数学（統計）で論理的に推論するのは，その一部を切り取った世界です．その範囲で得た数学（統計）的推論の結果を，系全体の中で解釈できる論理的な思考が必要です．
正しい数学（統計）推論で得られた結果でも，複雑な全体系で非論理的に利用されるとしたら，社会を誤った方向へ導く主張に，数学が加担してしまうことになります．PCR検査の規模拡大は有病率の低い集団ではすべきではないというのは正しい主張ではありますが，その主張の根底にあるPCR検査の性能から見直し，これを論理的に考察してみましょう．

■有病率とは
日本感染症学会の定義によると，有病率とは，「その疾患をもっている人数の全人口に対する割合」ですが，日々発表される厚労省の新規陽性者数と検査数のデータから，日本の有病率を計算できるように，有病率$$x_{0}$$の解釈を次のようにします．
（定義）$$有病率=有病罹患数/累積PCR検査数$$
　　　　 　　　$$有病罹患数＝累積検査陽性者数－累積回復退院者数－累積死亡者数$$
これにより，日時（$$T=$$5月15日）の日本の有病率を求めると$$x_{0}=0.58$$％になります．
ここでは，陽性者=罹患者と見なしています．
この検査集団の陽性率($$T$$)と罹患率($$T$$)は，7日平均（8～１５日）を用いて，
$$陽性率(T)=陽性者(T)/検査数(T)=6288/92167=0.068$$，
罹患率(*)$$(T) =陽性者(T)/累積検査数(T)=6288/13015244=0.0005$$

日時$$T$$の有病罹患数$$(T)$$を別の定義で表現してみましょう．有病罹患状態は，14日位で回復（陰性になる）します（運悪く死亡の場合もありますが，少数のため無視します）．今日$$T$$の有病罹患者（感染源となる罹患）の中には，$$t$$日前に罹患した者も残っています．そこで，次の定義が成り立ちます：
有病罹患数$$(T)=\displaystyle \int_{0}^{T}$$罹患数$$(t)p_{a}(T-t)dt$$，
ここで，$$p_{a}(t)$$は，陽性保持確率（病気の減衰関数のような性質）で，（付録３）の大規模調査の結果に報告されています．病気の感染初日を推定するのは大変難しいのです．PCR検査で見つかった日が感染日という訳ではないでしょう．感染から5日目あたりが，感染者が最も多くウイルスを放出するので，その頃が最も発見され易いのではないかと思います．
病気減衰関数の半減期は約10日ですので，コンボリューション積分は次のように近似できます：
有病罹患数$$(T)=10×罹患数(T)$$．この集団の累積検査数で規格化すると．
$$有病率(T)=10×罹患率(T)$$が得られます．
注*）感染症学会の定義では，罹患率の分母は，「集団の感受性のある人数」ですが，ここでは「集団の人数」としています．

■PCR検査の感度と特異度
PCR検査の感度$a$とは，罹患者をPCR検査で陽性（$$+$$）と正しく判定する確率のことで，真の罹患者でもPCR検査が陰性（$$-$$）（偽陰性）と判定される確率は$$1-a$$程度あります．検査の特異度$$b$$とは，非罹患者を正しく陰性（$$-$$）と判定する確率のことで，非罹患者を陽性（$$+$$）（疑陽性）と判定する確率は$$1-b$$程度です．

確率$$a , b$$は１に近いほど，優秀な検査になります．従来の議論に用いられてきたこれらの数値は，$$a=0.70, b=0.99$$ですが，昨年の英国ONSによる大規模調査（付録３．)で判明した数値は，$$a=0.95(0.85 ~ 0.98)$$，$$b=0.9992$$です．
低い有病率の集団でPCR検査対象を拡大すると，莫大な偽陽性が出て医療崩壊につながるので，有症状者や濃厚接触者に限定して検査を行っているとの主張がありますが，英国ONS調査の感度と特異度を採用すると，この主張の根拠が覆えることを検証します． 

■ベイズ推定による有病罹患の内訳

この集団の罹患率を$$p(罹患)=x$$，とします．この集団で，PCR検査が$$+$$判定のとき，罹患者である確率$$p(罹患|＋)$$，および，$$-$$判定のとき，罹患者である確率$$p(罹患| - )$$，などを推定しましょう．
$$p(罹患| + )=p( + |罹患)･p( 罹患) /p( +) =a･x/( a･x+(1-b)( 1-x)) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) x/\left( (1-a)x+b\left( 1-x \right) \right) $$， 
$$p(非罹患|+)=p\left( + |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( + \right) =(1-b)(1-x)/\left( (1-b)(1-x)+a \cdot x \right) $$,
$$p(非罹患| - )=p\left( - |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( - \right) =b\left( 1-x \right) /\left( b(1-x)+(1-a)x \right) $$，
下に$$x$$を変数とするグラフを示します．ベイズの定理は線形システムなので，重ね合わせができ，罹患状態を束ねた状態で定義される有病率$$x_{0}$$を入力にしても良いでしょう． 
■集団の有病率 $$x=0.006$$に対して，感度$$a$$，特異度$$b$$を変えて比較
（１）$$a=0.95, b=0.9992$$（英国ONS）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.9:0.1$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.9:0.0003$$
（２）$$a=0.7, b=0.99$$（従来）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.3:0.7$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.3:0.002$$
PCR検査が$$+$$判定であるときに，真陽性の確率$$p(罹患|+)$$と，偽陽性の確率$$p(非罹患|+)$$を比較すると，従来用いられている感度，特異度では，偽陽性確率が真陽性確率の$$2.3$$倍もありますが，英国ONSの数値では，逆に1/10になり，医療崩壊を懸念する根拠にはなりません．
いずれにしろ，陽性確定までにPCR検査は2度行われ，さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．

次に，真陽性の確率$$p(罹患|+)$$と偽陰性の確率$$p(罹患|-)$$を比較すると，
（１）では，$$1:3 \times 10^{-3}$$，（２）では，$$1:7 \times 10^{-3}$$で偽陰性は小さい確率です．これを人数で比較するには，陽性率$$y=0.07$$，陰性率$$1-y=0.93$$を，それぞれ，$$p(罹患|+)$$と$$p(罹患|-)$$に乗じます．
（１）では，$$真陽性人数:偽陰性人数=1:4 \times 10^{-2}$$，
（２）では，$$真陽性人数:偽陰性人数=1:9$$
この集団の陽性率は$$7$$％と低いので，陰性集団が大多数で，偽陰性の確率が小さくても偽陰性者数は多いとの主張もあります．確かに，従来の数値（２）を用いると，真陽性者の9倍もの偽陰性者がいます．しかし，数値（１）を用いると，偽陰性者の数は1/100で，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

■PCR検査数は十分か
ここに引用した２つの図は，1日の$10^{6}$人あたりの（横軸）検査陽性数：（縦軸）検査数の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは日本のものより縦軸で25倍，横軸で16倍大きいのでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間経過とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を拾い出す十分な検査が行われているようです．英国の例を見ると，始めは，陽性者が多く検査数が間に合わないほどでしたが，現在みられる検査数を増しても陽性者が一定となる状態は，十分な検査数が確保されている証拠です．日本の例で，検査数と陽性者数の増減の比例が見られる傾向は，検査数を増やせば，陽性者数も増加する可能性があります．
これらの図は，2020.1.25～2021.5.25の期間のもので，赤細線は，日本の図では，陽性率5{\%}と10{\%}の勾配，英国の図では，0.5{\%}と２０{\%}の勾配を示しています．
これらのグラフは，https://ourworldindata.org/coronavirus-testingから引用しました．

■付録－－－－－
付録１．ベイズの定理
条件付き確率についての「ベイズの定理」とは次のように説明できます．
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
ただし，記号の意味は例えば以下の様です．
$$p(X)$$:$$X$$が起こる確率 
$$p(Y|X)$$：$$X$$が起きる条件下で，$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きる条件下で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

付録２．PCR検査の原理
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を40回程度繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です．

付録３．英国ONSのcovid-19感染の大規模調査
英国国家統計局（ONS)によるcovid-19の大規模感染調査は，パイロット調査としてイングランド（2020.4末）で開始されました．7月以降，規模を拡大し，住所リストから世帯のランダム・サンプリングを行い，8月には，2週間ごとにテストされるサンプルを，イングランドで15万人，ウエールズ，スコットランド，北アイルランドで各1.5万人の規模に拡げました．調査は，小児の症候性および無症候性感染の有病率と発生率を知るため，2歳以上の子供を含みます（参照：covid-19学校感染調査）．16歳以上の成人の20{\%}は血液サンプルの提供を求められました．2020.7.31～9.10の6週間で，208,730の検体調査を行いました．偽陽性は症状のない人で発生すると予想されましたが，調査研究のデータからは，症状の有無によらず同じでした．血液サンプルは，オックスフォード大学で，抗体検査，IgG免疫グロブリンのテストをしました．
PCR検査に関する知見は；その感度が，85{\%}～９８{\%}(95{\%}である可能性が最も高い)にあり，特異度は，99.92{\%}でした．
綿棒スワブの検体採取は，適切な監督下で行えば，自己採取でも医療従事者が直接採取した場合と同様の正確な結果になることも報告されています.

引用データ

1)厚生労働省 
2) Coronavirus (COVID-19) Infection Survey, UK Statistical bulletins
3) Keeping up with COVID-19, Rachel Thomas;
https://plus.maths.org/content/keeping-covid-19
4) https://ourworldindata.org/coronavirus-testing

2021年3月に，2021年のアーベル賞の受賞者が発表されました．ラズロ・ロヴースLászló Lovász（ハンガリー科学アカデミー・レニェイ数学研究所）とアヴィ・ウィグダーソンAvi Wigderson（プリンストン高等研究所）です．
プレスリリースによると，「理論計算機科学および離散数学への基本的な貢献，および，これらの分野を現代数学の中心的な分野として確立するのに果たした主導的な役割」が評価されました．
アーベル賞は，2002年にノルウェー科学アカデミーによって設立された数学で最も権威のある賞の1つです．ノルウェーの天才数学者ニールス・ヘンリック・アーベル（1802–1829）にちなんで名付けられ，この分野の発展に多大な貢献をした科学者に毎年授与されます．

2021年の受賞者について，ステクロフ数学研究所，シカゴ大学（米国）の数学科アレクサンドル・ラズボロフ教授による解説記事を要約紹介します．
「トリニティオプション-科学」第6号（325），2021年3月23日号
https://elementy.ru/nauchno-populyarnaya_biblioteka/435811/Troitskiy_variant_Nauka_6_325_23_marta_2021_goda

離散数学は，有限の離散的オブジェクトの特性を研究します．その重要な部分は，伝統的には組み合わせ論と呼ばれ，「純粋」数学で生じる構造に動機付けられています．たとえば，組み合わせの観点から，トポロジーの基本である複体の概念は，複体の面に対応する有限集合の閉じたファミリーにすぎません．組み合わせの抽象化は顕著な結果をもたらし，「有用な」（つまり，基本的な数学に適用される）組み合わせ論は，数学界で常に重視されてきたのは当然です．

離散数学は，「ハンガリーの数学」と長い間関連しており，その最も活発な支持者および宣伝者は，ポール・エルデシュでした．ラズロ・ロバースは1948年にブダペスト（ハンガリー）で生まれ，この数学的文化の中で育ちました．特に，彼はかなり早い年齢でエルデシュに会いました．そしてこれは彼のその後のキャリアと展望に非常に大きな影響を与えました．ラズロ・ロバースは，ポール・エルデシュの直接の後継者と見なすことができます．

　　　　　　　　　ラズロ・ロバース

理論情報学の形成
理論計算機科学，または，コンピュータサイエンスは，一般に「計算の複雑さの理論」の基礎が築かれた1970年代頃に独立した分野として出現しました．この分野では，大まかに言えば，アルゴリズムの存在の問題，または多くの場合，それらの効率に与えられた制約を伴うアルゴリズムの非存在が研究されます．

その名称にもかかわらず，理論計算機科学は厳密に数理科学であり，そのすべての成果は，数学の他の分野と同様に，厳密な定義，定理，および補題の形で定式化されています．それにもかかわらず，開発の内部論理とともに，理論情報学もまた，実際のアプリケーションによって大部分が導かれ，時には非常に具体的であります．他の「半応用」分野と同様，それに対する「純粋」数学者の態度は，穏やかではあるが長い間警戒していたことは明らかです．

アヴィ・ウィグダーソンは，1956年にハイファ（イスラエル）で生まれました．彼の学生時代は，理論計算機科学，特に独立した分野としての計算の複雑さの理論の形成に費やされました．プリンストンでの大学院での研究中，アヴィは，複雑性理論の創設者の1人である彼の学術顧問Richard JayLiptonの影響を大きく受けました．ロバースの場合と同様に，理論計算機科学が彼の人生の仕事になりました．

　　　　　　　　　アヴィ・ウィグダーソン

両受賞者の主な成果の1つは，数十年にわたる両方の分野の成熟と形成の過程で，彼らの科学的研究と国際的な教育および普及活動が大きな貢献をしたことです．
理論計算機科学は，コンピュータが操作する対象のほとんどが離散的であるという自然な理由から，離散数学の成果，アイデア，概念を積極的に利用しています．その多くは「純粋な」数学では需要がありませんでした．一方，理論計算機科学のニーズは，離散数学の全く新しい分野の創造につながっており，これは科学の歴史の中で最も成功した共生関係の一つであると思います．この分野から他分野への「アイデアの移転」における最大の功労者は，今年のアーベル賞受賞者なのです．
「純粋」数学者や数学者との関係も，より良い方向に変化しました．たとえば，ラズロ・ロバース（ちなみに，ロシア科学アカデミーの外国人会員）は4年間（2007〜 2010年）国際数学連合の会長を務め，プリンストン高等研究所（IAS）でのアヴィ・ウィグダーソンの役職は数学学校に属しています．この道を歩み始めた当初は，どちらも考えられないことでした．これは，抽象数学の多くの分野に密接に関連する問題，アイデア，定式化が両分野に蓄積され，多くの場合，抽象数学自身の発展に影響を与えることによって，多かれ少なかれ自然な形で起こったことです．この点において，ラズロとアヴィは誰もが認めるリーダー的存在です．

離散性から連続性へ
離散数学の特徴として，連続的ではなく有限的な対象への関心が高まっていることを前述しました．ラズロ・ロバースは，正反対の仮定に基づいた非常に重要なプロジェクトの創設者の一人であり，おそらく主人公です．その結果，非常に大きなグラフやその他の組み合わせ対象物は，10進法の分数が無理数の近似値とみなされるのとほぼ同じ意味（ロバースのアナロジー）で，幾何学的または代数的な性質を持つ自然な連続構造の近似値とみなすことができることがわかりました．その結果，美しく一貫した理論が生まれ，当然のことながら組合せ論だけでなく，代数学，解析学，測度論，統計力学，エルゴード理論など，数学や物理学のさまざまな分野と驚くほど関連していることがわかりました．

ラズロ・ロバースは，優れたモノグラフのLarge Networks and Graph Limitsを書き，すぐにこの分野の古典的なテキストになりました．興味のあるすべての読者にお勧めします．

疑似乱数理論
アヴィ・ウィグダーソンに最も関連するトピックに名称を付けると，疑似ランダム性の理論でしょう．最初の動機から始めると，最も重要なアルゴリズムの多くが本質的に確率的なことです．つまり，作業で乱数検出器を使用します．ただし，絶対的なランダム性はまれであり，実際には，いわゆる疑似乱数発生器がほとんどの場合使用されます．これは，アルゴリズムがそのような置換に「気付かない」ことを期待して，決定論的手順によって生成されたランダムビットとして渡されます．

擬似乱数理論とは，大まかに言えば，この希望に理論的根拠を与えようとするもので，さまざまなアーキテクチャやパラメータを持つ発生器を構築し，それらが必要な特性を持つことを数学的に証明することができ，同時に，これらの対象や概念は，計算複雑さの理論において，まったく独立した別の用途があることや，対応する構造が，たとえば代数幾何学のような，数学のきわめて古典的な分野に関連していることも，すぐに判明しました．アヴィ・ウィグダーソンは，この分野で誰もが認めるリーダーです．特に，最も重要な構成要素（Nisan-Wigderson発生器）と，複雑さの理論における顕著な影響（Impagliazzo-Wigderson定理）の両方があります．

Kneser仮説
ラズロ・ロバースは，クネーザー予想の証明があります．クネーザーグラフは，代数的組み合わせ論で発生する非常に自然な有限グラフで，タスクは，その色数を計算することです．つまり，エッジで接続された頂点が常に異なる色になるように頂点に色を付けることができる最小の色数を計算します．

おそらく，最適な着色を作成するのは簡単です．問題は，それを改善できないことを証明することです．この問題は，25年近くの間，組合せ学的な努力を必要としていましたが，1978年にロバースが発表したエレガントな論文で，厳密に離散的な絵全体を多次元の球体に浸し，実数位相幾何学の基礎的な結果の1つであるBorsuk-Ulamの定理を適用することで解決されました．この証明から，今日では位相幾何学的組合せ論と呼ばれる学問全体が発展し，その方法によって，他のアクセスできない問題の数々が解決されました．

解の系

証明の複雑さの理論では，数学の定理や，あるグラフが与えられた数の色に着色できないという主張，あるコードにエラーが含まれていないという主張など，さまざまな自然な主張の効果的な証明が可能かどうかを研究します．最も重要な証明系は，いわゆる解の系であり，それに基づくアルゴリズムが最も広く実用化されているからです．

解の系を研究する方法はかなり昔から知られていましたが，2001年にEli Ben-SassonとA. Wigdersonが研究するまでは，せいぜい私的なものでした．本研究では，このような証明を分析するための驚くほど簡単な一般的手法を，幅と呼ばれるもう一つの複雑さの尺度の関与に基づいて提案しました．この論文は，証拠の複雑性に関する理論のパラダイムとなり，多くの新しいアイデアやコンセプトを生み出しました．

イベルメクチンは，北里大学特別栄誉教授の大村智博士が１９７４年，静岡県・川奈のゴルフ場近くで発見した微生物が生み出す「アベルメクチン」をもとにした化合物（誘導体）で，アメリカの製薬会社のメルク社との共同研究で，もともとは家畜やペットの寄生虫，回虫などの治療薬として１９８１年に開発されました．イベルメクチンは，家畜の寄生虫や皮膚病，イヌのフィラリア症などの特効薬となり，動物抗生物質として２０年以上にわたって売上高世界トップを維持する記録的なヒット薬剤です．

人間のオンコセルカ症 （アフリカ・中南米・中東などの河川流域で蔓延していた河川盲目症）に効果があっただけではありません．その作用の範囲は驚くほど広いことが判明しました．線虫，ほとんどの昆虫，ダニに効果があります．そして，多くの寄生虫（またはそれらが運ぶ病気）は動物から人間に伝染するので，寄生虫のペットを取り除くことも重要な仕事です．そして，人々はオンコセルカ症や他のフィラリア症に苦しんでいるだけでなく ，1億人以上が桿虫症に感染しており，私たちが忘れていた疥癬とアタマジラミは世界のどこでも消えていません．イベルメクチンはこれらすべての病気に適応されます．イベルメクチンはノーベル賞を受賞した英雄的な薬です．

ーーー

■以下のサイトより引用します

イベルメクチンはコロナ治療に有効か無効か　世界的論争の決着に日本は率先して取り組め : NEWS特集 : 記事・論考 : 調査研究ＰＯＩＮＴ ■北里大学の大村智博士が発見した抗寄生虫病の特効薬イベルメクチンが、コロナウイルス感染症（ＣＯＶＩＤ−１９）にwww.yomiuri.co.jp
　河川に生息するブユ（ブヨ、ブト）がヒトを刺した際に，ミクロフィラリア（回旋糸状虫）という線虫をうつし，それが体内で繁殖して失明する人が多数出ていた．この治療に役立てようと，１９７５年に大村博士がメルク社のウィリアム・キャンベル博士と共同研究を進め，オンコセルカ症や脚のリンパ腺に線虫がはびこって太いむくみが出るリンパ系フィラリア症（象皮症）の特効薬としてイベルメクチン（薬剤名はメクチザン）を開発した．世界保健機関（ＷＨＯ）の研究者は「これまで出てきたどの熱帯病薬剤と比較しても，けた外れに優れた効果を持つ」とイベルメクチンを高く評価し，メルク社と北里大学に協力を求め，１９８７年から熱帯地方の住民に無償で配布することにした．何よりも年に１回，錠剤を水で飲むだけという簡単な服用法がＷＨＯの評価を高めたポイントだった．この特効薬が出てきたため，盲目になる人が続出していたオンコセルカ症は急速に減少し，コロンビア，メキシコなどでは，オンコセルカ症を撲滅したと宣言している．その後，ダニによる疥癬かいせん症や糞線虫症など重篤な風土病の予防・治療薬になることもわかり，イベルメクチンは世界中に広がった．臨床現場では，副作用がほとんど報告されないことも評価を一層高めた．大村・キャンベル両博士は，この業績を評価され，２０１５年にノーベル生理学・医学賞を受賞した．

■ＣＯＶＩＤ－１９の大流行で浮上したイベルメクチン
　イベルメクチンは今，新型コロナ（ＣＯＶＩＤ－１９）のパンデミック（世界的大流行）で再び世界中の注目を集めている．試験管レベルの研究で，新型コロナウイルスがヒトの細胞内で増殖する際に，ウイルスのたんぱく質の核内移行を妨害し，増殖を抑制することがわかったからだ．

　ＷＨＯは２０２０年３月１１日，ＣＯＶＩＤ－１９のパンデミックを宣言し，世界中に厳戒態勢を求めた．しかし，感染が拡大しても有効な治療薬がないことから，中南米・中東諸国を中心に，イベルメクチンをＣＯＶＩＤ－１９治療に投与する事例が広がった．

　最初に臨床試験の結果が発表されたのは，アメリカ・南フロリダの４病院での臨床試験だった．２０年６月に発表された試験結果によると，イベルメクチン投与患者１７３人の死亡率は１５.０％で，非投与群１０７例の２５.２％と比べて有意（ｐ＝０.０３）に優れているというものだった．

ーーー

■北里大学病院の治験

新型コロナウイルスに対するイベルメクチンの現状・世界的の状況と北里大学の取り組み

■以下は，セルゲイ・グラゴレフによる記事から抜粋

Герой и злодей • ЗадачиБезопасное для животных и людей лекарство от паразитов —elementy.ru

日本の科学者大村智が伊東・川奈で土壌を採取

土壌から 分離した放線菌Streptomyces avermitilisの二次代謝産物である 8つの成分を発見しました．45年間，森林は伐採されていません．
長い間，この種のバクテリアは他の場所では見つけることができなかったようです．これは生物多様性の保全を支持する大きな根拠です．ジャイアントパンダや ミンククジラだけでなく，土壌や植生がある場所ならどこでも重要です．

アベルミクチンは，マクロライド系抗生物質に関連する 16員の大環状ラクトンで，それらの品種の多くは，この放線菌と密接に関連する種の放線菌から得られ，次にそれらから多くの半合成誘導体が得られ，そのうちの約5つが駆虫薬として使用されました．

詳細は，Andy Crump（2017）のレビューを参照ください．
Ivermectin: enigmatic multifaceted ‘wonder’ drug continues to surprise and exceed expectations

https://www.nature.com/articles/ja201711.pdf

数学の未解決問題は無数にあります．
未解決の数学の問題のリスト（書ききれないので以下をご覧ください）

Открытые математические проблемы — Википедияru.wikipedia.org
このリストに挙がっているものだけでも，あまりにたくさんあるので驚くでしょう．
挑戦してみたくなるものもあるかもしれません．

実際に，数学上の未解決問題は，無数に存在します．そのうちから，ここには，リーマン予想のようにその証明結果が数学全域と関わりを持つような命題，P≠NP予想のようにその結論が現代科学，技術のあり方に甚大な影響を及ぼす可能性があるような命題，問いかけのシンプルさ故に数多くの数学者や数学愛好家達が証明を試みてきたような有名な命題を７つ列挙します：

以下の7つの問題はミレニアム懸賞問題と呼ばれ，クレイ数学研究所によってそれぞれ100万ドルの懸賞金が懸けられています．
P≠NP予想
ホッジ予想
ポアンカレ予想（解決済み）
リーマン予想
ヤン-ミルズ方程式と質量ギャップ問題
ナビエ–ストークス方程式の解の存在と滑らかさ
バーチ・スウィンナートン＝ダイアー予想（BSD予想とも）

真空ギャップを通り抜けるフォノンのトンネリング。左側に入射する音波は、表面に交流電場を生成し、右側の2番目の物体の原子の同期振動を生成します。Phys.Rev.Lett.105,125501より
https://elementy.ru/novosti_nauki/431440/Mozhet_li_zvuk_peredavatsya_cherez_vakuum?from=rxblock　
2010 年10月27日• イゴール･イワノフ

■固体媒体で見られる新しい現象、つまりフォノンが真空（空隙）を介して、右の固体から左の固体に「ジャンプ」することが説明されています。音波は薄い真空の隙間を乗り越え伝わり、熱は通常の熱放射が伝えるより何十億倍も効果的に真空を介して伝達できます。
[訳者注）真空中を熱が伝わる様式は放射（輻射）のみと思い込んでいました．魔法瓶は壁の中に真空層があるために，真空中は熱伝導がなく放射だけなので熱流の遮断ができます．熱放射は真空中を伝搬できますが，それ程高温でない物体からの熱放射は小さいものです．物質の熱は原子の振動ですので，原子の振動を伝えることができれば非常に高効率な伝達でしょう．この発見の面白さはここにあります．ここで引用されているphys.rev.letters（フィンランドのグループ）によると，近接場熱伝達は音響フォノンが真空中をトンネルする現象で，フォノンによって誘起されるエバネッセント波が固体間を結合するので離れた誘電体間で起こり，いわゆる電流加熱でもないようです．近接場放射熱伝達の測定法はよくわかりませんが，以下の論文（入手していません）が引用されています．A. Narayanaswamy, S. Shen, and G. Chen, Phys. Rev. B,78, 115303 (2008)］．

音波とは、物質の原子が平衡位置を基準にして同期的に振動することです。音が伝播するためには、これらの振動を支える物質媒体が必要です。真空中では、音はそこには存在できないので、伝搬することはできません。しかし、最近になって発見されたこの現象は、音の振動は、サブミクロンの厚さの真空隙間を突き抜けて、固体から固体へとジャンプすることです。この効果は「真空フォノン・トンネリング」と呼ばれ、Physical Review Letters誌の最新号に掲載された2つの論文で説明されました。結晶格子の振動は音だけでなく熱も運ぶため、真空中での熱伝導が異常に大きいことに注目が集まっています。

新しい効果は、結晶の音波と電界の間の相互作用によって起こります。１番目の結晶格子の振動は、結晶の端面に到達し、その表面近くに交互の電界を生成します。これらの場は真空ギャップを越えたもう一方の端面で「感じられ」、2番目の結晶の格子振動を起こします（図1を参照）。全体として、フォノン（結晶格子振動の「量子」）が1つの結晶から別の結晶にジャンプし、その中でさらに伝播するように見えますが、もちろん、２つの結晶間の真空空間にはフォノンは存在できません。

発見者は、効果を説明するために「トンネリング」という言葉を使用しました。この現象は、量子粒子がエネルギー的に禁止された領域を飛び越えるときのトンネリングをイメージしています。ただし、この新しい現象は古典物理学で完全に記述でき、量子力学の関与をまったくないことを強調しておく必要があります。これは、変圧器、誘導ホットプレート、ガジェットの非接触充電装置などで使用される電磁誘導の現象に少し関連しています。固体で起こるなんらかのプロセスで電磁界を生成し、電磁界は、非放射的に（電力の損失なく）真空ギャップを介して別の固体に伝達され、そこで応答を引き起こします。両者の違いは、電磁気学のインダクタンスでは電流（つまり電子の動き）が「働く」のに対し、真空フォノン･トンネルでは原子そのものが動くということです。

このような結晶振動と電界が効果的に結びつく具体的なメカニズムはいろいろあるでしょう。フィンランドの研究者による理論論文では、この目的のために圧電素子（水晶などの電場で変形し，かつ変形すると電荷を生じる物質）を使うことを提案しています。加えて：効果的に真空ギャップを突き抜けフォノンが伝わるには、 "対向 "フォノン、交流電場と "エスケープ "フォノンの間の共振同調が必要です。計算によると、物質の現実的なパラメータの下では、このような共鳴が実際に存在し、特定の入射角でフォノンが100%の確率でトンネリングさせられることが示されます。

図2. 走査型トンネル顕微鏡の針の先端にある最後の原子と基板との間の熱交換が異常に強い。原子は基板上に電荷を誘導し、原子の熱ジッタを追従して基板上にフォノンを発生させ、その過程で原子からエネルギーを奪う。 Phys.Rev.Lett.105，166101より

別の論文では、物理学者たちは、一見まったく技術的な問題を研究して、議論されているこの効果に行きつきました：走査型トンネル顕微鏡の針の最先端の熱は、冷たい基板（図2参照）に（触れることがない）運ばれるのか？繊細な実験方法を用いて、彼らは針の先端の文字通り最後の原子の温度を測定することができ、驚くべき事実を発見しました：この原子は、針ではなく、基板の温度でした！これは、基板と先端の最後の原子の非接触熱交換が（真空を通して！）先端の残りの部分の針よりもはるかに強力であったことを意味します。

このようなことから、通常の熱放射だけ考えても、かなり不十分であることが判明します。研究者らは、針から基板への熱伝達は、熱放射が作り出すことができるものよりも数十億（！）倍も効率的であると推定しました。このことは、詳細な測定結果と相まって、真空中のフォノンのトンネル現象がここでも起こっていることを示しています。

論文の著者は、この効果のメカニズムを次のように説明します。金属表面近傍に置かれた電荷は、金属に電荷を誘起します（静電気の問題では、仮想電荷イメージ）。初期電荷が、例えば熱振動によって揺れている場合、誘起された電荷もまた同じ周波数と振幅で揺れます（電子は原子よりもはるかに軽いという事実のため、原子のそれぞれの動きには "適応 "する時間がかかります）。その結果、基板の表面にある種の電子塊が現れ、「熱い」原子のように揺れる。この塊は、基板上の原子の振動を励起しエネルギーが費やされる。それは、電子塊から、したがって、電気力によって電子塊としっかり接続されているの元の原子の熱を奪う！　これが、針の残りの部分が暖かい場合でも、先端の最後の原子は、クールダウンされるメカニズムです。

どうやら、応用はいろいろありそうです。新しい効果は、特定の状況で以前に考えられていたよりもはるかに効率的なので、熱伝達の観点から興味深いものになります。この観察は、マイクロメカニカルデバイスの設計や、多結晶圧電体サンプルの熱伝導率の研究において非常に重要なものとなるでしょう。また、圧電部品と金属部品を組み合わせたマイクロデバイスでは、電子が活躍します。これは、真空を介して電子とフォノンの間で、ある物質から別の物質へのエネルギー移動を迅速に行う現象のすべては、まだ探求されていません。

■Источники:
1) Mika Prunnila, Johanna Meltaus. Acoustic Phonon Tunneling and Heat Transport due to Evanescent Electric Fields // Phys. Rev. Lett. 105, 125501 (14 September 2010); текст статьи находится в свободном доступе в архиве е-принтов под номером arXiv:1003.1408.
2) Igor Altfeder, Andrey A. Voevodin, Ajit K. Roy. Vacuum Phonon Tunneling // Phys. Rev. Lett. 105, 166101 (11 October 2010).

См. также:
Структура электромагнитных полей в веществе оказалась сложнее, чем считалось ранее // «Элементы», 29.11.2005.

Игорь Иванов

4. 時空の構造
これらの考え方は、時空の構造に深く根ざしています。2+1次元時空の境界の粒子論から始まり、3+1次元時空の重力論に至りました。時空の次元の一つがどこからともなく現れたのです。この次元は、2+1次元の粒子の相互作用から出現しました。

そして、これは時空が最も基本的な概念ではないということを意味しています。それは、より基本的な概念によって生成され、その法則は、研究対象から観察者の一定の距離の後にのみ有効になります。例え話をしてみましょう。湖面を観察したとします。波が見えたり、水面に浮いている虫が走っていたり。湖の表面は透明度が高く、非常に描写しやすいように見えます。確かに、波の伝搬や表面張力などを記述する方程式を書くこともできます。さて、水面の構造をもっと詳しく調べたいと思ったとします。顕微鏡で見ると、以前のように水面がはっきりと観察されていないことがわかります。そして、電子顕微鏡で見てみると、水の蒸発分子が絶えず表面から出てきて、その場所は空気中の水の分子が凝縮したものに取られていることがわかります。よくよく考えてみると、水の表面が十分に明確に定義されていないことがわかり、個々の分子のレベルで起こる現象をなんとか含めなければならないことがわかりました。同様に、時空は近距離では明確に定義された概念ではなくなります。 明確に定義された概念は、境界に存在する粒子であり、時空は集合的な特性としてのみ出現します。

もし我々が負の曲率を持つ時空の中だけに住んでいるとしたら、我々の宇宙で起こっているすべてのことを理解するためには、その中の粒子の振る舞いを記述する境界層の適切な理論を作くることで十分でしょう。

しかし、興味深いのは、すべての利用可能なデータから判断すると、巨視的なスケールでは、私たちの宇宙の時空は、残念ながら、正の曲率を持っています。現時点では、正の曲率を持つ時空の重力場を同様に記述できる可能性があるかどうかはわかっていません。このような記述が存在し、それを見つけることができれば、ビッグバンの特異点問題は解決するでしょう。

 https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/25571

Juan Maldacena,　
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

3. これらの謎を解く
3.1. ひも理論
量子力学と重力は、あまりうまくいっていない2つの理論です。物理学者たちは、この二つの理論を整合性のある理論にまとめようとしてきました。私たちが遭遇するほとんどの物理現象は、重力の影響を無視してもいいし、量子力学の影響を無視してもいいようなものなので、日常生活の実用上、量子重力の理論を開発することはあまり重要ではありません。一方で、ビッグバンの最初の瞬間に宇宙の起源を理解しようとするならば、一貫した理論が必要です。そもそも量子力学と重力の両方が重要なのです。これが、量子重力の理論を見つけるための大きな動機の一つです。

ひも理論は量子重力の理論です。量子力学と重力をまとめて管理している。それが正しい理論なのかどうかはわかりませんが、我々が持っている理論の中では最も有力な候補です。それは，「ひも理論」と呼ばれますが、そのわけはここでの議論で重要ではありません。重要なのは、それが量子重力の理論であるということです。

3.2. ひも理論におけるブラックホール
ひも理論では、ブラックホールを考えることができる。いくつかの特殊な状況下で、これらのブラックホールの微視的な記述を見つけることが可能です。技術的な理由から、一定の負の曲率を持つ時空の中に存在するブラックホールを理解する方が簡単です。このような時空は、平面空間の最も単純な一般化で、平らな空間は曲率がゼロ、正の曲率を持つ空間の例は球体の表面です。図１では，一定の負の曲率を持つ２次元空間の「地図」を見ることができます．また，ゼロ，正，負の曲率を持つ時空を考えることもできます．負の曲率を持つ時空は、実質的に無限大に境界を持っています。粒子は有限時間内に無限大に行き、有限時間内に戻ることができますが、これは時間の流れが異なる位置で異なるため、遠くに行くほど時間の流れが速くなります。

図１：このエッシャーの描画は、双曲空間の幾何学を捉えようとしたもので、双曲空間を円盤に投影したものです。元の双曲空間では、それぞれの図は同じ大きさなのですが、投影の歪みの影響で、円盤の境界に行くに従って小さく見えます。実際には，円盤の境界は内部のどの点からも無限の距離にあるのです．世界地図を平面上に表現する場合も同様の歪みがあります．標準的な投影［訳者注）メルカトール図法のこと］では，地図上では極点付近の領域が不釣り合いに大きく見える．ここの双曲空間の投影では，逆の効果があり、双曲空間の大きさは無限大なのに、境界付近の領域がどんどん縮小されて投影されるので、全体が円盤内に収まって見えます。

1997年に、私はこの空間における重力物理学の全体が、境界上の普通粒子の理論で記述できると推測しました。これは、ガブサーS. Gubser，クレバノフ I. Klebanov，ポリャコフA. Polyakov，ウィッテンE. Witten らによってさらに発展しました。詳細はやや複雑ですが：境界理論は、私たちが理解していなかった重力理論を、私たちが理解している普通の素粒子理論と同等のものにします。さらに重要なのは この境界理論が 量子力学の原理に従うことです。

内部のブラックホールは、境界にある粒子と比べて熱状態にあります。ブラックホールのエントロピーは、これらの粒子のエントロピーに過ぎません。時空幾何学の「素粒子」とは、境界に存在する粒子のことです。

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

2. ブラックホールと量子力学
次に驚いたのは、量子効果が研究されたときです。量子力学では、真空は単に粒子が存在しないだけではありません。真空は非常に興味深い状態で、常に粒子のペアが生成されたり破壊されたりしています。平らな空間では、エネルギーが保存されているので、粒子の純生産はありません。生成された粒子はすべて、非常に早く消滅しなければなりません。1974年にスティーブン・ホーキング博士は、地平線が存在すると、もはやそうではないことを示しました。地平線の近くに正のエネルギーを持つ粒子と負のエネルギーを持つ粒子ができてしまうのです。負のエネルギーを持つ粒子はブラックホールに落ち、正のエネルギーを持つ粒子は飛び去る。平面空間では、負のエネルギーの粒子を持つことができないので、このようなことはありえません。しかし、地平線の反対側では、遠くの観測者から見て負のエネルギーを持つ粒子が、地平線の内側の観測者から見て正のエネルギーを持つことができます。正味の効果は、ブラックホールが粒子を放出することです。放出された粒子は、ブラックホールの質量に反比例する温度を持つ熱分布を持っています。太陽質量のブラックホールでは、この温度はこの効果を測定するには小さすぎます。もしブラックホールが空の空間にあったら、ブラックホールはゆっくりと質量を失い、小さくなるでしょう。質量の小さいブラックホールの方が高温になる可能性があります。1018キログラム（山脈の質量）の質量を持つブラックホールは、1000度の温度を持ち、白く見える。1ミリワットの電球1個分の光を出すことになる。その質量がどんどん小さくなるにつれて、その温度は上昇し、おそらく完全に蒸発するまで、どんどん速く蒸発していきます。実際、数キログラムの質量をブラックホールに崩壊させた場合（実際にはとても難しいことですが）、1ミリ秒もしないうちに完全に蒸発し、核爆弾よりも多くのエネルギーを放出します。

ブラックホールのこの熱的性質は、2つの謎を生み出します：1) 何がエントロピーを生み出すのか？2) 情報パラドックス？
これらについて詳しく説明しましょう。

2.1. ブラックホールのエントロピー
通常の物理学では、熱的性質は常に構成要素の運動から生じます。例えば、空気の温度は、空気分子の平均速度に関係しています。これと密接に関連した概念として、"エントロピー "と呼ばれるものがあります。エントロピーは、すべての構成要素の運動に関連する無秩序の量です。エントロピーは熱力学の法則で温度と関係しているので、システムのミクロな詳細を知らなくても計算できる。ホーキングとベッケンシュタインは、ブラックホールのエントロピーは、地平線の面積をプランク長の2乗で割ったものと同じであることを示しました。巨視的なブラックホールにとって、これは巨大なエントロピーです。このエントロピーにブラックホールの寄与が含まれていても、熱力学の法則は有効であることがわかりました。ブラックホールの「構成要素」が何であるかが全く分かっていないため、非常に不可解な結果となっています。ブラックホールは時空の穴なので、その構成要素を見つけることは、時空幾何学の最も基本的な構成要素を見つけることと密接に関係しています。

ブラックホールのエントロピーは体積ではなく面積に比例するというのは非常に興味深いことです。1990年代初頭、トホーフトHooftとサスキンドSusskindは、量子力学と重力を含む理論では、系を記述するために必要な構成要素の数は、系を取り囲む表面の面積よりも大きくてはならないことを提唱しました。このことは、時空が普通の固体とはかなり異なることを意味しています。ほとんどの実用的な目的のためには、このエントロピーの束縛はそれほど厳密ではありませんが、時空のある領域は、その領域の境界に住む構成要素によって記述できることを示唆しているので、理論的には興味深い意味合いを持っています。

2.2. 情報のパラドックス
これまでブラックホールはいろいろな方法で作れることを述べてきましたが、結局はいつも同じブラックホールになってしまうようです。物理学では、通常、異なる初期状態から始めると、最終的には異なる状態になります。時々、その違いは非常に微妙なものですが、違いがあります。例を挙げてみましょう。2枚のお皿を用意して、片方にAの文字を書き、もう片方にBの文字を書きます。最初の概算では、最終的な結果は同じで、たくさんの破片が割れていることになる。しかし，破片を詳しく調べれば，どの文字が書かれているかが分かります．

そのうちの一つをブラックホールに放り込んだとしましょう。どうやら、ブラックホールはホーキング博士の放射線を放出して完全に蒸発してしまうらしい。ホーキング博士の計算では、この放射は完全に熱的で、ブラックホールの初期状態とは無関係のようだ。つまり、元々プレートの上にあった文字の情報を完全に復元することはできなさそうです。

これは非常に難解な学術的な問題のように思えます。私たちはいつも物事を忘れているので、そんなことは気にしていません！（笑）。なぜこの問題が非常に重要な問題なのかというと、量子力学では、このプロセスを支配する法則は、原理的に情報を復元できるようなものでなければならないと教えてくれているからです。だから、情報の問題を解決することが、量子重力の一貫した理論に必要なのです。そのような理論は、情報の謎を解決しなければなりません。

ホーキング博士を含む多くの著名な物理学者は、これは不可能だと考えていました。彼らは、ブラックホールが本当に情報を破壊していると考え、量子力学を捨てなければならないと考えていました。彼らは、量子力学と重力は根本的に相容れないものであり、正しい理論は情報が失われないことを暗示する量子力学の原理に従わないと考えていた。

この疑問を考えることで、弦理論や素粒子物理学の分野で興味深い進歩を遂げてきました。

ーーー続く

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/3_Solving_These_Puzzles

Black Holes and the Structure of Space-Time • БиблиотекаBlack holes are very puzzling objects that are predicted by gelementy.ru
Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

1. ブラックホール
ブラックホールは、アインシュタインの一般相対性理論によって予測された最も魅力的な天体の一つです。ブラックホールには興味深い歴史があり、時空の性質の理解を深めるために多くの理論的な驚きの源となってきました。

まず、ニュートンの重力理論を考えてみましょう。ここ地球の表面では、重力の力を感じることができます。石を上に投げると、重力の力で石が下に戻ってきます。では、物を上に投げても下に落ちてこないようにすることはできるのでしょうか？はい、できます。秒速11km以上の速度で投げると、地球の重力場から離れてしまいます。この「脱出速度」は、地球の質量と半径に依存します。もし地球がもっと質量があり、同じ半径であれば、脱出速度はもっと高くなります。では、もし、光の速度よりも脱出速度が速いほど密度が高く、質量のある物体があったとしたらどうなるだろうか？そうすると、光が逃げられなくなり、それは黒く見えます。例えば、大きさが

より小さい星は黒く見えるでしょう。ここでG_{N}はニュートン定数、cは光速です。計算式に慣れていない方のために、いくつか例を挙げてみましょう。地球の質量の物体がブラックホールになるためには、その大きさが1cm以下でなければならない。太陽の質量を持つ物体は、1km以下の領域に集中していなければなりません。このことは1800年代にP.ラプラスによって指摘されましたが、誰も注目していませんでした。

1905年に特殊相対性理論が登場して、光の速度は他の普通の速度とは違うことがわかりました。それは宇宙の速度の限界であり、光より速く進ませることができるものはないのです。アインシュタインの相対性理論は、空間と時間が密接に結びついていることも教えてくれます。時間の流れは、お互いに相対的に移動している観測者によって異なります。あなたが通りのそばに立って車が通るのを見ているとしましょう。車に乗っている人の時間の流れは、あなたの時間の流れとは異なります。2 つの別々の街灯が同時に赤になるのを見たとしましょう。運転手にとっては、同時に赤になることはないでしょう。これはもちろん、光が両人の目に届くまでの時間を考慮に入れた上でのことです。両者とも光の速度で進んでいる光を見ていますが、時間の流れ方は異なります。時間は相対的なものであり、光の速度は絶対的なものである。私たちは通常、光の速度よりもはるかに小さい速度で移動し、私たちは非常に正確に時間を追跡していないので、これは私たちにとって非常に小さな効果であるため、これは逆に直感的に思えます。これは、粒子加速器では常に見られる効果です。粒子は光速に近い速度で移動しているときには、はるかに長く生きています。

空間と時間は、一つの概念である時空にまとめられています。時間は、お互いに相対的に移動している二人の観測者によって異なる知覚をします。どちらの観測者も同じ時空を見ています。この二つの観測者の観測を関連付けるための正確な公式があります。

重力の話に戻りましょう。重力には、ガリレオによって発見された非常に特殊な特徴があり、真空中では、羽と石が一緒に落ちる。これは他の力では起こりません。電場の中の粒子は、その質量や電荷が変われば、異なる動きをする。ニュートンの重力理論では、すべての粒子が同じように落ちるのは、重力の力が質量に比例するからです。これを "等価原理 "と呼ぶこともあります。

アインシュタインは、ニュートンの理論では重力が瞬間的に伝播するので、ニュートンの理論は特殊相対性理論と両立しないことに気づきました。1915年、アインシュタインはこの問題を、等価性の原理も自然に取り入れた方法で解決しました。彼はこの理論を一般相対性理論と名付けた。彼は、重力は時空の湾曲に起因することを提案しました。湾曲した時空の中の粒子は最短の線に従う。湾曲した空間上で最初は平行な線は、後になってお互いに向かって移動するかもしれない。例えば、地球の赤道にある2本の子午線は、最初は赤道で平行だったが、北極で交差する。時空の形は、その上を移動する物質に依存しています。一般相対性理論は、時間の流れが重力場に依存していることを暗示しています。したがって、同じ建物の最上階と最下階に住んでいる二人の人は、時間の流れが違って見えることになります。下の階に住んでいる人の方が時間の流れが遅くなります。これは、この地球上の建物にとっては非常に小さな効果であり、1/1015の効果です。私たちが学んだことは、巨大な物体が空間と時間をゆがめるということです。特に、これは巨大な物体の近くの時間は、遠くの時間よりもゆっくりと流れることを意味します。

物理学者は常に最初に最も単純な状況を研究しようとします。そこで、一般相対性理論が発明されて間もない1916年、カール・シュワルツシルトという若いドイツ人が、アインシュタインの方程式の最も単純な球対称解を発見しました。これらの方程式は、点状の質量によって生成される幾何学であると考えられていた特定の幾何学を記述しています。その幾何学が何であるかを語るのではなく、その特徴の一つである静止した時計がチックする速度に焦点を当ててみよう。太陽の表面にある時計は、遠くにある時計よりも100万分の1の速度で動いています。中性子星の表面にある時計は、遠くにある時計の70%の速度で動いています。この場合、大きな効果があることがわかります。シュワルツシルトが発見した解は、「中心」にある時計が完全に止まってしまうことを示しています。当初、ほとんどの物理学者は、これは物理的ではない結果であり、過度に単純化された解析の産物だと考えていました。

さらに研究を進めると、シュワルツシルトの解の「中心」は、実際には完全に滑らかな表面であることがわかりました。時空を旅している観察者は、この領域を何の違和感も奇妙さも感じずに通過することができます。ブラックホールの外にいる人は、落下してくる観測者からの信号が、すべての実用的な目的のために、最終的には消滅するまで減速することを見ています。静止した時計がゼロに減速する表面は "地平線 "と呼ばれ、この地平線は戻りがない点を示し、この表面を横切った観測者は、再び出てくることができず、内部の「特異点」に押しつぶされてしまいます。特異点とは、非常に高い時空の曲率の領域で、彼は引き裂かれてしまいます。アインシュタインの理論におけるブラックホールの大きさは、今でもニュートンの理論でラプラスが計算した式で与えられていることが判明しましたが、物理的な解釈は大きく異なっています。

ブラックホールは、太陽の数倍の質量を持つ星が核燃料を使い果たし、その重力の下で爆発することで、天体物理学的な過程で形成されることがあります。宇宙にはブラックホールが存在することを示す多くの観測的証拠があります。これらの天体物理学的ブラックホールには、大きく分けて2つのタイプがあります。太陽の数倍の質量を持つものと、恒星が崩壊してできたものです。ブラックホールは黒いので、なかなか見ることができません。運よくブラックホールの中にガスが落ちてくることがあります。ガスが落下すると、このガスは熱を帯びて独特の放射線を発しそれを検出します。このガスは、ブラックホールを周回している別の星から来ることもあります。つまり、お互いに公転している2つの星があって、一方の星が崩壊してブラックホールになったとすると、もう一方の星からガスが出てきます。そして、もう一方の星からのガスがブラックホールに落ち始めます。また、銀河の中心には、もっと質量の大きなブラックホールがあります。これらは10億個の太陽の質量を持っています。これらのブラックホールに物質が落下すると、熱を帯びて放射線を発し、それが最終的には地球上の私たちによって検出されます。私たちのような大きな銀河はすべて、中心にブラックホールがあると考えられています。

この講演の焦点は、天体物理学的なブラックホールの説明ではなく、ブラックホールが時空の構造に与える影響を探ることにあります。

アインシュタインの理論によれば、ブラックホールは時空の穴であり、一度落ちたら二度と戻れない。ブラックホールに投げ込まれたものは永遠に失われる。ブラックホールは非常に興味深い普遍的な性質を持っています。星がブラックホールに崩壊したとき、その最終的な形は質量と角運動量の2つのパラメータだけに依存します。つまり、ブラックホールは普遍的なものであり、ブラックホールを形成した物質の特異な詳細な性質に依存しないのです。最初の星の化学組成に関係なく、常に同じブラックホールを得ることができます。つまり、ブラックホールは重力の理論だけに依存しており、他の力の詳細な性質には依存しないのです。

ブラックホールのもう一つの特異な特徴は次のようなことです：ブラックホールが関与しているプロセスがあるとします。例えば、2つのブラックホールの衝突を考えてみましょう。ブラックホールが衝突して、より大きなブラックホールを形成する。ちなみに、この過程では重力波を出すことができ、それを測定しようとしている検出器があります。この過程を計算するのはかなり難しく、複雑な方程式を解かなければなりません。それでも、いくつかの簡単な結果があります。最終的なブラックホールの面積は、最初のブラックホールの面積の合計よりも常に大きい。面積は常に大きくなる。これは「面積定理」と呼ばれ、1970年にホーキング博士によって証明された。