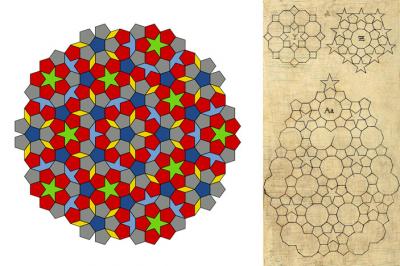
カバーの図は,「美しい幾何学」p.76-84,p84準結晶より引用
ロジャー・ペンローズは,ブラックホールの研究で2020年のノーベル物理学賞を受賞しました.
ここでは,ペンローズのタイリングと準結晶を話題にしましょう.
参考:Alexey Panov、Pyotr Panov "Kvantik" No. 9,2019,アーティストAnnaGorlach
No.7と No.8の記事は,すでに別項で取り上げましたので,そちらをご覧ください.
■ ロジャーペンローズの非周期モザイク

ロジャーペンローズ.
写真:Biswarup Ganguly,Wikimedia Commons; CC-BA-3.0
準結晶の発見に先んじて,数学者の準備はできていた.
1960年代に,数学者は新しいオブジェクト-非周期モザイク-を発見し,研究を始めました.
モザイクとは,平面を完全に埋め尽くすような多角形のタイルで作られたパターンのことです.
非周期モザイクは,どのような平行移動でも自分自身に重ね合わせできないものです.
非周期モザイクの中で最も有名なのはペンローズモザイクです.このようなモザイクの断片を図22に示します.
これは,いくつかのタイプのポリゴンを使い特定のルールに従って組み立て,平面全体を埋め尽くします.
これは,宇宙の調和に掲載されたケプラーによる絵(図23)とよく比較され ます.
ペンローズ自身は,「彼は私がやったことに近いことをしようとしましたが,うまくいかなかった」と述べています.
*)ケプラーのトリアコンタヘドロンは,現代の結晶学のシンボルの1つです.
図:22(左)ペンローズモザイクの断片.
図:23. 宇宙の調和から.
別のタイプの非周期なペンローズタイリングについてもう少し詳述します.
それらは2種類の菱形で構成されています(鋭角36°の 痩せたものと鋭角72°の太いものです).
そのうちの1つを図24に示します.もちろん,前号の記事の図18ほど対称的ではありません.
並進で自分自身と重ね合わせができず,回転対称軸もありません
[訳注:局所的な回転対称はありますが,全域的な回転対称はありません].
ただし,繰り返し五角形の星が表示され,72°= 360°/ 5回転するとそれぞれが重なります
[訳注:局所的な5回回転対称],さらに,これらの星は2つのクラスに分けられ(図25),
一方のクラスの星は別のクラスの星と36°= 360°/ 10の回転だけ異なります.
図:24. 鋭角36°および72°の菱形のモザイク
有限数の平行四辺形からなる各領域は,モザイク内で無限に繰り返し,36°回転したものも無限に繰り返します.
図:25. 異なる色の星は36°回転だけ異なります
ここで,ペンローズモザイクの物理的特性について少し説明します.
■ アラン・マッケイ:モザイクの回折
アランマッケイ.
写真:Julyan-cartwright、Wikimedia Commons; CC-BY-SA-3.0
Alan McKayは,標準的物理実験手法を非標準的数学オブジェクトであるペンローズモザイクに適用することを提案しました.モザイクの各頂点を小さな円[ドット]に置き換えたドットパターンを縮小し,ドット間の距離が光の波長程度にしました.このミニチュアにレーザー光を入射し,シェヒトマンの実験のように,回折パターンは10回対称となることを得ました*).マッケイの論文は,シェヒトマンが最初の実験を行った同じ1982年に発表されました.
シェヒトマンがマッケイのこの仕事について知っていれば,彼はそれを参照し,彼の業績の早期承認が得られたところですが,シェヒトマンは当時マッケイの発見に気付いていなかったと言います.
[*)訳注:このような標準的物理実験は,オプティカルトランスフォームといいます.
縮小されたドットパターンがらの回折像が得られます.
ドットパターンと回折像の関係は,互いに2次元のFourier変換の関係にありますが,
厳密に言うと得られる回折像は位相の情報が打ち消された振幅の絶対値2乗になります.
そのため,回折像の対称性には必ず対称心が生じます.
回折像の対称性は5回対称ではなく10回対称になります.]
■ トリアコンタヘドロン(菱形30面体)とヘキサコンタヘドロン(星型60面体)

ロジャーペンローズとロバートアンマン.
写真:Ludwig Danzer; MarjorieSenechalの記事「アンマンの奇跡」より
ペンローズの非周期タイリングの3次元アナロジーがあります.
そのようなモザイクの1つが,RobertAmmannによって発見されました.
これらは,前号の記事の図16の下部に示されているものとまったく同じ,
細長い平らな2種類の菱形の平行線から組み立てられています.
五角形の星が2次元のペンローズモザイクでよく見られるのと同じように(図24および25),
菱形30面体(トリアコンタヘドロン)は,アンマンの非周期空間モザイクや,60面の菱形の六面体でよく見られます.
星型60面体(ヘキサコンタヘドロン)は,菱形の多面体のリストにはありませんが,これは12個の凹所がある非凸多面体であるためです(図26).

図:26. 黄金比菱形[訳注:対角線比が]から組み立てられた星型60面体(ヘキサコンタヘドロン)
その後,物理学者は菱形30面体(トリアコンタヘドロン)と星型60面体(ヘキサコンタヘドロン)の形で実際の準結晶構造を作ることができました.
最後に,ヘキサコンタヘドロンとペンローズのモザイクに関するいくつかの演習を行います.
• 60個の黄金比菱形を使用してヘキサコンタヘドロンを作りましょう.また,トリアコンタヘドロンと菱形のフェドロフイコサヘドロンの両方が,このヘキサコンタヘドロンの12個のキャビティすべてにきちんと収まっていることを確認してください.
• トリアコンタヘドロンとヘキサコンタヘドロンがアンマンのモザイクによく見られるという事実について話しました.実際,ヘキサコンタヘドロンは20個の細長い平行6面体で構成でき,トリアコンタヘドロンは10個の細長い平行6面体と10個の扁平平行6面体で構成できることを確認してください.
• ペンローズタイリングの十分に大きな部分では,痩せた菱形の数に対する太い菱形の数の比が黄金比φ= 1.618に近いことが証明されています.
図24を使用して,このステートメントを確認しましょう.
• ペンローズモザイクは,他のすべての多面体と同様に,菱形で構成されているためゾーン[訳注:晶帯]もあります.今回のゾーンは,無限に続く菱形のチェーンです.各菱形は、共通の側に隣接する2つがあり,これらの側は平行です.