ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.17］ No.051
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号に引き続き双曲面分割の話です．

■エッシャーの「極限としての円」のシリーズが生まれるまで

コクセターとエッシャーは1951年の国際数学会で出会いました．
1958年にコクセターはこの分割を掲載した論文をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_0_m?1423875894

エッシャーの双曲面分割作品のシリーズ１は直線魚のモチーフでした，
天使と悪魔など，このシリーズの作品群があります．
そして，シリーズ3の洗練された作品に至り完成します．

■次に示すのは，エッシャーの作品「極限としての円3」です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_1_m?1423875894

白い線で分割されたタイル張りは，複数の正多角形による準正則タイル張り
[4,3,4,3,4,3]のように思うかもしれません．
しかし，白い線は直線ではないのです．白い線は，双曲世界のフチの円周と
直交しません（80°で交わる）．実は，右図に示される黒い線が直線です．
右図のように正8角形のタイルが頂点で３つづつ集まる正則分割{8,3}と
見るのが正しいのです．エッシャーの作品は，黒い線は顕に出さずに
白い線を見せて見事に数学的に正確で芸術的な作品に仕上げています．
このエッシャーのトリックについては，コクセターが論文で指摘しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.10］ No.050
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユークリッド幾何，楕円幾何，双曲幾何
色々な幾何空間があります．大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．これら3種を，平面を例にとり比較します．
（１）我々の常識の通用するのはユークリッド平面です．
ご存知のように，ユークリッド平面では，直線外の1点を通る平行線は唯一本だけ引けます．
（２）球の表面は楕円幾何平面の例です．地球の表面だけを想像しましょう．
地球自体は，3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面の例です．
楕円幾何平面の直線は大円（球の中心を含む平面による球の切り口）です．地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，これは地球の大円上の線分のことです．地球は3次元ユークリッド空間の物体ですから，地表の2点を地球内部を通る直線で結べば最短距離でありますが，地表だけの2次元平面では大圏コースが最短です．球表面の異なる２つの大円は必ず2点（直径の両端）で交わります．そのため楕円幾何平面では．平行線はありません．また，地球儀の緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面では，ある直線に対する直線外の1点を通る平行線は無数に引けます．双曲幾何平面は楕円幾何平面のように閉じていないので，イメージを持ちにくいのですが，ポアンカレがうまいモデルを提唱しました．このモデルはポアンカレの円盤モデルといいます．双曲幾何の世界を表すのに円盤を用い，この世界の直線は円盤のフチに直交する円弧とします．このように定義された世界では，ある直線に対する直線外の1点を通る平行線は無数に引けることがわかります．

■3種の幾何平面で，平面の正則分割を考える
さてこれからやることは，それぞれの幾何平面で，正多角形のタイルによるタイル張りを考えることです．このような問題は，平面の正則分割とも呼ばれます．
それぞれの幾何平面での多角形は，それぞれの幾何平面の定義による直線で囲まれているものです．それぞれの幾何平面で，3角形の内角の和Sは，S=π（ユークリッド平面），S>π（楕円平面），S<π（双曲平面）になります．
正p角形が頂点でq個集まってタイル張りがなされている状態{p, q}で，正p角形の内角の和を表す式を等号で置くと　(2π/q)p=(p-2)S　が成り立つので，
1/p+1/q=1/2　（ユークリッド幾何）
1/p+1/q>1/2　（楕円幾何）　
1/p+1/q<1/2　（双曲幾何）
となります．それぞれの幾何平面で，許される{p,q}の整数解を求めると，以下のことがわかります．
（１）ユークリッド平面での正多角形によるタイル張りは，正3角形，正4角形，正6角形で可能．｛3,6｝．｛4,4｝，{6,3}が解です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_0_m?1423315106
（２）楕円幾何の平面では，正6角形以上の正多角ではタイル張りができません（閉じた立体になりません）．
調べてみると，正5角形のタイルでは，頂点に3つのタイルが集まるもの{5,3}，正4角形のタイルでは，頂点に3つ集まるもの{4,3}，正3角形のタイルでは，頂点に5つ{3,5}，４つ{3,4}，３つ集まるもの{3,3}が作れます．結局，5種類の正多角形によるタイル張りがあり，これらはプラトンの正多角形に対応した球面立体です．ここでは｛5,3｝に対応するもののみ掲載します．黄色い球面正5角形が頂点で3つ集まっているものです．黄色いタイルに5mの対称性があるとき，赤で塗った三角形を中心から見込むような万華鏡を作るとこの映像が再現できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_1_m?1423315106
（３）双曲幾何の平面では，正則分割は無限にあります．
例として｛6,4｝と{5,4}のものをとりあげ掲載しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_3_m?1423315106
例えば，{6,4}の映像を3角形の万華鏡で作るには，
下図の中心に頂点のある三角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧の鏡を使います．しかしながら，この円弧は数学的に反転円として定義されているのですが，現実の光学法則では火線という収差があるので，あまり奇麗な万華鏡映像にはなりません
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_4_m?1423315106

■円盤の中の不思議な世界
私たちの宇宙は膨張していることが知られています．
遠方の宇宙のフチの後退速度はものすごく，光速に達すると，
こちらに光はやって来ません，そこが宇宙の果です．
宇宙銀河の回転速度は，宇宙のフチに行くほど大きく
高速で運動する世界の長さは，我々から見ると縮んで見えます
つまり，宇宙は双曲幾何の世界に似ています．
双曲幾何の円盤の内では，円盤のフチに近づくほど空間が縮みます．
この世界では，直線に沿って旅する自分自身もフチに行くほど縮むので
いつまで歩いても世界の果てに到達できません．
同様に，円盤の中心に近いほど距離が大きくはかどるので，
円盤の外から見ている我々には，直線が円盤の中心方向に膨らんで見えます．
一方，円盤内の世界にいる者にとってはこれが最短距離で直線なのです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.03］ No.049
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１種類の形（2等辺3角形）の赤色と黄色のタイル（赤タイルと黄タイルは互いに鏡像）
で作ったタイル張り模様を鑑賞しましょう．
1種類のタイルで，平面をタイル張りすると，必ず周期的なタイル張りになってしまう
と思い込むのは間違っています．確かに，
Fig.4　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_5_m?1422741853　や
Fig.5　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_6_m?1422741853
のような周期的なタイリングはすぐ思いつきます．
しかし，
Fig.2　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_1_m?1422741853　や
Fig.3　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_2_m?1422741853
のように非周期なもので，平面をタイル張りするものがあります．
Fig.2は中心に回転対称があるタイリング模様で，点群5mの対称性です．
Fig.3は，２つの目がある螺旋パターンのタイリングで，
水平線は映進面だと思うかもしれませんが，このパターンには周期がありませんから
映進操作はできません．螺旋の目の間（中心）に対称心があります．

さて，ここで万華鏡で作られるタイリング模様
Fig.1　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_0_m?1422741853
の登場です．
この万華鏡を生む3枚の鏡は１つの頂点では点群を生成しますが，他の２つの頂点では点群を生成しません．
従って平面を赤と黄色の市松模様で埋めることはありません．
全体の代数系は，群より緩いもの（特殊な亜群）になってしまいますから非常に複雑です．
対称操作は局所的で，独自の作用域と値域があり興味深いものです．
作用域，値域の制限のために，一つのタイル全体が無傷で写像されるパターン内の位置と，
部分が写像される位置があり，このような複雑なタイリング模様ができます．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊
ご感想コメントなどを，
http://blogs.yahoo.co.jp/tanidr/16430597.html　あるいは　以下のメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.01.27］ No.048
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１．万華鏡の美しさが我々の心をとらえる理由は，対称性とカオスの共存
完全な秩序は美しいが，死の世界のようだ．
一方，乱れは千変万化し同じ光景を見るのは一度きり．
そして現象は，いつ起こるかわからない．だから
我々は，はらはらしながら期待し目が離せない．
万華鏡は，秩序の中に乱れもある．生命も，秩序とカオスのただ中にある．
万華鏡の中を降りゆくガラス屑　定まると見し運命にカオスあり

２．対称性
それでは，まず対称性についての考察を始めようと思います．
対称性は自ずと決まるものとして，あるいは合理的なデザインとして生まれます．
環境や境界条件，自然科学の法則が，
その環境下の物質構造やふるまい/現象の対称性を自ずと決定する．
（例）人体，生物，乗り物，結晶，自己組織化，建築物．蜂の巣，花弁の形，柱状節理，etc．
■空間に関する対称性（１点の周りの対称性と周期）
タイル張り，壁紙模様，正多面体，結晶構造，エッシャーの版画．
■時間に関する対称性
時間反転．音楽（J.S.バッハ），詩の韻律，リズム，同期現象．
■現象の対称性
性質空間の対称性．因果律の対称性．

３．対称性はなぜ快いか？
インクの染みは汚らしいが，乾かないうちに紙を折り鏡映対称の染みになると美しく見える．
そしてなんだか想像力を駆きたてる（ロールシャッハ・テスト）．なぜ美しく感じるのだろうか．
私はその理由は次のようなものではないかと思っている：
物や事に対称性があると，我々の脳がその全貌を把握するための情報量が圧倒的に減る．
例えば，結晶とアモルファス（ガラス）で，それらの構造（構成する原子の位置）を
記述しようとすると，規則的な繰り返しのある結晶の方が圧倒的に単純だ．
人間の脳は，整理された少ない情報量だと負担が少なく，快いと感じるのではないだろうか．

４．鏡
万華鏡の話がテーマなのだが，ご存知のように万華鏡は合わせ鏡でできている．
万華鏡の対称性は，鏡映のみにより生成されたものに限ります．
我々は鏡をのぞきこむと何か変な気持がするものだが，以下のような話があります：
太古の時代は，我々の世界と鏡の中の世界の行き来ができたそうだ．＊

＊注）このようなことは4次元の世界なら実際に可能である．例えば，3次元空間で
右の手と左の手は，互いに鏡像になっている．右手が我々の世界にあり，
左手が鏡の世界にあると想像してみよう．左手が鏡の世界を抜け出して
我々の世界のなかで，右手と重なろうとしてもできない相談だ．
ただし，4次元空間なら左手の中身を裏返して，右手と同じにすることができる．
2次元の紙に描いた線画の右手と左手が，いくら紙表面の上で移動しても
ひったり重なることはできないが，紙を折り返す（3次元空間での操作）ならば
重ねることができることは実験で確かめられる．

話を戻すと，鏡の中の生き物とこちらの世界の生き物は仲良く一緒にいたのだそうだ．
ある夜，突然，鏡の世界の住人達が我々の世界で好き勝手を始めるようになった．
そして人々は，鏡の中の住人の正体が「混沌」であることに気付いたという．
そこで，黄帝が魔力によって「混沌」を鏡の世界に閉じ込め，
姿や動きも我々の世界の模倣しかできないようにした．*1)
呪文の効果が切れて，鏡の世界の住人達が勝手に動き出すことが将来起こるかも知れない．
そのようなテーマの小説に*2,3)がある．私は幻想怪奇小説が大好きです．

*1)Turbulent mirror, J Briggs & F. D. Peat, 訳：高安秀樹，高安美佐子
*2)パイプをすう男，M･アームストロング，幻想と怪奇 1（ハヤカワ）
*3)わな，Ｈ・Ｓ・ホワイトヘッド，怪奇幻想の文学(新人物往来社)

混沌の中から湧き出るように次々と生まれてきたさまざまなものが宇宙を形作った．
このようなプロセスを神の技と語られることもあります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.30］ No.044
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年もあと2日になりました．私は部屋の大整理掃除で3日間も満足にパソコンを開けません．
皆様には，よい年末でありますように．そして良い年をお迎えください．来年もよろしく．

クバンチックの問題は如何でした．私が一番好きなのは，第2問のビリヤードの問題です．
この問題に関する連想考察は，近いうちにぜひ書きたいと思っています．

さて，私は毎年「とっとりサイエンスワールド」で万華鏡のワークショップをやらせてもらっています．
正月まもなく（1月16日，PM3～）多摩センターでも開催しますので，お近くの方はご参加下さい．
詳細は，sgktani@gmail.com　にお問い合わせください．
これからメルマガでも，万華鏡の数学について何回か連載するつもりです．
ここで紹介する万華鏡のキットは，「その道の達人派遣事業」の時に開発し，
各地の学校を回り子供たちと作った万華鏡（当時は2種類）がもとで，
その後品種を増やしてできたものです．
-----
◆万華鏡の原理（１）
万華鏡は合わせ鏡の原理を使っていることはご存知ですね．fig1を見てください．
平行な合わせ鏡で挟まれた室（黄色）は1次元に無限に繰り返しています．
室内にある赤い物体もfig1に示したように繰り返します．
黄色い部屋の隣はその鏡像（左右が逆）．合わせ鏡で挟まれた黄色い部屋を（黒），
隣の鏡像の部屋を（白）と思うと，黒白の帯（1次元の市松模様）ができますね．
今度は，合わせ鏡のなす角度を平行でなくθ°とすると，
市松模様の帯は直線ではなく円を描くように延びて行きます．
円の反対側で市松模様がうまくつながるためには，
黒白のペアの数が整数でなければならない．
これは360°/2θ°＝n（整数）となります．これは，万華鏡の発明者
スコットランドの物理学者ブリュースターが1817年に提出した特許にあります．

FIg.1
以上の説明は2枚鏡の合わせ鏡でしたが，複数鏡の合わせ鏡でもできます．
3枚鏡の場合を考察しましょう．fig2には鏡が作る3角形の図です．
3角形の頂点で2枚の鏡が出会うわけですが，それぞれの頂点で，鏡のなす角度は
360°を偶数で割り切る角度である必要があります．3角形の３つの頂点で
この条件が満たされているなら3角形のタイルで平面が市松模様に張り尽くされます．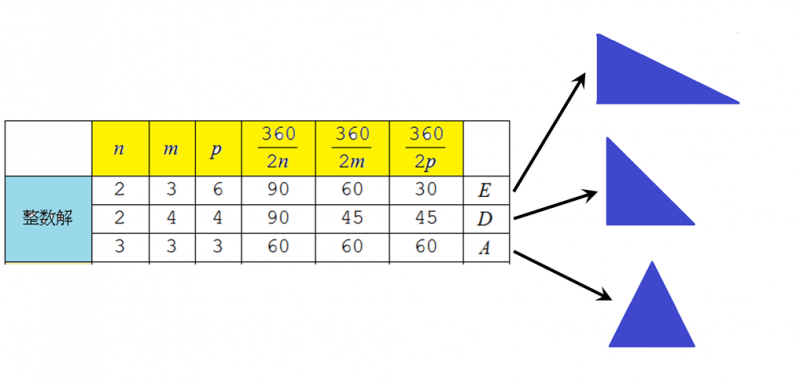

Fig.2
3つのどの頂点でも整数解を持つ場合は，平面をきれいに埋め尽くす市松模様ができます（3種類あります）．
1つの頂点でも整数解にならない場合には，市松模様は乱れますが，これも万華鏡としては美しいものです．