ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.04.07］ No.058
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
最近，我々のfacebook数学月間の会
https://www.facebook.com/sgk2014
に，Nishiyama氏から正方形の辺の長さの1/nを作る方法に関する
plusマガジンの以下の記事の紹介がありました．
https://plus.maths.org/content/folding-numbers?nl=0
皆様，正方形の折り紙を用いて試してみてください．
plusマガジンの記事は，下図の中に生じる黄色い２つの３角形が
互いに相似であること，直角3角形である（三平方の定理が成立）こと
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagak.jpg

を用いて，次の関係式を導びきます．
$$y/2＝k/(1+k)$$　
この関係式に，$$k$$の値（位置）として，得られた$$y/2$$の値（位置）を
代入するたびに，次の$$y/2$$の値（位置）が求まります．
$$k=1/2$$　→　$$y/2＝1/3$$
$$k=1/3$$　→　$$y/2＝1/4$$
$$k=1/4$$　→　$$y/2＝1/5$$
　　......
このようにして繰り返せば，一辺の長さの$$1/n$$まで順番に作れます．
正方形の上の辺に$$k$$の位置をとると，右側の辺に$$y/2$$に位置が決まります．
このように続けると，$$1/2，1/3，1/4，･･･$$の位置が正方形の周りを
ぐるぐる周りながら順次現れるのが大変面白いです．
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagaki.jpg

https://plus.maths.org/content/sites/plus.maths.org/files/articles/2015/haga/hagakj.jpg

さて，紙の形が長方形の場合は如何でしょうか？
手紙を３つ折りにして封筒に入れるときにこのようなことが必要になります．
長方形の辺の1/3を作る方法では，Takakubo氏からの以下の２通りの情報が
寄せられました．以下の図をご覧ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_1_m?1428237203
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/61/16622661/img_2_m?1428237203
これらは一般の長方形（辺の比が１:√2に限らない）で使えます．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.31］ No.057
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も桜が咲きました．関東地方は良いお花見日和です．
皆様のまわりは如何でしょうか．満開の桜はいいですね．
桜吹雪も私は好きです．年に一度の良い季節です．
一斉に花だけ咲く桜は確かに異常です．闇を背景の夜桜は怖いようですし，
森の中でただ一人，満開の桜の中に居れば，坂口安吾の小説にもあるように
気が変になりそうですね．
桜の花は，見事な5回対称をしています．今回は花見の季節という事で
平面図形の5回対称を観賞しましょう．今回は気楽にご覧ください．

（１）点群
桜の花びらの対称性は正5角形の対称性と同じで，
点群でいうと記号5mで表現します．これは，5回回転軸と鏡映面mとから
生成される点群だという意味です．図を見て下さい．
赤い5角形は，正五角形の中心に立てた5回回転軸を示します．
赤い線分は鏡映面を示します．鏡映面が１つあれば，5回回転軸のために
5枚の鏡映面が生じ，これらの鏡映面の交線が5回回転軸になっています．
ここで生じる5枚の鏡映面はすべて同じ性質です．それは5回回転軸で
互いに変換されるべきものだからです．
（群論の本では，すべての鏡映面は同じ共役類に類別されると表現されます）
群という言葉を出しましたが，あまり気にすることではありません．
5回回転軸と1枚の鏡映面mの操作を組み合わせ，次々新しい対称操作を
生んでいくことを，どんどんやっていくと，それまでに得たものと
同じ対称操作になってしまうことがわかります．
点群5mの例では，異なるものは10個の対称操作で全てです．
これら10個の対称操作で点群5mの対称操作の集合は閉じているといい．
点群5mの位数は10だと言います．
群となる条件は，集合が閉じているだけではありませんが，細かい定義は省略し，
ここでは，5回対称軸とそれを含む1枚の鏡映面だけで
10個の対称操作が生まれ，それで閉じていることを鑑賞ください．
点群と書いているのは群5mは1点を不動点にするものだからです．
出発点となった5回回転軸と1つの鏡映面を点群5mの生成元と言います．

老婆心ながら注意をうながしたいのは，奇数回転軸の点群で点群に生じた
鏡映面はすべて同一の共役類に入り，5mなどと記述すことです．
5mmではありません．
偶数回転軸の場合は，例えば，2mmのように記述し，鏡映面は
２つの共役類に分かれます．これらの違いは共役類の類別のためで
結晶学の本にときどき誤りが見受けられますのでご注意ください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_0_m?1427715627

（２）部分群
点群5m（位数10）の部分群に点群5(位数5)や点群m（位数2）があります．
部分群は上位の群の対称要素を落とすことで得られます．
操作mを落とすことで点群５が，操作5を落とすことで点群mが得られます．

（３）5回回転対称性は，並進と両立しない
均一な2次元平面を，互いに独立なベクトル a, b を用いて
na+mb となる格子点（n,m）で，デジタル化したものが結晶空間です．
すべての格子点（n,m）は同値ですから，結晶空間は周期的です．
ベクトル a, b を並進ベクトルと言います．格子点を多角形のタイル
で表現すると，平面のデジタル化は平面のタイル張りの問題になります．
ここで，正五角形のタイルでは隙間なく平面をタイル張りできないことを
確認しましょう．結局，結晶空間（今考察中のものは2次元ですか，3次元でも）
では5回対称性は存在し得ないことがわかります．

（４）フラクタルのタイル張り
正五角形でフラクタルのタイル張りをしてみましょう．
この図には隙間だらけですが，隙間をさらに2種類のタイルを使って
埋めることを考えるとペンローズのタイル張りが得られます．

（５）黄金比
正五角形の中に次々と組み込まれる小さな正五角形には，黄金比1:x　
が随所に表れています．そのため，たいへんまとまりの良い感じの
図形になります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_1_m?1427715627

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/49/16607149/img_2_m?1427715627

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.24］ No.056
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
私が通潤橋（熊本県上益城郡山都町）を訪れたのは，2007年10月のことでした．
22日は，午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業，
午後は先生方と人形浄瑠璃注）観劇を経験しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_4_m?1426898367
－－－－－
注）人形浄瑠璃は，清和文楽館
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
で観賞しました．山都町の人形浄瑠璃の始まりは，江戸時代の嘉永年間（1850年ごろ）で，
山都町（旧・清和村）を訪れた淡路の人形芝居の一座から，
浄瑠璃好きな村人が人形を買い求め，技術を習ったのが始まりといいます．
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました．
良い話です.民衆の文化の高さに感激しました．三人で一体の人形を操ります．
首（かしら）と右手を操る「主遣い（おもづかい）」，左手を操る「左遣い」，
足を操る「足遣い」です．人形も触らしてもらいました．
－－－－－－－－－－－－－

■通潤橋
阿蘇山の南側のこの付近の地形は，島のように台地があり，台地から台地への移動が
大変で平家の落人が隠れ住むのに好都合だったようです．
台地（白糸台地）に農業用水を引くのが大変です．
水は台地のがけ下に汲みに行かなければなりません．
時の惣庄屋「布田保之助（ふたやすのすけ）」は，白糸台地に水を引くための
水路橋”通潤橋”を，肥後の石工たちの技術を用いて1854年に建設しました．
通潤橋は，石造りアーチ水路橋で，長さ75.6m，高さ20.2m。幅6.5m．
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています．
通潤橋の写真（放水事に撮影k.Tani）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_0_m?1426898367
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_1_m?1426898367

通水管の写真(撮影k.Tani)
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_2_m?1426898367

長さ約127m．石をくりぬいた１尺（30cm）四方の函渠（圧力のかかる管水路）．
管と管の繋ぎ目には，振動吸収と漏水防止のための漆喰（しっくい）が塗られている．
さらに，通水管には5～6ケ所に地震対策のための板（緩衝材）を挟んでいる．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/tuusui.html
通潤橋は両側台地より低いので，サイフォンの原理で出口で水を押し上げています．
通潤橋の高さから流入側台地は7.5m高く，流出側台地は5.8m高い．
→http://www.geocities.jp/fukadasoft/isibasi/tsujyun/kaisetu.html
通潤橋は，今でも周辺の田畑を潤しています．
放水は，通水管に詰まった堆積物を取り除くために行うものです．

「通潤橋史料館」　に行くと，どのようにアーチ石橋を施工したかわかります．
川の中に写真のような木枠を大工が組んで石工が石を置きました．
アーチ橋の高さを台地の高さまで上げられなかった理由は，
この木枠をこれ以上の高さにする木材がなかったためという事です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/28/16586128/img_3_m?1426898367

石橋の木枠を外す最終段階は，橋の中央に白装束を纏った布田翁が鎮座し，
石工頭も切腹用の短刀を懐にして臨んだといいます．

これから，アーチ曲線の数学の話をしようと思っています．
写真で見えるアーチ曲線を型どっている石の並びについてです．
アーチの頂点にある石を”かなめ石”と言います．
アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です．
それでも下の木枠を外すときは，とても心配で責任者は命がけだったでしょう．
ーーーーーーー

さて，石積の橋の形，アーチ曲線に関して考えましょう．
アーチの両側の根元はしっかり固定しなければなりませんが，
アーチの上の石の重さが重ければ重いほどアーチの石は互い押し合い引き締め合うので，
橋は大きな荷重に耐えられるのです．石積みは引張力に抗する力はないが，
石積の石に働く力はすべて圧縮力だけなので接着の必要はなく安定構造になります．
石は圧縮に強い材料ですからアーチ型の橋には最適です．ただし，アーチ根元の支点部には，
大きな水平力が発生するので，それとつり合う大きな水平反力が必要です．
山で挟まれた峡谷などはこの点では最適な立地条件でしょう．
通潤橋の根元をしっかり押さえつけている重そうな石積の写真を見てください．

■空き缶を積んで作ったアーチ
私が真剣に積んだのですが，できるのはどうしても缶5個のアーチまででした．
5個の缶で缶同志の接点は4点．すべての接点で同時につり合っていなければなりませんから，
とても難しいことです．もし，6個以上でアーチが出来た方は新記録です．ご一報ください．
缶の周りにラップを巻いていますが，摩擦力を増すためでアーチのつり合い条件を変えるものではありません．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/46/16586546/img_1_m?1426979031

ここから先は，釣合の5つの一次方程式を連立して解く線形代数の話になりますから
省略します．興味ある方は以下でご覧下さい．
http://blogs.yahoo.co.jp/tanidr/16586546.html

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.17］ No.055
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
とうとう桜の花も咲きだしました．やるふりだけの中身のない政治や仕組みに呆れます．
メルマガくらいは，実質のある楽しんでいただけるものをと心がけようと思います．
ご希望コメントなどをお寄せください．

■振幅の大きな2重振り子の動画がyoutubeなどに色々あります．
大変滑稽な動きをしますのでまずご覧ください．
http://blogs.yahoo.co.jp/tanidr/16560015.html
にはインターネットから拾った2つの例を掲載しています．
第１の動画は実験，第２の動画はシミュレーション結果です．
なぜこのような話をするのかと言えば，
２重振り子は，振幅の小さいうちは，皆が見たことのある自然な振動をしますが，
ある程度以上の振幅になると，とても不自然な滑稽な動きになるからです．
振幅が大きいときは，始めのスタート位置（初期値）によって結果が変わることにも気づくでしょう．

■このような系（エネルギーが保存される）の運動は，
ラグランジュ関数（運動エネルギーと位置エネルギーの差）に対する
オイラー=ラグランジュ方程式を解けば決定できます．
ラグランジュ関数　L(x(t),x'(t)，t)は，座標x(t),速度x'(t)，時間tの関数です．
オイラー=ラグランジュ方程式というのは変分原理とも呼ばれ，
ラグランジュ関数の時間積分（これを作用積分といいます）が
停留値となるようなx(t)の経路を見つける方法です．
ここでは，代表して変数はx(t)しか記述していませんが，
実際は自由度の数だけ変数があり，
これと同じ数だけオイラー=ラグランジュ方程式ができます．
エネルギーが保存される系では，ラグランジュ関数は作れるのですが，
オイラー=ラグランジュ方程式は，一般に解けません（解を関数で書けません）．
昔，私達が物理学で演習したのは，解のある特殊なケースばかりだったのです．
注）振幅の小さい範囲では，x(t)やx'(t)の2乗まで残す近似で，
線形な微分方程式の固有値問題に帰着します．
詳細はhttp://blogs.yahoo.co.jp/tanidr/16560687.html

■問題は振幅の大きいときの運動を知る方法です．
これは解析的な解が得られないので，
今日のようにコンピュータが使えるようになって数値計算ができるようになりました．
そのためのプログラムは，次のような手順です．
現在の位置と速度をx(n),x'(n)とします．
x(n)，x'(n)から加速度x''(n)を得るのは，オイラー=ラグランジュ方程式を使います．
一方，x'(n+Δ)＝x'(n)+x''(n)Δ，　x(n+Δ)＝x(n)+x'(n)Δ　ですから，
x(n), x'(n), x''(n)から，時間ステップΔ後の x(n+Δ)，x''(n+Δ)が更新できます．
このようにして，初期値から，逐一運動の様子を求めていきます．

■力学系を記述するラグランジュ方程式は存在するのだが，
解を関数で記述できない（解けない）方程式が大多数です．
系の運動を支配する法則（ニュートン力学）は明確なのに，
解が関数で記述できないのです．コンピュータによって
運動は逐一決定できますが，常識と違う予想もつかない挙動が起こる．
分岐やカオスです．このようなことを指摘したのはポアンカレでした．

・1766　オイラー「変分法の原理」
オイラー，　ラグランジュ
・1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ
・1900　ポアンカレ
可積分の方程式はごくわずか
大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．
－－－－－－
可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

力学系を記述するラグランジュ方程式は作れるのだが，これが解けるとは限らない．
物理の演習では，解けるものしか扱わなかったのです．
実際の世の中は，解を関数で記述できない（解けない）方程式が大多数．
系の運動を支配する法則（ニュートン力学の方程式）は明確なのに，
解が関数で記述できないのだ．でも，コンピュータによる数値計算により，
運動は逐一決定できる．しかも，予想もつかない挙動が起こる．
このようなことを指摘したのはポアンカレでした．

1766　オイラー「変分法の原理」
オイラー，　ラグランジュ

1800　ラグランジュ「解析力学」
エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる
オイラー，　ハミルトン，　ヤコービ

1900　ポアンカレ
可積分の方程式はごくわずかで，大部分の方程式は非可積分（関数で記述できない）
ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．

可積分　→　予測可能，安定な軌道　互いに独立な因果列
非可積分→　カオス的　　　　　　　干渉し合う因果列

分岐理論

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.10］ No.054
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今回はホットなニュースです．
■錯視のシンポジウム
http://cmma.mims.meiji.ac.jp/…/jointrese…/demosillusion.html
International Symposium on Psychological vs Mathematical Approaches to Optical Illusion
が，明治大学中野キャンバスで，2015年3月4-6日に開催されました．
興味があるテーマでしたので多くのセッションを聞きたかったのですが，
私の時間の許す5日の14:00~17:20のセッションだけ参加しました．
https://www.facebook.com/sgk2014?fref=nf
注）
3月12-14日に明治大学駿河台キャンバスでサテライトミーティングがあるようです
http://www.mims.meiji.ac.jp/seminars/another/2011/20120313.html
ーーーーーーーーーーー
聴講したセッションの座長はYasushi Yamaguchi,
講演は次の3件；
Masanori Idesawa, A model for explaining tha anomalous motion illusion.
Akiyoshi Kitaoka, Color-dependent motion illusion in stationary images:
What causes illusory motion?
Stuart Anstis, Illusion of motion perception.
ーーーーーーーーーーー
会場は，明治大学中野キャンバス，5Fの新しい楕円型の階段ホール．
参加者は若者が多く４０人程度であった．この国際シンポジウムのオーガナイザーは，
Kokichi Sugihara(明治大学), Akiyoshi Kitaoka(立命館大学)です．
注）
明治大学は，2008年度，「現象数理学の形成と発展」グローバルCEOプログラムに採用された．
数学系では，東京大学，京都大学，九州大学，明治大学が採択されている．
大学院先端数理科学研究科，現象数理学専攻は2011年に開設，2013年に中野キャンバスがオープンした．
明治大学には錯視美術館（大学と少し離れた淡路町）があり，毎週土曜日だけ開館している．
博士前期課程では，学生1人に対し正副3人の指導教員が広がりを持った研究指導を行う．
後期課程では，学生の研究テーマに応じて，モデリング，シミュレーション，
数理解析の3分野から1人づつ計3人の指導教員がチームを組んで多角的な研究指導を行うという．
現象数理学は，微分方程式のモデルで定量的に記述し，コンピュータでシミュレーション．
分岐理論でなぜ違いが生じるのかを理解する．金融工学，進化ゲーム理論，錯視の仕組みなどが，
数理モデリングを通じて理解ができる．修了後の進路は，
ビッグデータを扱うIT系企業，金融機関，教員など．米国の例では，
投薬タイミングなどを分析して医師らにアドバイスする病院ポストなどまで広範である．

2006年の文科省科学技術政策研究所「忘れられた科学－数学」で
数学と他分野との共同研究実施に向けた体制整備が叫ばれた．
数学と諸科学の連携研究は，米国MAMでも盛んに報じられており，
活発化している数学の分野である．これが純粋な数学と呼べるかの疑問はさておき，
高性能のコンピュータと数値計算の発展により可能となった新しい分野である．
エネルギー散逸のない系を記述するオイラー=ラグランジュ方程式は存在するが，
その大部分は解けない（関数で書けない．非可積分という）．
学生時代に教科書で扱ったのはごく特殊なケースなのだ．
これらをコンピュータを用いて数値的に解くことになる．
安定軌道がなくカオス的で分岐が生じる現象が注目される．
同様にビッグデータを解析する統計学でもコンピュータが活躍する．
日本数学協会が，６月7日午後に予定している講演会（於大東文化大学）
「ヒトとモノづくり数学－10年目の数学月間」でも，
数学月間の経緯と並べて錯視を取り上げることになっている．
ーーーーーーーーーー
■静止画なのに動きを生じる錯視
見ているのは静止画なのに動きが出る（なぜ時間の要素が入る）のか？
と不思議に思うでしょう．見る側に原因があります．目の空間認識は，
TVのようなラスタースキャンではないが，サッケード運動，ドリフト，
中心視と周辺視の切り替わり，網膜の周期的なリセット，等々により，
これらは時間の関数だからです．私は形の認識の仕組みに興味があります．
図形の対称性を見て快いと感じるのは，単純なサッケードになるからだろうと考えていました．
そして今回，これは錯視と表裏一体の現象であると気付きました．図形の認識にかかわる
測度量で時間の関数であるものが，動きのある錯視を生む原因になるようです．
動きを生む錯視にも色々あります．北岡の回転する蛇に見るように，
黒/暗灰/白/明灰/黒/･･･の明暗のストライプで，白から黒の方向に動くように見える現象が，
色相のストライプでも起こり，周囲が明るいときと暗いときでは動く方法が逆になる．
このようなデザインは処々で活用されています．
http://www.ritsumei.ac.jp/~akitaoka/rotate.html
同じものを見ていても，全域的回転を認識するか局所的回転を認識するというように
注目現象が異なることがあります．どちらかを認識すると他方は見えないのです．
これは亜群の集合で核となる部分集合をどれに定義するかの問題と類似しています．
■青・黒ドレスの色が変わる
動きは生じない錯視の例として，青・黒の横縞のドレスが白・金の横縞に変わるのが，
このシンポジウムの紹介を兼ねて3月4日の夕方のTVニュースで取り上げられました．
youtube動画やtwitterなどで，この原因が，右脳，左脳による個人差だというような
説が流れていますがそれは嘘です．周囲の明るさに依存して変化するのです．
色相変化ではγ特性が効いています．
宮澤賢治が注文の多い料理店序文で「はたけや森の中で、ひどいぼろぼろのきものが、
いちばんすばらしいびろうどや 羅紗 や、宝石いりのきものに、
かわつているのをたびたび見ました」と言いましたが，これは錯視ではありません．
でも黄昏の光できものの模様が変わって見える錯視はあることでしょう．
フィルタリングや非線形γ特性などは，画像処理で日常使われているものですが，
これらも錯視を生む場合があります．
Stuart Anstis(University of California)は，動きを生む錯視の原理が理解できる例を
以下に掲載しています．http://anstislab.ucsd.edu/illusions/

■2重振り子（振幅の大きいとき）

微小な振幅であるならば，解析的な解があり，あまり複雑でない周期的な運動になることを前回に学習しました．
しかし，振幅が大きくなると，ラグランジュ関数 L の近似ができませんので，ラグランジュ方程式は解けません．
しかし，将来，誰かが巧妙な方法で解くのではないかと期待し，最悪そのような解析的な解は存在しないとしても，
振動範囲が小な場合と本質的に大差はないのではないかと想像するのが自然なことでした．
系のラグランジュ関数 L は全く正しいし，ラグランジュ方程式も正しいのですから，
解析的に解けないと言っても心配ないのではと思うでしょう．

しかし，実験ではとんでもない現象が見られました．
コンピュータを用いた計算が高度になり，力ずくで動きのシミュレーションがなされるようになりました．
正しい方程式は実在するのですから，関数による軌道記述は出来なくても，動きは逐一決定されるはずです．
しかし，初期条件（初期値）により，予想もつかない挙動が見られます（カオス）．

◆第１の動画は実験
スタートする初期値によって運動の様子は異なります：

◆第２の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1

■2重振り子（振幅の小さいとき）

図のような2重振り子の運動です．今回は物理演習のようになりましたが，
数式に囚われる必要はありません．重要なのは，振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので，2種類の周波数の振動が重畳
された運動になる．つまり，関数で記述できる安定な周期的な運動になる
という事です．そして，これに対比される次に話題になる振幅の大きい
2重振り子運動では，運動は関数で記述できず，予想もつかない
とんでもない運動をするということです．

◆それでは，振幅の小さいときの2重振り子の学習をしましょう．
ここでは，ラグランジュ関数やラグランジュ方程式を説明せずに用いています．
これらを学習したい方は，EMANの物理学などが参考になります．

m1の座標は

これは，Oから釣り下がる長さ l の糸と
mから釣り下がる長さ l₁ の糸の和であるからだ．

この2重振り子のラグランジュ関数Lは

Tは系全体の運動エネルギー，Uは系全体の位置エネルギー
解Φ，ψ を求めるには，次のラグランジュ方程式を解かねばならないのだが

解析的には解けない（関数で記述できる解がない）ので，
Φ，ψ の振動範囲を微小に制限して（Φ，ψの2次までを残す近似），

この近似した L=T-U を用いて，ラグランジュ方程式を解く．
これは解けるのだが物理の演習問題なので（参考）に示し，結論だけ述べる．
結論
Φ, ψ は，以下の2つの固有ベクトル（基準振動）の重畳（線形結合）で表せる．　

微小振動の範囲では，Φ，ψは，それぞれ２つの固有振動の重ね合わせであるということは，
それほど複雑な振動ではない．いずれにしろ周期的な振動である．
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
（参考）

続く⇒　振幅の大きい場合

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.03.03］ No.053
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
3月になりました．皆様，お元気にお過ごしでしょうか．
母が救急車で入院した1月には，硬い芽のようだった病院の梅も，
今はすっかり咲いてしまいました．白梅でした．
病院は遠方なのですが，見舞いにほぼ毎日通っています．
ここの梅の花の咲くのが見られるとは思っていませんでした．
でも，お陰様で無事に日々が過ぎています．

無限に繰り返す周期的な空間を結晶空間といいます．
このような空間を，正多面体（あるいは半正多面体）を組み合わせて，
すきまなく充填する様式を観賞しましょう．
これは立体パズルとしては難しいものですが，自然界ではめずらしくありません．
美しい鉱物結晶の構造として，結晶学の常識になっています．
空間分割の対称性，空間群の研究は，数学者ではなく
フェドロフなどの結晶学者や鉱山技師が偉大な業績を残しています．

■立方体（1種類）を積み重ねた周期空間から始めましょう．
Fig.1の4列目の最上行（右上隅）にあります．
http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16535749&no=1
（これらの図はPOV-Ray，v3.7を用いて作成しています）

1列目の図は，立方体と正8面体を重ねて表示したものです．
これらの2つの正多面体は互いに双対*の関係にあります．
（*立方体の面を頂点に，頂点を面に変えたものが正8面体）
立方体のサイズを固定して，正8面体のサイズを連続的に変化してみましょう．
第1列の上から下へ，正8面体のサイズを徐々に小さくしています．
そのとき，立方体と正8面体の共通部分として得られる半正多面体が第2列．
これら半正多面体の名前をシュレーフリ記号*で書くと，
第2列の上から順に［3,8,8］,［3,4,3,4］,［4,6,6］です．

*)記号の見方：例えば［3,8,8］は，頂点のまわりが，
正3角形，正8角形，正8角形で囲まれているという状態です

■第3列は，それぞれの多面体を2次元に配列させて作ったシート．
第3列の上段図には小さい正8面体，中段図には大きな正8面体を立てる穴が，
下段図では，正８面体ではなく同じ半正多面体［4,6,6］用の穴ができます．

■第4列に，空間を隙間なく埋め尽くす正多面体の組み合わせを示します．
第4列の最上段図は，立方体のみでできる配列．
立方体だけで隙間なく空間を充填した構造は単純格子といいます．
第２，第３の行に，正8面体の穴に正8面体を詰めて空間を充填する様式を示します．
これらも格子としては単純格子と同じです．
第４の行は，多面体［4,6,6］のみで空間を充填できることを示します．
このとき出来上がる構造は体心格子と呼ばれます．

■ペロブスカイト（CaTiO3）構造
Fig.1の下から2行目の配列構造を見てください．
正8面体と［3,4,3,4］多面体の組み合わせで，空間が充填されています．

Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/79/16539279/img_3_m?1425130572
正8面体の中心にTi原子，［3,4,3,4］多面体の中心にCa原子，
各多面体の頂点にはO原子を配置すると，ペロブスカイトの結晶構造が得られます．

余談ですが，この構造は，強誘電体や超伝導物質と係わりがありますし，
地球マントルの高密度物質の構造とも係わりがあります．

■ダイヤモンド構造
Fig.3
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_0_m?1425310851
こんどは，正8面体の稜を共通にして，平面シート状に並べます．
もちろん，正8面体だけでは空間の充填は出来ませんので，
正4面体の隙間がたくさんできます．正4面体の隙間はFig.3の緑のシートが
積み重なったようになり，頂点で８つの正4面体がつながり（シートが重なるため），
正4面体と正8面体の比率は2:1です．
空間の充填パズルはこれで正解なのですが，ついでにダイヤモンド構造を作ってみます．
Fig.4
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_1_m?1425310851
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/07/16541407/img_2_m?1425310851
正8面体（間隙）を取り囲む緑の正4面体の半分だけ使い，
各頂点で４つの正4面体がつながるようにします．
ダイヤモンドの結晶構造は， このような正4面体の配列が繰り返し，
青い正4面体の中心と頂点の位置に炭素原子を配置した構造*です．

*)正4面体の中心にある炭素原子から，4つの頂点方向に4本の結合が伸びています．
正四面体のどの頂点も4つの正4面体と規則正しくつながつているので，
正4面体の頂点の炭素原子からは，周りの４つの正4面体の中心にある炭素原子に向かって，
同様に4本の結合が伸びています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.24］ No.052
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
球表面を平面に投影するステレオ投影
地球儀を2次元平面の地図に

■性質1:　円は円として写像される
ステレオ投影というのは，球表面の点 Z(ξ，η，ζ)を，
北極 Nと結んで，南極 Sでの接平面 Π上の点 z=x+iyに投影することです．
N(0,0,1)，S(0,0,0)を直径とする球面の式は，ξ^2＋η^2+ζ^2=ζ　であり，
この球面はリーマン球と呼ばれます．
Z(ξ，η，ζ)は, (0,0,1）と（x,y,0）を結ぶ直線上にあるので，
ξ=x(1-ζ), η=y(1-ζ), これらを球の式に代入すると，ζ＝r^2/(1+r^2）となる.
ただし， r^2=x^2+y^2 である．　まとめると；
ξ＝x/(1+r^2) ，η＝y/(1+r^2)，ζ＝r^2/(1+r^2）
逆に解くと，x=ξ/(1-ζ)，y=η/(1-ζ)，r^2＝ζ(1+r^2）
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_2_m?1424438241
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_3_m?1424438241

平面上の任意の円の方程式は　a(x^2+y^2)+bx+cy+d=0　である．
この円の方程式の x, yに，上記の表式を代入し，
ξ^2+μ^2＝ζ(1-ζ)を用い整理すると
(a-d)ζ+bξ+cη+d=0　が得られる．
この１次式は平面を表し，球表面との交線は円となる．従って，
「平面上の円は球面上の円から投影され」この逆も成立することがわかる．
以上で証明は終わりですが，直観的な説明を補足します．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/95/16518295/img_4_m?1424438241

リーマン球上の円は平面Ωで球を切った切り口で，PQはこの円の直径です．
△NPQおよび△Nqpは，直径NSを含み，円の直径PQおよびpqを含む平面です．
図に示すように両三角形でα，βは互いに等しく，両三角形は互いに相似です．
PQを直径とする円に相似な円が，平面Π上にqpを直径として投影されるでしょう．

■性質2:　ステレオ投影は等角写像
複素関数 f が，複素平面領域 D のあらゆる点で微分可能*なら，Dで正則といいます．
*微分可能とは，どの方向からその点に近づいても同一の微分係数が確定することで，
微分係数が０や∞になる点は特異点といいます．
正則関数による写像は等角写像*です．
*写像された像が歪んでも，微小部分の角度は元の像の角度と変わらない．
ステレオ投影(複素平面からリーマン球面への写像 f )は，正則関数なので，
任意の点z0で交差する曲線の投影結果も，
それらの交差角度が保存されたまま投影されます（等角写像）．
（f(z1)-f(z0))/(f(z2)-f(z0))=(df/dz)(z1-z0)/(df/dz)(z2-z0)=(z1-z0)/(z2-z0)
ただし，z1,z2→z0 で成立．
lim arg(f(z1)-f(z2))=lim arg(z1-z2))
偏角について成立するこの式は，微小領域で写像による角度が保存されることを示す．
Fig.1に示した横倒しの地球儀のステレオ投影の様子を見ると
平面に投影した地球の下側半分の子午線は，大変歪んでいるが
互いに直交している状態は変わっていないことがわかる．

■諸科学への応用
等角写像は工学の色々な分野で利用されている．
色々な境界条件に合うようにする等角写像は，流体力学で活躍している．
何度でも微分可能であるという複素関数の性質も
我々の身の回りの現象を記述する方程式で頻繁に利用されている．

ご感想やコメントなど，以下のブログあるいはメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.17］ No.051
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
前号に引き続き双曲面分割の話です．

■エッシャーの「極限としての円」のシリーズが生まれるまで

コクセターとエッシャーは1951年の国際数学会で出会いました．
1958年にコクセターはこの分割を掲載した論文をエッシャーに送り，
これがエッシャーの「極限としての円」の作品群を生むことになります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_0_m?1423875894

エッシャーの双曲面分割作品のシリーズ１は直線魚のモチーフでした，
天使と悪魔など，このシリーズの作品群があります．
そして，シリーズ3の洗練された作品に至り完成します．

■次に示すのは，エッシャーの作品「極限としての円3」です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/08/16506608/img_1_m?1423875894

白い線で分割されたタイル張りは，複数の正多角形による準正則タイル張り
[4,3,4,3,4,3]のように思うかもしれません．
しかし，白い線は直線ではないのです．白い線は，双曲世界のフチの円周と
直交しません（80°で交わる）．実は，右図に示される黒い線が直線です．
右図のように正8角形のタイルが頂点で３つづつ集まる正則分割{8,3}と
見るのが正しいのです．エッシャーの作品は，黒い線は顕に出さずに
白い線を見せて見事に数学的に正確で芸術的な作品に仕上げています．
このエッシャーのトリックについては，コクセターが論文で指摘しています．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.10］ No.050
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユークリッド幾何，楕円幾何，双曲幾何
色々な幾何空間があります．大きく分けて，ユークリッド幾何空間と非ユークリッド幾何空間です．非ユークリッド幾何空間には，楕円幾何，双曲幾何の支配する幾何空間があります．これら3種を，平面を例にとり比較します．
（１）我々の常識の通用するのはユークリッド平面です．
ご存知のように，ユークリッド平面では，直線外の1点を通る平行線は唯一本だけ引けます．
（２）球の表面は楕円幾何平面の例です．地球の表面だけを想像しましょう．
地球自体は，3次元ユークリッド空間の物体ですが，表面だけなら楕円幾何平面の例です．
楕円幾何平面の直線は大円（球の中心を含む平面による球の切り口）です．地球上の2点間の距離が最小のものは大圏コースと呼ばれますが，これは地球の大円上の線分のことです．地球は3次元ユークリッド空間の物体ですから，地表の2点を地球内部を通る直線で結べば最短距離でありますが，地表だけの2次元平面では大圏コースが最短です．球表面の異なる２つの大円は必ず2点（直径の両端）で交わります．そのため楕円幾何平面では．平行線はありません．また，地球儀の緯線のようなもの（小円）は大円でないのでこの世界では直線になりません．
（３）双曲幾何平面では，ある直線に対する直線外の1点を通る平行線は無数に引けます．双曲幾何平面は楕円幾何平面のように閉じていないので，イメージを持ちにくいのですが，ポアンカレがうまいモデルを提唱しました．このモデルはポアンカレの円盤モデルといいます．双曲幾何の世界を表すのに円盤を用い，この世界の直線は円盤のフチに直交する円弧とします．このように定義された世界では，ある直線に対する直線外の1点を通る平行線は無数に引けることがわかります．

■3種の幾何平面で，平面の正則分割を考える
さてこれからやることは，それぞれの幾何平面で，正多角形のタイルによるタイル張りを考えることです．このような問題は，平面の正則分割とも呼ばれます．
それぞれの幾何平面での多角形は，それぞれの幾何平面の定義による直線で囲まれているものです．それぞれの幾何平面で，3角形の内角の和Sは，S=π（ユークリッド平面），S>π（楕円平面），S<π（双曲平面）になります．
正p角形が頂点でq個集まってタイル張りがなされている状態{p, q}で，正p角形の内角の和を表す式を等号で置くと　(2π/q)p=(p-2)S　が成り立つので，
1/p+1/q=1/2　（ユークリッド幾何）
1/p+1/q>1/2　（楕円幾何）　
1/p+1/q<1/2　（双曲幾何）
となります．それぞれの幾何平面で，許される{p,q}の整数解を求めると，以下のことがわかります．
（１）ユークリッド平面での正多角形によるタイル張りは，正3角形，正4角形，正6角形で可能．｛3,6｝．｛4,4｝，{6,3}が解です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_0_m?1423315106
（２）楕円幾何の平面では，正6角形以上の正多角ではタイル張りができません（閉じた立体になりません）．
調べてみると，正5角形のタイルでは，頂点に3つのタイルが集まるもの{5,3}，正4角形のタイルでは，頂点に3つ集まるもの{4,3}，正3角形のタイルでは，頂点に5つ{3,5}，４つ{3,4}，３つ集まるもの{3,3}が作れます．結局，5種類の正多角形によるタイル張りがあり，これらはプラトンの正多角形に対応した球面立体です．ここでは｛5,3｝に対応するもののみ掲載します．黄色い球面正5角形が頂点で3つ集まっているものです．黄色いタイルに5mの対称性があるとき，赤で塗った三角形を中心から見込むような万華鏡を作るとこの映像が再現できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_1_m?1423315106
（３）双曲幾何の平面では，正則分割は無限にあります．
例として｛6,4｝と{5,4}のものをとりあげ掲載しました．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_3_m?1423315106
例えば，{6,4}の映像を3角形の万華鏡で作るには，
下図の中心に頂点のある三角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧の鏡を使います．しかしながら，この円弧は数学的に反転円として定義されているのですが，現実の光学法則では火線という収差があるので，あまり奇麗な万華鏡映像にはなりません
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/93/16488893/img_4_m?1423315106

■円盤の中の不思議な世界
私たちの宇宙は膨張していることが知られています．
遠方の宇宙のフチの後退速度はものすごく，光速に達すると，
こちらに光はやって来ません，そこが宇宙の果です．
宇宙銀河の回転速度は，宇宙のフチに行くほど大きく
高速で運動する世界の長さは，我々から見ると縮んで見えます
つまり，宇宙は双曲幾何の世界に似ています．
双曲幾何の円盤の内では，円盤のフチに近づくほど空間が縮みます．
この世界では，直線に沿って旅する自分自身もフチに行くほど縮むので
いつまで歩いても世界の果てに到達できません．
同様に，円盤の中心に近いほど距離が大きくはかどるので，
円盤の外から見ている我々には，直線が円盤の中心方向に膨らんで見えます．
一方，円盤内の世界にいる者にとってはこれが最短距離で直線なのです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.02.03］ No.049
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１種類の形（2等辺3角形）の赤色と黄色のタイル（赤タイルと黄タイルは互いに鏡像）
で作ったタイル張り模様を鑑賞しましょう．
1種類のタイルで，平面をタイル張りすると，必ず周期的なタイル張りになってしまう
と思い込むのは間違っています．確かに，
Fig.4　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_5_m?1422741853　や
Fig.5　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_6_m?1422741853
のような周期的なタイリングはすぐ思いつきます．
しかし，
Fig.2　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_1_m?1422741853　や
Fig.3　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_2_m?1422741853
のように非周期なもので，平面をタイル張りするものがあります．
Fig.2は中心に回転対称があるタイリング模様で，点群5mの対称性です．
Fig.3は，２つの目がある螺旋パターンのタイリングで，
水平線は映進面だと思うかもしれませんが，このパターンには周期がありませんから
映進操作はできません．螺旋の目の間（中心）に対称心があります．

さて，ここで万華鏡で作られるタイリング模様
Fig.1　http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/556602/97/16430597/img_0_m?1422741853
の登場です．
この万華鏡を生む3枚の鏡は１つの頂点では点群を生成しますが，他の２つの頂点では点群を生成しません．
従って平面を赤と黄色の市松模様で埋めることはありません．
全体の代数系は，群より緩いもの（特殊な亜群）になってしまいますから非常に複雑です．
対称操作は局所的で，独自の作用域と値域があり興味深いものです．
作用域，値域の制限のために，一つのタイル全体が無傷で写像されるパターン内の位置と，
部分が写像される位置があり，このような複雑なタイリング模様ができます．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊
ご感想コメントなどを，
http://blogs.yahoo.co.jp/tanidr/16430597.html　あるいは　以下のメールにお寄せください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.01.27］ No.048
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
１．万華鏡の美しさが我々の心をとらえる理由は，対称性とカオスの共存
完全な秩序は美しいが，死の世界のようだ．
一方，乱れは千変万化し同じ光景を見るのは一度きり．
そして現象は，いつ起こるかわからない．だから
我々は，はらはらしながら期待し目が離せない．
万華鏡は，秩序の中に乱れもある．生命も，秩序とカオスのただ中にある．
万華鏡の中を降りゆくガラス屑　定まると見し運命にカオスあり

２．対称性
それでは，まず対称性についての考察を始めようと思います．
対称性は自ずと決まるものとして，あるいは合理的なデザインとして生まれます．
環境や境界条件，自然科学の法則が，
その環境下の物質構造やふるまい/現象の対称性を自ずと決定する．
（例）人体，生物，乗り物，結晶，自己組織化，建築物．蜂の巣，花弁の形，柱状節理，etc．
■空間に関する対称性（１点の周りの対称性と周期）
タイル張り，壁紙模様，正多面体，結晶構造，エッシャーの版画．
■時間に関する対称性
時間反転．音楽（J.S.バッハ），詩の韻律，リズム，同期現象．
■現象の対称性
性質空間の対称性．因果律の対称性．

３．対称性はなぜ快いか？
インクの染みは汚らしいが，乾かないうちに紙を折り鏡映対称の染みになると美しく見える．
そしてなんだか想像力を駆きたてる（ロールシャッハ・テスト）．なぜ美しく感じるのだろうか．
私はその理由は次のようなものではないかと思っている：
物や事に対称性があると，我々の脳がその全貌を把握するための情報量が圧倒的に減る．
例えば，結晶とアモルファス（ガラス）で，それらの構造（構成する原子の位置）を
記述しようとすると，規則的な繰り返しのある結晶の方が圧倒的に単純だ．
人間の脳は，整理された少ない情報量だと負担が少なく，快いと感じるのではないだろうか．

４．鏡
万華鏡の話がテーマなのだが，ご存知のように万華鏡は合わせ鏡でできている．
万華鏡の対称性は，鏡映のみにより生成されたものに限ります．
我々は鏡をのぞきこむと何か変な気持がするものだが，以下のような話があります：
太古の時代は，我々の世界と鏡の中の世界の行き来ができたそうだ．＊

＊注）このようなことは4次元の世界なら実際に可能である．例えば，3次元空間で
右の手と左の手は，互いに鏡像になっている．右手が我々の世界にあり，
左手が鏡の世界にあると想像してみよう．左手が鏡の世界を抜け出して
我々の世界のなかで，右手と重なろうとしてもできない相談だ．
ただし，4次元空間なら左手の中身を裏返して，右手と同じにすることができる．
2次元の紙に描いた線画の右手と左手が，いくら紙表面の上で移動しても
ひったり重なることはできないが，紙を折り返す（3次元空間での操作）ならば
重ねることができることは実験で確かめられる．

話を戻すと，鏡の中の生き物とこちらの世界の生き物は仲良く一緒にいたのだそうだ．
ある夜，突然，鏡の世界の住人達が我々の世界で好き勝手を始めるようになった．
そして人々は，鏡の中の住人の正体が「混沌」であることに気付いたという．
そこで，黄帝が魔力によって「混沌」を鏡の世界に閉じ込め，
姿や動きも我々の世界の模倣しかできないようにした．*1)
呪文の効果が切れて，鏡の世界の住人達が勝手に動き出すことが将来起こるかも知れない．
そのようなテーマの小説に*2,3)がある．私は幻想怪奇小説が大好きです．

*1)Turbulent mirror, J Briggs & F. D. Peat, 訳：高安秀樹，高安美佐子
*2)パイプをすう男，M･アームストロング，幻想と怪奇 1（ハヤカワ）
*3)わな，Ｈ・Ｓ・ホワイトヘッド，怪奇幻想の文学(新人物往来社)

混沌の中から湧き出るように次々と生まれてきたさまざまなものが宇宙を形作った．
このようなプロセスを神の技と語られることもあります．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.30］ No.044
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年もあと2日になりました．私は部屋の大整理掃除で3日間も満足にパソコンを開けません．
皆様には，よい年末でありますように．そして良い年をお迎えください．来年もよろしく．

クバンチックの問題は如何でした．私が一番好きなのは，第2問のビリヤードの問題です．
この問題に関する連想考察は，近いうちにぜひ書きたいと思っています．

さて，私は毎年「とっとりサイエンスワールド」で万華鏡のワークショップをやらせてもらっています．
正月まもなく（1月16日，PM3～）多摩センターでも開催しますので，お近くの方はご参加下さい．
詳細は，sgktani@gmail.com　にお問い合わせください．
これからメルマガでも，万華鏡の数学について何回か連載するつもりです．
ここで紹介する万華鏡のキットは，「その道の達人派遣事業」の時に開発し，
各地の学校を回り子供たちと作った万華鏡（当時は2種類）がもとで，
その後品種を増やしてできたものです．
-----
◆万華鏡の原理（１）
万華鏡は合わせ鏡の原理を使っていることはご存知ですね．fig1を見てください．
平行な合わせ鏡で挟まれた室（黄色）は1次元に無限に繰り返しています．
室内にある赤い物体もfig1に示したように繰り返します．
黄色い部屋の隣はその鏡像（左右が逆）．合わせ鏡で挟まれた黄色い部屋を（黒），
隣の鏡像の部屋を（白）と思うと，黒白の帯（1次元の市松模様）ができますね．
今度は，合わせ鏡のなす角度を平行でなくθ°とすると，
市松模様の帯は直線ではなく円を描くように延びて行きます．
円の反対側で市松模様がうまくつながるためには，
黒白のペアの数が整数でなければならない．
これは360°/2θ°＝n（整数）となります．これは，万華鏡の発明者
スコットランドの物理学者ブリュースターが1817年に提出した特許にあります．

FIg.1
以上の説明は2枚鏡の合わせ鏡でしたが，複数鏡の合わせ鏡でもできます．
3枚鏡の場合を考察しましょう．fig2には鏡が作る3角形の図です．
3角形の頂点で2枚の鏡が出会うわけですが，それぞれの頂点で，鏡のなす角度は
360°を偶数で割り切る角度である必要があります．3角形の３つの頂点で
この条件が満たされているなら3角形のタイルで平面が市松模様に張り尽くされます．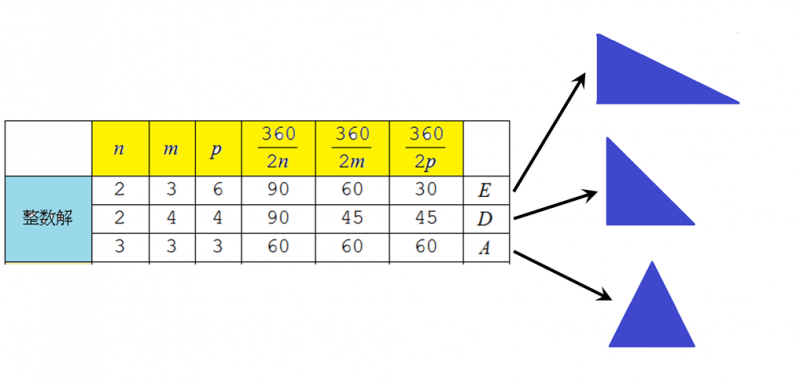

Fig.2
3つのどの頂点でも整数解を持つ場合は，平面をきれいに埋め尽くす市松模様ができます（3種類あります）．
1つの頂点でも整数解にならない場合には，市松模様は乱れますが，これも万華鏡としては美しいものです．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.23］ No.043
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
«Квантик»クバンチク（量子っこ）というロシアの生徒向けの雑誌を知りました．
http://kvantik.org/
数学，言語学，物理学などの自然科学の疑問や問題を楽しく学ぶ新雑誌のようです．
onlineでは12ページまでしか出ていないので，その先は購入しなければなりません．
クバンチクで現在出題されている「4つの課題」を紹介します．
出来た人は解答を　kvantik@mccme.ru.　に送ると独創的な解答は公開されます．
面白い問題で私は出来ましたよ．問題もさることながら，
ロシア語の題意を解釈するのに時間がかかってしまいました．
翻訳を載せておきますのでご挑戦ください．

（第1問）監獄からの脱出
T字型の監獄で．2m幅の堀で囲まれている．1.9mの板が2枚ある．
ジャンプは出来ない．どのように脱出するか？
（第2問）ビリヤード
1:2のテーブルの真ん中の位置に球を置いて，テーブルの角のポケット
にビリヤードで（反射させて）玉を入れることは可能か？
（第3問）如何にしてビンをぶら下げるか
2本のマッチと50cmの糸がある．
これらを用いて水入りのビンを棚の縁（角ではない）にぶら下げなさい．
（第4問）物体の警護
物体点のまわりに，哨兵を何人か配置し，
物体にも哨兵にもこっそり近寄られることの無いようにすることはできるか？
ただし，各哨兵は，選んだ一つの方向だけまっすぐに100ｍだけ見ることができる．

解答は載せません．以下は，私からのヒントですーーー
１．Tという形がポイントです．
２．可能です．
３．マッチ2本をどう利用しますか
４．哨兵3人で済みますね．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.16］ No.042
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
パターンがどんどん内部に繰り込まれて行くデザインのいくつかを紹介します．
これらはフラクタルと呼ばれる性質と関係があります．
葛飾北斎（１８３０年代前半）の富嶽36景，神奈川沖の絵の
波しぶきを見たことがおありでしょう．あるいはこの季節の
すっかり葉を落とした木立の先が美しく枝分かれしていたり
雲や海岸線の輪郭が，拡大しても拡大しても同じような
形が現れてくるのにお気づきでしょう．
同じ形が繰り返し内部に繰り込まれているような仕組みを
フラクタルと言います．
フラクタルの詳しい説明は後回しにして
今回は応用されたデザインの例を鑑賞しましょう．

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_0_m?1418046938
グラスのこちら側の円が凹レンズになり，向こう側の円模様を
レンズ円内に縮小して映し出しているのが面白い．
（リュミナルク製）

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/16/16306916/img_2_m?1418046938
五芒星と黄金比　外部と内部の比(1+√5)/2＝1.618:1

http://blogs.yahoo.co.jp/tanidr/GALLERY/show_image.html?id=16306916&no=1
レオナルドの星型8角形　外部と内部の比1+√2：1

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.09］ No.041
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆皆様，お元気でお過ごしでしょうか．選挙が迫り慌ただしい日々ですね．
大事な選挙です．私はもう期日前投票を済ませましたよ．
先週土曜日には，河合弘之弁護士の作ったドキュメンタリー「日本と原発」を
見てきました．皆様の近所でも有料試写会（自主上映）がきっとありますので，
ぜひご覧になることをお勧めします．
「原発は複雑系なので，事故が雪崩を起こす弱点（ここを攻撃されると過酷事故になる）
が思わぬところにある．その引き金となるのは，地震・津波だけではない」と，
メルマガ006に掲載したことがあります．ぜひお読みください．
バックナンバーはブログにもあります．私は，原発だけは止めたいと思っています．
高木仁三郎さんと「宮沢賢治をめぐる冒険」でお話したとき（1997年）のことが
昨日のように思い出されます．この本は，市民科学者として活躍した高木仁三郎さんが
羅須地人協会に打ち込んだ賢治と重なって見える良書です．
これら数学以外のことは，ブログの方に掲載することにしましょう．
ーーーーー

◆双曲幾何の円盤世界
Fig.1の灰色の円盤内の世界は，双曲幾何の世界です．
この世界の直線は，世界の果て（外周円）に直交する円弧
－例えば，Fig.1の赤い円－です．もちろん直径のような本当の直線も
灰色世界の円盤の外周円に直交しますのでこの世界の直線です．

赤い円で2分された灰色世界の左側と右側は
赤い円を反転円として，互いに反転鏡映像になっています．
Fig.1　
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_1_m?1418046545

2つの平面鏡と１つの円柱鏡で作られる万華鏡（Fig.2）を見てください．
赤く塗った3角形の各辺は，この円盤世界の直線です．
赤く塗った3角形の頂角は，30°－45°－90°．内角の和は165°で180°に
足りませんが，この円盤内の世界は双曲幾何の世界なので当然です．

赤く塗った3角形の辺を紙面に垂直な方向に伸ばした3角柱を考えると
平面2枚と円柱鏡からなる万華鏡ができます．
円柱鏡が生む映像は数学的な反転鏡映像としますと
Fig.2のような円盤内の分割（ポアンカレ万華鏡像）が得られます．
塗られた3角形と白い3角形は鏡映の度に入れ替わるので市松模様です．
Fig.2
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/67/16306967/img_0_m?1418046545

実際に作ってみました．ポアンカレ万華鏡を再現するのは困難です．
円柱鏡での光の反射（物理的）は，数学的な反転操作とは異なり
厳密な数学的な反転鏡映は，光学的には実現できないのが残念です．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.12.02］ No.040
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先に，「007_インドラの網と反転円」で言及したことがありますが，
円による反転鏡映について，その性質や利用例を鑑賞しましょう．

◆円による反転鏡映の性質
下図に赤い円による反転鏡映の代表的な例を２つ示します．
・反転円をよぎる直線aを反転すると，反転円の中心を通る円Aになる．
・円bを反転すると，円Bになる．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_0_m?1417183249

この性質を知っていると，色々なことに利用できます．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_3_m?1417183249
例えば，このような図形はアルベロス（靴屋のナイフ）
といいますが，この中の幾何学世界の面白さなどです．

下図のアポロニウスの窓の中にある黄色の円とピンクの円は，
緑色の円を反転円として，それぞれ反転円内の黄色とピンクの円が
鏡映像になります．これらの鏡映像は平行な直線（黒）に挟まれた
領域内に入ります．
平行直線の左はアポロニウスの窓の外周円の反転鏡映，
平行直線の右はアポロニウスの窓内にある左側の大きな円（灰）の
反転鏡映像です．なぜなら，外周円も左側の大きな円（灰）も
反転円の中心を通っているので，鏡映像はどちらも直線になるからです．
アポロニウスの窓内にある初めの黄色い円もピンクの円も，外周円と
内部の左側の大きな円（灰色）に接しているので，
それらの反転鏡映像でもそのような状態が保たれています．

このようなことがわかると，以下のパップスの定理が導かれます．
アルベロスの中で，右側の大きなピンクの円の上に生じる
黄色の円（ω1），続いて生じる灰色の円（ω2），の系列を考えると，
「円ωnの中心と直径ABとの距離は円ωnの直径のn倍である」
（パップスの定理）ことがわかります
以下の図は，ω2の場合の例です．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_2_m?1417183249
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/78/16304278/img_1_m?1417183249

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.11.25］ No.039
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆平面のブラベー格子は５つのタイプがあることを036号で学びました．
ここに示す繰り返し模様のそれぞれは，どの格子に対応しますか？
日本の伝統文様には，美しい繰り返し模様がいろいろあり，それらは
着物や食器，籠バック，インテリアなどと色々な所で見られます．
これらの模様には，どのような対称性があるかを鑑賞しましょう．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_3?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_4?1414573530

http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/545271/32/16234632/img_5?1414573530