ブログ倉庫

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.03.07］ No.157
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
桜もずいぶん早く咲いているのを見かけますね．皆様のところでは如何でしょうか．
今回もダ・ビンチの星型を取り上げますが，「星型小12面体」とも呼ばれる形を見てみましょう．
イメージ 1
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_0_m?1488810835
シュレフリの記号で書くと｛5/2，5｝です．
（注）シュレフリの記号｛p,q｝というのは，
正p角形の面が，頂点でq個集まっているような正多面体を表す記号でした．
この形は，東京都庭園美術館，朝香宮邸，姫宮の部屋の照明器具にも使われている美しい形です．
芯になるのは正5角12面体で，その12個の正５角形の面の上に，それぞれ正5角錘を取り付けた形をしています．
正5角錐の頂点は，それぞれ，正12面体の面に対応していますから，
頂点を結んでできる図形（赤の多面体）は，正12面体に双対な正20面体です．
2次元の断面を見ると，以下の左図の様な星型正多角形（ダビデの星）が見えます．
イメージ 2
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_1_m?1488810835
上図の図形は,星型5角形（ダビデの星）と星型8角形（ダ・ビンチの星型）です．
それぞれの図にある赤い輪郭線（それぞれ正5角形と正8角形）は，
凸多角形（凹所のない多角形）で，赤い輪郭線の多角形内部に，黒い線分で描いた図形が星型です．
左のダビデの星を見て下さい．
星型正5角形の辺をA→B→C→･･･→Aと1周りたどると，
辺の向き（→）が2回転することがわかります．（あるいは，
「5角形の頂点を１つ飛ばしで辿って，2周して始めの頂点に戻る」
ということもできます）
このような星形を｛5/2｝と表記します．
（もし，1点の周りが2x360°という世界があれば，この星型は凸多角形になります）
星型８角形でも同様で，この図形は｛8/3｝です．

■さて，星型正多面体を見て下さい，正5角錐の頂点の周りに，星型正多角形{5/2}が，
5個集まっていることがわかるでしょう．
従って，この星型正多面体をシュレフリの記号で書くと{5/2,5}となります．

このダ・ビンチの星型は，「星型小12面体」とも呼ばれます．
イメージ 1

シュレーフリの記号で書くと｛5/2，5｝です．
（注）シュレフリの記号｛p,q｝というのは，正p角形の面が，頂点でq個集まっているような正多面体を表す記号でした．
この形は，東京都庭園美術館，朝香宮邸，姫宮の部屋の照明器具にも使われている美しい形です．芯になるのは正12面体で，その12個の正５角形の面の上に，それぞれ正5角錘を取り付けた形をしています．正5角錐の頂点は，それぞれ，芯となる正12面体の面に対応していますから，頂点を結んでできる図形（赤の多面体）は，正12面体に双対な正20面体です．
この星型多面体の面は，以下の左図の様な星型正多角形（五芒星）です．
イメージ 2

　Fig.　星型5角形（五芒星）と星型8角形（ダ・ビンチの星型）

それぞれの図の赤い輪郭線（それぞれ正5角形と正8角形）は，
凸多角形（凹所のない多角形）で，赤い凸多角形内部に星型が作図されています．

■五芒星（図左）
星型正5角形の辺をA→C→E→B→D→Aと1周りたどると，
辺の向き（→）が2回転することがわかります．あるいは，
「5角形の頂点を１つ飛ばしで辿って，2周りすると始めの頂点に戻る」
ということもできます．
このような星形を｛5/2｝と表記します．
（もし，1点の周りが2x360°という世界があれば，この星型は凸多角形になります）
凸多角形では，1周すると辺の向きは360°回転し，正n角形では，頂点で360°/nずつ回ります．従って，正n角形の頂角（内角）は180°-360°/nです．五芒星の頂角は36°で，正n角形の頂角が36になるのはn=5/2ですから，五芒星を｛5/2｝と表記するのは妥当でしょう．

星型８角形でも同様で，この図形は｛8/3｝です．

■さて，星型正多面体に戻りましょう．正5角錐の頂点の周りに，星型正多角形{5/2}が，5個集まっていることがわかるでしょう(例えば，頂点Aの周りに右図のような五芒星の板を5枚集める)．芯に正5角形の穴の開いた五芒星の板を，各頂点で5枚ずつ組み合わせると，この立体を作ることができます．
従って，この星型正多面体をシュレーフリの記号で書くと{5/2,5}となります．
イメージ 3

デザルグの定理とは
「⊿ABCと⊿A'B'C'があり，AA'，BB'，CC'を通る直線が1点Oで交わるなら．
直線ABとA'B'の交点P，直線BCとB'C'の交点Q，直線CAとC'A'の交点Rは，同一直線上にある」

 このデザルグの定理の証明は，実はとても難しいのです．3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります．
ところが，下図のように，この図形を平面（2次元）と見ずに，立体（3次元）にあると見ると，ごく当たり前のことを言っていることに気づきます．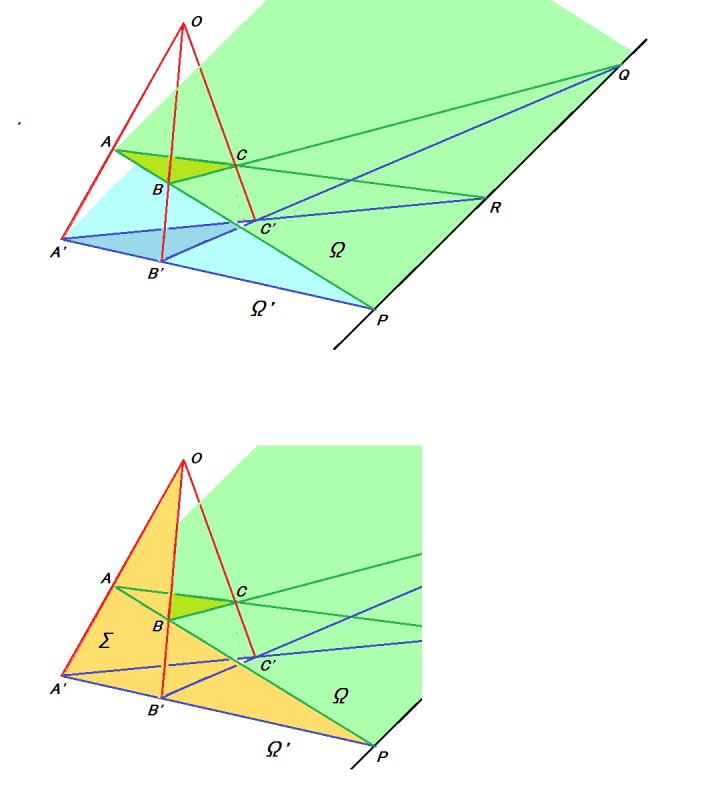
２つの平面Ω（薄緑）とΩ’（薄青）が交差しており，△ABCは平面Ω上に，△A'B'C'は平面Ω'上にあります．
光源Oから出る光が，△ABCの影を△A'B'C'に作っています（辺ABの影が辺A'B'）．
従って，O，A，B，A'，B' は，同一平面上にあり，この平面をΣ（薄燈）と名付けます．A，Bを通る直線も，A'，B'を通る直線もこの平面Σ上にあり，P点で交差します．
一方，A，B，Pは平面Ω上に，A'，B'，Pは平面Ω’上にあります．
結局，P点は平面Ωと平面Ω’の交線上にあることになります．
同様にして，QもRも，平面Ωと平面Ω’の交線上にあり，デザルグの定理が証明できました．

■デザルグの定理は，2次元で証明するのは難しいが，3次元では証明が要らないほど自明なのは何故でしょうか．
3次元でこの図のような模型があったとして，これを2次元に射影する（高さ方向をぺちゃんこ）と，直線が交差する状況は変わらないのですが，長さや角度の情報が失われてしまいます．△ABCと△A'B'C'は，それぞれ別の2次元平面にあったものですが，ぺちゃんこにされて1つの平面（紙面）に入ってしまいました．
私たちは，高い次元（2次元の世界から3次元の世界）を想像するのは困難です．デザルグの定理でこれを思い知らされます．
■デザルグは，17世紀初頭のフランスの数学者，建築家．透視図法を発展させた射影幾何学の祖です．ダビンチなどの画家たちは，遠近法や透視図法を古くから用いていましたが，その数学を固め射影幾何学の本を出したのはデザルグが最初です．
その後，射影幾何学が本格的に研究されるのは，200年後の19世紀中葉，ポンスレー（フランスの数学者．ナポレオンのロシア遠征に従軍し，ロシアで捕虜のときに射影幾何学を研究した）を待たねばなりませんでした．
射影幾何学自体，作図など重要な応用がありますが，やはり，19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました．

デザルグの定理とは
「⊿ABCと⊿A'B'C'があり，AA'，BB'，CC'を通る直線が1点Oで交わるなら．
直線ABとA'B'の交点P，直線BCとB'C'の交点Q，直線CAとC'A'の交点Rは，同一直線上にある」

このデザルグの定理の証明は，実はとても難しいのです．3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります．
ところが，下図のように，この図形を平面（2次元）と見ずに，立体（3次元）にあると見ると，ごく当たり前のことを言っていることに気づきます．
イメージ 2

２つの平面Ω（薄緑）とΩ’（薄青）が交差しており，△ABCは平面Ω上に，△A'B'C'は平面Ω'上にあります．
光源Oから出る光が，△ABCの影を△A'B'C'に作っています（辺ABの影が辺A'B'）．
従って，O，A，B，A'，B' は，同一平面上にあり，この平面をΣ（薄燈）と名付けます．A，Bを通る直線も，A'，B'を通る直線もこの平面Σ上にあり，P点で交差します．
一方，A，B，Pは平面Ω上に，A'，B'，Pは平面Ω’上にあります．
結局，P点は平面Ωと平面Ω’の交線上にあることになります．
同様にして，QもRも，平面Ωと平面Ω’の交線上にあり，デザルグの定理が証明できました．

■デザルグの定理は，2次元で証明するのは難しいが，3次元では証明が要らないほど自明なのは何故でしょうか．
3次元でこの図のような模型があったとして，これを2次元に射影する（高さ方向をぺちゃんこ）と，直線が交差する状況は変わらないのですが，長さや角度の情報が失われてしまいます．△ABCと△A'B'C'は，それぞれ別の2次元平面にあったものですが，ぺちゃんこにされて1つの平面（紙面）に入ってしまいました．
私たちは，高い次元（2次元の世界から3次元の世界）を想像するのは困難です．デザルグの定理でこれを思い知らされます．
■デザルグは，17世紀初頭のフランスの数学者，建築家．透視図法を発展させた射影幾何学の祖です．ダビンチなどの画家たちは，遠近法や透視図法を古くから用いていましたが，その数学を固め射影幾何学の本を出したのはデザルグが最初です．
その後，射影幾何学が本格的に研究されるのは，200年後の19世紀中葉，ポンスレー（フランスの数学者．ナポレオンのロシア遠征に従軍し，ロシアで捕虜のときに射影幾何学を研究した）を待たねばなりませんでした．
射影幾何学自体，作図など重要な応用がありますが，やはり，19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2017.02.21］ No.155
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユニット折り紙で作ったダビンチの星型の続きです．これは，
芯に置いた正8面体の各面に正3角錘が乗っている形です．Fig.4
星型の頂点を結ぶと芯にある正8面体に双対な正6面体ができます．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/19/17902919/img_0_m?1486823996

このユニット折紙では，正３角錐の面は正3角形ではなく直角3角形です．
そして，各面はツートンカラーになっています．
対称性を調べると，芯の正8面体の頂点方向に（x,y,ｚ軸）4回回転対称軸，
各正3角形の面に垂直に3回回転対称軸，2つの4回回転軸の中間（同じことだが，2つの3回回転軸の中間）に
2回回転対称軸があります．色の変化を調べると，
4回回転軸により4色の置換，3回回転軸により3色の置換と1色の保存，
2回回転軸により2色の置換と2色の保存が起こります．

この図形には4回軸があるので，色置換の操作も含めて完全な対称性にするには，
塗り分けには4色用いる必要があります．
3回軸の方向から見ると3色見え，見えないもう一色は，
3回軸で保存され，3回軸に垂直な面の大円上にあります．
3回軸の方向は4本あり，3回軸それぞれは，軸に垂直な大円上の色を保存するので，
結局，塗り分けには全部で4色使うという言い方もあります．

■写真(Fig.5)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_0_m?1487566646
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_1_m?1487566646

この星型は，立方体の6つの面に，正3角形の面で出来ている正4角錐が乗っています．
芯になる立方体の1辺の長さを１とすると，星型の頂点の高さは√2/2，
もし，星型頂点の高さを立方体の辺の長さの1/2に短縮すると，
星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります．
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_4_m?1487566646
(Fig.6)左が星型正24面体，右が菱形12面体

展開図は色々なものができますが，作りやすいものにするのがよい設計です．
星型24面体と菱形12面体の展開図を比較して見て下さい．（Fig.7）
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_6_m?1487566646
美しい形ですので作って見ると良いでしょう．

■正20面体を芯にして，正3角形の各面の上に正3角錘（正4面体）を乗せた星型が，星型正60面体です．
正3角形の面が10個集まっている点と3個集まっている点（頂点）が交互にある星型です．
1枚の連続した紙に展開図を描くことはできません．