ブログ倉庫

トレミーは2世紀のギリシャの天文学者プトレマイオスのことです．地球中心の天動説を確立したので有名です．トレミーの定理を導きました．

トレミーの定理（Ptolemy's Theorem）とは，円に内接する任意の４角形 ABCD で，AB･CD＋DA･BC＝AC･BD　が成立することです．高校の幾何ででてきた懐かしい定理です．

 

 

 

 

 

 

 

 

 

 

トレミーの定理を，以下のような特殊な円に内接する4角形＝長方形に適用すると，ピタゴラスの定理　a･a+b･b=c･c　が証明できます．この意味で，トレミーの定理はピタゴラスの定理の拡張定理と言えます．

 

 

 

 

 

 

 

 

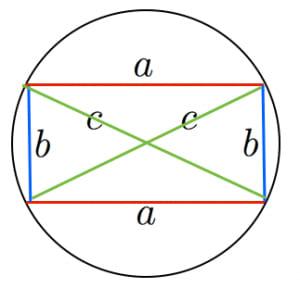
さて，トレミーの定理の証明には，三角関数を使うなど色々な方法がありますが，素朴に，下図の2つの図に示す3角形の相似を用いてやってみます．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

両辺を足し合わせると　AB･CD+BC･DA＝AC･(BP+DP)が得られます．

<<KVANTIK>>, No.11, 2020; Фёдор Ниловフョードル・ニーロフより抜粋

https://kvantik.com/extra/parall/

セミパラレル図形

白い正方形は一斉にペチャンコにすると図形をコンパクトにできます．不思議ですね．

 

 

 

 

 

 

 

 

 

 

 

 

 

パラレルニクという多角形は，下図のどちらかの性質を持ちます．

 

 

 

 

任意の平行多角形はパラレルニクである．下図に示す例は5角形の平行多角形の例です．

 

 

 

 

 

 

 

次の図は，中央に任意の３角形（緑）があります．その外に白い正方形を３つ作ります．それら頂点は，6角形になり，その外に白い正方形を３つ作ると，また6角形が得られます．同じ色の多角形の面積はすべて等しく，4角形はすべて台形です．この定理は，2001年にアメリカの数学者D. DeTemple と M. Hudelsonが証明しました．

 

 

 

 

 

 

 

 

 

 

 

また，中央の３角形をどんな平行多角形に置き換えてもこの定理が成り立つことも発見しました．以下の図は，中央に平行４角形，平行５角形にした例です．

 

 

 

 

 

 

 

 

 

https://elementy.ru/nauchno-populyarnaya_biblioteka/435457/Kvantik_9_2020

«Квантик» No9, 2020に，アレクサンダー・ペレペチコによる次の問題があります：

１．サーシャは，1日2回，朝と夕方に，物忘れ治療薬を飲まなければならないのですが，忘れることもあります．続けて 2 回服用した後は，必ず忘れずに服用し，2 回服用しなかった後は，服用を忘れます．過去 1 日にちょうど 1 錠服用している場合は，次回服用する確率は1/2とします．

サーシャが，ある時点から完全に薬を飲むことを忘れてしまう確率はどれくらいありますか? ずっと飲み続けている確率は？

 

 

 

 

 

 

 

 

２．酔っぱらいは居酒屋と彼の家の間の道路に立ち，1 秒ごとに同じ確率でランダムな方向に道路に沿って 1m ステップします．家に着いたり居酒屋に着いたりすると，そこにとどまります．

家まで 3m，居酒屋まで 7mの距離にある場合，彼が帰宅できる確率はどれくらいですか．

 

https://elementy.ru/problems/

立方体の上の面の対角線にレールがあり，下の面の対角線（上の面の対角線とは直交）にもレールがあります．下のレールの端（頂点）と上のレールの中点（面の中心）とを結ぶ長さの「線分」があり，この線分（長さを変えない）の両端はレール上をすべることができます．線分が包絡線となり囲む図形（リノイド）の表面の形を推理してください．

立方体の1辺の長さを2aとすると，リノイド体積はいくらですか．

なかなか難しいですが，線分の動きを頭の中でシミュレーションした以下の図が参考になります．

 

 

 

 

 

 

 

 

 

 

 

立方体の1辺の長さを2aとすると，線分KFの長さはa√6です．
図のような，座標系で考えます：

 

 

 

 

 

 

 

 

 

 

$$K(x_{K} , 0, -a), F(0, y_{F} , a), M\left( x, y, z \right) $$とします．
$$\overrightarrow{KM}(x-x_{K} , y , Z+a), \overrightarrow{FM}(x, y-y_{F} , z-a)$$
なので，次の方程式が得られます．
$$\displaystyle \frac{x-x_{K } }{x}=\displaystyle \frac{z+a}{z-a}=\displaystyle \frac{y}{y-y_{F } }$$
これを解いて，　　$$x_{K}=\displaystyle \frac{2ax}{a-z} , y_{F}=\displaystyle \frac{2ay}{a+z}$$
一方，　$$\left\{ \begin{array}{@{\,} c @{\, } }
KF^{2}=x_{K}^{2}+y_{F}^{2}+4a^{2} \\[0mm]
KF=a\sqrt{6}
\end{array} \right. $$ 　⇒　 $$x_{F}^{2}+y_{F}^{2}=2a^{2}$$　であるので，$$x_{F} , y_{F}$$を代入して，
$$\left( \displaystyle \frac{2ax}{a-z} \right) ^{2}+\left( \displaystyle \frac{2ay}{a+z} \right) ^{2}=2a^{2}$$　 ⇒　$$ \displaystyle \frac{2x^{2 } }{\left( a-z \right) ^{2 } }+\displaystyle \frac{2y^{2 } }{\left( a+z \right) ^{2 } }=1$$
このリノイドの水平（すなわち軸Ozに垂直）断面の方程式を得るためには， 
zの値を区間$$\left( -a, a \right) $$でスライスする． 
この方程式は，半軸に$$x=\left( a-z \right) /\sqrt{2}, y=\left( a+z \right) /\sqrt{2}$$を持つ楕円の方程式になる．
楕円の面積$$S$$は，　$$S=\pi \cdot \displaystyle \frac{\left( a-z \right) }{\sqrt{2 } } \cdot \displaystyle \frac{\left( a+z \right) }{\sqrt{2 } }=\displaystyle \frac{\pi }{2}\left( a^{2}-z^{2} \right) $$
ゆえに，リノイドの体積$$V$$は，　$$V=\displaystyle \frac{\pi }{2}\displaystyle \int_{-a}^{a}\left( a^{2}-z^{2} \right) dz=\displaystyle \frac{2\pi a^{3 } }{3}$$ 

 

 

 

厚労省の公表値を用いて，日本の有病率を求めると0.6%，検査陽性率は5%程度です（5月14日時点）．このデータを用いて，ベイズ推定を用いPCR検査結果の考察をします．PCR検査の感度$$a$$と特異度$$b$$により，この結果は大きく変わります．PCR検査の感度$$a$$と特異度$$b$$は，従来の定説の0.7と0.99よりはるか高い，0.95と0.9992であることが，最近の研究で知られています．

今日のPCR検査で$$+$$判定の者には，罹患（真陽性）と非罹患（偽陽性）があります．同様に，今日のPCR検査で$$-$$判定の者にも，非罹患（真陰性）と罹患（偽陰性）があります．つまり，今日，罹患となった者には，真陽性と偽陰性があります．そして，今日の罹患者の病気期間は11日間とすると，今日の罹患者は，11日間先まで罹患者であり続け感染源となります．これを有病罹患と定義します．今日の有病罹患者は，11日前から今日までの罹患者の累積となります．11日を過ぎれば，PCR検査$$-$$となり，回復非罹患者（今日の非罹患者＋11日より以前の全検査数-累計死亡者）になるとします．ここで，PCR検査で$$-$$判定で，罹患であるのは，検査の確率の視点での話で，必ずしも，無症状の感染者と一致するものではありません．
日々発表される新規陽性（罹患）者数を累積すると，累積陽性者数になるので，差分としての新規陽性者数は，罹患率に似た傾向ですが，罹患率そのものではありません．ここで定義する有病罹患者は，日々の新規罹患者と病気期間（発症してから陰性になるまでの病気減衰関数$$A(t)$$）のコンボリューションとして得られます．
$$有病罹患者(T)=\displaystyle \int_{0}^{T}罹患者(t) \cdot A(T-t)dt$$

あるいは，$$現罹患者数=累積陽性者数-累積退院･回復者数-累積死亡者数$$で定義できます．

有病罹患者（現罹患者）

国内発生状況．厚労省（2021.5.15現在）

$$有病率(5.15現在）=有病罹患者数(5.15現在)/累積PCR検査数=5.8×10^{-3}$$
$$陽性率(5.15現在）=陽性者数(t)/PCR検査数(t)=5.2×10^{-2}$$

PCR検査の感度$$a$$と特異度$$b$$が与えられ，集団の有病率$$p(罹患)=x$$が与えられると，この集団で，PCR検査が+と判定されたとき罹患者である確率$$p(罹患|＋)$$，および，-と判定されたとき罹患者である確率$$p(罹患| - )$$を推定できます．
$$p(罹患| + )=p\left( + |罹患 \right) \cdot p\left( 罹患 \right) /p\left( + \right) =a \cdot x/\left( a \cdot x+(1-b)\left( 1-x \right) \right) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) \cdot x/\left( (1-a)x+b \cdot \left( 1-x \right) \right) $$，

従って，この集団の陽性率を$$p( + )=y$$とすると，有病率は，以下のように表現できます．
$$p(罹患)=p(罹患| + )･y+p(罹患|-)･(1-y) $$
$$x=a \cdot x \cdot y/\left( a \cdot x+\left( 1-b \right) \left( 1-x \right) \right) +\left( 1-a \right) \cdot x\left( 1-y \right) /\left( \left( 1-a \right) x+b \cdot \left( 1-x \right) \right) $$

$$有病罹患者(T)=\displaystyle \int_{}^{}罹患者(t) \ A(T-t)dt$$
病気減衰関数$$A(t)$$の半減期はおよそ10日ですので，近似的に，有病罹患者数(t)は本日の罹患者数(t)の10倍としたもので，この等式が成立/

特異度は，$$b$$>0.99（0.999）との説もあり$$b=1$$として，$$a$$を求めると，$$a=5.2×10^{-2}/5.8×10^{-3}=8.9$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 

■条件付き確率についての「ベイズの定理」とは次のように説明できます．$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$ 
ただし，記号の意味は例えば以下の様です．
$$p(X)$$：$$X$$が起こる確率
$$p(Y|X)$$：$$X$$が起こり，かつ$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きた後で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

■PCR検査の精度
「新型コロナ検査，どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）」によると，以下のようです：
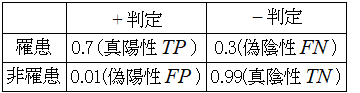
PCR検査の感度とは，罹患者がPCR検査で陽性（＋）と正しく判定される確率のことで，あまり大きくなく0.7程度です．真の罹患者でもPCR検査で陰性（－）（偽陰性）と判定される確率が0.3程度あります．
検査の特異度とは，非罹患者を正しく陰性（ー）と判定する確率のことでかなり高く0.99程度です．従って，非罹患者を陽性（＋）（偽陽性）と判定する確率は稀で0.01程度です．

有病率（現罹患者の比率）$$x$$が小さい集団では，非罹患者が大部分を占めるので，PCRで偽陽性の確率は0.01と非常に小さいとはいえ，PCRの偽陽性者数は多くなり，医療崩壊につながるという主張があります．しかしながら，陽性確定までにPCR検査は2度行われ，2度とも偽陽性となる確率は$$10^{-4}$$，1万人に1人です．さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．あるいは，PCR検査の感度のために偽陰性者をたくさん生むという主張もあります．確かに，検査数に比例する偽陰性者を出しますが，検査しない状況と変わりなく，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

（注）罹患者とは，真に感染しており現在感染源となるものと定義します．これには，PCR検査で陽性（真陽性）と判定されるものと，陰性（偽陰性）と判定されるものとを含みます．非罹患者とは，もともと感染していないか，回復した感染者で，感染源とならないものです．非罹患者はPCR検査で陰性になるのが原則ですが，例外（偽陽性）も0.01あります．有病率＝罹患者数／(罹患者数＋非罹患者数)　は，有病率の定義です．

 

 

 

 

 

■PCR検査の原理 
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です． 

 

■有病率の考察
日本疫学会の定義によると，有病率とは，ある時点で，疾病を有している人（罹患者）の全人口にたいする割合です：
（定義）有病率＝その時点の罹患者数／集団の人数
この有病率と混乱しそうな概念に，罹患率というものがあります：
（定義）罹患率＝ある期間の新規感染者数／集団内の感染感受性のある人数 

毎日発表される，COVID-19の新規感染者数は，罹患率の概念に近いが，罹患率に換算するのに必要な分母の「感染感受性のある人数」が不明です．ワクチン接種などで，感受性のある人数が減れば罹患率は上昇します．もし，その日の検査数（偏りのあるサンプルで，恣意的変動はある）を分母にするなら，その日の陽性率が得られます．
日々の新規感染者数や検査数は，恣意的な変動があるので，7日の移動平均をとり陽性率を定義します．検査の対象集団は症状のあるものや濃厚接触者なので，サンプル集団には陽性側に偏りがあります．

有病率，罹患率，陽性率は，時間で変化する関数で，感染拡大の指標になりますが，それぞれ意味合いが異なります．大雑把に言うと，陽性率は有病率の差分のような統計量です．

公開データから計算できる有病率$$p(罹患) $$を以下の2通りで定義することにしました．
（定義１）本日の有病者数＝累積陽性者数－累積回復者数－累積死亡者数
　　　　　本日の有病率＝本日の有病者数／累積検査数

厳密に言うと，累積陽性者数には非罹患者の陽性数（偽陽性）も混じりますが，累積回復者数を減じるので，これは相殺すると思われます．

有病率の分子からは回復者などが除外されるので，陽性率＝陽性者数／検査数よりも常に小さい値になります．

COVID-19の新規陽性者は，2週間隔離（症状の程度により，病院，宿泊施設，自宅などに）されますので，死亡者は無視して，本日の新規感染者は続く2週間は罹患者と見なされます［罹患期間を10日間とする見解もあります］．そして，2週間後にPCR検査が2度陰性になれば回復者に入ります．そこで，死亡者を無視すると次の定義も成り立ちます．便宜的に，新規感染者とは新規陽性者と同義語とします（厳密にいえば，偽陽性者が含まれるのですが，除去の根拠となるデータがありません）．

（定義２）本日の罹患者数＝日々の新規感染者数を2週間前まで遡り総和．
正確には，陽性持続曲線を用いて，新規感染者数と陽性持続曲線のコンボリューションとなります．
陽性持続の半減する期間はほぼ10日です．

英国国家統計局（ONS）は，オックスフォード大学，マンチェスター大学，英国公衆衛生サービスNHS，ウェルカムトラスト，IQVIA，グラスゴー・ライトハウス研究所，バイオセンター・ミルトンケインズと協力して，イングランドでパイロット調査を2020年4月に開始し，8月からは，サンプルのサイズを拡大し2021年3月まで大規模調査をしました．英国の４地域ベースのランダムな世帯サンプリングをし，得られた偏りのあるサンプルを英国全人口に外挿するには，多層回帰および事後層別化（MRP）を用いました．同じ世帯に対し長期間のCOVID-19検査を実施（最初の4週間は毎週，その後は毎月の検査）し，症状の有無にかかわらずCOVID-19の有病率と罹患率を，ほぼリアルタイムで観測し，病気期間（陽性持続確率）の関数を得ました．PCR検査の感度$$a$$と特異度$$b$$についても新しい知見が報告されました：$$a=0.95(0.85～0.98)$$，$$b=0.9992$$．スワブ採取が適切な監督下で行われれば，自己採取でも医療従事者が直接採取した場合と同様に正確な結果になることがわかりました．

COVID-19 Infection Survey: methods and further information，26 March 2021

 

 

 $$p_{a}(t)$$

 

 

 

 

 

 

 ■陽性率の考察
$$t$$時点の陽性率($$t$$）は，その時点でCOVID-19の検査で陽性となった人の割合です。現在のCOVID-19感染症は、鼻と喉から採取した綿棒で、症状の有無にかかわらず、SARS-CoV-2が陽性であることを意味します。これは、発生率とは異なります。発生率は、特定の期間における新しいポリメラーゼ連鎖反応（PCR）陽性の症例のみの測定値です。

ここで，陽性率$$p(+)$$に用いるべき数値を検討します．恐らく，毎日発表される検査陽性率（7日の移動平均された新規感染者数／7日の移動平均された検査数）を用いるのが適当でしょう．これは感染者数の微係数のようなもので，感染流行の傾向をある程度反映し注目すべき数値です．しかし，検査対象の制限（偏りがあるサンプリング）があり，かつ，サンプル数は少ない状況にあります．東京都の場合は，全人口1,400万人の集団に対して，症状のある集団1,000人程度を毎日サンプリングしています．日々の検査陽性率の4月14日時点の，厚労省の全国データを用いて，（検査）陽性率，$$p(+)=0.06$$を採用することにします．

引用）
1.厚労省データ，東京都データ，
2.COVID-19 Dashboard by the CSSE at Johns Hopkins University 

■問題：以下の２つを推定しましょう．ただし，ベイズの定理を使います． 
事前確率として，有病率を$$ p(罹患)＝x=0.003$$を用います．

（１）PCR検査で陽性と判定されたとき，罹患者（真陽性）である確率を求めなさい．この確率は，検査の「陽性的中率」と呼ばれます． 
$$p(罹患|+) =p( +|罹患) p(罹患) /p(+) =0.7x/(0.7x+0.01(1-x)) =$$
$$=7x/(6.9x+0.1)$$

（２）有病率を推定しなさい．
陰性と判定されたものの中に，見逃された罹患者（偽陰性）のいる確率は：
$$p(罹患|-) =p( -|罹患) p(罹患) /p( -) =0.3x/(0.3x+0.99(1-x)) =$$
$$=3x/(-6.9x+9.9)$$

集団の有病率$$x$$を変数に，$$p(患者|+)$$と$$P(患者|-)$$のグラフを示します．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

従って，全人口に対して推定される有病率は，陽性率$$p(+)$$，陰性率$$p(-)=1-p(+)$$とすると，
有病率$$=p(罹患|+) p( + ) +p(罹患|-) (1-p(+) )$$　なので，

事前確率として有病率$$x=0.003$$を用いた場合は，真陽性の確率0.174，偽陰性の確率0.0009で，さらに，陽性率$$p(+)=0.06$$を用いると，真陽性の罹患者に，見逃された罹患者（偽陰性）を加えた有病率は$$0.174×0.06+0.0009×(1-0.06) =0.011$$と推定されます．

■PCR検査数は十分か

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

引用）
3.https://ourworldindata.org/coronavirus-testing

 ここに引用したのは，検査陽性数／1日（横軸）；検査数／1日（縦軸）の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは100万倍大きい（数値では30～20倍）のでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を全部拾う十分な検査が行われているようです．英国の例を見ると，始めは，陽性者がたくさん出て検査数が間に合わないほどでしたが，現在は十分な検査数が確保されていることがわかります．日本の例では，検査数と陽性者数の増減が微妙なバランスにあり，英国のグラフに見られる検査数を増やしても陽性者数が一定となる部分が見られません．検査数を増やせば，陽性者数も増加する可能性があります．

COVID-19では，無症状の罹患者が感染源となることが知られています．症状のあるグループだけをサンプリング対象にした限定されたPCR検査では，無症状の感染源は抜け落ちています．自由に活動する無症状の感染源がどの程度のウエイトかも未知ですので，PCR検査のサンプリング対象の拡大をはかるべきです．

■継続的検査のイギリス流戦略

引用文献）

4.https://plus.maths.org/content/testing-testing-schools
5.Assessing the impact of secondary school reopening strategies on within-school COVID-19 transmission and absences: a modelling study，Trystan Leng，etal.

英国では3月8日に学校を再開するにあたり，接触者継続的検査SCTという対策を決めました．英国JUNIPERコンソーシアムの研究者達が，数学モデルを用いて種々の検査戦略のシミュレーションをした結果です．

クリスマス前（閉鎖前）の生徒は，学年別「バブル」の一員として学校に通っていました．ある生徒が陽性と判定された場合，その「バブル」内の全員が10日間の自己隔離になります．この戦略は，学校内はもとより周囲コミュニティ内の感染伝播も防げる利点がありますが，多くの学校で生徒を欠席させるという欠点があります．

生徒が学校に行けない日数を減らすために，イムノクロマトグラフィー（LF検査）を使用した新しい戦略（SCT検査）が提案されました．COVID-19の症例が特定されると，その「バブル」内の他の生徒は，①「10日間の自己隔離」か，②「7日の間，毎日LF検査を受けて，その日の検査が陰性ならば学校に通う」のどちらかを選択します．この戦略の目標は，多くの生徒たちが学校に通えるようにすることにあります．生徒は，学期の初めにLF検査を2回受け，陰性である場合にのみ通学します．

■イムノクロマトグラフィー検査

イムノクロマトグラフィー（LF検査）は，抗体が配置されたセルローズ膜繊維の端に，採取した検体を滴下し，検体中にCOVID-19の抗原があるなら，それが抗体と反応しながらセルローズ繊維を移動し所定位置でキャプチャーされ呈色します．

LF検査はPCR検査よりも感度が低いかもしれませんが，30分以内に結果が出ます．ウイルス量が最も多く，感染性が最も高いと考えられる時点（感染してから約5日後）には，LF検査でCOVID-19陽性となる確率は十分高い［LF検査は，感度も特異度も95%以上との説もあります］のです．人々が感染を避け家にいるだけという状況から，活動できるように，常に検査を続けフィードバックを行うSCT検査への転換をしました．

■数学モデルで介入をシミュレーション

COVID-19に感染した中学生の12ー31％が，症状を発症すると考えられており，発症すると無症候よりも感染性が高いのですが，無症候の感染力はよくわかりません．このように未知の不確実性があるので，シミュレーションのモデル作りでは，パラメーターに不確実性を採り入れ，点推定ではなく範囲を推定しています．

ダイソンのグループ（レンら）は，それぞれ200人の生徒からなる5つの「バブル」で構成されるモデルを作成し，色々な検査戦略：何もしない；学年グループを隔離；SCT検査；毎週の集団検査；両方検査の組み合わせ；のそれぞれを，7週間にわたって毎日の時間ステップでシミュレーションしました．

もちろん，「SCT検査と毎週の集団検査の組み合わせ」が，欠席日数と感染数の両方を減らす最も効果的な戦略です．

検査をすれば，無症候性のCOVID症例が多数特定できます．しかし，組み合わせ検査の戦略では，7週間の半期の終わりに，生徒1人は平均して25回の検査を受けます．検査費用もかかり，若者の同意が必要です．毎日子供たちの鼻に綿棒を突き刺すのは素晴らしいことではありません．それらはトレードオフにあります．この調査は，パンデミックの際に政府や学校の指導者が下さなければならない難しい決定を浮き彫りにしています．ライブパンデミックの前例のない挑戦に対処するには，数学モデルが活躍します．

英国はロックダウンを間欠的に実施しました．長期にロックダウンを続ければ感染は減りますが生活ができなくなります．どのくらいの期間のロックダウンをどのくらいの期間を空けて実施するのが良いかのトレードオフも，感染拡大モデルでシミュレーションしています．英国の100万人当たりのPCR検査数は日本の20倍～30倍もあります．パンデミックを乗り越え現在の有病率は日本より小さい値に下がっています．

実効再生産数を減少させるには，次の3つを減少させることです：①感染者が感染力を持つ期間，②感染者が1日当たりに接触する人数，③感染者の接触で感染する確率．感染→潜伏期間→発症期間→検査→隔離の期間内でCOVID-19は感染します．COVID-19は，潜伏期間でも感染し，発症のない無症状も感染力があることが判明しています．「感染者が感染力を持つ期間」を短くするには，検査で早く感染者（有症状，無症状とも）を見つけ早く隔離することです．