note.com投稿記事

■2008年8月4日に上智大が主催した数学月間参加プログラムで，
「感染症対策における数理モデルの役割」大日康史（国立感染症研究所）
という講演がありました．
数理モデルによる感染拡大のシミュレーションは，新型インフルエンザやバイオテロなどの対策の有効性評価に必要です．数理モデルには，SIRモデル，ibm（IndividualBasedモデル），Ribm（Realibm）などがあります．本研究で用いたRibmとは，実際に調査した個人の移動，所在の記録データ（首都圏では88万人）にもとづき，6分ごとに人々の接触状態（感染の機会）が定義されるものです．新型インフルエンザには，種々のタイプがあり鳥類間の感染は起こるが，鳥から人への感染は血液の濃厚接触などの場合に限られる（豚と人の感染するインフルエンザのタイプは似る）．人に感染した場合に，人から人への感染が始まり拡大していく．[注）Covid-19は，また別のタイプで異なる数理モデルの開発が必要です]

このシミュレーションに用いたのは，例えば，以下のシナリオでした：
（第１日）初発例が外国で感染．（第３日）帰国．帰宅後（八王子）感染性を持つ．（第４日）出社（丸の内）．発症．（第５日）国際医療センターに受診．東京都健康安全研究センターで検査診断．（第６日）対策へ：
このシミュレーションの結果として，
首都圏への感染拡大の様子や全国への拡大の様子が示されました．どのような対策（外出自粛，地域閉鎖，休校，住民全員が予防服用，....）をとると効果があるかを予測できるシミュレーションでした．

この現実的なシミュレーションのシナリオには，首都圏での人の動き（動態調査）のデータが使われています．
このような，人々の接触を考慮した感染拡大のシミュレーションはミクロなシミュレーションといいます．これに対して，統計集団としての陽性率，罹患率などのマクロな量の変化を追うのはマクロなシミュレーションといいます．

■つぎは，英国のハスルミアで行われたスマホアプリを用いた動態調査の実験です．インフルエンザ感染拡大のミクロなシミュレーションに必要な動態調査は，スマホアプリを開発して2018年になされました．それは以下のようなものです．
英国の全国的な市民科学実験は，BBC Pandemicというアプリを使いました．このアプリは，App StoreまたはGoogle Playからスマートフォンにダウンロードできます．
アプリを使用して，ボランティアは次の2つの研究に参加できました：
（1）サリー州の町ハスルミア（ロンドンの近く）に焦点を当てたもので，それはかなりの数の人々を登録するキャンペーンでした．ボランティアのスマートフォンの位置の連続3日以上の追跡を許可を得て実施します．
（2）英国全体の規模の大きい調査は，許可を得てボランティアが選んだ24時間にわたりボランティアの毎時の位置（1km^2のメッシュ精度）を記録します．

各研究期間の終わりに，ボランティアはその期間中に遭遇した人を入力するように求められます．

記録された移動データと自己申告した接触データとで構成された国のデータセットのみを取り出します．このデータを使用して，インフルエンザの蔓延に関する数学的モデルを開発し，それによってインフルエンザのパンデミックがどのようにイギリス全体に蔓延するかをシミュレートするのが仕事でした．

このバーチャルの大流行は，イギリス南部のサリー州にある町ハスルミアで始まり，番組シナリオに従い，BBCドキュメンタリーのプレゼンターはバーチャル実況をしました．ハスルミアで収集した詳細なデータは，バーチャルな国内感染爆発の火種となるハスルミア内の感染爆発のシミュレートに使用されました．結果の感染拡大地図（Kissler，Klepac, Tang, Gog，2018）を見るとロンドンで始まった感染は，何の規制もしなければ1週間でニューカッスルまで広がるようです．

 ■しかし，Covid-19では全く違う（まだわからない）

パンデミックの感染拡大は，インフルエンザとコロナウイルスで似ているようで，非常に異なるところが多いのです．上で述べたミクロなシミュレーションは2018年以前のCovid-19出現前のインフルエンザに対するものであることを再度強調しておきます．ご注意ください．
Covid-19はかなりの潜伏期があり，何の症状も示さずに感染している可能性があります．発症までに，インフルエンザの場合は数時間，コロナウイルスの場合は数日かかる可能性があります．そして，無症状の感染源があるので非常にやっかいです．潜伏期の考慮は本質的に重要で，単純なSIRモデルではなくSEIRモデルになることを，Gogらが指摘しています．そして，Gogらはインフルエンザで開発した感染モデルと全く違う感染モデルを作らなければならずまだ研究中です．

なかなか面白い手頃な問題を引用します．

（問２）

3人の農民が宿に入り，休憩と食事をしました．彼らはホステスにジャガイモをゆでるように命じた後，眠りました．ホステスは客を起こさなかったが，ゆでたジャガイモをテーブルに置いて去りました．
まもなく，彼らのうちの一人Aが目を覚まし，自分の分け前を食べ，そして再び眠りに落ちました．
それから二人目の農民Bが目を覚まし，ジャガイモを数え，1/3だけ食べてまた眠りに落ちました．
それから，三人目の農民が目を覚まし，自分が最初に目を覚ましたと仮定して，ジャガイモを数えて1/3だけ食べました．
それから彼の仲間たち全員が目を覚まし，まだ8つのジャガイモが残っているのを見ました．3人はこれからそれぞれ何個のジャガイモを食べれば，最終的に公平に同じ個数のジャガイモ食べたことになりますすか？

(問３)

数学者は庭のプロットでヤギを飼っています．彼は，20 mの長さのロープの一端を結び付け，他端はヤギの首に結びました．ロープの中間は，フェンスに沿ってスライドできるリングにするワイヤーに沿ってスライドできるリングを通してあります（図を参照）．結局，ヤギは移動できる範囲にある草を全部食べました．ヤギの到達範囲の境界となる弧を描きなさい．
図の説明　
дерево（木）　，кольцо（リング）

クバンチクの問題は，小中学生が対象ですが無理のない興味ある問題です．
第一に必要なのは，問題の意味を理解する読解力です．

■クバンチクの問題１（私の解答例）
クバンチクの問題は解答が定まるとは限りません．解答は5択の選択肢があります．クバンチク問題１として前回紹介したのは解答できる問題の例でした．私の解答例をここに掲載します．

●問２
全体をXとして，Aが食べた後の残りはX(2/3)，続いてBが食べた後の残りはX(2/3)^2，さらにCが食べた後の残りはX(2/3)^3＝8個でした．
従って，Cは4個食べ，Bは6個食べ，Aは9個食べています．
Aの9個は全体の1/3に相当します．B,　Cも9個づつ食べられますので，Bは後3個，Cは後5個食べられます．こうして8個の残りはBとCが食べてなくなります．

●問３

===============================================================

■クバンチクの問題２

今回はクバンチクの問題２として，新たな例題を３つ紹介します．これらはみな2016年の年間ツアー(毎月4~５題を出題）で出されたものです．
挑戦してください．私の解答は，C，D，D です．

●問：島で
島の成人男性の40％と成人女性の60％は未婚です．島の成人人口のうち，結婚していない割合はいくらですか（一夫多妻制および同性婚は島では禁止されています）？

解答選択肢
A. 48％
B. 50％
C. 52％
D. 68.5％
E.結婚について考えるのは早すぎる

●問：都市計画
図は，ある都市の道路地図を示しています．合計2つの環状道路（共通の中心を持つ2つの円）と，この中心で等しい角度で合流する6つの道路があります．バーシャ（名前）は，AからBへの行き方を考えています．外部環状道路または内部環状道路を通る2つのルートのうちどちらが短いですか？

解答選択肢
A.同じ
B.内側の円
C.外側の円
D. 2つの円の半径の比率に依存
E.地下鉄はまだ速いです！

●問：平均速度
2つの山村AとBの間の道路は，上り坂または下り坂のどちらかになります．古いバスは，上り坂では平均時速30 km / h，下り坂では平均速度60 km / hです．AからBまで行き来する通しの平均速度はいくらですか？

解答選択肢
A.時速40 km
B. 45 km / h
C. 50 km / h
D.明確な答えを得るための十分なデータがない
E.古いバスは間違いなく道で壊れます

私はこの問題が気に入っています．中学生向きですが，読解力と身に着いた科学的な常識があれば解けます．算数・数学というのは，数式の記述や論理の学習が目標ですが，そんな堅苦しい学習よりも必要なことは，生活や遊びで自然に身に着いた，読解力と常識が大事だと思います．

次の「アルプスを渡る」の問題では，以下の5つ（とりわけ出だしの２つ）がポイントです：
①題意を正しく理解する読解力→山頂を越えろとは言っていません．
②糸巻に糸を巻くなど生活の遊びの場で，自然に身に着いた力学感覚（力のバランスや手応え）★←特に大事
③円錐の展開図がひらめく（最短距離を引くのは展開だから）
④状況を読んで，2√2≒3と大胆に近似（融通の利かない数学バカでは行き詰る）
⑤半径2√2の円に内接する正3角形の一辺の長さは（ここだけが数学）

★物理学や円錐曲線などを知っている必要はありません．子供の頃に，積み木や水遊びや泥んこ遊びなどで，自然に体感したことのある手応えのことを，私はここで常識と言っています．
別に，物理や数学で数式を習わなくても，手応えが身についていれば，簡単に箸で豆をつかめるし，卵を握りつぶしたりはしません．職人は，器用にガラス細工をします．これは流体の粘性など面倒な計算をしても無駄なことで，その時の手応えで瞬時に反応できないと知識は役に立ちません．色々な分野で同様な身に着いた常識が大切でしょう．私は教室で知識を学ぶよりも，身についている手応えが一番大事だと思っています．
最近の子供は，ゲームやバーチャルな世界で間違った手応えを身に着けていますし，実際の泥んこの手応えや積み木のバランスや卵の殻の複雑な手ごたえを身に着けていないようです．大人になって機械設計をしても，構造の強度の感覚を持ち合わせていない．常識が身に着いていれば，直感（見た目でわかる）でわかる不安定なものを作ってしまう（計算結果がとんでもない数値になってもおかしいと思わない）．
さて，この問題では，円錐の斜面に糸を巻くときの手ごたえをイメージしましょう．とがった頂点を通るように糸を巻いたり，山麓の円周に糸を巻いたりを，安定にできますか？斜面のどこかを経由するとき一番きつく糸を巻きつけられるはずですね．

■問：「アルプスを渡る」
一定の傾斜角45度の円錐形の山のふもとに人々が集まりました．山の高さは2000メートルです．グループは、山のふもとの正反対の地点に行きたいと考えています（図の点Aから点Bに移動します）．AからBへの最短ルートは...

この仕事で地獄行？　もう降りようよ．

解答選択肢（私は，Bを選びました．皆様はどうですか）
A.　4.5 km
B.　5 km
C.　5.5 km
D.　6 km
E.　6.5 km

いろいろな多面体の見える万華鏡（立体万華鏡と呼びましょう）を作ります．アルミ板やプラスチックの鏡は像がきれいに映りますが，ミラー紙(厚手0.25ｍｍくらい）を用いても，ここで取り上げているような立体万華鏡は良好に作れますので，チャレンジしてみてください．

球面正多面体は，アラブの数学者，アブル・ワーファ（1000頃）に始まります．球面正多面体｛p,q｝は，球面正p角形が，頂点でq個集まっているもので，球面正p角形の１つの内角は2π/qです（図D）．
そして，球面p-多角形の辺はすべて大円であることに注意しましょう．

ここで具体的に取り上げるのは，正12面体に相当する球面正12面体＝球面｛5,3｝多面体です．

メビウスは多面体万華鏡を発明します（1850）が，これは，球面p-多角形を，2p個の球面直角３角形に分割することを使います（図A）．
分割された3角形の角度は，π/p，π/q，π/2，このような直角3角形を(p,q,2)と記述します．
万華鏡は，３角形（赤く塗った）の各辺となる大円を鏡にすると得られます．
（A）メビウス万華鏡になり，正5角形の面を10個の直角3角形に分割しています．
（B）正5角形の面を5個の2等辺3角形に分割しています．Bには，Aに存在した鏡映対称面が１つ消えています．
（C）赤く塗った正3角形の周囲の辺の大円を鏡に置き換えて万華鏡を作れば，正20面体の映像が見えます．

では，AとBを作ってみましょう：展開図は，前号の［正12面体の見える万華鏡を作ろう］に掲載してあります．

A(左写真)　　　　　　　　　B(右写真)

p.132～p.133　美しい幾何学より

正12面体や球面正12面体は，正５角形（あるいは，球面正５角形）の面12枚が囲んでできる立体です．
3枚鏡の組み合わせで万華鏡を作り，正12面体や球面正12面体が見える万華鏡を作りましょう．
正12面体の点群（対称性）を生成する3枚の鏡に，次のものを選びます．
（Aタイプ）１つの正5角形の面を10個の直角3角形（若草色）に分割し，
その領域を立体の中心から見込む「3角錘」が万華鏡になります．
（Bタイプ）１つの正5角形の面を５つの2等辺3角形（水色）に分割し，
その領域を立体の中心から見込む「3角錘」が作る万華鏡になります．

（Aタイプ）　　　　　　　　　　　　　　　　　　　（Bタイプ）

作製したそれぞれの万華鏡で見られる映像を対応させて掲載します．
どちらも正12面体の映像が見えますが，両者の正5角形の面を観察して比較しましょう．
Aの映像では直角3角形10個で正5角形の１つの面を作っていますが，Bの映像では2等辺三角形5個で正５角形の１つの面を作っているのがわかります．

■正12面体および球面正12面体の見える万華鏡（Aタイプ）の作り方

ミラー紙（厚さ0.25mm以上が良い）に次の展開図を描きます．青色の部分を使います（赤線に沿って光の窓を作ります）．赤線の円に沿って切ると「球面正12面体像が見える光の窓」，赤線の直線に沿って切ると「正12面体像が見える光の窓」ができます．どちらかを選びます．辺OHが共通につながるように3角錐（鏡面は三角錐の内側）を組み立てます．完成した万華鏡は△KAHから覗きます．

「美しい幾何学」球面正多面体とメビウス万華鏡p.133~p135に，この万華鏡の説明があります．

フィボナッチ数はいろいろな所に現れます．この記事はThomas Koshyの著書からの引用で，2018.09.25発行のメルマガSGK通信No.234のリメイクです．
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2018.09.25］ No.234
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
フィボナッチ数列は次のように定義されます．
F(n)=F(n-1)+F(n-2)．F(1)=1，F(2)＝１として数列を作ると
１，１，２，３，５，８，13，21，.......の数列が得られます．

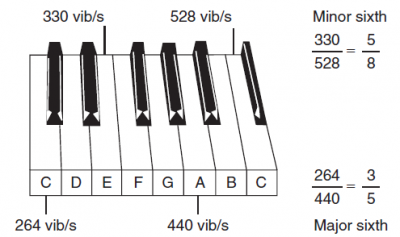
ピアノの鍵盤は，フィボナッチ数と音楽のつながりの可視化の良い例です．
鍵盤上で１オクターブとは，２音の間の音程で高音の周波数が低音の2倍になっていることです．鍵盤でいうと，1オクターブは，５つの黒鍵と８つの白鍵，合わせて13の鍵で構成されます（図）．この5つの黒鍵は2つのグループをなしています；一方は2鍵よりなるグループ，他方は3鍵よりなるグループ．

1オクターブに入る13の音は，西洋音楽で最も一般的な音階であるクロマチック音階(半音階)を作ります．クロマチック音階に先行して，2つの他の音階；5音からなるペンタトニック音階と8音からなるダイアトニック音階がありました． お馴染みの"Mary had a Little Lamb” と “Amazing Grace” は，ペンタトニック音階を使い演奏でき，また， “Row, Row, Row Your Boat” のメロディーはダイアトニック音階を使い演奏できます．

長6度と短6度（6つ離れた音，および，5+1/2離れた音）は，耳を最も喜ばす2つの音程(和音)です．長６度は，例えば，音CとAから成る：それぞれの音は，1秒当たり264と440の振動数で（図），264/440 = 3/5はフィボナッチ比であるに注目しましよう．
短6度は，例えば，1秒当たりの振動数330と528の音であるEとCから構成され，それらの比もフィボナッチ比です：　330/528 = 5/8.
［訳注）自音の音程は1度という．1オクターブの音程は8度である．］

これがどうして私の手元にあるのか思い出せません．
その他にも球状のものや，いくつか組木のパズル(箱根細工と呼んでいました）で子供の頃遊んだのを覚えています．それは遠い昔のことで，いつの間にか失くなってしまいました．複雑な組木もあったように思い残念です．なぜかこの組木だけが，今私の手元にあります．多分，この組木を手に入れたのが一番新しいためでしょう．この組木はとてもシンプルですが，職人のすばらしいアイデアだと思います．

全体の対称性は立方晶系の最も対称性の高い点群です．
4回対称軸が3本，3回対称軸が４本，2回対称軸が6本あります．
（鏡映面はたくさんありますが表示略）．

全体はこのような同じパーツが6個で出来ています．

3回対称軸に沿って引き抜くことができ，二つに割れます．
写真は3回軸に沿って引き抜き開いて（内部をこちらに向けて）並べたところです．

 ２つのパーツは互いに対掌体（右手と左手，あるいは逆まわりの風車）です．3回軸に沿って引き抜けるのは，この分解写真を見ると理解できるでしょう．
対称性を考えないと，引き抜く方向がわからず難しいパズルです．
３つのパーツでできた風車のような形を一体として引き抜くのがミソです．（この方法がわかっていても，特に，分解と逆の組立てのときは，手作業的にはなかなか難しい．手が3本欲しいということになります）
３つのパーツは一体として扱わなければ，互いに組み合っているので，バラせません．3回対称軸は４本あるので，引く抜く方向は4通りありどれでも可能です．

(図）4回対称軸の方向から見る↓　　　　　　　　　　　　　　　　　(図）3回対称軸の方向から見る↓

（図）3回軸（上下方向）に沿って引き抜く↓（今度，動画にしたい）

■この組木は，x平面，y平面，z平面がかみ合っているという見方もできます．それぞれの平面は２つのパーツからなります．
直交するx平面，y平面を作り，z平面の部品の１つだけ（下側）は置けるが，残り１つ（上側）をどう入れるかと，普通の人は苦闘します．
この手順では入りません．3つのパーツで組んだ風車型を一体として扱うのがミソでした．

(図）最後の１つはどうしても入りません．↓

■今回の記事は，2020年3月30日にマリアンヌによってプラスマガジンに提出されたエッセイの解説です．
How can maths fight a pandemic?　By Marianne Freiberger　，https://plus.maths.org/content/
プラスマガジンの編集者，マリアンヌフライバーガーは，2020年3月24日にGogにインタビューしました．
エッセイの全文翻訳（by KT）は数学月間ホームページに掲載しておきます

これは大変長いエッセイで読み難いので，ここにレジメを作成しました．
このエッセイの書かれた3月30日ころは，Covid-19の感染について未知なことばかり（感染させるが症状の出ない保菌者など）だったでしょう．しかし，2.5か月経過した現時点では，これらは皆さんの常識になりましたね．最後に出てくる医療崩壊をさせないための断続的なロックダウン方法のシミュレーションは参考になるかもしれません．

■ケンブリッジ大学の疫学者ジュリア・ゴグGogは，2月の初めに，数理科学センターの通常の職務を辞し，緊急事態のための科学諮問グループ（SAGE）に結果を報告するモデリンググループ，SPI-Mに専念することになった．
SPI-Mは，インフルエンザパンデミックへ備えてこれまで活動をしてきたのだが，現在はCOVID-19のパンデミックに焦点を絞った活動をしている．ゴグは，王立協会が率いる全国コンソーシアムの運営委員会にも所属し，このパンデミックに対処している．

SPI-Mの仕事は，次に何が起こるか，さまざまな介入でそれがどのように変化するかを，予測できる数理モデルを開発し働かせることだ．COVID-19パンデミックがどのように進展するか？社会的介入はどのような影響を与えるか？これらのモデルはどのようなものか？それらは正しいのか？

COVID-19パンデミックの報道については、こちらをご覧ください：https://plus.maths.org/content/tags/covid-19

ーーーーーーーーーーーーーーーー

 ■SIRモデルとは(訳者補足)
S   感受性保持者数，（感染可能な数）
I　感染者数，（患者数）
R 免疫保持者数，（回復患者数）

全人口Nは一定と仮定して，N=S+I+R　が成り立ちます．
SIRモデルの方程式は次のとおりです．

これら3つの式の意味は：
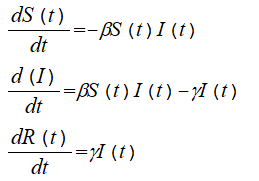
（１）（感染可能な数）の増加速度は，（患者数）と（感染可能な数）の積に比例する．比例定数βは感染率．
（２）（患者数）の増加速度は，（感染可能な数）の増加速度から，（回復患者数）の増加速度を減じたもの．
（３）（回復患者数）の増加速度は，（患者数）に比例する．比例定数γは回復率．

SIRモデルの詳細については，以下の記事https://plus.maths.org/content/mathematics-diseasesをご覧ください．

S, I, Rの間の状態遷移をブロック図で描くと上図のようです．
このモデル（単純SIR）で得られる結果は，下のグラフのようです．

S：青い線，I：緑の線，R：赤い線

赤い線は，「始めは免疫のあるものが誰もいなかったが，全員免疫ができて終わる」という当たり前の特別面白くない結果ではあります．
ーーーーーーーーーーーーーーーーーー

単純なSIRモデルは，寄宿学校の生徒などの単純な母集団に対して適切な予測を提供しますが，複雑な母集団に関しては，さまざまな母集団ごとのSIRモデルを繋ぎ合わせます．
実際には，これに色々な介入が加わるのですが，この影響を詳細にシミュレートするには，SIRモデルよりもさらに洗練されたモデルが必要です．

接触がカギ
このようなモデルの世界の背景で，非常に重要なのは人の接触パターンです（いわゆる動態調査）：誰が誰にどのくらい会ったか．例えば，BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります．人々は，彼らの動きを追跡するアプリをダウンロードし，出会った人々（すべて適切に匿名化されている）を追跡するように求められます．モデルに組み込むこのような接触データは数値の配列（ 行列 ）です（下図を参照）．

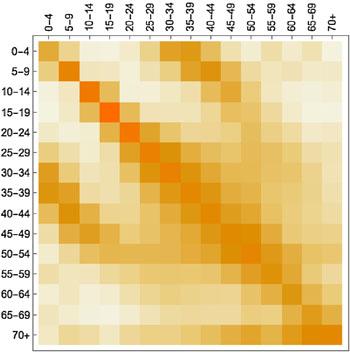
異なる年齢グループ間の平均的な接触を表示する接触行列．濃い色はより多くの接触を示します（ここでは，理解しやすくするために，数値ではなく色が使用されています）．Contagion! The BBC Four Pandemic – The model behind the documentary．
学校閉鎖などの特定の社会的介入が，感染拡大にどのように影響するかを確認するには，介入に関連する部分を削除または縮小して，接触データを適宜調整してみます．

学校要因を完全にオフにするのは現実的とはいえません．減じるだけです．学校外で子供たちは，他のルートがあり（祖父母と混ざってしまう可能性など）ます．これは，考慮に入れるべき追加の接触が発生していることを意味します． 教師のストライキ中に起ったことなどの既存データは，接触データを補正し介入による流行への影響予測に役立ちます．

モデルが現実的であるかどうかは重大な問題です．COVID-19は新しい病気．既存モデルは季節性インフルエンザのために開発したもので，コロナパンデミックモデルは誰も作っていませんでした．COVID-19とインフルエンザとではモデルのどこが違うのかを調べなければなりません．

パンデミックのダイナミクスは，インフルエンザとコロナウイルスで似ていますが，違いもあります．
COVID-19はかなりの潜伏期があり，何の症状も示さずに感染している可能性があります．発症までに，インフルエンザの場合は数時間，コロナウイルスの場合は数日かかる可能性があります．
モデルに関して言えば，これは，SIRではなく，SEIRのモデルになることを意味します．Eは「露出」．
クラスEの人々は感染していますが，まだ症状は出ていません．クラスEの人は，他人に感染させる人と感染させない人に分けられます．すべてのモデルは近似であり，インフルエンザの場合は，目的によってSIRを回避できることがよくあります．ただし，コロナウイルスの場合，潜伏期間を無視すると，近似が非常に悪い．特に，短期予測のときは，これを考慮する必要があります．

COVID-19については，私たちが知らないことが他にもたくさんあります．1日目や2日目の感染力など，詳細はわかりません．不完全なデータからそれを推測するのは非常に難しい．中国や他の国のデータがいくつか（クルーズ船からのデータは非常に興味深い）あり，限られた情報から推測するのに最善を尽くしています．十分な情報がない場合，モデラーは不確実性を取り除くために，最も重要な未知数は何か決定します．これがモデリングで非常に重要なことです．

明日，何人の患者が出るか予測するなら，多くのことを知る必要はなく，現時点では指数関数的増加です． しかし，第2波が発生するかどうかを予測するには，非常に異なるいくつかのことを知る必要があります．

長期予測で重要なパラメータは，疾患の再生産数（1人の患者が平均何人に感染させるか．多くの場合，R_0と表示される）です．これは 感染速度に関連する．COVID-19の場合，R_0は2~2.5の間にあると推定されます．モデラーは，可能な値の範囲ごとにモデルを実行し，対応する予測の範囲を考えます．

感染したが病気ではない
多くの疫学者が知りたいもう1つの重要なパラメータは，集団内での感染の症例数で，これには，病気にかかったが症状を示さない人々の症例数も含まれます．無症候感染者数は，睡れなくなるほどの多数で，これを知ることは，私たちの出口戦略にとって非常に重要です．とGog氏は語りました．

現在の指数関数的成長を止める要素が2つあります．

1つは，学校の閉鎖や身体的な距離をとるなどの介入うぃして接触率を減らすことです．
2つ目は，罹患感受性のある人をなくすことです．病気になったらしばらくの間免疫があるので，無症候性を含む真の症例数を知ることから，罹患感受性の高い人々のクラスがどれほど速く減少するかがわかります．
議論されている集団免疫のメカニズムは，罹患感受性のある人数が減少するにつれて，病気の指数関数的成長が平担になり，指数関数的減衰になるという仕組みのことです．

幸い，無症候性に関するデータは知ることができます． 病気に罹ったか罹っているか抗体検査が実施されています．これらの第一波は当然NHSスタッフにのみ公開されます．

では何が起こる？
何が起こるか誰も正確に言うことはできません．地平線に見える大きな望みはワクチンの到着です．これは，集団に免疫を備えるもう1つの手段です．最も脆弱な人を優先的に，最小限のダメージでどのようにその目標に到達させるかです．誰もが同意するのは，これには長期的な犠牲が伴うということです．「1週間だけシャットダウンして，この状況がなくなることを期待することはできません」「社会的距離の措置が早すぎる場合，感染かまだ残っていて，集団免疫はありません．現時点では，ヘルスケアシステムが容量を超えないようにするために，シャットダウンせざるを得ませんが，これは恒久的な戦略ではないことは十分に認識しています」とGog氏は語る．

先週 ，Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では，季節変動も考慮して，再発の問題について詳細に検討しました．呼吸器疾患の発生は，秋と冬に悪化する傾向があります．季節性インフルエンザの発生と同時に，ヘルスケアシステムにさらに大きな負担をかけます．キスラーと彼のチームは，そのような季節変動を反映する要因を含むSEIRモデルを使用しました．社会的距離測定の効果は，COVID-19の基本的な再生産数が最大60％減少することでモデルに反映され，中国で観察されたものと同等です．

この最新の研究の結論は，必ずしも明るいものではありません．
「シリアルロックダウンの期間を検討しています」とGog氏は言います．（医療崩壊が始まろうとしているときにロックダウンするという考え）英国のナイチンゲール病棟NHSのことは，noteの記事の1号に書きましたので，そちらをご覧ください．

社会的距離（ロックダウン）の断続的な期間の長さと頻度の仮定（米国の数値に基づく）のシミュレーション．

これらのグラフは，断続的な社会的距離（青色の領域）の下でのウイルスの有病率（黒い曲線）と重症なケース（赤い曲線）を示しています．最初と3番目のグラフには，季節的な強制がありません．2番目と4番目の季節の強制．ケア能力臨界は，水平の黒い実線で示されます．最初の2つのグラフは現在の米国の救急医療能力でのシナリオ，3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです．再生産数の最大値は冬期は2であり，夏期は1.4です．この図は，キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からです．

悲観的状況の中に，希望の光がいくつかあります．1つは，COVID-19の重症例に対して，投薬と良い治療プロトコルが，ある時点で追いつく可能性があることです．これで，NHSへの負荷の軽減でき，重症患者のケアができるます．

もう1つの希望の光は，軽度で無症候の感染者が，想定されているよりもはるかに多い（多くの人々がすでに病気になり免疫力がある場合）かもしれません．私たちはこれが事実かどうかわかるまでは，ルールを守って家にいるだけしかできません．

 3Blue1Brownのyoutube動画をご覧ください．

コーヒーカップの表面に，3つの家と３つのソース（ガス，電気，水）があり，
パイプラインが交差しないように，３つのソースと3つの家を繋ぎます．
いくら頑張っても交差箇所が1つできてしまいます．

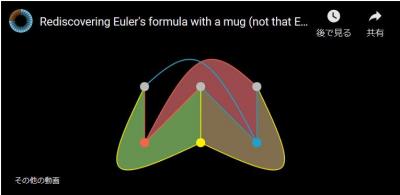
 頂点の数V，辺の数E，面の数Fとすると，V-E+F=2　がオイラーの多面体定理ですが，
図のように面（領域）の数は４つ（黒い地の部分も１つと数えます）で，
6－８＋４＝２とオイラーの定理が成立しています．
３つの家はそれぞれ３つのソースに結ばれるわけですから，辺（パイプライン）の数は９本ありますが，頂点６と面の数４ですから，最後のパイプラインはどうしても繋げません．

さてここで，コーヒーカップで実験をしている理由がわかります．
コーヒーカップの取っ手の部分をうまく使うのです．取っ手の中を通り抜けるパイプラインと取っ手の上を這わせるパイプラインで立体交差になります．

コーヒーカップは，穴が１つある浮袋のような位相表面です．先のオイラーの多面体定理は穴のない位相表面に対する表現なので，穴の開いている位相表面では定理が少し変わります．
注）トーラスでは，面の数が2つ減り，頂点の数が3つ減り，辺の数が３つ減るので，V-E+F=0　が成り立ちます）

このような教育グッズがたくさんあり提供されるようすが，国民数学祭NMFのサイトで見ることができます．