note.com投稿記事

Интервью с Семёном Гиндикиным
«Троицкий вариант» №10(229), 23 мая 2017 года

撮影は，Natalia Demina

Natalia Demina が，Semyon G. Gindikin（ロシア系アメリカ人の数学者、教師、数学の普及者）に，モスクワ生涯数学教育センターで，インタビューをしました．
反ユダヤ運動が才能ある若者にどのように影響したか，I. M. ゲルファントのセミナーについて語る．

О том, как отразилась на талантливых ребятах антисемитская кампания, о семинаре И. М. Гельфанда Наталия Демина поговорила с Семёном Григорьевичем Гиндикиным, российско-американским математиком, педагогом, популяризатором математики. Беседа с этим веселым, остроумным человеком состоялась в Московском центре непрерывного математического образования.

--------- 以下用紙抜粋---------- 

◆ピーター・セルゲイビッチ・ノビコフは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学の力学数学学部（мехмат）で反ユダヤ主義について話し始めるのが嫌いでした。数学者になり、「暗い20代」を強い人々が生き残ることができたという例です. それは本当ではない。これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に本物の数学者になることができたように私には思えます. 私は本当にラッキーでした。まず第一に、すぐに私の仲間と素晴らしい数学者の両方が私の近くにいることがわかったからです。

◆ イスラエル・モイセービッチ・ゲルファントについて一言いただけますか? 彼のセミナーに参加したことがありますか？

- もちろん。彼の90歳の誕生日に、これらのセミナーに関する記事を書きました。ゲルファントはこれについて議論するのをためらっていましたが、ランダウの物理学セミナーが彼のセミナーに強い影響を与えたように私には思えます。ある時点で、ゲルファントは物理学を学びたいと思っていたので、セミナーでは多くの物理学のプレゼンテーションがありました。レフ・ダビドビッチ・ランダウはイスラエル・モイセビッチ・ゲルファントをやや見下そうとしたと思います。

ランダウを初めて見たときのことを正確に知っています。これは1955年のことです。関数解析に関する会議があり、国内で最高の数学者がすべて集まりました - モスクワでの大きなイベントです。その時まで、実質的に会議はありませんでした。最初は戦前に行われました。モスクワ全体がこの会議の開会式に参加しました。そして、イスラエル・モイセエビッチはそこで君臨しましたが、彼のセミナーではいつもより少し控えめに振る舞いました。最初の報告は、ランダウによって行われました。そして、彼らはそれぞれのパートを完璧にリードした 2 人の偉大なアーティストであることがわかりました。その時までに、Israel Moiseevich は Bob Minlos と一緒に、経路積分と呼ばれるものを考え出していました (Bob は私の友人であり、素晴らしい人物であり、数学者でもあります)。

Landau の報告の後、Gelfand は、これらの積分はおそらく場の理論を作成する正しい方法であると彼に非常に穏やかに説明しようとしました。そしてランダウはこっそりと彼に答えました：「イズレール・モイセエビッチ、鶏は秋に数えます（捕らぬ狸の皮算よ）」。このフレーズは、ピョートル・セルゲイヴィッチ・ノヴィコフが好んで言ったことを覚えています。

ところで、私は、レニングラードで開催された数学会議 (1960 年頃) で、ゲルファントとランダウの間の別の会話を目撃しました。I. M. と一緒にネフスキーに沿って、Baltiyskaya Hotel の近くを歩き、Landau に会いました。真剣な現代数学を再び適用する可能性についての話題が会話の中で生じたことを覚えています。I. M. はいくつかの例 (ローレンツ群の表現だと思います) を引用しましたが、L. D. は断固として彼に同意しませんでした。彼は、何年にもわたって「数理物理学の方程式」に関するセクションがあったが、物理学への本格的な数学の重要な応用を知らないと述べた.

今日、現代の理論物理学でどのような精巧な数学が使用されているかを見ると、ゲルファントが正しかった可能性が高いように思えます。どうやら、ランダウは将来の物理学における数学の役割を過小評価していたようです (私の物理学者の友人から聞いたところによると、おそらく彼の学生の何人かはこれに多額のお金を払ったようです)。

ゲルファントのセミナーに戻ったら、私の見解を繰り返します。イスラエル・モイセービッチが民主主義を認めなかったことに多くの人が腹を立てた。彼にとってセミナーは、ある意味で彼の人生の本業でした。

第一印象は、セミナーのすべてが即興であるということでした。セミナーは大幅に遅れて始まりました。Gelfand 氏は、セミナーを待つことがコミュニケーションの最適な時間であると説明しました。これは、人々が（無意識のうちに！）互いに話し合う、科学的コミュニケーションにとって貴重な時間でした。

そのような完全に意識的な混乱は、彼の性格の特徴でした。彼はすべてを時間通りに行う必要があるとは考えていませんでした。彼は、自分にとって都合の良いことをする権利を獲得し、一般に受け入れられている規則を考慮しないと信じていました。少し大げさですが、あなたは素晴らしい人なので、導かれるように振る舞う必要があります。そして、これは最良の結果をもたらします。礼儀正しさは、イスラエル・モイセヴィッチの強みではありませんでした。しかしいつもではない。彼は誰とどのように話すかを知っていました。それでも、彼はスターリン時代を生き抜いた男でした。しかし、しばしばある時点で彼は崩壊し、すべての宝石外交は裏社会に陥りました.

セミナーに関しては、彼にとってそれは人生の主な仕事でした。それは彼自身が数学のほとんどを理解した場所であり、彼は他の人にこの数学を理解する機会を与えたと信じていました. そして、彼は完全にリラックスしていました。彼の態度は、すべての人に適しているとは限らなかったかもしれませんが、このセミナーから利益を得たいと思った場合、他の人が支払わなければならない種類の賛辞でした.

セミナーの数日前、彼はセミナーの内容について考え始めました。ゼミにいた有名な数学者で、普及にも携わったポール・ハルモス（ポール・リチャード・ハルモス）の思い出がある。セミナー、ゲルファントとの交流、彼がクレムリンをどのように案内したかについての章全体があります。そこでハルモスはセミナーに来て、綿密なレポートを作成しました。彼は偉大な達人であり、彼の本は高い教育レベルで書かれていました。そして、ここで外向きに-ある種の完全な障害：Gelfandは、スピーカーに発言権を与える代わりに、彼に質問をし、他の人と話します。

しかし、ゲルファントの世界モデルでは、そのような無秩序はありませんでした。最初のセミナーは彼にとってトランスのようなものでした。彼は数学を際限なく聞く準備ができていました。このため、彼は交霊会のように、導かれたように振る舞いました。そして、誰もがそれを気に入ったわけではありません。さらに、数学者は他の人のためにゲルファントに腹を立てることがありました。

しかし、イスラエル・モイセビッチは、名誉ある教授に「あなたは何も理解していない！」と言うことができれば、常に信じていました。-これは、彼が彼を平等に扱っていることを意味します。そして、彼が丁寧に彼に話しかけると、彼は彼を人として、そして確かに数学者として保持していないことがわかります。それがスタイルでした。

Gelfandは、人々が自分のキッチンに入るのを許可した場合、数学をどのように聞いたか、それについてどう考えたかを隠さなかった場合、そのように振る舞う権利があると信じていました。これは、このセミナーの心理学を再構成したものです。すでに説明しました。外国の数学者にとって、ゲルファントのセミナーに出席することは、ボリショイ劇場に出席することと同じくらい義務的でした。それはその娯楽の一部でした。

私が西側でアーノルドとマスロフと一緒に行った最初のことの 1 つは、モスクワとレニングラードでの一連のセミナーの開会式でした。彼女のアイデアは、モスクワのセミナーのスタイルを伝えようとする試みでした。西洋では、セミナーは短い純粋にビジネス的なものです。若い科学者たちは大学院での研究を完了し、博士号を擁護し、独自の軌跡に沿って世界のさまざまな場所に行きました。そしてモスクワでは、彼らは永遠に残りました。彼らはどこにも連れて行かれず、実際、彼らの専門分野で働くことができず、「箱」に座って、夕方にはアーノルドまたはゲルファンドのセミナーに来て、彼らの職業生活の最良の部分が始まりました。

そして、その学校は永遠のように見えました-それは決して終わらない学校でした. しかし、それは皆の個人的な選択であり、彼らは予期せずそこで厄介になる可能性がありました... I.M.にとってセミナーは本当に彼の人生でした. 私が見つけられなかった困難な時期がありました。しかし、大学とステクロフカを追放されたとき、彼が戦った唯一のことは、セミナーを開いたままにすることでした。

彼はセミナーで見知らぬ人が現れて最前列に座る様子を語った. 彼らはショルダーストラップを着用していませんでしたが、すべてが見えました。クルチャトフ研究所で働いていたミハイル・アレクサンドロヴィッチ・レオントヴィッチから、「私服を着た男が歩いていて、肩に何か青いものを持っている」という非常に適切なフレーズを聞いた。

生物セミナーもありました。これも面白かったです。私たちが若い頃、私たちはすべてを理解していると思っていました-どうすればそれを少し改善できるか、そして人々がそれほど引っ張られないようにすることができます.

Izrail Moiseevich はこれらのセミナーをほとんど欠席しませんでした。非常に気分が悪いとき、彼はしばしば彼らを導きました。かつて、実験として、彼が私と A. A. キリロフにこのセミナーを行うように指示したことを覚えています。セミナーは短く、素晴らしく、すぐに終了し、すべてのレポートはスムーズに進み、誰にも邪魔されませんでした。しかし、それはゲルファントのセミナーではありませんでした!

すでにアメリカにいますか？

— いいえ、モスクワです。アメリカでのセミナーについても、ご希望があればお伝えできます。私はラトガース大学でイスラエル・モイセービッチと一緒に仕事をしました。そして、このセミナーは行きませんでした...

――社会に民主主義がなければ、科学は正常に発展しないという命題があります。一方、スターリン主義ロシアにおける数学の隆盛は、このテーゼと矛盾するように思われる現象です。これらの「メールボックス」、「鉄のカーテン」がなければ、ゲルファントのセミナーはそれほど成功しなかったでしょうか?

- いいえ。Gelfand のセミナーの成功は、主に彼の人柄によるものだと思います。彼はこの数学的生活様式を発明しました。私は、モスクワの数学が独特で、他に類を見ない現象であったことを強調します。私たちの会話の時までに、私が行ったことのない場所と私が見たことのないもの。しかし、私はこれを他の場所で見たことがありません。この現象の起源と性質は、別の議論のトピックです。

数学は単なる科学ではありません。私にとっては、最高の状態で、ハイアート、音楽、詩に近いです。アルキメデスの時代から適用された側面は、しばしば重要で注目に値するものでした。権力者との関係は異なり、長い歴史があります。数学がアテネで栄えたのにスパルタでは栄えなかった理由、プラトンが未来の王たちのアカデミーで数学を教えた理由、ギリシャの衰退とともに幾何学が消えた理由、ギリシャから多くを奪ったローマは数学なしでした...

ソビエト連邦では、数学は生物学や言語学と同じようには破壊されませんでした。一番上には、政府の問題、主に軍事的な問題を解決するために、少なくともしばらくの間、数学が必要であるという幻想があったからです。多くの人にとって、当時の数学はそのようなはけ口でした。まず、この世界ではなく、「眼鏡をかけた」若者が常にそこに引っ張られていました。一方で、マルクス・レーニン主義に言及せずに記事を書くことができる、比較的非政治的な場所はほとんどここだけでした。他のどの科学でこれを行うことができますか?

そして、一般的に民主主義は複雑なものです。彼女の原始的な理解は、彼女の不在よりもはるかに優れているわけではありません. 彼らが理解しているように、彼らの権利のために戦う暴徒。民主主義の大部分を大金で買う能力...

- 民主主義に関するテーゼの確認は、科学の分野で最も先進的な国が民主主義の例と見なされている国であるという事実である可能性があります: 米国、英国、フランス、ドイツ。

-主なことは、これらの国の若者は数学があまり得意ではないということです. それが問題です！私が推測するように、あなたはさまざまな数学者に会いました。そして、ユーリー・イワノビッチ・マニンのように、人道的に才能のある人々を何人見ましたか? 非常に人道的に才能のある人々は、しばしば数学に進みました。他の地域に行くのはほとんど自殺行為でした。

ソ連で何が起こったのですか？数学は、通常の状況下では、通常の社会では絶対に数学に入ることはなかったであろう一定数の人々を食い物にしてしまった。この国に数学に専念する準備ができている若者がどれだけいるのか、私は今でも驚いています. 米国では同様のことは何も起きていません。民主主義があるように見えますが。

- アメリカでは、数学サークルが盛んに行われていないのですか? 最近、アメリカでは子供向けの数学的教育が発展しているという記事がありました。アメリカ全土で非常に多くのサークルが作成されており、子供たちが数学に興味を持っているということです...

「見えない。誰が言っているのかわからない。

――丸ごと記事でした。もしよろしければリンクを送ります... [2]

- しましょう。あなたが知っている、彼らはしません。しかし、去った人々のほとんどは、私たちがソ連で行ったことを開始する必要があると考えていました。サークル、数学の学校...アメリカでは、これらすべてが利用可能ですが、これは比較的小さいです。ソ連では、まだ行くことができる「誘惑」はありませんでした。素晴らしい音楽があり、素晴らしいアーティストが登場しました。選択肢はあまりありませんでした。

アメリカでは、数学を勉強した人は銀行やビジネスに行きます。そして、私は悲しみでそれをする人を知っています. しかし、社会におけるそのような価値観。彼らは家族や将来を犠牲にしたくないので、そのような選択をしなければなりません。私の見解では、数学をするのにより助長している国があります。いいえ、この社会の好みの尺度では、純粋な科学はかなり低い位置にあります.

— 科学や数学の大衆化に関わった経緯を教えてください。Kvant にすばらしい記事があります [1] . このコラボレーションはどのように始まったのですか？

- 私はオリンピック関係者です。さまざまな種類のオリンピックに常に参加してきました。これには常に関心がありました。数学の普及は、さまざまな数学サークルへの参加を通じて自然に生じました。

科学の大衆化の中で、私は自分自身のために別のニッチを思いついた. 「物理学者と数学者の話」という本が生まれた最初の記事は、数学の歴史に関する記事でした。当時、数学の歴史は公式イデオロギーが数学に圧力をかけようとするトロイの木馬でした。

そして、私はこのトリックを思いつきました。私は、数学についてのように、数学の歴史について書こうと決心しました。みんながガウスの最初の2つの発見について理解できるように、正直に書くことにしました。ガウスは、彼が数学者になることをまだ決めていなかった時代に、ほぼ男の子として、通常の 17 角形の構築に関する作業を行いました。数学。

そして、私はそれを正直に受け止めて、この証明をどこからでもどこへでも書いてみようと思いました。それがクヴァントでの私の最初の出版物でした。そして、それは良い考えだったと思います。それから私は互恵の法則について書きました。

数学者は最も興味深い思想家ではありませんでした。難しい問題やパズルを解けるメガネ男子がいたからです。でもすごい人もいました。そして、私が最初に書いた人物はブレイズ・パスカルでした。

そして始まりました。私は普及者の役割を選びました。私は数学史家ではなく、数学史を語る数学者です。

セミョン・ギンディキン (1984) (「TrV」No. 10 (229), 05/23/2017)
セミョン・ギンディキン (1984)
- 現在、そのようなアクセスしやすいスタイルで、科学に関する本物の科学者の話が不足しています。

- アクセスしやすいだけではありません。つまり、科学の人間的側面です。私たちはすでにこの方向に進んでいたので、ある少年またはその両親が私に何か言ってくれたことを思い出しました。私の記事について、「彼は偉大な科学者を人として語る」と言われました。そして、それはまさに私の自己注文であり、私が望んでいたものでした. 数学の普及の分野での私の仕事はしばらく続きましたが、その後終了しました。

- なぜ？最後の記事は、1985 年から 1986 年に Kvant で公開されましたか?

「それから私は別のことを書きました。私はロシアを離れました。他の言語で書きたくないことに気づきました。数学について英語で書くことはできますが、ノンフィクションの物語や本はできません。たまに講義で話します。私はまだこれらすべてに興味があります。

- 雑誌はたくさんありますが、ロシアには同じKvantが存在します。仕事を続けたいですか？

— 今日の Kvant が何であるかはわかりませんが、当時は単なる人気のある科学雑誌ではありませんでした...

- 過ぎ去った時代...

— アメリカで開催された Gelfand のセミナーについては十分に話しませんでした。アメリカでのセミナーは失敗しました。イスラエル・モイセビッチは楽観主義者でしたが、うまくいかないと確信していました。私はこの失敗にとても腹を立てていたので、行くことさえしませんでした。第一に、モスクワでのゲルファンドのセミナーは無期限に続く可能性があり、その後、夜にモスクワを散歩しました。先日、レニンスキー大通りを車で走っていたとき、昔の考えがよみがえってきました。毎週月曜日は苦痛でした。

そしてアメリカでは反射神経があります。カップルが終わったら、全員が立ち上がって去りました。廊下で出会った方法を覚えています。まったく理解できなかったゲルファンドを完全に失いました。

アメリカの同僚に最初に言ったのは、私は I. M. Gelfand の教師ではなく、彼についての苦情は受け付けないということでした。しかし、イスラエル・モイセビッチはあらゆる種類のトリックを投げ出しました。そこでの生活のすべての民主的な性質のために、セミナーで話す人に「何も理解していない」と言うのは習慣的ではありません。そしてゲルファントは、「はい、彼は素晴らしい人物であり数学者です。私は数学者として彼にこれを話しました。」

非線形方程式を扱った有名で非常に優秀な数学者、Martin David Kruskal がいました。これは、I. M. と同じ強さと気質の男です。 Gelfand が Kruskal の宿題を出したことがあります。彼はレポートを作成し、優秀な学生のように最初の机に座って、マスターの先生が彼に電話するのを待ちます。そして彼は別のことを話します... クラスカルはゲルファントに思い出させます：「イスラエル、あなたが私に仕事を与えたことを覚えていますか？」I.M. は彼にすべてを覚えていると厳しく言います。そして時間が経ちます。ペアがなくなると、全員が去ります。マーティンは再び彼に思い出させます。I. M. は、彼がこれに興味を失ったと彼に話します。しかし、クルスカルのような男でさえ、そのような態度を理解するユーモアのセンスに欠けていました...

それにもかかわらず、セミナーは引き続き運営されており、さまざまな人がそこに来ました。そして、私ははっきりと理解していました。別の言語でいくつかのことを行うのは非常に難しいということです。一番下の息子が結婚したとき、突然、息子の結婚式で外国語を話すのはただの悲劇だと痛感しました。「シンメトリー」という本（この本は非常に数学的な本です）の冒頭で、ヘルマン・ヴェイユは私に非常に近い言葉を言いました。

- ロシアでの科学の普及は盛んです。人気のある科学の講義や科学の祭典に参加する人がますます増えています。同時に、優れた科学はもはや成り立たなくなり、科学に対する一般の関心が高まっているようです。もしかしたら、科学は人々にとってある種のはけ口になるのでしょうか？

- プロレベルではなく、アマチュアレベルで普及が行われています...

「科学者もこれをやっています。たとえば、ゲルファントの孫は講義をよく読んでいます。

- 私は彼の博士論文の監督者でしたが、彼の論文が何について書かれているかはよく知りませんでした. ミーシャはおしゃべりがうまい。教育的能力は彼の祖父から彼に受け継がれました、それは素晴らしいです!

ロシア社会はますます西洋社会に似てきており、同じ価値観を持っていますが、これは非常に危険なことです。科学者が後援を必要とするとき、それは非常に危険です。応用もいいのですが、文化にとって基礎科学はとても重要だと思います。絵画は常に抽象的だったわけではなく、音楽は必ずしもメロディーなしではありませんでした。

数学も比較的遅く抽象化されました。80歳までに、数学のような私たちの生活の驚くべき現象の何かを理解したいと思っています. 今日、このすべてについて書くとしたら、社会の生活についてすべてを説明する強力な教えがあったソビエト時代の生活がどれほど良かったかについて話すでしょう。

また、ある時点ですべての数学者が、あることを研究し始め、別のことを研究しなくなる理由についても考えます。たとえば、17 世紀になると、誰もが突如として微分積分や積分計算、つまり解析幾何学を取り上げるようになったのです。そして、これらの分野で働いている膨大な数の数学者がいました。世紀ごとの分布さえありました-各世紀に何人の偉大な数学者がいました. 18世紀にはほとんどいませんでしたが、6人の名前を付けることができます.

なぜピエール・ド・フェルマーだけが数論に従事し、次の世紀になって初めてこれに関心が現れたのですか? 不明。物理学者はこれを理解しています。彼らは、素粒子の理論や場の理論を、それが可能だと思われる瞬間に構築したいと考えています。あるいは、日本人が首都を放棄して新しい首都を建設したように、なぜ数学者は特定の分野の知識を放棄するのでしょうか?

— 数学的オブジェクトは、ある種の理想的な世界に存在すると思いますか?

「存在は危険で曖昧な言葉です。しかし、少なくともある時点で、何かがあなたの選択を後押しし、目的が達成され、定理が証明されると信じ込ませるような感覚を避けることはできません。数学は、最低限、論理的な結論を伴う形式的な真珠のゲームです。上のどこかからたくさん来ているような気がします。偉大な人でさえありませんが、平均的な数学者です。

詩人たちは、詩がどこから来ているのかを理解しようとし続けました...なぜ、特定のアイデアが数学者の生涯を悩ませているのでしょうか? I. M. Gelfand がこのことについて教えてくれました。もちろん、彼に会うことは私の人生の主な成功です。偉大な人がとても近くにいると、彼はあなたを悩ませ、時には些細なことをあなたに話しますが、一時的なものはすべて排除されます. そして、この人が別の世界と直接通信したことがわかります。これについては他に説明がない場合があるためです。彼はどのようにしてこれまたはあれを知ったのですか？

あなたは彼と一緒に本を書きました。彼は扱いが難しいと聞きました。

「彼と一緒に仕事をするのは難しくありませんでした。でもまた… 50年前に聞いていたら、彼と一緒に仕事をするのは無理だと言っていたでしょう！あなたが彼の家に来ると、彼は電話で誰かと話し、それから別のことをします。私はあなたに、彼は仕事を組織するという点であまり自分自身をコントロールしていなかったと言いました. それはあなたが望む誰のためでもあります。彼は、おそらく、私に向かって叫んだことはなく、誓うこともありませんでした。私自身、性格が悪いのでしょう。

最近、モスクワの数学者の 1 人が、I. M. Gelfand がかつて彼に (彼を仕事に呼んだとき)、Semyon Gindikin と一緒に仕事をすることの否定的な側面について話すことができると言ったことを思い出しました。でも今日、あなたがそのことを私に話してくれたとき、私は少し驚きました。その瞬間、この殻がすべてなくなったとき、彼は数学について話し始めました...そしてそれは奇跡でした! 特にしばらくすると、これの価値が理解できます。

今、私は以前に彼にしようとしたことを何とかすることができました. この本以外にも、かなりの数の作品を書いています。その時、いくつかのことがうまくいかなかった理由がわかりました。

あなたは現在教えていますか、それとも引退しましたか？

-正式にはまだ引退していません。しかし、私は健康上の問題を抱え始めました。両手がうまく動かない。新しい技術がたくさんあるので、ボードに書くのをやめる時が来たと思います。どうやら、もうすぐ教え終わるらしい。

- 何を教えていますか？

- 私の教育​​活動は狭い枠組みの中で行われています。これはモスクワ大学でも、プリンストン大学でもハーバード大学でもありません。それでも、ここの学生の入学はあまり良くありません。しかし、私は最善を尽くそうとしています。私はよく旅行をし、さまざまなイベントで数学について話すのが好きです。日本やオーストラリアに共著者がいると、全く違う人生が開けます。

- あなたが持っている？

- もちろん。そういう意味で、私は世界の一部になりました...

— ロシアの数学は、この解散によって何かを失ったり、得たりしたと思いますか?

— 他のどの国でも、モスクワにあったような数学的生活の集中はないと思います。しかし、常識の観点からは、すべての数学が巨大な国の 1 つの中心に集中することは悪夢のように見えます。そして、モスクワに原爆を投下してすべての科学を失う可能性があるという理由だけでなく、一般的に。しかし、結果は素晴らしかったです。

今日でも、モスクワ生涯数学教育センターの建物の周りを歩いていると、よく知っている数学者や数学学校や数学大学の卒業生にいつも会います。昨日、ここで働いている女性が私に近づき、50 年前に私が第二高校で彼女を教えていたことを思い出させてくれました。モスクワのような数学者の集中は、どこにも見当たりません。パリでは夏に集まることもあります。しかし、1990 年代初頭以前にモスクワにあったようなものは、どこにもありませんでした。しかし、それは消えました。

はい、ロシアの数学は存在し続けています。数学を教え、学び続けている人がいるからです。私たちが会話をしているMTsNMO、ドゥブナのサマースクールがあります - これらすべてが存在します。そして、世界にはそのようなプロジェクトはあまりありません。数学の教え方を知っている数学者がここに残っていますが (私の仲間はほとんどいなくなりました)、これを行うのは非常に困難です。

ニュージーランドやオーストラリアにも行ったことがありますが、シベリアやコラ半島の景色も悪くなく、若い頃に欠けていたという感覚はありません。はい、私は多くの外国の数学者を見たことがありませんでしたが、ここにいた人たちは本当に楽しかったです。私はこの偉大な時代の同時代人であったことを嬉しく思います.

ピーター・セルゲイビッチは素晴らしい人でした。彼に会えてとても幸運でした。彼は数理論理を学び、素晴らしい数学者になりました。しかし、彼の才能の輝きは、記事でも講演でも十分に伝えられていません。多くの優れた数学者と共に、彼は特異点でした。あらゆる点で最も賢く、最も興味深い人物。彼のアパートの壁に「前代未聞」のアーティスト（フォーク、クリモフなど）の絵を見たのを覚えています。

彼は驚くほどオープンで、あらゆるトピックに関する会話を喜んでサポートしました。私は P.S. が行っていたこととはかけ離れた (そして彼にとってあまり興味深いことではありませんでした!) ことを選択しましたが、何年もの間彼に十分近いことをしようと試み、数年間彼と一般セミナーを行い、関連して出版しました。これらのいくつかの記事、さらに論理に関する本「Algebra of Logic in Problems」を書きました。

すぐに、イスラエル・モイセビッチ・ゲルファンドに会いました。そして、私の学生生活のほとんどは、私の 2 人の主要な数学教師の 1 人である Gelfand の周りで過ごしました。もう一人はイリヤ・イオシフォビッチ・ピャテツキー・シャピロでした。それもまた嬉しい出来事でした。

私は、人々がモスクワ州立大学のメフマートで反ユダヤ主義について話し始めるのが本当に好きではありません。私が例として挙げられているのは、彼が数学者になり、強い人々が「黒い20代」で生き残ることができたということです.それは本当ではない。私は、これらの出来事によって人生が完全に台無しになった多くの人々を知っています。そして、入ることを許されなかった人々は、絶対に真面目な数学者になることができたように私には思えます.本当にラッキーでした。まず第一に、すぐに私の同僚や素晴らしい数学者が私の近くにいることがわかったからです。

— Я увидела в «Википедии», что Вы не поступили в МГУ. Вы стали жертвой антисемитской кампании?

— Так я подозреваю. Я никогда не пытался собрать точные доказательства, но...

— Золотая медаль — и не быть принятым на мехмат?!

— Золотая медаль, а еще вторая премия на Московской математической олимпиаде, и не приняли.

— Вас на экзамене заваливали?

— Да, конечно, заваливали!

— Давали сложные задачи?

— Просто нерешаемые. Либо ты знал решение задачи, либо решить ее не мог. Это был не экзамен, это было собеседование. Но мой год был уже сравнительно вегетарианский. Если за пару лет до меня при таких начальных параметрах на мехмат не поступал никто, то в тот год поступили уже несколько человек. А у меня была золотая медаль — и разочарование. Я немало слышал об антисемитизме при приеме, о том, что происходит, но думал, что у меня есть запас прочности и меня это не коснется.

— А как Вы решили, куда поступать, если не в МГУ?

— У меня не было особых советчиков, у меня была довольно простая семья. Я настолько был настроен на мехмат и уверен в положительном исходе... В итоге я поступил в Ленинский пединститут. И более того, для медалиста было уже поздно поступать на физико-математический факультет. Это был случайный выбор от полной безысходности (в 16 лет!).

Я начал учиться на дефектологическом факультете, там было что-то связанное с математикой. Семестр я там проучился. Потом с большим трудом меня перевели на физмат. К тому времени к моей судьбе уже подключились несколько математиков. В учебе в педагогическом институте было много положительных сторон. Во-первых, там работали несколько очень хороших математиков. Из них наиболее ярким был Пётр Сергеевич Новиков. Знаете ли Вы его сына Сергея Петровича?

— Конечно!

— Пётр Сергеевич был удивительным человеком. Мне так повезло с ним встретиться. Он занимался математической логикой и был совершенно фантастическим математиком. Но яркость его таланта не передается полностью ни через статьи, ни через лекции. При множестве хороших математиков он был сингулярной точкой. Умнейший, интереснейший человек во всех отношениях. Помню, на стенах его квартиры я увидел картины «неслыханных» художников (Фальк, Крымов...).

Он был удивительно открыт, охотно поддерживал разговоры на любые темы. Хотя я выбрал заниматься вещами далекими от того, чем занимался П. С. (да и не очень интересными ему!), я много лет пытался сделать что-нибудь достаточно ему близкое, несколько лет вел с ним общий семинар, и опубликовал в связи с этим несколько статей, и даже написал книгу по логике «Алгебра логики в задачах».

Довольно скоро я познакомился с Израилем Моисеевичем Гельфандом. И больше всего моя студенческая жизнь проходила около Гельфанда, которого я считаю одним из двух главных своих математических учителей. Другим был Илья Иосифович Пятецкий-Шапиро. Это был тоже счастливый случай.

Я очень не люблю, когда начинаются разговоры про антисемитизм на мехмате МГУ; меня приводят в пример, мол, он-то стал математиком и сильные люди могли выжить в «черное двадцатилетие». Это неправда. Я знаю многих людей, которым эти события полностью сломали жизнь. И мне кажется, что те, кому не дали поступить, могли стать абсолютно серьезными математиками. Мне действительно повезло. В первую очередь потому, что довольно быстро около меня оказались и мои сверстники, и замечательные математики.

— Вы учились в Педагогическом институте им. Ленина. Вы встречали там Юрия Визбора, Юлия Кима и других?

— Конечно, я многих из них знал, хотя и не очень близко. Многие мои однокурсники стали поэтами, замечательными артистами. Это был один из бонусов той жизни. Культурная жизнь бурлила и интересовала меня, но я участвовал в ней ограниченно, тратя основное время на математику. Рядом был туризм, который увлек меня на всю жизнь.

Там были хорошие очень математики, и там были замечательные ребята, которые поступили туда по разным причинам. Там учился, например, Петя Фоменко, известный режиссер... Вдруг вспомнил, как оказался в конце 1960-х в Алибеке на горных лыжах с Петей Фоменко. Он только что ушел с Таганки. Вижу его на втором этаже двуспальных нар, читающего «Бесов» и уверявшего меня (пессимиста), что он поставит это! А еще его фантастические экспромты... Кстати, и Визбора я встретил — на лыжах, на Кольском полуострове. Он был уже звездой! Мы успели поговорить один вечер, а на следующее утро он страшно сломался, пытаясь съехать с крутого ледяного склона.

— Можете несколько слов сказать об Израиле Моисеевиче Гельфанде? Посещали ли Вы его семинары?

— Конечно. Я написал статью про эти семинары к его 90-летию. Израиль Моисеевич неохотно это обсуждал, но мне кажется, что на его семинары оказал сильное влияние физический семинар Ландау. Гельфанд в какой-то момент хотел заниматься физикой, и поэтому на семинаре было много физических докладов. Я думаю, что Лев Давидович пытался несколько свысока смотреть на Израиля Моисеевича.

Я точно знаю, когда увидел Ландау в первый раз. Это было в 1955 году. Была конференция по функциональному анализу, на которую съехались все лучшие математики страны, — большое событие в Москве. До того времени практически не было конференций. Первая проходила еще до войны. Вся Москва пришла на открытие этой конференции. И Израиль Моисеевич там царствовал, но вел себя чуть сдержаннее, чем обычно на своем семинаре. Первый доклад делал Ландау. И это надо было видеть, это были два великих артиста, которые прекрасно вели свои партии. К тому моменту Израиль Моисеевич придумал вместе с Бобом Минлосом то, что они назвали континуальными интегралами (Боб — мой друг, замечательный человек и математик).

После доклада Ландау Гельфанд пытался ему очень мягко объяснять, что, наверное, эти интегралы — правильный путь для создания теории поля. А Ландау хитро ему отвечал: «Израиль Моисеевич, цыплят по осени считают». Помню, что эта фраза понравилась Петру Сергеевичу Новикову, который сказал: «Да И. М. любит считать цыплят весной!»

Кстати, я был свидетелем еще одного диалога Гельфанда и Ландау во время математического съезда в Ленинграде (около 1960 года). Мы гуляли с И. М. по Невскому, около гостиницы «Балтийская», и встретили Ландау. Помню, что в разговоре опять возникла тема возможности применения серьезной современной математики. И. М. приводил какие-то примеры (кажется, представления группы Лоренца), а Л. Д. был категорически с ним не согласен. Он говорил, что много лет существует раздел «Уравнения математической физики», но он не знает ни об одном существенном применении серьезной математики к физике.

Сегодня мне кажется, что Гельфанд скорее был прав, если посмотреть, какая изысканная математика применяется в современной теоретической физике. По-видимому, Ландау недооценил роль математики в будущей физике (я слышал от моих друзей-физиков, что, возможно, некоторые его ученики дорого заплатили за это).

Если вернуться к семинару Гельфанда, то повторю свою точку зрения. Многих раздражало, что Израиль Моисеевич не допускал никакой демократии. Для него семинар был в некотором смысле главным делом жизни.

Первым впечатлением было, что всё на семинаре происходило экспромтом. Семинар начинался с огромным опозданием. Это Гельфанд объяснял тем, что ожидание семинара было лучшим временем для общения. Этот был ценный для научной коммуникации час, когда люди (поневоле!) разговаривали друг с другом.

Такая абсолютно осознанная неорганизованность была чертой его характера. Он не считал нужным делать всё вовремя. Он полагал, что заслужил право делать то, что ему удобно, и не считаться с общепринятыми правилами. Несколько утрируя: раз ты великий человек, то нужно вести себя так, как тебе ведется. И это даст лучшие результаты. Вежливость не была сильной стороной Израиля Моисеевича. Но не всегда. Он понимал, как и с кем говорить. Все-таки это был человек, который пережил сталинские годы. Впрочем, часто в какой-то момент он срывался и вся ювелирная дипломатия проваливалась в преисподнюю.

Что касается семинаров, для него это было главным делом жизни. Это было место, где он сам понимал большую часть математики, и он считал, что дает другим возможность разобраться в этой математике. И там он был абсолютно раскован. Его манеры, которые, может быть, не всех устраивали, были такой данью, которую должны были заплатить остальные, если хотели получить бенефиты от этого семинара.

За несколько дней до семинара он начинал обдумывать, что на нем будет. Есть воспоминания Пола Халмоша (Paul Richard Halmos), известного математика, занимавшегося также популяризацией, который бывал на семинаре. Там есть целая глава о семинаре, о взаимодействии с Гельфандом, как он его по Кремлю водил. И вот Халмош пришел на семинар, подготовил тщательно доклад; он был большим мастером, его книги были написаны на высоком педагогическом уровне. А тут внешне — какой-то полный беспорядок: Гельфанд задает ему вопросы, разговаривает с другими, вместо того чтобы дать слово докладчику.

Но в модели мира Гельфанда этого беспорядка не было. Сначала семинар был для него как транс, он был готов слушать математику бесконечно; для этого он, как на спиритическом сеансе, вел себя так, как ему велось. И совершенно не всем это нравилось. Причем иногда математики обижались на Гельфанда за других людей.

Но Израиль Моисеевич всегда считал, что, если он позволяет себе сказать какому-то заслуженному профессору: «Ты же ничего не понимаешь!» — то это означает, что к нему он относится хорошо, как к равному. А если он с ним вежливо будет разговаривать, то получается, что он его за человека не держит, и уж точно не за математика. Таким был этот стиль.

Гельфанд считал, что если он допускает людей в свою кухню — не скрывает, как он слушает математику, что он о ней думает, — то имеет право вести себя так. Это моя реконструкция психологии этого семинара, я ее уже описывал. Для любого зарубежного математика посещение семинара Гельфанда было не менее обязательным делом, чем посещение Большого театра. Это было частью такого entertainment’а.

Одной из первых вещей, которую я сделал на Западе вместе с Арнольдом и Масловым, было открытие серии трудов семинаров в Москве и Ленинграде. Ее идеей была попытка передать стиль московских семинаров. На Западе семинары — это короткая чисто деловая вещь. Молодые ученые закончили аспирантуру, защитили PhD и отправились в разные места мира по своим траекториям. А в Москве они оставались навечно. Их не брали никуда, фактически они не могли работать по специальности, они сидели в «ящике», а вечерами приходили на семинар Арнольда или Гельфанда, и начиналась лучшая часть их профессиональной жизни.

И та школа казалась вечной — это была школа, которая никогда не кончалась. Но это был личный выбор каждого, там могли неожиданно нахамить... Для И. М. семинар был действительно его жизнью. Были трудные времена, которых я не застал. Но единственное, за что он боролся, когда его выгнали из университета и из Стекловки, — это сохранить возможность работы семинара.

Он рассказывал, как на семинаре появлялись и садились в первом ряду незнакомые люди. Они погон не носили, но по ним всё было видно. Я слышал от Михаила Александровича Леонтовича, который работал в Курчатовском институте, очень меткую фразу: «Идет человек в штатском, а у него что-то синее на плечах».

Еще был биологический семинар. Это тоже было интересно. Мы по молодости думали, что всё понимаем — как можно было бы это чуть-чуть улучшить и чтобы людей так не дергало.

Израиль Моисеевич эти семинары почти не пропускал; часто он их вел, когда очень плохо себя чувствовал. Помню, один раз в качестве эксперимента он нам с А. А. Кирилловым поручил провести этот семинар. Семинар прошел коротко, с блеском, быстро закончился, все доклады шли гладко, никто никого не прерывал. Но это не был семинар Гельфанда!

— Уже в США?

— Нет, в Москве. Про семинары в США, если Вы хотите, я тоже могу рассказать. Я же с Израилем Моисеевичем работал в Ратгерском университете (Rutgers University). И там этот семинар не пошел...

— Есть такой тезис, что наука не может нормально развиваться без демократии в обществе. Между тем расцвет математики в сталинской России — феномен, который, казалось бы, противоречит этому тезису. Если бы не было этих «почтовых ящиков», «железного занавеса», то семинар Гельфанда не был бы таким успешным?

— Нет. Думаю, что успех семинара Гельфанда был прежде всего обусловлен его личностью. Он придумал такой способ математической жизни. Подчеркну, что московская математика была уникальным, неповторимым феноменом. К моменту нашего разговора где я только не был и чего только не видел. А вот этого я нигде больше не встречал. В чем истоки и природа этого феномена — тема для отдельного разговора.

Математика — это не только наука; для меня она в своих лучших проявлениях ближе к высокому искусству, музыке, поэзии. Ее прикладные аспекты со времен Архимеда часто бывали существенны и замечательны. Взаимоотношения с власть имущими бывали разными и имеют давнюю историю. Почему математика цвела в Афинах, но не в Спарте, почему Платон учил математике в Академии будущих королей, почему геометрия исчезла с закатом Греции, а Рим, взяв многое из Греции, без математики обошелся...

В Советском Союзе математика не была разгромлена так, как биология или лингвистика. Потому что наверху была такая иллюзия (может, и не совсем иллюзия!), что математика хоть на какое-то время нужна для решения государственных задач, в первую очередь военных. Для многих математика в те времена была такой отдушиной. Во-первых, туда всегда тянулись молодые люди «в очках», не от мира сего. А с другой стороны, э

«Кот Шрёдингера» №1–2(39–40), 2018，Математика как очки より
数学者Igor KricheverにGrigory Tarasevichがインタビュー

Igor Krichever:
宇宙の法則は内部のどこかで保護されているように思えてならない．

■証拠に基づく世界
数学者は日常生活の中でどのように決定を下すのですか？誰と結婚するか，休暇にどこに行くか，夕食に何を買うか，ジャーナリストとの会合に同意するかなど．このような問題の解決には，スーパーコンピューターが1日動作しても足りない複雑な多基準モデルの構築が必要です．そのような場合，数学者はどのように行動するのでしょうか？

皆さんと同じです．私は，人生においては数学者も普通の人でなければならないと信じています．そして数学はこれを妨げるべきではありません．

知り合いの数学者の多くは，どんな決定も痛々しいほど受け入れます．そして，それを痛々しいほど後悔します．私にとってすべて簡単なことです．子供の頃，両親が読んでくれたマルシャークの詩（*注）を覚えています．猟師の網に引っかかった鳥についての物語です．鳥は猟師に言います：私は小さく，一口で食べてしまう肉しかありません．放してください．私はあなたに貴重な３つのアドバイスができます．持っていないものを後悔する必要はありません．

私はこのルールに従い，何が欠けているのかではなく，何が先にあるのかを考えようとしています．しかし，これは私が数学者であるということと関係はありません．

（*訳者注）サムイル・マルシャークは，「森は生きている（12か月）」で，私たち日本の子供にも知られている児童文学者，詩人です．ここに引用されている鳥と猟師の会話は，詩「愚かさの物語」の一節にあることを探し当てました．たいへん哲学的な詩なので，私の語学力では十分に理解ができないのですが，概略は以下のようです：３つのアドバイスがあるというので，猟師は鳥を自由にしてあげます．３つのアドバイスとは：
持っていないものを後悔する必要はありません．
過去を取り戻すために無駄なことをして血を流さないよう．
ナンセンスを信じるな世界に奇跡はありません．
ということでした．鳥は猟師をだましたようです．

Самуил Маршак　サムイル・マルシャーク
Сказка о глупости　「愚かさの物語」

http://www.world-art.ru/lyric/lyric.php?id=4351

確かに，引用されている一節があります．
Я ростом с ноготок, Всего комочек пуха Да мяса на глоток. 
Пусти меня на волю, Доволен будешь сам.
Хороших три урока Тебе за это дам.

Запомни мой совет;
Жалеть о том не надо,
Чего уж больше нет.

この詩全体は，上記ウエブサイトをご覧くださいーーーーーーーーーーー

■数学は、考え方を変えますか？

「数学はあなたに考えることを教えます．どんなステートメントも批判的に知覚し，それが何で構成されているか，それがどのように受け取られたか，そしてそれから何が続くのかを分析することを教えます．「証明する」の意味を，人々が常に理解しているとは限りません．
レーニンの古典的な言葉「マルクスの教えは真実であるので全能だ」は，数学者の観点からすると，悪循環です．そのような発言は信頼できません．
数学は私たちにすべてのことを当然と思わないように教えています．丸ごと信じることはできません．

私はアメリカのコロンビア大学でたくさん働きました．
初等数学のコースでは：数式を与え，生徒に何かを計算させます．その後，上級コースが始まります．これは証明がベースのコース，つまり，証明とは何かを説明するコースです．すでに証明されているか，証明されているものから直接派生した要素の連鎖に，ステートメントを分解することは素晴らしい芸術です（*注）．これは長くて難しい旅であるに違いありません．特に，学生時代ではなく，大人としてこの芸術を理解し始めた場合はなおさらです．
（*訳者注）あるステートメント（声明，命題）を，証明済みとその証明から派生するものの連鎖に分解することは，論理的な推論に必要な構造化です．

■ロシアの学校では，「人文科学」という言葉がよく使われます．これは賢いようだが，正確な科学との関係が築かれていないのです．数学を必要としないのでしょうか？

数字を操る機能としての数学は，おそらく必要ありません．統計は社会学や心理学で使われていますが．私の意見では，思考を発達させる科学としての数学は誰もが必要としています．

個人的な例を挙げましょう．私の孫は第57学校の数学の授業を卒業し，現在は高等経済学部の言語学部で勉強しています．数学は彼にとって非常に有用であり，モデルを構築し，何かを計算します．数字を操る算術はまったく役に立たなかったと信じています．彼は論理的に推論し，パターンを特定し，構造化することを学びました．それが最も重要なことであり，算術能力ではありません．退屈な算術は数学ではありません．

繰り返しますが，これは証拠に基づく考え方です．数学は良い眼鏡のようなものです．絵がぼやけないように世界をよりはっきりと見たい場合は，数学を学びましょう．

■信仰と公式

ここでは，厳密な証拠に基づくことがいかに重要であるかを繰り返します．数学的思考は道徳的な選択をするのを邪魔しませんか？会議で手を挙げて，道徳的に間違った決定に反対する必要があるとしましょう．人はこれをしません：論理的な根拠が十分ではないと言って...

この場合，数学的証明を持ち出す必要はないと思います．これは市民の勇気の問題です．あなたの人間の感性で，これが正しいとか間違っているとか感じます．

道徳的な選択は数学的な正当化を必要としませんか？

おそらくそうではありません．宇宙の法則は私たちの内部のどこかで保護されているように見えることがあります．数学は，独自の規則と公理に基づいて，純粋に内部法に従って発展しているように思われます．実験や観察は使用しません．論理のみを使用します．これらはゲームのルールです．しかし，結局のところ，数学は現実の世界を不思議な方法で表現していることがわかりました．つまり，自然の法則は私たちの思考の中に非常に深く隠されています．どのように？誰によって？なんで？私にとって，これは私が答えを見つけることができない謎です．ここであなたは神について考え始めさえします．誰かがそれを私たちの中に置いたのです．おそらく，道徳の法則は同じカテゴリーのものです：それらは私たちの内側のどこかにあります．あなたは何かを信じ，あなたの良心に従って，あなたの考えに従って行動します．少なくともそれが私がそれを理解する方法です．

信仰と証拠の必要性は互いに矛盾していますか？

はい，それらは矛盾しています．しかし，私の仕事では，私はしばしば原則に導かれます：それは美しいので，それは正しくなければなりません．これらは形式化できない概念です．何かがあるという信念，私たちの世界を定義する調和．ただそれを神の奇跡についての素朴な考えと混同しないでください．むしろ，それは世界の正しさへの信念です．私はそれを持ってます．

あなたは世界が正しく配置されていると信じますか？それともあなたはそれを知っていますか？

「信じる」または「知っている」と言うのは完全に正しいわけではありません．私は自然の法則が合理的であると信じています．同時に，私たちの社会の世界は私には深く間違っているように見えます．それは間違った方向に進んでいます．すべてが悪化します．しかし，おそらくこれはただの時代への不平でしょう．

私たちの世界の何が問題になっていますか？例を

人々の考えがシフトし引き裂かれているのは間違っているように思えます．これは特に子供に顕著です．彼らが一人でいることはますます難しくなっています．人々はただ座って考える時間がますます少なくなっています．それは正しくありません．しかし，それは避けられないことだと私は理解しています．

進歩はありませんか？

進歩はそれが進むところに行くのは，自然なプロセスです．それが正しいかどうかはわからない．私はそれが好きではありません．誰もが本は死ぬだろうと言います．本は何か他のものに置き換えられるでしょう．私はそのようなことは好きではありません．しかし，これについて議論することは，風に逆らって唾を吐くようなものです．

避けられない事故
当初は，世界の構造における偶然と必然性の比率をインタビューのメイントピックにしたかったのです．たとえば，シュレディンガーの猫の運命は，粒子の完全にランダムな振る舞いによって決定されることが知られています．そして，ローレンツ蝶はブラジルで羽ばたき，それによってテキサスでハリケーンを引き起こします．それが非常に複雑であっても，非常に異なる現象の間に因果関係があるという事実についての話です．あなたの意見では，チャンスと必然性はどのように相関していますか？

新しい数学的解決策を提案するとき，あなたは創造するようです．しかし，その一方で，あなたはただ何であるかを発見します．会議で，私の偉大な同僚は，詩人がその行を書かなければ，それは二度と現れないだろうと言いました．しかし，あなたが定理を証明しなければ，遅かれ早かれ他の誰かがそれを証明するでしょう．結局のところ，それなしでは，あなたは先に進むことができません．ある意味で，これは必然性であり，数学の発展における予定説です．ここにはランダムなものは何もありません．

しかし，ランダム性は時間の文脈に存在します．発見が今日行われなかった場合，それは後，たぶん5年後，あるいは50年後，あるいは150年後かもしれません．科学の発展は事前に決定されていますが，科学が進む道はほとんど偶然です．

物理プロセスの数学的モデルを構築する場合，ランダムな要素はどの程度重要ですか．

それはすべて，モデル，実際のプロセスの必要な単純化の程度に依存します．コインを投げるとしましょう．実際，表または裏がでるのは常に事前に決定されています．それは，体の初期位置，指によって加えられる力，風，および他の多くの要因に依存します．しかし，表裏のどちらかが偶然にでると想定します．これは実際のプロセスの近似です．十分に正確な場合もあれば，そうでない場合もあります．

あなたの伝記では，偶然と必然性はどのように相関していますか？

私の人生はかなり退屈で，まっすぐです．私がモスクワ州立大学のコルモゴロフ寄宿学校を卒業した後，すべてが比較的明確でした．したがって，おそらく，私は人生における事件の重要性を誇張する傾向はありません．私には，すべてが論理的であり，一方が他方に続いているように思われます．ランダム性は，一般的な背景の小さな波紋です．

あなたがこの寄宿学校に行き着かなかったら？

わかりません...私はタガンログで最高の学校の1つであるチェーホフ学校で勉強しました．数学の先生が，コルモゴロフ寄宿学校に入学した元生徒と一緒に私を連れてきました．もしこれが起こらなかったら，私はモスクワにたどり着くことはなかっただろうし，私の人生は違ったものになっていただろう．しかし，これを証明するのは非常に困難です．私はやはり数学者になると思います．道のりが長くなるでしょうけれど．

物理学など，他の分野の科学者になることもできます．

はい，私は現在の専門分野の数学物理学者です．しかし実際，私はもちろん数学者です．そして，物理学が常に私にとって問題の発生源であったというだけです．

昔々，上司，そして同僚で友人のセルゲイ・ペトロヴィッチ・ノヴィコフと私はボソン弦の量子化の問題に取り組みました．そして彼らはよく言いました：結果として物理理論が何を得るのかは不明であり，任意の代数曲線のために私たちが思いついたローラン-フーリエ基底は数学に永遠に残ります．

同時に，私は問題は外の世界から来るべきだと信じている数学者のその部分に属しています．原則として，それらは最も興味深いものです．過去20〜30年間で，数学の最も注目すべき成果が物理学から生まれたアイデアに関連していることは不思議ではありません．

今日の日本でも，大学教育はグローバル化，ユニバーサル化に対応する必要があり，高校教程で学ぶべきミニマム数学の内容やその達成度テストも適切なものでなければならない．これらの議論は教育数学の研究集会の記事をご覧ください．カリキュラム改革はいつの時代でもなかなか難しい．
改革では今日の数学（統計学やデータ解析など）に目配りする必要があるでしょう．６0年前に遡り，その時代に議論された新数学教科書改革；ソ連，フランス，欧米の先行事例を知ることは大事ではないでしょうか．以下の記事(アレキサンドル･ブヘトフ)からコルモゴロフの改革は何だったか学びましょう．

Падение преобразователя: четыре вопроса о реформе Колмогорова
Александр Буфетов, профессор РАН
«Троицкий вариант» №2(346), 25 января 2022 года

Падение преобразователя: четыре вопроса о реформе Колмогорова • БиблиотекаПятьдесят лет назад в советских средних школах появился учебнelementy.ru
■学校教育の数学コースの改革の一環として，アンドレイ・ニコラエヴィッチ・コルモゴロフが編集した幾何学の教科書がソビエトの中等学校に登場したのは60年前だった．

10年制学校の6年生から8年生向けの幾何学の教科書

学校の数学授業を20世紀の数学に近づけたいという願望は，戦前から叫ばれており，1950年代に活発に議論されました． この論説の著者が10歳の少年の頃，学校の数学の授業が17世紀の数学者の業績(*)で終わっているのを，どこかで偶然読み，非常に驚いたことを覚えているという． その後に行われたことを知る時間はいつあるのでしょうか？（*訳者注）ニュートン，ライプニッツ，デカルト，ベルヌーイ，フェルマーなどの時代.
この論説の著者の生まれる20年前も，アレキサンダー大王の継承戦争の時代の数学者の業績(*)で学校の幾何学コースが終わっていることを知っていたら，もっと驚いたことでしょう．（*訳者注）アレキサンダー大王の死は紀元前323年です．アルキメデス，ピタゴラス，ユークリッドなどの時代．

ユーリ・アレクサンドロヴィッチ・ネレチンは次のように書いています．「私たちの3次元空間は，私たちの考え方と同様に，その時以来，あまり変わっていません」しかし，私たちの3次元空間の考え方が，ユークリッドやアルキメデスの考え方と同じではありません．その時代には，ベクトル計算，平面運動の分類，第5公準の独立性の証拠がありませんでした（ユークリッドの第5公準の解釈はロバチェフスキーの驚くべき業績です）．3つのトピックのうち，キセリョフの注目すべき教科書（改革前の好評な教科書）で触れられているのはそのうちの1つだけ(ロバチェフスキーの幾何学は，キセリョフの教科書の余白に現れています）です．それ以来，学校のコースでの議論はこれ以上詳細にはなりませんでした．その一方，学校の幾何学コースにベクトルと幾何学変換が欠けているのは古くさいとの認識は，戦前からありました．

改革の主な熱狂者の1人は，RSFSRの教育副大臣であり，解析関数の理論に関する古典的な大学の教科書の著者であり，多くの言語に翻訳され，今日まで積極的に使用されている著名な数学者Алексей Иванович Маркушевичアレクセイ･イヴァノビッチ･マルクシェビッチでした．

1960年代初頭，コルモゴロフは改革の作業に参加しました．彼のリーダーシップの下で，新しいカリキュラムが作成され，その後，彼自身が共著者の小さなチームと協力して，非常に短い時間で，代数と解析入門と，幾何学に関する新しい教科書を書きました．

しかし，特に幾何学の教科書は厳しい批判を受け，批判は改革全体に広がりました． 1978年，ソ連科学アカデミーの数学科は，数学の教科書と学校のカリキュラムの現状は不十分であると認識し，コルモゴロフの改革は公式に却下されました．

一方、コルモゴロフによって編集された代数と解析入門教科書は，学校に残り，ソビエト連邦時代を無事に生き延びました．昨年，卒業前と卒業のクラスのための教科書の第26版が出版されました．幾何学の教科書の方は，取り返しのつかないほどの後退をしました．
コルモゴロフの改革は，西側の改革，つまり米国の新数学，そして特にフランスの急進的な数学の近代よりも比類のないほど穏やかでした．たとえば，フランスのリセウムの大学院クラスの1972年の幾何学教科書の目次を開いてみましょう：ベクトル空間，線形写像，多重線形形式，行列式があります．

フランスの最新数学の研究は，膨大な（そしてあまり簡単に見ることができない）文献に結び付けられている．詳細なモノグラフ「新数学の政治史」が最近米国で出版されました．3)
Yu.A.Neretinの注目すべき最近の論文は，コルモゴロフの改革に捧げられています．4)

3） The New Math: A Political History by Christopher J. Phillips. University of Chicago Press, 2015.
4） Ю.А. Неретин, Реформа Колмогорова математического образования, 1970–1980-е годы. arxiv.org/abs/1911.06108

------------------------------------------------

コルモゴルフ　wikiより抜粋ーーーーー
(1903年4月25日 - 1987年10月20日）は、ロシアの数学者。確率論および位相幾何学の大きな発展に寄与した。彼以前の確率論はラプラスの『確率の解析的理論』に基づく古典的確率論が中心であったが、彼が『測度論に基づく確率論』『確率論の基礎概念』（1933年）』で公理主義的確率論を立脚させ、現代確率論の始まりとなった。
1931年に彼はモスクワ大学で教授になり、1935年に、コルモゴロフはモスクワ大学で第1代議長になった。1939年に、彼はソ連科学アカデミーの正会員に選出された。ーーーーーーーーーー

結局，コルモゴロフの教科書改革は失敗でした．改革が不徹底の原因背景について種々論じられています．ここで取り上げたАлександр Буфетовブヘトフの論説の後半部分でも，４つの問題点が語られています．
例えば，数学に割り当てられた時間の15〜20％の大幅な削減．8年制から10年制への移行にともない，なぜ時間を短縮されたのか​​わかりません．週に６時間の数学を決めたのは誰でしょうか？幾何学試験の廃止を決定したのは誰でしょうか？
制約がいろいろあったようです．コルモゴロフが非常に急いでプロジェクトを進めたのは何故でしょうか？健康問題もあったようです．費用も少なかったようです．しかし，当時の時代背景や状況の理解が十分にできていない筆者にはわからない点が多く，現時点でのこれ以上の深入りは止めておきます．もう少し調べる必要があります．
詳細な調査を掲載している別の論説も以下にあります：

Реформа Колмогорова (Kolmogorov reform)mat.univie.ac.at

Замыслы Колмогорова о школьном курсе геометрии • ВидеотекаПоселок Московский, 29.06.2009. Конференция лауреатов Всероссelementy.ru

Вспоминая Колмогорова • ВидеотекаПоселок Московский, 04.07.2006. II конференция лауреатов Всерelementy.ru

 https://elementy.ru/nauchno-populyarnaya_biblioteka/431665/Aleksandr_Shen_Uchenikom_Kolmogorova_ya_ne_byl?from=rxblock

 Александр Шень: «Учеником Колмогорова я не был» • БиблиотекаАлександр Ханиевич Шень — кандидат физико-математических наукelementy.ru
■50年代後半から60年代前半にかけて，さまざまな人々が，微分積分，幾何学変換，ベクトル代数，組み合わせ論，確率論（および統計），複素数，集合論的アプローチ，数理論理学を，詰め込む可能性について議論しました．学校のカリキュラムは，現在のプログラムから何かを省略する必要があり困難な問題です．リストのほぼすべての要素を押し込むことが比較的合理的な方法でできました（統計，積分，および論理を除く）．しかし，いくつかの夢を犠牲にしなければならない難しい決断でした...
幾何学変換で不変となる量に注目していろいろな幾何学（ユークリッド，非ユークリッド，アフィン，射影，トポロジー等々）が定義できます．幾何学的変換の概念に基づいて幾何学のコースを作成するというアイデアは，1905年にエミール･ボレルによってフランスで成功裏に実装され，ソビエト連邦では戦前でも詳細に繰り返し議論されました．ベクトルは，キセリョフにも，ニキチンの初等教科書（コルモゴロフの前身）にも，1969年のポゴレロフの教科書にも含まれていないが，コルモゴロフの改革の枠組みの中で学校の幾何学コースに入りました．

■ポゴレロフの教科書が完成し，使用されました．これは，早くも1969年に行われた可能性があります．

Atanasyan-Butuzov-Kadomtsev-Poznyak-Yudinaの教科書，A.D.Aleksandrov-Werner-Ryzhikによる教科書が書かれ発売されました．教科書の全連合大会が開催されました．

作家が誰にでも好かれることはないのと同じように，1冊の教科書が誰にでも愛されることはありません．すべての教科書には欠点があることがわかります．Wernerによると，教師は教科書を選択できました．1980年代初頭，サンクト・ペテルブルグ市のさまざまな地区で3つの異なる教科書が使用されました．

 https://note.com/sgk2005/n/naa3e06512eb1

ガウス積分

$$I^{2}=\displaystyle \frac{1}{4}\displaystyle \int_{- \infty }^{ \infty }\displaystyle \int_{- \infty }^{ \infty }e^{-(x^{2}+y^{2})}dxdy=\displaystyle \frac{1}{4}\displaystyle \int_{0}^{2\pi }\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdrd\theta =\displaystyle \frac{2\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-r^{2 } }rdr$$
$$r^{2}=X$$とおく，　$$2rdr=dX$$
$$I^{2}=\displaystyle \frac{\pi }{4}\displaystyle \int_{0}^{ \infty }e^{-X}dX=\displaystyle \frac{\pi }{4}$$, $$I=\displaystyle \frac{1}{2}\sqrt{\pi }$$
--------------------------------------------
$$\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\sqrt{\displaystyle \frac{\pi }{\alpha } }$$
$$\displaystyle \frac{d}{d\alpha }\displaystyle \int_{- \infty }^{ \infty }e^{-\alpha x^{2 } }dx=\displaystyle \int_{- \infty }^{ \infty }dx\displaystyle \frac{d}{d\alpha }e^{-\alpha x^{2 } }=\displaystyle \int_{- \infty }^{ \infty }dx(-x^{2})e^{-\alpha x^{2 } }$$
$$\displaystyle \frac{d}{d\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }=\sqrt{\pi }\displaystyle \frac{d}{d\alpha }\alpha ^{-1/2}=\sqrt{\pi }\left( -1/2 \right) \alpha ^{-3/2}$$
$$\displaystyle \int_{- \infty }^{ \infty }x^{2}e^{-\alpha x^{2 } }dx=\displaystyle \frac{1}{2\alpha }\sqrt{\displaystyle \frac{\pi }{\alpha } }$$

フレネル積分　　$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{ix^{2 } }dx$$を求めなさい． 
ただし，$$S(x)=\displaystyle \int_{0}^{x}\textrm{sin}t^{2}dt$$, $$C(x)=\displaystyle \int_{0}^{x}\textrm{cos}t^{2}dt$$もFresnel積分と呼ばれる．
ただし，$$S( \infty )=C( \infty )=\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }$$を既知とすると，
$$I=\displaystyle \int_{0}^{ \infty }e^{ix^{2 } }dx=\displaystyle \int_{0}^{ \infty }\textrm{cos}x^{2}dx+i\displaystyle \int_{0}^{ \infty }\textrm{sin}x^{2}dx=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }\left( 1+i \right) $$が得られます．
（参考）Gauss積分　$$\displaystyle \int_{0}^{ \infty }\textrm{exp}[-t^{2}]dt=\sqrt{\pi }/2$$

－－－－－－－－－－－－－－－－－－－－－－－－－－－
これを複素積分法で計算してみます： 
$$I=\displaystyle \int_{0}^{ \infty }\textrm{exp}[ix^{2}]dx=\displaystyle \int_{0}^{ \infty }\textrm{exp}[-(e^{-i\pi /2})x^{2}]dx$$
$$z=xe^{-i\pi /4}$$とおくと，$$dz=dxe^{-i\pi /4}$$だから，　$$I=e^{i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{Re^{-i\pi /4 } }\textrm{exp}[-z^{2}]dz$$

被積分関数$$\textrm{exp}[-z^{2}]$$は，周回積分の領域$$C$$で正則だから，コーシー・リーマンの定理により周回積分は０になる：
$$0=\displaystyle \int_{(C)}^{}\textrm{exp}[-z^{2}]dz=\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz+\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz$$
$$z=te^{i\theta }$, $dz=dte^{-i\pi /4}$, $dz=d\theta iRe^{i\theta }$$
$$C_{1}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}\textrm{exp}[-z^{2}]dz = e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}e^{-i\pi /2}]dt=e^{-i\pi /4}\displaystyle \lim_{R \to \infty }\displaystyle \int_{0}^{R}e^{it^{2 } }dt$$
$$C_{2}$$
$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}\textrm{exp}[-R^{2}e^{i2\theta }]e^{i\theta }d\theta =$$
$$=\displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}e^{-R^{2}\textrm{2cos}2\theta }e^{-iR^{2}\textrm{sin}2\theta }e^{i\theta }d\theta \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}\textrm{cos}2\theta }|d\theta \leqq $$
$$ \leqq \displaystyle \lim_{R \to \infty }iR\displaystyle \int_{-\pi /4}^{0}|e^{-R^{2}(4\theta /\pi +1)}|d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\displaystyle \int_{-\pi /4}^{0}e^{-(4R^{2}/\pi )\theta }d\theta =\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left[ \displaystyle \frac{e^{-(4R^{2}/\pi )\theta } }{-4R^{2}/\pi } \right] _{-\pi /4}^{0}$$
$$=\displaystyle \lim_{R \to \infty }iRe^{-R^{2 } }\left( 1-e^{R^{2 } } \right) /\left( -4R^{2}/\pi \right) =\displaystyle \lim_{R \to \infty }i\pi (1-e^{-R^{2 } })/4R=0$$

$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{3})}^{}\textrm{exp}[-z^{2}]dz = \displaystyle \lim_{R \to \infty }-\displaystyle \int_{0}^{R}\textrm{exp}[-t^{2}]dt=-\sqrt{\pi }/2$$
従って，$$\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{1})}^{}=-\displaystyle \lim_{R \to \infty }\displaystyle \int_{(C_{2})}^{}$$ より，
$$\displaystyle \frac{\left( 1-i \right) }{\sqrt{2 } }\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\sqrt{\pi }/2$$
$$\displaystyle \int_{0}^{ \infty }e^{it^{2 } }dt=\displaystyle \frac{1}{2}\sqrt{\displaystyle \frac{\pi }{2 } }(1+i)$$

オーギュスタン・ジャン・フレネルFresnel（1788-1827）は，ナポレオン時代のフランスの数学者です．

■フレネルレンズ

フレネルレンズの概念（断面図はwikiより）

フレネルは，フレネルレンズ(1819)やゾーンプレートに名前が残っています．注）ブリタニカ（https://www.britannica.com/technology/Fresnel-lens）によると，レンズの表面を同心円状のリングに分割するというアイデアはFresnelよりも古く，Georges-Louis Leclerc de Buffon（1748）で，フレネルは，1821年に灯台レンズの製造に採用したとあります．ビュフォンもフランスの数学者で確率論の実験「ビュフォンの針」で有名です． 

灯台の凸レンズは巨大で重いのが問題でしたが，フレネルはフレネルレンズを採用してこの問題を解決しました．今日ではプラスチックを用いることで，この原理を使った平板レンズが，ルーペなどの小さいものから，太陽光集光用の大型の製品まで作られています．

https://www.ntkj.co.jp/products/#lens1

 製品情報 | NTKJ Co., Ltd. - 日本特殊光学樹脂日本特殊光学樹脂株式会社(NTKJ)より

■ゾーンプレート

フレネルゾーンプレートは，単色の光を集光することができます．X線や光や電波は，皆，電磁波の仲間ですが，ゾーンプレートは，屈折させて集光するレンズが作れないX線に対しても集光することができます．

 STXMで使われるX線の集光（バークレイALS，BL5）

■アンテナとフレネルゾーン

フレネルゾーンは，無線通信でも使われる言葉です．無線通信で「見通しが良い」ということは，送信アンテナと受信アンテナの間に障害物がなく，お互いにアンテナが見通せるという意味ではなく，フレネルゾーンが確保されている状態を指します．フレネルゾーンは，送信アンテナと受信アンテナの位置を軸とする楕円体の形で，第1フレネルゾーン，その外側に，第2フレネルゾーン…と広がっていき，隣り合うゾーンの位相は互いに反対です．

私の家の立地では，携帯４Gの電波強度が非常に弱いので，屋外にドナーアンテナを設置してもらっています．私の場合では，800MHz（18バンド）ですが，例えば基地アンテナからdの距離があるとすると，第1フレネルゾーン半径r_1は，r_1＝√(λ･d)/2=9.7mとなります．ただし，λは800MHz電波の波長37.5cm，d=1,000mを用いた．第1フレネルゾーンの楕円体の60%程度が確保できれば良い通信状況と言えますが，この途中で障害物が邪魔をするのです．一般的な話をすれば，地上から高い位置に受信アンテナを設置できれば，第１フレネルゾーンの60%確保がしやすいということになります．

フレネルゾーン計算ツール | 株式会社サーキットデザインwww.circuitdesign.jp

レンズアンテナと反射型アンテナ

電波望遠鏡，衛星放送アンテナは，良く知られるように反射型のパラボラアンテナが使われます．これは，特定の方向からやってくる平行電波を集光する反射型アンテナです．しかし，ゾーンプレートの原理を使って集光するアンテナもあります．

一寸，脱線しますが，ルネベルグレンズは，球形の誘電体レンズ（同心殻で誘電率を変化させている）で，マイクロ波電波を屈折させて集光するレンズアンテナです．球体が乗っているレーターの写真を見たことがおありでしょう．私は昔，衛星放送受信用のルネQアンテナを使用していました．残念ながら今は販売されていないようです．

■フレネル反射率

フレネルは若くして（39歳）で亡くなりましたが，フレネル反射率は死の4年前の発表（1932）です．

物質の表面や界面で反射や透過する光の電場の振幅は，電場の界面平行成分と電束密度の界面垂直成分は連続になります．
物質0と物質1との界面を問題にするとき，この界面で反射される電場の振幅の比ρをフレネルの振幅反射率といいます．エネルギー反射率はρ^2です．
屈折率の低い物質から高い物質に向かう界面で反射するときには，ρが負になりますが，これは振幅の位相が180°変わることを意味します．エネルギー反射率はρの2乗なので負にはなりません．

■フレネルは，光学の分野で色々な研究をしました．そこで現れる数学「フレネル積分」の話をするのが，実は本題ですが，長くなったので，稿を改めて別の機会にします．

Maxwell方程式　[c.g.s.単位系使用] 
$$rot\overrightarrow{E}=-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{B } }{ \partial t}$$    (1a)    電場$$\overrightarrow{E}$$
$$rot\overrightarrow{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$ （変位電流）    （1b）    磁場$$\overrightarrow{H}$$
$$div\overrightarrow{B}=0$$    （1c）    磁束密度$$\overrightarrow{B}$$
$$div\overrightarrow{D}=4\pi \rho$$ (空間電荷)    (1d)    電束密度$$\overrightarrow{D}$$

弱い場では，線形応答が成り立つ： 
$$\overrightarrow{B}=\mu\overrightarrow{H}$$ (透磁率$$\mu=1$$の物質を対象とする)    (2a)    magnetic susceptibility$$\mu$$
$$\overrightarrow{D}=\varepsilon \overrightarrow{E}$$    (2b)    dielectric constant$$\varepsilon $$
$$\overrightarrow{j}=\sigma \overrightarrow{E}$$    (2c)    current density$$\overrightarrow{j}$$，conductivity$$\sigma $$
---------------------------------------------------- 
参考） [MKSA単位系の場合]
$$ \bigtriangledown \times E=-\displaystyle \frac{ \partial B}{ \partial t}$$
$$ \bigtriangledown \times H=\displaystyle \frac{ \partial D}{ \partial t}+j$$
$$ \bigtriangledown \cdot B=0$$
$$ \bigtriangledown \cdot D=\rho $$
ベクトルポテンシャル，スカラーポテンシャルの定義
$$E=- \bigtriangledown \cdot \phi -\displaystyle \frac{ \partial A}{ \partial t}$$
$$B= \bigtriangledown \times A$$
---------------------------------------------------- 
公式　$$[ \bigtriangledown \times \left[ \bigtriangledown \times E \right] ]= \bigtriangledown \left( \bigtriangledown \cdot E \right) - \bigtriangledown ^{2}E$$を使うと，
(1a,b)　→ $$ \bigtriangleup \overrightarrow{E}=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{E } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}$$， $$ \bigtriangleup \overrightarrow{H}=\displaystyle \frac{\varepsilon}{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{H } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{H } }{ \partial t}$$ （３）
（３）の解  → $$\overrightarrow{E}=\overrightarrow{E}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$，$$\overrightarrow{H}=\overrightarrow{H}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$ 　　　（４）
解（４）は，条件（５）の下で成立する．もし，変位電流がなければ，（５）の右辺第２項はない． 
$$\left( \displaystyle \frac{2\pi kc}{\omega } \right) ^{2}=\varepsilon -i4\pi \left( \displaystyle \frac{\sigma }{\varepsilon } \right) $$ (5)
(4)を(1a,b)に代入（$$\sigma =0$$の物質を対象とする．）： 
$$\overrightarrow{k} \times \overrightarrow{E}_{0}=\displaystyle \frac{\omega }{2\pi c}\overrightarrow{H}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
kE_{x} \\[0mm]
0
\end{array} \right] =\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
H_{y} \\[0mm]
0
\end{array} \right] $$ (6a)
$$\overrightarrow{k} \times \overrightarrow{H}_{0}=-\displaystyle \frac{\omega }{2\pi c}\overrightarrow{E}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
-kH_{y} \\[0mm]
0 \\[0mm]
0
\end{array} \right] =-\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
E_{x} \\[0mm]
0 \\[0mm]
0
\end{array} \right] $$ (6b)
$$\displaystyle \frac{c}{n}=\displaystyle \frac{\omega }{2\pi k}$$ (7)
$$\displaystyle \frac{H_{y } }{E_{x } }=\displaystyle \frac{\omega \varepsilon }{2\pi ck}=\displaystyle \frac{2\pi ck}{\omega }\left( =\displaystyle \frac{\varepsilon }{n}=n \right) $$ (8)
$$n^{2}=\varepsilon $$, $$\displaystyle \frac{H_{y } }{E_{x } }=\sqrt{\varepsilon }$$ (9)

境界条件

物質１と物質２の境界では，電束密度の界面垂直成分，電場の界面平行成分が連続することがMaxwell方程式から導ける．
$$D_{1z}=D_{2z}$$ $$ \Leftarrow $$ $$div\overrightarrow{D}=0$$ (10a)
$$\displaystyle \int_{}^{}(D_{2z}-D_{1z})dxdy=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}D_{z}df_{z}=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}div\overrightarrow{D}dV=0$$
$$E_{1x}=E_{2x}$$ $$ \Leftarrow $$ $$div\overrightarrow{B}=0$$ (10b)

$$\displaystyle \int_{}^{}(E_{1x}-E_{2x})dx=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}(rotE)_{y}df_{y}=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \int_{}^{}\displaystyle \frac{ \partial B_{y } }{ \partial t}df_{y}=$$

$$=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial }{ \partial t}\displaystyle \int_{}^{}div\overrightarrow{B}dV=0$$

垂直入射
$$E_{1x}+E_{1x}^{R}=E_{2x}$$
$$H_{1y}+H_{1y}^{R}=H_{2y}$$ $$ \Rightarrow $$ $$n_{1}\left( E_{1x}-E_{1x}^{R} \right) =n_{2}E_{2x}$$
$$\displaystyle \frac{H_{1y } }{E_{1x } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$-\displaystyle \frac{H_{1x}^{R } }{E_{1x}^{R } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$\displaystyle \frac{H_{2y } }{E_{2x } }=\sqrt{\varepsilon _{2 } }=n_{2}$$
振幅反射率 $$\displaystyle \frac{E_{1x}^{R } }{E_{1x } }=\displaystyle \frac{n_{1}-n_{2 } }{n_{1}+n_{2 } }$$， $$n_{1}<n_{2}$$で位相反転
振幅透過率 $$\displaystyle \frac{E_{2x } }{E_{1x } }=\displaystyle \frac{2n_{1 } }{n_{1}+n_{2 } }$$
--------------------------------------------------------
$$n_{1}, n_{2}$$が実数なら，$$\displaystyle \frac{\left| E_{1x}^{R} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }+\displaystyle \frac{\left| E_{2x} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }=1$$
-------------------------------------------------------- 
$$\displaystyle \frac{ \partial \rho }{ \partial t}+div\overrightarrow{j}=0$$
$$\displaystyle \frac{ \partial }{ \partial t}div\overrightarrow{D}=4\pi \displaystyle \frac{ \partial \rho }{ \partial t}=-4\pi div\overrightarrow{j}$$
$$div\left( \displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+4\pi \overrightarrow{j} \right) =0$$
$$rot\overrightarrow{H}=\displaystyle \frac{\varepsilon }{c}\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$
第１項：第２項の寄与率＝$$\varepsilon \omega :4\pi \sigma $$
$$\omega \gg \displaystyle \frac{4\pi \sigma }{\varepsilon }$$ $$\to $$ 誘電体

４．特異値分解の数学

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n

簡単のために，m=5，n=3として，具体的に演習してみましょう．

今回は，昔，私がリコーで関わった懐かしい実験の話をして，特異値分解の数学の話への導入にしたいと思います．まず，実験の話をしますが，私がSTXMに係わったのは，2000年～2004年で，もう20年も前のことです．その後の進歩は著しいに違いありません．当時，実用になるSTXM装置は，Hitchcoch博士が，サンフランシスコ，バークレーのALS（Advanced Light Source）に建設した，BL5.3.2（bending magnet光源利用）　とBL7.0.1（undulator光源利用）の2台だけでした．後年，岡崎の分子研のUVSORに，やはり，Hitchcock博士がSTXMを建設しました．

（注）放射光とは初耳の読者もおられるので，放射光施設とは何かを簡単にお話しておきます．ドーナツのような真空リングの中を，光速に近い速度に加速された電子が回転しています．回転するといっても電子の軌道が円形というわけはなく，リングの要所要所に偏向磁石bending magnetが配置されていて，偏向磁石の所で電子は曲げられるので，電子の軌道は多角形です．電子が方向を変えるときには，電磁波（白色光の光やX線）を放出します．これが放射光で，いろいろな測定に放射光を利用します．リングの電子蓄積エネルギーとはリング内を回転する電子のエネルギーのことです．ALSでは1.9GeV，兵庫県のSPring8では8GeVです．蓄積エネルギーの大きさは，放出される放射光のエネルギーの最大値を決めるので，SPring8は硬X線の光源，ALSは軟X線の光源となります．
放射光の光源は，偏向磁石bending magnet光源とundulator光源とがあります．undulatorというのは周期的に配列した磁石のことで，蓄積リングの電子軌道の直線部に挿入します．周期的磁場で電子は蛇行運動をしますが，その軌道のFourier変換に相当する波長のX線（準単色光）が放射されます．

さて，STXMに使うALSの放射光リング（蓄積電子のエネルギーが1.9GeV）は，軟X線の光源です．軟Ｘ線の領域は10^2eV～10^4eVの範囲で，炭素など軽元素の1s（K殻電子）の励起（光電効果による電子の放出）は，このX線の領域にあります．硬X線と違い，軟X線は空気で減衰しますからその測定は，He置換した真空チェンバー内で行います．炭素の1sの吸収スペクトルNEXAFS(吸収端近傍の吸収微細構造)は，分光して単色化したX線ビームを薄膜試料に透過させ，その吸収を測定して得ます．スキャンするエネルギー範囲は，280eV～310eVで，スキャンステップは0.1eVですので，スペクトルは300点ほどのデータ数になります．

目次
これから始まるこのテーマの話には4つの側面があります．
第１は，ニュースとしての一般向け報道．
第２は，STXMの装置の仕組み．
第３は，材料科学の側面．炭素1s吸収端近傍の吸収スペクトルNEXAFS．
第４は，データ解析の数学．特異値分解．

技術者向け教育の場合にお話しするのは，第１，２の部分です．第４の部分は，Hitchcock博士らの開発したaXis2000というソフトウエアを用いるので，数学を意識することはないのですが，今回は，特に，第４の数学の話に注目することにします．番号順に順を追って話ます．

１．一般向け報道

せっかくの記事ですが，技術の解説が正しくありません．ここで言及しているデータベースは無関係で，この記事はピントがずれているのが残念です．

２．STXM（ScanningTransmissionX-rayMicroscopy）装置

放射光X線をFresnel Zone Plateで，試料薄膜上にフォーカス（22nmΦ）させ，その微小ビームを試料薄膜に透過させ，微小ポイントの吸収スペクトルを測定します．スペクトルを得るには入射するX線のエネルギーを280eV～310eVの範囲で，0.1eVの分解能で変化させます．これは，色を変えて見る実験に例えるとわかりやすいでしょう．同じ材料薄膜でも，赤い色を透過させてみた場合と青い色を透過させてみた場合とでは異なるでしょう．試料薄膜（ミクロトームで加工した厚さ100nmの切片）上をラスタースキャンすることで，そのエネルギーで見た薄膜の吸収画像が得られます．
薄膜に入射するＸ線エネルギーを280eV～310eVの範囲で変えて測定した300枚ほどの吸収画像をスタックすれば，薄膜試料の各点(x, y)の吸収スペクトルμ(x, y)が，point to pointで得られたことになります．試料上の空間分解能は約30nm，スペクトルのエネルギー分解能は0.1eVという高性能な測定です．私たちは装置を使う純粋ユーザーでしたが，私は，このような装置を開発したHichcock博士グループの技術と装置の仕組みに興味を持ちました．ここでは，STXM装置の重要な要素であるゾーンプレートとその制御についてとり上げましょう．

ゾーンプレートの焦点距離は波長で変わります．入射するX線ビームのエネルギーがスキャンされれば，そのつど瞬時にフォーカスしなければなりません．これは，レーザー干渉計とゾーンプレートの載るピエゾステージで行われます．試料点の（x, y)スキャンは試料台のピエゾステージで行われます．
BL5.3.2はbending mgnetからの放射光（undulator光源よりは光強度は弱い）ですが，照射された点の有機物はダメージを受けますので，できるだけ高速で測定します．そして，試料の変質がなかったかどうか測定前後でチェックする測定ルーチンもあります．X線のエネルギーを変えて測定した吸収画像をスタックしたとき，サンプル位置のずれがあれば自動修正できます．

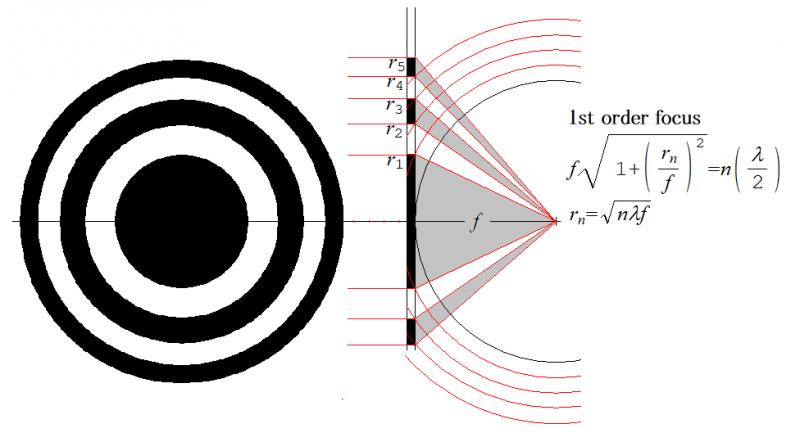
以下で，STXM装置で最も主要な素子であるFresnel zone plateについて，詳述しましょう．zone plateは，外径45000nm，最外輪帯幅35nm程度のものです．下図のゾーンプレートは，波長λのX線の単色光を集光します．黒い部分はX線を通しません．例えば，中心の黒丸はダイレクト光をストップし，輪帯環の白い部分を通過してくる行路長　f+λ/2，f+3λ/2，f+5λ/2，････のものが，焦点距離fに集光できます．

 このようなフレネルゾーンプレートの後ろにOSAという絞りを置いて，行路差λずつの光線（１次のフォーカス）のみが試料位置に集光するように調整します．

 入射X線のエネルギーを変えたときのゾーンプレートの焦点距離の調整は，レーザー干渉計を用い精密制御されています．

３．炭素の1s電子の吸収端直上の微細構造スペクトルNEXAFS

電子写真で使われるトナーは，カーボンブラックとか顔料色素で出来ていると思っている人がほとんどでしょう．実際には，このような黒やカラーの色素だけでなく，樹脂，ワックス，電荷制御剤など，複数の有機物分子が，1粒のトナー中に分散されており，それらの分散状態は，トナーの性能に影響を与えます．設計通りの分散状態が実現しているか評価することが必要です．高精細トナー1粒のサイズは数μmという微細さで，その中の物質の分布状態を30nmΦの分解能で調べる必要があります．しかも，混合されている物質は，皆，有機物ポリマーで元素分析をすれば，どれも主成分は炭素です．つまり，炭素が骨格のよく似た有機分子が混合している状態の分布マップが知りたいのです．これを化学状態マッピングといいます．

下図には，色々な物質の炭素1s電子のNEXAFS吸収スペクトルを載せました．X線のエネルギーを変えて観察した透過像も載せています．例えば，①カーボンブラックの分布する場所は292.5eVのX線エネルギーで見ると吸収が大きいため白っぽく見え，②ワックスの分布する場所は，287.8eVで見ると吸収のためX線の透過が悪く白っぽく見えます．同様に，③樹脂の分布する場所は，284.3eVのX線の透過像では白っぽく見えます．
エネルギースキャンにともなう画像変化のパラパラ動画を作って見るとわかりやすく面白いものです．

 化学状態（元素分析ではない）という意味は，トナー中に分散している物質は，すべて有機分子（どの分子もほとんど炭素元素で出来ている）なので，元素分布のマッピングでは差がありません．炭素原子が骨格の有機分子の吸収スペクトルは，炭素の1sの吸収端285eV付近にあり，その炭素原子がどのような化学結合状態にあるのか（1重結合か，2重結合か，π電子系か，どのような官能基と結合しているか）により，吸収端から高エネルギー側に観測される吸収スペクトルの微細構造（NEXAFSという）に違いがでます．
トナー中の有機ポリマー分子の分布マップを得るには，化学状態マッピングがどうしても必要になります．
元素に特有な特性X線を検出すれば良い元素分布マッピング［TEM（分析電顕）でも，放射光でも，微小領域の蛍光X線分析は普及している］と，化学状態マッピング［微小領域のpoint to pointで炭素1sのNEXAFSの測定が必要］は，全く異なる技術であり，我々の目的には，STXMでの実験が必要でありました．

リコーが，Adam P. Hitchcock（McMaster University）博士が開発したALS（バークレー，AdvancedLightSource）のBL5.3.2に設置されたSTXMで共同研究を行ったのは，2000~2004年のことです．

実験で得られるデーターセットは，試料表面の座標を（x, y）とすると，試料表面のラスタースキャンと，透過させるX線のエネルギーωのエネルギースキャンを行って，point to pointで収集した吸収スペクトルμ(ω；x, y)です．
再度たとえ話をすると，膜を透過する光のコントラスト像は，光の色を変化させると透過光の像のコントラストが変わって見えるというわけだ．

このような，データセットの収集と解析は，Hitchcock博士の開発したソフトウエアaXis2000を用います．この解析のために用いる数学は，特異値分解です．この先は，４．特異値分解の数学に続きます．

４．特異値分解

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n
簡単のために，m=5，n=3として，続編で演習してみましょう．続く...

参考-----
特異値分解を使いますが，特異値分解の概念図は以下のようなものです．

以下の拙著の第3章p64～p84から抜粋転載しました．

https://www.amazon.co.jp/dp/4774143936?tag=note0e2a-22&linkCode=ogi&th=1&psc=1

■特異値分解

複素行列$$A(m \times n),m \ge n$$は，適当なユニタリー行列$$U(m \times m)$$と$$V(n \times n)$$を用いれば，
$$UAV^{ \dagger }=\mit\Sigma $$，あるいは，$$A=U^{ \dagger }\mit\Sigma V$$に分解できる．これを，Aの特異値分解という．
(ただし，$$V^{ \dagger }$$は$$V$$の共役転置行列．$$A$$が実数行列の場合は転置のみ$$V^{'}$$）．

$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$

ここで，$$\sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$を$$A$$の特異値と呼ぶ．
$$r$$は$$\textrm{rank}(A)$$に等しい．

$$AA^{ \dagger }=U^{ \dagger }\mit\Sigma VV^{ \dagger }\mit\Sigma ^{'}U=U^{ \dagger }\mit\Sigma ^{2}U$$,      $$ \because \Sigma \Sigma ^{'}=\Sigma ^{2}(m×m) $$
$$AA^{ \dagger }$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$m-r$$）
$$A^{ \dagger }A=V^{ \dagger }\Sigma ^{'}UU^{ \dagger }\Sigma V=V^{ \dagger }\Sigma ^{2}V$$,      $$ \because \Sigma ^{'}\Sigma =\Sigma ^{2}(n×n)$$
$$A^{ \dagger }A$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$（０の個数は$$n-r$$）

線形写像 $$ y=Ax  (x∈C^{n}，y∈C^{m})$$があり，それぞれの空間でユニタリ変換； 
$$ x'=Vx$$, $$y'=Uy$$をすると，$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている．

■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して，
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める．
特異値分解ができたら；$$UAV'=\Sigma$$，$$A=U'\Sigma V$$が成立している．
（$$A$$は実行列なので，$$U，V$$は直交行列となり$$U'＝U^{-1}$$などの性質がある．）
最小2乗法は，$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる．
$$\textrm{rank}(A)=r≦n<m$$とする．$$\Sigma (m×n), V(n×n), U(m×m)，x(n×1)$$の型であった．

$$r=n$$の場合を考える．

$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$,　$$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから，
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方， 
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って，$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると，第1項は0になり，第２項は残差の２乗を与える，

$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る．

１．結晶空間群．結晶点群

結晶は周期的な内部構造を持ちます．周期的な離散空間を＜結晶空間＞と言い，
その対称性は<結晶空間群>で記述します．結晶空間群の種類は，3次元では230種類です．
3次元の周期構造の幾何学的な表現を＜格子＞と言ったり，その数学的な表現を＜並進群＞と言ったりします．
結晶空間の中で，格子分だけ移動しても，周囲の状況は移動する前の状況と全く同じなので，無限に繰り返す結晶の中で自分がどこにいるか区別できません．そこで，格子分だけ移動した点はすべて同値とみなして，
無限に広い結晶空間を１つの単位胞の中に畳み込んでしまうことができます．
あたかも，無限に続く時間を，時計の文字盤（12時間）に畳み込んでしまうのと同じです．
＜単位胞＞（有限図形）の対称性は＜点群＞で記述でき，3次元の＜結晶点群＞は32種類です．

（注）＜結晶点群＞の対称操作は周期性と両立しなければならないので，ただの点群とは異なり，
回転対称は２，３，４，６回軸に限定されます．

格子を法として（あるいは，並進群を核として）準同型写像をすると，結晶空間群の230種類を，結晶点群の32種類に還元できます．

 $$\mit\Phi /T \cong G$$ ,     $$T \vartriangleleft \mit\Phi $$    ($$\mit\Phi $$結晶空間群，$$T $$並進群，$$G$$結晶点群）

２．双対空間．コンボリューションのFourier変換．Curieの原理（因果律）

結晶格子をFourire変換すると逆格子が得られます．結晶格子（$$r-$$空間）と逆格子（$$R-$$空間）は，Fourier変換で移り変わる互いに双対な空間です．結晶の電子密度関数$$ρ(r)$$とそのFourier変換F(R)は，1:1に対応し，両者の対称性は同じです．

電子密度分布$$ρ(r)$$により散乱されるX線の散乱振幅は$$F(R)$$で，$$ρ(r)$$のFourier変換にほかなりません．観測される散乱強度は$$|F(R)|^{2}$$で散乱振幅$$F(R)$$の位相情報は失われます．

 $$Tr[\rho (r)]=F(R)$$,     $$Tr[\rho (r)*\rho (r)]=|F(R)|^{2}$$

結晶の対称心の有無にかかわらず，観測されるX線散乱強度には，対称心が生じます：$$|F(-R)|=|F(R)|$$，これをFriedel則と言います．

Friedel則は，もっと大きい次のCurieの原理の一部です．

原因である「結晶構造の対称性」は，結果である「その結晶で生じる現象の対称性」に反映される．

（例1）結晶構造に，4回対称性が存在すれば，Ｘ線回折像の対称性に，少なくとも4回対称性は反映される．しかし，Ｘ線回折像に4回対称性が存在しても，結晶に必ずしも4回対称性が存在するわけではない．
これを回折対称の上昇という．

（例2）Ｘ線回折像に10回対称（5回対称⊗Friedel則）があったとしても，その原因たる結晶構造に5回対称性があるとは限らない．結晶構造の5回対称性は周期性（結晶の定義）と矛盾するのであり得ない．しかし，周期性を外せばあり得る．準結晶のモデルは，非周期のペンローズ・タイリングで実現できる．

３．点集合とベクトル集合．ホモメトリック

結晶構造（点集合）の対称性と，回折強度像（点集合のベクトル集合が作るスター）の対称性の関係を考察しましょう．両者の対称性では，回折強度像の対称性が高いわけで，与えられたベクトル集合から点集合を推理するのは，面倒な逆問題になる場合がある．

一般に，回折強度像の対称性から結晶構造の対称性は，一意に定まらず，同一の回折強度像を与える結晶構造が複数存在する可能性があります．これらをホモメトリック構造という．
下の2つの図は，1次元のホモメトリック構造の例［Patterson(1944)］．
（注）この図の見方は，1次元の単位胞が全円周（長さ1）です．図中に描き込まれた長さは円弧に沿って測ります（弦の長さではない）．円周（長さ１）のどこか1点で切って，線分（長さ１）に延ばします．この線分を1次元のタイルのように並べていくと1次元の周期的な図形になります．この図形には黒い点が並んでいますが，2つの図形で黒点の配列は異なります．それにもかかわらず，出現する黒点間の間隔の種類は2つの図形で同じになります．

PCR検査の統計と論理　　　　　　　　　　　　　　　谷　克彦

（要旨）
◆PCR検査の感度と特異度は，遥かに1に近い確率でした．偽陰性や偽陽性を理由に検査数をコントロールする理由は成り立ちません．検査を拡大し有病者を発見し早期隔離しましょう（感染から5日目頃が最もウイルスを放出し，有病者の半減期は10日位です）．◆日本の陽性率は7%と計算できますが，最近の変動の勾配（末尾に掲載）から見ると10%を越えたように見えます．このグラフがそのように見えるのは，検査数を抑制しているために陽性者数のオーバーフローが起きている証拠かもしれません．
---------------------------------

COVID-19パンデミックは，実効再生産数を1より低下させると鎮まります．この対策は，次の３つの数値を下げることです；①感染者が感染力を持つ期間，②感染者が接触する人数，③感染者との接触で感染する確率．そして，それぞれに対する施策は以下のようです；
①感染者を早期に発見し隔離する．このためにPCR検査の拡充が必要．
②効果的なロックダウンの期間，地域，方法を，シミュレーションで予測し戦略的に介入する．
③ワクチン接種で，感染感受性のある人の割合を減らす． 

COVID-19に感染すると，次のような経過になります． 

感染（陽性）→潜伏無症状期→発症期（無症状もありうる）→回復（陰性）or死亡
陽性の期間［潜伏無症状期＋発症期（無症状もありうる）］は，「罹患者」が感染源となる有病状態なので「有病罹患」と呼ぶことにします．感染源となる「有病罹患」（症状の有無にかかわらず）を早く発見し隔離する必要があります．
有病罹患者の発見はPCR検査でなされます．検査の目的は蔓延率の推定だけではなく，感染源となる有病罹患者をできるだけ早期に探し出し隔離するという緊急な役割があります．検査対象を限定し，検査の陽性的中率を上げることが検査の目的になってはいけません．
実世界の現象は，多数の原因と結果が複雑に絡んだ因果関係をなし，数学（統計）で論理的に推論するのは，その一部を切り取った世界です．その範囲で得た数学（統計）的推論の結果を，系全体の中で解釈できる論理的な思考が必要です．
正しい数学（統計）推論で得られた結果でも，複雑な全体系で非論理的に利用されるとしたら，社会を誤った方向へ導く主張に，数学が加担してしまうことになります．PCR検査の規模拡大は有病率の低い集団ではすべきではないというのは正しい主張ではありますが，その主張の根底にあるPCR検査の性能から見直し，これを論理的に考察してみましょう．

■有病率とは
日本感染症学会の定義によると，有病率とは，「その疾患をもっている人数の全人口に対する割合」ですが，日々発表される厚労省の新規陽性者数と検査数のデータから，日本の有病率を計算できるように，有病率$$x_{0}$$の解釈を次のようにします．
（定義）$$有病率=有病罹患数/累積PCR検査数$$
　　　　 　　　$$有病罹患数＝累積検査陽性者数－累積回復退院者数－累積死亡者数$$
これにより，日時（$$T=$$5月15日）の日本の有病率を求めると$$x_{0}=0.58$$％になります．
ここでは，陽性者=罹患者と見なしています．
この検査集団の陽性率($$T$$)と罹患率($$T$$)は，7日平均（8～１５日）を用いて，
$$陽性率(T)=陽性者(T)/検査数(T)=6288/92167=0.068$$，
罹患率(*)$$(T) =陽性者(T)/累積検査数(T)=6288/13015244=0.0005$$

日時$$T$$の有病罹患数$$(T)$$を別の定義で表現してみましょう．有病罹患状態は，14日位で回復（陰性になる）します（運悪く死亡の場合もありますが，少数のため無視します）．今日$$T$$の有病罹患者（感染源となる罹患）の中には，$$t$$日前に罹患した者も残っています．そこで，次の定義が成り立ちます：
有病罹患数$$(T)=\displaystyle \int_{0}^{T}$$罹患数$$(t)p_{a}(T-t)dt$$，
ここで，$$p_{a}(t)$$は，陽性保持確率（病気の減衰関数のような性質）で，（付録３）の大規模調査の結果に報告されています．病気の感染初日を推定するのは大変難しいのです．PCR検査で見つかった日が感染日という訳ではないでしょう．感染から5日目あたりが，感染者が最も多くウイルスを放出するので，その頃が最も発見され易いのではないかと思います．
病気減衰関数の半減期は約10日ですので，コンボリューション積分は次のように近似できます：
有病罹患数$$(T)=10×罹患数(T)$$．この集団の累積検査数で規格化すると．
$$有病率(T)=10×罹患率(T)$$が得られます．
注*）感染症学会の定義では，罹患率の分母は，「集団の感受性のある人数」ですが，ここでは「集団の人数」としています．

■PCR検査の感度と特異度
PCR検査の感度$a$とは，罹患者をPCR検査で陽性（$$+$$）と正しく判定する確率のことで，真の罹患者でもPCR検査が陰性（$$-$$）（偽陰性）と判定される確率は$$1-a$$程度あります．検査の特異度$$b$$とは，非罹患者を正しく陰性（$$-$$）と判定する確率のことで，非罹患者を陽性（$$+$$）（疑陽性）と判定する確率は$$1-b$$程度です．

確率$$a , b$$は１に近いほど，優秀な検査になります．従来の議論に用いられてきたこれらの数値は，$$a=0.70, b=0.99$$ですが，昨年の英国ONSによる大規模調査（付録３．)で判明した数値は，$$a=0.95(0.85 ~ 0.98)$$，$$b=0.9992$$です．
低い有病率の集団でPCR検査対象を拡大すると，莫大な偽陽性が出て医療崩壊につながるので，有症状者や濃厚接触者に限定して検査を行っているとの主張がありますが，英国ONS調査の感度と特異度を採用すると，この主張の根拠が覆えることを検証します． 

■ベイズ推定による有病罹患の内訳

この集団の罹患率を$$p(罹患)=x$$，とします．この集団で，PCR検査が$$+$$判定のとき，罹患者である確率$$p(罹患|＋)$$，および，$$-$$判定のとき，罹患者である確率$$p(罹患| - )$$，などを推定しましょう．
$$p(罹患| + )=p( + |罹患)･p( 罹患) /p( +) =a･x/( a･x+(1-b)( 1-x)) $$，
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) x/\left( (1-a)x+b\left( 1-x \right) \right) $$， 
$$p(非罹患|+)=p\left( + |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( + \right) =(1-b)(1-x)/\left( (1-b)(1-x)+a \cdot x \right) $$,
$$p(非罹患| - )=p\left( - |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( - \right) =b\left( 1-x \right) /\left( b(1-x)+(1-a)x \right) $$，
下に$$x$$を変数とするグラフを示します．ベイズの定理は線形システムなので，重ね合わせができ，罹患状態を束ねた状態で定義される有病率$$x_{0}$$を入力にしても良いでしょう． 
■集団の有病率 $$x=0.006$$に対して，感度$$a$$，特異度$$b$$を変えて比較
（１）$$a=0.95, b=0.9992$$（英国ONS）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.9:0.1$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.9:0.0003$$
（２）$$a=0.7, b=0.99$$（従来）を用いた場合 
　$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.3:0.7$$
　$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.3:0.002$$
PCR検査が$$+$$判定であるときに，真陽性の確率$$p(罹患|+)$$と，偽陽性の確率$$p(非罹患|+)$$を比較すると，従来用いられている感度，特異度では，偽陽性確率が真陽性確率の$$2.3$$倍もありますが，英国ONSの数値では，逆に1/10になり，医療崩壊を懸念する根拠にはなりません．
いずれにしろ，陽性確定までにPCR検査は2度行われ，さらに，抗原検査の併用もありますから，偽陽性の誤判定リスクは回避可能です．積極的にPCR検査の対象を拡大し，感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません．

次に，真陽性の確率$$p(罹患|+)$$と偽陰性の確率$$p(罹患|-)$$を比較すると，
（１）では，$$1:3 \times 10^{-3}$$，（２）では，$$1:7 \times 10^{-3}$$で偽陰性は小さい確率です．これを人数で比較するには，陽性率$$y=0.07$$，陰性率$$1-y=0.93$$を，それぞれ，$$p(罹患|+)$$と$$p(罹患|-)$$に乗じます．
（１）では，$$真陽性人数:偽陰性人数=1:4 \times 10^{-2}$$，
（２）では，$$真陽性人数:偽陰性人数=1:9$$
この集団の陽性率は$$7$$％と低いので，陰性集団が大多数で，偽陰性の確率が小さくても偽陰性者数は多いとの主張もあります．確かに，従来の数値（２）を用いると，真陽性者の9倍もの偽陰性者がいます．しかし，数値（１）を用いると，偽陰性者の数は1/100で，PCR検査対象を拡大しない理由にはなりません．検査を拡大すれば，拾い出せる陽性者は検査数に比例して確実に増加します．

■PCR検査数は十分か
ここに引用した２つの図は，1日の$10^{6}$人あたりの（横軸）検査陽性数：（縦軸）検査数の散布図で，日本（上）と英国（下）の例です．英国の散布図スケールは日本のものより縦軸で25倍，横軸で16倍大きいのでご注意ください．散布図パターンを比較すると特徴的な違いがあります．時間経過とともに，右横あるいは右下がりに伸びる部分では，検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり，縦に伸びる部分では，陽性者を拾い出す十分な検査が行われているようです．英国の例を見ると，始めは，陽性者が多く検査数が間に合わないほどでしたが，現在みられる検査数を増しても陽性者が一定となる状態は，十分な検査数が確保されている証拠です．日本の例で，検査数と陽性者数の増減の比例が見られる傾向は，検査数を増やせば，陽性者数も増加する可能性があります．
これらの図は，2020.1.25～2021.5.25の期間のもので，赤細線は，日本の図では，陽性率5{\%}と10{\%}の勾配，英国の図では，0.5{\%}と２０{\%}の勾配を示しています．
これらのグラフは，https://ourworldindata.org/coronavirus-testingから引用しました．

■付録－－－－－
付録１．ベイズの定理
条件付き確率についての「ベイズの定理」とは次のように説明できます．
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
ただし，記号の意味は例えば以下の様です．
$$p(X)$$:$$X$$が起こる確率 
$$p(Y|X)$$：$$X$$が起きる条件下で，$$Y$$が起こる確率
$$p(X \cap Y)$$：$$X$$かつ$$Y$$が起こる確率
ベイズの定理は，$$X$$（原因）が起きる条件下で$$Y$$（結果）が起きる確率$$p(Y|X)$$と，$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です．

付録２．PCR検査の原理
PCR(ポリメラーゼ連鎖反応）を利用して，わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を，1983年にマリスが発見し1993年のノーベル化学賞を受賞しました．
RNAに対しても逆転写酵素によりDNAを合成し，DNAの複製反応が利用できます．ターゲットDNA鎖全体の複製ではなく，ウイルスを特徴づける断片の複製をします．これが，パウエル社が発表（1987）したRT-PCR技術です．PCR検査は，検体に含まれるCOVID-19ウイルスの微量なRNAから，逆転写酵素を用いて，cDNAを合成し，温度サイクル処理を40回程度繰り返し，cDNAを検出可能な濃度まで複製するというものです．このようなPCR検査の原理から，検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが，含まれていなければ誤混入がない限り増幅物は全く生じません．すなわち，特異度の高い検査です．

付録３．英国ONSのcovid-19感染の大規模調査
英国国家統計局（ONS)によるcovid-19の大規模感染調査は，パイロット調査としてイングランド（2020.4末）で開始されました．7月以降，規模を拡大し，住所リストから世帯のランダム・サンプリングを行い，8月には，2週間ごとにテストされるサンプルを，イングランドで15万人，ウエールズ，スコットランド，北アイルランドで各1.5万人の規模に拡げました．調査は，小児の症候性および無症候性感染の有病率と発生率を知るため，2歳以上の子供を含みます（参照：covid-19学校感染調査）．16歳以上の成人の20{\%}は血液サンプルの提供を求められました．2020.7.31～9.10の6週間で，208,730の検体調査を行いました．偽陽性は症状のない人で発生すると予想されましたが，調査研究のデータからは，症状の有無によらず同じでした．血液サンプルは，オックスフォード大学で，抗体検査，IgG免疫グロブリンのテストをしました．
PCR検査に関する知見は；その感度が，85{\%}～９８{\%}(95{\%}である可能性が最も高い)にあり，特異度は，99.92{\%}でした．
綿棒スワブの検体採取は，適切な監督下で行えば，自己採取でも医療従事者が直接採取した場合と同様の正確な結果になることも報告されています.

引用データ

1)厚生労働省 
2) Coronavirus (COVID-19) Infection Survey, UK Statistical bulletins
3) Keeping up with COVID-19, Rachel Thomas;
https://plus.maths.org/content/keeping-covid-19
4) https://ourworldindata.org/coronavirus-testing

2021年3月に，2021年のアーベル賞の受賞者が発表されました．ラズロ・ロヴースLászló Lovász（ハンガリー科学アカデミー・レニェイ数学研究所）とアヴィ・ウィグダーソンAvi Wigderson（プリンストン高等研究所）です．
プレスリリースによると，「理論計算機科学および離散数学への基本的な貢献，および，これらの分野を現代数学の中心的な分野として確立するのに果たした主導的な役割」が評価されました．
アーベル賞は，2002年にノルウェー科学アカデミーによって設立された数学で最も権威のある賞の1つです．ノルウェーの天才数学者ニールス・ヘンリック・アーベル（1802–1829）にちなんで名付けられ，この分野の発展に多大な貢献をした科学者に毎年授与されます．

2021年の受賞者について，ステクロフ数学研究所，シカゴ大学（米国）の数学科アレクサンドル・ラズボロフ教授による解説記事を要約紹介します．
「トリニティオプション-科学」第6号（325），2021年3月23日号
https://elementy.ru/nauchno-populyarnaya_biblioteka/435811/Troitskiy_variant_Nauka_6_325_23_marta_2021_goda

離散数学は，有限の離散的オブジェクトの特性を研究します．その重要な部分は，伝統的には組み合わせ論と呼ばれ，「純粋」数学で生じる構造に動機付けられています．たとえば，組み合わせの観点から，トポロジーの基本である複体の概念は，複体の面に対応する有限集合の閉じたファミリーにすぎません．組み合わせの抽象化は顕著な結果をもたらし，「有用な」（つまり，基本的な数学に適用される）組み合わせ論は，数学界で常に重視されてきたのは当然です．

離散数学は，「ハンガリーの数学」と長い間関連しており，その最も活発な支持者および宣伝者は，ポール・エルデシュでした．ラズロ・ロバースは1948年にブダペスト（ハンガリー）で生まれ，この数学的文化の中で育ちました．特に，彼はかなり早い年齢でエルデシュに会いました．そしてこれは彼のその後のキャリアと展望に非常に大きな影響を与えました．ラズロ・ロバースは，ポール・エルデシュの直接の後継者と見なすことができます．

　　　　　　　　　ラズロ・ロバース

理論情報学の形成
理論計算機科学，または，コンピュータサイエンスは，一般に「計算の複雑さの理論」の基礎が築かれた1970年代頃に独立した分野として出現しました．この分野では，大まかに言えば，アルゴリズムの存在の問題，または多くの場合，それらの効率に与えられた制約を伴うアルゴリズムの非存在が研究されます．

その名称にもかかわらず，理論計算機科学は厳密に数理科学であり，そのすべての成果は，数学の他の分野と同様に，厳密な定義，定理，および補題の形で定式化されています．それにもかかわらず，開発の内部論理とともに，理論情報学もまた，実際のアプリケーションによって大部分が導かれ，時には非常に具体的であります．他の「半応用」分野と同様，それに対する「純粋」数学者の態度は，穏やかではあるが長い間警戒していたことは明らかです．

アヴィ・ウィグダーソンは，1956年にハイファ（イスラエル）で生まれました．彼の学生時代は，理論計算機科学，特に独立した分野としての計算の複雑さの理論の形成に費やされました．プリンストンでの大学院での研究中，アヴィは，複雑性理論の創設者の1人である彼の学術顧問Richard JayLiptonの影響を大きく受けました．ロバースの場合と同様に，理論計算機科学が彼の人生の仕事になりました．

　　　　　　　　　アヴィ・ウィグダーソン

両受賞者の主な成果の1つは，数十年にわたる両方の分野の成熟と形成の過程で，彼らの科学的研究と国際的な教育および普及活動が大きな貢献をしたことです．
理論計算機科学は，コンピュータが操作する対象のほとんどが離散的であるという自然な理由から，離散数学の成果，アイデア，概念を積極的に利用しています．その多くは「純粋な」数学では需要がありませんでした．一方，理論計算機科学のニーズは，離散数学の全く新しい分野の創造につながっており，これは科学の歴史の中で最も成功した共生関係の一つであると思います．この分野から他分野への「アイデアの移転」における最大の功労者は，今年のアーベル賞受賞者なのです．
「純粋」数学者や数学者との関係も，より良い方向に変化しました．たとえば，ラズロ・ロバース（ちなみに，ロシア科学アカデミーの外国人会員）は4年間（2007〜 2010年）国際数学連合の会長を務め，プリンストン高等研究所（IAS）でのアヴィ・ウィグダーソンの役職は数学学校に属しています．この道を歩み始めた当初は，どちらも考えられないことでした．これは，抽象数学の多くの分野に密接に関連する問題，アイデア，定式化が両分野に蓄積され，多くの場合，抽象数学自身の発展に影響を与えることによって，多かれ少なかれ自然な形で起こったことです．この点において，ラズロとアヴィは誰もが認めるリーダー的存在です．

離散性から連続性へ
離散数学の特徴として，連続的ではなく有限的な対象への関心が高まっていることを前述しました．ラズロ・ロバースは，正反対の仮定に基づいた非常に重要なプロジェクトの創設者の一人であり，おそらく主人公です．その結果，非常に大きなグラフやその他の組み合わせ対象物は，10進法の分数が無理数の近似値とみなされるのとほぼ同じ意味（ロバースのアナロジー）で，幾何学的または代数的な性質を持つ自然な連続構造の近似値とみなすことができることがわかりました．その結果，美しく一貫した理論が生まれ，当然のことながら組合せ論だけでなく，代数学，解析学，測度論，統計力学，エルゴード理論など，数学や物理学のさまざまな分野と驚くほど関連していることがわかりました．

ラズロ・ロバースは，優れたモノグラフのLarge Networks and Graph Limitsを書き，すぐにこの分野の古典的なテキストになりました．興味のあるすべての読者にお勧めします．

疑似乱数理論
アヴィ・ウィグダーソンに最も関連するトピックに名称を付けると，疑似ランダム性の理論でしょう．最初の動機から始めると，最も重要なアルゴリズムの多くが本質的に確率的なことです．つまり，作業で乱数検出器を使用します．ただし，絶対的なランダム性はまれであり，実際には，いわゆる疑似乱数発生器がほとんどの場合使用されます．これは，アルゴリズムがそのような置換に「気付かない」ことを期待して，決定論的手順によって生成されたランダムビットとして渡されます．

擬似乱数理論とは，大まかに言えば，この希望に理論的根拠を与えようとするもので，さまざまなアーキテクチャやパラメータを持つ発生器を構築し，それらが必要な特性を持つことを数学的に証明することができ，同時に，これらの対象や概念は，計算複雑さの理論において，まったく独立した別の用途があることや，対応する構造が，たとえば代数幾何学のような，数学のきわめて古典的な分野に関連していることも，すぐに判明しました．アヴィ・ウィグダーソンは，この分野で誰もが認めるリーダーです．特に，最も重要な構成要素（Nisan-Wigderson発生器）と，複雑さの理論における顕著な影響（Impagliazzo-Wigderson定理）の両方があります．

Kneser仮説
ラズロ・ロバースは，クネーザー予想の証明があります．クネーザーグラフは，代数的組み合わせ論で発生する非常に自然な有限グラフで，タスクは，その色数を計算することです．つまり，エッジで接続された頂点が常に異なる色になるように頂点に色を付けることができる最小の色数を計算します．

おそらく，最適な着色を作成するのは簡単です．問題は，それを改善できないことを証明することです．この問題は，25年近くの間，組合せ学的な努力を必要としていましたが，1978年にロバースが発表したエレガントな論文で，厳密に離散的な絵全体を多次元の球体に浸し，実数位相幾何学の基礎的な結果の1つであるBorsuk-Ulamの定理を適用することで解決されました．この証明から，今日では位相幾何学的組合せ論と呼ばれる学問全体が発展し，その方法によって，他のアクセスできない問題の数々が解決されました．

解の系

証明の複雑さの理論では，数学の定理や，あるグラフが与えられた数の色に着色できないという主張，あるコードにエラーが含まれていないという主張など，さまざまな自然な主張の効果的な証明が可能かどうかを研究します．最も重要な証明系は，いわゆる解の系であり，それに基づくアルゴリズムが最も広く実用化されているからです．

解の系を研究する方法はかなり昔から知られていましたが，2001年にEli Ben-SassonとA. Wigdersonが研究するまでは，せいぜい私的なものでした．本研究では，このような証明を分析するための驚くほど簡単な一般的手法を，幅と呼ばれるもう一つの複雑さの尺度の関与に基づいて提案しました．この論文は，証拠の複雑性に関する理論のパラダイムとなり，多くの新しいアイデアやコンセプトを生み出しました．

イベルメクチンは，北里大学特別栄誉教授の大村智博士が１９７４年，静岡県・川奈のゴルフ場近くで発見した微生物が生み出す「アベルメクチン」をもとにした化合物（誘導体）で，アメリカの製薬会社のメルク社との共同研究で，もともとは家畜やペットの寄生虫，回虫などの治療薬として１９８１年に開発されました．イベルメクチンは，家畜の寄生虫や皮膚病，イヌのフィラリア症などの特効薬となり，動物抗生物質として２０年以上にわたって売上高世界トップを維持する記録的なヒット薬剤です．

人間のオンコセルカ症 （アフリカ・中南米・中東などの河川流域で蔓延していた河川盲目症）に効果があっただけではありません．その作用の範囲は驚くほど広いことが判明しました．線虫，ほとんどの昆虫，ダニに効果があります．そして，多くの寄生虫（またはそれらが運ぶ病気）は動物から人間に伝染するので，寄生虫のペットを取り除くことも重要な仕事です．そして，人々はオンコセルカ症や他のフィラリア症に苦しんでいるだけでなく ，1億人以上が桿虫症に感染しており，私たちが忘れていた疥癬とアタマジラミは世界のどこでも消えていません．イベルメクチンはこれらすべての病気に適応されます．イベルメクチンはノーベル賞を受賞した英雄的な薬です．

ーーー

■以下のサイトより引用します

イベルメクチンはコロナ治療に有効か無効か　世界的論争の決着に日本は率先して取り組め : NEWS特集 : 記事・論考 : 調査研究ＰＯＩＮＴ ■北里大学の大村智博士が発見した抗寄生虫病の特効薬イベルメクチンが、コロナウイルス感染症（ＣＯＶＩＤ−１９）にwww.yomiuri.co.jp
　河川に生息するブユ（ブヨ、ブト）がヒトを刺した際に，ミクロフィラリア（回旋糸状虫）という線虫をうつし，それが体内で繁殖して失明する人が多数出ていた．この治療に役立てようと，１９７５年に大村博士がメルク社のウィリアム・キャンベル博士と共同研究を進め，オンコセルカ症や脚のリンパ腺に線虫がはびこって太いむくみが出るリンパ系フィラリア症（象皮症）の特効薬としてイベルメクチン（薬剤名はメクチザン）を開発した．世界保健機関（ＷＨＯ）の研究者は「これまで出てきたどの熱帯病薬剤と比較しても，けた外れに優れた効果を持つ」とイベルメクチンを高く評価し，メルク社と北里大学に協力を求め，１９８７年から熱帯地方の住民に無償で配布することにした．何よりも年に１回，錠剤を水で飲むだけという簡単な服用法がＷＨＯの評価を高めたポイントだった．この特効薬が出てきたため，盲目になる人が続出していたオンコセルカ症は急速に減少し，コロンビア，メキシコなどでは，オンコセルカ症を撲滅したと宣言している．その後，ダニによる疥癬かいせん症や糞線虫症など重篤な風土病の予防・治療薬になることもわかり，イベルメクチンは世界中に広がった．臨床現場では，副作用がほとんど報告されないことも評価を一層高めた．大村・キャンベル両博士は，この業績を評価され，２０１５年にノーベル生理学・医学賞を受賞した．

■ＣＯＶＩＤ－１９の大流行で浮上したイベルメクチン
　イベルメクチンは今，新型コロナ（ＣＯＶＩＤ－１９）のパンデミック（世界的大流行）で再び世界中の注目を集めている．試験管レベルの研究で，新型コロナウイルスがヒトの細胞内で増殖する際に，ウイルスのたんぱく質の核内移行を妨害し，増殖を抑制することがわかったからだ．

　ＷＨＯは２０２０年３月１１日，ＣＯＶＩＤ－１９のパンデミックを宣言し，世界中に厳戒態勢を求めた．しかし，感染が拡大しても有効な治療薬がないことから，中南米・中東諸国を中心に，イベルメクチンをＣＯＶＩＤ－１９治療に投与する事例が広がった．

　最初に臨床試験の結果が発表されたのは，アメリカ・南フロリダの４病院での臨床試験だった．２０年６月に発表された試験結果によると，イベルメクチン投与患者１７３人の死亡率は１５.０％で，非投与群１０７例の２５.２％と比べて有意（ｐ＝０.０３）に優れているというものだった．

ーーー

■北里大学病院の治験

新型コロナウイルスに対するイベルメクチンの現状・世界的の状況と北里大学の取り組み

■以下は，セルゲイ・グラゴレフによる記事から抜粋

Герой и злодей • ЗадачиБезопасное для животных и людей лекарство от паразитов —elementy.ru

日本の科学者大村智が伊東・川奈で土壌を採取

土壌から 分離した放線菌Streptomyces avermitilisの二次代謝産物である 8つの成分を発見しました．45年間，森林は伐採されていません．
長い間，この種のバクテリアは他の場所では見つけることができなかったようです．これは生物多様性の保全を支持する大きな根拠です．ジャイアントパンダや ミンククジラだけでなく，土壌や植生がある場所ならどこでも重要です．

アベルミクチンは，マクロライド系抗生物質に関連する 16員の大環状ラクトンで，それらの品種の多くは，この放線菌と密接に関連する種の放線菌から得られ，次にそれらから多くの半合成誘導体が得られ，そのうちの約5つが駆虫薬として使用されました．

詳細は，Andy Crump（2017）のレビューを参照ください．
Ivermectin: enigmatic multifaceted ‘wonder’ drug continues to surprise and exceed expectations

https://www.nature.com/articles/ja201711.pdf

数学の未解決問題は無数にあります．
未解決の数学の問題のリスト（書ききれないので以下をご覧ください）

Открытые математические проблемы — Википедияru.wikipedia.org
このリストに挙がっているものだけでも，あまりにたくさんあるので驚くでしょう．
挑戦してみたくなるものもあるかもしれません．

実際に，数学上の未解決問題は，無数に存在します．そのうちから，ここには，リーマン予想のようにその証明結果が数学全域と関わりを持つような命題，P≠NP予想のようにその結論が現代科学，技術のあり方に甚大な影響を及ぼす可能性があるような命題，問いかけのシンプルさ故に数多くの数学者や数学愛好家達が証明を試みてきたような有名な命題を７つ列挙します：

以下の7つの問題はミレニアム懸賞問題と呼ばれ，クレイ数学研究所によってそれぞれ100万ドルの懸賞金が懸けられています．
P≠NP予想
ホッジ予想
ポアンカレ予想（解決済み）
リーマン予想
ヤン-ミルズ方程式と質量ギャップ問題
ナビエ–ストークス方程式の解の存在と滑らかさ
バーチ・スウィンナートン＝ダイアー予想（BSD予想とも）

真空ギャップを通り抜けるフォノンのトンネリング。左側に入射する音波は、表面に交流電場を生成し、右側の2番目の物体の原子の同期振動を生成します。Phys.Rev.Lett.105,125501より
https://elementy.ru/novosti_nauki/431440/Mozhet_li_zvuk_peredavatsya_cherez_vakuum?from=rxblock　
2010 年10月27日• イゴール･イワノフ

■固体媒体で見られる新しい現象、つまりフォノンが真空（空隙）を介して、右の固体から左の固体に「ジャンプ」することが説明されています。音波は薄い真空の隙間を乗り越え伝わり、熱は通常の熱放射が伝えるより何十億倍も効果的に真空を介して伝達できます。
[訳者注）真空中を熱が伝わる様式は放射（輻射）のみと思い込んでいました．魔法瓶は壁の中に真空層があるために，真空中は熱伝導がなく放射だけなので熱流の遮断ができます．熱放射は真空中を伝搬できますが，それ程高温でない物体からの熱放射は小さいものです．物質の熱は原子の振動ですので，原子の振動を伝えることができれば非常に高効率な伝達でしょう．この発見の面白さはここにあります．ここで引用されているphys.rev.letters（フィンランドのグループ）によると，近接場熱伝達は音響フォノンが真空中をトンネルする現象で，フォノンによって誘起されるエバネッセント波が固体間を結合するので離れた誘電体間で起こり，いわゆる電流加熱でもないようです．近接場放射熱伝達の測定法はよくわかりませんが，以下の論文（入手していません）が引用されています．A. Narayanaswamy, S. Shen, and G. Chen, Phys. Rev. B,78, 115303 (2008)］．

音波とは、物質の原子が平衡位置を基準にして同期的に振動することです。音が伝播するためには、これらの振動を支える物質媒体が必要です。真空中では、音はそこには存在できないので、伝搬することはできません。しかし、最近になって発見されたこの現象は、音の振動は、サブミクロンの厚さの真空隙間を突き抜けて、固体から固体へとジャンプすることです。この効果は「真空フォノン・トンネリング」と呼ばれ、Physical Review Letters誌の最新号に掲載された2つの論文で説明されました。結晶格子の振動は音だけでなく熱も運ぶため、真空中での熱伝導が異常に大きいことに注目が集まっています。

新しい効果は、結晶の音波と電界の間の相互作用によって起こります。１番目の結晶格子の振動は、結晶の端面に到達し、その表面近くに交互の電界を生成します。これらの場は真空ギャップを越えたもう一方の端面で「感じられ」、2番目の結晶の格子振動を起こします（図1を参照）。全体として、フォノン（結晶格子振動の「量子」）が1つの結晶から別の結晶にジャンプし、その中でさらに伝播するように見えますが、もちろん、２つの結晶間の真空空間にはフォノンは存在できません。

発見者は、効果を説明するために「トンネリング」という言葉を使用しました。この現象は、量子粒子がエネルギー的に禁止された領域を飛び越えるときのトンネリングをイメージしています。ただし、この新しい現象は古典物理学で完全に記述でき、量子力学の関与をまったくないことを強調しておく必要があります。これは、変圧器、誘導ホットプレート、ガジェットの非接触充電装置などで使用される電磁誘導の現象に少し関連しています。固体で起こるなんらかのプロセスで電磁界を生成し、電磁界は、非放射的に（電力の損失なく）真空ギャップを介して別の固体に伝達され、そこで応答を引き起こします。両者の違いは、電磁気学のインダクタンスでは電流（つまり電子の動き）が「働く」のに対し、真空フォノン･トンネルでは原子そのものが動くということです。

このような結晶振動と電界が効果的に結びつく具体的なメカニズムはいろいろあるでしょう。フィンランドの研究者による理論論文では、この目的のために圧電素子（水晶などの電場で変形し，かつ変形すると電荷を生じる物質）を使うことを提案しています。加えて：効果的に真空ギャップを突き抜けフォノンが伝わるには、 "対向 "フォノン、交流電場と "エスケープ "フォノンの間の共振同調が必要です。計算によると、物質の現実的なパラメータの下では、このような共鳴が実際に存在し、特定の入射角でフォノンが100%の確率でトンネリングさせられることが示されます。

図2. 走査型トンネル顕微鏡の針の先端にある最後の原子と基板との間の熱交換が異常に強い。原子は基板上に電荷を誘導し、原子の熱ジッタを追従して基板上にフォノンを発生させ、その過程で原子からエネルギーを奪う。 Phys.Rev.Lett.105，166101より

別の論文では、物理学者たちは、一見まったく技術的な問題を研究して、議論されているこの効果に行きつきました：走査型トンネル顕微鏡の針の最先端の熱は、冷たい基板（図2参照）に（触れることがない）運ばれるのか？繊細な実験方法を用いて、彼らは針の先端の文字通り最後の原子の温度を測定することができ、驚くべき事実を発見しました：この原子は、針ではなく、基板の温度でした！これは、基板と先端の最後の原子の非接触熱交換が（真空を通して！）先端の残りの部分の針よりもはるかに強力であったことを意味します。

このようなことから、通常の熱放射だけ考えても、かなり不十分であることが判明します。研究者らは、針から基板への熱伝達は、熱放射が作り出すことができるものよりも数十億（！）倍も効率的であると推定しました。このことは、詳細な測定結果と相まって、真空中のフォノンのトンネル現象がここでも起こっていることを示しています。

論文の著者は、この効果のメカニズムを次のように説明します。金属表面近傍に置かれた電荷は、金属に電荷を誘起します（静電気の問題では、仮想電荷イメージ）。初期電荷が、例えば熱振動によって揺れている場合、誘起された電荷もまた同じ周波数と振幅で揺れます（電子は原子よりもはるかに軽いという事実のため、原子のそれぞれの動きには "適応 "する時間がかかります）。その結果、基板の表面にある種の電子塊が現れ、「熱い」原子のように揺れる。この塊は、基板上の原子の振動を励起しエネルギーが費やされる。それは、電子塊から、したがって、電気力によって電子塊としっかり接続されているの元の原子の熱を奪う！　これが、針の残りの部分が暖かい場合でも、先端の最後の原子は、クールダウンされるメカニズムです。

どうやら、応用はいろいろありそうです。新しい効果は、特定の状況で以前に考えられていたよりもはるかに効率的なので、熱伝達の観点から興味深いものになります。この観察は、マイクロメカニカルデバイスの設計や、多結晶圧電体サンプルの熱伝導率の研究において非常に重要なものとなるでしょう。また、圧電部品と金属部品を組み合わせたマイクロデバイスでは、電子が活躍します。これは、真空を介して電子とフォノンの間で、ある物質から別の物質へのエネルギー移動を迅速に行う現象のすべては、まだ探求されていません。

■Источники:
1) Mika Prunnila, Johanna Meltaus. Acoustic Phonon Tunneling and Heat Transport due to Evanescent Electric Fields // Phys. Rev. Lett. 105, 125501 (14 September 2010); текст статьи находится в свободном доступе в архиве е-принтов под номером arXiv:1003.1408.
2) Igor Altfeder, Andrey A. Voevodin, Ajit K. Roy. Vacuum Phonon Tunneling // Phys. Rev. Lett. 105, 166101 (11 October 2010).

См. также:
Структура электромагнитных полей в веществе оказалась сложнее, чем считалось ранее // «Элементы», 29.11.2005.

Игорь Иванов

4. 時空の構造
これらの考え方は、時空の構造に深く根ざしています。2+1次元時空の境界の粒子論から始まり、3+1次元時空の重力論に至りました。時空の次元の一つがどこからともなく現れたのです。この次元は、2+1次元の粒子の相互作用から出現しました。

そして、これは時空が最も基本的な概念ではないということを意味しています。それは、より基本的な概念によって生成され、その法則は、研究対象から観察者の一定の距離の後にのみ有効になります。例え話をしてみましょう。湖面を観察したとします。波が見えたり、水面に浮いている虫が走っていたり。湖の表面は透明度が高く、非常に描写しやすいように見えます。確かに、波の伝搬や表面張力などを記述する方程式を書くこともできます。さて、水面の構造をもっと詳しく調べたいと思ったとします。顕微鏡で見ると、以前のように水面がはっきりと観察されていないことがわかります。そして、電子顕微鏡で見てみると、水の蒸発分子が絶えず表面から出てきて、その場所は空気中の水の分子が凝縮したものに取られていることがわかります。よくよく考えてみると、水の表面が十分に明確に定義されていないことがわかり、個々の分子のレベルで起こる現象をなんとか含めなければならないことがわかりました。同様に、時空は近距離では明確に定義された概念ではなくなります。 明確に定義された概念は、境界に存在する粒子であり、時空は集合的な特性としてのみ出現します。

もし我々が負の曲率を持つ時空の中だけに住んでいるとしたら、我々の宇宙で起こっているすべてのことを理解するためには、その中の粒子の振る舞いを記述する境界層の適切な理論を作くることで十分でしょう。

しかし、興味深いのは、すべての利用可能なデータから判断すると、巨視的なスケールでは、私たちの宇宙の時空は、残念ながら、正の曲率を持っています。現時点では、正の曲率を持つ時空の重力場を同様に記述できる可能性があるかどうかはわかっていません。このような記述が存在し、それを見つけることができれば、ビッグバンの特異点問題は解決するでしょう。

 https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/25571

Juan Maldacena,　
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

3. これらの謎を解く
3.1. ひも理論
量子力学と重力は、あまりうまくいっていない2つの理論です。物理学者たちは、この二つの理論を整合性のある理論にまとめようとしてきました。私たちが遭遇するほとんどの物理現象は、重力の影響を無視してもいいし、量子力学の影響を無視してもいいようなものなので、日常生活の実用上、量子重力の理論を開発することはあまり重要ではありません。一方で、ビッグバンの最初の瞬間に宇宙の起源を理解しようとするならば、一貫した理論が必要です。そもそも量子力学と重力の両方が重要なのです。これが、量子重力の理論を見つけるための大きな動機の一つです。

ひも理論は量子重力の理論です。量子力学と重力をまとめて管理している。それが正しい理論なのかどうかはわかりませんが、我々が持っている理論の中では最も有力な候補です。それは，「ひも理論」と呼ばれますが、そのわけはここでの議論で重要ではありません。重要なのは、それが量子重力の理論であるということです。

3.2. ひも理論におけるブラックホール
ひも理論では、ブラックホールを考えることができる。いくつかの特殊な状況下で、これらのブラックホールの微視的な記述を見つけることが可能です。技術的な理由から、一定の負の曲率を持つ時空の中に存在するブラックホールを理解する方が簡単です。このような時空は、平面空間の最も単純な一般化で、平らな空間は曲率がゼロ、正の曲率を持つ空間の例は球体の表面です。図１では，一定の負の曲率を持つ２次元空間の「地図」を見ることができます．また，ゼロ，正，負の曲率を持つ時空を考えることもできます．負の曲率を持つ時空は、実質的に無限大に境界を持っています。粒子は有限時間内に無限大に行き、有限時間内に戻ることができますが、これは時間の流れが異なる位置で異なるため、遠くに行くほど時間の流れが速くなります。

図１：このエッシャーの描画は、双曲空間の幾何学を捉えようとしたもので、双曲空間を円盤に投影したものです。元の双曲空間では、それぞれの図は同じ大きさなのですが、投影の歪みの影響で、円盤の境界に行くに従って小さく見えます。実際には，円盤の境界は内部のどの点からも無限の距離にあるのです．世界地図を平面上に表現する場合も同様の歪みがあります．標準的な投影［訳者注）メルカトール図法のこと］では，地図上では極点付近の領域が不釣り合いに大きく見える．ここの双曲空間の投影では，逆の効果があり、双曲空間の大きさは無限大なのに、境界付近の領域がどんどん縮小されて投影されるので、全体が円盤内に収まって見えます。

1997年に、私はこの空間における重力物理学の全体が、境界上の普通粒子の理論で記述できると推測しました。これは、ガブサーS. Gubser，クレバノフ I. Klebanov，ポリャコフA. Polyakov，ウィッテンE. Witten らによってさらに発展しました。詳細はやや複雑ですが：境界理論は、私たちが理解していなかった重力理論を、私たちが理解している普通の素粒子理論と同等のものにします。さらに重要なのは この境界理論が 量子力学の原理に従うことです。

内部のブラックホールは、境界にある粒子と比べて熱状態にあります。ブラックホールのエントロピーは、これらの粒子のエントロピーに過ぎません。時空幾何学の「素粒子」とは、境界に存在する粒子のことです。

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

2. ブラックホールと量子力学
次に驚いたのは、量子効果が研究されたときです。量子力学では、真空は単に粒子が存在しないだけではありません。真空は非常に興味深い状態で、常に粒子のペアが生成されたり破壊されたりしています。平らな空間では、エネルギーが保存されているので、粒子の純生産はありません。生成された粒子はすべて、非常に早く消滅しなければなりません。1974年にスティーブン・ホーキング博士は、地平線が存在すると、もはやそうではないことを示しました。地平線の近くに正のエネルギーを持つ粒子と負のエネルギーを持つ粒子ができてしまうのです。負のエネルギーを持つ粒子はブラックホールに落ち、正のエネルギーを持つ粒子は飛び去る。平面空間では、負のエネルギーの粒子を持つことができないので、このようなことはありえません。しかし、地平線の反対側では、遠くの観測者から見て負のエネルギーを持つ粒子が、地平線の内側の観測者から見て正のエネルギーを持つことができます。正味の効果は、ブラックホールが粒子を放出することです。放出された粒子は、ブラックホールの質量に反比例する温度を持つ熱分布を持っています。太陽質量のブラックホールでは、この温度はこの効果を測定するには小さすぎます。もしブラックホールが空の空間にあったら、ブラックホールはゆっくりと質量を失い、小さくなるでしょう。質量の小さいブラックホールの方が高温になる可能性があります。1018キログラム（山脈の質量）の質量を持つブラックホールは、1000度の温度を持ち、白く見える。1ミリワットの電球1個分の光を出すことになる。その質量がどんどん小さくなるにつれて、その温度は上昇し、おそらく完全に蒸発するまで、どんどん速く蒸発していきます。実際、数キログラムの質量をブラックホールに崩壊させた場合（実際にはとても難しいことですが）、1ミリ秒もしないうちに完全に蒸発し、核爆弾よりも多くのエネルギーを放出します。

ブラックホールのこの熱的性質は、2つの謎を生み出します：1) 何がエントロピーを生み出すのか？2) 情報パラドックス？
これらについて詳しく説明しましょう。

2.1. ブラックホールのエントロピー
通常の物理学では、熱的性質は常に構成要素の運動から生じます。例えば、空気の温度は、空気分子の平均速度に関係しています。これと密接に関連した概念として、"エントロピー "と呼ばれるものがあります。エントロピーは、すべての構成要素の運動に関連する無秩序の量です。エントロピーは熱力学の法則で温度と関係しているので、システムのミクロな詳細を知らなくても計算できる。ホーキングとベッケンシュタインは、ブラックホールのエントロピーは、地平線の面積をプランク長の2乗で割ったものと同じであることを示しました。巨視的なブラックホールにとって、これは巨大なエントロピーです。このエントロピーにブラックホールの寄与が含まれていても、熱力学の法則は有効であることがわかりました。ブラックホールの「構成要素」が何であるかが全く分かっていないため、非常に不可解な結果となっています。ブラックホールは時空の穴なので、その構成要素を見つけることは、時空幾何学の最も基本的な構成要素を見つけることと密接に関係しています。

ブラックホールのエントロピーは体積ではなく面積に比例するというのは非常に興味深いことです。1990年代初頭、トホーフトHooftとサスキンドSusskindは、量子力学と重力を含む理論では、系を記述するために必要な構成要素の数は、系を取り囲む表面の面積よりも大きくてはならないことを提唱しました。このことは、時空が普通の固体とはかなり異なることを意味しています。ほとんどの実用的な目的のためには、このエントロピーの束縛はそれほど厳密ではありませんが、時空のある領域は、その領域の境界に住む構成要素によって記述できることを示唆しているので、理論的には興味深い意味合いを持っています。

2.2. 情報のパラドックス
これまでブラックホールはいろいろな方法で作れることを述べてきましたが、結局はいつも同じブラックホールになってしまうようです。物理学では、通常、異なる初期状態から始めると、最終的には異なる状態になります。時々、その違いは非常に微妙なものですが、違いがあります。例を挙げてみましょう。2枚のお皿を用意して、片方にAの文字を書き、もう片方にBの文字を書きます。最初の概算では、最終的な結果は同じで、たくさんの破片が割れていることになる。しかし，破片を詳しく調べれば，どの文字が書かれているかが分かります．

そのうちの一つをブラックホールに放り込んだとしましょう。どうやら、ブラックホールはホーキング博士の放射線を放出して完全に蒸発してしまうらしい。ホーキング博士の計算では、この放射は完全に熱的で、ブラックホールの初期状態とは無関係のようだ。つまり、元々プレートの上にあった文字の情報を完全に復元することはできなさそうです。

これは非常に難解な学術的な問題のように思えます。私たちはいつも物事を忘れているので、そんなことは気にしていません！（笑）。なぜこの問題が非常に重要な問題なのかというと、量子力学では、このプロセスを支配する法則は、原理的に情報を復元できるようなものでなければならないと教えてくれているからです。だから、情報の問題を解決することが、量子重力の一貫した理論に必要なのです。そのような理論は、情報の謎を解決しなければなりません。

ホーキング博士を含む多くの著名な物理学者は、これは不可能だと考えていました。彼らは、ブラックホールが本当に情報を破壊していると考え、量子力学を捨てなければならないと考えていました。彼らは、量子力学と重力は根本的に相容れないものであり、正しい理論は情報が失われないことを暗示する量子力学の原理に従わないと考えていた。

この疑問を考えることで、弦理論や素粒子物理学の分野で興味深い進歩を遂げてきました。

ーーー続く

Juan Maldacena,
Institute for Advanced Study, School of Natural Sciences Princeton,
New Jersey 08540, USA

https://elementy.ru/nauchno-populyarnaya_biblioteka/25568/3_Solving_These_Puzzles

Black Holes and the Structure of Space-Time • БиблиотекаBlack holes are very puzzling objects that are predicted by gelementy.ru
Скачать видеозапись (avi): Часть 1 (160 Мб), Часть 2 (170 Мб), Часть 3 (195 Мб)

1. Black Holes
2. Black Holes and Quantum Mechanics
3. Solving These Puzzles
4. The Structure of Space-Time
5. Bibliography

1. ブラックホール
ブラックホールは、アインシュタインの一般相対性理論によって予測された最も魅力的な天体の一つです。ブラックホールには興味深い歴史があり、時空の性質の理解を深めるために多くの理論的な驚きの源となってきました。

まず、ニュートンの重力理論を考えてみましょう。ここ地球の表面では、重力の力を感じることができます。石を上に投げると、重力の力で石が下に戻ってきます。では、物を上に投げても下に落ちてこないようにすることはできるのでしょうか？はい、できます。秒速11km以上の速度で投げると、地球の重力場から離れてしまいます。この「脱出速度」は、地球の質量と半径に依存します。もし地球がもっと質量があり、同じ半径であれば、脱出速度はもっと高くなります。では、もし、光の速度よりも脱出速度が速いほど密度が高く、質量のある物体があったとしたらどうなるだろうか？そうすると、光が逃げられなくなり、それは黒く見えます。例えば、大きさが

より小さい星は黒く見えるでしょう。ここでG_{N}はニュートン定数、cは光速です。計算式に慣れていない方のために、いくつか例を挙げてみましょう。地球の質量の物体がブラックホールになるためには、その大きさが1cm以下でなければならない。太陽の質量を持つ物体は、1km以下の領域に集中していなければなりません。このことは1800年代にP.ラプラスによって指摘されましたが、誰も注目していませんでした。

1905年に特殊相対性理論が登場して、光の速度は他の普通の速度とは違うことがわかりました。それは宇宙の速度の限界であり、光より速く進ませることができるものはないのです。アインシュタインの相対性理論は、空間と時間が密接に結びついていることも教えてくれます。時間の流れは、お互いに相対的に移動している観測者によって異なります。あなたが通りのそばに立って車が通るのを見ているとしましょう。車に乗っている人の時間の流れは、あなたの時間の流れとは異なります。2 つの別々の街灯が同時に赤になるのを見たとしましょう。運転手にとっては、同時に赤になることはないでしょう。これはもちろん、光が両人の目に届くまでの時間を考慮に入れた上でのことです。両者とも光の速度で進んでいる光を見ていますが、時間の流れ方は異なります。時間は相対的なものであり、光の速度は絶対的なものである。私たちは通常、光の速度よりもはるかに小さい速度で移動し、私たちは非常に正確に時間を追跡していないので、これは私たちにとって非常に小さな効果であるため、これは逆に直感的に思えます。これは、粒子加速器では常に見られる効果です。粒子は光速に近い速度で移動しているときには、はるかに長く生きています。

空間と時間は、一つの概念である時空にまとめられています。時間は、お互いに相対的に移動している二人の観測者によって異なる知覚をします。どちらの観測者も同じ時空を見ています。この二つの観測者の観測を関連付けるための正確な公式があります。

重力の話に戻りましょう。重力には、ガリレオによって発見された非常に特殊な特徴があり、真空中では、羽と石が一緒に落ちる。これは他の力では起こりません。電場の中の粒子は、その質量や電荷が変われば、異なる動きをする。ニュートンの重力理論では、すべての粒子が同じように落ちるのは、重力の力が質量に比例するからです。これを "等価原理 "と呼ぶこともあります。

アインシュタインは、ニュートンの理論では重力が瞬間的に伝播するので、ニュートンの理論は特殊相対性理論と両立しないことに気づきました。1915年、アインシュタインはこの問題を、等価性の原理も自然に取り入れた方法で解決しました。彼はこの理論を一般相対性理論と名付けた。彼は、重力は時空の湾曲に起因することを提案しました。湾曲した時空の中の粒子は最短の線に従う。湾曲した空間上で最初は平行な線は、後になってお互いに向かって移動するかもしれない。例えば、地球の赤道にある2本の子午線は、最初は赤道で平行だったが、北極で交差する。時空の形は、その上を移動する物質に依存しています。一般相対性理論は、時間の流れが重力場に依存していることを暗示しています。したがって、同じ建物の最上階と最下階に住んでいる二人の人は、時間の流れが違って見えることになります。下の階に住んでいる人の方が時間の流れが遅くなります。これは、この地球上の建物にとっては非常に小さな効果であり、1/1015の効果です。私たちが学んだことは、巨大な物体が空間と時間をゆがめるということです。特に、これは巨大な物体の近くの時間は、遠くの時間よりもゆっくりと流れることを意味します。

物理学者は常に最初に最も単純な状況を研究しようとします。そこで、一般相対性理論が発明されて間もない1916年、カール・シュワルツシルトという若いドイツ人が、アインシュタインの方程式の最も単純な球対称解を発見しました。これらの方程式は、点状の質量によって生成される幾何学であると考えられていた特定の幾何学を記述しています。その幾何学が何であるかを語るのではなく、その特徴の一つである静止した時計がチックする速度に焦点を当ててみよう。太陽の表面にある時計は、遠くにある時計よりも100万分の1の速度で動いています。中性子星の表面にある時計は、遠くにある時計の70%の速度で動いています。この場合、大きな効果があることがわかります。シュワルツシルトが発見した解は、「中心」にある時計が完全に止まってしまうことを示しています。当初、ほとんどの物理学者は、これは物理的ではない結果であり、過度に単純化された解析の産物だと考えていました。

さらに研究を進めると、シュワルツシルトの解の「中心」は、実際には完全に滑らかな表面であることがわかりました。時空を旅している観察者は、この領域を何の違和感も奇妙さも感じずに通過することができます。ブラックホールの外にいる人は、落下してくる観測者からの信号が、すべての実用的な目的のために、最終的には消滅するまで減速することを見ています。静止した時計がゼロに減速する表面は "地平線 "と呼ばれ、この地平線は戻りがない点を示し、この表面を横切った観測者は、再び出てくることができず、内部の「特異点」に押しつぶされてしまいます。特異点とは、非常に高い時空の曲率の領域で、彼は引き裂かれてしまいます。アインシュタインの理論におけるブラックホールの大きさは、今でもニュートンの理論でラプラスが計算した式で与えられていることが判明しましたが、物理的な解釈は大きく異なっています。

ブラックホールは、太陽の数倍の質量を持つ星が核燃料を使い果たし、その重力の下で爆発することで、天体物理学的な過程で形成されることがあります。宇宙にはブラックホールが存在することを示す多くの観測的証拠があります。これらの天体物理学的ブラックホールには、大きく分けて2つのタイプがあります。太陽の数倍の質量を持つものと、恒星が崩壊してできたものです。ブラックホールは黒いので、なかなか見ることができません。運よくブラックホールの中にガスが落ちてくることがあります。ガスが落下すると、このガスは熱を帯びて独特の放射線を発しそれを検出します。このガスは、ブラックホールを周回している別の星から来ることもあります。つまり、お互いに公転している2つの星があって、一方の星が崩壊してブラックホールになったとすると、もう一方の星からガスが出てきます。そして、もう一方の星からのガスがブラックホールに落ち始めます。また、銀河の中心には、もっと質量の大きなブラックホールがあります。これらは10億個の太陽の質量を持っています。これらのブラックホールに物質が落下すると、熱を帯びて放射線を発し、それが最終的には地球上の私たちによって検出されます。私たちのような大きな銀河はすべて、中心にブラックホールがあると考えられています。

この講演の焦点は、天体物理学的なブラックホールの説明ではなく、ブラックホールが時空の構造に与える影響を探ることにあります。

アインシュタインの理論によれば、ブラックホールは時空の穴であり、一度落ちたら二度と戻れない。ブラックホールに投げ込まれたものは永遠に失われる。ブラックホールは非常に興味深い普遍的な性質を持っています。星がブラックホールに崩壊したとき、その最終的な形は質量と角運動量の2つのパラメータだけに依存します。つまり、ブラックホールは普遍的なものであり、ブラックホールを形成した物質の特異な詳細な性質に依存しないのです。最初の星の化学組成に関係なく、常に同じブラックホールを得ることができます。つまり、ブラックホールは重力の理論だけに依存しており、他の力の詳細な性質には依存しないのです。

ブラックホールのもう一つの特異な特徴は次のようなことです：ブラックホールが関与しているプロセスがあるとします。例えば、2つのブラックホールの衝突を考えてみましょう。ブラックホールが衝突して、より大きなブラックホールを形成する。ちなみに、この過程では重力波を出すことができ、それを測定しようとしている検出器があります。この過程を計算するのはかなり難しく、複雑な方程式を解かなければなりません。それでも、いくつかの簡単な結果があります。最終的なブラックホールの面積は、最初のブラックホールの面積の合計よりも常に大きい。面積は常に大きくなる。これは「面積定理」と呼ばれ、1970年にホーキング博士によって証明された。

https://elementy.ru/nauchno-populyarnaya_biblioteka/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

漠然とした質問の性質
AS：私の友人は、基礎物理学の現在の状態を、コペルニクス理論が出現する前の時代と比較できるかどうか尋ねています。惑星の動きを予測することを可能にしたプトレマイオスシステム[訳者注)天動説]がすでにありましたが、その背後にある現象の物理学の理解はありませんでした。今は、方程式の背後にある物理的な意味が現れるのを待っていると言えますか？

DG：もちろん、私たちは何かを待っています。おそらくホーキングは私たちが何を待っているのかを正確に教えてくれるでしょう。しかし、ご存知のように、歴史が正確に繰り返されることは決してありません。私たちは未来が何であるかわからないので、私たちの時間を過去にあったものと比較することは非常に困難です。

AS：あなたが今構築している新しい基本理論には多くの希望があります。それは万物の一種の究極の理論になるはずです。しかし、新しいコンセプトが最終的なものになると考える理由は何ですか？今、重力の性質とは何かを尋ねているのなら、なぜ疑問が生じないのでしょうか、弦の性質は何ですか？等...

DG：自然！あなたがそれらを形成するとき、質問は非常に曖昧です。「自然とは何か」という質問は曖昧すぎて、ほとんど哲学的です。たとえば、私たちの多くは、微細構造定数［訳者注）微細構造定数とは、水素原子のスペクトル線の分裂を説明するときにアーノルド・ゾンマーフェルトにより導入された］が1/137である理由を理解したいと思っていますか？これは適切な質問です。しかし、そのような明確な質問への回答を受け取ったとしても、漠然とした質問のいくつかはより正確な定式化を見つけ、より正確な回答を必要とするため、私たちはまだ満足できません。答えを求めているすべての質問に答えることができたとしても、新しい質問が生まれます。これが科学の歴史です。そして、これは無期限に続きます。しかし、おそらくいつか私たちは、非常に満足のいく答えを見つけて、やめるでしょう。私はこの問題にとらわれません。おそらく、決定的な理論、「万物の理論」があります。しかし、そうでないかもしれない。だれも知りません。

自分自身を計算する世界
SP：数学は自然を表現するための言語であり、普遍的でなければならないとおっしゃいました。物理学で使用される分析法の言語を数値法に置き換えるという最近発表された提案についてどう思いますか？結局のところ、方程式を書く能力を奪われているので、これの背後にはまったく異なる哲学があります。

AS：はい、一部のプログラマーは、私たちの世界が計算可能かどうかに常に関心を持っていますか？

DG：コンピューター...現代のコンピューターの数値計算能力は驚くべきものだと思います。そしてもちろん、それらは理論物理学者が今日働く方法に強い影響を与えました。多くの人はもはや微分方程式を解こうとはせず、単に数値的にシミュレートします。そのため、一部のコンピューター科学者は、この傾向を限界まで押し上げています。

SP：スティーブン・ウルフラム、例えば？

DG：その通りです。Wolframは実際には計算の専門家であり、物理学者ではありません。彼は私の友人であり、私たちが会ったとき、私は彼に非常に強い議論をしました。彼は落胆したと思います。

SP：あなたの間で公開討論をするのは素晴らしいことです...

DG：私たちもそう思いますし、実際に議論するつもりですが、それはまだうまくいきません。

AS：私のコンピューターの友達はよく尋ねます：量子論はある意味で世界の基本的な離散性と同等であると言えますか？連続体の古典的なアイデアは現実の世界に関連していますか？

DG：いいえ、量子力学は離散理論ではありません。多くの人が無限大を非常に複雑な概念だと考えています。19世紀以来、世界のすべてのものが離散的で、有限で、計算可能であるべきであることを示す試みがなされてきました。ただし、無限大は非常に強力な概念です。そして、私は本当にそれをあきらめたくありません。

実際、計算手法は現在、幼児期に開発されています。20〜30年前のデバイスの機能と比べると、今できることは驚くべきことのように思えますが、将来の機能と比べると何もありません。コンピュータはまだそれほど賢くはありません。

そして、ウォルフラムについて話す文脈で特に興味深いもう1つのことは、完全に古典的なままである思考の性質です。私たちが計算アルゴリズムについて話すときに使用または考えるすべてのコンピューターは古典的です。しかし、過去10年間で、量子力学を使用することにより、計算、さらには実際のコンピューターの構築にも信じられないほどの可能性があることに気づきました。この方向にはすでに目覚ましい進歩があります。私の研究所は現在、量子コンピューターとコンピューティングのための量子力学システムの使用に関するプログラムを実装しています。また、場合によっては、従来のコンピューターよりも指数関数的に優れたパワーを得ることができることがすでに証明されています。

したがって、ある意味で、世界が独自の状態を計算していることは完全に真実です。これだけが量子力学の制御下で起こります。これは量子コンピューターであり、古典的なコンピューターではありません。そして、あなたのコンピュータの友達のほとんどは、量子力学について何も知りません。したがって、彼らはこれらすべてを50年前の観点から議論しており、強力なコンピューターは複雑な問題を解決できると言っています。そろばんの前に座って、現代のプログラミングの利点について話すようなものです。非常に原始的です。

弦理論には真の競合はありません
SP：弦理論と競合する理論について何が言えますか？

DG：実際、弦理論には本当の競合はいない。これが、非常に多くの人々が弦理論に取り組んでいる理由です。強い競争相手がいたら、他のことに取り組んでいる人もいるでしょう。重力のループ理論には何かがありますが、量子重力の理解など、限られた問題の枠組みの中でさえ、あまり成功していないように思えます。そらは古典的な重力を再現することさえできません。

SP：単一の理論の開発にそれほど多くの労力を費やすのはリスクが高すぎませんか？

DG：弦理論は、実際には特定の理論というよりもパラダイムだと思います。さらに、弦理論と場の量子論の間には非常に密接な関係があります。実際、この2つを区別することはさらに困難です。場の量子論は、強い相互作用、弱い相互作用、つまりすべての自然の力を説明するために使用されるツールです。したがって、弦理論には、このような幅広い問題に対処するための強力な競争相手はありません。そして、ある意味で、弦理論は代替手段ではないので破壊することはできませんが、逆に、ご存知のように、一般に受け入れられている物理学の理論的基礎として機能する場の量子論と密接に関連しています。

来たるべき物理学の革命について話すとき、私は弦理論を完全理論とは考えていません。私たちはまだそれが何であるかを理解しようとしています。そして、私たちはすでにそれに成功しているとは思いません。しかし、私が言ったように、私は革命が進行中であると信じています。そうは言っても、弦理論は根本的に新しいものではなく、実際には古い物理学と密接に関連しています。そして実際、私たちはすでに、核力をよりよく理解するために、すべての基本理論であると主張する、いわゆる弦理論の主要なセクションの1つを使用しています。したがって、弦理論は私たちの観察に関連しているため、反駁することはできません。

SP：では、理論的基礎だけでなく、弦理論の研究には直接的な観察の動機がありますか？

DG：それは理論的なつながりの問題です。弦理論はあなたがしなければならない多くのことに非常に役立ちます。あなたはそれを宇宙論の分野の研究に適用することを試みることができます、あなたはそうすることができます-核物理学をよりよく理解することを試みること。数学やゲージ理論へのリンクを調べることができます。若い研究者ができることはたくさんあります。

基本的な物理学における人々の仕事の方向性を決定するものについて話す場合、これらはまだほとんどない重要な実験結果（それらが現れることを願っています、少し待ってみましょう）、またはエキサイティングな領域のいずれかです。弦理論には強力な競合概念はありませんが、人々が取り組むことができる良い問題を提供します。本当にそうです。

量子対相対性理論
AC：「時間の簡単な歴史」、スティーブン・ホーキング（スティーブン・ホーキング）、ロジャー・ペンローズ（ロジャー・ペンローズの ）による「皇帝の新しい心」、「エレガントな宇宙」グリーン・ブライアン（ブライアン・グリーン）などのノンフィクションの本から-その弦理論は一般相対性理論と量子論の間の矛盾を解決する試みであると結論付けることができます。この印象は正しいですか？

DG：非常に異なる本...実際、これは弦理論が有用であることが証明された問題の1つにすぎませんが、それを解決することは当初の目標ではありませんでした。弦理論は核相互作用の理論として始まりましたが、それは（カントの力学と相対性理論の間の矛盾を取り除いたこと- AS）は弦理論の最も重要な成功の1つです。そして、矛盾を含まない量子力学的相対論的不変式論であるという事実により、それが成功を収めたことは間違いありません。弦理論のブラックホールは、量子力学の原理に違反するクレイジーなオブジェクトではありませんが、通常のオブジェクトは弦理論にとって大きな成功を収めています。ホーキングのような男でさえそれを認めなければなりませんでした。ホーキングは何年もの間私に説得されましたが、彼は同意しませんでした。彼は一般相対性理論の量子力学が深刻な問題に直面していることを固く確信しており、私たちは量子力学を変えなければならないでしょう...

AS：そしてペンローズは一般相対性理論を変えたいと思っています...

DG：ペンローズは数学者で物理学者ではありません。真面目に受け止めてはいけません。ホーキング博士は自分が間違っていたと認めた 弦理論のおかげで、量子力学を変える必要がないことがわかってきました。これは弦理論にとって大きな成功です。そして、その理由の1つ、理論的動機の1つ（実験的証拠ではなく理論的動機！）は、まだ正確な予測を行うことができないにもかかわらず、人々を弦理論の軌道にとどめるものであり、概念を解決できるという事実です。パラドックス。これは物理学の発展にとって非常に重要です。量子力学もパラドックスを背景に発生しました。一方では古典物理学であり、他方ではボーアの原子モデルには互換性がありませんでした。これは理論的な問題であり、量子力学によって解決することができました。

そして、私たちはこれから何を得るでしょうか？
AS：あなたが話している基本的な物理学の新しい革命は、原子力や半導体の発見のようなものに、私たちの世界を変える何かに、いくつかの重要な社会的変化をもたらすでしょうか？

DG：誰が知っているのか...わかりません。実際、基本的な科学的知識の開発よりも、テクノロジーやアプリケーションを予測することははるかに難しいと思います。テクノロジーを予測し、科学を知っていても科学がどのように使用されるかを予測することは非常に難しいビジネスであり、関係する要因が多すぎます。

AS：しかし、そのような変化の可能性を期待していますか？

DG：実際、私たちがすでに理解し、実験でテストし、確認を受けたものについて質問するのもよいでしょう。たとえば、素粒子の標準模型や核相互作用の理解についてです。それらのアプリケーションはどうですか？たとえば、量子色力学の応用について何度も聞かれました。記者は常にこの質問に悩まされています：「これの用途は何ですか？」そして、私は何も考えることができません。

しかし、歴史は、あなたが何も考えられないときでさえ...同じ量子力学を取りなさい-量子力学の用途は何ですか？ハイゼンベルグに量子力学の使用法を尋ねた場合、彼がトランジスタやレーザーについて教えてくれるとは思えません。しかし、それらは現れました。アプリケーションを予測することは非常に困難です。20世紀に私たちが達成した基本的な相互作用の信じられないほどのレベルの理解でさえ、まだ何かにとって有用か有害かわかりません。新しい武器、新しい薬、または新しい道具は作られませんでした。しかし、誰が知っているでしょうか？技術を予測することは非常に困難です。誰もトランジスタを予測しませんでした。IBMが1950年代にコンピューターについて考えたとき、彼らはコンピューターを、ラップトップの処理能力を備えたこのホテルのサイズの建物と考えていました。

応用科学としてのビッグバン
SP：あなたの講義には、理論物理学全般、特に弦理論が「好奇心からだけでなく、私たちの世界の起源を理解しているかどうかを知りたいから」発展しているという声明があります。個人的には、研究の主な動機は好奇心ですが、世界の起源の問題は実用的だと思いますか？

DG：もちろん、主な動機は好奇心です。これが基礎科学を前進させるものです。しかし、好奇心を通じて得られた質問への回答が、ある意味で有用である場合、科学者は誰でも大きな道徳的満足を得ることができます。それで、私は物理学の基本法則の新しい知識を他の科学分野に適用することについて話しました。

最も注目に値するアプリケーションの1つは宇宙論です。そのため、弦理論家は宇宙論者や天体物理学者と多くのことを話します。宇宙論者たちは現在、ビッグバンとビッグバン自体の後の宇宙の発達の初期段階を理解しようとしています。そして、この分野では、私たちの関心のある領域が重なっています。したがって、弦理論で私たちが尋ねる質問を理解せずに、包括的な宇宙論や宇宙の歴史を構築することはできません。

しかし、弦理論の他のアプリケーションもあります。これは弦の物理学者をとても幸せにします。特に、私たちが新しい数学を発見しているという事実。または、核の相互作用について異なる考え方をする能力。これにより、計算を改善できます。これはすべて非常に満足のいくものです。この理論は科学の発展に不可欠なステップであり、量子力学と同じように多くの用途があります。

何を読むか
AS：そして最後の質問です。弦理論の一般的な説明を探している人にどのようなアドバイスをすることができますか？あなたの講義では、「二重性」、「量子測定」、「ゲージ理論」など、かなり複雑な用語を使用しています。多くの人にとって、これは完全に理解できないように聞こえます。一般の人に何をすすめますか？

DG：あまりありません。ブライアングリーンの本があります...

SP：エレガントな宇宙のことですか？

DG：はい、そして2冊目の本はすでに書かれています- 「宇宙の構造：空間、時間、そして現実の質感」。リサ・ランドールによって書かれた、余分な次元についての良い新しい本があります- 「ワープする宇宙―宇宙の隠された次元の謎を解き明かす」。私自身、このような公開講座をもとに小さな本を書くつもりです。しかし、あなたが知っている、良い人気のある科学の本を書くことは非常に難しいです。そして、Barton Zwiebachによって書かれた、弦理論の学生のための良い教科書があります。これは、場の量子論をまだ研究していない物理学の学生向けに設計されたこの種の最初の教科書です。そして、これはとても良い本です。

［訳者注↓］

https://elementy.ru/nauchno-populyarnaya_biblioteka/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

思考プロセスはどのように進んでいますか？
AS：弦理論（ひも理論）では、弦のアイデア自体が現実の良いモデルですか、それとも単なるイラストですか？
DG：弦理論の観点から現実を説明することは、粒子の観点から場の量子論を説明することに似ています。量子色力学（核力の理論）では、クォーク、グルーオン、およびそれらの間の距離に関して便利な説明があります。しかし、これはおおよその説明にすぎません。場の量子論の観点から、量子色力学のより良い説明があります。弦理論では、実際には最初の記述だけがあり、2番目のより正確な記述はありません。特定の側面なら弦理論の多くの説明がありますが、多かれ少なかれ完全な説明は、ある時空で動く弦に関するものだけです。弦理論では、場の量子論の経路積分に相当するものはまだありません。これ以上の基本的な定式化がなく、これは弦理論におけるテーマの1つです。

SP：しかし、ひもとしてのこの説明は、実際の物理的な直感に役立ちますか？

DG：はい、もちろんです。

AS：個人的に仕事をしていく上でより頼りにするのは、物理的直観と数学的直観のどちらでしょうか？

DG：それらを区別するのはかなり難しいです。数学は言語であり、非常に発達した言語です。私たちが考えるとき、私たちは視覚的なイメージで操作します。しかし、私たちは思考を言語で整理し、数学は非常に高度な言語形式です。したがって、理論物理学者は数学的に考える傾向があります。しかし、もちろん、思考のプロセスがどのように進行するかを正確に説明することはできません。私はそれをしようとさえも思いませんし、多くは無意識のうちに起こります。

数学の現実は宇宙人が証明する
SP: 数学は言語だとおっしゃいましたね。自然を言語で記述する際に、私たちはこの記述を発明したのでしょうか、それとも自然現象の根底にあるのは数学的法則なのでしょうか？例えば、ガリレオにとっては、そのような疑問はありませんでした - 彼は、自然の本は数学の言語で書かれており、誰が書いたかは非常に明白だと述べました。

DG：私たちが自然や数学を発明していると言うのは間違っています。それどころか、私たちは自然によって発明されました。同時に、私たちは自発的に現れなかったと思います。いいえ、私たちは私たちが神によって創造されたとは信じていません。私たちは自然の一部として進化してきました。ですから、自然環境の中で生き残るために進化してきた私たちの心が、自然を十分に理解するために必要な能力を発達させてきたのは当然のことです。違った結果になったとしたら不思議です。したがって、ほとんどの数学者はある程度物理学者であると思います。物理学者は現実の世界を説明し、自然界に存在するものを発見します。そして数学者は一般的に同じことをします。学者アーノルドがこれについてどう思っているかを尋ねる人もいるかもしれませんが、ほとんどの数学者は自分たちが物を発明するのではなく、発見すると信じていると思います。

プリンストン大学の同僚で有名な物理学者ユージン・ウィグナーは、「自然科学における数学の不可解な効率性」を好んで話していました。私は彼に同意していないし、理解できないことは何も見ていない。数学は、自然を理解し、その中で最適な生存を実現するためのツールとして、私たちが創造した（あるいは自然進化によって進化した）言語から成長してきました。だから私は、数学は本質的に自然の一部であり、それを発見していると考えています。数学が自然を記述するのが得意だという主張は、ほとんど同語反復に近い。

ちなみに、これは実験的に検証することができます。私はこれについて数学者と話し合いました-私に同意する人もいれば、同意しない人もいます。このように確認できます。いつの日か、銀河の反対側にある別の文明とのつながりを確立するとしましょう。世界は1つしかないので、私たちとほぼ同じ物理学を持つことに誰もが同意します。（そして、彼らが私たちよりも弦理論をよりよく理解することを願っています。）しかし、私たち自身に問いかけましょう：彼らは同じ数学を持っているでしょうか？一部の数学者はノーと言います、彼らは完全に異なる数学を発明することができます。しかし、私はそうは思いません。彼らの数学は私たちの数学と非常に似ていると思います。実はその歴史も彼らの数学の発達は私たちとほぼ同型であるでしょう。もちろん、わずかな外部の違いも可能です。しかし、何世紀にもわたる規模を見ると、彼らの数学は同様の道に沿って発展するでしょう。いつかこの仮説を検証できることを願っています。

人類原理の認識論的悲観論
SP：これはかなり楽観的な見方です。人類の将来がどうなるかはまだ分からないからです。

DG：そうですね、それでも勝ちます。私たちの手法が課題に適さないという指摘はありません。それらは完璧に機能していて、私たちはすでに驚くべき結果を得ています。では、なぜ悲観的になるのか？ロシアでは悲観論者になるのが流行なのは知っています。また、科学者の間だけではありません。ビジネスパーソンの間でも見たことがあります。

SP: 講演の中で、人類学的な原理に非常に批判的なご意見がありましたが、どのようにお考えでしょうか？しかし、あなたが今言ったことは、同じではないにしても、少なくとも人類学的原理の精神で推論することと非常に似ています。

DG：いや、そうでもないですね。もちろん、人類学的原理には一定の論理があります。私たちはここに座っているので、私たちは生きているので、私たちの世界は私たちの存在に必要な一定の性質を持っていることを意味します。しかし、私の直感がこれを教えてくれます。歴史がこれを教えてくれます。私たちの存在のために特別に作られたように見えるものは、最終的には自然な説明を得ることができるでしょう。

たとえば、氷は水よりも軽く、その表面に浮かんでいるという事実を考えてみましょう。それは私たちにとって非常に重要です。氷が浮かなければ、夏には海が溶けず、生命が発達しません。これは人間原理によるものと言えます。水は確かに非常に珍しい液体ですが、今日、私たちは化学のおかげでその特性を理解しています。実際には、原子物理学、化学、生化学、生物学、そして最後に、生命とそれに基づく私たちの心さえも、ご存知のように、量子力学、電磁気学によって記述されています。これは信じられないほど強力な理論の例であり、原則として-もちろん実際にはありませんが、原則として-電気的相互作用の力を除いて、任意の仮定と自由パラメーターは含まれていません。非常に簡単な理論と1つの数字で、水、有機物、生命のすべての性質を計算することができます... まさに反人類主義の勝利です。

100年前は、科学で生命を説明することはできないと多くの人が考えていました。今は基本的なレベルで生命を理解していると考えれば、十分な理論を持っています。もちろん、原子から始まって、脳を構築して理解することはできません。そしてもちろん、すべての仕組みを理解するために必要な方法を開発するには、長い時間が必要になります。しかし、その理解は最終的には恣意的な要素を持たない理論の上に成り立つ。私の考えでは、人々はしばしば、非常に難しい質問に答えることができないために、自分たちの力への不信感から、議論を求めて人類学的原理に目を向けることがあります。しかし、歴史を見れば、解けないと思われる質問でも、最終的には答えが出てくることがわかります。

もちろん、それらはいくつかの点で正しが-いくつかの質問には答えることができません。宇宙の発展には多くの事故があり、科学がそれらを説明しようとして失敗することがあります。たとえば、ケプラーは、太陽系の惑星軌道の半径を計算できると信じていました。彼は正多面体の美しいシステムを構築し、そこから半径のセットを取得しました。そして、それらは太陽系の軌道のサイズに似ていましたが、軌道半径を予測することは、1年後-2007年5月13日の午前11時のモスクワの天気を予測するようなもので、これは計算できるものではなく、計算しても面白くありません。

もちろん、基本量として物理法則に含まれている私たちの世界のパラメータは、同じランダムな性質を持っていることが判明するかもしれません。これは、人類原理に従う人々が言うことです。この可能性は捨てることができません。人々は無力感からこれらの考えにたどり着くのではないかと思います。そうすれば、歴史は彼らが間違っていたことを示すでしょう。しかし、それらが間違っていることを証明する唯一の方法は、過去に起こったように、予測力を備えた実用的な理論を提供することです。したがって、たとえば、物理学が生命を説明できる科学を証明する唯一の方法は、DNAの構造の発見、量子力学、原子物理学、生化学などの理解でした。

SP：それで、あなたは辛抱強くなるようにアドバイスしますか？

DG：一生懸命働くことをお勧めします。

空間の次元は実験的な課題です

AS：主に実験材料を扱う多くの物理学者や天文学者は、これらの多次元理論は物理的現実からかけ離れていると信じており、現実世界の科学というよりは数理ゲームです。

DG：たぶんそうです。科学は興味深いものです。なぜなら、予測力のある発見をするまで、誰も答えを知らないからです。だからそれは実験の問題です-時空は多次元です。多くのモデル、特に弦理論では、これが当てはまると想定しています。これらはおそらく非常に小さい寸法であり、見るのが難しいと考えられています。ただし、これらが十分に大きく、観察にアクセスできる可能性があることを除外していません。これは純粋に科学的な質問です。

今日、天文学者や天体物理学者は、アインシュタインによって開発された非常識な数学的理論をほとんど認識しています。そしてそれを認識すれば、時空は動的な物体であり、次元の数の問題は科学的な問題であることが理解できます。これらの寸法の一部は非常に小さく、検出が難しい場合がありますが、正直な方法はそれらの存在を確認することだけです。

正しい科学的アプローチは次のとおりです。物事をより深く理解することがあなたに新しい質問を提起し、新しい可能性を開く場合（たとえば、一般相対性理論のように）、これらの新しい質問と可能性を探求する必要があります。弦理論の場合、追加の次元が必要な理由はおおいにあり得ます。しかし、これは未解決の科学的問題です。現在、それらの存在の確固たる証拠はありません。しかし、これは常に当てはまります。新しいアイデアに対処するのは簡単ではありません。

大型ハドロン衝突型加速器が優れている理由
JV：あなたの講義で、CERN大型ハドロン衝突型加速器（大型ハドロン衝突型加速器、LHC）の建設現場-弦理論の検証のための最も有望な装置であると述べました。ただし、そのエネルギーは、アメリカのテバトロンなどの既存の加速器のエネルギーよりも1桁高いだけです。大統一のエネルギーが少なくとも10桁高いのに、なぜ1桁のステップだけが根本的に新しいデータを取得するのに役立つと思いますか？

DG：この加速器は、標準モデルの予測を完全にカバーするために必要なエネルギーのスケールへの脱出を初めて可能にするので、非常に重要です。

もう一つの重要な理由は、新しい物理学、新しい基礎物理学に関連した効果がこのエネルギースケールで現れ始めることを示す、非常に説得力のある実験結果が多数存在することです。このようなエネルギーでは、弦理論の重要な要素である量子（超対称）時空の新しい次元が発見されると期待されている理由を説明します。新しい対称性、新しい量子時空次元が、LHCで達成可能なテラ電子ボルトのエネルギーで最初に発見される可能性を支持する3つの独立した議論があります。

これらの議論の1つは、相互作用の組み合わせに由来します。力の統一の簡単なスキームは、超対称性の存在を必要とします。これは、LHCで利用可能なエネルギーのオーダーのエネルギーで顕著になりますが、これを確実に予測することはできません。

2番目の議論は、重力が強いスケールとそれが非常に弱い核スケールとの間の巨大な格差を理解しようとすることと関係があります。繰り返しになりますが、超対称性は、このスケールの大きな違いを自然で美しい説明にしています。

最後に、宇宙物理学から学んだことは、宇宙に存在する物質のほとんどは、目には見えないが重力を感じる暗黒物質という未知のタイプに属しているということです。暗黒物質が構成するかもしれない粒子をたくさん発明することができますが、標準モデルの超対称版では、暗黒物質の候補となる粒子が自動的に存在することが保証されています。これらの粒子がLHCで観測可能な質量を持っていれば、宇宙の物質の9割が何からできているのかがすぐにわかります。

これらは3つの非常に強力な議論です。超対称性の兆候がどこでどのように観察されるかについての証拠や正確な予測はありませんが、定性的なレベルでは、超対称性の発見を支持する非常に説得力のある議論があります。だから私は50：50で誰とでもこれに賭ける準備ができています。そして超対称性が発見されなければ私はたくさんのお金を払わなければなりません！

---続く---

https://elementy.ru/nauchno-populyarnaya_biblioteka/izbrannoe/430285/Devid_Gross_Derzhu_pari_chto_supersimmetriya_budet_otkryta

2004年5月のノーベル物理学賞を受賞したDavidGrossがモスクワを訪れました。彼は、弦理論と理論物理学の今後の革命について公開講演を行うために、王朝財団と国際基礎物理学センターの招待を受けて来ました。講義の前に、DavidGrossはElementsWebサイトからの質問に答えました。

デイビッド・グロスへの質問は次のとおりです。
セルゲイ・ポポフ、天体物理学者、モスクワ州立大学の研究者、アレクサンダー・セルゲイエフ、ジャーナリスト、ラジオ・リバティの科学オブザーバー、ウェブサイトElements

左から：セルゲイ・ポポフSP、アレクサンダー・セルゲイエフAS、デイビッド・グロスDG（写真：オルガ・レビナ）

数学と物理学はそれほど異なる科学ではありません
セルゲイ・ポポフ：グロス教授、私たちの会話は、主に現代の理論の複雑さとそれらで使用されている概念の問題に触れたいと思います。したがって、最初の質問は、素粒子物理学の分野で働く若い科学者、理論物理学者からです。現代の理論物理学者が数学の最新の研究を知り、過去10〜20年にわたって出版されたオリジナルの数学記事を読むことの重要性を教えてください。それとも、ほぼ同じ時間スケールで発行されたモノグラフに精通するだけで十分ですか？

David Gross：それはあなたが扱っている問題に部分的に依存します。弦理論のいくつかの分野では、物理学者は自分たちで新しい数学を発明することを余儀なくされています。そして、彼らは数学者と非常に緊密に協力しています。彼らが直面している課題のいくつか（および行われている発見）は、数学者が以前は知らなかった新しい数学的構造の出現につながります。そのため、弦理論のいくつかの分野では、物理学と数学が協力して、本だけでなく元の記事でも読むことが不可能な新しい数学を発見しています。

素粒子物理学は多くの現代数学を必要としますが、何か新しいものを発明する必要はありません。しかし、現代の物理学（場の量子論と弦理論）は、50年または100年前よりも数学の最先端にはるかに近づいています。

アレクサンダーセルゲイエフ：これは、物理学者が数学的解析を発明したニュートンの時代と比較できますか？

DG：そうですね、時代は変わりつつあります。現在、多くの人々が数学と物理学の両方に従事しています。そして、ニュートン自身が惑星の動きを理解するために新しい数学（数学的解析）を発明しなければなりませんでした。しかし、多くの点で、これはかなり珍しい時期です。これは19世紀にはすでに当てはまりました。その後、偏微分方程式の理論が生まれました。波の伝播、熱伝達を説明する最初の場の理論の構築に必要でした。フーリエ、ラプラスのような数学者は、物理学を理解するために新しい数学を発明しました...

しかし、20世紀の終わりに、初めて、新しいタイプの非常に緊密な協力（物理学者と数学者の間）が登場しました。私は数学と基本的な理論物理学をそれほど異なる科学とは考えていないとだけ言っておきましょう。結局のところ、物理学者のような数学者も、本質的に自然の中で起こる現実の何かを発見します。

弦理論はロシア的です

SP：その場合、弦理論は今日の数学者にとって最も刺激的な主題であると言えますか？それとも、他にも同様に有望な分野はありますか？

DG：弦理論と場の量子論は非常に密接に関連しています。当初、数学は場の量子論から強力な後押しを受け、その作用は弦理論でも続いています。もちろん、物理学と数学がうまく相互作用している他の分野もありますが、弦理論で起こることほどよく似ているものはありません。

ご存知のように、私はカリフォルニアで理論物理学研究所を運営しています。毎年何百人もの物理学者が集まって、共通のトピックに取り組んでいます。そして昨年の秋、弦理論の数学的構造に関するプログラムがあり、参加者の半数は世界をリードする数学者でした。弦理論家と数学者は非常に緊密に協力しています。これは本当に素晴らしいです。そして、これは非常にロシア的です-物理学に近づき続けるロシアの数学者の伝統のように。ゲルファンドを覚えています...
SP：そしてアーノルド..。
DG：はい、これらは良い例です。アーノルドの仕事は主に力学系などの古典物理学に関連していました。

[訳者注]ロシアの数学の特徴はオイラーの流れをくむというか，物理に密接しているようです．対話で言及された本を以下に引用します：

関数とグラフ (ゲルファント先生の学校に行かずにわかる数学 1)www.amazon.co.jp1,400円(2021年02月02日 07:27時点 詳しくはこちら)
Amazon.co.jpで購入する
古典力学の数学的方法www.amazon.co.jp9,900円(2021年02月02日 07:27時点 詳しくはこちら)
Amazon.co.jpで購入する
量子力学は学校で教えられます
SP：弦理論の数学は非常に複雑です...

DG：複雑なのはその目新しさのためだけです。ニュートンにとって数学的解析は非常に困難でした。そして、ご存知のように、ハイゼンベルグが量子力学（行列力学とも呼ばれる）を発見したとき、彼は行列について聞いたことがありませんでした。しかし、ハイゼンベルグはなんとか関係式を書きました。「それはマトリックスのように見えます！」と言われて、彼は：「マトリックスとは何ですか？」と応じました。したがって、ハイゼンベルグにとって、行列（マトリックス）は非常に困難なものでしたが、今日では大学で教えられています。

SP：弦理論の数学ツールは、時間の経過とともにアクセスしやすくなると思いますか？結局のところ、何と言っても、たとえば経路積分は通常の積分よりもはるかに複雑です。

DG：すべて時間の問題です。

SP：人々はこれらの難しいことに慣れているだけですか、それとももっと理解しやすいアプローチを発明していますか？

DG：アイデアが最初に浮かんだとき、開拓者自身でさえそれをよく理解していません。新しい概念を十分に理解して生徒に教えることができるのは、多くの場合、長年の研究の後でのみです。時にはそれは数世代かかる。たとえば、多くの物理学者はまだ量子力学に苦労しています。私たちはまだそれを正しく教えるのに十分に理解していません。そしてこれは80年が経過したという事実にもかかわらず。そして、1930年代に書かれた量子力学に関する最初の教科書を見ると、それらはひどいものです。教科書は時間とともに良くなります。彼らは改善を続け、高校生に量子力学を教え始めると、彼らはより自然に感じ、それをよりよく理解するようになります。

ほら、他の分野でもまったく同じことが起こっています。力学や電気と磁気に関する最初の記事と教科書は非常に複雑でした。アインシュタインが電気と磁気を研究したとき、彼は苦労しました。結局のところ、それは大学の4年生でしか教えられず、それでも非常に難しい記事と見なされていました。そして今や私たちは学校で電気と磁気を普通に習います。

---続く

[訳者注）この節の放射線医学に関する内容は不十分です．iwjの以下のyoutube動画をお勧めします．]

https://iwj.co.jp/wj/open/archives/233698

「内部被曝の影響は、これから出てくる」 放射線治療の第一人者が語る、被曝問題の隠された真実～岩上安身によるインタビュー 第517回 ゲスト 西尾正道氏 第一弾 | IWJ Independent Web Journal　北海道がんセンター名誉院長で、臨床医として約40年もの間、放射線治療に携わってきた西尾正道氏は、3.11後、全国各地で内iwj.co.jp

なぜ放射性セシウムが必要ですか、それを不注意に扱うとどうなりますか？ 

セシウム137は、強力なガンマ線源として工学や医学で使用されています。医師は、腫瘍の領域に放射性薬物のエンドウ豆を置くことによって前立腺癌の治療をします-ガンマ線はそれを焼き切ります。また、工学の分野では、構造欠陥の探索から種々のタンク内の充填レベルの決定まで、さまざまな測定にガンマ線が必要とされています。放射性セシウムを含む機器の普及は、無知や不注意と相まって、悲惨な結果をもたらす可能性があります。捨てられた機器の無責任な所有者が放射性元素の入ったシリンダーから取り出すのを忘れて、ゴミ捨て場行になったことが時々ありました。そこから他のスクラップと一緒に冶金工場に運ばれ、精錬されることもあります。その結果金属が放射性物質になり、危険なバッチが見落とされると、最悪の場合、悲劇を招くことになります。

最悪の事態は1985年にブラジルの都市ゴイアニアで起こりました。そこで、地元の診療所は新しい建物に移転し、一部の機器が古い建物に残りました。診療所は建物の所有者に借金を負っており、裁判が進行中で機器が差し押さえられていましたが、セキュリティが十分でなく、社会的責任の低い二人が機器を盗み、部品のためにそれを解体し売りました。部品の中には放射性セシウムを含むアンプルがありました。泥棒はアンプルを売ることができず、お祭りに持ち帰り、彼らが発見した-夜に青く光る素晴らしい結晶について自慢しました。

近所の人は奇跡の粉を歯につけて味見をしたり、肌にこすりつけたり、ポケットの中でつまんだだけの人もいました。そして、しばらくして、人々は病気になり始めました。医者は症状にはほとんど注意を払わず、いつもの「何かを食べたからか、アレルギーがあるからか」と言っていましたが、病状が悪化し、被害者の中の誰かが、粉末を医師に見せると、すぐにすべてが理解されました。全体で200人以上の人が苦しみ、4人が放射能病で亡くなった。

ブラジル人が自分たちの過失と文盲のために苦しんだとすれば、クラマトルスクの家の住人は無実の被害者で、恐ろしい事故の犠牲者であります。複数のマンションの入居者が長期にわたって体調不良を訴え、数人が血液がんで死亡した。結局、1989年には検査が行われました。建物の壁に埋め込まれたセシウムのシリンダーを発見した。調査の結果、このボンベは70年代に消えていて、どうやらコンクリートを作るための砂利の中にあったらしい（セメント工場にはセシウムの器具がある）。このコンクリートは不運な壁に注がれたのです。

1997年の事件は死傷者には至りませんでした。ジョージアの兵士たちは古いソビエト軍の兵舎を解体しました、そして彼らの一人は磨かれた金属の美しくて暖かいシリンダーを見つけました。幸いなことに、彼はそれを開けませんでしたが、彼のポケットに入れました。兵士が放射線熱傷を受けた後、発見の性質が明らかになりました。

セシウムは薬ですか？
［訳者注）ここの話題のセシウム治療薬はほとんど与太話です．著者も懐疑的記述をしています．誤解を招くといけないので念のためお断りします．］
ルビジウム（「化学と生命」第9号、2020年参照）と同様に、医学者は精神疾患の治療にセシウムを使用しようとしてきたが、成功していないようだ。文献には矛盾する証拠がある。例えば、躁鬱病患者の血液中のセシウム含有量は、健康な人に比べて低く、治療後に症状が改善した患者に比べて低いという研究者もいます。しかし、他の人は、違いを見つけることができません。いずれにしても、これらの研究は20世紀後半に上演されたもので、今では話題性がありません。腫瘍学者の間では、セシウムはかなりスキャンダラスな名声を得ています。

事実、代替医療の支持者たちは、人が塩化セシウムを服用する、いわゆる高アルカリ性癌治療法を推進しています。この方法の達人によれば、セシウムは腫瘍細胞に濃縮され、そこで細胞を破壊するアルカリ性環境を作り出します。この方法の批評家は、この方法には化学的または生物学的根拠がないことを指摘しています。さらに、塩化セシウムを提案された用量、1日6グラム、さらには静脈内投与で食物と一緒に定期的に摂取すると、心臓の働きに深刻な問題が生じ、頻脈とその停止さえ引き起こします。さて、米国食品医薬品局は、承認された方法の数に癌のセシウム療法を含めなかっただけでなく、時々手紙を送ります、この方法の危険性についての警告。しかし、支持者は主張します：科学的根拠はそこに非常にあり、結果は認められた薬の結果より悪くはなく、時にはさらに良くなります。しかし、この紛らわしい話の本質を理解するためには、詳細を掘り下げる必要があります。

https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

福島事故後、放射性セシウムはどうなりましたか？
原子炉で発生する放射性同位元素の中で、セシウム137が最も有害なのは、第一に、セシウム137の量が多いこと、第二に、半減期が30年以上で、放射能汚染が長く続くことによります。たとえば、2011年の福島事故では、約20kgの放射性セシウムが放出されました。これは莫大な量です。このような放射性セシウムの放射能は9〜36 PBq［訳者注）ペタという単位は10^15です］、つまり1秒あたり数千万の崩壊［γ線光子が出ます］です。

福島の事故は、放射性セシウムの最新データを研究者に提供しました。原子炉の爆発で放出されたセシウムは、可溶性の化合物ではなく、鉄とケイ素の酸化物を主成分とする粒子の形で放出されました。どうやらこれらの粒子はかなり安定しているようです。いずれにしても、事故から1年後に、福島の学校の校庭から採取した土壌サンプルからも容易に発見されました。事故現場から数百キロ離れたタケノコの表面やシイタケの笠から放射性セシウムを含む単一粒子が検出されたが、その多くはタケノコの葉屑や切り株に付着した茎の先端から検出された。そして、タケノコやキノコの果肉の内部では、放射性セシウムは観測されなかった。このことは、放射性セシウムの移動性と植物組織への移行能力がやや誇張されていることを示唆している。

福島の原子力発電所の爆発後に散乱した粒子のオージェ分光分析（「化学と生命」第11号、2020年）
電子顕微鏡とオージェ分光法を用いて、サンプル中の元素の分布マップを得ることができます。福島の原子力発電所の爆発後に拡散した粒子をこの方法で分析すると、それらは主に酸化鉄に、シリコン、塩素、亜鉛、放射性セシウムを含むものでした。Scientific Reports、2013年8月30日

セシウムで汚染された土壌はどうか？
汚染された物や土壌を埋葬地に送ることで、小さな地域を埋め立てることができますが、原子力発電所での原子爆発や大事故は、放射性元素が畑や森林に散らばり、必然的に食物になってしまうため、主に農業の大惨事になります。セシウムの場合、この汚染がバックグラウンドレベルになるのに何十年もかかります。広大な農地を開墾したり、使用をやめたりすることは事実上不可能です。なぜなら、これらの土地で労働者として生活している膨大な数の人々を再定住させる必要があるからです。したがって、わずかに汚染された土地での生産が停止されることはなく、結果として生じる汚染された製品をきれいな製品と混合して、許容可能なレベルの放射能となります。

しかし、他の方法もあります。セシウムは植物に存在する必然性はないので、植物組織におけるセシウムの存在は単なる運の問題です。さまざまな種とさまざまな種類の飼料草で実施された実験は、それらに入り込むセシウムの蓄積は10倍以上も異なる可能性があります！　季節的にも同様の変動が見られます。葉や茎の成長が活発な夏の初めには、葉や茎の成長が終わる頃に比べてセシウムの量が著しく少なくなります。このおかげで、通常の農法を変えることなく、品種の選択と正しい農業技術のおかげで、汚染された土地でも比較的きれいな生産を受けることが可能になりました。遺伝学者が努力すれば、農家は土壌からセシウムをほとんど吸収しない品種を自由に使えるようになるだろう。原発の事故で汚染された土地ばかりになれば、そのような種に頼ることになってしまうが．．．。

しかし、研究者は汚染された土地をきれいにするためいろいろな方法を試しています。たとえば、福島の事故後、次のようなジレンマが発生しました。この県の住民は野生のキノコやベリーを採取するのが大好きです。さらに、それは彼らにとって重要な収入源です。しかし、セシウムを蓄積するハーブを育てることで畑をある程度きれいにすることができるが、この方法は森林では機能しませんが、キノコがその仕事に対処できる可能性があります。

横浜国立大学の研究者は、この仮説を確認しました。彼らは、セシウムが腐敗した落葉落枝に蓄積し、その含有量が菌類のバイオマスに比例することに気づきました。新鮮な葉にはセシウムが含まれておらず、キノコは処理中にすでに危険な金属を土壌からごみに汲み上げるという考えが生まれました。次に、彼らは菌類の成長に最も適した条件を作成することを決定し、汚染された森林の実験エリアの土壌を厚い木材チップの層で覆いました。確かに、わずか6か月で、キノコは土壌から放射性セシウムの半分を吸い込み、腐った木に濃縮しました。

ただし、一部の木は土壌自体からセシウムを吸引するのが得意であるため、これはすべての木で機能するとは限りません。これは、蜂蜜の研究におけるドイツの実験によって証明されています。したがって、すでに1988年以降、土壌放射性セシウムの菜種蜂蜜への変換係数は2％を超えませんでした。そして、針葉樹の新芽を食べているアブラムシからミツバチが集める甘露蜂蜜の場合、係数ははるかに高かった。その後のトウヒの針葉と若い芽の分析により、それらに高含有量の放射性セシウムが含まれていることが明らかになりました。土壌から蜂蜜への放射性セシウムの最も高い変換係数は、ヘザー蜂蜜で観察されました。土壌の含有量と比較して、40倍も多いことが観察されました。

セシウムで汚染された土地での山火事は危険ですか？
広島と長崎へのアメリカの原爆投下から75年後、マヤック事故から63年後の現在、チェルノブイリと福島の地域には、放射性セシウムで汚染された土壌に2つの大きな森しかありません。最初のケースでは、それらの面積は3000平方キロメートルであり、2番目のケースでは400平方キロメートルです。2011年11月の福島の森林地域では1平方メートルあたり1MBq以上でした（自然のバックグラウンドは数十万分の1です）。森林から落ちた放射性元素は森林から消えず、そこで崩壊し続けていると考えるのが論理的で、放射性セシウムはこの例です。

おそらく、それは森のゴミに蓄積し、そこから針葉に入り、枯れていくと、実際にその場所から移動することなく、ゴミに戻ります。そして、火事が発生すると、この場で放射性粒子が灰に変わり、火事の場所から遠くに散乱する可能性があります。しかし、それらはどこまで行くかを簡単に体験できます。両方の汚染された森林の松やもみの針を集め、木の下にゴミを捨て、セシウム塩の溶液（もちろん非放射性）に浸し、それらを燃やし、燃焼生成物を吹き飛ばすのに15〜20メートルの高さのパイプを通します：これは、山火事で炎が舞い上がる状況の再現です...

この実験は、2018年にミズーラ（モンタナ州）の米国森林局消防研究所のブースで実施され、非常に重要な結果を受け取りました。特に、ごくわずかなセシウム（3％以下）だけが煙とともに残り、残りは火の場所に散らばった灰の中に残っていることが判明しました。そして、セシウムの煙の粒子は遠くまで飛ぶことはありません。圧倒的多数で、それらは大きく、直径は10ミクロンです。したがって、消防士が最も危険にさらされています。

この結論は、2020年4月から5月にチェルノブイリゾーンで発生したひどい山火事の際の実践によって確認されたようです。メディアの報道によると、ゾーン外の過剰な放射線レベルは認められませんでした。また、京都大学の研究者による実験では、汚染地域のごみは高温で燃焼する必要があることが示されました。そうすると、放射性セシウムがボトムアッシュに集まり、低い燃焼温度で煙の粒子が濃縮されます。

［訳者注）ここでのテーマは，量の多い放射性セシウム汚染に関するものです．放射能は消せないのですが，農作物に取り込まない方法はありそうです．放射性セシウムからのガンマ線は外部被ばくに関与しますが，ベータ線やアルファー線を放出する核種は細胞に取り込まれると深刻な内部被ばくに関与します．例えば，トリチウム水は大きな問題です．］

ーー続く

セシウムはどのようにして原子力施設に行き、そこで何をするのでしょうか？

セシウムは2つの理由でそこにある可能性があります。第一に、放射性セシウムは、ウランが原子炉で核分裂するときに生成されます。そのようなセシウムはまだましな方です。結局のところ、それは強い放射能と長い寿命を持っているので、原発事故後の長期的な悪影響につながるのは放射性セシウムです。そして第二に、原発を設計するエンジニアは、セシウムを核または熱核施設に意識的に配置します。その理由は、電子管の陰極にセシウム層を塗布すると、電子の仕事関数が急激に低下するためです。つまり、追加の努力をしなくても、このようなランプの電流が増加します。原子力施設はそれとどのように係るのかだろうか？

惑星間宇宙工学の開発者は、原子力発電所がなければ、太陽系の惑星へ宇宙船の飛行は不可能であると確信しています。ただし、このような施設では、熱を地球に適用できる電気に変換するという原則は使用できません。この寸法では、蒸気エンジンを宇宙に配置することはできません。そのため、1970年代には、ソビエトのライプンスキー物理・電力工学研究所とクラスナヤ・ズヴェズダ研究・生産協会の技術者が、別の原理に基づいてトパーズ核施設を設計しました。

熱は熱放射によって直接電気に変換されました。対応するデバイスは電子ランプであり、電子は加熱された陰極から飛び出して冷たい陽極に飛んで、回路に電流を供給します。陰極は原子炉の熱で加熱されます。そのため、陰極にセシウムの層があれば、電子電流は何倍にもなります。

しかし、どのようにしてセシウムを熱陰極に保つのですか？このために彼らはそのようなトリックを思いついた。電極間のギャップは非常に小さく、数百ミクロンです。したがって、セシウムは陰極に堆積しませんでしたが、その原子からのガスはこのギャップを通してポンプで送られました。いくつかの原子は最終的に陰極表面に到達し、陰極表面からの電子の脱出を促進しました。「トパーズ」のテストは1987年と1988年にそれぞれ衛星「コスモス-1818」と「コスモス-1867」で成功しましたが、チェルノブイリ事故後、この種の作業は削減されました。彼らはアメリカ人と協力して再開しましたが、90年代後半にこのプログラムも終了しました。

セシウムは、核物理学SB ASソ連の研究所からノボシビルスクの物理学者によって発明された施設で同様の役割を果たしたが、発電のためではなく、全く別のタスクのためのものである。彼らは、加速器で使用するために、負に帯電した水素イオンのビームを生成する必要がありました。正イオンを作る方法は多かれ少なかれ明らかであるが、それは原子をイオン化することが必要である - 光で電子を引き裂くために、例えば。しかし、どうやってマイナスイオンを作るのか？このようなイオンは、電子管の陰極に水素分子を衝突させることで得られる。それを残して電子を拾うことによって、分子はその安定性を失い、すぐに水素原子とマイナスイオンに崩壊します。陰極にセシウムをコーティングすることで、電子が逃げやすくなり、水素イオンが何十倍も生成されやすくなることがわかりました。

現在、熱核科学者はそのようなイオン源を使用したいと考えています。彼らの仕事は、燃料、つまり重水素原子を加熱して、プラズマに入るときに冷却しないようにすることです。そして、加熱するということは、原子に高速の動きを与えることを意味します。ただし、中性原子の加速はイオンよりもはるかに困難です。そのため、イオンを作り、分散させ、中和するという発想が生まれました。中和は他の原子との衝突で行われますが、電荷が正の場合、イオンの速度が速いほど衝突の確率は低くなります。電荷が負ならばそうではありません。そのため、ITERAの建設に伴い、強力なマイナス水素イオン源を作ることが急務となり、セシウムを使わずにはいられなくなりました。このようなソースでは大電流が予想されるため、セシウムを含む陰極だけでなく、その層を常時再生するシステム全体が必要となる。開発されています。

セシウムは宇宙エンジンで使用されていますか？
いいえ、アメリカ人は加速されたセシウムイオンのジェット気流を宇宙船に提供しようとしましたが、成功しませんでした。現在、宇宙イオンエンジンの作動流体はキセノンであり、これはセシウムと同じくらい重い。

https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

油田ではなぜ、何立方メートルものセシウム塩溶液を井戸に流し込むのか？［訳者注］自然に存在するセシウム同位体は安定な133で，放射性セシウムではありません．まず安定なセシウムの利用の話の続きです．

そのような塩は、現代の掘削流体のユニークな成分であることが判明し、専門家が年間生産量と見積もっているセシウム50トンの半分以上を必要としています。掘削泥水は、掘削プロセスの間に井戸に直接汲み上げられます。これは複数の機能を持っています。その中でも特に重要なのは、掘削によって破壊された岩石を持ち上げることと、地層中の流体によって破壊されないように井戸内に反圧を生じさせることです。そのためには濃い泥が必要で、密度を高めるために、粘土のような充填材を追加します。
しかし、別の方法として、重くて均質な流体を使用するという方法もあります。セシウムは自然界に存在するすべてのアルカリ金属の中で最も重いので、セシウム塩を水に溶かしたものが使われます。実際、ギ酸セシウムはこのような塩として機能します：その溶液の密度は、水の密度の2倍を超えており、2.2 g/cm^3に達することがあります。また、ギ酸塩は分解しやすく、ある程度の量のセシウムで汚染することを除けば、環境に全く害を及ぼさないというメリットがあり、危険なことではありません。

ギ酸セシウムを掘削流体にする歴史は1999年までさかのぼります。その時にトータル社が抱えた問題からです。1997年には、北海の英国領エルジン・フランクリン油田の掘削を開始しました。石油は地表から約6キロ下にあり、貯留層の圧力と温度は前例のないほど高く、1000気圧以上、摂氏205度にも達しています。1999年までに7つの井戸が掘削され、2つの井戸には貯留層からの油の流れを増やすために壁に穴が開けられていました。

すべての井戸に、欠陥のあるエレベータ・ストリング（油を地表に送り出すパイプ）が設置されていることがわかりました。どうすればいいのか？井戸を殺して新しい井戸を掘るのか？そこで、エンジニアは別の方法を考え出しました：井戸を一時的にシャットダウンし、パイプを取り出し、ハンガーを変更し、すべてを元のラインに戻す。同じ泥で井戸を浸水させて殺してしまっうのですが、この場合は泥を使うことができませんでした。油田の油層は砂岩で構成されており、粘土の粒子が気孔に堆積し、それを詰まらせる可能性があります。これは、塩水が修理に必要であることを意味します：その密度を確保できる固体粒子ではなく塩溶液です。しかし、当時は臭化亜鉛という塩しか使えませんでした。この溶液は深刻な腐食を引き起こすだけでなく、海の生物を死滅させるほどの量の亜鉛が海に流れ込む可能性があります。何らかの無害な液体を探す必要がありました。

そして、会社にとって幸運なことに、遠くないスコットランドのアバディーンで、キャボット・スペシャルティ・フルイーズ社が所有する4,000m^3という十分な量のギ酸セシウム溶液のバッチがあったことです。この液体を借りて、一つづつ井戸を埋めて修理して、液体を汲み上げて別の井戸に送りました。このような丁寧な処理のため、貴重な液体はわずか10％しか失われていませんでした。全体としては、1つの井戸につき100万ドルの費用がかかりました。これは、不良品のバネを工場から出荷した品質管理部の社員とこのようなバネを導入した管理職の給料よりもはるかに高いものでしょう。

それ以来、油田労働者は掘削泥水の成分としてギ酸セシウムを頻繁に使用します。高密度で安全なギ酸セシウムは、掘削時間を2～4週間（掘削の複雑さにもよりますが）短縮し、機器の消耗を抑え、腐食速度を低下させ、油回収量を増加させます。最も重要なことは、作業員や環境に無害であることのおかげで、そのような掘削油は油田での環境に優しい作業のための新しい基準になりました。

ーーー続く

Цезий: факты и фактики • БиблиотекаЦезий — это первый элемент, открытый благодаря спектроскопии:elementy.ru
https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

A.Motylyaev 「ChemistryandLife」 No。11、2020

1860年、シュヴァルツシルトのミネラルウォーターサンプルの発光スペクトルを研究していたロバート・ブンセンとグスタフ・キルヒホフは、その中に明るい青色の線を発見しました。その元素を "空色 "という意味のラテン語のcaesiusからセシウムと呼びました。医師はすぐに新しい元素を使おうとしましたが、あまり成功しませんでした。20世紀には、セシウムは光を励起しやすいことがわかったため、荷電粒子の崩壊生成物を分析するための検出器をはじめ、さまざまな光学機器に使われました。［訳者注）ヨウ化セシウム（NaやTlドープ）は，ガンマ線で発光するシンチレータとして安価に販売されています．］

唯一の天然の同位体であるセシウム133が存在し、大きな原子質量、電子殻がシンプルなので、セシウムガスは、現在世界の時間を設定する超精密時計の動作体となりました。［訳者注）自然に存在するのは安定な安定な同位体だけですが，2011年の原発事故で放射性の同位体137などが環境に放出されました．セシウム時計については，現代の標準時計をご覧ください］https://note.com/sgk2005/n/n5a0079b99920

また、触媒としての役割も証明されています。しかし、時間が経ち、生産量が増え、新しい応用（時にはかなり議論の的になることもある）が見だされています。

グリーンエネルギーの創造者たちは、なぜセシウムに注目しているか。
材料科学者はセシウムペロブスカイト太陽電池に大きな期待を寄せています。少し前の2009年には、いわゆるペロブスカイト太陽電池への関心の波が押し寄せ始め（化学と生活#7、2019参照）。今ではそれは津波のようです。結局、太陽光を電気に変換する効率は14％とかなり許容範囲内になり、シリコンを導入したペロブスカイト電池では28％という記録的な効率になっています。ソーラーパネルの技術者は、これらのセルが安価に作られる方法に非常に魅力を感じており、専門家はペロブスカイトの大量生産が開始された後、ソーラーパネルの価格が急落すると予測している。そして、もう始まっています! 　中国企業のMicroquantaは2020年8月、小州市に70ヘクタールの工場を開設し、年内に20万平方メートルの純ペロブスカイトセルを生産すると発表しています。ドイツでは2021年に、イギリスのオックスフォード・フォトボティクス社の技術を用いたタンデム型シリコンペロブスカイトセルの生産を開始します。
ーーーーー
［訳者注）以下のmicroquantaのサイトをご覧ください］https://www.pv-magazine.com/2019/10/24/microquanta-achieves-14-24-efficiency-with-large-area-perovskite-solar-module/

Microquanta achieves 14.24% efficiency with large-area perovskite solar moduleThe four-year-old Hangzhou-based business says it already haswww.pv-magazine.com
ーーーーー

しかし、これらの成功はすべて、ハロゲン化鉛にメチルアンモニウムなどの有機カチオンが結合した有機無機ペロブスカイトで達成されました。実践では、これらの化合物は太陽光や大気中の水分の影響を受けてあまり安定ではないことがわかっています。その上、技術者たちは、そのような化合物の効率を向上させるための手段をすでに使い果たしており、理論的な限界に非常に近づいています。そして2015年には、有機カチオンを金属に置き換えるためのアイデアが生まれました：セシウムは、その外殻電子が簡単に分離する性質［訳者注）水素様原子］から、そのような選択がなされました。こうして無機セシウム系ペロブスカイトが登場しました。

セシウムには、量子ドット（光を放出したり吸収したりできるナノ粒子）と、太陽電池の2つの用途があります。5 年間で、セシウム・セルによる光から電気への変換の効率は 5 からほぼ 20 ％ （実験室のサンプルで）、実験者のデータではなく、認証機関のデータでは - ちょうど 15 ％ 未満まで増加しました。まだ理論上の限界からは程遠く、実際には道半ば、改善の余地は十分にあります。しかし、これらの素子の安定性は、まだ多くの問題があります。国際電気標準会議の加速規制下でテストされた最高のセルは、規制下では少なくとも1000時間は持たなければならないのに対し、240時間で10％の効率低下を示した。材料科学者は安定性を高めるための多くのツールを持っています。現在の主要課題は、安価なセシウムペロブスカイトセルで、高価なシリコンセルよりも日光の変換効率をよくすることです。これが実現しないと、すべての努力が報われません。

ーーー続くーー
安定な同位体セシウムの利用の話から始めました：
今回は，太陽電池への利用の話でした．
次回は，「油田掘削での利用」

Академик Георгий Сергеевич Голицын　ゴリツィン
«Природа» No6, 2007
https://elementy.ru/nauchno-populyarnaya_biblioteka/430479/Portret_neizvestnogo_K_300_letiyu_Leonarda_Eylera

レオナルド・オイラーは18世紀の偉大な科学者です。その前世紀の偉大な科学者はアイザック・ニュートン、そして、次の世紀はオイラー（1707–1783）であったことは確かです。オイラーは、現代の数学の主要な分野を提唱開発しました：変分法、複素変数の関数理論、解析的整数論、特種関数の理論。彼は、天体力学理論、流体力学、弾性の理論などに関する数多くの研究を残しました。A.S.プーシキンによる「テーブルトーク」では ,オイラーについてのセクションがあります。

1730年から1740年に統治したアンナ・イオアナブナの甥であり、将来の皇帝ジョン6世となるイワン・アントノビッチの誕生時に、宮廷はオイラーに王位継承者のための星占いを命じました。オイラーは占星術を信じていなかったので、最初は拒否したが、宮廷の要請を受けました。ホロスコープを作成するためのルールを知っていたオイラーは、イワン・アントノビッチのためにそれを作成しました。ホロスコープは酷いものであることが判明したため、オイラーはあえてそれを使用せず、別の非常に成功したものを提案しました。一年後、エリザベタ・ペトロヴナは赤ん坊の王を退位させシュリッセルブルク要塞に幽閉し、（ミロビッチ中尉がイワンアントノビッチを釈放しようとしたとき）1764年にエカテリーナ2世の密令で殺されました。オイラーは優秀な計算機でした。1783年の彼の死後、誰かが「オイラーは死んで計算をやめた」と言いました．

■1972年3月、レニングラード水文気象研究所の大気物理学部長であるデイビッド・L・ライヒツマン教授から、惑星大気の力学に関する講義を2週間で4回行うように招かれました。
私（ゴリツィン）は週に半日2回忙しく、残りの時間は美術館で過ごし、街を歩き回りました。ネフスキープロスペクト近くのルビンスタイン通りに部屋を提供してくれた友人のネイルBと滞在しました。

ある日、モスクワ駅近くのネフスキーにある古着屋に行きました。1階にはあらゆる種類の衣類があり、2階には絵画やその他のオブジェがありました。そこには、巨大な金箔の額縁に入った大きな暗い肖像画があった。漆喰が所々落ちていましたが、まともな状態でした。近づいてみると、その肖像画にはレオンハルト・オイラーが描かれていることがすぐにわかりました。オイラーの肖像画は、無名の画家の無名の人物の肖像画として売り出されていた。キャンバスは所々破れていたり、絵の具がボロボロになっていたりしていました。この肖像画は買わないと一生後悔すると実感しましたが、それは、93ルーブルで 50カペイカだった。

私はそのようなお金を持っていませんでした（当時、理学博士の給料は月に400ルーブルでした）。ネイルに足りないものを借りて、翌朝の開店に行きました。支払った後、なぜそんなに安い価格なのかと尋ねました。店員は私がラッキーだったと言った。肖像画は3か月以上店にあり、最近15％割引にしたと。したがって、肖像画の元の価格は110ルーブルだったのです。

フレーム付きの肖像画の重さは15キログラムで、裏には指の太さのロープが付いていました。ネイルは彼の肩に肖像画を掛け、私たちは彼の家に行きました。翌日、私はモスクワに向けて出発しました。ネイルが私に同行しました。車掌が、120×140cm巨の大な絵を車内に乗せないと言い、私はそれをコンパートメントの頭上の荷物棚に置くと言いましたが、確かに、棚ははるかに狭いのです。チェックインする時間がありません。電車が出発する約10分前です。ネイルは送ってくれると約束し、電車に沿って歩いて行ったが、数分後戻って、肖像画が別の車の前デッキに乗せたと言いました。私はボロゴエで、肖像画が乗客の出入りを妨げないことを確認し、モスクワでは私が最初に電車を降りることにしました。車掌には5ルーブルを支払いました。

モスクワのレニングラード駅で、重くて公共交通機関が不便だったので、一人では家にも仕事場にも肖像画を運ぶことができないのに気づき、保管室に渡しました。駅にある十数台のロッカーのうちで、そのような大サイズのものを受け入れられるのは最も遠くにある1台だけでした。数日後、私は研究所「カジク」に、絵を持ち込みました。

肖像画は明らかに修復が必要な状態でした。いとこのイラリオン・ウラジミロヴィチ・ゴリーツィン（ロシア人民芸術家、芸術院議長会会員、2003年の国家賞受賞者）に電話してみました。 イラリオンは、ペトリーヌ時代からの家族の肖像画をすべて保管しており、その中のいくつかは、この事件の少し前にトレチャコフ・ギャラリーで修復したものです。プロの修復業者の電話番号を教えてくれました。汚れを落とし、新しいキャンバスの裏に貼り、落ちていたところを塗り直して、すべて70ルーブルでできました。似顔絵は新品同様に良くなりました!　 右下隅には署名がありました：I. Konig, 1881.

肖像画は私のオフィスの壁に取り付けられました。USSR科学アカデミーの大気物理学研究所の所長である学者のアレクサンダー・ミハイロヴィッチ・オブホフがそれを見に来て、それを賞賛した後、突然「ゴガ、私に肖像画を売ってください」と言いました。数秒経過の後、私は次の返事を返しましたが、それには数十年後の今でも驚いています。「アレクサンダーミハイロヴィッチ、あなたはすでにあなたのオフィスに必須で良い肖像画をぶら下げていますが、これはそれより芸術的に優れ、政治的に間違っています。」オブホフはうなって立ち去り、このトピックに戻ることはありませんでした。

1973年、科学アカデミー250周年記念式典の準備が始まりました。その年の雑誌『自然』9号には、V.I.ヴェルナドスキーの論文「科学アカデミーの最初の年」が掲載されており、父パヴェルの息子キリル・パブロヴィッチ・フロレンスキーの資料に基づいて作成されています。他の肖像画の中で、私はレオンハルト・オイラーの自分の肖像画を見ました。キャプションには、E. ハンドマン（1756年、バーゼル大学）の肖像画が掲載されています。

スイスのこの街でオイラーは生まれ、1720年から1724年にかけて上記の大学でヨハン・ベルヌーイの数学の講義を受けた。若きオイラーは毎週土曜日に彼と数学の話をし、子供のニコラスとダニエルと仲良くなった。この二人は1724年にサンクトペテルブルク・アカデミーへの招待状を受け取り、翌年には同アカデミーに入学しています。オイラーは本当に一緒に行きたかった。しかし、彼が招待を受けたのは翌年の1726年12月でした。ニコライ･ベルヌーイが、かの地の気候に慣れることができなかったため、アカデミーに空席が発生したからです。オイラーは1727年5月に20歳でロシアに来て、1741年までここに住み、数学と力学の約80の論文を作成しました。

1740年、アンナ・イオアンノブナ皇后が亡くなりました。幼児ジョン6世の下の摂政は彼の母親アンナ･レオポルドブナでした。彼女の治世の数年間、ロシア国家の情勢は完全に混乱、アカデミーは1年間給与を支払わなかった。1741年オイラーは、ベルリン科学アカデミーを組織た若いプロイセン王フリードリッヒ2世（後にグレートの愛称で呼ばれる）の招待を受け入れた。オイラーが数学教室長に就任。彼はベルリンに25年間滞在しました。1759年には、このアカデミーの初代学長であるモーペルチュイ（力学における最小作用の原理の発案者として知られていますが、オイラーの貢献が大きい）、モーペルチュイの死後、オイラーはアカデミーのマネージャーに任命されましたが、フルードリッヒは給料を上げませんでした。厳格なフリードリッヒは、常に服装が正式でないオイラーを非常に嫌っており、これは数年間続きました。

王位に就くと、エカテリーナ2世はすぐにサンクトペテルブルクアカデミーに注目をしました。ベルリンでの25年間を通じて、オイラーはサンクトペテルブルクでの出来事を追跡し、アカデミーのメンバー、特に彼が常に支援していたロマノソフとの広範な通信を維持していました。エカテリーナは、首相であるN.I.パニンに、どうしてもオイラーをロシアに戻すように指示し、彼はベルリンでの給料よりもはるかに高い給料を約束され、1766年7月にオイラーと彼の家族はぺテルブルグに戻りました。ここで過ごした最後の17年間で、彼は約400点の論文を作りました。

（続く）－－－－－

ハンドマンと私の肖像画では、オイラーは明らかに生命のない右目をしています。これには独自の物語があり一度は聞いたことがありますが、今は正確なリンクを与えることができません。1740年代か1750年代には、パリのアカデミーが帆船のマストの配置を競うコンテストを発表しています。オイラーは長年造船業に携わっており、大会に参加したかったのですが、コンテストの論文提出期限が迫っていた。ついに彼は計算のために座り、丸3日間机から離れませんでした。その間、彼は他の人が少なくとも1か月を費やしたであろう計算を完了し、賞を受賞しました。しかし、彼は目を失った。第二の目で、レナード・オイラーはすでにサンクトペテルブルクで盲目になりました。それから彼は彼の長男に彼の仕事を口述した。オイラーの子孫はまだサンクトペテルブルクに住んでいます。

1981年1月、私はソ連科学アカデミーの対応メンバー3名の代表団を率いて、「気象・気候予測モデルのための大気プロセスパラメータ化に関する国際シンポジウム」に参加しました。ワシントンDCのすぐ北にあるメリーランド大学コンベンションセンターで開催されました。そこから私は同僚の海洋学者オーウェン・フィリップス氏（ボルチモアのジョンズ・ホプキンス大学教授）に電話をかけました。1時間足らずでワシントンからボルチモアまで 送ってくれました。地球惑星科学専攻では、回転流体の対流に関する講義を行いました。講演会の後、私はもう一人の同僚である有名な乱流研究者のスタンリー・コルシン（Stanley Corrsin）という研究所の友人を訪ねました。彼と一緒に、私は偉大な流体力学の写真の肖像画を見ました：ジョシュア・レイノルズ、乱流の科学の創始者、ルートヴィヒ・プラントル、セオドア・フォン・カルマン、ジェフリー・テイラー、そして、レオナルド・オイラーの肖像画の小さなカラー写真を見せてくれました。コルリジンは、"科学と芸術の歴史の中で、こんなに素晴らしい題材を個人的に所有することができるのか？"と質問し、どうすればいいと思っているのか聞いてみました。答えは、"科学史博物館か、せめて科学アカデミーに渡した方がいい "というものでした。私には、その後、前述の流体力学者の肖像画の写真が郵送されてきました。

コルジンの事務所を出ると、世界的に有名な力学者であるトゥルースデル教授に会いました。その本の多くは、1960年代と1970年代にロシア語に翻訳されました。この教授の主な趣味はレナナルド・オイラーの人生と仕事の研究であることを私は知っていました。コルジンは私たちをお互いに紹介しました。幸いなことに、私はオイラーの肖像画の写真の別のコピーを持っていました。私はこれをトゥルースデルに渡し、飛行機に遅れたことを謝罪し、必要に応じてフィリップスとコルジンが私の住所を持っていると言いました。

当時、まだメールもファックスもありませんでした。約1か月後、トゥルースデルから手紙を受け取りました。彼は、私が偉大な科学者のこのような素晴らしい肖像画を持っていたことがどれほど幸運であったかについて、ほぼ文字通りコルジンの言葉を繰り返しました。彼は次のように書いています。「あなたがこの肖像画を継承したと仮定させてください。」彼は続けて、この肖像画の最初の所有者が誰であったかについて2つの提案をしました。最初の可能な所有者である彼は、啓蒙された慈善家であるアレクサンダー・ミハイロヴィッチ・ゴリツィン副首相（1722-1806）を指名しました。もう1人は、当時の有名な科学者であり、すべてのヨーロッパのアカデミーのメンバーであり、エルミタージュの絵画や芸術作品を購入するエカテリーナ大王の主な代理人であり、フランスとオランダのロシア大使であるドミトリー・アレクシーヴィッチ・ゴリツィン（1734-1803）である可能性があります。彼については別の話があります。

（訳者注）著者名も含めて，ゴリツィンが3人も出てきて私も混乱しましたが，皆別人（ゲエオルギィ，アレクサンダー，ドミトリー）です．

トゥルースデルは、オイラーの肖像画が3か月以上誰も興味を持たなかったため、古着屋で割引価格で購入されたと聞いてがっかりしました。1989年12月にアカデミックA.M.オブホフが亡くなり、すでにUSSRの科学アカデミーの正会員であったので、1990年1月1日から私は大気物理学研究所の所長に任命されました。最初の2年間、私は古い小さなオフィスを研究所と気候理論部門の責任者として維持しました。オイラーの肖像画がそこにありました。1991年の終わりに、USSRの崩壊、ソビエト連邦の共産党の主導的役割の廃止、そして部屋を空ける必要性とともに、私は小さな古い事務所を空け、壁からウラジミール・イリイチ（レーニン）のかなりまともな肖像画を取り除き、そこにレナルド・オイラーの肖像画を置きました。

2000年末までは肖像画の関連することは何も起こりませんでした。その全容は不明のままでした。2000年12月、モスクワ石油ガスアカデミーの数学教師である末娘のマーシャは、パイプ内の非定常ガス運動に関する博士論文の防衛戦に臨んでいました。彼女の結果によると、パイプの2つの場所で希薄化波の振幅と通過時間を測定すると、ガスパイプライン（例えばウクライナ）からの不正なガス抽出の場所と量を特定することができました。防衛に成功した後、出席者全員が部署に招待され、少しお祝いをしました。論文評議会のメンバーであるグレブ・ミハイロフ教授は、何気なくレオナルド・オイラーのことを口にしていた。マーシャはすぐに、父親が科学者の大きな肖像画を持っていると答えた。教授は珍しく興奮して、この肖像画を見ることができるかどうか尋ねました。マーシャは彼に私の電話番号を教えてくれました。翌日、彼は私に電話し、私たちは彼が私の研究所に来ることに同意しました。「この肖像画を見てもいいですか？」マーシャは私の電話番号を教えてくれた。次の日、彼は私に電話をかけてきて、私の研究所に来ることになりました。

到着すると、グレブ・コンスタンティノヴィッチは、オイラーが彼の人生の主なテーマであると言いました。ソビエト（後にロシア）委員会の事務局長、そして流体力学はサービスです。本職はオイラー。これまでサンクトペテルブルク、ベルリン、スイスの彼のアーカイブは完全に解かれていませんでした。レオンハルト・オイラーの遺産に関する国際委員会のメンバーとして、毎年1ヶ月間をスイスやドイツで過ごしており、その活動は後を絶たない。「この素晴らしい肖像画に出会えて何と嬉しいことでしょう。2、3日でロシアでの歴史が調べられると思います」と、ミハイロフ教授は別れを告げました。

その日のうちに電話が鳴った。興奮したグレブ・コンスタンチノビッチが次のように言っていた。1875年、ロシアアカデミーは創立150周年を迎えていました。その中でも特に目立つメンバーの肖像画があることが決まった。オイラーの肖像画は、ドイツの画家ヨハン・ケーニッヒに依頼され、彼は1756年のバーゼルの肖像画の非常に正確なコピーを作成しました。 その後、このコピーやコピーから、質が著しく低く、色調が異なる多くの新しいコピーが作成されました。このような二次コピーは、モスクワ大学、ロシア科学アカデミー学長の応接室にあります。

1881年にケーニッヒによって実行されたこの命令は、最初にサンクトペテルブルクのワシリエフスキー島にある科学アカデミーの建物に吊るされました。1889年は、プルコボ天文台の開館50周年の年でした。オイラーは天体力学の分野でも多くのことをしていたので、彼の肖像画はこの天文台に贈られました。1918年、天文台は革命家船乗りによって2度略奪されました。54年後、私はネフスキーのコミッションショップで「不明」の暗い肖像画を見たのです。

［訳者注］量子力学の数学的基礎(ノイマン）がベルリンで出版されたのは1932年，みすずから日本語訳の出版がされたのは1957年です．ソボレフ達がスミルノフ主催のセミナーで勉強したのはこの本でした．ディラックのデルタ関数を厳密に扱うにはルベーク積分やヒルベルト空間の理論を基礎に置くことが必要でした．ソボレフの名はソボレフ空間に残っています．
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

Семен Кутателадзе，«Наука из первых рук» №1(86), 2020　より

https://elementy.ru/nauchno-populyarnaya_biblioteka/435305/Sobolev_iz_shkoly_Eylera

数学は思考の形を研究します。最も一般的な意味で、微分はプロセスのトレンドを決定し、積分はトレンドの将来を予測します。

現代の人類は、積分と微分なしでは思考ができません。ニュートンとライプニッツによって、微分積分が発見され、この概念を使用して、オイラーは変数の新しい数学を育て、多くの独創的な発見をし、驚くべき公式と定理の数えきれない集大成を行いました。

200年間、解析学はニュートン、ライプニッツ、オイラーの微積分にとどまりましたが、20世紀に入ると、古典微積分は分布の理論へと進化していきます。近代解析学の主要な対象は、ルベーグの意味での積分と、S.L.ソボレフの意味での微分であります。古典的な微分と積分の操作対象とならない一般的な依存関係のために、これらは定義されています。ルベーグとソボレフは、積分と微分への新しいアプローチを提案し、数学の影響力と応用の範囲を大幅に拡大することで歴史を作りました。

歴史上の人物や発見は、歴史的な並立と分析に値する。数学の賜物は、先生から生徒に受け継がれます。この交互に続く連鎖こそが、数学スクールの物質的な担い手で、ソボレフは、レオンハルト・オイラーにまで遡るスクールに属しています。

オイラーからソボレフへ
人間は物理的な物体であり、４次元時空の世界線で部分的に表現できます。オイラーの世界線の大部分はロシアに属します。スイス出身のオイラーは、ロシアに第二の故郷を見つけ、サンクトペテルブルクに住みました。数学の "ダ・ヴィンチ "たる彼は、ずっと前にロシアの精神の不可欠な部分になっていました。

スイスの数学もロシアの数学もありませんが、ロシアには数学があり、国家的な数学の伝統があり、国家的な数学スクールがあります。我々の同胞は、オイラーをロシアの数学スクールの創始者と考えることを誇りに思っています。

オイラーの努力により、ペテルブルクは18世紀に世界の数学の中心地となりました。 ダニエル・ベルヌーイはオイラーに次のような手紙を書いて、時代をリードする科学雑誌となった有名な「サンクトペテルブルクアカデミーのコメント」の話をしています。この出版物は何度か名前を変え、時を経てIzvestiya RAN (Mathematical Series)となりました。サンクトペテルブルク科学アカデミー紀要にはオイラーの論文473本が掲載されており、オイラーの死後1830年まで何年もの間、順番に掲載されていました。

サンクトペテルブルクの家。ここにL.オイラーは住んでいた。撮影：M.パンフィロフ 。オイラーのサイン。ロシア科学アカデミーアーカイブのサンクトペテルブルク支部

19世紀の初めに、数学的思考の中心はフランスに移り、ラプラス、ポアソン、フーリエ、コーシーが活動しました。生み出される数学の新しいアイデアは、ハリコフ帝国大学から合法的に取得した卒業証明書を剥奪され、パリに留学したM.V. オストログラドスキーによって受け入れられました。オストログラドスキーがフランスで獲得した名声と、科学アカデミーに提出された多くの彼の回想録は、ロシアでの彼の功績を認識させ、彼はすぐにロシアの数学のリーダーとして認められるようになりました。

[訳者注）ベクトル解析のガウスの定理のことを，ロシアではガウスーオストログラドスキーの定理と呼ぶのをロシアの物理本で見たことがあるでしょう]

［訳者注）オストログラドスキーがハリコフ帝国大学の博士号を拒否した状況はwiki参照］

オストログラドスキーは、ロシア科学にとってのオイラーの重要性を十分に認識していた。オイラーの遺産を出版するという問題を精力的に提起したのは彼でした。「オイラーは、近代解析学を創始し、それだけでも彼のすべての前任者を合わせたよりも豊富で、それを人間の心の最も強力な道具にした 」とオストログラドスキーは書いています。全28巻の出版は10年以内に完了する予定でしたが、当時も現在も科学アカデミーはそのための資金を確保できず......。

ロシアの有名な数学者や力学者の多くは、M.V.オストログラドスキーの影響を受けています。その中には、オストログラドスキースクールのサンクトペテルブルク支部のチェビシェフ、リアプノフ、ステクロフがいた。チェビシェフの教え子には、コルキン、マルコフらがおり、ソボレフの大学院の顧問となったギュンターはその下で学んでいた。ソボレフは、V.A.ステクロフやA.M.リャプノフの弟子であるV.I.スミルノフを、彼の第二の師と考えていた。ソボレフの科学的系図の華麗なる連鎖はこのようなものでした。

"1951年、セルゲイ・リヴォヴィッチはモスクワ国立大学で数学物理学の方程式の講義した。メモを取る時間がないほど、鮮かで素早い講義だった。生徒たちはスローダウンと彼にメモを送ったが、10分ももたずに、また夢中になり始めた。セルゲイ・リヴォヴィッチは授業中に気を散らすことはありません。とても律儀で、自分の講座を自分のテキストを使って明瞭な講義をしました。［訳者注）リヴォヴィッチは，ソボレフの父称。名前だけでなく，名前と父称で尊敬をこめて呼ぶのがロシアでは普通］
私たちは彼の試験を受けることを恐れませんでした。彼は学生が主題を知っていることを確認し、すぐに成績を上げました。
当時、私たちはソボレフが有名な数学者であることをすでに知っていましたが、もう一つの仕事である原子力研究所で彼がどのような責任を担っているのかは知らなかった。”ーー物理学と数学の博士号、RRCクルチャトフ研究所の教授、最高科学責任者、IVM RAS V. I. レベデフーー

1930年代のロシアにおける数学
大発見とは、自然には発生しないが必然のマイルストーンである。必要性はチャンスが密集した雑木林を通り抜けていく。ソボレフの発見は、世界と国家の数学の大躍進の年に属していました。

20世紀は当然のことながら自由の世紀と見なされます。自由とは、個人間の対立を解決する方法を反映した歴史的概念であり、多様性に制限はなく、集団的共存の形態を制限します。歴史的な環境は、すべての勝利とすべての悲劇の不可欠な要素です。

レニングラード大学の学生時代。S.L.ソボレフと同志のS.A.クリスティアノビッチ、教師のV.I.スミルノフ。

民主主義の社会制度の発展は、人々の精神生活のあらゆる側面の解放と同時に起こりました。数学は、自由な思考の科学としての本質を明らかにしました。

微分方程式を解くという概念を改訂するというアイデアは、20世紀初頭の数学的な雰囲気の中で身につけられました。1957年の彼の業績を理解するにあたり、ソボレフ自身は次のように述べています。”偏微分方程式を満たす関数を見つけるさまざまな問題を研究する過程で、必要な次数の連続導関数を持たない関数のクラスを使用することが有用であることがわかりました。どこにでもありますが、ある意味では方程式の実際の解を制限しています。このような一般化された解は、さまざまな関数空間で自然に求められ、時には完全であり、時には新しい「理想的な要素」を導入することによって特別に補完されます”。

科学は、個々の解から関数空間、その中の演算子、そして解の要素の研究へと移行していきました。
これらの一般化された解が、いつ古典的な意味での解になるのかという問題は、この考察下では独立したものとなりました。

私たちが見ることができるように、ソボレフは、カントールの集合理論に基づいて、彼の理論とヒルベルトの考えとが不可分に結びついていることを示しました。

ソボレフがこの問題に注目したのは、集合関数論に基づいて数理物理学の方程式へのアプローチを見直す必要があるというルベーグの考えを推し進めたギュンターと関係があることは間違いない。

ソボレフは、スミルノフ主催のセミナーで関数解析の考え方を紹介されました。そのゼミで、量子力学の数学的方法についてのJ・フォン・ノイマンの古典書を研究したのがきっかけでした。ノイマンのアイデアはまた、スミルノフのセミナーの別の参加者の興味を喚起しました。ソボレフの大学の友人であるL.V.カントロヴィッチは、K.フリードリヒの関数の概念を拡張する問題に専念し、中等度周期分布の一般化された微分の記述を含む2つのノートを1935年にソ連のDANに発表しました。

親しい友人であり、同じセミナーの参加者でもあるソボレフとカントロヴィッチが、関連する話題でお互いの研究を知らなかったことは、絶対に信じられないように思えます。しかし、後にこのエピソードに触れたことは二人とも一度もありません。当時、ソボレフとカントロヴィッチの間には一時的な疎遠感があったことは明らかであり、彼らは最後まで温かく心のこもった友情を保っていた。その本質は、レニングラードとモスクワの数学界で当時繰り広げられていた非常に鋭い政治的な出来事を理解することによって理解することができます。

この国の数学界の状況は、当時の一般的なモラルとあまり変わらなかった。北の都の旧教授に対抗して「レニングラード数学戦線」が展開された。主な攻撃対象は、ペトログラード数学会を率いたギュンターであり、理想主義と実践からの離脱を全面的に非難され、「公共生活における反動的」「科学における保守的」という烙印を押されていた。ギュンターへの痛ましい告発を含む1931年3月10日の「レニングラード物理数学協会の再編成に関するイニシアチブグループの宣言」に署名した人々の中には、カントロヴィッチがいる。ギュンターは、部門の指導者を去り、悔い改めの手紙を書くことを余儀なくされたが、「唯物論の数学者」とも呼ばれた。ステクロフも理想主義者の中にランクされました。ソボレフとスミルノフの名誉のために、彼らは彼らの指導者の公の迫害に加わっていませんでした。教師と生徒の科学的見解の明らかな近さは解毒剤として役立ちました。

モスクワでも老教授たちは嫌がらせを受けていた。ムスコビテスもカントロヴィッチを論争に巻き込もうとしたが、彼はルージンへの攻撃を控え、ソボレフは残念ながら「ルージン事件」に関する学術委員会の活動に積極的に参加した。

 ロシアの数学の悲劇は普遍的なものだった。その勝利はまた、普遍的なものであった。

ソボレフと原子爆弾
人間の力は、理想的な無形の価値を創造し伝達する能力にあります。数学は、無謬の知的技術の最古の技術を保持しています。根拠のある計算の科学と芸術、数学は文化の中心に位置しています。思想の自由は、個人の自由の必須条件です。世界観の基礎である数学は、自由の基礎となり保証人となります。オイラーとそのスクールの最高の代表者の仕事は、これの無数の例を提供しています。ソボレフの運命も例外ではなかった。

20世紀に入って、人類は第一次世界大戦と第二次世界大戦の扇動者を止めることができずに、安全な存在の境界線に来た。抑止力は自由の保障人であるが、アメリカとロシアの原爆製造は、科学の驚異的な力、つまり人類生存の最後の予備軍であることを示している。数学者は、このプロセスに同僚が参加していることを誇りに思う。ノイマンとウラムはマンハッタン計画で働き、ソボレフとカントロヴィッチは国内のエノモルモズ計画に関わっていた。 

今日では、核兵器開発の歴史に関わる文書のほとんどが機密解除され公開されており、あの英雄的な時代の熱気を感じることができます。

我が国における原子力事業の開始は、1942年9月28日付のGKO令No 2352号「ウランに関する事業の組織化について」に関連づけられています。 数ヶ月後、GKOは、原子力エネルギーの研究のためにソ連科学アカデミーの第2研究所を組織することを決定した。クルチャトフは、研究所の管理と原子問題に関するすべての作業を任されました。すぐにクルチャトフはソボレフを副官に任命し、キコインのグループに加わり、同位体分離のためのカスケード型拡散装置を用いたウラン濃縮を担当した。

特別フォルダーには、1945年8月のクルチャトフとキコインの報告書が入っています。 この文書の前文には次のように書かれています。

"海外で知られている4つの原子爆弾（ウラン235とプルトニウム239）の製造方法のうち、「ウラン235とプルトニウム239の製造方法」と「プルトニウム239とプルトニウム239の製造方法」の2つを紹介します。ウラングラファイトボイラ法、ウラン重水ボイラ法、拡散法、磁気法、第二研究室の第一人者（学識経験者のクルチャトフ、ソボレフ、科学アカデミーのキコイン、ボズネセンスキーに相当するメンバー）は、これらの最初の3つの方法について、第二研究室は現在、施設を設計し、建設するのに十分なデータを持っていると考えています。”

早くも1946年には最初のガス濃縮器が製造され、大量生産が可能になりました。ガス状六フッ化ウラン濃縮実験開始 その仕事は、膨大な数の多様な科学的、技術的、組織的な問題を解決しなければならず、ソボレフの本業となった。ソボレフは、プルトニウム239とウラン235の両グループで働き、計算機の組織化と指導、工業用同位体分離の規則の開発、損失削減の責任者、その他多くの組織的・技術的な問題の解決を行った。原子力プロジェクトでの彼の役割は大きくなっていた。

1949年8月29日、セミパラチンスク近郊でRDS-1の実験が行われ、そのちょうど2ヶ月後には、800人以上の参加者が原爆計画に参加していたことが明らかになりました。ソボレフはレーニン勲章を受章した。

1949年半ばには、第2研究室は「LIPAN-科学アカデミー計測研究所」に改称されました。LIPANでは、ソボレフは、彼の人生の主要な本、"数理物理学における関数解析のいくつかの応用 "を書いた。

原子計画はソボレフの科学的、個人的な可能性を豊かにした。計算数学は、彼の人生の最後まで彼の仕事の中心を占めていました。1952年から1960年までは、モスクワ国立大学の計算数学科を率いました。すでにシベリアで、ソボレフは、その普遍性の驚くべき美しさ、立方式の理論を構築しました。ソボレフは、古典的な近似法と分布理論の概念を統合しました。

LIPANでの仕事は、ソボレフの数学の理解に新たな明るい色を加えました。彼によれば、多くの問題において重要なのは、解決策があるかどうかという抽象的な問題ではなく、合理的な近似変形を規定の期限までに具体的に提示することであることに気付いたのは、この頃だったそうです。

新しい微分-新しい微積分
ずっと前の1755年に、オイラーは関数の普遍的な定義を与えましたが、それはほぼ200年間、最も一般的で完璧なものと考えられていました。彼の有名な微分積分のコースで、以下のように書いています：

"ある量が，他の量に依存し，他の量が変化するときに、変化を受けるなら、前者は後者の関数と呼ばれる。この呼称は非常に広範で、ある量を他の方法で決定するすべての方法をカバーしています。したがって，もし x が変数量を表すならば，何らかの方法で x に依存するすべての量，すなわち x によって決定されるすべての量は，その関数と呼ばれる．

 ソボレフの研究は、微分方程式の解の概念の再考に関連している。

ソボレフはコーシー問題を汎関数空間で解くことを提案した．すなわち，関数としての解を理解するのを止めた．ソボレフは、プロセスの挙動のすべての積分特性が使える場合でさえ、微分方程式を解いたものとして考えることを始めた。この場合、時間の関数としての解は未知であるだけでなく、存在しないこともあります。予測の重要な原理の質的に新しい理解が科学に入りました。

ソボレフの一般化された導関数はオイラー関数の概念には該当しない。ソボレフが提案した微分は、数学的数量の相互依存性の新しい理解に基づいています。一般化された関数は、あらかじめ選択されたサンプル関数のクラスのすべての代表に対するその効果の積分特性によって暗黙的に定義される。

ソボレフは、関数分析を数学物理学に応用した先駆者の一人であり、1935年に理論を発表した。 10年後に独立して同じ考えに到達したローラン・シュワルツの研究により、新しい微積分が一般に利用可能になり、代数学、幾何学、位相幾何学の多くの進歩的な考えを利用した、優雅で強力で極めて透明性の高い分布の理論として発表された。

17世紀の微分積分は、古典力学の一般的な見解と切り離せないものである。一般化された関数の理論は量子力学と結びついています。

特に強調したいのは、量子力学は古典力学の単純な一般化ではなく、新しい法則に基づいた科学的な世界観を表しているということです。古典的な決定論と連続性は、量子化と不確定性に取って代わられました。二十世紀の人類は、自然過程の理解度の全く異なるレベルに達しました。

現代の数学理論も同様である。現代の論理は、アリストテレスの論理を一般化したものではありません。バナッハ空間の幾何学は、ユークリッド平面幾何学の一般化ではありません。現代の微積分となった分布理論は、微分方程式による物理過程の数学的記述の技術全体を激変させた。

ニュートンとライプニッツの発見は、何世紀にもわたって続いてきた微分・積分の前史を総括し、新たな研究への道を開いた。ルベークとソボレフの業績は、創意に富んだ先人たちの反省を継続し、現代の数学者の道を照らすものであった。

ソボレフは未来を聞き、自分のスペースを持って人々に贈り物をしました。彼の発見は、数学における多くの革命的な変化のきっかけとなりました。

ソボレフは最後の一連の数学研究では、オイラー多項式の根の微妙な特性に専念していました...

"セルゲイ・リヴォヴィッチを見た多くの人は、彼がハンサムだったと言うだろう。背が高く、エネルギッシュな動き、素早い足取り。彼の演説は常に非常に明快で、優れた論争家とみられていましたが、めったに論争しなかったのは、彼が正しいことが多かったからかもしれません。セルゲイ・リヴォヴィッチは常に慈悲深く、他人の意見を尊重しました。

ソボレフは優秀なプロモーターであり、様々な聴衆の前で講演していました。たまたま小学生に関数解析とは何かを説明したとき、彼は最も難しいことにまで言及しせんでしたが、非常に明確でわかりやすく数学のこの分野の立場と重要性について生徒たちに伝えることができました。”ーーАкадемик, д. ф.-м. н., советник РАН Ю. Г. Решетняк, ИМ СО РАН

Редакция и автор благодарят Е. С. Соболеву, пресс-секретаря Президиума СО РАН О. В. Подойницыну, сотрудников библиотеки ИМ СО РАН, директора издательства Т. Н. Рожковскую за помощь в подготовке публикации.

В статье использованы материалы из архивов семьи С. Л. Соболева, Института математики им. С. Л. Соболева СО РАН, Президиума СО РАН.

Литература
1. Атомный проект СССР. Документы и материалы. Т. II: Атомная бомба 1945–1954 / Ред. Рябев Л. Д. М.; Саров: Наука, 2000.
2. Кутателадзе С. С. Сергей Соболев и Лоран Шварц // Вест. РАН. 2005. Т. 75, вып. 4. С. 354–359.
3. Нейман, Иоганн фон. Математические методы квантовой механики. М.: Наука, 1964.
4. Николай Петрович Дубинин и XX век / Сост. Дубинина Л. Г., Овчинникова И. Н. М.: Наука, 2006.
5. Сергей Львович Соболев. Страницы жизни в воспоминаниях современников / Ред. Рамазанов М. Д. Уфа: ИМВЦ УНЦ РАН, 2003.
6. Смирнов В. И., Соболев С. Л. Биографический очерк [Николай Максимович Гюнтер (1871–1941)] // Гюнтер Н. М. Теория потенциала и ее применение к основным задачам математической физики. М.: ГИТТЛ, 1953. С. 393–405.
7. Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука, 1974.
9. Соболев С. Л. Избранные труды. Т. 2. Новосибирск: Ин-т математики СО РАН, 2006.
10. Философские проблемы современного естествознания / Ред. Федовеев Н. П. и др. М.: Изд-во АН СССР, 1959.
11. Эйлер Л. Дифференциальное исчисление. Л.: Гостехиздат, 1949.
12. Lutzen J. The Prehistory of the Theory of Distributions. New York etc.: Springer, 1982.
13. Schwartz L. A Mathematician Grappling with His Century. Basel etc.: Birkhauser, 2001.

［訳者注］19世紀には，数学がその源泉として物理学と一体でした．ニュートンは自分の力学の研究のために新しい数学（微分や積分）が必要で，自分で開発しました．ニュートンは物理学者兼数学者です．ストークスの数学も現実の物理現場に対応する中から誕生し実験現場に適用されました．今日，高度に分化し抽象化した数学を数学の中で扱うことだけに興味をもつ数学者を，私は嫌いです．数学者が現場に足を入れることを願います．このエッセイを私が好んで読んだ理由はここにあります．
**********************

科学者の研究に対する評価
J.ニュートンによって始められた光のスペクトルの研究は、W.H.ウォラストン、J.フラウンホーファー、J.F.W.ハーシェル、C.ホイートストン、J.H.ストークスの研究によって発展しました。黒体放射のH.R.キルヒホフの研究も有名です。化学者R.W.ブンゼンと彼の実験的研究は、スペクトル線の反転効果の発見、フラウンホーファー線の説明、物理学、化学、天文学のための重要なスペクトル分析法の創出につながりました。

同時代のW.トムソンは、J.G.ストークスの物理学のこの分野への貢献について書いています。彼は、ストークスの太陽化学と恒星化学の原理が、ここ8、9年の間、公開講座で概説されていたことを思い出しました。ブンゼンとキルヒホフ（ストークスとは独立して理論を発見した）の研究は応用されて、太陽には鉄、マグネシウム、その他の既知の金属が存在することが示されました。すでに何年も前に会話の中でストークスは、太陽スペクトルの暗い線によって、太陽大気の化学的性質について結論を出すことができるという考えを表明していました[8, p.114]。

同時にストークスは、地球の基準表面［訳注）ジオイド面を近似した回転楕円体］、質量、軸を中心とした自転の角速度によって地球の外部重力場を決定するという問題も解決しました。この問題の解答可能性を証明し、ポテンシャル理論の最初の境界問題として、圧縮されたスフェロイドの収縮の二乗のオーダーの相対誤差を持つ近似解を与えた。楕円体のストークス問題のかなり正確な解は、1945年にイタリアのP.ピツェッティとロシアのM.M.モロデンスキーによって与えられた。

ケンブリッジでは、自然科学や技術科学における数学的手法の使用が奨励され、ストークスもまた、それらを広く活用していました。これは、ヴァイルが指摘したように、ベクトル解析とテンソル解析のすべての積分定理が、座標 x_i で囲まれた空間にある r 次元（方向性のある）多様体上の次数 r の微分形に対するストークスの一般定理の特別な場合であるという事実に現れていた [9, p. 192]。

実際、ストークスは数学の発展に重要な貢献をしました。ベクトル解析の主要な公式の一つであるストークスの定理は、ベクトル場の回転を、閉曲線を境界とする有向曲面上で面積分したものが、元のベクトル場を有向曲面の境界の閉曲線上で線積分したものに等しいという彼の名を冠した定理で、1849年にW.トムソンによって得られました。J.G.ストークスは、半収束無限級数の指摘をし、無限級数の完全収束（絶対収束？）や限定収束（条件収束？）を研究しました。
[訳注）収束する無限級数には、絶対収束級数と条件収束級数（半収束級数）があります]

1848年、J.G.ストークスはドイツの数学者F.L.vonザイデルとともに、級数と級数の一様収束の概念を科学的に導入しました。彼は純粋な数学だけでなく、物理学の様々な分野（力学や光学）、天文学や工学への応用にも興味を持っていました。漸近解析におけるストークス現象、流体力学におけるストークスパラメータとベクトル、微分幾何学における彼の定理、光学におけるストークス線、結合、せん断、Navier-Stokes方程式、ストークスドリフト、ストークス電流と波動関数、流体力学におけるストークス境界層などが科学の歴史に登場しています。

彼の研究結果の修正は、ストークスの科学におけるメリットを損なうものではありませんでした。P.N. レベデフ と彼の教え子である N.P. ネクレパエビム は、音響ストークス波とキルヒホッフ波の公式の係数の正確性に疑問を持ち [10, p.349]、W.G.ブラッグは、ストークスのインパルス理論（加速された電子がエーテル中でインパルスを発す）では、X線と電子の交換性を説明できないと指摘し、R.E.ミリカンは、液滴の運動法則がストークスの法則と一致するのは、連続的な媒体の場合だけであることを強調しました。その他にもストークスの研究結果に対する多くの議論が起きました。

ストークは晩年も研究を続けていましたが、レントゲンの発見を乗り越えることができませんでした。1898年には「X線の性質について」という論文の中で、陰極ビーム粒子の制動の結果として反陰極（陽極）上での短時間の電磁的インパルスを理論的に扱おうとしました。ドイツの物理学者J.E.ウィーチェルトと同様に、J.G.ストークスは、X線が非常に短い波長の発光であることは、X線の発生モードから明らかであるという結論に達しました。

科学のオーガナイザー、教育者としてのストークス
生前、ストークスはM.ファラデーからE.ファラデーに至るまで、イギリスの著名な科学者たちに囲まれていました。まだまだスターダムの瞬間を待っていたラザフォードら。

ストークスは最後の日が来るまで、科学的な出来事に関心を持ち、批判的に（いつも評価が正しかったわけではないが）評価していました。例えば、W.トムソンのように、J.K.マクスウェルの 論文に対しては寡黙でしたが、W.レントゲンによるX線による発見はすぐに認め急いで手紙で知らせました。

ストークスとその仲間たちは、精密科学と応用科学の発展、物理現象の解明方法の解明、自然哲学と科学的知識の区別、経験的活動と科学的活動の区別に多大な貢献をしました。彼や彼のような人たちのおかげで、大学教育の質が将来の研究者のニーズに沿ったものになリ、ストークは何十年も講義をしました。マクスウェルも彼の意見に耳を傾け、やがてストークの親友となりました。

ストレットの回想によると、ストークの講義や実験は彼に感銘を与え、教えることについて多くの有益なことを教えられたという。ストークスのコースの学生が、自分たちが理解していない光学現象の解明を彼に訴えたとき、彼は大抵の場合、親身になって対応してくれました。

19世紀後半と20世紀初頭の英語教育の伝統では、まず、生徒に説明する際には、自分自身がその質問を理解しているかどうかを確認することが大切だと指摘しています。第二に、クリアーの形を探すときに... プレゼンの... 新しいアイデアが浮かんできます。第三に、学生の質問は思考を刺激し、私たちがいつも標準的な方法でアプローチしている現象を新しい視点から見させてくれるので、創造的な思考にも役立ちます[11, p.261]。かつてストークがやっていたことです。

彼のコレクションから、ストークスは、学生が物理学や数学の問題に関連する1つまたは別の問題を解くことを勧めます。そのうちの一人は、等高線上の積分が、等高線を通過する流れの大きさに関係していることを証明することを提案した。今日では、このためにはストークスの定理を証明する必要があると言われていますが、ストークス自身はその証明を発表したことはありませんでした。1854年、トライポサス（ケンブリッジ大学の優等学士号取得のための公開試験）に合格したとき、ストークスの大学院生だったマクスウェルは、気体中の速度による分子の分布の問題を解きました。

1887年から1892年まで、ストークスはケンブリッジ大学の国会議員の一人であった。そのような責任ある立場にもかかわらず、合理的な心と冷静な性格のためか、下院での発言はほとんどせず、注意深く聞き役に徹していました。

強い宗教的信条を持つ家庭で育ったストークは、保守的な価値観と人生の信念を堅持していました。1886年にはヴィクトリア・インスティテュートの会長に就任しました。ダーウィンの進化論からキリスト教の原則を守るために設立されました（ストークスもダーウィンの進化論を批判していた）。また、イギリスと外国の聖書協会の副会長を務め、その宣教活動を支援していました。

1851年、ストークスはロンドン王立協会の会員となり、その後その幹事となり、1885年～1890年にはロンドン王立協会の会員-社長となりました。1849年から1903年までケンブリッジ大学のルーカス教授。1852年に光の研究で王立協会からラムフォード・メダル、1893年にはコプリー・メダルを受賞。ストレットのおかげで、1889年には男爵に昇格し、フランス学士院からアラゴ勲章を授与され、ロシア帝国軍医学校のメンバーとなりました。

ストークスのスタイルを評価し、彼についての本を書いたJ.ラーモアは、次のように述べています：ストークスの極端に慎重な研究発表の特徴は 質量で捉えた物質の性質と規則性に言及した定義の一般的なトーンで、正確さ、厳格な定式化は、分子という概念を使用することも必要としないようです [12, p.329]。

ストークスの仕事は、当時の科学文化の有機的な一部となりました。19世紀や20世紀の科学者たちがストークスの仕事を数多く紹介していますが、彼らの研究でストークスの研究結果に磨きがかけられ、発展したことは、彼の努力が無駄ではなかったことを証明しており、現代の科学のさらなる進歩を刺激する肥沃な材料となっています。

科学の古典の遺産
ストークスの発見-まず、ストークスの法則、ストークスの定理、ストークス・シフト、ストークスの方程式とそのパラメータ-は、科学技術の世界に入り込み、外国とロシアの科学者の開発活動を活性化させた。1909年にN. ボーアがレイリー理論を指定してストークス法にも言及していることを思い出していただければ十分です。

J.G.ストークスの存命中、彼の科学研究はM.ファラデー、J.C.マックスウェル、D.P.ジュール、H.R.ヘルツ（彼らはそれぞれ1867年、1879年、1889年、1894年に他界）、W.トムソン、W.ラムジー、J.W.ストラット、そして他の同僚たちによって続けられました。彼らとの会話や議論の中で、彼は新しいアイデアを得て、豊かになり、インスピレーションを得て、創作活動の中でさらなる発見をするきっかけを得ました。

彼の発見は、ストークがいなくなった後も科学者たちの想像力をかきたて、新たな成果へと導きましたが、今度は量子論と相対性理論の観点からです。H.A.ローレンツ、M.K.E.L.プランク、A.アインシュタイン、N.ボーア、A.A.マイケルソン、R.E.ミリカン、A.H.コンプトン、A.F.ヨッフェ、Y.I.フレンケル、S.I.バビロフなどの20世紀の科学者たちが、J.G.ストークスの思想の発展に貢献してきました。

ストークスは研究に関する本を書かなかったが、王立協会、英国科学振興協会（1869年に会長に就任）、ヴィクトリア研究所などの科学団体の論文発表数では、最も多作であった。彼の研究の成果は論文に反映され、各国の同僚との文通の対象となった。

ストークスの著作は、『数学・物理学論文』（1880-1905）の5巻に集められて出版されたが、そのうちの最初の3巻は彼自身が編集したものである。最後の2巻は1905年に彼の死後に出版されたもので、ストレットが書いた死亡記事が掲載されています。

1907年には、ストークスの簡単な伝記と、J.ラーモアが作成した彼の科学的な書簡が2巻で出版されました。また、若い才能を奨励するためにストークス財団（英語や外国人科学者による講演講座）も設立されました。

ジョージ・ガブリエル・ストークスは1903年2月1日、ケンブリッジで83歳で死去した。ミルロード墓地に埋葬されている。残念なことに、彼の墓は妻と二人の子供の墓とは違って保存されていません。ストークスの名誉を冠して命名されたのは：CGS単位系の粘度単位、月と火星のクレーター、鉱物ストークサイトです。

Литература
1. Клейн Ф. Лекции о развитии математики в XIX столетии. Т. 1. М., 1989.
2. Столетов А. Г. Собрание сочинений. Т. 1. М.; Л., 1939.
3. Погребысский И. Б. От Лагранжа к Эйнштейну. М., 1996.
4. Стрэтт Дж. В. (лорд Рэлей). Волновая теория света. М., 2015.
5. Эйнштейн А. Собрание научных трудов. Т. III. М., 1966.
6. Творцы физической оптики: Сборник статей. М., 1973.
7. Эйнштейн А. Собрание научных трудов. Т. I. М., 1965.
8. Кирхгоф Г. Избранные труды. М., 1988.
9. Вейль Г. Математическое мышление. М., 1989.
10. Лебедев П. Н. Собрание сочинений. М., 1963.
11. Капица П. Л. Эксперимент. Теория. Практика. М., 1981.
12. Тимошенко С. П. История науки о сопротивлении материалов. М., 1957.

1 Ротор векторного поля показывает, насколько и в каком направлении закручено поле в каждой точке.

2 Луи Мари Анри Навье (1785–1836) — французский математик и механик, один из основоположников теории упругости, с 1824 г. член Парижской академии наук.

3 Кинематическая вязкость — отношение динамической вязкости плотности среды к жидкости, дает понятие о ее вязкости под действием силы тяжести (измеряется вискозиметром по времени вытекания из калиброванной емкости).

4 Аберрация света — изменение видимого положения светила в небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли.

5 Михаил Сергеевич Молоденский (1909–1991) — советский геофизик, гравиметрист и геодезист. Разработал теорию использования измерений гравитационного поля Земли для целей геодезии. Предложил метод астрономо-гравиметрического нивелирования, новый метод определения.

6 Николай Павлович Неклепаев (1886–1942), ученик П. Н. Лебедева, исследовал вместе с ним поглощение акустических волн, преподавал в Московском университете, затем был ассистентом при кафедре физики Саратовского университета.

7 Институт Виктории (или Философское общество Великобритании) был основан в 1865 г. как ответ на публикацию книги Ч. Дарвина «О происхождении видов...». Институт Виктории пользовался значительным успехом в конце XIX в., когда Дж. Г. Стокс был его президентом (с 1886 г. до своей смерти). Максимальное число членов — 1246 человек — было в 1897 г., но быстро упало до менее чем трети от этого количества в первые два десятилетия XX в. Дж. К. Максвелл неоднократно приглашался для вступления в институт, но, хотя он и был набожным евангелистом-христианином, он отказался от приглашений из-за узости тематики и консерватизма института.

ストークスの光の波動理論の研究
ちょうどこの頃の科学の世界では、物理学の機械化や弾性理論の基礎とともに、光の波動説が生まれ、O.J.フレネルの「準固体エーテルは動く物体に部分的に付随する」という仮説が出て、エーテルの数学的な理論も登場してきました。このような展開の中で、ストークスは重要な役割を担い、特に光学の発展に大きく貢献しました。ストークスは生涯にわたって光の波動理論の支持者であり続け、適切な数学的装置を使用し、実験はニュートンとほぼ同じ条件で行われました。［訳注）ニュートンは光の粒子説でした］

上図は，ストークスシフトの概念図．これは、吸収スペクトルと放出蛍光スペクトルのずれを示しています．横軸は波長です．蛍光スペクトルは吸収スペクトルより波長が長い．

ストークス（彼の多くの同時代人と同様に）は光の収差、ニュートンリング、光の干渉と偏光、および媒質を通過する波動、スペクトルなど光学現象を研究しました。ストークスの波動理論への貢献は非常に大きい。彼の学生であるストレットは論文「波動光学理論」で、J.G.ストークスを（O. J.フレネルに次ぐ）引用数2位としました。 [ 4、p.206]

1852年、ストークスは電磁波の偏光ベクトルを表す量を提案しました。彼によって導入されたパラメータは、列ベクトルであり、光強度の次元を持つています。詳細なパラメータは、総強度、偏光度、および楕円偏光度を使って、インコヒーレント光や部分偏光を記述できます。

ストークスは、蛍石（フルオライト）の観察中に発見した発光も扱っています。同じ1852年に、ストークスは、フルオライトによって放出された光線は吸収された光線よりも屈折が少ないという結論に達しました（後にE.K.J. vonロンメルとS.I.バビロフによって一般化された）。蛍光の波長は励起光の波長より長い。ストークスにちなんで名付けられたこの規則は、蛍光（フォトルミネッセンス）の量子性を示すものだったのです。

1879年、ロンメルは、スペクトルの一部で放射周波数が励起光の周波数よりも高いことを発見しました。ストークスの法則と矛盾するスペクトルのそのような部分は、反ストークス線と呼ばれていました。ストークスは、ニュートンが提案したクロスプリズムの方法に続き、クロスフィルターの方法による発光の観測を導入し、発光を利用した近紫外領域の検出・研究方法を提案しました。

1905年、アインシュタインは彼の記事「光の出現と変換に関する発見的観点について」で次のように述べています [ 5、p.103]。光が量子で構成されている場合、ストークス規則からの逸脱は2つの理由で可能です。1つは、単位体積あたりの量子の数が多い場合（励起された光の量子は多くの励起された量子からエネルギーを受け取ることができます）。第二に、発光中に放出された量子のエネルギーが励起量子のエネルギーよりも大きい場合。

ストークスの時代には、発光に関する研究は偶然の性格を持つものでした。バビロフはその基礎研究に人生の30年を捧げました。ストークスの法則の限界を決定し、熱力学の第二法則の始まりとストークスの法則を関連付け、発光の絶対収量を定式化し、その種類を分類し、放射体の性質に関連づけたのは彼でした。そして1950年には「光の微細構造」にまとめている。その少し後にバビロフは、主にストークスのルールを含むいくつかの一般的な法則を発見したにもかかわらず、発光は物理学の人里離れた島のままであると書いた。アインシュタインがストークスの法則の意味を説明できたのは、1905年の量子論に基づいてのことです。1913年にはボーアの原子構造の量子論によって、発光の全分野、そのすべてのセクションの主要な特徴が明らかになりました[6, p.335, 338]。

エーテル理論のどれが正しいと考えられていますか？
ストークスは長寿だったので、エーテルのいくつかの理論の変遷を見ました-エーテルとは、その振動が可視光を含む電磁波として現れるような一種の万能媒体です。O. J.フレネル、O.L.コーシー、W.トムソン、H.A.ローレンツ、J.A.ポアンカレ、M.C.E. L. プランク、等がエーテルの解釈を提案しました。ストークスも関心がありました。

異なる科学者の考えにおけるエーテルは、均質性、圧縮性などの程度、および軌道上を移動するときに地球によって運び去られる程度が異なっていました。エーテルの特性についての理解に応じて、科学者はマクスウェルの方程式をさまざまな方法で解釈しました。ご存知のように、ストークスとトムソンはそれを抑制して扱いました。エーテルの否定は、アインシュタインによる相対性の理論の後です。

特に、フレネルはエーテルが非圧縮性であるという仮説を提唱しましたが、それは物質中を透過するのが困難である横方向のせん断を可能にします。ストークスは、樹脂のように、エーテルは急速な変形の間は剛体のように振る舞い、惑星が動くときはプラスチックのように振る舞うという事実によってこの困難を説明しました。1839年、コーシーは収縮するエーテルの理論を作りこのモデルを改善、これは後にトムソンによって洗練されました。

1845年に収差の理論（ある基準座標系から別の基準座標系に移るときの光の伝播方向の変化）を作りました。ストークスは、地球が移動するときに周囲のエーテルも運び去ると仮定して、その結果、地球表面のエーテルの速度は惑星の速度に等しくなります。科学者は、いっしょに運ばれるエーテルの動きが、惑星を取り巻く空間とそれが静止している領域の両方で渦なしの特徴を持っていることを認めました。ストークスによれば、エーテルは硬くも柔らかくもあり、通常は液体媒体のような振る舞いをします。

銀河のエーテル風の流れによる地球表面の流れの架空図（左）（1- エーテル圧力が上昇したゾーン; 2- エーテル圧力が低いゾーン; 3- 海からの水分捕捉のゾーン; 4- エーテルのトロイダル渦が冬に大気を捕捉する）、および、科学者が自然界にエーテルを探せなかったことの風刺画。

ストークスは、収差効果について次のような説明を提案しました。地球の表面から一定の距離になると、エーテルの巻き込み部分とエーテル全体の速度差が現れるはずで、この差により、光学素子に当たる光波の前面が回転してしまう。これが収差を惹き起こします。ストークスは、エーテルの運動が渦なしの速度ポテンシャルの形であることを証明する計算で説明を補足しました。その後、プランクはストークスの理論を肯定的に捉え、それを救おうとしたが、役に立たちませんでした。

ストークスは、エーテルの巻込み程度が、その密度の違いだけに依存するのではないことも指摘しました。エーテルは物質の中に入ると圧縮され、離れると希薄化して物質の粒子に引き寄せられることが予想されます。弾力性のあるエーテル論は、非常に長い間、科学界に根付いていました。実際、ストークスをはじめとする当時の著名な物理学者たちは皆、その性質や本質を一般的に解明することに取り組んでいました。

1846年、ストークスは次のように書いています：我々は、よほどの理由がないと、エーテルが地球の固体質量の中を完全に妨げられずに移動するのを信じることができません。しかし、それを正しいと考える理論をチェックする決定的実験は非常に有用であろう[7, p.235]。1881年、A.A.マイケルソンは、J.G.ストークスが仮定したように、エーテル風が地球によって運び去られることを実験で確立したように見えた。しかし、エーテル否定の結論はまじかに迫っていました。

ストーク自身も、エーテルの概念に固執した彼の同僚も、その本格的な理論を作ることができません。I.フィゾーの発言によると、1851年に提示されたエーテル仮説の中には多かれ少なかれ可能性はあるが、どれも証明されたとは考えられません[6, c.214]。10年後のストークスは、仮説の長所と短所について議論を続けたが、彼自身はこれが成功するとは期待していませんでした。

ストークの死後、1905年には、アインシュタインは、相対性理論と光速不変を提唱しました。その結論によると、これらの前提条件は単純で矛盾のない移動体の電磁気学を構築できる。光を運ぶエーテル」の導入は、余計なものに見えます[7, с. 8]。この瞬間から、ストークスの理論だけでなくエーテルに関する数多くの理論がその価値を失うことになりました。

■今回の節では，ストークスの研究のうち，光の波動論とエーテル仮定を扱います．前者は成功しましたが，後者は無意味でした．

偏光状態を表示するストークス・パラメータ，反ストークス線については，
訳者が別稿で解説する予定です．

科学者であるストークスは、数学から美的快楽と実用的満足感を得た。半収束級数の指摘、完全収束または限定的収束の無限級数の研究、整数列と級数の一様収束の概念の導入、ベクトル解析に取り組んだ。彼が提案した最も重要な公式の一つは、彼の名が冠されたストークスの公式です。

［訳注］
ベクトル場の回転を閉曲面上で面積分したものは、ベクトル場を閉曲面の縁で周回線積分したものに一致するというものです。

ベクトル場A(x,y,z)とは、平面あるいは空間の各点でベクトルが定義されているものです。例えば、天気予報で風の向きと強さが矢印で描き込まれたマップをよく目にすることがあるでしょう。
ベクトルの回転は，上の式でrotAと書かれているものですが，ベクトル解析は別の稿にまわします。話をもとに戻します。

1849年には友人のトムソンがストークスからこの公式を入手しています。ストークス自身は、1849年から1882年まで毎年行っていた数学の試験にこれを含めることが有用であると考えていました。 1910年には、ドイツの理論物理学者A.I.W. Sommerfeldがストークスの結論を4次元空間に一般化しました。J.C.マクスウェルは、彼の論文 "On Faraday Force Lines" (1885-1886)で、ストークスの結論をベクトル解析の重要な定理として、C.F.ガウス、J.グリーン、M.W.オストログラドスキ、W.トムソン、そしてもちろん、J.G.ストークスの名を冠した。

当初、科学者たちは、液体や気体の力学と固体の力学には共通点がないと考えていました。しかし、1845年、ストークスは固体と粘性液体の共通の性質を発見しました。固体物質の可塑性が高まると弾性が低下し、固体は液体状態になっていくという結論です。ストークスの考えは価値あるものであることが証明され、その後の一連の科学的研究を刺激しました。

フランスの科学者L.M.A. ナビエ, O.L. コーシー, S.D. ポアソンなどが粘性流体の研究に成功しました。ストークスは1849年に彼の論文「移動する流体の内部摩擦の理論と弾性固体の平衡と運動について」で、粘性流体と気体の微分方程式を導出することによって、ナヴエの理論を補完しました（分子の概念とは無関係です）。これらは今日ではナビエ・ストークス方程式として知られています。この科学者に敬意を表して、CGS単位系で動粘度の単位は、後にストークス（ロシア語表記：St、国際St）と呼ばれるようになりました。国際単位系では、粘度のSI単位はm^2/sです。

ストークスは層状境界層の理論も構築しました。彼は乱流における層流の遷移の事実を確立した - 最初は液体の流れる水道管や物体に対して（研究は抵抗の値に境界層の剥離の影響を研究するために実施された）。時を経て、船、航空機、タービン、蒸気機関の高速化に起因する乱流の理論が大きく発展しました。

科学史家 I.B. Pogrebyskii が定義したような、物理的側面への注目、実験結果の考察、運動の明確な運動学的描写、オリジナルの動的原理の網羅的な定式化、これらすべてが、理論の成功した応用と組み合わされて、ストークスの研究は粘性流体の理論に関する更なる研究の主要な出発点となりました [3, p.127]。

分子間の距離や分子間の相互作用による液体速度の不規則な成分を無視して、ストークスは液体粒子の近傍での液体の平均的な規則速度のみで計算しました。彼が粘性流体の運動方程式を導出することを可能にしたのは、流体粒子のひずみ速度の6つの成分に対する応力の6つの成分の線形依存性に基づくと仮定したからです。

流体を連続的な媒体として考えたストークスは、「内部摩擦」の概念を採り入れ、その計算に基づいて、円柱内の粘性流体の回転に関して、ニュートンの解析を修正した。ストークスが示したように、ニュートンの間違いは、液体中の隔離された各層の外部表面と内部表面に作用する摩擦力のモーメントの代わりに、力そのものを考慮したことである。ニュートンは、流体粒子の1回転の時間が円筒状の層の半径に線形に依存することを発見し、ストークスの結果から、時間は半径の2乗に比例することがわかりました。その結果、円筒管内の定常流における粘性非圧縮性流体の流量についても、ハーゲン-ポワズイユ式を理論的に説明できるようになった。やがてストークス自身も、速度の時間変化の法則を記述した微分方程式を得ました。

1851年、科学者は、束縛されていない粘性流体の中で、そのゆっくりとした均一な運動の間に小さな固体球に作用する抗力Fの公式を導出しました。ストークスの公式はＦ＝６πＲηｕ形です。ここでＲとｕは球の半径と速度、ηは流体の動的粘性係数で、この法則は非常に小さな半径でも真であることが判明し、A.アインシュタインは後に糖分子の半径を測定するためにこれを使用しました。

ストークスの法則は、新しい研究で広く使われました。私は、A.アインシュタインによるブラウン運動の計算、J.J.トムソンによるイオンの電荷の決定、R.ミリカンによる電子電荷の決定を思い出します。ミリカンの実験と自身の実験を分析した結果、ミリカンがストークスの公式で誤って空気粘度の値を使ったので、素電荷を正確に決定することができなかったことがわかりました。このチェックの結果は、ストークスの法則の正しさの確認になりました。

論文 "移動する流体の内部摩擦の理論について" (1845) で、ストークスは物体が等時性振動を起こすのは、小さな変形範囲では、物体に生じる応力が変形量に比例するという事実によることを示し [4, p. 116]、橋梁のたわみについても研究しました。ウェールズの鉄道橋の崩壊を知り、変形したときの鋳鉄の脆さが原因であると解明しました。ストークスの橋梁の動的たわみに関する研究は、工学的な応用研究に近いものです。
弾性の理論を扱い、弾性体と塑性体を考察し、自然界では弾性と塑性は切り離せないものであり、実際には両者の間には急激な変化はないと考えました。

ストークスはまた、液体の中での音の吸収についても研究した。しかし、彼は粘性を散逸（散逸）メカニズムと考えながらも、熱伝導率を考慮に入れていなかったため、彼の分析は不完全なものでした。しかし、J. R. von マイヤー、J. P. ジュール、H. L. F. von ヘルムホルツがエネルギー保存法則を発見（当初は不信感を持って科学界に受け入れられていた）をするまでは、これを解決できませんでした。

ストークスは科学活動の初期の頃から、主要な力学者、流体力学者としての地位を確立していました。F. E. ノイマン、J.A.ポアンカレ、P.M.M. デュエム、T.レヴィ＝チヴィタ、M.V.オストログラドスキー、P.L.チェビシェフのように、彼は力学の理論的基礎の開発に貢献しました。同時に、弾性理論は、彼によって開発されました。 1860年代までに。若いジョージ・ストークスは、ケンブリッジの科学界で、理論力学、数理物理学、水力学の熟練した研究者として、光学の専門家として、同時に新世代の科学者たちの辛抱強く親しみやすい教育者としても知られるようになりました。

ジョージ・ガブリエル・ストークスの生誕200周年の節目に
«ПРИРОДА» №1, 2020，ロバート・シュチェルバコフより，
教育学博士（エストニア，タリン）

https://elementy.ru/nauchno-populyarnaya_biblioteka/435633/Dzhordzh_Gabriel_Stoks_klassik_matematicheskoy_fiziki_KhIKh_veka

J.G.ストークス（1819-1903）は、アイルランド出身の英国の数学者、機械工学者、物理学者：理論力学、流体力学、弾性理論、振動理論、光学、数理物理学、数理解析。彼はロンドン王立協会の会員であり、その秘書兼会長を務め正確な科学を推進した。

19世紀のイギリスでは、数学的分野とともに物理学的分野も発展しました。伝統的な自然哲学（当時は自然科学と呼ばれていた）から、独自のアプローチと方法を持つ独立した科学、物理学が誕生し、最初の物理研究所が誕生しました。

彼の同胞の多くと同様に、J.G.ストークスは、19世紀の自然科学の中心地であったケンブリッジの伝統を大切に守り発展させました。理論的な力学と光学の問題を解くために、まず第一に数学的方法を用いることです。研究に実験を適用することはごくまれでした。

科学者としてのストークスの形成

プロテスタント福音司祭ガブリエル・ストークスの6人の子供の末息子であるジョージは、1819年8月13日にアイルランドの村で生まれました。

家族は宗教的であり、彼の兄の3人は後に司祭になりました。そして彼自身、科学に専念し、生涯を通じて世界に対する彼の宗教的な世界観を保持しました。

1835年には 16歳のジョージはイギリスに渡り、ブリストルカレッジに入学しました。2年間の見習い生活は、彼の数学的能力の開発に重要な瞬間であり、ケンブリッジでの彼の研究のために自分を準備するのに役立ちました。1841年、ストークは大学で教育を受け、ケンブリッジでは教職にも就き、1849年には数学のルーカス・チェア（世界で最も権威のある学術的地位であるルーカス数学教授を、記録的な54年間務めた）を受けました。当時はJ.ニュートンが会長を務めていました。

ストークスは66年間の科学的活動において、機械工学と光学の古典的な研究から、地球の重力場、仮想エーテル、スペクトル分析の応用まで、彼の世紀の物理学のほぼすべての分野をカバーしました。ただし、電磁気学だけは彼の興味の外になりました。これらの科学分野では、ストークスは、数学的方法のエキスパートだったので非常な成功を収めました。

F.クラインが強調したように、イギリスの数理物理学は、ストークスとウィリアム・トムソン［訳注）やはりアイルランド出身で同時代の物理学者］がケンブリッジの若い才能に現れて以来、途切れることなく華麗な上昇を続けました。ストークスは1837年から死までの66年間、最初は研究者として、次に教育者および管理者として、ケンブリッジに住みました。優しい個性で、彼の広範で継続的な非常に有益な活動を行いました [1, p. 259]。

ストークスは、ケンブリッジのペンブローク大学の部屋で数学を応用して実験を開始しました。1871年から1872年にかけて、イギリスの科学者たちがオックスフォード研究所や（J.C.Maxwellの努力により）ケンブリッジ大学のキャベンディッシュ研究所などの物理学研究所を設立したのは、正確な体積測定の必要性が高まってきたからに他なりません。52歳のストークスにとっては残念ながら、少し遅かった。

開所当時、J.K.マクスウェルの研究室を訪れたA.G.ストレトフによると、当時、物理学の研究は長い間、数学のコースに含まれており、物理学のための特別な学科の存在は、その用語自体と同様に新しいものでした。1871 年までケンブリッジでは数学の一部としての光学と化学の一部としての熱の章だけが教えられていました。電気と磁気の広範な科学は全く教えられていませんでした [2, p. 342]。

おそらく、このことが、数学、理論力学、光学、仮想エーテルなどの科学活動の方向性と、そのような英国の科学者（ストークスを含む）の選択ができたのでしょう。ストークスは時折、今日の基準では最も単純な実験的調査を用いて、彼が既に行った理論的な結論を徹底的にチェックしました。

ストークスの研究における力学と流体力学
J.G.ストークスは、J.グリーン、W.トムソン（ケルビン卿）、W.J.M.ランキン、O.レイノルズ、J.W.ストラット（レイリー卿）らとともに、数学的手法の開発に成功した。- 数学的方法の開発に成功し、古典的な数学物理学の発展に貢献し、当時の物理学や工学の問題に数学を適用した。その世代の科学者のおかげで、熱伝導、拡散、弾性と運動の安定性の理論、振動と波動の過程、光学、電位理論と電気力学の多くの問題を解決するために数理物理学の方法が開発されました。これらの方法は、現代の物理学、工学、産業界に関連しています。

J.G.ストークスの親しい同僚、教え子、友人たち。
左から、J.C.マックスウェル、J.W.ストラット（レイリー公）、W.トムソン（ケルビン公）。

コンスタンチン・ボグダノフ
「クォンタム」2014年第4号、第5号、第6号、第7号、第8号

エンペドクレスは、2500年前にシチリア島に住んでいた古代ギリシャの哲学者、医師、司祭でした。

エンペドクレスは、万物は土、空気、火、水の4つの要素で構成されていると考えました。愛と憎しみ、あるいは好きと嫌いという二つの対立する力は、これらの要素に影響を与え、それらを統合しあるいは分離し無限の様々な形を作る。

私たちの時代は、物質は原子と分子で構成されていることを誰もが知っており、エンペドクレスの推論は、笑われてしまいますが、エンペドクレスが語った無限の多様な自然は、分子および原子の化学反応に置き換えることができます。

そして、愛と憎しみ、共感と反感はどのような関係があるのでしょうか？
例えば、一枚の紙がコップ一杯の水を愛したり、マッチが石けんを憎んだりすることは、どのようにしてできるのでしょうか？

有名なレオナルド・ダ・ヴィンチが言ったように、真実を判定する唯一の基準は実験であるから、これらの質問に答えるために、簡単な実験を設定しましょう。

実験1.一枚の紙は水の入ったグラスを好むのか？

厚手の紙から一辺15cmの正方形を切り取ります。壁のカレンダーのカバーはこの目的に最適です。水道水の入ったグラスを取り、それを四角い紙で覆い、そっと裏返し、紙をグラスにしっかりと押し付けます。

グラスを裏返し、水の動きが止まったら、紙の保持をやめて手を横に離します。私たちがすべてを正確に行えば、一枚の紙は水の入ったグラスからはがれず、いわばそれに引き付けられます（下の写真を参照）。エンペドクレスは正しい。一枚の紙が水の入ったグラスに恋をしました？なぜこのようなことが起こるのでしょうか？

実験2.なぜマッチは石鹸を嫌うのか？

大きな容器（料理やゼリーの下ごしらえ用のトレー、直径30cm以上の深鍋や鍋、バケツや湯船でもOK）を持っていく。石鹸液の残りを洗い流し、冷たい水道水で満たしておきましょう。次にマッチを持って、その頭を任意のシャンプーに一瞬だけ浸してから、このマッチを水面にそっと置いて離します。マッチの頭が水に触れた「石けんスポット」からすぐに離れるのがわかります（下の写真）。それはまるでマッチがエンペドクレスの言葉を借りれば、石鹸液を嫌って純粋な水に寄り添うかのようだ。なぜ？

実験１と実験２を説明するためには、まず、エンペドクレスの要素の一つである空気が何であるかを知る必要があります。人間は空気なしでは生きられないことを誰もが知っています。私たちの体は空気中に含まれる酸素を必要としています。空気の存在を検出するのは非常に簡単です。これを行うには、あなたが紙のシートを持ち、団扇のようにそれを振ると、移動する空気を顔に感じるでしょう。

 地球の表面の上にある空気の層の厚さ-約100キロ。この地球の空気層は大気と呼ばれています。空気は水の約1,000倍の軽さですが、大気はかなり大きな力で私たちの体の表面のあらゆる部分を押しています - １平方センチメートルあたりの力は、１kgの重さに等しいのです。この圧力を大気圧といいます。

山上の大気の厚さは海上よりも薄いので、山上の高いところの空気は圧縮されておらず、気圧が低いということになります。例えば、エルブルス山の頂上では、気圧がソチの半分になっています。

気圧は登山時だけでなく、気温や湿度の変化でも変化します。モスクワの気圧がトゥラ［訳注）モスクワの南100kmにある］よりも低くなると、トゥラからの圧縮された空気がモスクワに向かって移動し始め、南風が吹きます。そのため、気圧を測定することで、天気予報に役立ちます。

フランスの有名な科学者ブレイズ・パスカルは、登山中に気圧の存在を証明し、その低下を実証した最初の科学者です。さらに、パスカルは最初の機械式計算機を設計しました。圧力測定の単位（1パスカル＝1N/m^2）とプログラミング言語の一つにパスカルの名前がついています。

実験3.水から空気を作る方法は？
これは大人の目の前で行うのが一番です。ビニール袋に少量（30ml）の水を入れ、空気を絞り、上部でしっかりと縛ります。そして、袋を電子レンジに入れてスイッチを入れます。数秒後に袋が膨らみ始め、約1分後には電子レンジのほぼ全容量を占めるほど膨らみます。

袋がかなり熱くなることがあるので注意が必要です。2つの質問に答えてください。
1.密閉された袋の中の空気はどこから来たのか？
2. 密閉された袋の中に水を入れていない場合、電子レンジはスイッチを入れたらどうなるでしょうか？

この実験と実験１の説明("一枚の紙はコップの水が好きなのか？") の動画があります。

実験３「水から空気を作るには」では、エンペドクレスの一つの要素（水）から別の一つの要素（空気）が生まれました。実験では、水と空気は熱したり冷やしたりするとお互いに変化し、なんとなく似たような感じになることがわかりました。電子レンジで加熱すると密閉された水の入った袋が膨らんでしまう理由がわからなかった方は、こちらで解説しています。

実験４．グラスはなぜ歌うのか？

この実験は、大人の目の前でやった方がいいと思います。実験には2つの同じグラスが必要です。片方は半分を水で満たし、もう片方は空けておきます。空のグラスの足（スタンド）を左手でテーブルの表面に押し付けます。次に右手の人差し指を水で湿らせ、空になったグラスの上端に沿ってゆっくりとまわしながら、端の指の圧力を少しずつ高めていきます。圧力が十分であれば、この指の円運動で音が出ます。次に、半分が水で満たされたグラスで同じことをします。水の入ったグラスが低い音を出すのが聞こえてきます。

2つの質問に答えてください。
1. なぜグラスが歌い始めるのか？
2. 歌うグラスに水を入れると音程が下がるのはなぜ？

この実験の動画は、Quanticsのウェブサイトに掲載されています。https://old.kvantik.com/files/materials_2014_06.html

イギリスの科学者ロバート・フック(1635-1703)は1660年に、力とそれが引き起こす固体の変形を結びつける法則を発見しました。この法則は、現在ではフックの法則と呼ばれていますが、身体の弾性変形は力の大きさに正比例するというものです。ラテン語では、フックはこの法則を次のように記しています。"Ut tensio, sic uis" 文字通りの意味は "力と同じくらい伸びも同じくらい" 当時、科学者たちは、他人に流用されることを恐れて、発見を暗号化することがありました。フックは彼の法律のラテン語の言葉からアナグラムを作った - アルファベット順に文字を並べ替えた。"ceiiinosssttuu". 彼は1676年にこのアナグラムを発表し、1678年に解読しました。

フックが残した多くの発見や発明の中でも、彼の最も重要な技術的発明である、当時としては前例のない精度を持つ懐中時計について言及しなければなりません。1日1分の誤差を達成しました。このような高い精度を確保するために、フックはアンカー機構（図1）とスパイラルスプリング（図2）を時計のデザインに取り入れました。フックの発明以前は、時計は15分以上の誤差で進んだり、遅れたりするので、毎日巻かなければなりませんでした。19世紀末までにフックのゼンマイ時計は改良され、その精度はさらに10倍に向上し、船乗りは正午の時刻を確定し、海上での経度を0.5度の精度で知ることができるようになりました。

実験４「グラスはなぜ歌うのか」では、ガラスの縁に沿って濡れた指を動かすとガラスが鳴りました。ガラスは川の砂でできており、他の岩石（花崗岩、大理石、石灰岩など）とともに地球の地殻の一部であることが知られています。このように、ほとんどすべての固体は、エンペドクレスの「土」の要素と考えることができ、そのすべてが音源となりうる。では、なぜ固体の接触が音の発生につながるのか、その疑問に答えてみましょう。

実験4 "グラスはなぜ歌うのか？"

グラスがなぜ歌うのかを理解するためには、まず音とは何かを理解する必要があります。これは別の記事で取り上げますが、今のところは「音は空気の振動である」と言っておけば十分です。

固体の振動を伝達して、空気が振動することがよくあります。例えば、人が話すと声帯が喉の中で振動して声が出る。人がギターを弾くとき、弦を揺らしたり、捻ったり、指で叩いたりして音を出します。少し違うのは、バイオリンを弾いた時の音です。ミュージシャンが弓で弦をこすると、摩擦で弦が引っ張られている状態になりますが、弾性力はそれを引き戻す傾向があり、この力が摩擦力を超えるとすぐに、弦は戻り繰り返され、音が聞えます。

歌うグラスは、バイオリンとほとんど同じです：グラスの縁に沿って指を走らせると、皮膚の小さな凹凸がグラスにまとわりついて、グラスが振動します。バイオリンの弦との違いは、これらの振動がミクロなもので、目で見ることができないことです（指で感じることはできますが）。しかし、グラスの中に水がある場合は、グラスの水面に波が現れるのを見ることができます。これは、ガラスが本当に振動していることを意味します。

実験を成功させるためには、ガラスと指が油っぽくないことが重要です（摩擦力がここで働くので）。

水の入ったグラスの方が水の入っていないグラスよりも低い音がするのはなぜでしょうか？
正確な説明は簡単ではありませんが、おおよその現象は次のように説明できます。
空気の振動をゆっくりとさせるような音が、私たちには低く見える。
ここで、バネ振り子で、バネに重りをつけたものを想像してみましょう。Kvantikのサイトに投稿された動画では、プラスチック製のバネとミカンで作れるバネ振り子の振動を確認することができます。経験上、ミカンのあるバネは、ない場合に比べて、はるかに振動数が小さいことがわかります。実際、荷重が大きくなるほど、バネが元の位置に戻るまでに時間がかかります。グラスに水を入れると質量が増えるので、ミカンをくっつけたときのバネのように振動数が小さくなります。

http://kvantik.com/files/materials_2014_07.html

ーーー

2つのフォークを取り、それらを組み合わせ、それらの間の隙間に木製のつまようじを刺します。次に、この構造をガラスのゴブレット（または背の高いグラス）に置き、つまみでガラスの端にのみ触れるようにします（右の写真を参照）。同時に、構造物が落ちないように、端にしっかりとぶら下がるようにしてください。これが実際に実行できるという事実は、Kvantik Webサイトのビデオに示されています。

次に、2つの質問に答えましょう。
1. 　2つのフォークと1つのつま先の構造が非常に安定しているのはなぜですか？
2.　この構造の重心はどこにありますか？

古代ギリシャの有名な科学者アルキメデス（紀元前287～212年頃）は、彼の2世紀前に世界の根源を4つの要素としたエンペドクレスがいたアクラガス（現在のアグリジェント）の町から100キロ離れたシラクーサ（シチリア島）に住んでいました。アルキメデスは幾何学が好きだったので、いくつかの物理法則を発見し、そのうちの1つには彼の名前が付けられています。

アルキメデスの法則は次のように述べています：液体（または気体）の中に沈められた身体は、身体によって変位された液体（または気体）の重量に等しい力を受けます。紀元前1世紀に生き、ユリウス・シーザーの時代にローマの水道橋を設計したローマの建築家ヴィトルヴィウスの書物から、世界は初めてアルキメデスの法則を知った。ヴィトルヴィウスによると、アルキメデスは入浴中に自分の法則を発見し、その直後に裸で家から飛び出し、ギリシャ語で「見つけた！」という意味の「ユリイカ！」と叫び始めたという。

アルキメデスが発見した同じように有名な法則に「てこの法則」があります。古代ギリシアの作家プルターク（45-127）は、アルキメデスが「てこの法則」を利用しようとした珍しい方法を伝えます。アルキメデスは、友人でもあり身内でもあるギエロン王に、与えられた力でどんな重さでも動かすことができると書いたことがあります。要するに「支点をくれたら世界をひっくり返す」ということです。

アルキメデスは、物体の重心の概念を最初に導入し、三角形や平行四辺形の形をした平たい物体の重心の位置を求めた。忘れてしまった方のために、物体の重心とは、その物体の重力の力（地球に引き寄せられる力）が集まる点です。覚えておきましょう。

壁に打たれた釘に物体を吊るすと、数回の振動の後、物体は静止し、その重心は懸垂点の下、つまり懸垂点から垂直に下っていく線上にある。この重心の性質を利用して、図に示した図形の重心の位置を求めてみましょう（Kvantikのサイトの動画も参照してください）。まず、A点から物体を吊り下げ、落ち着いたらA点を通って赤い線を縦に引きます（右図のように）。次に、同じようにB点から物体を吊り下げて青い線を引きます（右図のように）。この図の重心であるC点で線が交差していることがわかります。多くの場合、物体の重心がこの物体の外にあることもあります。Kvantikのサイトに掲載されている動画を見ると、2つのフォークを繋いだ時の重心が2つのフォークの間にあることがわかります。

実験5　 なぜフォークは落ちないのか？

2本のフォークをつまようじで固定した構造が、ガラスの端に置いたときに非常に安定していることを示しています。安定している理由は、構造物の重心が支点の下にあるからです（左の図で重心が青、支点が赤で表示されています）。この説明が本当なのかどうかは、もう一回実験してみると（Kvantikのサイトの動画を見てください）わかると思います。

実験６　ボールはどうしてグラスの中に入るのか？

卓球のボールとグラスを持って、テーブルの上にあるように置きます。手などでボールを触らずにグラスに入れることは可能でしょうか？ボールをテーブルの端に押し付けて、グラスでキャッチするなどは禁止です。実際にこれが可能であることは、Kvantikのウェブサイトに掲載されている動画でも紹介されています。

では、2つの質問に答えてください。
1. 　グラスの中にボールを引きあげ保持する力は何か？
2. 　この実験は、グラスの壁が上に伸びている形状でも可能でしょうか？

実験6 　ボールはどうやってグラスの中に入ったか？
グラスを逆さにしてボールにかぶせ、グラスを回転させる。ボールがグラスの中で回転するようにグラスの壁をボールに押し付け続けます。グラスの口（首）の近くでは壁が先細りになっていて、その傾斜のために横だけでなく上にもボールを押し上げます。ボールの立場で見た場合、それは、遠心分離機や回転木馬のように、ガラスの壁に強く押し付けられ、グラスの軸から最も遠い領域（グラスの壁）に押し出されます。（動画を見るとよくわかります）https://old.kvantik.com/files/materials_2014_08.html

口（首）が拡大しているグラスの場合、この方法は適していません：ボールはグラスから排除されます。

アーティスト アルチョム・コシュチュケヴィッチ

参照
コンスタンチン・ボグダノフ氏による大衆科学講演会「私たちの中の物理学」，2007年12月13日，モスクワ，ФИАН

http://video.elementy.ru/fian/Bogdanov-fpff.mp4

https://elementy.ru/nauchno-populyarnaya_biblioteka/izbrannoe/432676/Chetyre_stikhii_Empedokla

https://elementy.ru/kartinka_dnya/53/Dvoynoe_lucheprelomlenie?from=rxblock
2016年5月11日 • Pavel Plechov　
この記事は簡単なので入門にはよいのですが，あまり正確ではありません．結晶光学については，物の記事で解説します．

岩塩haliteと方解石calciteの結晶
写真は、岩塩とアイスランドスパー（方解石）の結晶の大きな断片を示しています。外見上、それらは類似していますが、光学特性が大きく異なります。

岩塩結晶は立方晶系に属します。光は方向に関係なく同じ速度で結晶を通過します。このような結晶は、光学的に等方性と呼ばれます。

一方、方解石結晶は顕著な光学的異方性を持っています。結晶に入った光線は2つの互いに垂直に電場が振動する光線に分かれ、異なる速度で結晶内を移動します。一方の光線の速度は、もう一方の光線の速度より11.5％高速です［訳注：光軸に垂直に伝播する異常光のこと］。このため、複屈折、または複屈折の光学現象が発生します。各光線には独自の屈折率があり、結晶内で異なる方法で屈折します。結晶のある点に入った光線は、結晶内で異なる経路をたどり異なる場所に出て、そのうちの1つは遅れて現れます。写真は、方解石の後ろにある「кальцит」の刻印が二重に見えるのに対し、岩塩の後ろにある「Галит」の刻印では何も起こらないことを示しています。

-----
［訳注］もう少し正確に言うと，方解石の結晶構造は，３方晶系（光学的には１軸性です）．光軸方向に進む２つの偏光は同じように進む（分かれません）．それ以外の方向に進む光線は複屈折を示します．複屈折の大きさは，光軸に垂直な方向に進む光で最も大きくなります．
結晶内を伝搬する２つの偏光は，通常光と異常光と呼ばれます．通常光の伝播速度は結晶内のどの方向に伝播しても同じです．
ここで，使われている光の速度とは伝播する光の位相速度のことで，物質の屈折率をnとすれば，物質内で光の速度は1/nになります．
-----

一枚の紙にカルサイト結晶
箱の中の紙の上に横たわる方解石結晶による複屈折。
en.wikipedia.orgからの写真

偏光面を回転させて方解石の複屈折を見る
結晶の方位に対する偏光面の方向によって方解石の複屈折の大きさが変わります：en.wikipedia.orgからの描画

複屈折の効果は、1669年にデンマークの科学者エラスムスバルトリン（1625-1698）によって最初に説明されました。彼はそれをアイスランドからの船員によって運ばれたアイスランドスパーの結晶で見つけました。E.バルトリンの出版は、「神は1つの無生物を創造したので、それだけでは2つになることはできない」という同時代の人々からの大きな批判を引き起こしました。方解石の複屈折の現象そのものが、アイザック・ニュートン、クリスチャン・ホイヘンス、ジョージ・ストークスなどの科学者を悩ませました。19世紀初頭、トーマス・ヤング（1801）とオーガスティン・ジャン・フレネル（1820）による光の理論に関する研究により、アイスランドのスパーの効果が理解できるようになり、開発の可能性が開かれました。結晶光学の誕生です。

ウィリアムニコールは、1829年に最初の偏光器を設計し（したがって、偏光器はしばしばニコルプリズムまたは略してニコラと呼ばれます）、1851年から1854年にヘンリークリフトンソルビー卿は最初の偏光顕微鏡の設計を提案し、多くの分野で科学的革命を引き起こしました。偏光顕微鏡を使用すると、さまざまな鉱物や合成材料の複屈折など、物質の多くの光学定数を定量的に測定できます。［訳注：岩石を構成する鉱物の同定に使われたのが歴史的な用途です］

写真©アレクサンダーSigachev commons.wikimedia.org
サンプルはAEFersman MineralogicalMuseum

「回折の物理理論におけるエッジ波の方法」
Konstantin Bobrov, "Popular Mechanics" No. 9，2020　に，
「ロシアが起源の重要な発見と発明」という記事が載っていました．
ここには，医学・生物学，物理学，材料デバイスなどの現在発展し実用化されている科学技術で，ロシア発祥の研究が12例紹介されています．
その中で私の興味を惹いたものの第一位は，ステルス・テクノロジー（1962）の起源です．そこで，少し調べてみました．
ステルス戦闘機の技術は軍事研究ですが，1962年のUfimtevの論文は「回折の物理理論におけるエッジ波の方法」ウフィムツェフ（1962年出版）という，基礎的な電磁波回折散乱方程式で，X線散乱の論文と同程度にたいへん地味な装いです．
この論文の著者の，Peter Yakovlevich Ufimtsev（1931年生まれ），電波工学者，物理学者，数学者です．彼はさまざまな形状の航空機に対するレーダビームの散乱面積を計算できる方程式を作りました．散乱面積（レーダー反射断面積RCS）とはレーダ反射が作る飛行機の像がどのくらいの大きさかというもので，現在最新鋭のステルス機F-35などでは，野球ボールや雀位の大きさと言います．1960年代初頭に、彼が開発したエッジ波法は、推測がまだ多かったことと，散乱面積を小さくする構造は、空気力学の原理と両立せず，戦闘機の運動性能を低下させるので実用性はないと考えられていました．

したがって、Ufimtsevの論文はソ連では重要とは見なされず，世界に公開されました．この論文に注目したのは，デニスDenis Overholzerです．
1970年代初頭にロッキード社のオフィスで働いていた若いデニスは，ロシア語ができたので，ソビエト連邦で出版された技術出版物を調べることが仕事でした．デニスは高度な工学教育を受けていたため，Peter Ufimtsevの科学的研究に興味を持ち，深く掘り下げ英語に翻訳しました．
「回折の物理理論におけるエッジ波の方法」ウフィムツェフ（1962年出版）

デニスはこの論文の重要性を上級管理職に訴えましたが取り上げられず，その後，デニスはエンジニアリングスタッフに直接渡しました．その分野の真の専門家であるエンジニアリングスタッフは，Ufimtsevの仕事の重要性を理解しました．

Ufimtsevによって発見されたアルゴリズムは，ステルス技術を使用して製造された最初の航空機であるF-117ナイトホークの設計に使用され，これは1981年に離陸しました．

Ufimtsevの論文は，防空レーダーから飛行機を事実上見えなくする方法を説明しています．翻訳者のデニス・オーバーホルツァーは，技術的に有能な人物で米国の偉大な愛国者でありました．彼は，Ufimtsevの仕事がアメリカ空軍に前例のない機会をもたらすことにすぐ気づきました．ソビエト連邦は，この論文を秘密にしなかったので，アメリカは完全に合法的に技術を手に入れたのです．

ソビエト連邦がステルス技術の利点を認識したのは，米国がすでにナイトホーク航空機を完全に使用していた1980年代の終わりになってからでしたが，それはすでに手遅れでした．さらに，ミハイル・ゴルバチョフの時代の冷戦雪解けになり，ステルス機は不要になりました．

1990年はソビエト連邦の存在の最後の年でした．Peter Yakovlevich Ufimtsevにとっても1990年は転機で，当時ソビエト連邦科学アカデミーの無線電子工学研究所で働いていた彼は，カリフォルニア大学の客員教授として，アメリカ合衆国に招待を受けました．

彼がアメリカに到着したとき，デニス・オーバーホルツァーは彼に会いに来ました．しかし，Ufimtsevは，ロッキードの競合-ノースロップグラマンとの契約になり，アメリカのB-2爆撃機の戦闘能力の改善に取り組み始めました。

Peter Yakovlevich Ufimtsevの生涯と運命，そしてステルス技術の歴史全体は，科学者に対する国家の不注意がもたらす深刻な結果の典型的な例です．1990年代，ソビエト後のロシアでは「頭脳流出」が深刻な問題となりました．何万人もの有望な科学者，エンジニア，技術者が，お金だけでなく，より注意深く敬意を払う態度を求めてロシアを去りました．

残念ながら，この問題は今のところ解決されていません．国内科学への資金提供には多くの要望が残されています．そのため，若い科学者たちは西側に，そして今では東側にも向けて出発しています．米国，そして中国にも，彼らの知識は需要があります．

以下のサイトを参照しました
https://en.topwar.ru/162805-russkij-stels-kto-razrabotal-tehnologiju-samoleta-nevidimki.html>

補足
レーダーの仕組み：
電波が機体に当たり、機体表面に誘導電流が発生する．
誘導電流から電波が発生する（これは反射波となる）
見えなくするには：
電波が来た方向へ電波を反射しなければ良い（あらぬ方向へ受け流す）．
金属は電波を反射し易いので，電波を反射し難い・吸収する物質に換える．
厚さ1/4波長の表面と裏面から反射させて，反射波同士を打ち消し合わせることも可能である．
ステルス機の形は多面体を思わせるが，どちらから見ても来た方向に電波を戻さず横に受け流すにはこのような形が良いのだろう．

光学的ステルス
可視光で見えなくなる隠れ蓑のような衝立が2019.12にカナダの企業から発表されたのを覚えている方もおられるだろう．可視光に対するステルスも研究されている．

Алексей Левинのエッセイ（ИСТОРИЯ НАУКИ，14.10.2016）
http://www.csmonitor.com/Books/Book-Reviews/2015/1209/The-Invention-of-Science-tells-the-story-of-the-shaping-of-the-modern-world

ウートン著 科学の発明：科学革命の新しい歴史

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．
この著書についてのアレクセイ・レビンのエッセイ（ИСТОРИЯ НАУКИ • 14.10.2016）から抜粋編集。

■ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年

ニコラウス・コペルニクスの モノグラフ「天球の回転について」が、ニュールンベルクの出版社 Johann Petraeusから出版されたのが1543年です。ウートンは2つの理由から、コペルニクスの1543年を科学革命の開始とする従来の見解に異を唱えています。
第一の理由は、太陽を不動中心とする（地動説のこと）コペルニクスモデルは、ケプラーとガリレオの後の17世紀の初めになってから、革命の要因になれるからです。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、その物理的な基盤が不確かだと思いました。たとえば、砲弾がどの方向にも同じ距離を飛ぶという当時の事実は、地球回転の仮説を反駁するに十分でした。1580年代と90年代には、天文学界のコペルニクス信者は3人以下でした。しかも、そのうちの1人、ドイツのクリストフ・ロスマンは、最終的に敵の陣営に移りました。第二の理由は、コペルニクスのモデルが、アリストテレスと古代の天文学者から受け継いだ、地上世界とは全く異なる月以遠（天上界）の世界の絶対不変の概念をそのまま保持したからです。ご存知のように、この概念は17世紀に完全に拒否されました。
コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象で、すべての天体は大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は、毎晩、天で同じ経路をたどり、明るさも変化しません。彗星は唯一の例外で、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者になるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月にこの星が完全に消滅するまで、輝きが徐々に薄れていくのを追跡しました。彼は1573年に、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusavimemoriapriusvisaStella」を出版し、彼の観察を説明しました。そのため、ブラーエはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見たのです。この現象は、11月6日に韓国、2日後に中国で記録されました。これより古い1054年の超新星観察は明月記や中国，アラビアで記録されましたが、ヨーロッパでの記録はありません。

その数年後、彼は、彗星は月以遠の世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定をすることを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積しました。これは、品質と幅の点で、ヨーロッパだけでなく、中国やイスラム教徒の最高の天文台でこれまでに行われたすべての観測をはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することを、ケプラーが厳密に証明できたのはこれらの材料を用いてであり、それによってコペルニクスモデルの弱点が修正されました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。
この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていました）。ウートンが提案する科学革命の最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。
科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較します。 16世紀の終わりの、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく解釈された夢は未来を予測すると信じていました。彼らは、地球は動かず、宇宙の中心にあるという公理を受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたと思われますが）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの著作、または、おそらくそれらのポピュラー書に限定されていました。 彼らは、個人的な図書室に、2～3ダースの本を持っていました。

1730年頃までの150年間を早送りで見ます。当時、同じ社会的および教育的地位を持つ英国人は、フランス、イタリア、ドイツ、さらにはオランダの同時代の人よりもはるかに優れた科学的知識を持っていました。おそらく、彼らはすでに望遠鏡と顕微鏡を通して見る機会があり、太陽系の機能がどのようなものかを知っていました。彼らは良い時計や、おそらく水銀気圧計を持っていて、それを使って天気を追跡していました。彼らは魔女、狼狼、魔法使い、または彗星関連の前兆を信じていませんでした。彼らは、虹が神の啓示ではなく、雨滴が日光を屈折させる結果であることをよく理解していました。彼らは蒸気エンジンについて聞いたり読んだりしていて、おそらく仕事でそれらを観察していました。彼らは目に見えない生物がたくさんいること、心臓は機械式ポンプのように血液を送り出すことを知っていました。彼らは未来を予測する可能性を否定し、おそらく聖書の奇跡を詩的な比喩と見なしました。彼らはニュートンを世界で最も偉大な科学者であり、進歩と科学への熱狂的な信念であると考えました。彼らの図書室は数百、さらには数千冊にのぼり、現代人類があらゆる点で古代世界をはるかに超えたことを疑いませんでした。

ウートンは科学の発明（この本のタイトル）を可能にした知的道具立ての出現と進化をたどります。さまざまなヨーロッパ言語による発見と出現の重要なアイデアから始めます。このプロセスの開始は、彼の意見では、クリストファーコロンブスや他のスペインの航海士の旅が、中国ではなく巨大な新大陸への大西洋横断ルートを開拓したことを、ヨーロッパが知った16世紀初頭です。「アメリカ発見が幸せな偶然だったとしたら、それはさらに驚くべき偶然、つまり発見の発見につながりました」（p.61）。この結論は奇妙に思えるかもしれません。結局のところ、最大の地理的発見は以前にあり、アフリカ沿岸のポルトガル人の航海ではないでしょうか。しかし、彼らの旅は、新しいルートに沿っているとはいえ、すでに知られ予想されている目標への旅と認識されていました。そして、これは決して地理分野に留まりません。コロンブス以前の時代のルネッサンス精神の著名人は、失われた古代の文化的価値を取り戻そうとしましたが、新しい知識の誕生には至りませんでした。さらに、「カトリックの宗教、ラテン文学、アリストテレスの哲学は、新しい知識がまったく存在しないということを共通認識にしていました」（p.74）。知ることができるすべてはすでに知られており、時間の経過とともに蓄積された破損したテキストと誤解釈の修復が研究対象となりました。繰り返す循環過程としての歴史認識が支配していたのが１6世紀です。華麗なイタリアの歴史家でマキャヴェリの友人であるフランチェスコ・ギチャルディーニは、「過去に起こったことはすべて、将来も繰り返されるだろう」と書いています。当然のことながら、そのような態度は、17世紀の初めにフランシス・ベーコンを始めとする、磁気学の研究者ウィリアム・ヒルベルト、ヨハネス・ケプラー、ガリレオ・ガリレイの発見が影響を与えるまで、知識の絶え間ない進歩の可能性を考慮する余地を締め出していました。

発見のアイデアを「育てる」ことは多くの結果をもたらしました。それは、16世紀の前半に、3次方程式、4次方程式の解法の探求に関連し始まり、その後、数学以外の研究にも広がり、誰が先に発見したかの議論が活発になりました。「このような論争は、知識が公になり、進歩的で、発見指向になったことを明確に示しています」（p.96）。17世紀には、個々の著者を発見に帰属させ、それに応じて、その著者の名前を認定された発見に冠するという伝統が生まれました。たとえば、ボイルの法則として知られている理想気体の法則は1708年にこの名前を受け取り 、ニュートンの重力の法則は1713年にこの名前を受け取りました。

----------------------------------------------------------------------------------------------------------------------------------------------

前号から始まったデビッド・ウートン（ヨーク大学の歴史教授）の表題の著書の紹介の続きです．
アレクセイのエッセイ（ИСТОРИЯ НАУКИ， 14.10.2016）より抜粋編集しています．
今回は17世紀あたりまでの科学の流れを概観します．

http://www.csmonitor.com/Books/Book-Reviews/2015/1209/The-Invention-of-Science-tells-the-story-of-the-shaping-of-the-modern-world

まず，前号のレジメから
■ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年

ニコラウス・コペルニクスの モノグラフ「天球の回転について」が出版されたのは1543年です。
ウートンがこの年を科学革命の開始とする従来の見解には，賛成しません。前号ではその２つの根拠を述べました。

このパラダイムは、1572年11月11日に最初の衝撃を受けました。その夜、ティコ・ブラーエは、
カシオペア星座の明るい星に気づきました。彼は、1574年3月にこの星が完全に消滅するまで、毎日観測を続けました。
ブラーエは、彗星の軌道は天球の運動とは異なるので、彗星は地球の大気圏内の現象とした当時の説を否定し、
彗星も月以遠の宇宙世界に属していることを証明しました。
ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点と宣言します。
ウートンが提案する科学革命の最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）
の出版された1704年です。

ウートンは科学の発明（この本のタイトル）について，
その発明者の名を冠して呼ぶようになったヨーロッパの歴史にも言及します。
それは、17世紀のことです。たとえば、ボイルの法則として知られている理想気体の法則は1708年に、
ニュートンの重力の法則は1713年にこの名前を受け取りました。

■15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。
コペルニクスは、すでにプトレマイオス世界を改訂しました（具体的には1514年）。
地球を固体の球と見なし、その表面には海と海が点在するものです。地軸の周りを１日に1回転します。
この視点は当時非常に新しく、まだ共有できいませんでした。
たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。
居住地は丸い島のようにこの表面から突き出ており、その形は半球で、決して球ではありませんでした。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。
アメリゴ・ベスプッチが赤道を越え南緯50度のブラジルの海岸に航海した後で初めて現実になりました。
この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版され、
ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。
それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマンが
地球の表面を完全な球とした新しい地図を描きました（1507年に公開されたWaldseemullerの地図では、
コロンブスによって発見された大陸を、アメリカと名付けられました）。
ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかったでしょう」。

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。
これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、
前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。
TubingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉は、フクシア属の植物に名前が付けられています）。

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。
どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。
当時のグラフィック印刷技術の向上があって出版が可能になりました。
フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、
各植物が彼の本のページに描かれていると考えたのは偶然ではありません。
これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。
実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、
中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、
早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、
共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。
15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、
幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。
視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、
特にアルブレヒト・デュラーによって使用され、開発されました。
彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。
しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。
彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、
初期の科学界の集団心理学の基礎となりました。
彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。
1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。
そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、
ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。
彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。
その中にはDoge Leonardo Donato自身が含まれていました。
上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、
彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。
数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。
この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、
天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、
ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。
最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、
1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、
木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。
彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。
コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているかの説明の説得力がありませんでした。
これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本
「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。
同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、
新しく発見されたジュピターの衛星をメディチの星と名付けました。

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。
英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、
ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。
しかし、ハリオットは彼の結果をまったく公表しませんでしたし、
マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、
科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、
ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。
1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。
その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。
実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。
6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、そこまででした。
（惑星の輪についての最初の明確な声明は、1655年にChristian Huygensによって行われました）
1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、
実際には太陽系の8番目の惑星であるネプチューンを星座Virgoの恒星（固定星）と思いました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙では
存在できないことを完全に理解していました。それらは、太陽中心理論（地動説）によって自然に説明されました。
プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、
これらのオプションの間で明確な選択はできませんでした。
前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、
後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。
対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、
月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。
ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、
ローマのコッレジオロマーノイエズス会アカデミーの教授，そしてグレゴリア暦の創設者の1人に知らせました。
これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、
「有能な天文学者はプトレマイオスのシステムを守ることができなかった」。
ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

*************************************

ウートンは、すべての追加補充された発見のアイデアをヨーロッパの文化分野に含めることが、科学発明の基礎となった体系的な認知革新の重要な要因になったと結論付けています。歴史的に、彼らの最初の製造業者は、新しい土地を説明した地図製作者でした。このプロセスでは、数学者がすぐに参加し、次に解剖学者、植物学者、天文学者、物理学者、化学者が加わりました。彼らは皆、印刷機を利用して、テキストや図を正確かつ大量に再現することを可能にしました。「その結果、革新的で批判的で競争力のある新しいタイプの知的文化が出現しましたが、同時に正確さと信頼性に重点が置かれました」（p.107）。この文化は科学的活動の基礎を形成しました。

15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。コペルニクスは、すでにプトレマイオス世界の改訂を開始（具体的には1514年まで）していました。地球を固体の球と見なし、その表面には海と海が点在するものです。この球は、両方の極を結ぶ軸の周りの空間空間で回転し、１日に1回転します。この視点は当時非常に新しく、誰もがまだ共有できいませんでした。たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。居住地は丸い島のようにこの表面から突き出ており、その形は半球に近づいていますが、決して球になることはできません。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。彼女は、アメリゴ・ベスプッチが赤道の南50度を離れてブラジルの海岸に航海した後で初めて、彼らと実際に衝突しました。この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版された後、ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマン地球の表面が完全な球の表面のように見える新しい地図を描きました（1507年に公開されたWaldseemullerの地図では、コロンブスによって発見された大西洋横断の土地は最初に大陸として表され、アメリカと名付けられました）。コペルニクスはこの概念に精通しており、彼の反省の中でそれを信頼していました。したがって、この場合の新しい地理は、新しい天文学の誕生の前提条件になりました。ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかっただろう」。（p.143）

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。 これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。 ）、TubingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉で、フクシア属の植物に名前が付けられています）。

画像1

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。当時のグラフィック印刷技術の向上により出版が可能になりました。フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、各植物が彼の本のページに描かれていると考えたのは偶然ではありません。これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

画像2

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。 15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、特にアルブレヒト・デュラーによって使用され、開発されました。彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、初期の科学界の集団心理学の基礎となりました。彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。その中にはDoge Leonardo Donato自身が含まれていました。上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているの説明の説得力がありませんでした。これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。 同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、新しく発見されたジュピターの衛星をメディチの星と名付けました。

画像3

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。しかし、ハリオットは彼の結果をまったく公表しませんでしたし、マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。 1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。 6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、それで終わりです（惑星の鳴動についての最初の明確な声明は、1655年にChristian Huygensによって行われました）。 1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、実際には太陽系の8番目の惑星であるネプチューンである星座Virgoで「固定星」を観察しました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙に存在できないことを完全に理解していましたが、それらは、太陽中心理論（地動説）によって自然に説明されました。プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、これらのオプションの間で明確な選択はできませんでした。前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、ローマのコッレジオロマーノイエズス会アカデミーの教授、そしてグレゴリアンカレンダーの創設者の1人に知らせました。これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、「有能な天文学者はプトレマイオスのシステムを守ることができなかった」（p.226）。ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

画像4

金星の段階の発見と分析は、ウートンが科学の相対論的歴史学の支持者、特にトーマス・クーンとの論争において重要な位置を占めることを可能にします。それらのすべては、科学的知識がその生産に関与する特定のコミュニティの信仰の対象であると考えています。このことから、科学的信念のさまざまな「シンボル」のキャリア（Kuhnによると、代替パラダイムの支持者）はコンセンサスに達する可能性がほとんどないことがほぼ自動的にわかります。したがって、パラダイムの変化は、クーンが科学革命と呼んでいる科学コミュニティ内の対立に関連しています。ウートンが書いているように、「クーンの科学革命の構造の後、科学の歴史家は科学内紛争の研究に焦点を合わせてきました。この傾向は、そのような論争は事実上すべての主要な科学的発見によって必然的に生じ、科学理論を競合する概念に置き換えることは決して避けられないという仮定から生じた」（p.246）。しかし、金星の相（変化段階）の発見はまさに望遠鏡の発明の必然的な結果となり、そのおかげで、天文学界は遅滞なく、ほぼ完全にそして多くの議論なしに、プトレマイオスの理論を放棄しました。ウートンが強調するように、そのような状況は典型的です。これは、科学の歴史学における相対論的イデオロギーとは対照的に、経験が科学の進歩的な進化における決定的な要因になる可能性があることを意味します（そして、原則として役立ちます！）。これはウートンの主要な結論の1つであり、本全体で何度も繰り返され、他の多くの例で確認できることは簡単にわかります。

コペルニクスの素晴らしい業績に加えて、ウートンは科学革命に重要な役割を果たしたさらに2つのモノグラフをあげます。 これらは、1543年にオランダの医師AndreasVesaliusによって発行された解剖学の教科書「Dehumanicorporisfabrica」と、前年に発行された植物のリファレンスブック「DescriptionofPlants」（「Dehistoriastirpiumcommentariiinsignes」）です。 ）、TübingenLeonhartFuchs大学の医学教授によって作成されました（彼の名誉が、フクシア属の植物に名前が付けられています）。

彼らは、人間の臓器と植物界を研究し、ガレンと他の古代の古典の多くの間違いを訂正しました。どちらの本にも高品質のイラストが多数含まれています（ベサリウスは250、フックスは512）。当時のグラフィック印刷技術の向上により出版が可能になりました。フックスが、根や茎から葉、花、種子、果物に至るまで、そのすべての部分の綿密なスケッチで、各植物が彼の本のページに描かれていると考えたのは偶然ではありません。これもまた、ヨーロッパの科学の形成におけるグーテンベルクの偉大な発明の非常に重要なことを示しています。実際のところ、それははるかに早く現れ始めました。たとえば、13世紀にヨハネスカンパヌスによって作成され、中世に手書きのコピーで知られているユークリッドの原論のラテン語の翻訳は、早くも1482年にヴェネツィアで最初に印刷されました。ウートンが書いているように、共通の利益と共通の価値観を共有する国際的な科学コミュニティの出現を可能にしたのは印刷媒体でした。

科学革命はまた、数学の可能性と課題の新しい理解によって準備されました。 15世紀半ば、イタリアの偉大な建築家であり芸術研究者でもあるレオンバティスタアルベルティは、幾何学的な視点の理論を構築しただけでなく、芸術と科学の両方の基盤としての数学の主要な役割を宣言しました。視覚芸術の問題に幾何学を適用する彼の方法は、ピエロ・デッラ・フランチェスカ、特にアルブレヒト・デュラーによって使用され、開発されました。彼らの仕事は、17世紀に数学の一分野として出現した射影幾何学の創造への道を開きました。しかし、すでに16世紀になると、地図製作者、土地調査員、エンジニア、金融業者、そしてもちろん天文学者が数学を習得し始めました。彼らはますます数学化された物理学の出現への道を開き、17世紀に至ります。

ウートンはさまざまな発見の説明と分析に言及しています。観察と実験に基づいて得られた新しい知識の価値認識は、初期の科学界の集団心理学の基礎となりました。彼は、望遠鏡で行われるガリレオガリレイの天文学的研究に多くのスペースをさいています。1609年の春の終わりに、ガリレオはオランダの眼鏡技師によって発明された望遠鏡について学びました。そして8月初旬、彼はオランダ人がそのような鏡筒をヴェネツィアに売りに出そうとしていると聞き、ガリレオはワークショップに駆け込み、吹きガラスで作る凸型と凹型のレンズの実験を開始しました。彼の回想によれば、数週間後、彼は8倍の鏡筒を手に入れ、8月25日にヴェネツィアの貴族に仕事でデモンストレーションを行いました。その中にはDoge Leonardo Donato自身が含まれていました。上院はすぐにガリレオに2倍の給料とパドヴァでの生涯にわたる教授職を提供した。

その後、ガリレオは天文学に熱心に取り組みました。秋の初めに、彼は月の観察を始め、彼が彼自身のワークショップで組み立てた20倍の望遠鏡を用いて続けました。数か月以内に、ガリレオと彼の助手は約100個の望遠鏡を作りましたが、高品質の画像が与えられたのは12個以下でした。この巨大な作品は、最も価値のある成果をもたらし、ガリレオは月の海、山、火口を見て、天の川が多くの星と星の塊で構成されていることを発見しました。これらの発見の中で最も有名なのは、ガリレオが木星の近くにある4つのかすかな星に気づいた1610年1月7日に起こりました。最初は普通の星と間違えましたが、翌週、木星に対してずれているのを見て、1月15日、これらは木星の周りを回っていることに気づきました。この真に革命的な突破口に達した彼は、木星が太陽周回軌道に沿って動くときも、静止しているときと同じように周回する衛星を運んでいると結論付けました。彼の発見により、彼はコペルニクスの理論に対する当時の広範な異議を弱体化させました。コペルニクスの理論は、太陽を周回する地球に月がどのように追いついているの説明の説得力がありませんでした。これは、地球が軌道運動の唯一の中心とは見なせないことを示し、プトレマイオスの宇宙にとって不都合な驚きでした。

ガリレオはそのような注目に値する発見で彼の優先順位を固めることを急ぎ、3月に550部ほどヴェネツィアで印刷された本「SidereusNuncius」に掲載しました。 それはトスカーナのコジモ2世の大公に捧げられ、ガリレオはその庇護を得ました。 同じ理由で、彼はトスカーナを統治したメディチ王朝に敬意を表して、新しく発見されたジュピターの衛星をメディチの星と名付けました。

新作はヨーロッパのセンセーションを巻き起こし、その作者を望遠鏡の唯一の父として有名にしました。英国人のトーマス・ハリオットは1609年7月末に月の望遠鏡による観測を開始し、ドイツ人のサイモン・マリウスは11月に空を見始め、おそらく1、2か月後に独立して木星の衛星を発見しました。しかし、ハリオットは彼の結果をまったく公表しませんでしたし、マリウスが公表したのは1614年のみでした。そのため、ガリレオは、光学天文学に関する世界初の出版物の著者として、科学の歴史に名を残しました。 Johannes Keplerは、すでに4月に、プラハ、次にフィレンツェとフランクフルトで発行された「Dissertatio cum Nuncio Sidereo」という手紙で、ガリレオの結論を支持しました。ガリレオは惑星運動のケプラーモデルの支持者ではなかったので、これは注目に値します。

ガリレオの新たな名声により、彼は故郷への帰還を首尾よく交渉できました。 1610年7月に「トスカーナ大公の哲学者兼数学者であり、ピサ大学の主任数学者」に任命され、9月にフィレンツェに移りました。その少し前に、彼はトリプルスターの形で土星を観察しました。それは彼が緊急に発表されたアナグラムで概説しました。実際、彼は望遠鏡の力が不十分なために見ることができなかった土星の輪の反射を見ました。 6年後、彼は2つの半楕円で囲まれた球の形で土星をスケッチしましたが、そこまでです（惑星の輪についての最初の明確な声明は、1655年にChristian Huygensによって行われました）。 1612年12月28日と1613年1月28日、ガリレオは、現在私たちが知っているように、実際には太陽系の8番目の惑星であるネプチューンを見つけましたが、星座Virgoの恒星（動かぬ星）と思いました。

新月近くの三日月に似た薄い三日月。ガリレオは、金星のそのような段階が単にプトレマイオスの宇宙に存在できないことを完全に理解していましたが、それらは、太陽中心理論（地動説）によって自然に説明されました。プトレマイオスモデルでは、金星の軌道は太陽軌道の内側にあるか、太陽軌道の外側にあり、当時の観測では、これらのオプションの間で明確な選択はできませんでした。前者の場合、金星の円盤の明るい部分はその半分を超えることはできず、後者の場合、円盤は常にほぼ完全に照らされたままでなければなりません。対照的に、コペルニクスのシステムでは、金星は地球の軌道の内側で太陽の周りを回転するため、月の円盤のように、円盤を完全に照らし、完全に暗くすることができます。ガリレオが観察したのはこの段階の変化であり、12月にケプラーと有名な天文学者クリストファークラビウス、ローマのコッレジオロマーノイエズス会アカデミーの教授、そしてグレゴリアンカレンダーの創設者の1人に知らせました。これらの観察が1611年5月にClaviusの同僚であるOdovan Maelkotによって確認された後、「有能な天文学者はプトレマイオスのシステムを守ることができなかった」（p.226）。ウートンが指摘するように、天文学界からのそのような反応は、科学革命がどこまで進んだかを非常に明確にしています。

金星の段階の発見と分析は、ウートンが科学の相対論的歴史学の支持者、特にトーマス・クーンとの論争において重要な位置を占めることを可能にします。それらのすべては、科学的知識がその生産に関与する特定のコミュニティの信仰の対象であると考えています。このことから、科学的信念のさまざまな「シンボル」のキャリア（Kuhnによると、代替パラダイムの支持者）はコンセンサスに達する可能性がほとんどないことがほぼ自動的にわかります。したがって、パラダイムの変化は、クーンが科学革命と呼んでいる科学コミュニティ内の対立に関連しています。ウートンが書いているように、「クーンの科学革命の構造の後、科学の歴史家は科学内紛争の研究に焦点を合わせてきました。この傾向は、そのような論争は事実上すべての主要な科学的発見によって必然的に生じ、科学理論を競合する概念に置き換えることは決して避けられないという仮定から生じた」（p.246）。しかし、金星の相（変化段階）の発見はまさに望遠鏡の発明の必然的な結果となり、そのおかげで、天文学界は遅滞なく、ほぼ完全にそして多くの議論なしに、プトレマイオスの理論を放棄しました。ウートンが強調するように、そのような状況は典型的です。これは、科学の歴史学における相対論的イデオロギーとは対照的に、経験が科学の進歩的な進化における決定的な要因になる可能性があることを意味します（そして、原則として役立ちます！）。これはウートンの主要な結論の1つであり、本全体で何度も繰り返され、他の多くの例で確認できることは簡単にわかります。

ウートンの著作を紹介したアレクセイのエッセイを読んでいます（続きです）．1730年頃までの150年間を早送りで見ます。当時、同じ社会的および教育的地位を持つ英国人は、フランス、イタリア、ドイツ、さらにはオランダの同時代の人よりもはるかに優れた科学的知識を持っていました。おそらく、彼らはすでに望遠鏡と顕微鏡を通して見る機会があり、太陽系の機能がどのようなものかを知っていました。彼らは良い時計や、おそらく水銀気圧計を持っていて、それを使って天気を追跡していました。彼らは魔女、狼狼、魔法使い、または彗星関連の前兆を信じていませんでした。彼らは、虹が神の啓示ではなく、雨滴が日光を屈折させる結果であることをよく理解していました。彼らは蒸気エンジンについて聞いたり読んだりしていて、おそらく仕事でそれらを観察していました。彼らは目に見えない生物がたくさんいること、心臓は機械式ポンプのように血液を送り出すことを知っていました。彼らは未来を予測する可能性を否定し、おそらく聖書の奇跡を詩的な比喩と見なしました。彼らはニュートンを世界で最も偉大な科学者であり、進歩と科学への熱狂的な信念であると考えました。彼らの図書館は数百、さらには数千冊にのぼり、現代人類があらゆる点で古代世界をはるかに超えたことを疑ったりしませんでした。

ウートンは科学の発明（この本のタイトル）を可能にした知的道具立ての出現と進化をたどります。さまざまなヨーロッパ言語による発見と出現の重要なアイデアから始めます。このプロセスの開始は、彼の意見では、クリストファーコロンブスや他のスペインの航海士の旅が、中国ではなく巨大な新大陸への大西洋横断ルートを開拓したことを、ヨーロッパが知った16世紀初頭です。「アメリカの発見が幸せな偶然だったとしたら、それはさらに驚くべき偶然、つまり発見の発見につながりました」（p.61）。この結論は奇妙に思えるかもしれません。結局のところ、最大の地理的発見は以前にあり、アフリカ沿岸のポルトガル人の航海ではないでしょうか。しかし、彼らの旅は、新しいルートに沿っているとはいえ、すでに知られ予想されている目標への旅と認識されていました。そして、これは決して地理分野に留まりません。コロンブス以前の時代のルネッサンス精神の著名人は、失われた古代の文化的価値を取り戻そうとしましたが、新しい知識の誕生には至りませんでした。さらに、「カトリックの宗教、ラテン文学、アリストテレスの哲学は、新しい知識がまったく存在しないということを共通認識にしていました」（p.74）。知ることができるすべてはすでに知られており、時間の経過とともに蓄積された破損したテキストと誤解釈の修復が研究対象となりました。繰り返す循環過程としての歴史認識が支配していたのが１6世紀です。華麗なイタリアの歴史家でマキャヴェリの友人であるフランチェスコ・ギチャルディーニは、「過去に起こったことはすべて、将来も繰り返されるだろう」と書いています。当然のことながら、そのような態度は、17世紀の初めにフランシス・ベーコンを始めとする、磁気学の研究者ウィリアム・ヒルベルト、ヨハネス・ケプラー、ガリレオ・ガリレイの発見が影響を与えるまで、知識の絶え間ない進歩の可能性を考慮する余地を締め出していました。

発見のアイデアを「育てる」ことは多くの結果をもたらしました。それは、16世紀の前半に、3次方程式、4次方程式の解法の探求に関連し始まり、その後、数学以外の研究にも広がり、誰が先に発見したかの議論が活発になりました。「このような論争は、知識が公になり、進歩的で、発見指向になったことを明確に示しています」（p.96）。17世紀には、個々の著者を発見に帰属させ、それに応じて、その著者の名前を認定された発見に冠するという伝統が生まれました。たとえば、ボイルの法則として知られている理想気体の法則は1708年にこの名前を受け取り 、ニュートンの重力の法則は1713年にこの名前を受け取りました。

ウートンは、すべての追加補充された発見のアイデアをヨーロッパの文化分野に含めることが、科学発明の基礎となった体系的な認知革新の重要な要因になったと結論付けています。歴史的に、彼らの最初の製造業者は、新しい土地を説明した地図製作者でした。このプロセスでは、数学者がすぐに参加し、次に解剖学者、植物学者、天文学者、物理学者、化学者が加わりました。彼らは皆、印刷機を利用して、テキストや図を正確かつ大量に再現することを可能にしました。「その結果、革新的で批判的で競争力のある新しいタイプの知的文化が出現しましたが、同時に正確さと信頼性に重​​点が置かれました」（p.107）。この文化は科学的活動の基礎を形成しました。

15世紀後半から16世紀初頭にかけての地理的な発見は、もう1つの重要な結果をもたらしました。コペルニクスは、すでにプトレマイオス系の改訂開始（具体的には1514年まで）した。地球を固体の球と見なし、その表面には海と海が点在するものです。この球は、両方の極を結ぶ軸の周りの空間空間で回転し、１日に1回転します。この視点は当時非常に新しく、誰もがまだ共有できいませんでした。たとえば、15世紀には、地球はより大きな半径の水球の表面に浮かぶ球と見られました。居住地は丸い島のようにこの表面から突き出ており、その形は半球に近づいていますが、決して球になることはできません。

何世紀にもわたって、このような地球の「モデル」は、当時の地理的概念と概ね一致していました。彼女は、アメリゴ・ベスプッチが赤道の南50度を離れてブラジルの海岸に航海した後で初めて、彼らと実際に衝突しました。この旅の説明は、ベスプッチの手紙「Mundus novus」（「新世界」）が1503年に出版された後、ヨーロッパで知られるようになりました。この手紙はわずか4年で29版になりました。それに基づいて、地図製作者のマーティン・ヴァルトゼーミュラーとマティアス・リングマン地球の表面が完全な球の表面のように見える新しい地図を描きました（1507年に公開されたWaldseemüllerの地図では、コロンブスによって発見された大西洋横断の土地は最初に大陸として表され、アメリカと名付けられました）。コペルニクスはこの概念に精通しており、彼の反省の中でそれを信頼していました。したがって、この場合の新しい地理は、新しい天文学の誕生の前提条件になりました。ウートンが書いているように、「コペルニクスの世界観はベスプッチなしでは起こらなかっただろう」。（p.143）

wikiより拝借

Алексей Левинのエッセイより抜粋　ИСТОРИЯ НАУКИ • 14.10.2016

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．

'The Invention of Science' tells the story of the shaping of the modern worldThe central subject of this vibrant work is not really the inwww.csmonitor.com

ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年。

ニコラウス・コペルニクスの モノグラフ天球の回転について（ニュールンベルクの出版社 Johann Petraeusから1543年に出版）。

ウートンは2つの理由から、コペルニクスの1543年を革命の開始とする従来の見解に同意しません。第一に、太陽中心（地動説のこと）［正確には太陽不動］コペルニクスモデルは、ケプラーとガリレオの研究の後の、17世紀の初めになってから天文学革命の要因になりました。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、それが物理的な基盤を持っていることは否定しました（たとえば、砲弾がどの方向にも同じ距離を飛ぶという事実からも、地球回転の仮説は反駁できたと信じられました）。1580年代と90年代には、コペルニクスは天文学界に3人以下の信者しか持っていません、さらにそのうちの1人、ドイツのクリストフ・ロスマンは最終的に彼の敵の陣営に移りました。第二に、コペルニクスのモデルは、アリストテレスと古代の天文学者から受け継いだ地上世界とは根本的反する、月を越える（天上界）世界の絶対不変の概念をそのまま保持しています。ご存知のように、この概念は17世紀に完全に拒否されました。

コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象でした。すべての天体は、大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は毎晩、天の同じ経路をたどり、明るさと数の両方で変化しません。彗星は唯一の例外でしたが、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者であるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月に完全に消滅するまで、その輝きが徐々に薄れていくのを追跡しました。その前から、彼は1573年に出版され、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusævimemoriapriusvisaStella」で彼の観察を説明しました。そのため、ブラヘはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見ました。（11月6日に韓国で、2日後に中国で、日本でも記述があります）。

左：TychoBraheの著書「DenovaetnulliusævimemoriapriusvisaStella」からの星座Cassiopeiaの描画。 超新星は文字Iでマークされています。
右：スペクトルのさまざまな部分のフレームを合計して得られた超新星の残骸のスナップショット。 チャンドラ望遠鏡のウェブサイトで、この残骸が2000年から2015年の間にどのように変化したかを見ることができます。
http://mvshelter.blogspot.ruからの画像

数年後、彼は、彗星は月を越える世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定を実行することを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積してきました。これは、品質と幅の点で、ヨーロッパだけでなく、中国とイスラム教徒の東の最高の天文台でこれまでに行われたすべてをはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することをケプラーが厳密に証明することを最終的に可能にしたのはこれらの材料であり、それによってコペルニクスモデルの主な弱点を修正しました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていましたが、真に無限の宇宙には中心はありません）。ウートンが提案する最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。

科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較することを提案しています。 16世紀の終わりに、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく理解された夢は未来を予測すると信じていました。彼らは、地球が動かず、宇宙の中心にあるという公理として受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたでしょう）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの研究、またはおそらくそれらのポピュラー書に限定されていました。 彼らはまた、個人的な図書館-2、3ダースの本を持っていました。

https://elementy.ru/nauchno-populyarnaya_biblioteka/431670/Vsego_lish_stepeni_dvoyki

И. Акулич，«Квант» №2, 2012　に２の累乗の大きな数を求める問題があります．

（問題） 

$$S = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{63}$$

$$S$$の値を計算しなさい．

$$2 S = 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{64}$$

$$2S-S＝S=2^{64}-1$$

計算機を使えば，$$2^{64}-1=18446 744 073 709551615$$ と計算できるでしょう．
計算機が無くても，許容できる精度でおおよその答えを見つけることができます。原則として、日常生活では（そしてほとんどの自然科学では）2～3%の誤差が許容されます．
$$2^{64}$$をどのように概算したらよいかという問題です．

 $$2^4 = 16$$，$$2^{10} = 1024≒1000=10^3$$　だから，

$$2^{64}＝2^4・(2^{10})^6≒16・(10^3)^6$$

しかし，この誤差はかなり大きい．結局，1024を1000に置き換えること続けて6回．
このため，1.024倍の誤差の6乗$$1.024^6$$の誤差になります．

1よりも何倍も小さい数xについては、次の近似式を使うと精度が高い．

$$(1 + x)^n ≒ 1 +n･x$$　これを使うと，

$$(1+0.024)^6≒1+6×0.024＝1.144$$

従って，$$2^{64}≒16･10^{18}･1.144=18304･10^{18}$$　と補正します．その結果，

$$S≒2^{64}≒18,304,000,000,000,000,000,000$$となり（18304の後ろに0が18個），
これは正解と1%未満の誤差になります．

■注

１．数字を2のべき乗の和で表すのは，数字を2進数で表すときに必要になります．

たとえば，$$2^{10}+2^9+2^8+2^7＋2^6＋2^4＋2^3+2^2＝2042$$，　2進数で表記すると$$11111011100$$

２．この問題の最初の式は，次の一般式の$$m=64$$の場合になります．

$$2^m = (2^{m–1} + 2^{m–2} + ... + 2^0) + 1$$

３．次の性質も役に立ちます：

$$10^{10}＝(2･5)^{10}＝2^{10}・5^{10}$$

$$2^{10}>10^3$$，　$$5^{10}<10^7$$

Григорий Мерзон, «Квантик» №5, 2020　より

この記事の図には，不要なものもありましたので，必要なものだけ掲載します．文章は冗長ですので私が全部書き換えました．解が1つしかないような記述も私は気に入りません．要するに，この問題は，以下の図（ラクダと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れという主旨です．パズルの問題として予備知識なしで考えるとなかなか難しいかもしれません．

この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

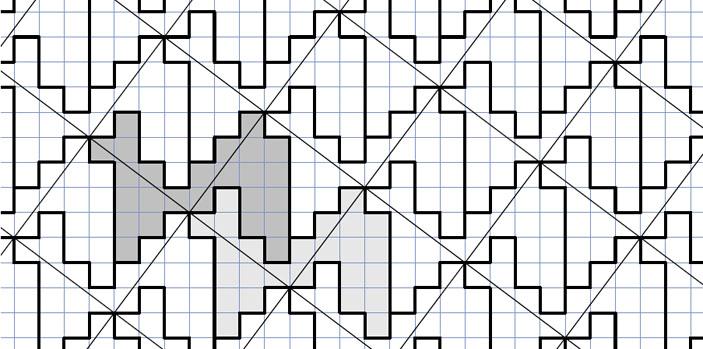
このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞と呼びます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の答ですが，私は答えはこれだけではないことを指摘しておきたいです．

ラクダが3分割できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Григорий Мерзон, «Квантик» №5, 2020

この記事の図はすべて掲載しますが，文章は冗長ですので私が全部書き換えました．要するに，この問題は，以下の図（らくだと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れということです． 

 この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞とよぶます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の回答ですが，私は答えはこれだけではないことを指摘しておきたいとおもいます．

ラクダが3等分できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

そして彼が帰宅したとき、クヴァンチクは上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
のエッセイのまとめです．今回は短いが，彼の最も言いたかったことはここにあるのでしょう．最後に私（訳者）の感想を述べます．

そして今、第四の定理について、少しだけ、多分最も恐ろしいことを話します - "教えても、誰も興味を示さない”。この問題のいくつかの断片はすでに話しました。人々は有限群の研究に興味を持たなくなりました。やる人が減ってきて、テキストという形で保存されてきた知識の塊が不要になり、誰も読めなくなってきている。これは数学の多くの分野を脅かす不幸でもあります。

数学の分野によっては運がいい分野があります。例えば、グラフ理論と組み合わせの理論は同じです。本気でやり始めるにも、ほんの少し学べばよい。少し勉強して、数学オリンピックの問題が解ける。一歩踏み出して、未解決の問題があり、～やったーとなります。しかし、数学の多くの分野は、本当に美しく、それをやりたいと感じるためにも、あなたは多くのことを学ぶ必要があります。そして、その道中では、他にも多くの美しいことを学ぶことができます。しかし、道中で出会うこれらの美しさに気を取られてはいけません、そして、最後には、まさに迷路の中で、美しさを見て、そして、多くのことを学んで、この分野の数学ができるようになっていくのです。そして、この難しさは、そういった部分の問題です。数学の分野が発展するためには、それに従事しなければなりません。全ての困難を乗り越えて、そこに登って、その後もやり続けるというのは、多くの人には面白いはずです。そして今、数学はその難易度の高みに達しており、多くの分野で人知の限界が大きな問題となっています。

人類がこれらすべての問題にどのように対処するのか-私にはわかりませんが、それは興味深いものになるでしょう。

実はそれだけです。

訳注）感想：私は、このエッセイで例にあげられている有限群の問題に興味があります。しかし、この分野は数学者たちは興味を失っているようです。それは、数学の確立された分野で，これ以上研究するのは人間の理解できる限界だからです。これを乗り越えるのは、他のすべての分野の知識もマスターしている数学者ができる仕事でしょう。それを乗り越えられる人がいるのか，その人知はもう人間業ではないのか。そして、たとえ誰かが乗り越えても他の誰にも理解できず，その結果に誰も関心をもたないという状況が恐ろしい．

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
3番目の定理-何かがわかっている場合、それは隣人には説明できません。

これらはまさに現代の数学で最も燃えている問題であり、おそらく最も誇張された問題です。人は何かを証明しましたが、その証明を他の人に伝えることはできません。または、彼が本当にそれを証明したことを他の人に納得させます。この範疇で最初の例であり、一般に最も有名なのは、4色問題です。しかし、これはまだここで発生する最も困難な状況ではありません。ここで、4色問題について少しお話しした後、さらに異常な状況を示します。

図： 5.
4色問題とは何ですか？これはグラフ理論の質問です。グラフは、エッジで接続されたいくつかの頂点です。これらの頂点を平面上に描画し、エッジが互いに交差しないようにそれらをエッジに接続できる場合、フラットと呼ばれるグラフが得られます。グラフカラーリングとは何ですか？トップスはさまざまな色で塗装しています。エッジに沿って隣接する頂点が常に異なる色になるようにこれを行った場合、色は正しいと呼ばれます。できるだけ少ない色でグラフを正しく描きたいです。たとえば、図5には、ペアで接続された3つの頂点があります。つまり、どこにも移動できません。これらの頂点は、必ず3つの異なる色になります。しかし、一般的に、このグラフを描くには4色で十分です（3色では不十分です。確認できます）。

百年の間、問題がありました：平面上に描くことができるどんなグラフも4色で着色できるというのは本当ですか？誰かが信じて4色で十分であることを証明しようとしましたが、誰かが信じずに4色では不十分な例を考え出そうとしました。また、そのような厄介な問題もありました。問題は非常に簡単に定式化されます。したがって、多くの人々は、軽薄な数学者でさえ、それに襲いかかり、それを証明しようとし始めました。そして、彼らは膨大な量の疑惑の証拠または疑惑の否定を提示しました。彼らはそれらを数学者に送り、新聞で叫んだ。私は4色の問題を証明しました！」 -そして誤った証拠のある出版された本さえ。要するに、ノイズが多かったのです。

結局、K。AppelとV.Hakenがそれを証明しました。ここで、証明のスキームについて説明します。同時に、この証拠が他の人には説明できない理由もわかります。人々は、フラットグラフがどのように機能するかを真剣に研究することから始めました。彼らは数十の構成のリストを提示し、すべてのフラットグラフでこれらの構成の1つを見つける必要があることを証明しました。これは証明の前半です。そして、証明の後半-これらの構成のそれぞれについて、それがグラフにある場合は、4色で色付けできることを確認できます。

より正確には、証明は反対からさらに進んでいます。グラフを4色で着色できないとします。前半から、リストからいくつかの構成があることがわかります。その後、これらの構成のそれぞれについて、そのような推論が実行されます。グラフにこの構成が含まれているとします。捨てましょう。誘導により、残ったものは4色に塗られます。そして、残りを4色でどのように着色しても、まさにこの構成をペイントできることを確認します。

カスタマイズ可能な構成の最も単純な例は、他の3つだけに接続されている頂点です。グラフにそのような頂点がある場合は、最後に色を付けたままにしておくことができることは明らかです。他のすべてに色を付けましょう。次に、この頂点がアタッチされている色を確認し、4番目を選択します。他の構成の場合、推論は似ていますが、より複雑です。

さて、これはどのように行われたのですか？このように多数の構成のそれぞれが常に手でペイントされていることを確認することは不可能です-時間がかかりすぎます。そして、このチェックはコンピューターに割り当てられました。そして、彼は多くの事件を調べて、これがそうであることを本当に確認しました。その結果、4色の問題が証明されました。

当初はこんな感じでした。厚い本に記録された推論の人間的な部分には、すべてが着色されていることの最終チェックがコンピューターに委ねられ、コンピュータープログラムのテキストさえも与えられたというフレーズが付随していました。このプログラムはすべてを計算し、すべてをチェックしました-実際、すべてが正常です。つまり、4色の定理が証明されています。

すぐに騒動が起こりました-そのような証拠は信じられませんでした。結局のところ、証拠のほとんどは人間ではなくコンピューターで生成されたものです。 「コンピュータが間違っていたらどうしますか？」 -そんな偏狭な人たちが言った。

そして、この証明の問題は実際に始まりましたが、それらはコンピューターの部分ではなく、人間の部分にあることが判明しました。証拠に欠陥が見つかりました。もちろん、複雑な検索を含むこのような長さのテキストにはエラーが含まれている可能性があることは明らかです。これらのエラーは見つかりましたが、幸いなことに修正されました。

ヨハネスケプラー

コンピュータ部分は残り、それ以来、同じ種類の検索を行うだけで、プログラムを書き直しさえして、複数のコンピュータでチェックされました。結局のところ、正確に何を列挙すべきかが言われれば、誰もが独自のプログラムを作成して、結果が期待どおりになることを確認できます。たとえば、証明にこのような大規模なコンピュータ列挙を使用することは問題ではないように思われます。どうして？しかし、同じ理由で、4色の問題の例ですでに明らかになっています。つまり、人間の証拠よりもコンピューターの証拠の方がはるかに信頼されており、少なくはありません。彼らはコンピューターが機械だと叫びました、そして突然それはどこかで故障し、道に迷いました、そこで何かが間違っていました...しかしこれはただありえません。コンピュータが誤ってどこかで誤動作し、エラーが発生した場合（0が誤って1に置き換えられた場合）、これによって誤った結果が生じることはありません。これは結果につながりません、それはプログラムが最終的に壊れることだけです。コンピューターが実行する典型的な操作は何ですか？彼らは、そのようなレジスターからそのような番号を取得し、そこに制御を移しました。当然、この数に1ビットの変更が発生した場合、制御は誰にも移されませんでした。そこにいくつかのコマンドが書き込まれ、すぐにすべてが破壊されます。

もちろん、コンピューター用のプログラムを書く際にエラーが発生する可能性がありますが、これはすでに人為的なエラーです。人はプログラムを読んで、それが正しいかどうかを確認することができます。人は他人の証明を読んで、それが正しいかどうかを確認することもできます。しかし、人間はコンピューターよりも間違っている可能性がはるかに高いです。他の人の十分な長さの証拠を読んでいて、それに間違いがある場合、あなたがそれに気付かない可能性があります。どうして？まず第一に、証明の作者自身がこの間違いを犯したので、それはそれが心理的に正当化されることを意味します。つまり、彼は偶然にそれをしたのです-これは原則として、典型的な人がそのような間違いを犯すことができる場所です。これは、この一節を読んで、それに気づかないことで同じ間違いを犯す可能性があることを意味します。したがって、人間による証明の人間による検証は、コンピュータプログラムの結果を他のマシンで再度実行して検証するよりも、信頼性の低い検証方法です。 2つ目はほぼすべてが正常であることを保証し、1つ目はどれほど幸運かです。

そして、この問題（人々が書いた数学のテキストの誤りを見つけること）では、それはますます困難になり、時には不可能にさえなります-これは現代の数学の深刻な問題です。あなたはそれと戦わなければなりません。まだ誰も知らない。しかし、問題は大きく、現在発生しています。これにはいくつかの例があります。これはおそらくあまり知られていませんが、最も近代的なものの1つです。これはケプラーの古い仮説です。彼女は三次元空間にボールを置くことについて話します。

図： 6
まず、2次元空間、つまり平面で何が起こるかを見てみましょう。同じサークルを作りましょう。それらが交差しないように平面上にそれらを描くための最良の方法は何ですか？答えがあります-あなたは六角形の格子のノードに円の中心を置く必要があります。このステートメントは完全に些細なことではありませんが、簡単です。

3Dでは、どのようにボールをしっかりと詰めますか？まず、図6に示すように、平面上にボールを配置します。次に、図7に示すように、同じ層の別の層を上に置き、止まるまで押します。次に、同じ層の別の層を上に置きます。直感的には、これは3次元空間にボールを置くための最もタイトな方法です。ケプラーは、このパッケージは3次元空間で最も密度の高いパッケージでなければならないと主張しました（そして最初に作成したようです）。

それは17世紀に起こりました、それ以来、この仮説はそれだけの価値がありました。 21世紀の初めに、その証拠が現れました。そして、あなたの誰もがそれを手に入れて読むことができます。インターネット上のパブリックドメインにあります。この記事は200ページです。それはある人によって書かれ、コンピュータ計算だけでなく、純粋に数学的な推論も含まれています。

図： 7
まず、著者は数学的な推論を使用して、問題を有限数のケースをチェックするように減らしようとします。その後、時々コンピューターを使用して、彼はこの有限の、しかし非常に多くのケースをチェックし、すべてが収束します、そして-万歳！ -ケプラーの仮説が証明されました。そして、これがこの記事の問題です-誰もそれを読むことができません。それは重いので、場所によっては検索が本当に完了したかどうかが完全に明確ではないので、それを読むのは単に退屈だからです。 200ページの退屈な計算。人はそれを読むことができません。

一般的に言って、誰もがこの記事にはこの定理の証拠が含まれていると信じています。しかし一方で、これまで正直にチェックした人は誰もいません。特に、この記事はピアレビューされたジャーナルに掲載されていません。つまり、自尊心のある数学者は、「はい、すべてが正しく、ケプラーの推測が証明された。」

そして、これは唯一の状況ではなく、これは数学の他の分野でも起こります。最近では、セット理論、モデル理論、さまざまな分野で未解決の問題のリストに出くわしました。そして、ある仮説に対するコメントがあります。それは、このような記事で反駁されていると言われていますが、誰もそれを信じていません。

これが状況です。その人はその声明を証明しましたが、それを他の人に伝えることも、他の人に伝えることもできません。

最も恐ろしい例は、もちろん、有限の単純なグループの分類です。必要に応じて、それらが何であるか、グループが何であるか、有限グループが何であるかを正確に定式化することはしません。有限グループはすべて、ある意味で、単純なグループと呼ばれる単純なブロックから組み立てられます。これは、小さなブロックに分解することはできません。これらの有限の単純なグループは無限にあります。それらの完全なリストは次のようになります。これらは17のエンドレスシリーズであり、最後に26の個別のグループが追加されます。これらは個別の方法で構築され、どのシリーズにも含まれていません。このリストには、すべての有限の単純なグループが含まれていると言われています。この仕事は数学にとってひどく必要です。したがって、70年代に、その解決策に対するいくつかの特別なアイデアと希望が現れたとき、さまざまな国、さまざまな機関の数百人の数学者が問題を攻撃し、それぞれが独自の作品を取り上げました。いわば、このプロジェクトのアーキテクトがいて、これらすべてをまとめて1つの証明にまとめる方法を大まかに想像していました。人々が急いで競争していたことは明らかです。その結果、彼らが行った作品は合計で約10,000の雑誌ページになり、それが出版されたものです。また、プレプリントまたはタイプライトされたコピーのいずれかの形式で存在した記事もあります。私自身、そのような記事をやがて読みました。この完全な証拠の注目すべき部分が含まれていますが、公開されることはありませんでした。そして、これらの10,000ページは、さまざまな人によって書かれたさまざまなジャーナルに散在しており、さまざまな程度の理解力があります。これに関係がなく、この理論の設計者ではない一般の数学者にとって、10,000ページすべてを読むことは不可能であるだけでなく、非常に困難です。証拠の構造そのものを理解します。そしてそれ以来、これらの建築家の何人かは単に死にました。

証明は誰も読めないテキストの形でしか存在しないが、分類が完了したことが発表され、次のトラブルにつながった。新しい数学者は、有限グループの理論に行く気がありませんでした。これを行う人はますます少なくなっています。そして、50年後には、この証拠で何かを理解できる人が地球上にまったくいないということが起こるかもしれません。伝説があります：私たちの偉大な祖先は、すべての有限の単純なグループがこのリストにリストされており、他にはないことを証明する方法を知っていましたが、今ではこの知識は失われています。かなり現実的な状況。しかし、幸いなことに、この状況が現実的だと思っているのは私だけではないので、彼らはそれに苦労しており、彼らは特別なプロジェクト「有限の単純なグループの分類の証明に関連する哲学的および数学的問題」を組織したとさえ聞いた。この証拠を読みやすい形にしようとしている人々がいます、そして多分いつかそれは本当にうまくいくでしょう。これらすべての困難をどうするかを考えようとしている人々がいます。人類はこの仕事を覚えているので、最終的にはそれに対処します。しかし、それにもかかわらず、他の同様に複雑な定理が現れる可能性があり、それは証明できますが、誰も読むことができず、誰も誰にも言うことができないという証拠です。

Дмитрий Германович Фон-Дер-Флаасс, «Квант» №5, 2010
Gorgiasの2番目の定理は次のようです-
何かが存在する場合、それは人にはわかりません。
ここで、このカテゴリに分類される文の例をいくつか示します。

集合理論に問題がありました。「選択の公理は本当ですか？」のような質問をする権利はあるのでしょうか？矛盾することなく数学をやりたいだけなら、原則として、選択公理を受け入れることも、それが真実ではないことを受け入れることもできます。どちらの場合でも、私たちは数学を開発することができ、ある場合にはいくつかの結果を、別の場合には他の結果を得ることができますが、矛盾は決してありません。

しかし、今は状況が異なります。明らかに、結果があり、その答えは明らかに存在し、明らかにそれは明確に決定されていますが、人類はおそらくそれを知ることは決してないでしょう。最も単純な例は、いわゆる（3 N + 1）問題です。これについては、これから説明します。自然数を選択しましょう。偶数の場合は、半分に分割します。そして、それが奇数の場合は、3を掛けて1を足します。結果の数値についても同じことを行います。たとえば、3から始めると、次のようになります。

7から始めると、プロセスに少し時間がかかります。いくつかの小さな数から始めて、このチェーンはかなり長いことが判明するかもしれませんが、常に1で終わります。どの自然数から始めても、そのようなチェーンを構築すると、常に1になるという仮説があります。これは（3 N + 1）-問題です-この仮説は本当ですか？

すべての現代の数学者はそれが正しいと信じているように私には思えます。そして、無謀にもそれを証明しようとさえします。しかし、誰も成功しませんでした。そして何十年も経過しています。したがって、これは魅力的な課題の1つです。もちろん、真面目な数学者はそれを軽蔑します-まるで楽しいパズルのようです。何がそこにあるのか、そこに何があるのか​​を知る必要が誰にあるか​は不明です。しかし、軽薄な数学者は、仮説が真実であるかどうかにまだ興味を持っています。それが証明されないうちは、ここで何でも起こり得る。まず、この質問には明確なyesまたはnoの答えがあることは明らかです。自然数から始めて、1に到達するというのは本当か、本当でないかのどちらかです。ここでの答えは、公理の選択や人間の意志に依存しないことは直感的に明らかです。人類はこの質問に対する答えを決して知らないという仮定があります。

ベルンハルト・リーマン
もちろん、誰かがこの仮説を証明すれば、私たちは答えを知るでしょう。証明するとはどういう意味ですか？これは、自然数が1に収束する理由を彼が説明することを意味し、理由を私たちに明らかにするです。

誰かが73桁の数字がまさにそのような特性を持っていることを証明するかもしれません。それからこのチェーンを実行することによって、私たちは間違いなく任意の大きな数字を得るでしょう。または、このチェーンが別の場所でループすることを証明します。繰り返しますが、これが仮説が間違っている理由になります。

しかし、たとえば、私にはひどい悪夢があります。この命題が真実であるが、理由がない場合はどうなるでしょうか。確かに、この命題には、ある人が別の人に理解して説明できる理由はまったくありません。そうすれば、私たちは答えを知ることは決してありません。残っているのは、すべての自然数を繰り返し、それぞれの仮説をテストすることだけだからです。そして、これは当然、私たちの力を超えています。エネルギー保存の法則は、有限の時間内に無限の数の操作を実行することを許可していません。または光の速度の有限性。一般に、物理的な法則では、有限の時間内に無限の数の操作を実行して結果を見つけることは許可されていません。

多くの未解決の問題は、この領域に正確に関連しています。つまり、原則として、彼らは本当にそれらを解決したいと考えています。それらのいくつかは決定する可能性が高いです。リーマン仮説という名前を聞いたことがあると思います。たぶんあなた方の何人かはこの仮説が何を言っているかを漠然と理解しているでしょう。個人的には漠然と理解しています。しかし、リーマンの仮説では、少なくともそれが真実であることは多かれ少なかれ明らかです。すべての数学者はそれを信じています、そして私は彼らが近い将来それを証明することを願っています。そして、まだ誰も証明も反証もできないという命題がいくつかあり、仮説においてさえ、2つの答えのどちらが正しいかは定かではありません。人類は、原則として、これらの質問に対する回答を決して受け取ることはない可能性があります。

Дмитрий Германович Фон-Дер-Флаасс (1962–2010)カバー写真より
数学者が、例えば複素関数を研究するとき、複素数が実数の対であること、実数が有理数の無限集合であること、有理数が整数の対であることなどをいちいち思い出すわけではありません。出来上がったいろいろな数学対象を使っています。しかし、非常に長い話になりますが、原理的にはすべてのものは基礎から組上がっています。

では、数学者は何をするのか？彼らは、これらの数学対象のいろいろな特性を証明します。何かを証明するためには、すでに何かを知っている必要があります。何よりも、一人の数学者が得た結果が他のすべての人に受け入れられるためには、どのような初期特性から議論を始めるかの完全な合意がなければなりません。

これらの初期特性のいくつかを書き出す（それらは公理と呼ばれる）ことから始め、多くの複雑な数学対象の他のいろいろな特性を証明します。しかし、自然数では困難があります。正しいと直感的に感じる公理から導くことができないが、それにもかかわらず真実と思える自然数に関する命題があることが判明しました。

すぐに疑問が湧いてきますが、この性質が自然数にも当てはまることをどのようにして知ることができるのでしょうか？困難な問題です。自然数の公理しか扱えないのであれば、多くのことを語ることは不可能です。例えば、自然数の任意の無限部分集合について語ることはできません。それにもかかわらず、人々はそれが何であるかを想像し、これらの部分集合がどの特性によって決定されるか直感的に理解します。したがって、公理から推論できない自然数のいくつかの特性について、人々はそれらが真実であることを知ることができました。自然数のある性質を明示的に示したのは、おそらく数学者のクルト・ゲーデルが最初で、それは直感的には真実である（つまり、数学者はそれが真実であることに異議を唱えない）が、当時受け入れられていた自然数の公理からは推論できないということになる。

部分的、実際には非常に大きな範囲（数学のほとんどの分野）で、この問題は、慎重にすべてを集合に持ちこんで、直感的に正しいと思える集合理論の公理のいくつかを書き出すことによって対処されました。

言ってみれば、連想の公理。もし、いくつかの集合の集合があれば、次のように言うことができます：この集合からこれらの集合のすべての要素を含む集合を形成しましょう。このような集合が存在することには、合理的な反論はありません。また、もう少しトリッキーな公理もあります。ここでは、集合理論の中で、原理的に疑問視される可能性のある3つのトリッキーな公理を考えてみます。

例えば、こんな公理があります。要素をたくさん有すると集合で、それぞれの要素上のある関数の値を曖昧なく決めることができるとします。この公理は、この集合の各要素にこの関数を適用すると、集まったものが再び集合を形成するというものです（図2）。最も単純な例：xをx^2に変換する関数なら、自然数の集合があれば、それをそれぞれの正方形に入れるイメージで、また自然数の集合に対応させます。 直感的に理解できる公理ではありませんか？もし、これらの関数が非常に複雑な方法で定義されると、集合が非常に大きくなる恐れがあります。また、私たちの関数が明確に定義されていないことは証明できるが、集合の各要素についてこの関数の具体的な意味を計算することは非常に難しい、あるいは無限に難しいという状況もあり得ます。何かしらの答えがあることは確かで、それは曖昧なものではありません。このような複雑な状況でも、この公理は適用可能と考えられており、集合論の問題の源泉の一つは、このような非常に一般的な形です。

図3
一方では自明、他方では問題をもたらす第二の公理は、この集合のすべての部分集合を抜き出せるという公理です。ある集合があれば、その集合のすべての部分集合からなる集合が存在するという。有限集合の場合は当然のことながら N個の要素の有限集合があれば、それは2^N個の部分集合しか持ち得ないことになります。基本的には、全部書き出すことも可能です。最も単純な無限集合でも問題はありません。1,2,3,4,5,6,7などの自然数の集合を取ってみましょう。自然数の集合のすべての部分集合の族が存在することは、なぜ明らかなのでしょうか？要素がわかっているからです。自然数の部分集合を想像するにはどうしたらいいのでしょうか？取り出す要素には１を、取らない要素には０を対応させる。この配列が無限に続く２進数であることを想像してみましょう（図３）。［訳注）いくつか抜き取った状態は0.1010････など頭に０．をつけて無限に続く2進数で表現できる］これで、実数は自然数の部分集合とほぼ同じであることがわかります。 すべての実数が順に並ぶことを直感的に知っているので、それらは実線として明確に表すことができます。与えられた集合のすべての部分集合の集合に関する公理も成り立つのです。

さらに考えてると、ちょっと怖くなってきますが、数学者は、この公理は常に実行されると信じています：我々がある集合を持っている場合、それはまた、そのすべての部分集合が存在することを意味します。そうでなければ、何かを構築するのは非常に困難になります。

そしてもう一つ、最初は信じていなかった公理があります。その名を聞いたことがあるかもしれません。「選択の公理」です。様々な方法で定式化することができ、非常に複雑なものもあれば、非常にシンプルなものもあります。今から、選択公理の定式化の方法をお話ししますが、その中で、それが正しいことが本当に明白になります。いくつかの集合を用意しておきましょう。それらは実際には重なっているかもしれませんが、それは重要ではありません。 簡単に言えば、それらはまだ重なっていないかもしれません。そうすれば、これらのセットを全部まとめたものを作ることができます。これはどういうことかというと、その要素はこれらのものになる、つまり、それぞれの要素から1つの要素を取り出して、それらすべてで1つの集合を形成する（図4）。集合から一つの要素を選択するそれぞれの方法は、これらの集合から作られるものの要素を与えます。

もちろん、これらの集合の中に空集合があり、そこから選択するものがない場合、作られるすべてのものも空になります。そして、選択の公理は、そのような完全に明白な事実を主張します。これらの集合がすべて空でない場合、作られるものは空ではありません。これは明らかに、選択の公理が実際に正しいという事実を支持する最も強力な議論の1つです。他の定式化では、選択の公理はこれほど明白に聞こえません。

すべての数学を集合理論の言語に翻訳しようとして、数学者が命題をどのように証明するかを観察すると、多くの場所で、数学者はそれに気付かずにこの公理を使用していることがわかりました。これに気がつくと、別の命題に分ける必要があることが明らかになりました。私たちはそれを使用していたので、どこかからそれを取り出さなければなりませんでした。それを証明するか、これが基本的な明白な事実であり、それを公理として使用することを許可されていることを宣言する必要があります。これは本当に基本的な事実であり、他のすべての事実だけを使用して証明することは不可能であり、反論することも不可能であることが判明しました。したがって、それを受け入れる場合は、公理として受け入れます。そして、もちろん、受け入れる必要があります。

ここで大きな問題が起こりました。この事実が明確な形で定式化され、「使用できます」と宣言されるとすぐに、数学者はすぐにそれを使用し、直感的には全く非自明な命題を多数証明しました。直感的に間違っているように見える命題すら証明しました。

選択の公理を使用して証明された、そのような命題の最も衝撃的な例は以下です。ボールがあります。それをいくつかのピースに分割し、これらのピースから2つのまったく同じボールが作れます。ここで「いくつかの部分に分割する」とは、たとえば7とすると、各点ごとに、これらの7つの部分のどれに該当するかの話で、これはナイフでボールを切るようなものではありません。はるかに難しい場合があります。たとえば、これは想像するのは非常に難しいですが、ボールを2つにカットする方法なら、座標が有理数であるすべての点を1つのピースに取り、もう1つのピース（無理数の座標を持つすべての点）も作ります。各点について、どのピースに分類されたかがわかります。つまり、これはボールを2つのピースに合法的に分割したものです。しかし、これを視覚化することは非常に困難です。これらの各ピースは、遠くから見ると、まるでボールのように見えます。これらのピースの1つは実際には非常に小さく、もう1つは非常に大きくなりますが。そこで、選択した公理の助けを借りて、この方法でボールを7つのピースにカットできることを証明しました。次に、これらのピースを少し動かして（つまり、空間内で動かしたり、歪ませたり、曲げたりすることなく）、もう一度組み立てて、2つのボールを得ることができます。当初のものと同じです。この命題は証明されていますが、やや風変わりに聞こえます。しかし、それにもかかわらず、数学者は、選択の公理のそのような結果を完全に放棄するよりも我慢する方がよいことに気づきました。他に方法はありません。選択した公理を放棄すると、それをどこでも使用できなくなり、多くの重要で美しく直感的な数学的な結果が証明できないことが判明します。結果は安全に証明できるようになりますが、同時にそのような異常な結果もあります。しかし、人々は多くのことに慣れており、これらの異常にも慣れています。一般的に、現在選択されている公理には問題がないようです。

集合理論の一連の公理があり、数学があります。そして多かれ少なかれ、人間が数学でできることはすべて、集合理論の言語で表現できるようです。しかし、ここでは、ゲーデルが算術の時代に発見したのと同じ問題が発生します。私たちの集合の世界（すべての数学の世界）を説明するかなり豊富な公理のセットがある場合、それらが真実であるかどうかを知ることは決してできないという命題があります。これらの公理から証明することはできず、反論することもできません。集合理論は強力に発展しており、今ではこの問題に最も近いものです。いくつかの問が非常に自然に聞こえる状況に直面することがよくあります。それらに対する答えを得たいのですが、答えも未知で、公理から導き出すこともできないことが証明されています。

何をすべきか？集合理論では、彼らはどういうわけかこれに対処しようとします。つまり、彼らは新しい公理を考え出そうとします。人類にとって直感的に明らかなことはすべて、20世紀の初めに開発された集合理論の公理にすでに還元されているように思われますが、まだ何か他のものが欲しいことがわかりました。数学者は直感をさらに訓練して、いくつかの新しい命題が何らかの理由ですべての数学者に突然直感的に明白に見えるようにし、それらを使用できるようにするでしょう。

もちろん、これがどのように行われるのかはわかりません。非常に複雑な命題があります。まず、集合理論を深く掘り下げて、それらが主張する内容を理解し、次に理解する必要があります。 これらの命題は、実際に直感的に明白であると見なすことができ、公理と見なすことができます。 これは、数学の最も神秘的な分野の集合理論が現在行っていることです。

Dmitry Germanovich Fon-Der-Flaass "Kvant" No. 5、2010

https://elementy.ru/nauchno-populyarnaya_biblioteka/431269/Teoremy_sofista_Gorgiya_i_sovremennaya_matematika

Dmitry Germanovich Fon-Der-Flaass（1962–2010）が早すぎる死を遂げました。クバントの読者はこの名前に何度も会ったことがあります。クバント誌はしばしば彼の問題を発表しました。ドミトリー・ゲルマノビッチは大きな科学で成功を収めましたが、それは彼の活動の一部にすぎません。彼は、学童のための数学オリンピック、全連合および全ロシアのオリンピック、そして近年では国際審査員を務めました。彼はさまざまな数学キャンプや学校で講義を行い、国際数学オリンピックロシアチームのトレーナーの一人でした。この文は，2009年に全ロシア子供センター「Орленокオルリョノク（わし）」で、D.Fon-der-Flaassが行った講演に基づいています。

■古代のソフィスト、ゴルジウスは、三つの定理を立てたことで有名です。第一の定理は、世界には何も存在しないということです。第二の定理は、もし何かが存在するならば、それは人間にはわからないということです。第三の定理は、もし何かが認識可能であるならば、それは隣人には言い表せない。
言い換えれば、何もありませんし、何かがあれば、それについて何も知りませんし、何かを知っていても、誰にも言えません。
これらの三つの定理に四番目を追加します。何かを言うことができたとしても、誰も興味を持ちません。
これらの四つの定理は、実は、現代数学の主要な問題です。

ゴルジウスの第一定理
世界には何も存在しない。数学の言語に翻訳すると、数学は理解できないことをしています。ある意味、これは真実です。結局のところ、数学的なものは世界に存在しません。私たちは皆、自然数が何であるかを知っています。それらは1，2，3，4，などです。そして、私たち全員が「など」という言葉の意味を理解しているという事実は大いなる謎です。 「など」は「無限に多い」数を意味するからです。この世界には、無限に多くのものが存在する余地はない。しかし、私たち全員が自然数について考えるとき、私たちは皆同じことを考えていると信じています。私は7の次は8と思うが、あなたも7の次は8と思う。私が19を素数と思うが、あなたも19を素数と思う。この対象物は世に存在しないようですが、私たちはそれを知っており、私たち全員が同じことを知っています。もちろん、これは数学的な謎ではなく、哲学的な謎なので、議論は哲学者にさせます。幸いなことに、私たちは数学的対象の概念を持っているだけで十分で、それらについて考えるすべての人にとって同じです。だから数学が可能なのです。しかし、哲学的な大きな問題は残っています。

数学者が、これを厳密に考えようとすると、問題が発生します。それがこれからお話しすることです。それらが人類の記憶に出現したのはごく最近（過去100年間）のことです。

自然数に加えて、数学にはもっとたくさんのことがあります。ユークリッド平面があり、そこにあらゆる種類の三角形、角度を描き、それらについての定理を証明します。実数がある、複素数がある、関数がある、もっと恐ろしいものもある...。19-20世紀の変わり目（もちろん、それは少し前に始まった）で大きな転機がありました。人々は、多様な数学的対象の全体は、単一の概念 （集合の概念）に還元できることに気付きました。確かに、単純に「集合」とは何か、「など」とは何かということを直感的に理解していれば、基本的にはすべての数学を構築することができます。

問題は、集合で何ができるかということです。集合が存在する場合、それはどういう意味でしょうか？つまり、私たちの世界、数学的対象の世界のどの要素についても、それがこの集合に含まれているか否かを尋ねられたら、はっきりした答えを得られることを意味しています。答えは明確で、私たちの意志とは完全に独立しています。これは、集合を使ってできる最初の基本的なことで、要素が集合に属するかどうかを調べることです。

もちろん、集合自体は何らかの方法で構築する必要があります。そして、最終的には、すべての豊富な数学的対象がそれらから構築されます。それらはどのように構築されるでしょう？たとえば、空集合Øを作成できます。この集合に属しているかどうかに関係なく、どの要素について質問しても、答えは常に「no，属していません」となり、空集合はすでに一意に決定されています。空集合に関するすべての質問は即座に答えられます。

そして、空集合だけしか含まない集合{Ø}を作成できます。繰り返しますが、この集合があるとはどういう意味ですか？これは、どの要素についても、それがこの集合に属しているかどうかを判定できることを意味します。そして、この要素が空集合である場合、答えは「yes」、この要素が他の要素である場合、答えは「no」になります。したがって、この集合もできました。

ここからすべてが始まります。より直感的な操作をいくつか使います。 2つの集合がある場合は、それらを結合できます。これは、一方または他方の集合の要素を含む集合があると言えます。繰り返しますが、要素が結果集合に属するか否かという質問に対する明確な答えができます。だから私たちは結合を築くことができます。等々。

ある時点で、無限に多くの要素が存在する集合があることを宣言する必要があります。自然数があることを知っているので、無限の数が存在すると信じます。自然数の集合も利用できることを宣言します。無限の集合が現れると、整数を定義できます。整数は、ゼロまたはマイナス記号の有無にかかわらず自然数のいずれかです。これはすべて、集合理論の言語で行うことができます。

有理数を定義できます。有理数とは、分子と（ゼロ以外の）分母の2つの数値のペアです。それらの間に加法と乗法を定義する必要があるだけです。そして、そのようなペアが同じ有理数と見なされるときの条件は何でしょうか。

実数とは何か？これが興味深いステップです。たとえば、それは無限小数であると言うのも良い定義でしょう。無限小数とはどういう意味ですか？つまり、各自然数は実数に含まれます。

ところで、数学者は実数をこのように定義するわけではありません。我々がすでに押さえた有理数の集合を見れば、厳密には実数の集合よりも小さいものであることを宣言しておきましょう。これは非常に厄介な定義です。実は、以前の定義と非常に似ています。例えば実数3,1415926だとすると (無限の数の連鎖が続いている)例えば、それよりも小さい有理数は何でしょうか？小数点以下の端数を切ります。3.14という数字が出てきますが、考えた実数よりも小さいです。小数点以下第4位の端数を切ると3,1415個になり、これも考えている実数よりも小さい有理数が1つ増えます。自分の数よりも小さい有理数をすべて知っていれば、その数だけで決まることは明らかです。そのような絵を視覚的にイメージすることができます。直線はすべて実数で、その中でどこかに私たちの未知数があり、その左に私たちの未知数よりも小さい多くの有理数があります。他の側のすべての有理数は、それよりも大きくなるだろう。これら2つの有理数の間に1つのチップがあることは直感的に明らかで、このチップを実数と呼ぶことにします。集合の概念から始まって、数学全体が少しずつできていきます。

 
plus magazine（November 5, 2020）を要約した

11月18日の東京都のCOVID19新規陽性者数は493人となり，指数関数的な増加予測グラフに乗りました．予断を許さない状況になりました．
ここで紹介する（plusmagazine，Nov.５，2020）記事は，マスク着用の効果とエアロゾルを介しての伝染を予防するための換気について語っています．たぶん，皆様の常識になっている事実の確認で新規性はないので，この記事は圧縮して紹介します．

■　COVID-19を引き起こすウイルスは、主に大きな液滴と小さなエアロゾルを介して伝染する。これらは、呼吸、会話、咳、または笑いの際に排出され、「ウイルスを含む小さな呼吸エアロゾルは、呼吸によって生成された二酸化炭素と一緒に、換気の流れによって部屋の周りに運ばれる」とリンデンらは論文で言う［Paul Linden, Rajesh Bhagat, Stuart Dalziel, and Megan Davies　Wykesによる］。「換気が不十分だと二酸化炭素濃度が高くなり、ウイルスにさらされるリスクが高まる可能性がある」

オフィス、病院、レストランなどの多くの近代的な屋内スペースの換気システムはさまざまです：　風と熱によって駆動される自然換気、または機械システムによります。混合換気は、空間内の空気を十分に混合して維持することを目的とし、置換換気は、部屋の上部から暖かい空気を抽出し、床近くの通気口から冷たい空気を供給することで、より涼しい下部ゾーンとより暖かい上部ゾーンを生成します。

COVID-19の感染に関しては、空気を混ぜることは望ましくない。「混合換気は、すべてを空中に浮遊させてかき混ぜることを目的としています」とリンデン氏は説明します。「置換換気ならば、私たちが吐き出す暖かく潜在的に危険な空気は天井に上がり、そこで抽出することができます」。

置換換気を使用しても問題が発生する可能性があります。部屋にさまざまな熱源がある場合、呼気は暖かい天井層の下に閉じ込められ、他の人によって再び吸い込まれる可能性があります。

人々の呼気の正確な挙動と病気の伝染におけるその役割を予測することは非常に難しいので、リンデンと彼の同僚は、流体力学研究所（ケンブリッジ大学の数学科学センター）で実験を行いました。

■　呼吸、会話、笑い
人がじっと座って息を止めているときでさえ、彼らの体の熱は天井に上がる暖かい空気のプルームを生成します。人が呼吸を始めたり、口を開いて話したり、歌ったり、咳をしたり、笑ったりすると、吐き出された息が2番目のプルームを生成します。伝達に関しては、この2番目のプルームが本体のプルームに同伴されて天井に運ばれるのが最善です。

もちろん、空気は見えませんが、リンデンと彼のチームは、暖かい空気を追跡できる画像技術を使用しました。「誰かが暖かい空気を吐き出すと、温度と密度の変化を見ることができます。それは光を屈折させ、あなたはそれを測定することができます」とバガットは説明します。

チームが作成した画像を以下に示します。左側の画像では、人は静かに座って鼻から呼吸し、中央の画像では通常の音量で話し、右側の画像では笑っています。各画像では、体のプルームが穏やかに上昇していることもわかります。3つのケースのそれぞれで、吐き出されたプルームが体のプルームに吸収されていないことがわかります。

上段の写真はマスクなし．下段の写真はマスクありです．

■　実験と数学

このような実験は非常に重要ですが、実験はリンデンと彼のチームの研究の一部に過ぎません。同様に重要なのは、ガスやその中の汚染物質の挙動を記述する数学モデルで、ウェルズ・ライリーの方程式があります。これは、空気感染性の病気にかかっている人と部屋を共有することで感染する人の予想される数I　を推定しています。

ここで、Sは、部屋の中で病気にあらたに感染可能な人の数であり、Γは部屋の中の既に感染している者がウイルスを排出する率を記述し、qは一人当たりの平均呼吸率、tは人々が部屋を共有している時間幅を記述する。Qは部屋の換気率、つまり新鮮な空気が部屋に入る率です。

この式をよく見てみると、Qが大きいほど（部屋の換気が良いほど）感染する人の数Iが少ないことがわかります。ウェルズ-ライリー方程式は、換気 Q は空間全体で均一であることを前提としており、リンデンと彼のチームが示したように、これは通常、人や家電製品によって生じる空気の流れも問題になり現実にはそうではありません。しかし、ウェルズ-ライリー方程式（他の多くの関連する数式とともに）は、現実の生活をより正確に記述する、より複雑なモデルの一部を形成するでしょう。

■　結論

置換換気システムは、適切に設定されている場合は、より良い選択である。
マスクは有益である。

この研究はまた、もう一つの興味深い可能性を示唆している。ウイルスを含んだエアロゾルは、私たちが息を吐くCO₂と同じように振る舞うので、部屋のCO₂レベルは警告システムに使える。CO₂レベルは非常に簡単に測定することができ、それが高い場合は、空気感染のリスクも高くなるので、リンデンらは、信号機のような警報システムを考えている。