note.com投稿記事

 
■NHS Nightingale Hospitalについて
NHS＝国民保険サービス，Nightingale Hospital＝臨時救急病院≒野戦病院
イギリスのNHSは4つの地域区分（イングランド，スコットランド，ウエールズ，北アイルランド）があります．イングランドのナイチンゲール病院は，London（4,000床）にオープン(4月3日)を皮切りに，7つ目のSunderland（460床）は日産自動車工場近くに整いました．Covid-19患者の数に北東部の病院が対処できない場合に限り使われます．「人々が社会的距離を保ち，あるいはワクチンができ，この病院を使わないですむことを願っている」とNewcastle病院のNHS局長は語りました（Sunderland Echo紙）．
Stay at home, protect the NHS, and save livesがスローガンで，
イギリスは，3月23日に3週間の全土封鎖に踏み切ったが，まだピークが去らないとしてさらに3週間の延長しています．4月19日現在．累積確認患者数は90,629，累積死者数は14,399に上りますが，一日の感染者の広がりは減少始めたようです．封鎖と並行して，PCR検査から抗体検査に転換し，抗体検査の大規模実施（現時点で1万3729人1日3万5000件の能力がある）と「NHSナイチンゲール病院」の設立を進めました．
クリミア戦争(1853-1856)で野戦病院の衛生状態の改革を行ったナイチンゲールは，『看護覚え書』，『病院覚え書』など多くの著作を残し，そこにはワンルームの病院設計図もあり，高い天井まで延びた3層の窓，3層目の窓を開放し換気，ベッドの間隔，等々要点が記されています．
NHSが設立した病院は，ナイチンゲールの病院概念が活かされた臨時救急病院≒野戦病院だからこう呼ぶのでしょう．
■ナイチンゲールについて（以下のウエブサイト記事を参照しました）
草の実堂；https://kusanomido.com/study/history/western/21987/　
ナイチンゲールはクリミア戦争(1853-1856)で野戦病院の衛生状態を実践改革し死亡率を低下させました．帰国後のナイチンゲール・チームはバーリントンホテルに集結し，戦時の報告書をもとに病院の状況分析をして，数々の統計資料を作成，改革のためにつくられた各種委員会に提出しました．特に，死亡原因ごとに死者の数をひと目で分かるようにレーダーチャートの発明があります．
1860年にナイチンゲールが看護専門学校（ナイチンゲールスクール）を設立したのは広く知られていますが，ナイチンゲールが統計学者であることはあまり知られていません．疫学研究の元祖です．1859年にイギリス王立統計学会の初の女性メンバーに選ばれ，アメリカ統計学会の名誉メンバーにも選ばれました．ナイチンゲールは90歳で亡くなりますが，晩年50年間はほとんどベッドの上で，本の原稿や手紙を書く活動でした．その病因はブルセラ病に感染したこと（by D A B Young，Florence Nightingale's fever，1995)でした．

ブルセラ病については，次号に続きます．

 
ナイチンゲールが50年間ベッドでの仕事を余儀なくされ，死因ともなったのは，クリミア戦争時に流行したマルタ熱（ブルセラ症）であることが明らかになった．D A B Young，Florence Nightingale's fever，(BMJ VOLUME 311 23-30 DECEMBER 1995)
ーーーーーーー
■ブルセラ症（brucellosis）
NIID国立感染症研究所https://www.niid.go.jp/niid/ja/kansennohanashi/513-brucella.html，および，wikiを参照した．－－－－
ブルセラ症はマルタ熱とも呼ばれる細菌に感染して起こる人獣共通感染症．クリミア戦争でマルタ熱が流行したことで世界的に注目されたが，紀元前400年頃のヒポクラテス著書にブルセラ症と思われる疾患がすでに記載されている．現在でも，世界中で毎年50万人を越える家畜ブルセラ菌感染患者が新規に発生（食料や社会・経済が家畜へ依存し，家畜ブルセラ病が発生している国や地域）発生している．マルタ熱の原因菌として，イギリス軍の軍医Sir David BruceによりB. melitensis が分離（1887）されて以降，種々のブルセラ属菌が発見されている．ヒトへの感染が報告されている主なものは，B. melitensis （自然宿主：ヤギ，ヒツジ），B. suis （ブタ），B. abortus （ウシ，水牛），B. canis （イヌ）の4菌種である．日本では，過去に牛のB. abortus感染が流行し問題になったが，家畜衛生対策の徹底により，1970年を最後に国内家畜から菌が分離された例はない．感染動物の加熱殺菌が不十分な乳・乳製品や肉の喫食による経口感染が最も一般的である．ヒト－ヒト感染は極めてまれである．
ブルセラ属菌は敵国の兵士や住民に罹患させて能力を低下させる生物兵器としても研究・培養された．アメリカは1942年、ソ連は1978年に兵器化を実現した．

■サビノワとリユドミラ物語．Екатерина Савинова и Людмила Сенчина
Приходите завтра「明日来なさい」(1963年，ソビエト映画)は，1540万観客の大ヒット映画（ロシア語）です．シベリアの寒村からИнститут имени Гнесиных モスクワの音楽学校に入ろうと出てきた才能ある少女の物語です．重い荷物を背負って一人で都会に出てきた元気で愉快な純粋な少女です．しかし，モスクワに来たときは既に遅く入学試験は終わっていました． 少女の役名はФросяフローシャ．これは実在のЕкатерина Савиноваサビノワの伝記映画で，サビノワ自身が主演し歌います．あの声はサビノワしか出せません．私がこの映画を知ったのも彼女の3.5オクターブ出るという魅力的な声の歌を耳にしたからです．音楽学校の玄関で有名なソコロフ教授に何度か訴えます．ついに引き出した教授の返事が Приходите завтра!「明日来なさい」でした．教授に学校のオーデトリウムで聞いてもらえた彼女の歌声がすばらしい．教授もフローシャの純粋さと素晴らしい声を見抜き，何とか入学させようと動きます．この映画はサビノワが自分で主演した愉快で楽しい映画で，私はとても好きです．しかし，残念ながら，その後のサビノワは，ブルセラ病（生牛乳を飲むと牛から感染する）が重くなり鉄道自殺（1970年，43歳）してしまいます．

興味深いのは，1963年にウクライナで高校生時代に，Людмила Сенчинаリュドミラ・センチナはきっとこの映画を見たのではないかと私は想像します．リュドミラは成功して，ロシア人民芸術家歌手になります．彼女は今年の1月25日に，ペテルブルクの病院で死去（６７歳）しました．
リュドミラは，高校を卒業して，歌手になるために，ウクライナからレニングラード（現ペテルブルグ）に出てきました．でも，そのとき音楽学校の試験は終わっていたのです．よく似た話があるものですね．サビノワと違うのはペテルブルグに親戚がいたことです．
リュドミラの代表曲は，Песня Золушкиシンデレラの歌
－－－－－－－

 
新型コロナウイルスCovid-19の感染拡大が止まりません．皆様お元気でお過ごしでしょうか．現在，日本では「人と人との接触機会を８割減にしよう」との呼びかけがなされています．規制を遵守し感染機会を減らすことはこの時期非常に重要です．

8割減は，感染拡大の転換点であるとされています．その根拠となる手法の総説には，例えば，「感染症流行の予測：感染症数理モデルにおける定量的課題」（西浦・稲葉；統計数理，第54巻第2号，461-480，2006）があります．しかし，接触機会8割減が転換点であるという具体的なシミュレーションはまだ見ておりません．

いろいろな感染症はそれぞれの特異な伝染状況があり，それに合わせた数理モデルを作る必要があるので一般論ではかたづきません．Covid-19の感染拡大に対しての数理モデルと，感染率，ウイルスの活性期間，患者の死亡率，感染者が感染源になりうる期間，等々の係数を仮定する必要があります．Covid-19は，まだ解明されない特異な感染の振る舞い（無症状の保菌者が感染源になる，感染回復後も再度感染する，等々）があり，完全な数理モデルができず確定的予測は困難です．
今回，石黒真木夫が，簡単な仮定に基づくCovid-19の特徴を考慮した数理モデルを作り，教育的なシミュレーション結果を得ました．その詳細は．「NPO数学月間の会」のホームページhttp://sgk2005.saloon.jpにありますのでご覧ください．

■ここでは，数式を用いずに，石黒の数理モデルとシミュレーションの内容要点を紹介します．

（１）ある人口集団を未感染者，ウィルス感染源，免疫獲得者，死亡者に分類し，未感染者がウィルス感染源の一員と接触したときにある感染確率で未感染者が感染してウィルス感染源となるものとする［実際は，Covid-19では，人－物ー人の感染ルートもあるといわれる］．

（２）ウィルス感染源のウィルス拡散は14日間つづき，14日目に「死亡率」に従って死亡者と免疫獲得者に分かれ，免疫獲得者はもはやウィルスを拡散することも再感染することもなくなる［実際は，再感染するケースも稀にある］．

（３）このモデルでは時間の経過とともに未感染者は単調減少，免疫獲得者は単調増加するので，感染の流行はかならず止まる．しかしそれは集団全員が感染した後である．

（４）感染確率と死亡確率を適当に与えればシミュレーションは簡単である．いまの計算機をもってすれば人口集団の各個人の命運をたどるミクロ・シミュレーションもさして難しくないが，以下で紹介するのは未感染者やウィルス感染源集団の大きさの変化を追跡するマクロ・シミュレーションである．確率的な現象の「期待値の動き」を追いかける決定論的なダイナミクスを採用する．ミクロ・シミュレーションをして，算術平均の変化を見るとマクロシミュレーションの結果に「誤差」が乘ったような動きになるだろうと考えられる．

（５）感染が感染源と未感染者の接触でおきるので，接触規制で感染源率を下げて「医療崩壊」は防ぐことは可能だが，これは未感染率を「高止まり」させ，規制をはずすと残った未感染者が感染する事態が発生することを示している．接触規制で再流行時期を遅らせて得た時間的余裕を有効に使って致死率を下げることが重要．それができないと、結局は死者の数は減らせないということになる．

■石黒の数理モデルを用いたシミュレーション・プログラム（Excelファイル）は，NPO数学月間の会のウエブサイトhttp://sgk2005.saloon.jpに公開しています．各自このファイルをダウンロードし，パラメータも色々変えてシミュレーション実験をすると面白いだろう．各種規制の効果は接触機会数に乗じるパラメータを変えて見ることができます．
感染者数のピークが過ぎても，揺れ戻しの感染者数の小さなピークが観測され，このような波動を繰り返しながら収束に向かうことがわかるでしょう．

 
私は3月24,26日のメルマガまぐまぐ(311,312号)で以下の内容の発表をしました．－－－－－
3月21日の厚労省の公表値を用いて，罹患率＝発症患者/PCR検査数と定義すると，罹患率は，約5%になります．しかし，PCR検査の，感度と特異性（酒井健司，朝日デジタル）の情報を入れてベイズ推定した罹患率は5.9%になりました．この推定値の増加は，主としてPCR検査感度に原因があり，実際の罹患者を取りこぼすためです．（注）この数値は，PCR検査を受けた限定されたグループをサンプルとしているために，一般の集団に対しては少し割り引いた数値になるでしょう．－－－－－
今日，PCR検査数も増加したので4月23日厚労省のデータを用いて，再計算をしてみました．どのように変わったでしょうか？
ただし，PCR検査数が増加したといっても（多少はPCR検査を受ける条件の緩和があるかもしれませんが），陽性の確率が高いサンプル集団について検査が行われている状況は変わりません．
カバーの図を見てください．ここで推定する数値はあくまでもサンプル集団に関するもので，一般集団に対してはいくらか割り引いた数字になるでしょう．
ーーーーーーーーーーーーーーーーーーーーー
■条件付き確率についての「ベイズの定理」とは次のようなものです．
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です．
p(X)　　Xが起こる確率
p(Y|X)　Xが起こった後でYが起こる確率
p(X∩Y) XかつYが起こる確率
ベイズの定理は，X（原因）が起きた後でY（結果）が起きる確率p(Y|X)と，XとYを入れ替えた確率p(X|Y)を結び付ける定理です．
ーーーーーーーーーーーーーーーーーーーー
■新型コロナウイルスに対するPCR検査数は，厚労省の発表https://www.mhlw.go.jp/stf/newpage_11012.html　で，4月23日現在，
135,983人になりました（1月前の3月21日の数字の7.5倍です）．
PCR検査数　　　　135,983
PCR検査陽性者数　  11,919
陽性者のうち発症患者（陽性者∩発症患者）7,315人
発症患者/PCR検査数＝罹患率　と仮の罹患率を定義すると，罹患率は約5.4%です．
陽性率＝陽性者数/PCR検査数＝0.088　，陰性率＝0.912　と定義できます．

■PCR検査の精度
新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）に基づき，次のように仮定します．PCR検査の感度というのは，罹患者がPCR検査で陽性＋と正しく判定される確率のことで，あまり大きくなく0.7， 罹患者でもPCR検査が陰性－となる（偽陰性）の確率は0.3程度．
検査の特異性により，非罹患者が＋（疑陽性）と判定される確率は0.01だそうです．

■これらの仮定の下で，以下の２つを推定しましょう．ただし，ベイズの定理を使います．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．
p(罹患|+)=p(+|罹患)p(罹患)/p(+)=0.7×0.054/(0.054×0.7+0.946×0.01)=0.80

＋(陽性)でも検査感度のせいで罹患者をとりこぼすことが多い．また，非罹患者の割合が大きいので偽陽性の数も無視できない．この2つの原因が，＋判定でも罹患者である確率を80%（前回79%）に下げている．

（２）罹患率を推定しなさい．
p(罹患|−)=p(−|罹患)p(罹患)/p(−)=0.3×0.054/(0.054×0.3+0.946×0.99)=0.017
－（陰性）と判定されたものの中に見逃された患者である可能性は1.7%（前回1.6%）ほどある．

従って，サンプル集団で推定される罹患率は0.088×0.80+0.912×0.017=0.086
すなわち，8.6%(前回5.9%)と推定できます．

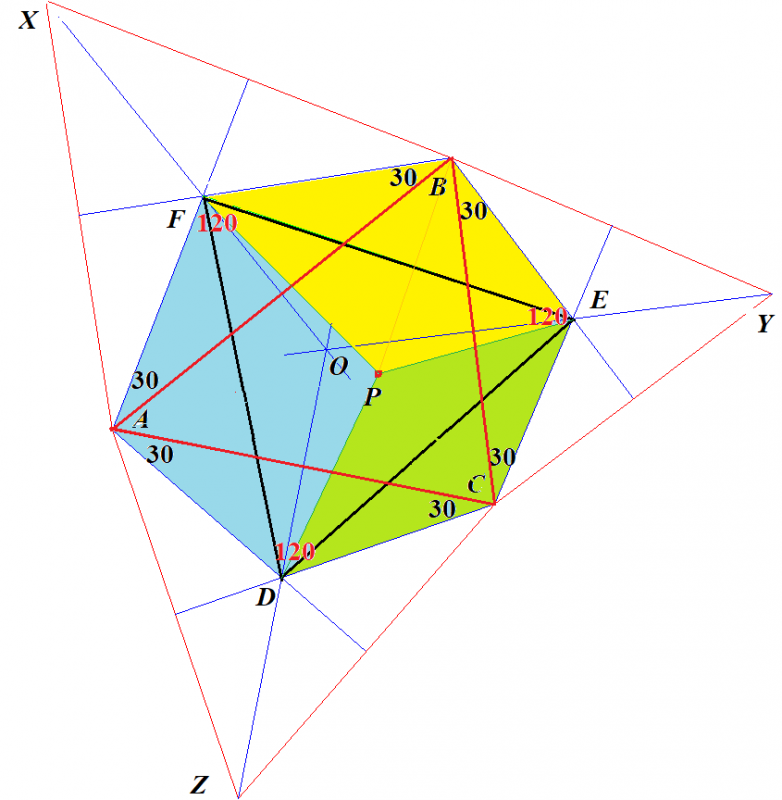
ナポレオンが発見したといわれるナポレオンの定理とは次のようなものです．

ーーーーーーーーーーーーーーーーーーーーーーーーー
ナポレオンの定理
任意の⊿ABCの各辺上に正3角形を作図し，それら3つの正3角形の重心をD，E，Fとする．D，E，Fを結んでできる⊿DEFは正3角形である．
ーーーーーーーーーーーーーーーーーーーーーーーーー

なかなか美しい形の定理ではありませんか，ナポオンの名を冠するのにふさわしい定理だと思います．ただし，ナポレオンが発見したかどうかは記録がなくわかりません．

ナポレオン (1769 －1821) は数学好きです．
陸軍幼年学校で，代数，三角法，幾何などを勉強し，数学で抜群の成績をおさめ，1784年にパリの陸軍士官学校に入学．数学が役に立つ砲兵科へと進みます．騎兵科，歩兵科でなく砲兵科に進んだのも戦術の時代の流れを見据えての決断でしょう．砲兵司令官，将軍，皇帝になりました．この時代にフランスには多くの数学者がいました．ラプラス，モンジュ，フーリエなどが近くにおり，エジプト遠征 (1798 年) にはモンジュやフーリエが同行しました．
ナポレオンは数学が大好き，このような幾何問題を考えるのが楽しみで，きっと定理を発見したのだと私は想像します．

証明

与えられた任意の3角形を⊿ABCとします．
その各辺上に作図した正3角形のそれぞれの重心がD,E,Fです．
点Oは⊿ABCの垂心（⊿ABCのそれぞれの辺の垂直2等分線が交差する点）で，点D，E，Fは，この垂直2等分線上にあります．

色々な角の角度は図中に記入してあります．我々が証明すべきことは，⊿DEFが正3角形であることで，例えば，∠DFE=60を証明すれば済みます．考えてみてください．

ヒントは，∠BFE=∠BXC　　と　　∠AFD＝∠AXC　を証明することです．

正3角形であるための必要十分条件は「３つの内角すべて（すくなくとも2つの内角）60°」です．

図形の対称性から，内角の１つが60°であることを証明すれば済みます．

これは，補助線1本引けば自明です．三角関数を使って計算で証明する方法もありますが，補助線1本で自明になるのが幾何の醍醐味です．

■さて，ここに出てきた６辺形には面白い性質があるのを見つけました．

この６辺形の中にある正3角形の中に点Pを中心になるように，正3角形の外の6辺形の部分を折り込むことができます．

4月25日，10:30から，Zoomを用いてリモートでの同志社中学校のDo★MATH博物館の見学がありました．10分間ほどの休憩をはさんで1時間ほど園田先生が出演され，見学会と，一太刀切りでハートや星形を作ったり，誕生日を当てる数あてカードを楽しみました．今年は，「数学月間」のイベント（毎年7月22日に実施し今年は第16回）もリモートで実施することになりそうです．

誕生日（1～31の数）を当てるには，4x4の数字が書かれた5種類のカードを見て，自分の誕生日が書かれているカードを選び出します．そして，それらのカードの左上の数を足し合わせると誕生日が当たるのです．
なかなか不思議ですね．この原理を今日は解説します．

■これからの説明は，誕生日を当てるゲームの変種で，15までの数を当てるゲームについて語りましょう．ゲームの実施方法も，数字が書かれてあるカードを選ぶのではなく，数字が書かれたカードの上にマスクをかぶせて当てようとしている数が見えているかどうか訊ねる方法になります．この両方のゲームとも同じ原理（2進数表記）を利用しています．

4x4の16個のマスに0~15の数字が書かれたカードがあります．このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる．これをマスクカードを変えて4回行えば，相手が心の中で思っていた数が当てられるというのが，この数当てのゲームです．

どのような仕組みがあるのでしょうか．秋山久義さんが，2019年7月のパズル懇話会で発表されています．今日は，秋山久義さんの発表「数当てカードの諸相」から引用して，その仕組みを解説します．

まず，16個の数の配列は，ランダムに配置したふりをしていますが隠れた規則があります．
例えば次の２つの方法があります．
（１）左右対称の位置にある2つの数字の和は常に15になる．
（２）回転対称（2回対称あるいは点対称）の位置にある２つの数字の和は常に15になる．

 このために右半分（あるいは左半分）を知れば，全部の数の配置がわかります．つまり，相手の意中の数がマスクに隠されて見えない場合は，その数との和が15となる数の方が見えているのです．

さて，0~15の数を2進数で表すと次の表のようになります．下図をご覧ください．a,b,c,dはそれぞれ2^3，2^2，2^1，2^0の桁に相当します．

2進数表示で3桁目を表すマスクカードがa，2桁目を表すマスクカードがb，というように4枚のマスクカードができます．
それぞれの数の上に乗る4種類のマスクカードで，2進数表示の１のところに孔を開ける（逆に統一してもかまわないが）ことにします．
例えば，13に場合は，aとbとdのマスクカードに孔（網掛け部分）をあけ，ｃのマスクカードには孔はあけません．

以上で，仕掛けの準備ができました．

これで，質問を開始して，数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます．
見えないといったマスクカードは
（１）の場合には裏返して重ね／（２）の場合は180°回転して重ねるのです．

結局，4枚のマスクカードを重ねたものは，
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです．

同じ正３角形（正6角形）格子［あるいは，正３角形２つよりなる平行4辺形格子とみてもよい］のパンチングメタルを2枚重ね合わせました．
この図の状態は，2枚の格子どうしのなす角度が2θ＝30°になった場合です．初めの正3角形（正6角形）の格子より大きな新しい周期の格子が出現しているのがわかりますか．

■正方形格子（網目）を2枚重ねた場合を考察してみましょう．
(Coincidence-site-lattice)

両方の網目が重なった位置に，新しい網目の格子が見えて美しい．

2枚の正方形の格子（正方格子という）どうしの傾きを変えると，ときどきこのような新しい格子が現れます．もとの格子の互いに直角な２つの並進ベクトルをa，ｂとすると（正方格子ならa=b），
もとの格子は，格子点 na+mb，（n,mは任意の整数）の集合です．
同じ正方格子を２枚傾けて重ねて，新しい周期の２つの並進ベクトル x, yが生じています．これらの図の状態は，

（上図）x=2a+b，y=a+2b ．（下図）x=3a+b，y=a+3b（面心格子，２格子点胞）

この基底変換を行列で書き，行列式を求めると３（左図），8（右図）ですので，新しくできた格子はもとの格子と比べて面積で3倍（左図），8倍（右図）粗くなっていることがわかります．

格子というのは，並進ベクトルの作る群＝並進群の”図的表現”です．2枚の格子の干渉で生じた新しい格子の周期は，もとの格子の粗いサンプリングになっているわけで，新しい格子は，もとの格子の部分群になります．

格子が重なって，拡大された（粗い）格子が見える現象は，干渉（ビート）と同じことです．
実際に，２つの原子網面が重なって，このようなビートが見えることは，電子顕微鏡で格子像の観察をするときにもよく起こります．
結晶は周期的な構造をしているので，周期的な空間は「結晶空間」とも呼ばれます．エッシャーの繰り返し模様や，壁紙模様などで，周期的空間の実例をたくさん目にしていると思います．

■2つの正方格子の平行なずれによる干渉（モワレ縞） 

 それぞれの正方格子の周期をλ１，λ２とすると，新しい周期Lは
1/L=1/λ1−1/λ2　の関係があります．

私は，子供のころ家にあった織物検査器というもので遊んだことがあります．これは，標準となる格子模様がガラスに刻んであり，織物にこのガラスを重ねると繊維の周期とのビートで縞模様が観察できます．1mmの中に何本繊維があるかとか，織り方が均一でなくどの程度乱れているかが，モアレ縞からわかります．

次の写真は，工事現場のネットが折り返されて2重になっているために観察されるモアレ縞です． 

昨年9月に表題の本（技術評論社）を出版しました．この本の構成は8つの章からなり，全章を通して万華鏡で繋がっています．1,2章は有限図形の対称性（点群）．3,4章は周期的な空間の対称性（平面群）．これらの映像は，万華鏡で作り出すことができます．5章は万華鏡．6章は円による反転という数学的な鏡を用いた万華鏡．7章はフラクタル操作という数学的な鏡を用いた万華鏡です．8章は東京ジャーミイで，イスラミック・デザインを鑑賞します．写真撮影にご協力いただいた東京ジャーミイの本屋さんにも本書を置いていただいています．

■この本に，第9章を続けて書くとすれば，イスラミック・デザインになります．イスラムデザインの特徴は，黄金比（すなわち5回対称や10回対称）がちりばめられていることです．しかし，5回対称性と2次元（あるいは3次元)世界の周期性とは両立できませんから，ちりばめられている5回（あるいは10回）対称性はロゼット内部だけに局所的に作用し，世界の全域を支配するものではありません．そのため，あたかも我々の住む3次元に高次元宇宙が投影しているようで不思議な魅力を感じます．イランのDarb-i Imam寺院（1453）の壁には,その500年後にヨーロッパで発見されるPenroseタイリング［自分の中に自分と同じパターンが繰り込まれる］と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています．イスラムの繰り返し模様は準結晶や基本領域が分割されて写像される万華鏡と似たところがあります． 

 
病院でMRI(核磁気共鳴イメージング)を撮ったことがある方もおられることでしょう．私も3年前にMRIの診断を受けたことがあります．お陰様で現在は絶好調です．このMRIの記事はそのころ書いたものです（記事の中で1.5Tの静磁場と記述しましたが，3年たち3.0Tの装置の普及も多少進んだようです）．
MRIの測定中に聞こえる”カタカタ”や”ビー”というほとんど冗談かと思うようなふざけた音は何でしょうか？　あれは，1.5T（テスラ）という強い磁場中で装置が動くために，あたかもスピーカーと同じように装置が振動して出す音です．それにしてもなんとかならないものか？振動しないようにガッチリ作るのは，今でも何トンという重量ですから無理なのでしょうが．

さて，画像の分解能を良くすれば，測定時間は増えるわけです．しかし，
分解能を上げて，かつ，測定時間も短縮できる「圧縮センシング」という数学的な方法があり，これに言及するのが後編の主題です．その前に，前編では，まず，MRIの装置の仕組みについてお話しましょう．
■プロトン（水素の原子核）はスピンを持ち,磁石の性質（核磁気）があります．強い静磁場下に置かれたプロトン核磁気は，磁場に沿ってだいたい向きが揃い，歳差運動している状態です．歳差運動の周波数（ラーモア周波数という）は，磁場が強いほど高く，MRI装置の静磁場は1.5T程度と超強力なので，ラーモア周波数は64MHｚ（ラジオ電波の周波数領域）程度です．
静磁場下のプロトンに，このラーモア周波数の電波が照射されると吸収共鳴が起こり，核磁気の歳差運動の振幅（周波数は変わらない）が増大しほとんど横倒しの状態で回転（古典論的なイメージ）しています．
一方，歳差運動をしているプロトン核磁気からは同じ周波数の電波が放射されるので，これを検出することができます．
■生体組織は，水をはじめ水素原子と結合した分子からなる組織です．
つまり，プロトン（水素の原子核）核磁気は組織の至る所に分布していて，
その水素の属する組織の環境（診断される情報）がそのプロトン核磁気の性質（緩和現象）に反映されています．
すなわち，核磁気の歳差運動の縦緩和，横緩和という現象は，そのプロトン（水素）が含まれる（結合している）組織内の状態で違いが出ます．
緩和というのは，電波の照射を止めると，励起されていた核磁気の歳差運動が定常状態に戻ることで，静磁場方向の核磁気成分の復元緩和を「縦緩和」，静磁場に垂直面内の成分の減衰緩和を「横緩和」といいます．
組織の各点で，これらの緩和定数を測定し，マップに表示できれば，
診断に役立つ組織の特徴を反映したイメージングになります．
■さて，組織画像の位置情報はどのようにして得られるのでしょうか．
これがなければ画像として見ることができません．断層測定をするには，検出器に到来する電波が，１つのスライス平面から来るものだけ集める必要があります．このためには，静磁場の他に傾斜磁場を印加します．
傾斜磁場はさきほどの静磁場とは別で，ペアのコイルによって発生する
（数十mT/m程度の強さ）もので，たとえば，ｚ軸方向の静磁場があり，加えて，z方向に沿って変化する傾斜磁場，x方向に沿って変化する傾斜磁場，y方向に沿って変化する傾斜磁場の3種類があります．
傾斜磁場があると，空間内で磁場の大きさが一定になるのは平面になります．例えば，静磁場方向と同じz方向の傾斜磁場を印加すると，磁場一定の平面はz軸に垂直な平面です．
プロトン核磁気のラーモア周波数は，磁場の強度に比例するので，
共鳴吸収する電波の周波数をスキャンすれば，z軸に垂直な各断層平面に並ぶ核磁気からの電波を順次採取することができます．
次に，各断層面内の(x,y)位置情報はどのように得たらよいでしょうか？
断層内のプロトンの歳差運動を励起した後に，x傾斜磁場，引き続きy傾斜磁場の印加を行うとします．
x傾斜磁場印加でx軸に沿って歳差運動の周波数が変化し，その場所から放射される電波のx座標情報（周波数エンコーディング）が得られます．
ｘおよびｙ傾斜磁場の印加でy軸に沿って歳差運動の位相が変化し，
y座標情報（位相エンコーディング）が得られます．
傾斜磁場を印加して，空間の位置情報を得，画像化を可能にしたのは，
Lautergur（1972）の発明で，2003年のノーベル賞を受賞しました．
■緩和時間の測定は，歳差運動の励起後，照射電波を切って行うので，
立ち上がり時間も考慮した電波照射の複雑なパルスシークエンスになり，
256x256画素の測定でもかなりの時間を要します．高分解能画像を得るには，正攻法で行うならさらに細分化した画素数の測定が必要になり膨大な測定時間になるでしょう．
これを解決し，MRIの高分解能かつ高速化を実現したのは，
後編で言及する予定の「圧縮センシング」という数学方法です．

2017年の数学月間懇話会（第13回）の講演の一つとして，ブラックホールの形を見る（池田思朗）をとりあげました．ブラックホールはなんでも引っ張り込み光も脱出できません．しかし，ブラックホールの穴に荷電粒子が引き込まれるときに電波やX線が放出されるので，ブラックホールの形は，この放出される電波を観測（地球上の6地点の電波望遠鏡を結んで電波干渉計を作り，電波の強度とその位相を観測）して，それらのデータをFourier変換すると形が見えるはずです．しかし，Fourier変換に用いる観測データは，地球が宇宙空間で旅した範囲の観測点で得られるのは圧倒的に限られたデータしかありません．

ブラックホールの穴画像を$$x$$，観測されたデータを$$y$$とすると，$$y=Ax$$
（行列$$A$$や，形式的な逆行列$$A^{－１}$$は線形演算子で，Fourier変換やその逆変換のことです）．
行列Aが正則ならば逆行列を両辺に左から乗じて，$$x=A^{-1}y$$と簡単に解くことができるのですが，$$y$$の次元$$N$$は非常に小さく，$$x$$の次元$$M$$は非常に大きい（行列$$A$$は$$N$$x$$M$$行列でランク落ち）ために解けません．多数（$$M$$個）の未知数のある$$x$$を解くのに，式の数（$$N$$個）が少ないので，不定解になります．もし，解$$x$$にたくさんの0要素（スパース）があるとしランクを下げれば，一意解を持ちます．なぜこのようなスパースな解が合理的なのかは難しいのですが，我々のまわりの画像は統計的にスパースなようです．この方法は，LASSO（Least Absolute Shrinkage and Selection Operator）といいます．数学的には，$$x$$がスパースであるという条件を，$$Σ|x_{i}|$$が最小という条件にして，最小2乗法$$||y-Ax||^{2}$$　を解き，少ない観測値$$y$$から$$x$$を求めます．このための数学には，ラグランジュの未定乗数法が適用できます．

■圧縮センシング
このような手法は，医学画像（MRIなど）解析で用いられており，高速で高解像度の画像が測定できる圧縮センシングとして役立っています．得られる画像の解像度を上げるには，観測空間でも細かくたくさんのデータを収集し，それらを用いてFourier変換を行うのが正攻法です．これは情報理論でシャノンのサンプリング定理（注）と呼ばれるものであります．

しかし，実際には画像内で急峻な変化がある場所は少なく大体がだらだら変わっています．そのような性質のある実際画像では，観測空間内を細かい分解能で測定するのは時間がかかり過ぎてもったいない．観測空間の少数の点だけのデータで十分なのです（この考え方はjpgなどの画像圧縮と同じ）．得られる画像は至る所0（スパース）という仮定は，大胆であるが良い結果をもたらします．

観測空間のサンプリングをナイキスト・レート（注）より細かく行う場合はオーバーサンプリング，ナイキスト・レートより粗い場合はアンダーサンプリングと呼ばれますが，画像がスパースという条件があれば，アンダーサンプリングのデーター集合を用いて解像度の高い原画像が再現できるのです． 解のスパース性を利用するこの手法は，医学画像（MRIなど）の撮影で利用でき，高解像度の画像を短時間で得られるようになりました．
ーーーーーーーーーーーーーーーーーーーーーー
（注）シャノンのサンプリング定理（1949年)

アナログ信号をあるサンプリング・レートでデジタル化すると，元のアナログ信号に含まれる周波数成分のうち，サンプリング周波数（ナイキスト間隔とも呼ばれます）の1/2の周波数成分までが再現できます．ナイキストは，サンプリング定理を1928年に予想していました（シャノンの証明が広く知られています）．

デジタル音源のサンプリング周波数は44.1ｋHzが使われていますが，この周波数でサンプリングすれば，人間の耳が聞き分ける高音限界といわれる20kHzの音まで十分に再現できるからです．
ーーーーーーーーーーーーーーーーーーーーーー

特定方位に切り出した水晶Quartzの両側の面に電圧をかけると結晶は変形します．逆に両側から力をかけると両端に電圧（分極）を生じます．この性質を圧電効果といいます．圧電効果は，結晶構造に対称心がある場合には生じません．なぜなら，結晶中のいかなる方向に電圧（分極）ベクトルが生じたとしても，対称心に矛盾するからです．

所定の方位で所定の厚さに切り出した水晶片の両面に交流を印加すれば，水晶片は振動します．水晶片の共振の起こる周波数で安定な発振器を作ることができます．水晶振動子（通常32.768kHz＝2^15Hzの水晶音叉）を用い，精度の高いクォーツ時計が作られており，実際の標準時計もこれです．
現在の時間標準は，セシウム（133Cs）の原子時計と定められました．原子時計とは，水晶時計を含む総合システムで，水晶発振器の周波数の校正標準に原子の状態遷移の周波数を用います．
セシウム原子は，最外殻の電子が１つ（水素原子型）なので，解析的にエネルギー準位の計算ができます．磁場を印加して縮退している準位を分離させた状態で，基底状態から励起状態への遷移を起こさせると，マイクロ波領域の9.192631770GHzのエネルギーで遷移します．そこで，水晶発振器により，この近傍のマイクロ波を発生させ，セシウム原子による吸収が最大になったときの水晶発振器の周波数を，9.192631770GHzであると校正しています．
ちなみに，GPS衛星は，ルビジュウムの原子時計を積載しています．最近はMEMS(Micro Electric Mechanical Systems)技術により，ルビジュウムの腕時計の開発も進んでいるそうです．
長さの標準は，地球の経線の1/4を10,000mと定めたのが始まりでした．しかし，1983年に，真空中の光速でこれを定義することになりました．1mの定義は「光が真空中を1/299,792,458秒間に進む長さ」です．長さの標準も時間に基礎を置くことになったのです．
数学と基礎科学，谷克彦（数学文化15号P82より抜粋）

シュロ縄で柵の竹竿を結びました．庭師は男結びと言う方法で結ぶそうですが，私は簡単にランニング・ノットという方法で結びました．実は，シュロ縄の扱いが大変だったので，一番作業の楽な結び方をして，後でこの結び方の名前を調べたら，ランニング・ノットという方法であることがわかりました．
ランニング・ノット（あるいは，スリップ・ノット）と言われる所以は，竹竿を通してから紐を引っ張って締めると結節ノットが移動して，自然に竹竿の周りの輪が締まるからです．結節になる輪から紐の両端が同じ方向に出ていますから，竹竿を通してから紐の一端を引っ張ると，輪が締り結節になると同時に，他端も同方向に引かれるので，両側から輪を締め，自分自身を締め緩みを防止しする一番シンプルな結び方になります．
ランニング・ノットの結び方で紐の両側を引っ張ると，輪の中に竹竿がなければ手品のように紐は結び目が出来ずに解けてしまいます．比較のために，もやい結びを見てみると，結びの両側を引っ張ると結節ノットは移動せず輪が出来てしまい，竹竿の周りを締める結び方にはなりませんし，竹竿がない状態で，もやい結びの紐の両側を引っ張ると解けずに固定した輪を残して結び目が出来てしまいます．

紐の始まりを竹竿の周りのランニング・ノットから始めて，柵を組んだ竹竿に巻きつけ固定し，紐の最後もランニング・ノットで収めようとするとなかなか難しい．巻いてきたひもが緩まないように締めながら出口の結節になる結び目を作る必要があるからです．
シュロ縄は水に湿らせた方がしなやかでよく締まります．シュロ縄を繰り返ししごいていると，縄に毛玉のような塊や細い箇所ができますから注意しましょう．

今回は，紐の両端をそれぞれ別の場所で固定したので，使いませんでしたが”かます結び”という方法もあります．これは紐の両端を結ぶ結び方です．

アラビア文字の各文字は数を割りあてられています．このシステムのことはアブジャドabjadと呼ばれ，十進法のインド数字が採用される以前は数値を表現するのに使われていました．また，単語や文章の数値はシンボリックな意味があります．
例えば，「アッラー」は66，このアナグラムの「ラーレ（チューリップ）」も66で，同じ数値ですので，チューリップ模様はジャーミイの装飾に使われます．

クンデカリを構成するピースの数も意味があります．例えば，ドアの文様を構成するセグメント数の165ピースは，「アッラーのほかに神はいない」，
66ピースは，「アッラー」を意味するそうです．

■私はアブジャドのことは聞きかじっただけで，正確な記述ではないかもしれません（アブジャドのことをご存知の方教えてください）．
私の理解した考え方だけおおざっぱに述べると，アラビア語でも，アルファベット（英語）で計算する数秘術のように，単語（スペル）の文字の数値を総計し，その単語の数値が決まります．ただし，数値を対応させるのはアブジャドに対してで，アラビア文字そのものに対してではないそうです．

（注）世界には，ギリシャ文字（ラテン文字，キリル文字，...），漢字，アラビア文字，などいろいろありますが，アラビア文字は子音を表記する文字に母音も含めるようで，文字も独立の場合と単語の中に使われる場合で異なるようです．漢字や速記文字なども記号全体で一定の意味もつのに似ています．単純なアルファベットではなくアブジャドという文字体系に数字を対応させます．

■クンデカリ技術で作られたドアを構成するピース数の意味

以下の写真のドアの文様の数値227は，次のようにして数えるそうです．この数値のシンボリックな意味は知りません．

面積１の正方形の数14個　→1x14=14
面積２の長方形の数11個　→2x11=22
面積３の長方形の数13個　→3x13=39
ーーーーーーーーーーーーーーーーーー　
　　　（全図形数）38個　　 　　75（全面積）
　　　　　　　　　x4
　　　　　　－－－－－
　（枠のピース数）152　＋（面積数）75　=227（全ピース数）

クンデカリKundekariという技術は，接着剤も釘も使わず木のピースを組み立てていく技術です．イスラム模様の装飾のある説教壇（minbar），ドア，家具に用いられます．12世紀にアナトリア地区で生まれたこの技術は，その地のセルジューク帝国，オスマン帝国時代に洗練されました．杉，薔薇，梨，クルミ，黒檀，リンゴなどの木材が使われます．木材ピースを溝とホゾで組み立てるので．各ピース間は2~3mmのギャップがあり，それぞれのピースの膨張伸縮で歪みが生じることがありません．接着剤や釘で固定された作り方よりも，湿気などに対する耐久性があり，ひびが入らず700年持つといわれます．ジャーミイのドアは，5cm位の多くのパーツをクンデカリの技術で組み立てています．そしてさらに，このドアーを構成する木材ピースの総数は，数秘術的な意味があるそうです．
⇒数秘術的な意味については，アラビア文字のアブジャド数に続く．
（参考文献）クンデカリについては，Mugla Journal of Science and Technology, Vol2,No2,2016,110を引用

■ダイヤモンドの価値は，4C［Carat重量，Color色，Cralityキズ，Cutカット］で評価されます．ここでは，数学的に興味のあるカットのプロポーションについて述べました．ラウンド・ブリリアン・カットのダイヤモンドが最も輝くようにしたプロポーションを理想カットといいます．理想カットは1919年にベルギーのMarcel Tolkowsky(数学者でダイヤモンドのカッター)が計算しました．今なら，コンピュータもあるし，光線追跡のソフトウエアもある時代で，理想カットの形（プロポーション）を見つけることは容易でしょうが．1919年にどのように計算したのか，興味深いことです．多分，閉じ込められた光線が全反射を繰り返す光路に注目したのでしょう．

ダイヤモンドのブリリアン・カットの各部の名称を図に記載してあります．正面の平らな面をテーブル面，上半分をクラウン，下半分をパビリオンと呼びます．真ん中のガードル面に対してクラウン斜面のなす角度をβ，パビリオン斜面のなす角度をαとしました．

テーブル面の左隅Aに入った光線（赤色）が,ダイヤモンド内部を進み，後方の左パビリオン斜面で全反射され，次に，右パビリオン斜面で全反射され，テーブル面右隅Bに戻り，前方に出て行く光線もありますが，テーブル面右隅Bで一部は反射され内部に戻る光線（青色）になります．この光線は全反射を繰り返し内部に閉じ込められることになります（青色）．
この図で追跡した光線は，テーブル面の左隅Aから出て，テーブル面の右隅Bに達する左右対称の光路です．ダイヤモンドの屈折率n≒2.417を用いて，この光路のテーブル面での入射角φ，屈折角γに対する屈折の式，sinφ＝n･sinγ　から，左右対称になる入射角φ（テーブル面の垂線と入射光線のなす角）を求めると，21°になります．というのは，左右のパビリオン間でテーブル面と平行になる光路ですから，左のパビリオン斜面での反射の法則（反射角αはパビリオン角αに等しい）から，γ＝90°ー2α＝8.5°となることが決まるからです．ここで，パビリオン角α＝40.75°を用いました．

■屈折率の高い媒質中に光が閉じ込められるのは，全反射を起こし易いからで，ダイヤモンドの全反射の臨界角θ（入射角でいうと）は，sinθ=1/nだから，θ＝24.4°（反射面から測った反射角で言うと，65.6°）です．
テーブル面の出口で反射されて内部に戻った一部の光線は，パビリオン面とクラウン面で全反射を繰り返し内部に閉じ込められます．パビリオン角α＝40.75°，クラウン角β＝34.50°というのは実によくできた設計です．
全反射によりブリリアン・カット内に閉じ込められた光線の経路は，一周すると，これに平行な経路に戻ることを証明するために，次の作図をしてみました．BC(赤色)の直線はダイヤモンド内部で全反射を繰り返す光線（青色）を外に引き伸ばしたものです．その代わりに，ダイヤモンドも反射面を共通にしてつないで並べました．結局，全反射を4回繰り返すと光線が平行になるということは，このように配置したダイヤモンドが４つで回転角が0に戻る（初めの向きと同じ）ことからわかります．

■カットの形を評価するには，そのカットの形を磨き直して理想カットにするとしたら，重量がどれだけ減るか（カット減点%）で表します．カット減点5%までは理想カットと見做されます．さて最後になりましたが，トルコフスキーの理想カットのプロポーションを表紙の図に示しました．トルコフスキーはガードル厚には言及せず，ナイフ・エッヂだったそうですが，現実にはナイフ・エッヂは作れず，ガードル厚は必要です．
■（注）ラウンド・ブリリアン・カットとは，58のファセット面を磨き上げた形（キューレットも1面と数えます）です．ダイヤモンドは立方晶系の結晶ですから，複屈折はありません．また，光の分散もそれほど強くなく上品です．虹色にぎらぎらするようならキュービック・ジルコニアなどの疑いがあります．
クラウン面の高さや，パビリオンの深さが最適でないと，テーブル面の中が暗くなります．

ある折り紙の本に正5角形の作り方がありました．
複雑な手順なので整理して原理だけ説明しましょう．
正5角形の中心角72度を作るミソは，以下のようです．
これで，Θは72°になることを証明できますか？

答，72°になりません．
約71.56...°です．

この折り紙手順で作れる角度は，72°に非常に近いので
実際の折り紙工作では非常に良い方法といえるでしょう．
でも，幾何の命題としては正しくないのです．

話は別になりますが，
正5角形を，コンパスと直線定規で作図できます；
例えば　http://www.natubunko.net/zukei/png/penta03.png
ここから図を引用しましょう．

さてそれでは，この作図を折り紙の手順で追いかけてみましょう．
折り紙の手法で，「円を描く」というのは，可能でしょうか？

コンパスの使い方には２通りあます；
１）所定の長さを所定の方向にとる．
２）２つの円の交点を求める
（与えられた2点から，それぞれ与えられた距離だけ離れた点を求める）．

このうち，1)は折り紙手順で可能ですが，2)は折り紙手順で不可能ではありませんが工夫がいります．折り紙の手順で，正5角形の作図を追いかけてみると，(4)の段階で，２つの円の交点を求めることが必要になり，ここが困難です．でも不可能ではないようなので，皆様，挑戦されて，もし，うまい方法を発見したら教えてください．

まったく別の方法でも，折り紙で正5角形を作ることができます．例えば，表紙の写真は定幅紙（帯）を用いて正5角形を折ったものです．この場合はどのような手順の作図になるのかを考察してみてください．このような折り紙は手順が全部完成してからつじつまが合うように最初から調整しますから，漸近的に正5角形を得る作図のようなもので，無限の手順がかかるので幾何学の作図としては認められません．

折り紙では近似的な正5角形（星型）が出てきましたが，これから扱うのは数学的に厳密な正5角形についてです．
半径１の円に内接する正5角形の1辺の長さを求めましょう．
この正5角形の1辺の長さをxとします．
△BACと△ADCは相似(相似比が黄金比Φ)で，形は2等辺三角形(等辺xとすると，底辺Φ･x)です．Φ･x＝x＋(x/Φ)　ですから，Φは黄金比の方程式
　Φ^2ーΦー１＝0を満たします．この方程式の解（Φ>1のもの）は，Φ＝(1+√5)/2　です．

■次に，△BCEと△BOFとが相似であることを利用し，
1：(Φ･x）＝OF：CE=(1－y)：(x/2)　が成立するので，　y＝1ー1/(2Φ)　
ただし，y＝√[(x/Φ)^2－((Φ･x)/2－x/Φ)^2]＝√[x^2ー(Φ･x/2)^2]＝x√[1－(Φ/2)^2]　
x＝y/√[1－(Φ/2)^2]＝[1－1/(2Φ)]/√[1－(Φ/2)^2]＝(√[10－2√5])/2＝1.1756

■　作図
半径１の円に内接する正5角形の一辺の長さｘ＝(√[10－2√5])/2を作図する方法
（証明）ピタゴラスの定理を2回使います．

私は，yahooブログ 「数学と社会の架け橋<数学月間>（2012.5～2019.3）」に，発行している同名のメルマガまぐまぐのバックナンバーを保存していました．メルマガはテキストなので，必要な図はどこかに保存したもののリンクを張らねばなりません．そこで，必要な図や写真はyohooブログに保存していました．しかし，昨年yahooブログが閉鎖しましたので，ブログ機能はlivedoorブログと数学月間の会のホームページに引っ越しました．
テキストは移動できたのですが，移動できなかった画像や写真があります．yahooブログに張ったリンク先が消えてしまったので後の祭りです．
今回Noteを始めて，それらの記事中から面白いものを優先し，図を作り直し再現しようとしています（新規の記事も並行して随時書きます）．お付き合いのほどよろしくお願いします．記事の候補全体は，数学月間の会ホームページにありますので訪問ください．その中で再現すべき記事のリクエストがありましたらお寄せください．まだNoteの使い方になれないので皆さまのお気づきのことをお教えください．記事に数式が必要なこともありますが，Texが使えないようなので，まとまった数式は画像にして埋め込むことにしています．

今回再現するのは，以下のメルマガの記事です．
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2018.10.23］ No.238
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日は，たいへん古典的だが，重要な証明問題を扱いましょう．
ギリシャの幾何学者達が研究した不可能作図とは
以下のものがあります．

（１）与えられた正立方体の2倍の体積の正立方体を作れ
（２）与えられた円と同じ面積の正方形を作れ
（３）任意に与えられた角を3等分せよ
これらは，定規とコンパスだけを有限回使って作図できるか？
ということです．

■なぜ作図できないか
（１）は，2の3乗根の作図が必要です．
（２）の円と同じ面積の正方形を作る方針を以下の図に示します．

どうしてこの作図ができないのかわかりますか？
与えられた円の半径をrとします．まず，円と同じ面積の長方形を作りましょう．もし，縦r，横aの長方形が作れたら，r･a=x^2　となるxの作図は可能です．問題は，円の面積と同じ縦 r，横 a=πｒの長方形を作るところで，
円周の半分の長さπrの線分を作図する方法が，定規とコンパスではないからです．無理数πが作図できません．

■直線定規とコンパスだけを有限回繰り返し用いて作図できる長さは
２つの有理数の，加法，減法，乗法，除法，開平だけです．
作図方法は，以下をご覧ください．
条規とコンパスで作図
開平を繰り返せは，2のべき乗根（4乗根，8乗根，．．．）は作図できますが，例えば，立方根は作図できません（この証明は難かしいのでスキップ）.

（３）任意の角度の3等分が作図できないわけ．
角度3等分の方程式は　x^3-3x-a=0　で，
例えば，与えられた角度が60°ならa=1の方程式です．
60°の3等分の方程式は，x^3-3x-1=0　となりますが，この3次方程式は，p+q√r　（ただし，p,q,rは有理数）の型の解を持たないので
この角度の作図は，定規とコンパスでは不可能です．
もちろん，60°の3等分の20°は存在しますが，
定規とコンパスだけを使う方法では作図できないということです．
詳しくは，以下をご覧ください．

■任意の角度の3等分
任意の角度∠XOYの3等分がなされたとします．

フィボナッチ数列F(n)は，1,1,2,3,5,8.13,21,34，.....のような数列です．
F(n)=F(n-1)+F(n-2)　と再帰的に定義されます．
この数列は，いろいろな所に現れます．得られた数列が，フィボナッチ数列であることを証明するには数学的帰納法を用います．
今回は，その典型的な例として，抵抗ラダー回路を取り上げましょう．

■抵抗ラダー回路

ラダーとは梯子のことで，梯子型に抵抗を並べた回路を，抵抗ラダー回路といいます．例えば，表紙の図は3段のラダー回路です．

A-Bの端子（入力側）から見たインピーダンスをZ_i，
C-Dの端子（出力側）から見たインピーダンスをZ_oとします．
この3段のラダー回路は，A-B側（入力側）にR1の抵抗があるが，C-D側（出力側）にはないので，左右対称ではありません．入力側から見たインピーダンスと出力側から見たインピーダンスの比から，減衰率Z_i/Z_o≡Aが定義されますが，A>1なのでこの回路はアッテネータ（減衰器）として使えます．
抵抗値をすべて同じR1=R2＝１とすると，
ラダーの段数mを増やしていくと，減衰率A(m)＝F(2m+1)/F(2m-1)は，2/1，5/2，13/5，34/13,...とフィボナッチ数列が出てきます．
（参考）n=1から3までの計算は以下にありますのでご覧ください．
証明は数学的帰納法を使う練習になりますので，各自試みてください．

■ラダー回路の応用例
ラダー回路は，アナログ信号が入力されたときに，そのアナログ信号の大きさを，瞬時に8水準に分類する（8ビットのデジタル化）回路（これを8ビットのAD変換といいます）に使われたりもします．次の図をご覧ください．

コンパレータが7個並列に並んでいますね（カスケード結合）．
入力信号の大きさを８水準に分類するのは，7個のコンパレータの働きで，
その境界値となる７段階の基準電位をそれぞれに供給します．
この７つの基準電位を発生するのが，一番左の直列に並んだ抵抗ラダー回路です．nビットのAD変換には(2^n）-1個のコンパレータと基準電位がいります．

■正5角形の性質
正5角形の中に相似な2等辺3角形（頂角36°）が次々に組み込まれていく様子を見てください．赤い2等辺3角形→緑の2等辺3角形→青い2等辺3角形の順です．2等辺3角形の辺の比率は，いつもΦ：1で，Φは正5角形の対角線（星形の辺），1は正5角形の1辺です．このとき成立する方程式，Φ2－Φー１=0を解いて（Φ>1をとる），Φ＝(1+√5)/2＝1.6180･･が得られます．Φは黄金比の値です．

■正5角形の実用作図法
この作図はつぎの式が成り立ちます．AH=HB=1/2，MH=√3/2　であるので，PH=(√3ー1)/2，従ってPB=(√[(√3－1)2＋1])/2＝(√[5－2√3])/2
AB/PB＝2√(65－26√3)/13＝1.6138･･･
この作図法は，イスラームのタイル作図で便利ですが，厳密な正５角形ではありません．しかし，誤差は0.26%なので実用上問題ない恐るべき精度です．

 ■厳密な正5角形の作図
AB=1，AH=1/2，PH=1　ですので，AP＝(√[1＋22])/2＝√5/2
従って，QP＝(1＋√5)/2＝Φ
この作図で得られるのは厳密に正5角形であることが証明されました．

■折り紙で作る正5角形(1)の精度
この図は折り紙で正5角形を作る原理を示しました．y=3xの直線とx軸のなす角θを求めると，θ＝arctan3＝71.5651･･°　となりますが，正5角形では72°になるべきです．この誤差は．0.6％ですのでかなり良い精度と言えましょう．他の角度は，72.1087（0.2%），72.6524（0.9%）程度です．（カッコ内は誤差）

■折り紙で作る正５角形(2)の精度
折り紙の一太刀切で大変作り易い星型です．この原理は以下の図を見てください．正5角形（星型）の一辺の中心角は360°/5＝72°ですから，一太刀切りに対応する中心角は36°です．
以下の図を見ると，一太刀切りの中心角は，35.783°(36°からのハズレは-0.6%)to,36.870°（+2.4%）に収まっています．

60÷5(7-5)＝？
この答えは24ですか6ですか
60÷5x2＝？と聞かれれば，24と迷わず答えられる人が，なぜ6と答えたくなるのでしょうか．これは５と()の間にxが書かれていないことが心理的に影響すると思います．
5(7-5)は文字式のような錯覚に陥り,ひとまとめにして数値を出したくなります．÷とxの演算が並んだ式は，前から順番に演算するのが決まりです．割り算を使わず掛け算だけで書き直すこともできます．例えば，
60÷5x2＝60x(1/5)x2　のようにです．
60÷5(7-5)＝を，分数で書いてみましょう．しかし，5だけが分母に来るのか，5(7-5)が分母に来るのか不明確です．(60/5)(7-5)のことなのか，60/(5(7-5))のことなのか，かっこを1組追加すれば明確になります．

逆ポーランド式に，二項に対する演算の繰り返しとして計算手順のグラフを書くと，解釈の異なるそれぞれの計算手順は表紙カバーの図のようになります．

■さて，文字式の場合は係数と文字の間のx記号は省略されるのが普通です．9a^2÷3a＝の答えは，3a か，3a^3　のどちらが正しいのでしょうか？
雰囲気的には3aですが，式の機械的な記述は曖昧です．
このような曖昧さを避けるために，()を用いて明確にすべきです．
9a^2÷(3a)＝3a　あるいは，(9a^2÷3)a＝3a^3　のようにはっきりさせましょう．

■ここまでの記事を，私がメルマガに掲載したことがあります．すると，以下のコメントを読者からいただきました．この問題はなかなか面白いですね．ここに掲載させていただきます．

理学系では『省略演算の優先』を意識している傾向がいくつか見られます。たとえば化学業界では省略演算は優先することが国際的なルールとして明記されていて、先の計算は６と答えなければならないように定められているそうです。
また、物理学のフィジカルレビュー誌の投稿規定にも同様な省略演算の優先が書かれているということですので、こちらも６と答えることが義務付けられていることになります。
算数の世界では、帯分数の計算部分に同様な様子が見られます。{以下テキストの都合上帯分数には()をつけ、整数部分と分数部分の間に『と』を挟みますが、実際には無いものと思ってください}
(２と1/3)×3　は，２+1/3×3　なら，+より×優先なので　=2+1=3　と計算するはずですが、実際には省略演算である+を先に行い、7/3×3=7　と計算します。
ところで、マセマティカで計算すると、メルマガの計算は24が出力されるようです。ソフトのいくつかは24を出力すると聞いています。
以下は想像です。
理学系では古くから省略演算を優先する感覚があったため、そのようなルールが少なくとも上記の物理化学ではルールとして明記された。数学はともかく算数でもそのように教えている部分がある。
一方で後発の計算機業界ですが、こちらはそもそも昔は省略演算は文法違反でエラー扱いでした。それがハードが強力になり対応可能となった時に、理学系の慣習など頭になく、ただ省略演算を補うだけだったために、結果24と計算するソフトが多いのではないかと。実際、カシオの関数電卓では、古い機種では24を答えに出し、新しい機種で６を出力するケースを確認しています。おそらく化学業界あたりから苦情が来てユーザーニーズに合わせたのではないでしょうか？
数学では化学業界と違って国際組織が演算順序をルールとして明記するなんて多分やってないと思います。×が+に優先するなことすら学会による明文化はなく慣習によるものだと思われます。明文化されない以上慣習として定着するまではどちらが正しいとは言い切らないのが無難に思います。ただ、化学業界のルールでも但し書きとして、『ただし、誤解を招かないよう括弧を十分に補うことを推奨する』とあるそうですから、メルマガの式は
(60÷5)(7-5)　なり、60÷(5(7-5))　なりにするのが大人の対応ということになりそうです。

エンゼルフィッシュの縞模様やヒトデの星型はどうしてできるのでしょうか？
コンピュータの発明や暗号解読で有名な天才数学者アラン・チューリングが，”The chemical basis of morphogenesis”という論文を1952年に発表しました．今日，受精卵が細胞分裂を繰り返し分化し生物組織が出来ていく胚発生過程は遺伝子情報にプログラムされていることは公知です．1952年にチューリングが発表した理論は，「反応拡散系」が条件を満たせば，パターンや構造を自己成長形成するというものです．反応拡散系と言うのは，２つの物質（モルフォゲンと呼ぶ）が，反応し合いながら組織を介して拡散するもので，初期状態は均一であったものが，ランダムな外乱により，物質の濃淡の波が生じその波が生物の形や模様をつくりだすというものです．この数式でつくり出される模様は「チューリング・パターン」と呼ばれますが，コンピュータ・シミュレーションで描き出すと，条件により，動物の模様にそっくりな縞模様が出現したり，ヒトデの形を作ったりします．手の指が形づくられていくのは，その設計図が遺伝子により決定されているからと考えられていますが，もしかしたら，「指の形成はチューリングの理論のように波がつくっているのではないか」という論文が最近発表されたそうです．遺伝子はからだの構造の基本を決める設計図で，例えば，肺の形成の初期に気管支の分岐などを作るが，細かい肺胞の形成まではその設計図には書かれておらず，チューリング理論のように，現場の細胞同士のやり取り（反応と拡散）で作り上げられて行くのだろうと，近藤滋氏は言っています．

1952年に提唱されたチューリング理論は，現実の生物分野でそのような実験的証拠がなかったので，その後長い間，机上の空論と思われていました．1995年，近藤滋は，海洋エンゼルフィッシュのポマカンサスには，縞模様が皮膚に固定されていないことを発見しました．体の成長とともに，単純に比例して拡大する哺乳類の皮膚のパターンとは異なり，ポマカンサスの縞模様は，体の成長にともなうパターンの連続的な再配置が起こる．そして，縞間のスペースが維持されるという実験事実を観測しました．

実際，チューリング理論に基づくシミュレーションは，成長とともに形成されるパターンを正しく予測できたので，この理論の正しさを支持するものです．

■　チューリングの反応拡散系方程式
存在する２つの物質（モルフォゲン）が，反応したり拡散したりするのは，遺伝子情報で制御されるわけでもなく単純な化学反応で，以下の連立方程式で記述できます．u(t,r)，v(t,r)は振動し，いろいろな形が形成されます．

■チューリングの反応拡散方程式の解の安定性を調べる数学について
（解が不安定（暴走）では，縞模様ができません）
数式を多用することができませんので，ここでは，言葉で説明するにとどめます．⇒　Texによる数式追補http://sgk2005.saloon.jp

反応項 f，g はそれぞれ物質の濃度 u, v の関数で，平衡点の周りでテーラー展開（1次の項まで）して線形化します．このような連立線形微分方程式の性質は，ヤコビアンと呼ばれる行列Aで決まるが，この行列Aの固有値の実部がすべて負であれば，解は安定になります．
行列Aの固有値を求めるのは面倒なので，条件を緩くして，行列Aの対角要素の和（固有値の和に同じ）が負であるとし，さらに，拡散係数も0の場合から始めると，結局，f_u＋g_v<0が得られます．
これは，f_uとg_vが異符号で負の絶対値が大（促進剤と阻害剤が拮抗して働き，若干，阻害剤が強い）の条件を意味し，このようなときに縞模様が形成されます．

表紙写真のグラス（リュミナルク製）のデザインは，こちら側の模様の円が凹レンズとして働き，向こう側の模様の円を円内に縮小して映し出すので，あたかもアポロニウスの窓のようです．

■映像が果てしなく繰り返す「インドラの網」
網の上に置かれた真珠は互いに反射し合って，他の真珠を映しだすだけでなく，映っている他の真珠の映像の中に自身の姿をも映しています．世界全体が真珠一つ一つの上に映り，またその姿が別の真珠に映り，これが永遠に続くのです．「インドラの真珠」D.マンフォード, C.シリーズ, D.ライト, 小森洋平 (翻訳)，日本評論社は，美しく興味深い数学の本です．

この美しい図形の２次元版は，「アポロニウスの窓」ApolloniusGasketとも呼ばれます．
互いに 接し合う3つの円に接する第4の円を描くのですが，これを次々と繰り返して，どんどん小さくなる円で埋め尽くされる円盤内の世界はフラクタルです．
4つの円の曲率（半径の逆数）をa,b,c,dとすると，
2(a^2+b^2+c^2+d^2)=(a+b+c+d)^2 という，デカルトの発見（1643）した定理が成り立っています．
（参考）⇒三角形の七不思議 (ブルーバックス)， 細矢 治夫

■反転によるフラクタル構造

2つの円β，γが互いに接し，かつそれらがアポロニウスの窓の外周円Ωとも接しているとき，これらの接点を通り外周円と直交する円（赤色）を考えましょう．すると，この円で分断された2つのアポロニウスの窓の世界（若草色と黄色）は，この円（赤色）を反転円として，互いに鏡像（反転鏡映）となっています.　もし反転円がどんどん小さくなれば，
その小さな領域に大きな世界がどんどん繰り込まれていくので，不思議なフラクタル世界 の美しさが見られます．表紙の図はこのような様子を表しています．色々な反転円を考えれば，無限にある大小さまざまな大きさの円は，
みんな同じ大きさであるとも言えます．それゆえに，円盤内の世界は無限に広いと言い張るのも良いでしょう．

上図は　Cinderellaというフリーソフトを用いて描きました．

■円による反転

中心Oの半径rの円による反転は，反転円外の点r1を反転円内の点r2への写像
で，反転像どうしは，r1･r2=r^2を満たします．
もし，反転円の円周上に点があれば，反転像は元の点と同じ位置です(r1=r2=r）．
反転操作では，円は円に写像されます．もし，反転円に直交するような円周の円をこの反転円で反転すれば，同一の円の上に写像されます．したがって，円周に直交するような反転円で分断された円の２つの部分は，反転円によるそれぞれの鏡像になります．

反転円が直線なら，反転鏡映は普通の鏡映像になります．
直線鏡の組み合わせで作られる映像は，良く知られた万華鏡ですので，反転円を用いたインドラの網の鏡映像も拡張された万華鏡の映像とみなせます．

■仏教では，「宇宙の一切のものが,一切のものの原因になっていて，
無限の過去からの無数の原因が，どの一人にも，それぞれ反映されている」と考えます．これはまさに単純な因果列ではなく複雑系の考え方ですね．
宮澤賢治に「インドラの網」という小品があります．インドラの網目に縫い付けられた珠玉は，互いに映じ合うと同時に，自分自身も輝いています．

この項目は，反転円の幾何学のほかに，フラクタル，複雑系，双曲幾何の円盤モデル，エッシャーの不思議な世界，万華鏡，などに関連があります．
これらは順次取り上げる予定ですが，拙著「美しい幾何学」技術評論社(2019.9刊）をご覧いただけると幸いです．

■円による反転鏡映の性質
①反転円の円周上の点は，反転しても元の点と同じ位置．
②反転では，円は円に変換される（直線も半径∞の円の仲間）
下図に反転円（赤い円）による，反転鏡映の例を示します．
●図１・反転円Oと交差する円Cは，交差の２点を共有する円cに変換される．
●図２・反転円Oと直交する円Cは，自分の上に変換される．
円周に直交するような反転円で分断された円の２つの部分は，反転円によるそれ
ぞれの鏡像になる．
●図３・反転円Oの中心を通る円Aは，直線aに変換される．
特に，円Bが反転円Oと交差する場合は，交差する2点をよぎる直線ｂに変換される．
③反転円が直線なら，普通の鏡映像になります．
直線鏡の組み合わせで作られる映像は，良く知られた万華鏡です．
反転円を用いたアポロニウスの窓も拡張された万華鏡の映像と言えるでしょう．

■反転の利用

反転の性質を使うと，パップスの定理の様な難しいものを簡単に証明できます．

このような図形はアルベロス（靴屋のナイフ）といいます．
この中に面白い幾何学があります．

円弧αと円弧βに挟まれたア
ルベロスの領域に，互いに接す
るように円のチェーンω0, ω1,
ω2, … があるとき， 円ωnの
中心と直径ABとの距離は円ωn
の直径のn倍である．
（パップスの定理）

［以下の証明ができます］
円ω2の中心は，線分ABから円ω2の直径の2倍だけ離れていること．
① 点Aから円ω2へ接線を引く．両接点を通りAを中心とする円γは，円ω2
と直交します．（なぜなら，円の接線は接点での半径と直交するから）
② γを反転円にして，色々なものを反転してみましょう．
円ω2 は自分自身に．円α，β は，それぞれ 直線α’，β’に，
円ω1，ω0 は，それぞれ円ω1’，ω0’に，なります．
③ 円ω2，ω1’, ω0’の直径はすべて同じだから，パップスの定理が証明
された． （なぜなら，平行な直線α‘とβ’に挟まれているから）

■楕円幾何平面の正則タイル張り
球表面が球面正p多角形タイルで{p,q}のように張りつめられているとき，1つのタイルの中を2p個の直角3角形に分割できます．この直角3角形を鏡室とする万華鏡を“メビウスの万華鏡”と名付けます．このときの直角3角形（鏡室）の内角は，それぞれ π/p，π/q，π/2で，この直角3角形を（p,q,2）と略記します．

■双曲幾何平面の正則タイル張り
ポアンカレ円盤の双曲幾何平面が，双曲正p多角形で{p,q}のように張りつめられているとき，１つのタイルを2p個の直角3角形に分割できます．この直角3角形を鏡室とする万華鏡を“コクセターの万華鏡”と名付けます．
双曲面の｛6,4｝正則分割を例に，直角3角形(6,4,2)(赤い3角形）を図（左）に，対応する“コクセターの万華鏡”の映像を図（右）に示します．

■双曲面{6,4}分割の場合の“コクセターの万華鏡”を作る

双極面{6,4}分割の映像を，3角形の万華鏡で作るには，双曲面直角3角形(6,4,2)を用います．この3角形の2辺は平面鏡，残りの1辺は円盤のフチに直交する円弧鏡よりなります．この円弧鏡は，数学的には反転円として定義できるのですが，現実の円柱鏡の反射には収差があるので，数学の定義のように鮮明な万華鏡映像を作るのは困難です．

■エッシャー作品の生まれるまで

　　（１）　　　　　　　　　　　　　　　（２）　　　　　　　　　　　　　　　　　　（３）

(1)コクセター：直角3角形(6,4,2)による双曲面の｛6,3｝分割の細分
(2)エッシャー：直線魚のモチーフ
(3)エッシャー：「極限としての円Ⅰ」CircleLimitⅠ

コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました．1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り，これがエッシャーの「極限としての円」の作品群（Ⅰ～Ⅲ）を生むことになります．

*By S.H.M.Coxeter
Crystal Symmetry and ItsGeneralizations (published in the Transactions of the RoyalSociety of Canada in 1957).

■エッシャーのトリック（引用先：コクセター論文）
M.C.エッシャーの「極限としての円」Circle limit IIIを鑑賞しましょう（図左）．
この円盤内は双曲幾何の世界（ポアンカレの円盤モデル）です．
この円盤内を旅する人は，円の縁（世界の果て）に近づくほど時間がかかる．つまり，［世界の果てに到達するには無限の時間がかかる］ようになっています．
この世界で定義される直線（最短時間で移動できる経路）は，円盤世界の縁で直交する円弧です．
エッシャー作品（図（左））の円盤は，魚の流れを示す白い線で分割された双曲面の[4,3,4,3,4,3]分割のようにも見えますが，実は，図（中）に示すような，黒い線で分割した{8,3}正則分割です．
白い線は，双曲幾何の円盤世界の縁に80°で交差し，直線ではないのです．
図（中）の正8角形の黒い線がこの円盤世界の直線であることは，図（中）に書き込んだ赤い円弧（いずれも円盤縁で直交する円弧）を見れば理解できるでしょう．

双曲平面の正８角形タイルは，双曲平面の直線（円盤の縁で直交する円弧）で囲まれています．
タイルの大きさは円盤の縁に行くほど小さく見えますが，円盤内は無限に広い双曲幾何平面なのですべて同じ大きさです．
１つのタイルの中には4匹の魚がおり中心に4回軸があります．
正8角形の頂点には3回軸があり，魚の白い流れは3回軸の場所に集まっています．
エッシャーは｛8,3｝分割に用いる直線をわざと隠し，白い流れが分割であるようなトリックを見せます．もちろん，白い流れの円弧（直線ではない）に関して鏡映対称はありません．

参照：「美しい幾何学」p.142,143

■パイレックス・ガラスとは

シリカガラスSiO2の軟化点は1700°Cと高温です．ガラスには明確な融点はありません．初めから乱れた構造ですから液体状態の固体ともいわれます．固体での変形が起こるのは軟化点～1900°Cあたりまでで，それ以上の温度では液体になります．シリカの正4面体ネットワーク中の所々にCaイオンやNaイオンが入ったものが，ソーダーライムガラス（青板ガラスとも呼ばれる）で，ガラスの融点も軟化点も下がり成型が容易になります．しかし，Naの熱振動振幅は大きく，ガラスの熱膨張率は大きくなります．ホウケイ酸ガラスは，ホウ素Bを添加したガラスで，ナトリウムNaの量を減らせるので，熱膨張率を小さくできます．これがpyrexパイレックスガラス（Corningの商標）で軟化点は820℃位で，Nonexという非膨張ガラスの処方も開発されました．パイレックスガラスは，キッチンのベーキング皿にも，温度計にも，ビーカーなどの理化学機器にも，1949年に完成したパロマーのヘール望遠鏡の巨大鏡（回転放物面）にも使われています．この巨大鏡はパイレックスガラスの直径5mのガラスのキャストディスクで20トンもあります．この巨大なガラスのキャストディスクの製造では，アニーリング・オーブンに入れて10か月もかけて徐冷したそうです．これを現場に運び凹面（回転放物面）に研磨しました．

■パイレックス・ガラス製造中止
2008年3月14日に パイレックス・ロール板の生産中止をコーニング社は決めました．パイレックスと言えば耐熱ガラスの代名詞で，理化学機器にも使われていますが，望遠鏡用の 大きなガラスも作らなくなりました．どうなることか心配です．
今日，コーニング社の製品は，スマートフォン用のGorillaGlassというカバーガラスやエレクトロニクス用の薄い強化ガラスにシフトしたようです．

以下の写真はコーニングガラス博物館の様子で面白そうです．

https://media-cdn.tripadvisor.com/media/photo-m/1280/19/bd/64/98/corning-museum-of-glass.jpg

力学系を記述するラグランジュ方程式は作れるのだが，これが解けるとは限らない．
物理の演習では，解けるものしか扱わなかったのです．
実際の世の中は，解を関数で記述できない（解けない）方程式が大多数です．
系の運動を支配する法則（ニュートン力学の方程式）は明確なのに，解が関数で記述できないのだ．
でも解は存在するのです．コンピュータによる数値計算により，運動は逐一決定できる．
しかも，予想もつかない挙動ーカオスーが起こる．このようなことを最初に指摘したのはポアンカレでした．

ーーーーーーーーーーーーーーーーーーー
●1766　オイラー「変分法の原理」
　　　　（オイラー，　ラグランジュ）

●1800　ラグランジュ「解析力学」
　　エネルギー散逸がない系は，オイラー＝ラグランジュ方程式が作れる．
　　　（オイラー，　ハミルトン，　ヤコービ）

●1900　ポアンカレ
　　可積分の方程式はごくわずかで，大部分の方程式は非可積分（関数で記述できない）
　　ニュートンの法則に従う系の運動は，可積分と決めつけてはいけない．

可積分　→　予測可能（安定な軌道）　互いに独立な因果列
非可積分→　カオス的　　　　　　　　干渉し合う因果列
ーーーーーーーーーーーーーーーーーーー

■2重振り子の例

上図のような2重振り子の運動です．今回は物理演習のようですが，
数式に囚われる必要はありません．重要なのは，振幅が小さい範囲なら
運動は線形の微分方程式に近似できるので，2種類の周波数の振動が重畳
された運動になる．つまり，関数で記述できる安定な周期的な運動になる
という事です．そして，これに対比される次に話題になる振幅の大きい
2重振り子運動では，運動は関数で記述できず，予想もつかない
とんでもない運動をするということです．

（注）ここでは，ラグランジュ関数やラグランジュ方程式を説明せずに用いています．
これらを学習したい方は，EMANの物理学https://eman-physics.net/analytic/lagrange.html
などが参考になります．

2重振り子のラグランジュ関数は正確に作れます．
次に，ラグランジュ方程式を解かねばならないのだが，これが解析的には解けない（関数で記述できる解がない）．

◆振幅の小さいとき
Φ，ψ の振動範囲を微小に制限して（Φ，ψの2次までを残す近似）解く．
これは解けます（物理の演習問題）．
計算の詳細は以下に載せました．http://sgk2005.saloon.jp/blogs/blog_entries/view/46/ddf8d815a70840c192d0532618218407?frame_id=54

結論
ラグランジュ方程式（連立方程式）を微小振動の範囲とし線形近似したので，解のΦ，ψは，それぞれ２つの固有振動（基準振動）の重ね合わせになり，それほど複雑な振動ではない．いずれにしろ周期的な（予測できる）振動になります．

◆一般論（振幅の大きいとき）
振幅が大きくなると，ラグランジュ関数の線形近似がなり立たないので，ラグランジュ方程式は解析的には解けません．でも解は実在するはずです．
将来，誰かが巧妙な方法で解くのではないかと期待しつつ，得られたその解は，解析的ではないにしろ振動範囲が小な場合と本質的に大差はないのではないかと想像するのは自然なことです．
系のラグランジュ関数 は完全に正しいし，ラグランジュ方程式も正しいのですから，解析的に解けないと言っても心配ないのではと思うでしょう．
これが誤りであることを証明したのがポアンカレでした．

現代は，コンピュータを用いた計算が高度になり，力ずくで動きのシミュレーションがなされるようになりました．正しい方程式は実在するのですから，関数による軌道の記述は出来なくても，動きは逐一決定されるはずです．
しかし，初期条件（初期値）により，予想もつかない挙動が見られます（カオス）．ともかく，そのような運動の実験とシミュレーションの例を，youtube動画で見てください．とんでもない現象が見られます．

◆第１の動画は実験
スタートする初期値によって運動の様子は異なります：

◆第２の動画はシミュレーション
Double Pendulum Chaos Light Writing (computer simulation) 1

ドアや家具や壁に見られるイスラムの美しい模様を作製する技術は千年以上の歴史があります．イスラムのデザインの特徴は，対称性の高い星型がちりばめられていることです．
繰り返し模様全体を支配する対称性は，17種類の平面群のどれかであるはずだし，並進（周期性）と両立しうる回転対称は，2,3,4,6回軸に限られるはずです．しかし，イスラムの模様の中に散らばる星形は対称性が高いのです．高い対称性はもちろん模様全域に作用はできません．その星形の内部にだを作用域とする局所的なものです．

上図の模様を例にとると，8回対称の青い星型が，正方形格子の周期で配列していることがわかります．青い星型にある8回対称性は，青い星型内部と緑の周囲領域，草色の星形5角形の領域までは有効ですが，オレンジ色の８角形までは有効ではありません．
青い星の中心にある8回対称軸はオレンジ色8角形の付近では，4回対称軸に低下してしまいます．これは，周期的な平面では8回対称軸は存在できない（正8角形のタイルでは平面を張れない）から当然のことです．
ある点のまわりの対称性という言葉は注意が必要で，その点周囲の「局所的」対称性を指す場合もありますが，平面「全域」で有効な対称性を指すのが普通です．この例では，青い星型の対称性は8回対称ですが，この星の中心にある回転対称軸は4回対称軸です．
このパターンの単位胞は，オレンジ色の8角形の中心を結んでできる正方格子の１つの内部です．

■Girihタイル（装飾線が描かれたタイル）

イスラムの繰り返し模様の壁はGirihタイルという手法で作れます．
正方形と正8角形を組み合わせた平面のタイル張りの例を，下図(a)に示します．このテッセレーションは，シュレーフリの記法で（4,8,8）と記述されます［１つの頂点のまわりに，正4角形，正8角形，正8角形が集まっている状態］．

(b)図は，正4角形および正8角形の内部に装飾線を描いたGirihタイルです．
平面をGirihタイルでタイル張りしておいて，タイルの縁の輪郭を消すと(c)図のパターンが得られます．
デザインを作れる以下のウエブサイトがありますのでお試しください．
https://girihdesigner.com/

■ここで，始めに掲載したイスラムの模様も，上の例と全く同じであることを確認してください．
始めに掲載した模様の正4角形タイルや正8角形タイルの形は，草色の星型の中心を結んでいくと明らかでしょう．正4角形や正8角形の内部の装飾線はどのようなものであるかもお確かめください．

私たちは，ものごとを考え解決困難なときに，次元を１つ上げて（失われている視点を一つ加えて）見ると，思わぬ解決策にはっと気づくことがあります．たとえば，今，新型コロナウイルス禍にあり，医学・疫学的視点と，経済活動視点の２つの視点に集中して，この危機を乗り越えようと必死の活動がなされています．しかし，政治的視点がなおざりにされています．不安定な遺伝子のウイルスはやがて消滅し我々は生き残るでしょうが，見えない次元に無関心でいると，そのときの社会体制は，監視や権力集中の社会に変貌しているかもしれません．歴史学者のハラリ氏は，そのように警告しています．パンデミックが変える世界ユヴァル・ノア・ハラリとの６０分：
https://www.dailymotion.com/video/x7tjaoq

視点を上げる（次元を上げる）効果は，デザルグの定理を考えるとよくわかります．
ーーーーーーー
デザルグの定理とは
「⊿ABCと⊿A'B'C'があり，AA'，BB'，CC'を通る直線が1点Oで交わるなら．
直線ABとA'B'の交点P，直線BCとB'C'の交点Q，直線CAとC'A'の交点Rは，同一直線上にある」

ーーーーーーー
高校とき幾何の教科書にこの問題が載っていました．
このデザルグの定理の証明は，実はとても難しいのです．3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります．
ところが，下図のように，この図形を平面（2次元）と見ずに，立体（3次元）にあると見ると，ごく当たり前のことを言っていることに気づきます．

２つの平面Ω（薄緑）とΩ’（薄青）が交差しており，△ABCは平面Ω上に，△A'B'C'は平面Ω'上にあるとイメージするのです．
光源Oから出る光が，△ABCの影を△A'B'C'に作っています（辺ABの影が辺A'B'）．従って，O，A，B，A'，B' は，同一平面上にあり，この平面をΣ（薄燈）と名付けます．A，Bを通る直線も，A'，B'を通る直線もこの平面Σ上にあり，P点で交差します．
一方，A，B，Pは平面Ω上に，A'，B'，Pは平面Ω’上にあります．
結局，P点は平面Ωと平面Ω’の交線上にあることになります．
同様にして，QもRも，平面Ωと平面Ω’の交線上にあり，デザルグの定理が証明できました．
高校の教科書では，このような証明は厳密でないとみなされるせいか，チェバやメネラウスの定理を使ってあくまでも平面図形として扱われます．

■デザルグの定理は，2次元で証明するのは難しいが，3次元では証明が要らないほど自明なのは何故でしょうか．
3次元でこの図のような模型があったとして，これを2次元に射影する（高さ方向をぺちゃんこ）と，直線が交差する状況は変わらないのですが，長さや角度の情報が失われてしまいます．△ABCと△A'B'C'は，それぞれ別の2次元平面にあったものですが，ぺちゃんこにされて1つの平面（紙面）に入ってしまいました．
私たちは，高い次元（2次元の世界から3次元の世界）を想像するのは困難です．デザルグの定理でこれを思い知らされます．

■デザルグは，17世紀初頭のフランスの数学者，建築家．透視図法を発展させた射影幾何学の祖です．ダビンチなどの画家たちは，遠近法や透視図法を古くから用いていましたが，その数学を固め射影幾何学の本を出したのはデザルグが最初です．
その後，射影幾何学が本格的に研究されるのは，200年後の19世紀中葉，ポンスレー（フランスの数学者．ナポレオンのロシア遠征に従軍し，ロシアで捕虜のときに射影幾何学を研究した）を待たねばなりませんでした．
射影幾何学自体，作図など重要な応用がありますが，やはり，19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました．

千川論文［千川純一，ひょうご科学財団］は，実用化も期待でき興味深いが難解なので，ここで解説を試みます．厳密な記述は原著論文を参照ください：
・Chikawa et al.,"Hair growth at a solid-liqid interface as a protein crystal without cell division", Progress in Crystal Growth and Characterization of Materials, Volume 65, Issue 3, August 2019, 100452
・Chikawa et al.,"Cancer development in the hair spectra by X-ray
fluorescence using synchrotron radiation",International Journal of Cancer,  in press

■千川論文の意義
毛根にある毛球から毛髪は成長してきます．毛球の中は液体で，毛髪の成長は，あたかも，固液界面で成長する無期結晶のようです．固液界面には毛母細胞［毛球と毛幹（毛髪のこと）の境界］があり，その液体側の毛球に，S, K, Ca, Srなどの元素が偏析し，血液から毛母細胞に流入する元素量と，成長した毛幹の元素量が等しい状態が維持されています．
毛髪の成長は，純化学的過程（化学ポテンシャルの勾配が成長を駆動する）で行われることが示されました．［細胞分裂で成長するときのように遺伝子の関与もなく，チューリング反応拡散系と同じように純化学的な過程です］

この平衡関係から毛髪の元素濃度は血液の元素濃度から計算できるので，毛髪の分析をすると毛母細胞のイオンチャンネルの開閉の記録（癌の発生と成長に密接に関係している）が分かるというのがこの研究のミソです．

臨床データとリンクし収集した多数の毛髪の分析が実施されました．
毛髪１本の毛根から先端へとＸ線蛍光分析をし，種々の元素の分布するパターンのデータを収集しました．これらを解析し，大気汚染（黄砂）による心筋梗塞，脳梗塞の死亡率の増加の原因も毛髪分析で示されましたが，特に重要な結果は，癌発生の機構とCaの分布パターンが関係のあることを見出したことです．

■毛髪のCaの分布と癌発生のメカニズム
Caが不足すると，副甲状腺ホルモン(PTH) が分泌され，PTHが各細胞の「受容体」に結合すると，細胞のチャンネルが開いてCaを取り込むので，毛髪カルシウムは正常値を超えます．他方，血清Caが正常値以下に低下すると，小胞体に備蓄のCaを使うために別のチャンネルが開きます．これら２種類のチャンネルの開閉の記録が毛髪Ca 濃度に残されています．
情報伝達の主役であるカルシウム(Ca)の毛髪濃度は，毛母細胞のCaチャンネルが閉じた状態の正常値と，その5倍も高いPTH制御Caチャンネルは開いたときの値があります．また，正常値以下で小胞体の備蓄Ca量制御のチャンネルが開いた状態も起こりますが，これらは識別できます．
癌患者の毛髪を先端から毛根へと分析すると，癌の種類によらず，癌は必
ずPTH 制御チャンネル開のCa高値で発生し，癌成長とともに１～２年かけて正常値に降下し，さらに，小胞体の備蓄Ca量制御のチャンネルが開くCa正常値未満の状態(癌の「成熟」と呼ぶ)が続くことがわかりました．即ち，癌の発生から成熟までが，毛髪に特有のパターンとして記録されるわけです．

■（注）放射光実験の方法
毛髪の元素分析は，2003年から千川純一らが実施しており，臨床とリンクし採取した多数の毛髪分析のデータを集積しました．放射光を用いる蛍光X線分析は，毛髪一本で長さ１ｍｍ以下でも精密に測定できます．放射光施設利用にボトルネックはあるものの，毛髪だけ提供すれば済むので，人体に安全な診断方法であります．
血液は採取した瞬間の結果しか知ることができないが，毛髪には過去の記録が残されていて［１カ月に約１cm成長］変化のパターンを知ることができるところが，この方法の優れたところである．
さて，毛髪1 本（直径は100μm 程度）中のX 線照射点から出てくる蛍光X 線を観測すれば，その点に含まれる元素を検出することができますが，毛髪の元素濃度を得るには，蛍光X線強度を照射された部位の体積（質量）で規格化する必要があります．これにはそのとき観測されるバックグランド強度を用います．バックグランドは毛髪母体のタンパクによる散乱X 線（小角散乱領域ではない．コンプトン散乱が主体）で，一定の方位にセットした検出で，散乱X線も蛍光X線も測定できます．これらの比をとれば毛髪の太さや形状によらない値になり，濃度指標が得られます．

このマガジンの数学月間とは題名に違和感を感じている方もおられるでしょう．「数学月間」とは7/22－8/22のひと月を指します．この期間は22/7＝3.14･･･（π）と22/8＝2.7･･･(e)に因みます．
日本の数学月間は，（故）片瀬豊さんの提案により2005年に日本数学協会が7/22-8/22を数学月間と定めたことに始まります．2005年の発足以来，ボランティア・ベースながら，毎年，「数学月間」の初日7/22に，「数学月間懇話会」を開催し，啓蒙的な講演を一般市民に対し実施してきました．2020年の7月22日にも第16回の開催予定です．今年は，集会の実施は困難が予想されるので，初のZOOMによるリモート開催の計画です．
「NPO法人数学月間の会」のホームページhttp://sgk2005.saloon.jpに情報を随時掲載します．
（注）2005年から始まった「数学月間の会（代表：片瀬豊）」は，昨年から，「NPO法人（理事長：岡本和夫）」になりました．このような数学月間活動は米国MAMに学んで始めたものですが，米国MAMのように国家的行事として行うべき性質のものです．現在は個人寄付金とボランティア・ベースで実施していますが，活動を社会に波及させたいものです．「NPO法人数学月間の会」は，数学同好会ではありません．数学の内部にとどまらず社会の諸分野に横断的に呼びかけ活動し，「社会と数学の架け橋」を目指します．情報を共有しましょう．仲間に入りませんか．
問い合わせ先や詳細はhttp://sgk2005.saloon.jp にあります．
ーーーーーーーーーーーーーーーーーーーーーーーーーー

■米国MAM(Maths Aeareness Month)はレーガン宣言から始まった

全文を掲載します．どなたの草稿か知りませんが，格調高く今日でも心を打ちます．米国MAMのスタート時は月間行事ではなく，週間行事MAWでした．

原文は以下にあります．
https://www.gpo.gov/fdsys/pkg/STATUTE-100/pdf/STATUTE-100-Pg4430.pdf
----------------------------------------------------------------------
アメリカ合衆国大統領による宣言5461
｢国家的数学週間」1986年4月17日
宣言(National Mathematics Awareness Week)

およそ5000年前，エジプトやメソポタミアで始まった数学的英知は，科学･通商･芸術発展の重要な要素である．ピタゴラスの定理からゲオルグ･カントールの集合論に至る迄，目覚ましい進歩を遂げ，さらに，コンピュータ時代の到来で，我々の発展するハイテク社会にとって，数学的知識と理論は
益々本質的になった．社会と経済の進歩にとって，数学が益々重要であるにも拘わらず，数学に関する学課が米国教育システムのすべての段階で低下する傾向にある．しかし依然として，数学の応用が医薬，コンビュータ･サイエンス，宇宙探究，ハイテク商業，ビジネス，防衛や行政などの様々な分野で不可欠である．数学の研究と応用を奨励するために，すべてのアメリカ人が日常生活において，この科学の基礎分野の重要性を想起する事が肝要である．上院の共同決議261で，国会が1986年4月14日から4月20日の週を，
国家的な数学週間に制定し，この行事に注目する宣言を出す事を
大統領に要請した．今日，アメリカ大統領，私ロナルド･レーガンは，
1986年4月14日から4月20日の週を国家的数学週間とする事を，ここに宣言する．私はすべてのアメリカ人に対し，合衆国における数学と数学的教育の重要性を実証する適切な行事や活動に参加する事を勧告する．
その証拠として，アメリカ合衆国の独立から210年の西暦1986年の４月17日，ここに署名する．ロナルド･レーガン(Ronald Reagan)
----------------------------------------------------------------------

長くなりますので，活動の様子は省略し，年度別テーマのリストを掲載します．（注）2017年からMSAMに変わりました．追加されたSはStatistics統計学です．

■MAMの年度別テーマの推移
http://www.mathstatmonth.org/mathstatmonth/msamhome

1986数学----基礎的訓練
1987美と数学の挑戦
1988米国数学の100年
1989発見のパターン
1990通信数学
1991数学----それが基本
1992数学と環境
1993数学と製造業
1994数学と医学
1995数学と対称性
1996数学と意思決定
1997数学とインターネット
1998数学と画像処理
--MAWからMAMへ------
1999数学と生物学
2000数学は全次元に
2001数学と海洋
2002数学と遺伝子
2003数学と芸術
2004ネットワークの数学
2005数学と宇宙
2006数学とインターネット保全
2007数学と脳
2008数学と投票
2009数学と気候2013持続可能性の数学
2010数学とスポーツ
2011解明進む複雑系
2012統計学とデータの洪水
2013持続性の数学
2014マス，マジック，ミステリー（Martin Gardner記念）
2015数学はキャリアを駆動する
2016予測の未来
2017年より，MSAMがテーマになる
注）略語表
MAM：Mathematics Awareness Week
MAM: Mathematics Awareness Month(4月)
AMS：American Mathematical Society米国数学会
MAA: Mathematical Association of America米国数学協会
SIAM: Society for Industrial and Applied Mathematics工業応用数学会
ASA: American Statistical Association米国統計学協会
JPMB: Joint Policy Board for Mathematics米国連結政策協議会
*）2006年から、ASAが加盟することになった．

■編集後記
数学月間は数学者のものではなく，一般人が対象です．数学は，ものごとの本質を追求し，装飾を剥ぎとり，その本質をあぶりだします．
出来上がった抽象化された概念体系（定理）を，数学者は美しいと感じます．数学とは，そのような理論体系であるべきことは確かです．
しかし，このようにして出来上がった抽象的な数学を見せられても，
一般人は興味が湧かない．そこで，数学月間は＜数学と社会の架け橋＞として，数学が実際の課題に使われていることを示して行こうと考えています．
かつて，物理学の現場で数学が生まれている時代がありました（ニュートンの微積分もその例です）．数学は自分の生まれた源泉を離れて抽象化に専念していることに，著書の前文で警鐘をならしたのはクーラントとヒルベルトでした．源泉に立ち返って数学を見るときっと共感を感じることでしょう．

大学の数学では，完成され抽象化された数学を，数学科の先生が教えます．
これは，数学科の学生に対する教程としてはオーソドックスなものですが，
数学科でない学生には不親切であります．工学，薬学，経済学など，
それぞれの専門に適した数学の基礎教程が必要でありましょう．

安倍内閣が今週にも通過させようとしている検察庁法改正案は，権力分立の精神に反し憲法違反です．以下のメルマガを発行した2015.9.22のことを思い出しました．
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2015.09.22］ No.082
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
戦争法案が多くの世論を無視して強引に可決してしまいました．
本来，違憲である法案が国会に出されること自体あり得ないことですし，
国会の議論でもまともな答弁がなされていないことは誰の目にも明らかです．
政府の宣伝機関になったNHK始め大手メディアの罪はたいへんに重い．
さて，翁長沖縄県知事の国連人権理事会で演説に期待しよう．大手メディアの世論操作に負けてはならない．
イギリスで投獄を覚悟してインドの独立を主張したガンジーの姿が重なって見えます．
ーーーーーーーーーーーーーーーーー

■戦時中の“科学朝日（1944年3月号）”「特集・戦争と数学」

https://twitter.com/oburo72　自由古書園「海つばめ」さんの写真借用

 戦争一色の特輯：南方の科学　飛行機　精密機械と兵器　戦車と偽装
防空の科学　潜水艦　戦争と数学　航空母艦　基地建設と進攻兵器...

 －－－－－－－

この特集号には，多くの著名な数学者が寄稿しており大変興味深い．
その中で，巻頭の弥永昌吉先生の論説が群を抜いており，言論も不自由であったろう戦時下に，実に立派な意見を展開しておられます．
さらに，数学月間の考え方と同じ所も見受けられ我が意を得たりの感があります．まず，弥永論説（対話形式）の概略を紹介します．

1年くらい前から始まった戦時下の米国の数学動員（米数学協会の記事の記憶）が紹介されます．遅ればせながら日本でもこのような動きが始まっています．
ーーーーー
米国の数学動員
委員長（モース）の下に６つの委員会がある
1.工業技術，2.航空力学，3.弾道学（ノイマン），4.確率統計，5.計算法，6.暗号解読
１は数学と工業の連携強化，2,3は微分方程式，高射砲の照準や電波兵器の数学，４は大量生産管理，5は計算機．
ーーーー以下抜粋－－－－－
■数学は魔術ではなく，合理的なものの中でも最も合理的なものですから，使い方も合理的でなくてはなりません．
この際，数学者の側で，数学を使えば何も彼も容易にできるというようなことを言いふらしたり，まだ十分の研究を積まないのに現場の人たちのやり方が悪いと言ったりするようなことは一番いけないと思います．
ーーーーーーー
■大和魂が第一でも，それだけでは戦争に勝てないことがだんだんわかってきて，科学研究の動員が必要になった．
第一次大戦では「化学」，第二次大戦では「物理」→「数学」が必要だ．
米の他，ソ連，独，伊でも同様な数学動員の状況がある．
ソ連は，コルモゴロフ（確率の基礎）飛行機の乱流，ヴィノグラドフ（整数論）などがスターリン科学賞を受賞した．
ドイツからは，開所したばかりの米プリンストン研究所などに科学者が流出しており，米国に最も豊富な人材が集まっている．
ーーーーーーー
■学問としてお留守にならず，その品位を下げぬような動員の仕方をすることが，戦争に勝つ道であると信じる．
日本では，それぞれの分野が功を急いだせいかも知れませんが，
学問が専門化しすぎて，それぞれ孤立化する危険がある．
この機会に横の結びつきが強化されるのは良いことだ．お互いに学問の理解を深め，基礎理論の整備進展，新理論の展開という方向へ導かれれば日本の学問全体にとってもこんな有り難いことはない．
ーーーーー
■問題解決のためにも，数学では個々の小さな問題をそれぞれに突っつくよりも，根本的なところまで遡って考えた方が，大きな成功を収めることがよくあるのです．
この戦争のために，目先のことばかりを考えてよいのでしょうか．
長期建設戦」ともなれば，文化が直接ものを言うことがますます多くなりましょう．世界中のだれが見ても頭を下げるような高い立派な文化を我々が戦いつつ築きあげて行くことがぜひとも必要です．
この頃，この点について偏執な，浅慮短見の説をなす人があるのを慨いて，
渡辺慧さんはそれを「文化的敗北主義」と言っている．

2014年の米国の数学月間MAMのテーマは，Mathematics, Magic, and Mystery　でした．

このMAMのテーマは，Martin Gardner (1914-2010)の生誕100年を記念したものです．
ガードナーのことは，『サイエンティフィック・アメリカン』誌に，コラム「数学ゲーム」を25年に渡って連載したのでご存じの方も多いでことしょう．MAM(2014)のサイトに掲載されている組み紐のパズルに挑戦してください．

http://www.mathaware.org/mam/2014/calendar/braids.html

■魔法の三つ編み組み紐　（James Tanton）

James Tantonのウエブサイトは　http://www.jamestanton.com/?p=1072

■次のパズルはどうでしょうか．

これは可能ですので，チャレンジされてください・

こんにゃくでこんな形にした料理がありましたか？

回答は以下にあります．

■それでは，次の四つ編みは実現可能でしょうか？

■可能なことを証明するのは簡単です．作って見せればよい！しかし，不可能であることを証明するのは難しい．何度も試行して失敗すれば，不可能と思えるかもしれません．しかし，もう一度試してみたらうまくいくかも知れない．

4つ編の組み紐の完成例が左図です．4本の紐の上端と下端がそれぞれ閉じている状態で始めて，このような完成例にすることが可能でしょうか．この四つ編み組み紐の完成例には，交差点が全部で12あります．上から出発して，左から来る紐の上に右から来る紐が乗る交差点を̟⊕，左から来る紐の下に右から来る紐が潜る交差点を̠⊖として，図示したのが左図です．12の交差の後，四本の紐は，上端での順番と下端での順番とが同じになります．全体で，⊕が８個，⊖が4個ですので，全体のIndexは＋４と定義します．

いろいろな四つ編みを試してみてもIndexを０にできないようです．
まだ詰めが必要ですが，これが四つ編みで組み紐を完成できない理由のようです．

同じことをやってみると，三つ編み組み紐の場合は，交差点数６で，3本の紐の上端での順番と下端での順番が同じになり，Indexは０になることがわかります．

（参考）http://www.jamestanton.com/wp-content/uploads/2012/03/Cool-Math-Newsletter_June-2013.pdf

■「30年以内に震度６弱以上の地震が起こる確率は，横浜市が78％で最も高く，九州では大分市が54％」などと言われていました．あくまでも確率ですから，いつ地震が起きるかはわかりません．熊本の方が先に大地震が起きてしまいましたね．このような確率はどのようにして出たものでしょうか？(このSGK通信を書いた2016.７時点の数字)

震度（揺れ方）6弱といっても，震源が浅い場合もありますから，
震度が大きいものが必ずしも巨大地震（マグニチュードMが大きい）とは限りません．

■地上の被害は震度（揺れの程度）に比例します．
地下の岩盤には色々な原因で歪が蓄積していき，岩盤の耐えられる歪の限界を超えると，岩盤がポッキリ折れて地震が発生するというイメージです．岩盤が強靭なほど溜め込める歪エネルギーの限界は大きく，限界まで溜め込んだ岩盤が地震で放出するエネルギーは大きい（地震のエネルギーの対数がマグニチュードM）．
地震は破壊現象なので，限度まで歪を蓄えた岩盤がいつどこで破壊するかを予知することは不可能だが，破壊が始まってからの前駆現象を少しでも早く観測することは可能です．

■日本の地震の発生メカニズムを調べると，大雑把に言って2つのタイプがあります．
１．海溝型（海洋プレート沈み込み境界）
Mは大きい巨大地震で，頻度分布は数十年～100年．
２．内陸型（陸側プレート内）
震源は地下5～20kmと浅い．Mは小さいが震源が浅いので，直上の被害は大きい．頻度分布は数百年ー数十万年．
日本で起きた最近の大地震は，内陸型です．
1923年の関東地震，2011年の東日本大震災，心配されている東海地震や南海トラフ地震は海溝型です．

■地層に残る地震の記録や，古文書の記録を調べると，日本の各地で，数多くの地震が繰り返し起こっていることがわかります．この地震発生の繰り返し周期はどうなのか，地震発生の予測のために，経過年に対する地震頻度の分布を調べてみます．過去の地震記録はどのような分布と合うでしょうか．地震は破壊現象なので発生確率はランダム（ポアソン分布）が予想されます．沈み込むプレートに引き込まれた陸地が時折り弾性反発するモデルは，Brown酔歩時間の分布(BPT)が予想されます．

全国を250kmのメッシュに切り，その地に影響を与える活断層起因の地震やプレート境界起因の地震で，地表の震度が６弱以上となる地震について発生確率を算出します．
メッシュに切った各地の30年以内の震度6弱以上の地震発生確率を着色した地図が以下のサイトにあります：　
http://www.j-shis.bosai.go.jp/map/

■ここで用いられる地震の発生確率の定義では，分布密度関数を積分した全面積を確率１とします．
現時点は分布密度関数内のどこかですが，現時点から分布密度関数の０となる将来時点までの積分値に対する，現時点から30年先の時点までの積分値の比の値が30年以内にその地震が発生する確率となります．
現時点がどこか（過去の最新活動時期が不明）わからない場合には，地震の発生が「ポアソン過程」に従うとします．

地震は繰り返し発生しますが，正確な周期があるわけではありません．
今日地震が起こらなければ，明日地震が起こる確率は、今日より高くなる
今日より明日，明日より明後日と大地震がやってくる確率はどんどん高まって行きます．

（注）地震のマグニチュードMとその発生確率は，べき乗測が成り立つことが知られています．
被害の大きい巨大地震（Mの大きいもの）も，発生数は少ないですが必ず起こり，その時の被害は甚大です．
ここで話題にして来たのは，時間（年）の経過に対するある大きさ（震度８弱）をもたらす地震の発生確率に関するもので，べき乗測とは別の話です．

■さて，地図を見てください．日本の活断層の話に移りましょう．
赤い線は活断層です．関東地方では，高崎-熊谷-深谷の西側を流れる荒川に沿いに走り，荒川は江戸区で東京湾に注ぐ．断層地帯の荒川上流は長瀞など風光明美な処です．富士山側の活断層は，諏訪-甲府-富士山の西側を富士川沿いに走り，駿河湾に至ります．活断層は繰り返し地震を起こしており注意が必要です．

DNAの2重らせん構造が解明されて，ノーベル賞を受賞したのは1962年のことです．
受賞者の一人ワトソン博士は，後に本（二重らせん，講談社文庫（1986）)を出版し話題になりました．
もう旧聞に属しますが，今回はこの二重らせんがテーマです．

カバーのDNAの図はlivedoorblog美惑星フィロソフィアからお借りしました．
このブログの主は存じ上げませんが，SARS，MERSが同定されてまもないころ（2015年6月）に，コロナ･ウイルスは，一本鎖のRNAリボ核酸でアビガンか効きであることに言及されています．

DNAの2重らせんの話がしたくなりました．

■Rosalind Franklin，ロザリンドは，ロンドン大学のキングス・カレッジに職を得て，Ｘ線結晶学者としてDNA結晶の構造解析を行っていた．DNAには水分含量の差によって2タイプ（A型とB型）があることを明らかにし，それらを別々に結晶化し，X線回折写真撮影に成功した（1952年）．X線構造解析では単結晶をつくることがとても大事で，難しい仕事です．物質によっては方法をいろいろ変えてもどうしても結晶が育たない（微細な沈殿になってしまう）ので，私もずいぶん苦労し断念したことがあります．
撮影したX線回折写真を見れば，X線結晶学者なら，らせん構造があることはすぐわかります．
らせんのピッチや周期はすぐ計算できます．
しかし，彼女のまとめた非公開研究データのレポートは，予算権限を持つクリックの指導教官のマックス・ペルーツが入手し，クリックの手に渡ってしまいます．一方，ウイルキンス（彼女が赴任する前からDNAの研究をしていた）は，
ケンブリッジ大学キャベンディッシュ研究所のワトソンとクリックに彼女の撮影した写真を内緒で見せてしまいます．
ワトソンは，複製の能力のあるDNAのモデルを考えていたので，彼女の写真を見て2重らせん構造モデルを確信します．

■ワトソン，クリックの論文は，Nature（1953.4.25）に掲載されます．同じ号に，ロザリンド・フランクリンらの論文，
ウイルキンスらの論文を，同号に同時掲載の体裁（合わせて３篇）をとっています．
ワトソン，クリック，ウイルキンスがノーベル賞を受賞したとき（1962），
フランクリンはその4年前に37歳で亡くなっています．

■X線構造解析の定石は，回折像の逆Fourier計算し，DNAの詳しい構造を見つけることです．ロザリンドの時代にはコンピュータはなく，Fourier合成の計算は，数表Beevers-Lipson短冊を用いて行う手計算（多分機械式のタイガー計算機でしょう）でありました．また，試料たんぱく質の結晶化も不十分で，回折像のスポットもぼんやりしている写真しか撮影できませんでした．
良い結晶を作製して，X線自動回折系で6,000個もの反射スポットを得て，コンピュータで計算し精密な構造を得るのは1981年になってからです．

◆Matt Parker：エジンバラ・フェスティバルでは切符完売のコメディ・ショーを持ち，ロンドン数学会の人気講師という権威ある肩書きも持つのは，マット・パーカーただ一人だろう．
彼は，数学とコメディという彼の２つの情熱の混合に没頭している．
オーストラリアの数学教師であったが，今はロンドンに住み，コメディと数学コミュニケータをしている．
彼は，数学への情熱を，著書，ラジオ，TVショー，新聞，学校訪問，ライヴ・コメディ・ショー，そして時折の街頭パフォーマンスで広めている．
彼には，ロンドンのクイーン・メリー大学の数学フェローという公的契約もある．

⇒ 　http://www.standupmaths.com/
--------
◆マット・パーカーが鮮やかに演じる「27枚のカード・トリック」の背景には3進法がある．しかし，見ているとそんな背景は思いもつかず，楽しくも不思議である．
ビデオの後半で，マットがトリックの仕組みに3進法が使われていることを解説するので納得できる．この27枚のカードトリックはマーチン・ガードナーが1956年に発表したものだ．マットはこの発展として47枚カードのトリックを演じるが，7進法を使うものであってマットの発明である．
　Martin Gardner； Mathematics, Magic and Mystery（ドーバー,1956）

27枚カードのトリックは次のように演技される：
　観客に任意のカード1枚（例えば，スペードA）を選ばせ，27以下の数字（例えば18）を選ばせる．演技者は，選んだカードが何んであるか知らない．選ばれたカードを含む27枚のカードは十分に混ぜられ，裏向きの束に積み上げられている．演技の最後には，27枚のカード束の上から18番目の位置に，選ばれたカードを移動しておく必要がある．つまり，スペードAの上に17枚のカードがあるようにしたい．
　この演技のプロセスに，3進法が利用されている．
3進法で17を表すと17=2x3^0+2x3^1＋1x3^2で，221と表記される　(ここでは，１の位から先に表記していて，慣れている表記と逆順なのに注意せよ)．
演技者は，27枚のカードを，3つの山に，1枚づつ配り分けていく．選ばれたカードがどの山に入っているか聞いてから，出来上がった3つの山を，さりげなく重ね合わせる．
再度，同じ操作を繰り返し，結局全部で，操作が3セット繰り返されて，得られた3つの山を１つの束に重ね合わせると，不思議なことに求めるカードは，上から18番目に置かれている．
このトリックのミソは，3つの山を重ねる順番にある．重ねる機会は3回あるのだが，各回，どの山を上（Top=0），中（Middle=1）,下（Bottom=2）　の何処に置いたら良いか？
さりげなく手際が良いので見分け難いが，マットの仕組み説明で良くわかる．18番目に置くには,17の３進法表記221を使い，求めたいカードの入っている山の位置を，1回目は底（Bottom），2回目は底（Bottom），3回目は中（Middle）になるように積み上げるのだ．もし，10番目の位置に置きたければ，9=0x3^0+0x3^1+2x3^2　で，3進法表記では　001なので，1回目，2回目，3回目の積み上げでは，Top,Top,Middleの位置に置くようにすれば，求めるカードは10番目の位置になる．

国立数学博物館MoMath(National Museum of Maths)は，米国唯一の数学博物館で，
ニューヨークのマディソン・スクエアに，2012年12月15日オープンしました．
ここには30以上の対話型の展示があります．

ホールの展示で目立つのは，正方形の車輪の3輪車が滑らかに走る光景(動画の2分半経過ごろ)です．
たいへん興味深いので，床面の曲線がどのような形であるかを計算してみました．
ここに掲載する結果（Fig.1）は，2013年7月22日の数学月間懇話会（第9回）で
谷が発表したものです．

■Fig.1　四角い車輪

　　床の形状

ついでに，応用問題として計算した3角形の車輪の結果を（Fig.２）に掲載します．

■Fig.2　三角の車輪

床の形状

注）2013年10月2日に開設された東京理科大学「数学体験館」にも，同じような4角い車輪の車の展示があります．

今年の「とっとりサイエンスワールド」は，新型コロナウイルスのため急遽中止になりました．残念です．

とっとりサイエンスワールド---美しい数学・楽しい算数---は，鳥取大学，地域学部，矢部敏昭教授（現副学長）が中心になって2007年にスタートし，今年で第14回でした．発足時は，東部（鳥取市）だけの開催でしたが，すぐに西部（米子市）と東部の2か所で開催するようになり，4年目からは，西部，東部，中部（倉吉市）の3会場で開催に広がりました．鳥取県，鳥取県数学教育会が主催，鳥取県教育委員会，各地区教育委員会が後援し，小・中学校の先生方が活動の中心になっています．多数の高校生，短大生のバランティア参加もあり頼もしい．いまやすっかり地域から愛されるイベントになり，子供，両親から老人までが楽しみに集まる数学フェスティバルとなっています．

 この13年の間に，豪雪被害の年も，台風被害の年も，倉吉地震の年もありましたが，乗り越えて毎年開催することができました．2020年は中止せざるを得ない状況は残念なことです．

 とっとりサイエンスワールドは，毎年夏休みの日曜日に開催（無料のイベント）されます．昨年の例では，鳥取(7/28)，米子(8/4)，倉吉(8/25)に開催され，各会場に1,000人程度の参加者があります．私も万華鏡のワークショップで参加しています．万華鏡作りの参加者は3会場で400人ほどの子供や大人です．

■数学まつり
多くの人々が数学に関心をもつようになるイベントを数学月間では応援しています．講演会，講習会，数学カフェ，ワークショップ，様々な活動形態がありますが，子供たちが楽しめて数学感覚が身に着く”数学まつり（フェスティバル）”というのがあり，英国のMMPでも米国のMAMでも大変人気があります．

国立数学博物館MoMath(National Museum of Maths)は，米国唯一の数学博物館で，ニューヨークのマディソン・スクエアに，2012年12月15日オープンしました．ここには30以上の対話型の展示があります．
東京でもMoMathのような常設の数学展示のあるものは，科学技術館，リスーピア，東京理科大「数学体験館」(2013年オープン）などがあります．一度見学されると良いでしょう．

Do Math 同志社中学校数学博物館www.facebook.com

■同志社中学校数学博物館　Do★Math

同志社中学校数学博物館　Do★Mathは，2016年6月にオープンしました．Do★Mathは，生徒以外にも，一般市民にも公開されています．
一つの学校の教育の場で実現した，米国のMoMath（数学フェスティバル）や，米国の地域の数学サークル活動を思わせる意欲的な活動です．今年の数学月間懇話会（ZOOMによるリモート開催の計画．詳細が決まり次第http://sgk2005.saloon.jpに掲載します）のテーマの一つとして，Do★Mathを園田毅先生（同志社中）にご案内いただく予定です．

これはオーボールという赤ちゃんのおもちゃです．球の表面は互いに接する大きい円20個と小さい円12個でできています．円を正多角形にすれば，いわゆるサッカーボールの形です．つまり，小さい円は正5角形，大きい円は正6角形に対応します．

（問）大きい円と小さい円の半径の比は？

球面多面体の正多角形の辺は球の大円でできていますが，多面体の正多角形の辺は直線でできています．この多面体の1つの頂点の周りには，正5角形，正6角形，正6角形が集まっています．このような多面体は［5,6,6］(シュレーフリの表記法)と記述します．正3角形の面だけが頂点で５つ集まっているのは正20面体で｛3,5｝と記述します．正20面体の頂点を切って（切り口は図の白い面），残りの面が正6角形になるようにすると，多面体［5,6,6］が得られます．

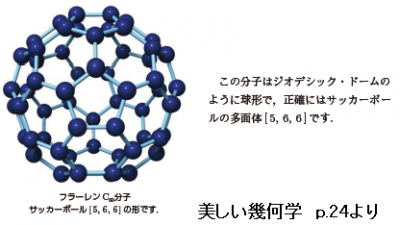
これは，上図のC60［フラーレン（60個の炭素原子からなる）分子．青球は炭素原子C］と同じ形です．

■さて，問の答えですが，オーボールの大きい円と小さい円は，フラーレンの正6角形と正5角形に対応することがわかります．
下図を見てください．

辺の長さの等しい正5角形と正6角形の外接円(内接円)半径比が答えです．計算すると　1:1/2sin36°≒1.176：１

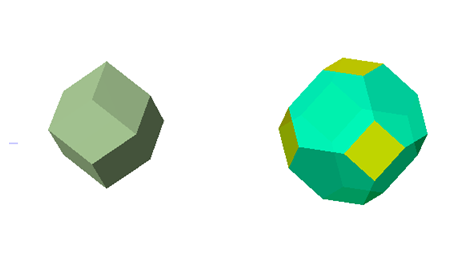
 ■次の図に示す「組み合わさった立体」は，正20面体（水色）と正12面体（黄色）が組み合わさっています．それぞれの多面体のサイズは，辺の中央でちょうど重なるようにしました．入り組んで組み合わされている多面体は，正20面体｛3,5｝と正12面体｛5,3｝です．これらの正多面体は互いに双対です．
（注）｛3,5｝←→｛5,3｝のように，面の形と頂点に集まる数を入れ替えると，”互いに双対”な多面体が得られます．
サッカーボールもオーボールも，正20面体由来の正6角形（正3角形）の面と正12面体由来の正5角形の面からできています．サッカーボールの面に対応する頂点をもつ双対な多面体を作ると菱形30面体が得られます．
（注）正５角形の面に対応する頂点間と正6角形の面に対応する頂点間が，それぞれ菱形面の対角線になります．
下図の「組み合わさった多面体」で，黄色い頂点と水色の頂点を結ぶと菱形30面体が得られます．
菱形面の１つを赤い線で図に記入しました．この菱形面の対角線比は黄金比です．

多面体の見える万華鏡

reciprocalという言葉があります．経済などでは，互恵的とか対等とかいう意味で使われます．
結晶学では，結晶格子crystal latticeに対して，逆格子のことをreciprocal latticeといいます．
両者の関係は，多面体でいうと，面を頂点に，頂点を面に変換した多面体
（これを双対dualな多面体という）の関係と同じです．

例えば，シリコンの結晶格子は面心格子で，ディリクレ胞を描くと菱形12面体（左図）です．シリコンの逆格子は体心格子で，ディリクレ胞を描くと［6,6,4］半正多面体［いわゆるケルビン立体］（右図）です．

結晶格子中のデリクレ胞と逆格子中のデリクレ胞は，このように互いに双対です．格子latticeに対して逆格子reciprocal latticeとはうまく名付けたものです．
もちろん，対称性はどちらも同じ，正6面体（角砂糖）と同じ対称性です．菱形12面体と［6,6,4］半正多面体（ケルビン立体）の形が見える万華鏡を作りました．この万華鏡は，左から覗くと菱形12面体が，右から覗くとケルビン立体が観察され，両者の対称性は同じであることを理解するのに役立ちます．

ーーーー

(注）用語（ディリクレ胞，格子，逆格子，面心格子，体心格子，半正多面体）は，説明なしに用いたので，別の機会に補足説明をいたします．

参考　「美しい幾何学」　　今，試し読みができるようです．
p.44～ 45　万華鏡で作る多面体
p.60～ 62　ディリクレ胞，格子

「美しい幾何学」

◆立方面心格子→菱形12面体
面心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると「菱形12面体」が得られます．

◆立方体心格子→半正多面体［4,6,6］（ケルビン立体とも呼ばれる「切頂正8面体」の一つ）
体心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると，この立体が得られます．

．

■格子というのは，無限に続く周期的構造の＜幾何学的表現＞です．格子点に置くのは繰り返される単位モチーフです．格子点に本当に点を置くのは一番単純な構造です．面心格子の格子点に本当に原子を配置した構造は，銅やアルミニウムなどの金属結晶で知られています．体心格子の格子点に本当に原子を配置した構造は，鉄，タングステン，セシウムなどの金属結晶で知られています．

■格子からディリクレ胞を作る手順を見ると，ディリクレ胞とは格子点１つが占有する多面体の形なのがわかります．
従って，格子点にディリクレ胞を配置すれば，空間が隙間なく充填されるのは明らかです.
そして，ディリクレ胞の対称性（点群）に格子の対称性が現れています．

図は省略しましたが立方体（角砂糖）を積み上げた形，菱形12面体や，ケルビン立体，は周期的空間を隙間なく埋め尽くすことができます．これら３つの対称性は同じです．

◆純粋に数学的に空間充填構造を導くのはとても大変なことですが，結晶学者は昔から知っていました．
自然科学の分野に数学への源泉がいろいろありました．結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．

今年（2020年）のとっとりサイエンスワールドは，新型コロナウイルスのために残念ながら中止になりました．
2017年のとっとりサイエンスワールドin倉吉は，8月27日に開催されました．1,250人の来訪者があり，例年のように盛況でした．万華鏡ワークショップは30人クラスを4回実施し120人が作りました．2016年は，鳥取サイエンスワールドの終わった直後，翌々日に倉吉地震がありびっくりしました．多くの方が避難生活をし，サイエンスワールドの会場だった梨っこ館もガラス天井が落ちたそうです．隣のプールは2017年7月20日になってやっと利用開始にこぎつけました．白壁土蔵群，赤瓦館でも地震の被害がありました．

2017年に，その赤瓦二号館を訪れたとき見つけた御殿まりの写真です．

これらはみんな一人のご婦人が作ったものだそうです．お会いしたいものでしたが，残念ながら不在でした．
どれも美しく良いできですね．
正4面体群：正6面体群（正8面体群）：正12面体群（正20面体群）のどれがあるでしょうか？

Q1：さて私は，正6面体群（正8面体群）と正12面体群（正20面体群）のうちのどちらを選んだでしょう？

私が選んだのは，前者の方でした．

参考に，これと同じ対称性の図形を掲載しましょう．

これらはともに，半正多面体［4,6.6］ですが，立方体のx,y,zの方向に，4回軸があり，体対角線の方向に3回軸があります．2回軸のある方向も確認してください．（注）シュレーフリの記号［4,6,6］は，頂点の周りに正4角形，正6角形，正6角形が集まっていることを示しています．
結局，これらは皆，球面正6面体｛4,3｝や正8面体｛3,4｝と同じ対称性（点群）になります．（注）{4,3}もシュレーフリの記号と呼ばれますが，正4角形が頂点に３つ集まっていることを示しています．

Q2:　球面正12面体｛5,3｝や菱形３0面体の御殿まりを見つけましょう．このなかにありますか？

これらの対称性（点群）は，正12面体やその双対の正20面体と同じです．

一番下の立体の形は，菱形30面体です．菱形30面体は，12･20面体（半正多面体［3,5,3,5］）と双対な多面体なので，対称性としては，上の3つの立体はすべて同じです．
別項目・サッカーボール（フラーレン）に関連記事があります．

Q3:　この他に，半正多面体［6,3,6,3］があります．探してみましょう．

ーーーーーーーーーー

美しい幾何学，p21，p46，p48　が関連します．ご参照ください

平面張り詰めができる凸５角形タイルの形は，フランスの数学者マイケル・ラオがコンピュータを使い，全部で15種類を数え上げ（2017）決着したようです．このような数え上げの問題が難しいのは，演繹的な数学が使えないからです．
　米国サンディエゴの主婦マジョリー・ライスが，タイル張りの問題を知ったのは，1975年のScientific American 誌のマーチン・ガードナーのコラムでした．平面のタイル張り，別の言い方をすれば，一つのタイルで平面を分割する（テッセレーション）問題です．
　平面のタイル張りは，任意の３角形，任意の４角形タイルで可能，凸７角形以上では不可能です．凸６角形の場合は，全部で３タイプのタイル形で可能なことをラインハルトが証明しました（1918）．残されたのは凸５角形の場合で，1975年のガードナーのコラムには，ラインハルトの５タイプと1967年にカーシュナーが発見した３タイプの計８タイプが掲載されていました．ところが新しいタイプがまだあったのです．
　マージョリ（フロリダ州生まれ）が，高等学校で数学を学んだのは１年だけでした．
1945年，結婚しワシントンD.C. に移り，幼い息子と一緒に，その地で商業デザイナーとして働き，後にサンディエゴに移住します．数学が楽しみで，黄金比とピラミッドに魅了されていたといいます．子どもたちが学校に通っている間に自分も読めるようにと，息子達にScientific American の定期購読を許しました．
　この問題では，５角形タイルのタイプ分けがとても難しい．連続変形によりどちらのタイプにも属するタイルがあるし，同じタイプでも出来上がったパターンが全く違うように見えたりもします．彼女は発見に驚き喜んで，自分の仕事をガードナーに送りました．ガードナーはそれをペンシルバニア州のモラヴィアン・カレッジのタイリング問題の専門家であるドリス・シャトシュナイダーに送ってくれました．シャトシュナイダーは，彼女の発見が正しいことを確認したのです．彼女は，張り詰め可能な４つの新しい凸五角形タイプと，それらによるほぼ60種類のテッセレーションを発見しました(1977)．1975年以降にマジョリーの４種を含む計７種が発見されていま
す．最後に発見(2015) された15番目は，やはり周期的なものですが，単位胞が12個の５角形で構成される大きなもので，発見にスーパーコンピュータが使われました．
マジョリーは2017年７月２日94歳で亡くなりました．認知症のため，５角形タイリングの問題がついに完結したのを知ることはありませんでした．ワシントンにある数学協会のロビーの床タイルに，彼女の発見した５角形テッセレーションの１つ（エッシャー風の絵）が見られるといいます．

マジョリー・ライスについては，Natalie Wolchover の記事
(Quantamagazine, 2017）
https://www.quantamagazine.org/marjorie-rices-secret-pentagons-20170711/
をご覧ください．
注） 凸５角形タイルの非周期タイル張りに関しては，３回以上の任意の回転対称のものが作れることが知られています．

■エッシャーの繰り返し模様のようなモチーフをつくる

平行4辺形や平行6辺形タイルは，平面を敷き詰めることができます．

（１）平行4辺形とは下図の（A)のような形です．
これらは，向かい合った平行な辺どうしは同じ長さです．
向かい合った辺どうしを突き合わせて平面を敷き詰めることができます．
向かい合った辺に同じような変形を加えて図案のモチーフを作ります．
エッシャーの作品の2羽の鳥はこのようにして作られています．

（２）平行6辺形で平行な辺どうしが同じ長さの図形は下図の（B),（C)のような形です．
これらは，向かい合った平行な辺（同じ色に着色）どうしを突き合わせて平面を敷き詰めることができます．
向かい合った辺に同じような変形を加えて図案のモチーフを作るとエッシャーの様な繰り返す絵が作れます．私は，ハロウイン魔女を作って見ました．

（３）平行８辺形以上になると平面を敷き詰められないのは何故でしょう？平面は２次元ですから独立な並進ベクトルは２つa，b です．a，b を２辺とする平行４辺形が平面を充填する並進の単位（単位胞）となります．３つの平行辺のある6辺形もタイル張りが可能ですが，2次元平面内の3つ目の並進ベクトルをcとすると，a，b，c の間に c=b−a の関係があり自由はききません．4つ目は作れません．

■一つのタイルを配置するときに回転を許すと，凸６角形タイルで平面の充填ができるものは，以下に図示する３つのタイプがあります．

(注)任意の４辺形は，180°回転したものと組み合わせると平行６辺形になります．任意の3角形も，180°回転したものと組み合わせると
平行4辺形や平行6辺形になるので，平面を敷き詰めることができます．

■凸5角形によるタイル張り4種を発見した主婦マジョリー・ライスの話は，別の機会にします．凸5角形の場合は全部で15種類をコンピュターで数え上げ2017年に至り決着しました．

「美しい幾何学」p.68～71

１．立方体（角砂糖）を積み重ねて，空間を隙間なく周期的に埋めることができます．下図の出発点にある黄色い立方体（シュレーフリの記号で｛4,3｝）を並べた図がそれです．このときの空間充填では「立方単純格子」ができます．
２．立方体の頂点を切り落とした（切頂といいます）立体を考えましょう．頂点の切り口は正3角形で，立方体の正方形の面が正8角形になる位置で切頂します．すると，下図の2番目のように，切頂正6面体（シュレーフリの記号で［3,8,8］）と正8面体｛3,4｝が組み合わさって空間を充填することがわかります．

３．下図の3番目は，立方体の切頂の切り口がさらに大きくなった場合です．立方体の正方形の面は45°回転した小さな正方形になります．このときは，正8面体｛3,4｝と半正多面体［3,4,3,4］（あるいは6・8面体と呼ぶ）とで空間を充填することがわかります．

4．切頂でできる正3角形をさらに大きく，切り口が正6角形になる位置で切頂します．このとき，組み合わされる２つの立体は同じ形になります．つまり，切頂正8面体（あるいは半正多面体［4,6,6］，ケルビン立体とも呼ぶ）だけで，空間を充填できます．このときの空間充填では「立方体心格子」ができます． 

■図の３番目，半正多面体［3,4,3,4］と正8面体｛3,4｝の組み合わせの図で，正8面体だけを抜き出すと，以下のように頂点でつながっています． 

このような構造は，ペロブスカイト CaTiO3 という物質の結晶構造に見られます．正８面体の頂点に酸素原子Oがあり，正８面体をつないで骨組みを作っています．　正８面体（青色）の中心にはチタンTi原子，骨組み中の空いた穴（黄色）の中心にはカルシウムCa原子があります．
　ペロブスカイト構造は，強誘電体や酸化物高温超伝導材料などの結晶構造に見られます．また地殻を作るケイ酸塩鉱物MgSiO3（カンラン石など）はマントル下部の超高圧下でこの構造になることが知られています．

美しい幾何学，p.63,64をご覧ください．

■ドリルが動かなくなったので分解しました．こんな減速機構になっています．グリスの詰め替えをしましょう． 
先端のカバー内に遊星歯車による減速機構があります．

表面に見えている3個の歯車（歯数20，遊星歯車と呼ぶ）の中心に，モーターからの回転軸（歯数6，太陽歯車と呼ぶ）が入ります．この3個の歯車は，周囲の円（歯数48，リング歯車と呼ぶ）とも接しています．
中心軸（モーターのシャフト）が右回転すると，3個の歯車は左回転し，この3個の歯車を乗せている台は，周囲の歯に沿って右回転します．

■原理図を以下のサイトからお借りします．この原理図の歯数は，私のドリルの場合とは違いますのでご注意ください．https://www.monotaro.com/s/pages/readingseries/kikaikiso_0112/​

■私のドリルの減速機構に戻りましょう．
中心の回転軸が右回りに1回転すると，台は6/48=1/8だけ右回転します．
このドリルでは，このような機構が2段になっていました．
つまり，３つの遊星歯車を載せている回転台の中心軸（出力軸）に，また6枚歯の歯車が付いていて，これが2段目の入力となっています．
こうして，下段の同様な遊星歯車に回転を伝えるので，結局，(1/8)^2＝1/64だけ減速することになります．
遊星歯車は入力の回転軸と出力の回転軸は同一線上にあるので，このように段数を重ねることができます．

■遊星歯車を，toyotaプリウスでは，うまく使っています．
ガソリンエンジンにつながっているのは遊星歯車の台，発電機につながっているのは太陽歯車，モーター（車輪）につながっているのは，外周のリング歯車です．3つの歯車のうちの１つをロックすると残りの2つ間で回転の伝達が起こるので，切り替えて，いろいろな使い分けができます．

遊星歯車機構とTHSのしくみ - まっつん総研連絡用ブログ《免責事項》 自分なりに調べたことを書いていますが、間違っている点があれば資料と...matsun-ri.cocolog-nifty.com
以下の図は上記サイトからお借りしました．

■歯面に垂直なカの伝達のできる互いにかみ合う歯面の曲線については，別の機会に取り上げます．

■５つの正多面体（プラトン立体）のうちで，最も面の数が多い（球に近い）ものは正20面体です．正３角形の面が20個でできています．最も対称性が高いものという言い方も間違いではありませんが，互いに双対な正12面体と正20面体は同じ点群です．互いに双対な正6面体と正8面体は同じ点群です．
（注）正多面体とは，正多角形（正p角形）の面でできていて，どの頂点の周りも同数の面（q個の面）が会している立体です．この立体を，シュレーフリの記号で｛p,q｝と記述します．pとqを入れ替えた正多面体どうしを互いに双対と言います．

正多面体（プラトン立体）は，正4面体{3,3}，正8面体{3,4}，正6面体{4,3}，正12面体{5,3}，正20面体{3,5}の５つしかないことは証明できますから，面数20より多い正多面体が存在するはずはありません．
しかし，例えばゴルフ球のディンプルはいくらでもたくさん作れるように思えなす．正多面体の面を分割し続けると，いくらでも球に近い正多面体が作れるように思うかもしれません．しかし，そのようなことが可能なはずがありません．ここで作るいくらでも球に近い多面体は，面が正多角形からわずかに歪むので，正多面体ではないのです．

正20面体の１つの正3角形の面を４つの三角形に細分化します．このとき，中心の三角形は正3角形ですが，その周りの3つの3角形は正3角形から歪むのを確認ください．以下，細分化の操作を繰り返すたびに，面の数は4倍ずつ増加します．そして，細分化された面で正3角形のものは，初めの正20面体の面の中心にあるものだけです．だから，正20面体を細分化して，球に近い多面体を作っても，その対称性は正20面体と同一（細分化しても対称性は上昇しません）．素性は隠せないのです．細分化された多面体の面は正3角形ではないので，細分化でできる多面体は正多面体ではありません．（この細分化で用いたjavaプログラムは郡山彬氏が作成しました）

美しい幾何学p.23より

表紙は結晶空間のイメージです．同じ造作の部屋が無限に並んでいるホテルです．電子を1個だけ入れたら，電子はどの部屋に居るべきでしょうか？どの部屋にも同じように出現せねばなりません．電子の存在確率は結晶空間の周期をもった関数であることが知られています．

一種類の多面体を積み重ねて空間を充填します．許されるのは平行移動のみとします．

これを考えるのは「格子」を考えるのと同じことです．3次元の場合は，独立な移動方向は３つあります：それらのベクトルをa, b, c としましょう．
na+mb+lc，（n,m,lは整数）を格子点といいます．無限に続く格子点全体を格子と呼びます．ベクトルa, b, cの組みを対称性で分類したものがブラベー格子と呼ばれ，2次元では5種類，3次元では14種類，4次元では74種類ります．

無限に繰り返す「周期的空間」（「結晶空間」とも呼ぶ）の幾何学的表現が「格子」です．周期的空間は，点の集合と考えるとデジタル化された空間といえます．（注）整数全体は可算無限個の世界です．

■格子からディリクレ胞をつくる

ディリクレ胞は格子点1個の占有領域です．単位胞とは少し意味合いが異なります．物理ではウイグナー＆ザイツ胞と呼ぶことが多いです．ボロノイ分割と似ているところもありますが，ボロノイ分割と異なり格子の分割に限定しています．

立方体（角砂糖）を積み上げたような格子の場合に，ディリクレ胞の作り方を説明します．手順を見ると，ディリクレ胞とは格子点１つが占有する多面体の形なのがわかります．格子点にディリクレ胞を配置すれば，空間が隙間なく充填されるのは明らかです.
そして，ディリクレ胞の対称性（点群）に格子の対称性が現れています．

◆立方面心格子→菱形12面体
面心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると「菱形12面体」が得られます．

◆立方体心格子→半正多面体［4,6,6］（ケルビン立体「切頂正8面体」の一つ）
体心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると，この立体が得られます．

図は省略しますが立方体（角砂糖）を積み上げた形と，ここに示した菱形12面体やケルビン立体は周期的空間を隙間なく埋め尽くすことができ，これら３つの対称性は同じです．

■格子というのは，無限に続く周期的構造の＜幾何学的表現＞でした．格子点に置くのは繰り返される単位モチーフです．格子点に本当に点を置くのは最も単純な構造，面心格子の格子点に原子を配置した構造は，銅やアルミニウムなどの金属結晶で，体心格子の格子点に原子を配置した構造は，鉄，タングステン，セシウムなどの金属結晶で知られています．

◆純粋に数学的に空間充填構造を導くのはとても大変なことですが，結晶学者は昔から知っていました．
自然科学の分野に数学への源泉がいろいろありました．結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．

美しい幾何学　今，試し読みができます