note.com投稿記事

 
■NHS Nightingale Hospitalについて
NHS＝国民保険サービス，Nightingale Hospital＝臨時救急病院≒野戦病院
イギリスのNHSは4つの地域区分（イングランド，スコットランド，ウエールズ，北アイルランド）があります．イングランドのナイチンゲール病院は，London（4,000床）にオープン(4月3日)を皮切りに，7つ目のSunderland（460床）は日産自動車工場近くに整いました．Covid-19患者の数に北東部の病院が対処できない場合に限り使われます．「人々が社会的距離を保ち，あるいはワクチンができ，この病院を使わないですむことを願っている」とNewcastle病院のNHS局長は語りました（Sunderland Echo紙）．
Stay at home, protect the NHS, and save livesがスローガンで，
イギリスは，3月23日に3週間の全土封鎖に踏み切ったが，まだピークが去らないとしてさらに3週間の延長しています．4月19日現在．累積確認患者数は90,629，累積死者数は14,399に上りますが，一日の感染者の広がりは減少始めたようです．封鎖と並行して，PCR検査から抗体検査に転換し，抗体検査の大規模実施（現時点で1万3729人1日3万5000件の能力がある）と「NHSナイチンゲール病院」の設立を進めました．
クリミア戦争(1853-1856)で野戦病院の衛生状態の改革を行ったナイチンゲールは，『看護覚え書』，『病院覚え書』など多くの著作を残し，そこにはワンルームの病院設計図もあり，高い天井まで延びた3層の窓，3層目の窓を開放し換気，ベッドの間隔，等々要点が記されています．
NHSが設立した病院は，ナイチンゲールの病院概念が活かされた臨時救急病院≒野戦病院だからこう呼ぶのでしょう．
■ナイチンゲールについて（以下のウエブサイト記事を参照しました）
草の実堂；https://kusanomido.com/study/history/western/21987/　
ナイチンゲールはクリミア戦争(1853-1856)で野戦病院の衛生状態を実践改革し死亡率を低下させました．帰国後のナイチンゲール・チームはバーリントンホテルに集結し，戦時の報告書をもとに病院の状況分析をして，数々の統計資料を作成，改革のためにつくられた各種委員会に提出しました．特に，死亡原因ごとに死者の数をひと目で分かるようにレーダーチャートの発明があります．
1860年にナイチンゲールが看護専門学校（ナイチンゲールスクール）を設立したのは広く知られていますが，ナイチンゲールが統計学者であることはあまり知られていません．疫学研究の元祖です．1859年にイギリス王立統計学会の初の女性メンバーに選ばれ，アメリカ統計学会の名誉メンバーにも選ばれました．ナイチンゲールは90歳で亡くなりますが，晩年50年間はほとんどベッドの上で，本の原稿や手紙を書く活動でした．その病因はブルセラ病に感染したこと（by D A B Young，Florence Nightingale's fever，1995)でした．

ブルセラ病については，次号に続きます．

 
ナイチンゲールが50年間ベッドでの仕事を余儀なくされ，死因ともなったのは，クリミア戦争時に流行したマルタ熱（ブルセラ症）であることが明らかになった．D A B Young，Florence Nightingale's fever，(BMJ VOLUME 311 23-30 DECEMBER 1995)
ーーーーーーー
■ブルセラ症（brucellosis）
NIID国立感染症研究所https://www.niid.go.jp/niid/ja/kansennohanashi/513-brucella.html，および，wikiを参照した．－－－－
ブルセラ症はマルタ熱とも呼ばれる細菌に感染して起こる人獣共通感染症．クリミア戦争でマルタ熱が流行したことで世界的に注目されたが，紀元前400年頃のヒポクラテス著書にブルセラ症と思われる疾患がすでに記載されている．現在でも，世界中で毎年50万人を越える家畜ブルセラ菌感染患者が新規に発生（食料や社会・経済が家畜へ依存し，家畜ブルセラ病が発生している国や地域）発生している．マルタ熱の原因菌として，イギリス軍の軍医Sir David BruceによりB. melitensis が分離（1887）されて以降，種々のブルセラ属菌が発見されている．ヒトへの感染が報告されている主なものは，B. melitensis （自然宿主：ヤギ，ヒツジ），B. suis （ブタ），B. abortus （ウシ，水牛），B. canis （イヌ）の4菌種である．日本では，過去に牛のB. abortus感染が流行し問題になったが，家畜衛生対策の徹底により，1970年を最後に国内家畜から菌が分離された例はない．感染動物の加熱殺菌が不十分な乳・乳製品や肉の喫食による経口感染が最も一般的である．ヒト－ヒト感染は極めてまれである．
ブルセラ属菌は敵国の兵士や住民に罹患させて能力を低下させる生物兵器としても研究・培養された．アメリカは1942年、ソ連は1978年に兵器化を実現した．

■サビノワとリユドミラ物語．Екатерина Савинова и Людмила Сенчина
Приходите завтра「明日来なさい」(1963年，ソビエト映画)は，1540万観客の大ヒット映画（ロシア語）です．シベリアの寒村からИнститут имени Гнесиных モスクワの音楽学校に入ろうと出てきた才能ある少女の物語です．重い荷物を背負って一人で都会に出てきた元気で愉快な純粋な少女です．しかし，モスクワに来たときは既に遅く入学試験は終わっていました． 少女の役名はФросяフローシャ．これは実在のЕкатерина Савиноваサビノワの伝記映画で，サビノワ自身が主演し歌います．あの声はサビノワしか出せません．私がこの映画を知ったのも彼女の3.5オクターブ出るという魅力的な声の歌を耳にしたからです．音楽学校の玄関で有名なソコロフ教授に何度か訴えます．ついに引き出した教授の返事が Приходите завтра!「明日来なさい」でした．教授に学校のオーデトリウムで聞いてもらえた彼女の歌声がすばらしい．教授もフローシャの純粋さと素晴らしい声を見抜き，何とか入学させようと動きます．この映画はサビノワが自分で主演した愉快で楽しい映画で，私はとても好きです．しかし，残念ながら，その後のサビノワは，ブルセラ病（生牛乳を飲むと牛から感染する）が重くなり鉄道自殺（1970年，43歳）してしまいます．

興味深いのは，1963年にウクライナで高校生時代に，Людмила Сенчинаリュドミラ・センチナはきっとこの映画を見たのではないかと私は想像します．リュドミラは成功して，ロシア人民芸術家歌手になります．彼女は今年の1月25日に，ペテルブルクの病院で死去（６７歳）しました．
リュドミラは，高校を卒業して，歌手になるために，ウクライナからレニングラード（現ペテルブルグ）に出てきました．でも，そのとき音楽学校の試験は終わっていたのです．よく似た話があるものですね．サビノワと違うのはペテルブルグに親戚がいたことです．
リュドミラの代表曲は，Песня Золушкиシンデレラの歌
－－－－－－－

 
新型コロナウイルスCovid-19の感染拡大が止まりません．皆様お元気でお過ごしでしょうか．現在，日本では「人と人との接触機会を８割減にしよう」との呼びかけがなされています．規制を遵守し感染機会を減らすことはこの時期非常に重要です．

8割減は，感染拡大の転換点であるとされています．その根拠となる手法の総説には，例えば，「感染症流行の予測：感染症数理モデルにおける定量的課題」（西浦・稲葉；統計数理，第54巻第2号，461-480，2006）があります．しかし，接触機会8割減が転換点であるという具体的なシミュレーションはまだ見ておりません．

いろいろな感染症はそれぞれの特異な伝染状況があり，それに合わせた数理モデルを作る必要があるので一般論ではかたづきません．Covid-19の感染拡大に対しての数理モデルと，感染率，ウイルスの活性期間，患者の死亡率，感染者が感染源になりうる期間，等々の係数を仮定する必要があります．Covid-19は，まだ解明されない特異な感染の振る舞い（無症状の保菌者が感染源になる，感染回復後も再度感染する，等々）があり，完全な数理モデルができず確定的予測は困難です．
今回，石黒真木夫が，簡単な仮定に基づくCovid-19の特徴を考慮した数理モデルを作り，教育的なシミュレーション結果を得ました．その詳細は．「NPO数学月間の会」のホームページhttp://sgk2005.saloon.jpにありますのでご覧ください．

■ここでは，数式を用いずに，石黒の数理モデルとシミュレーションの内容要点を紹介します．

（１）ある人口集団を未感染者，ウィルス感染源，免疫獲得者，死亡者に分類し，未感染者がウィルス感染源の一員と接触したときにある感染確率で未感染者が感染してウィルス感染源となるものとする［実際は，Covid-19では，人－物ー人の感染ルートもあるといわれる］．

（２）ウィルス感染源のウィルス拡散は14日間つづき，14日目に「死亡率」に従って死亡者と免疫獲得者に分かれ，免疫獲得者はもはやウィルスを拡散することも再感染することもなくなる［実際は，再感染するケースも稀にある］．

（３）このモデルでは時間の経過とともに未感染者は単調減少，免疫獲得者は単調増加するので，感染の流行はかならず止まる．しかしそれは集団全員が感染した後である．

（４）感染確率と死亡確率を適当に与えればシミュレーションは簡単である．いまの計算機をもってすれば人口集団の各個人の命運をたどるミクロ・シミュレーションもさして難しくないが，以下で紹介するのは未感染者やウィルス感染源集団の大きさの変化を追跡するマクロ・シミュレーションである．確率的な現象の「期待値の動き」を追いかける決定論的なダイナミクスを採用する．ミクロ・シミュレーションをして，算術平均の変化を見るとマクロシミュレーションの結果に「誤差」が乘ったような動きになるだろうと考えられる．

（５）感染が感染源と未感染者の接触でおきるので，接触規制で感染源率を下げて「医療崩壊」は防ぐことは可能だが，これは未感染率を「高止まり」させ，規制をはずすと残った未感染者が感染する事態が発生することを示している．接触規制で再流行時期を遅らせて得た時間的余裕を有効に使って致死率を下げることが重要．それができないと、結局は死者の数は減らせないということになる．

■石黒の数理モデルを用いたシミュレーション・プログラム（Excelファイル）は，NPO数学月間の会のウエブサイトhttp://sgk2005.saloon.jpに公開しています．各自このファイルをダウンロードし，パラメータも色々変えてシミュレーション実験をすると面白いだろう．各種規制の効果は接触機会数に乗じるパラメータを変えて見ることができます．
感染者数のピークが過ぎても，揺れ戻しの感染者数の小さなピークが観測され，このような波動を繰り返しながら収束に向かうことがわかるでしょう．

 
私は3月24,26日のメルマガまぐまぐ(311,312号)で以下の内容の発表をしました．－－－－－
3月21日の厚労省の公表値を用いて，罹患率＝発症患者/PCR検査数と定義すると，罹患率は，約5%になります．しかし，PCR検査の，感度と特異性（酒井健司，朝日デジタル）の情報を入れてベイズ推定した罹患率は5.9%になりました．この推定値の増加は，主としてPCR検査感度に原因があり，実際の罹患者を取りこぼすためです．（注）この数値は，PCR検査を受けた限定されたグループをサンプルとしているために，一般の集団に対しては少し割り引いた数値になるでしょう．－－－－－
今日，PCR検査数も増加したので4月23日厚労省のデータを用いて，再計算をしてみました．どのように変わったでしょうか？
ただし，PCR検査数が増加したといっても（多少はPCR検査を受ける条件の緩和があるかもしれませんが），陽性の確率が高いサンプル集団について検査が行われている状況は変わりません．
カバーの図を見てください．ここで推定する数値はあくまでもサンプル集団に関するもので，一般集団に対してはいくらか割り引いた数字になるでしょう．
ーーーーーーーーーーーーーーーーーーーーー
■条件付き確率についての「ベイズの定理」とは次のようなものです．
p(Y|X)p(X)=p(X∩Y)=p(X|Y)p(Y)
記号の意味は例えば以下の様です．
p(X)　　Xが起こる確率
p(Y|X)　Xが起こった後でYが起こる確率
p(X∩Y) XかつYが起こる確率
ベイズの定理は，X（原因）が起きた後でY（結果）が起きる確率p(Y|X)と，XとYを入れ替えた確率p(X|Y)を結び付ける定理です．
ーーーーーーーーーーーーーーーーーーーー
■新型コロナウイルスに対するPCR検査数は，厚労省の発表https://www.mhlw.go.jp/stf/newpage_11012.html　で，4月23日現在，
135,983人になりました（1月前の3月21日の数字の7.5倍です）．
PCR検査数　　　　135,983
PCR検査陽性者数　  11,919
陽性者のうち発症患者（陽性者∩発症患者）7,315人
発症患者/PCR検査数＝罹患率　と仮の罹患率を定義すると，罹患率は約5.4%です．
陽性率＝陽性者数/PCR検査数＝0.088　，陰性率＝0.912　と定義できます．

■PCR検査の精度
新型コロナ検査、どれくらい正確？　感度と特異度の意味（酒井健司，朝日デジタル）に基づき，次のように仮定します．PCR検査の感度というのは，罹患者がPCR検査で陽性＋と正しく判定される確率のことで，あまり大きくなく0.7， 罹患者でもPCR検査が陰性－となる（偽陰性）の確率は0.3程度．
検査の特異性により，非罹患者が＋（疑陽性）と判定される確率は0.01だそうです．

■これらの仮定の下で，以下の２つを推定しましょう．ただし，ベイズの定理を使います．
（１）PCR検査で陽性と判定されたとき，罹患者である確率を求めなさい．
p(罹患|+)=p(+|罹患)p(罹患)/p(+)=0.7×0.054/(0.054×0.7+0.946×0.01)=0.80

＋(陽性)でも検査感度のせいで罹患者をとりこぼすことが多い．また，非罹患者の割合が大きいので偽陽性の数も無視できない．この2つの原因が，＋判定でも罹患者である確率を80%（前回79%）に下げている．

（２）罹患率を推定しなさい．
p(罹患|−)=p(−|罹患)p(罹患)/p(−)=0.3×0.054/(0.054×0.3+0.946×0.99)=0.017
－（陰性）と判定されたものの中に見逃された患者である可能性は1.7%（前回1.6%）ほどある．

従って，サンプル集団で推定される罹患率は0.088×0.80+0.912×0.017=0.086
すなわち，8.6%(前回5.9%)と推定できます．

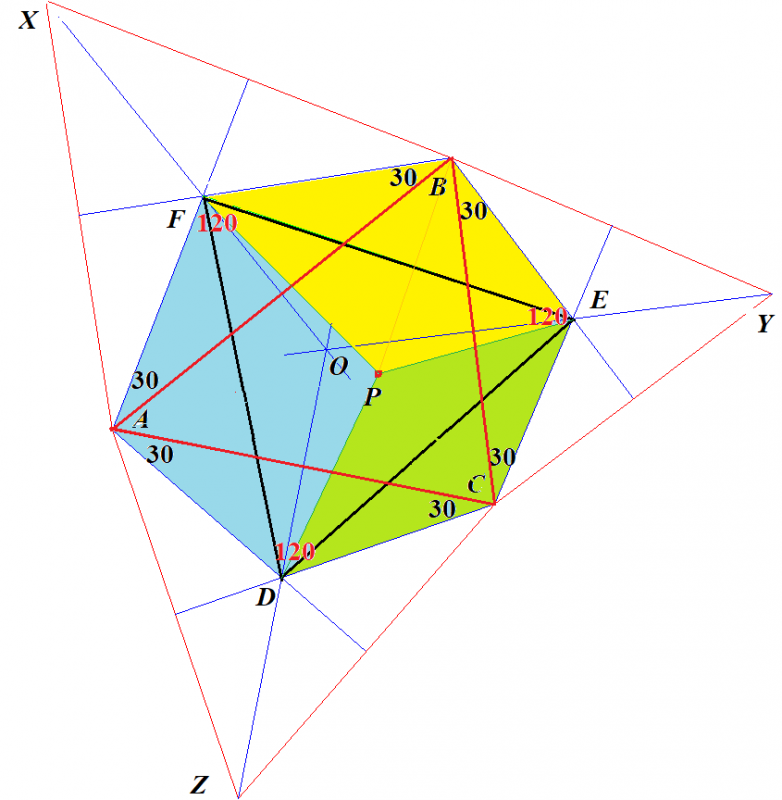
ナポレオンが発見したといわれるナポレオンの定理とは次のようなものです．

ーーーーーーーーーーーーーーーーーーーーーーーーー
ナポレオンの定理
任意の⊿ABCの各辺上に正3角形を作図し，それら3つの正3角形の重心をD，E，Fとする．D，E，Fを結んでできる⊿DEFは正3角形である．
ーーーーーーーーーーーーーーーーーーーーーーーーー

なかなか美しい形の定理ではありませんか，ナポオンの名を冠するのにふさわしい定理だと思います．ただし，ナポレオンが発見したかどうかは記録がなくわかりません．

ナポレオン (1769 －1821) は数学好きです．
陸軍幼年学校で，代数，三角法，幾何などを勉強し，数学で抜群の成績をおさめ，1784年にパリの陸軍士官学校に入学．数学が役に立つ砲兵科へと進みます．騎兵科，歩兵科でなく砲兵科に進んだのも戦術の時代の流れを見据えての決断でしょう．砲兵司令官，将軍，皇帝になりました．この時代にフランスには多くの数学者がいました．ラプラス，モンジュ，フーリエなどが近くにおり，エジプト遠征 (1798 年) にはモンジュやフーリエが同行しました．
ナポレオンは数学が大好き，このような幾何問題を考えるのが楽しみで，きっと定理を発見したのだと私は想像します．

証明

与えられた任意の3角形を⊿ABCとします．
その各辺上に作図した正3角形のそれぞれの重心がD,E,Fです．
点Oは⊿ABCの垂心（⊿ABCのそれぞれの辺の垂直2等分線が交差する点）で，点D，E，Fは，この垂直2等分線上にあります．

色々な角の角度は図中に記入してあります．我々が証明すべきことは，⊿DEFが正3角形であることで，例えば，∠DFE=60を証明すれば済みます．考えてみてください．

ヒントは，∠BFE=∠BXC　　と　　∠AFD＝∠AXC　を証明することです．

正3角形であるための必要十分条件は「３つの内角すべて（すくなくとも2つの内角）60°」です．

図形の対称性から，内角の１つが60°であることを証明すれば済みます．

これは，補助線1本引けば自明です．三角関数を使って計算で証明する方法もありますが，補助線1本で自明になるのが幾何の醍醐味です．

■さて，ここに出てきた６辺形には面白い性質があるのを見つけました．

この６辺形の中にある正3角形の中に点Pを中心になるように，正3角形の外の6辺形の部分を折り込むことができます．

4月25日，10:30から，Zoomを用いてリモートでの同志社中学校のDo★MATH博物館の見学がありました．10分間ほどの休憩をはさんで1時間ほど園田先生が出演され，見学会と，一太刀切りでハートや星形を作ったり，誕生日を当てる数あてカードを楽しみました．今年は，「数学月間」のイベント（毎年7月22日に実施し今年は第16回）もリモートで実施することになりそうです．

誕生日（1～31の数）を当てるには，4x4の数字が書かれた5種類のカードを見て，自分の誕生日が書かれているカードを選び出します．そして，それらのカードの左上の数を足し合わせると誕生日が当たるのです．
なかなか不思議ですね．この原理を今日は解説します．

■これからの説明は，誕生日を当てるゲームの変種で，15までの数を当てるゲームについて語りましょう．ゲームの実施方法も，数字が書かれてあるカードを選ぶのではなく，数字が書かれたカードの上にマスクをかぶせて当てようとしている数が見えているかどうか訊ねる方法になります．この両方のゲームとも同じ原理（2進数表記）を利用しています．

4x4の16個のマスに0~15の数字が書かれたカードがあります．このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる．これをマスクカードを変えて4回行えば，相手が心の中で思っていた数が当てられるというのが，この数当てのゲームです．

どのような仕組みがあるのでしょうか．秋山久義さんが，2019年7月のパズル懇話会で発表されています．今日は，秋山久義さんの発表「数当てカードの諸相」から引用して，その仕組みを解説します．

まず，16個の数の配列は，ランダムに配置したふりをしていますが隠れた規則があります．
例えば次の２つの方法があります．
（１）左右対称の位置にある2つの数字の和は常に15になる．
（２）回転対称（2回対称あるいは点対称）の位置にある２つの数字の和は常に15になる．

 このために右半分（あるいは左半分）を知れば，全部の数の配置がわかります．つまり，相手の意中の数がマスクに隠されて見えない場合は，その数との和が15となる数の方が見えているのです．

さて，0~15の数を2進数で表すと次の表のようになります．下図をご覧ください．a,b,c,dはそれぞれ2^3，2^2，2^1，2^0の桁に相当します．

2進数表示で3桁目を表すマスクカードがa，2桁目を表すマスクカードがb，というように4枚のマスクカードができます．
それぞれの数の上に乗る4種類のマスクカードで，2進数表示の１のところに孔を開ける（逆に統一してもかまわないが）ことにします．
例えば，13に場合は，aとbとdのマスクカードに孔（網掛け部分）をあけ，ｃのマスクカードには孔はあけません．

以上で，仕掛けの準備ができました．

これで，質問を開始して，数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます．
見えないといったマスクカードは
（１）の場合には裏返して重ね／（２）の場合は180°回転して重ねるのです．

結局，4枚のマスクカードを重ねたものは，
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです．

同じ正３角形（正6角形）格子［あるいは，正３角形２つよりなる平行4辺形格子とみてもよい］のパンチングメタルを2枚重ね合わせました．
この図の状態は，2枚の格子どうしのなす角度が2θ＝30°になった場合です．初めの正3角形（正6角形）の格子より大きな新しい周期の格子が出現しているのがわかりますか．

■正方形格子（網目）を2枚重ねた場合を考察してみましょう．
(Coincidence-site-lattice)

両方の網目が重なった位置に，新しい網目の格子が見えて美しい．

2枚の正方形の格子（正方格子という）どうしの傾きを変えると，ときどきこのような新しい格子が現れます．もとの格子の互いに直角な２つの並進ベクトルをa，ｂとすると（正方格子ならa=b），
もとの格子は，格子点 na+mb，（n,mは任意の整数）の集合です．
同じ正方格子を２枚傾けて重ねて，新しい周期の２つの並進ベクトル x, yが生じています．これらの図の状態は，

（上図）x=2a+b，y=a+2b ．（下図）x=3a+b，y=a+3b（面心格子，２格子点胞）

この基底変換を行列で書き，行列式を求めると３（左図），8（右図）ですので，新しくできた格子はもとの格子と比べて面積で3倍（左図），8倍（右図）粗くなっていることがわかります．

格子というのは，並進ベクトルの作る群＝並進群の”図的表現”です．2枚の格子の干渉で生じた新しい格子の周期は，もとの格子の粗いサンプリングになっているわけで，新しい格子は，もとの格子の部分群になります．

格子が重なって，拡大された（粗い）格子が見える現象は，干渉（ビート）と同じことです．
実際に，２つの原子網面が重なって，このようなビートが見えることは，電子顕微鏡で格子像の観察をするときにもよく起こります．
結晶は周期的な構造をしているので，周期的な空間は「結晶空間」とも呼ばれます．エッシャーの繰り返し模様や，壁紙模様などで，周期的空間の実例をたくさん目にしていると思います．

■2つの正方格子の平行なずれによる干渉（モワレ縞） 

 それぞれの正方格子の周期をλ１，λ２とすると，新しい周期Lは
1/L=1/λ1−1/λ2　の関係があります．

私は，子供のころ家にあった織物検査器というもので遊んだことがあります．これは，標準となる格子模様がガラスに刻んであり，織物にこのガラスを重ねると繊維の周期とのビートで縞模様が観察できます．1mmの中に何本繊維があるかとか，織り方が均一でなくどの程度乱れているかが，モアレ縞からわかります．

次の写真は，工事現場のネットが折り返されて2重になっているために観察されるモアレ縞です． 

昨年9月に表題の本（技術評論社）を出版しました．この本の構成は8つの章からなり，全章を通して万華鏡で繋がっています．1,2章は有限図形の対称性（点群）．3,4章は周期的な空間の対称性（平面群）．これらの映像は，万華鏡で作り出すことができます．5章は万華鏡．6章は円による反転という数学的な鏡を用いた万華鏡．7章はフラクタル操作という数学的な鏡を用いた万華鏡です．8章は東京ジャーミイで，イスラミック・デザインを鑑賞します．写真撮影にご協力いただいた東京ジャーミイの本屋さんにも本書を置いていただいています．

■この本に，第9章を続けて書くとすれば，イスラミック・デザインになります．イスラムデザインの特徴は，黄金比（すなわち5回対称や10回対称）がちりばめられていることです．しかし，5回対称性と2次元（あるいは3次元)世界の周期性とは両立できませんから，ちりばめられている5回（あるいは10回）対称性はロゼット内部だけに局所的に作用し，世界の全域を支配するものではありません．そのため，あたかも我々の住む3次元に高次元宇宙が投影しているようで不思議な魅力を感じます．イランのDarb-i Imam寺院（1453）の壁には,その500年後にヨーロッパで発見されるPenroseタイリング［自分の中に自分と同じパターンが繰り込まれる］と同様なパターンがすでに見られることをPeter LuとPaul Steinhardtが報告しています．イスラムの繰り返し模様は準結晶や基本領域が分割されて写像される万華鏡と似たところがあります． 

 
病院でMRI(核磁気共鳴イメージング)を撮ったことがある方もおられることでしょう．私も3年前にMRIの診断を受けたことがあります．お陰様で現在は絶好調です．このMRIの記事はそのころ書いたものです（記事の中で1.5Tの静磁場と記述しましたが，3年たち3.0Tの装置の普及も多少進んだようです）．
MRIの測定中に聞こえる”カタカタ”や”ビー”というほとんど冗談かと思うようなふざけた音は何でしょうか？　あれは，1.5T（テスラ）という強い磁場中で装置が動くために，あたかもスピーカーと同じように装置が振動して出す音です．それにしてもなんとかならないものか？振動しないようにガッチリ作るのは，今でも何トンという重量ですから無理なのでしょうが．

さて，画像の分解能を良くすれば，測定時間は増えるわけです．しかし，
分解能を上げて，かつ，測定時間も短縮できる「圧縮センシング」という数学的な方法があり，これに言及するのが後編の主題です．その前に，前編では，まず，MRIの装置の仕組みについてお話しましょう．
■プロトン（水素の原子核）はスピンを持ち,磁石の性質（核磁気）があります．強い静磁場下に置かれたプロトン核磁気は，磁場に沿ってだいたい向きが揃い，歳差運動している状態です．歳差運動の周波数（ラーモア周波数という）は，磁場が強いほど高く，MRI装置の静磁場は1.5T程度と超強力なので，ラーモア周波数は64MHｚ（ラジオ電波の周波数領域）程度です．
静磁場下のプロトンに，このラーモア周波数の電波が照射されると吸収共鳴が起こり，核磁気の歳差運動の振幅（周波数は変わらない）が増大しほとんど横倒しの状態で回転（古典論的なイメージ）しています．
一方，歳差運動をしているプロトン核磁気からは同じ周波数の電波が放射されるので，これを検出することができます．
■生体組織は，水をはじめ水素原子と結合した分子からなる組織です．
つまり，プロトン（水素の原子核）核磁気は組織の至る所に分布していて，
その水素の属する組織の環境（診断される情報）がそのプロトン核磁気の性質（緩和現象）に反映されています．
すなわち，核磁気の歳差運動の縦緩和，横緩和という現象は，そのプロトン（水素）が含まれる（結合している）組織内の状態で違いが出ます．
緩和というのは，電波の照射を止めると，励起されていた核磁気の歳差運動が定常状態に戻ることで，静磁場方向の核磁気成分の復元緩和を「縦緩和」，静磁場に垂直面内の成分の減衰緩和を「横緩和」といいます．
組織の各点で，これらの緩和定数を測定し，マップに表示できれば，
診断に役立つ組織の特徴を反映したイメージングになります．
■さて，組織画像の位置情報はどのようにして得られるのでしょうか．
これがなければ画像として見ることができません．断層測定をするには，検出器に到来する電波が，１つのスライス平面から来るものだけ集める必要があります．このためには，静磁場の他に傾斜磁場を印加します．
傾斜磁場はさきほどの静磁場とは別で，ペアのコイルによって発生する
（数十mT/m程度の強さ）もので，たとえば，ｚ軸方向の静磁場があり，加えて，z方向に沿って変化する傾斜磁場，x方向に沿って変化する傾斜磁場，y方向に沿って変化する傾斜磁場の3種類があります．
傾斜磁場があると，空間内で磁場の大きさが一定になるのは平面になります．例えば，静磁場方向と同じz方向の傾斜磁場を印加すると，磁場一定の平面はz軸に垂直な平面です．
プロトン核磁気のラーモア周波数は，磁場の強度に比例するので，
共鳴吸収する電波の周波数をスキャンすれば，z軸に垂直な各断層平面に並ぶ核磁気からの電波を順次採取することができます．
次に，各断層面内の(x,y)位置情報はどのように得たらよいでしょうか？
断層内のプロトンの歳差運動を励起した後に，x傾斜磁場，引き続きy傾斜磁場の印加を行うとします．
x傾斜磁場印加でx軸に沿って歳差運動の周波数が変化し，その場所から放射される電波のx座標情報（周波数エンコーディング）が得られます．
ｘおよびｙ傾斜磁場の印加でy軸に沿って歳差運動の位相が変化し，
y座標情報（位相エンコーディング）が得られます．
傾斜磁場を印加して，空間の位置情報を得，画像化を可能にしたのは，
Lautergur（1972）の発明で，2003年のノーベル賞を受賞しました．
■緩和時間の測定は，歳差運動の励起後，照射電波を切って行うので，
立ち上がり時間も考慮した電波照射の複雑なパルスシークエンスになり，
256x256画素の測定でもかなりの時間を要します．高分解能画像を得るには，正攻法で行うならさらに細分化した画素数の測定が必要になり膨大な測定時間になるでしょう．
これを解決し，MRIの高分解能かつ高速化を実現したのは，
後編で言及する予定の「圧縮センシング」という数学方法です．

2017年の数学月間懇話会（第13回）の講演の一つとして，ブラックホールの形を見る（池田思朗）をとりあげました．ブラックホールはなんでも引っ張り込み光も脱出できません．しかし，ブラックホールの穴に荷電粒子が引き込まれるときに電波やX線が放出されるので，ブラックホールの形は，この放出される電波を観測（地球上の6地点の電波望遠鏡を結んで電波干渉計を作り，電波の強度とその位相を観測）して，それらのデータをFourier変換すると形が見えるはずです．しかし，Fourier変換に用いる観測データは，地球が宇宙空間で旅した範囲の観測点で得られるのは圧倒的に限られたデータしかありません．

ブラックホールの穴画像を$$x$$，観測されたデータを$$y$$とすると，$$y=Ax$$
（行列$$A$$や，形式的な逆行列$$A^{－１}$$は線形演算子で，Fourier変換やその逆変換のことです）．
行列Aが正則ならば逆行列を両辺に左から乗じて，$$x=A^{-1}y$$と簡単に解くことができるのですが，$$y$$の次元$$N$$は非常に小さく，$$x$$の次元$$M$$は非常に大きい（行列$$A$$は$$N$$x$$M$$行列でランク落ち）ために解けません．多数（$$M$$個）の未知数のある$$x$$を解くのに，式の数（$$N$$個）が少ないので，不定解になります．もし，解$$x$$にたくさんの0要素（スパース）があるとしランクを下げれば，一意解を持ちます．なぜこのようなスパースな解が合理的なのかは難しいのですが，我々のまわりの画像は統計的にスパースなようです．この方法は，LASSO（Least Absolute Shrinkage and Selection Operator）といいます．数学的には，$$x$$がスパースであるという条件を，$$Σ|x_{i}|$$が最小という条件にして，最小2乗法$$||y-Ax||^{2}$$　を解き，少ない観測値$$y$$から$$x$$を求めます．このための数学には，ラグランジュの未定乗数法が適用できます．

■圧縮センシング
このような手法は，医学画像（MRIなど）解析で用いられており，高速で高解像度の画像が測定できる圧縮センシングとして役立っています．得られる画像の解像度を上げるには，観測空間でも細かくたくさんのデータを収集し，それらを用いてFourier変換を行うのが正攻法です．これは情報理論でシャノンのサンプリング定理（注）と呼ばれるものであります．

しかし，実際には画像内で急峻な変化がある場所は少なく大体がだらだら変わっています．そのような性質のある実際画像では，観測空間内を細かい分解能で測定するのは時間がかかり過ぎてもったいない．観測空間の少数の点だけのデータで十分なのです（この考え方はjpgなどの画像圧縮と同じ）．得られる画像は至る所0（スパース）という仮定は，大胆であるが良い結果をもたらします．

観測空間のサンプリングをナイキスト・レート（注）より細かく行う場合はオーバーサンプリング，ナイキスト・レートより粗い場合はアンダーサンプリングと呼ばれますが，画像がスパースという条件があれば，アンダーサンプリングのデーター集合を用いて解像度の高い原画像が再現できるのです． 解のスパース性を利用するこの手法は，医学画像（MRIなど）の撮影で利用でき，高解像度の画像を短時間で得られるようになりました．
ーーーーーーーーーーーーーーーーーーーーーー
（注）シャノンのサンプリング定理（1949年)

アナログ信号をあるサンプリング・レートでデジタル化すると，元のアナログ信号に含まれる周波数成分のうち，サンプリング周波数（ナイキスト間隔とも呼ばれます）の1/2の周波数成分までが再現できます．ナイキストは，サンプリング定理を1928年に予想していました（シャノンの証明が広く知られています）．

デジタル音源のサンプリング周波数は44.1ｋHzが使われていますが，この周波数でサンプリングすれば，人間の耳が聞き分ける高音限界といわれる20kHzの音まで十分に再現できるからです．
ーーーーーーーーーーーーーーーーーーーーーー