
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
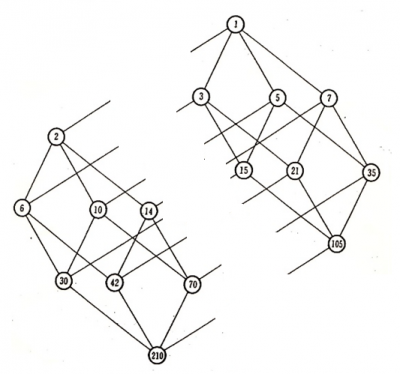
2019.10.26に開催した数学月間企画講演会では,約数の構造をわかり易く表示するグラフ(亀井図)を取り上げました.例えば,210の約数の系統的な構造を示すグラフは以下のようです.
210は4つの互いに素な素数の積210=2・3・5・7から出来ているので,4次元超立方体と同じこのような構造になります.210の約数は,自分自身の210と1を含めて全部で16個ありますが,系統的に並べると上の図のように整理できます.
頂点1のレベルには1個,頂点2のレベルには4つの素数,頂点6のレベルには2つの素数の積で4C2=6個,頂点30のレベルには3つの素数の積で4C3=4個,頂点210のレベルは4つの素数の積で1個です.4次元の超立方体には対称心があり,互いに点対称な頂点の積は210になることも理解できます.
このようなグラフは,数学のいろいろな分野で出会います.半順序を表現するハッセ図というのは,このグラフを逆順に描いたものと同じです.
210の約数の構造といえば,210をトップに置き逆順(ハッセ図と同じ)に並べる表示もありでしょう.
約数の構造に関しては,数学Aの研究課題として高校生にもなじみやすいものであるし,このグラフは高次元立方体の理解にも役立ち興味深いでしょう.
(注)数学ではハッセ図と呼ばれるものですが,美しくバランスのとれた4次元立方体は,亀井のアルゴリズムで描けるので亀井図とも呼ばれます.
4次元の超立方体の1つの次元(例えば,素数2の方向)を消すと,3次元の立方体の2つに分離します(下図).同様なことを,それぞれの3次元立方体で考え,例えば,素数7の方向の次元を消すと,3次元の立方体は2次元の面(例えば1-3-15-5)に分離します.このような性質は高次元の超立方体の成り立ちの理解に役立つでしょう.
(演習)2310=2・3・5・7・11ですから,2310の約数の構造を示すグラフを描いてください.これは5次元の超立方体になるはずです.
解答
(演習) $$420=2^2・3・5・7$$ の約数の構造を示すグラフを描いてください.
←wikiより
■3Dへ
Broone橋にある記念プレート,
Hamiltonが4元数を発明したときこの橋の下を散歩していた.
数学者William Rowan Hamilton卿はDublinのTrinityCollegeが産んだ最も著名な子であろう.
彼は最後の20年,複素数が2次元の回転を表すのと同様な
3次元の回転の表現を捜し求め,人生の最後にHamiltonは,4元数という答えを見出した.
$$q=a_{0}+a_{1}i+a_{2}j+a_{3}k$$
ここで,$$i^{2}=j^{2}=k^{2}=ijk=-1$$, $$a_{0}, a_{1}, a_{2}, a_{3}$$は実数.
複素数でしたように,4元数を幾何学的に記述し,回転の表現に用いよう.
今度は2次元でなく3次元の回転だ.
$$i, j, k$$は,3次元内の単位平面:$$i$$は$$yz$$平面,$$j$$は$$xz$$平面,$$k$$は$$xy$$平面で,外側向き法線はそれぞれ$$ x,-y,z$$方向である.
$$i, j, k$$は,3次元空間の単位平面という幾何学的解釈ができる.
点$$ a=(a_{1},a_{2},a_{3}) $$を,角βだけ原点を通る$$b=(b_{1},b_{2},b_{3})$$軸の回りに回転してみよう.
2つの4元数$$q_{1}, q_{2}$$を$$b, \beta $$から作る.
$$q_{1}=\textrm{cos}(\beta /2)+\textrm{sin}(\beta /2)(b_{1}i+b_{2}j+b_{3}k)$$
$$q_{2}=\textrm{cos}(\beta /2)-\textrm{sin}(\beta /2)(b_{1}i+b_{2}j+b_{3}k)$$
$$a$$($$x,y,z$$方向の単位ベクトルの線形結合)に,これら2つの4元数を乗じて
$$a'=q_{1}aq_{2}$$
この積で得られる点$$a'$$は$$a$$を与えられた軸の回りに角度$$\beta $$だけ回転したものだ.
複素数は平面内の回転記述,4元数は3次元空間内の回転記述に用いられる.
ダブリンの橋の下を通りかかったとき,Hamiltonのひらめきは,
3次元で物体を回転させる最も効率の良い方法であることがわかった.
だが彼の新しい乗法で,だれも幸福にならなかった.
物理学者Kelvin卿は4元数のことを:”....美しく巧妙だが,とにかく,これに触れるものには,純粋邪悪である...と評した.
とりわけ厄介なのは,2つの4元数を掛け合わせるとき,答えがかける順番で変わることだ.この特性を非可換という.
Hamiltonの積則をみれば,$$ij=k, ji=-k$$が示せる.
もし,$$i, j, k$$を単位平面のように扱えば,Kelvinや彼の同時代の人々を困らせた特性は直接導ける.
■映像を生活へ
Hamiltonの発明はいまや多数の物体を動かしたり,運動の創出へのグラフィック応用に使われる.コンピュータグラフィックで最も重要なツールの2つは,変形と補間である.
補間とキーフレーミング技術は,物体の初めと終わりの形と位置の特定と,その間の様子をコンピュータに計算させることだ.以下に示す映像のように:
一連のフレームにわたって徐々に変形するティーポットの形
諸君は,未発達のへびのアニメーション(Richard Wareham製作)を見ることができる.
ここではへび全体が,いくつかの特定な点の運動から,
補間を用いてコンピュータで作られた.
[訳注:ファイルのダウンロード先は略]
変形は単純なものから複雑なものを作り出す方法だ.
下の映像のように,変形球を覆っている布は,
普通の球面で起こる同じ光景を数学的な変形をして得られる.
変形も補間も速くて安定な数学的技術を必要とし,
4元数関連の手法がこれを提供する.
http://plus.maths.org/issue42/features/lasenby/sphere.png
http://plus.maths.org/issue42/features/lasenby/deformed_sphere.png
■ガーラムを信じさせる
http://plus.maths.org/issue42/features/lasenby/motioncapture1.jpg
http://plus.maths.org/issue42/features/lasenby/dots.jpg
http://plus.maths.org/issue42/features/lasenby/skeleton.jpg
データは体の色々な部分に付属しているリフレクターの運動からキャプチャーされる.....
....骨格は,データに数学的にフィットさせる.
上で記述したテクニークは古典的なアニメーションでも基本的なツールである.
漫画キャラクターでは,我々はその結果が信じられるのはとても幸せだ.
しかし,人間のアニメーションでは,たちまち偽者とわかってしまう.
現実味ある動きを作り出すにはモーションキャプチャーが必要になる.
ロードオブザリングズのフィルムバーションから,ガーラムのような
多数のキャラクターを作るにはモーションキャプチャーによる.
これらは,身体,頭,肩,ひじ,ひざなどの回転点に,本当の人のリフレクターを付加して作られる.それぞれは,多重のカメラによってフィルム化されリフレクターの位置の変化をコンピュータに記録する.
骨格は3次元データでフィットされる.
最後に,上に記述された技術はすべて,骨格上に具体化し,生活し,呼吸し,動くキャラクターを作り出す.
もしまだ諸君がタイトルロールを完全に見るために留まっているなら,首尾よい映画作製で使われた種々の製作タレントに気づくだろう.作者,ディレクタ,俳優,衣装デザィナー,プロップビルダー,....
これらのクレジットリストが続々流れる.
しかし一つの名前がしばしばタイトルロールから忘れられている-数学だ.
今日の映画の多くは,光線追跡の幾何学,4元数による空間内の回転なくしてはできない.
次回は,あなたの映画シートで,CGスペクタクルを楽しむために,数学に対してポップコーンを掲げよう.ショーの隠れたスターへ.
(訳:KT)
-----------------------
著者
http://plus.maths.org/issue42/features/lasenby/jl_small.jpg
Joan Lasenbyはケンブリッジ,トリニティカレッジで数学を専攻し,
電波天文学グループ物理学科のPhDをとった.
マルコーニの企業で短期間働いた後に,大学に戻り,現在,
ケンブリッジ大学工学部の信号処理グループの講師や
トリニティカレッジの研究のディレクター,研究員である.
彼女の興味は,コンピュータビジョン,コンピュータグラフィックス,
画像処理,モーションキャプチャと幾何代数の分野にある.
Maths goes to the movies By Joan Lasenby
Submitted by plusadmin on March 1, 2007
http://www.plus.maths.org/issue42/features/lasenby/index.html
今回も,MMP,plusマガジン42号の筆者KTによる翻訳です(2回に分けて掲載).
数式が読みにくい場合は,数学月間の会http://sgk2005.saloon.jp,社会を支える数学科学でご覧ください(ホームページではTexを用いている).これは,2007年の数学月間懇話会で配布したものです.この後の13年でコンピュータビジョンの分野は非常に進化しましたが,原理の紹介には非常によく書かれたこのエッセイが役に立ちます.
------------------------------------------------------------------
ポップコーンは手に入れたか?よい席は選んだか?座り心地は良いか?それではタイトルロール....
■数学が誇らしげにプレゼント....
映画の中の信じられないほど真に迫ったコンピュータで作られた映像に皆な驚く.ジュラシック・パークの恐竜,ロード・オブ・ザ・リングズの不思議 ---- 特に,ガーラムの出演者 --- は,数学なしではできなかったということを知らない人が何と多いことか.どのようにして,これらの驚くべき映像が作られるのだろう?
コンピュータ・グラフィックス,コンピュータ・ビションは大きな課題だ.この記事では,完成作品に使われる数学のいくつかを簡単に概観する.最初に映画の世界を創造し,次にそれを生活へ持ち込もう.
■場面を作る
pblk0001.png
最初の対象物は,三角形のような単純多角形よりなる針金骨格として作られる.
コンピュータ生成映画を作る第一ステップは,物語中のキャラクターや,
それらが棲む世界を創造することだ.これら対象物のそれぞれは,
接続された多角形(通常は三角形)で構成された表面として作られる.
各三角形の頂点は, コンピュータメモリにストアされる.
どの三角形のどちらの面が,物体やキャラクターの外側であるかを知ることは重要だ.この情報は, ストアされている頂点の順番として,右ネジの規則に従い記号化される.これで,どちらが外か一意に決まる.
[頂点の順番に従い,三角形の周りを右手の指を人差し指,中指,..と回したとき]
諸君の親指が向いているのが三角形の外側だ.例でやってみよう.
三角形(A,B,C)の外側方向(外側法線)は,三角形(A,C,B)の外側方向と反対であることがわかるだろう.
pblk0002.png
右ネジ規則で定義された(A,B,C)の外側法線は(A,C,B)とは反対方向
pblk0003.png
諸君の視点からファセット面までの光線を追跡しよう.光線は反射して光源を通過するか?
いまや対象物の表面は三角形の針金網だ.網のコンポーネントのそれぞれを彩色する準備ができた.
我々がモデル化している光景のライティングを,実際と同じにすることが重要である.これは光線追跡と呼ばれるプロセスを用いなされる.視点から物体へと遡り光線追跡し,反射させる.もし,目から出た光線がファセット面(針金網三角形の中の一つ)で反射され,光源を通過するなら,そのファセット面は光源に照らされ明るい色,もし,反射された光線が,光源を通過しないなら,そのファセット面は暗い色の影付をする.
光線を特定のファセット面まで追跡するには,表面を数学的に記述し,光線とファセット面の平面とが係わる幾何学方程式を解くことが必要になる.これはベクトルを用いなされる.光景の3次元座標系に,視点となる原点(0,0,0)を加える.
ベクトル v =( a, b, c ) は,原点から発し座標 a, b, c で終わる矢である.
例えば, v にスカラー2を乗ずるのは,規則 2v =2( a,b,c )=(2a, 2b, 2c ) に従い行う.
2v は v と同じ方向で2倍長い矢だ.
表現 λ v を見よう. λ は変数(言い換えれば,任意の実数).これはもはや,ある長さの矢ではない.長さが変数になったのだから.矢の方向だけを表している.別の言葉でいえば,この表現はベクトル v を含む直線を表す.
それは我々の視点からベクトル v の方向に発する光線を記述する.
三角形のファセット面で定義される平面は,3つの情報で表現される:
3頂点のうちの1つの位置頂点 $$a_{1}$$と, $$a_{1}$$から $$a_{2}$$へのベクトルと, $$a_{1}$$から $$a_{3}$$へのベクトルである.
下の囲みの中に,目とファセットで決定される面から発する一本の光線の方程式を与える.
光線がファセットをよぎるか否か,何処でよぎるかを知り,反射された光線の方程式を計算するには,
これらの2式を解かねばならぬ.
------------------------------------------
-------------------------------------------
(光線追跡の数学の詳細は,Turner Whittedの革新的な論文 ”影付け表示のための改良された照明モデル”,
Communication of the ACM,Vol.23,Isuue6に見ることができる.)
光線追跡は現実味ある光景を作り出すことができるが,たいへん遅い.
これはコンピュータが作る映画の製作には用いることができるが,コンピュータゲームのようにリアルタイムで照明を変化させることが必要な場合問題である.
影や火線束(コースティク)[収差による回り込みでできる光像],多重反射のような複雑な現象は,モデル化が困難で,動的あるいはもっと巧妙な数学的な手法,事前計算放射輝度伝搬(PRT)やラジオシティ(R)が使われる.
pblk0004.png
コンピュータゲームDOOM3,Neverwinter nights はダイナミックライティングが必要だ.
■必要なのは若干の想像力
光景,照明が出来てしまえば,監督が”アクション!”と叫び,キャラクターが動き出すのを待っばかりだ.いまや,数学がイメージに命を吹き込むのを確かめよう.
最も基本的な物体の動きの一つは,与えられた軸の回りの与えられた角度の回転である.
座標幾何学は,回転後の物体各点各点の位置を計算するツールを提供する.だがこれらのツールは効率的で高速であることが重要だ.これらのツールを見るにあたり,数学授業に一寸立ち寄って見る....
[この後,複素平面のこと,複素数に虚数iを乗じると反時計回りの90度回転になること,などの説明があるが略]
........
1806年にアマチュア数学者Jean Ribert Argandは複素数とiに幾何学的な解釈を与えた.複素数を乗ずることは,幾何学的には回転を表す.
■3Dへ
pblk0006.png
Broone橋にある記念プレート,Hamiltonが4元数を発明したときこの橋の下を散歩していた.
数学者William Rowan Hamilton卿はDublinのTrinityCollegeの最も著名な子であろう.
彼は最後の20年,複素数が2次元の回転を表すのと同様な,
3次元の回転の表現を捜し求め,人生の最後にHamiltonは,4元数という答えを見出した.
⇒次号に続く
中西達夫さんの「スパゲッティを巡る旅」は,スパゲッティを適当に砕くと,破片の長さの分布がどのようなものになるかという興味ある実験でした.
興味おありの方は,「数学文化」第21号(2013年)をご覧ください.数学月間懇話会(第10回,2014)でも講演していただきました.このとき観察される「べき乗則」は,社会の関心事の一つである「地震」でも見られます.
地震のテーマはメルマガNo.031('14/09/30)に,複雑系原発の事故雪崩のテーマは「数学文化」第16号(2011年)やメルマガNo.006('14/05/15)に掲載しました.今回は地震のマグニチュードと頻度のべき乗則の話です.
地震のマグニチュードMはエネルギーの対数です.マグニチュードを決めるのにリヒターが発案した当初の定義は便宜的なものでしたが,現在ではもっと理屈に合ったモーメント・マグニチュードが採用されています.
(注)震度というのはその地の揺れ(加速度[ガル])の程度をもとにした段階区分です.
地震で解放されるエネルギーは,生じた断層面の面積×平均変位×地層の剛性の積です(大雑把にいえば生じた断層の長さに比例します).
生じた断層の長さが長い方が解放されたエネルギーは大きいし,
地層の剛性が大きいほど大きな歪エネルギーが蓄えることができます.
これらを踏まえ,起こりうる地震の最大エネルギーを見積もるとM9.5程度と考えられています(1960年のチリ地震ではM9.5が観測されている).
地震のマグニチュードMと発生頻度(回/年)nの間にn=10^{a-bM}の関係があるのを,グーテンベルクとリヒターが発見しました.a, bはその地域の地層の剛性などを表す定数(b≒1)ですので,地震のマグニチュードが1つ大きくなるごとに,地震の頻度(回数)は1/10に減ります.ゆえに,これを「べき乗則」とも言います.
地震では,多発しやすいマグニチュードというものがありません(中心値があるようなガウス分布やポアソン分布ではない).べき乗則では,大きな地震ほど少なくはなりますが,M9あたりも起こり得ます.めったにないことですが,そんな巨大な地震に見舞われたなら壊滅的で,大きな地震の被害コストは莫大です.
地震被害コストの総額=Σ被害コスト(Mの関数)×発生確率(Mの関数)
を小さく抑えるのが,最善のリスク対策です.
工場の品質管理を考えましょう.不良品の多くでる日と少なく出る日がありますが,不良品の個数とそのような数の不良品を出す頻度の分布は,ガウス分布,ポアソン分布,ワイブル分布などの中心値を持つ分布ですから,中心値を出した普通の日の対策を検討すればよいわけです.
しかしながら,分布がべき乗則の場合は全く異なります.
頻度は小さいけれど致命的な被害を惹起する巨大地震に対して,
被害が最小となるように備える必要があります.
広域を汚染し人間の尺度に合わない百年もの年月要する原発事故の被害コストは致命的です.原発の再稼働は止めましょう.
クリーン・ルームの塵のサイズ分布も「べき乗則」だと言われています.
もし正規分布に従い,頻度の高い塵サイズがあるなら,そのサイズの塵の発生に特化した対策ができるのですが,「べき乗則」では特別な対策は困難です.幸いなことにこのケースでは,大きなサイズの塵が桁外れに大きな被害コストを与えると言う訳でもありませんし命に係わることもありません.
べき乗則は,大規模停電,原発事故,ハリケーン被害などの複雑系でみられます.べき乗則は,小さな事故が雪崩をうって全体に広がる性質と関係があります.関連テーマのバタフライ効果は稿を改めます.
■砕いた破片の分布関数を求める実験は,中西氏の実験したスパゲッティやクラッカーのほかに,凍ったジャガイモを投げて砕く(南デンマーク大,1993年)などいろいろあります.砂山が雪崩を起こす限界傾斜の実験も面白いものです.これらでも「べき乗則」が確認されました.
◆揺動させる
もう一つの重要なモデリングパラメータはランダムジグリングである
(プログラム中にrandomJiggleと記す).
「各鳥の周囲の鳥の平均飛行方位の査定が,いつも正確になされている訳ではない」という事実を考慮に入れる.プログラムが時時刻,各鳥の方位を更新するとき,ランダムジグリング変数により与えられる範囲内のランダム角に調整される.
10°より小さいrandomJigle値なら,群れは最終的に一方向への一体運動になる.randomJiggleを180°にセットすると系は塵微粒子のブラウン運動の
シミュレーションと同じになる.
ガス分子の例のように,このモデルをさらに自然に近づけるいくつかの方法がある.このヒントのいくつかはプログラムファイルの末尾にある.
◆単純さと速度
モデル記述で重要な因子は,用いるアルゴリズムの効率である.
”アルゴリズム”の起源は,アラブの数学者al-Khowarazmiの名前であるが,
”仕事を完成させるための一連の指示”を意味するようになった.
鳥の群れの例で用いたアルゴリズムは,おそらくそれほど自然ではない.
本当の鳥は,他のすべての鳥の位置を記録し,
自身と他のすべての鳥間の斜辺距離を計算し,
正確に5m内のものを選択し,
それらの進路の算術平均の方位に向けて舵を切るなどということはしない.
これらのステップは,追従が容易で,望ましい結果が得られるので,モデルとして選ばれたのだ.これは,なかなか冗長な方法だ.
一つの鳥から他のすべての鳥までの距離を計算しなければならない.
これを順番にそれぞれの鳥について,各時間ステップごとに行う.
高速なデスクトップコンピュータでも,鳥の数が500より大きいとシミュレーションはゆっくりゆっくり進む.
そこで,モデルのデザインでは,仕事をどのように達成するかを考える必要がある.可能な限り速いアルゴリズムを使うか,系でできる限り現実の方法に近づけるか,効率は悪いが仕事が達成できる方法にするか.
プログラミングで,しばしば,特定の仕事部分のアルゴリズムを関数にするのは良いアイディアだ.こうすればプログラム内で特定の計算が必要になったときいつでも呼び出せる.
(鳥の群れのコードを見れば,MeanHeading()関数でこれがなされる
のを見るだろう.)
見守る間にシミュレーションがずっと速く走るようにしたければ,
プログラムを2つの段階に分割するとよい.
最初は,コンピュータを貪り尽くすようなすべての計算を通して行い,
各時間ごとに系の状態を別々な行列として記録する.
この計算の後は,例えば1000回の時間間隔の行列リストの束のような3次元行列に行き着く.
シミュレーションを一回通しで行えば,すべての情報が保存される.
第二のステージは時間ステップごとに順番に表示する
(今度は計算処理のために待つ必要はない).
あたかもアニメーションを見るのに,行列の本の頁をパラパラするようなものだ.我々は,鳥の群れの単純なシミュレーションに絞ってきた.
コンピュータプログラムの構造,特定の仕事をするアルゴリズムや関数の記述などのコンピュータモデリングの重要な様相が浮彫りになるからだ.
このように単純なモデルでも,複雑で大変自然に近い群れのふるまいが作れる.これはまさに,動物研究者が作ろうとし,理解しようとした鳥の群れのふるまいや,魚の群れのコンピュータモデルだ.
例えば,Iain Couzin博士が動物のふるまいを理解するために巨大グループのコンピュータモデルを使つている.彼のモデルは,この論文で見てきたものとまったく同じ原理に基づいており,同様の複雑性がみごとに出現する.
モデルはさらに複雑になっており,(我々の2次元平面を超え)
3次元で動き,冗長だが現実に近い各個体のふるまいを制御する規則の集合を持つ.
-------------------------------------------------------------------------
◆Iain Couzin
イアンは,プリンストン大学とオックスフォード大学の両方に拠点を置く
動物行動の専門家だ.バッタから魚,鳥に至るまでの群れのダイナミックスのコンピュータモデルを作った.
彼の研究は,如何に動物の群れが集団としての決定をなすか驚異的な特徴を見いだすことと,アフリカの政府機関の行うバッタの致命的な群移動コントロールを手伝うことだ.最近まで,イアンは群れがどのように肉食動物の
アプローチに反応するかに集中していた.
諸君はイアンの研究の詳細を
http://www.princeton.edu/̃icouzin/で読むことができる.
下の映像は彼のモデルの一つから作ったビデオの静止画だ.
BBCのドキュメンタリシリーズ”肉食動物”で使われた.
http://plus.maths.org/issue42/features/dartnell/SimImage.jpg
------------------------------------------------------------------------
◆重力モデル
この種類の粒子運動モデリングの拡張は,画面をよぎって伸びる効果を含めることである.このわかりやすい例は,重力である.
重力は消えそうなほどわずかかもしれないが,太陽の重力の影響は非常に長距離まで達する.processingを使い単純な重力モデルを作るには,太陽としてスクリーンの中心に小円を描き,他のすべての点から太陽までの方位と距離を計算する関数を記述する.これで,諸君のモデル化した世界にある
粒子が影響を被り速度を変じる重力を計算できる.
ランダムな位置に置かれランダムな速度を持った惑星でシミュレーションを初期化し,これらの太陽の周りの円弧運動をアニメートしよう.
次の時間ステップのこれらの位置は,現在の重力と速度で決定される.諸君はプログラムを,各惑星が後ろに軌道の軌跡を残すように変更することもできる.
(draw()関数BYの背景コマンドを取り除く.ラインの始めに//でコメントにする).
http://plus.maths.org/issue42/features/dartnell/collision.jpg
Fig. 何十億という星がアンテナ銀河の衝突の間に形成された.
下に示した銀河衝突モデリングで色々見いだそう.
このイメージはハッブル宇宙望遠鏡で撮影された(NASA提供).
太陽系の表示のために,各惑星の円軌道を生む速度を注意して解く必要がある.太陽系の圧倒的な支配力,太陽の重力だけを含めば,第一近似で正確なモデルができる.だが,巨大ガスの木星は他の惑星に注目すべき影響を与える.このような二次的な効果を含めるなら,さらに正確なモデルができる.
水星の軌道を完全に観察に合わせるには,もっと複雑なレベルが必要で,
アインシュタインの相対性理論-これはNewtonの重力の法則よりも,
ある特定の状況では正確-を含める必要がある.
繰り返すが,モデリングのコツは,無視できない詳細の最小量を巧妙に考慮することだ.月面に人を着陸させたアポロプログラムは,単純な Newtonの重力モデルで地球と月の影響以外のすべてを無視した.
すべての粒子が互いに相互作用するもっと大きな重力系ダイナミックス
のモデリングは,非常に高速なコンピュータを使い膨大な計算が必要で,
極端な”計算浪費”である.
しかし,そのような数値シミュレーションも多くの研究者にとって
極めて重要だ.例えば,下の枠中に,2人の主導的な研究者の仕事に焦点を合わせ,過去と未来の数十億年のイベントを見ることができる.
世界を打ち砕く衝突を通して月が作られ,我々自身の銀河と我々に最も近い隣人銀河が,巨大な重力で引き合い,数十億年の先に互いを分裂させられるであろう.
----------------------------------------------------------------
◆Robin Canup
ロビンはテキサスのサウスウエスト研究所の宇宙科学者だ.
彼女は月がいかにして形成されたかに興味を持ち,
太陽系生成の初期に,若い地球がより小さい原始の惑星に衝突した時の
イベントから月が生まれたという理論をテストした.
彼女のコンピュータモデルは衝突の熱で地球全体が融け
大量の岩が宇宙に放出され,その多くは衛星の軌道でに合体し月になった.
http://www.boulder.swri.edu/̃robin/でもっと多くを見ることができる.
http://plus.maths.org/issue42/features/dartnell/Moon_impact1.jpg
-----
◆John Dubinski
ジョンはトロント大学で全銀河のダイナミックスを研究している宇宙物理学者.我々の銀河,天の川,アンドロメダと呼ばれるらせん銀河の隣人は
重力的に互いに引き合っていて,500,000km/時間でお互いに向かって落ちて行く.
ジョンはスーパーコンピュータを使用し,これらの2つの巨大な銀河が合体し始め,2つの星が互いに引き裂かれるときに星の大きな帯を引き裂き始める約30億年後の時間をモデル化した.驚くべきことに,このすべての混乱にもかかわらず個々の星の間のギャップは非常に大きいため,実際には一つも衝突はないであろう.
我々の太陽の運命は不確実である.太陽は銀河間の宇宙の暗虚に排出されるか,混合銀河の密集しているコアに飛び込むかである.諸君は,
http://www.cita.utoronto.ca/̃dubinski/tflops/で,
地球の夜空の景色も含めて,さらに色々な映画を見ることができる.
http://plus.maths.org/issue42/features/dartnell/galaxy1.jpg
-----
◆著者:Lewis Dartnell
著者のルイスはオックスフォード,クイーンズ・カレッジで生物科学を専攻している.現在[訳注:2004年当時],生命科学と実験生物学の数学と物理センター,学際科学のロンドン大学センターの生物学的複雑系モデリングの
4年間のMRes-PhD課程にいる.彼は宇宙生物学の分野で研究している.
火星の放射線レベルのコンピュータ・モデルを用い,火星の表面付近で
生命が生きられるかの予測をし,最近ニュースで報じられた.
彼はデイリーテレグラフ/ BASFの若手科学ライター賞などを4回受賞した.
彼のポピュラーサイエンス本,宇宙での生活:初心者向けガイドは,
2007年3月に出版された.彼のウェブサイトで多くの作品を読むことができる.(訳:KT)
proccessingという使いやすいオープンソースのプログラムがあります.私も使っています.現在はver.3.5.4が出ています.これで何ができるか粒子モデルの紹介です.
この記事は,英国MMPのplusマガジン42号(2004)の翻訳(訳:KT)です.
http://plus.maths.org/issue42/features/dartnell/index.html
Matrix: Simulating the world Part I - Particle models by Lewis Dartnell
鳥の群れが黄昏空に飛び交う様,魚群が敵をかわす様を見たことがあるなら,その完璧に振り付けられた動きに驚愕したことだろう.この行動は,
複雑に思えるかもしれないが,コンピュータでそのモデル化を行うのは,
それほど難しくはない.Lewis Dartnellが諸君自身のシュミレーションの
実地ガイドをする⇒経験不要.
粒子モデルにより,鳥の群れの運動,銀河系誕生,原子分子の物質構成,
などをシミュレート!
■マトリックス[訳注:1999年アメリカ映画]
世界をシミュレート 第1部---粒子モデル
モデルの構築は,科学や工学の多くの研究分野の核心である.
モデルの本質は複雑な系の表現であり,複雑な系のふるまいを理解するのに
異なった種々の方法で系の単純化がなされてきた.例えば,航空技師は,風胴テストのために戦闘機のミニチュア模型を作るかもしれないが,現代は,数学モデルをコンピュータ上でたいへん高速に走らせるモデリングが,ますます盛んになっている.超音速気流のコンピュータモデルは,信じられないくらい複雑だが,プログラムのデザインとシミュレーションは非常に基礎的な原理に基づいている.
モデルのふるまいに関するこの論文の前半で,たいへん興味深い自然系研究のコンピュータモデルが,いとも簡単にプログラムできることを述べる.
先端研究にこのようなモデルを用いている科学者の何と少ないことか.
◆はじめよう
http://plus.maths.org/issue42/features/dartnell/fish.jpg

Fig.1 どちらに行くのか?魚の行動をシミュレートする方法を見出せ.
これは,数学的なモデリングとコンピュータ・シミュレーションへの体験入門である.だが,プログラミングそのものの学習には深入りしない.これまでにプログラムを見たことがないとしても,心配は要らない.
シミュレーションのすべては,このウエブサイトでJavaビデオとして見ることができる.もし諸君がコンピュータプログラミングをすこしやったことがあるなら,この論文で用いた全コードをダウンロードして,改良したり調節したり試してみたいだろう.これらのシミュレーションを書いたり,アニメーション作りに用いたソフトウェアはプロセッシングと呼ばれ,無料でダウンロードでき,PCやMac バージョンで利用可能だ.
プロセッシングはコンピュータ科学者とアーティストの協力でリリースされ,自分で容易に改良や開始ができる.http://processing.org/download/index.html
プロセッシングが使われた世界中の種々のプロジェクトすべてのリストを
ホームページで一見されたし.http://processing.org/
よいモデルを組み立てる本質は,複雑な問題をいかにうまく単純化し,
系の重要な特徴を抽出し,モデルのふるまい解析を混乱させるものは取り除くように考えることだ.
例えば、ライフル銃から発射された銃弾弾道の単純なモデルは,明らかに重力の影響を考慮する必要があるが,空気抵抗のわずかな影響は無視してよい.この場合の空気抵抗は,2次オーダーの効果と呼んでよい.
別の系のモデリング,航空機の翼による揚力では,空気の影響を無視することはできないが他の因子は無視できる.
コツは,そのふるまいが理解しやすいように,モデルをできうる限り単純に保つことと,意味のない結果が生じないように重要と思われる因子をあまりカットしないようにし,入力因子の一つを変えて全系の応答の影響を見ることとのバランスにある.
この最初の論文のすべての例は,各点が空間内を色々な規則に従い動き回る粒子モデルとして知られるものである.
◆箱の中のガス分子
最初のモデルは,箱につめられたガス分子の大変基礎的な物理シミュレーションだ.見やすく単純にするため正方形内に閉じ込められた2次元粒子とする.この場合の物理は簡単である.各粒子は,箱の壁に当たるまで,
出発したときと同方向・同スピードで直線運動し続ける.壁に衝突すると,粒子は跳ね返り方向を変えるがスピードは変えない.映画と同じで,この論文のアニメーションは流体の運動を印象づけるフレームのシリーズからなる.
プログラムの仕事は各粒子の位置,方向,スピードを各時間ステップごとに前のステップの情報に基づき計算することである.この論文のすべての例では,各時間ステップごとのデータを配列または行列に蓄える.
行列の各行は異なる粒子に関する必要な情報を蓄える.このガスの例では,各粒子の状態は4つの数で記述される.
これらのうちの2つは平面内の位置(x,y)である.残りの2つは,粒子の運動の2成分を記述する.これらはdeltaX, deltaYと呼ばれる(”X位置の変化”,”Y位置の変化”の意).粒子の速度も定義する.
この場合の行列は4つの列と,全粒子に対する十分な行数を持つ.
シミュレーションの各時間ステップごとに,各粒子の位置(x,y)は,その速度に依存した更新を受ける.このプロセスのモデルを記述するプログラムの構造は,かなり直接的である.
どのように機能するか一般的な要点がつかめるかコードを見てみよう.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules.pde
最初にするのは,モデルの最も重要なパラメータ(含まれる分子の数,各粒子の位置と速度の情報を格納する行列など)
の定義である.次に,プロセッシングは,世界の大きさ-この例では正方形,アニメーションのフレームレート-を決め,シミュレーションのセットアップをする必要がある.
それからシミュレーションの初期化をする.これはデータを蓄える行列で,各粒子の初期位置,速度の必要な情報を順次蓄える.今回は,粒子のランダム散布を選んだ.
次に,トルコ石色の背景と各粒子の(x,y)位置に置かれた赤い円で系の現状を記述するコードがある.
最後に,シミュレーションの中核,アップデート関数が来る.
各時間ステップごとに,この関数は,行列中の各粒子に順番にあたり,時間ステップ内に,その速度が箱の境界を越えその粒子を飛び出させないかどうか計算する.
もし飛び出すなら,箱の壁で跳ね返り,粒子速度は変化するが,そうでなければ,その速度ベクトルで決められる距離だけ前進し続ける.
かくして,各粒子は新しい位置と新しい速度ベクトルをもち,行列は新しい値にアップデートされる.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules_web.jpg
Fig
箱に閉じ込められたガス分子のモデル.Java始動には映像をクリック.
全プログラムは,粒子が系をアップデートした後,再び描画し,
粒子はもう一度アップデートされ,これが繰り返されるように,
ループにセットされる.高速な現在のコンピュータでは,
これがたいへん高速に行われるので,ガス分子のスムーズなアニメーションになる.
この絵はプログラムのJAVAバージョンを開くようになっているので,
プロセッシングソフトウエアをインストールしなくても,動作を見ることができる.
この過剰に単純化したモデルは,2つの問題点があることに気づくだろう.第一に,我々のプログラムではdeltaX,deltaYに整数値だけ使っていること.このため粒子が動ける異なる方向の多くがなくなってしまう.
粒子のいくつかは,両サイドでバウンドし往ったり来たりするので,完全に水平や垂直に動くのが見られる.
第二に,このコードは,分子間の相互作用を考慮していない.分子は決して互いに衝突せず,箱の中を跳ね回るだけで,
完全予測可能である.周期的に,はじめがそうであったように,全分子が外向きに散らばる前に,真ん中で密なクラスターが形成される.これは明らかに部屋の中の空気分子では起こらないことだ.
空気分子は絶えず互いにぶっつかりあい予測不可能な運動を生み出している.
もし諸君が,少しコンピュータプログラム知っているなら,この単純な例をスタートとして,もっと洗練され現実的なものを作りたいと思うだろう.これをどのように行うかの若干の助言は,プログラムファイルの末尾にある.
運動のモデリングのもう一つの例に移ろう.今度は,粒子の相互作用の規則がもう少し複雑である.
◆鳥の群れ
モデル化する系は鳥の群れである.分子の例のように完全に独立に動くのではなく,各粒子は他の粒子の動きに反応して動く.
同様な標準構造をガスのプログラムにも用いるだろう.
最初はパラメータと世界の大きさを決め,全粒子の位置と速度を初期化する.次に,系の現在の状態を表示する関数のループをまわし,
次のタイムステップでの系の変化の計算を行う規則を実施する.
最初の例は,閉空間に閉じ込められた粒子の運動のシミュレーションをねらった.
今度は,開かれた戸外で飛ぶ鳥がどのように群れを作るか調べるのが関心事だ.エッジがあるような世界は困る.なぜなら,そのような人工的な特徴の周りでは,シミュレーションが適切にふるまわないであろうから.
モデリングの共通のコツは,世界空間を,粒子が左から去れば右から現れる,上下も同様[周期的境界条件]に世界空間を定義することだ.
上下は互いにつながりチューブのよう.左右端を丸く曲げてつなぐ.
ドーナツの表面の世界のようだ(数学ではトーラスという).
http://plus.maths.org/issue42/features/dartnell/flocking_index.html
Fig
鳥の群れモデル.単純な規則の集合が,他の鳥との相互作用を定義し各粒子の運動に作用する.燈色の円は視野範囲を示す.イメージをクリックすると
シミュレーションのJavaバージョンが走る.
再スタートは[Ctrll]+[F5](Windows)または,[z]+[R](Mac).
このモデルでの第二の発展は,直線運動を続ける粒子のかわりに,
鳥たちは互いに相互作用をし近隣者に依存し飛ぶ方向を変化させることだ.
各時間ステップごとに,プログラムは,次々に各鳥を選び,選んだレンジ内で他のすべての鳥の飛行方向の平均を計算し,選んだ鳥はこの方向に舵をとる.
ランダムに選んだある鳥の視野レンジの場を燈色の円で表示させる.
プログラムで値を蓄える変数はeyeSight.
プログラムがどのように機能するか一般的な要点を拾い上げるため,
コンピュータ・コードを一寸見てみよう.
http://plus.maths.org/issue42/features/dartnell/Flocking.pde
次に左のイメージのシミュレーションを走らせて見よう.
始めはランダムであった鳥たちの運動が,直ちに秩序のある振る舞いに変わる.
鳥の巨大な群れが,大体同じ方向に飛び行くように自己組織化される.
孤立した鳥が一団の中に引き込まれる.そして時折2つの大きいグループがお互いに近づいて迷うとき,個々の鳥は他の群れに参加するために引き剥がされる.2つの雲がスムーズに混ざり合うようだ.
ちょっと迷って,そして次に新しいグループの先頭が決まる.
この設計された行動を本当の鳥一団の動的関係と比較してみよう.
これを書く時点で,あるホップベースの飲物の英国テレビで放映されている素晴らしい広告がある.
夕映え空のツバメの群れに魅せられる.タグ ライン「属します」で終わる.
この広告はYouTube から見ることができる.たとえすでに消されていたとしても,他の鳥の群れビデオを見いだすのは全く容易であろう.
http://www.youtube.com/watch?v=RHHfynLYW1I
Fig 巨大スケール鳥群れを示すYouTube広告
この運動は優雅な振り付けに見える.
個々の鳥が次に何処に飛ぶか正確に知っているように見える.
鳥の巨大な流れが,滑らかに調和し一斉に方向を変える.
群れの中にリーダーはいない.基本計画もない.
すべての決定はグループ力学だけで決まる.
何千という群れをなす鳥の魅了される複雑さのすべては,
最近接の隣を越えた残りのグループが何をするかを知ることなしに,
個人が行動するというたいへん単純な規則から発する.
これはボトムアップ制御として知られる.
単純な規則で相互作用している個体から,
たいへん複雑なグループ行動が出現する例だ.
たくさんの動物,ミツバチ,スズメバチ,アリ,シロアリ,...が,
この種の「群れ知性」を使う.
しかし,群れの振る舞いの基礎となっているこれらの単純な規則は異常な環境では,まったく馬鹿な行動を惹き起こすことがある.
自分自身ではまだ試す機会がなかったが,友達の友達から,
諸君が羊の一団と一種にやれる面白いトリックの信頼できる情報を得ている.
羊達の前で突然走ったとする.羊達は脅威を察知し動き去ろうとする.
まだ可能な限り,諸君の隣人に近い状態を保って,同じ方向に動作することが最も安全であるという規則は働いている.
もしあなたが羊より少し速く走り続けるなら,あなたは追いつき,
そして一団の中央を通過して先頭で今走っている.グループの動的力学が,
侵略者から逃げ出すという初期の個体の決断から引き継がれていて,
あなたは,群れ全体をあなたの後ろに従えていることになる.
◆コウモリとタカ
プロセッシングソフトとこのモデルのプログラッミングコードをダウンロードしたら,グループ全体のふるまいにどのように影響するかモデルのある特徴をいじることができる.
例えば,鳥同士は何処まで見えているのか,eyeSight変数はたいへん重要なパラメータだ.我々のプログラムでは,この変数は20にセットされている
(とりの視野を表している燈色の円の半径が20単位).
このパラメータは諸君の望む如何なる値にもセットできる.
2つの異なるシナリオを見てみよう:
”コウモリのように目が見えない”eyeSightは1とする.
もう一つは地図をよぎって見渡せる”タカの目”eyeSightは100とする.
下の2つのリンクの図をクリックすればjavaが動き,どちらのシミュレーションも見ることができる.
http://plus.maths.org/issue42/features/dartnell/eyeSight1_web.jpg
http://plus.maths.org/issue42/features/dartnell/eyeSight100_web.jpg
Figコウモリのように目が見えないeyeSight=1 タカの目eyeSight=100
第一のシナリオでは鳥たちは相互作用をまったくしない.だから実際は世界空間内でランダムに走るガス分子と同じだ.
第二のシナリオでは,鳥たちはグループの反対側にいる個々の鳥の飛行方向に反応するくらい,たいへん遠くまでコミュニケーションする.グループのふるまいはたいへん速く一体化した固まった運動になる.
どちらの場合にも,少なすぎるか多すぎる相互作用のために,すべての複雑な群れのふるまいは失われる.
系のアウトプットはこのパラメータにたいへん敏感である.気体的ふるまいと固体的なふるまいの間にある種の相転移がある.興味あるダイナミックスの見地ではどちらも死んだも同然だが,自然ではeyeSightの値がこれら両極端の中間値のときにのみ緊急行動が起こることが見られる.
このエッセイは,2020年3月30日にマリアンヌによってプラスマガジンに提出されたものの翻訳(by KT)です.
How can maths fight a pandemic? By Marianne Freiberger ,https://plus.maths.org/content/
■ケンブリッジ大学の疫学者であるジュリア・ゴグは,「人生は長期間同じように過ごすことが許されない」と語った.ゴグ自身の人生は2月の初めに突然変化した.彼女は数理科学センターの通常の職務を辞し,緊急事態のための科学諮問グループ(SAGE)に結果を供給するモデリンググループであるSPI-Mに専念することになった.
SPI-Mは,インフルエンザパンデミックへ備えて活動をしてきたが,現在はCOVID-19のパンデミックに焦点を当て活動が引き継がれている.ゴグは,王立協会が率いる全国コンソーシアムの運営委員会にも所属し,パンデミックに対処している.
SPI-Mの仕事は,次に何が起こり,さまざまな介入でそれがどのように変化するかを予測するのに役立つ数理モデルを開発し使用することだ.COVID-19パンデミックがどのように進展し,我々の生活している社会の介入はどのような影響を与えるのか.これらのモデルは何か,それらは正しいか?
モデル
COVID-19パンデミックの報道については、こちらをご覧ください:https://plus.maths.org/content/tags/covid-19
諸君は意識しないで,数理モデリングを使っている可能性は十分にあります.COVID-19の感染数が3日ごとに2倍になると聞いて,きっと予測計算をしたことでしょう.今日$$ x $$件があり,この傾向が続くと,
3日間で$$ 2x $$件,6日間で$$ 4x $$件,9日間で$$ 8x $$件,一般的に,3 $$ n $$日で$$ 2 ^ nx $$.
このように急増加して今回の災害に至りました.
この外挿は単純ですがモデルの基本的な要素,時間の経過とともに起こる変化の一般的な性質を表す数式と,変化の正確な形状を特定するパラメーターがわかります.
この例では,時間の経過とともに指数関数的に増加し,この増加の急峻さは2倍に増加する時間パラメーター(3日間)で決まっています.
ーーーーーーーーーーーーーーーー
SIRモデル
$$ S $$を感染しやすい人の数,$$ I $$を感染した人の数,$$ R $$を回復した人の数とする.
SIRモデルの方程式は次のとおりです。
$$ \displaystyle \frac {dS} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle-\beta SI $$
$$ \displaystyle \frac {dI} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle \beta SI-\nu I $$
$$ \displaystyle \frac {dR} {dt} $$ $$ \displaystyle = $$ $$\displaystyle \nu I $$
ここで、$$ \beta $$は感染速度で,$$ \nu $$は回復速度, $$ d / dt $$という表現は,時間の経過に伴う変化率を表すため,$$ dS / dt $$は時間の経過に伴う感受性の数の変化率の意味.
数値$$ R_0 = \beta / \nu N, $$($$ N $$は母集団のサイズ)は、疾患の基本的な複製数と呼ばれる.
SIRモデルの詳細については,この記事https://plus.maths.org/content/mathematics-diseasesをご覧ください.
ーーーーーーーーーーーーーーーーーーーーーー
長期の予測や介入の影響を詳細にシミュレートするには,さらに洗練されたモデルが必要です.短期予測,長期予測,学校閉鎖など特定の介入効果のシミュレーション,さまざまな目的のためにさまざまなモデルが設計されています.モデルが異なっても,それらのモデルは1910年代以降のアプローチであるSIRモデルに基づいて構築される傾向があります.
SIRモデルの背景となる考え方の理解には,すべての人を,病気にかかりやすい(S),感染している(I),回復し免疫がある(R)のどれかの集団に属するとします.人が,SクラスからIクラスに,IクラスからRクラスに,進む方法を数式によって記述します. これらの方程式は,病気の感染率と回復率にも依存します. Iクラスの人口が少ないモデルから開始し,時間の経過とともにモデルを進化させて,病気がどのように広がり,人々が回復して免疫力を得て治まるかが見られます.
単純なSIRモデルは,寄宿学校の生徒などの単純な母集団に対して適切な予測を提供します. より複雑な母集団に関しては,さまざまな地理的場所やサブ母集団を表す個々のSIRモデル(個々の町や学校など)を繋ぎ合わせます.
接触がカギ
背景で非常に重要なのは人の接触パターンです:誰が誰にどのくらい会ったか.これに関する情報は,社会混合研究から得られます.例えば,BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります.人々は彼らの動きを追跡するアプリをダウンロードし,彼らに出会った人々(すべて適切に匿名化されている)を追跡するように求められます.このような接触データは,モデルに組み込まれている数値の配列( 行列 )(下図を参照)によって数学的に表されます.
異なる年齢グループ間の平均的な接触を表示する接触マトリックス.濃い色はより多くの接触を示します(ここでは,マトリックスを理解しやすくするために,数値ではなく色が使用されています).図は論文
Contagion! The BBC Four Pandemic – The model behind the documentaryから許可を得て使用.
学校閉鎖などの特定の社会的介入が,病気蔓延にどのように影響するかを確認するには,介入に関連する部分を削除または縮小して,接触データを適宜調整してみます.
ただし,「学校要因を完全オフに切り替えるのは現実的とはいえません.子供たちがまだ学校に通っているので減じるだけです」とGog氏は言います.「そして明確なガイダンスがない場合,学校外の子供たちは他の方法などや,祖父母と混ざってしまう可能性があります.これは,考慮に入れるべき追加の接触が発生していることを意味します.それらの範囲での推測になります」. 教師のストライキ中に何が起こったかに関する情報などの既存のデータは,接触データを補正し介入による流行への影響を予測するのに役立ちます.簡単に言うと,これが疫学モデリングの仕組みです.
だが,モデルは正しいか?
英国,ヨーロッパ,さらには世界全体を表すように設計された壮大なモデルは1つだけではありません.代わりに,さまざまなことを実行するように設計された多くの異なるモデルがあり,SIRモデルのコンパートメントアプローチは支配的なパラダイムですが,モデルの性質は依然として異なる可能性があります.完全に確定的なものもあれば,ある程度のランダム性を含むものもあれば,特定の要因の役割を示すために1回だけ実行されるように設計されているものや,不確実性に直面して予測の範囲を取得するために何度も実行されるものもあります.
大きな問題は,モデルが現実的であるかどうかです. 1つには,COVID-19が新しい病気で,既存モデルは季節性インフルエンザのために開発されたものなのです.「私たちのモデルは,みなインフルエンザから始まったもので,コロナパンデミックモデルは誰も作っていませんでした」とGog氏.COVID-19とインフルエンザのためとでは構築した典型的モデルで何が違うのかを調べなければなりません.
パンデミックのダイナミクスはインフルエンザとコロナウイルスで似ていますが,違いもあります.1つは,COVID-19にはかなりの潜伏期があるということです.人は何の症状も示さずに感染する可能性があります.「インフルエンザの場合は数時間かかるかもしれませんが,このコロナウイルスの場合は数日かかる可能性があります」モデルは,SEIRモデルを用いることを意味します.E「露出」が追加されます.このクラスの人々は感染していますが,まだ症状はありません.Eクラスは,人に感染させる人と感染させない人にさらに分けることができます.すべてのモデルは近似であり,「インフルエンザの場合,目的によってはSIRを回避できることがよくあります.ただし,このウイルスの場合,潜伏期間を無視すると,近似が非常に悪くなる.特に,短期予測のときは,これを考慮する必要があります」とGog氏は語った.
これは,単純SIRモデルによる典型的な結果で,感染しやすい(可能性がある)人の数は青,感染した人の数は緑,回復した人の数は赤で表示されます.
COVID-19について私たちが知らないことが他にもたくさんあります.「1日目や2日目の感染力など詳細はわかりません」.「不完全なデータからそれを推測することは非常に困難ですが,現在,中国や他の国からのデータがいくつかあり,クルーズ船からのデータも非常に興味深い.限られた情報から推測するために最善を尽くしています」 十分な情報がない場合,モデラーは不確実性を取り除くために何が最も重要な未知数か決定します—これがモデリングで非常重要なことです.
1つのパラメーターの重要性は,実行しようとしていることに厳密に依存する場合があります.「明日何件の発病があるかを予測するためには,多くのことを知る必要はありません.現時点では指数関数的です」.「しかし,第2波が発生するかどうかを予測するには,非常に異なるいくつかのことを知る必要があります」
長期予測の重要な数値は,疾患の基本的な再生産数です(多くの場合,$$ R_0 $$と表示される).人口の全員が疾患感受性がある(かかる可能性がある)と仮定すると,感染者が平均して感染させる人の数(それは 伝送速度に関連する,上記の枠記事を参照).COVID-19の場合,これは2から2.5の間にあると推定されます.モデラーは,可能な値の範囲ごとにモデルを実行し,対応する予測の範囲を考えます.
感染したが病気ではない
現在,多くの疫学者に必要なもう1つの重要な数は,集団内での感染の真の症例数で,これには,病気にかかったが症状を示さなかった人々の症例数が含まれます.「無症候性の数は,私が現時点で睡れなくなる数です.これを知ることは,私たちの出口戦略にとって非常に重要です」とGog氏は言います.
現在の指数関数的成長を減らすことができるものが基本的に2つあります.「1つ目は,学校の閉鎖や身体的な距離などの介入により接触率が変化することです」とGog氏は述べます.「指数関数的プロセスを変える2番目のことは,感受性の枯渇です」 病気になったことでしばらくの間免疫があり,無症候性を含む真の症例数を知ることで,感受性の高い人々のクラスがどれほど速く小さくなるかがわかります.議論されている集団の免疫のメカニズムは,感受性の数が減少するにつれて,病気の指数関数的成長が平らになり,その後指数関数的減衰になることを意味します.
幸いなことに,無症候性に関するデータを知ることに関しては望みがあります. 人が病気にかかっているかどうかを知ることのできる抗体検査をしていますが,これらの最初の波は当然NHSスタッフにのみ公開されます.
しかし、不完全な情報があったとしても,モデリングの予測は,特に不確実性の範囲を考慮して提示する場合,暗闇の中で突き刺すだけではありません.優れたモデルは,私たちが持っているすべての関連情報で構成されています.優れたモデラーは,モデルの制限とモデル内の不確実性を注意深く追跡します.多くの場合,可能なパラメーター値の範囲を含み,予測の範囲につながります.これは,さまざまな介入戦略の下で発生する可能性のある将来のシナリオの範囲です.予測は完璧ではありませんが,私たちが持っている情報を使用して実行できる最善の予測です.
では何が起こるのでしょうか?
誰も何が起こるか正確に言うことはできません.地平線に見える大きな望みはワクチンの到着です.これは,群れの免疫を構築するためのもう1つの手段であり,最も脆弱な人を優先的に保護するオプションを備えています.問題は,最小限のダメージでどのように自分自身をそのポイントに到達させるかです.
誰もが同意することの1つは,これには長期的な犠牲が伴うということです.「1週間だけシャットダウンして,この状況がなくなることを期待することはできません」とGog氏は言います.「それはまだここにあり(社会的距離の措置が早すぎる場合),集団の免疫はありません.現時点では,ヘルスケアシステムが容量を超えないようにするためにシャットダウンせざるを得ません.しかし,これは恒久的な戦略ではないことは十分に認識しています」
先週 ,Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では,季節変動も考慮して,再発の問題について詳細に検討しました.呼吸器疾患の発生は,秋と冬に悪化する傾向があります.季節性インフルエンザの発生と同時に,ヘルスケアシステムにさらに大きな負担をかけます.キスラーと彼のチームは,そのような季節変動を反映する要因を含むSEIRモデルを使用しました.社会的距離測定の効果は,COVID-19の基本的な生殖数が最大60%減少することでモデルに反映され,中国で観察されたものと同等です.
この最新の研究の結論は,必ずしも明るいものではありません.社会的距離の1期間では、救急医療能力が圧倒されるのを防ぐのに十分ではありません(調査では,英国ではなく米国の救急医療能力を調べましたが,英国でも同様の結果が当てはまります).「[この調査によると]シリアルロックダウンの期間を検討しています」とGog氏は言います.「批判的なケアが始まろうとしているときにロックダウンするという考えです.しかし,英国で起こっていることは,NHSが規定を拡大しているため,ロックダウンがより短く,それほど深刻ではなく,あまり頻繁ではないことです」
これらの社会的距離の断続的な期間がどれだけ長く,頻繁に異なる仮定(米国の数値に基づく)になる可能性が高いかを,論文から抜粋した以下の図に示します.
これらのグラフは,断続的な社会的距離(青色の領域)の下でのウイルスの有病率(黒い曲線)と重大なケース(赤い曲線)を示しています.最初と3番目のグラフには,季節的な強制がありません.2番目と4番目の季節の強制.クリティカルケア能力は、水平の黒い実線で示されます.最初の2つのグラフは現在の米国の救急医療能力のあるシナリオであり,3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです.基本再生数の最大値は冬期は2であり,季節的なシナリオでは夏期は1.4です.この図は,キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からのものです.許可を得て使用.
悲観的状況ですが,希望の光がいくつかあります.1つは,COVID-19の重症例に対する投薬とより良い治療プロトコルが,ある時点で到来する可能性です.これは,人々が短期間で病気にならないことを意味し,NHSへの圧力を軽減します.社会的距離を縮める措置の深刻さの多くは,NHSが崩壊しないようにする必要があるため,深刻な病気の人々を効果的にケアすることができ,短期間の過酷な措置が少なくなる可能性もあります.
もう1つの希望の光は,軽度で無症候性の感染者の未知な総数です.これがモデルで想定されているよりもはるかに高いければ,より多くの人々が病気になり免疫力があれば,上記の図が示唆するほど見通しは悪くありません.私たちはこれが事実であることを期待し,それがわかるまでは,ルールを守って家にいるだけです.
この記事について
Julia Gogはケンブリッジ大学の数理生物学の教授です.彼女は,その結果を緊急事態用科学諮問グループ (SAGE)にフィードするモデリンググループSPI-Mのメンバーです.彼女は王立協会が率いる全国コンソーシアムの運営委員会のメンバーでもあり,COVID-19パンデミックに対処しています.
プラスマガジンの編集者,マリアンヌフライバーガーは,2020年3月24日にGogにインタビューしました.
http://plus.maths.org/issue42/features/foster/LCH_web.jpg

テームス川にかかるロンドンシティホール.内部の巨大な螺旋階段ケースに注目.映像©Foster + Partners
■Foster+パートナーズについて
Foster+パートナーズは,Norman Foster とシニアーパートナーグループ
が指導する国際的に著名な建築スタジオである.
ロンドンのガーキンGherkin(キュウリ)として知られる建物や,この
ロンドンシティホールや,大英博物館の大広場の屋根のようなランドマークは彼らの設計です.地上最大建設の一つワシントンDCのスミソニアン研究所の中庭,ロンドンのウエンブリースタジアム,北京国際空港第3ターミナル(龍のイメージ)なども手掛けています.
大英博物館の大広場の屋根 ガーキンの全貌
■Foster+パートナーズのプロジェクトがもつ共通点は:巨大
巨大は,環境に最大限の影響を与えます.巨悪のデザインとならずにすむかどうかは,微妙なバランスの技であります.
建造物は構造的に健全で,美的に快いものであるだけでなく,
設計規制,工費の制約,目的に良く合うこと,エネルギー効率の極大化
など,多角的に満たさなければなりません.デザインの過程は,複雑な最適化問題になります.この問題を解く方法が,モダーン建築術と古代エジプトの建築術とでは異なるのです:
先進的なデジタルツールが,制約の膨大な配列を分析統合し,最適解を見出します.数学は建設される構造の形,要求される物理的特徴を記述できます.数学はコンピュータの言語で,モデリングのすべての段階の基礎になっています.
■ロンドンシティホール
ロンドンシティホールは,ロンドン市長,ロンドン議会,大ロンドン当局を収容します.ガラスの使用と内部の巨大ならせん階段が,透明性と民主的プロセスへの親近感を象徴しているかのようです.
外見の強いインパクトは,この建物の奇妙な形です.
テムズ川の土手の上に置かれて,建物は川原の小石を思わせます.
その丸みも民主的な理想を思わせます.けれども,ガーキンと同じように,
形が決められたのは,みかけの形のためだけではなく,エネルギー効率を最大化するためでもありました.
これを実現する1つの方法は,建物の表面積を最小にすること(望まない熱の損失と流入を防ぐことができる)です.諸君は,体積が同じあらゆる形の中で,球形が最も表面積が小さいことを知つているでしょう.
これが,ロンドンシティホールが球に近い形をしている理由です.
建物を非対称にしたのもエネルギー効率に貢献しています:南面のオーバーハングが,ここの窓を上階の床で陰にして,夏季の冷房需要を低下させる.
ガーキンの場合と同様に,コンピュータ・モデリングで建物の中の気流が如何動くか把握でき,自然の換気が最大になるように建物内の形が選ばれました.実際,この建物は冷房を必要としないといいます.
同程度のオフィススペースのエネルギーに比べ,たつたの1/4と伝えられます.
螺旋階段さえ,単に審美的理由で選ばれたのではありません.それらの分析の一部として,ロビーの音響効果,人々の声が適切に聞こえるような建物をSMG(専門家モデリンググループ)は設計しました.
初期の音響効果は,広いホール内をエコーが跳ねるという状態でひどく,
何らかの対策が必要だったが,Foster+パートナーの過去のプロジェクトの1つが手がかりを提供したのです:
ベルリンの Reichstag は大きいホールがありますが,大きい螺旋の傾斜路があり反響が起きません.SMG はロンドンのシティホールに同様な螺旋階段のモデルを作り,Arup Acoustics会社がこの新モデルの音響効果を分析しました.諸君は,以下のアニメーションで,音が階段後ろに閉じ込められ,エコーが減じるのを見ることができます.このアイデアは最終設計に採用されました. (アニメーション © Arup Acoustics)
https://plus.maths.org/content/sites/plus.maths.org/files/Flashfix/arup.mov

arup.mov1.62 MB
◆この記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者が翻訳し若干編集しました.原著エッセイを,3つに分割して(その1)に当たるものです.
◆専門家モデリンググループ(SMG)について
Foster+パートナーズの専門家モデリンググループ(SMG)は,De KestelierとPetersがメンバーになっており,1997年に設立された.SMGの仕事は,建築家を助けて,プロジェクトのバーチャルモデルを創造することだ.
「通常,チームは概念を持って我々のもとにやって来る」と,De Kestelierは語る.「それはスケッチのようなものであったり,より発展させたものであったりする.そこで我々は,CADツールを用いるかツールを開発し,モデル作りで彼らを助ける」
http://plus.maths.org/issue42/features/foster/populated_surfaces.jpg
パネルを収めた数学的表面.映像提供 ΕBradyPeters
コンピュータの助けを借り,その物理から外観まで,建物のほぼすべての様相を設計することができる.コンピュータ モデルで,建物の周囲を風が流れる様や,建物内部の音波の反響をシミュレートできる.グラフィックプログラムで,異なった数学的な表面を探究し,それらに異なった柄のパネルをはめてみることもできる.
そして,これらのモデルから手に入る情報のすべては,近年の建築 CAD ツールで最も重要な発明であるパラメトリックモデリングに連動できる.
http://plus.maths.org/issue42/features/foster/gherkin_model.jpg
30St Mary Axeの建築モデル.
映像 © Foster + Partners.
パラメトリックモデリングは,1960年代からあった.しかし,建築家がその力をフルに利用できるようになったのはつい最近である.
モデルは,諸君が建物に加えた変化により影響を受ける他の特徴を再計算せずに,建物のある特定の特徴をいじることを可能にする.
これはたいへん強力なデザインツールである.ガーキンを例にとろう.もし,建物をもっとスリムにしようと思うなら,他の何らかの特徴が犠牲になるだろう.外側ライニングカーブやダイヤモンド型の角度など再計算が必要となる.これはまったくたいへんな仕事量で,もしなされたとしても,手書きであれ再プログラミングであれ,新しいスケッチを描きなおさねばならない.
パラメトリックモデルはこれらのすべてを諸君のためにやってくれる.
変えないようにしようと決めた特性は固定されたままで,幾何学的特徴を色々変えることができる.モデルはスプレッドシートのような働きで,建物の特徴を変えることは, スプレッドシートの項目を変えるようなものだ.変化に応じ,ソフトウエアは先に決めた関係を保ちつつ,モデルを再度生成する.
丁度スプレッドシートがそのすべての項目を再計算するように,SMG によって提供されたデジタルのツールが装備され,デザインチームは短期間のうちにデザインオプションの莫大な範囲を探検することができる.チームは建物の幾何学的な特徴を変えて,変化がどのように・・・例えば気流,あるいは音響特性・・・に影響を与えるかを見ることができる.
建てるのが難しいようなどのような複雑な形でも,探究することができ,単純な形へと分解することもできる.必要な材料はどれほどで,
コストはいくらかもすばやく見積ることができる.
複雑な形がほとんど建設不可能であったためと,最良な環境へ適合させる科学を充分使いこなせなかったため,数十年前には実現不可能であった建物を建設できるようになった.
◆ガーキン [ガーキンとは”キュウリ”のこと]
http://plus.maths.org/issue42/features/foster/gherkin_wind_web.jpg
ガーキンの周囲の気流のモデル.映像 © Foster + Partners.
ガーキンは SMG が関与したプロジェクトの1つで,形がどのようにして制約を満たすように選ばれたかがわかる主要な例である.このビルは30St mary Axe の公式名称で,高さ180m(ナイアガラの滝の3倍の高さ).他の高層建築に比べて,3つの際立った特徴がある:
形は方形でなくむしろ丸い.膨らむ中央と先細るトップ.螺旋のデザインに基づいている.これらすべてが,純粋に審美的特徴となることに容易に気づく.だがそれだけでなく,これらは特定の制約を満足させている.
ガーキンサイズの建物の主要な課題は,周囲を吹き抜ける気流だ.
ベースから旋風がまきおこり,近隣地域を不快な地にする. この問題を扱うために,SMG は,建築家に乱気流の数学に基づき建物の空気力学特性を
シミュレートするコンピュータモデルを使うように助言した.
モデルは円筒状が方形のものより空気の流れへの応答が良く,旋風を減らすことを示した.中央が太く16階で最大直径に達するものが,スリムなものより風の低減の助けになるということもわかった.
強風でくちゃくちゃにならないとしても,高層ビルの隣に立つのは恐ろしい.高層ビルは諸君を小さく見せ,低い建物の輝きを奪い,日光を奪い取る.これらの効果を最小に抑えるのは,ガーキンの特有な形である.
膨らんだ中央と先細のトップは,下からトップが見えないようにする.
かくして,諸君を小さいとは感じさせないし,太陽と他の景観も底から覗き込める可能性がある.
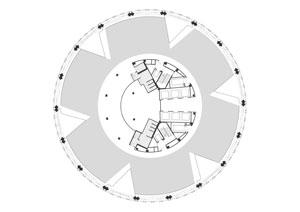
ガーキンの床面プラン. 映像 © Foster + Partners.
最初に決めたことは,ガーキンが可能な限り持続可能な建物であるべきということだ.そしてこれは,自然な換気(エアコンの節約のため)と自然の日光照射(光熱費の節約)を最大にする形の選択を意味する.6つの三角形のくさび形を,建物の内部に貫入するように各フロアの円形プランから切り取る.これらは光の井戸の役をする.
それらが作る光線は,自然の喚気を促進する.しかしながら,くさび形はお互いの直上には位置していない.空気力学のモデリングは,1つの床のプランが下の床のに対して数度回転していると,換気が最大になることを示した.それで,くさび形が作るシャフトは建物を昇る螺旋を作り,建物の外形により起こる空気の流れと,最適に相互作用する.くさび形のファサドの窓が自動的に開いて,新鮮な空気を建物に引き込む.慎重に選んだ幾何学の結果として,この建物は,同程度の他の建物に比べて,エネルギーが50%削減されたという.
http://plus.maths.org/issue42/features/foster/gherkin_inside.jpg
ガーキンの内部.三角形のくさび形は,床面プランから切り取られる.
それらは,光の井戸の役をするし,喚気も促進する.映像 © Foster + Partners.
◆この記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者が翻訳し若干編集しました.
原著エッセイを,3つに分割して(その2)に当たるものです.
ガーキンの全貌.平面パネルが曲面を近似していることに注意.映像 © Foster + Partners
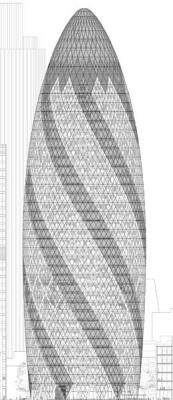
ガーキンやロンドンシティホールや,他の多くのFoster+パートナーズの作品がたいへんモダーンに見えるのは,外側が曲面であるためです. しかし,曲面を作るのはとても困難で,建設費が高くなります.そこに幾何学者のチャレンジがあります:単純な形から作る一番良い方法は何か?
「これが我々の主たるチャレンジの一つだ」とDe Kestelier(SMGメンバーの一人)は語ります.
「我々のプロジェクトの実に99%は,いかなる曲面も使っていない.
例えばガーキン,1種類の曲面パネルはトップにあるレンズのみだ.
建物が曲面という印象は,多数の多角形の平面パネルで曲面を近似的に作ることで生じる.パネルが多いほど錯視も真実味をおびる」
複雑な表面を記述するこのような平面パネル解を見いだすのが,SMGの仕事です.De Kestelier が説明するように,幾何学[その形]は,しばしば経済により決定される:「我々は矩形に近いパネルを使う傾向がある.なぜならそれはいっそう経済的であるからだ.資材をカットするとき安くなる」
三角形では,多くの材料ロスがあるが,矩形に近いとロスが少ない.
また,矩形に近いと構造が少ないので,視覚的にもさらによい.これは,
表面が完全に矩形から成り立っているロンドンシティホールで実証されました.
実際,ロンドンシテイホールは,理想的な幾何学形と建設容易さのバランスがよく取れている例です: 扱い難い丸い形はスライスに切ることにし,スライスの一つ一つは,僅かに傾いたコーンで容易に数学的に記述できて平面パネルでの近似も容易です.
■合理的な設計
数学的な方程式で記述されるコーンのスライス,トーラス,球などの表面は,しばしば,SMGデザインの基礎となります. これらを,バーチャル・モデルの創造に使うときに,数学的に生成される表面はコンピュータ上で容易に表現できるのでたいへん利点があります.
たくさんの個別座標を蓄え記述する構造ではなく,方程式を蓄えるだけでよい.表面の正確な形は方程式のパラメータを変じて制御できます(例として下図を見よ).[記述に必要なメモリが圧倒的に少なくなる]
平面解はやはり比較的容易に設計できる:ソフトウェアはオリジナルの表面のノードポイント集合に直線を引くようにする.
http://plus.maths.org/issue42/features/foster/surfaces_web.jpg
これらの表面は,関数z=e^-a(x^2-y^2) のグラフである.ここで,
3次元座標系は,x,y,z(上向き)軸であり, a は表面の形を決める.
第一の表面はa=1 ,第二の表面はa=5 ,第三の表面はa=7 .
数学的に定義された要素の集合からなる複雑な構造を考えるのは,
バーチャル世界では有用ではない:建物モデルから実際の建設手順のガイド作りを支援する合理化のこのプロセスは,もう一つの SMG の仕事の重要な部分だ.
同様に,数学的な完全性は,実用性のために道を譲る必要がある:「2~3週間前のことだが,楕円の一部である壁のプランのことで私のところに来た建築家がいる」とDe Kestelierは語った・・・
もちろん楕円は数学的には描くのは易しいのだが,それをさらに合理化することを望むのはなぜか?
私は楕円の弧を3つの円弧に合理化することを決めた.理由は,壁の建設でコンクリート壁用の型が要るためだ.これは全体の形を建設するのに多くの型パネルを使ってなされる.もし諸君が正確に楕円にしたいなら,すべての型パネルは異なっていなければならない:楕円の周囲を進むと,楕円の曲率はたえず変化しつづけるのだから. もし楕円をやめて3つの弧にするなら,諸君が必要とするのは,3セットのパネルだけで,各セットのパネルは同じである.
これならずっと簡単になる.「 数学者に理想的なものは,建築家に理想的であるとは限らない」
http://plus.maths.org/issue42/features/foster/museum.jpg
英国博物館の屋根.設計Foster+パートナー
■博才の人
SMG が,建物の外見と気流・音響のような物理現象の双方をモデル化するには,コンピュータプログラミングを使う.幾何学[形]の理解は,デザインと建設プロセスに直結する.
「建築家でなく数理科学の専門家なのか? SMGメンバーの8人中7人が,プロの建築家だが,専門的知識は,複雑な幾何学,環境シミュレーションからパラメトリックなデザイン,コンピュータ・プログラミングにまで及んでいる.グループの8番目のメンバーはエンジニアで,主プログラマーである.
こみいった数学に基づき,物理的特徴をモデリングするとなれば,
チームはしばしば専門コンサルタントを使う.チーム内で予備的な解析を行ない,もしさらに知りたければ別の解析を行う.「我々は,専門コンサルタントとデザイナー間の接点となる」とPetersは説明する.
純粋数学,幾何学は如何? どれぐらい複雑なのか?
「オフィスに1Aレベルの本がある」と,De Kestelierは語る.結局のところ,それはすべて建設可能な構造を作ることに関わり,古典幾何学を越えるものはここでは用いない.
SMG の大部分の活動には数学が付随しているのだが,彼らのデザインとは,
仕事に対して制限を与えるものであるとPetersとDe Kestlierは主張する.
「悟るべき重要なことは,我々はアーキテクチャで働くプログラマーではなく,プログラミングをするアーキテクトだということだ」とDe Kestlierは語った.
Petersも同意する:「我々の主な仕事はモデリングではない.
プロジェクトのパラメータは何かを理解し,噛み砕き定義できる規則にする.我々は,何処に適応性があり何処に制限があるかを理解できるようにする」 制限の最適化と建設可能な物体の創造.もちろん,建築家はいつもそうしてきたし,PetersとDe Kesteierも建築の仕事は本質的には変わっていないと思っている.
現代のデジタルツールにより,今日の建築家は,過去の世代には夢であったデザインオプションの領域も探索できるようになっただけだ.
形と模様,科学とコンピュータの言語として,これらのツールを自由に使えるようにしたのは数学だ.数学は確かにその料金を取り戻している.(訳:KT)
-----------------
◆編集後記
ガーキンとロンドンシティホールを設計したFoster+Partnersについての記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者(KT)が翻訳し若干編集しました.
原著エッセイを,3つに分割して(その3)に当たるものです.
Perfect buildings: the maths of modern architecture
By Marianne Freiberger
http://plus.maths.org/issue42/features/foster/xavier_brady.jpg

Xavier(左)とBrady(右)はFoster+Partnersのモデリング専門家メンバーである.プラス編集者は,ロンドンの数学と芸術ブリッジ会議(2006年)で,二人に出会った.ブリッジ会議の詳細はウエブサイトにある.
Marianne Freiberger(プラス編集者)
◆ところで,ガーキンに良く似た超高層ビルが新宿にあります.2008年に完成した東京モード学園が入っているコクーンタワーです.コクーンとは繭のことですがどちらかというとセミに似ているビルです.設計は丹下都市建築設計です.新宿で大変目立つビルです.