note.com投稿記事

Грегори Чейтин　科学の世界«В мире науки» №6, 2006

数学と物理学
数学と物理学は完全に異なるものと一般に思われています。物理学者は、実験と観察の結果に基づいて世界を説明します。ニュートンの法則であれ、量子物理学の標準モデルであれ、宇宙を支配する法則は、経験的に確立され、論理的に証明するのではなく、実験的にのみ検証できる公理と見なされなければなりません。数学者は、ある意味で世界から独立しています。彼らの結論や定理、たとえば整数や実数の性質は、私たちの周りの現実にまったく依存していません。数学的な真実はどの世界でも真実でなければなりません。それでも、類似点があります。物理学、そして一般的に自然科学では、科学者は観察結果を昇華させることによって法則を生みだします。それから、結果の法則から観察結果をどのように推定できるか示します。数学でも同様のことが起こります。数学者は計算実験の結果を公理に圧縮し、それらから定理を推定します。

ヒルベルトが正しければ、数学は閉じたシステムであり、新しいアイデアの場所はありません。数学のすべてを説明する静的な閉じた理論があり、それは独裁者のようになります。数学を発展させるには、創造のための新しいアイデアと範囲が必要です。いくつかの基本原理から考えられるすべての結果を推測するために最善を尽くすだけでは十分ではありません。個人的には、オープンシステムの方が好きで、厳格で権威のある考え方は好きではありません。

1956年にハンガリーから脱出し、その後イギリスで科学の哲学に従事したイムレ・ラカトスも、数学は物理学のようなものだと信じていました。彼は、実験が数学にとって異質ではないことを示すために、準経験性の概念を導入しました。たとえば、1742年に、Christian Goldbachゴールドバッハは、2を超える偶数は2つの素数の合計として表すことができるという経験的な結論に達しました。ゴールドバッハの推測は、10^{14}までの数で正常にテストされていますが、厳密には証明されていません。数学は準経験的であるように私には思えます。言い換えれば、それは物理学（本当に経験的です）とは異なりますが、おそらくほとんどの人が考えるほどではありません。

新しい公理
新しい公理を追加するという考えは、数学者にとって異質ではありません。たとえば、ユークリッドの5番目の仮定を考えてみましょう。直線の外側に選んだ任意の点を通る指定された直線に平行線な直線は、1つだけ描くことができます。何世紀にもわたって、幾何学は、ユークリッドの他の仮定に基づいてそれを証明しようと頭を悩ませてきましたが、失敗しました。最後に、数学者は、5番目の公理を置き換えて、曲線空間の非ユークリッド幾何学、特に球面形と鞍形を得ることができることに気づきました。他の例としては、論理学における除外平均の法則や集合論における選択の公理などがありますが、これはほとんどの数学者が進んで証拠として使っています。しかし、それを認めず、いわゆる直観主義的な論理や構成主義的な数学を探求する科学者がいます。数学はまだ絶対的な真理の一枚岩のシステムになっていないことが判明しました!

もう一つの非常に興味深い公理は、「PはNPと等しくない」という文で、PとNPは課題クラスの名称です。NPクラスには、提案された解を非常に迅速にチェックできる課題が含まれています。例えば、「数字8633の因数を求める」という問題では、提案された解「97と89」を簡単な掛け算ですぐに確認することができます。（「速い」には厳密な定義がありますが、ここでは詳細は重要ではありません）クラスPは、事前の想定がなくてもすぐに解ける課題です。誰も答えを知らない問題は、どんなNPクラスの問題でもすぐに解けるかどうかということです。(数8633の因数を素早く求める方法はないのでしょうか？)つまり、クラスPとNPは同じなのでしょうか？これは、クレイ数学研究所のミレニアム賞問題リストにある項目の一つで、それぞれ100万ドルの賞が与えられています。

ほとんどのコンピュータ科学者は、PがNPと同等ではないと確信しているが、厳密な証拠はまだ見つかっていない。このような仮定の真偽は多くの経験的証拠に支えられているが、それを前提にして公理として受け入れられるのだろうか。それこそコンピュータの専門家がやっていることです。確かに、広く使われているいくつかの暗号システムの信頼性については疑問が残ります。
ハッキングできないと考えられていますが、誰もそれを証明することはできません。

実験数学
物理学と数学の交差点で、実験的な数学が生まれました。多数の例のコンピュータ処理による新しい数学の法則の発見です。このアプローチは、短い証明ほどの説得力がありませんが、長くて複雑な証明よりも説得力があり、場合によっては非常に受け入れられます。この概念は、過去に、ヒューリスティックスと数学の準経験的性質の強力な支持者であるジョージ・ポリヤとラカトスの両方によって支持されてきました。これは、2002年に発行されたStephen Wolfram（Stephen by Wolfram）の著書「NewKind of Science»（A the New Kind of Science）」に適用され、正当化されています。

大規模なコンピューティングは非常に説得力がありますが、それは証明の必要性を排除しますか？はいでもありいいえでもある。計算と証拠は、さまざまな種類の証拠を提供します。特に重要なケースでは、証明に誤りが含まれている可能性があり、コンピュータの計算は、残念ながら、想定されている結論を反証するような反例を見つける直前に停止されることがあるので、両方とも必要だと考えます。

議論された問題は非常に興味深いものですが、解決にはほど遠い。ゲーデルの証明に関する記事が発表されてから50年が経過しましたが、2006年の今でも、その不完全性がどれほど深刻なのか、それが原因で数学的方法を修正すべきかどうかはまだわかりません。おそらく50年以内に答えが見つかるでしょう。

追加の文献：

・Leibnizの章については、Men ofMathematicsを参照してください。ETベル。再発行します。タッチストーン、1986年。
・数学の準経験的見解のより完全な議論については、数学の哲学の新しい方向性を参照してください。ThomasTymoczkoによって編集されました。プリンストン大学出版局、1998年。
・ゲーデルの証明。改訂版。E.ネーゲル、JRニューマン、DRホフスタッター。ニューヨーク大学出版局、2002年。
・実験による数学：21世紀のもっともらしい推論。J.BorweinとD.Bailey。AK Peters、2004年。
・ゲーデルの哲学と彼の作品とライプニッツの作品との関係については、不完全性：カートゲーデルの証明と逆説を参照してください。レベッカゴールドスタイン。WWノートン2005。
・メタ数学！：オメガの探求。グレゴリィ・チェイチン。パンテオンブックス、2005年。
・数学者の経歴は、スコットランドのセントアンドリュース大学の数学統計学部のウェブサイトで入手できます。
・グレゴリィ・チェイチンのホームページ。

ロシアの義務教育は6歳から17歳までの11年間の一貫教育です．この年代の生徒が読む科学啓蒙雑誌も各種あり，いろいろ工夫されており面白く自分で深く学ぶこともできます．

 ●「科学の世界で」

月刊誌、ロシア版サイエンティフィックアメリカン。2003年から発行されています（それ以前は1983年から1993年に発行されました）。

●知識は力

1926年1月にティーンエイジャー向けの月刊ポピュラーサイエンス&アドベンチャーマガジンとして創刊し、困難な発展の道を歩んできました。戦後、「冒険」の要素を失くし、「働く若者に人気の科学雑誌」になりました。60年代の初めにかけて、人道的知識の割合が増加しました。
「科学と社会の架け橋」として、あらゆる年齢や専門分野の人々との交流を重視しています。

●量子っ子　クバンチク

2012年から発行されている、あらゆる年齢の好奇心旺盛な学童のための月刊イラストマガジン。数学、物理学、言語学、生物学、化学の面白い話や問題があります。

●量子　クバント

学童と学生のためのソビエトとロシアの人気のある科学、物理学と数学のジャーナル。1970年から発行されています。アカデミアンP.L. Kapitsaは、「KVANT」の創刊という提案をしました。アカデミアのIKKikoinがジャーナルの最初の編集長になり、アカデミックのA.N.Kolmogorovが最初の副編集長になりました。

高校生とその教師、および中学生を対象としています。
「Quant」セクションのタスクは、通常、6年生から学者まで、誰にとっても興味深いものです。

●トリニティオプションサイエンス

「TrV-Science」はロシアの人気科学新聞です。2008年4月1日から2週間ごとに発行されています。

●コマーサントサイエンス

出版社「Kommersant」の情報速報。Kommersant新聞と一緒に配布されます。2011年から（断続的に）公開されています。

●シュレーディンガーの猫

2014年10月から発行されている月刊「科学祭」。

●科学と生活

ロシアとソビエトのイラスト科学の月刊誌。1890年に創刊され、1934年に更新されました。

●サイエンスファーストハンド

科学の学際的なジャーナル。2004年以来、世界最大の科学センターの1つであるNovosibirskAcademgorodokで発行されています。ロシア語の印刷版は年に6回発行されます。Science First Hand （英語の電子版）は年に3回発行されます。

●ポピュラー機械

2002年から公開されています。1902年以来発行されているアメリカの人気科学雑誌PopularMechanicsのロシア版。

●可能性：化学。生物学。薬

学生と教師のための月刊教育雑誌。2005年から生産。

●可能性：数学。物理。コンピュータサイエンス

学生と教師のための月刊教育雑誌。シリーズ「数学。物理。情報」は2005年から発行されています。

●自然

ロシア科学アカデミーの月刊自然科学ジャーナル。1912年1月から公開されています。

●化学と生命

月刊科学誌。1965年に「Chemistry＆Life」という名前で創刊されました。1997年以来、「化学と生命-XXIセンチュリー」というタイトルで出版されています。

●科学技術の最新情報（販売終了）
雑誌「現代の大都市のハイテクライフスタイルについて、革新と科学的発見について」、アメリカの雑誌ポピュラーサイエンスのロシア版。2002年から2009年に終了。
●エコロジーとライフ
エコロジーアンドライフマガジン（販売終了）
月刊の科学教育誌。1996〜2012年に公開されました。

今年の数学月間（7月29日）は，稲葉寿氏（東大）の表題の講演をZOOMでお送りしました．covid19の感染拡大第３波に見舞われている今日，お読みいただくと役に立つと思います．gotoトラベルは，それぞれR<1を保っている複数の状態（都市）の相互作用により，R>1に変わる可能性を誘発する危険な政策です．

■これまでに人類はいろいろなパンデミックを経験してきました．1918年のインフルエンザ（スペイン風邪）は4000万人以上の死者，2015年のＨＩＶ感染者は3670万人，マラリアは年間3億～5億人の患者を生む．最近のSARS，エボラなどの新興感染症や，再興感染症などにより感染症撲滅という1980年代までの楽観論は消滅しました．人口増加，都市集中，環境破壊などによって，感染症流行リスクはますます増大しています. 現在COVID-19は予断をゆるさない状況です．

■感染症の数理モデルは，SIRモデルを基本とします．これは，ケルマックとマッケンドリックが提唱(1927)したものです．全人口をS（感染感受性のある集団），I（感染者集団）,　R（免疫のできた回復者）の３つのグループに分け，それらのグループ間の相互作用（遷移）を数式で記述し数理モデルができます．
数理モデルは，感染拡大の様子を予測でき，種々の介入（ワクチン接種，隔離，接触制限，ロックダウンなど）を行うことで，感染性人口を絶滅させる（感染源にならないようにする）対策の策定に必要です．

COVID-19では，もう少し進化させた，SEIR数理モデルが必要です．これは，E（潜伏期間にある感染者集団）が加わったモデルです．特にCOVID-19は，Eグループのものが感染源になることや，免疫のできた回復者の免疫が消えることなどがわかり始めており，一筋縄では行かないモデリングになります．

■基本再生産数R0（R-naught)
感染感受性のある集団に居る一人の感染者が，その全感染期間に再生産する（感染させる）2次感染者の数を基本再生産数R0と定義します．全員感受性のある集団で，1次感染者数，2次感染者数，3次感染者数，･･･と等比級数で増加するときの公比がR0です．
R0は患者数と感染感受性のある人（未感染者）との接触回数に比例するので，環境状況でこの数値は変化します．感染が広がると未感染者が減り，実際の集団には免疫のある人も混ざった状態になるので，全員感受性がある集団で定義したR0よりも小さいR（実効再生産数）が期待できますが，適切でない介入があれば，逆にRの増加もあり得ます．
結局，R>1であればその集団の感染者人口の成長率は正になり，流行は拡大していくが，R<1であればその集団の感染者人口の成長率は負であって流行は自然に消滅する．何らかの介入をして，すみやかに，R<1とすることが対策になります．

■多状態のSEIRモデル
集団に2つの状態（例えば，学童と社会；病院と社会；東京と地方；大学と社会；等々）がある場合は，それぞれにSEIRモデルを作り，さらに２つの状態間の相互作用を考える複雑なモデル（コンパートメント・モデルという）になります．２つの状態にはそれぞれの実効再生産数Rがあります．
現実に近い多状態SEIRモデルを作り，その次世代行列の最大固有値として，Rを計算します．そして，どのような介入（例えば，ワクチン接種，ロックダウン，外出制限，休校）をすれば，Rが下げられるかを検討します．
集団の２つの状態のRが1未満であるため，感染が制御されているように見え，通常の生活に戻り始めるかもしれません．
イギリスでも約200万人の大学生が全国から復帰し，フレッシャーズフルー［注）フレッシャーズフルーとは，大学で最初の数週間に新入生が発症した一連の病気に付けられたイギリス英語］のようなCOVID-19感染拡大が懸念されるそうです．若者が無症候で感染を広げる最悪モデルでは，学年末までに96％感染と予測されました．学生集団は軽症ですが，体力の弱いスタッフや周囲のコミュニティと相互作用をするコンパートメントモデルでシミュレーションし，いろいろな介入施策の検討がなされています．
［注）Isaac Newton Instituteによって実施された「感染症のパンデミックのダイナミクスを理解する上での数学的および統計的課題」（IDP）　https://www.newton.ac.uk/event/idp］

日本でも，東京と他都市のRが，それぞれ１をわずかに下回っている状況ですが安心はできません．東京と他都市の相互作用により全体が増加し１を超えるRになる可能性はあります．

■免疫は持続するか
もし，回復したものの再感染を許容するモデルにするならば，新規感染率に対する，回復者再感染率の比をσとし，σR0＜１なら収束に向かいます．
従来の感染症の常識では，免疫を得ると再感染はしないということを前提にしていますが，COVID-19に関しては，再感染をしないような免疫が獲得できないかもしれません．免疫抗体が数か月で減衰するという報告が中国やスペインからなされている状況です．もし，免疫が獲得できないのであればワクチン自体が成立しないことにもなります．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
次回の数学月間企画講演（第3回）のお知らせ
「3Dジグソーパズルのデザインと数学」
手嶋吉法（千葉工業大学）
12月26日（土），15:00～17:00，参加無料です．
ZOOMにてリモートで実施します．多くの皆様の参加をお待ちします．
ホームページhttp://sgk2005.saloon.jp/　で申し込みができ，
参加登録されると，実施日の1週間前までにZOOMのURLをお知らせします．
主催：NPO法人数学月間の会

■大発明たる所以
色々な分野でフーリエ解析（フーリエ変換）が使われます．現在の科学におけるフーリエ変換の貢献は偉大です．フーリエ変換なしでは何も考えられません．例えば，時間とともに変化する信号$$f(t)$$は，いろいろな周波数$$ω$$のサイン波の信号の振幅が時々刻々変化するものを重畳$$\displaystyle \sum_{}^{}a_{n\omega }(t)\textrm{sin(}n\omega t)$$して表現できます．線形システムというのは，時間の関数の入力$$f(t)$$があれば$$A･f(t)$$が出力され，入力に，$$f(t)$$と$$g(t)$$があれば，$$A･(f(t)+g(t))$$が出力され，いわゆる重ね合わせが成立します．入力信号も出力信号も，重畳成分のいろいろな周波数のサイン波に分解できるというのがフーリエ変換です．分解された個々周波数のサイン波ごとに，ある周波数帯域を除去するフィルタを通すなどして，それらの出力を再び重畳する信号処理が可能です．

赤外吸収IRスペクトルの測定を例にとりましょう．これは，サンプルを透過する光はどのような波長で吸収されるかの測定です．光の波長を順次スキャンし分光しながら測定する方法は普通ですが，FTIRという方法では，分光せず白色光をマイケルソンの干渉計でインターフェログラムにし，これに対するサンプルの吸収を測定して得たデータをフーリエ変換をすれば，波長スキャンのときと同様に吸収スペクトル測定ができます．

結晶学では，結晶空間と逆空間という互いに双対な空間を扱いますが，この両空間は互いにフーリエ変換で変換し合う空間です．イメージが把握できるように，双対という概念に簡単に説明しましょう．例えば，正6面体と正8面体は互いに双対な立体です．この両立体は，面を頂点に，頂点を面に取り換えると互いに移り変われる立体です．置き換える面と頂点の関係とは，結晶格子の基本ベクトルと逆格子の基本ベクトルの関係と言い換えることができます．

■さて，フーリエ級数（展開）とフーリエ変換は，同じ性質のものなのですが，細かいことをいうと違いもあります．

フーリエ級数展開は：
周期的などのような波形も、単純な波形（サイン波）の重ね合わせとして表すことができます。
フーリエ変換では：
周期的でない波形を扱えます．ここで用いる単純な波形（サイン波）の周波数は，フーリエ級数のときのように離散的な倍音のみではなく，周波数のステップが細かくなり，級数は積分になります．

■ジョセフ・フーリエは，熱が固体中をどのように移動するか（熱伝導現象 ）を数学的に研究しました．この研究のために，新しい数学的方法を開発しました．これがフーリエ解析の始まりです．

彼が熱伝導に興味を持ったきっかけが，いつのことだか定かではありません．北アフリカにいたときに生じたと推定しているのは，以下のエッセイです．

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
1798 年, フーリエはナポレオン のエジプト遠征に科学顧問として, モンジ ュやマリ ュ スとともに同行し， エジプトでは考古学上の調査や， カイロ学士院の創設に力を注ぎ，カイロ学士院の書記官にも選出されました． ナポレオンは 1799 年にパリに帰還しますが，フーリエはその後 2 年間エジプトに残りました.　1801 年, フーリエはフランスに帰還し, 再び諸工芸学校の解析学の教授になりますが，翌年 2 月にナポレオンはフーリエをイゼール 県の知事に任命しました．以下のエッセイによると，熱伝導研究の開始は 1802 年頃らしいとされています．

タイトル未設定www.kurims.kyoto-u.ac.jp
1807，1811年 に論文で，連続物体の温度分布の問題を解いており，フーリエ展開公式を導いています．

彼の研究結果は1822年に、熱の解析理論（Theorie analytique de la chaleur)に掲載され、そこでは、複雑な物理問題をより単純なものに分解して解析する方法が示されました。

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
フーリエは，複雑な波形を単純な波形の重ね合わせとして表せることを示しました．一般に，古典的な系を説明する方程式は，これらの単純な波のそれぞれについては簡単に解けます．フーリエは，これらの単純な波形を重ね合わせて，複雑な問題全体の解を得る方法を示しました．数学的に言えば，フーリエ級数は，周期的な任意の関数を単純なsin波の種々な高調波（倍音）の重ね合わせとして表す方法で，フーリエ解析は調和解析とも呼ばれます．（下図参照）

周期的でない任意の波形の場合は，整数倍音の高調波の重ね合わせではなく，連続的に変化する高調波の積分で表現するフーリエ変換の概念に拡張できます．

フーリエ解析の登場フーリエ解析の登場energychord.com

■20世紀半ばにコンピューターが登場するまで，自然の複雑さに立ち向かう武器は，フーリエ解析でした．フーリエ解析の出現以来，科学者はニュートン力学の法則や他の基本的な方程式を直接適用して解ける単純な問題だけではなく，複雑な問題にもそれを使用して解くことができました．19世紀のニュートン科学の偉大な成果の多くは，実際には，フーリエによって最初に提案された方法を使用しなければ不可能でした．その後，これらの方法は，天文学から機械工学まで，さまざまな分野の問題を解決するために使用されました．現在は，画像処理などでコンピュータを用いた高速離散フーリエ解析が行われています．

■ジャン・バプティスト・ジョセフ・フーリエ（1768-1830）
フランスの数学者．オセールに生まれ，9歳で孤児となる．若くして数学の才能を発揮した．フーリエは教会学校や軍人学校で教育を受けた後，フランス革命にあう．彼は数学教師として働いたが，生涯を通じて政治の世界で活躍した．1794年にはテロの被害者を保護して逮捕されたが，ロベスピエールの死後，獄中から釈放され，パリの有名なエコール・ポリテクニークの創設に参加し，その地位はナポレオン政権下での昇進の橋頭堡となった．ナポレオンに同行してエジプトに行き，下エジプト総督に任命された．1801年にフランスに帰国すると，州知事に任命された．1822年にはフランス科学アカデミーの常任書記官に就任し，フランスの科学界で影響力のある地位に就いた．熱伝導の論文は1807，1811年．フーリエ解析の本の出版は1822年．

Q．正4面体を，平面を切り口に，合同な２つの図形に分割すること．

この問題を考えるのに，まず，正四面体の対称性から説明を始めましょう．図を見てください．正4面体の回転対称軸を調べると，3回回転対称軸が，各頂点にあります．2回回転対称軸は直角に対向している稜の中点を通ります．正4面体の場合は対称心もあるので，2回回転対称軸は，4回回反軸の性質もありますが，今，この問題で必要なのは2回回転対称軸の性質で十分です．鏡映対称面もありますが，この問題では関係ないので略します．

正4面体を，平面で切って，2つの合同な部分に2分割するのですが，対称性を考慮すると，2回回転軸を含む平面で2分割すると，合同な２つの部分に分割できることが理解できるでしょう．例えば，以下の2つの解答例を思いつきます．ついでに，Q．それぞれの例の場合に，その切り口の形はどのような図形でしょうか？という問題も追加します．

解答例１（指で挟んでいるのが，2回軸の正4面体への入口と出口）

解答例２（指で挟んでいるのが，2回軸の正4面体への入口と出口）

■さて私が言いたいのは，「解答例はそれだけでしょうか？」ということです．

実はそのような解は無数にあります．一つの直線を含む平面は無数にありますから，どれも解になります．下図（正4面体の1つの2回回転軸の真上から眺めた図）をご覧ください．黒い線が表現する平面は解答例１，赤い線が表現する平面は解答例２の場合です．2回回転軸を含む平面は無数に作れるので，例えば緑の線も解答例になります．

私がこの問題を作ったのは，対称性の概念は，物事を見通し良く整理して理解するのに役立つことを示したかったからです．

■Fourier変換
フーリエ解析のときに触れた事柄をまとめておきます：

$$F(\nu )=\displaystyle \int_{- \infty }^{+ \infty }f(t)e^{-2\pi i\nu t}dt$$
$$f(t)=\displaystyle \int_{- \infty }^{+ \infty }F(\nu )e^{2\pi i\nu t}d\nu $$

関数$$f(t)$$のフーリエ変換を$$F(ν)$$といい，$$F(ν)$$から$$f(t)$$に戻る変換をフーリエ逆変換といいます．

変数$$t，ν$$は実数です．積$$ν･t$$は無次元なので，変数$$t$$の空間と，変数$$ν$$の空間は，互いに双対な空間になります．フーリエ変換は，互いに双対な空間同士を結びつける線形写像です．フーリエ変換を用いると，同じ現象を，異なる世界（空間）で見ることができ，現象の理解に威力を発揮します．

適用例
事例１．$$t$$を時間とすると，$$ν$$は周波数ですから，フーリエ変換は，時間空間から，周波数空間への線形写像になります．
事例２．もし，$$t$$を実空間とすると，$$ν$$は逆空間になります．

■ラプラス変換

ラプラス変換はフーリエ変換とよく似ています．歴史的にはフーリエ変換より先だったのですが，フーリエ変換の紹介を先にしてしまいました． 

$$ {\displaystyle F(s)=\int _{0}^{\infty }f(t)\mathrm {e} ^{-st}\mathrm {d} t} $$

$$ {\displaystyle f(t)=\lim _{p\to \infty }{\frac {1}{2\pi i } }\int _{c-ip}^{c+ip}F(s)\mathrm {e} ^{st}\,\mathrm {d} s} $$

（第一の式）$$F(s)$$を$$f(t)$$のラプラス変換といいます．関数$$f(t)$$は実数 $$t ≥ 0$$ について定義されており，積分範囲は$$0≦t<+∞$$になっています．ここで， $$s$$ は複素数（2 つの実数 $$σ, ω$$ を用いて $$s = σ + iω$$ と書ける）．もし,$$s$$を純虚数$$s=iω$$とすれば，フーリエ変換になります．
（第二の式）$$c > 0$$ として，関数 $$F(s)$$ から元の関数 $$f (t)$$ を計算することを逆ラプラス変換といいます．複素平面$$s$$での積分をするので難しそうですが，複素関数論の定理が役に立ちます．複素平面内の積分経路を閉曲線となるように広げ，内部にある特異点の留数の総和を求めれば計算できます．

ラプラス変換は，$$0≦t<+∞の$$実数の空間から複素平面$$s$$への線形写像です．
なぜ，このような面倒な変換が必要なのでしょうか．それは，微分方程式を解くのに有用です．ラプラスは，1812年の著書で，微分方程式の解法に使っています．

ラプラス変換，逆変換を，次のように簡略表記することがあります．
$$ {\displaystyle F(s)={\mathcal {L } }[f(t)]} $$
$$ {\displaystyle f(t)={\mathcal {L } }^{-1}[F(s)]} $$

■ラプラス（1749-1827），フーリエ（1768-1830），ヘビサイド（1850-1925）
フーリエはラプラスより20歳若いのですが，どちらもナポレオンに仕えて，大臣や知事を任命され政治の場でも活躍したところが似ています．
ラプラス変換は，後の演算子法（ヘビサイド）や複素関数論とのつながりがありますので，ここでまとめて紹介しましょう．

ヘビサイド（英国人）は，ラプラスよりも100年後の時代の電気技師ですが，微分方程式の解法に演算子法という素晴らしく便利な方法を開発（1880-1887）しました．これは，微分方程式を代数のように簡単に解く手法です．しかし，その解法の導出過程は数学的厳密さを欠いていたため，当時の数学者から非難されました．ヘビサイドは，「数学は実験的科学であり，定義が先にくるわけではない」，「私は消化のプロセスを知らないからといって食事をしないわけではない」と言ったそうです（wikiより引用）．

その後，ヘビサイドの演算子法は，ラプラス変換により理論づけがなされました．今日，私たちが，微分方程式を解くのに，ラプラス変換をして，周波数空間に移り，そこで簡単な代数計算をして，それをラプラス逆変換して，私たちの世界の時間の関数の解を得るという手順を使います．

ヘビサイドはユニークな天才です．1884年に，当時は20の式から構成されていたマクスウェル方程式を，今日知られる4つのベクトル形式の式に直したというのもとても興味深い逸話です．

■コーシーの積分定理

閉曲線$$C$$および，その内部で$$f(z)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$

■ローラン展開と留数

関数$$G(s)$$に，極（分母が0となる特異点）がある場合，例えば，１つの極$$s_1$$の周りで，次のようにローラン展開ができます．$$s_1$$が$$n$$次の極とすると，
$$G(s)=\displaystyle \frac{a_{-n } }{\left( s-s_{1} \right) ^{n } }+\displaystyle \frac{a_{-\left( n-1 \right) } }{\left( s-s_{1} \right) ^{n-1 } }+ \cdots +\displaystyle \frac{a_{-2 } }{\left( s-s_{1} \right) ^{2 } }+\displaystyle \frac{a_{-1 } }{\left( s-s_{1} \right) }+a_{0}+a_{1}\left( s-s_{1} \right) + \cdots $$
この展開中の係数$$a_{-1}$$を留数と言います．

実は，$$G(s)$$を複素関数と見たとき，極$$s=s_1$$で，$$G(s)$$は正則ではありません．$$s=s_1$$を内部に含むような閉曲線$$C$$に沿って左回りに1周$$G(s)$$を積分すると
$$\displaystyle \int_{C}^{}G(s)ds=2\pi ia_{-1}$$  となります．これを留数の定理といいます．

さてこれらの証明は，難しくはありません．興味おありでしたら，親切な解説をしているyoutube動画がありますので，そちらをご覧ください．

関数をローラン展開すると，いろいろな次数の項がでて来ますが，閉曲線に沿って1周積分すると，なぜ-1次の項の係数（留数）だけが残るのか不思議ですね．youtube動画で証明を確認ください．たいへん都合の良い便利な性質です．

■いろいろな場面で，いろいろな積分をするのに，留数定理を使います．「道具としての数学」の代表でしょう．複素関数論は活躍しています．

話は変わりますが，ちょっと似た手法で，ラプラス逆変換をするときに，部分分数に展開します．以下の例題をご覧下さい．

複素関数$$G(s), s=x+iy$$を，ラプラス逆変換するときに，$$G(s)$$を部分分数に展開することが必要になります．

コーシー (1789-1857)、リーマン (1826-1866)

これも19世紀の数学で重要な発見の一つです．「数学が社会（科学技術も含まれる）とどのように係わるかを知る」のが私たちの目的で，数学の勉強会とは別物です．そのような視点で見ても，複素関数論は19世紀に確立した重要な数学分野で，広い応用をもちます．そこで，この数学概念の意義を理解できることを目指します．

私たちの使う関数論は19世紀の数学で確立しました．先に，Fourierフーリエ級数（変換）,Laplaceラプラス変換を取り上げましたが，もう少しだけ複素関数に言及する必要があります．今回は，コーシー-リーマンの方程式を取り上げます．

複素平面（$$x$$軸が実数，$$y$$軸が虚数）に定義域$$D$$をもつ複素関数$$f(z)$$を考えましょう．この関数は領域$$D$$で正則（微分可能）であるとします．微分可能な関数ですから，この領域$$D$$で連続であることはいうまでもありません．

ある点$$z∈D$$での微分は，$$ｘ$$軸に沿って（$$x$$で偏微分）行う微分係数と，$$y$$軸に沿って（$$y$$で偏微分）行う微分係数がありますが，複素関数$$f(z)$$が正則であるとすると，どちらの微分係数も一致し，点$$z$$での微分係数は確定しなければなりません．
関数$$f(z)$$が$$D$$で正則とは，定義域$$D$$のすべての点$$z∈D$$で微分係数が確定する（微分可能）ことです．

関数$$f(z)$$に領域$$D$$での正則性を要請します．定義域内のすべての$$z=x+iy$$に対して，

$$\displaystyle \frac{df(z)}{dz}=\displaystyle \frac{ \partial u}{ \partial x}+i\displaystyle \frac{ \partial v}{ \partial x}=\displaystyle \frac{ \partial u}{ \partial (iy)}+i\displaystyle \frac{ \partial v}{ \partial (iy)}$$が成立します．$$x$$で偏微分しても，$$iy$$で偏微分しても等しい．
実部と虚部をそれぞれ等しいとおいて，
$$\displaystyle \frac{ \partial u}{ \partial x}=\displaystyle \frac{ \partial v}{ \partial y},　 \displaystyle \frac{ \partial v}{ \partial x}=-\displaystyle \frac{ \partial u}{ \partial y}$$が得られます．これをコーシー-リーマンの方程式（条件）と言います．

逆に，コーシー-リーマンの方程式が成立するなら，複素関数f(z)は正則であることが証明できます．
従って，複素関数が正則であるための必要十分条件は，コーシー-リーマンの方程式が成立することです．

■閉曲線$$C$$とその内部で，$$f(x)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$　←コーシーの積分定理

（コーシーの積分定理の証明）
$$\displaystyle \int_{C}^{}f(z)dz=\displaystyle \int_{C}^{}\left[ u(x,y)+iv(x,y) \right] \left( dx+idy \right) =\displaystyle \int_{C}^{}\left( udx-vdy \right) +i\displaystyle \int_{C}^{}\left( udy+vdx \right) =$$

$$ =\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial v}{ \partial x}+\displaystyle \frac{ \partial u}{ \partial y} \right) dxdy+i\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial u}{ \partial x}-\displaystyle \frac{ \partial v}{ \partial y} \right) dxdy=0 $$

（参考）
$$\displaystyle \int_{C}^{}\displaystyle \frac{f(z)}{z-z_{0 } }dz=f(z_{0})\displaystyle \int_{\mit\Gamma }^{}\displaystyle \frac{dz}{z-z_{0 } }=2\pi if(z_{0})$$

■正則な複素関数$$f(x,y)＝u(x,y)+iv(x,y)$$はその実数部$$u(x,y)$$あるいは虚数部$$v(x,y)$$のどちらか一方を知れば他方は決まってしまう．

例えば，虚数部$$v(x,y)$$を知り，コーシー-リーマンの方程式を使うと，実数部$$u(x,y)$$を求めることができる．

例えば，以下のyoutube動画には，このような問題の演習があります．

■応用について

実数部を知って虚数部を求める例として，私のやった実験の話をします．

複素屈折率を　$$ \tilde{n}(\omega )=n(\omega )+iK(\omega ) $$と書きます．$$ω$$は光の周波数で実数．複素屈折率$$ \tilde{n}(\omega ) $$は，複素数値をとり，実数部$$n(ω)$$と虚数部$$K(ω)$$があります．
実数部の$$n(ω)$$は反射率に，虚数部の$$K(ω)$$は吸収率に関係があります．

反射率を測定し$$n(ω)$$を知り，$$K(ω)$$を計算し吸収率を求めます．このとき，実数部$$n(ω)$$と虚数部$$K(ω)$$を結ぶのは，クラマース-クローニッヒ変換です．$$ω$$は複素数ではないので，コーシー-リーマンの方程式にははなりませんが，$$ \displaystyle \frac{\tilde{n}(\omega )}{z-\omega } $$は実軸より上側で正則（$$ω$$は極）なので，コーシーの積分定理を使うと，クラマース-クローニッヒ変換を導くことができます．

$$0=\displaystyle \int_{}^{}\displaystyle \frac{n(z)}{z-\omega }dz+i\displaystyle \int_{}^{}\displaystyle \frac{K(z)}{z-\omega }dz=P\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{z-\omega }dz-i\pi n(\omega )+iP\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(z)}{z-\omega }dz+\pi K(\omega )$$
$$\left\{ \begin{array}{@{\,} c @{\, } }
-\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{Z-\omega }=K(\omega ) \\[0mm]
\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(\omega )}{z-\omega }=n(\omega )
\end{array} \right. $$

 
セルゲイ・ネテソフ, "SCIENCEFIRSTHAND" №3（88）,2020
ノボシビルスク州立大学自然科学部，バイオナノテクノロジー，微生物学およびウイルス学研究所長

前半の章（以下の３つ）は略
■先駆病原体SARS-COV-2，■コウモリから人間へ，■人への道，

■エピデミックを止める方法
病原体の最も重要な特徴は、感染の基本再生産数（R0）で、まだ感染していない集団で，1人の患者から感染する平均人数のことです。通常のインフルエンザウイルスのR0は0 1.4まで、そして新しいコロナウイルスで、おそらく3から5までです。この指標は徐々に変わりますが、感染拡大は国によって定義がわずかに異なるためです。

ドイツ連邦共和国は、第１波の流行克服では最も成功した国の1つです。2020年5月には、ドイツの研究によると，患者の隔離も、マスクなしの社会的距離も、学校の閉鎖も、R0減衰に効果がありませんで。最大の効果は、大規模なイベントの禁止、過酷な導入、罰金、マスク体制、および集中的なコミュニケーションが行われている組織の閉鎖から得られました。これらの措置の結果、実効再生産数は1を下回り、流行は収まり始めました。

ドイツでの抗流行対策の早期導入と広範なテストは、ウイルスの実効再生産数を迅速に低下させ、多くの死亡を防ぐのに役立ちました。
（National Geographic、2020年5月1日）

同様の状況がオーストリア、ノルウェー、イタリアおよび他のヨーロッパ諸国で観察されました。そこでも、学校の閉鎖は効果がないことが判明し（学童は教育機関の外で積極的にコミュニケーションをとっています）、流行を止めるための有効な介入は、マスク着用、集団行動停止、社会的距離を置く、患者の隔離でした。同時に、そのような措置がすぐに導入されず、完全ではなかったスウェーデンでは、主に高齢者の死亡率はヨーロッパで最も高いものの1つでした。そして、イラン、イラク、サウジアラビアでは、検疫措置が弱まった後、病的状態の第二の波が始まりました。

バルセロナ（スペイン）の診療所にいるCOVID-19の患者。
写真：フランシスコアビアホスピタルクリニックデバルセロナ

抗流行対策の有効性の最も顕著な例は、サンフランシスコとニューヨークという2つの最大のアメリカの都市の行政の行動で見られました。サンフランシスコ政府（カリフォルニア州知事および市長）は3月16日、州が自己隔離、マスクの着用、事業活動のほぼ完全な停止などの厳しい検疫措置を課していると発表しました。ニューヨークでは、同じことがわずか6日後に行われました。その結果、米国で最大の都市で2か月以内に約2万人が死亡しましたが、2番目に人口密度が高く13番目に人口の多いサンフランシスコでは35人しか死亡していません。これは、抗ウイルス予防策の採用が少し遅れただけでも、その結果がどれほど広範囲に及ぶ可能性があるかを明確に示しています。

ニューヨーク市では、コロナウイルスと診断された死亡患者の77％が糖尿病、肺疾患、高血圧や喘息などの心血管疾患も患っており、死亡者の1.5％のみが比較的健康でした。参考までに、米国では約66％の人が太りすぎまたは非常に肥満であり、コロナウイルス感染による死亡のリスクが高くなっています。また、ニューヨーク市の成人人口の約半数が高血圧です。

■Covidかどうか？
コロナウイルスはRNA含有ウイルスに属し、リボ核酸自体に加えて、脂質とウイルス特異的タンパク質も含み、さまざまな方法で診断できます。第一に、患者の鼻咽頭からのサンプル中のウイルス自体の成分の存在による：RNA（逆転写PCR、RT-PCR）およびウイルス抗原-表面Sタンパク質（免疫学的測定法）。

SARS-CoV-2ウイルス粒子では、スパイクSタンパク質がはっきりと見え、そこからウイルスの名前が付けられました。透過電子顕微鏡法。画像：NIAID

別の方法は、体の免疫の構成要素、例えば、特定の抗体ができているかを評価することです。これを行うには、症状の発症と同時に現れる、患者の血液サンプル中のIgMクラスの「一次」抗体の含有量が測定されます。過去に疾患に罹ったかは、「二次」IgG抗体の存在によって識別できます。これらのテストは、酵素免疫測定法を使用して実行されます。

2020年8月20日の時点で、157の異なる検査システムがロシアで登録されました。126はコロナウイルスに対する抗体を検出し、31はウイルスRNAです。しかし、なぜ、そのような多数のシステムで、診断の信頼性を論じるのでしょうか？

第一に、ウイルスRNAの試験システムを使用する場合、鼻咽頭から材料を正しく採取することが非常に重要です。さらに、ウイルスRNAの分離と保存のために、特別なサンプラーを必要とする特別な液体にすばやく入れる必要があります。第二に、今日、テストが実行される多くの研究所がありますが、テスト手順のすべての段階で正しく実行されるわけではありません。

患者の鼻咽頭からCOVID-19テスト用の生物学的材料を採取します。写真：フランシスコアビアホスピタルクリニックデバルセロナ

第三に、上気道からRNAを検出する可能性は、鼻咽頭からのウイルスの「逃避」のために、病気の後期に減少します。最後に、RT-PCRテストでは、患者が回復した後でも、長期間にわたって陽性の結果が得られることがよくあります。その理由は次のとおりと考えられます。体は生きているウイルスではなく、ウイルスRNAの断片を循環し続けます。

ウイルス抗原の信頼性の高いテストシステムが開発され、最近医療現場に導入されましたが、状況によってはウイルスRNAの結果が陰性または不明確な場合に正確な診断を行うことができるため、患者の正確な診断に有用であることがすでに示されています。

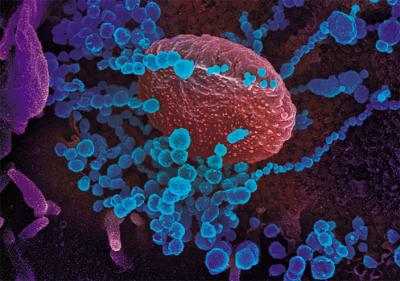
実験室培養におけるSARS-CoV-2ウイルス粒子（青い物体）。この株は、米国の患者から分離されています。走査型電子顕微鏡写真：NIAID

IgG抗体の検査システムに関しては、ARVIを引き起こす一般的なコロナウイルスに感染していて、検査システム自体が十分に特異的でなかった場合、検査システムの中には偽陽性を示すものもあります。その結果、私たちの人口のほとんどがSARS-CoV-2に対する抗体を持っているように見えるかもしれませんが、最も特異性の高い検査のデータから判断すると、この割合はまだ10〜12％を超えていません。

一方、IgG抗体を持っていなくても、ウイルスに対する免疫防御が欠如しているわけではありません。個々の保護を評価するための追加の検査は、免疫細胞が活性化され、サイトカイン誘導が検出される特異的Ｔ細胞免疫の有無の判定であります。しかし、このような診断や抗体解析の複雑さやコストは比類のないものであるため、限られた規模の科学研究でのみ使用されます。 

ほとんどの場合（症例の40〜90％）、COVID-19は無症候性または軽度であるが、中程度の重症度の疾患では、体温が上昇し、ODSの1つ以上の臨床徴候を示しています：乾いた咳、急速または困難な呼吸、味覚と嗅覚の喪失、血中酸素飽和度の低下。重いフォームが特徴です：38℃以上の体温、脱力感、食欲不振、下痢、筋肉痛、肺炎の記録された徴候。感染してから重篤な症状が現れるまでには、実際には約2週間かかります。（ニューイングランド医学ジャーナル2020年5月16日号）

問題は、今日のロシアでは、外国で行われているように、実際の患者からの対照サンプルとCOVID-19に感染していない人々からの陰性血清の広範なパネルを使用して実施された、すでに適用されている診断法の特異性と感度の比較分析のためのデータをパブリックドメインで持っていないことです。そして、そのようなデータは、特定の診断ツールの購入を決定する際に、ロシア保健省と地域の保健当局の両方で役立ちます。質が大切で安ければ良いというのもではないからです。

感染性物質による人間の感染の実験は、世界のほぼすべての国で犯罪です。したがって、ヒトに対するウイルスの感染量、すなわち、疾患を引き起こすために体内に侵入しなければならないウイルス粒子の数はまだ決定されていません。病人が単位時間あたりにどれだけの量のウイルスを環境に放出するか、テーブルやボタンなどの家庭用品の表面に接触しているときに指に付着するウイルスの粒子の数は不明です。しかし一方で、ウイルスが環境内でどれだけ迅速に、どのような条件下で不活性化されるかがわかりました。このための実験は、倫理基準に違反しませんので。

たとえば、デンマークの科学者は、感染者が多く、これらの人々が病気の最初の症状を感じる前でさえ、下水でコロナウイルスを特定しました。同時に、人をテストするときと実質的に同じテストが下水域のウイルスを検出するために使用されます。しかし、それらはサンプル中のウイルスRNAの存在を明らかにするだけであり、「生きている」ウイルス粒子ではないことを常に覚えておく必要があります。したがって、研究者は、細胞培養物中の生きたウイルスの実際の検出とPCR試験の結果を時々検証する必要があります。

以下続く･････

■治療薬は？，■ワクチン接種を受けるか？否か？，■氷山の隠れた部分

Сергей Нетесов，«Наука из первых рук» № 3(88), 2020　より

■治療薬はどうか？
残念ながら、2020年1月以降、治療用抗体を含む新薬の模索が続いていますが、COVID-19に対してウイルス特異的効果が証明された有効な薬剤はまだありません。

米国食品医薬品局（FDA）で事前承認を受けている製品は、RNAポリメラーゼのウイルス酵素阻害剤であるレムデシビルのみです。エボラの治療のために開発されたこともありましたが、その効果はあまり期待できませんでした。

SARS-CoV-2による肺炎患者の第1陣が、早くも2020年2月に中国で正式に服用を開始したが、その時点では効果が証明されていません。しかし、後にアメリカで行われた2つの臨床試験では、重症期間が15日から11日に短縮され、致死率が20～25％低下するという結果が出ています。しかし、他の2つの臨床試験では、これらの結果は確認されていません。レムデシビルは現在、米国ではCOVID-19治療薬として承認されていますが、ロシアでは登録されていません。

他の薬の有効性も研究されています。インターロイキン-6（IL-6）阻害剤は、免疫反応や急性炎症反応を調整する低分子で、患者の免疫系が「制御不能」のときに、いわゆるサイトカインの嵐を防ぐのに役立ちます。そのような薬には、モノクローナル抗体に基づくトシリズマブが挙げられる。イタリアの医師によると、それは肺炎を予防することで病気の経過を改善し、病気の初期段階で有効です。

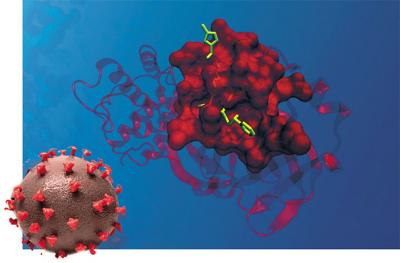
SARS-CoV-2ウイルスプロテアーゼの主酵素と潜在的阻害剤の組み合わせの分子モデル．X線構造解析による．
写真：ツヴィティリオ・クロメナーレ
左：SARS-CoV-2ウイルス粒子．芸術的な構成．写真：NIAID

英国の医師によると 、抗炎症作用と免疫抑制作用を持つ合成グルココルチコステロイドであり、古くから知られているはるかに安価な薬剤であるデキサメタゾンは、サイトカインの嵐を抑制し、重篤な疾患の死亡率を低下させることができます。英国では、この薬は非常にうまく機能しましたが、COVID-19の軽度の症例では、その使用は禁じられています。

抗マラリア薬ヒドロキシクロロキンと抗生物質アジスロマイシンの組み合わせも、ウイルスによる肺炎の治療にテストされました。前者は肺の炎症反応を抑え、後者は付着細菌感染を予防すると考えられていました。しかし、この組み合わせの第一成分の効果のなさを指摘する多くの出版物があり，テストに終止符が打たれました。さらに、ヒドロキシクロロキンとアジスロマイシンは、それ自体で心血管合併症による死亡のリスクを高める可能性があり、このような問題を抱える人々は特にコロナウイルスに対して脆弱です。

免疫不全状態の重症インフルエンザの治療薬として、2015年に日本でアビガンという名前で登録されたファビピラビルをベースにした薬剤に大きな期待が寄せられました（催奇形性効果のため、妊婦には使用できません）。この物質は、レムデシビルのようなRNAポリメラーゼの阻害剤であり、ヒトウイルスではなくRNA含有ウイルス酵素のみに作用する。2020年2月に中国でCOVID-19患者を対象とした臨床試験が開始され、3月に薬効が発表されましたが、その後の説明はありませんでした。

ファビピラビル/アビガンのライセンスは2019年に失効しており、2020年夏にはロシアのメーカー3社からコロナウイルス感染症治療薬として位置づけられている「コロナビル」「アビファビル」「アレプリビル」の3つのファビピラビル系薬剤が国内向けに発売されています。9月には、これらの処方薬がロシアの最低生活レベルに匹敵する価格で小売販売されました。

その有効性については、最近日本でコロナウイルス患者を対象としたファビピラビルの臨床試験の第3フェーズが完了し、平均的な重症度で、摂取により病気の期間が14.7日から11.9日に短縮されることが示されました。これらのデータは、ロシアのパイロット研究の結果と一致しています。中程度および軽度の疾患では、ファビピラビルは「臨床的回復期間を約3.5日短縮し」、鼻腔からのウイルス排除を加速し1～3日短縮することができます。全治療には、体重に応じて40錠1.5～2パックが必要です。

赤外線非接触温度計を使用して人々の健康状態をチェックします。インド。写真：グウィディオンM.ウィリアムズ

■ワクチン接種を受けるや否や？
2020年8月末現在、世界で約160の候補ワクチンが開発されており、そのうち約50は臨床試験のさまざまな段階にあり、そのうち9つはフェーズ３にあります。この段階では、通常、多施設で慎重に管理された研究で、安全性を判断し、実際の流行における薬剤の予防効果を評価するために、大規模な患者グループ（少なくとも1〜3千人）の参加を得て実施されます。

同時に、ロシアと中国の2つのワクチンは、フェーズ３の臨床試験が終了するまで、国レベルでの限定的な使用が許可されました。これは前例のないケースです。

まず、これは、コロナウイルススパイクタンパク質の遺伝子が挿入されたゲノムに第5血清型のアデノウイルスをベースにした中国企業CanSinoBiologicsのワクチンです。フェーズ３の臨床試験は、サウジアラビアの保健省と協議して、サウジアラビアの何万人ものボランティアを対象に8月に開始されました。しかし、早くも2020年6月25日、中国国防省は、一部の軍隊の医師にワクチン接種のために、このワクチンを1年間使用することを正式に承認しました。これが任意接種なのか強制接種なのかは不明です。今日、このワクチンが、アデノウイルスワクチンの中で最も「先進的」なワクチンです。

2つ目の「冬ツバメ」は、M.V.ロマノソフ記念・モスクワ疫学・微生物学研究センターとモスクワ疫学・微生物学研究センターが共同開発した2成分ワクチン「スプートニクV」です。このワクチンは、モスクワの疫学・微生物学研究センター（Gamaleya Research Center for Epidemiology and Microbiology）とロシア国防省の48中央研究所が共同で開発しました。また、コロナウイルス蛋白質遺伝子Ｓを組み込んだアデノウイルス（第５、２６回ヒト血清型）をベースにするこのような方法論に基づいて、この研究センターでは、これまでに我が国のエキゾチックエボラおよび中東呼吸器症候群に対するワクチン候補が開発され、フェーズ1およびフェーズ2の臨床試験に合格しています。

このような組換えワクチンはすべて、比較的無害なウイルスをベースにしており、これらのウイルスは、人体内での繁殖能力を弱める（減衰させる）か、あるいは奪うかのいずれかです。実際、このようなウイルスは、ＤＮＡやＲＮＡワクチンの場合のように、病原体の遺伝物質を細胞に送達し、特異的な免疫応答を誘発するためのベクターとなります。このようなウイルスが細胞に入ると、そのDNAが放出されて細胞核に入り、そこでメッセンジャーRNAが合成され、コロナウイルスの表面Sタンパク質を含むウイルスタンパク質が組み立てられます。これらのタンパク質が細胞膜に組み込まれると、細胞は免疫原性になります。つまり、体内で特定の免疫を形成することができます。

スプートニク Vワクチンの特定のアデノウイルスベースに関しては、これらのウイルスが人体での増殖能力をどのように失ったかについての情報はありません。

「スプートニクV」の正式登録は、2020年8月11日に発表されました。これは、臨床試験のフェーズIIIの開始とフェーズ１〜２の結果の公開のほぼ1か月前です。その後、この登録は条件付きで、2021年1月1日まで有効であることが発表され、最終的な登録は、最大4万人が参加することになっているテストの完了後に行われます。

マスクの少女（「サイエンス・ファースト・ハンド」第3号（88）、2020年）写真：ニックアンダーソン

2020年の夏に、コロナウイルススパイクタンパク質をコードするメッセンジャーRNAに基づくさらに2つのワクチンがフェーズ３の臨床試験用にリリースされました。1つは米国の革新的なバイオテクノロジー企業であるModerna社が、もう1つはドイツのBionTech社、米国のPfizer社、中国のFOSUN Pharma社が共同で開発しているワクチン、そして中国で国有製薬企業の参加を得て開発された不活化ウイルスSARS-CoV-2をベースにした3種類のワクチンです。

これとは別に、Sタンパク質遺伝子が挿入された組換えワクチンも注目に値します。これもアデノウイルスに基づいて作成されていますが、ヒトではなくチンパンジーに基づいています。オックスフォード大学（英国）で、英スウェーデンの製薬大手AstraZenecaと共同で開発されました。ステージ３の臨床試験は、8月初旬にブラジル、米国、南アフリカで開始されました。これらのテストのいくつかはロシアで実施される予定との情報があります。

なぜ開発者の中には、組み換えワクチンの基礎としてサルアデノウイルスや希少なヒトアデノウイルスの血清型を選ぶ人がいるのでしょうか？実は、最近の研究によると、かなりの割合の人がすでに共通の血清型5に対する抗体を持っている可能性があるということです。例えば、このような抗体は、がん研究プロジェクトの一環として中国で調査された人の67％、中国の青海省の子供の75％以上、米軍の新兵の4分の1にも見られた。また、このアデノウイルスをベースにしたワクチンが、以前に接触したことのある人にどの程度効果があるかは不明です。

ワクチン製造の世界的リーダーの育成に関連し最低限の宣伝と「PR」をしているのは：米国に本社を置く国際的なバイオ製薬企業メルク・シャープ＆ドーム、英国グラクソ・スミスクラインに本社を置く国際的な企業、免疫生物学的製剤の多国籍メーカーであるフランスのサノフィ・パスツール

ロシアでは、さらにいくつかの候補ワクチンが様々な拠点で開発されており、その中には、Rospotrebnadzorの国立ウイルス学・バイオテクノロジー研究センター「Vector」（Koltsovo、ノボシビルスク州）、A.A. Smorodintsevインフルエンザ研究所（サンクトペテルブルグ）、M.P. Chumakov免疫生物学的製剤の研究開発のための連邦研究センター（モスクワ）などが含まれています。また、ロシアでワクチンを生産するために、外国の開発者との交渉が進んでいます。ということで、2021年には選択肢が出てきます。

■ワクチンの2ショット
「スプートニクV」の使用説明書には、臨床試験のフェーズ１の結果から、発生頻度の点で有害事象（AE）は、頻繁かつ非常に頻繁に発生していると見なせます。ワクチン接種後、次のAEが記録されました：一般的な障害と反応注射部位：高体温、痛み、浮腫、ワクチン接種部位のかゆみ、無力症、倦怠感、発熱、ワクチン接種部位の皮膚温度の上昇、食欲減退。神経系障害：頭痛、下痢。呼吸器系、胸部および縦隔器官からの障害：中咽頭の痛み、鼻のうっ血、喉の痛み、鼻漏。現在の臨床試験でワクチンの投与量を減らすことにより、これらの現象を減らすことができる可能性があります。

実際のワクチンの保護効果は、20年9月に始まったフェーズ３の臨床試験で検討されるためまだ評価されていません。この場合は破られましたが臨床試験のフェーズ３は通常のアルゴリズムで行います。フェーズ２の試験では、通常、薬剤の投与量が変化するが、既に公表されているスプートニクVの臨床試験結果では、そのようなデータは得られていません。

ワクチン「Gam-COVID-Vac」（「ScienceFirstHand」No.3（88）、2020）

フェーズ３に関しては、独自の規則があります。各テスト参加者には「幸福」の特別な日記が与えられ、セラピストが割り当てられます。すべてのテスト参加者は少なくとも4つのグループに分けられ、そのうちの1つはワクチンの代わりにプラセボを投与され、もう1つは同様のワクチン製剤、3つ目はワクチン自体、4つ目は可変用量などです。スプートニクVの場合、前例のないことに直面し、臨床試験のフェーズ３の開始を待たずに、2020年9月8日、ロシア保健省は、ワクチンの最初のバッチを民間循環に放出する許可を発表し、地域を含むリスクグループからの集団の大量ワクチン接種が計画されています。

ちなみに、「スプートニクV」の指示には、子供だけでなく、主なリスクグループである60歳以上の人（75歳以上の人の死亡率は20～30％）にもワクチンを使用してはいけないと書かれています。

ここまでnote公開･･･････････････

■氷山の水面下
2020年のSARS-CoV-2コロナウイルスのパンデミックは、人間のスクリーニングでは前例のないものです。このウイルスが、さまざまな人々の生物と病原体、主に季節性インフルエンザや他の急性呼吸器ウイルス感染症を引き起こすものと相互作用で，多くの問題が明らかなったのは驚きではありません。

たとえば、インフルエンザの発作を起こし、流行中に健康を維持することで、感染を回避できたと考えています。ただし、この場合、インフルエンザウイルスは、明らかな病気の兆候を引き起こすことなく、上気道の少数の細胞に感染し、そこで「わずかに」増殖する可能性があります。そしてこれが事実であるならば、SARS-CoV-2の場合にすでに証明されているように、ワクチン接種された人々でさえ感染の無症候性の保因者である可能性があります。

COVID-19患者は、最初の症状が現れる2日前に感染を広げ始めます。病気が無症候性である場合でも、感染した人々は、呼吸、くねくね、または咳だけでなく、糞便によっても、最大2週間ウイルスを環境に放出する可能性があります。そのため、ウイルスの存在について陰性の検査を行った後にのみ、患者は検疫から解放されます。

問題の反対側：現在、人類は原則として呼吸器感染症の90％を診断することができます。しかし、少なくともロシアでは、実際にはこれを行っていません。急性呼吸器ウイルス感染症とインフルエンザの診断は、症状によってのみ行われます。そして、ARVIの症状のほとんどはほとんど同じであるため、これは冒涜です。ただし、インフルエンザはほとんどの場合、鼻水が出ずに消えますが、これはCOVID-19を含む他のいくつかの感染症では一般的です。ARVIの特定の原因（病因）についての答えは、正確な実験室診断によってのみ与えられます。現在は可能ですが、有料です。ARVIのPCR診断は、強制医療保険の資金調達には含まれていません。

「寒さ」やインフルエンザの特定の症例は目で判断されるため、わが国で実際に特定の病原体に一度に感染したARVI患者の数を概算することすらできません。そしてこれは、これらの感染のそれぞれからの真の損傷を評価することと、最も危険で疫学的に重要なものを決定することの両方を防ぎます。したがって、インフルエンザウイルスを除いて、これらの病原体に対する新しいワクチンや抗ウイルス薬を開発したり、それらの進化の長期的な傾向を追跡したりすることはありません。したがって、ARVI病原体のグループに新しいウイルスがどのように補充されているかにすぐに気付かないのは当然のことです。

フランス。 2020（ "Science First Hand" No. 3（88）、2020）
フランス。2020年の写真：Jacques Paquier

ただし、一部の国では、関連する研究がいわゆるパイロット都市で実施され、PCRを使用して、いくつかのポリクリニックからのSARSの兆候があるすべての患者のサンプルが分析されます。はい、それは非常に費用がかかります。1つのサンプルのそのような分析は、現在7〜8千ルーブルの費用がかかります。しかし、病原体の全範囲を見ると、どの感染症に対してワクチンを開発する価値があるかが明らかになります。

ちなみに、これらの病気の原因のうち、細菌感染症はわずか20％、残りはウイルス性です。今日のワクチンはインフルエンザに対してのみ開発および生産されており、ARVIの病因におけるその割合は10〜15％です。さらに、一部の国では同じコロナウイルス感染がより一般的です（15-30％）。そして、これらの「習慣的な」コロナウイルスは無害とはほど遠いです。COVID-19のように、重度を含む3種類の病気があり、感染自体の結果と機械的換気による二次性肺炎の両方で死亡する患者もいます。

もちろん、ARVIのすべての患者に対して一般的な診断を行ってそのようなウイルス感染を検出することは意味がありません。特定の抗ウイルス治療がないため、これまでのところ症状があるだけです。通常の治療コースは、診断自体よりも約7倍安くなります。ウイルス感染の場合、上記の理由で選択的研究を行う必要があります。どのワクチンを開発し、どの診断をCHIに導入する必要があるかを理解するためです。

モスクワでのそのような研究は、適切に組織された場合、1年以内に数千人の患者をテストするために約1500万ルーブルを必要とします-モスクワの「3ルーブルノート」の価格または最も高価なベントレークロスオーバーではありません。しかし、保健省はそのような提案に対する答えを1つだけ持っています-お金がありません。

新しいコロナウイルス感染によって引き起こされたパンデミックが私たちに教えてくれた主な教訓は、実際、私たちはウイルスの流行と感染一般についてほとんど知らないという理解です。それは、そのような将来の出来事に備える方法と、それらに対処する上で効果的に行動する方法を私たちに教えなければなりません。そして、それはCOVID-19自体についてでさえありません。それは、危険な季節的な感染ではありますが、別のものになる可能性があります。自然界に動物や鳥がいる限り、新しい未知の病気のパンデミックのリスクは残ります-「野生の」病原体の自然の貯蔵所。

そして、私たちが本当に人口を保護したいのであれば、私たちが今しなければならない最初のことは、私たちがまだ病気であるもの、私たちの中で最も危険なSARSを引き起こす病原体、ロシア人を見つけることです。モスクワ、サンクトペテルブルク、ノボシビルスク、クラスノダール、イェカテリンブルク、カザン、ウファ、ウラジボストークなど、SARSが特に多い主要都市でモニタリング研究を実施するためには、まず、健康問題の解決に今よりも有能かつ効果的に多くのお金を費やす必要があります。他の百万以上の都市と同様に。

SARS-CoV-2に関しては、明らかに、抗流行作用だけでそれを根絶することはほとんど不可能でしょう。おそらく、少なくとも効果的なワクチンが広く実践に導入されるまで、それは人間の集団で循環し続けるでしょう。しかし、私たちはまた、この病気を簡単にまたは無症状で経験し、おそらく免疫を持っている人々の層が徐々に増えています。ワクチン接種は彼らの数を増やすべきであり、そうすれば流行は減少するでしょう。

その間、マスマスキングと社会的距離は感染の拡大を減らすことができ、それは人口の最も脆弱なセグメントを保護します。厳しい対策（企業、学校、大学、カフェ、レストラン、ショップの仕事をやめること）に戻ることは経済の崩壊につながり、ひいてはヘルスケアの状況を悪化させることになることを心に留めておくべきです。

文献･････　　略