2019年4月の記事一覧

 Fig.1

 菱形30面体と12・20面体とは互いに双対な多面体です．双対の説明はFig１に図示しました．さらに，12・20面体は互いに双対な正12面体と正20面体とを重ねたときの共通部分でもあります．

注）Fig.1の重な合わせでは，共通部分はサッカーボール［5,6,6］の半正多面体ですが，正20面体のを少しづつ大きくしていくと，［5,3,5,3］の半正多面体（12・20面体）になる点があります．

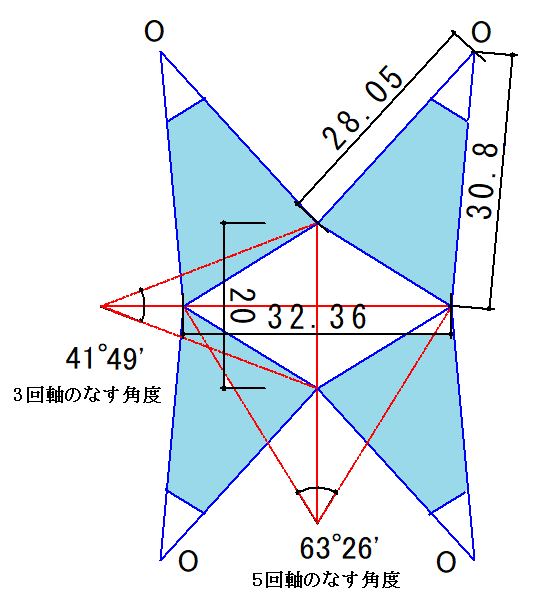
菱形30面体の頂点は，正12面体の頂点（3回軸の位置）と正20面体の頂点（5回軸の位置）とから構成されています．菱形面の短対角線（正12面体の正5角形面の辺長）をaとし，長対角線（正20面体の正3角形面の辺長）をbとすると，a:b=1:Φ＝2:1+√5　の黄金比です．正12面体の頂点のうちの8個を使い，一辺Φaの立方体を内接できるので，正12面体の外接球の半径は，R₁₂＝√3Φa/2です．
一方，正20面体の外接球の半径は，R₂₀=(b/4)√(10+2√5)です．

寸法をa=2，b=1+√5，Φ=1.618にすると，R₁₂=2.80，R₂₀=3.08が得られます．
実際の製作は展開図に記入した寸法（10倍）にすると作り易いです．

ミラー紙（厚さ0.25mm程度の厚紙）を使って，展開図の鏡を作りピラミッド（内側が鏡）のような形に組み立てます．O点は立体（ピラミッド）の中心に相当し，O点の周囲は光の窓になります．覗くのは菱形面（ピラミッドの底面）の外部からです．

針金で正4面体ABCDを作り，持ち手をつけて，正4面体をシャボン液の中に浸してからゆっくり引き上げると，どのような面にシャボン膜ができるでしょうか？
実験してみてください．針金枠の正4面体の面にシャボン膜ができると思いますか？

多分，正4面体の中心Oと正4面体の辺でできる三角形，例えば，△OABなどの膜ができると思います．正4面体は辺が6個ありますから，このような膜は6枚あります．
Oから正4面体の各頂点へ，線分OA,OB,OC,ODの4本がありこの線分が３つのシャボン膜の境界になります．
（１）Oから正4面体の各頂点に向かう線分同士のなす角度は何度でしょうか？
（２）△OABのような６つの膜が1点で出会うOのような点が必ずできるでしょうか？
（３）正4面体の４つの面の面積合計と，△OABの面積x6とでどちらが大きいでしょうか？
（４）どのようなシャボン膜の形のつり合いが実現するでしょうか？
色々な疑問が起こり難しい問題です．実験してみて推測してみましょう．

 針金の枠が立方体のときは，どのような膜の形になるでしょうか？

実験してみると下図のような膜ができると思います．
このような膜の形ができることを説明してください．

1976年，ドイツのRegensburg大学のKurt Fischerは，神経の生理学モデルを研究し，フィボナッチ数の発生をここでも発見した[177]．神経繊維に沿って移動するインパルスは，ナトリウムまたはカリウムのイオンに由来し，n>=2の細胞からなる同一の膜貫通孔を通って流れる．微量のカルシウムイオンCa²⁺が孔に入ると，孔内のナトリウムイオンNa⁺の流れを止めることができる．
これらのイオンは，細孔の入り口を除いて，それぞれ1つまたは2つの細胞を占有することができ，これらの２つの状態をそれぞれ１あるいは２と標記する．図3.39は典型的な孔の状態で，0と表示したのは空の細胞である．

ナトリウムは，孔のいずれの端でも出入りすることができるが，カルシウムは孔の左側でのみ出入りできると仮定する．その結果，孔内のカルシウムイオンは，この孔を通るナトリウムの流れを妨げる．
ロシアの数学者Andrey Andreyevich Markov （1856-1922）にちなんで名付けられたこのマルコフ確率過程は，ツリー構造で表すことができる．木の頂点は細孔の可能な状態を表し，そのエッジは状態間の可能な遷移を表す．たとえば，図3.40に，5つの空でない細胞を有する孔の様々な可能な状態を示す．
図３．４０

ツリーは2種類の頂点で構成されていることに注意せよ．すなわち，右端のセルに1，あるいは，右の2つのセルの中央に2があるものだ. レベル5のすべての状態は後者で，状態の右側にカルシウムが存在するため，ナトリウムイオンの右への移動がもはや実行可能ではない．図3.41に図3.40のツリー骨格が描かれている．これは図2.1のフィボナッチツリーに非常に似ている．いずれの図からも，5つの空でない細胞を有する孔は，レベル5に5=F₅個の状態を有することがわかる．
図３．４１

一般的に，n個の空でない細胞を有する孔は，レベルnにF_n個の状態を有する．これは，レベルnの状態数がフィボナッチ再帰関係を満たすことからわかる．

1963年，カリフォルニア州サンノゼにあるサンノゼ州立大学のS.L. Basinは，”電気ネットワークに関心のある人々まで，我が友フィボナッチから逃れることはできない”[23]と書いた．ここでは，フィボナッチ数が電気ネットワークの研究にどのように現れるか示そう．

今年の桜