note.com投稿記事

Т-квадратelementy.ru
このフラクタルは、T定規の形をしています（英語ではT定規をT-squareと呼ぶそうです）。レース模様のようです。

始めに与えられた辺の長さ１の正方形（暗い部分）の中心に,①辺1/2の正方形を白く塗ります。次に，②正方形の4つの頂点を中心に，①の正方形の辺の1/2の辺の正方形を白く塗ります。このように繰り返し，次の世代で追加する正方形は，前の世代の正方形の頂点を中心に，辺の長さは前の世代の1/2にします。
無限回繰り返したときにできるフラクタルのフラクタル次元は，
log_{2}4 = 2　です。

無限に繰り返すと，始めに与えられた正方形のどの点をとっても、その近傍には白く塗りつぶされた点があり，始めに与えられた正方形のほとんどすべてが白くなり，残りの領域は0に等しく，フラクタルは始めに与えられた正方形（面積１）全体を占めます。しかし、塗りつぶされた部分の境界の長さは無限です。

(訳者による要約)

単純群とは，自明な正規部分群以外の正規部分群を含まない群です．乱暴な言い方をすれば，自然数では素数のようなものです．有限群を単純群の積で表すのは，自然数を素因数分解するイメージです．

（定理）有限単純群は次のいずれかと同型である．
１．素数位数の巡回群
２．5次以上の交代群
３．Lie型の単純群
４．26個の散在型単純群

 １～３は系列ですが，どちらにも属する群も存在し，この分類は重複を許すものです．４は系列に属さず存在する群なので散在型と呼ばれます．モンスター群は散在型単純群に分類されます．この記事の趣旨はこのような数え上げの問題では分類完了と言い切れないということで，有限単純群の分類に踏み込んで理解する必要はありません．

 この分類定理は，10年を越える500以上もある論文を繋ぎ合わせて得られる結論ですが，論理の繋ぎにギャップがある可能性はあり．分類に抜けがないとは言えません．理論全体を理解している人は10人いるかどうかで，今後とも証明が完全であることを証明できるかどうか疑わしいと言うことです．

結晶点群は32個ですが，この中の単純群は1,2,3,4(mod2),-1,mで，1は例外,3以外は位数2です．

ーーー 

■数学は何処へ行くより３， Brian Davies（ロンドンキングスカレッジ）

https://elementy.ru/nauchno-populyarnaya_biblioteka/164681/164685

これから説明する3番目の危機も、不必要な複雑さに関連していますが、ある意味ではもっと深刻です。この場合、私たちはコンピュータは使いませんが、「純粋数学」におけるコンピュータの証明が容認できない理由です。私が提供する例は、現代数学の中心的な分野の1つである群論に関連します。

1970年代に、100人を超える群論専門家が一種のコンソーシアムを結成し、単純な有限群の完全な分類を目標にしました。この問題は非常に骨の折れるものとして提起され、その解決策は、純粋数学で「フロー法」と「分業」を使用した唯一の例です。ダニエル・ゴレンシュタインの指導の下で、問題は「パッケージ」に分解され、世界中の数学者のさまざまなグループに割り当てられました。10年間の集中的な作業の後、3つの可算無限の系列族と、26個の散在型で構成されるすべての有限単純群の完全な分類をまとめることに成功しました［訳注）約500編の論文］。 「モンスター」と呼ばれる最高位数の散在型の存在は、コンピューターの助けを借りてのみ証明することができました。 幸いなことに、この問題をめぐる危機は、群分類の詳細に立ち入ることなく議論することができます。有限単純群が何であるかを知る必要さえありません。

1980年代には、群分類自体と同じくらい興味深いことが起こりました。外向きのポジティブな変化です。コンピューターを使わずに「モンスター」の存在を証明する方法の発見です。さまざまな数学者グループの努力を組み合わせて、模索された証明の大規模な研究を実施することが決定されましたが、期待される結果の代わりに、以前に受け入れられた証明の多くのギャップが特定されました。ほとんどの穴にはパッチが適用されていましたが、1990年に単純な有限グループの完全な分類が得られたという記述は時期尚早であると見なされるほど、深刻であることが判明しました。時が経つにつれて、このギャップはアシュバッハーとスミスの証明で埋められ、再びその証明は非常に正しいように見えました[3]。この最終的な証明の20巻のうち、これまでに公開されたのは不完全な5巻だけであり、これは定理が「証明」されてから四半世紀後のことです。詳細については、[3]、[27]を参照してください。プロジェクトに最も関心のある参加者の1人であるミハエル・アッシュバッハーは、いつの日か新しい有限単純群が発見される可能性を排除していません。
その特性がすでに知られているどれかに関連しているなら、大したことではありませんが，
アッシュバッハーは、根本的に新しい有限単純群である可能性を排除していません。その場合は、分類に関するすべての作業を最初から始めなければなりません [4]。Jean-Pierre Serre は用いられる証明の正しさと完全さに懐疑的であることを記しておきます [24]．

アッシュバッハーは、証明は「外見は十分に強い」と考えています。それは、特定された欠点が、証明のメインラインに影響を与えることなく、適度な量の追加作業でこれまでに修正できたからです。残念ながら、これは証明が正しいことを意味するものではありません。証明の強さは、そのリンクの最も弱いものによって決定されます。これまで、ドロップされたリンクが比較的簡単に新しいリンクに置き換えられたという事実は、これが将来何度も成功することを保証するものではありません。

個々のスレッドの切断があるネットワークの形の証明をイメージしましょう。ネットワーク全体の整合性を脅かさないで、どこかにハエが這うのに十分な大きさの穴があることは排除できません。ハエ（この場合は有限単純群）の大部分は捕らえられますが、すべてではありません。

数学的知識を相互に関連する事実のウェブと比較するという考えは、線形論理の役割を減らし、数学的証明の問題を確率論的平面に移します。これは必然的に不必要な複雑な構造につながります。この考えは新しいものではありませんが、数学者自身が向かうのは比較的最近です。同様の類似点は、特にアシュバッはー [4]によって与えられており、「古典的な数学」とは対照的に、データを整理するさまざまな方法が豊富な、情報集約型の科学としての現代の数学と生物学の類似点を示しています。

有限単純群の最終分類案の完成（徹底的な最終報告書を発行するという意味で）に関しては、自然な老齢化で主要な参加者を失ったために危機に瀕しています。さらに10年後、それらのほとんどは生命や数学から消え、分類を完了するのに十分なほど問題を深く理解している科学者は少ないでしょう。しかし、プロジェクトが徹底的な最終報告で終わったとしても、少なくともマルチボリューム証明の主要な行を理解していると主張する権利を持っている数学者は、おそらく世界に10人もいないでしょう。

したがって、次のような状況になります。数文で定式化された問題の解決には、数万ページのテキストが必要です。証明は完全に書き留められておらず、一貫して書き留められているわけではなく、おそらく書き留められることはなく、最後に、1人の個人が完全に理解することはできません。しかし、得られた結果は重要であり、群理論の枠組みの中でさまざまな問題を解決するために広く使用されていますが、その正確性は依然として大きな問題です。

もちろん、群分類の問題を解決する簡単なアプローチができる可能性もあります。しかし、同じように、これが起こらない可能性もあります。アシュバッハーは、（まだ記録されていない）利用可能な証明の推定全長が過去四半世紀で減少していないという事実を考えると、比較的単純な証明の可能性について懐疑的です。チューリングの研究から、証明が定式化よりも何倍も長い定理があることがわかります。実際、これら2つの長さの比率は任意に大きくすることができます。コーエンは、「中程度に複雑さの数理論の基本問題でさえ、圧倒的多数が合理的な理解を超えている」と確信しています[13]。したがって、将来的には、この種の新しい発見のみが期待できます。

https://elementy.ru/posters/fractals/Levy

このオブジェクトは1906年にイタリアのエルネスト･セサロによって研究されましたが、その自己相似性とフラクタル特性は、1930年代にフランス人のポール･ピエール･レヴィによって研究されました。このフラクタルの境界のフラクタル次元は、 1.9340にほぼ等しい...。しかし、これはかなり複雑な数学的結果であり、正確な意味はわかっていません。

華やかなフォントで書かれた文字「C」に似ていることから、レビィCカーブとも呼ばれます。よく見ると、レヴィの曲線がピタゴラスの木の冠の形に似ていることがわかります。

バリエーション
歪んだ曲線は、各ステップで等角線の右三角形の代わりに他の右三角形を使用することによって得られます。

Levyレヴィ Cカーブの別バージョンは、セグメントではなく文字Pで開始する場合に作成できます。以下は、このカーブを作成する最初の3、8、および11番目のステップです。

レヴィ島は、正方形を基準にすると得られます。

https://elementy.ru/posters/fractals/Pythagoras

上記ウエブサイトの図を利用していますが，説明文はわかりやすくするために書き換えています．

この図形は正方形ばかりでできています．３つ組の正方形が囲む3角形が直角3角形なので，ピタゴラスの定理が成立するので，ピタゴラスの木と呼ばれます．

この構成規則のため木全体が制限されるので，最大の正方形を1とすると，木は6×4の長方形に収まります。したがって，その面積は24を超えません．各ステップで，正方形の辺は1/√2倍に縮小され（面積は1/2）ますが，生じる縮小された正方形の数は2倍ですので，いつも同じ面積が追加されて行きます．このため，木の領域は無限大になるはずです．しかし実際には，正方形がかなり速くから重なり始め，領域がそれほど速く成長できません．それは有限ですが，正確なことはわかっておらず，これは未解決の問題です．

３角形の底辺の角度を変えると，木の形が少し異なります．そして，60°の角度で，3つの正方形すべてが等しくなり，木は平面上で周期的なパターンに変わります．

正方形を長方形に置き換えることもできます．そうすれば，木は本物の木のように見えます．そして，いくつかの芸術的な処理により，かなりリアルな画像が得られます．

https://elementy.ru/posters/fractals/Sierpinski

このフラクタルは、1915年にポーランドの数学者シェルピンスキーVaclavSierpinskiによって記述されました。これを作るには、正3角形の内部に、中線3本を引き、生じた4つの小さな３角形の中央の1つを捨てます。次に、残りの3つの三角形のそれぞれについて同じ手順を繰り返します。この図は、最初の3つの手順を示しています。

Sierpinski三角形を作る手順

中央の３角形を捨てることは、Sierpinskiの３角形を作る唯一の方法ではありません。「反対」のやり方も可能です。最初は「空の」三角形を取り、その中の中線で形成される３角形を作り、3つの角の三角形のそれぞれで同じことを行います。最初は、図は大きく異なりますが、反復回数が増えるにつれて、それらはますます互いに類似し、無限回繰り返す極限では両者は一致します。

Sierpinski3角形を作る「反対」の手順

Sierpinski3角形を得る次の方法は、次の反復の一部に縮小された自分を置き換えることで幾何学的フラクタルを構築する通常の手順にさらに似ています。各ステップで、ポリラインを構成するセグメントが3つ折れのポリライン（最初の反復で形ができた）に置き換えます。この3つ折れを右と左に交互に置き換えて行きます。8回目の反復でフラクタルに非常に近いものが出来上がっています。

Sierpinski３角形を得る別の方法

しかし、それだけではありません。Sierpinski３角形は、平面上の点のランダム歩行の種類の1つの結果として得られます。この方法は「カオスゲーム」と呼ばれています。他のいくつかのフラクタルはそれを使って構築することができます。

カオスゲーム

「ゲーム」の本質は次のとおりです。正３角形をA1 A2 A3とします。任意の始点 B0が与えられます。３角形の3つの頂点の1つがランダムに選択され、もしA1が選ばれたとすると、B0とA1の中点B1 がマークされます。同様に、次にA2が選ばれたとすると、B2がマークされます。その後、A3が選ばれたとすると、B3がマークされます。つまり、前の手順で何を選択したかに関係なく、三角形の頂点がランダムに選択されるたびにマークされる点がジャンプして生じます。驚くべきことに、シェルピンスキーの三角形がすぐに表示されるようになります。以下に、100、500、2500ポイントがマークされたときに何が起こるかを示します。

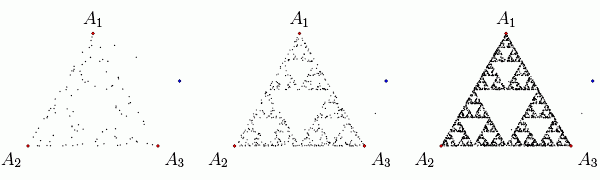
カオスゲーム：100、500、2500ポイント

いくつかの性質

フラクタル次元$$log_{2}3=1.584962･･･$$。 Sierpinski３角形は、自分自身を1/2に縮小した3つのコピーで構成されます。それらの相対位置は、グリッドセルが半分になると、フラクタルと交差する正方形セルの数が3倍になるようなものです。つまり、$$ N( δ/2)= 3N(δ)$$です。最初のセルサイズが1で、フラクタルがそれらの$$N_{0}$$と交差する場合（$$N(1)=N_{0}$$）， $$N(1/2)=3N_{0}，N(1/4)=3^2N_{0},･･･， N(1/2^k) =3^k$$ $$N_{0}$$。　　　したがって、$$N(δ)$$は$$ (1/δ)^{log_{2}3} $$に比例しており、フラクタル次元の定義により、次元は$$log_{2}3$$に等しいことがわかります。
Sierpinski３角形の面積はゼロです。これは、単一の、非常に小さな円でさえ、フラクタルに収まらないことを意味します。つまり、最初の方法で構築を開始した場合、内部全体が３角形から「取り出され」ました：各反復のたびに、残っている領域は3/4倍されます。つまり、ますます小さくなり、0に収束します。これは厳密な証明ではありませんが、他の構築方法も、この特性が真実であるという確信を高めるだけです。
コンビナトリクスとの予期せぬつながり。$$2^n$$ 本の線があるパスカルの三角形で、すべての偶数を白で、奇数を黒で着色すると、目に見える数字はSierpinski３角形を形成します。
オプション
Sierpinskiによるカーペット（正方形、ナプキン）。正方形のバージョンは、1916年にVaclavSierpinskiによって記述されました。彼は、自己交差することなく平面上に描くことができる曲線は、このスカスカの正方形のサブセットと同形であることを証明することができました。３角形のときと同様に、正方形はさまざまなデザインから取得できます。右側は古典的な方法です。正方形を9つの部分に分割し、中央の部分を捨てます。次に、残りの8つの正方形についても同じことが繰り返されます。

Sierpinskiカーペット、最初の5回の繰り返し

３角形と同じに、正方形の面積はゼロです。シェルピンスキーカーペットのフラクタル次元は、3角形と同様に算出し　log_{3}8

シエルピンスキーのピラミッド。Sierpinski３角形の3次元類似物の1つ。起こっていることの3次元性を考慮して、同様に構築されます。1/2に圧縮された最初のピラミッドの5つのコピーが最初の反復を構成し、その5つのコピーが2番目の反復を構成します。フラクタル次元はlog_{2} 5です。図の体積はゼロです（各ステップで、体積の半分が破棄されます）が、表面積は反復ごとに保持され、フラク​​タルの場合は最初のピラミッドの場合と同じです。

メンガーのスポンジ。Sierpinskiカーペットの3次元空間への一般化。スポンジを作成するには、手順を無限に繰り返す必要があります。繰り返しを構成する各立方体は、27個の1/3に縮小された立方体に分割され、中央の立方体とその6つの隣接する立方体が破棄されます。つまり、各立方体は20個の新しい立方体を生成します。これは3分の1です。したがって、フラクタル次元はlog_{3} 20です。このフラクタルは普遍的な曲線です。3次元空間の曲線は、スポンジの一部のサブセットに対して同形です。スポンジの体積はゼロですが（各ステップで20/27倍されるため）、表面積は無限大です。

表紙の3D図形は，コッホピラミッドと呼ばれます．
https://elementy.ru/posters/fractals/Koch

コッホの雪片

この図は，最初に研究されたフラクタルの1つです．これは，1904年のスウェーデンの数学者Helge vonKochの論文に初めてでたKoch曲線の3つです．この曲線は，連続ではあるが至る所接線を引くことができない線の例として提案されました．このような特性を持つ線は以前から（Karl Weierstrassは1872年）知られてはいましたが，Koch曲線はその構造の単純さで注目に値します．

コッホ曲線の作り方　以下の操作を無限に続けます．

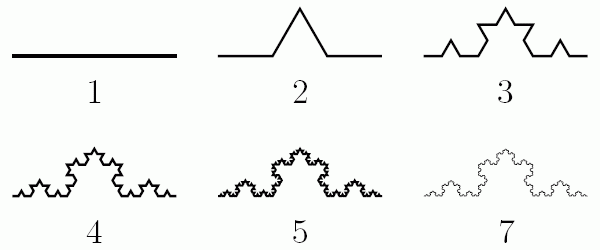
コッホ曲線の基本的な特性
0.拡大しても拡大しても同じパターンがでて来ます。

1.連続ですが、至る所で微分できません（接線が引けません）。

2.無限の長さを持っています。元の線分の長さを1とすると、各ステップごとに；　1，4/3，(4/3)^2，．．．．のように長さが増えていきます。nステップごの線の全長は(4/3)^nですから、n→∞で全長は無限大になります。

3.コッホの雪片が囲むのは有限な領域ですが、その周囲が無限であるというのは不思議です。興味のある方は、面積を計算してみてください。

始めにあるのは面積S_0の正3角形１つ．step１で出来るのは，2つの正3角形を重ねたダビデの星形（ピンク色の星形）．この面積S_1は，中心の正6角形［面積は(2/3)S_0］と外側の小さな３角形［面積は(1/9)S_0］が6個です．S_1=S_0［2/3＋6(1/9)］．step3では，青色の小さな正3角形［面積S_0x(1/9)^2］が2×6個分付け加わります．S_2=S_1+2･6･S_0(1/9)^2．このように継続していくと，面積は単調に増加一方ですが，付け加わる面積は指数関数的に減少し，n→∞で面積はある値に収束するはずです．

4.フラクタル次元はlog4 / log3 =1.26･･･
自分の中に1/3に縮小した自分が4個入って次の世代ができる

美しい幾何学p159,160

https://elementy.ru/posters/fractals/H-fractal

Hフラクタル
文字Hの形の図形からすべてが始まります。Hの垂直な線分と水平な線分の長さは等しくなっています。
次ステップで、図の4つの端のそれぞれに、半分に縮小されたコピーが描画されます。
次ステップで，両端にあるのは，4分の１に縮小された16個のHです。
このように無限に繰り返して、フラクタルは視覚的にほぼ正方形を埋めます。

Hフラクタルはどの場所でも密。つまり、正方形の任意場所のいくらでも小さい近傍に、フラクタルがあります。よく見ると、各文字Hが、同じステップで完成した独自の小さな正方形に含まれていることがわかります。

Hフラクタルは正方形を埋める（空間充填曲線）ので、そのフラクタル次元は2で、すべてのセグメントの全長は無限大です。

Hフラクタルを構築する原理は、電子マイクロ回路の製造に使用されます。複雑な回路内の多数の要素が同時に同じ信号を受信する必要がある場合、Hフラクタルの適切な反復セグメント端に配置し、接続します。

オプション
Mandelbrotマンデルブロの木は、線セグメントではなく長方形でできた厚いHを描画することで作られます。

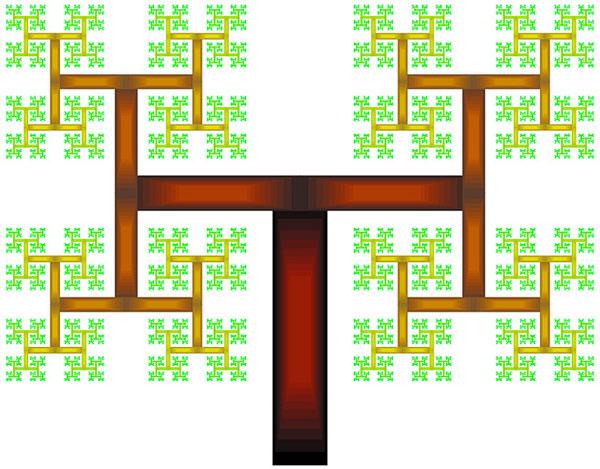
www.flickr.com/photos/29915793@N08からの画像
平面の一部を埋める線のいくつかの例（空間充填曲線）は、1890年にイタリアの数学者ジュゼッペペアノの論文に初めて登場しました。Peanoペアノは、曲線と正方形が等しい性質（点集合と見なす場合）である、つまり「同じ」密度の点を持っているということの視覚的な説明を見つけようとしました。この定理は、Georg Cantorカントールによって、彼が創始した集合理論の枠組みの中で証明されていましたが、この直感に反する新理論の結果は、大きな懐疑論を引き起こしました。ペアノの例（セグメントから正方形への連続写像）は、カントールの正しさの良い確認となりました。

ペアノ曲線、最初の3回の繰り返し
不思議なことに、ペアノの論文には1つのイラストも含まれていませんでした。ペアノ曲線という表現は、特定の例ではなく、平面または空間の一部を埋める曲線を指す場合があります。

下の曲線（ヒルベルト曲線）は、1891年にデビッドヒルベルトによって発表されました。見ることのできるのは，私たちの念頭にある数学的オブジェの有限回近似です。本当の曲線は、無限回の操作後にのみ実現します。

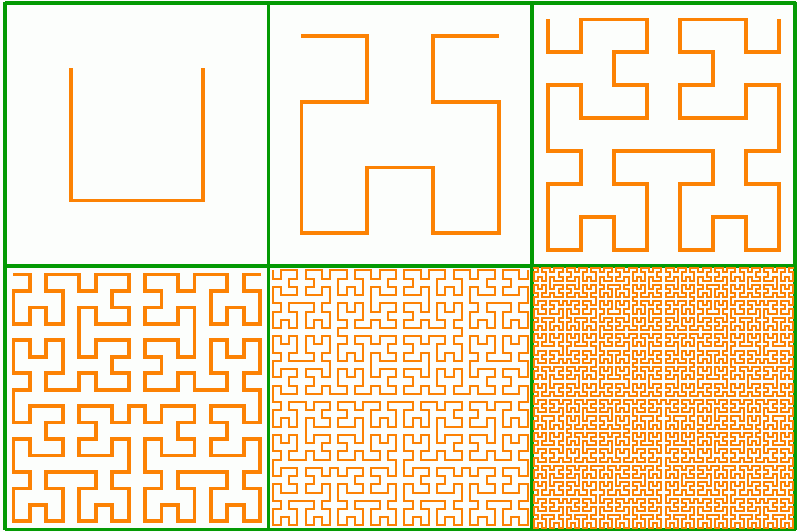
ペアノ曲線の変種-ヒルベルト曲線、最初の6回の反復

ゴスパーカーブ、またはゴスパー雪片（ビル ゴスパー）：

ゴスパーの曲線（雪片）

そして、そのような線の三次元版もあります。たとえば、3次元のヒルベルト曲線、またはヒルベルトキューブ：

カリフォルニア大学バークレー校のコンピューターサイエンスの教授であるCarloH.Séquinによって作成された、3Dヒルベルト曲線のエレガントなメタリックバージョン（3回目の反復）。 www.cs.berkeley.eduからの画像

このようなモデルは、64個のプラスチック製コーナー配管を用い自分で作れます。

ヒルベルトのプラスチックキューブ（2回目の繰り返し）。momath.orgからの画像

モーペルテュイは，
「始状態から終状態への運動経路には，作用と呼ばれる積分量が定義でき，作用が最小となる経路が実現される．これが物理学のみならず，万物の運命を決める外界の原理である」
という着想－”最小作用の原理”(1744年)を得ました．たしかに，現実の運動では，しばしば作用が極小になりますが，正確には，「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります．
オイラーは，モーペルテュイの作用量の定義を積分に拡張し，最小作用の原理をさまざまな力学課題に適用できるようにし，”最大，または最小の性質をもつ曲線を見出す方法”（1744）を発表しました．これを読んだ若きラグランジュは変分法を発明し，オイラーに手紙（1755）を送ります．オイラーは，ラグランジュの方法を採用し，”変分法の原理”（1766）を出版します．変分法で導かれる運動方程式が，オイラー＝ラグランジュ方程式といわれる所以です．その後，ラグランジュは，”解析力学”（1788)を出版します．その序文に「本書には図は一つも出てこない．...所定の手続きに従い進める代数計算だけだ．...」と高らかに宣言します．こうして，複雑な力学問題も解ける一般化された手法が確立されます．
変分法は，19世紀のハミルトン，ヤコービにより完成に至ります．ハミルトンは，系の状態を表示する空間に，座標と速度を座標軸とした相空間を導入し，「作用量は最小化や最大化するのではなく，停留化する」ことを示しました．
１つの物体は，座標x,y,zと速度x˙,y˙,z˙を変数に持ち，その状態は6次元の空間の１点で表現できます．同様に，N個の物体よりなる系は，6N次元の空間の１点で表現できます．この空間を相空間といいます．系のエネルギーを
H(xi,yi,zi,xi˙,yi˙,zi˙)，i=1,2,･･･,Nとすると，エネルギーが保存される運動の軌跡は，相空間内の超平面H(xi,yi,zi,xi˙,yi˙,zi˙)=hに含まれます．超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです．解けるかどうかは別として，周期解（軌道）が存在することは，証明（1986年）されています．（文献10）
■　最小作用の原理の理解には，ホイヘンスの光の波動説の説明が参考になります．ホイヘンスは，空間は見えない媒質で満たされており，光は波紋（球面波）が拡がるように伝わると考えました．波面上の各点はまた新たな波源となり，そこを中心として新たな波紋が広がって行きます．生じた無数の波紋は重なりあったり打ち消しあったりの結果，新しい波面ができます．これは多数の波面の包絡面で，この面に垂直な方向に光は進むと考えます．この様なプロセスで決定された方向は，作用を停留値にするものです．

量子力学の世界の運動には，軌道の概念がなく，電子などはランダムに動き回ります．しかし，我々の日常（マクロ世界）では，電子の運動でも軌道はあります．ここで，マクロ世界でも物体はランダムな経路をとれるとしてみましょう．あらゆる経路に実現可能性があるが，各経路の実現率は，それぞれの確率に従う．これらの確率は，波紋が伝播するときのように互いに干渉し合い，その結果として現実の経路が決まってくると言うわけです．最も確からしい経路は，近くからの干渉の最も少ない経路であって，これがちょうど作用積分を停留化するもののようです．「ファインマンの原理」（文献10）
■　運動方程式が解ける問題を”可積分な問題”といいますが，実際は，”非可積分の問題”がほとんどです．ニュートン力学は，可積分で安定な周期軌道が解になる特殊な範疇を扱っています．一方，非可積分の問題からは，カオスが生じます．１つの軌道は，1本の因果列の存在を意味しています．単純な世界は，今日の現象（原因）１が明日の結果１につながり，今日の現象（原因）２が明日の結果２につながる世界ですが，一般には，今日の現象のすべてが，明日のある結果１の原因になりうる複雑な世界です．バタフライ・エフェクトという映画＊）があったようですが，今日，上空で蝶が羽ばたいたことが，遠い未来に竜巻きを起こす原因の一つになるかも知れません．「風が吹けば，桶屋が儲かる」世界です．この世界は，独立な因果列はないので，周期的な軌道にはなりません．コンピュータを用いて，すべてのステップを計算していけば，結果を予測できるのですが，遠い先の結果は予測もつかないものになります．「最小作用（停留値）の原理」は，ニュートン力学も含むが，このようなカオスも含む原理であります．
＊注）過去に戻れる能力を持ったエヴァンは，過去に戻りやり直すことにする．しかし，過去に戻り選択肢を変えて始めた人生は，どれも，自分を含め自分が愛する誰かが，幸せではないものだった．
 
■　最小作用の原理の起源といえば，1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません．「決まった二点の間を，始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です．ライプニッツの提案により，ベルヌーイはこの問題を海外の数学者にも公開することにしました．ベルヌーイは，ライプニッツの友人で，ニュートンとライプニッツの微積分の先取権論争にも加わり，ライプニッツを応援しています．きっと，ニュートンを困らせてやろうと思ったのでしょう．ところがこの問題を受け取ったニュートンは，「当時，造幣局の仕事で忙しく疲れて帰宅したが，問題が解けるまでは寝なかった．とは言っても朝４時までには解けてしまった」と日記に書いています．そして，解答を匿名で返したということです（文献１，5）．

最速降下曲線の答えは，円板の縁（１点）に目印をつけ，直線上を転がしたときに，目印が描く”サイクロイド曲線”です．ホイヘンスが振り子時計に用いたあの曲線です．

■　解析力学の手順
力学系を記述するラグランジュ関数 を求め，ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと，オイラー＝ラグランジュ方程式が得られます．簡単な系のラグランジュ関数は，（運動エネルギー）－（位置エネルギー）の型になりますが，複雑な系では，位置エネルギーが速度に依存することもあります．
ラグランジュ関数は，電磁場に置かれた荷電粒子にも定義され，光（電磁力学）も力学も統一して扱える原理であります．変分原理から，ニュートンの運動方程式は導出されます．その上，変分原理はニュートン力学よりさらに一般化された外界の原理です．（文献１１）
20世紀に入り，量子力学が誕生するときにもこの原理が手がかりになりました．光や物体の運動が，作用積分を停留化するような，手の混んだ経路を選択するというのは，何と不思議なことでしょう．

（文献）
１．物理と数学の不思議な関係，マルコム・E・ラインズ（青木薫訳），ハヤカワ文庫,　2004
５．古典物理学を創った人々，エミリオ・セグレ（久保亮五，矢崎裕二訳），みすず書房，1992
１０．数学は最善世界の夢を見るか？，エクランド（南條郁子訳），みすず書房, 2009
１１．理論物理学，カンパニエーツ（山内恭彦，高見穎郎訳），岩波書店, 1964

（「数学文化」谷，NO.15(2010)，p.79-87　より抜粋）

ストローと輪ゴムで凸多面体を作ります．
輪ゴムの働きは，結節点でストローの長さを変えないように固定しますが，ストロー間の角度は固定しません．つまり，このような構造を建築ではトラス構造と言います．

皆様の常識通り，２次元の多角形では，３角形は安定で，４角形は安定ではありません.

多面体の面がすべて３角形で出来ていれば，変形しない多面体になりますが，１つでも3角形でない面（４角形や，5角形や，....）があると変形が起こる多面体になります．
例えば，以下の多面体は，すべて３角形の面で出来ているので安定です．

これらが安定なことは，皆様の経験通りで感覚的にわかるでしょう．オルルクは１つだけ4角形の面を含む以下の模型を提案しましたが，実験するとこれも変形してしまいました．

これらの事実は，力学的には常識で自明と思いますが，数学的には証明が必要で，自明なものほど証明は難しいものですが，コーシー＆アレクサンドロフの定理が関係あります．

今回の記事は，KVANTIK，No3（2018）のDmitry Panov, Alexandra Pushkar, Dmitry Chebasov の記事を参考に作成しました．

 
フリーマンダイソンFreeman Dyson（1923年12月15日ー2020年2月28日）
フリーマン・ジョン・ダイソンは、イギリス・バークシャー生まれのアメリカ合衆国の理論物理学者、宇宙物理学者、サイエンスライター。ケンブリッジ大学トリニティ・カレッジ卒業、コーネル大学大学院中退。プリンストン高等研究所名誉教授。 若くしてダイソン方程式を発表、量子電磁気学の完成に大きな寄与をなした。（wikiより引用）

1949年に彼は、トモナガと独立してシュウィンガー、ファインマンによって提案された、当時の量子電磁気学である量子場理論のさまざまな定式化が実際に同じ理論の説明であることを示しました。これにより量子電磁気学が定式化されました。　　繰り込み理論＝renormalization theory
（ヴァレリー・アナトリエビッチ・ルバコフの開会の辞2009.3.23より抜粋）
＊訳注）朝永、シュウィンガー、ファインマンはノーベル賞（1965年）をもらいましたが、ダイソンは受賞を逃しましたね。

■訳者（私）の意見
  二酸化炭素は温室効果ガス（地表から放射される赤外線を閉じ込める）でありますが，水蒸気の温室効果は二酸化炭素に倍するほど強力です．大気中にある水蒸気や二酸化炭素は地球大気に広がり地球を包み地球全体としての温暖化を起こすでしょう．それでも，水蒸気や二酸化炭素の濃度には場所により濃淡があります．飽和水蒸気量は気温依存しますので，寒いほど水蒸気量は少なく温室効果は減少するので，寒いところはますます寒くなります．水蒸気の豊富にあるところの温室効果は水蒸気が主体となります．
大気中の二酸化炭素量だけが地球全体の温暖化に結び付けるのは，その他のもっと重要な温暖化原因を故意に見落とすことになります．二酸化炭素を減らしたが温暖化は解決しないということが起こる危険があります．二酸化炭素を削減するために原発が必要という我田引水な理由で原発稼働がなされてきたのは間違いです．

それでは，ダイソン博士の講演を拝聴しましょう．
https://elementy.ru/video/20/Ereticheskie_mysli_o_nauke_i_obshchestve

２．土地管理と気候
これから5つの問題について私は異論を述べます。
最初の異論：地球温暖化をめぐる現在の誇張されたヒステリックな宣伝です。ここで私は、気候モデル専門家の聖なる兄弟と、気候モデルにより予測された数値を信じる惑わされた市民の群衆に反対します。もちろん、私はこの分野の専門家でないので話す資格がないと言われます。しかし、私は気候モデルを研究し、それらの能力を知っています。このモデルは、流体力学の方程式を解き、大気と海洋の流体運動を非常によく記述します。しかし、この方程式は，雲、ほこり、化学、畑、農地、森林の生物を説明することはできません。この方程式は，私たちが住んでいる現実の世界を説明できません。現実の世界は泥だらけで乱雑で、私たちがまだ理解していないことがたくさんあります。科学者がエアコンの効いた建物に座ってコンピューターでモデルを実行する方が、防寒着を着て沼や雲の中で実際に何が起こっているのかを測定するよりもはるかに簡単です。その故に、気候モデルの専門家は自分たちのモデルを信じてしまうのです。

地球上のいくつかの場所で、気候が実際に温暖化していることは間違いありません。私は，この温暖化が問題を引き起こしていないと言っているのではありません。明らかに問題は起こっています。私たちはそれをもっとよく理解すべきです。 この問題がひどく誇張されていると言いたいのです。これを語り，貧困、感染症、公教育、公衆衛生、陸と海の生物の保護など、緊急でもっと重要な他の問題から目をそらさせ，お金を奪っています。 とりわけ、戦争と平和と核兵器の問題についてもお話します。

地球温暖化の問題は、その重要性が誇張されていますが、興味深い問題なので、少しお話します。大気や生物圏における炭素の流れを詳細に理解するには、多くのパラメーターの数値を測定する必要があります。たくさんの数字と混同したくないので、1つの数字だけを覚えておいてください。覚えておいていただきたいのは、年間1/3mmです。次に、この数字の意味を説明します。砂漠、極地の氷、都市、道路、駐車場などではい地球の土地面積の半分を想像してください。農地、森林、沼地など、さまざまな種類の植物を支える土壌で覆われています。毎年、地表のこの半分は、その二酸化炭素の一部を吸収してバイオマスに変換します。それを大気中に放出します。バイオマスの増減を測定していないため、この割合がどれだけ大きいかはわかりません。バイオマスは生き物であり、すでに死んだ生き物の残骸でもあります。私が覚えておくように頼んだ数字（年間1/3mm）は、化石燃料を燃やすときに放出されるすべての二酸化炭素の吸収によって、地表の半分で起こるバイオマスの厚さの平均増加です。

これらの計算の意味するところは、土壌による大気中の炭素の吸収が非常に良好な速度で進行する可能性があるということです。大気中の二酸化炭素濃度の上昇を止めるには、土壌バイオマスを年間わずか1/3mmだけ増加させる必要があります。肥沃な上層土はバイオマスの約10％を占めるため、1年に1/3mmのバイオマスの増加は、1年に約3ミリメートルの表土の増加に対応します。耕作回避など農業慣行の変化は、同様に急速なバイオマスの増加につながります。土を耕さずに作物を育てれば、より多くのバイオマスが根に行き、それが地面に残り、より少ない大気に戻る炭素は少なくなります。遺伝子工学を通じて、根のバイオマスがより高い品種を入手すれば、明らかに、達成することができるでしょう。土の厚さの成長がさらに速くなるように。これらの簡単な計算から、二酸化炭素の大気への放出の問題は気象学の問題ではなく、土地管理の問題であるという結論が導かれます。大気と海洋のコンピュータモデルでは、土地をどのように管理するかを予測することはできません。

地球全体の規模でバイオマスの平均増加を計算することはできないかもしれませんが、この問題を局所的な側面で検討しましょう。この将来の可能性を想像してみてください。中国は、石炭の燃焼に大きく依存する産業大国として発展を続けていますが、米国は、土壌バイオマスの増加によって排出される二酸化炭素を吸収することを決定しています。植物や木の生きている部分に蓄積できるバイオマスの量は限られていますが、土壌に沈着できるバイオマスの量を制限するものは何もありません。大規模な土壌増強は、遺伝子操作された作物の経済的パフォーマンスに応じて、有益な場合とそうでない場合があります。しかし、少なくとも、石炭を燃やすことによって中国が豊かになる可能性については、非常に議論の余地があります。一方、米国は、大気が中国の鉱山から米国の土壌に炭素を自由に輸送できるようにし、大気中の二酸化炭素を一定に保つことによって土壌を貯蔵することにより、環境を祝福しています。化石燃料と気候変動についての予測を聞くとき、このような機会は検討する価値があります。コンピュータ技術が過去50年間に君臨したように、バイオテクノロジーが次の50年間に地球上で最高に君臨する場合、気候ゲームのルールは根本的に変化します。大気中の二酸化炭素含有量は一定に保たれます。

フリーマンダイソン，2009年3月23日，モスクワFIAN

気候変動についての公開討論に耳を傾けると、私たちの知識の巨大なギャップ、私たちの観察の不完全さ、そして私たちの理論の表面性に驚かされます。私たちの地球生態学における多くの基本的なプロセスの理解はまだ乏しい。それらをよりよく理解した場合にのみ、地球の現在の状態を正確に診断することができます。病気の人の世話をするのと同じ方法で地球の世話をしようとすると、最初に病気を診断し、次にそれを治療する必要があります。このためには、生物圏で起こっているプロセスを観察し、それらのパラメーターを測定する必要があります。

大気中の二酸化炭素濃度の増加は、気候と非気候の2つの重要な結果をもたらすことは全員が同意します。1つは、大気中のエネルギーの放射伝達の物理的変化であり、2つ目は、陸上および世界の海の植生の生物学的変化です。これらの結果のどれがより重要であるか、またこれらの結果が個別にまたは一緒にか、有益であるか有害であるかについての意見は異なります。物理的影響は、降水量、雲の被覆、風の強さ、温度の変化に現れます。これらは通常、一緒に積み上げられ、誤解を招く用語「地球温暖化」と呼ばれます。湿った空気では、二酸化炭素によって引き起こされる放射輸送の変化は、水蒸気のはるかに強い温室効果によって本質的に相殺されます。

二酸化炭素の影響は、空気が乾燥している場所で重要であり、空気は通常、冷たい場所でのみ乾燥します。 二酸化炭素の温暖化効果は、空気が冷たく乾燥している場所で最も強く、主に熱帯ではなく北極で、主に夏ではなく冬に、そして主に昼間ではなく夜間に発生します。 温暖化は、暑い場所を暑くするのではなく、寒い場所を暖かくします。 この局所的な温暖化を世界平均で表すことが、人々に誤解を生じさせています。

大気中の二酸化炭素の濃度が生物学的に非常に重要である本当の理由は、この濃度が非常に低いことです。晴れた日の午後に太陽の下で育つトウモロコシやその他の穀物の畑は、地上1メートルの二酸化炭素を約5分ですべて吸収します。対流と風によって空気が継続的に混合されない場合、トウモロコシは成長を停止します。大気中の二酸化炭素の約1/10は、毎年夏にバイオマスの成長に費やされ、毎年秋に大気に戻ります。これが、化石燃料の燃焼の影響を植物の成長と衰退の影響から切り離すことができない理由です。
数千年の時間スケールでしか利用できない炭酸塩岩と深海を除いて、短い時間スケールで生物学的にアクセスできる炭素に5つのプールがあります。これらの5つのプールは、大気、陸上植物、陸上植物が成長する土壌、海洋植物が成長する海の表層、および化石燃料の実証済みの埋蔵量です。大気はこれらのプールの中で最も小さく、化石燃料は最も大きいが、5つすべてが同等のサイズです。それらはすべて互いに強く相互作用し、それらのいずれかを理解するには、それらすべてを理解する必要があります。インテリジェントな土地管理によって、大気中の二酸化炭素の増加を止めるのに必要な量である年間40億トンの炭素が土壌プールの成長を増加させられるかどうかはわかりません。確かに言えることは、これは理論的な可能性であり、真剣に検討する必要があるということです。

地球温暖化の科学的および経済的側面について私が知っている議論のほとんどは、最も重要な問題を回避しています。これは科学的な問題というよりは宗教的な問題です。そのような世界の世俗的な宗教-それは環境主義と呼ぶことができます-それによると、地球上の人々の役割は経済管理者の役割であり、私たちの贅沢の無駄で地球を台無しにすることは罪であり、正しい方法は可能な限り経済的に生きることです。環境倫理の基本は、世界中の幼稚園、学校、大学の子供たちに教えられています。環境主義は社会主義に取って代わり、主要な世俗的な宗教になりました。この宗教には強力な倫理的基盤があります。科学者や経済学者は、仏教の僧侶やキリスト教の説教者たちに、私たちの自然の生息地の破壊は悪であることに同意することができます。鳥や蝶を注意深く保護することは祝福です。グローバル環境主義コミュニティは非常に強い道徳的立場を持っており、より良い未来への希望の道に沿って人間社会をリードしています。自然への希望と尊敬の宗教としての環境主義は、真剣にそして長い間やって来ました。これは、地球温暖化の危険性を信じているかどうかに関係なく、私たち全員が共有できる宗教です。

しかし、残念ながら、環境保護運動は、地球温暖化が何よりも地球の生態系を脅かしているという信念の信条の1つとして採用されています。これが、地球温暖化についての論争が非常に熱く激しくなっている理由です。地球温暖化の危険な影響に懐疑的な人は誰でも環境の敵であると国民は信じています。今、私のような懐疑論者は、そうでなければ大衆を説得するという困難な課題に直面しています。これらの懐疑論者の多くは熱心な環境保護主義者です。彼らは、地球温暖化への一般的な執着が、今日私たちの惑星をすでに脅かしているはるかに深刻な危険から国民の注意をそらすのを恐れて見ています。例えば、環境に対する真に深刻な脅威は、世界の人口の制御されていない成長から来ています。しかし同時に、人間の人口の幸福の増加と出生率の低下の間には強い正の相関関係があります。

20世紀の後半、メキシコが豊かになると、メキシコの平均的な家族の人数は7人の子供から2.5人に減少しました。アイルランドやイタリアなどの繁栄しているヨーロッパ諸国の家族規模はさらに急速に減少しています。世界の人口を安定させ、地球を保護する最も簡単な方法は、すべての人を豊かにすることです。先進国は一般的に人口が安定しているか減少しており、環境に配慮する余裕があります。ベルトルト・ブレヒトが三文オペラでずっと前に述べたように、「最初のコムト・ダス・フレッセン、ダン・コムトは道徳的に死ぬ」、「最初に餌を与え、次に道徳が来る」。環境にとって最悪のことは、産業技術の助けを借りずに、成長し、飢え、貧しい人々が土地に住もうとしていることです。中国とインドの政府が地球温暖化との戦いよりも貧困との戦いを優先するとき、彼らは道徳的にも科学的にも正しいといえます。