note.com投稿記事

Алексей Левинのエッセイより抜粋　ИСТОРИЯ НАУКИ • 14.10.2016

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．

'The Invention of Science' tells the story of the shaping of the modern worldThe central subject of this vibrant work is not really the inwww.csmonitor.com

ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年。

ニコラウス・コペルニクスの モノグラフ天球の回転について（ニュールンベルクの出版社 Johann Petraeusから1543年に出版）。

ウートンは2つの理由から、コペルニクスの1543年を革命の開始とする従来の見解に同意しません。第一に、太陽中心（地動説のこと）［正確には太陽不動］コペルニクスモデルは、ケプラーとガリレオの研究の後の、17世紀の初めになってから天文学革命の要因になりました。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、それが物理的な基盤を持っていることは否定しました（たとえば、砲弾がどの方向にも同じ距離を飛ぶという事実からも、地球回転の仮説は反駁できたと信じられました）。1580年代と90年代には、コペルニクスは天文学界に3人以下の信者しか持っていません、さらにそのうちの1人、ドイツのクリストフ・ロスマンは最終的に彼の敵の陣営に移りました。第二に、コペルニクスのモデルは、アリストテレスと古代の天文学者から受け継いだ地上世界とは根本的反する、月を越える（天上界）世界の絶対不変の概念をそのまま保持しています。ご存知のように、この概念は17世紀に完全に拒否されました。

コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象でした。すべての天体は、大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は毎晩、天の同じ経路をたどり、明るさと数の両方で変化しません。彗星は唯一の例外でしたが、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者であるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月に完全に消滅するまで、その輝きが徐々に薄れていくのを追跡しました。その前から、彼は1573年に出版され、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusævimemoriapriusvisaStella」で彼の観察を説明しました。そのため、ブラヘはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見ました。（11月6日に韓国で、2日後に中国で、日本でも記述があります）。

左：TychoBraheの著書「DenovaetnulliusævimemoriapriusvisaStella」からの星座Cassiopeiaの描画。 超新星は文字Iでマークされています。
右：スペクトルのさまざまな部分のフレームを合計して得られた超新星の残骸のスナップショット。 チャンドラ望遠鏡のウェブサイトで、この残骸が2000年から2015年の間にどのように変化したかを見ることができます。
http://mvshelter.blogspot.ruからの画像

数年後、彼は、彗星は月を越える世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定を実行することを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積してきました。これは、品質と幅の点で、ヨーロッパだけでなく、中国とイスラム教徒の東の最高の天文台でこれまでに行われたすべてをはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することをケプラーが厳密に証明することを最終的に可能にしたのはこれらの材料であり、それによってコペルニクスモデルの主な弱点を修正しました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていましたが、真に無限の宇宙には中心はありません）。ウートンが提案する最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。

科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較することを提案しています。 16世紀の終わりに、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく理解された夢は未来を予測すると信じていました。彼らは、地球が動かず、宇宙の中心にあるという公理として受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたでしょう）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの研究、またはおそらくそれらのポピュラー書に限定されていました。 彼らはまた、個人的な図書館-2、3ダースの本を持っていました。

https://elementy.ru/nauchno-populyarnaya_biblioteka/431670/Vsego_lish_stepeni_dvoyki

И. Акулич，«Квант» №2, 2012　に２の累乗の大きな数を求める問題があります．

（問題） 

$$S = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{63}$$

$$S$$の値を計算しなさい．

$$2 S = 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{64}$$

$$2S-S＝S=2^{64}-1$$

計算機を使えば，$$2^{64}-1=18446 744 073 709551615$$ と計算できるでしょう．
計算機が無くても，許容できる精度でおおよその答えを見つけることができます。原則として、日常生活では（そしてほとんどの自然科学では）2～3%の誤差が許容されます．
$$2^{64}$$をどのように概算したらよいかという問題です．

 $$2^4 = 16$$，$$2^{10} = 1024≒1000=10^3$$　だから，

$$2^{64}＝2^4・(2^{10})^6≒16・(10^3)^6$$

しかし，この誤差はかなり大きい．結局，1024を1000に置き換えること続けて6回．
このため，1.024倍の誤差の6乗$$1.024^6$$の誤差になります．

1よりも何倍も小さい数xについては、次の近似式を使うと精度が高い．

$$(1 + x)^n ≒ 1 +n･x$$　これを使うと，

$$(1+0.024)^6≒1+6×0.024＝1.144$$

従って，$$2^{64}≒16･10^{18}･1.144=18304･10^{18}$$　と補正します．その結果，

$$S≒2^{64}≒18,304,000,000,000,000,000,000$$となり（18304の後ろに0が18個），
これは正解と1%未満の誤差になります．

■注

１．数字を2のべき乗の和で表すのは，数字を2進数で表すときに必要になります．

たとえば，$$2^{10}+2^9+2^8+2^7＋2^6＋2^4＋2^3+2^2＝2042$$，　2進数で表記すると$$11111011100$$

２．この問題の最初の式は，次の一般式の$$m=64$$の場合になります．

$$2^m = (2^{m–1} + 2^{m–2} + ... + 2^0) + 1$$

３．次の性質も役に立ちます：

$$10^{10}＝(2･5)^{10}＝2^{10}・5^{10}$$

$$2^{10}>10^3$$，　$$5^{10}<10^7$$

Григорий Мерзон, «Квантик» №5, 2020　より

この記事の図には，不要なものもありましたので，必要なものだけ掲載します．文章は冗長ですので私が全部書き換えました．解が1つしかないような記述も私は気に入りません．要するに，この問題は，以下の図（ラクダと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れという主旨です．パズルの問題として予備知識なしで考えるとなかなか難しいかもしれません．

この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

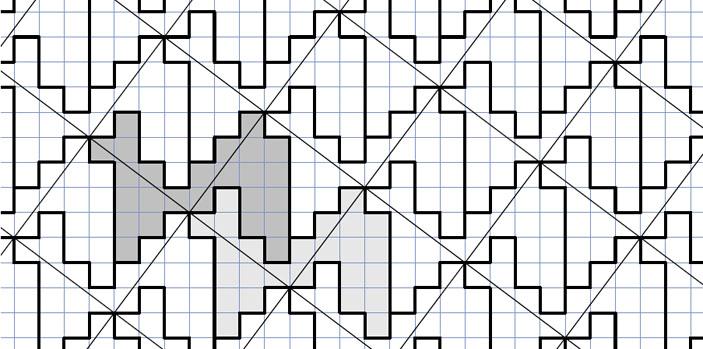
このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞と呼びます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の答ですが，私は答えはこれだけではないことを指摘しておきたいです．

ラクダが3分割できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Григорий Мерзон, «Квантик» №5, 2020

この記事の図はすべて掲載しますが，文章は冗長ですので私が全部書き換えました．要するに，この問題は，以下の図（らくだと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れということです． 

 この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞とよぶます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の回答ですが，私は答えはこれだけではないことを指摘しておきたいとおもいます．

ラクダが3等分できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

そして彼が帰宅したとき、クヴァンチクは上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
のエッセイのまとめです．今回は短いが，彼の最も言いたかったことはここにあるのでしょう．最後に私（訳者）の感想を述べます．

そして今、第四の定理について、少しだけ、多分最も恐ろしいことを話します - "教えても、誰も興味を示さない”。この問題のいくつかの断片はすでに話しました。人々は有限群の研究に興味を持たなくなりました。やる人が減ってきて、テキストという形で保存されてきた知識の塊が不要になり、誰も読めなくなってきている。これは数学の多くの分野を脅かす不幸でもあります。

数学の分野によっては運がいい分野があります。例えば、グラフ理論と組み合わせの理論は同じです。本気でやり始めるにも、ほんの少し学べばよい。少し勉強して、数学オリンピックの問題が解ける。一歩踏み出して、未解決の問題があり、～やったーとなります。しかし、数学の多くの分野は、本当に美しく、それをやりたいと感じるためにも、あなたは多くのことを学ぶ必要があります。そして、その道中では、他にも多くの美しいことを学ぶことができます。しかし、道中で出会うこれらの美しさに気を取られてはいけません、そして、最後には、まさに迷路の中で、美しさを見て、そして、多くのことを学んで、この分野の数学ができるようになっていくのです。そして、この難しさは、そういった部分の問題です。数学の分野が発展するためには、それに従事しなければなりません。全ての困難を乗り越えて、そこに登って、その後もやり続けるというのは、多くの人には面白いはずです。そして今、数学はその難易度の高みに達しており、多くの分野で人知の限界が大きな問題となっています。

人類がこれらすべての問題にどのように対処するのか-私にはわかりませんが、それは興味深いものになるでしょう。

実はそれだけです。

訳注）感想：私は、このエッセイで例にあげられている有限群の問題に興味があります。しかし、この分野は数学者たちは興味を失っているようです。それは、数学の確立された分野で，これ以上研究するのは人間の理解できる限界だからです。これを乗り越えるのは、他のすべての分野の知識もマスターしている数学者ができる仕事でしょう。それを乗り越えられる人がいるのか，その人知はもう人間業ではないのか。そして、たとえ誰かが乗り越えても他の誰にも理解できず，その結果に誰も関心をもたないという状況が恐ろしい．