note.com投稿記事

これはオーボールという赤ちゃんのおもちゃです．球の表面は互いに接する大きい円20個と小さい円12個でできています．円を正多角形にすれば，いわゆるサッカーボールの形です．つまり，小さい円は正5角形，大きい円は正6角形に対応します．

（問）大きい円と小さい円の半径の比は？

球面多面体の正多角形の辺は球の大円でできていますが，多面体の正多角形の辺は直線でできています．この多面体の1つの頂点の周りには，正5角形，正6角形，正6角形が集まっています．このような多面体は［5,6,6］(シュレーフリの表記法)と記述します．正3角形の面だけが頂点で５つ集まっているのは正20面体で｛3,5｝と記述します．正20面体の頂点を切って（切り口は図の白い面），残りの面が正6角形になるようにすると，多面体［5,6,6］が得られます．

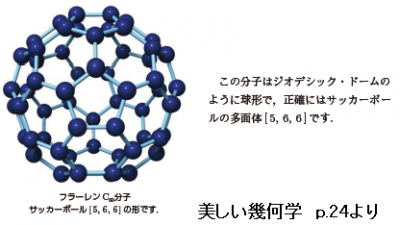
これは，上図のC60［フラーレン（60個の炭素原子からなる）分子．青球は炭素原子C］と同じ形です．

■さて，問の答えですが，オーボールの大きい円と小さい円は，フラーレンの正6角形と正5角形に対応することがわかります．
下図を見てください．

辺の長さの等しい正5角形と正6角形の外接円(内接円)半径比が答えです．計算すると　1:1/2sin36°≒1.176：１

 ■次の図に示す「組み合わさった立体」は，正20面体（水色）と正12面体（黄色）が組み合わさっています．それぞれの多面体のサイズは，辺の中央でちょうど重なるようにしました．入り組んで組み合わされている多面体は，正20面体｛3,5｝と正12面体｛5,3｝です．これらの正多面体は互いに双対です．
（注）｛3,5｝←→｛5,3｝のように，面の形と頂点に集まる数を入れ替えると，”互いに双対”な多面体が得られます．
サッカーボールもオーボールも，正20面体由来の正6角形（正3角形）の面と正12面体由来の正5角形の面からできています．サッカーボールの面に対応する頂点をもつ双対な多面体を作ると菱形30面体が得られます．
（注）正５角形の面に対応する頂点間と正6角形の面に対応する頂点間が，それぞれ菱形面の対角線になります．
下図の「組み合わさった多面体」で，黄色い頂点と水色の頂点を結ぶと菱形30面体が得られます．
菱形面の１つを赤い線で図に記入しました．この菱形面の対角線比は黄金比です．

多面体の見える万華鏡

reciprocalという言葉があります．経済などでは，互恵的とか対等とかいう意味で使われます．
結晶学では，結晶格子crystal latticeに対して，逆格子のことをreciprocal latticeといいます．
両者の関係は，多面体でいうと，面を頂点に，頂点を面に変換した多面体
（これを双対dualな多面体という）の関係と同じです．

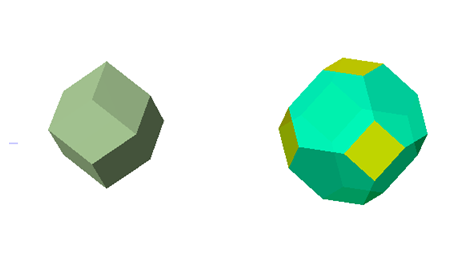
例えば，シリコンの結晶格子は面心格子で，ディリクレ胞を描くと菱形12面体（左図）です．シリコンの逆格子は体心格子で，ディリクレ胞を描くと［6,6,4］半正多面体［いわゆるケルビン立体］（右図）です．

結晶格子中のデリクレ胞と逆格子中のデリクレ胞は，このように互いに双対です．格子latticeに対して逆格子reciprocal latticeとはうまく名付けたものです．
もちろん，対称性はどちらも同じ，正6面体（角砂糖）と同じ対称性です．菱形12面体と［6,6,4］半正多面体（ケルビン立体）の形が見える万華鏡を作りました．この万華鏡は，左から覗くと菱形12面体が，右から覗くとケルビン立体が観察され，両者の対称性は同じであることを理解するのに役立ちます．

ーーーー

(注）用語（ディリクレ胞，格子，逆格子，面心格子，体心格子，半正多面体）は，説明なしに用いたので，別の機会に補足説明をいたします．

参考　「美しい幾何学」　　今，試し読みができるようです．
p.44～ 45　万華鏡で作る多面体
p.60～ 62　ディリクレ胞，格子

「美しい幾何学」

◆立方面心格子→菱形12面体
面心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると「菱形12面体」が得られます．

◆立方体心格子→半正多面体［4,6,6］（ケルビン立体とも呼ばれる「切頂正8面体」の一つ）
体心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると，この立体が得られます．

．

■格子というのは，無限に続く周期的構造の＜幾何学的表現＞です．格子点に置くのは繰り返される単位モチーフです．格子点に本当に点を置くのは一番単純な構造です．面心格子の格子点に本当に原子を配置した構造は，銅やアルミニウムなどの金属結晶で知られています．体心格子の格子点に本当に原子を配置した構造は，鉄，タングステン，セシウムなどの金属結晶で知られています．

■格子からディリクレ胞を作る手順を見ると，ディリクレ胞とは格子点１つが占有する多面体の形なのがわかります．
従って，格子点にディリクレ胞を配置すれば，空間が隙間なく充填されるのは明らかです.
そして，ディリクレ胞の対称性（点群）に格子の対称性が現れています．

図は省略しましたが立方体（角砂糖）を積み上げた形，菱形12面体や，ケルビン立体，は周期的空間を隙間なく埋め尽くすことができます．これら３つの対称性は同じです．

◆純粋に数学的に空間充填構造を導くのはとても大変なことですが，結晶学者は昔から知っていました．
自然科学の分野に数学への源泉がいろいろありました．結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．

今年（2020年）のとっとりサイエンスワールドは，新型コロナウイルスのために残念ながら中止になりました．
2017年のとっとりサイエンスワールドin倉吉は，8月27日に開催されました．1,250人の来訪者があり，例年のように盛況でした．万華鏡ワークショップは30人クラスを4回実施し120人が作りました．2016年は，鳥取サイエンスワールドの終わった直後，翌々日に倉吉地震がありびっくりしました．多くの方が避難生活をし，サイエンスワールドの会場だった梨っこ館もガラス天井が落ちたそうです．隣のプールは2017年7月20日になってやっと利用開始にこぎつけました．白壁土蔵群，赤瓦館でも地震の被害がありました．

2017年に，その赤瓦二号館を訪れたとき見つけた御殿まりの写真です．

これらはみんな一人のご婦人が作ったものだそうです．お会いしたいものでしたが，残念ながら不在でした．
どれも美しく良いできですね．
正4面体群：正6面体群（正8面体群）：正12面体群（正20面体群）のどれがあるでしょうか？

Q1：さて私は，正6面体群（正8面体群）と正12面体群（正20面体群）のうちのどちらを選んだでしょう？

私が選んだのは，前者の方でした．

参考に，これと同じ対称性の図形を掲載しましょう．

これらはともに，半正多面体［4,6.6］ですが，立方体のx,y,zの方向に，4回軸があり，体対角線の方向に3回軸があります．2回軸のある方向も確認してください．（注）シュレーフリの記号［4,6,6］は，頂点の周りに正4角形，正6角形，正6角形が集まっていることを示しています．
結局，これらは皆，球面正6面体｛4,3｝や正8面体｛3,4｝と同じ対称性（点群）になります．（注）{4,3}もシュレーフリの記号と呼ばれますが，正4角形が頂点に３つ集まっていることを示しています．

Q2:　球面正12面体｛5,3｝や菱形３0面体の御殿まりを見つけましょう．このなかにありますか？

これらの対称性（点群）は，正12面体やその双対の正20面体と同じです．

一番下の立体の形は，菱形30面体です．菱形30面体は，12･20面体（半正多面体［3,5,3,5］）と双対な多面体なので，対称性としては，上の3つの立体はすべて同じです．
別項目・サッカーボール（フラーレン）に関連記事があります．

Q3:　この他に，半正多面体［6,3,6,3］があります．探してみましょう．

ーーーーーーーーーー

美しい幾何学，p21，p46，p48　が関連します．ご参照ください

平面張り詰めができる凸５角形タイルの形は，フランスの数学者マイケル・ラオがコンピュータを使い，全部で15種類を数え上げ（2017）決着したようです．このような数え上げの問題が難しいのは，演繹的な数学が使えないからです．
　米国サンディエゴの主婦マジョリー・ライスが，タイル張りの問題を知ったのは，1975年のScientific American 誌のマーチン・ガードナーのコラムでした．平面のタイル張り，別の言い方をすれば，一つのタイルで平面を分割する（テッセレーション）問題です．
　平面のタイル張りは，任意の３角形，任意の４角形タイルで可能，凸７角形以上では不可能です．凸６角形の場合は，全部で３タイプのタイル形で可能なことをラインハルトが証明しました（1918）．残されたのは凸５角形の場合で，1975年のガードナーのコラムには，ラインハルトの５タイプと1967年にカーシュナーが発見した３タイプの計８タイプが掲載されていました．ところが新しいタイプがまだあったのです．
　マージョリ（フロリダ州生まれ）が，高等学校で数学を学んだのは１年だけでした．
1945年，結婚しワシントンD.C. に移り，幼い息子と一緒に，その地で商業デザイナーとして働き，後にサンディエゴに移住します．数学が楽しみで，黄金比とピラミッドに魅了されていたといいます．子どもたちが学校に通っている間に自分も読めるようにと，息子達にScientific American の定期購読を許しました．
　この問題では，５角形タイルのタイプ分けがとても難しい．連続変形によりどちらのタイプにも属するタイルがあるし，同じタイプでも出来上がったパターンが全く違うように見えたりもします．彼女は発見に驚き喜んで，自分の仕事をガードナーに送りました．ガードナーはそれをペンシルバニア州のモラヴィアン・カレッジのタイリング問題の専門家であるドリス・シャトシュナイダーに送ってくれました．シャトシュナイダーは，彼女の発見が正しいことを確認したのです．彼女は，張り詰め可能な４つの新しい凸五角形タイプと，それらによるほぼ60種類のテッセレーションを発見しました(1977)．1975年以降にマジョリーの４種を含む計７種が発見されていま
す．最後に発見(2015) された15番目は，やはり周期的なものですが，単位胞が12個の５角形で構成される大きなもので，発見にスーパーコンピュータが使われました．
マジョリーは2017年７月２日94歳で亡くなりました．認知症のため，５角形タイリングの問題がついに完結したのを知ることはありませんでした．ワシントンにある数学協会のロビーの床タイルに，彼女の発見した５角形テッセレーションの１つ（エッシャー風の絵）が見られるといいます．

マジョリー・ライスについては，Natalie Wolchover の記事
(Quantamagazine, 2017）
https://www.quantamagazine.org/marjorie-rices-secret-pentagons-20170711/
をご覧ください．
注） 凸５角形タイルの非周期タイル張りに関しては，３回以上の任意の回転対称のものが作れることが知られています．