2019年8月の記事一覧

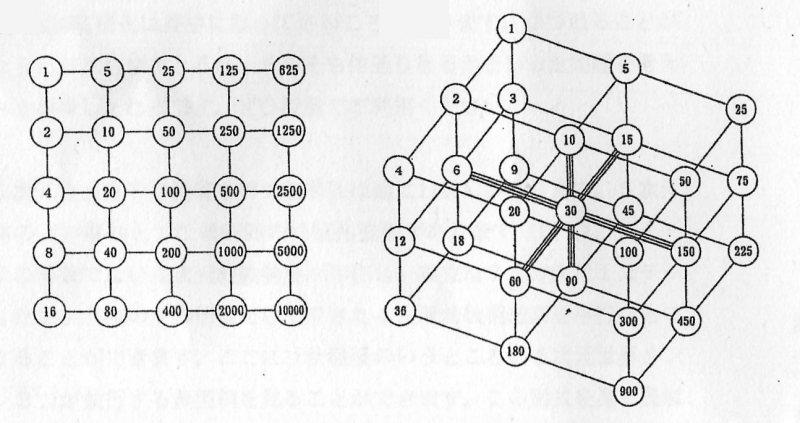
■2次元，3次元の格子点に配置された約数構造
左図の2次元格子｛2ⁿ･5^m｝は，素数２および５が生成する２つの1次元格子｛2ⁿ｝と｛5^m｝の直積で生まれる．10の2次元約数構造が，それぞれ格子点に配置されたものとみなせる．

右図の3次元格子｛2^p･5^q･3^r｝は，３つの素数2,5,3がそれぞれ生成する1次元格子｛2^p｝，｛5^q｝，｛3^r}　の直積で生まれる．これは，30の立方体約数構造が，3次元格子点に配置された構造とみなせる．

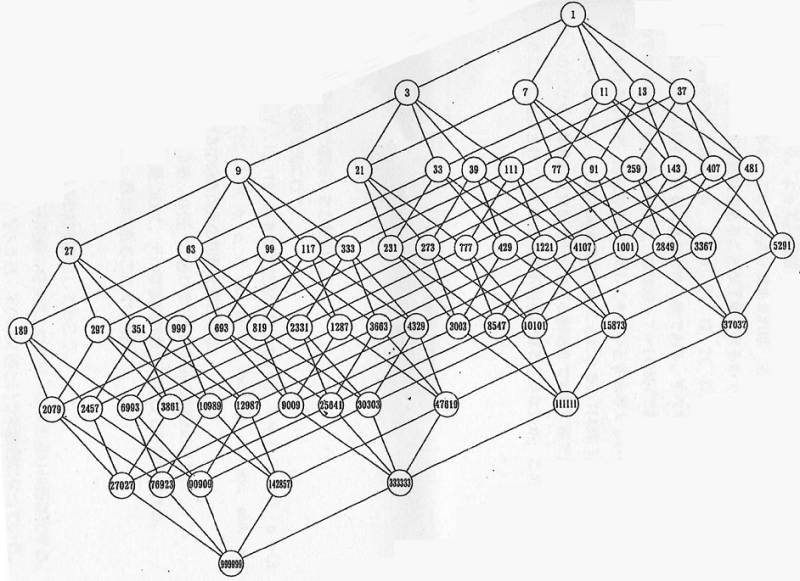
■4次元約数構造を，新設した1次元格子の格子点に配置してできる4次元＋1次元格子の約数構造で，この格子点は37037（右端の4次元超立方体）の約数構造と，新設した素数3の1次元格子｛3ⁿ｝との直積で得られる．