note.com投稿記事

By Julia Gog, Rachel Thomas, Marianne Freiberger

私たちは，伝染病の実効再生産数Rについて考えることに慣れてきました．これは，1人の感染者によって感染する人の平均数です．以前の記事で見たように，Rは伝染の様子かを理解するのに役立ちます．R> 1は流行が拡大することを意味し，R = 1は横ばいであることを意味し，R <1は流行が減少することを意味します．

（私たちがニュースで耳にする実効再生産数Rは，流行の過程で毎日変化します．基本再生数R0とは違います．）

ただし，Rが教えてくれないことの1つは，物事がどれほど速く変化しているかです．これは，Rがレートではないし，関連する時間スケールがないためです．たとえば，ある疾患でR = 2の場合，流行が拡大することはわかります（R> 1であるため）． HIVやTBのような病気では，ある人が次の人に感染させるまでに数か月または数年かかる可能性があります．R= 2としても，時間の経過とともにの成長が遅いことを意味します．ただし，インフルエンザ，または，はしかの場合，感染がはるかに速く，日数のスケールでは，R = 2は非常に急速な成長を意味します．

感染流行の成長率はどれくらいですか？
疾患の成長率は，感染症の数が日々急速に変化する速さを捉える自然な方法です．疾患の症例の増加は，指数曲線を使用してモデル化されます．

$$N（t）= {\rm constant} \times e^{\lambda t}$$
ここで，$$N$$はケース数であり，日数で測定した時間$$ t $$に依存します．$$ \lambda $$は，1日あたりの疾患の成長率と呼ばれるものです． （$$ e $$という数値は，約2.719に等しい数学定数であり，指数関数的成長と密接に関連しています．）
上記の曲線の例では，HIVの成長率は1日あたり$$ \lambda $$ = 0.002で，はしかの場合は1日あたり$$ \lambda $$ = 0.06です．この例の両方の疾患が同じ再生産数を持っているにもかかわらず，これは翌月に大きく異なる結果をもたらします．

以下の対話機能を使用して、さまざまな成長率で疾患の進行がどのように変化するかを調べることができます（スライダーを使用して$$ \lambda $$の値を変更します）。--略

COVID-19のパンデミックの間，新しい症例数と新しい死者数が毎日報告されています．これらは3月と4月上旬に英国で増加し，ここ数週間で減少しているのを見ました．増加率が正の場合，毎日新しい感染数は増加します．増加率が0の場合，新しい感染数は一定のままです． 流行を抑制し続けるために必要なことは，成長率がマイナスになることであり，それゆえ新しい感染数が減少することです． 新しい感染数が昨日から3％減少した場合，その増加率は、およそ，1日あたり$$ \lambda $$ = -0.03です． （これは完全に等価ではありませんが，$$ \lambda $$の一般的な値の適切な近似値です．成長率は実際には複利のように機能します．ここで確認できます．）

Rと成長率のどちらが優れていますか？
実効再生産数$$ R $$と成長率$$ \lambda $$はどちらも，疾患の成長を理解するための有効な尺度です． それぞれに適した用途を概説します．
--------
◆再生産数：R 
Rは、流行を止めるために必要な介入の強さを理解するのに自然であり、制御手段を計画するためにより適切です。例えば：

R = 1.5は、感染率を3分の1に減らす必要があることを意味します。
R = 2は、影響を受けやすい人々の半分にワクチン接種する必要があることを意味します（この計算については、注＊）。
したがって、Rは、流行を止めるために必要な将来の介入の強さを予測する直感的な方法を提供します。

R> 1指数関数的成長
R = 1フラット
R <1指数関数的減衰

R感染発生の数で，レートではありません。時間スケールは含まれていません。

Rは実際には簡単に測定できませんが、感染の時間スケールがわかっている場合は、モデルを使用して適合させることができます。原理的には、だれが誰から感染したかに関する正確な疫学的データによって推定することができますが、これは通常の設定では通常は実行できません。

◆1日あたりの成長率：$$ \lambda $$
成長率は、ケースが時間とともにどのように変化するかを考えるのに自然です。例えば

$$ \lambda $$ = 0.01 /日は、ケースが1日あたり約1％増加することを意味します。
$$ \lambda $$ = -0.02 /日は、ケースが1日あたり約2％減少することを意味します。
成長率は、現在何が起こっているかをよく説明しています。今日特定の数がある場合は、明日、翌日などに何人になるか予測できます。

$$ \lambda $$> 0指数関数的増加
$$ \lambda $$ = 0フラット
$$ \lambda $$ <0指数関数的減衰

 成長率$$ \lambda $$は、通常COVID-19の日数で与えられる率です。

成長率$$ \lambda $$は、ケースまたは死亡の時系列データから比較的簡単に推定できます（ただし、少数については以下を参照してください）。単純なアプローチは、ログに記録されたケースの勾配を見つけることです。時間とともに変化する成長率、または不均一な人口を考慮に入れることができるより高度なアプローチには、再び流行モデルのフィッティングが含まれます。
--------
病気の発生率が非常に低い場合や、調査しているコミュニティの人口が非常に少ない場合など、症例数が少ない場合、再生産数と成長率の両方を推定することは特に困難です。その場合、日々の変動が病気の根本的なパターンを簡単に覆い尽くす可能性があるため、成長率についての不確実性が大きくなります（したがって、信頼区間が広くなることが期待されます）。

どのようにしてRから成長率に、またはその逆に到達しますか？
Rと成長率の正確な関係は単純ではありません。次の感染までの各タイミングを考慮する必要があります。大雑把な近似は

$$ R = e ^ {\lambda T} $$
ここで、$$ T $$は平均生成時間です。感染から次の感染までの時間です。
さらに高度な数学も知りたい
これはすべて、制御手段と病気にかかりやすい人の数があまり速く変化していないことを前提としています。

1人の感染者に続いて、感染後の時間を$$ \tau $$（日数）で示します。彼らは平均して他の$$ R $$に感染し続けます。これらのそれぞれについて、感染のタイミングは確率密度関数$$ f（\tau）$$で分散されます。次に、（数学の学部生のための演習！）$$ R $$と$$ \lambda $$は次のように関連付けられます。

$$R ^ {-1} = \int _ {\tau = 0} ^ {\infty} e ^ {-\lambda \tau} f（{\tau}）d \tau $$
これはラプラス変換または生成時間分布のモーメント生成関数と非常に密接に関連しています。

生成時間の特定の分布（ガンマ分布など）の場合、これは簡略化できることがあります。生成時間を$$ T $$のように正確に一定にすると、$$ R = e ^ {\lambda T} $$が回復しますが、これは実際の多くの感染症のかなり大まかな近似です。

$$ f（\tau）$$は、潜伏期間などの生物学的事柄や、症状があるときに他の人とまだ混合しているか、自己隔離しているかなどの社会的要因に依存します。

詳細については、WallingaとLipsitchによるこのペーパーを参照してください。
----------

この記事について
レイチェルトーマスとマリアンヌフライバーガーはPlusの編集者であり、ケンブリッジ大学の数理生物学の教授であるJulia Gogと共同でこの記事を作成しました。 Gogは、その結果を緊急事態用科学諮問グループ（SAGE）にフィードするモデリンググループSPI-Mのメンバーです。彼女はまた、王立協会が率いる全国コンソーシアムの運営委員会のメンバーであり、COVID-19パンデミックに対処しています。

by Rachel Thomas and Marianne Freiberger

伝染病の実効再生産数Rは，母集団の異なる部分で異なる値を持つ可能性があります．Rは，感染した人が他に感染させる平均人数でした．社会のさまざまな部分（たとえば，地理的区分，病院や介護施設など）ごとに，R値が異なる場合は，これらのさまざまな構成要素がどのように結びついているかを考慮する必要があります．ご想像のとおり，これにより計算が複雑になります．それでは，その数学をさらに詳しく見てみましょう．

その記事の例を続けましょう．人口を2つのグループに分割したものを検討します．介護施設や病院の患者またはスタッフなどの「病院」というラベルのグループと，残りの人口の「コミュニティ」と呼ばれるグループです．コミュニティのRは0.8，病院のRは0.7としましょう．

これら2つのグループを独立個別なものとして検討することはできません．コミュニティの人々が病気になったときは病院に移動するし，病院や介護施設のスタッフが無意識のうちにウイルスをコミュニティに持ち込むことがありえます．これら2つのグループ間の病気の伝染を考慮する必要があります．仮定として，コミュニティでの感染が続いてかつ病院で0.4の新しい感染を引き起こし，病院での感染が続いてかつコミュニティで0.2の新しい感染を引き起こすとしましょう．これで，病院およびコミュニティに関して，それぞれの内部と両者間での感染で4種類があることがわかりました．

 ■病院に1000人の感染者がいて，地域社会に1000人の感染者がいる場合，新しい感染例はどれほど発生しますか？

有用な発見と警告
数学的詳細に入る前に，例を見て，表から直接読み取れる情報を確認しましょう．左側の列の数値を合計すると1.2になります．これは，コミュニティの感染者が平均して感染させる人の総数です．そして，右側の列の数値を合計すると0.9になります．これは，病院で感染した人が平均して感染させる人の総数です．このようなテーブルの列の数値を単純に合計すると，状況によって，起こっていることの有用なヒントが得られます．

列の合計が両方とも1未満になる場合：列内の数を合計すると，両方の列で1未満になる場合，つまり，平均して1人未満の人が感染することになります．全体のR値が常に1未満になることを示しており，この病気が制御されていることになります．

列の合計が両方とも1を超える場合，各列の合計が1を超える場合，すべての列について，つまり，すべての感染が平均して複数の人に感染することになります．全体のR値が常に1より大きいことを数学的に示すことができ，病気の新しい感染が指数関数的に増加することになります．

列の1つが1を超え，列の1つが1未満の場合，難しい状況になります．この状況では，全体のRを計算して，疾患が制御下にあるのか，制御不能なのかを知るには，数学の知識が必要になります．例題は，この場合です． 

世代を超えて
この例で，もう少し数学の詳細を説明します．コミュニティの元の感染者数には$$ I_ c（0）= 1000 $$，病院の元の感染者数には$$ I_ h（0）= 1000 $$の記号を使用します． 1つのグループの第1世代の新しい感染を計算するには，そのグループ内で生成された新しい感染の数（つまり，元のコミュニティ感染によって引き起こされた新しいコミュニティ内感染$$ R_ {cc} I_ c（0）= 800 $$）と，他のグループからの新しい感染の数（つまり、病院での元の感染によって引き起こされた新しいコミュニティ感染$$ R_ {hc} I_ h（0）= 200 $$）が必要です．次に，コミュニティの第1世代の新しい感染，$$ I_ c（1）$$，および病院の$$ I_ h（1）$$の計算は次のとおりです．

$$I_{c}(1)=R_{cc}I_{c}(0)+R_{hc}I_{h}(0)=800+200=1000$$
$$I_{h}(1)=R_{ch}I_{c}(0)+R_{hh}I_{h}(0)=400+700=1100$$

fig

$$I_{c}(2)=R_{cc}I_{c}(1)+R_{hc}I_{h}(1)=800+220=1020$$
$$I_{h}(2)=R_{ch}I_{c}(1)+R_{hh}I_{h}(1)=400+770=1170$$

fig

このようにして，未来の世代に対して順次計算を進めることができます．

中間のステップをして，初期状態の感染数でｎ世代の感染数を記述するのが効率的です．

$$ I_{c}(2)=R_{cc}I_{c}(1)+R_{hc}I_{h}(1) =R_{cc}(R_{cc}I_{c}(0)+R_{hc}I_{h}(0))+R_{hc}(R_{ch}I_{c}(0)+R_{hh}I_{h}(0))$$ 
$$=(R_{cc}^{2}+R_{ch}R_{hc})I_{c}(0)+(R_{hc}R_{cc}+R_{hh}R_{hc})I_{h}(0) $$

$$ I_{h}(2)=R_{ch}I_{c}(1)+R_{hh}I_{h}(1) =R_{ch}(R_{hc}I_{h}(0)+R_{cc}I_{c}(0))+R_{hh}(R_{hh}I_{h}(0)+R_{ch}I_{c}(0))$$
$$=(R_{ch}R_{hh}+R_{cc}R_{ch})I_{c}(0) +(R_{hh}^{2}+R_{hc}R_{ch})I_{h}(0)$$

$$ \left( \begin{array}{@{\,} c @{\, } } I_{c}(1) \\[0mm] I_{h}(1) \end{array} \right) =\left( \begin{array}{@{\,} cc @{\, } } R_{cc} & R_{hc} \\[0mm] R_{ch} & R_{hh} \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } I_{c}(0) \\[0mm] I_{h}(0) \end{array} \right) =\left( \begin{array}{@{\,} c @{\, } } R_{cc}I_{c}(0)+R_{hc}I_{h}(0) \\[0mm] R_{ch}I_{c}(0)+R_{hh}I_{h}(0) \end{array} \right) $$

 $$\left( \begin{array}{@{\,} c @{\, } }
I_{c}(2) \\[0mm]
I_{h}(2)
\end{array} \right) =\left( \begin{array}{@{\,} cc @{\, } }
R_{cc} & R_{hc} \\[0mm]
R_{ch} & R_{hh}
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
I_{c}(1) \\[0mm]
I_{h}(1)
\end{array} \right) =\left( \begin{array}{@{\,} cc @{\, } }
R_{cc} & R_{hc} \\[0mm]
R_{ch} & R_{hh}
\end{array} \right) \left( \begin{array}{@{\,} cc @{\, } }
R_{cc} & R_{hc} \\[0mm]
R_{ch} & R_{hh}
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
I_{c}(0) \\[0mm]
I_{h}(0)
\end{array} \right) $$

$$\left( \begin{array}{@{\,} c @{\, } }
I_{c}(n) \\[0mm]
I_{h}(n)
\end{array} \right) =\left( \begin{array}{@{\,} cc @{\, } }
R_{cc} & R_{hc} \\[0mm]
R_{ch} & R_{hh}
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
I_{c}(n-1) \\[0mm]
I_{h}(n-1)
\end{array} \right) =\left( \begin{array}{@{\,} cc @{\, } }
R_{cc} & R_{hc} \\[0mm]
R_{ch} & R_{hh}
\end{array} \right) ^{n}\left( \begin{array}{@{\,} c @{\, } }
I_{c}(0) \\[0mm]
I_{h}(0)
\end{array} \right) $$

$$I(n)=MI(n-1)=M^{n}I(0)$$

 （訳者注）

$$PMP^{-1}=\left( \begin{array}{@{\,} cc @{\, } }
\lambda _{1} & 0 \\[0mm]
0 & \lambda _{2}
\end{array} \right) $$と対角化できれば，$$PM^{n}P^{-1}=\left( \begin{array}{@{\,} cc @{\, } }
\lambda _{1}^{n} & 0 \\[0mm]
0 & \lambda _{2}^{n}
\end{array} \right) $$

全体のRは？
線形代数を使用すると，伝染病の成長をより明確かつエレガントに表現できます．

たとえば、次世代マトリックス$$ M $$の固有値と呼ばれるものを見つけることができます．これらは2つの数値$$ \lambda _1 $$と$$ \lambda _2 $$であり，対応する固有ベクトル$$ v_1 $$と$$ v_2 $$があるため，行列による固有ベクトルは，固有値倍だけ拡大されます．

$$Mv_ i = \lambda _ i v_ i $$
そして、誘導で示すことができ、固有ベクトルに$ M $を繰り返し適用すると、次のようになります。
$$ M ^ k v_ i = \lambda _ i ^ k v_ i $$
もう1つの有用な線形代数の事実は、ほぼすべての行列で、固有ベクトルが線形に独立していることです。これは、1つの固有ベクトルが他の固有ベクトルではないことを意味します。そして実際、これらの2つの固有ベクトルの線形結合として任意のベクトルを書くことができます。 （この事実を真実にするには、固有値と固有ベクトルに複素数を許可する必要があります。詳細はこちらで読むことができますが、これについては気にしない理由を少し後で明らかにします。）
つまり、コミュニティと病院の元の感染数で構成される感染ベクトル$$ I（0）$$を次のように記述できます。

$$ I（0）= av_1 + bv_2 $$
次に、次世代の新しい感染症は次のようになります。
$$I（1）= MI（0）= aMv_1 + bMv_2 = a \lambda _1v_1 + b \lambda _2v_2$$
そして、新しい感染の$$ n $$世代は次のようになります。
$$I（n）= M ^ nI（t）= a \lambda _1 ^nv_1 + b \lambda _2 ^ nv_2$$
線形代数からの別の結果によると、次世代行列のエントリはすべて正の実数であるため（負の数に感染させることはできません）、（大きさの点で）「最大」の固有値もaになります。正の実数。私たちはみな指数関数的成長に精通しているので、世代数が増えるにつれて，$$I（n）$$の式がその支配的な固有値を含む項によってどのように支配されるかがわかります。
実際、この支配的な固有値が、そのような次世代行列で表される区分化されたシステムのRの全体的な値と同等であることを示すことができます。そして最終的に、システムは、対応する固有ベクトルによって表される2つの設定間の感染の分割に落ち着きます。

$$ \left( \begin{array}{@{\,} cc @{\, } } 0.8 & 0.2 \\[0mm] 0.4 & 0.7 \end{array} \right) $$

この例では、次世代行列の固有値
1.04と0.46（小数点以下2桁に四捨五入）です。したがって、この区分された母集団の全体的なRはR = 1.04です。そして、何世代にもわたる感染症の後、新しい感染症の約45％が地域社会で発生し、新しい感染症の55％が病院で発生します。 （これは、支配的な固有ベクトルが（0.84、1）であり、1.84のうちで0.84が45％，1が55％ですからわかります）

Rでわかること
この例では、人口を2つのグループに分けています。病院（介護施設を含む）とコミュニティです。しかし、介護施設、病院、地域社会など、より多くのグループを区別したい場合はどうでしょうか。または、いくつかの地理的地域間で？数学は、任意の数のグループに分割された母集団に拡張できます。次世代マトリックス（モデルでは2x2）の次元はグループの数まで増加し、グループのいずれか2つの間の感染の伝達のエントリと、各グループ内で生成された感染の個々のR値が含まれます。そして、上で紹介した数学は今でも機能し、全母集団の全体的なRは次世代行列の主要な固有値です。

前の記事で直感的に調査したように、区分化された母集団の全体的なRの値は、次世代行列の個々の数値の値よりも常に大きくなります。これは、任意の数のグループに分割された母集団について数学的に証明できます。支配的な固有値である全体のRの計算は、線形代数を使用すると簡単ですが、頭の中で行うのは簡単ではありません。上の図の例で示したように、グループ間およびグループ内の透過率の値がすべて1未満であっても、覚えておくべき重要なことは、全体のRが1より大きい場合があることです。確実に計算する必要があります。

何世紀も前に、数学者は整数の特性と整数間の関係を研究はじめました。 現在、数論として知られている数学の分野である数の研究は、最も古い数学分野の1つです。それは深く魅力的な問題に満ちた豊かな歴史を持っており、その多くは何世紀もたっても未解決のままです。

そのような問の1つに、完全数があります。 完全数とは、その約数の合計に等しい整数です。たとえば、$$ 6 $$は$$ 2,3 $$と$$ 1 $$で割り切れ、合計$$ 1 + 2 + 3 = 6$$にも等しくなります。同様に$$ 28 $$ は，$$ 1,2,4,7 $$と$$ 14 $$で割り切れ、$$ 1 + 2 + 4 + 7 + 14 = 28$$と等しくなります。その神秘さで、完全数は数学者も非数学者も同じように魅了します。

完全数とユークリッド
完全数の物語は、2300年以上前に、これまでに発行された最も影響力のある数学的著作の1つである”Elements“原論で始まりました。ギリシャの数学者ユークリッドは、紀元前300年頃に生まれ、プトレマイオス1世の統治下でアレクサンドリアの教師として完全数の研究をしました。

ユークリッドは幾何学だけと思われがちですが、実際は数学の多くの分野を研究しており、数論も彼の研究分野のうちです。原論の第9章の最終命題で、ユークリッドは次の命題を証明しました。

例で説明しましょう。数値$$ 1 $$（ユニット）から始めて、後続の数値に$$ 2 $$を掛けて、数値のシーケンス$$ 1、2、4、8、16 $$を取得します。これらの数を足し合わせると、素数$$ 1 + 2 + 4 + 8 + 16 = 31 $$に到達します（素数は、それ自体と$$ 1 $$だけで割り切れる数です）。ユークリッドの結果は、合計$$ 31 $$にシーケンスの最後の数$$ 16 $$を掛けた値が完全数であると述べています。つまり、$$ 31×16 = 496 $$が完全数です。

確かに：$$ 496 $$の約数は$$ 248、124、62、31、16、8、4、2 $$および$$ 1 $$です。

$$1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496$$
実際、$$ 496 $$は$$ 6 $$と$$ 28 $$に続く3番目の完全数です。

ユークリッドの驚くべき結果は、新しい完全数を発見する確実な方法を提供し、後続の数学者の世代に影響を与えました。ただし、問題点はあります。最後に完全数を得るには、合計の結果（この例では$$ 31 $$）は素数でなければなりません。しかし、これは常に当てはまるわけではなく、それをチェックするにはかなりの量の計算が必要です。今日でも、数学者は新しい素数を特定する方法を模索しています。

完全数とニチョマコス
私たちの物語の次の主要なプレーヤーは、Nichomachusです。ギリシャのもう1人の哲学者であるニチョマコスは西暦150年頃の人で、有名なピタゴラスによって始められた思想学校の主要メンバーでした。ユークリッドとは異なり、ニチョマコスは彼の結果の証明提供をせず、彼らの真実を主張しました。

したがって、彼の完全数への影響は、命題ではなく、むしろ彼の作品「算術入門」で提示した数の分類ー過剰数、不足数、完全数ーにあります。

ニチョマコスによると、不足数$$ n $$は、約数の合計が$$ n $$に満たないもので、過剰数$$ n $$は、約数の合計が$$ n $$を越すものであり、前述のとおり —完全数$$ n $$には、合計が正確に$$ n $$となる約数があります。 当然、すべての数はこれらの3つのカテゴリのいずれかに分類されます。

ニチョマコスは、このように数字を分類しただけでなく、不足数も過剰数も完全数よりも質が低いと主張しました。

多すぎる場合、過剰、過多、誇張、虐待が発生します。少なすぎる場合は、欲求不満、デフォルト、困窮、不足が生じます。そして、等しい場合、美徳、公正、妥当性、美しさ、そしてそのようなものを生み出します。

実際、その後の思想家はしばしばニチョマコスの分類に従い、完全数を特定の神の質を持つものとして扱いました。たとえば、4世紀の神学者聖アウグスティヌスは、神の都で次のように書いています。「6はそれ自体が完全な数であり、神がすべての物を6日間で作成したからではなく、その逆です。数が完璧だからだ」

別の例として、10世紀のドイツの詩人であるHrotsvitは、完全数を「主要な数」と呼び、彼女の劇「サピエンティア」の最初の4つ、つまり$$ 6、28、496、$$および$$ 8128 $$について論じています。したがって、ニチョマコスは、独自の方法で今日でも続く完全数を神格化するという伝統が生まれました。

完全数とイブン・アル・ハイサム
ユークリッドの死後1200年以上の間、私たちは中東を旅し、完全な数に関する別の結果を得ました。ペルシャの数学者イブン･アル･ハイサムは、物理学や光学から数論や幾何学に至るまで、さまざまな分野を研究していました。特に、彼は数学的な方法の事例研究としてユークリッドの要素を熱心に研究しました。

完全数に関する限り、イブン･アル･ヘイサムはユークリッドの命題の逆も真実であると最初に示唆したようです：完全数を生成するためのユークリッドのプロセスは、実際にはすべての完全数を生成し、完全数はすべて偶数です（このシリーズの次の記事を参照してください）。イブン・アル・ヘイサムはこの結果を完全に証明することはできませんでしたが、完全数の完全な特徴付けを試みた最初の数学者でした。その後の多くの数学者たちは、イブン・アル・ヘイサムの研究を模倣しようとして、さらなる進歩を期待したが、完全な特性が明らかになるまでさらに700年待たなければならなかった。

完全数とオイラー
レオンハルト・オイラー、1707年から1783年。 ヨハン・ゲオルク・ブラッカーの肖像。

1707年に生まれたレオンハルト・オイラーは、今まで生きてきた中で最も多作な数学者の一人です。 実際、数学のほとんどすべての分野で彼の名前が付けられており、数論も例外ではありません。オイラーは、完全数を生成するためのユークリッドのアルゴリズムが実際にすべての偶数を生成することを証明しました。

そのため、完全数は、ユークリッドによって導入された形式の素数と正確に1対1で対応しています。 さらに、オイラーは8番目の完全数を特定しました— この200年で発見された最初の新しい完全数です。

 $$（2^30）(2^31－１)＝2305843008139952128$$

完全数の発見の間に経過した長い期間を考えると、一部の数学者は、これ以上は発見されないと自信がなくなりました。 確かに、ピーター・バーロウは、数論の初歩的な調査で、「オイラーの完全数」は現在知られている最大の完全数で、おそらくこれまでに発見された中で最も大きい数と言った。 というのも、役に立たないだけの完全数を、さらに探す可能性は低いからです。しかし、ピーター・バーロウは18歳で亡くなり（9番目の完全数が発見される21年前）ました。 数論の進歩と新しいテクノロジーの時代は、想像を絶するほど大きな完全な数を特定することが現実的に可能性となりました。

今日の完全数
早送りし今日に戻りました。これまでに51の完全数が発見されました。 最大の数字は49,724,095桁です（すべてのリストはここ）。 さらに印象的なのは、ちょうど1年前に発見された50番目の完全数よりも300万桁以上多いことです。 この進歩は、図1と2に示されている現象である数学とコンピュータサイエンスの強力なパートナーシップの結果です。

もちろん、完全な数値を計算することは、それらについての事実を証明することとはまったく異なります。 ほぼ毎年新しい完全数も発見されていますが、多くの疑問でさらに研究が必要です。

奇数または偶数のすべての完全数を共有する共通の特性は何ですか？
完全数は無限にありますか？
奇妙な完全数はありますか？
数え切れないほどの数学者が、発見的な議論や専門的な事例のいずれかを用いて、これらの問に迫っています。 しかし、一般的な答えはとらえどころのないままです。 次の2つの記事「完全に偶数」と「完全に奇数」では、これらの質問に対する実質的な結果を要約し、解明し、結び付けて、おそらく最も奇妙な完全の定義に数学者と非数学者を同様に引き付けるという最終目標を掲げています。

 ［plus magazineより． submitted by Marianne on February 5, 2020］

by the Plus Editors Rachel Thomas and Marianne Freiberger.

この数週間によく聞く2つの言葉に，集団免疫と基本再生産数$$R_0$$と呼ばれる数（R noughtと言う）があります。

基本再生産数
COVID-19などの感染症を考えると，$$R_0$$は病気の基本再生産数です．つまり，集団のすべての人が病気への感染感受性がある場合，感染者が感染させる平均人数です．COVID-19の場合，この数は現在2から2.5の間にあると推定されています．季節性インフルエンザの場合，0.9から2.1の間です．そして，はしかの場合，それはなんと12から18です．

$$ R_0 $$が十分に大きいと，病気が急速に広がるのがわかります．たとえば，$$ R_0 $$が2の場合，1人の感染者が次のような新しい感染の増加を引き起こします．

第1世代：新しい感染$$ 2 $$
第2世代：新しい感染$$ 4 $$
第3世代：新しい感染$$ 8 $$
第4世代：新しい感染$$ 16 $$

$$ n $$世代の新しい感染は$$ 2 ^ n $$です．患者の感染性が続くのが1週間だとすると，この率では，全世界の人口（78億人）は32週間強で感染します．

基本再生産数$$ R_0 $$が1未満の場合，非常に異なる描像になります．例として，$$ R_0 = 0.5$$とします．明らかに，感染した人は半分の人に感染させるとはできませんが，これは平均であることを覚えておいてください．つまり，10人の人が 他の5人に感染させる，または100人が他の50人に感染させると想定します．前と同じように，最初に感染者が1人いると仮定すると，新しい感染の数は次のようになります．

第1世代：新しい感染$$ 0.5 $$
第2世代：新しい感染$$ 0.25 $$
第3世代：新しい感染$$ 0.125 $$
第4世代：新しい感染$$ 0.0625 $$

$$ n $$世代の感染は$$（0.5）^ n $$件の新しい感染があります．世代の数$$ n $$が大きくなるにつれて，この数はますます小さくなり，病気は消滅します．

$$ R_0 = 1 $$の場合はどうでしょう？ この場合，病気は風土病endemicになります．常に集団に存在しますが流行epidemicはありません．

実効再生産数
それでは，はしか，あるいは季節性インフルエンザの株いくつかは$$ R_0 $$が1より大きいのに，なぜ全世界がずっと前にこれらの疾患に感染していないのでしょうか？その理由は，集団のすべての人に感受性があるとした場合の感染した人が感染させる平均人数が$$ R_0 $$でしたが，その世界にいた人は免疫力がなく，予防ワクチンがない条件です．実際には，他の場所で病気に感染した人が，これまでにその病気がなかった世界に入ったからです．

$$ R_0 $$が$$ 2 $$の場合，前述のように，最初は感染者の数が急激に増加します．

しかし，いったん人が病気から回復したら，彼らは（うまくいけば）ある程度の免疫を獲得するでしょう．つまり，しばらくすると，完全な感受性のある集団ではなくなります．集団の一部の人々が影響を受けない理由は他にもあります．彼らは他の理由で免疫があるかもしれないし，あるいは，ワクチンがある場合彼らはそれを接種したかもしれないし，他の集団から隔離されているかもしれません．

 実際の状況では，病気の実効再生産数を調べる必要があり，$$ R $$で表します．一部の人が免疫を持っている（または他の介入が行われている）集団で感染者が感染させる平均数です． もちろん　$$ R_0 $$と$$ R $$は関連しています．病気に感受性のある集団の割合を$$ s $$と書くと，

$$R=sR_0$$
例として，集団の半分だけが感受性がある場合，$$ s = 0.5 $$，$$ R = 0.5R_0 $$になります． この場合，$$ R_0 $$が$$ 2 $$以下の場合，$$ R $$は$$ 1 $$以下であり，病気は伝染病になりません． ワクチン接種であれ，社会的距離であれ，あらゆる介入の理想的な目的は実効再生産数を1未満にすることです．

集団免疫
これは，集団免疫とどう関係があるのでしょうか？集団免疫の背後にある一般的な考え方は，多くの人々が免疫を持っている集団では，病気の感染が広がらない．それによって免疫のない人々を守るので，この集団は脆弱な個人を保護します．

それでは，集団免疫を獲得するには，集団の何人が免疫を必要とするのでしょうか？ 病気の基本的再生産数が$$ R_0 $$で，1より大きいため，伝染病の脅威になると想像してください．私たちが見てきたように，実効再生産数$$ R $$が1未満の場合は，この病気はやがて消滅します． したがって，集団免疫を達成するには，実効再生産数$$ R $$を1未満にする必要があり，$$ R = sR_0 $$，$$ s $$は感受性のある人口の割合なので，

これを並べ替えると、

$$s <1 / R_0$$
つまり，集合中の感受性のある人々の割合を$$ 1 / R_0$$未満にする必要があります．これを実現するには，何人の人々が免疫力を必要とするのでしょうか．感受性の高い人の割合が$$ s $$である場合，感受性のない，つまり免疫のない人の割合は$$ 1-s $$です．

$$s <1 / R_0 $$　ということは，　$$1-s> 1-1 / R_0$$
集団免疫を達成するには，少なくとも人口の$$ 1-1 / R_0 $$の割合が免疫を持つ必要があります． $$ R_0 $$が2.5（COVID-19の推定値の上限）の場合，これは少なくとも免疫力のある集団の$$ 1-1 / 2.5 = 0.6 $$，60％に相当します．

 どうやって達成するか？理想的には，人口の少なくとも60％にワクチン接種することです．ワクチンがなければ，このレベルの免疫が病気になり免疫されることによって自然に達成されることを期待します．しかし，多くの人がCOVID-19で亡くなっているので，感染を増やすと免疫力が高まるという知識に自信をもって，集団全体に適用できません．

世界中の多くが現在封鎖されているのは，脆弱な人々と私たちの医療システムを保護する必要があるからです．皮肉なことに，封鎖とは，私たちの多くが感染したことによる免疫力を獲得していないことを意味します．

それでは，この最悪のシナリオで何をすべきでしょうか？ 1つのオプションは，ワクチンができるまでロックダウン状態を維持することですが，それは1年以上かかる可能性があります．もう1つは，間欠的なロックダウンを行って，流行の急増をヘルスケアシステムの重要な能力より低く保つことです．

現時点では，誰も将来何が起こるか正確には知らないのです．私たちの知識にもとづく推論は，パンデミックの経過を予測しようとする数学的モデルに基づいています．私たちの現在の苦境から最善の出口戦略を見つけるために，緊急の呼びかけが科学モデリングコミュニティに出ています．

上記の計算は，ワクチン接種に関する重要なメッセージも送信します．これは，病気の予防接種を受けている個人を保護するだけでなく，何らかの理由で予防接種を受けず，したがって脆弱な人々も保護します．予防接種はあなたのためだけではなく，集団全体のためです！

クバンチク8月号には宇宙速度の話が載っています．

https://kvantik.com/issue/pdf/2020-08_sample.pdf
その書きだしは以下のようで，人類最初の宇宙飛行士ガガーリンの時代を思い出しました．

■セルゲイ・パブロビッチ・コロレフが率いるソビエトの科学者、設計者、エンジニア、労働者のプロジェクトは、1957年に見事な勝利を収めました。
10月4日、彼らは最初の人工地球衛星を軌道に打ち上げました。
1961年4月12日、最初の宇宙飛行士、ユーリ・アレクセービッチ・ガガーリンを送り出しました。有名なガガーリンの第一声，«Поехали!行くぞ！»が世界中で響き渡り、人類は宇宙時代に突入しました。
宇宙のテーマは急速に広がり、ロケット、宇宙服、無重力、第一宇宙速度、第二宇宙速度という新しいテーマと概念が登場しました。
私たちの世代の少年たちは皆、夢の中で宇宙飛行士の宇宙服を試着しました。無重力については別の機会に話しますが、ここでは宇宙速度についてとりあげます。
最初の人工地球衛星は直径58 cmのボールであり、「ビープ」音の信号だけを送信しました。しかし、第一宇宙速度に達しました！
その1年後の1959年1月2日、Luna-1宇宙船は月へと第二宇宙速度で飛行しました。
2006年1月19日に米国の自動惑星間ステーションNew Horizo​​nsが最高速度16.26 km / sで地球を脱出、太陽との相対速度は45 km /秒でした。これは地球の軌道運動の方向に打ち上げられ地球の公転速度が加算されています。

■第一宇宙速度
オブジェクトを水平方向に発射し地球の周りを円軌道で周回させる速度です。オブジェクトを発射する高さが高いほど、この速度は遅くなります。 たとえば、国際宇宙ステーションは400km高度で7.6km/sの速度で周回します。
月は地球から384500 kmの距離で，1 km/sの速度で周回します。 地表からなら7.9 km / sの速度に対応します。これを、第一宇宙速度と呼びます。
同様に、地球は太陽の周りを30 km/sの速度でほぼ円形の軌道で公転しています。
衛星の速度がその高さの第一宇宙速度よりわずかに速い場合、その軌道は楕円になります。地球の周りのすべての衛星と太陽の周りの惑星は、楕円軌道です。 そして、彗星の軌道も楕円形で、非常に細長いので、彗星は軌道に沿って「暗闇の中へ」飛び去り、時折のみ太陽のそばに戻ります。

第二宇宙速度
惑星の重力に打ち勝ち、その周りに閉じた軌道を残すために宇宙船に与えられなければならない速度ですが、惑星に戻らず、無限に飛んでいくことが想定されています。地球の近くでそのような速度を持つ物体は、地球の近くを離れて太陽の衛星になります。
第二宇宙速度は、第一宇宙速度の≈1.4倍です。

第三宇宙速度
地球の引力だけでなく、太陽の引力にも打ち勝ち、太陽系を去ることができる最小速度です。
地球の公転速度の√2倍ですが公転速度を差し引く(地球から見た相対速度）と、　(√2-1)･30km/s≒12km/s
地表から打ち上げる場合は、地球の引力を振り切る必要があるので、
16.6km/s

■地表から水平に発射された砲弾は重力に引かれて地表に落下する (A)。
射出速度を上げても第一宇宙速度未満ならいつかは地表に落下する (B)。
第一宇宙速度で打ち出された場合は円軌道の人工衛星となる (C)。
それ以上の速度では楕円を描く (D)。
第二宇宙速度以上の場合は地球の重力を振り切る (E)。

数学月間懇話会（第16回），第3日目（2020.7.29）にZOOMにて表題の講演がありました．

■感染症の流行－現代社会最大のリスク要因
>1918年のパンデミックインフルエンザ（スペイン風邪）は4000万以上の死者，日本で
も40万程度の死者と言われる．
>2015年のＨＩＶ感染者は3670万、新規感染者210万、エイズによる死者110万
>マラリアは、全世界で年間に3億～5億人の患者、150万人～270万人の死者（90％はア
フリカ熱帯地方）
●新興感染症（ＳＡＲＳ，ＢＳＥ（ｖＣＪＤ）,高病原性鳥インフルエンザ, Ebolaなど）、
再興感染症（結核、性的感染症、薬剤耐性の進化etc.）などによって、感染症撲滅に
関する1980年代までの楽観論は消滅。
人口増加、都市集中、環境破壊などによって、感染症流行リスクはますます増大.

●COVID-19は？

■モデリング

人口をSusceptible, Exposed,　Infective, Recovered等の部分人口にわけて相互作用をモデル化する

介入（ワクチン接種、隔離、接触制限など）によって，「感染性」人口を絶滅（感染源にならないようにする）

 Kermack and McKendrick I (1927)

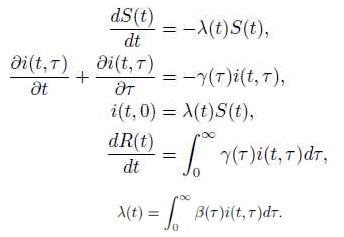
ケルマックーマッケンドリックのエンデミックモデルは
偏微分方程式の境界値問題として定式化される(Inaba 2001, 2016)

■基本再生産数R0（R-naught)

なんらかの病原体(ウイルスや細菌など）に対してすべてが感受性
(susceptible)を有する個体からなるホスト(宿主）人口（個体群）集団に
おいて典型的な１人の感染者が、その全感染期間において再生産する２
次感染者の期待数を基本再生産数(basic reproduction number)とよび、
R0で表す．

感染人口を世代毎にみて、1次(初期）感染者(primary cases)、2次感染者
(secondary cases)、3次感染者等を継続的に考えた場合、R0は等比級数
的に変化する各世代の感染者サイズの公比である。

Diekmann, Heesterbeek & Metzによって1990年に数学的な定義が確立．

R0の推定値例
現在では，従来考えられたよりも数字の分散はずっとおおきく，桁違いの数字まで観測される．
生物的にきまる感染確率・感染性期間と環境によって決まる接触頻度の積なので，
数学的定義はともかく，実際の流行への応用に際して，非常に解釈が難しい数字でもある．

■例

S:感受性人口、I:感染（性）人口、R:回復・隔離人口、
β: 伝達係数、γ: 回復・隔離率（１／γ＝平均感染性期間）

 侵入のモデル（線形化）
• 感染人口の初期成長（マルサス法則）：　
• 感染人口の初期成長率：
• 世代時間Ｔ（二次感染までの平均待機時間）：
• 侵入条件(invasion threshold)

 ■多状態モデルの例題ー2状態ＳＥＩＲモデル

 ホスト人口を、明らかに最終規模の異なる二つの集団（学童とそれ以外）
に分割してＳＥＩＲモデルを適用（インフルエンザの場合）
状態１＝学童、
状態２＝それ以外
潜伏期間、感染性期間は同一と仮定

 多状態SEIRモデル

 －－－－－

■モワレMoire：The superposition of two regular nets produces a secondary enlarged net of the same shape.
2枚のグレーチング（格子模様）を重ねたとき，グレーチングの拡大像らしきものを見たことはありますか？

これはモワレ現象の一種です．決して格子の穴の一つが拡大されて見えるわけではありません．
2枚の全く同じグレーチング（格子模様）を重ねたとき，両者の方位が互いに少し傾いているので，モワレ縞を生じます．
これは，2枚のグレーチング模様が運よく重なった場所の周囲はよく光を透過するので明るく見え，模様の重なりがずれている場所の周囲は，透過光が少なく暗く見えることによります．重なる場所の出現は周期的ですから，重ね合わせ像のコントラストには周期的な分布ができます（ビート，うなりのようなものです）．見かけの拡大率は，重ねたグレーチング間の傾きがわずかだと高倍率，傾きが大きいと低倍率に見えます．

さてこの3枚の写真のそれぞれは，全く同じ2枚のグレーチングが平行移動（傾きはなく）して重なっている状況です．これらの写真を見ると，やはり2次元的なビート・パターンが生じているのですが，全く同じグレーチングが平行にずれても，新しいビート・パターンは生じないはずです．ではなぜこのようなビート・パターンが生じたのでしょうか？
それは，2枚のグレーチングの間にスペース $$D$$ があるために，観測者から視差（パララックス）があり，前方のグレーチングよりも後方のグレーチングを小さく見込むためです．これは，わずかに寸法の違うグレーチングを重ねたのと同じ現象なので，このためにビート・パターンが生じているのです．

■考察
では，計算してみましょう：ノギスの副尺の原理を思い浮かべると良いでしょう．

本当のグレーチングの格子のサイズ　$$a$$
2枚のグレーチングの間隔　$$D$$
視点から表面のグレーチングまでの距離　$$L$$
後ろのグレーチングの縮小割合　$$δ/a≡q<1$$
として，生じるビートの周期　$$T$$　を求めて見ましょう．
$$a/(D+L)＝(a-δ)/L$$　より　$$δ/a＝D/(D+L)$$
$$T≡n･a=(n+1)(a-δ)$$より　$$δ/a＝a/(T+a)$$　⇒　$$T=a(1/q-1)$$　← $$D, L$$ を消去した
　　あるいは，　$$T=a(L/D)$$　← $$q$$ を消去した
さて，この例で生じた新しいビートの周期は，　$$T=5a$$　のように観測されます．
従って，$$L/D=5$$　が得られます．あるいは，$$1/q＝6$$，つまり　$$δ/a=1/6$$　です．

2枚の同一なグレーチングの間隔$$D$$で重ねたとき生じるビートが，もとのグレーチングのn倍に見えたら，観測点から表面のグレーチングまでの距離は$$L=n･D$$です．これは間隔$$D$$が既知の時，距離$$L$$ を計測する道具に応用できます．
ただし，$$n=1,（T=a）$$はモアレとは言いません．$$a/2$$周期の均一なコントラスト分布です．

Maxwell方程式（c.g.s.単位系による）
$$\textrm{rot}E=-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial B}{ \partial t}$$　　　　　　　　　　　　　　　　$$E$$電場 （１）
$$\textrm{rot}H=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial D}{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma E$$ $$H$$磁場 （２）
$$\textrm{div}B=0$$ $$B$$磁束密度 （３） 
$$\textrm{div}D=0+4\pi \rho $$ $$D$$電束密度，　$$\rho $$電荷密度 （４）
変位電流，空間電荷がなければ，（２），（４）式右辺の第2項はなくなる．
弱い場では線形応答； 
$$B=\mu H$$, ただし，$$\mu =1$$の物質を対象とする． （５）

$$D=\varepsilon E$$ （６）
$$J=\sigma E$$, $$J$$電流密度 （７）
$$\mu $$magnetic susceptability,
$$\varepsilon $$dielectric constant, 
$$\sigma $$electric conductivity, 

（１），（２）から，
$$ \mit\Delta E=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}E}{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial E}{ \partial t}$$, $$ \mit\Delta H=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}H}{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial H}{ \partial t}$$ （８） 

鏡の中の世界（鏡の後ろの世界）と我々の世界を考えるととても奇妙な感じになります．この不思議な気持ちを以下の文章はよく表しています．引用しましょうーーー

遠い昔，鏡の中の世界と人間の世界とはいまのように別々にはなっていませんでした．その頃は，鏡の中の生き物と人間とは色も形も全く違っていましたが，皆仲よく一緒に暮らしていたのです．鏡を通り抜けて二つの世界を行ったり来たりすることもできました．しかし，ある夜，なんのまえぶれもなしに鏡の中の生き物が地上を侵略し，人間の世界は無秩序になってしまいました．そこで人間は，鏡の中の生き物の正体が＜混沌＞そのものであることに気づきました．＜混沌＞の力はとても強力なので，黄帝の魔力以外には彼らを鏡の中に戻すことはできません．そこで，黄帝は鏡の中に混沌を閉じ込めておくため，人間の姿や動きを機械的に模倣するような呪文をかけました．－－－－－鏡の伝説，J.ブリッグス，F.D.ピート，ダイヤモンド社より

■科学知識が浸透した現代でも，鏡が恐ろしいと感じられるときがある．「生殖と鏡は数を増すので，神秘な恐ろしさ」と言ったのは誰だったか．
鏡に向かうと自分の影（＝鏡像）が見える．自分の右手を上げれば，影もて手を上げる．ただし左手だ．「自分はここにおり，向こうは影だ」と，自分だけは知っている．しかし，非常によくできた理想的な鏡であったとしたら，この様子を見ている傍観者には，どっちが本物でどっちが影かが見分けられない．もし，自分の後ろにも鏡があったら，その鏡には，後ろ姿の自分が映っている．これは合わせ鏡になるから，前の鏡には，後ろの鏡自体も映る．しかも，前の鏡に映った後ろの鏡の映像には，自分の後姿が映っている．前の鏡に映った後ろの鏡の中を，さらによく見ると，ああ，前の鏡が映っており，しかも自分の前姿の影つきだ．このようにして，２枚の合わせ鏡の中に立つと，映像がつぎつぎと繰り込まれていくのがわかる．自分の前姿と後姿が際限なく繰り返されている無限の世界に出会う．鏡を覗き込む傍観者には，どれが本物で，どれが影だかわからない．このように際限なく（=無限）繰り返される周期性を，格子と呼んだりする．格子の世界を歩いて行くと，繰り返し繰り返し同じ風景が現れる．どこまで歩いても，無限に続く格子の世界．ここには端というものがないのだから，番地もつけられない．いやになってしまう．このような世界は実際にある．結晶の世界がそれである．結晶は原子や分子が並んでできた構造単位が，整然と繰り返し配列しできている．結晶は有限な大きさだから，端はあり，本当の無限に続く格子ではないが，原子や分子は非常に小さいため，繰り返し数は莫大で，10^{22}個も続く．実用的には，無限に続いているとみなしても良いだろう．

■鏡の魔力を楽しめるもう一つの例を引用しますーーー
パイプを吸う男の話［原作：マーティン・アームストロング（英）］より

ある田舎に老人が一人で住んでいた．老人といってもまだ逞しい．人はめったに通らないさびしい道とそこにある小さな家を想像してほしい．庭には草が茂り，家は木立に隠れている．男の居間には５面窓がある．夕方，男は居間の机に向かって座る．外はだんだん暮れていく．地平の空は，赤い夕日の残りに染まるが，すぐに天空から闇が降りてくる．外が暗くなると，自分の影がガラス窓に映るようになる．窓が５面あるので，５つの自分の影が映る．外は真っ暗，木立の枝をゆする風音が聞こえる．男はタバコに火をつける．５つの影もみんなタバコに火をつける．こうして夜が更けていく．毎夜毎夜のことだ．ある晩のこと，男はいつものようにタバコに火をつけた．いつものように，４つの影もタバコに火をつけたが，一番左の影が火をつけたのはパイプだった．.....．ーーー

万華鏡をのぞくあなたに，今夜何が起こるか？万華鏡内部にある無限の世界に引き込まれたりしないか．.....これがエピローグです．

■万華鏡の起源は，物理学者ブリュースター卿の特許（1817年）です．私は，これからいろいろな角度の合わせ鏡の実験をしようと思います．それらはどれもワークショップで作ることができます．
合わせ鏡の組み合わせにより，規則正しい周期的な壁紙模様（対称性は平面群で記述される）を作るものもあり，秩序が乱れる壁紙模様もあるが，どちらも美しいものです．万華鏡を作って合わせ鏡の生成する平面群を鑑賞するのがこれから先の主題です．しかしその前に，不思議な鏡の魔力についてもう少し楽しみましょう．

■私の前に鏡があるとします．私の姿が鏡に映っています．ただし，鏡に映った影は私の方を向いていますから，影の左手は私の右手が映ったものです．つまり，鏡の中の世界は，私のいる鏡の前の世界が映ったものですが，左右が逆になった世界です．そのような，左右が逆の世界が鏡の中（鏡の後ろ）に広がっています．鏡の前の世界に居る私が，こっそり鏡の後ろに回ったとしても，鏡の後ろにある影と重なることは不可能です．影は左右が逆になっていますから当然です．鏡の後ろには，私たちの世界と左右が逆の世界が広がっているわけだが，その世界は，現実には私たちの世界の中にあるのです．とても恐ろしいと思いませんか．先ほど，鏡の後ろに回っても，左右が逆だから影と重なることはできないといいましたが，4次元の世界を動くことができれば，左右が逆転している影に重なることは可能です．
鏡の中の世界と我々の世界の混沌がとても不思議な感じがするので，いろいろなSF小説のテーマに使われています．

この記事は数を記憶する方法 https://note.com/sgk2005/n/n15dcfd723999 の続編です．

藤井聡太君の活躍はすごいですね．彼の頭には自分の棋譜はもちろんのこと数多くの棋譜が記憶されており，盤面の映像として取り出せるのでしょう．2019年，5月19日の日本数学協会の講演会の一つに，田村聡子氏（大阪市公立小学校教諭）の講演「ソロバンを取り入れた算数」がありました．
今日の学校教育は，教科書からはみ出たことは一切できない，指導要領にないことは入る余地のない時代だそうです．そのうえ，ソロバン塾よりも公文に行ってしまう時代で，ソロバン教育はなかなか大変です．

私も小学生の頃，ソロバン塾に数か月通ったことはあります．たし算ひき算しか出来ない初級ですので，上級者の技には感嘆するばかりです．その脳の働き方は想像もつきません．
田村先生の話によると，数字がソロバン珠の配列パターンで見えるそうです．私も暗算の時はソロバンを見ていた方が楽ですので，その状態はなんとなく想像できます．

2014/06/10発行のメルマガ13号で，「数を記憶する方法」という英国のエッセイを紹介したことがありますが，3.141592653589793238462643383...などの数字の列が，色彩豊かな色の列として見える人がいるそうです．
記憶術でも，こじつけのストーリをつくり，それを映像化して記憶するという方法があるそうです．どうも映像で覚えるのが決め手のようですね．私にはかえって面倒でその良さがわかりません．
日本語では語呂で覚えることはよくやります．英語の語呂合わせは日本語よりも面倒で，この点では日本語の方が有利なようです．

√5＝2.2360679は「富士山麓オウム啼く」とやる方が，各数字を同じ韻を踏んでいる言葉と結び付け（例えば），oneワン＝バンbun，twoトゥー＝シューshoe，threeスリー＝ツリーtree，fourフォー＝ドォーdoor,.....などとやるより優れているでしょう．

■ソロバンの上級者は，数字でも英語のアルファベットでもピアノの楽譜でも，ソロバン珠の配列パターンで見えるそうです．ソロバンの上級者になると，英語にも音楽にもこの能力は役立つそうでうらやましい限りです．
読み上げ算や読み上げ暗算では，ものすごいスピードで読み上げるのを
聞き逃さず，聞き分け，記憶する．その集中力がすい．
試験会場の自分の座席とスピーカーの位置で，聞きやすい座席位置と聞きにくい座席位置があるそうですが，その違いが明瞭に出るほどの極限状態の集中力です．
場所は指定されているので始めは運ですが，間違った人が抜けて前に詰めるときは，聞きやすい場所を見抜ける人は皆，そこを狙っているそうです．
そろばんの頭の使い方と集中力はいろいろなことでも役立つでしょう．

産業(化)社会

産業化社会では物が豊富でなんでも売っているので，人々は受身になってそれを享受するようになりました．ものを買うだけの都会の消費生活です．その昔，私たちは手に入らないものを工夫して作るのが楽しみでした．しかし今や，個人では作れない高レベルのものが安く売られている時代です．少年の頃のラジオ作りをやったあの楽しみが奪われたのです．コンピュータもマイコンと呼ばれた時代は楽しんで作りました．今でも作る人もおりますが，高性能なものがデザインも良く作るよりも安く手に入るとなれば，やる気がなくなります．TVの修理にしても，基板ユニット部品を丸ごと交換するので，エンジニアは自嘲をこめて自分をチェンジニアと呼ぶ時代です.　産業化社会は，都会の消費者のように豊富な物品を享受する受身の生活を浸透させました．

産業(化)社会の後に到来する脱産業社会

脱産業化社会は情報化社会になるらしいのですが，産業化社会を享受しすっかりやる気を失った受身の人間が大多数の社会ですので，主体性のない腑抜け社会，バーチャルの社会であります．はやく本当の情報社会を作りたいものです．
今や，政治も文化も，スポーツ観戦と同じ，自分がやっている気になるだけのバーチャル社会であります．主人公たるべき国民が観客化しているのです．TVはこのような受身の人間の洗脳支配に使われています．そのようなものでは情報社会になり得ません．本当の情報化社会になれば，それぞれ個人が自分で考えそれを発信できる社会になるでしょう．

現状のＴＶは限られたコメンテータやタレントが支配し，メジャーな情報がすべてを押しつぶし隠ぺいしています．マスコミ・メディアは隠れた問題を発掘し木鐸となる勇気はなく，叩ける弱いものに集中攻撃をする．なんと骨のないことか．それでも一応，何でもかんでも情報はそろえてあります．その豊富さは，逆に自分がやらずとも専門家がいる，あるいはすでに周知のことなのだと思わせることで，やる気を失わせガス抜きをしてしまう．あるいは，自分で研究して作らなくても既にあるということで開発意欲を消してしまう．逆説的な言い方をすれば，自分が選手ではないのに，ワールドカップやオリンピックで戦っているつもりになるばからしさに似ている．最大の問題は，民主主義の主体たるべき国民が観客化していることで忌々しい限りです．選挙でも変わらない，何をやっても変わらない政治に対する無力感が，観客化した受身の人々をますます増加させています．

私たちは正規分布の一点ではない

投票所が閉まって，まだ1票も開票されていないのに当選確率のでるバカらしさを見てください．少なくとも自分の入れた投票が開票されてからにしてほしいものだ．大体，世論調査というものや統計は，個人を正規分布の1点としか見ないのです．個人の個性は無視されます．RDDの世論調査も投票所の出口調査も，私は聞かれたことがありません．私の意見はどこにも反映されていないのだが，そんなことにかかわらず大勢は決まっているという現実がある．世論調査や選挙報道は，集団の統計量（巨視的な数値）だけに関心があり，私たち個人の微視的な考慮はできません．また，統計量は因果関係を論ずる論理的なものでもありません．皆様が今関心をお持ちの新型コロナ感染拡大を例にするなら，巨視的と微視的の視線の違いは，疫学統計は集団の巨視的な数値として死亡率や感染率を取り扱うが，患者の治療にあたる医師は担当する患者一人一人に目を配るというところです．
現状のビッグデータ解析は，手の届かないところから運命の決定が下りてくるようで気持ちが悪い．まだまだ不確かであります．このような未成熟情報化社会のマイナス面が，選挙投票率を低下させ，政治への関心を低下させています．さらに，国会で論争もなされない議会軽視がこの風潮をさらに助長しています．

しかし，情報社会は我々個人が主体的に発言できるプラス面があるはずです．声の大きいマスメディアに支配させていてはいけません．脱産業化時代になろうとしているのに，受身の享受体質ではいけません．個人が統計集団の中の1点ではなく，個人がそれぞれ自分で考える時代である必要があります．

(参考)産業化社会については，中岡哲郎の論説をご覧ください．

$$0$$と$$1$$だけが並んでいる語を考えます．そのような$$n$$桁の語を$$n$$-bit語と呼びます．
Q：連続して$$1$$を含まない$$n$$-bit語はいくつあるでしょうか？
A：
(1)　$$n=1$$のとき，そのような語は，$$0,　1,$$ですから，計2個あります．
これを$$a(1)=2$$と書きます．
(2)　$$n=2$$のとき，そのような語は，$$00,　01,　10$$で，$$a(2)=3$$個です．
$$11$$は$$1$$が連続するので条件に合いません．
(3)　$$n=3$$のとき，そのような語は，
$$n=2$$のときの語の末尾に$$0$$を付加した，$$000,　010,　100$$の$$a(2)$$個と，
$$n=2$$のときの末尾に$$1$$を付加したものと言いたいところですが，
$$１$$の連続を避けるために，$$n=1$$のときの語に$$01$$を付加し，$$001,　101$$の$$a(1)$$個です．これらは，互いに背反するので，この両ケースを合わせて，$$a(3)=a(2)+a(1)=5$$　となります．

■連続した1のない語の数の数列$$a(n)$$は，このような手順（一般の$$n$$で成立）で作れ，$$a(1)＝2, a(2)＝3, a(3)=5,･････$$と続き，
結局，$$a(n)=a(n-1)＋a(n-2)$$が得られます．
これはフィボナッチ数列の再帰的な定義そのものです．
フィボナッチ数列$$F(n)$$は，$$1,1,2,3,5,･････$$ですから，この問題の$$a(n)$$は
3項目から始まるフィボナッチ数列です．$$a(n)=F(n+2)$$

Q：それでは，連続した$$111$$を含まない$$n$$-bit語の数はいくつでしょうか？
A：
これも同様な議論で，$$a(n)=a(n-1)+a(n-2)+a(n-3)$$　となることが証明できます．

Q：$$n$$個のコインを順番に投げて，連続して表がでない確率を求めよ．
A：連続して表の出ないに相当する語の数は$$a(n)=F(n+2)$$でした．
$$n$$個のコインを順番に投げて実現する状態数は$$2^n$$ですから，求める確率は$$F(n+2)/2^n$$となります．

練習問題
Q：
1ドル札と2ドル札のみを使い，$$n$$（整数）ドルを払う方法の数$$B(n)$$を求めましょう．（同じ種類の札は区別しませんが，札の出る順番は区別します）

A：
１．$$n=$$1のとき：2ドル札は0枚で，1ドル札1枚出すしか方法はありません：
　　方法$$｛1｝$$のみで，方法の数は$$B(1)=1$$
２．n=2のとき：2ドル札0枚なら｛1,1｝，2ドル札1枚なら{2}で，
　　方法の数は　B(2)=2
３．n=3のとき：2ドル札0枚なら｛1,1,1｝，2ドル札1枚なら｛2,1}，{1,2}で，
　　方法の数は　B(3)=3
４．n=4のとき：2ドル札0枚なら{1,1,1,1}，2ドル札1枚なら{2,1,1},{1,2,1},{1,1,2}，2ドル札2枚なら{2,2}で，
　　方法の数は　B(4)=5
（注意）同じ種類の札は区別しませんが，違う種類の札が出る順番は区別しています）

これらの結果を考察すると，
B(n)はB(n-1)の方法に1ドル追加したものと，B(n-2)の方法に2ドル追加するものとの和になる．
2ドル追加の方法に{1,1}を追加する方法があると思う人がいるかもしれないが，追加する２つの１のうちの始めの１は，B(n-1)個の方法に繰り込まれ，すでに存在し，それに1を追加することは，すでに前者の項に含まれている．ゆえに．
B(n)=B(n-1)+B(n-2)
かくして，この方法でnドル支払う方法の数の再帰的な定義が得られました．
これはフィボナッチ数列
1, 2, 3, 5, 8, 13, 21, 34, 55, ･････
の定義と同じです．

(注)この記事は，Fibonacci and Lucas Numbers with Applications, Thomas Koshy, Wiley, Ch.4 を参考にしました．

■お知らせ
7月22日～8月22日は，数学と社会の架け橋＝数学月間です．この期間は，22/7=3.14（π）と22/8=2.71（e）に因みます．毎年，7月22日に数学月間懇話会を開催していますが，今年（第16回）は集会ができないので，
ZOOMを用いリモート（参加無料）で行います．

数学月間期間内に，次の4つの講演を行います．
●7月22日，15:00～16:30，AstronomyとAstronautics（ケプラーから宇宙エレベータまで），八坂哲雄（九州大学名誉教授）
●7月23日，15:00～16:30，Do★MATH同志社中学校数学博物館の紹介，園田毅（同志社中）
●7月29日，14:00～15:30，感染症の数理モデル，稲葉寿（東大）
●8月22日，15;00～16:30，X線や中性子で見る表面・界面，桜井健次（元物質・材料研究機構）
主催●NPO法人数学月間の会
参加方法●会員でなくても参加でき，無料ですが事前申し込みが必要です．
氏名，メールアドレス，参加日，を明記して，sgktani@gmail.comまで申し込むか，http://sgk2005.saloon.jpでオンライン参加申し込みができます．
後ほど，各回のミーティングIDとパスワードをお送りします． 
***************************************************************************************************

7月22日（月間初日）には，八坂哲雄氏の表題の講演があります．
今回の記事は，八坂哲雄氏の講演の予備知識になるように書きました．

■ケプラー

地動説の始まりはコペルニクス（1510年）です．地動説を支持したガリレオやケプラーはコペルニクスの死後の20～30年後に生まれます．ケプラーは1571年生まれで，1599年にティコ・ブラーエのもとで働き始めますが，ティコ・ブラーエはその1年半後の1601年に亡くなります．ティコ・ブラーエは20年以上の長きにわたって正確な天体観測を行ってきた偉大な観測者です．
ケプラーはティコ・ブラーエの観測記録から火星の記録をもらい，太陽に対する火星の軌道の解明を手掛けました．天体の逆行運動を合理的に説明でき地動説に立ち，円軌道を仮定し解明を進めましたが，どうしても観測値と$$８’$$の誤差がでます．苦心の末，ケプラーは火星の軌道は円でなく楕円であることを発見しました．ケプラーの発見した惑星の軌道に関する３つの法則は（1609年，1618年）：
第1法則
惑星の軌道が円ではなく楕円である．太陽の位置は楕円の焦点の1つである．当時，惑星の運動は円であると信じられていたが，火星のデータは円では説明ができなかった．
第2法則
「面積速度一定の法則」
面積速度とは，惑星の位置ベクトルと速度ベクトルの外積なので，ニュートン力学の「角運動量保存の法則」に同じ．
第3法則
惑星の公転周期の2乗は，軌道の長半径の3乗に比例する．
公転周期の長さは楕円軌道の長半径のみに依存し，楕円軌道の離心率に依存しない．楕円軌道の長半径が同じであれば，円運動でも楕円運動でも周期は同じになる．

これらの3つの法則は，ケプラーの死後（13年後）生まれたニュートンによるニュートン力学（万有引力）で，すべて導くことは容易ですが，ニュートンがやったように，逆に，ケプラーの法則からニュートン力学を作るのは非常に難しいことです．ニュートンの天才が必要でした．

■静止衛星から宇宙エレベータ

皆さん，BS放送（波長25mmのマイクロ波）の電波を受信するパラボラアンテナは，例えば，東京では，方位角224°（南西），仰角38°に向けます．これは，赤道上空にある静止衛星の方位です．

静止衛星は，赤道上空約$$ｈ＝36,000$$[km]の静止軌道にあり，地球の自転と同じ周期で公転しているので，地球から見ると静止しているように見えます．地球の赤道半径は，約$$R=6,400$$[km]ですから，静止軌道の半径は，約$$r=R+h＝42,400$$[km]，静止軌道の一周$$2πr＝266,000$$[km]を，周期$$T＝24$$[時間]で回りますから，秒速$$3$$[km/s]となります．
地球の自転と同じ角速度で地球の周りを公転する静止衛星は，静止軌道上で遠心力と地球に引かれる重力が丁度釣り合っています．衛星が地球から見て静止（衛星の公転の角速度を地球の自転の角速度と同じに保って，つまり，角速度$$ ω＝2π/T＝7.3×10^{-5} $$[rad/秒]）している状態で，もし衛星の軌道半径が静止軌道のより小さくなれば衛星は地上に落下するし，静止軌道の半径より大きな軌道半径になれば衛星は地球から離れていきます．それでは，静止衛星を上・下（地球から遠くなる・地球に向かう方向）にすこしづつ伸ばしていけば，静止衛星で長く伸びたものが作れるでしょう．これが宇宙エレベータの原理です．これを実現するために，どのような研究がなされているでしょうか，八坂哲雄氏の講演を聞きましょう．

宇宙エレベータの発案は，宇宙旅行の父，ソ連のコンスタンチン・ツィオルコフスキー（1895年）です．軌道エレベータ，ヤコブの梯子などの呼び名もあります．

漫画が面白いので，問題を訳してみました．問題３は難しいです．

■空間的な想像力を練習してみませんか？
数学，プログラミング，物理学など，科学技術のさまざまな分野で役立ちます．
ステレオメトリ（空間幾何学）の知識がなくても解決できるいくつかの問題を次に示します．

１．平面で立方体をカットして，切り口が3角形や4角形にするのは簡単です（図参照）．
切り口が正6角形になるようなカットの仕方を描きなさい．

２．立方体「キューブ」は3×3×3個の単位立方体からできています．
次のものを描きなさい；
a）中央の立方体と中央の立方体と共通の面を持つ立方体で構成される「ハリネズミ」．
［（訳注）「ハリネズミ」とは，中央の立方体に面でくっついている立方体を含む立体の形と解釈します．エッジだけではない］
b）角の立方体を取り除いたときの「ハリネズミ」．
c）「キューブ」から「ハリネズミ」を削除するとどうなりますか．

３．問２のばらばらの「ハリネズミ」で空間全体を埋めることは可能ですか？

４．四面体のそれぞれの面ごとに，面に平行な2つの平面を描きます．これらの平面は四面体をいくつの部分に分割しますか？

ロビンソンは，円形の無人島に流れ着きました．ロビンソンが海岸の小屋を出て，西に3 km，南に4 km移動した後，彼は海岸に出ました（その日は小屋に戻りました．）．翌日は，ロビンソンは小屋を出て南西に１0 km行くと海岸に出ました．1日後，ロビンソンは海岸沿いに島を一周することにしました．彼が歩く一周の距離はどのくらいありますか？

A.約16 km
B.約31 km
C.約63 km
D.約113 km
E.正解は異なります。

■解答です．図を描いて考えましょう．

最初の日は，AからBに行きます．（その日はまたAに戻ります）次の日は，AからCに行きます．A,B,Cは海岸にある点ですから，この3点を通る円の中心を求めれば円の半径rがわかり，島の全周囲は2πrとなります．

解答は，Dです．

この問題で紛らわしいのは，最初の日はAの小屋にもどると書いていないところです．（小屋にもどる）というのは私が補足しました．次の日の出発点をBとすると，非常に大きな円になります．半径51kmで全円周320kmになります．無人島の探検なのだから，小屋はAしかないのでしょうが，紛らわしいのではっきり出発点に戻ることを書いてほしかったです．

この問題は作図で解くのが良いと思いますが，座標を用いて計算で解くこともできます．西，南の方向を＋にした座標で書くと，A(0,0),B(3,4),C(10/√2,10/√2）で，円の中心(a,b)，半径rの円の方程式(x-a)^2+(y-b)^2=r^2

に，A,B,Cの座標を入れた3つの式を連立させて解き，半径rを知ればよいのです．

Fibonacci  and Lucas Numbers with Applications, Koshy，p.37-38より

フィボナッチ数は，いろいろな分野に現れます．
面を密着させた2枚のガラス板（スタックと呼びます）は，図に示すように，4つの反射面を備ています．
［訳注）表面反射；２の裏側，４の裏側は考慮しないようだ］

光線がスタックに入射し，$$n$$回反射$$n \ge 0$$をするときの異なる反射経路の数$$a_{n}$$を求めたい． (L.Moser and W.Wyman，1963年) 

$$n=0$$なら反射は起こらない．図3.26に示すように光はガラス板を通り抜けるだけであり，$$A_{0}=1$$. 
図3.26

反射が1回あるものは，２つの異なる経路があるので$$a_{1}=2$$；図3.27． 
［訳注）表面反射は数えていない］

2回反射が起こる場合には，３つの可能な経路がある；$$a_{2}=3$$；図3.28．
3回反射するなら，５つの可能な反射経路があり，$$a_{3}=5$$；図3.29．
同様に，$$a_{4}=8$$;図3.30．

一般的に，光線が$$n$$回反射されたとして，最後の反射が面1または面3で起こるなら，その前の反射は面２か４で起こらなければならない；図3.31．

面1上で$$n$$番目の反射が起こる経路の数は，$$n-1$$回の反射後に面1に到達する経路の数に等しい．
このようなパスは$$a_{n-1}$$個ある．
$$n$$番目の反射が面3で起こったとすると，$$(n-1)$$番目の反射が面4で起こらなければならない．
このような光線は面4に達する前に既に$$n-2$$回の反射をしていなければならず，
そのような経路は，定義により$$a_{n-2}$$個である．
したがって，加算原理により，$$a_{n}=a_{n-1}+a_{n-2}$$，$$a_{1}=2$$および$$a_{2}=3$$である．
ゆえに， $$a_{n}=F_{n+2}$$． 

異なる媒質間の界面をよぎつて進行する電磁波は，運動量保存則が成り立たない．運動量保存則は，一様な媒質中で成り立つからである．この場合，運動量の界面接線成分は保存されるが，界面法線成分は変化する．このため，界面で屈折が起こる．屈折の法則とは，運動量の界面接線成分の保存の表現である： 

 $$p_{0t}=p_{1t}$$  →　$$p_{0}cos\theta _{0}=p_{1}cos\theta _{1}$$

X線で用いる入射角（grazing angle)$$\theta _{0}$$，屈折角$$\theta _{1}$$の定義は，それぞれ，界面と光線のなす角である［光学で，一般に用いられているのは，”界面の法線”と光線のなす角なので，特に注意を要する］．

$$n_{1} \equiv \displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{cos\theta _{0 } }{cos\theta _{1 } }$$
物質１の屈折率は，真空に対するものとして定義され： \\
$$n_{1}=\displaystyle \frac{p_{1 } }{p_{0 } }=\displaystyle \frac{hk_{1 } }{hk_{0 } }=\displaystyle \frac{\lambda _{0 } }{\lambda _{1 } }=\displaystyle \frac{c}{v_{1 } }$$
$$v_{1}=\displaystyle \frac{c}{n_{1 } }$$であることがわかる．$$v_{1}$$は，物質１中の電磁波の位相速度．
$$E=E_{0}exp\left[ i\left( \omega t-2\pi kz \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{2\pi k}{\omega }z \right) \right] =E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{n}{c}z \right) \right] $$
$$n$$を複素数にすると：$$n=(1-\delta )-i\beta $$ 
$$E=E_{0}exp\left[ i\omega \left( t-\displaystyle \frac{1-\delta }{c}z \right) \right] exp\left( -\displaystyle \frac{\omega \beta }{c}z \right) $$
$$\displaystyle \frac{\left| E \right| ^{2 } }{\left| E_{0} \right| ^{2 } } \equiv exp\left( -\mu z \right) =exp\left( -\displaystyle \frac{2\omega \beta }{c}z \right) $$
１）虚数部$$-\beta $$は，線吸収係数$$\mu $$に比例：
$$\mu =\displaystyle \frac{2\omega \beta }{c}=\displaystyle \frac{4\pi \beta }{\lambda }$$ $$ln\displaystyle \frac{\left| E_{0} \right| ^{2 } }{\left| E \right| ^{2 } }=\mu z$$ をoptical density という．
２）実数部$$1-\delta $$は，位相速度$$v$$と関係がある．$$\delta $$が正で大きくなれば，位相速度は増加： 
$$v \equiv \displaystyle \frac{\omega }{2\pi k}=\displaystyle \frac{c}{1-\delta }$$

X線に対する物質の屈折率が$$n<1$$になること

古典的原子モデル（原子核を中心に電子が公転している）を考え，
Lorentz振動子モデル（原子核＋と電子ーが互いに束縛されて振動している）を適用する．
X線電場により，原子核に束縛された電子が振動する運動方程式：
電子の電荷：$$-q$$，　X線電場： $$E=E_{0}exp\left( i\omega t \right) $$
$$\ddot{r}=-\mit\Gamma \dot{r}-\omega _{0}^{2}r+\left( \displaystyle \frac{-q}{m} \right) E_{0}exp\left( i\omega t \right) $$
$$r=\displaystyle \frac{(q/m)}{\omega ^{2}-\omega ^{2}_{0}-i\mit\Gamma \omega }E_{0}exp\left( i\omega t \right) $$

分極$$P$$，分極率$$\chi ,j$$は電子の番号（単位体積に$$N$$個あるとする）
$$P \equiv \chi E=(-q)\displaystyle \sum_{unit vol}^{N}r_{j}=-\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{unit vol}^{N}f_{j}E_{0}exp\left( i\omega t \right) $$
ただし，
$$f_{j}=\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega _{0j}^{2}-i\mit\Gamma _{j}\omega }=\displaystyle \frac{\omega ^{2}\left( \omega ^{2}-\omega _{0j}^{2} \right) }{\left( \omega ^{2}-\omega _{0j}^{2} \right) ^{2}+\mit\Gamma _{j}^{2}\omega ^{2 } }+\displaystyle \frac{\mit\Gamma _{j}\omega ^{3 } }{\left( \omega ^{2}-\omega _{0j}^{2} \right) ^{2}+\mit\Gamma _{j}^{2}\omega ^{2 } }i$$

原子散乱因子（atomic scattering factor）の定義：
$$a$$原子の原子散乱因子$$f$$とは，$$a$$原子に属する$$n$$個の電子に対して$$f_{j}$$を総和したものである．
$$f=\displaystyle \sum_{an atom}^{n}f_{j}=f_{0}+\mit\Delta f ' +i\mit\Delta f '' $$
$$f_{0}$$は，原子中の電子数$$n$$（原子番号）；$$\mit\Delta f ' $$,$$\mit\Delta f '' $$は，異常分散項という．

マクロな光学定数の定義： 屈折率$$n$$，誘電率$$\varepsilon $$，分極率$$\chi $$
$$n=(1-\delta )-i\beta $$,    $$\delta , \beta \sim 10^{-6}$$,   $$\delta ( \sim 10^{-6}) \propto N$$
$$\varepsilon =\varepsilon _{1}+i\varepsilon _{2}$$
$$D=\varepsilon E=E+4\pi P=\left[ 1+4\pi \chi \right] E$$
$$\varepsilon =n^{2} \approx (1-2\delta )-2i\beta $$
$$\chi =-\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{unit vol}^{N}f_{j}$$

原子内の電子はそれぞれの$$\mit\Gamma _{j}(\omega ), \omega _{0j}(\omega )$$を持ち，$$\omega _{0j}<<\omega $$の電磁場追従ではそれぞれの位相遅れを生じる［特に，原子核に強く束縛されるK殻電子は顕著］．これが$$\omega \approx \omega _{0j}$$近傍で，”異常分散”を起こす．$$j$$個の電子は吸収端の振動数$$\omega _{0j}$$から高振動数側に分布する多数の振動子の集まりと見なせる．
（１）$$\omega <<\omega _{0}$$ 光と物質
$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{in unit vol}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega ^{2}_{0j}-i\mit\Gamma _{j}\omega } \cong 1+4\pi \displaystyle \sum_{in unit vol}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega _{0j}^{2 } } \right) $$
$$n \approx 1+2\pi \displaystyle \sum_{in unit vol}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega _{0j}^{2 } } \right) >1$$
（2）$$\omega _{0}<<\omega $$ X線と物質
$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{in unit vol}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega ^{2}_{0j}-i\mit\Gamma _{j}\omega } \cong 1-4\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) $$
$$n \approx 1-2\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) <1$$ $$N$$: (電子数　$$ \textrm{in unit volume)=} $$電子密度

単位体積中の電子数　$$N$$
Fig. X線電場により，原子核に束縛された電子が振動する．
振動ゆらぎ分だけ分極し双極子が生じる．

■10回（5回）対称のタイルを周期的に並べる

10回(5回)対称は，周期的に並ぶことができません．周期的に並べることが可能な回転対称軸は，2回，3回，4回，6回対称に限られます．
10回(5回)対称タイルを周期的に配列したイスラームの繰り返しパターンを調べましょう．もちろん，5回対称軸が周期的に並んでいるはずはありませんので，自然に並べるのにうまい工夫があるはずです．このようなパターンはイスラームに特徴的で，ジャーミイのいろいろな所で見かけます．

10回(5回)対称は周期性と矛盾しますから，それぞれの10回(5回)対称が支配するのはタイルの内部だけです．

このタイルの描き方を習得するのにだいぶ工夫をしました．
作図手順の足跡として，赤色の作図補助線を残しておきましたから，
皆さんも工夫してこの図を描いてみてください．

まず，中心にある円の円周を10等分することから始めます．
円周の10等分は中心角が36°の作図で，前回に正五角形（中心角72°）の作図をやりましたから，それを応用して円周の10等分を作図してください．

この長方形のタイルが単位胞になり，これを並べることにより繰り返しパターンが作れます．

この繰り返しパターンの平面群はP2mmです．

10mmという対称性の高い部分（正10角形）があります．もし，そのような対称性が全域に作用するなら，繰り返し（周期性）ができるわけがありません．10mmという点群の作用はそれぞれの赤い円内の領域に限られるので，周期性と両立できるのです．このようなイスラーム・パターンは色々な所に見受けられます．

次に，この繰り返しパターンを３つの部品によるタイル貼りと解釈してみましょう．つまり，図に示したように正10角形タイルと，ピンクのタイルと黄緑色のタイルの3種類です．
今日は，この3種類のタイルで平面が隙間なくタイル貼りされていることを確認してください．

■応用例

周期的な2次元平面では，互いに独立な並進ベクトルを2方向とれます．
これら2本の並進ベクトルが挟む平行４辺形を単位胞といいます．
並進ベクトルの組み（単位胞の形）を対称性で分類したものがブラベー格子です．
2次元のブラベー格子には，図に示す5種類があります．
そして，それぞれに対応する格子の図も掲載しておきました．

■さて，以下に伝統文様を10種挙げました．
図中に赤色ベクトルで，並進の周期を描き込んであります．
図中に描き込んだ並進ベクトルの位置はいろいろ可能で，図示したものは一例です．赤色ベクトルの選び方もいろいろ可能ですが，
単位胞の形（赤色ベクトルで囲まれた平行4辺形）が
（A）正方形，（B）長方形，（C）120°の菱形，（D）任意角度の菱形，　
の4種類のどれかにあてはめるようにとれます．
2次元のブラベー格子の5種類のうち，（E)一般形の平行4辺形に属する伝統文様は，ここの例には挙げていません．
Q．それぞれの伝統文様は，A,B,C,Dのどのタイプに属するでしょうか．

詳しくは，美しい幾何学，p86～88