note.com投稿記事

科学の発明：科学革命の新しい歴史・1

Алексей Левинのエッセイより抜粋　ИСТОРИЯ НАУКИ • 14.10.2016

ヨーク大学の歴史教授，デビッド・ウートンが表題の著書を出版しました．

'The Invention of Science' tells the story of the shaping of the modern worldThe central subject of this vibrant work is not really the inwww.csmonitor.com

ウートンは、科学革命の開始と終了の正確な日付を提唱しました：1572年と1704年。

ニコラウス・コペルニクスのモノグラフ天球の回転について（ニュールンベルクの出版社 Johann Petraeusから1543年に出版）。

ウートンは2つの理由から、コペルニクスの1543年を革命の開始とする従来の見解に同意しません。第一に、太陽中心（地動説のこと）［正確には太陽不動］コペルニクスモデルは、ケプラーとガリレオの研究の後の、17世紀の初めになってから天文学革命の要因になりました。16世紀の主要な天文学者は、コペルニクスモデルが天体の動きの計算を容易にすることは認めましたが、それが物理的な基盤を持っていることは否定しました（たとえば、砲弾がどの方向にも同じ距離を飛ぶという事実からも、地球回転の仮説は反駁できたと信じられました）。1580年代と90年代には、コペルニクスは天文学界に3人以下の信者しか持っていません、さらにそのうちの1人、ドイツのクリストフ・ロスマンは最終的に彼の敵の陣営に移りました。第二に、コペルニクスのモデルは、アリストテレスと古代の天文学者から受け継いだ地上世界とは根本的反する、月を越える（天上界）世界の絶対不変の概念をそのまま保持しています。ご存知のように、この概念は17世紀に完全に拒否されました。

コペルニクス前後の近代初期のヨーロッパの天文学は、非常に安定した研究対象でした。すべての天体は、大空で周期的な動きをし、それは永遠の世界秩序の現れと考えられていました。星は毎晩、天の同じ経路をたどり、明るさと数の両方で変化しません。彗星は唯一の例外でしたが、アリストテレスに続く科学者たちは、彗星を純粋に大気中の現象であると考えました。

このパラダイムは、1572年11月11日に最初の打撃を受けました。その夜、未来の偉大な天文学者であるティコ・ブラーエは、カシオペア星座の明るい星に気づきました。彼は、1574年3月に完全に消滅するまで、その輝きが徐々に薄れていくのを追跡しました。その前から、彼は1573年に出版され、ヨーロッパ中に衝撃を与えた本「DenovaetnulliusævimemoriapriusvisaStella」で彼の観察を説明しました。そのため、ブラヘはヨーロッパの科学者として初めて、星に予期しない変化が発生する可能性があることを発見しました（現在知られているように、彼は超新星爆発を見ました。（11月6日に韓国で、2日後に中国で、日本でも記述があります）。

左：TychoBraheの著書「DenovaetnulliusævimemoriapriusvisaStella」からの星座Cassiopeiaの描画。超新星は文字Iでマークされています。
右：スペクトルのさまざまな部分のフレームを合計して得られた超新星の残骸のスナップショット。チャンドラ望遠鏡のウェブサイトで、この残骸が2000年から2015年の間にどのように変化したかを見ることができます。
http://mvshelter.blogspot.ruからの画像

数年後、彼は、彗星は月を越える世界に属していることを証明しました。これらの発見により、ブラーエは天体の動きの膨大な量の正確な測定を実行することを目的とした研究プログラムを創始しました。デンマークの王フレデリック2世の寛大さのおかげで、ブラーエはエーレ海峡のヴェン島にウラニボルグ天文台を建設し、ユニークな観測器具とアシスタントの助けを借りて、21年間、星、惑星、月と太陽の観測の膨大なアーカイブを蓄積してきました。これは、品質と幅の点で、ヨーロッパだけでなく、中国とイスラム教徒の東の最高の天文台でこれまでに行われたすべてをはるかに上回りました。惑星が楕円軌道で太陽の周りを回転することをケプラーが厳密に証明することを最終的に可能にしたのはこれらの材料であり、それによってコペルニクスモデルの主な弱点を修正しました。これらの状況を考慮して、ウートンは新しい星の発見とティコ・ブラーエの天文学的研究の始まりを科学革命の出発点として宣言します。この年代学は、コペルニクスの英国の支持者で、天文学者、数学者のトーマス・ディッグスの活動とよく合っています。彼は1576年に、宇宙空間が無限に広がり、星が地球から任意に遠く離れている可能性があることを最初に認めた人（ただし、ディッグスは依然として太陽を宇宙の中心と見なしていましたが、真に無限の宇宙には中心はありません）。ウートンが提案する最後の瞬間は、ニュートンの「光学」（反射、屈折、屈折、光の色の扱い）の出版された1704年です。

科学革命がヨーロッパの文化に与える影響の規模を明確に示すために、ウートンは、さまざまな時代の住民の知識と認識を比較することを提案しています。 16世紀の終わりに、典型的な高学歴のヨーロッパ人（英国の紳士）は、ほぼ確実に魔女と狼狼の存在を認め、錬金術と占星術の信頼性を疑うことはありませんでした。彼らは、自然は真空を恐れ、磁石はニンニクの影響でその力を失い、殺人者の存在下で死体が出血し、彗星は災害の前兆であり、正しく理解された夢は未来を予測すると信じていました。彼らは、地球が動かず、宇宙の中心にあるという公理として受け入れました（おそらく、彼らはコペルニクスについて何か聞いていたでしょう）。彼らはアリストテレスを人類の歴史全体の中で最大の知的権威と見なし、彼らの自然に関する知識は、プリニー・ザ・エルダー、ガレン、プトレマイオスの研究、またはおそらくそれらのポピュラー書に限定されていました。彼らはまた、個人的な図書館-2、3ダースの本を持っていました。

２の累乗の概算法

https://elementy.ru/nauchno-populyarnaya_biblioteka/431670/Vsego_lish_stepeni_dvoyki

И. Акулич，«Квант» №2, 2012　に２の累乗の大きな数を求める問題があります．

（問題）

$$S = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{63}$$

$$S$$の値を計算しなさい．

$$2 S = 2^1 + 2^2 + 2^3 + 2^4 + ... + 2^{64}$$

$$2S-S＝S=2^{64}-1$$

計算機を使えば，$$2^{64}-1=18446 744 073 709551615$$ と計算できるでしょう．
計算機が無くても，許容できる精度でおおよその答えを見つけることができます。原則として、日常生活では（そしてほとんどの自然科学では）2～3%の誤差が許容されます．
$$2^{64}$$をどのように概算したらよいかという問題です．

$$2^4 = 16$$，$$2^{10} = 1024≒1000=10^3$$　だから，

$$2^{64}＝2^4・(2^{10})^6≒16・(10^3)^6$$

しかし，この誤差はかなり大きい．結局，1024を1000に置き換えること続けて6回．
このため，1.024倍の誤差の6乗$$1.024^6$$の誤差になります．

1よりも何倍も小さい数xについては、次の近似式を使うと精度が高い．

$$(1 + x)^n ≒ 1 +n･x$$　これを使うと，

$$(1+0.024)^6≒1+6×0.024＝1.144$$

従って，$$2^{64}≒16･10^{18}･1.144=18304･10^{18}$$　と補正します．その結果，

$$S≒2^{64}≒18,304,000,000,000,000,000,000$$となり（18304の後ろに0が18個），
これは正解と1%未満の誤差になります．

■注

１．数字を2のべき乗の和で表すのは，数字を2進数で表すときに必要になります．

たとえば，$$2^{10}+2^9+2^8+2^7＋2^6＋2^4＋2^3+2^2＝2042$$，　2進数で表記すると$$11111011100$$

２．この問題の最初の式は，次の一般式の$$m=64$$の場合になります．

$$2^m = (2^{m–1} + 2^{m–2} + ... + 2^0) + 1$$

３．次の性質も役に立ちます：

$$10^{10}＝(2･5)^{10}＝2^{10}・5^{10}$$

$$2^{10}>10^3$$，　$$5^{10}<10^7$$

ラクダを３つに切る方法は？

Григорий Мерзон, «Квантик» №5, 2020　より

この記事の図には，不要なものもありましたので，必要なものだけ掲載します．文章は冗長ですので私が全部書き換えました．解が1つしかないような記述も私は気に入りません．要するに，この問題は，以下の図（ラクダと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れという主旨です．パズルの問題として予備知識なしで考えるとなかなか難しいかもしれません．

この図（ラクダ）を見ると，うまく組み合わせれば，エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます．それは下の図のようになります．ラクダのモチーフが周期的に繰り返されていることがわかります．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

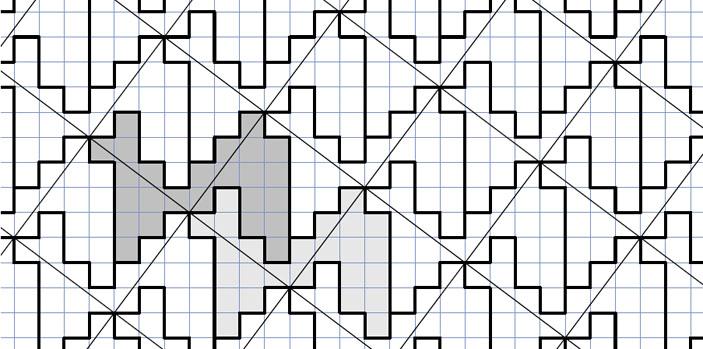
このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞と呼びます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の答ですが，私は答えはこれだけではないことを指摘しておきたいです．

ラクダが3分割できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

ラクダを３つに切る方法は？

Григорий Мерзон, «Квантик» №5, 2020

この記事の図はすべて掲載しますが，文章は冗長ですので私が全部書き換えました．要するに，この問題は，以下の図（らくだと言っている）を3つの部分に直線で切り分けて，それらを組み合わせて正方形を作れということです．

一つのラクダの頭に注目すると，右斜め上に次のラクダの頭があり，それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります．

この周期はいくつかというと，3,4,5の直角3角形（この記事ではエジプト3角形と呼んでいる）にあてはめると，周期が５であることがわかります．

このエッシャーの周期的な絵（寄せ木細工）のような繰り返すラクダの壁紙は，斜めに置かれた1辺が５の正方形を周期にしています（私の説明流儀では単位胞とよぶます）．

従って，以下のように３つの部分に直線で切れば，組み合わせて1辺５の正方形が作れます．

これがこの問題の回答ですが，私は答えはこれだけではないことを指摘しておきたいとおもいます．

ラクダが3等分できる範囲にあるならば，単位胞の正方形はずらす（平行移動）ことが可能で，答えはこれだけではなくたくさんあります．

そして彼が帰宅したとき、クヴァンチクは上の図は「ピタゴラスモザイク」といって，ピタゴラスの定理の証明になっています．これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです．

アーティストAlexeyVayner

ソフィスト，ゴルジウスの第四定理

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
のエッセイのまとめです．今回は短いが，彼の最も言いたかったことはここにあるのでしょう．最後に私（訳者）の感想を述べます．

そして今、第四の定理について、少しだけ、多分最も恐ろしいことを話します - "教えても、誰も興味を示さない”。この問題のいくつかの断片はすでに話しました。人々は有限群の研究に興味を持たなくなりました。やる人が減ってきて、テキストという形で保存されてきた知識の塊が不要になり、誰も読めなくなってきている。これは数学の多くの分野を脅かす不幸でもあります。

数学の分野によっては運がいい分野があります。例えば、グラフ理論と組み合わせの理論は同じです。本気でやり始めるにも、ほんの少し学べばよい。少し勉強して、数学オリンピックの問題が解ける。一歩踏み出して、未解決の問題があり、～やったーとなります。しかし、数学の多くの分野は、本当に美しく、それをやりたいと感じるためにも、あなたは多くのことを学ぶ必要があります。そして、その道中では、他にも多くの美しいことを学ぶことができます。しかし、道中で出会うこれらの美しさに気を取られてはいけません、そして、最後には、まさに迷路の中で、美しさを見て、そして、多くのことを学んで、この分野の数学ができるようになっていくのです。そして、この難しさは、そういった部分の問題です。数学の分野が発展するためには、それに従事しなければなりません。全ての困難を乗り越えて、そこに登って、その後もやり続けるというのは、多くの人には面白いはずです。そして今、数学はその難易度の高みに達しており、多くの分野で人知の限界が大きな問題となっています。

人類がこれらすべての問題にどのように対処するのか-私にはわかりませんが、それは興味深いものになるでしょう。

実はそれだけです。

訳注）感想：私は、このエッセイで例にあげられている有限群の問題に興味があります。しかし、この分野は数学者たちは興味を失っているようです。それは、数学の確立された分野で，これ以上研究するのは人間の理解できる限界だからです。これを乗り越えるのは、他のすべての分野の知識もマスターしている数学者ができる仕事でしょう。それを乗り越えられる人がいるのか，その人知はもう人間業ではないのか。そして、たとえ誰かが乗り越えても他の誰にも理解できず，その結果に誰も関心をもたないという状況が恐ろしい．

ソフィスト，ゴルジウスの第三定理

Дмитрий Германович Фон-Дер-Флаасс，«Квант» №5, 2010
3番目の定理-何かがわかっている場合、それは隣人には説明できません。

これらはまさに現代の数学で最も燃えている問題であり、おそらく最も誇張された問題です。人は何かを証明しましたが、その証明を他の人に伝えることはできません。または、彼が本当にそれを証明したことを他の人に納得させます。この範疇で最初の例であり、一般に最も有名なのは、4色問題です。しかし、これはまだここで発生する最も困難な状況ではありません。ここで、4色問題について少しお話しした後、さらに異常な状況を示します。

図： 5.
4色問題とは何ですか？これはグラフ理論の質問です。グラフは、エッジで接続されたいくつかの頂点です。これらの頂点を平面上に描画し、エッジが互いに交差しないようにそれらをエッジに接続できる場合、フラットと呼ばれるグラフが得られます。グラフカラーリングとは何ですか？トップスはさまざまな色で塗装しています。エッジに沿って隣接する頂点が常に異なる色になるようにこれを行った場合、色は正しいと呼ばれます。できるだけ少ない色でグラフを正しく描きたいです。たとえば、図5には、ペアで接続された3つの頂点があります。つまり、どこにも移動できません。これらの頂点は、必ず3つの異なる色になります。しかし、一般的に、このグラフを描くには4色で十分です（3色では不十分です。確認できます）。

百年の間、問題がありました：平面上に描くことができるどんなグラフも4色で着色できるというのは本当ですか？誰かが信じて4色で十分であることを証明しようとしましたが、誰かが信じずに4色では不十分な例を考え出そうとしました。また、そのような厄介な問題もありました。問題は非常に簡単に定式化されます。したがって、多くの人々は、軽薄な数学者でさえ、それに襲いかかり、それを証明しようとし始めました。そして、彼らは膨大な量の疑惑の証拠または疑惑の否定を提示しました。彼らはそれらを数学者に送り、新聞で叫んだ。私は4色の問題を証明しました！」 -そして誤った証拠のある出版された本さえ。要するに、ノイズが多かったのです。

結局、K。AppelとV.Hakenがそれを証明しました。ここで、証明のスキームについて説明します。同時に、この証拠が他の人には説明できない理由もわかります。人々は、フラットグラフがどのように機能するかを真剣に研究することから始めました。彼らは数十の構成のリストを提示し、すべてのフラットグラフでこれらの構成の1つを見つける必要があることを証明しました。これは証明の前半です。そして、証明の後半-これらの構成のそれぞれについて、それがグラフにある場合は、4色で色付けできることを確認できます。

より正確には、証明は反対からさらに進んでいます。グラフを4色で着色できないとします。前半から、リストからいくつかの構成があることがわかります。その後、これらの構成のそれぞれについて、そのような推論が実行されます。グラフにこの構成が含まれているとします。捨てましょう。誘導により、残ったものは4色に塗られます。そして、残りを4色でどのように着色しても、まさにこの構成をペイントできることを確認します。

カスタマイズ可能な構成の最も単純な例は、他の3つだけに接続されている頂点です。グラフにそのような頂点がある場合は、最後に色を付けたままにしておくことができることは明らかです。他のすべてに色を付けましょう。次に、この頂点がアタッチされている色を確認し、4番目を選択します。他の構成の場合、推論は似ていますが、より複雑です。

さて、これはどのように行われたのですか？このように多数の構成のそれぞれが常に手でペイントされていることを確認することは不可能です-時間がかかりすぎます。そして、このチェックはコンピューターに割り当てられました。そして、彼は多くの事件を調べて、これがそうであることを本当に確認しました。その結果、4色の問題が証明されました。

当初はこんな感じでした。厚い本に記録された推論の人間的な部分には、すべてが着色されていることの最終チェックがコンピューターに委ねられ、コンピュータープログラムのテキストさえも与えられたというフレーズが付随していました。このプログラムはすべてを計算し、すべてをチェックしました-実際、すべてが正常です。つまり、4色の定理が証明されています。

すぐに騒動が起こりました-そのような証拠は信じられませんでした。結局のところ、証拠のほとんどは人間ではなくコンピューターで生成されたものです。「コンピュータが間違っていたらどうしますか？」 -そんな偏狭な人たちが言った。

そして、この証明の問題は実際に始まりましたが、それらはコンピューターの部分ではなく、人間の部分にあることが判明しました。証拠に欠陥が見つかりました。もちろん、複雑な検索を含むこのような長さのテキストにはエラーが含まれている可能性があることは明らかです。これらのエラーは見つかりましたが、幸いなことに修正されました。

ヨハネスケプラー

コンピュータ部分は残り、それ以来、同じ種類の検索を行うだけで、プログラムを書き直しさえして、複数のコンピュータでチェックされました。結局のところ、正確に何を列挙すべきかが言われれば、誰もが独自のプログラムを作成して、結果が期待どおりになることを確認できます。たとえば、証明にこのような大規模なコンピュータ列挙を使用することは問題ではないように思われます。どうして？しかし、同じ理由で、4色の問題の例ですでに明らかになっています。つまり、人間の証拠よりもコンピューターの証拠の方がはるかに信頼されており、少なくはありません。彼らはコンピューターが機械だと叫びました、そして突然それはどこかで故障し、道に迷いました、そこで何かが間違っていました...しかしこれはただありえません。コンピュータが誤ってどこかで誤動作し、エラーが発生した場合（0が誤って1に置き換えられた場合）、これによって誤った結果が生じることはありません。これは結果につながりません、それはプログラムが最終的に壊れることだけです。コンピューターが実行する典型的な操作は何ですか？彼らは、そのようなレジスターからそのような番号を取得し、そこに制御を移しました。当然、この数に1ビットの変更が発生した場合、制御は誰にも移されませんでした。そこにいくつかのコマンドが書き込まれ、すぐにすべてが破壊されます。

もちろん、コンピューター用のプログラムを書く際にエラーが発生する可能性がありますが、これはすでに人為的なエラーです。人はプログラムを読んで、それが正しいかどうかを確認することができます。人は他人の証明を読んで、それが正しいかどうかを確認することもできます。しかし、人間はコンピューターよりも間違っている可能性がはるかに高いです。他の人の十分な長さの証拠を読んでいて、それに間違いがある場合、あなたがそれに気付かない可能性があります。どうして？まず第一に、証明の作者自身がこの間違いを犯したので、それはそれが心理的に正当化されることを意味します。つまり、彼は偶然にそれをしたのです-これは原則として、典型的な人がそのような間違いを犯すことができる場所です。これは、この一節を読んで、それに気づかないことで同じ間違いを犯す可能性があることを意味します。したがって、人間による証明の人間による検証は、コンピュータプログラムの結果を他のマシンで再度実行して検証するよりも、信頼性の低い検証方法です。 2つ目はほぼすべてが正常であることを保証し、1つ目はどれほど幸運かです。

そして、この問題（人々が書いた数学のテキストの誤りを見つけること）では、それはますます困難になり、時には不可能にさえなります-これは現代の数学の深刻な問題です。あなたはそれと戦わなければなりません。まだ誰も知らない。しかし、問題は大きく、現在発生しています。これにはいくつかの例があります。これはおそらくあまり知られていませんが、最も近代的なものの1つです。これはケプラーの古い仮説です。彼女は三次元空間にボールを置くことについて話します。

図： 6
まず、2次元空間、つまり平面で何が起こるかを見てみましょう。同じサークルを作りましょう。それらが交差しないように平面上にそれらを描くための最良の方法は何ですか？答えがあります-あなたは六角形の格子のノードに円の中心を置く必要があります。このステートメントは完全に些細なことではありませんが、簡単です。

3Dでは、どのようにボールをしっかりと詰めますか？まず、図6に示すように、平面上にボールを配置します。次に、図7に示すように、同じ層の別の層を上に置き、止まるまで押します。次に、同じ層の別の層を上に置きます。直感的には、これは3次元空間にボールを置くための最もタイトな方法です。ケプラーは、このパッケージは3次元空間で最も密度の高いパッケージでなければならないと主張しました（そして最初に作成したようです）。

それは17世紀に起こりました、それ以来、この仮説はそれだけの価値がありました。 21世紀の初めに、その証拠が現れました。そして、あなたの誰もがそれを手に入れて読むことができます。インターネット上のパブリックドメインにあります。この記事は200ページです。それはある人によって書かれ、コンピュータ計算だけでなく、純粋に数学的な推論も含まれています。

図： 7
まず、著者は数学的な推論を使用して、問題を有限数のケースをチェックするように減らしようとします。その後、時々コンピューターを使用して、彼はこの有限の、しかし非常に多くのケースをチェックし、すべてが収束します、そして-万歳！ -ケプラーの仮説が証明されました。そして、これがこの記事の問題です-誰もそれを読むことができません。それは重いので、場所によっては検索が本当に完了したかどうかが完全に明確ではないので、それを読むのは単に退屈だからです。 200ページの退屈な計算。人はそれを読むことができません。

一般的に言って、誰もがこの記事にはこの定理の証拠が含まれていると信じています。しかし一方で、これまで正直にチェックした人は誰もいません。特に、この記事はピアレビューされたジャーナルに掲載されていません。つまり、自尊心のある数学者は、「はい、すべてが正しく、ケプラーの推測が証明された。」

そして、これは唯一の状況ではなく、これは数学の他の分野でも起こります。最近では、セット理論、モデル理論、さまざまな分野で未解決の問題のリストに出くわしました。そして、ある仮説に対するコメントがあります。それは、このような記事で反駁されていると言われていますが、誰もそれを信じていません。

これが状況です。その人はその声明を証明しましたが、それを他の人に伝えることも、他の人に伝えることもできません。

最も恐ろしい例は、もちろん、有限の単純なグループの分類です。必要に応じて、それらが何であるか、グループが何であるか、有限グループが何であるかを正確に定式化することはしません。有限グループはすべて、ある意味で、単純なグループと呼ばれる単純なブロックから組み立てられます。これは、小さなブロックに分解することはできません。これらの有限の単純なグループは無限にあります。それらの完全なリストは次のようになります。これらは17のエンドレスシリーズであり、最後に26の個別のグループが追加されます。これらは個別の方法で構築され、どのシリーズにも含まれていません。このリストには、すべての有限の単純なグループが含まれていると言われています。この仕事は数学にとってひどく必要です。したがって、70年代に、その解決策に対するいくつかの特別なアイデアと希望が現れたとき、さまざまな国、さまざまな機関の数百人の数学者が問題を攻撃し、それぞれが独自の作品を取り上げました。いわば、このプロジェクトのアーキテクトがいて、これらすべてをまとめて1つの証明にまとめる方法を大まかに想像していました。人々が急いで競争していたことは明らかです。その結果、彼らが行った作品は合計で約10,000の雑誌ページになり、それが出版されたものです。また、プレプリントまたはタイプライトされたコピーのいずれかの形式で存在した記事もあります。私自身、そのような記事をやがて読みました。この完全な証拠の注目すべき部分が含まれていますが、公開されることはありませんでした。そして、これらの10,000ページは、さまざまな人によって書かれたさまざまなジャーナルに散在しており、さまざまな程度の理解力があります。これに関係がなく、この理論の設計者ではない一般の数学者にとって、10,000ページすべてを読むことは不可能であるだけでなく、非常に困難です。証拠の構造そのものを理解します。そしてそれ以来、これらの建築家の何人かは単に死にました。

証明は誰も読めないテキストの形でしか存在しないが、分類が完了したことが発表され、次のトラブルにつながった。新しい数学者は、有限グループの理論に行く気がありませんでした。これを行う人はますます少なくなっています。そして、50年後には、この証拠で何かを理解できる人が地球上にまったくいないということが起こるかもしれません。伝説があります：私たちの偉大な祖先は、すべての有限の単純なグループがこのリストにリストされており、他にはないことを証明する方法を知っていましたが、今ではこの知識は失われています。かなり現実的な状況。しかし、幸いなことに、この状況が現実的だと思っているのは私だけではないので、彼らはそれに苦労しており、彼らは特別なプロジェクト「有限の単純なグループの分類の証明に関連する哲学的および数学的問題」を組織したとさえ聞いた。この証拠を読みやすい形にしようとしている人々がいます、そして多分いつかそれは本当にうまくいくでしょう。これらすべての困難をどうするかを考えようとしている人々がいます。人類はこの仕事を覚えているので、最終的にはそれに対処します。しかし、それにもかかわらず、他の同様に複雑な定理が現れる可能性があり、それは証明できますが、誰も読むことができず、誰も誰にも言うことができないという証拠です。

ソフィスト，ゴルジウスの第二定理

Дмитрий Германович Фон-Дер-Флаасс, «Квант» №5, 2010
Gorgiasの2番目の定理は次のようです-
何かが存在する場合、それは人にはわかりません。
ここで、このカテゴリに分類される文の例をいくつか示します。

集合理論に問題がありました。「選択の公理は本当ですか？」のような質問をする権利はあるのでしょうか？矛盾することなく数学をやりたいだけなら、原則として、選択公理を受け入れることも、それが真実ではないことを受け入れることもできます。どちらの場合でも、私たちは数学を開発することができ、ある場合にはいくつかの結果を、別の場合には他の結果を得ることができますが、矛盾は決してありません。

しかし、今は状況が異なります。明らかに、結果があり、その答えは明らかに存在し、明らかにそれは明確に決定されていますが、人類はおそらくそれを知ることは決してないでしょう。最も単純な例は、いわゆる（3 N + 1）問題です。これについては、これから説明します。自然数を選択しましょう。偶数の場合は、半分に分割します。そして、それが奇数の場合は、3を掛けて1を足します。結果の数値についても同じことを行います。たとえば、3から始めると、次のようになります。

7から始めると、プロセスに少し時間がかかります。いくつかの小さな数から始めて、このチェーンはかなり長いことが判明するかもしれませんが、常に1で終わります。どの自然数から始めても、そのようなチェーンを構築すると、常に1になるという仮説があります。これは（3 N + 1）-問題です-この仮説は本当ですか？

すべての現代の数学者はそれが正しいと信じているように私には思えます。そして、無謀にもそれを証明しようとさえします。しかし、誰も成功しませんでした。そして何十年も経過しています。したがって、これは魅力的な課題の1つです。もちろん、真面目な数学者はそれを軽蔑します-まるで楽しいパズルのようです。何がそこにあるのか、そこに何があるのかを知る必要が誰にあるかは不明です。しかし、軽薄な数学者は、仮説が真実であるかどうかにまだ興味を持っています。それが証明されないうちは、ここで何でも起こり得る。まず、この質問には明確なyesまたはnoの答えがあることは明らかです。自然数から始めて、1に到達するというのは本当か、本当でないかのどちらかです。ここでの答えは、公理の選択や人間の意志に依存しないことは直感的に明らかです。人類はこの質問に対する答えを決して知らないという仮定があります。

ベルンハルト・リーマン
もちろん、誰かがこの仮説を証明すれば、私たちは答えを知るでしょう。証明するとはどういう意味ですか？これは、自然数が1に収束する理由を彼が説明することを意味し、理由を私たちに明らかにするです。

誰かが73桁の数字がまさにそのような特性を持っていることを証明するかもしれません。それからこのチェーンを実行することによって、私たちは間違いなく任意の大きな数字を得るでしょう。または、このチェーンが別の場所でループすることを証明します。繰り返しますが、これが仮説が間違っている理由になります。

しかし、たとえば、私にはひどい悪夢があります。この命題が真実であるが、理由がない場合はどうなるでしょうか。確かに、この命題には、ある人が別の人に理解して説明できる理由はまったくありません。そうすれば、私たちは答えを知ることは決してありません。残っているのは、すべての自然数を繰り返し、それぞれの仮説をテストすることだけだからです。そして、これは当然、私たちの力を超えています。エネルギー保存の法則は、有限の時間内に無限の数の操作を実行することを許可していません。または光の速度の有限性。一般に、物理的な法則では、有限の時間内に無限の数の操作を実行して結果を見つけることは許可されていません。

多くの未解決の問題は、この領域に正確に関連しています。つまり、原則として、彼らは本当にそれらを解決したいと考えています。それらのいくつかは決定する可能性が高いです。リーマン仮説という名前を聞いたことがあると思います。たぶんあなた方の何人かはこの仮説が何を言っているかを漠然と理解しているでしょう。個人的には漠然と理解しています。しかし、リーマンの仮説では、少なくともそれが真実であることは多かれ少なかれ明らかです。すべての数学者はそれを信じています、そして私は彼らが近い将来それを証明することを願っています。そして、まだ誰も証明も反証もできないという命題がいくつかあり、仮説においてさえ、2つの答えのどちらが正しいかは定かではありません。人類は、原則として、これらの質問に対する回答を決して受け取ることはない可能性があります。

ソフィスト，ゴルジウスの第一定理の続き

Дмитрий Германович Фон-Дер-Флаасс (1962–2010)カバー写真より
数学者が、例えば複素関数を研究するとき、複素数が実数の対であること、実数が有理数の無限集合であること、有理数が整数の対であることなどをいちいち思い出すわけではありません。出来上がったいろいろな数学対象を使っています。しかし、非常に長い話になりますが、原理的にはすべてのものは基礎から組上がっています。

では、数学者は何をするのか？彼らは、これらの数学対象のいろいろな特性を証明します。何かを証明するためには、すでに何かを知っている必要があります。何よりも、一人の数学者が得た結果が他のすべての人に受け入れられるためには、どのような初期特性から議論を始めるかの完全な合意がなければなりません。

これらの初期特性のいくつかを書き出す（それらは公理と呼ばれる）ことから始め、多くの複雑な数学対象の他のいろいろな特性を証明します。しかし、自然数では困難があります。正しいと直感的に感じる公理から導くことができないが、それにもかかわらず真実と思える自然数に関する命題があることが判明しました。

すぐに疑問が湧いてきますが、この性質が自然数にも当てはまることをどのようにして知ることができるのでしょうか？困難な問題です。自然数の公理しか扱えないのであれば、多くのことを語ることは不可能です。例えば、自然数の任意の無限部分集合について語ることはできません。それにもかかわらず、人々はそれが何であるかを想像し、これらの部分集合がどの特性によって決定されるか直感的に理解します。したがって、公理から推論できない自然数のいくつかの特性について、人々はそれらが真実であることを知ることができました。自然数のある性質を明示的に示したのは、おそらく数学者のクルト・ゲーデルが最初で、それは直感的には真実である（つまり、数学者はそれが真実であることに異議を唱えない）が、当時受け入れられていた自然数の公理からは推論できないということになる。

部分的、実際には非常に大きな範囲（数学のほとんどの分野）で、この問題は、慎重にすべてを集合に持ちこんで、直感的に正しいと思える集合理論の公理のいくつかを書き出すことによって対処されました。

言ってみれば、連想の公理。もし、いくつかの集合の集合があれば、次のように言うことができます：この集合からこれらの集合のすべての要素を含む集合を形成しましょう。このような集合が存在することには、合理的な反論はありません。また、もう少しトリッキーな公理もあります。ここでは、集合理論の中で、原理的に疑問視される可能性のある3つのトリッキーな公理を考えてみます。

例えば、こんな公理があります。要素をたくさん有すると集合で、それぞれの要素上のある関数の値を曖昧なく決めることができるとします。この公理は、この集合の各要素にこの関数を適用すると、集まったものが再び集合を形成するというものです（図2）。最も単純な例：xをx^2に変換する関数なら、自然数の集合があれば、それをそれぞれの正方形に入れるイメージで、また自然数の集合に対応させます。直感的に理解できる公理ではありませんか？もし、これらの関数が非常に複雑な方法で定義されると、集合が非常に大きくなる恐れがあります。また、私たちの関数が明確に定義されていないことは証明できるが、集合の各要素についてこの関数の具体的な意味を計算することは非常に難しい、あるいは無限に難しいという状況もあり得ます。何かしらの答えがあることは確かで、それは曖昧なものではありません。このような複雑な状況でも、この公理は適用可能と考えられており、集合論の問題の源泉の一つは、このような非常に一般的な形です。

図3
一方では自明、他方では問題をもたらす第二の公理は、この集合のすべての部分集合を抜き出せるという公理です。ある集合があれば、その集合のすべての部分集合からなる集合が存在するという。有限集合の場合は当然のことながら N個の要素の有限集合があれば、それは2^N個の部分集合しか持ち得ないことになります。基本的には、全部書き出すことも可能です。最も単純な無限集合でも問題はありません。1,2,3,4,5,6,7などの自然数の集合を取ってみましょう。自然数の集合のすべての部分集合の族が存在することは、なぜ明らかなのでしょうか？要素がわかっているからです。自然数の部分集合を想像するにはどうしたらいいのでしょうか？取り出す要素には１を、取らない要素には０を対応させる。この配列が無限に続く２進数であることを想像してみましょう（図３）。［訳注）いくつか抜き取った状態は0.1010････など頭に０．をつけて無限に続く2進数で表現できる］これで、実数は自然数の部分集合とほぼ同じであることがわかります。すべての実数が順に並ぶことを直感的に知っているので、それらは実線として明確に表すことができます。与えられた集合のすべての部分集合の集合に関する公理も成り立つのです。

さらに考えてると、ちょっと怖くなってきますが、数学者は、この公理は常に実行されると信じています：我々がある集合を持っている場合、それはまた、そのすべての部分集合が存在することを意味します。そうでなければ、何かを構築するのは非常に困難になります。

そしてもう一つ、最初は信じていなかった公理があります。その名を聞いたことがあるかもしれません。「選択の公理」です。様々な方法で定式化することができ、非常に複雑なものもあれば、非常にシンプルなものもあります。今から、選択公理の定式化の方法をお話ししますが、その中で、それが正しいことが本当に明白になります。いくつかの集合を用意しておきましょう。それらは実際には重なっているかもしれませんが、それは重要ではありません。簡単に言えば、それらはまだ重なっていないかもしれません。そうすれば、これらのセットを全部まとめたものを作ることができます。これはどういうことかというと、その要素はこれらのものになる、つまり、それぞれの要素から1つの要素を取り出して、それらすべてで1つの集合を形成する（図4）。集合から一つの要素を選択するそれぞれの方法は、これらの集合から作られるものの要素を与えます。

もちろん、これらの集合の中に空集合があり、そこから選択するものがない場合、作られるすべてのものも空になります。そして、選択の公理は、そのような完全に明白な事実を主張します。これらの集合がすべて空でない場合、作られるものは空ではありません。これは明らかに、選択の公理が実際に正しいという事実を支持する最も強力な議論の1つです。他の定式化では、選択の公理はこれほど明白に聞こえません。

すべての数学を集合理論の言語に翻訳しようとして、数学者が命題をどのように証明するかを観察すると、多くの場所で、数学者はそれに気付かずにこの公理を使用していることがわかりました。これに気がつくと、別の命題に分ける必要があることが明らかになりました。私たちはそれを使用していたので、どこかからそれを取り出さなければなりませんでした。それを証明するか、これが基本的な明白な事実であり、それを公理として使用することを許可されていることを宣言する必要があります。これは本当に基本的な事実であり、他のすべての事実だけを使用して証明することは不可能であり、反論することも不可能であることが判明しました。したがって、それを受け入れる場合は、公理として受け入れます。そして、もちろん、受け入れる必要があります。

ここで大きな問題が起こりました。この事実が明確な形で定式化され、「使用できます」と宣言されるとすぐに、数学者はすぐにそれを使用し、直感的には全く非自明な命題を多数証明しました。直感的に間違っているように見える命題すら証明しました。

選択の公理を使用して証明された、そのような命題の最も衝撃的な例は以下です。ボールがあります。それをいくつかのピースに分割し、これらのピースから2つのまったく同じボールが作れます。ここで「いくつかの部分に分割する」とは、たとえば7とすると、各点ごとに、これらの7つの部分のどれに該当するかの話で、これはナイフでボールを切るようなものではありません。はるかに難しい場合があります。たとえば、これは想像するのは非常に難しいですが、ボールを2つにカットする方法なら、座標が有理数であるすべての点を1つのピースに取り、もう1つのピース（無理数の座標を持つすべての点）も作ります。各点について、どのピースに分類されたかがわかります。つまり、これはボールを2つのピースに合法的に分割したものです。しかし、これを視覚化することは非常に困難です。これらの各ピースは、遠くから見ると、まるでボールのように見えます。これらのピースの1つは実際には非常に小さく、もう1つは非常に大きくなりますが。そこで、選択した公理の助けを借りて、この方法でボールを7つのピースにカットできることを証明しました。次に、これらのピースを少し動かして（つまり、空間内で動かしたり、歪ませたり、曲げたりすることなく）、もう一度組み立てて、2つのボールを得ることができます。当初のものと同じです。この命題は証明されていますが、やや風変わりに聞こえます。しかし、それにもかかわらず、数学者は、選択の公理のそのような結果を完全に放棄するよりも我慢する方がよいことに気づきました。他に方法はありません。選択した公理を放棄すると、それをどこでも使用できなくなり、多くの重要で美しく直感的な数学的な結果が証明できないことが判明します。結果は安全に証明できるようになりますが、同時にそのような異常な結果もあります。しかし、人々は多くのことに慣れており、これらの異常にも慣れています。一般的に、現在選択されている公理には問題がないようです。

集合理論の一連の公理があり、数学があります。そして多かれ少なかれ、人間が数学でできることはすべて、集合理論の言語で表現できるようです。しかし、ここでは、ゲーデルが算術の時代に発見したのと同じ問題が発生します。私たちの集合の世界（すべての数学の世界）を説明するかなり豊富な公理のセットがある場合、それらが真実であるかどうかを知ることは決してできないという命題があります。これらの公理から証明することはできず、反論することもできません。集合理論は強力に発展しており、今ではこの問題に最も近いものです。いくつかの問が非常に自然に聞こえる状況に直面することがよくあります。それらに対する答えを得たいのですが、答えも未知で、公理から導き出すこともできないことが証明されています。

何をすべきか？集合理論では、彼らはどういうわけかこれに対処しようとします。つまり、彼らは新しい公理を考え出そうとします。人類にとって直感的に明らかなことはすべて、20世紀の初めに開発された集合理論の公理にすでに還元されているように思われますが、まだ何か他のものが欲しいことがわかりました。数学者は直感をさらに訓練して、いくつかの新しい命題が何らかの理由ですべての数学者に突然直感的に明白に見えるようにし、それらを使用できるようにするでしょう。

もちろん、これがどのように行われるのかはわかりません。非常に複雑な命題があります。まず、集合理論を深く掘り下げて、それらが主張する内容を理解し、次に理解する必要があります。これらの命題は、実際に直感的に明白であると見なすことができ、公理と見なすことができます。これは、数学の最も神秘的な分野の集合理論が現在行っていることです。

ソフィスト，ゴルジウスの第一定理

Dmitry Germanovich Fon-Der-Flaass "Kvant" No. 5、2010

https://elementy.ru/nauchno-populyarnaya_biblioteka/431269/Teoremy_sofista_Gorgiya_i_sovremennaya_matematika

Dmitry Germanovich Fon-Der-Flaass（1962–2010）が早すぎる死を遂げました。クバントの読者はこの名前に何度も会ったことがあります。クバント誌はしばしば彼の問題を発表しました。ドミトリー・ゲルマノビッチは大きな科学で成功を収めましたが、それは彼の活動の一部にすぎません。彼は、学童のための数学オリンピック、全連合および全ロシアのオリンピック、そして近年では国際審査員を務めました。彼はさまざまな数学キャンプや学校で講義を行い、国際数学オリンピックロシアチームのトレーナーの一人でした。この文は，2009年に全ロシア子供センター「Орленокオルリョノク（わし）」で、D.Fon-der-Flaassが行った講演に基づいています。

■古代のソフィスト、ゴルジウスは、三つの定理を立てたことで有名です。第一の定理は、世界には何も存在しないということです。第二の定理は、もし何かが存在するならば、それは人間にはわからないということです。第三の定理は、もし何かが認識可能であるならば、それは隣人には言い表せない。
言い換えれば、何もありませんし、何かがあれば、それについて何も知りませんし、何かを知っていても、誰にも言えません。
これらの三つの定理に四番目を追加します。何かを言うことができたとしても、誰も興味を持ちません。
これらの四つの定理は、実は、現代数学の主要な問題です。

ゴルジウスの第一定理
世界には何も存在しない。数学の言語に翻訳すると、数学は理解できないことをしています。ある意味、これは真実です。結局のところ、数学的なものは世界に存在しません。私たちは皆、自然数が何であるかを知っています。それらは1，2，3，4，などです。そして、私たち全員が「など」という言葉の意味を理解しているという事実は大いなる謎です。「など」は「無限に多い」数を意味するからです。この世界には、無限に多くのものが存在する余地はない。しかし、私たち全員が自然数について考えるとき、私たちは皆同じことを考えていると信じています。私は7の次は8と思うが、あなたも7の次は8と思う。私が19を素数と思うが、あなたも19を素数と思う。この対象物は世に存在しないようですが、私たちはそれを知っており、私たち全員が同じことを知っています。もちろん、これは数学的な謎ではなく、哲学的な謎なので、議論は哲学者にさせます。幸いなことに、私たちは数学的対象の概念を持っているだけで十分で、それらについて考えるすべての人にとって同じです。だから数学が可能なのです。しかし、哲学的な大きな問題は残っています。

数学者が、これを厳密に考えようとすると、問題が発生します。それがこれからお話しすることです。それらが人類の記憶に出現したのはごく最近（過去100年間）のことです。

自然数に加えて、数学にはもっとたくさんのことがあります。ユークリッド平面があり、そこにあらゆる種類の三角形、角度を描き、それらについての定理を証明します。実数がある、複素数がある、関数がある、もっと恐ろしいものもある...。19-20世紀の変わり目（もちろん、それは少し前に始まった）で大きな転機がありました。人々は、多様な数学的対象の全体は、単一の概念（集合の概念）に還元できることに気付きました。確かに、単純に「集合」とは何か、「など」とは何かということを直感的に理解していれば、基本的にはすべての数学を構築することができます。

問題は、集合で何ができるかということです。集合が存在する場合、それはどういう意味でしょうか？つまり、私たちの世界、数学的対象の世界のどの要素についても、それがこの集合に含まれているか否かを尋ねられたら、はっきりした答えを得られることを意味しています。答えは明確で、私たちの意志とは完全に独立しています。これは、集合を使ってできる最初の基本的なことで、要素が集合に属するかどうかを調べることです。

もちろん、集合自体は何らかの方法で構築する必要があります。そして、最終的には、すべての豊富な数学的対象がそれらから構築されます。それらはどのように構築されるでしょう？たとえば、空集合Øを作成できます。この集合に属しているかどうかに関係なく、どの要素について質問しても、答えは常に「no，属していません」となり、空集合はすでに一意に決定されています。空集合に関するすべての質問は即座に答えられます。

そして、空集合だけしか含まない集合{Ø}を作成できます。繰り返しますが、この集合があるとはどういう意味ですか？これは、どの要素についても、それがこの集合に属しているかどうかを判定できることを意味します。そして、この要素が空集合である場合、答えは「yes」、この要素が他の要素である場合、答えは「no」になります。したがって、この集合もできました。

ここからすべてが始まります。より直感的な操作をいくつか使います。 2つの集合がある場合は、それらを結合できます。これは、一方または他方の集合の要素を含む集合があると言えます。繰り返しますが、要素が結果集合に属するか否かという質問に対する明確な答えができます。だから私たちは結合を築くことができます。等々。

ある時点で、無限に多くの要素が存在する集合があることを宣言する必要があります。自然数があることを知っているので、無限の数が存在すると信じます。自然数の集合も利用できることを宣言します。無限の集合が現れると、整数を定義できます。整数は、ゼロまたはマイナス記号の有無にかかわらず自然数のいずれかです。これはすべて、集合理論の言語で行うことができます。

有理数を定義できます。有理数とは、分子と（ゼロ以外の）分母の2つの数値のペアです。それらの間に加法と乗法を定義する必要があるだけです。そして、そのようなペアが同じ有理数と見なされるときの条件は何でしょうか。

実数とは何か？これが興味深いステップです。たとえば、それは無限小数であると言うのも良い定義でしょう。無限小数とはどういう意味ですか？つまり、各自然数は実数に含まれます。

ところで、数学者は実数をこのように定義するわけではありません。我々がすでに押さえた有理数の集合を見れば、厳密には実数の集合よりも小さいものであることを宣言しておきましょう。これは非常に厄介な定義です。実は、以前の定義と非常に似ています。例えば実数3,1415926だとすると (無限の数の連鎖が続いている)例えば、それよりも小さい有理数は何でしょうか？小数点以下の端数を切ります。3.14という数字が出てきますが、考えた実数よりも小さいです。小数点以下第4位の端数を切ると3,1415個になり、これも考えている実数よりも小さい有理数が1つ増えます。自分の数よりも小さい有理数をすべて知っていれば、その数だけで決まることは明らかです。そのような絵を視覚的にイメージすることができます。直線はすべて実数で、その中でどこかに私たちの未知数があり、その左に私たちの未知数よりも小さい多くの有理数があります。他の側のすべての有理数は、それよりも大きくなるだろう。これら2つの有理数の間に1つのチップがあることは直感的に明らかで、このチップを実数と呼ぶことにします。集合の概念から始まって、数学全体が少しずつできていきます。

空気の清浄化：屋内をCOVID安全に

plus magazine（November 5, 2020）を要約した

11月18日の東京都のCOVID19新規陽性者数は493人となり，指数関数的な増加予測グラフに乗りました．予断を許さない状況になりました．
ここで紹介する（plusmagazine，Nov.５，2020）記事は，マスク着用の効果とエアロゾルを介しての伝染を予防するための換気について語っています．たぶん，皆様の常識になっている事実の確認で新規性はないので，この記事は圧縮して紹介します．

■　COVID-19を引き起こすウイルスは、主に大きな液滴と小さなエアロゾルを介して伝染する。これらは、呼吸、会話、咳、または笑いの際に排出され、「ウイルスを含む小さな呼吸エアロゾルは、呼吸によって生成された二酸化炭素と一緒に、換気の流れによって部屋の周りに運ばれる」とリンデンらは論文で言う［Paul Linden, Rajesh Bhagat, Stuart Dalziel, and Megan Davies　Wykesによる］。「換気が不十分だと二酸化炭素濃度が高くなり、ウイルスにさらされるリスクが高まる可能性がある」

オフィス、病院、レストランなどの多くの近代的な屋内スペースの換気システムはさまざまです：　風と熱によって駆動される自然換気、または機械システムによります。混合換気は、空間内の空気を十分に混合して維持することを目的とし、置換換気は、部屋の上部から暖かい空気を抽出し、床近くの通気口から冷たい空気を供給することで、より涼しい下部ゾーンとより暖かい上部ゾーンを生成します。

COVID-19の感染に関しては、空気を混ぜることは望ましくない。「混合換気は、すべてを空中に浮遊させてかき混ぜることを目的としています」とリンデン氏は説明します。「置換換気ならば、私たちが吐き出す暖かく潜在的に危険な空気は天井に上がり、そこで抽出することができます」。

置換換気を使用しても問題が発生する可能性があります。部屋にさまざまな熱源がある場合、呼気は暖かい天井層の下に閉じ込められ、他の人によって再び吸い込まれる可能性があります。

人々の呼気の正確な挙動と病気の伝染におけるその役割を予測することは非常に難しいので、リンデンと彼の同僚は、流体力学研究所（ケンブリッジ大学の数学科学センター）で実験を行いました。

■　呼吸、会話、笑い
人がじっと座って息を止めているときでさえ、彼らの体の熱は天井に上がる暖かい空気のプルームを生成します。人が呼吸を始めたり、口を開いて話したり、歌ったり、咳をしたり、笑ったりすると、吐き出された息が2番目のプルームを生成します。伝達に関しては、この2番目のプルームが本体のプルームに同伴されて天井に運ばれるのが最善です。

もちろん、空気は見えませんが、リンデンと彼のチームは、暖かい空気を追跡できる画像技術を使用しました。「誰かが暖かい空気を吐き出すと、温度と密度の変化を見ることができます。それは光を屈折させ、あなたはそれを測定することができます」とバガットは説明します。

チームが作成した画像を以下に示します。左側の画像では、人は静かに座って鼻から呼吸し、中央の画像では通常の音量で話し、右側の画像では笑っています。各画像では、体のプルームが穏やかに上昇していることもわかります。3つのケースのそれぞれで、吐き出されたプルームが体のプルームに吸収されていないことがわかります。

上段の写真はマスクなし．下段の写真はマスクありです．

■　実験と数学

このような実験は非常に重要ですが、実験はリンデンと彼のチームの研究の一部に過ぎません。同様に重要なのは、ガスやその中の汚染物質の挙動を記述する数学モデルで、ウェルズ・ライリーの方程式があります。これは、空気感染性の病気にかかっている人と部屋を共有することで感染する人の予想される数I　を推定しています。

ここで、Sは、部屋の中で病気にあらたに感染可能な人の数であり、Γは部屋の中の既に感染している者がウイルスを排出する率を記述し、qは一人当たりの平均呼吸率、tは人々が部屋を共有している時間幅を記述する。Qは部屋の換気率、つまり新鮮な空気が部屋に入る率です。

この式をよく見てみると、Qが大きいほど（部屋の換気が良いほど）感染する人の数Iが少ないことがわかります。ウェルズ-ライリー方程式は、換気 Q は空間全体で均一であることを前提としており、リンデンと彼のチームが示したように、これは通常、人や家電製品によって生じる空気の流れも問題になり現実にはそうではありません。しかし、ウェルズ-ライリー方程式（他の多くの関連する数式とともに）は、現実の生活をより正確に記述する、より複雑なモデルの一部を形成するでしょう。

■　結論

置換換気システムは、適切に設定されている場合は、より良い選択である。
マスクは有益である。

この研究はまた、もう一つの興味深い可能性を示唆している。ウイルスを含んだエアロゾルは、私たちが息を吐くCO₂と同じように振る舞うので、部屋のCO₂レベルは警告システムに使える。CO₂レベルは非常に簡単に測定することができ、それが高い場合は、空気感染のリスクも高くなるので、リンデンらは、信号機のような警報システムを考えている。

次世代行列

疫学において、次世代行列（じせだいぎょうれつ、英: next-generation matrix）は、感染症の流行に関する区画モデルの基本再生産数を得るのに用いられる。個体群動態においては、構造化個体群モデルの基本再生産数を計算するのに用いられる[1]。マルチタイプの分岐過程でも、同様の計算に用いられる[2]。

次世代行列を用いて基本再生産数を計算する方法はDiekmann et al. (1990)[3] と van den Driessche and Watmough (2002)[4]によって与えられた。次世代行列を用いて基本再生産数を計算するために、集団全体を n 個の区画に分割し、はじめの m 個を感染集団の区画とする。時刻 t における区画の個体数を$$ {\displaystyle x=(x_{1},\dotsc ,x_{n})^{T } } $$とおき、流行モデル

$$ {\displaystyle {\frac {dx_{i } }{dt } }={\mathcal {F } }_{i}(x)-{\mathcal {V } }_{i}(x)\qquad ({\mathcal {V } }_{i}(x)={\mathcal {V } }_{i}^{-}(x)-{\mathcal {V } }_{i}^{+}(x))} $$
を考える。ここで $${\displaystyle {\mathcal {F } }_{i}(x)}$$ は i 番目の区画における新規感染の発生率を表しており、$${\displaystyle {\mathcal {V } }_{i}^{+}(x)}$$ は他のコンパートメントから i 番目の区画への遷移率を、$${\displaystyle {\mathcal {V } }_{i}^{-}(x)}$$ は i 番目の区画から他の区画への遷移率を表している。このとき

$${\displaystyle {\mathcal {F } }(x)=({\mathcal {F } }_{1}(x),\dotsc ,{\mathcal {F } }_{n}(x))^{T},\qquad {\mathcal {V } }(x)=({\mathcal {V } }_{1}(x),\dotsc ,{\mathcal {V } }_{n}(x))^{T } }$$
とおけば、上のモデルは

$$ {\displaystyle {\frac {dx}{dt } }={\mathcal {F } }(x)-{\mathcal {V } }(x)} $$
と書くこともできる。いま $$x0$$ を感染症のない定常状態とする。このとき $${\displaystyle {\mathcal {F } }(x)}$$ と $${\displaystyle {\mathcal {V } }(x)}$$ のヤコビ行列は $$x0$$ において

$$ {\displaystyle D{\mathcal {F } }(x_{0})={\begin{bmatrix}F&0\\0&0\end{bmatrix } },\quad D{\mathcal {V } }(x_{0})={\begin{bmatrix}V&0\\J_{3}&J_{4}\end{bmatrix } } }{\displaystyle D{\mathcal {F } }(x_{0})={\begin{bmatrix}F&0\\0&0\end{bmatrix } },\quad D{\mathcal {V } }(x_{0})={\begin{bmatrix}V&0\\J_{3}&J_{4}\end{bmatrix } } } $$

となる。ここで F と V は

$$ {\displaystyle F={\begin{bmatrix}{\frac {\partial {\mathcal {F } }_{i } }{\partial x_{j } } }(x_{0})\end{bmatrix } }_{1\leq i,\,j\leq m},\quad V={\begin{bmatrix}{\frac {\partial {\mathcal {V } }_{i } }{\partial x_{j } } }(x_{0})\end{bmatrix } }_{1\leq i,\,j\leq m } } $$

で定義される m 次正方行列である。このとき K = FV −1 は次世代行列と呼ばれる。その最大固有値、すなわちスペクトル半径 R0 = ρ(K) がこのモデルの基本再生産数である。

コロナウイルスとの生活（氷山の水面下にあるもの）

■氷山の水面下

2020年のSARS-CoV-2コロナウイルスのパンデミックは、前例のないものです。このウイルスが、季節性インフルエンザや他の急性呼吸器ウイルス感染症を引き起こすウイルスと相互作用をし、惹き起こす多くの問題が明るみに出たのは意外ではありません。

例えば、インフルエンザの予防接種を受けて、流行期に健康を維持していれば、感染を回避できていると考えられます。それでも、インフルエンザウイルスはまだ上気道の少数の細胞に感染している可能性があり、明らかな病気の兆候を引き起こすことなく、そこで「軽く」増殖しています。もしそうであれば、SARS-CoV-2のケースですでに証明されているように、ワクチンを接種した人でも無症候性の感染キャリアになる可能性があります。

COVID-19の患者は、最初の症状が現れる2日前に感染を広げ始める。無症状の場合でも、感染した人は呼吸やくしゃみ、咳だけでなく、糞便と一緒に最大2週間ほど環境中にウイルスを放出します。そのため、患者はウイルスの検査で陰性になって初めて隔離所から解放されるのです。

現在、人類は呼吸器感染症の90％を診断することができます。しかし、少なくともロシアでは、実際にはこれを実施していません。急性呼吸器ウイルス感染症ARVIとインフルエンザの診断は、症状によってのみ行われます。そして、ARVIの症状のほとんどはほとんど同じであるため、これではわかりません。インフルエンザはほとんどの場合、鼻水が出ずに消えますが、これはCOVID-19を含む他のいくつかの感染症でも一般的です。ARVIの特定の原因（病因）についての答えは、正確な実験室診断によってのみ与えられます。これは可能ですが、現在有料です。ARVIのPCR診断は、強制医療保険の資金調達には含まれていません。

「かぜ」やインフルエンザの特定の症例は目で判断されるため、わが国で実際に特定の病原体に一度に感染したと思われるARVI患者数を知ることはできません。これらの感染のそれぞれからの真の損傷を評価することと、最も危険で疫学的に重要なものを決定することの両方を妨げます。したがって、インフルエンザウイルスを除いて、これらの病原体に対する新しいワクチンや抗ウイルス薬を開発したり、それらの進化の長期的な傾向を追跡したりすることができません。ARVI病原体のグループに新しいウイルスがどのように侵入しているかにすぐに気付かないのは当然でした。

フランス． 2020（ "Science First Hand" No. 3（88）、2020）
2020年の写真：Jacques Paquier

ただし、一部の国では、関連する研究がいわゆるパイロット都市で実施され、PCRを使用して、いくつかの総合病院からのSARSの兆候があるすべての患者のサンプルが分析されます。それは非常に費用がかかり、1つのサンプルのそのような分析は、現在7〜8千ルーブルの費用です。しかし、病原体の全範囲を見ると、どの感染症に対してワクチンを開発する価値があるのかが明らかになります。

ちなみに、これらの病気の原因のうち、細菌感染症はわずか20％、残りはウイルス性です。今日のワクチンはインフルエンザに対してのみ開発および生産されており、ARVIの病因におけるその割合は10〜15％です。さらに、一部の国では同じコロナウイルス感染がより一般的です（15-30％）。そして、これらの「習慣的な」コロナウイルスは無害とはほど遠い。COVID-19のように、重度を含む3種類の病気があり、感染自体の結果と機械的換気による二次性肺炎の両方で死亡する患者もいます。

もちろん、ARVIのすべての患者に対して一般的な診断を行ってそのようなウイルス感染を検出することは意味がありません。特定の抗ウイルス治療がないため、今のところ症状があるものだけです。通常の治療コースは、診断自体よりも約7倍安くなります。ウイルス感染の場合、上記の理由で選択的研究を行う必要がありますが、どのワクチンを開発し、どの診断をCHIに導入する必要があるかを理解するためです。

モスクワでのそのような研究は、適切に組織された場合、1年以内に数千人の患者をテストするために約1500万ルーブルを必要とします。モスクワの「3DKマンション」の価格ほどで，最も高価なベントレークロスオーバーほどではありません。しかし、保健省はそのような提案に対する答えを1つだけ持っています-お金がありません。

新しいコロナウイルス感染によって引き起こされたパンデミックが私たちに教えてくれた主な教訓は、実際、私たちはウイルスの流行と感染一般についてほとんど知らないということです。それは、そのような将来の出来事に備える方法と、それらに対処する効果的行動方法を私たちは学ばねばなりません。そして、それはCOVID-19自体についてだけに留まらず、危険な季節的な感染ではありますが、別のものになる可能性があります。自然界に動物や鳥がいる限り、新しい未知の病気のパンデミックのリスクは残ります-「野生の」病原体の自然の貯蔵所。

そして、私たちが本当に人口を保護したいのであれば、私たちが今しなければならない最初のことは、私たちがまだ病気であるもの、私たちの中で最も危険なSARSを引き起こす病原体、ロシア人を見つけることです。モスクワ、サンクトペテルブルク、ノボシビルスク、クラスノダール、イェカテリンブルク、カザン、ウファ、ウラジボストークなど、SARSが特に多い主要都市でモニタリング研究を実施するためには、まず、健康問題の解決に今よりも有能かつ効果的に多くのお金を費やす必要があります。他の百万以上の都市と同様に。

SARS-CoV-2に関しては、明らかに、抗流行作用だけでそれを根絶することはほとんど不可能でしょう。おそらく、少なくとも効果的なワクチンが広く実践に導入されるまで、それは人間の集団で循環し続けるでしょう。しかし、私たちはまた、この病気を簡単にまたは無症状で経験し、おそらく免疫を持っている人々の層が徐々に増えています。ワクチン接種は彼らの数を増やすべきであり、そうすれば流行は減少するでしょう。

その間、マスマスキングと社会的距離は感染の拡大を減らすことができ、それは人口の最も脆弱なセグメントを保護します。厳しい対策（企業、学校、大学、カフェ、レストラン、ショップの仕事をやめること）に戻ることは経済の崩壊につながり、ひいてはヘルスケアの状況を悪化させることになることを心に留めておくべきです。

Литература
1. Bendavid E., Mulaney B., Sood N. et al. COVID-19 Antibody Seroprevalence in Santa Clara County, California // MedRxiv. 2020. DOI: 10.1101/2020.04.14. 20062463.
2. Logunov D. Y., Dolzhikova I. V., Zubkova O. V. et al. Safety and immunogenicity of an rAd26 and rAd5 vector-based heterologous prime-boost COVID-19 vaccine in two formulations: two open, non-randomised phase ½ studies from Russia // Lancet. 2020. V. 396. N. 10255. P. 887–897.
3. Moghadas S. M., Fitzpatrick M. C., Sah P. et al. The implications of silent transmission for the control of COVID-19 outbreaks // PNAS. 2020. V. 117(30). P. 17513–17515.
4. Peccia J., Zulli A., Brackney D. E. et al. SARS-CoV-2 RNA concentrations in primary municipal sewage sludge as a leading indicator of COVID-19 outbreak dynamics // MedRxiv. 2020. DOI: 10.1101/2020.05.19.20105999.
5. Zhanga R., Li Y., Zhang A. L. et al. Identifying airborne transmission as the dominant route for the spread of COVID-19 // PNAS. 2020. V. 117(26). P. 14857–14863.

著者について
Sergey Viktorovich Netesov- ロシア科学アカデミーの対応するメンバー、生物科学の博士、ノボシビルスク州立大学自然科学部のバイオナノテクノロジー、微生物学およびウイルス学の研究所の責任者。国際的に引用されたジャーナルと10以上のモノグラフで150以上の出版物の著者。生物医学の分野でロシア政府賞を2回受賞。

コロナウイルスとの生活(先駆病原体ウイルス）

«НАУКА ИЗ ПЕРВЫХ РУК» №3, 2020
Sergey Viktorovich Netesov
- Corresponding Member of the Russian Academy of Sciences, Doctor of Biological Sciences, Head of the Laboratory of Bionanotechnology, Microbiology and Virology, Faculty of Natural Sciences, Novosibirsk State University.

公式の統計から判断すると、パンデミックの最初の6か月におけるSARS-CoV-2コロナウイルスの犠牲者の数は、2009年から2011年の1年半の悪名高い豚インフルエンザの流行を越えました。さまざまな推定によれば、7〜14億件の症例のうち、15万人から50万人が死亡しました。COVID-19については、9月の公式症例数は3,300万人を超え、死亡者数は100万人を超えました。[訳者注）11月26日現在，症例数6,030万人，死亡者数142万人]

SARS-CoV-2は、人類にとっては困難な問題であることが判明しました。一方、COVID-19の大流行では、当初から前例のない急速な証拠の積み上げとこの問題に関する科学出版物数の増加を惹き起こしている（2020年6月の初めまでに、その数は20万を超えました）、WHOは150以上の候補ワクチンを登録しました。一方で、この病気の原因物質に対して本当に効果的な薬はまだ1つも現れておらず、SARS-CoV-2と身体との相互作用のメカニズム、および広範な病理学的症状の出現はまだ研究中です。

過去数か月にわたって、専門家は新しいコロナウイルス感染について多くの有用な情報を学んだだけでなく、私たちが慣れ親しんでいる急性呼吸器ウイルス感染症（ARVI）についても、たとえば、以前はあまり注目されていなかった無症候性のよく知られた現象など、違った見方になりました。現在、このような現象はコロナウイルスだけでなく固有のものであることが明らかになりました。

私たちがパンデミックとの戦いから学び、どのように進むかを考える時が来ました。いずれにせよ、人類の最優先事項は、この病気が日常生活と経済に与える影響を最小限に抑えるために可能な限りのことをすることです。

■先駆病原体SARS-COV-2
今世紀の初めまで、コロナウイルスは通常の季節的なSARSの原因になっていましたが、2000年代になり状況は変わり始めました。非定型肺炎の原因物質であるSARS-CoV-1は、2002年11月に中国の広東省で最初に「特定」されました。それはコウモリのコロナウイルスに由来し、その中間の宿主は明らかにヒマラヤのコガネムシ（ウィーバーラ）だったようです。これらの動物は、コーヒー［世界で最も高価なコーヒーの品種の一つであるliuvak kopiになる］の果実を食べ、肉が美味しく、毛皮も美しい。その内臓や体の部分は、中国の民間療法で使用されています。そのため、かつては中国など東南アジア諸国で集中的に飼育されていました。コウモリから、そして次に人間にもたらされたウイルスの偶発的な適応は、2003年に世界37カ国で8000件以上の感染と800人近くの死をもたらしました。

SARS-CoV-2が属するOrthocoronavirinaeサブファミリーは、広範なCoronaviridaeファミリーのメンバーです（Science First Hand No. 3（88）、2020）。

SARS-CoV-2が属するOrthocoronavirinaeサブファミリーは、広範なCoronaviridaeファミリーのメンバーです。それはいくつかの亜属を含む4つの属で構成されています。これらのうち、SARS-CoV-2、SARS-CoV-1に加えて、重度の急性呼吸症候群（SARS）を引き起こす2002- 2003年のSARSウイルス、および中東を引き起こす肺肺炎の原因物質であるMERS-CoVは、人間にとって特に危険です。呼吸器症候群。他のヒトコロナウイルスは、肺および中等度のARVIの原因物質です

MERS-CoVは、2012年にサウジアラビアで最初に特定されました。これは、エジプトのロゼットコウモリコロナウイルスに由来し、中間宿主である片こぶのラクダを通過した後、ヒトに感染し始めました。この病原体は8年間（2012年9月から2020年1月まで）、実験で確認された感染症例を2.5千件以上引き起こし、そのうち約800件（35％以上！）が致命的でした。ラクダと接触した人のほとんどが病気になりましたが、人から人への感染の事例も知られています。韓国でのこの病気の発生は広く知られ、1人の患者から150人以上が連続して感染しました。

■コウモリから人間へ
コロナウイルスは1960年代半ばに発見されました。その名前（ラテンのコロナから'太陽コロナ'）は、英国のウイルス学者で顕微鏡学者のジューンアルメイダによって電子顕微鏡で最初に見られたウイルスの形状に由来します。「クラウン」は、表面タンパク質、スパイクによって形成され、膜貫通受容体（アンギオテンシン変換酵素2（ACE2、またはACE2）の分子）に結合することにより、ウイルスが細胞に浸透することを保証します。

同じ1960年代以来、長い間人間に感染してきた一般的なコロナウイルスが徐々にわかってきました。それらのうちの2つはアルファコロナウイルスNL63と229Eです。さらに2つ-ベータコロナウイルスHKU1およびOC43。後者には、SARS-CoV- 1SARSウイルスと現在のSARS-CoV-2が含まれます。

過去10年間、中国とアメリカの科学者たちは、コロナウイルスを含む数十種類のカブトコウモリウイルスのゲノムを詳細に研究してきたので、かなり早く新しい病原体を特定することができました。2020年1月10日までに、中国疾病管理予防センター（北京）の専門家は、患者から得られたSARS-CoV-2の9つの分離株のゲノムを解読した。新型ウイルスは、SARS-CoV-1（約79％の類似度）とMERS-CoV（約50％の類似度）の両方とは遺伝的に異なることが判明した。その違いは非常に深刻です。

SARS-CoV-2を分離する（ "Science First Hand" No. 3（88）、2020）
米国で最初の症例からSARS-CoV-2（球状ウイルス粒子、青）を分離します。粒子の内側に黒い点が表示されます-ウイルスゲノムの断面。透過電子顕微鏡法。写真：疾病管理センター

ただし、SARS-CoV-2はスナッフボックスの悪魔［訳注）キノコ］ではありません。その特徴づけられた分離株はすべて、2018年に中国東部で発見された2つの既知のコウモリコロナウイルスに遺伝的に近く（88％以上の類似性）、このウイルスのヒト細胞との結合部位は、SARSウイルスのものと類似していました。少し後に、RatG13株がコウモリで同定されました。これは、新しい病原体にさらに近く、96％以上の類似性があります。

SARS-CoV-2の最初の8つの完全なゲノムは、互いに99.98％以上同一であり、ヒト集団における最近の出現を示しています。同時に、コウモリがこのウイルスにとって「孵卵器インキュベーター」であったかどうかはまだ決定されていません。このウイルスの起源については多くの仮説が提唱されていますが、最も現実的なのは、ウイルスが人間にとって病原性になり、中間宿主、おそらくパンゴリン（アルマジロの遠い「相対的」）の生物を「通過」するというものです。

SARS-CoV-2の人工的な起源をめぐる論争については、この理論に賛成して、「ソファーに座った」ウイルス学者は、2015年のNature誌の記事に記載されているハイブリッドを指摘しています。これはコロナウイルスの自然な進化を模倣する実験に言及しています。この研究の主な目的は、SARS-CoV-1ウイルスのスパイクタンパク質をコードするわずかに修飾された遺伝子が挿入されたコウモリコロナウイルスの1つです。主な変更は、科学者がそのゲノムにヒトACE2受容体への結合に関与する領域を挿入したという事実にありました。

北京の動物園のコウモリ（Science First Hand No. 3（88）、2020）
コウモリは、人間にとって潜在的に危険な多くのウイルスのキャリアですが、コウモリ自体は病気にならず、ウイルス感染で死亡することもありません。写真は北京（PRC）の動物園のコウモリです。写真：愚かなウサギ、トリックスは子供向けです

この組換えウイルスは、ノースカロライナ大学（米国）で構築され、ウーハンウイルス学研究所（PRC）でテストされました。そのようなキメラの特徴は細胞培養でテストされ、それが人間にとって潜在的に危険であることが判明しました。ちなみに、Gain-of-Functionという英語名のこのような実験は、過去10年間で2回禁止され、世界の科学界によって2回許可されています。

ただし、このハイブリッドウイルスは、パンデミックなSARS-CoV-2とは大きく異なります。遺伝的類似性は87％以下です。別の「陰謀」シナリオによると、別のコウモリウイルスであるRatG13が誤ってウーハンの中心から放出される可能性があり、SARS-CoV-2の類似性ははるかに高くなっています。

陰謀研究は魅力的で非常に伝染性の高い活動ですが、新しい感染性物質の起源と拡散に関する有能な科学的調査とは異なり、病原体との戦いには役立ちません。

たとえば、人間と接触して生活しているさまざまな動物のSARS-CoV-2に対する感度をテストすると、犬、豚、鶏、アヒルの生物では再現性が非常に低いが、フェレットや猫ではよく再現され、呼吸管によって、そして感染した動物から人間へ。これはデンマークや他のいくつかの国のミンク農場で起こり、ミンクは人間からのウイルスにしか感染できませんでした。したがって、コロナウイルス感染の可能性のある貯蔵所として、野生動物と家畜をさらに研究する必要があります。

人への道
ウイルスは、人間と家畜のすべての感染症の70％以上を引き起こします。工業用抗ウイルスワクチンがなければ、人間の寿命ははるかに短くなり、人類が動物性食品を提供することは非常に困難になります。

数十年前、いわゆる新規または新たな感染症はすべて、野生動物から飼いならされた動物、そして人間への「飛躍」による動物病原体の適応進化の結果であることが示されました。人間と動物のウイルスゲノムの分子遺伝学的研究によって証明されるように、これは、はしか、おたふく風邪、風疹、C型肝炎、HIVの古くから知られているウイルスに関しても当てはまります。したがって、戦略的な目的のために、人間の病気を防ぐために、最も危険な病気に対して動物にワクチンを接種するだけでなく、野生動物の病原体の全範囲を特定するためのモニタリング研究を実施し、その後、人間の新たな感染を防ぐための対策を開発する必要があります。

家畜の産業繁殖において、野生の親類の病原体から動物を保護することも同様に重要です。同時に、閉鎖状態でのみ家畜を飼育する必要があり、生きた動物を販売するための「野生の」市場は禁止されるべきです。現代の養鶏場では、空気がフィルターを通って鳥に入り、労働者は完全に着替え、飼料は消毒されます。中国の同じ手のひらのシベットも、コウモリがそこに行けないように、閉鎖された保育園でのみ飼育されています。

X線に対する物質の屈折率は１より小さい

真空の屈折率は１です．例えば，ダイヤモンドの屈折率は2.42で，物質の屈折率は，波長589.3 nm（振動数$$5×10^{14}$$Hz）の光（ナトリウムD線589.0nmと589.6nmの平均値）で測定するのが慣例です．屈折率nの物質に入ると光の位相速度は真空中の光速の1/nで伝播します．屈折率が１より小さいならば真空中の光速より速くなると心配する必要はありません．ここでいう光速は位相速度のことです．物質（ダイヤモンドでも）の屈折率は，X線領域では，1よりわずかに小さく$$n=1-δ，δ～10^{-6}$$になります．何故でしょうか？

■X線，可視光，電波などは，電磁波（振動電場）の仲間です．可視光に比べてX線の周波数は$$10^4$$倍も大きく，30keVのX線の周波数は$$10^{19}$$Hzです．
ダイヤモンドに限らず，物質は原子が集まって構成されており，物質が振動電場に置かれると，物質中に種々の振動する双極子が生じ，これらが物質の置かれた振動電場と同じ周波数で振動し，同じ周波数の電磁波を放射します．これが物質による電磁波の散乱現象です．
物質中に生じる分子分極やイオン分極による双極子の固有振動は赤外や可視光の領域にあります．これらの種々の分極は赤外や可視光領域の誘電率（振動電場に対する応答）に寄与しますが，振動電場の周波数が高くなると，これらの振動は追従できずに次々に落ちていきます．特に，X線の周波数域になると，原子内に束縛されている電子の振動による「電子分極」だけが追従できます．

さて，電子分極だけに注目しましょう．原子内のいろいろな軌道に束縛された電子の固有振動数は10^15Hz程度（この振動数の付近では共鳴が起こります）です．

$$n^{2}=\varepsilon =1-4\pi \left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) \displaystyle \sum_{j=1}^{N}\displaystyle \frac{\omega ^{2 } }{\omega ^{2}-\omega _{0j}^{2}-i\mit\Gamma _{j}\omega } \cong \left\{ \begin{array}{@{\,} cc @{\, } }
1+4\pi \displaystyle \sum_{j=1}^{N}\left( \displaystyle \frac{q^{2 } }{m\omega ^{2}_{0j } } \right) & for \omega <<\omega _{0} \\[0mm]
1-4\pi N\left( \displaystyle \frac{q^{2 } }{m\omega ^{2 } } \right) & for \omega _{0}<<\omega
\end{array} \right. $$

以下の式を見ると，（１）電子の固有振動数よりはるかに小さい周波数の可視光の領域では，屈折率は１よりわずかに大きく，（２）束縛電子の固有振動数より遥かに大きい周波数のX線領域では屈折率は１よりわずかに小さいことがわかります．

結局，電子分極だけが振動に追従できるX線領域での物質の屈折率nは，１よりごくわずか小さいことになります．

■応用
X線に対する物質の屈折率は１より小さいので，空気中（≒真空中）から，物質表面へ臨界角以内ですれすれに入射するX線ビームは，表面で全反射します．X線を曲げるレンズの光学系は作れませんが，全反射を使うと，適当な形状のミラーを組み合わせてX線ビームを集光させる光学系を作ったり，光ファイバーのようなX線導波路を作ったりすることが可能になります．

全反射するX線は，スキンデプスと呼ばれる物質の極表面しか侵入しませんから，極表面の分析に利用できます．
物質の深さ方向に種々の屈折率層の積層モデルを作り，フレネル反射率をシミュレーションできます．これは，種々の入射角で反射率の測定を行い，物質表面の深さ方向の情報を得る反射率測定実験で利用されています．

コロナウイルスとの生活（治療薬，ワクチン）

Сергей Нетесов，«Наука из первых рук» № 3(88), 2020　より

■治療薬はどうか？
残念ながら、2020年1月以降、治療用抗体を含む新薬の模索が続いていますが、COVID-19に対してウイルス特異的効果が証明された有効な薬剤はまだありません。

米国食品医薬品局（FDA）で事前承認を受けている製品は、RNAポリメラーゼのウイルス酵素阻害剤であるレムデシビルのみです。エボラの治療のために開発されたこともありましたが、その効果はあまり期待できませんでした。

SARS-CoV-2による肺炎患者の第1陣が、早くも2020年2月に中国で正式に服用を開始したが、その時点では効果が証明されていません。しかし、後にアメリカで行われた2つの臨床試験では、重症期間が15日から11日に短縮され、致死率が20～25％低下するという結果が出ています。しかし、他の2つの臨床試験では、これらの結果は確認されていません。レムデシビルは現在、米国ではCOVID-19治療薬として承認されていますが、ロシアでは登録されていません。

他の薬の有効性も研究されています。インターロイキン-6（IL-6）阻害剤は、免疫反応や急性炎症反応を調整する低分子で、患者の免疫系が「制御不能」のときに、いわゆるサイトカインの嵐を防ぐのに役立ちます。そのような薬には、モノクローナル抗体に基づくトシリズマブが挙げられる。イタリアの医師によると、それは肺炎を予防することで病気の経過を改善し、病気の初期段階で有効です。

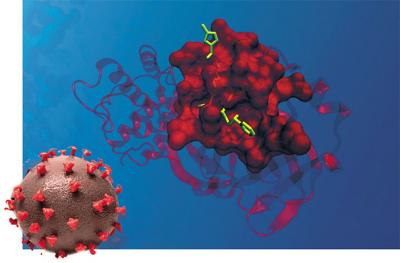
SARS-CoV-2ウイルスプロテアーゼの主酵素と潜在的阻害剤の組み合わせの分子モデル．X線構造解析による．
写真：ツヴィティリオ・クロメナーレ
左：SARS-CoV-2ウイルス粒子．芸術的な構成．写真：NIAID

英国の医師によると、抗炎症作用と免疫抑制作用を持つ合成グルココルチコステロイドであり、古くから知られているはるかに安価な薬剤であるデキサメタゾンは、サイトカインの嵐を抑制し、重篤な疾患の死亡率を低下させることができます。英国では、この薬は非常にうまく機能しましたが、COVID-19の軽度の症例では、その使用は禁じられています。

抗マラリア薬ヒドロキシクロロキンと抗生物質アジスロマイシンの組み合わせも、ウイルスによる肺炎の治療にテストされました。前者は肺の炎症反応を抑え、後者は付着細菌感染を予防すると考えられていました。しかし、この組み合わせの第一成分の効果のなさを指摘する多くの出版物があり，テストに終止符が打たれました。さらに、ヒドロキシクロロキンとアジスロマイシンは、それ自体で心血管合併症による死亡のリスクを高める可能性があり、このような問題を抱える人々は特にコロナウイルスに対して脆弱です。

免疫不全状態の重症インフルエンザの治療薬として、2015年に日本でアビガンという名前で登録されたファビピラビルをベースにした薬剤に大きな期待が寄せられました（催奇形性効果のため、妊婦には使用できません）。この物質は、レムデシビルのようなRNAポリメラーゼの阻害剤であり、ヒトウイルスではなくRNA含有ウイルス酵素のみに作用する。2020年2月に中国でCOVID-19患者を対象とした臨床試験が開始され、3月に薬効が発表されましたが、その後の説明はありませんでした。

ファビピラビル/アビガンのライセンスは2019年に失効しており、2020年夏にはロシアのメーカー3社からコロナウイルス感染症治療薬として位置づけられている「コロナビル」「アビファビル」「アレプリビル」の3つのファビピラビル系薬剤が国内向けに発売されています。9月には、これらの処方薬がロシアの最低生活レベルに匹敵する価格で小売販売されました。

その有効性については、最近日本でコロナウイルス患者を対象としたファビピラビルの臨床試験の第3フェーズが完了し、平均的な重症度で、摂取により病気の期間が14.7日から11.9日に短縮されることが示されました。これらのデータは、ロシアのパイロット研究の結果と一致しています。中程度および軽度の疾患では、ファビピラビルは「臨床的回復期間を約3.5日短縮し」、鼻腔からのウイルス排除を加速し1～3日短縮することができます。全治療には、体重に応じて40錠1.5～2パックが必要です。

赤外線非接触温度計を使用して人々の健康状態をチェックします。インド。写真：グウィディオンM.ウィリアムズ

■ワクチン接種を受けるや否や？
2020年8月末現在、世界で約160の候補ワクチンが開発されており、そのうち約50は臨床試験のさまざまな段階にあり、そのうち9つはフェーズ３にあります。この段階では、通常、多施設で慎重に管理された研究で、安全性を判断し、実際の流行における薬剤の予防効果を評価するために、大規模な患者グループ（少なくとも1〜3千人）の参加を得て実施されます。

同時に、ロシアと中国の2つのワクチンは、フェーズ３の臨床試験が終了するまで、国レベルでの限定的な使用が許可されました。これは前例のないケースです。

まず、これは、コロナウイルススパイクタンパク質の遺伝子が挿入されたゲノムに第5血清型のアデノウイルスをベースにした中国企業CanSinoBiologicsのワクチンです。フェーズ３の臨床試験は、サウジアラビアの保健省と協議して、サウジアラビアの何万人ものボランティアを対象に8月に開始されました。しかし、早くも2020年6月25日、中国国防省は、一部の軍隊の医師にワクチン接種のために、このワクチンを1年間使用することを正式に承認しました。これが任意接種なのか強制接種なのかは不明です。今日、このワクチンが、アデノウイルスワクチンの中で最も「先進的」なワクチンです。

2つ目の「冬ツバメ」は、M.V.ロマノソフ記念・モスクワ疫学・微生物学研究センターとモスクワ疫学・微生物学研究センターが共同開発した2成分ワクチン「スプートニクV」です。このワクチンは、モスクワの疫学・微生物学研究センター（Gamaleya Research Center for Epidemiology and Microbiology）とロシア国防省の48中央研究所が共同で開発しました。また、コロナウイルス蛋白質遺伝子Ｓを組み込んだアデノウイルス（第５、２６回ヒト血清型）をベースにするこのような方法論に基づいて、この研究センターでは、これまでに我が国のエキゾチックエボラおよび中東呼吸器症候群に対するワクチン候補が開発され、フェーズ1およびフェーズ2の臨床試験に合格しています。

このような組換えワクチンはすべて、比較的無害なウイルスをベースにしており、これらのウイルスは、人体内での繁殖能力を弱める（減衰させる）か、あるいは奪うかのいずれかです。実際、このようなウイルスは、ＤＮＡやＲＮＡワクチンの場合のように、病原体の遺伝物質を細胞に送達し、特異的な免疫応答を誘発するためのベクターとなります。このようなウイルスが細胞に入ると、そのDNAが放出されて細胞核に入り、そこでメッセンジャーRNAが合成され、コロナウイルスの表面Sタンパク質を含むウイルスタンパク質が組み立てられます。これらのタンパク質が細胞膜に組み込まれると、細胞は免疫原性になります。つまり、体内で特定の免疫を形成することができます。

スプートニク Vワクチンの特定のアデノウイルスベースに関しては、これらのウイルスが人体での増殖能力をどのように失ったかについての情報はありません。

「スプートニクV」の正式登録は、2020年8月11日に発表されました。これは、臨床試験のフェーズIIIの開始とフェーズ１〜２の結果の公開のほぼ1か月前です。その後、この登録は条件付きで、2021年1月1日まで有効であることが発表され、最終的な登録は、最大4万人が参加することになっているテストの完了後に行われます。

マスクの少女（「サイエンス・ファースト・ハンド」第3号（88）、2020年）写真：ニックアンダーソン

2020年の夏に、コロナウイルススパイクタンパク質をコードするメッセンジャーRNAに基づくさらに2つのワクチンがフェーズ３の臨床試験用にリリースされました。1つは米国の革新的なバイオテクノロジー企業であるModerna社が、もう1つはドイツのBionTech社、米国のPfizer社、中国のFOSUN Pharma社が共同で開発しているワクチン、そして中国で国有製薬企業の参加を得て開発された不活化ウイルスSARS-CoV-2をベースにした3種類のワクチンです。

これとは別に、Sタンパク質遺伝子が挿入された組換えワクチンも注目に値します。これもアデノウイルスに基づいて作成されていますが、ヒトではなくチンパンジーに基づいています。オックスフォード大学（英国）で、英スウェーデンの製薬大手AstraZenecaと共同で開発されました。ステージ３の臨床試験は、8月初旬にブラジル、米国、南アフリカで開始されました。これらのテストのいくつかはロシアで実施される予定との情報があります。

なぜ開発者の中には、組み換えワクチンの基礎としてサルアデノウイルスや希少なヒトアデノウイルスの血清型を選ぶ人がいるのでしょうか？実は、最近の研究によると、かなりの割合の人がすでに共通の血清型5に対する抗体を持っている可能性があるということです。例えば、このような抗体は、がん研究プロジェクトの一環として中国で調査された人の67％、中国の青海省の子供の75％以上、米軍の新兵の4分の1にも見られた。また、このアデノウイルスをベースにしたワクチンが、以前に接触したことのある人にどの程度効果があるかは不明です。

ワクチン製造の世界的リーダーの育成に関連し最低限の宣伝と「PR」をしているのは：米国に本社を置く国際的なバイオ製薬企業メルク・シャープ＆ドーム、英国グラクソ・スミスクラインに本社を置く国際的な企業、免疫生物学的製剤の多国籍メーカーであるフランスのサノフィ・パスツール

ロシアでは、さらにいくつかの候補ワクチンが様々な拠点で開発されており、その中には、Rospotrebnadzorの国立ウイルス学・バイオテクノロジー研究センター「Vector」（Koltsovo、ノボシビルスク州）、A.A. Smorodintsevインフルエンザ研究所（サンクトペテルブルグ）、M.P. Chumakov免疫生物学的製剤の研究開発のための連邦研究センター（モスクワ）などが含まれています。また、ロシアでワクチンを生産するために、外国の開発者との交渉が進んでいます。ということで、2021年には選択肢が出てきます。

■ワクチンの2ショット
「スプートニクV」の使用説明書には、臨床試験のフェーズ１の結果から、発生頻度の点で有害事象（AE）は、頻繁かつ非常に頻繁に発生していると見なせます。ワクチン接種後、次のAEが記録されました：一般的な障害と反応注射部位：高体温、痛み、浮腫、ワクチン接種部位のかゆみ、無力症、倦怠感、発熱、ワクチン接種部位の皮膚温度の上昇、食欲減退。神経系障害：頭痛、下痢。呼吸器系、胸部および縦隔器官からの障害：中咽頭の痛み、鼻のうっ血、喉の痛み、鼻漏。現在の臨床試験でワクチンの投与量を減らすことにより、これらの現象を減らすことができる可能性があります。

実際のワクチンの保護効果は、20年9月に始まったフェーズ３の臨床試験で検討されるためまだ評価されていません。この場合は破られましたが臨床試験のフェーズ３は通常のアルゴリズムで行います。フェーズ２の試験では、通常、薬剤の投与量が変化するが、既に公表されているスプートニクVの臨床試験結果では、そのようなデータは得られていません。

ワクチン「Gam-COVID-Vac」（「ScienceFirstHand」No.3（88）、2020）

フェーズ３に関しては、独自の規則があります。各テスト参加者には「幸福」の特別な日記が与えられ、セラピストが割り当てられます。すべてのテスト参加者は少なくとも4つのグループに分けられ、そのうちの1つはワクチンの代わりにプラセボを投与され、もう1つは同様のワクチン製剤、3つ目はワクチン自体、4つ目は可変用量などです。スプートニクVの場合、前例のないことに直面し、臨床試験のフェーズ３の開始を待たずに、2020年9月8日、ロシア保健省は、ワクチンの最初のバッチを民間循環に放出する許可を発表し、地域を含むリスクグループからの集団の大量ワクチン接種が計画されています。

ちなみに、「スプートニクV」の指示には、子供だけでなく、主なリスクグループである60歳以上の人（75歳以上の人の死亡率は20～30％）にもワクチンを使用してはいけないと書かれています。

ここまでnote公開･･･････････････

■氷山の水面下
2020年のSARS-CoV-2コロナウイルスのパンデミックは、人間のスクリーニングでは前例のないものです。このウイルスが、さまざまな人々の生物と病原体、主に季節性インフルエンザや他の急性呼吸器ウイルス感染症を引き起こすものと相互作用で，多くの問題が明らかなったのは驚きではありません。

たとえば、インフルエンザの発作を起こし、流行中に健康を維持することで、感染を回避できたと考えています。ただし、この場合、インフルエンザウイルスは、明らかな病気の兆候を引き起こすことなく、上気道の少数の細胞に感染し、そこで「わずかに」増殖する可能性があります。そしてこれが事実であるならば、SARS-CoV-2の場合にすでに証明されているように、ワクチン接種された人々でさえ感染の無症候性の保因者である可能性があります。

COVID-19患者は、最初の症状が現れる2日前に感染を広げ始めます。病気が無症候性である場合でも、感染した人々は、呼吸、くねくね、または咳だけでなく、糞便によっても、最大2週間ウイルスを環境に放出する可能性があります。そのため、ウイルスの存在について陰性の検査を行った後にのみ、患者は検疫から解放されます。

問題の反対側：現在、人類は原則として呼吸器感染症の90％を診断することができます。しかし、少なくともロシアでは、実際にはこれを行っていません。急性呼吸器ウイルス感染症とインフルエンザの診断は、症状によってのみ行われます。そして、ARVIの症状のほとんどはほとんど同じであるため、これは冒涜です。ただし、インフルエンザはほとんどの場合、鼻水が出ずに消えますが、これはCOVID-19を含む他のいくつかの感染症では一般的です。ARVIの特定の原因（病因）についての答えは、正確な実験室診断によってのみ与えられます。現在は可能ですが、有料です。ARVIのPCR診断は、強制医療保険の資金調達には含まれていません。

「寒さ」やインフルエンザの特定の症例は目で判断されるため、わが国で実際に特定の病原体に一度に感染したARVI患者の数を概算することすらできません。そしてこれは、これらの感染のそれぞれからの真の損傷を評価することと、最も危険で疫学的に重要なものを決定することの両方を防ぎます。したがって、インフルエンザウイルスを除いて、これらの病原体に対する新しいワクチンや抗ウイルス薬を開発したり、それらの進化の長期的な傾向を追跡したりすることはありません。したがって、ARVI病原体のグループに新しいウイルスがどのように補充されているかにすぐに気付かないのは当然のことです。

フランス。 2020（ "Science First Hand" No. 3（88）、2020）
フランス。2020年の写真：Jacques Paquier

ただし、一部の国では、関連する研究がいわゆるパイロット都市で実施され、PCRを使用して、いくつかのポリクリニックからのSARSの兆候があるすべての患者のサンプルが分析されます。はい、それは非常に費用がかかります。1つのサンプルのそのような分析は、現在7〜8千ルーブルの費用がかかります。しかし、病原体の全範囲を見ると、どの感染症に対してワクチンを開発する価値があるかが明らかになります。

ちなみに、これらの病気の原因のうち、細菌感染症はわずか20％、残りはウイルス性です。今日のワクチンはインフルエンザに対してのみ開発および生産されており、ARVIの病因におけるその割合は10〜15％です。さらに、一部の国では同じコロナウイルス感染がより一般的です（15-30％）。そして、これらの「習慣的な」コロナウイルスは無害とはほど遠いです。COVID-19のように、重度を含む3種類の病気があり、感染自体の結果と機械的換気による二次性肺炎の両方で死亡する患者もいます。

もちろん、ARVIのすべての患者に対して一般的な診断を行ってそのようなウイルス感染を検出することは意味がありません。特定の抗ウイルス治療がないため、これまでのところ症状があるだけです。通常の治療コースは、診断自体よりも約7倍安くなります。ウイルス感染の場合、上記の理由で選択的研究を行う必要があります。どのワクチンを開発し、どの診断をCHIに導入する必要があるかを理解するためです。

モスクワでのそのような研究は、適切に組織された場合、1年以内に数千人の患者をテストするために約1500万ルーブルを必要とします-モスクワの「3ルーブルノート」の価格または最も高価なベントレークロスオーバーではありません。しかし、保健省はそのような提案に対する答えを1つだけ持っています-お金がありません。

新しいコロナウイルス感染によって引き起こされたパンデミックが私たちに教えてくれた主な教訓は、実際、私たちはウイルスの流行と感染一般についてほとんど知らないという理解です。それは、そのような将来の出来事に備える方法と、それらに対処する上で効果的に行動する方法を私たちに教えなければなりません。そして、それはCOVID-19自体についてでさえありません。それは、危険な季節的な感染ではありますが、別のものになる可能性があります。自然界に動物や鳥がいる限り、新しい未知の病気のパンデミックのリスクは残ります-「野生の」病原体の自然の貯蔵所。

文献･････　　略

コロナウイルスとの生活（感染を止める，検査）

セルゲイ・ネテソフ, "SCIENCEFIRSTHAND" №3（88）,2020
ノボシビルスク州立大学自然科学部，バイオナノテクノロジー，微生物学およびウイルス学研究所長

前半の章（以下の３つ）は略
■先駆病原体SARS-COV-2，■コウモリから人間へ，■人への道，

■エピデミックを止める方法
病原体の最も重要な特徴は、感染の基本再生産数（R0）で、まだ感染していない集団で，1人の患者から感染する平均人数のことです。通常のインフルエンザウイルスのR0は0 1.4まで、そして新しいコロナウイルスで、おそらく3から5までです。この指標は徐々に変わりますが、感染拡大は国によって定義がわずかに異なるためです。

ドイツ連邦共和国は、第１波の流行克服では最も成功した国の1つです。2020年5月には、ドイツの研究によると，患者の隔離も、マスクなしの社会的距離も、学校の閉鎖も、R0減衰に効果がありませんで。最大の効果は、大規模なイベントの禁止、過酷な導入、罰金、マスク体制、および集中的なコミュニケーションが行われている組織の閉鎖から得られました。これらの措置の結果、実効再生産数は1を下回り、流行は収まり始めました。

ドイツでの抗流行対策の早期導入と広範なテストは、ウイルスの実効再生産数を迅速に低下させ、多くの死亡を防ぐのに役立ちました。
（National Geographic、2020年5月1日）

同様の状況がオーストリア、ノルウェー、イタリアおよび他のヨーロッパ諸国で観察されました。そこでも、学校の閉鎖は効果がないことが判明し（学童は教育機関の外で積極的にコミュニケーションをとっています）、流行を止めるための有効な介入は、マスク着用、集団行動停止、社会的距離を置く、患者の隔離でした。同時に、そのような措置がすぐに導入されず、完全ではなかったスウェーデンでは、主に高齢者の死亡率はヨーロッパで最も高いものの1つでした。そして、イラン、イラク、サウジアラビアでは、検疫措置が弱まった後、病的状態の第二の波が始まりました。

バルセロナ（スペイン）の診療所にいるCOVID-19の患者。
写真：フランシスコアビアホスピタルクリニックデバルセロナ

抗流行対策の有効性の最も顕著な例は、サンフランシスコとニューヨークという2つの最大のアメリカの都市の行政の行動で見られました。サンフランシスコ政府（カリフォルニア州知事および市長）は3月16日、州が自己隔離、マスクの着用、事業活動のほぼ完全な停止などの厳しい検疫措置を課していると発表しました。ニューヨークでは、同じことがわずか6日後に行われました。その結果、米国で最大の都市で2か月以内に約2万人が死亡しましたが、2番目に人口密度が高く13番目に人口の多いサンフランシスコでは35人しか死亡していません。これは、抗ウイルス予防策の採用が少し遅れただけでも、その結果がどれほど広範囲に及ぶ可能性があるかを明確に示しています。

ニューヨーク市では、コロナウイルスと診断された死亡患者の77％が糖尿病、肺疾患、高血圧や喘息などの心血管疾患も患っており、死亡者の1.5％のみが比較的健康でした。参考までに、米国では約66％の人が太りすぎまたは非常に肥満であり、コロナウイルス感染による死亡のリスクが高くなっています。また、ニューヨーク市の成人人口の約半数が高血圧です。

■Covidかどうか？
コロナウイルスはRNA含有ウイルスに属し、リボ核酸自体に加えて、脂質とウイルス特異的タンパク質も含み、さまざまな方法で診断できます。第一に、患者の鼻咽頭からのサンプル中のウイルス自体の成分の存在による：RNA（逆転写PCR、RT-PCR）およびウイルス抗原-表面Sタンパク質（免疫学的測定法）。

SARS-CoV-2ウイルス粒子では、スパイクSタンパク質がはっきりと見え、そこからウイルスの名前が付けられました。透過電子顕微鏡法。画像：NIAID

別の方法は、体の免疫の構成要素、例えば、特定の抗体ができているかを評価することです。これを行うには、症状の発症と同時に現れる、患者の血液サンプル中のIgMクラスの「一次」抗体の含有量が測定されます。過去に疾患に罹ったかは、「二次」IgG抗体の存在によって識別できます。これらのテストは、酵素免疫測定法を使用して実行されます。

2020年8月20日の時点で、157の異なる検査システムがロシアで登録されました。126はコロナウイルスに対する抗体を検出し、31はウイルスRNAです。しかし、なぜ、そのような多数のシステムで、診断の信頼性を論じるのでしょうか？

第一に、ウイルスRNAの試験システムを使用する場合、鼻咽頭から材料を正しく採取することが非常に重要です。さらに、ウイルスRNAの分離と保存のために、特別なサンプラーを必要とする特別な液体にすばやく入れる必要があります。第二に、今日、テストが実行される多くの研究所がありますが、テスト手順のすべての段階で正しく実行されるわけではありません。

患者の鼻咽頭からCOVID-19テスト用の生物学的材料を採取します。写真：フランシスコアビアホスピタルクリニックデバルセロナ

第三に、上気道からRNAを検出する可能性は、鼻咽頭からのウイルスの「逃避」のために、病気の後期に減少します。最後に、RT-PCRテストでは、患者が回復した後でも、長期間にわたって陽性の結果が得られることがよくあります。その理由は次のとおりと考えられます。体は生きているウイルスではなく、ウイルスRNAの断片を循環し続けます。

ウイルス抗原の信頼性の高いテストシステムが開発され、最近医療現場に導入されましたが、状況によってはウイルスRNAの結果が陰性または不明確な場合に正確な診断を行うことができるため、患者の正確な診断に有用であることがすでに示されています。

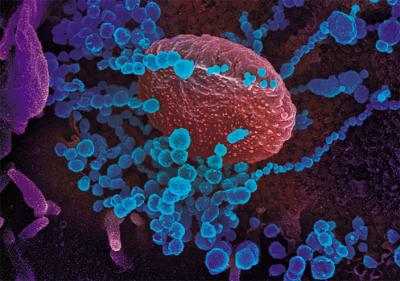
実験室培養におけるSARS-CoV-2ウイルス粒子（青い物体）。この株は、米国の患者から分離されています。走査型電子顕微鏡写真：NIAID

IgG抗体の検査システムに関しては、ARVIを引き起こす一般的なコロナウイルスに感染していて、検査システム自体が十分に特異的でなかった場合、検査システムの中には偽陽性を示すものもあります。その結果、私たちの人口のほとんどがSARS-CoV-2に対する抗体を持っているように見えるかもしれませんが、最も特異性の高い検査のデータから判断すると、この割合はまだ10〜12％を超えていません。

一方、IgG抗体を持っていなくても、ウイルスに対する免疫防御が欠如しているわけではありません。個々の保護を評価するための追加の検査は、免疫細胞が活性化され、サイトカイン誘導が検出される特異的Ｔ細胞免疫の有無の判定であります。しかし、このような診断や抗体解析の複雑さやコストは比類のないものであるため、限られた規模の科学研究でのみ使用されます。

ほとんどの場合（症例の40〜90％）、COVID-19は無症候性または軽度であるが、中程度の重症度の疾患では、体温が上昇し、ODSの1つ以上の臨床徴候を示しています：乾いた咳、急速または困難な呼吸、味覚と嗅覚の喪失、血中酸素飽和度の低下。重いフォームが特徴です：38℃以上の体温、脱力感、食欲不振、下痢、筋肉痛、肺炎の記録された徴候。感染してから重篤な症状が現れるまでには、実際には約2週間かかります。（ニューイングランド医学ジャーナル2020年5月16日号）

問題は、今日のロシアでは、外国で行われているように、実際の患者からの対照サンプルとCOVID-19に感染していない人々からの陰性血清の広範なパネルを使用して実施された、すでに適用されている診断法の特異性と感度の比較分析のためのデータをパブリックドメインで持っていないことです。そして、そのようなデータは、特定の診断ツールの購入を決定する際に、ロシア保健省と地域の保健当局の両方で役立ちます。質が大切で安ければ良いというのもではないからです。

感染性物質による人間の感染の実験は、世界のほぼすべての国で犯罪です。したがって、ヒトに対するウイルスの感染量、すなわち、疾患を引き起こすために体内に侵入しなければならないウイルス粒子の数はまだ決定されていません。病人が単位時間あたりにどれだけの量のウイルスを環境に放出するか、テーブルやボタンなどの家庭用品の表面に接触しているときに指に付着するウイルスの粒子の数は不明です。しかし一方で、ウイルスが環境内でどれだけ迅速に、どのような条件下で不活性化されるかがわかりました。このための実験は、倫理基準に違反しませんので。

たとえば、デンマークの科学者は、感染者が多く、これらの人々が病気の最初の症状を感じる前でさえ、下水でコロナウイルスを特定しました。同時に、人をテストするときと実質的に同じテストが下水域のウイルスを検出するために使用されます。しかし、それらはサンプル中のウイルスRNAの存在を明らかにするだけであり、「生きている」ウイルス粒子ではないことを常に覚えておく必要があります。したがって、研究者は、細胞培養物中の生きたウイルスの実際の検出とPCR試験の結果を時々検証する必要があります。

以下続く･････

■治療薬は？，■ワクチン接種を受けるか？否か？，■氷山の隠れた部分

コーシー-リーマンの方程式

コーシー (1789-1857)、リーマン (1826-1866)

これも19世紀の数学で重要な発見の一つです．「数学が社会（科学技術も含まれる）とどのように係わるかを知る」のが私たちの目的で，数学の勉強会とは別物です．そのような視点で見ても，複素関数論は19世紀に確立した重要な数学分野で，広い応用をもちます．そこで，この数学概念の意義を理解できることを目指します．

私たちの使う関数論は19世紀の数学で確立しました．先に，Fourierフーリエ級数（変換）,Laplaceラプラス変換を取り上げましたが，もう少しだけ複素関数に言及する必要があります．今回は，コーシー-リーマンの方程式を取り上げます．

複素平面（$$x$$軸が実数，$$y$$軸が虚数）に定義域$$D$$をもつ複素関数$$f(z)$$を考えましょう．この関数は領域$$D$$で正則（微分可能）であるとします．微分可能な関数ですから，この領域$$D$$で連続であることはいうまでもありません．

ある点$$z∈D$$での微分は，$$ｘ$$軸に沿って（$$x$$で偏微分）行う微分係数と，$$y$$軸に沿って（$$y$$で偏微分）行う微分係数がありますが，複素関数$$f(z)$$が正則であるとすると，どちらの微分係数も一致し，点$$z$$での微分係数は確定しなければなりません．
関数$$f(z)$$が$$D$$で正則とは，定義域$$D$$のすべての点$$z∈D$$で微分係数が確定する（微分可能）ことです．

関数$$f(z)$$に領域$$D$$での正則性を要請します．定義域内のすべての$$z=x+iy$$に対して，

$$\displaystyle \frac{df(z)}{dz}=\displaystyle \frac{ \partial u}{ \partial x}+i\displaystyle \frac{ \partial v}{ \partial x}=\displaystyle \frac{ \partial u}{ \partial (iy)}+i\displaystyle \frac{ \partial v}{ \partial (iy)}$$が成立します．$$x$$で偏微分しても，$$iy$$で偏微分しても等しい．
実部と虚部をそれぞれ等しいとおいて，
$$\displaystyle \frac{ \partial u}{ \partial x}=\displaystyle \frac{ \partial v}{ \partial y},　 \displaystyle \frac{ \partial v}{ \partial x}=-\displaystyle \frac{ \partial u}{ \partial y}$$が得られます．これをコーシー-リーマンの方程式（条件）と言います．

逆に，コーシー-リーマンの方程式が成立するなら，複素関数f(z)は正則であることが証明できます．
従って，複素関数が正則であるための必要十分条件は，コーシー-リーマンの方程式が成立することです．

■閉曲線$$C$$とその内部で，$$f(x)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$　←コーシーの積分定理

（コーシーの積分定理の証明）
$$\displaystyle \int_{C}^{}f(z)dz=\displaystyle \int_{C}^{}\left[ u(x,y)+iv(x,y) \right] \left( dx+idy \right) =\displaystyle \int_{C}^{}\left( udx-vdy \right) +i\displaystyle \int_{C}^{}\left( udy+vdx \right) =$$

$$ =\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial v}{ \partial x}+\displaystyle \frac{ \partial u}{ \partial y} \right) dxdy+i\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial u}{ \partial x}-\displaystyle \frac{ \partial v}{ \partial y} \right) dxdy=0 $$

（参考）
$$\displaystyle \int_{C}^{}\displaystyle \frac{f(z)}{z-z_{0 } }dz=f(z_{0})\displaystyle \int_{\mit\Gamma }^{}\displaystyle \frac{dz}{z-z_{0 } }=2\pi if(z_{0})$$

■正則な複素関数$$f(x,y)＝u(x,y)+iv(x,y)$$はその実数部$$u(x,y)$$あるいは虚数部$$v(x,y)$$のどちらか一方を知れば他方は決まってしまう．

例えば，虚数部$$v(x,y)$$を知り，コーシー-リーマンの方程式を使うと，実数部$$u(x,y)$$を求めることができる．

例えば，以下のyoutube動画には，このような問題の演習があります．

■応用について

実数部を知って虚数部を求める例として，私のやった実験の話をします．

複素屈折率を　$$ \tilde{n}(\omega )=n(\omega )+iK(\omega ) $$と書きます．$$ω$$は光の周波数で実数．複素屈折率$$ \tilde{n}(\omega ) $$は，複素数値をとり，実数部$$n(ω)$$と虚数部$$K(ω)$$があります．
実数部の$$n(ω)$$は反射率に，虚数部の$$K(ω)$$は吸収率に関係があります．

反射率を測定し$$n(ω)$$を知り，$$K(ω)$$を計算し吸収率を求めます．このとき，実数部$$n(ω)$$と虚数部$$K(ω)$$を結ぶのは，クラマース-クローニッヒ変換です．$$ω$$は複素数ではないので，コーシー-リーマンの方程式にははなりませんが，$$ \displaystyle \frac{\tilde{n}(\omega )}{z-\omega } $$は実軸より上側で正則（$$ω$$は極）なので，コーシーの積分定理を使うと，クラマース-クローニッヒ変換を導くことができます．

$$0=\displaystyle \int_{}^{}\displaystyle \frac{n(z)}{z-\omega }dz+i\displaystyle \int_{}^{}\displaystyle \frac{K(z)}{z-\omega }dz=P\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{z-\omega }dz-i\pi n(\omega )+iP\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(z)}{z-\omega }dz+\pi K(\omega )$$
$$\left\{ \begin{array}{@{\,} c @{\, } }
-\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{Z-\omega }=K(\omega ) \\[0mm]
\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(\omega )}{z-\omega }=n(\omega )
\end{array} \right. $$

コーシーの積分定理と留数

■コーシーの積分定理

閉曲線$$C$$および，その内部で$$f(z)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$

■ローラン展開と留数

関数$$G(s)$$に，極（分母が0となる特異点）がある場合，例えば，１つの極$$s_1$$の周りで，次のようにローラン展開ができます．$$s_1$$が$$n$$次の極とすると，
$$G(s)=\displaystyle \frac{a_{-n } }{\left( s-s_{1} \right) ^{n } }+\displaystyle \frac{a_{-\left( n-1 \right) } }{\left( s-s_{1} \right) ^{n-1 } }+ \cdots +\displaystyle \frac{a_{-2 } }{\left( s-s_{1} \right) ^{2 } }+\displaystyle \frac{a_{-1 } }{\left( s-s_{1} \right) }+a_{0}+a_{1}\left( s-s_{1} \right) + \cdots $$
この展開中の係数$$a_{-1}$$を留数と言います．

実は，$$G(s)$$を複素関数と見たとき，極$$s=s_1$$で，$$G(s)$$は正則ではありません．$$s=s_1$$を内部に含むような閉曲線$$C$$に沿って左回りに1周$$G(s)$$を積分すると
$$\displaystyle \int_{C}^{}G(s)ds=2\pi ia_{-1}$$ となります．これを留数の定理といいます．

さてこれらの証明は，難しくはありません．興味おありでしたら，親切な解説をしているyoutube動画がありますので，そちらをご覧ください．

関数をローラン展開すると，いろいろな次数の項がでて来ますが，閉曲線に沿って1周積分すると，なぜ-1次の項の係数（留数）だけが残るのか不思議ですね．youtube動画で証明を確認ください．たいへん都合の良い便利な性質です．

■いろいろな場面で，いろいろな積分をするのに，留数定理を使います．「道具としての数学」の代表でしょう．複素関数論は活躍しています．

話は変わりますが，ちょっと似た手法で，ラプラス逆変換をするときに，部分分数に展開します．以下の例題をご覧下さい．

複素関数$$G(s), s=x+iy$$を，ラプラス逆変換するときに，$$G(s)$$を部分分数に展開することが必要になります．

ラプラス変換

■Fourier変換
フーリエ解析のときに触れた事柄をまとめておきます：

$$F(\nu )=\displaystyle \int_{- \infty }^{+ \infty }f(t)e^{-2\pi i\nu t}dt$$
$$f(t)=\displaystyle \int_{- \infty }^{+ \infty }F(\nu )e^{2\pi i\nu t}d\nu $$

関数$$f(t)$$のフーリエ変換を$$F(ν)$$といい，$$F(ν)$$から$$f(t)$$に戻る変換をフーリエ逆変換といいます．

変数$$t，ν$$は実数です．積$$ν･t$$は無次元なので，変数$$t$$の空間と，変数$$ν$$の空間は，互いに双対な空間になります．フーリエ変換は，互いに双対な空間同士を結びつける線形写像です．フーリエ変換を用いると，同じ現象を，異なる世界（空間）で見ることができ，現象の理解に威力を発揮します．

適用例
事例１．$$t$$を時間とすると，$$ν$$は周波数ですから，フーリエ変換は，時間空間から，周波数空間への線形写像になります．
事例２．もし，$$t$$を実空間とすると，$$ν$$は逆空間になります．

■ラプラス変換

ラプラス変換はフーリエ変換とよく似ています．歴史的にはフーリエ変換より先だったのですが，フーリエ変換の紹介を先にしてしまいました．

$$ {\displaystyle F(s)=\int _{0}^{\infty }f(t)\mathrm {e} ^{-st}\mathrm {d} t} $$

$$ {\displaystyle f(t)=\lim _{p\to \infty }{\frac {1}{2\pi i } }\int _{c-ip}^{c+ip}F(s)\mathrm {e} ^{st}\,\mathrm {d} s} $$

（第一の式）$$F(s)$$を$$f(t)$$のラプラス変換といいます．関数$$f(t)$$は実数 $$t ≥ 0$$ について定義されており，積分範囲は$$0≦t<+∞$$になっています．ここで， $$s$$ は複素数（2 つの実数 $$σ, ω$$ を用いて $$s = σ + iω$$ と書ける）．もし,$$s$$を純虚数$$s=iω$$とすれば，フーリエ変換になります．
（第二の式）$$c > 0$$ として，関数 $$F(s)$$ から元の関数 $$f (t)$$ を計算することを逆ラプラス変換といいます．複素平面$$s$$での積分をするので難しそうですが，複素関数論の定理が役に立ちます．複素平面内の積分経路を閉曲線となるように広げ，内部にある特異点の留数の総和を求めれば計算できます．

ラプラス変換は，$$0≦t<+∞の$$実数の空間から複素平面$$s$$への線形写像です．
なぜ，このような面倒な変換が必要なのでしょうか．それは，微分方程式を解くのに有用です．ラプラスは，1812年の著書で，微分方程式の解法に使っています．

ラプラス変換，逆変換を，次のように簡略表記することがあります．
$$ {\displaystyle F(s)={\mathcal {L } }[f(t)]} $$
$$ {\displaystyle f(t)={\mathcal {L } }^{-1}[F(s)]} $$

■ラプラス（1749-1827），フーリエ（1768-1830），ヘビサイド（1850-1925）
フーリエはラプラスより20歳若いのですが，どちらもナポレオンに仕えて，大臣や知事を任命され政治の場でも活躍したところが似ています．
ラプラス変換は，後の演算子法（ヘビサイド）や複素関数論とのつながりがありますので，ここでまとめて紹介しましょう．

ヘビサイド（英国人）は，ラプラスよりも100年後の時代の電気技師ですが，微分方程式の解法に演算子法という素晴らしく便利な方法を開発（1880-1887）しました．これは，微分方程式を代数のように簡単に解く手法です．しかし，その解法の導出過程は数学的厳密さを欠いていたため，当時の数学者から非難されました．ヘビサイドは，「数学は実験的科学であり，定義が先にくるわけではない」，「私は消化のプロセスを知らないからといって食事をしないわけではない」と言ったそうです（wikiより引用）．

その後，ヘビサイドの演算子法は，ラプラス変換により理論づけがなされました．今日，私たちが，微分方程式を解くのに，ラプラス変換をして，周波数空間に移り，そこで簡単な代数計算をして，それをラプラス逆変換して，私たちの世界の時間の関数の解を得るという手順を使います．

ヘビサイドはユニークな天才です．1884年に，当時は20の式から構成されていたマクスウェル方程式を，今日知られる4つのベクトル形式の式に直したというのもとても興味深い逸話です．

正4面体の２分割

Q．正4面体を，平面を切り口に，合同な２つの図形に分割すること．

この問題を考えるのに，まず，正四面体の対称性から説明を始めましょう．図を見てください．正4面体の回転対称軸を調べると，3回回転対称軸が，各頂点にあります．2回回転対称軸は直角に対向している稜の中点を通ります．正4面体の場合は対称心もあるので，2回回転対称軸は，4回回反軸の性質もありますが，今，この問題で必要なのは2回回転対称軸の性質で十分です．鏡映対称面もありますが，この問題では関係ないので略します．

正4面体を，平面で切って，2つの合同な部分に2分割するのですが，対称性を考慮すると，2回回転軸を含む平面で2分割すると，合同な２つの部分に分割できることが理解できるでしょう．例えば，以下の2つの解答例を思いつきます．ついでに，Q．それぞれの例の場合に，その切り口の形はどのような図形でしょうか？という問題も追加します．

解答例１（指で挟んでいるのが，2回軸の正4面体への入口と出口）

解答例２（指で挟んでいるのが，2回軸の正4面体への入口と出口）

■さて私が言いたいのは，「解答例はそれだけでしょうか？」ということです．

実はそのような解は無数にあります．一つの直線を含む平面は無数にありますから，どれも解になります．下図（正4面体の1つの2回回転軸の真上から眺めた図）をご覧ください．黒い線が表現する平面は解答例１，赤い線が表現する平面は解答例２の場合です．2回回転軸を含む平面は無数に作れるので，例えば緑の線も解答例になります．

私がこの問題を作ったのは，対称性の概念は，物事を見通し良く整理して理解するのに役立つことを示したかったからです．