
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
http://twitpic.com/8qlket に,√2=2 というパラドックスが提起されています.
このパラドックスの原因は,非常に興味深いので,ここで考察することにします.
問題1
一辺の長さ1の正方形の対角線の長さは√2ですが,上図のように,X軸方向に1,y軸方向に1動く経路(n=0)を考えると長さは2になります.以降,このような折れ曲がり経路を繰り返して行きます(n=1, 2, 3, 4,・・・・∞).折れ曲がりを繰り返して行っても,いつも経路の長さは2で変わらないことがわかるでしょう.このような碁盤の目のような経路の長さは,マンハッタン距離と呼ばれることもあります(マンハッタンの市街の道は,碁盤の目の様だそうです).マンハッタン経路は,n→∞で対角線に限りなく近づきますので,√2=2 というパラドックスになります.
どこがいけないでしょうか?
問題2
同様な問題に以下の様なものがあります.https://note.com/keyneqq/n/n2ead38a59af5
半径1の円の円周は2πです.半径1の円に外接する正方形の一辺の長さは2ですから,半径1の円周のマンハッタン距離は8です.n=0から出発してx方向,y方向への折れ曲がり数を繰り返しマンハッタン経路は,限りなく円周に近づきますが,マンハッタン距離は8のままです.
従って,2π=8,すなわち,π=4となります. どこがいけないでしょうか?
■さて,これらの問題に見られるパラドックスは,どこに原因があるのでしょうか?
これらのすべての曲線はいずれも連続であることは確かです.碁盤の目に沿って辿るマンハッタン経路を∞回細かく繰り返した曲線は,至る所ギザギザで,微分不可能な曲線になっており,曲線の長さを微分係数を用いた積分で定義することができません.2点間(x1,y1),(x2,y2)のマンハッタン距離の定義は|x1-x2|+|y1-y2|で,碁盤の目(メッシュ)を細かくすればするほど,マンハッタン経路はいくらでも目的とする曲線に近づけることはできるのですが,マンハッタン距離は不変です.
(メッシュで定義される碁盤の目のデジタル世界でも,差分により微分係数が定義できますが,そのときもユークリッド距離を用いて定義します)
マンハッタン経路で定義される曲線は,無限回折れ曲がりを繰り返すことで,目的とする曲線にいくらでも近づきますが,マンハッタン距離が変化するわけはありません.
繰り返しの手順を見て,折れ線のフラクタルとみなしフラクタル次元を求めると,この折れ線の次元はやはり1次元になりました.折れ線の幅がフラクタル次元を生むというような説明も見かけましたが,そうではなくフラクタルはこの問題では関係ありません.この問題で人を驚かせるパラドックスの原因は,単純に距離の定義の違いによるものです.
定義が違うものなので違って当然なのですが,2つの曲線は限りなく近づいて行きますので,定義の違いを忘れて同じ長さだと思ってしまうのが間違いの源です.
半径1の円に内接する正5角形の1辺の長さを求めましょう.
この正5角形の1辺の長さをxとします.
△BACと△ADCは相似(相似比が黄金比Φ)で,形は2等辺三角形(等辺xとすると,底辺Φ・x)です.
Φ・x=x+(x/Φ) ですから,Φは黄金比の方程式 Φ2ーΦー1=0を満たします.
この方程式の解(Φ>1のもの)は,Φ=(1+√5)/2 です.
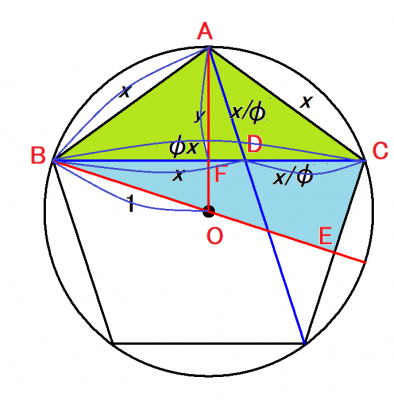
■次に,△BCEと△BOFとが相似であることを利用し,
1:(Φ・x)=OF:CE=(1-y):(x/2) が成立するので, y=1ー1/(2Φ)
ただし,y=√[(x/Φ)2-((Φ・x)/2-x/Φ)2]=√[x2ー(Φ・x/2)2]=x√[1-(Φ/2)2]
x=y/√[1-(Φ/2)2]=[1-1/(2Φ)]/√[1-(Φ/2)2]=(√[10-2√5])/2=1.1756
■ 作図
半径1の円に内接する正5角形の一辺の長さx=(√[10-2√5])/2を作図する方法
(証明)ピタゴラスの定理を2回使います.
■ 万華鏡への応用
■OECDのPISA(Programme for International Student Assessment)国際的な学習到達度調査で,日本の急激な読解力低下(2018年)が指摘されています.PISA調査は15歳(高校1年)を対象に,読解力,数学的リテラシー,科学的リテラシーの三分野について,3年ごとに実施する調査で,国立教育政策研究所が担当しています.
直近の2018年の試験では,読解力が前回の8位から15位に落ちました.
■日本の読解力の平均得点は504点で,OECD加盟国(移民など多数含む)の平均(487点)は上回ったものの,前回(2015年)から12点下がりました.内訳は408点未満の低得点の生徒の割合が全体の約17%を占め,前回調査から4ポイント増えている.生徒の6人に1人が十分な読解力を持っていないことになる.これほど低得点層が増えたにもかかわらず,平均点の低下は少なかった.これは,文章を解さない児童が増えたが,十分な読解力を備えた児童も同時に増える「二極化」が進んでいるということを意味します.得点分布が,平均中央に山を持つ標準的なグラフでなく,中央の左右に2つの山ができるグラフへと変化しました.
そのような変化は,少なくとも2つの因子が存在することを意味します,本来の読解力だけでなく,影響を与えるもう一つの因子なんでしょうか?それは家庭の経済力かもしれません.現在の日本社会では,貧富の2極化も進んでいますから.あるいは,文科省の言うようにデジタル機器への適応の問題である可能性も否定はしません.
■PISAは,紙に手書きで解答する方式から,パソコンで入力する方式に変更(2015年)したそうです.文科省は「日本の生徒は機器の操作に慣れていないことが影響した可能性がある」と分析しています.パソコンを介したテストの方式を私は良く知りませんが,まず,ディスプレイに問題文が表示され,次に進むと問が表示され,これに応えるという後戻りのできない方式ではないでしょうか.これに解答するのはかなり難しくなる.印刷物を介したテストでは,問を見てからまた問題文に戻り確認して答えるというやり方をすると思います.文科省の分析が,このようなテスト方式の変化のためであるというなら私もそうだろうと思います.しかし,「順位が落ちたのはパソコン入力に戸惑ったせいだ」との分析であるなら間違っていると思います.パソコン利用では,紙のときと違い,読解力だけでなく記憶力など総合的に影響し難しいテストに変わったかもしれません.
折り紙も数学ですが,この雪の結晶を折るアルゴリズムは複雑でわかりにくいです.
写真の1,2は完成した雪の結晶を,表面から見た写真(1)/裏面から見た写真(2)です.
(1) (2)
■スタートに用いるのは,以下に示す6角形の折り紙(3)です.完成品を見ながら,
折り紙(表面側から見て)に,谷折りすべき線(赤色)/山折りすべき線(黄色)を描き込んでみました.
(3)
この線の通りに,谷折り/山折りをして,(4)に示す中間体が作れますから,
試行錯誤して,(4)図のような中間体を作るのを目標にしましょう.
(4)中間体
■中間体(4)の表面側に出た6か所の山尾根の部分を,平らに広げて帯状筋を作る.
この帯状筋の形成のときに,新たに山折りとなる箇所を,
折り紙(3)に青緑色の線で示しておきました.
中間体の山尾根をつぶして帯状筋にするところは,注意深くやりましょう.
■金沢に来ていますが北陸の海は8日は荒れ模様でした(この日はサンダーバードが運休しました)。海の色の変化が美しい。虹の撮影は小梁さん。
■ここは勧進帳の舞台です.腹芸とは相手の心を思いやり察することです.忖度は権力と利益が結びついていて汚いもので,人情や腹芸とは違うと私は思います.

中谷が雪の研究を進めたのには,シベリア出兵の時代で,雪や着氷などが軍事研究として必要だった背景がありますが,実際にやった中谷宇吉郎の雪の研究は基礎研究です.
この地に雪の科学館を設計した建築家は磯崎新です.
■氷の結晶模型はH-O-H分子が水素結合で連鎖しており,平面ではありませんが6角形が見えるでしょう.氷の結晶の内部構造の6回対称性が,樹脂状結晶成長にも反映され,成長した雪片の外形(「雪は天から送られた手紙である」というように上空の環境で様々な形の雪片が見られます)は,どれもすべて6回対称です.
中谷宇吉郎雪の科学館
ダイヤモンドダストの実験.
過冷却の霧(氷点以下なの水(液体)の状態を保っている)の中に,氷結の核となるダストを吹き込むと,一瞬にして水滴の霧が氷晶の霧となる.氷は光を当てるとキラキラして(屈折・分散・反射が強く起こる)ダイヤモンドのように輝く.
*私は自販機でお茶を買い蓋を開けたとき一瞬でペットボトル内が凍るのを見ました.私の記憶では季節は夏だと思うのですが,自販機のペットボトルはギンギンに冷えていて過冷却だったのでしょう.
*実験の動画を撮影しyoutubeに置きました.
鈴木大拙
■機械に何でも頼ると機心machine mindsになる.
A machine mind is a calculating mind. Such a mind is not clean and pure.「荘子」の外編
■You cannot understand yourself simply by thinking about yourself.
You can understand yourself better by understanding others.
〇△□
ドアや家具などに見られるイスラムの美しい模様は千年以上の歴史があります.
イスラムの星のデザインは,対称性の高い星型が配列しているのが特徴です.
繰り返し模様全体を支配する対称性は,17種類の平面群のどれかになるし,
並進(周期性)と両立しうる回転対称は,2,3,4,6回軸に限られます.
しかし,イスラムの模様に散らばる星形は対称性が高いのです.高い対称性はもちろん全域に作用はできず,その星形の内部にだけ作用する局所的なものです.
上図の模様を例にとると,8回対称の青い星型が,正方形格子の周期で配列していることがわかります.
青い星型にある8回対称性は,青い星型内部と緑の周囲領域,草色の星形5角形の領域までは有効ですが,
オレンジ色の8角形までは有効ではありません.
青い星の中心にある8回対称軸はオレンジ色8角形の付近では,4回対称軸に低下してしまいます.
これは,周期的な平面では8回対称軸は存在できない(正8角形のタイルでは平面を張れない)から当然のことです.
ある点のまわりの対称性という言葉は注意が必要で,その点周囲の「局所的」対称性を指す場合もありますが,平面「全域」で有効な対称性を指すのが普通です.この例では,青い星型の対称性は8回対称ですが,この星の中心にある回転対称軸は4回対称軸です.
このパターンの単位胞は,オレンジ色の8角形の中心を結んでできる正方形の格子で作られるタイル1つです.
■Girihタイル
正方形と正8角形を組み合わせた平面のタイル張りの例が下図(a)です.この例のテッセレーションを,(4,8,8)と記述します[1つの頂点のまわりに,正4角形,正8角形,正8角形が集まっている].
(b)図は,正4角形および正8角形の内部に装飾線を描いたGirihタイルです.
平面をGirihタイルでタイル張りしておいて,タイルの縁の輪郭を消すと(c)図のパターンが得られます.
■ここで,始めに掲載したイスラムの模様も,上の例と全く同じであることを確認してください.
始めに掲載した模様の正4角形タイルや正8角形タイルの形は,草色の星型の中心を結んでいくと明らかでしょう.
正4角形や正8角形の内部の装飾線はどのようなものであるかもお確かめください.
Volume 90 Issue 50 | p. 64 | Newscripts
Issue Date: December 10, 2012
マイケル・フリッケ博士(オハイオ州のBoehringer Ingelheim's Ben Venue 研究所の化学者)は,2011年の化学ノーベル賞受賞者シェヒトマンの準結晶を知り,自宅の新しいパティオのデザインにこれを用いることを思いつきました.そしえ,フリッケは1年がかりで2012年11月にパティオを完成しました.
1200個の特製のコンクリート舗装石を準結晶パターンに配置したものです.
写真は,子供が準結晶タイル張りのパティオに立っているところです.彼のTシャツには「悪役のようにゆったり」と書かれています.
フリッケは,パティオに使う2種類の舗装石(太った菱形と痩せた菱形)の木製型を作製しました.木型を使用して彼は1日に15枚のコンクリート舗装石をキャストし,10か月生産した後,ペンローズの非周期タイルと呼ばれるパターンに配列し始めました.
この配列を作るのは「忍耐が必要」だったようです.準結晶が広く受け入れられるまでに,シェヒトマンが嘲笑や猜疑を乗り越えたように.
夜明け前の空の色が美しい.桔梗の色とオレンジ色の消えるところが良い.
新年おめでとうございます.2020年も宜しくお願いいたします.蕎麦好きな私ですが,年越し蕎麦を蕎麦屋で食べたのは初めて,除夜の鐘を撞きに行ったのも初めてです.行列があれば止める主義の私ですが,今回はどちらにも並んでしまいました.