note.com投稿記事

フーリエ解析（1822年）

■大発明たる所以
色々な分野でフーリエ解析（フーリエ変換）が使われます．現在の科学におけるフーリエ変換の貢献は偉大です．フーリエ変換なしでは何も考えられません．例えば，時間とともに変化する信号$$f(t)$$は，いろいろな周波数$$ω$$のサイン波の信号の振幅が時々刻々変化するものを重畳$$\displaystyle \sum_{}^{}a_{n\omega }(t)\textrm{sin(}n\omega t)$$して表現できます．線形システムというのは，時間の関数の入力$$f(t)$$があれば$$A･f(t)$$が出力され，入力に，$$f(t)$$と$$g(t)$$があれば，$$A･(f(t)+g(t))$$が出力され，いわゆる重ね合わせが成立します．入力信号も出力信号も，重畳成分のいろいろな周波数のサイン波に分解できるというのがフーリエ変換です．分解された個々周波数のサイン波ごとに，ある周波数帯域を除去するフィルタを通すなどして，それらの出力を再び重畳する信号処理が可能です．

赤外吸収IRスペクトルの測定を例にとりましょう．これは，サンプルを透過する光はどのような波長で吸収されるかの測定です．光の波長を順次スキャンし分光しながら測定する方法は普通ですが，FTIRという方法では，分光せず白色光をマイケルソンの干渉計でインターフェログラムにし，これに対するサンプルの吸収を測定して得たデータをフーリエ変換をすれば，波長スキャンのときと同様に吸収スペクトル測定ができます．

結晶学では，結晶空間と逆空間という互いに双対な空間を扱いますが，この両空間は互いにフーリエ変換で変換し合う空間です．イメージが把握できるように，双対という概念に簡単に説明しましょう．例えば，正6面体と正8面体は互いに双対な立体です．この両立体は，面を頂点に，頂点を面に取り換えると互いに移り変われる立体です．置き換える面と頂点の関係とは，結晶格子の基本ベクトルと逆格子の基本ベクトルの関係と言い換えることができます．

■さて，フーリエ級数（展開）とフーリエ変換は，同じ性質のものなのですが，細かいことをいうと違いもあります．

フーリエ級数展開は：
周期的などのような波形も、単純な波形（サイン波）の重ね合わせとして表すことができます。
フーリエ変換では：
周期的でない波形を扱えます．ここで用いる単純な波形（サイン波）の周波数は，フーリエ級数のときのように離散的な倍音のみではなく，周波数のステップが細かくなり，級数は積分になります．

■ジョセフ・フーリエは，熱が固体中をどのように移動するか（熱伝導現象）を数学的に研究しました．この研究のために，新しい数学的方法を開発しました．これがフーリエ解析の始まりです．

彼が熱伝導に興味を持ったきっかけが，いつのことだか定かではありません．北アフリカにいたときに生じたと推定しているのは，以下のエッセイです．

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
1798 年, フーリエはナポレオンのエジプト遠征に科学顧問として, モンジュやマリュスとともに同行し，エジプトでは考古学上の調査や，カイロ学士院の創設に力を注ぎ，カイロ学士院の書記官にも選出されました．ナポレオンは 1799 年にパリに帰還しますが，フーリエはその後 2 年間エジプトに残りました.　1801 年, フーリエはフランスに帰還し, 再び諸工芸学校の解析学の教授になりますが，翌年 2 月にナポレオンはフーリエをイゼール県の知事に任命しました．以下のエッセイによると，熱伝導研究の開始は 1802 年頃らしいとされています．

タイトル未設定www.kurims.kyoto-u.ac.jp
1807，1811年に論文で，連続物体の温度分布の問題を解いており，フーリエ展開公式を導いています．

彼の研究結果は1822年に、熱の解析理論（Theorie analytique de la chaleur)に掲載され、そこでは、複雑な物理問題をより単純なものに分解して解析する方法が示されました。

Анализ Фурье • Джеймс Трефил, энциклопедия «Двести законов мироздания»Любая волна сложной формы может быть представлена как суммаelementy.ru
フーリエは，複雑な波形を単純な波形の重ね合わせとして表せることを示しました．一般に，古典的な系を説明する方程式は，これらの単純な波のそれぞれについては簡単に解けます．フーリエは，これらの単純な波形を重ね合わせて，複雑な問題全体の解を得る方法を示しました．数学的に言えば，フーリエ級数は，周期的な任意の関数を単純なsin波の種々な高調波（倍音）の重ね合わせとして表す方法で，フーリエ解析は調和解析とも呼ばれます．（下図参照）

周期的でない任意の波形の場合は，整数倍音の高調波の重ね合わせではなく，連続的に変化する高調波の積分で表現するフーリエ変換の概念に拡張できます．

フーリエ解析の登場フーリエ解析の登場energychord.com

■20世紀半ばにコンピューターが登場するまで，自然の複雑さに立ち向かう武器は，フーリエ解析でした．フーリエ解析の出現以来，科学者はニュートン力学の法則や他の基本的な方程式を直接適用して解ける単純な問題だけではなく，複雑な問題にもそれを使用して解くことができました．19世紀のニュートン科学の偉大な成果の多くは，実際には，フーリエによって最初に提案された方法を使用しなければ不可能でした．その後，これらの方法は，天文学から機械工学まで，さまざまな分野の問題を解決するために使用されました．現在は，画像処理などでコンピュータを用いた高速離散フーリエ解析が行われています．

■ジャン・バプティスト・ジョセフ・フーリエ（1768-1830）
フランスの数学者．オセールに生まれ，9歳で孤児となる．若くして数学の才能を発揮した．フーリエは教会学校や軍人学校で教育を受けた後，フランス革命にあう．彼は数学教師として働いたが，生涯を通じて政治の世界で活躍した．1794年にはテロの被害者を保護して逮捕されたが，ロベスピエールの死後，獄中から釈放され，パリの有名なエコール・ポリテクニークの創設に参加し，その地位はナポレオン政権下での昇進の橋頭堡となった．ナポレオンに同行してエジプトに行き，下エジプト総督に任命された．1801年にフランスに帰国すると，州知事に任命された．1822年にはフランス科学アカデミーの常任書記官に就任し，フランスの科学界で影響力のある地位に就いた．熱伝導の論文は1807，1811年．フーリエ解析の本の出版は1822年．

感染症の数理モデル

今年の数学月間（7月29日）は，稲葉寿氏（東大）の表題の講演をZOOMでお送りしました．covid19の感染拡大第３波に見舞われている今日，お読みいただくと役に立つと思います．gotoトラベルは，それぞれR<1を保っている複数の状態（都市）の相互作用により，R>1に変わる可能性を誘発する危険な政策です．

■これまでに人類はいろいろなパンデミックを経験してきました．1918年のインフルエンザ（スペイン風邪）は4000万人以上の死者，2015年のＨＩＶ感染者は3670万人，マラリアは年間3億～5億人の患者を生む．最近のSARS，エボラなどの新興感染症や，再興感染症などにより感染症撲滅という1980年代までの楽観論は消滅しました．人口増加，都市集中，環境破壊などによって，感染症流行リスクはますます増大しています. 現在COVID-19は予断をゆるさない状況です．

■感染症の数理モデルは，SIRモデルを基本とします．これは，ケルマックとマッケンドリックが提唱(1927)したものです．全人口をS（感染感受性のある集団），I（感染者集団）,　R（免疫のできた回復者）の３つのグループに分け，それらのグループ間の相互作用（遷移）を数式で記述し数理モデルができます．
数理モデルは，感染拡大の様子を予測でき，種々の介入（ワクチン接種，隔離，接触制限，ロックダウンなど）を行うことで，感染性人口を絶滅させる（感染源にならないようにする）対策の策定に必要です．

COVID-19では，もう少し進化させた，SEIR数理モデルが必要です．これは，E（潜伏期間にある感染者集団）が加わったモデルです．特にCOVID-19は，Eグループのものが感染源になることや，免疫のできた回復者の免疫が消えることなどがわかり始めており，一筋縄では行かないモデリングになります．

■基本再生産数R0（R-naught)
感染感受性のある集団に居る一人の感染者が，その全感染期間に再生産する（感染させる）2次感染者の数を基本再生産数R0と定義します．全員感受性のある集団で，1次感染者数，2次感染者数，3次感染者数，･･･と等比級数で増加するときの公比がR0です．
R0は患者数と感染感受性のある人（未感染者）との接触回数に比例するので，環境状況でこの数値は変化します．感染が広がると未感染者が減り，実際の集団には免疫のある人も混ざった状態になるので，全員感受性がある集団で定義したR0よりも小さいR（実効再生産数）が期待できますが，適切でない介入があれば，逆にRの増加もあり得ます．
結局，R>1であればその集団の感染者人口の成長率は正になり，流行は拡大していくが，R<1であればその集団の感染者人口の成長率は負であって流行は自然に消滅する．何らかの介入をして，すみやかに，R<1とすることが対策になります．

■多状態のSEIRモデル
集団に2つの状態（例えば，学童と社会；病院と社会；東京と地方；大学と社会；等々）がある場合は，それぞれにSEIRモデルを作り，さらに２つの状態間の相互作用を考える複雑なモデル（コンパートメント・モデルという）になります．２つの状態にはそれぞれの実効再生産数Rがあります．
現実に近い多状態SEIRモデルを作り，その次世代行列の最大固有値として，Rを計算します．そして，どのような介入（例えば，ワクチン接種，ロックダウン，外出制限，休校）をすれば，Rが下げられるかを検討します．
集団の２つの状態のRが1未満であるため，感染が制御されているように見え，通常の生活に戻り始めるかもしれません．
イギリスでも約200万人の大学生が全国から復帰し，フレッシャーズフルー［注）フレッシャーズフルーとは，大学で最初の数週間に新入生が発症した一連の病気に付けられたイギリス英語］のようなCOVID-19感染拡大が懸念されるそうです．若者が無症候で感染を広げる最悪モデルでは，学年末までに96％感染と予測されました．学生集団は軽症ですが，体力の弱いスタッフや周囲のコミュニティと相互作用をするコンパートメントモデルでシミュレーションし，いろいろな介入施策の検討がなされています．
［注）Isaac Newton Instituteによって実施された「感染症のパンデミックのダイナミクスを理解する上での数学的および統計的課題」（IDP）　https://www.newton.ac.uk/event/idp］

日本でも，東京と他都市のRが，それぞれ１をわずかに下回っている状況ですが安心はできません．東京と他都市の相互作用により全体が増加し１を超えるRになる可能性はあります．

■免疫は持続するか
もし，回復したものの再感染を許容するモデルにするならば，新規感染率に対する，回復者再感染率の比をσとし，σR0＜１なら収束に向かいます．
従来の感染症の常識では，免疫を得ると再感染はしないということを前提にしていますが，COVID-19に関しては，再感染をしないような免疫が獲得できないかもしれません．免疫抗体が数か月で減衰するという報告が中国やスペインからなされている状況です．もし，免疫が獲得できないのであればワクチン自体が成立しないことにもなります．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
次回の数学月間企画講演（第3回）のお知らせ
「3Dジグソーパズルのデザインと数学」
手嶋吉法（千葉工業大学）
12月26日（土），15:00～17:00，参加無料です．
ZOOMにてリモートで実施します．多くの皆様の参加をお待ちします．
ホームページhttp://sgk2005.saloon.jp/　で申し込みができ，
参加登録されると，実施日の1週間前までにZOOMのURLをお知らせします．
主催：NPO法人数学月間の会

ロシアの科学啓蒙雑誌・新聞

ロシアの義務教育は6歳から17歳までの11年間の一貫教育です．この年代の生徒が読む科学啓蒙雑誌も各種あり，いろいろ工夫されており面白く自分で深く学ぶこともできます．

●「科学の世界で」

月刊誌、ロシア版サイエンティフィックアメリカン。2003年から発行されています（それ以前は1983年から1993年に発行されました）。

●知識は力

1926年1月にティーンエイジャー向けの月刊ポピュラーサイエンス&アドベンチャーマガジンとして創刊し、困難な発展の道を歩んできました。戦後、「冒険」の要素を失くし、「働く若者に人気の科学雑誌」になりました。60年代の初めにかけて、人道的知識の割合が増加しました。
「科学と社会の架け橋」として、あらゆる年齢や専門分野の人々との交流を重視しています。

●量子っ子　クバンチク

2012年から発行されている、あらゆる年齢の好奇心旺盛な学童のための月刊イラストマガジン。数学、物理学、言語学、生物学、化学の面白い話や問題があります。

●量子　クバント

学童と学生のためのソビエトとロシアの人気のある科学、物理学と数学のジャーナル。1970年から発行されています。アカデミアンP.L. Kapitsaは、「KVANT」の創刊という提案をしました。アカデミアのIKKikoinがジャーナルの最初の編集長になり、アカデミックのA.N.Kolmogorovが最初の副編集長になりました。

高校生とその教師、および中学生を対象としています。
「Quant」セクションのタスクは、通常、6年生から学者まで、誰にとっても興味深いものです。

●トリニティオプションサイエンス

「TrV-Science」はロシアの人気科学新聞です。2008年4月1日から2週間ごとに発行されています。

●コマーサントサイエンス

出版社「Kommersant」の情報速報。Kommersant新聞と一緒に配布されます。2011年から（断続的に）公開されています。

●シュレーディンガーの猫

2014年10月から発行されている月刊「科学祭」。

●科学と生活

ロシアとソビエトのイラスト科学の月刊誌。1890年に創刊され、1934年に更新されました。

●サイエンスファーストハンド

科学の学際的なジャーナル。2004年以来、世界最大の科学センターの1つであるNovosibirskAcademgorodokで発行されています。ロシア語の印刷版は年に6回発行されます。Science First Hand （英語の電子版）は年に3回発行されます。

●ポピュラー機械

2002年から公開されています。1902年以来発行されているアメリカの人気科学雑誌PopularMechanicsのロシア版。

●可能性：化学。生物学。薬

学生と教師のための月刊教育雑誌。2005年から生産。

●可能性：数学。物理。コンピュータサイエンス

学生と教師のための月刊教育雑誌。シリーズ「数学。物理。情報」は2005年から発行されています。

●自然

ロシア科学アカデミーの月刊自然科学ジャーナル。1912年1月から公開されています。

●化学と生命

月刊科学誌。1965年に「Chemistry＆Life」という名前で創刊されました。1997年以来、「化学と生命-XXIセンチュリー」というタイトルで出版されています。

●科学技術の最新情報（販売終了）
雑誌「現代の大都市のハイテクライフスタイルについて、革新と科学的発見について」、アメリカの雑誌ポピュラーサイエンスのロシア版。2002年から2009年に終了。
●エコロジーとライフ
エコロジーアンドライフマガジン（販売終了）
月刊の科学教育誌。1996〜2012年に公開されました。

証明可能性の限界（３）

Грегори Чейтин　科学の世界«В мире науки» №6, 2006

数学と物理学
数学と物理学は完全に異なるものと一般に思われています。物理学者は、実験と観察の結果に基づいて世界を説明します。ニュートンの法則であれ、量子物理学の標準モデルであれ、宇宙を支配する法則は、経験的に確立され、論理的に証明するのではなく、実験的にのみ検証できる公理と見なされなければなりません。数学者は、ある意味で世界から独立しています。彼らの結論や定理、たとえば整数や実数の性質は、私たちの周りの現実にまったく依存していません。数学的な真実はどの世界でも真実でなければなりません。それでも、類似点があります。物理学、そして一般的に自然科学では、科学者は観察結果を昇華させることによって法則を生みだします。それから、結果の法則から観察結果をどのように推定できるか示します。数学でも同様のことが起こります。数学者は計算実験の結果を公理に圧縮し、それらから定理を推定します。

ヒルベルトが正しければ、数学は閉じたシステムであり、新しいアイデアの場所はありません。数学のすべてを説明する静的な閉じた理論があり、それは独裁者のようになります。数学を発展させるには、創造のための新しいアイデアと範囲が必要です。いくつかの基本原理から考えられるすべての結果を推測するために最善を尽くすだけでは十分ではありません。個人的には、オープンシステムの方が好きで、厳格で権威のある考え方は好きではありません。

1956年にハンガリーから脱出し、その後イギリスで科学の哲学に従事したイムレ・ラカトスも、数学は物理学のようなものだと信じていました。彼は、実験が数学にとって異質ではないことを示すために、準経験性の概念を導入しました。たとえば、1742年に、Christian Goldbachゴールドバッハは、2を超える偶数は2つの素数の合計として表すことができるという経験的な結論に達しました。ゴールドバッハの推測は、10^{14}までの数で正常にテストされていますが、厳密には証明されていません。数学は準経験的であるように私には思えます。言い換えれば、それは物理学（本当に経験的です）とは異なりますが、おそらくほとんどの人が考えるほどではありません。

新しい公理
新しい公理を追加するという考えは、数学者にとって異質ではありません。たとえば、ユークリッドの5番目の仮定を考えてみましょう。直線の外側に選んだ任意の点を通る指定された直線に平行線な直線は、1つだけ描くことができます。何世紀にもわたって、幾何学は、ユークリッドの他の仮定に基づいてそれを証明しようと頭を悩ませてきましたが、失敗しました。最後に、数学者は、5番目の公理を置き換えて、曲線空間の非ユークリッド幾何学、特に球面形と鞍形を得ることができることに気づきました。他の例としては、論理学における除外平均の法則や集合論における選択の公理などがありますが、これはほとんどの数学者が進んで証拠として使っています。しかし、それを認めず、いわゆる直観主義的な論理や構成主義的な数学を探求する科学者がいます。数学はまだ絶対的な真理の一枚岩のシステムになっていないことが判明しました!

もう一つの非常に興味深い公理は、「PはNPと等しくない」という文で、PとNPは課題クラスの名称です。NPクラスには、提案された解を非常に迅速にチェックできる課題が含まれています。例えば、「数字8633の因数を求める」という問題では、提案された解「97と89」を簡単な掛け算ですぐに確認することができます。（「速い」には厳密な定義がありますが、ここでは詳細は重要ではありません）クラスPは、事前の想定がなくてもすぐに解ける課題です。誰も答えを知らない問題は、どんなNPクラスの問題でもすぐに解けるかどうかということです。(数8633の因数を素早く求める方法はないのでしょうか？)つまり、クラスPとNPは同じなのでしょうか？これは、クレイ数学研究所のミレニアム賞問題リストにある項目の一つで、それぞれ100万ドルの賞が与えられています。

ほとんどのコンピュータ科学者は、PがNPと同等ではないと確信しているが、厳密な証拠はまだ見つかっていない。このような仮定の真偽は多くの経験的証拠に支えられているが、それを前提にして公理として受け入れられるのだろうか。それこそコンピュータの専門家がやっていることです。確かに、広く使われているいくつかの暗号システムの信頼性については疑問が残ります。
ハッキングできないと考えられていますが、誰もそれを証明することはできません。

実験数学
物理学と数学の交差点で、実験的な数学が生まれました。多数の例のコンピュータ処理による新しい数学の法則の発見です。このアプローチは、短い証明ほどの説得力がありませんが、長くて複雑な証明よりも説得力があり、場合によっては非常に受け入れられます。この概念は、過去に、ヒューリスティックスと数学の準経験的性質の強力な支持者であるジョージ・ポリヤとラカトスの両方によって支持されてきました。これは、2002年に発行されたStephen Wolfram（Stephen by Wolfram）の著書「NewKind of Science»（A the New Kind of Science）」に適用され、正当化されています。

大規模なコンピューティングは非常に説得力がありますが、それは証明の必要性を排除しますか？はいでもありいいえでもある。計算と証拠は、さまざまな種類の証拠を提供します。特に重要なケースでは、証明に誤りが含まれている可能性があり、コンピュータの計算は、残念ながら、想定されている結論を反証するような反例を見つける直前に停止されることがあるので、両方とも必要だと考えます。

議論された問題は非常に興味深いものですが、解決にはほど遠い。ゲーデルの証明に関する記事が発表されてから50年が経過しましたが、2006年の今でも、その不完全性がどれほど深刻なのか、それが原因で数学的方法を修正すべきかどうかはまだわかりません。おそらく50年以内に答えが見つかるでしょう。

追加の文献：

・Leibnizの章については、Men ofMathematicsを参照してください。ETベル。再発行します。タッチストーン、1986年。
・数学の準経験的見解のより完全な議論については、数学の哲学の新しい方向性を参照してください。ThomasTymoczkoによって編集されました。プリンストン大学出版局、1998年。
・ゲーデルの証明。改訂版。E.ネーゲル、JRニューマン、DRホフスタッター。ニューヨーク大学出版局、2002年。
・実験による数学：21世紀のもっともらしい推論。J.BorweinとD.Bailey。AK Peters、2004年。
・ゲーデルの哲学と彼の作品とライプニッツの作品との関係については、不完全性：カートゲーデルの証明と逆説を参照してください。レベッカゴールドスタイン。WWノートン2005。
・メタ数学！：オメガの探求。グレゴリィ・チェイチン。パンテオンブックス、2005年。
・数学者の経歴は、スコットランドのセントアンドリュース大学の数学統計学部のウェブサイトで入手できます。
・グレゴリィ・チェイチンのホームページ。

証明可能性の限界（２）

数値Ω
Ωの発見に向けた第一歩は、ライプニッツのエッセイが出版されてからちょうど250年後に出版された有名な記事でした。1936年、ロンドン数学協会プロシーディングスに、アラン・チューリングが単純なユニバーサルコンピューティングマシンの数学モデルを発表しました。さらに、彼はコンピュータ・プログラムが停止するか否かの判断が可能かどうか疑問を持ちました。これが有名な停止問題の定式化です。

数値Ωは、数学未知な部分を表しています。有限長のコンピュータプログラムは、この数の有限数のビットしか決定できません。後続のものはすべて、あいまいな暗闇の中に残ります（画像：www.sciam.ru）

オメガの中は暗闇！

もちろん、プログラムを実行すると、最終的には停止していることに気付く場合があります。基本的な問題は、プログラムが停止しない場合に、いつあきらめて停止するかを決定することです。多くの特殊なケースでは解決できますが、チューリングは一般的な解決策がないことを示しました。アルゴリズムも数学理論も、どのプログラムが停止し、どのプログラムが停止しないかを決定することはできません。（このチューリングの状態の近代的な証明は、サイエンティフィック・アメリカンのウェブサイト上で見つけられます。）ちなみに、私は現代的な意味で「プログラム」という言葉を使用していて、それはコンピュータプログラム自体の全体と、それが処理するデータを意味しています。

数値Ωに向けた次のステップは、考えられるすべてのプログラムのセットを検討することです。ランダムに選択されたプログラムが停止することはありますか？停止確率は Ωです。まず、プログラムをランダムに選択する方法を決めましょう。プログラムはビットの列であるため、後続の各ビットの値を選択するには、単にコイン投げをします。プログラムには何ビットを含める必要がありますか？コンピューターが次のビットを要求しなくなるまで、コイン投げをします。数値 Ωは、このようなランダムなビット列が導入されたときに、マシンが停止する確率です。（数値Ωはプログラミング言語の選択に依存しますが、この数の驚くべき特性はプログラム言語によりません。言語を選択すると、Ω はπや5のような特定の数値をとります。）

数値Ωは確率を表すため、ゼロより大きく、1より小さい必要があります。一部のプログラムは停止し、一部は停止しません。バイナリコードで記述されたΩの数は 0.1110100...のようになり、小数点以下のビットの列は還元不可能であり、それら自体も還元不可能な数学的事実であることがわかります（各事実は特定のビットが0か1かです）。

Ωの決定方法

数値Ωがどのように決定されるか理解するために、簡単な例を考えてみましょう。特定のコンピュータのすべてのプログラムのうち、停止するのは3つだけで、それぞれ110、11100、11110、これらは、それぞれ3、5、5ビットの長さであるとします。我々はランダムに連続する各ビットの値を決定するためにコインを投げ、それらの各々の確率は1/2です。各プログラムの確率は

$$1/2^{3}, 1/2^{5} , 1/2^{5}$$, です。次に、そのようなコンピューターのプログラムを停止する確率は、次の式によって決定されます。

$$Ω = 1/2^{3} + 1/2^{5} + 1/2^{5} = 0.001 + 0.00001 + 0.00001 = 0.00110$$

［訳注）1/2^{3}は10進数表現，0.001は2進数表現です．他も同様］

ここで、2進数は、3つの停止プログラムの1つをランダムに選択する確率を表します。プログラム110が停止するため、1100や1101など、110で始まる3ビットより長いプログラムは考慮しません。したがって、それぞれの合計に0.0001を追加しません。

このように開始にプログラム110が含まれる、長いプログラム（1100など）すべては，停止すると見なします。言い換えると、プログラムデータは停止した後、それ以上のビットを要求しないので自己制限的です。

数Ωは無限の合計として定義でき、長さがNビットの各プログラムはΩに$$1/2^{N}$$だけ寄与します。言い換えると、停止する各Nビットプログラムは、Ωのバイナリ表現のN番目のビットに1を追加します。停止したプログラムに対応するすべてのビットを合計することにより、Ωの正確な値を取得できます。このように数値Ωは√2やπのように正確に計算できるように見えますが、そうではありません。数値Ωは厳密に定義されており、非常に具体的な意味がありますが、実際には解決策がない停止の問題を解決するので、計算することはできません。具体的には、Ωの最初のN ビットを知ることで、最大N ビットの長さのプログラムが停止するかどうかを判断できます。つまり、ΩのNビットを見つけるには、少なくともN ビットの長さのプログラムが必要です。Ωで特定のビット数を定義できないことを示唆しているわけではないことに注意してください。たとえば、コンピュータプログラム　0、10、および110が停止することを知っていると、Ωの最初の3ビットまでと言えます。0.111の形式です。重要なのは、Ωの最初のNビットは、Nビットよりも大幅に短いプログラムを使用して計算できないということです。

最も重要なことは、 Ωが無限の数の還元不可能なビットを与えることです。有限の長さのプログラムは、何十億ビットも含まれていても、残りのビットを決定するのに役立ちません。残りのビットは無限にあります。言い換えれば、公理の有限集合に対して、この集合を使用して証明できない真実の数は無限です。

数値Ωが非圧縮であるのはなぜか？

数値が非圧縮であること、つまり、最初のNビットがNビットより短いプログラムで決定できないことを証明してみましょう。チューリングの停止問題に照らして、Ωの特性を分析しましょう。Nビット長までのプログラムは、それより短いプログラムでは問題を解決できないという命題を使用します。

Ωの非圧縮性を実証するために、最初のNビットを知ることで、Nビットまでの長さのプログラムのチューリング問題を解くことができることを示します。N ビット以下の長さのプログラムでは、Ωの最初の N ビットを計算できないことがわかります。(もしそのようなプログラムが存在するならば、その助けを借りて、最初のNビットΩを計算して、Nビットの長さのプログラムのチューリング問題を解くのに使うことができます。)

それでは、ΩのNビット知ることで、停止問題を解くことができ、Nビット長までのプログラムのうち、どのプログラムが停止するかを決定することができるかを見てみましょう。一歩一歩やっていきましょう。Ｋステップでは、各プログラムをＫ秒間実行し、停止したプログラムの数によって、停止する確率$$Ω_{K}$$を決定します。Ωが全てのプログラムを用いて算出されるのに対し、最終的に停止するプログラムのサブセットのみを用いて取得されるため、Ωよりも小さいが、Ｋが増加するにつれて、$$Ω_{K}$$の値はΩに近づき、$$Ω_{K}$$の最初のビットの多くがΩの対応するビットと等しくなります。 $$Ω_{K}$$とΩの最初のNビットが一致する場合、これは、Nビット長までのすべてのプログラムが考慮され、遅かれ早かれ停止することを意味します。

(他にもNビット長のプログラムがあったとしたら、後段Kで停止してしまい、$$Ω_{K}$$がΩよりも大きくなってしまうので、あり得ない)。

つまり、Ωの最初のNビットを知ることで、Nビットまでの長さのすべてのプログラムの停止問題を解くことができます。今、Ωの最初のNビットの長さがNビットよりも有意に短いプログラムで検出できるとしましょう。そして、$$Ω_{K}$$を計算するプログラムと組み合わせて、Ｎビット以下のプログラム長を求めることで、Ｎビットまでのすべてのプログラムの停止問題を解決することができるが、上記のように、そのようなプログラムは存在し得ない。したがって、Ωの最初のＮビットを計算するためには、ほぼＮビットの長さのプログラムが必要となる。これは、数Ωが非圧縮性であること、すなわち、適用できないことを認めれば十分である。(大きなNビットの場合、NビットからほぼNビットへの長さ短縮は重要ではありません)。

Ωという数が受け入れられないことから、包括的な数学的理論が存在し得ないことは、次のとおりである。無限のビット数Ωは、ビット列よりも単純な、いかなる原理からも導き出すことのできない数学的事実の無限集合（選択された各ビットが１であろうと0であろうと）である。このように、数学の複雑さは無限であるのに対し、「世界の万物」のいかなる個々の理論も有限の複雑さを特徴とし、その結果、数学的真理の世界の豊かさをすべてカバーすることはできない。これまで言われてきたことから証明に意味がないということではありませんし、私は決して論理的な推論に反対しているわけではありません。実際、説明不能な原理（公理）は、常に数学の一部である。Ωという数字を見ただけで、今まで考えられていたよりもはるかに多いことがわかります。

数学者は何でも証明しようとする必要はないのかもしれません。彼らは真実ではない事実については、新しい公理を追加するべきです。問題は、彼らが説明不能であることを理解し、証明できないことを認めることです。しかし、厳密な証明ではなく、常にもっともらしい推論を用い、新しい法則を導き出して新鮮な実験データを理解しようとする物理学者とは異なり、数学者は決してあきらめることはありません。数学は物理学に似ているのだろうか？

概要：還元不可能な複雑さ
＊ゲーデルは、数学にある不可避の不完全性を示しました。厳密に証明できない真の命題があります。特異数Ωはさらに大きな不完全性を明らかにし、有限の公理集合から推論できない定理が無数に存在することを証明しました。

＊Ωという数値は厳密に定義されており、非常に具体的な意味がありますが、有限のコンピュータプログラムを使用して計算することはできません。

＊数値Ωの特性の分析は、数学者が新しい公理を仮定する必要があることを示しています。これは、物理学者が実験の結果を一般化し、論理の助けを借りて証明できない基本的な法則を導き出すときに行うことです。

最も公正な選挙

アイク・アコピアン АЙК АКОПЯН • МАТЕМАТИКА • 21 КОММЕНТАРИЙ

https://elementy.ru/problems/2390/Samye_spravedlivye_vybory

さまざまな形式の選挙がいたるところで実施されています。選挙結果が有権者の意思をあまり反映しない場合もあれば、大多数の意志を反映する場合もあります。選挙を数学の観点から検討し、このプロセスに2つの自然で明白な特性を要求すると、予期せぬ結論が得られることを示します。しかし、最初に、選挙とは何を意味するのか、そして選挙の正義とは何かを形式化しておきましょう。

複数の候補者が選挙に参加し、各有権者がこれらの候補者の特定の評価、つまり、候補者を有権者の個人的な好みの降順で並べたリストを持っていると仮定します。ワシントン、フランクリン、ジェファーソンの3人の候補者がいる例を考えてみましょう（ただし、以下のすべての推論は、もっと多くの候補者でも有効です）。その場合、ある有権者の評価は次のようです。「フランクリン>ワシントン≥ジェファーソン」。すべての候補者を優先度の高い順に1行に並べることができるこのような評価は、推移的と呼ばれます。

私たちが慣れ親しんでいる選挙では、各有権者が候補者の1人だけに投票を行う、たとえば、ある有権者がジェファーソンに投票したい場合、これは彼の評価が「ジェファーソン>フランクリン=ワシントン」のようになることを意味します。

選挙制度は、「大多数の意見」を反映した評価を出力するべく、すべての投票を評価する方法であると理解します。もう少し数学的な言葉で言えば、選挙はすべての有権者の好みを入力として受け、これらのデータに基づいて集合の好みの評価を出力する機能です。

このようなシステムの特殊なケースは、ロシア（日本でも）で使われている各候補者の総投票数です。別の特殊はケースは、例えば、候補者のランダムな最終選択で、これは投票者の意見がまったく考慮に入れられません。

選挙制度が公正と呼ばれるために必要な特性は何でしょうか？
まず、すべての有権者が2番目の候補よりも1番目の候補を好む場合、最終結果はこれを反映する必要がある、つまり、最終選挙手順は、1番目の候補が2番目の候補よりも高くなるのが論理的です。このプロパティは、全会一致と呼ばれます。第二に、これも非常に論理的ですが、最終評価における2人の候補者の相対位置は、有権者の好みの評価による相互位置にのみ依存し、他の候補者の位置に依存するべきではありません。これは、選挙結果で、一方の候補者が他方の候補者を追い抜いたことが判明した場合、3番目の候補者が投票に追加（または除外）された場合もまったく同じ結果になることを意味します。2番目のプロパティは、無関係な選択肢からの独立（またはバイナリ独立）と呼ばれます。

これらの2つの特性を満たす選挙は、公正であると見なされます。

課題
これらの定義を満たす唯一の公正な選挙制度は独裁である。つまり選挙の結果が一人の人の好みによって完全に決定され（そして、他の人の好みはまったく考慮されない）システムであることを証明しなさい。

ヒント1
結果は3人以上でも当てはまりますが、3人の候補者による選挙で行うのが最も簡単です。

ヒント2
最初はすべての有権者が個人的な評価でリンカーンを最初に置き、フランクリンを最後に置いたとしましょう。そのような評価で最終的な選挙結果はどのようになりますか？有権者がリンカーンとフランクリンの場所を次々と変え始めたら、選挙結果はどのように変わるでしょうか？

解答
有権者が6人しかいないとします。まず、候補者が2人だけの場合にどうなるかを考えてみましょう。ワシントン（W）をジェファーソン（J）と競争させ、フランクリン（F）をしばらく忘れます。

すべての有権者がジェファーソンよりもワシントンを好む場合（つまり、評価がW≥Jの場合）、全会一致規則に従った公正な選挙の最終手順は、W≥Jになることに注意してください。この平凡な状況を図1に示します。.逆に、すべての有権者がワシントンよりもジェファーソンを好む場合（すべてJ≥W）、明らかに、ジェファーソンもワシントンを打ち負かす必要があります。

図1.

それでは、ダイナミクスで何が起こるかを見てみましょう。誰もがワシントンに賛成している状況から始めて、有権者が順番に個人の評価を変更し始めたらどうなるかを見てみましょう。最終結果はどのように変わりますか？
最初はワシントンが勝つことは明らかであり、最終的には、すべての有権者が好みを変えると、ジェファーソンが勝たなければなりません。最終手順で結果が逆転する、ある有権者i（私たちの場合は、1≤ i≤6）があります。私たちの場合では、i=4（図2）。

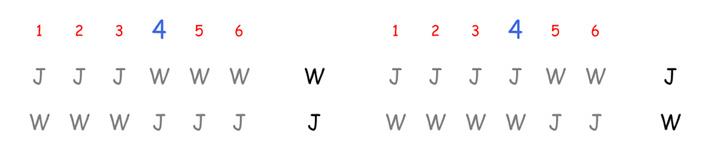
図2.

フランクリンを思い出して、図2の左側のケース（主要な候補者のランキングでW≥Jの場合）を考えてみましょう。フランクリンは、i<4の場合投票の真ん中に位置を占め、i≥4の場合に最下位になるとしましょう（図3）。選挙結果はどうなりますか？フランクリンが入る前に、ワシントンがジェファーソンを倒したことを思い出してください。私たちの選挙は公正なので、この結果は、バイナリの独立性のために変わるべきではありません。また、すべての有権者についてJ≥Fであることがわかります。全会一致プロパティから、最終結果もJ≥Fである必要があります。したがって、最終手順はW≥J≥Fとなります。

図3.

もし4番目の有権者がWとJを入れ替える決定した場合、この有権者はペア（W,J）のキーであり、個々の評価の相対位置（J,F）と(W,F)は変わらないので、最終結果はJ≥W≥Fに変わります（図4）。主要な有権者の個人的な評価は、最終的な評価と一致することに注意してください。

図4.

このキー有権者がどれほど強力であるかを理解するために、他の有権者の票を変えることによって選挙の結果に影響を与えようとしましょう。たとえば、フランクリンとジェファーソンの個人的な評価の場所を交換します(図5)．結果は変わりましたか?

図5.

個々の評価におけるWとFの相対的な位置は変更されていないため、W≥Fは最終手順に残ります（無関係な選択肢からの独立性のため）。また、JとWの相対位置は変更されていません。つまり、最終手順ではJ≥Wになります。結果はまったく変更されず、ジェファーソンが常に勝ちます。そしてこれは、4番目の有権者が、彼の個人的な評価でジェファーソンを1位にした唯一の人であるということです。キー有権者の個人的な評価がJ≥Fである限り、この問題に関する他の有権者の意見は最終的な投票結果に考慮されないことがわかります。

では、何を証明したのでしょうか。候補者のペア（この場合はワシントンとジェファーソン）について、他の人の意見に関係なく、投票結果で3番目の候補者の位置を明確に決定するキー有権者がいることを示しました。

しかし、候補者の任意のペアのキー有権者の存在から、独裁者の存在自体は導かれません。理論的には、このキー有権者は候補者のペアごとに異なる可能性があるためです。それにもかかわらず、キーは常に同じ有権者であることが判明しました（正確には、彼が実際に評価におけるFの位置を指示しているためです）。これは、上記と同様の推論を実行することで簡単に示すことができます。このキー有権者による評価が最終的な選挙結果を完全に決定することが判明しました。

あとがき
上で議論された問題は長い間古典的な結果でした。これは、1951年の論文で、アメリカの数学者で経済学者のケネス・アローによって最初に定式化され、証明されました。今では、民主主義の不可能性またはアローのパラドックスについてのアローの定理と呼ばれています。
一般的なケースの完全な証明は、J.Geanakoplos，2005にあります。
Arrowの不可能性定理の3つの簡単な証明https://link.springer.com/article/10.1007/s00199-004-0556-7

この定理は実際には次のように述べています。人々の好みが独立していて一過性であり（評価を表す）、選挙が全会一致と、無関係な選択肢からの独立の原則を尊重する場合、他の評価に関係なく、個人の評価が結果を完全に決定する独裁者が常に自動的に存在します。これらの条件を少し緩和しても、たとえば、独裁者ではないにしても、選挙の最終結果における任意の2人の候補者の相対的な位置を常に決定する「拒否」する権利を持つ人が常に存在することを示すことができます。

定理が成立するために必要な有権者の選好要件は、通常のアプローチと呼ばれます。このアプローチでは、個人の好みは量的ではなく質的に考慮されます。つまり、いくつかの選択肢は他の選択肢よりも優れている、悪い、または同等である可能性がありますが、ある選択肢が別の選択肢よりどれだけ優れているかを判断する手段はありません。

これらの条件はすべて、非常に論理的ですが、実際には常に満たされているわけではありません。たとえば、基本的に選挙の特定の客観性の要件であるバイナリ独立（無関係な選択肢からの独立）の原則（候補は互いにのみ比較され、他のコンテキストでは比較されません）は、非常に簡単に破られます。100人の有権者がいて、その個人的な評価が次のように分布している状況を想像してみてください。25人の有権者の評価はW> J> F、40人の有権者の評価はJ> F> W、残りの35人の有権者の評価はF> W> Jです。いずれにせよ、選択はバイナリ独立の原則に違反します（W、J、またはFが勝つ場合を個別に検討してこれを示すようにしてください）。

この例は、一般に、候補者が3人以上いる場合、大多数の「意見」が互いに矛盾する可能性があることも示しています。公的選択の理論におけるこの現象は、コンドルセパラドックスまたは公的選択の循環的性質と呼ばれます。これは、社会全体の観点から（つまり、「選挙」の結果を合計した後）、次の逆説的な状況が発生するためです。W> J> F> W> ...、にもかかわらず各有権者の個々の好みは一時的なものであること。

このパラドックスは、2段階の投票システムで重要です。最も明白な例は、米国大統領選挙です。そこでは、各党（共和党と民主党）の候補者が最初にいわゆるプライマリーを通過します。そこでは、各党から1人の候補者が選ばれ、主要な大統領選挙で党を代表します。

今年の民主党の初等協会では、主な戦いはバーニーサンダースとジョーバイデンの間でした。ジョー・バイデンが予備選挙で勝利し、選挙で民主党の候補者になります。彼は現職の共和党大統領ドナルド・トランプと競争するでしょう..。コンドルセのパラドックスはアメリカ社会の好みで起こっているのかもしれません：トランプ>バイデン>サンダース>トランプ> ...そして、バイデンは世間の心にあまりないので、すべての選挙の結果は選挙の第一段階（プライマリー）の結果に依存することがわかりますトランプよりも優先され（サンダースよりも優先されますが）、サンダースはトランプよりも優先されます（バイデンよりは優先されませんが）。そして、この状況では、大統領選挙に参加したバイデンは（プライマリーではサンダースよりも好ましいため）、トランプに負けます。したがって、ある意味で、民主党が選挙に勝つチャンスがあるにもかかわらず、あまり好まれない民主党の候補者を指名することは「より有益」です。しかし、そのような場合の世論を評価する問題は、社会学の分野に属します。

ーーーーーーー
（参考）11月4日現在

証明可能性の限界（１）

https://elementy.ru/nauchno-populyarnaya_biblioteka/430319/Predely_dokazuemosti

グレゴリー・チェイチン
「科学の世界で」2006年第6号より

ゴットフリート・ライプニッツが、「形而上学の議論」(1686年)で、最初に表現した複雑さとランダム性の考え方と、現代の情報理論におけるそれらの確認から、数学が「すべての中で最も一般的な理論」を作ることは不可能です。

1956年、Scientific American誌は、Ernest NagelとJames R.Newmanによる記事「Gödel's Proof」を発表しました。2年後、その著者は同じ名前の本をリリースしました（まだ再版されています）。当時はまだ子供でしたが、ニューヨーク公立図書館で本を開いたときのスリルを今でも覚えています。

Kurt Gödelゲーデルが、数学を使って、数学自身の可能性の限界を示していることに私は驚いた。彼は、数学の完全な理論の存在についてDavid Hilbertヒルベルトが約1世紀前に行った命題に反論しました。数学的論理の規則を一貫して使用することにより、数学のすべての命題を導き出すことができる究極の公理系はあるか。ゲーデルは、この方法では証明できない真の数学的命題が存在することを示しました。彼の結論は、「この命題は誤りである」と「この命題は証明できない」という2つの自己関連のパラドックスに基づいています。（ゲーデルの不完全性定理の詳細については、 Scientific Americanを参照してください。）

有限のコンピュータプログラムを使用して、計算できない特定の厳密に定義された数Ωの存在は、真の命題を厳密に証明できる包括的な数学システムを作る希望を打ち砕きました。（画像：www.sciam.ru）

私は生涯を通じてゲーデルの証明を扱い、半世紀後、自分の本を出版しました。ある程度、これはNagelとNewmanネーゲルとニューマンの本の私のバージョンですが、ゲーデルの証明はその主要なテーマではありません。私の仕事は、情報を測定し、いくつかの数学的な事実は複雑すぎるために理論に詰め込むことができないことを証明することに基づいています。私のアプローチによると、ゲーデルは氷山の一角を発見しただけです。有限の公理体系からは証明できない正しい数学的定理が無数にあります。

複雑さと科学の法則

ライプツィヒに記念碑が建てられたゴットフリート・ライプニッツは、300年前にアルゴリズム情報の多くの特性を予見していました（www.uni-leipzig.deからの写真）

1686年、ライプニッツの哲学的エッセイDiscoursdemétaphysique形而上学の議論が出版されました。提起された問題は：特定の法則によって記述できる事実を、どの法則にも従わない事実からどのように区別するか？
彼のエッセイの4章で、ライプニッツは非常に単純で深遠な考えを表現しました。理論は、それが説明するデータよりも単純でなければなりません。そうでなければ、何も説明しません。科学法則の概念は、それが無制限のレベルの数学的複雑さを許容する場合、意味がなくなります。なぜなら、事実がどれほどランダムで乱雑であっても、法則を定式化することが常に可能だからです。逆に、一部のデータを説明する単一の法則が複雑すぎることが判明した場合、問題のデータは実際にはどの法則にも従いません。

アルゴリズム情報の現代の数学理論は、複雑さと単純さの概念の正確な定量的定義を与えることを可能にしました。従来の情報理論は、情報をエンコードするために必要なビット数によって情報量を定義します。たとえば、単純な「はい/いいえ」の回答をエンコードするには、1ビットが必要です。対照的に、アルゴリズム情報量は、データを生成するために必要なコンピュータプログラムの長さによって決定されます。プログラムを格納するために必要な最小ビット数は、アルゴリズムデータ情報量と呼ばれます。たとえば、自然数1，2，3，...　の無限のシリーズには、アルゴリズム情報がほとんど含まれていません。シリーズのすべての数は、短いコンピュータプログラムを使用して取得できます。計算を完了するのにかかる時間や、使用するメモリ量は関係ありません。プログラムの長さ（ビット単位）のみが重要です。（もちろん、アルゴリズム情報量の正確な値は、選択したプログラミング言語によって異なりますが、この記事で説明する問題については、これは関係ありません。）

別の例として、3.14159...に等しい数πを考えてみましょう。そのアルゴリズム情報量は少ない：すべての符号を順次計算するには、かなり短いアルゴリズムですむ。しかし、100万文字のみを含むランダムな数値、たとえば1.341285 ... 64は、はるかに大量のアルゴリズム情報によって特徴付けられます。そのような数字には定義構造がないため、それを書き込むために必要なプログラムの長さは、数字自体の長さに近くなります。

科学理論は、観察結果を予測するコンピュータプログラムのようなものです。有用な理論は、実験データの昇華です。いくつかの法則と方程式を使用して、さまざまな現象の全世界を記述することができます（画像：www.sciam.ru）

（...で置き換えたすべての数字をプログラムに含める必要があります。）このような数字の列を計算できる短いプログラムはありません。プログラムは圧縮できず冗長性もありません。最善の方法は、そのまま書き出すので、このような列は、還元不可能またはアルゴリズム的にランダムと呼ばれます。

上記は科学法則や事実との関連は如何でしょうか？
アイデアは、プログラマーの目を通して科学を見ることです。科学理論は、観察の結果すなわち実験データを予測するコンピュータプログラムのようなものです。この見方は、2つの基本原則に基づいています。最初の（Occam's razor「オッカムのかみそり」）によると、いくつかのデータを説明する2つの理論のうち、より単純なものが優先されるべきです。言い換えれば、最良の理論は、観測結果を計算するための最短のプログラムです。ライプニッツによって示された2番目の原則は、現代の用語では次のように言います。ビット単位のサイズが説明するデータ量に等しい理論は、完全にランダムなデータを記述できるため、役に立ちません。有用な理論は情報の削減を提供します：データを理解することは、それらを短いアルゴリズムの説明に圧縮することです。理論が単純であるほど、現象の本質をよりよく理解できます。

十分な理由
コンピュータプログラム登場の2世紀半前に生きていたライプニッツは、現代のアルゴリズム情報の概念に非常に近づいていました。ライプニッツは、すべてがバイナリコードの形式で表現できることを知っており、最初のコンピューティングデバイスの1つを作成しました。複雑さと単純さの概念を考慮して、彼はコンピューティングの巨大な可能性を認識していました。ライプニッツが知っていたすべての要素を組み合わせていたとしたら、彼はおそらく自分の哲学の基礎の一つである十分な理由の原理（起こったものにはすべて理由がある）を疑っていただろう。ポジションが真であれば、何らか真の理由があります。しかし、日常の喧騒の中で、信じられないことが起こります。理由が常にわかるとは限りません（おそらく、推論の連鎖が長すぎて混乱しているため）、神のみぞ知る。それですべてです！

数学者は、常にすべてを証明しようと努力しているため、ライプニッツの十分な理由の原理を無条件に受け入れることは間違いありません。たとえ定理の真実が明白であり、何百万もの例がそれを確認したとしても、数学者は依然として一般化された証明を必要とします。そして、アルゴリズム情報の概念は、知識の出所と限界についての哲学的推論に驚くべき貢献をすることができます。それは、いくつかの数学的事実が理由もなく真実であることを示しており、十分な理由の原理に異議を唱えています。以下に示すように、還元不可能な数学的事実は無数にあり、その真実はいかなる理論によっても説明ができません。それらは計算上還元できないだけでなく、論理的にも還元できません。これらの事実を「証明」する唯一の方法は、理由なしでそれらを公理として認識することです。

「公理」の概念は、論理的な還元不可能性と密接に関連しています。公理は、私たちが自明であると考え、かつ単純な原理から証明できない数学的提案です。すべての数学理論は、公理から導かれる定理で、これは、ユークリッドが2000年前に行ったことです。幾何学に関する彼の著書は数学的な表現の手本になりました。

古代ギリシャでは、他の方法ではなく、この方法で投票するように仲間の市民を説得するために、あなたの理由を述べる必要がありました。これがおそらく、ギリシャ人が数学的な提案は証明されるべきであり、経験的に推論されるべきではないという考えに至った理由です。（ギリシャ人とは異なり、メソポタミアとエジプトの初期の文明は実験に依存していたようです。）論理的推論の方法は非常に実り多いことが判明しました。現代の数学、数学的物理学、そしてコンピュータ構築技術を含むすべての精密科学は、現代の数学と論理機械の助けを借りて作られました。
私は2千年かけて構築した数学とすべての科学のアプローチが失敗だったと主張しているのでしょうか? ある意味そうです。私の反論例は、論理と推論の限界を示し、証明できない数学的規則の無限の流れの源を、私が「オメガ」Ωと呼ぶ数に担わせることです。

存在の矛盾の理論（その２）

こうして、3千年ぶりに、数学者は彼らの分野の最も深い基礎を研究することに近づきました。そして、奇妙な構図が浮かび上がりました。数字ファンは、計算を行うルールを明確に記述することを学び、パラドックスによって生じる疑念を排除するために、使われた根拠の「正当性」を証明すれば済みました。そして1920年代の前半までに優れた研究学派を形成した偉大なヒルベルトは、一連の論文で数学の基礎の研究計画（後に「ゲッティンゲンプログラム」の名前が付けられた）を講演しました。最も単純化された形式で、それは次のように表すことができます。数学は、特定の公理体系から導き出された一連の結果として表すことができ、次のことを証明できます。

１．数学は完全です。すなわち、いかなる数学的な記述も、その分野自体の規則に基づいて証明または反証することができます。
２．数学は一貫しています。受け入れられている推論の規則に違反せずに、いかなる命題も証明すると同時に反駁することは不可能です。
３．数学は決定可能です。つまり、ルールを使用して、それが証明可能であるか反駁可能であるかどうか、任意の数学命題について調べることができます。

実際、ヒルベルトのプログラムは、すべての数学的な質問に答えるための、または少なくともそのような存在を証明するためのいくつかの一般的な手順を開発しようとしました。科学者自身は、彼が作成した3つの質問すべてに対して肯定的な答えを確信していました。彼の意見では、数学は確かに完全で、一貫性があり、解決可能でした。残ったことはそれを証明するだけでした。

さらに、ヒルベルトは、公理的方法が数学だけでなく、科学一般の基礎にもなり得ると信じていました。1930年に、彼の記事「自然と論理の認識」で、彼は次のように書いています。

科学のさらなる発展のために、ヒルベルトと彼の学派は成功したでしょうか？彼が信じていたように、すべての数学（および科学全体）が公理のシステムに還元された場合、一般的な論理規則に従ったプログラムに従って、元の命題から次の命題を実証する（つまり、定理を証明する）ことがコンピューターでできます。

ヒルベルトの理論が実現されれば、24時間稼働するスーパーコンピューターは、ますます多くの新しい定理を継続的に証明し、World WideWeb上の無数のサイトに投稿します。数学に続いて、「公理の時代」は物理学、化学、生物学に広がり、そして最後に、人間の意識の科学に変わります。私たちの周りの世界、そして私たち自身は、そのような場合には多少異なって見えるでしょう。

しかし、「普遍的な公理化」は行われませんでした。世界の数学者が数十年にわたって取り組んできた、非常に野心的で壮大なプログラム全体が、単一の定理によって反駁されました。それは、当時わずか25歳のKurt Gödelゲーデルによってでした。

1930年、ケーニヒスベルクのウィーンサークルが主催した会議で、彼は”論理計算の完全性”に関する発表をし、翌年の初めに、”Principia Mathematica と関連システムの根本的な困難”に関する論文を発表しました。彼の仕事の中心は、数学のさらなる発展において基本的な役割を果たす定理の定式化と証明でしたが、不完全さについてのゲーデルの有名な定理は、「どのような一貫した公理システムであっても、受け入れられた公理系内で、証明または反証することができない命題が存在する」と述べています。このように、ゲーデルはヒルベルトの最初の命題に否定的な反応を示しました。興味深いことに、ヴェルナー・ハイゼンベルグは同じ会議で「因果関係の知識と量子力学」について講演しました。このレポートで、”不確定性原理”の最初のアプローチが提示されました。

■ゲーデルの定理

それから四半世紀が経過しましたが、ゲーデルが何を証明したかについての議論は続いています。特に熱狂的な議論が疑似科学界で起こっています。「ゲーデルの不完全性定理は本当にユニークです。神々の存在から理由の欠如まで、"世界のすべて"を証明したいときはいつでも言及されます」と、優れた現代数学者V.A.Uspenskyは書いています。

多くの推測はさておき、科学者はゲーデルの評価で二分されました。ラッセルに続いて、現代の数学論理の基礎となるこの有名な定理は、この分野以外の研究にほとんど影響を与えないと信じる人もいます。

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

新しい定理を絶えず証明し続けるコンピューターの幻想に関しては、そのような活動の意味に多くの専門家から、大きな疑問が投げかけられています。確かに、数学にとって、証明された定理の定式化だけでなく、その理解も重要です。これにより、さまざまなオブジェクト間の接続を識別し、どの方向に進むことができるかを理解できるからです。そのような理解がなければ、形式化された推論ルールに基づいて生成された定理は、一種の「数学的なスパム」にすぎません。これは、モスクワ州立大学の数学論理および機械と数学のアルゴリズム理論部門のメンバーであるアレクサンドル・シェニの意見です。

ゲーデル自身も同様の方法で推論しました。数学の基礎の完全性を破壊したとして彼を非難した人々に、彼は、「実際には何も変わっておらず基礎は揺るぎないままで、彼の定理は論理の鉄の法則に支配される科学分野で、直感と個人的なイニシアチブの役割の再評価につながっただけ」と答えました。これには何かメリットがあるというわけではありません。

ゲーデルとアインシュタイン（写真：「科学の世界で」）

存在の矛盾の理論（その３）

ゲーデルの定理
それから四半世紀が経過しましたが、ゲーデルが何を証明したかについての議論は続いています。特に熱狂的な議論が疑似科学界で起こっています。「ゲーデルの不完全性定理は本当にユニークです。神々の存在から理由の欠如まで、"世界のすべて"を証明したいときはいつでも言及されます」と、優れた現代数学者V.A.Uspenskyは書いています。

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

ゲーデルとアインシュタイン（写真：「科学の世界で」）

ーーー

しかし、一部の科学者は異なる意見を持っています。確かに、論理的に推論する能力が人間の心の特徴（少なくともその主なツール）であると考える場合、ゲーデルの定理は私たちの脳の限界を直接示しています。無限の思考力を信じて育った人が、その力の限界についての論文を受け入れることは非常に難しいことでありましょう。

むしろ、私たちは自分の精神的能力の思考限界について話すことができます。多くの専門家は、論理的思考の根底にある計算の「アリストテレス」プロセスは、人間の意識の一部にすぎないと考えています。彼の他の分野、「非計算的」分野は、直感、創造的な洞察、理解などに責任があります。そして、心の前半がゲーデルの制限に該当するとしても、後半はそのような枠組みから解放されます。

この観点の立つ最も一貫した支持者である数学と理論物理学の著名な専門家、ロジャー・ペンローズは、さらに進めて、創造的意識行為の実現にかかわる非計算的性質のいくつかの量子効果の存在を示唆しました。彼の同僚の多くは、人間の脳に仮想の量子メカニズムを与えるという考えに批判的ですが、ペンローズと彼の共同研究者は、その存在を確認する実験スキームをすでに開発しています。

ペンローズの仮説の多くの結果の1つに、量子コンピューターの出現がコンピューティング分野の途方もないブレークスルーであるとしても、現代のコンピューティングデバイスに基づいて人工知能を作るのは基本的に不可能であるという結論があります。事実、どのコンピューターでも、人間の意識の形式的で論理的な「計算」活動を詳細にシミュレートすること以外はできず、知性の「非計算的」能力にはアクセスできません。

これは、75年前に発表された若いゲーデルの数学的定理によって引き起こされた自然科学と哲学的論争のほんの一部にすぎません。他の偉大な同時代の人々と一緒に、彼は人に自分の周りの世界と自分自身を異なって見させました。

ゲーデルの定理、相対性理論および量子論の創造を含む、20世紀の最初の3分の1の最大の発見は、過去2世紀の科学的研究に基づいて創造された自然の機械的決定論の構図の限界を示しました。宇宙の発展の道と道徳的義務の両方が根本的に異なる法則に従うことが判明しました。そこには、取り返しのつかない複雑さ、不確実性、偶然、そして不可逆性があります。

しかし、科学革命の偉大な結果は、すでに述べたものに限定されません。20世紀の初めまでに、ラプラス-ニュートンの決定論思想は、社会科学の発展に大きな影響を与えました。すべての要素が厳格な法則に従い、厳格な機械的構造の形で自然を表現した古典的な自然科学の先覚者に続き、現在の状態を知れば未来を明確に予測することができ、司祭、社会科学者は不変の法則に従い、所定の方向に発展する人間社会を描きました。そのような世界像を保存するための最後の試みの1つは、明らかに、「唯一の真の科学的教義」の概念に取り組んだマルクシズム-レニニズムであり、その一部は「歴史の物質主義的理解」でした。「大きな工場」のような社会主義社会を構築するというレーニンの考えを思い出すだけで十分です。

宇宙の自然科学の全体像に定着していた複雑さ、ランダム性、不確実性についての考えが、徐々に、社会科学や人間科学に浸透し始めました。社会では、個人の自由という現象を通じて、不確定が実現します。歴史的プロセスを複雑にし、普遍的な発展の不変の法則に従わないのは、自由で予測不可能な選択をする主題としての自然界の人間の存在です。

しかし、わが国の複雑な世界の新しい構図の取得は非常に困難でした。これに気付くのは間違いありません。70年間支配していたイデオロギーは、普遍的な権威秩序の哲学としてのラプラス型の決定論に引き寄せられました。厳格な階層法に支配されている社会工場の支配的なソビエトの官僚機構が決して離さなかった夢の中心に、この事前決定の原則がありました。

したがって、複雑さ、多元性、多様性に関しては、それが相対性の理論、量子力学、遺伝学、サイバネティクス、社会学的研究、心理分析などであるかどうかにかかわらず、イデオロギー検閲のメカニズムがすぐに働きました。これは、自然と社会の両方からの自由へのすべての言及を排除することを目的としていました。

悲しいかな、不活性な遺産は、今でも多くの同胞や同時代の人々の心を暗い影として支配しています。これは、共産主義の教義の終焉によって空けられた場所を埋めるために、当局によって開始された新しい「国民的イデオロギー」探求の苦悶によって証明されています。

このようにして、クルト・ゲーデルと彼の偉大な同時代人たちは、頭上の星空と私たちの内なる道徳法則、そして私たちが住む社会を、新しい方法で私たちに見せました。

Александр Музыкантский，«В мире науки» №3, 2007

存在の矛盾の理論（その１）

アレクサンダー・ムジカンツキー, 「科学の世界で」2007年第3号より

訳者より口上：私はラッセルのパラドックスがよく理解できません．その簡易な解説は，次のような表現で語られることが多いのでここから始めましょう．

アレクサンダー・ムジカンツキー, 「科学の世界で」2007年第3号より

訳者(SGK)より口上：私はラッセルのパラドックスがよく理解できません．その簡易な解説は，次のような表現で語られることが多いのでここから始めましょう．

町の人々は，自分で自分の髭を剃る（Ａ）か，剃らない（Ｂ）かのグループに完全に2分割できます．どちらの集合にも属さないという人はあり得ませんし，両方に属するということも不可能です．そして，床屋も町の人のうちに入りますから，（Ａ）or（Ｂ）のどちらかの集合に属します．床屋が自分に課したルールで，他人の髭を剃ることができるのは（Ｂ）に属する人に対してです．床屋自身はどちらの集合に属していてもかまいません．もし，（Ａ）に属していれば，自分の髭は自分で剃りますが，（Ａ）の人のひげは剃らないという床屋のルールに反します．もし，（Ｂ）に属していれば床屋の手で髭を剃りますが，自分＝床屋なので，自分で剃ることになり（Ｂ）に存在することが矛盾になります．

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
訳者のウォーミングアップはここまでにし，
Александр Музыкантский，В мире науки，№3, 2007
によるゲーデルの紹介に入りましょう：

■20世紀の最も優れた発見といえば、アインシュタインの相対性理論、量子力学、ハイゼンベルグの不確定性原理などです。しかし、多くの著名な科学者（数学者や哲学者）は、前世紀の科学的思想の最大の成果の中にゲーデルの定理を含めています。物理学分野の画期的な進歩が、人間の心の自然の新しい法則への理解をもたらすなら、ゲーデルの仕事は人間の心自体の動作原理をさらによく理解する可能性で、私たちの時代の世界観と文化に大きな影響を与えました。

ゲーデルとは誰か？
Kurt Gödelゲーデルは1906年4月28日、オーストリア-ハンガリーのモラヴィアの都市ブルノ（当時はブルンと呼ばれていました）で生まれました。18歳で、彼は最初に物理学を学んだウィーン大学に入学しましたが、2年後に数学に転向しました。このような科学的関心の変化は、主にバートランド・ラッセルの著書「数学の哲学の紹介」の影響下で起こったことが知られています。科学者としてのゲーデルの形成に大きな影響を与えたもう1つは、ウィーンサークルの活動への彼の参加でした。これは、1920年代後半から1930年代半ばまで定期的にウィーンに集まった、数学者、論理学者、哲学者などの優秀な科学者の集団です。ルドルフ・カルナップ、オットー・ニューラス、ハーバート・フェイグル、モリッツ・シックなどの科学者は、さまざまな時期にウィーンサークルの活動に参加しました。哲学的な積極性の形成は、彼らの活動に関連しています。サークルのトピックスは、自然と社会の知識のうち、科学的知識のすべてをカバーしていました。さまざまなヨーロッパの科学センターで開催された国際会議では、20世紀の基本的な科学的知識の形成で、ウィーンサークルが果たした卓越した役割がありました。ゲーデルは、木曜日のサークルのほぼすべての会議と、彼が主催する国際会議に参加しました。オーストリアでのサークルの活動は1936年に中断され、そのリーダーであるモリッツ・シュリックがウィーン大学の階段でナチスの学生に殺されました。サークルのメンバーのほとんどは米国に移住し、ゲーデルも移住しました。時が経ち、彼はアメリカ市民になり、プリンストンの高等研究所で働き、同じ都市で1978年に亡くなりました。これが彼の人生の輪郭です。職場の友人や同僚は、彼を閉じた人、痛々しいほど傷つきやすく、周囲の世界から切り離され、完全に彼の考えに没頭している人であったことを思い出します。

Kurt Gödel（1906-1978）．写真：「科学の世界で」

世界の論理的理解が、ゲーデルの人生の中心を占めていたという事実は、彼の伝記の奇妙な詳細によって証明されています。1948年、アメリカ市民権の取得の問題が決定されたとき、ゲーデルは、決められた手順に従って、アメリカ憲法の基本に関する口頭試験のようなものに合格しなければなりませんでした。彼はすべての科学的良識をもってこの問題に取り組み、文書を徹底的に研究し、憲法に違反することなく合法的に独裁権を確立することができるという結論に達しました。そのような発見は、彼がテストを受ける役人と話し合うとき、テストに失敗させるだけです。彼はもちろん、合衆国基本法の彼の理解を政治思想の最大の成果であると考えました。彼が市民権を取得したときにゲーデルの2人の保証人の1人として行動したアルバート・アインシュタインは友人です。少なくとも誓いが立てられるまで、彼の議論の展開を延期するように彼を説得しました。その後、歴史は興味深いエピローグとなります。四半世紀後、別のアメリカ人、ケネス・アローは、ゲーデルがアメリカの憲法を研究して到達した命題を一般的に証明したことでノーベル賞を受賞しました。

ゲーデルは何を証明したか？
ゲーデルの名前を不滅にした定理の提示に進む前に、1920年代の終わりまでに数学が直面した問題、正確には、19世紀と20世紀の変わり目に際立っていたその断面を簡単に話す必要があります。それは「数学の基礎」と呼ばれました。
最初に、幾何学の学校コースに立ち寄る価値があります。それは今日まで、2000年以上前に書かれたユークリッドの「原論」を大部分繰り返しています。伝統的な教科書では、最初に、平面上の点と線の特性に関するいくつかの命題が与えられ、そこから「アリストテレス」論理の規則［訳注）三段論法］に従った論理的構築によって、さまざまな重要で有用な幾何学的事実（定理）が推論されます。たとえば、公理の1つは、たった1本の直線が2点を通過すると主張しますが、平行線は無数にあるとする別の公理（ロバチェフスキーが非ユークリッド幾何学で拒否した有名な第5の仮定）もあります。公理の真実は、明白なものと見なされ証明は必要ありません。ギリシャの幾何学の特徴は公理から定理を導くことです。
19世紀の終わりに、ユークリッド原論のすべてのギャップ（数学者の厳密さと推論の正確さの観点で）が埋められました。
ドイツの数学者David Hilbertの本「Foundations of Geometry」は、最新の研究の結果となりました。
ユークリッドの方法の成功は、科学者に彼の原理を数学の他の分野に拡張することを促します。幾何学の後に算術の番が来ました。1889年、イタリアの数学者ジュゼッペ・ピアノは、最初に算術の公理を定式化しました。これは、ばかばかしいほど明白に見えました（ゼロがあり、各数字の後に別の数字が続くなど）が、実際には完全に網羅的です。彼らは幾何学において偉大なギリシャ人の仮定と同じ役割を果たしました。このような記述に基づいて、論理的推論を使用して、基本的な算術定理を得ることができました。
同じ時期に、ドイツの数学者ゴットリーブ・フレーゲはさらに野心的な問題を提起しました。彼は、研究中のオブジェクトの主な特性を公理的に承認するだけでなく、推論の方法を形式化、体系化することを提案しました。これにより、特定の規則に従って、記号のチェーンの形で数学的な推論を書くことができました。フレーゲは彼の結果を「算術の基本法則」で発表しました。その最初の巻は1893年に出版され、2番目の巻はさらに10年間の努力を必要とし、1902年に完全に完成しました。
おそらく、数の科学の発展で最も劇的な物語の1つは、フレーゲの名前と科学的研究に関連しています。第2巻がすでに印刷されていたとき、フリーゲは若い英国の数学者バートランド・ラッセルから手紙を受け取りました。ラッセルは、同僚の素晴らしい結果を祝福しながら、それでも著者の注意を引いた1つの状況を指摘しました。陰湿な「状況」は「ラッセルのパラドックス」であり、後に広く知られるようになりました。
自分自身を要素として含まない集合の集合は、自分自体は要素として含まれるか。フレーゲはすぐに謎を解くことができませんでした。彼は、印刷されていない彼の本の第2巻に、苦味に満ちた言葉を追加するしかありませんでした。「科学者にとって、発見することほど望ましくないことはありません。やっと完成した仕事の基盤が崩壊したこと。バートランド・ラッセルから受け取った手紙は、私をまさにそのような立場に置きました...」苦しんでいる数学者は、大学を卒業し、理論を正すために多くのエネルギーを費やしましたが、それはすべて無駄でした。彼は20年以上研究しましたが、算術に関するこれ以外の論文を書きませんでした。

しかし、ラッセルは、すべての数学をカバーし、フレーゲのアイデアと仕事に正確に依存して、当時知られているすべてのパラドックスのない正式なシステムのバージョンを1902年に導き出すことができました。Principia Mathematica（Alfred North Whiteheadと共著）という本で発表された彼の結果は、実際には論理の公理化になり、David Hilbertは、これが「科学を公理化するためのあらゆる努力の頂点と見なせる」と信じていました。
数学者が彼らの分野の基礎に強い関心を持っているもう一つの理由がありました。事実、19世紀と20世紀の変わり目に、集合理論に矛盾が発見され、そのために傲慢な「集合理論のパラドックス」が生み出されました。これらの中で最も有名な—ラッセルの有名なパラドックス—は、残念ながら、それだけではありませんでした。さらに、ほとんどの科学者にとって、新しい奇妙な発見が当てはまらないことは明らかでした。集合理論は数の科学の建物全体が建てられている基礎の役割をしているので、ヒルベルトが言ったように、この発見は数学の世界に「壊滅的な影響」を及ぼしました。「これらのパラドックスに直面して、私たちは今の状況が長い間耐えられないことを認めなければなりません。考えてみてください：数学（信頼と真実のモデル－概念と推論）は、研究し、教え、適用することが無意味であることになります。では、数学的な思考自体が破綻した場合、どこで信頼性と真実を探すことができるでしょうか？ヒルベルトは1925年6月の数学者会議の彼の報告で嘆きました。

ーーー

１．数学は完全です。すなわち、いかなる数学的な記述も、その分野自体の規則に基づいて証明または反証することができます。
２．数学は一貫しています。受け入れられている推論の規則に違反せずに、いかなる命題も証明すると同時に反駁することは不可能です。
３．数学は決定可能です。つまり、ルールを使用して、それが証明可能であるか反駁可能であるかどうか、任意の数学命題について調べることができます。

1930年、ケーニヒスベルクのウィーンサークルが主催した会議で、彼は”論理計算の完全性”に関する発表をし、翌年の初めに、”Principia Mathematica と関連システムの根本的な困難”に関する論文を発表しました。彼の仕事の中心は、数学のさらなる発展において基本的な役割を果たす定理の定式化と証明でしたが、不完全さについてのゲーデルの有名な定理は、「どのような一貫した公理システムであっても、受け入れられた公理系内で、証明または反証することができない命題が存在する」と述べています。このように、ゲーデルはヒルベルトの最初の命題に否定的な反応を示しました。興味深いことに、ヴェルナー・ハイゼンベルグは同じ会議で「因果関係の知識と量子力学」について講演しました。このレポートで、”不確定性原理”の最初のアプローチが提示されました。

■ゲーデルの定理

数学者は、「ゲーデル以前」の時代に、彼らの定理を証明していたように、今日も証明をしています。

ゲーデルとアインシュタイン（「科学の世界で」より）