note.com投稿記事

オーギュスタン・ジャン・フレネルFresnel（1788-1827）は，ナポレオン時代のフランスの数学者です．

■フレネルレンズ

フレネルレンズの概念（断面図はwikiより）

フレネルは，フレネルレンズ(1819)やゾーンプレートに名前が残っています．注）ブリタニカ（https://www.britannica.com/technology/Fresnel-lens）によると，レンズの表面を同心円状のリングに分割するというアイデアはFresnelよりも古く，Georges-Louis Leclerc de Buffon（1748）で，フレネルは，1821年に灯台レンズの製造に採用したとあります．ビュフォンもフランスの数学者で確率論の実験「ビュフォンの針」で有名です． 

灯台の凸レンズは巨大で重いのが問題でしたが，フレネルはフレネルレンズを採用してこの問題を解決しました．今日ではプラスチックを用いることで，この原理を使った平板レンズが，ルーペなどの小さいものから，太陽光集光用の大型の製品まで作られています．

https://www.ntkj.co.jp/products/#lens1

 製品情報 | NTKJ Co., Ltd. - 日本特殊光学樹脂日本特殊光学樹脂株式会社(NTKJ)より

■ゾーンプレート

フレネルゾーンプレートは，単色の光を集光することができます．X線や光や電波は，皆，電磁波の仲間ですが，ゾーンプレートは，屈折させて集光するレンズが作れないX線に対しても集光することができます．

 STXMで使われるX線の集光（バークレイALS，BL5）

■アンテナとフレネルゾーン

フレネルゾーンは，無線通信でも使われる言葉です．無線通信で「見通しが良い」ということは，送信アンテナと受信アンテナの間に障害物がなく，お互いにアンテナが見通せるという意味ではなく，フレネルゾーンが確保されている状態を指します．フレネルゾーンは，送信アンテナと受信アンテナの位置を軸とする楕円体の形で，第1フレネルゾーン，その外側に，第2フレネルゾーン…と広がっていき，隣り合うゾーンの位相は互いに反対です．

私の家の立地では，携帯４Gの電波強度が非常に弱いので，屋外にドナーアンテナを設置してもらっています．私の場合では，800MHz（18バンド）ですが，例えば基地アンテナからdの距離があるとすると，第1フレネルゾーン半径r_1は，r_1＝√(λ･d)/2=9.7mとなります．ただし，λは800MHz電波の波長37.5cm，d=1,000mを用いた．第1フレネルゾーンの楕円体の60%程度が確保できれば良い通信状況と言えますが，この途中で障害物が邪魔をするのです．一般的な話をすれば，地上から高い位置に受信アンテナを設置できれば，第１フレネルゾーンの60%確保がしやすいということになります．

フレネルゾーン計算ツール | 株式会社サーキットデザインwww.circuitdesign.jp

レンズアンテナと反射型アンテナ

電波望遠鏡，衛星放送アンテナは，良く知られるように反射型のパラボラアンテナが使われます．これは，特定の方向からやってくる平行電波を集光する反射型アンテナです．しかし，ゾーンプレートの原理を使って集光するアンテナもあります．

一寸，脱線しますが，ルネベルグレンズは，球形の誘電体レンズ（同心殻で誘電率を変化させている）で，マイクロ波電波を屈折させて集光するレンズアンテナです．球体が乗っているレーダーの写真を見たことがおありでしょう．私は昔，衛星放送受信用のルネQアンテナを使用していました．残念ながら今は販売されていないようです．

■フレネル反射率

フレネルは若くして（39歳）で亡くなりましたが，フレネル反射率は死の4年前の発表（1932）です．

物質の表面や界面で反射や透過する光の電場の振幅は，電場の界面平行成分と電束密度の界面垂直成分は連続になります．
物質0と物質1との界面を問題にするとき，この界面で反射される電場の振幅の比ρをフレネルの振幅反射率といいます．エネルギー反射率はρ^2です．
屈折率の低い物質から高い物質に向かう界面で反射するときには，ρが負になりますが，これは振幅の位相が180°変わることを意味します．エネルギー反射率はρの2乗なので負にはなりません．

■フレネルは，光学の分野で色々な研究をしました．そこで現れる数学「フレネル積分」の話をするのが，実は本題ですが，長くなったので，稿を改めて別の機会にします．

Maxwell方程式　[c.g.s.単位系使用] 
$$rot\overrightarrow{E}=-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{B } }{ \partial t}$$    (1a)    電場$$\overrightarrow{E}$$
$$rot\overrightarrow{H}=\displaystyle \frac{1}{c}\displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$ （変位電流）    （1b）    磁場$$\overrightarrow{H}$$
$$div\overrightarrow{B}=0$$    （1c）    磁束密度$$\overrightarrow{B}$$
$$div\overrightarrow{D}=4\pi \rho$$ (空間電荷)    (1d)    電束密度$$\overrightarrow{D}$$

弱い場では，線形応答が成り立つ： 
$$\overrightarrow{B}=\mu\overrightarrow{H}$$ (透磁率$$\mu=1$$の物質を対象とする)    (2a)    magnetic susceptibility$$\mu$$
$$\overrightarrow{D}=\varepsilon \overrightarrow{E}$$    (2b)    dielectric constant$$\varepsilon $$
$$\overrightarrow{j}=\sigma \overrightarrow{E}$$    (2c)    current density$$\overrightarrow{j}$$，conductivity$$\sigma $$
---------------------------------------------------- 
参考） [MKSA単位系の場合]
$$ \bigtriangledown \times E=-\displaystyle \frac{ \partial B}{ \partial t}$$
$$ \bigtriangledown \times H=\displaystyle \frac{ \partial D}{ \partial t}+j$$
$$ \bigtriangledown \cdot B=0$$
$$ \bigtriangledown \cdot D=\rho $$
ベクトルポテンシャル，スカラーポテンシャルの定義
$$E=- \bigtriangledown \cdot \phi -\displaystyle \frac{ \partial A}{ \partial t}$$
$$B= \bigtriangledown \times A$$
---------------------------------------------------- 
公式　$$[ \bigtriangledown \times \left[ \bigtriangledown \times E \right] ]= \bigtriangledown \left( \bigtriangledown \cdot E \right) - \bigtriangledown ^{2}E$$を使うと，
(1a,b)　→ $$ \bigtriangleup \overrightarrow{E}=\displaystyle \frac{\varepsilon }{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{E } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}$$， $$ \bigtriangleup \overrightarrow{H}=\displaystyle \frac{\varepsilon}{c^{2 } }\displaystyle \frac{ \partial ^{2}\overrightarrow{H } }{ \partial t^{2 } }+\displaystyle \frac{4\pi \sigma }{c^{2 } }\displaystyle \frac{ \partial \overrightarrow{H } }{ \partial t}$$ （３）
（３）の解  → $$\overrightarrow{E}=\overrightarrow{E}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$，$$\overrightarrow{H}=\overrightarrow{H}_{0}exp\left[ i\left( \omega t-2\pi \overrightarrow{k}\overrightarrow{r} \right) \right] $$ 　　　（４）
解（４）は，条件（５）の下で成立する．もし，変位電流がなければ，（５）の右辺第２項はない． 
$$\left( \displaystyle \frac{2\pi kc}{\omega } \right) ^{2}=\varepsilon -i4\pi \left( \displaystyle \frac{\sigma }{\varepsilon } \right) $$ (5)
(4)を(1a,b)に代入（$$\sigma =0$$の物質を対象とする．）： 
$$\overrightarrow{k} \times \overrightarrow{E}_{0}=\displaystyle \frac{\omega }{2\pi c}\overrightarrow{H}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
kE_{x} \\[0mm]
0
\end{array} \right] =\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
0 \\[0mm]
H_{y} \\[0mm]
0
\end{array} \right] $$ (6a)
$$\overrightarrow{k} \times \overrightarrow{H}_{0}=-\displaystyle \frac{\omega }{2\pi c}\overrightarrow{E}_{0}$$ $$ \Rightarrow $$ $$\left[ \begin{array}{@{\,} c @{\, } }
-kH_{y} \\[0mm]
0 \\[0mm]
0
\end{array} \right] =-\displaystyle \frac{\omega }{2\pi c}\left[ \begin{array}{@{\,} c @{\, } }
E_{x} \\[0mm]
0 \\[0mm]
0
\end{array} \right] $$ (6b)
$$\displaystyle \frac{c}{n}=\displaystyle \frac{\omega }{2\pi k}$$ (7)
$$\displaystyle \frac{H_{y } }{E_{x } }=\displaystyle \frac{\omega \varepsilon }{2\pi ck}=\displaystyle \frac{2\pi ck}{\omega }\left( =\displaystyle \frac{\varepsilon }{n}=n \right) $$ (8)
$$n^{2}=\varepsilon $$, $$\displaystyle \frac{H_{y } }{E_{x } }=\sqrt{\varepsilon }$$ (9)

境界条件

物質１と物質２の境界では，電束密度の界面垂直成分，電場の界面平行成分が連続することがMaxwell方程式から導ける．
$$D_{1z}=D_{2z}$$ $$ \Leftarrow $$ $$div\overrightarrow{D}=0$$ (10a)
$$\displaystyle \int_{}^{}(D_{2z}-D_{1z})dxdy=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}D_{z}df_{z}=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}div\overrightarrow{D}dV=0$$
$$E_{1x}=E_{2x}$$ $$ \Leftarrow $$ $$div\overrightarrow{B}=0$$ (10b)

$$\displaystyle \int_{}^{}(E_{1x}-E_{2x})dx=\displaystyle \lim_{ \mit\Delta z \to 0}\displaystyle \int_{}^{}(rotE)_{y}df_{y}=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \int_{}^{}\displaystyle \frac{ \partial B_{y } }{ \partial t}df_{y}=$$

$$=\displaystyle \lim_{ \mit\Delta z \to 0}-\displaystyle \frac{1}{c}\displaystyle \frac{ \partial }{ \partial t}\displaystyle \int_{}^{}div\overrightarrow{B}dV=0$$

垂直入射
$$E_{1x}+E_{1x}^{R}=E_{2x}$$
$$H_{1y}+H_{1y}^{R}=H_{2y}$$ $$ \Rightarrow $$ $$n_{1}\left( E_{1x}-E_{1x}^{R} \right) =n_{2}E_{2x}$$
$$\displaystyle \frac{H_{1y } }{E_{1x } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$-\displaystyle \frac{H_{1x}^{R } }{E_{1x}^{R } }=\sqrt{\varepsilon _{1 } }=n_{1}$$, $$\displaystyle \frac{H_{2y } }{E_{2x } }=\sqrt{\varepsilon _{2 } }=n_{2}$$
振幅反射率 $$\displaystyle \frac{E_{1x}^{R } }{E_{1x } }=\displaystyle \frac{n_{1}-n_{2 } }{n_{1}+n_{2 } }$$， $$n_{1}<n_{2}$$で位相反転
振幅透過率 $$\displaystyle \frac{E_{2x } }{E_{1x } }=\displaystyle \frac{2n_{1 } }{n_{1}+n_{2 } }$$
--------------------------------------------------------
$$n_{1}, n_{2}$$が実数なら，$$\displaystyle \frac{\left| E_{1x}^{R} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }+\displaystyle \frac{\left| E_{2x} \right| ^{2 } }{\left| E_{1x} \right| ^{2 } }=1$$
-------------------------------------------------------- 
$$\displaystyle \frac{ \partial \rho }{ \partial t}+div\overrightarrow{j}=0$$
$$\displaystyle \frac{ \partial }{ \partial t}div\overrightarrow{D}=4\pi \displaystyle \frac{ \partial \rho }{ \partial t}=-4\pi div\overrightarrow{j}$$
$$div\left( \displaystyle \frac{ \partial \overrightarrow{D } }{ \partial t}+4\pi \overrightarrow{j} \right) =0$$
$$rot\overrightarrow{H}=\displaystyle \frac{\varepsilon }{c}\displaystyle \frac{ \partial \overrightarrow{E } }{ \partial t}+\displaystyle \frac{4\pi }{c}\sigma \overrightarrow{E}$$
第１項：第２項の寄与率＝$$\varepsilon \omega :4\pi \sigma $$
$$\omega \gg \displaystyle \frac{4\pi \sigma }{\varepsilon }$$ $$\to $$ 誘電体

４．特異値分解の数学

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n

簡単のために，m=5，n=3として，具体的に演習してみましょう．

今回は，昔，私がリコーで関わった懐かしい実験の話をして，特異値分解の数学の話への導入にしたいと思います．まず，実験の話をしますが，私がSTXMに係わったのは，2000年～2004年で，もう20年も前のことです．その後の進歩は著しいに違いありません．当時，実用になるSTXM装置は，Hitchcoch博士が，サンフランシスコ，バークレーのALS（Advanced Light Source）に建設した，BL5.3.2（bending magnet光源利用）　とBL7.0.1（undulator光源利用）の2台だけでした．後年，岡崎の分子研のUVSORに，やはり，Hitchcock博士がSTXMを建設しました．

（注）放射光とは初耳の読者もおられるので，放射光施設とは何かを簡単にお話しておきます．ドーナツのような真空リングの中を，光速に近い速度に加速された電子が回転しています．回転するといっても電子の軌道が円形というわけはなく，リングの要所要所に偏向磁石bending magnetが配置されていて，偏向磁石の所で電子は曲げられるので，電子の軌道は多角形です．電子が方向を変えるときには，電磁波（白色光の光やX線）を放出します．これが放射光で，いろいろな測定に放射光を利用します．リングの電子蓄積エネルギーとはリング内を回転する電子のエネルギーのことです．ALSでは1.9GeV，兵庫県のSPring8では8GeVです．蓄積エネルギーの大きさは，放出される放射光のエネルギーの最大値を決めるので，SPring8は硬X線の光源，ALSは軟X線の光源となります．
放射光の光源は，偏向磁石bending magnet光源とundulator光源とがあります．undulatorというのは周期的に配列した磁石のことで，蓄積リングの電子軌道の直線部に挿入します．周期的磁場で電子は蛇行運動をしますが，その軌道のFourier変換に相当する波長のX線（準単色光）が放射されます．

さて，STXMに使うALSの放射光リング（蓄積電子のエネルギーが1.9GeV）は，軟X線の光源です．軟Ｘ線の領域は10^2eV～10^4eVの範囲で，炭素など軽元素の1s（K殻電子）の励起（光電効果による電子の放出）は，このX線の領域にあります．硬X線と違い，軟X線は空気で減衰しますからその測定は，He置換した真空チェンバー内で行います．炭素の1sの吸収スペクトルNEXAFS(吸収端近傍の吸収微細構造)は，分光して単色化したX線ビームを薄膜試料に透過させ，その吸収を測定して得ます．スキャンするエネルギー範囲は，280eV～310eVで，スキャンステップは0.1eVですので，スペクトルは300点ほどのデータ数になります．

目次
これから始まるこのテーマの話には4つの側面があります．
第１は，ニュースとしての一般向け報道．
第２は，STXMの装置の仕組み．
第３は，材料科学の側面．炭素1s吸収端近傍の吸収スペクトルNEXAFS．
第４は，データ解析の数学．特異値分解．

技術者向け教育の場合にお話しするのは，第１，２の部分です．第４の部分は，Hitchcock博士らの開発したaXis2000というソフトウエアを用いるので，数学を意識することはないのですが，今回は，特に，第４の数学の話に注目することにします．番号順に順を追って話ます．

１．一般向け報道

せっかくの記事ですが，技術の解説が正しくありません．ここで言及しているデータベースは無関係で，この記事はピントがずれているのが残念です．

２．STXM（ScanningTransmissionX-rayMicroscopy）装置

放射光X線をFresnel Zone Plateで，試料薄膜上にフォーカス（22nmΦ）させ，その微小ビームを試料薄膜に透過させ，微小ポイントの吸収スペクトルを測定します．スペクトルを得るには入射するX線のエネルギーを280eV～310eVの範囲で，0.1eVの分解能で変化させます．これは，色を変えて見る実験に例えるとわかりやすいでしょう．同じ材料薄膜でも，赤い色を透過させてみた場合と青い色を透過させてみた場合とでは異なるでしょう．試料薄膜（ミクロトームで加工した厚さ100nmの切片）上をラスタースキャンすることで，そのエネルギーで見た薄膜の吸収画像が得られます．
薄膜に入射するＸ線エネルギーを280eV～310eVの範囲で変えて測定した300枚ほどの吸収画像をスタックすれば，薄膜試料の各点(x, y)の吸収スペクトルμ(x, y)が，point to pointで得られたことになります．試料上の空間分解能は約30nm，スペクトルのエネルギー分解能は0.1eVという高性能な測定です．私たちは装置を使う純粋ユーザーでしたが，私は，このような装置を開発したHichcock博士グループの技術と装置の仕組みに興味を持ちました．ここでは，STXM装置の重要な要素であるゾーンプレートとその制御についてとり上げましょう．

ゾーンプレートの焦点距離は波長で変わります．入射するX線ビームのエネルギーがスキャンされれば，そのつど瞬時にフォーカスしなければなりません．これは，レーザー干渉計とゾーンプレートの載るピエゾステージで行われます．試料点の（x, y)スキャンは試料台のピエゾステージで行われます．
BL5.3.2はbending mgnetからの放射光（undulator光源よりは光強度は弱い）ですが，照射された点の有機物はダメージを受けますので，できるだけ高速で（dwell time 2msec）測定します．そして，試料の変質がなかったかどうか測定前後でチェックする測定ルーチンもあります．X線のエネルギーを変えて測定した吸収画像をスタックしたとき，サンプル位置のずれがあれば自動修正できます．

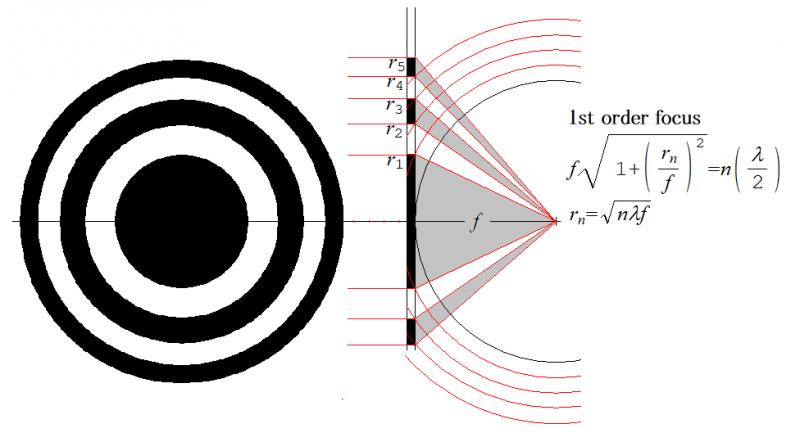
以下で，STXM装置で最も主要な素子であるFresnel zone plateについて，詳述しましょう．zone plateは，外径45000nm，最外輪帯幅35nm程度のものです．下図のゾーンプレートは，波長λのX線の単色光を集光します．黒い部分はX線を通しません．例えば，中心の黒丸はダイレクト光をストップし，輪帯環の白い部分を通過してくる行路長　f+λ/2，f+3λ/2，f+5λ/2，････のものが，焦点距離fに集光できます．

 このようなフレネルゾーンプレートの後ろにOSAという絞りを置いて，行路差λずつの光線（１次のフォーカス）のみが試料位置に集光するように調整します．

 入射X線のエネルギーを変えたときのゾーンプレートの焦点距離の調整は，レーザー干渉計を用い精密制御されています．

３．炭素の1s電子の吸収端直上の微細構造スペクトルNEXAFS

電子写真で使われるトナーは，カーボンブラックとか顔料色素で出来ていると思っている人がほとんどでしょう．実際には，このような黒やカラーの色素だけでなく，樹脂，ワックス，電荷制御剤など，複数の有機物分子が，1粒のトナー中に分散されており，それらの分散状態は，トナーの性能に影響を与えます．設計通りの分散状態が実現しているか評価することが必要です．高精細トナー1粒のサイズは数μmという微細さで，その中の物質の分布状態を30nmΦの分解能で調べる必要があります．しかも，混合されている物質は，皆，有機物ポリマーで元素分析をすれば，どれも主成分は炭素です．つまり，炭素が骨格のよく似た有機分子が混合している状態の分布マップが知りたいのです．これを化学状態マッピングといいます．

下図には，色々な物質の炭素1s電子のNEXAFS吸収スペクトルを載せました．X線のエネルギーを変えて観察した透過像も載せています．例えば，①カーボンブラックの分布する場所は292.5eVのX線エネルギーで見ると吸収が大きいため白っぽく見え，②ワックスの分布する場所は，287.8eVで見ると吸収のためX線の透過が悪く白っぽく見えます．同様に，③樹脂の分布する場所は，284.3eVのX線の透過像では白っぽく見えます．
エネルギースキャンにともなう画像変化のパラパラ動画を作って見るとわかりやすく面白いものです．

 化学状態（元素分析ではない）という意味は，トナー中に分散している物質は，すべて有機分子（どの分子もほとんど炭素元素で出来ている）なので，元素分布のマッピングでは差がありません．炭素原子が骨格の有機分子の吸収スペクトルは，炭素の1sの吸収端285eV付近にあり，その炭素原子がどのような化学結合状態にあるのか（1重結合か，2重結合か，π電子系か，どのような官能基と結合しているか）により，吸収端から高エネルギー側に観測される吸収スペクトルの微細構造（NEXAFSという）に違いがでます．
トナー中の有機ポリマー分子の分布マップを得るには，化学状態マッピングがどうしても必要になります．
元素に特有な特性X線を検出すれば良い元素分布マッピング［TEM（分析電顕）でも，放射光でも，微小領域の蛍光X線分析は普及している］と，化学状態マッピング［微小領域のpoint to pointで炭素1sのNEXAFSの測定が必要］は，全く異なる技術であり，我々の目的には，STXMでの実験が必要でありました．

リコーが，Adam P. Hitchcock（McMaster University）博士が開発したALS（バークレー，AdvancedLightSource）のBL5.3.2に設置されたSTXMで共同研究を行ったのは，2000~2004年のことでした．

実験で得られるデーターセットは，試料表面の座標を（x, y）とすると，試料表面のラスタースキャンと，透過させるX線のエネルギーωのエネルギースキャンを行って，point to pointで収集した吸収スペクトル（optical density）$${μ(ω；x, y)t}$$を得ます．$${I/I_0=e^{-\mu t } }$$
x,yのスッテプは50nmで各ステップでの測定時間は2msec，TEM用のメッシュに置いたサンプルの厚さは80nm，
CのNEXAFS測定でのエネルギー・ステップは；0.3eV（282.0～284.2eV），0.1eV（284.3～286.0eV），0.4eV（286.2～292eV）です．
再度たとえ話をすると，膜を透過する光のコントラスト像は，光の色を変化させると透過光の像のコントラストが変わって見えるというわけだ．

このような，データセットの収集と解析は，Hitchcock博士の開発したソフトウエアaXis2000を用います．この解析のために用いる数学は，特異値分解です．この先は，４．特異値分解の数学に続きます．

４．特異値分解

試料はn種類の物質で構成されており，それぞれの吸収スペクトルは既知とします．この試料薄膜の各点（x, y）ごとに，吸収スペクトルが測定されています．この測定されたスペクトルは，各物質の吸収スペクトルをそれぞれの存在量で重みをつけた重畳になっています．課題は，各点(x, y)で，その点に存在する物質量を求める課題になります．
エネルギースキャンの点数はm（実際は300点ほど），混合される物質種数はnです．m>>n
簡単のために，m=5，n=3として，続編で演習してみましょう．続く...

参考-----
特異値分解を使いますが，特異値分解の概念図は以下のようなものです．

以下の拙著の第3章p64～p84から抜粋転載しました．

https://www.amazon.co.jp/dp/4774143936?tag=note0e2a-22&linkCode=ogi&th=1&psc=1

■特異値分解とは

$${m}$$行$${n}$$列($${m\geq n}$$) の任意の実行列$${A(m\times n)}$$は，$${A=U^{T}\mit\Sigma V}$$，$${UAV^{T}=\mit\Sigma}$$のように分解できる．

ここで $${U ，V}$$ は，それぞれ $${m}$$次，$${n}$$次 の直交行列．$${\mit\Sigma(m\times n)}$$ は，対角成分が正 （$${\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r >0}$$，$${r}$$は$${A}$$のランク）で，それ以外の成分はすべて 0の行列である．このような分解を特異値分解 (singular value decomposition) と言い，任意の行列に対して可能であることから，工学や物理学でしぱしば活用される．特に，行列$${A}$$が$${m=n}$$である場合が固有値分解であり，分解された$${\mit\Sigma}$$の対角成分を固有値と呼んだ．固有値問題の拡張が特異値問題で，固有値に対応する概念が特異値である．

もちろん，これらの分解は$${A}$$が複素行列である場合にも成り立つ．実行列の場合は，$${U,V}$$は直交行列だが，複素行列の場合はユニタリー行列で，例えば，$${U}$$の逆行列は，転置行列$${U^{T } }$$でなく，共役転置行列$${U^{\dagger} }$$になる．この場合も特異値はすべて正である．一般に，エルミート行列（対称行列）の固有値は実数で，異なる固有値に属する固有ベクトルは互いに直交する．
$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
& & & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$

■線形写像 $$ y=Ax  (x∈C^{n}，y∈C^{m})$$があり，それぞれの空間でユニタリー変換； 
$$ x'=Vx$$, $$y'=Uy$$をすると，$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている．

 ■特異値分解の手法

実行列$${A(m\times n)}$$に対して，$${AA^{T } }$$や$${A^{T}A}$$ を作ると，これらは，それぞれ$${m}$$次，$${n}$$次の実対称行列になる．この実対称行列に関する固有値問題を考えよう．行列$${A(m\times n)}$$のランクは$${r=rank(A)}$$であるから，$${rank(AA^{T})=rank(A^{T}A)=r}$$である．従って，これらの実対称行列は$${r}$$個の固有値とそれらに対応する固有ベクトルを持つ．異なる固有値に属する固有ベクトルは互いに直交することが知られている．

 実対称行列$$AA^{T}$$と$$A^{T}A$$を考える：

$$ AA^{T}=U^{T}\mit\Sigma VV^{T}\mit\Sigma^{T}U=U^{T}\mit\Sigma ^{2}U $$，$$ \because \Sigma \Sigma^{T}=\Sigma ^{2}(m×m) $$

$${(AA^{T})U^{T}=U^{T}\mit\Sigma^{2 } }$$，$$AA^{T}$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}$$

固有ベクトルは，$$U^{T}(m \times m)=\left( \begin{array}{@{\,} c @{\, } }
u_{1} \\[0mm]
u_{2} \\[0mm]
\vdots \\[0mm]
u_{r} \\[0mm]
\vdots
\end{array} \right) $$

$$A^{T}A=V^{T}\Sigma^{T}UU^{T}\Sigma V=V^{T}\Sigma ^{2}V$$,      $$ \because \Sigma^{T}\Sigma =\Sigma ^{2}(n×n)$$

$${(A^{T}A)V^{T}=V^{T}\mit\Sigma^{2 } }$$，$$A^{T}A$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}$$

固有ベクトルは，$$V^{T}(n \times n)=\left( \begin{array}{@{\,} c @{\, } }
v_{1} \\[0mm]
v_{2} \\[0mm]
\vdots \\[0mm]
v_{r} \\[0mm]
\vdots
\end{array} \right) $$

 このようにして，$${A}$$の特異値$${\sigma _{1}, \sigma _{2}, \cdots , \sigma _{r } }$$や，特異値ベクトル$${U^{T},　V^{T } }$$を求めることができる．

 ■特異値分解の応用

$$ A=U^{T}\Sigma V=\left( \begin{array}{@{\,} c @{\, } } u_{1} \\[0mm] u_{2} \\[0mm] \vdots \\[0mm] u_{r} \\[0mm] 0 \end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } } \sigma _{1} & & & & 0 \\[0mm] & \sigma _{2} & & & \\[0mm] & & \ddots & & \\[0mm] & & & \sigma _{r} & \\[0mm] 0 & & & & 0 \end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } } v_{1} & v_{2} & \cdots & v_{r} & 0 \end{array} \right) = $$

$$=\left( \begin{array}{@{\,} ccccc @{\, } }
\sigma _{1}u_{11} & \sigma _{2}u_{12} & \cdots & \sigma _{r}u_{1r} & 0 \\[0mm]
\sigma _{1}u_{21} & \sigma _{2}u_{22} & \cdots & \sigma _{r}u_{2r} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
\sigma _{1}u_{r1} & \sigma _{2}u_{r2} & \cdots & \sigma _{r}u_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } }
v_{11} & v_{21} & \cdots & v_{r1} & 0 \\[0mm]
v_{12} & v_{22} & \cdots & v_{r2} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
v_{1r} & v_{2r} & \cdots & v_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) =$$

$$=\sigma _{1}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{11}v_{11} & u_{11}v_{21} & \cdots & u_{11}v_{r1} & 0 \\[0mm]
u_{21}v_{11} & u_{21}v_{21} & \cdots & u_{21}v_{r1} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{r1}v_{11} & u_{r1}v_{21} & \cdots & u_{r1}v_{r1} & \\[0mm]
0 & & & & 0
\end{array} \right) +\sigma _{2}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{12}v_{12} & u_{12}v_{22} & \cdots & u_{12}v_{r2} & 0 \\[0mm]
u_{22}v_{12} & u_{22}v_{22} & \cdots & u_{22}v_{r2} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{r1}v_{12} & u_{r2}v_{22} & \cdots & u_{r2}v_{r2} & \\[0mm]
0 & & & & 0
\end{array} \right) + \cdots +\sigma _{r}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{1r}v_{1r} & u_{1r}v_{2r} & \cdots & u_{1r}v_{rr_{ } } & 0 \\[0mm]
u_{2r}v_{1r} & u_{2r}v_{2r} & \cdots & u_{2r}v_{rr} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{rr}v_{1r} & u_{rr}v_{2r} & \cdots & u_{rr}v_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) $$

ここで，特異値は大きい順$${\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r >0}$$に並べてあるので，この展開は良い近似になる．例えば，$${A}$$を画像データとすると，最大の特異値$${\sigma_1}$$に関する行列だけ用いる情報圧縮（次元圧縮）ができる．

ベクトル$$U^{T}(m \times m)=\left( \begin{array}{@{\,} c @{\, } }
u_{1} \\[0mm]
u_{2} \\[0mm]
\vdots \\[0mm]
u_{r} \\[0mm]
\vdots
\end{array} \right) $$や$$V^{T}(n \times n)=\left( \begin{array}{@{\,} c @{\, } }
v_{1} \\[0mm]
v_{2} \\[0mm]
\vdots \\[0mm]
v_{r} \\[0mm]
\vdots
\end{array} \right) $$などは固有ベクトルであるので，それぞれの空間で互いに直交しているが，ベクトル$$u_i$$や$${u_j}$$は，互いに直交しているわけではない．

 
■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して，
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める．
特異値分解ができたら；$$UAV'=\Sigma$$，$$A=U'\Sigma V$$が成立している．
（$$A$$は実行列なので，$$U，V$$は直交行列となり$$U'＝U^{-1}$$などの性質がある．）
最小2乗法は，$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる．
$$\textrm{rank}(A)=r≦n<m$$とする．$$\Sigma (m×n), V(n×n), U(m×m)，x(n×1)$$の型であった．

$$r=n$$の場合を考える．

$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$,　$$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから，
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方， 
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って，$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると，第1項は0になり，第２項は残差の２乗を与える，

$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る．