note.com投稿記事

 http://imgur.com/qjjlkGm

無限に食べられるチョコレートをご覧ください．不思議ですね．
How to eat chocolate indefinitely [fixed]109159 views and 3505 votes on Imgurimgur.com

◆7×9の板で1コマが幾何学的に消滅する
これは2014年の米国MAMで取り上げられたマジックです．
http://www.mathaware.org/mam/2014/calendar/areapuzzles.html

まずは，アルゼンチンのマジシャン，ノルベルトジャンセンによるプレゼンをご覧ください．　http://youtu.be/3PszMaZ5Ipk

7x9のエリアにタイル片が配置されています，断層に沿って滑らせ
上部の左3コラム分と右4コラム分を入れ替えると，不思議なことにタイルが１つ減ります．
この操作を繰り返すたびにタイルが1つづつ減り３つまで減らせます．
タイルが1つ減っても，2つ減っても，3つ減っても，
元通りの7x9枠内にタイルはきちんと配置され変わらないように見えます．
これは不思議ですね．どうしてタイルが１つづつ余るのでしょうか？

ビデオを観察していると，タイルが消滅する原理がだんだんわかってきます．原理の理解を助ける図を以下に作成しました．
青色の面積がだんだん減じているのがわかります．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/11/15935811/img_1?1405218032

このおもちゃを作製して見ようとする方は，この原理図を参考にしてください．
数学マジシャンの使っているタイルのパーツは目地が太いですね．
私の原理図には，目地はありませんが，作製するときは目地の効果も考慮すべきでしょう．
結局，断層をはさんだある行だけ，1コマ縦の長さが1/7だけ縮むので，
7コラムあるから面積としては1コマ分取り出せることになります．

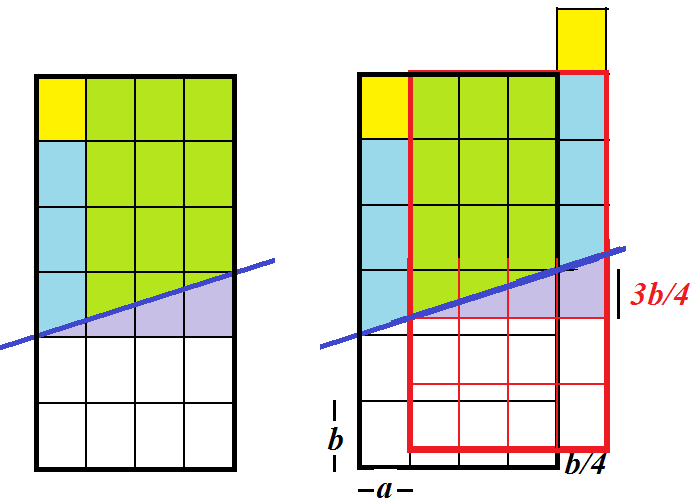
◆なぜタイルが１コマ減るのか
左のコラムと右の3列を入れ替えると，１コマ減る．
１コマの高さをbとすると，断層を挟んでb/4だけ縮みます．
ただし，右端のコラムの断層ではコマ間の目地が消えるのが残念！
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_3?1405215030

◆真ん中を取り除いたお札が再現できる
http://youtu.be/-h0AXeLIHqQ　　

 お札の中心を取り除いて，裏向きにして並べると
完全な1枚が再現できたように見えます．
真ん中が消えるとは，あり得ないことが起ったように見えます．
数学マジシャンの使っているお札の裏面には
再配列したときに完成するようなお札の裏面の絵が描いてあるので
お札が再現したように錯覚します．以下の原理図を参考に作製してください．
http://blogs.c.yimg.jp/res/blog-09-2d/tanidr/folder/497823/96/15937596/img_0?1405215030

今回も以下のメルマガのリメイク版です
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.06.10］ No.013
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆数を記憶する
http://plus.maths.org/issue31/features/eastaway/index-gifd.html
Rob Eastaway

今回は，2004年の英国MMP，plusマガジン31の記事の翻訳（byKT）です．
肩のこらない読み物なので長文ですが全文掲載し，さらに新たに，編集後記を追加しました．

2004年3月, Kent のDaniel Tammet が，π（パイ）を小数22,511位まで暗唱してみせ，
ヨーロッパ新記録が達成された．この仕事を完了するのに5時間を費やした．
それでも，日本の後藤裕之が1995年に達成した小数点以下42,195桁のやっと半分である．

［訳注：その後の2006年10月3～4日に，16時間28分をかけて，
原口　證（当時60歳）が100,000桁を暗誦している．ギネス社申請中とのことだ．
http://www.worldrecord314.com/pi01.html
原口の方法は，数字を1,000桁ずつ区切り，語呂合わせで物語として暗記するもの．
今回の物語のテーマは「世界旅行」．北海道に住んでいる武士が全国各地を歩いて
いるうちにいろいろな人物や物件に出会い，10万桁にもなれば，
朝鮮半島を通り過ぎてシルクロードまでたどりつくストーリーになっているという．
柴田昭彦http://www5f.biglobe.ne.jp/̃tsuushin/sub1.htmlによる］

人間はいかにしてこのような信じられない（むしろ無意味な）記憶の業績を
やり遂げるのだろうか？　それらから学べるものが何かあるだろうか？
数字を覚えていなければならぬもっと実際的な必要性---
例えば，南京錠のコード，キャッシュカードの暗証番号---などもある．

◆記憶と数
記憶は諸君が考えるために重要だ．諸君はほとんどすべての活動に記憶を使用する．
記憶は事実と名前を学ぶために必要だが，新規に身体技能を獲得するためや，
冗談を言うためにでさえ必要となる．素質はそれぞれの人によって大変異なる．
同じ人の記憶能力も仕事によって大変違う．例えば，数を良く記憶する人が，
ジョークも覚えているとは限らない（私は苦い経験がある）．
数を覚えているという特別な素質はどこから来るのだろう？

数学者は他の人より数を覚えているようだが，
この領域で卓越した能力を持っことが数学者になるための必須条件ではない．
例えば，Daniel Tammetは，数字の順番を記憶するすばらしい能力を，
数字を色と映像として”見る”ことに置き換えている．
彼にとってπは数字の抽象的なセットではなく，物語か映じられるフィルムのように現れる．
Tammetは，稀有だが詳しい記載のある症候群---共感---と呼ばれるもので，
感覚のある一つが刺激されると，他の感覚も反応を引き起こすのだ．
共感はさまざまな様子で現れる．ある人達は，数字にさらされるとき，多重の感覚の反応を得る．
有名なロシアの”記憶男”Shereshevskyは，数字2は常に暗い矩形として見えるさまを記述している．
私は別の人間で，数字４はトマトの味とリンクしている人に出会ったことがある．
彼らにとってこれらの関連に理屈はない．共感は，記憶をしようと思ったときに自然な利点がある．
なぜなら，脳は，感覚と結びついたものを長期間記憶しようとするからだ．
出来事や物体は，音や映像や素材や特に匂いに結びついているときに，さらに記憶し易くなる．

ほとんどの人と同じく諸君も匂いに関する奇妙な経験があるだろう．
例えば古い家具の匂いをかぐことが，遠い過去に起こった何かを思い出させる．
匂いは記憶と特別に強い結合がある．多分，匂いを扱う脳の部分が，
長期記憶を形作ると考えられている海馬と近いためだろう．もし諸君が，
何かを記憶しようとするとき，わざと特定の匂いに囲まれるようにすれば，
後に思い出す必要があるとき，その匂いは記憶を引き出すのに役立つ可能性が高い．
記憶と感覚の間のこのリンクは，勉強の助ける記憶術の基礎である．
数を記憶しておくためによく提案される方法は，各数字を韻を踏んでいる言葉と結び付ける方法である．
oneワン＝バンbun
twoトゥー＝シューshoe
threeスリー＝ツリーtree
fourフォー＝ドォーdoor
......
このアイデアは，抽象的な数字を付随するイメージと音とともに，実質のあるものに変える．
もし，数字24を覚えていようと思ったら”シュードア”と覚え，正面ドアを蹴っ飛ばす絵を描く
（このイメージはなぜか容易に記憶される）．
ドアをける記憶は数字２４より長く維持されるだろう．私が１週間，数を覚えていようとするとき，
私はすぐにイメージを考える．思い出すにはただそれを数に変換するだけだ．

明らかにこれは小さい数を記憶しておく助けになるテクニックであろう．
しかし，もし何桁かの数を記憶する必要があるなら，信じられないほど厄介である．
1492は，bun-door-wine-shoe．この順番を記憶するのに必要となるイメージ---
オドビンスの［ワイン］店にパンを投げ込む適切な事件---を思い浮かべようと奮闘する．
もっとよい方法がきっとある....

◆数の記憶の数学的アプローチ
数を良く覚えている人のほとんどは，何らかの感覚的経験によるわけではない．
数が彼らにとって意味をもっているということはありそうな理由である．
数学者はここに強力な有利さがある．なぜなら，本職で数にさらされているので，
数の特徴に親しんでいるからだ．数学者に4832を見せる．彼らは，
その数字はどのような種類（4桁，偶数）か直ちに認識できる．
時には，数学者は数で遊ばずにはいられない．
この場合，4832を4×8=32と言っている自分を見出すかもしれない．
この種の遊びは，数字の意味付けを助け覚えやすくする．
数で遊ぶというこの衝動の有名な例がある．記憶で有名だった
Alexander Aitkenアレクサンダー・エイトケンは，エジンバラ大学の数学教授で，
かつて以下のようなコメントをした：
私が散歩している時に，モーターカーが通り過ぎ，登録ナンバーが731なら，
それは17×43と観察せざるをえない．....折襟に数字のついたバスの車掌を見ると，
その数字を２乗してしまう．....これは故意ではなく，どうしてもそうしてしまうのだ．
....時々は，数字が811のように特徴をまったくもたないものもある．
時には41のように諸君ご存知の多くの定理に登場するものもある．
さて，どっちが興味深い数字だろうか？

数学的な特性により数を記憶する最も有名な例の一つに，
病院に友人のRamanujanをたずねた時の数学者G H Hardyの話がある．
Hardyはタクシーできて，Ramanujanに挨拶した後お詫びを言った．
”私のタクシーナンバーは， 1729 だった．あまりぱ っとしな い数 ですみません.”
”それは逆です．1729はたいへん興味深い．”とRamanujanは言った．
”それは２種類の答えがある2つの立方体の和の最小の数字だ．”
（1729=12^3+1^3，または，10^3+9^3 ）

しばしば，数字の背景にあるパターンと意味が努力なしに心に残るだろう．
それほどでなくても，数字を意識的に記憶する方法の基礎になりうる．
諸君はそれらを暗証番号や電話番号の記憶に使うかもしれない．
これらはもっと長い数にも適用できる．例えば，この数を覚えてみよう．
10秒間の猶予がある：15222936435057

書いて覚えようとするなら，多分苦しむだろう．数の短期間の記憶保持は通常7桁までである．
これより長いものは，最初の数桁より先は覚えられそうもない．
（上の例では，たいがいの人が15222は簡単に覚えるが，それ以降はごちゃごちゃになってしまう）
今，数学の頭になってみよう．諸君は，数字のパターンのなかに，
それをもっと簡単に覚えるものを見つけることができるか？
おそらくここの仕事を単純化する複数の方法があるだろう．もし見つけたなら，
仕事をなんでもないものにしてしまう一つの特別なパターンがある．
実は，数字が二桁づつに分解されて，15 22 29 36 43 50 57,７つの対は
だんだん大きくなる順に並んでいる．諸君がすることは始まる数字と規則を覚えればよい．
[訳注：７ずつ増えていく数列]

◆πの記憶
すべての数がそんな都合のいいパターンとは限らない，だがどの数のなかにも，
数学的な意味のある数のサブグループがあるものだ．
実際上はランダムな順序と思える数πに適用して見る．ここにπの始めの100桁を記す：
ほとんどの人は，一桁の数字の列として覚えることはできないだろう．
だが，もし諸君が面白い数の固まりを選び出すなら，仕事はもっと容易になる．
3.141592653589793238462643383...
例えば，最初の10桁は連番14-15を含む，足すと100になる数65-35，
後の方には偶数のクラスター846-264がある．これらはともに，二番目以降の数を
逆転すると（864は846，246は264になる）単純な数列になる．
これらのパターンにリンクさせ，数学的ストーリーを組み立てることができる．
これはプロフェッショナル記憶者が使う種類のアプローチだ．彼らは，
それを他のテクニック－数字を，文字に置き換え言葉にするなど－と結びつけている．
良く使われる数字と文字の対応規則は：
1 becomes the letter T (a single downstroke),
2 is n (two downstrokes),
3 is M (three downstrokes),
4 is R (r is the fourth letter of four!),
5 is L (L is the Roman fifty, which is close...),
6 is J (J is a bit like a backwards 6),
7 is K (K is like two sevens stuck together),
8 is F (a cursive f resembles an eight),
9 is P (P is a backwards 9),
0 is Z (Z is for zero).

πは次のように始まる M-T-R-T-L-P-N-J-L...，思いつきで母音を時々入れる
（これは数字にカウントしない）．例えば，My TuRTle oPeN JaiL....，
諸君の亀が牢やぶりするイメージを描く．ほら，πの最初の９桁を記憶出来た．
これを42,187桁続ける．世界記録は諸君のものだ．幸いなことに諸君が記憶演者になるか，
あるいは物理学，数学，天文学の非常に特別な分野を追求する予定がない限り，
πを３～４桁以上記憶している必要性はなく，
この重要な数のその程度の桁を思い出すときには，忘れにくい文章がある．
”May I have a large container of coffee?" [コーヒー大カップをいただけますか］
この文中の各単語の文字数を数える．πの数字が小数７桁まで現れていることがわかるだろう．
［訳注：日本語では，“産医師異国に向かう....”などとやるのです］

最後に，覚えていたい数字が何であろうとも，πでも，歴史の日付でも，
ナンキン錠のコードでも，最も忘れ難い記憶術は，諸君が諸君自身のために発明するものである．
諸君のアプローチがどんなに風変わりでも問題ではない．
それが諸君のために働くならそれで良いのだ．（訳：KT）

■編集後記（KT)

折り紙も数学が必要ですが，この雪の結晶を折るアルゴリズムは複雑でわかりにくいです．写真の１，２は完成した雪の結晶を，表面から見た写真（１）／裏面から見た写真（２）です．

（１）                                                  （２）

■スタートに用いるのは，以下に示す6角形の折り紙（３）です．完成品を見ながら，折り紙（表面側から見て）に，谷折りすべき線（赤色）／山折りすべき線（黄色）を描き込んでみました．

（３）

この線の通りに，谷折り／山折りをして，（４）に示す中間体が作れますから，試行錯誤して，（４）図のような中間体を作るのを目標にしましょう．

（４）中間体

■中間体（４）の表面側に出た6か所の山尾根の部分を，平らに広げて帯状筋を作る．この帯状筋の形成のときに，新たに山折りとなる箇所を，
折り紙（３）に青緑色の線で示しておきました．
中間体の山尾根をつぶして帯状筋にするところは，注意深くやりましょう．

 3Blue1Brownのyoutube動画をご覧ください．

コーヒーカップの表面に，3つの家と３つのソース（ガス，電気，水）があり，
パイプラインが交差しないように，３つのソースと3つの家を繋ぎます．
いくら頑張っても交差箇所が1つできてしまいます．

 頂点の数V，辺の数E，面の数Fとすると，V-E+F=2　がオイラーの多面体定理ですが，
図のように面（領域）の数は４つ（黒い地の部分も１つと数えます）で，
6－８＋４＝２とオイラーの定理が成立しています．
３つの家はそれぞれ３つのソースに結ばれるわけですから，辺（パイプライン）の数は９本ありますが，頂点６と面の数４ですから，最後のパイプラインはどうしても繋げません．

さてここで，コーヒーカップで実験をしている理由がわかります．
コーヒーカップの取っ手の部分をうまく使うのです．取っ手の中を通り抜けるパイプラインと取っ手の上を這わせるパイプラインで立体交差になります．

コーヒーカップは，穴が１つある浮袋のような位相表面です．先のオイラーの多面体定理は穴のない位相表面に対する表現なので，穴の開いている位相表面では定理が少し変わります．
注）トーラスでは，面の数が2つ減り，頂点の数が3つ減り，辺の数が３つ減るので，V-E+F=0　が成り立ちます）

このような教育グッズがたくさんあり提供されるようすが，国民数学祭NMFのサイトで見ることができます．

このエッセイは，2020年3月30日にマリアンヌによってプラスマガジンに提出されたものの翻訳（by KT）です．
How can maths fight a pandemic?　By Marianne Freiberger　，https://plus.maths.org/content/

■ケンブリッジ大学の疫学者であるジュリア・ゴグは，「人生は長期間同じように過ごすことが許されない」と語った．ゴグ自身の人生は2月の初めに突然変化した．彼女は数理科学センターの通常の職務を辞し，緊急事態のための科学諮問グループ（SAGE）に結果を供給するモデリンググループであるSPI-Mに専念することになった．

 SPI-Mは，インフルエンザパンデミックへ備えて活動をしてきたが，現在はCOVID-19のパンデミックに焦点を当て活動が引き継がれている．ゴグは，王立協会が率いる全国コンソーシアムの運営委員会にも所属し，パンデミックに対処している．

SPI-Mの仕事は，次に何が起こり，さまざまな介入でそれがどのように変化するかを予測するのに役立つ数理モデルを開発し使用することだ．COVID-19パンデミックがどのように進展し，我々の生活している社会の介入はどのような影響を与えるのか．これらのモデルは何か，それらは正しいか？

モデル
COVID-19パンデミックの報道については、こちらをご覧ください：https://plus.maths.org/content/tags/covid-19

諸君は意識しないで，数理モデリングを使っている可能性は十分にあります．COVID-19の感染数が3日ごとに2倍になると聞いて，きっと予測計算をしたことでしょう．今日$$ x $$件があり，この傾向が続くと，

3日間で$$ 2x $$件，6日間で$$ 4x $$件，9日間で$$ 8x $$件，一般的に，3 $$ n $$日で$$ 2 ^ nx $$．

このように急増加して今回の災害に至りました．

この外挿は単純ですがモデルの基本的な要素，時間の経過とともに起こる変化の一般的な性質を表す数式と，変化の正確な形状を特定するパラメーターがわかります．

この例では，時間の経過とともに指数関数的に増加し，この増加の急峻さは2倍に増加する時間パラメーター（3日間）で決まっています．

ーーーーーーーーーーーーーーーー

SIRモデル
$$ S $$を感染しやすい人の数，$$ I $$を感染した人の数，$$ R $$を回復した人の数とする．

SIRモデルの方程式は次のとおりです。

 $$ \displaystyle \frac {dS} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle-\beta SI $$
 $$ \displaystyle \frac {dI} {dt} $$ $$ \displaystyle = $$ $$ \displaystyle \beta SI-\nu I $$
 $$ \displaystyle \frac {dR} {dt} $$ $$ \displaystyle = $$  $$\displaystyle \nu I $$
ここで、$$ \beta $$は感染速度で，$$ \nu $$は回復速度， $$ d / dt $$という表現は，時間の経過に伴う変化率を表すため，$$ dS / dt $$は時間の経過に伴う感受性の数の変化率の意味．

数値$$ R_0 = \beta / \nu N, $$（$$ N $$は母集団のサイズ）は、疾患の基本的な複製数と呼ばれる．

SIRモデルの詳細については，この記事https://plus.maths.org/content/mathematics-diseasesをご覧ください．

ーーーーーーーーーーーーーーーーーーーーーー

長期の予測や介入の影響を詳細にシミュレートするには，さらに洗練されたモデルが必要です．短期予測，長期予測，学校閉鎖など特定の介入効果のシミュレーション，さまざまな目的のためにさまざまなモデルが設計されています．モデルが異なっても，それらのモデルは1910年代以降のアプローチであるSIRモデルに基づいて構築される傾向があります．

SIRモデルの背景となる考え方の理解には，すべての人を，病気にかかりやすい（S），感染している（I），回復し免疫がある（R）のどれかの集団に属するとします．人が，SクラスからIクラスに，IクラスからRクラスに，進む方法を数式によって記述します． これらの方程式は，病気の感染率と回復率にも依存します． Iクラスの人口が少ないモデルから開始し，時間の経過とともにモデルを進化させて，病気がどのように広がり，人々が回復して免疫力を得て治まるかが見られます．

単純なSIRモデルは，寄宿学校の生徒などの単純な母集団に対して適切な予測を提供します． より複雑な母集団に関しては，さまざまな地理的場所やサブ母集団を表す個々のSIRモデル（個々の町や学校など）を繋ぎ合わせます．

接触がカギ
背景で非常に重要なのは人の接触パターンです：誰が誰にどのくらい会ったか．これに関する情報は，社会混合研究から得られます．例えば，BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります．人々は彼らの動きを追跡するアプリをダウンロードし，彼らに出会った人々（すべて適切に匿名化されている）を追跡するように求められます．このような接触データは，モデルに組み込まれている数値の配列（ 行列 ）（下図を参照）によって数学的に表されます．

異なる年齢グループ間の平均的な接触を表示する接触マトリックス．濃い色はより多くの接触を示します（ここでは，マトリックスを理解しやすくするために，数値ではなく色が使用されています）．図は論文

Contagion! The BBC Four Pandemic – The model behind the documentaryから許可を得て使用．

学校閉鎖などの特定の社会的介入が，病気蔓延にどのように影響するかを確認するには，介入に関連する部分を削除または縮小して，接触データを適宜調整してみます．

ただし，「学校要因を完全オフに切り替えるのは現実的とはいえません．子供たちがまだ学校に通っているので減じるだけです」とGog氏は言います．「そして明確なガイダンスがない場合，学校外の子供たちは他の方法などや，祖父母と混ざってしまう可能性があります．これは，考慮に入れるべき追加の接触が発生していることを意味します．それらの範囲での推測になります」． 教師のストライキ中に何が起こったかに関する情報などの既存のデータは，接触データを補正し介入による流行への影響を予測するのに役立ちます．簡単に言うと，これが疫学モデリングの仕組みです．

だが，モデルは正しいか？
英国，ヨーロッパ，さらには世界全体を表すように設計された壮大なモデルは1つだけではありません．代わりに，さまざまなことを実行するように設計された多くの異なるモデルがあり，SIRモデルのコンパートメントアプローチは支配的なパラダイムですが，モデルの性質は依然として異なる可能性があります．完全に確定的なものもあれば，ある程度のランダム性を含むものもあれば，特定の要因の役割を示すために1回だけ実行されるように設計されているものや，不確実性に直面して予測の範囲を取得するために何度も実行されるものもあります．

大きな問題は，モデルが現実的であるかどうかです． 1つには，COVID-19が新しい病気で，既存モデルは季節性インフルエンザのために開発されたものなのです．「私たちのモデルは，みなインフルエンザから始まったもので，コロナパンデミックモデルは誰も作っていませんでした」とGog氏．COVID-19とインフルエンザのためとでは構築した典型的モデルで何が違うのかを調べなければなりません．

パンデミックのダイナミクスはインフルエンザとコロナウイルスで似ていますが，違いもあります．1つは，COVID-19にはかなりの潜伏期があるということです．人は何の症状も示さずに感染する可能性があります．「インフルエンザの場合は数時間かかるかもしれませんが，このコロナウイルスの場合は数日かかる可能性があります」モデルは，SEIRモデルを用いることを意味します．E「露出」が追加されます．このクラスの人々は感染していますが，まだ症状はありません．Eクラスは，人に感染させる人と感染させない人にさらに分けることができます．すべてのモデルは近似であり，「インフルエンザの場合，目的によってはSIRを回避できることがよくあります．ただし，このウイルスの場合，潜伏期間を無視すると，近似が非常に悪くなる．特に，短期予測のときは，これを考慮する必要があります」とGog氏は語った．

これは，単純SIRモデルによる典型的な結果で，感染しやすい（可能性がある）人の数は青，感染した人の数は緑，回復した人の数は赤で表示されます．

COVID-19について私たちが知らないことが他にもたくさんあります．「1日目や2日目の感染力など詳細はわかりません」．「不完全なデータからそれを推測することは非常に困難ですが，現在，中国や他の国からのデータがいくつかあり，クルーズ船からのデータも非常に興味深い．限られた情報から推測するために最善を尽くしています」 十分な情報がない場合，モデラーは不確実性を取り除くために何が最も重要な未知数か決定します—これがモデリングで非常重要なことです．

1つのパラメーターの重要性は，実行しようとしていることに厳密に依存する場合があります．「明日何件の発病があるかを予測するためには，多くのことを知る必要はありません．現時点では指数関数的です」．「しかし，第2波が発生するかどうかを予測するには，非常に異なるいくつかのことを知る必要があります」

長期予測の重要な数値は，疾患の基本的な再生産数です（多くの場合，$$ R_0 $$と表示される）．人口の全員が疾患感受性がある（かかる可能性がある）と仮定すると，感染者が平均して感染させる人の数（それは 伝送速度に関連する，上記の枠記事を参照）．COVID-19の場合，これは2から2.5の間にあると推定されます．モデラーは，可能な値の範囲ごとにモデルを実行し，対応する予測の範囲を考えます．

感染したが病気ではない
現在，多くの疫学者に必要なもう1つの重要な数は，集団内での感染の真の症例数で，これには，病気にかかったが症状を示さなかった人々の症例数が含まれます．「無症候性の数は，私が現時点で睡れなくなる数です．これを知ることは，私たちの出口戦略にとって非常に重要です」とGog氏は言います．

現在の指数関数的成長を減らすことができるものが基本的に2つあります．「1つ目は，学校の閉鎖や身体的な距離などの介入により接触率が変化することです」とGog氏は述べます．「指数関数的プロセスを変える2番目のことは，感受性の枯渇です」 病気になったことでしばらくの間免疫があり，無症候性を含む真の症例数を知ることで，感受性の高い人々のクラスがどれほど速く小さくなるかがわかります．議論されている集団の免疫のメカニズムは，感受性の数が減少するにつれて，病気の指数関数的成長が平らになり，その後指数関数的減衰になることを意味します．

幸いなことに，無症候性に関するデータを知ることに関しては望みがあります． 人が病気にかかっているかどうかを知ることのできる抗体検査をしていますが，これらの最初の波は当然NHSスタッフにのみ公開されます．

しかし、不完全な情報があったとしても，モデリングの予測は，特に不確実性の範囲を考慮して提示する場合，暗闇の中で突き刺すだけではありません．優れたモデルは，私たちが持っているすべての関連情報で構成されています．優れたモデラーは，モデルの制限とモデル内の不確実性を注意深く追跡します．多くの場合，可能なパラメーター値の範囲を含み，予測の範囲につながります．これは，さまざまな介入戦略の下で発生する可能性のある将来のシナリオの範囲です．予測は完璧ではありませんが，私たちが持っている情報を使用して実行できる最善の予測です．

では何が起こるのでしょうか？
誰も何が起こるか正確に言うことはできません．地平線に見える大きな望みはワクチンの到着です．これは，群れの免疫を構築するためのもう1つの手段であり，最も脆弱な人を優先的に保護するオプションを備えています．問題は，最小限のダメージでどのように自分自身をそのポイントに到達させるかです．

誰もが同意することの1つは，これには長期的な犠牲が伴うということです．「1週間だけシャットダウンして，この状況がなくなることを期待することはできません」とGog氏は言います．「それはまだここにあり（社会的距離の措置が早すぎる場合），集団の免疫はありません．現時点では，ヘルスケアシステムが容量を超えないようにするためにシャットダウンせざるを得ません．しかし，これは恒久的な戦略ではないことは十分に認識しています」

先週 ，Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では，季節変動も考慮して，再発の問題について詳細に検討しました．呼吸器疾患の発生は，秋と冬に悪化する傾向があります．季節性インフルエンザの発生と同時に，ヘルスケアシステムにさらに大きな負担をかけます．キスラーと彼のチームは，そのような季節変動を反映する要因を含むSEIRモデルを使用しました．社会的距離測定の効果は，COVID-19の基本的な生殖数が最大60％減少することでモデルに反映され，中国で観察されたものと同等です．

この最新の研究の結論は，必ずしも明るいものではありません．社会的距離の1期間では、救急医療能力が圧倒されるのを防ぐのに十分ではありません（調査では，英国ではなく米国の救急医療能力を調べましたが，英国でも同様の結果が当てはまります）．「［この調査によると］シリアルロックダウンの期間を検討しています」とGog氏は言います．「批判的なケアが始まろうとしているときにロックダウンするという考えです．しかし，英国で起こっていることは，NHSが規定を拡大しているため，ロックダウンがより短く，それほど深刻ではなく，あまり頻繁ではないことです」

これらの社会的距離の断続的な期間がどれだけ長く，頻繁に異なる仮定（米国の数値に基づく）になる可能性が高いかを，論文から抜粋した以下の図に示します．

これらのグラフは，断続的な社会的距離（青色の領域）の下でのウイルスの有病率（黒い曲線）と重大なケース（赤い曲線）を示しています．最初と3番目のグラフには，季節的な強制がありません．2番目と4番目の季節の強制．クリティカルケア能力は、水平の黒い実線で示されます．最初の2つのグラフは現在の米国の救急医療能力のあるシナリオであり，3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです．基本再生数の最大値は冬期は2であり，季節的なシナリオでは夏期は1.4です．この図は，キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からのものです．許可を得て使用．

悲観的状況ですが，希望の光がいくつかあります．1つは，COVID-19の重症例に対する投薬とより良い治療プロトコルが，ある時点で到来する可能性です．これは，人々が短期間で病気にならないことを意味し，NHSへの圧力を軽減します．社会的距離を縮める措置の深刻さの多くは，NHSが崩壊しないようにする必要があるため，深刻な病気の人々を効果的にケアすることができ，短期間の過酷な措置が少なくなる可能性もあります．

もう1つの希望の光は，軽度で無症候性の感染者の未知な総数です．これがモデルで想定されているよりもはるかに高いければ，より多くの人々が病気になり免疫力があれば，上記の図が示唆するほど見通しは悪くありません．私たちはこれが事実であることを期待し，それがわかるまでは，ルールを守って家にいるだけです．

 
この記事について
Julia Gogはケンブリッジ大学の数理生物学の教授です．彼女は，その結果を緊急事態用科学諮問グループ （SAGE）にフィードするモデリンググループSPI-Mのメンバーです．彼女は王立協会が率いる全国コンソーシアムの運営委員会のメンバーでもあり，COVID-19パンデミックに対処しています．

プラスマガジンの編集者，マリアンヌフライバーガーは，2020年3月24日にGogにインタビューしました．

■今回の記事は，2020年3月30日にマリアンヌによってプラスマガジンに提出されたエッセイの解説です．
How can maths fight a pandemic?　By Marianne Freiberger　，https://plus.maths.org/content/
プラスマガジンの編集者，マリアンヌフライバーガーは，2020年3月24日にGogにインタビューしました．
エッセイの全文翻訳（by KT）は数学月間ホームページに掲載しておきます

これは大変長いエッセイで読み難いので，ここにレジメを作成しました．
このエッセイの書かれた3月30日ころは，Covid-19の感染について未知なことばかり（感染させるが症状の出ない保菌者など）だったでしょう．しかし，2.5か月経過した現時点では，これらは皆さんの常識になりましたね．最後に出てくる医療崩壊をさせないための断続的なロックダウン方法のシミュレーションは参考になるかもしれません．

■ケンブリッジ大学の疫学者ジュリア・ゴグGogは，2月の初めに，数理科学センターの通常の職務を辞し，緊急事態のための科学諮問グループ（SAGE）に結果を報告するモデリンググループ，SPI-Mに専念することになった．
SPI-Mは，インフルエンザパンデミックへ備えてこれまで活動をしてきたのだが，現在はCOVID-19のパンデミックに焦点を絞った活動をしている．ゴグは，王立協会が率いる全国コンソーシアムの運営委員会にも所属し，このパンデミックに対処している．

SPI-Mの仕事は，次に何が起こるか，さまざまな介入でそれがどのように変化するかを，予測できる数理モデルを開発し働かせることだ．COVID-19パンデミックがどのように進展するか？社会的介入はどのような影響を与えるか？これらのモデルはどのようなものか？それらは正しいのか？

COVID-19パンデミックの報道については、こちらをご覧ください：https://plus.maths.org/content/tags/covid-19

ーーーーーーーーーーーーーーーー

 ■SIRモデルとは(訳者補足)
S   感受性保持者数，（感染可能な数）
I　感染者数，（患者数）
R 免疫保持者数，（回復患者数）

全人口Nは一定と仮定して，N=S+I+R　が成り立ちます．
SIRモデルの方程式は次のとおりです．

これら3つの式の意味は：
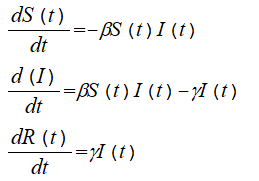
（１）（感染可能な数）の増加速度は，（患者数）と（感染可能な数）の積に比例する．比例定数βは感染率．
（２）（患者数）の増加速度は，（感染可能な数）の増加速度から，（回復患者数）の増加速度を減じたもの．
（３）（回復患者数）の増加速度は，（患者数）に比例する．比例定数γは回復率．

SIRモデルの詳細については，以下の記事https://plus.maths.org/content/mathematics-diseasesをご覧ください．

S, I, Rの間の状態遷移をブロック図で描くと上図のようです．
このモデル（単純SIR）で得られる結果は，下のグラフのようです．

S：青い線，I：緑の線，R：赤い線

赤い線は，「始めは免疫のあるものが誰もいなかったが，全員免疫ができて終わる」という当たり前の特別面白くない結果ではあります．
ーーーーーーーーーーーーーーーーーー

単純なSIRモデルは，寄宿学校の生徒などの単純な母集団に対して適切な予測を提供しますが，複雑な母集団に関しては，さまざまな母集団ごとのSIRモデルを繋ぎ合わせます．
実際には，これに色々な介入が加わるのですが，この影響を詳細にシミュレートするには，SIRモデルよりもさらに洗練されたモデルが必要です．

接触がカギ
このようなモデルの世界の背景で，非常に重要なのは人の接触パターンです（いわゆる動態調査）：誰が誰にどのくらい会ったか．例えば，BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります．人々は，彼らの動きを追跡するアプリをダウンロードし，出会った人々（すべて適切に匿名化されている）を追跡するように求められます．モデルに組み込むこのような接触データは数値の配列（ 行列 ）です（下図を参照）．

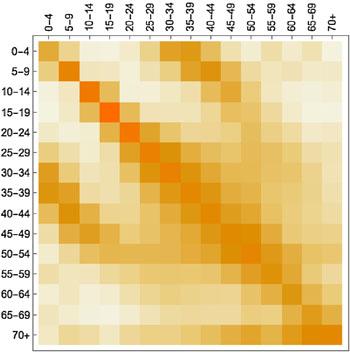
異なる年齢グループ間の平均的な接触を表示する接触行列．濃い色はより多くの接触を示します（ここでは，理解しやすくするために，数値ではなく色が使用されています）．Contagion! The BBC Four Pandemic – The model behind the documentary．
学校閉鎖などの特定の社会的介入が，感染拡大にどのように影響するかを確認するには，介入に関連する部分を削除または縮小して，接触データを適宜調整してみます．

学校要因を完全にオフにするのは現実的とはいえません．減じるだけです．学校外で子供たちは，他のルートがあり（祖父母と混ざってしまう可能性など）ます．これは，考慮に入れるべき追加の接触が発生していることを意味します． 教師のストライキ中に起ったことなどの既存データは，接触データを補正し介入による流行への影響予測に役立ちます．

モデルが現実的であるかどうかは重大な問題です．COVID-19は新しい病気．既存モデルは季節性インフルエンザのために開発したもので，コロナパンデミックモデルは誰も作っていませんでした．COVID-19とインフルエンザとではモデルのどこが違うのかを調べなければなりません．

パンデミックのダイナミクスは，インフルエンザとコロナウイルスで似ていますが，違いもあります．
COVID-19はかなりの潜伏期があり，何の症状も示さずに感染している可能性があります．発症までに，インフルエンザの場合は数時間，コロナウイルスの場合は数日かかる可能性があります．
モデルに関して言えば，これは，SIRではなく，SEIRのモデルになることを意味します．Eは「露出」．
クラスEの人々は感染していますが，まだ症状は出ていません．クラスEの人は，他人に感染させる人と感染させない人に分けられます．すべてのモデルは近似であり，インフルエンザの場合は，目的によってSIRを回避できることがよくあります．ただし，コロナウイルスの場合，潜伏期間を無視すると，近似が非常に悪い．特に，短期予測のときは，これを考慮する必要があります．

COVID-19については，私たちが知らないことが他にもたくさんあります．1日目や2日目の感染力など，詳細はわかりません．不完全なデータからそれを推測するのは非常に難しい．中国や他の国のデータがいくつか（クルーズ船からのデータは非常に興味深い）あり，限られた情報から推測するのに最善を尽くしています．十分な情報がない場合，モデラーは不確実性を取り除くために，最も重要な未知数は何か決定します．これがモデリングで非常に重要なことです．

明日，何人の患者が出るか予測するなら，多くのことを知る必要はなく，現時点では指数関数的増加です． しかし，第2波が発生するかどうかを予測するには，非常に異なるいくつかのことを知る必要があります．

長期予測で重要なパラメータは，疾患の再生産数（1人の患者が平均何人に感染させるか．多くの場合，R_0と表示される）です．これは 感染速度に関連する．COVID-19の場合，R_0は2~2.5の間にあると推定されます．モデラーは，可能な値の範囲ごとにモデルを実行し，対応する予測の範囲を考えます．

感染したが病気ではない
多くの疫学者が知りたいもう1つの重要なパラメータは，集団内での感染の症例数で，これには，病気にかかったが症状を示さない人々の症例数も含まれます．無症候感染者数は，睡れなくなるほどの多数で，これを知ることは，私たちの出口戦略にとって非常に重要です．とGog氏は語りました．

現在の指数関数的成長を止める要素が2つあります．

1つは，学校の閉鎖や身体的な距離をとるなどの介入うぃして接触率を減らすことです．
2つ目は，罹患感受性のある人をなくすことです．病気になったらしばらくの間免疫があるので，無症候性を含む真の症例数を知ることから，罹患感受性の高い人々のクラスがどれほど速く減少するかがわかります．
議論されている集団免疫のメカニズムは，罹患感受性のある人数が減少するにつれて，病気の指数関数的成長が平担になり，指数関数的減衰になるという仕組みのことです．

幸い，無症候性に関するデータは知ることができます． 病気に罹ったか罹っているか抗体検査が実施されています．これらの第一波は当然NHSスタッフにのみ公開されます．

では何が起こる？
何が起こるか誰も正確に言うことはできません．地平線に見える大きな望みはワクチンの到着です．これは，集団に免疫を備えるもう1つの手段です．最も脆弱な人を優先的に，最小限のダメージでどのようにその目標に到達させるかです．誰もが同意するのは，これには長期的な犠牲が伴うということです．「1週間だけシャットダウンして，この状況がなくなることを期待することはできません」「社会的距離の措置が早すぎる場合，感染かまだ残っていて，集団免疫はありません．現時点では，ヘルスケアシステムが容量を超えないようにするために，シャットダウンせざるを得ませんが，これは恒久的な戦略ではないことは十分に認識しています」とGog氏は語る．

先週 ，Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では，季節変動も考慮して，再発の問題について詳細に検討しました．呼吸器疾患の発生は，秋と冬に悪化する傾向があります．季節性インフルエンザの発生と同時に，ヘルスケアシステムにさらに大きな負担をかけます．キスラーと彼のチームは，そのような季節変動を反映する要因を含むSEIRモデルを使用しました．社会的距離測定の効果は，COVID-19の基本的な再生産数が最大60％減少することでモデルに反映され，中国で観察されたものと同等です．

この最新の研究の結論は，必ずしも明るいものではありません．
「シリアルロックダウンの期間を検討しています」とGog氏は言います．（医療崩壊が始まろうとしているときにロックダウンするという考え）英国のナイチンゲール病棟NHSのことは，noteの記事の1号に書きましたので，そちらをご覧ください．

社会的距離（ロックダウン）の断続的な期間の長さと頻度の仮定（米国の数値に基づく）のシミュレーション．

これらのグラフは，断続的な社会的距離（青色の領域）の下でのウイルスの有病率（黒い曲線）と重症なケース（赤い曲線）を示しています．最初と3番目のグラフには，季節的な強制がありません．2番目と4番目の季節の強制．ケア能力臨界は，水平の黒い実線で示されます．最初の2つのグラフは現在の米国の救急医療能力でのシナリオ，3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです．再生産数の最大値は冬期は2であり，夏期は1.4です．この図は，キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からです．

悲観的状況の中に，希望の光がいくつかあります．1つは，COVID-19の重症例に対して，投薬と良い治療プロトコルが，ある時点で追いつく可能性があることです．これで，NHSへの負荷の軽減でき，重症患者のケアができるます．

もう1つの希望の光は，軽度で無症候の感染者が，想定されているよりもはるかに多い（多くの人々がすでに病気になり免疫力がある場合）かもしれません．私たちはこれが事実かどうかわかるまでは，ルールを守って家にいるだけしかできません．

これがどうして私の手元にあるのか思い出せません．
その他にも球状のものや，いくつか組木のパズル(箱根細工と呼んでいました）で子供の頃遊んだのを覚えています．それは遠い昔のことで，いつの間にか失くなってしまいました．複雑な組木もあったように思い残念です．なぜかこの組木だけが，今私の手元にあります．多分，この組木を手に入れたのが一番新しいためでしょう．この組木はとてもシンプルですが，職人のすばらしいアイデアだと思います．

全体の対称性は立方晶系の最も対称性の高い点群です．
4回対称軸が3本，3回対称軸が４本，2回対称軸が6本あります．
（鏡映面はたくさんありますが表示略）．

全体はこのような同じパーツが6個で出来ています．

3回対称軸に沿って引き抜くことができ，二つに割れます．
写真は3回軸に沿って引き抜き開いて（内部をこちらに向けて）並べたところです．

 ２つのパーツは互いに対掌体（右手と左手，あるいは逆まわりの風車）です．3回軸に沿って引き抜けるのは，この分解写真を見ると理解できるでしょう．
対称性を考えないと，引き抜く方向がわからず難しいパズルです．
３つのパーツでできた風車のような形を一体として引き抜くのがミソです．（この方法がわかっていても，特に，分解と逆の組立てのときは，手作業的にはなかなか難しい．手が3本欲しいということになります）
３つのパーツは一体として扱わなければ，互いに組み合っているので，バラせません．3回対称軸は４本あるので，引く抜く方向は4通りありどれでも可能です．

(図）4回対称軸の方向から見る↓　　　　　　　　　　　　　　　　　(図）3回対称軸の方向から見る↓

（図）3回軸（上下方向）に沿って引き抜く↓（今度，動画にしたい）

■この組木は，x平面，y平面，z平面がかみ合っているという見方もできます．それぞれの平面は２つのパーツからなります．
直交するx平面，y平面を作り，z平面の部品の１つだけ（下側）は置けるが，残り１つ（上側）をどう入れるかと，普通の人は苦闘します．
この手順では入りません．3つのパーツで組んだ風車型を一体として扱うのがミソでした．

(図）最後の１つはどうしても入りません．↓

フィボナッチ数はいろいろな所に現れます．この記事はThomas Koshyの著書からの引用で，2018.09.25発行のメルマガSGK通信No.234のリメイクです．
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2018.09.25］ No.234
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
フィボナッチ数列は次のように定義されます．
F(n)=F(n-1)+F(n-2)．F(1)=1，F(2)＝１として数列を作ると
１，１，２，３，５，８，13，21，.......の数列が得られます．

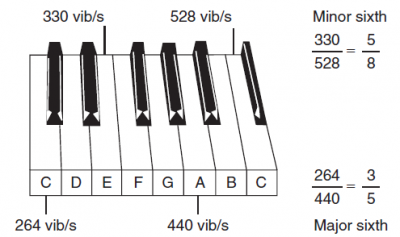
ピアノの鍵盤は，フィボナッチ数と音楽のつながりの可視化の良い例です．
鍵盤上で１オクターブとは，２音の間の音程で高音の周波数が低音の2倍になっていることです．鍵盤でいうと，1オクターブは，５つの黒鍵と８つの白鍵，合わせて13の鍵で構成されます（図）．この5つの黒鍵は2つのグループをなしています；一方は2鍵よりなるグループ，他方は3鍵よりなるグループ．

1オクターブに入る13の音は，西洋音楽で最も一般的な音階であるクロマチック音階(半音階)を作ります．クロマチック音階に先行して，2つの他の音階；5音からなるペンタトニック音階と8音からなるダイアトニック音階がありました． お馴染みの"Mary had a Little Lamb” と “Amazing Grace” は，ペンタトニック音階を使い演奏でき，また， “Row, Row, Row Your Boat” のメロディーはダイアトニック音階を使い演奏できます．

長6度と短6度（6つ離れた音，および，5+1/2離れた音）は，耳を最も喜ばす2つの音程(和音)です．長６度は，例えば，音CとAから成る：それぞれの音は，1秒当たり264と440の振動数で（図），264/440 = 3/5はフィボナッチ比であるに注目しましよう．
短6度は，例えば，1秒当たりの振動数330と528の音であるEとCから構成され，それらの比もフィボナッチ比です：　330/528 = 5/8.
［訳注）自音の音程は1度という．1オクターブの音程は8度である．］

正12面体や球面正12面体は，正５角形（あるいは，球面正５角形）の面12枚が囲んでできる立体です．
3枚鏡の組み合わせで万華鏡を作り，正12面体や球面正12面体が見える万華鏡を作りましょう．
正12面体の点群（対称性）を生成する3枚の鏡に，次のものを選びます．
（Aタイプ）１つの正5角形の面を10個の直角3角形（若草色）に分割し，
その領域を立体の中心から見込む「3角錘」が万華鏡になります．
（Bタイプ）１つの正5角形の面を５つの2等辺3角形（水色）に分割し，
その領域を立体の中心から見込む「3角錘」が作る万華鏡になります．

（Aタイプ）　　　　　　　　　　　　　　　　　　　（Bタイプ）

作製したそれぞれの万華鏡で見られる映像を対応させて掲載します．
どちらも正12面体の映像が見えますが，両者の正5角形の面を観察して比較しましょう．
Aの映像では直角3角形10個で正5角形の１つの面を作っていますが，Bの映像では2等辺三角形5個で正５角形の１つの面を作っているのがわかります．

■正12面体および球面正12面体の見える万華鏡（Aタイプ）の作り方

ミラー紙（厚さ0.25mm以上が良い）に次の展開図を描きます．青色の部分を使います（赤線に沿って光の窓を作ります）．赤線の円に沿って切ると「球面正12面体像が見える光の窓」，赤線の直線に沿って切ると「正12面体像が見える光の窓」ができます．どちらかを選びます．辺OHが共通につながるように3角錐（鏡面は三角錐の内側）を組み立てます．完成した万華鏡は△KAHから覗きます．

「美しい幾何学」球面正多面体とメビウス万華鏡p.133~p135に，この万華鏡の説明があります．

いろいろな多面体の見える万華鏡（立体万華鏡と呼びましょう）を作ります．アルミ板やプラスチックの鏡は像がきれいに映りますが，ミラー紙(厚手0.25ｍｍくらい）を用いても，ここで取り上げているような立体万華鏡は良好に作れますので，チャレンジしてみてください．

球面正多面体は，アラブの数学者，アブル・ワーファ（1000頃）に始まります．球面正多面体｛p,q｝は，球面正p角形が，頂点でq個集まっているもので，球面正p角形の１つの内角は2π/qです（図D）．
そして，球面p-多角形の辺はすべて大円であることに注意しましょう．

ここで具体的に取り上げるのは，正12面体に相当する球面正12面体＝球面｛5,3｝多面体です．

メビウスは多面体万華鏡を発明します（1850）が，これは，球面p-多角形を，2p個の球面直角３角形に分割することを使います（図A）．
分割された3角形の角度は，π/p，π/q，π/2，このような直角3角形を(p,q,2)と記述します．
万華鏡は，３角形（赤く塗った）の各辺となる大円を鏡にすると得られます．
（A）メビウス万華鏡になり，正5角形の面を10個の直角3角形に分割しています．
（B）正5角形の面を5個の2等辺3角形に分割しています．Bには，Aに存在した鏡映対称面が１つ消えています．
（C）赤く塗った正3角形の周囲の辺の大円を鏡に置き換えて万華鏡を作れば，正20面体の映像が見えます．

では，AとBを作ってみましょう：展開図は，前号の［正12面体の見える万華鏡を作ろう］に掲載してあります．

A(左写真)　　　　　　　　　B(右写真)

p.132～p.133　美しい幾何学より