note.com投稿記事

写真の石垣は美しいですね．石積みの改修は番号をふって再現するのでパズルのようです．素晴らしい石工の技です．
ボロノイ分割のような網目で各所の釣り合いの条件を書いて計算できたとしても物づくりの役にたちません．石工の技術は直感と身に着けたバランス感覚そのものです．ガラス職人は熔けたガラスの粘性の手応えに反射的に反応し細工をします．機械の設計でも常識や力学感覚が身に着いていない技術者の計算まかせはとんでもなく危うい．
私たちは，幼児の頃に，積み木をしたり水遊びや泥団子などで遊び，物の柔らかさや脆さ，それを扱うバランス感覚，力学感覚を自然に身に着けました．物理や数学を学ぶよりもこの常識を身に着けることはとても大事なことだと思います．壊れやすいものを不器用に扱う若者が増えています．もっとも，理論と器用さは関係ないようで，教授でも子供より不器用な人はたくさんいます．

■通潤橋のアーチと通潤橋のアーチの数学に関し，私はnoteに以下の2つの記事を書きましたがあまり目につかなかったようです．
https://note.com/sgk2005/n/n5eccdef5315a
https://note.com/sgk2005/n/n4356f184665d
リンク切れになっているウエブサイトやブログもあるので，再度，概要を紹介をしましょう．

表紙の写真は，石積みの美しい橋，通潤橋（熊本県，山都町）です．アーチの形は懸垂曲線，放水の軌跡は放物線です．逆さにした懸垂曲線のグラフをアーチに重ねてみました．

鎖の両端を持ち水平に広げたときに，鎖が作る曲線が懸垂曲線です．鎖の各部分は重力で下向きに引かれ，鎖の一つ一つの繋ぎ目はどこも引張あって釣り合っています．この形の上下をひっくり返すとアーチができ，アーチの各部に働く力はすべて圧縮力になります．アーチには圧縮力しか働きません．石たちは自分の重量で互いに押し合い，圧縮され引き締め合います．接着されていない石積みは引張力ではバラバラになりますが，自分の重量で圧縮され良く締まります．石が割れると困りますが，石は圧縮力には強いのです．すべての荷重がかかるアーチの根元には，大きな水平反力が必要ですが，山に挟まれた峡谷などは建設するのに最適な立地条件です．

■私が通潤橋（熊本県上益城郡山都町）を訪れたのは，2007年10月のことでした．22日は，午前中に潤徳小学校3,4年生36人に万華鏡づくりの授業，午後は先生方と人形浄瑠璃を観劇しました．
最近の通潤橋の様子は，以下のウエブサイトにでています．2016年の熊本地震で被災し，修理工事中だった2019年5月にも豪雨で石垣の一部が崩落しましたが，2020年3月までに工事を終え，翌4月から4年ぶりに放水を再開しているそうです．
通潤橋の近況ですが，山都町のウエブサイトよりhttps://d38mttjwbmxw55.cloudfront.net/files/6c2868f8-675e-4dac-b6f3-079b3d5bf224_l.jpg?1585873042

阿蘇山の南側のこの付近の地形は，島のように台地があり，台地から台地への移動が大変で，平家の落人が隠れ住むのに好都合だったようです．
台地（白糸台地）に農業用水を引くのが大変です．
水は台地のがけ下に汲みに行かなければなりません．
時の惣庄屋「布田保之助（ふたやすのすけ）」は，白糸台地に水を引くための水路橋”通潤橋”を，肥後の石工たちの技術を用いて1854年に建設しました．通潤橋は，石造りアーチ水路橋で，長さ75.6m，高さ20.2m，幅6.5m．
橋の上部にサイフォンの原理を応用した3本の石の通水管が敷設されています．

◆通水管
長さ約127m．石をくりぬいた１尺（30cm）四方の函渠（圧力のかかる管水路）．管と管の繋ぎ目には，振動吸収と漏水防止のための漆喰（しっくい）が塗られている．さらに，通水管には5～6ケ所に地震対策のための板（緩衝材）を挟んでいる．
通潤橋は両側台地より低いので，サイフォンの原理で出口で水を押し上げています．通潤橋の高さから流入側台地は7.5m高く，流出側台地は5.8m高い．
通潤橋は，今でも周辺の田畑を潤しています．
放水は，通水管に詰まった堆積物を取り除くために行うものです．
「通潤橋史料館」　に行くと，どのようにアーチ石橋を施工したかわかります．川の中に写真のような木枠を大工が組んで石工が石を置きました．
アーチ橋の高さを台地の高さまで上げられなかった理由は，
この木枠をこれ以上の高さにする木材がなかったためという事です．
石橋の木枠を外す最終段階は，橋の中央に白装束を纏った布田翁が鎮座し，
石工頭も切腹用の短刀を懐にして臨んだといいます．

写真に見えるアーチ曲線を型どっている石の並びについて話しましょう．
アーチの頂点にある石を”かなめ石”と言います．アーチ状に一列に並んだ石達は自分の重さで互いに締め付けあい安定になっておりセメントなど不要です．それでも下の木枠を外すときは，とても心配で責任者は命がけだったでしょう．布田翁も石工頭も命がけで臨んだのがよくわかります．
近年の熊本地震でも残ったのは，その堅牢さ（石の配管の修理をしたと聞きます）の証明です．
2007年当時の「通潤橋資料館」のウエブサイト資料がなくなりましたので，http://www.kumamotokokufu-h.ed.jp/kumamoto/isibasi/ab_sakus.html
のウエブサイトより以下の説明図を引用しました．

■人形浄瑠璃
http://seiwabunraku.hinokuni-net.jp/wp-content/uploads/img/about/s_06.jpg
人形浄瑠璃は，清和文楽館で観賞しました．山都町の人形浄瑠璃の始まりは，江戸時代の嘉永年間（1850年ごろ）で，山都町（旧・清和村）を訪れた淡路の人形芝居の一座から，浄瑠璃好きな村人が人形を買い求め，技術を習ったのが始まりといいます．
清和文楽は農家の人々が農業の合間を縫って練習や公演を行い伝承されてきました．良い話です．江戸時代の庶民の文化の高さに感激しました．三人で一体の人形を操ります．首（かしら）と右手を操る「主遣い（おもづかい）」，左手を操る「左遣い」，足を操る「足遣い」です．人形も触らしてもらいました．

■空き缶を積んで作ったアーチで実験

私は真剣に積んだのですが，どうしても缶5個のアーチまでしかできませんでした．5個の缶で缶同志の接点は4点．すべての接点で同時につり合っていなければなりませんから，作るのがとても難しい．もし，6個以上でアーチが出来た方は新記録です．ご一報ください．
缶の周りにラップを巻いていますが，摩擦力を増すためでアーチのつり合い条件を変えるものではありません．

5個の空き缶を積んで作ったアーチです．左右対称ですから，左半分だけ解析しましょう．缶の中心を①，②，③と名づけます．すると，缶同士の接点は，線分①－②の中点と，線分②－③の中点にあります．線分①-②，線分②-③には，それぞれ圧縮応力f_{1}, f_{2}があります．すべての缶は点で接触しており，モーメントは考える必要がありません（トラス構造）．線分①-②，および線分②-③の水平となす角度をそれぞれα，βとしてつり合いの式を立てます．各缶には下向きに力gがかかっています．つり合いの式は，①点，②点，③点でx, y成分ごとに書きます．

$$ f_{1}, f_{2}, r_{x}, r_{y}, g $$が，ゼロででない解であるための必要十分条件は，行列式がゼロとなることでした．この行列式を計算すると，
$$ tanβ=3tanα $$　の関係が得られます．
この釣り合いの結果は，①から測った曲線に沿った距離$$ s $$と，その点の接線の傾きtanθが比例する　$$ tanβ/3＝tanα/1=tanθ/s $$の関係（懸垂曲線で導ける）と一致します(下図参照)．

懸垂曲線のグラフ（赤）と放水軌跡のグラフ（緑）を表紙の写真の上に重ねました．ご鑑賞ください．アーチの形とアーチの屋根の左右の石の詰め物を見て，この橋の安定なバランスに感動するなら，あなたは常識の力学感覚が身に着いていると思われます．
 

By Marianne Freiberger; plus magazineより　

今，学校の再開が注目されていますが，もう1つのパンデミックの課題にも直面しています．今月と来月，全国の大学が秋学期を開始します．

約200万人の大学生が全国から選択した教育機関に動きだします．フレッシャーズフルー*)［*注）フレッシャーズフルーとは，大学で最初の数週間に新入生が発症した一連の病気に付けられたイギリス英語．］の感染は大学のキャンパス全体に簡単に広がる可能性があります． COVID-19では，若者が無症候である可能性が高いということから，発生しても迅速に発見されない可能性があります．若者のCOVID-19は深刻な病気になる可能性は低くいのですが，学生より脆弱な可能性のあるスタッフや周囲のコミュニティと混ざり合うため，大学での流行は無視できないリスクとなります．

大学を可能な限り安全に保つのに，何ができるでしょうか？ 7月に2つのオンラインブレーンストーミングセッションがありました．Isaac Newton Instituteによって実施された「パンデミックの感染症のダイナミクス：感染症のパンデミックのダイナミクスを理解する上での数学的および統計的課題」（IDP）　https://www.newton.ac.uk/event/idp　の一部で，数学者と教育省および高等教育機関の代表者が集まり，数学がいくつかの問題の敏速な解決にどのように役立つかを確認しました．

数学者が提供しなければならないのは，数学モデルを使用してさまざまな状況下で病気の広がりをシミュレートし，緩和策が感染拡大にどのように影響を与えるか確認することです．

「この問題の見方で，数学は学際的なタペストリーの一部になりたい」と講演者でサウザンプトン大学のレベッカ・ホイルは言いました．「すべての答えがあると感じているわけではありませんが，そのパッチワークの一部を提供します」

■ベースライン
病気が典型的な学生集団にどのように広がるか，IDPの会議で，Ellen Brooks Pollockはブリストル大学のチームの仕事について報告しました． チームは、2010年に実施された社会的接触調査のデータとブリストルの学生の家庭の状況に関する匿名の情報を使用して，学生の接触パターン（誰が、どのくらいの頻度で会うか）を把握しました． チームは，学期の初めに到着したときに学生が通常どこから来るのかを見て，COVID-19に感染して到着する学生の数も推定しました． 彼らは，この情報を確率的コンパートメントモデル*)https://plus.maths.org/content/how-can-maths-fight-pandemic　に組み込みました．
このモデルによると，ブリストルの学生の約20％が最初の学期中に感染する可能性があり，大学生活が通常どおり継続する場合，約74％が学年末までに感染することを示唆しています．新入生は感染率が最も高く，発生の初期段階を促進します．ブリストル大学では，他の多くの大学と同様に，新しく到着した学生が好む宿泊施設であるホールは，さまざまな混合場所になるため，1年目の期待と社交への熱意を考慮すると驚くべきことではありません．

モデリングは，発症の症例と比較して，気づかれずに忍び込む無症候性の症例が，どれほどの感染性であるかに依存することも示しました．上記の結果は，無症候性が対症療法の約半分の感染性であるという仮定（入手可能なデータに照らして妥当な推定値）に基づいています．しかし，ブルックス・ポロックと彼女の同僚は，この相対的な感染率の他の値も試し，流行の最終的なサイズがその数に非常に敏感であることを発見しました．たとえば，無症候性の人が症状を示している人と同じくらい感染性があると仮定すると，学生の約96％が学年末までに感染します．

すべてのモデルと同様に，ブリストルのチームによって開発されたモデルは，仮定に基づいており限界があります．これについては，https://www.medrxiv.org/content/10.1101/2020.09.10.20189696v1.full.pdf　この論文に書きます．大学の流行は，本当にリスクがあることを確認しています．これらの発生をよりよくシミュレートするために，無症候性の症例の感染性に関するより多くの研究が必要であることを示唆しています．

■テスト、テスト、テスト
今では誰もが知っているように，エピデミックを回避または少なくとも軽減するには，感染の連鎖を早期に断ち切ることです．したがって，大規模な大学が独自の学内テストおよびトレースシステムを導入することは理にかなっているでしょう？ IDPセッションは，まさにそれを調査しているウォーリック大学のチームからも聞いた． チームは，接触パターンを反映するネットワークと組み合わせたコンパートメントモデルを使用して，ワーウィックキャンパスでの病気の蔓延をシミュレートしました．

IDPセッションで報告された最初の結果は，最も効果的にするために，テスト＆トレースがスムーズに機能する必要があることを示唆しています．症状を発症する十分な数の人が実際に行ってテストを受け，症状がでるまでとテスト＆トレースシステムの遅延を短くする． これらの問題の両方で，学内のテスト＆トレースシステムが明らかに役立ちます．

潜在的に危険な無症候性の症例を見つける唯一の方法は，学生の体全体の定期的なテストを実行することです．問題は，そのようなプログラムが効果的であるために，学生はどのくらいの頻度でテストされる必要があるかということです．これはブリストルの研究が検討したもう1つの問題であり，モデルによるとその答えは少なくとも2週間ごとです．

すべての英国の大学にスケールアップすると，これは多くのテストを意味し，問題はそれらすべてのテストがどこから来るのかということです．一部の大学は独自のラボを使用してテスト能力を構築していますが，ほとんどの大学はこれを行うことができません．そのため，大学のテストでは，現在医療従事者や症状のある人々のために確保されている国の能力を利用する必要があります．

テストに関する現在の問題を考えると，より経済的なアプローチを検討することも理にかなっています． 「検討するかもしれないのはバッチテストです」とHoyle氏は説明します． 「アイデアは，サンプルを組み合わせて一度に複数の人をテストすることです．そのテストが陰性に戻った場合，個別のテストを行う必要はありません．陽性のバッチにあった人を個別にテストするだけで済みます．多くの人を定期的にテストできるかもしれません」

IDPセッションの参加者は，個々の機関がどのような種類のテスト体制が彼らに適しているかを見つけるために使用できる適応モデリングツールを作成することを目的として，テスト＆トレースモデルに取り組んでいます．モデリングはまた，大学での流行が周囲のコミュニティにとってどれほど危険であるかについてのより多くの考えを私たちに与えるでしょう．危険性が高い場合は，国の政策でこれを考慮に入れる必要があります．国の試験能力の一部は，実際に大学のために確保する必要があるかもしれません．

その間，教育機関は，テストで陽性となった学生をどうするかについても考える必要があります．モデルでは，これらの人々は感染性がなくなるまで検疫に入ると常に想定されていますが，現実はそれほど単純ではありません． 20歳の子供に，家から遠く離れた小さな学生部屋で2週間自己隔離するように言うと，規則の違反やさらに悪いことに，深刻なメンタルヘルスの問題につながる可能性があります．誰もが家に帰ることを期待している学期の終わりにテストが行われる場合，これはさらに悪いことになります．モデラーだけでなく，学生の福祉や支援を担当する人たちにもやるべきことがあります．

もちろん，大学が実施できる手段はテストだけではありません．対面教育と学生間の接触を減らすことは，他の2つの明白なオプションです．これらについて詳しくは，
https://plus.maths.org/content/going-back-uni-during-pandemic-part-ii

ブライアンデイビス，ロンドンキングスカレッジ
Notices of American Mathematical Society 52,No11(2005)12月
Элементы，数学は何処へ行くより抜粋翻訳（１）：　
https://elementy.ru/nauchno-populyarnaya_biblioteka/164681/Dokazatelstva_s_ispolzovaniem_kompyutera

コンピューター支援で証明された主要な数学的定理の最初の例は，1976年にAppelとHakenによって証明された4色定理でした．これは2つの理由で，多くの数学者を大いに心配させました．第一に，機械が実行した計算のすべてを，手動で再チェックすることなしに証明の正しさを検証することは不可能であると主張されました．当時，「正しい」定理の証明は，ほとんどすべての数学者にとって，まだ完璧に見えました．証明の偶発的なエラーの可能性は認識されましたが，それらを修正するのは時間の問題であると考えられました．もう一つは，一部の数学者は，その定理が正しいかどうかではなく，なぜそれが正しいと見なされるのかについて考え始めたからです． 本質を理解していない証明は彼らに興味がありません．

4色定理は重要な応用がなく，長い間，面白い逸脱と見なされていました．おそらく，誇張された関心が高まったのは，この定理の単純な定式化のせいでしょう．しかし，時が経ち，コンピューターはますます利用可能になり，コンピューターの証明が広く受け入れられるようになりました．
最も新しい事例，ケプラー問題をここで取り上げます．

ケプラー問題は，最大平均密度となるように，同じ直径の球体を3次元空間に最も密に充填する方法を見つけることです．期待される解決策は昔から知られおます．1998年，トムヘイルズは，幾何学的分析と複雑なコンピュータ計算を組み合わせて，ケプラー問題に対する厳密な数学的解決策を見つけたと発表しました．ジャーナル"Annals of Mathematics"は，この論文を審査のために受け入れ，この分野の20人の主要な専門家からなる委員会を立ち上げ,専門家の委員会は，全体的な戦略を決めるためにプリンストン大学で会議を開始しました．数年が経過し，レフェリーは徐々に委員会を去りました．そして2004年の初めには，記事のレビューを続けられなくなりやめることが最終的に決定されました．ジャーナルの編集委員会は，論文の「理論的部分」を公開し，「コンピュータに基づく部分」をより適切なジャーナルに送るすることを決定しました．ジャーナルの編集委員会のメンバーであるロバート・マクファーソンは，このような論文に対するジャーナルの編集方針は破綻したことを認めた．

王立協会の会合では，コンピュータプログラムの操作の正しさを正式に証明し，それによってコンピュータを使用して証拠を調べる手順を明確にする可能性について活発な議論が行われました．マクファーソンによれば，コンピュータプログラムの正しさを証明するための実際の技術を提供できる人は学術評議会にいなかったので，問題を明確にすることはできませんでした．プログラムは，正式な数学的正しさの専門家による評価の必要性を念頭に置いて作成されたものではないので，これが大きな妨げとなりました．

証明の理論的部分に含まれるアイデアを完全に実装する完全に新しいプログラムを「ゼロから」作成することは可能です．しかし，この可能性は，専門家のレフェリーグループにとって耐え難いものとして却下されました．これは，他の科学分野のプロジェクト（土星へのカッシーニ宇宙探査機など）を完了させるために必要な労力の価値を認めている数学者はほとんどいないからです．

レフェリーの過程で，実行される計算は非常に具体的で特定の問題に特化しているため，引き出された結論を他の同様の問題に適用することはほとんどできないことが明らかになりました．

特に，ケプラーの問題は，互いにさまざまな相互作用を起こすランダムな形状とサイズの異なる物体の大規模なシステムの最小静止エネルギーを決定する問題と密接に関連しています．このような最小化の問題の例は非常に多く，個別の数値手法を開発してコンピューターで計算するので，１つづつが別物でこの分野の理解は不可能です．数学的モデリングを除いて，これらすべての問題を解決する他の方法がない場合，これらの問題のほとんどはそれほど興味深いものではありません．ただし，ケプラーの問題自体は，エラー修正コードの理論などの重要な他のいくつかの問題と関係があります．

コンピューター支援の良い面としては，コンピューターが純粋な数学者を面倒な日常的な計算から大幅に解放したことです．これは，いくつかのカテゴリに分類できます．数式処理は，絶望的に長い計算を変換することができ，さまざまな分野で広く使用されています．カオスの力学系の研究は，数値実験なしには進展しなかったでしょう．カオス現象の存在が19世紀の終わりにアンリポアンカレによって発見されたのは事実ですが，主題を理解と進歩は，コンピューターの開発を待たなければなりませんでした．自己結合行列と非自己結合行列のスペクトルの振る舞いの大きな違いは，数値実験の結果として明らかになり，現在、それ自体が厳密な数学の分野として研究されている疑似スペクトルの新しい分野を生み出しました．特に高次非線形微分方程式の分野では，コンピューター法のみが解の存在を証明することを可能にしました．

モーペルテュイは，
「始状態から終状態への運動経路には，作用と呼ばれる積分量が定義でき，作用が最小となる経路が実現される．これが物理学のみならず，万物の運命を決める外界の原理である」
という着想－”最小作用の原理”(1744年)を得ました．たしかに，現実の運動では，しばしば作用が極小になりますが，正確には，「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります．
オイラーは，モーペルテュイの作用量の定義を積分に拡張し，最小作用の原理をさまざまな力学課題に適用できるようにし，”最大，または最小の性質をもつ曲線を見出す方法”（1744）を発表しました．これを読んだ若きラグランジュは変分法を発明し，オイラーに手紙（1755）を送ります．オイラーは，ラグランジュの方法を採用し，”変分法の原理”（1766）を出版します．変分法で導かれる運動方程式が，オイラー＝ラグランジュ方程式といわれる所以です．その後，ラグランジュは，”解析力学”（1788)を出版します．その序文に「本書には図は一つも出てこない．...所定の手続きに従い進める代数計算だけだ．...」と高らかに宣言します．こうして，複雑な力学問題も解ける一般化された手法が確立されます．
変分法は，19世紀のハミルトン，ヤコービにより完成に至ります．ハミルトンは，系の状態を表示する空間に，座標と速度を座標軸とした相空間を導入し，「作用量は最小化や最大化するのではなく，停留化する」ことを示しました．
１つの物体は，座標x,y,zと速度x˙,y˙,z˙を変数に持ち，その状態は6次元の空間の１点で表現できます．同様に，N個の物体よりなる系は，6N次元の空間の１点で表現できます．この空間を相空間といいます．系のエネルギーを
H(xi,yi,zi,xi˙,yi˙,zi˙)，i=1,2,･･･,Nとすると，エネルギーが保存される運動の軌跡は，相空間内の超平面H(xi,yi,zi,xi˙,yi˙,zi˙)=hに含まれます．超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです．解けるかどうかは別として，周期解（軌道）が存在することは，証明（1986年）されています．（文献10）
■　最小作用の原理の理解には，ホイヘンスの光の波動説の説明が参考になります．ホイヘンスは，空間は見えない媒質で満たされており，光は波紋（球面波）が拡がるように伝わると考えました．波面上の各点はまた新たな波源となり，そこを中心として新たな波紋が広がって行きます．生じた無数の波紋は重なりあったり打ち消しあったりの結果，新しい波面ができます．これは多数の波面の包絡面で，この面に垂直な方向に光は進むと考えます．この様なプロセスで決定された方向は，作用を停留値にするものです．

量子力学の世界の運動には，軌道の概念がなく，電子などはランダムに動き回ります．しかし，我々の日常（マクロ世界）では，電子の運動でも軌道はあります．ここで，マクロ世界でも物体はランダムな経路をとれるとしてみましょう．あらゆる経路に実現可能性があるが，各経路の実現率は，それぞれの確率に従う．これらの確率は，波紋が伝播するときのように互いに干渉し合い，その結果として現実の経路が決まってくると言うわけです．最も確からしい経路は，近くからの干渉の最も少ない経路であって，これがちょうど作用積分を停留化するもののようです．「ファインマンの原理」（文献10）
■　運動方程式が解ける問題を”可積分な問題”といいますが，実際は，”非可積分の問題”がほとんどです．ニュートン力学は，可積分で安定な周期軌道が解になる特殊な範疇を扱っています．一方，非可積分の問題からは，カオスが生じます．１つの軌道は，1本の因果列の存在を意味しています．単純な世界は，今日の現象（原因）１が明日の結果１につながり，今日の現象（原因）２が明日の結果２につながる世界ですが，一般には，今日の現象のすべてが，明日のある結果１の原因になりうる複雑な世界です．バタフライ・エフェクトという映画＊）があったようですが，今日，上空で蝶が羽ばたいたことが，遠い未来に竜巻きを起こす原因の一つになるかも知れません．「風が吹けば，桶屋が儲かる」世界です．この世界は，独立な因果列はないので，周期的な軌道にはなりません．コンピュータを用いて，すべてのステップを計算していけば，結果を予測できるのですが，遠い先の結果は予測もつかないものになります．「最小作用（停留値）の原理」は，ニュートン力学も含むが，このようなカオスも含む原理であります．
＊注）過去に戻れる能力を持ったエヴァンは，過去に戻りやり直すことにする．しかし，過去に戻り選択肢を変えて始めた人生は，どれも，自分を含め自分が愛する誰かが，幸せではないものだった．
 
■　最小作用の原理の起源といえば，1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません．「決まった二点の間を，始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です．ライプニッツの提案により，ベルヌーイはこの問題を海外の数学者にも公開することにしました．ベルヌーイは，ライプニッツの友人で，ニュートンとライプニッツの微積分の先取権論争にも加わり，ライプニッツを応援しています．きっと，ニュートンを困らせてやろうと思ったのでしょう．ところがこの問題を受け取ったニュートンは，「当時，造幣局の仕事で忙しく疲れて帰宅したが，問題が解けるまでは寝なかった．とは言っても朝４時までには解けてしまった」と日記に書いています．そして，解答を匿名で返したということです（文献１，5）．

最速降下曲線の答えは，円板の縁（１点）に目印をつけ，直線上を転がしたときに，目印が描く”サイクロイド曲線”です．ホイヘンスが振り子時計に用いたあの曲線です．

■　解析力学の手順
力学系を記述するラグランジュ関数 を求め，ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと，オイラー＝ラグランジュ方程式が得られます．簡単な系のラグランジュ関数は，（運動エネルギー）－（位置エネルギー）の型になりますが，複雑な系では，位置エネルギーが速度に依存することもあります．
ラグランジュ関数は，電磁場に置かれた荷電粒子にも定義され，光（電磁力学）も力学も統一して扱える原理であります．変分原理から，ニュートンの運動方程式は導出されます．その上，変分原理はニュートン力学よりさらに一般化された外界の原理です．（文献１１）
20世紀に入り，量子力学が誕生するときにもこの原理が手がかりになりました．光や物体の運動が，作用積分を停留化するような，手の混んだ経路を選択するというのは，何と不思議なことでしょう．

（文献）
１．物理と数学の不思議な関係，マルコム・E・ラインズ（青木薫訳），ハヤカワ文庫,　2004
５．古典物理学を創った人々，エミリオ・セグレ（久保亮五，矢崎裕二訳），みすず書房，1992
１０．数学は最善世界の夢を見るか？，エクランド（南條郁子訳），みすず書房, 2009
１１．理論物理学，カンパニエーツ（山内恭彦，高見穎郎訳），岩波書店, 1964

（「数学文化」谷，NO.15(2010)，p.79-87　より抜粋）

ストローと輪ゴムで凸多面体を作ります．
輪ゴムの働きは，結節点でストローの長さを変えないように固定しますが，ストロー間の角度は固定しません．つまり，このような構造を建築ではトラス構造と言います．

皆様の常識通り，２次元の多角形では，３角形は安定で，４角形は安定ではありません.

多面体の面がすべて３角形で出来ていれば，変形しない多面体になりますが，１つでも3角形でない面（４角形や，5角形や，....）があると変形が起こる多面体になります．
例えば，以下の多面体は，すべて３角形の面で出来ているので安定です．

これらが安定なことは，皆様の経験通りで感覚的にわかるでしょう．オルルクは１つだけ4角形の面を含む以下の模型を提案しましたが，実験するとこれも変形してしまいました．

これらの事実は，力学的には常識で自明と思いますが，数学的には証明が必要で，自明なものほど証明は難しいものですが，コーシー＆アレクサンドロフの定理が関係あります．

今回の記事は，KVANTIK，No3（2018）のDmitry Panov, Alexandra Pushkar, Dmitry Chebasov の記事を参考に作成しました．

https://elementy.ru/posters/fractals/H-fractal

Hフラクタル
文字Hの形の図形からすべてが始まります。Hの垂直な線分と水平な線分の長さは等しくなっています。
次ステップで、図の4つの端のそれぞれに、半分に縮小されたコピーが描画されます。
次ステップで，両端にあるのは，4分の１に縮小された16個のHです。
このように無限に繰り返して、フラクタルは視覚的にほぼ正方形を埋めます。

Hフラクタルはどの場所でも密。つまり、正方形の任意場所のいくらでも小さい近傍に、フラクタルがあります。よく見ると、各文字Hが、同じステップで完成した独自の小さな正方形に含まれていることがわかります。

Hフラクタルは正方形を埋める（空間充填曲線）ので、そのフラクタル次元は2で、すべてのセグメントの全長は無限大です。

Hフラクタルを構築する原理は、電子マイクロ回路の製造に使用されます。複雑な回路内の多数の要素が同時に同じ信号を受信する必要がある場合、Hフラクタルの適切な反復セグメント端に配置し、接続します。

オプション
Mandelbrotマンデルブロの木は、線セグメントではなく長方形でできた厚いHを描画することで作られます。

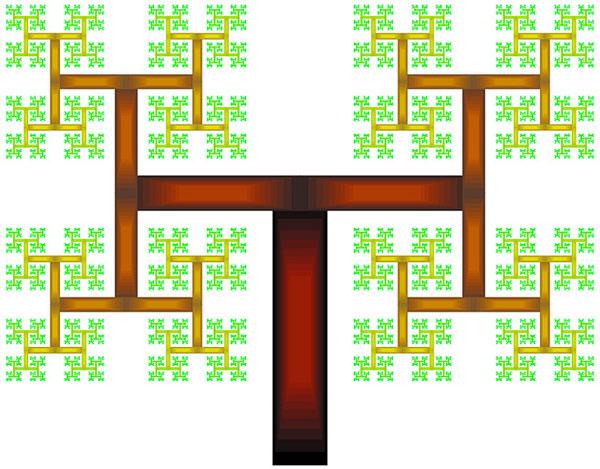
www.flickr.com/photos/29915793@N08からの画像
平面の一部を埋める線のいくつかの例（空間充填曲線）は、1890年にイタリアの数学者ジュゼッペペアノの論文に初めて登場しました。Peanoペアノは、曲線と正方形が等しい性質（点集合と見なす場合）である、つまり「同じ」密度の点を持っているということの視覚的な説明を見つけようとしました。この定理は、Georg Cantorカントールによって、彼が創始した集合理論の枠組みの中で証明されていましたが、この直感に反する新理論の結果は、大きな懐疑論を引き起こしました。ペアノの例（セグメントから正方形への連続写像）は、カントールの正しさの良い確認となりました。

ペアノ曲線、最初の3回の繰り返し
不思議なことに、ペアノの論文には1つのイラストも含まれていませんでした。ペアノ曲線という表現は、特定の例ではなく、平面または空間の一部を埋める曲線を指す場合があります。

下の曲線（ヒルベルト曲線）は、1891年にデビッドヒルベルトによって発表されました。見ることのできるのは，私たちの念頭にある数学的オブジェの有限回近似です。本当の曲線は、無限回の操作後にのみ実現します。

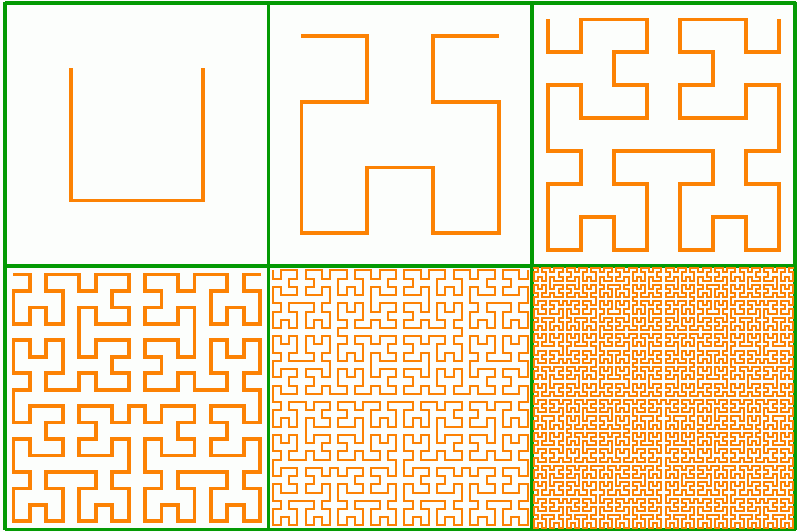
ペアノ曲線の変種-ヒルベルト曲線、最初の6回の反復

ゴスパーカーブ、またはゴスパー雪片（ビル ゴスパー）：

ゴスパーの曲線（雪片）

そして、そのような線の三次元版もあります。たとえば、3次元のヒルベルト曲線、またはヒルベルトキューブ：

カリフォルニア大学バークレー校のコンピューターサイエンスの教授であるCarloH.Séquinによって作成された、3Dヒルベルト曲線のエレガントなメタリックバージョン（3回目の反復）。 www.cs.berkeley.eduからの画像

このようなモデルは、64個のプラスチック製コーナー配管を用い自分で作れます。

ヒルベルトのプラスチックキューブ（2回目の繰り返し）。momath.orgからの画像

表紙の3D図形は，コッホピラミッドと呼ばれます．
https://elementy.ru/posters/fractals/Koch

コッホの雪片

この図は，最初に研究されたフラクタルの1つです．これは，1904年のスウェーデンの数学者Helge vonKochの論文に初めてでたKoch曲線の3つです．この曲線は，連続ではあるが至る所接線を引くことができない線の例として提案されました．このような特性を持つ線は以前から（Karl Weierstrassは1872年）知られてはいましたが，Koch曲線はその構造の単純さで注目に値します．

コッホ曲線の作り方　以下の操作を無限に続けます．

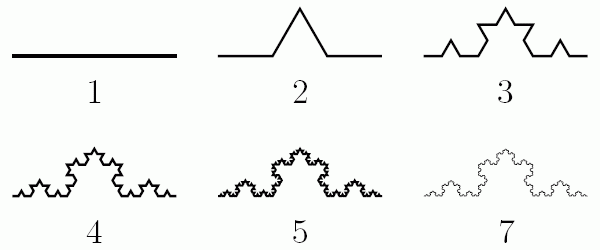
コッホ曲線の基本的な特性
0.拡大しても拡大しても同じパターンがでて来ます。

1.連続ですが、至る所で微分できません（接線が引けません）。

2.無限の長さを持っています。元の線分の長さを1とすると、各ステップごとに；　1，4/3，(4/3)^2，．．．．のように長さが増えていきます。nステップごの線の全長は(4/3)^nですから、n→∞で全長は無限大になります。

3.コッホの雪片が囲むのは有限な領域ですが、その周囲が無限であるというのは不思議です。興味のある方は、面積を計算してみてください。

始めにあるのは面積S_0の正3角形１つ．step１で出来るのは，2つの正3角形を重ねたダビデの星形（ピンク色の星形）．この面積S_1は，中心の正6角形［面積は(2/3)S_0］と外側の小さな３角形［面積は(1/9)S_0］が6個です．S_1=S_0［2/3＋6(1/9)］．step3では，青色の小さな正3角形［面積S_0x(1/9)^2］が2×6個分付け加わります．S_2=S_1+2･6･S_0(1/9)^2．このように継続していくと，面積は単調に増加一方ですが，付け加わる面積は指数関数的に減少し，n→∞で面積はある値に収束するはずです．

4.フラクタル次元はlog4 / log3 =1.26･･･
自分の中に1/3に縮小した自分が4個入って次の世代ができる

美しい幾何学p159,160

https://elementy.ru/posters/fractals/Sierpinski

このフラクタルは、1915年にポーランドの数学者シェルピンスキーVaclavSierpinskiによって記述されました。これを作るには、正3角形の内部に、中線3本を引き、生じた4つの小さな３角形の中央の1つを捨てます。次に、残りの3つの三角形のそれぞれについて同じ手順を繰り返します。この図は、最初の3つの手順を示しています。

Sierpinski三角形を作る手順

中央の３角形を捨てることは、Sierpinskiの３角形を作る唯一の方法ではありません。「反対」のやり方も可能です。最初は「空の」三角形を取り、その中の中線で形成される３角形を作り、3つの角の三角形のそれぞれで同じことを行います。最初は、図は大きく異なりますが、反復回数が増えるにつれて、それらはますます互いに類似し、無限回繰り返す極限では両者は一致します。

Sierpinski3角形を作る「反対」の手順

Sierpinski3角形を得る次の方法は、次の反復の一部に縮小された自分を置き換えることで幾何学的フラクタルを構築する通常の手順にさらに似ています。各ステップで、ポリラインを構成するセグメントが3つ折れのポリライン（最初の反復で形ができた）に置き換えます。この3つ折れを右と左に交互に置き換えて行きます。8回目の反復でフラクタルに非常に近いものが出来上がっています。

Sierpinski３角形を得る別の方法

しかし、それだけではありません。Sierpinski３角形は、平面上の点のランダム歩行の種類の1つの結果として得られます。この方法は「カオスゲーム」と呼ばれています。他のいくつかのフラクタルはそれを使って構築することができます。

カオスゲーム

「ゲーム」の本質は次のとおりです。正３角形をA1 A2 A3とします。任意の始点 B0が与えられます。３角形の3つの頂点の1つがランダムに選択され、もしA1が選ばれたとすると、B0とA1の中点B1 がマークされます。同様に、次にA2が選ばれたとすると、B2がマークされます。その後、A3が選ばれたとすると、B3がマークされます。つまり、前の手順で何を選択したかに関係なく、三角形の頂点がランダムに選択されるたびにマークされる点がジャンプして生じます。驚くべきことに、シェルピンスキーの三角形がすぐに表示されるようになります。以下に、100、500、2500ポイントがマークされたときに何が起こるかを示します。

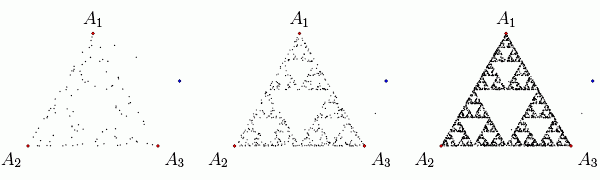
カオスゲーム：100、500、2500ポイント

いくつかの性質

フラクタル次元$$log_{2}3=1.584962･･･$$。 Sierpinski３角形は、自分自身を1/2に縮小した3つのコピーで構成されます。それらの相対位置は、グリッドセルが半分になると、フラクタルと交差する正方形セルの数が3倍になるようなものです。つまり、$$ N( δ/2)= 3N(δ)$$です。最初のセルサイズが1で、フラクタルがそれらの$$N_{0}$$と交差する場合（$$N(1)=N_{0}$$）， $$N(1/2)=3N_{0}，N(1/4)=3^2N_{0},･･･， N(1/2^k) =3^k$$ $$N_{0}$$。　　　したがって、$$N(δ)$$は$$ (1/δ)^{log_{2}3} $$に比例しており、フラクタル次元の定義により、次元は$$log_{2}3$$に等しいことがわかります。
Sierpinski３角形の面積はゼロです。これは、単一の、非常に小さな円でさえ、フラクタルに収まらないことを意味します。つまり、最初の方法で構築を開始した場合、内部全体が３角形から「取り出され」ました：各反復のたびに、残っている領域は3/4倍されます。つまり、ますます小さくなり、0に収束します。これは厳密な証明ではありませんが、他の構築方法も、この特性が真実であるという確信を高めるだけです。
コンビナトリクスとの予期せぬつながり。$$2^n$$ 本の線があるパスカルの三角形で、すべての偶数を白で、奇数を黒で着色すると、目に見える数字はSierpinski３角形を形成します。
オプション
Sierpinskiによるカーペット（正方形、ナプキン）。正方形のバージョンは、1916年にVaclavSierpinskiによって記述されました。彼は、自己交差することなく平面上に描くことができる曲線は、このスカスカの正方形のサブセットと同形であることを証明することができました。３角形のときと同様に、正方形はさまざまなデザインから取得できます。右側は古典的な方法です。正方形を9つの部分に分割し、中央の部分を捨てます。次に、残りの8つの正方形についても同じことが繰り返されます。

Sierpinskiカーペット、最初の5回の繰り返し

３角形と同じに、正方形の面積はゼロです。シェルピンスキーカーペットのフラクタル次元は、3角形と同様に算出し　log_{3}8

シエルピンスキーのピラミッド。Sierpinski３角形の3次元類似物の1つ。起こっていることの3次元性を考慮して、同様に構築されます。1/2に圧縮された最初のピラミッドの5つのコピーが最初の反復を構成し、その5つのコピーが2番目の反復を構成します。フラクタル次元はlog_{2} 5です。図の体積はゼロです（各ステップで、体積の半分が破棄されます）が、表面積は反復ごとに保持され、フラク​​タルの場合は最初のピラミッドの場合と同じです。

メンガーのスポンジ。Sierpinskiカーペットの3次元空間への一般化。スポンジを作成するには、手順を無限に繰り返す必要があります。繰り返しを構成する各立方体は、27個の1/3に縮小された立方体に分割され、中央の立方体とその6つの隣接する立方体が破棄されます。つまり、各立方体は20個の新しい立方体を生成します。これは3分の1です。したがって、フラクタル次元はlog_{3} 20です。このフラクタルは普遍的な曲線です。3次元空間の曲線は、スポンジの一部のサブセットに対して同形です。スポンジの体積はゼロですが（各ステップで20/27倍されるため）、表面積は無限大です。

https://elementy.ru/posters/fractals/Levy

このオブジェクトは1906年にイタリアのエルネスト･セサロによって研究されましたが、その自己相似性とフラクタル特性は、1930年代にフランス人のポール･ピエール･レヴィによって研究されました。このフラクタルの境界のフラクタル次元は、 1.9340にほぼ等しい...。しかし、これはかなり複雑な数学的結果であり、正確な意味はわかっていません。

華やかなフォントで書かれた文字「C」に似ていることから、レビィCカーブとも呼ばれます。よく見ると、レヴィの曲線がピタゴラスの木の冠の形に似ていることがわかります。

バリエーション
歪んだ曲線は、各ステップで等角線の右三角形の代わりに他の右三角形を使用することによって得られます。

Levyレヴィ Cカーブの別バージョンは、セグメントではなく文字Pで開始する場合に作成できます。以下は、このカーブを作成する最初の3、8、および11番目のステップです。

レヴィ島は、正方形を基準にすると得られます。

https://elementy.ru/posters/fractals/Pythagoras

上記ウエブサイトの図を利用していますが，説明文はわかりやすくするために書き換えています．

この図形は正方形ばかりでできています．３つ組の正方形が囲む3角形が直角3角形なので，ピタゴラスの定理が成立するので，ピタゴラスの木と呼ばれます．

この構成規則のため木全体が制限されるので，最大の正方形を1とすると，木は6×4の長方形に収まります。したがって，その面積は24を超えません．各ステップで，正方形の辺は1/√2倍に縮小され（面積は1/2）ますが，生じる縮小された正方形の数は2倍ですので，いつも同じ面積が追加されて行きます．このため，木の領域は無限大になるはずです．しかし実際には，正方形がかなり速くから重なり始め，領域がそれほど速く成長できません．それは有限ですが，正確なことはわかっておらず，これは未解決の問題です．

３角形の底辺の角度を変えると，木の形が少し異なります．そして，60°の角度で，3つの正方形すべてが等しくなり，木は平面上で周期的なパターンに変わります．

正方形を長方形に置き換えることもできます．そうすれば，木は本物の木のように見えます．そして，いくつかの芸術的な処理により，かなりリアルな画像が得られます．