note.com投稿記事

 
セルゲイ・ネテソフ, "SCIENCEFIRSTHAND" №3（88）,2020
ノボシビルスク州立大学自然科学部，バイオナノテクノロジー，微生物学およびウイルス学研究所長

前半の章（以下の３つ）は略
■先駆病原体SARS-COV-2，■コウモリから人間へ，■人への道，

■エピデミックを止める方法
病原体の最も重要な特徴は、感染の基本再生産数（R0）で、まだ感染していない集団で，1人の患者から感染する平均人数のことです。通常のインフルエンザウイルスのR0は0 1.4まで、そして新しいコロナウイルスで、おそらく3から5までです。この指標は徐々に変わりますが、感染拡大は国によって定義がわずかに異なるためです。

ドイツ連邦共和国は、第１波の流行克服では最も成功した国の1つです。2020年5月には、ドイツの研究によると，患者の隔離も、マスクなしの社会的距離も、学校の閉鎖も、R0減衰に効果がありませんで。最大の効果は、大規模なイベントの禁止、過酷な導入、罰金、マスク体制、および集中的なコミュニケーションが行われている組織の閉鎖から得られました。これらの措置の結果、実効再生産数は1を下回り、流行は収まり始めました。

ドイツでの抗流行対策の早期導入と広範なテストは、ウイルスの実効再生産数を迅速に低下させ、多くの死亡を防ぐのに役立ちました。
（National Geographic、2020年5月1日）

同様の状況がオーストリア、ノルウェー、イタリアおよび他のヨーロッパ諸国で観察されました。そこでも、学校の閉鎖は効果がないことが判明し（学童は教育機関の外で積極的にコミュニケーションをとっています）、流行を止めるための有効な介入は、マスク着用、集団行動停止、社会的距離を置く、患者の隔離でした。同時に、そのような措置がすぐに導入されず、完全ではなかったスウェーデンでは、主に高齢者の死亡率はヨーロッパで最も高いものの1つでした。そして、イラン、イラク、サウジアラビアでは、検疫措置が弱まった後、病的状態の第二の波が始まりました。

バルセロナ（スペイン）の診療所にいるCOVID-19の患者。
写真：フランシスコアビアホスピタルクリニックデバルセロナ

抗流行対策の有効性の最も顕著な例は、サンフランシスコとニューヨークという2つの最大のアメリカの都市の行政の行動で見られました。サンフランシスコ政府（カリフォルニア州知事および市長）は3月16日、州が自己隔離、マスクの着用、事業活動のほぼ完全な停止などの厳しい検疫措置を課していると発表しました。ニューヨークでは、同じことがわずか6日後に行われました。その結果、米国で最大の都市で2か月以内に約2万人が死亡しましたが、2番目に人口密度が高く13番目に人口の多いサンフランシスコでは35人しか死亡していません。これは、抗ウイルス予防策の採用が少し遅れただけでも、その結果がどれほど広範囲に及ぶ可能性があるかを明確に示しています。

ニューヨーク市では、コロナウイルスと診断された死亡患者の77％が糖尿病、肺疾患、高血圧や喘息などの心血管疾患も患っており、死亡者の1.5％のみが比較的健康でした。参考までに、米国では約66％の人が太りすぎまたは非常に肥満であり、コロナウイルス感染による死亡のリスクが高くなっています。また、ニューヨーク市の成人人口の約半数が高血圧です。

■Covidかどうか？
コロナウイルスはRNA含有ウイルスに属し、リボ核酸自体に加えて、脂質とウイルス特異的タンパク質も含み、さまざまな方法で診断できます。第一に、患者の鼻咽頭からのサンプル中のウイルス自体の成分の存在による：RNA（逆転写PCR、RT-PCR）およびウイルス抗原-表面Sタンパク質（免疫学的測定法）。

SARS-CoV-2ウイルス粒子では、スパイクSタンパク質がはっきりと見え、そこからウイルスの名前が付けられました。透過電子顕微鏡法。画像：NIAID

別の方法は、体の免疫の構成要素、例えば、特定の抗体ができているかを評価することです。これを行うには、症状の発症と同時に現れる、患者の血液サンプル中のIgMクラスの「一次」抗体の含有量が測定されます。過去に疾患に罹ったかは、「二次」IgG抗体の存在によって識別できます。これらのテストは、酵素免疫測定法を使用して実行されます。

2020年8月20日の時点で、157の異なる検査システムがロシアで登録されました。126はコロナウイルスに対する抗体を検出し、31はウイルスRNAです。しかし、なぜ、そのような多数のシステムで、診断の信頼性を論じるのでしょうか？

第一に、ウイルスRNAの試験システムを使用する場合、鼻咽頭から材料を正しく採取することが非常に重要です。さらに、ウイルスRNAの分離と保存のために、特別なサンプラーを必要とする特別な液体にすばやく入れる必要があります。第二に、今日、テストが実行される多くの研究所がありますが、テスト手順のすべての段階で正しく実行されるわけではありません。

患者の鼻咽頭からCOVID-19テスト用の生物学的材料を採取します。写真：フランシスコアビアホスピタルクリニックデバルセロナ

第三に、上気道からRNAを検出する可能性は、鼻咽頭からのウイルスの「逃避」のために、病気の後期に減少します。最後に、RT-PCRテストでは、患者が回復した後でも、長期間にわたって陽性の結果が得られることがよくあります。その理由は次のとおりと考えられます。体は生きているウイルスではなく、ウイルスRNAの断片を循環し続けます。

ウイルス抗原の信頼性の高いテストシステムが開発され、最近医療現場に導入されましたが、状況によってはウイルスRNAの結果が陰性または不明確な場合に正確な診断を行うことができるため、患者の正確な診断に有用であることがすでに示されています。

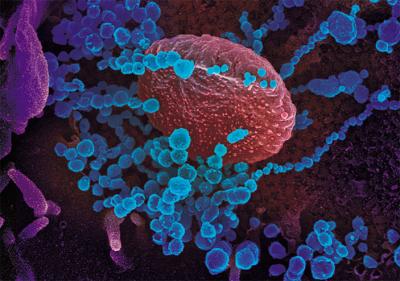
実験室培養におけるSARS-CoV-2ウイルス粒子（青い物体）。この株は、米国の患者から分離されています。走査型電子顕微鏡写真：NIAID

IgG抗体の検査システムに関しては、ARVIを引き起こす一般的なコロナウイルスに感染していて、検査システム自体が十分に特異的でなかった場合、検査システムの中には偽陽性を示すものもあります。その結果、私たちの人口のほとんどがSARS-CoV-2に対する抗体を持っているように見えるかもしれませんが、最も特異性の高い検査のデータから判断すると、この割合はまだ10〜12％を超えていません。

一方、IgG抗体を持っていなくても、ウイルスに対する免疫防御が欠如しているわけではありません。個々の保護を評価するための追加の検査は、免疫細胞が活性化され、サイトカイン誘導が検出される特異的Ｔ細胞免疫の有無の判定であります。しかし、このような診断や抗体解析の複雑さやコストは比類のないものであるため、限られた規模の科学研究でのみ使用されます。 

ほとんどの場合（症例の40〜90％）、COVID-19は無症候性または軽度であるが、中程度の重症度の疾患では、体温が上昇し、ODSの1つ以上の臨床徴候を示しています：乾いた咳、急速または困難な呼吸、味覚と嗅覚の喪失、血中酸素飽和度の低下。重いフォームが特徴です：38℃以上の体温、脱力感、食欲不振、下痢、筋肉痛、肺炎の記録された徴候。感染してから重篤な症状が現れるまでには、実際には約2週間かかります。（ニューイングランド医学ジャーナル2020年5月16日号）

問題は、今日のロシアでは、外国で行われているように、実際の患者からの対照サンプルとCOVID-19に感染していない人々からの陰性血清の広範なパネルを使用して実施された、すでに適用されている診断法の特異性と感度の比較分析のためのデータをパブリックドメインで持っていないことです。そして、そのようなデータは、特定の診断ツールの購入を決定する際に、ロシア保健省と地域の保健当局の両方で役立ちます。質が大切で安ければ良いというのもではないからです。

感染性物質による人間の感染の実験は、世界のほぼすべての国で犯罪です。したがって、ヒトに対するウイルスの感染量、すなわち、疾患を引き起こすために体内に侵入しなければならないウイルス粒子の数はまだ決定されていません。病人が単位時間あたりにどれだけの量のウイルスを環境に放出するか、テーブルやボタンなどの家庭用品の表面に接触しているときに指に付着するウイルスの粒子の数は不明です。しかし一方で、ウイルスが環境内でどれだけ迅速に、どのような条件下で不活性化されるかがわかりました。このための実験は、倫理基準に違反しませんので。

たとえば、デンマークの科学者は、感染者が多く、これらの人々が病気の最初の症状を感じる前でさえ、下水でコロナウイルスを特定しました。同時に、人をテストするときと実質的に同じテストが下水域のウイルスを検出するために使用されます。しかし、それらはサンプル中のウイルスRNAの存在を明らかにするだけであり、「生きている」ウイルス粒子ではないことを常に覚えておく必要があります。したがって、研究者は、細胞培養物中の生きたウイルスの実際の検出とPCR試験の結果を時々検証する必要があります。

以下続く･････

■治療薬は？，■ワクチン接種を受けるか？否か？，■氷山の隠れた部分

コーシー (1789-1857)、リーマン (1826-1866)

これも19世紀の数学で重要な発見の一つです．「数学が社会（科学技術も含まれる）とどのように係わるかを知る」のが私たちの目的で，数学の勉強会とは別物です．そのような視点で見ても，複素関数論は19世紀に確立した重要な数学分野で，広い応用をもちます．そこで，この数学概念の意義を理解できることを目指します．

私たちの使う関数論は19世紀の数学で確立しました．先に，Fourierフーリエ級数（変換）,Laplaceラプラス変換を取り上げましたが，もう少しだけ複素関数に言及する必要があります．今回は，コーシー-リーマンの方程式を取り上げます．

複素平面（$$x$$軸が実数，$$y$$軸が虚数）に定義域$$D$$をもつ複素関数$$f(z)$$を考えましょう．この関数は領域$$D$$で正則（微分可能）であるとします．微分可能な関数ですから，この領域$$D$$で連続であることはいうまでもありません．

ある点$$z∈D$$での微分は，$$ｘ$$軸に沿って（$$x$$で偏微分）行う微分係数と，$$y$$軸に沿って（$$y$$で偏微分）行う微分係数がありますが，複素関数$$f(z)$$が正則であるとすると，どちらの微分係数も一致し，点$$z$$での微分係数は確定しなければなりません．
関数$$f(z)$$が$$D$$で正則とは，定義域$$D$$のすべての点$$z∈D$$で微分係数が確定する（微分可能）ことです．

関数$$f(z)$$に領域$$D$$での正則性を要請します．定義域内のすべての$$z=x+iy$$に対して，

$$\displaystyle \frac{df(z)}{dz}=\displaystyle \frac{ \partial u}{ \partial x}+i\displaystyle \frac{ \partial v}{ \partial x}=\displaystyle \frac{ \partial u}{ \partial (iy)}+i\displaystyle \frac{ \partial v}{ \partial (iy)}$$が成立します．$$x$$で偏微分しても，$$iy$$で偏微分しても等しい．
実部と虚部をそれぞれ等しいとおいて，
$$\displaystyle \frac{ \partial u}{ \partial x}=\displaystyle \frac{ \partial v}{ \partial y},　 \displaystyle \frac{ \partial v}{ \partial x}=-\displaystyle \frac{ \partial u}{ \partial y}$$が得られます．これをコーシー-リーマンの方程式（条件）と言います．

逆に，コーシー-リーマンの方程式が成立するなら，複素関数f(z)は正則であることが証明できます．
従って，複素関数が正則であるための必要十分条件は，コーシー-リーマンの方程式が成立することです．

■閉曲線$$C$$とその内部で，$$f(x)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$　←コーシーの積分定理

（コーシーの積分定理の証明）
$$\displaystyle \int_{C}^{}f(z)dz=\displaystyle \int_{C}^{}\left[ u(x,y)+iv(x,y) \right] \left( dx+idy \right) =\displaystyle \int_{C}^{}\left( udx-vdy \right) +i\displaystyle \int_{C}^{}\left( udy+vdx \right) =$$

$$ =\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial v}{ \partial x}+\displaystyle \frac{ \partial u}{ \partial y} \right) dxdy+i\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial u}{ \partial x}-\displaystyle \frac{ \partial v}{ \partial y} \right) dxdy=0 $$

（参考）
$$\displaystyle \int_{C}^{}\displaystyle \frac{f(z)}{z-z_{0 } }dz=f(z_{0})\displaystyle \int_{\mit\Gamma }^{}\displaystyle \frac{dz}{z-z_{0 } }=2\pi if(z_{0})$$

■正則な複素関数$$f(x,y)＝u(x,y)+iv(x,y)$$はその実数部$$u(x,y)$$あるいは虚数部$$v(x,y)$$のどちらか一方を知れば他方は決まってしまう．

例えば，虚数部$$v(x,y)$$を知り，コーシー-リーマンの方程式を使うと，実数部$$u(x,y)$$を求めることができる．

例えば，以下のyoutube動画には，このような問題の演習があります．

■応用について

実数部を知って虚数部を求める例として，私のやった実験の話をします．

複素屈折率を　$$ \tilde{n}(\omega )=n(\omega )+iK(\omega ) $$と書きます．$$ω$$は光の周波数で実数．複素屈折率$$ \tilde{n}(\omega ) $$は，複素数値をとり，実数部$$n(ω)$$と虚数部$$K(ω)$$があります．
実数部の$$n(ω)$$は反射率に，虚数部の$$K(ω)$$は吸収率に関係があります．

反射率を測定し$$n(ω)$$を知り，$$K(ω)$$を計算し吸収率を求めます．このとき，実数部$$n(ω)$$と虚数部$$K(ω)$$を結ぶのは，クラマース-クローニッヒ変換です．$$ω$$は複素数ではないので，コーシー-リーマンの方程式にははなりませんが，$$ \displaystyle \frac{\tilde{n}(\omega )}{z-\omega } $$は実軸より上側で正則（$$ω$$は極）なので，コーシーの積分定理を使うと，クラマース-クローニッヒ変換を導くことができます．

$$0=\displaystyle \int_{}^{}\displaystyle \frac{n(z)}{z-\omega }dz+i\displaystyle \int_{}^{}\displaystyle \frac{K(z)}{z-\omega }dz=P\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{z-\omega }dz-i\pi n(\omega )+iP\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(z)}{z-\omega }dz+\pi K(\omega )$$
$$\left\{ \begin{array}{@{\,} c @{\, } }
-\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{Z-\omega }=K(\omega ) \\[0mm]
\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(\omega )}{z-\omega }=n(\omega )
\end{array} \right. $$

■コーシーの積分定理

閉曲線$$C$$および，その内部で$$f(z)$$が正則であれば，$$\displaystyle \int_{C}^{}f(z)dz=0$$

■ローラン展開と留数

関数$$G(s)$$に，極（分母が0となる特異点）がある場合，例えば，１つの極$$s_1$$の周りで，次のようにローラン展開ができます．$$s_1$$が$$n$$次の極とすると，
$$G(s)=\displaystyle \frac{a_{-n } }{\left( s-s_{1} \right) ^{n } }+\displaystyle \frac{a_{-\left( n-1 \right) } }{\left( s-s_{1} \right) ^{n-1 } }+ \cdots +\displaystyle \frac{a_{-2 } }{\left( s-s_{1} \right) ^{2 } }+\displaystyle \frac{a_{-1 } }{\left( s-s_{1} \right) }+a_{0}+a_{1}\left( s-s_{1} \right) + \cdots $$
この展開中の係数$$a_{-1}$$を留数と言います．

実は，$$G(s)$$を複素関数と見たとき，極$$s=s_1$$で，$$G(s)$$は正則ではありません．$$s=s_1$$を内部に含むような閉曲線$$C$$に沿って左回りに1周$$G(s)$$を積分すると
$$\displaystyle \int_{C}^{}G(s)ds=2\pi ia_{-1}$$  となります．これを留数の定理といいます．

さてこれらの証明は，難しくはありません．興味おありでしたら，親切な解説をしているyoutube動画がありますので，そちらをご覧ください．

関数をローラン展開すると，いろいろな次数の項がでて来ますが，閉曲線に沿って1周積分すると，なぜ-1次の項の係数（留数）だけが残るのか不思議ですね．youtube動画で証明を確認ください．たいへん都合の良い便利な性質です．

■いろいろな場面で，いろいろな積分をするのに，留数定理を使います．「道具としての数学」の代表でしょう．複素関数論は活躍しています．

話は変わりますが，ちょっと似た手法で，ラプラス逆変換をするときに，部分分数に展開します．以下の例題をご覧下さい．

複素関数$$G(s), s=x+iy$$を，ラプラス逆変換するときに，$$G(s)$$を部分分数に展開することが必要になります．

■Fourier変換
フーリエ解析のときに触れた事柄をまとめておきます：

$$F(\nu )=\displaystyle \int_{- \infty }^{+ \infty }f(t)e^{-2\pi i\nu t}dt$$
$$f(t)=\displaystyle \int_{- \infty }^{+ \infty }F(\nu )e^{2\pi i\nu t}d\nu $$

関数$$f(t)$$のフーリエ変換を$$F(ν)$$といい，$$F(ν)$$から$$f(t)$$に戻る変換をフーリエ逆変換といいます．

変数$$t，ν$$は実数です．積$$ν･t$$は無次元なので，変数$$t$$の空間と，変数$$ν$$の空間は，互いに双対な空間になります．フーリエ変換は，互いに双対な空間同士を結びつける線形写像です．フーリエ変換を用いると，同じ現象を，異なる世界（空間）で見ることができ，現象の理解に威力を発揮します．

適用例
事例１．$$t$$を時間とすると，$$ν$$は周波数ですから，フーリエ変換は，時間空間から，周波数空間への線形写像になります．
事例２．もし，$$t$$を実空間とすると，$$ν$$は逆空間になります．

■ラプラス変換

ラプラス変換はフーリエ変換とよく似ています．歴史的にはフーリエ変換より先だったのですが，フーリエ変換の紹介を先にしてしまいました． 

$$ {\displaystyle F(s)=\int _{0}^{\infty }f(t)\mathrm {e} ^{-st}\mathrm {d} t} $$

$$ {\displaystyle f(t)=\lim _{p\to \infty }{\frac {1}{2\pi i } }\int _{c-ip}^{c+ip}F(s)\mathrm {e} ^{st}\,\mathrm {d} s} $$

（第一の式）$$F(s)$$を$$f(t)$$のラプラス変換といいます．関数$$f(t)$$は実数 $$t ≥ 0$$ について定義されており，積分範囲は$$0≦t<+∞$$になっています．ここで， $$s$$ は複素数（2 つの実数 $$σ, ω$$ を用いて $$s = σ + iω$$ と書ける）．もし,$$s$$を純虚数$$s=iω$$とすれば，フーリエ変換になります．
（第二の式）$$c > 0$$ として，関数 $$F(s)$$ から元の関数 $$f (t)$$ を計算することを逆ラプラス変換といいます．複素平面$$s$$での積分をするので難しそうですが，複素関数論の定理が役に立ちます．複素平面内の積分経路を閉曲線となるように広げ，内部にある特異点の留数の総和を求めれば計算できます．

ラプラス変換は，$$0≦t<+∞の$$実数の空間から複素平面$$s$$への線形写像です．
なぜ，このような面倒な変換が必要なのでしょうか．それは，微分方程式を解くのに有用です．ラプラスは，1812年の著書で，微分方程式の解法に使っています．

ラプラス変換，逆変換を，次のように簡略表記することがあります．
$$ {\displaystyle F(s)={\mathcal {L } }[f(t)]} $$
$$ {\displaystyle f(t)={\mathcal {L } }^{-1}[F(s)]} $$

■ラプラス（1749-1827），フーリエ（1768-1830），ヘビサイド（1850-1925）
フーリエはラプラスより20歳若いのですが，どちらもナポレオンに仕えて，大臣や知事を任命され政治の場でも活躍したところが似ています．
ラプラス変換は，後の演算子法（ヘビサイド）や複素関数論とのつながりがありますので，ここでまとめて紹介しましょう．

ヘビサイド（英国人）は，ラプラスよりも100年後の時代の電気技師ですが，微分方程式の解法に演算子法という素晴らしく便利な方法を開発（1880-1887）しました．これは，微分方程式を代数のように簡単に解く手法です．しかし，その解法の導出過程は数学的厳密さを欠いていたため，当時の数学者から非難されました．ヘビサイドは，「数学は実験的科学であり，定義が先にくるわけではない」，「私は消化のプロセスを知らないからといって食事をしないわけではない」と言ったそうです（wikiより引用）．

その後，ヘビサイドの演算子法は，ラプラス変換により理論づけがなされました．今日，私たちが，微分方程式を解くのに，ラプラス変換をして，周波数空間に移り，そこで簡単な代数計算をして，それをラプラス逆変換して，私たちの世界の時間の関数の解を得るという手順を使います．

ヘビサイドはユニークな天才です．1884年に，当時は20の式から構成されていたマクスウェル方程式を，今日知られる4つのベクトル形式の式に直したというのもとても興味深い逸話です．

Q．正4面体を，平面を切り口に，合同な２つの図形に分割すること．

この問題を考えるのに，まず，正四面体の対称性から説明を始めましょう．図を見てください．正4面体の回転対称軸を調べると，3回回転対称軸が，各頂点にあります．2回回転対称軸は直角に対向している稜の中点を通ります．正4面体の場合は対称心もあるので，2回回転対称軸は，4回回反軸の性質もありますが，今，この問題で必要なのは2回回転対称軸の性質で十分です．鏡映対称面もありますが，この問題では関係ないので略します．

正4面体を，平面で切って，2つの合同な部分に2分割するのですが，対称性を考慮すると，2回回転軸を含む平面で2分割すると，合同な２つの部分に分割できることが理解できるでしょう．例えば，以下の2つの解答例を思いつきます．ついでに，Q．それぞれの例の場合に，その切り口の形はどのような図形でしょうか？という問題も追加します．

解答例１（指で挟んでいるのが，2回軸の正4面体への入口と出口）

解答例２（指で挟んでいるのが，2回軸の正4面体への入口と出口）

■さて私が言いたいのは，「解答例はそれだけでしょうか？」ということです．

実はそのような解は無数にあります．一つの直線を含む平面は無数にありますから，どれも解になります．下図（正4面体の1つの2回回転軸の真上から眺めた図）をご覧ください．黒い線が表現する平面は解答例１，赤い線が表現する平面は解答例２の場合です．2回回転軸を含む平面は無数に作れるので，例えば緑の線も解答例になります．

私がこの問題を作ったのは，対称性の概念は，物事を見通し良く整理して理解するのに役立つことを示したかったからです．