メルマガ

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2022.12.06］ No.451
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
なかの数学まつりは，初めての試みでしたが，予定通りに3回の実施ができました．
第2回は11月26日，第3日は11月27日に実施しました．
コロナの第8波やインフルエンザに注意し，定員制で，マスク着用，検温，消毒なども実施し
無事に開催できました．小学生の参加では，親子で参加や姉妹で参加された方もおられます．
学校の事業とは違う参加型の体験で，みんな楽しい時間になったと思います．
このイベントの告知は，数学月間の会ウエブサイト，中野区の72か所の施設に配ったチラシが主体です．
参加者にどの経路で知ったか聞いたところ，児童館，高齢者会館，地域センターに設置したチラシとの
回答がありました．ウエブの区民ニュースを見た方もおられました．中野区掲示板は200か所もあり
とても貼って回ることはできませんが，中野駅や中野ZERO付近の掲示板は見られているようでした．
数セミイベント情報にも掲載しておりますが、小中学生はこれを見ることはないようです．
我々は組織的な広報手段を持ちませんが，ある程度の参加者を得て楽しく快適に実施できたのは
参加者の口コミ応援が貢献していると思われます．ありがたいことです．
数学月間の会の会員ボランティアの協力に感謝いたします．

さて，第2回，第3回の内容についての解説に移ります．
以下のウエブサイトの記事を参照ください．次々にリンクが出てきますので
クリックして，図やYouTube動画もご覧になるとよくわかると思います：

（第2回）正多面体を作ろう
https://note.com/sgk2005/n/n891019aa6da0

（第3回）エジプト紐であそぼう
https://note.com/sgk2005/n/n8304931cfec7

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2022.12.13］ No.452
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
450号で始めた「瞬間の時間単位」の具体的な内容に言及しようと思います。

　時間単位　と　起こる現象の代表例
マイクロ秒　　　水滴の分離
ナノ秒　　　　　表面原子の動き
ピコ秒　　　　　結晶格子振動
フェムト秒　　　電子，プロトンの移動
アト秒　　　　　オージェ電子放出
ゼプト秒　　　　原子核内反応
ヨクト秒　　　　素粒子の生成や崩壊

それぞれの項目の詳細は以下のリンクに書きました。ご覧ください。
https://note.com/sgk2005/n/n966d425aa31e　ミリ秒
https://note.com/sgk2005/n/nc22e83bd9bad　マイクロ秒
https://note.com/sgk2005/n/n74b4c6c0e460　ナノ秒
https://note.com/sgk2005/n/n543634f4f445　ピコ秒
https://note.com/sgk2005/n/n8ab495be1fda　フムト秒
https://note.com/sgk2005/n/nfea6ba2f2e14　アト秒
https://note.com/sgk2005/n/n8fb86846aa6b　ゼプト秒
https://note.com/sgk2005/n/nf2d930b4c3dc　ヨクト秒

時間が量子化されてこれ以上は分割できないというような最短時間（時間の量子）が存在するのか，
それとも，時間は連続なのかどちらでしょうか．量子化できないことの証明があるらしいのですが
私はわかりません．もしあるとすれば，光がプランク長を移動するのに要する時間（プランク時間）
のオーダー 10^{-44}秒でしょう．

ロシアの科学ジャーナル「エレメント」から、以下のポスターがでています．
イラスト入りでよくまとまっています．ご参考に．
https://old.elementy.ru/posters/moment

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
ご感想やコメントを以下のブログあるいはメールにお寄せください．
☆NPO法人数学月間の会(SGK)＝数学と社会の架け橋
　連絡先：sgktani@gmail.com
　https://note.com/sgk2005
　公式HP: http://sgk2005.saloon.jp/
☆発行システム：『まぐまぐ！』 http://www.mag2.com/

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2022.12.20］ No.453
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
瞬間を測る時間の単位を見てきました．こんどは，原子核レベルの小さい距離を測る単位はどうでしょうか。

原子核とその構成粒子は非常に小さいため，フェムトメートル( fm )の単位を用います。1fm = 10^{-15}m
これは、ナノメートル nm(分子の典型的なサイズ) の 100万分の 1（ 10^{-6} ）です。
陽子または中性子のサイズは約 1 fm 程度、さらに小さく重い粒子があります。

素粒子の世界のエネルギーも小さすぎてジュールJでは測れません。
代わりに用いるエネルギーの単位は電子ボルト( eV ) です。
定義によると，1eVは，1つの電子が 1ボルトの電位差を通過するときに，電場で獲得するエネルギーです。
1eV は約 1.6×10^{-19} J です。
-------------------
注）電子の電荷は約 1.6×10^{-19}クーロンで，1アンペアの電流が1秒間で運ぶ電荷が1クーロンです．
1クーロン の電荷を1ボルト の電位差に逆らって動かすのに必要な仕事が１ジュール．
1ジュールは，１ニュートンの力で1メートル動かすときの仕事でもあります．
-------------------
電子ボルトeVは，原子や光のプロセスを記述するのに便利です。
たとえば，室温の気体分子は，約１/40eVの運動エネルギーを持ち，
可視光の光量子は，約 1eV のエネルギーを持っています。

原子核や素粒子の内部で起こる現象は，さらに大きなエネルギー変化を伴います．
メガ電子ボルト ( MeV )，ギガ電子ボルト ( GeV )，さらにはテラ電子ボルト ( TeV ) がここで使用されています。
例えば，陽子や中性子は，数十MeV の運動エネルギーで原子核内を移動します。
陽子の内部構造が顕著になる陽子-陽子衝突や電子-陽子衝突のエネルギーは数GeVです。
現在知られている最も重い粒子であるトップクォークを生成するには，約1TeVのエネルギーで陽子を押す必要があります。

距離スケールとエネルギースケールの間に対応関係を確立できます。
波長 L の光子のエネルギーの計算は: E =c h/L
ここで，cは光速，hはプランク定数（約 h=6.62 10^{-34} J･s です。
光子だけでなく,スケール Lで物質を研究するときに, 対応するエネルギーの推定に適用できます。
「微視的」単位では,1GeVは約1.2fmフェムトメートルのサイズに相当します。

アインシュタインの有名な式 E_{0} = mc^{2}　によると，質量と静止エネルギーは密接に関連しています。
素粒子の世界では，この関係は最も直接的な方法で現れます．十分なエネルギーを持つ粒子が衝突すると，
新しい重い粒子が生まれ，静止している重い粒子が崩壊すると，質量差が結果の粒子の運動エネルギーに移行します。

このため，粒子の質量も一般に電子ボルトで表せます (より正確には，電子ボルトを光速の2乗で割った値)。
1 eV はわずか 1.78×10^{-36}kg の質量に相当します。
これらの単位で, 電子の重さは 0.511 MeV, 陽子の重さは 0.938 GeV です。
多くのさらに重い粒子が発見されています。これまでの記録保持者は, 質量が約170 GeV のトップ クォークです。
質量がゼロでない既知の粒子の中で最も軽いニュートリノは, 数十meV (ミリ電子ボルト) しかありません。

引用：https://old.elementy.ru/posters/collider,加速器（Ускоритель；Accelerator）

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2022.12.27］ No.454
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今年も残り少なくなりました。次回のNo.455は，年が変わり2023年になっています。

どうぞ皆さま良い年をお迎えください。
今回紹介するこの本，数学は外界を認識するのに必要であるにもかかわらず，
嫌われているのは何故かがわかります。そして，数学の授業が
17世紀の微分積分あたりで終わっていて，その後の発展した分野に触れておらず
つまらないものになっているということに私も同感です。
---------------------------------------------------
愛と数学-隠された現実の心 Edward Frenkel (著)
 
Love and Math: The Heart of Hidden Reality
https://old.elementy.ru/bookclub/book/410/Lyubov_i_matematikaより翻訳

«Любовь и математика». Главы из книгиold.elementy.ru
序章
私たちの隣には秘密の世界があります - 美しさと調和に満ち，私たちの世界と密接に絡み合った隠された平行宇宙です．これが数学の世界です．そして，私たちのほとんどにとって，それは目に見えないままです．私の本はこの魔法の世界への招待状です．Edward Frenkel

訳者注）隠された世界とは外界（森羅万象の法則の世界）のことです．「数学によってのみ外界が認識できる」と言った，デカルト，ホッブスを思い出します．

次のパラドックスを考えてみましょう：数学は私たちの日常生活に織り込まれています。インターネットで買い物をしたり、ウェブで必要な情報を見つけようとしたり、テキスト メッセージを送信したり、GPS デバイスを使用したりするたびに、数式やアルゴリズムを利用します。その一方で、数学はほとんどの人に畏敬の念を抱かせます。詩人ハンス・マグヌス・エンツェンスベルガーの言葉を借りれば、それは「私たちの文化の盲点であり、エリート、少数の学習者だけが、地位を確立できたエイリアンの地」となっています。「小説を読んだり、絵を眺めたり、映画を見たりすることを考えただけで、耐え難い苦痛を感じる人に出会う」ことはごくまれですが、「理性と教養のある人々」が、「軽蔑とプライドが混ざり合って」、数学は「退屈」で「拷問」または「悪夢」にすぎないとしばしば言います。

この異常を説明するものは何でしょう?
私の意見では、これには2つの理由があります。第一に、数学は他の科目よりも抽象的であり、そのためアクセスしにくい。第二に、私たちが学校で学ぶのは、数学のごく一部でほとんどが千年以上前に開発されたものにすぎず、それ以来、数学は信じられないほど進歩しましたが、私たちのほとんどは、どんな宝物が隠されているのかさえ気づいていません.

学校で、フェンスの描き方だけを教えられ、レオナルド・ダ・ヴィンチやピカソの作品を見せることのない「美術の授業」に強制的に出席させられたと想像してみてください。これをしながら芸術を鑑賞することを学ぶことができますか? 芸術についてもっと知りたいですか？
おそらく次のような答えになるでしょう：「学校の美術の授業は時間の無駄だった。 フェンスをペイントする必要がある場合は、適切な人を雇うだけです。」 ばかげているように聞こえるかもしれませんが、それが今日の数学の教え方です。 同時に、偉大な絵画の巨匠の作品は誰でも利用できますが、偉大な巨匠の数学は 7 つの封印で秘密のままです。

しかし、数学の魔法はその美しさだけにあるわけではありません。ガリレオの有名な言葉、「自然界の書物は数学の言葉で書かれている」は誰もが知っています。数学は、現実を説明する方法であり、私たちの世界がどのように機能するかを理解する方法であり、真実のゴールド スタンダードとなっている普遍的な言語です。科学と技術が社会の発展に重要な役割を果たしている私たちの世界では、数学はますます明確な力、富、進歩の源になりつつあります。したがって、この新しい言語を流暢に話せる人は、進歩の最前線にいます。

数学に関する一般的な誤解の 1 つは、数学は「ツール」としてのみ使用できるというものです。たとえば、生物学者は実験を設定し、データを収集してから、このデータに対応する数学的モデルを構築しようとします (おそらく数学者の参加を得て)。この形式の協力は重要ですが、数学は実際にはもっと多くのことを私たちに提供してくれます。根本的な突破口を開き、完全なパラダイム シフトを意味する発見を行うことができます。これは、数学の助けがなければ不可能です。
たとえば、アルバート アインシュタインが重力によって空間が曲がることに気付いたとき、彼は方程式を使用してデータを記述しようとはしませんでした。実際、そのようなデータはまったくありませんでした。当時、私たちの空間が湾曲しているとは誰も想像できませんでした。誰もが私たちが平らな世界に住んでいることを「知っていた」のです。しかし、アインシュタインは、重力と加速度が同じ効果を持つという彼の洞察と合わせて、これが彼の特殊相対性理論を非慣性系一般化する唯一の方法であることに気付きました。これは、アインシュタインが50年前の数学者バーナード・リーマンの業績に頼るだけで達成できた、数学の分野における最高レベルの知的飛躍でした。
人間の脳は、2 次元を超える湾曲した空間を想像できないようにプログラムされています。それらを研究して説明する唯一の方法は、数学を使用することです。あなたはどう思いますか？アインシュタインは正しかった！私たちの宇宙本当にねじれています。しかも拡大中。これが、私が話している数学の力です。

そのような多くの例は、物理学だけでなく、他の科学分野でも引用することができます (それらのいくつかについては以下で説明します)。歴史は、数学的アイデアが科学と技術をますます急速に変革していることを示しています。最初はもっぱら抽象的で難解なものと考えられていた数学的理論でさえ、後に応用問題を解決するために不可欠になることがよくあります。最初は数学に依存していなかったチャールズ ダーウィンは、後に自伝の中で次のように書いています。それをマスターした人々は、理性を働かせる追加のツールを備えているように私には思えます。私はこれが将来の世代のための優れた指示だと考えています。

子供のころは、私は隠された数学の世界があることを知りませんでした. ほとんどの人と同じように、数学は無味乾燥で退屈な科目だと思っていました。しかし、私は幸運でした。高学年で勉強しているときに、この魔法の世界を開いてくれるプロの数学者に出会いました。数学は無限の可能性に満ちており、優雅さと美しさにおいて詩、絵画、音楽に劣らないことを学びました。私は数学が好きになりました。

親愛なる読者の皆さん、この本の助けを借りて、私の先生や指導者が私にしてくれたことをあなたにもしたいと思います： 数学の力と美しさをあなたに明らかにし、私がかつてなんとかしたように、あなたがこの魔法の世界に入るのを助けることです．たとえあなたが「数学」と「愛」という言葉を同じ文で決して使わない人の一人であったとしても、数学が私の肌に浸透したのと同じようにあなたの肌に浸透し、世界のイメージは永遠に変わります。

数学の知識は他に類を見ません。物理的な世界に対する私たちの認識は常に歪められますが、数学的真実の認識は歪められません。これらは客観的で、永遠で、揺るぎない真実です。数式または定理は、性別、宗教、肌の色に関係なく、どこにいても誰にとっても同じことを意味します。千年後も同じ意味を持つ。しかし、さらに驚くべきことは、それがすべて私たちのものであるということです。数式の特許を取得する権利は誰にもありません。これらの数式はすべて私たちのものであり、共通のものです。この世界には、これほど深く洗練されていると同時に、誰もが平等にアクセスできるものはありません。そのような知識の貯蔵庫が実際に存在することは、ほとんど信じられないほどです。この知識は、少数の「選ばれた者」だけに与えるにはあまりにも価値があります。それは私たち一人一人のものです。

数学の重要な機能の 1 つは、情報の順序付けです。これが、ヴァン ゴッホのブラシの跡を単なる絵の具の塊と区別するものです。3D プリンティングの出現は、私たちが馴れ親しんでいる現実の根本的な変化を示します。物理的なオブジェクトの領域から、すべてが情報とデータの領域に流れ込み始めます。3D プリンターのおかげで、PDF を書籍に、MP3 を音楽に変換するのと同じくらい簡単に、情報から物質を作成できるようになります。このすばらしい新世界では、情報を整理して順序付けする方法として、また情報を物理的な現実に変換する手段として、数学がさらに重要な中心的な位置を占めるようになるでしょう。

この本では、過去 50 年間に数学で出現した最も偉大なアイデアの 1 つであるラングランズ プログラムについて話します。ラングランズ プログラムは、多くの人が数学の大統一理論と考えています。この魅力的な理論は、代数、幾何学、数論、解析、量子物理学など、光年離れているように見える数学の分野間の深いつながりの網を織り上げています。これらの地域を数学の秘密の世界の大陸として想像すると、ラングランズ プログラムは、私たちをある大陸から別の大陸へ瞬時に移動させ、また戻すことができるテレポーテーション デバイスのようなものです。

ラングランズ プログラムは、現在プリンストン高等研究所でアルバート アインシュタインのオフィスを持っている数学者、ロバート ラングランズによって 1960 年代後半に開始されました。このプログラムの根底には、対称性の理論があります。同時に、その基礎は、20 歳で決闘で殺される直前に、フランスの天才によって 200 年前に築かれました。その後、フェルマーの最終定理の証明を定式化することを可能にしただけでなく、数と方程式の理解に革命をもたらした別の驚くべき発見によって、それは豊かになりました. さらに別の鋭い洞察力は、数学には不可解なアナロジーと比喩に満ちた独自のロゼッタ ストーンがあることを示しました。数学の魅惑的な土地を流れる小川としてのこれらのアナロジーに従って、インスピレーション、深いアイデア、驚くべき啓示など、ほとんど注目されていない数学の側面を見ることができるように、これらすべてについてお話ししたいと思います。数学は、真実を求めて無限に飛び交う身近な空想の境界を打ち破る方法です。無限理論の創始者であるゲオルク・カントールは、「数学の本質はその自由にある」と書いています。数学は、現実を分析すること、事実を探求すること、それらが私たちを導くところならどこでもそれらに従うことを私たちに教えてくれます. 教義や偏見から私たちを解放し、私たちの革新的な可能性を養います。このように、数学が私たちに与えるものは、主題そのものをはるかに超えています。

しかし、この贈り物は善にも害にも利用できるため、数学が現実世界に与える影響に常に注意を払う必要があります。たとえば、世界的な経済危機は主に、金融市場で不適切な数学的モデルが広く使用されたことによって引き起こされました。多くの意思決定者は、自分自身の数学的無知のために、これらのモデルの本質を完全には理解していませんでしたが、システム全体の崩壊につながるまで、彼らの貪欲さだけに導かれて傲慢にモデルを適用し続けました. 彼らは、誰もブラフを開かないことを期待して、情報への非対称アクセスの利点を悪用しました. 多分、別の例を見てみましょう。1996 年、米国政府が任命した委員会は秘密会議で、消費者物価指数の計算式を変更しました。消費者物価指数は、課税、社会保障、健康保険、およびその他の指数による支払いを決定するインフレの尺度です。何千万人ものアメリカ人の利益が影響を受けましたが、新しい公式とその結果についての公の議論はありませんでした. そして最近、この式を「裏口」として使用して、舞台裏で米国経済に影響を与えようとする別の試みが行われました.

数学に精通した社会では、この種の秘密取引ははるかに少ないだろう. 数学は、厳密さと知的な正直さに事実への依存を掛け合わせたものです。今日の数学に支配された世界では、少数の権力者の恣意的な決定から身を守るために必要な数学的知識に、私たちは皆自由にアクセスできるべきです。数学のないところに自由はありません。

* * *

数学は、芸術、文学、音楽と同じくらい私たちの文化遺産の一部です。私たち人間は、未知のもの、新しい目標の達成、宇宙とその中での私たちの場所の知識に対する生来の欲求を持っています. 残念ながら、コロンブスのように新しい大陸を見つけたり、月面に最初に足を踏み入れたりする必要はもうありません。しかし、私たちの世界の未知の不思議を求めて海を泳いだり、宇宙に行ったりする必要はないと言ったらどうでしょうか? それらは私たちの目の前にあり、日常の現実の繊維と絡み合っています。ある意味、彼らは私たちの一部です。数学は宇宙の流れを導き、あらゆる曲線や形の背後に隠れ、小さな原子から巨大な星まであらゆるものを支配しています。

私の本は、この豊かでまばゆい世界への招待状です。数学の教育を受けていない人のために書きました。数学が難しすぎて何も理解できないと思っているなら、数学が怖いけれど、同時に本当に知っておく価値のある何かがあるか知りたいと思っているなら、この本はあなたのためのものです.

数学を理解するには、何年もかけて勉強しなければならないというのはよくある誤解です。一部の人々は、それを理解する能力を持たずに生まれてきたと信じています。これには同意できません。私たちのほとんどは、太陽系、原子と素粒子、DNA の二重らせんなどの概念について聞いたことがあるでしょう。これらのことを初歩的に理解するために、物理学や生物学の特別なコースは必要ありません。そして、これらの複雑なアイデアが私たちの文化、私たちの集合意識の一部であるという事実に誰も驚かない。 同じように、誰もが数学の重要な概念とアイデアを理解できます。それらは適切に説明する必要があるだけです。そうすれば、数学の学習に何年も費やす必要がなくなります。多くの場合、退屈な手順を飛ばして問題の核心にたどり着くことができます。

問題は、全世界が惑星、原子、DNA について話しているにもかかわらず、対称群、「2 たす 2」が必ずしもそうではない非標準的な数体系など、現代数学の魅力的なアイデアについてはほとんど誰も教えてくれないことです。いわゆるリーマン面のような 4 つの美しい幾何学的形状を作成します。トラだと言い張って、小さな猫を見せているようなものです。しかし、実はトラは全く別の動物です。ウィリアム・ブレイクが雄弁に言ったように、その「驚くべき対称性」を理解できるように、その素晴らしさをすべてお見せします.

私はあなたを誤解させません: この本を読んだ後、あなたはすぐに数学者になることはありません. しかし、誰もが数学者になるために努力すべきだと言っているわけではありません。ですから、いくつかのコードを覚えれば、ギターでかなりの数の曲を演奏できるようになります。世界一のギタリストになれるわけではありませんが、あなたの人生を豊かにしてくれます。この本では、長い間隠されてきた現代数学のコードを紹介します。そして、あなたの人生を豊かにすることをお約束します。

私の教師の 1 人である偉大なイスラエルの Moiseevich Gelfand は、次のように述べています。酔っぱらいに 2/3 と 3/5 のどちらが大きいか尋ねても、彼は答えられません。しかし、質問を再定式化すると、ウォッカ 3 本に対してウォッカ 2 本、5 本に対してウォッカ 3 本のどちらが良いか、すぐにわかります。もちろん、3 本に対して 2 本です。

この本での私の目標は、すべてを理解できる言葉で説明することです。
訳者注）マーフィーの法則で、「言葉が通じなければそれは数学」と揶揄的に定義されている．

また、抑圧的な政権に直面して数学が自由の防波堤となったソビエト連邦での私の生活についてもお話しします。当時ソビエト連邦で施行されていた差別政策のため、私はモスクワ州立大学に受け入れられませんでした。目の前でドアがバタンと閉まりました。私はのけ者でした。しかし、私はあきらめませんでした。講義とゼミのために大学に忍び込んだ。数学の教科書を独学で勉強し、夜更かしすることが多かった。最終的に、システムをだますことができました。彼らはドアを通らせてくれませんでしたが、私は窓から飛び込みました。結局のところ、人が恋をしているなら、彼を止めるものは何もありません。

2 人の素晴らしい数学者が私を彼らの庇護の下に連れて行き、私のメンターになりました。彼らの指導の下、私は独自の数学的研究を始めました。私はまだ研究所の学生でしたが、すでに未知の境界を突破しようとしていました。それは私の人生で最もエキサイティングな時期であり、差別的な政策がソビエト連邦で私の専門分野の仕事を得ることができないと確信していたにもかかわらず、私は好きなことをしていました.

しかし、私には驚きが待ち受けていました。私の最初の数学的研究は密かに国外に持ち出され、有名になりました。その結果、21 歳のとき、ハーバード大学の教授として臨時のポストに就くよう招待されました。奇跡的に、同じ頃、ソビエト連邦でペレストロイカが始まり、鉄のカーテンが崩壊し、ソビエト市民は海外旅行の機会を得ました。それで、博士論文を擁護することさえできなかった私は、ハーバード大学の教授になり、再びシステムをハッキングしました。その後、科学の道を歩み続け、ラングランズ プログラムの最前線で研究を行うようになり、過去 20 年間にわたってこの分野の発展に貢献することができました。この本では、著名な科学者によって得られた驚くべき結果の説明を見つけることができます。

しかし、何よりもまず、この本は愛についてです。私はかつてこのビジョンを持っていました: 数学者が「愛の公式」を発見し、これが映画 Rites of Love and Mathematics の始まりとなりました。この映画を上映するたびに、誰かが必ず「愛には公式があるのですか？」と尋ねます。

私の答えは、「私たちが発見するすべての式は愛の式です。」結局のところ、数学は、存在するすべてのもののまさに中心に浸透し、文化、大陸、世紀を通じて私たちを結び付ける、永遠で計り知れない知識の源です。私たち一人一人が、この世界とお互いへの愛に新しい意味を与えるこれらのアイデア、公式、方程式の魔法のような美しさと絶妙な調和を見て、感謝し、賞賛できるようになることを夢見ています.

読者へのアドバイス
私は、この本の数学的概念を最も初歩的で直感的な方法で提示するためにあらゆる努力をしました。ただし、いくつかの部分が数学で過負荷になっているように見える場合があることは理解しています (特に、第 8 章、第 14 章、第 15 章、および第 17 章の断片)。最初の読書で、理解できない、または退屈だと思う資料をスキップすることは何も悪いことではありません (私はしばしばこれを自分で行います)。後で戻ってきて、新しい知識を身につけていると、はるかに理解しやすくなっていることに気付くかもしれません。ただし、これは通常、次に説明する内容を理解するためには必要ありません。

何かについて混乱するのは完全に正常であることを強調することは非常に重要だと思います. 数学をしているとき、私は 90% の確率でこの感覚に陥っています。私の世界へようこそ! 混乱 (時には絶望さえも) は、数学者なら必ず伴う感情です。しかし、この状況には明るい面もあります。すべてが明確で、ほとんど努力することなくすべてを整理できるとしたら、人生がどれほど退屈になるか想像してみてください。数学をこれほどエキサイティングなテーマにしているのは、混乱を克服したい、理解できないものを理解したい、未知のベールを取りたいという私たちの願望です。そして、私たちが理解したかったことを理解したときの個人的な勝利の感覚は、経験とコストを正当化します.

この本では、技術的な詳細ではなく、全体像と、さまざまな概念と数学のさまざまな分野の間の論理的なつながりに焦点を当てています。多くの場合、より詳細な議論はメモに記載されており、有用な資料へのリンクや追加の読み物への提案も提供されています。ただし、脚注は主要な資料を理解するのに役立ちますが、安全にスキップできます (少なくとも最初の読書では)。

式の使用を最小限に抑え、可能な場合は口頭での説明を選択しました。しかし、本の中のいくつかの公式を見逃しても大丈夫です。

数学用語についての警告: この本を書いている過程で、私は驚いたことに、数学者によって特定の方法で使用される特定の用語が、非数学者にとってはまったく異なるものを意味する可能性があることを発見しました。これらは、「対応」、「表現」、「構成」、「ループ」、「多様性」、「理論」などの用語です。そのような誤解が生じる可能性がある場合はいつでも、私は追加の説明を提供しました. また、可能な限り、いくつかの数学用語を他のより理解しやすい定義に置き換えようとしました。単語が理解できないと思われる場合は、本の最後にある用語集をいつでも見ることができます。

私のウェブサイトhttp://edwardfrenkel.comにアクセスしてください。ここには追加の資料があります。また、この本の印象を共有したい場合は、私にメッセージを送信することもできます (私のメール アドレスはサイトに記載されています)。私はあなたのフィードバックに感謝します。

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.01.03］ No.455
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━ 　
2023年になりました。新年おめでとうございます。
今回のメルマガは、前回の続きで、数学者Edward Frenkel著の「愛と数学」-隠された現実の心 の紹介です。
歳を跨ぐ形になりましたが、この本の主張は、「数学者ではない一般の人に数学への共感を広げようという数学月間の趣旨」と一致します。
数学月間の考え方は、この本のどこに共感するのかをまとめてみましょう：
数学は、社会のあらゆる分野を支えて（いろいろな分野で登場します）いますが、一般の人は数学を嫌って避けようとします。
それは、数学が孤高で孤立しているからです。マーフィーの法則で、「言葉が通じなければそれは数学」と揶揄されたりします。
数学者は、出来上がった論理体系の数学を教えるだけでなく、相手のいろいろな分野に入り込みその分野の数学を組み立てて
見せる必要があります。数学科への数学があるように、工学、薬学、医学、経済、などにはそれぞれの数学があります。
ユークリッドやニュートン、ライプニッツの数学に留まらず、それ以降発展した数学分野をどんどん取り入れる必要があります。
定義、定理、証明の形式を軽視するものではありませんが、その繰り返しの簡潔な数学ではなく、その数学の適用分野や
その数学の発生現場も十分に言及してほしいと思います。
数学者には論理としての抽象的な数学が醍醐味でしょうが、一般の共感を得て普及するには、
数学は物理学の一部であると見た方が良いのです。この本の著者もそのように述べていたと思います。
前回の趣旨を数学月間流に解釈すると以上のようです。

次に、今回の趣旨を述べるのですが、素粒子の例がほとんどで冗長です。数学月間の会ホームページに移ってお読みください。
https://sgk2005.saloon.jp/bbses/bbs_articles/edit/232/d86e61800257d893cd1018ad509a8e1f?frame_id=328
https://sgk2005.saloon.jp/　は、年末にリホームしたいへん読み易くなりましたので、ぜひご訪問ください。

今回の部分の趣旨を一言で述べると、Edwardがなぜ数学を好きになったかが述べられています。
それは、優れた指導者に巡り合ったことから始まり、幸運な特殊なケースです。
素粒子物理に興味を持っていた子供が、良き数学指導者に会い、SU(3)群の学習へと導かれるわけです。
これは、Edwardの場合の例で、人によって必要とするものはそれぞれ異なり、数学のどの分野の話でもあり得ますので
これ以上の言及は避けます。
（注）SU(3)群とは、3次のユニタリー行列の作る群　

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

第1章
どうやって数学者になるの？方法や手段はいろいろあると思います。これが私(Edward Frenkel)にどのように起こったかをお話ししましょう。

驚かれるかもしれませんが、学校では数学が嫌いでした。いいえ、「嫌われている」という言葉は強すぎるかもしれません。数学があまり好きではなかった。数学はつまらないと思いました。すべてのタスクを熱心に完了しましたが、なぜこれを行っているのかわかりませんでした。クラスで話し合った資料は、私には無意味で役に立たないように思えました。私は物理学、特に量子物理学に魅了されました。私は、この主題に関するすべてのノンフィクションの本をむさぼり食いました。私はロシアで育ちましたが、そのような文献を入手することは問題ではありませんでした。

量子の世界に魅了されました！古代から、科学者や哲学者は、宇宙の基本的な性質を説明することを夢見てきました。すべての物質は原子と呼ばれる小さな粒子で構成されている。原子の存在は 20 世紀初頭に証明され、ほぼ同時期に、科学者は各原子がその構成要素に分解できることを発見しました。原子は原子核であり、その周りを電子が回っていることがわかりました。原子核自体は、図のように陽子と中性子からできています。
-----------略-------------------

ゲルマンによれば、クォークには「アップ」と「ダウン」の 2 種類があります。中性子と陽子は、アップ クォークとダウン クォークのさまざまな組み合わせによって形成されます。中性子は 2 つのダウン クォークと 1 つのアップ クォークで構成され (図 1.2)、陽子は 2 つのアップ クォークと 1 つのダウン クォークで構成されます (図 1.3)。

図1.3.陽子のクォーク構造

これはすべて非常に明確でした。しかし、陽子と中性子が不可分の粒子ではなく、さらに小さな粒子で構成されていることを物理学者がどのように推測できたのかは、私には謎のままでした。

1950 年代後半、科学者たちはハドロンと呼ばれる多数の素粒子を発見しました。中性子と陽子はハドロンのクラスに属し、物質の構成要素であり、日常生活で大きな役割を果たしています。残りのハドロンについては、その目的は明らかではありませんでした。科学者たちは、それらが何のためにあるのか（または、研究者の一人が言ったように、「誰がそれらを注文したのか」）をまったく理解していませんでした。宇宙には非常に多くの種類のハドロンが存在するため、影響力のある物理学者であるヴォルフガング パウリは、物理学が植物学に変わりつつあると冗談を言ったことさえあります。科学者たちは、ハドロンの分類に秩序をもたらし、ハドロンの振る舞いを支配し、この驚異的な多様性を説明できる根底にある原理を突き止めようと必死に努力しました。

ゲルマンと独立したユヴァル・ネーマンは、素粒子の革新的な分類を提案しました。どちらも、ハドロンが自然に小さなファミリーに分類され、それぞれが 8 ～ 10 個の粒子であることを示しました。これらのファミリは、オクテットおよびデキュプレットと呼ばれます。同じファミリーに属する粒子は、似たような性質を持っています。

私が当時好きだった人気の本では、オクテットは図を使って描かれていました (図 1.4)。

図1.4.オクテッドのダイアグラム

図では、陽子はp + (プラス記号は正の電荷を示す)、中性子はn 0 (ゼロはこの粒子が電荷を持たないことを意味する) で表され、ギリシャ文字の奇妙な名前を持つ残りの 6 つの粒子があります。

しかし、なぜ 7 と 11 ではなく、8 と 10 の粒子なのでしょうか? 私が自由に使える本では、この現象の首尾一貫した説明を見つけることができませんでした。それは、ゲルマンによって開発された神秘的な理論に言及しています - ある種の「八正道」(仏教の聖なる八正道に似ています)。しかし、この理論が何であるかはどこにも述べられていませんでした。

この誤解は私を悲しくさせました。物語の重要な部分は、私の目から隠されたままでした。この謎を解明したかったのですが、方法がわかりませんでした。

幸いなことに、私たちの家族の古くからの友人から助けがありました。私は約 15 万人が住むコロムナという小さな工業都市で育ちました。コロムナはモスクワから約 115 キロ、電車で 2 時間強の場所にあります。私の両親は大規模な重工作機械工場でエンジニアとして働いていました。

コロムナは、2 つの川の合流地点に建設された古代都市です。それは1177年に設立されました（モスクワの設立からわずか30年後）。コロムナの建築遺産にはいくつかの美しい古い教会があり、コロムナ クレムリンの壁は今でも過去の歴史を思い起こさせます。しかし、コロムナは教育的または知的センターとは言えません。当時、市内には学校の教師を養成する小さな研究所が 1 つしかありませんでした。この教育機関の教授の 1 人である数学者の エフゲニー・エフゲニエビッチ・ペトロフは、私の両親の親友でした。ある日、母は通りで彼に会いました。彼らは長い間お互いに会っていなかったので、当然のことながら、彼らには多くの話題がありました。ママはいつも友達に私のことを話すのが好きだったので、彼らも私を無視して会話をすることはありませんでした。科学に興味があると聞いて、

- 私は彼に会わなければなりません。それを数学に置き換えてみます。
母は反対しました。彼は量子物理学を勉強したいと思っています。
「心配しないで」とエフゲニー・エフゲニエビッチは答えた。

彼らは会うことに同意した。私はあまり楽観的ではありませんでしたが、それでもエフゲニー・エフゲニエビッチと一緒に仕事をしました。

私はもうすぐ 15 歳になり、最後から 2 番目の 9 年生を終えようとしていました (1 年生をスキップしたため、クラスメートより 1 歳年下でした)。40代のエフゲニー・エフゲニエビッチは、フレンドリーで気取らない人物の印象を与えました。眼鏡をかけて無精ひげを生やした彼は、数学者という私の考えを具現化したものでしたが、彼の大きく開いた目の鑑定的な表情には、すぐに注目を集める何かがありました。彼らは好奇心を放ちました-彼は彼の周りで起こったことすべてに興味を持っていました。

エフゲニー・エフゲニエビッチは私を数学信仰に改宗させる狡猾な計画を本当に持っていました。私が彼のオフィスに入るとすぐに、彼は次の質問で私を驚かせました。

— 量子物理学が好きだと聞きました。ゲルマンの八正道とクォークモデルについて聞いたことがありますか?
はい、私はいくつかのポピュラー本で読んだことがあります.
しかし、このモデルが何に基づいているか知っていますか?
科学者はどのようにしてこれらのアイデアを思いつきましたか?
SU (3)群って何か知っていますか？
 SU (3) 群に精通していない場合、どのようにクォークモデルを理解できますか?
*****************訳者注）*************
SU(3)群とは3次のユニタリー行列の作る群です。２次の行列が，パウリの４つの行列の線形結合で表現できるように，３次のユニタリー行列は８つのゲルマン行列の線形結合で表現できます。ここで登場する８という数字はSU(3)を生成する 8 つのゲルマン行列とかかわっています。
*****************************************

彼は本棚から数冊の本を取り出し、それらを開き、数式で満たされたページを見せてくれました。上記のようなおなじみのオクテット図に気付きましたが、それらは単なる美しい写真ではありませんでした。図は、一貫性のある詳細なプレゼンテーションの一部でした。

もちろん、式自体は何も理解していませんでしたが、これらのページで、私を真剣に悩ませていた質問への答えを見つけることができることがすぐにわかりました。気づきの瞬間でした。公式と言葉に魅了され、言葉では言い表せない、これまでなじみのない感覚に襲われました。エネルギー、インスピレーションが沸き起こるのを感じました。これは、音楽を聴いたり、なじみのない写真を見たりして、印象に残っているときに感じる方法です。「うわー！」という一つの考えが頭の中で渦巻いていた。

- 数学は学校で教えてくれるものだと思っていたでしょう - エフゲニー・エフゲニエビッチは続けました。彼は頭を振った。「いいえ、ここです」と彼は本の「真の数学」の公式を指さした。量子物理学を真に理解したい場合は、ここから始めるべきです。ゲルマンは美しい数学的理論でクォークの存在を予言しました。実際、それは数学的発見でした。
――でも、なかなか難しいですよね…。
式は本当に威圧的に見えました。
- 心配しないでください。最初に学ぶべきことは「対称群」です。ここからすべてが始まります。数学や理論物理学の大部分は、この概念に基づいています。私はあなたにいくつかの教科書をあげます。それらを読み始め、理解できない文に印を付けます。週に一度、あなたと会って、読んだ内容について話し合うことができます。

彼は私に対称群に関する本と数冊の本をくれました。彼らは、いわゆるp -進数 (私たちが子供の頃からよく知っている通常の数とはまったく異なる数体系) とトポロジー (基本的な幾何学的形状の科学) について話しました。エフゲニー・エフゲニエビッチは非の打ちどころのない趣味を持っていることが判明しました。彼はトピックの完璧な組み合わせを見つけたので、私はこの神秘的な怪物 -数学 -をまったく新しい視点から見て、恋に落ちました。

学校では、２次方程式、初歩の微分、基本的なユークリッド幾何学、三角法などを学びました。私には、すべての数学がどういうわけかこれを中心に展開しているように思えました-問題は時間の経過とともにより複雑になる可能性がありますが、それらは常に、私がすでに慣れ親しんでいるすべての同じ一般概念の枠組み内にとどまります。しかし、エフゲニー・エフゲニエビッチの本は、私にとってまったく異なる世界を開きました。

私はこの瞬間に転向しました。

2より大きい偶数は、2つの素数の和として表すことができます。

https://old.elementy.ru/trefil/21143/Problema_Goldbakha

Проблема Гольдбаха
old.elementy.ru

最も単純な数学的ステートメントが、証明するのが最も難しい場合があります。フェルマーの最終定理が最終的に証明されたのは、定式化から数百年後の 20 世紀の終わりになってからのことです。数学者がこれまで証明できなかった、フェルマーの定理にいくぶん似た別のステートメントがあります。これはゴールドバッハ問題と呼ばれ、このステートメントの定式化は非常に簡単です。2 より大きいすべての偶数は 2 つの素数の和として表現できるということです。(素数 とは、1および自分自身以外では割り切れない数です。したがって、2、3、5、7 は素数ですが、4 (2 x 2)、6 (3 x 2)、9 (3 x 3) はそうではありません。) このステートメントは、1742 年に Christian Goldbach によって最初に提唱されました。このことから、偶数 10は、7 + 3 の和として書くことができます。ここで、7 と 3 は素数です。あまり知られていないゴールドバッハの主張のもう 1 つの定式化は、9 以上の奇数は 3 つの素数の和として表すことができるというものです (たとえば、13 = 7 + 3 + 3 = 5 + 5 + 3)。
ゴールドバッハがこの予想を提唱して以来、数学者は、フェルマーの最終定理と同様に、この予想が正しいことを疑いませんでした。しかし、フェルマーの定理とは異なり、誰もそれを証明できたと主張したことはありません。この問題を解決するための正面からのアプローチがあります - 長い間、このステートメントをより大きな偶数で順番にチェックするコンピュータープログラムを実行することです。このようにして、定理が間違っていたとしても、その定理を反証することができます。でも、プログラムが次のステップでテストする数が規則の最初の例外になるかも知れないという単純な理由で証明できていません。実際、ゴールドバッハの問題は、少なくとも 100,000 までのすべての偶数に対して真であることがわかっています。
1930 年代に、ロシアの数学者のグループが、任意の偶数をn以下の素数項の和として表すことができるような有限のnが存在すること、およびゴールドバッハ予想が偶数の大規模なクラスに当てはまることを確立しました。しかし、定理の証明はまだ見つかっていません。
なぜ数学者はフェルマーの最終定理やゴールドバッハの問題のような問題を解くのに多くの時間を費やすのでしょうか? 結局のところ、これには実際的な意味はなく、彼らの決定から利益を引き出すことはできません。私の意見では、これは非常に古く、人間の活動の非常に特徴的なものであり、自明で議論の余地のない真実の探求です。哲学者たちは何千年もの間、真実を探し求めてきました。数学者は、純粋な論理に基づくシステムを操作することで、そのような真実を発見したいと考えています。そして、これらの証明を達成するのが非常に困難であるという事実は、おそらく、数学自体の特性ではなく、論理の性質そのもの、つまりこの信頼できず、変化しやすい世界で真実を見つけることが不可能であることによって説明されます.

---------------------------------------------------------

10=3+7
12=1+11=5+7
14=1+13=3+11=7+7
16=3+13=5+11
18=1+17=5+13=7+11
20=1+19=3+17=7+13
22=3+19=5+17=11+11

9=3+3+3=1+3+5
11=3+3+5=1+5+5
13=3+3+7=3+5+5
15=3+5+7=5+5+5=1+7+7
17=5+5+7=3+7+7=1+3+13=1+5+11=3+3+11
19=1+1+17=1+5+13=3+3+13=1+7+11=3+5+11=5+7+7

ーーーーーーーーーーーーーーーーーーーーーーーーーー
クリスチャン・ゴールドバッハ、1690-1764

ドイツの数学者。プロイセンのケーニヒスベルク（現ロシア・カリーニングラード）生まれ。1725 年に彼はサンクトペテルブルクで数学の教授になり、3 年後には将来の皇帝ピョートル 2 世の家庭教師としてモスクワに来ました。ヨーロッパ旅行中、ゴールドバッハは、ゴットフリート ライプニッツ、アブラハム ド モアヴル、ベルヌーイ家など、当時の主要な数学者の多くに会いました。彼の論文の多くは、スイスの偉大な数学者レオンハルト・オイラー (1707–83) とのやり取りから生まれました。私たちが現在ゴールドバッハの問題と呼んでいる主張は、1742 年にゴールドバッハからオイラーへの手紙の中で最初に提起されました。

数学の醍醐味は、次の2点にあります；
①現象を支配する数学を見出す．これは物理学に近い
②数学の論理を展開する．
軌跡を求める問題の着眼点も，この2点にあります．特に，物理や機械に近い着眼点①は興味深いもので，私は軌跡を求める問題は特に好きです．
代表例として，単純な 問題１を作りました．挑戦してください．

■問題１
円A，Bの半径をそれぞれ１とし，２つの円の間は１/2だけ離れているとします（つまり，ABの距離は3/2です）．円Aの円周上の点P，円Bの円周上の点をQとし，P，Qは，長さ１のジョイントPQで結合されています．つまり，この構造は， 

$${AP＝PQ=QB=１AP＝PQ=QB=１}$$ 
の３セグメントからなります．点A，Bは固定点ですが，A,P,Q,Bのジョイントはピボットです．PQの中点Rの軌跡を調べなさい．

問題１の構造と思考実験

ヒント
この問題を方程式やベクトルで解き，軌跡を式で表すのは，なかなか困難ですが，見ただけで直感でわかる軌跡の性質がいくつかあります：
この解の軌跡は，上下対称、左右対称であるはずです．
A円上の点Pは限られた範囲（円弧）上しか移動できません．B円上の点Qに関しても同様です．ただし，ABの距離とセグメントPQの長さによりだいぶ様相が変わります．

■実験してみましょう．
図２に実験結果を掲載します．軌跡の曲線はリボンのような形です．

図２２円が重ならない場合の実験結果

■円A,Bが一部重なる場合の例

図３２つの円が部分的に重なる場合の軌跡の例

これらのリボンのような軌跡は，単純な式では表現できません．どなたか挑戦してみては如何でしょうか．

■下図は2つの円の距離をパラメータにして軌跡の曲線の変化を示した一例です．

■　拡大縮小に使われる仕組みーパンタグラフ

点Oは固定点．Oを含む４つのピボットがあり，辺は平行４辺形を保ったまま自由に変形できる．このとき常に，O，P，Qは一直線上にある．
Pの描く図形とQの描く図形は相似であり，相似比は，OP：OQである．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.01.24］ No.458
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
群の概念の発見で，まず第一に名前が出てくるのはガロアです。
しかしながら、ガロアが群概念を突然発見したわけではありません。
5次方程式の解の代数的な公式を作ろうと探し求めた何百年もの課題があり
どうやらそのような解を代数的に記述するのは不可能らしいと思いはじめ，
不可能の証明に取り組み始めた時代になりました。

5次方程式が解けないという表現は，誤解されがちですが，正確に言うと；
一般の5次方程式には、5つの複素数解が存在し，それらの数値はいくらでも正確に求められるのですが，
方程式の係数の間の四則演算とベキ乗根を求める演算を用いて，解を記述することができない
（代数解がない，あるいは，解の公式がない）という意味です。

ガロアが突然群の概念を発見したわけではありません。
ガロアの前の研究に，ラグランジュ，アーベルの伏線がありました。そして，ガロアの発見に至ります。

さらに，ガロアの遺稿の価値を見出し数学的に検証したリウヴィルの研究1846年は重要です。
リウヴィルは，統計物理学のリウヴィルの定理やエルゴード理論の人だと思っていましたが
ガロアの概念の発見では大変な貢献者です。
（注）統計物理学のリウヴィルの定理とは，相空間（数学の位相空間と混乱するので，
ガンマ空間と呼んだ方が良いかもしれない．粒子数Nでは６N次元の空間）を，
運動する粒子の分布関数の体積は保存されるということ。

ガロア以降の群概念の発展は，我々には重要です。
特に，これらはジョルダン，ヘルダーの貢献によります．
結晶空間群が含む並進群が正規部分群であることを利用して，商群を作り，
結晶点群に準同型に対応させる仕組みの基礎は，ジョルダン1869，ヘルダー1889が作りました。
こうして，様々な科学の分野に群論が適用されるようになりました。
これらの詳細について，イアン･スチュアートの著書を引用して
https://note.com/sgk2005/n/n9c9c98cb2344
に書きましたので，ぜひご覧ください。

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.01.31］ No.459
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
無限大とは非常に大きな数ではありません．無限大は特定の数よりも大きく，つまり，自分自身よりも大きいのです．
それゆえに，アリストテレスは，これを無限に続くプロセスと見なしました．
しかし，カントールは，無限にも大きさ（濃度）があることを証明しました．
可算無限（有理数の集合が例）と非可算無限（実数の集合が例）があります．

今回のメルマガでは，
イアン・スチュアート著； 偉大な数学者の生涯と発見
(Ian Stewart. Significant Figures: The Lives and Work of Great Mathematicians)
（ロシア語訳）出版社「アルピナ ノンフィクション」、2019年
が，カントールの章だけ以下のサイトに公開されています．
https://old.elementy.ru/bookclub/chapters/434568/Znachimye_figury_Glava_iz_knigi

これを抜粋し訳したものを，以下のサイトに置きます．
長くなりますので，以下のサイトに移動してお読みください．
https://note.com/sgk2005/n/n49deb1f56903

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.02.07］ No.460
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
◆お知らせ
数学月間の会のウエブサイトhttps://sgk2005.saloon.jpは12月にリニューアルし，お陰様で多くの方々がアクセスされています．
さらに，2月初め（先週）に，新しいURLのサイトhttps://sagk2005.orgの開設も行いました．
現在は，これら両方のサイトを見ることができる状態です．今後は，旧サイトの更新は行わず，新サイトのみ更新します．
どうぞ，新サイトにご訪問ください．現在、旧サイトへのアクセスは日に千件程度，新サイトへのアクセスはゼロです．
（新サイトのURLをお知らせするのは、今回が初めてですので当然ですね）どうぞ新サイトをご利用ください．
引っ越し先の新サイトURLが十分に周知されれば，旧サイトは閉鎖する予定です．

◆今回のメルマガのテーマは，フォノニクスという科学技術についてです．
音波は，空気や物質中の振動の伝播のことで，熱振動も物質原子の振動ですから音波の仲間に入ります．
量子化された音波をフォノンと言いますが，フォノニクスで，音波を一方向だけに伝える物質や，
熱を一方向だけに伝える物質を作れます．
弾性率の異なる素材の交互積層の超格子（周期構造はバンドギャップを生む）や，ナノチューブが材料に利用できそうです．

超音波を集束させたり，一方向だけに流す超音波ダイオード，超音波整流器．
コヒーレントな熱波を作ったり，熱流ダイオードなどが実現可能なようです．
これらは医学や精密機械分野に有用ですが，
光学的な不可視マント（ステルス航空機）のような超音波の不可視マント（ステルス潜水艦）
のような軍事利用と結びつきそうな技術でもあります。

フォノニクスは音波を操る技術分野で，これはフォトン（光子）を操る技術分野をフォトニクスという
ことに倣って作られた述語です．
物質の振動（音，熱）の量子がフォノンで，振動周波数の高い熱振動までもフォノニクスに含まれます．
フォノニクス（フォノン）の分類は，次のように振動の周波数で行われ，
(１)超低周波音域；15Hz未満，
(2)可聴音域；15Hz～20kHz，
(3)超音波音域；20kHz～100MHz，
(4)極超音波音域；100MHz～100GHz，
(5)テラヘルツ熱振動音域；100GHz～100THz
の領域にわたります．これらの分類がなされる所以は，フォノンの周波数は，励起される物質のサイズに関係があり，
それぞれのフォノンの特性が異なるからであります．

この先の詳細は，https://note.com/sgk2005/n/n6c1624e3ffbf
に書きましたので，noteのサイトに移動してお読みください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.02.14］ No.461
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━ 
地震、大規模停電、原発事故などの複雑系は、些細な原因により生じた故障が次々と雪崩を起こし、系全体に広がり大規模な災害を生みます。
複雑系には、予期できない特性があり、そのような特性の出現を予測することは非常に困難です。

複雑系の研究は、現代科学の最も重要な分野の 1 つです。複雑系は、多くの独立した要素からなり、それぞれが他の要素と相互作用する系として定義されます。たとえば、砂の山は複雑系で、1粒の砂を押すと、山を構成する他のすべての砂粒に圧力が伝わり、これらの砂粒が応答してわずかに変位します。証券取引所は、買い手と売り手の行動が変化するにつれて、買い手と売り手が行動を変える複雑系です。他の要素の動作の結果として要素の動作が変化する系は、複雑適応系または自己調整系と呼ばれ、証券取引所はこの例です。

高速電子計算機が登場する前は、複雑系を研究することは不可能でした。これらの系は、通常の数学で扱うには大きすぎ、複雑すぎます。複雑適応系のコンピューターでの研究の最も重要な結果は、予期しない特性という概念でした。砂山を例に取ると、砂粒を積み上げていくと、遅かれ早かれ新しいタイプの行動が突然現れます。山全体の100 万分の 1 の砂粒を追加すると雪崩が発生するとします。この動作は、雪崩前に起こっていた圧力伝達現象とは根本的に異なります。つまり、この100万個目の砂粒１つで、「より多く」という概念ではなく、「別」の特性出現に変わります。

予期せぬ特性の重要な特徴は、それが徐々に現れるのではないことです。言い換えれば、1 粒の砂が雪崩の 100 万分の 1 の部分を形成することはなく、そ１粒を同様の部分に追加して、100 万粒の砂の山に雪崩を発生させることができます。100 万分の 1 の砂粒に到達するまでは雪崩はまったく見られず、1粒追加後突然雪崩が発生します。

意識や内省などの心の特性は、多くのニューロンの系の予期しない特性であり、多くの砂粒で発生する雪崩のようなものであるというのは興味深いことです。もしこれが本当なら、神経系の進化は「より多く」から「別」の特性になるポイントに近づいています。

今日の科学が直面している大きな課題の 1 つは、個々の要素の特性に基づいて、系の予期できない特性の出現を予測できるかということです。現時点ではそれは不可能です。結局、予測は不可能なことかもしれませんが、複雑系の研究が進み、その特性発現の解明ができる可能性もあります。

引用：百科事典「科学の性質．宇宙の200の法則」，ジェームズ・トレフィル

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.02.21］ No.462
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━

■数学月間とは　　　　　　　　　　　　　　　　　(たに・かつひこ/NPO数学月間の会）
米国のMAM（数学月間）は，上院の共同決議「1986年４月14～20日を数学週間とする」に基づくレーガン大統領宣言で1986年にスタートした．レーガン宣言は格調高く，「およそ5千年前に始まった数学的叡智は進歩を遂げ，今日の社会を支えている」と述べ，すべてのアメリカ人に対し，数学と数学的教育の重要性を実証する活動への参加を要請している．米国が国家的行事のMAMを決断した背景には，国民の数学力の低下で，産業力も低下するとの焦りがあったといわれる（小林昭七「顔をなくした数学者」）．1950年代の日本は，Dr. Demingの品質管理手法を，TQCやQCサークルに発展させ，生産性向上を達成していた．1980年NBC放送はIf Japan Can, Why Can’t We?と呼びかけ，Dr. Demingのセミナーが米国で展開されたが，さらにこれを数学全般の啓蒙MAMへと発展させたのは米国の叡智であった（竹内淳実）．バークレーの地域数学サークルなどの学校外活動も効果を上げている（小林昭七）．米国MAMは，数学系学協会が参加するJPBM（Joint Policy Board for Maths）が，毎年，社会を反映した数学テーマを選定し，4月に種々の数学イベントが展開される．国民からの事後評価も受ける．時局の数学を，種々のレベルで学習できるウエブ・サイトが充実し，そこにエッセイや論文が集積され，数学を基礎から最先端まで，学生が独習できる優れたガイドになる．日本の数学月間（7/22-8/22）は，片瀬豊（表紙写真）の日本数学協会への提案(2005年)でスタートした．片瀬豊は，日本版JPBMが国家的行事として数学月間を展開すべきだと考えていた．「数学月間」活動は，数学同好者の内部にとどまらず，数学が係わるあらゆる分野を横断し，一般市民に働きかけ，数学（論理）が社会を支えている事例を踏まえ，数学への共感を獲得することを目的としている．
■孤高な数学では共感を得られない
理系でも数学と結びつきの薄い分野に生徒が流れる傾向がある．数学まつりを実施しても，教材の基礎にある数学へ言及することは少ない．「数学によってのみ外界（森羅万象の法則の起源）が認識できる（デカルト，ホッブス）」のだが，数学はこのように避けられ嫌われている．数学への共感が得られない原因を考えるに，数学の孤高姿勢にある．完成した数学体系を学べというのではなく，相手の現場に立ち入り数学論理を見出し適用して見せることで共感が得られる．教育数学においても各学科分野にふさわしい数学を提供するのが良い．マーフィーの法則で，「言葉が通じなければそれは数学」と揶揄的に定義されるようではいけない．完成された数学体系は美しいが，それぞれに，その数学概念が生まれた源泉があり，その過程を見せること，および，その数学の適用現場を見せることが共感に繋がる．数学者でない一般社会人の共感を得るには，地に足がついているという意味から，数学は物理学の一部であると考えた方が良い．（クーラン&ヒルベルト「数理物理学の方法」，イアン・スチュアート「無限をつかむ」）．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.02.28］ No.463
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━

YouTube動画で色々な発明開発の動画があり，製作過程の面白さに惹かれてつい見てしまいますが，そのほとんどが時間の無駄です。
永久機関もあれば，まわりくどく原理がなんだかなぁとがっかりするものです。このようなものには次の２つのタイプがあります：
①投稿者自身が，意図的にトリックがある（詐欺，マジックの部類）ことを自覚している。
②投稿者自身が発明と信じていて，改良を進めればものになると思ってい
る。

①は詐欺の部類です。これはアイディアが面白ければ，受け狙いと割り切て，マジックのように楽しめばよいのです。しかし，かなりの人が騙されるようです（見る人の知識不足が原因です）。
ここで，私が気になるのは②の場合です。
視聴者のコメントを見ると大部分（９割）は肯定的で賞賛さえしています。その一方，正しい批判的コメントや親切なアドバイスも少数（１割程度）だがあるのは救いです（他人が一所懸命にやっていることへの否定や批判は言い難いし，そのようなコメントへの返信を見ると，発明者当人は聞く耳を持たないようです）。

当人は真摯に取り組んでいるとしても，このような動画は，多くの人を発明者と同じ泥沼に引き込むし，無駄な投資をさせたりするでしょう。
このようなことが起こる原因は，発明者の物理のその分野の知識不足にあります。発明品の不思議に見える動作原理は，生半可な知識の混沌とした状態の利用です。よく利用される現象の例は，ファラディやマックスウェルをはじめとする多くの科学者により既に解明された電磁誘導；コイルの周りで磁場が変化すればコイルに電流が生じ，電流が変化すれば磁場が変化するという現象です。この現象は，広大な応用分野をもち，モーター，電子レンジ，リレー，トランス，回路まで含めればほとんどの電子デバイスを作り出しました。ワイヤレス給電などもこの現象の利用です。抵抗に電流が流れれば加熱されるのは、既知の別の現象です。
「配管のそばで磁石をモーターで回転させて，配管に誘導電流を発生させ加熱する」という暖房装置のYouTube 動画があります。見世物として面白いと思う多数の視聴者がいます。これが石油の節約だと信じている人もいます。私はモーターを回転する電力で抵抗過熱をした方がよほど良いと思います。
開発を続けエネルギー変換効率の改良を進めれば，シンプルな現存装置に帰着してしまうことが見えています。

原子炉をボイラーの熱源代わりにする原子力発電もこの部類に入ります。100万kWの原発を１日稼働すると約3.7kgのウラン235が核分裂し，引き取り手のないおびただしい放射性核種が生じるというのに。

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.03.07］ No.464
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━

「数学の弁明」．原題「Апология математики」(初版2007)，2017年に第2版が出版されています．著者はウラジミール・ウスペンスキー（Владимир A. Успенский）．著名な数学者A.N.コルモゴロフの弟子で数学者，言語学者，1966 年から 2018 年まで，モスクワ大学の数理論理およびアルゴリズム理論の学部長．
この出版物は読者から高く評価され，2007 年の「新世界」賞を受賞しました．数学と人文科学の間の障壁を克服し，非数学者が数学の基本的な概念と問題のいくつかに親しむことができます．

■先行する似た題名の本に，次のものがあります．そちらの本は，英国の数学者G.H.ハーディが1940年に出版したもので，全く異なる内容です．
そちらの本の内容もnoteの別の記事として取り上げていますので，そちらをご覧いただければ幸いです．https://note.com/sgk2005/n/n9fbb5b7fd9de

■ウラジミール・ウスペンスキーの本Апология математикиの内容に触れましょう：

第 1 章 ワトソン対ホームズ
第 2 章 ピタゴラスの定理とフェルマーの定理
第 3 章 未解決の問題と解決不可能な問題
第 4 章 長さと数
第 5 章 円と正方形
第 6 章 質量の問題とアルゴリズム
第 7 章 ガリレオのパラドックス、コルタザール効果、および量の概念
第 8 章 神話における平行線現実と数学
第9章 100万ドル問題
第10章 計量幾何学から位置の 幾何学へ
第11章 位置の幾何学からトポロジーへ
第12章 私たちの宇宙はどのようなものになるでしょうか?
第1章の付録 読者の意見
第3章の付録ゴールドバッハ問題の歴史について
「集合」「順序組」「対応」「関数」「関係」 の概念について

以下のサイトで公開されている内容から抜粋します：

Читать онлайн «Апология математики (сборник статей)», В. А. Успенский – Литрес
Читать онлайн книгу «Апология математики (сборник статей)» ав
www.litres.ru
現代社会では，どんな専門分野にも数学が係わっています．「数理物理学」を筆頭に，「数理生物学」,「数理言語学」，「数理経済学」，「数理心理学」等々．今や数学は流行の職業になっています．

これは，数学の応用の計り知れない可能性のためです．数学は，人文科学と見なされてきた分野にも浸透しています．

数学は，現実に適合した一般的でかなり明確なモデルを提供します．これは，他の科学によって提供される一般的でなく漠然としたモデルとは対照的です．

自然科学と人文科学の区分がいつまでも続くとは限りません．数学が自然科学に帰属することの反省が起こっています．数学は物理学の一部であると言われますが，物理の世界の特性記述に数学が成功したからで，人文科学の他の分野でも同じ成功を収めるに違いありません．

数学の人文科学への係わりについて

列車の乗客は窓越しに無数の白い羊の群れを見ています．そして，彼らは
電車に横向きに黒い羊がいるのに気づく．「ぁぁ，ここにも黒い羊が！」と 一人が叫ぶ．「片面の黒い羊が少なくとも 1 頭はいる」と，別の数学者が彼を訂正します．
この逸話は，過度の正確さが有害であり，適切な内容認識を妨げる可能性があることの例です．ここには，人文科学と数学の間の双方にとって有益な対話の基礎が​​あります．この対話では，数学者が（人文科学）非数学者に教えたりしませんが，構文構造の構築の正確さがいかに重要であるかの共有がなされます．数学者は，論理的枠組みを理解する能力を非数学者に伝えようとしています． 一方，非数学者は，不正確さの重要性の考えを数学者と共有します．非数学者は数学に対して，その論理的枠組みを包み込む肉付けと文脈の両方が，言及された枠組みと同じくらい重要であると示しています． 非数学者は，周囲の世界は不定形で曖昧であるため，数学的に正確な文言よりも，不正確で曖昧な文言の方が適切に反映されると思っています．
数学者と（人文科学）非数学者は異なる思考スタイルを持っており，異なるスタイルに触れることで両者が豊かになります．たとえば，「公理に明示的に記録された情報のみ推論に使用できる」という数学で広く普及している公理的方法の研究は，厳密な思考の習慣を植え付けます．そして，「無限集合の性質」を知ることは想像力を育みます．歴史家は公理的方法や無限集合を必要としないと思うかもしれません．しかし，思考と想像力の厳しさは彼の思考の妨げにはなりしません．
一方，数学の方にも学ぶべきことがたくさんあります．
人文科学者は数学者より他人の意見に寛容です．数学的な概念は明確に定義されていますが，人文科学的な概念は曖昧です． それゆえ，私たちの曖昧な世界を説明するのに適しています．
私たちは，情報を冷静に伝達する機能に関心があります．それは文言に具現化されます．国内プログラミングの創始者の一人であるアンドレイ・ペトロヴィッチ・エルショフは，これを「ビジネス散文Деловая проза」と呼びました． ビジネス散文には，特に，自然科学のテキスト (主に数学)，法律のテキスト，事務のテキストおよび指示（マニュアル）が含まれます．ビジネス散文は私たちの生活の中でますます重要な位置を占めるため，母国語のレッスンや，感情を伴わない純粋な情報に特化した特別クラスで教えられる可能性があります．
ビジネス散文を教えることは，ビジネステキストの正しい編集と正しい認識のスキル，つまり，言葉で考えを正しく表現し，言葉で表現された考えを正しく解釈する能力を養成します．

（私のコメント）
数学は物理学の一部であるという思いは，私も同様に実感しています．
しかし，人文科学にも，数学の浸透が進んでいるのは事実です．
むろん，以前から数学の人文科学との係わりはありました．A.A.Баpсов（モスクワ大，数学）は，ロシア語文法，正書法の提案を行いました(1755）．
数学の論理は，自然科学も人文科学も係わります．数学を人文科学に帰属させても不思議ではありません．
ブラックボックスとしてAIが用いられる現代では，現象の数学モデルを作ったり，得られた解析結果を解釈するのは，正しい読解力が必要であると思います．解釈次第でとんでもない結果も恣意的に導くことが可能ですから．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.03.14］ No.465
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
先週は、京都大学の教育数学研究集会3/6-9に参加しました．そこで，ChatGPTとDuolingoの話がでました．
皆様はご存じだったかもしれませんが、私はこれらを知りませんでした．
ウエブで探して使ってみるとどちらも非常に面白い．
ChatGPTとは対話型のAI，Duolingoはゲーム感覚で英語の学習ができます．

さて，今回のメルマガで取り上げるのは，デュードニーのタイル張りパズルです．これは；

正3角形を多角形に分割してそれらの全部品を組み合わせて正方形が作れます．このようなことのできる最小の分割数はいくつですか?
この問題は、1905 年 2 月 1 日と 8 日の問題で Henry Dudeney によって Daily Mail の読者に提示されました。
寄せられた何百もの回答の中で、正解は 1 つだけでした。4 つの部分で十分です。

https://etudes.ru/models/dudeney-dissection/
上記のリンクにあるアニメーションを見ると正解がわかります．しかし，この解の仕組みを見つけるのはなかなか難しいので，解説用の図を以下に２つ作りました．重ねた図形の2回回転対称性に注目すれば，非常に簡単に解けます．

Fig.1　正方形と正3角形は同一の面積です．2つ並んだ正方形と２つ並べた正3角形を，それぞれの中点の上で重ね合わせます．この点は2回回転対称軸があります．これだけでは，重ね方にまだ任意性がありますから，正3角形を連ねて作った帯の上側の辺，下側の辺が，それぞれ，２つ並べた正方形の右側の正方形の右側の縦の辺の中点，および，左側の正方形の左側の縦の辺の中点を通過するようにします．これらの条件は同時に満たされることは，2回回転対称性から明らかです．

Fig.1

Fig.2

Fig.2を見ると，正方形の中は、赤，黄，緑，青のパーツで構成されることがわかります．一方，正3角形は，赤，黄，グレーのパーツで構成され，正3角形と正方形は面積が等しいから，部品の面積について，グレー＝緑＋青　の等式が成立します．従って，正3角形も赤，黄，緑，青のパーツで構成できることがわかります．

https://etudes.ru/etudes/reuleaux-triangle/

■円以外に，定幅曲線はあるでしょうか？
上記のリンクの動画をみるとわかります。

ルーロー・フランツ（1829—1905）は、ドイツの科学者で、初めて（1875年）、機構の構造と運動学の主な問題を明確に定式化しました。工学的物体の美学の問題をとりあげました。
正3角形を考えましょう。各頂点で、辺の長さに等しい半径の円弧を描きます。この曲線はルーロー3角形と呼ばれます。これは定幅曲線であることがわかります。円の場合と同様に、2 つの接線を描画し、それらの間の距離を固定して回転を開始します。ルーローの３角形は常に両方の線に接しています。実際に、1 つの接点は常にルーローの三角形の「角」の 1 つにあり、もう 1 つは円の反対側の弧にあります。これは、この曲線図形の幅が常に円の半径、つまり元の正３角形の辺の長さに等しいことを意味します。

ルーローの3角形で作ったコンベア

奇数の正多角形で定幅曲線図形を作る

非対称の定幅曲線図形

マツダのロータリーエンジン

映写機の機構への応用

定幅曲線は無限に作れます
頂点の数が奇数の任意の正 n 角形は、ルーロー３角形が構築されたのと同様な方法で，定幅曲線を構築できます。イギリスの 20 ペンス硬貨は、7 角形の上に定幅曲線が描かれています。

非対称曲線も作れます。交差する線の任意のセットを考えてみましょう。セクターの1つを考えてみましょう。この扇形を定義する線の交点を中心として、任意の半径の円の弧を描きましょう。隣接するセクターを取り、それを定義する線の交点を中心にして、円を描きましょう。半径は、曲線の既に描かれた部分と連続して続くようにします。次々と続けていくと、この構造は、曲線が閉じて定幅になることがわかります。要証明

定幅曲線はすべて、周囲が同じです。同じ定幅の円とルーローの３角形を比べると、円は最大面積、ルーロー３角形は最小面積。周囲の長さは円でもルーロー3角形でも同じです。要証明

■ルーローの３角形は、数学界でよく研究されます。この幾何学図形は、力学で興味深い用途があることがわかりました。
マツダ RX-7です。ほとんどの量産車とは異なり、(RX-8 モデルと同様に)ヴァンケルのロータリーエンジンを使っています。内部の配置をみると、ローターに使われているのはルーローの３角形。これと壁の間に3つの部屋が形成され、それぞれが燃焼室になります。ここで青いガソリン混合物が飛散し、ローターの動きにより圧縮され、点火され、ローターを回転させます。ロータリーエンジンには、ピストンの場合にあるいくつかの欠点がありません。回転が直接軸に伝達され、クランクシャフトを使用する必要はありません。

■これが映写機に使われているクラムシェル機構です。モーター軸は均一に回転します。スクリーン上に鮮明な画像を表示するには、フィルムをレンズに 1 フレーム通過させ、止まり、再び急激に引き抜く、という作業を 1 秒間に 18 回行う必要があります。 . クラムシェル 機構が解決するのは、この動きです。これは、正方形に内接するルーロー３角形と、正方形が側面に傾かないようにする二重平行４辺形を使います。反対側の長さが等しいので、すべての動きの間、中央のリンクは底面と平行のままで、正方形の辺は常に中央のリンクと平行です。グラブの爪の動きは正方形です。

文献
Болтянский В. Г., Яглом И. М. Выпуклые фигуры. — М.—Л.: ГТТИ, 1951.
Радемахер Г., Теплиц О. Числа и фигуры: Опыты математического мышления. — М.: ОНТИ, 1936. — (Библиотека математического кружка; Вып. 10). — [Переиздания: 1938, 1962, 1966, 2020].

Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 84—85, 319—320.

「定幅曲線」の他の研究

・https://etudes.ru/etudes/drilling-square-holes/?ref=calso

・https://etudes.ru/etudes/wheel-inventing/?ref=calso

ビデオ⁠⁠「回転するルーロー3角形」で、定幅の特性形状について話します。正方形の穴を開けるのに役立つのは、定幅の最も単純な図形，ルーロー３角形です。この「３角形」の中心を特定の経路に沿って移動すると、その頂点はほぼ正方形を描きます。

https://etudes.ru/etudes/drilling-square-holes/

⁠得られた図の境界線は、角の小さな　部分を除いて、厳密にまっすぐになります。 線分を延長しコーナーを追加すると、正確に正方形になります。

上で説明した図形を得るには、ルーロー３角形の中心を、4 つの同一の楕円弧を繋いだ軌道に沿って移動する必要があります。楕円の中心は正方形の頂点にあり、半軸（正方形の辺に対して45°）は、$${k(1+1/\sqrt{3})/2}$$と$${k(1-1/\sqrt{3})/2}$$、ここで$${k}$$は正方形の一辺の長さ。

角を丸くする曲線も、正方形の頂点を中心とする楕円の弧で、その半軸（正方形の辺に対して45°）は、$${k(\sqrt{3}+1)/2}$$と$${k(1/\sqrt{3}-1)/2}$$の長さです。
角が丸まったために減少した面積は正方形の約2%です。
ルーロー３角形のドリルを使い、角がわずかに丸みを帯びた正方形の穴をドリルで開けることができますが、正方形の辺は完全にまっすぐです。

そのようなドリルを作ることは難しくありません。断面がルーローの三角形に似ていて、刃先はその頂点と一致します。
難点は、前述のように、ドリル中心の軌道が 4 つの楕円の弧で構成されなければならないという事実にあります。視覚的には、この曲線は円に非常に近いが、円ではありません。そして、工学で使用されるすべての中心がずれた異なる半径の円は、厳密に円の中で動きを与えます。

1914 年、英国のエンジニア、ハリー ジェームズ ワットは、そのような掘削する方法を考え出しました。表面的には、彼は、「ドリルが自由に浮いている」状態でカートリッジに挿入された、ドリルが入る正方形の形のスロットを備えたガイドテンプレートがあります。このようなカートリッジの特許は、1916 年にワット ドリルの製造を開始した会社が保有していました。

四角いガイド枠に配置されたルーロー三角形にドリルをしっかりと取り付けます。フレーム自体はドリルに固定されています。ドリル チャックの回転をルーローの３角形に伝える必要があります。
この技術的な問題を解決するのに役立つのは、通りを通過するトラックの底でおそらく何度も見たことがあるデザイン、カルダン シャフトです。このプログラムは、ジェロラモ・カルダノに敬意を表してその名前が付けられました。

ジェロラモ・カルダノ1501年～1576年
1541 年、皇帝カール 5 世が勝利を収めて征服したミラノに入ったとき、カルダノ医科大学の学長が天蓋の横を歩いていました。示された名誉に応えて、彼は王室の馬車に2本のシャフトのサスペンションを供給することを提案しました。そのようなシステムのアイデアは古代にまでさかのぼり、少なくともレオナルド・ダ・ヴィンチのコーデックス・アトランティックスには、ジンバルを備えた船のコンパスの図があります。このようなコンパスは、明らかにカルダノの影響なしに、16 世紀前半に広く普及しました。Гиндикин С. Г.「物理学者と数学者についての物語」

これでドリル​​の準備が整いました。合板のシートを取り、... 四角い穴を開けます！すでに述べたように、正方形の辺は厳密にまっすぐで、角だけがわずかに丸みを帯びています。必要に応じて、すりで修正できます。

文献
・Weisstein E. Reuleaux Triangle.
・Гиндикин С. Г. Рассказы о физиках и математиках. — М. : МЦНМО, 2006.
・Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 84—85, 319—320.

「定幅曲線（図形）」の他の研究

Круглый треугольник Рело / Этюды // Математические этюды Рассмотрим правильный треугольник (с равными сторонами). На к etudes.ru
Изобретая колесо / Этюды // Математические этюды Может ли повозка ехать без тряски по ровной поверхности на не etudes.ru
 

ジェームズ・ワットの蒸気機関の発明以来，円の動きを直線の動きに変換するヒンジ機構を構築することが課題でした．
色々なヒンジ機構を組み合わせてできる運動の軌跡の問題は，私の特に好きな分野です．円による反転を作図できるヒンジ機構は，
最も興味のあるものです．
この装置の仕組みは，https://etudes.ru/etudes/lipkin-inversor/?ref=calso にある動画を見れば理解されるでしょう．
証明は２つのペン先と反転円の中心は常に一直線上に乗りますから，この時出来る2つの相似な三角形に注目すれば容易です．

■説明が遅れましたが，円による反転の定義を以下に示します．

引用：美しい幾何学

■1864 年に、フランス軍の工兵部隊の将校であるポセリエ (Charles Nicolas Peaucellier, 1823-1913) の個人的な手紙で、反転円機構は初めて報告されましたが、彼はメカニズムの詳細を提供しませんでした。1868 年、P. L. Chebyshev の学生、Lipman リプキン (1846-1876) が、反転円機構を発明しました。彼の詳細な記事は 1870 年に出版され、1873 年になってようやく、リプキンの研究を引用したポセリエの記事が登場しました。

反転円機構（その美しさと優れた機械的特性をもつ特別なヒンジ機構）は、エンジニアリングで多くの用途が見出されています。
引用: https://etudes.ru/etudes/lipkin-inversor/?ref=calso

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.03.21］ No.466
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
ルーローの3角形という形があります．これは，正3角形の各頂点で正3角形の辺の長さを半径として円弧を描き，
これら３つの円弧で囲まれた形です．ルーローの3角形は定幅曲線です．
https://etudes.ru/etudes/reuleaux-triangle/　のサイトにあるアニメを見れば，ルーローの3角形の形や
それが定幅曲線であるという意味が理解できるでしょう．

円はもちろん定幅曲線ですが，ルーローの3角形も定幅ですから，
アニメにあるように，どちらもベルトコンベア用のコロに使えます．
ベルトコンベアは地面と平行な動きをしますが，ルーローの3角形のコロの中心の軌跡は波を打ちます．

奇数の正多角形からも同様な定幅曲線を作れ，定幅曲線の外周の長さは同じという性質があります．
また，非対称な定幅曲線も作ることができます．

最も単純な定幅曲線であるルーローの3角形をガイドに沿って運動させることで，いろいろな装置を作ることができます．
このアニメでは，マツダのロータリーエンジンと映写機の機構に使われていることが紹介されていて興味深い．
（注）ルーロー・フランツ（1829—1905）は、ドイツの科学者．幾何学図形と運動機構を研究しました．

ルーローの3角形は，正方形の穴をあけるドリルの歯にも利用されています．
1914年，英国のエンジニア，ハリー ジェームズ ワットは，そのようなドリルを考案し特許をとりました．
https://etudes.ru/etudes/drilling-square-holes/　のサイトにあるアニメを見れば，その仕組みをよく理解できるでしょう．

今回の記事は，幾何学概念である図形の運動（軌跡）が，色々な機械を作り出す例を紹介することでした．

今回の記事の内容の詳細や図は，数学月間の会のHPをご覧ください．
https://sgk2005.org/bbses/bbs_articles/view/232/98ee6233dfe52dd32de7602e9b3f82c0?frame_id=328
https://sgk2005.org/bbses/bbs_articles/view/232/d2d592f20b8032d1c0af70aea42240ed?frame_id=328

以下のサイトもとても参考になります：
http://ikuro-kotaro.sakura.ne.jp/koramu2/16479_t8.htm

自動車のワイパーが故障していても，普段なら気にならないのですが，雨の日には大変困ります．私はワイパーが故障している車を雨の日に運転して死ぬほど大変だったことを思い出します．ワイパーは疎かにできません．

２つのワイパーの扇運動は，１つのモーターの回転運動で生み出されます．
多関節ヒンジ機構の応用例に，自動車のワイパーがあります．
フロント窓にある2つのワイパーの同期方式には位相の異なる種々のものがありますが，ここでは２つのワイパーの動きが同位相であるようなヒンジ機構をとりあげます．
固定されたヒンジは，A,B,Cにあります。点Aの周りの回転運動は，このヒンジシステムにより，固定されたヒンジ点B，点Cを中心にした扇運動に変換されます．巧妙なヒンジ機構をご覧ください．

https://etudes.ru/etudes/windscreen-wiper/
上記サイト（Etudes）にある動画を見ると仕組みが良くわかります．

以下のサイトの図も参考になります．
https://book.etudes.ru/articles/wipers/

平面上の関節ヒンジ機構に関する数学的研究は、ジェームズ ワットによる最初の蒸気機関の発明で始まりました。 19 世紀、ロシアの偉大な数学者パフヌーティ・ルヴォヴィチ・チェビシェフは、これらの研究において重要な役割を果たし、私たちの時代に続いています。

21 世紀には、「署名定理」が証明されました。どんな署名でも、この署名を望むだけ正確に複製する平面のヒンジ機構が存在するという定理です。

署名定理には、工学と設計において多くの実用的な応用があります。 鋳造部品の製作や精度の高い動きのロボットの製作など、複雑な形状を精密に再現できる機構の製作に使用できます。 また、この定理は、メカニズムと機械の動作理論の重要な要素です。

チェビシェフは色々な機械のヒンジ機構の動作軌跡の研究をした。彼は初の歩行機械の発明を行った。宇宙ロケットの制御でも、ソ連はコンピュータは遅れているが、機械的制御が進んでいると言われた時代があった。これは、チェビシェフ以来の伝統によるものだ。
歩行機械の仕組みがどのようなものか、以下のサイトにある動画を見ると良くわかります．
円運動をキノコの帽子型（歩行する足の軌跡）に変換する「ラムダ・メカニズム」がミソです．キノコの帽子型の軌跡をたどる足をつければできる．

https://sgk2005.org/bbses/bbs_articles/view/26/a8442c2c249394d42c8ad839c315e51a?frame_id=76

音は空気の振動で，音の高低は振動数（周波数）で決まります．音楽で使う音は，周波数の（離散的に）決まった幾つかの音です．つまり，2つ以上の音が快く調和して聞こえるのは，構成要素であるそれぞれの音の周波数の比ができるだけ簡単な整数比であることが必要で，そのような音の集合の中を音の高さ（周波数）の順に並べたものが音階です．２つの音の周波数比が最も簡単なのは，２倍あるいは1/2倍で，そのような2つの音の比は「オクターブ」といいます．1オクターブの中に半音12個の音を選ぶと，それらから選んだ2音の周波数比ができるだけ簡単な整数比になるようにできました．これが音階で，これは大変な発明だったと思います．単音の集合としての音階を次の２つの公理を満たすとして，数学的に定義しましょう：

音階の中に周波数 $${f}$$ の音が存在すれば，周波数 $${2f }$$と $${f/2}$$ の音は常に音階に存在する．（オクターブの存在）

任意のメロディーを，音階中の任意の音から始めることができる．（移調が可能）

このような2つの公理で定義された音階は，平均律といいます．平均律音階{$${f_n}$$}は，公比$${q}$$（半音階）の等比数列であることがわかります．

2音の周波数比が簡単な比であれば純粋な和音になりますが，厳密にいえば，平均律にはオクターブ以外に純粋な和音はありません．つまり，平均律音階の音はオクターブ以外は，簡単な比というのは近似的なことで，厳密ではありません．完全5度 (全音３つと半音１つ）とは，周波数比が 3/2 の 2 音のことで，例えば，C(ド)-G(ソ)，G(ソ)-D(レ)，D(レ)-A(ラ)，A(ラ)-E(ミ)などの間隔です．純正律ではこれらの周波数比は3/2にできます．

1オクターブは12の半音で構成されますから，平均律では$${q^{12}=2}$$，すなわち，$${q=2^{1/12}＝1.0595}$$　[2の12乗根]で，$${q}$$は半音に相当する公比．　平均律の完全5度音程の周波数比は　$${q^7}$$です．したがって，平均律の完全5度では $${q^7=2^{7/12}=1.4983...≠3/2}$$　となり，純正律の3/2=1.5　とは，ほんのわずかですが違います．

同様に， 完全4度（全音２つと半音1つ）の音程，例えば，E(ミ)-A(ラ)，A-D，D-G，G(ソ)-C(ド)，C-F，B-Eの周波数比は，純正律では4/3にできますが，平均律では4/3とわずかに異なります：$${q^5=2^{5/12}=1.3348...≠4/3}$$．4/3=1.3333ですから，この差もほんのわずかです．

バイオリンには，G,D,A,Eの４弦があります．調律はA線を440（あるいは442）Hzに合わせた後，それぞれの弦を完全5度の間隔に合わせるので，純正律になっています．
ギターは最も低い第6弦Eから第3弦Gまでと，第2弦Bと第1弦E間を完全4度の間隔に，第3弦と第2弦間は長3度に調弦するそうですが，純正律をつくれます．
１オクターブを12 のステップに均等分割することは，ピアノの鍵盤を作るには必要で，ピアノは平均律ですが，平均律は純正律の非常に良い近似になっています．

以下の表の純正律の音の周波数は，オクターブ，および，完全5度と完全4度の音程が簡単な整数比にするという条件で計算しました．

-----

参考文献

https://note.com/sgk2005/n/nc5534e950cfa

https://www.mathedu.ru/files/news/books/matematicheskaya_sostavlyayushhaya_2019.pdf

http://www.enjoy.ne.jp/~k-ichikawa/junseiritsu.html

ロシアの数学月間

数学月間懇話会（第19回）2023のお知らせ

日時●7月22日，13:30ー17:00（開場13:00）
場所●東大駒場キャンバス，数理科学研究棟002教室

テーマ●新型コロナの数理モデル研究について
総合司会●稲葉寿（東京学芸大）
●パンデミックで活躍する数理モデル；国谷紀良（神戸大学大学院システム情報学研究科）
●新型コロナウイルス感染症のデータサイエンスと政策科学；土谷隆（政策研究大学院大学）

主催●NPO法人数学月間の会（理事長：岡本和夫）

ーーーーーーーーーーーーーーーーー

 会場参加費●1,000円（ただし，学生・生徒，および，当会会員は無料）．
会場定員のため，事前に会場参加登録をしてください．
登録方法●氏名，メールアドレス，会員種別 を以下のウエブサイトに登録する：
参加者数が定員になり次第，受付は停止します．
リモート参加（無料）をご希望の方は，同ウエブサイトで事前にリモート参加登録をしてください．
数学月間の会ウエブサイト●https://sgk2005.org/  
最新の情報は，上記ウエブサイトでご確認ください．

問い合せ先●sgktani@gmail.com
 ***************************** ************************

上記ウエブサイトはロシアの多面体模型のウエブサイトです。そのサイトの主旨は次のように語られます：科学はショーとして提示できますが，数学のショーは難しい。数式は一般の興味を惹かないからです。数学のショーを成り立たせる有力テーマは，多面体です。多面体の紙模型は，空間の性質や対象物の幾何学を認識させるのに有効です。 紙模型は，曲面でなく平面とエッジで構成され，厚紙で作れます。

2022年11月26日（数学まつり第2回）に，我々も「多面体を作ろう」を実施しました。このときは，正12面体と星型小12面体を取り上げました。これらの多面体を作り，立体の体積や，その立体のを分割して幾何学構造を理解するワークショップでした。小梁修（osa工房）による立体模型です。

数学まつり第2回の内容は，以下のサイトで見ることができます：

https://sgk2005.org/bbses/bbs_articles/view/24/618d4f4e4684317b3551a483d4f99fc5?frame_id=37

20世紀の科学的発見で，最も偉大な業績とされるべきものは何でしょうか．おそらく，量子力学の誕生でしょう．量子力学は，ミクロの世界（原子や粒子のレベル）で起こることを説明するだけでなく，トランジスタやレーザー，超伝導や原子工業など，新しい技術を生み出したのです．ちなみに，数学者は，量子力学を記述するための適切な数学ツールを開発し，量子力学に大きく貢献しました．水素原子に関する最初の量子方程式は，シュレーディンガーの依頼で数学者ワイルが解いたのだ．同様の問いを19世紀の科学についてすれば，答えは明白．マクスウェルの方程式を中心とした電磁気学の誕生である．もちろん，ここでも熱力学や統計力学の創始などの他の目覚ましい成果も忘れてはならない．しかし，マクスウェルの方程式によって電気を「制御」する時代が到来し，蒸気の時代から電気の時代に引き継がれたのだ． 電気力学の分野では，マクスウェルに先立ち，エルステッド，アンペール，そしてもちろんファラデーという優れた先達がいた．彼らは，電気力学の基本法則を実験的に確立していた．彼らは，誘導電流，磁力線，自己誘導現象などを発見した．しかし，この分野で最も印象的な功績は，「場」の概念を導入したことだろう．電気や磁気は，いわば空間のすべてに「浸透」している．空間に「プローブ」としての電荷や電流がなくても，電場や磁場は空間に存在しているのだ．電場や磁場という２つのベクトル場は，空間座標および時間にも依存する．マクスウェルは，実験結果をもとに，これらの場が従う方程式系を導き出した．この方程式ができるまでの道のりは，実に長いものだった．というのも，適切な力学的アナロジーを見つけるのに長い時間がかかったからである．トムソン（ケルビン卿）とマクスウェルを導いた主なアイデアは，理想的な非圧縮流体の渦流のアナロジーでした．電場や磁場は，流体で質量のない物質，つまり最も希薄なエーテルであり，空間全体を満たし変動するものと考えられていた．

$${\displaystyle \frac{ \partial H}{ \partial t}=-c  \textrm{rot}E}$$, $${\textrm{div}H=0}$$

$${\displaystyle \frac{ \partial E}{ \partial t}=c  \textrm{rot}H}$$, $${\textrm{div}E=0}$$

*訳者注）$${ E(x,y,z,t), H(x,y,z,t)}$$は，それぞれ電場ベクトル，磁場ベクトルで，空間の座標と時間の関数です．$${ \textrm{rot}E}$$や$${ \textrm{div}E}$$は，それぞれ，ベクトル場での回転，発散と言われる演算でベクトルを出力します．

このアイディアは，有名な数学者デカルトに遡る．彼は同様の基礎の上に物質の渦理論を構築しようとしました．機械的なアナロジーは発見的な目的を果たしたが，現代の電磁気学の教科書には今やその痕跡すらない．しかし，方程式そのものに，回転rotと発散divという形で，渦と非圧縮性に関する響きが残されています．マクスウェル方程式の2つの重要な結果は，電気通信技術の発展と時空に関する現代物理概念の形成に基本的な役割を果たしたました．これにより，光の電磁気的性質が明らかになり，1888年，ヘルツは電磁波を発生させる方法を発見した．その直後，ポポフやマルコーニがヘルツのアイデアを利用して，遠距離の無線通信を実用化した．マクスウェル方程式のもう一つの重要な帰結は，相対論的力学である．ポアンカレがローレンツ群と呼んだ4次元時空の線形変換の10個のパラメータ群に関して，マクスウェル方程式がその形を保つことが判明したのである．一方，3次元空間におけるニュートンの第2法則の方程式は，同じく10個のパラメータに依存するガリレオ変換群を許容している．相対論的力学の基本的な考え方は，力学と電気力学を調和させるために，ガリレオ群をローレンツ群に置き換えるべきだというものであります．相対論的力学の考え方は，現代の空間と時間の理解を形成し，マクスウェル方程式は電気力学の数学的基礎となっただけでなく，世界の物理的全体像の整合性を維持することを可能にしたのです．

引用：МАТЕМАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ Редакторы-составители Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнинp.30-31

アイルランドの首都ダブリンのブルーム橋には，「1843年10月16日，この場所で，ウィリアム・ローワン・ハミルトン卿が散歩中に，天才的な洞察力で，四元数の乗法を決める公式、$${i^2 = j^2 =k^2 =ijk =-1}$$ を発見し，橋の石に書き込んだ」という石版がある． この規則は，実数の4倍体である四元数（クオータニオン：ラテン語でクオータとは「4」という意味）の掛け算を決定することができる．
四元数$${q =(a; b; c; d)}$$は，分解$${q =a +bi +cj +dk}$$と見なすことができる．ここで$${i, j, k}$$はブルーム橋の公式の「虚数単位」である．現代に至り，突然，人間とともにクォータニオンが宇宙へ飛び立った．1960年代末，宇宙船の設計者は，技術的に宇宙船にコンピュータを搭載できるようになった．地球の管制センター，宇宙飛行士とともに，コンピュータは宇宙船をコントロールしなければならない．コンピュータに求められる条件は，耐衝撃性，軽量性，高速動作，十分なメモリなどの非常に厳しいものだった． コンピュータに求められる主な仕事は，宇宙船の座標と方位を計算することで，当時，方位表現の基本的方法として，オイラー角を使う方法と回転行列法の2つがあった．しかし，いずれも実用上大きな欠点がある．第一の場合は，オイラー角による船の位置の記述が縮退してしまい，方位制御がうまくいかなくなるという危険性が生じる．また，百分の一秒，千分の一秒単位で情報を更新する必要が，軌道投入，宇宙船の降下などのアクティブな局面で必要だが，当時の計算機では対応しきれない．
こうした問題を回避する解決策を見つけたのは，中央実験機械製作設計局（S.P.コロレフの旧ОКБ-1）のスタッフたちだった． 科学者とエンジニアは，3次元空間の動きを四元数という「4次元」の言語で記述することで，オンボードコンピュータに実装できる計算しやすいモーションコントロールシステム（СУД）の開発を可能にした．3次元空間の動きは，四元数の構成要素である通常の数への代数演算（加算と乗算）として表現できる．四元数のСУДでは，記述の縮退の危険や，三角関数の値を計算し続けるためにコンピュータに負荷をかける必要がない． СУДのコースは宇宙飛行士の宇宙訓練の一環であり，すべての候補者が四元数を勉強しなければならない． 四元数による姿勢パラメータの表現は，明快さに欠けるので，通常，宇宙飛行士は訓練中に何度もリハーサルを行い，四元数を含むパラメータの制御値を暗記している． 宇宙で最も困難で責任のある作業のひとつに宇宙船のドッキングがあるが，軌道上での異常事態の1つで，四元数を「読む」能力が役に立ったエピソードを紹介しましょう．
3度目のミッションに臨むアレクサンドル・セレブロフ宇宙飛行士は，アレクサンドル・ビクトレンコとともにミール宇宙ステーションでクヴァント2号モジュールを実施する機会を得ました．自動ドッキングプログラムはすでに開始されていました．
その時，突然オンボードコンピュータのメモリがオーバーフローし，パワージャイロ（ジャイロダイン）が停止しました．手動でのアプローチとドッキングに切り替えなければならなかった．ビクトレンコはステーションの姿勢を制御し，セレブロフはスクリーンに映し出されるプロセスパラメーターを監視していた．
四元数制御システムは，その効率の良さから国際標準となり，特に国際宇宙ステーションで使用されている．3次元グラフィックスやゲーム制作のための重要なツールでもある．

引用：МАТЕМАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ 
Редакторы-составители Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин
 p.24-25

最も抽象的で思索的な科学理論が，しばらくして（時には相当な！）非常に実用的な事例の基礎となることがあり，たった一つの応用からの恩恵が，科学史におけるオタク数学者のコストの何倍にもなる...ここに多くの例の一つを挙げます．
19世紀前半．カザン大学学長ニコライ・イワノビッチ・ロバチェフスキーは，「仮想幾何学」を提案する．ユークリッドの2千年の幾何学が存在していたというのに，この幾何学では三角形の内角の和が180度にならない．狂気の沙汰としか言いようがない．同じ頃，ドイツの偉大な数学者カール・フリードリッヒ・ガウスも同様のアイデアを思いついたが，その成果を発表するのを恐れていた．ドイツの数学者ベルンハルト・リーマンが，ユークリッドの幾何学とロバチェフスキーの幾何学の両方を含む一般理論を構築し，数学の純粋な抽象部分であるリーマン幾何学が登場した．アルベルト・アインシュタインは，リーマン幾何学に基づく特殊相対性理論（STR），一般相対性理論（GTR）を完成させる．核反応の計算はすべてSTRに基づいており，GTRは長い間，美しいが実生活には役に立たないおもちゃと思われていた．GPSナビゲーターは，ナビゲーションシステムをサポートする軌道上の衛星に非常に正確な時計を要求する．衛星の速度が速いため，軌道上の時計は地球上とは異なる動きをするのです．しかし，それ以外にも，この種のGTR効果には，時空の非ユークリッド幾何学に関連した特有のものがある．もし，ある瞬間にこのような効果の考慮を「オフ」にすると，1日の間にナビゲーションシステムの表示に約10kmの誤差が生じます． つまり，我々の空間がわずかに非ユークリッドであることを一瞬でも忘れると，溝やビルの壁にぶつかることが確実なのです．

Паршин Алексей Николаевич

p.12

現代の生物学では，大きなDNA分子を本のように一文字ずつ「読む」ことはまだできません．その代わりに，科学者はゲノムのどの部分から切り取られたのか分からない短いDNA断片の配列を解読しています．このような大量のDNA断片からゲノムを組み立てるプロセスをシークエンシング（sequencing）と呼びます．
 
10億個のジグソーパズルを組み立てるようなもので，3世紀以上前に開発された数学的理論に基づいている．

18世紀前半．
大数学者レオンハルト・オイラーが「ケーニヒスベルクの橋の問題」を解決し，川と二つの島に囲まれたケーニヒスベルクでは，現存する7つの橋をそれぞれ一度だけ通過して出発点に戻ることはできないことを証明しました．このようなグラフの経路はオイラーサイクル（Eulerian cycle）と呼ばれる．オイラーサイクルの存在問題は，グラフの各頂点から偶数個の辺が出ているか，奇数個の辺の出る点がある場合は２つという，非常に単純な判定基準を持つ．オイラーサイクルを見つける問題（ZEC）は，非常に大きなグラフであっても，かなり速く解決される．

 19世紀後半．
数学者William Hamiltonは，ZECに似た問題として，グラフの各頂点を1回だけ通る閉じた道（ハミルトンサイクル）を見つける問題（ZGC）を考えた．

20世紀後半．
ZECとは異なり，ZGCは効率的な解法アルゴリズムが知られていない問題の代表格であることが立証された．

20世紀末から21世紀にかけて．
1990年代半ばに細菌ゲノムが，2001年にヒトゲノムの塩基配列が決定された．この作業は，スーパーコンピューターのアルゴリズムがZGCをベースにしていたため，時間とコストがかかるものだった．この10年間で，数学者はZECに関連した高速アセンブリー法を開発した．
そして 現在，生物学者たちは，哺乳類の各生物種のゲノムを組み立てるという基本的な課題に取り組む準備を進めている．
 
Певзнер Павел Аркадьевич
p.13

数学は，科学，技術，経済など多くの領域で重要な役割を果たしています．
問題の定式化と解決，予測の作成，モデルの構築，新しい技術の開発などに役立ち，私たちの理解と世界の変革の可能性を大幅に拡大しています．
ーーーーーーーーーーーーーーーーーーーーーーーーーー
生物学では，生物を研究します． 天文学では，天体を研究します． 化学では，物質の種類とその相互変換を研究します．私たちは現実世界で何かを観察し，測定し，特定の条件下で特殊な実験を行い（ただし，天文学では行いません），それらの結果をもとに説明的なパラダイムを構築します．それは科学の進展の重要なマイルストーンとなります．しかし，数学では，何を研究しているのでしょうか？その答えの1つは，実際の対象であるかのように扱えるアイデアを研究しているということです．

それぞれのアイデアは，利用される可能性のあるあらゆる文脈でその形を保持するために十分に堅牢である必要があります［訳者注：数学はどんな分野や局面でも，独立して適用できるということ］．同時に，それぞれのアイデアには他の数学的なアイデアとつながりを持てる豊かなポテンシャルが必要です．最初のアイデアのコンプレックスが形成されると，これらのアイデア間の関係も数学的な対象となり，抽象の巨大な階層の最初のレベルを形成します．この階層の最下部には，物事自体の思考イメージやそれらを操作する方法があります．驚くべきことに，高レベルの抽象概念さえも何らかの形で現実を反映することがあります．たとえば，物理学者が得た世界の知識は数学の言語でしか表現できません．
現実世界の理解に数学がどのように応用されるかを理解するためには，数学をモデル，理論，およびメタファー［隠喩］の3つのモードで考えると便利です．
数学的モデルは，特定の現象のクラスを定量的または定性的に説明しますが，それ以上のことを主張することはありません．
定性的なモデルは，安定性や不安定性，アトラクター（初期条件に依存しない平衡状態），相転移（複雑なシステムが2つの相または異なるアトラクターを持つ2つの盆地の間の境界を越えるときに起こる現象）などの現象の理解に役立ちます．
理論とモデルの違いで最も重要な点は，理論の主張は広範であることです．理論を創造し続ける力は，物質的な世界とは独立して存在し，数学的な道具でしか認識できないものです．
数学的比喩は，それが認知のための道具であると主張する場合，ある複雑な現象群をある数学的構成要素に例えることができると仮定します．
数学理論は，作業モデルを構築するための招待状であり，数学的隠喩は，私たちが知っていることに思考を誘うものである．もちろん，この区分は厳密でも絶対でもありません．
構造的な観点から見ると，数学の発展は言語の発展と並行して行われます．数学と言語の両方が，現実（客観的に存在する範囲で）と観察可能なものとの間の橋渡しとなります．すなわち，現実が意識にどのように反映されるかを示します．

私は，科学，特に数学が私たちの文明の推進力ではないと信じています．科学のおかげで私たちは地図や機械を持っていますが，科学は私たちの行くべき方向や行くべきでない場所を決めるものではありません．科学が決定できると考えることは，知識を魔法の一形態と見なす古代的な認識の時代に戻ることになります．
［訳者注：すべてが不確実な世界．トランスサイエンスの時代に，科学や数学で決定できると思うのは幻想でしかない］
その時代では，日食を予測したり，未知の結果がどのように解決されるかを予見した人は，象徴的な表現を操作して出来事を引き起こす魔術師と見なされました．実際には，思考の生物学的な機能は，自発的な反応を引き起こすことではなく，それらを防ぐことにあります．
かつて，巫者やシャーマンは，部族の居住地や出来事，住民などを直接的にではなく，可能性の空間を記述していました．巫者は実用的な問題の解決には関与せず，それは部族の指導者が行っていました．ただし，指導者は自身のシャーマンやアドバイザーに耳を傾け，行動の選択において彼らの助言を受けていました．
有名な古代の例として，リュディア王クロイソスの物語があります．彼はペルシャとの戦争に備えてデルフォイの神託に助言を求めたところ，「クロイソスよ，ギリシャを渡るならば，偉大な王国を破壊するだろう」と答えられましたが，具体的にどの王国を指しているのかは明確にされませんでした．クロイソスはギリシャを渡り，結果として敗北しました．
［訳者注：ギリシャはエーゲ海をはさんでリュディアの対岸にある．デルフォイの神託とは，巫女が神懸かり状態となり，予言の神アポロンの言葉を語るものである］
数学は現実世界の位相空間や可能性の空間を記述し，この位相空間における可能な軌跡を決定する法則や，特定の位相軌跡を選択するために必要な条件を研究します．
Манин Юрий Иванович
МАТЕМАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ, p.40-41
応用：文明
数学： 数学一般

数学コンポーネント（あるいは，数学要素）МАТЕМАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯという本を紹介したことがあります．この本は，ロシア科学アカデミーのステクロフ数学研究所から出版され，2015年に2017年に受賞しました．今見ているのは，2019年に大幅に増補された367ページの電子版です．この本の特徴は，現代社会で使われている技術がどのような数学とかかわりがあるかを解説していることです．違和感のある書名は，応用例とそこで使われる数学要素ということを表しているようです．
どのような応用事例があり，どのような数学要素があるのか整理し，結果を一覧できるようにしました．応用例の後ろの（）内の数字は，本のページを表しています．１つの応用例に，複数の数学要素が対応している場合があります．全部の表を作ると膨大になりますので，数学要素「確率と組合せ」のところだけを表にしました．

解析
コンピュータ断層撮影（20）；地図上の経路長の決定（64）；
滑らかな線（80）；実用的な無限大（94）；うるう年（160）；
音楽とモジュロ演算（202）；航空機工学の数学的翼（208）；
造船の数学（212）；信号処理：波からバーストまで（228）；
水平線までの距離（308）；地図投影（342）

初等幾何学　解析幾何学
ロバチェフスキーの "狂った"幾何学からGPSナビゲーターまで（12）；
クォータニオンが宇宙へ（24）；コーナーリフレクター（44）；
パラボラアンテナ（46）；腎臓結石を砕く（48）；
カーブの曲がり方（52）；鉄道車両の車輪対（53）；
自動車の前輪操舵（54）；ねじ継手（56）；地平線までの距離（60）；
飛行機の飛行軌道（61）；地図からの経路長の決定（64）；
地図の折り畳み（65）；最短経路（66）；地下鉄の駅の深さ（67）；
遠近法（68）；A4フォーマット（70）；パノラマブック（74）；
蜂の巣のハニカム（76）；定幅図形（84）；
プラスチックカップの幾何学（86）；
シュホフの塔（88）；チップス（90）；ピザ･スライス（91）；
オレンジの皮の体積(92)；円錐フルート(93)；三次元世界の方位(106)；
衛星ナビゲーション（110）；北極星（112）；虹（118）；
色空間（122）；イメージの拡大縮小（128）；
不可能図形（129）；装飾文様（130）；地図投影（136）；
万華鏡（150）；サッカーボール（154）

幾何学と位相幾何学
ロバチェフスキーの「狂った」幾何学からGPSナビゲーターへ（12）；
音波の伝播（14）；コンピュータ・トモグラフィー（20）；
グラフェン（32）；回転曲線（52）；歯車（58）；飛行機の軌跡（61）；
遠近法（68）；プラスチックコップの幾何学（86）；
ピザ･スライス（91）；地図投影（136）；サッカーボール（154）；
幾何学的結晶学（214）；ゆがんだ世界（222）

論理学．数学の基礎
可能性を記述する言語としての数学（40）；高速算術（166）；
数学と論理（242）；複雑性理論（262）

代数学
四元数列は宇宙へ(24); 暗号技術への数学の応用(36)；
三次元世界における方位（106）;
イメージ算術（126）；装飾文様（130）；
≪15≫のゲーム（148）；万華鏡（150）；高速算術（166）；
音楽とモジュロ演算（202）；幾何学的結晶学（214）

数論
暗号技術への数学の応用(36)；
周期蝉(79); 算術トリック(146); 高速算術(166); 複素数論(262)

微分方程式．数理物理の方程式．最適制御理論
音波の伝播（14）；最適制御（26）；力学の数理モデル（28）；
電磁気学の方程式（30）；理論物理学と現代数学（34）；係留（62）；
純粋区間（98）；パターンはどのように起こるか（178）；
航空機工学の数理翼（208）；定幅図形（319）

力学
交通流の数理（18）；力学の数理モデル（28）；歯車（58）；
三次元世界における方位（106）；航空機工学の数理翼（208）

確率論．数理統計学
故障の検出（22）；暗号技術における数学の応用（36）；
量子コンピュータ科学（38）；短い待ち行列の選択(50);
テストの精度 (51); ランダムウォーク (170)；
パターンはどのように起こる（178）；言語統計学（186）；
音楽とモジュロ演算（202）

離散数学
ケーニヒスベルクの散策からゲノムの再構築まで(13);
インターネットの数学(16); 交通流の数学(18)；
暗号技術における数学の応用(36)；滑らかな線（80）；≪15≫ゲーム（148）

今年も数学月間（7/22～8/22）の暑い夏が始まります．
この3年リモート開催ばかりでしたが今年は集会を実施します．
covid-19の第9波が進行中で，covid-19の研究会でクラスターが起きてはしゃれになりません．
もちろん，定員に余裕をもって安全に留意し開催します．

リモートに慣れて，すっかり出不精になったので，暑い夏に外出するのは，今年はことのほか大変です．
会場には自販機はありませんので，熱中症にならないように水筒持参は必須です．
集会でもリモートでも参加できますので，どうぞご参加ください．
ただし，定員内人数であることの把握のため事前参加登録は必要です．

■講演会2つを紹介します．
――――――――――――――――――――――――――――――――――
（１）数学月間懇話会（第19回）
日時●7月22日，13:30ー17:00（開場13:00）
場所●東大駒場キャンバス，数理科学研究棟002教室
テーマ●新型コロナの数理モデル研究について
総合司会●稲葉寿（東京学芸大）
●パンデミックで活躍する数理モデル；国谷紀良（神戸大学大学院システム情報学研究科）
●新型コロナウイルス感染症のデータサイエンスと政策科学；土谷隆（政策研究大学院大学）
主催●NPO法人数学月間の会（理事長：岡本和夫）
詳細や参加登録方法は https://sgk2005.org/ にあります．
QRコード１
リモート（webex）で参加する場合のURLは以下です（リモート参加登録を済ませてください）：
QRコード２
――――――――――――――――――――――――――――――――――
（２）日本学術会議公開シンポジウム
「数学教育の変遷～数理・データサイエンス・AI時代における数学教育の変革及び女性人材の登用に向けて」

日時●8月2日，13:00-17:00

NPO法人数学月間の会は，この公開シンポジウムを後援しています．
詳細や参加登録は以下のサイトをご覧ください．
https://www.scj.go.jp/ja/event/2023/346-s-0802.html

QRコード３
引用したQRコードやポスターを見るには、https://sgk2005.org/ あるいは，
https://note.com/sgk2005/n/n49ebb919fef6?fbclid=IwAR1m6ShaaQbSdi4ZuS-F4feALktVC-uZxlA9TzDPvt_AJ4soRTbGoOsjm3c
などをご覧ください．

日本の「数学月間」は7/22ー8/22です（22/7≒πと22/8≒eに因みます）．日本の数学月間は2005年に始まりました．米国の数学月間は1986年に始まりました．米国が1986年に，上院の共同決議に基づくレーガン大統領宣言で，国家的な行事としての「数学月間」MAMを決断した背景には，国民の数学力が低下し，米国の産業力も低下するとの焦りがあったといわれます（小林昭七『顔をなくした数学者』）．
日本も，今日，同様な状況にあり，国家的行事の「数学月間」が望まれます．

1950年～1980年の日本は，Dr. Demingの品質管理手法をTQCやQCサークルに発展させ，生産性向上を達成しました．
米国で無名だったDr. Demingを1950年に日本に招聘し8日間の第1回セミナーを実施したのは，日科技連，日本企業の先見の明でした．1951年にはデミング賞が創設され，Dr. Demingの統計学に基づいた品質管理手法が日本企業に普及していきます．「PDCAサイクル」などという言葉をどこかで聞いたことがおありでしょう．

当時の米国企業では，フレデリック･テーラーの競争原理が支配していました．品質より生産量を競い，作業能率を重視しました．四半期/半期の損益報告を重視し長期的な展望を持てない欠点がありました．
これに対して，ウィリアム･エドワーズ･デミングは協力によってもたらされるwin-winの状況を基礎に置きました．顧客が望むものは信頼できる品質であり，何事も目的意識をもって行動すれば必要な結果はすべて得られると解きました．
これは，私には，数学学習の前に，その数学の応用を知り目的を明確にするという数学月間の心に重なって見えます．

統計学者デミングの品質管理手法に，米国に先んじて注目したのは日本企業の叡智でしょう．協力精神に基づき，終身雇用，年功序列賃金，労使協調などの導入された制度は日本に合っていました．
品質管理の統計的手法は，マネージメントにも全社的に展開されTQC，日本企業の躍進の時代をもたらしました．私が新入社員で入社した1970年には，工場では皆ZDのバッチを付けていた（ZD運動）ことが思い出されます．
その後に続く，QCサークルなどの活動で目的を明確にして協力する体質が作られて行きました．

1980年になると米国では日本に学べとばかりに，NBC放送は, 1980年， If Japan can... Why can't we?というドキュメンタリーを放送し，米国でもDr. Demingのセミナーが展開されるようになります．
しかし，この時，これに留まらず，もう一歩進め，数学全般の啓蒙「数学月間」MAM活動へと発展させたのは，一歩先に行く米国の叡智でした（竹内の証言）．
こうして，米国の「数学月間」の開始を告げるレーガン大統領宣言は1986年に出されます．米国の数学月間は1986年（1999年までは週間）に始まり1999年に月間（4月）になり，2017年からは数学・統計学月間になりました．この潮流は米国の叡智そのものと言えるでしょう．現代社会は統計学に依存しています．そして，数学は理工学だけでなく，人文科学にも浸透して来ました．統計学は，特に，人文科学でも重要なツールです．

表題テーマの「数学月間懇話会（第19回）」を，2023年7月22日，13:00-17:00，東京大学数理科学研究科棟002教室にて実施しました．主催はNPO法人数学月間の会（理事長：岡本和夫）です．
以下の２つの講演（それぞれ90分）により構成され，総合司会を稲葉寿（東京学芸大）が行いました．（注）2020年の数学月間懇話会で実施した講演：感染症の数理モデル，稲葉寿（東大）も参照

(1)　パンデミックで活躍する数理モデル：國谷 紀良（神戸大学大学院システム情報学研究科）
(2)　新型コロナウイルス感染症のデータサイエンスと政策科学；土谷隆（政策研究大学院大学）

今回は，講演（１）を紹介します．講演（２）は次号で紹介します．
（注）2021年の数学月間懇話会で実施した講演：新型コロナウイルス感染症と統計数理， 土谷隆（政策研究大学院大学）も参照

講演（１）國谷 紀良（神戸大学大学院システム情報学研究科）
■まず，感染症の数理モデル（集団内での感染症の流行を表す微分方程式など）の研究史の概略紹介がありました．
SIRモデルとは，集団が３つの部分集団$${S，I，R}$$で構成されるとして，それらの集団の増減を微分方程式で表したものです．ここで，$${S}$$は，感受性（感染可能性）のある集団，$${I}$$は，感染中で他人を感染させる力のある集団，$${R}$$は，回復集団（再感染はしないと仮定）です．
感染率$${\beta}$$，回復率$${\gamma}$$とすると，SIRモデルの基本微分方程式が得られます：
$${S'=-\beta SI}$$,    $${I'=\beta SI-\gamma I}$$,    $${R'=\gamma I}$$
これは，ケルマックとマッケンドリックが1927年に発表した論文「感染症流行の数学的理論への貢献」によります．
感受性のみの集団に侵入した１感染者が算出する新規感染者数を「基本再生産数」$${R_0}$$といい，$${R_0>1}$$のときに流行が起こります．
感染症の種類，ウイルス株，国や地域によって$${R_0}$$は独特の数値を持ち，麻疹は12-18，インフルエンザで1.2-1.4ですが，covid-19では2.4-3.4でした．　

果樹園における感染症の伝搬を，格子点上の隣接する木から感染する確率を$${p}$$として，モンテカルロ法によるパーコレーションの研究をし，流行の臨界値を研究したのは，ブロードベントとハマーズリー（1957）でした．

SEIRモデルは，感受性$${S}$$の集合から感染$${I}$$の集合に移る間に，潜伏期$${E}$$の集合を入れて得られます．このとき，$${E}$$から$${I}$$への遷移確率$${\varepsilon}$$を入れます．微分方程式は次のようになります：
$${S'=-\beta SI}$$,   $${E'=\beta SI-\varepsilon E}$$,   $${I'=\varepsilon E-\gamma I}$$,   $${R'=\gamma I}$$

SEIRモデルを日本の流行初期(2020/1/15)～2/29）のデータに適用して，基本再生産数$${R_0}$$を推計すると，$${R_{0}=2.6}$$が得られました．

■緊急事態宣言などの介入の効果検証
不要不急の外出自粛，飲食店，映画館，デパートなどの休業，テレワークの推進などが行われ，「接触8割減」が提唱されました．

第1回目緊急事態宣言（2020/4/7-5/25）では，期間中に実効再生産数が減少し，期間の最後で最小値になり，期間終了解除後にリバウンドが現れました．感染率の減少割合$${r^{*}=0.86}$$，　実効再生産数$${R_{c}=(1-r^{*})R_{0}=0.36}$$

■無症候感染を含むSEIRモデルは，次のようになります：
$${S'=-(\beta_{1}E+\beta_{2}I)S}$$,   $${E'=(\beta_{1}E+\beta_{2}I)S-\varepsilon E}$$,   $${I'=\varepsilon E-\gamma I}$$,   $${R'=\gamma I}$$

SRIRモデルを用いて，流行の抑制に十分な発症者隔離率$${\nu}$$を求めます．ソーシャルディスタンスによっても，発症者隔離によっても感染率の減少効果はみられますが，介入の組み合わせが効果的であることを示すマップ（横軸：ソーシャルディスタンスによる感染率減少効果，縦軸：発症者隔離による感染率減少効果）が得られました．
検査隔離のある状態モデルでは，偽陽性による隔離と真陽性による隔離の２つの部分集団が追加されたものです．

■数理モデルはワクチン接種法の検証にも適用した．
COVID-19に対し，累積死亡者数を最小化するためのワクチン1回目と2回目の最適な接種間隔を，構造化感染症モデルによって調べ，
ファイザーとアストラゼネカを想定したパラメータでは，いずれも接種間隔が3～4週間よりも長い方が良いという結果を得た．
感度分析では，仮想的なワクチンの2回目の意義が大きいほど，短い接種間隔が最適であるという示唆が得られた．

■研究中課題
均質ではない集団（年齢構造化など）にSIRモデルを適用したり，出生と死亡を含むSIRモデル，平衡解の大域安定性の問題，周期解の存在など興味深い問題の研究も行っている．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.08.01］ No.484
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
明日8月2日は，日本学術会議公開シンポジウム「数学教育の変遷」で，数学月間についての講演をさせていただきます．
貴重な機会ですので，私は4点（数学月間の心）に絞り話そうと思います．

第1点：
数学月間の起源，背景米国が1986年に国家行事としての数学月間を始めたのは，
「・・・社会と経済の進歩にとって数学が益々重要であるにも拘らず，
米国教育システムのすべての段階で低下する傾向にある．・・・すべてのアメリカ人に対して，
合衆国における数学と数学的教育の重要性を実証する適切な行事や活動に参加することを勧告する．・・・」
レーガン宣言によります．
国家的な行事ですから，毎年4月は，大学，学校，研究所，などそれぞれの立場で数学月間の活動を実践する義務があります．
日本は1950年から米国の統計学者Demingを招聘し品質管理の手法を展開しました．
Demingの思想は，競争でなく協力の体質をはぐくみ，1980年には米国を抜くことになります．
米国はこれに危機感を感じ，日本ができたことがなぜアメリカにはできないと，米国でもDemingの統計的品質管理が見直されます．
米国が賢かったのは，統計学的品質管理にとどまらず，数学一般の啓蒙である数学月間を始めたことです．
日本の数学月間は2005年に片瀬豊が始めました．

第2点：
数学的基礎を疎かにしない米国のＡＩ教育．読解力が重要コンピュータやソフトウエアが発展し，
統計もＡＩもブラックボックス化しています．ChatGPTもその例です．ブラックボックスを操るのでは実に危うい．
すくなくともAIの専門教育では，数学の基礎を疎かにしない米国を見習うべきです．
線形代数，確率論，情報理論，物理学などの基礎を押さえることが必要です．
さて，AIや統計をブラックボックスとして扱うと，とんでもない結果を導くこともできます．
解釈には常識や読解力が必要です．これらは社会で自然に身に着くものですが，
定義の幅を利用した論点ずらし，部分否定と全否定のすり替え，必要条件と十分条件をわざと区別しないなどの詭弁がまかり通り，
またマスメディアの報道自体が信用できない社会です．
言葉で考えを正しく表現し，表現された考えを正しく理解するために，ビジネス散文教育が必要です．

第３点：
数学は他分野と連携しよう19世紀には，物理学で生まれた微分方程式の解法が解析学を発展させました．
そしていまや数学は，物理学だけでなく人文科学にも浸透して来ました．
数学は孤立して存在し得る特性があり，純粋数学はこれが誇りでもありました．
しかし，他分野との連携がなければ数学の発展はないと考えます．
マーフィーの法則で「言葉が通じなければそれは数学」と揶揄されるようではいけません．

第４点：
応用現場で数学的構成要素を見つける他分野との連携は，教育数学にも必要なことです．
社会主義では抽象的な理論よりも具体的に適用場をもつ理論をこのむようです．
例えば，群論でもドイツやヨーロッパのように抽象群論ではなく，ソ連では結晶空間群（フェドロフ），
磁性構造を記述できる黒白群（シュブニコフ），幾何空間に特性次元を付加した色付き空間群（ベーロフ），
群の拡大理論を用いた一般群（コプツィク）など物理学に応用の根を張ったものになります．
現場に根を張った数学理論を見つけだすということは，教育でも配慮されています．
ロシアで盛んな数学オリンピックもそうですし，科学アカデミーのステクロフ数学研究所発行の『数学的構成要素』にもみられます．
この本は我々の周囲の森羅万象が数学と無縁でないことを，応用事例で示しています．
興味を惹くような先端科学などの86の応用事例が掲載され，それぞれどのような数学が使われているかがわかります．

7月22日の数学月間懇話会（第19回）の報告の続き：
(2)　新型コロナウイルス感染症のデータサイエンスと政策科学；土谷隆（政策研究大学院大学）

■2000年1月から2021年末まで（前半戦：デルタ株まで）

　　　　　　　　　　　　　　　　　　　　　　　　東京都新規陽性者
10月以降下がるのはワクチンの効果．
12月増加するのはオミクロン
発症者数＝5日後の新規陽性者数×0.65(非常に役に立つ経験則)
（オミクロンやBA.5では数値が変わるが類似式が成立）
［今日の発症者数は，5日後の新規感染者数に因果関係があるので当然の予想される経験則である］

　　　　　　　　　　　　　　　　　　　　　　　　実効再生産数
［緊急事態宣言下では，確かに実効再生産数は減少する］
■2023年5月まで（オミクロン株ー5類移行まで）

　　　　　　　　　　　　　　　　　　　　　　　東京都新規陽性者
■ データを振り返る

1．(2021/10/3時点)
デルタ株流行
・行政が把握した国内感染者累積
1,704,845名（都内375,973名），死亡者17,736名(都内2,954名)
・世界に大きな広がりを見せる．特に欧米では流行が激しく，より多くの人命が失われる．社会にとっての大きな脅威．
・国や地域による感染態様の違いが大きい．
・ワクチンが急速に普及しつつあり，国内的にはデルタ株の脅威は去ったように認識されていた．
・特効薬がない．
・いろいろと謎が多い．

２．（2022/7/15時点）
オミクロンBA1流行
・行政が把握した国内感染者累積
10,118,297名（都内1,733,041名），死亡者31,565名(都内4,594名)
・1月からのオミクロン株の流行で国内的には大変だった．
・欧米では，オミクロン以降，規制を緩めて以前の社会が戻りつつある．
・国や地域による感染態様・医療対応の違いが大きい．
・デルタ株までとオミクロン株では状況が大きく変化した
・オミクロンの変異株BA.5の大流行がはじまった．

３．（2023/5/8日時点）
・行政が把握した国内感染者累積
33,803,572名（都内4,388,360名），死亡者74,694名(都内8,126名)
・2022年末から2023年初頭にかけての第8波が到来した．
・第5類への変更が行われた．

■　陽性率についてのデータ
無症状者のモニタリング検査
2021年8月の東京の陽性率 0.3%　 (デルタ株)
2022年2月の東京の陽性率 9%　 (オミクロン株)
このデータからは，21年８月時点の新規感染者の低下傾向は，集団免疫ではなくワクチンの普及による．22年2月以降は集団免疫形成の効果が出ていると推定される．

■　推定の方法

次の階差方程式を用いる：
$${I(t+1)=I(t)+\beta(t)I(t)-\beta(t-D)I(t-D)}$$
人口を$${N}$$とする．$${S(t)+I(t)+R(t)=N}$$ の条件がある．
$${t}$$ 日目の未感染者数$${S(t)}$$　　
$${t}$$ 日目の感染者数$${I(t)}$$
$${t}$$ 日目の回復者数（＋死亡者数；回復者は再感染しない）$${R(t)}$$
未感染者が減少すると感染能力$${\beta(t)}$$の減少効果となるから
$${\beta(t)}$$を$${\beta(t)(S(t)/N)}$$で置き換え補正する．

デルタ株
社会にまん延することはなかった．まん延したら手の施しようがないのでとにかく感染者を増やさないことに社会として力を注いだ．
いくつかの流行の波が去っても免疫を持っている人は高々10％程度．
社会の集団としての免疫は結果的にワクチンによって人工的に実現された．
オミクロン株
デルタ株までに比べて感染者数が大きく増えた．一方，比較的重症者が少ないことが指摘され，また，南アやイギリス等で流行が2ヶ月程度でピークアウトし大きく減少することが報告されていた．
これは，社会の多数が免疫を取得したためと解釈できる．（これに近いことが起こっていると考えられることを日本のデータで検証する．）

■ 感染発病のモデル
感染してから潜伏期間が約5日あり，感染者は感染してから5日目から9日目位まで感染源になり得る．この期間を世代期間$${D}$$［感染源となり得る日数］という．
PCR検査には3あるいは4日目から11日目位まで陽性が出る可能性がある．
行政が把握する感染者（新規陽性者）の85％は， 発熱等の有症状であった．
行政が把握している感染者の10倍程度$${C}$$の感染者がいる．つまり，
行政が発表した感染数に対して，実際の感染源になりうる感染者数（未発症の感染者含む）は$${C}$$倍いる．
既に７－８割の人が免疫を持っている（2022年3月下旬で）．
これらの，潜伏期日数，世代期間，実際の感染者数と行政の把握している感染者数の比などの数値を，モデルによるシミュレーションと実際のデータをフィットして推定した．
特に，オミクロン株に対しての潜伏期間は2-3日，世代期間は2日程度で，非常に早く感染が広がると言われているが，データに見られる正月3ヶ日での遅延を解析し，潜伏期間5日，世代期間7-8日を得た．この違いは，感染源と感染者を特定する疫学的調査に基づかず，統計的にデータをフィットしたのですべての感染経路が考慮できているためである．

「幾何級数（指数関数）的に成長する」という言い回しは，日常語でよく使われる．数列 $$ \{b_1, b_2, b_3, ……..\} $$で，$${b_{n+1}=b_{n}q}$$のような数列を幾何級数と呼び，$${q}$$は公比である．次のようにも書ける$${b_n=b_1q^{n-1 } }$$

$${q>1}$$なら数列は増加し，$${0<q<1}$$ なら数列は減少する．

幾何級数的に説明できるいくつかの例を見てみよう．１．チェスの起源に関する最も有名な伝説がある．昔々，古代インドで，セッサという賢者が新しいゲームのルールを考案し，シェラム王にプレゼントした．王は魅了され，ゲームの考案者に自分の報酬を選ぶよう招いた．彼は自分の報酬を次のように選んだ．王様は，ボードの最初のマスに小麦を1粒置く，2番目のマスに2粒，3番目のマスに4粒というように，次のマスには前のマスの2倍の麦粒を置かなければならない．幾何級数的な増加である．$${b_1=1}$$，$${q=2}$$という「ささやかな」要求を満たすことは不可能だった．地球全体の収穫を何千年もかけて行わなければならない量である．

２．幾何級数の想像を絶する成長は，ただ紙を折るだけでも感じることができる．二つ折りにすると紙の厚さは2倍になり，それを二つ折りにすると4倍になる．すぐに実践できる実用的な可能性がなくなってしまう．一枚の紙を42回折ることができたと仮定すると，その厚さは地球から月までの距離よりも大きくなる．

３．数列が減少する性質の例：冒頭の図のように歯車の連鎖を作ってみよう．歯車の連鎖は前の連鎖の5倍遅く回転するとする．この連鎖は十分に長いと仮定する．もし，最初の歯車の車軸を高速で回転させ始めたとしても，最後の歯車は実質的に回転しない．例えば，連鎖に17個の歯車があり，最初の歯車が1秒間に1回転するとすると，「20年後」最後の歯車は1/1000回転もしない．だから，壁に永久に固定したも同然である．この先何年もの間，動かないのだ！これは儚い人間の人生から見れば，実用的無限といえる．「指数関数的に成長する」という表現は，これに非常に近い意味を持つ．

もしパラメータ$${n}$$が離散時間であるなら，$${b_{n+1}=b_1q^n}$$の式は，時間における量の急激な変化の記述とみなすことができる．高速連続過程では，$${y(t)=bq^t}$$の形の関数が現れ，これは指数関数と呼ばれる．したがって，関連する用語は指数関数的成長である．

応用：私たちを取り巻く世界
数学：幾何級数

『数学的構成要素』p.94-95より抜粋

オレンジを買ってきて半分に切った．
オレンジの半分に，皮と果肉のどちらが多いか見た目で わかりますか？

この質問は奇妙に思える．なぜなら，皮はオレンジの端の薄い層なのだから．しかし，球の端にある比較的薄い皮は，他の部分と同じ体積を持つことが分かった．例えば，直径10cm，皮の厚さ1cmのオレンジの場合，全体の体積のほぼ半分が皮の体積である．調べてみよう．半径$${R}$$と$${r（r＜R）}$$の2つの球を考える．
小さい方の球の体積が，大きい方の球の体積の半分になるような球の半径は？半径 $${R}$$の球の体積は$${V_{R} = 4/3 \pi R^3}$$
題意の$${r}$$を見出すには
$${V_{r}=V_{R}-V_{r } }$$       $${4/3 \pi r^3 =4/3 \pi R^3 -4/3 \pi r^3}$$
これから，$${R^3 =2r^3}$$ が得られる．すなわち，
$${r=R/ \sqrt[3]{2} \fallingdotseq0.79R\fallingdotseq4/5 R}$$
このように，球の体積の半分が，半径の1/5の表面近くの層に集中している．図のオレンジでは、果皮と果肉は等しい．

嫌な薬を飲むように子供を説得するにはどうしたらいいのだろう？
数学的なトリックがある．うまくいったら、薬に加えて、詳細説明も飲み込ませることができる．
混合薬を円錐形のグラスに注ぎ，「病人」に半分飲むように勧めると，たいていの人は「半分」を自動的に「半分の高さ」だと思い込み，グラスの中身の$${7/8}$$，つまり，ほとんど全部を飲むだろう．
実は，液面が約$${1/5}$$下がると，グラスの半分が飲み干される．
これは，オレンジの例で計算したのと同様である．
証明は，球の体積の公式ではなく，同様な円錐の体積の公式に置き換えるだけだ．これは，どのような形の円錐グラスでも成立する．

応用：日常生活
数学：円錐、円錐の体積

『数学的構成要素』p.92ー93　より抜粋

18世紀前半，ヨハン・セバスティアン・バッハの『平均律クラヴィーア曲集』が出版されました．平均律音階というのは，隣り合う音の周波数比$${q}$$を一定にして，1オクターブを12の音で構成したものです．
例えば，周波数$${f}$$の音から始めると，
$${ \{ f,  fq,  fq^2,  ….,  fq^{12}=2f \} }$$　，13番目の音はオクターブとなります．
$${q^{12}=2}$$を解くと，$${q=\sqrt[12]{2}=1.059463…}$$

隣り合う音の周波数比$${q}$$を一定にした（平均律）ことで，どの音から始めても同じ音階の平行移動ができ（移調ができる），図のようなピアノの鍵盤が作れるのです．黒鍵，白鍵すべてで隣り合うもの同士が半音階（周波数比$${q}$$）になっています．
バッハの平均律が凄い発明というのは，簡単な周波数比になる2音は心地よく響き和音を作るわけですが，完全5度，完全4度などの和音を良い精度で近似できるからです．
自分自身の音との間隔を完全1度といいます．完全5度とは，例えば，A（ラ）とE（ミ）のような純正律なら周波数比が$${2:3}$$になるような2音の間隔で，平均律では，$${q^7=1.4983 \fallingdotseq3/2}$$の周波数比です．
完全4度とは，例えば，E(ミ)とA（ラ）のような純正律なら周波数比が$${3:4}$$になるような2音の間隔で，平均律では，$${q^5=1.3348 \fallingdotseq4/3}$$の周波数比です．
このように，平均律の和音の響きは，純正律と異なりますが，非常に良い近似になっていることがわかります．

応用：音楽
数学： 幾何級数、無理数
『数学的構成要素』p.96-97；ただし，説明は全面的に変えた。

色々な種類の楽器（弦楽器、管楽器など）は，数学の観点からは，すべて，音源が弦の振動というモデルで表すことができます．

古代では，モノコード（単一弦）が，科学的な装置としてだけでな，楽器としても機能しました．モノコードは木製の共鳴器で，その上に弦が張られ、2点で固定されています．弦の発音部分の長さは，スライド式スタンドによって可変です．

弦の特性（材質、張力）が変化しなければ，振動数$${f}$$は弦の長さ$${l}$$に反比例します：$${ f ∼ 1/l}$$
例えば，同じモノコードを2つ用意し，片方を基準とし，もう片方のモノコードで，弦の発音部分の長さを変え，色々な音程［2音の差］作ったとします．
純正律には，ユニゾン［弦長比１］，オクターブ［弦長比1/2］，クイント［弦長比2/3］，クオーター［弦長比3/4］（ユーフォニー*の高い順に並べた）があります．*［ユーフォニーとは調和の良さのこと］
弦の周波数は弦長に反比例するので，それぞれの基本音の周波数は，オクターブで２倍，クイントでは3/2倍，クオーターでは4/3倍異なります．

■現実に起こる弦の振動は基本周波数のみではありません．同時にいろいろな倍音が発生します．両端が固定された弦の振動は，基本音とこれらの倍音の重ね合わせになります．弦の両端の他に，$${n}$$個の節のある定在波は弦を$${n+1}$$等分するので，基音の周波数を$${f}$$とすると，倍音の周波数は$${(n+1)f}$$になります．従って，弦の周波数の完全集合は$$ \{f, 2f, 3f, 4f, …. \}$$です．

■弦楽器の音色は，周波数の集合だけでなく，種々の倍音の音量比も関係します．一般に，倍音の音量は主音より小さく，倍音の次数が増加するにつれて減少します．また，主音と倍音の調和も関係し，倍音の次数が小さい方が良く調和します．

オクターブだけ異なる２つの弦は，弦長が2倍異なり，長い方の弦の周波数集合を$$ \{ f , 2 f , 3 f , 4 f , ... \} $$とすると，オクターブ高い弦の周波数集合は$$ \{ 2 f , 4 f , 6 f , 8 f , ...\} $$となります．
2番目の集合は1番目の集合の部分集合なので，オクターブ異なる２音は，似た音として知覚されるのはもっともなことです．

２つの楽器が同一音を発するユニゾンとは異なり，オクターブ異なる場合は音量（振幅）に違いができます．
オクターブでは，音量（振幅）は，長い方の弦の「偶数」の倍音に対してのみ変化し，その主音$$ \{ f \} $$あるいは「奇数」の倍音$${ \{3f , 5f,  7f,...\} }$$については変わりません．

クイントを考察しましょう．クイントとは弦長の比が2/3になった場合ですから，純正律の完全5度の和音です．
$$\{f , 2f, 3f, 4f, ...\}$$が長さ$${l}$$の弦の周波数集合とすると，長さ$${2l/3}$$の周波数集合は，$$ \{ \frac{3}{2}f, 2 \frac{3}{2}f, 3 \frac{3}{2}f, 4 \frac{3}{2}f, …. \}$$となります．
短い弦の基本音$$\{ \frac{3}{2}f \}$$は，長い弦の倍音中にはないことがわかり，オクターブのユーフォニーの説明にクイントは当てはまりません．

しかし，音の知覚には，まず基本音の比較があるので，もし，長さ$${2l}$$の架空の「統一」弦を考えると，その周波数集合$$ \{ \frac{f}{2}, 2\frac{f}{2}, 3\frac{f}{2}, …. \}$$の中に，弦$${l}$$と弦$${\frac{2}{3}l}$$の基本音，および，それらのすべての倍音が現れることがわかります．

重要なのは，架空の「統一」弦の長さが$${2l}$$であることです．
この$${2l}$$という長さは，長さ$${l}$$とクイント弦の長さ$${\frac{2}{3}l}$$の最小公倍数です．
統一弦の倍音の調和のとれた世界に，両方のクイント弦の周波数を取り入れることで，聴き手は音の良さとまとまりを感じます．

クイント弦の周波数を直接比較することもできます：
弦長$${l}$$に対しての周波数集合$$\{f, 2f,  3f,  4f,  ...\} $$，弦長$$\{\frac{2}{3}l\}$$に対しての周波数集合$$\{\frac{3}{2}f,  2\frac{3}{2}f,  3\frac{3}{2}f,  ...\} $$でありました．
短弦のすべての「偶数」倍音は，長弦の倍音ですが，短弦のすべての "奇数 "倍音は長弦の倍音ではありません．
これらの短弦の「奇数」の倍音が，ハーモニーが不完全である理由です．クイントは調和しているが、調和の程度はオクターブより劣っているのです．
クオータの和音（完全4度）も同じように分析されます．
弦の長さが$${l}$$と$${\frac{3}{4}l}$$の場合，統一弦の長さは$${3l}$$になります．その結果，クオーターは純正律になりますが，クイントよりも調和がとれた音にはなりません．
弦の音を基本音と倍音の合成音として数学的に表現するということは，周期関数を倍音の$${sin(nx)}$$, $${cos(nx)}$$の和で表すことを意味します［長さ$${l}$$で両端固定の弦の振動はFourier級数で　$${\sum_{n}^{} a_{n}sin(2n\pi x/l)}$$］．
この和は，構成倍音とは大きく異なることがあります．シンプルなトーンが，豊かで表現力豊かな音色を構成します．

応用：音楽
数学: 比例、和声分析
『数学構成要素』p.98-101のテーマより．
ただし，説明は全面的に変更しました．

［追記］

私の手元には「楽器の音響学」安藤由典があります。例えばバイオリンなら弦の振動が源ですが，実際に楽器から聞こえる音は，共鳴体の胴の振動で，楽器の良し悪しは胴の特性で決まります。共鳴周波数の間隔が完全5度に近いと良いような説があります。バイオリン4弦の開放弦音のスペクトルでもそれぞれの弦で倍音の出方は異なります。G線では倍音次数とともに始めは増加が見られます。

GPSやGLONASS(ロシアの衛星測位システム)受信機が，軌道上の衛星から座標を受信すると考えるのは間違っている．第一，衛星はあなたの座標を知らないし，第二に，衛星はメッセージを，あなただけでなく全員に，一斉に「宇宙から」送信している．では，ナビゲーターはどうやってあなたの座標を決定するのでしょうか？衛星ナビゲーション・システムには，宇宙と管理の2つの主要機能がある．宇宙機能は，地球の周囲に均等に衛星を配置することである．地球上にある管理機能は，すべての衛星で「システム全体」の時刻を同期させ，単一の座標系を使用することを保証する．各衛星は，メッセージ送信時の衛星の座標と送信時刻を含むナビゲーションメッセージを継続的に送信している．このようなメッセージを受信した受信機は，衛星までの距離を次のように計算することができる：$${d =(t^{(pr)} - t^{(otpr)})c}$$この式では，信号の移動時間（送信時刻$${t(otpr)}$$から受信時刻$${t(pr)}$$まで）に無線信号の伝搬速度，すなわち光速$${c}$$を乗じている．一方，直交座標系であなたの座標を$${(x; y; z)}$$とし，送信時の衛星の座標を$${(x1; y1; z1)}$$とすると，衛星とあなたの距離$${d_1}$$の2乗は$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2}$$である．受信機が同時に2つの衛星からナビゲーションメッセージを受信した場合，受信機はあなたの座標$${(x;y;z)}$$を求めることができる．

$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2 =d_{1}^2}$$
$${(x - x_2)^2 +( y - y_2)^2 +(z - z_2)^2 =d_{2}^2}$$
$${(x - x_3)^2 +( y - y_3)^2 +(z - z_3)^2 =d_{3}^2}$$

ここで，$${(x_i; y_i; z_i)}$$は$${i}$$番目の衛星の座標で，$${d_i}$$は衛星までの距離である．このシステムの幾何学的解釈は以下の通りである．ある衛星からのメッセージ は，あなたがいる地点を中心とし，衛星までの距離を半径とする球を定義する．

これら2つの球体の交点は，一般的に言えば円である．第3衛星からのメッセージはもう1つの制約（もう1つの球）を追加する．それらにより，あなたの座標は決定される．3つの球が共通の点を持つということは，システムの構成そのものから導かれる．２つの「形式的な解」(円と3つ目の球の交点)のうちの１つは題意に適さず，もう一つがあなたの座標である．記述した衛星 ナビゲーションシステムのスキームは単純化されているが，現実にはもっと複雑なモデルを使う必要がある．例えば，記述された方式は誤差に非常に敏感である．主要な誤差の一つは，時計の精度の影響である．

衛星の時計はナビゲーション・システムの地上局と通信し時間を修正する手段を持たない．もし，時計がシステム全体の時刻と0.001秒ずれているとする．光速は秒速30万キロメートルであるので，衛星までの距離に300キロの誤差が生じる！記述したシステムでは，もし解があったとしても，あなたの場所は違うものになるだろう．幸いなことに，このような問題も克服可能である．たとえ時計の精度がわからない，例えば，受信機の時計がシステム全体の時刻より（未知の）$${δ}$$だけ遅れているとしよう．メッセージを受信した瞬間の読みは$${t^{(pr) } }$$である．ナビゲーターは，衛星までの距離を$${d =(t^{(pr)}-t^{(otpr)})c}$$と「仮定」する．これは真の距離$${d +δc}$$より小さい．座標$${(x; y; z)}$$と新しい未知数$${r =δc}$$を求めるには，別の方程式が必要である．4つの衛星からのデータがある場合に次のようなことができる：

$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2 =(d_1 +r)^2}$$
$${(x - x_2)^2 +( y - y_2)^2 +(z - z_2)^2 =(d_2 +r)^2}$$
$${(x - x_3)^2 +( y - y_3)^2 +(z - z_3)^2 =(d_3 +r)^2}$$
$${(x - x_4)^2 +( y - y_4)^2 +(z - z_4)^2 =(d_4 +r)^2}$$

この問題の解を幾何学的に解釈すると次のようになる．受け手は半径$${r}$$の球の中心であり，その球は外部から（時計が遅れていたため）半径$${d_i}$$の4つの球に接しており，その中心は衛星である．このような球が存在し，その中心があなたの位置である．(図はこの問題の2次元バージョンを示している．半径$${r}$$の円が3つの円に外部で接している)．このシステムを使って座標を計算することで，ナビゲーターは，座標が得られ，追加の "ボーナス "として，ナビゲーターはシステム全体の時間の値を受け取り，時計を修正し，正確な時刻をあなたに伝えます！

応用：ナビゲーション・デバイス
数学: 球、座標法、方程式系
『数学的構成要素』p.110-111より

2次元の世界のGPSなら２つの衛星，3次元の世界のGPSなら３つの衛星が最低必要だということです。

コンピュータで表現された画像に対し，加算，減算，乗算，べき乗の演算ができます！フォトショップやSNS用の写真加工のツールなど，ビットマップ画像を扱うコンピュータプログラムは，この算術演算に基づいています．
ビットマップ画像は，スクリーン上の発光画像として表現することができ，
(ピクセル）で構成される長方形の表です．それぞれのセルには，3つの基本色（赤，緑，青）の明るさを表す数値セット$${(r; g; b)}$$が格納されており，この数値でピクセルの色が決まります．$${(r, g, b)}$$の各数値は1バイト［８ビット］として格納，つまり，値の範囲は0から255$${(=2^{8}-1)}$$までの整数です．

0の値は，その色がないこと，255の値は，その色の明るさが最大であることを意味します．
例えば:
$${(0; 0; 0)}$$ - 黒ピクセル，$${(255; 255; 255)}$$ - 白ピクセル，
$${(255; 0; 0; 0)}$$ - 赤ピクセル，$${(0; 100; 0)}$$ - 暗緑色ピクセル，$${(200; 200; 0)}$$ - 黄色ピクセル．

画像に対する算術演算は，ピクセル単位で成分ごとに行われます．等しい位置にあるピクセル $${(r_1; g_1; b_1)}$$と$${(r_2; g_2; b_2)}$$の場合，それらの和は$${(r_1 +r_2; g_1 + g_2; b_1 +b_2)}$$で，積は$${([\frac{r_{1}r_{2 } }{255}]; [\frac{g_{1}g_{2 } }{255}]; [\frac{b_{1}b_{2 } }{255}])}$$となります．
加算で255を超えれば255とし，積の定義で，括弧［］は数の整数部だけを表示します．一般に，加算は明るい点を生成し，乗算は明るさを減じます．
例えば，絵に白い背景を加えると，絵全体が白くぼんやりする．
色のついた絵に「黒い正方形」を乗ずると，正方形の「ブラックホール」ができる．
緑の三角形$${A}$$と赤の円$${B}$$とすると；

これらの演算を適用した直後の結果にはがっかりさせられる．
緑の三角形$${A}$$と赤い円$${B}$$があるとして，
$${A＋B}$$の和は交点に黄色のスライスを作る．
（訳者注：白の地の部分はすでに255なので，すでに飽和している）
もし， "ハーフイメージ "$${0.5A＋0.5B}$$を作ると，三角形と円の形は変わらないが，色は変化する：図形の交叉は暗い影になり，残り部分は明るくなる．積$${AB}$$では，図形の交叉が暗くなり，他の部分は元の色を保つ．
しかし，単色灰色マスク（つまり黒から白のある階調の画像）を使えば，実用的な問題の大部分は「算術的」に解くことができる．
黒と白のマスク$${M_A}$$ と$${M_B}$$ を考えてみよう．$${A}$$ と $${B}$$ にマスクを乗ずると，物体そのものが白くなり，白い背景が黒くなる．
さらに2つのマスク，$${\overline{M_{A } } }$$と$${\overline{M_{B } } }$$はその「反転」であり，黒と白が入れ替わる．

 画像Aにマスク$${M_{A } }$$を乗ずると，黒い背景に三角形の画像ができ，画像Bにマスク$${\overline{M_{A } } }$$を乗ずると，黒い三角形が丸で切り取られる．
結局， 画像$${AM_A + B \overline{M_{A } } }$$は，赤い円$${B}$$上に緑の三角形$${A}$$を重ねたものになる．同様に，$${BM_B + A \overline{M_{B } } }$$ は，緑の三角形上の赤い円を重ね合わせたものになる．
上記のマスクは白黒だったが，"真の "灰色マスクも使われる．たとえば，重ね合わせた画像を半透明にするために使うことができる．黒と白のマスクの直線的な組み合わせである2つの灰色マスクは，円に三角形を重ねた半透明の重ね合わせを作り出す．$${A(0.7M_{A} +0.3 \overline{M_{B } }) + B(0.7 \overline{M_{A } } +0.3M_{B})}$$

また，モノクロ写真をシャープにする「べき乗」など，1枚の画像だけで作業するときに便利なツールもあります．
基本的な操作は，個々のピクセルに対する処理という最も単純なモデルで考えたのですが，周囲のピクセルの色を考慮してピクセルの色を変更するツールも使用されています．例えば，色の平均化は写真をぼかす効果を与えます．

応用：画像処理
数学：算術演算，ベクトル
『数学構成要素』p.126-127より　

<<音楽とは，無意識になされる魂の秘密の代数演算である>>ヨハン・セバスティアン・バッハと同時代に生きた解析学の創始者の一人であるゴットフリート・ライプニッツが，クリスティアン・ゴールトバッハ宛の書簡(1712年4月27日)の中に，この偉大な言葉を書いたのは今から300年前である．今日，数学が提供するのは，既存の音楽作品を研究し，その知識を生徒たちに伝えるためのアプローチだけではない．新たな創造の可能性，音楽を「構築」する新たな方法も提供している．音楽は楽譜を使って保存され伝達される．楽譜には，音程，開始時間，演奏時間，音量，演奏される楽器などの情報が含まれている．連続するシーケンスをどのように変形すれば，オリジナルと同時または連続演奏しても面白く魅力的なメロディーになるだるうか？対位法人間が幼少期に習得する最も単純な数学演算は足し算と引き算である．音楽家が教わるメロディの最も単純な変換は移調である．移調とは，音楽シーケンスの各音符の音程を，固定された一定の音楽単位（半音）だけ変えることである．複数の声部がある場合，ある声部を他の声部に対し相対的に移調することは，「垂直対位法」と呼ばれる．セルゲイ・イヴァノヴィチ・タネーエフの著作『厳密な書法による可動対位法』（1906年）において，一般的な対位法を記述する数式形式が提示された．以下は，この教科書に掲載されている垂直対位法の「モデル」例である．

最初は2つのメロディ・パターン（声部）がある．上の はそのままで，第2声部が1クオート下がる．

*訳者解説）１クォート下がるとは，完全４度下がることである．ハ音記号の楽譜は中心線がC音である．左側の楽譜の第2声の音はCで始まるが，右側の楽譜の第2声の音はGで始まり，完全4度下がっている．第2声の左側の楽譜のメロディは，右側の楽譜では完全4度下がってそのまま再現される．ーーーーーーーーーーーー

そして，次はヨハン・セバスティアン・バッハの作品からの一例で，「平均律クラヴィーア曲集」（1744年）の第1部にあるホ短調 のフーガである．これは2つの19連打の部分と4連打のコーダ（終結部）で構成されている．第2楽章は，第1楽章のほぼ正確な垂直対位法で，両声部がずれている．たとえば，第1楽章（第16-17-18小節）と第2楽章の（第31-32-33小節）の２つの断片を比べてみよう．

第1声部と第2声部の位置が変わっているのは容易にわかる．高声部が下方に，低声部が上方に移動しているのだ．つまり，それぞれの声部に異なる垂直対位法が適用されている．アルベルト・シュヴァイツァーが書いているように，バッハの作品は長い間過小評価されてきた．それは彼の作品の音符が，深い音楽的内容を伴わない，単に形式的に美しいテキストとして認識されていたからである．しかし，歴史は，形式的な構成がとっても驚くほど耳に美しいものであることを証明している．

モジュロ$${n}$$（$${n}$$を法とする算術）

音階における音符の周期性は，数学における周期集合とよく似ている．これは作曲における形式的な数学手法を生み出した．整数の世界では，等号の概念の特別な拡張がある：2つの整数$${a}$$および$${b}$$は，その差$${a - b}$$が$${n}$$で割り切れる場合，つまり，$${a≡b（mod n)}$$である場合，自然数$${n}$$を法として(モジュロ$${n}$$として)等しいと呼ばれる．これを用いて，偉大な数学者C.F.ガウスは，新しい構造modulo $${n}$$演算（1801年）を提案した．この算術に従い，数は足し算，引き算，掛け算，そして時には 割り算もできる．

例えば，モジュロ$${ｎ}$$が12であれば，この算術にはちょうど12種類の数が存在することになる．これら12種の代表は次のように選ぶ．自然数を12で割った余り$$ \{0, 1, ..., 10, 11 \} $$を代表とするのである. 演算の例：8 +5 ≡ 1, 　8 ･ 5 ≡ 4。半音階スケールとの類似性：半音の12音からなる1周期は，1オクターブ．第1オクターブのD音に12半音を加えると，第2オクターブのD音になる．オクターブは調和することが知られている．ーーーこのアプローチは1844年にさかのぼる．その作者であるフランスの音楽学者カミーユ・デュルトは，一様に調律されたピアノでは，多くの音程が12段階の周期に分けられることを指摘した．このことから，音程に対する演算は「モジュロ12」と定義された．このような考え方を作曲に応用することで，アメリカの作曲家ミルトン・バビットは，いわゆる「集合論」（1992年）という音楽理論全体を作り上げ，数学論文に発表した．

和声分析

最も単純な倍音は，三角関数$${1，cos kx，sin kx}$$（$${k}$$は任意の自然数）である．これらの関数は，数学と音響学の両方で特別な役割を果たしている．以下の問題は調和解析の基本的な問題である： 与えられた関数を三角級数の和として表現すること，与えられた性質を持つ関数をそのような級数の和として求めること（例えば，ある初期条件と境界条件を満たす微分方程式の解）．

*訳者注）Fourier解析のこと．

音楽音響学では，これらの問題の第一は，H.L.F.ヘルムホルツによって提案され，ドーム型共振器（「ヘルムホルツ共振器」）のシステムを用いた音の研究方法で，これによって音のスペクトル組成を決定することが可能になった．第二の問題は，加法合成の出現のきっかけとなったことである．加法合成は，20世紀の音楽における最も輝かしいトレンドの1つである．この様式は，多数の単純な倍音の重ね合わせによって得られる人工的な音で構成されている．現代のコンピューター技術の水準は，機械的な装置を使わないことを可能にしている．特に，フランスの作曲家ジャン＝クロード・リッセは、このスタイルで確固たる地位を築いている． 鐘の音を思わせる電子音のセットを手に入れた．これが 彼の作曲した『Mutations』（1969年）の基礎となっている．

確率論

確率論的手法の作曲への応用は，ジャニス・クセナキスによって提唱された．クセナキスはエンジニアとして訓練を受け，ル・コルビュジエのもとで働き，建築家として認められるようになった．一方，彼は生涯音楽に携わり，著名な作曲家となっただけでなく，音楽学者・理論家にもなった．彼の仕事，業績，情熱を統合していたのものは，至るところで数学的手法を応用したり，応用の機会を探したりしていたことだった．例えば，直線の動きを利用するというアイデアは，1954年の音楽作品『メタスタシス』では，弦楽器の連続的なグリッサンドとして，ブリュッセルで開催された万国博覧会「Expo-58」のフィリップス・パビリオンでは，屋根の表面を直線で構成したことに共通している．

選択された数学的モデルに従って楽曲がダイナミックに展開するというアイデアは，その後何年にもわたり彼によって発展させられた．このモデルはランダムな過程によって定義され，ある瞬間に作者が意図した信号スペクトルや空間上の音量分布などが得られるように選択された．クセナキスの音楽的マニフェストは，著書『形式化された音楽』（1963年），ロシア語訳（2008年）である．特にこの本では，集合論，確率論，情報理論，ゲーム理論といった数学の分野を，音楽の作曲や研究に応用することを探求している．

アルゴリズム論

よく知られているように，アルゴリズムとは，有限のステップ数で目標を達成するための実行者の行動順序を記述した命令の集合である．同じアルゴリズムが入力データに順次適用される場合，そのようなプロセスは反復と呼ばれる．数学では，反復プロセスの最も一般的なバリエーションは，逐次近似の方法によって問題の解を見つけることである．また， "探索的 "と呼ばれるあらかじめ決められたゴールのないプロセスのバリエーションがある．日常生活においても，反復プロセスは珍しくない．例えば，現在の銀行預金に年利が発生すると，次年の預金額が増える．（複利と呼ばれる）．

応用：音楽

数学： 調和分析、モジュラー算術、確率論、アルゴリズム

『数学構成要素』p.202-205　Амосов Григорий Геннадьевич

$$ \{1, m_y, m_x, 2 \} \Longleftrightarrow \{I, H, V, R \} $$

階段の上にあるスイッチからでも，階段の下にあるスイッチからでも，１つの電灯のon/offができるようにするには，3路スイッチを2個つかいます．片切スイッチを直列に2個用いても，2つのスイッチが揃ってoff状態になっているときは，どちらか１つのスイッチをonにしても点灯することはできません．そこで，3路スイッチが登場するわけです．片切スイッチを2個直列にした状態は，2つの片切スイッチの間は１本の線で結ばれていますが，２つの3路スイッチの間はいつも2本の線で結ばれる状態であるのがミソです．引用している回路図をご覧ください．3か所から1つの電灯をon/offするには，３路スイッチ2個の他に4路スイッチを１つ加えることで可能になります．実は，何か所からでも1つの電灯のon/offをするには，3路スイッチ2個の間に，必要なだけ4路スイッチを追加すれば良いのです．これを証明しようとして表題の真理表を作りました．２つの3路スイッチ$$ A=\{1, 0\}, B=\{1, 0\} $$を直列に繋いだ時の真理表です．2×2の4つの状態があり，その中のon状態1，およびoff状態0は2つづつあります．例えば，Aのスイッチがどちらの状態にあっても，Bのスイッチの操作で全体をonにもoffにもできることがわかります．2つの3路スイッチの間に４路スイッチ$$ C=\{1, 0 \} $$を入れたとしますと，$${C=1}$$のときに作った２つの直列な３路スイッチA，Bの真理表が，$${C=0}$$にすると0と1が反転します．4路スイッチをいくつ増やしてもこのどちらかの真理表が実現するわけで，どの4路スイッチを操作しても全体をon/offできることがわかります．4路スイッチの性質がよく理解できれば，次の練習問題はすぐ解けます．

（練習問題）4か所から１つの電灯をon/offできる結線図を考えなさい．

［解説］スイッチには以下の種類があります．片切スイッチ　（1回路1接点）両切りスイッチ（2回路2接点）３路スイッチ　（1回路2接点）４路スイッチ　（3回路スイッチの機能を持った両切りスイッチ）これらのスイッチの違いと使い方については，以下のpanasonicのウエブサイトjpn.faq.panasonic.comでの説明がわかり易い：

４路スイッチの内部構造はどうなっているのでしょうか？

2つの3路スイッチを結ぶ2線の間に４路スイッチを置き，2線の結合を切り替えるわけですが，2つの状態しかありませんから，この切り替えでon/offが必ずできます．この切り替えは4路スイッチをいくつ増やしても同様に成り立ちます．このように，4路スイッチの機能はわかったとして，どのような機構にすれば4路スイッチを実際に製造できるのか気になります．ウエブを探しても，実際の内部構造の写真や図は見つかりませんでした．実物を分解したことは私はないのですが，以下の「たくのこWeb」www.kakunoko.comに想像図が載っています．このような可動構造なら作れそうですね．多分そうでしょう：

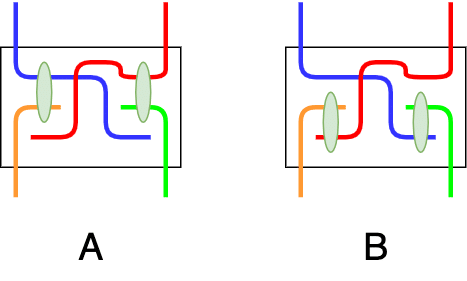
（注意）住宅の配線に付けられたスイッチの交換には電気工事士の資格が必要です．私は電気工事士ではありません．

以下のサイトにある問題をグラフを使い解いてみましょう：

https://tomari.org/main/java/senkeikeikaku.html　線形計画（シンプレックス法）

ある会社が、A、Bという製品を売り出している。　それらを製作するための材料はプラスチック、アルミ、ゴムである。
それぞれ１個を製作するために必要な材料の量は下の表のとおりである。

このとき、手持ちの材料の範囲内で売上高を最大にするためには、A、Bをそれぞれいくつ作ったらよいか？

製品Aを$${x}$$個，製品Bを$${y}$$個作るとする．
この時の売上高を評価関数$${f(x,y)}$$にし，これを最大にする$${(x,y)}$$を求める．

$${f(x,y)=2x+3y}$$

可能集合（可能領域）は，以下の制約条件で決まる
$${x+2y≦14}$$ ,  $${x+y≦8 }$$ ,  $${3x+y≦18}$$, $${x≧0}$$, $${y≧0}$$ 
可能領域を囲む頂点は，５つあるが，可能領域外頂点は５つである． 

領域は凸多面体であるので求める極値は頂点にあり，
$${(2, 6)}$$のとき，最大値$${f(x,y)=22}$$となる．

行列表現

これを　$${A=\left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right)}$$, $${x=\left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right)}$$,  $${b=\left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right)}$$,  $${c=\left( \begin{array}{@{\,} c @{\, } } 2 \\[0mm] 3 \end{array} \right)}$$　　と表現すると，
制約条件は　$${Ax≦b}$$となり，$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$
この制約条件下で，$${c^{T}x}$$を最大にする$${x≧0}$$を求める問題である．

$${x≧0, Ax≦b}$$のもとで, $${c^{T}x}$$を最大とせよ．　

$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$

$$\left[ \begin{array}{@{\,} ccccc @{\, } }
1 & 2 & -1 & 0 & 0 \\[0mm]
1 & 1 & 0 & -1 & 0 \\[0mm]
3 & 1 & 0 & 0 & -1
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
z_{1} \\[0mm]
z_{2} \\[0mm]
z_{3}
\end{array} \right] \le \left[ \begin{array}{@{\,} c @{\, } }
4 \\[0mm]
8 \\[0mm]
18
\end{array} \right] $$

この例題は，2次元（2変数）の例題であるが，問題を一般化して$${n}$$次元の問題が考えられる．

■$${n}$$次元の問題に対するDantzigのアルゴリズム
可能集合の１つの頂点を選ぶ．
可能集合の辺に沿って頂点から頂点へ移る．
普通，頂点には$${n}$$本の辺があるが未知の最適解に近づく方向を選ぶ．
やがて，どの辺に沿って移っても最適解から遠ざかる特別な頂点に到達する．その頂点が最適解である．

問題を一般化して$${n}$$次元の問題（制約条件$${m}$$）を考えると，
$${m×n}$$次の行列$${A_{mn } }$$を用いて，$${z=A_{mn}x-b}$$と置くと，

$${A_{mn}x-z=b}$$なので，条件式は$${A_{mn}x-z≦b}$$，すなわち

$${\left[ \begin{array}{@{\,} cc @{\, } }
A & -I
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x \\[0mm]
z
\end{array} \right] \leqq b}$$

$${\left[ \begin{array}{@{\,} cc @{\, } }
A & -I
\end{array} \right]}$$ は２つの行列を横に並べただけの行列で，$${m×(m+n)}$$次元の行列であり，

$${\left[ \begin{array}{@{\,} c @{\, } }
x \\[0mm]
z
\end{array} \right] }$$は，ベクトル$${x, z}$$を並べただけの$${m+n}$$次元の新しいベクトルである．もちろん$${b}$$は$${m}$$次元のベクトルである．

$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$

$$\left[ \begin{array}{@{\,} ccccc @{\, } }
1 & 2 & -1 & 0 & 0 \\[0mm]
1 & 1 & 0 & -1 & 0 \\[0mm]
3 & 1 & 0 & 0 & -1
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
z_{1} \\[0mm]
z_{2} \\[0mm]
z_{3}
\end{array} \right] \le \left[ \begin{array}{@{\,} c @{\, } }
4 \\[0mm]
8 \\[0mm]
18
\end{array} \right] $$

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2023.10.24］ No.495
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
レスキューで用いられる●コイル巻きもやい結びと●3重もやい結びの話です．
私は，今回，高所作業の用いるために，レスキューの動画を見て学習しました．
結び目の構造を理解するのはなかなか難しいです．
写真や動画が多数ありますので，以下のサイトに移動しお読みください．
https://note.com/sgk2005/n/n06057985856b

■秋の企画講演（第12回）が近づきました：
日時●11月18日（土），13:30ー16:00（開場13:00）
場所●東大駒場キャンバス，数理科学研究科棟002教室
テーマ●固有値問題で解く日本の国民経済-大規模データ版
13:30-15:00講演● 松原望（東京大学名誉教授）
15:10-16:00討論（質問と解説）
主催●NPO法人数学月間の会（理事長：岡本和夫）
会場参加費●1,000円（学生・生徒，および，当会会員は無料）．
会場でお支払いください．
遠方の方のためにwebexによるリモートも併用することになりました．
リモート参加費●1,000円（学生・生徒，および，当会会員は無料）．
リモート参加費は，数学月間の会ゆうちょ口座に事前にお支払いください．
webexのパスコードをご連絡します．詳細は https://sgk2005.org/ をご覧ください．

会場参加もリモート参加も以下のサイトで事前登録をお願い致します．
https://sgk2005.org/

■数学月間企画講演（第13回）のお知らせ
日時●2024年１月20日（土），13:00-17:00
場所●東京大学数理科学研究科棟002教室
プログラム●
●結晶格子と非周期タイル貼り，河野俊丈（明治大学総合数理学部教授）
●超音速ノズル流の基礎と気体レーザーへの応用，佐藤浩之助（九州大学名誉教授）
主催●NPO法人数学月間の会（理事長：岡本和夫）
参加費（会場およびリモート）●1,000円（ただし，学生･生徒，当会会員は無料）．

参加登録（会場およびリモート共通）は ，以下のサイトで事前にお済ませください．
https://sgk2005.org/

■2024年3月の土日に，中野ZERO，生涯学習課主催の「こどもカーニバル」に連携し
数学ワークショップを企画中です．テーマのご提案やボランティア参加を募集します．
問い合わせ先●sgktani@gmail.com

「アルゴリズム」という言葉は，ペルシャの偉大な科学者アル＝フワリズミの名前に由来する．アル＝フワリズミは，9世紀に数位システム［10進法数表記］を記述した（代数学という言葉も同じ著作に由来する）．
イスラム黄金時代の数学（9 世紀から 10 世紀）は，ギリシャ数学 (ユークリッド，アルキメデス，アポロニウス) とインド数学 (アリヤバータ，ブラフマグプタ) の上に発展し，分数を含む完全な小数位システムの開発，代数学の最初の体系的な研究，幾何学と三角法の進歩など，重要な進歩があった（10～12世紀）．
https://academic-accelerator.com/encyclopedia/jp/mathematics-in-the-medieval-islamic-world　参照◆

整数や有理数を演算するアルゴリズムは，数値アルゴリズムと呼ばれる．
アルゴリズムの対象は一般化されて，グラフ，配列，テキスト，スケジュールなど任意の離散データ（グラフ，配列）を扱うものにも及ぶ．
これらは，K.ゲーデル，А. A.マルコフ，P.S.ノヴィコフ，A.チューリング，A.チャーチといった前世紀の偉大な数理論理学者の著作で定義され，計算できる厳密な理論が作られた．
Математическая составляющая, p.262-275参照◆

アルゴリズムは，広義には，完全に定義されたルールの集合で，有限時間でゴールに到達できる手順を定めるものである．

一つの問題を解く手順にも異なる色々なアルゴリズムがある．また，ある問題に対する同じアルゴリズムであっても，問題　に与えられた数値に応じて効力が変わる．アルゴリズムの質を数値化することは容易ではない．

アルゴリズムの「質」を，ある「複雑さ関数」によって測定することが，この複雑さ理論の目標である．

あるアルゴリズムでの試行回数を測定してみると，特定のある入力値の場合には偶然にも1回で答えが出たりする．２つの異なるアルゴリズムを比較した場合，与えられた特定の入力値に対して試行回数が逆転することもある．このようにアルゴリズムの複雑さの尺度を決めるのは非常に困難な問題である．アルゴリズムの複雑さは，最悪のケースを評価の対象として決める．

その複雑さを数値で完全に定義することは難しい．
このため，普遍的尺度は，古典的な計算理論の枠組みの中で，次のレベルの一般化としてのみ導入できる．これは，チューリング・マシンのクロック・サイクル数と呼ばれる．チューリング マシンは，1936 年に英国の偉大な数学者 A. チューリングによって提案された抽象的なコンピューティング デバイスで，直感的には，これは目標を達成するために必要な基本的 (分解不可能な) ステップ数である． プログラムの動作期間全体にわたって，プログラムに含まれる命令の実行数をカウントすることと理解することもできる．これは実行の数であり，命令の数とは異なる．後者はいわゆるコルモゴロフ複雑性であるが，ここでは考慮の対象としない．

これを説明するために，２つの整数（例えば，630と300）の最大公約数gcdを求める例を考察する：
（方法1）最大公約数は$${2･3･5＝30}$$である．
　　　

（方法２）それぞれの数を素因数分解する．
　　　　　$${630=2･3^2･5･7}$$
　　　　　$${300=2^2･3･5^2}$$
これから，最大公約数$${2･3･5=30}$$が得られる．
それぞれの数の約数構造を整理するのに，亀井図（多元構造図）は有用である．
両方の数に含まれる互いに素な辺$${2,3,5}$$で生成される平行6面体の頂点が共通な約数を与える．最大公約数は30．

　　　　　　　　　　亀井図による630と300の約数構造の表現

　　　　　　　　　　　630と300公約数部分のグラフ

（方法３）ユークリッドのアルゴリズム（互除法）を使う．
630＝2･300+30
300＝10･30+0
従って，最大公約数は30である．
（注）ユークリッドのアルゴリズム
$${a<b}$$のペア$${(a,b)}$$に対して，$${b}$$を$${a}$$で割って余りを出す： $${b =h･a +r}$$ここで$${0≦r≦a-1}$$．次に，このアルゴリズムをペア$${(r, a)}$$に再帰的に適用する： $${a}$$を$${r}$$で割り，$${a =u･r +s}$$となり，再帰的にとは，$${(a,b)}$$を$${(r,a)}$$で置き換え手順を継続することである．これを$${(0,d)}$$の形になるまで続ける．このとき得られた$${d}$$が最大公約数である．-----------------◆
ユークリッドのアルゴリズムが正しく機能するのは，$${gcd(a, b) =gcd(r, a) =･･･＝gcd(s, r) =...}$$だからである．最大公約数は，この変換手順の不変量である．従って，最後のペア$${(0, d)}$$は最大公約数$${d}$$に帰着する．
$${(a+r)≦(2/3)(a+b)}$$が常に成り立つので，組の数の和は指数関数的に減少し，このアルゴリズムは$${f (n) ≈ 10n}$$反復で収束する．
これは，$${a}$$ と$${b}$$ の表記におけるビット数 $${n}$$ の一次関数である．
関数$${10n}$$が，多項式である（指数関数ではなく，ある$${C, d＞0}$$に対して$${C･n^d}$$の形をとる）という事実は重要である．
現代の複雑さ理論では，（最悪の場合の）複雑さの見積もりが多項式（速く計算できる）であるアルゴリズムのクラスは多項式（ "P "）と呼ばれる．