日本の数学月間

■数学を体験，数学祭り

多くの人々が数学に関心をもつようになるイベントを数学月間では応援しています．講演会，講習会，ワークショップ，様々な活動形態がありますが，子供たちが楽しめて数学感覚が身に着く”数学まつり（フェスティバル）”は，英国のMMPでも米国のMAMでも，とっとりサイエンスワールドでも大変人気があります．学校カリキュラムの補完ではなく，数学力を伸ばす地域の数学サークル活動，学校の昼休にみんなが参加できる数学ゲームなどが，米国の学校で効果を上げています．

国立数学博物館MoMath(National Museum of Maths)は，米国唯一の数学博物館で，ニューヨークのマディソン・スクエアに，2012年12月15日オープンしました．ここには30以上の対話型の展示があります．東京でもMoMathのような常設の数学展示のあるものは，科学技術館，リスーピア，東京理科大「数学体験館」(2013年オープン）などあります．

 ■同志社中学校数学博物館Do★Mathは，2016年6月にオープンしました．キャンバス移転の2010年に，全教科が専門教室をもつ方式が採用され，数学科も6つの教室（数学１，2，3それぞれ専用の教室がある），メディアスペース（博物館として展示）があります．博物館には，「見る読むゾーン」，「触れる体験ゾーン」などがあり，特に，触れる体験というのは，この時期最も貴重だと思います．ピタゴラスの定理，$$Σn^2，Σn^3$$，正4面体の2分割，ソーマキューブ［体積$$3×3×3$$のキューブを7つのパーツ（体積4のパーツ6個と体積3のパーツ１個)で組み立てる］などの手で触れ体験できるパズル，誕生日当てゲーム［2進数の利用］，ハノイの塔などさまざまあります．展示物は，教職員が製作したものや，生徒が自由研究で製作したものもあります．写真のシェルピンスキーのフラクタル模型は，授業で生徒たちが牛乳パックを用いて１辺14cmの正4面体を１つづつ製作したものを合体させて作りました．

米国のMoMathや，数学サークル活動を思わせるこのような意欲的な活動が，単独の学校の教育の場で実現しました．ここは，授業で使用しますが，生徒が昼休みなどに親しむこともできます．さらに一般市民の見学も受け付けています．手で触り自分で体験することは数学や科学への出発点になります．

数学月間懇話会（2020.7.24）はzoomで実施され，Do★Mathを園田毅先生（同志社中）にご案内いただきました．

大変暑い夏でした．皆様お疲れのことと思います．どうぞご自愛ください．
2020年の数学月間（第16回）は，新型コロナウイルス感染拡大のため，
例年のような集会は困難と思われたので，ZOOMによるリモート実施の方針を固め，
準備の一環としてyoutubeチャンネル「NPO法人数学月間の会」を3月末に開設しました．
4月初めには，昨年度実施の講演ビデオはすべてこのチャンネルにアップロードを終えました．
今年度の講演ビデオもこのチャンネルにアップし，会員外にもすべて無料で公開しています．
今後このyoutubeチャンネルの充実をはかって参りますので，皆様，育成のご協力お願いいたします．

■さて，2020年の数学月間は7/22～8/22の間にZOOMのメリットを活かして分散型で実施しました．
ZOOMのメリットとは，時間と場所の制約がないことです．講演者も参加者も遠方からでも参加でき
日時も自由がきくので，４件の講演を数学月間の期間内に分散して行いました．
講演時間それぞれ2時間に延び十分にとることができました．
欠点は，参加者がインターネットとZOOMをやる方に限られることですが，これはや無負えないことです．
これを補うために，すべての講演ビデオをyoutubeブランドチャンネルに公開しました．
数学月間の1月間に実施した講演は以下の通りです：
7/22，宇宙エレベータ，八坂哲雄，
7/23，同志社中学校の数学博物館，園田毅，
7/29，感染症の数理モデル，稲葉寿，
8/22，X線・中性子で見る表面・界面，桜井健次
種々の話題があり，なじみのない分野の方々にも伝わるように
平易な解説記事をホームページに掲載しますのでご覧ください．

■月間最終日の8月22日,17:00～17:20に，
学術会議，数学教育分科会委員長の真島秀行先生より，追加プレゼンがありました．

この緊急提言の趣旨は，統計の教育カリキュラムの実効性を高めることにあります．
高校カリキュラムには，数列，ベクトル，統計が含まれており，
統計学はセンター試験に出題されるのだが，選択者は少ない．
たまたま，新型コロナのニュースで統計データが国民の目に入る昨今の状況を見ると
統計教育への関心を高める良い時期である．
令和4年から始まる新学習要領で統計学をきちんと教育するには，
教える側の先生への講習等の準備を始める必要がある．

数学月間企画講演の第3回は，12月26日(土)，15:00-17:00に，27名の参加で実施しました．
この1年間は直接の会合ができず，物足りなさの残る年度でした．とくに，インターネットをやらない会員各位にはご不便をおかけします．ここに年度後半の概要を報告いたしますのでご利用ください．なお，内容詳細は，NPO数学月間の会HPの記事，および，そこにあるリンクからyoutubeに公開した講演動画をご覧ください．
■企画講演（第3回）3Dジグソーパズルのデザインと数学，手嶋吉法（千葉工大）
３D ジグソーパズルとは立体ジグソーパズルのことですが，市販されている地球儀ジグソーなどは，球表面の地図ですので，２Dジグソーになり，３Dジグソーではありません．3Dジグソーパズルの起源は，2000年の池上裕司氏（理研，機械設計）の発明だそうです．講演者もこの直後に理研に在籍し池上氏とともに研究しました．現在も大学で研究テーマの一つとしておられるとのことです．今回の講演内容は，町屋佑季氏（修士論文）の研究に関わります．3Dジグソーパズルは，ピースが全部ばらばらに分解できるものでなければなりません．例えば，3×3×3 のジグソーパズルは，ばらならになる27個のピースよりなります．

３D ジグソーパズルのヒントは，日本の伝統的な継手（柱を繋ぐ技術）「四方継」にあります．池上式３D ジグソーパズルは「四方繋」を応用して作られました．ジグソーの仕組みをみると，「溝」と「ほぞ」は，常にかみ合っているわけですから，このかみ合わせ部分を1本のパイプで表現すると，ジグソーパズルの構造は空間のパイプの組み合わせとしてモデル化できます．

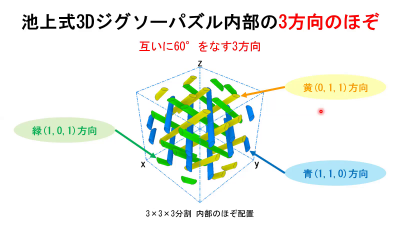
上図のような，無限に伸びたパイプの組み合わせで作られた周期的な構造は，その対称性を空間群で記述できます．この構造例では，空間群は$$Im\bar{3}m$$ で，ジグソー立方体の点群は $$m\bar{3}m$$であろうと推察されます．

町屋佑季氏は，作った3×3×3，4×4×4，5×5×5などの各３Dジグソーパズルを分解し，それぞれを構成するピースの形の種類と個数を分類し報告しています．これらの結果を，立方体内のサイト・シンメトリーとその同価ピースの個数という視点で再検討すると，非常に興味深い知見が得られると思います．

■第1日（7.22) 目付字・目付絵の数理トリックとその400年史，秋山久義（パズル研究家）
「目付字」，「目付絵」とは，類似した多数の候補から，客が心の中で選んでいるものを当てる遊びで，直接的でなくyes/noで答えられる数回の質問で当てる数学マジックです．秋山氏の研究によると，平安時代末期には公家の間で遊ばれていたといいます．藤原資隆の「簾中抄」に「いろはの文字くさり」の記述があるのがその証拠です．
これらの遊びの原理は，2進数にあります．2進数で,11111と書けば，$$ 2^{4}+2^{3}+2^{2}+2^{1}+2^{0}=31 $$のこと，つまり，5桁の2進数で31までの数が記述できます．

例えば，塵劫記の「椿の目付字」（左図）を例にしますと，花弁に書かれているどれかの字を当てるには，その字が出現する花のある枝に書かれた数値を足し合わせます．「椿の目付字」には5つの枝があり，それぞれの枝には，1,2,4,8,16の数字が書かれています．例えば，「正」の字なら，2,4,8の枝にある花弁に出現するので，「正」の字に対応する数字は14．もし，14は「正」という対応表を持っていれば当てることができます．同様に，花弁に「不」の字がある花の枝は，4,16なので，「不」は20に対応します．これらの5つの枝1,2,4,8,16は，2進数の各桁に対応するわけで，意中の字が出現する枝を質問によって知れば良いのです．質問の仕方には色々な演出が考えらますが，意中の字の存在する花が枝１にあるか問い，yes/noの答えを聞くと，全部で32の候補があったとして，候補は半分に絞られます．次に枝２での有無を聞くとさらに半分に絞られ，このように繰り返し，枝16での有無を聞くと，結局，5回の質問で32分の1と絞られ一意の答えが得られます．
講演者の考案・改良した五角形の数地盤とマスクを使用する数あてマジックでは，当てる数字の候補の半分を常にマスクで隠し，半分がの穴あき窓から表示されます．マスクを5回回転させながら数が見えるか見えないかを問うことが，椿の目付字の5回の質問に相当します．マスク内での穴あき窓の配置に対称性をうまく利用するなどの非常に洗練されたマジックに仕上がっています．もちろん，この数あてマジックの源泉は2進数にあります．その400年の歴史は，平安，室町，江戸，明治，大正，昭和のそれぞれの時代の世相を絵柄に反映し変遷しました．講演と併行して歴史資料として貴重なコレクションの紹介もなされました．

■第2日（7.31) 新型コロナウイルス感染症と統計数理，土谷隆（政策研究大学院大学）
本講演が行われた時点で行政が把握していた累積国内感染者は，約903,324名（都内210,610名），死亡者は，15,175名(都内2,288名)でありました(2021/7/30現在)．今，振り返ってみれば，この時期は第5波の成長途上で，この半月後に第５波のピークを迎えます．これは，7月23日～8月8日のオリンピック開催による人流増加が関係すると思えます［小池都知事が言うようなTV観戦によるスティホームの効果は疑問です］．新型コロナウイルス感染症の流行が，欧米でなぜ激しいかなど，まだ未知の部分が多く残されています．
従来のSIR，SEIRモデルついては，昨年の稲葉講演（数学文化No.35）を参照ください．土谷講演は，判明したコロナの病態を考慮したSIRモデルに関します．それは，感染力を表現するパラメータ$$β(t)$$に，感染能力の保持期間$$D$$を入れたことと，感染力は未感染者の割合にも比例するので，$$S(t)/N$$を$$β(t)$$に乗じたことです．
ここで，$$S(t)$$は感染感受性のある者，$$I(t)$$は感染力保有の感染者，$$R(t)$$は免疫保有の回復者，$$N$$は全人口です．
感染者の変動：$$I(t+1)=I(t)+β(t)I(t)S(t)/N-β(t-D)I(t-D)S(t-D)/N$$
未感染者数の変動：$$S(t+1)=S(t)-β(t)I(t)S(t)/N$$
免疫保持者の変動：$$R(t+1)=R(t)+β(t-D)I(t-D)S(t-D)/N$$
感染して$$W_1$$日で発症，それからさらに$$W_2$$日後に行政によって発表されるとします．

［つまり，感染日は不明だが，$$W_1$$日経過して，PCR検査で発見される．このとき，発症している場合もあれば無症状の場合もある． 症状の有無にかかわらず，感染から$$D$$ 日間感染力を有する．PCR検査日から陽性判定され発表日までの行政遅れは，$$W_2$$ である．これらは，発表データから推定されるが，$$W_2$$ は数日程度，$$D=15$$日程度で，$$W_1$$と$$D$$が特に知りたいパラメー タである］

感染から発表まで行政遅れ$$W_1+W_2$$の存在と，全感染者のうちの$$1/C$$だけを行政は把握できるとし，これを行政的感染者と呼びます：$$P(t+W_1+W_2 )=β(t-1)I(t-1)/C$$．
行政的感染者のうち割合$$r_0$$が発症するとします．$$t$$日の新規感染者が発症するまでに$$W_1$$日の遅延があるので，$$t$$日の発症者数$$H(t)$$は，次のようです：
$$H(t + W_{1}) =r_{0} β(t - 1)I(t - 1)/C$$．
行政で発表されるデータを使い推定するので，行政発表の遅れ$$W_2$$や行政的感染者の概念を導入する必要がありました．発表された新規感染者のデータを用い推定を行い，以下のパラメータが得られました：
$$D=15$$日（感染して人に伝染させる期間），$$C=23$$（行政が把握している感染者の何倍くらい実際に感染者がいるか），$$C=23$$は6月時点のもの，7月22日時点では$$C=8$$まで下がっている）．$$W_1+W_2=9$$日，$$W_1=5$$日，$$r_0=0.6$$．

［$$W_1=5$$というのは，感染して5日目がウイルス放出量が最も多くPCR検査で発見されやすい（数学文化No.36,p.66）という事実とよく一致する］

これらに基づいて$$β(t)$$を推計します．$$β(t)$$が１を境にして，感染の拡大/縮小が決まります．感染拡大が起こると，介入がなくても行動変容や自粛が起き，感染は縮小するが，緩むと$$β(t)$$はまた増加する傾向があります．適切な介入やワクチンの影響は$$β(t)$$の減少となって現れます．モデルに基づきどのような介入をすれば感染の縮小が起こるか予測することができます．
わかりやすいモデルの構築は，意思決定責任者と専門家のイメージの共有を促進し，国民の信頼と納得感に直結するので重要です．

■第3日(8.7) 回折対称の上昇，松本崧生（金沢大学名誉教授）
結晶は原子で構成されており，原子を点と見做すと結晶は点の集合です．結晶の対称性（空間群で記述）は，点集合の対称性に他なりません．結晶で観測される現象の対称性には，その舞台となった結晶の対称性が反映されねばなりません（因果律）．しかし，それを超える対称性を持つことを禁じているわけではありません．結晶によるX線回折という現象でも，結晶構造の点群を超えた回折対称（点群）が現れます．結晶からの散乱波は結晶構造のFourier変換であり，観測されるのは散乱振幅の絶対値の2乗（位相情報は失われる）であるので，回折強度像には必ず対称心が生じます（Friedel則）．回折像の対称性にFriedel則を超えた対称の出現を回折対称の上昇と言います．観測される回折像の対称性が結晶構造の対称性と信じ込むと，誤った構造解析を進めることになります．
この問題は，結晶モデルとしての点集合の対称性と，点集合で定義されるベクトル集合（任意の2点を結び，そのすべての端点を原点に移動し重ねたもの）の対称性の関係と同値です．ただし，結晶は周期的構造なので点集合は有限集合を採用できますが，ベクトル集合では困難な問題が残されています．同一のベクトル集合を持つが，異なる点集合の構造となるものをホモメトリック構造と呼びます．

図は，1次元のホモメトリック構造の例で，Patterson（1944）が提案したものです．１次元の周期（単位胞）を長さ１の円周で表し，円周上の点配列は，1次元の周期構造モデルになっています．図には円周に沿って並んだ任意の2点の距離が書き込まれています（距離は円弧に沿って測り，弦ではありません）．この2つのモデルを比較すると，ベクトル集合は同一ですが，点の配列構造は異なることがわかります．
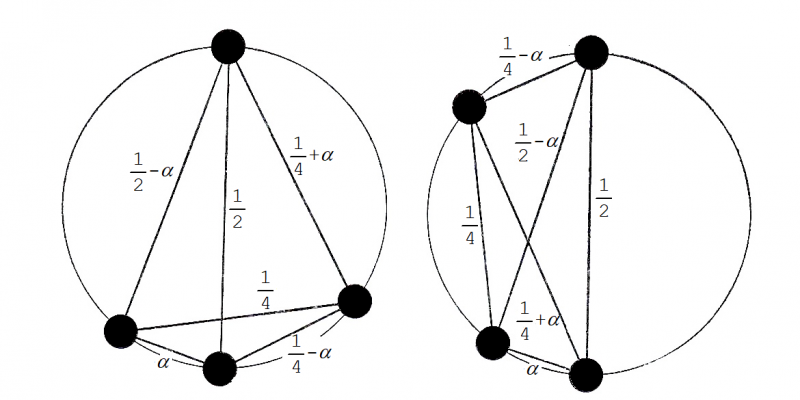
このような1次元構造を組み合わせて，2次元や3次元のホモメオリック構造を作れます．
1次元の８点系モデルで，ホモメトリック構造を系統的に導く講演者の研究が紹介されました．

回折対称の上昇は，空間群の対称要素を特殊点に作用させたときの同価点集合の対称性上昇と関係があります．空間群より高い対称を示す軌道をリストアップした講演者とWondratschekらの出版（1984,2015）「結晶空間群の非特性軌道」の紹介もなされました．

■第4日（8.14) スマホやタブレットで数値計算，山崎純一（元 大学非常勤講師）

MATLABは優れた計算ソフトウエアですが，非常に高価（私はMATLAB互換な無料のscilabを使っている）です．今は，ほとんどの学生がスマホを持っている時代で，スマホにはMATLABを無料でインストールできクラウドで使えます．講演者は，学生が実験のデータ解析やグラフ作成にスマホでMATLABを使うことを奨励し実践して来ました．講演者の用意したMATLABのスクリプトを，数学月間ホームページの「みんなの広場」http://sgk2005.saloon.jp/lobbyに掲載しておき，ここから，自分のスマホのMATLABにコピー＆ペーストして，数値計算を体験出来る企画でありました．

MATLABは線形代数の数学概念の把握に非常に役に立つと思います．連立方程式を解く，固有値問題を解く，特異値分解をする等の計算を通じて，これらの数学概念の理解を深めることができます．線形代数の学習の助けになるようなMATLABスクリプトのライブラリを充実する数学月間のプロジェクトがあっても良いのではないでしょうか．皆さんの作成した教育的なスクリプトを，この「みんなの広場」に投稿して共有の輪を広げましょう．
このように，数学教育でもMATLABの併用は，数学概念の具体的な理解に役立てることができます．もちろん，実地のデーター解析にもどんどん活用しましょう．包括的なライセンスでMATLABを学生全員に使用させる大学もあります．学生が折角もっているスマホやタブレットをゲームに使うだけでなく，スマホをツールにして数値計算に親しむようになることは，まさに，数学月間の狙いでもあります．

ミノカズヤ（IMAGINARY）

NTT，DOORを用いて作る「数学月間の会バーチャル会議室」でおなじみのミノカズヤ氏にVR(バーチャル･リアリティ)の講演をお願いしました．必要な機材は，ゴーグルと手に持つコントローラ［例えば，Oculus2（3万～4万円）］，および，画像処理の速いゲームPC．VRに登場させるアバター（自分の分身になるキャラクター）の作成にはVroidStudio，立体作成や3Dモデリングには，Blenderなどのソフトウエア（これらは無料）を用います．このようにして作成したオブジェクトを，PCのSteamというプラットホームにインポートし動かします．VRでワークショップなどを行うには，Steam上でNeosVRというアプリを用います．ワークショップや数学博物館の開催など，いろいろな可能性がありVRの発展が期待できます．
VRでは，3D空間に図を描き，これを物体のように回転させたり，自分が内部に入って観察したりできます．VRのキャラクターである自分の視線で世界がどの様に見えるか，逆に，周りからキャラクターである自分がどのように見えるかをカメラを切り替えて映し出し，VRの丁寧な説明がありました．ZOOMを介して自分のPC画面で見ているので，実際のVRとは異なるリアリティとは思いますが，その雰囲気は理解できました．

ゾム・ツールは，米Zometool社の製品（日本総代理店：イメージミッション木鏡社）で，多面体の作製に便利です．ノード（球）は1種類ですが，所定の角度に孔が開いていて，結合棒で繋いで多面体が作れます．球には62個の孔［正20面体の面（3回対称位置）の20個，正20面体の頂点（5回対称位置）の12個，正20面体の辺（2回対称位置）の30個］があります．これらの2面角は大概の多面体を作るときに有用です．4次元多胞体の3次元投影模型なども作ることができます．

河野俊丈（明治大学）

このテーマは，Kavli IPMUにおける数学と宇宙物理の協働研究に関わる．
ガリレイ変換に従う古典力学では，すべての慣性座標系で一つの絶対時間が支配するので，光速は座標系の移動速度の影響を受ける．一方，ローレンツ変換に従う特殊相対論では，どの座標系でも光速は不変（実験事実）としたので，時間は個々の座標系で異なる固有時間$${t'=t\sqrt{1-(v/c)^{2 } } }$$となる．座標系の移動速度$${v}$$が光速$${c}$$に近づくと，その座標系での時間の流れは遅れ，逆に，$${v \ll c}$$ではガリレイ変換の結果$${t'=t}$$に一致することがわかる．
ローレンツ変換に従う真空時空では，計量$${ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2 } }$$が保存されるが，
質量エネルギー分布があるために生じる空間の歪（曲率）は，アインシュタイン重力場方程式により記述されるが，特に，太陽のような天体が作る球対称の重力場に対しては，シュバルツシルト計量が保存される．この時空の光線は，シュバルツシルト計量を保存し，時間が最小となる経路（フェルマーの原理）を進むので，光線経路の偏角を容易に知ることができる．

アインシュタインリング(NASA)

大きな重力場を有する天体の傍らを通過する光線は，その重力場が空間を歪ませているため，時間が最小となる経路をとると曲がっている．重力レンズとは，重力場が示すこの効果を言う．大きな重力場のある天体の輪郭にリング状の光（アインシュタイン・リング）が観測されたり，実際に存在するのは１つのクエーサー（準恒星）であるのに，これが複数個に観測されたり，像が歪むなどの現象が起こる．これらの現象は，身近な光学現象で見られる光線の集まる火面（コスティック；caustic）の形成と同じである．1点の光源から発した球面波の波面は，途中にグラスなどがあると，その表面で反射や屈折を起こし，折り返され方位を変えた複数の球面波の波面になり，波面が重なり光線の集中する火面が形成される．同様な現象が，重力場でも起こり，波面が折り返され重なり，歪んだ光線の集まる火面の像が観測される．
遠方宇宙にあるクエーサーや銀河からの光が，途中で巨大な重力場を通り，観測者Oに達するのだが，像は観測天球面T上にあり，光源は遠方宇宙の天球面S上にある．観測者O，観測天球面Tの点，遠方宇宙の天球面Sの点の3点は，重力場による曲率のある世界の測地線上にある．光線は途中の重力場で曲がるために，実際に光源となったクエーサーや銀河が存在するのは，観測像の延長上ではない．

クエーサー，および銀河の像（NASA）
我々が観測するこのクエーサーの像は，火面が引きちぎられて5つに見えるものだが，これらが同一光源からの像であることの証拠は，それらのスペクトルが同一であることによる．なぜ５つに引きちぎられて見えるのかというのは，特異点理論が関わる．２つの天球面間に，なめらかな写像T→Sを考えよう．火面形成に関与する波面の集合は写像の臨界点集合で，カタストロフィー理論（ルネ・トム他）によると，写像の特異点の型は①折り目(fold)，②カスプ（尖った点；casp）の型があり，臨界点集合の折り目の外側では写像によってSの1点に写されるTの点の個数は1個であるが，臨界点集合をよぎるたびに２ずつ増加するので，一般には上のようなTの点の個数は奇数となる．この写真のクエーサー像と銀河像は，それぞれ，5個および3個の像に観測されている．
特異点理論は，宇宙観測データの膨大な解析と協働して，宇宙の重力場やダークマター，ブラックホールの分布を知ることにもつながる．

立木秀樹（京大）

イマジナリーキューブとは，直交する3方向（立方体の３方向の辺）に沿って見る（射影する）と，立方体と同じに見える立体のことで，図に示す正4面体や，HとTなどの立体があります，HとTは，立木氏が開発したイマジナリーキューブ・パズルで現れる立体です．

HもTも1辺１の立方体に入るイマジナリーキューブとすると，1辺２の箱の中に8つのイマジナリーキューブが収まるのは当然ですが，3個のHと６個のTのイマジナリーキューブ計9個を収めるのがこのパズルです．これは，面と面を合わせて空間充填された状態で詰め込まれます．４つのTの頂点が集まる位置にできる窪みにHが突き刺さるように入り，Tの層に挟まれてHが入り，この構造での個数比はH:T=1:2です．空間群でいうとP6/mmmの積層構造になります．無限に続くこの結晶構造から1辺２の立方体の箱に収まる部分を切り取るのは，3回回転対称軸を立方体の体対角線に一致するようにすると得られます．

このイマジナリーキューブの発想は，フラクタルから生じました．イマジナリーキューブ立体図形をフラクタル配置で拡げたものは，やはりイマジナリーキューブになることが，数学的帰納法で証明できます．正4面体から作ったシェルピンスキー4面体（シェルピンスキー・ガスケット）は，やはりイマジナリーキューブであり，Hから作ったフラクタルもTから作ったフラクタルもイマジナリーキューブであります．これらをイマジナリーキューブの辺方向から少しずれた方位で投影した図には，大変美しい形がときどき見られます．3Dプリンターでこれらのフラクタル模型を作ったり，また，正4面体を集めてシェルピンスキー4面体の工作をし，大学から中学までの各レベルの数学学習に合わせて活用しました．数学的帰納法は級数で導入するのが普通ですが，フラクタル図形で導入するのも自然で理解し易いようです．正4面体のイマジナリーキューブ・フラクタルの京大オブジェや，フラクタル日除けを作りました．フラクタル日除けは，日除け自体の熱容量が小さいので熱を貯めないなどの利点があり，酒井敏教授（人間・環境学研究科）がキャンバスに建設しました．太陽光線による影が，イマジナリーキューブになるという特定方位の瞬間は，実際にはないが，フラクタル木漏れ日は気持ちの良いものです．